What does the order of a filter do?
One of the essential steps in signal processing is getting rid of unwanted noise from the signal. A signal could be composed of multiple frequency components. Real-life signal (signals from audio, video etc.) consists of various frequencies.
This notebook would demonstrate signal denoising. First, I will take a clean signal consisting of only one frequency component. I will add noise to it. I will then filter the signal by removing unwanted frequencies.
import matplotlib.pyplot as plt # matplot lib is the premiere plotting lib for Python: https://matplotlib.org/
import numpy as np # numpy is the premiere signal handling library for Python: http://www.numpy.org/
import scipy as sp # for signal processing
from scipy import signal
from scipy.io import wavfile
from __future__ import print_function
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
from IPython.display import Audio
#for filter
from scipy.signal import butter
from scipy.signal import lfilter
from scipy.signal import freqz;
def create_sine_wave(freq, sampling_rate, total_time_in_secs = None, return_time = False):
'''Creates a sine wave with the given frequency, sampling rate, and length'''
# if the total time in secs is None, then return one period of the wave
if total_time_in_secs is None:
total_time_in_secs = 1 / freq
# Create an array from 0 to total_time_in_secs * sampling_rate (and then divide by sampling
# rate to get each time_step)
time = np.arange(total_time_in_secs * sampling_rate) / sampling_rate
# Could also generate this signal by:
# time = np.linspace(0, total_time_in_secs, int(total_time_in_secs * sampling_rate), endpoint=False)
sine_wave = np.sin(2 * np.pi * freq * time)
# or, once the sample is made:
# time = np.linspace(0, len(s) / sampling_rate, num=len(s))
if return_time is False:
return sine_wave
else:
return (time, sine_wave)
def compute_fft(s, sampling_rate, n = None, scale_amplitudes = True):
'''Computes an FFT on signal s using numpy.fft.fft.
Parameters:
s (np.array): the signal
sampling_rate (num): sampling rate
n (integer): If n is smaller than the length of the input, the input is cropped. If n is
larger, the input is padded with zeros. If n is not given, the length of the input signal
is used (i.e., len(s))
scale_amplitudes (boolean): If true, the spectrum amplitudes are scaled by 2/len(s)
'''
if n == None:
n = len(s)
fft_result = np.fft.fft(s, n)
num_freq_bins = len(fft_result)
fft_freqs = np.fft.fftfreq(num_freq_bins, d = 1 / sampling_rate)
half_freq_bins = num_freq_bins // 2
fft_freqs = fft_freqs[:half_freq_bins]
fft_result = fft_result[:half_freq_bins]
fft_amplitudes = np.abs(fft_result)
if scale_amplitudes is True:
fft_amplitudes = 2 * fft_amplitudes / (len(s))
return (fft_freqs, fft_amplitudes);
Our noiseless signal contains only one frequency component, i.e. 50 Hz. We add noise to the clean signal by adding two additional frequency components, one of 70 Hz and 150 Hz.
sampling_rate = 16000
freq = 50 #original freq
total_time_in_secs = 0.5 # signal lasts 500ms
clean_signal = create_sine_wave(freq, sampling_rate, total_time_in_secs)
add_noise150 = create_sine_wave(150, sampling_rate, total_time_in_secs)
add_noise70 = create_sine_wave(70, sampling_rate, total_time_in_secs)
time = np.arange(total_time_in_secs * sampling_rate) / sampling_rate
#add the signals and divide by the number of signals to normalise the final output.
signal = (clean_signal + add_noise150 + add_noise70)
fig, ax = plt.subplots(1,2, figsize=(15,6))
ax[0].plot(time, clean_signal)
ax[0].set_xlabel('Time [s]')
ax[0].set_ylabel('Amplitude')
ax[0].set_title('Clean Signal (50 Hz)')
'''
ax[0,1].plot(time, add_noise70)
#ax[0,1].set_xlabel('Time [s]')
ax[0,1].set_title('Signal of 70 Hz')
ax[1,0].plot(time, add_noise150)
ax[1,0].set_xlabel('Time [s]')
ax[1,0].set_title('Signal of 150 Hz')
'''
ax[1].plot(time, signal)
ax[1].set_xlabel('Time [s]')
ax[1].set_ylabel('Amplitude')
ax[1].set_title('Noisy Signal')
plt.show();
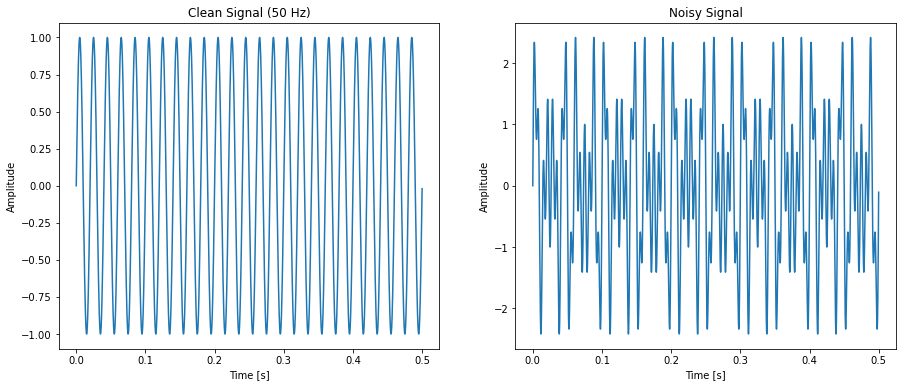
Our objective is to eliminate the noise from the noisy signal and restore it to the original (Clean) signal. We will first investigate what frequency components are present in the noisy signal.
#observe the frequency components in the signal
fs, hs =compute_fft(signal, 16000, n = None, scale_amplitudes = True)
fig,ax=plt.subplots()
ax.plot(fs[:200],hs[:200])
ax.set_xlabel('Frequency [Hz]')
ax.set_ylabel('Normalised Amplitude')
ax.set_title('Spectrum of the noisy signal');
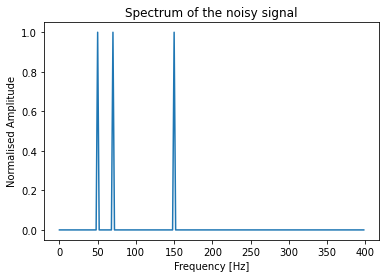
In the plot above, we observe that the noisy signal consists of 50 Hz, 70 Hz and 150 Hz. Now, our objective is to design a filter to get rid of any frequency components other than 50 Hz (the frequency of the clean signal)
I designed an FIR (Butterworth Low Pass) filter (Using Python packages) to filter out unwanted noise components. I choose FIR over IIR because the hardware realisation of FIR is easier compared to IIR.
Our cutoff frequency will be little more then 50 Hz to take care of the transition width between passband and stopband. I have set it to 55 Hz.
def butter_lowpass(cutoff, fs, order=5):
nyq = 0.5 * fs
normal_cutoff = cutoff / nyq
b, a = butter(order, normal_cutoff, btype='low', analog=False)
return b, a
def butter_lowpass_filter(data, cutoff, fs, order=5):
b, a = butter_lowpass(cutoff, fs, order=order)
y = lfilter(b, a, data)
return y;
Let us try to retreive the original clean signal with a filter of order 1
#interact(filterAndPlot, order=widgets.IntSlider(min=1, max=7, step=1, value=11));
fs = 16000
cutoff = 55 # desired cutoff frequency of the filter, Hz
order = 1
y = butter_lowpass_filter(signal, cutoff, fs, order)
fig, ax = plt.subplots(2,2, figsize=(17,12))
#plot freq response of noisy signal
Fs, Hs =compute_fft(signal, 16000, n = None, scale_amplitudes = True)
ax[0,0].plot(Fs[:200],Hs[:200])
ax[0,0].set_ylim([0,1.2])
ax[0,0].set_title('Spectrum of Noisy Signal')
ax[0,0].set_xlabel('Frequency [Hz]')
ax[0,0].set_ylabel('Amplitude')
# Plot the frequency response.
b, a = butter_lowpass(cutoff, fs, order)
w, h = freqz(b, a, worN=8000)
ax[0,1].plot(0.5*fs*w/np.pi, np.abs(h), 'b')
ax[0,1].plot(cutoff-5, 0.53*np.sqrt(2), 'ko')
ax[0,1].text(cutoff+10, 0.53*np.sqrt(2), "Magnitude at 50 Hz")
ax[0,1].axvline(cutoff-5, color='k')
#ax[0,1].set_xlim(0, 0.5*fs)
ax[0,1].set_title("Frequency Response of Low Pass Filter of Order 1")
ax[0,1].set_xlabel('Frequency [Hz]')
ax[0,1].set_ylabel('Amplitude')
ax[0,1].set_xlim([0,1000])
ax[0,1].grid()
Fs, Hs =compute_fft(y, 16000, n = None, scale_amplitudes = True)
ax[1,0].plot(Fs[:200],Hs[:200])
ax[1,0].set_ylim([0,1.2])
ax[1,0].set_title('Spectrum of Filtered Signal')
ax[1,0].set_xlabel('Frequency [Hz]')
ax[1,0].set_ylabel('Amplitude')
ax[1,1].plot(time, signal, 'b-', label='Noisy Data', alpha=0.2)
ax[1,1].plot(time, y, 'g-', linewidth=2, label='Filtered Data')
ax[1,1].plot(time, clean_signal, 'r-', linewidth=2, label='Original Signal', alpha=0.5)
ax[1,1].set_xlabel('Time [s]')
ax[1,1].set_ylabel('Amplitude')
ax[1,1].grid()
ax[1,1].legend();
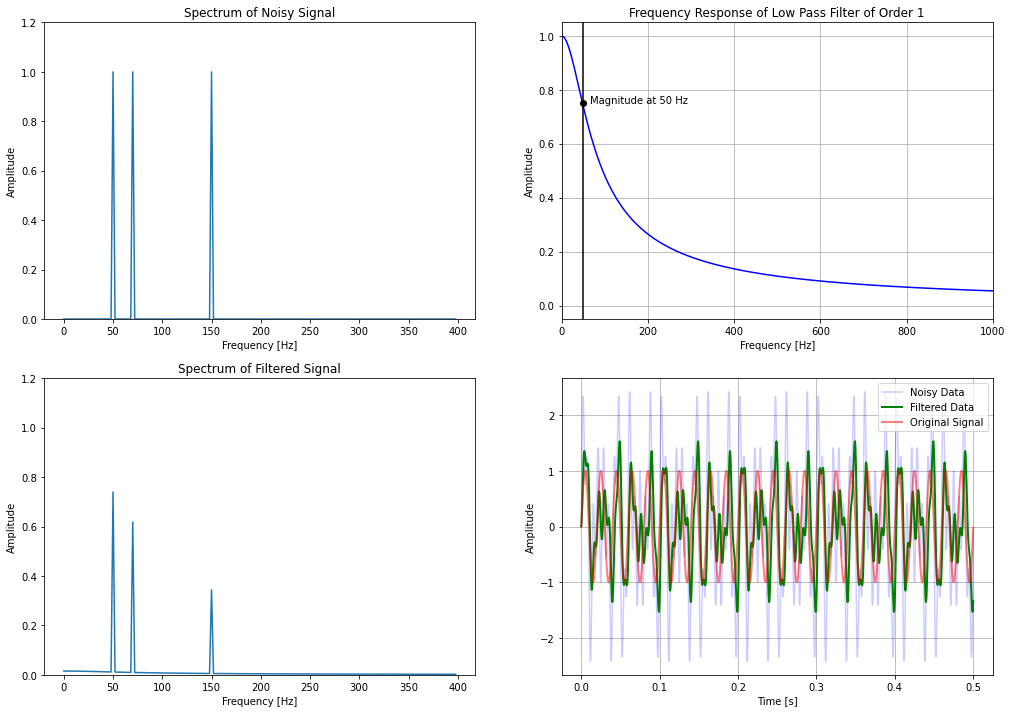
The frequency response of the filter is far from idle. As we can see in the top right plot, frequencies beyond 50 Hz will still appear in the signal, although with lower amplitude. Consequently, the filtered signal in the bottom right plot hardly looks like the original signal. Also, observe the black dot in the top right plot. It shows the magnitude at 50 Hz and the same magnitude is observed in the frequency response of the filtered signal (bottom left plot)
To improve the frequency response, we will need to increase the order of the filter.
fs = 16000
cutoff = 55 # desired cutoff frequency of the filter, Hz
order = 5
y = butter_lowpass_filter(signal, cutoff, fs, order)
fig, ax = plt.subplots(2,2, figsize=(17,12))
#plot freq response of noisy signal
Fs, Hs =compute_fft(signal, 16000, n = None, scale_amplitudes = True)
ax[0,0].plot(Fs[:200],Hs[:200])
ax[0,0].set_ylim([0,1.2])
ax[0,0].set_title('Spectrum of Noisy Signal')
ax[0,0].set_xlabel('Frequency [Hz]')
ax[0,0].set_ylabel('Amplitude')
# Plot the frequency response.
b, a = butter_lowpass(cutoff, fs, order)
w, h = freqz(b, a, worN=8000)
ax[0,1].plot(0.5*fs*w/np.pi, np.abs(h), 'b')
ax[0,1].plot(cutoff-5, 0.60*np.sqrt(2), 'ko')
ax[0,1].text(cutoff+10, 0.60*np.sqrt(2), "Magnitude at 50 Hz")
ax[0,1].axvline(cutoff-5, color='k')
#ax[0,1].set_xlim(0, 0.5*fs)
ax[0,1].set_xlim([0,1000])
ax[0,1].set_title("Frequency Response of Low Pass Filter of Order 5")
ax[0,1].set_xlabel('Frequency [Hz]')
ax[0,1].set_ylabel('Amplitude')
ax[0,1].grid()
Fs, Hs =compute_fft(y, 16000, n = None, scale_amplitudes = True)
ax[1,0].plot(Fs[:200],Hs[:200])
ax[1,0].set_ylim([0,1.2])
ax[1,0].set_title('Spectrum of Filtered Signal')
ax[1,0].set_xlabel('Frequency [Hz]')
ax[1,0].set_ylabel('Amplitude')
ax[1,1].plot(time, signal, 'b-', label='Noisy Data', alpha=0.2)
ax[1,1].plot(time, y, 'g-', linewidth=2, label='Filtered Data')
ax[1,1].plot(time, clean_signal, 'r-', linewidth=2, label='Original Signal', alpha=0.5)
ax[1,1].set_xlabel('Time [s]')
ax[1,1].set_ylabel('Amplitude')
ax[1,1].grid()
ax[1,1].legend();
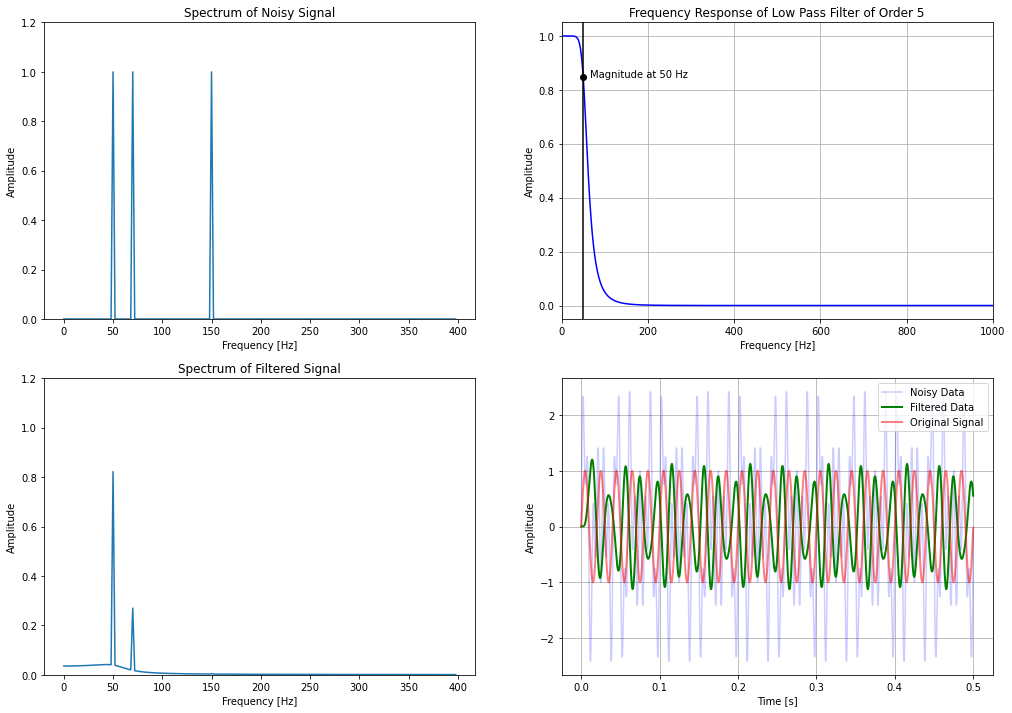
The frequency response with an order 5 filter is better relative to order 1. The frequency response at 150 Hz is almost 0. But we still have a significant amplitude at the frequency of 70 Hz. We will again increase the order and try to minimize the magnitude of 70 Hz component.
fs = 16000
cutoff = 55 # desired cutoff frequency of the filter, Hz
order = 7
y = butter_lowpass_filter(signal, cutoff, fs, order)
fig, ax = plt.subplots(2,2, figsize=(17,12))
#plot freq response of noisy signal
Fs, Hs =compute_fft(signal, 16000, n = None, scale_amplitudes = True)
ax[0,0].plot(Fs[:200],Hs[:200])
ax[0,0].set_title('Spectrum of Noisy Signal')
ax[0,0].set_xlabel('Frequency [Hz]')
ax[0,0].set_ylabel('Amplitude')
# Plot the frequency response.
b, a = butter_lowpass(cutoff, fs, order)
w, h = freqz(b, a, worN=8000)
ax[0,1].plot(0.5*fs*w/np.pi, np.abs(h), 'b')
ax[0,1].plot(cutoff-5, 0.59*np.sqrt(2), 'ko')
ax[0,1].text(cutoff+10, 0.59*np.sqrt(2), "Magnitude at 50 Hz")
ax[0,1].axvline(cutoff, color='k')
#ax[0,1].set_xlim(0, 0.5*fs)
ax[0,1].set_xlim([0,1000])
ax[0,1].set_title("Frequency Response of Low Pass Filter of Order 7")
ax[0,1].set_xlabel('Frequency [Hz]')
ax[0,1].set_ylabel('Amplitude')
ax[0,1].grid()
Fs, Hs =compute_fft(y, 16000, n = None, scale_amplitudes = True)
ax[1,0].plot(Fs[:200],Hs[:200])
ax[1,0].set_title('Spectrum of Filtered Signal')
ax[1,0].set_xlabel('Frequency [Hz]')
ax[1,0].set_ylabel('Amplitude')
ax[1,1].plot(time, signal, 'b-', label='Noisy Data', alpha=0.2)
ax[1,1].plot(time, y, 'g-', linewidth=2, label='Filtered Data')
ax[1,1].plot(time, clean_signal, 'r-', linewidth=2, label='Original Signal', alpha=0.5)
ax[1,1].set_xlabel('Time [s]')
ax[1,1].set_ylabel('Amplitude')
ax[1,1].grid()
ax[1,1].legend();
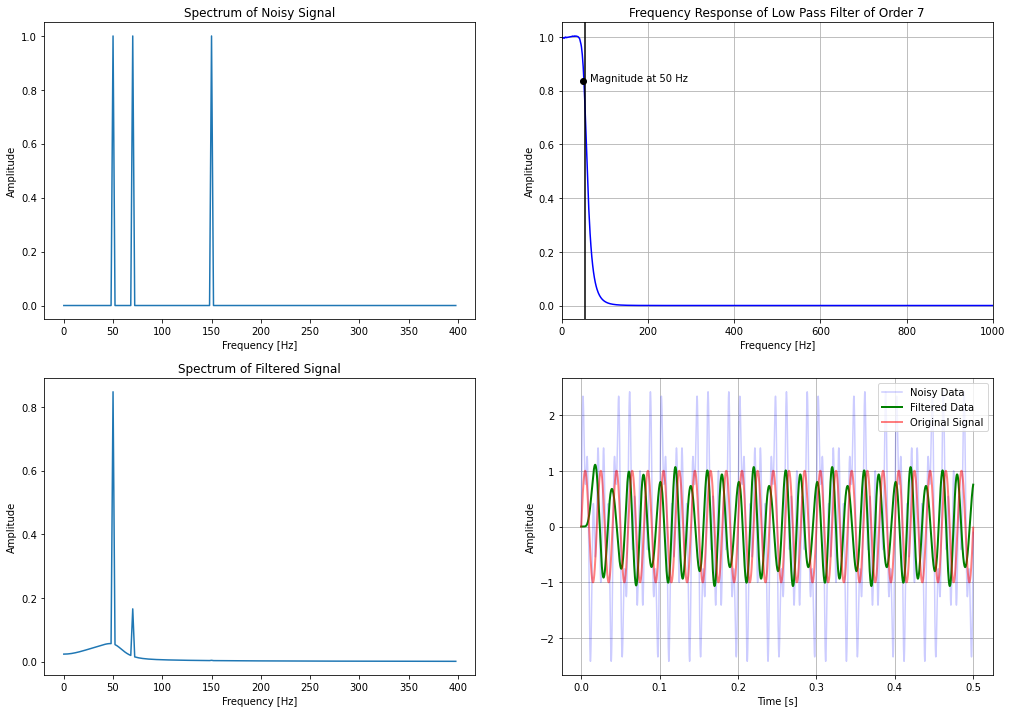
With an order 7 filter, the magnitude of frequency at 70 Hz is much lower compared to the fundamental frequency of 50 Hz.
The previous analysis was on a synthetic signal where we incorporated some noise. Let us try the above analysis on a audio signal recorded at 41 KHz. This audio signal captures a human breathing sound of inhalation followed by exhalation. According to research literature, useful information in an inhalaiton-exhalation lies after 1024 Hz. Hence. we use a high pass filter, to remove low freuquency noise from the audio signal.
sr,y=wavfile.read('FVC-1.wav')
audiosignal = y/np.max(y)
#audiosignal = audiosignal-np.mean(y)
time = np.arange(len(audiosignal)) / sr
fig, ax = plt.subplots(1,1, figsize=(5,4))
ax.plot(time, audiosignal)
ax.set_xlabel('Time [s]')
ax.set_title('Audio Signal');
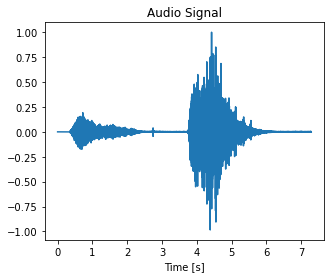
Below, we can hear the raw signal as recorded by a smartphone microphone
audio = Audio(data=audiosignal, rate=sr)
audio
<audio controls="controls" >
<source src="data:audio/wav;base64,UklGRiTQCQBXQVZFZm10IBAAAAABAAEARKwAAIhYAQACABAAZGF0YQDQCQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHAAAA+f8AAAAAAAAHAAAAAAAHAPn/AAD5/wAA+f8AAAAAAAAAAPn/AAAAAAAAAAAAAAAA+f8AAAAAAAAAAAcAAAAAAAAA+f8HAAAAAAAAAAcAAAAAAAAAAAAHAAAAAAAAAAAA+f8AAAAA+f8AAAAAAAAAAAcAAAAAAAAA+f8HAAAAAAD5/wAAAAAAAAcA+f/5/wAABwAAAAAAAAD5/wAAAAAHAAcAAAAAAAAAAAD5/wcABwAAAAcA+f8HAAAAAAD5/wAAAAAAAAAA+f8OAAAABwD5/wAABwAAAAAA+f8HAPn/BwAHAA4ABwDq/wAABwAHAPL/AAAAAAAA8v/q/wcA+f8AAPL/8v/y/wcAAADq/w4ABwAOAAcADgAHAPn/BwAOAAcA8v8OAAAA8v8AAA4ABwDy/wcA+f8AAPL/AAAWAAAAAAAHAA4AAAAHAAAA+f/5//n/DgD5/wAAAAAAAAAA6v/5//n/BwAAAAcA+f/y/w4A+f8HAA4ABwDq/77/1P/b/+P/HQAHAM3/6v8HAEIAFgAHAAcAkf++/5H/iv/F/wAALADy/zsAMwDb/7b/r/+v/6D/DgAOAM3/6v8WAAAADgAHAJn/kf/F/xYABwAdADsA1P/5/yUA+f++//L/DgDj/+r/6v9CADsAQgDy/3v/AABZAGAA+f8OADMABwAzAA4ABwAWAEoABwDb/w4AHQBRAFEAOwDy/wAAUQAlAPn/LABCADsALAAHACUAAAAWACUABwBCAGAAWQBRAEoA2//b/x0AFgAlAGcAWQD5/7b/DgBZAAcADgCv/6//4//y/xYAHQBCAPL/r/9d/+P/+f+2/83/QP9s/5n/1P/5/wcA+f+R/2z/OP+R/+P/8v/b/4L/tv/U/6D/mf/U/wAA2/90/2z/1P8dACUA4/+n/+P/2/+g/7b/6v8AAMX/zf++/wcAWQAlAL7/mf/b/+r/DgAAADMAQgBgADMABwCFAFEAHQDj/zsAYABZAGAAFgBRAEIAjABgAH4AmwBCACwAHQCFAGAAfgAHALb/+f9ZAH4ALACqAB0Akf+R/77/JQAsADsAoP90/4r/4/8lABYAvv9d/6//tv+2/6//+f8OAL7/+f8HAOP/r//U/77/2/87ABYAJQD5/9v/2/8dAHYADgDb/wcA+f/5/xYA2/8WABYAvv/q/wcAdgAzAL7/zf/F/9v/BwAHAPn/JQDU/83/iv/q/6MA6v8AANv/mf/F/xYAhQBnAFkA2/+2/8X/FgD5//L/ZwAWAFkAQgDIAOUALAAAAJn/8v8AAAcAOwDq/77/DgBRAFkAUQCZ/6//mf/F/0oAHQBCAKD/R/+Z/xYAAACC/1b/kf/j/9v/mwB2AFkA2/9l//L/kf9ZAFEAAAAOAE7/r/9gAIwAMwAHAOr/AABs/5n/uQBgACUAtv/U/6f/QP/5/6MALADJ/vX+bP9CABYAoP9CAKD/e/8x/xYAjADj/+P/R/+g/5n/4/9+AFEAmf8i/9v/QgBZANv/MwBgAK//DgCMAIUA4//5/yUAzf97/+P/bwCFADMAoP92AJQAFgB7//L/zwBs/5n/MwBnANv/gv87AL7/xf/j/5QAUQCn/4r/e/92ACUAQgBCAPL/dP8p/0oAUQB+AEoAJQC2/0f/4/9gAHYAZf/F/1EAMwCK/zH/jABCAKf/Tv/U/1EAe/+2/xYAAADb/9v/4//b/4L/kf8WACUAHQAOAGAAJQDy/wAA6v+v/0D/JQCMAEIAtv87AMgAVv9W//L/YAAzAOP/AACv/zMA2//b/4UAhQAOAHv/tv+R/+r/UQBRAGAA8v9CACUAgv/F/ywAOwAOAB0AdgAzAHv/kf8zAGcABwDb/w4A1P8i/6//mwCMALkAJQCv/+P/r//N/+r/DgDq/8X/HQD5/83/YAC5AA4Aiv/j/yUA1P/j/4UAfgDy/6//p/9vAO0A2/9H/77/FgCv//n/NwEdABv/6v/5/yUAQgDj/13//f5A/4L/WQDAAPL/e/+C/6f/p/87APQABwBl/0IAfgB7/4L/bwB2ADMA8v+FAN4AsgBKAIr/jACjAPn/fgDXAG8AoP9RAH4A1P8sAEoAFgCZ/6//qgA+ATcBjADb/ywAoP9A/x0AYAB+ANv/owALAQ4AfgBZAB0Ae/9l/wcAUQD0AFEAFgAsAL7/Tv97/wAAAACZ/2z/8v++/1kAqgAHAGX/jv5A/1b/BwAdAKD/OwAx//X+vv+qAAAA0P7f/in/zf/j/6oAmwAWAKf/5/5l/7b/LADj/zMAOwBW/6D/QgDPAAAAQgBZAED/iv90/9v/LABRAG8Azf/b/77/+f9+AGcAUQCZ/+r/FgAx/zMAfgBvACUAZf87ACUAQgBKAAAAYAAlAAAAvv92ACUAtv8OAM3/JQDb/yUAWQBCAGAASgB2AAAA4/+2/5sAXAF+AM3/oP8AAJn/8v+UAMAAlADy/w4A2/9gAIUA2/87AAcAiv+R/4L/Xf+g/zMAZwDF/5n/JQAOAEf/Vv8WANv/2/8i/zH/YADy/5n/3/7j/1kATv8zADMABwDF/+r/8v+n/28A4/8HABYA+f8WAAcA7QAlANv/5QAzAJH/AAA7AGcAbwDeAFwBbwAAAOr/6v8OAA4AhQDtAAMBe/90//QAbwDU/+P/5QAzABP/FgAAAEoAdgDj/yUA+f9O/3v/dgAlAK//MwBnAAAA5/7u/hYAxf/U/6oAFgB0/4L/fgDeADMAxf8M/5H/Xf/Q/kIAKAHXAMX/vv/j/8X/HQAdAHYAR/9//iwAhQCv/wT/oP8lACL/QP/b/zMA+f9H/wcAqgCn/3f+E/+n/77/LABZACgBFgAb/wcAWQCMALb/vv8HAFb/e/+yAPEBjABl/1b/SgDb/0D/CwFvAOr/E/8i/8AAOwDU/ywA5QCg/wT/bP8lAEIAOP9gAFEA+f8x/7b//AAAAM3/1P+5AJn/hv6c/vL/yADJ/jsAUQCn/2z/Iv9+ABYAHQC+/ywAzf/9/qf/HQBgAE7/8v/j/3YALAAb/7kAHQCg/9T/PgHIAE7/2/9KACgBQP/9/l3/p/8WAM3/GQFCAPL/Zf9nAJQAG/9d/wz/1P+V/mz/FgD5/xIBZf/q/8X/p//F/0f/zf90//n//AD8AIr/Xf9nAMsB7QCC/wAAr/92AA4ALAD0APQAowAi/wAAhQA7AOP/dgCMAEf/+f/N/3YAoP/Q/gcAgv9s/5H/fgBvAJn/7v4i//L/vv+n/+P/XAFKANv/fgBKAM8Akf8WAB0AVv8b/28AvQH0AO0AsgCfAdT/wv5+ANcAmwCC/2AAlADN/4r/LACjAOr/BP9l/xkBowBvANT/owAsAFL+1wA3Aer/yf5O/zsAzf/b/zsAXAHq/yn/kf/F/0IALAAZASwAiv/F/6//OwD9/n/+zf+C/1L+gv9nAMAA/ACK/w4AoP9w/l3/kf9s/9/+E//F/6D/vv+n//X+DP+K/x0AsgC+/w4AFgC+/yL/jv7b//n/UQDF/8X/8v+g/2cAUQALAVEAjACFAAcAsgAzAJABTQG2/4r/hQBvAFb/FgDlANcAlAALAQcA1P8WAEoAfgCZ/94AqgDy//3+Wv7q/xYAoP8i/x0AyAC5AMAAyACMABP/Mf++/w4AAACFAMgAe/9s/w4A/ADtADsAoP/N/7b/tv9cAeUAJQB7/7b/SgC+/1EAiv/F/5H/Kf8AAPn/1wBZAEIAOwDu/v3+OwALAfL/QP+K//L/BP8x/88AUQCK/9D+QP90/1b/tv/5/0IAbP8WAMAADgCk/rP+zf/F/yUA1P9vAED/4/3U/1wBawGyANcAdgAWAKD/AADEASgBQP9s/1kAdgBcAZABKAEHADH/bP9VAXYCEgG9AW8AdP/b/6//lAA7AIL/pP5RAAMBfgAwAaoAdgB0/3v/OwA7AK//E/8HAJQAQgDlAMAAzf/n/lL+Mf/5/4UAQgCFAFkAMwDAACUALABw/ib+jv44/7IAHQA3AW8A2P6Z/34Ap/9w/kD/e/8p/4r/HQBnAH4AQP+r/nv/p/9H/2j+s/4dAHYAr/8AALb/R/9d/3v/FgDq/w4Agv+Z/6oAlACZ/yL/wv66/rkA5QD5/9T/oP8dAIr/5/65AHIBbwDq/5H/8v8lADsAoP+n/0oA+f8OAJQAegE3AQcAG/+bAN4AQgDpAQsBjAAzAGX/SgDPABIBfgDf/o7+WQA3AX4A5QBNARYAiv++/5QA/ADXAJH/+f1O/3T/BwDeADsAhQAdAIL/FgBcAfQAzf/9/kD/2//U/4L/0P7F/0oAlAAsAKD/owC+/7P+yf6C/2AAZwBCACL/oP/PABYAuQAdAMX/UQC2/0oAZf/j/58B7QAdAMX/6v9ZADMAFgDy/2cAfgD5/wMBmwBRAGX/OP8dAKD/yACR/zMALADY/oL/BP/y/7b/DgAdAPL/JQDIAJsA0P62/zj/Mf+6/o7+WQAHAIwAPgFZAPL/wABRAL7/WQBRABYAQgBd/5H/8v+v/8AAkf8AAOr/G/9KAED/LAB2ADMA1wAx/3D+p//tAAcAmf/j/2X/r/9W/+P/FgCv/0IA8v9nAIwACwGYAR0ATv9A/zH/bP8x/9/+2/8sAIUAmwBRAKMA6v9l//3+Kf9//vX+DgAdAD4BRgF+AAT/yf6K//L/OwA7ACEBawHAAMAAiQGqAMX/oP/1/jj/mwCUAOr/OwAHAO0AgQGuAYUAnP6c/sL+/f6v/5sABwCZ/wT/Zf+FAIwAywGUAE7/r/9O/3YA9AC2/5H/iv9s/4r/QP/IAJABfgBKAEoAlAAAAIwArgH5/9D+Lf57/8AAAAC2//3+YAAOADsANwEHAIL/Hv79/rb/4/+jAPL/Kf8m/i3+bP9O/x0AlABo/l3/6v/tAFUBJQCyAIr/mf/C/mz/fgAoAYkBp/+K/xYARgEdADMAwACbAO0Ap/8HAL7/8v/XAAcAS/4M/wAA4//PAKoASgBW/3f+jv6Z/0IA7QDTAcgATv9s/wcAZwAzAGj+BP/PAMgAUQBnAHYA1wDIAGAAGQEM/x7+0P4p/6oAGQH0AG8AJQAT/3D+Mf/q/2cABwCR/yUAUQDN/2cA8v/u/l3/mf+g/7kAsgByARIB+f9gAKv+LABvAMX/1wBd/4L/OwAhARkBuQALAbIAbP+O/sL+4/9gABYAmwBd/0D/S/62/Yr/JQDb/2X/QgAx/+7+2P6K/88AXf9A/zz+S/5s/x0AbwAdAK4B/ACr/mX/QgCqAGsBLABW/9D++f9kAXYAuQC2/6D/bP+r/owAhQB+AOr/Xf8sAHv/xf9s/zH/Tv+K/1EA+f+jABv/mf+5AHv//ABs//X+MwBnAAMBe/9CAN4A4/8lAM3/JQCFAGX/dgD0ABYArgHIABv/Mf/F/4wAZwCR/5H/LADb/6oAe/+g/yUAQP++/2H+1P/q/34A9ADC/k7/Kf+5AA4AOP92ADsAYACZ/+P/qgAOAPn/fgDy/4kB0wEWAAAAbwBVARIBKAFZAPn/R//q/xIBOwCbAPn/Iv9//iEBjAJGARkBOP88/h7+5/50/07/p/9RAM3/fgC9ASUA6v9W/2j+5/6R/5ABmAEp/83/OwAT/4L/AABgAAAAr/8sAGAABwB2AMX/xf+g/7P+QP++/2sBp/+v/7b/G/8sANT9Kf9RAAAAe/++/+P/UQCYAWcAAABa/mX/mf/y/64BRgG9Aef++f3q/28A0wGJAd/+9f7y/34AGQGJAT4BMf/u/kP+BP9nAJQAMAH5/5z+zf+MAJn/OwBCANT/9f7j/88AjACfAWQB/ACbALIA4/8+AbIAbP9KAMn+2//q/2sB1wL/AekBAADC/jj/dgBCAJsAvv+G/pn/bP+g/6//oP+MABkBfgC2/8gAYABd/yUA/f4AAHYAmf9vAGz/Zf9w/rr+IQF2AO0A/wHb/13/Wv6g/cgAEgGFAHT/8v08/mH+7v4wAXoBQP9H/9j+/f4B/uf+tQE7AGz/iv+jAHYAJQBgAHv/E/9S/iL/dgBvAG8AfgDF/9T/uQBVAYEBuQAE/zH/r/+R/+P/4/9kAb7/Mf8AAHv/uQBgAIUA2/9s/6D/OwADAQsBwAAdAG8ALf4T/+UA4//0ABIBZAG9ATMA3/6MAM8Agv/5/+f+oP8dAEP+/f6FAAMBawFs/0/9DP9W/+P/dgCC/6f/OP3C/rIAqgAkAiUAQP8I/ob+yADtAK4BegF0/4r96v+qAjADBwKz/qT+Q/6z/nIBJQBRAmACaP6c/uP/mwLxAVkAaP4m/r7/oP/4AVUBcgFCAOP9s/6v/4kBKAHb/6//QP8M/xIBWQBKALkAcP5W/9T/QP9gAFwBtv/q/xYA+f/U/w4AbwKR/3T/jAAdAHIBiv9//tD+QP+jAGAAG//y/0IA0P5//qv+OP8+AXYAIv++/c39tv9A/ywAuv7q/2AAYABkAfL/YAIDAYUA2//5/1kA4//4AZABywHtAE0BkAFgAtMBZAGbAKT+AwELAZ8BIQEsALP+yf62/zMATQF2AIEBVv+z/ur9Xf8HACn9Zf0X/Dz+WQADAWz/BP81/gH8qP2c/n4A1P8M/wz/Hv7J/ur/ZwCyACwAq/4B/qv+yADTASwCYABRABP/5/7tAK/9OP8sADj/BwCFAAMB6v/j/wT/Iv8T/9j+UQDeAAsBfgB0/28Akf/b/5ABowCuAd4AnwGBAVkA6QHaAXID3gCZ/4EBbwLTAQT/yAA7ADsApgGFAIEBEgH0AJ8BgQGmAcQBZf9L/L79Hv4t/g4AAACjAOUAUQDF/wH+Mf8T/wz9PP6R/eP9Yf79/vn/Iv/1/q/9QP8b/8n+r/+6/jj/yf5d/13/R/8WAFwBkf8I/s3/WQDtAN/+vv2k/pQAQgBZAHYAaP7F/2j+wv7N/zj/9f5a/qD/sgB9AvEBIQEzAOP9d/6UAG8Axf8OApgB+f/XAAMBlAKbAtoBnwFs/wMB9ADU/x0Aq/6n/0oADgAsAGsBKAGyAAcAE/9RAJsAAwFs/x7+oP31/rIAuQBrAaMAnP6+/TsAawEoA94CbwDU/8X9d/7C/lb/CgP4AdD+R/84/5QAxAEwAz4DR/9s/4r/Jv5D/qoAyAB7/9v/SgAhAQcAqgAT//n9jv6k/sX/QgAoAYb+T/2V/qD/FgDJ/mH+yf6G/tj+1P9O/34A1wBl/5H/4/9cATMCnwHIAED/xf8WABYAUQBCADj/PP4zAnYCmwLPAsAAYACv/+r/Q/5gACwAMwD9/uP9owCg/QcAzwBZAGQBjACv/9D+5QAoA+UCtQEkAv38Mfsp/eUAMAOMAt4CBP+bAN4A7QAzABIBWALc/aD/qgAOAAsBhQDN/e78Xf3C/pX+8v0OAAAAp//u/nYA/ACBAc3/6v39/KT80P5w/koAZf+z/ib+Mf9O/zsANwNVAZABMwDIAFEAjABA//L/qgAe/koAS/6UAHT/HQAsAhYAhQI3AYL/9f5s/4wAYAJZAEoADgBA/Rv/Xf84/1kABwAp/8gCtQGqAKMA/AAoA0D/uQBVAbb/Xf8p/QH+1wDtAA4CcgHU/2ACZAFVAVwBsgBD/jX+Kf97/9v/Xf/tAjMAegE3AVkAawHc/er/kf+R/ygBKANyAyQC2/9A/2j+tv+8A5n/LAC+/wAAIQGfAR0Cjv5gAHv/kf+D/Wj+qgBa/tT/nP7U/47+Iv/XAPL9r/8x//L9Hv7J/hv/oP2+/7UBCwHC/sX9hv6K/Uv+BP/f/h0ALABs/6v+d/43AZABSgDC/qT8Zf9W/yL/uv7u/oEBZAE3Aef+yAAwAXv/hv4OACQEMwIhAfL9Zf0i/9/+wACz/rr+xAGUAKv+dP8sAhkDsgDtAFkAoP9A/4P92P4lAFUBjABl/9T/Vv9d/xIBcgMzBE0BOP/5/yL/oP+UAN/+kf04/83/TQHeAEoAuQCD/Qj+tv0SAZcD+AHy/6/9JQDAAHv/cP7tAEIA1P90//3++f/5/88Cgv+O/r7/3gBvACwAgv/j/5gBKf8hARv9Wv6O/uP9vQH8AGACJv5o/jj/oP8lAMsB5QKR/07/F/7tAPwAsgC5AHf+R/9d/1r+yABCAhIB5QCR/ygBBP/f/vn/pgF9Al3/Vv+d/HD+q/7N/8QBVQF9Ajj/9f6n/ywA6QGqABP/BP/y/a//8v+fASQCRgFcAZX8YACyAB0ASgBO/+UAxf83ASwArgEHAPwACwHq/cX/e/9RAJsAOwKMAC3+mf3F/QH+MwDPAokD7QLn/mH+EPxW/yEBgv/q/5z+0P4I/kYBdgA3AXoB2//j/3v/EgF6AZ8BaP6qAJn/8v3eADsAjACqANcAzwCBA6oC5QB3/uP9UQA3AeIBzf2k/hYA8v+QAXoB1P+r/mH+cPxH/ywCUQJGARf+jvzq/V3/iv+c/uP9d/7U/Zz+dgDPAm8Cuv6o/f3+f/4e/m8AKAFcAfn/BP+MAHoB1wKMAhYAtv/U//L/sgAoAcsB5/6Z/1kAqgAWArIAowJl/wj+PP4i/ywAIv/tAIr9kf/Y/qv+dP/Y/FkAxf0M/6//fgBcA4wAOP/U+4r9lACn/7b/RgH0AOP/bwD0ABUENwMWAB7+aP4hAf8BMwJVAXYA+AEhAd/+2gE4/0P+mf8M/TABsgCYAU0Bvv3y/WX9ZwAOABP/Tv/Q/ob+AADF/3/+yADC/h7+r/07AGcCLACmARIBLACjAOUA8v8lAIb+Q/6Z/2AALATxAd4AQgBa/qoAcgGMAFb/s/5CACwAd/4+AZH/Vv+MAA4A/wFA/34AlACV/kf/Kf+K/zMC7QJA/9/+fgC1AVL+bP8OAnv/8v8lAJsAzwBRAq4Bxf/N/dz9HQB2ABIBiv8HABYALALLAc3/8QElAC3+G/1O/yEB+AF+AA/+aP5l/34AkAHtBEoAzf3F/wz/zwBcAVwBYACFAJz+Kf2K/cAAvAMSAa//2PzQ/v8BiQE7ACL/AwGZ/aD7F/5+ANoBjAC+/2X99vzF/0D/SgBGAUf/mf2g+yL/nwFvAgcEKAH9/jH95/wt/jsClAKK/6T+oP3eAPn/XAFyAxYAMwDb/4EBUQL8ALb/g/2G/ND+3gCUAJQA1P3c/R0AQgI7BEYB3P0p/6f/Nf5rASwCTv8e/lr+dP0e/sQBgQFnABf+d/7pAeUCBwQ3AX/+Kf+r/s398v3lAPwAXf2c/rkAZwDEAVkABP3q/f3+QgKjApgBYwOV/lr+nP7b/6MCQP8i/xf+/f5KAnYEUQIOAiQCT/2O/h0AxAHeAHT/tv/J/pH/5QBvAIb+7v6R/a/9Hv5cAb0BS/7Y/jH/RgFrAYwAqP0i/779YfwT/9z9WAKbAA4Agv/C/hkBaP52ACwAuQAZAVkAoP+g/SL/zf/iAQ4A0P7PAPL9zf/tAm8CtQMwA5QA2//j/47+SgBH/w/+R/8p/ekBPgO1ATABPP65AP3+Yf75/9D+hQC+/3/+E/2g/XYAqgCFAgMBHQBvAIb+TQE7At4CmwA4/dj+AAAHAHYACwHf/sX96v1CAGsBkAGqANz98v/8AMX/Wv6g/xv/2PzN/fL/egFgAKYB2gFgAO0ADgJgAH4AMAHy/yQCtQG9ATsCyADXAvgDNwMzArr+bwD5//L9MwAzAMAE+AP4AX4ALABvAvn/QgBa/lEAR/9E/FL+xf/XAH4AqgDQ/gz/5/yr/nIBegFNBZQC1P13/Dj9Jv7u/lb/WQBvAFkAIQFKAhkDSgK9AUP+DP+UAKT+QP8E/139Zf3Y/iL/+f1o/in/Hv6O/jH9LAC2/7b9r/8Q/O783PtE/HT/YAByAQMBmf9a/l3/Tv+UAJQApgHIALb/DgAsAIUA1wBRAt/+bwAWAD4B4gGC/2sB+f/0AGz/jACMACwAuQCk/pn/MAF6AxYAQP/eABYCXAFS/hP/r/9l/9cA8v9h/ssB+f/1/hv/CwFVA3oBRgE8/l3/kf+z/k7/6v3f/NT/dgJgAHIB3gA+AcX/mf3n/vn99vzy/Rv/Xf9cAdcAQgDq/0P+hvzq/XYAUQB2AP3+ZwCO/gz/yAIsANT/UQCYAU7/G/3/AUIEegPb/4b+HQLiAQcCWQBZAPADSgLN/1r89f7EAdj+3gCbAqoAf/7f/q//Zf9//sn+bwAzAHT/1P+C/3v/7v5h/Lb9JQAWAsQB4gGBA6D/gQHaAX/8OP35/5sC2gG5APQA9ABCApQCJAJvAEf/G/8m/nf+bwIOApsAZAHf/Ef9uQA7AqYBxAFcAb79cPzN+Q/+DgAsAAsBpPyR/Sn9Uv5KAPgBfQKC/2H8YfzN/2AA6v9w/u0AAADY/sn+6v1RACL/NwNRBuEF1wLy/0f9HvzN/9/+mAEoAUD/Zf+V/g4CzwB0/9/+Afyk/g4A1wA7AiL/HQAb/9T/jACc/g4Ar/3tAOIB/AAwA88ATv/PAFwBbwC5AgMDZwJgAK//wAKQA0ICAwF0/xf+zf8OACwCEgEsAIL/mfsi/wMBGQNgBJQCOwBP+536R/0I/l39D/57/5sAQgCmAQsBDgBCAEP+kf+yAJAB3gA4/13/nP66/h0CLAIt/pn/BP9l/6YBcgFRBKoA0P5A/xP7kf/xAa//WQAt/pX+4//u/Bv9Uv4x/ZH/r/9L/rr+cP5l/ZX8LAALAaYBwAAt/Lf7Jv5RANT/yABCADcB8v/U/ZQArgHtBKoCwABNAYr/FgLtArkCNwPEAc3/dP3q/fEB7QJKAtv/owA+AUD/KAO5AoUAbP9d/zH9E/3N/yb+FgKYAZsAE/8I/NT9S/xA/xIBEgHeAJX+OwBKAL79oP2O/qv+CP6d/Fr8Jv7lAG8AmAFVAQcAjABW/RP9Jv61AcsB6QHpAXD+AwH0ACwCJQAE/07/6v2C//n9ZwDC/gMBFQSBAf8B5QDeAIr9+f2g/Tj9DgDn/psAjADaAcsBsgAKAywCyALLAeP/VQHTATABCwGXA/gD7QI7AH/8vv+UAED/Kf+YAU0F/AL4Aaf/7vzf/E/9R/8i/zj/Zf9a/JH7Nf75/dD+oP+K/5z+vv1O//b81P2QAYwC+f84/4UAyfxs/af/HQJ9AqoACgMzABYA+ANRAvgBDgJGATcB7QB2AP3+Tv/lAEYBR/8HAIwCIQFd/+f8uv6g/6//qgDJ/Bf+Iv9S/qj9xf8+A83/Nf5a/Dj9tQG1ATcBegMHAjj/Lf7r+6YB+AMoAdcAmAGbAmAA8QEp/9cAzwJ0/wsBiv2+/1ECtQELAVb/CgNNAe7+9f4P/r7/dgBnABkDjAIWADz+DP1nADj/jAAzAqD//f4F+3D8BwBvAHoB4gHF/ZX85QDU/94AWQCr/sX9QP3tABIBgQMwAbP8Hv4p/2sBaP72/MX/mf/j//wAmwK5Ak0BMwDq/cL8Wv7lAHv/0PzC/o7+lAC5An4AE/+c/gsBHQDiARkDBP8B/rP8cP6bAEYBuQK+/zH7PPxw/uIB+AP/A00DUv4p/6D/fQJGBVECywEp/5sAKf84/8gE0wM7BKMCIv+mAZABawFyA5ABEgHeANv/G//j/zABJQC2/Tz+mf81/k/9LfxnAJ8BvQHxAQ/+Mf+R/9z9Af4sAuUA1P81/lr8oP1l/8QDvv/xAe0AG/8x/xv9DgL9/or/DP0p/c3/zfuO/tj+Zf/lAFL+OP2o/QT9zfsI+l3/XAHF/zj/ePpL/t/+SgDlAk7/gv+G/ib85/oP/ukBOwT0BMAAUv5RAFUBAwGYAcQBpP7U+xf8Zf/AAsgA9ABkAaoA1P+v/R0AHQIzAIb+EPwE/8gCXf9KALP8Zf2bAPX+mwKqAssF8AUDA2j+hv7eAu0CVQG2/xIDAwFgBPQCZAGmA4EBpgNVAZcDMANCArb/hv52AJsAawEb/6v+1PtcASwCLAJ9BDH/BP9s/Wz/fgBO/8L+Kf+MAMgA9AKFAJX+MwCr/AH6DP2UADcFwARgAOf+zf9A/xIB/ADu/B7+Xf1w/Nj8/AAoA3IBOwCV/Ev83P08/in9Wv4x/QT/yf4m/vwAYfw4+5n53PnU/RkB9ABH/0D/7v5o/jz8kf9ZAN4Atv9h/Jz+EgHlAlwB8v+5AJn/5/7U/1kABwSXA+0CDgAM+07/DgIKA5ABWAJgBOkDSgBd/1UBZf9kARIBcgHlAO0CxAHc/VEAbwCQAygDRgFKAHYCpgGR/U7/qgBgAjX+qP03AWAAegH8AML+awEWAvwAtQHb/5H/T/1L/uIBLAC2/4wA5/zy+3f+hQAdAq//BwDF/aD9tv3q/RIBe/+YAWz9hvxa/gz9Xf1p/M8AIv92AG8C+f0OAOIBEgO1AQz/qgBw/nT9kf1d/WQBDgAWAlgClf6MAF3/G/9+AGQBQP/f/mcADP/9/i3+tv8T/5sAtQEB/igBxAEOAJsAf/7Y/ukBlAJnAmsBQP/y/13/7v52ALUBtQFd/aj9DgCqALECR/9l/2cACP5kAbUB7QBZANz9G/3N/fQANwHTAZn/mf1RAPwALARYAmsBLAK+/ef8iv2jANoBmAE+A4EBjv6c/kP+Kf2g/4L/tv+D/cn8CwEAAFgC2gGBAbIAf/oM+2n8DgA7AlUB6v8ZAYkD1wL4AeP9Zf+V/vb8E/9cAVgEQgKFAGj+8v8WABYAMwA8/h7+/fxD/vX+rgFKAIL/mwCqAN4AoP83ARP/4/01/G8AMAMSA4EHhQTiAaf/dP+Z/0oANwN9AgMB4gMDBTADuQQdAq//e/9yAc8ATv8HAnYAG/84/8AASgJS/h7+SgBP+2n8R/9O/5sAYACg/Yb6Nf4b/8AAcP6d/Pn9r/vy/f3+XAGbAK//Lf6G/psADgCZ/3/83/yo/RP/PgFGBR0EMAO5AHD8Hv4m/lECVQMZBUYDtQNcBbkAbP1E/NcAQP/AAE7/mf+1AZsAXAET/aMAQ/5h/KT+Mf1h/sn+hQDaAYUAjv41/kf9BP9ZAB0C5QK1A88ES/7J+Mn6CwHIAjsCMwKmAYUC0wEm/kP+OwAAACL/5/70AN4C1gTu/u7+Xf8B/rUDowAlAKD99vxh/lkAbgZ2BB0Cq/41/Dj9kf/IArUDJQAm/IP7R/+mAfEB5QK5ACgBbP35/bkAQgByAdv/yf4i+xP9q/6O/jz+Af4AAHD8f/yV/iEBWAK1AUIAOP1w/ur9s/zc/fb8DP/eAPL/nwFnAEf/UQBcAcgCwAJYBDMEOP/u/lUB8v/Y/hP9d/5L/hv/AwPlAmAC9ABCAL795QAkBEoAf/75+775CPxKAmcCMwAsAPn/qP2z+nD+hQIsBIwCywF+AEv+/f4p/dj+2gHtAnT/R/kt+vb8SgBjA4wE2gO9AdD+Kf1a/rr+owB//hP9S/wQ/B0AAACfAygDMwBl/xv/3gIKA9oBMwILASb+p//N/5ADDgZvBG8CXf38AtYE5QJkAd4AEgNRAokB2P4OAHYAmf8p/zcDgQN//GH6T/uZ/R7+SgIHBEv+wvpe+0v8zf2Z/YL/G/+O+r772Pqg/6oAE/1//r77G/t0/TMAOwLtArkABwD9/sn+R/1D/lUDoP8e/P368v2FAigH1giXBQsBiv2K/zsArgEwA8ACsgD1/pn9tv+MBAcGlwOXA28CyfzxAeIB4gNNA1396QEDAa4BIv++/Vr+xAG1BZsACwG5BLUBf/4E/xf8ywGjApz+7v5l/TsAHQD8AB0AKAHq/yb+p//u/rIAHv4x/Rf+awFcAfL96v+g/xYADP0F+4UACwGQASwAMf/TA+kBHQI7Ak0BPP79+jz+nP7j/4L/Kf8dAIUAAf5D/k0Bgv/8AGX/Iv/F/2X92P7n/pX8e/04/ZH9vv+D/dD+9f6FANcC0wOUBAT9F/y6/jj9e//tAMQDVQMx/2QBiv0M/TABZwCQAe0ATQNGASEBiQNgAH/+7v74AQcCuQKyACn/sgB9AhUEe//y/6YD2/8i/+0AXAEOAjcBLAKMAD4BZf+2/QT/BP1NAd4A/AB0/2n8wvyz+s39Hv5h/mz/mf+5ABIB5QCv/6f/mf8T/139uvoP/ukDLAI4/9j+xf9S/jj/ZAEDA64FegNrA6D/Tv9KALr+G/+o+5H9wv4p/c39DgJrA3IDsgCc/s8CZwBVAc8AdgADARP9jvzC/DcD+wS6/t/8Q/7lAEYDbwJ2AFwBuQDU/2j+Vv3AAhIFHQSC/0D7Vv0M++P9pP4x/9YEvv/c/R7+/ABnBgoFXAMi/zX+1P9h/l3/zf+6/tj8hvyV/hYCogRRAvwA/AAWAu0Avv+g/6T+E/9L/CL/WQBnAMsBqP2+/XYAxAFH/0v+PP6O/GX/YAQhA5sAQgKbBM8Cjv5H/fb6lf4t/i3+tQEHAgcGWQCR/UIAq/5w/rkAwv4i/QH+6v+fAdD8cP5W/br+kf97/0YDjv66/mj+BP8M/aD9oP9//pQCnwEkAnYCtQO1Acn+tQHpAUoAxf17/wMB3gBcA2AEAwNnApABtv/U/70BTQW9ATX+pgFS/B78iQE+AyQC3P3q/Z36Uv7pAaoCmwCg/QcCe//TAUkEzwIX/oUA0P5A+TABawNGA839pgPPBGQB4gFo/hv/zfvEAZH98v38Auf+F/rF+8gC3P2R/wH+E/1S/Kv8T/3N+aT8s/4+AVr+OwBnANcAlAD2/Of47vijAuP/Zf8dABv/gQH8AssF+APeAhIDAAAb/xYA5QBvAkoALALn/tv/yARvBJQEmf1nAFUBMAFCBDcDbwBw+hv58vkx/3IBrgHy/wH8+fta/s8ASgJyA3/+G/uR+6/7f/52AML+wv6G/Nz9PgFRAAMBOP9E/NT5lf78AJsA9ABo/gz/Kf9CAOkB1wAm/Pb8PPx//iQE+wRYBCL/q/7Y/ogFwAS+/Yb+Zf2O/lr+pgNJBigFqgJH+UT40P7xAQcEUQLXALwDoP0x/cgA/f74AbUBZAGR/2j+fQQKA+0CpgF3/rUDxAEZAfL9Vv/0BJcDTQP5/R7+3PtP+779E/3aAQ4EJAIwAaoAd/5W/3/8Vvtp+ur9CgNCAPQAWQDlACn94/2r/jj7pP7y/1gCHQJW/zj/d/5H/U7/Hv71/iEDmAHF/U7/gQFs/7kAE/9VARIBUQCqAnoBVQOjACwCSgJKAN4AOwCxApADHQCQAXIF2gOYASUAfQLy/7P+0P4ZAeIDRgG5ABv9f/6O/qD//f5RAFUD5QA3AWj+yf7u/NcAIQElAKYDbwCFAAj+cgGQBfQCOwCmAaoCXAEDAYwCgQFp/Bf+PPzu/vwCYwPPBDMAVv/eAPL9dPuO/r7/Zf1A+7r+nP7Q/m8AR/3lAGz/wABp/Pb0S/rY/vQCwv66/E7/7v4ZAZn/aP5gAMQBs/5E+mX97v6QAZ8BBP92AnYAJATeBKMAnP5L/vwA3Pu+/XYAzwAhA9oBZwCg/Xv9Kf8B/h7+0wFrAdT/xf+uAS3+oP1CAvwAnwPAAAH+7vwq+6//hQLiASUAlACyAD4BpgEVBOUEDgK5AGX/Xf+FAPwCbwJW/RD8EgFcA64DIQFa/KD9p/8HAKYBmwLIAh0A9vzc/Qj+fgCZ/4r//fyg+fn/lf4+A2AGuQTwA5H/e/93/P3+R/3f/t4ErgHN/y3+xf8sAgMD5QJ7/yb8RPzq/00DLAD5/3v/jv7U/w/+GQPU/0T8E/st+lwBVQMDBeIDpP5E/K/9E//xAVECYAIM/3v5Wvw4/88EhQJCABIBmf+v/9cAawXtAoUCMf1h+l3/fQIsBpsCZwDf/AH8lADIApQEMAOjAP38qPnC/v8B+f+uAb0BPgFcAQoDAADj/ZQAG/2O/AT96v+1AS3+NwE3A94CZwI8/tH6s/jG+RP72P7TARv/mf0f+jH5/fjJ/t4CWQBw/p34bP0B/vn//wGv/YUAWvot/MgErgPXAsAEuQRYAkD/qgCBA6oCHQQSA13/g/2JAZQCOwLU/9/6G/2C/+0CWAIdBgoFt/nJ9p365/yV/AsB4/+6/Jn9qgCIBaII6QWBAUoAS/7U/S362PxjA1EG3gKuA7EGxAHIBDsAzf3Y/Ef98QHF/QsB0wEdAmcA3PvF/dcAMwAi/Yb+0P6yAOr/Kf1p+sL6FgA7AGsBJv5E/GAAE/3u/PQARgEWAt4C3/4M/7kEawMsAowCQgRyAxv/E/9//lkAhQJYCJMIjAQKBdj+F/41/Mn+JARW/6YBPgG3+4P7Wv75/7b/yf4T+x784/++/7ECXAGR/88C2Pz5+3T/F/yv/ekB8AMDAy8FawVa/tz9Kf/EAXYEFgL4Ab7/6v9VAVkAuQD0AvEBdPse/ML8Mf83A0oC9AL1/t/8Nfwb+2z/E/+g/UoAQ/6z+oP7UQC9AYUAcP5o/lgEvQG1ATMAMf0+Aef86/ssAMQD/AKbAjcBmf/iASUACwEE//3+Jv4Q+n/8cP7Q/koAPgH1/tz7vvuc/lr6R/v4AR0Af/6K/wAAMfsM/RIBWALTA5z+9f5W/e7+0wVgAlUDSgLn/uUAFgKfBTcBaP5A/x7+fgAkAiEFXAMlACL9pPzy/8sDogaBAR78UvwHAN4CVQG+/bb9Ofmk/NMBdP1rA7wD4gHY/lr8Hv50/8gCLACv/8L8jAAsAg/+0wHN/3f+5/7y/WsB8AW5BqIEYAAi/yb+DP8zAmsByf66/mQBTv+FBC8HdgRYArr8F/xw/Jn/iQFgAjsAq/5W/ywAxAFRApsAOPv5/br8pP6MAK//pgObAhIF0wEzAiQC8v/0AJH71P0oAfEB4/+D+5n/UQIDAw4EywG5BNj+pPgt/Bv/OwSMAAH+lfop/TMA4/mqAEoAAACqALf7+f+qAE0D6QHu/GX97vqk/Dj7JvyV/gX7LAAE/7r8nP6MAK4DtQGuAXv9tv0zAGX//ABS/vn7lf4DAxIBowKBBaYDjATj/wT95/z9+oL/nwG8Ax0GRgW8A837afyg/3D+QgL5/8n8R/+K/0oAEgG5ACQCBwAdAowCqgILAWz7tQFs/R7+cgPU/+UAr/2bAG8ANwEvBXIBYAB7/3oBrgPwA2AEDgC6/pABLALU/wH8BP/2/Cb8ZwKqAjoGUQQE/dj4r/u5ADH//f44/1b/wv7j/SwAhQKBAZADmwK+/3/8Zf0DA9T7cP77BCAHhQSr/q4B6v8zAmz/pgGxBHT/XANL/nT5VvnF/fAD7QDQ/uf+bwASAz4D6QE3AYwAyfy39dj4dP2O+rP8pP5kAQ4Cp//F/3v9hvzy+1b7/fyMAFECwv4T/2j+VvvN/e0AQ/4x+xv/3/7q/wAAF/5GA0YBXf8T+yL5G/9w/mz/p//F/3YCf/4X/H/+kf0HAPn/tv2uAU0DIQMhA1QHWAL2/Lb/tv2bAlgCGQPEA9T9tQH8AowEtQX0BCEFhQDiATMCS/79/nT99f5GAUoACgWXB1EGqgDY/Ib8Iv3EAygBRPyv/YUCdgLtAM8EFgIDA9z9lfom/kT89AC1AZ8ByAC1AbkCNfyv/Q/+g/0x/3T9hQBVAfX+mf0f+p38G/1h/goDOP8dAtMB3/zXAAcAUv6o/c37uv7xAdcA9f6yAGcCOwKuAzABHQDb/+f6uvyfAZsCegOUBCUAbP/N/xP/VQF7/aoA6v/J/kYB/f4p/1r8fQJNAQz/kAOv/3f8EPpD/rP8T/t0/8gA8QG5AE0DOwJZAIEBnwFcAcsDEgXq//L9QP3Q/igDJAh2CsAEywH4Ad/+hQAoBaIE7QIHALb//fyD+6oCVQMhA0YBVv1d/QH+WQAb/wcAq/44/bb9rPqz/gj8NfxyAY78uvxd/RYCVQO+/07/kvnf/mcAe/8VBKoA/ADy+zn5q/yv+5n/ZwRCBpsCqP0m/uP7f/iO/KMAIv+d/HT7QP3U/aj9JAQzBC3+1P1a+kf9KAGYAf8DpP57/XT7hQC4CIUE5QZyA/EBOwLF/fgDp/+D/er9t/tGAw4E7AaUADH9kAPj/R0AJv4p/5n/xvcM/zME0wVVA/n9UvyD/TMAtv+BA2cEMAPEA6YDOwDj/+IDTv9L/CL5YfwvBQ4CWv66/MX9CP4m/t4A0wHiAVL8ivszAJn/MAFVAWn8ivuk+O7+bgaG/lECmwT/AVECAwFNBRUEAwPAApH/1fdp+H/81PnABJMKVAeuAxv/0Pzu/PQAIQMKA2z9zftD/pH/PgPaA/AD7QB7+6/7s/wdAJQCLAD/AQMD8QGD/Sn9dgCv/QT9mfvQ/t4CHQJNA1ECCwHIACL9KANrBywA1wK+/yn/tv8X/gcGnwPq/9/6kf1GA4L/xf+UALr86/fC+JX8TQFw/Ir5OPsq+1L+S/6MAPX+0Pzu+ML42P6V/rkAlASMBiEDfgCBAZQAowDaAYwAQ/5o/kf9BP96AZ8DbggDBbwDegPC/DcBfQLJ/gT/LAI7Aq/9+AMsAhIFkAW+/88Evv1w/iL/F/6yAEP+Yf79/D4BoP9s/xf+BP2c/lr4Af6v//3+e/9h/Ef/3P3c/RP91P1//jH9vANkASUAWAJW/3oDmwAdAO0CBwAkAv381P8KA4UAjAKD+1wBkAFw/NMDjAK1A4wAqP2BAU7/zf9VAUoAGQMhAef8iv1H/5AFlAL4AVwDLALPBC3+kf9D/uP7gv/9/jH/mf+1AzMEtQOuAdcAPPzJ+Lr8wAAsBtoBKAGg/eP7Wv7C/GcE/AKuAaD/9vr1/s3/2//5+zz4Uvop/7UFkwgDBRIBXf3g+Nj8xf/tAOkB/fwB/uf+WQB6AyEDIQOC/7b/r//EAX0G2P44+6T+kf9CAPn/OwSbBBf+5/68A7wDEgEi//L7H/p3/GAAMAH4A9MDPPxa/Bf+4QWiBk0B/wOs+rr8gv/f/sgCCPy8A5AFcP7aAX0C6QUsBPn/sgBL/sgCRgGg+wj+2P5RBFwF0wMSA839nfzq/Rf+7vxh/Of+mf+o+2H+AwEzAp8BG//eAKT6ePiZ+0P+mf9S/HD6E/tvAMQDHQR6A0oAAfz5+8X9wACJA0f/Tv9s/eP3hvyYAXoD1P9h/AAArPrU+d/8S/6uAVL85/44/9/6PPrc+5n/Vv2bAIP90fowAWAARgESAWcEqgRh/PQAJQAWAowCpPyxAtz9zwJJBDADKwhGBa0Hgv/pAU0DPgEvBbkC8QH/AQcEuQT7BFEAYARcAzAD3gbaBzMMLAAi/Vr8rgEsBGH8oP9w/P38UQAzBHYI2gnLB3D+g/ny+yb6Vv25AqoCfQQP/jH7DP3J/nD86QHeBiwAXAE1+v34Af7pAZ8BwvzC/Dz4T/eV+k/9/fx+AAcCKAN+AOP93gCG/lkAD/4x+2n4pgG8B1b/QgDTAf8D/f4b/w/+qPfq/9YEUQRnBGACOwIP/kv8gQGD/XYAsgAM/4EFpgEOBqoCiQG5BgX7vv3EAx0GZwZKACgD/ADeAPn93Pn9/sL6pP4wASn9BfsQ+kD/q/wI/nv9+fkB+rf36/kx+e78r//n/FkAr//n/M37uvxa/n/8PP6fAaIGawU7BEkIegHU+8n67vpNAZsEIQEdAkIA0P4m/jz6vAXhB28COP32+DH9wv4DBx0G7QJw/pX4s/p09xYAhQJe+3IBBwJgAqoGywM7AqYBhQBS/sAAwv4p/QMDOPvY/ssDWQAzAsL8lf5gBHoF/wOR/4P9Af5l//gBwvqk+iQCFgD/A6YDuQLj/er95QJCANoFQgQdAOP9kf+YAZ8DJARVAYUEpPwM+xIBqgJcAywAE/vJ+lwByALq/dD+qgY3A7wFYAQT/5QCYf4ZA/b6rPpJBg4EsQQWAPwCOwBa+jsA8QEDAT4BmwAP/ssDgQEt/A/+bPt//M35DP/7BKYBLALC/L77zfu6/gMHRgOFAOr9kvl2ACEBCP6UADn5E/sM/Rf+ZwT1/mcCXf0I/vQAVvlO/+v54/1KAMX9WAiUAtD8/fyD/R7+AACQA1wBZwAX/Hf+RgdnBlQFiv/C/GH8BfswA0YF/wPC/AX70Pz2+IUC0wWUBLUBAfyO/A/+fQKMBmcEE/8q+zH5jADaA2sBdgKmAd4AR//lAAMDKAGD/XD+tv+O/BP/IAc7BEf9uvxs+yb8yfwWAIL/lADIAE0BKAPu/toBMfvj+dj6dP2QAXT/yAT5/Yr9bwBgBHoDkAHpA4r7OP0X/lEGxAdgAs8Cyf7IAJgBPgOQAdMB6v9KADsCd/7/AfwC2gO9Aaf/r/t/+KD/AADC/s8C/AIe/mn8E/92AiUAaP4OAt/+vv2k+qj5uv4e/CUA8v/f/uUGtQHj+9/+egFrAy3+d/6bAJX65QRcAzMAIQN3/BYCcPj5+cQBgQH5/177NwMsANoDsgDj/4wCuQDy/3/4FgDU+6YBywFw/OIDSgCmA6MCEgVnBB0EiAUlAGAClAQ7ALwDuQQP/okDZwAKAzX+nfo3ARv9+APeADME5QBH+5gBZf8E/xD6mfuK+ZH9Kf2k9owAbwRcAUv8iQElAHv/R/8M+bwDWALTBcsJq/5P+a/55QDaAfQEwASFAmACT/1P+a//kAlyA/8F0wFl+eD2t/f/A5H9Lf5YAsn8Hv7b/9z90fqO/Fb/JAKJAWMDUQAi/Sn9Jvwt+gz7qgTwA/gBBwDc+4P7NwEDBSQCywEDBVEEMf9cBYEDdgZ2BhkBMAN3/Of+3gCFBBIDaweMCD4DRgfb/94Ayf6R/9/+r/+5BBf8Wv4M/Wn82gMkAnf8DgAF+6z21wASAfL/Nf4p/e78OP8SAaMACgPC/gz//fyZ+Uf9Q/4+ARP9f/gp/zH/qgLiA5H9gv/y+7f58vfY9uv7f/7j/dX3t/l3/GH+KANL/Kv86QG6/OP9SgJl/+76EPx7/R7+cgH/AYwElwNYAu0E1gSbBAAAVv9s/2z/OgbWBscG9Ab/AUD/E/+UBNMFHQRcA3T/4gEoAWsFMwqmA+P/BP/f/kf9iQEKBUYFdgKo+8L6Mf1VAc3/Q/57/4wAiv08+gAAKAGo+1b59f4DAfgBqgB//AMBHv7j/cACQgJyBWcEiQM3A+P/NwdnBHv7PP4T+1gCAwVl//ADRgM+BSn/2P5JBkD/H/ZP8Qj62P5CAFEEtQE3AfL73Pf69775xf/n/s37HvzJ9sX7HQb7Bi8F7vz5++P35/aqANYEkAOG/DH75/ZgABUInweECsL8yfrc9Sb4XAG6/DsCxf2h94b6RPziAe0AcP6mAxv/CPqv++f8Hv50/y8FegNyBTcFmwBZAOP/NwUwA94EjAQi/6//iQObCFEGrQkgBzsA/f6V+nD+oP/U/zz+rPiv/e74BP3LBzcJwwtnAK/5TPKK+eEFDgJ2BEIACwEQ+GX7bwSg//AHEgMZAZn9iQEvC3oFkwaYAfn7ZftKAvEBDPu1A/8DEgGFAgMFgQcp/ywAMAF/+NT9hQQOBMQB8v8HAj4D9AADAZsAHv4i/S74g/3TAYwAJAR6A1QFNwOc/gj8jADEA3/+wvqO+ML+3gBkAUIAvv2jAKv+cP4i+5z+EgOv/30EcgHQ/I7+PP5KAPX+BP9VAdcANf7f/GX/bP1vAIwGRgUlAFL8rgFvBH0EIQUOAHYAYADR+s39iQH4BbUJhQL1/gj4rPRa/oED8AW9AeUCWAQx+a/5DP1h/lL+jvwkAr77DPs1/v388QG3+0oA8QH1/t4AH/rN/cL+YAByAQcEwAZCAA/+RPi3+UD7iv8sBA4AbwAq+6z6zfsX/g4GvAWJA6D/r/mS+Rv7Tv+JAaj9SgBA+7P6CwH1/mcEBwDc/R0CbwCmA8QF/wEx+zH7ivek/DME/AADAY74T/lo/mAEwwtnBjAD+f1a/rkCYwMkBP3+5/oT/2sDjARyB+0EE/8b+UD/MwSUBCsKkf2R/7wFQgDwBQoFxAGc/hf8Zf1RAg4EDgZJBF39Lf5d//QE/ABcBTMIjACiCOIBiv9NB0kIE//2+GX9vvfF+yQCqgTIAjsA2/+BAZQEp/+UApn5Vvlw/IP1mAEdAmz79vSH9jj7S/pgALUDUQZs/0P+CP7v9vn9iQOUAMb5yfYb9U/3XAHaA+0CrgMKBSUAe/la/Az5kftNAcX9XAM7ALr+CwHy+28EMwQ1/sn+Yf50/4wAcgf0BtMD1gQX/JX4EPz9/lwDGQN9BHIBwvxkAZABJv6MAHIBdPeS8zX4uv4OApsAWASG/lr+3Pvr+3IFYf7xAXT9NfxNB0ICKAF2BMsHzf/j97r81P3u/LkGeQmfB0IGBP07AP36s/6bBIwCHQRW+1ECTv+1AYUGQ/7u/mX7Yfjj94UA6QXADIUGMwAwARv1fPXc9Sb8hvrq/0ICU/a5ApsEyAQKBU7/QPlp9ML4CP6bBPgDLwlRBAn27vy5BtIHLAQwAyQEDPsX/L7/R/0rCCEF6v3R+pz+TQVrAYEJvAWUApn/Jvj2+rf3xf+UBGQBfQTiA13/vAMVBlgEDghnAnv/dgAsAqf/+f90/5X4yAAT/6D9PgM7BGcG3gAQ+rr6R/2g+Vr+Jv4p/d/+r/vPAND+CgXaARv5jAKG/sX/WAbtBAYIlwWJAfwA3gBYBFwDxf+S9775kAl2BgMFEgO2/RIB1PmD+Tz+F/5a/v36JvyfA7kGYAIb+zX2CPqo+5X+gQX4A2MDyABRAOIDBwJNAQz9S/qD+y3+ywE8/r7/5QLIALwDnwHxAeUEOfmo9dj2PPha/tD+PP4B+ur/GQFs/UP+8vkP/rkAAwG+/doB+AX5/6/9qPkP/hIBdgBGBfsEMAESA3oFzwbwA/QE2gUi/8sBDP2mA8QD6QH0CH/2xvlE/NT/BgqxBDcFAf6R/TH/iv+qAjABr/9a+tX3sQJyBWH8qP1w/IwCSQT4AR0CuvpKAmz/8v+MCIkBQP/C/HD6E/25BGMHQgQM/1773gD0AHIDVAWYAfX+PPzy/X0CPgfHBr7/2Po4+x/4+f2qBigJs/5m8/L74PiG/vAFOwQOAib6WvoM+0ICvAWFBjz+g/vC+qT8CgW5ALEKhQIDA0IEpPiz/CL9iQEx+2QBzwYvBeIBaP70AC36e/0T/2H8FPkI/tT9iv0hBSEBHv6K++r97QA+Az4DsQL2/HD6jvwI+goDSQi1BS3+t/s8/Fb7QgIdCBkJjAT2/CL58vfu/AMFjABrA3T/4/2n/6H3/AK2/4UA2gPJ+Lf34/3wBSEFywf4BVwBiv+c/jMAbwLF/47+hQJL/CL/vAPLByQIAwUkAqj5s/wx+0f95QJRBHIBRgHf/qzyr/eh90D/ywVA/6f/F/wQ/Nj4DP/AAOr//fyz9HT75QDpBZcDyASk/KH3bfcu9rUD3gKiBvL9r/td/xP7qgDN/dMDOwA8/Bv7NfiK+bIAQgQm/sX/7vzAAAH+3P0sACQCgQVGA/8Ds/zPBtMFG/96BWMFcgXIAj4F3gbpA88AdgZuBukDjAaxAvX+BwDC/m35egP7CIwIRQlH//n7Kvng+MgCnwH7BoEHr/mO/Fb7wv6UApsCfQYzAI78G/+K/1b9xAFW/1r83/q+//n7T/dVAe780wWbALP48vmv9woFbwA5+TMASgBe9b711PklAPgBZwJCAs370wUoA/sGvAPY/BIDS/b29qj92gMKCZcFUQJ6A8gC0Pxw/igDxwj7CAoF0wOuAbr+FgCqAOf6DP30Ag4ATQFcAd4CxAdjA5QEBP+d+mj+hv7Y/s33CPiK/3oFeQexBHIDcgPPAL774PjU//QAzfmbANoDRgcvBw4CbP88+lb/3gKMAnf+YfzJ/Dz8Jvwt/mcEe/2h99T7GQEhAwoDHQDJ/AH+d/x7/Rv7bPu6/nD6xvm6/MACtQPIAGcE7QJ7/aD9BP9+AP8BmAGMApQC3/7C/v8BRgGjAvwAKf2jAM35mf0hBRYAogQsAjADyAJh/HD6f/zN+8L6Hv6z+NcCoP/aAR0I/f65Alr+EgfN/3v9hQDn+qoCG/8HBm8Civ+2/9/8DP2UAEIGe/1h/M37VQNRAkYBywGd+nIDTv/Q/qYDwAbxAfb0lfj9+qMCZwaMAgMFKf0E/TcF5QJ0/8gCWAK++2X7qP2mBRP/U/QM+Uv+KAM7AmsFdgbeBKj9Nfw+Ay8FYwMm/Bf6WvRE+mz/vAVRBPn/sQSg+TcB3gC8A0YBcPa+/Zz+YAR7/4L/r/81/k/9mfn1/pMGXAXf+oUA1wIwAzABjALq/3v9mwSv/TsC1wJvBLIANfxL/lb5owDlABkB7QAOAt4C/wXaCQMHowIx9WH6afwB/FEAoPufAbkEHQbPAnT/DgbaATX4pPqs+nj6BP93/iL9oPkzAMsBjvwlAFb/ivuW9nT3E/2FAvgBiQHn/t/6YfyG+g4ALASpCssDUvqxAqv8s/o4/Qj8s/zF/1EE0wNGBaoIagvwBZn7r/k1+kv0uvw3BUYD3gLU+zz84gMZCToGZwD9/DMANfwQ9psAMAOUBIkDkf3j/SUAyABW/8X78v/ABs8CbwSFAMACvAN2BMAIiv3wBZcFgv+fAygBcgW9AVEEfQZh/iwCsgBCAIEDAwetDyQIuQKc/sn6H/qg+WcC7v6c/psAYAAoA7EEgQWJA1QFbP+v+3/+bP1A+xD8t/uc/owAr/sB/gT/zf1RAEoCZf08+p32OfUi/RP/OwS1B+7+xvlL+If0XvtE/Mn8LwWMBFEEMwBrAbkE+ANGA6oAR/3n+l750PxcAxIBBwTY/OD2IveS94EB4/1w/kIAxf8sBp8DnP48/ob88vvN97f5ZwALASEFsQJvBBkDIQHpARv/jv47AGsF7QT7CAj+CPw3AxIDegPF/bECxvkq+2sDbwJcAQ4CrQmMAFb79ALEBW8CcgcKA9T7AAD5/xf8cfSR/VwHvQGqAIEF1wADA4gJiQOz+GX5Iv/j9zX+ywHeBp8FfgBrARv7WQC5AkIIs/zn/gMBT/sVBDj/gQkx/d/8nwEF+8sBLADWBv3+QgTeAgH0fPXU+2AEmwLy/+UAHQIq+ZX6H/pP+cX9Xf1RAt/+NwNW/zX8xf14+hf4wvzEBWX98v/2/Pn/Zf+o+VEChvrIACwGEgdYBKMASQTj/94ABwDtAED/lfz9+DH11PtuDJcNtQXEB7r8qPnn+qf/hQRgAA/+E/sB+jj7BwRjA1gGwAKz/pn/t/n8AkoCHQb/Bx0C5QbaAwMBMAHU/yUA1P8SBf8HPgV9Bir7kf16AaMA6QnXAhUIqQrAANj8wvbg9NT9Jv7U+V77cPwsAgj+xAGZ//b8S/6Z8y72UvymATMAe/th+CL3ku9/+OUAyfo3AYr7zf0M/RYC4gHj+WX9FPmV/lkAdgg3BTMCkAG6/B0AbP2iBFEAcgWqBHv9uQIZAV8I5QbpA0f/lf65BvQA6/tS/lUBBwRa/tD8WATEA+IDiAUDBQcE0gexCmcA+flH+6T80wH8AtcCAwV2AjcFhQK5AKoE1wLXAMb5ivdw+iwCQgp2CvAFnP53/qj99va6/PgD2gGqBuIDG/8lAIkD3/679C740fjTAYkDuv7XAlr+T/cJ9Cb6nP6mAer9XvkQ+i36Yf6FAOP/iv0I/rP2Wvg+A1QFvAVyA4b+0fg4/c37PP7WBJcFhQTQ/AcCvQHlBG4GMf+uAY720fLq/VQFkwZyB9MBjvj9/ML+2gNJCtMDVv1A+5X4T/30BBkFgQUKA6z6G/nlAJH/8QH0AGX/JAT2+qD9xfuO/JH/E//TBXIBdgC393T3F/op/W8Ce/87AIP7GQEWAEoA+AHXAt4Ct/f2/K//wACuA/gBIv84/ZL5JvwdBPEBnwN9AhIHXAcDAUD/T/nC+gj8Q/5JBk0D4/+MBFEAYwWmA3v/wAIT/TABKf9CAvwCDgCn/77/eQeFAg/+mfuuARYCywGmCSEFnP5W+U/9hvqG/FwDtv8SA7P+CP7LBbwDywl5CS38Bfky89j2xAEKBQMHywNvAO0ArgHq/bUBqgAb+e74Xvce/HoBhQBRAOv7f/ju/BP7Vv38AJ8BfgBS+nD+h/Z/9BP/lwMvCVQHRgWD/ev7zf/LAW4KDggsBO0A2Pz0BBkHrgXHCCwE6/la9I78YAJ9BrEIGQNvAtD+Vv07AGAGxwbN/Rv3AfS6+sgCTQfWCE0HsQSK/0D7yAQGDEICowAI/gX3D/4sBEYDTQfwA2z/Wvp79/wA/ALlBtoDPP6k+AH2wvqK+b7/HQLhBfn9uvwM+6j1qgBl/fAJ0wWUAH4AYfpNBVr6MAN2Bt/6qPnK8rf7KAWbBEIG3QqZ/xf8kAMm/u0A7QSv+6j3f/xs++787QS1B1EA7v4hAa//Af75/+UMuQSV+IP7nfo596j3jAKyAOIBhQaQAQAANfwOAq/9u/Zp+v3+cgElAIUG/fxL/lQFVv9P+/L35QA4/28Ap/+G/uf8Iv8zCBv/4gEm/sgAmf04+zcDD/7ACHYGLAQx/Uf9gQOfA94I/AA7Apn/mAFnAG8AzwQhBfQGgv//AQj+g/0wAZsAFgD1/sgArgESBY7+jvh7+1L8QP2iBjcFRgPeAtz3Wv5gAn/46/tw/of4d/5S/kIE8AeUAlEAcPi++zH7/ACjANz9bwBP/c3/WAaBB5n9qgJ3/tj+0PyYAW4KBP0zBKMC4gOUAlEGxAV4+Jz+PgHlBJX+ePpA+Qj8yfraAd4IuQZ5C7f5vvdH+9T9BP+5ADz+vvXiAaf/Q/4M/wcEBP/Y+jsC9AIoCxIDLf4Q+Hv5/wOmBfQGIQOjADH5g/v/AcAEIQPJ/pn7Yf5yB/AJbgyUAl39r/2z/qYFRgOUAnv9D/7n/Dj/jw+ECnoBqPtt+QH+F/4SAcAAYfw8+sb53PV+AEkE2Pzy/dX1dPsb+0v+CwHR9F737viMAuIBzwRgBlb5+vXk76Hz9f4GDoANuAiMBIr9uv63+/EBdPvY/P8BMf1NAwMBrQcRC60JgQdh+sL2zftP+U/1OPtH/SEBegEkAtT/Bfu1A3T/Nfp790T89f41+FEAtv/2/ED7Yf4kBG8C5QJH/8L+8AP0BOv7kAE+B+0Civ1W9zH/pPrU/3oFzf1jA/QEJASo+aXyXve++aj5nP61CekHPgHr90D1AwEsBkIEBwYoCeP9H/jXAGcIqQ65BkIAOwJ2An0CDgggCXkHmg6xBNT9+fuk/sACxAHwA/n7+AVW/6/5BwbwA1wBbfnJ/mH+Zf2FBDcFzwDY/hv9nfrF+zH57QKS+Tj71wIP/n0CF/xA/zH7RgNrAcb37QLIAh7+bfd0/7r+E/1H/8X9fgCk+NT9lAAx/4wIHQq1A2n6CPr/AY7+yACjApX+RgfTA2H6Cfb5+TcBZf1yBTMMfgCR+1r4cPh2ALUDDgRkAcX/8vlH/SUAXf05+WL0AfxA/+UI1gT5/6T8u/afAbkErQneAgz5ivWd+Hf+gQeiDCgJfQJI83f8q/4VCEkO0wP7BH/+Uvw3AfsGF/rG96z6egF2CPAHAwlrAbkEZfmK+U/3kAMZC1f1+f2MAJMM7BBNB2AAAfw1/jcDCgVL/iwGPgVNBf8BpgM2C7UJzwZl+XzzF/rwBfsGFQYVBMAAvvmo+9/+s/4zAtX16/Xr8Xf8PgeJAzoICgP2+O/w+fmO/MQDoP8E/d/+9vimBXT/hQLABoEFbP/N80v4vvfF/2MLOgoGCLwH9vq+9e74R/9VAVr+XANW+5L53/qH+Lr6/f52AtoD+wS5BvL/V/OD/QoDZwKMAtz9dPnu+Ef9D/77BP8HHA61B8gANwMHAJn9bfdO/4r9CwGFBv38S/zV95n7mwLeAoL//f4zACUAFQSC/3/8vv8wAZsGCgVNATMAkfswAR0CiAUKBZn/yACG+noDAwHPAE0HCglyDfn5WvYq9WX1R/0M+8gCCgszCnD+pPQx9YEDqgTLA4wGxf9l/0T4Af5rAxUGsQhcA3D+pPiO+HD8uQI8+pH/WALb/3oBmftJCIkBUvw4//b6qPe/8cn6Xf9s/77/gQE3A/QAkAF9AhIFywV9AjH7ePQX+Gj+xwaxCrUHfQR//Ib+Nfot/N4CawXACB7+g/2O+jcJ3RA+CcQB/vJm8bTwiAVJCGMD1wAX/F3/G/3ABPX+egHn+uP3F/hi9s8KxwpL/hD6qP17+Q4EzwabAgYISgI3BSwCnwXpB30GPgtGBzABq/6BA1gIdgDc/TME1P0E/zMGxwYdAsQBMf9e+Z32pPreBJsAIv/G+Yr/3gQkAtT/fPWk/CL55/gAAAcE2gHC/PwAD/6Z/34ALAKjAm8A9vih93YCTQf0BJH7kvc59yL/qgjEBZn/QP+V/NX1EPaG/LEERgNT9o/s/vB0+eP//wM3AxD8RPbK8lb3jABKAKYFSgCZ9W317vrF/UYB/wkoA4P9xAHWBCQGYwds+9z5XAO4CIwKSgDpB0YDkvkM/SQG5BJFC4wAMfu++1wB/wexBukFSgAb/XT7MftYBk0LhBADAaz4t/eK+fQCbwIzBJn/MwDn+KD9tQOECrUJ8vfLASQCgQOg/7b/6QGO9sX7OPtvANoBCgnlCHv7DgLeADj93PmS+dXze/npBV39jAAX+qD/cPxI7ywEkAN3/If0Afiv+6T+IA9gAhIBh/hi7uf4xf/ADOEJ/wN6ARf4lvaUAOkDywMSB7kE3gRGAS8FzwgsAPQCIQGR+1r4T/d+AGz/4/s8/ogFZwaFAl77lvDY+MgAowJZAKYFMAEU83TzafRgAMcI0hFjC8L6oP9YBt4CXf9qCYwO/wd9Ah0GDgSpDNoHVvny//3++Af/ATMGrQuBAf8DyfxP+xv3UvxGAWH+D/5h/h0A8vth/AH4JvTv9KT+tv8Q/L7/DP3/BQYIZf+JAeP/2PwhATz+JQAvBYgHpgXj92n6sQbhC8sHwAA+AQz/Af5CAkf/T/tL/Bf8lfwm/IEBvv1h/MgABfUQ9KH3p/+9AXj0+vcT+zj7/AKQBZ8DZwIwA478G/Vl/QMDF/7/AdoFHQbABFUBOwI8/lb/gQHEA4UICgmeC4wCjv5UBYkDQP+5AhP94/mmA+IBxwiuBXIJQgpE+sgEBP3G+VL8Xf99CmQBEgWxBF39t/d48vbyU/Y7APgHWAiBAcACMf1o/iQGtQHeAAz5U/Tg9lEENwmBA7UDe/3g+NXzoP8KCxIHfQTiAXT3f/RgBOkDgv9p+Kj1S/iO/OkFPP5NAT4BS/wq++7+AwNS/gMFYwd9BDcBKAHJ+F73Mfs3Aa0LywUcDhIBafbf/OP5bgiFCLUDhQAI/iEDiQEI/jH9rgHu/oP9iQGo+SL5Lf6z/B0CKAFE/KD73PsX/MQB/wEq9x7+Hv6O+BD8uv6XCccIrgEb/5n9tQOFBNT/3P1w/IEBLfwp/90MawdcB9z7nfig/Z34QgYoAaD9pgPn/Mb52P5NBzz+vvlS+p30T/lGBXoDivvAAkYBOP0x+UT87QI1/AMD5QLu+gH8wABd/9T72gcdBLkAiAvtBLIAbP8m/rECXf9jA4UCu/ZP+Yr/6v/pBcsLjwsrCBf8s/of+Cb+pguR/Sb8gv+3+wj+fQTABhIDxwamBzsADPdP+5QAlws6DKoEQP/g8BP7mAE+CxgPEgESAfn5dPn9/O78VAXpA2z7uvj9+OIBdgSC/175KvN4+t/6lvbn/HD+xAFGBYL/9AS6/hf8Kf0t+vALsQhyCRUE6QH0BPL5BwBl/W8Elf5l/8sNCgmMCt4GTv8B9tj2Zf2FAEoAfQQvCXkHQgAB+mcAowDu/pn1ivV0+d/6pgE3AeUMgQdw/vEBD/5o/t/8+fte9xf6PgXj/1wBXANP+775hvrTA1wJtQXaA5QEp/9VAxUElfgM+f34t/nc9XYCBgyqBlsNTQs6CKYHkwo7BOv7DPnLAWMFtv/TA9oBJAg3A7UBG/sQ+LUBBwByBcL+AwFl+zH98AP+9Gj+VAX9/HD4NfQj9eP9Nf6r/pn7Lf7LA0v+dgLU/a//Yf5E+u7+Xf2K/7b9Yf6g+WX7mAEsAAT/jvg4+9T/ZwADAfEBrgFw/gz5afbJ+Mn68AOBAXD4Vvkf9jLzhvxgBmQBZwJW/5n36/mbABUIsQJ0+6/5Iv/lAEIGUQQe/u0EpgMGCLEGbggsBCn/owK8B9INiQNyBwH8CPot/Nz5zwjpA54JpgEi+XT7Wvx3/H/4MwK+/VL8f/qz+B0E4gNcBW4GyfpW9zz+PgGz/vsEHQjC/rb/D/6bAFwB/wGiCGcKpg0M/Vr0R/vC+jX8Yf6xAnoDEPqG/ML+mAF5CekBYwN//E/5dPle+dcA7QIKB88AEgE59aj5mwLEAzoMLweiBgX5zwJ2BNT/OgbF+8X7e/sdBuUEQgSICR78FPm1AQMBQP3c/aT83Pst+vQGFQ56BZX85/jG87fxg/1cAxIDnwHTAzH5jvbr+cL8SQjaA3YEjvqO+gcCdP2BAR0AKf/g9pb2G/9JCjIQkwh2CMQBlf5l//3+bwB//t4EIAdCBkkEVQFgAur9Nfr9+or/nwPY/kjzv/HY+Mn+wAJZAKD7Uvob/zX6afrJ/kj3rPop/dT5f/5cB8sJiA3wB9D8LARYBk0HtQM8/A/+9AL4A6T6owLpB9oFvAvj/2H88QHN/9H6offQ/KMAq/50++0CAwM1/kD9oPmo+Uv+2/899hkBsQZRBDX+4PIx/wj+hQLwA+UAvAdcBcsBT/vTA2sHGQXPBAH8mfk7AvAFpgXSBw4Cs/5l/ef8mf2bAJQE6Qf5/wz3T/s1+GX9LAR0/wH+Zf8p/5n9d/x9BMsBwv55B0D9F/zN+2z9PgUgC7QPkAWC/7f7DP13/J8FIA0dCt4IYAbu/Hj0KAMhA4EHagupDBUME/+1AR/y5PFA/ZQA5Qj4A1b/e/nF/ewILAQKA4wE3PdT7tnspPZp/Or/6QV0/wz/Jv769wX3F/6+/f34OflW/Sr7s/Tf/o7+cP4ZA8gEyALQ/FEAHv6R//QABghUCUIEZAHG9dz5DgBNB9/+tv95Cdv/hQS399/+VAc+A0II1PtNAaT8HQBH/8X9Lw3EAXT7wvwx+2X5sQRcB1wB2PosAPQEqPtGA6v8YwMe/lr6DgR7/R0Amfeo+cACKAuqAhIBYAIT/S3+KvWr/qIE6QeQAQAARPwm9tH6Kvdh/AX7ZwAZAR0AQgC8A0kGZwJrA/b6CPpt9Tz4Vv0sAvsGSQgdCuUKGQc8+KoA5QJVAfQAzf0sAoEBYwVRAlb9Vvu2/dz7Ivv9/GsD/wE1/J8B0fiD+RkBXAdJBJ38R/t09R/41P2JA4wCYAQDCSwE2Pqv++kBF/p/+i8HhAzSCbwDoPmA8Ff1kfth/AoDsgDy/d/6Nfw3A+0EgA8ZC6D/TPBP81b/h/iD+4b+iAUt/oUApgWv+9MFVA2xBJn7oP+6/Jn9wv6bAD4DNwMZDaYHjACV/HoDr//n/qIIqP25AIwC1gS2/b75KAPU++r9DP/pBQoF4/k4/xP7Xvm6/Dn55/Zt9cn2Jv7ABO0EBwRnAMX7r/ct/MX/CPph/DsAPP6o/csFWAiBBXv/f/SS9WH6lwPACkEMRQnxAX/8xvki/7b9vv3EAUf/2gEKCfgDSQSIC7kCjAAx91r4VAW6/hf84/m1AZ8FAACK+9T7DgRcASgF7QLc+0f91Ptl+eTxh/jHCCgHxAXWChkHLwWv/dz7e/8sBAMFXvc8/AT9+AGfA1wDng8SB4wGS/wJ9gH6ZwBFDQoFVQGc/l73MvO3++kHSQwZCz4Dp/+Z/5QCVAUVBP38zfuR/UkEEQ1MD3kJ/AL/A/L/3gBKArUHrgPtAHYC3P0VBisMGQ3pAfn/3PlP/cAAWvYDASb8QP2g+Qz1rPjn/sQD5PNT9nv54/nR+rf5S/bN96z6mu9T9P38wAR5B+UCmfm6+N/++veV/igDRgFnAAz7XvsVBG4QDgwdCnIH/AAHAt/8Iv97/zcDkAFNAQ4GmwJ9DukBpPh7/cL+YwVW+zX4BflNAZX8Nfb5/xv/q/44+xf+Iv/tAgYI1P3C/msDBP+MANv/KAHLAZn7HQBRBhIHSQQKA777sgB2Bjz+3/6g/5AB8vc19nTxt/fWBhkDTQn/Ab7/Nfqz9gXz5/KUBHYAWALIBFQJOwSJAcQHs/z9+s333PmK983/Jw99BPsEIAu8BywCqP2Z+3v5QPs+AZsC2P6mBWj+tPCR/a4DkAUsBgoDlwN/+gH2sPNp9jX4yfiG/B/6VQHaAdoBng2xDAMFe/+H+Az30fhh+jcFywvPBu0EHQJJBLwLsQyiBLr4lfp//GX/fQY3B2sHtQNW/VP2nfw7BLkGvv2Z9ef61fO2/64FlAAOBtoDSQY4+8b5Xf3y9UoAYAQhBfAJSQio++vtkvcoARkHSQroDSQIgPIj9aH3yfr/BV8M8Aez/gcE4/ms+IUGjAQ7AsQD9f7y+8L4IQE2DSgBVv+YAZgB0fo8+p8BTv+XCSwEpP6v/Zn9pP5p+Hf+Vv3y/VwFQP9s/6MCoP8rCPn72PbU/fL7wABgAAoJ2P7U+9j8YfyC/zX2MAF0/+78jACfA+v7f/ovCT4FzwLq/a/76/eK+9cAZAESA+0AKf9a8rf3egUzBu7+xAOtCWAABwTeCEf7g/Mm/hj0DPdGBfQGpgkZAQYKBwIJ9pH9mf1rAX4AYwmUBGX1DPuV/n/8hvxrAxf8Hv6qBP38QggKB3ILOgqH+Bf6XvN099cCtA2IEYUEr//n+AX10PzaAekBXAN+ADz+6/sT/VwFrQdgANj24/kJ9or/RQ+fA7wDVQMe/H/8R/3IAv8DVv+z+sL+QgamCcAIDP0u9nv5Lfzb/9oHpgVE+FP4PPry+dv/vAMb/UzyR/mMADsARgUKAyn9Q/62/UD7jvqbAj4DG/tD/vgDWw3U+6T4YwXC/rEOgQnIBHkHywPJ9rftHv5p9DH/egMsBkkIh/j7BIr58vv/AVb9Jvyz+k0FNwOiCOUGdgCV+Hj6G//5+7UFWAhUBx0CqgZRBBYCKAX5/8QDdP3u+hv7xAOfB6YBuQTy+5X6LvL68W4GcgnWDJQE7/Qy80T24/2v/SwCXf++96D/pP7TA+kFZwIwA6T0vvf7BM8EkAd6BcAENf5l+1UD5/4i//L92P6d+h/6BwRh/lkAPP75/Xv7/fzPBIr9E/2S+az64/nr+b7/NwPC/q/7XAeBBfsIRQkOAED5T/nTA8gCOwRjBaoCOwDAAAMHLwUzBtMFF/zG9y72VQNFCz4FQgi5BgoH/f7F/2cA6/uUABT3Nf7pASwEMwKS98QHjAyxBL77GPTN97D1H/Z/+gz5mwSXBV39ivt//vAJ/wGv+VryePrTBaoEkAll+94CxwpRAvgD7QKtCd4Ch/jF/bkGogiMAlwBRgFNAxkDmAGBAa/9mwCC/+r9JQAhAeP/SPfy/W8CYAB9BCwA3P29AXoD5/pW994AuQIP/oUEeQubCOP/2PyIBxID/wH0Brf5bP30BrEKkAemAfALIQVH+1r8jAL/BW8Amf+L86j1yfgF+9/+lf7DCZX+rPiD+fn54/nU+f32Xu1h/AMDYATeBrUBG/1e92LyCPghAxkFkAOG+uP3Jvo7AmX/zf2R/472Nfp3/iEDKf0T/Yr7zfkI/Dn5Lf6g/24ILAZnBKIG9AbtBIEBOP8x/eIDcgGqADz+XwogDwoHkAPC/GACxwYzBu7+6QHTARP/vveZ9wcA2PxGAzMAywe8BbwF7AgB/KMCiQGMAMX/XAHF/Qz3NwFjA1gEwARvAkIAfPMm9t/+afTv9gX7Wvq++dD8mf/5+6IEsgBE+OvxF/abAJ38UQJKAlP4ofVH+Z8Bpgu0D4wIUv5P/Vr+qP0DB88Kiv3y95X+nfwe/igFgQV9BLUDVQP/Ac39afrc+X/+NwcgB9D+T/Pg9BD6fQKeE3UMdP8u9ofySPci+x0GOgo4/VPyf/YSAzoOKAvEBUD7t/WZ+xf8YAL/CZsKnP7r+UD7dgCMBHIB3gge/v32mf0gCY8TmgwKC0/5wvDc+b71jvzIAFUDIAfEBdMFFQgKC0II9wvlACb4mwK6/ob6FPlA/eUEgQfpB7r+QPvj+xID1g61Bd4CJALc9wXvoe2v/UD/qgJp/IfyFPci9xUE+AUOCLP+wvZp9Lf1IQVL/qMC5QTtAkD7afzN/2359wn0CE0F9AJNC7wR5QpKAuf8dgqQA7UBBwKUBPAHwvrC9s31g/2V/hf+LALAAgcEbPtE9Lv2OPsF+0D3Iv2d+pb0Zf2d9pL1hv6uA7UDmfvXAhUGzwjSBxP/mwQhBVUBbPuK+VUDlwXEB4UAf/Zw+p36cgdQDrUJ/wlNAWn46/Wc/m8CVQF7+R/wSPUn8rb9HQpS/pgBgv8M+e0CLAY+B9MBDPnj+3YEmwibCLUBFPda+kD9Nf6z/gMJAhFnAlECbwJYAoUIJAS5AhYALwWbBi74RPA59/EB9ADaAR0E6v/f+hf8wADn/gYIvAdS/rP4pPYT/yr74gOQCUv+vvvF+779BP9gBsAIbgaJAYUCqgJw+msFNg0VCHYAmftW/0D/E/2o+xD62//8AnoD2gMZAx0IIQHY/iwCF/xE+kD/iv+v9139cP4OABkDmfcm+hYAMwC2/8AC5QiMBKIE+AUSAfX+EPx//Dn3T/ug/177Lwf3CbUFxf3PAlECnfh6BRYC5QQzAtz9KAez/HYAIv/g9Hf8yfzIAiQKiAUOBhIBAwN+AJH9yACk+ET6qPFa9gz9DgLwB7P6YAQE/fL5IvdX7Zn9Lfy5AtcC9vZA+8sBJAK79uv3mfvG9cAAG//r9RIBLAIzBiQEQgZqC0D/nfqs8ML22PYm/JcH6v3LBbEEbgrHCBP/qgD2+Mn82PTy9TcDWARYCg4Givsi/ZgBFgIVCA4MIAeQB+kHRgV6A/L/0gvpCTH/EgfeAP3+owIdAIkDUQaqAPQCnwOR/d4Ggv96BVAOQgKV/MLylvQX9pQCAg2xDpMM7vwI/q/71gQVCJn/CwHK8ib8xwiIDY8TsQII+uvzzfljA7r+IQWmAYb8ZfnU+9YE6v/aAaoA7vr29NnyhvwB+q4DGA/XAJX69vJX7zn5zf/N/6z2R/ts+xT3oPv8AgoLWAIzAqj9f/rJ+sb1EPxP9xIBsQYDAbUBawOaDIgL4Q95B2X9cgfhBw4Ah/Ze+xYALARuCtD+jALlBqf/G/+W9vgBBgop/3v9DPct+g4Atv8Y9PbuCPwi/8sFWAbpBW8CBfsJ9C7q3PkwA1QFqQrtBOUAe/1h+vL72PoQ+OP5WviFAPEB1gg6DAT9D/729Pr1T/lA/aYFDgIOBAz9yAR7/5L5f/5m88n6hQBqCbgMgQeMCP36iv03AcX9Zwbj/UD/dP8I/g0OKwqXB/QC5QJZALb9Ywk+BT4JqgTF/QT//wFcCRkFRgfEB64FDgKd/B0AjAKbAE0DFgCo+5H7AfyMBm8ATv9S/kDzBftT+Pn/0gdP+9/84/kf8gz3CP7q/2z//ABd/RIB8AMhA9YE1P12AI72KvPU+zMCNhFcCYQKMwY4/WQBiv12AgH8Lf4wAa//hQjj/0IAbPsj9Vb5cfQDAT4B2gFgBPn5cgFs+zMCIv9s+z4JwvZp9rfx0fKZ/UYBGQ3lBkUP9ApYCkUJUvpgAuv5Yfwi+0D7TQkoB8MRWAjq/94At/MX+E/1r/n4Awz9cgE8/JH7yAJ3/BP9v/Pn9hD4ku/r9Wnyp/+jAob8vv8m+iUA9f6fAdoFuQCMAJH/1P3u+Fb59vyR+1wB1ggSA3YEHQTC/nIFywfpCYEDmwAzBor5JvbC/n0IUAwSAV3/DP0SAWsFXf+UBJcDlwMF9Vfz1wIT+wMFF/6s+NcCzfuUBAT/d/7iATH5oP9/9uf8BwRKAN4IlAStCSwEBwR+AI76AwmMAKoCXvth/BkLywfaB6YBWALn+Lb9GQW6/IkBpgPlANz5BwBrBbr+Wvxs+3D4jABgBqMC0wM4/Sb+pPwq+0D/H/r8AK0J3gbEB/gHSQRnBG35XvtYBtMDBwYHAEf9rgEzAj4DjARqCWsDcPwi/YP7uQbWBnv9e/1e9xv77vwP/uv7ivtrAVP2dPl7/Tz+Yfqk9HYCLASICToGg/nU+VP2Jvwb+6T6S/5vAOkHXAOtB1UD+AHWBo78dgJw+AH4RgEx9x0CEgOC/1EE9ALtBKD5ZvNa+Lr6pPaw9QMHmwSBA2z/Oe9L+uf+1gTN+/L1dgDK9J38SQabCv8NNwM8+DH5FgIKA+UILwfWBNMFbwA3BZAFUQSxBtv/uQLhBb7/3/5T+Lf57v6FBH0O1giJA8gExAV2AvL9CPyK99T5s/wF+0T6tv8+BUD9dgCBBxIHDgh0+az2dgBrBYEF1P1a/NT71PnN+2cA6v+qCOgLtQVGBRID8w4ZDekJwwse/uD4ivXC+P8Bpg0GEpcJrQeXB4EFqgKBAfn9ZvMn8kv2XAHaB5X80wFp/L/zjABW9yPvOfV794P5wvQu9toDZwZw/gn2wvjQ/goDsQhnApsGYwND/rkA5/7HBpcD2geBB2X/qgDWBkURxAUe/hv/Hvwb/536afYI+lr45/q2/bb/zwrEA8L8Lfql7nj21gSXBQT9e/2V/kv+6QkSBRkFIQVH/SwEBftCAs8IMAMWAkT6jAKO/g4KXAXG9bUD+AHoCxUIvAVRBpn3t+9b6jX46QG4ClQHPPjr+UT8pPwSA9oD4gN9BHT5PP6g/zABOwLj+av8yvRW+xkDiQMOBED9SQSqAMX9WAKR/YwAOP+V/kYF7AayAP7wkvGW8rr6QgBl9b7/UvpcAcAIYAAVBhD8FPlp9qT27vqFAEkES/7U/WH4s/5jA2X/KwgOCEv+kf2D+dT/iQMrCNUSZwI+B/wABffPAJn3ZwC5ANz5tv9s/3oDSQwKB/QAzwYsAKzyofefBXYGsQa5BHoF6v2o86z6QgCFCPsEZwQzBrwFuAxRCD4FUv5a+I74CfaFAuUI+f2z/mX90P6IBbwJ/wfC/LP2UOti9D4DZwzSE07/4Phs/dz5f/zY/PL/lACv+x/6r/eMDLEOOP3AAC74sgDTAQX7H/pE9jsE8ANcBaYDLf69AX/8OP2qAMgCuA7lCJn76/viA54L4/9GB6oE/f4KBa//TQmtBy8PNwG78Az7EPjWBH0EE/t7/V71f/qr/s37LwXY9r/zT/PJ9iEF+vdH/8r0mfPN98ry4gEb/SgHxAFVAUUJuQDsCgcEOffy9bb9wAY4/wMHYwtcA4gHwvzIAPADdgLHBvX+VAftBLwF6QUhAV77h/Rw+kD9LwWFAsQFTQOo/eUC4/8M/wsBsQLc+777yfpyA/ALkAXiAR/0GPBA9Yr5uQD4ByAL7Aq1B7wD4QWMAjn54Pbq/aYDeQ2MDG8EEQnXAHf8bwDPArUHhv7U+VkA9wtGB2H+uQC+9RP7rPjv9jH7G/0gB+v3nwEkBPb6q/wQ8mX1MfeC/zAD7QLXAsAAOwCz/qYD0gfIBLr4PPq79JLzbP/XAHoBvv9S/Fb7GQP8Anj6JvRW/+r/jvbN+yrzh/b9+qj7pPqD9Uf/Vv2z+h0C/wNnBs8Gmf9i9Gn0/we8BV39YALPAEIEkAFnBDsAiQOiEKYF+AUZB8cKQQ6jACL/2PzU+VkAlAD5/cgCdgS+/VQFQgYM+7r6CPoM/Y76RgEkCJz+rgGz+vbw2PQF99/6Mf1YBOEJmwQkBmMFvv3R+s3/Pge5ApH9pgHDCa0J/wnWCE0DYwPXAv8B4/sZBewIzwgzDnYKEQuK/5QA3P2D+WcCEgG1BeP/rPoT/wsBVQNrA9MBtv1H+139t/vr91r6dP0e/pn7G/vy/Vb/Uvzr++v5bP9jBRIBvAUI/uUAVAX2/AcAqgbSC/8FFQh6AQMBKwymBQ4ESgLy/ZX6H/D29EYHNwcVCtoBVvmO+Hjymf3Y+Mb5e/lt99T7LfzSCUkGKAlgBr71/fby+aT8sQS1C/ALxAf/BdMDQP2xBD4HNwPj/6//kAXu/v8FOgjAAmQBDPlA/S3+vv9CAmX7cPyg/SEBHQQ3AXv/kvXn9tj6nfhD/rEEnwf1/in9UQBqC+EN0PzN+ZLz2fLr97v2HQB9Cn0KWAZnAET83gCV/M33T/1P+Zn34/l/9hv/1wCc/tMDAfpH+UT6S/ZP/Yr9G/+UAOf60Pwm+uD2qP07AB0AR/2Z/w/+Vvug/QH8Kf+c/koC/frN/Y8RQQxYCJH/vvdgAD4BEgEwA/QCvAMi/zj7qgR9DJcPHQqZ+cb5tQF9BjMKSgJyAe78XvNL+K4BAwlqCRIFivs7AiQIyAT0Agj4t/sx9ajz6v/U+8L+VQOz/hP/HQTpAbP89vb5+XT5PPqV/o76G/+2/YEDRgXtAhUI1P0q9wz7BwAHAvQKfQraAZ8BmwAZBZMIYwc+AyL/Vvm2/ekH7QTWBKYDhv48/ur/DghqD90M2ge5AFr6NfreAuUEBP08/lb9T/0WAowIeQ3hCc8E6/kb9Vb7cPzn/lgCIv1L/Ib+LfyS+TX6g/uv+wMBAwOfA8X78/EJ9k/79ASXB6j7r/uUACL31P16BbwF6QP690oAJv6v+4EDSQTq/5L54gNl/2sDywUM+70BdgZyBzX6ivfc/d/82P70AAcGPgUoCUkGs/aZ+WMH7ArtBND8jv71/msBywXAABUGWASR+xf4AfoHADABKAOV/ET6qPnJ9qv+GQE+AVL+nfQY8l7zlfp9AnYCZf1e97r6yfq5Aq0LmwgKBRYAf/6o99cCJAjn/rUB1P9VAVECEgP/BbUF/wXhBWn6XvsB/HT7RQk4/0YBjv5l+aT6I/UDAxkBIv+6/tD+AwO9AQAAjvqZ+07/7AaJA9T/fQooCUoCQQyMBn/8wv41+Cn9Af6JA4EHWQA+BXIF6QEsBB0CrPKA7D3ys/hH+dT9kAW6/r79uv4f+qz2E/tw/uf47vhH+3oBKwhgBIL/R/vU+zcBUv5NBVQNpgVS/M37VQGmAUIG+wg7Ain9u/Yi92sFlwmbBjsCWQDpATj7YAJRBNv/vQE1/lb9dPs7AD4FmwDu/qD/g/26/igBKAUVBhkLlwke/DX8H/pL/vgB3gAx/5X81gYGCBIBiQPWCpcDwACZ+wX3wAAsAsgCkvmO+pABf/yg/QMDGQVGAWj+WQDy+/L54gN2AAT9PgGMBOf8oPvpA7f7TQHeAJz+rQfAArwFOgwVBiQCvveW9owA3PsM/dH2yfxa/uv1owLlCGcKJAKR/UT2oPvIAiQC7QIB+nT/ivn5+UoAhQQOCoUIDgJE/MQDiQHABmsFJvxa+N/6YwNgAvQAFgLLASb8BwTtAD4BlwNl+Zn7FPUP/vQEJARRCKIEfQS5AE0B3/4I/v8B3PmR/VgCVvubAKMCcgfsDFgKYwcb+W3zxfuk/hv7ywXHDB0EAfr29OP5ivnwA5sCBfmJAQz/VQN2Ah0C8Avq/zX8i/NX8QAAd/xd/Vr2Kf3eBv8DUA4oCSAHSQR7/9T5I/Fl+1b7bfe9AVwBf/7hBcAEE//u/LUBxf88+DX44/sdBJADIv+3+7wD5QLR9jH3lfriA/ADhQT7BgoDiv0sAHIJngmiDv8N3gRgAKj9RPrTASwE5/7PAhkD7QL4AcQH5QbPAHoDhAqfBwj6e/u388bvT/vABM8C+f2++wLwbfnEAeEFHQo+BaoE5/pw+gcAAwEp/S38rPjG7YP5QgiqCF8I6QdRAAz7hvxo/kICQgZnBOP9yACFAmsB2P6d+tz7r/vu/oUEogRKAnYGKAEX/M8CDgAM/TsAQgJp/ND8SgJ0/wj4PPgP/n/8XAEzAin/3gAVBBUG/AAX/lr+Mf26/PX+iv1GAywC1wBH/4f0jAKk/m33NwEkBCQQ1gimAaMC2PaH+MX/MwCZ/07/VQOBBR0E6QMoCV8ILAAM+xTzr/ev/TH/xwhFDcAI2P7j+xP9fgBe+0v2S/zC+LIAsQJw/JsCafrn/FEAivvq//QASQY8+s31VQFvAMn8VveD+Yf48v/SCccIGQf/Bcn8tO5/9Mn4Tv9S/qD7hv7c80/7hQQKB64Duvi79NH0Mf1VA7IAqgL9/Kz0T/nc/fAJTQuTCKYFPPxD/jcDqQqeCZMIBwBe+Qj+dgIcDAYQRQun/zH/3PtH/SsIwAzEB3v7xf3F/xYCCgWqCL0BePjr+xD6zflCApMIywHLBXIFmwIE/RT3q/7N9Vr8BwR2BNoH5/4U+eD48vtW/x0GVQM3AZADdgBs/UoCvAfiAcX7qPXc+Xf8vv+8A5QA/AA4+wH+6v87APgFfQSz/rv2yfiG/Pb6OPvN+/n5dPs7BHIF1wL0BAMBQPlw+CwAPgeQBcgC4//C+nf+/f50+3YExAeqBDcFXAUZB1UDH/r29L71R/sOAmMDp/9d/ef8R/vC/lgCBwIb/9j0FPUB+uP5f/yV/MX/Xf8F+Uf9vQGTBssLVQGQAzMCfPW+++v3+fkDCbULBgoDBWcCzwDF+yL/AwWJAQ4AiQMdBv8DfQSmAxP9E/uS94r7PgVcC3YIDgB6AQz7FPdH/77/pgFZADj7fgCMAvn/lwVrB7kEmAGW9gH8BwKuAdMF6v/lBpcDyAJjB5QAYwmUBIEBBwBw/CgDs/6Z/4r/RPwB/nD8zwTEAwT9FQjTAw4EgQE59dX3RPj/Adj6pPovBYP9wAL0Ai8FOgh7+3T9AwWg+4P5uvqZ/TADWARNC1gILwnHBhv75/aO9ML49voI/EIEOgiBCfsKYAYsBvb8Xvtl+6npzfO1AVQFBwRl+88A1wK9AeUCkfuv++r9JvzF/5gB3QoHBm33SPX680v+WAhnBjcBowA4/y3+0Pzr+f8BkwjXAvL72P4VCGcM7QTC/Ff1YvZT+PL3dPms+IwCTQHEAzsCuv5a/k/1Jvzg+Ov7GQHy/6T8WviK/ZH/SQRcAZ8FMwTTBcMJZwDy/a/9cgnaBaMANwMSAYEHgQWIBUkGzwKqBKD5dPEOAHoF3gTc/Vr66QE+AcQFEPxE9Dn3S/Rl9+P5lAA3A8gAWQAOAPgD9AIm+kv2DPk3AScNvA0DBx0E3Pvr9wH+awO1CYEHfQjWBiL/PgGFAOkFyAQ4/2n8wvr4A0YHYwc4/0f5DP8b+xD4KAEzAgcADP3r80/93gjhCz4DsPGl8OD0MfX29qYDwwvPBBv/WvzC/IUAtv8b+zj9tQFVARf+Xf0i/RYAXAcVBGj+EgO6/ob6nP5E/NIJVAvb/yQChQAHBPn/kf1kASEB6QUOAs35bPu3+WH63gCk/H0GtQda/noB4gH8Al3/iv9W+y740fhO/1wFMwLtBPQE4gPc+VwBeQcOAhkFr/0SA7EE/wH0Aj4FRQkI/Jb2Vv+r/uUALAD5/eUCEPpH/47+f/6MCJz+tv1E/OP95/6QA58HiQFs/9T72PiH9Kj9jAKMBMAIZwj/CSAJ4QcdAOv5JvjC+Cr3lfg5+XIBuAjPCPAJvQG1AyL3bfGO8vPvoP10+f38mwbwBXkHrgHY+Ib6yfwAADz8u/Yi/aH1dPdS/vsETQ2AD78QRgUVBPAD/f6v+wz7QgDy/zsCsQRnBDoI7QRw+uf6NwGQA07/RgE7Aq/9JQD4A0YDrPT+7ofuMvFA+7r8lAKuAXT91P23+8AA+AGG/O78WvYb9yb+DPtH/+P/YABYBg4E3/7XAiALkw6eC8sHvAX1/m8Azf/y/z4Llw8SB/n7nwFUCQYI/wMB+gj46v1s+/QA8AMDA6YFDPsHAA/+e/lGA+v3afSs9jz8xwj0AokBbP3j+5AFnP52AvQGvANuBpsCAwNVA58DVv/Q/Bf+r/8oBZQEKAMb/9D+uQCYAcgAg/04/2QBtv9W+YP5oP2+/zMCFPki90IAd/w3AWQByAI6CuUAxf8q+aD7/ALiAaYFiQHU/Yr9/f6bAPQEZf9a/hf68vmmAyn/Ng3/De0EzwLN+6D93/x7+f70EPLy9fb8Xf28Bf8JxwYlACb4T/kB+Bf+Iv3f/Of84/1CAkT8Hv7q/y3+q/6UAmcCawWqBOUCSQQQ+qT8cP7g+Hv/OgYDB28EoP1CAv8BbP1A/wj8iv+++xkBJALTATcJpgGQAWAA1wAoAWAGpgkzCA4GOPsQ/Hv/BwCz/jMAuvyk/tcCcP6fA5sG/wdO/0jzvvfxATMAmf+v+/70d/yg+zcB1P/n+EoAcP5A+5n7tv0KA/gFBwJKAjcDhv6h96T0Lfp6A+ENkAWUAGcAR/tjBaYJJAwoCz4HlwVs/cn8bwLlCh0GowBKAtj6IvtGAeIDjAA+BToKlAQKBdcAwvqh93j2G/tW+5QAegO3+UoA/AB2AD4HzfujACL9f/qXBfL/uQIKBd4CTQEsAIEBKANH/br8Vv/8AP8LxAH9+uf4pPi+/az6zf+O/IP70Pw4/SL/QP1KAAj8pfIU81P2F/hA/c379vyK/br+ZwBCAGcIEgET+yn94PZE+N4ADgSaDMsNbwAOAur/Q/5A/9j85QqMCIP9Kf9A/zcDdgAT++f6zfs7AtT9zf2QB/8Be/nG+dz7ePqR/1QF9ADq/xIDowJS/oP3lfzTA/AD4QnsBuwGnwUP/g4CMwIzADH9wvwwAXoD6v/eBisOzf3j+fn9/AAKBTH94Pj9+rr8ivsX+k/71gSXA5n5kf35/QsBoP9a+ML2u/YdAk0Bzf03ATsA6v9W/64Ftv0e/C3+wvan/zcFQgrACLkGuQDG8yr1R/1RBsn+R/u39wz3uv7f+ssDYwXwAwj8pezN9QH63/4sBgT/egFd/9X38v9RBKYLSQxrA1gEq/4B/rEC+AeuBRkBXwq1B18Ingn7BF8K7QQm/ur/owLSBw4KhQRYBGsFfgAsBCwEvANJBPgFVAcp/VgCxANh/rb/RPom/lr6ofeMAA/+2gM6CIL/zwD1/tH6r/dI83T9bP3f+n/+Lfy6/I74OPvY/N4CkAX2+iwAXf9gBBUEg/lo/tH6XAE3Afn7EgNCAoUCKvth+tcA5QRRBhf+T/2uAxIHQgQ4/9X3sPVW/TABxf1nAFECQPlW+Qz7KAEGDkkO6QP9/Bv74/8+B0IADgYM/zX0Zf059aMC2Q1yCa0HAABUBcL+R/uUAG31ofMi+7b9XAUOCD4FHQRo/kT60fZl+cX91P9nAC3+jAKbBjoKdgTQ/IL/1PkM+3IDFQYvCZMIrQf8APn5ZAGmA8X9JAQHBN4CVA3PBgoDawHj+9D89vgsAgYIHQbHCFEExf3n/CL/cPziAZcF5/z2/N4ClwX7CMcITQHc9frznP7XAOUG8AuuAf36S/ZX9Sr1T/1jBwoDEgHj+/b6t/tL+M39Xvli9Hj6PPrV9X/4xvm6/j4BXf2bBNz9pP5h/IPv7/ZE9qD94/2k/hYCPPrXAIP9HQA3A+UAIQGd+jH/CwGZ+4b+UQLWBMQFJv5w/uUAlARNATH7FQhqCU0HdgJP/er/NwEHBqT+uv61BxkHegGz+oL/MwjlDgINDgJyA0ICIv1S+sb5GQX7CNMFHQRNBTsA5QJKAkT4TQfwBZH/BwDJ+Fb7iv3eAJ8BNwH0AEYF+wbq/8n+7QSn/yr3ePhT+K/9sgDLBd4A0PyfARD8hvwB/J8DvAdgAqT8s/ZW9x/6uvxH+Rv9UvxI9RDyjvgsAmcCwADN9UT2zf1P/Yb8QgB2AEv0sPWW9mH4XAXlAhkDBP/u+m4GHQCd/CL/Yf4wA9MB7AiiDBkF/AIWAqD7nP52Ahv9mwDABKIIrQkvD2YUwwuZ/9/61P+R+6oCKAtl/4r7tv2K+aT+2ROwGK0L+AEHADH7qPfb/5gByADY/GX5afYI/LwNyws7Auv3u/ao+5X+uAjsBi8H2gdw/sryRPhnBFr+/f47AMsDKAfEBXIDmf/0AGX5bfe39/QAiA1UC+EJ1wAb/aD7Yfgi97fxMfd4+K/5awWXA9IHLw2mCVUDWvQX+o72yvRL/Ev2qgDiAbUDD/5a+BID/ABRAIUE2gcM/QT9qP0m9Ir9VQOQAfn/bwIdAigBTQN9CGMD5/SV+Az35/pgBuEFvQHn/CwGVAd//vL/T/0X+k/9CwHLA2cIWAZ0+W3vsPMAANoDXwoNDqYJzwhYAsgCxAHf/F73Yu5E9JH7Bgg9E6IQlwl3/KT8kAOo/Tz+2P6D+wcAwvxvBFwJMwC2/RDyrPJT+Lb/vAfQ/nT7s/a+9835e/lD/or/JARl/dz5Iv2C/1UDlfwe/F39mf8HBOUEoggVBiEBJQBRAKv+ZwbHCk0HpgUb+9j6s/q39wT/rgN2BHoFyADN+R0A/AIGCOEFyfrc+cn2SgDhBcAAOP/XAEIAF/pT+D32xfsQ/J36Zf9GAdYK7Abr+779yfo1+Mn8pPqv9x7+2gV6A4wAMwTlAj4BqgBYBJcJfQRrAU7/E/0KAwsBIQFnCM8ApPyqAqMCIQGxBFwFJATeBLUBKf0Q+GX7VvtD/kUL0gvwCWQBZf/q/8359ARUBxkBIQEe/kD7Hvw7BAMH9ACqBPAJTQfTAcn6r/vg+ET4Hvyh9536T/19AtoBNfzTAxYAxfslAKD7bPu2/yr7wv4dBpcFJAZcAfX+8v39+gj+dgKuA6IIVA3aC/cLtQG+/1ECAfry++P7gQGQA+78RgcvCVwBnwH0AgoF6QHf+gX5e/83AUD9zf3Q/okBYfgx9ZX8Lf5yBTcHuQTtAP38WvwDA/QEp//5/fb8AwNCAhYC3gJ2AvL9mfnf/oEB7QIHAAMFafzc/cAIQgRGBVP0PfAF8bvwxf3N/c3/2gWK/4P77QBW/dz9Vvn29kf5yfgHAt4CcgOfA7ECZf3c+e78lfpS/rkAhQCFBCAHRgdYBFL+qP1s/64BegHPAK/9S/RM8uD26QESBwcG6v/u/nT9g/neBJgBMAF0+yPvoffU+6YDgQl2CEkI/f6Z/5QClf5CAqv8aP4WAKD/wwk2CzYN7QQT/Qj8Zf8p/1L+kAEM/8AAQP3tAiQCyAIp/8r0+ftS/LUBFgAwARP/h/jeBJsGiQNVASr3Mfmv/yb+XAsvCfgDegHY9Hf+fQSbCBUI4gOjAC72vvmJAZ8FagkvCSEDlfha9CL5afZt98sD/wd3/sn+XANh/Hj6U/i+/WX/awWBB8X7aP4M/RIHywOd9uP79vzPCGMJCglTFbEORgf2/ET64gGR/+kFsgCBAxELKAMKB5sEMwR0/1L8sQLj/xIB1ggoCbEE/wF//Ir7cPYm/MX9pPy8A/sEMwyBAbP+/f7q/fL/e/uz/G35Nfw59dT7lwPlAIwCnfyG/gT9mwDq//QA/ABW+zX+s/he+2j+Zf1CAnT/s/yJAWX7xftA/7P81wLr+YP5Wvpp9gj+hQAZA/b8nfaA8M7vH/hW++P//wWbBKj9QP3c+VL+QgIM/3oFiQEB/iwAsgDwCbEMPgftBLP+3/4B/or9PgnDDUgUKAssArUJawfwC8sH/wXeApL3gv8i/0IEkwzaBdIJsQQWACQCePgM/8sB4/sm/E/7JvyH+GH+mwJyAw4A9vIf8Ir3JAJgApQCfQLj+9j6wv79/nD86/tP+xkD5QYHBMQB5/zF+6D97vyiBKIIGQHiAxP9wvzN/5ABVAlw+Gn27vxZAOEFqgCuAQAAq/x/+Cr3ZfveAHoFQgDU/QT/T/1vAq/9yfgLAS3+5QDABH0CJQAM/e74NfT9/FEAwAYHBowAYASjAG4GzwS1AWsB0fqO+Ef5xAEODJMKQgQ7BIr/bgaUBIwAZAGZ9U/7GPQx+xUEvQGxDvX+PPqo98b3YAJA+6T8FPcb97r8kfsT+7756QG1AaT++AH7BrEKsQIb/cn8bPvU+aD/ZwLg+B0A+AOBBScR1gpjB28Axf15BzX8T/0DA0j3E/vc+4wAJAj/A30IhvzC+pcDyALpATX+BgrQ/N/66QdRAH0IcgOg/9D8Vv3aBcgAxAWmB9oFDP/N/bECwvyn/z4DIQPn/Cn/SQQI+nT5d/z2/Az3MffC+h/4WARGBRkDuQTaAe7+g/c8+p38tv2c/m8EUQIm+lr8VvujANYETQeiBCQIgQcSAS8HawV9CJn/6/nC+Kj7ZwhrBxkJ3/whBdYIq/zIBAj+MAPEB5ABTv9s/Vr+Yfgj853ys/5CBML8yfzu/BP7QPnU+U7/XAHU+V71CPwp/U7/2Pyk+iL/QPVl/a/9uvqqBAH+mwJW/28AxAEb/5H9Vvll/+78HQTq/3IDPgXXAFkA7/Ln/JL5/wELAef6qgKL8w/+/fq+/bEGRPoe/J36dgBA/0D1F/zu/PL7JALABg0OuQKk/pQAr/lGBXIHDgz/C+IDhQhJBN4EVAshA88Epgu6/sgA7AafA3YAxf2tB8MLDgJZAMQBg/k8/CL9EgckEBUGdPfR7nD+e/ug/1wBf/yuBdT5CwGUArEI4Q+C/837BfO+9c397v6+/zABfQpNC0YDkfsF+yL7BftA+QH6kAVJCuEL9AAE/0IIrPoM+/r1Ku8Y9Lr62gdd/X/+7QI4/9cCyATsBqMAzf1w9uvxt/dvAtcAkAXhC6YB+wjtBGoLOgZI9139jvZYAvQEywVjBYUAMwh+AEf/hvof+Cr7hvrF+5X4NfxGA/QEXf2+/ZgBE/vj9wj46v1JBGAGQgZH+0/7dPta8sX9SgCJAV8IOgYVBuf+r//lAp8BeQdrBQX7UvyZ/YUAmAHU//QIhQLpB8QDYfiyALIA+wSv+0D/dP+o+9/+NfTN/eIDMwxgBJn11ffC+Lb9PPqFBisIVAflCK/7lAJKAN4AMf8B+BYABP0DA+UEFQT/BxkBCgP5+x78mwL1/rP+Ivn9/v8DiQFd/R/4Zfng9M33mAEVCFwH4/08+ET8awNS/q/7F/4e/Pn7h/iv/d4ENwNd/WH6+AEDA3IFTQcVBMsBd/xw/jABNwMSBWMFF/7N+0YBpP7j/7kCXwh2BrwFBwag/xP/S/rlAIUCfQIOCCb+xvnn+ML++AMoBTMKqgZ6A/3+FPkJ9noBXwzpB2cEyfpA/f364PiQBcgEmwYX/Nz3CwFcA7wHLAT4B/8D3/pW+xj0BfXC/pAFhQR0/Y786/tA/zsEQgpgBoP9hQav+9z7tQMzAuUCPfTJ/kP+iQPzECsMZwpW/c3/Nfgb+QcEbP8HAKT+YAK+/+r9WvxH+SL7wvid/Of++f1w/rP27vz8Ap8Fngki+9H6V/VX8wMBuAxxEUIKEgWd+N/6QgBRCJMIkANnABD47QC2/SgHdgSR/WMDXvsx/eP3R/sb+9H2WvrF/0oClf57/9j2FPe6+ib6mAHj/1b98vlt91kAwvolAMgExf8zBGj+9AgKBQAAWv7N87f59vxyCUYHOP/Q/I78bgbHCOkFBwK6/Ir5AfgF9VwDHAy5AgX7KvnY/MX/NfyFAv8Hzf1vAv36xf+XBdT7F/45+a4BOP/tAhUMAgv3CcgCmwSBAcgA+APSCQMH6QGqAF774/83B/MOLhNjD94CG/nf/CL7zfMT+1b/AwO6/lL+kwaz/OP9lvY18m31BfvU/ZX46QEp/aT6Kvtd/yb2be+Z90v4AACv+3kJHQjeAPsGkvUm+lr8QPVd/ZX+JAYGCsAIJBAE/9X3KAHeApADZAHwB7EGEgOk/Ib8MAEHBLP6G/EoA8gEsQQ+BbEKzg7R+vbymvHv9Pb8/wF2AhkDwAb4B/n/OPu5Alr+CPqv+9/8tQObCtYOKwhZANj+fPWw8b/z+f/hBz4DbgpJCL8Q7Azf+pn9G/sb/SL7tv+fB1wFmwRGBaoCuQJCCKv8OP+xAlb/mwT0AqkMmwJS/m8EOfNl9177DP2Z/Sb6RgOv/5H/2/8x/y38QP2G/Fr2BwQE/7P64Pis+O7+Xvcm/gH86/VL+jcB1grABlb7mfud+lb5d/7C/qoAs/zc9fbyRgEgB+kDuQI4/QMFHQCFBPsEvv97/Zn5Yfou9rkE0wVQDt4Ikvl3/tz1uQCk/lL6AwVUBa4FvAXeBgoFJAKFANj+KvuO/tMBWQDxAVUDS/z1/hkDiv9UBfAD7AwkBnT9YADn9tT5F/pjBRkF+AHlADn5PgO2//QA3gIZBUIC6v1RBEv+0wEdAEIAiQFL+BD6F/6jArkC0wOxBiwE6v3V99D8fQKn/5ABZwIhBbkGFPlH+fb89f4wA+r9ZwCd+jX0uvjN/fX+PgMGCn/84Piv+xv7rgF6ASwEvvsB+rP8f/YAALkCFQi1BSr70wO9AWsBSQaQAW8CQP/C/NoBE/0M+28AZwDIBIgHnwUzBv8BhQBs//b6TQXeApn9Qgb8AKoALfxh/MsB7v6UBFQF1wKqAkkG9AKO/rP4PPqJAQz75QLeBK4DKAfQ/uP3cPzLBR0CjADpAz4HiQEQ/Nj+9vzj/TH/xAMhAxkBTQHN92H4iv/U+dT7nwVKAgH89vz/Aa4BuvyK+Y76dPes9vb8yfyFAiwECP6z/iwAGQXEBVEA5QBw/DH3HQBnBs8EXAWuA6MATQEOAMsHVA3IAjH7yfbu/P8DEgVuCDsE2/+2/y3+cP7EBTcFrPhA9aj7RPzN+WX/ZAFh+rP65QD8AkICKAHY/rv0PfCs9jX6Yf6K/9z9cgHY/vL34/WZ9+UAr/2o92cA0wPlBDABkf1KALP+ePqG+vwAbgZVA7kAHQZ5CdYEOP+qBHYGxAO5AOUCkwyMBJgBcgNVAe0EfgDC/tMFUQZNAXv/jAB9CLUDBwDLB1ECKf/r+zz+9ALY/NT9bwB0/1b9Q/4kApADRgFs+139egPwCeEFBP/n/AH0Jvi+/aIEbwKv+cL+1P0SAQMDogibCqoCQPnn+C3+yfqyAKT8MwKk/uD2lwOjAGML2gfR9lL6kvkB+KD9WASXCRkF4/vu+mX5QPsi+yb8AACbAmsHbgh5CTcFTQF2AHf+Hv6C/94CVAWiBN4AqP2UBBIFQ/5KAqf/Hv4e/P36Uv5RAH0C/fyg+9j8Iv+G+hD6rPgq9e764PgHAh0I/wG6/CL7xvlT+Mn6cP5rA8X7uvpnAsQF5QSC/0v6e/1yAXT5jv4zAv8DGQdGA7EIUQZuCEII/f7TAeUA5/5w/sAA+wRRAOf+ZwTTBVwF8AcdAPL3ZfVl+Xf+bPtnAq4BhQK4CCEFaP6r/G8AU/gu9tz9SQjiAcn83gLY/HIFwAb8AJ8FiQEI+rf30fZH/3oBqPkM/SL7QPlw/BkDTv+k+vb6e/m2/9/+5QRVAdD83/rv9LP8MwCbBEIExf+V/uP/oP9nBIgLQgrIBKT8oPtL/OkFgQeqAGsD1P3R+s39pgGIC2MLkf9e+2n8RgPpB2sD+AMoBTX+Lfps+zj/9AbTA00BvQFRBpAJ0P5D/mj+e/uG/n0CzwKTBsAIrgE7BKoEbP9E+M3zoPmd/ML+zwbhC9IHyAQi/9j4E/uS+eP5+f1h/GX7hvrlACQIKAEi/3IDLABw/FL83Pug/zADR/9h/L79qgKJA6/9zf0dAA4AmwJcATH9vv0B+hD2rPjF/X0GogaqAlkAdP8i/Y74Jv6K+y74ofe++RUG/wfHBtoF0wEE/dj84/dw/GMF6/kB/PADPgWfA88AJQCR/0f7g/vABKoCtQWxBuEFqgbTAY78dPWK/TMAdPsE/0ICiQE7BNIHMAPxASgB9f6G/mH+rgGBASwArgGBA58FTQEwA8X/UvzIACL7uQB2BvAJUQRS/mz9Vvl9Aq4DQgamBfL73PF88wz/6QPSBzYLuApyAWQBZwAHAn0C+f9s/3f+iQHF/TcFjARRCMsDSPdw/B/6DgIoB8gEegWYAXj4kvk1/Nz9d/66/AsBUv6G/lb7vv059/L5Zf/r+YEF/ADXAED9T/vJ+sn2+ftp+pQA+AHAALkA+AUOBsgCHv5p8vL18vl7/5MKgA3pCXoBivnf+or70P7n/r79Vv2Z/YgJZwa5BFEG5QBS/j4Bkf+G/KoCwAIgC7EE/fwkAgMD2gOjAPQA/ACqBGj+/fxCAPn9hv6d+hv9/AByA6//F/o1+jj99f44/5z+afxh+nj4dP3c++74Tv9a/gj+mwQZAeP/zf97+TH9DP3u+t4CD/6z/oQKWvz2/KoABP0rCDsCyfwU+bb9EgMkBMQDKAHIBH/8afiv+W8AZwSFAgX7xfvABEICTQMOAKoGogby/2z7ofeR/a/9QgLtAscMPREzAAH8S/xW9235OfmZ/csJJAZKApsClwPpB+kFwv4WAAT/Afby93/6dgCfA4EDsQJA/ygBHQAHANv/FgAE/+P9UQDn/KT4jvj9+Nj82Pyd/O0ACgUdAhf8DP+6+Hv/RgOZ/cQDAfxd/Qz9bfnN/YgF/AJH+z4FHQI7BCsKJAZfCvAHlf4e/Fb96v9VA0oCvAPLBSgFLARUBcsBuQC5ADj92gOuAygDVQH29o76wvx89U/7GQXlCC8FEgHj+aHz9vpt89T7rgV9AvcJVv87As8Gf/6g/wMDmf9a/HT/bwK8B8QH/wl9BlgEr/9L/pAFYAICC/gDT/vF+9X1PPrc/SgJQgiqAnoBqPvJ/kv60PyR/W31wvh0+8L8uv6bAoP9DP1NAa/9nwGyAPsEegHG94r//wGG/uP9r/9H/8L+VvnJ+Ir/8v9d/235qP25BgcEIv1A+Rf6JvS/81b5Kf1s/wX7qgBGA0IE3gS++/38Zf0oA1wDYwWpDMgEvQET/+wIiAlyB/AFCP7eBjMEOghGA3oDAwn9+tz9xf1nBqIKjArPCnoBGQXR9uv16v+r/PwAyf6MAuf+0PymA+r/ZwAvBfAFpPis9s35IvnIBJsGzwAI/KMA9f4M+WX/6QUOAiL50wF2BBIDRgWV/qj5NfwdBMQBYAI7At/+RPzc93/8qP0ZA8QBe/kT/b7/BwBs/YEB3gBs/yn/FPVd/30G1wLxAeUCiQMq+WX5LfpA/VECawF3/ib+9AjHBtoF+f1W96/9FPVp9gX5EgGxCg4C/f4B/iEBTv93/ND80fgsAsACWvz5/xIHZwb4BYgH6v1GARv5V/Ov+Tj/8A2XB/gH+AXXAJgBg/04/2X7Zf3Y9DH59ASjAsAIzf8B+hD63PNE+noDLwXIBPQCdPnC+owAjvw3A8n+Wvry/Tj/lwV7/z4H6QcSAR7+Vvcx/Wj+GQmBB30GyAQb9z30au6v+ZcD4QUKCfQKwwlnCG8C3Pnb/7f5NfzpASb+iQGbBtoJ5QbWBoEB5/ry9xv9Hv7y+24M0g2v/fL7NfxL+C3+ywH5/Sr7dP3N+0T2NfrsCOEL5QAsAFb3kvVo/gj+EPyBASwCT/eV/DH9LwfsDGAEtQeYAYwA3/z9/rEGwwlYBvgByAKr/uEHFQjPBOIDlwWqCBYCMAPLBVwDIvvaAZ8BqgDLBcL6ePj2+Gz/kf2O/igD1Psb+zz6GQFKAigFnwFE9DX6afrj+zH/MwCUBAMDlwmMCIkDogT4BbkA4/m8BWMD6QGMBlwFEgdRAJn/S/ry/13/afhH+dj6TQVs/TMCBwAq+ZH7h/Ly9TH7pPzv9tD8qPfc9QT/lfjb/9H2CfYsAJH71wAhA1r+2Pzu/Pr14/kdBCgDnwHiAX0CDgKUAn0GZwLr+5sCCgNvAn0KbwTj/+UCpPYY8tD8XAGJA5H/2P5jA9j4qPmBA/n/lwX/AYP3R/lw/Aj8WvYm/J8B1wLQ/mcCIAlCAB0I9ALC+ML+G/04+zj9QgSuAbb/Zf/IAvwCCPrAAOv5DPsVCOEF/wdYAhYARPx0+e78Wv5GAwcACgM4/58Fjw3F/Zn/ZwD9+nT/7QA8/mcEOwQVBBUEnfoGCLwFRPzLAwT/WvYt+u0AYABuBmAGqgYb/8X7KAXj/7kEwAgSATz6kAPEB0IAuQRs/Uv8aP5D/jcFlASMCukJEgNNAcQDegWUADH97/JW+7b/mfk7BAcCbgj4A3v9NwVd/d/+JAI3Azz+7v6Z//n5HQRNAXYAXAFS+qv8Vv30BP8LywW1ASwAMfed9M33ZfkWABP9yfwSBRIF+AX4Axv5xvmR+5nzcPzu/owCIAuuBRkFcP75/QH+jv7c9+v1Iv+R/fQKhQZ9CKYD1fOS+Zn1EgGxBvgDmfnJ+hIFKf+mBfwCiQM1/nD2+fth+l3/cgeBBQj+6v04/2cAgQX7Ci8LpgMx/Sb8F/rC/toFyfxL+sX/XAdMD1gOIAvIAnT/dgDU/4b+E/+uBa4BJv6R/3/+nwVrAZn7CPoQ9jH79vrC+hP93/52Ahv95O9B8R/4yfj5+9H4hvzJ/AH6JvoM+xYCbwIb/U/3FgKiBvsEnwfTAzcBPP4LAZH9vQEDB8cGlwMB/M8EyARKAvsEgQM3AcgCWAZ2AigHRgU3AzcFjvo4/X/+EPoT/5z+SgCbBFEGHQIe/Fr+Vv0p/Yb8Hv5CAkv+5/6r/Nj8/ACg/SUAvv9O/4EBLfwp/a/9oPk4/0f/jvzC/h78awP4BRkHwATV94f4MvN092j+CgMZC3oFcgM4+xv7xfth/kkELAA3AX/64/0WAF3/BwC6/mz9CfAx9R/62gHLCS8H8AnF/8gAvvd88Tj/G/9JBKIETQVYAhkB9AixBJH/zfl0+1b53/zsBtYGywmtCWMFPgEoBbkCpP6r/lEA3P1p+vgHkwZNAwYImwr0BDsADgTPAFEIYAZrBSQEmf8kBIP5dP3LB4wCkftt9zLz5/SMAP8FHQiTCmMJoP8I+Kz4F/hW94vz1fP29nD+KwixBtYEbP+v/6v+jvYU+Tn5OP2Z/fEBDgTpAbULpgUZAaD9Cfal8rP07vxnBK0L+wqiDigFmfnu/FL8nP7lBn0GBwD4B9D+rPgm/gz7VAcSBcn8Vv2s+nYAHQr4B88GsQZ3/HT/jvwb+9cALAAoA8X7OP0HAKoCMwaFAhUEkf2mA8sDr/mmA58D2PymAdj+f/77Cm4MwwlVASb4BfXC9jX+4gECC1wHMwifBX/+awWo+5b2S/ZH+0v6vvnlAib+gv8x+xv7e/9gAt4CPPq+/b7/R/9VA2MFmAG5AKz4RPLy+XD6VQPeBv8FawfpAxYCLfx0/Uv4yfzaA6z4s/zu/F75oP8x/Yb6NfzF+x78AwPlAAz/wAKZ97r44/0E/fb81PmK++f8pgWbBowG2/9p/F3/ePa+/dH6OwLLCQoHKAdJBAYMQgBZAJX63PXn/gz9LALABo8LcgEB/hT5DP9YBsAC7Ag1/JX6FPkx/ZH7xf0kBmn2AACR/zH5q/wb+1EABwT0BED/Vvte9ZL3e/2BA4ANrQdvAnv/LvgB/jMGiAflAlb9Yfx3/hUEwAQ6CPsG9AhqC779mf8zBvL/5/y2/aD9iAetB94CwALc+4b+f/rj/fAF+AUdAMb5r/dp8qD9iQMVCrUHZfsb9xD2uQC5AIwCHv4B/h0Chvy5At4GnwdrAxkD6v3lADcF/fxnAvgBZwrwC5H/lAAzBJcDlABnBjABlACfAdH6mwCz+qD5s/i+9aD/7QAzALwFUQj9+lr6+fsU9fn9F/qR/d4COP1rAYUCnwN0/3IB+f8b/zsC0fqXA1wDmwAkBLECywMsAOr9qPcE/c3/ywEoB8QDbgrpB8ACegPABKD79vhgADX8SgK2/0v+7v7N+9cCRgPpA4UAXAHU/Uv+5QSd+gMDXAfQ/Bf8Nf6jAlwBcgdfCAMF8v+3+U0DOP0KAyAJbwBrB2sBRPqd9sb5xvlP+RYCOP3IAuP95/hL/vr19voT/Rv3Zfn8AkIAF/zC/mn0yfxH/wz7kAOQA9MB3PtW+1P4MwTPBk/7AwGv+fgBlwl2BgMHhQaz/tX1Xf1W958DgQswAwcCtv/hB6oEIAer/gz5Vvm77t/6hQCiCPAJBP3J+Lf1F/y2/br+p//0AOUE+fmv+xYCvv+uAc3/JAIe/r75Yfhi9v3+QgR1DDMIqgAwAS746v/wBa4Bp/9w/ML6NfpcAeUCTQUdAgj8YfyG/IEBxf/Q/m334/nJ/Dz6RgNkAbkGe/8Q+GX5+flCAhIF+wrIApsAG/0q+1UBSgD0BhkFKAlrATX+nwXtAs8KqgLpAU0DWvztAssBZwY2DwYMGQUdBCEBzf9YBDsAHQbWCMgE2gf/A0oCyADN/3/8zf8sBBIB5QjwB4EB4gESAcX/7QAx/c3/ywO3+0f97vxyAZsGiAXXAM33DP2z+mn4rPjq/aoCf/gM+dXxMvEi+3f+F/6d+B0AU/g59a/7uvhH/0D7Hvx49OTzQP9A/3IFFgA3A3T/D/6iBAsBAwfpBekB0fh//FwB3gB2CJAJ8AUX/h0ESgJyAeUEQP/r+zX0zf1nAs8EHA7eBqD/G/n5+fb8Tv/iAbP+jABa/IkBTQPC/pQEuvzf+vQAXAfEAYEBMwSV+GX9LviH+ML6nfhH/XD+YwMhAUkGYf6k+Lr6f/aR+/wAxAO2/T4DDgQ+A8sBOP0DBaoCgQUoAc8AmwK+/WcER//aAcgCJAL8Aor9fQTIALkAtQEx//X++f3TA3j6JvzJ/k/9rgPlAFEE7v4m/vEB0wWFBtz9XAF7+Tz8QgSD+1L+3gJ6AxIDjAauBQMF+AW2/cL+tv8hAYkBUQDEAUoAGQVRAkIA4/vq/ZsCBP1+ACr7Vvsx/zAByfyV/FwBkftCBJn/9f5o/q/56/tW/+wGBwCQCYr96/eIBaoCVA3sDK0JtQGUAJX+OwDiA+v54/8599/6DgKQAfQEqgDeBAz7p/99ArP+2gP5+8n8YfxyAVwBs/zLAUoAUvzy+w4EHQIDAx0ENfpL+hD6WvQi91UBcgMKB3YE3/4m/L77HQLC/mH+s/ybAt4GdgR6BR7+Yf5w/OUC/ADn/i8F/vSH+Bf+Vv0+BVwDdP88+FL6Q/7u/KT+pPwB/sQBNwOc/o7+FgIWAO0CLf4m/HD+3/r2+GAAKAnABkEOEgVP+/X+mfWo+YUAMwC6/IUEiQNS/mMFG/9rATAD6QEm/hYCUQJ0+3IHs/5nAsMJWQAdBJAB+fuD/a4Dg/km+oUCWQCFBHIB9AIZA9YGXAf5/4UCAwObAgH8ePYX/LwFcgUkBOkFyABJBogHFgCJAbUDcPzV9Wn4LfxKAGsB4//C/n0CyATf/uP9kfsF95X+KAFw/psI7Aa6/Ef/xftE+qf/F/xl+ev7bP0B/k0BIQGuA0IElfr2/OkBZf/R+nYChQBt+YwGCP7IAB0Ewvi+/WACVAWg/70B3/4lACb+bfOD+8n67vwHAhkFjACuASwCafJ49nv7q/zlAHIFMwIZAS8HbP2c/kIETQGv/0D/AAAAAJAD/wHEAxUGHQIoAxYARPxH+wT97vrY/oEJlAK5BmAEcPhjA1QHOwLY/mL21e9i9m35fgBRCOIDvv93/IwCtQH/AS3+H/gQ/Kv8ZAEdBrEIpPp//KYB1PtNBSQCjAT/AaT+ZwLEAbUJDgyiCAH+e/ny90v0zfn0AAcAg/1gBCL/JQAOCPAHjAjy+2n2JvTj9a/5/fiXA+0Auv5d/8X95QBCBDADAfrc+wz5MwBvBPb83/5w/AoDVQGbBJsEq/y2/xT32PaC/z4FhQSqBokDbwKxCAH+Nf7F/1UBpgPtAAT/Iv37COUGuQRyB8QFkAMm/oEFiQE7AuUA5/j/AQ4ECguMCGX92Pgt+vEBCP43Ac8AtQHpA6/5KAFCCMACQP1h/JX4nfhnAJQAOwJd/9MBQgBw/MQBBfsDAeIBLvgM++f+/ADtAkYBkvki/3T7H/r7BBIFuQZP/dT7f/yZ/bkAIv+qBjcDvAUsBor/iQEKBWcAyfxNBQAA8v2jAk0Bkf01/oUCVv/xATX+oPvF/1EAqgBW/dYEhQQI+H/4R/u6/ED/SQQzBpAFlASg/d/+T/tw/NcANf5fCJAJ1wJL/HD6I/V//G4IJv56BQcE2P7b/yUAmwhcAf388vu6+nD8qgKjAH4AuQRa+q/7XvXj9TsCiQMdBIwAywXABAAAd/xe9/b6cfS37yb4rgEoBx0KbwRH+8L+dPuS+Vb/ZwD8AsAABP+s+uv7gv/9/j4Df/wI/KD/Kf1RBKIK7AhUCRkL1wI1/BD8zwDLA7EC5QYoBdIJOgwi/2AAywMWAK4FcgcwAXIFqgTF+xP96/fj/8QFlABYBpH9KvuD90v4tv2O/rgM2gVZADH9JvYI+B7+ZwSMAMX/cPj5/Wz/xftJBrwF6QNE+qz4F/r2/BkB1PvEAW8CBwJl/c39UQSR/5n/5/q++RP9Zf2D/Yb6wvwWAhYCmAGpChUG0P4i/Srz6/s7AKMAlASz/IwEXwjIAOIBiQEq+WH4lf7q/5MG4gPLAYL/1Pn7BGMDkf+QAX/8CPp//Or9qPWO+msBVQMWAvn5wv4X+pL5OP0M+Zn/xf3J/oL/cPwsAvn/wvyR+/n5f/hL+Mb5+fvAAtcCFQQVBAoDVAXF/6oCdP/Q/sACtv3F/wz77v70ACQC8Ak+B64FMwKIBVwFnguxCjj72PpT9sX7lwNjBREL0gcI/Jn1h/jn+jMKjApgAi8FFPeK9yn9T/3pAx7+zf9E/HT34/0P/hkDZwaQB+0A2P6xAm8CWAZl/0f/LAD8AigD/fx0//n5LAJCCNoJrQ3HBsgCkf31/mz/9Ag6CO76ywEP/pn/UQZCAgsBegPwB/EBHQR2Aob6+fsB/P8DiAVrA8X/S/xp+tH44gHn/LkCngkP/p8BXAEB/pH/5QB0/+7+9f57+TMAFgCfAcsFHv4SB0D/2PghAVr8/AKQA2MFMANKAK4B3PeZ/QMBXAUhAcX7iv0q9U/91Pnf/KoEpPq+/UT4KvmXA00B5/wI/FL6yvSk/vgBPgOpDPQAKAFvAtT78QG2/+78/fxw+pX4wvxs/aj9PgOk/k/7Zf0b/0D9UvxL/u761Plh/Ir5XvveArUFlARgABIFAwHC+GX/SgKUAhUGuQR3/i8HywcSASQC4/0zADH5Afbq/e7+GQFnBnIDXf/7BH/+lf7eANj63/5H/fL9DP2+/RIHIQWmBf8FywG5AlECVQGr/Ov71PvQ/mcCdP9YCIwGTQFl/9j6sgAm/lr8F/qr/jsEG/0p/Zn7RgH4AfL9UQCV/E/9XvmR/bUD/ACmAbr6pPqD+T32WQDsBlAKDgzPBnv/uvwp/5z+kf8OAssDYwVCAjMGtQNRAi8HDP1E/KYBGQO2/8QBOwR7/Tj/oPsAAIP7ePY7AmH6QP16A58BegVNAQcAQ/4i+1L+yAKMAqoA/wHJ+lb7Iv8f+psAD/47ADoGXf//BYEF9vxl/YL/jv6v/fn93/zXAEf/jvwDAXT/bP9yA4UEiQMsAAj+3/yC/9j8mf0VBH0ElwVKAKoGkAemBTcJgv92BJADuQQoC6IINwlrAXv/3gD9/qMAywWtB9cACwEoAzz+RgE7An/+OwDPAPn9jvwx//n5nfzC+qzyLvhp+jME9AR//JX6jvpp/Az9Vv/U+QX5T/nZ8uP3nP4X/s3/LfzR8n/0wvybANMBegHPBG4GD/7b/7UDMwAt/mn4Cfbu/psESQQRCfQAjvyo/bP6RgPwB24GbwTU/1b5hv4+AYwE7QQ8/HT/4Pgt+iEBvANYCMAEwADaA3IL+AMVBGsD4/ek/Dz6mfkZA1b7PPxw/jLzG/3LA8n8tQHpB9MBmwBE+h/yQ/5P/fn9AACd9kf7/fpa+lwBnwOxBAj+xfvj/ywE5Qa1A+UGdPuS90v8jviQATADQgZ2BKYD6QUDAyAH+AN3/s373PuV/PAFwwl2AigBHv5//HYCD/6o+9MDUvxRAukHTQeADbUF3/4f+mX76/uFAJADUv6R/dj8JAJjBd4AlABW/cn2xvfy90IAe/+FAEkGZf34AbUBBP1S+mn81P0lAKIGPgcZC5ABJAILAZX60wOXA/EB+AVcBSL7t/ez+GX5WAJgAiwAxAOYAbUH+wqXBTsCNfob9eTzKf1O/1EENwkB/rb/Vv2BAQcGgQE7BPb6CPpW/xD4EPxNBeIDe/2O/Nj++f//BQoFAwXaATz+Bfsb9YUABwR6BYEDdgIkBv36h/jF/dj+dP+xCM8CoP3WBgH+ZftS/mn6yALDCfADkAW1Aw/+DP++/RkD5QjtBNj+t/vj9+f+XAe5BukFJv44+7P42PYHBHkJoggvCQT/Pfao98L6lfqqABIBgv9uBj4DMwYdCEYBE/+6+nv7vv94+jH9egF0+ZQAxAN+ABUEowAx+9z9FgDN+9/+DPuv/aMAEPz0AjADZf2V+gH83/xRBOkDpP5jA8X/7QAWArf78v22/y3+FQQ3A3YACwFS/qv+e/8dBJcDBwAe/nv77vq++/wAwvy78hjy4PR3/MsBsQSeCfwCwv4B+ib2AfwX/nv9e/s3A9MD/wN9Cl3/dP13/vb4G/8oA0UJzgxuBpn/DPfN+zj9Zf/WBIwAzwJE/Kj9awFgAFUDafwJ9v328v/pAd4GsQr0AgH+s/jn+K/7Lfps/bb/BP/PBjME8v9GA0oCJAJH/8AA1P8zANMB5/yr/ob+Af50/1UB9wmMCLUFnwPq/1gClfrN/ygBqPtUByEDtv1cAZsAXf2MAjcFqP0oA88EowCMAnT/1P88/Pb0Tv83Ae0A9wl5CaYHrgPaAXv9Vv3F/83/+AGD/RUEOwTq//QGrgPeACgBr/1w/oUACwET/9j+vAUVBh0Aivl790D9S/x3/sQDZwJh/jn3dPeg/SgFmwi9AWz/5/wm+tv/BwDy/34Ahv4I/Bv7BwQSB/QIkAebAnoBE/ssAEoA3P2C/7P8f/50/8QDpPwQ/Hv93PcLAZQAzf8p/833nfzIAjcBLAKg/3/6DP1KADABiQP8AmX3CPyG/rP8kwztBNoBLwVs/bwFrQflAIkBJQDr+U/5oPsq+5gB2gP5+Uv4cPrU/WAA4/3n/rr6EPoI+ir5QgByAU7/0fjN8Uj36v+JA7wD+wZ9Bur/kAG2/Rf8cgPtAvgDsQTIAq/9Yfox+1L8gQNgBN4ATv/2/EICegP/AZcJGQV7/Y76ePYOABIHcgdRCJ8HsQJw/h0AxvmmA2sFR/tNB77/cgEOCKf/DgIx/xf+WvyxAiEBjv6yAAz3Xvtp/M3/pgPeAs8EkAVyAdz7YAA1/DH5xvnF/Xf+ZAFcBSn/mwLF+/34Zfnj+zADEgHlCAcA4/chAf3+Xf84/6j7QPk1+rECDgQdCNYGIQHpAXT9NwUsBg4A8AOQAVL+LAJ9BqMCQP0m/L77lfpgAsMJawemA/ADBfv+8Fr8Mf0dADoGWvz5+83/gv9CALEEdgKqAsQBDPXC+m4GPgHq/2z70fTj/aMAzf8hA/ADMwKo/XIBBwSJA1gCrPqd9l71PP5nBnIFvAlGA2cAywGmAZAHDgbhBcgCnwFgAIUEQgr/BX0I3gL9/FUBxf9p/M8E3gL8AGsHkf+BA3YCe/ta+pL3UvoP/s8AEPx2ABf+nfquAZn5Uvoi+dj2E/uH9sX9jAQHAE/5pPrU+aT6BP9A9QH6OP+V/t4AEgMZAQz75/zC8o74YADeAFQHwAJl/8X/egNL/EIAG/+6+vL/+vMt+uUApP5jAy8HBwII/u0CAACmA1UB9vo8/lL8xf+MBCgDxAfeCFECIQPpBTABlf7Q/psAZwblBGcElwVGAw4ELALc/SUAAwPq/YwAzwIkBkIKEgVnBmcCOP+5AoUCiQPABCQEMf+V/jz+cPprAdMDHQTLB/b8zf3/BWQBbwLeAJ36G/2v+/34UQBcA/8BcgOfAYUAdgbU/Xj62gPc/VgCNwMi/Y7+Zf9GAygFQgTu/lUB1wJgAsQBdP03AVEA0fig+RkBEgP0BBIBT/3q/Sb6t/nC+u7+bP81/qz6ivm6/lkAEgNl/534ivcB/Mn+ZwDlBrkGfQIE/0f5vv2QBSQCQgIZBUYHiAWUAML+Jvrn/pn9oPl9AmcCXAEHBHoFyALc/ev5F/iZ+QX3mfvJ/uP9/f5d/e7+3gC5Aq//1P9KAJn/6QGg/bIA8AXlBIUCD/6k+OP3f/7PAuIDwAZ5B+IBYf5gAO0CogTIBEf9afjy/UIAcgEwAzADaP7699XzGPQT+5ADZwovBQMBmAEQ/Dz8JQCn/0/7s/gm9uP5UQJrA3IHGQNW+5n/Hv48/g4CKAFh/qT+LAAM/cX/d/79+Hv9qP3Y+ib+5/gu+E7/d/xKAqYH3gDu/Jz+RPqg+58BG/la/oUAxf+QCQoFSgLEAfn5h/hNAQsBfQSiCrwDNwEOAqoE2gF9Aq4DIv8E/5H9zwJUBaIGXAUHAGQBBwD8Atz9s/y5BmACywFGBXIBzf/8AtT/8v/eBg4E4gHF/9z5BfkDATcDmwbaC9MBqP0q+zH73gDAAg4CE/+K+xvzq/xGB3IBDgSZ/0D5/fy+/TMAyALu/kf5d/xO/28AgQND/gj+5/6V/ukBuAjTBVb5wv7EARYChQbSB2MFqgDb/8X/WAJVAfQG9AIX+mACmwRnAqoGpgW++f38jAJa+pz+AwOg+Yr5zfki+0kKRgcZAYEBZfk1+PL9F/5H/zsCnfqD+0IEmwQdBkkKkAG+/QcAMf2uBSQEaP6Z/5sA5QI3A5n/t/un/8n+Wv6UBOEFiv0q+6j7mfUF+1UB/fx7/4gHwAAF+0f7uvz8At4CbwI3A/EBTQHj/6/9egPhBXIDEgHtAIUELf4+AZ8B3P2QA6MABP26+nD63/6YAX4AKf/j/cL8/fhH+bP6EPiZ/XT9jvxO/+P/rgHaAyQEGQO8A6D7EPp7++P5SgC8BQcEbwCqAu76d/wdACL58v/f/oP90wGFAqoCYAIM//r1CPph/g4CwAgzAtv//f4i9+f4FgAKB8cO9ws7BBYApgFKAnoBkwYsAJ36cPyK+TsASQrdDCQGKf+V/nv76v9gBMQB3gJA/fr3dPsx/4wCMwJl/WAA4gP1/rUBvQF3/B788vcf9Ef94QdUBRkDDgBl/zsEuQJ//uP70fpE+o76Vvs7Al8IAwWBASL//fx+AFUBhv4M/5QAtQXLAbb/jAbTAdT97vzc9+P56/sI/JsCXAOjAkIE7QJA/cn+OwLQ/GAEJAaUAGsBmftW9+r9qP1NARwOgQduCkkKpgFRBvAFZAE3AXYE1PviAXkJIQMZBbIA1PtL/DX+jv7tAAMBFgIoA478bP8x/6j7bP0q9530XvUx+wcEHQAdAm8ABfuG+jz85/56AZsI3P3y+/b84/nU/xP9RPpA9RP9DgAhAwMHMwDxARD68vtgAmAAZwJ2BP3+nfhl/zH/AAADAzH/RgEkApsEIQV2BDMERgHpAxP/YABvBEf9F/5S/u7+dgKQBUYFnwNRBmcCPPyk/AT/qgCjAML63PtL/tj4e/0SA3T/zwLIAAH4sgCv/9H44gEsAtH6r//AAFb3tv2jArUFVA9YCLIAHQLc96z06QH5/cn+7Aav/Wz/GQX5/x0G/wl0/3D64/eK9WX98QEx/94CMwCk+KD7egG5AsAEnwGH+AT9BP9S/k/98vnn/uP9OwBCAOf8sQL/AQz7cPw7AAcADgQHAnv9awP4A5H/9ACBAdMDUQBW+bP6tv9vAG8AQgQE/+kDeQdS/jMCBwSO/pQCFQZGARIH+wRZADADLAC5AsgE3gA8/p8D8v8x/4wCBP/XAp8DWQBD/r7/bPth+hP9hv6K//36RPzy+6/92/8lACwAiv9RAB7+7QBgBCgBoP2z/PL5Vvt0/7ECMf9/+hv/6v22/aIEhQTPAsQFG/0I+lb9F/gt/FUBPgGO/lEAs/6+/5AFMf/EA1gEhvxd/az6Vv2fAeP/EgEwA5gBAAAOADH9q/xvAlgCKf0b/1kAd/6JA58HAwXy/yQCjAJA/2AGDgS9AYr/V/M8+n0GogjhC5MIbP22/fEBpP6mBU0FS/p0/Rv7dPuTCHYGMAHtAHT3G/f8AsAA1P/hBSb+nfpCAoEBQgTwB1b5s/ZA+0D7CgW4CIUGLAYOAL73d/yZ+xT5p/+D/aT8JAIHBpgB/ABo/lb5cPz5+Sb8R//C/Nj8QP3F/9/+d/4sAHD83/pt95n5zf8zAtYEXAFnAE/7cPr9+oP9Bwa5AlUBGQGmAYP9wvx3/rb/XwgvCXIHZwKyAML+ZAHPAqD/5QS+//L/hQRKAm8EDgSv/bP8mAFNA28ExAfABH/8Afrj+fn9hv4B/g4A6QFRAs3/lwPeAEv+R/uD9QH64gF//gj+UAybCIUG6QeD+6/5mffr8QX3MwIrCMsJ1giv/6D7iv3N+z4Hmwgb/YL/CPou+OUAMwKxBH0IFgKk/Kv+PgMgB/QCTQHn/sL8bP3f/u0CZwAkAgsBF/59BDoGgQMM/1kA8QE8/qYBawOmAdoBtQUzBCwAgQPj/cn8owK9AcQBZwLF/aj7F/5A/W8Czf+6/PQCIv26+PL9QP1A+3v/QP32/KYDjAII/qYDOwLC/u0Cs/qC/94CcPoB/oL/r/0sAiQIEgUoBWsD7vzf/hkDuQCR/7r+kvmK/dD8jvoi/TH/6v8b/+0EkAOfAcsBs/oq98X7bP0X/G8CVQHq/ywC1Pv9/ML8Zf3wAx7+4/03A5X+r/viAaMCr/9GAaMAqP0i+7kAD/5l/TAD1P8zAk0FLwVnAJsCcgX4Ac3/AfyV/DX8xfst/EoAgv9//mH+6/kAABkDyABvAOP/1P39/Of6Bfkq+ef68v+iBIEHTQHaAX4ABfszAqYBR/+YATj9H/raAX0IGQdNBeP99vby/WQBBwR9CvgDDgCR/0f7Kf1yA8sB9f5s/xf+0wHTBbEEUQAdAgz//frN/Sn91wLTAyb+UQASAW8AsQSv/9/+DgJgBE0HSgCjAiwCIQFrA/8BsgDIAmAEq/w7AAcATQGfAaD76v1s/3YCd/6+/+P7pPgm/qH3Wvbu+G354PhW+/X+AwFcB64DlfxW/Sr7d/xA/83/9AY6CIwAkf35/6YDywd5B2cCBP3C/tT9r/0zCDcDBP/1/jH36/sHAp8BawFVASn9r/uZ/yn92P5jBcX/jv5ZAM37QgISA6T8DgKFBMAAcgdyBYP90wOMBOf+q/7XApQAegP4BVEALAYwA7b9Nf7U+2QBiQH5+8395QL0BgMHpgWZ/1b5UvyD++v3PPry/c37s/59BKMA+f32+or1xvMB/Aj+R/9YBLP83/xS/mz/KAP0AJn/vQEkBDsA5QR5B2sD1gbLAxIDxAfLB94IcgexAsX9kfsi+6T+UQTeAuUAiv9W/Qz7g/10/4b+7v6z+OP13PmbACgBawHn/gH6q/5L+mz9qgQkAsgAQP+o/aj9bwDC/vQAjAJ7//EB0wNd/6YBMwSk+sL8HQA4/TMCrgWBAyUAuv6r/pn9r/9RAoEB2gGv/Rv/2P66+qD/BP+r/H/82/+O/tz9IQFh/ur/mAG1ASUASgIZAzcDXAVvAFUByAA4/aT8Tv99BOwI3QyfBy8FGQXQ/kv8s/z2+lr8uQLTATsEQgRW/4wCePoB9vL5s/zEA5QEkf+K/W8CF/53/JsAhv4dAob+kf21Ax0ESgLy/x0ASgD4Ad4AKAHPBIkD6QXWBNj+vv/N/6v+sgAhBTADAwF9Av3+MwKbAsX/Mf2r/Gj+ivlD/m8AXf1W/bb/KAE8/ND8+f2Z/+7+3PsF+779owAi/xP/Jv6jAB7+5/ru/Mn+LADY+tj87QD0AgMFMf1S/Lr++fnC/KD/Q/7tANcAoP8KBTMGWvz29rP2T/d3/CUAWQBCBtYEtv3ABND+e/km/jn10fYWArkG/wfeBiUASgDwA0v+f/zQ/E/5xvn9/toBjAozDLUBlABo/sL8kf+R/1wBKAEe/or9gv8wAXoDAwWMADH//wEoAUIAmAHpAXT9oPlw+NT9ogRUCVgGe/3XAgT/DPmO/DX8/f7j/wz/Xf+IBTcD3/5h/gX5e/12ALP+vv9CAm8AQgDPAi3+ZAELAZX8vANYBBkH1gozAnf8wvy2/2z/uQI7BHD+2/+XAzMGmwYkBHD+pPzf/OP59vzpASgBhv5h+uvz7viO/ML62gH0BIUC1wLY/Cr5Iv+k+pH7wAAX/iL/WALj/3f+kAdjBeUCHQRA/2sB0wOFAssDawFW+478Zf12AE0DogRcA9D+e/0e/HD8t/tw/Az51PvF/2sBkAOxAsQDR/uv+4r7RPxnAqYBVQEAABYC6QHhBS8H3gT5/8399ATlBiwGkAW1A2z7tv0dBM8ErQmTBsX/Zf+MAD4BmwSBAWX/mwAp/Qj+awMzAFL6d/zC+l75Yf4OALr89ABkAQAABwKk/LP8rPoT++f+9ALLA/EBwAauAav+fgDC/gMBPgWFAmcE2gk3A0IEmwRVAe0CGQFNAaf/4//aAdMBKAPq/8X/LADr++f8F/xh/lwBXvuR+5z+afw4/dj8Mfnf/Gz9t/lA/RIB8QGK/1r+3/yd+gj+5QAhAWsBmwL7BJsCDP8m/s35R/1rAfb86QPEBXv/sgDq/1EA7QAE/Vb3OfmD/f3+gQV2Bu0Axf35+b73T/3AAH0GgQkWAML+DP+o/b0BBwYvB6YFHQJl/Qz/tQPEA/QCbgZNAd/86/uG+owCWAR2BK4Bhv5a/qD5F/ha+koApP4I/l3/7vi+9dj6Xf9L/GH8vvlL+kf/0P5A//3+OwCd/Nj6r/3lAPAFNwN2AvEBDgDLAwoDuvxs/SUAWQD/B9YIsQQGCAoFR/3pAeIDKAFCBOr93gB2CNMFyATABA4Ag/shAwsBDgADCZgBG/tCAGX9JvwVBPwCYAJ6AZH7DP8OAJX8rgP5/xv7LAQx/839bwJs/139Wv7U/Rf8+f+XA3IDjAKYASL9YfyV+ED5S/xa/rwFhv5l/f3+S/57/34AFQRrA0oCVvsm+s351PshAQMBf/4e/lr+xvnU/1ECXAEhBUP+Afak+rP8DgA+B9oDegOg/6T8aP7EAaMCMf/LAZQCTQMkBiwGRgOn/5L5f/7/AzMCcgVyBbb/0Pzj//36yfz0ALP+zf/pBbkE3P3tBFwBcPw8+u76Xvsm+hkF/wOYAbUFnwdGBZADDgIm/uf6g/0DAXoBSQRRAP3+YfxjBaoIxf0zBCgBoffq/woFKf9rA7r8f/ho/hv9UQKiBM8Af/x0/476iv3j/zH31wBRBuUABwBvAiL9mf9vACL73/yr/Jn9s/7eAm8EEgXEA4wCZf3R+qT+qP2R/28A+AGqAMX/hv62/4L/2Pyk/Mn4YfxgAIkD8APpAzsAYfzc/Uf9H/r69xP9cPxcA2sDuQCxBGQBFgKV/Pn7OPuR/Yb8BfvwBbwD8AXtBKv8OwB+AN/6Af4DA3T/1wJnAtH6f/7C/lb/awOR/wT9aP4lAKD7gv+uATz8r/9S+k/7MAFgAhUIXwiiBKYBKf0i+f38R/+fAa4DGQEoAwMDiQFcA58BMAGfBRIDpP7iAXD+2PiG/pn9PgHaB5sAYAJKAor/0wHAAKv8G/35/cL4Yf7n/k/9p/8M/94A3gKXAwAAgQGS9xT1dP3N+YwCKwpcBbkAXf8M/fX+OwTHBoEDe/tS+jn5afwSAXID/wElAAMBkfvJ/pcFogTeAGX/E/9O/3f8kvnU/ef+gQF9BFwBd/5vAj4BiQG8B4r/Q/7lACr5nfwhBRIDWAQb/7P4tQFyA+EFTQXq/Qj8Xf0i/f8B+wyxCO0C4gEx/5X+3/50/Uf7nfxo/iQCqgL0ABkDdgAb+8X/e/1e+5n/F/pw+iwCkAczBK4D6v+9AVwDlfhl/+f+bwIdBOv76QEdAiwE/wMkAnD81feZ/aT8+f9nApX+F/66/hP94/soA5gBq/y++4b6xAVYBBv9oP1A//wA9AAoBQT/DgLlBrECyAKn/zH/Hv6v/+UAFgL/A00HAwVH/y8FXAeBBVEADP13/qD9JvyD+zsCagnHCKoGJQBP+ygBxAGBBcACVvmR+yr34/eUADH/QgBjBfL5bPtyByUA5/7U+xv79ADtAHv/QP2fATcB5QKbAo7+tQV+APn7iv8T/Yr9oP0p/Sn9IQHWBFwDLAAOAFEAbPsM9x/2t/th/Jz+BwAm+gz9DgDtAssFkAX4AyL9Wvgx/0f9bPtrA1b9QPt2AHoDVQG5AOUCzwC5ACwCZf9t9xv7wvyO/vQEYwnaB1kA5QBW+2X7r/3b/8sB/wE3BdcAkAHlBOUGMwLj/zH9t/v1/iEBoghgAsX73Pl0/fADuQKxAk7/6/tP/eP/dgSIC24Gd/6S91736/t//OUGXwhfCIwEhvqV/Jn9lf4dBiQIVQFCAP38LfpH/ygBDgAx/7b9hv7LASUAWQCR/xP9IQFrAaj9yAB0/aj5lACZ/6YDHQR0/Yr/2Pr9+Fb/Tv9L/mcCBP++/00DNfy6/A/+LfrN+zX+6/sb/7b/e/uMBN4G1P/5/3f+/fx7/7r+LAC9Aaf/3gIwAaf/IQV6Be78+fkdAF3/DgR9BED/lADJ/OP7Lfyg/3YEJAbLAYL/NwV7/3T9Vv0e/BID0wUKBywG0wMkBOEFtQEp/7wD/wGr/rIAVQEKAzcHUQTIAjsEhQR+ALr4S/qg/er/mwA+AWMFiQN3/gT9t/nj96T8Hv7C/Of68vvN+8L8mAEsAMAAq/4X+tT5E/vr+2z9dP01+r79egG9ASwERgU8/tj+3gKz/Of+kAHu/qT+mf9L/m8AlALTAyEFQP8T/Vr6QPst/uUAUQBa/mcAvvv9/okB3gDxATABAf6r/CUAjAA3AwAAZwCbBB0IUArTBfgDqgQb/0v64gHtAP8BsQRGA1wDsQThBdj+XANs/R/6Jv5A+6//cPw8/h0ANf5P/cgAywPU/+7+Vv08/M39GQNVAx0EWASR/7f7LfwOAuIBlwP7BOP/yACfAwz/TQHtAEv60Pz9+in/jAZNA6v+WvyV+hP9qgDQ/iwAPP4x+zX+rgNyBa4D0wE1/Ef7OPu2/cAAr/9VAd/+UQIoB1EE1gR6A3v/r/9JBCQE4/8b/dz5Zfsp/Yb8lADpA30COwSqAv3+OwJ7/9T55/yjAAAA1P90+8L41P0zAtMDawOUAor/7QB/+iL3lwMWAuP/5QLlABIBp/9d/3/+3/wM/zn5OffY+hP9lwXaB5cJLAKV+tT5h/aV/rUBbwIDA5z+D/5CAh0AIv9YAlr+NwFvAmsDuQTeAPX+egMVBBf+QgJKADMAdgZYBogFowA1/E7/hv6fAYEHbP+FAL0BXf1CAJADcgNJBAoDOwCjAl75mflO//n9nwESBaf/rPgZAZQAYwPpBcX/Kf0x+Xv7bP/wBdMFLAIb/QH8Jvyg+7r+5/5nArb/kAHTA9MDrgGv+Yr5EPz9/r77zfs7AIr9bP25AEP+cgEdBB7+Mf+bAmMFywVrA6T8r/l//Pn9bP9UBQYK9ALaA2z/R/2BAwcAyAKMBCwCbP3c+1L81P1gAj4DRgX8AuP/VQG5AOP/QgBZAH4AD/4OAvQCaP78AFb/F/7u/oP7DPfQ/FL+3P3LAxv/3gCr/G31e/c5+Sb4vvfEAQ4AE//EAX/8lfx7//n/d/wb/9T9CPyg/83/Xf9d/dT/Yf7U/zoGegMhAxIBKf1cAYUAOPvj/X/+jv7aBbEE8v+xAob8dPmMAJX+6v9vAET8E/+G/uf8SgLlBGAC0wE1/lb9ZfuO/joGzwI+BxUE2PqO/g4CHQKBBdYKLAS+/8gAe/+bAm8CbPtA+0v+s/5ZAH/+hQRRCNMDQ/6g+yn9VvfN9cL4Yf6BBdMDZAHEA0YB4/0B/Kj3RPps/9oD+AHtAGcE8AV9CEIE3/oI+mH+Vvk1/kIGiAcZBUT87vwWACwE4gG2/Sb6mfubAnIBiAf7BDj9qPsx+ZH7CP5RAIEFpgW1AbkEXf9E+jX++f2jABkFuQRvAEf/RgH8AIwAbwK+/2cAOwTiAbwDTQHf/DsAJv6v/TADf/4ZAVwJIQOmAZgBpPgm+O78PPhA+8L+qP3lAuUAbgZ6BXT7PP7R+lb5T/3j+6f/4gMsAqoCRgH4AWsFuQL0ACgDlwPU/5QCFgKK/+0EhQAx/y8FLAbwB3IHlABw/okBG//j/2z/kf1yAVgCQgRgApn/awHN++P3QPvF/Q4AhQISAdD+Iv2s+I78OP0t/DcFowBS/s8Ce/3j/dcA9vx0/zsC2Pz0AEICjASqCFUB+f84/2X9wvzu/kIC2gPIAC3+lAJd/XT9QgDJ/n0Czf8m/HYAbP88+jj70fohAUoCjv6bAB0C2gOk/gT9d/7tAsgCjACFALr8IQPtBGsDrgOFBukHKAEm/nf8mwCJA3YCFgKO/oL/bwLY/hP/GQPU/+v70fjG9wT9tQNcAdD84/26/H/8MfsF+wsBmwJh/PL7MAFGA8sDiQEHAHYA4/+c/tD+MwAzAOr9xf/EBcsFLARKAgsB7QAp/w4AbwBl/YP9gv+z/uID2gfLBVgEuv6D9532mf2yAGcCPgUSAZn/GQG+/xv91P3Y/uf6T/vy/TH/MwKBAdv/HQJ9AlkA5QD8AJsCiQOk/hf+Vv35/TcFsQgSBWsBtQPPAhIBAAAI/qD/Lf5/+l77+AGIBUoACP4DA4UA0P7G+Zb0e//XAAT/0Pxw+sX78vn5+y3+7QLAAmsD0wFS/jH/wADAACr5NfyG/k7/nwHq/0IA4QWqCHv/wALlAhYAqgLy/f3+FgIp/bP+wAaFAg4EowKG/Bv7cPwLATj/ywMwAyb+0P5O/9j60Pyv/yb6ePq3+QT/MAHaAU0BjAAzAsn8PPwi/SgDtQPPBK4DHQJ6BQH+RPzY+v36D/4sALUBNwexCGACHQQp/8L6kf0B/pz+zwAM/ywAJAKqAssBjvz5/xD6Mfmo/WH+iQPb/yL/SgADAWX97vx0/8gA0wHy/zsADP0dAF3/egF9BlUBJQDb/+r/RgMdCFgEzwDq/xf6PP7IAg/+hQC2/2z7XAF0/zj9afw4/UoCbwBKADsA/fzY/DMAJvyV/gsB6/nJ+h78lACmA28CvQHXAO76S/y5Av3+JAIM/zj9dgAsAAcCvv/IAtcAivmk+iUA3gDABgoLHQblCO0C6/kB+rf7YACBAywC6v/N/6v+3/6qAs8EZwI3AQH+mf34Adj+iv39/ib8r/kF+xYAkwjsCukF4gFCAHoB1P84/1UBzf/C/Jz+AwGqBi8JOP/9/i3+RPqqAoUEDgI7BP38Ofl3/qf/vQHU/zH/BP0X/iUAVv0DAR0AUQC+/Xf+NwHAArEE2//tANT7t/tvACn/kf1+ANT/9vpRAuP/7QDPBCwAowCbACwCKAOyAOv7S/pP+fn/4QdfCKIEYAAsAET8E/1h/sQBpgNO/5X6ZfvABDcFLAIi/0T6U/iV/DH7mfszBMgCxf9A/Yr9Ivt3/HD+cPx2AsQFrgNW/2j+UvwE/zX+3/wP/n/6AABRAFUDLwUoBVQHvQEX/mj+gv/n/lgCqgCQAQ4CHQC5Aq4BxAHTAQMDIv8kAnYEnwFnBM8A9vxS/gMBMwCfAcL+E/8m/gj6pPx3/JsCfgBs/2ACIQEzBEYDyf6K/w4EHvyZ+dT5G/mqAJcD4QXsBjoG7QRYAt/8mf2K/6D9Nf6r/j4D2gfaB28CLf6K+aj7dP9A/bECPgPLAaYFuQaUBNoDQP9H+QH6PPwDA4EH1gQ7Ar7/0PwAACUADP0P/sL6s/jQ/iEF/wFKAmACgv8I/E/5AwNKAlb/mwCv+R/6qgDq/28CkwgzAs8CSgJ3/oUCqP3G+Yr78v0T/3IB0wEwAUkEAwHF/R78hvwb/5z++f22/TsCDgJvAIwCiv8i/+76zfsX/mX9egMi+7P6Kf9S/t4C3P1E/HD4Mfl0/2sBXANZAKIECgPn/N/8S/xA+8n6cPz5/eUABwL/A5QEgQl2CmsBkf9/+uv3/fzC/g4CvAlUB4UEWAan/7kCYwNw/toBbwIB/tD+KAMWAhkHRgUI/lr+afzLAYwEIQE7BNj+uvx7/476yALPBjsCcgP8ArkC4gOYAUD7QP1//Jn5wvy+/ywEEgdcA2X//ACz/Cn9jv7Y+gX7+f01/jH/GQWbAi8FWAJE/Of6T/nJ/GX5Xf2YAeP/Mf8dAHT/rgGQAzz6zftD/hv/jAYZA6v+TQPc+9j4d/53/DcDDgQkAq4DVAXeBLUBAwGc/i38DPkt/BP91wLeBrkA1wBKAn/+Xf2z/qT8DgRCAGX/WAZnAED9Uvo8+DH7LwnlCGMD5QLj/WX/bP39/jj/OP/b/xv/Yfyz/DcB/ABcAwsBmwAoAdj+r//j/xP9+f+jAEj3afpD/gj8MAMsBgcCHQbtAOv7DgC6/L79p/+O/s35kvkF+3oBpgNA/8QBe/kI/tv/AfwwA8gAxAFgBKMAS/7b/7P6Afir/CL//ACQB/AHnwMvB7b/r/2+/3/+LAQDAWX7vv3IAIwA6QPpAd/+S/4M+3T5Vv2qBvAFr/9L/jMAWv7Q/Dz60fjF/av+QP0AAOwGwARyBVkA4/t9As39kAGqAhYCgQNH/6v+Q/6FAhUEZwIX/mz98v34AS8HfQSxBtYEF/wX+tz9nfo4/4wAZftVA/QCMwKXAwcAe/+iBM39R/vEB5n/nfwSAQAAvQHN/5H/jAKxAp8BXAEM/cQDMwhcA88E6QFa/h7+3P0OBOEHjAJ2AvL78vW2/30ChQCxBokD4/3n/i74mfvJ/lr8BP/EAywEPP7N/aj5QPmZ9XT3s/wB/sAAt/v1/pn/4gOuAQz/zf8F93/2u/YX/uUCFQTiA4EDE//U/X0Cf/5NBSEFBP/U/34AIv/eBB0GBP/lBEoC/f5NAZgBbwLEA0IAiv0lAK4BTQWBAdMBsgAWAMAAYf50/07/rgNJBK4FZwAi/8X/WvrPACwEGQNcBUkGbP9NAZADcP7PAPEBpP62/WACZAFw/mj+wABNAQAAvv+6/in/1P8x/+762PyG/B7+5/5d/aoAR/uZ/fb8Vvds+0YDlf6k+KD96/eR/Vb/s/xcBQ4GuQRW+6T4xvnf+qj9lfwzAJsA9Ab7BqoEAwdZAED/g/1a/M3/8v+MAPADRgOMBDMKbwS+/er9hvqs+j4FiAUHAmcEsgCc/qj9qPsm/O0Ae/+9ATMCF/w7BLEC8v3lAD4DXAP8AEYBe/+k/q//+AEDAcsB9AaIBcACEgVS/mj+LAK6/DME5QDIAvgHYfwQ/MQBfgCV/G8AS/r5+TABXf/9/ukBHQbN/QH6nfgF+Rf8S/4ZBXIDwAAM/0f9f/wWArwFEgHY+lr89AAzAK0HsQTN+1L83/wx+Qz9BwQOAP8BnP72+gz/jv5kAUkEkf01+sX96/lL/qIENwOmAfn9uvxl/0IEdgauBcACUQAB/BT5QPvN/RkBOwTLAR0C7Aar/lb/NwOk/GX9rPph+DX+PgU+BbkCtv9W/+r/F/gX+M372P7/ASEDEgOC/z4Bvv9W/4UEhQL9/hD8afzq/cQBBgjXAlEAbwDJ/Or9Vv8LARYClAJrAX0EJASjAAAAZfu3+yb6WvrJ/Or/owDq/ekBKAHAAP3+Wv7j/wj+1P/j/QH6hvr9+oP9MwRrAZX+Nf5W+aD7tQGJA30E3gTu/NT75QDQ/ib+PgMoA8gAdP8I+ib+wADPAlQF7QRnBs8EhQRNA5cD2//1/ib+DP+UAoUAVQPXAqMAlwNfCA4ChQKv/2X3nP459y36MwRCAHIB7QS1Afn/kAPY/lb9s/7C/pH/8v/U/58DBwQdANMB/f7iAbkCYf4p/QMBrgPEAVUBmf2jAk/9wvr5/0v6yfzC/kP+p/+fBcAAF/wOALr4rPr1/l77oP1nAtD+bwBCAkD72P7U/Sb8NwE8/or7Kf81/mcAogiuA4UCWAKO/GX9QP+fASQCyACV/vgBSgB7/X4A+f3tAOUCpgHeBp8De/la/GX5e/ebAML+s/6uAcn+1P+xCIUEDgDr+zn3KAGBAZsEDgYkBjcDKAHAAt/+Awf/AQsBFgJs/4EDjACJAzoG1gY3Ac3/4/1h/G8CZAGmA9cCE/0M/dT/vAPhBXIBtv/N/ZX8zftS/FkAegPSB+IBogR9Agj8/fwt/CwAzfn2/KD/jABYBrEIvAcM/2cAMfsb+Vb/mwCMANoBegVNAxUEmwCR/VL8cPgp/dT/ZwRYCm4G6v+6+ib6qPm6/gMFf/79/Nz9wvy1AW4GmwLN/fb46/Em+O0AIQW8AzABp/8P/h7+Jvrn/Ev+Jvox+7r+OwBcA7EC8AO8AyL/3gC++7b/PgMSAVUBmwQKB1b/r//9/CgDbwIM/+UG/ACmAdcCMf1s++kDZf3N+e0CG/3tAMAA3Pse/kf/Iv8WAM39jvp7/YP96v0AACEBMf9W/wH+dP0I/psCVAVgAG8C3Psb/VEA/f7xAbkAmf8M/fsECgUKBSgHvv1T+NT7Yf5A//8JlwU4/xv9rPYB/M8AHQCjAnoD6/sF+ZL5bP+fBVwH5QJp/N/6RPRL+Lb9PgEsBAsB1P90/1wBF/7C+p38iv/C/nYCwAQhBZ8F2/92ApQCnfxE+jX8hvp2AE0NNg3ODKIKyf5p+Gj+T/39/g4G9AT0AIr/e/8b/64F8v+v+2n63PfIAJsC2gMdBsQFuv4b/f38S/g8/ssBxf9//koC+f9a/tcA1PvN/woFMwJCApQA5/6K/U/7tv3N/UoA9vwb+8gA+f+xAm8EZf/5+f38QPsX/jADPPzy/2QB1wKuBd4EvQFs+4r5CfZA/YEHRgfLBygHFgIOAHYAiQGbAoUCG/8E/VkAvv9vBCQI/AJ0/0f9zfcu+MX/0P5YApQEiv+FAE0B5/6o/ef8bfm3+77/DP8zAjcDWv5ZANcCPgOxBHoF2gF3/OUAD/4hAWsD1PtVAfQEMAOFAoUEwv4t/k0B/f6JAQMBXAGK/7IA3/7F/5QAjvqK/f3+JQASAbwDaP4i+QT/f/qV+A/+lf5CAN4CIv9//okBCwGV/kf79vaS+er/CP6bArEGwv6O/MQDXf/f/lQHOwAx/wj+nfyFALP81Pta+gj8XAGbAj4B5/7b/5n/f/pe+yUAUQDQ/gMBaP6k+q4BWv5//hUEp/9+AP8DMwRCACgFBghrA+r/EPyg/xIFeQdrBVQHHQZZAOr/xf1KABUGSQQzAtT/afru/p8FfQhnBokD+f9I95X6wv50/0YDaP6z+Pb8QPsB/H0EYwM3AZn9hvy3+2j+GQPq//QALAAx+wz5rPp7/TcDPgMOAJH9kfuK/6YDBggoA+kD9ADc9Xj4nfzJ/hkB2gE4/6MCfgAi/5n/yfoX/nT9ivsx/YUGFQQb/5QEowKr/lL8f/zY+Dj7Yfzn/q4DPguiDF3/PgEI/hv/dgY+A9cAzwBw/Bf84QX/AfADMwLq/fEBawFYAoED+wQt/K/7R/us+hkDVQGK/8QDDgAf+tT/afzj/cn+rPru/kf/NwMsBJQC5QAzBAMBNf4sANz75/6C/3D+E//8AgcCpgVUBe787QK6/lr8AwP/AYUC4QVA/RD4CPxD/k0D4/2z/H/8BP3pAYUCIQNGA6YFs/7C/ND8DPvU+3T7gQEsBmMF6QEzBFr+r/3wA5gBTQX8Ahv9DP+jAqYBxwb7BgsBVQEi+/36bP8oA1QFTQeFBrkA1wD5/+f+uvx//tcAlABcA5sE2gE4/TMAlf4p/7r+mfmg/ZX8wv4DAbUBbwKbAvgBF/wB/jX8tv0oATX+3/4HALkAdgDLAwcC1P+v/Tj7mf8wAc8CowAM+yb8bP8p/YwAqgLC/G35t/mg/UoAr/85+Uv6s/pp/OUAnfxH/1EA4/+r/msBNf57+c37f/oM/zsAawOuA/sGZwSUAEYD4/0zAtMBUQQOBJsCAwPeAPsEcgUzBm8CyARyAe0AyAJkAQcE6QEOBkIEJAI8/oEBZwAP/iEDg/vr+bP8ywF6AUIGdgAQ+t/+zf0dBBkBegF0/Y78bP1h/GAAEPxa/lEAZwI4/0oANf4WAG8CUvy+/139Uv7f+jH7Nfrj+3f+QPvj/3YACgM8/hP/yfbc9QH81fdA/Z38iQMlAHD+DP/u+l39EgGuA7P+tQFKAG8A4/3LA0kG1wAsBML8HQC1AWcEbgZuBgMHkAGO/jz+cgWqAnoDcgGK/4EBEgPpBdoBZwTC/sL6uvop//sE+AW8A5H/jALF/9j+Q/6Z/7f7wv4wAXf80wUhA70BOwDF/x0CrgO1A/n/DgKG/Pn/3gD0AGQBZf9KAOf8PgWXBVwFQgbpAe78H/q2/83/pgFGA7kAMf8i/4P5LfyYAb7/fQI4/UD/QgAt/Az9G/26+mn2CPyD/br+ZAGn/+D4OfcX/C74CP6jAOr9q/5KAN4CMf9A/QX5DPkm/pz+gv9vBDcDOwQ+BeP7jvxs/fwAyATtBLEGiQOfAyQCWQAF+7P4WviS+QT/ogaMDrgI6QPu/q/7ePo4/3YA1Pmn//L9R/0LAUIG/wNgAOkBQ/4hASn/YAJvAKD98v/U/VEAIQPeBr0BE/8zAuUETQFvAqMARPpO//X+yAQgB6IIywOc/tT/R/kb+8393gD5/6oE+AP4A0ICIvnF+3/4Hv70AO0C6QGBAUoC+ftkARf+jvzn/MX9qPuG/h0EOwKfA3YAxf+K+Rf+zf17+wcA2P4kAk7/ZwCv/TMAsQIkAqj9KvtO/5X6xf+fA6YHOwBh/hYAt/dnAA4E8QEsACEBWv6r/jsAwACuAfQC+wYT/aT8AABCAv3+s/5VAYP7uv5VAaYJSQi8AyUAt/vr+zMAYwWqANoByfqr/H0E+AeMCPgDsQJl/fgB4/90//3+zfsb/ZQA/wMsArgIEgGK/f3+Xf0X/uP9Mf85+YwAxAFH/94CuQLF/177zfmO+Bf++f22/xkBSgD0AMX7Lfw4/wH+wv4hA5n/pP5S/sL8E/2++9j+QgCK/6f/LAJw/sgCKANw+mcAEgH0ACwCNwPTAbb9lf7U+zX89ABVAwcCJAILASn/8v2c/hYCBwDC+o76kf8x/SL9QgDn/GX/jAKZ/b77CwFvAJX+R/+R/zcBYALEA/EBbP/j/Wn8E/1W/1UDGQXiAR0A/fzF+yEBRgN2Aur9kf99Ak7/7QIDAUoAcgWfA5gBKAOqAnv/LAJGATsAsQTeAm8EMAOK/5QCkANrA58DJARgAAz/mf8AAGAELARRAF75RPyC/+r9IQV9BNcCvAMhAc3/OP93/qj9Nf79/NT/bwLy/Tz63/y2/8L+mwA7ArUBMAE8/q/5d/w3AQT/e/0t/jz8nfgM+6/9BP/aAf3+T/0I/gz/6v81/v3+ZAHXABv/DgBgAIL/QgKJAUv+7QBo/h7+XAXTAzADAwOJASgFpgX0AvX+9vzc+6/7pPxNAT4FbwJjA13/T/34ATj/hv52AAz9qP3XAv38OPveADMAqgLTA6f/nP7u/jj7YfziAZAFPgcvBeP/9vr2+qD7f/5GAYEBAwNUBVgCyf5ZALr+zfuz+Ir78vuk/rwDgv8+A5ABYfwM/Sr5nfhH/0f/MwAHBN/+sgCc/hv9OwCMAAsBuQDIAHv99AJ6A4EDxAPaAfwALfy2/3YA/wMzBA4EEgEdAkIG9vrf/oL/NfzlAH0C/wMOBrUD2/8dAlr+zwAWAl3/Mf2G/Bv9e/1cBRkFpgF4+v36yf6bAOUCIQEDA5H9oP3N+6v+DgD5+7IANf5H//n/e/1E+o78bP9GA/gFR/+k/Fr89f75/30EbwLPAlEElfzF/fn/RgXTBbEEIQOBAXT//AASBS8FXwqJA8sBJQDF/4wCcP43Adv/wvyK+1ECYf7N/aMCq/43AaYDmwTu/JsCYACd+KD7S/gq+Xv5WAIVBCQCXAOUAvL/Vv8hAZX8e/8E/Tj9EPxL/lUDKf/LAd4AqgB7/cn6YfyjAkIEQgIM/835qgJh/lL8BP97+WH6R/1h/n0CywM8+jH92PpD/j4Ftv3Y/t/8Ivt0+wMBYAAT/2cC1wAZAe0CAwnlBHoFZwLc+yL9NfyyANoBxwa1B+UAOP1//jX+1wAvBcsBkf8B/Fb9nfqd+r77lfqK/d/6tv2+/wcElASbADH9QPvn/Fb9OwCd/MgAdgC2/dMDsgCBAS8FkAFd/8ACAAC1ASAHRgXtAIr/tv2z/EkEYAJNBaYJcgW5AIr7iv3tAJQEoP8OAN/8g/sdBBYC1gZjB4L/g/mz/LP8jvymAcn+YAAt/qYBKAEsAGcIYAZRAur/G/1P96j95QAb/xEJIAnEA5gB9AAVBIgHdgJs/Yb+/f4P/rkCMwi4CEEMRgPF+/b6CPiR+zj9SgI7BM3/Nf7TAcQBhQKBAzX6Vvmg+c35pPxW+zX+MAFcAfL/EgF0/8n8kfvY+KMArgND/mX/3/pA+4wC5QDC/iL/PP5A+/L54/kT/8gEHQSbAv36F/hH+az45/woATMC2/+z/P368v/J/p38JAJ7/Y781P+Z+Yb8mwb8Al3/QgKO/mn8Uv5W/3YCXAWxBMgCjADaA6oGbwBGAa4F4/+v/SwC+wQCC4gLmwR6A58Btv+1AQcCHQJW/xv9SgBrA+EHiAn7BLb9Wvo4+5X6Zf+uAR0CAwf0BOUAvv/F/Sn9g/26+q/7S/7F/xYCQgKUAiEDWALj/1EA6v1W/8374/X1/in9+f3aA3YAEPxH/cX9yfjn/pH/G/+MAAj8OPsm/MX9bP2G/CL5R/tP+aH3s/7iAy8HBwYKA2X7wvoI+hf6wvxA/dcCdP+2/4kDtQPEAz4FTv/y+88ACPz8AmMFAwNRCDMG+wRRBgMDS/5w/r733PlKAtYEpgkRCTADGQGfAZ360fpA/Vr80foM+4wAOwJYBKoEcgG3+S3+bP2v+U0DsQLaAwoDmAE3Ad4GOwS3+3T/G/kX/hUG/wW1BXYE1wCUAJQEq/6k/mX7JvxH/wT9gQNYBlwBMf9W/ZL5YAA8/lb7bPvR+ob8S/ph/C36IQOFAkf9Iv0b+R7+QP2c/gz93/wm+jj7Iv9+AM8GMwBNA3YCf/5nAEv88v0sAFUB7QRyBwMDIQO+/xP/KAFa/Pb6cPyyAHoFPgszAoP9bP0i+Sb86v+XA8ACUQY3ASwA7QB+AKoCcP5KADH5G/s7AAcGngvlDE0LXAFVAfL51Pun/9v/rgObArkCWAIKB94CYAaXBd/+Mf0x+dz5/fwsBKYDwAaJAYP9HQBw/uP95/hW+0v6iv3U/+kBMwIDAfwAqPn5/Y7+nP6v/WH+d/x0+zH94/sOBhIBJAJo/sb1kf0i/2cCqgY3BTj7hvyV/HD8+AMkBpQEBfvc+3T/qgLACPQKWAYoAxIB9vxNAcQBzwCn/8QDYAKbAFEG2gPEA1EAuv6bAiQGwAKUALP+Lfpd/zj/kftw/HT/9vzTAQ4E+AH/Awj86/v2+lr+tQEi/a/5t/nC/Gz/+AUP/pH/Iv++97778v1CBAcEgQPY/jX+Zft/+h0Ae/szAgcAqPvy/VEA4gEZA1QHbP8b/8AAMf9a/gT/ywFKAEoC1wCfAdMDcgHQ/lkA1wJ2AsAAJQD8AOIBvAPf/Dj9/f5h/gcAuvyv/6/9Jv6R/er9cgM+A5gBtv0b/0D7T/2Z/6D7f/7Q/Lr+r/tH+5sALACqBNMDJQDN/zX8s/pS/lwBkf1/+nf8S/wM//sE0wWjAkoAwvyV+lb7oP2Z/wT/uQQdAkD9CP6V/AMBZwKxBDADsgBA/6T8hv7TAbUFEgNUB3IDPP4zAjMAGQVfCN4GmwDN/xf+5/pcAdoFMwiUAs8ALAB7/94Aiv0I/Mn8dP8x/8AEPgeXBcgCVvvY+E/3BfuK/aMA6QMzALr80P50/+f6vv87AND8Yfx3/HD+7v7lBigDqPur/BD4+vX2+hID0wNyBbwFKAHY/rr82/+g/bb9awHF/dD+zwIAADz+WAJs/9D+gQEE/Qj+xAHc+478UQRl/wcAmAET/XT/awM7BHf+Hvx4+Lr4mwBjByAH4/35/zsCYwM6CiALIQHV9534Lvi1AfcJhQjlBFwBAwM3A58FzwRyAw/+ivmc/oEBzwQhA0YD/wWjAOf8VQHF/7kAWAjq/Qz7QP+d+nD+wAIHAn4A4/3F+7P+AACbAjMEbP+z/O76UvyC/zcDuQK9Ad4A8vur/Dj/G//J/mX/8v2yAJADbP+K/wAAkf3n/N/8mf3u/hYAZwAm/or/EgFh/k/9XAGJAyEB/wWbAkv+NwNjBeUCzwBNAeP7BP9A/6MCSQYZA+EFVv+1AbkC9ADC/qT+GQM4/WAARgOBBdoDMwDf/jj9wv4DAQcEs/4+AYwAwv4wAygDQgKZ/Wz9zftP/RYCogSMAHD+kf/u+oP95QBVAxf+r/1+APb88AOuAwT/WALtBMn8IvdL/AH+yADTAav+nfzY/uIB2P7F/yQCVv1p+H/4QPk1+mX/BwAOAJ8DawOZ/5n9BwDq/V3/DgCc/pn/G//AAgMDvAUOBGcC9ABw/pAByf6fBU0F2//5/6v+UQCZ/1EAE/+1Axv/G/2jAgj+jAIHBEoCMwDIAAT9DPd3/FwBiAf0Akf/pPx/+G8AYAKqAGMDMAP2+lr8s/4x/SgDQgCO/B7+tv8b+6/7PgOQBVEGegPxARv9bPt0+/L7/f4i/Sr7Kvls/1kASgCFAgT/5/5S/ND8OfnN97b97v7Q/F39Mf2k/J8BYfxS/koClf7q/9j8SgAvBdMFzwB7/UIAmAFVAYL/UQIzAg4EmwDq/f8DLARrA+UCKAdjA3/80Px//q4DqgabBPX+4/10/dv/ywPPBu0E3/4e/lL8lAJgBoEDwv5KANMBVv1NB1QH8QEkAkoChv6Z/+kFcPy+/64FtQVnBKMCAwN7/SEBQgAoAbb/1P92AML6fQK6/gX7q/xL/GX7xf1KAuv7e/0i++f6q/xa+qT6Ivc8+r77dP0E/dz9wvyd/EIABfs1/jz+8vuZ/QT9Kf3lAPwCpP7AAO7+afzF/fL/UQCxBMsHMwI7AgH+rgG5BIEDFQSR/yL/Vv9CArkEsQokBBf+mf8e/AcCbwIzAigDqgSYAaoAdgK6/or/LfxVASEDcgNjA4b+4/+n/6oE4/8zAAMDPP59AsgApP6Z/58BOwBVAfEB7vzY/ib8Mf0hAfgBJAII/Fr6uvzN/Zn/0wPpAa4BwALN+yL79vwI/nf+9ADJ/tT7Mf+yAHYC7QDWBDMCR/39/Pb8jADC/PL7Mfk4/Sb+DPv0Ag4Cvv97/dj8s/qg+3T9E/ts+/36lfxh+L794gFh/N/+fQJvAM37UQC6/Ev+iAeUAEv+0wHLAWz9AwGBBfgBbwRcA4UCIQOmBXIFcP6v/5ABOwJgAlwDrgGFArkGsQLeAlwBR/+K/cX9QgDQ/lECWAI3A/gFhQSmAbIAVv++/UD/iv9nAAz9LABKAkv+0wU+Bx0AXAHxATj9uQBVAdD+owJZADj9CPoF+8X/CPzN/ZcDGQMSAZgBdP2z+O7+d/7j+5H7zfmh9wH6JARVA+kHYAYi/6j93PkHAiQCMf+K/zj/Iv92ApADZwAgB1UB9f5ZAFb9pgGqArECLADAAlgCsgD0AigDEgP5/00BG/+g/TcBMwCz/mz/0wPXAkIC0wN//sn+NwPTBUoCnwElAK/3QPdl+QcCRgXeBMgCPPztAEYDyAIzAMQBUQBl/S3+9f7HBpcDqgBl/X/8kf/F//AD4gGJA00DrgEWAFL+kf/q/x0C8v3N+0P+RgNnAv3+TQFA/c37dP3Q/kYBwAJNAQz/tQHAAokDSgBd/dD+q/xS/sX9QP0b/6//KANrAzcDLAAp/yn/f/yk/rb98vu6/PL/4/87AP8B1P0P/u78PP6Z/fn5tv+K/Xv90wNZAK/9UQBH/eD4s/qD+8n8kf8kAoUAjv7xAQcCIQGuARkB4/sE/TsA4/+UBGcE/AL9/kYBDgQsAFwDLAAB/mcAdgAdAK4BbwIx/5H/kf9vADX+bP0DAQ/+IQFRBFb/3gIsBBP96v0ZA/gBZwAKBcsD8v/eArwDmwJ6BaoEWAJnBJQAhQDxAU0B+AFl/zMCpgMsAAj+Xf9//uf+KAEI/sn+ZwB3/gj8afx0/VL6Nfpl/TH7xfsx/wT9g/sE/Vb9e/shAWj+r/kP/sL8EPyK/bkC4//8AML+vvn4ATH/hQKjAq//EgEb//wAiQFYBNT/wAKqAAj6kf90/+kDSgJKABYA1P8oAw/+NwHaAUv+Kf9A/7kCRgVJBjADMAHy/wMBYAIhAdMFOwRyAyQEAACjAvsExAPeAmcCzf/b/64BowJrBWAC+AGQAQT91P9GAcn+9f4oAcL+Q/6bAML6jvqr/vwAPgNrA94AWv7y/5n78vuz/NH6OwCv/Uv8uQDeADH/ZwIwA2sBJASR/6v8Xf1a+k/9Uv4I/LP+/AD4A58D/wHq/2H+lf5e+2z9OP3aATsA3/xcA7799ACQAZX+tv39/Mn+xfv4AQMBYAKMAvQAMwLC/kYFMwJ0/yQCOwJ6AU0BWAJH/3YAxf+v/fb8gQPWBGj+QgIHAo7+iv3N/dj8nfrQ/AH8NfiD+3D+f/yr/m8CkAEsAAcCBP0i/cX/e/2qALb/2/84/1kAgQEWAiwCWvw7AGAA0wE7Aqv8r/0i/WAAmwAwAaYB8v/J/h/6R//lAvL/iv+v/fL7QP3F/4wAWQCFAGX/q/w1/tMBgQG5AjADd/yg+3f+/fyMAMsDOwL1/p8BIQNA/5QAIQE7ADj/iQHlAHYATQXEA8sBMAFnArb9E//eAtz7jv71/nT9hQBgBk0FRgH4A3/+Xf9P/Xv7wv4x/1wFvQHU/YwATQHN/d4ARgMX/HT/Zf8B/PEBcgPeADsCAwEi/Vr+dP3r+WX75/w7AJQCDP0p/5z+Zf3aAY7+2P5CAgsBCPqg/1gED/5h/sL8wvzr+xYCFQQ+AdcCR/3y+6/9fQQHBD4BQgCs+nv7Kf16A+kBHQD1/vn5bP9gAMAAIQMhA4wAIv3U/Vb/8v83AUYFyALN/+0AMf99As8GcgP5/7b/3P01/hkDWAaFBssFdP/f/H0CyAIhAeIBMwIx/5sAIQOmAcQBGQE7BLr+QP3EAzz+Iv//AQ4AUQJnBAcA4/+5BJ8BR/9H+yL7FgB2AlQHpgXaAcgAuv5w/u0ATQVGAV39Zf8X/sAC1gTPAO7+S/5d/9/+QgBS/uP/mwBP/bUB6v1s/Zn9s/oOAJz+7v6YAcX/zf0p/yEB+f3u/qv8T/vAAqIETQOjALb/dP0i+/n9kf0sALIAzwLwBUIClwMAABv7r/2k/tD8G/8p//b6r/8kAs8CNwPf/kf9pPoi/SEB9f61AWACyfyk/lb/BfsB/Ib+9f7LAVEEbwIoAVr+/ACYAYb+2gEi/fn7mwDAAvQC7QJjA8n+gv9rARkDVQGfAe0Ce/3EA/sEowJVA2H+aP5vAAcChQDj/9j+Lf7C/lr+vQEkAq4DEgMi/yn/f/yz+sn6LfzAAPn/F/5vAJQApgFCAnT9G/sx/TH7NfzTARkBtQGQA0ICOwIzAgMBpPxa+KD5LfyG/qMCtQFVASQEEgGC/77/PP6G/mn6F/iZ/fL/E//5/X/8r/sx/dz9lf6mA3IBBP32+gz7G/9kARkBKf3f/pX+PPy5AFUD9ALiAekBDgC5AgoDLAKbBmsFsQbEBWsDyARZAJz+LAJcAdoD0wUvBfgFiQFjAyUA1P19AqMAZf90/VEAfgDAAm8Ayfxh/kD7FgJs/07/8QEi+yr72PyUACQCjASk/uP7wv48/uP/yf52Aor/T/22/5n/dP8dAFkAAwHeAuP9BwCO/gT/5QCv/eUCyABA/c37wACqAH/+Uv4X+nv9yfyFAPn/hQLIBB7+Iv9O/3D+JvoHALP+Zfvj/+f8uQCn/8QBJAZJBJQAe/0I/H/+ZwYSAzsArgEAANT9cgEsBDsEcgeYAQT/5QIZA6v+YABVAf8BQgaUAp8DfgA7ADsAZf/IADz+PgFP/QsBUQKmA2cGjv4b/xv9fgDF/yL7Uv5gAH0CrgHxASgBuQAM/Vb9ZAHIAEYBAABw/rIAogRCAg4AAAAHAF3/8QE+A/n9uv6V/BP/mwJnAOP/e/1e+RD4PgFVAb0BDgDc+cX/MwCjAFb9PPq++ef4kfvC/rwFFgLN/bb/XAGbAML+Vv8m/Nz9BP/N/XIB9AJgAvwCUQLq/yb+7vwp/Q/+2P6C/4EDyALPAOIDiQGfAd4Ae/sm+t/+dgDU/RIBfQJrA5QEOwSjABD8Wv7C/mMDGQdJBJQC4/32/ND+sQJgBN/+d/zC/FkAxAP/Ba4D1Psm+jH5qPtl/yQCvv8x+QcAcgF0//QCLf4B+B/4kvkT+6oAgQEhAb79bPveAOIB0wPaBWsDS/xA+779xftGAfAH0wNh/mcCUQA7AmcIpgVyA1L+s/zq/ZgBjALaA5cDiv0E/3/82Pxo/rP+gv8p/8ACNwEZA8ACOP/9/nD+hvy2/QcAwvyjAOIBs/we/PX+yf4oAa4DDP8wAd4AS/6K/UD/Iv+O/PL9AfxRAG8AOwL/A4EBQgJO/3YCpPxp/CUA3/zIAt4EuQIAAAoDmf+K/QoDNf5KADMEpgFw/kT8qPvN/a4DmwQVBIwEwACk/k7/JQAvBe0EowCc/n/8UvwzAJcFcgFvAsAEe/9KAG8Ae/8AAGMDZwBl/Q4CBwA8/hf+f/6MADMC1wAX/lb9uvqZ+0/9Mf/TARYAKf96A6YDwvzu+kf5XvcM+47+wAAhAw4EOwCZ//QEIQMi/Vb9uvoX+mcClwXSBysKKAWfAe0ALfwx/WACGQF9Bh0IHQJrA5ADmwIkAukD/AIT//X+E/t0/SgD0wH8ACUAmf/U/wcA7vwm+u78OP1//m8AT/31/rP+jvwzAML+Kf1H/fn7E/s4/fQA1P/eAHT/zfuV/Kf/S/6O/HoBMf3j+28A2P79/rb/aP4Q/MX/oP/n/DsAmAF3/s35hvo8/BYAowK9AaYB+f/J/gz9e/s1/sAEvQHY/kf/EPq6+lb/AwOUAu0EqgKK/xUEYAJUBWsHqgIt/nT9dP8B/n/+mAEkBjMI9AYvBdoDnP4b/aYBLAL0BMsD2Pyk/D4D6QE+ARIF1wC+/58B6QEi/8sBXf+++8AEKAUVBpcD1P9w/sn6jv4OAMX/Jv7q/+0AbwJRBMQBHQKk/sL8T/v2/E7/jvzF/R0CiQMHAKMAlf5o/sAAPPzu+uP9QgCc/koAJARnArr+4gHxARf8Iv8E/QH8FgDN/e7+yAAwAbkAxf3C/uIDRgHC/CgBmf/F+3/+dP3n/igDRgNKAFL+4gEe/pX8TQOFApgBgQF+ACgBIQPLA3IDlwPy/3/+BP9d/+0EHQa9Ad4CLAKjAjcFFQT/AfX+nP5P+9j8lAAkAhIDsgAsAuP/TQPlAt/8e/tL+kP+QP/aAZsA9AALAXv/+AHY/r7/d/wX/AH++f2bAA4C3gRvADX86v3b/zj7f/7q/yL7QgBa/kf7d/ybAHT9g/10/zz8FgAb/c3/Uv5H/WAAg/0T/cn8QP8B/K//CwEOAIL/1P/lAnT9RgGg/0IAlACZ/Q4ABwDpAdz9vQESA1gCVQFVAaoCKf9RABv9zwIWAh0CmwL5/4UEQP8HAtcAAwH0AHv9S/7N/4wCqP1gAvgBOwKbBFwByf7c/fX+2PjN/RYA7QJ9AqoCLARA+5H9Ivtl/dz9ZAGbAqT+9ACv+cn+OP2G/uP7AfaC/8n+tv1s/4wEQP08/C38S/jIACn/6v0m/JQAuQDJ/sL+FgKQBdD+3gL5/YL/lAB//tcAQgCxBHD+LAI+ATMCQgJCAJsEEPwsADj/CP7C/t4ArgHc/T4Djv5W/8L+HQDj/3v9sQLEASgBawHEAzz86v+1A7IABwSBAer/qP3IBH4ANwPEB7UD2gVh/iwEXf9W/cQBCwH0An4AhQQI/toBiQOn/2QBZwIOAmn6+f/q/Qz9OwB0/9T9OP1VAXD83gBNAaYBYABa/t4AJvyqAJsAlf4U+Rv7/f4WACAHvAMvBZH/+f2r/gj+hQKv/c37nfph/tT99AKeCSgDqgDc/dH6R/tvAL795/zq/8n+3/zF/fADKAFGAQ4A/f4I/gH+VQFP/dv/6v+qAAj+Nf78AND89ALABLkASgDWBKT+dP1VA9T9Xf9W/9T/hQCFBOIDAAB9AiQC3gK6/rkC6QFGAZQCDgASAw4ACgXxAXv/OwDj/4kBp/+fBZz+mf/XApX+r/8DAa4BMfvf/o7+PP6R/yL9/f5S/E7/+f8P/i3+s/7n+gz9hQJH/dj6HvyUAOf8+f1s/1L6JvzU/fwAiv2UAvwAnfrtAGQBlACz/AH+RPyv+4UArgGUAKv+pgFa/O7+YAIHAK//Af4hAUf/XAMSBb0Bxf1E/A4A1P3EAf8D6QOQA3oDJALEAfsIJAR3/pX+4/8SAX0EfQj4A94CegEi/4P9zwBgBM3/cgEhA/n/fgAZAxkBZwDiAZsAqP04/d4A7vxl/bIAe/0M/WQBDgTf/qoA9f5H+zz+Nf7j/zz8Af5l/U/5gv/8AGj+9vwB/uv5XvujAmcALABNASUAQPvF+1EADgCjAJ8BMAEp/bb/2/9D/pQCBwaiCKoCuQTWBJH/WAKqAEIACwGJAx0Atv+FBpQEVQEWAtYGkAFs//EBuv62/2z/BwAM/W8A4gMX/qj9hv7U+7f5TQPABukBVQHF/fn5F/xVAX/+Jv5s/xf+kf07AtYGQP8b/zj/qPuG/GcA/wFd/9MDXAHy/3IDQgLj/TX8hv72+Lf5zwBnBDcBzf/XAH/8Iv2Z/cL+Vv/XANv/Wvzn/uUCkAHu+qoAtv/9/HIDegOiBDADcgN7/zX+vQFRBOkFsgC2/3T7Kf3pA1wF5QLLAfgBrPq6/Az/1P/N/xYAyALAAGMDJQBA/Qz9r/9//BT57v4F+9z9kf8OArEERgFs/zH5OP1h/mX99vof+g/+6/sLARkBPP7J/pX+kfta/IUAQP+FAjj/xf+5AB7+bwCD/QcAKAFyAZH/UQDtAgH+Vv/J/qoAMAGBAeID7QAoA4EBegGg/5H9fgCR/T4BMwTpA+0CfQJKAu78FgJCBK4BpgPEAeUAzf9cAyQC9f5yA8sBHQDtAOUAe/2V/hIDEgGv/0f9gv9+AED/ZwBa/tj+bP9P/Rv7mwBL/k/3zfta/Bf+iQEkBJsACPwX/kT8Nf6g/13/DP2Z+wH+oP12ANoB/AJ+AED9sgA3AQsBcgNjAyL/2/+UANT9ZwCjAkf/kf3EAWcCNwPiA4UCrgET/3v/pP4M/ywA4gEDAer9PgF+AL0BmwSXA2AEOwTeAHD8Vv9RAgMBkf+FAA4C5QJNBZcFrgWqAg4ApPwp/ZcDIQG2/2H+bwCmAdv/FQaFArr+DP90/bf7Uv4HBFL+S/7F/az6OP2+/5cDq/5H/f38RPpH+cX7dgJgAFUBfgDY+gz7oP+K/0v8JQDn/jj9R/0b/1UBdgKUBIb+G//aASwCpgFL/ur/Hv4E/9cA1wBrAc8CjARA/3YAOwI1/qj9Uv4x/wj+/AD4AW8ApgPxAXf+Vv/AAED/UQD4AcgAcgFgAO0CsQI1/sAAOP+K+w/+mwAdAHYCtQOUAE0B2gEDAV39iv0dADH9Xf1//B7+wACJAywEsgBRADX82Pzc/bkA7QJ7/TH9F/zF/Vb/MwKfAwAADP97+yr7BP2v/77/HQB2AE7/bwLpAQMDWAIp/yb+Jv7j/Q4A/AIT/1gCFQR+APgBWQBD/jH/AwHaATcDlABa/nf+hvyMAG8CdP/F/e78WvwX/iQCXAFnAHYAOP+g/4L/vQH/AZ38d/xo/gT/IQFKAMX/kf+qAFb/BP/PArUBHQQsApn/IQEi/y3+uvyyAG8ACwFyAf38BwAWAKYBFgLTAbkCmf/j/S3+mwJO/yL9SgA1/vX+Kf8lANcABwDu/v38rgGbBBkDQgAB/vn9EPxo/lEAxAEkAur/RgE3AXYCEgFO/5QAgv++/77/ZwCYASQCJQC6/mAAR/+n/6D/Kf8DAeP/Xf90/88AUQCc/nf+q/zQ/pX8qP0DATsAbwL/AXoBEPyK/ef+8v2BAeP9r/+UAHYA/f4p/9cA9f5cAaMAcgEDA9oDLAI+AfEBgv8P/in/9AAzACgDEgNGA0IENwNyAdv/LALq/3/+Tv+FBLkC2/+bAkD/2/+r/jj/5/65AE0DOP8zAL0Bxf/U+13/Iv/c/VwBd/5CABYCIQGC/8393/xl+zj7tv3LAbIA6v8dAM3/AABw/h7+pP44/3/+lf6qAIwCdP/j/XYAgv/N/4P96/vtAFwFLAQsArkC1P9H/ev7Jv7XAMQBbwAm/F39WQDlAiL/mf04/139CwGYAfX+dP8AAKT8qP0oAQcCsgDC+kv80P4b/wsBLAAE/xIBgQHY/uIBegMwAbr+Jv5W/V77e/2v//EB9AL8ApsAbP2G/jj/E//F/8sBnwHtAIEBBP/F/dD+R/++/1kAmAGFAEv+Kf+9AWcCTQNRBAMBFgBCAuIBAwE3AcAAgv9CAMsBowIVBJADTQGQAVEA1P/F/83/zwLlAv8B5QDaAW8A2/8SAd/8wvyR/XD+JQBvAnYCp//Q/vb8uv7Q/pX+CwE+AWcAhv6O/FL6mfth/HD+RgG2/3T/dP22/QAAjv4t/kv+5/wX/HT95/4+AbUBWQDf/o78pPyZ/SEBWAJrAwMDT/1o/pQCEgPxATADOwDQ/iwAQ/7TA+EF0wGk/pn90P7U/9cA8QGXAyQEuQJ0/wz/Tv8LAcX/Wv6R/1b9DP/iATsEJAKQAzcD8v10/+P/1wAHAMACMwIE/yEBWQD2/AH8mAF2AKoAZwLj/6oAKf8x/3T/jAD8AmACOP9H/a/9r/2+/VEAsgAx/8X/3/x7/QMBiQP8AjsAKf97+7f7vvtH/eUAJQD1/lr+/f4T/2sDvAO5ACgBAf7y/X4A4gHaAZsCowDf/HT/ywEHBFgE3gIwAa//GQFGAdoBYAL4AeP/Lf4I/t/+FgBnALkAHQBa/hP9AAAWAJsAyAA8/B/6CPq3+wz9LALEAQ4A8QEOACn/F/5W/YP5cPz1/m8ANwVjBbEGTQMwAbP+iv1s//wA+AG1AUkEcgEOABIDegXAAmcA6v/n/OP/wAL/AZsACgPAAsn+q/4e/sL8Vv0p/0P+yf7q/5n/Hv50/6YBYAD0AED/7vx0/SUA5/53/FL+S/4WAPQASgD8APQAhQBl/wAApgHLAf3+uvy2/aD9iv9gAmsBZwJCAkP+F/z9/Hf+5/65ACEBqgAdAKD9xf17/a//jAJnAE0BDgDr+8L6D/7TAUoAawF6AR0AqgDlALkCLAJgAukB3/47AMgAAf5a/vQAqgK5AuUCFgJ2AGAA9AC1AXYCmwJ//Ef7Yf4I/hYCbwLIAnoB0P6O/vb8Iv/J/B782P70AMsDmwLpA4wCUvx0+Uv6kfuO/PL/ywFkAdMBdgIKA9oDxAOz/hv7BP3y/cn+sQLABMQBOP8I/iUABwIdAh0CIv8hAYUCWv6Z/Yr/kf+g/9D+q/xL/jj/DP/eALUBzf+R/Yr7HvzC/gsB4gPTAV3/CP6v/aj9dP+qAs3/dP+2/3v/awGMBPQEwAISA5X+3/wlANcCEgO1AcQBxAHaA9MBJv5o/oUAXAFs/3D+Hv6k/pz+JQA3A4kDxAGk/DX4wvp0/Tz8dP+UArIA8v8HAFwB2gEWAOf+g/2d/Jn94/8DAywGRgXtAHD+xf9NAdv/mf8ZAYwAp/+5AM8CKAVYBGsBTv/n/oUABwAM/w4A1wAI/rP+bwJCAmAEogQOAsX/QP17/YL//ACMAq4Bq/44/wz/Mf9ZAAMBdgAi/4L/qPse/Dj/DP+n/83/kf9p/Ev8+fvu/HoBJQAB/uP7Mf2+/77/BwCn//n/Lf5+ADMAyf4wAWz9DP2c/lUBowJnAh0EPgFw/hf8Kf1O/1EA5QAsAAAAQgCbADMAIQMdAlb/qP2d/AT/xf/XAIkBSQQOAg/+hv4b/UoAowDq/0oCXAM7BAsBcgGJA8ACDgCd/BP9G/8WAq4BBwTeBmMFqgLu/M39SgDq/9/8Jvw7ANcCqgLC/gcADgCd/Aj6IvtH/3oBFgLF/fn95QAwAYr/2P4sAMX/+f3C/IkB/AJNAUYBDP93/owAUQAT/xIBsQKqAmsBSgA7AA4Ae/2z/ED9iv10/wMBJAISAQMBe/+G/hYAGQHY/nT77vwi/9T/2/+jAk0BlADEAZn/q/5o/kv+Bfv9/gMDLAKJAXoBegET/z4Buv53/iQCtQHeAAMBmwL4ARkBpgE+A/EBUQK9AQAAowL0ApAB9AByAfwAHQK5AtMBMwB0/WX9R/1O/x0AD/6Z//wA9ACg/1b/bwCD/aT62PhS/CgB2gFKAPX+/wGV/lb9OP8ZAXoDq/6D+9D8/wGMAp8BrgE7AsQBD/75/00B/AJGAxYAVv3N/Rf+OP2Z/7ECHQTeAIwA9f5A/X/+dP2k/Lr8BP+6/l3/7QAlAMn+p/8LAQz/uv4x/zX+bP8dAuIBLAALAUYBLf57/1kA8v9KAu0CDgJH/zz+Af5rAX0CJALq/177Kf9KAEYBPgHU/6/9R/0HAI7+awHiAU7/Xf0X/mz/D/6z/nD+zwAsAhkBbwBo/r79Mf8e/pX+QgK5AKv+HQCbAH4Axf8I/lEAQgQDBQ4CbP+C/1b/5/4p/8gAmAF+ALP+TQEKA94CXAFE/K/9jv5P/cX90P4B/u789f6Z/aT+VQEDAdv/2P7F/Tz8/fy5AB0CqgCQAaMAUv4zAAMDwADAAAMDYACK/zAD3gQhA3oDhQJ7//n9+f9ZADsArgMSA7kAxf8DAcn+/f7EAZX+Zf2g/1ECOwCr/kv8g/mD++r9xf8p/xkBiv84/TH/g/0M/QH+nfxw/Gj+sgBGAVL+DP31/nT/p/9KAKf/EgEKA4EBYAISA7kApP6v/eUAtQU+BaoCPgG1AVgCGQGBA/8DUQIAAJn9YAC1A4UG1gSXA/8BIv9L/r794gNrA28AXAFA/wAAVv97/2sBGQPpARv/gv+6/qoAoP+o/VwBCwF3/vn90P5a/tj+6v9d/wsBEgPeAmH+KvtW+xD8iv0sAMQBkf+Z/zH/9f7tAB0C1P8B/Of8lfwI/oUAIQEoAaMAEgG2/5H/mf9RACb+E/2v//3+/AC9AWj+Nf7AAPX+Jv7f/nD+PP7y+w/+WQC1AVwBuQCqAB0AEgHf/Aj8qP3U/wcCNwHiA8QDfQJcAQH+3/5vANcA/ALPArkCxAGc/vL9GQHPAnYARgFl/9D+6QGBARIBLAAoAYkBqgByASEDowDU/dT/dgCYAcAAzf2k/Ir/GQOYAbUBAwNvAAH+tv0X/lkAzwB3/rr+SgCZ/1L+jv5w/ob+G/++/6oAbP+G/u7+Zf8WABYAKf+v/RP9E/sp/fwAMwBgAMn+Mf9vAGAA7QDq/77/0P6g/XD+EgPXAtv/xf97/8AA8v/y/ywAmAFyA28AR/+mAd4Akf/Y/oL/lAKjAtMDCgMdAkoAoP1H/YP9lACZ/00BOwKqAAcAZAEKA2sBVQO6/kT8f/7J/sn+QP/tAGz/r/9RAMsBawEzAlEApPyv/4kBlALaAbUBHQDJ/nv9Hv6BAUoAawEAAH/+JAKJA34ACwHwA7IAbwDAAKv+cP4E/S38Hvwp/QcAUQLPAmACmAE8/gT9q/5L/sX9T/10/QH+G/8LAWcAxf3N/Vb95/4hAx0CFgKmAcQBEgG+/X/+Uv7f/jcBEgMZA2AEawNZAL0BLAAx//X+4/22/wAASgBrAYUAVv8x/xv/G/1s/cX9Zfuc/or/hv53/r79sgAsAsgA+f3c/c39dP9RAvgBbwKQASUA0P4oAfgDOwLIAKMAWQDeAMAC1wISAQAAzf/1/pH/NwHtAK//DgDq/5sAAwMWAmcC3/6Z+7b9Nfyz/NT/OwDY/jcB8QHiAUkEZf+o/WH+3/rJ/ML+lf7xAZcDFgBGASEDtv2G/nf+Mf3AAIwARgOuA/8B1wAHAJH//f7U/0/9BwD1/hf+gQGqAB0E1wIHAAcA9f53/Ir7DP3U/VUB6v/Y/s8Akf+C//L/4/8T/wz/Uv7f/M3/owAi/3YA+f83AbIAiv8lAB7+yf71/qYBHQKFACL/wvyV/iL/HQI7ANj+nP48/Jn/7QCFAhv/d/5W/XD67v5ZAMgCcgEm/o783P2+/1b/mwJNAXYAJQCr/P3+ZwKbAt4CQgKqAJH/sgBkAXYCNwO+/aT8Iv8wA+UGGQXEAxkBbP3f+pX+uQDj/zMA+f2Z/4EDWAYhATH9Nf7u+ib6+f12AvgB0wEoARf8+ftyASgBS/6n/y3+F/7n/ur/EgFs/8AAsgB7+6/9yAIe/m8A0wNZAGsBIQNVAVr8pP7PAJH/LABNATcBHv5KAjsCmwBRBJQEyADJ/AAAbwD5/yQCsQJO/1L+hQAE/U7/KAMSA5n/DP9GAQH+Kf/EATsAE//xAUf/1PvN/94AYACZ/88AwAKBARIBxAHU/1wBHQR0/2H+KAOmAWX/hQKBAaD/Zf8sAMgA8QHiA5QAmf9cATAB2Pzc/RkBpP7C/vn/MwIAAK//Kf9H/Rv/vv9O/9T7OwD8ACb+YALpAaT+s/xs/fb8jv6FAED/WQAzANT/kf/Q/t4AsgBA/3D+UvyZ/b7/9ADPAN4A8v/C/tcAWQD8AHv/pP7F/br8rgPABM8EzwKV/pn/zf9CAtv/cP5A/6j9R/+QAdMF8AUdBCL/Uvx0/5n9mwCQAfX+lAD8AKv+hv5KAnf+BP0p/zj90P4sAFUBrgF+ADz+ivv2+qz6QP13/JX8VQGO/n/+bwJ9Apn/oP17/aT8xf/N/5gBkAEhAd4Cr/3IAAcC1wAzAsQDOwTaAX0EowALAfgBgv8zApsAnwFNAYwAmAGxAmcAyfxnAM39R/1RANz9gv8AAOf+Xf31/vQAZf2V/kv+dP0e/n/+mAEWAJH/4/90/5QA/wEsAFL+JALEA8sF1wIhAbkCzf1W/+r/BwBGA70Bp/8hASgFrgMOAiUAYf6n/5X8d/zj/+P/+f2G/hf+qP0AAFL8nfpS/tT9Kf01/tz9mf3u/JH9HQA7ANcA3gAT/dD8jv7c/dcAcgPPAk0BBwA7AJsAQgIZA5cDKAHn/gAAWQDXAjMESgIhAaoAhvwP/jsCMAHIAmsBDgBkATsApP5CAO0CAwMWAmcAd/41/FL8mf/wAzoG5QSZ/zz8iv/tAjcD5QK1A3oBUv7Y/HT/1wDq/6oAaP65ADMC9AAlAM8AmAH9/Hf8jvzq/QAAKf83AW8AUvzC/JH/WQC9AXYA1Ptw/ML+9vzq/3oDVQHq/R78Nf6+/3T/Mf8WAMgATQE1/h78lAB2AiEBIv/y/0oAS/6Z/5sCPgOBA30CTv+fAT4DRgE7AFECDgIHAGcCTQGyAAMBNwHPAkoCEgGYAZsC+f8p//3+QgCjApH/xf2v/0IA+f39/iEB/ACuARYAzf+2/yUAdP81/LkA2gE8/pX+Zf/IACQC1wKmAfQAIv+r/ur9hv6fA4EBNf5l/+7+pPxd/64BOP2V+v36Nf5d/9T9Tv9H/wz9qPsm+O74pP5a/nT7s/xl/2j+QP3n/kIAmwBcAX/+afyC/zMAHQCqAJQCOwCR/8sBUQC1ASgBiQMZA3IBpgPeAlwBq/5h/k/7gv+MAqj9AwGbApgBr/99AqYBMf3f/uv7Zf2g//EBywHb/5ADcgH8AGsBLAKD/cL6LAIOAuIBYALEAxYCRgMdBJX8p/9KAJH9wvyyAPEBLf4DATX+Vv/f/hf+JQAp/TX+vv04/TH//ALY/gj+VQHu+h78OP3N/e7+CP7U/88AtQMkBLwD1wDXAE7/mftRAH4A2/+2/xYAmf9CAKIEgQVgBmACFgB//Kv+awNa/koAxAG9AQ4ArgEwA9v/tv/q/TH/Xf2mAaYDwv6xAn0CZf8b/zcBpPwi+4UAzwCbApADRgMx/yn9g/1s+yn/ogTpA/n/xAEkAgMBgQGMAMgAhv7b/x0Ar/2qACwCkf8sACQEgv9S/noB3/5yAfQCMwLN/0D95/4M/5n/JQBS/gX7/fyV/jz+LAKXAxkDiv/y/fn9F/wI/vX+r/9vAJH//fzy+w4AZAFnABIBsgBo/vX+9ACuA30GSgJW/Vb73/xA/5z+dgD0BDcFdP+n/1b/jv7XAm8APP7n/sgAvv8X/psAIv8E/V3/HQKc/vwAlAQx/0f93/75/3f+4gFgAlL+AwH4Ac8A1P/EA7kCE/2UAN4CZAGUAOUAE/2o/cAAFgBJBPsElwM1/qv8/wFyAbb/6v1H/wH+iv/4AaYBNwVnAtD+G/tA/QT/+fvj/8gAYf7N/XoBqgBKAPL/Afw1/v3+2gHj/+r97QAI/or9mAGqAAT9fQLwA4wC2gMsAnT/zf2jApsCjAKUAvL9afxO/ywERgOFBGsFkAH9/C38Iv1A/UoCOwIHAu0CYAKyAK/7d/z2+rf5bPvJ/Lb/vQEkAmz/UQC6/pX+dP9W+Xv5F/oE/f8BAwFcAZQC9f63+9T/Xf9yAcACiv3PAEYDlwVnAhP9Iv9W/13/qgJyBYkB7QJgAor9BwDeAL0BZwBKAHoBHQDtALkChQAx/xYC+f35/ZgB1P+Z/6MADgBO/xkBgv+6/vL9s/7y/zX80P75/7b9QP/XAHYAuQC6/uP5BflE/PL/3/4DASEBbP0b/xYAOwDXAD4DJQCG/C3+Xf8sAPwAegFH/ef+HQJVAb0BbwSqBNj+2//j/2H+Xf8WAO7+pP5kAb79s/7iAQoDVv8e/N/+Uvxa/uIBZwIzAFEAnP7r+6YB7QAb/1b/owJcA0IAFgKFAH4AwAI+BZABxf/aA00BrgFjAz4DCgOmAeUAYAB0/x0CpgWYAT4DawXj/1r+g/0m/kICjAKV/rb9D/5l//wAxf+JAWcAzf0t/AH8f/5S/jH/DP8X/oP94/1D/tj+FgB//jj/6/sb+9v/+f/lAu0EoP9//Mn8e/kQ/IwAXAHEAzcD9AJvAjMClwNGA94AzwCn/6T6kf0SAVUBawV2BhkDjABA/6D9/fzF/6f/yfxS/lL+qP2+/4kBhv6K+1b7bfnc+9/+AwE3AQ4A1wDlAIwCnwHq/wz9wvph/JX+qgQKB2AEUQJH/4UAlwMwA6MCdgJVAQAAYAB+AFgCxAGV/ib+2PwWAGQBzf/tAOIB5QD5/ZH9lf7iAcX/Vv+K/7794gGk/pH9sgALAbECsQT4ARP/Uv7c+8AAywGqAu0Etv81/mACxAOYAdoBG/vc96D5LfqK/8gCrgW8A9j+dP0p/2H8wvo1/Bv53/xl/UD9RgF6AaMAqP3y/bUB4gNyAf8BZAEi/zcBnP4wAVEE9AA3AWsDGQNJBJsGGQUHBnIDPgGQAU/9Vv3j/QsBegVYBPwCrgPXALr8PPwp/XID6QEM/b79Nfyc/rb/DgCuAbP+Nfiv+TsAawNCBE7//f5d//L7t/uo/Zz+Yf66/IP7EgNJBM3/HQC+/3v/JQCUAFEAmAFE/AX71P0e/ukB+f8KA8AGMwSuAYUA4//n/MX7T/tO/2QBEgEdAHIBQgRW/YP7Yf4AAAsBMAOJAQH+NwG+/Qj++f+fAVECtv0WArwDmwJVA+IDVv+r/j4DZf/lAPQCdgRVA5gBowKg/2AAbwDN/4L/DgRGAxv/fgD5/d4Auv6R/TMAAf4AAOP/owDEATMAPPxh+rP8G/9yAaT+hvwX/Ir7BP8oAWACuQLY/qv8CP7c/SL9mwB2AIb+CwEp/+r/LADy/5sAt/uz/s8AGQEVBNMDOwIi/aj7afxd/fX+YAA4/dT56QFNA/8BGQVrAdj+r/ug+av8G//AAKMC2/97/XYCXAGUAMsBnP78AHYAYf7J/mH+fgBvAiQCQgJGA9cCowDj+6v8BwBL/o7+6v8dAhUEKAOJAUf/Hv7f/mH+CP62/zj/dP8DAUYBgQFO/zj/BwDn/nYA3gAp/zX+JQAsAFkAPgGr/hYAJQCyALIA6v84/478Kf+G/nYALAIAAGX/WQB9AuP/vv8I/v38Kvur/CgDfQIkBJQCq/6o/Rf+8v9RAN4ATQHtALkAIQVcBYEBWQAx/br8OwAkAn0EkAUZAwsB4/8M/7IArgMoAYr/OP9P/TH9wv5KAhIBzf93/sL8Nf5yAZ8DCwFL/tT7Jv4T/9T/ZAHU/U7/qgB7/Wz7S/6UAOf8NfyfATsEjATPAkf9oPsi/Vr+g/0M/5QAvv9gAIUCxAVyAzsAmf17+1r+ZAFnBBkFPgEhAZQAafx//tj+vv1KAssB9f43Ac39ivtW/ef8owJ6ATX+wAA4/+7+vQEdAOv7tv2D+x783gBGAQoDegFNAbP+ivuk/mAAlAQgByEDiQG+/9z95QBvAFb/QgKJAZgBMwT/ARkBDgAe/mACNwX7BJQCHvwI+ob+E//tALUD4/8sAND+r/+mBaMCVv+z/NH6D/6+/xYCMwZ5B1wDd/5gAAcCSgAx/0P+Iv9s/0D/jADLA2sDG/8M/0v+XAHeAr79kf9H/6/7vvvF//8BbP9A/Sr7CP6z/C381P8b/4r/afxl/XIBmwAm/tT7hvzJ/s39Mfs4/f38mfst/vEBzwK2/yL9tv0dAJgBZwLN/3D+6/v2+kIAtQOqBAcC4/90/0oA4/9RAsAEYAJGA7UBdgIzBHYEnwOMAAAAJv5a/u0A6QM7BJ8DlwOqANv/kAEkAs8AS/4WAE0FBwQSASn9g/szAED/2PyjADcDgQFVATMAUQS1BWH+Jvxl++0AZwIm/q//r//c/ef+QgAi/c8A/wFW/2z/dPvy/SUAzf3N/28AqP22/3v9Yfo7AK4BUQCn/1kAIQE4/w/+bP8M/+7+dgDn/koAXAGjAuUCxAELAYb8oPuR/SL/HQD4AywE5QB9Anv/Lf4kAsX/jvx//qf/LAKMBPgFuQSn//3+Jv6O+lb7oP/q/7kCsQYSBbkCsgCK/Wz7FgDAAIr/oP8SAWsFYAQ7BIUAs/6g/bf7lf5w/psCCgPaAXYCOwCmAeP/zf9RAjcB4/1A/YL/Jv5+AHIBQP0M/QcAlwMZBZ8F0wHQ/GH8f/7q/7P+q/72/B78r//xAX0CTQOqAJn9Zf9RAHf+Kf22/VL8g/3f/hv/yASmBbUB2//F/9D+Uv4T/4EBsgBd/dj+T/0WAOUC6v+mAQoDKAFh/Dz8E/3J/AcA/f4b/6D/Zf9gAJH/1wC2/aj7Yf7y/88CBwT4AeP9Af4p//3+yf5nAMAAuvxl/+P9pP7WBDcBF/50/13/6v2V/jH9d/5L/jz8vv+MAGACFgJh/Cn9egGMAFUDqgKz/Pb89vzY/g4CHQK5AKYBhQDu/k7/7v74AeUAzwB0/6v8zf/tAK4DZwS5AB789vpS/s3/owCUAAsBkf/U/zsE9ADn/lL+RPoX/E7/MwDy/94ALAIDA+IBtQGuAUD77vz0AN/+VQGyAPX+0wGbAgcCEgP0ArkAQP8E/XT9HQB7/6oA1wCuAfgBzwCQAXv/mf8t/KT81P2K+7UBCgW1BUYDhQDn+nT7gv9h+g/+s/6UAGcCxAGMBnoDJQBe+zz4Lvh7/SEDRgEhBaoEHQD1/in/kf9a/jH/xf9l/3YClARgBFgEzwAHADX+zf3tAnoD+ANgBtoDAwHLA4L/BwADA/8BNwVD/mz/dgJKAOUALAAhATsA/ALj/8n+R/9o/tv/pP4wA9v/tv10/6/7uvyg/3oBMwDf/hf+CP4AABv/Vv2g/dcAvv8M+8L+5/xh+tT9jv56AXoBlAA4/WX9q/4e/hv/s/5s/8n6/AASBXIBNwWFAqD9Iv0X/in9jABnAAz9QP+MAnIFegHj/1ECd/63+2j+Kf+R/zMAvv9s/70BegEt/Gz9iv+FAL0BMwTwA1wBCwEt/or/zf+mAXoFUQJA/zMAywEsBMAEMwJ9ArIAUQAOAjsCVQMkAtz98v/EA0YBIQF7/dj6afox+9/+uQDTAR0Af/75+7f76/n2/DsAkfst/LP6DPmg+3v/uQC5AH4A9vxl+4b+TQHn/oUAiQFh/iUAyAJnAqMCcgGv/8X/UQA7BJcDiQHWBFEEZAG1A00DrgHLA4L/Af7lAIUC7QL/ATsCkAM+A77/BwAt/NT7lf7r+zsCywUZAwAAVv0m/J38LALAAGj+FgDu/lb9xfvu/qMAKAMSBd4CYAJrAUYDlf4B/goD7QBCAEP+e//AABYCMAOqBLkGcgPXAjz8Nfx+AFr89vwM/bb/kAHj/zMAcP5S+sL4F/qk+gT9vvug+Y764/1vABP/MwCk/hf65/i++2z7xfun/9cAtQNYBH0CqgB2AiEDAwF6AdMD1gT0APwCsgA1/m8CgQHAAuUGTQcLAav+8v08/jcBWALXAib+oP8WAB/6Yf7EAQH+oP/j/6j7AfxL/iwArgE3AXoBvv90/eIB4/8T//EB1P0p/Y7+ZwLeBIEFnwNVAfX+F/69AQ4CRgemBaoAwv6G+sn8IQHEA3IDKf/5+WH+SgDIADsEYAC+/6/7g/fj/e0AOP0M/ZH7hv4OAjX8AfzC/Lf7DP3J/kIAOwJvAHf+awG5AOUAwvwb+b79yf6g//wCEgMZAfwCSQTpAQsBWQDJ/rb94/83AZH/5QKUAqMCBwbaAaT8Uvob/0YDPgNRAukB4gF0//n/8vta/iQCtv3TAWsFpgP8AH/+uvz5/QcA+f/N/5H/GQXpBfgDrgM1/qv+vv92AOIBSgKQAwMBQgK5AmcC6QEOAJz+Hv7aAXv/qgCFAgj+Jvzy+/b81P0OAEf/2P4T/5X8HvxA/aT+7vw5+bP8UQDj/zMCqP0X/lkAQP2K/4UA6QFKADsAFgIDAyUALf4zAKv+0wPPAkf/AwEHAAH+owCMBuIDmAGv/Xv7Vvt//q4DsgD/Aaf/9vxL/pH/2gGFAqoCaP5d/YL/UQJKAtv/uv6K/cX/hQJGA64DOwTF/wz/sgBGAVgEegH2/I780wHeAiwELAJP/Xv/EPyg/TH/MwAZAdj8vv26/psAIQGC/9j6Xvsb/QX5UvyR/3YC9AJKAJsCWQDN/cAAnP6o/VUDMwJd/ywEgQPLAcQDXAPTAXD+ZwJVA/wCiAeBBZsCe/+g//L9hQBgBNcCywGG/u0ANf4E/0IECwEhAVkAE/2G/kYB3gKQBQsBbPsB/Nz5bPt2APL/jAQhBTMANwO+/ywAEgF/+v36tv1H+8n8qgI3AZsELALY/I78R/kE/bIAiQEdADsApPxe+6D9BP2YAZn/4/3J/Gn8egFYBHoDMf97/1r+Vv0m/rP+4/93/lgCRgH8AEYFHQDJ/sL+8QH0BKoC9AQoASb+CwGxAjMANwMzBowA+ANGAz4DSQZKAjsCuv5W/TX+cP5KApcFmwJl/Rv/5/rn+k7/jvrY/H/+4/vy/bIAjAAB/n/8T/uO/M39wv7c/WX94gGYARv/Xf/U/Vb9BP/C/sAAbwQHBIUA1wB9Amn8/fgf+h/6T/0+AcAAfgCc/kT8E/+6/mj+kf0i/WH+6v2+/S3+3gCk/r79RPyZ+0oCZAHLA88IrgPU/4r9f/xa/tMBiQMWAjsCQgDlAI7+zwCIBSgB+AVgAhv9p/+yAKoCKAPLBfL/R/8AAK//7QKMAFwBPP6O/vn/Yf7AADcBLAB0/30CzwILAWX/OP0i/1UBrgGn/00DogSd/I7+MwBW/9MDzwRyAwMBDgCK/av+PgOiBDj/8vun/2H6iv0dAnf+Mf/F/UP+AAD4AZsAcP7F/az65/j9+Ib+2/9//BYAhQDY/r79OfmO+ib8s/pH+yn/5QC2/6f/tv2K/wH+g/vr+fb6mAHb/ygBBwRgAvQCvAMoAd/+Vv8i/woDAwMkBP8FowKiBPQCQgKFBj4FOwJ6A1UBLf4WAnT/ZAFNBbkAtQObApgB4gPiAVgCzwLU/2X9bwBA/ef8wv5a/PEBAwOQAUICawGv/4b+zf3y/Xv/DP8dAoL/1Pt0/28AuQAoAcn+r/s1+ib6S/47BA4GKANvAHv9G/2K/3f+mf2k/qD/+fsp/7kC7v71/nf+UQB3/qT+2/8t/vQCGQWuAav82//j/a/75QL8ANj+F/6g/Wj+bwAkBH0CTv9o/kYBBwJCBOEFq/x7+br6qPfn+u0AbgbHBjsCQP/U/Tz+6v3n/rr8E/0OAJX+cgNRBtoDMwDJ/Ev8q/xgACEDIQNrA4gHzwhrBaoCkf3f+nv7aP6UAOUCjAjwBaMCVQMAAFr+Mf3q/cL+PgGJAzABLAIOApgBbPtP+9MB3P29ARIF+AFNAfgB8v+O/uP/vvuV+jH9+AOBAXT9EgG++wj6wvzIAjcDuQAE/ev1zf21A/wCBwDF/2cAR/ts/XIBZwJrAc8Aiv2C/9oFlAQZA/8BXAP8AKf/mwCK+3v7g/0E/30C7QL0AsgCCPwx+3/+CP4dAED/kfuZ+9v/2P5ZACwCjv7Y+qD5+f+v/xP/8v+5AA4AnwEKBUYBZwY3Adj6D/57/6//2/8hBXIDPgUsAsn+BP8b/YwCmwD8ABUEgv/u+mj+sgCJAe0ETQF0/V77pPzU/TX+vAPWBv3+QP0hAZn9gQFGBcsDkAHj/6z6dPkHAO0CwARyAZ8D1wAb+xYAjv5D/uUAXAGfAfADvAO+/839PP5ZAJX+VQESA7P+CwFVAbP+BwIsAvn9OP9NAfwAAwGJAaoCvQFW/6oAKAEm/BP9Af62/d4AYADwAw4EkAFd/5H9yf5//tcAF/6n/xf+H/pD/qf/bwKC/yn/8v8T//L9hvz1/hv9hQA3ATcBxAN6AZQA6v1S/P38Mf1H/xkDtQMKA4UCSgCZ/x0CCgNgBE0Byfx3/uf8Tv8OAH0CYAKz/uUA9vxO/wAA2gH/AQcA+AEi+Xv5r/8sAAT/QgIsAAH6Jvyk+or9FgJRBPgB1Pv5/2QBvv2fATsEZf8E/zsAF/z5/wMD5/4zAED/JQBgAG8ADgauA0oAUQCR/aT6uvyd/Cb+HQQOAqD/e//Q/Ov74/8sAAAAXAFKAGAChQL8AHT/dP13/JH91PvF/ywEZf0LAUkE1wCfAbr+4/se/tcAJQAdALr+9vzY+qT4cP6yALUBwAaUAgcAyABs/x0AFgC2/x0AfgBO/4kBjALwBfsIsQIE/2H8r/2yALECAwfpBxUEuQB0/5H9e/9A/zj9qP12AIwA/f70Ag4E/wGV/jH/gv+k+p36xf2v/WX9dP1W+5n/CgMLAcn+zf3F/0P+/fxvAL0Bs/wB/HT96v3aBVwHQgCd/L77lfyFAJcDlwNyBSgD3gD0AGX/MwRyAbb97QCR/0ICmwQZA/ADZwaMAFL+xAHpAccGkAP/AfL/qPslAPwA6QFYAnYAd/xH/7ECJQCbAmX/zf2O/uv7Tv8DAR0AbP/1/mj+3/xP/Z38PP5W/5ABwAJH/9oBmf8m/hv/5/53/ib+uQSUANj+cgHj/3D+Jv52AIr7sgDlAlL+2gGUArr+vvk8/JH73/zN/yL/nwFA/8AARPyv+UICOP9d/TMA7v5s/00BxAEkApQEEgGR/9v/Wv6JA3oBOwJJBiQEhQYSAzH94/+XA+IBlATEAe76mwAI/ib++wTlBEYFcgF//H/6r/uK/xYClf75+9D8KvnG+ZH9CP4x//wAr/2R+/L/ZwAX/iUAZwCK+/36Ivt7+5X+EgEKA3oBiQOMBMsDZwRRAkf/jvwT/w/+tv8DATj/EgXLAx0CowBH//3+xfsm/hf+WQAwAZz+Zf2K/SgDAwNO/6T6U/g8+iL9nwF6AXIDMwRa/v38MwDAAsQBdP9S/jj/xAMZA94AyAL0Au0Af/4OAB0AWAIDBXIDfgAsAPQCIv2C/5cDgv8b/4b+3/yz/uUE4gM3BT4DaP7n/Dn5DP/4AW8C6QMhAUv8OP2yACwAywMWAmj+LADu/vn74//j/0f/OwKv/yL/8v2UAOkBMwJCBO0C4/8t/Ev+r/2xAj4H7QDj/Uv+6v+6/pH/bP9S/Fb9uv6+/+kBhQb/A+r9ivti9qH32Py1AYwEDgSBA+P9mfse/s8A2/8dANv/cP59BKYDHQAdAH4Ae/8OAO7+afwb/+r9vv8kAjMC/f6g+5X6F/zXALkAZAFh/hP/4/2V+v38T/2g/SUAWAZ+AMn+JAKyAJsC3gK5BEYBHQCUAGsBTQV5BywGWv7F/wcEIQM+BS8FhQISA94CIv++/ygDyALq/4b+qgCJAXT/5/6r/k0BfQJp/Hj6r/0t/qD9E//PAFUBDgSfAZn7Hvwp/aT+G/0I/noBGQHeAEP+cgEhBXYE2P4b+QX5Zfu6/v3+1wLEA6MCmf9D/jMA0Pxl+775f/pH/R0CAwXpAw4EowLC/C36Mf2v/YwAegEsAu0A5QAzAPX+QgKqAvQEjv4OAB0CQ/7tAML+2P6c/koCS/6r/goFEgFrATz+1P1vADMCyABA++r9yAKqAq/9/f47AGn8gQFGAZsATQftBEf/mf0SAVb/9vzu/M37Vv+FAGAEfQLF/0oC6v9d/aD9f/7U+9z9d/6+/7UD6QFyAe7+Afy6/lb/kf2bAIwCawMDA1UDgQOD/Tn50frJ/Dj9egNcA/QAHQJl/Qz9dP8hARIBR/+2/Xv9Bfs8/J8DDgDQ/Az/bP2n/64D/wNVA70B3/6++0D99AA7ALb9Zf2g/9v/rgMZBxIDkf8T/cL6r/sDASEDvAOXAwT/uv4b/9/+dgCZ/4UAYADlANMDegPtArIA0P6O/qYBuQCr/noDywGC//X++f+C/9j+5/6G/Fb/SgAlAED9FgC5BKf/Hv7Y/BT53PsdAk0BzwIdBMgAWv7j/9oBYACYARP/kf+JAU0HvAnLAx0EZAHC/gT9D/62/TcBHQR//lUDbwQWAiQCnwEhAY7+OP3f+vL5qPs8/lL+hv5H/3/+yfyR/88AwvwI/nf8Zflh+uP9Q/5h/p8Bd/4e/JH9uQADAZn/oP9L/mj+1P/eAs8ERgcoA3D8QP+C/wH+oP/f/iL/1wD0ABUEDgaiBLkCq/xA+0D/BP8hAR0EowCYAZQCAf6Z/bP+LAJnBAMDgQNgAur/vQG1AVb9nwEhA6T8s/5jA7UDkAXWBIr//f6n/2z/uv7AAKoEHQQhAWAAGQN2ANMBr/8b+RP9lf4x/aT+MAOR/3D+QP/r+2z/nP5A/1L8R/vf/Nj6+fvc/c8Alf4OAu0AE/t0/aD9Mftw/rUDQgAZARkB5QDlAJz+QP9p+tj69f4WABIBIAd2BqT+UQB+AIr9jAA+A0P+qP0i/3T9f/zY/nYCkAH8AukDMAPIAJgBKf1W+XYAPgHxAYkDYASv/4L/GQOMAOkBpgGJA0D/0P4OBAcCrgNCBCEDTv/9/ob+7vxVAy8FnwNCAmcAVv0X/Hv/JQAwAVL+r/tKAHIBwAL4AwcAWv5O/0v8q/wAABP96/vj+yL7uv5CAJX+jv4T/fn9q/4I/qD/CP7q/QH+jv4Q+lr6HQAI/vEBlwWbAsL+/wGMAK4BhQaYAbUBJQCuA6oC/wFJBEICowDn/FgCgv99BJMGsgBgBJADCgNA/wcCdP+z/qD/ePrF+6j7OwBRAmcGvAWqAhkBQPvN+/n5Uv5RAgz/HQA3AQT/xf9kAXv/9AAx/wT9kf1l/b0BvAMkAuUA5/xw/GAAmAG9Ac8A7v6r/iwANwHiAd4Axf35/bkAKAMZA6oAlf4SAWsB2/9vBBkBS/7tAK/9r/3PAFECYf5W/00Bhv6YAR0CkAMwAXv/GQGc/koANwGBAWz/dgLTAWj+fQJgAIr/p/8LASQC/wFGAeUA6QGv/1r+5/p0+4b+Mf/f/B7+Nf7N+88AowBKANv/Q/6g+TH7FgAT//gBXf13/Cb6r/kB/gz/3gJGAyEFJQDy/wAA3P1CAiEB3gDY/kf/FgC9AZ8DVQO8A/wA+AGMAg4ErgMAANj++f0b/Tj9hQDLAUoC5QJCAIb+mf8E/YP7qP39/O78yfoQ/PwAKAF+AA4Azf13/N/+0P4e/nD+g/2v+9z7CwEOBGMDZwAE/07/ZwBJBP8Bxf3u/nv/mf0OAIEDCwEoARIDtv8OAFUDMwCqAB0CYAALAUf/Q/4I/lb/nwGFAgAAbP0lAJX+BP+qAEf/8QG5BFgC4//TATH/G/0t+gH65/5vAKoECgWFBNcCiQGk/n/8qgAe/tcAlAJs/9D+gQF2Auf8Af5W/XT9f/4LAW8CXf/tAkoAJv7U/yL/Bfu6+tT/zf3y/cAAlwNRAukByALj/Yr9DP9H/yn/8QH4AQ4A6QHpAfQAoP/eANT9nfoM/wcCdgAP/nf+p/+1Ae0APP4e/M3/pgNl/er9ywEWADz8s/x7/9j+2gFrATsAmwLaB8gEr/9rA139Uvqk+uv7IQEOBsMJ9AT0AsgABP9S/BYAqgQp/QAA3gI7Ap8D6QUkAlL8nwE4/0v+BwJ7/3D8yf7wA8gA5/47ALr+yfwE/z4D9f5e+139PPob+zMEJAQT//n/xf8m/Bf8CwFvAC3+2gHLAY7+p//eBE0Dr/8sAJ38YfyK/7UD7QAb/1UDMf35/SQC3gA+AX0CZAFa/h0AIv/F/YP7S/5cAdT/OwQZARv9Jv7b/+f+QP9JBA4CpgH/AbP+pP5nAEIAzf1p/Dz+yAJJBMAGvAeuAZQAAACv+wz9mAEdApn/RgFvADABogb4A9oBgv9h/qT+jvwdAOUCoP8T+xkBsQIM/6oCE/9p/Bv/E/9A/TsAUQB0+Tn5BP/IBN4CG/9+ADj9mfkI/uf+OwA+BXYCF/7Y/v8BKf3u/AsBmf/LAZ8DWAafA4UAIv++/R0AQgIdAor9iQFKABD8vv/xAUoCF/5CABP/Zf0OAlkA5/w1/p8B8vu6+kP+q/xA/4EB1wC2/XT/ywFW/Yr7QP3F/0f/lALEA4b+SgBRAB0AIQEwA8QDmf32/Gz/awEZA30EzwD5/3oFawP5/5H/tv9e+R/6dP/F/QMByABh/nv/egEm/r77iv2+/28AyfyjACL/PPxW/yL/R//8AHoDBwAwA7wFlACyAG8CgQPIAKYBxAN6AcgAyf5L/M39nwHU/1b/vAOjAv3+OP2yALIAZf3PAPL9DPs8/tz7H/i2/RYCnP5vAvEBbP0e/rr+owBW/wAAZwAB/jH/xAPEAyUAlAAi/dz7JQDiA28EEgPaBcACyf6fAcgAQP+FAKD/Zf3u/sACMwIb/x0Atv+6+vb6dP0X/hkBXAP8ACb+PP5P/Rf8WvzN/4UABP+JAXT/xf9cAc8AqgDq/28COwB7/4EBAwNRAiEDKAUi/wcCxAM7AGz/nP4i/wj8Iv8WAD4BMAPLAdMBWvy+/QAAS/5w/qMAXf8t+tj88v3q/VEAjABw/lb/pgHtAIwAKf8zAg4CLAC5AGX9afwi/xkBFgBcAxUE0P57/5sCuQKBA+0EEgF0/Xv/YACr/gMBnwMOBHIDFgI+ATH/DgCmAWsBRgE7BMQDOwBCApgBMf9a/or/Yf7Y/lwDiQNGAygBQgD5/Sb86v0x/WH+KAHlAuP/DgAZAXf8dP1o/vn9aP66/t/+DP3tANoBPP4m/hf+r/2k/Dz+vv9ZAOP/pP6z/Ef79f6v/Uv8OP/b/5n7s/o7AJH/iv9RAGX/vv3n/N/+9f7F/5X+Lf50/5sC1gTb/yL/DgTIAlkAawN9Atj+FgAzAoUC3gb/B0ICBwBVAXIBYf61ASwEmAEdAt4C3gIWADsCpgH5/Zn/p//c/Tz+gQPeAigByAJZAPn9xf3N/Xf8Jv4x/1L+tv8wAWz/wvwT/+0CywNCAGz9e/te+eP9NwFcARIDhQDF/UP+8QGQAwT/Vv2V/I78f/6qAj4FBwLtAHv/Lf6O/PL7lfzC/PQAAwGjADsC6QEE/2z94/+K/Sn98v17/T4BzwDy/9oB/AB6AUoCbP9P/WcABwDJ/mMDfQLlAJsAJQDXAJsAqgI3AcsBnwOfA0oCkf/AAFkAp//n/lEAMAFZADsC+AGjAqYDqgLb/wAA+f9d/Rf+Hv6V/nv/qgB7/+P9QgAOAE0BSgLlAOP/Mf2o/dz9E/1W/5n/Lf7F/dcAbwLTAcsB2P6G/tD+HQCbAC3+bwCbANcAKAHy/0oA6v2o/br+nwFNA6oA7v6c/ssBgQFgAIUAkf++/7r8nfyk/r7/1P9ZAGQBOwBgAgcAG/1h/sn8qP3f/tj+QP9RAkkElADn/tT9S/zn/v8BbwDC/hkBZAGFArwHSQifAaD7vvlw+t/+ywFcAZgBIQNCBowGfQLU/9D8zfcQ+mj+fgBJBD4DVQE7AC3+8v1H/Tj9Hv7U/xYAs/4SAXIDTQM7Arb/d/48/q//2//PALwDrgFd/3f+kf+r/lL8OP/tAiEFvAOQA94ALfxL/Az5ePodANj+Kf1S/qoA6QHAAs8C5QBs/y38T/tH/e7+jACyAAMBbP9A/wj+vv3lAMn+LABjAyQCHQJRAuUAKAGmAXv9pPyC/0P+dP9rAxIDuQL8AvQA6v2R/Xf+wvzY/oUAG/+n/00BAwGn/+0ACP4x+478xf2yAMQB+AFVAbr++f1L/iEBowL8AMQBegHeAE0BdgBgAIwAFgBH/wcA9AKMBIUCDgLlAuUAmf10+0v8tv0zAPQAsgC9AcsBiQFl/w4AwABo/kf7/fhH+/b8kf/EAZABQgLxAd4AdP+uATcBnfyZ+777f/6mAZADRgMsAukB7v4e/pX+bwCJA+IDXAOuAxID4//q/XD8OP0E/7b/e/8i/94CUQSQA5sAMf+5AN/+JvwF+xf+Uv6C/2QBFgDtArkCDP9W/SL/pP7U/2ACPgGMBPwCtv/1/pz+AwGmAekD9ATIBNMDDgBd/4wAoP+z/iL/vv8M/4L/ZwKxAoEBhv5E/HD8QP39/qD/+AGMAAH8S/oB/CL9Af7tAAT/d/4e/uf+EgF+ALIATv/IAPwAUQDj/xv/fgDn/sL+Vv9NASQCYAKiBJcDDgQOAhP/Kf1s/WAA9vwX/oUAHQBnAsAAuQAzAigDxAGC/5X+G/tw+s39GQEkAkoCzf/N/9v/mf39/sL+bP9//jj9Yf7pAe0CbwDAACb+F/4t/Bv9HQIhA64Dyf44/fX+PgFyAZsApgEM/zsAsgAHAGACYAKJAVwByAAWAOUAhQAp/zsALAAE/8X9oP07AigD6QFcAS3++f3y/U7/JAJvAAT/6v9h/lr+4/2d/Dz+jv7N/9v/WQCJATsCgQEE/yb+xft0/UD/MwCqAJ8B7QIm/iwAEgF7/5QAzf0i/4kB6QFNAdoB+AEdAFUBbwCZ/Zz+Zf/N/3YCVQMsAj4BxAFKANT9G/87AIUA5QA7AtoBywE7Auf+QP+MAL7/iv/5/yQCRgNcAyEBBP9d/zj/bP+qAOr/mf8dACL9zf1+AEYBTQHq/4L/R/2+/Wz/OP++//L9e/1S/q/9Q/62/8X/6QH4AR7+S/41/u78BP3C/lEATv9W/2X/gv+QAQMDCwHq/yUAZf0i/WAALALlAn0E/wM7AHYABwJnALkAdgDb/yn/bwBrBdYEPgOUAJn9oP+Z/zH/PP4x/88AnP7Y/jcBMAG2/YP7oPuv/QMBuQAM/3D+QP0p/S3+Zf1o/noBRgEi/1b/BP8I/mAAQP9L/nYCIQHy/XYARgNjA4wCHQJh/tD8bwCZ/+UAQgIAAPL//AD/A0oCrgEWAn/83/pE/HD+bwD8ACgB4/+6/t/+oP+g/0oAsgAE/6/9d/4E/0D/cgEhARkBUQDC/Ir9cP6MAJ8B4/9+AL7/Zf+6/gz//ADIADz+t/uk/DH9d/4sAPwAiQFrAaYBbwD0ANoBwABRAAcAEgHlAAz/SgBcAXoBfQKuA2sD3gLEA9MBwAC9AbECOwIwAbIAE//y/zz+D/5cASEDrgNrAZsAuQCJAZQAaP5l/+kBRgHC/or/6v9s/1r+e/0T/QsBOwRnACUAAwFgAN4AXAGK/6D9iv3R+hv7oP/AAgoDKAFS/l39G/8b/wAAfgDC/k/9hvxw/ob+OwBnADX8r/tL/DMA9AAsADMC5QAzALb/6v8b/ygB8QHU/SL/VQEZAZABwAIhAdv/PgHeAK//4gEZA3IBhQJgABP9g/35/VL8+ftCAOIBXAE7Atj+S/wi/7r+G/96AaMAaP5H/Wz/9AAOAs8Cmf9p/AT/dgBvAJQCywEDAZsCYwOQAWcCowC+/a//Kf/j/2cCCgO9AYEBUQAB/pn/+AFcAfEBcgPq/6f/egGg/3f+Tv/1/rP+vQEhAywC8QE+Adj8s/7F/7b9MAE3AVgC8QEKAxkDAAAHAO7+oP/j//QAAwEoA9oDowCn/2X/ZwCr/nIBwAJcAdoBNf4Q/Ov7Q/5w/r7//wH1/lL8UvwE/XT7OP2R/47+AAAwARv/Tv83AaT8Xvur/i3+4/39/uUAtv/8AJsC2/87Av8B/f7u/pz+Q/53/lUBGQHj/+r/Af7q/4EDxAPPALb/Kf0Q+q//KAP/AeIBNwFW//n/5QLU//3+5QAt/qv+dgIwAywC8QGUACn/QP9+AAMBVQF9AvwAZf/AAEYBDgBCAA4AAf7C/mAACwHiA3IDYAAB/lb70Pzq/S3+6v8AAJQAHQBh/nv/FgBw/tj89vpe+xv9/f4b/6f/EgH1/tT9Zf0i/13/5/5A/0D9wv6YATABSgAhA5ABCwGuAVL+kf8DASgB3P22/3YCAwH4AyQEiQOXA8sB+f2V/msBAABW/zABrgF+AGcCnwFVAbUDOwJ3/tT9Kf+G/Aj+EgHq/0oA6v8I/Nj6iv2c/hf+Zf3J/IP7r/12AML+8v8ZA5QAVvu6+gz9oP1s/zcBzwDPAqYB8v04/58BawGK/6v+hv5O/9/+iv/xAQsBuQB7/6v+PgH/AfwAfgCg/wT/+f/IAIkBuQLAAmsBAwEWAiQCKAGBAWsBOP90/8AADgDLARUExAE3AQ4Chv4I/pn/PP7F/30ClADj/x0Ckf+2/cX/SgCyAGAA4/97/3YA9ACV/v3+9ABnAOf+AAB7/zj/fgBH/Rv91wDU/6j9RgHAAJz+0wH8AOr/MwDc/eP5E/vj/ygBgQF2An4AG/2n/2cACP7f/mj+jvzn/koCIQEoAUIAQP8dALb/8v+v/3T//AASA3oD5QQOBEoAhv6K/ygBMwLlBLwDmAFZAF39vv2QAfwCowC2/+7+S/5nAFgCZAEAABf+bPta/AMBMAOjALkAgv/C/Gj+q/72/ND+gQEwAekDYAQWAGX/OwA1/oP9q/6g/Sn/qgDAAEYBVQMOBIr/e/++/9z9f/7U/dT9zwDtAukBQgCMACwAD/4x/xP/kf/aAX4AMAEwA7UDFgKR/zH/R/++/ywCPgM+A1gCIv8E/4wAHQI3AbkAcgEdAGAABP+v/3oBXAEb/1r8QP1d/Tz+E/8WAKMAlAC2/5n9R/8WABYAjv5a/O78wvwp/8QBmAGqAFwBPgEm/vwAzwJgAJ8BlAAI/hf+dP9//pz+HQLIAjMCJAL0AFL+CP5L/hP9Yf5gAKv+Wv59ArIAF/5h/vn7r/vf/s8AfgCBA8ACDP9ZABYATv/u/iL9S/xs/2AElASuA8AE6QGK/6//nP4zAM8CYAJcAfgBzwIHAjcBPgFs/77/SgBnAE0FogaXA1kA7v7f/OP7bP/u/vX+bwAp/w4AWAISA2cCbwBH/4b+R/1l/X/8QP9GAcn+kf13/q4BZwJ9AnoBYABvAJQAdgL0AlwD2/+k+v362P78AKYBAwOJAQ4AfgBvAOP9s/z1/vb85/yjAGH+HvwB/JL59vp3/r792Pwp/br8q/7TAQMBD/5W/d/8Vvth/iwC9AC5ADAB9f7j/30CFgDY/rkAuQDEAVEEMwTxAf8BzwBA/Uf9Lf5D/gAALAKUAHT/YAKmAcgA8QG2/5z+3gCQARYAiv/y//L/vv8dAt4CVQHIAJz+bwDIBIgF7QJRADMAQgDPAKYBmwJ6AQz/wv4b/07/UQAlAOP//wGJASUALADJ/kT8qPtH/cX7Bfu2/bP+bwA3AQT9mfuD/cn83PuR/Uf/Jv4E/5H/G/1L/v3+afzY/K//r/8T/58BFgJKAGQBtv+d/Dj/wAD9/qf/yADN/0IABwKjADz+sgD0AI7+ywHeApQAcgEkApH/kf/PAFb9jvxkARUElwPtBBIDOwCbADsAAACUAIUClAAX/tcADgSbAtcAmwKBASgBAwGK/2cAbwIdAlL+E/8wA5sCVQFcA7UBT/0I/HD8tv3EAdYEEgHQ/gAAtv1H/XT/lf5W/SL99vx3/Ib+egG2/wAAdgAe/in9jvw8/GH+ZAGFADj/oP/N/7P+qgCfAW8A9AJGAYL/dgDIAHYAyACqApsCWARcBQcCbwAOAmcAQgAWAvQAcgGUAt4COwKQA8ACAf6R/S3+xf2+/zABr/8I/nf+hv7J/qMAWQAlAOP/lf4b/Uf9vv8P/lb97v6yAMsB8QHEARIBxAEx/wj+Q/5h/owAlABrAX0C2gGUADAB2/+K/cgAZwLF/xv/4/88/pn/GQPaAYwC2gNd/+f8DgDAAGX9f/7IACL/TQHlBJgBHQDPAv3+Xf0OAKT+f/5gAoEDp/+jALUBe/+n/xv/q/4E//L/fgBKAKMCKAOZ/cL8uv4I/u7++f08/mj+Zf/j/1r+9AByAUf/wvyd+jz8DP8zAE0BhQAt/mj+iv3j/VEALABH/xP/s/7Y/uUAMAEsABYAnP5//rb/lABGATsCQgS8A1wB7QAAALr+fgBcARYCcgVrBRYCKAFvAh0AAwEDAywArgFcARP/7QAsBJADdgD5/6D9s/wp/4EB7QD5/6D/q/yR/4UE/wELAVECTv+V/pH/Mf08/Ib+FgCO/n/+tv/J/rkAqgJNAcAA5/4e/N/63P0zAIr9Hvxe+0f9+f8x/9/+5/6z/jj/9f66/iUAKf+v/dj8hvx7/Xf+QP+r/iEB5QIhAXv/E/8i/xYA5QK9AaoAVQO8A1wBrgHaAXf+BP/0AGcAHQAoAdv/5/4ZA4EDmwLeAn4AE/8E/yL/PP4i/5H/6v3J/hYCFgIdAG8CywGUAIkBp/+2/UD/owLXAD4B/wEHAGcA/ACbAvQAIv8p/a/7+f3AANMD2gNYAnYAOP+K/2cAbP9P/Rv9xfvj+7796v8dAsQBHQCV/gH+qP1h/vL/OwC6/qj9LABgAGj+3P10+wj8mf8dAED/cgEHAmH+uv4b/5H9S/4x/eP7kf0p/5n/6v90/2X/BP9W/5n93PuR/88ABwB2AE7/7v6C/3D+Q/7PAPQCNwET/8gAhQCqAPgBnwESAa//YABKAPQAegNyA9cCXAFd/+P/MwLIAlECcgHaAYEBMwAzAtoB/wFvAkD/R/+Z/8L+R//PABkDOwJRALIAHQDQ/nYAqgKmAbb/QP0m+lL81wALAXoBUQKYAer/+f+qAHD+Xf8t/rP6Uv61AXIBzwBvADH/5/5ZAE7/uv6jAIr//fzC/nv/s/6JAf8Biv8T/+P/r/3Q/M3/G/+Z/Sb+uv5o/vn/FgIlANMBsQTLAQj+E/3c+837zwCXA4wCkAGUAHf+2//EA8ACtQGqAML+Nf5cAbwDQgBNAdMBtv9VAeUC6QGJAaIE2gFl/30CUQLiAbECCgNCApsEywW9AUYBegF3/kv+owB+AEYBfQL8ADsAVQHPAE/9T/0t/B/62P5VAfL/2P44/dz5zfcM+478JvxH/3v/QP1l/6f/Hv4HAKf/cPxL/Dz+Nf7N/4EBUQAOACUAvQF2AoUCQgKR/34AywEZASQCkANgAjH/d/7PAPQAxf9VATj/wv78AF3/BwA7ApsCbP/Q/mX/2Pzn/okBMf/c/eP/Mf9S/iUAHQAOALUDxAOUAAoDfQIe/pH9/f47AFgCrgOfAaYBAwMHAj4BzwIHAkf//AAHAlb/bwAKA2sB9ABA/yb8r/3aAWACZAFJBIkBT/01/pz+qgCMAnv/JvwX/q//dP9NAXYEowJ//kv+mf31/sAA8v88/kf92P4e/tj+zwDY/hD8afyR/5H/7v5KAAz/hvxA/R7+QP10/1wBGQFyAeIBr//q/TsAG//9/qYBWQAZAQoDyAJ2AgMDdgLb/8AA1wCr/I7+mAFl/94AFQSUAuUAKAGc/jX+nwFnAA/+gv+MACL/7QBjA28Atv9gAOr9Iv+UAoEBFgIZBW8C4/8HAssBZf/0AHIBlf7XACgDRgGjAhkD9f57/bP+xf0p/wMDjAAQ/Dj9Hv4m/NT7CPxw/OP9hv5D/ob+s/4F+xv5afw8/jj/R/8OAOIB/ACFAK//6v1A/XT9BP9NAU0DlAIZAVgCNwNyA7UDiQGO/tz9F/75/UYBtQVRBJgB5QCc/sL+3gCv/6v+0P62/yb+9f5JBKMC7QAsALP8q/wb/Rf8PPzq/9MBDgIwA/8B6v8b/+P9Vv12ABIB8v8zALIAIQHaAekBAf5D/nYAnP6+/xIDawMHAsAAvv3R+vL7s/5d/5ABDgLb/x0Aiv+2/cX93/6Z/QT9wv4zAO0AXAFrAUIAJQCn/6j9R/vY/PQAtQF2AlgCzf/u/kIA3gCR/yUAFgJs/0P+WQCR/yL/PgGBAQAAVQPTAZX8f/5nAEf/uv52ABv/r//pA7kCBwA+AfL/YfqO/NT/3P1A//EBpgHxARUEawF//j4BVQHJ/u7+PP4p/fX+UQI3AzMCowJnADj/owCMAGsBHQCK/Sb+bwCxAmACZwCFANv/jv4x/77/mwDIAM3/R/97/4UAbwB2AKoCkAMZAQj+6v3Q/pX+8v3j/Wz/VQFNATsAGQHEAZgByAAsAFEAzf+O/or71P34AWcAgv/PAHIBXAFRAjcBIv/U/9/+mfvj/TMCSgD5/30CVQG+/7b/3P1S/Fr+/f5a/owAZAGO/nv/sQI7AFb/RgE1/rP8Wv7C/kD/7QDEAY7+dP9RAkoA5QCxAhkBZf/y/wAATv+bAH0C8QEHApsCFgBW/9T/r/8AALkAtQGg/2z/mAGmATABp/8E/839Xf0I/uv7dP0zADMATQHLAWX/zf1L/ur92P6jAEoAoP2R/xkDsQIwAwAAJvyg/UoAYAAsAnIFwAIp/9v/wAASARIDSgBp/DX+BwBZAFkAEgGO/s39tv+2/2MDNwUDAfb8r/t4+mH8CwFnAND+tv92AGz/hv57/zj/3gCMABP9g/31/u7+Uv6+/3oBkAHy/5z+oP/IAEoCegGyANcAzwAdAGH+r//0AFECrgOFAq//q/50/4b+zf/lAukB2/8HAgsBlf7IAMsBGQG1AcsBq/7Q/uUA4/1//lEEZwRnAt4C1wC6/h0AYAAI/okB+ANd/1L+LADF/0oAWAL9/nf8gv/9/uP9VQGqAq//Yf6+/cL8Af7F//L/G/8HADcBgv/y/64BWQAsAAAA4/8sAOUAmwL/ATsCnwElAN4AkAHPAN/+p//IAK//+f9d/5H9Uv6yAFUB9AD0AKD95/op/XD+1P1D/r79EPxs/Yr/zwD/ASQCyf5s+6v8T/uG/FwBYAKfAc8AoP97/dv/6QG2/4L/vv+z/iUAVQN2AsQBxAEAAIL/mwDXAMX/dgAzAGAAegE3AU0BEgHPAEf/+f3y/fX+awH/AcgAWQBH/779xf9+AN4AywF7/13/MwCYAe0A4//eAAH+uv6UAHT/rgEzBEICoP+n//L9+fth/uUATv/eAAMDLAAwAaMCxf9d/Xv92Pyk/IkBiQOJARYCzwD9/HD8d/4i/6D/NwGc/tz75/7j/ywAywP8Atj+hv48/jz85/yV/u7+4///AR0CPgG9ARYCJAK9AYwAE//Y/MX7DP8kAuIBRgNNAwAAWQAZAUD/mf9nAMn+d/6JAYEByf5ZAPwAnP6r/rP+E/87AEoAFgC2/58BE//y+7P+nP6G/nv/4/9ZAIwAGQFl/9D+NwHeAHT/BwBh/vL9HQBcAd4ALAC5ALkA/wHaAT4BZAFs/x7+Wv4p/8X/MwD5/2cAFgKjAowAIv+g/3f+7v47ACwA5QD0ALUBfQJkASUA3/4X/or99f6QAaMCfQSxApH/OP9O/4r/oP9KAn0CdgCMANv/mf9cAW8ClABvAJQANf6V/kICNwMHArUB8v3C+k/9vv97/28AEgH5/aD92/+o/cX9Tv+z/N/6d/wsAG8ATQHiAUD9f/wm/uf8Mf3j/1kA3gD0AB0A2//C/pH/q/7y/5QCbwJyAa//DgJ6Adj+HQDU//X+ZwC5AvQC4gOxBP8BpP75/Yr9Uv5yA6IEbwIkAukBvv++/dT/1P+g/9oBSgISA4ED8QH5/Zn9e/9//vn/pgGqAKoAXAE7AAAACwEHABP93/xKAKMAVQFVAQz/uv5w/gj++f07AO0AAABd/6T+r/90/5H/MwDU/5H/p/9W/8X/1wB0/2H+dP8AADH/SgDEAZ8B1wJKAsX/dP8sAA4AowDaARIBwv5o/n/+wv4hAVUBBwBGAaMCYABa/rP+Uv4m/lEAawHj/4UAlf7Q/EoAawHPAFEAawHeAGz//wG9ARkBowJZAND++f9s/zsA3gL4A28CFgCR//3+zf99An0CfQKFAkIAVv8p/07/mf+2/xP/PP5l/4b+Jv4p/yb+pP53/q/7uvxvAGz/dP2O/lL+QP3j/zMAhvwB/tv/kf1w/rUBMwDj/9cCAwFa/qv+S/7Q/MAALwXwA1wDmAEx/a/7DP+jAP3+hv4t/lr+FgBcA4UEvAP8Aqv+qPu2/ZQA8QHeAHYAWQBL/hf+vv9cAbwDUQR2Ag4CNwGK/2j+p/96AZsA+AEwASUAUQLxAWcAyf6k/hD8uvwOApsC3gISA7kA7v4+AVUBs/yV/FL+afwx/doBpgGBAbkC9f50/Vb/Uv4I/HD+ywFyAekBNwFa/nv9r/0m/Bv7+f2C/+r/CwFW/wT/QgB2ALP+lfwT/Rf+QP8lAJn/3/53/oP7T/tA/zABXAHb//L/BwDb/7IAYAB7/0v8oPuR/R0AcgNrA8ACowLIAOP9Vv8oA+kBR/+C/6//6v9rA0IE3gKQA7b/8vtl/eUAmwI+AyQGqgK2/Sb+q/yK/SEDzwSfASUA2P5S/Ef/sQQoA0YBiQFP/Wn8YADaATcBegHXAKT+xf9+AFr+QP+QAT4BwAADAb7/2P7PAFUB/ABjAwMDyf6k/O78Vv2K/2cCTQP4A0IEfgD9/DH/uQAb//L9yf7q/Tz+8QFnAhIDdgLb/8X9/fw1/jH9nP61AXYA8v/xAb0BfgDPACwAxf13/u7+Nfzu/tMBKf+g/8QBzf+g/zcBJQAx/zABLACD+839/f6Z/fL/2gFyAbb/wABD/mX9CwEHAMn+r//1/jH9hv5gAAMBGQGZ/837ePqZ/QAAWALAAsAAZf+V/uf+yAC1AfQAp/8b/5n/bwADA+UCMwK1Ac3/xf9vAH0CNwNyAwoDyAC2/zMA4gF2Av8BnwF2AKT+5/43AVgCJAJNATX+wvwi/+P/p/83ARIBQP2d/Bv/5/6n/28ALfyv+0IAOwBnAA4ClACg/Qj+Xf8e/uUAwAJl/6v+lABZAA4CLASbAKj97v4lAGAA4gGYAc3/Tv+v/4UA2gE3A9cAUv6g/X/+/wFVA9oBHQCg/6f/3gCMAP3+kf+C//3+Lf5vAMAC0wF2AhkBQP9a/qv8t/uG/DMAUQK9ATAB6v9H/bP86v0t/l3/3gCMACn/MwC1AXYAPP7f/Pb6DPvn/vL/NwEzBMgCzf8AAE0BE/8T/SL/DP+6/m8ABP9W/4wC7QIOAPQAowIdAPQAZAEp/9j+ZAESAcAAOwTPAq//4/9NAaD/FgCjAOr9JQD0AhYCIQEwA/EB+f96AW8Alf6R/yn/yfxH/6oAlADEAf8BCwHF/9cA6v8WABYCkAGv/wT9NfxD/pn/qgDXAOUAPgPiAYL/BP/N/0f/Mf1l/UD9Kf+fAa4BgQHaAeP/AfzY+jz8Wv78AA4CoP/b/7kAzf/y/83/Wv6k/GH+3/4M/1ECawG+/Zz+mwDy/wcA4/+d/Dj9cgG+/7r+mwCFAK//SgAdAGn8vv2v/+f8Hv74AVwBBwBGAZQAWQDPAPX+BP2G/jABpgEDA2sD1wC+/4kB6QHeAAcC7QL/AYUCYAL/AWsDmwJZAOr9e/9VAx0CNwE7AvwARgEzAtv/1P13/sL+7vxw/owABwD0ADH/Kf1H/7IAf/72/Mn+Vv8HAAMBf/72/Lr+aP4X/jABvQGn/9T/LADC/m8ArgGD/aT8Yf7Q/qMAywHXAJH/+f9a/nf80P6K/yL/DgIZA94AYABNAer/0P4AAPL9Lf5NAYEBYAKmAz4DR/+2/ZH/yACUAvwCRgHC/tT9iv1W/zcD6QWbAsL8OP2z/mAAbwIWAjH/Hv5O/4r/pgNyBRkBe/2r/OP98v+qAlgCIv90/7P+xf34AcACFgCO/qj9EPyZ/bUBawF0/5z+BP1l/f8BQgJCAAcA6v0t/B7+ZAFs/7r+Mf/5/z4DGQNZAML+FgDq/dj8/AAzAlECIQP0APX+3gDq/zX+owBcAU7/6v9RAh0CWAKqAk7/mf1o/jj/8QGMAur/afxp/HD+R/9rAU0BSgD9/hf+kf9vAHv/9vxW+3/88v9nArkCSgKYAUf/S/7u/jz+2/8kAvQCiQN2BFEC6v/IAED/3P0HAFECnwHTAZsCMwLIAgsBaP6z/q//wv4i/4UAegEDA30CAACc/kf/R/9RAN4C1wCZ/3oBHQDn/kf/yACjAAcAcgEp/9T/XAGO/i3+r/9cAbkADgD9/vb8mf10/Yb89vxD/gcAqgBS/jX8E/1o/vX+iv/U/8L+QP+c/n/84/3U/ef8S/6MAHYCmwKbAiEBfgCQAZsADgAsALr+1P1KAO0C4gNYBKYDYAKn//38QP1ZAAcEGQXAAm8AsgCR/yUATQNcAXv9mfu3+0D9kAGqBE0BMwDy/zz8UvwSARYCQP8m/lL8Lfz5/dT9DP2+/70BG/9w/nv/ZwAzAL7/9f6K/0oC9AA1/uP9Iv+R/wcCqgRGBRUE+f/J/vn/owIZAzMCtQFO/1b/iQFrA7ECAwF//u781PsX/A4AbwLiA0oAOPs4+8L8+f3C/oUAWQAx/9j+Yfzc+83/BwK5ACwAzwAb/77/jAJ2AlgElwPq/x7+wv7aAQoDSQRCBB0CqgBO/ywARgHXAFgCjAJ+ABv/jv4T/yUAiQGr/kT8+f2v/R7+sgB+AKj9D/62/dT7wvwm/vn90P5KADj9uvx7/w4AqgDTAW8AcPx0+6j78v2jAkkEsQL8AG8AMwDAAMAAdgDlAMgASgA3ATABwABnAmACMAGC/6/9E/3F//8DvAP8AoEBr/1w/DX8vv2qAFgCTQEb/zMAR/8p/7kAr/8i/839zf2V/tMBogRNA2cCbwCr/i3+bP+jAO0AkAEhAfL/bP9RADcBMwIwAT4ByAAT/+0A/f5h/koAXf1H+5H9iQFYAnYCxAHf/DH9HQCo/Vb9vv8OAMn+r/+2/9z9ywGUADz63Psx/xkBwAK8A5sCnwEoAUv8r/ssAD4B+f/1/qf/nwGfA3YC+f9+AGsB3gCbABIB1wA+AQ4C9AAdALIA2/8OAGsBWQCqADcB7QCMAGcAegHxASQCqgAi/1b/DgCR/zj/GQGMAAMBuQKjAML+3/6V/n/+BwALAQMBvQEZARP9Vv1W/yL9Mf2r/gMBVQHIALkA5/69AZ8BpP71/q//AACZ/1UB3gDIAIUCwACFAA4CkAHlAIwAkf2G/AH+jv5W/zcBPgOMABv/f/66+qD7PP4e/oP95/4e/nv7xf26/h0AdgLN/8L8JvzY/hYAp/+g//X+fgCyAHoBAwGG/hYAqgB2ACUAR//q/w4A+AG8A+IDEgOv/7b9d/52AH4AbP+jAH0CpgNcAxkB8v0t/vn/MwIhBQMF4gPLAYUAJQB0/3YAKAEE/2j+SgLtBP8D+AFvAJn/kAFNAR7+Xf8oAU0BhQCg/+P9OP22/X/81P1gAE7/G/9KAhkBdP/N//n9Xf31/hv/t/vn/Dz+RPxgAGcEGQPIAA/+g/3j/yEBiv+G/HT94/2g/RYA9ADAAND+f/yO+n/8iv/5/2cABwDU/1b/1P+2/+P/FgCZ/9/+xf1O/9cAwALtAnoB5QCUAoEFmwTiAef+Wv4dAJ8BbwISA1UD7QBvAJcDwATPAlr+Zfuk/hkDYwX4BUIEowCk/lr+pP7q/3/+wvyK/eIBrgUsBogFRgF0/ZH7E/sm/E/9OP+bAOIBDgLtAO0AMf8B/L77hvwb/br+kAHiAQAAE//U/Wz9lf7Y/gH8Ivtw/Kv+ywG5Am8C9f7u/Hf89vxW/9/+Af4E/f3+3gB2ANcAs/71/ur/Zf9NAUYB1wBKAEv+Lf4WADsCUQIKA4kDLAISAdcAIQGv/+r/Vv/C/Gz/rgMvBX0EhQJ+AJX+zf2Z/Xv/YASUBIUAE/+qAGQBE/+r/vwAMwI+Afn/8v8OAukDowBP/er9Vv8zAHYAHQD1/qv+mf+k/qD9Nf5o/hP/3/4AAMQBvQF6AX/+s/yK/V39f/yZ/eIBvANCAnT/e/0E/7b/lf6R/f3+/wGBAaf/5/50/8X/pP4m/lr+R/8OAAcA9ABcA0ICzf9KAE0B1wAx/2z/Mf8hAQoDQgAT/xYAmAH8ABkBtQESAVwBdP93/pX+Vv+BAdoBkAEOABf+Q/71/sX/BwB+ACgBvv9gANoBhQBH/8L+bP2R/a//bP92ABkDmwLj/8n+mf08/CUAegHXACEBKf+2/8gA5QBA/779/f5nABkBrgFYAmsBbP9A/Zz+5QD0ACUA7v7PAMAC7QLXANj+D/7C/DX+WQADAzMEKAGG/sX9hv4+ASQCMf/y+3f8uv50/2QBSgLpAXYAXf08/MX9Vv+r/Hf8oP87AGX/Hv5D/h0AcgHn/tj87v7AADsACwEHAhIB1wAI/ob8Hv7eAAMDvQELAYwAQgLEA3oDZwSQA6oA0Pyd/BP//ABrA6oC9ADaAWcCmAFNAbECfQJnANj+Hv41/tT/+AFrAQcAs/71/ur/vv/U/9v/GQHXAO0AgQFgAk0DhQBd/yL/Mf/j/2z/Iv++/88AzwA+AWACEgO2/w/+bP/n/gsBYAAI/L753/om/jMA+f+o/ZX8G/2R/UD9DP8+ASn/xf0T/XD85/wX/Ef70PyYAe0CSgAhAaf/1P3AAL0B1wCJAfgBIQHIAiwEIQMOAk0BoP+V/r0B2gHTAWsFZwYKBSEDHQKBAWMDOwJh/ib+Mf/b/w4AawMoA6D/f/7c/Rv/dgC5AC3+CP44/6v+6v/0AM8Af/7Y/Jn7qPt7/XYAiQNyAWz/yf6Z/z4B5QDIAHf+cP78AHv/Zf8DAaf/Lf5h/oL/Iv+R/8gADgB2AoEDkf9H/YL/qgC+/5H/2PwE/YwAmAHXAD4B0wGR/yUA4gEhARYAFgBCAFwBogTPAhYAYADf/q//zwJgAr7/p/8E/3D+ywF6A+kBdgBnAKf/jv4m/pn7R/3IAFb/7v7q/13/pPx//Hf+yf6Z/TH7jvpA/dcClAJs/8n+3PvC+BT5Xf1S/lkAGQO+/6D/4gE7AC3+sgCyADj9kf+FApADQgYsBuIBdP/U/2H+DgD/A+UC6QHeAoUELAb4BW8CHv5O/6oAQgCuASwCHQA4/9v/dgCjAqYD2gH9/jz+0P6c/sX/WQAi/y3+vv3y/X4AwAJRAn4AQ/4b/Sn9pP6jACUAmf/Y/pn9/ACUAhIBUQCc/o783/p3/M39Iv/AADj/lf6FAGsBhv5l/Zn7xvlw/H/8E/2k/jsAkAHPAAAAG/0I/n/+q/yV/q//mwBvAFwBiQFgAk0DoP8AAJgBLABS/rUBlATaA88EKAN2AjsCkAGc/iwAnwX0AlUBvQEHArUBywGMAuUAZwLeAqoAnwGxAjsAr/2R/Uf90P7iAd4ADP+5ABIBbP/F/3/+PPwp/ef+pP4B/mcAVv9//pQAzf+FAOr/f/50/aj9BwA3AaMC3gDu/P38Wv5O//wCnwMoAbP+t/sX/DH/sQIwA8QBzf/y/Zn9Vv9NAaMAR/8M/UT8Af5cAaYDUQJO/9j+iv+O/s391Pse/K/9Iv/PAJ8B8QEb/5H9zf/wA/AFuQLU/Tz8Vv0lAEoCBwKQA5cDXAHAALEE7AZ2BBIDFgCz/iEBBwI+AVgC1wJvAJn/Vv+O/jcBywHY/h0AAwE7AAcCyAIE/9D8Hv7U+177OP+UAED/6v8LASwA/AAAAJX8ZfsT/er/DgBCAIUAS/5D/l3/0P79/mAAiv3F+5H/EgEkAnoBVv/f/iL/1P+n/zsA9f5p/Cb+awFVAcgAcP4x+3D8Xf+JAbEChQKV/k/9DgAAABYABwCk/hYAGQH9/pQAMwS1BW8EzwJgAC3+jAB2AGcAOwS1BYkBQP9kAXIBTQESATMAAADy/zz++fuD/SQCkAG6/rb/kf2R+0D9Hv7y/Vb/R//9/Pn7Iv3f/gAAdgDQ/Ib8oP1W+xP91wDEARYADgBd/Tz8hQDXALb/QgA8/n/8mf8wAW8AsQJcAxIB2gGBA8ACdgK9Acn+1P/LAz4DJAJnAtMBfgAZAfwAGQEKA9oBsgDeAFUDYAJnAAAAf/y3+xv9LAAoAQMBawFl/8X9s/7AAMsBzwJ+AKv+sgCxAuIBG/8X/vn9tv2K/QT/TQMSB+0EmwLaAa//4/3Y/IP7jvwZATj/nfyz/kIA2//N/5sA6v3q/XT93/om/Lb/5QAt/r79tv17/f3+Hv41/Ef9F/6v/ZsABwQsBJ8DkAEB/gH+6v+C/wj+uQCQAQAAwALPBC8FzwTpA6//r/3y/1kAnwHpA7UDR/9RAGQBe/39/oEB+AHTAaoC+AFgAssDsgBRABkBzf/F/7kA/ACFAj4FzwLPAEYBHQD9/lkACgNRAvgDegOV/ob+ZwDlAML+d/7C/M37Vv/5/34AEgHXAIr/Zf/j/Uf7dP08/rr88vsm/nD+/fxa/rP+DgB6Adj+f/p//EoAJv75/fL/d/7U/bb/lf7U/SgBcgFl/64BCgOv/6D99vwT/b0BHQauA9j+zf2R/3IB6QNCBP8BCwFh/rr8zwAKA4EB6v+K/a/9VQGUBJAFpgPeAEv+G/2G/tv/3gBKAkoCFgBa/rkAuQIb/y38Wv61ASEDMwQ3A6MAWQAb/0/92Pxh/kD/bP2z/p8BVQOuAzABLfwM+WX7e/9gAowEnwWmAdj83Pt0+/38f/7N/dj8R//eAqMCQgLPAAH+4/0t/pH9gv/TARYAHv5a/i3+BP1o/rb/7v6jAk0FFgIhAZADDgJh/qf//f5E/Bv/HQLTAeIBNwGR/Tz+XAHb/wz/UQCyAKD/p/9vALkAhQBW/83/dgCG/gX7Ivs1/okBgQXIBLUBLAD9/pX+Iv/q/7b/8v3F+y38Uv6uAc8E9AJW/zz+0Px0+9D+tQO8A5sCSgII/rP8Kf90/Wj+6QHAAL7/FgKxAmQBwAJ2Aq//oP8m/sX7vv9GA1UBAwGuAXT/+f17/7P+Kf8dAs8ATv90//L/r/0M/QsBowCz/o7+/f6r/jMA+AGO/qj9e/8I/vL9UQIDAzcBPgHc/cX7s/4LAQ4A9AADA70BfQIhA5QAXAGBAYb8q/wdAuUC/ADPAgcE7QK8A8sBOP1h/L79F/75/7kCkAF7/8X/gv+v/X/8CPwF+2X7Mf+BA4EDowAP/gj83/xl/Y7+vQHXAPX+s/4lAKoCKAWqBLkAzf+c/qD95QCUBJADXAN2BEoAqP3N/Wj+E//4ASEDIQEsAhYALfxw/E7/e/+UAK4BYf44/d/8vv38ALUD8QEE/13/yf6K/1gCmwIB/gj8PP4b/0ICrgUoBdMDpgG2/TH7Jv4hA4wCnwFgAvQA1P9VAVUD7QC6/lb94/sT/cL+VQFNA94CNwGjADMAr/++//3+F/4T/07/7vzq/+ID+AGMACQCSgJ2ALIAOP9a/hIBhQKbAn0C/wF0/zX+d/4x/ZX8Kf2k/iwAIQGmAa4DvAP1/gT9hvz5+ZX40frb/yEB7QDIAAj+1P26/qj9D/6fAZ8Bs/zC/B0A9ADLAaoCBwCR/SL/BwALAbUDKANH/6T+AAA7AN4CbwT0AiQCPgEi/6T+9f6Z/Xf+rgH/ATcBawO5Anv/r//Q/v36OPv9/vn/PgH/AwMDDP8t/h7+Xf0AAN4AoP0T/QcC1wL0AIkDgQOC/8n83P0x/z4BbwKjAIkBIQNcAav+hQAkAmAAr/8m/t/8Kf+jAHYAkAOQA+7+g/3y/f38wv4+AzsCDP+6/vn9RPzj/SUAAf6R/+kB7v6k/noBiQHf/nv9Kvst+ob+TQHTAcgCxAFO/13/4//q/Wj+bP/9/sgAFQTtBHIDiQP5/xf8Kf9cAXv/LABgAqT+1P0WAvEBLALwA/EBHv5O/+r/Vv0E/1EANf5o/pABZwBA/+0A9ACUAjADowCc/r7/kf+Z/28CLAKZ/6v+jv57/YkBpgPj/4r/4//U/zABSQQkBLkABwB7/x78kftw/tj+WQCJA7EETQMZAQ/+hvwI/pn9+ft3/hYCIQHtALkAKf+z/Bv5BflA/XIBDP93/vgBrgNcA/gB0P4T+wj8afrR+tcASQSQA5ADqgQZAYUAmwCR/yn/6v0t/nf+PgG1A4EFRgXXAGz7Kvkt/Lr+KAHAAu0A/f5H/4r/Nf7F/eP7MflS/FkAOP+6/pQA2P5p/HT/YABh/koA5QD9/oUAYAI4/3D+TQGmAVgCfQS8A70BRgMoA+0AGQFyAZ8BawPABNcCKAMHAl39G/9rAYUAmAHEAWz/DP+jAE7/+f3F/+0Ajv6C/xYCd/6V/Pb8e/tW+wH+Mf9W/aMAfQSbAk7/F/5E/GX5OP2qALUBcgMSAZz+Wv4HAHYAzwBCAOP9FgASAQ4ATQHiA9cCQP9CALIAzf+5AAcAmf3j/Uv+DP2Z//QCHQJ2AG8C5QJKANT9iv32/Of6xf3AAEoCPgVgBFUBawF6AQ/+d/zQ/lb/Kf/lAsgEWATtBGcCs/6C/ywA/fyR/SUAbP+YAfAFjASFAsQBOP3J+vn9+f/N/5AD8APU/1EARgHj/S38UQCg/2H8D/5s/2sBOwSUAor9qPtS/GX7HvwOABIBIQHIAPL93/zU/RP/T/2v/UIAxf8T/6f/sgADAd4C4gGo/Xf8zf3Q/sgASQQwAw4CNwXaA3f+1P/tAiwA2/+yACL/GQFcBZcDuQByA6YB5/wi/cn+4//pAUYDgQHPADsCFgB7/fn98v2O/jsA9ACjAEoAqgBKAJH/2P6g/6//BP8OACn/xf/F/4r9Kf13/jj/OP1D/hYABwCYAdoBlf6d/PL9R/3Q/CL/XAFGATABmwCO/mcAcgF//p384/+FAtv/r/+YAWMDBwS1AdT/S/6c/jMAgv+qAOIDZwQkBKIEMwT/A6YB4/22/a//ZwIKAwcCMAGbAEIC+AOFApgBQgI8/kT8cP5W/8gAMAMhA47+kf0e/jX86v3pATABKf8wASgBOwD/AbEC7v4e/H/8d/7eADcBIQGR/+P/e/+g/cX9jv7Y/pz+7QJ2BOUA+f1E/Bv73/ru/Dj9Wv6qAIr/r/9vAqMAd/7XADMA2P7iAbkCYACUAKMA5/4AAJ8BMf8OAIEDcgFRAO0C2gNgAigBZf9o/s8AXAMsAnv/lf7C/FL8wv7LAWsDPgM3A00B9AB2ApQAkf/tANv/r/3y/64BbP0M/ef8bfmr/sgEfQQ+A4kBBfta9lr6yfx7/UD/Kf1l+av8GQMzAvn/d/5S+rP4s/zIAKMCHQa8BbkAQP+c/pn9wv7AANcACwFcA7ECzwBVAZQCNwFO/0P+mf2jANcCNwHb//wAR/9s+/b6afyv/V3//wG5AN/+YADn/oP7Zf0M/2n86/uR/Tz+6v9YBEoCaP6V/tz9bP0B/mAAnwGqBAMFRgHy/0IA5QBKAKMACwGUAiQCZAEDA/wCvQFO/2j+3/43ARkBE/9W/2j+zf0b/0f/Vv0X/mX/yf5s/xIB5/5l/Tz+nfxo/iwAUv4M/dj+vv9H/zsCJARjAz4B/f6V/F39uQCqAmcEPgPpAQsBQP97/7kAawH8AOP/9f7XALEEbwQdAuIBDgCd/GH8+f2O/j4BgQNkASn/nP50/SL9zf+jAAcA8QE3AWX/7QAlAIr9oP1D/uP9Kf9kAQsB7QDIApcDywELAUD/lfzF/xYC0wFCArECsgC2/Vr+nP5o/hv/yABRANT/awM7BJgBiv+g/QX7hvzu/vn9LACMBPQCWv4p/2j+OP2v/xv/r/2Z/+UCLALpAc8CF/6s+pn74/vq/X0CvQGG/s8AtQNRAjMAiv9d/Wn8Jv5KAA4CYAK9Abr+Xf0sAIL/T/0WAKMCVQGjAi8FxAG2/Rv9ivsM+6f/yAIdAOkBdgYOBFUBmAGK/9z9dgDj/2j+NwOIBe0CdgI7Al3/yf7q/5sAMAG5ArEEOwTlAiQCXAHN/fn7R/2+/Y7+zwADAf3+IQPlBAAA/f4HAHv7s/qMABv/D/56AXT/rPot/uUAs/we/vX+wvwX/h0CSgL0AMQBWv44+8L8Vv1E/I7+QgJ9AtD+yf6+/9D+zwDxAVUBtv8zAP3+qP3y/1b/OPvf+l3/zf8+Ae0CDgKyAPn/R/9//Gj+kf+z/gsBEgN6AfQAKAHu/gz/MAFRAlECTQVyBekBrgHtArkCzwKmA2cAJv4OAMQDIQWQBSEFrgG5AEYBegFKADMAZwAi/zX++f/eABf+Mf8hAcX/zf0i/a/5WviZ/c3/dP/lAJQAKvsT+/n9IvuG+pn9bP0T/XoDuQSJAaMC+f+o+wT9zwAWAPQAawV2BIEDUQSQAZz+iv9yAe0ArgEkAqoCQgKjAAcCyACG/gz/vv9d/eP9yADj/xkBlAA1/Bf67v4OAJH9AwOuA3T9g/sB/gH+HQD0Asn+OP0OAAcAq/6FArwDyf4I/jsAbwDeAFECMwJRADX+/f4AAIUAGQFO/+f+RgFrAyEBcP6Z/8X/G/8kAg4Exf/f/u0A5/57/6oCmwAX/r7/uv75/fwCVAUDAWX/MAG+/Uf7d/5s/88AyAT4A7kA2/+K/6v+e//tAj4DuQB+AGQBsQKXA3ID+AHN/6f/2//u/pH/VQFNAXT/r//AADj9OPtL/L77dP3N/47+Uvwx/XT9RPqR+/L9uvof+hv9Mf3q/c8A6v/N/Zz+q/57/aT+WQBH/2z/hQD0AFgCSgKQAXIB3gBKACUAAAAHArwFegWUAukBrgFw/iL/jALeAHYAVQMHApn/lwOqBGz/f/6n/xv9qP3TAVUBjADpA+IDzf3q/c8AKf8dAGQBcgGyANcAtv9S/qMAjAAsAKYBGQOqAjMAdP8wAer/G/01/jX+d/y6/Kv+dP/LAVwDwv7c+779Vv2o+8n+OP+6/IL/MAEB/vL9lADn/qD95/4p/83/6QFRAsAA9AAOAj4Br//y/3oBHQLU/yL/sgBnAEIC/wOyAEP+yACbAHD+TQMvBzsCQP++/4r9Zf+iBOUCuv4oAW8AXvu2/7EEEgG+/64B6v0F++7+rgHpAbUD/wEt/Fb7bP0Q/KT8lABZAFL+R/92AJQATQFjA2ACPP5p/HD8QP2bAFgEYwNs/13/kf8T/aD/egNyAVr+zwAsAs8AYwPTAf38G//4AR7+uvw7ACn/CP6MAhUEYAC2/1b/S/7F/wMBqgCK/3T/mf2D/SUAlACn/+7+1wCUAvL/T/3j/0YBbP+FAFECzf+r/r7/DP2G/sAC1wCc/ssB0wGR/ZQAsQI1/l39FgCZ/e78bwLTARv/5/7N/Yb8tv0ZAa4BRgHIACL/f/6V/jz+7v6v//n/7QAHAPL/qgKqAuf+cP4dAMn+HQD/A1UD6QF2AgcAoP3b/3oByf7U/yEDG/9l/RkBDgJNAyEFiQEQ/OP7Xf1s/dT/9AJkAXf+OP+jANv/kf+FAML+BP3q/ZH/MwBvABID7QLy/5n/oP1W+wH+0P6Z+2X96QPtBJQCAwN0/8L6mftl/Wz9jv6JARkBjACQA/wC7v4T/aD7hvp//jcD8APtAqMCrgFD/sL8QP2v/TH/5QDPAgoD3gJjA+IBjv6d/Nj8Kf1vANYE2gWqBA4EMAGZ+4r97QCv/6oACgMkAkIAlAK5AHv91wCMAKv8Lf5GAX4AfgA7AkIAKf1a/mj+g/3j/2X/tv0E/5H/2/96ASEBAADN/3YAZAGfAXIBMf9A/+r/iv3y/RIBxAE7AoEDzwLlAjMC4/84/Vr8cPz9/Ef/tv9gALkAawHj/777VvvU/V3/4/1P/fL9q/6G/lkAKAFd/77/6v3r+0D9VQHTAUIAKAEOAEP+dP/PApADbwQ+BTsCPP5W/5gB/ACxArkCMwAOAIkDNwNvAtoDUQC2/YL/GQFnAJ8D4gM4/839OP1s/Qj+BwC2/0v+Hv6D/Sn/9AASARkB3gDF/dT7mf13/iwAQgK+/4b+jADN/7b95QCFBOUABP9H/zX+yf7EAR0CmwB2ApsAQP2v/WX/Nf4WAAcEpgHj/zMAqgCn/8L+3P3c/W8A/AD5/ygBSgJs/9/+uv6R/6oCFgJO/xv/LACD/UD/4gNGA8X/Xf9s/wz/FQRrBfwCiQFL/nT7nP78AvEB/ABrAaoABwBYAgMDWAKFAH/8bPtD/gsBZwAZAfwAbP92APgBowBa/tD+3/w8/OP/JQDU/0ICNwF7/U/9yf5o/oUA7QJo/pH73/44/5z+sQIOAiL/1wBs/5H92/+uAb7/Zf92AJn/FgAsAvgBegEOBKYBvv0E/TH9Tv/AADMA3/6yAM8APP6c/s3/lf5o/pn/Uv5L/hv/0P7N/YL/LACo/TH/5/5a/Nz9QgK5BHoDcgH1/q/9Mf8M/9/+WAKjApQAWQCqAMQBdgKYAcX/cgFrAzsAe//TAaD/5/7TATABXf+FAGcAQ/7y/ygBNf5w/rUB7QAWALUBYACc/qT+xf2r/MX9pP7n/rIAtQEsAhkDywET/x0AwADC/rP+lf62/SUAKANKABv/MwIoAdz94/0p/3/+YABkAWz9jvyr/rb9OP1vANT/G/tp+s37Zf0sAGQBOwDf/pn/f/5S/s8AoP9H/zABjACv/+kB3gJrA/AFogTXAH4A+AOBAw4CbwK2/6oAegUZB/QEDgTiAUP+xf9RAOf+9ABgAnYA2gEzBBIBNf5a/ib+3P2g/9/+afzu/pgBAwELAdv/Zf13/k7/g/10/U7/2P4B/tcA/ADn/tcA8v/N++P9ywELAcgAXAEB/rP8UQCg/7b9zf9s/7b9xf9NAQAA6v9+ALr+xf2+/3YAiQFgAq//kf0i/2QBqgAWAmACDP/F/4kBDgIDAzADMwA1/igB/wFvACwCxAFa/iEBMAND/qD9ZwA4/28A1wIAACL9f/5w/jz8wv5gAB0AMwK9AWz9UvzQ/l39Wv4LAdD+bP3N/yUAE//LAVECMwBl/2cA8v+qALwDRgHY/hv/q/6D/QT/jAIVBP8D2gG2/3T/HQAi/6MAHQKz/pH9uv75/TH/wAJnAHv9Mf/y/XD8/wHPBGX/Iv35/av8QP0zAiEDawEZA+0AyfwP/l3/g/3q/+kBSgDLAQcEZwKMAK4Bkf9d/YUAwABh/nIBuQB3/Ef/mAHJ/gj+3gC2/QH8EgF2ADj/CgOjAK/5f/y6/vb6UvzU/zz+iv2qADX+PP6MAowAs/zn/q4BOP+FAFgC7v7U/UD/bP1h/jADawOmAcAC7QJZADMCegNH/5H/xAFd/4r/kAPeAvL/bwC5AF3/0wFcA7IAZAESAfL9xf8wA/QA2P7y/8L+G/2FAFgCXf9CAB0AIv2g/Tj/S/5S/r0ByACg/fX+gv/Q/Or9DgB3/gH+r/9RAO7+sgBGARP/MwAE/2z98v8WAqYBMAEKAwcCBP/N/1b/cP78ADcB2/+uAaMC/f5w/q4BZAFnAPQAp/8e/t4AfQLXAE0BGQFs/+r/AwHb/0f/hQAlAHYANwPEA8sBIQFd/1r+/ABVAU7/p//0ABP/QP8kAsAAKf/tAE7/2PzaAYkDbP+v/yUAq/yO/FkA3/79/ssBmf9l/cAAGQN0/9T/HQDc+0v6jvxh/jMAPgXTA9D+aP5S/i38xf2fAQcAFgDPAsAA3P3XAEIAJvwp/34AYf5W/5gBGQG5ALkCqgBw/Nz9tv9w/u0AIQEE/c399ABVARkBpgFs/2X9YACFAlwBowKFAAj6uvolALIAAADLA1wDDP9d/0oAzf8hATsAbPvu/JgBbwAM/1ECkAPPANcAp/8P/kYBmAG6/lwBWASbACb+mwBYAgMBDgJRAs3/6QFVA5sAhv7PAL0BSgBnAjMCQgA3ATcBNf6c/vgBOwJrAQ4CdgJGARkBG/84/Vr+iv/5/2cAjAKfARkBZwJ2AGcA2gFnACL/mwDlAGX/oP+UAP3+jv5o/tj8Mf/lAtcClAAWAigBlfyd/HT9oP31/gz/Wvw4/TcB9ABS/jj/Kf8x+0v+egG+/2AAPgHIADH/1P8p/538Yf5s/5z+e//j/zz+7v4+A3IFiAX8Amz97vqr/Lr+bwDPAokBYf6c/hkBmAEZAbECr/8p/Y7+nP5gAFgEywX0AAH+nP6r/Ib8yACYAZsATQM3A2sB0wGBA3YA0Pwt/or9gv+fBaoIUQbAAtT/1Psq+8n+CwHEATcDvQEWAEYBiQEx/UD70P6g/aj9RgHeAHT/cP63+6j5T/vJ/Bv7zf1nArb/+f2C/07/wv7C/jz+Jvwp/Uf/QP96AT4De/9w/ND+AAD9/toBtQPf/jj9p/8dAG8ALACo/WX7OP+YAVL+/ACQA1b/1P3n/lL++f03AVgC/f5gAOUAWv7XAMQD8QFGAWACQP/N/VgCmwR9AvwCVQFp/Mn8iv8DAf8DIAcHAoP98v/J/hv/bwJkAUf/xf+K/0/9bP04/9j8r/tO/5QA9ACfAV3/LfxW/X/+CPxs/XYABP8e/k7/Jv6K/Tj/WQDJ/or/sgB7/fn/2gN2AsAAdgCc/oP7Uv7iAXv/+f/0AjsAbwAKA/QA6v+BA3YEtv+UAIEB2P4hAfQCEgE3AeIDhQJvAGcCTQG6/koCdgJKAH0CHQBh/Pn9qgKuAQz/jADc/Xv7vv3n/pn9QgDAAsX/hv6O/rP8Jv52AiUA3Ptp/Jz+JQD4A58HxAPtAN/+3/ps/d4CTQW5BHYEnwE4/cn+bwB2ALwDtQOk/nT95QB2AmcCmwJa/nD4rPjn+hf8jADWBCQCE//f/k/72PpCALUBr//q/0D/S/z5/R0CJAIzAowCQ/4P/g4ELAQOAsQBMwAAAD4DgQWQAfQATQP5/3T/VQN2AqT+E/9l/+P/CgWIBRYAF/41/kv8Iv0HAoUCR/+O/gj8rPrN/Xv/p/8HANT/cPzn+vb8cP7AAGACYACv/Sn/oP97/z4BVQEE/839Mf8P/q//vAOiBJQCIQF2AAH82PyjALIAqgAzAk0BdP2c/owAiv17+zj9qP1CAH0ElAKV/gH+pP6g/Xv/JQDY/q//kf+Z/w4AEgGUADsARgFA/y3+PgEzAj4BTQOjAiL/aP6K/6//1wBJBBYCtv0b/6D/mf92AoEDOP8E/XIBPgEHAMsB9ADn/tj8DP0B/p8BHQSyAPL9Nf7F/e78LAB9AoUCUQLq/0D9hv5cAVwBZAHY/pH7WvxVAeUE9ARJBpADUv7f/Kv+iv/iAfgD6v93/pgBDgTTA4UEGQPu/Bv7q/w1/uP//wGMAjcBawGyAPn9jv6Z/1L8Ivsi/QT/gv+MAJgBLAByAZQA6/s1/GX/dP+c/igBYAKC//L/ZAET/yUA0wH5/77/3gL4AzcBowB//l77dP3aAcQDVQOxAqf/3P1ZAD4BG//1/nD+yfzN/QT/AABVAXYCiv/2+qv8Yf44/1wBe/+g/Tj9Kf2+/er9PgHEAQH+R/0P/lb/lALiA0IAWv6v/8X/7v56AYwEdgL0AGcAMwB2Av8D+AGk/jj/E/97/zsCRgN9BNoDegEE/Xv7p/8WALkAuQIDAX/+R//TAVwBSgL0Avb8uvpnAJgB2gEoBdoD8v/c/U7/6v2v/TABTv9L/vwAHQLlAHoBawEB/Fr6/f5vAPn/kAEzAI7+gv/j/c35vvs3AeUAOwASAdD+Lf4LAWsBXf/C/pn9zflh/H0CFgIZA7EC3/5L/t4AbwKC/13/BwCD/Zz+pgHeApcDVQP0AMn8Afyr/pn/tQPWBrUDHQB7/f38r/26/hv/dP0lAN4CiQHxAbUBQgA1/sX9BP9RALkCqgCG/j4ByAKBAUoAkf9d/6YBpgOxAkICxAObApQALACg/+P/ZAG5AjsC3gIsBO0Awvy+/QT/r//0AJn/D/7C/koA+f/AAv8DYf44+3D6jvoB/GAA5QJd/6//OwBD/gcAwACr/qD9Tv9W/3T95QCUBE0DdgKuAUP+0PyG/gT/8v3eALwDEgH0AOkBEgEoAZ8Be//F+5X80PxL/FkAAwP0APL/Tv8E/aj9KAEZAXT9Zf1d/aD/XAPiAX/+r/2UALr+Zf2uAaoC8v+jAJ8BBP97/5gBCwEb//EBywHq/U7/OwALAdMB7QIlAGH82//EAWcA3/5P/f38Jv6BAcsD2gF6AVb/dPvY/K/9uv4dACwALADq/xYChQKbAG8Alf6z/Kj9PP6+/6oCgQW5BM8AyAAp/3/8mf8lAPX+xf+9AVUDjADlACUAYfzq/YL/e/+jAAoDdgDQ/Ir9CP5D/or/lABW/Sn9HQBs/zH/hQDtANz90PzC/PL7OP+fAfwAUQBnAED/oP04/4UADP9cASQEowAi/0oAHQA3AbkCowJ7/0IAcgP0AJQAGQMWAqMADgKqAqMA/ACuAWH+aP6qAJz+xf1rAR0E5QB+AMQBT/0e/Of+uv5p/Kv+wAAT/z4BZwKV/vL98v8t/jj9hv79/pH/MAPlBJH/9f4OAjABQgCbADMAKf9ZAKYB/AAzAnoD0P4b/aMAJQB7/8gAQgCG/g4AgQFh/sX9FgAP/ib8cP6G/v38Mf9kAVEAuQD0AGX98vun//QA0P4OAJgBZwC+/ywCvQGC/4EBoP9h/DH//AJGAz4DZwSuATX+e//j/yUAkAP4Af3+tv/eAt4EsQIDAwMB3/xD/tD+Af6QAbwFKAUwAZQA4/9//BYApgEm/nD+dP9W/xYAWAIsAP38Yf62/9D+p//AAL79Kf12APgBPP6k+qD7yfzQ/sAA+f/f/vn/SgCG/tD+mwAB/q/7Uv6R/wcA0wGxApsAG/92AIL/pP7iAbUBF/50/2sBpgEzAhkDRgF7/Xf+HQAwASQESQRZACL/mf+D/Xf+hQLEA8sBSgKYAcX9D/7eAFUBgv8b/+P/dgAsArUB9f4p/07/5/yr/CwAyAKmAfQCMwQM/+P7tv3J/ur/awELAQj+Kf2g/9D+iv87AtT/iv2+/88AMf8E/4r/2Pwm+qj9aP57/fEBlAKZ/3f+wv5H/UD9lAAzADH/AwMZA/3+SgAhAZX+cP4lADMAUQBGBYwGNwGyAGAC8v8sAGMD5QIsAq4D/wH1/gAARgH9/tD+TQEwAYEBDgRnBO0AoP8LAer/Tv/5//X+Kf2R/Vr+/f4kApsEdgKz/k7/0P79/H/+Uv4M/er9hQDIADH/hQAb/zz6rPpP/RP9Zf26/nD+S/7tALECVv9L/Ib8Vvv9/P3+hvzU+xv/MAO9ARIBGQPj/4r9Tv+R//X+1P9W/1b/bwKIBWAE6QGJAfX+F/5cAZQCrgEzAmsDIQNGAfgBOwJnAH0CXAMdAlECWAJVAfX+5/57/1r+sgBcA4wCYAJ9AukBPP4X/Jz+kf+mAR0CCP5L/Ib+p//u/lb/mf84/ZX8kAH/AwcE/AIp/WH4afiK+2z/wAIVBMgCzf+FAG8Azf3j/77/5/zU+wT/xAFcAWMFEgXU/5n9F/xE/HT/cgFZADMAKAGbAAz/VQGqAh0AG/9D/v3+uv7U/64B/f4i/3YAgv+v/8gANwFyAbIAuv5H/RP9BP8E/2cAKAPlAND+Zf9vAIL/4/1S/kP+QP13/vn/UQDPAvgBYf41/jH/wv6G/A/+FgBD/oL/0wEsApADmwSjAK/7Xf1l/5X+xAF6A4r/QP/iAWcCqgJgBAoDD/44/5gBDgBVAbkCIv8T/aMAnwHb/5QAfQJZAE7/5QIwAfn9d/4x/6MAuQJVASn9f/yg/w4Agv+FBD4FWQDn/uP/bwCFAK4Blf5a/MX/uQCqAPwCWAQlAB78+f1a/kv+PgEOAoUA1wD0AED9BP0ZAdMBbP+V/jj/R/0E/x0C/ACbAE0BNwE8/gH+e/+k/kIAawHu/nf+2gHtAHT9S/4LAUf/6v3iATsCHQJrAa/7Lfqo/ZQAjACv/8sB1wA8/noBrgHQ/pH/G/84/TH9bwAkAokBiQPaAav8T/3PAH4AYAJ9BvADQgB+AFEADP+1AdoDHQBO/zABuQDIAFEE/wMe/sn+mf+K/fL/UQKbApABhQB0/WH6lf5rAav+tv+YAQ4AR//U/9D+zf0OAK//RPwWAHYE4gF+AMX/mf1p/OP9QgCMAH0EgQX5/4r/AwH1/qD9e/+FAP3+uQBjAyEDgQPxAdz9yfwi/6//CP4i/1EA4/9kAUIC/f6r/Mn+QgBo/jX+DP/U+2H8OwBGAfADWARs//363PuG/mX9DP3Q/hf+e/+mAzMENwOmA1UB3/qo+TH9Nf5kAbEE8QF7/8gAOwC2/br+BwJW/9/8yABZAEf/UQLtANT9pP50/3f+BP/TAdT/ZfsE/Wj+cP5CAPwALADtAFUDPgHy/Sn90foF+xv/zwDxAdoDtQNCADH/CgN2AAH82Pzq/RkBogQSBXYCAAAOADX+QP/lBDsEDP/F/Zz+jv50/28CYAI1/pn91P+YAe0E7QSqABv9PPxA+/b6OP8HAnoBbwBa/hP7E/0DA30EbwKc/hf8FPl4+tT/oP9ZAHoBPP7U+2X/SgJCAH4A/ACG/ML6Vv8WANT/gQOQAwz/mf3y/zH/fgCuAzcBVv8wAc8CmAEOAFwBTv9d/SEBBwILAUkEPgUhAaT+zf9cASgBzwIoA4L/6v/j/wz9q/74AcQBuQBgAukDkAF+AJgBaP4t/lb/Jvwt/BkBZwRRAuIBiQGK/a/71P3q/8QBUQQwAUD9D/7F/4L/Yf6g/+f+Xf08/iL/zf8lAE0BMwDc+1r8Lf7y/TABywHJ/vL9cP4M/0v+1P+MAtT/e/26/uP//wPLBVECjABH/5sALALiAcAEZwL1/iQClAThBVQFDgQhAwcAowDxAVUBxANNA+IBYAIdAqYBMf/1/kD//f6mAfgBE/9h/vL/Kf+o/br8VvuO+gj8BP/n/hP/WQDq/Zn7bPs1/DX+vv/lAKv+e/v1/h0A8v2R/xYAq/6d/MX9BwJ6A+EFyAR7/07/2P6G/s8AGQHlANv/CwG5AqD/HQC1AxUEBwTPAP38zf22/3oBhQIKAzsCoP1P+6f/NwPABGMFOwJs/1b9OP3U/8AASgLtAnoBcgE+AeUAKAFkAUf/Kvtl+yn/vQE7BH0GxAN7/WX5kvmO+kf90wFGAcAAmAHq/wT9uvzU/3f+q/xL/h7+Zf2jAKYBtv8oAa//RPys+pH9/AK8AzcDVQHj+/n7G/90/V3/MwJKAur/vv2g/3v/xf+yABP/R/3U/TH9CP5gAtMDuQK6/sL8zfsT+8n+/AAWAG8ACwFRAPwAsgCC/1L+Hv50/WX7Q/4HApsC9AL0AokBKf/5/dT/FgDY/iL/Lf7J/gMB5QLlAgMBawFyAav+QP8hAcgAYAIzAj4BZf/Q/mcC6QE+AVECQP84/V3/JQD/AVQFpgUSAxv/gv9ZAKT+8v/c/RP7OP+QAX0CTQMKAz4Dr/+Z/TH9DPv9/BYA2/+JAQcCQgDQ/iL9Yf5D/gz/JQA1/tT9wABCBAMDGQFO/8n8jvxd/34ADgDXApsCWQDq/8QBowKn/8AA/ABA/Uf/r/8M/1UDtQUkBiwCWQAb/8n6Mf8HBOkBwABgAigB+f8oAZsCWAKuAc8CR/8X/mQBmAGJATcDPgFH/er96v+qAH4AwALXAo7+oP3U/cn+TQGbAN/+f/7c/Uf9hvzY/pn/F/x0++f8Hv7u/sAApgFo/i382Pwb+/38FgD9/gT/e/3C/sL+1P1cAfwA4//b/yb+uvzC/lgCywPXAND+dgAWAK4BKAPaAUYBoP8I/qf/mwKmBZsEEgEDAZH/QP9KAKYBmwTPBNcChQDf/psAIQPEAQcCWQBd/UP+bwCuA5ADTQNVAaD93P3N/xYAuv75/9v/0Pyk/DH/Tv8x/zcBLACK/cX79vqK+wj+2/9a/qj92P6z/pn9Uv5w/pX86/sf+tH6oP8LAdoBPgEE/13/zf22/SwA8v9nAA4Aiv/XANv/nwG1AQj+5/5RANMB+AMVBJABG/9s/1UBlAAp/0YBzf/q/7EChQKjAiwCZwISAZH/DgKYASL9T/1l/5QAHQQoBSgDwAB2AAMB5/6r/uP/OP/f/sAA1wI7AgoDyAIP/vL9Kf+G/kIADgLiAdT/FgAHADz+gv9GAWj+LfxA//X+2P7tAG8Azf8t/hP/DP+D/cX/gv+R/XT/BwB0/Vr+ZwDIAF3/Uv5gAB7+T/2+/xv/+AFYBFECDgBO/yL/r/1h/oEBPgEM/9D+cP7f/lUBQgIHAKj9Lf75//n/QgB+AIL/G/9A/ZX83/6jAqIEMAHq/R7+wv5gAA4ChQJcA1EAF/5d/7IAqgTlAjj/7v6D/U7/2/90/+kB4gF9AgoDvv8t/kP+dP/IAFb/nP6V/hf+7v75/5gBzwQhA4b+D/75/av+JQCbANMBzwBd/3v/Iv9gAlgEvQGJAcAAyf5W/Yb+JAKmAUIAkf8M/58B6QHj/5n/Iv/q/9D+qP07ANv/tv+2/7P+4/8M/yb+q/5H/7IAtQGn/1r+q/4x/ZX+e/+K/yUAlACBA3oBjv7n/l39gv8ZA5QAR/92ABkBawPaAYUATv+6/M3/jADPAJsCWQCC/6oATQEOAvQAG//n/vn9cP52AJ8BMAO9AcgA3gDq/TX+zf9NAXoBf/50//wAQgLLA28ClAAlAI7+D/4OAFEAIQGr/kD/1wC6/nIBOP++/a//iv+K/wj+D/4b/5z+oP1A/7r8qPv2/Kj7dgCFAnYABP3c+ZX8Vv+jAHIBwv6+++P9q/4OAHYCJQD1/kf9Jv69AekBYwMHAqv+DgCUAEYBRgP4ARkB+f9d/30CiQEAAGcClAB2AN4CfQLpAUD/0P4AADABIQV6A7r+1P0X/iwAegEoAdcCQgL0AMsB+f+6/pH/Vv87AH4AcP6C/8AAvQFCBJQAr/2r/LP6G/8sAuIDSQR//ur95/4t/Ev+Mf8i/zcBWQDF/3T/hQCjAsgAq/5P/QX75/zAAP8BegMWArr++f0P/k7/rgH0APX+zf2o/cAAtQHEAeIBzwCYATH/xfuz/FL+AwFgBLwDEgP5/779jABRAKYBZwIm/jX89f6fAe0EnwUzAqMAzf0t/qD9D/7aAwoDsgC2/wH+DP/F/2H++f+MAP3+f/72/N/+zwCk/uP9Wv6V/mX/R/2k/tcAYf5nADH/Nf70ANT/owBGASUA/f6k/EP+fQLXAgcEUQSuAaoATv/j/w4CfQJNA/gBoP+MAg4EcgMVBKYB+f8WAIL/9ADIAnoDcgXEAUP+R//C/vwAQP/F/2MDMwBH/4L/PP4x/w4AFgB6AVEAD/5d/bb91wDb/yb+Zf8P/pn9s/4b/zsAXf/J/F39kf0t/nv/Yf5H/5H/T/1p/P38mf0b/xIBxAFKAM39Lf6g/eP9Kf84/zsC9ACyAFEC8v9VAWAApP50/yL9QP1d/5QAuQSqBB0AKAFvAND+MAHy/9/+owAZAXYAE/9W/6MCCgO8A/QEXf8B/r79nfwOAsQDnwMwAWj+7QDPAMAAwAIOALP8kf1l/b7/KAFcAaYD6v8T/+r98vtW/7IATQFKAEP+G/0b/WX9p/8wAaMANwF//Nj6e/0T/ygD8QF7/13/9vyK/bP+5/6fAXYAtv2yAIUChQLIAlkADgBS/lb9wADTAfsEXAVYAv8BDP+r/msBZf8x/0oAR/9gApsExAVJBPX+bP3F+6D77v6g/0oAMANnAiEBr/+z/Kj9xf1d/zMCQgDC/g/+Nf7tALUB2gGyAJ38f/6FAM8A7QIAAJz+4/1W/XIBjAKuA+0C2Pw4/aD//f7IAPwAOwCZ/4P96v2K/Vb9zwASAZgBRgOC/yL9yfzF+xf+mf8hAQcCDP/u/vn/iv9RAG8AOP90/f38WQByA5cDsQJ0/zj/cP5p/Ef/ZAGMBGAE9ACFAAT/lf4AAHT/dgBgApH/lf4T/6MA0wNKAgsBs/57+4b8hv4SAVUD5QAlAFkAlfwt/iwARgF9Ahv/Xf0p/cL+iQG9Af8BqgL5/9z9mf9kAeUCHQKjAFL+S/zQ/jcBQgSbBHoBZAF2AOP/1wDIAJ8BVQFw/ur9iv9kAS8FOwQSARv/0fox/VwB0wGJA/wAkf9RAF398v3U/fb8kf8m/gj+CwG6/hf+QgBD/rr+T/0X+vL7dPtS/qYBUQDeAAz/Wvzf/Ev+Nf7J/mX/CP4M/br8MwAwA/8DNwPU/Uv8OP39/iwCEgGuATABNf4lAFUBIQEOAhIB/AADASgB4gG6/vn/egP8AO0AOwAI/rkAvQEsAu0CJQD9/jz+BP9NA7wD/AJGA2z/Lf6MADsApgHAANj+lAC+/2AAqgL4AfwC+AEe/lEALAB7/2QBDP/j/6f/Tv/8AEf//f5d/9j+owCFAGz9oP/N/0P+DgDN/4UAs/7y+/L9BP9O/2sB1P+R/cL8WvwWAA4CZwLxAaT+CP7Q/s39xf9kAZH/Xf/F/Y7+1P9RAPQE0wMhAQAAHvzY/Kf/ZwAZAVwBTQEzADH/gQHLAyQCpgEzALP8zf13/h0AHQTABPgD/AAb/zsA6v9ZABkBVv8M/7P+1P21AVwDHQKfAWH+F/4I/tj8R//y/6YBywGZ/a/9E//Y/s3/LAB+AEoA6v3c/Yr9Uv6bApQCKAGn/9T9jv62/+UA7QILAUP+Nf6K+0P+OwKqAq4D3gC2/8L+Wv75/2z/Uv6O/t/+0P43AfwAIQGyAND+Af4B+qj9TQFNAVEE5QKqAB7+lfyr/Nz9wv57/2AAmAEgB4wE5QAZAWX9hvw4+w/+YwPLA8gEjAQ7Ap8Bd/7U++P/DgJ2ApABvv/IAkoCKf/F/6v+p//eAIr/pgHAALb/zwD9/rr+Kf0e/ND+HQDTASgDVQEi/x78qPtd/Xv9f/6z/iL/+f/Q/hv/IQGBAQMBlf5l/e7+PP4dAL0BQgJ9BG8CjADAAGX/dgCmA8QD/AILASUAQgJKAtYEzwQx/zz+4/2k/tcC5QK1AfQAUQAlAA/+S/4P/r77d/zy/c3//wHaAWAAVv/9/in9Jvpa+gj8q/zu/lgCqgR6A7r+7vwi/Xv/OwJL/qD9Nf6V/MAAqgQzBmAEHv6v+/n93/5NAZQC/wEsAi3+f/6FANoBGQXiAR0ABwAT/Rv/OwJcA8sDxf/Q/gAA+f3/ASgF4gObAo7+R/0T/1EAKANYBG8CZAEP/tT9tQG9AQoDWAKR/7P+d/5cAZQCmwDn/t/8EPx//hv/DgCUAs8AMf+++3j6lfxL/L7/AABh/v3+vvuZ+7P89vxnAJsC7QCR/XT72Pop/ZX+mf+5AB7+iv9O/3f+VQNRAjsA0P6K+0D9kf8SA4wGXAOuAU0B+f1L/sgA/AIKBUYDmAEwARIB6QMSAywCjAJKAEIAbP8LAR0CegFjA8QBTv/j/7UBFgIWAk0BQgBD/hf8cP6yAD4DkAMdAE7/nP4M/dz9p/+YAa4BAf7U/Tj/jv4hAQsBkf+K/1b7EPoi+3f80wHAAiwAd/6o+9D8+f+2/88AbP/N+2X7WvrC/qYDGQMzApX+6/uV/E/9AwHTA+P/Jv72/K/9AwOuA/8D0wGK/TH93/wI/koCEgOjAg4E5QAdAMQBowJNA0YBGQPXAor/OwB0/zMAWAT4AyED5QIZAWQBQgD8AAcEVQF//jj/dP83Af8BOwJcA+P//f6g/3/+zf8B/tT9FgCMAFwBQP9s/er/xf+G/q//R/2Z/XT/mf/8AJX++f1l/TX8nP4x/4UArgM+AZz+8v8E/Y7+OwAM/5QCBwB0/1EAR/0OAHIBhQDiAVL+R/0HAMn+DgJYBDMC6v9L/Ir7DP0P/lkAzwBO/2AC+f8B/m8AKf8ZAer/E//b/7b9p/8oA+IDlwPXAFr8dP2Z/1ECrgP0ACEBRgFcA5QEcgF6AXYAVv1W/Yr9GQEdBLUBmwKYAb7/MAFh/uP/iQEE/3IBQgBKAJgBLf7U/wMB2/+qACwAIv+qAMAClAQZA1L+Hv6K/dz9QgDj/xIBgQH8ANoBBwJkAcX/lf5h/nv96v0b/0D/YABgAEP+pP6MADMAZf8P/pH97vwp/d/+T/3u/t4AcP66/vX+q/5S/lL8bP1w/n4AzwLy/9cAtQGk/mH+E/8AALkAkf8lAEoAs/7XAn0COwBNAc39Iv9gAKMA0wEsAL0BegHn/q/9f/4LAUYBTQHEATsAQgAwAXoBLAKyAA4AjAC5AAMDdgIhAZABtv92AFwBuQDXAMAABwRnBM8A1P9L/gH8Q/7j/1kAvAObAjsAe/90/83/4/tP+wj+4/uZ+6D9Vv0OAMAA7v4T/xv9lfw1/AH8r/1w/JH9xf9//B78oP2z/v8BJALAABv/q/5H/+r9gv9KAhIBcgHxAcX/WQBgAPgB/ALlANcA+f2O/Fb/CwFgBK0HawNW//L9/fwlAFb/DgAsAIP9OwAT/0oAGQXwA9MBFgAX/jX+hv5ZAFECHQADAU0BOwAZA6YDXAM3Aaj9g/3Y/iwAlAI3A+IBMwKUAP3+Nf50/6oAtv3f/k7/tv2v/5H/4/1o/nf+Iv8p/zz8S/5w/nT9e//Y/LP+gv/j/c3/Zf3N/QcAAf7f/m8ApP6O/ob+3/6FAvQCegMWAt/8lf7XADABgQOJAS3+Q/5a/j4BXAXEBaIE9f6+/dT/QP9nAvgBXAESAbP+MwBkAQsBpgHXALb/egHy/ywCegXiAzADG/1h/GX/MwDtAnIB7QBnALb/KAMSBWcCjAAi/Yr5QP1o/gsB+AMsAlEEUQB//Az9VvvQ/rIA4/8OAJn9T/0sAO7+Uv4sAAH+6v0E/Tj9yABgAN4A1P32+mz9Kf0E/Tj/hQC2/4r/8v9d/xf+2P7PANv/XAHPAAT/wAB3/rIAQgTIAiwCHv5D/oUCEgPEAwMDXAEwAeP/r/8sAiEBIQOIBZsABP8p/dD8UQCjAGACZwC6/CL/hv6R/yEFqgDf/M39EPqG/M3/YACbAsQBSgDC/DH7s/6v/6D/NwHU/3D+7QDxAfwCJATIAjj/ZftW/V3/OwBgAvwAmwDaAT4B3gA3AXYAZf/u/r7/LAC6/lkAfgDN//QCowDj/aT+G/13/noBbwKiBEICIv+UALb/GQPEA8gAXAF0/SL/SgLaATMGmwblArIAE/1w/HYA+AG8AwcCpP6YAaMAKf+uARv/Zf2R/dT7Kf/AAPQAsgB3/Gz94/sb+3D+dP0E/x0A3/6k/i380fpP/br+hQCK/5X8aP66/Dz8oP/5/yEB9f4m+rr6PP7PAtYErgH5/8X7g/l2AP8BUQI+BT4BPP4M/TH9AwEhA/QELAQZAdcCegOmARkFGQVnAKT+3/x//ssB1gSFBssDuQKbAFL+oP/Y/hv/MAESAVwBTQHPAJH/Nf7lAE0BbwBcAXv9Iv0LAaoADgIzAsgAAwHu/rkAuQJCACEBbwD2/MX/AAAp/w4CEgG1AZH/F/7j/1b9R//tAHT9lf7J/r779f66/gz/cgHu/JH9g/35+wT9WvzY/ED9Xf2K/x0ClACMAMn+ZfsI/Lf79f6UAkkEUQRA/5n9Xf+yAJcD+ANrAef+zf16ASQGBgiiCFECnfz2/Jn7EgE+Be0C7QIzAE7/bP/F/2MDiQMhAW8Aq/w8/Gj+Iv30AqIERgEWAML8afyZ/X/+oP8DAdcAvQEzAKD/VQOUANT/bP9p/BP9T/2n/ygDvAMkBPQAr/1KAAAADgA7AE/96v22/wcAe/87AGsBDgCk/u78uvjr+dz98v9RAmAA6v9S/kT80PzC+q/9kf9d/8sBbP+G/mAAMwC9AVECSgCR/7P+dP92ArkCJAQ+Ax0AUQIoA7kC4gEOAJsA3gC5AM8CJAQhAwcABP0WACUAp//TAa//IQFVAbkAVQEsAND+xfvq/QsBQgCg/7r+oP+UAHD+zf3C/vL/4gGMAP3+D/6G/CwAywFa/lr+OP1l/QsBlAJGA5QAgv9gABf+bP+uAav+5/7AAHT/R//u/sgAZwDj/5ADmAH1/jX+CPyc/mQBLABNAbIAyf44/83/wABH/5n/mf9a/hYAPgFYBOEFAwOK/3v9Kf+o/Wn8JQDeACwCRgPeAtYEbwRrAXT93PvF/ZH9G/8dBDMEKAMZAYb8bPsm/qYDOwTeAvQC4/9h/rb/IQEWAiQCxf/Y/sL+xf8wA3IDVQNNA/L9Xvmk/FwBwARKAr79Q/7C/PL9dP8OAA4Cr/0m+mH69vxKAND+vv3N/WH+r/9l//X+Af71/pX+UvzJ/JX8g/0wAZQA/ACQBXoDNwEt/sL8CwHU/wAAlADXADADywFRAiwG3gSJAZn/KvvF/WsBdgKQBfgDMwL9/o7+jALTATAD3gQM//36q/wHAFwD3gQzBND+EPxL/h7+tQG5BCEB/f6r/in/8v3J/oUCegG9AVkADP3c/er9s/6qAFwBkAFs/7b9p/8M/9cAMAET/QAA4/+r/rkAWQD8AHT/DP1o/gz/BwBrAWX//wEZAaT6Xvs1/mQBmwKg/wj8OPst/Nz99AAhAwsBnfot+v38bwAsBAoD2gGZ/eP7Wv6G/mcAiQFCAukB+f2O/IEBzwZjByEDVv9S/q/7qP2C//EBAwcWAiL/2//9/t4AQgKqBHoD4/0m/B78EPxrAZ8D/wHAAhf+ivvF/xYCrgF3/sX78vtW+3f+xAOMBDcFxAHy+xP7oPsB/vL/HQJGA9v/+f9KAB0A9AJ2AssBwADQ/hv//AD4A6MCT/35+/b8Tv+1A+0CBwIAAHv9Lf6R/YUADP9H++r9hQCjAGQBQgI4/zz8G/uK/e0A4gObBM8AuQDY/sb5ivsLAWMFRgfPBNoBNf7f+gH8nP5nAvwCDgBCAHIBZAHiAZQCFgLf/vn7yfz9/ukBWAJgAjsCpP5e+zX8YACUAv8BZAGfAZH/gv9a/t/86QHxAZsAvv8p/YP9pP7XAEICWQC+/9cAf/5RAGQBTv8wAXT/E/2K/fn9mwDpA/8DfQQ+Ae76ivsE/WcAYAT8AJQA+AG+/x0A6v+fAYEBMf1P/XD+CwEWAt4A2gGjAtv/nfyr/Nj8Yf7b/4kBTQF2AKoAuv4e/rP8xfs4/fn9uvwt/GH+lwMOBED/9f5A/e78T/1P+2X/sQJcAcgAgv92AMsDmwCv//3+S/59BPADAwNgAgj+1P/5/zH/EgWfBSgDAwPQ/pQAOwJKACEBpP6qAPsEywOmA28COP9VAZsAbP0OAGcAZAFnAoUCIQXTAV39f/z2/IkBGQOg/4b+xf0E/WX/IQGYAaYB5/4x/Yb8Mf3XADMAE/8B/nv7R/26/kf/4/+g/7r+g/tL/KoAGQHlAEIAjv7y/Xf8mftE/E7/CgOMAoL/HQBl/+P95QB2AHoBVQF0/Sb8QPtZAKoEawOxAmcAjvzc/Yr/LAAwAw4AXf/u/kD90wESAe0AhQIx/0D/0wHIAMAA2/8p/3oB6v2C/5cD1wB6AwcCZf0lAGAAZf+QAaMCgQMzAqD/UQBO/94AogSqAKv+4/26+u78R/8OAlEEZwL8ALr+Zf2C//3+dP3u/rP8T/ta/mcAxAPTA2sBKf90+0D99f4i/7kCuQBZAIwEYAKQAeUAhv65AFb/Wv5cAW8A6QFnBFQF1gZGAe78RPxw/JgBsQISA6oENwF7/8AAJQBs/5z+Nfw8/owAXAHTASwAxAEE/9z7HQBcAZQA5QBD/rP8Kvvr+bP+/f7LAa4FbP/q/6f/7vyg/w/+Kf0M/TH9BwJnAsAAQgQdAK/7Jv4M/e7+zwDAAFUDqgIOAv8B3/6jACQCOP8+ATsAaP4oAQoDfQbtBFkAoP8x/6//ywHIAvQC1wLj/yL/OwBgANoBNwH8AHv/PPwI/LP6Vv0sAjMCGQF//jH9wvwE/aoAUQI+ASL/kfta+nv9DgCUAs8Cxf+g/dz7/f7AAnIDtQOZ/+v5e/uFAM8C0wXIAt/+bP3r+7b/lf5//qYBd/5w/rUBZAEdApQCqgAdAJX8Mf1CAIb+0wHTA8gA3/4Q/KT6d/5yA1wFNwOg/+P/vv/1/hIDtQO1AZsADPuo+7kA6QHEAywCp//j/SL98QFrA5gBPgNZAHf8yfwt+iL7Iv9KAB0CiQGK/xP9vvll+6T+WQAWAtD+Uvy6/qMAiQFKAEf/Hv75+139MAGxAiwCZwJl/139Tv+2/9oDywUhAyQCmf8WAEf/tv1gADAB1wKJAYb+RgGqAoUCqgTpAQT/UQDc/Xf+CwFCABYCtQEWAGcA7v7XAK4Be/2z/q//Vv9nAg4C8QFnAKj7Afz9/Gz/ZwTTAYr/OwAM/9oBJAJH/5n/Xf2r/Jn/nP7lAJcDLAIwA6oAaP5w/mH8Zf8oA6YBywFh/u764/2R/UoCWAaYAU/96/lE+u7+UQL0Ag4Ef/4e/OP9bP1JBOkBjvxS/nT9S/4lACEBLASMBNMB5QL5/Uf7uv6n/1gElwPu/kv+uv75//8B2gG5AIP9zfnY/vwC7QQ3BWAALf53/Gz7bP1kAR0E4gMHALP86v1d/aMAKAWqAlEA/fyd/BIBNwOXA28APP6Z/e78XAFnBDcDOwLJ/gj8uv6bALwD6QXIApgBJv5H/ZQANwGJAwoDp/9W/Yb8kf+BA4ED/AJyA47+Hvzu/Nz94gPTA8X/Yf5W++r9QgC6/ukBFgAT/dj+xftS/Bv/Iv+UAm8CaP4i/R/6hvpd/6f/6QEHAH/6qP1ZAPQAKAPLASn/3P3n+u786v+1AfQEzwDf/qv+vvvY/msDCgPEAZn/nfzN/2cAlAA+AS38iv1RADMARgMWAtv/JAJS/nT7cPyz/JABBwK1AXoD5QB7/34AIv+n/w4CHv7J/sX/d/5CBCgFRgMDAfL7S/zn/n4AMwZYBhkBXf8B+vb4dP3xAYUGtQUkAmcAZf26+tT9Q/5kAdcCdP2k/hIBsQTPBIkBuv7R+h/6PPxNAYUEtQcSBRv9lfoi+ef6r/96A30ExAElAIr/3/7IAJ8BKf1L+hv9E/+fAbEEZwSxAhYACwF+ABP/ywHpAfgB9ALb/6j9+f+bAHID2gV2BIL/FPmv/fQAhQCUAkIAmf1d/7UBOwBNAUoARPyR+0f7mf3f/hv/owL0AJX+SgDn/Gz9IQF7/4r/s/5w/ND8T/0sAKYB4/0b/yn/zfs1/kf/tQH/A4wAdgB2AJn/sgBa/gT9DP81/mz9qgKIBaoEogTAANz9Nfwi+zz+GQE7BPgF3gK1AYwAt/tH/dv/+f+UAvEBkAG9AaoAawOBAyEB9AC6/DX+2gWfBWAG5QTU+wX7xfuk/tMFEgP8AvEBbP3N//wAmAHaATH/3/qG/IL/gQGBA6oAQgAt/KD5D/6MACEDMANo/u783/w4+3T/9AALAfEB7vzj/fL/Q/5RAAcAe/0I/Ev8/f4oAWACJAKQAQAA5/6Z/Qj+owJyA64DEgNvABP/E/3Y/L0BlwObANcAhQDlAv8DogQ+BYP9Kvt0+7r6UQDXAiQCRgNCAND+tv/N/x0CBP/y+1L+2/8hAZcDGQE4/8gAbP9nAHT/wv6C//X+1wCbAN/+Xf+g/+r/lwMDAywAIv2V+v3+MAH4AWsB/fxh/P38Uv59ArkEPgPF/3f8E/t7/doBtQP0AGz/Kf8p/eP/hQDb/7kAmwBcASwAzwLlAnv/Yf4i/c39vQGxArP+KAGMAqYBZwCR/aT+iv0+AbkEEgHeAPL/Mf1gAPgD5QKyALr8CPwzAHIDXAeqBI7+2/+z/in/cgGqAPwCRgEe/nD+pP47ANMBDgDAAML+4/mK/WcA/AIoAzH/xf0q+6j78v+mATMCFgAf+Pn5xf8AAKIElwM+AU0Btv2C/zcBYf71/pn9T/38ADsAfQTwB+IDgQFw/t/8S/wQ/E0BMwabBKMCLACz/iQCVv9L/gMBQP3r+777BP9yA28C0wPIAqv8IvsM/Uv+8QGR/6/7BP2k/BIBLALTAbUDvv3Y+qD72PqO/s8CmwC+/6v+CP7b/139wAAsAjX+d/w5+QH8OwLaAygDUQJL/s39bP/AACEFmwCg/UD/Nf7EAeUElwVcBX4AhvzY/kD/yADAAowCqgR2ACn96v/EAYUCegHN/1b/DP0t/AMBEgNGA7IAS/xS/nT/Yf5CAAsB/f7c/QH+4/9vAC3+Kf+K/zj/8v/j/Q/+S/7n/Nj+WQDtAG8AXf2K/RIBDgAOAJABWv6c/pz+yf5KAN/+2/9d/3v9hv6jAGcC3gQ3AUT8OP2G/M3/tQNJBHIDLf7n/DMArgEoA7EEnwFW/zsAKAHLA6oC7QBrA00DyAJCAoUARgOJA7P+kf1KACwCkAFvAB0EfQbLATABiv+d/M8AwAA4/8sBtQFCADsAbP8OAFL+Bfvj/fn9p/9NBVUDOwA8/gj6CPob/Uv+6v8T/47+aP7J+mz9awGMAA4Aq/7J/CL/fgDF/7kCQgAB/kP+EPxd/z4BiQEHBPQCXf9S/gT/xAE3AwAAywFgAJX8e/+R/30C9ASv/xP9YfzY/PL/dgCmAyQGiv/q/WAAaP6bACwC+f+c/nT92P7lAFECZwQsBJ8BbwAm/iL9QgAwAU0BIQGqAFEC/ADb/+UCPgEt/mz9Mft//n0CgQPeAv3+Xf3F/cX9pP4OAKD9kf01/rP8AADq/4r/DgCD/Vb90PzF+9/8Vv9CAnIF6QEE/R7+d/5KAJABxAFrAQT//ABcA5QCiQE+AV3/p//8AkoCUQJ2AhkBMAEWAE0BiQE1/jMA6QEAAFEAbP/5/ZH9mf+XA7wFQgSyAPb8Ofmo+5z+OwBGA8sB/f4X/psAhQJ6ARkBaP72+DH7QgKYAQ4C1wLC/MX7afy3+/n/uQCbAlUDPP7Y/mj+iv1rAYkBnP6O/sL89vzlACwC2gUDAwT9f/yo+xP/pgN9BJQCMwCZ/b79kf/IAP8DxAFvAKoAcPzY/mAChQKmAyQCKf+R/Wn8pP5YBCEFxAMt/qj5JQBnAp8BAACd+kD7Mf3J/rkEUQZYBL0BpPq++Q/+Wv4b/3oBDgC2/3oBbwBKAiwCHQLXAOP5zfnF/QcCogZnBPn/CwFgANT9PP5rAZsEAADU+wH+oP3f/ukDNwPIAt4CBP2G+gj8Jv5vAk0DlADN/WH69f7iA8AAUQAi/538aP62/13/nwEHAiEBKf/F/UoCEgMSAQMBKf8x/cL+hv4i/3YEgQVjA8X9S/x2ALb/6v/y/9j8q/7b/839gQHxAQAADgCO/Ef9Kf0Q/N4A+f/9/iEBwv62/2QB9AD0AOr/D/41/MX7BwA7BEICbwTPAgj+UQBW/34AjALXAGAA+f1P/aYBSgKxAs8EMwCg/Q4Atv8zAK4BMwAOAN/+Uv4zAJsAWARJBFr+q/zj/br+PgHPAqoCvv+G/NT9d/wzAAoFRgE7ALIAq/57/70B4/+C/47+vv2g/Yb8egFnAjABXAEX/i3+CwGQAXYAe//J/qj9G/uK/YwAawFJBJsCZAEoAZz+mf0T/Vb9aP5s/0YDdgYHBBIDWAJ7/R78cP7J/iEBywGFAPwClACZ/77/9f7EAU7/8v3eAPgBiQF6AwoDhQCZ/ef6AAADAWACiQPy/xkBvv9d/4kBKANyA4wAQ/4oATMCPP7N/47+DP2r/jX8E/+jAtMBqgBw/uUA7QC6+kf7DP1s/T4BvQGC/47+d/wB/EP+9f7PAJX+EPyC/3v9Yf7EA/EBR/8x/aD7G/39/I7+qgI7At4AHv54+qf/kAMLAXYAOP9H/+r/yf4ZAZgBUQBCAur/HQCXA+r/mf9kAXT/JQBGAeIBwAK9AYUC/wFd/9oBSgJ6AWACr/+K/Qz/cgHeAqYDXAMhA0f/Uvy+/QT90P6uAc8AzwAdAo7+PPz1/vQARgHr+3v5XvtS/BIBOwQvBbkE1P8I+v34+f1gAvEBwAAsAgcAcP7aAX0CJAR2BFEAvv2D/d/++f+fATsEwARgAP3+G/9H/XYA/AK5Ain/jvwb/Tz83/6BAUoATv+n/zX+Iv0T/5gBCwHY/Aj8jvzY/B0CWAQkAp8D5QDU+wH+ZwC1Ac3/CP6jAkYD2gObBmsDPgEWAPn7Wvxd/6D/HQLEAw4ErgN7/b79nwHU/6YBTQET/fn9hv7IAM8EVQF//tj6Afgx/af/wAJnCNMFuv6O/Nj6JvwAAKYBkAXAAmz/gv84/f8B/wVyAa//Mf8x/dMBSQRRBEkG+AGr/nf84/mC/7kCvQGxBJsAQ/4dAP36pPzu/tD8Kf8E/+f+KAFKAGQBQgKv/br6OfkT+5QAkAPpBWMD9vz9/Gj+g/0hASwCxf/5//n/vQFjA28CFgBS/h7+3/6+/dz9awPiA5QC4gHq/Rf+HQDAAA4AjAByAbP+iv3b/3YAzf9ZAH/+8vs4/Vb/r/84/1kArgGC/2X/dP9A/Y7+1P+g/83/dgDu/h7+vv/xAfgDDgILAZX+E/04/x0AXAH5/0P+PP6K/zsARgFkAa/9yfxE/Cb8DP8OApQC7QCFAIUAdgAT/6T+R/+6/AH+NwHXACEDWAQOAowAgv/Q/gT/5/7F//EBegEwAWz/CP5vAB0A/ABCAmX/Iv1//AH+gQG1ASwA9AJnAu7+5QDb/wcAMAPeAA4AbP8E/wsBXAHEARkD1wBCAPgDWAK8AzcFLADF/Uf9wv6UADcBDgLxAbP+q/7b/7791P8LAYUAhQCk/kP+oP2O/DMAsgD9/Fb9yfpH+1gCEgNkAU0BXf1L/Cb+fgASBfQCIv+z/sL8qP3/AWMDawP/AVL+bP1W/0IExwY3A77/nP4B/KD9kAHtAJsCGQHu/kD/CP6K//wAAwPIBM3/XvvU/e7+jAIdBhIDgv9p/Cr7Iv1VA5sGKAUDATX+DP+k/pgBwAJcAaMA4/2g+9D81wBNA5QEDgKG/JL57vpCAJADfQKFAGn8RPqV/EP+DgDeAGz/wvwp/eUAGQOmAXv/zwBd/3f+hv7U/cgA/wEoAWz/3/5A//X+kf8hASQCxAGQAaf/oP8WAIr/R/9a/Nj8Jv6k/qoAnwEsAvwAQP97/U/98v04/4EBtv+C/zsAjv5W/1kAG/8X/i3+Iv35/xYCmAGQA4kBGQGjAFb9pPxA/a///wHIAqYB/ACUANcAdgCg/2cAyf6v/28A/f7j/xkDQgQSAeP/lf6D/dD8nP4hA8QBhQAHAH/+VQEzApn/uv5H/0IAcgF6A64D9ACr/Cb86v1H/VUBYwN9AgMD/wEhAUf/f/6V/jz+tv2n/7IAqgIKBwoFMAFl/az6zfmd/GACWATXAlEA2//u/u7+6v8p/8n+5/7u/n/+kf/iAUoCuQDlAFr+oPl//HIBmwIsBJ8DDgCD/UT8QP2+/7kC1wKg/+f+OwC2/13/mwL0ArP+6/tp+mn8zwJ2BrkG4gP9/rP87vq2/YkD0wNNAQT/nfwi/woDTQPXAsX9lfoM+3D81wBNA1QF8AN3/sn6Mfsx/f3+Zf9o/rb/7v6k/igBlAI7Aqf/G/04+zH98v+MAFUDZwSBA00BJv6k/FL8pP5VAWcCvQEoAYkB7QJrAyEBSgDY/gT9f/xd/5sEZwYZBekBMf+6/Lr8/fwP/lwBPgF0/+P/MwL8APwAFgKjAKv+9vo8+pX8fgAkBG8E3gAm/M353P2BBZ8HQgYzAtD88vlw+q/9XAGfA2ACyAA3AXYAE/9+AFwB5/44+8L68v2BAcQFZwYOArb9e/t/+ur9xANvBL0Bjv57/Uv+XAGuAzsCowCR/ZX6IvuK/7UDXAW5AgH+t/t/+uP9ZAHTAXYCZwCV/Lf7pP6FAP8BAwN6AY7+CPzn/EYB3gRGBRUEMf94+lr6S/wDAXkHcgkHBOP9LfwT/WH+GQE+AzsCQgCjABYCzwIZA8X/3P0WAFkAxf3J/sgCbwISAUIAWv41/KT+LAKXA/QErgGg/QX7pPwb/x7+xf9yAaoA5QDlAg4CIv/N/dj+8v0B/k0DuQR6A6MCpP7j+/38cP4OAM8AdgJjAzcBxAEzAMn8xf1w/ib8ivt0/+0CawP/Ax0CbP1E/KT8Kf25ADsEYAJl/6v+bP2k/hkB9AIkAiL/d/4WAE0B3gL0BIUCG//F+9/6r//PAh0EKAOR/0v+R/1l/eIB+ANnArkAaP5d/TMAywFKACL/hvzj+/38OP9gBIwGrgOK/Tn3rPYe/FkAMwSqBsgCAf7f+oP5t/uO/in/Af5H/Yr/zf9CAP8DvAO+/1b76/le+8X9oP+9AX0EGQP8AIL/3P0b/wz/Lf5GAcQBmwAkAq4BRgFgAIr/hQA4/1b/cgG5ADcBkAHu/psAbwILAVkAfgBkAQT/DP0AAAMD+AFgAFb/8v3u/uP/gQEKA88C8v+d/L77S/zN/zsCxAO5Avn/6v/b//3+iv1a/vL/1wDlABYCpgE4/5n/nP7Y/oUA6v/y/bP+fgBCAAAAVv+k/k/9JQA+A6YBdP8t/vb8/fot/Kf/6QF+AOP/RgHLAZ8DbwJL/k/95/xP+0/99AC8A7EEFQT8ABv9iv1A/wAAIQF2ApgBwAK5BMsDbwIzAFL+9vzJ/Ev+awGuAbECjATiA9MDR//Q/Dz+BP/f/lb/UQDJ/gT/xf+MANcAlf7U+yL9bP+C/1EAVQE3AwsBxf+FAAj+9vwQ/Hf8pP7U/wz/QgDTA3ID/ABd/+7+9f5a/hv/yACUAGj+Zf2V/jj/6v/y/wT/Iv+V/hv/zf/y/av8cPwi/TH/IQGYAR0AnP4I/sX9G/1W/bP+OwD8AtYEjASbAr7/lf5ZAPQCDgSqAnYArgEkBD4F1gQHBDADPgET/9D8BP8+Ax0ETQO9AZQAlAA3AYEBiQFnAN/+7vxS/Mn+RgFNAw4EawMWAAT9bP2K/dD+1wB6AfEBGQHY/hP/pgGfAWQBZAHJ/hf83/oE/ZgBLwVUBZgBiv3j+6D7g/3tApcDbwB//uf8vv13/gAAHQKQAY7+zfuD+wz/owLlAMAA6v+K/Xv9mf2MAM8CQgLaARIBYf5d/Uv+kAHLBUIE/wFnAH/+yf6JAXoDOwIZAUIAOwJnBDMEgQFd/Uf9r/1D/vwARgN2ApQAPgF+AEP+Jv4AAIUA+f+C/+7+1P/IACQClALPAOr94/lA+/EBiAX4A2cADP+c/lb9Yf5nAKf/Yf5d/6//zwDiASwAnP6v/Rv/2/9//k/9S/wI/t4C7QQ3Aav+nfw4+2X91P8DAer/DP8m/vL9Q/5s/wsBr//n/sX9pPx3/okBuQLXAGH+uvzf/Nz9PgH/A/EBDP+g/Wj+AAAHAtcC8QEHAm8ANf41/oUA7QIdBLwDEgFL/q/7pPxKANoBYAK1AWAAG/8M/5QAGQMSA9/+uvqd+Mn6f/7AAPwCqgIlALP+0P4p/5H9cPzj/aj9CP6bAMQBzwIOAr7/bP/C/hf+OP+2/1EAawEwAQMBTQELAQsBLAAx/34AvQGuASEBwADIAIL/S/41/uf+7QBvArUBGQGUAMX9e/39/l3/SgDj/3YAEgHF/w4AAAB7/2X/Mf08/EoATQH5/8gCawNvAE7/BwDAAOkB0wFd/yL9Yf4LAaYByAKQA00DGQNnAP387vzN/UP+lAAZA8ACMwDN/bb9Vv/q/1kAmf14+lb7afxA/4wCAwN2AML8H/rj+9j+owB6AbP+/fy3+xP9uQCUAmcChQDu/ob+mf9A/xYCxANRAq4BJQDb/34AowIKAx0EMwQKA8sBdP9vACQCVQPiAWz/T/3q/eUA6QO8Bc8CLAAm/ob8pPy+/+IBmwAAAGz/r/9gALUBEgN6A6MAjvxP+2H+2gPIBPEBQP+R/aD9ZwBCAsACywGG/pn7CPw7AGACzwJkAef+G/04+8n8wAD8Av8BR/8Q/LP6Uvw7AKoC4gESAYL/Mf3n/JH/KAEwAVkAe/3J+tj6Mf/7BJcH4QWK/175Vvm++3T/sQQSB30EMwBS/O76xf2jAFECfQIhAe7+G/9l/88A+AN6Aef+cPwb+0P+owL0BOUEHQKo/U/7G/kx/YUCkAPAAvn/PP6r/vQAywHlAkf/xfsT/er9zwADA+0CbwCV/kv+Iv97/wsBYwMWAiwC8QHxAX0CGQEHAKT+lfwX/h0C0wPABK4DHQIOAssBPgFZACUA5QAlADX+dP1W/VEATQMzArUBgQHQ/qT8qPu6/K//4/90/4wAtQFrAaD/aP5h/mj+dP1p/Hf8DP8+A9MF+AOFADX+YfyD/cAADgLb/6j9PP5ZAFwDpgO5ACb+yfpp+h7+/wGbBM8CjACZ/+f+nP5L/qT+owD/AaD/dP3f/BP/bwJvBDAD3/6K+7r6+f3EAWAGUQabAHv9EPyZ/fQALAISAb0BJAKyAEv+iv1kAekDogSUAn/+uvxl/Rv/IQHPAvwCfgBs/UP+iv+FAIL/4/2z/jH/Zf/n/vn/qgAHAnYCyAAdAGX92Pxa/pn/mAEhA/gBZf9s/88AVQNJBM8CZwDc/fn9wv4OAGQBKAH0ADABlAI7An4ADgD5/eP90P7Q/B7++AF6A/wCe/+Z+4P7lfx3/rUBtQF3/mn8QP1W/3oBSgIlAAT9qPsI/ssBkAPLAzsC5/7F+xv9RgFyAygFAwOZ/XD8jv7IAD4DtQM7ADX+zf3N/SwATQMoBRIBMfuD+Z36Hv5kAYkBmf93/nD8d/zQ/jMA1wK9ASn9RPqo+R78Xf8SAQMDWATIABv95/wt/v8BjAQZA7kAq/6O/jsA0wGqBOEFPgOg/+f8yfyR/0oCcgOqBMACZf+k/uf+sgDPAhIDKAHu/jj93P1KADMCcgNyAXIBtQFD/hD8yfxd/58BEgOmAc8AKf+Z/TcBIQN6ASb+uvxp/Kv+dgKxAvwCuQDf/Fb7wv68A7EEDgL9/pH9oPsP/igBhQC2/2H+q/5NAR0CUQC2/xf+uvyd/F39dP+5AFEC5QB7/fn7qPsM/d4AtQNVA83/vvtE/Kj9wv43AaMCmwJNAWz/Iv/b/wcAZAEHAsgAgv84/+7+8v8hAy8FHQSFAFb9Nfyr/lECnwPTAV3/oP3Y/KD/3gL7BFwDMf8B/PL7G//PAL0BiQHIAtMB1P39/Fb/GQPLA1ECHQCk/v38vv1RAgoF5QRvAEf9afw4/QMBuQK9AY7+Hvy6/Jz+OwD/ATMC9ABl/xf8R/u+/cgAawOJAdT9xf0T/Xv9uQBVAygFSgJA/WH8lf6bADsCEgGZ/2X/Vv2G/mAA1wI3BfwCOP9E/Ib8pP6qArwDZAH9/hv9zf3J/kICpgMSARP/jv5a/qT+3gCBAdMBWQAX/lr+JQD0AOr/1wCUAGX/Mf8x//L/4gEHAlEAzwCn/x7+xf3y/8gC0wGg/6v+Zf+g/x0CwAIsAB7+Mf0p/wcAlAA7ANcAzwJ9ArkAnP6Z/XT9AAA3ASgBpgGFAL7/R/+bAPwAWQAdAF3/DP/N/0YBIQHPAMn+nfzQ/HD8R/3q/zMCHQJW/9/8OP2v/wcCEgPEAYb+Xvs1+pH9TQGYATcBmf9d/yQCdgTPBEYDIv+Z+/L7iv12ANcC3gS1BYwCLf6K+/b8OwAsAsgC+AOxAmX/5/5VAXoDhQKFAGH+iv1s/QAA/wO5BNoB3P04/6oARgFgAvgB3gAe/lr8g/vN/d4AFgKMAtcAyf53/Lf7kf21ASQEcgEt/o78oP1ZAK4BtQFRALr+Nf5o/u7+2gFnBJABaP7n/Bf8OP2MAFwDDgSQA34AF/4B/GH84/+YAbUBBwB3/gz9oP2n/6YBEgMHAGn88vtA/Qz/pgHTAaD/uv4b/QH84/12ADsAf/4E/34AEgGuAUICLALIAML+5/xA/TMAegGfAYwCNwPxAaT+oP22/5gB9AAm/jj93/6FAAcCuQL4AVb/QP01/FL8QP9cAQMBR/84/6D/iv8OAPQA4gG+//L9Xf+JARkBzwDlAGX/Vv9L/g/+BwB2Ah0EtQNjA/EB3P3J+ib87v75/4L/gv/PABYCtQHj/5z+Iv8M//L9wv7b/5sAUQB+AN4AhQCn/2n8uvzXAKYDDgQKA+UAr/04/TsAMAPAAr0BRgHeAJsAQgDAAKYBgQHb/wT/D/7J/ssBBwSBBU0DD/5w+vn5f/5rAwMDowBA/aD7OP2Z//8B2gFd/2X9qP2o/af/xAH0AO0ADgAT/wH+Zf1l/xkD5QQoA6oADP8t/mj+pgF6A+0CtQGz/gz9uv4+AXYCfQKR/wz9Vv0i/70BbwI3AcL+hvzY/O7+qgCuASEBZwAlAJz+Af52AMsDEgNH/1L8KvvU+13/BwRyBRkDXf93/v3+QP+z/r79Uv5L/o7+cgFVAywCfQKMAqoAtv3u+t/82gFrBa4FQgQlAIr7Lfo8/PQAWAS8BVUDUQCC/+7+Wv48/nf+6v1o/rP+lACxAq4DuQQsAsn+mfuS+Wn6Zf0WAhkFsQQWAqD/8v1s/Xv9D/5l/4r/mf8lAGX/HQDTAcsBHQD2/IP7Kf1KAMQDXAU+A0f/kfvu+qT+6QFjA94CAwFH/8X9r/1RAJQCDgKqABP9IvtE/Dj/xAOIBSgD+f2k+lL6yfybAH0EAwVgADH9EPy2/b0BJAQdBIUCJv4B+sX7bwCiBIEFYwWJA47+T/3N/6oCHQRjA13/nfzJ/HT91wC5BCgHuQTq/wj+jvx7+1b9nwG8A6MCnP7c+139e/99ArkCmf8t/BD6E/0wAZQC4gPlAnf+dPus+nD85/5+AIUCHQK+/9z93P0hASEFbwRRABv9G/tl/Z8BlAQvBb0BQP39+kP+4gOMBm4GAwMX/hD8pPzu/oUCUQRNA9cADP/f/v3+p/8sAMX/OwByAQcC2gHpAdMBAACg/RD8r/tL/Pn9lABNA9YEzwKz/l77YfoX/P3+hQDeAPn/Vv1p/Hf+KAHTAd4Axf1S+qD57vr5/Q4ClAT0Akf/cPy6/F3/2gFVA2QBOP0X+v36LAD/BdIHnwXLAe78g/vj/YkBfQTIBJ8DiQFA/5X+FgAKA4gFpgMp/5X8bPt//lEE1gYoBVEAUvzy+3/+VQPABvsEZwAI/DX6Mf1NAQcEJATlABv9T/vu/JsAAwUzBgoDJv6++4P9yf5+ABYCpgFd/9j8ivtp/HT/SgKxBE0DdP+6/BP7dPvq/bIArgGg/6/73/rJ/DsARgMzAin/LfzR+nD8WQBNA1gEowJH/w/+d/7U/8sBKAMkAoUAOwCBAbkCxAFyAfEBGQFW/0f/zwCfAbUBsgCQAQoDowD9/H/8DP9CABYAyADTAVkANf5w/gz/6v8M/7b9Hv6+/zcBnwHXAsQB5/6d/Lr8/f4zAOP//f79/in/ZwCQAVUBzf/u/t/+Wv71/uP/RgFNAWz/Mf1W/Q/+Lf52ALUB3gK1AQj+afxw/K/9bwD4ASwC5QKUAC3+7vx7/X4AkAH0AKD/Zf9CAGsBdgL8ArUBpP6k/Of8pP5rAdoDVQPEAXT/3P1l/Rf+JALwAzMCE/9E/Mn8sgA+A7EC6QHF/8L8kfvq/XoB2gMVBJgBBP+K/b79mf8kAk0DXAHU/Xf8q/5vAuEFJAbtAl3/F/ys+qj9nwGuA4kDnwGMAAAApP7Y/IP9DgAZAZsAXf+n/6oAowAdAL7/hv6++6D7Hv4SAVEEhQSQAbr+pPwF+7P8YACxAtcCTQGbAF3/Uv6g/4wAbwBh/l39lAC8AxUE4gF7/3f+Nf6G/uP/gQHpASwCXAHN/yn/Lf57/TX+mf9ZAIkBtQEHAB7+/fx3/jj/lf6r/mz/KAHpAZsA6v+yAEf/DP0M/UP+9ACuA+kD7QLaAXT/iv35/UIAowIdAtT/S/4i/+UCOwS5AhIBuv4P/pz+LACqAvwCZwJRAsgA2/+2//n9Q/4WAFUB1wIdAiL/Lf7q/8gCkAM3ASn/QP1H/er/egFnAh0C5/6k/Or9JQBgArkCZAEp/yL9G/3C/PL9IQGBAUf/6v3C/ED9Iv+v/w4AbP9L/h78lfox/e0AowIOApn/pPxh/M39bP9RAoUEIQMp/5X8afzc/ekBxAXhBUkEzwCG/M396QEoAx0EegPlADH/Yf7j/6oCPgU3BW8CdP9s/UT83/y5ANoDWAT/AXT/DP8OAOIBXAEdAJX+pPxh/KT+fQKqBDME3gCd/ED7Jv6FAjMEuQJs/6T8/fwP/pH/CwHeALIA5/7U/bP+r//IAM8AMwAT/9z9q/xP/af/EgHXAAT/Vv2g/a//YAJrA+0AE/2g+b75/fyMAEYDBwR6Aw4AcPyg+/L9VQHAAnYCEgEAAJX+Xf2o/WAApgMoA94A2//5/1EAlABnAH4A6v93/qD9cP5GAZ8D+AMOAmH+Zfv2+o78LAA3A0oCKf+6/ND8Wv7lAJcDzwIM/3D8EPyz/Fb/4gGfAfwAJQBa/pn9lf6jANcCNwP0AGH+PP7q/70BCgPLA/wCSgA4/Uf9FgDIAj4DVQHb/5X+r/+fAUICNwOBAQ/+BP2G/in/mwAHAuIB/wGC/3/8jvxW/1gCvAOqAsAAIv9S/mz/iv/IALUBjABW/3f+tv/PAHoBcgELAd4Auv7U+5X8uQCBA64DAwFw/qT8e/s1/jMClwOQASb+t/ug+8n89f6MAlwDfgB0/Rf84/0ZAQoDpgM+AVb9Afrg+E/9lwP7BowG6QHj+536e/1kAc8EnwPU/7f74/kT/f8B7QSuA9v/hvyG/FL+jAAkAhkBJQBl/3/+Q/4HAJsCVQO5AjAB5/4I/LP8oP9NAfQCbwLPAM3/xf9vAHYAr/+k/hYAEgGZ/7b/sgBVAUICBwKyADj/iv04/Yr/HQJrA4wCBwAX/n/8f/wx/9MBYAJVAQ4AcP6D/Yb+DgAoAcAAYf5a/HT9AACuAQoDYAJH/0v8t/s8/p8B0wP7BIED9f7N+5n7iv3lAPwCqgJyAWAA7v5w/uP/QgIZA/8Bzf+Z/TsAxAP0AjcBgv+6/Az7oP3pAU0FxAUKA13/kftL/KD/tQGxBIwEegET/+v7xvl7+1b/jALXAhkBdgDb/5QAkAFZAFkAbP9p/ED7Mf0OAAoDNwNyAaMAe/26/F3/JAJnBE0DdgAI/t/8R/0AAP8BnwGR/0/9tv3Q/sAAhQKFAjcBHv4I/Ir92/9yAW8CgQEZAWz/5/zU/YUASgJGA3oDqgL4AR0Ahv6r/mAAfQKqAlEC0wEDAeUAxAHAAhYCbP88/pz+gv+jAhIFjASFAo7+VvvF/dcAUQK1A7kCOwAx/TX8DP0x/+0A7QAlADX+CP44/5H/Mf8x/zz+G/1W/TX+JQCjADj/aP4sACgBvv9o/h7+2/8ZASgByAC5AHv/aP78AEYDQgK+/6/9oP17/5sALAKBA00Bjv4E/Vb9p//TAXYC+AFs/7f7e/uV/sAA3gKFBOkBJv4m/ML8dP+jAJH//f50/77/egGjApADywMx/9/66/vc/Y7+vQG5BG8ElALb/5X+Xf9s/zj/jAADAeP/cP7c/V3/AwGbAA4A+f+2/Vb96v/4ASEDSgKz/tT7oPtp+nf8rgG1AzsETQO9AWAAqP2G/E7/SgC2/x0Axf9yAbkCUQLEAVEAd/7c/XD+BP9kASwEuQQZAzsAuvwI/Ib+/f5CAGcCGQE8/o78lfyv/94C1wIkAmX/oPvC+qT8xf+mAW8Amf0t/Lr8QP9RAu0CmAFCANT9RPzF/UoA1wIHBDMCZf/C/n/+DP+bAGsBfQKfAf3+Yf5CAFEChQTlBA4Cf/4q+wX7T/0T/zcB6QM3AxP/xf0E/2cAkAF2ANz9wvzY/Bf+MwLtBLECwv7r+6/7BP9GA/8FXAW5AFL+DP/9/owAsQIwAwMDPgEp/77/dgCv/yEBUQKBAUoAG//U/94AYADU/6MAhQD5/a/7CPyr/q4BawFD/nT9WvzJ+qj7R/1vAGACfgD5/Xv9Zf0p/SL9Vv2r/in/f/4i/4wAcgGUApABIv+2/TX8Vv2jALECRgObAn4Ahv5o/mj+f/5cAZQCkAFnAnIBqgDeAL7/1P8+Aa4ByADAAIwAhQAoAUoC5QKQAbb/Vv+fAU0DQgRrA+0A2/9//sX9BwCbArUBuQDj/7r+zf+2/6f/0wFRAoL/e/1P/ZX+lADlADsA0P5W/ZX81P3b/4kBwAI3ARv/8v0T/Qz9yf4zAPQAAwF//or9xf1w/igBlALPAPn9q/xw/Ib+TQFrAZsA9f5s/X/+BwCqAA4C5QJnAqMAoP2r/Bv/DgJjA6MC1wAdAMX/HQAdAoEDfQLAAOP/q/5S/or/uQCmARYC/ADY/vn9f/6MAKMCgQG2//3+Kf04/QcA8QF6A/QCtv/F/UD9d/6YAbUDxAMwAXT9F/w1/vQAqgIoAz4BIv/N/dj8Nf4dAlEEsQLIAK/9Ivsi/W8AWAISA4kBlf4M/Yb86v30AMgCnwOjArP+s/yR/ZH/IQOJAyQChQB0/Yb8bP/0AlwDzwJvAvQAdP++/yEB1wLlAhYAE/9s/7P+mf8oAVwBZwLtAL79f/7Y/pz+WQCFAOP/fgCo/RD8e/8sALb/vv9A/+7+bP+Z/9/+QP90/yL/1P92AA4AZAEzAkYBJQDu/NT79vzn/AcAHQQZA3IBbP8Q/Dz8G/2z/Of+VQELAeUAHQAb/yL//f7U/UD97v4dAPEB9AKyAJz+/f75/+0ADgILAVwBbwILAT4BywE7AHT/jv4m/p8B9AJYAnYC+f9L/jz+f/5nAAMD3gK5APX+oPvC+oP9JQAOAvgBSgAt/oP9T/1L/jcBawG2/5X+Af7F/3IDdgK+/5X+Mf1H/8AA5QBgAt4CXAGyAMAAiv8AANv/qgCBA/8D5QDU/Tj9QP1W//wAPgFcAQ4Ag/0T/Tj/ZAHLA3oDkAHU/9T9bP1a/v3+RgHwA30CMAHtAPL/JQBCAmcCRgHpAVb/3P0hAWsDlAKUAH/+4/0T/77/MAFcASwAiv9o/o7+DgASAfQAqgAM/+f8yfx7/ef+hQCBAZsAJv5d/Rv9tv0X/r79+f/XAGz//f7f/mH+E//f/rP+MAG5AKD/8v8i/47+Xf8lAGz/wv5o/qoAmwJYAkIClADN/br6S/rJ/PwAyAR9BFgCVv/5+yb8yf7PACwCYAKfAZ8BBwKMAkYDSgKbAOP/Kf/N/3oB5QJGBbEGywMM/5H9Zf+5AuUE5QK2/3T/DP/c/QT/fgCfAUICdgCr/ob+F/48/mz/bP+R/0D/g/35/ZH/lADEAVkADP2k/Gz9Zf3n/hYA7QDiAdT/Xf1W/Uv+Kf9gAM8ALAD9/mn8vvvj/U7/kf9gAKoAjv7C/Cn9dP9gArECIQFA/3/8kfu6/jADIQWJA3v/dP08/l3/8QHaA2sD+AEdAHT/IQHLARkBLALpAYUA3/7N/V3/iQE7AjABcgFrASwA+f+2/83/AwFkAX4ARgHlALP+DP8p/13/NwGyAAcAEgG5AFkAPgFcAUIAkf+c/qj93/7lAKMCIQMdAAT9oP1l//gBkAPeAGX/kf9A/e78f/6G/koA8QF2AOP/tv/y/UP+dP+R/6//cP5L/tT/jABNAZAB8v8t/or9Iv3j/d4A/ALeAowC2/9a/GH8dP3f/kYB/wGMALb/0P5//sAArgElAAz/+f3N/SwACwFcATMCmwBo/in9Xf0T/+IBPgPAAuIBtv/y/S3+Tv9vAEYBwABKABYA2P71/sAAwACMAIEBSgBW/zj/5/5nAEICUQL8ANT/DP8i/9v/GQGqAn0Czf8t/ob+tv/xAcsBxAE+A70Bjv4P/pn/jAD/AVgCFgBa/i3+xf1vAJcDdgK9AVkAE/3r+2z98v+uA/gDhQA4/w/+F/4OAN4AMAG5AHf+Hv5nACQCpgN6A1UBlf6R/a/9hv6QAQMD9AIHAk7/f/47AH4Ar//j/0IAjADj/4P9e/vc/TcBXAFZAIb+Zf0P/kv+q/4AAMX/OP8i/839BP0M/U/97v7AAMgA6v8AAGcAvv8AAAAAG/8lAL7/+f2r/gcAegFyA88CyADF/5X+SgC5Av8BlACZ/6f/dgAZATcBNwEhAe0A5QA+AX4A9f6n/xIBnwHiAVwBlADIAPL/G/+MAEoAYACFAJz+kf9cAekBDgJyAcgA+f/n/gj+pP7tAGACLAIdAoUA9f4x/wj+Hv5CAJn/jv6K//3+BwAoAcL+3/5d/yn9CPyG/Kj9FgDEAd4AQP/Y/Kj7jvyk/nYAbwBnAFb/4/13/or/hQC5AED/uv6R/5n/lAC1ASEBdgCg/9v//ADAABYAMwBcASQCdgL/AQcAd/75/e7+MAGJA+UCHQB//lr+dgAdAsQB/ABvAML+R/04/4EBEgOQAwMBqP3J/DH9xf+8A/gDRgNRAhv/nfx7/X4ARgOBAxkB1P/C/qD9Hv47AAcC+AH0AED/5/4lAMAA2/+Z/7r+OP0m/sL++f9NAWAAdP/u/oP9UvzC/Ir9OwBcA64D6QF3/rP6oPk8/Jn/gQHEAX4A7v6v/0IADP/5/w4AR/8HAAT/lf43AbkCfQI7An4AE/81/mz9uv5VAbUDcgOfAQ4Alf4i/28AAwELAYL/Zf10/Yr/BwJGA/EBMwBs/7P+1P1d/b79QP/tAGsBqgDF/5H/DgAoAfwAdP9S/tz9Wv6n/6MAPgFCAjMChQCK/zH/G/8WAOIBpgHU/yn/S/7C/iwAFgD5/6//e/8WAPn/Mf+yAIkBVv81/rb9Q/52AMAAdP/y/1kAhv7Q/lEAXf88/iUADgIkAjsCqgDf/gz/G/8b/6oAXAFGAVwBNwE+AUoACwHpAYEB5QCR/zH/lACMAvQCowI+AXYALADJ/tj+iv9nAK4BbwKuAcgAQP8e/gcACwGYAaMCxAHu/lb9oP0i/64BMwIDAer/QP+O/hv/RgFKAjMCAwHJ/qj9dP2K/cX/WAKbAkoA/fyo+6D9DgAlALb//f6O/v3+Mf93/lL+p/+g//3+Q/4E/TH9uv7N/zsA1wBvAE7/Wv6g/Sb+p/8WALIAcgFKABP/Yf6g//gBfQKYAfQAmAFVARIB4gHaAcACOwTpAwMDvQH0AH0CQgTaA3YCGQF0/wAAbwJnBIEFOwTeAFL+D/6c/pH/awF2Ag4CKAHu/mz9DP/8AMQBegFA/7P8+fsp/TcB/wPtAuUAqP0M++P79f4LAXoBAwHF/9D+xf0M/b79p/8OAGz/G/+D/aT8tv3J/nT/AwFCAC3+QP17+5X8oP+UAH4A8v9W/Wn6R/t//n0C3gRvAlL+bP10/b79sgAOAtoBIQET/3f+1P/TAYkD4gM7AkIADP9s/+kB/wNvBEYDGQFl/5z+Tv9yAT4DHQTtAgMBmf8m/uP/GQMOBBIDEgFh/nv9OP/y/zsAmwAHAEf/Q/6g/er9R/8hAcsBowC6/u786/t3/P3+XAEWApABR/9E/Ir7T/0P/lb/mAHTAaYBdgAB/vn94/8WAEoA5QBd/9z9zf39/r0BQgTtAlb/wvwt/KT+nwEKA3oDqgJZAHf+iv1S/uUARgFO/0v+Hv53/hYA/wF6A+kDNwFa/JH71P2C//gBJAJ+AM3/DP90/Xv9Iv+2/1kAywEDAw4Czf9H/X/8nP6qAJABUQCg/Xf8/f6JAZ8BoP8E/f38OP1L/lUBYAL8ABYAUv5L/C38vvs4/TMA3gBRAFEAxf93/uf+8v+K/0D/4/+R/2X/kf/9/mcAYAIsAsAAMf+V/n4AxANYBMACZAHb/5n/MwD5/7UB2gM3A2ACZAGR/83/owAzAGQBDgKFAPL/kf8E/wcAJAJGA30Cr//Y/AT95/52ABIBTQFRAHT/9f5L/jMAmwDN/1UBZwJRAGH88vnn+sX/mwJyAUf/hv7n/u7+sgCbAMn+nP7C/lL+S/4e/hP//wFvAuIB8v8B/Gn6uvxNAfADlAKK/5z+QP/q/5sA5QD5/0P+6v1W//wALAIkAh0Aiv8zAO0AOwL/AQsBsgAWAK//EgGfAWsBawFCAGAA2gEdAqYB6QFGAZQAJQDu/ur/ywEkAnoB6v9D/gH+4/8zAq4B1P88/p38R/0sAGQB8v8T/9/+s/7j/6f/BP/XANcAG/8i/zj/s/5l/wsBFgJgAmsBOwAAAB0AmwAZASgBowDj/3v/zf8hAaYBjAAHAPn/kf+2/5H/0P66/gT//f6UACgBR/9//lr+uv5A/3v/hv4m/pn/GQGbAnIB9f7y/bP+6v+K/8X/ZwDIAPgBqgJRAp8B+f+G/k7/dgASAWcCzwLpAXoByAAWAPn/p/8x/1EAJQAP/k7/EgE+AaYBhQCg/2cAR/8E/Yb8BP3C/iEBFgJVAVEAmf9S/mj+dgAoAXoBNwG2/9cABwLeAGAAyABW/9j+BwDAACQCiQFvABkBhQBA/2X/DgBRADcBHQIoAX/+jvwQ/Kj9tv8WAM8AVQEHAMn+Wv6D/TX+JQCqAM3/d/5A/a/9MwCYAW8Ahv6K/eP9jABYArUB6QHTAXIB4gFNAYb+qP04/zsAZwJVA9MBZAGBAfwAVQH8AAcA8v9O/9T/ZwLiA3IDyAKbACn9qPvJ/KD/7QK1A9oBEgFvAF3/hQDEASwAQP9RAB0Akf/n/o7+HQA3Abb/nP6R/9T/BwCqAHYAOP8T/6D/QP9d/2H+mf2O/u7+oP+qALkAdP8B/hv91P0p/+7++f8+AcgAxf/N/wcA2P48/ib+d/7J/rr+cP47AAoDAwOMAlkAOP0b/dD+MwBcAYkBhQBvAJQAYADN/9T/WQCmAXYC+f/j/Rf+vv+xAh0E4gEOAED/8v2C/wcCUQLEAX4AcP7Q/gcAHQD0ABYCegE4/xP9vvv9/GAAhQKYAQ4Avv0F++P7vv0OADsC0wEx/4P9oP3j/Yr/BwBd/+P/uQBRAL7/Vv84/1kAHQD0APQCFgIi/wz9qP3j/zMCHQKqAHv/G/8AAJgBjAKjAP3+pP7Q/uUAtQGFAFEAUQAAADABMwA1/kf/AAALATsC0wHXANv/G/+6/tv/UQCv/1kA2gFrARkBgQHq/4r/6v8T/2X/FgDb/6oA6QGfAZQATv9H/+0AiQHAAPL/yf4B/gz9mf3N/yEBSgIOAt4Ae/9W/UT8PP6R/2z/owB7/6v+Vv9L/s39lf79/r7/mAH0ABv/3/7U/d/8S/4M/6v+iv/N/6D/ZwAOAAj+dP0t/k7/QgDAAL0BFgKuAcgAIv9P/br86v3XACwEyARvAnT/e/1P/UD/ZAG5AjcDUQIlAND++f9vAIUAGQHIACwALABKAKoA2gGuAbIAwAASAZsAzwBkAXIBLAKBAU7/Lf7n/jMABwISA0IC4gEhAdv/tv84/47+e/87AN4AQgKBAbP+yfxw/ED9sgCfA28CdgBD/lr8Zf0OAE0BrgH8AOP9yfxa/pH/9ADLAVwBzwAOAHT9d/zC/iEBjAJ6Abb9Bfvr+3/+hQLPBGcC5/50+1r6Xf3XAMsBvQEhARP/dP2g/RP/xf/j/6f/vv/8ADcBjADIAH4AIv+C/5sA4/9//q/9DP8SAygF4gNGAYP9g/tA/TAB+AOuA4wA8v01/rr+bwAkAj4BBwCn/yn/G//N/wAABwDF/+r/8v+v/1EAfgDPAIwAR//Y/l3/Zf/y/x0CZwLpAWsBr/+V/or9xf25AJADlASQAygBZf8e/vn92/+9AaMCQgISAYUAhQBl//X+1P8zACwCQgIsANT/Vv/Q/jsATQHlADsAUv6K/QT/sgC9AdMBYADc/ef8CP7y/yEBPgG5ACUAnP6G/Bf+GQEHAnoBBwAT/7r+QP2V/Jn/gQH0AHoByABH/9/+d/5W/0oAXf93/jH/QgDF/4r/FgCR/6f/1wAzAE7/2P4T/fL9mwBvAL7/xf/f/n/+bP90/6//yABCAIL/p/9d/6//WQAzAGcANwEwAVkA4/+C/6//TQE+A0kENwMAAGz9+f2qAMgCiQPpAWH+9vzC/jsCbwR6A6oAPP4x/ef8QP+FApADEgOyAOr9LfwX/Jz+tQFNA4wCr/8t/vX+jADxAcQBHQAi/yL/BP9KANMByAIhA4EBwv7C/Gz9AADlAlwDOwK9AQcA5/7Q/nD+7v4T/xf+iv9VAQ4Ahv7j/cL+bwADAcX/wv7C/tT9OP1s/S3+AAADAdT/0P6n/7b/mf8DAQsBr/++/Vr8Tv96AxkDQgDq/1EAvv/9/kv+5/75/w4Azf8LAZABmf+6/uP/ZwDU/8n+bP0I/gz/2P44/2z/HQDxAWACsgAp/zj9Mf17/zMAfgCqAOr/uv7Y/hYAkAGxAnYCzwCV/kv+0P4LAa4DlALN/0v+wv6UAN4CvAPTA94C8v9s/SL9Iv+JARID6QPLA00Bjv6g/WH+dgBVAdMBcgHN/2X/vv8oAVwDYwO1AZX+DPt0+9/+JAKmAygDxAGjABYAe/+C/83/Kf8I/mz9Zf0i/6YBBwIhAfn/yf7N/fb84/uV/LP+2//tAIEBZf9L/Pn77vy6/n4A1P9S/sL8Lfyz/I7+TQFgAg4CuQAt/ob8DP3Y/qoAYAKjAkYBMwDN/w4A2/8sAJ8BIQMDA/QAOwCQAbwDegPpAfwA/f6D/Tz+YADIAvQEFQRVAXD+7vyk/s8A9ALiA+0CMwDU/TX+zf+yAH4AQgCZ/wcAfgDtAHYClAJKAg4CdgBP/VL8qP13/owA1wI+A+UCBwCk/A/+8v+n//L/gv+O/mH+S/6V/sAAfQL8ALr+cPwX+sL6hv47AigFvAX8APn7nfqd+jH9lADLAaMCmwIHAIb+dP9ZAK4BJALAAGX/wv4HAPwCWARcAxkBBP+v/e78s/61AZsEkAXiAZz+yfwq+3T9VQHtAjADNwGz/BP7PPwI/u0AgQFRALr+r/0I/nf+mf8lAB0A3gCv/9z92P4b/47+iv+g/w4AdgA4/+7+bwAhAVwBOwKqAJn9lfzy/cgAsQLiAZn/r/0Q/KD7E/+xAsACtQFvAJH/pP4T/cn8pP6UADcB2gGFAJz+s/6C/2cA/ACbANv/9ACmAU0BqgKxAhIBMAFvAAj+DP9CAq4D4gP/Af3+oP9RAvwCegOuAxkBp/9RADsAhQCUAA4A2/+5AHYCMAOUAlkA+f3f/BP9pP6jAJQCfQI7AFL+3P1d/+P/Q/4i/Y788v10/9D+bP8ZARYAmf08/Hv79vyK/8X/2/87AKj9G/st/ND+GQFVAfn/BP88/gT9pPwe/mcABwI7AiEBTv/f/tT/jACjAEf/mf1O/58BWAKJAzMCuQB+ADsAjACyACEBTQFKAowCWAKBAbb/q/6O/qoA9AJvBPADcgFgAK//yf4LAUoCsgDlAK//oP/pAVwBHQCFAIwAgv+C/2X/mf+UAAsB5QAdAIb+afzY/Nj+Kf84/w4AlACqAAT/DP2g/c39q/wM/XD+lf4M//L/r/8sAJQALABnAF3/Mf0i/aT+kf9RAK4BmwLTAYwAXf+C/6MARgF6AXYAiv/J/jH/uQDEAd4C0wGc/kv8OP0OAH0CDgKg/0D/bP/F/7b/0P7u/gcAowCyADsA/f79/jH/6v/eAOIBXAFS/rP8Zf07AKoCfQJ2AOr/bP/j/dD+AACFAN4A1wA4/3/+nP5w/tv/mwADAbIAtv8I/rb9JQBkAVwByAD1/l39F/57/0YB/AIdAkoAgv9S/vn9uQD0ArkCgQEZAdcA1wBvAK//9ACQAfwAnwGUAqYBPgGQAXoBmAFZAE7/+f9cAfgBOwLTAWcAKf/J/nT/lAAoAb7/oP8+AVwBdgD9/jj9Q/5RAHYAAwEDAaMAAAAp/xf+0Pzc/UoAhQJcA+IB5/4I/mz/3gCxAukBjv4p/e7+RgEdAgMBDgDj/07/DP/b/wAAFgCfAX0C8QEM/0T8F/z9/Dz+AABkAYUA0P7F/Xf+6v8wAekBdgAt/nD8Iv3F/7IA+f9RAH4A+f8WACwAGQESA9oD7QJ6AbP+Iv2V/tMBNwWfBWsDAABL/iL/sgBRAjADMwIDATcBwAByASEBWQA7AjABmf0X/Hv9owCuA8sDBwLb/0T8Mfts/cAAdgLLAZgBwACc/pH9g/0e/mcA/ABnAFkAR/9W/0IAYABgAFkASgAhAUD/Iv3J/s3/EgFkAV3/3P1D/lb/lADEAcX/Kf0x/U7/lAD0AGAApP6g/6MAr//5/Uv8R/t0/T4BlAJjA/gBKf+V/Ef7mf16AVwDSgJ0/0f9Q/6FAEoC7QLaARv/zfvC+tz9wAKqBEkEzwJ6AfL/T/3C/Ev+tv8lAOP/uv79/gMB2gEdAmQBkf8X/lb9Kf2k/igBBwJGAb7/8v39/IP9pP5ZAJ8BuQCv/zj/0P4p/6D/zf++/1kAhQBRAO0ATv+g/fX+SgAhAQsBG//C/vQAfQLpAQcCQgLj/4P9Wvzf/M3//AIOBMgCOP88/P38Xf96AaYBJQB0/eP7F/6JASEDCwEB/l39Jv6Z/Zz+OwDy/z4BhQAm/s39Hv7j/64DlwOn/wj+Vv2o/Zn/9AAoAT4BwAC+/4UAcgHAAN4AkAFRAMX/Iv9L/vn/IQEoASEBUQBW/wAAwABZAOr/dP+n/2cAgv8X/sL+Xf9A//L/KAFkAcgAp/9d/d/8f/7C/qD/mAGMADj/f/5w/sAAvQFCADH/Kf/Y/k7/fgCJAe0Ad/7Q/ET83P22/4kBKAOFAvL//fzj+3T9sgCmAUoAQ/41/I78nP7IAN4CRgNVAVEA4/+K/2AAjABZAL7/9f6g/yEBsQJGA5QCZAFd/0f/nwFnApgBEgF+ABYA9ABNARkBfgAM/6f/pgE7AlUB2/+c/gH+yf78APgBawHAAL7/bP+V/sX9Kf+jALkAe/+Z/bb9AADAADsAjACUADMAe/9o/gT/RgHEAUIAnP4p/e78nP5VAfwCPgMSAa/9CP4LAQMDDgKr/nT7HvyK/1UBJAI7Ak0B6v9H/7P+wv4WAEIAsgCuAfgBZAFkARkBLAC+/x7+Af50/4wAiQGMAs8CqgL0ApgBgv8m/lr+4/+JAfEBqgBZAIwAawGxAlgC2//c/Qz/5QDpAdMBfgCC/07/Xf+UAOIBvQE+AUIADP+G/nD+Xf8LAZABhQB7/7b/ZwDtAGsBHQA8/g/+CP5S/l3/DgBgAO0AowCC/5z+BP3Q/AT/gQFnAt4A9f5D/s39T/1o/l3/nP5D/ob+kf+mAe0CiQFA/x7+3P2c/q//BwC2/x0A1P8x/6oAIQFZAIUAVQHaAeIBKAG2/4r/xf+2/zMAowCbALIAnwH/AWQB9AAzACwAMAESAaoADgCR/7IAegHEAfgB9ABO/3/+Zf+fAeUC/wGyAB0AHQBl/5H/GQFGAdcAfgCv/0f/R/9D/mH+tv+FADMC7QKyAPn9e/2V/hYA7QBgAAz/xf3Q/GX9JQBkAUYBqgBO/7r+iv8ZATABdgBH/5X+S/6Z/Qj+fgBgApgB1wDb/+f+oP8sAK//YABGAVkAWQB0//n9d/6C/wcAlABNAYwAmf9O/5H/MwALAX4A3/5O/4L/e/9yAbUBSgBKADH/4/2O/kf/dgCbAgMDkAGUADH/aP50/6oAUQCv/zsAtv8HAEYB/ACUAH4Aq/4t/gcAZwBNAYEBoP8t/gH+lf57/ygBrgEDAaMAkf88/t/+Kf+K/3oBFgJcAX4AHQC2/+7+Q/53/rb/iQGbAtMBlADJ/kv+4//IAEIATv8E/zH//f7C/oL/gv8x/0oAqgCv/wj+s/wT/br+1P9O/+7+2/9ZABYAR/97/a/9Xf/Y/qT+tv+qAPgBFgKMAND+6v3c/XT/kAFnAr0Bxf8t/kv+1wBgAiwCEgGC/8X/e/9A/5QANwEHAJn/YABKALIAMAHAALb/0P41/rb/YALiAXYA3gADAdT/DgDIAIwAJQDn/o7+FgBVAR0C4gOQAyEBkf8M/3T/BP9L/k7/bwAAAAAAvQEkAoUAxf8b/wH+kf08/BP92gEkBNMBwv5l+5L5AfyV/mz/AAAx/1b9Hv7PAJgBawFnAKj9RPwi/UD98v17/3v/QgAWAowCjAIzAhYAwv50//n/mwBKAFr+cP4DATMCZwLtAvEBZwD9/lL+xf+QAZ8BKAF6AXYAIv+C/ywAvv+Z/3T/S/5O/7kAEgH4AWsB2/90/3v/Hv4B/vn/pgFvAlgC1wBw/s39G/+1AVUDuQIZAUoAHQAE/0f/r//U/6MAVQHLAYUAjv4e/in/UQCQASEB0P6g/VL+Vv8sACgBhQBW/8X9vvuz/B0AxAHxAb0Btv/N/WX9F/5l/1wBtQFCACUAxf/5/00BtQHAAN4A3gBA/47+Q/4lAAoDUQQoAygBFgDJ/mX/wADAAEoA/AADAZsAegEZAc8APgHeAJQAcgFGAVkA9AA3AX4AyAALASUAGQHpAfQA1P8E//3+LACjAHv/EgGJAxIDVQEWAI7+Xf2G/Bv7EPwe/m8AgQPaA4wA4/1l/XT9r/3U/dj+q/7y/UD9zf1CAA4Awv4P/ur9Uv4T/4L/zf9vAMX//f5S/jX+oP96Ab0BmwDU/4r/oP+2//L/9AADA8QDVQN6A9oBp/90/2z/BwD/ASgD7QKMAjMCawH/AVECvQFyAdT/d/6g/0oCegP4A+kD7QBw/tj+e/+bAAsBOP9s/wsBkAFcAeP/Q/6O/gcA8v/Q/s39T/0X/iL/gv/1/q/9S/wI/Nz9mf9KAIUAIv9s/Sn9E/2r/GX96v2G/jsAtv/C/oL/gv9o/rP+Tv+r/n/+f/44/w4AsgBcAZQCwAJs/7P8OP2g/6YBGQMOBDADMAHC/i3+bwA7Ak0DHQTXAsAAR/8b/34AuQLlAmAAS/5h/u0AIQN6AzsC/ABZANj+8v1w/oL/lAD4Ab0BMwAE/wH+Kf/8ADcBuQBCAGX/DP8M/9/+bP87AOUAEgG2/xv9cPyZ/br+1P8SAXoBQgBO/9D+PP41/gz/R/+z/nv9AfwI/qYBIQPxAdv/8v2V/Hv9Vv+UAM8AnwHxAXYAbP/q/S3+r//q/ywAlACqAFkAmAFyA5ADrgHF/0D/0P4i/2cAUQJcA5QCzwAHADMALAD8ANMBEgPXAmsBbwBd/+r/sgC5AMAAnwEDAZn/AAA7AE7/pP4E/2X/AwESARv/Yf7j/bb9Nf4i/8X9PPxH/Xv/xAHTAdv/Mf2R+4P7WvzY/owAFgAWAHv/9vyz+kf7q/4dAhYCBwCR/1r+cPwX/DH9lf5H/4UAvQGqAmsBjv6g/dz9d/5CACgBHQBnAJgBEgFCADMAmwAwAdcAZwAhAWcC9AK9AYwA4/+K/58BrgNVAz4DTQM7AmcA7v5A/4UA0wFYAvwCyAIoAX4Azf/9/lb/7QAWAlEC/AD9/jH/DgAOAPn/4/9D/pX8Vv3N/5sCGQN2AOr91P1w/sX9xf1L/rP+zf97/w/+OP2g/Uv+QP+bALb/Nf7Y/N/8yf5gAFkAmf/9/uf8AfxW/YL/RgFCAhYCIQEOAM398v1W/wcANwGFAiwCYAAhAWACrgGK/+P9Tv9jAwcGiAXLA6oAaP7C/hIBbwL0ANT/dgDeApAFkAXPAk7/s/zY/K//SgK1A5cDkAFA/0f9Mf22/8QBsQKbApgBoP8e/ib+3/6g/34AEgHb/1b/DP90/5ABBwIoAaf/Uv4b/fn9WQCuAYkBmf9o/pH9D/6O/ur99f4dAAMBcgFZAGH+r/1H/V392P7Q/tz9R/1o/t4AhQJKAh0As/6D/Y78Iv26/qoAyAIVBFECxf8B/jj9Xf9vAssDGQMoAfX+s/4ZAWsD/wOJA4UCGQEOAHT/SgCUAhIDwAI7AlEAOP8lAA4CTQObArIAkf9l/1b/1P9rAbECNwH5/4L/Iv/N/wT/3P2z/psAmAFnAtMByf6v/ZH9Zf0b/+0AMwBs/zsAMwB2ADMAS/44/Qj+jv7C/h0AbwAdAM8AUQBo/pH9BP39/GX/rgGQAe0Agv+2/VL+jv6V/kIAPgHIAG8AbwDf/q/9cP5gALUB7QAx/7r+dgBkAekB9ALLAX/+/fxD/hYAywGbAhkDbwJ7/wT9D/43AZAD8APEAZz+qPsX/EoAvAMKBcACBP/Y/Lr8Hv6C/94A8QG5AnoB0P4T/Yr9r/8OAEf/f/7F/WH++f9cAR0CvQG+/3f+3P2g/br+e//y/zABDgKYAdv/D/6z/t4AxAEwAVkAbP9w/sn+SgDLAd4CTQNRAhYAVv0B/Aj+jABkAZQCnwOYAUv+Kf13/vQAegGK/zz+D/6K/cL+kAFvAoEBgv+G/Pb6Nfw1/sAAbwJyAQ4ATv/N/Tz8g/0i/5H/vv9s/77/lADlADMAowBvAHD+Wv50/77/hQA7AqMClAL/ATsAyf66/qD/IQFcA/ADNwOmAQT/Zf1//sgAnwGbApcDKAOyAHD+6v39/gsBAwEHAAT/hv7U/28CxANnAr7/g/0i/c394/9rAcQBywHXANT/f/7q/fL9wv47AMQB2gEdAFr+yfxA/XD+p/9GAYEB/f4t/Cb8Zf2n//QA5QC2//L9yfzu/E7/lACZ/2H+Q/75/X/+r//5/1EAuv48/kf/wv5S/rP+Kf8OAK4BhQKmAU7/Uv5s/8AAcgGqAEIALABO/zMANwOMBPADMAOjAowAxf1d/Yr/9AIdBAMDegGyAGcA6v/XADABQgBs/yL/4/8SAfgBMAGMAEIAf/7Y/AT9nP4zACwC9AJkAUf/s/zy+4P9R/+jAN4AowAOAEf/uv66/nD+CP5//pn/sgCFAGX/Wv7Q/m8AegFcAQz/Uvyd/DsAIQMSA2QB5/5H/eP9HQAdApQCDgK5AAT/zf0E/X/+7QAWAoUCWALlAEP+Jv47AD4BdgCC/6//BwCFAG8AlABGATcB6v/1/pX+CP6C/wsBXAHtABIBIQEzAPL/Vv/u/nf+yf6n/wMBHQKjAAAAGQGmASgB7QBH/9D8s/wi/yQCEgMoA64Bmf8m/kf9jv4ZAZQCawH0ACwAWv5L/or/HQAzANcAMwB+AHoBcgE3AW8AVv9//v3+2//AAJABHQJnAoUCgQHn/r79lf6yALECiQN9AhYAzf2V/Ib+kAE3A8gCZwBS/gH+8v+1AfgBcgHj/6v+Uv4P/iL/TQF9At4CJAJKACL/cP5w/jH/mf8T/5z+wv4M/94AzwI3A3IBBP+g/Tz8HvyR/VkA6QE3AeP/dP87ABYAzf/5/0IA1P/q/7kAfgBd/zz+7v6FAG8CNwN2AsAABP+G/jz+p/+fAT4DegNVAWX/iv/eAMAAMwAzAEoAMwD5/2cAgQHlAkICLABw/gj+bP++/xP/e/+FAKoAG/+6/g4AkAFkAbb//f5A/fL7nfyV/hkBDgJKAq4BoP/J/Ir7dP3y/+UAXAEZAcX/yf7U/Sb+xf/AAK//jv4m/gH+BwDxASwCMAHb/8X94/tw/Fr+CwGMAmQBG/8b/yL/Nf5d/xYABwBgAA4ALf6+/a//awF2AuIBhQBH/1L+DP0I/gcCHQRVA88Alf7F/UP+JQBYAoEDAwOYASn/QP1S/m8ArgEHAkYBwAD5/7P+7v4lALkAzf9O/1kAYAB7/9v/BwBo/mX9mf3N/Yr9QP17/4EDjARgAkf/bP3n/Dz8xf3AADsC2gHlAIUALAC2/77/jABNAZgBPgHIAA4AMf8b/w4A7QCqAFEAVv97/2sBuQIdAvn/jv5H/X/8nfxS/q4B1wK9AbkAgv/2/LP6rPrY/Ir/PgGuAfQAs/7n/Jn9aP41/gj+Kf+R/7r+s/7U/0YBIQF7/1L+Iv8M/7P+r/+bAIkB5QBO/4b+Kf/5/00BMwLiAcAA7v7q/dj8oP3y//8BMAMsAvL/S/50/Zn9xf9kAcQBVQEAAE7/1P9nAOr/Vv9d/4wAJAIdAjcB+AHAAokBQgCMALkAHQALAaoCPgPpAQAA/f4i/wcAAwFcA6oERgNgAAj+E/04/QT/dgBgAB0ASgC5AIEBbwA8/iL9Zf2v/Xf+3gCuAWcAS/4X/tD+3/7u/iL/9ABGAaD/DP9ZAPEBEgNgAmX/wvyr/Lb/JALtAg4CXAEhAaoAXAHEAQcCyAC+/94AawEOALP+9f47AEYBqgB2AAMBBwJKAlUBFgBL/q/9S/6C/ywASgDAAP8BGQOUAs8ACP7J/Ev+YACuAc8CuQIZAUoAqgC9AVwBs/79/Bf+DgDeAJAB4gHeAOr/p/8i/3f+F/4B/hP/lACyAMgAzwBD/or76/vN/dv/uQC5APQABwAP/vb8S/6v/0oAlAB+AKoADgAi/7P+e/++/zMAywHEAe0AmAFGAxkDvQGg/6v+BwC5AJ8BKAOQA3IB2//j/9v/2//0AEoCWAIdApsAMf9o/jX+tv96AfEBmf9d/YP9uv7lAP8BMAFA/5n9qP0t/rb/TQFkATsAJv4x/fn9Tv+R/7b/dgDXAJQAp/+Z/zj/D/72/Lb9+f+mAeIBKAFkASEBdgAi/779F/5d/wMBTQFnAKf/dgB6AVUBmAG1ATsAd/53/r7/IQHlAAcAfgBNAbkAxf8dAH4A7QADAWAA0P5D/nv/4/+qAMQB2gHXAIL/f/5a/s3/OwBvALIA3/6D/Yb+sgCmAdoB0wGFAP3+1P0t/kf/BwCUAD4BfQLiAUoAgv8p/6//mwDEAYkB/f4i/cX9e/+qABYCawObAm8ApP6k/k7/pP4P/gT/QgCn/13/TQGFAokBWQCR/6v+8v35/dT/4gEkAlUB9ACyAIL/2P7F/ywAe/92ACwCjAJGAc3/LAB2ANv/uv4p/8AAFgAM/4UArgHPAOr/e/8i/5n96/tE/PX+fQLEA88C+f81/AH6ZfuV/jAB7QIWAvn/xf10/QT/+f/AAHYA7v5H/YP9sgCMBP8FtQMsAIr9jvwT/Rv/cgFnAm8C4gGQAQsBmwDAAMAAuQBgAMAA/AC+/xf+Hv6+/1kAFgDF/ywAAADu/k7/yAD8ALP+yfxE/H/8kf1H/64BdgIHArkA+f2o+0T61PvF/zMCYAKyADX+jvxP/aD/EgELAdT/6v0E/Sb+zf8LAer/Iv3J/N/+YADU/9T/ZwAlAGX/Wv4E/yUALACn/7b/iv+6/pn/UQDq/0f/bP/AAIEBTQESAfQAgv+z/gAANwEZASwADgCFAFUB3gBs/3v/owBYAnID+AH9/mH+tv9rAdcCmwLXAFr+s/zj/doBvAOFAt4ATv+6/gT/JQD0AKoA2P6v/cL+2/+qADABAwE4/yL9q/zy/aD/vv9d/77/mf8P/ur9R/97/6T+q/7b/0IAR/9a/tD+E/+v/Tj9Tv+yAKoANwEkAvEBoP8x/V39ZwD4AZgBtQFKAkoCGQEsAL7/1wA7AowCjAIsAj4BsgCmAYwCTQOJAwMDcgFnAEoASgByASwC9AKqAqYBhQC+/6YBVQNcA64B3/7Q/Bf+kAHaA/AD2gEM//38Iv2k/hIBowLaAT4BzwBH/6/9G/2g/av+5/5H/2cASgDQ/l39dP3c/QT9hvx0/QT/tv8p/4b+4/1l/U/9zf2G/nD+r/1D/qf/FgBKAG8A4/88/in9e/2z/s8AjAJVA28CsgDf/o7+AABKADMAEgFYAu0CJAKyAJsAawE+AeUATQG9ASgBIQG1AWcCqgKQAWcA4/+C/zH/2//EAdMDlASXA/wAjv4P/v3+dgCmAb0BAwGbAEoAgv/u/tT/mwCFAFkAJQDq/6T+6v3U/Rv/SgA7AOP/Yf7U/Wj+5/4B/hv9Xf1L/gAAIQGQAfwAQP+V/Lf7f/wE/fL9dP+qAGQBHQJcAVEAf/4i/er9uv66/uf+1wDEAVwBSgCK/3v/Vv+2/4UABwJkAcX/oP8AACUAFgCMAK4BDgJvABP/Mf92AJgBWAKqApgBQgCv/zsA1wASAfwAVQG9AQMBAACg/1kAIQE3AQMBmwDU/6D/yAAzAlECsgD9/sX9s/xa/Cb+awEZAwMDWAKv/0T8QPur/Fb/dgBA/7P+r/8sACwAIQE+AbP+zfte+0/9iv/IAKoAdgDeACwAXf+k/o7+gv+g//n/UQCjAO0AmwD5//n/fgBgAN4AIQF+AJn/6v/8AMsBfQLTAcgABwBnAJQAsgBZAKf/hQCJAbkCyAI7AhIBXf+6/pn/rgFvAuIBZwCC/0oAKAFNAdMBZAFA/9D+dP8zAHYAqgCQAdoBEgF3/nf8R/0zAJQCGQOBAeP9Ivsq+6/9dgDTAfQAs/44/Y78qP1ZAMsBNwFs/zj9s/pH+c37UQAZA1ECkf9h/lL+jv7Q/uP/jABl/8n+e//b/3f+tv0E/94ArgGfAcQB3gCK/3v/tQGqAiUAZf2R/WAA8QGxAtoDVQMHANT99f7tANMBKAEoATcB2//Y/tv/nwH4AWQBRgEDAVb/Jv4T/7IAyAAOAL7/kf+K/3v/8v8dAF3/CP41/oL/4//j/yUAlAAb/yL9cPxP/TH/JQByAaoCXAHU/c377vz9/qf/4/8DATAB6v/f/oL/YABZAA4Ap/+v/3v/Mf+jAHYCFgLIAFkAxf/C/o7+Tv/tABYCpgGbABYAp/9l/1EArgFYAvQA7v7q/Xv9PP5d/34AfQLLA2cCdP9A/aj9bP97/3D+BP+mARID+AFZAOr/bP8e/pn9f/6bAAMBmwAoAU0BowAp/zz++f0I/lr+DP9CANcAPgHLAcgAaP7n/N/8Kf3y/XYA/ALaA6MCkf8x/UD92P70ANoBowDQ/nf++f/pAZADIQMwAa//hv6k/mz//AAHArUB5QDb/0IAKAGuAf8BgQEzAKf/IQEZA4EDxAHF/0D/JQCmAVECMwKBASUA8v8SAVEClAJyAQcAbP8WAGcAHQBKAPQApgELAWz/aP7Q/g4A3gC5ACwAmf8T/6v+Vv8dAHv/Wv5L/gT/xf9RAKD/7v4B/kD9xf0X/qv+2//aAZAB9f4E/Sn9dP+FAAcAHv6d/JX8D/4DAdcCHQLU/xf+bP26/sgAmAEoAWX/zf3j/f3+r/8zAD4B2gG5AJH/Zf/q/zsAOwAhAcQB/AAM/zz+QP+QAZcD8AOqAowAXf84/yUA3gCfAQ4CywF6ARkBiQFGATAB0wFCAqYBdgAAAHYAXAGBASwC0wEAAGH+wv5NAYEDVQOBARYA3P1//Bv9gv/EAcQB7QC+/wT/mf3J/Jn9Vv+MAB0Ap/8E/yL/p/8AAKD/T/3f+ir7xf30ADADawOMAs3/Xf0E/cX9jv6V/or/WQDAAKMAmf/F/1EALACC/y3+6v17/64ByAIwAbr+/fx//Ef9Mf+9AZsCGQET/yL/2/9s/7P+3/75/wAAR/+v/8gAwAAHAGAAsgBgACUAKAEWAlUBhQAlAFkA4/9H/z4BPgP0AgMB+f/F/zH/iv9vALUBBwJcAaMABwAM/5H91P3F/zABNwELAdT/Wv4M/94ASgISAd/+4/1L/iL/Vv+MAMQBawGUAHYAEgGFAH/+T/01/qD/HQBRAJsAUQAi/4b+E/+2/77/0P4t/ur9mf3F/S3+3/7J/uf+2//U/3T/Xf/9/jX+vv0t/l3/FgC+/3T/p/+n/6D/dgByAcQBlADY/u7+lAAzAoUC4gEoASwAE/+z/oL/9ACbAuUCywHAAM3/7v4x/2QBrgNyAyUAuvzY/KD/DgKxAn0CYAKQAV3/6v1S/lb/ZwADAU0BKAEsAED/gv9+AMAA+f8E/6T+PP4p/9cARgE+ATsAjv6o/Yr9D/4p/zMAZwA7AIUAQgBw/n/88vtP/Zn/AwG5AHv/d/5l/aj9Vv/IADAB1P88/pH9Yf6bAAcCvQGFACL/Wv5D/lb/KAEsAuIBwABKAH4AUQAAAOr/UQCqAH4AAACg/4UAvQGJAYUA8v/y/3YAKAFyAa4BGQEHAA4AKAEzAokB8v++/xkB6QGfAXIBrgGfASEBlAAOAKf/Tv+v/6oAdgAM/1r+d/7Q/jsA/AAHAMn+yf6Z/wT/Zf2O/KD9iv92AAcAR/+k/jz+5/7XAMsBHQD5/Uf9Kf9cAfgBRgEWABv/xf1D/m8AmwJ6A2cCZAFvAPX+Zf3y/bIAGQMoA+0A/f5h/gT/lAAsAowCNwGK/9/+Kf/y/3YAlADj/6v+Uv6n/5gBJALEASgBJQDY/l39R/0i/5gBegMkBIUCxf8e/jz+Vv/y/0oAKAGJAcAA3gDEAbUBHQAe/i3+AAADAfn/gv8sAJQA4/+k/kf/AwGfAVEAq/7c/aD9Q/6K/0YBmwKFAt4A3/4t/nD+G/8lAKMAGQGYAfwAxf/b/1UBFgLTAaoAXf/Q/pX+QP9cAZADNwMSAXv/pP5a/kf/yADiAfEBUQB7/4r/Vv9d/2AARgFnAL7/8v/j/4r/DP+6/nf+Uv7J/iUATQEwAXYA4/8T/3/+0P6C/zsAhQBKALIAMAHeAA4Ae/84/9/+oP9VAYUCSgKfAfQAAACr/g/+r//xAd4C0wFnAAT/g/0p/Tz+mwCmAaYBZAH5/5z++f1L/sn+yf53/gT/DgAlAKf/4/8lAOP/oP9W/6f/2/+UALUBWAKmAQz/Vv3c/WcANwPPBPADGQF7/13/vv8OAGcA1wCJAcQBZAESAQ4AdP+K/9v/LACn/3T/r/8WACwAbP+O/qD98v2+/4UAmwAoARkB2//y/Yb8yfxD/iwAkAFCAnoBwv4b/b79Vv/5/4L/7v7f/sX/UQDy/zj/Yf6v/dT9hv6g/z4BJALeADz+nfzf/Cb+/f57/wAAsgCqANv/R//1/gz/cP5w/tT/kAG1AVEAXf+6/q//dgBZALIAgQEkAvgBDgKYASEBlADU/9v/1wAHAg4C4gEHAlgCLAI+Aa//7v6g/0IA3gCFADj/Q/4p/wMBvQEZAc3/lf4T/X/8Vv0i/+UATQHXAIr/vv0T/ZH9Lf7Y/jH/iv87AHYAJQCR/4b+dP10/aT+tv8p/y3+f/6R/ywAJQAi/1L+Q/4t/tD+R//Y/h7+CP5a/iL/ZwDAAOUAmwA7AK//0P5h/h7+2P7j/zcBHQKjAnYCIQFgAMX/p/9RANcAXAFRAhkDyAL/AdMB4gHlAFb/0P7F/yQCdgTtBDME6QEM/yb+G/9+AN4A1wBVAf8B6QGUABP/Yf6z/kf/r/8OAJQA1wCFAPn/5/4B/jz+hv5L/pz+iv/F/5H/bP8p/+f+d/5L/vX+e/8i/8n+dP9nAJQAtv8B/vb86v0lAB0CWAL0AF3/D/4B/gz/ZwCQAf8BMwJVAR0AOP/n/lb/r/8WABYAmwBVAeIB8QESAR0A7v5S/jz+oP9KAoEDIQMsAjcBxf9//mH+xf9VAQcC9ALTA7UDvQG+/6f/sgBGATABrgF6AdcAYAAdAEIA4/8HAHIBfQKfAWz/1P3y/dD+R/9A//3+R//j/yUAHQB7/yb+Kf1W/c39q/6R/7IA4gFyAQAAHv4T/Q/+gv9gAFkAfgAhAbUBHQLAAPX+jv44/3YAgQFvAukBjADU/+r/1wCBAYkB1wD5/3v/Xf9s/5H/HQCjAM8AmwAZAcsBXAEHANj+Yf5D/kP+nP5RAOkBrgFRALP+Uv5l/zcBBwK5AH/+/fwB/n4ABwKBAbb/f/7q/R7+DP/U/4wAqgDAABIBjAAi/x7+hv71/rP+Uv4E/28A/ABNAQsBZwCR/8n+3/4E/yL/iv/8ACQCvQEWAP3+G/8b/yUAyABgANT/Tv8HAHIBxAElAN/+aP7J/vL/9AC9ARkB+f+k/ib+7v62/6MAIQHlADMAFgAzAFkAhQCR/7r+hv6k/hv/r/9+AO0AVQFNAVkAdP+6/u7+FgBZAAT/bP1W/Rv/rgHXAtoBiv+R/Qz96v2v//QAiQGYAfwA+f+z/rb91P1A/34AWQB+AGsBJAIdArkAOP9D/uP9Nf6Z/6YB/AJ6AxID6QGZ/2X9Kf3f/vQAtQG9AUICiQOBA4UCIQHf/oP9r/2n/2sB6QHiAaYBpgHAAF3/0P4T/3v/8v+qAJsA2/8T/9/+Kf8T/9/+q/6z/jH/Tv8b/8n+wv4T/3T/AAAAAAcAWQDq/9D+iv39/E/9Q/5nAG8CKAPaAQT/e/3U/cL+OP9s/34AcgHIAIr/uv5L/g/+CP5a/oL/IQEdAnYC2gGv/8n8qPsE/V3/gQEdAq4BKAESAQMBlAD5/3v/1P/IAPEByAIZA4UCRgFRAA4AUQASASQChQLAArkCJALIAHT/e/9gAMQBJAJRAlECXAHN/x7+zf13/rb/IQFRAn0CKAGZ/3D+xf2D/bb9lf7U/ygBtQH8AJH/4/04/Tj9vv2V/nv/uQCqABYAe/+G/mX9QP08/pn/3gDAAEoATv+O/vL9BP1l/TX+kf/XAE0B7QAOADj/S/5S/oL/tv/Q/n/+5/5gAGsBtQGuAcgAYAD5/4L/Vv+2/8gACwEsAIL/HQB6Ac8C1wK9AR0Aq/79/h0AQgDy/ywA1wDEAc8CEgP/AR0AE/+C/3v/5/4p/zMANwGBAe0A7QD8ALb/d/4P/sL+1P9cAeUCwAJcAd/+Zf0t/mz/6v9nAHoB/wHiAfwAr//Y/rP+nP7C/tv/cgH/AQMBdP9//hv/8v8AAGX/PP7F/bP+ZwAkAkoC6v9W/fn72PzF/2ACVQN2AoUACP7Q/ED9DP+MABIBGQFKAJsANwGBAfwAkf8b/wAAZAG1AR0CowJvAvwAZf/1/iL/HQDAANMBZwIsAtoBawEwAQAA2P7F/fL9BP8dAHIBvQFrAZH/vv39/IP9bP+UAPwAmwCv/9D+Yf4X/g/+d/5A/7kApgFrAfn/nP5D/mj+E//j/88ATQELAbkA1P93/uP93/6jAGsB3gAdACwAlABgAJH/D/4p/dT9oP96ARYCxAHtADj/Xf3C/K/9bP/0AMsBpgFZAEv+Kf1D/gcAzwBgAJH/6v+fAbEC4gHU/9z9oP1A/zcBHQKbAqMCiQFvAHT/Zf/q/3YA3gD0AO0AmwCqALIAUQBl/8L+dP8WAGcAowCyAFkAMf93/kD/Xf8P/uP9e/8oAVUBUQCR/13/uv5a/v3+fgD/AekBVQF+ALb/tv9W/0D/+f/eAHIBAwFRAGcAowBnAFb/zf17/Wj+dgAOAukBSgCv/XD8BP1a/rP+S/6z/lEAvQFGAbb/vv08/C38zf3y/yEByAAlAIUABwAE/wH+iv0m/hP/NwFRAiwC/wGBAXoBSgBw/r79wv65AHYCFQS1A+UAJv7F/dT/2gHLAVkAxf9gAGQBegHXAKD/6v17/Qj+bP8DAUIClAJrAcX/CP7U/ZX+dP8SAdMBegGyAJQAGQGUAKD/Iv/U/ygBJALeAmcCmwCr/ur9lf7U/zcBEgNyA00Bd/5d/dj+YABGASgBoP/Q/pn/XAFgAoEBG/8i/d/84/3b/+IB1wK9AeP/jv7c/a/93P39/mcA5QBgAJn/dP+n/9/+Nf6O/hv/QP++/z4BDgKfATsA7v5S/vn9PP4T/9v/lAD0AAMBjAAb/1r+f/6C/8AAfgAWAIr/gv8sAOUAyABO/w/+6v1H/3IBGQMwA3IByf6K/av+zwBvAqoC6QFZAI7+F/5l/4wA9ACJAbUBRgGUADsAbwAzACL/cP5l/8gAEgEhAcgAyADlAFkAZwAWAOP/8v9ZABkB/AC5AB0Atv8AALIAKAFGAe0AJQAAAAAAHQCUAO0AfgCZ/+7+Kf8HAH4AdgAOAIr/DP+n/28AQgCK/yL/tv8zAAAAlf5P/a/9Zf/tAPwAMwDF/w4AqgD0AMX/Af6k/CL9bP96AZQCuQLaAU7/bP1P/aT+sgDpATsCIQF7/7P+Xf8zALb/nP5S/r7/vQGMAvEBJQDc/TH9T/3q/XT/EgHXAtcCjADU/X/8Zf1l/wsB6QHEASgBwAAsAIr/pP5a/qD/awF2ApQC8QGFAIL/gv+2/1b/Wv53/koA6QFCAmQBBwDn/qD93P10/1EALADU/xYAMwCn/2j+Q/6K/3YAzwCUAAAAyf41/jH/fgD0ANT/hv5//mX/xf97//L/BwC2/9T/QgDIAJsA6v8E/9j+DP9l/7b/BwDlADABcgE+ASgBPgFKACn/Af6r/mcARgESAc8ANwFNAbkAIv/f/tT/yAD8AIUAbwBCAEIASgBnAFkADgDN/ywAAwFGASgBbwC2/2X/gv9W//3+2/+fATsC7QAx/yb+lf7b/2cAzf/9/o7+p/+1AWcCmAGv/2H+d/71/mX/2/9CAKMA3gCMAPL/Jv4b/aD99f7IANMBpgF2AGX/d/41/i3+Jv6z/hYABwIZA4EDYAIAANz9tv04/6oASgIwA4EDbwJ+ABv/3/4OAHoBdgKjAh0CwACZ/5n/dP8x/0f/oP+bAGsB4gHaAfQABP9W/Zn9wv6bAMsBDgLLAZQAr/84/0f/wv5a/vX+zwBYAmACKAEp/w/+3P3N/8gAiv9S/ib+UQBkATsANf7Q/Gn8bP1RAG8C6QEM/7P8hvzq/bb/5QCFAML+Vv0E/VL+zf+jACEB/ACUAEoADgD5/0IAfgBgACUAbwBVAWACawPEAz4DiQGC/wz/xf8LAaYBtQFYAsAC1wJkARP/oP22/aD//AD0AOr/nP6o/b79Kf8lANv/aP6D/Rf+BP/N/wAAdP+O/vn9Nf5A/zsAfgAzAKD/BP8m/hf+kf/8AE0B1wAWAHT/Vv+n/2cAmwCK/+P9G/2V/h0ATQHTAdcAiv+c/k7/tv/f/ur94/2r/v3+bP+Z/3T/9f4T/xYAjABO/2X9T/3n/vQAkAFgAAT/q/5O/zsAowB0/3D+nP50/94AmAGuAVUBHQCK/3T/6v92ADsALAAsAL7/kf8lAOUAtQHaAa4BXAFgAED/Wv7u/mcAWAJGA28CNwH5/83/+f/AABkBbwCg/13/sgCuAZAB9ABgAOr/3/5//h0AvQHiAYwAyf66/qf/yACQAcQBAwGK/6T+Yf71/sX/9AAHAqYBUQAM//X+tv++/9/+Yf6V/kf/JQB2AH4ASgCZ/+f+Jv4B/nf+/f7b/4UAQgD9/tz9Hv4OAE0BlAAM/xf+nP7F/xIBXAHAAOP/Xf+K/9T/hQAoAfEBrgEZAaMAr/+K/9T/uQC1ATMCywHXAGcAfgD0AJ8B2gEDASwAOwDlADcB9ADPAE0BxAGQAfwAowBCANv/5QBRAmACCwEdAKoAKAHtAKoAmwAWANT/1wD0AuIDUQKg/1L+hv71/iwAegEWAgsBvv97/83/BwAT/4b+q/5s/w4ADgAAANT/iv/Y/ob+Wv7Y/qf/xf/j/8X/xf/N/0f/q/66/kD/ZwCyANT/BP9w/gT/DgAZAcAA7v7q/br+qgBrAZQAQP+6/mX/oP/y/2AAbwAdAGz/DP+K/4wA5QBKAHv/dP9gAIEBiQFZAOf+CP6G/qD/TQEdAmsBzwDlAJAB/ADy/3v/gv/b/zsAzwCBAQcC6QFrAUIAR/+z/iL/owB6ASgB+f8x//3+9f6O/o7+dP++/0f/yf4p/+r/6v8b/1L+xf3y/dD+xf9kAfEBuQAE/4P9dP3n/kIAEgGyABYAmf9O/9v/BwDq/07/bP8sALkAbwBd/3v/FgC5ADsA9f4P/tD+EgG5As8CyAAp/zH/jACuATABxf9L/i3+Vv9cAdcCuQK1AWcAVv/Q/kv+aP4E/6//qgA3ASEBHQB0/xP/BP8T/0D/DgAHAKf/q/4P/o7+bP/j/3v/0P4I/mj+2//lAFEA3/4b/S383P12ABYChQBA/dT7bP1KAK4BHQL4Ad4AOP+r/k7/DgDIAN4ABwB7/7b/zwCxAhkDmAGFAA4ABwB+AJsAdgDIADcBGQH0AKMA+f8OANcATQFCAI7+PP5W/+UAOwIkAqMA7v5h/iwABwKBAeP/nP4m/n/+Vv92AHIBVQH5/xP/E/+Z/4L/0P7u/k7/SgDeAB0ABP/U/Wz9F/7U/7IAdgDF/9j+s/4M//L/jABCAED/q/5d/88APgGFAL7/uv4P/vL9Tv8oAVgCJAIoAd4AYADq/yL/E/+R/5n/8v/PAFwBXAEwAbkAuQD5/7P+3P0i/58BTQPpA1gCLABo/mH+kf/tAJgBmwCn/9T/awGqArkCIQET/+P98v0p/34AawFcAbIABP+K/b79Mf+UAMgA8v/1/kP+6v2G/k7/qgAwAbIA1P9a/kv+bP9vAAcAoP+n/6D/xf8AAH4AUQCv/wT/q/4i/2AAnwFvAg4CYABo/tj8pPyO/iwCmwRgBMsBf/6d/CL9Vv+uAU0DyAK5AIb+lf6UAKYB1wDY/rb93P10/70BGQP0AoEB0P5h/Ev8q/6jArEEXAPAABf+f/zC/EP+OwAoARkBRgFrAQMBTv9A/fb8Af48/lr+Mf/0AIUCWAKMAGX9dPvr+7P+/wESAxYC1P8t/g/+dP/8ANoBegFnAHT/Yf6G/q//MAHpAYkBZwAi/3/+DP9+ACgBEgEWADH/pP6V/mAAUQKUAmsB2//9/jj/Xf/F/wMBnwFGAWAAdP+2/1UBhQJYAhIBkf8T/4r/FgB2AFEAp/84/x0ApgFCAnIB2//1/kP+Jv7f/rb/9AB6ARkB4/8E/wz/DgDlAGcAoP+C/34AlAAAAOP/HQAlAM3/JQD8APEBrgHeALkAjAAlAF3/G/8sAEoCBwSuAyEBHv4x/Sb+LAC5AuIDyAKn/zH9Vv2C/3oBRgFZAF3/OP+g/w4ALAAp/wH+qP2O/t/+QP+MAJ8BVQFO/y3+4/1L/nT/3gCYATsAS/7U/er/2gHiAYUAs/6k/rb/fgBCAK//BwDIAHoBPgELAcAABP+K/Zn9mf+mAeIBnwFyARkBSgAE/1L+hv6R/8gAkAGYAQcAq/53/uf+R//n/oL/QgCFALkAmwA7ACn/5/5s/6f/9f7Y/lkAFgJCAqoAG/88/rP++f/tAOUAUQC5AMsBpgET/7P8BP1d/z4B4gGYAWcAR/+z/gz/gv+v/5H/iv+5AJgBTQGqAKD/Tv/y/zsAOwCZ/9j+nP71/jsAXAFVATsAKf8p/5QAtQFrAeP/Hv6R/f3+XAFKAtMBwACUAN4AowD0AD4BiQGjADMAKAGYARIBG/8B/kv+2P6v/wsB0wFZAF39r/ur/KT+6v9gALIAvv/N/dj8Vv2O/rP+d/7J/pH/HQBCALIAUQAi/1r+d/6k/gT/4//PAHoB3gCC/xv/iv+Z/5H/e/9RAB0CsQIsAqoABP9S/uf+uQB9Au0CgQEdAG8A+AF9AigBmf9O/w4AmwDlADcB2gH/AcQBEgHF/zH/R/+qAP8BHQKYAYwAgv/f/g4ARgE3AWcAZwCQAQsBkf9//tD+xf8dAAAAMwDAAIL/Wv4B/qD9Iv0i/XD+DgCyAPX+Iv3C/F39cP6g/wcAuv6D/TH9Hv4i/2X/r//5/8X/gv/F/83/FgBZAB0A9f6Z/Xv9QP/aAd4CZwJgANz9d/wT/SL/AwEkAsQBwACZ/9D+E//N/w4A4/8OAJsAMAHeAAcAZf97/5sAHQKxAsQBowB2AHIBDgJGAQ4ATv/q/3oBxANnBJQCAwEZAQ4CrgHb/wT/r/+qAKYBOwL4AfwAr/90/4L/7v66/k7/6v97/+7+R/8AAMX/mf++/wz/zf1p/Bv9G/87AMgANwFkAc3/Hv4P/sn+1P9RAIwAhQDb/+7+pP5CAJ8BDgL4ATsAxf1L/B7+XAEDA28CBwDC/pX+OP8zAAcAkf9A/zj/Zf+K/+P/sgBNAaYB6QH0ALr+Iv2r/jABFgLpAVwB9AA7AGz/Xf8WAM8AqgAhATsClAIWAk0BqgC+/zj/5/5//u7+MwDpAWACXAE7APn/oP/J/t/+7v7Y/jH/WQA+AXYAq/6G/Bf8G/1//h0ATQFNAUD/kf2K/X/++f+UAPQAUQCk/gj+q/4AANcAKAHEAb0BmwDN/6D/dP/U//wAFgIsAvQAZwCfAVECIQFs/3D+D/4e/rb/nwGxAjADfQJrAQAAf/7U/VL+1P92AJsAPgG1ATcBQgD9/hv9/fwb/9oBTQP/Aa//Wv7f/ur/GQGBAUIA3/53/rb/VQFnAoUC4gGUAPX+F/4m/vn/DgISAw4Ctv81/gj+DP+v/3YAIQHPAMn+Kf1//vL/dgC+/xv/3/4P/ib+HQAhA4EDPgGc/v380PxW/Zz+DgCBASQCmAHy/9j+jv5w/jj/1P/IAGsBzwDb/y3+Iv1P/XD+sgBgAkoC7QBW/4b+7v75/4UALACO/sX9Tv/eADABzf+z/qT+uv5d/zsAawFNAaMAUQCZ/7P+tv2z/sgA0wFcAQMBrgGfAX4ATv9O/xYAXAHXAnID3gLtAHv/gv/F/9T/ZwAoAUICwAIsAmsBHQAp/9D+9f4M/+f+QP9ZAD4BCwGjAJn/D/7C/Of8hv4AACgBPgGUAAT/tv1a/s3/MwBO/1b/8v/q/8X/p/84/xP/oP8DAZ8BHQCO/ur99f4WAAsBHQLtAJX+Mf1a/ur/OwBnAFEA1P81/nv9f/5KAKYBvQFcAbIAkf+c/uf+R/++/ywAJQB+AD4BjALIAq4BLABs/1b/E/+V/lb/BwL4A4wE7QIdAEP+Xf0X/nT/5QDaAcQBAwHy/2z/r//b/9v/8v9l/5z+F/5S/mz/sgCqAJH/mf++/1b/OP90/6D/Vv/J/pX+Mf9vAJ8BmAELAXv/cP4x/2z/4/9KAKMAWQCv/4r/3/5w/jX+R/9yAbEC6QEAAGj+Lfwx+3T9CwHlAlgCjABd/1b/Vv/U/wAAAAD5/yUAGQGfASgBWQD5/wAAyABGAc8AqgByAcgCmwL8AF3/Kf8WAHIBmwKFAmcCnwHF//X+bP+UAL0BtQFyAQcCFgKMAN/+Yf53/v3+vv/lAFwBSgBA/2j+Wv5a/ib+0P4dANcAAADn/g/+1P13/hP/5/48/nD+gv/tAJgB5QB0/7b9Yfwi/SL/YAC9Ad4CwAKqAGX9PPzU/SUAgQEHAqYBJQBD/nv9yf6bAHIB9ACv/8n+uv71/gcAGQE3AW8A3/7U/XT9wv4DAf8BDgKQATcBYABA/zj/wADPArEC/AA4/3f+bP9GAVgCvQF2APL/xf+R/9T/QgD8ANcAQgCUAAAAUv72/NT9zf9CAFb/lf5d/2cA9ACUAKD/Kf9d/0oAMwBL/lr8nfwb/4EBowIHAs3/e/1S/L791wCbAg4C8v/5/b79aP5s/6oAyAAzAL7/Tv/5/4kBdgLpAW8Akf8M/+7+FgASAU0BnwFVAVkAiv9s/7b/BwBgADABqgJVA/gBG/9s/TX+bwCjAgoD4gHj/9j+dP8LASQCpgGMABv//f4zAO0AowAWADsAhQBnAJH/OP97/3v/4//0AB0CZAGc/qv8E/0t/gAAqgJjA5ABQ/6k/I7+7QBcATMAIv+c/nf+Mf9KADABegESAR0Ajv7N/ZX+sgDLAd4AHQD5//L/Mf/J/oL/hQCBAXIBWQCr/vL9lf4AAKYBSgKmAYr/bP2g/dv/lADU/+r/3gDAAAz/CP7N/Yb+/f7F/xkBPgEwASEBRgHb/9T91P3N/00BjAAAAGX/p/+jADMCFQQSA77//fxA/U7/mAGbAiQCEgEx/3f+2P6n/94A2gE+AWX/Uv5w/koADgLEAQAAhv6v/R7+qgDXAhID9AAP/hP9Q/4HAIwA7QC9AVECvQHb/2H+d/50//n/owCJAcQB1wDN//L/hQDIACwAkf/5/+0AjADu/gT/qgCQAe0ATv+6/h0A7QBvAIL/0P4I/u78tv0lAMsBgQHIAIwABwB//gz9qP2C/8gAKAHEAQMBE/93/q//TQE3AZsA8v+K/6v+lf4lAE0BkAGjAOP/BP9S/n/+DgCQAfQAgv90/ef8Nf7lALkC/wGMAP3+nP4b/zMAgQGYAW8Ae/+2/xYAJQCMACEBKAGbAOP/QP/J/mz/qgAoAX4Amf9l/0f/2P5h/tj+r/8HAFb/CP6R/b79R/9nABYA1P+K/+7+Lf66/qf/R/9o/t/+3gCYAVEA3/4b/0IAtv+V/mj+uv6K/3oB5QKqAssBHQDJ/vL9g/08/sX/iQF9AnoDXAN6AQz/kf0e/sX/egF9Au0C6QHq/6T+Kf+yAJ8BxAHAAFEAmwBNARYC/wGYARkBQgCz/i3+E//8AFwDMwSQAxYCoP+2/Wj+CwEDA3YCtv9H/U/90P7F/7IAwAKXA2sBAf4X/ED9Zf9gALIADgD5/Y78g/2MACgDowIsAPb8BfsB/Of+TQFCAtoBAAA8/qv89vyc/rb/mwDlACgByAAlAOP/SgB+APn/bP/J/mz/dgB6AfEBgQHXAAcATv9//lr+Yf5l/8gAywFRAtcA3/7u/J38Lf7F/+P/nP53/kD/AAAdAEoAXAE+AfX+nfy6/NT9/f6bAH0CywMHAv3+bP0e/lEACwHPAB0Alf7y/Wz/4gH0AiQC4/9l/YP7mfuc/psCyARcAxkBQP+2/Tj9S/6qAL0BCwGn/zj/xf/AAKYBEgH5/+f+Yf5L/mX/GQEWAvEBjAC+//X+q/6R/00B/wGbAFb/BP9d/0D/AAA3AZgB0wHlAlEEPgOv/y38kfsI/igBegMsBDMCR//J/qoAlAKxAkIABP35++786v+fA7EEmwIx/779Wv5H/2cARgHEAekBzwB0/0f/JQA7AlwDuQJKAGX9E/3u/h0COwT4A1ECYACr/jX+R//XAHoBQgBw/hP9Af5vAKMC/wMhA1kA0PzF+6j9e/+v/2j+qP1o/sX/qgDXAMX/Hv5H/Tz+r/9H/y3+1P2V/mAAFgIzAmAAD/6G/CL9QP/8AOkBfQK5AoUCiQFA/6D9aP5nAJABNwGFAIr/gv8SAQ4CnwElADH/Zf/F/6D/q/4e/kf/IQFRAk0B/f4I/u7+sgB6AQsBxf9w/rb9Uv7eAMgCzwKmAUoAKf/C/ob+Yf7y/4kBOwL/AbkAxf8p/7P+9f7y/6MAUQCR/x0AkAH/AdcAXf9L/nT9F/7U/w4CyAI3Abb/cP4t/gT/UQCJAdcAG//Q/sX/3gCYAfQAp/+r/kD/1wAwAWAAtv+v/2z/2P71/nYA2gHTAcAA0P5s/Xv9BP9GATsCIQHJ/iL9Xf1h/jH/Iv/j/aj9yf6MACQCOwKqADX+Lfxe+0/9GQFGAz4D/wFnAHf+OP3F/aD/xAF9AiQCHQIsAlwBiv9o/n/+Mf+UAPwATQEdAjsC4gGJAXoBZwAx/+r9qP2+/6YBfQLpASEBbwBs/1r+qP2G/qD/WQAdAMX/dgAZARkBQgAOAEIAiv93/hf+QP/lAHoBRgGjAJH/s/4T/8AAQgJvAr0BCwEp/9D8afw1/nYApgGMAjMCZwDN/Uv8+f2Z//n/gv8E/13/tv+2/6f/r/97/6D/jv6D/XD+FgCQAQ4C/wF+AEv+xf2n/9MBFgJcATMAr//1/hv/AwHpAVUB/ACuAU0BZf9o/qf/zwA7AMX/qgDTAeUATv9W/4UARgFgAGX/R//1/sn+OP9gALUBnwGFAL7/BwCg/3f+Nf5A/1wBSgL/AVEAWv7F/cn+KAFgAp8BIv8M/e78yf4zAgcEwAKC//382Pxh/m8ApgFyAdT/6v2o/X/+4//AAGcAQgC+/5X+zf1a/uP/ywHlAgcCJQAP/hv9tv3q/yQCIQOUApsAe/8AAJAB6QHEAXIBbwAx//X+bwA3AfEBhQJRAsgA5/66/ur/7QCqAAsBqgAi/xf+nP70ALECuQKyAEP+jvx3/Lb9e/8wAZABgQGjAJn/7v48/vL9D/7n/iUAEgFrAfwA2/9A/83/6v9O/8L+2P5O/3T/OwB6ASwCCwEb/7P+e/8WAE7/wv4m/q/9pP7q/wMBPgEwAWcAKf81/hf+OP8sAPL/e/8HAOr/LAC5AM8ACwGyAO0A6QGUAjABOP/C/s3/gQG5AhIDrgHq/0f/Xf+Z/zMA7QByAQMBBP+K/R7+xf+qAKMAMf/n/E/7g/sP/uUA/wHPADH/pP6c/jX+Af79/hYA8v+r/i3+DP+yACQCmwKfAb7/1P1l/U7/LAL/A5sCdgDU/7b/bP+n/2AAlABkAaYBPgFvAGz/Vv8WAGsB6QH/AaoA2P7J/mcAgQH8AG8Ar/+Z/0oAEgFGAaoAYAAzANv/tv8lAFwBLAKJAZQAXf8e/jH9mf1gAJQCqgKmAYUAdP++/QH8Zfs8/Hf+IQFgAjcB3/7y/QH+Af6Z/V39/fwX/I78F/6qANMBwAAp/0D9yfzN/e7+gv9CALkA1P8t/uP9tv/0AN4AHQAzAIwAbP/Y/or/7QAdAsAC7QKmAYr/+f2r/mQB4gMsBGsBJv7u/Nj+owISBRIFNwP0AKv+Zf2v/Xf+iv/eAHYC3gJCAokBbwAx/1b9PPwM/ZX+lAAWAm8CpgE4/9z9Af4t/kP+xf2k/uP/jACqACn/Xf1S/Fr8mf1s/zcBUQLlAKj98vsE/RYAJAIdAlwBDgDu/nf+Iv8oASEDAwNVAaoAjADPALUBOwLeAqMC5QBH//n/vQGqAtcCDgJkAbIA3gDLAf8B2gGuAYUCdgK5ADH/7v5CAOkB9AJrA5sCHQB//u7+owAWAvEBowDC/pn9zf2+//EB9AJRAmAAIv/y/Wz9Nf57/+UA5QDj/+7+3/4i/3v/ZwAdAKv+Xf2Z/TH/bwB+AJn/xf/q/5z+1P3j/Wj+G//j/5QAwACn/9T9Zf2z/t4A4gFrAZQAOP+k/kf/ZwCQAfgBEgGn/9D+3/4LAVUDVQOuAer/Vv/1/qf/pgGmA7wDTQHf/jX+e/+MALUBuQK5AvgBp/9D/iL//AAOAk0B6v8x/yn/kf/XAD4BQgBW/47+F/4B/mH+OP/y/+r/E/+r/ur97vxP/dj++f8b/zX+Lf7J/qD/Vv84/+r/+f8M/8n+Kf9CAAMBAwHtAGcAWQBW/9/+4/9VARYCPgEsAKf/BwDy//L/4/+R/13/e/9CAKMATQFVAaMAXf+V/u7+Vv8WADcBDgIDAfX+oP0t/r7/7QBkAaoA8v8AAN4AMAFRAAT/uv4x/13/4/8DASwCpgEOAAT/Iv++/0IAqgDPAFkAdP8x/zj/AADeADMAcP4M/S3+wAB6AVEAIv+z/mH+Q/6g/zABnwHlADsAqgALAYUAnP6o/d/+7QD0AigDkAEHADj/Tv8lAHoBhQJ6AQAAyf66/sX/6v/U/4L/iv9W/8X/WQAsANv//f6Z/UT8G/0b/yEBXAFvALkAUQDY/vb8s/x7/bP+fgBCAqoC7QDf/gj+QP+5AHIBmwD1/vL9lf6MAHoBDgIZAdv/1P8sAHIBJAJyAQcAKf/Y/pH/cgGqArkCowL8AmsBpP6o/d/+1wBGAYkBowJRAqMAr//b/yUA8v/N/5QAawHTAdoBCwHy/0f/JQCFAA4ASgCqAM8AOwDb/wAAFgCZ/7r+Af75/WX/NwHxAbIAyf57/f38e/2V/uP/JQCz/jH9Vv2z/vL/UQCK/w/+/fzn/AH+kf+jACEB2/9A/S381P04/4r/zf/5/83/Hv5W/XD+lABgAm8CxAEOAJX+Q/4p/zMAcgEZA5cDYALN/7P+oP+5AFwBYAJ6A6MC9ADPAKMCcgPEAXv/jv5l/wMBXAPPBLwDzwA1/qD9f/5CAJgBrgH0AFkAfgCFAKf/5/6O/lb92PzF/fX+8v+K/1L+1P13/pn/wAB+AGz9lfoq++r9FgBGATABXf/f/JH7Uvxh/hYAFgAM/47+G/+2/wAAOwBRAA4AaP7Y/AH+SgCqABP/s/5CAJABywGYAZ8BGQHb/4L/FgCUAN4AMAE3ATAB+AEZA4UC/ABKAKoAnwHaAVgCmwIdAj4B5QDaARYCdgIZA0oC1wD5/w4AFgBnAPEBLARvBCgB4/2K/ef+QgB6ATsCxAGjALr+kf1S/tT/qgBl/8399vzF/SUAVQGYAWcAD/7U+7P6PPxA/wMBzwAi/0f95/xd/bb9cP6g/4L/xf3r+777hv5kAa4BMAGBAbkApP4T/er9MwA3ATcBowB2AHYAzwCfAVgCQgJGAYwALADAAOIB/AL0Av8BEgFCAMX/gv9CAPQAhQLLAzcDUQLIAIL/Vv9nAIwCuQSfA6f/jvyG/DH/awEDAygDRgH9/mH+kf+FAKYBhQJVAUP+Uvz9/Of+yAByAWsBbwAP/hv92P7XACgBQgDJ/l39s/wM/WH+WQD4AaYBkf+6/I760fq+/WQBawMhAw4AlfxP+5X8Iv9ZALkAMwBA/xP/tv8DAcQB4gGuAcAAYf7Y/A/+TQGiBHoF2gO5AKD9nfwp/00DPgVYBCQCbwDY/hf+dP9yAcACZwIoAYwAkf+k/jj/fgCMAOr/AAAb/y3+Xf+YAZQCNwFD/iL7S/rJ/MgAxAPEAxIBZf1/+ob6vv3IABIBDgB7/07/3/7U/bb9cP7Y/pz+Wv6c/jj/uQBrATMAcP6K/R7+Wv5//tT/vQFRAqMAVv9W/yn/Zf/AAGcCzwLpAYUAkf++/wMBjALeArkCAwMhA/8BBwCK/1EAcgH8Ap8DOwLlAGsBYALTAcX/hv4t/gH+BP9GAZ8DkANkAXv/D/7f/BD8CPw4/a//6QG9AQ4Aq/7F/WX9q/yG/Ev+WQCUABP/f/7C/u7+DP8E/wz/nP66/lb/4/9CAKMA1wAzALb/pP4P/mj+DgB2Au0C5QAp/Vr8D/5nAGAC+AE3ASUA7v48/nv/TQGQAfQA+f8lAJQAawFKAtMB5QCMAEYBOwI7Ar0BPgGjAMgAxAHlAnYCCwEHAPL/3gDaAbkCxAH5/5z+3P13/tT/+AGBAxYCcP6g+4P73P1ZADMCLAIHAJH9AfzJ/DX+dP+R/zz+BP3n/C3+kf8LAekBEgEm/gz7G/sm/jcBCgOMAlb/Hvzr++f+rgH0AhIDyAJyAXD+jvxl/R0AawH4AYwCxAElAJz+wv5gAA4C4gEzAGH+CP4sAKoCwALlACn/3P32/Gz9fgC1AyQEFgJW/8X93P26/ur/cgFgAowCRgEx/839zf0p/8gAxAH4AZAB+f88/mz94/0T/w4AHQBA/13/AABgAOr/R/97/07/F/5A/Tz+uQBRAt4Af/7Q/B78wvzJ/n4AnwHxAc8AHQDn/s39kf01/u7+QP9vAJgBSgLEAdcAQgCg/wz/tv/8ALUBegHAANoBfQLiAX4AVv9D/l39nP7XACgDiQNvAgcAQP3C/A/+jACFAvQC6QFd/3f8CPw1/pQAxAFKAhYCfgAi/0f/3gC1AaMAMf9O/yUAegE+A1wDBwJgAOr/WQDIANcAxAHXAv8B5QDlABIBJQCg/4UALAIHAvQA9ACqAE7/mf1D/r7/7QDlAM3/BP8t/hf+pP4b/wj+Vv17/Y7+UQDlAOP/3P2r/GH8E/2K/fL9Q/4M/28ARgEwAU7/Hv7y/Xf+f/50/94A/ACjAIr/BP9D/u7+lADpAQcCqgC+/5H/JQAAAN4A5QBgAN4AawFKAh0CMwK9AZgBKAElADMAEgFcAyEFywXlBAcCG/81/lb/0wGUBFQFbwRKAgAATv9KAPgB/wG5AKoAegHTAYkBjABW/7b9yfwm/gMBfQIDATj/Uv79/Cb85/zy/S3+f/5A/0f/kf/5/4L/4/3N+0f7PPxa/nYApgEWAn4A1P3Q/Cb+1P+yAD4BAwF0/779mf1H/4kBWAJrATsAVv+O/jj/jAB+AAAA+f/U/+7+BP9vADsCwALAAP3+6v08/koASgIoA28CkAESAQMB1wDy/4b+pP4oAVUDHQQhAw4C9ADb/yUA7QCYAaMAHQBNASwCvQF+AGAAqgCFAKD/pP7Q/nT/tv8lANcAsgBd/yb+Q/5s/8gA3gCv/yb+Vv2D/Xf+p/+R/zj/8v8wAeUA/f50/fn9gv/j/9v/vv8x/3f+jv7y/9cAHQAp/wz/OP/9/n/+3/7F/5sA+f9h/nT9mf1h/in/fgAWADX+Yfw8/Pn9bP92AHoBPgHn/oP9Xf3C/jMAjADiAdMBuQC+/7b/wADaAUICdgI7AlkAzf8oAaoCmwIDAQcAkf8p/+P/HQIzBAcENwET/5n92Pw1/g4AiQEWAlgCNwG6/mX9Lf4p/8n+2/9kASEBvv8t/rr+HQDj/wT/nP7f/o7+G/9CADMAVv9o/sL+DP90/x0A9AA3AQAAG//f/tD+6v2+/d/+HQAlAIr/kf8i/xv/Tv/F/0oALABd/8L+Uv75/ZX+xf8wAe0AMwAdAAcA4/8WAPwA4gFCAssBJAIHAssBPgE7AGAAMAFYAvEB/ABnAJ8BVQN6A8AC1wCK/1L+wv7XAM8CkAOFAqoAcP6+/av+WQASAaMALADy/wz/Hv7f/gAAFgBh/mz9+f1//rP+Mf87AL7/CP6d/Kv8E/2K/f3+bP+k/sX9r/31/s3/Vv8i/9/+PP6V/s3/JQA4/5H9Iv08/s3/LAJgAjMAAf4i/cn+/AAOApAB1wAdAMX/UQASATAB/ACQAb0BTQGFAFkAjAASAbkC+APTAygBf/5S/jH/1P8OAFEAbwBCAOP/uQDlANT/Vv+k/lr+Q/6G/l3/MwAwAbUB3gBl/3D+4/3J/kIAMAH4ATMCywHPADj/oP3c/eP/4gHLAQ4A5/4E/5sAZAEoAbkAgv8m/gH+gv8zAGz/OP+Z/w4AMwDq/5n/bP+R/3v/G//Q/gz/lACuATcBFgDY/qT+R/9O/+P/5QCBAfEBkAE3AZsA8v8lANcANwFVAYwC8AOmA0YBe/9O/zsAMwIkBPsECgMDAYUAuQAoARkBnwFrAb7/CP6z/kYBBwKjAPL/vv/Y/gj+cP6n/0D/pP6R//wANwET/3v96v04/5sAwAAT/8n8Lfwx/8gClwPtAnoBIv9w/JH7qP3IAP8BNwGMAIUAAAC+/zMAHQB7/wz/MwBkAe0Aiv8b//n/zf9l/0f/Kf/f/or/VQH4AQMBZf8p/0D/Yf6g/X/+xf8OAO0AqgKXA7UBZf+6/qv+pP6R/88ABwL8AoUCBwI+AUoAmf+Z/1kApgFgAlwBwAC5ACgBKAHXAOP/S/4t/mX/GQHeANT/R/+r/sX9/fwe/mcAcgF2ADH/6v1w/Bf8r/0zAE0BuQCg//X+3/6c/i3+Uv6z/tv/9AASAfQAwABnAJH/2P7C/k7/r//U/wMB0wGYAaMAHQBRAHT/cP57/8QBjAJVAbkALAAi/5X+BP/PAFUBwABnAGAAiv8m/tj+HQC5AMAAPgE+AcX/f/71/h0AoP/1/pH/RgGYAVkAbwCjAK//S/6r/jcBsQKJAcgATQEZAdT/Xf87ACUAKf8p/28A2gE7AgMBtv8b/wz/+f+qAAsBawFrAUoAuv62/WX9vv0T/zABJAKuAQ4AMf8x/yn/Kf/1/t/+Jv4m/hv/FgBA/wH+pP5O/13/5/4i/wcAhQDq/xP/wv5h/uf+lAAdAoEBiv8m/pX+gv+Z/8X/5QBvAukBzwBRACUAQP81/t/+HQCqACUADgDeADABvv9h/pz+OwA7ApQCMwKbAMn+CP6G/s3/NwH8AhID2gFgAPn/HQCMADcBPgGmAfwAmwC5ADMA2/+FAG8ChQLAAN/+F/6G/mX/owD8AFEAuv4x/cX9r/+YATMCuQDy/RP7RPpa/Nv/tQFNAa//0PxP+8n84/9cAX4As/6Z/RP95/xa/r7/MwBW/9D+Iv/n/tj+OP/PAOUA/f5l/dz9iv8OAKMA1wBKAAz/lf5d/2AAsgBRALIAWQC5AGQB4gGmASwABwAlAPQABwJcA3oDvQFRAAcAJAJvAvQAZwAZAVgCMwIHAtMBxAGJATcBrgFNAUD/oP2z/oUArgE7AtMB1wBW/6/9nfxs/Sn/iv90/77/zf9d/yb+Xf1H/SL97vyv/cX/ZwDj/13/s/48/jz+uv4E/13/1P9nAPn/uv6r/pn/zwCFAE7//f6C/2cAUQBCALkA+f/1/in/ZwD8AAcA/f66/qT+3/5gAK4BNwFvALIAEgFnAPn/owBkAQsBwAD/AfwCpgHF/4UAFgIOAq4B6QEHAokBIQG9AZQCUQL/AUICdgIoAUD/iv/0AKYBowBs/x0A7QCjAAsBiQGUAAT/3P13/v3+/f4i/8n+Q/79/E/9s/6C/1b/nP5a/mX9DP0m/gAAHQC2/dz7Hvxa/iwA5QA7ALP+QP2r/Dz+qgBnAh0CdgCr/jz+kf+fASEDSgIsAEv+S/6g/1UBCgNGA0oC5QBRAIwAmAFKArUBlADy/3YAvQE3A64DawMdAn4A2//U/zMAjABrASQCqgIZA2MDhQLXAKMAsgAdAKD/fgCBAekBfQIdAsgADP9L/or/9AB6AZABZAGjABP/F/6G/rP+CP5H/aj9Kf8lACwAIv90/R78dPt//ML+BwCg/3D+oP3n/GH8lfzN/QT/OP+2/5QAVQFRAFL+e/1l/aj9wv4wAZsCSgKbAED/xf8sAJH/wv5H/6oABwJvAhkBdP8I/vn9kf/LATsCNwE3AVwBNwGMAHYA5QDIAKoAfgD8APQAMwBgAEYBJAJRAm8CdgLxAWAAKf+v//QA2gGmASEBYADq/zMAowC5AOr/QP+K/5QAdgCg/0f/uv6v/f38oP2z/kf/nP7y/dz94/1//kf/iv/U/RD8lfzf/mAA6v/C/h7+hv79/iUAKAHAAKf/uv50/00BBwIhAQAAG/8T/6//9AB2AlgCVQHXAOUAqgA7ADMAMwCZ/07/sgDlAnoDkAEzAE7/Vv0Q/Fb9owBcA3oDiQHN/6v+PP5D/v3+HQBvALkA/ADpARkDfQKjAN/+vv2g/bP+sgCjAtcCOwJGAQAAG/81/tT9Jv7C/nT/4/9O/2j+Lf5w/lr+bP39/IP9BP+Z/7P+Lf4I/k/9hvz2/HD+mf92ANcAYADY/u78Kf17/58BZwIkAoEB5QBZAEIA3gCjAIwAcgH8AmcEDgTIAgsBxf+g/+UAwAKJAxkDvQHeAGcASgA7AKoAuQCn/6f/mwA3AXYABwAsACwAxf8b/xP/yf6c/ob+bP8zAOr/tv8WAN4ALAAb//n9Af5d/8X/xf8OAM8AMAG5AL7/nP6Z/U/9aP4dACgBwACK/3f+4/01/oL/UQC+/2H+R/0E/TH9Af66/gz/bP+C/6//LACMAOP/wv53/qf/egF6AYUA7QD/AR0CyADN/xYAPgEKA1gEYAQ3A3oBFgBRAIEBlAKmA3oD6QGjALkAnwEzAjsCpgESAaoADgAlAN4AowCZ/1b/sgD4AWsB4/84/0D/uv4P/qD9Hv4b/9T/WQAWAJn/Mf+K/wAAMf/y/fn9E/8AANcA3gBCAAz/8v1w/tv/zwCjAFkAOwBgAOr/Kf/1/hP/1P8dACUA2/+g/zj/3/57/5H/gv+C/wcAZwAOAM3/6v/eAOUAmf8t/hf+Kf/tAJsCMAOMAmAAlf5S/or/7QCYAfEBywEOAoUCWALXAIL/E//U/2sB8QGMAmcCMAGn/+7+SgBrAXIBuQB2AFkA2/+2/yUA7QAzAF3/G/8b/6D/Vv/C/lr+wv7N/xIBtQEOAK/9hvyD/Wz/bwCyAGAAxf+V/sX9hv7F/xYAbP8p/77/JQD5/zH/lf6V/rr+nP5w/uf+iv8sAJH/nP6k/lL+S/4i/2cAsgC+/yb+G/0I/sX/ZAGfAaoAQP8X/i3+Kf8wAbECfQL0AKD/DgA3Ab0BMAHIAMAAhQCbAEYBdgLtAv8BjADU/+P/OwByAaoCdgKuAWcABP+V/nT//ABCAlEC3gA4/zz+Uv5A/88A4gHtAIL/s/5s/6MASgAx/3f+s/5s/28AowCC/5H9jvyv/Zz+Mf8p/+f+Iv8T/5X+iv0M/Qz9/fzn/JH9S/48/o7+9f7J/tz9Vv1S/qf/Mf8B/qT+UQCJAeUAr/9H/wT/Iv/y/2sBWAIdAr0B6QE7AtoBCwE7ACwAyACBAR0COwKFAnYCnwELAYUAYAA7ABYAjACBAfQCNwOYAcX/Zf/5/1EAFgAWAAsB/wH4AfwAQgDj/2z/dP8HAKMAKAEoAc8ACwGQAZABMwAM/yL/gv8sAJQAUQDq/4L/Iv+Z/0IAOwDj/6D/OP9//ib+8v3F/Qj+yf5d/5H/G/9w/hf+mf1l/Sn9vv3Y/rb/JQDb/1b/s/66/qT+uv4i/3T/bP9O/wAAlAALAeUAFgB7/zj/dP/b/0oAlABrAUoCdgKJARYAIv8T/wAA9ADTAUoCbwJ2AiwCrgHXADMA6v9gACEBPgE+AWQBiQFkAeUAbwBCAHYAfgAAAJn/xf9KAAsB0wHpAaoA2P4t/vX+r/+C/0IAegESAUD/8v0e/vL9zf1w/pH/JQDq/2cAwACv/0D96/uk/Aj+BP+v/34AAABl/6D/4//9/pH9Xf26/s8AIQEOACL/Tv/5/xYAZf9w/ob+2P50/3YAZAFyAbIAmwAOABv/S/5D/pH/NwEWAmQBzwDtAEYBPgHtANcAmwBnAB0A/AAdAiQC/wHpAfgBTQHtACgBZAGJATcBIQGfAcQBGQHeAE0BvQGQARIBbwC+/wAAowC9AZQCvQGK/0P+5/7U/ywAWQBVAXIBYABl/+f+Kf+6/pX+mf92APn/yf7J/l3/r/9A/5z+jv6V/tj+9f5l/77/BP+k/rr+wv71/nv/HQBRAPn/wv4t/iL/jABrAYEB3gCK/xP/MwCJAcQBqgBs/xv/6v8+AW8C5QL4AZsAFgBKACUAgv8x/4L/jAC9AbkC9ALLAQAALf4m/or/1wCmAWsBCwHeANcA/AAwAbIAp//9/gz/bwDEATMCDgL8AL7/pP4t/mj+3/6Z/34AXAFVAWAA3/5d/Rv98v2g/88AMwDu/hf+tv2o/c39Uv5W/8X/Zf/J/gj+xf3j/R7+Q/7Y/tT/mwDXAAcAd/4E/WX9Xf8ZAdoBCwEzACwADgBRAKMAQgDF/wAAAwHiAdMB1wAsAL7/xf9nABIBkAEZAaoAZwBZAFkALABvADsA+f87AN4A5QBCAAAADgCMAM8AwABRAPn/1P9l/0D/Vv8OAMAA3gB2AK//G//Q/v3+Mf9l/7b/dP9A/13/vv/b/zH/q/41/ur9Yf44/2AAmwCg/+7+f/4I/uP9nP7j/34AoP88/gj+0P6n/x0AQgD5/wz/q/5l/0oA/ACMAF3/s/4x/5QAVQEhAW8ALACUALIAowAhAZgBAwFvAGcAowCjACwAWQCfAc8CZwJNAbkAfgBRAIwAAwGMAK//vv83AYwCDgJKAHT/6v9CAMgAqgDq/+f+yf7j/+0AegFnAKT+3P13/mX/iv+O/rb96v3C/hYAsgCjAEf/OP0t/Ev81P3b/88AQgBW/wz/gv+C/07//f6z/kD/xf87ANv/Zf90/83/JQDU/5H/oP8WABYA+f/y/8X/AAB2AO0A/AAZAQMByACqAJQAowDIACgBcgGYAVwBMAGYATsCUQIZAdT/AAALAbUB8QHTAVwBRgFcAQsB7QCFAPn/e/9d/wAAYAALARIBjABvAPn/6v+g/7r+mf1P/VL+vv/AAHYA8v+2/zj/Wv4I/gj+D/5L/tD+4/9RAB0AIv9h/o7+d/5L/kv+pP4p/3T/8v+5AIwAZf93/pX+G/+g/ywAUQAzAOP/YAD0AE0BNwFKAPn/Vv8x/0oAmAFvAm8C4gH0ADMAbP/F/8AAtQEkApgBMAHeALkAMwAdAG8AGQFrASgBCwGjAG8Axf9O/6//lADeAFEAdgDPAFwBqgDy/wAA4//N/3T/+f+jACgBTQEDAaMA1P+C/13/e/9H/zj/4/8WAOP/1P/5//L/1P9W/5z+hv6G/k7/QgCUADMAaP5A/eP91P+YAXIB4/9o/mH+5/62/3T/cP5o/kD/1wADASwA9f4B/jz+q/6Z/ywAZwCFAEIAZf+c/pX+OP/q/yUAbwBgAIwANwGBAeUAkf9//jj/kAGjAgcCwAAOABYAWQDPAPwAVQEwAQsBEgEhAXIBpgGQASEBuQCMABkBGQE3AcsBPgEsAFb/BwBVAYkB7QBZACwAFgBKAH4ASgAi/y3+hv6+/8AASgBO//3+Tv++/1kAqgDy/xv/Lf4P/nD+aP4b/xYAAwHlACUAzf8b/47+xf17/UP+Mf9nAOUASgDu/h7+Uv4b/77/4/87AOP/mf90/xP/Kf8T/6//dgB2AH4AfgBZAPn/iv+Z/ywA5QAhAcAAAABA/2z/ZwBrAXIBhQAlAAcAkf+Z/5n/mf9vAAsBzwBRAA4AUQBnAAcAkf+Z//L/YADPAOUA1wAdAHv/oP/U/7b/Xf9d/wcAjAB+AAcAOP8T/3v/1P87APn/R/9//uP9Yf4zAK4BXAEHANj+jv6z/t/+Mf+g/28AwAD8ABIBFgAE/2j+7v4zAJQASgBgAKMAzwASAfwAwACjAKMAjAD5/07/Tv9KAJABWALxAd4A4/9H/yn/Mf9W/6//mwByAWsB3gCZ//L93/wM/aT+bwDeAKMALAAp/w/+Xf3N/av+9f7u/mz/YADAANv/hv6G/sn+lf5D/lL+d/6r/nT/hQBVAbIAQP+c/sn+jv4B/nD+p/+yAO0AsgA7AHv/DP8p/4L/kf+2/4wAcgF6AdcA8v97/6//DgDlAHoBTQHlALIAbwBvAN4AIQFcAQsBSgAzANcAtQEOAigBLADy/1EAwADtAN4ALAAdAMgAyAAsANv/AAAdAFkA+f+2/wAAbwBNAZ8BZwCr/tT9Q/57/1EAzwDIAJQAbwD5/xP/1P3q/RP/LABZABYAgv+r/nf+jv6Z/yUA+f+C/zj/gv9s/07/5/4p//L/5QCfAT4BHQBo/s39/f4wAdcCGQO9ATMAp/8AAD4BPgG5AKoAsgAwAb0B4gFrAc8A+f++/4UAnwFgAkoCiQEOALr+lf7b/58BowIsAhkBQgAAACwAHQBCAJQAwADIAFEA8v87AHYAwACUAA4A6v+n//n/lACMAMX/Vv9l/5n/QgBgAGAAOwCMAJQAVv+k/sL+vv+bADMAXf9d/4L/4/9gAEIA8v8b/9D+/f5H/1b/OP+Z/9T/DgCR/9D+q/50/0oA8v+C/0D/iv8lAFkAQgAsAAcA8v/U/9v/LABnAJsAzwC5ADsA+f9nAGQBHQKBAXYAiv9A/6D/YABrASwCOwJ6Ac8AfgB2ALIAEgESAe0AhQBCADcBkAEwAXYA1P/U//n/LABKAKMAjACqAJsA8v9W//3+dP8WAGcAHQAdAHYAqgCMAB0Akf+k/mj+7v75/wMB3gBKAPn/R/+6/uf+/f5O/1b/QP9d/wT/wv7f/mX/Zf9o/qj9zf2r/hv/3/7Q/sL+BP9W/zj/G/+k/ob+q/4E/07/Kf9W/9T/AACC/zH/Kf+g/5QA3gCyADsAiv+n/6MARgFkAbkAAAAHAPL/ZwCQAX0CbwKmAWAA2/9CAMgAgQFVATAB9ADlAIEBEgGFABYAOwDeADAB/AC5APQA3gCFAMX/R/+Z/4UA0wEkAj4BoP93/pX+Xf9vAO0AsgCMAJQAZwCg/wT/yf4p/6f/Zf8b/5X+aP7n/qf/6v/n/g/+1P08/jz+1P3j/WH+OP9A/9D+4/3n/JX89vwI/gT/oP9O/1b/xf9W/1L+E/2r/Nz9mf+jAO0AmwAAAKf/iv++/wcAQgBgAAcAQgAoAeIBSgJcAZQASgBRAOUAawHxAdMBgQFrAcsB0wGBAVwB3gCyAGcAUQCqALUB7QL0AsQBSgDF/xYA/ABNAU0BuQDN/x0AhQD0AM8AfgBvAEIALACg/+7+q/6R/w4Akf/1/rr+G/8i/9D+Nf6+/Yr9iv1S/tj+jv7q/Wz9T/2K/aD9Xf17/dz9lf5d/yn/r/32/GX9xf2G/lb/dgA3ARYAlf4B/mj+mf/AAIEB4gEhAQcA+f+yAIkBegHlALIAPgHaATsCUQJ6AcAAdgADAUoCAwPXApgBYAAWAEoACwHxAUICDgI+AVkAOwADAWsBuQAOAKf/QgA+ARkBowBvAMgAqgAWAOP/vv+2/4L/iv/j/+r/p/97/6f/gv/Q/g/++f3Q/or/mf8M/1r+Uv6G/ib+CP5S/pz+uv6G/sL+2P6V/pz+s/4T/yn/s/6V/sL+2P7f/kf/JQCbAAcAMf+6/hv/dgCJAaYBRgG5AGcAzwAZAe0ACwFrAfEBFgLEASEB1wADAe0AmAFKAkIC8QGQAVwB9ABgAAcAYAASAcQB4gFNAXYAHQBZAEoADgCC/6D/owAZAdcA+f9H/7b/ZwC5AFEAZf/Q/n/+OP8zAFkAhQA7APL/4/9O/9D+0P4E/+P/uQDeAHYA1P9d/0D/iv+C/6f/4//5/9v/iv8HAEoA1P+C/4L/r/8OACUADgB0/7r+yf5W/2AA1wCjAFEAHQC2/77/DgAdAMgAzwC5AH4ABwBKAOUAEgHeAIwAowA3AWQB8QFNAQ4Azf8dALUBdgKmATsAmf8OABkBrgHEAbUBqgC2/7P+uv7q/xIBpgHlAM3/Zf+v/ywAZwCZ/1r++f0p//QAvQGjALr+6v1D/qf/uQDIAB0AZf8i/9D+9f57//n/ZwB2AK//QP8b//3+iv/q/7b/R/9l/83/ZwB+AL7/Zf84/0f/tv9CAKoAyACFAFkA6v+K/+P/zf/b/+r/+f9vAMgA1wBKAHT/OP+2/0IA7QBNARkBWQCR/7b/LACFALkA5QBvAOr/DgBnAAMBPgESAZsAMwAAAPn/lABgANT/dP9W/wcAYACMAJQAlADj/47+zf3q/Rv/FgDPANcAzf+G/nv9Mf2o/ZX+BP/9/qv+q/4M/13/Mf9w/s39OP04/aj9lf4HAJsAzf9o/r79Uv4x/07/bP8p/8L+5/5O/0IAjABCACUAQgA7ALb/e//b/28AhQCyAMgAqgDtAPwAawFcAX4AQgCbACgBVQESAcgAyAADAWsBmAH8AHYAUQCbAM8A9ABrAa4BvQEhAZsAdgBRAGAAhQDPANcA9ADtAOUA3gCFAB0AHQCUALkAqgAdAIL/dP+v/x0Avv+Z/8X/r/++/yn/pP41/ur9Yf5l/zsAOwCR/9D+Nf50/d/8QP1a/or/1P+K//X+Yf4t/hf+Jv5h/in/2/8OAHT/F/6Z/Tz+tv+yAIUAvv/Y/in/UQBcAUYBLABO/5H/NwFKAuIB5QDq/4L/HQCQARIDcgN9Ak0BAABs/9T//ADlAjcDYAJ6AVkAOwB2APQANwG5AJsAwAA3AXoBZAEZAVEAZf+z/sn+4/9NAekBkAFCAGj+G/3j/RYAPgHAAIL/BP/n/kD/bP+K/9T/iv+R/3v/vv8dAA4A4/+K/zH/3/4b/3v/WQCFAOP/OP+6/hP/dP8OAGcAbwBKAHT/hv7j/TX+Zf9gAKMAfgDj/4L/Vv9d/5H/BwCqAN4AowDj/3T/kf9gAFwBawGyAPn/lADiAZQCJAJVAcgAqgD0AHIB0wHiAcsBegFGAd4A3gBNAcsBJAJrAR0AQP+n/8AAxAFkAcX/Yf4e/in/OwBKACL/PP7N/Sb+Mf/y/x0Akf/Y/gj+qP3j/Tj/jACjAK//f/6r/nT/bwC5AHYA6v9d/3v/MwCJAWAC8QGMACn/s/5O/zsAEgFVARkBlAAWAHYA1wASAWcAG//Y/pH/dgCUADMAr/9H/yL/iv/q/w4A8v9H/zH/G/8i/77/UQCMAIUAQgAAAIr/yf6V/hP/2/+yAJABvQEhAQ4A3/6z/sL+Kf+v/wAAyACbAOP/1P/5//L/OP9//kP+hv4p/+P/WQAOAKD/5/7C/jH//f4E/wz/Vv8OAG8AdgAWAKf/kf/b/xYAbwBvACUAJQCqAEYBpgFkAX4AYAC5AHoBiQGqAJQAzwAZARIBIQF6AXoB7QCjAMgAhQAdAOP/fgALAcgA6v9O/3T/AABCAAAAJQAAAKD/E//C/iL/4/+UABYABP8t/tz9jv4lAEYBXAGUAAT/cP6r/uf+OP+g/6//r/8WAG8A5QDeAPL/s/6+/c390P7j/3YASgCn/9D+1P35/dj+r//y/9T/p/8p/8L+d/4i/28AEgHPAPL/5/66/jj/1P+bAIUAZwBvAHYAyACbACwAdP8i/2z/zf8sAIUAAwGJAXIBDgBD/ur9QP8hAVECmwKYAaD/uv4E/w4AEgFcASEBwACMAFkAowAwAekB+AH0AM3/Xf9RAK4BdgJ2Aq4BWQCZ/+r/GQH/AfEBZAEOAIL/dP/N/+0AywHTAZQABP8X/nf+e/9RAGAA4/+C/yn/BP/9/vX+2P4M/7P+pP44/07/Xf97/6//dP/Y/ib+PP79/kf/Kf/n/vX+Mf84/xP/9f4M/wT/0P7f/u7+G/+R/x0AUQCK/8L+S/66/nT/xf8HAAcAMwAHAPn/4/+v/5H/2/+FAKMAbwBgALIA/ADeAIwAjACMAIwAqgCUAKoAowDeAIkB/wHiARIBOwDy/5QAIQEZASEB/AAhAWsB7QB2AIr/Kf/j/2AA5QD0AO0AMAEoAX4Agv+G/jX+9f4sAN4AZwDj/8X/kf/J/nD+9f7y/9cAsgDq/6v+8v1//gcA5QCjAGX/zf3j/Rv/lAALAVEAoP97/w4AfgBZACwAvv+6/o7+Mf92AK4B2gEDAeP/5/6G/mX/ZwB6AUYBZwAlAAAADgC+/77/+f+jAPQA9ADtAH4AQgDb/9T/QgCqAO0AmwDj/83/1P/b/0oAQgAsAPn/AABvAHYA1P+k/vn9/f7eAJ8BGQEAADj/Vv+K/4r/zf/U/zsAmwBCAB0Ar/9A/5n/dgDPAFkAVv/f/pn/FgAsALb/dP8sAHYAMwDj/3T/Iv8i/yL/Kf9W/5n/HQCqAOUAjACC//3+p/9+APwA9AB+AGAAfgAzAFkAlADPAIkBywFyAe0A/AAoAXIBTQGbAGAAzwAOAmcCxAGjAKf/6v8ZAb0BrgEoAX4AqgDXAPwAQgAb/9/+OP+2/6f/r/+R/6//e/9O/zH/5/7f/ob+yf4E//X+9f4T/xP/aP4P/rP+4/9nAAAADP9a/mj+BP9l/5n/Mf+V/v3+OP90/yn/nP6k/sn+bP+K/2z/Kf/Y/mX/p/8p/+7+Zf9vALkAzf/C/tD+r/9gANcAsgBCANT/BwADAYkBIQEAAGz/2/+jAEYBiQF6ASEBsgAsAB0AZwDlAGsBnwGYAZABTQEwAd4A+f+2/wcAuQBVARIByACjAGcAdgAsAIr//f4i//n/fgBgAEf/f/66/l3/QgBvAL7/wv5//vX+Vv9W/yn/Tv9CAN4AdgCR/6T+jv7Y/jj/Vv90/wcAuQDXADMAQP9w/tj+gv8dAGAAFgAWADMAYAC+/+f+Uv6V/vn/wACUAB0AFgCyAKoAoP+k/ur9uv47AN4A/AB2AB0AHQBRAA4AdP8x/4r/SgDXAOUAfgBgAIUACwHXAAcAr/8HABIBMAHlAJsASgAOANT/1P/b/zsAQgBnAHYAAAC2/4r/8v/q/4L/E//u/tv/lACyACwAzf+2/1b/DP8M/83/5QDpAaYBLADC/n/+kf/AALUBrgE+AVEAZf+Z/9v/MwBnAPQAkAFNAW8Avv8WANcAwAC+/7r+s/6K/34A3gBnALb/Mf/9/tD+0P4b/13/r/+2/xv/PP5a/vX+MwDeAKD/Nf6K/Xf+oP9ZALkAUQAzALb/Xf8p/07/4/8sAG8AAACg/wcAwABVAbkA7v7c/Y7+WQCfAUYB6v+c/ib+q/6Z/+r/r/+R/7b/OwAdAED/wv6V/jH/FgAzAFEAYACUADsAE//C/hP/LABkAZABVQESAaMAhQADAYkB6QF6AfwANwE+AfQAlADAAIEBxAGfAXIBPgFVARIBBwBH//3+mf/XABkBEgG5AEoAxf/1/pz+wv6n/6oAPgHeAOr/Kf/J/tT/hQDq/xP/lf6v/94A9ACjAPL/gv8p/9/+5/4T/+r/AwG9AUYB1P+c/mj+7v5s/5n/Iv9H//n/1wAhAQcA/f5h/ob+wv4E/07/r/9RAEoAHQCC/zj/Kf8b/07/Xf/q/88AHQJgAlUBLAAx/2z/lAA3AUYBXAFkAfgBfQL/ATABmwD0AJgBmAEoAYUAjABcAQ4CBwKJAYwAAAB+AJsA4/8x/5n/5QD/ATsCVQH5//3+9f6C/0IAbwAHAPn/HQBZAHYAUQBCAB0AXf/C/sn+OP9KAN4AZwB7/9/+Xf/F/4L/E/93/i3+s/4lAEYB/ACn/0P+3P08/t/+R/90/77/r/9d//X+/f5l/2X/5/4t/lL+Zf+qAMsBegFRAO7+xf01/or/IQHEASEBwAC5AN4AZwDb/0oAKAG1AUYByADeAAsBIQH0ALkASgC+/7b/MwDlAOUAJQCn/w4AIQFrAZQAmf8T/yn/R/84/9v/mwDAAJsAJQC2/6f/QP/n/mX/DgBZADsAWQB+ANv/BP9a/qv+p/9KAHYAZwAdACL/S/5S/hv/+f8lAM3/2P4t/ob+Kf+Z/2z/lf41/kP+7v6n/4L/2P4X/vn9pP4T/+7+/f4E/2X/xf97/4r/iv9d/3v/Xf9s/77/BwCUAO0AyACbAHYAqgDlALkAZwAdAHYATQHEAUYBjABZAEoAbwBRAEIAsgALAYEBawF2AJn/DP9l/6MAGQHAAG8AjAA+ARkBWQBs/0D/+f/tAMsBrgELAVkAbwAHAGX/Tv+Z/xkBMwL/AYUADP+O/sX/CwEDATMAjv5L/lb/7QCBAUoA5/53/tj+E/9A/9/+BP9W/xv/G//9/hP/QP90/07/cP5d/b79Tv/lAGQBjAB7/9/+pP6k/gz/mf+MADABTQHtAFEAQgAlAG8AAABd/9v/wACQAYkBmwC2/3T/6v/0ABkBHQBA/3T/hQD8AAAAR/+n/28AGQGjAOP/2P6z/oL/ZwAwAe0AsgB+AG8Agv9h/i3+DP+yAK4BtQGqALb/Xf+g/6f/Tv8i/2z/FgCMALkADgAx/5X+s/79/lb/zf87AHYA2/9A/7P+Kf9CAO0AjACC/5z+lf50/w4AmwAlAA4AWQCFAIwA+f/U/5n/tv/N/7b/zf+qAGQBKAFZAJz+F/79/vQAbwIdAu0A1P+v/w4AUQAlACUAZwDAAKoAUQD5/x0AGQFyAdcA4/8M/3T/yAAZAX4AKf/Y/gcANwGmAd4Ap//u/gT//f6R/w4AowA3AaMAAACr/ib+yf7F/zsA6v90/1b/8v8AANv/QP8M/2X/+f9KALb/e/+v/5sA7QCbAFkAZwB2AA4ADgD5/34AEgFyAYkBowAdAA4AyABGAUIAR/+C/4wAFgJ2AlwBFgDu/nf+wv6n/wMB0wHxAU0Bmf93/mH+G/+qAFUBZwBW/3v/9ABvAqYBkf8t/vL9Tv/XACEB1wA7AOP/MwCMAEoAZf8i//L/lABZAMX/OP+R/5QAAwH8AOP/2P7J/vX+Xf/F/1kAmwBvAM3/3/6G/gT/4/9CADsA+f/y/zsAwACMAFb/Q/5L/gAArgHxARIBMwAzAJQAmwB+ADMA8v8sAFkAZwAzAOr/WQD0AOUA+f/Y/hP/dgB6AUYBr/9S/i3+tv9VAVwBlABW/5X+d/79/qf/UQDlAPQA7QB2ALb//f4M/2z/p/+g/77/sgCQAYkBOwAE/5X+wv6n/ywAWQCqAO0A7QBvAFb/jv41/jj/1wBNAfwA1P+R/w4AMwBCAJn/E/84/+r/owC5AFEAHQAdAAAAdP8M/0f/zf+MAJsAAADF/9v/JQCUAHYAmf/J/sn+LABGAYEBRgF2AAcAVv+z/tD+4/8wAfEBnwFCAJn/OP/U/6oAdgA7ALb/DgCFAJsAUQCZ/5n/LAB+APL/xf/q/1EAQgAb/2H+8v3n/kIAsgA7ACL/Uv4t/jH/oP9l/0D/Mf+n/4L/wv41/kP+R/92ADsAiv8T/8n+Mf8T/yn/kf8dAJsAbwD5/xv/f/7J/s3/MwAHAJH/Vv/j/9v/e/8b/zH/vv9gAFEA+f9CAHYAyAC5AG8Avv90/zMAyACBAa4BTQHlAJQAQgCFAAMBgQF2AmACawEOANv/7QDEAb0BsgDq//L/1wCYAVgCbwJVAWAA6v/5/77/iv8WABkBawHAANv/oP8lAG8AuQBKAM3/Xf/9/pH/MwCjAEIAoP8T/7P+5/5d/wAALAC2/3D+vv26/g4AzwAdAHD+Vv10/Xf+p/9CANT/Vv/Q/pX+/f79/vX+5/7Q/gT/gv8WADMADgAi/779bP01/r7/9AALAQ4ABP/Y/k7/tv+K/2X/Tv9l/7b/r/+C/6f/xf8WAHYAOwDF/7b/OwAsAEf/DP9W/28AxAH/AfwAOP9//jj/dgA+ATABqgCUAO0AMAE3AZsAOwB2ALIACwEwAfwAEgF6ASgBqgAlAPn/bwDAAPQA3gCMAFEAOwBgAFkAFgDq//L/+f+2/07/G/+R/83/r/+Z//X+/f44/zj/mf+n/6//p/9l//3+3/4E/3T/6v8OAL7/OP9O/3T/mf/N/9T/8v9CABYAoP9s/2X/tv/F/6//Xf+n/0IAhQCFAIr/0P5S/gT/fgBkAXIBDgAE/7P+OP++/4r/dP/U/34AzwDlAG8AMwAlACUAAADN/x0AhQDPACEBgQEDAZQAbwBvAG8AJQBCAJsAZAGQAdcAhQCqABkBawHAACL/Uv7Y/rkAfQJCAk0BUQDF/0oAuQCUAK//Kf8OADABtQFyAfQAowBgAKf/7v44/3YAywHpAXIBWQAT/+f+dP9ZAEoAoP9W/x0AEgH8AIUAvv9s/4L/e/9s/07/tv8dADsAsgB+AAAAkf8E/wz/s/7Y/qf/UQBvAIr/BP8T/4L/Zf/Q/nD+uv6v//n/WQAHALr+Jv6V/ur/CwHtADMA4/90/wT/pP7Y/ur/NwEWArUBhQBW/8n+3/4p/77/YAALAVwBNwGFAGz/uv7Q/rb/wAAhAdcAbwCbAKoA+f9A/+7+xf8DAT4BXAE3AWAAp/8x/8X/wABVAYEB1wAAADH/G//N/6oA3gBZAAAAoP/F/83/Kf/Q/in/LADlAMgAZwAzAM3/Vv+r/n/+E/8AABkBXAH8AG8A8v+R/6f/R//J/k7/OwDLAcsBsgDF/4L/mwD0AFEATv8b/wcAMAHaAWsBhQDq/9T/vv/N/5n/2/8hASQCSgIZAWX/cP6k/oL/YACMAH4AwAD0ABIBjADb/1b/BP8i/6D/SgASAb0BgQGMABv/hv5H/x0A5QDAAGcAQgBCAJQAlACUAFkA6v+v/2X/Iv/f/vX+dP/b/83/e/9A/zH/OP8p/5X+Q/5a/ob+QP9d/zj/Mf/f/o7+8v0I/in/WQDAACUAMf/Y/uf+Tv9RAN4AyAAlAM3/4/8WAKMAwAAwARkBOwCR/9T/PgE7Ag4CdgD1/tD+e//8AJABuQC2/07/FgAoAWQB7QDU/zj/Kf9H/8X/bwBNAdoBnwFRACn/5/4x/wAA3gDpAR0C2gE3ATMAvv+K/w4A3gBrASgBuQDtABkBCwEAAP3+9f4OACgBIQHIAM3//f4b/zj/Mf84/4r/SgBZAE7/6v1W/X/+HQDAAPL/Wv5s/er95/5d/zH/s/4p/83/xf8T//L9kf35/fX+Zf97/wcAsgAZAWAA3/50/cX9oP+fAcAC2gFKACL/pP7u/k7/fgDLAR0CvQGbACn/nP4i/1kAPgESAaMAdgALAVwBuQBKAAAA1P8sAO0ArgEOAtMBGQE7ANT/LADlAAcChQIdAjcBJQC2/7b/dgCQAUoCDgKUAFb/e/+UAIkBvQFRALP+Wv4i/6MAZAHlAGz/Lf4m/nf+pP5//pz+Iv/N/9T/BP9w/lr+jv5D/in9nfyR/UD/OwDb/8L+xf2K/Tz+3/79/tj+hv7f/vL/jAAWAED/7v6Z/3YAuQBRALb/kf+R/+r/GQF2AiED6QFKAEf/Xf/XABYCzwIdArkAOwCUANMBZwKuAaoAsgAhAZ8BQgI7AvEB7QAHAM3/8v/8AL0B4gEZAZH/s/4p/94ALALLAZsAVv+G/kv+aP5l/5QAPgEwAWcAoP/Y/hf+mf0B/v3+p//y/wcA1P8T/1L+CP7y/QH+CP4B/t/+8v8WAFb/e/1//HT9DP9gAEoAdP/Y/qT+BP9O/6f/4/++/ywAqgDXAMgA1wCuAdoByACg/4L//AB9AowCpgHeAMgAkAHIAgMD4gEOABP/xf/PAHIBtQGBASgByABgAAcAFgAOAPn/1P9l/6D/QgC5AKMA1P8b/7P+nP7n/kf/kf/q/wAA+f/b/6D/Vv/1/sn+f/5S/ob+gv/AAAMBwADU/7r+Wv4I/vn9Lf79/mcACwGjAJH/jv48/sL+Iv9A/2X/iv9ZAMAAQgCK/8L+yf6R/x0AFgDy/2AA9AD0AG8Ap/9H/9v/7QDTAbUByAAWAAcAdgCFACwASgADAZ8BEgHy/5n/1P+MAOUAdgAAAE7/Xf/j/wcAAACZ/4r/+f87ACUAAADb/wAAFgDb/w4AMwCUAJQAoP97/8X/AAAlAOr/BwAsAB0AZwCjAIUAAAA4/0D/+f8dAHv/wv5o/pz+2P5d/5QAAwGFADH/CP6G/kf/DgBRAOr/vv+R/ywA7QCyAAcAXf9O/+P/mwAwAYEBiQH0AGcAdgCyAPwAyABKAFEAlAC5APwAKAHIAGcASgBgAKoAWQC+/0f/Vv8dAKMAAAA4/5H/DgAWAJn//f7J/pX+2P6n/28AbwCg/wz/BP9H/0f/BP/9/gT/Kf9H/83/bwBvADMAkf+6/o7+2P5s/6f/vv9KACwAzf8lAEIA4/9W/4b+nP5W/6//LAC5AD4BPgFKAED/yf7J/nT/lACYASQCmAHPAFkAHQAOAAAAjAAwATcBEgF6AfEBrgESATsA6v9gAD4BQgIdAk0BOwDb/4wAEgE3AaMALAAsAGcAqgBvAEoAFgDy//L/1P+v/07/9f7n/jH/QP9A/2X/bP9d/8L+Af62/Sb+/f6C/77/oP8b/2H+F/5w/u7+dP/5/0IAlABZAJH/OP9W//L/YACMAN4AmwBCAA4ALACyAAMBRgEhAaoAZwAlAFkAegFKAlECawGMANcAEgESAZsADgCFAGsBQgJgAssBwAAlACUAWQC5AIUAyABGAVUBqgAx/9D+bP9vANcAOwDb/6f/oP90/xP/uv4M/6f/HQAlAND+mf0x/fn9gv9KADsAmf9A/+7+cP5S/qT+dP9s/0f/gv/b/ywAp//1/ob+aP5O/8AAxAFkAdv/uv7n/tv/bwBZAEoACwGmAYkBVQHXAHYAUQA7AGAAowDeAEYBQgKxAv8BuQB0/2z/2/9RANcATQG1AVUBwAAzAIL/9f4E/+P/sgAhAaoAvv9l//X+d/6c/lb/bwAhAc8AHQAT/9T99vzn/Aj+kf+qAGsBxAFyARYAr/3r++P7Xf2K/zABLAIHAnYAyf4I/mj+Iv/U/+r/vv/y/zMAPgEzAsQBFgA8/ur9Mf/PAOkBUQK9Ac8ADgC2//n/LAAsAEIAsgD0AKoAbwAOAJH/3/53/tj+zf8DAXIBCwEHAKT+tv2K/Qj+/f4OAKMAlADb/zj/nP48/sL+Kf+Z/w4ASgCjACUAbP/C/o7+Iv+R/0IAuQDAAJsABwDU/+r/p/9O/2X/8v+qACEBCwHXAGcAxf+n//L/fgCbAEoAMwCUABkB9AB+AB0Axf/N/w4AowBcATABUQDb/yUAjACFALIAPgEwAUoAkf+R/9v/LAAlADMAAwGJAT4BFgDC/hf+Uv6K//wAvQH0AIL/3/5O/9v/Tv9h/g/+5/5RAE0BegGFABv/iv3J/AH+SgDTAVUBxf8e/rb9yf4zAJgBvQGFADj/cP66/l3/tv8zAG8AhQDAAKoAsgAsAAT/5/57/yUAGQHTAZAB8v8t/or9PP7b/0YBvQGuAfwAoP+O/ib+0P4HAIUAjADPAGQBKAFnAKD/BP9l/yUA9ABrAWsBCwFRACUAJQAOAPL/6v8zAEoASgAzAIwAsgBZAMX/BP9s//n/dgC5AA4AXf9O/x0AmwCjACwAmf+v/6D/gv+n/4UACwGMAOP/DP9H/xYAhQA7AIL/0P5o/mz/qgB6AYEBowCn/9j+q/7Q/tv/wADeAMgAWQDq/1b/oP+bAD4BAwHj/yL/bP9ZALIA5QD8AGAAkf90/34ARgFkAQ4Ahv6z/pn/uQDtAM8AmwDN/wz/aP7Q/lb/Zf+K/7b/2//F/9v/r/9s/9j+F/6c/gAAEgEZAQ4Aq/4m/rP+Zf8zALIAhQBZAFEAUQC+/6T+nP50/0oA7QD0AMgAlABCANv/bP84/0D/+f8LAekBQgJyAR0ATv/9/sX/KAEHAkICpgG5ADsADgD5/x0A9ABkAWQBXAEZAdcAWQDy/83/+f8WACwA5QBcATcBDgDQ/iL/jABrAd4Axf8T/3T/QgCjAIwAtv/9/u7+R/+v/2X/Q/7F/Yb+zf+UACUAR/93/gH+Jv5h/gT/bP+C/13/yf5//nf+7v6Z/6//vv/F/9v/JQD5/1b/3/4x/wcAIQHaAbUB1wCg/9j+yf4x/9v/MAHlAmsDwALeABv/2P5H/zMAdgBgAMAAIQG1AXoBlACR/9D+7v4x/8X/hQBkARYCegElABP/0P5H/8X/8v8OAAcAHQCyAD4B1wCg/8n+s/6v/9cAzwCMAAcAVv8E/13/sgBkAYwAMf9D/o7+bP/q/w4A+f97/xP/OP/U/x0AOP9a/lL+2P6+//n/ZwB+AF3/hv4t/nT//ABGAT4BbwDb/3v/Tv+g/yUAzwA+AbUBEgEHAPL/SgDtALkAHQAsAPQAmAFNAXYAvv+R/xYAqgCyAKoAQgAdAKoAlADN/5X+hv5W/0oA/ACUAB0AMf+G/nf+BP8WAFEAUQC2/yn/5/6G/uf+e/+v/4L/r/9KALkAWQCv/4r/xf87AKD/R//y/4UAPgELAc8A3gCjADsAvv/j/2AAYAAWAB0AZwDIAMgAwAADAbkADgD1/nD+wv7N//wAGQFGAWQBNwEzAO7+aP5o/nv/fgBNAekBtQH8AM3/9f66/hv/tv92ADABXAHIAL7/Vv9l/7b/p/+K/+r/DgAWAKD/Tv8x/yL/Tv9l/77/tv+K/2z/bP9W/9/+s/71/vL/ZwBKAA4AQP/n/hv/p/8AAPn/AAAWALIA7QBKAOr/QgB2AA4Azf9RAAsBRgEwAYwAzf97/6D/jADTAQ4CCwG+/8n+Kf8WAMAA5QAHAEf/mf/tAGQBYAAp/0P+d/57/7IAPgHIAIL/Yf4b/ywAmwA7AJn/gv9s/5H/8v+yAMgAzf8x/07/r//N/+P/QgBnAB0AHQAzACwAHQB7/7b/QgDU/9/+PP4x/1EA7QDeADMAoP/Q/uf+tv8dAM3/s/6G/hv/iv+v/6D/LAAlAHT/mf8AABYAkf9H/x0A5QDlAEoA4/8OABYAMwCUAPwAuQC+/2z/bwCfAdoBZAHXAIwAQgAWAG8A7QAZAbkA6v9l/5H/MwBkAQcCXAFvAMX/e/90//n/fgB+AFEA8v8zAJQAjACbAJQAjADq/+7+pP7N/64BOwJVASUAR//Y/jj/JQDPACEBZwBH/wT/Iv+R/1kAwAA7AAz/d/71/gcAdgCZ/8L+cP5o/vX+2/+MAEIAwv50/aj9jv79/iL/mf8WAOr/Vv8M/6//AABd/1b/oP8lAGAA6v8WAKMAuQCMAHYAYACbADcBTQE3AeUAmwAZAWQBCwEwAVUB3gAzAM3/YAALATABZAEOAqoCTQGK/yL/+f8wAbIAUQD8ALUBnwFCAF3/9f4E/83/wACfAU0B+f9A/5H/6v+2/0f/Zf9l/13/tv/y/28AWQCK/8n+d/6k/in/bwDXALb/f/5L/mX/UQDIAIUAmf8X/t/8zf3U/2QBIQFl/5z+uv4b/83/MwCK/2H+3P0T/wsBZAGUAOP/FgAWAF3/E/9l/yUAfgB2AMgA/AD8ADcBcgESATMADP9W//QAZAFrARkBqgDXAKMAYABCAJsAKAE+Aa4ByADQ/nf+kf9yATMCRgFZAIr/DP/C/hv/4//q/9v/OwAwAfwAvv/9/qT+9f4M//3+6v+qAIwA1P+K/6D/Tv+r/jz+hv71/lb/DgCbAFEABP+g/Wz9Lf44/1EA9ABKAJX+oP0I/v3+tv+n//3+lf7Y/nv/3gCQATMANf4x/Sb+BwBkAUICQgIoATH/+f3f/s8AQgK5AmcCZAHU/wz/BwD4AbkCgQF+APQAxAHiAQMBMwDy/wcA1wAHAkoCegGjAHYAqgBKAFb/R/+MANoBHQJNAeP/R/9W/7b/lACjAGAAOwBgADsAQP/J/sn+Tv/5/0IAZwCn/+7+Wv4X/rP+Kf+n/9v/Tv9L/vb80PxD/s3/hQDb//3+jv6+/YP9cP7y/2AAVv/C/t/+e/90/9j+BP8T/0f/1P9ZACgBhQD1/nf+R/92AKMAWQAWACUAZwCUABkBmwCg//3+Zf9GATMCbwLxAYUAXf+V/pH/awEOAoEBXAFcARIBkAEkAkoCCwH9/qj9aP78AOUCfQRgBB0CMf9W/Vr+4//0AO0AjACyAGAAsgD8AEoAs/5d/Zn9Tv8DAe0ALABA/0v+T/0x/Uv+QP+C/wz/DP/u/qv+9f4M/9j+Hv6+/UP+Kf/U/8X/Mf/J/o7+Yf4E/6//AAB0//X+vv9nAG8Azf+C/13/Mf+K/zMAkAGYATsATv9A/zMAyAC5AN4ACwHlAPQA9ACUAB0Axf9ZAN4AGQFcAcQBMwKmAQsB1wAoAfQAfgBGAa4BegHAAIwAVQGuARkBWQAsAOP/Kf/Q/koA8QHEAWAAwv6r/uf+3/6v/2cAWQAb/x7+Uv7Y/vX+BP9O/wT/cP5D/v3+JQAzAAT/Nf7y/c39d/6Z/28AdgC+/07/Tv9l/3v/6v+qACEBbwCC/7b/ZwAZAVwBTQEhAVEAOP84/34AmAEOAuIBGQFKAKD/kf+FAL0BmAHAAIUAFgDq/8AAawHEAZAByACUAMgAWQCZ//n//AADAVkABwDIAA4CdgLxAU0BdgAi/1L+Kf+yAJ8BmAFNAdcAJQD5/9T/1P9d/zz++f3n/hYAmwBKABP/Lf41/qv+DP+V/qD9Mf0P/kf/8v/y/9T/Xf+k/mH+S/4M/4L/0P5D/qv+QgCmAf8BAwG+/xv/7v57/4wA2gGYASwA+f92ACEBKAGFAJsAIQGqAKD/6v8SATsCOwL0AEIAdgAZAfwAqgCqACwAOwADARYCowI7AnoByACUAKoA7QADAZsAqgA3AfEBJAJkAdcAuQDIAB0AG//n/pn/WQALARYC0wHq/0f9PPxd/QT/SgBgAA4AXf8B/v38kf3C/ob+iv0E/aj9q/5O/0D/CP5a/F77NfxD/nT/Kf/J/t/+7v6r/pz+wv5a/vL96v31/kIA1wDtALkABwC6/pz+8v83AYkBwAAzAMAAVQHIAB0AbwAZAXIBvQHpAT4BbwDq//n/sgDeADABLAKqAlgCyAB0/3v/OwC9AW8CHQIoAVkAowD8AAsBfgBZALkA7QC5AEIAlADPAM8AuQCUAFEAKf+O/nT/mwDtAA4A9f4i//L/2/8M/2j+Nf7Q/sX/fgBKALP+vv3c/av+Xf9O/+7+f/5//in/SgDb//X+G/9H/1b/wv6z/kf/AABKAA4AWQDy/7P+3P3J/n4AcgF6AdcAOwBd/9/+bP9nAPQACwHXAH4AZwAAAHYA7QCFAHYA6v8zANcAAwFkAT4BmwBW/+7+mf9gANcA3gCqAFkAdgBZAMgACwFKAFb/9f5d/6//UQALAfEBywFnAED/q/66/v3+AABNAbUBWQCk/kP+yf6Z/9T/8v+Z/wT/3/6Z/5sAr/8B/vL92P6g/77/Zf+K/77/mf+R/6D/9f4I/i3+OP8lAGcA3gAoAcAAQP/N/VL+iv9ZAG8AQgA7AHYASgBCAKoA6v/J/n/+6v/XAG8AdgDPAIkB5QCn/0D/oP92AMAAwACbAMgAzwDtAFwBNwH0ALkAzwASASgBPgE+AXoBMwJ2AhYCkAHtAOUA5QDeAN4A9AA3AfQAlAA7AJsAVQFVAWcAXf8p/0f/8v9+AEoA5/57/cX90P4sAGAAFgBs/0v+qP2g/cn+Iv9//nf+q/5o/gj+PP4p//L/BP/N/a/9Yf7u/qD/uQCbAMX/pP4m/v3+dP9A/4L//ABVAZsAjABCAFkAfgCqABkBcgE+AaMAawFKAmcCrgHPADMAzf9RAIkBVQOQA2AC3gDU/7b/FgCJAVgCxAG2/0v+QP/aAXoDwAIZAbP+g/3N/bb/rgG9AZQAXf/U/7IATQHPACwATv8X/lr+Zf/tADcBMAHlAOP/pP50/Qj+R//b/9D+S/7Y/jH/dP8p/07/3/4m/ur9d/5A/zj/R/9l/0f/Wv4B/sL+tv+MAH4AhQAOAFb/bP8HAJsA2//f/jj/zwDEAbUBNwH0AO0A1P/N/34A5QDlAH4APgFyAfwA1P+R/1kAUQDAAKMAbwAHAL7/hQDeAKMAvv+Z/zMAjABnAEoAqgBRAJH/Xf9CAPQAZwDU/94ADgLEAdcAbP/9/hP/Kf/y/2AAjAAlAGcAVQELAc3/yf4X/r79F/5s/+UA5QA7ACL/cP5L/nv9tv0b/xYAxf/1/gT/p//U/yn/hv5L/n/+PP5D/mX/ZwCbAPn/p/9l/6T+Hv5h/pH/5QCfAXIBfgAb/y3+jv4HAPQAjADN/07/tv9+AKMAhQA7ANT/MwDlANcA8v8T/13/6v8dALb/4/8SAaYBkAH8AM8AOwB7/13/vv8DAd4AZwBcATMCUQKYAcAAMwB7//3+iv/lAIkBiQG9Aa4BEgG2/3D+Nf4i/xYAowD8AJsAJQDN/9T/OP9//pz+Mf9vAGAAoP/u/rP+9f7f/in/Iv90/0IAIQFkAfn/Nf5H/cX9q/50/wAAYADPALIAlABCAED/r/0E/S3+QgDEAeIB0wG1AfQAkf9S/pz+bP9+AJgBbwJnAu0Amf/F/zABywFrAQMB1wDlALIAwACMAL7/R//N/7IA9AAZAbUBYAKuAVb/Iv0p/Yb+HQCQAaMCqgLAAP3+7v4HACUAMf84/77/UQAsALkA4gFrASwA/f4T/4L/Mf9l/wAAzwCjAHT/Xf/5/6//DP/f/gT/7v7n/uP/wAAWALP+q/4WAGcAKf97/XT9s/6v/6MA9ACyAHT/Uv4E/9T/+f9s//3+iv++/+P/fgDXAH4AbP9l/5sAawFVAYUABwDb/4L/OP/N/+UAiQHEAdoBCwGK/7r+Xf9NAWACFgKjAED/G/+C/6oAMAHtAJQA+f8zAJsAwACUANv/mf+C/07/r/+jAIEBIQEOAMn+D/6G/tT/RgHIAFb/D/6+/Qz/uQCYAT4BHQBL/lb9tv3Y/ur/LACv/xv/QP++/1EASgC+/+f+jv57/3YATQFyAd4AFgCC//n/9ABkAbkASgCyANcAZwBCANcAxAGQAYwAp/8p/13/gv+5AFgCywEx/0f9jv4SAaYBOwDQ/qT+Zf9RABIBIQGZ/139QP1d/xkBnwGbAGX/wv6V/o7+jv7u/gz/tv8zAH4AYACZ/7b/Mf8P/in9mf1A/34AyAA7ABYAzf9A/3/+Hv4I/s39nP7j/9cAdgBd/7r+f/7n/pn/zwDLAUYBbP8t/pX+vv/XALUBHQIZAW8AuQB6AXYC+AHtAEIAsgCuAVECfQIHAlgCOwJ6AXYAOP9W/34AjAL/A3oDcgEx/9j+OwCBAUYB+f+z/mH+4//xAXYC9AB//gT9Vv26/jMAlADF//3+yf4x/6D/5/6o/XT9jv6R/9T/6v8OAM3/yf53/pX+Uv7c/Qj+DgCYAZAB8v/n/kf/Vv9A/wT/dP9l/13/8v8DAaYBzwDy/2z/DgAdAGcANwEwAeUAWQCjADABiQFcASEBbwBH/0f/yAAZA4EDDgIWANj+OP9CAOkBKAPIAigBAAAOAB0A8v/5/zsAwAC5AMAAVQGmAe0AR/+c/t/+Xf/b/4UAKAEhAVEAVv/J/kv+F/7j/br+zf/5/6//G/9l/4L/s/5s/br82Pz5/b7/5QAoAQ4ApP62/a/9Nf4E/yUAmwBZAPL/tv+K/x0AJQCK/3v/gv8WADABMwJnAhIBKf/J/kIA8QEdAmsBQgBl//L/9ABnAnoDjAKqAMX/xf9CAPQApgGuATcB9ACUAJsAWQBCAJQAEgGJAfQAsgDPAPwAowAdADsAhQB+AH4AVQGuAQsBtv9H//L/QgAWAKD/DgAOAM3/4//5/34AQgAb/0P+Af4I/sn+FgDIAOr/Yf75/av+Mf+k/hf+d/4i/5H/vv+2//3+vv1l/aT+MwDU/xf+/fyo/Tj/HQBCAEIAWQBs/wj+kf08/s3/mwCMADsA6v+v/77/fgDeAO0A3gCyADcBgQELAX4ADgAdALIA+AEKAwMD2gFvANv/p/9nAGQBUQKFAmQBlABRAMgAqgDAADABTQF6Ac8A1wDXAIwADgDy/0IAOwDIAMgA3gAWAGX/2/9CAO0AmwBnANT/QP+r/qT+gv+g/ywAFgCMAHYAyf62/dz9Xf++/0f/7v4p/wz/jv4T/6f/Mf8p/Vr8vv3q/94AUQCZ/5X+xf0x/YP9Uv7C/uf+QP/j/9T/bP8b/+f+S/7U/Vr+R//5/zMAQgAsAGcAUQAWAIwA7QC5AOr/tv8dAGcA9ACmAYUC/wHXAMgARgFKAhYC5QAzACUAlAAoAVECYwNNAyQCzwC+/07/dP/5//wAawH8AG8AqgBrAWsBhQBl/4b+F/4P/rr+qgCBASUAyf5L/n/+Iv9s/6D/QP/c/SL9qP3u/k7/DP8i/+7+Uv4E/br8Q/6n/6D/9f4m/mX9mf26/n4ANwGMAE7/Yf5//jX+Nf5s//wAtQF6ARIBqgBnAA4Axf9W/wz/AAC9AQMDuQKQAYwAYADlAGQB4gFYAjsCVQHXAE0BbwLXAmACBwLEAWQBmwDeANoB2gGqAM3/YAAZAUYBfgAOAA4AAAAHAK//8v++/8n+Jv7U/dz9f/57/3YA/AD5/yb+3/y6/P38Zf01/qT+lf5D/rr+2//N/5z+Vv0x/Q/+7v7j/zsAOwC+/4b+Wv66/nv/SgDXAPwAJQBl/13/jABGAbkAJQAzAHYAHQBRAN4A5QAdAAcAIQG1AZABUQCv/1EA3gD8AAMBXAFNAc8AjACyAM8AYACZ/w4AxAFRAssBEgF2AIr/5/6Z/7kAVQFNATABsgCK/xf+Xf3Y/t4AiQHAAIL/nP4P/kP+R/8HAJH/f/7N/TX+d/6V/u7+Xf/U/yL/Hv7j/cL+vv/F/13/lf6g/WH+uQBRAsQBE/84/XT92P5gAFUB2gGBATsAyf7Y/sX/mwD0AAsBegHeANv/gv/5/88AEgEoAbUB+AHLARkBHQAlAH4APgEWAuUCEgNRAoEBjACqAKoAjAAZAbUBWALpAVwBNwE+AfQADgB7/6f/OwAhAcsBVQEdABP/hv66/rb/WQAzAK//OP9H/xP/yf66/sL+/f4M/+7+Zf9CAIUAtv/U/d/8Kf1o/hYAyACMADH/PP4m/rr+r//U/6D/bP+R/9T/vv8x/+7+Mf/U/7kA9AD8AEoAkf/f/kv+nP5W/zcBbwK5AjsCSgCG/sX9Q/5O/34A3gADAVwBcgGJATAB1wAOAIL/QP/N/7IA3gBGAXoBawGqAB0AUQA7APn/Vv9W/w4AhQDAAJsAdgD5/zj/3/4M/8X/dgDPAEoAXf8T//3+Vv/j/5QANwHlAOP/R/+R//L/4/8dALkAGQHPAPn/xf/y/34A7QALAZABuQCv/0f/gv9gAN4AGQGBAf8BkAE3AbkAFgBH/0P+2P4zAIEBywHLAaYBhQAi/8393P2c/g4AgQF6AYwA7v4P/nf+dP9CAEIAoP/9/in/iv/j/wcA4//q/3T/E/+g/zMAzwDlAFEA6v+2/zMAwAADATcBdgDj/xYAbwCyAAsBawHaARYCRgFgABYA+f/y/0IAhQB+AG8AhQA3AZ8BCwHb/zH/7v6O/k7/fgALAU0BVQESAW8A9f7j/TX+OP+FAPQA3gDtAM8AqgBZAMX/DP9//nf+Kf8lAKMAmwA7APn/FgAOAJn/Iv/1/iL/Vv9d/w4AAwHtAA4A2P75/R7+d/4p/6//4/9RAHYAfgDq/9j+vv1d/Vr+iv+qADABdgD5/9v/e/9d/0f/e/8zAAsBnwELAQAAkf+Z/w4AmwBcAbUBuQB0/7P+7v7U//wAkAG5AIr/lf5h/u7+r/8sAM3/R/8i/2z/6v+K/yL/OP8M/1b/tv8sAJQAr/+G/mj+Zf+jAMgAQgAWANT/r//U/wcASgAdAAAAMwCqALkAyADIAEoAhQC5ABIB/AA7AKf/mf9nAN4AgQGuAZQA4/+v/+P/MwAlAB0A8v/F/6D/gv+v/+P/8v/j/83/p/9A/xP/R/+R//n/FgAsAFkAxf/J/nD+2P4zAD4BIQFRAAz/pP7Q/k7/8v+yAEYBhQBl/9D+BP9O/yL/E//J/tj+Xf/F/0IAUQB0/2j+Uv7n/u7+7v4E//3+Iv/Q/t/+mf8HAEIABwAT/zX+8v0I/u7+6v+yAD4B/ABKAJn/Mf/C/qT+7v62/6MAMAEOApQC0wEWAMn+d/5h/v3+JQAoAeIBKAG+/0f/Mf9A/6f/SgAOAHT/3/7n/tv/SgCMAEIAxf8x/zH/QgBrAfgBmwBH/wT/4/83Ab0B8QEoAQAAG/97/1UBYAI7AlwBuQCFAHYAKAGYAXoBjAD9/vX+QgC9ASwCTQHU/xv/Xf+2/zsAgv/9/qv+lf6g/5n/QP+c/g/+wv7b/8gAqgCR/3/+4/3U/Wj+G/9+AHoBmAEDAb7/5/48/gz/QgDIAN4AdgCyAN4A7QCqADsAlACjAIUAZwDj/8X/ZwBVAXIBwABRAFkAjAAWAEf/OP+g/ywAhQDlAMsBpgF2AKD/bP/N/+P/OwAwAb0BRgEdAA4A9AAhAXYAFgB+APwAwADb/6f/UQASAZABKAEWAKv+Af4b/34A9AAWADj/DP8b/wz/f/5w/pX+Tv/U/4r/Iv9S/lL+3/6v/77/G//1/vX+E/8i/xv/p/9nAKMAyAAzAE7/nP7n/g4ACwH/ASwCDgKQAXIBCwHy/5H/tv9+AIEB5QJ6A8ACNwGg/8n+wv7F/ygBMwLxAUYBBwBA/zj/Iv+2/wcAuQAwAfQADgAM/8n+DP/F/28ACwGqACUAkf9W/9T/FgB2ADMALACv/2X/LAD8AGQB/AD5/+7+Kf9RAJ8BLAJNAeP/Wv48/pH/ZAFCAnoBowBd/4b+Lf6r/vn/ZwCyADMAoP+n/8X/HQDj/2X/s/5w/gT/OwAwATABfgCg//3+wv6n/5sA/AAzAF3/e//j/zsAkf84/5H/8v87AB0AAAD5/6D/Vv+n/yUAbwCn/yn/Kf9d/4r/Zf8OAIUAYABW/8L+Iv+2/0oABwDF/6f/p/8zAOUAKAFgAP3+PP6c/jMAnwEOAtMBAwFCAIL/R/9s/+r/7QC9AZABbwDN/4r/4/92AO0AVQHXAIUAhQCqAHYAzf/b/5sAsgBRAA4A6v9RAH4AhQA7ACwAJQDq/0oADgCK/zH/E/++/zMAOwBZAGcAvv+z/pX+E//U/zsAxf8p/6v+q/7Y/sX/5QDtAGcAdP+V/q/9oP3Y/iwANwELAZsAWQB7/6v+4/3q/f3+UQCBAZ8BGQFCACL/0P71/iL/kf9ZACEB3gD5/9j+Hv7f/h0AAwH0ABYAZf/Y/in/2/92AOUAqgA7AF3/5/79/jj/HQASAbUBxAH8AA4Agv+6/lr+E/9ZAK4BBwKYARIBdgDN/9/+cP6r/oL/1wAsArEC0wEzAMn+0P7F/88AAwGUAHYAtv/J/pz+Zf/IAAsBmwCFAGcA2/9O/zj/kf9l/4r/HQB2AAsBAwF2APL/Vv+6/pz+xf/tABIBZwBs/9j+DP/q/7IAmwDq/zH/9f4E/0D/mf+2/9T/kf8x/7r+hv7Y/u7+E//9/t/+E/9s/4L/Mf/u/tj+BP9W/4r/e/+C//L/HQC+/2z/mf+5AMQBvQEwAR0Aiv+2/wAAlADtAEYBFgJRAiQCNwHy/wcAUQDPAEYBVQGYATABKAEwAfQAzwB+AFEADgCn/4L/hQD4ATMCPgG2/+f+bP9CAMAAyAAdAHv/r/9ZAOUAGQHXAFEA2//b/xYADgAWADsAOwD5/07/BP+2/8gAMAGjAGz/jv5L/mH+Mf9vAAMBWQBs/8L+cP4X/qj9Af79/hYAYABCAMX/hv50/Tj9Nf4x/5n/oP+v/zMA8v8b/2H+3/57/6D/JQBCAMAANwHlAJQAHQDU/0oAXAEsAjsCcgGUACwAYADtAKYBowLPAjsCawGFAGAA1wBkAaYBXAEZASgBkAH/AQ4CPgFCALb/oP8HAIwAEgHtAOUA5QCMAMgAYAC+//3+d/7Q/or/uQAZAbIAr//C/mj+Af6G/iL/Vv+C/0f/Xf+g/2z/f/6D/TH9oP2z/pn/JQAzADj/r/2z/Nj81P1l/5QAsgDU/3/+3P0B/uf+8v87ADsAr/84/13/xf+FAAsBAwFgANv/r/+v/xYAmwDXAKMAuQDeAPQAuQAsADMAJQAsAG8AKAEHAmcC+AFgAKv+Wv6g/00BSgKmAbkAMwCZ/13/e/9KABkBGQFnAAcAmf8b/zj/+f9kAZgBGQFCAJH/e/+r/sL+vv/PAJ8BVQElABv/jv5o/qv+lf6V/in/mf+2/5n/yf4P/pH9bP01/lL+Yf6O/nf+3/7C/jz+xf0I/kD/AADN/7r+CP5S/jH/OwC5AJQAHQAOADMAjAB+ABYASgCFABIBTQF6ASQCZwJKAjABOwD5/5QAtQEsAmcCHQKBAQsB7QDeAGcAfgADAWsBMAEOAJn/SgAhATABZwD5/zMAYADy/yL/cP5//nv/uQC1AXoBlACn/+7+7v66/rP+e//PAJgBmwAx/1L+pP50/wAA2/+C/77/6v87ANv/Kf/f/vX+gv9l/0f/R/+g//L/mf/1/i3+d/6g/88AqgBO/wH+6v0M/wcAuQBZAK//dP9d/0f/3/4i//n/5QBrAeUA8v+g/6f/8v9KAG8AmwDXAIkBywEwATsAr/9RACEBawE+ATcBkAG1AVUBLACK/77/WQC1AUICiQGMAAcAhQDXALkAZwAdAGcASgA7AG8AdgCUAJsAowBCANT/8v8SAeIBNwEAAAT/mf+jANcAfgDj/7b/1P9KAM8AIQGbAJn/Xf8x/yL/G/9A/+P/HQCK/9D+wv66/t/+Mf8p/xv/0P7Q/gz/Iv9H/2z/dP8M/8L+yf4T/6//LABvADMAmf8b/13/MwD8AMgAp//f/uf+2/83AX0CfQIZAZH/5/4b/83/YABvAO0AXAESAWcA1P/q/1kAfgCn/9j+uv79/vn/yACFAM3/7v5//hP/Vv+g//n/HQBgAL7/9f6k/sn+JQBNAZAB1wBW//3+tv/AAE0B5QBKANT/QgDtAPQAsgAdAMX/4/8sADsADgBnAO0AyAAWAOf+jv4i/3YAXAHXAPn/BP/J/gz/dP8dAIwAwACjACUAXf8E//3+2//PAMgAAABA/3T/JQAoAZ8BcgFnAGX/Mf+C/0oAZwBgAB0ASgBvAIUA1wBKAPL/oP+n/9T/AABRAIUAYAC2/0f/E/+n/ywAYACFAAcAdP/n/v3+bP/b/x0ASgCUAGcA+f8HACwAFgC2/0f/dP/y/4UA1wDlALkADgDy/zsAZwAdAMX/2/9CAOUA7QCjAGcALACv/wz/Tv/F/1kAyADAAG8A4/9d/yn/r/8OACwA+f/b/1EAbwCyAHYA1P+R//L/bwAHAK//Xf/F/+0AawEoATMAR/9O/0IAfgD5/yn/3/4AAD4BkAGyAFb/pP5W/0IAjABZAOP/+f8dABYAmf/n/uf+p//XAIkB7QC2//X+9f5H/3v/dP+v/5sAVQH0AL7/Yf5//r7/XAH/AWQBQgAM/0f/1P+FAH4AAACMAE0B2gESAQcAgv+2/1EAWQAsAB0AmwDlABIBsgB7/6v+nP75/1UBXAGbALb/iv+2/2z/R/9l/7b/8v/F/zj/f/5D/n/+gv87AAAAG/8m/ib+nP4x/wT/S/75/bP+gv+v/4L/2P7J/tD+f/5w/nD+/f7q/1kAUQB0/yb+D/53/nT/WQBZABYAgv+g/w4AOwAsAEoAlABnABYAHQDXAJgBrgEwAVEAAADPAK4BDgLTAdcALAAzAM8AiQHLAb0BZAFVAQMBSgCR/zH/zf/lAHIBXAHAADMAzf84/wz/BP9A/7b/LADPAMAABwDf/mj+DP+K//n/1P+Z/6f/kf84/8L+3/5H/0IAsgAsAGX/Yf48/pz+gv9RAIwAUQCv/07/5/6G/kv+5/62/4wAowDU/yn/d/79/l3/mf+C/2z/MwCqALkA8v9H/8L+/f7U/3YAyAAWAPn/UQDIAJsA8v+g/8X/lADlANcAQgAsAJsAEgEwAWAAkf+K/wMBwAJcAwcCYACn/8X/owDXAOUA/AB6AUoCfQKBAa//2P6R/wsBnwFkAc8AbwCjAMAAYABW/yn/1P+5ADABfgCv/2X/JQDXAHYAkf/Q/v3+xf9vAG8A2/9d/2z/JQCFAOr/Tv8b/13/FgAsAPn/LABgANcAdgAx/3D+Yf6C/xkBrgE+ASwABP/J/iL/Tv9l/3v/e/9s/4r/Xf9W/4r/kf97/wz/yf6k/t/+dP/N/4L/wv6V/oL/yAAwAbkAmf/Q/vX+p/9+AAsBMAFcASQCHQIoAer/wv4b/88AyAJcA30CNwF+AJsAmwAOAIr/AAAhAfgBOwKYAbIASgDy/6f/QP8T/5H/jACQAXoBOwC6/kv+9f7F/xYAe/8T/3T/JQBRAPL/G/9o/rP+dP8sAAAAQP+r/t/+kf/5/5H/wv6O/hv/OwAsAE7/nP48/v3+tv/N/0D/wv71/tT/bwA7AHT/q/6k/hv/+f8WAGX/3/4p/+r/FgDU/1b/Xf+Z/8X/kf8M/zj/xf/lAL0BgQF2ACL//f4HAE0B0wEwAYwAWQC5AGsBNwHeAPQAgQHpAVUBfgAHALIAywEkAoEB2//f/mz/zwCYARkBDgB0/9v/jACbANv/OP+C/0oAzwCUAKD/q/7Q/nT/xf+C/+7+gv92AD4BMAEsADj/Yf6V/lb/JQBnAOr/AAD5/+P/2/97/3v/8v9KAEIAoP9O/77/ZwAhATABQgD9/rP+QP8AAJQASgDq/77/WQDAAEoAbP8T/9v/sgD8ACwAxf/b/wcAQgAdAA4A6v8AAFEAyACjAAcAvv8WANcAqgA7AOP/AABnADsAXf/Y/l3/LABVAXoBowBl/6T+/f7F/6MAhQBgAIwA1wC5APn/Kf9w/gz/bwByAXIBwAB+AIUAYACn/8L+Lf7C/psAHQJYAgsB/f6o/Zn9hv6+/4wAKAGfAYkBjADC/or9bP2V/lEA7QCbALb/OP9d/07//f5L/jX+9f4dAMAAYABl/2H+Uv6z/iL/Iv9H/7b/HQB+AOP/QP/J/v3+6v+5AM8A6v8T/9D+1P/tAMgAJQBl/1b/r//j/wcA6v/b/0oAlABKAOP/Zf9l/x0AjABnALb/DP9H/9v/dgCUAOP/Mf/u/nT/ZwDeANcAYADj/9T/e/8p/xP/r/+FAN4AMAHlAKoAOwCZ/xv/7v7U/+0AHQJYAk0B1P+G/n/+bP+UADcBCwGUAH4AhQBZALb/DP8b/4L/hQB6AdMBegGFAMX/Vv9A/13/6v/XAPgByAKFAt4AIv+k/kD/ZwBcAa4BgQFyASEBjABKAAcA8v8sAH4AmwCUAIUAyABkAWQBUQDJ/kv+BP9KAPwAJQD1/mj+wv7U/8gAzwDy/6v+6v3q/XD+BP9A/8X/owAwAbkAdP+V/n/+OP8WAGAAdgB2AMAA5QCjAAAAIv9A/wcAGQG9AVwB7QCbAKMAqgBCAB0AfgA+Af8B6QH8AB0Avv9RAD4BegEoAYwADgBCAMAAwABvACwAOwCqAPwASgD9/nD+3/7F/7kAEgF2AKD/5/7C/uf+BP9d/77/lADtAMAAFgAi/9j+yf4b/yn/dP8OAM8AAwFCAED/Jv4t/hP/HQCFAAcAXf/C/rP+2P7f/ob+S/7n/tv/ZwAdABv/Jv7U/Rf+wv79/u7+5/79/k7/gv9s/yn/3/7Y/uf+5/79/u7+gv9+AO0A5QBnANT/vv8dADsAOwAHAB0AEgEdAjsCiQGqAFEAqgD8ABkBowAzAH4ANwHpAXIBJQDf/v3+8v+5AO0AFgBs/2X/zf/5/4L/uv48/rr+mf/b/77/oP++/zsASgBW/yb+CP4p/8AAnwESAeP/iv8dAIwAbwC+/4r/AABNAR0CZAGFAE7/Zf9vAEYBZAF2AA4ALADeADcByAAWAKD/+f92AH4AdgBvACwALADq/wcAZwC5AFwBXAHIALb/5/50/+UAHQJvAr0BAwG5ALIAqgCMAKMAzwCBAekBmAGqAAAADgBgAMgAdgDj/2X/Xf8lAKoAbwBl/1L+Uv5W/w4A4/+z/tT91P2c/nT/xf/j/yL/0P6c/s39Xf1H/TX+r/+yAIUAdP9w/ur9Uv7n/tD+q/44/1EANwELAaf/Wv5a/oL/3gBNAe0AQgAHAIwAIQEhAQ4AR/+2/94A0wFyAaoAQgCUAPwAzwBZAPL/BwBZAN4A/AB+AAAABwCqAO0AQgBA/9D+mf/PACgBsgAAAMX/ZwDIACUA3/7q/X/+LACBAcQBjAAi/2j+q/57//L/LADb//L/QgAHAIL/wv6k/in/p/+n/07/Tv/y/1EABwAE/6j9dP1//jMA9AAzALr+T/2o/Qz/6v/j/0f/yf5d/zMAFgAi/+P91P3f/mcAZAFkAaMAmf+g/77/2//q/6f/LADlABIBlADq/+r/lAAZAd4AFgCg/6//QgD0ABkBhQCR/2X/zf9vAJQAHQCv/4r/8v8OAPL/tv+n//n/OwBZAOP/gv97/9v/hQB+AGcAWQAWAGAAlAC5AHYA8v8AAIUAPgEoAZsALABKAOUAPgEoAaoAWQAHAAAAFgCZ/+7+Mf8sAFwBFgIwAeP/DP8T/1b/Xf+C/9T/uQCBAXIBhQCZ/07/zf+qADAB7QCbAJsAwABNAfQAZwDj/w4A/ABcAZgB3gB+ADMASgCUAEoAbwBRAFEAowCFACwA2/+g/8X/mf+C/6f/tv8sADMA2/8b/6v+wv5d/28AhQDU/8L+S/4x/5sARgHIAPL/R/9A/wcA7QDtAKMAWQCFADAB5QBnADMAZwBGAZ8BiQHtADsASgCFAMgAqgBgADMAfgADAdcAWQDF/7b/FgBnAIwAHQDF/wAAZwC5AH4AoP9H/9v/7QC9AUYBHQBs/4r/fgA3ATcBhQC2/w4AmwDIAEoAiv+g/zsAKAELAQAA2P6V/nT/MwBvAMX/DP/n/in/dP8x/8L+f/6G/kD/+f/b/3T/Iv8i/0D/Kf/J/pX+Iv/5/88A5QBgAMX/QP9l/83/AAAlAB0ABwBRAG8AUQAlAOP/2/8lAHYAZwDU/2X/OP90/6D/mf/j/9v/8v/y/2X/Mf/9/hv/r//b/77/tv+2/zsAzwDPAAAABP+G/qv+r/9RALkA5QCUAGAAFgDb/2z/Mf8b/3v/+f8WACUA1P+g/2z/Kf/1/qv+wv4i/6f/BwDj/yL/S/4e/ob+Iv/N/5H/E/+6/t/+OP8i/yn/yf79/s3/jADAANT/7v7n/qf/wABcAYwAkf84/5H/yABcAc8AAACv/xYAzwDeAFkA1P+g/+P/SgB2AHYAhQCyALkAMwBl/3D+hv62/7kATQHIAMX/Tv+v/w4Azf9O//X+Kf9RAD4BIQEsAN/+hv7Y/pn/OwAHAOP/8v9KAIUAYADq/2z/xf9gAMgAowBKAFkAYACqAO0AbwDy/+P/OwDIAAsBowAWAAcAFgBnAEIAp/9O/07/FgDeAKoAvv8T/zj/mf+n/0D/yf44/ywAEgFNAd4A6v8E/xP/Zf/q/+P/DgCbAO0AIQFRAMX/dP/5/94APgFrAfQAowCFAOUAzwCMACwAgv+2/yUAUQBCABYAp/++/zMAfgBnANT/Tv8b/0D/QP9s/2X/QP9l/77/FgDF/07/Iv9O//L/YAB+AIUAQgAzACwAHQDj/8X/ZwADAXoBgQH8ADsA4/8dAKMAGQEDAcgAqgDlABkBAwF2AOP/kf/y/6oA5QA+AbkAQgAsAAcALADF/4r/dP/q/6oA9ADAAPL/oP/j//n/zf9d/9/+BP/N/7IA3gAlAF3/BP9s/+P/r/8p//3+e/9gALIAOwD9/jX+uv6K/1EABwAx//X+kf8zABYAkf+V/ob+dP8AAB0A1P9O/2z/zf/j/77/Vv8p/5H/WQC5ALIALACv/8X/AACFAJsAdgB+AGAAlAB2ACwA8v+Z/yUAmwDAANcAWQDb/6f/FgBgAEoA1P+C/wAAQgB2AA4ATv/Y/gz/kf8OAFkA6v+g/6f/+f8OANv/e/8b/3T/zf/5/9T/gv+C/+r/WQCqAFEAmf9d/2z/FgB2AJsAuQB2AGAAQgBgAGAAWQBCAFEAwACqAIwAjACFAM8A5QCUAB0Axf8dAKMA9ADXAEIAxf8HAKMAmwBZAM3/R/+R/xYAowDtAIUAOwAlAAAADgCZ/3T/vv9RAAsByABRAL7/mf/F/zMAMwBO/yL/Xf9CABIBEgFvADH/Yf5L/gz/6v9RAPL/gv90/07/Vv8b/6T+Yf5w/iL/6v/j/6D/Zf9A/2X/QP/Y/sL+Iv/U/0oAYAAOAIL/p/8HAEIABwCK/6f/UQBVAXIByADq/6f/YAADAWQB5QAlACUA3gDEAcsBAwElANv/SgALAVwBGQH8ABIBRgGBAQsBFgBl/6f/1wDiASwCegGyACwAZwDPAKoAfgAzAIUATQHpAbUB7QAdAJH/vv8sALkA5QDtAAMBEgHPACwAp/8p/2z/DgBnAFEADgDU/4r/zf8lAPL/kf9W/2z/zf8OANT/Xf9A/4L/BwAlAPn/iv8p/5H/4//F/3T/e/+R/zsAzwB2APn/Kf/Y/mz/UQCjAFkAvv+Z/zMAmwDIACUAZf9A/83/ZwCMAEoAmf+C/7b/BwBCAAAA1P+2/6f/xf+C/yL/BP9d/0oA3gDXAEoAoP9A/1b/gv+g/8X/Tv+K/0IAuQDlAG8A2//F/9v/+f8AAJH/gv++//L/LADj/zj/DP97/9T/BwCK/wz/G/+C/7b/iv/9/n/+7v5l/83/e/+V/nD+/f7b/xYAVv9S/gH+lf4AALkAZwCg/9/+bP8AADMADgB7/4L/LACUAM8AZwCv/9v/bwCqADMAkf9A/wAAMAGfASEBzf8T/xP/xf+MADsAXf+z/hP/HQCqABYAR/8i/4L/LAAAAED/f/5L/oL/1wAoAVEABP/Y/mX/OwB+ALb/9f7J/rb/owDIAG8Ap/+R/+P/JQAzAOr/MwCFAMAAwADq/zj/G//5/wMBRgGUAIL/G/9l/x0AdgA7ANT/Tv9H/77/p/9l/xv/G/+2/2AAbwCR/+7+cP7Y/qD/6v9ZAEoAqgDeAHYAiv93/lL+DP9vAPEBjALiAfQAJQDU/83/1P/b/0oAMAHxAUoCxAHAAKD/Tv8AAAMBmAFkARkBqgCFAIwAUQC2/0f/oP+5AHIBRgG5AK//dP+2/w4ADgCn/1b/Vv8WAHYAjAAOAHT/Zf/F/x0A8v/U/13/Vv/U/0IAfgBZAFkAJQAHANT/iv97/3v/2/9KAMgAlADb/3v/Tv+v/w4A2/+n/2z/iv8AAA4A4/9O/+f+Zf/y/ywA+f90/3v/4/9vALkAMwCZ/6f/LACUAIUALADq/zsACwF6Ae0AUQDq/wcAzwD0AJQA+f/q/9cAegFrAX4AbP8E/6f/uQDtACwAQP/Q/or/sgDIADMAG/+G/tj+zf+jAG8AAAAE/9j+QP97/6f/Mf9W/8X/HQBgADsAxf9s/6f/tv/F/5H/Zf+R/9v/SgAdAL7/OP84//n/hQCFAMX/Vv9H/5H/LAAzAAcA1P90/13/oP+Z/3T/p/8dAJsAyABvALb/Vv9d/7b/SgCMALIAzwDIAOUAuQAAAJH/bP/F/5sAgQHaAXIBqgDj/6//tv/q/+r/UQCUAMgAAwGyAFkAdP9A/6f/OwC5AIwAMwAOAJsA7QCqAAcAdP84/w4ACwE3AcgA1P+Z//L/3gAoAaMAxf8x/4r/LADPAG8AQgAlAGAAzwCMAPn/OP/1/nv/YABvAHYA+f/U/yUAJQAdAFb//f7C/in/xf8zAGcADgAlAFEAhQB+ADMAvv+v/9T/HQBnAJQAyAADAa4BgQELATMA2/9gAPQAnwFGAcAAfgDAAAMBTQHeAA4A8v8lACgBpgFkAYUA+f9KAGAAbwDb/yn/OP8AAOUA5QAOACL/q/5H/+r/DgCg/9j+9f6v/1EAQgCK/9j+Kf8HAH4AdgC2/13/kf8lAH4AWQDq/8X/OwCjAN4AQgBH/xP/+f8DAQsBUQAp/5z+9f62//L/dP/n/sL+kf/5/5n/2P7j/UP+E//F/83/Kf/f/u7+mf/U/13/s/5//kD/HQCUAKMAMwDy/0IASgCMAEoAr/+v/+P/wAD0AN4AsgBgAIwAqgCFAM3/R/9O/7b/HQBKAEIAzf9O/zH/G/+z/mj+aP66/l3/2//b/3T/uv41/gj+Yf7Y/t/+R/+K/9T/HQAWAMX/R/8M/07/FgCyAOUAowB+AH4AfgCFAEIA4//y/28A5QAhAcgAdgAOACUAbwAsAOP/gv+K/83/YACqAFkAxf9H/1b/r/8sAA4Ap/97/6f/OwCbAJQAJQCg/5H/+f+jALkALAAAAAAAqgBcAU0B5QBgABYAQgCbAJsAbwAOAFkAmwC5AJsA8v/N/4r/6v8sAAcAoP/f/uf+Mf/F/5n/Iv/J/pX+7v4p/yL/uv5w/rr+QP+K/3v/7v6c/rr+bP/q/wcABwBl/2z/vv8AADMASgBRAG8A7QD8AMgAJQC2/83/dgAoARkBqgBCAEoAqgD8AMgAHQB0/83/qgAhATcBmwDN/4r/AAB+AMgAUQDN/ywAmwADARIByABvAFkAZwB+AFkABwAHAFEA3gD0ALkAUQAlAGAAuQDXAG8ABwCZ/5n/SgC5AIUADgBl/zH/mf/N/+P/gv8M//X+e/8WAOP/Xf+z/mj+7v6K/5H/Xf/1/uf+Xf8AAEIA+f+2/3v/2/8HAFEAjAAsAGcAjACjAFEA8v8WAKoAcgGuAU0BZwDy/+r/WQAoATcB9ACUAIwAIQFkASEBfgCZ/3v/LAAZAa4BRgFZAK//r/8AAGcAdgBgAFkAqgD0AJQA+f8M/+7+vv+qAO0A1wBvAL7/r//q/1EAbwBZAEIALAD5/5n/bP97/+P/BwA7AFkASgDq/6f/dP8p/4L/bP/5/1EAhQDPACwAQP+c/ob+5/4WALIA3gBnAKf/bP8i/13/R/97/3v/vv87AA4A8v+v/2X/oP/U/77/8v/j/w4ADgDy/9v/bP9H/2X/UQCFAGcA2/9H/2X/xf+FAIUAWQDN/13/mf8OAEoADgDj/8X/LACbAM8AowAOAJH/AABnAM8AAwFCADsAFgBCAG8AHQC2/07/tv9gAN4AyABnAK//Mf9H/3T/p/+K/4r/Tv9O/4r/p/+C/4L/p/9H/2X/Tv9O/9v/4/8AAKD/Iv8T/07/2/9RAJQAOwDb/6//1P8HABYADgCg/6//xf8HABYA4/8HANv/6v/j//L/zf8p/+f+E/++/2AAlAAdAIr/Vv+2/zsAWQDU/xP/G//j/7IATQH8AOr/bP9d//L/dgCUAGAAJQAzAEoAowCMAGcAFgCv/9T/zf/y/w4AOwBKAEIAAABd//3+wv4x/wAAmwDAACwAe/8E//X+R/9O/0D/bP+2/34A7QCjAPL/Mf8i/4L/DgCFAJsAsgC5AKoAOwCZ/zH/Mf+2/0IAqgCUAPn/zf/U/wAAFgCn/yn/3/44/+r/MwA7AM3/bP9s/6//2/9s/07/OP/U/7IA7QDAAPn/r/8HAGcAqgCUAAcAFgCUAD4BiQH8AJsAMwCqABkBCwHIAEIAbwCyADABRgHeAHYABwDb/+P/1P/N/x0ASgBKAA4A1P+Z/2X/Tv84/yn/Xf/j/9T/8v+K/0f/dP90/5n/QP9W/8X/LAB+ADMAp/8p/yL/2/9+AIUASgDq/9v/zf/U/7b/r//q/wAAQgAlAOP/xf+v/6//tv+K/5n/AAAsAEoABwC2/4L/iv/F//n/HQA7AGAAjAB2AGcAowCjAN4AwABRAEIAlABcAZ8BiQH8AJQAzwBcAZ8BMAGMACwAowAhAYEBAwFKAAcAr/8dADsAJQD5/+P/JQBZACwAZf/f/qT+BP+2/xYA+f+R/1b/Vv+v/4L/OP/n/sn+Xf/U/1kAfgDy/+P/2//F/9v/gv+R/wcAjADlANcAfgDj/77/8v9RALkA3gCUAHYAhQBnAJsAbwA7ACUAHQBRAEIALAAdAEoAjACjAIUA+f97/3v/2/9CAFkA2/+R/5n/+f+jAG8A2/9l/xP/r/9RAJQAdgAlAOP/1P8WAPn/tv+Z/77/ZwD8APQAZwDU/4L/zf8AABYAzf+Z/+P/OwCFAGcA8v8p/wT/QP+n/2AAYABvAAAAp/+n/zj/OP9d/4r/6v8dACwAMwAAAMX/mf++/+P/8v/q/9T/vv+g/w4AbwCbAFEA1P9s/3v/zf/y/0IA8v/F/77/2/8lAKf/dP8x/xP/Xf+C/5n/mf+n/6f/dP8E/6T+jv7J/oL/LADb/13/9f71/oL/1P+n/xP/uv71/r7/hQCjANv/R/8E/4L/WQA7ACUAp/+v/0oAyADAAAcAoP9W/+r/qgD0AG8AAADb//n/jAB2ADsA4//N/wcASgAdAK//xf8HAKMAyACFAAAAp//N/wAAQgAWANv/BwB+APQA/AB2AMX/dP/N/2cAyADlAKoAYAAlAB0AWQBvAG8AowB+AEoAZwA7AA4ADgAdABYABwAdADsAQgBRAFEAHQDF/3T/gv/5/2cAdgBCANv/r//U/0oAwABnAL7/OP9d/wAAuQDlAHYABwC2/+P/+f/j/13/E/+K/ywAqgDIACwAOP/9/gz/mf/N/9T/8v/N/1kAbwBvAOP/Iv8i/1b/UQD8APQAYACv/4r/oP8AACUABwDq/wAAhQCbAFkALACK/3T/tv/b/yUA+f8zAG8AUQAzAM3/1P8lAKoAAwGMACwAzf8HAKMA3gASAaoAQgAzAFkAjABnAFEAWQBCAEoAowDIAM8AowA7AL7/r/8AAGAAlAAOAAAAFgCUAPwAdgDN/xP/QP/b/6MAzwBCAMX/p/8zAGAAHQCK/0f/Xf/5/4wAYAAWAJn/zf8AANv/Xf/Y/jH/oP9KADMAoP9d/yn/mf/q/9T/bP/1/gz/gv8OAB0Avv8p/8L+BP9s/+r/1P+R/6f/e/++//n/4/9O/zH/mf8OAKMAQgDb/3T/mf9CAM8A/ABZAPn/xf87ALkAqgCqAEIAQgC5AO0AmwAOAIr/iv8OAMAA1wCUAFkAAAAzAA4Azf90/0f/2/9vAN4AowAlAMX/p//N//n/xf+K/4r/r/9CAFkAFgC2/8X/4/8dAGcA1P9O/9/+R/8dAJQAjADb/3T/OP90/6f/vv+v/6//HQAzADsA+f9d/0D/dP+Z//L/FgC+/6D/tv/5/wcA8v+Z/xv/R//b/4UAuQAzAE7/BP9l/yUA9ACMAA4Ar/90/wcAMwAlAPL/2/9nAMAAfgAOAIr/e/8HAHYAuQBvACwALAAdABYAp/+K/6//LACyALkAmwAsANT/vv+Z/3T/e//y/2cAowCUAOr/oP+R/6D/vv+n//n/FgB+AGAAxf+C/zj/zf9KAFEA+f9l/3T/6v9CAEIAxf9l/5H/AAC5AHYABwCC/xv/r/8lAM8A1wBgAOr/kf/N//n/MwAdAAAALAAdAFEAhQAOAPL/r/+n/wAAAAAAAIL/p/9CAKoAyAAzAGX/Iv+R/yUAlAAsANv/6v9CAMAAwABZAKD/p/9RANcA9AD8AHYAbwDlAMgA5QCjAIUAowDPAOUAowBZACUASgBKAIwAbwAzAB0A6v/b/83/AAAAAPn/+f/q/83/gv90/4r/oP+Z/8X/2//y/w4A8v+n/07/Xf+n/yUAfgB+ADsA2/+n/6D/r//y/1EAsgDPAGcA4/+K/2X/4/8WAB0AHQDN/wAAWQBKAK//DP+V/qv+Vv/F/wcAp/9d/yL/Kf+K/3v/vv+v/9T/+f/F/77/kf/b/yUAbwBgADMAOwBvAKoAfgCUAG8AfgC5AAMBNwHXAH4ADgDN/9T/HQBvAKoAyACFAFEABwDU/5H/QP8p/13/8v+MAKMADgAp/3D+nP5O/83/6v+Z/4L/vv9CAJQAHQBW/9j+G//F/34AyABgADMAAAAzAGAAHQAzAPL/zf87AFEAOwBZADsA4/+v/2z/Tv+C/7b/AADy/4L/oP+g/77/8v+R/2X/E/8i/5H/6v8dADsADgCR/6f/zf/N/wcAHQDy/x0AQgB2AOUAzwDeAIUAFgDU/9v/QgCbADcBCwHXAH4AQgBZAG8AqgB+AGcAMwBZAHYAhQBZANv/r/++//n/6v8HAAcA8v+2/5H/kf+K/8X/2//y/77/iv9H/2X/xf8OADMAFgDj/5H/xf/q/w4A4/+Z/77/2/92AKoAqgBRAOr/p/+K/6D/tv8AAPn/SgA7ALb/OP/1/kD/vv8zAFEAOwDU/5n/2//5//L/2/+2/77/LACjALIAbwAWAMX/HQBvAKoAuQCFAH4AUQBnAGcAOwDq//n/fgDtADABowAAAED/G//b/7IAPgEwAcAAJQAHACUAQgAAALb/6v9CAJsAuQB+AB0Ap/9s/5H/8v+FALkAyACyABYAxf+2/6f/zf87AH4AYACjAKoALAA7APL/xf/y/83/DgD5/wAA4//j/wcAzf/b/3T/bP9l/3v/1P++/8X/e/9W/2z/kf+2/+r/2/+n/4r/Zf/U//n/LAAlAK//gv97//L/WQB2AG8AMwDN/3v/xf8AAFkAWQDU/9T/vv/F/w4ABwDb/3T/gv+Z//L/SgAdAAcAvv+2/6//mf97/07/mf/j/28AZwDN/1b/Kf9d/83/LAAOAK//e/+Z//n/HQDF/2z/Mf+g/0IAmwBnANT/p/+v//n/LAAsAPL/DgBCAGcAsgB2AEoAAADy/+P/FgB2ALIAEgGqAFkA1P+v/wAASgCMACwA2/+g/9T/LACFAB0AZf8b/yL/vv8HANv/e/+C/4L/oP+n/5H/gv9W/4r/bP+v/4L/dP+n/6//FgAdAEoA+f/N/2z/Tv+R/5n/YACMAJQAZwAAAAcA+f/5/wAABwDb/77/6v8lAFkAlAAsAL7/zf+v/9v/FgBCAGAALAAsAGcAYABCACUAHQBgAJsAfgBZAIwAqgD8APwAsgBnANv/SgDIABkBPgHeAMgAowB+AG8AUQB2AKMAyAC5AFkAFgDb/xYAZwAzAA4Azf/N/9v/BwAWAPL/tv9H/1b/oP8HADsAAAAAAJH/kf/q//L/LADj/5n/zf8zAIUAUQDy/5H/xf9KALkAlADj/2z/QP/U/0oAMwDU/2X/tv/y/xYA8v9H/wT/E/97/wAABwDq/5n/bP90/0D/R/9s/3T/kf/q//L/r/+R/13/bP/F/wAABwDq/6//tv/y/wcAJQDb/6D/mf+2/x0AMwBRACwA+f8lAAcAAAC+/6//zf8HAH4AdgA7AA4ADgAOAPn/+f/N/83/HQCbAKMASgDU/3v/gv+2/ywAUQB2ADMASgB2AEIAJQCn/9T/MwB2AJsAWQAHAM3/DgBZAIwAWQAlANv/6v87AFEAlABKACwA8v/j/xYAMwBRANv/tv9l/6D/LAAzADMAAADN/77/4//j/+P/p//U/ywAHQAHAIL/dP+g/+r/dgB2AAAAiv9s/6f/1P/q/wcA8v/q//L/2/+2/5n/r//F/9T/4/8dAFEAYABnACwA2//F//L/FgBZAGAAhQCUAFEAJQC+/6//6v9gAN4A7QDeAIUAjACjAEoAQgAAAOP/OwBZAMAA5QB+AEIAzf+g/6D/2//q//n/LADU/83/e/90/3v/R/84/yL/e/+K/9v/1P90/07/R/+C/4r/r/9l/3v/mf+v/yUAAAAAAIr/Mf8x/1b/tv8OAIwAdgBCACUABwDy/5H/Tv84/13/HQDAAMAAdgC+/yn/Iv+C/83/+f8lAEIAbwBZAA4Amf9W/2X/1P+FANcAzwB+ADsAHQAOACUA8v/U/+r/LAD8AAsBdgD5/3T/mf/5/5sAyAAsAOP/oP++/w4AFgAOAOP/xf/F/9T/HQAHAM3/tv97/83/2//q/9v/iv+K/5H/xf++/8X/tv/F/0IAOwDb/3T/E/9W/wAAZwCUAOr/Zf+K/+P/hQCFAFkA+f/N//L/UQCjAG8AhQCMAKMAfgBCADsAOwBgAKMA5QD8APQAsgC5AHYAQgBnAEoAdgCFAHYAZwCbAMgAfgAWANv/oP+v/+r/DgBCACwAMwBKAFkAOwDb/5H/Vv+n/wcAQgCUAKMAlABvACwABwDj/+P/LABZAJsAzwDlALIAQgAOAPn/+f/y/xYAHQA7AG8AWQBgANT/iv++/9v/FgDb/3v/Kf9l/8X/HQBvANT/dP8i/yL/kf+2/w4A4//y/xYALAB+AIUAYABCAB0A6v9nAKMA3gAhAeUAsgAlACUAbwCyAOUA7QBvANT/4/+n/8X/AADj/9T/tv+K/6f/tv++/6D/Mf9l/6D/zf/U/+r/xf+K/6//iv/q/wcABwA7AEIAWQBKACwAFgAdACUAlADXADABCwGFAB0Axf/q/ywAmwB2AFkASgAdAB0A4/++/4r/vv/j/zMAOwDj/13/Mf9l/0f/oP97/2X/oP9O/1b/Xf84/zj/OP8x/6D/4/8AAOr/e/8x/yn/kf8HADsABwCg/3T/iv+v/6//vv/y/x0AhQB+AAAA2/+K/6f/tv++/+P/+f8zADsAHQCR/3v/R/+Z/ywAMwBZAMX/zf/F/6//2//U/8X/r/8OACUAfgCFAAAAvv+v/+r/QgCjALkAjAAlAAAAOwCUAMAAwACUAEIAfgCqALIAfgBKAEoAWQB2ACwA4//b/w4AbwC5AH4ADgDF/83/BwDU/3v/E/8i/77/OwBZACwAxf97/4L/dP9s/3T/tv/j/0IAZwBCAA4Ar/++/6f/zf8OAEIAjACUAIUAOwAlACUAOwAWACUABwAOAIUAWQBRAPL/vv+K/3T/BwDj/w4ADgD5/w4Axf/N/6D/dP9l/13/kf+Z/83/FgDy/9T/p/+R/6//xf/q//n/xf+2/7b/4/8zAGcAlABKANv/tv/F/+r/HQBRAAcAxf/b/xYAJQA7APL/iv+n//L/HQAOAA4Axf/N/77/bP97/07/gv/q/yUAFgDF/4L/gv+2//L/LAAdALb/dP++/wAAWQA7APL/p/+Z/ywALABCAPn/dP+Z/wAAZwB+AAAAZf97/6D/FgBKAPL/oP97/9v/YABvAMX/bP/n/kf/8v8dAGAAvv+K/6f/xf/5/7b/mf97/5n/8v8dAAcA2/+v/4r/mf+2/77/+f8lADsAYAAzANT/kf+g/77/UQCqAEoAFgDj/+r/JQBKAEIAHQDy/yUAUQBZADsA8v/U/77/BwAdADMAAADN//L/+f8sAEoAZwA7AA4AAAAHAB0AJQBvADMAOwBnAKoAGQEhAd4AJQC+/9v/SgDIAN4AwACqAMAAzwCjAFEAAADb/8X/4/8WAEIAQgBKACwA2//F/5n/mf+2/6D/vv/q/xYAJQDq/4r/e/+R/6f/+f/F/77/AAAOAGcASgDj/9T/r//b/9T/mf+g/6//AABgAH4AFgC+/3T/Xf/U/+r/4/+v/3v/Zf97/83/zf+R/yn/7v7n/jj/zf/y/6f/BP+k/u7+gv8lABYAtv+v/5n/8v9nAGAALADb/9v/JQBRAHYAowDXACEBRgESAbkAhQCUAIwAhQBRAEoAsgD8AEYBAwGyAFEA2/8AADMAWQBZADsADgAzADsAFgAHAFb/Vv+Z/8X/WQA7APL/mf8x/5H/2//b/9v/gv+C/6D/1P8OAPL/BwDj/83/6v8sAEIAYABgAPL/xf+g/wAASgB+AGAA1P/U/6f/8v9CAPn/tv/N//L/FgAdAOP/zf+Z/7b/vv+Z/7b/+f9RAHYAdgDq/6f/vv8AAGAAlACMAFEASgAzAGAAfgBZAEoAFgAsADsAZwCjAKoAfgA7ABYAQgCbAJQASgD5/83/HQBgANcAwABgAGAAAAA7AA4A2//j/6//SgBvAG8ALACZ/6//r/+v/9T/oP+2/0IAYABnAPL/iv+K/6//QgCMAH4AUQAzADsAZwBZACUA8v/j/wAAQgCyAIUAZwA7APL/AAAdAHYAhQBRAAcAkf+Z/wAASgCMAH4A+f8AAA4AAAAlAA4A8v/q/x0AZwB+AG8ADgDN/5n/iv/j/0oAfgCjAMgAdgBCAPL/p//5/1kAhQBgAEIAJQBCAJsAyACFAOr/vv8AAH4AqgCbAEIA6v8HAEoAlABnAA4A8v/q/x0AMwDq/8X/zf/b/+r/HQAOAOP/2//F/8X/6v8HANT/2//b/83/tv+g/7b/tv/U/3T/Zf+K/7b/JQA7APn/bP8T/wz/Mf+C/7b/dP97/13/bP++/0D/OP8E/zj/Tv9W/2X/G/+n/6//1P+n//X+aP6k/jj/r/9KAAcAzf90/4L/oP+g/6f/mf/q//n/mwCbAH4AUQDU/8X/oP8AAGAA9AASAQsBCwF2ABYA1P+2//L/JQBvALIAyADeAFEA+f++/3v/FgA7AFEAJQDb/w4AFgBZABYAmf97/5H/JQBgADsADgCn/6D/8v9CAFEAOwDF/6D/vv+v/+P/1P++/5n/mf+v/7b/kf+R/2z/9f4M//3+bP+R/5n/mf8E/wz/BP97/9T/vv90/yn/Zf+g/ywADgCg/3v/R/+C/w4ALAA7AB0A8v9CAFEAYAA7ABYA+f8HAEIAYACqAGcAWQAzACwAZwBKAFkAFgDq//L/OwCjAJsAfgDj/6D/4/8lAIUAbwAWADMADgAHAGAASgA7ADMALABnAGcAfgBgAEoAOwAsAFkAMwAlAG8AUQBvALIAbwBnACUA+f8zACUAOwDj/77/4//N/9v/zf/F/77/+f/5/9T/bP8x/zj/QP+v/7b/tv+R/5H/tv+n/7b/bP90/6//+f9CAFkAJQAOAPn/DgA7ABYAQgA7AG8AjAB2AG8ALAD5/6//p//j/xYAAAAHAAAAxf/b/wcAHQDb/4L/Iv8b/0D/gv/q/6D/iv+Z/1b/dP97/3v/r//U/+r/JQBRAAAA2/+2/2z/Zf++/1EAdgCFAGcAJQAdAEoAYAAlAOP/1P8lAJQAzwDAAGcABwAOAGAAlADPAN4AmwB2AJQAbwB2AFEADgAzACUAbwCMAIUAfgBgAJsAjACqAGAALABKAEIAdgBnAFkAWQBgAJsAqgCMAG8AHQAWAFEASgBZAGAAdgBnAFEAWQAdAOP/zf/F/+P/BwAzAG8AdgBCANv/xf+2/83/1P+K/yn/Mf+n/9T/JQDb/0f/QP8b/zH/bP97/3v/4/87AFEAJQCZ/yn//f5A/77/dgC5ALIAhQAzAEIAWQBnAFEAUQBRAMAAPgE+AVwB3gBvADsAJQCMAKoA1wD0AMAAqgB2AG8AdgCFAJsAdgBCABYAAAA7AH4AZwAzAPL/1P+v/6D/2/+R/5n/2//U/6f/kf9l/zH/p/++//L/4/+R/7b/gv+Z/5H/Xf9d/07/Zf/N/wAABwDy/6f/mf9W/zj/Tv+K/4r/r/+Z/zH/Mf8b/2X/e/9d/1b/BP8M/xv/QP+C/4r/dP9l/2z/kf90/4r/r//U/x0AOwBCAAcADgAOAA4AZwBvADsAWQDPABkBXAFcAcAAdgBnAH4A1wDeAPQA3gCqAKoAhQBvAIwAuQCUAIUAfgBRAHYAWQBRAOP/iv/F/w4AjAB+AA4Aiv9s/77/LABKAOr/tv+n/wAAQgDy/3T/Tv97//L/SgAdAM3/Zf9H/6D/oP+v/6D/bP+C/6f/e/9A/zj/Vv84/zH/gv+n/9v/xf9s/yL/2P4p/5H/6v8AAMX/r/+2/9T/2//U/6D/kf+Z/9v/UQCUAKoAUQAdAPL/FgBnAG8AWQBCAFEAwAAoAd4AfgD5/8X/LACyAPwAyADIALkAzwD8AM8AOwDb/+r/BwCbAPQA5QDAAJsAdgAlANT/xf/b/1EAfgBgAJsAbwBvAFEADgDq/8X/FgBZAG8AdgCFAFkAYAAsANT/2//b/x0AJQAHAM3/r//b/9v/tv+Z/13/QP90/07/Vv9O/zH/Kf9d/5n/p//F/3T/dP84/yn/p//b//n/xf/b/9T/zf/5/9T/tv+C/5H/AAAOAAcA8v+R/+P/4//F/9v/p//N/9T/8v/q/7b/dP9O/07/gv+v/13/dP9O/yn/dP+C/77/1P+v/4L/Tv97/9T/1P/F/77/zf8sAIUAqgBgAAcABwA7AGcAsgCqAFkAfgDeADABPgH0AGcAJQAsAEoAlADeAOUAwACqAIUAWQA7ACUADgDb//n/QgBRAH4AfgAzAAAAp/+g/6//zf9KAIwAjABCAA4A8v/y/zMAMwD5/wAAAAD5/ywAQgA7AEIAOwAOAAAAAAD5/+r/mf+g/7b/AAAdABYAFgCK/0f/Kf8M/zj/Zf+K/8X/8v/N/77/Zf8T/9/+s/4E/13/8v9ZADsAAAB7/13/dP/F//L/tv/b/83/UQC5AJQAbwC+/6D/4/8zAGAAdgBZAA4AWQCUAMgAyACMAEoAHQAAACwAUQA7AJQAmwCjAKoAdgBKAAAA2//U/+r/DgBgAKMAmwBRAPL/xf+v/6//tv++/77/DgAzAFEAQgDq/+P/4/8AAAAAHQD5//n/FgAdAHYAdgBRACwADgDq/9T/AAAAAAAAJQBnAIUAfgAHAKD/kf+g//L/JQAWAPL/xf/U/wcAFgAOAM3/mf+v/wAAbwBgAFEA6v+g/9v/+f9CAB0AAADU/6//6v8WAFkAQgAsAPn/zf+n/5H/8v/j/+P/xf+Z/+P/FgAzABYAoP9d/07/Vv/q/9T/oP+Z/07/xf/q//L/oP9O/13/oP8lABYA4/+n/5n/1P8HAA4Azf+g/6D/FgB+AJsAOwDq//L/BwAsAAcA6v+2/83/OwCFAH4AbwA7AAcAFgD5/wAA8v/5/yUAUQBZAEIAZwAzABYA6v++/9v/JQBKABYAzf97/9T/6v/y/+r/Vv9d/4r/1P87AA4Amf9d/0D/dP+Z/6f/+f/F/+r/6v+n/6//mf/U/83/zf/b/+r/OwBCAAcA1P/b/wAAQgB2AEoAMwAWACUAbwBgAG8AdgCMAM8AowCUAGAAWQB2AIUAzwDIAPwAAwELAQMBWQBCACwAhQAZAeUA1wC5AGAAbwCFAGAAZwAzAEIAYABvAG8AFgAzADMAJQDq/9T/DgAlAHYAYAAAAKf/iv/N/ywAOwD5/77/Zf+C/5n/mf/N/6//vv/y/9T/8v++/4L/oP9s/4r/bP/F/wAA+f8dAKf/mf+C/+P/DgC2/wAA+f8AAEoAUQAWAOP/oP/U//n/+f8dAMX/+f87AIwAuQBnAFEAJQBKAGcAZwBCACUAMwBZAIwAowCMACwAJQAsAA4AJQBKADMAhQB+AFEAQgC+/+P/1P/F//n/AAAOANT/vv+R/6//2//N/5n/E//9/jH/iv/b/5n//f7J/tj+Xf+2/3v/Mf/C/sn+R/+K/13/Iv/n/gz/Tv9O/3v/Zf8p/1b/Vv9d/4r/Vv9O/2X/Zf90/4L/4/8HAAAAvv90/5n/1P8dAEIAAADU/9v/BwAsACwAMwBCAFEAlAC5AJQAhQBRAAcALAA7ADsAMwBKAIwAqgCjAFkAHQAAAAAAJQBZAH4AjAAzAOP/xf+n/yUAUQBZACwA4//q//n/OwDy/77/bP9W/5n/zf/y/5n/iv9l/3T/oP/N/9T/kf+K/07/Tv9d/5n/2//j/wAA8v/F/83/8v/j/+P/mf+R/x0AQgCFAFEA1P/b//L/LAA7ACwABwDU/w4AFgBKADMA2//y/9v/BwAlAB0ADgAlACwAAAA7ADsAOwBnADsA+f/5/9v/6v9ZAGAAMwAWABYAHQBZACwAr/++/7b/JQBgAA4ABwDq/9v/+f8AAPn/AAAsAHYAWQAWAAAA2//5/ywAOwBZAH4AqgDIAMgAfgAlABYABwAHAFEAdgB+AJQAbwAdAPn/1P8AAFkAmwCMABYA+f/U/ywAdgBRAG8AAAAOAJsAwACyAGAA+f/j/w4ALAB+AFkAHQB+AJsAhQB+ADMAMwAsACwASgDj/wcAWQCjALIAdgBCAPn/FgAOAPL/r/+g//L/BwA7AOr/r/+2/6f/tv+v/4L/gv+v/8X/6v/b/77/kf/F/8X/vv/y/9T/DgDb//L/MwA7ADMA2//q/77/+f87AEoAUQAlADMAJQA7ACUA+f/b/8X/HQBnAG8AQgD5//L/JQBKAEIALADy/7b/+f8zAEoAJQAOAB0AHQBnAFEAMwAHAPL/SgCUALIAuQCyAHYAmwBnADsAWQAlAFEAdgCbAM8AzwCjAEIA+f8AAPn/SgCqAIwAZwD5//L/LABKAH4AOwAAAB0AOwB+AIwAWQA7ABYASgBvAG8AdgBgAFkAJQBCACwAOwBnAEIAfgBnAFEAQgA7ACwAFgAlAAcAQgBvAGAAQgAAAL7/2/8WAB0AMwAOANv/oP/U/wAA2//q/5H/Zf+C/5n/1P/N/6f/tv++/77/2/+v/zj/E/8x/3T/p/++//n/2//F/77/mf97/wz/QP9d/7b/MwAHAOP/bP+C/9v/4//y/6//mf90/+r/MwDy//L/p/+v/9T/vv/N/7b/p/+v/9v/BwAHACwA8v/N/6f/iv+Z/6f/+f8AAPn/8v/5/ywAMwDq/2z/Iv8x/83/SgBgAPn/bP9H/3T/4//b/7b/Zf9l/83/8v/q/5n/Tv9W/6//tv/N/77/bP97/5H/kf+R/5n/kf/b/wAA1P+v/0f/Mf9O/4r/AABCAFkAZwAdAMX/r/9W/3T/r/++/wcAJQBgAFkAHQAdANv/iv9l/2z/zf9CAG8AOwAdALb/gv/F/6D/p/+R/5H/+f8lACwA+f/j/8X/p//y/+P/2//j/+P/AADy/xYA6v/b//L/zf/b/9v/+f8HAA4AFgDy//L/6v/y/wcAAADb//n/6v/b/9v/4//U/9T/4/+n/83/r/++/wAA6v/5/8X/tv++/wAAJQBCAFkAFgAdAA4AOwAlAB0AJQBCAIwAmwDlAKMAYABKABYALABZAHYASgBRAGcAbwCjALIAfgBCAAcAAABRAIUAwACjAEoA+f/y/0oAZwAzACwAAADN/yUAYABnADMA4//N/6D/vv/U/83/6v8AAEIAWQA7AAcA1P/y/xYAHQAdAAcA4//N/9T/xf/F//L/HQAAANT/xf9s/5n/tv++/6D/Kf97/6//+f8OAHv/Kf9A/6D/8v8lAOr/p/+2/wcALADj/8X/mf/j/zMAmwCjADsAJQAOAFEAZwBnAEoADgA7AEoAdgCjAIwAfgAzAPn/DgAlAH4AmwBKABYA8v/b/0oAlAAzAB0AAADy/2AAYAA7AAcA1P8AABYAAADj/6D/kf++//L/+f/U/wcAFgAWAB0A4//y/wcADgAdAM3/r//y/w4AUQA7APL/4//b/yUAUQBCABYA1P/N/wcAJQAAAMX/gv9s/6//+f8sAB0Avv/j//L/6v/y/6//tv/U/yUAUQBKAGAAFgDU/9v/zf/b/x0AJQBgAGcAYACbAHYAbwA7APL/AABCALIA3gCUAGAASgBCAKMAowBvADMA8v9KAHYAjACUADMABwAlACUAJQAsANv/4/8AAOr/MwAAABYAFgDj/8X/dP+v/+r/OwAsAOr/vv+2//L/AAAOAIL/gv++//n/UQAdAPL/zf/b/w4AQgDy//L/8v+v/+P/4//5/+r/+f8OAA4AAADU//L/r//F/9v/JQBRAEoAUQAdANv/dP/N/9v/JQBgAEoAowBZAGAALADj/9T/zf8zAHYAowCMAGcAOwAHAPn/1P8dAFkAhQCFADMADgAWAB0A+f/b/5n/tv/5/wcALAC+/3v/gv+v/xYAHQDb/4r/bP+Z/9T/xf+2/5n/iv+2/9T/AAAAAAAA6v/U/9T/8v/y/9v/AADq/0oAUQAsAFkA1P+R//L/FgBCAFkAHQAHAMX/2/8AAOP/JQD5/+P/DgDq/wAABwDq//n/p/+2/+r/2//5//n/8v+v/5n/oP+n/+P/zf++/wAA4/+2/+r/1P/U/9T/xf/N/9v/DgC+/6//vv+2/+P/6v/N/5H/oP+Z/xYAOwAAAA4Ar/+Z/83/LABZAAAAr/++//n/OwBgADsADgD5/zMAMwBRADMABwAdAOr/OwAsAB0AbwAsAB0AMwAHAA4AHQAdACUA8v/b/+P/AAA7AA4AFgD5/7b/BwAWAB0AHQDj/9v/BwBvAGcASgAOAMX/8v87AHYAWQBRACUALABnAJQAowA7ABYAOwBgAG8AowCFAEoAMwAdAEoAUQBZACwASgBgAGcAbwBnAG8A6v8AAPn/2/8AAAcAFgDq//n/r//q/x0AHQAsAAAA6v/b//L/8v/q/4r/r//b/9v/LAAdAOr/gv+g/2z/Xf+v/6//1P/F/9v/p/97/13/BP84/07/Tv+K/2z/gv+K/13/e/+n/7b/iv9s/07/dP/F/w4AOwAOAAcA+f/j/+r/BwAOACUAFgA7AG8AdgDXAMgAhQBCAOP/FgB2AJQAyACqAEIAZwBZAGAAUQAHAAAALAB+AHYAlABKAPL/AAAOABYAAADq/wAAUQBKAEoADgDU/+P/1P/j/+P/+f8HABYAHQAWAOr/vv/j//L/AAD5//L/6v/N/9T/+f+2/4r/oP97/77/1P/U/8X/Vv9H/07/r//N/5H/r/+R/3v/oP++/6f/e/+C/4r/tv/y/wAADgDy/77/vv+v/77/FgA7ACUA2/+g/6D/AABCACUAAACR/6f/4/8zADsA6v/F/4r/JQCMAGcAQgC+/3v/p/8OADMAMwAHAOr/BwAzACUALAD5/7b/xf/b/yUAMwBvAEIA1P/y/+r/DgBRAEoAHQAWABYASgBnAFEAUQAlABYA+f8zAHYAbwB2AB0A8v8OABYAYABRABYA+f+v/9v/LABnAG8AUQA7ACwAWQBCADsA8v/y//n/DgBgAFkAZwBCADsAOwAzACwADgAHABYAUQBgAFkAFgAWABYA8v8dAAAA2//q//n/BwAdAA4A+f/j//n/2/++/5H/iv/F/7b/FgAHANT/tv+Z/9T/zf/y/6D/e/+n//n/MwAdAAcAvv/j/9T/zf/N/77/4//y/xYA+f/b/83/8v8sABYA2/+n/7b/2/8WADsADgDN/+r/AAAHAPn/xf/j//L/HQAHAK//p/+g/9v/BwDy/wAA6v/y/x0AJQDq/77/zf/y/0IAbwBgAEIAHQAdAB0ABwDj/wcAYACbAKoAZwAWAKf/p//j/w4AUQBKADMAMwAOACUAMwD5/6//mf/b/ywAWQBvAFEA2//U/+P/4/8OAL7/+f8zAAcAJQDb/77/DgAlACwADgDF/+r/8v8OACUAzf++/83/BwBCACUA8v+n/5H/xf/5/wcA6v+v/9v/+f8lACwA4//b/6f/xf8AACwALADj/83/xf/q/x0AWQAzAPn/8v/y/+r/8v/b/83/BwAOABYAAADy/wcAAAAOAMX/vv+v/wcAZwBCAEIAr//F/x0AYADIAGcAAADN/w4AhQCUAIwAQgD5/yUAMwBCADsA4//F/+P/JQBRADsAJQAOABYA+f8OACUAQgAsAB0AJQDq/wAA4//y/x0AHQAzAAcABwAHADMAOwAOAOr/xf8AAAcALAAlAOr/4//q/xYA+f/y/83/p/+n/6f/8v/U/8X/xf+C/6D/Zf9O/5H/kf+g/6D/p//N/8X/1P/y/8X/r//N/wcABwD5/w4A+f/y/wcAAAAAACUAFgAAAPL/8v8sAB0AQgBRACUAMwAzAEoAQgAsAAcA+f8AACwAWQBRAEIAFgDy/83/4//y/wcAFgAOAAAA1P/j//L/MwAHAPn/FgD5/1EAWQAzAAcAAABCAFEAfgBvAB0AJQBnAHYAZwAzACwALAB+AIwAYABnAB0AOwBgAGcAUQAdABYAHQBKADMALAAlADsAFgAAACUAzf/N/9v/2/8dAA4A4//b/8X/vv/j//L/vv+2/6//4/9KAFkAZwAHAMX/zf++//n/DgAOAM3/BwAlAPL/DgCv/7b/tv++/+r/zf/U/9T/6v/j/9T/p/++/9v/6v/5/83/zf+Z/7b/6v/q/w4A+f/U/9v/vv/F//L/r/+n/9T/8v8lABYABwDj/9v/8v8HACUA+f/U/9v/6v8OAA4AFgDy/9v/LAAsADMAFgDb/yUAYABZACwAAADy//n/LABRABYA8v/5/yUAdgB2ACUA4//F/77/HQBKAAAABwAWABYAMwBRACwA8v8AAA4A+f8sAAAA4//5/+P/FgAAAA4AAADN/83/tv/U/+r/BwDy//L/1P/F/7b/p/+v/5H/zf++//L/6v/F/9T/AAAOAJH/r/9s/3T/AAAHAA4A4//N/9T/BwAHAAAA8v/y/wAAHQBKAB0AAADy/w4AJQBKACwABwAWADsAdgAlAB0A2/++/w4AQgBZAEoAUQAHABYAFgAsACwAAAAlAOr/LABRADMAHQDy/+r/zf/b/+r/HQAWACwAWQAzADMA2/++/+P/DgA7AB0Azf++/wAALAA7ANv/r//N/9v/JQAOAKf/iv+R/6D/1P++/4L/Xf9W/7b/zf+2/3T/Mf8b/2X/p/+R/5H/Vv9l/2z/e/++/4r/gv+R/6//oP+n/7b/mf/b//L/BwDy/6//p//F/yUALAAlAPn/AAA7AFEAowBRANT/4/8HAGcAqgCbAFEALAAzAH4AmwBnACUA+f8dAGAAhQBgAEIADgAHAFEAYABKABYABwDy/+r/6v8OAOr/4/8WAM3/+f8OAAAA4/++/9T/tv/U/+P/4//b/+r/BwAAAPL/2//N/+P/AAAOACwA1P/q/wcAFgAzAA4A8v+v//L/JQBKAFkAHQDq/wAAQgBCAFkADgD5/wcAOwBvADsAFgD5/xYAMwCFAH4ALAD5/9T/6v8sAHYAdgAzANv/8v87AH4AlABvACwABwBZAIUAmwBZAA4A1P/N/zMAYABvAEoALAAOACUADgAWAB0A2/8lAAcA4/8AABYAbwBgAEoA8v/N/9T/4/9gADsABwDN/6f/AAA7AIUAOwDb/5H/p/8WAB0ALADj/5H/mf/b/x0ALAAWAKD/Xf+R/wAAMwBCAPn/xf+Z/83/AAAHADMA2//5//n/JQBnAEoAYAAOAOr/1P8AACwAQgBvACwAHQAAAPL/FgBKAB0AAADb/5n/BwBCAG8AbwAAAL7/tv8AAGcAWQAAAL7/oP+v/+P/MwDj/6D/r/+Z/+r/6v8AAAAAr/++/7b/zf/y/ywAOwAHAOP/1P/y/+P/LAAlANv/1P/F/wAABwD5/+P/xf+v/6//6v++/9T/zf+n/wAA+f/j/9v/zf+v/77/vv+n/+P/AAD5//n/1P+v/6f/zf/F/6//p/+R/5n/vv/U/+P/6v+2/6//zf/y/x0A8v/F/4L/iv+v/wcALAAHABYA1P8AAAcABwBKAAAA2//b//n/MwBZAFEASgAHACUAWQBKAGAAMwAlAAAASgCUAIwAjABZADsAHQA7AEoAZwA7AEIAYABKAGcALAAdAPn/FgAdAB0AUQAsAGcAWQA7AFEABwDF/wcAYAB2AKMASgD5/9T/zf8WAGcAUQD5//n/zf/N/x0AUQAsAOP/p/+K//L/OwBCACUAtv+K/7b/DgBCAB0Avv+C/5H/zf8HAB0A1P+R/7b/4/8sAB0Atv+R/07/dP/y//L/8v/N/3T/iv/U//L/OwAWAKD/kf+v/9T/DgAsAKD/bP+v//L/UQBRACUAp/+K//L/QgBgAFEAHQDU/wcAFgAlACUAxf8AAAcAHQBZAB0ABwD5/xYAOwBKAEIADgAAAOP/BwBKAFkAQgAWADsAFgAzAGAAMwAdAOP/8v8lAFEASgAzAB0ADgAzADMAOwA7ACwA+f8dABYA+f8HAA4AJQAsAG8AWQBKABYAr/+v/77/2//y/w4A+f/q/w4ALAAlANv/mf9W/4r/p//j/xYA4//F/4L/6v8HAPn/LADN/9v/4//U/x0ADgDq/7b/iv+g/wAAQgBZACUAvv/F/w4AHQBKAB0Axf/q/wcAHQAzAPn/r/+n/wAALAA7AEIAFgAOAPL/BwAlACwADgAOACwAMwB2AG8ASgAdACUAOwBZAJQAZwBZACUASgCFAIUAZwAzAGAAWQCUAIwAbwAzANv/LAAlADMAMwAlAAcA4/8lACwAJQAHANv/vv++/wAALAAzAPL/vv+C/4L/BwAdAAcA4/97/5n/2/8sACwA2/+Z/4r/zf/5/zsALADq/7b/tv/b//L/FgDy/9T/zf/U/xYABwDy/+r/r//q/wAADgBCAPn/8v/j//n/QgA7AB0Atv+Z/+P/FgBCADMAxf+v//n/LABgAGAA4/+R/83/4/92ALIAQgAWAM3/AABCAFkAUQD5/+r/2/8WAGcAZwBgABYA+f/5/77/DgAlANv/2/++/8X/DgAlAAcA8v+g/6D/zf/b/83/oP+n/5H/p//U/8X/mf+g/6D/vv/b/83/1P+Z/6//oP+g/8X/1P/y/5H/tv+g/83/8v/U/wAAp//N//L/6v/q/9T/tv+v/+r/AAAOAOP/tv++/+P/BwAWACUA6v+2/9v/DgAOACUA4/++/+P/r/8AACwADgAOANT/+f/5//n/MwDq/77/vv/j/zsAJQA7ACwA1P/5/w4AHQAzADMAJQAWACwAJQBCAFkAUQAlAAAA+f8dAEoAHQAlAOr/1P/y/yUAdgAzAPL/p/+2/77/BwAdAPn/FgCv/wAAJQAOADsALAAzACUAFgAsAEIA2/8zACwA6v8WANv/HQAOAEoAZwAAAA4AHQAsADsAHQAHAB0ABwAdAPn/1P8WACUALAAOAPL/1P/q/x0AWQBRAA4A4/+2/+r/JQAzAB0Axf+n/6D/vv/q/9v/1P++/6//zf/q/+r/2/8AAM3/xf/q/9T/8v8sADsAAAAHAMX/r//j/xYAFgDb/wcA6v8HAAAA+f8AAOP/JQAdAEoAJQDF/83/4/8sAFEAFgDq/6D/oP8HAEoAQgAWANv/dP++/xYA8v8HAOr/tv+g/+r/8v8HAOr/iv+Z/2z/oP/b/xYAMwAlAAcAxf/j/9T/8v/5/+r/8v+2/wAA+f/y/x0A6v8AAPL/1P/y/w4ABwDU/+r/1P8HACUAHQA7AAcA8v/b/x0AAAD5/xYABwAlAA4AJQBKAEIAFgBRACUAJQA7APn/LADb//L/AAAzAEoAFgAlAA4AJQD5/xYA+f/N/wAA+f87AEIAHQAdANv/oP/y/wAAHQAWAB0ALADF/+P/4//q/w4AJQDj/9v/2//N/ywAAAAWAOP/2//y/8X/8v/F/+r/6v/y/9T/vv/N/83/DgD5//L/1P+v/6f/2/8dAOr/+f8AAM3/6v8WAPn/BwAsAPL/HQAWAOP/JQA7AFEAUQAdACwASgA7AEoAYAAzAEIAWQBCADMAQgA7AFEAUQBCAFEADgAdAB0AWQBZADsAMwDy/1EAJQBRAFEA+f8sAB0AMwAWACwADgBKAEoAQgBZAMX/JQD5/ywAUQDb/ywABwBKAG8ASgAlAPn/HQAWAEIASgAsADMAOwAlAAcADgAWADMAWQAzAPn/6v/5/xYAHQAOACUADgDy//n/JQAlAAcAQgAlAOr/8v/b/wAALAAHAB0AAAC2/6//xf/5/+r/AAAAAOP/DgDU/xYALADy//L/xf/q/x0ALAA7AEIALAAAAAAAJQAWAB0AHQAWAFkAQgBZAFkAFgAHABYABwAHAEoAHQAHAOr/BwAsADsAOwDj/+P/xf/U/w4AJQAsAAAA2//j/+P/8v/5/+r/BwAAADMALAAdAAcAtv/b/9T/+f/y/wAABwDy/zMA6v/j/wAA2//F/9T/1P++/xYAJQAAAOP/r/+g/6//vv/q/9T/p/+g/3v/vv/q/9v/2/+g/4L/oP+K/6//1P/b/8X/oP+n/4L/xf/q/9v/8v+v/6//p/++/9T/AADy/9v/xf/F/x0A6v8AAAcA1P/b/9v/BwD5/x0ADgAHADsAFgAdACwABwAOACwADgA7AEoABwAlADsASgBvAFEAOwBCABYAFgAdADsAYABKAFEASgAOACwAWQAzAGAAMwDq//n/8v8lACwAHQDq/9v/4/8HAA4ABwAzANT/tv++/83/xf++/8X/e/+K/4L/1P/U/6//vv97/6f/tv/U//L/1P/U/6D/xf/F/5n/zf+2/3v/e/+2/+P/8v8HAM3/bP9d/77/2/8HAOr/r//F/3T/xf/q/8X/xf+R/6//vv/N/xYAFgDU/+r/vv+v/83/xf/5/9v/zf+v/83/DgAdAB0AAAAAANv/8v8zADsAMwAOAPn/6v/b//n/AAAAAPL/xf/5/+P/8v8HAA4ADgDU/83/r//q/+P/8v8AAK//r/+2/9v/FgDy/8X/4/+g/8X/+f/N/83/tv/F/8X/4//N/+r/4/+v/9v/2//y/+P/6v++/8X/AADy/w4AAAAAAOP/AAAOAOr/6v/U/yUALAAlAEIAHQA7ACUAFgAOAAcAOwBCADMAQgAsAA4AUQA7AAcAAAD5/w4AAABCACUAFgDb/83/HQAHAHYALAAWAB0AAAAsAAcASgAOACwAQgDy/yUAOwBZAG8AUQAdACUAFgAOAGcAjABnAEIALAAdAEoAUQBKADsAOwBRACUAHQAOACUALAAdAFEAAAAAAAcALABgADsAQgDj/wAABwAWADsADgAsAOP/DgAlAAcAJQAsACwAHQBZABYADgAdADsAWQA7ADsAFgAOAB0AYABRAFkAJQDU//L/DgBnAIUAWQAOAAcA4/8dAJQAbwBnACwAJQBKADMAdgCFAFEAUQAsACwAOwAsAG8AZwBZACUABwAOACwAWQBRADsA+f8OAOP/8v87ACwAJQD5/9T/tv/N/9T/BwAsACwADgDN/9T/xf/U//n/AAD5/9T/xf/q/wAADgAlABYAFgDF/+P/AADb/yUALAAHAOr/1P++/wAAHQD5/xYA4//N//n/DgAzACwAFgAAAPL/AADj/+r/LAAAABYABwDb//L/zf8WACUA8v/5/+P/BwDy/+P/DgDj/+P/8v/q/+P/4//j/+r/BwDb/83/8v/F/9v/8v8AABYAAADy/8X/xf8AAA4ADgAlABYAzf++/wcA8v8AACUA6v/q//n/FgAWABYAFgD5/w4A8v/q/wcA2//b//n/2//b//n/2/++/+r/tv/b/wAAvv/y/9v/2//y/9v/2//b/+P/zf/y/+P/6v/j/9v/zf/b/xYA4//y/+P/xf/U/wAAFgAsAEIAJQBCAFEAOwAsADsAAAAlACwAHQBnACwAQgA7AEIAJQAlAEoADgAWACwAWQBCAFEAUQBRAEIAQgBRAAAAFgDy/xYAQgAsAEoABwDF/8X/4//j/wcABwAAAM3/xf8AAPL/+f/y/9T/vv/b/wAAHQAHAOP/4/+v/83/AADj/7b/r/++/6//zf/U/8X/1P+2/7b/zf/j/+P/vv/F/6//zf/U/9T/zf++/9T/tv+n/5n/zf/F/83/2/+2/77/zf/q/9v/DgDj/5n/tv+Z/8X/8v8AAPL/6v/N/+P/4//U//n/6v/y/+r/vv++/9v/4/8HAOr/BwD5/6f/8v/F/wcA8v+Z/+P/xf/U/+r/zf++/77/tv/b/+P/6v8WAPn/8v/b/9T/vv/U/wAA6v/j/+r/xf++/wAA+f/q/wcA+f/5/w4AFgAOAM3/4//q/+P/LADq/+P/2//b/ywAOwBRABYA4//b/x0ALAAdACUABwAlABYASgBRACUASgAzACUALAAWACwAQgBCAEIAHQAsAAcADgBCABYALAA7ADMALAAAAA4AJQAWAB0ABwDb//n/FgAsAFEALAAAAOr/8v8AABYAHQAAAA4A8v8OAB0ABwAlAA4AMwAWAPL/QgAdAAcALADq//n/LAAOAAAA4//5//L/FgBgACwABwAAAPL/AAAzAAcAHQAlABYASgBCAEoAJQAOACUAOwAzACwALAAOAB0AJQAlAA4AFgAWAA4AHQDy/zMALAAzAEIAFgBKACwALAAlAPn/BwAHACwAQgAWACUAFgD5/wcAAADU/9T/8v8OACUABwAAANT/2//y/+P/HQAWACUAHQDq/wcAxf/F/+P/zf/y/9T/8v8lAA4ABwDy//n/2//U/w4A+f/j/wAAAAAHAA4AFgAWABYALAAlADMADgD5/yUADgAsAA4ADgD5/+P/DgDq/wcADgAAAPn/AAAdAA4A4//y/+r/vv8AAAAABwAOAOr/HQAAAPL/LAAdAAAABwD5/83/6v8HAPn/AAD5/xYAMwAAACUABwAWADMADgBRADMAMwAlAB0AMwAdAEoAHQAdAB0AAAAzAB0AFgBCAFEALAAzADsALABRACUALAAsAPn/JQBZAH4AbwBCAB0ABwAOAFEAQgAOADsADgAWADsA+f8dAB0ABwBCAA4A8v8AANv/6v/U/9v/DgAOAB0ADgDq/9v/2//q/wcA6v/b/9T/zf/q/+r/FgDy/+r/4//b/w4A+f/5//L/8v+2/8X/6v/U/w4A+f8HAOr/4/8AAOP/FgDj/8X/8v/b/+r/+f/U//n/LAAHABYABwDb/w4AHQD5/wAA4//U/+r/1P8WAAAA4/8sAPn/BwD5/wAAAADy/w4A1P/q/+P/8v8HANv/1P/U/+r/xf/N//L/1P+n/77/xf+n/7b/1P/b/6D/xf+n/6//zf+n/9v/r/+2/7b/tv/5/83/2/+2/4r/r/+2/8X/6v/U/77/1P+n/4L/kf97/4r/tv+g/5n/p/+Z/5n/p/+2/5H/r//j/6D/p/+g/5H/vv+n/+r/BwDN/77/2/8HAM3/2//F/6f/zf++/wAADgDb//n/2//N/+r/8v8sABYAzf/j/+P/4//y/w4A+f/F/77/4//5/wAAHQAHAPL/xf/5/xYA6v8AANv/2//F/9v/AADN//n/+f/5/ywA+f8HAA4A8v8dAOr/+f8lABYAOwBCADMAJQAlACUAMwAsADMALAAdADMALABKACUAJQAzABYADgAAACwADgD5/wAAAAAzAA4AJQAzAOP/BwAdAAcAAAAAABYA1P/j/xYA1P/y/w4A+f/5/wAAFgAWAA4AHQA7AA4ABwAzACUALAAWACUAJQAHADMALAAlACwAQgAzAB0AMwAOABYADgAOACwAQgBKAEIAQgAsAB0AFgAzAB0ADgAOAA4ALAAzAGAAZwBCADMAHQAHACwAMwBKAGAAOwBZACUAFgBCACwALAAWAPL/4//5/wcADgDq/9v/+f/y/+r/BwAAAAcAJQAHAB0AAADb//L/8v8AAOr/+f/y/+r/+f/j//L/BwD5/+P/4//b/+r/+f/q/+P/2//N/83/6v/y/wcAAAAOAAAA1P8WANv/+f/5/7b/8v+2/9T/BwDj/w4A+f/y//L/2//q/wAA1P++/+P/2//j/wAA+f/j/+P/BwAOAAcAJQAAAOP/BwAAAAcA8v8HABYA8v8OACwABwAAABYADgAOAAAAFgAOAAcABwAAAB0AJQAzAAcAFgAsAPL/LAAzABYAMwAWAAAAJQD5/wAADgAHAA4ABwAlAAAAFgAWAAcADgAOACwADgAlABYA+f8dAAcABwAWABYA+f/y/wcA8v8WABYABwAWAPL/AAAHACUAJQAdAEoAJQAlADMASgAlADMAOwAlADsAHQBRAFkASgBRADsASgAlABYAHQAWAAcAHQAdAAcALAA7ADMAAADq//L/xf/j/xYABwAdABYAHQAsACwAFgAHACwABwAHAAcAAAA7ACwAMwA7ACUAJQAsADsALAAsACUAJQAsAB0ALAAlAB0ALAA7ABYADgAsAPn/OwAdAOr/AADb/x0AJQA7ACwAFgAdAB0AFgAHADsA6v/5//n/+f8OANv/+f++//L/BwAHABYA4//y/+P/8v/b/wAA8v/y/x0A+f8OAAcA+f8OABYADgAOAAAAAADq/9T/1P+2/+P/4//j//L/zf/b/9v/1P8AAOP/tv/U/7b/xf/U/7b/1P++/9v/+f/j/+P/1P/U/77/tv/F/6f/vv/N/9v/+f/F/8X/xf+2/83/vv/N/77/xf/F/7b/xf+v/77/vv/U//n/4//y/w4AAADb/+r/BwAHAOr/HQAOANT/JQAlACUAOwAOACUAHQAlADMABwAAAAcA8v/y/xYAFgAdACwAAAAWAB0A+f8WAAcADgAlAB0AHQDy/9v/+f8OAPn/DgAdANv/BwD5/w4AJQDy/w4A2//y/w4ABwA7ADMABwD5/9v/1P8HAPn/HQAdAPL/8v8AAAcA+f8dAPL/FgAOAOP/DgD5/wAADgAzACUAFgAdAA4AHQAsAB0AJQAlAOr/8v/q/+r/+f/y//L/2//y/83/1P/q/+P/xf+2/7b/mf/N/77/1P/q/8X/6v/b//L/AAAHABYA+f/q/+P/8v/q/+P/4//5/wcA1P/5/w4ADgAHAPn/AADU/wcADgAWAB0AAAAlADMAOwAWAB0AQgAdABYAJQAOAB0AMwAWAB0A6v8WADsALABgADMAJQAOAPn/BwDy//n/+f/y//n/DgAWABYAQgAdAA4ALADq/+r/6v/N/6//2//U/6//1P++/+r/8v8OADMAFgAHAOP/+f/q//L/BwAAAOr/+f8AABYAMwAHAA4AHQAlAA4AJQAHAOP/FgDq/wAADgAOAA4AFgAdAPn/FgAOANv/8v/b/7b/8v/5/wAA6v/q/xYA+f8dABYABwAWABYADgAWAA4A+f8lAA4AFgAdACwAQgA7ACwAFgAHAAcA+f8dACUAAAAlAAcAHQAOAAAAQgAAABYA+f/y/yUA8v8HAAAA6v/5/wAABwAWAPn/8v/U/9v/6v/y/xYABwAAAM3/8v8WAPn/MwAlAPn/JQAWAAAAFgDy/xYADgAAABYA1P8OAPL/6v8dAPn/DgD5//n/+f/q/wAABwAOAPn/AADb/9v/AADq/+r/4//b//L/8v/5/wcAHQAWAPL/LAD5/9v/FgDy/w4AHQD5/+r/6v/5//n/HQAHAPn/DgAdABYAHQAdAOP/JQAdAOr/+f/N/wcABwD5/xYA+f/5/xYAQgBCAAAABwDy/9T/4//U/9v/vv/b//L/8v/5/+P/DgDU/+P/8v/N/+P/r//b/9T/4//5/9v/1P++/+r/AAAWAPn/+f8AAMX/4//b/wAAAADq/xYA2/8OAPn/2/8lALb/tv/q/7b/2/++/6//tv+2/9T/1P/U/9T/1P+n/77/tv+R/8X/xf+n/6f/vv+v/83/zf+v/7b/tv+n/7b/1P+n/83/p/+Z/9v/oP/j/+r/tv/j/9T/zf/N/+r/1P+2//L/6v/5//n/4//j/+P/AADj/wAAFgDU/8X/xf/F/9T/AADq/wcADgD5/ywA8v/5//n/zf8OAPn/8v8OAOr/BwAAAOr/+f8AAB0AJQA7ACUALAAWADMASgAdAEIALAAsACUALAAzADsASgA7ACUAHQBKACwASgAlAA4ALAAsAG8AMwAzACUAOwAsAAcASgAWACUALAAsAA4AAAAAAAcAHQAAAAAAAAAHAPL/AAAHAAcABwAHAB0ABwAdAAAABwDy/+P/DgDN//n/8v/y/ywADgAOAPn/8v/j//L/FgAAAAAAAAAOAB0AJQAsAA4A8v/5/wcA+f8AABYALAAsABYA8v/5/wcADgAdAAcADgAOAAAAAAAdAAcAAAAWAPn/DgAWAAcABwAzACUAFgAzAAAADgAHABYAJQAWACwAFgAlAPn/DgAzADsAWQAzADsASgAzAEIALAAWACUAAAAOACwAHQAzADsASgA7ACwALAAlAAcA6v8HANT/zf/y/9v/+f8AAAcAAADb/wcAAAAHADMADgAWACUADgAHAAcAFgAdAB0AHQAOABYAAAAHAAcA+f8HAAAADgD5/wcADgAOAA4AFgAsABYALAAsABYAHQA7ACwAMwBZACwALAAlADMAOwBRAFEAOwBRABYABwAHABYAFgAAAB0A+f/q/w4AMwAlAA4AAADy/wcA+f8OAA4A2//5/9v/zf/b//L/FgAWABYA8v8OAOr/4//y/9T/4//N//L/6v8OACwAAAAWAA4A+f8OAA4A2//j/+r/4//j/wcA+f8HADMADgBRAB0AFgAdAAAALADj/ywADgDq/xYAAAAOAA4AFgAlACwALAAdAA4AHQAOAAAADgAOABYABwAdAA4ADgAWACUAAAAHABYA+f8zAAAAAAAWAAcAJQAsAEIAMwBCADMAUQAsAAcAOwAWABYASgA7AB0AOwAWAEIALAAlAEIA6v8lABYA6v8HAB0AFgD5/zMAFgAlAEIAMwAsAPL/DgAdAAAAFgAsAA4ABwDy/9T/AAD5//n/+f/q/wAA4/8AAAcA2//q//L/zf/N/+P/2//y/9T/6v/b/9v/BwDF/9T/xf+2/7b/r/8AAOr/6v8AAAcA+f8OAAAA6v/j/+r/+f/U/wcA8v8AAPn/1P/5/+P/BwDb/9T/zf/b/9v/p//F/77/xf/N/+P/+f8HAMX/xf/N/5n/xf+g/8X/1P++/9T/xf+n/4r/1P/F/9v/4//j//n/4//N/6//zf+2/6//vv+g/83/xf++/+P/1P/q/9T/2//U/7b/vv+g/83/p/++/+P/r/8HAOr/1P/q/83/xf/N/+P/6v8AAPL/6v/5/+P/2//j/9v/2//N//L/zf/N/+P/xf8HANT/tv/j/+P/AAAHAB0A+f/5/wAAAAAHAA4AFgAAAOr/6v8OAA4AJQAlABYAAAAHAAcA6v/5/9v/4//q//L/8v/b//L/zf/b//L/DgAWAPL/DgD5//n/+f/b/x0A6v/5/wcA2/8AAAAAFgAdACUABwAOAA4ABwAWAOr/6v/j//n/+f8HADMAOwA7ACwAJQAOAAcA6v8OAA4ALABZAB0AOwAzAA4AHQAzACUAAAAOAAAAFgAWAPn/DgDj/77/2//y//n/4/8OAAcAzf/N/77/2//b/+r/DgD5/w4A+f/5/+r/vv8AAPL/BwAdAPL/HQAHAAAAJQAOAOr/HQAsAPL/DgAWAB0AHQAAAA4ADgAOABYA+f8HABYABwAlACwAJQAHAPn/8v/y//n/+f/j/8X/+f/U/w4ALAAWADMAAAAHAAcAFgD5/yUADgAHADsA6v8dAAcAAAAdAAcADgAHAPL/6v8HAOr/4//U/9v/tv/q/w4AAAAWAOr/AADj/9v/1P/b/+P/4//j/9T/6v/N/+P/8v/5/+P/AAAAANv/8v/b/+r/2/8WAPL/BwAWANT/DgAAAPn/AAAHAPn/AADj/9T/+f/y/wcA+f/5//L/LAAWAAAAFgD5/w4ABwAdABYAJQA7ACwAHQAHAA4A+f8WAA4AOwBCADMAZwAWABYALAAOAB0AHQAdAAcAJQA7AEoAQgAzACwAAAAlACUAJQAzABYAOwAAAOP/+f/y/wAALAAAAOr/DgDU//n/BwAdACwAHQAdAA4AFgAdACwALABRAPn/FgAdAA4AUQDy/x0ADgAHABYAFgAWACwAOwAWAFkABwAlACwAOwBZADMAbwA7ADMALABgADMAHQBgAB0ALAAHAAAAFgAdACUAHQAWAAcAFgAWAB0ALAA7AAcABwAHAPL/FgAsADsAJQAlAA4AJQAlABYAHQAWACwAAAAHAPL/BwAlAPn/HQAHAPL/DgAWAA4AAAAOAPL/4//U/9T/6v/j/yUAOwDy/+P/+f/b/9T/BwAAANv/2//j/7b/xf/b//L/DgDF/9T/tv+v/83/zf8HAM3/1P/U/8X/tv/N/wcAtv++/9T/4/++/+P/AADU/9T/oP+R/7b/tv+g//n/tv+Z/9v/oP+2/77/6v/N/9v/6v/q//n/+f8OAMX/BwAAAAAAFgAAACUAJQAlABYAHQDj/wcAFgAAAA4A6v8OAA4ADgDy/+r/DgAdAPn/AAD5/9v/BwAAAA4AAAAAAAcAHQAWAEIAOwDq/1EABwD5/wAAAAAsAOP/FgD5/wAAAAD5/x0AFgAWABYAOwAHAA4AFgAlABYABwA7AA4A6v8dAEIA8v/5/w4AAAAlANv/AAAAAMX/BwD5/+P/4//q//n/xf/j/+P/vv/j/9v/+f/y/8X/6v/q/83/8v8OAPL/8v/5/+P/BwAOAAAADgDj//n/DgDj/9v/8v8dAAAA8v8WAPL/JQAdAA4AMwDj//L/8v/b/xYAFgAlABYADgAdAAcA6v8AACwAFgD5/+r/1P/b/wcA8v/j/wAA2//F/9v/2/8OAAcA+f8HAPL/+f/j/x0AAADj//n/4/8OAAcAUQAsAAcALADy//n/6v8HABYADgAWAAcA4//j/wcA8v8WACUAJQAHAPn/AAAOAFEAMwAzAA4ABwAzABYASgBKABYAHQAAAOP/DgAdAA4AQgAdAAcA+f/j/w4ABwAlACUABwDy/+r/HQAlACwA8v8OACwA6v8HAB0ASgA7AB0AOwAHAMX/BwAlAB0ABwD5/+r/zf8HAAAADgAWAAcA+f/N//n/8v8OACUAAADq/+r/1P8dAEIABwAsAMX/6v/j/7b/FgDq/wAADgD5//L/8v/j/wcA+f/y/xYAzf/j/8X/xf/5/wcABwAAAOP/r//q//L/DgAWAPL/6v/N/9T/DgAOAAcA6v/N/+r/mf/j/w4A2/8HAOr/AADy/+r/+f/y/xYAAAD5/9v/xf/y/+r/6v8OAOP/6v/q//n/2//N//n/1P8HAA4ABwD5/+r/DgDq//n/FgAAAAAAFgAAABYALAAWADMAFgAHAAcAHQAdABYAHQAAAAcADgAOADMAJQAWACUADgAdAAcA8v8zACwAQgA7AAAADgD5/xYABwDU/+r/6v/j//L/DgDj//n/HQDj/9v/1P/5/xYABwDy/9v/zf++/9T/4//y/9v/zf/U/9v/4//U/83/4//y/83/AADb/7b/AAD5//L/6v+v/6//1P+v/9T/8v/y/wcA1P/N/9v/zf/q//L/1P/U/77/xf/j//L/xf/b/wcAxf+2/9T/+f/j//n/8v+2/9v/1P8WAPL/xf/5/77/xf/b/+P/FgAHAPL/8v/U/+r/BwAdACUABwAWAB0AHQAOAB0AMwAzACUALAAOAPn/BwAHADsADgBKADMADgAzAAAALAAWADsAQgAOAA4AMwAzADsAYAAOABYADgAAAPn/8v8lAB0AHQAAAOr/8v8HABYAOwAWAA4ABwDj/ywALAAzADsAOwAWANT/DgAsABYAHQAdAAcA8v/q/xYAFgAWAEIAJQAAAAAABwDy/w4ALABKACwAAAAHABYAFgAzAHYABwAWAB0AAAAzADsAdgAWAEIAMwAWAFEAHQB2ADsAQgAsAAcAQgAWADsALAAlAAAAFgAlAAcAQgAsAB0ADgAOAPn/8v8WAAAA+f/F/9T/6v++/9T/AADq/9v/8v/F/9v/zf/U//L/6v8AANv/1P/5//n/+f8lAA4ABwAHAOr/FgDj/x0ADgDq/yUA4/8WAOr/4/8HANT/BwDj/9T/+f/5/wcAAAAOAAcAAAAHAA4AHQAOAB0AFgDy/+r/8v8HAPn/MwA7AA4AHQAWACwAUQBCABYAJQAdAPL/DgAlAA4AQgBRABYAOwA7AB0AMwAWABYAAAAOADMADgAOACwALAD5/w4ADgDN/zsAHQAlAEoA2/8HAPL/FgBRAEIAfgBKACwAHQAsACwAAAAlAPL/8v/b/9T/HQAOABYABwAOANT/xf8AAM3/FgAOANT/6v/q/+P/8v8WAAAABwAHAAcAFgAWACwAMwAsAAcA+f/j/9T/DgAdAA4AMwD5//n/AADN/ywADgAOACUAzf/5//n/6v8OAA4A+f/5/9T/6v/U/9v/DgDU//n/zf/N/8X/r/8OANv/xf/q/8X/tv/5/9v/8v8HAL7/6v+v/6//BwAAAB0ADgDN/9T/2//q/wAA4/8dAOP/2/8WAPn/LAAzAFkAHQDy//L/zf8WACUAHQAlAA4A+f/j/+r/HQAWAOP/HQDq/7b/vv8AAAcAzf8dAOr/4//q/83/+f/N//L/BwAHANv/4//5/+r/JQDy/+r/6v/j/+P/4//5/83/BwDy/9v/xf++//n/1P/y/9v/xf/N/+P/+f8AABYA4//5//n/8v/y/+r/DgAAAAAAAADq/wAAzf/F/ywABwD5/w4Atv+Z/8X/+f/U/+r/6v/N/83/xf/j/+P/1P+2/9v/vv/F/+r/tv/q/77/2//q/83/8v/j/w4A8v/b/+P/1P++/8X/2/++/7b/xf/U/6f/tv/N/77/xf+2/6D/oP+2/7b/p//F/83/r//F/6//oP+v/83/2//F/9v/p/+2/9T/1P/j/6f/tv/U/6//tv/N/9v/AADq/+r/AADU/+P/2/8AABYA8v/5/wcA4/8AAB0AJQAHAAAALADq/yUAMwAHAAAABwA7ANT/AAAOAB0AOwAdAFEA+f8lADsALAAsAB0AOwD5/wAAAAAAACUAMwBgABYAHQAdAPn/SgBKAEoALAAOAB0A+f8WABYABwDy/x0AAAAOAH4AFgAzACUA8v8sAA4ALAA7AFkASgAdACwALAA7AEoAWQBRAEIAMwAWAB0AQgBCAEoASgAWABYADgAlADsAWQBZAPn/DgAAAAAAMwAdABYAAADj/9v/+f8WACUAQgAHAOP/4//N//n/DgAlADMA4//U/9T/1P/y/+P/1P/j/9v/zf/b/+P/6v/b//L/+f/N/83/1P/y/x0ABwDy/ywAFgD5//L/1P8zACwALAA7AAcAFgAsACUAMwA7AAAABwDy/+P/8v8AADsAJQAWACwA+f/U/xYAFgAlADsADgAlABYAJQBZAEIAFgAlAAcAAAAdABYALAAdAB0AMwAdADMAUQA7ADsAJQAdABYAHQBCACUALAAlADMADgAAACwAMwBCAEIAWQAdAB0AFgAWABYADgAzAAcAQgAAAA4AMwAWAEoAAAAHAA4AMwAdADMASgAlADsA8v8dAAcABwAsACUAUQAAAOP/BwDb/9v/DgDy/wcA6v/q/w4A6v8AAPL/4//j//L/2//b/xYAFgAsABYA+f8HAB0AQgAOABYAMwAAADsAOwAOACwA8v8OACwADgAzABYAAAAAAOr/+f/y/+r/6v8AAPn/FgAdAAcAHQAHAAcAFgAdAPL/8v8AAL7/4//y/+r/6v/y/+r/1P/U/+r/+f/U/wcAzf/j/wAAxf8lAPn/6v/5/9v/8v8HADMAMwAlAAAA6v/q/xYAJQAWAB0ADgAOANT/2/8OAOP/AAAAANT/1P++/83/2/8OAA4A8v/q/8X/6v/5/+r/4/8AAAAA8v8dAA4ABwAAABYAHQAOAAAAAAAsABYAHQAlAPn/2//q/w4AFgAOAB0ALAAWAPn/DgAWABYAMwAHAPL/4//j/wcABwAdAA4AAADj/+P/4//F//n/8v/b/8X/vv/F/9v/2//N/9v/vv+C/5n/1P+2/9v/1P+v/77/kf+K/6f/2//b/+P/1P+n/6D/vv/b/7b/4/+v/6D/kf+Z/+P/tv/j/8X/vv/N/6f/xf/y/x0A6v8AANv/oP/j/9v/4//y/9T/vv++/5n/oP+n/9v/6v/N/9T/oP+n/7b/zf/U/9T/vv+g/9T/2/8HAPn/FgAHALb/vv/F//n/zf8OAPn/1P8HANv/FgDq/ywADgDb/yUA2/8WAAcADgAsAAAABwDy//n/DgAzACwAJQAOAOP/8v/U/83/LAAOAPn/DgDF/+r/BwAAACwA+f/U/+P/6v/j//n/HQDy//L/BwD5/w4ALAAdADsAMwAAAA4AFgAHAAAA+f8lAAcADgAsAA4AJQAlADMABwAlADMAFgA7AA4ALAAzAFEAbwBvAGcAWQBZACwAWQBCAEoAOwAWADsA8v8OADsAJQAzADMABwAOACUAHQBCACUASgBCADMAMwAlADsAQgAsACwAQgAOAFEASgBKAGcAFgBgAEIAJQBKADMAJQAsAH4ASgBCAHYASgB2AGAAQgBCADMAWQBRADMAOwA7ACUALAAlACwAMwAWACwABwAOAB0A+f8lAAcAFgAWAAAA4//F/9T/zf/j/+r/4//N/9v/4//y//L/4//5/83/2//y/wAAAADq/wAA1P/U/+r/6v8HAPn/AAAHAM3/zf/q//L/DgAAAPL/+f/j/w4AFgAOADsALAAdAAcAJQBCADsALAAsAAcA6v8lAPn/LAAWAAcAUQAAAB0A+f/5/w4A8v8OAPn/6v/q//L/6v/b/9T/8v8AAOP/zf/N/9T/zf8OAOr/AAAAAM3/2//U//L/BwAdAOr/6v/q//n/AAD5/wcAzf/b/9v/AAAHAAAAOwAlAAAAAADq//n/MwAWAPL/8v/j/8X/4//q/wAABwC+/+P/zf/U/+P/2//j/77/zf+C/77/zf++//n/tv/q/+P/zf/b//n/BwDj/xYAAADj/+P/4//y//n/BwAOABYAAAAAAAcA8v/y/+P/4//j/7b/zf/N/+P/DgAHAAcAAADq/+P/8v/5/xYABwAHAPn/8v/5//L/LAAdACUABwD5/wcA+f8dAAAAJQAOAPn/AADq/wcA8v8dAB0AAADq/83/8v8HAPL/AAAHANv/8v/j/+r/4//j//n/1P/U/83/FgAOAPn/DgDN//L/8v/j/w4AFgAWABYAFgAdAAcA+f/b//L/AADb//L/6v/y//n/+f/5/9T/1P/j/9v/6v8OAPL/6v8WAAAA8v/b/+P/6v/q/wAABwAHAAAA+f8HAPL/4//j/+P/8v/q/wAABwAAAAAADgAAAPn/8v/b//L/4/8HAAAA8v/5//n/DgAAAB0A8v8AACUADgAHAPL/6v/j/x0AAADq//n/6v/j/8X/BwDN/wAABwDb/w4Avv/j/9v/xf/5/wAAAAD5/xYAAAAHAAAAAAD5//L/AADj/w4AHQAOABYAHQAdACwAJQAsADsAAAAOACwAFgDq/wcALAAlAB0ALAA7APL/JQAAANv/MwDj/+r/AADb/wAAAAAHAPn/4//5/+P/6v/q/+P/BwAAAPn/6v/5/+P/1P8zACUABwAOAAAA4//y/wAADgAWAOr/+f/y//n/DgAHABYAAADy/yUAJQD5/x0ABwDj/+r/+f/5/+r/8v8HAA4ABwAlAB0AHQAHAAAABwD5/wAA8v8AAAAABwD5/x0AJQDj/x0AAAD5/ywA8v8WAPn/8v87AA4A+f8AAOP/BwAHAPL/+f/b/wAABwDU/wcAAADq/+P/6v/U//n/HQAOACwABwD5//L/JQAsAA4AMwAOAEIAFgBKAEIAAAAsAB0ALAAAABYAAAAlAB0A8v8lAOr/DgD5//L/+f/q//n/+f8HAPn/JQAAAAcAHQD5/w4AFgD5//L/FgAWAB0AJQAlACwABwAWAAcABwD5/9T/8v8AAPL/BwAOAPn/AAAHAPL/2//q/wAA8v8HAAcA8v/5/wAABwAAABYADgAsACUABwAsAPL/JQAlABYADgAAAA4A+f8WADsALAAWACUA8v8HACUABwAHAPL/+f/5/wcA8v8HAA4A6v/5/+r/+f/5/x0ADgAOAB0AJQAsACUAMwAdACUAHQAdAEIAMwAOABYA8v8AADsABwAlABYAAAD5/wcAFgDy/wcA+f/b/+r/8v++/+r/+f+2/83/4//U/9v/4//b/wcA6v/y//n/2/8HAPn/BwDy/9v/4//y//n/4/8OAAcA6v8OAOr/1P/b/83/2//q/9v/xf/q/77/zf8WANv/AADq/+P/2//U/+P/6v8WAOP/DgAHAOP/MwAOAOr/BwDy/wAAAADU//L/8v/5//L/4//b//L/AADq/wAA8v/5/wcA6v/q/wAA8v8HAA4AAAAAAOr/DgDy/xYAHQD5/xYAAAAHAOP/8v8dABYAFgAWAB0ADgAlAB0AFgA7AEoAOwBKADsAMwAzACwASgAdACUAHQAAAEoAMwAlADsAAAAlACUADgAdAAcAJQD5//L/AADb//n/DgAzAAcA4//q/wcAFgAHACwADgAWACwADgDy//L/+f8OAB0A+f8OAB0A+f/5//L/zf/U/wAA8v/y/+r/xf/q/+P/+f8zABYAFgAWABYAAAAlABYAHQAzAPL/OwAlAAcAHQAHABYAAAAOANv/6v/5/+r/FgAAAPL/8v/q/+r/+f/5//n/2/++/9v/xf/j/wAA2//y//n/2//5/wcA4/8OAPn/zf8HAOP/4//y/83/1P/q/wcA4//b//L/AAD5//n/HQAsADMADgAOACUA6v/b/wAA1P/N/+r/4//j/83/4//U/9T/6v/y//n/zf/b/8X/xf+v/6//2//N/+P/zf/b/+r/vv+n/77/xf/N/+P/2//N/+r/AADy/+P/+f8WAPL/+f8AANv/6v/y/wcA6v8AAA4A8v8OAPL/FgAsAOr/8v8AAOP/DgDq/+r/BwDj/x0AAAAOAB0AAAAOAAcAHQD5//n/+f/q/ywAAAAWAAAAzf/5/9T/xf/b/+P/zf/F/83/2//U/7b/4//U/9v/6v/U/77/2//5//n/+f/y/xYA6v/5//L/xf8HAOP/DgAOAPn/MwAWAPL/BwAsAOr/+f/5//n/FgAOACUABwD5/wcAHQAOABYABwD5/wcA+f8AAA4A+f/N//n/8v/b/w4A2//b/wAA6v8AAB0A8v8AAA4A+f/5/9v/8v/5/w4AHQAOAB0AAAAWABYA6v8lACwABwAdAA4ADgAsACwAQgAzABYAMwAzACwAUQBKAB0AJQAlAAcAMwA7AB0AJQD5//L/DgAWAB0ALAA7ADsAOwAWACwAFgDq/x0A6v/5/wAA+f8zAAAADgAAANT/4//b//n/8v8AAAAA+f8OAPn/8v8OAB0ABwA7ACwALAA7ABYAQgAWAA4ALAAAAAcAJQAWAAAAJQAsADMAJQAWAB0ABwAdAB0ADgAOAPn/8v/5/w4ADgBCAEIAFgA7ABYAJQAsAAAAFgAOAOr/4//5/x0ADgDj/yUAHQAAACUA+f/5/+r/AAAAAAAAFgAOADsABwAdABYAFgAzAA4AQgAOAB0AJQAsACwAAAA7AA4AAAAWAPL/LAAWAPL/JQAWADMAFgAAAB0A+f8lAB0ADgA7ACUADgAOAA4ABwAOAAAABwDy/+r/AADj/9T/2/8AAPn/8v/b/+P/6v/U/9v/+f/y/9T/BwAAAPL/AAAHAPn/AAAWAOr/JQAWABYAFgD5/x0ADgAOAB0AQgAzAEIALAAAAAcAAAAlACwAMwAsAA4A+f/5/x0A+f8HACUA6v/y/wcA+f/y/83/2//j/9v/4//5/wcAzf/N/+r/1P/N/+P/4//N/9T/2//N/83/AADb/83/2//b/wAA6v/5/wAAxf/q/+r/4//N/8X/6v/b/wAA4//N/83/zf8WANv/6v/b/7b/1P/F/9v/mf/U/+r/p//b/83/1P/j/+P/+f/b/83/+f/5//L/8v++/83/2//q//L/2//5/wAA6v/5/9v/6v/b/8X/6v/j/8X/1P/b/83/6v/y//L/8v/q/+P/4//y/9v/1P++/+P/2//5/zMAJQAOAPn/DgAAAPn/DgAOAOr/zf8HAOr/8v8HAAcAHQD5/wAAFgDy/wcA6v/j/yUA+f8WAB0ADgBCAB0AHQAOAAcAHQAWAAcADgAlACUAMwBnADsAJQAlAB0AUQBRADsALABKADsALAA7ADsAYABKAG8ASgAsAFkAOwAlADsAJQD5/w4AJQBCACwAUQBgACwAQgAlADsALAAzACwA+f8dACUAJQAsADMALAAzAB0AFgAAAAAAFgAOAB0ADgAOAAAA8v8OACUADgAlACUAAAAOAAAADgDq//n/6v/5/x0A2/8OAPL/+f/y/83/HQDU//n/HQDU/wAA6v/y/wAAAAAHAPn/DgDN//L/AADj/wcA+f8HAPn/FgD5//n/FgDj//n/4//q//n/AADj/w4ADgD5/yUA6v/y/+P/2//5/+P/xf/q/xYA8v8OAAcA8v/j/+r/HQAAAB0ADgAHABYAAAAzAAAA4//5/83/zf/j/+r/xf/N/83/xf/b/9v/+f8OAAcABwAOAPn/FgAOAOP/4//U//L/zf/q/+P/1P/5/83/+f/U//n/DgAHAPn/vv8HANv/DgD5/77/DgDb/w4ABwDq/w4A1P++/9v/4//U//n/4/8HAA4A6v8WAAAA2//q/+P/zf8AAOP/+f8AAK//+f/b/+P/6v/b/+P/zf/j/+r/+f8HAA4AAAAWAAAAAAAWABYAFgDj/xYAAAAHACwADgAdAAAABwAHAA4AFgAWAAcABwAHAPn/JQAlADMAHQDy/xYAHQAzAEoAHQA7ADMAAAA7ACUAJQBCADMAOwAsADsAOwAlAFEAMwAzAGcADgAlAEIAJQAdAPn/HQD5/xYALAAlADMABwAOAAAABwAAAB0ALAAHAA4ADgDy/7b/2//b/+P/BwDq/xYAJQAlADsAHQAOAAAA6v/5/w4AFgAAAAAA+f8HAPn/BwAWAAAAFgAWADMABwAHAAAA6v/y//L/+f/N/wAAAADj/+P/4//5/+r/DgDq//L/8v/5/w4A4/8AAPn/xf/F/+P/2//j/9T/vv++/6D/zf/U/6f/oP+v/5H/gv++/9T/vv/F/9T/vv+v/8X/1P/U/9v/zf++/9v/tv/N/+r/zf/U/9v/zf/U/+r/AAAOAAcA2//b/9v/1P/y//L/6v/b/8X/6v/F/7b/8v++/9v/+f/U/9v/4/8dAAcA2//5//L/AAAWAAcAAAAAAPL/FgAOAPn/HQAWAB0ALAA7ACUAMwAzAA4AMwAlADMAOwAlACwAQgAzACwAQgAWACUAMwAAAAAALAAWAB0AMwAOAAcA8v8OAA4A+f8WAAcAFgAAAAcAFgD5/xYAJQAlAA4A6v8AAA4A6v8OAB0AAAD5/+P/6v/y//L/2/8AAAAA2//5/+P/6v/j/+r/6v/j/9T/8v/y/8X/AADb/+P/8v/j/w4ABwD5//n/BwAOAA4A+f8AAB0AHQAHAPL/AADj//L/HQAWAPn/FgAdAPn/FgAdAB0ABwAWAPn/8v8WAAAADgDq//L/6v/j/w4A+f8dABYA+f8OAPL/4/8WAAAA8v8dAAAA8v8HACUAAAAWAB0A4/8lAA4AFgAlABYAMwD5/wAAHQAsABYABwA7APn/HQAzAAAAAAD5/wcA8v8dAB0ADgAOAOr/BwDq/wAAAAC+/+P/2//b//n/8v/y/+r/6v/j/+P/4//b/9v/xf/b/wcAxf/U/wAAtv/U/9v/6v/q/+r/4//U/wAA1P/j//L/4/8AAOP/1P++/+r/4//U/9v/8v8AAPL/BwDq/w4A8v/y/wAAtv8HAPn/2/8HABYA+f/y/x0AAAAlAOP/6v87APn/JQAdAPL/AAAAAAcAHQDq//L/JQAHABYAMwAlACwAOwAzAB0AAAAWADMAFgAlAB0AHQAOAA4AHQDy/xYAFgAdADMAFgAWAB0ABwAOADsALABRAEIAJQAlAPn/DgAOABYAMwAAAOr/JQDy//n/BwAAACwA4//y/+r/2//5/9v/AADq/+r/DgAHAAAAJQAsABYAFgAOAB0AFgAOAPn/DgAWAAcASgBCAB0AHQAlACUAFgAlACUADgAHAB0AAAAOACwADgAdACwADgAOAEIAJQAdADsAFgAOAA4AHQAzACUADgAdADMADgAOADMAHQAHABYADgAlAAAAJQAWAPn/HQDb/wAADgAAABYAAAAWAAAA8v8WAB0ABwAAAAcAAADq/x0AFgAHAAAA2/8OAOr/+f/5/83/4//y/wAA8v/5/9v/6v8AANv/6v/5/+P/1P/q/77/tv/b/8X/tv/j/+P/zf/j/9v/4//q//n/2//q/9T/zf8HAM3/4//U/83/6v/j/+P/4//5/8X/6v8HANv/4//N/+r/6v8AABYAAAAWAAAAHQAdAPL/DgD5/wcAAAAAAA4A4/8WAAcADgAWAOr/AAD5/w4A+f/5/w4AAADy/9v/AADq/+r/HQAOAOP/FgAAAOP/OwAAAAAAJQAAAA4AAAAsAB0AFgAWAA4AJQAdAEIAMwAzADMALAA7ACUALAA7ADsAMwBCABYAFgAsADsAOwAOAB0ADgAAAPn/QgAdAA4AOwDq/wcA6v8OACUAHQAzAA4AJQAdAAcABwAlAAAAHQBKAAAABwAOAPn/DgAWAOr/+f8AAPn/6v/y/+r/vv8WABYA4//y//n/4//F/wAAFgAAAAAAAADy/77/+f8HAPL/HQDy/w4ADgD5/x0A8v8WAAAA+f/b/83/4//q/wcA1P/5/+r/6v/5/9v/1P/5/+r/2/8AANT/BwDy/+r/FgD5/wAA4/8HAAAALAAlABYAFgDy/wAAAAAdAAAABwAWABYAAAAsAB0AJQAsAAAAUQD5/xYADgDy/w4Azf8dAPL/6v/q/9v/8v/y/wAA8v/5/83/8v/j/8X/zf/b/6f/tv/j/6D/2//U/+r/zf/U/9v/oP/y/6f/8v/U/6f/4//U/wAAr//5/83/1P8WANT/DgDb//n/2//b//L/tv/y/9v/8v/j/9T/AAAHAA4ABwAOAPn/4//U/+P/6v/b/wAABwDb/9v/2//U/83/zf/b/8X/xf/U/83/2//q/83/zf/y/9T/6v/y/9T/8v/N/9v/BwD5/w4A8v/b/xYAAAAHAAcABwAzAAcAQgA7APn/HQAWAA4ADgAAAAcAAAAAAAAA+f/y/wAA+f/y/wcA8v/j/+r/AAAdAAAAAAAOAPL/6v8OAAAAHQAdAA4AQgD5//n/BwDq/w4A+f8HAAcADgAdAPn/6v/5/w4AFgAAAAAAAAAHAA4A6v/5/wAABwAdAA4ADgAHABYALAA7ACUADgD5/w4AFgAHADMADgAWADMAHQAsADMAMwAlADMAHQAsACwABwAWAA4AHQAWAAAADgD5//n/6v/q/xYA4/8AABYAxf/q/+r/6v/5//L/+f/y/wcA+f8WAPn/zf8HAPL/AAAAAAcAJQAWAA4AHQA7AAAADgAOABYAHQAWABYA+f8dAAcAJQAlABYAOwAlAAcAAAAOAOr/FgDq/9T/+f/5/w4AAAD5/9T/AADq/+P/AADq/wcA+f/5/+r/BwD5/+P/BwD5/+r/6v/5/+P/4//5//n/1P/q/77/vv/j/9T/4//F/+P/xf/F/9v/vv/q/+P/2//j//n/zf/j/+r/r//q/9v/zf/5/+r/xf/q/+P/4//q/83/4//b//L/FgD5/+r/DgDy/+r/AADq//n/8v/q/9T/2//j//L/AAAAAAAABwAWAPn/AAAOAA4AAAAAAAcABwAWABYALAAsACUALAA7ADMAUQBgAFEAfgBZAFkAWQBKAFEAUQBZAEIASgA7ADMAYABCAEIAOwAsADsAMwBgADsAUQBgACwAWQAdADMAJQAWADMADgAsAAcAOwAsAPn/JQDq/+P/DgDq/+r/DgDN/9v/AADN/83/4//U/7b/2//U/+P/4//q/wcA6v/y//L/DgDb/wcAFgDq/zsA8v/j//L/8v/y/+P/BwDb/+r/1P/U//L/2//5/w4AAAD5/zMAHQBRADsAFgBKAAcAMwAzAEoAOwAlACUA+f8lAA4AFgAAAAcAAAAAADMADgAsAPL/+f/q/+P/BwAHACUA4/8WAAcAFgAlAA4AMwAOAB0A+f8AAPL/4/8AAOr/8v+2/+r/xf+v/9v/r/+2/8X/2/++/+P/2/++//n/2//b/+P/4/8AAPn/6v/y/+r/8v/5//n/8v/q//L/1P/5/+r/8v8dAPL/AADy//n/8v/j/9v/1P/q/wAADgD5/wAA6v8HAAAADgAlAAcABwD5//n/6v8OAB0AFgAHAPn/BwDy/xYAHQD5/+r/+f/q//n/HQAWAB0ALAAdAAcAFgAWAA4ALAAlAAcAMwAsAAcALAAdACwAJQAsAA4ALAAdANv/FgDq/xYAJQAHADMAFgAWAAcAHQAsABYAOwA7ABYAHQAOACUAJQD5/wcADgAdAAcAFgAOAAcALAAAACwAOwAAAB0AHQAHAA4ADgAOAPL/+f/5/+r/8v/5/xYA4/8OAB0AAAAsAPn/FgAHABYADgD5/wAABwAlAPL/FgD5/wAAFgDF/w4A4//N/wAA6v8AAPn/BwAlAPn/FgAWAAAAFgD5//n/AAAAAOr/zf/N/83/1P/N/9T/vv+v/9T/tv/U/9v/xf/b/7b/4//j/9v/8v/y/yUA6v8HAOr/6v8lANv/HQAOAPn/8v/q/w4A1P8AAA4ABwDj/9v/DgDj/9v/8v/q//L/8v/F/+P/1P+n//L/+f/q/+r/+f8OANv/6v/5/8X/zf/q/7b/tv/b/7b/1P+2/6//4/+v/9T/6v/F/83/6v/q/+r/8v/N/9v/1P/b/+r/4/8AANT/4//b/9T/AAD5/wAA+f8AAOr/4//y//n/8v/j/+P/2//q/9v/6v8AAOP/AAAAAPL/8v/5/yUAHQAWAB0AFgAdAA4ADgAWAA4AAAAAAB0ADgAAAAcAAAAHAOP/6v8AAAAABwD5/w4ABwAHACUADgAdAB0A+f8OAA4AAAAdAA4ABwAWAB0AJQAOAOP/AADy//n/HQAAAA4A+f8OAAcA8v8OABYAOwAHACwAQgAdAEIAHQAWABYAFgAdAB0AJQBRACwAFgA7ACUAMwBCACUAMwAsACUALAAWADMASgAdADsAMwAzAEIALAAzACUAHQAlADsAOwAsAB0ABwD5/wcADgAAAAcADgAlAAAA2//j/+P/AAAAABYAJQDq/wAAOwAHAPn/DgDy//L/DgAWAB0AJQAHAAAA2//b/xYA2//j//n/6v8HAPL/8v/b/9v/6v/N//n/8v/5/wcA8v8AAMX/4/8OAM3/BwAAANT/BwDU/wAABwDb/xYA4//y/+r/6v/j/+P/+f+2//n/8v/j/+r/4//U/7b/4//b/wAA+f8AAAcA8v8AAAAAFgAHACUADgAdABYA+f8zAAAALAAzAPn/JQAHAA4AJQD5/wcAAADq/x0AJQAAACUAJQAWABYAFgAHAAcAQgAAABYAFgDN/wcA8v/5/+r/DgAOAOP/4/+2//n/4//U/9v/2//q//L/DgD5/x0ABwDy/w4ABwD5/wAADgDy/wcAAADU/wAA+f/q/wcA1P8AAPn/AAAlAA4ADgDq/+r/+f/y//L/HQAHABYAFgD5/xYAAAAAAPL/DgD5//L/AAD5/wcA2/8WAPn/4//b//n/BwDj/w4A+f8dAAAABwAAAAAADgAAABYADgBZAB0AMwAlAAAAQgAAABYADgAOACwAAAAlAB0ABwAWAPn/JQAWADMAUQAdAEoAOwBCACwALAAsACwAOwAdAEoAMwAsAB0AJQAOABYALADy//n/1P/q/+P/8v8HAPn/8v/j/wAA8v/y/+P/AADj/+r/BwDN/wcABwAWAA4A+f/5/9v/4//5/83/xf/j/9v/2//F/8X/xf+2/77/tv+v/+P/6v/U/+P/2//j/8X/6v/b/9T/+f/y/wcA6v/5/+r/4//5/+r/6v8AACwADgAsACUAHQAWAOr/BwAOAAcA6v8HACUAAAAWACUAFgAWAAAAFgAOAPn/JQAlAAAAAAAOAOP/BwAWAAcAFgD5/wcA8v/5/+r/2/++/83/+f+v/w4ABwDb/w4A2/8HAAAA4/8AAPn/FgAAAOr/+f++/+P/4//U/wcA1P8AANT/zf8HAOP/4//5/xYA8v8HAB0ABwAOAA4AJQDy/xYAMwAHACwALAAOACUAMwAdACUAHQAsADMALAAWAA4ADgAAACUAMwAzAPn/DgAdAOP/FgDy/+r/AADy//n/+f8WAAcA+f/5/wAAAAAAAAcADgD5//L/2//j/+r/2//5/wcALAAzAA4AAAD5/9v/8v/y//n/DgDy/x0A6v/q/w4A8v8lAAcA+f8HAOP/xf/j/77/xf/U/6//1P++/8X/vv/F/83/2//N/9v/8v+2/wAAxf/N/+r/xf8AANv/4//j//n/6v/q//n/4//y/9v/4//q/9T/8v/5/w4AHQAAAB0A+f/5/xYA8v/5/+r/JQAWAAcABwAOAB0A6v8WABYALAAdAA4ALAAAAAcAFgDy/+P/HQAOAA4AJQAWACwAMwAWABYAHQAAAB0ALAAzADsAQgAWAAcAJQAAAB0AFgAOABYAHQAOAAcADgDy/wcA+f8WAB0ABwAOAPL/8v/5/wAABwAWAA4ALAAOAA4ADgAHAB0A6v9CADsAFgAzAA4AFgDq/wcALAAHAAAAJQAWAAAAMwAWAAcA+f/y/wAA4//q//L/AADy/+P/8v/q/w4ABwAAAA4A6v/5/+r/+f8OABYADgAHACUAAAA7AEIADgAWAAcADgAWADMAFgAlADsAHQAdADMAOwAWACwABwAdAEIA+f8HAB0AHQAOAB0AJQAWAAcADgAOAPL/+f/q//n/+f/b/wcA+f/q/wcA+f8AAAcAAAD5/wAA+f/b/+P/4//j/+r/1P+2/77/vv+2/9v/vv+v/83/p//F/+P/tv/U/9v/1P/j//L/8v/q//n/8v8OAAcA4/8AAOr/+f8HAA4A+f/5//L/AAAAAOr/+f/b/+r/6v8WAAAA2/8AAMX/BwAHAAAA+f/j/x0A2/8HABYABwAWAAcABwD5/w4A+f/5//L/6v/j/9v/AADy/+r/4//N/+P/8v/j/+r/2//b//L/2//j//n/2//j//n/8v/j/9v/6v/N/9v/2//q/wAAzf/q/8X/zf/b/9T/AADb/wcA2//q//L/zf8dAPL/8v8HAOr/BwAdAAAADgAWAPL/HQAlACUAJQAzAAcABwAOAOr/6v/b/xYA+f8OABYA8v8dAAAAMwAAAPn/FgAlADMA+f8sACwAQgAlADMAOwAzAGcAHQBCADMALABCACwAMwA7ADMASgBRACUAWQAWAAcAHQDq/w4ABwDj/+r/JQAWACUAFgAdACwAHQAsAPn/QgAdAAAAJQAAAAcADgAHAAAAHQDq//L/HQD5//L/8v/U/+r/2//b/+P/xf/q/+P/6v/U/83/8v/U//n/4//b/+P/4//5//L/tv/N/+P/vv/j/6//p/+v/9v/2//N//L/tv/F/8X/8v/b/8X/6v/U/+P/8v8AAPL/4/8OAAAA2//5/+r/6v8OABYABwAOAB0AHQAlAAcAMwAHAAAAFgAWABYAFgAzAAcALAAdABYADgAOAFEAHQAzACUAHQDy/yUAJQDb/yUABwA7ABYAFgAzAPn/HQAWAB0AFgAdAAcA8v8WAAAA6v8HAOr/xf8AAPL/BwAAANv/AADj//L/+f/j/+P/8v/q/9v/2//5/wAA+f8OABYAJQAlAA4A+f8WAB0ALAA7AAcAJQAlAPn/AADq/9T/2/++/+P/2//U/w4A2/8HAPn/4/8sAM3/BwAlAOP/BwAAAAcAAADj/wAAHQAdADMADgD5//L/8v8OAAcA6v8WAAcA1P8sAA4ABwAsAAcALAAAAB0ALAAzAEoAFgAsACwAFgAsAEIAJQAzACUAJQA7APL/JQAlAAcAJQAlADMA+f8OABYA6v8dAAAADgAlAAcAQgAWADsAJQAWADsADgAWAPL/DgD5//L/DgD5/w4ABwAzABYABwAWAOP/6v8dAOP/BwAlAAAAHQD5/w4A1P/U/wcAFgDy/9T/AADF/+r/xf++/+P/vv/j/8X/xf/y/+r/xf8AAM3/6v8OANT/BwDq/9v/DgAAANv/HQAHAAAAAAD5/ywA4/8dAAAADgAOANv/8v/N/x0A6v/j//L/1P/b/+P/2//U//n/xf/b/9T/vv+n/5n/xf+2/83/8v/b/+P/BwD5//n/AADb/9v/8v/y//n/+f/q/wAAAAAOAAcA4//y//n/+f8WAB0ABwAHAPn/HQAOAAcAMwAHAA4ABwAWAAcA6v8WAB0ABwAdADMAFgAHABYADgD5/x0ADgAOAB0ABwAdAA4ABwAOACUALAAsACwAJQAsAEIAWQA7ACwAMwA7ACUALAAsABYALAAsACwAFgAWAAAAJQAsAAAALADy/wcALAAOACUADgAHAAAADgAzAAcA8v8sAPn/8v8OAL7/1P/j/77/2//j/9v/2//N/8X/4//j/9T/2/++/9T/1P/b/9T/vv8WANv/8v8dAOr/FgDb//L/DgDq//n/8v/y//L/DgD5/wAA8v/5/xYA+f8lAA4ALAAdAPn/HQAAAPL/AAA7AAAAAAAWAPn/JQAAAB0AJQAWAB0AFgAHAPn/HQDy/wAA+f8AACwA+f8OAAAA6v8lAAcA2//b/wAA1P/q/w4Azf/y/+r/6v8AAM3/DgDy/+P/FgD5//n/DgAHAAAA+f/U/+P/8v/q/wAABwDb/+r/+f/j//n/6v8OADMABwAOAA4AAAD5/+r/DgD5/+P/8v/y/w4A+f8HAA4A4//j/+P/xf/U/wcAAAAdAAcA+f8AAA4AJQAHADsADgDj//n/DgAAANv/FgD5/+P/DgAAAPn/BwAOAPL/6v/5/+r/8v/j/77/1P/U/83/8v/b//n/+f/F/9v/2/++/9T/1P/j//n/1P/5/wcA8v8AABYAFgAHADMAAAAHAAcA1P8WAB0AHQAOAPn/BwAOABYABwBKAAAABwAsANT/QgAlAOP/LAAHADsAFgAdAEoA8v8lADMADgAWADsAFgDU/x0A8v/5/x0A+f8WAAAA8v/y/ywAJQAOADsAHQAlACwAJQAdAAcADgAdAA4AFgAlAA4AHQAHAAAAJQAHABYAHQAAAB0AFgD5/xYAHQAAAA4AJQAdACUADgAsAOr/8v8lANv/BwAAAA4A+f8AAOr/1P8OAOP/DgAHAAAA2//y/yUABwAlANv/DgAdAPn/JQAsACUAHQAdAB0ASgA7ADsAOwAHAB0AJQAWACUA8v/y//n/6v8HANv/DgD5/9v/4//F//L/2/8AAOP/6v8HAAAALAAlADMAHQAlACwAFgAHABYAJQAlACUAAAAsABYADgAWAPn/2/8AAAAAxf/y/83/1P/b/9v/6v/y/xYA1P/U/+P/xf/j/+P/4//j//L/8v/U/+r/6v++//L/4//U//n/8v8HAPn/6v/j//L/8v/q//n/AAAHABYAFgAHABYA8v/5/yUADgAdACUALAAlAEoALAAlAFEAFgAAAA4ALAAHAA4ABwDq//L/8v8HAPn/FgDj//L/FgDq/+P/6v/b/77/8v/y//n/AADj/9v/8v8AAOP/+f8AABYA6v8HAB0A+f8AAPn/DgDj//n/AADb/+P/DgAAAOP/FgAWAAcAFgAdAOP/4//b/8X/BwDq/9v/1P/U/83/p/+R/5H/r//F/8X/zf/N/77/+f/q/8X/2//j/8X/4//q/6D/tv++/8X/zf/N/9v/1P/b/7b/2/8AAOP/2//y/9v/6v/y/+r/FgDN/6//+f/N/77/6v++/+P/2//F/+r/1P/y/83/6v8WAM3/BwAlAOr/AAAdAAcAAAAOACUA+f8HAPn/8v8lAPn/JQAzAA4AJQAAAPn/BwDq/w4AAAAHABYADgAsAAcABwAWABYA+f8AAAcA8v8dABYA+f8AAB0AFgAOACwADgD5/w4AAAAWAAAAFgA7APL/QgAHAPn/YAAWAAcADgAlAAAAFgAHAA4ADgDy/xYA4/8WAA4ABwAlAAcAHQAWACUAFgAsAEIAJQAOACUABwAlADsAUQBCAAAAHQD5/ywAFgAlADsA+f8WANv/AAD5/wAADgAHAAAA6v8OAAAALAAHAPn/HQAOACUADgD5/wAA8v8AACwAAAAHAPn/1P++/9T/8v/b/w4A+f/y/+r/zf8HAAcA+f8OAB0AFgDq/wcALADq/w4ABwDy/xYAAAAsAAcAAADy/9v/AADN/wcA+f/F/wcA1P/q/wcAzf8OAPn/2/8OAAAA+f8dAA4A4/8WAPn/4/8OAPn/+f/5/9v/+f8OAOP/BwAAAOP/BwAAAB0AFgAAACwAAADq/xYAFgAAAA4ADgAWAPL/4/8dADsAFgDy/zMA8v8AACUAvv8OAOr/2/8AAMX/1P/N/9v/4//U/9T/2//F/9T/6v/b/9v/4/8AAPn/DgAHAPn/HQAlAB0AJQAsAOr/HQAlABYAMwAOACUAAAAHACUA+f/q/9T/2//b/+P/+f/j/83/4//j/83/4//y//L/+f8OAAcA1P8HAA4A8v8WAOr/4//q//L/1P/b/9v/xf/q/9v/8v/q/9v/4//b/wcA8v/5/wAA6v8HAA4A+f8HAB0ADgAHAOr/8v/5/+r/HQAHAPL/FgAOAB0AFgAOADsAHQAHABYABwAOAA4AHQBKAA4AJQBRAAAAOwBRAAcALAAWADMAOwAHAEIAAAAOADMA4/8lAA4ABwAHABYASgAHAA4AFgAWABYAJQBKACUAJQAlAA4AJQAzABYAQgAzAA4AQgAzAFEALAAOACwA8v87AEIADgBRACwADgAOACUAMwAlAEIAHQA7ADMAHQBCACwAOwAsACwAWQA7AEoAMwAOADsA+f8OACwA+f9CAAcADgAHAOP/FgD5/yUALAAWADsAFgAdAA4ABwAdAAAALAAdACwAMwAdADMAFgAdAA4ALAAWAAAAHQDq/xYADgD5/wcADgDy/+r/+f/j/xYA4/8OAA4A1P8WAAcAAAAAAAcA8v8HAAAA4/8AAOr/4//y//L/2//y/9v/vv/j/8X/2//y/8X/6v8HAPL/4/8OAPn/8v8dAAcADgAAAB0A8v/y/wAAxf8HAPn/+f8HACUAHQDN/xYA8v/j//L/6v8dAPn/6v8AAPL/8v8OAPL/zf8AANv/zf8AANT/8v8HAOP/AADb//n/4//F/+P/zf/N/83/8v/N/9T/2/+2/8X/r/++/7b/vv/F/6D/zf/F/8X/zf/j/+r/vv/y//n/zf/U/9v/1P/j/+P/6v8OAA4A8v8HABYA+f/j/+P/AADj//L/HQDj/77/zf/F/7b/zf/b/+P/xf+g/6f/e/+R/6f/1P+2/7b/zf+K/9v/2//j/83/vv8WAOP/6v/y//L/AADy/wcAAAAOADsAJQAWACUADgAzACUALAAzABYALAAzADsALAAdACUASgBCAEoAYAAsAB0AMwAsACwAQgA7ADMAJQA7ADMAJQAzAB0AMwA7AA4ABwAsAPL/HQAsAPL/LADy/wcAHQAHAA4ADgAlAAcALAAOABYAAAD5/zsAAAAOABYAAAAsAA4ABwAdAA4ALAAWAAcADgD5/x0ADgDq/+P/4//q//n/BwAOAPn/+f/q//L/HQDq/wcA6v/N/wAA6v8HAAcA4/8AAA4A4//5/x0AAAAHAAAABwDj//L/6v/b//L/xf8HAOP/2/8AANT/6v/y//L/4/8OAOr/8v8dAPL/8v++/6//zf/q/8X/4//y/77/+f/F/+P/vv+C/8X/p//U/83/zf/q/77/tv/N/6//tv/5/+r/AADq/+P/BwDy//n/2//N/9v/zf/N/+r/8v/N/77/AADb/83/6v+v/83/1P/b/wAA+f8OAAAA6v/b//L/BwDy/w4A4//N/+r/4/8AAOP/1P/q/+P/8v/j/wcAAADb//L/DgDq/+r/DgDF//L/6v/b/+r/zf8dAA4ADgAAABYAHQDj/x0ADgA7ACUAFgBRAAAADgAzACUADgDy/ywAJQD5/ywAOwAAADMAFgAHADsA8v8dACUA+f8OAAAAFgAHABYAOwAzADMAMwAWACwALAAzAGAALABCAGcAWQBgAGAAZwBCAGAAbwBnAGcAdgCFAFkAbwBgAGcAWQAsAHYASgA7AEIAHQA7ACwASgAlACwAQgAsACwAHQBnAB0ABwAzAAAAJQAdADMAMwD5/w4ASgBCAEIAQgAsAEoAHQAdACwADgAOABYAJQAOACwAFgAHABYAOwAdAAcAQgAAAB0AFgAAAB0A+f8AAAcA8v8AAA4AJQAlAPn/JQAOAA4AMwAAACwA+f8AAA4AHQAzAAAAHQDq/w4ADgDy/yUA6v/5/+r/AAAsANT/FgAlAMX/AADq/9T/8v/5//n/1P/U/8X/1P+v/83/6v/F/w4Atv/F/+r/2/8AALb/xf+2/9T/6v+2/9T/zf++/9T/xf/U/+r/8v8OAM3/2//5/+P/2//q/+r/4/8OAOr/BwDy//L/DgDj/0IABwAOAEIADgDy/+P/8v/j/wcAAAD5/+r/6v/q/+r/2/++//n/4/8AANT/xf/b/77/8v/q/9v/vv/N/9T/vv/U/77/p/+g/77/vv/F/+P/2//U/9T/2//q/77/zf/U/8X/8v/U//n/DgDU/9T/1P/y/wcA4/8AABYA2/8HAB0A+f8WACwABwD5/wcA1P8AAAAA6v8OAAcAAAAOAA4A4/8AAPL/+f8WAPn/JQAOAAAAOwAWABYABwDb/wAA2/8AAB0A8v8dAPn/FgAOAPL/4/8AAAcA2/8WAAAA+f/5/wcAAAD5/w4A+f8dAA4AFgAOAB0ALAAOADMALAAHAOr/FgAOAOP/8v8OAOr/4/8OAPn/6v/5/wcA+f8HACUA+f/y/+r/6v8HAPL/+f8HAPL/DgAWAAcAAAAHAAcA8v/y/wAABwDy/wAAAAAWABYA8v8WAOr/DgAdAAcAFgAHAPL/+f8OAAcA+f/N/wcA1P/j/ywAp//N/+r/vv+2/9v/+f/j/+P/1P/b/9T/6v++/+P/4/+n/wcAzf+2/9v/1P/b/9v/8v/y//L/AADb/+r/4//b/yUA+f/q/+r/zf/q/+r/BwDb/+r/2/+v/+r/6v/j/+P/2//N/9v/vv/N/+P/zf/U/8X/4//q//n/AAAAAOr/2/8WAPn/FgAdAAAAAAAOAA4A+f8HAPL/BwD5/wAAHQAAABYADgAAAAAAAAAAABYAAADy/zsADgAHABYA8v8AAAcA+f8dABYA+f8zACUAHQAzACUAHQAWAA4ADgAWAAcABwAWAB0A+f8HAPL/AAAsAPn/FgDb//n/DgD5/yUAzf/q/wAAFgAOAPn/BwAHAB0ABwAdAA4AFgAWAB0AHQDq/xYADgDy/wcAJQAWAA4AHQAOAPn/8v8OAPn/+f8AADMALAD5/ywAMwAzADsAHQAsAB0ADgAOAAAABwDb/wcAFgDy/yUA+f8HAA4A4/8lAAcAxf8sAB0AAAAsAPn/LAD5/xYAHQD5/zMAAAA7AA4ADgAdAA4AAADq/w4A2/8WACwAMwAzAEIAMwAzACwADgBgACUAQgAzADMAQgD5/zsAMwAsAPn/FgAOAA4AAAD5/yUA2/8sAB0A8v8lABYAFgAHABYAAAAWACUA+f8AACUABwAsADsAHQAlAAcALAAWAA4AOwAsAA4ADgA7AAcA2/8sACwAJQAsADMASgAlADMAMwAdABYALABKAA4AHQA7ACwADgAdAAcA4/8dABYAFgAHACUAJQAzADMA8v8lAAAAMwAsAAcALAAAAB0AFgAHAAAABwAlAAcADgAWABYABwAWAA4ADgAOAOr/FgAdAPL/HQAOAOr/+f/y//n/6v/5/x0Azf/5//L/6v8sAPL/+f/q/wAAAAAHABYA+f8sAOP/AAAOABYADgD5/w4A1P8dAOr/AAAsAPn/JQAHACUAJQAAAA4AHQDy/wcAFgAAAA4AAAAWANv/8v8AAPn/+f/j/xYA+f/q/9v/8v/b/+r/AADb/wcAAAAOAPn/+f8dADsAFgAWACUABwBCACwAHQAWACwALAAWACwABwAOAAcAFgDy/9v/6v/b/9T/zf/y/9T/1P/U/+P/8v8OAAAA2//q/+P/DgD5//n/8v/5//L/1P/y/9v/8v/y/+P/xf/U/9T/r//q/+r/2//j/+r/1P/b/+P/2//j/9v/zf/q/+r/4/8WAOP/4//y/+r/4//b/+r/xf/5/7b/r//N/6f/xf+g/9T/oP9s/5H/p//F/5n/vv/F/7b/xf/F/83/1P/N/8X/1P++/83/FgD5/9v/1P/q//L/1P/5/8X/+f/q/9T/JQDj/xYA8v/5//L/2/8dAMX/8v/j/8X/6v/j/+r/8v/q/9T/+f/q//n/AAAWAB0ABwAWAB0ALAAlAEIAJQAOACwALAAOACUADgD5/w4A6v8HAPL/6v/U/+r/2//q/xYAxf8AANv/+f8AAPL/BwCv/w4AAADj/x0AFgDy/yUA8v/j/ywA+f87AAcABwAHABYAUQD5/0IAFgDq//n/8v/q/77/DgAWAPL/4//y/wAA6v/q//L/AADy/wcABwAAACwAHQAdACUADgA7AFEAJQAlACwAHQAWABYAFgAOAAAA6v8AAB0A+f87AB0ABwAOANv/HQD5/wcADgD5/zMA8v8OABYAJQAsAAcALAAHAPL/DgAOAAAA8v/y/wAA4//y/xYA+f/y//L/+f/y/9v/8v/j/9v/8v/j/w4A6v/U//L/zf8OAAAA6v/q/+r/+f++/wAA1P/U//n/4/8AANv/6v/j/+P/2//N/+r/1P/F/7b/8v/q/9T/8v/U/+P/4//j//L/2/8OAB0AAAD5/+r/DgAAAOr/AAAOABYABwAzAAAAJQBKAOr/OwAdAAcALAAHAB0AHQAOAAAAFgAWADMASgAOACUAHQAsAAcABwAWAPn/QgAHACUAHQAHAA4AAAAlAPn/OwAAAOr/DgDy/xYAAAAWAAcALAAdAPL/FgAOAA4AJQBRABYABwAOABYAJQAWABYAJQAOAPL/HQDq/x0AJQAHACwAAAAHAA4AHQAOADsAHQAsADMA4/8WAAcAJQAOABYAAADF/wcA8v8AAPn/BwDy//n/HQD5/x0AJQAHADMAQgAWACUAMwBCAEIAYABZADMAZwBCADsASgAzADMAQgBCAA4AMwA7ADsASgAHADsAOwAsAEoAHQAlADMAOwA7ADMAQgAdADMAMwAWAAcAFgAHAPn/DgDb//n/FgAOAA4A+f/U/w4AAADF/zMA4//j/wcAzf8AAOP/6v/b/9T/2//U/83/1P/q/8X/6v/j/9v/+f8HAA4A8v/y/wcAAADb/+r/4//U/8X/2//y/77/+f/q/77/1P/j/9T/zf/y/77/tv/N/9v/1P+g/9v/6v/N/+P/xf+v/7b/4//y/9T/6v/N/9v/4/+v/wcAtv+Z//L/p/+2/77/r/++/+P/6v/N/+P/zf/b/+r/4/++/9T/4/+2/+r/8v/q/+P/6v/y/8X/1P/5/83/p//y/9T/xf/j/83/1P/N/9T/1P8HAOr/zf/5/+P/1P/y//L/zf/b/+P/8v8AAM3/2//j/wAAHQDj/w4A2/+2//n/1P8AAAcA8v/b//n/8v/y//n/xf/q/8X/6v/U/+P/FgC+/9v/oP/F/9T/zf8AAOP/+f/N//L/+f/j/wcABwAAAOr/BwAHANv/+f8WAPL/DgAOADMAWQAlADMAMwAsADMALAAlABYAJQAlADMABwAsAFkADgAsADMASgBKADMASgBCAFEAQgBKACwASgBRADsAbwAzAFEAZwBnAFkASgBnAFEAYABZAFEAJQBnAEIAMwBnADsAbwBvACwASgBZAA4AOwAsADMAYABgAG8AMwBKACwASgAlAB0ASgAOAFEAMwAlAA4ADgAdABYALAAzAFEAFgBgAEoADgAzAB0AJQAdABYAAAAzAB0A6v/5//L/8v8OABYA+f8AAAcA6v/j//n/1P/q/w4A2/++/83/r//j/9v/vv8OAPL/4//q/wcA8v/j//n/vv/b/7b/2//y/+P/+f/b/83/tv/N/9T/6v/F//L/1P/U/wAAxf/5/wAAAADq/9v/zf/y/9v/4//j/6//BwDb/xYA6v/U/wcAtv/b/+r/6v/q/x0A6v/q/wAA4/8AAPL/8v/j/xYAFgAOAM3/BwAHAKD/+f/U/+r/1P/U/+r/tv/N/77/zf/F/77/zf/b//n/1P+2//n/4//F/wcA4//b/wcAAAAHAA4A4/8AABYA6v8HAB0A+f/N/wcAAAC2/x0AFgDy/x0A4/8AAA4ABwAHAPn/MwAHACUAFgAWACUABwAWANv/FgAHAPn/MwAOAPn/AAAOAPL/+f/y/xYADgAHAPL/6v/q/9T/FgDy/+r/FgDj//L/+f/N/+r/6v/5/wAA8v8WAOP/AAAHADMAHQAHAB0A8v8sAA4AHQAAAA4ADgAOADsAFgBvAB0AHQAlAAAAJQAdADsAHQAlAA4AAAAlAB0ADgAHAAAAJQAOAAAAHQDy/wAA+f8sAPL/AAAlAPL/SgAWAA4ADgAHAPn/2/8WACwAFgAdAB0A8v8dAOP/8v8lAOr/FgAOAAcALAAdAAcAAADy/wcABwD5/+r/2/8HAAcAFgAdABYADgAdAAAA8v8HAPL/AADy//n/FgAAAOr/FgAHAOP/8v/j/w4ADgAHAPL/HQAOAM3/+f/5/wAAAAAAAAcABwDF/9T/4//F/wcA2//q/9v/+f/5/8X/8v/F/xYAAADU/yUA4//5/x0AAADq/9v/AADq//n/+f/U//L/AAAWAPn/+f/q/8X/6v/j/9T/2//j/+r/8v/y/+r/2//j/+P/+f/q/+r/HQDU//n/+f/y//n/zf8HANT/+f8WAAAAJQAAAPn/AAD5/x0AFgDy/wAADgD5/+P/WQAsANv/MwAAAPn/+f8HAAAABwAAAOP/DgAAAB0A+f8HAAcAAAAlAAAAFgD5//n/+f/5//L/8v8lAPn/AAAAAOr/8v8AAPn/8v8WAA4ADgAlAA4ADgAdAB0AHQAWAPn/DgAWAPL/HQBCAA4AFgA7AA4AFgAWAAcAHQAdADMAQgAsACUADgA7AEoAJQBCADMAJQAsAB0ASgBRACwASgBKADMAMwBRAFkAWQBKAEoAbwAlAGAASgAlAGcALAA7AB0AHQAsAA4AHQAWAB0ABwAdAPn/DgAWAAcAFgDy/wcA6v8dACUADgAWAAAAJQAAAPn/BwD5/wAAFgAOAPn/AADy//n/zf/q/+r/zf/y/+P/BwAHAAAAAADq/+r/4//q//L/+f8HAAcABwAAAOr/8v/j/wAADgD5/+r/2//5/9v/4//q/+r/6v/N/+P/8v/j/+r/8v8HAAcAAAAlANv/8v8lAOr/BwAHAPL/xf/j/wcA+f/j/9T/1P+2/9v/1P/j//L/2/++/8X/8v8AABYA6v/5/9T/zf/b/+P/BwDj//L/4/8HAAAA6v/y/w4A+f/5/zsA8v8sABYAJQAzAAcAQgAlACwAAAA7ACwADgBCAB0AQgAWADMAJQAWADMAFgAsAB0AMwA7AEIAJQAWAB0ADgAOABYAHQAHAA4AAADb/+P/zf/F/9T/zf/F/77/1P/N/9T/1P+v/7b/zf/N/83/6v/j//n/2//j/xYAzf/U/83/p/+n/7b/vv+g/77/r/+g/6//oP+v/9T/p/+2/9T/2//j/83/BwDq/7b/AAAsAOP/6v/5/6//xf/N/+P/4//b/9T/zf/F/8X/xf/b/+r/tv8AAOP/4/8HAOP/8v/F/9T/vv/b//L/2//y/8X/8v/U/9T/6v/q/wAA2//y/wAA2//y/wcA1P++/8X/tv/U/9v/4//5/9v/+f/j/+r/4//j/xYA8v8HAPL/+f8OANT/+f8AAAcA+f8HAAcA6v8AAPL/+f8OAPL/6v8AAOr/tv/j/8X/4//j/6D/4/+n/9v/zf+2//L/tv/y/+P/+f/q/9T/+f/N/+P/6v/5//n/8v+v//L/+f++/x0A+f/5/wcADgAAAAcAAAD5/wAA+f87AB0AHQAHADMA6v/j/zMA2/8AAPn/AAAAAPL/BwAWAAAAFgA7AA4AJQAHADsAHQDy/w4A6v/j//n/JQDy/xYAHQAOAAcAAADq/w4AAADU/0oA8v/5/w4A6v/q/9v/8v/U//L/8v8lAOr/+f8sAAAAFgC2//n/AADj/ywABwDj/w4AHQAAAB0AAADy/xYABwDy/xYAAAAHAB0AAAAHAOP/+f8AAPn/6v/j/xYA6v/q/x0A6v/y/xYAAAAOAA4AMwAzAAAAJQAdAPn/FgAlAPn/HQAWAB0AJQD5/0oAHQAlADsAHQAsAA4AHQAOABYAFgAsACUAFgBgACwAJQA7ADMAMwBKAGcAHQBCAEoAOwBgADMALAAdAEoALAAHAGAAOwAdACwALAAsADsAMwA7AEIAFgAsAB0AHQAsACUALAAWAPn/BwAlAA4ASgAsADMALAD5/ywABwAlABYAFgAWAOr/AADy/wAA4/8dAAAA+f8sABYAMwAWAAcA6v8HAAcAHQAzAAcAZwAlAAAALAAOAB0AAAAlADMABwAzADsAHQAzABYALAAWAAcALAAlABYA+f8zACUADgAsACwALAAWACUABwAWABYAFgAdAA4ADgDj/wAAHQAWABYAAAAAAAAA8v8OAPn/AAAsAPn/HQDj/83/AADb/+r/8v8WAPn/+f8WAPL/4//b/wAA8v/5/wAA+f/5/wcAFgDb/+r/HQAOAOr/AAAAAM3/1P/y/wAA6v/y/9v/zf8HAOP/4//y/+r/DgDq/9v/DgAHANv/4//j/8X/2//5/+P/xf/b/83/2/++/77/4/++/7b/1P/b/9v/6v/5/+P/2//y//L/4//5/wAABwDq//n/BwDq/w4ADgAOAB0ABwDy/wAABwAHAB0ADgAsAEIALAAsAB0AHQAzACwABwAsAA4ABwAzAPn/DgAHAOP/JQAOAPL/HQAAAAcAAADq/wcA4/8AAAcAAAAWAAcABwAAACwABwAAABYADgAHAOr/8v/j/wcA8v/y//L/6v8AAOr/+f/j/wcADgD5/wcABwAOAPL/DgAdABYAHQAOAB0ABwD5/ywAFgAHAA4A+f8HANT/4/8AANT/+f8AAPn/BwD5//n/4//b//n/8v/5/+r/BwDq/+r/AADN/wAA6v8AAA4A8v/5/wAA1P/q/w4Avv8WAOr/2/8WAPL/AADq/xYADgAOAAAAAAD5/wAAHQAAAPL/1P8OAOP/6v8AANv/DgDj/9v/AADy/wAADgAAAB0AAAAHAPn/DgAdAPn/DgD5/w4AAAAdAAcADgAsAPn/HQAHACwADgAWAB0A+f8OAAAA8v/y/xYA6v/5/wcA+f/j/w4AJQD5/wAA8v8WAOP/AAAWAPL/FgAWAAcAAAAsAOr/HQAdAAAABwDb/yUADgAHAA4A6v8AAEoAJQAOADMAJQAzABYAJQAdAB0ADgAsACwABwA7APL/BwD5//n/HQDq/wcADgAHAAAAAADy/wAA8v/j//n/1P/q/83/xf/F/7b/6v+n/77/vv+v/83/vv/U/6//4//j/6//4//j//L/+f/y/+r/2//U/9v/8v/U/wAABwDF/9v/6v/b/w4AFgD5//L/6v/j//L/+f8HAOP/4/8OAAcADgAdAEoABwAAAEIALAAdADsAYADy/ywAWQAWAEoAHQAsACUALABKACUALAAsABYABwAlACUALAAWAAcAHQAlABYADgAlABYADgAAAAcABwAOAB0ADgAHADMAJQAOADMA+f/y/wAA6v/5/w4ABwDj/wAA+f/q//L/+f/y/+r/2//j//n/8v8AABYAAAAdAPn/1P8zANv/6v8lANv/AADq/+P/6v/5/9v/AAAAAOr/AADj/x0A1P/b//n/vv/q//n/2//q//n/8v8OAPL/BwDy/+r/8v/5/ywABwAdAA4AQgAdACUAMwAWAFEAAAAsAAcA+f8WAAAAFgDq/w4ADgAAAPn/BwDy/9v/6v/N//L/6v/q//L/zf/N//L/4//F/+P/+f8AAPn/8v8AAPn/AAAAAPL/AADy/9v/HQAAANT/8v+v/83/1P/N/+P/r//F/8X/2//b/8X/2//N/+P/6v/q/+r/8v/j/9T/1P/b/9T/8v8HAL7/4//F/6f/8v/F/6f/tv+g/6f/8v++/+P/4//N//n/zf/b/8X/6v/j/+P/6v/N/+P/2//q/9v/BwD5/9v/6v/j//n/1P/y/wAAAAAAAA4ALAAHABYAMwAOABYAUQAlAB0AHQAWACUALAA7AB0ALAAWACwAMwAWACwAHQAdAPn/FgDy/+P/FgD5/x0ADgD5/zsAUQAOADsAMwAOADMAFgAHAPL/HQAAAPL/MwAdACUAAAAdAPn/DgAsAAAALAAAAAAADgDy/wAAAADy/wAABwAWAB0ALAAdAPn/HQDy/+P/AADq//n/6v/j/+r/AAAHAA4AAAAAAB0A6v/y/9v/4/8HAOP/6v/b/9T/1P/q/8X/r//5/77/4//q/8X/2/++/9T/zf/j//L/6v/j/9v/1P++/+P/1P/j//n/AADb/wAABwDy/x0A6v/y//L/AAAHAOP/2//F/9v/zf/j/+r/8v/y/wcABwDy/w4A8v8WAPn/AAAHAPL/HQDU//n/+f/j/w4AAADj/wAADgAWAA4A+f8HANv/AAD5/wAABwDj/w4A6v8WAA4AAAAlAAAABwAOAB0ABwAOAAAAAAAHAPn/AAD5/wcADgD5/wAAFgAHAB0ALAAsAA4ADgAOABYAJQAHACUAAAD5//n/4/8AAAcAAAAHAB0AHQAdABYAAAAAAAAAAAAlABYAHQBCAA4AFgAsADsALABKAGAAUQBZACwAWQA7AFEAWQA7AGAAYABZAEIAOwAdAEIAMwAsAA4AHQBKADsASgAlACUAHQAzAB0AJQBRADsASgBKAFEASgA7AEIAYAAzAFkAQgBCAGAAJQBvAFEAQgAsADsAMwBZAGcASgCFACUAYAA7ADMAUQBKAFEALAAsAB0AdgAWADMASgAlADMAHQBKAAcAUQBKADsAYABKADMALAAlAB0AOwAHADsAAAAlAEoABwAzAA4AFgAHAB0ABwDy/w4ABwAWAAcAFgAAAAcA+f8AAPL/AAAAANT/+f/q//L/zf/y//n/tv8OAPn/+f8AAB0AFgD5/yUAAAAHAA4AAAAAAAcAFgD5/wcA2//j/x0A4//5/wcA6v/5/wAA4//y/wcA4//q/9v/4//5/+P/8v/5/+P/AADy//L/AADU//n/6v/j//n/+f/q/+P/AADb//n/+f/q//L/6v/j/83/zf/N/9v/tv/N//n/6v/j/8X/zf++/8X/xf/F/6//p//N/7b/tv/F/9T/2//b/77/zf/q/7b/zf/j/77/+f8AAK//6v/U/+r/BwDb/w4A2//U/9v/6v/b/+P/8v/U/+P/zf/5/+P/4//5/+r/4/++/7b/vv/y/83/1P/y/+r/BwAHAOP/2//y/6f/2//N/6f/2//F/83/tv+n/5H/r/+g/5H/xf++/8X/r//q/9v/r//q/9T/zf/N/9v/1P/N/9v/6v/b/83/6v/N/83/2//y//n/+f/q/9v/FgD5/+r/FgDy//L/8v/5//L/+f/j//n/8v8AANv/6v8AAM3/BwDj/wcA+f8AAOr/+f8WAAcAJQDN/w4A8v/b/wcABwDj/wcAAADy/xYAFgAsANv/JQDb//n/DgD5/+r/vv/b/9T/6v+Z/x0Axf/j/9v/vv/b/4r/2/+n/9T/1P/b/5n/8v+2/+P/AACn/w4Amf8AAJn/2//F/+P/AADF/wcA1P8HAKD/HQC2/+P/6v/b//L/6v8dAM3/DgDb/0oA2/87ABYALABZAAcAZwAAAGcABwBCAAAADgDq/xYAAADj/zsAr/8WAIr/OwDb/yUABwAWADsAzf9KAM3/SgC+/1kAxf9gACwAFgBZALb/bwCv/4UAp/9gAOP/DgAHAPL/YACR/6MAXf+FAKf/MwAzAPL/HQCn/1kAgv/AAKD/YACg/3YAxf8sAPL/1P8lACn/dgBO/4UAe/9gAK//JQAsAIL/jAAp/3YAbP+MAJn/UQDN/9v/WQAx/+UA9f7eAAz/mwCK/83/MwBA/94AKf/0ACn/EgH1/tcAQgCZ/2cA3/6mAdj+4gFd/4wC4/tvArUBYfwKBTX63gQE/YEBMAFA/aMC2PwKBUf7mwLj/7P+TQNL/IkDdP2QATsAE/+BASL/AwGn/94Ae/8+Aaf/sgBRAKf/egH9/jcBLAAdAFEALACMAM3/dgAOADMADgBKAAAAQgAOAB0AUQDy/5QAvv9ZAEoA4/9RAAAAWQAdADMAOwAlAB0AFgBCAAcAWQAOAEIAJQAAAEIA1P8zAPL/BwAOAPn/FgAAAB0A1P8HANT/8v/j//L/2//U/yUAxf8WAAAABwAHAB0AHQAHADMA+f8dACUALAAsAEIAMwAsACwAHQAlACwADgAWADMABwAzAOr/QgD5/wcAHQDN/2AA6v9RAAcAJQBKACUAUQD5/1kA8v9ZAAAALAAzAOr/LADN/0oA4/87AAcABwAsAOP/MwD5/x0ADgAzAA4ADgDq/yUA6v/5/wcAtv8dALb/FgC+/+P/2//U//L/tv8HANT/FgDU/wcAxf/y/wcA+f8WANv/HQCg/yUABwDj//n/6v/5/+P/DgDU/wcAzf8dANT/BwAOAL7/QgCn/w4ABwDq/xYA+f/q//L/6v/y/wAAvv8HAL7/1P/y/9v/8v/b/9v/8v/F/9T/AACn/+P/xf8AAK//tv8HALb/BwDN/wcA1P/N/83/6v/q/9T/LADq/zMAAAAHAPL/8v/j//n/LADq/1EABwAlAB0AQgAWABYASgDU/x0AAAAOAAcADgDj/wAA2//F/x0Ar/8HAM3/+f/b/9v/HQC+/wcA1P/5/+P/8v/j/9T/zf++/w4Ar/8AAOr/6v8HAPL/AADF/w4ADgDF/9T/+f++/w4A1P/j/9v/tv8lAL7/6v/5/7b/8v/y/9v/FgD5/xYA+f/q/+r/1P/5/7b/+f/N/8X/1P8lAJn/zf9CAGX/QgC2/xYA6v/N/0oAiv9gAL7/BwAAAMX/MwCv//n/2//q/w4A8v8lAB0Azf9KAAAA6v8sAPL/MwDq/zMAHQDy/x0ABwAWACUAAAAHAB0AAAAlAOr/OwAOAOP/WQDj/ywAOwAdAGAAAABZABYA8v9KAM3/ZwDb/w4AHQC+/2AA1P9gAA4AFgAWAOP/DgDj/zMAvv8dAPn/DgAHAEIAHQDF/2AA8v8sABYAUQAHADMAQgDq/1kAAABgAPL/WQBgACUAYAAHAEIA+f8sAAcADgDN/+r/DgDj/zsA8v8sAOP/FgAzAAAAFgAOACUA+f8OANv/LAAWAPn/4//U/xYA1P8zANT/JQAWAMX/JQC2/xYA+f/y/w4A8v8HANv/8v/5//n/1P8OAAAAFgDy/wAAJQDU/0oA8v8lACUAFgBZAPn/LAAHAEIAFgAlADMALAAzAA4AMwDq/zMABwBKADMALABRAPL/ZwDF/0IAMwDj/2cA6v8sANv/BwA7AMX/+f/y/wAA4//y//n/AAAdAPn/HQDq/xYAQgAHACUAAAAAANT/FgDb/w4AAAC+/1kAp/8lANv/6v/j/6D/UQCC/zMA8v/b/w4Ae/8sAOr/tv/5/+r/6v8AAKf/DgDq/+P/4//F//L/iv8dAIr/6v/q/6D/LACv/wcAr//U/9v/vv8HAJn/1P8AAKf/HQDq/6//HQCC/x0A1P/b/zsAr/8OAM3/DgDy/+P/FgDj/83/FgDU/9T/FgC2/yUAp/8OAAcAzf/y/77/QgCg/yUA6v/U/9v/zf8WAMX/MwDj/zMABwDy/ywA1P8lAOr/BwDq/wcALADb/xYAAAAAAAAA1P8WAPL/8v8dAM3/2/8OAOr/AAAWAPn/FgAHAAcAAAAlAA4ADgAsAM3/FgD5/ywA+f8AAB0A1P8dALb/AAC2/+P/1P/y/wAAr/9KAK//QgAAAOP/OwCn/yUA8v/y/ywAtv/5//n/tv9gAMX/8v8OAM3/AADj/x0AoP9RAM3/BwD5/77/WQCZ/2cAvv9CABYA2/9vAM3/UQDF/0IAFgAWAEIAHQAdAA4AZwDF/zMA8v9CADsAzf9ZAPL/JQAdACwAHQAAAEoAQgBKAAcAHQAdAAAADgDy/w4Avv/b/wcAvv9ZAL7/BwBKAL7/QgDF/xYADgC+/xYABwDU/+P/DgCn//L/zf/q/w4A8v8zANT/DgDy/9T/LADj//L/AADN/wcAvv/N/x0Axf8AAAAA2//y//n/FgDU//L/8v+v//n/2//F//L/2//j/9v/DgDy//L/+f8AABYA1P8dAPL/+f/5/83/FgDF/zMA+f/N/x0Avv8dAM3/2/8AAKf/FgDq/wAA4//U/+r/6v8HAK//AAC+/+r/BwDU/yUAzf/5/83/vv++//L/8v/j/wAAoP8HAOr/1P8HAPn/8v/y//n/4/8WANT/BwAdAMX/LAAdAIr/JQD5/9v/SgDF/0IA6v8dAEIA1P87APL/MwAOAB0AOwBRAAcAMwBKANT/bwDj/x0ABwDb/ywABwBCAOr/QgDb/w4ALADb/0IA4/8sAAAAHQAdAOr/HQAAADsADgAAAB0A8v8AABYA+f/q/wcAHQAdACUALAAsABYAOwAzAB0AWQD5/zMAAAAAADsA6v9vAOP/FgD5/wcAZwDy/4UAAABCACUADgBvAOP/ZwAdABYAQgAWAAcAJQAWAA4AWQDy/yUAHQAHACwALAAAAAcAQgAOADsAJQAAACwAMwAWAEIAWQA7AG8AQgA7AEIAOwAWAFkAJQAHAFEADgAzAA4ALAD5/+r/DgDy/w4A2/9CACUABwAzAA4AAAD5/wcADgAAAOr/+f+2/yUA4//q/w4Axf9nAM3/QgAHAL7/MwCv/wcAoP/q/+r/zf8OAOP/FgAAAA4Azf8OAOr/+f/q/+r/JQDF/ywAzf8sAMX/6v9CAJn/SgDU/wcA+f/b/wAA6v/y/+P/UQDF/w4A8v/y/83/p/8WAM3/AADF//L/vv8HAAAA2/8OAKf/QgCv/+r/+f+2/zMA2//y/9v/+f/5/+P/6v/U/+r/1P8dAOP/xf8WAOP/8v/5/wcA+f+2/zsA8v/q/yUA8v8lAMX/FgAsANT/QgDy/wcAQgDq/1kA+f8HAGAA1P87APn/HQAOAAAAJQDU/ywAFgAlABYA+f/U/1EAvv8HAGAAgv9vAK//JQBCALb/OwDN/w4A8v8AAB0AJQDj/ywA1P/b/ywAr/9CAOP/LADj/wcA+f/U/xYAmf8sAL7/JQDj/9v/HQC+/yUA1P/q/+r/+f/b/wcAxf/y//n/2/9CAKD/OwDq//n/HQDN/x0Atv8HAOP/BwAHAM3/FgAAAMX/r/8OAPn/2//5/9v/1P/y//L/AAD5//L/AAAHAPL/AAAAANT/FgDy/wcA8v/b/wAA1P8lAAcA4/8OANT/8v8AAK//8v/N/9v/BwCR//L/8v+2/xYA6v8OACwAr/8lANT/r/8sAL7/QgDb/9T/LAC2/yUAAAAAAEIAAAAHAEoA6v8sAB0ABwA7APL/QgAWACwA+f8WAPn/HQBCAM3/YAC+/ywADgDU/0oAxf8HAPL/BwDb/wAA4//y/9T/6v8HAKD/WQDU/xYA6v/j/w4Avv9CAKD/LADF/83/HQC+/w4A6v8HANv/LADN/wAAxf+v/wcAiv8zAL7/FgDj/7b/MwC+/ywA1P/5/+r/8v8sAPn/HQAAACwA6v8OABYABwAOAA4ALADj/wcAAAAHABYAAAAAAOr/+f/j//n/DgDy/x0A6v/q/xYAxf8dANv/DgAWAL7/SgCv/x0AAADF/1EA1P8AANT/8v/N/8X/8v/U/9v/mf8zANT/xf8OAL7/DgDU/x0ADgDy/0IA4/8dAOP/2/9KAOP/HQAsANT/+f8sAAcA6v8sAOr/AAAzAPn/AAAAABYALAAlACUAMwAWABYADgAOAAcABwBCAB0AOwAsADMADgAHACwA2/8dAPn/FgAOAAAASgD5/x0ADgD5/w4AFgD5/x0ABwDj/1EA4/9RACUA+f9vAMX/ZwAdANv/OwDy/ywABwBCADsALAAOACwAJQAHADsA4/9KAAAAHQBRAPL/MwDy//L/AAAsAPL/MwAzAOP/HQAAAB0A+f9RAAcAOwAWAOP/lAC+/ywAFgDN/zsABwAlAB0ALAAWAAAA2/8WACUAAABRACUAJQBKADMAQgAzABYAMwAOAEIAJQAsADMA4/9vABYADgAlAPL/SgAHABYALADN/wAABwDq/0IA8v8AAOP/+f8sAK//FgDj/+P/8v/N/wAAtv/j//L/4//y/+P/6v/y/+r/BwDj/wAA+f/b/xYA6v8dALb/AAAAAMX/JQDN/w4Axf/N/+P/xf/U/+P/8v/F//L/1P8sAPL/+f8lANv/SgAHAA4ADgDq/yUA+f8dACUA2//y/+P/BwAHAOP/HQDq/wcA8v/U/wAA4//j/9v/1P/q/+r/4/8HANv/4//j//L/+f/y/zMA2/8sACUA8v8lADMALAAOABYA+f8dANv/AAAAAPL/+f/y/yUAp//y//L/1P++/+P/6v+g/xYAoP/b/9v/p/8dAK//AAAlAL7/BwDq/9v/HQAAAAAALADy/wAAHQDN/x0A+f/b/wAAvv/5/6//8v/y//n/DgD5/x0Axf8WAOP/+f/5/+P/+f/j/+P/p//5/83/4/++/77/8v++/+P/zf/N/8X/BwCZ/9T/2/+g/+r/mf/b/83/BwDF//L/8v/F/w4AoP8OAK//tv/b/6f/+f+2/wcA8v/q/yUA6v/5/wAA6v8OAPL/4//j/wcA4//N/x0Ar//5//L/2/8HANv/DgC+/+r/2/++/9T/6v8AANv/6v8lAPn/zf8sAOP/LADy/+r/SgCg/zsAAAAHAB0A8v8sANT/YAAzAB0AQgAAAB0AHQAlAA4AUQAOACwABwDy/ywAvv9CAPn/6v8lAAAAWQAlACUAMwAdAAAAMwAdAB0AJQAlACUAFgBnAOr/UQAsAPL/dgAOAGcAOwAzAEIAMwBgABYAYABvAA4AUQA7ABYAZwAHAFkAHQAdAHYA6v9ZAB0A+f8zACUALABKAB0AMwBZAAAAMwAWAB0AFgAOAA4A6v8OAA4AAAAAAA4A6v87AOr/JQAWANT/OwDb/zMABwBCACwABwBZANv/LAAWAA4AHQAAACwAMwAHAPL/4/8AAB0ABwAzAAcAJQAHAAcADgAHAB0AAAAAAAAAHQAAACUABwAdAAAADgBCAMX/DgDj/9v/BwAdANv/HQD5/6D/WQCg/xYADgCv/zsA1P/U/+P/AACn/+P/zf+v//n/oP/j/9v/zf/b/9T/4//j/wAA2//5//n/zf8WAM3/6v/b/83/DgCv/+r/6v/b/+r/BwDq//L/FgDU/zMAxf8zAPn/2/9nANv/SgAHACUALAAWAA4ABwBKAPn/QgD5/x0A+f8HADMA6v8lANT/MwAHAOr/JQDN/yUAAAAHAA4Azf8dAAcABwAOAMX/2/8HAOP/6v/5//L/AADb/w4A+f/F/ywA1P8HAAcA6v8sAPL/LAAAAPn/QgD5//n/OwDb//n/FgD5/xYAvv8lAPL/6v8lAL7/AAC+/wAA2//U/zMAr/8sABYAzf8lAOP/6v/5/wcAJQDy//n/BwAdAPL/4//5/9T/2//N/w4A4//q/xYAtv8dAAcABwAWAOP/MwAWAOr/BwAAAPn/LAD5//L/FgD5/wcA8v8AANT/2/8HAOP/8v/y/9v/AAAlAL7/6v/j/83/HQDF/xYA8v/j/zsA8v8zAPn/6v8zAPn/FgAHAB0AFgD5/0oAHQAWACUABwAHANT/DgDy//n/OwD5/ywAFgDN/wAA2//q//n/AAAWAAAAMwDq/+r/+f/j/w4A4/8lAPL/6v/y/9v/1P/b/wAAtv8AAMX/6v8dAMX/JQDq/83/8v8AAPL/DgDj/83/4//N/x0A1P/y/wcAvv/j/w4A2//b/xYA2/8AANv/BwAsAM3/FgDN/9T/6v++//L/2//q/83/1P8OANv/4//N/+P/8v/N/+P/xf+v//L/6v+v/w4A8v/j//n/1P8OAMX/2//5/w4ADgDj//n/+f8OANv/FgAAAPn/+f8HAB0Axf8zANT/AAAHAMX/AAC+/wcAxf/F/83/vv/b/6D/6v/q/7b/1P/U/8X/xf/y/wcA2//b/wAA4/8HAAcAJQAsAOr/JQAHAA4AMwDj/w4AHQDN/ywAHQDj/zsAzf8OAOr/6v9gAMX/SgDN/9T/LACv/zMAAABCAAcAAAAzAAAAJQDj/yUADgAHAAAAJQD5//n/DgDU/0IAzf8zACUA8v8WAOr/HQDU/x0ABwBKABYAHQBgAPL/dgAOADMAMwA7AFEADgCFADMAbwAzAEIAfgAlAIUAWQBZAGAASgA7AEoAUQAsACUABwAHACUAOwD5/2AAHQAzAGcABwBnAPL/SgA7AB0AOwDq/28AFgA7ADsAMwBZAAAAJQAzAPn/DgBZAPL/OwAOAA4AfgD5/0IAFgDy/yUA8v87AEIALABCABYAMwAlACwAMwAdAFEADgAlABYAYAA7AA4AUQDy/zsALAAsAOr/DgD5/8X/LADU/yUADgAdAA4ADgAlAOP/+f++/wAA6v/5/9T/4//U/6//DgDb/wAA8v/y/wcA8v/j//L/r//q/x0A6v8OAK//8v++/+P/+f+v/wAA1P8HANv/DgAAABYAFgDb/x0ABwAdAAAABwDq/w4AJQDj//L/4//5/w4A4//N//L/r/8OAAAA4//5/9T/AADN/9v/r/8AAL7/r/8dALb/DgDb//L/+f/U/+P/tv/y/83/2//F/9v/AADj//n/1P/y//L/zf/q/+r/4/8OAPn/8v/q/+P/FgC+/wAABwDN/zsAAAAAAOr/6v/y//L/8v+v/x0Ar//j//L/e/8HAK//zf8AAM3/4//N/9v/6v/j/wAA8v/j/x0ADgAsAPL/BwD5/9v/OwD5/wcADgAAAAcADgAAAB0AFgDb/yUAHQAWACUAJQAOABYAHQAWACwAFgA7AB0ADgBCAEIABwAdABYA8v8WAAcAAADN/wAABwAAAB0A8v/5//n/1P/N/wAAxf/y/wcA2/8HAOP/8v/q/+r/r//N/wcAvv8HAPL/AAAOALb/HQDy/8X/DgD5/9T/6v8WAKD/8v/y/6f/FgD5/yUA4//j//L/+f8AAPL/MwD5/ywAJQDy//n/AADy/+P/JQAHAOr/DgAWAOP/AAD5//n/+f/5/yUA8v9CAB0AHQA7AAAA6v8WADMA6v8dAOr/+f8dAPn/OwDq/wAADgDU/ywA4/8AAA4Azf8WAMX/zf/b//n/DgD5/xYA8v8lAOr/8v/F/8X/2//U/w4Azf8OAPL/HQDj/+r/MwDN/wcAvv8AAPL/xf8OAOP/4//b/9v/1P/b/83/DgD5//L/JQAOAAcA2/8HAOr/HQAOANT/DgDb/wcAJQAAAB0ADgAHAAcA4/9CAA4A+f8zAOP/HQAdAA4AFgAOACwAHQAWABYAFgAHACUA6v/5/x0A8v8dABYAOwAAANv/DgAHAA4AFgAOAOr/HQAHAB0ABwAAABYA6v9KAAAAFgA7APL/FgAHACUABwAOACwAFgAWAB0A8v8AACwA+f8sACUALADy/wAAJQD5/w4A4/8sAAAA4//5/wAAHQDy/yUAAAC+/9T/+f8WAA4AAAAdAA4ADgAzAPn/BwAAAB0AJQAlAAcAHQAzAPL/WQAdAAAAJQAHADMA6v8lAB0A+f8sAOP/BwAAAAAAMwAOACwAFgAAAAAADgAlAPL/6v8HAB0AAAAOAA4ABwDq/wAABwDb/wAA1P/j/8X/8v/N/9T/HQDF/zMAAAAHAPL/4/8AAM3/AADN/wAAr//y/+r/oP8OAKf/1P/b/83/+f/b/9T/8v8AAPL/FgAAAPn/BwD5/+r/4/8AAPn/+f8lAOr/DgAHAOr/FgDy/yUAHQAWADMALAAdABYAAADy/yUABwAlAAAABwDy//L/BwC+/zMA2/8OADsA6v8sAA4AJQD5/wcADgDN//L/JQDy/wAAFgDy//n/+f8lABYAHQBCABYALAAzAB0ALAAsACUAFgAdAB0A4/8HAAcAAAAOAA4AHQDy/wcABwAAAB0AAAAOACUA4//5/w4ABwAOAOP/FgDy//n/AADU/w4Atv/b/w4Atv8OAAAA8v8lAPL/AAAOAA4A+f/5/wcA6v8OAPL/FgAWAOP/6v8HAAAA2/8sAAcAAAD5/+P/AADj//L/+f/5/9T/8v/j/w4ADgAHACwA+f8dAPn/DgDq/83/8v/q//n/6v8HAOr/AAAlADMA6v/y/xYA2/8dANv/DgD5/83/FgC2/+r/8v/U/+P/2/8dAPL/4/8HANT/DgAWAL7/AADF//L/SgDy/xYA6v/j/wcABwAWAM3/xf/U/9T/6v/q/9T/4//j//n/DgDj/wAA8v8AANT/zf/5/9v/BwAAAAcA+f/y//n/6v8AABYABwDb//n/zf/b//L/AAAAAPL/8v/F//L/xf/b//L/6v8HAM3/6v8AAOP/2/8WAOP/4/8HAPn/HQDb//n/HQDU/83/FgAAAAAAJQAAADMAAAAAAAcA+f8WABYAMwAdACwADgDq/wcA+f/U/wAA4//U/xYA+f8HAOP/4/8lAAcALAAzACwA+f/y/0IAJQAlADsAFgAWAB0AFgAWACwAWQAdADsAZwAOAFkAMwA7AFkABwBCABYAHQAAAPn/OwDq/+P/FgAHABYADgAAABYADgAzAAcA+f8AAOP/HQAOADMAHQAWAB0A2/8sAOr/tv8sAMX/4/8WAMX/FgC+/+P/JQDU//L/1P/5/9T/+f8HAOr/BwDb//L/DgAHAPn/JQAOADsAMwAWACwAJQBKAAAADgAWADMADgAWACwA6v8sAOr/AADq/wcAAADU/ywADgAWAAAAHQAWACUA8v/y/x0A2//y/9T/LADy/9v/HQDU/wAADgAOAPn/HQAOACUAHQAOAEIADgA7AB0A+f8dADsAQgAHADMAJQAlACwADgAlABYAAAD5/w4ADgAWAPL/+f/q/+P/AADb/+r/tv/j/83/p//q/8X/8v/j/+r/AADq//L/8v/U/9v/+f/U/wcA2//b/w4A2/8OAAAA4/8lAA4AAAAsAOP/LAAWAAAAQgDq/ywADgAlABYA8v8AANv/JQDj//n/DgDq/wAA6v8HAPL/2//q/+P/AAAWAPn/BwD5/+P/4//N/8X/2/8AAPL/8v/b/+r/BwDq/wcAAADj//n/AADy/wAADgD5//n/8v/j/wAABwDj/+r/8v++/+P/+f++/+r/AADb/wAAzf/N/+r/zf/y//n/2//q//L/4//5/9T/2//U/9T/DgDU/yUAHQDq/xYAzf/5/9v/HQAlANT/DgDq//L/BwAAAPL/JQAOAA4ADgDb/ywAAAAAAAAAAAAdAPn/QgAsAAAAAADq/+r/BwDj/w4A6v/b/xYA2/8OANv/8v8OAPn/+f/5//n/8v8zAPn/AAAHAPn/BwAOADsA8v8sAAAAJQAlAPL/LADj/x0AJQAlAA4AHQA7AAAADgAOAPn/DgA7AA4AHQAAAPn/BwDF/xYABwAAABYA+f/q/9T/4/8OABYA6v8AAOr/HQAWAOr/JQAAAAAA6v/5//L/xf/q/wAABwDU//L/6v/5/x0Axf/U/+r/6v8HANv/+f8AAKD/zf/U/9T/AADj/w4A4//N/wAA4//F/+r/JQDU/9T/1P/U/+r/zf/q/77/zf/b/7b/1P/U//n/6v/N/9T/4/8AAOP/2/8AANv/+f/y/83/xf/F//n/1P/N//L/6v/b/77/2/8HAPL/4//j//L/2/++/+r/1P/q/+P/+f8dAPL/HQDj/+P/+f/5/yUABwAWAAAAFgAzACwAJQAsAB0AHQA7APL/JQAdAOP/FgAAAOr/8v8HANv/DgAOAA4AMwDy/w4AFgAWABYAAAAWAAcA+f8HAAcADgAOAOr/BwDq/+P/6v8AACUAFgBCAAcADgAOAPL/LAAWAA4AHQAWAPn/LAAHAA4ALADU/zMABwDU//n/AAAHAAAADgAWADMAHQBKACUADgA7ACwAOwAOAB0AFgAOACUAMwAsACUAUQAdACUAQgAWACUAYAA7ADsAQgAWAEIAMwA7ADMAQgBKACUAQgAWACUABwAsAFEA+f9KADMAAAAzACUAJQAWAB0AFgDq/x0AJQDy//L/2//5/+r/8v8sAPL/BwAdAB0AHQAzADsAHQA7AA4AHQBCADsAWQAdADMAMwAdAFEASgAzACwASgA7AEIAbwAzADMAQgAlADsAOwAsACwAHQAdAPn/+f8WAPL/+f/q/wcAAADj/yUA+f8OAB0ADgAlAOr/+f8AAPn/AAAHAOr/2/8WAA4AAADq/xYAJQAAAB0AAAAOACUADgAWACwAMwAsAB0AAAAHAAAAFgAWAB0AJQAsAB0ABwAsABYADgAOAAcASgAdAB0AOwDy/wAABwAHAB0A1P/5//n/6v8dAOr/4//j/+P/4//q//L/6v/y/9v/+f/N/6//1P+2/77/6v/j/8X/8v/U/83/2//N//L/2//j/wAA4//N/9T/4//N/+r/8v/N/wAA2//N/wcA4//5/wAABwD5//n/FgDj/xYA8v/j/wcAzf8lAOP/vv8HAMX/1P/j/9v/vv/F/7b/zf/U/6D/1P/F/77/1P/U/8X/tv/j/wAA6v/F/wAA8v/5/wcA+f8OALb/4//y//L/BwAAAAAAAAAzAAAAFgAOAA4ABwDU/yUA2/8AAA4Azf/q/9v/+f/U/wcA4//j/wcAzf/5/+r/4//q//L/4//U//L/4//b//L/4//N/9v/tv8HAPL/8v8sAOP/LAD5/xYALAAAAFEAFgAzACUABwAlABYA6v/5/ywA4/8HADsALAAHABYAHQD5/w4AAADj/9T/8v/j/+P/4/+v/9v/2//N/9T/zf/j/83/1P/y/8X/zf/N/+r/AADF/wAAAADj//n/4//N/6//1P++/8X/r/+g/83/tv/N/8X/vv/F/6f/p/+2/77/oP+2/77/tv/b/83/r/+v/6f/xf/U/7b/2//N/7b/tv+n/8X/xf/j/+P/xf+n/6//tv+Z/77/oP+v/7b/oP/q/8X/xf/j/5n/vv/F/83/6v+v/83/1P+n/6//2//U/9T/+f/b/wcABwAAACUAHQAdABYADgAOAPn/8v8dAPn/6v8HAPL/BwAHAPn/AADy/wcAJQAOACUAJQAsADsAAAAzACwAMwAsADsAZwAOACwAOwAsADsAUQAlACUAUQAOAGAAOwAOACUA+f8sAEIAHQAzAGAAFgAsADsAJQBZAFEASgBRAH4AQgBgAFkAQgBnAFEAZwA7AGAASgAsADMADgAlACwAMwAWADMAAAAOAB0A+f8WACwAQgAWAEIALAAdABYALABgAAcAQgAzADMADgAlAGAALABRABYAHQAsADsAQgBRAG8ASgBKAFEASgAdAFEAQgBRAFEAQgBvACwAUQA7AFEAWQA7AJQAYABnAG8ASgBKAFkAUQBRAFkAYABRAEoAWQA7AFkASgBCADsALAAzABYAOwAWAB0AJQAzADMAAAAlAAAALAAWAAAAQgDy/wAAFgAWAB0AAAAzAB0AAAAsAA4AHQAzAAcADgAOAAcAJQAsACUAHQAWACUAJQAsAEIAFgAsADsAHQAzACwASgAWADMAUQAHAB0AJQAOAAcADgAdAAcA4/8HACUAHQAzACwAHQAHACwABwAWABYAAAAzAPn/AAAAAAcAAAD5/x0A1P/y/xYA8v8sAA4Avv/y/77/xf/5//L/DgDy//L/4/8HAOr/+f/5/83/AADF//n/2//q/9v/tv/b/83/2//N/9v/oP/N/77/r/+2/3T/2/+2/77/xf+v/5n/vv/F/77/2/+R/77/e/+Z/9v/oP++/8X/xf+n/7b/r/+2/6D/vv/F/6f/xf+n/7b/vv++/7b/zf+2/6//r/+R/8X/p/+n/9T/zf/U/9T/zf/F/7b/r//b/83/xf/j/8X/2//U/9v/4//F/9v/vv/F/9v/xf/U/8X/xf/j/9T/2//U/9v/+f/F/9T/+f/y/wAABwDy/9T/+f/j/+r/1P/U//n/vv/q/83/4//j/9T/8v/F/+P/8v8HAPL/+f/j/+P/2/+v/9T/tv/F/9T/6v/U/9v/8v/b/+P/6v/q/83/8v/j//L/BwDq/wcA+f/y//L/4//U/9v/2//j/83/2/8WAPL/8v8AAOP/6v8HAOr/BwAAABYAHQDy/w4A1P8AANv/1P/5/7b/+f/q/+r/BwAOAB0A+f/5/zMAHQAdACwADgAdAB0AMwAWAB0AJQAHAB0A+f8dAOr/AAAsAOr/JQAWAA4AFgAWACUABwD5/wAABwAHAA4ABwAWAB0A+f8OAAcAAAAWAAAADgAWAPn/HQDq/+P/FgDy/zMABwAAADMAHQBCAB0AHQAHAPn/8v/U//n/4//5//n/6v/5/9v/6v/j/+r/AADy//n/AADy/+P/+f8OAOr/FgAlAB0AMwAOACwAJQD5/yUALAAOAEIALAAWACwAFgAsAB0AJQA7ABYAJQAzAEoALABCAEoALABCADsALABCADsALABKAB0ALABRABYAHQAdADsAQgAdAFkAWQBKAFkAHQA7ADMAFgAlAAcAJQAlACwAJQAWACwAFgAsAB0ALABCACwALAAlAB0ABwAAAAcAHQAWAAcAFgAOABYA6v8OAB0A+f8lACwAWQA7ABYAMwA7ACUASgBRABYAJQAsAB0AAAAdABYADgAzAB0AHQAHAA4ABwAWACUAJQAOAAAAFgDy/wcA+f8WADMAFgAsAPn/4/8AABYAHQAdAA4AAAAdAA4A8v8OAAAABwAOAPn/JQAAAAAA4//j//n/4/8HAOP/8v/N/8X/1P+2//L/2/8HABYA+f8AAOr/AAD5//n/BwDN/+r/AADy/wcA4/8HAOP/2//b/83/+f/F//L/4//y/wAA6v/j/9v/DgDq//n/6v/q/+P/4//y/9v/AADq//n/AAAOAA4A+f/5/+r/FgDq/wcAAADj/+r/4//5/6//6v/y/8X/+f/U/w4A4//N//L/2/8OAOP/JQAlAPn/JQDU/w4A+f/q/x0A1P/q/9v/8v8AAPL/AADq/wcA6v/y//n/+f/5//L/JQDj/9T/6v/j//n/xf/q/9v/8v8WANv/6v/b/9T/1P/U/9v/xf/U/9T/vv/F/83/2//5/9T/1P/F/77/2//F/9T/1P/y//L/8v/j/+r/xf/F/+r/6v/5/9v/BwDy/+r/BwDj//n/8v8HAAAA8v8HAAAA8v/q/wAA6v/y/wAA6v/b/+P/AADy/+r/FgD5/9v/4//q/wcA8v8AAA4ABwDy/wAADgDq/wcA8v8AAPL/BwAOAOP/JQDq/wcALAAAACUAHQAAACUALAAWACwA6v/y/x0ADgAsAAcADgAlAAcAJQAWABYALADy/x0ABwDq/yUABwAWAB0ABwDy/xYABwDy/x0A4/8WABYA8v8OAOr/4//U/9T/2//j//n/+f/b/83/2//j/wcAAAAdABYA4//5/+r/4//5/9v/8v/y/+P/FgAAAOP/4/++/wAA2//j/wcAzf/y//L/DgAAANv/AAD5//n/BwAWAOr/AAAWAOP/+f8HAOr/6v/b/+P/6v/N//n/2//U//n/8v/5/+P/AADy/wcA+f8AACUABwAlAAAABwAHAAcAHQAAABYAHQAsAB0AMwAOAAAAMwAOACwALAAWADMABwAWACUABwAsAAcAFgAlABYAMwAlACUAHQA7ACUABwD5/x0AHQDy/yUABwAAABYAHQA7ADMAOwAzACwAQgAsAB0AOwAzADMALAAzACwAMwAsADsAOwAHAFEADgAOAEIADgAzAB0AHQAWABYAAAAAAAcABwAHAPL/FgDj/wAA6v/N/wcA+f/q/wcAAADq/w4A6v/U/wAA4//q/9v/4/8HAAAAAAAHAAcAHQAdAB0AJQAdAAcAAAAOAAcAAAAAAAcA+f8OABYAFgAsACUAAAAHAEIAFgA7AB0AAAAlAB0AJQD5/xYAAADy/+P/8v/q/9T/FgDq/wcAFgAHAB0ADgDy//n/FgAAAB0AFgAlAAcA8v/5//n/AAD5/x0ABwAAAAcAFgDq/wcA+f/y/1EAAAAdAA4ADgAdAB0ADgD5/x0A+f8sAAAA4/8AAPL/AADy//n/+f8OAOr/+f/5/w4AFgD5/x0ABwAdAAcAHQAWAB0AJQAOADsAJQA7AA4AFgAlABYAFgAWAB0A+f8sABYAAAAHAAcABwAHAB0A6v8HAOP/6v8lANv/+f8lAPn/DgAWAAAALAAdACUAHQAWAB0AMwAsAB0AHQAAACUAAAAWABYABwAsAA4ADgAHAAcA+f8WAOP/+f/5/8X/JQDq//L/6v++/+P/tv/U/9T/zf/b/83/1P/F/6f/1P+2/5n/zf/F/83/6v/b/7b/1P/F/7b/vv/N/77/tv/U/8X/8v/b/8X/1P+2/7b/zf++/77/6v/F//L/AADq//L/2//U/9v/2/++/+r/4//b/+r/2//y/+r/+f/5/+r/BwDq/+r/AADj/wcABwDy//n/1P/q/wAAAADy/w4A6v/b/wAA1P/5/9v/1P/y/83/4//U/9v/4/+2/9v/6v/U//L/6v/q/w4A2/8HAB0A8v8dAPn/LAAWANT/DgAAAA4A6v8HAPn/zf8AANT/AAD5//n/AADb/w4A6v/U//n/2//j/xYA+f8OAOP/8v8AAMX/BwDj/+P/8v/U/9T/6v8OAOr/1P/y/+P/vv/b/83/2//U/9v/8v/q/+P/zf/b/+P/AADq/wcAAADq/w4A6v8HAOr/8v/5//L/BwDq/wAAAADj//L/DgDy/wAADgAOAPn/AAAHAPL/+f/b/w4AAAAOACwABwAdAPn/AADy/x0A+f8AACUA4//y/+r/FgAAAAAADgAOABYAAAAHAPn/LAAOABYAMwDq/xYAFgAWAA4AFgAzACUAFgAOAB0A+f87ACUALABRAAcASgAOAEIAWQAzAG8AAAAsADMAAAA7AEIALAAlADMAFgAWACUAHQAlACUA+f/5/w4A6v8lAB0A6v8OAA4AHQAOAPL/FgAHAAcAMwAdAAcAHQAWAAcAJQAlAB0AAAAWAA4A8v8dAPL/6v8WAA4AFgAsAOr/BwAHANv/BwD5/yUABwAOAA4ADgAHAAcAHQDU/w4A4//y//n/2/8zAPn/JQAWAAAAJQAHADMAOwAzADsAHQAOABYAHQA7AEIALABCAAcA8v8lAA4AMwBCAEIASgAsADsAHQBKADsAOwAzAOr/JQAOAPL/+f8WAPn/DgAHAPn/HQDy/wAA4//y/+r/8v8AAPL/DgD5/wAA4//q/9T/+f/q/8X/8v/b/+P/6v8dAM3/8v8OAOP/HQAHAA4A+f/y/wAABwDq//n/+f/q/wcA6v/U/9v/JQD5/w4AJQDy/wcA4//5/+r/8v8lAA4AFgAsAAcAMwA7AA4AMwAHAA4A+f8HADMABwAOAAcA+f8WAB0ABwAsAA4AHQAzAB0AJQD5/w4ABwAHAA4AAAAAAPn/BwAOACwAHQAlACUAOwAlABYAMwAzACwAJQA7ACUAMwBKAB0AHQAdACwAQgAsACwAOwAdAPL/HQAWAOP/HQAWACUALADj//n/+f8OABYAAAAAAPn/4//q/x0AAADj//n/4//y//L/8v8OAPL/4//5//L/+f8HAPL/BwAAAPL/JQAAAAAA8v/j/xYAAAAHABYAFgAHAAAAAADy/+r/8v8AAOr/4//j/9T/2//q/83/6v8AAPL/6v/y/wAAxf/y/+P/zf/b/6//4//b//L/+f/q//L/6v8AAPL/4//b/+r/4//j/9v/8v/q/7b/zf++/77/1P/q/+P/1P/F/77/r/+2/77/oP++/77/vv/j/8X/4//y/6//2//j/9T/6v/j//L/6v/N/77/4/+v/9T/2/+2/9v/p//q/8X/zf/F/6//xf+g/8X/oP/F/6f/oP+n/7b/xf++/9T/mf/b/6D/vv/j/7b/4//F/+r/tv/U//n/2//j/+P/1P/q/wcA6v8AANv/6v8AANv/8v8HAOr/2/8AANT/+f/5//L/BwDj//L/+f/j/9T/6v/q/+r/AADU//n/4//F/wcA8v8HAPL/6v/y/8X/6v/N//n/+f/j/xYA4//5/wAAAADq//n/DgDy/wAA6v8AAPL/JQAzAAAAJQAdAB0ADgAsAEIAFgA7ADMAMwBKACwASgBKADMAWQAsADsAYAAzAFkAUQA7AFkAOwB2AFEAQgB2AGcAYABRAG8AJQAzAGAAMwBZAFkAQgBnAEIAOwBnAA4AOwAsACUALADy/zMA8v8dACUADgBKAA4AFgAlABYAFgAzAB0AOwBZACUAFgAsACUAHQAzAAcAFgAlAAAAAAAdABYASgA7AB0AUQAHADMALAAzAEIALABnADMASgA7AEoAWQAdAFEAUQBCAEoAOwBgADsAHQBKACwAQgAzADsASgAsAEoAOwBCADsAMwAdACwALAAsAEoAQgBgADsALAAlAA4AJQAOABYAAADq/w4A+f8dAAcA6v8lAM3/AAAAAMX/1P/F/+P/vv/q/6//vv/N/6D/1P+2/+P/zf+v/6//oP+Z/5n/1P/F/77/xf/N/83/4//N/wAA+f/y/+P/tv/b/8X/6v/5/wAABwDN/9T/1P/F/9T/6v/F/wAA8v/5/ywA4/8HAPn/8v8OAAAABwDy/w4ADgDj//n/AADy//L/zf/N//n/1P8OAAcA1P8HANv/8v/b/+P/8v/F/9T/zf/N/8X/2//N/7b/vv++/+P/1P/U/9v/4//U/8X/tv/q/+P/4/8OANv/6v/j/wAA2//q/9v/p//j/6//4//N/9v/6v/F/+P/1P8AAPL/+f/5//L/4//y/9v/xf/y/7b/1P/N/7b/2//b/9v/6v/j/9T/AADy/+r/AAAAAOr/AAD5/wcABwDN/wAA1P/N//L/2//q/9T/1P/5/+r/AADq//n/DgDU/wcA8v8HAOr/6v8dANT/HQAAANv/AAAHAA4ADgAWAPn/FgD5/+r/BwAAAPn/HQAOAA4AMwAAABYAFgAHAAcA8v/j/xYA+f/b/+r/zf8AAOr/BwAAAOr/8v/b/wAA8v8dAA4ABwAOAA4AJQAdACUAFgAsAPn/BwAOAAAABwDj/ywABwAWAB0ADgA7AA4AOwAdACwAOwAOAEIAMwAlAEIAJQAHACUADgAdACUAAAAdAAcAHQAHAA4AOwDy/w4AJQAAAAcAFgAOAA4AJQAAABYAAAAdACUABwAzAAAA6v/q/+P/BwAWACUAFgAdAA4ABwAdABYADgAWACUAHQAlAEIAOwAzAB0AMwAWAAAALAAsADMAHQAlACUAAAAOACUADgAHAPn/BwAHAPL/DgAHAA4A+f/y/+P/1P/5/83/+f/b/+P/FgD5/9T/xf/y/83/+f8HAPn/AAD5//L/1P8AAAAAAADy/9v/DgAWAOP/FgDj/8X/DgDb/w4AAADq/wcA+f/5//L/AADq/xYAFgAHAPn/AADy//L/JQD5/yUADgAHABYABwAlABYADgAWABYA+f8sAAcADgAdAAAAMwAdABYA8v8OAAcAFgAdAPL/FgD5/w4ADgAWABYA+f8dAA4ADgAHABYAHQAsACwAJQAzACUAFgAlADsAHQAdADMADgAdAEIAJQBRAEIAMwAzAB0AHQD5/wcABwAAABYAFgAHABYALAAdABYA+f8HAOr/BwAHAA4AMwAHADMAFgAWAAcADgAdAAAAQgAHAB0ADgAAABYABwAzAAcAOwAWACUALAAAAEIABwAsABYAAAAOAAAAFgDj/x0ABwAHAAcA+f8OAPL/DgD5/wcA6v/q/w4A6v/j/9T/AADq/wAAAAAAAB0A6v8dABYA4/8OAA4A4/8HAAcA+f8OAPn/JQAHAPL/JQAOAA4AHQAdAAAA8v8HAAAA2//q/wAA2//j/wAA4//q/+r/6v/y/9v/+f/q/wcA8v/N//L/zf/y//n/2//5//L/xf/b/wAA1P/U//L/4//j/9v/2//q/+r/4//j/wAA2//j/+P/zf/y/8X/2//5/+r/4/++//L/6v/U//n/2//j/9T/1P/q/8X/zf/j/9v/xf++/83/zf/q/+r/4//q/+r/8v/y/+r/zf++/83/4/++/9v/2//N/+P/2/8AANv/+f/b/9T/6v++/9T/xf/j/9T/6v/q/9v/8v+2/+r/1P/j/wcA2//5/wAA8v/y/+r/+f8OAA4A8v/q/w4A8v8OAPL/4//5/77/+f/b/83/4//q/wcA8v/5/+r/BwAdAB0AHQD5/+r/AADj/+r/FgAAABYAFgD5/9v/2//b/+P/8v/b/wAA1P/5/wcA6v8lANv/BwAWAPL/HQAHAPn/DgAOANv/AAAOAPn/BwD5/wAA+f/j/wAAAADq/wAA8v8AAAAAAADb/9T/8v/N//L/8v/y/w4A+f/5//n/+f/U/9v/1P/y/+r/6v8HAPL/DgAHAPL/2//5/+P/4//y/9T/FgD5/yUAJQD5/xYA8v/b/9T/2//b//L/4/8AAAAAAAAHANv/BwDq//L/FgAHAAAAJQAOAA4AHQDq/xYAAAD5//L/BwAWAA4AHQAHADMAAAAsABYAAAAdAAAAHQDq/ywABwAsACUAHQBKAPn/SgAHAAcASgAlACwAMwA7AAAAMwAWAPn/AAD5/w4AAAAAABYAJQAAADMAFgAAABYA4/8HANv/6v/5//L/+f/y/xYA+f8AAPL/8v/5/wAADgAdAFEAFgAlAAAADgAzAAcAJQAWABYABwD5/w4AFgAWAA4ABwAAABYAFgAOABYAAAAOAB0AFgAlAAcABwAHAOr/6v/j/wAAAAAOAB0AHQAlABYAFgAdAAcAHQBKAA4AOwBKAAAAJQAlABYALAAzABYAQgAsAAcAUQA7ADsASgA7ABYADgAdAB0AHQAWAA4AFgAAAAcAOwAlADMAJQAdAA4ABwAzAAcAJQAOAPn/DgD5/wAA+f8WAAcADgAsAB0AAAD5/wcA+f8HAPL/+f8AAPL/BwAAAPn/AADq/+P/1P/U/9v/zf8HAA4A2/8AAB0ABwAlAB0AFgAAAPL/AAD5/x0ABwAWAA4A8v8lACUADgAWAA4A8v8WABYAFgAWAOP/JQAWACUAOwAsAB0ADgAdAA4AJQAWAB0AOwAdAB0AFgAAAAcABwAAABYA+f8AAB0ADgA7ABYAFgAsAAAAFgAAAA4AFgAAAAAABwAOAPL/AADN/83/2//U//n/zf/y/8X/2/8AAOr/8v/y//n/1P/5/9v/8v/j/83/AADF/83/6v/q/9T/8v/U/83/8v/U/+r/4//q/+r/4//F/7b/1P/F/+P/2//b//L/zf/j/9v/zf/y/9T/2//q/9v/+f/q//L/BwDy/wcABwDN/wAA8v/F//n/2//q/9T/6v/q/8X/8v8AAPL/8v8OAPn/6v8HAPL/4//y/wAA2//j/+r/xf8AAA4A8v8lAAAAJQAdAAAAJQAHADMAJQAlADMABwAHAAAABwAHAAAADgAAAOP/BwAAAPn/4//j/wAAAAAOAPn/BwD5/+r/8v8WAAAA8v8WAOr/FgAdAAAADgAAAOr/4//j/9T/AADq//n/+f/U/+r/4//b/+P/4//q/9v/4//U/9T/4/++//L/zf+v/+r/tv/b/+r/4//j/9T/1P/j/+P/+f/5/8X/8v/j/+P/2//j/+P/4/8OAOP/BwD5/9v/1P/b/83/xf/b/77/2//F/9v/zf/U/9v/vv/j/83/2//q/9T/2//y/77/zf/y/8X/6v/F/83/xf/F//n/4/8OAPn/1P8AAPL/4/8HAPL/+f8AANv/HQD5/+r/HQDy/wAA+f/5/wAA8v8WAA4A+f8HAPn/AADy/9T/+f/y/+r/8v/j/wAA8v8HAAAAAAAWAAAABwDy/+P/+f/y/9v/8v/b/+r/6v/b/x0AAAAHAB0ALAAdABYAHQAHAB0AHQBCACUAOwAzACUAMwAlAGAAMwBRADsALABvAEoAdgB2AG8AdgBgAGcAbwB2AIwAZwBnAGAAWQBvAFEAbwBgAEoASgBCADsAOwBRAEIAQgBZAFEASgBvAEoASgBgACwAUQAsAFEAWQAzAFEASgA7AEIAOwAsAGAAMwAzAFEAOwBRADsAYABKAFkAWQBKAFEAMwBRACUALAAlAB0AOwAWABYAFgAsABYAHQAOAPn/FgAdACwADgAWAAcADgD5/xYAOwAWAEoALAAdAAcADgAsAA4AOwAlADMAJQAdAB0ADgAOAPL/HQAOABYAHQAAAAAAAADq/+P/+f/y/wcAAAAHABYAAAAOAB0ADgAOAPn/4/8HAA4A8v/5/wAA+f8HAPL/HQDy//L/QgDy/zMA+f/b/wAAzf/j/8X/BwDq/9T/4//q/wAA8v/5//L/2/++//L/2//U/+P/2//U/83/1P++/+P/oP/N/77/tv/q/6D/2/++/8X/zf/F/9v/1P/U/+r/AACv/9T/tv+v/9v/vv/j/83/zf++/8X/4//b/83/1P/q/77/zf/q/+P/zf++/9T/vv+g/9v/1P/q/+r/1P/y/9T/+f/q//L/6v/N/9v/xf/j/9T/2//b//L/6v/y//L/2//5/+P/BwDb/+P/+f/U/wcA4//j//n/4//q/wAA+f/y/+r/1P+2/77/1P++/9T/2//j//n/6v8OAA4A+f/y//n/6v/5/w4A6v/b/9v/8v8AAPn/+f/5//n/DgAWAB0AFgAHAB0AAAAdACwAFgAdACUAHQAOAEIAJQAdAEIAJQBKABYAHQAzAA4ALAAdAA4AFgAHAAcA+f/j//n/4//U/wAA6v/5/w4A8v8AAPn/FgAOAA4ADgDb/wcA+f/y//L/6v/y/+P/DgDy//L/+f/j//n/2//y//n/1P/U/+P/6v/5/+r/8v/5/8X/AADq//L/AADb/wcA6v/q/+r/+f+2/77/+f+v/+r/1P/F//n/1P++/77/r/+g/8X/oP/F/8X/oP/U/6f/xf/F/8X/1P/F/9T/vv/N/6f/zf/U/6//xf+R/7b/tv+R/77/oP+2/9T/zf+2/8X/6v++/7b/1P+2/6//vv/F/77/vv/U//L/6v/j/9v/2//q/+r/8v/q/9v/8v/q/+P/6v/q//L/4//y/wcABwD5/+P/AADq//n/+f/b/9T/zf8AANv/1P/5/9v/6v/b/9v/AADj/+r/DgDj/+P/8v/b//L/6v/q/+r/zf8AAAcA4//5/wAA+f/j//L/2//j/w4A8v8AAPn/8v/y//L/DgAHACUADgAlAGAAJQAsAEoAFgAWACwAMwAzAB0ALAAsAEIAOwBKADMAFgBZACwALABnADMAOwBvACwAOwBKACwASgAzAEIAQgAzAFkAUQA7AFkASgAzAGAAUQBZAFkASgBKAFEAZwBgAGAASgBgAFkAMwBgAG8AYABKAFEAOwAsAGcAQgBCAGcAOwBgAFEAWQCFADMAQgBKADMAUQA7ACUASgBKACwAWQAdAFEASgAAAEIABwAdADMAHQAlAPn/FgD5/xYAHQAdADsA+f8HAB0AAAAWAB0AAAAOAPn/BwAOAAcAOwAWACUAFgDy/w4AAAAlAFEAQgBKAFkAJQAzACwAFgBKADMAWQBgACUAHQAsACwAFgAWACwAMwAdACUAFgAdAAcADgAlAA4AJQAlACwAJQAzACwAHQAlACUAHQAsADsABwAdACUAJQAlACUAJQAAAAcA6v/y/w4AFgAOAAcADgD5/x0A+f/N//L/8v8dACUA8v8dAAAA6v8AANT/1P/5/+r/8v8WAOP/8v/q/9T/4/+2/9T/1P+2/9v/8v/j/9T/6v/N/83/2//U/83/2//N/9v/8v/b/+P/8v/5/+P/6v8AAPL/4//5/9v/zf/j/83/1P/N/+P/zf/U/+r/2//5/9v/+f/U/9T/4//U//n/zf/j/9T/xf/q/83/vv/N/+r/4//b/9v/8v/y//L/6v/q/9v/6v8AAM3/+f/5/+r/DgDy/wcAAADq/wAAAAD5//n/DgD5//L/AADj//L/8v8AACUAAADb//n/4//y/wcA4/8WANv/8v8WANT/DgD5//n/FgAOACUAHQAOAPL/DgD5/wcAMwAOACUABwAHAB0ADgAlAAAAAAAHAPL/FgDy/wcADgDj/wcAAADq/wAA8v/q//n/AAD5/w4A6v/y/wAAzf/q/+r/8v8AAPn/8v/q//n/+f/q/+P/2//U/9T/1P/b/83/2//U/6//4/+2/8X/4/+v/9T/1P/U/9T/vv/y//L/4/8OAOr/8v8AAOP/BwC2/83/xf+2/8X/tv/q/77/zf/b/9T/xf/F/8X/tv/b/6//2//U/8X/4//N//n/6v/N/+P/2//b/+P/4//b/9v/4//q/+P/4//y//n/6v8HAA4AJQAOAA4ADgD5/wcA6v8AAAAA4/8AAOr/2//U/9v/6v/j//L/4//q//n/zf8AAOr/2/8HAOr/FgAWAA4AJQAWABYAJQAzACwAQgAOABYAOwAOADsAQgA7AGAAOwBCADMAMwBRADsAOwAzACUAFgAsAA4A8v/b/77/vv+2//n/AAAHACwAMwBRABYA2//N/8X/vv/q/wcAMwBRAA4AFgAAAAcA8v/U/77/zf8sAA4AHQAOAPL/zf+n/8X/vv/j/wAAMwBRAB0AMwAAAPn/zf+2//L/4/8WACwAMwAsAAcA2/+2/83/zf/j/wcAMwAsADMAJQAAAPL/6v8dAAcALABCADMAMwAdAB0A+f8HAAcAAAAHADMAJQAlADMA+f/y/+P/6v8AABYAJQA7ADMAHQAWAA4AAADb/w4ABwAdACUAHQBCAPL/+f/b/9v/AAAAACUAFgAWANv/DgAWAMX/AAAHAPL/JQAdAB0ALAAsAFEAQgAlABYALAAlACUASgA7ADMAWQBRABYAJQAsABYASgBZACUAOwAdAAcAOwAWABYAMwAdACwAJQAsACwAFgAsAA4A+f8lAA4AHQAlAPn/FgAAAPn/FgAlACUADgAWACwABwAAACwAFgAOACUADgAsACwAFgAOAAAAFgAOAAcAMwAlABYAMwAOAB0AJQAHAB0AAAAOACwAHQAWACUAMwDy/yUAHQAHADsADgAWAAcAFgAHAPL/+f/N/+r/zf/F/83/2//b/+P/+f/q/+r/1P/y/9v/xf/b/+P/+f/U/9T/2//F/9T/6v/j/+r/4//j/wAA6v8AAAAABwAAAAAAJQD5/wAA+f/y/wAA2//j/+P/+f/5/+r/AADy//n/BwAHAPn/4//q//L/6v8AAAAA6v/5/+P/8v/y/+r/BwAHABYADgAAABYAAAAAAPn/FgAWAAAAHQAAAAcADgD5/xYABwD5//n/+f/q/xYAJQAAAAcA6v8AAAAA8v8OAA4ADgAAAAAABwDy//n/8v/y/+P/6v8AANT/+f/N/83/4/+2/+r/xf/U/9T/vv/q/7b/zf+g/7b/2//F//L/xf+n/6f/oP+2/77/r/++/77/tv++/8X/xf+v/8X/vv+v/83/tv/F/83/oP+g/5n/oP+v/6D/tv+2/6//tv/N/8X/p/+2/6f/p/+n/8X/tv/F/+r/2//q/9v/2//b/83/zf/U//n/6v/q//L/zf/q//n/2/8HAPL/6v/q/9v/8v/N//L/BwDb/+r/+f/q/9v/AADq/8X/+f/y//n/8v/y/wAA4//j/+r/2//q/w4ABwAOAA4A6v/5//n/+f8HAA4ABwAOAA4ABwAsAB0AJQAsACwAFgAsADsAHQAsADsAFgAOACUADgAWACUAJQAWAFEAYAAlAFEAOwAdADMAHQAzADMAJQAsADMA+f8WACwAAAAzAB0ALAA7AAcALAAlACUALAAzADsADgAzACUAJQAsABYAMwAzAB0ALAB2ADMASgB2ACUASgA7ACwAOwAdADMAOwAsAEoAOwBKAEoALABZADsAbwBnAGAAdgAsAGAAOwBRAFEASgBgADsAUQBRAFkAMwBRADsAJQB+AEIASgBvACwAOwBKAB0AHQAsAPn/+f/5/wcA+f/j/w4A8v/q/wcABwD5//L/AADN/+r/+f/j/+r/1P/U/9v/2//U/+P/1P/j/9T/vv/F/77/2/++/+r/6v/j/wcA4/8AAOr/8v/y/9v/8v/b//L/4//y//L/6v/5/9T/8v/j//L/+f/U/wcA2//j//L/4/8HAA4AJQAOAA4ADgDq//n/DgD5/xYAJQAOACwAFgAlACUAAAAlAB0A+f8dAEIAFgA7ACUAHQAlAAcALAAlACUAJQAdAA4ABwDy/wAA+f/U//n/8v/q/+r/DgAAAPn/DgAAABYA8v/5//n/DgAdAA4AJQAWAA4ABwAlAAcA8v8zABYAHQAlABYAMwAdABYADgAAANv/BwAdAPn/HQAHAAcAAAAWAA4AAAAHAMX/+f/U/9v/AADq/wcA8v/y//n/4//N/+P/tv/U/wAA8v8OAPn/+f/5/+r/6v/5//n/BwAHAPL/HQD5/xYAFgAAAB0ABwAzACwAFgAlABYAFgAlACUAQgBRADMASgAzABYAMwAWACUAJQAWADsASgAzACwAUQAzADMASgAOADMAJQAOADsAJQAWAB0AFgAAAAcABwAHABYA6v8AAAcA8v8HAOr/+f/y/9v/DgDy/+P/8v/y/+r/+f/b/+r/4//U/w4A4/8AANT/6v/q/77/DgDN/xYA8v/y//L/vv8HAM3/8v8AAA4A8v/q/wAA4/8OAPL/6v/q/9v/6v/y/83/zf/b/83/1P/F/7b/tv+g/6f/r/+g/8X/vv+2/7b/xf/N/9T/AADb/9v/4//j/9v/zf/b/83/4//b/9v/2//b/9v/8v/U/+P/8v/N/+r/vv/b/8X/r//N/77/xf+2/9v/tv++/9T/6v/b/9T/AADN/9T/2//F/7b/xf++/83/6v+2/+P/2/+v/77/xf+2/5n/xf/F/6D/4//b/77/2//N/8X/zf/U/+P/8v/q//n/6v/5//n/6v8OANT/AADq/8X/2//N//n/2/8HAPL/1P/y/+r/1P/U/+P/vv/U/+r/AADj//n/DgDq/wAA2//q/+P/8v/5/9v/FgAAAPn/AADy/+r/2/8HAA4ABwAlAAAA8v/5/wcABwDy/w4A1P/j//L/zf/y//n/+f/5/wcAHQAAAAAADgDj//L/AAAAABYADgAWAAAAFgDq//L/DgD5/zsALAAdAAAADgAAAOr/4//5/xYAAAAlAA4AAAAAAAAA+f/y/wAA8v8OAAcAJQAdAAAALAAHACUALAAAACUAJQAWACwADgAAAB0AAAAOACUABwAWADMAMwBRADMAMwAzADMAUQA7AFkAUQBRAG8AOwBKAFEAJQBKAEoAQgBRADsAYABCADMAWQA7ADMAQgBCADMAQgAzACwAJQAzADsAMwBCAB0ASgBCAEIAUQAzAEoAFgAlADMALABRAEIAFgAdADsAAAAzACwA+f8OAAcABwDq/wAAAAAHAA4A+f8OAOP/AAAHAPL/+f/j//n/6v/5/+P/8v8HAPL/+f8HAA4A+f8OAAAAFgAAANv/AADb//L/AAAHAAAAAAD5/wAAFgAAAEoAOwAzACwAJQAWAOr/LAAOACUAJQAOACwAHQAsACwAMwAHABYAAAD5/x0ADgAzADMAJQAdAB0A+f8WACUAAAAHAPL/AADj//n/8v/q/w4A+f8lABYADgAsAA4AHQAdAA4ALAAWAAAABwDy//n/6v/q//n/4//b/wAA6v/y/w4A4/8OAOr/4//q//L/BwDq/w4A8v/U/9T/+f/b/9T/8v++//L/2//q/9T/1P/q/77/4//q//L/4//5/83/2//j/8X/+f+n/+P/6v/N/+P/+f8AAOP/HQDq/wAAAADq/x0A+f8dAAcAAAAHAAcAJQAOAAcAHQD5/wcABwAHACUA8v8dAB0ABwAOAPL/AADb//L/AAAWAAcAFgAzAA4AQgAdAPn/BwAdABYAJQAOAPL/FgDy/w4ABwDy/+P/1P/N/83/DgDj/xYAAADb//L/2//b/9T/6v++/83/2//b/+r/xf/q/+P/2//q//L/6v/5/wAA6v/q/+P/6v/q/9T/zf/F/7b/tv/b/+P/xf/U/77/vv/F/8X/1P++/9v/tv+2/9v/4//j/83/2//b//L/6v/5//L/8v/y//n/AADF/+P/zf/U//n/+f8AAPn/+f/q/w4A8v/5//n/8v8AAAcAJQD5/x0ADgAlAB0A+f8dAOr/FgAdABYAFgAdAB0AJQAdAAcAAADq/w4A+f8HAAAAAAAOAPL/JQAWAAAAFgAlAA4AFgAdAAcAHQAWABYADgAAAPn/FgAAAA4AMwAAAB0ALAAWAAAABwAOAPn/BwAAAAcADgAOAB0AAAAAAAcA8v/y/+P/4//U/9v/8v/b/wcA+f/j/9v/4//N/9T/AADN/+P/6v/y//L/BwAHAOP/BwDN/+r/4//y//n/8v8WAPn/JQAOABYAHQAWAB0ABwAWAB0AHQAdADsAAAAlACUAAABCAAcAJQAsAAAAAAAWABYADgAOABYAFgD5/xYA4//5//L/4//y/+P/DgDj/w4A8v/y//n/+f8WAOr/FgAAAB0AJQAWABYABwAsAA4ADgAdADMABwAzAEIAFgAsAA4ADgAAAAcAAAAHABYALAAzAAAAAAAHAAAA8v8zAPn/8v/5/9v/DgDq/ywA8v8HAB0AAABRAAcAOwAHAA4AHQDq/ywA8v8AAAAA+f8AAA4A+f/y/xYA6v8lAAAAAAAWAAAAJQD5/x0ABwAAAEIAFgAWADMABwAWADMADgBCACwAJQBCAB0AQgAdAB0AOwAsACUADgBRAB0AJQBKACwAMwAsADsAJQAWACUAHQAOAA4ADgD5/wcABwAHABYABwD5/+r/6v/q/wAA4//q//n/4//y/+P/6v/b/+r/4//U/+r/vv/q/9v/zf/q/7b/xf/b/9T/4//U/9T/6v/q/wAADgAAAAcA+f/y/+r/zf/b//L/2//y/+P/4/8AAK//+f/y/7b/AADF/+r/4//q//L/zf/y/8X/6v/y//L/AADq//L/AAAAAPL/DgDy//n/6v/5/+P/4/8dAPL/AADy/wAAzf/b/wAAtv/q/9T/4//U//n/4//b//n/2/8HANT/BwDj//L/AADq/xYA4/8WAOr/BwD5//n/BwDb/w4A6v8AANT/FgD5/9T/HQC+/wAAAADj/wAA8v/b//L/4//q/w4A2//5/8X/zf/b/6//8v/y/9v/AADj/9v/AAC2/9v/xf/F//n/vv/5/83/xf/5/9T/1P/N/9v/zf/U/+r/4//j//n/+f/j/+r/AADb/+r/+f/N/wAA4//U/wcA6v8AAAcA8v/y/wcA+f/y/wcABwAHAAAA8v8AAAAABwAlACwAOwAOAAAA8v/5/wAA4/8WABYAMwAlADsAOwAlAEIADgA7AAcABwAWAAcAJQDy/w4A+f8dACUALAA7AB0AQgAsACwALAAdACUAMwAlAEIAMwAdADsALAAlACUAMwAWADMAHQAWAB0A+f8WAAAAHQAWADMAJQAdADsAAAAsAAAA+f/y/wAADgDy/x0A+f8WAAAABwAAAOP/MwAHAA4ADgDq/wAABwAWAB0AFgAOAA4AFgAsACwADgAzADMA8v8sAB0AAAAOAAcABwAAACwAHQAlAA4AJQA7AAcAHQD5/wAABwAHAA4ALABCADMAUQAlACUAMwAHACwAMwAlAEoASgBCAEoALAAlACUAHQAzAFkAOwBCADMAOwBKAB0ALAAdACUA+f8WACwA8v8sACUAFgAHAAAA2//j//n/1P/5/9T/2//y/wcADgAdAAAAAAAWAOP/BwD5/xYADgAWAA4AAAA7APL/HQAOAPn/8v/q/wcA1P/5/wcAJQD5/wcADgC2/+P/zf/b/+r/2//5//L/6v8dAPL/+f8WANT/BwD5/wAAFgAHAAcA8v/y/wAAFgAAAAAAAAAAAOr/6v8AAOr/AADy/wAA1P/y//n/1P8dAPL/8v8AANv/+f/q/+P/AADy/+r/BwDq/83/AAD5//L/BwDq/+r/2//q/wAA+f8dAAAA8v/y/9v/6v/b/wAADgDy//L/8v/5/+r/8v8HAOr/8v8HAPn/+f/5/w4A4//b/wAA+f8WAAcAAAAHAAcAFgAdAA4ABwA7AAcAAAAdAOr/HQAHAOr/FgD5/wAABwDy/wAADgDq//n/AADq/+r/+f8AANT/8v/q/+P/BwD5/w4ABwAAAPn/AAD5/+P/6v/q//n/8v8AAAAABwAOAAAA6v/b/w4A8v8AACUABwDq//n/6v/j/yUAAAAWAA4A6v/q/8X/2//F/+P/6v/5/+r/1P8AAOP/8v/5/9v/2//y/+r/AADj/83/8v/b/+r/6v/j//L/2//j/+r/+f/q/9T/6v/j/+r/6v/y/wAA4/8HAPn/6v8OAPn/8v8AABYA6v8lAB0ABwD5/+r/JQDN/w4ABwDq/x0A+f8WAOP/+f/q/9T/2//j//n/1P/y/8X/8v/5/+P/+f/5/+r/zf/5/9v/4/8AAPn/2//5//L/4/8OAMX/8v8AAOP/AAAOAPL/4//5/9T/8v/y/+r/DgDq/9v/+f/5//n/HQDy/wAABwDy/w4AAADq/+r/6v/U/+P/xf/y/wAAAAAdAPn/AADb//L/8v/q/wAAAAAAAOP/BwAHAOP/AAAHAM3/+f8OAPn/DgDU/+r/zf+2/77/tv++/6//zf+2/8X/xf/U/9v/xf/q/7b/zf/U/8X/1P+g/7b/vv++/9T/6v/j/9v/4//y/wcA4/8OAAcA4/8HAPL/+f/q//L/BwDy//L/AAD5//n/DgD5/xYABwAHACUAAAAlABYAJQAHAAcALAAAAAcAFgAlACUAMwAsACUAOwAsADsALAAsAFkAYABgAHYAZwBnAFEAWQBnAGAAdgBKAGAAUQBCAG8AUQA7AEIAOwAWAFkAOwA7AFkAHQA7ADMAJQA7ADsAOwBRACUAMwAsAAAAMwAWADMAFgAdABYA+f/5/8X/6v/F/wcA+f/j/ywA6v8OAAAAAAAAAOr/+f8HAOP/6v/y/9T/DgD5//L/6v/y/+P/6v8lAOP/LAAHAA4ALADb/xYA8v/y/wAA+f8dAAcAFgAlACUAHQAzAEoALAAdADMAHQAAAB0AHQAOAPn/+f8OAPn/DgAzABYAJQAsAPn/DgAAAA4AFgAWADMAFgAsAB0AAAAAAA4AJQAdADMAHQAlACUABwAHAPL/+f/q/+r/6v/y//n/6v/5/+P/AADy/+r/FgAHAAcABwAdAA4AAAAOABYA4//y/x0A8v8AAOr/6v/y/9T/8v8AAPL/AADy/wAAFgDb/w4ADgAAAAcA8v8OANT/6v/b//n/JQAOAB0ADgAdAOr/6v/j/+r/+f/F/+P/zf+2/9T/1P/F/9v/xf/U/+P/vv/5/9T/4//q/9v/6v/U/9v/AAAWAAAABwDj/wcA4/8AACUA+f8zAPn/HQAlAAAAJQAdAPL/6v8zACUALAAlADMAMwAHACwADgAWAA4A+f/5/x0A8v8HACwA8v8dAOr/8v8AAPL/AAD5/xYA8v8HAAAADgAdAPn/BwD5//n/2//q//n/8v8OAPn/8v/U/9v/4//U/+r/zf/y//n/4//5//L/8v/j/9v/1P/b/9T/2//q/+r/8v/b//L/2//U/+r/2/8AAOr/AADy/9v/8v/U//L/1P/b//n/4//j/83/4//j/9T/6v/F/+r/2//F/wcA6v8AAOr/8v8HANT/+f/q/+P/4//b//n/+f/y/+r/6v/y/9T/AAAOAOP/DgDb//L/+f/N/wAAzf8AAPn/AAAlAPL/BwAOAAcA+f8WAA4AAAAAAAAAFgDq/xYAFgAAAPn/8v8AAPn/+f/y//n/4//q//n/8v/j//n/BwDb/+r/BwAAAPL/DgAAAOr/6v8AAAcA1P/y//n/1P/b/+r/6v/y/wcAFgAWAPL/8v/y/+r/6v/q//L/6v/j//L/BwDq//L/AAAAAPn/6v/y/wcAAAAWACwADgAsABYADgAOAPL/DgAAABYA+f8HAB0ADgAWAAAA+f/y/x0ABwAOAA4ABwAWAA4AJQAOACwAHQAlACwAFgAdAAAAHQAWAA4ALAAWAPn/BwAsAB0AHQAWAPn/+f/q/wAAJQAdAAcABwAOAOr/8v8OAA4A+f8AAAcA6v8AAPL/FgAWAOr/FgAAAAcADgAsADMAFgA7AAAAAAAHAA4ALAAWACUAMwAdACUALAAOABYA+f8HAA4ADgAsAA4AOwAsAB0AHQAOABYAAAAdAAcADgAWAA4AJQD5/w4ABwDq/wAA4//5/w4ADgAWACwAAADy/yUA+f8HADMAHQAsADMAJQAsACUAHQAzACUALAAzACwAJQAHAB0AMwAWAAAAHQAHAPn/QgAdACwALAAlACwAHQAzABYAHQAAAAAAFgAdAA4ADgBCAA4AHQAlAB0AJQAsACwAHQAdAB0AMwAWAA4A8v8AAAAA6v8HAPL/DgDy/w4A4//U/wAAxf8AAOr/DgAOAA4AHQAOACUA6v8OAA4AAAAHAA4AHQAAAA4AFgAAAAcADgAAAA4AAAAHAAAABwAAAPL/FgDj//n/+f/5/wAA4/8AAPL/4//b/wAA+f/j//L/2/8AANT/1P/y//L/AAD5/+r/2//5/+r/8v8WAPL/6v/y/+P/2//y//n/8v/q//n/1P/F/9v/zf/5/+P/+f/5/8X/BwAHAPn/+f8lACUA+f8lAA4AFgAlAB0AJQAAAPL/FgDj//L/HQD5/x0AMwAzACUAOwAOAB0ASgAOAB0AAAAHAAcADgAlAAAABwAdAB0ABwAWAA4ADgAOAOr/+f/y//n/6v8AAPn/4//b/9v/+f/N/9T/zf/j/9v/xf/U/9T/1P/b/9T/r//U/77/zf/j/8X/6v/N/+r/tv/b/+P/xf/5/7b/+f/U/83/4//F/8X/mf/F/7b/tv/N/+P/1P/N/9T/tv/j/9T/6v/U/9v/4/++/9v/1P/5//L/4//b/9T/xf++/8X/4/8OAPL/+f8AAAAA2//5/wcA6v/5//n/AADy/wcA+f/5//L/AADy/9T/8v/U/+P/2//N//L/8v/U/+r/+f/U/wcADgAOAPL/4/8HAPn/8v8AAAcA4//y/+r/1P/j//L/6v/y/+r/+f/q/9v/FgDq//n/BwAAAAAA1P/q/9T/2//q/+r/zf/b/+P/r/+2/9T/6v/F/9v/1P/N/+r/+f/y/9v/+f/q/wcA+f8AAPL/xf/q//L/4//N//n/1P/b//L/xf/5/9T/8v8AAOr/HQAWACUAJQAzACUAHQAzABYAHQAdAEIALAAOAB0ABwAWAB0ALAA7ABYAJQAHAB0AFgAHADsAFgAdACUAJQAlADMAUQAlACUAJQA7AB0ALAA7ADMASgAlACwADgBCAAcADgBRABYAWQAzADMAQgBKADsASgBRABYAQgAsAFkAJQA7AGAAJQBZADMAYABRADMAQgBKADMAJQBnAEIAQgBgAFkAZwBRAFEAbwBCADsAQgAzAEIAMwBRAGAALAAdADsABwAAACUAHQAzADsAQgAOAA4ADgAHAAcA+f8HAAAAAADq//n/AAD5/w4AAAAOAA4AFgAAAAAAHQDy//n/DgAAAAAA6v8dAAcA+f8sAAAADgAlAAAABwAdAA4ADgAAAAcABwAAAB0A8v8AAOP/+f/U/9T/AADF/wcA+f/5/wcA4//b//n/BwAHACUAAAAOAPL/4//j/+r/8v/N/wAADgDy/+P/AADq//n/4/8AABYA6v8OAPn/BwDq//L/6v8AAPL/AAAlAAcAFgD5/xYA6v/5/wAA6v8OAOr/AADq/wAAAADy/9T/4//N/77/2//N//L/vv/j//L/4//F/9v/BwDb/w4A+f/y/9T/1P/j/9v/4//y/+r/tv/j/6f/tv/N/8X/6v/j/77/r//F/5n/tv/N/7b/xf/b/83/6v/b/9v/+f/U//L/+f8dAPn/HQAlAAcAJQAHACUA4/8HAAcA4/8WAPn/JQAHAOr/FgAHAOP/FgAWAPn/+f8WAAcA+f8HAAcAAADy/x0ADgAlABYAMwAzABYAQgAHADsABwAOADMAHQBKAA4AOwAzAA4AHQAlAB0AHQAsAB0AHQAzACUABwD5/9T/+f/j/wAABwDj/wcA2//U/+r/6v/N/+r/2//b//L/8v/b/83/4/+v/83/vv++/7b/xf/j/77/AADU/+P/4//F/+P/8v/y/+r/8v/5//n/1P8AAAAA4//y//n/2//j/xYA6v8WAPL/6v8OAOr/BwAAAOP/+f8AANv/AADq/+r/8v/b/+r/2//q/+r/1P/U/+r/xf/b/+P/zf8AAOr/2//5/+r/1P8AAOr/AAD5/+r/AADq/wAA2/8AAOr/1P/j/+P/BwDq/wAAAAAAAPL/8v/y//L/DgD5/w4Azf/F/+P/xf/q//L/8v8AAAAADgD5/w4AFgD5/x0A+f8AAPn/6v/y/+r/+f/5/x0ADgAHAPL/AAAHAOr/BwDU/wAA+f/y/wAA8v8AAOP/8v/N/8X/4//y/+r/FgAHAOr/HQDU//n/FgD5/ywADgAWAB0ABwAlABYADgAWAAcAFgAAAPn/FgAHACwAMwAWACUAHQAOABYAAAAHAAcAFgA7APL/HQAlAAAASgA7ACUASgAlADMAOwAAAFEAQgAlAEIAMwAzAAAAOwAzABYAJQAHAA4ADgAsACwAJQAWAA4AFgAWABYADgAsAA4AMwA7ACUAOwAWACwALAAdACwASgA7ACwAWQA7ACwAQgBCAEIAOwAOAA4AOwAlAAcAHQAWAAcADgAdAAcAAAAAAAAABwAAAAAA+f8OAOP/8v8WAPn/HQAAAAcABwDq//L/+f/y//n/DgD5/w4AJQD5/w4AFgAAAB0A+f/5/xYA2/8OABYA+f8WADMAJQAHACUABwAHACUALAAdAPL/6v/5//L/HQAdAPn/JQAOAPn/BwAlAPn/+f8OAAAAFgAHABYAAAAWAA4AAAAWAPn/+f8AAB0AHQAsACUALAD5/xYAFgD5/0IADgBKABYALAA7AAcAMwAdAEoALABKADMAQgAsADsASgAAAFEAFgAdAA4AAAAdAAAALAAAAAAABwD5/wcAAADq//L/6v/y//n/6v/y/+P/2/++/+P/1P/U/9v/zf/b/83/4//U/9T/vv/U/8X/tv/U/8X/4//U//L/2//N/+P/4//U/8X/1P/F/83/2//5/+P/+f/b/+r/+f+v//L/xf+2/+r/xf/U/+r/2//y/9v/zf/5/77/+f8WANv/AAAAAOr/6v/b/+P/+f/j/wcAFgD5/+r/vv/j/9v/xf/b//L/4//b/xYA6v/y/w4A2/8dAOr/BwAHAOr/HQDb/wAA+f8AAA4ABwD5/wAAAADq/yUA6v8HAPL/4//5/9T/+f/N/+r/1P/N/9v/4//j/9v/AADj/wcAFgDy//n/HQAHAB0ABwDy/ywA4/8AAAAA1P/q/wcAAADU//L/1P/b/9v/8v/y/wAAMwAdAEIALAAOAAAA8v8HAOr/AAAAANT/BwAAAOP/4//F/7b/iv+g/6f/tv/b/7b/zf/b/6//1P/q//L/JQAAAPn/+f/j/+P/4//5/+r/6v/q/9v/zf+2/83/zf/b/83/xf/q/+P/+f/U/9T/2/+2/77/1P/N/6//1P/q/83/1P8HAOP/xf8AAM3/AADy/9v/6v/N/wcA6v/5/w4A4//N//n/2//U/wAA4/8WAPn/DgAAAOr/+f/j/x0ADgBCACwAOwAsAAcAFgDy/w4A+f8dABYAHQAWAAAAFgAAAPn/2//y/+r/6v8WAB0A6v8AAAcA1P/y/9v/1P/y//n/4/8WAA4A8v8OAMX/8v/q/9T/BwAAAAcAAADy/+P/+f/5//n/DgAdAPn/HQAOAPn/JQDy/x0AFgAdAEoAJQAzABYAFgAzAB0AFgAOABYAOwAsACUAMwAsAB0AHQAOAAcALAAOAA4ALAA7ACUAFgAHAAAAFgAWACUAHQA7ACwAHQAzAA4AJQAzAFEAQgBKAEoALABCACUASgBRADsAOwAsAEIAJQAzADsAMwBRAEIAOwBCADsASgBCAEIASgBCAFkAYABZAGcAUQBgAGAAWQBgADsAOwBCADsAOwAsACwALAAlACwALAAzAA4ADgA7ACUAJQBKACwALAAlAA4AFgAlAB0AFgAWABYAAAAOABYADgAlAPn/+f/y/9T/FgAOACwALAAWADsAHQAWAAAABwAOAAAAHQAOABYAFgAsACUAHQAzAAAADgAWAA4AHQD5/xYA+f/b/wcA+f8WAAcADgAsAAAAMwAlAA4ALAAdAB0AHQAOAB0AQgAHAAcALAAAACUAJQAWADsAJQAzACUAAAAdAB0ABwAHAA4A4/8OAPn/4/8sAPn/FgAHAPn/AADj/xYABwAOADMAMwAWAAAA+f/y//n/AAAOAPL/8v/y/9T/6v/y//L/2//y//L/1P/y//L/8v/q/wcALADy/w4ABwD5/wcAAAAOAA4AAAAAAB0ABwAWAAcA8v/q/+P/BwDy/w4AHQD5//n/8v/j/9T/xf/F//L/tv/U/+P/zf/j/8X/tv+n/6//p/+v/6//tv/F/83/xf/F/8X/oP/q/9T/2/8HAOP/4//q//L/zf/q/9T/1P/U/77/6v/b//L/8v/q/w4A8v/j//L/zf/q/+P/xf/b/+r/8v/N/wAA2//q//L/2//y/7b/+f/N/77/2//F/83/zf/5//L/8v/U/9T/6v/j//L/8v8AAM3/xf/q/+r/4//5/wAA+f/b/+P/+f/b/9v/2//y/9v/zf/y/+P/1P/b/9v/zf/U/83/4//F/6//4/+v/6//8v/j/9v/1P/U/77/zf/j/6//8v/b/+r/BwDb/xYA8v/5/+r/6v/y/+r/AADb/wAA6v/5/w4A8v8dAAcAAAAWAAAA2//q/wAA6v/y/w4AAAAAAAcAFgAdABYALAAAAAcAFgDq/wAAAAAHAPL/6v/y/9T/6v/y/+P/6v8HAA4ADgAOAAAAJQD5/+r/BwD5/wAAAAAAAPL/8v/y/9T/8v8AANv/AAAAAAAA6v/j//n/1P/b/9v/6v/5/+r/HQDj//L/AADU//L/4/8HAPL/6v/y/9v/6v/q/+r/4//b/9T/DgAAAPL/DgD5/+P/4/8WAAcAHQAsAPn/DgAdAAAAAAAWAPL/BwAHAA4ALAAAAA4AAAAAAB0AJQAWACwALAAWACwAHQAdACUABwAdABYADgAdAA4ADgAWACUAFgAOAB0A8v8dAAcAAAAWAPn/BwDq//n/2//b/xYABwD5/+r/+f/5/+P/DgAAANv/+f/q//L/+f/5/wcA6v8WAPn/+f8WAAcAHQAOAA4ABwAOABYADgAWABYAMwAHABYALAAdABYALABZABYALAAsAAcALADy/xYADgDj/w4AAAAHAPn/6v8HAOr/DgAdAAAAJQAWAAAA8v8AAAAA4/8AAPL/DgAAABYAJQD5/w4ABwAlAPL/AAD5//L/HQDq/x0AHQAdAB0AHQAOACUALAAWADsAAAAzABYABwBKAA4ADgAOAB0AFgAzADMAMwAlAAcAFgAHABYADgAOAOP/DgD5//n/JQDy/xYA6v/y//L/6v/y/9T/2//j//L/1P/5/+r/+f8AAPn/+f/N/xYA2/8AACUAAAAWAA4ADgDb/xYADgAOABYABwAdAPn/HQAAAAcAAADj/xYA2//j/wcAAAAHAAcABwAdACwAFgAWAA4AJQAdACwAOwAHAA4AJQAOAAcAMwAlAB0AJQAOAB0AJQAOAA4ADgAdABYABwAlAAcAAAAAAPL/+f/y/w4A8v/5/wAAAADy/+r/HQAOABYALAAlAAAADgAHAAAAFgDy/w4ABwAOAA4AFgAWAPL/HQAHAA4ABwAHAOr/8v8HAM3/+f/5//L/8v/b//L/8v/b/+P/6v/b//L/1P/U/9v/1P/5/+r/8v8HAPL/1P/b/+r/4//5/+r/AADj//L/DgDN//n/6v/q//L/+f8sAAAADgAWAA4A8v/5/w4A+f8dAAcAHQAdABYAHQAdAAAA4/8AANT/6v/j/wAA4//y/xYA1P8AANv/4//j/9v/8v/U/wAABwAAABYABwAAAB0ABwAlAAcA4/8WAPL/BwAOAA4AFgAAACwA8v8AAA4AAAAWABYAFgAOACUAHQAdABYAAAAOANv/DgD5/9T/HQDU/wcA+f/U/+r/1P8AAOP/BwAWAOP/2//N/83/2//U/83/2//N/+P/1P/b/wcAzf/N/+r/1P/b//n/8v/q/wcAAAAAAAcAAAAAAAAA+f8OAB0AAAAOAPn/+f8HAOr/BwD5/+r/+f/y/wAAAAAWAOP/BwD5/9T/HQDj/+P/8v/U/wAA2//U/+P/4//5//L/BwAWAAAA1P/5/+P/2/8HAPL/AADb//L/8v/j/xYABwAOAPn/8v8HAAAAAAAHAAAA4//j/+r/AAAAAAAAAAAOAAAABwBKACUAJQAlAAcAFgAAAB0AHQAHACUAAAAAAPn/8v8sAAcAHQAOAPn/JQAAAAcABwAHAA4AFgA7ABYAFgAlAAAALAAOAA4ALADy/0IADgAsAFEA+f9gADsAOwA7ACwAMwAOADMAFgAlAEIAHQA7AEoAJQA7ACwAMwAsAA4AOwAdACUAJQAOAB0AAAAdAB0AAAAdAB0A+f8WABYABwAdAA4ADgAzAAAA4/8AAOr/AAD5/+r/4/8AAAcADgAdABYAFgDy/zMALAAlACwAFgAlAAcAJQAzAEoAMwAWACUAHQAdAB0AMwAdACwAHQAWADMAFgAOADMALAAlAA4AHQAzAPn/HQAWAAcADgAHAAcABwAWAPn/LAAlACwAMwAWAB0ADgAdAAAA+f8HABYAAAAdADMABwAWAPn/+f/q//L/8v/q/+r/xf/5/+r/4/8AAOP/DgAHAAcADgDj/+r/2//q/9v/4//q/+P/8v/N//L/4/8AAPn/6v8HAL7/6v/b/9T/1P+2/83/vv/F/83/vv/U//n/AAAOAAcAHQAHANv/6v/F/77/xf/b/9T/4//5//L/4//U/77/oP+g/5n/tv+n/9v/4//F/wcA2//U/9T/6v/y/9v/1P/F/83/p//F/9T/2//b/+P/8v/U/+r/6v/b/+r/1P/U/83/xf/U/9v/6v/5//L/4//q/wAA+f/5/w4A+f/U/+P/4//y/w4A8v/y/wAA4//y/+P/4//5/+r/FgAAAPL/8v/y//L/zf/y/+r/+f/y//L/+f/U//n/6v8AAPn/+f8OAB0AFgAdACUABwAOAOr/HQAWAPL/OwAlABYALAA7ACwAFgAsAAcA8v8OABYADgAHAAcABwAHABYAHQAWAAcABwDy//L/BwAHACwAHQAdAB0AFgAdACUAHQAWAEIAMwAzADMAQgA7AB0AJQAHABYAHQAOAB0AJQAdAB0ADgAOADsAFgAdACwAAAAOAPn/+f8sAAAADgAWANv/AADj/+P/DgAAAAAADgAOAAAABwAAAAAABwAAAAAAJQAOAAcAOwDq/wcADgDy/xYAFgAsAAAAJQAOAPL/JQAAACwAFgDy/xYA+f/q//n/BwAHAPL/AAAAAOr/+f/5//n/6v/5//n/BwAlAAAABwAHAA4ABwAOABYABwAOAAAAFgDy/wAA2//b//n/1P8OAPL/4//j//L/4//b//n/+f8HAOP/AAD5/wAAAADq//n/+f8HAPn/JQAWAA4ALAD5/w4ADgD5/xYA6v/q/wAA4/8OAPn/AAAOAOr/DgDj//L/BwDb/wcA8v/q/wcA+f8AAPn/AADq/+P/AADj/wcA6v/j//n/zf/q//L/4//b//n/4//b/+P/4/8HAPL/+f8AAOP/4//b/9v/HQAWAAcAFgDq/w4AAADq//L/6v/y/9T/2//j/9v/8v8HAOr/DgAWAAAABwDy/x0A6v/y/zMA4//y//L/2/8AANv/DgAsAA4ADgAHAAAA6v/y//n/FgD5/wAAFgDq/wcA+f/j/9T/8v/q/wcA+f/q/wAA1P8HANv/DgAHANv/FgDy/x0AHQAOABYADgAAACUAHQAHAA4AAAAlAPL/DgAAAPn/DgDb/ywABwD5/wcA4/8AAPL/1P/5/+r/6v/5/9v/+f/q//n/8v/j//n/2//q/9v/4//y/+P/6v/b/8X/2//b/83/4//5//n/2//j/+P/8v/N/+r/AADq/wAA2//5/w4ADgAlABYAFgAOACUAHQAlAB0AAAAdAA4A8v8HAAcAAAAOAB0AFgAHABYAHQAOAPn/DgAAAPL/8v/j//n/6v/y//n/4//5//L/zf/y/+P/2//5/+P/AADq/+r/4//5/x0A1P/5/+P/6v/y/83/DgDy//L/DgAHAOr/AAAAAOP/+f/5/+r/+f8WAPn/DgAOAAAAFgAOAPL/AAAOAPL/JQDq//n/JQDb/x0AJQAOAPn/HQAHAAAAFgAAACwAAAAOACUAFgAWAA4A+f/5/w4A8v8AAOP/DgAHABYAHQD5/x0A+f8WAAcAFgAWAB0ALAAOACwABwAWAB0ABwAAAAAADgAlACUAFgAzABYAHQAWAPL/DgD5/+P/LAAHAA4ALADq//n/6v8HAPn/BwAHAAcAJQAdAB0A4/8HAPL/6v/5/9T/6v/j//n/zf/5/+r/2/8WAPn/AAD5//n/8v/j//n/AADq/wcA4//y/wcABwAsAAcAFgAHAPL/4/8AAAAAzf8WAPn/1P/q/9v/2//y/83/AAAHANv/BwDj/+P/1P/j/+r/+f8HAOr/HQDy/wAAFgDq//n/AAAHAPL/DgAdAAAA8v/5/xYAFgAsACwAAAAlADMALAAdADMALAAzACwADgBCAB0AOwA7ACwAUQAlAEIAQgBZABYALAAzAOr/HQAOACUAAAAWACwA8v8dADsALAAWAB0AJQAlABYALAAWAB0AFgAAAB0ADgAOABYALAAlACwAHQAWAA4ABwA7AAcALAAsAA4AJQAWACwAFgBKADMAFgAlAB0AJQAOABYA+f8HAAcADgAlACUAJQAHAAAAAAAOAPn/+f8OAAcA+f/U/9v/2//U/9T/6v/U/83/2//N//L/2//q/wAAAAD5/wAABwDb/w4A+f/5/xYAAAAdAA4ADgAdAAcADgAsADMALAAOACUAJQAdACUADgAlAAAABwAdAAAABwAWAAcAAAAWANv/8v8OAPL/DgAHABYAHQDj/wAAFgD5/wcAAAAWAB0A8v8AAOr/4/8AAOr/AAAHAPn/+f/5//n/4//5/9v/2//5//L/+f/q/wcA4//y//L/8v/5/+P/DgDq/w4A8v/5/wcA6v8OAPL/+f/y/+P/2//b/+r/+f/5/+r/AAAWAOr/6v8HAM3/+f/y/+r/4//j//n/2/8HAPL/+f/5//L/2//j/w4A4//q/wAA2//j//n/zf/5/9v/zf/b/+P/6v/j/wcA8v8OANv/4//j/9v/FgDj/xYA4//5/wcA1P/j/9v/2//N//L/8v8AAAAA8v8HAPn/6v8OAAcA8v8HAPL/FgDy//L/AADy/+r/6v8AAOP/DgDq/wAA6v/y/x0A4/8dAPL/AAAAAOP/8v/F//n/2//j/wcA4/8AAOP/2//N/9T/8v/N/xYAFgD5/yUADgAHAA4AAADy/xYA8v/y/wcA8v/y/wcABwDy/wcAHQAOAA4ADgDj/wAA4//5/xYA6v8WAOP/DgAAAAAAJQDy/x0ABwAdAAAAAADy//n/LAAAACwAJQAHACUAJQAOACUADgAHAB0ADgAdAA4AHQAOABYAFgAWABYAAAAWAOr/DgAWAAAAFgAAAB0A+f/q/wAA+f/j//n/BwDq/9v/6v/j/77/vv/N/9v/4//y//n/4//y/9v/2//5//L/6v/b/+P/xf+2/+P/1P/N/w4A8v/q/+r/2//5/9T/+f/q/9T/8v/j/wAAzf/y/+P/2//y/6//2//b/9v/4//U/83/1P/j/9v/zf/b/9v/zf/N/83/2//F/9v/2//N/+P/2//b/83/1P/U/83/8v/y//L/BwD5/ywADgAWAEoA+f8WAAAAAAAAAPL/BwDj/wAA1P/j/+r/8v8AAB0AHQDq/x0AAAAHAB0A8v/5//L/AADy/+r/AADy/wcAFgAAAB0AAAAHAPn/2/8OAOP/6v8dACUAAAAWAAAA+f8HAAcAHQAHACwAFgAWACwADgA7AB0ALAA7ABYASgAWAB0ASgAlADsAMwBRACUAOwAzABYASgAOAEIAOwBKACUABwAsAAcAJQAdADsABwAlAB0ADgAlAB0ALAAdAEIADgAsABYAAAAlAB0ADgAOACwABwAlABYALAAdAB0AMwAdADMAFgBRAEIAUQBKADsAOwAWACUAJQBCACwAUQBZAEIAOwBRADsAHQBCABYAMwAzACUAHQAsADMALAAzABYAOwAWAB0AMwAWACwALAAzAB0AJQAzAAAADgA7AA4AJQA7ACUAMwAlADsAJQAlADMA+f8HAAcABwAHAAcALADq//n/AADq/wAA2/8OAPn/8v8dAAAAAAD5/wAA8v/y//L/8v/q//L/8v/5/wcA6v/q/+P/4//j/wcA2//F//L/2/8AAOP/AAAWANv/BwD5//L/AAAAAPn/8v/5//L/8v/y//L/4//j//L/zf/q/wAA6v/q/w4ABwDq/w4AAAD5/+r/8v/y/9T/8v/j//L/2/8AAB0A6v8OAPL/AAD5/+P/DgDy/wAADgDq//L/+f/q/wAAAAAHAOr/1P/j/9T/6v/y/+r/AAD5/w4A6v8HAAcA4/8dAAcA6v8AAOr/1P/b/83/1P/F/+P/BwDN//L/4//U/9v/6v/U/77/6v++/+r/2//j/+r/2//y/8X/8v/q/+r/+f/y/9T/4//F/77/8v++//L/zf/F/9v/xf/N/+P/zf/N/+r/vv/b/6f/vv+n/7b/zf+n/+P/r//b/77/zf/N/6//4/+2/83/2//b/9T/xf++/+r/vv+v//n/xf/b/9T/vv/U/8X/xf/q/8X/8v/q/83/FgDU/+r/2/++//L/2//y//n/4//5/+r/6v8HAAAAFgD5//n/8v/q/w4A6v8OAAAA8v8WAAAAFgBCACUAOwAlAB0AQgDy/zMALAAOACUADgAOAAAADgAWAAcA6v/q/9v/4//U/wcA6v/j/xYAvv/y/+P/8v/5/+r/BwDq/wAA1P/q/9v/2//b//L/8v/q//n/zf/y/+P/AADy/wAAFgDN/x0AAADj/yUAFgAWAAAAFgAOAPL/JQAAABYALAAOADsAJQAlACUALAA7ADMAMwAlABYAFgAzAB0AQgA7ADsAWQA7ADMALAA7ADMAMwAdADsAHQAHADMAHQAzABYAFgAOAB0AHQAdACUAAAAzAA4AJQAsAAcAQgAOACwABwDq/wAA8v8AAPL/HQAHAA4AFgAHAB0ADgAOAA4ADgAWABYABwAlACwALAAWAAcAAADq/w4AAAAOAA4ALAAsACUAMwD5/zsAFgAOADsAHQAlAB0AOwAHABYAMwAzAEIALABRADsALAA7ADMALAA7AEoAJQAWACUADgAWAB0ALAAsAPn/JQAlAPn/BwAOAA4ADgAlADsAJQAsACwAJQAsAA4AHQAlAA4AJQAzADsALAAzAFEAMwAlAFEAHQAlAEIADgAdACUAHQAlAB0AHQAlAAAAHQAHAOr/DgD5/9v/4/8HAMX/8v/q//n/LAD5/yUA+f8OAPn/6v8AAPL/+f/5/wcA6v8AAOr/AADy/xYADgDy/x0A6v8dAOP/6v/5/9v/DgD5//n/4/8AAOr/AAD5/wAADgDy/w4ADgAWAAcABwAAAPL/8v8HAAcA8v8AAAAA+f/5/w4A+f/q/+r/4//5//n/6v/y/wAA+f8AAPn/8v/q//n/AADy/+P/8v/j/8X/8v/j/9v/6v/5/+r/AAAWAAcA+f/U/wcA+f/5/+r/8v8HANv/AAAHAOP/+f8WAOP/AADy//n/+f/b//L/zf/j/9v/4//U/+P/BwDj/wcA6v/j//L/8v/y/+r/2//U//n/8v/q//L/1P/5//n/6v/5/9v/6v/U/+P/1P/b/+r/zf8HAOr/AADy/9T/4//U/+P/1P/q/83/4//b/9v/8v/F/9v/1P/b/77/4//b/8X/2/+v/77/2//q/8X/4/8AANv/6v/U/+P/8v/q/x0AFgDq/wAAAAD5//n/+f8HAOr/6v/5//n/AADb//n/8v/y//L/xf/5/7b/xf/y/83/4//N/83/2//U/6//2//j/8X/4//q/83/1P/5/9v/6v/5//L/4//b/wcA4//q//L/2//q/+P/6v/b/77/4//b/9T/6v8AABYAAAAsAPL/6v8OANv/DgD5/wAAAAAOABYA8v/5//L/4//b//n/8v/q//n/BwDj/wcADgDy/x0A2//5/+P/4/8AANT/AADU/9v/AAD5/wAA+f/b/9v/4//y/9v/4/8OAOr/+f/q/+r/AADy//L/zf/j//L/BwD5/9v/2//q/+r/zf/y/+P/zf/j//n/4//j/wcAAAAOANv/4/8HANv/8v8AAAAAAAD5/w4ADgDq/wAADgAHAAcAAAAOAAcAAAAHAB0ADgAOAAcABwAWAAAAOwAsADMAOwAOACUAJQA7ACwALAAdAB0AHQAzAB0AAAAdAPn/HQAOABYADgD5/ywAHQAsACUAMwAdACUAOwAdAB0AHQAsAB0ALABCABYALAAlACUAUQAlAEIAOwAWAB0ABwAsAB0AFgAWACUALAAAAB0ADgAdABYADgAzAA4AJQBCADMAJQBKAEIALAAWAA4AHQAlAA4AHQAzAAAAFgAdAAcAMwAsAA4AJQAdAB0AQgAdACwAOwAWADMAOwAWADMAQgBCAEIALAAzAFEAMwAWADsAHQAzAEIAQgA7ABYAOwAAACUALAAAADsADgAWADMAFgAOAPL/1P/y/wAA2//y/wAA4//5//L/8v8AAOr/6v/5//n/2//N/8X/xf+2/77/xf/F/+r/xf/F/8X/tv/U/77/4//U/8X/8v/y//L/BwDy/wAAAADb/w4A+f/y/wcAHQAWAB0AOwAsACUAJQBCAA4AFgAHAPn/+f8AAA4A2/8WAPL/8v8AAPL/+f/b/wcA4//q/wAA4//N/+P/+f/N/wAA8v/5/wAAAAAdAAAAAAAWACwAJQAdACwAFgAsACUABwBCACwALAAzAEIAUQAzAEoAMwAWADsAQgAsADMALAAsADMAFgAzADMAMwAsAEoASgBCAEIALABgADsAUQBKABYAJQAsACwADgAdAA4AJQAsAA4ADgAAAAAA2/8HABYA8v8WABYAFgAWAAAABwAAAAAAHQAOAB0AHQAlADMAMwAsAB0ALAAWACUAMwAWABYAMwAsACUALAAOAAAADgAsABYAFgAWAAAALADj//n/DgDN/wcA1P/U/+r/zf/q/+P/8v/b/9v/1P/N/9v/xf/F/6//r/++/83/zf/F/77/xf/q/7b/vv/U/6D/xf+v/5H/vv+n/77/vv+n/8X/xf/F/6f/zf/U/8X/1P+g/8X/tv/N//L/tv/j/9T/1P/b/+r/AADN/wcA+f/q/w4Azf8AAPL/6v8lAPL/8v/y/+r/4//j/wcA1P/b/wAA4//5//L/6v/b/6//zf++/6//6v++/83/zf+2/9v/vv/U/83/1P/b/7b/1P/F/8X/zf/b/8X/xf/N/7b/6v+n/77/zf+v/9T/tv/F/83/1P/N/77/r/+2/6//tv/q/8X/zf/j/9v/4//j//L/AAD5//n/8v/j//n/BwAOAAcAAAD5//n/+f/5/wcA8v8HAPL/+f8OAAAALAAHAA4AFgDj/wcABwAWAA4A4/8WABYA+f8OABYAAADy/+r/+f8AAPn/BwD5/w4AAADy//L/6v/y/8X/8v/j/wAA6v/F/w4Avv/b//n/+f8AAAAAFgAAABYAAABCABYAFgA7APn/LAAAAB0AMwAOABYAAAAsAAcAHQBCAOP/DgAOAAAAJQAHACwAJQAOACUAJQAsAA4ABwAHABYAJQAdACwABwDy//n/DgAAABYAJQDq/wcADgD5/wcA8v8OAAAAAAAWAAcAHQAWADMAFgAWACUADgAdACUALAAsADsAMwAzADsAMwAzAB0AFgAsADMALAAzAB0AJQAdAA4AMwAdACwAJQAdADMAHQAWACUALAAsAA4AHQAzAPL/DgAHAPL/FgDy/ywAFgAHADMAHQAlABYAJQAdAA4AJQAdAB0AFgAWAAcADgAWAA4AFgAWAAcAFgAdAAcAJQAWAA4AQgA7ACwAMwAWAAcADgAzAA4ABwAsAA4AHQAHAB0AHQAAAA4A8v8WAPn/DgAWAAAAAAAAABYA8v8AAOr/8v/q/+r/AADq//n/vv/U/9v/vv/U/wcA4//N/wAA2//y/83/6v/j/83/AADU//L/2//b//L/2/8AAAAABwAAAOP/+f/5//L/FgAHAPL/6v/5//n/1P8AAAAA8v/y/+r/FgDq//n/AADy/w4A6v8AAAcA4//5/wcAAADj/w4ABwAOAA4ABwAdAPn/FgAHAAcAJQAlACUADgAdAA4AJQAOACUAOwDq/wcADgAAAA4ABwAHAAAAHQAWAAAABwD5//L/+f/5/9T/zf/y//L/+f8HAAcA1P/q//n/4//5/wAAAADy/wAA8v/5/wAAAAAWABYADgAOABYABwD5/xYADgAOADMAFgAOAB0AAAAOAPn/BwAsAB0ADgAlAA4ABwAdAPL/FgAWAAcAHQAdAAcA+f8lAA4AFgAlAB0ABwD5//n/+f8HAPn/FgAAAA4AHQD5/xYABwAHAPL/+f8AAAcA8v/y/x0A4/8HAAAAAAAWAPn/BwAOAAAA+f8WAPn/HQD5/+r/FgDq/wcA8v8AAPn/4//5//L/4//b/+r/1P/b/83/8v/y/+r/AAD5/wcA2/8AAPn/6v8AAPL/BwAHAPL/6v8dAPL/AAAHANT/6v/U/+r/4//y//n/6v/5/+r/+f8HAPn/6v/5/+r/+f/5//L/AAAHAAAAAAAOAPL/AAAWAA4AHQAHAAcABwDq/xYAFgAOACUAAAAOABYABwAAABYADgD5/w4AAAAdAAAAAAAWAOP/BwAHAAcADgDy/wAA8v/q//n/6v/U/9v/6v/U/+P/4//q//n/2//j/+P/8v/q/+r/4//y/w4A6v8WAAAA8v/y//n/AADy/w4AAAAOAB0AFgAAAA4ABwAAABYA+f8OAOr/DgAlAPL/FgAWAPn/AAAOAA4ABwAHAB0ABwAHAAAADgAOAPL/HQDy/w4A8v/5/w4A4/8OAOr/8v/y//n/AADb/wcA6v+2/8X/vv/y/9T/6v8HAM3/+f/U//n/DgDj//L/8v/j/83/6v/U//L/8v8HAA4A4/8AAOr/FgDy/+r/DgDy/w4ADgAOAPn/HQAlAA4A8v8WAAAA6v8OANv/+f/y/wAADgD5/+r/8v/5//L/FgD5/w4AJQAOAA4ADgAAAPL/BwD5/9v/DgD5/+P/FgAHABYABwAWAB0A1P/5//L/2//j/xYALADy/wAAAADq/+r/8v/5/wAAFgAHAAcADgAHAPL/+f/5/+r/AAAHAPn/+f8AAPL/+f8WAPn/DgAdAAAABwD5/wcA+f8HAAAA+f8dAPL/FgAOAAAAAADb//L/2//y/+r/8v8OAOr/FgAAAPL/DgDb/wAAFgAAABYADgAOAAcABwAdAB0AHQAsACwAMwAzAB0ABwAAAB0ADgAlACwABwAWAPn/+f/5//n/+f/y/wAA4//5//L/4/8HAPL/2//y//n/+f8AAAAABwDy/9T/BwD5/+r/AAD5//L/8v/5/+P/4//y/wcA6v/y/wAA1P/j/+r/6v/U//L/xf++/+P/r//b/7b/xf/b/+P/BwDj/wAA+f/j/+P/1P/b//n/4//5//n/+f8OAAcA+f/b/w4A4//5/xYA4/8OAPn/DgAAABYALAAWAA4AAAAWABYADgAOADMADgAdACUAFgAsAAAADgD5//L/4//q/wcADgAOAPL/HQDy/wAA+f/N//n/2//y/w4A+f8dAB0AFgAdAPn/HQAOAAAADgD5/xYADgAdACwAHQAzABYAHQAdABYADgAHAB0AAAAAAAcA+f8HAPn/BwAAAPn/8v/j/wAA1P/b/+P/1P/b/83/8v/N/+P/+f/U//n/4/8AAPL/6v/y/83/8v/y/+P/+f8HAAcA8v/q/+P/AADq/+r/BwDb//L/DgAAAAcAAAAAAA4AAAAOAAcADgAWAAcAJQAOACwAOwAzAFkAMwAzADMAQgA7ACwAMwAzACUAJQAzAA4AMwAlACUAOwAAAB0ABwAWACwABwA7ABYALABZAAcAMwAzAAcAMwAsAB0AOwBCACwAMwAHABYADgAHACUADgAlABYAFgAOAA4ABwAHACUABwAWAAAAFgAWAPL/DgD5/wAA8v/y//n/+f8HAAAABwAHAAAA8v8HAPL/6v8HAAAAFgAdAA4AJQAzACUABwAHAB0A+f/5/wAA6v/q/+r/4/8AAA4A4//j/9v/zf/b/83/zf/b/9T/2/8OAOP/6v8AAM3/8v/q//L/6v/j//L/8v8AAAcABwD5/xYA+f8HAPn/4/8WAOP/FgAOAPL/BwDq/ywAHQAAAAcAHQD5/w4AFgDb/w4A8v8lABYAAAAzAA4AJQAWACwALAA7ACUAMwBCAAAAMwAsAA4ADgAlAAcADgAsAPL/HQAAAAAABwAHAB0A+f8OAA4AAADy/xYAAADq/yUAHQAsAB0ABwAlAPL/AAAOAPL/DgAHAAcABwD5/wcA+f/5/wAABwAAAPL/AAAHAPn/+f8HAAcA+f/j/w4AAADq/w4A6v/5/w4ABwAWAAcAHQAAAAcAFgDy/xYA+f/y//n/6v8HAPn/BwAWAPn/DgAWAPn/AAAdAAAA+f8WAB0AAAAHABYA+f8dACUAHQAsAB0AJQAOAAAAHQAWAAAA+f/5//n/1P/5//n/2/8AANv/AADj/+P/+f/y/wAA1P8OAMX/6v8AAL7/FgDU/9T/4//N/8X/1P/b//L/8v/b/wAA8v8HAAAADgAHAPn/8v/U/wAAxf8AAAAAzf/j/9v/4//N/+r/4//b/+P/2//b/+r/1P+v/9T/vv/N/9v/8v/5/+r/+f/5/+r/1P/y/+P/xf/j/wcAvv/F//n/tv/y/+r/xf/5/83/xf/U/9T/AADb/+P/BwDj//n/DgAAAOP/BwAOAPL/BwD5/9v/vv/N/9T/2//b//n/AADU/+r/6v/j/83/AADq/8X/8v/j/+r/1P/U/wAAAADU/wcABwAAAPn/+f8AANv/8v/N/+P/AAD5//n/8v/5/9T/AADq/+P/6v/b//n/+f8OAAAA8v/5//n/AAAWANv/+f8AAM3/BwDU//n/6v/y/wAA+f/y/9T/BwC+/+P/4//U/+r/zf/5/+P/1P/b/+r/vv/N/8X/zf/y/8X/2//j/+r/6v8OAPn/BwAHANv/+f/j/wAA4//q/+r/4/8OAA4AHQAOAB0ABwAOACUALAAlAA4ALAAlACwAJQAlABYAAAAWACUAFgAlAB0AHQAOABYAFgD5/ywAFgAdACUABwAdAPn/BwAAACUADgD5/xYA8v8WAAAAAAAWAAAAFgAOAA4ABwAOABYADgAWAAAAFgAWAPn/LAAlAB0AAAAOADMAFgAdAAAADgDq/wcAJQAWABYA+f8WAPn/AAAAAPL/AADU/+P/6v/j/+P/4//y/+r/8v8AAOr/BwAAAPn/FgDq/xYABwDj/wAABwAAAB0AFgD5/x0AHQAzAB0AOwAlAAAAJQAAADMA+f8AACUAAAAdAAcAFgAOAAAADgAAAPn/BwAHAB0AHQAOABYAFgAlABYAQgAWAA4AJQD5/zMAHQBCAEIALABKAPn/JQAsAA4AJQAHACUAMwAsACwALAAzAB0AMwAzABYAHQD5/yUAJQAOACUAJQBRACUAWQBZACwAUQAdACwAOwAsACwAQgBCADsAZwBCACwAJQA7ACUAHQBKACwALAAsAB0ADgAHACwALAAHAB0ABwD5/wcAAAAdAA4AHQAHAA4AJQDy/wAA6v/j//n/4//q//n/AADb/9T/DgAOAOr/JQAWAPn/BwDy//n/AAD5/wcA+f/y//n/4//j/+r/AAAHAPL/4//j//L/2//y/w4A8v/y/+P/4//y/9T/+f/q/83/AADj/+P/BwDU/9v/BwDj//L/4//U//n/4/8HAPL/6v/y/9v/8v/y//n/6v8AAOr/4//5/9v/8v/j//L/AADq/wAAAADy/+r/2//q/8X/1P/U/6D/6v/U//n/+f/N/+r/zf/q/8X/4//j/83/+f/b/9T/2//N/9v/2//N/wAAzf/U//L/vv/y//L/4//5/+r/4/8WAOr/+f8WANT/6v/U/9v/2//j/+r/8v8AANv/6v/U/+r/AADy//n/8v/5/wAAFgAsAB0AHQAsACUAAAAdADMAFgAAAA4ABwDb/xYAFgAOACUABwAWAPL/DgDq/+P/LAD5/xYAAAD5//n/AAAHAPL/HQAOAPn/FgAlAPn/HQAlAAAADgDy//n/8v/5/+P/6v8OAOr/+f8HAPn/AADy//L/FgDq/w4AHQDy/+r/+f8dAAAADgAOAA4ABwAAADMADgAAAAcAAAAAAAAAAAD5//L/BwAAAOP/8v/y/9v/1P/j/+P/4//b/+r/4//F//n/6v/U//L/6v/b/+r/6v/y/wcA+f8OAAcABwAWAA4AFgAHAA4A+f/j/wcA6v/y/xYA+f/5//n/8v/q//n/8v/y//L/2//5/9v/AAD5/9v/AADb/+r/6v/5//n/4/8HAPn/8v8AAAAAFgAlAPn/BwAOAAcAFgD5/yUAAADj/x0A+f8AAAAA+f8AANv/BwAAAOr/BwAHAPn/8v8OAAcA+f8HAOr/2/8HABYADgAWAPL/AAAHAPL/DgAOABYAAAAWABYAAAAAAPn/DgD5/xYALAAAAB0AFgAHAAcAAAAHAPL/+f8OAAcA+f8HAAcA6v8HAA4ABwAdAA4AFgAAAA4AHQAWADMALAAzACUAJQAWAAcAHQAOAA4AFgAlABYAFgAsAAAA+f8AAAAAFgAHAB0AHQD5/xYALAAlACUAMwAHACUASgAdAFEALAAzAA4AAAA7AAcALAAWADMAMwAHADsAFgAWAB0AJQAOAA4ALAAWADMALAAdABYAFgAAABYABwD5/yUABwAOAAcA+f8OAPn/DgDb/9T/+f/N/+r/4//b/+r/4/8HAPn/4/8HAAcA4/8AAAcA6v/q//L/4//q//L/+f8OAAcAFgAsACUADgAWACUAAAAWAB0ADgAHAA4AHQAOAAAAAAAHANv/FgAOAPn/AADU/+r/6v8AAAAAFgD5/9v/HQAAAOP/8v/y/+P/8v/5/wAA+f/y//L/4//5/9v/8v8AAPL/AAAOAAAA8v/5//L/AAD5/+r/JQDy/+P/AADy/w4ADgAOAAcA+f8dAA4AAAAHAAAA+f/y/+r/AAAAAPn/AAD5/wAADgAHAOr/BwAdAPL/JQAWAPn/AADy/wcA8v/y//L/6v/q//n/AADj//n/8v/q/+P/6v8HAOP/4/8AAOr/1P8HAAcA8v/5/+r/HQDj//L/BwDb/xYA4//5/+r/zf8HANT/8v/5/+P/DgDq/9v/4//N/9T/8v/U/+r/8v/N/+P/1P/b/9v/xf8AAOr/6v/y/+P/+f/y//L/8v/j/+P/8v/j/+r/8v/j//L/BwDy/wAAFgAAAPn/6v/5/9T/AAAHAPn/HQD5/wcA8v8dAAAA6v8dAPn/FgAOAA4A4//5/w4A+f8AAOr/AADj/+r/+f8AAAcAAADj//n/BwDj//n/4//y/+P/BwAlAAcAAADy/xYA4/8AAA4A6v8AABYAHQAHAAAAFgAlAAcAFgAWAAcAHQAOAPn/BwAWABYAJQAdABYA+f8HAAcA4/8AAOr/+f/y//L/DgD5/w4AAADq//L/2/8AAPn/8v8HAPL/DgAAAAAAFgDb//L/BwAAAAcA+f8AAOr/6v/q/+r/8v/q/wcA6v/5//L/4//j/9T/AADq/w4AFgAAABYA8v/y//n/+f8HAPn/8v8HAOP/DgAOAPn/DgD5/x0A8v8OAPL/AAAHAOr/MwAAADMABwAlAEIAAABKADMAJQAWACwALAAsACUALAAdACwASgAAAGAAQgAdACwAFgAlAPL/DgAHAAAA4//b/wcA2//y//L/8v8WABYAAAAOAA4A8v/5//L/4//5/w4AFgAOAB0AJQAHAOr/AAD5/wAA+f/q/wcA+f/q//n/DgDq/9v/8v/q/wAA+f8AAAAA4//5//L/1P/5/+P/4//5/+P/JQAAAB0AFgAHAB0A2/8AAPL/FgAHAAcAJQDy//n/6v/y/+P/AAAAAA4AFgD5/xYADgAHAPn/BwAWACUAFgAzACUAAAAzAA4AHQAAAAAAHQD5/x0AHQAAAA4AJQAWABYAFgAWAAcABwAdAAcAHQAWAAcAHQAOAA4AJQAHABYAHQAOACwAJQAlAB0AJQBCABYAMwAsABYAMwAWADsAMwAlAB0AAAAHAOr/+f8AAA4A4//y/w4A1P8HAA4AMwAWAB0AHQDj/wcA4//q/wAA8v8OAPn/4/8WAPn/8v/y/+P/FgDU//L/DgDN/+r/4//U/9T/zf/U/+r/8v/y/+P/AADb//L/FgDq/xYA6v8AAA4A6v8HAPn/+f/q/+P/+f8AAOr/DgD5/+P/AADj/wcABwDy/wAA8v8WAAcA+f8dAPn/+f8OAPL/8v/j/wcAAADU//n/4//q//n/8v8OAOP/1P/5//L/1P/q//n/zf8AAPL/zf/N/83/2//F/+r/2//5//n/6v/y//L/DgDb/wAA+f8OACwAAAAOAAcAFgDy/wAABwAAAAcABwAWABYAFgAOAAAA+f8WAAAA+f8AAAAA+f8AAAcA4/8AAOP/6v8OAPL/8v/5/+r/1P/y/wAA+f/q/+r/AAAAAA4AFgAOAA4AFgAdAA4AFgAzABYAFgAWAA4ABwAWACwADgAlAAAA+f8AAPL/BwAHAA4ABwAOAAAABwD5//n/FgDq/wAADgAAABYAAAAOAAcA8v8AAPL/+f8HAA4A+f/y//L/2//5/83/1P+2/6//zf++/+r/vv++/9v/r/++/+P/1P/j/9T/2//j/6D/4//N/83/2//F/9T/oP/N/9v/vv/F/+P/1P/F/9T/2//b/9T/6v/N/83/8v++/9v/4//N//n/2//q/+P/xf/5/9v/2//q/9T/1P/b/+P/BwAHAPn/JQAOABYABwDy/wAA+f8AAPL/AAD5//L/6v8AAA4A6v8WABYABwAOAA4ADgAdACwA+f8HAB0AFgAdABYAJQAOAAAAJQAHAAcADgAsAB0AAAAOAOr/+f/N//n/HQD5/yUAHQAdADMAHQAzAEoAFgAdABYABwAdAB0AJQD5/wAAFgAlABYAHQAlABYAFgAdACwAHQAsADMAHQA7ADsAMwBKADsALAAzABYALAAdAA4ADgAAAA4ABwAOACUAHQAWAAcA+f8AANT/8v8AAPL/8v/b/wAAAAAOAAAABwAAAOr/BwAHAB0ADgAsAB0AFgAOAAcAJQAHABYAFgAOABYAOwAdAB0AMwAHACUAFgAdACUALABCABYASgBKACUASgAsAA4ADgAWAA4AJQAsABYAOwAlACUAQgAzADMASgAzAB0AOwAdADsAQgA7AEIAOwBCACwAQgAzADMAQgAlACwAMwAzADMAOwBCADsAFgAOACUALAAOACwAOwAHAA4AAAAHAA4AFgAOAAAADgAHABYADgAAAPn/+f/5/xYA6v/j//n/2/8AAPn/BwDy//L/FgAAAPL/4//y/9v/zf/j//L/zf/F/9v/xf/U/9v/2//y/9v/4/8AAOP/+f8AAOP/1P++/+r/zf/F/+r/1P/j/+r/1P/j//n/2//q/wcA1P/5/wAA2/8AAPL/4/8OAAcA+f8lABYA+f8HAA4ADgD5/x0ABwDy/wcA6v/5//n/BwDq/wAAAADy/w4A2//5/+r/xf/U/+r/2//y/w4A4//y/9T/AADy/+r/8v/j/9T/2/8OAOP/AADy/9v/6v/j//L/+f/5//n/FgDy/wAA8v/j/wAA6v8HAPn/DgAHAOr/AADq//n/8v8HAPL/2//y/+P/2/8AAPn/6v8HAAcAAAAAAPn/BwD5//n/AAAAAAcABwAOACUAMwAAAB0AFgAAAA4A6v/y/wAA8v/q/xYA8v/q/w4AAAAdAPL/DgAAAPn/AADq/xYA4//b/+P/zf/N//L/4//y/wAA6v/5/+P/6v/j/+P/+f8OAOP/4//b/9T/+f/b/xYAAAAWADMAAAAdAB0AFgAHAAcAAAAOAB0ALAAlABYALAAlACUAJQAdAAAAAAD5/xYAFgD5/x0ADgAOAPn/+f/5//L/8v/y/yUA2/8AAA4ABwAOANv/FgDF/9T/+f/N/wAA4//U/83/4//N/83/4//b//L/xf/j//n/8v/q//L/8v/q/wcA4/8OAAAA8v/5/+r/8v8AAA4A1P/5/9v/4//5//L/AADq/xYA4//j/+r/BwAOAPL/JQAWAB0AFgAWAAAADgAAAA4AJQDy/yUA6v/5/wAAAAAdAAAAHQAAAAAA4//U//L/4/8AAAAAAAAAANv/6v/y/+P/DgAAAAAA+f/j//n/8v/y/+P/AAD5/+P/FgAAAAAABwAWAB0AAAAsAA4AFgAOAAAAHQAAAA4A8v8AAA4A+f8WAAAAHQAWACUAMwAHAA4A+f/y/wAA+f8AAPn/1P/j/+P/2//5//n/FgAAAOP/FgDy//n/DgDj//L/2//j//L/1P/q/9v/6v/y//n/AADb//n/FgAHACUAHQAOADMADgAWACwAAAAOACUAHQAlAAcADgAlAOP/AAD5/+r/DgD5/w4AJQAWAAcAFgAHAPn/DgAOAAcADgD5//L/BwAAAOr/8v/y//n/BwDy//n/DgAAAPL/6v8HAPL/+f8sAAcA+f/5/wAAAADy//n/DgAHAAcAHQAWAA4ADgAWAA4ADgAAABYAFgAdACwAHQAzACUAJQAOABYAAADy/zMA8v8HAB0A+f8OAPL/AADy//L/+f/U/9v/4//q/+P/8v/q/83/6v/y/+r/DgD5/9T/+f/y/83/6v/j//L/BwDq//n/4//U/+r/zf/y//n/6v8AAOr/+f/y//L/+f/y/wAA4//b//n/4//b/wcAAAAHAAAABwAWAPn/AADj/wcA8v/q/w4A8v8HAOP/BwAOAAAAAADb/wAA6v/b/wAADgD5/wAADgAHAAAAAAAAAAcAFgAHAB0A6v/5/xYA6v8HAPL/AADy/+r/DgDy//n/+f8HAA4A6v/q/wAA8v/q/wcA+f/U/9v/FgAHAAcAJQAWAA4ABwAWAB0AHQAdAB0ALAAlACwAJQAlADMALAAlACwAHQAlACwABwAlADMAHQAzADMAMwA7AA4ALAAzAOr/DgAWAOr/JQAOAA4AFgDy/xYABwAHACwAHQAdACUAFgAsACwADgAWAAAA+f8OAA4AFgAHAPL/8v/5/wAAAADy//n/AAD5/w4ABwAOAA4AHQAlAAAAFgAdAB0ADgAOABYA4/8AAPn/6v/y//L/AADq//L/6v/b/9T/8v/j/+P/4//F/+r/6v/q/9T/zf/N/77/zf/b/9T/1P/y/+P/+f/N/9v/+f/F/x0A4//y/wcA4/8WAOr/+f/5/9v/2//q/9v/2/8AAPL/6v/q//L/4/8HAA4A+f8HAPn/DgDj/wcA+f/F/+P/8v/5/9v/+f/5/wAA8v/q/wcA8v8OAAcABwAdAAAADgAOABYAJQAWAAAAAADq//n/+f8AAB0AAAAAAPn/8v/5/wcADgAOABYABwDq/+r/BwAHAAAADgDy//n/FgDy//n/AADy//L/4//5/+P/+f8HAOr/8v/q//L/1P8HAAcA+f/5/+r/+f/F//L/AADy/wcA+f8OAAAABwAOAAcAHQAdAAAAFgAWACUALAAlAFEAJQAdAA4AJQAlAAAASgAdADMAMwAsAFkAHQBCACwAAAAWACwAFgAlACwAHQA7ABYAJQAlAA4ABwAsADMABwAsAAcAAAAOAPn/BwD5//n/BwAWAA4AJQAlAB0ABwAOADMAFgAsACwAFgAWAA4A+f/q/wcA8v8OAA4AFgAsAAcAMwAzAAcAAAAHAA4AAAAWADsADgAWACwA8v8OACUA+f8HAAAADgAAAOP/DgAHAOr/BwD5/+r/BwD5/xYABwAHAA4A6v8WAAAADgAzAB0ALAAWABYAAAAOABYAHQA7AA4AMwAsAA4AJQAOABYAMwA7ACUAMwAlABYAFgAWAA4AFgAsAA4AHQAdABYAFgAOACwA+f8lABYABwAlAAAAOwAzACwAMwAWACwADgAOAA4A2//5//L/4/8AAPL/BwD5/wAABwDq/+r/4//b/8X/1P/F/8X/zf/U/wAA2/8AANv/xf/b/7b/1P/b/9T/2//y/9v/1P/b/9T/1P/b//n/6v8HAAAA+f8AAOr/DgDj/83/zf/U/+P/2//b/9v/6v/q/9v/2//j/9v/8v/y/wAAAADj/+r/8v8HAOr/BwAAANv/+f/b/wAA6v/5/wAA2//5/9T/1P/b/+P/1P/j/+P/zf/b/83/6v/b/83/1P/q/+P/1P/y/9T/AADj/wAADgDb/wcA+f8HAPL/8v8HAPn/BwAAAAAA8v/5/x0ADgAWABYAJQAzAB0ALAAAAAcALADy/x0AAAAHADMABwAHAAAA4//q//L/AAAAAOP/BwD5/9T/6v/j/+r/4//y/+P/4//b/9v/8v/U/+r/4//j/77/2//b/6//1P+v/9T/vv+2/+P/2//b/8X/zf+2/+r/4//q//L/zf/5/8X/zf/F/8X/1P/N/9v/xf/b/6//1P/b/7b/1P/N/83/xf/b/8X/xf/b/8X/4/++/6//r/+n/6//xf+2/7b/xf+n/77/tv/F/83/vv/F/7b/1P/N/9T/6v/b/9v/2//q/9T/4//j/9T/+f/q/9v/8v/j/+r/8v/q//L/AAAAAAAA+f/b//n/DgD5/xYADgDy/wAAAAAOAB0AHQAWABYALADq/wAABwDq/xYAHQAWACUAMwAAAAcADgDy/yUAHQAzAEIAJQA7ADsAHQAzADMAJQA7ADsALAAWADsALAAdAEIAMwAsACwAMwAsADMAFgAOAB0AJQA7AAcAHQAdAAcAHQAdADsALAAdADMALAAAACwAHQAOACwADgAlAAAALAA7AB0AUQAWAA4AHQAHAAAADgAdABYAHQAAABYAJQD5/xYAHQAdADsAJQAsACUAJQAWABYAHQAdADMAFgAsABYADgAzAAcAMwAWABYADgD5/xYA6v8WAA4AFgAsABYAFgAOAA4A+f8WABYA+f8AAA4ABwAHABYABwAOAAcAHQAHAAAADgDq/wAA+f8AAAcAFgAHAPL/HQAHAB0AFgAAAPn/+f8AABYAOwAlAB0ALAAWABYAJQAsACwAFgAdAB0AHQA7AAcAHQAsAAAADgAHAA4AJQAHAA4ADgDy/zMALAAsAEoAHQAdAAcABwAAACwADgD5/w4A2//5/wAAHQAOAAcADgAHAA4A6v8dAA4AFgAOAAAAFgDb/wAA+f/5/x0AHQDy/9v/+f/N//L/6v/U/wcAAADj//n/+f/q//n/8v/j/+P/+f/q//n/AAD5/wcA2//N/83/2//U/7b/4//F/83/zf/F/9T/vv8AANv/xf/q/83/6v/q/wAA+f8HAAAA6v8AAPL/AAAWAPL/AAAlAA4AJQAsACUAJQAOAEIAFgAlADsAFgAzAB0ASgAlACUAMwAlADsAHQAlABYADgAAAPn/JQAHACUAHQAAABYAAAAOACUAFgAAADMAAADb/wcA4//y/wAAAAAHAPn/+f/5//L/AAAHAAAALAAAAPn/AAAHAAcA2/8dAA4AFgAHABYALADq/x0ABwAWACUA8v8OAPn/AAAAAAAAFgDj/wAAFgD5/x0A4//j/wcAzf/y//L/4//y/9T/4//U/+r/DgAAAB0ABwAOAAAA+f8AANT/8v/q/wcAAAD5/w4A8v8AAAAA+f/U/+P/6v/y/wcADgAWAPL/6v8AAOP/1P8HANv/6v/5//L/8v/y/x0A+f8dAOr/8v8WAOr/BwDq/wcA8v/y//n/1P/b/9T/4//U/9T/4//b/77/8v/U/9v/DgDq/x0A+f8HAA4ABwAlABYAFgAAACUAHQAHACUAFgA7ACwAHQAzADMAJQAOADsAMwAWACwAHQAOAB0ABwAdADMADgAWAA4ABwAWAB0ALAAOAB0ADgD5/wAAAAAOAB0AJQAOAAcAAAAAAA4A+f/b/w4AHQAAABYA8v/j/+r/+f8OAAcADgAHAAcA+f8AABYA6v8AAA4A1P/5/+r/2/8AAOP/+f8WABYA8v/5/wAAAAAAAAAAFgDy/wAA+f8AAOr/AAAdAPL/FgD5/w4AHQAWAAAABwAOAOr/FgAOABYAHQAOAB0AFgAdAA4ADgAWAAAAAAAdABYAAAAOAA4A6v/j/+r/8v/b/+r/AADq//n/6v/j//n/+f/q/+P/AADq//n/6v/5//n/6v8AAPL/+f/y/+r/+f/q//n/AADj/+r/6v8HAOr/6v8HAPL/AADj//n/8v8HAAcA+f8dAPn/LAAHAB0ADgAOABYA+f8lAPL/HQAWAA4ADgDq/wAA8v8OACUAFgAOAA4A8v8AAAAAAAAHAOr/+f8AAPL/4//5/83/2/++/9T/+f/y/w4A2/8AAOr/BwDq//n/HQD5/xYA1P8AAOr/4/8HAPL/8v/q//n/4//y//n/AAAHAAcAFgAWABYABwAHAAAA+f/5//L/BwAOAPn/DgD5/wAA+f/j/wAA1P/5/wAA8v/y/+r/+f/b/+r/2//q//L/xf/q/+r/xf/y/+r/6v/5/+P/AADy/wAA2//y//L/2//5/+r/+f/y/wcA8v8HAAAA8v8HANv/+f/y/wAA+f/5/9v/+f8OANv/+f/b/+r/xf/j/+r/zf/q/9T/8v/j//n/2/8HAPn/4/8OAM3/AADy//L/AAAAAOr/4/8HAOr/FgD5/wcABwDU//n/6v/b/+r/+f/j//L/8v8AAPn/+f/5/+P/FgDj//n/+f/U/wcA6v/5/+r/AADy//n/8v/F//L/1P/q/+P/1P8AANv/+f/5/9T/FgAHAPn/DgDb/wAA+f/q/yUABwAAABYADgAHADMAJQAlAFEAFgAdACwAJQAdAB0ALAAdACwALAAsACwAFgAzAB0A6v8WAB0AAAAOACwAHQAlACwAHQAlAA4ABwAsAAcAAAAdAA4ADgAOAB0AJQAlAB0ABwAdAB0ALABCADsAMwA7AEIAJQAzABYABwAdABYAFgAsADMA8v8AAA4A6v8AAOP/4//5/9v/BwDy//n/FgDy/wcA6v8AAAcAAAAHAOP/BwDb/9v/BwDj/+r/+f/y//L/DgDy//n/JQDq//n/DgAHAAcAFgAOAAcABwD5/w4A6v8HACUAMwAlAA4AUQAlACwAOwAlADsABwAsADMAHQA7AB0AFgAWAAcAFgAdAAcADgAAAAAA8v/q//L/6v/q/+r/AADj/wcABwDq/wcA8v/q/+r/+f/U/8X/+f/y//L/AAAAAOr/+f8HAA4AFgDy/wAADgDy/wAAJQAWABYADgD5/wcA+f8AAAAA+f8OAPL/6v/b/wAADgDq//n/+f/5/+P/2//y//L/8v/j//n/8v/b//L/2//U/77/vv/j/8X/4//q/9T/8v/j/+P/2//U/9T/xf/F/9T/4//j//L/2//U//L/8v/j/+r/6v/q/+P/BwAdAA4AHQDy//n/AADq/x0ABwAAABYAAAAOAAcAAAAHAPn/+f/b//L/8v/q/xYAAAAOACUADgAlABYA+f/y/wcAAADy/wcA+f8HAA4ABwAWAPL/FgD5//L/AAD5/wcABwAdAPL/+f8OAPL/6v8AAPn/AAAWAPn/DgDy/wcABwDy/wcAAAAWAAAAFgD5/xYADgDy/ywAHQAsABYALAAOAPL/AADy//n/+f8HAAAA4//5/wAA6v/y/9v/4//q//n/+f/q/w4A2//q//n/8v/j/+r/+f/j/+P/+f8AAMX/4//j/+P/6v/b/9T/1P/q/7b/6v/b/9T/8v/q/wAA8v/y/+P/AAAAAOr/8v/5/+P/AAAAANv/+f/q/+r/8v/5/+P/6v/y/w4ADgD5/x0A+f/y//L/BwDy/wAAAAAAAA4ABwAlAPn/FgAlAPL/AAAsAAcABwAOAOr/HQD5/x0ALAAWAAAADgAlABYAJQDy/ywADgDq/wAAAAAOAPn/JQAdAA4ABwDy/9T/6v/q/wcALADy/xYAHQDy/w4ADgAAAAAAAAAWAPn/DgD5/9v/FgDy/+r/BwAWAPn/BwAOABYAFgAAADsADgAAAB0AHQAWABYAFgAOAB0AHQAlAB0ADgAsADMAFgA7ADMAOwBCADsAOwAHACwAFgAlAAcABwAWAAcAHQAOACUA4/8dAB0ADgAlAEIAMwAWADsABwAzAPn/LAAsAA4AMwAWAEIA6v8AAAAAAAAAABYAJQAHADMADgAlAB0ADgAAAA4A+f8HAA4AHQAdAOr/JQDU//n/AAD5/wcA6v/5/9v/BwDq//n/6v/j/wAA8v/5/9T/2//N/9v/8v/b/9v/AADb/+P/6v/q//L/2//q/83/6v/F/9v/2/+v/+r/xf/j//n/1P/q/9T/zf/j/83/1P/q/+r/BwAHAAAABwAOAB0AFgAHABYADgAWAA4AAAD5/wAA+f/N/wcA8v8HAB0ADgAzAAcABwDy/xYA6v8OAB0A8v8WAAcAHQD5/w4ALAAAACUAOwAWADMADgAWADsAHQA7ACUAUQAlADMAOwAdAEIADgBCACwAHQAdAB0AAADq/wcA+f8zACUAFgAdABYAHQAHAA4AJQAHAAAAHQAAAAcADgD5//n/AADy/w4AAADy/+P/8v/y/9T/JQAAAAcAFgAOABYAFgBKABYAFgAHABYAAAAdAB0ADgAzAPn/OwDy/w4AMwD5/yUAHQAlACwAOwAzADsAJQAsADMADgAWACUADgAWACUALAAdAOP/JQAHACwALAAHADsABwAsADMAMwAHACUAHQAOACUA+f8WAOr/FgAOAAcAHQD5//n/8v8HAPL/BwDy/+r/+f/y//L/4//y/+r/4//j//n/8v/j/9T/tv+n/77/xf++/+P/2//j//n/1P/b/+P/4//y/+r/2//y/+P/2/8AANv/6v/5/+P/+f/j//n/2//5//L/2//5/8X/4//U//L/4//q//L/zf8AANT/4//F/83/2//U/9T/xf/5/+r/4//q//L/1P/b/9v/4//j/9T/4//F/+P/vv+2/8X/r/+n/7b/tv/N/83/tv/q/6//2//F/+r/8v++/wcAvv/b/83/1P/N/77/6v++/8X/zf/N/6//6v/F/83/6v/N/+r/xf/b/9T/6v/y/9T/6v/U/9v/+f/y//n/4//b/9v/1P8HANT/6v/b/6f/zf+2/9v/6v/j/+r/+f/j//L/BwDq/wcA6v/q/9v/4//y/9T/+f/b/+P/BwDj//L/+f/b/77/xf/b/9v/6v/j//n/1P/b//L/1P/5/+r/BwAAAPL/BwAAAPL/8v/y/+r/+f/y/x0A+f/y/wcA4/8AAOP/8v8AAAcABwAAAB0AFgAOACUAHQAlACwA+f8lACUAFgBCACUALAAzABYAHQAzAB0AHQAlAB0AJQAWAPn/FgAOAB0AQgAzADsADgA7ADsAJQBKAB0AFgAOABYALAA7ADMAQgAzACUAMwAdACUAFgAWAA4AFgAsACUALAA7ABYAJQA7ACUASgAsADsAOwAHACUAJQAAAPn/6v/b/wcA4/8OAB0A+f8AAPn/DgD5/yUAAAAWAAcA8v8WAAAALAAOAA4AHQAzACUAJQAWAAcABwAAACUAAAAlAPn/BwAdAOP/HQAOAAcABwAdAB0ABwAWACwAAAAHADMAAAAsACwAFgAWAA4AJQAzABYABwAWAPL/LAAlABYAJQAdACwADgA7AB0ADgAlAA4ADgAOABYAHQAlAAcAFgAWACUAQgAWAEIAFgAWAB0A8v8lAPL/BwAWAAcADgD5//n/8v8OAB0AFgAzAB0AFgAsAA4AJQAWAPn/FgD5/yUAFgDy/w4A+f/j//L/+f/q/wcA8v8OAAcA8v8HAAAAFgAHABYA+f8HAPL/2//y//n/DgDj/wAAzf/b/wAAzf/5/83/zf/b/83/8v/q/wAAAADy/wcA4/8AAA4A6v/q/8X/2//y//L/8v/5/wcABwD5/9v/8v++/9T/2//b/+P/xf/y/+P/6v/y/w4AHQDq/+r/8v/5/+r/JQDy/+r/LADb//L/AADq/wcADgAOAAcAHQDy/wAABwDU/w4A1P/j/+r/1P/b/9T/8v/U//L/AADq//n/+f8HAOr/8v/b/+r/4//q/xYA8v/5/wAA+f8AAAcADgAOACUADgAHABYAHQAOAAcADgAOACwABwAOABYA+f8OAPn/AAAAAOP/AAAAAAcAAAAdAA4ADgAlABYAFgAHABYAFgAWACUAHQAdABYABwDq/wAABwD5//n/FgAdAAcAAADj//L/8v/q/wcA8v8HAA4ABwAWAAcAFgDy/w4AFgAHACUAAAAWAA4AAAAHAA4AJQAHABYABwAAAAAAAAAHAOP/2//5//L/4/8AABYADgDq/w4A6v/q//n/AAAAAMX/6v/N//L/+f/y/yUA2/8AAOr/4//N/83/2//N/+r/4/8OAOP/AADy/9T/+f/F//L/6v/y//n/8v/y//L/2//U/9T/tv/y/9T/1P/b/8X/2//F/+P/4//j/+P/2//b/+P/6v/q//L/+f8AAAcAFgD5//L/4/8OAAAA+f8lAOr/JQDb/wcAHQDN/yUA8v/5/wcA+f8HAA4AHQAHAA4AFgAOAAAAFgAOABYABwAOACUAAAAAAAcABwDy/wcAAAAAAPn/BwAdANv/HQD5/9T/BwDq/wAADgDy/+P/AADy//n/8v/q//n/6v/5//n/4//q/wcA+f8WAAcA+f8AABYAHQDy/xYABwAWAAcA4/8OAPL/8v/5/wAA8v8HAB0AFgAWAPn/HQAWAAcAMwAWACUAHQDy/w4ADgAAAAcAAAAWAAcAFgAWAPL/DgAHAPn/HQAAAAcADgDq/x0AJQD5/x0ALAAdAB0ADgAOAA4ADgAlABYAHQAWAAAAHQAWABYADgAHAAcABwAOAB0AMwAAAA4AHQAAABYADgAlABYAFgAzAAcAFgBCAB0ADgAOABYADgAHAB0AHQAlACUAFgAWABYA+f8AAA4ADgAlABYAHQAAAPL/BwD5/83/2//q/9T/+f/b/wAA2//j/wcAxf8HAOr/6v/j/+r/+f/b//L/2/8AAOr/4/8HAPn/4/8HAAAA2/8WAOr/BwAAAAAAHQD5/wcA4/8WAAAA+f8dAAAA8v8WACUAJQAsABYAHQD5/wAAAAAOAA4A8v8lAPn/+f8AABYAAAD5/x0A6v8AAAcABwAAAA4ABwAHAAcA8v8HANv/8v/q/+r/BwDy/wAA+f8OAAcAHQA7APn/FgAAAAcALAAOADsAJQAOAAAAHQAHAAcAHQDy/x0ABwAdAAcAFgAsAAAAHQAOACwABwAsACUABwAzAAAAHQAAAOr/+f8AAAcADgAdABYAMwAAAAAAHQAAAA4ABwAHABYAAAAAAAAA6v/5//L/DgAOAPn/HQAAAPn/HQAdACUAFgAdABYAAAAAAAcADgD5/wcAJQAdABYABwAOAA4ADgAWACUA8v8HAAcA6v8HAAAAJQAOAAcAFgAAAPL/+f/5/9v/+f8AAAcA8v/y//L/2//b//n/+f/j/xYA8v8AAA4A+f/q//L/AAD5/wAAzf8OAPL/6v8AAAAAAADj/wcA4//5/9v/4//j/+P/BwDq/wcAAAAAAPL/AAAAANT/6v/q/9T/6v/y/+r/6v/y/+r/6v/5/8X/1P++/7b/vv+v/+P/p//N/9T/vv/b/8X/zf/F/7b/p//F/7b/xf/j/8X/1P/F/83/zf/N//n/zf/F/9v/xf/U/9v/+f/b/9v/zf/N/9v/zf/5/9v/BwD5//L/8v/j/wAA4//5/77/4//j/+r/AADN/9v/zf/N/6//xf++/9T/zf/U//L/1P/j/+r/+f/U/w4A6v8HABYA6v87AOr/BwAHAOP/+f/q/wcADgAHAAAA+f8HAAcAAAAWAOr/4//y//n/BwAOAAcA+f8HAOP/FgAAAPn/LAAOAB0AAAAWAB0AAAAHAB0AAAAAAAAADgAOAB0AHQD5/wcA1P/y/9T/4//j/+P/FgDq//n/4/8AAOP/+f/q/+r/AADF/yUAAAAHAB0ADgAAAOr/DgAAAAcAJQD5//L/8v/F/xYA+f8AABYAAAAlAPn/JQAOAB0AAAD5/w4A4//y/+P/+f/q/wcAFgAHAAcA8v8OAAcAFgAOAAAADgAAAPn/+f8WACUADgBCAB0AJQAsAA4ALAAHACwAFgAlAB0AFgA7AA4AHQD5/w4AHQAHAA4ALAAdAAAADgDy/wcA8v8WABYAAAAdAA4AHQAdACUAJQAAAPL/LADy//L/AADq/wcAAAAOAB0AFgAAADMABwAAAAcA+f8sAAcAMwAlAA4ADgAHAAAA+f8OAPL/AAAOAA4ABwAHAB0ALAAHACwAHQAAAEIADgAWAB0AHQAAAA4AAAAAAB0A+f8dAA4ALAD5/wcABwD5/ywA8v8dAOr/+f/5//L/DgDU/w4ABwDq/xYABwDy/xYABwAHAAAA+f/5/w4AFgAHAB0ADgAlAB0ALAAdAB0AMwAdADMAHQBCACUAJQBCADMAOwBCAEoAOwBKAEoAMwAWABYADgAzACUAMwBCAB0AUQAWAB0AMwBKAEIALABCAB0ALAAWADMAQgAlAEIAOwAzADMAJQAOADMALAAdABYADgAWAAAAHQAWAOr/AAAHAPn/BwAWAA4AHQAWAA4AHQAOAB0AFgAWAPL/6v/q/83/FgDq//L/AADj/wAA2//y//L/1P/q/w4A2//b//n/zf/b/8X/4//N/77/1P/b/9T/1P/5/9T/8v8OANv/2//y/83/1P/b/9T/6v/b//n/8v/U/9T/2//F/77/zf++/77/tv+2/6//zf/U/83/1P/N/8X/xf++/9T/1P/F//L/r//U//L/vv8AANv/6v/q/9v/+f/U/9v/2//j/wAA4//b//L/1P/y//n/+f8HAAAABwDq//L/8v/U//L/4//F/9v/6v/j/+r/AAAHAPL/+f/q/+P/2//j/+P/+f/q//L/6v/j/w4A2/8HAAAA4/8OANT/+f8HAAcADgAWAB0AAAD5/wAADgD5/w4AAAAOACUABwAOACUADgAHACUADgAAABYABwAWAA4ADgAdAAAAAAAHAA4ABwD5/wAA8v8AAPL/BwAHAAAALAAOACwAJQAAABYA+f8HABYA6v/5/wAABwAWAPn/DgAHAAcA+f/j//L/AAAlABYAFgAAAPL/BwAAAA4ADgAdABYAHQAsAA4ADgAAAAcADgAOAB0AHQAlAB0AMwAzABYAJQAsACwAHQAWABYAFgAAAAcAFgD5//n/AAD5/wAADgD5/w4ADgAHAAAA2/8AAOP/4/8AAOr/+f8AAAAA+f/y/+P/AAD5/wAA4/8OACwAAABCAAAA+f8HAAcABwAAACUAFgAHAAAADgDj/wAA+f/5/yUA+f8HAAAAAAD5/yUADgAOACUAFgAOAAcAHQDq/x0A+f/5/ywA+f8dAPn/HQD5/wcAMwDq/w4AAAD5/w4ABwAWAAcAAAAlAA4ALAAzAA4AMwAWAAcA+f/5/wcA8v8dAA4AHQAOAAcADgDq/xYA6v8AAAAA2/8AAOr/FgDq//n/DgDj/wAA4/8AAOP/+f8OAPL/6v++/9T/zf/U/83/1P/U/77/AAAHABYADgD5//n/4//q/9v/2//y/9T/2//b/83/1P/j/wAABwDy//n/+f++//L/AADN/x0A+f/N//n/6v/y//n/8v/y/+P/8v8OANv/2//5/+P/+f8HAAcA8v8OABYA6v/y/wAA2//j/wAA6v/5//L/6v/y//L/+f8AAPn/AAAAAA4AHQDy/xYAFgAHAA4ADgAWAA4AMwAAABYALAAAAA4AAAAHAB0ALAAWAA4AFgD5/w4AFgAdACwAJQAsABYAHQAzAB0AJQAdACwALAAzADMA8v8zAAcA+f8WAPn/FgDb/wAABwD5/xYADgAdAPn/BwAOAB0ADgDy/wAABwDy/+r/HQD5/w4ADgAHAA4A6v8dAAAAAADy//L/BwD5/xYAHQAWAAAAFgAHAB0ADgAOAB0A6v8lAB0AAAAHAPn/8v/q/wcA+f8AAAcA2/8AAAAA8v8WAOP/8v/y/+r/BwDq/w4AAADj/wAA1P/b//L/2//5//L/8v8AANv/4//j//n/AADy/w4A1P/j//n/2//j/+P/6v/b/+P/+f/5/+r/8v/j/+P/4//j/+r/4//q//L/4//F/83/r//b/8X/vv/q/6f/xf/F/6f/vv/U/8X/tv/U/77/1P/q/83/1P/y/9T/4/8WANT/+f8WAOr/BwDy/+P/6v/U/+P/2//5/wcA+f/5/+r/6v/q/+r/DgAdAAAADgD5/wAA+f8AACwA8v/y/wcA8v/j//L/6v/5/w4ABwAOAB0AHQD5/wcAHQAOABYAFgAlAB0AJQAdAB0AOwAdACUAMwAsAEIAFgAWABYAAAAlAAAABwAHAAcAFgAWAB0AHQAzAAcAHQAWAAAADgAAADMAFgAlAEIAHQAsACUA+f8sACwADgAlADMASgAlADsAHQAWAAcADgAlABYALAAOAB0AFgAOACUAHQA7ADMAMwAlAEoAHQAWADsAHQAlAA4AJQAzACwAQgAdACUAOwAWAB0AFgAsAAAABwAHANv/JQAOACUADgAWAA4A8v8WAPn/JQAHAAcADgAAAB0ABwAWAAAAJQAlAPn/AAAdAAAADgAAAPn/JQAOACUAFgAAAAcADgAWACUALAAOABYAAAAOAA4AFgAlACUAHQD5/wAAFgAHABYAMwAdAB0ADgAWAAcADgAsAAAAHQAOAPn/DgAWABYAFgAOABYADgDy/xYA+f8dAAAA+f8sAOr/BwD5/wcABwAHAAAA8v8WAPn/HQAWAPn/BwDy/9v/4/8HAPn/AAAWAPn/+f8AAOP/AAAHAOP/+f/q/+P/4//q/x0A2//5/wAAxf8dAOr/4/8HANv/6v/U/83/6v/y//n/BwDU/+P/6v/b//n/BwAHAPn/FgAAAB0AAAD5/w4A+f8lAAcAFgD5//L/DgDU/wAADgD5/wAAAAD5//L/BwDy/+P/8v/j/+r/2//5//n/xf8AAPL/2//q/+r/6v/5//n/6v/5/9v/8v/j/9v/AADj/+r/AADq/9v/4//j/+r/6v/y/+r/8v/b/+P/4//N/+P/zf/U/77/zf/q/+P/8v/5/w4A2/8AAPn/6v/y//n/FgDj/wcA8v/j/+P/6v/j/83/8v/q/9v/+f8WAM3/2//j/8X/8v/j/+r/BwAAAAcABwDb//L/AADq/+r/AAD5/+r/BwD5/wcAAADy//L/8v/j/9v/+f/U//L/1P/N/+P/zf/q/9v/2/++/83/tv+n/9T/vv/F/+P/8v/b//n/1P/F/83/oP/F/7b/zf/U/83/8v/U/9v/2//N/9v/2//N/9T/8v/j/8X/1P/q/9v/1P/b//n/zf/N/wcA6v/y/+r/8v/U/77/2//N/83/1P/q/77/xf8AAMX/4/8HAOr/+f/q/+r/+f/b//n/AADy//L/8v/y/+P/8v8HAAcAAAD5/wAA8v/5/xYA6v8AAAAA+f8dAAAAMwAlACUASgAdADsAJQAzADMAHQA7ADMAQgBKADsASgAzABYASgAlADsASgAlADsAHQAdACUAJQAdACUAMwAlACwALAAdABYAFgDy/x0AJQAlADsAJQAWAAcAHQAAABYAFgAAAA4AAAAOAAAADgAdAAAAJQAWAA4AJQD5/yUAAAAHABYA6v8zAAAAFgAdABYADgAHAB0A4/8dAPn/DgAAANv/AADb/+r/+f8AAAAABwDy/w4A4//5/ywA6v8HAA4AFgAAABYADgAHAPL/4/8WAOr/DgAWAAcA8v8AAAAA8v8sAAcABwAOAAAA8v8WAA4A8v8AAPn/BwDb/wAADgAWABYAFgAlAB0AMwAHACUAHQAAADMAHQAsADMAHQAdAA4ADgAsACwADgAlACUABwAzAA4AFgAdACwALAD5/zsADgAWABYADgAlAPn/BwAWABYADgAdAPn/DgD5/9v/BwDU/wcABwAHAA4ADgD5//L/DgDq/wcA8v/5/wAA+f8AABYABwAdACUA8v8WAAAAJQAdACUAJQDj/wAA6v8AAPn/JQAOAPL/FgDy//L/6v8OAAAABwAHAB0AHQDq/wAA8v8WAAcADgAWAPL/FgAAAOr/AADy/wAABwAAACUABwAdACUABwAdAAAABwAOACUALAAOABYAFgAHAAAADgDq/xYAHQDq/x0ADgDy/wAA6v/y//L/8v8OAPn/BwAHAPn/FgDj/wcA+f/U//L/4/8WAPL/FgAWAOr/HQDy/wAA+f8dAA4A6v8dAPL/BwD5/wAAAADq/wcA+f8HAAAA6v/y/wAA2/8HAOr/2//5/83/6v/U/wcA2//N/+r/vv/q/+P/8v/b//n/2//b/+r/vv8HAOP/4//5//L/8v/j//n/6v/U/+P/4//j/+r/8v8dAAcA+f8OAPL/2/8AAPn/+f8WAPL/FgD5/wAABwAOAB0A2/8lAPn/BwAHANv/FgDq/w4A6v8AAAcA8v8OAOr/+f8OABYA8v8dABYABwAsAPL/+f8AAAAADgAHABYADgAOACwADgAAACUABwAHACwAJQAAAAcAFgAOAA4AJQAOAAcAJQAdACUAFgAlACwAHQAzAB0ABwAHAPn/HQAHAPL/JQDy//L/FgAAABYA6v/q//L/zf/q/+P/xf/U/77/xf/N/83/1P+g/83/2/+2/9T/2//F/77/4//q/9v/4//q/+P/2//j/+r/6v/5/w4AAADq/9T/2//5/wAAAAAWAA4ABwAdAAcAFgAAAPn/+f/5/w4A6v8AAAAAzf/q/wcA4/8HACwAFgAsACUAHQAsAB0AAAAlAB0A+f8dAAcADgAHAB0AJQD5/yUALAAdACUAMwAlAB0AJQAOABYADgAdADMAHQAdACUABwD5/wcA+f8OAPL/+f8HAOP/DgDb//L/6v/5/yUA8v8AAOr/4//j//L/4//q//n/8v/5/+r/DgDj/xYADgDj/w4A6v/q/9v/AADj/9v/8v/j/w4A8v8AAB0ADgAAAAcADgDq/w4ADgDy/wcA4//5//L/2//5/83/8v/5/9v/BwDy/9v/8v/b//L/8v++//n/4/8AAB0AAAAzAOr/AAAHAPn/AAAAACUABwAdAAcAFgAlAPL/HQAWAOr/HQAWAPn/QgAlAB0AMwAHAA4AFgAdADMAJQAzADsADgAlAB0ABwAdAB0AFgAOAA4AJQAlAPn/LAAWAA4ADgDq/zMABwD5/w4A4/8AAAcA4/8AAAcA4/8HAOr/6v8OAAAA6v/y/wcA8v8WAB0AAAAlACUAHQAlAA4AJQAdABYAFgD5/w4A+f/5/wAA+f8OAAcAFgAzAB0AHQAWANv/8v8HAOP/+f/y/+P/4//q//L/zf/y/+r/4/8AAPL/FgD5//L/DgDq/wAAAADq//n/AAAHAPL/8v8HANv/8v8AAOr/6v/j//n/BwD5/wcAHQAAABYADgAHAB0ADgAzAAcAHQAdAAAALAAlAB0AJQA7ABYAHQAOABYAHQDy/wcABwD5/+r/FgAHAOr/AAD5/wAA8v8WAPL/AAAdAPL/FgAdAAcAHQAlABYAJQAAAAcAFgD5/wAADgAAAPn/AADy/wAAAAD5/wcABwAAAA4A+f/5/wcAAAAlAPn/DgAHAPL/DgDy/xYA6v/5/9v/zf/5/9v/+f/j/wAA8v/j/wcA+f/U/+r/+f/j//n/AAD5//n/8v8AAA4A2//j/+r/tv/b/8X/1P/y/83/zf/U/77/zf/b/77/vv+v/83/tv/F/9v/tv/b/7b/4//N/7b/zf++/9v/xf/U/9T/2//b/83/1P/b/wAA+f/j//L/1P/N/w4A+f8AAB0A+f/y/+r/DgAAAAAADgD5/wcADgAHAPL/FgDy/wcALAD5/x0A8v8OAAcA6v8WAPL/DgAdAAAAAADy/wAA+f8AAA4A+f8HAAcA+f8HAPL/+f/5/+P/zf/U/8X/zf/q/8X/2/+2/7b/xf+v/9v/xf/N/83/zf/q/77/1P/j/83/8v8dAAcA+f8WAAcA6v/5/wcABwAHAAAADgAOAOr/BwDy/+r/AADy/ywA8v/5/yUA4/8OAAcA8v8HABYABwD5/x0AAAAHAA4A6v/q/wcADgAHAB0AHQAWAB0AFgAlACwAHQAdAB0ADgAzAEIAOwBKADMAMwAlAB0AJQAzAEoALABCADsALAAzADMAQgAWABYADgAsAEoAMwAWACUAHQD5/0oAHQAlADMADgAWAA4AHQAWADMAFgAlADMADgAHAPL/DgDy/w4AAAD5/wAA8v8OAPn/BwAOAPn/BwAAAOr/DgAdAB0AHQAOAAcA+f/5//L/BwD5/w4ADgDy//L/AAD5//L/+f/j/x0A8v8AABYA8v8sAPn/FgAWAA4ADgAlADMA+f8zACwAJQAlAAAAFgAHAAAADgAWAPn/FgAdAAcADgAWAPn/+f8OAPn/HQAAAPL/BwAAAAcAFgAlAAAAHQAHAPn/+f/5/wcA+f8sAA4AFgAdACUALAD5/zsAFgD5/xYAFgAlAB0AJQAdACUADgAzACUAAAAdAPn/JQAOAA4AFgD5/wAA+f8HAOP/JQAdAPL/MwAOAAcADgAdAB0ABwAsAAcAAAAHAAcALAAHABYAAAAAAAcA6v8dANv/4//j/8X/6v/U//L/6v/j/+r/6v/y/9T/BwD5/+r/AAD5//L/8v8OAAcAAAAWAAcAAAD5/+r/6v/5/+r/8v8OANv/6v/5/+r/FgAWAA4ABwAHAAcA6v8AAA4A8v8AAAAA4/8AAPn/FgAsAOr/DgAHAOP/+f/5/wAA4//y/wAA6v/j/9v/4//j/+P/4//j/+P/+f/y/+P/AADN/+P/6v/U/w4A6v/5/wAA4/8HAPL/8v8HAB0AHQAOAA4A8v8HAAAAAAAdACUAJQAlACUA+f8dABYABwAWAPL/AAAAAAcAHQAWAAAAAAAOAPn/BwAOAPn/+f/y//n/8v/j//L/2//U/+r/6v/y/9v/AADq/+r/AADq//L/1P/U/77/tv/U/77/vv/U//L/xf/j/9v/tv/y/77/tv/b/8X/tv/N/9v/r/++/9T/tv/b/9v/1P/j/8X/8v/b//L/BwC+/wcAAADy/x0A+f8lAA4ADgAlAPn/JQAHAPn/BwDj/wcAAADy/wcA2//j/9T/vv/b/77/1P/b/9v/1P+v/83/4//U/9v/8v/N/9T/6v/5/+r/vv/b/83/zf/y/+P/2//j/9v/zf/5//L/2//5//n/6v/y/+r/8v8HAPn/FgAOAB0AJQAdABYABwAsABYABwAOAB0AAAAOADMADgAdAAAAJQA7ABYAHQAsABYAAAAzAA4AJQAWAAAAHQAAACUAAAD5//L/+f8OAPL/DgAHAPn/BwAHAAAABwAOAPn/+f8AAPL/BwAHACUALAAOADsADgAAADMA6v8AAA4AAAAsAAcADgAWAA4AFgAdADMAAAAsADMAFgBgADsAMwA7ADMAHQAWACUALAAzAEIAUQAdADsAQgAHACUALAA7ACwAOwBCACUAMwAsACUADgAsAB0AFgAzAA4AHQAlAA4AHQAOAB0AFgAHAAcA8v8dAAcAAAAHAAAADgAHAB0AJQAWAA4ALAAHABYAJQAHACwAAAAzACUA8v8WAAcABwAlAB0ADgBCAB0ALAAlAA4ALAAWAEIAMwAsADsAQgAzAB0AOwAAAA4ADgAAAAAA+f8WAAAADgAdAAcA8v8HAAcA+f8OABYAFgAsACwAJQAWAAAADgAHAAAAFgD5/+r/FgAHAA4AHQAWAB0ADgAdAA4ADgAlAAcADgAOAAcAAAAdAAAA+f8OAOr/+f8AAAcA+f/5/w4AFgAHAAcAJQAOAAAALAAWAA4ADgAAAPn/6v8WAAcA+f8dAPn/AADy//n/2//j/77/r//q/6D/zf/q/9v/2//q//n/1P/j/+P/6v/U//L/1P/b/wAAvv/y/9T/4//q/83/+f/j/9T/8v/5/9v/1P/j//L/4//j/+r/AADq//n/FgDy//n/6v8AAM3/2/8AAM3/AADy/+r/4//5/wcA6v/q//L/AADU/+P/2//j//n/8v/5//n/6v/j//L/+f/y/+P/+f/y/+P/BwDj/+P/8v/j/wAADgDy/w4A+f/q/wcA6v/y//n/+f/5/wAA+f/5/wAA2//q/+r/4//y/+r/+f8AAPn/AAAAABYA4//q/xYA1P8OAAAA6v8HAOr/AADb/+r/AADq//L/+f/5/wAAAAAOAA4A+f8WAAAAFgAHAPn/BwAAAAcAAAAHAOr/+f/5/wAA2//q/wAAzf8HAOr/+f8AAPn/HQAAAA4ABwAdAAcAFgAOAAAAAAAWAAcAAAAlAPL/JQAlAAcAFgAWAA4ADgAzAA4AJQAHAAAADgDy/xYABwAWABYA+f8AAAAA6v8OAA4A8v/5/+r/BwDy/+r/8v/q//n/+f/q/9v/1P/N/+r/zf/N//L/4//j/+r/8v/q/8X/1P/q/9T/2//b/9v/xf/b/+r/4/8AAL7/vv++/8X/1P/U/+P/xf/j/9v/xf/U/83/1P/b/8X/4//b/9T/+f/U/9v/2//j/+P/6v/q/+P/6v/b//L/2//y/+P/6v8AANv/4//N/+r/zf/j/+r/xf8HAPL/4/8HAAAA4/8AAPn/AAD5/wAAFgAHABYAFgAWANT/AAAAAPn/DgDq/x0A+f/q/w4AAADy//L/2//y/9v/zf8AAOP/DgD5/xYAFgAHACUA8v8sAOr/DgAdAPL/HQAWADsAHQAzAA4AJQA7ACUAUQA7ADMAHQAzAB0AHQAdAAcAHQAlAFkAOwAdADsALAAlADMAMwAzACwAFgAlABYABwAlACUADgAWABYAFgAAACUADgAdAEIAAAAdAAAAAAAHAAcALAAOAB0AAAAAAB0ADgAWAB0ADgAWAB0AFgAAAA4AFgDy/zMAHQAOAAcAAAAzAPn/HQAlAPn/BwAAAPn/AAD5/wAADgDy//n/6v8dAA4A+f/5/+P/DgDj//n/FgAOAPL/DgAWANT/+f/5/wcA6v/q//L/+f8HAPL/LAAAAPn/BwAAAAAABwAAAAcAJQAHACUAAAD5/w4AAAAOAPn/DgAHAAAA4//5//n/8v8OAPn/DgAAAAcAHQAHABYA8v/5/wcA6v8WAAcA8v/5/wcAFgAWABYABwA7ABYAFgAlAA4AJQAOADMAFgAOABYAFgAzAA4AQgAOAAcAHQD5/x0AJQBKADMALAAsACUALAAOACwAJQAWAEIAJQAOABYAJQAdABYADgAWAB0ADgAlAAAABwAOAAcAFgD5/xYADgAWAAcAAAAAAPn/AAD5/ywAFgA7AA4A+f8WAAAAJQAOACUAAAAWABYA+f8WAPL/BwD5/w4A6v8OAAcA8v8dAOr/JQD5//L/BwAdAAcA4/8WAOr/BwD5/wAAFgAdACUABwAdAPL/6v8HAOP/+f8lAPn/LAAzAAcAAADU/+r/8v/y//L/AADj/+r/AADq/xYA+f/5/wAA+f/y/w4A+f/q/xYA4/8OAA4A8v8OAAAAAAAHAAcA6v/q/8X/2/8AAOr/6v8OAOr/xf/b/9T/8v/b/+r/8v/q/83/1P/q/7b/4//N/83/8v++/77/6v/j/8X/4//U/9v/2//U/9v/1P/q/9T/2//N/9T/2//q/+P/4/8HAOP/6v8AAPL/8v/j/+r/6v/b//n/1P/j/wcA4//5//n/AADy//L/BwDj/+r/BwDq/9v/+f/j/+P/BwDy//n/+f/q/wAA6v/y/w4A2//y/9v/+f/y/77/AADU/83/+f/U/+P/AAAOAAcA6v/j//n/4//q/9T/2//j/9T/AADy//n/BwAdAA4AHQAlAPn/AADq/wAA+f/q/wAA8v/q/+r/6v/y/+r/4//5/+P/2//q/9T/2//j//L/4//b/9v/2//q/9v/4//q/9v/4//y/+r/1P/j/+r/4//5/wcABwAAAPL/DgAOAOP/+f/y//n/FgAWAB0AAAAAAPL/AADy/wcAHQD5/wAABwAdAPn/AAAWAPn/FgAOABYABwAWABYAOwAsAB0AMwAHABYAAAAAAA4AJQAdADMAOwAOAEIAJQBKAEoAMwBKACUAMwAdAEIAHQAdAFEAFgAsADsAHQAzAEIAJQBCACwAMwA7AB0AMwAOAB0ALAAdABYAFgAdADMAOwAHACwAAADj/ywABwAdAB0ABwAdAAAAFgAdAAcAFgAOABYA8v/j/wcA6v/j//n/AADq//n/+f/q/wAA+f/5//L/6v/j/+P/1P/j//n/6v8OAPL/8v/j/8X/4//N/+P/2//U/9T/zf/j/+P/2//5/+P/6v/y/9T/8v/5/xYABwDy/w4A+f8HAAcA+f/y/wAADgDy/wAAFgD5/xYAHQDq/wAAHQAHAAAAJQAlAAAADgAdABYABwAOACUALAAdAB0ABwD5/w4ABwAdAAAA+f/y//n/+f/q/xYA+f/5//L/FgDq/+P/HQDj/ywAFgAHADMAHQAWAAAADgAOABYA4//5/xYA+f8dAPn/AAAOAAcAHQAdAAcAAAAOAAAABwAOAAcAAAAAAAAAAAAdAA4AFgAOANv/DgAOAOr/DgDy//L/HQAAAB0ABwAAAAcA1P/y//n/4//q/+P/1P/y/wAA6v8OAOr/6v/q/9T/+f/5//L/8v8AAPL/6v/j/+r/BwAAAB0A+f/y/wAA+f/y/x0AHQDy/xYAAAAAAA4ABwAWACwAHQAOACwABwAzADsABwAdAAAABwAWAPn/FgAOAAAAFgDq/9v/6v/j//L/AAAHAAcABwAWAAcABwAAAOr/AAAAAPn/+f/q/wcA+f8AAB0AAAAdAA4ADgAdAAcALAAHAAAAFgD5/w4A8v/y/wcABwAHAPn/AADy//n/+f8AAAAA2//y/+P/4//y/83/4//b/8X/zf/q/9v/xf++/77/xf+v/8X/tv/U/9v/tv/b/77/zf/b/9v/8v/b/9v/2//U/+P/AAAHAPL/6v8AAAAA4/8AAAcA2//q//L/1P/q/9T/1P/y/+P/+f8OAAcAAAAWAA4AJQAlACUAMwAWAB0A+f8OAB0ADgAOAAcAAAAHAAcA+f8WAPn/DgAlABYAFgAOAB0A+f8OAB0ABwAOAB0AHQAWAA4A+f/5//L/BwAHAAcAFgAHAAcA+f8AAAAAAAAAABYAHQAWAB0A8v8WAAcAAAA7ABYAHQAdAAcAJQDj/wcAFgD5/yUADgAdAA4ADgAWAPn/BwD5/wAADgAAAB0AHQDy/wcA+f/q/xYALAAWAAAADgAAAAAABwAWAB0AAAAAAPL/BwD5/9v/BwDy/w4ADgAHAAcA2/8WAAAAFgAlAAcALADq/xYAHQDq/wAABwAdAAAAFgAdAAcABwAOAPL/HQAdAPn/OwAdABYAJQAdAAcAAAAHAOr/BwAOAA4ALAAOAB0AJQDq/w4A8v8HAOP/1P/5/83/+f/F//L/1P/F/wcA2/8lAAAA+f/y/9T/8v/q//n/BwAHAPL/AADj//n/AAAAAA4A8v/5/+r/4//U/+r/1P/j//L/6v/q/+P/6v/b/+P/1P/U/83/1P/F/9T/xf++/8X/kf/F/7b/4/+2/6//2/+v/83/zf/U/83/6v+2/83/2/+2/+P/vv/b/83/2//b/8X/zf++/+P/4//q/+r/AADb/+r/BwDj//n/+f8HAPL/BwAAANv/FgDy//L/+f8WAPn/2//5/9T/4//j/+r/BwDy/w4AAADy/9v/6v8AAOP/BwD5/wAABwDy/9v/2//y/83/4//5/wAAAADy/w4ADgAAAAAABwAWABYAHQAdAAcAAAAOAA4AFgAAAAAA+f/j/ywAHQAlADsAJQAdAB0AMwAdACUAOwAlABYAHQAHACwASgAHADsAOwAlAEIAOwAlACwADgAWABYA+f9CAPL/BwAHAOr/JQDy/x0AHQAlAAcAHQAWAOr/MwD5/wcA+f8OACwABwAWABYAJQAOACwALAAWACwAJQAsACUABwAOABYAAAAdABYALAAzACUAMwAWABYAHQAWABYADgAHACUADgAdABYAAAAlABYAFgAWAA4AAAD5/w4ABwD5/wAABwD5/wcA8v/q/wcAAADy/9v/6v/b/9T/FgDy/+P/AADb/+r/6v/5/+P/zf/q/8X/2//U/83/4/++/77/zf++/+P/8v/b/+r/4//b/9v/6v/y//L/6v/y/x0A6v8HAA4A6v8dAPn/BwAOAA4AFgAOAB0ABwAOAOr/AAAOABYAJQD5/w4ADgAdACUALAAdACUAQgAWADMAFgAWADMAFgAdABYALAAWABYAJQAOABYADgAOADMAFgAWACUABwAOAA4AFgAHAAAA+f8AAPL/8v8HANv/4//5/wAA6v8AAPL/+f8AAPL/FgDy/x0AHQAsACwAHQAsAAAAFgD5/yUAAAAdADsABwAzAA4ADgAOAB0ADgAdABYAHQAWAA4ALAD5/zsAJQAdACUA+f8WAPn/AADq/wcAHQAWAB0AHQAlAB0AHQAsAB0ADgAsABYAFgAdAAAA8v8OABYAAAAdACUAJQAWABYAFgAWAA4A6v8OAB0AJQAdACUAFgAWAA4A8v8OAAAADgAWAA4AHQD5/wAADgAWAAcADgAOAAAAJQDq/wAALADy/wcADgD5//n/2//q/w4A6v8OAAcA8v8OAPn/FgD5/wcADgAAAA4AAAAWAPL/FgAWABYAFgAHAB0ADgAOAPL/8v/5/9v/6v8AAOr/+f/5/+r/8v/y//L/zf/y/77/vv/y/9v/6v/j//n/zf/b/9T/1P++/83/6v+Z//n/xf/5/wAA2/8WAK//DgDF/8X/6v+n/+r/1P/j/9v/BwDj//n/BwDb/wcAzf/q/9T/xf/y/9v/xf/N/+P/vv/q/+r/4//q/+r/BwDj/wAA8v/5/w4AAAAAAAAA+f8HAPL/8v8WAPL/BwDq/xYAMwAHACwA+f8OAB0AFgAlAAAADgD5//n/8v8HAB0A8v/5/xYA+f8HABYAJQAWAAAAHQD5/wcADgAOAA4AFgAlAAcALAAlACUALAAzABYADgBCABYASgA7AB0AOwAdACUASgAdAB0AMwAOADsALAAdAEIABwAAACUADgAHAAcABwAHAOr/DgAlAB0AJQAdACUABwAWAA4AHQAWAA4AFgD5/w4ABwAWAOr/BwAWAOP/FgDy/w4A8v/b/w4A4/8AAAAA+f8AAAAAFgAzAB0ADgAsAAcAFgAWAB0ABwAAAB0A+f8OAPn/+f/q/+r/BwDy/wcA8v8OANT/4/8AAM3/DgDU//n/BwDU//n/zf/U/8X/zf/N/9v/+f/j//n/zf/5/+r/xf/j/77/6v/b/83/4//U/+P/2//j/wAA+f/b//n/6v/j//n/8v/5/+r/8v/y//n/+f8OAA4A6v8HANv/2//5/9v/AAAAANv/+f/5//L/BwDy/wAA6v/b//n/6v/b/+r/6v/j/83/1P/U/77/+f/N/+P/8v/F/8X/zf++/5n/tv+g/7b/vv/F/77/p//j/6f/2//b/7b/4//b/9v/1P/j/9T/DgAAAPn/6v/b//L/2//q//L/4//j//n/4//j/+r/4//U/9T/4/++/77/xf++/77/zf/N/9T/tv/U/+P/zf/b/9T/6v/F/9T/4//F/wcA4//y/w4A6v/q/+r/+f/b/+P/FgD5//L/HQAOAPn/FgAAAAcABwD5/x0ABwAWAA4AAAAOABYAFgAdAEIAAAAlABYA+f8zAB0ALAAlABYAFgAOABYADgAHAB0AJQAdAEoAFgAlAB0AFgAsAA4AOwAlAEoASgAlADMAHQAWAB0ALAAlADMAJQAzADsAFgAWABYAHQAOAB0AOwAdAB0AJQAsADsAHQAlAB0AHQAsACwAMwA7ADMAOwBKAA4ALAAsAA4ALAAOABYADgD5/w4AFgAdADMADgAlAEoAMwBCABYAHQAWAAcAAAAOAB0ABwAdAPL/DgAOAAcAJQAOACUAAAAHAPn/FgAWAOP/LAAOAOr/DgD5/+P/BwAWAA4AFgAHAPn/DgAHAAcADgAWAB0AAAAOAA4A1P/y//n/6v8AAPn/DgD5//L/+f/q/wAA+f8HAA4ABwAAAAAAAADy//n/BwAlAPn/FgAdAA4AFgD5/w4ABwD5//n/BwD5//L/BwD5/+r/8v8HAPL/+f/q/83/+f/q//n/8v/j/wcA4/8OAA4AAAAdAOP/FgD5//n/FgD5/xYA4/8HAOP/6v/q/9T/BwDF/9v/1P++/+r/xf++/9v/1P/y/+r/2//y/+P/BwD5//L/6v/b/9v/zf/F/9T/zf/U//n/tv/N//L/tv/5/wAAzf8OAB0A+f8WAA4AAAAAAAAABwAAABYAFgAHAAcA8v/5/wAA8v8OAA4AAAAHAPn/BwD5/wAABwAWACUADgAWABYAFgAWACUAJQAdABYAJQAWAPn/AADq//n/+f8AAPL/+f/5/+r/6v/y//L/+f8OAA4AJQAOAA4ADgAHAB0A1P8AAPn/1P/q//n/8v/q/wcA2//y/wAA8v8HAAAA8v/q/wAA+f8AAA4A8v8HACUAFgAlAA4ABwAdACUAMwAdABYADgAHAAcA8v8AAPn/6v8HAAAAAAAOAAcAFgAHAA4AJQAdABYAHQAWAPn/+f/y/+P/BwAOAA4AFgAWAPL/4/8HAPL/+f8HAAAADgAAAA4ADgD5//L/BwDy/wAABwAAACwADgAWAAcA+f8AAPL/+f/j/wcA+f/q/wcA8v/5/xYABwAAAPn/6v8HAAcAAAD5/xYAAADq/x0A8v8AABYABwAAAPn/AADy/+r/6v/5/+P/4//q/83/4//j/9v/4//y//n/4//j/9v/4//q//L/6v8HACwABwAOABYABwDy/wAAAADq/xYAAAAHAAAA+f8AAOP/DgAAAAAAAAAAAA4A6v/5//n/4//q/wcA8v8WACUABwAdAOr/FgAWAPn/FgAAAAcA8v/q//n/AAD5//n/+f/y//L/+f8OAAcA+f/y//L/1P/q//L/4/8WAA4A8v8dAAcA8v8HAAAAHQAWABYAHQAOAA4AFgA7ABYAFgAWAA4AOwAWAEIAJQAdADMAJQBRACUALAAlACUAQgAsAEIAMwA7ADsAOwBCADsAWQBCADsAMwBRAEoALAA7ADsAQgBCADsASgAzACwASgAsADsAQgBCADsAFgAsADMALAA7ACwAJQA7ADMAJQAdAB0ALAAdAAAAFgAzAB0AMwAdABYAOwAHAAAAHQAAAOr/DgAHAPn/HQAOAB0AJQAdACUAFgAHABYAFgAAAOP/JQBCAA4AWQA7AA4AJQAHABYABwD5/x0AFgD5//n/FgAOACUAFgAHACUA8v/5//n/+f8AAPn/FgDy/wAAHQD5//n/8v/b/wcA+f/j//n/tv/j/+P/4//5/9v/BwDU/9v/6v/j/+r/2/8HAPL/AADy/+P/+f/b/wcAFgAAAAAA6v/b//n/+f/j/+r/8v/5/9T/AAAOAOP/8v/j/+P/zf/j//L/vv/U/9T/2//q/+P/AAD5//n/HQAAAOr/2//F/77/tv/U/9v/4//j/9v/2//N/9v/4//U/8X/6v/U/77/6v/b/8X/xf/U/7b/zf/U/83/2//b/+r/zf/q/83/r//F/6//vv/U/83/r//U/7b/vv/N/77/6v/F/8X/4//N/7b/8v/j/9T/DgDy/+r/4//q/8X/2//5/+r/8v/U/9v/2//b/9T/BwDb/8X/AADj/wAA2//q/+r/2//5/77/+f/5/+P/8v/F/8X/zf/U/9v/1P/b/8X/xf/j/77/1P+2/6//4/+2/77/2//U/7b/4//b/8X/8v/N/9v/4//F/9T/zf/N/+r/1P/b/+r/2//y/+r/8v/5//L/8v8HAA4A8v8OAAAAFgAHAPL/FgAHAAcADgAsAAcADgAdACUAMwAHACUABwAOABYAFgAdABYAHQAAAB0ADgAdACwAJQAsABYAJQAzACUAHQAsACUAOwAlACwAQgAOABYADgDy/wcAFgAAADMAFgAdACwAHQBZADsAQgAsADMAJQAWACwAJQAzADMAQgAHAEIAUQAdAEoAHQAWAB0AHQAAACwAHQAHAEIAOwAzACUAMwAsACUALAAsACwAFgAlACwAAAAsAB0ABwAzAAcAJQAOACUALAD5/ywAFgAWADMALAAlADsALAAsADMAHQBKACwAHQAWABYADgAOACwAQgA7ACwAUQA7ADMASgBKADsAOwBCADsAQgAsAEoALAAsAEoAQgAsADMAOwAOABYAHQAlABYAJQAWABYAJQDq/wcA+f/q/+r/8v/q/+P/8v/F/9T/xf++/8X/zf/q/9T/1P/U/+r/8v/q/wAA+f/y/wAA4/8AAPL/zf/N/9T/2//N/+r/2//q//n/2/8HAPn/6v8AABYAAAD5/yUA6v/y/xYABwAlAAcAAAD5/+P/AAAAAPL/2//y/9T/2//q/9T/DgDy/wAAAAD5/wcAAAD5/wAAFgD5/x0AAAAAAAcA1P8AAPn/AAAAAPn/4//U/9v/r//j/9v/4//j/8X/1P++/7b/r/+v/77/tv/F/83/2//j/+P/1P++/+P/1P/b/9v/vv/5/83/xf8AAL7/1P/F/6//1P/F/83/2//b/6//1P/b/83/4//N//n/+f/b//L/6v/U/+r/8v/b/wcA1P/y/wAA1P/y/+P/+f/b/+r/+f/q/wAA2//5/+P/1P/y//n/8v8AAA4AAAAHAPL/2//q//n/8v/y//n/FgAHAAAABwDq/wcA+f8WAA4ABwAdAPL/8v8HACwALAAdACwAMwAzACwAQgAzADMALAA7ADMALABZAEoAQgBZAEIAMwBKADsAMwA7ADMALAAlADMALAAsADMAMwA7ADMAHQAzACUALAAzADMASgAlADMAQgAlACUAMwAOACwALAAOADsADgAWABYAAAAAAB0AMwAAACwAJQAWABYALAAdAB0AMwAHAA4A6v/5/+P/6v8AAM3/4//j/9T/vv/q/83/zf/b/83/xf/N/+r/xf/y/8X/zf/U/77/1P+n/83/vv/j//L/1P/j/9T/1P/F/8X/1P/q/9T/8v/b/8X/8v/j/9v/2//j/+r/6v++/83/1P++/6f/tv/F/4L/vv/N/8X/4//U/+r/8v/U/9v/8v++/8X/xf/U/+P/tv/q/9v/vv/j/+P/2//j/9v/4//b/8X/2//5/+r/xf/j/8X/tv/F/9T/4//F/9T/xf/N/9v/1P/j//n/AAD5/wAABwAHAAAABwAHAAcAAAAHAPL/DgD5/+r/FgDy/w4A+f/5/wAAAAAHAPn/FgDy/wAA8v8OAAcA6v8HAPn/BwD5/w4A8v8AAA4A+f8lAA4ABwAAAAAA4//j/+r/BwAWAAcALAAHAAcABwD5/wAADgAWAPn/+f8dAAcAFgAlAA4AJQAOADsAQgA7AEIAFgAzABYAJQAzADMAWQA7AFkALAAsADsALAA7AB0AMwBKACwAQgA7ADsAWQA7AEoAJQAsAEIADgBCACwADgAlAB0AJQAWACwAHQAdAB0ADgAlABYAFgAOABYADgD5/yUAMwAOABYAFgAWACwADgAzADsAHQBCAB0ALAAOACUAHQAAADsAFgAzAB0AHQAlAOr/DgAWAOr/BwAlAAcALAAdAA4AJQAHAA4AFgAHAB0AHQAzADMAJQBRAB0ALAAsAA4AMwA7ADMAJQBCADMAMwAAAB0AJQAHAEIA+f8zACUAAAAsAA4AHQAWABYAHQAzAA4AHQAOAAAAJQAWADsABwAWACwABwAHAPn/BwD5//L/AAAHAOr/DgAAAAAADgDq/yUADgAHAA4AFgAHAPL/JQAlAAAADgAzAPn/BwAOAAAA6v/y/x0A6v8OAPL/6v8HAPn/JQAOACUA6v8WADMA+f87ABYAHQAWAB0AMwAdAEoAMwA7ADMALAAsAA4AFgAdADMAUQA7ADsASgAsACwAHQAWAA4A6v8lAA4A+f8OABYABwAAAPL/+f8HANv/BwD5/9v/+f/q/wAA4//5//L/8v/y/9v/AADN/83/1P8AAPL/8v8lAPL/LAAWAAcADgD5/yUA+f8WAAcAFgAWAPn/JQDy/wAAAAAAAA4ABwAdAA4ADgAAAA4A6v/j/wcA+f/5//n/BwD5/wAADgD5//L/AAAOABYABwAOAPn/+f8AANT/AADq//L/FgD5/wcAAAAHAPn/BwAHAAcABwD5/x0ABwAWAA4ABwAHAA4A+f8AAB0A8v8OANT/8v/5/8X/AADb/+r/+f/y//L/6v/q/83/zf/N/+P/1P/q/wAA1P/y/+P/vv/b/9v/1P/U/83/zf/b/83/zf/F/9T/+f/F/9T/xf/U/+r/r//q/8X/tv/y/8X/2//b/8X/8v/U/8X/1P/U/9v/xf/j/+r/xf/b/9v/6v/q//n/8v/y/wAA+f/5/+P/8v/5/9T/6v8AANT/8v8OAOr/8v/N/+P/4/+2/+P/4/++/+P/8v/N/9T/2//F/77/tv+2/77/mf+2/9T/r//F/7b/p/++/6f/xf++/5H/vv+2/5H/r/+n/5n/xf++/6f/tv+Z/6f/mf90/7b/iv+Z/83/r//N/7b/p//N/8X/zf/y/9v/2//j/8X/6v/N/83/+f/b/9T/zf/N/9T/1P/U/9T/4//N/wcABwDj/w4A+f8dAAcA6v8HANv/8v/j/+P/8v/5/wcAAAAAAPL/DgAAAAcAHQAlADMABwAdAA4AAAAlAAAAAAAsACUADgAHAB0AJQAOAEIALAAOADMAHQAWABYAJQAWADMAQgAdACwAMwAHABYAFgAHADsAJQAsACwAJQAsAB0AHQAsADsAJQAsAAcAHQAsAA4AJQD5/ywADgAAADMADgAlAAAADgAdABYAFgAAAB0ABwAzAEIAHQA7ACUAFgAlAAcAAAAsAPn/AAAOAOr/DgAOACUABwAHAB0AFgAWAA4ADgAAAB0ABwAdAAAABwAWAMX/BwDq//L/+f8AAPn/6v8dAPL/BwD5/+r/8v8AAAcAHQAzAPn/JQAOAA4ADgAHABYAAAAlAAAADgAdAPn/AAD5//n/AAAAABYAHQAWAB0ADgAWAAAAAAAHAA4AHQAOACUAFgAlACwADgAdACwAHQAAACUAJQAWADMAHQAdAAcAFgAdACUALAAOAEIAHQAWACwAFgAdAAcAMwAWACUAJQAAACUA8v8HAAcAFgAAAAcADgDq/w4A4/8AAPL/2//5/+P/6v/5//L/6v/y/+r/AADy/wAAAAAHAB0AFgAzAPn/+f8HAPn/+f8dAPn/+f8lAA4AOwAOAB0AFgAAABYA6v/5/yUALAAOACwAAAAHAB0A+f8dAPn/6v/y//L/8v8AAAAAAAD5//L/BwDb/9v/8v/j/+P/4//q/wcAAAD5/yUAFgD5/w4AHQDy/wcADgAAAA4A8v8zAPn/DgAsAA4AMwD5/x0AFgAHAB0ABwAHAAcADgAOACUAJQAOAAcABwAOABYADgAOABYAAAAHABYADgAdAAAALAAsAA4AMwAWAA4AAADy/wAA4/8HAAAA8v8HAPn/HQDy/xYAJQDq/x0ABwAHAAAABwAHAOr/HQAHAAAAAAD5//n/6v8HAAAA+f8HAAAA8v/5/wAAAAAWAA4ABwAOAPn/AAD5/+r/BwD5/yUAFgDy/zMADgAHAA4A4/8HAOr/8v8lABYAHQAHACwABwD5/zMA8v8HAAAA8v/y//L/FgD5/wcALAAdAAAADgAWAAAADgAdACUAHQAdAB0AFgAAAA4AHQAlAB0AAAAOABYAJQAWAA4ADgAHAPn/4//5/+P/8v8HAOr/8v/j/+r/BwAHAPL/DgAHANv/BwAOANT/8v/q/9T/8v/q//n/8v/5/wAA8v/q//L/+f/U//L/AADj/+P/1P/N/+P/zf/y/wAA6v/y/+r/8v/j/9v/4//q/+r/+f/j/7b/2//U/9T/2//b/9v/2//q//n/HQD5/wcA+f/q/w4A+f/y/wAA+f/q/wAA+f/5/wcA2//y/+P/4/8HANT/4//y/+r/6v8AAAAABwAOANT/6v/y/9v/+f/q/9v/zf/5//n/AAAsAAAA+f/5//n/+f/5//L/4//y/wcA8v/j/+P/1P/U/9v/6v/b/9v/2//j//L/zf/y/9T/4/8AANT/HQAAAOr/8v/j//n/2/8AAAAA+f8AAPL/8v/j/9T/6v/U/8X/AADb/9v/AADj/+r/+f/5/+P/AADy/+P/AADj//L/+f/j/+P/2//N/+r/xf/U/+r/xf/y/+P/8v/5/+P/6v/q/+P/6v/q/+r/AADj/wcADgD5/wcAAAAAAOP/+f/q/9T/BwDy/+P/+f/b//L/BwAAACUAHQAHAA4AFgDj/wcAAAAHAB0A1P8lAOr/8v8dAOP/JQD5/wcABwAAAA4A+f8dAA4AJQA7ADMAFgAdACUADgAHAAAAFgAWAAAA+f8AAAcA+f/5/w4AAADq/wcABwDU/+P/AADN//L/BwDj//L/BwDy/wAABwAAACUABwAOABYADgAdAA4ALAAzAB0ALAAsACwAOwAsACwALAAWACwALAAOAB0AMwAdACwALAAzADMAJQAlABYAHQAdABYAHQAsAAAAJQAzAB0AQgAHABYA8v/q/wcA6v8WAA4AHQAOABYA8v/j/wcAAAAlABYABwAAAPn/6v/q/wAABwAOAA4AHQD5/w4AAADy//n/BwAdAAAAHQAdABYABwD5/9v/8v8WAOr/HQAWAA4ADgDy/wAA6v8AAPn/8v8lAPn/BwAlAPL/+f8AAAAA8v/5/xYADgAAAPn/AADy/wcADgAAABYADgAdAA4AHQAOAPn/HQD5/x0AFgAHADMA+f8HAPn/8v8HAPn/DgAOABYA8v/q//n/4//j//n/+f/N/9v/AADq//n/6v/y//n/4/8OABYAAAAAAAAAAADU//n/+f/y/wcA+f/y/9T/6v/b/+r/2//j//n/1P8WAOP/8v/5/83/6v/q//L/AAAHAPL/DgD5//n/FgAHAAcA+f8WAAcADgAzADMAHQAlABYA+f8dABYAFgAWAAcAAAAOABYAHQBCABYA+f8AAAAAHQAdACwASgAlADsAJQAsACUABwA7AB0ALAAOABYAHQAAAAcA+f8OAAcAFgAAACUABwD5/xYA+f8dAA4AAADy//L/1P8AABYA+f8WAA4A8v8HAPn/8v8HAM3/AADU/9T/AADN/w4A4//b/9v/+f/q//n/FgDb/w4A+f8WAAcAHQAdAA4AJQAHABYA+f8dAAAA4/8HAB0ABwAHAB0A8v8AAAcAAAAHACUABwAWABYADgAlAPL/QgAWACUAMwAOACwADgAHAA4AJQAWADMAFgAlACUABwAdAAcADgAOADsADgAWAB0A6v8OAPn/AAD5/wAAFgAHAAcABwDq/wAADgAWAA4AAADy//L/AADb/wAAAADj//n/+f8HAOr/+f8WAA4ABwAHAOr/2//N/83/8v/b//n/4//b//n/6v/q//L/+f/5/wAA1P/5/wAA6v8AAPn/4//5/xYA8v/5/wcA+f/q//L/4//y//n/4//q//L/AADy/wcA6v8HAPL/1P/y/77/+f/b/9T/8v/b/9v/2//q/9v/6v/j/wAA8v/5/xYA4//5/+r/8v8AAOr/AAAAAOr/AADq/+r/DgD5//n/AADy//L/8v/y/w4A+f8OAB0ABwAAANv/AAAAAAcAJQAHAAAA8v/5//n/FgAlAAcAJQAHAAAAJQAWABYAAAAdAA4ABwAsAAAAJQAAACUAJQAAAB0A+f8AAOr/AADq/+r/6v/y/+P/4/8OANv/DgAAAAAABwAAAAcA4//q/9v/8v/b/+P/2//N/83/xf/b/83/8v/q/83/vv/b/7b/xf/F/7b/8v/b//n/8v/q/9T/1P/U/8X/1P/N/+P/1P8AAOP/zf/y/9v/6v8OAAAA+f8HAAcALAAAABYAAAAOAB0AHQBZAPn/LAAdAPn/DgAAABYABwAdAPn/DgD5/w4AHQDy/wcA2//j/wAA8v8WAPn/AAAlAM3/AADj/+r/JQDN/xYA+f/F/+r/1P/q/+r/1P8AANv/2/8dAOr/+f/q//L/DgAWACUAAADy//n/DgDy/w4ABwAAAA4AAADy/+r/LAAAAPn/BwD5/+r/DgAOAOr/DgDq/w4A8v/j/wAAAAAOAAcAJQAHAAAAAAAdAPn/+f8AANT/AADb/9v/4//b/9T/8v/j/wcADgDq/w4A8v8HAPL/BwAAAPL/JQDq/wAA4/8AAAcA4/8AAPn/8v/U/wcA+f/j/w4A8v/b//L/DgAOAA4AFgAWAA4AHQAlAB0AFgAlABYAAAAdAB0ADgAOAB0ASgA7AEoAOwAHAA4ADgAsAB0AOwA7AA4AMwAWAA4ADgAdADMAHQAsAB0ADgAAACUAHQAHAB0A+f8AAPL/6v/5//L/BwDq//L/FgD5//n/+f/y/9T/6v/U/83/8v/b/xYA6v/5/yUA+f8zAAcAAAAdAAAA8v8WAPL/+f8OAPL/OwAHAPL/FgAAAPn/6v8HAPL/AAAOAAAABwDq/wAADgAHAAcAAAAOAA4ABwAsABYADgAzAAcA+f8HAOr/8v/b//n/DgDy/xYA8v/5/w4A+f8AAAAADgAOAAAADgAlAAAAFgAlAB0ADgAAADMA8v8WACUABwAWABYAJQAAABYABwAAAAcAAAAlAA4AFgAlABYAJQAsAB0ALAAzACUABwAAABYAFgAdACwAHQAHAA4A4//5/wcAxf/5/+P/1P8HAAcA+f/y//L/+f/b/9T/BwDq/+P/+f/q/9T/8v8AANv/6v/q/83/1P/5/9v/+f/y/9v/8v/N//n/1P/q/w4A+f/y/wAADgDj/wAA8v/y//L/4//q/9v/4//q//L/4//y/+r/6v/q//L/AADj//L/2//q/+P/2/8AAPn/FgAAAPn/6v/y/9v/2//5/6//2//5/9T/+f/q/wcA4//q/wAA1P/5/9v/4//q//L/6v8AAA4A4/8zAAAADgAzAPn/OwAHABYAJQAAAB0ABwAWACUAFgAHAB0AAAAWACUABwAsABYALAAzABYAQgAOABYAHQAHACUADgAWABYADgAdACUABwDy/wcA+f8AAPn/BwDq/9T/AADb//L/8v/q/9T/4//q/77/8v++/+P/1P/N//n/zf/5/83/6v/y/9v/8v/q//L/8v8HAAAADgDq//L/AAAHAAcA+f8zAOP/FgAdAPL/MwD5/yUAHQAWACUABwAWAAcABwAdAAcAAAAzACUALAAsACUAHQAWAB0AAAAdAPn/HQAdAPn/JQDy/wAAAADq/x0ALAAWABYABwD5/x0AAAAWAA4A+f8HAAAAFgAWAB0AHQAOAOr/FgAlABYAOwAlACUAHQAsACUALAAsABYALAAWADMADgAOACwA8v8WAPn/+f8HAPL/+f/b/+r/2//U/9T/8v/j/83/6v/F/83/1P/U/+r/zf/b/8X/xf/N/8X/6v/q//L/6v/y/wAA2//U/+P/6v/q/9T/4//b/83/+f/q/+r/+f/y/wAA4//5//L/+f8WAOr/AADj//L/4//j/w4A2/8HAOr/4/8AAOr/AADq//L/8v/5//L/6v/5/+r/AAAOAPn/DgAdABYADgDy/x0A8v/y/w4A4/8lAPn/AAAAAOr/+f/5/wcA6v8AANv/8v/5/+r/4//N//L/2//j/wAAAADq/xYABwAWADsA6v8lAA4A2//y/w4AHQAHACwAHQAdAAAA8v8dAAAAFgBCACUAFgAlAAcAHQBRACwAHQAdAAAAFgAHAB0AMwAAAB0AHQAdACwAFgAOAB0ADgAHABYABwAOAB0AJQAdACUAJQAdAAcABwAOAB0AMwAHACUADgAHACUADgAWACUAOwAdADMABwAHACwAFgAWAPn/DgDy/xYAJQAWACwAAAAHAB0AHQAdACUAFgAdAAcAJQAzAB0AJQAOABYABwAHAOP/BwD5/9v/6v/N/wAA6v8HAPL/+f8HAPL/FgDy//L/1P/y/wcA6v8AACUAFgAHABYA8v8HAA4AAADy/xYAAAAAACUABwAzABYAAAAOAB0A8v8lAB0A+f87AAcAJQD5//n/HQD5//L/4/8AAAcAAAD5//n/4//U/8X/6v8HAOP/AAAAAOr/6v/5//L/AADy/+r/8v/b/wAA6v/y//L/4//j/+P/1P/F/+P/6v8AABYA8v8AAPn/2//5//n/AADq//L/AADF//L/6v/q/+P/4/8HAAcADgAOAA4ADgAsAA4AQgAOAOr/FgD5/x0A+f8zAA4A+f87ABYAFgAsABYADgAlAPn/FgAAAAAAFgAAAB0A8v8WAPn/DgAWAPL/HQAHAAcAAAAWACUABwAlAA4A4/8OAAAA8v8HAAAADgAAAPn/AAAHAAcA8v8AAA4A6v/5//n/8v8HAAAAAAAAAA4A+f8sABYA+f8zAAAALAAOAAAAJQAAAAAAAAAHAAAABwAHAAcAAAAAAPL/6v8AANv/6v/5/+r/DgAHABYADgDq/x0A4//y/xYA6v8OAOr/8v8HAPn/8v8AAAcA6v8OAPn/AAAHACUAJQAWACwABwAdAA4A8v8lAA4A6v8AAPn/DgAHAAcABwDq/wcA2//y/+r/4/8AAOP/6v/b/+P/6v/q//n/+f/j//L/2//q/9v/2//5/77/AADj/+P/8v+2/9v/p//N/+P/tv/b/+P/2//j/8X/1P/b/83/4//N/9v/1P/N/+r/6v/q/9v/6v/q/83/4//U/83/xf+2/9v/xf/q/8X/zf/j/77/+f/U/w4A6v/b/+P/vv/b/8X/AADF/+r/BwDy/wAAAAAlAPn/BwAOAA4ABwAWACUADgAOAPn/DgAOAPn/4/8AAPL/4/8HAPL/6v/y//n/+f8AABYADgDy/w4A8v/q/wAA8v8AAOP/6v/q/+r/8v/y//L/4//U/+r/HQDq//n/BwDj/9T/6v/j/9T/+f/5/w4A6v8HAAcA8v8dABYAHQD5/wAAAADb/+P/6v/j//n/+f8AACwADgAWACUAFgAOABYA+f/y/w4A4//q/w4A4//b/+r/AAAAAAAABwD5//n/+f8HAAcABwAOAOr/DgD5/+r/HQD5/wcAHQAlAA4ABwAWABYALAAWAAAAAAAHABYAHQAWAAcABwAAAAAA+f/y/w4ABwDy/wAAHQAWACUAMwAWAA4AHQAHAAcAHQAAAAcABwAOAA4A8v8dAPL/BwAHAOr/DgD5/x0ADgAWACUAFgAzACwALAAsACwAHQAlADMAQgAsADsAHQAdAEIAFgAsABYAHQA7AB0ALAAsABYAMwAsAB0AOwD5/ywAOwAlACwAJQA7AAAAHQAlAPn/BwAdAAcADgAlAAAAMwAdADsAOwAsADsALAAdAAcAFgDy/+r/BwDj/+P/DgD5//n/DgAWAPn/BwAdAPL/FgD5/w4A+f/5/xYA4/8AAOr/FgDq/wcAHQDq/xYA4/8AAOP/+f8WAAAAFgAWAA4AFgAOAPL/BwD5/w4ADgAOAA4ABwAWAB0AOwAHACwAHQAOACUAHQA7AB0ALAAlAB0ADgAsADsA8v8zAA4AAAAzAA4ALAAdAAcAAAAAAA4A6v8WACUAHQAWAA4ABwDq//n/+f/5//L/+f8AAAAABwAHAA4A+f/5/+r/+f/q//L/FgD5/wAA6v/5/83/8v8HANv/FgDF//L/+f++/wcA4//j//L/4//y//L/BwAAAOP/+f/U/83/2//b/+r/zf/F/+r/4//U/+r/1P/j/+r/zf/b/8X/2//j//n/AADb/xYAAADq/wcA4/8AANv/zf/5/+P/DgAdAAcAAADy/8X/1P8AAM3/+f/q/77/8v++/+P/+f/q/w4AAAAAAOP/2//5//n/6v/y//n/+f/j/9v/8v/b/+r/6v/U/+P/1P/j//n/+f/y/wAAAADU/+r/AAD5/yUAFgAAACUABwAAAAcAAADq/+r/8v/5//L/6v/j/83/6v/5/83/1P/q/83/zf/U/+r/8v/U/+P/6v/N/83/AADj/+P/6v+2/9v/zf/y//L/zf/j/9T/4//j/w4AAAAHAAAA2//5/+P/BwDj/9v/8v/N/+r/2//N/+P/2//U/+r/8v/y/9v/+f/b/9T/+f/j//L/4//b/+r/1P/U//L/1P/j/wcA2//b//L/6v/q/xYA+f/y/wcA+f/y/+r/BwD5//n/BwAOAAAA+f8HAOr/+f8AAAAADgAHAAAAFgAdAB0ALAAlABYA+f8HABYAHQAsAB0AJQAlABYAHQAdAA4AFgAOADsAMwAsAEIAMwAlACwAOwAOACUAFgAzAA4A+f87AAcAMwAlAEIAHQAWADsAFgAzAAcAHQAOAA4AJQAsADMALABCACwAQgAsADsAOwBCAFEAFgAlACUAJQAWAEIASgAsADsAQgBZAEoAWQBnADsAOwBZAEIAUQA7ADsASgAlAEIAOwAzADsAMwAsACwAQgAdAB0AMwAzACwAOwAsABYAHQAdAB0AFgAlADsAJQAsADsADgAOACUADgAOABYA8v/y/w4ADgAlAPn/AAAOAPL/JQAWACUAJQAdAA4AFgAWABYAQgDy/xYAJQAOACwAOwA7AAAAFgAlAB0AFgAWABYAAAAAAAAA6v8AABYA4/8HAAcA6v/y/+r/AADj//L/+f/y//n/4//5/+P/6v8AANv/6v/q/83/2//N/+r/xf/U/9v/xf/y/8X/2/++/9v/2/+n/+r/2//q/8X/6v/b/9T/+f/b//n/xf/q//n/2//y//L/+f/y//n/AAAWAPL/+f8HAOr/8v/q/wAA+f8HAPn/AAAAANv/AADy/wAADgD5/wcAAAAHAAcABwAWAPn/AADy/+P/+f/q/wcABwDb//L/2//j/w4AAAAdAB0AHQAdAPL/BwDq/+r/AADq/+r/zf/5/+r/8v8HAOP/6v/q/9T/8v/q/9v/6v/b/+r/4//y/w4A4//y//n/8v/y/w4AFgAHAB0ADgAWAPn/DgAAAPL/4//U/+r/xf/5//L/+f/5/+P/4/+v//L/4//j//n/4//q/83/4//j//L/8v/F/+r/1P/N/+P/1P/j/83/2//q/9v/zf/y/wAA1P8HAPn/8v8AAOP/4//U//L/vv/b/+P/4//y/77/6v/N//L/6v/U/+P/zf/5/+P/AADb/+P/8v/b//L/xf/y/+r/+f/q/9v/DgDy/wcADgD5/+r/6v/U/+P/8v/j/wAA4//y//n/+f8dABYAJQAOAB0AHQDq//L/6v/q//L/1P/y/+r/2//5/+r/6v8AAAcAAADq/+r/4//b/9T/1P/j/9T/1P/j/9T/2//F/9T/zf/y/9v/r//5/9v/4//y//L/DgDj//L/+f/N/9T/xf/N/9T/p//F/8X/tv/b/77/xf/F/77/r/+2/7b/xf++/9T/+f++/wAABwD5/+r/8v8AAM3/BwAAAAAA8v8OABYA8v8lAPL/AAD5//n/BwDy//n/4//q//L/BwAHACUAHQAAAB0AHQAAAAcAHQAAAA4AAAD5/w4AAAAWABYADgAdABYAFgAWAPn/DgAzACUALABCAA4AHQA7APn/JQAdADsAOwAzAEIAHQBCADMASgBRADMAUQBKACwAOwBRAB0AUQAlACwAUQAdAEoALAAzAEIAMwAzAB0AOwAzACwAOwAzACwASgBKAEIAOwBKAGAAOwA7AEIALAA7AEoAQgAzACwAQgAdAB0ASgAOADMASgAHACwALAAOACUAFgAlAB0AJQBRAB0AUQA7ADMAUQA7AFkAMwAsAA4ALAAdAEoASgAHAEoADgA7ADsAQgAsAA4AUQAWAEIAOwA7ACwADgAzAB0AAAAWACUAHQAdABYALAD5/w4AJQDy/wcA4//q/9v/FgAHAAAAFgDy/wAA6v8HAPL/BwD5/+P/+f++/+r/6v/U/9v/2//N/83/zf+2/8X/vv/F/9T/r/+v/77/p/+v/77/tv+2/77/r/++/8X/vv/j/77/xf/U/+r/6v/U/+P/1P/b/83/6v/N/9v/+f/b/9v/zf/y/83/2//q/9v/DgDy/wcADgAHABYA8v/y/+P/6v/y//L/DgDy//n/8v/j/+r/xf8HAOP/AAAOAOP/LADy/w4ADgD5/w4ABwAlAA4AFgAWAA4ABwDy/wAABwDy/x0AFgAOACUAAAAWAPn/8v8HABYA8v8AACwADgAdAB0AOwAWAA4ALAAOACUA8v/5//n/4/8AAPn/8v/5/wcA6v8WAAcA6v8OAOP/BwDy//L/FgDq/xYA+f/y/wcA6v8OAPL/4/8AAPL/6v/q/9v/1P/y/+P/6v8OAPL/4/8AAOP/zf/j/+r/8v/b/+r/AAAAAPn/+f/y/+P/6v/y/wAA+f8OAPL/4/8lAPn/DgAzAAcALABCABYAJQAzACUAMwA7ACwAJQAOAAAAJQAsACUAFgAWADMAAAAdABYA2/8AAPL/4//5//L/AAAOAPL/FgAAAPn/AAAAACwA8v8HAAAA4/8AABYADgDj/w4A8v/b//L/4//U/9v/6v8AAAcA1P/y//L/xf/q/+r/xf/j/+r/zf/j/9T/1P/5/+r/4//q/+P/2//j//L/2//U/+P/1P/j/83/zf/U/+P/6v/q//n/2/8AAPL/8v8HAPL/AAAAAPn/+f8HAOr/+f/q//L/BwDj//L/4//y/wcAAAAdACwAFgAlADMALABCADMAHQAdAAAA+f87AA4AAAAdAAAAJQAAABYALAAHACUAJQAWADMALAAWAB0AAAAHAAcAAAAOAAAAAAAOACUADgAOADMALAAdACwAHQAOADsALAAsACUABwAWACUAFgAdAB0ABwAdAA4ADgAAAPn/AADq//n/+f8WABYAFgAWAA4ABwDy/x0A6v8HAPn/2/8dAM3/8v/y//L/AADU/w4A6v/q//L/2//5/+r/4//b/+r/AADj/w4AFgAAAB0ABwAWAAAADgAAAOP/FgDy/wAA6v8HAA4AAAAlAPn/DgAAABYAFgAOAA4AFgAdAB0ADgAOACUA8v8OAPn/BwAAAB0AHQAHAFEA+f87ACUAFgAzAA4AOwAHACwABwAOACUABwD5/wAAFgAWADMAFgAWAAcAAAAAABYADgDy/yUADgAOAB0AOwAlADMALAAHACUAFgAWAAcAFgAAAAcAAADj/wAA6v8AAAcA8v/5/w4ADgDy/wAABwAAAOP/+f8dAOr/6v8HAOP/8v/5/+r/DgAHAAAABwDj//L/BwAHAAAABwAHAPL/8v/q/wcA+f8OAA4ABwA7AAcADgAOAAAA+f/y/wAABwAWABYABwDj/w4A1P/b/wAA1P/y/+r/+f/j/+r/4//y/9v/4//N/8X/8v++/9v/1P/q//L/8v8AAAAADgD5/wAAzf8AANv/8v8AAMX/DgDj//L/6v/j/9T/xf/F/9T/8v/N//L/6v/b//L/1P/N//L/4//5/+P/zf/y/9v/4//N/+P/4//b/+r/6v/j//L/+f/j/xYA4//5/wcA4/8OAA4A8v/5//L/1P8HAOP/4//y/+P/AAD5/wcAAAAHABYABwDj/wcAAADq/wcAAAD5/wAA+f8AABYA4/8dAAAA8v8lAAcAMwAdAB0AOwAsACUAFgAWABYA+f8dABYABwA7AB0AHQAWAB0ABwAdADMAFgAlAAcAOwAAACUAOwDq/yUAFgAOAAAABwDy/+r/+f/j/wcA8v8AAB0A8v8OAPn/6v8AAOr/+f/j/w4A+f/q/xYA6v8HAPn/FgAOAPn/BwAAAAAA8v/y/+P/6v/U/+r/+f/5/w4A+f8AAA4A8v8OAA4A6v8lAA4ADgAHAA4ADgD5/xYA8v8OAAcABwAWACUABwAHACUA2//y/+r/6v/U/9v/1P/U//L/2/8AANT/6v/j/9T/4//q/9v/1P/y/77/4//q/6//zf/U/6f/4//U/83/6v/b//L/zf8HANv/2//j/77/AADN//L/+f/b//n/2//j/+r/6v/5/+P/BwDy/+r/DgDy/xYA8v8HAPL/+f8lAOP/HQAOAPn/BwAsADMAJQAdAA4ALAAAAEIAHQAAACwA+f/5//n/+f8AAAAA6v/b/+P/8v/U/+r/6v/b//L/8v/q//L/HQAAACwAFgD5/w4A2//q//L/+f8OACUAAAAsACUAFgAlAA4ASgAWABYALAAWAAcAFgAdABYAHQAOACwAFgAdABYAFgAzACUALAAWAAcABwAWAA4ADgAlAPL/AAAdAAAAAAAAAAcABwDq/+P/BwDb/9T/BwDj/wAAAAD5//L/4//5/9v/4//y//n/6v/5/wcA+f/q/wAABwDN/x0A4//j/wAA6v/y/9T/AADj/yUAAAAAADMA+f8sAA4ABwAWABYAFgAsAB0AFgAsAB0AHQAWABYABwAOAAcAHQDy/xYAFgDq/yUABwAsACUAOwAdAB0ALAD5/xYAHQAWAAAAJQDy/w4AMwAsAEoAMwA7AAcAJQAOAA4AHQAsACwAAAAlAAcAMwAWACwASgAlACUAJQBCAA4ALAAdABYAFgAAAEoAHQAlADMAHQAdAB0AHQAWABYADgAdACUALAA7ADsAFgAWAA4A+f8zAAcADgAdACUAMwAAAB0ABwAlAB0ABwAdAB0AQgAAAEIAHQAHAEIAAAA7ABYAMwAsAOr/MwD5/x0AMwDy/wAA6v8AAAAADgBCAAcADgDy//L/AAD5/x0AFgAOAPn/JQAOABYAOwAHACUAMwAzAA4AFgAWAA4ADgDq/wAA8v/q//L/DgAHAOr/FgAlAAAA8v8AAPL/8v/q/9v/2//j/9T/2//y//n/4//j/wAAxf/F/9v/xf++/6f/xf+2/7b/vv+v/9v/vv/U/+P/zf++/5H/xf/N/8X/2//N/83/xf/U/+P/1P/j/+r/xf/N/77/vv/5/9T/+f8HAAAAAADj//L/1P/q/+P/4//y/9v/+f/b/9T/+f/j/83/8v/y/9v/AADb/83/zf/F/9T/1P/q/+r/6v/b/83/zf/F/83/xf++/83/zf++/+r/+f/b/+P/8v/y/83/xf/j/83/2//j/9T/2//b/9T/1P/b//L/BwAAAPL/AADq/+r/DgDy//L/BwDy//n/AADy/w4AFgD5/wAA+f/5/wcAAADy/wAABwAWAAcA8v8OAAcAFgAHAPn/BwD5/xYABwAHAAAADgAOAPL/MwAOABYABwDy/x0ABwD5//n/+f/y/wcA+f8AACwA8v8HAB0A+f8dABYABwAHAPn/8v/5/xYADgAAAAcA+f/5/wAA8v/5/+P/4/8AANT/6v8HAPL/AADy/wcAHQAAAAAADgAWAPn/BwAdAOr/AAAHAPL/+f8AAA4A4//y/x0A6v8WACwADgAdAPn/BwAAAAAAHQAHAB0A+f8OACUABwAsACUAJQAsADsAHQAOACwALAAzABYAHQAsAA4AHQA7ADsALAAzADMADgAsAB0AFgAlAPn/DgAAAA4ADgAdAA4A+f8lAA4AFgAHAPn/FgAAAPL/DgD5/w4ADgDU//n/4//5/+P/2//5/7b/4/8AAOr/8v8AAOr/2//F/+P/4//N//n/zf/b/7b/1P/q/+P/4//F/9T/xf8AAOr/AAAHAAAAHQAOAB0AAAAlAA4AFgAWAA4AHQAdADsALAAsABYAJQAOAAAADgAHAPn/+f8OAPn/JQAWABYAFgAHAB0ADgAzACUAJQAHAAAAHQAHACUAHQAdAA4A8v8dAAcABwAsAAAAAAAAAPn/FgDq/wcAHQDj//n/DgAOABYABwAOAA4ADgAOAA4ABwAAABYAAAAAAAcA+f8AAOP/zf/j/+P/2//j//n/6v/q//L/6v8AANT/8v8HAOr/BwAHAAAA+f8HAOP/+f8WAAAAAAAOACwAAAAAAA4A6v/b/x0ABwDq/xYA6v8OAPL/FgAdAPn/MwAOAAcADgAHABYADgAAAA4ADgAOACUAJQAlABYAAADq//n/1P/y//n/4/8AAOr/BwAHAPL/8v/5/+r/HQAOAOr/DgD5/wcABwAWAAcAFgAOAA4AJQAHADMAFgAdACUAMwA7AB0AJQAdADMABwAWAAAABwAWABYADgAHABYA6v8OAAAADgAdAAAABwAOAPL/4/8OAPn/6v/b//n/4//b/xYA4//q/9v/4//y/+r/8v/F/wAA8v/j//L/vv/U/77/1P/j/83/AADj/+r/2//j/9v/zf/5/6f/zf/N/8X/2//j//L/xf/5/83/zf/5/9T/AADy/+r/6v/b//n/8v8AAAAA8v8zAOr/+f8OANv/FgDj/wAABwDq/wcAAAAWAPn/BwDj//L/DgAAAB0ABwAlAAcABwAdAOr/FgAHAA4AHQAAACUADgAHAAAABwAWAAAAJQAWAAcA4/8HAB0Azf8HAPn/8v8HAOr/8v/j//L/4//j/+r/2/8OAOP/AAD5/9T/BwDj//L/8v/b/wcAAAD5/yUAJQAHAA4ADgAOAAAABwAAAA4AFgAAAB0AAAAAAAcAJQAzAB0ADgAHAPn/AAAsAAcAMwA7AB0AHQAWACwAAAAsACUAFgA7ABYABwAdAB0AAAAOAA4ADgAlACwAHQAlAAcAAAAsAAAAHQA7AA4AHQAzAAcABwAOAPL/JQAWAA4AOwAHACwAOwAHAEIALAAsADMA8v8HAPn/FgAOAA4AJQD5/xYAFgAOAAAADgAAAAcALAAzAEIAMwBCACUAHQAOAB0ADgD5/yUA8v8AAPn/DgAWAPL/DgAOAA4A8v8AAPL/AAD5//L/BwDF/wAAAAD5/xYA6v8OAOP/8v8OANT/+f/b/9T/1P/F/wAA1P/5//L/1P/y/+r/6v+2/+r/4//F//L/4//5//n/BwAAAPL/BwDy/wAABwD5/x0AAAAOAB0A6v8OAAAA+f8HAAcAHQD5/w4AFgAHAB0ADgAdABYAAAAOAPL/6v/q/wcABwDq/w4A6v8AABYA4/8OAOr/8v8OAPL/HQAOADMALAAOACUAHQAsAAAADgAAAOP/DgAHAPL/BwD5//n/DgDq/xYA+f/y/xYA4/8WAPn/BwD5//n/DgD5/ywA8v8dACUABwAsABYADgAAAAcABwDy/9v/+f/b/9T/BwAAAPL/8v8OAOP/6v8AAOr/4//b//L/+f8HAAcAOwAHAAcADgDy/wAA6v8dAAAAAAD5/+P/+f8AAAAA4/8dAOP/6v/y/+P/BwDq/w4A4//5/+P/4//y/+P/AADj/wAA8v8WAAcA6v8HAPL/+f/b/w4ADgDq/+r/8v/y/9T/BwAHAAAA+f/j/+r/4//j/+r/4//y//L/+f8AAOP/4//U/9v/xf/b/9T/vv/j/83/4//F/+P/zf++/9v/vv/y/8X/6v/q/9T/2//b/wcAxf8HAOr/xf/U/83/AAD5//n/+f/5//n/+f/U/9v/zf/F/9T/zf8AANv/+f/q/83/+f/j/xYADgAOAB0A8v/5/+r/4//y/+r/DgAdAAcAHQAOAAAA6v/y/wAA2/8AAAAA6v/5/wcAAAAAAAcADgAOACUAHQAHACwAAAAOAAAA1P8WAAAA+f/j/+P/8v/y/+r/8v8HAPn/AADq//n/+f/y/wAAAAAdAOr/BwAOAAcAMwAAAA4AFgDy/wAAFgAHAA4A+f/j/+r/4//5/+P/8v/5/+r/6v/j/+r/zf8AAPn/8v8lAPL/HQAzAAcAHQAdAA4AHQAdAA4ALAAAAPL/DgDq/x0ADgD5/x0A+f8OAAcAAAAOAPL/+f8HAPn/FgA7ABYAFgAHAAcAJQAdABYAJQAsAAAABwAWAA4ADgAWADMAHQAdACwAFgAdAAcA+f8HAOr/DgAsAA4AHQAAABYAAAD5/yUAAAAAAAAA+f/y/wAA8v8OAB0ABwAsABYAAAAHABYAAAAAABYABwAAAAcAHQDj/w4A+f8AADsABwAzAA4ADgAWAPL/HQAHAA4ABwAAAAcADgAOABYAHQAAABYAAADq/w4ADgAAAPn/+f/y//L/zf/b/+r/1P/5/wAABwD5/83/AADq/9T/+f/y/wAA4//y/+P/zf/5/wAABwDj/x0A+f/q/wcAzf8AANv/AAAHANv/+f/y/w4A6v/q/wAA8v/q//L/+f/y//n/BwAOAPn/HQAHANT/AADj/+r/BwAAAPL/+f/5/9v/BwD5/+P/+f/5/wAA4//y/wAAAAAHAPn/BwDy//L/AADb/+r/+f/5/wAA+f8dAAcAAAAOAA4ADgDy/w4ADgAHABYAHQAdAAAAJQAsACUALABCADMAJQA7AAAAHQAlABYALAAOACUAHQAHAOP/AAAdABYAFgA7ADMAAAAWAA4ABwAHABYAHQAHAB0A+f8AACUAHQAWABYA8v/5/w4A8v8WAAcA+f/5/w4AHQAHAAcA6v/5//L/BwAOAAcAOwAlACwALAAlAB0ADgAdABYAAAAAABYAJQAlACUALAAWABYAHQAWACwAFgAHABYAHQAAAAAAHQDj/x0ADgDq/xYA8v/5//n/HQDy/+r/FgDy/xYABwAHAPn/8v8WAAcAFgAHAAcADgDj/wcAFgDb/wcA+f/q/wcA4//5/wAA6v/5/wcA4//b/wAA6v/q//n/6v/q//L/6v8AAOr/6v/5/w4ADgAdAB0AAAAdAPL/BwAWAPn/DgAOAPL/6v8OAPn/LAAHAPn/FgD5/w4ABwAWAPL/AADy//L/BwD5/wAABwAlANT/AAD5/9v/4//N/9T/zf/y/8X/8v/U/9T/+f/N//L/8v/5/9v/BwAOAAAADgD5/wcA+f8HAAAA8v/y/+P/BwAAAPn/BwAAAAcA6v8OAB0A4/8AAOP/2//q/wAAFgAHACwADgAOACUAFgAlAA4ADgAlAB0ADgAzACwAFgAzAB0AMwAlAAcAMwAHAAAADgAAABYAHQAzABYAFgAdAPn/FgAWAA4AFgAHABYA4//5/w4ABwAzAAcADgAAAAAAHQAWADsAFgAlABYAFgAdAAcABwAHABYAFgAAAPL/JQD5//n/DgDy/w4ABwAHAB0ABwDq/w4A8v8AAAAABwAWAOP/HQDN//L/+f/b/x0A6v8dAAAAAAAAAOr/4//q/83/vv/q/9T/AAAHAPL/2/8HAPn/zf/q/83/2//N/+P/1P/b/+r/xf/5//L/4//q/9T/zf/U/+P/4//q//L/4//5/w4ABwD5//L/BwDq/w4A+f/q//L/2//b/9T/4//j//n/8v8dAAcADgAsAAcADgAdABYA2/8sAPL/FgAsAPL/LADj/xYA8v8HAPn/6v8HANT/AADb/wcAzf/b/+r/6v/5/9T/4/+v//L/2//b//n/zf/b/+r/2//j/+r/8v8AAPL/8v/q//L/6v/5/+r/4//5/9v/+f/5//L/+f8AAPL/+f/N/+P/DgDF/wcA6v/j/+r/1P/j/9T/6v/j//L/8v8AAOr/+f8AAOr/JQAHAAAAJQAHAA4AAAD5/ywA+f8lAA4A+f8dAOr/JQD5/w4ADgD5//L/1P8AAOr/AAAHAAcAAADy//L/+f8AAPL/+f/5/w4ADgAdAA4AHQD5/wAAFgDq/ywA+f8HAAcABwAAAOr/JQDy/w4AAAAWACwAFgAsACUAFgAHABYAFgD5/wcADgDq/wAA6v8HAOr/+f8lANv/DgDU//n/AADj/yUA4//5//L/AADb/8X/AADU//L/+f/5/+r/6v8HAOr/+f/q//L/4//b/w4A1P/b//L/tv/j/+r/2//y//L/4/++/+P/+f/y//n/+f8OAOP/4/8HAAcAAADN/+r/4//j/wAA6v/q/9T/FgAHABYAOwAAAAcAAAAOAPn/DgAWAA4ADgD5/yUA+f/5/w4A6v/5/+P/8v/5/+r/8v/y//n/6v/j/wAA6v/N/+r/1P/b//L/4/8lAAAABwAdAOr/BwAAAAAA4/8HAA4A6v8HAPL/AAAHAA4AFgDy/+P/AAD5/+P/DgAAAAcA6v8HAAcA8v8dAPn/+f8AAAcA+f8AAAcA+f/q//n/FgD5/wcA+f/5/+P/AAAOAOP/DgD5/wcAFgAWAPn/+f8dAOr/BwAOAA4ABwAdACUA8v8OAAcA+f8OAPn/FgAsAAcAMwAHAPL/HQDy/w4A+f8WADMAFgBCAB0ALAAlABYALAAlADMAJQAzAB0ADgAlAEoAQgAdAEoAMwAdAA4AFgAOAAAAFgAdACUA8v8AAAcADgAAAAcALAAAAA4AHQAdAA4ADgAHAAAALAAHAAAAJQAWACUAJQAHABYAFgAdAB0AHQAsAEIASgA7ACwADgAzACUABwAdAPn/AAAOAAcABwAlACwABwAsADMABwAHAB0AJQAdAAcADgAHAA4AHQAWABYADgAOABYAOwAOAA4AMwAAAAcAJQAHAPn/HQAOAA4ADgAWAA4A8v8AAAcADgAAAB0AFgAOAAcA8v8HAOP/6v/y/w4ABwAHABYAAAAWAAAAFgAOAAcAHQAWAA4AFgAWAA4ADgDy/wcAAAAHADMAFgAAAB0AAAD5/x0AAAAHAOr/6v8OAOr/+f8HAAAAAAAHAAAAAADq/wAAAADj//n/8v8HAOr/+f8HAPn/AADq//n/8v/j/9v/2//U/+P/+f/5/wAA4//5//L/+f/5/+r/DgDy/9v/AAD5/9v/AAAAANv/8v/y//n/AADy//n/FgD5/+r/AAD5/wcABwAdABYAFgAdAA4A8v/b//L/4//y//n/AAAHAOr/AADy/+P/+f/y/+r/BwAAAAcAFgDq/wAADgD5/xYADgDj/+r/4//q/+r/2/8OAPn/8v8HAPL/DgD5//n/BwD5/w4A+f8AABYA4/8HAAAA+f8WAPL/BwD5/+r/AADy/wAA6v/b//n/4//j/wcAFgAAAA4AHQDb/wAA+f/y//n/2/8WAPn/AAAWAA4AFgAOAA4A+f8HAAcABwAAAPL/6v/5//n/6v8HAAcAHQAHAPn/6v/y/wAAAAAOAPn/MwD5/wcAFgDq/yUA8v8AAA4ADgAWAAcADgD5//n/6v/y/+r/8v8AAAAABwAdAB0ABwAOAPn/DgAdACUAJQAsACwADgAWAA4AFgAlAB0AJQAsABYAHQAsAA4ADgAHAPn/2//y//L/2//5/+r/+f8HABYABwAHAB0ABwAAAPL/AADy//L/DgAHAPn/+f8HAAcA6v8AACUA8v/5/9v/zf/y/+r/AAAAAA4A2//y/+r/zf8AAL7/+f/q/9v/AADq/83/xf/5/83/6v8AANT/AADb/77/8v/U/9T/4//N/+P/zf/U/83/zf/F/9v/2//F/+P/r//q/9v/6v8WAMX/2//N/83/tv+2/7b/tv/N/83/2//U/83/1P/b/77/6v/b/+r/2/+n//L/tv/N//n/6v/5//L/BwDy//L/AAAWAOP/4//q/+P/8v/j/wAA+f8OAAcA+f8AAPn/BwAWAAAA4/8HABYA8v8OAAcA+f/q//n/DgDb//n/+f/y/wcA2//y//L/+f/q/xYAJQDq/ywA+f8AACUAAAAOAPn/AAAHAA4A8v8OABYAAAAdAA4AFgAWAPL/BwAWAOr/DgAWAPL/FgAdAB0AHQAOAAcADgAAAB0AJQAOADMAFgAdAA4ABwAdABYAHQAzACUABwAzABYAMwAzABYAQgAsAB0AFgAWAAAABwAHAAAAHQD5/x0AAADy/yUAAAAHAB0AHQAHAAAAHQAAAA4AMwD5/wcADgAAACUAFgAlAA4AJQAHAOr/HQD5/xYALAAlADMAJQAdABYAJQAdAA4AJQAHAPL/DgAOAB0ADgAWAB0AAAAlAEIAMwAWABYAAAAAAAAA8v/y//n/8v/y//L/1P8HAPn/8v8AAPL/HQDy//L/DgAAAPn/4//j//n/BwD5//n/8v8AAOr/8v8AAPL/8v/y//n/8v8HAAAA+f/q/9v/xf/b//L/8v/y/wAA8v/j/w4A2/8AABYA4/8dAA4ADgAOAAcA+f/5/wcAFgAHAPn/MwD5//n/DgAAAA4A+f8OAB0ABwDy/wcADgAHABYADgAHAA4AOwAHACUALAAOACwAFgBKABYAMwBRAAcAOwAdACwAFgAWACUABwAWAAAAMwAHAA4AFgAAAB0A4/8dAPn/+f8WAA4ADgDj/x0A+f/5/wcA+f/5//n/BwDb//L/6v/5//n/DgAHAPL/AADU//L/1P/b/9v/2/8HAOP/6v/5/wcABwAdAAcABwAAAOP/HQAAABYAFgDy//n/6v/q/+r/BwAWAA4ADgAlAAcAHQAzABYAJQAOAB0AFgAdACwADgAdAPL/FgAOAAcAQgAOACwAFgAOADMABwAsAAcAJQAzAAAAOwAlAB0AHQAlACwAFgAdAB0ADgAHABYA8v/q/wAA+f/5/wcAFgDq//n/AADy//L/8v/y/+r/FgAdAA4ABwAdAA4A6v8AAPL/DgAdAAcABwDj/wAABwD5/wAA6v8OAAAAAAAWAPn/DgDy//n/+f/j/wcADgAOAAAAFgDj/+r/6v/j/wAA4//q/83/2//j/9v/2//N/77/1P/q/9v/BwDj//n/BwDj/+P/AAAAAM3/AADj/+P/6v/5/wAA2//5/9v/1P/j/+P/xf/j/+P/2//U/8X/+f/N//L/6v/y/+r/zf8AAMX/4//5/83/2//N/9T/2//N/9v/4//U/+P/1P/b/9v/zf/b/77/vv/j/8X/2//q/9T/+f/F/83/xf+v/83/vv/N/9v/1P++/+r/1P/U//n/4/8HANv/4/8HAAcAAADy//L/2/8AAOr/1P/q//L/2//y//L/4/8AAOP/AAD5/wcAFgD5/xYA6v8HAA4A+f8OAPn/BwAHAPn/DgAHAAcAJQAHAAAABwDb/+r/AAD5//n/DgAOAPn/8v8WAAcA8v8OAAAAFgAOABYAHQAAAA4ABwAWAPn/+f8HAAAABwAHAAcA6v8OAA4A6v/y//n/AAAAAPn/DgAdAB0ALAAdAB0AAAAAAAAA+f8dAAAAJQDy/wAALAAHACUA+f8dAA4ALAAlAAcAWQAWACwAWQAdACwAOwAzAEoAHQAsAEoAAAA7ADsAHQAzADMALAAsABYABwAdAAcADgAAAAAADgAAAB0AFgAWAPn/+f8AAAcA8v/y/xYAAAAOABYAAADU//L/BwD5/xYAFgAOAA4AAAAOACUABwAOAB0A+f8AAA4AFgAOABYAAAAOAA4A+f8dABYABwAAABYAAAAOAAcAAAAlAAAADgAHAAcADgD5/w4AHQAHAAcADgAHAA4ABwAWAPL/DgAWAOr/+f/q/+r/2//j/83/8v/5//n/FgDU/wAA+f/5/w4A6v8OAPL/6v/5//L/6v/b/+r/4//y//n/4/8WANv/4//y/8X/FgDj//n/FgDU/9v/+f/5/+r/HQDq/w4ADgDy/x0A4/8AAOr/+f8AANv/+f/q//n/AADb/9v/6v/F/9T/2//b/+r/4/8AAPL/8v8AAAcA8v/5//n/1P/y/9v/6v/b/+r/6v/U/9v/xf/q/9T/8v/y/83/2//U/9v/1P/5/+P/BwAOANv/AADj/+P/8v/j/w4ABwAHAAcAAAAOAAAAJQAOABYALAAdABYAFgAzAPL/LAAOAAAALAAAAEoAAAA7AEoADgBKACUASgAsACwAJQAdAB0ABwAsAAcAHQAsACwAQgBCAEIAZwBKADMAWQAsAEIAOwBKAFkASgBCADMAOwAWADMALAAzAA4AHQAzAAcAFgAHACwABwAdACUAFgAsAAcAQgAWACUAFgAAAB0ABwAOAPn/HQD5/xYAHQA7ADMABwAzAPn/HQAdAB0AFgAdAEIAAAAlAAcAAAD5/wAAFgDy/wcADgAAAAAA8v/5/xYA6v8AAAAA2/8AAPL/8v/5//n/8v/j/+P/6v/b/+r/6v/N//L/vv/b//n/tv/j/+P/xf/j/+P/2//5/8X/vv/U/8X/zf+2/9v/2//N/+P/6v/b/9T/xf/q/+r/2//5/9v/8v/y/wAAFgD5//n/6v/5/9v/6v8AAOr/8v/F/9T/2//N/+r/zf/b/9T/1P/y/83/+f/U/7b/6v/N/83/zf/j/8X/zf/b/77/zf/F/9T/1P/b/77/1P/q/83/6v/b/wAA2//b/9v/4/8HAOP/DgDq/+r/6v/j//L/1P/q/+P/1P/U/9T/vv/q/9v/xf/j/83/8v/y/wAA+f/5//L/8v8AAAAA8v/b//n/2//j//L/6v/q//L/AAD5/ywAAAAWACUADgAdAA4AMwAHACUAJQAOACwAJQAdAA4AJQAdADMALAAlADMAFgAWABYAHQAsACwAHQAdAB0AAAAOAA4ABwAdAAcABwD5/+r/MwDy/x0AHQDq/ywA+f8lACUADgAAAAAAFgAlACwADgAlAA4AFgAdAA4ABwAlACwAFgAzABYAMwAdAEIAOwAOACwABwAlAAcAMwAsACwAMwAWADsAAAAWAPn/HQAOACwAJQAHAEoAAABgADMAOwBKAB0ASgAWAFkAHQBKADMAHQBZAA4AQgAAACUALAAOADsAJQAdACUAMwAOACUADgAOACUAHQA7ABYAMwAdAAcAFgAAAAcADgAWAA4AFgAHAAcAFgAWAA4AJQAzABYAJQAzAB0AFgAdAPn/+f8AAPn/FgAOAPn/HQAAAPL/8v8AAAcA2/8HAPn/4//y/9T/4//j/wAA+f/5//L/8v/y/9v/8v/U/9v/6v/b/wAAAAAAAAcA+f8OAAAA2//q//L/+f/5/wcAAAAOAAAABwAOAPL/HQDy/yUAAADq/ywAzf8WAPL/6v8HAM3/+f/j//n/4/8AAAcA8v/5/+r/+f++//L/6v/j/wcAvv/y/wAAzf/5//n/1P8AAA4A+f/5//n/+f/j/9T/8v/j/9T/4//N/wAA6v/5/w4A8v8WAPL/AAD5/wAA+f/j/wAA4//5/wAA8v/j/w4AAADj/xYABwAAAPL/BwAAANv/8v8OAPn/+f8AAPL/DgDU/wAADgDy/wcA8v8OAOP/BwAsAB0AMwAHABYABwDy/w4ADgDy//n/+f/5/wAABwDq/+P/8v/U/wAAzf/j//L/xf8HAM3/6v/j/8X/6v/F//L/1P/b/9v/zf/q/77/zf/F/8X/4/++/+P/2/+2/wAA1P/j/+r/zf/j/9v/+f/j/+r/1P8AAOr/xf8OAOP/8v/N/+P/6v/b/w4A1P/y/9T/xf8AAOr/8v/y/+r/AAAAAPL/FgDq/+P/AADj//n/8v/j//L/4//N/9v/2//U/+r/8v8AAOr/8v/5//L/AAAHAA4AFgAOAAAAFgDj/+r/6v/F//L/xf/y//L/2//5/9T/8v/y/wAAFgAHABYA8v/5/wcAAAAHABYAAADy/wcABwAdAAAA4//y/+r/8v8HAAAABwAdAOP/BwAWAA4AJQAHABYAAAD5/wcAAAAHAAcA4//q/wcA1P8HAOP/4/8WAM3/AADq/+P/8v/j/xYA6v/5/wcA4//q/+r/4/8AAPn/+f8OAAcABwDq/+r/BwAHAAcAJQAAAOr/FgAWACUAFgAdACUAFgAsACUAQgAzAA4AHQAWAPL/BwAsAAcADgAHAB0ADgAOACUAAAAAABYA+f8AABYA8v/5//n/+f/q//n/BwDj/x0A4/8WACwA6v8lAPL/DgAdAPn/+f8AAAcAAAAdAPL/BwDq//L/AADj/x0A8v8WABYA1P8AAAcA8v/5//n/AAAAAAAAHQAOAB0AJQAdADsASgBCAEoAUQAsADsAMwAlAFkALABCAFkALABCAB0AHQAlAPn/DgAsACwADgAWAB0ADgAzACwAJQAWAB0AMwAOACUAHQAOAA4ADgAWAPn/JQAOAA4AMwAOABYAFgAWACUAFgAHABYAJQAdACUAHQAlADMAHQA7AEoALAAsAA4ABwAlACUAJQAzAAAABwAlAA4AJQAOADMAFgAOAEIADgAWAPL/FgAWAPn/FgD5/x0A+f8HAA4A6v8lAPL/AADq/9v/AADy//n/8v8OAOr/8v8AAMX/4//5//L/2//b//L/2//F/+P/4//N/8X/2//y/7b/2//j/83/6v++/+P/1P++/+P/zf/b/9v/tv/F/9T/vv/b/8X/1P/y/+r/BwDq/+P/AAAHAAAALAAWAAcAFgAWACwADgAzACwAFgA7ACwAQgAsACwAMwBCAB0ABwAzAPn/HQAlAA4AAAAOABYA+f87ACwAOwBCACwAHQAAAA4A+f8dADMAJQAlADMAJQAdADMAJQAzAA4AJQAdAA4AAADq/wcA1P8WAA4AAAAsAA4AJQD5/wAAAAAAAPL/6v8dAAcAFgD5/wcABwDq/x0AFgAAAPn/BwDq//L/DgD5/wcABwAAAAAAAADy//n/+f/q//L/6v/5/83/zf/5/9T/1P/U/83/4//U/+P/8v/U/wAA2//U/+r/vv/q/9v/1P/j/+P/4//F/9T/zf/b/+P/zf/b/+P/zf/N/+P/6v/N/+r/+f8AABYAAADy//L/6v/y/9v/AAD5/wAAFgDj/w4A8v/b/wcA8v/5/wAAFgAHABYABwAAAAAA2/8AAOr/HQAsAA4AQgAzACwABwAAAAcADgDy//L/DgDj/wcAAAD5/wAAAADy/83/BwDb//n/JQDq/x0A+f/q//n/8v/y//n/JQAOAA4AFgAHAAcA+f/5//n/BwDj/w4ABwDy/xYA8v8OAAcA+f8HAPL/BwAAAPL/1P/j/+P/2//j//L/4//U/wcA4//q//n/zf/U/9T/6v/y/+P/+f/5/83/BwD5/+P/6v++/8X/xf/b/+r/BwDq//L/DgDy/w4A8v8AAOP/zf/y/9T/2//q//L/FgAWAPn/BwDq/83/8v/j//n/BwAAAPn/BwAWAA4AJQAOABYADgDy/xYAJQAWAAAADgAOAAcAAAD5//L/6v/5/wcADgAdACUAFgAlADMADgAdAA4ABwAzAA4AHQAHAPn/AADy/x0ABwAHAAAABwAHAOP/8v/q//n/4//U//L/8v/j//n/8v/b/9T/2//j/77/8v/U/9T/2//F//L/xf/N/9v/4//j//n/4//N//L/tv/y/+r/1P/y/9T/6v/q/9v/4//y/83/6v8AAMX/1P/y/9T/4/8HAAAABwDq/w4ADgDy/yUABwD5/x0AFgAHAA4ABwAHAA4AAAAOACwALAAzACUAHQAdAAAAAAAOACUAHQAOAAcADgD5/wAALAAOAA4ADgAWABYAAAAdAAAABwAAAB0AFgD5/xYA+f8HAPn/FgAAAOP/+f/q/wcAAADy/+P/1P8OACUA8v/5//n/6v8HAAAAJQAdABYAJQAWABYAJQAlABYAJQD5/w4AFgAlACUADgAdAAAAFgAdAAcAHQA7AAcADgAlAOr/AADj/w4AFgAOACwAHQAdAPL/DgAOAA4AFgAdADsABwAWACUADgAWACUALAAlADMAQgAsADMASgAzACUAOwBZAFEAOwBZAEoAUQBnAFEAbwA7AEoAYAA7AGcAQgBKADsAUQBKAB0AZwAsADsALAAdADMAHQBCADMASgAsABYAFgAOABYABwAdAA4A+f8HAAcAAAAOAPn/8v/b/9T/2//j/+P/zf8dAPL/8v8OAPL/DgDy/wcA8v/q/+P/8v/5/9v/4//q//n/4/8OAOr/BwAHANT/BwDj//n/2//5/wAAxf/5//n/8v8AAB0A8v/q//n/xf/j/+P/4//j/8X/2//b/9T/1P/N//n/zf/N//L/zf/j/+r/4//q/8X/1P/U/83/1P+v/8X/r/+n/83/r//U/77/oP/F/77/oP+v/6//r//F/77/+f/j/+P/8v/5//L/8v8zAAAADgAHAPn/6v/q/w4A6v/5/9T/6v/j//n/BwAHACwA+f8WAOr/6v/y//n/DgAOAB0A4/8OAOr/AADy/9v/BwDy/wcADgAdAAcADgAOAB0ALAAWADsADgAOAA4ADgAOAAcA8v/5/x0ADgAlABYAAAAAAPL/+f8HABYADgAWABYAHQAdAA4AFgAWAAAA+f8AAPn/+f8AAA4AJQAdAB0AFgAWAAAA+f9CABYAMwBKAAAAOwAOADsAFgAOAEIAAAAdAA4ABwAWAA4AHQAWAPn/BwAlAB0AFgAOACwADgAsAA4AAAAlAAcAJQDy/x0ABwD5/xYAAAAAAAAADgDj/ywA8v8HAB0A1P/y/8X/HQDq/wAALAAdADsAAAA7AA4AHQAlAA4AHQAWACwAJQBCAA4ABwAdAA4AJQA7ADsAJQAlADMAMwAWACUALADy/w4A+f/b/wcA8v/y/83/4//q/9T/DgDq/+P/vv/U/83/kf/q/77/xf/q/+P/2//U/9v/xf/j/+P/6v/j/+P/6v/y/9T/8v/F/83/8v++/xYA2//q//n/xf8WAOr/6v/y//n/4/8AANv/2/8AANT/DgDj/9T/8v8AAOP/AAAOAOr/DgDj//L/6v/N/+r/6v/b//L/BwDN//L/6v/y/+r/1P/N/9v/zf/N/9T/p//q/77/tv/b/7b/1P/N/9v/zf+2/77/zf/F/9v/6v/b//L/+f/q/+r/AADN/+r/xf++//L/vv/5/+r/zf/5/wAA6v/b/9T/8v/q/9v/AADy//n/BwAdACUABwAAABYAFgAdADMAJQAzABYAHQAOAAcADgAAAB0A8v8sABYABwAdACUAHQAWADsADgAdAB0AHQAOABYADgAAACUABwAdAA4AHQAlABYAMwAWAA4AFgAdAAAA+f8AABYAFgAlADMAJQAlAA4AJQAdACwALAAWAB0ALAAsAB0ADgAAACUAAAAWACwADgAdAB0AFgAAAAcA+f8AAAcA+f8AAPn/8v/q/+r/4//q/9v/8v/q//L/AADj//n/2//y/wAA4//q/+P/2//j/+r/+f/U/9T/+f/b/+r/6v/y//n/8v/y//L/6v/y/w4A8v8WAAAA+f8WANv/6v/q/wcAAAD5//n/8v/5/+P/AADy/wcALAAWAAcADgAHAPn/8v/q//n/2//j//L/6v/j//n/AAD5/x0ABwAWAAAADgAOAPL/FgD5/wAA8v8AAA4A+f8WAAcAFgAOAB0AQgAlADMALAAlADsAHQAdADsAMwAzADMALAAWACwAQgAsAEIAJQAsACUAJQBZACwAMwAlABYAMwAWACUAMwAsACwAOwAWAAcAHQAHAA4AHQAHAAcAHQD5//n/+f8OAA4A8v8dAPn/AAAWAPn/AAD5//n/6v/y//n/8v/5/+r/8v/5/+P/BwDy//n/FgDb/wcA8v/j/+P/4//y/+r/FgAAAPn/6v/U/9v/8v8AAOP/BwD5/9v/AADj//L/+f/q/wcA+f8HAAAA6v/5//L/AAD5/wAAFgAdAOr/BwAHAOr/DgDb/wAAAAD5/w4AFgAWAB0AHQDy/yUAAAAdAB0A+f8HAOr/AADN/xYA+f/q/w4A2//q/9v/AADb//n/2//q/xYA2/8dAPL/BwAHAAcAMwAlAEoAMwAsAB0AHQAsACUAHQAsACwA+f8HAB0AJQAlABYADgD5/wcADgD5/wcAFgAHACwA+f8HAB0A6v8sAAcAHQAHAPn/MwDy/wAAAAAAAPL/+f8dAAAADgAOACUADgAAABYADgD5//L/DgAHAAcAAAAHAAcAAAAOAAcABwAAAAcAAAAAAAAABwAAAA4AFgAOAAAA1P/b/9T/8v/q//L/DgDj//n/4//b/+P/8v/y/+r/FgD5/w4AJQAAAA4ABwAAAPn/BwAOAAAADgAHABYABwAHAPn/+f8OAOP/FgDU/9v/AADN//n/2/8HAL7/4//y/7b/8v+v/9T/r//b/+r/+f8WANv/AADF/+r/6v/U/wAA+f/y/w4A8v/N//L/xf/b/83/8v/y/+P/HQDq//n/BwAAAPn/DgD5//n/BwD5/wcABwAsAA4AFgD5/xYA8v/b/wAA2//5/83/AAD5/+P/+f/q/+r/1P/5/+P/8v/y/w4A+f/b/wAAzf8AAOP/6v/5//L/AADq/wAA4//5/wcA8v/5/xYABwDb/+r/6v/q/wAA+f8AAAcA6v/y//n/+f/5//L/+f/U/+r/AADb/wAABwDb//L/8v/U/wAA+f/y/wcA4//5//L/+f8lAOr/HQAWAOP/8v/U//L/zf/y//n/4/8OAOr/4//b/+P/2//y//n/+f8AAA4ABwDy/ywA8v8WABYA2/8lANv/AAAOAAAABwDq/yUA8v8HABYAHQAlABYA+f/q/wAA4/8AAAAAFgAAAAAAFgC2/wAAAAD5/wAA+f8dAOr/DgAAABYAFgAHACwALAAzAAAABwD5//L/FgAHAPn/HQAdABYAFgAHADsAFgAsADMADgAOAA4AHQAWACUA+f8dAAcABwAsABYAMwAAADsAFgAWADMABwA7ABYAHQAdACUAJQAdAEIAJQAHACUAHQAWADMAMwA7ACwAOwAzACUAMwAdADMAOwAlACUAOwAdACUADgAdAB0A6v8sAAAABwAdAPL/DgD5/wcAHQAHAPn/AAAHAOP/HQAOAPL/LAD5/x0ADgAHABYA6v8dAPL/HQAsAA4AHQDq/wcAFgAHAAcAHQAOACwABwAOADMA8v8sAAcABwAWAAcADgAOADMA8v8OAA4A8v8WAAcAAAD5/w4AFgAAAAcAAAD5/wcA2//5//n/xf/5//n/4//b//L/2//N/9v/vv/F/9v/2//j/+r/zf/y/+r/2/8AAAAABwD5/w4A+f/q/w4A2//5//L/zf8AAPn/4//q/+P/zf/U/83/xf/b/77/2//N/9T/zf/N/9v/tv/q/6//tv/U/6//zf/F/8X/p//N/6f/r/++/77/1P++/+r/r//U//n/1P/y/+P/2//N//L/+f8AAPL/4//q/wAAAADy/yUAAAAOAAAA4//j/+P/AAD5/xYABwAOAAAA+f8WAPL/AAAHAPn/AAD5//n/8v/q//L/4//5//n/4//5/9v/2//j/+r/8v8OACwAAAAOABYA+f8dAAcAAAAdAAAAAAAAAAAABwAAACwAHQAOACwAJQAWABYAJQAlAB0AJQAHAA4AAAD5/w4A4/8WAAcA+f8dAPn/JQAdAB0ALAD5/xYADgAAACUALAAWAA4AOwAlABYAQgAlAB0ALAAsACUAJQAlACUALAAOADMAOwAOADMALAAdACwAJQAdAB0AJQAsABYADgAlADsAHQAsACUABwAdAAAAHQAAAPn/HQAdADsAHQBCADMAOwA7ACwAOwAWAB0AHQAsADMALAAHAB0ABwAHAB0AAAAOAA4ABwAAADMAAAAdACUA4/8zAAcAFgAsAB0A8v8OAB0AAAAlAPn/HQAOAPn/FgAOAPn/DgAOAOP/+f/U//L/2//5//L/AAAWAPn/JQDb/wcAAAAHAB0ADgAdAPL/DgDy/wAABwAAAAcA+f8OAPn/4//y/9v/r//q/9T/4//q/8X/+f/N/9v/8v/F/9v/6v/U//L/8v/j/wAAzf/b/+P/2//q/+r/FgDq/+P/DgDy//L/+f/y/+r/4//q//n/6v/q/+P/2//N/9v/8v/q/wAAzf/U//L/r//q//L/2/8AAPL/+f/y/+P/8v/y/wAA+f/5/wAA6v/b/+r/BwD5/+P/8v/5/9T/2//y/9T/8v/y/wAAAADy/w4A4//5/wAA4//y//n/8v/j/wcA+f8AAA4A8v/y/wcA4//q/ywA6v/y/wAA6v/5//L/AAAAAPL/+f8sAA4AHQAdAA4ABwAHABYAAAAsABYADgAWAA4ABwDy/wcA8v8sAA4ADgA7APn/AADy/x0AFgAHAB0AFgAdAOr/HQAHAPn/DgD5/wAAAAAAAPL/BwAAAOr/DgDy//L/+f8HAAAA+f8AAOr/JQAWAPn/FgAWAB0AAAAHAA4A6v8OAPn/FgAdAPL/HQAWABYAMwAOAAcAHQDy//n/BwAHAAAABwAlAPL/DgAAAOr/BwDb//n/BwDU//n/HQAOACUALAAsAA4ABwAsABYAJQAlACwAJQAWAB0A+f8AABYAJQAWACUAHQAOAAcA6v8dAAcAAAAWAPn/BwAHABYAAAAHAA4ABwAlAOr/8v/y/+P/+f/q/wAA6v/y//L/6v/U/9v/4//U/wAAzf/5/+r/4//5/9T/AADN/+r/AADq//L/BwAWAAAAAADy/wcA1P8AAB0A+f8WAAAAFgAzAAAAFgAWANv/HQAHAAcAHQAHABYAAAAdAA4AHQAlAB0AJQAsADMAHQAlACUAHQAHADsAFgAWADMAAAAlABYADgAAAAcA+f8AAB0ABwD5/+r/FgD5//L/+f/5//L/4/8dAPL/8v/5/wAAAADy//n/2//y/9v/2/8WAPL/DgAHAPL/FgDq/+P/+f8HAPn/6v8OAOP/2//j/+r/2//q//n/6v/5//n/+f/j/w4ADgDy/wcA2//b/+r/2//b/wAA8v/U/wAA1P/b//L/1P/q/+r/2//b/+P/1P/U/+r/2//y/+r/zf/5/+P/6v8AANT/4//U/+r/AADq//L/8v/q/9v/4//j//L/AAAWAAcAAAAWAPn/HQD5/w4AAAAAACwA8v8OAPn/AAAOAA4AJQAWACUAHQAOACwAHQAAACwA+f8OAB0ABwAlAAAAMwAOAPn/HQAOAPL/+f/5/83/FgDy/+r/DgDq//n/AAD5/wAAAAD5/w4A8v8HAOr/4//N/77/1P/U/+r/zf/q/9T/4//b/77/xf/U/83/r//q/7b/2//b/83/8v++//L/2//q/wAA4/8AAPL/vv/q/+r/1P8AAPL/6v/q//L/1P/5/wAA+f8AAPL/8v/q/wAA1P/5/9v/6v/5/+P/FgDj/wAA+f8AAOP/2//q/9T/4//F/wAA4//y/wcA+f8WAPL/AAAHAPn/AAAdAAAA+f8OAOr/AADy/9v/FgDy//L/FgAlAB0AFgAzAAAAFgAlAPn/BwAHAAcAFgAlABYAMwDy/wcADgD5/zMABwAWABYAHQAdACwADgD5/yUABwAWAAcADgAAAAcADgDy/ywAHQAWAB0AFgAOAAcAFgAOAPn/AAAOAPL/+f8HAPL/8v8HAOr/6v8AAAAA8v/y/wAA+f/y/wcAFgDq/wcA8v8HAAAA2/8OANv/FgAOAA4ALADy/x0ADgAWAB0AHQAOAAAAFgAAAAAAAAAHAB0ADgAWAPn/BwAlAB0ALAAOAB0AHQAHABYA+f8HAA4AAAAHAA4AAAA7AB0AHQAlAPn/LAAOAEIAHQAOAGAAJQA7AEIAQgAsADMAOwAsAEIAOwBRAEIAUQBRADMAWQBCADMASgBCADsALAAzAB0AFgAlABYAJQAsACUAFgAlAAcAAAAHABYAMwAWAEIAQgA7ADsAQgAdAAcAMwD5/yUAJQAWADMAJQA7ABYAHQAzAA4AHQAsAA4ALAAzAAAADgD5/wcADgD5/w4ABwAHAB0AFgAAAAcABwDy//n/BwAHABYA+f8WAAAA1P8OAOr/8v/j/8X/BwDj/9v/8v/U/9v/r//N/9v/tv/5/9T/1P/y/+P/+f/q/9v/1P/j/+r/4//b/+P/4//b/9T/2//b/9v/6v++/+r/2//N/wcAzf/q/wAA2//q/9v/2/++/9v/6v/F/77/tv/b/9T/1P/j/9v/zf/U/+r/xf/U/7b/xf/U/83/2//b/+r/zf/5/9v/4/8AAMX/2//N/9T/xf/b/9T/zf/F/7b/4/++/wAA+f/y//n/6v/y/8X/BwDq//L/8v/N/+r/tv/U/+r/+f8HAPn/BwAdAAAABwAdAPL/BwAAAPL/BwDq//n/BwAHAPn/AAAHANT/+f/5//L/BwD5/w4AAAD5/wAA8v8AAA4ADgAOACwAFgAHAA4ABwAAABYAFgAsACwAAAAWABYAHQAOACUAQgAHACwALADy/w4ABwAAABYA4/8WACUA6v87ADMADgAdAAcA8v/5/w4ADgAOAB0AHQAHAAAA+f8AAAcAJQAWAB0ALAAdACUAHQAWAB0ALAAWAAcAFgAOAAcAFgAWAAcAHQD5/wcAFgDy/wcAAAAOAPn/4//y/wcA+f8OAA4AAAAzAOr/BwAOANv/BwAAAPL/AAAHAPL/DgD5//L/AAAOAAcABwAOAAcAHQDb/wAA6v/U/w4A+f87ABYADgAHAPn/BwDy/xYA8v/q/wAA8v/5/xYABwAHAA4AAAAHAAcAFgAHACUAHQD5/xYAJQAHAA4A8v8HAOr/xf8OANT/+f8HAOr/BwDN/+r/BwDj//L/FgAHABYAAAD5/wAA2/8HAAcAAADq/x0AJQD5/x0ALAAWABYALAD5//L/+f/y/wAAFgDy/wAAHQD5/zsABwAdAAcADgAlAOP/DgDy/wcA6v/5/wcA8v/5/+P/FgD5/wAAFgAHAA4AHQDy/wAAFgDq/wAA4//5/+r/8v8dAAcAAAAHAOr/4//q/9T/+f/j/wAA8v/q/83/zf/q/9v/AADj/+r/1P/j/8X/xf/U/9T/1P/F/wcAzf8AANT/4//U/7b/AACv//n/xf/U/+P/2/8HANT/+f/j/wAA8v/j/+r/6v/U/+P/2//b/w4A4/8OAPn/AAD5/xYAHQDy/x0A8v/y/wcABwDj/w4ADgAWAB0AAAAsAB0AHQAWADMABwAdACwAFgBRACUASgAdACwAMwAWAEIAHQAlACUALAAOACwAJQAWADMAHQAdACUADgDy/zMABwAAACUADgAOAA4AHQAHAB0AHQAlAB0AOwA7ABYAMwD5/xYABwAdAB0AFgAdAPL/JQAAACUABwDj/wAA8v8HAAcAFgD5/wcAFgAOAAcADgAHABYAOwAHAB0AHQAOAB0ALAAOAAAAFgAAAA4A+f8sAB0ADgAWAA4ALAAAADMABwDy/+P/8v/5/9v/BwDq/wAA6v/q//L/1P8HAAcABwAHANT/1P/j/83/6v/j/x0A6v++/wcAxf/5/+P/6v/q/+r/8v/U/+P/r//N/6//xf/b/77/tv+v/9v/6v/j/8X/AADb/9v/FgDq/9v/8v8AAA4AFgDq/wcA6v/b//n/AADy//L/FgAHABYABwAOAOr/2/8HAAAA8v8AAA4A2/8WAPn/+f8AAOr/+f/b/xYA6v/y/xYABwAAAOP/+f/y//n/AAAdAAAA6v8AAA4AFgAHAA4AAAAAABYAMwAlACwAOwAWAA4AHQAdAB0AJQAzACUABwAOAAcAJQAHACUALAAAABYA+f8OAPL/DgAAAAAALAAHACwAFgAdAAcAJQAlABYALAD5/yUAFgAlABYABwAlAAcAFgAWAPn/BwAdAOr/AAAOAPn/FgAWAPL/AADy/9T/8v/b/wAA6v/N/9v/2/8AAAcAAADy/w4ADgAAAAAABwDy/9v/1P/b/9v/2/8AANT/8v/5//n/AADb/yUA4//q/wAA6v8HAPL/DgAHAM3/6v8HAL7/8v8AANv/8v/q/wcA6v/y/xYA6v/b/wcAFgD5/xYA+f/j/wAA+f8AAOr/BwAHAOr/DgAAAPL/8v/q/+r/6v/5/9v/tv/q/+P/8v8AANv/DgDF/77/6v+2/+r/+f/y/+P/8v8HAA4AJQAOAAcAAAAOAAAAFgAsAAcABwD5/w4AFgDy/wAADgDq/w4ADgAOAA4ADgAlAPn/FgAHAAcAFgAdACwAAAAWACUABwAHABYA2//5/wAA+f8WAAcABwDj/wcA6v8OABYA+f/y/9v/8v/F/wcA6v/q/wAAzf/N/9T/4//F/9v/1P8HAOr/6v/y/83/2/++/w4AAADy//L/BwAOAAcALAAlADMA4//5/xYABwDy/+r/DgDU/77/1P/j/+P/6v8AAB0AAADy/wAADgDq/77/AADj//n/2//q/wcA1P8dAOr/8v8AAPL/2//b/wcA2//b/9v/+f/F/9T/BwD5/wAA8v8OAPL/2//y//n/6v8AAAcA8v8sACUABwBCABYA8v8HAOr/FgAWAPL/DgAAAPn/AAAdABYA+f8AABYA8v/y//n/6v/y/7b/BwAdAPL/JQAAAA4AAAAAAAcADgAsAPn/JQD5/+r/SgAlAFkAQgD5/x0ADgA7AFkAQgAzACwALAAlAFEAOwAlADsADgAWACwADgAzADMAOwAsAAcAOwAOAA4AMwAOADMAFgAlADsAAAAWAAcADgAzACUAHQD5//n/DgAdAA4ABwAAANv/6v8lADMALAA7ACUAHQAWAAcAOwBKADMAFgAWACUAFgAdACUAFgAAAA4AOwAdABYAMwAdAA4AFgAWAAcADgAAACUAJQAHADMAMwAlAA4AMwAlABYAHQAAADsABwAAADMABwD5/xYA+f/y//n/BwA7AOr/BwAOAAAABwAOAA4A4/8HAAcAHQAHACwAFgDb//n/zf/q/+r/BwDq/9v/AADj/9T/4//5/83/4//b//n/6v/q/wAAzf/U/9v/8v/U/9T/1P/F/9T/AAAHACUAJQDq/x0Azf/b/+r/6v8OAPn/BwDU//L/4//q//n/HQAOAAAABwD5/xYAvv/y//L/6v/j/+r/AADU/wAA6v8AANv/JQAHAOP/DgDq/wcA+f8AAOP/4//F/+r/1P+2/wcAxf/5//L/FgAWAOP/DgDy/+r/4/8AAOr/+f8sACUA+f8AAA4A6v8HABYAAADj/wAA6v/b//L/8v/q//L/DgD5//n/1P/5//n/6v8dAAAA1P/j/wAA4//U/9v/AADb/+r/BwDq/wcAxf/N/7b/xf/5/+r/8v/F/8X/4//b/83/6v/j/83/1P/b/wcA6v/q/+P/zf/q//n/AAD5/wAABwAAAOr/8v8WAA4AFgAOABYAFgAOABYA4/8WACwAAAAWACUAJQDy/xYAJQAHAAcABwAHAOr/DgAzACwAFgAsACUA8v/5/x0AJQAWAA4ABwAHAAcAMwAdANv/+f8WABYABwBCADsA8v/q/x0AOwAAAAcA+f/5/xYADgBCAA4A1P8WACUA8v8sAB0A8v8sAB0ALAAOANv/BwAOACwAFgAOAAAAAAAWAAAA8v/j//n/AAD5/+r/tv/U/wAAAAAHAAAA8v/5//L/+f8AAOP/4//q//L/+f/j//L/4//U/wcA6v/j/+r/AADy/6//2//b//L/+f/q/9T/1P8AAPn/4//5/w4Azf/j//n/4//5/+r/2//U//n/xf/j/xYAFgAWAAAAFgD5/wAA2/8OABYA+f8lABYABwDy/xYA6v8WADMADgAAAB0AOwAWACUADgAHANT/6v8sAB0AAADN/+r/2//5/yUA+f/5/wAA4//j//n/8v/F/9T/8v/F/+P/zf/y/wAAzf/N/+P/DgDb/wcA8v/j/9T/zf8OAAAABwDb/wAA+f/F/wAADgD5/+r/AADy//L/AAAOABYADgDb/+r/BwDj//n/AAAHAAcAAADj/wAA6v/b/wAAxf8OAAAAAAAWAPn/DgAHAPL/4/8HAPL/AAAlAAcA8v/q/wAAJQAzABYADgAWADsALAAzACUAAAAWABYALAAOACUADgAOACwAFgAlAAAAAAD5/xYAJQAOAAcADgAWAB0AJQAOABYAAABKAEoAMwA7AAcALAAlABYAAADy/w4ALAAlACwAJQAHACwAQgA7APn/DgA7ADMAQgAOAPn/AAAWADsAQgAAAPn/HQAdACwAMwAOAPL/+f8AACwAFgD5/wcAMwBnAB0AHQAOAOr/HQAlACwADgDq/xYABwDy/yUABwDq/wAABwAsAPL/4/8WAOr/FgAlAOP/+f++/77/+f8AAAcAAAAAAA4AFgDj/83/vv/F/+r/+f8dAPn/2//y//n/+f/y/+P/1P/5/w4ABwAlAA4A6v8AANv/8v8WAPL/LAAlAOr/+f8lAPn/8v8lAPL/2/8lACwA6v/q/wAA2//U/9v/BwDb/7b/LAAAAMX/+f/U/6//vv8OAA4A1P/y//n/AAAlACwADgAHAOP/+f8zADMAFgAlADsAOwAsAM3/HQDj/9v/SgDy/wcAAAAdAB0A+f8OAAAAAADj//L/FgAsACUAHQAWAPL/1P/b/wcAAAAAAOP/DgAAAOP/HQD5//n/4//q//n/r//b/xYAJQAHANv/HQD5//L/FgD5/6f/vv8WANT/+f/5/wcALAD5/1kAMwDU/wAAOwDU/+r/MwDq/ywA+f8dACwAzf8OAPL/8v/b/wcAOwAHAEoAOwAOAA4A+f/q/w4AFgDb/wcAJQAAANT/AAAOAOr/BwDj/wcABwDy/+P/xf/j/wcAHQDU//L/BwDF/+P/DgAsAAAA8v8HAAAA6v8OACUA8v/j/wcADgDN/wcAAADj/xYAAAAOAPn/+f8dACwAAAAAAAAA2/8WAAcAvv/j/xYAtv/F/wcA2/++/7b/4//F/6f/6v/y/8X/2/8OADsA6v97//L/4/+n/w4A+f/5/wcAAAAAAOP/oP+Z/8X/xf8lAG8ABwC2/9v/8v8dAPL/2//y/6//JQBvAEIAMwAAABYA+f+2/wAALADj/9T/4//5/w4A8v/F/77/4/++/+P/2//j/wAA1P/y/wcAAADb//n/4//q//n/HQAzAPn/MwA7AOr/2/8sAB0ALABnACUAJQAOABYAMwAzAOP/BwAlAA4AZwAsAB0ABwAdAAAA1P8AAAcA2//F/zsABwAAAAAA6v/y/wAABwDj/zMAHQBCAEoABwDj/+r/FgDj/yUAAAAWACUAMwAHAOr/OwDq/wcAAABCAPn/vv87AOr/2//y/zsAJQAHACwAFgDy/7b/2//y/+P/+f/5/+P/+f++/6D/AAAsAPn/dP++/+P/4/8WAAAAvv+K/wcAQgAAALb/xf8dAOP/+f/5/6//xf/U//L/AADq/+P/xf8HAFEADgAAACUABwAAACwA8v+g/+r/QgAdAOr/oP/N/zMABwAzAEoAxf+v/xYAUQAlACwAFgCv//n/OwBKAAcAmf+g/8X/LABKADsAzf+C//L/FgAdAPn/tv+g/0IABwDN/ywAp//U/9T/AAA7ACUAOwD5/wcAzf9RAFEA+f8dALb/JQBZAFEADgAdADMAtv/y/yUASgDy/6f/OwBKAOr/6v8sABYAzf8zAFkAvv/U/1kAowDy/6f/OwDy/+P/FgAzANv/oP8zAGAAMwBCAFEA8v/q/zMAbwBZAB0AFgAWAAAAMwCFADsALADF//L/bwAWAGAASgAzADMA8v8sAHYABwDy/yUA4/9RACwAHQAlAPn/LAD5/xYA4//U/77/4//y/+r/HQCv/9v/kf/U//L/kf/j/8X/FgAWAA4Axf+2/xYA4//j/w4AWQDq/83/6v/5/+r/p/8HANv/r//j/2cAHQCR/ywA+f/N/+P/LABgAIr/vv8WACUAMwDj/wAAkf/U/3YAmf++/2AASgBZAB0Azf+K/7b/JQD5/wcAJQDy//n/4/8sADsAe/+g/zMA6v/q/0IADgD5/xYAQgDy/77/FgAWAK//HQDeACwA1P/j//L/6v8dAH4Azf+v//L/JQAzACwAJQCK/zH/AACjAA4AHQDF/6f/8v/b/2cAAACg/8X/FgBKAGAABwCn/+P/4/8lAL7/e/+v/yUAzwBKACUAFgD5/8X/kf9RAPL/iv9gAEIADgBgAEoAbP9d/zMAxf+n/83/hQAhAfL/2/9KAK//kf/y/x0A8v/j/zMAFgAdANT/SgBKAED/vv+C/xYAQgD5/0IAgv8AAIL/1P+jAA4AoP+n/4wA8v/U/2cA6v+R/+r/LADU/6f/OwBvAJn/r//j/83/tv/U/1kALAAHAM3/DgBZANv/tv97/9T/hQAdAAcAFgAOADsAHQDF/13/MwDy/5n/HQDj/0IAvv9RAKoAp/+K/yn/1P92AKMAWQAdACUAgv/y/1kAUQBs/+7+hQC5AG8AJQAWAAcATv8zAFEADgC+/wcAbwCC/4UAUQB7/+P/DgBKAHT/FgCyACUAZwBvAAcAXf97/2cASgCv/xYADgDq/9v/6v8HANT/dgA7AKf/8v/5/+r/+f+5AEoAdP9l/zj/UQD8AJQADgCZ/x0AAAAzAKMA8v9l/6//1wALAXYAtv/j/x0Aiv/IAN4Azf97/+P/zwCUACwA2//5/6//oP9+ALkAbwC+/wAAUQAOAEoASgDj/77/JQCMAHYAZwAHANT/WQDN/1kADgBs/0IAMwC5AFEAOwDb/6D/1P8HAKMAgv9RAH4AWQAHALb/HQDy/0IA2P4HAFkADgBCAKf/mwAOAM3/bP9vAMX//f5RAKoAqgBd/yUAzf+K/+r/BwAAACn/BwBKACwA1P9nAOr/QP9s/3v/8v8x/4UAUQAWAEIAmf/b/wz/BwDj/9/+bP9KALIA+f/5/wcADP+c/pn/WQBKAPn/FgAsAA4AlADj/9/+R/+C//n/hQCMACUA6v9CAPL/p/8M/9v/mwDF/wAA6v/AADMAe/8sAPL/Zf+z/iUAyACFAOP/6v8OAPX+WQDPABYA5/7y/8AAkf9ZAGAAhQAT/zj/UQDq/0IAYADeANT/WQCjAA4Atv+2/+UAZf+Z/8AA5QBRALb/JQDj/xYABwCMAA4AoP9ZADsAfgAWAAcAe/+Z/7kAbwBgACwAAAAsAEIAhQDq/3v/xf9vAIUAQgCqAM3/Xf8sALIAZwB0/8X/HQDy/zsAdgC+/zH/1P/IAGcATv/b/77/DgDtAEoAKf8p/zMAxf8zAEIAG//C/lkAZAG2/6//p/8p/+P/AwGJAa//S/4OAEYBiv/F/28AVv+n/88AEgEzAKf/1P+bAPQAoP8p/1EAbwDF/28AYAD1/iL/UQDAAOP/p/87APn/r//F/4UAiv+V/koARgGg/9/+yABRAOr/owCg//3+bP9nAIwABwC2/1kA2/84/2cAHQB0/6//oP9vAKoAr/8zAA4Ae/+C/w4AsgB7/1b/QgCFALb/MwDIACwAbP8b/88AOwC+/ywAAAB2ADMADgCZ/xYAAAAHALkAZwCK/5z+hQBGAfn/zf/u/n/+2/8ZAaoAiv8E/9v/G/8b/1UBkf9S/pn/3gCbAAz/DgDF/9/+QP+jAMAAS/4i/94AlACC/2z/Zf9A/8X/+f/q/6//e/8T/5QAOwDC/hP/DP/q/x0Atv+2/wcA5/7F/9cAYf4T/5sA6v/y/zMAvv8HADH/mf+jAP3+1P/XAHYAbP87ALIAuv5gAPQAZf8i/94AzwCZ/00B3gCv/3T/tv/5/6MAIQGK/wcAdgC5ADMAXf8hAYUAZf/y/wMBOwCv/7kA4/9O/wcAwAAp//n/4gFnADH/Mf8lAB0AsgC2/zj/fgAdAOUAYADy//X+lf5yAe0A7v5l/zAB+f+6/q4BzwAX/uP9QgAHAjH/OwD0AF3/Zf/IAIUCIv/5/Q4AbwCn/8AAnwFRAKD//f5yAVEA9f6qAM3/QP87AD4BHQCC/yn/MwBKANv/MwDY/jH/5QDEASUAyAB+ADX+F/70AEICjv7Q/qoAgQHb/4wAtQHq/Wz9gv/TAVEAkf/lAGAAbP9+ANMBOP/Q/o7+zf8OAgMBbP+R/z4Bgv8T/8gAWQB0/6MA6QHlABP/kf+BARP/3P2MAGQB0P4zAKYDMAHQ/tD+JQB0/w4A6QEp/9/+YAByAZABoP+O/nD+pP6+/zcB1wAsAIr/iv8sAEIAWQB3/pX+BwCv/5QAvQEZAZz+Kf/eANj+Yf6R/7kANwFZAG8AowBCANT/e//C/jH/uQAOAGQB/AKZ/3/+BwAdANT/Xf9CADMABwDxAdMBzf8B/kv+iv8lACQCZwCv/TsAgQFZAL7/UQAp/6D9fgCMAqMABP9KAMAAQP84/zAB1P9A/VkA6QGFACwAuQBH/4P9G//0ABIBwv5O/zAB3gBO/yn/ZAHF/3f+DP+jAMAAKf8zAPEB7QCd/Pn/KAE8/pQAxf8ZAQT/7v7eAnT/uv6c/hkBIQHN/X4A3gDU/9j+7QBNAdD+zf/j/3IBbwBH/+r/5/6K/5QANwF7/wT/zf+UAM8ASgBkAQz/+f0OAL0BqgB3/iEBBwCz/jcBEgGUAPL/jACFAIP9T/0WAk0D9ADb/3T/uv4b/1gCPgHq/2j+Kf2v//wCFQSC/wT/wvyK/3oDiv+v/839p/+1AVEC1wDF/1EA3P3lAFEALACMALb/JQAOAMACMAHf/nf+wv6QAYkBDP/q/7kA/wGZ/4b+CwFgAGAAJv4OAO0AOwA7ABYAtv88/k0BzwCv//L/3gJO/3f+2gEx/zsAE//lAH/+VQHlAgz9cP5vAB0EDP+2/RIB+f/u/pABIQN3/AT9mAGUAiL/xf1NAzcByfoSAW8CR/35/af/uQLu/tv/NwFP+6D97QSjAND8e/9H/wsBBP3iAaMCRPzu/Dj/yAJRAKYBjv71/pz+yf61AQT/CgPC/tj8G/+BAYUAnfw7AGAAhv7F/xIBQP83ATsANf6r/g/+0P5RANT/9f5yAWcATQF3/qT+DgJ2AEv+8v03AdT/zwCn//QCvQFA/Xv/dP9nAmj+vv/N/6oAiQGUAIwEoP9o/t/8VQGv/+f80wGqAHoDdP0dAPsEUv5h/vEBDP/j++0C1P8m/pQCzwCUAFr+bP/N/+r9+f2UApQCE/38AGsBJQBH/0D/hQDj+8L8pgHEA9/+4//xAXT7awG1A5387vwi/wT/fgCBA1gCxf3Y/KYBZAH5/dcCYwPF+4P9IQH/AQsBdP+bAur9/fxvBHoFD/72/PgBIv9a/sX/rgOuAUP+zwD4AZQA5/6mATj9Yf4+AcgC+AEP/vgBXf8AAKv+iv+UALb9pP6+/cgCLASuAaD/QgBP+1b9KAPf/ib8Zf92BnD+0wGQAU/9bP9e+xID8v1CAHYEtv/n/Ef/cgf9/JX41wAzAtj84gNNB0D7/fp9BJQCT/uz/owAxAHC/rEEpgXn+rP8T/3n/s8ALAZnAEv4pgFcB7b/hvziA3f+Vvm6/i8FmwKv/WQBsQR//hf8tQNd/xf8lf7pA3oBG/0VBCQCxf0dAJn/Jvgb/8gEMwCk/ur/ZwblAEf5jv7wBfL95/pVATMChQKg/wAA5QB6AV39R/8oAbP+uQB+AGMDmf2r/ssD+AEB/tD+TQVH/dj+Nf4T/7UFmf0T/zz+7QIoBUf/yfw4+3oDe/39/p8DkAHu/gz7rgPu/AAAIQMt/r7/PPrPABYC9AAp/1r+hQL9/iwA3P3F/wMF0foB/qYDR/1KAEP+5QIDA/n71P0hARkDxftCAqoEyf7J+hP/9ASg+5z+SQRyA7771wCbBNz77vwWAigDUvrLASwEKAF0/0f7xAFCAOf+7v7PADz+tv+JA4EB2gFo/jj9kf0dAnYCUQC6/uUAYAIi+9cAawNw/jMA1P3lAjMGAfzj/yQCQgBkASn9QgBo/uP/wAIsAm8Civ1h/v38ZAGJA139ZwCK/XT/wAKJAYUCq/xA/139oP/pARP9YATF/WH+VQNs/ZsAYABP+wMBPgHf/FEEr/3j/yUAWvzlBjsAF/p//gMFBfsOALwHIv0dAEv8lALJ/gH8bwTq/4kBCPw+A3IDDPn4AfgBOPsB/mcCOP/AArkEHQCz/qD7BwDY/hP9NwMsAn/+uQJNBx/69vozBmX/s/yr/owCS/wQ/PsMBwS39zz+yf5a/ND+9AYdBP346v28A5sELAAb/Sb+Yfp+AJABRgEzArr8hQBZAHf+7QDU/7r8zf3y/wMB0wFRAH/+BP0zApgBWvz5+VECDgby+dMB3gLq/XIB8v0oAYUC3P1S/rUBMfnq/z4JZAFS/l771wCZ/07/BwRCBFkAT/lnAJQABP1JBIEDZfvxASQE9f5RAHT9XAEsAgH8Jv43BcX9ywF5C0/70fg+Ad/+cPwsAq4BqgA4//n9ZwRYAnv/R/vu/kIAT/1a/mcCSgJd/yQGD/7Q/mQBG/07AFEAf/wt/joGQgCJAeUAlf78ALkCEPyV+IEDr/0p/4L/2gNO/4769ALj+6MAF/74Aaf/NfymA+kBQgLY+M39zf8ZAQMBXf9YBNT7bP8hAQAA2gGUAuf+jv4OBg/+QP93/mn6vAcoAxD4AACBBa4DtQGbAGcAtv10+eP9BgprAcb5hQb4A1b7YAAVBKj9Ofk4+4wI1ghE9DsAAg3U/TH9JAK++dT5mwLtBHIFHQCr/r7/Mf9yAc8E8v3+9Lb/iv2qBj4Pt/s1+Hv/3gJRAH0CKvld/b0B1Pn7CKMAHv4sBMQBf/wM/Z8FfPM8/BIH/AAOBrP+VQH8Avn7pgG9AdH2ePjPBlgId/zaAZAD8v8HAhf64/8e/i3+iQM7AG8EBwBCAKv+g/2r/tT9XAEP/jj/zwAsAIwAegF3/jz+RPxW/c8G9vyg/7kCUvw1/h7+Bgj5/773wvwzAv8FJQD0BhYARPav/zMA1wLwA4r/jAD9/jMCWAKuAQcEEPq3+wj+awNNC+v7R/2bBgAAPPry/07/7vrIArb/UQBW/wsBbggoAQX7CPg4/U/79ARyCaD7CwE8/kYBr/v5/YgHZfWK++0AZwJNAef+IQOg/QsB0fq++TH7FgCICWz7hvo7BG33ePpuCvL9Kf3C/lwB7AZl+SwA+ANP+Sr5ogSmBaD94/0dBDsEcPziA9cCBP2d/B0ENwGk+goL9ALj+dj8lwXTAc39GQnJ+O761P+xBJsKoff9/CEDTv87AmAGjAIx9Uv4fQR9AnT9VAcHBtj0qPszCh0AUvpA/5sAQgIb90T65QzwBY783/4dABP7G/l2BgoHcPru/G4GCgPu/vEBbP2v/TH7s/yXA/EBDgZH//QE3gQm+sn++fn0ArwD/ADy+w/+MwhH/8QHZf8OAkv6pPQcDNH6iQNCBCn9EgMt/F3/mfsWAoP7KAObAnj2Dgj8AkYBhQDj/aD5JviqBEoADP9nAmMHyADC9gMBd/7G+dMD/f4WAg4INfprAd/8/vS1A2sDBfn0At0O8vmjAqYFAfp6A/rz8vcOBvgDFgKXBcQFTv9nAAAAcPxl+fL32gFJDg4EUQDr+5QE2/899tkNBffy+dcCOwRbD4r9iQOk/lr80PwM/wT9Xf2xBDMAww19BkP+NfyO/N/+CPwQ+Cb+UA7q/zMGWARp9kv+FPfEASEFwAAsBi38uQLXAiL/Kf9p9vL/xf25Aq4Dmf+BBe0A3gYWACb4+fs8/gz9aglh/FP0YwlW++kFywXc+fL7Yf5cBfn7iQME/7r8QP/u+m8CiQP/Afb6ZwCfAUj3hQL/Bbf7/fyjAnT/Wv78Aq/9tQMM+cL4bwQx/3oDjvj7BrIAhQCfBXj2YwMF+cQBoP/Q/CgDwATF/zMA6Qmo8RIBPgV2AIL/uQBVAb77YAbY+iAJdgIi+bb9CwFrAyQCnwP9/OwKpPpA/xIDG/1VAXD6GQHq/8n+T/3kEGX/i/OJAXoBtv1l+UYHmfcHAtoByACtB/Lz2gMm/ODyZAEhBaIIjAY8+Bv/MwDy+1QFq/4t+kD5GQND/v8LDgII+I8TXvUp/ZcDH/aUANcAsQJl99D+7QJyBVwH5QAQ/Mn2vvt0/YL/9ABYAur9UQj4Bcb5yALV8/7ynglyA9T5OgpJBgj+jAaFAH/8g/0I/PLzH/pcC6UPSQgsAkoAyfrC+nYAwABS/Ir/qgCIB4r/fgDsCIf2zfswAcL+Wvo3AUICE/3aB0IGbfdP8ToKuvwq8+P7awdcC3Tz/wN5C/8BbfPeAr75yvKtCyr70wN0+zcFywswARf8Nf78AGbxGQls/Tj/NwVCBDX8g/lYDuvzJQAwAf8FWAYb9Vb/QP9H/zH7EgfIAJn9FgAdCC74EPbaBwj41gpgAgoFrPpl/a0L5/JuClb99vic/sAAJAwzBKMClf5cCRv36v3wDyL3DPeqBNv/9vzWCHILlAK6+Hv/cP6D/WACR/92AED1FgArEDcBmfXiAfn7S/RcBZsEywF09ZsAGBEX+O76qP0b9V772PoDAcQDbwSfA6YFbwRE9uIDuQLj+TcBmfvK9Jb2Lw+1CUf/ZwhO/wn2I/NGAZcLmAGV+pgBVQM+A6z4BP9p+hXpKAV6AfgDSQhCBt4AQPO5Bqv+Vv+h9/b40gvaB/gBVv+uBXD8QPsU9zcFHQjy/YgNahHr+0zujAyK/2L2tv1JBAoLpPZYBsgA7QLLBev7Ywfb/8n8BfG++YgPvAOg+WH+bwKbAqIELwcVBOP13euS+RUEUQLlCqIGT/kx/7EER/0B/Ov54gGK/XXrCg3DFWX1q/yxDnD4Qe0OBnIDrPqW9in/DgyK++D4CgkHBqz2+fsDA/38zflE+AoDmwowAcL8+f92Auv7E/9nBPX+0fZT9CgFAwlNCdz9mf1NA6z49ATPBBP9GPBgAogHwvwRCaz6rgFYBIUCvvsHAk0FpPjJ/okBMw6YAYwGrPg98P8JdgDtAsAG6QPu+Kj9/wX3C00DG/dT+Jn3TQksBPsKxvmT558Bdgq8BXT/F/yw8ywECgWyACL/s/K++e7+UQTLB2oLMfkJ8vL/+f3g8AMBUAoQ+ugLcgMSAUYBYvIb+4r7ofV7/csPlweMCAX75/jhDe766/Mf9kkG8Ata/owKChGS+az0Zww+ASL3YALj/7UDqgimCVAMq/728ML4cgWuA9cA+AdnBP38D/7U/2z/t/umAaIGqPVa9LEC4Ql7/3jwMwAHBNj6LAK4DtD+MvN6BfQGWvgN74UGUvw8/LgU2gNGAZn5EgPEAwz5wv7N/60Jbfn69XkN+ftF7JcP5BJ/+u74UQa6/If0XwhH/Vr+2PxnCIgH9vT7DKT8uvr/AXD+qP2H8gITIxJM7rv0wwmBBx/4WAKqBqzscfTODuQW6/vs6VAS3gLC9JMSnfx87bDzAwnLA9zz1gyBAbf7fgAvBbkAiOT8AkURS/ad9PcLNwf28Nj8kf/r+eDwtv+sGy8Pv+9a/MQDku8GCMAAe/vlCOP/Pgfn/gX5FPed+JsGxAemBWz7Xw4CERHuEQlGAXHwg/Xk7/sOpg3HCg4IwAjg7kTwKwgF+UEQ5QC6/AH6wAKbCtD8wAJm89j+F/amDYgRRPaiBhIHEPop/T4JEPxp/JQA+wzj+3YKDgyE7fADOfXPCin/G/XZG+UEReyk/IgF0fJP+3IHOgi07BT1dRRJDFL6oP+iBlTcBe3gFVsTR/+JAS8Jt/UY8FkAmgxP8Tj/AhUDARD8OwT69YPzqgYU+bf79wsgB5gBjASZ930C/fai5YEBvvv9/qD9KAfsDkv6kvMI/Hv3XvkkCAT9+wTY+O78VQPC/nYCuQIZA2bxQRBrA9T5lwki/9YI4QV9Cj4N9AJT8o78kwbf+k/1zwpRBqz6UBhuCKYH7QLZ7Cr7kAGD+V3/hAxvAC38XAFYBEoC1fOh9W8EuvpRCDoUjAAB9vrzbwTu/hP/OgjaB8flMfWSHPPv2gMKEfn7/fhYAgYKg/ki/aHz4gOD+cPs7A7eBu0EHBDY+Fb3Tv9p9mL2TOxs++0AMwYYD8sB1P/c9XD+OPvV9bP4h/gVBFgGQgjpBVr+pPSV/PsG+vdE9DcHQgSMAhENQgZH+Rj0dgSAD6YB4/UsAiL/xwhs/7/x4REf9PQAVxR/+HYAVv16A9z5T/sSA5X8iv16A8Ya2P7W5c3//AIx+8AAR/8M/X0GrgEZAyEFqPGuAYkDLvbTA6j9TQcWAjH3wAJ3/tz74PjXApH9VQP7Cv36LATg+Ovzt/m+/X0GqgIKD0oAFPP/A8AChvpP8xP/AwU19pH/PgssBFwDPgf5+d/8zfvN9+QUYfxh+toLMwCtC5QAWAgX/oUE0wNe8ysQjAJYBDMC9w3lBOvv5QpnCpcHVvfwCbgOkvde7y3+OgxgAL0BIv2lD5rxiv0gEb71OwJW+Uv+/vDQ/vAP7xfG7VHbjAoU7RIFIvs3AbwF++nHEssHQgSR+/QCzu/s5RkLS/7U+xv1NwOfBWH+E/84/7IAtO4VDlAKpPTeBsn4uvz4Bfb4Jv5jBQn09vjPCHj67xOtEVr8/wmk+h0A0wEj78n2Ag0m/Fb7+wQ3A3Qeivdh+iwAnuzPBKD7Bgp6AXT9SQbJ/oUGqgCuA8QFZf16AyL7W/DlAo76KAt1DP8FqP0N6XgdLwW3+TADHOcE/+D4nwHGHp8F+u0SB64DPfTW55sApgu06qEYtBNA/dz9UQIkCt3l1fNE+hvxs/yAEwIN2PpmFMgE3PXC8gX1Lw8e/JLvIAkkCG3zfQQgD0f7QPMb9xgR2P4Y8g4EmAFNCzX2ZwSqCGbpzfXaA9D8hvoZDaj7q/yJAQYK0gdh+MAGce4GCK4F/u5GAwz/xwjlCp8FOwTODJL1fPNJDvQEKAHEBZH7+vWXC9oFzwQX/Nj64Qc97sL8cgtNC7ULHvziASb2y+bHBiQEIvcrDKIKuQCv+w0QOwKh6+jug/OiCMsDKAPC/sQDhv6iBsMPhOvN9UHvJvhNB6j1G/0I/ED7r/t2AGMDQgaD96z4OwAU+Yr/fO0b+5MIRPiz9tMFzwpNC90Qh/aH6mLuYAQcEIgJgQHLA4UEXvFfCPQGf/5L+u7+/wtrBycTjAS6+njyAAA2CyEB5/pJCA0Q/AKQB+/0gQfG9fL7xhaQA4wGMfnWDLvuxfv0AD32bR4x9RT5nguo+TLlogrhC4DwuAqG+qYLOgZ4+PQGFPel5mAAIxKJASQCG//HBnXvPPjWBDn3hxM3CfADg/tl90YH1P+s+D3ungnACM7tcRFqCaz0Lfru+MgCe/sGDqIKUQZcA4vtOgY8/ET0cPiiBPQGivW4EogLWQBx9LjpgQk2C1gCBgybCi7sT/u/Du74WvpI88sJjAqZ9U0HywlNC+P1WvpCAgzz+fsDAyQC1Pu1CXv58vsb+470Nhdl+8QDkwy07sL2aP7J/qYJKhhVAdT9E/+c/uwM5QIy7SvpFgARD80cVA10/QH27vyQBVL+MwiL6zj/vAno8Pn9SQSqBgj4uvzj9UkEywFM8goPxw75/fvl5/gU91gCZhaz+AsBafwE/8gALfqR/7kADPsGCo8N1fNTIYAPZu0M/fPpaP6IB1gKDgBrBUkOR/1xE+vv9ACAF0jrafrr+yUAbPtQEisIreKR/yL3G/9yC/QMOwBe87jhKvO3HJb2iv1P+1r+BwaUAj4H7vrWDHjwwv7zElQFLvIDAyAVV/H0BBD8F/xW+6T+BwJS+jcDGPJJCGz9gv+V/If2G/tE+FAKpe5yBT4D9vQB/vL9bgp7+Uf75O/ABmsDF/hXGpn5T/d0/bEI5BJ7/WIVHvzs68gAxvcsBtoDnwGwFF4e8AVW+R0KYvA8/GoP6/MGCOwOVvv7EAMJafj5+xDyWvaD8doD9xPWDmcMoP0oCzXw5d+bBFAOiAeG+l8MQgrr8RP/GQnR9irvq/4I+pH7afyFBEwRZffC9Ir1+vHIANH2QPez9BTxlwVa8h/yIxTHBn3lmfu4EMfp2PymCQn02P6s+tT/WAh6BS3+fQ6QAbjrYf4RDXIJYvCMAMQFIAmz+kIAuiEF9VQLVA019JcFi/MF9a4BPg1jCQIRG/9T7jcJnP7j/ZcH5QAt/F8MYwkm+qYLJQD2+gXv3PHdFAILkAf3CWMFCPrTAQ4AXvf4BSb43P1RBOEJXf+PC54JL+YX+Ovzwvyw7TMMBR7c76H36OpfCBIHu/Sc/uDuPubF+7gWYwv0DB78HO/l4+f0fQTj+Zz+F/qhHqIMG/mqACb4gPAy6RUQywHR+pAJ4Qe0DQj+ogiS+Qz7vw6g+Q/+lAJcCwj+J/KeDXYCtPAVCNwcLwUE/4wESgLEAfb4ePZh/nYGuvpIGGX7oe1TIwMDwvRNBxUMAfSR/9YG3O/U+zz62Q+xBnXr+fsHALD1kwxyDY7+qPF56tYOwv6JA+UMEebc8TYLwvIF888Eqe0NDpMKSPW4Ds8AdPeXB1b/eex49D3sQPVjD4gLKAGTFFUD8+8ZDbb9U/IhARgX4Pik+lsNxvXLC87t4Pb7DNoBqQxi8DsAMhJ4+tv/1P/K9L75+fkcDq0PPfCs+LkEIvmXC94IG/P4B4P12PxiGT32HOtCACAPnhPwBUv+ww9e7SfwLhNM7vL9vAWn/4QMF/w+ByED6/u0DdYM5O3eAnEZseM591QFbgaMDkjz6QUF+xkB3/o7BJYVJOfC+IwIJvpe91MXuQTW51gGYf75+Qz/qQwwA3/2jAAGCML6RgNbFU/3hO1I9yMSpPoM/a/39vzCH8PssBj5/Vzgt/UF7y4TPfDsBrf7s/yaEPrxngvN+dnq7+q0D3YEEeqPGWcENwFTGQj60upW+Zn1xwhRBrwDngmZ908eiAVP9YP5Luy8CzLznP6pEiQIsgAsAHIJ5O/G79D+SQSK/xENcRXSBw4Clf4m+ITnMflJBHERkwgi/14aUQbk7XjwKvv667EKCRXy+yQQhQJnCOf4be8n8IP37AZl+V4iiAcQ/J4N7/JQDAH+3PlUDwH8ZffY/nIJkAG38zoOsQJ0/Sn99vTcIGH4+vObAjXwtQkB+AoP5BDn/PL3Uvrf/kDzlAIi/aUPNfqqAqwhCfY8+Lb9YvIU9+wKQP1YDBkF7/D6HK/3g/MLAXT1PfaS9UIGpgXvF9D8T/lfED4LhQQn6o7yDPsoB2btU/IyGE/5XAfDD8MJmwLV7+v5Ee766zcBLAZ//msBbP9gBlEAfOsM86H1uQAB/mH4AwliHZL5v+UNFF7v3O97+Xj4BRh/9PoUGxqK91EAYuzO7Xj68QGbBCsMzwCH+HkHLAYZCy8HyvKW9pAHPfZl/3oFuQLdDnT7vA8+BaMChBAQ+EkO8At9AhD8dPV0/fQAOgwrEvALV+1h+BELOP2k9lUDAABi7or93gZnDL/x3/ooAdnu8xZRBl71YvYf9iPzdgasGeDyyfpT7AcGqByk/kkOW+af3M37r/0T/9oLVvtP80IKqgR0HG4Kmuvs6aj1t/cQ+Osc7/Tu/qIG0PxfDh/ssQqtCTn1be3EBzYN0uatEeUKDPW07owCwAh877EE2gnY/t4C3yN7+RkBRRVq6vn/CfRmEJADr/08IxkFRgfy+fn7DPk26BzppP5l/Y76ux/hBWcC8vkHAL75ceZqDyPzRPBNBcoZFQ4y8VECq/yD+XH0HBKTFMgCTQECDYUCsOtJCp7kt/tQEHXvdgRjBXIBEPYOCg3t2PzzEvb8DBwb9VL68vMF9ewM6/HG8w3pjAabBFQRux+xCOUAsOshBXjy6/sZCfL5dgTr8fQCFBgJF9Xzs/JX8779vBH5+QoRGBMkBBjq0gc4/+bTHQRP+VEEuxP9/ssB0fgg6If4g/nU+aT+lvakH9YQuBCg/1fzt/Ot4CUAKu85Fi8JsPO7FXINogRa+k0Bh/jWBH/0KAkvD63ocPpQEs8AuviaDCTbwvw59Y729SdW/YgJhvxJDBUEU/LN94DmePKS7zsC+wpuEDMEtQNH+Qn0iv+76tj85/Zt9+r/xwyMCrf1EQnG8+P3OP1yBf4PePAgFUkQ9vpUCXoFBwC79IwK4/vLA/LzUOXQJc4S8AvvEXv7Kf0RCw/+cPbWDjLzMf2dGQ/+dP3HBuf2dQw7AAoJQCJL+EEQAfqo91UDM99T7ODwIBEZAVr8yws+A50XDgKo80T2g+9X8Tz44Q+AE2n4zwAWAm8AYwOo+WH8eeJl++wSOPtw+mcA/hEHAir7nwHv6hjyT/lYCrwN4PY6FJgB8/E7Ah/6g/tf32MDhA4f+GoReQdFDQcGs/T68UD1s/Sz/hUIYu6+/UwX2Rki+5LvHQD7BgIPkAG/FjMGKwr+Ff36WxUB9IjopPhvBEkGuA5WIsff3Pm/HIwEIvnu+rvw3teFAjnzVQM+Awj47xlU6r77vA2Z+0jp+92e6kv86QVE+oQWLwcM9zMIp//z8WH8Kwgm+scMvAv7CsL8nfIkBkHjNurY/BT1LwUjHAgtOhSmCzoOwONY5QH4JNs19MMLDgySGIkBwh86CnbdIvul7jn3yfp5C+QYcg0jFMgAcgtA81/p+fsQ9tYEmgwCEaIIvxDZEXT/3O8zCDMAk+eID30K5QZH/yAN8AP+6LP2+u07AgXzHQorEGAEmwqw8VAOwvYN75LvSQR1FOP5ixz0BuwI3Pko3AIP9+y85OUOUQRiFR0EBwaeCxj06Qeb37fxbPsE/1odnfL0DKD/qPsp/WX9xh4Q+ML+IvlT9K/7S/6hGrP2zft8FvPxuQSMBJLvYfyh7474bP81G4QKDgAT/yTbWQCs9CwA3Puw7W4GYw32Gdj6+ANM8BngBuvY/GX14PgbHo72gximCxkBngsF7yUAAu7WBlEAdggyEMoRlhvC8pABcPayAFsPbga1CQj83/5fFO8ZUvpw9pfksOnlAKIQBRoDB+UA4ejN/b79fPVyAZrnLvb+GVgILAKlHbTk9+ZT7PX+Iih160IKLAK/71L+2PyMBqj1yfox/agcNwX7CvIcv/M25NnoBfVt90wTNfz3CewOzgx1FiP17Aip5bDnSQapCj4BcfQvCR/4kAEuHTcHMvEzArDtRQvkEi7qNwG/81gCYhsgE3jyWAKD9/fiFRAb/V4cegUJ6nwSEgMB/P7u2P5E9nHwyhF9ClL+NfwdBp36be1P+ZbunfoE/VPylw0VBDMACwFx8I7y9vqV+DXyOgoVDlAW2guz9o78K+tm8y7yePgZBzoG1gSeD6cwvw6V/u/2SeOH9o74tA15DfAJ4gGpEJkcQe0HAGrs7OtUC1fvIAtYCvn/cP6V/p4P1emS+QILafSQB/7q0fKSGrb/Xf8b+2nw9vzy/3kNLAap6R0COgbC+vsSq/4p/5H/u/ZM6svkXwr0Bh0IXf2/FJcJceZEGUYDnfxA9470MhR094b6r/9d/Tn5EPrEB3j0zfOd8rP4eQ3IAs37FRL3Eyb85BAoBY/mvvcJ8gT9IQN+AI8VkxS4EnkNTv+K+0zmRejzFMAG3PmIEToOOgrq/8AG8AUR4u/s3gDj978WSBzlCuEJBfsAAFgM0gmd8rf5UO9i8NUa9AZrB4b+EPhgAhTv1gywGND+de278goPuvya7+UO7vz+8Fb/bwIREXj6nfAi+Ujv4/+Z96zs+AXPACEBgQEHBuwQHO+D76D5SO8K3iP1Pg9P+y4fcRPLAfwACehCBgH+qekF82X9OwQYGfYlmgw3B2cMnfZm5br6RPSh724KoRY2EUUNSBa8CQT9fd3R8GX97OWEDlECTQcZDcAE2RWn/wsBtOh93dz79f4E/c8GhBJ9DMQHJAQU62roMu336rsZuBRgAs8ICe6S7VgIyhkr4VPwwxFm8e8T3Q5YDEEQvvc7AP7yv+XEAXIHbfPu/pYTuA4n6rvw2P6r/ukFOPtqCWn62PZ/9G7jPgGlD+wSpg399oP3lw8VDqkO3gIj64fyw+pI91QNaRkYD4r33gSpCiQKNwOA7vPpEPRyAcgCf/YVCrgUagvvEQH8Uvrn9Jrx7QI+B24Me/1bERIFmwDoEdLmhO1A/3IDhvq9AfAH1fX7DLwLbhDn+AnwrQee6gH8UA7pAcL44Qm5Bo78Sx0zDiAJQ/7z7af/dP2t4sL6cB8M9S8LhBSlFxER09yiCsL0UOljC4wEEgdh+ogFIvkhAWIV4Pgx9a/9F/pP+2X1/wXXAJrpH/LG9YUIde1P98sPu/Q4/xf4F/zZ8pn1VxSbAD30PgfV81ECcRHo8MAEi+099J8DpgUODNMBeBfG85cDivsd39z5Ww1NCbfvZwSxBFEA6v2MDPgFauzz63IJDRQhAwgp/AIM92cAFenD5p36hx1FE2YUxf/WCk0DcgWmARzpbfMO4bEMGBFIIFAW6/XEA+P5Dga78nv9i/HJ+AIPBwaDIssFL+hw/EYFqeUF+z0ZIvkHBGoROfPK9M8EAwEb/ezpofVkAaj70gnrGMsNAfYvDTcHi/FJBNT/oe2xBKwbtQMZA7b/xAPVHHv7Afyc/qzy9xNP+Uzy6v/L5or9viCaGP8De/dQ6ccK7xGB3oPvhAwj7SQCKhifAc8GDPm/FML+UOvEAanjBwbaAe8ZPg8H14QKAf5U6CcN+hjR9kD1F/xw9mAGxAE2C0oAUO0U97wFWARfCPsQcP5S/oDyePBA/dXxtA+1A/7sngt+APQM8A3/C4wAudlh+EoA0wX+DycRdP+P8HoDvveTCIEBKAlmGP3+UAyxDPsI/foN7S3+jvwf+K4FkAXLA835CwGaENcAqgBh+Ef/PfY57YQO/AL+8FPwYf4rCMsDKAc6Bor7rO7Q/HoDQgJUDeERag85+bfz1fWo8eUEUQLSC1EGQPV5D18MvxYOAFDls/ht75nzlfppGXIJOe9UBe/w+f/0ABTxvQEkAmz9nfRYCMsBhO1A/63kK+noGbwJ+AdCBof4SQha+L7/qgIAAHUMnwEx+4fuWQBjDSsSxfvg8LgOcPqFBIQUKw5t69bZbfUb+zz84gGWFyb24/mPGcAEcPw19gn0OfO8CTz+7A7KGfQA9AQf8gT9YfwgCZAF8v+4CDH9khZjBfgF3/ro6K/9g/UX+pABLw29AVr45/SI3g3xZwaxAuUGHQoQ+sL4G/m/80j3H/LU//8FAf5YCBUQs/4Y7g3rqPGFBMX7FRIMJFgI0wVP/U/zxvmFACvpWvb7BIP9IA8VDuQScegc4yL5Xf84+yb0KiS8B2z/zflb7Lr84Oxw+mAEWw0c7b7/+hT/A8MLpepFD9IRM+PABngdZfn36n0KBwb4A6EW2PbLB9wk6PBE/JQAw+TN9+UAJAjsCgoN/wNyA+7+IvdM7HnkpPp88w4MiiKbBgXvJ+Yu7OvzmwrJ/Ff1BP/C/AUYqQqs+Az9fPVS+nv/q/yK+RP/afhw+Ef7D/6tD2oPdgag/6YDw+pc2mn8qQqFCKHxuvh8Gk0F7vgi917z/vLk83ILbP+pDnQijw2S8VjbIvle8woJERdyAc4MJxHOGFL6E/1M8OHo3/xjCxgVUQa0FUjtUQDWDl77ng1i9sn6FQowA0HlwAozBr797AzK8FwJR/sJGy8PgOTN+9D+BP9B6YgLkxKR/SsQNfbk7aXyNfBCCqYD1g5cC1P0/wmD96YB1fO14AH8E/uQA3f+FQZVAcn4Iv9w/okBzwJnBM3/wADC8jLrMvO2/Qz5dP9CBqz68AcsAqT+Lfwq+RT3lfyiDo7+cRPiA4DkbggJ8JX8Lhvy82cEdCDsFN0KZwIu7v341P+iCpYXi/FNB/sK1gQgCz4H5BQC7Or/DRh2Agz5IQUOAqLhhAwzDAMFNSGJAVEGsQh170D5W+4n7gMDMwCTBhwOTQsx/0UL7vr+5s8GHvz4B2YQ+AGlF2H6k+dRAjX6Yf4YEZH9ivnHEmz/LvT8Aify6A/7DiL7eRFp8I72dQ76FlASZfetCUv8f/6aDib4Dgh/9hHsBgipDEgW7vr5/xkNwvo7ACb28AUU9Y/kZhiLGL/xOfMWAsX/wv4gDaYNCgebCEj1BSL+EabgNwOx2yrzFQRgAu4j4PIc61Ps+wjsCh3f2PhJDk0F1etnDHUWI/M7Ak/1lvTG7zn1xhjc/VwDqRDzEvoYS/j9/H0MpPhj4iAHiAfv8icRMfnlBGQBR/vRF9j4qgSIB5MKdgYwAUEMjN/y+1EItBXCI7P2dRgOCPvp3/5jBTj9BfPY+HIF7x1FEdkRRgeT5YXbj+aA7Ib8eB0T+9IPdRLG8WcCuQLr7bnTJAgt+l/rhxOwENUYyfZe8fAHhvq85FPuowIRD8MNGQVnBs33kAM4/3v/kAXN+4f4kvc1/u/2XAWd+v34s/7HCLwRofe1BZX4lAAU+aXmrQ1E9pLvzg6xArTqbfM1/ogL2Q12CsYaWvzR8DX4XvXg+IfynfRS/mMPhv509Qj+wAQhBe0ATQeG/BkHX+sN560HQell9cAMivX7BIYjlfh/9rwNbfPR+Of2R/3hD8oRogRE/Kzype7F+476Jv6s+kgWVAv2/NEfqQzk8xnkv/FT+Ir5TQviA30Ce/ntAiARvv3lAK4FAvAx96/9Dga8CSgD9Ahw/If4XvGh9RD6iAsnGcoRagkx97UFF/Z9DtUWS/RCABvz9vgp/bgK5BJ9AkXgYuqpFqnlivX6Hs39u/Yq+cn+5Qyd+IEBZhDN8bwJZf2t6NHu+vW7GWsFzhDtAs8EWSuP8LDr6Ogf8I8NG/9mEDz+Zf1/9lr8eBvEBQoFO9PZ5GElRBcCESn/oPus9Nz5+fsF8831BfvdEqoCIvu0E7gWYwWUAI74Afxs/c7nUQYyENj6gPAB/qoGU/hMG3IJsOf4Afb2lf4gD5L1bfWBC5cP8++H7kT8cPr4BVr2wAJ9AjX8DQ5jB/8N9ATC/hD65/x3/IDuOP39/Lr4cgXWDOIDQP34A8cGH/h89Rv7Afi/8/gBuxfU+aYFqQxo/kkK/NcD2k0DngvKF3Qang8f9or59ArK7tT9dRT36AH+UAp8Gu8bZf3KEZPnTQVqDyrzzwjN9fANjAK0F4sUfQRFESHabfMQ9rwFPRMV5eUAbRZYCH/4zwZJBL/vHO2d+Ir/zfd9AvsOvAtl900B/fhW+xwOiAe2/TnxZwTn+HIN5BAN72ro0fQDCY72xwrY+jsAHQKS81cSqgDXANXrmfcOAq/7XAPv9C3+H/Je8fb61Ri2/1DrVxK+/6YNXiCFAIr1LAKZ9Sr5D/7AAHEVVAnhD5MQUv4y817xvANa+r7/SBS37zcFzSKICQoDx90y84r51e+eD+ELKANn45cP2gs57T0XAfzY+DbuNfBNCx/4AfpE+Cb8sQK3+Qz7s/Y595n9xvWd+sACmgwVEiMYhiWs9v70gQdw9v8FpPQsAFb5i+1JDIQQtA3N90T8h+pq7p34s/IZBcvm9vbLCZH/r/eR+0v2u+oX+HD6XxJQ65b2zhSP5uDw6v+TDA4ARPZW+av+JA7eBCsOEgM64aHtOgwkBkP+UQiBCzMGogblBBkNCRUm9lDvowK8CRkNSQyFBMsHNwHV9x0Gbfe07Az7Pg9QFEv81PvaBdj+3ghCBnT1xfst/M8A7AzVGr8OIv8x+/L5VxJQEC8FZf8X/AnyZf8KD1r6XwwVDF75wwmQCUv+Ng+v/dbdCehrAbgOgQdnAOD0FQa38TH54BeA7Mn4ywGo8bgWDB7j/TkYFPOm5PoWhOeE6/EBaR1xFxUSEyjWClcaIv1f64Dkau5JCo76FyNpI4ELOg70DP8BBe8y8RjsXvc+D24MkwhcCSgBsQKQBQH80uZU3gLuOwS8EVkAbfe8B28EDPUVDHwaqe9U3Lfx1wJ7+aT+bR5BEuD4n96P6gcCMuvlCmoJrO4gDU0FQfGxAsbxhs3d69z3SgCeCx78ERH/B9HuPfZ09/PxlAKECqkKQgaW8JrrR/2fA1f1Jvyh9bgQcCVL/Cr5zwQJ9oTlF/Z3/HT98AX3FcMVPgWV+oTphv4q+cgElw/q/SL5UvqTEOP91goDA8TYFO9jDw0StBNqC07/XAWS+YgPg/2YAcAKGO4CExkJeBnoCzH9HBCR+/AHde3j/8YUsQpUBXf8vAk27Bf2LwcsAvADAfyv/Tj92gN0+2sD/ADD6j3yLAT8AG351ga4Cs4M2eRm6eUAJ+5l+V3/xiCMAtH4jvgy7esYQelE8Az7zfvtAED3Fx/iAVPyGeTw5qj90PzABGkZDRbD6MLyTPK1A2X9G/EwA0/xcgkzDJoUvvsz38fnOuPeCCwEwvhJBo72gOo19E/5qPea7Qz3pfCJ0ED5BP0c76D9afyk+qXmYfpCAE/5G/f36uUAvvtnAvsMPeqXBxwW3PWk/MLwAfRuCIchkxSV+isKePjPAE/73PuWEQH0e/drATX+ViDkEmPaafSjAEf7lALy/48PQPOz/lcSDgZA/cbtafbr+6Xw1PnGHgz7ofM8IzkYVxDoFWH+ot11ED0Xi+9qD7EOMwyMCnwShBTc+WoNgQsVBqHznfBHJJ4LmfM5+YUAkwYSAfsKYfp7+6HrAuTf/nD+bgx8FNMBlfjaASUAXAWw9cDjCfDQ/nYGBP8OCsQBlwf5+QbnegWUABP7BuvJ/I8LlupnBDcJjvQx/5MMyAIO3x7+ngk8+LgQvvfaCX0KBP+lFwH2u/Lr83YCYAC1A7opEQ/u/hv5ivXwB9T/UO03AUkE7vocFlcclw9E9Pb2T/mL684OzwIDBUEOSO+QB17z2gHPBp32mhja4Nj+uAiL75sE0e5CBp34mwpA9TX0BCru+EwPSQiL5xIF9u65AHsiMwibAJABLwVrAQoN3RLR8in/ku96A1cQ8vewFJz+SQbsCpn1Awe8CQz1M+HG9fsSVxiIEZ4VxxBB79vURPQ7BJ34hxcNFBIF9AoI/nf8WAbg7CPx8Af68+0Cww/3EdYOsPNM8mcATA8E/bfxFRIdBFgEsBBQ7/cLpg2G/scMZf9UB4vtCfDxAdj+mhD3C2IZOgwx+SANjARO/+UIXf9A/3D+SQZFCX0Ivxy38frzVv0u7M0gAheBC3T/xvPY9FL86xqA7i74fQjj+zADT/Gv/8X7zus19CwADP9uCssNNwMhAT301e/+8FP4F/YRCewGr/mG/HYCpg2A8D3uPejPBAIP8vN8FoUGqPUwA3v5ePQx+6nnk+cn8AcALh+eC7P+xvGMAMX9s/q+/0j1Vv9T9jUlDRAu7Nz7Mu9i8MgAQCZ9DFb7s/q4CJoSqgS3GpH/f/jO7Q4GbzEoAZsAE//R9HYE+f/wCfQGMf2++88AUQSqBIr9U+zg+K/7H/LTAxgTVAVs/1fxw+jR+vDikf0NDsL0VA0dCNoLvxKH+Jb0uviP5rr40hE+D7gOvAU6Ds8IR/9b7sruwvZe7+kJhBTrGMYYsBL0AIvvT/sp/y7s4Pj/Czz+WxlQEsAKUQAJ7M8GQPUM+W8AXwhXEKkQrB/wDREJEPL68VgGlwXwCTMGcguTDHweGB3IBD4N2gFq4qT02Q0DCRwS5Qhd/7wRSQz9+n0CrPTR8mcIJvRvBD4JTQfoEUTwoe1W+4gLnfjJ+nUUgQfaB+0CSQTC9hjuNfSYARIFtQlXHMX/R/vOFisSF/gWAAH2v/H2+vrx9xF5DekJ0wEnDWMR7QCeDUDzYwVF4jrjrB0E/8cOjAox99/8cPyQB4P7kf3v6gH0dyfAAvsIYxEn7IwEG/VW+0YFogggEwn2ng3y/Yf46QcD4C8FhAxL9pEmPR1d/U0FjxNNA4DswAYKBU/13gTSE1AUE/sU9zn3AfKTCt4C8AcgC2j+dRYq8bTsFQb69aT0fQKTFAT9owKFCP34TPLr+XINUQIM/fQEWhvlDpoQ8xIu8LjnZwDzEODwmwKFAiL9pQ+iBvsORPqh8SEDIxKIB0IIvA92ALvyr/1xD2Pmd/69ARztahESA5oO9Ab/B5oMQePs5777tv22/4sUTQVGAXjydeUsBJL3afxp+GX3bfd1Dj0RXvFp9jfcXvtU6Cfs4/sS2ED/5PNQDmMJJvYJ8lvkS/o26Aj8cPp4+AX1DgINFED9lf736t3p/+TLATYPV+tYCL8SwARYCO781uXa4rTui+kt/Ov7afJfCCP1JBAdCDrldeun1A/+KwwOAlryde39/k/3e/+Z+Sb63/pjDw3x5OeC/1b7VAv2/FMVuvoz4Rzvyf5qDbDtqPVp9vQExAXeCCAL++c667f3r//j+1AOXwwwAVDvnuDJ+jnxLfwx9zz4eQm6+BD8u/b3DcL+9OOl6rvshxftABP/dQ7O6yb42fCZ99kR4Q1e83TxvA+D96j97xFe79H6yfwf+HUYeQn9+MX90Pxm57/zgQnc9SsWkxCw7w4A+f9h/q0LR/1L+Ir/hOcF+2X/5/qfB+P1e/k9EXQc3Pk98M7vY+BNB8QDk+tFCcQB7AyLGt4EAwOL8VL+zfM8+nUOAwfHEJsG7Aw4+7wDafqW8hwMMw6HHU0LXxT4A2z/KAV17zn1TPBGAzMIawVp9lb/kwrf/Ib+DP0KB+v1RPxNBQj6dgSXB8b3f/q5BKYB7BIvBaIINg/lBi8NOPt9BqkKkAltIkEU3P3IAuf0uA6DHt4A9AyS9bvu1giMCmL05/ocFLP+fBayAHT9KxQ97lr2t/e8CXz1g/FqDf36jwtkAW8ArQeXBX4A6/kDA0HxKvuJA9MFQP2X3OjqQPtyB/sEZu/n/uDymfsKD7r4pgXV9+jmhN/Q/LwRsPX3C4r36PBp9gj4r/kg6A4IWvZi8AcAYACIBx0Guvwc53zzXu8t/tEbpgm79MLyFPdI9zH/nwcp/R/6nhGH+K/3HQJNBdIJ389JBq0T1tsJ6tzz4QUz49LoyfiMABkFCfZ9DCvjjdWp5RjuuONm5x0Gi+fTAVwHAfT7BoP3ouHW3b/vi+kG66Xy6OpE9GACIAuXCwMDj+xq6A3tM+Oz+OkFg/OW8kHrH/pjC6H3LvCI5uXZNfKiCqf/oP0F7/7u6QFp8EjvWQAn8Anqbfkc7UkIcgd55Gnymfep61P4hQgY8PAFjvoc5f36S/6FBHf8Kf2t5PL9zfuW8FEICfBuBrEECPixCpoQu/BW/Tz+V+eBA1P4S/7lAF8MOfMy5/n5MuueD90Q7AguE7EGoulI9WcASQh6A6zuBRxP89H0aC+8AyPzGBG3+17tLhdvAET8FBQX+pH7DRoVELP2ZwLF/TLzqPsm/J4JiiJ79w3xVA9a9PsECPqw65cFCgNuCPoWXxB1DIscQPd48EYBX+maEIsY3Bg7PegXyw0jFv7qFgIcEsr0aRmGIywzqjmPC9z9i+3y+70BWxH+Dz4LtiaxAtwcmSLwAzoGS/pYDmcGLwXQLxclVv3oDSMWjw8NFkAcywutDe4lkw49HfcRFgB4FxQYBCYQG2AEkwiQB8sBTQntAH0KFQ5jDbsdyR/KF7Dz9+x7+V77NwMMHoEFmwo3Nusiey73CbDx5PHv8i8PAhE5ImIfmhCLEPkiPRNTF7QPFPeBB6oEJxXDEzs15yGL67EG3ggsAvQAoCKYLMsJ+AfWDOwSEBkrFvcNNf5JECMUVA3NKOkH0fabBkIAxf+HF2wwMhTEB+EN7BTqJl8QfPMJE0EUQgpYClb/eB1NATAB8A+mA9kRQPkkAkgenSF9AuUAFQ6E7VUBwxetCX0Ctv0rCrgWPgFl/zEeHBA+A+QYVAW5BEUTv/N8FDQzFQTpATYNPg3+HUUVtA0hBXD+S/alF3skSPWWEdoFkAPVEo78CPpp8igDFOvwB8AAfO0ZDT32mg6iBLP4/ubY9AoNsO8WAIUG+wpx8IDw1ghGAUzubfmMCvbwQ/7G+Qz/gPKz+I8P6/WZ+WPcSQRiGeTz7AhyB6zy/uyFBOv3V/NL9gLwlvTn/FgMMfnaAaHrdPnPAOHmNwNC2YwAPg2A5gMB/u70AoQKRPii55L1pP5Q77kGlAA7BO78ne79/Ib+6/mo90D5mfvr+YTnh+z99kT2Oe2L66j3vvVYBAj6h/hH+avRTdbV9Yvvx+cWAAz53Pv0Apb2lfrv7AXtuN8b913/UOVcCdj8QRTwDULXrQmxBvrrIv2o/Y78hQCMBO/0GPDC/D4HiAW37ef++wbr81gCOfUDB/oY8w46EKHxXvFCBlwJu+ybANAlZhC7Gb4myR8ZCcsBs/aD+ygJOfdyDVUBkwZWIkULtBP2+v/YMu8kCKUX3PUn8LUJDe238fL5uQTTBTvN6+0MHH/2NwU2Faz6h+wz2XD4IQUb8ZsGowBQ6WblMf0q8ffohBBCCCb6OfUI+GH6NfqUAMTcn9rW3X3jJArDC78WvvvD7or1Gd6s8pPr8Nzi2nXvcP4T/a0HouUv6AcCqPsK5Grsofc26l8OUQbh5PrzEPBN3BT3TBuMAi7yYvCe7B7+Rebo6Bf2a9pa9IkBkAOv+9nov++f0FHZZu+E5zj7jOX033YAQeup6W3tm9ub3XXpt/kdCowAVdoY7FjhXN50+y/m9+CX2h/sOuM18Pb2o9f69b/tB9MA1f/kreht9SPxZu1x9GDVseOW6mPmKu9N3vXPZu2+/x/0mhSiEj7mKOCt4I/o6/ck4+HofOlb8D4Jd/zIApL5zfHl4Qn27xu++xD4JvhF6jABD/4u8CsSKvPW4ewOKwhRAJn73gDn+M3xsQ6TCK/36/tl/4r/ZvEq+xjy4O6/Esn+7QIGCPsO1gjs61EGF/5i7NricPzZF4P9De9jA+IBq/59BP7qHQIk50zozhAI+Ef5cgWDHOP1JvRCCD3qbfMf7NXz5QAOCiQIQgRbD3YAWAR48PPxjxHu+DX6lwNL/jsE8xBJBtoDZwLs3fQAS/hE9vYbnweaELkGj+y/82IdowBX8yQG/fqMAAbrCRNbF4sYqRYC8G31V+92BMgCAweQCVQFBhBNC1gGuQRFCY/uX+nJ+kkQ2Rv2IeQQ2P6FCGX9KwyK9zsEDCCv/cYiNCuLEs0gfQyg+QMBag91EC8P3CC+HjEgJiGaDEkIkiCZJrgI+wpiHW0UvxBdKm0g/frODMwsoRxhI0o1uv6XBV0oWiMiJicTfQ4REaEeySVXHIcVsBJNDe4j0zjcIBcjHQrwCSAVrQeeES4TOCo1GX8ldzPYHwEdeQelHagcNSOvKrca/SMBI2EpRRV5E9gdUxXzENkZQCoPJ3AnxiAXI6UZ2B1eIEkGxwhJCH0Mwh3FKuAXeRVDK2Ev4yT6IPIe4/mz/IEJOCRHJsoZcCU+C1MXrQ2sF8oZBg5JEs8CUyMYE6QnFyHN+84QawEcGHkR7QCxDkkQ1gTdChMqjAot/p8HfPNH/dkTaguv+UD5kAW6/Hv3ng9p8gj6GQHa3sgC+f8m/EkKJv7o5G7hR//o6FvqzuuP5hHqdefn/Kjzj/C12onSxNZG2vL9TPA25J7m+90+4GveGtBk1OLSm9Vf4ZzNx+Fy4gfdHdWgxkzmYNGVyWvUftONzU/Cdtd20wjLjcnCxcDVg++14ufFOM430inKe8pf34nUt8AazinOptix4YThb9lHzKrXJNuM4ezlA9aU2RrI9cv+8iDkhOlE8ozXusWjzev3Vvn035Dgx93P1anlwvCX5Abh8+U64ZPhAu425t3rsPW2/VPuptyV+lTq/+Ly+xIHtOqt5LAUzfto/lQNoe+s9BTx9vDc/Uv2CPgsBn0MHQoVBgMBZu+BB28EhvqqAmLqBg4oBWcEjAwb9ZgBCgU4KjMOCgOXB/r1Bg6FAL8UuxeID+QQNhPpCaD7DRgLAa0HeB2kI9sqNRkYF9IJ3gjY/hv5iv/WCtghMSZhIUAmJim8Cbb/Vv0b/88C0gn+E90UxSwnEegVqBpW/dILywPhB3YAwAD7EgIZpy7JJfMSbhIx+zH5SQwP/qUThx+BCwweEyRmGkwX0gvaCYr//fxnDJ4RMSDrFicbSQ43A1cQ0fi4FKUbrQ+iEOEJSRAkBNX1hxVoM3/6KvMCEXUOtv/3D3wWs/JCCjMOJw/ZFzsxnhX+9EEMOe0E/XYCpRGFAJ8BpR2s+NEdXw7HCIQWofWA6vb6CROZ//APlALz8bwHvv1l9Sr7/wNvAIb6v/NXFMYaAADpATn5T/cJ8OkJjw9J4bTwgA3PCl8OfRDeAJ7qPeoDAf36G/3c8f7ulw1L+C4TOgYU8wcCj+q/7X3bfQhL/rP8Khr+7i8NTBNqFT4DQgAKA2rg8vtvAib8awVgBlb/7BBiExIDG/vWCukHV/MUFAX3LfoUHtYQuAiZ//gDkAWlD8oT+wzAAEkKkwx9CpH/ZwahGD3wagmeFXYAgQN9DhIF5OvpB7r4+AFXFI8Psx96BWACKhiiDCwEnwEB8oQM8xInFQ0WpPyhFjsAxvd9DF8I8Akb9YARAhcYE84OOe3rHMYixAWqBuP/RQlMEzEoIQV880wPoP0zCFEGgv/SDUD3QgThD30E7BD0APQCJv7q/bcYfQIzAk0H7QDY9kv0BRaSHIcXEROXC7EGlwVQFMYUSPcdAC4ZSQzN/evzbghP/TH/mhJB6e0CEBkDBUkKCwGd8uDsrgNcB6D7dgQwAXj6e/9CBr7/EQ3WBmn2Ogy4DCsKg/nY/GMHtv/3EdT/tv/HDGoLawGJAbwRbfeXCegNYwWaGjH/AwldJoUGtv9WJK0NDPWuAQYSHxsFGAwkkxSfBS748ANqF6kK/hFYArwN6Qfj+1MXOgq7EysU9vzj913/AfgJ9voW7xv+D8AI6Qc59bP0fQg9E84UAur9/Ioi4QuUAtYK6A0zAsL8H/T/A4AXOP/LBzMEgOwVCtH47+yEFiQELu4+Aev7Mued+Ir7OwKEFs3/E/83Ay/kyuj5/ejouvoOBlwJnR1fElAMyfZs+5/aFdvC8HHuORwZARAdhx9i8kIAEez02WDPgOzk63Hsgx6TEo7+T/2a6az0h+xR31DtLNVG1n3lYADPAib6ePTX1YfuLuwg4lXaWdMc76HxT/UKAxT58dA/ymrq0uIZ2uTvStMf7i4TNfjiAbjpusnFzofyyNsk2UIAceb5/S7y2uJP8SjcGOZe8RDy+utN3oTltO4SBQ4I7du85vDgCegkBG3tbfnE3trY+f957LHfWvQm+O/0nuwY6Jn15/gf9A7jv+n+8BzvY+Z53kzuVvfn/nIDawWW7vbwbulN5FUD8v1T9IDyUv46CAIZogR16R3dW+yICfL3Zwi/8Wj+KxCmAQITiQNW+/7mF/xb8Ev6NR0DAc4UYwXtApcDxusM/bwHnwEb/5YXyhv+ERkNAwMi94f2bP0zAhkDjwvYJeID9AihHP7y0P4E/4b+LATsDrMl+hxfDn/+vv9t8Yr/3Bp8GqoGgQV4H9ILrBl6AYjocgk9FckfeRX1KccQ+vH9/kv4EQ2xCpcL/g+AFSYdkAMkDk0NsQalGTIUhQSA7iUA9w2ECmoLOfP8AkgUdRREF/4VMAPs6zLt0fpqF9YGAweHHeEL7AjhC/X+OwKXBcX/UxkoBXYKUx8kBMMLDPew7/L7KwzACk0HahdnAMAIrgM6DLEI2eqV/Fb/ZhB5B+gTkiBNAUIEGPSQBzYPDPX7BIwGnfpH+6IOYwmK92n8uvyIBbEMWxUGEEj33gB4+FL+4RE8/IEJFQjEBUURvxhaG3IFwAYU9xYAkwpjAwkb3CJeGkUJBgiTEOgP4QUnEZoWqRSsFfcLXhr9H/oUOwQCEXgZuxusHSMSixRfDmkf7xtBFN4ClALnJaYNagvVEj4BqQrzGBEPyhW7H5AH/wsuFUUJJw8VCkT0T/28C2z/9wlQFBf8Xwo+B/b45/gR5msFIQNw+EIEbP9KAs35PuSJ2Dz4wvK86DX0F/qE7QfZ9vCo8Vb3OfE31sDfT/Vp9DfYE8z/2pDUf8WF11XY4tjA3XzpJ+hc2IzdANVgz4rC1ts+4CnITeLP3a3ezueR0JHMLNOQ2N7R4L/A1wrmrehj2jzLz9mwuibB58WZvGTKHdP27kzmzukg6BHkLNlpuZzNWdXE0u3TA9rl4YTrkvNk2M/h1uNOyDjItd4k5brD2tb+6CzdNfQJ7DDQkNYW1RXfT/He2YzbBNDE1iPpHddJ5XLgAuwr6S/e8+cy77HlMNIX+BHsWc/e1Vjh8OBq4DnvkvHf/pLtMvNGA5LzPuA+5N3jJOeqAMPkOfHg6r/liA25ArP8H/Do7u/wxvOH+GH+FgAq7y7qOe3J/q0HqgRB777/xAfN8dD+Ceyz/vgHt+/g9Cb4OghKAP8DuA7VEj4PG/2iDmcGsPWpDLEIdP2oGhwYsBJ4GWsBpgueCwYSZhabAEgWKhqDINwkQRTwCznzWw3NHCwEjhuDIp0lTBHj/YIohiOeFa0PLheDIiUASRDGIrsT2RcQG3EZ4Q/HDvoeJicYHY8NTA9FEZoQ/wmuBUcwhi0dAlECBg5AHoMctBG0F/cPRgfKF4MYeQ30ANj+ngmICZIahiMcGPsIng1IFmUgjxcN8ZX8+f96AXgXVxrrICcXWA5mFEkQ6A0b/yrxDgqTFLAY5BaSFioa3/wGCpMUDPuv/U0JNwmeC1sRzwZ5CVAMivcvC7QVF/7lBBIBQ/4KB88GKANNC3IH9vghAxYAXAv7DnUSSQQf8Dj/jv5eIg8ndQ4zBgz5lf7LA7r87+pm74r7sQqTEigJs/zj/1gK8QGW9LjrsPFp8o7yHQbHCtnmDPkRDTH3DgZyASL7Ce6K9VQLYw0kCuP/IBH0BBj0T/O6/PQMzwbSDfQMWvxQCnkRGQGg/ev5lwPiA7EGAg3HDpkc/g8hBaYFZfk65YfwgQfGGLAQ7QIgFccQfQxXGr8W4eT+6qD9uvoUFpMGagu8CdINOwCR+xwMW+x0+W8ANhGiCAcAZwYm/l8UCP4dAMn8/AByB2MHNhed8vwAAg0NEqwhpgl2CHkLOwStCT4DpPaeD1sVWhvGGuwMxhjSC4gRiBEVBFsPWA68DbcYqRbdFrgSnwVuCtYOZhgDCSALEBlUCZMS0g3ABowGzwQODEIK4Q9xGYwIHQoQH6kSIQOjAhwWQRJYCD4LXxJxFYgH2gkX+tIJNSNfEmMJNhH3EXkR0g8oB4oeqRJZAKYLeBvJIcMRTQ2+/XIHuBQdChgTmDSZHPQArCNrBbkC5xtyAVgIIBF5DTEkODIRFd4ENg3C9tj+MhJ5FdgrXiI4LKEWpgWaGnkLARvlDtcAwviqBGkZiA01GcoVfQ4b/X0GCRmaEkD1XvfKF9YEYw9jAwoD/w12AhIHe/9UDcn8ZhKAFWMHnSF/+JX8GQHV9z4NSQq8BXv/uBZMDzoMkAcn5pcDvvu77qUPyhNcBUICSBYzBOjuhQKmA2MF/frR8jMK8Af/C24I+f1fCPgH8vkY8NoDAwV//tT7tA8jEin9pgeO+kIGfgDtAH0IFgBuCIPzzhB9CMLw0g1YAnnq4OwZC84SSQ7oC7vyrPCxAl73kAltFo72Mu0M9SsQiAnsBlMZZwKS7S/iOg5EIdT7ww3n/iL5wv6O9Mod/wOS9Xv7zfvcHA4ImhCZ/ZfkowIf+DX+JQBw/G8CmwjKGcn+YAYVBAfdxvMx+6oIkwo3A6oIQgrzED3yu/S79Cr15/Iy8VEAcPyMDigHywlI9QLsX+k26GYOofOW8IvvBfFL+KYHQQ6e4P7mSd897sL2GOiS91Py4/1/9M3/VAdj5ojkpuKA6or1s/rEBWn2t/E8/vL5TOgR5A4IPgkHACwEFOsG6W7dNuY7BDcHtQHV63jyLvKh7zH9rPSa7z7eJOebAmcCIxSbCBHmG/Ol5mriXf399jn5Lvhe++juSPN9AkXkmwDABF7xs/zu/Hj2DtnD7jbu3t+A7NHwAwk721jfhBKK9c31i/ER4Lzok+nc8yr5UO0658brVOTK8BEJ2fAY8Ir1+99E8JH/Yfit6Cb6hAqd9EjpQetd/WPo1e9uDBHobfOBC7D1h/br8d3hUQLu+EzqrPq85vn9hQSo/QoH9vpg3fjUcfS38cL6F/j29LUF5QTDDQ4AgOrH5SfyiObD6GcKdgZa/PAHyw2D++P9/fjk6ef2x+lb5tcANwl2BGMHmhA1/uvz+vVF7FfzlABvBFP22gHN/bf16QG399j8u/CO9uTtau6K/a4Bixi376T6uQJI66zySOlW+ZQAdP899m8A8v018lb9vvWz8qT6WvrW5wT9mfXg8PX+k+t1Dujs9+DHBjLl7QDzEP38uOlx5v36puRp+jX8K+l/+NXv+wSiDGcKgQNm50HnV+v683f+OP8x+wj6rgE1/I7ywvhE+CfyJ+bv6lwD9AgoAdzv1fFl9Xns3ef+6HztU+5099MB8v3Z8O/uGdzW3ajx3PMx+WH6qelx6IQSVve77JPrAMsV5dnucPqqAqYHofXJ/qz4j+rWDqXqwvBP833nBule98sBK+NYDpX+6+9E9kj1uAq450Hr0fC3+58DLvAi//n5j+xe+7f5KvuD+ffqS/o592X5oP019C70gPDU+WcAmfvl5RztsQLC8oDyZwqjAi72Cfad9GbzW+bj+4vxofEWALvy6A949N4AWA4u9NoLjvrIBFr6s/bIAB/udRgkBLP2UQjf+m4KG/UhAQIPh/CZ9wcG6BGaDKkU4Q+p7Tn1BfMj6SQEXwgx9RwUhicnFx8ZdP328AXvRPKiDhkHOhJ2BrkGsBTY+FwBBfsvBxID3gasG07/gQvoDekFkvfEAZQCQPPdDrwLZhBqCwMDawGn/1f1PgMQGSUAKw61BQX1h+woAycXFQRxFSb+g/1mDgIP8ANT8kD34PIVBM4UQRiFAkkIuxe1A1r2HQA9G/AFEPzsDsIZwAKS930O2P7kEFAKGQGwFtoBzhRAINT/xu99BqUVegE5+QMB2gfLAUEYkiCPD60J/frsBtcCAfzaA6MAsQg6BsAKJh2+HmcGwvL9/GcMwAabAlEIjw1TFbgW8xhXEm8CR/1uCE/x+f8lM6oGjv77ELgK9xcgDVAMYATOED0RPgGmCQLs0wVTGY74BggVCGMDtv12AEUPwwueDav8jAQvDyEDKwry/YwCWAzc8xv/5QT3Cz0bLAapFFEIivVnBCcTBRqD90v6jAAY9OkBwxOtB8cGxwwb/xkFFPkHBuv3xu22/QH0OgrWDGMPmAHeAP8F0fqmA88CLAQF8bP4Xf+MCLgUAf7zElcUhQIVBCn/DgbG+bb9fQao+3kNxxCEDKIGCgfkEEIICgOqBIr7mfulEfQAAhVpJ7wDtOia4xf82PiPGUQXIQXwD5sKxhQn8nT5yABj5KzuMwJCAu8VGB30BhEPPfA+5tLoLfwQH1wDpP6BCaYBdgD/CaYF2P4M97D1xf0cEhUG1ffiAVfpWAzLA+fyRQ9UC6YHfPU9FU7/BfH8AJ3uPg08/Or/cRXG+Rf2tv9NCQMBAwEOBuvtzuv4A+0EpfIF+9YGMf1d/VEAmfkm9Ov58+0b9VgEqPk3BRIHxf2D77b/2glW9zMOMwJP8+Ttxut2Bnj0iv+d+oTlKAVA/9T/G/kQ/M8EFgLwCYP5VAWo86jxKAmz/kzwSPduBkP+7BKTEkIIW+aP5gH4mfPVGGAELfzy964BkwbtAGcGhOUI/vEBsQjvG8L+TPCc/moNeQ9FD8AMIvvS5hYC0g9fCMAGcgvN9W352gkb9WsFceiO9LEE0PzRFygLTv8i/VkAKN497Ov7hQKtD1b5sBKFBj0TqRRp+DADMuU25HYA5QYODI8P2gVh+lwDgQlRCIEBJ+ao81cWrBUVCpMUFQyV+isWVAXc8RXp3PtQEMsHcCeSGNUUYwm8CcsJnfJgBuXj4gFxHfn/5x3BKT4Nzutt9xf8nfIM/3YCeBdLHVQPwxNuDv8DFQan/4TpT/lRCCn9Mw6wFBAb/hNl/R/2h/R5DR8XNwX7BmYSmwqqCHEXWA6Z+Z8DogrhBUICyw/ZFaIG3RSIEXAfkAcb890Og/F0Gu4jMf1vACEBXhbsDK4DSQoSB/3+f/7hBXUUTA8zAiwAJAgqGt4A0gszCJ388AVq6lAMMw5gAN4EzwKDGlEESQoRD/gHQRKs8Ir/GQUT/csP/AARFSL/WvheGOv59w1bDWsDOgZb8A4KvAeEDFP4w+jHEpX4+AGqBgH6pgOA6E0L3Qpe84wAAu5I7c8E0RdrAYUA5QY589T7BfdL9Hv5I+3R9LgK4gNgBnT36OQzAnH0BfPpCS3+I++39Xv91evn/BP7Eebh4q3kMfl7/xEN4/3H6ZboVOa3+Zn5jABvAPvnfOvR9u0AXAcN7Tnvu+6J1toBrQei6YfwQPmd+nzrrPhcAfr3GOwK3rfzOfn+9E/51fHg9hjyyfad8v7mlvK06HT1ivVp8JH/EPLAAHT9cPb0DKXysO2K+xznRPYR4trYrQeZ+az4iv818rDvnP4e/Fjlbe3w5lP24/dm7VEADPN94VfpjvKi52Lu2Pph+NcCZwQy5XnooPtB8V73H/D28P38dgKXB/AF0fZL9N/8VN6W7FAKmAGs9H4AwxfzDigLt/FB5Uv6xAGJA3T1z9+386EaywmH8Ofy2PxW93j2Jv5M7Az5pgPJ+PEBUApuDor3yuyK96np6/uXBanvEQ0JF+f+QgRW/ZL32Pp889XzsOlH+akOI/XEATMIlvJNAejuZfnF+7XcT/n9+mcGQgJJBCsQdevv9s31WAI7AkD50wVH+Wj+Xf9qD2cAf/79+oDqH/oj8x/41wIYGdT98+kx+0UJgQmb4b/zFPWA8Of8CfZl/0jxx+N0813/WvKw66T0WAR47rf1KANX6dcCyvIC7Nz9DPM+5hHo8AdW+34ACP4u9DH5NfAoCWn2QetX76XyKwhYDrASj/CH9JLxL+KQBekJwAgVBg4IWAKXA2MRWASZ/1r6zu+XBaQj5Qy4EDkgQgg18OTtcg3vGXsoCRkrDLAaRB09HygJbgbj+1b78AfDD08mZz8kPxgV4Q09EUEQiAcZAV8MKxANFAMJWxGKIs0kHQp0+UkQQQ4GCu4huxfDC9Ugpgu4CKIQiAcKC2oN6A//AdUeZDCLGPYdBCZ1GCsK+wogFZIeWxnPCvMQlSW3GuMg5BYOALUD/ABQFPcROg4oBcoRoRjdEIQQg/VYDKoA3PkvBXILwwk8/m0UuAp5FZ8DT/3pAaIKIA+h9bEG4PLiAXkL0Rf+E8gC7xF87WAEzgwdCigHg/kF9aT6RBm6+k0LWw/sBjUbwACmBYr/afQm+pH9GQUzAsYYWxMt+qD9U/IQ+Jn7LATn/mn6IBOfA3INnweV/FP2yugvC8sNJARGAxf41fduDFwHE/8m9EjpiQHu+q4FhBSXCQXtUOfu/H4A+AdT9Fb9fQZi9I/wpeZI6b/v3/ob/4UAPROeCzj7zflH+UT2yuiW9pn5rQdYBDLvAAAC7sn8jvpL+uvzQeuFBHv3Lw/lCNIN2eze3WMFrPCz+I729Ag8/J38QQz9/gH4Seda+ofyzf2MAu7+8v8T/woJ5/bH5xHkv+286F3/AwO8A8sBV/HLAbf5XwpfCqz0AvDU/U0Dvvle+9z5wvDS7ET6+u8HBhIFFPn8AL7/BP2L7TMCAuxi8jcF3/5H+UHp2gm1C7f3Oe9P8S7yr/nU+csFrQ0hAXIBIvvwD1kAjA5e+5TbLADH5+jwTQ2EEPQAmAF0/bvyMwglADMAWxNJDA3rlvRA+Uv4yfbg9vL57Ocm+qjzZhT+F0T4KAHk7fPxmusn8jz4QPVw/pz+nwcoAfQA1P1b7GbtXvebAAYOpgv4A8AIkwgB9s3xHO8F9YP3vOCbBJIYHBA8/uzrT/ew86zyOuVT8JQEbRQyFIb+nfa78O/wlu5T9r73afJ48u8RBg4yFMklafZj5unePfad9PwCdRRi9iAJdQ61B1DrivdJCLf3sOns5/r3jvjsBlEAzwZw+EHnhOcj8RYCTQl1GM31qPGS82H8tQUY9NLqUO1JDNYKNgtxEzsC1tus9BkDqgQcGK/3Jv4B9GMDBghvALf3BuWbBkP+RgcnE7QV9AAU9yQGgQUGCqT8YATWBrQVDRQcEp8F3Pcb/Tn5ZhTwCeENlwcRCSMUFQrfKTkiXAHLA38dHBL/C4sS/wtUDd0UQBwREbQTtBNuCqoGRROeDRQWtxibCtkThQTACGX9ZwZUDcsLPR8VDD0V1RwBH9kZtQt2Ck0NsBQQJdsohxUjGvkk8SywGg0S1ggvB2IZ7A77EMIjtTjoExENYh95E0wVZAFUDcMPLxG/FuQUSynYHzgkERVt888AzhizJ7sbIiQJGYP5MR6ZJBEXbgoKDYQQ7AjmNUozDCAcFEkQog6MCPsM8h48JXT1Jxk8JTsvIigX/OQW4PaxDnsiuxVnAP70IxYzBgUWgBexBPvneO5UBaIKfx1FEaYHRPz1/iPzF/5UB58Fagm++SsMkAPPAjsEGPQ96rTsbwI6DE0JmwRw/O/uNf6R/0jzRt419JcHFO8hBeD4GeBf33HmgeLz69Hw0uhl+xv13e0+4C/mgOZn4+bRhdcQ8sva1es33n3bNM9Zywz1cej+5t7T9ckD3svmudcK2trWyM9x6iXVnMly3jPXpL+X2M/hKdBJ3QLmed7qyKfMgszI06fKq9G84NTIot3s593lC9BIutW6wr0o3CDg6dJG0iDgvOhQ4QPY/9hn3VLNNM/M1onQ4dyq36bcO80/zGPg18+N0UrVM9e52QPeud0Az6njQeWf0oe/Hd9U4jzFZ9cw2FvoY9xvzQfRNuy77CzXnuYw2nnkwN+a66LlIc4L1sbAFdvd61ftjva86H3hM9956tnoo9Vn45PpLNvD6hjsv+Um+F8I6+954EndNNF24WLwowBl9UjpOunV66D9nfZn4ZrtF/wH17Tkt/Wa77/xfeV0817t5O9u5y7sPPpa9E/9ce679C7ygQNxETj9s/q/5Rzthv7eBmH6JQDkGpQAaP4jGq0Tafi396j50glCBgj8gBez/hUMmRzAAFwDs/6l7sL6kh6DGKUTTQ33Cy8P0wNuDvsIG/u07uIBGBFjCxAbXh6XB4QShx8+B84QAfrO7Q/+rRN7KrkGeRP2JToKYwO+IBQcWvqBBUkSNhNXEB8dhBQVCisQywX3E1ccDRjSEToI9AIzCkgUag02FYMejxcRFwEbsyOvLmITJAaxDlEE+hrCHcIlryy7G8UksBgII2Uk2B+AE+UMtihAHjguWiNBDpoWkxCiBI8T+TA4Jh4vUyEFHgITUBa9ODEm4CE5FpYXRRG5M5pJVibCHTsEyw0fHUQlEyT5JgITgBldLp8HLSsfId0Oyh1lHsUk3P1tFG4OGQOdF7gSSysyFMoXzCxWKPIkgBEQI3EPhAyHGxwMux2eFTIUEB88IRAdoRQiIIMmSx9CBuQQEyrvG4wOuAj1K2wqE//CJ7QVNfouGQ0U8hx0HlIvNSEUFjgkqQ6SHKgmaR27HWoVGBUQH20YkTJSLy4hXiCIBcoZ2RnkGosS5BwfG2oJYSUUHFkv3ymiCsAIfBoKCfcNuTPZGZoYSQYGCiIihiNeFowGwwskDJ0fKhqaFm0c+xIvBVwLvAepDncliAuR/XYCUQgdBucl4yDZDQUekAnwDZ8Hpgn3CZ8FmhA1GzgkawNYCFwLdPkrECATlwW8DbAUJxMMJEQfdP8dBOr/FPe5BBwU1RYnDTUZUArHBq/5PfBjD6IItA88/FEAfyN9BnkLtyS8Be/00PyTBrwRvAeIDdj+nP7dDtIVRCG8C+r//fgoAU0DVBE5Fir7NwXiAfn/3gb+7s7jgPD/AyoamwKfA3gb7QDu+A3pSeEq9ZbsePYrDp8HrQtW+d/69vgK3NYGGQeh9Rf6DgDAAn/6wAIf+KT8w+jv6M399AahGL/xDe0ZAdzzPgXhC9z7HOdb5rkCJvw3AQj6qe3V8bDp4PYm9Az14Oxt7br4LwdGBRzru+yQ3Fvk2Pjg9HXriOgn7Hf8+fkn8Ov5PuYH3e3bzfvg+AXtoP/l3/PpOPvV67DttO7E3Cvpt/e79ETuSPEU90jrpfKL8cLyWN9/+OD4wN3C/ib8kAPQ/BHu19eI6Ojq0M+Q4K3iAADTAZsA4/tW+VfnRtAN51TeLvBnAF7ti+ny9XHsoPmbBqnrzucf7mX3lfxH/17zuviH7gPYqeMu9IEHIv+H7FP0RgFI8Rf4Vv2h6y7sFPWt6iDmJ/In6tH4G/HU+X/6peqS7TvbJOei50/xL+Ka7/387dcT/Z38L+KT54zdK+FA84Tpt+9NAYfq4eju+Knt6OTaAdT9cfL4BbvwU+zc9zLnUONB6Qj8YvTR+rsXxu/a3Ejru/Ks7Kj3T/sN56Hz8vdUCUf7OfVj4JDYsgDn9nIN0g0ODFb7kOAF7T4FJAiP7M8CU/SqAmcGjvhCCivtRPiK9w3t6O6O/OUCjv7hD3IDYfh/+pX6NfA18n/4q/5P+aXsJAjj/5byDPPh4BTrUO2+/+wIbfN89Z32bfkg4BTzxwjs4/bwxvftAMQHowLtBBD2LvQY8s7rpPz0BOv55BCXA0D3jv7TA28Ahd0x9VDlW+ohA4fykAGd+Ev+mfXR9Mb5X+cF7crwkvWW9pbwuQb3D0v0r/3z70TulACO9BIBluqE58MRPg14+t4AG/MOAq0H0P5BDHXrywEb9bjhMwj1/ofy5eOp7W3rpgOmBann5QC79hjqXvU4/4DkA97S6rTkI+3K7msDG/Xj9XoBv+mA6HHuLwen/8L4HQC78pX6BP2+++UAJAYx/Zb2egWQAxvzU/SR+/rxs/oDAeTt/vDF+3f+qPHO55byZu1T+P3+g/HN8TLtf/gC8EjxtQFQ6/Pt5PP29Aj+fQxqD0D7UOns43/2RPK8B/4P3PnF/w3t3PsQH4sYdP0q+VjfJN8KCzLzgQOZHrkACP4gCTbqCepUBzH1CfQU8T30zfdl+xf+uQBFC/7uivW++x0CJBAi/0f5sQbTBRkBeQku8q/3mfmBAUwP6BFYDmn0mhbAAvn73gDo6oEDi+3k84UCChFtFLIAGQ2mA2z9xvno5vbuRQ+0FfMOrPj+9KYFQgS8DZcDzwpCCNH0ivs2C8IfQRQF++juSQYNFkUVnR14I0gWj/B0//ALywMRCZsGMf9797UFVAXzEjIUZwDAAvb6bP2R+6j7agmLFM8GQfGD+TcJbgh6A7UJAfQR7GcCLw+eCzMOvh7tAmbpf/55E+0CS/y2/0YBXxThE6kWogqBA9H2RPAvDX0KYwk6BpIWbRom+JoOxiJ2AgT9FRBvAHT9e/0E/RkJyvQdAEEQdQxYCsb1FgJxFXgfqQqK9+ELkvUzAGoXJAo7AnHsPPz3EXUMiA+0GQYOmfeXBf4TxwZw/Ff1dPluBssN2CXDFdIHLxFB70f5WxPhD8QHMwByB5MGviCYNB0IrQfZG60J6xbkFCL/8vkvEUgULAa4FgYMTQ0dBC8Hfx9mDpMMfBa/EL8WXiLj/Sn/khiPDcAI4gOBCYwKNRkbIPMSKAdBFOERvv2FCKIEpROICbEIixzADK0PlwlyB4wAlAD7CIEFnSO+JqD9rQuHGeEHVxaaFscO2//0BIgF+AVlJBUOdRCWEaIKZwxKAJIY+AemCfsSxAGqCIr9KxDZD5MGYhkE/WH4UBRJDuP7hxlLJyEBSQYvCVEAF/7WBEUP8v1YCrgSpRFQGEkI3gSTCigH0gtJEBQUlh/rGsoXbhCBBbUD7QIwAXYA1hBXFHQiCCvvGRENww/pBZ7m+fvAApsCsQaMCCYdZwqLEKv8Bus6EpMQqPvTBcoRUA6LEqj9Uv4P/irzsQapDBkJ4gFFDxD6qPnOEjAB2PbY9tMFcgGAFX8dpgs7BCgDCgeO+s4WwATEARQYHA58FMsD4RMCDSn9dggnE5QCV+tyC7wPEgFL/u8TYASw70f9vAPNIjMCqe+YAdMDHvy3748PKwoU9y70/wGtD9IHDgiEClQTIvl/9AMBVAe/FFQHbga+/z4JsQrIABEP7QB5CxQUYf4RCw/+VvedH9YKF/5YCpb2T/c99icNUBY7Arf7cfCfBSgJqPfWBMAEr/35/b77tQMf+If4VQHv9EoCE/0f+BT1dP/GGGX7wvpA++/uvv9CBHf8tO7U/4r/GOy6+Ef/0foM93T3vOZE7lgIfQTTAR0COgr+8DrhQePs4xP/u/Jx7qj1Af5W/ZAHtQsv5m35+AHY9qbiAuoQ+J32Xhgm+OjsK+d20/rvQgL3Cd4CQedj5qYLHvw4+y8Feth21X0CNfSx3V77gPBRAL/xGeRbD93hgeBvAhzlyfaYAf7uIQGZ+Xzzzu9U6I7y5/oAAHHwPfZB6W3t9wvC+jLzXAEf+I/w7BIrFnD8OfHH593t5QLAArgIXvel6FASOgbxAUIE0wO1AWcEDRbhDY8TNu6JAVL8CeyEEAoDLAL5/dEXUA4uFVgKPfYNEo7+xwg1/JsKkwytB9kNogYQG+/yjASPDUT6CgNuBsYaPgUhBQITHQAJ8NIH+wpyASsUMwhkAW314/vhBU0DNwPg9kD/U/YB/BwMgBetB83xTQN88+P58A3oC2X77/TY/LPy0fDj/3EX8QEB/B78OPv5/RT54Qdm894COg6bBAX3Ag/ZFYHYBudQ61b7hQZP+9T7mAFBDNX3zhLEAVvqOfOe6IPvUAouG3z1FO84+wz9h/Iy73/+6O678FkAOgiqCFwJdQyg+5n3oP0Q8D3wzfX29pcDt/vD5hv5Yfwb9YsYqQyK/av+4PY599z5wAgM+7DvBftNAQLkqe+d9jrpuQas+Nv/9AT4AZQEYACz+Ans/vSE4bXiMfnlCNnspeYX/r753gSK9TbsFeek9KjzBP2LECfmU+5j5LXe+vdF6hkNxwjO5aT2nwN49qrft/km+qIEPg/D6g4EjAxa/Ari/ubj9478lALc75sGF/zr+6f/T/Ow7eTts/oN72X5Iv0rFjX8I+uz+tnk4PJx8JLtw+pVAd/6Ee6G+tH4dRCh9+Dsg/2P7sTey+Rq7u/y8vOs9JX+Ouvc96ISQe2t6nkJrO7Z5HT7/fbS6rfzcfBB69j6qPXR9H/4/fpb5Jrphvp089MB5/hcA5boa9SK9wz9J/LN8Zb0iOIV50YBVxwODHjyhOEY6uwM7QJCADj7h/ZI8yPvzwDIBI/wXvf29ufy1wJYDsId1e8J8Dn51e0p/bUBzhCK/1wBdgClEe8RdgjpA8PoLvIM+eEP/hdeHvcPRQ1uBofyDgaK/8gCtQFyBYEFTQXEAQIT8Ali7HoDJvaO+hD8bP9s/30G9wm++ToOu/bv7Pr1VQNfCgMFVv0X+pQC/vSg/47+QgIQ9pDeuvovC4wIIAdyBVEI+wYX/IvtSeVp9tH0U/A59+f2DgyUBA3p8OS78iQElvYsBKUPMu+1CVr009xs/zz6EPYU7WQB0P7U+5n7jvytB2X57QTG87r4JvTeBgkT4ebg8ir7qPXd6zn13PtrASb65O+H9v70PfYn7Fr+fO/Z6p4LgQW37fb0zfFI6YEHLu4F7XD8CfAn8o704Pg19LPy2Pav/7P+xAc98PbwIvsf7Lf3sOny/c39V+0Q8o7yOP/J/IzlseNvAo/sU/CfBWX74eil8C3+1uF2BJX4SPPPBpbqRgVd/3T3vvfJ9tD8Wv7tBO0CHBSFAtj49vYj9c3x7Ot0+y74fQKd9ND8ywFL+o7+J/AM/+jqLfwQ+rDvTQVm6xgRawe/8ZX++vFKAE/3tQnIBLv00wXk87UBBwBa9NMBKAPhC/sEMf95B58FCP6iDjcBXf0DBwnqIQHHEAYS8v9P99YMQgD7BM8Klfxq7M8AmwpfFDkWIQF08UDz7xkHACQEtQsy8x0EHBg1IxIH/wMdCEIAUQB6A+gPTxoDBToKjiEVCGj+qgJ9Chj0LwnzDjH/sx3zEsYWZhDdDlEGHQDsBrMb6BEX+kgeqQ7LC00DnhHoF8oR/SOEEtQqhBL7EPMUuv5JCv8LHBZbEYMgixaECh4teyiiCu8RixJNBW4MlSE8JUEYFCBhIWIZLAQrEhsiMhwiIqwdRyYQHRQW8h4MJJ0Xsx0jGKoIpRkzDs4YYh8uH4cbhxWwGiAV8iRaHagg7ieWEbgIyhG/GtEb4B+pFgoPqBxtHhUQVxA2EUgc7x3dDkQbGx4iKDgshAr3EaYFqPGwGi4VJxHnGyAVwiP6GuUEVA1iE1b9eQ3rGlsZBSChFAoRfQ7/AXTzfRCEEJsEiBHKEU4oLxFyAWYYfBYrDqkWFQztAJMSogamC9UaaSFqE/L9hBYMHGoXWxX/CQ4MWAhJChAdLhVfCg4IAg8UHKIKpgvu+vb0egF6AbsdIiZTI/L5lvZyCzz8eQvN/XD6RgX/CUYFkf3sBsAKqQy+/wsBjv7lAFwByvSs+McQnwcz11DpXvd/9JAJlhv7EET4GQGT65rlpgFp+Ff18v0f9hv7SPM3AcAETOxNCfLzMu0hBS38jAD8AFb9ne7R8qH3AwMM+aHrS/ai6ffsBgyLFpPrYvCR+1fvbwBRAG35auKa6VgIgQW6/GMJg/vH5bvuBfXAAv32R/kODFQHuQAB9v38pPhp9or5qeNI6xv79vQWAtUSCgsI+nH0oPk58Qrmt/sWAmrupuS05sb5MAF9BAXvv+2g+1/njviz+LP45/hw/p4Nnfav//rzdPk99IHaqPlm8fL3Hv7U+WMLGQkDCXv9TPIH1cTcZAHn/kIA9vom/iwAF/xp8pby7vrG7Qn21PtRBhscpRHu/nT/DPkb/wj6J+okBKD54/28B0YHeRMR7rTwIvv679z3lwuaEBvz3gLwC7fv1wLoETMAlfob8XXvLvhnABETxxBgAoQS+AcV5+P/UA7zDo8VUv5e9av+vAk1G9Ugd/wg3oTlhvwuHYcdRBtPGsX7q/x0/7gMIBUq8WX7g/0dAKkWaRkNDkD1GQFS/Gn0RgGmB3v/mwQOBv36SBSbAuf4FPOd+jX83e1eGI764PgVCJn9EQumB6IMvOR57PgH9vrlAkkGOwADBzIQnfrlDG4Mpejd4U/zuBCpCsYgxAWP7C4Tng2lEe7+RPgb9Xz1TQlqCf0h/wEQ+AcE7OviAe782e4DCfAJJvoWAFAKvxI8+Bju2gHZ8FDnH/SeEw4KRPzoC1fpt++PFbr+XvM+ART3oevV92cID/637cbvOP3aAc8CZAEf8KzsDPNt+TLx3gKqCMbxZwy9AV7zMuUh1BP/XAEU+WcES/ys9NH2hBDHDo70PfK37az2LALGFIQKJ/IZAyTjtPCIB5367Aih97EElvYM82cA1t3R8LEEnfg8/vQKuQTC9kTu7Ou83Ezoxu2B3vX+egPpCX/+3PmbAMLwF/xy2svkxvVB5zLx7v4m9lDpOfVf487rKdLZ6C70N9RJBrr4hQLo8Knj+vMn6tj2buMM9evxAuyF1/HM5POZ/dj2Cfb/BTboi+3k7VzcH/TS6oTjLvK3+5fmMutB8WveEtSQ1Cvjt+17+7r86/H27mX5wvC/8ejwHdnE0sDdLuz753D6+vEC4t3tIOIY8pX+qPeL8xXpXu3D7IDwtPBC31fxF/ZM6rzkot8u9PbwVOqZ+VvsZNiD8VvwdPkF+1DpogqT6Wrse/ee4pH7qgI+DygHKAVnCFr8g/XdEkUTzf0uEyEFrQvfJQwq1gZA/fL97OXWDHkVNgvsDkEMXAk9ERQexw4kBokDmwiqCPAPpRknD30I0g1cB0f9yhXvFakSfBgZC+Qa6BlbEfsSjw+kH+AVKwzsDrEMyR8MIFAWgBkIIXAtrBdUCaIQYAJEI4IoFBrbNNghxw5fDlIryhUI/s4a9vj9+lMbKhqWHdgr1RQ6DhQatxo9Fc31WxFQDtcCkhrYH60PwwtxD+IBuxkgCaEYXw5cBS4XbganKDIaxiDPArTuF/b68RgPxf0nFaYHxwrvFWcI8xQOAu76wvBp9KT+gBHsCt0Kjwv68Tz6V/U97i74cgl6BekDs/Qi95cHJvxcBQXzpeyx3QnsnhN0/5z+dgCH+NHwne4m+LwDT/NM6HXvX+Gr/oEBvOLR9Ir7hO2a7Rjq8Obc9xvz+91M6Fb9KvP+6H3nEeJW/88Ei+fH4YDqAf5i9Lzm0fid9EHvzufd6zj/Pe5T9Drrx+PeAtz1sPFI7dHy4gEv6KbgauhT+Fr84PL9+Jb24PDZ6PPrPP7G9U/1g/Pz55n1gOZQ55LzafCs8nTx5/Lw3Ofywvxm6+Txx+Hk5xTti+kg6If21gSZ9XHus/Lc80Xmw+Zy5Lf3pgVx7ovzJOXw5s8A5O915xf6g/Fx5vgBwABB7TXwLvR09QzzxvFE9i36zff/BfANnfgj70HxU/biATj/1fdT8IjoxAdQGKf/PPgq80/z/fhS+i3+T/uD98b3lwOtDx7+Nu7K8pL5UQK+/XETxwhQ500JNg1UBYkDXf88+g3prQmAD+f49wnlBmn8qgQ3AbwNVBGxDJADLwVaG6f/JArsCgX7uA4t/qoIkxAkDpsIYfo3ASAHwAiPExcfegN/9ssD0wNL+hkFjA45+SAJ6BO8EaEUG/sx/64FTQFjC3IHGQ0QHXQoIAvv9rwPKvNT7g4Kr/82FecdKAt1EiMY6BmxDtD+lfyiCKUXKxREG1ohGBE583D+3RJ1FNkbZwB//lr+tQttGi8RWA6k+hwSUBblCNnygPKsF+UEvvvKEUkSOgofGW4KIv/PBIgRAhVNAxQWVAfsDKUXWAKFBH0I+wYWAqkShx+sHycNWAqUAj4D7x1UBdYEYhvbKGwmBg6xBkf/BwDn/tYEhQjeBtEf8hy/GOAdAwmW6Mbtxw6FCPcRwApQCi8RdRQYF3TzeREDCfL3ZwYgDawVng+6KdkPe/1gAGAC1gSmCcQDBgryKkkGCgeXC0UVYwXv8tEXogSEEH0MSQZBEjYNiA96BWMJs/rAAGwk+wwDCf4VmfuPEQ4KKf1CCpMKgBWkHxsi9AL0BlUD4gH7CpoQhA4ZBcoV+wrrHosSxwi4EPEB2gX/BbgQPgebAgn20fT5+ToM+SLzFj4NPRX/B0Htxw7LC7sTHBaIDYQSKAV8GrEIohI+CXoFTQn0BKUd6QMgDSQMPg2tB+IBNgt9Ah7+NfrsFFb/zwrWBlfx7xMOAPQCcP6MBj0TPPiqBPwCkAVcBwz5lw1UEXD4r/8WANj4dRBYDscGlwOMBBUMvAu1C9T/Ag/XArTod/zsCvcTwwnLAeQcUxdd/cQH9f7eADLtiOhYDDLxMwwkEGn4PPxX8woJQPU8+l39CfQyFv4PPfR47ifyU/Jt8UTwkvmH+MX7zf/pAT4Dyfy397XcsPPf/L/xEgM27oDwwvzr9wLo1ucU76HrcPhi9N/80wNyC7EE8+1b7Ozdbt9m61b/+vfj9+EJG/OJAUwPkvP41jLlVvtt8+r9sQ56BXj6Pgtm8SHYTPIT+1Toeep6AW338vNp+Cb8lAQ1+BT5owJf6c7naP7u+DH7oPlM6nnkQ/4B/mbvzfHc+Sr3L+ZQCtz9PehI8Yr1Xu3W5d4AFO9w9lDv7OfV7bftQPNu528Cbfd6AcsHpgEnEQcEw+5+1xHqPfbz8WbtdgKeE7wD6/HAAhUQYuqH8PrzUvowAxHuwvAVBMb5Aurj90HrcPaK/ejspex09xkJbwIf9lf1kAGZ94/oFPNvAO74U+7R7mcEAg83AZMGGPKS9yb0IOo6CnD47vjdCpn5PfKo+Z345/Zu58DbgOzg6mn6Pgt2BFQPUAyZ957kKu+Z/9nyt/Nw/GcIPgPb/5AJawHY/ND8awHC/OgP3QzaAYgPhxeWGb756/W/5cLymwB2CKkQePTVGLwD9ABYBI/we//U+ToIcPa1AeEPFQ5ZAJ32/ABI92H6bfNL/goDjxO0Da0JZwpT9PgDE/sKBQ4IiA16A3D6UBArCE0HKOJu3470vAdUDx0IqRJrAQoLzwKH+GbzteAZ3gH4/g+5AKUR1RJQEmcAlvAb/eTtgO7K9MoVVBPhDZ0hQRbwB+r9OPvD6A3tXf/vE8sNxxAjGLkGMhqqBDLvpPbAAqj9WvaqCHIDTBN1Enf+VA/6FM331uN49AEblhvoC/4VEQu38fn5WAro7tD85Q4wAxT3SgLzFm8CFBz4A8rsDgIX+Pn7ChFBGIkBRgGi6doLERGs7O8RVAnr+7UDuxUp/x0C6BfV994E5BJCCqoAKvXn/i8JVAXWCIEJjw+TECATvw6+/837ePqD+9z1ixIUFBENIAtBEGcM+AH/DcffngvWDBTxdBwCCwIVHxluEhIBhQbABML6fQqeDcMT9vwM/XD6mf9eFkwZeQ3K8ovvF/bxAaIQNwOH8p7sI+0LAb0Bng3wA9nyvvfG77P+2//LB9H4CuQN7yb6cP5bDU0J8QGPF9z5TQuh8zLncgWX3FEEhQiXA+ID4/m7F+P5GQEGCP7q0ugj86UPJApS+jz+r/vh6OHiePQu7DsCMfsb8+gZAAC376/7f/Qd3wj4dPe379MFWvyPC93tIORB7dzx6O767Yr9sd+z/NINxfumAXkN5d+cz8bt4tp17SfmePoHBGbzbga6+L71fPEn7LXYDt2O+CL/DgAx/eTzw+Ss7Bf6afTW47/vSPf27sX98AUdAl39EPRt64vtZfvj+dz1zfud+IwKpPgY6kD56OyZ+3T5LvI18mX7AwXZ6nHwE/13/mH8nfQ1/rfvzuW/83Hq7QJgBkXspgGo9Qz7GQPS5CL7v+9U5qoAeeyH9mnwzuuXA3v5Rebw3pbwGeIX/FkAmu0DB4PxwvqH9Cb25Qx//jXyEPqjAJb0ywUdAor11fcOCKD9MvF5Ed0UuBCbBr71nfSYAbDxG/sRDVwDkxRA/yr79Abj96j35/yo+TH/XvlP+84MFPfPAPgHIvuz9Dz+4gMU794IVQGW9LUDfPWz8uf47AhxE0kMrQ0sBgH6FgJnCLwDcPgx9+P7IAsnGXYK+vGz/gYI8+Vx7KD92Q/J+rfzfyG4DA4IywmV+g3tmfM1/EYBkw70ADsCTv/dELECgQUSAyTfePgi+XINGBUzDosSfQ5JBC36f/id+DMCsOk+DycTvAs1HYUInR91DisWUBa+/Yr/7QSoHoMkXwpl9VQNIAd9BJMMNhGXBaD9qCAjGsoZmwRh+Dj9AfbhD+wQeRFvAtX3ahdqE1gGsQY8/FsPfQz7DIsYzfvgFdEdiQPOEssNKAd9Bnv3/wOiCFQTMSaECjABrQ2iECEFnRtWJAAA9vqO/IcT1RZuEmIfiBGL7/b41gzEBYYnqRhcCYwG0wXdFMsHPR3LB835d/6tDb4mhA4YHZoWawGV/oELcRF89bEC0ge8B8oVKxZQDJoMxAWr/DMGj+46CLgSzfXPCGAA9vpA+5b0QPP8AD4LWAIRF78YpP6BB7774O7aBwH0s/gq8/rtHAxW/4wE1gYDBS7yH/JA+TXyxvd/+MX9bfObBKoCLwlW/YDuxvUk37/vH/LR8noDMhjhBcb5Kf9l91P45O3Y9NLsKAXaAUD7XAc4/0jzZvEHBlzezun29Dz4KAFE+r8Qv/PG76zwfd1q4rD1g/dj4OLa4/c1+F7vNfqA6Mvgm9+A7pfmAu5e8VDvzu8C6OUIUd8z2cvmM+H+7BD4og7J+hD2R/tP/cPo2ewj8b/rTPDs5WX5rPqMAOkByvAg5pbuNfps/Vf1SPPK9Nj4vQFX6X/4/u6P5iPtePSxAkjzzf+l8JsA0wPC9Ev8PfR/9rP2nugc6RETmwYhBYwEpPQ27FfxogYu8rQN0glvAu78XAHOGD32FQxnBCrxjABBDPAD6/OQCQzzFPWG/lQF9w+k9IEF8QGD7zj94RNx8lze7QBx8jcJUBCbCOf2yujeAqH1oP8+A1EIw+5m8wIPRPy8C6v+4/3N90IAUxdYBI7+TQvLD+0Exf2jAtoJkvUrEoQMj/A2FxseERd5EZcJDPn5/84MZwZH+dYEUQSV+pMOyALsEiQQLwfr883xsx1nBiwCDQ51DvsEiAWeFfgHRPZ5B1sZCgf4B5sAgQXsEJn9uQDRFxEX9AoOBEf7+w5XFB0A9vQp/cL6f/a0EcMNVA+zHywEMfUB9iPvKAOPDcAGIQFcBUQf/hE8/BENbfN55CEDXf/oE2kh2Q0DCd0UeB8nD0kMQgBw+HkNERVQCvYh2ReG/pMUpgepEu0EoP12AHT5IBHHBv8LKAPlCMX9rgG8C/38tBPu/ssHVv8oA48XCger/hP93RDC/DISiAntBB8ZD/5cCwoDWxEoC5cL7xF//MMP5BBUBbvs2gNGAwH0DgT8AmoNMAH/B9YItQfN/7r4GPKl8n0KAwPLB6HzqgLIAJn5WhsdBEIEbfez+vQIQgiXAznxmwRIFOsaahX0CnD43/pS/kHxBgwKBXzzkAMVCFcYIxZcCREP2Pjv8jX8Ww8NGLgKMwR88c8GjwtUCeMgERXhByQCG/9rAxP7MAFEGU0Bs/xZADYL9h+pCksdngmA8kT6nfg3BWMDChHF/2sDmgyxBoMamwh9CHj2fO1KAjX4kwj7EBIDBwK4Dsn+Vvm4Cpn5YfxD/u74sQorDnT7fQZGBfL3TQ0P/n0ChAqK+9oFCgeXBW4GwAx8FKYLgQGiBsL6zfveCGMFBP/aAzkeBRbeBML6J/JI88LyKAfgF60LUAxQEisKKxKXDcAGT/fc8fAFUBJyC2AGLh0VBrkAJxGuA8ACng1qFfcT4QXc8/gDi/NUD1Ym+vN2CCMUywMb8wMDvxZnCOwIePC1A7QNF/hQFMcGDgT3Ee0CKf2Z84EB/wt9DLwDIQMsBAz9ePhQ788GMw5fCh/4/fwgCwoNVxAx9yL7SPOo/RD2i/N5CycRHBT5+4P98+X37H4AOP1h/M3xQPuyANIR/w2iBL75wvYY5mLqrQnf+nHsofEB/rkAdRCBA+782e5A8/AD1fdQClP4fQj69+HoPgFvAPL7xvm1AfvbS/zj+Z32JxnEA8b3AuK3+zLzW+4F+crwqPPz8af/zffWBlEEGPTs4zrrj/DL5i8Fv+9ZACQKsgB8ElPuh/Y98hHi6OZu53v3t+/y9xYCHQYhA2bznuhl+R/02tqV/hHu5eOD7/bwdgpP95sC9vYN5yb4V+9e+8L6Afh/9s7tEgHwCev54PRB67DvIvvD7IL//hEq+W3tbwCiDC72be2mAUf7f/b2/ND8Kvm07FkA5/z759j4KvHV9/ADde899m8AMfUq9bb/s/Tg9Jb0A9wc6XIFxAf2+LUDCgVgAkYHuQDXAmbtUvo19rv2awG+/20UvAVyAWLsCgnU/5fepPpa8mcEpPia72H8ZhLG+ZPf6PBn3UT40fR/+vQM5/L67frt7OXD5Nj0aur729noEPpvAEkGBunl38L4NfI96lDpw+7K6Ir3afyk9vn/EgEb+ccI+wpT7rDznuTc9xTtX+tnCs7vsQJ+APn7EQsI/hzj/vIgB7r6j+4u8Gn4JONL9KXyjADK8LzmZwJi7sMRzf818kv2u+oQ9DH9mwI4//gF0uBH+4gLBfu2/dXxePgU9TMEd/66+Ir/UQg+C0/9+f/7CCr56O6K+zbuxf9i9M7nDQ58Ei8F5/bABCgJ0P7aCR0EePgdBs39XvXy80T2qRLpBwsBSQqC/yL5MwYHBGH8dP9w/lUBhQTkGMcIywmbCHj4fgCd9H4Af/okCsMJawVHJHUQdgQM/831s/QHBIQKUAylE84WCgs4+8ML2/+tB2n8BfHGFjz8KAPJJ4cdhxXHDh0KWvTr76IQjAhcC5kmLxHN/60RzhhFC6MAT/Pn+uwIJw2pEoUGxxBwIVEAu/KpEukDf/ps+6zyQgLq/zMKNRuHHdz1H/JbFVUBvvXG9QsBOfkb978awiPEB9j8DgRA8+P/TQ0b/472bwCiCNIVuiOADdj4Luy++xkLeRENDnv9GA9jEbwD2gscEK0L+wpt92Lw7vzoE+MeQgYwAfAJGQG39e8X9w0q8YUGs/Rm7a0PRB15CRUGkfvpARkB1gY9G/bynwduBhf4RQnC/hwQagkzDsMVawM3AYELZwjwCTMOpgObAE7/Pgk2CzoU2gt9Agj4eehuEPMOgA+aGMn4KvMY8AYKeRUzBGMJQPnN+Sb47/CpEJQErPCz/nv5mfsu9mcEeBmS7QLwTQur/t3tivdfEAz1Xf/PCkf5U/Ab9fQKTO7f/KoErPpyB+/yIvnc/fb4d/wy7YzlmfmH7mbnT/mjAjH7TOZnADz+L9yA7BkDV+nZ6KoAMfX2+n0ErQcf9Lf3Uvzw5E/1t/sOAsQDLADlAprvYfw+CfPvNfaz9qLhDuOA6Az1fgB3/BvzxvOA8uTnvOBp+gH2reYu9kbaUOXc8bDzg/HX1c7jxu+mARkFyfjZ5sPkg/Ga8aT0T/cHBOf4LvAe/J4P9AI98LvuFO0q9aj3eQ+bAn/+G/m06PLz8+ez+H0C9vr+8Cb6ZwBE8lP0hOfA1yTd0fZm78gCNwmE67fzCex//k7/j/A58TnvFPnV7Z3wF/5w/Hz1V/Wk+KYHoPle+RET4Oxw+L777+i8C4P9E/1JELkG7vwp/Z8B5/oe/IDu0uaFCJMQT/vIAl8OZfuD/SgHiveS+Sr7DgTIBEkETyIqHEf7RPpx9BTr9wsZAVb95QAZBawj0wO0E7gUqgBd/aT46Qk3AUYHfgDLA+v1Yw0nG88ALhda/mn4kAWaEmIVXwiBAQAAzfvq/eAbUApT9GX7GA9l94P79Aj2/M0czwqwEBwUzf+v+3T9AAAm9GoJRBeMCAoJ5xvdDFECdPc7AAz3ptwSBWMNxwxiGy4buvhE+mQBku0e/Ovx6/F4+uwMvxiaFMAAXw6/EBHsuAhD/i7yg/PhCwUgqgTcGoQQLAKxCukDeQcI+sLwvw5EGXINTQXf/owCNwedF9oBePaYASrzvvnnGwEpVxARCf7y/fjHClgIkhhCADsADgKqBBQcpgnHChERnwOfA90K+AV2BhP9cfRCCmAAYwcrEmz/XAN//gcGUvrK9GcM0fgT/wMFR/28BcsHTyBxGY78kvnq/xD2kAURFZ386QGK/bkCxf/+E78areig+9YGixBjB7wRBRrN8zH1BfVvAvbyq/wm+qHt2/8kBCsQWxE5GO/2G/vg7ify0gnr87wRr/ku8DMK+xI3CdH2Mfv9/igDR/k+B5YZsBKPD/0f8w6bCvALZu/V8/L9Tv/eBhMqERVyA4cZFQSuAVwFoP0VDFQRywOBCbwL0hOQBxD61wLV8ZrrOg7jIEwZjh2V/in/HvyUAKIMSgA6DtH6FBbpBbfxGQ2MBsgAvvVP8SPxMhgcEH0KLhvDE2cEwv4GDEDzgv9S/uUEcP5H/RYxmhjhBycZNSM3CfgDKiDSE3wWXAXq/WoX5BofIbQRIAc+C1gIOgwqHBouvxr/C1EArgWMDIQK/hGEFAUazwQUICcPvv2zGwz7Iv2D+VEGXhqECkkQ6yAUFhIBUA5cBR/u4PDG9+f6tA18FuQUdP3r7Qz1sOlcAQoJbfHsBk8k/f4f9k7/+u/G85bo1ffd7cgAHQaw85sKUvqPD0nhb8/7BPrt0fqmA64BV++H8CgFdeP37HHmC9a14M3zFQYu8M3z/fi/8bP0kAEu6jXwtQEv4IP9bfm1AaT2EPIFFi/mRPgt+vrxkvWZ+zISs/xgBprxBfNW+28Cjw9I86z0/fYB9tH0VxQDB0ICERNX7+ER5QCh93kPdgaEDkD/2gulEUwZJA6PFZoUlfxfCtH6pRUuGbsZ7BQGDrcgfBanLlsPKAvkFnIH9hljEYMY5BYCD4saDRpPHm0aQgYYFV4ebhAZDeclmDboD5AF9huoIicVvA0rEI8RFQqKJrYyIBOGKZkcngvVFOMe2CUUGM4WaR3hE/4T5issBtv/ag/DDcACXwjnH7QNKh5NDQYKpgPLCVAW2fDR9Lvs6+2s+Isasx0NDpMQbfeH7mcKDBymCUIAX+UQ+IQMhBCeEWX7Zft0+4/uK+nzFhkJMfVx9D3u6+8j7aMANfjiASL5ZwKW8rnd9f6+92vaDtc96BLaPgOmBW31EPr42AbjHOPO52DdOuPo7hncx+kJ8BHo/94ixkba0fCX2ojg7s0L2NXpQt+/5xzlAfLO40DIcMmq3XrUl9yA5m/N1t1N4LXeqttx5mz7Zus4zsLFHd1K2XXrt+2C1Kjxmu8U7XHozNal6oHgtOZb6iHacPoGFLkCAuYq8xv12ext9ZLvjv7c+0/7kwgOCDYRRQ3f/CvrnfYwA+/2cPr3CfALUQhTH5MU+AEKCdz9hvxMD9EX2P5NA3UQxhgVDhwOViKW7nv/+h4ODAkdpyg1ISANbgylGxUSQP1yC3kN9w3ZDwwiNSVbEf0nSgKO+DYNdBqhFlUBEybwDdIHCCHlAGz/kAlD/rwLpRU2F6kQVAVYBvwAERP7CGX7e/krCG0eKAmWEfYbCwE97lEEDggGCEgWPRGQByAJXhi4DMQHUvrR8tT9yASfBSn/EQlNA/b8UQCuBUkE8vud+h0A5/hYBAILh+608B7+mhSmDR/6G/Pd5WnymwAKC3YEmfeuA7/tsd/AChD6Ive07E3aEPJG3jH7G/Mh3AX1Nu6Q1HLgOP/E2r3WoucC4kXgG/GP6LLROe214n7LStOa7VjjKNpl+27fZ9ns49bZLu5v097RBNDfxWrqqedQ6+nc5ddo0UPRgdxHxnfFjsMK3InQjNl86aPZn9ji1ObV5Lqj18jVP8rb0tvODt2F1XngPuK9zl64wc2yy2zEEtp95cPgkNK14rLTa9xK0c287sMh0OHeCMvm033d1t9vz1LN6dKc0/zXxNQs3fXJTeCI6K7O/Ndf4a3iaM+y1XXn/+DR8nnklM9n36nj8+nA2cfnmue45cgAoffg+IThTdiQ3OHoK+OQ3mbxJN8C7mL0oP2S98Pg8Oai533nW+bS6KrXV+tm8ffiiv/V9/fiuOHI28DjbfGS7Yf04/cU9U/5uQA3Adzxt+3671Dr+u2BA9Xtr/d5DRXp4PR48FL8CP6k+hQYKf3IAPgDcgm1AxTxOe0+5j32JvxmFKkUFBYcDNIVHyEx//MWLwuO9gn03QwyGgoJEBkNFpYbhxuTFIwEIAkCFycTngkhBUwXQCCAF3kVzCzpBw4ARQ0LAZoS2REkDAz3lwnKFwMDEQtlHn0CYAR8HsMRXwys+DMIh+qZ+UQX6QVpIxUIjwvZEysSXhxXFH0IQgaxDBkHViIBKcYUoRRWIN0M2gUcFLAQzwQGCmEhTxyTFDoUYhPADKwhSB5XEjka3Bg+C9YKGjC0D2MRviAQH1QT8AvaOIMgoRZbGbQNwv42FR4noRx0IugNsx/gFzkcPC1XGA4M4RFtGoARdCCNKeAdxhZSK70yhiVWIG0i8xo9H5IkWAYCD08isxuoGkQfuiFlKKUX5yU1IxEXySWYAR8hwiN7JCkoNhE1Idwi3zGAG8UqwhuaGBsouiNnO0cqazaWFx8Zjh3dFswyjhv+GXAn6jIBJzguCCvNHiocUAx8FuAVlDN+NwEf2ypMFzIUkiD7CrwLnRn6HmIdwxdsJts06ySSIisWR/0+D+wK7xtHKvko+DLKF48VryIeJRERdBoXLTQpeyaZIhcpuiMPLW0c8xBqEaUZaSOsHcQ2ZSpmGtwkDyudI/YbhxskDLb9FQ4qJOMe2CkqJoMeCCs5HhEVjh+/Dp4J0hGAEQkbtxh/JSIkJinjIGIdcCcCF1Mb8AcrFNIRsQjrJEAeEBtxGzwjqCQxINgjqyfDEzsE5QRvACsWKiIcFLsZ+hxME+AhMwgI+s4YKxJL/n0OuBZ5B1sRCgOtEdEbbRzvG/389ASQBxER/wnsFIwAwvxsLg0UHxlaJ4cXQ/6tEYoelw2zG9kRkAFh+MYaVxraA+0AAgvpB3D2OSJlICARiQMvB+kDjvbgGZcLRgVVA3UOVxAKBZoUQQyZ//L9IxQrCl8K/g9/HcoZF/y3Ht0SRQ0yFIEFKvnr+6IMUQCSIKgeZhQFFsn4bP1NCbgSARvLA0/x6At1EIMcdgiZ/94IG/FJCL/tbghBEGDdvAOPE7EOvA3lDJH/s/R7++EJU/Lg9FsNT/Eb/V77FQTIAFwBYwUz36HrpPrSC0j15/baCzLnFdv68+P9qetfCkf78+Xz70HrFgCH+CPr3eNa8nnkyfg5GLPyS/hX9QLuzuOO/q4FWOUX/LzmIOTK8JH9gQG46+DuPejO51frqP3r+Qz5bulg1+/ycPZL9EHjdt8636D5h/Bv2SEB2uD/4jz+HOXl39nw0t4tzYHiGdq53Vvixu1E7griRez03yzX4trA2YnSA9b/3CTlouWw7w3xy9hr2gPWo8+q16rVp85M5g3tIdiI3MTcmuVY4/zNUdt935nC8dJj6ObRKNZY5arTYNdR3dDRHeHa3pPpGeJLw3rWNMvvveLakNwTyOnWbuF60A7fUdvbzpDge8IpyLHZEMOyy9fLftXqzGPa5s3nx4/m18um3pvVn9Y/0n/HTdyC1KrbyM/X1zDWgeLw3lnXX+NQ4eXf1MQZ2GfXL+Bj5ljh5eNK17HjP9D40trYwNsH29PcptqZyDLl4PKA5izZAuax4zPXEerH3eXZAvD048vaCegc6yTnsOkf+tLsTdzr78Lw++Pg9KT8cfJF4knhlvQQ+vL35eE65/vnePiS+STlZwBI6YjibuVe80Dzku8+A5LtRPKh9Sb0uOG78Ev60fJGBcX9UQI2C9YQ3/rV8xf4kf9A/Sb+eQ30BtoHbhCvJHEPGQlW/2LyzfvPACL5u+4NDv8H4RNmDjcJ3ghh+msBMu/SCX0M7v5//K/7IAePEQILzg4cDjrriv9p+j4Jfi9aHaYJ6QUoBRgX+hq6+KYBJ/BX854LJxnjHtkRcRX36igDog4q9REJs/jlAq0R6AsRDyAHMfsY8r/tZuvg8JQAywP4BSsOfBKfBz4D1fPh4HD4MwKpCqoIsQyuAb73Mwal8LP+MANA+8b55QpUE7wFYhNw+Dn3E/+P7I/sivXpA9MD2PZw+KD9K+ma65sA5/zk7dzxAfIj72n6lwNh+pLzmAHn9ir5SQQwAZLv5POqBlPuMfuaDkoAwvZE9ET6UQgVDDcHXAVE9OTnEPhvBAH+vxJyB+/qOP9vBJz+KAOiCNz9muW391QH3/rODLP+XvN17VDrrPQR7LgQEgPN/3T9oP8vDQLsafx56LP2afztAqUTH/pJDkIELwuo930I7xMp/akShQLkFm4MCgtUCdj0FPc596IMs/Z//h0I3gT7BIQO2Q2/75n9h/TPBBUMagscEk/9Iv/N84kDywN2BogR5/4Q/PMajiOXC1Mb/f7G8dYI3RCEFCcP/hljEaMCfQa3IrQV1hD+D3/6Ag/vGXAhKxDWEC4hNhfdEOAVrQtl/0UPVA2BCUwVnR1CBqIS+xIVCIcTVv+tEY8LBRg5IhEVfx1xFakUdQ58FgYMtBUnF50ZTizYJ6AsXxB1EnkNuA4yGrgSryJQFucdEBmLFr4eHAxrB2AEww/HDFMXeBuwFLckORjHCj4PwhkzBjIQ/g/U/70waCvsFIQW0g+bABENYSHvF3AhkhblCmkddCh8HCYlMhT3C+wSuAwpLqQfKxb7EIsWbRzHEGITOhQ9G7QROCp8FGYSwh0dCKISQRZNC8gAwhu8BWYSnSWKIKQfwAwqGCALIxQcELQVLhPoEUAiVxzZEaIIOSAYF8MTFQRFFZkgcRMbKPcL9wnvHYQW+AedH4cVrRNIFpH7fBxBEnIDiAsCDSgJERd4G5cLMha1A1wDKAmxDsYUbwJ1FKUTUQJXFC8LUQimBwT9sBKpFmsF9w9TF7kEcB9JDKD9YwOO8l8U3RKzIZ4LLwmAFfb2DgRjA4EJzulI7V8IGBMzDNT//g+n//oWBwYJ7J3upfA6CrP86v8p/Vr2awN2BGsFLwexDnD2+f1iFWH+4QUT/ef8bwKBAYEJXAVbEa//dgTQ/mAEmwpnBCgFBe0nD94CZf//CTsEhQZP8zntpuRa/F71nfB0830KeQ0oAw4IuOUb+1vqFPcVCD30tv2D+UIABuksBkIE9OOG/ET80fb0AkgcUQaH9DABU/Zl+yEFMAMQ/JLtQetRALEMMwTLAUD7CP6UAqf/2Ppa9Kz4q/wt/B3hXAFbD8fjau4q7xP7mfcI/JgBjvJW9+TxCPyK/Uv+uvrC+jH1uOcB/F4a1gSL8/ALbwL0CPADhv6QAbEC1wI4+1wLoPsx9aD7nfwm/sAIAfph/DIQ+fkKB1L+Vvls/y3+qPFB6WnyYvLU/1r0SQqQCZQCgQGo9/QIafbj+aT2G/lH/Qj4H/hT8IwEHBBFC0v8/fyYAev54PBX9cX/VvlL+K/38vvq/bf7xf/n/Hv5nfA24nHqfO8X/jMGcP4m+sflivssApb0I/N/9r71t+1H+VP0nwU4/Sb64PjS6KjzyvJnCiQKvAWZ86jx1e/R8MAIw+5D/gH2J/JS+m33Xwgp/TXwCPrkELP+nwfv9NX3rQfV84wCnuTr9Vr6OwIFFkIEAwcb88rufPPv9ob65BamBUT8Mwzr+cAAf/gzDpH9v+2d+C/kBfe/DkESFQyMAHHqqPM7AuIB0fT9/Gz9y9iI6Lb9KwzaA4b8jvpb6Cvrf/gU9Yji+u3G91L8kvlJBq/3Nuzu/oTnv+/r8173+fkj7UTyCP466+nYmfVT8LfvFPkb+9j6/fas8vPvEeqt4ML+yvIQ+CgBBuGw8wz3rPL36A7fT/kn6nnodgY4/9j+W+z75STlBuPF+4fwt/P0Ahv5zuvaASrvJdUF81Dvt+8Q8vgHuQZa+F75Ivl3/tLsIvuP6n3h8NzV7/MSH/TY/pbw5Odx8HzzF/rz60v8GOgG37/n1fUx/b/t3O+F3b/lNuap5T3o/ubr+d3pRPJS/r/v8+Un6ELf+9948mbxXvUj8er9h+4y8fn9qt+L8QnyH+xx7nT1IQFA+Qj4zfm07HLede+w7zbuCfS+9wbnvOKFBtYOVv8Y7jbqy9gK3JL5ZhC6+uf4zwDi1q/5KwqFCCAHi/OP6G7j3gYcEGoT5QpUEY78sPO4CuD0NfiL79z7zwbEByQK+f9jBRP/9ABCBK4DQP2K+U/1DgogFfgBXwi2/2334QWd+pb2jAoM/3IFGQkoA4gFmf1NC30E+f8kCvsIUQTdDh0G5/iBBYUC1PuR/RgPogzsDrAQhA7/A6T8LhPSCZQE2gvZFd/+FQQvEUv2afr/AT4PYwNCCGYOyhOxDgYO0g90+SoaQRAKD+kFMhTNKL0B9hkrDscQBRgDA+EFHBANFPMQdCBQDsoRdRj7DK0RrQ/hCZcHuQb/Af4RuBCk/hEPixibAhIHKxD3C8QBMhBwIwoH2Q3DE8QHAg3GFKYNhA5xD3YAAg/wCcMXGBPj9dj4ZwZjD0UJTBVfCt4CNfymC4P9X+uIDxjwKvUB/lL69wlUBTYLwv4KB00BT/N56uHkLAYVDlEAngsGEJX6T/dA++P77QRt9fPpDfE3AwYSkAn6FssPR//N++DyAvDo6lEIbgZnCioa/g9rBSP1BwTc/eP5zudI9QoJvv9EGwMJ9Ao+ARvzlfys8l7tlu4rDssLcgu8ESAJHQAI+h0AZvNP8UkErQsF8WAA7xk+B1AKRQv4AU0DCPrg7Aj4TQGfA7EIBgxYCp4LAwFM8kYBkvlCCh8ZNfzsCIEL1hCzG/sE8QFL9uP1qgRcCdEZ8xbLC8gCPgvwCa0JNhU3AekD8xJTFToQORapCp8FtQutCdkV8v0jGhMq8xKmC/MQUxfR+ioa1RqTDC8Jlw36FhP9aR+ZILkEVvtYDgoLqgR7JrQPhBZXHrQXagu1ATISR/v1/hwUcRMoCVASoRxyC3kL/w0nEzoGIQF5EwMFXwpbFc8Eh/Cz+D4HEgOWFWMHzg4bGkUPKw7r+1gKIvkm+Az3JAIUGuIBVA01/CQEsQ5YBCPpPuJ8FmMD/wGtDVsPWQDN8xv9/uowAaD/1uc662MDZwo+BxwOgv/9+vrtPfLY+N3pPP4NEovrV+tqCeDuJvTN9xjyS/Z55j3wf/rc/cX9zfkf+J36fO8z3Unjw+KA8BD6BfHN9Vfz9vKL77zmfeeh9ejwReSw6Vvs5/Ic5cPuRPwn8Fvs/+Qu9LPyLvRA+Yfw9+qa6QMDZft95frrT/1P/cL61Pti9E/1awEvDZLxjvJt8+TrAfj2+BkNYfgB/EICivVCBjj/4gPG8xD2kwaz+sQDPgP9/C8L8AsU7b/zqP3J+rgMkxDOGuEJIQF1FJoQUQbDDR8Z9vwHAjUZAg37CisKhv4GCHEd3RZWIksdahHODIr94RHZGaEYlwtFDw0UHBZtHjoKVxKaFnQaQRj6GGoRvxRWJrsX8iqkKcIjFQx5D1IxWiNwK08agBFME5YVSB4IJSg6PzAxKsEv7i3JKTEqDCY4LAEfvAtPIocfLSUCRuY3BCobIhUGixKAFZEomSA9Ew49+SRLJ+4vUimLEpcNCRn0BgwiVAuOG10qaR0aKhQecR0vD/Yfjh3ZG6UdGx5eGpAJwxdGBWYOzhJ9CkEQMhBiF78OmhY2D+kBjvwB9lb/yuwb+18MrPiAEYgHrQ86CuDq/u5Y4dMBw+acz4DodgLR+I/oxw6/8837kvOp7U3cVdDeAKD5Wv7r7ZbwPuB55o/mqteO/qjz1uGrx8bv7QLv9Bzp19cS2izZYvT73Y/oZuch3A7jMNhv2W/ZOt3M1vrvpuLk5wnu5dut3CzdSd9kygfb3tHT1iDk2uK43wDVDts8x4nOhdsO45HILct55KfSl9j038fdBMZ/w5DW5d8azl6+hsdV1qrZ/cl61lXOvsTQ0bLNObiZwonM8sT80XvGc9DfyTzFnMtXvJjOGtC2yObJTs66zdvIXNSgxqi4Us/fxfLE09RLyUfGgsaC0tvILc2ZxkG0vsivyrXUTs44xDTJishDyYLUmM4Ix6bYYc0p0EbSEt7e2aS/0M+q38viIc4TzGjJS8Wy197bStGGy43TB9kv5u3bTdo701LLSs+3wEnjYuqr0R7Rdt097BXdN9ib3/TbIdrP0+3Tluwr6VTgiOht6xjswN9U4CThluhf3z7ksPGe4IvrlvQf9C/iMu+H8GroH/hr2qbk7/Dj+4fui+nC/IzhV/Pk86/9QPkY5p341ueL6V75+AGG+gH6Yf44++74PgHsDEoA5QTR+nD4PfIQ9sMXBggzCJsK/uh89UkOzffhD8UmKAtyBRjy+wSdH8sJVBMYFQj65/6QB6UPQCBbDf8NpRmeC54VDRaWETYRAgv+ETYN/hGaEoAPJxOECrQNdgrKF+seNwfpByMSbRTnHR8Z1RgmI5sIuAyhFIQSFyEgD8sHYwUGFKwf5yXqKjIWUBTVGKwdVxbDEYEFEgGLEtEdFy0mJcYcbg4sBJsENR04KNkNsymDGkkMGyboF+scgBtBED4FixL2G+QUySvXM4UzNSNXFu8beRN9DHcnLS9pH6cu2CNsJDgqmCx/J7gSQRpbFzwpMzneNbciZhwbJL8ccRPVGBI0ahdsJskrmRzMMlIl+TC/FGIXeBtUC38nuiNdMDEoIijENioiuiUpMu8V7xufOIgPahVzMmwsFylLH+k2ViQ5GFg7wh8qHAArDCQpKBsmAzScMdEh4B8qGnUUgiowNCMe4yRvN9QuuBTCGSIoqCKOHXgfkSqNL8g1sjOoHjQpAzrCIYscsyEfH9ITTyIWN4oqKTDiLqcsyhMuGT8wmDATKocVJh0kEAQmPzh6MjUjnhXOEgIVoj2zHZIYcB8BIQgvZR6KKl0mASdAIn8jdBryIEcsnhFFC0cuazJBFn8pvxQyGKgePCUHMVYkejaDJosaAwNTH6snHBKOI3kRLw98IDQt9w/NHtcxHifHEugPmSJCCBchPRVXEm0e/hNAJvgH1RxHIlUB+hj+E4b81gysGQMJeBfCIS8JRRUuF84SbRRT+LEC8Asx/8QHfQqQBc4WKxCo+ZsKFBS7G+ENYwv7DqH1QQwkEBv3ePpfCOgNZf8ZBysOLwfzEjz+7/L7Cl8Q4QlW/xf8YAa+/2X18A87Am35Mf9t8WQBvQHkEJMIUvybAqYJ0hF7/1L6NfqbAnv76v9t9YUCEQ+/5z4JkAcC8D4FEgHG8837rPoI/D4B4PZP+7TwqgAq+7TuDPfG83f+G/MLAd/6CPg6DLP2rerJ9t4Cg/vk7f/infJh+Lf54gHk73v9pP6D9Xj47+zc84PzcPi38XzpywV3/N7f/uxA/fb2RPRb7LTscej69WL009Tu+JLvRep/+L/xFPn43hv7ePIA1UHlouep7UT6FQYQ9DntMu897MPmSOnD6NnsyvA65Rv1nfz9/H3n4d508XXpAuZp8LzoFeE18KHrSO+w7YTlSO3Z6AnqI/Er6fDiG/Ff4yvh8vc+5iDe5On82abW9+LN86HzJ+gB9rXigdzV6bfzteCyz3nmHdUA0XniaP6P7BneyujI01nXGeKz/MPiu+rN8d/L7Olj4tre2uBG0M/dau735lfnAu7O40/5HO3A18fhl+a06uXd0uhf57Hjlu4v5EoCePSq363qEtDe35fmuvhl+Z/YMvG39Z7mUdkR5qXmZ+Eu8K3eJN+N1bHfcfCh7ZQCReqx3T7aKNYg6ifopeYZ2tnkau499m8AG/Hz8c7jmNbp2P70GPRI6Tz4++lx6oPv/vTz5T7mOfHH5ZPhJ+YHBIP9OfdE9sDhjOFj3vjc4ehl/ZsCEPLN8QH0de8J8lvmZvH68Vryvv8c7WbrG/sGCof2u+xX7fvdx+Um/OUEWvJE8o76/vIM+YwI3esf7I7yfePN8aXwlfy46T7k9+xQ4+Hmivnf/jPf2eT+7Of4De9X8wz5Pubj9Uzwk+fL4JH9YAS38Tn3sPVT8sb3DgZ49jnzEPrF/1b9zwADB4P1sOlM8rvy/uwKC5ABbfXR9gz1WAJW/TLrfOv99gzzVBP3Cev7kfvd7W3vNuy1CVkAdP0sAmn2nfbC/n0IYABCCkIGxfuh7/L5Tv/wBS4VmvGd9t0KAfxh/jMCQP0Q/L/t7vgvBWsHnhF4+PrzS/iK+3T7rPAf9nTxi/OS+Uv8DPl4+gj+kvOL6Q3v3Qov6IHYMf+t5hIDog6i5TnxPPzc9XLgMff8AJL16Oi4664DbfPTAWz7GOpj4Lzolu4R6n0OpgHU+znvqPl2CGruZfku7gzz0fbg9HXntObkFKMCRPqr/g4Aag0j8QXxxvE3ByoaoP++93v3mwgB+v70qPfU/YgJIv+eDyQKfx2pDKz6Zf2p6QX5uv60Fbb9uQbVFsn+Jvqa8eERuvpP858FgQMdBgoNHxnaAW4K2P7G+SgHbwRtFnINpgHu/NT/wwlFDxYCiAf7DlL8tA/lDK0HWw9NAcn22gVXFK4BXf2h67EKrRGD850XdghRAtoHFQxBFsAIcPp08/L9qPX/DZAHvvnEAZ8HMR73D90UZf8y82ACPgVKAoP9ixSuAccSfCB1FLohKvk7AKIQowB2CuwGTBXKFSsMKxArCGsBrQmEDNz5ogauAysUGyDy900LWw38Ap8FyvRgAjkWVAmk/IANbRRcC+UM3RDtBIgH7AY3A3YKyw/VEoEHLACg/ysONgtmEPochBAwA6kUGBnr+7sdHAy6+J8D/vIcDKYFUQZVA28EDRY9Ew0WiA+8ETj/YvIx95L37QQVBG4OQgjq/4AXDgg+AQoFSRJXGjIQPg+5BlMXBwBQDGoRWAIGDlr2dRQvES4blhFrA+QUFQSeE/b2jAZUCWAE6BGUBO8XCgWbBEj3G/tmEjIW9AiH8HEVxAe5AvcXWASbCgoPOwA19jMMIxT/DYARMhqdGeIBYxFQCmMHTya3HC4VlAL0BgoPNg1eGAoJTyAtIxwUASW7FWcIiQMgCfAJ0geAF+8ThxMqGGEhUxe8BZ4LnwUdBO8TBCg9EV8MvxouGXQoYhkyHLgWIAd9DkwRPRM1HUggtQn0DF8OPCMpKm0iCR9NB60P1gaSGKEaNgutEfL9vw5iFZ0XEyZXEEUTSRB89QIRHxn7BMAC2gXhEysW6A+IB7AQrRGbBnf+zf3IBHILYwVRAHwWQQzsEl8Mf/wJF7wNYARqCXUMvA33FbAUTQ2iCH0MDRLABhUQfQovBdYMkxTVHDYRrQ03B532PgcuGWoVUxnWCDMGFQrIAhkDcgGiBqYDAwdJDOENFRCLFHoBlvYgB9ILYw/7BhkN6BF8EuQQ0hNjBzbsGQfLBcb3bwDWDjIakhaSGGoLZhJ5C+f4S/pa8nT5LATj+0v2sBK3GNoD0wG6/HH0kvP5+UXqAfawEk0B+wz2H5sI7viS9YPvT/Hg7oUCMhSJASQIjA5VAXIBbRZ9CKLjLvjADJADJAxUE7ECww0VEj32PfIVDur/nuptFA4GS/x2BED9QQx2BMsH1P1i9pL3WAKFAAXzuv4q9zXwV/VXFnkH4O4ZBxUEsgC396T84/+uA+UEOwDVFKT2xvFKAuf0Pg3ZD0kE9ACk/mcAiv2s+C38DgokBD4Hwv5kAcMPWxVuBt3jdP1P8SDoixA+D532U/gi/R/uCgXU/f70cgE1/A3vOe0f+tnokvFW+zX2Xf0hAwHyW/DN+bEC2RGL89X1BfO+9233IOj0BkIEf/xa+CL7xvGg+00HmfcDAQ4A5/hF5o/we/uv93j4yfgm+tXtG/8OAsQDnfYN7zcBCuQ1/lb7wNfaBYkBf/ox/2H+fQ4Q8hHkV+3n+JH/UAqz/N/86Bnn/GLq8vc7BBT1FPeH8Bzv5QoVBBET6QHtAnYAGeJ86cfpGPC6+tYOmf1D/hIFlfrc92romfP+8Ov5mftE+hIB1gYNDo74MvM59T3yeer99gT/xvmv+5cDHQbW5dLo3/6d9F/fUO9ZAPn/r/+h8839SPGV+gH4hOPR9jn30fZF6rf3XvUv5r0BvAXr+4P7zwpL/nHoCfTEAXni7OcKDS/oS/jsCPb4Yfyo9XkRpgvG8+/0ZvNx8DH96v85894Cgv+/7WLqivn4AfLzqPsAANzzE/9FCRf2u/bj/ejouOlW/0f/2fLK7ML+Q/7d6YUAbgj667/lr/3U/dzv5/Rt+UT0rPqiDqHvrOwU+annf/TV9UICawXv9p384/3Z7Ir3lfq4600JfQoGEisIOfGbAh/sh+pRAs39xvmFBhwQZhKiDJsAEPpE9Ojweeom/CsQKAf0ANMBqPOP7rf7nfhP+f38JvymBxwMfQraCTH/QgIOAlryyu4y894AqgZYCHILq/zn9joMWv4R7j4L6Qmz9pX88AUM+3j47v5QCmX9oeu+9dLk2P6QB8L+IA9O/6oAJvig/a0L5QLN8yPxkAG3+4DqCfTu/tT9Ogrn+u0ASQiw8eP3kfuBAYUGOPvpAVwLDfHc+/QAofXIBFL6Xvsq7+HoKvnaAWcEyAL4AwYQpgGA7GcESPFt9aD52eorEOwGW/Cz9kf/KwrIAMbtKAlbE28E/AIDBxwQKvMU85H78+2O9u7+sgBw/mnwVAdXFnHsku9l+/b8mfmZ+8cGWAiBBSb0xvW79rwHWAQhA+UCDPk5+ev3uAxJBOERSQx9Av70NuxRBLkEUx0cDvgFegVfCG8C0fD99rPyDRDhCzoOSQgRCWElXw5W/yL99vZp8vgFKwzVEvcTCgv3C3v9IBHoCyfqxvnwDX0O9xUCF3wSd/z+7rP4lAQJGcQFcPhO/4b6KAtmHM4SDRCeC+kBIv+K9S8HT/kkCI4fHvyWE9wcXhzyHJQCzwZyA5MI5QYf8lr8NwMoCeQSogixCjcF/vSTBgMDH/RGBc31NfJA8/32AwXG9TYLHQLb/9IH8vvF//PxfQIq9530DPfz6bb9Jw1IFOEJgQFx6uv5Tv947pX8bfO8B+IDmfeyAI7+dP/34t3h6/Hj+771lvRQGCr7sOm+/V/rBe8m9DLvsO/V82bv1e2K/94Ge/t153D66QGL5z3wwvhQ7yb2QP1VA/8JZfk1+l71seOS+T32PehnBLkEIveD+xT1mvGA7D3yf/pi9J30zf0WAjH/xft47v7w1P1h+tj0Tv+o+2n4GQuQBQcE+f17+RYAKvtjA2MDLwWBAeD2CgMB/i368w7oEfX+F/jy/0f9QgQvCWMLTQP9+lgG9f52CAoPGBF//CUA+STZFbgQ0gt9ECb8kwzXLeERdQxMFzwhXf+lFzQrnRvhE8sBfx2lFU8gPCvVGj4FQRQmH9YKhit8IKoIDgRQGF4aeQ9oKVcc9wm8Ee8VXwqiBIgNdCT3EyAPwiUYERTx6BmuNpLxfRDsEBTv2RfrJBsarPYcDnwaqRblCFEEqQ499LUD/hMUFuUM/hXF/y7q6A99DiUAnwG+/br4yhWpGN4AZg5tFp36W/Dg9AH2SQh2BnkNDgJp9hv/uv6s7hHumwjg7u/sBfeBBcAIYAQvCW7nivlx8PvnyfY1+kf9V+0t/hXpI+9NAaD5zwJE8FfvAfKz+prxk+Vm827jfd8G587nuOOT6Tz6t/GW6nnqCeyI4OXf2fAR6Mrw9vrG77ndzuVL/EHp2uDl3/PtrPgJ9tj+w+x09y7yvdZM6HH06Oz76dnuouVi7MX9I/FC4WbvDe2I4v7yh+7K7uDu5/h49lTizufg6qHvseE65yb02//V86XstQN87Uv+YvJ56BD0wNvd7aD5yf4y8Yb6cgFp8FL6LvYc7cn2Xf8N5dHwzfNq5IDwCe6z9msBVv9l9aYD9u6e5v7y2eQq+YvnUOVrA1wFtv9P/TH7JvSA7iL3tv3R8pAFKvHF+4QUKvcKCcACs/Qr6x7+LhcCFbEGgOxuBgX7tQXGFFEGeQ8x+WAApgUVBoARUxcgC0D3SPPR9nkNnwdJBssL5QgGCMQFlwvdClQH1wIOBE0FJxVRBufyt/uXA60JG//hDUIKwv5nBvsKxxBQDsAGjA4UFl7vIvdyBWL2UvzwBwIXtQNBDBgRPPx1ELwP4/fLA1EEivsrDCQCYADwB+f+0g1bDRv1e/eV/PQGSRK/EkULawUcEigDpgnwBWj+eQ19Cs4M6QOwGhwQ9w0QGQILqgbJ9rUJOgg9FWYQHBhTH/n/RB9bD5L5uvqXAyr7S/q3JEkM1gpTG/8DR/vsDqkMFgKSGB0KkAfACnYC8A9xDz0bNg/EB4sSYAI3B+sWhxfoD7MhTBvhCRgR8A15ESQG/hHHEC8F5BQFHF4a9w0YE7wDxve1CQYM9vh6A6giFQ7g8s3/Bgp2BhUQpgtRCIr5/fyqBB/0/g+hHHILG/0sBnoDcg0JFa0J8w7/AfMOLARrBVEGcguPF0P+Zwrn+AH6wAqxDCALE/1NA4r1e/epCpsI5/YM85H/+f1s+5QCtv2R/5ABafjg+PEBGQmr/hT3De1i9pH/1grODEIE+AMm+AYKWvb29kv8zfEI+Az3HAzPBMQDbevg+A4I3PGz9ETwdPda8vwC5/bN9Y74oe3N/SPtzuda8vAHCgMb85H/1gyw7Qbjyfip70v6EgEAAE0DHBTSB1b/dgIx+UzyPtzK9NoDFQrsCP8Fvvk58ZX8yuzV99nu3e3k7y3+zwgDA5sGtOrc9dnsF/iZ+VDnywNT+Lb/ohKpEt/62e4B+HXvePaBB1QTSgIoCXUQCPxgAsn88AdyBzH7Og4zCA4CJv59BhUE2gECC833fQJ+ACwAJA5BErQPHQDy+e/qg/nlBtkPWw1W+bb9/wnKF9oHRQsUFBkFDPeyAMoZ8AdvAlQLbgxXFuQQYwUCE9UStQFUCX0INfy4DL4gcgO/EDEevAXDE30ItBO1CXoB7xPu/jUZ8xoYEYQMPRMIITj/8xBqE1gCtQndFr8arRGVJUsj3BqfB2cKWAb9+v0hXh4VEP4ZADN9EOEHIiitC+AbAhGBA6kMbhBpHRAd9iOlE7gK7vifAegLbP2XD6kUahWLEFsRvxJfCoEJkw6eC6MAvw4nG0kOpgnZE54RsBS4FtINGQtBGE8e7xekJ7ohwwt9BjX+vAVIGnUW0RsGDgAACg+XD9Ue2Q1xDzMCHvySGMAGKhrZGRUSnfr8AOUIOe2tEV4cOSJfENkTWxeAEzUZvAd4GewGJh09F4wIdCB1EoARbP+4Es8KxAdDM6Aif/5jC4oq2Q95B6kSRgNvAiAPrRPhDW0UhxkcFjYLkAOQBxf+kAnZGYUGMwThB7QRZg50/7QVywtS/hUIjv6k/M8EpgVVAd0K4Qc4+/36afpFCbEC4gMqHmAA4eik9IDyPe7Q/kf/puSz+qoEQe2K/TMAvvV//Hzx+u2F3SfmZwrG7b/zr/0g5K3cwNX04yPz4/ul6qPVm+ET/QLwidjd7T7g7smb2Unh5d/r7w3vQtuRxMnFl94h0lHXDeV62m7jfPGE53PS/cl+zVa+t7g32g7dWNnl4w7fC9LE2uzhVc75zBrKzcQYuePE4eaw6U3cM9uj2RvAs8NWxhvCC9ay0enSKOKB1pDeGd40z8TamMoayHPMUs840JjUouPX1fDil9p7xk3YJOFz1N7RM93a4v/k/97o4sveptx21WfZ6djIz1TmkNoO187tgOrd40HjLNsz4R3bsdn+6DvZZ9nK7oP1eeBF6PDinNPa4kzooulC3wT9BP+S9U/1kvEj68DdoPmI5ifuBft49G3t+u0gD9X3DgrwCSTlbeuW9l73ePJRBOP7MAH8AhT5gQNh+OkB5/i77NMBafBU3k/zFQgzAMMN8xYX/vL3IOh0/5AF9f5bEVfvcfAE/dYMvw70BOELCfbF/d4G+wxqD+ENqQoDByARrgU6BvQAf/ooAYgJtQXG9af/wwkrFs4UXAtFCxP7GPRt9Yf40gcvDVsNWAy2/zMC0fp4+AMF0fbY/jcFyw/QJSsS7AiC/6HxKAGpCuf+sQReFoATIxTKEVgOEQ3tAtj4s/apDBQeViBtIOgLUQRJDmsHzf8p/+kHRQsqGBchSBaTCuUGsQ4U9ZMIvA+w9d0ONgscEiMW9htXHOUMegXr+R0IZAEzCAoLQgQYF0cmCRkcGK8qywtGA9T/xAWpDpMMKiJ8GoQOZg6SGpsEiv8REWcGBwbiA5YXVxgfF6wVuQB5C30QGQXf/G8Clw1QDN0SnRc2C8AMXwxCCjMMixRtFm8CVA1IFhETXxAjEgoLpgWLFkEMsBTdEpsI0wOO/gYMPP6PEcYccRFmEHoBkAm8Db0BCP7TA6v+yARqCxkFIA/zEhERFgAM99cAawNyB4wIyhXwDcX99AqO/HoFvAN95/wAZwKICYEDjvrODmH6PgHSCUIKGPIk5YEJMvO3784MZf8n7KLjx9+77sL4Zu/O7+DyZut16xT5RPwj72DdcuSi39noT/3R7rDx7OV55GPe8OCV+Fvoqt8c77P8OfGUAO78uOWp42/RVdA31Lvs8vVP80f7ouVc2nniEeqX5s/f5eF53pDcOe26+Anw6OyA7H3ffeH74zLpz9+l5nv/otvK6H/6Be1164UAzwIs2efyqef37MX7Zfsx/abaePBe8yb6t/tnBJ3wLu4oCxT5KxSn/w4CW+5b6MYaMhDsChf8ZwpnCKkWBSKsGfcNH/gnE9oLAhXVIBcj5ydHMJ8yuBZeJBMmoCIqGCogOCQkCtc5lkw7MQM2kiQ6DmYWbSBONLw81zlYPcwq+SpyQDc6+SI9H9EbfyccR01Epj4gQElD1j/tN+MsWilJQfg8ykiTSdY9UE8OPyEyBC6TRy9G6jAdOyksrjy0UAFaBVHWPzo/gTZ+L2wsfUXtO9M2SjuqM55IqUPpOMEv1zVDMW87uEtUQFNSWTXqKqZCvTLuKdM0VD7MMrw+ykiiR3094jRsKscGxSxiSi0vzC6RMHAprCFzKrIz4yjCG20cxxICEdsoNScJH0gaXf+s+PALzhAiIqAopRVJErQPwAZL/McGsQ7K8PLzdRbwBcsFVxR2ALwJTBdNC0/xMfeIBzz4UvpuBm35CPhYAib8uv4y63j4zf1B4yfuBe+s8uTn1ueb4QXvuvyT6RXd9dOH+N7bus2e5C/kxutq5A3pQ83/1lTin9TP3bDpNuqQ1FHVEt471UrZ8vU8w2m9Ee6f0DfSPtxF4MTUsLT5xjfS96/a1tPSPqO91s/V0Mezw7PBkciHtXGx68BAxkmwIsJivf63rMExvAW4/6kFwuPEtLU1vwvQhsMRsf67aMcYubyv675PuNW+e8Biv1rBwsHxzB7Hcbk9uWzEzrAYt8XIt7wUvGHNE8hXusHL3MLVtLuzu71AxsK9YrdSxWHF9cfP35XL38Nhx4LISLoLzB3fo80o1snHxdBAxhPIWc9Sy6vRP8q82gfZ/uhg2RXdTsx1uJvZfstu30bcyNdR1xbZTd7T0q3m9N0o1uHkbe3p2BzlSPGQ3KntMfc34BbZ7OuL7/L3lfqo8wbny95u5XHstOjo7Ef/BfFX7xD6GQWs8C7ypPpd0ivhPfBT7gLu2gHEA6T4j/A34DX0GPIHArr8w+5E9JABxfsn5L8QVvk57zsEU+5I9UT42Q8CEUf9ogZbDQLu9vbKExv9SRC8CZz+bRZBEtkTvv149Pn9mf9cCxwMiAsgCQUc1SBNB60JSgBP/TcF+wSWGfsSYwlcCxgZxhr/BScRSQxMFV4YGyITKBQYdBzIBIscyhO0F14gTQF7JLAeYh8bGrQX4B2hHPoUrQfKHRQU0CnyIHgf1y3oD5cNiBFEIdgffycEKgwkFyfhPj5C/C8vPN8tViYfHyIgGyimOOlC+Dq1QP88uENdMuclpjwOOdswfUnePT84+D4WMbU66jAhMhsk/R+RMOw/bkf4PPtBmDQZOKAutjDqMuMsHinBKzZMyz6/R6sxcCeQNrMnMzvUJComui/BL7hB2j4sP+U7FjtIIPYb9iPSFQUiiiC3HmIb6ij1MawjiTSGJSYh1CTgHRwYhBTMLNEb/R+cJ0cw6yDlBvksrRNmFDkgpRsMJnQeSi/yIJkeSBbGFFAWgBPFKEsrlzwqJEQfzRyQB0kMsQiOG/AP8xboGbQZDzPQM3QidRDZEzz6Pgs9F3EX4x7HDqEWjv4VEqUbWxFtGg0a0CdeGo4b9iMQHUUNiBFxFRwQXhz2IQwgeQ8uG34t+hi0E6YNOwJqF5MGVA1EHZIasx0+AXUOCwF5CcsDgQEFGuvzsBCWEcsF0hNTGRwSnP7j+5H93RD0Cl4ahA4zCBQWxAGO8h/6sQ5x8vL1uQQvCz4H0PzZEbP8defc8dnwcfDn+j3yQPtl9dnubwLr8+zja9yA6pPlRerq//rvwvgb95vbSecu8L/p7OvT2k3c2eTh4kXmauzV9VTkfd825izZsd864wfXFefS4I3T4d741pTb3tvP2Qfd3tdR1bnZbukH2YXRy9oLzvnOo9WM4ffmRthLyYHYI+uA5ALqk+Fj2m/Vgdjd6ZPjIOR95bXeidId3aXmfeM96DrfPtjW42Lq3tmp4fThnubE3CzRUOO12j7eLuob9avNgtQ595Pl3t1q4Lfvp9K77mbvauBcBbTm1tk00UHlq/zR7kjxsOnO46H1xvF148rqu+oc6UHjZu/N93T7mu0R6gz3mu0DAcb1SOul7p3u6/XN+fQEU/An7LP+6QG+9/r3E/+fBSgB0fRS/GL26/lE9oPx4gOz/i8Jkw7v9qj1Xvls+9oJ3gj5+ysK/AKK9QINlw2pCuUGwvpe9aT4dgL3EfMWPgfPApX6EPjV6er/sBJd/cAMR/2g/UIKRQvsCrvyOfVI82btJv4rEqIGS/j0Bm35Mu+O9N/6vAVT9M3/vvd6AR8ZKveBA1773O+q3xneH/D69/AHBP2pDJL1ogR0/5rr3PtI6cLyJOf/AVb9bwB9BDrnLvYF7VL69vqh7azsLvaH8g/+tQcAAOP5eeZd/bv2WvgF+UTwOfUg6jX0DPv5/+P3S/pP99z3TQFl+bP8s/qs+mX3Qesj82X5vvkOABjwFOtE/N0Mtv8U8U/1JvRp9AXxmfek/C4TZwRI84L/xf/TAYTrofUx/br60fbg+DMCAfZs+6YB8vuL8e/2de3J+IEH9viiBAYInfx49u/qx+lCAvgBvQHf/sn2IQGIC2MFPP5fEpQE1PshAY8LGQdXEkgemuvn/pYR8Al5B8AAyw9GAx0IhBAOBJgBuAiqCIkDrgMGCJcLKf8x+wcGJAimCVb/U/Rs+7UJ2gmO9DsCUQDY/IwGOggbGpX6xAXWBprxoRptFmX/GO5a9toBNwEuExEL4Q8GECgBkww7BEv+fQxgAvL5bgZD/nYIOhCg+a/7oe88/sL2/vR1DvrtPPqD/b0BLwvZD8MJW+6O/IDsIv8zCBP/DgCP8CQGQQxjC+IBlwPN/y70AfjY9gAAzwgZCdj6+wTHCHIBlwMt/Aj+/vLv6njyr/neBkUTSQTD7EHvMfcQ+tMDOgry+dnyePjN9Vb5wvr2+u78Yfqk9N/6FPla9B0CJvovBaoGQPOO/Az3cPq++3D4BP9p9AH2qgh0/XD2wvzz6WH40wEI+HT5KvUm+gT/0wP/ARf+PfTv8i7wl+ZNA6kKDPs+BXT76/Va/qv+dPtw9lEEFPfO6xf2UQS8DSgFFQq1Bxf8V+/hBcQFbfkrCDMC4PRe7Y8XIAuK/YgROfUy8xD8awdyCWcK3QzLCX0CxwixDjsAFQblApQAyfwzBpMS5QAsBuQWkxAzCH0MLALR8KD/0gfwDQghqQrwB8MLLADwCaYLSQYHBK4B4/24EkAefx21B1sP/hHy9V8IkAUyGJAJUv7DDcMLpgs+AUUPdPdYDjMONfIF+5MQZR4u8N/8xwgHBtMFhBKIDUIGiiaiBp8B+AEyEDkYyf7HDIwEzwhBFKkUOhLHCnEXrBWADf4XvxLlCNoDivtCAiwG7vgdAFAKbfnODNkb/wlcA5MG9AgVBNYKbghjBWcEHQTZD+wGYAZXGMQHyAKXDZsGNwMHAlAWuAp//vsOIAlRAjIQEREx+00NZwBL9mMDCwFjBd/6JAjr+0oCwxeQCfn/oPkM/1b9q/549NH6VAW9AYgP5Qgi/0T2s/Lv9nH0jALc+8rs0wOPDbUHVAcdCB/6MuvU/WcCOfUb+6IKywNH+9D8kvdp8LTszf+R//L1WALwB8X/RPYI/Gj+VvuK/yQEQPkq8dz3OPtjBaYH8vt49jn1NfoZBTMIywu8BSr5lAQi/xDw5/av/WQBlf7PBs3/U/gHBBTrfO1MEXYKXvnwBWoNKAOO/lb5Hvzn9mX35QDn+KD9UQIdAIb+AACJAdnyrPKw9RTxQe8F+4wOowAKA777v++8B3v7w+zc900DcfIF9w4Ef/reAokDyw81+M35iAed8B7+2gHXAtz3PPyg/fb6WALLAQT96PD+F6v+U+5eGN0SlACp764DEe7u+poa/f4+CQoJXAfy9/wCoghX9TMAxu3PAEoCywMvB7P68Ae/8dMDG/0p/yQCGPQZA17tJAwOCvQI/wWH9JAJlvZyCWsHIQPWBOr/2gXXAkUPH/pZACb6Kf3kFhwQywvy9cAEdgZgBFobcgPn8jz8fQa++4QKhiVJBDMEJxNNBz4D1wJcCZ8BRRVAHJ4NtA+8D24OowB9EPcVdP9l+7QVsBa0Fy0vEROLFBUKrQc+D/b6TBVuDlASrRMvEVMhbgrACjsAivXlCrwN+wwUFoQSKhpFFWX7+w4vCVb7iAt4+Ef/XxJFCSQIeQkVELgQcgtUC/n9ZftfChkJ7xOhFPQMOhBA/ToMAwmD+YANwAqXA4wAwAKc/poU+hQ8+Kv8p/+FAl75OwLHCF75V+fk7Tj73PUI/rv2afRe9ekFSgLZ8s3xyvAu8CvngQFA+XoDNfrD4OP1BfFA89HuDPXD6Fry8+0y71r8z+Fx8HXn2PQN6VfvRPZj4Ej109Bg0R3dj+pX8TrpJ/CS7b71X+PC9lfrTs5Y28zWdeX28Ef/uvxJ57TsW+S/72n6z91u30jtZvGT527pKAH8AKbikNye5gblqPeI5A3toPtw/GMDHOW37w3lduF86c7p1ekj67fxBuNyAdz54PIm9ivrTOxe7T4DePhgBuIDku+L6T3o0fIQ8tT7Zu0dADsCVvfDC28AYAYF92LsrO4b8eEFzfd7/RUES/a8AxwOlf7g9qHzf/SxDOEJVxLdFOEHlw0ZDbAaXAE1/LEGT/W1B3kHBwKVIwssUQjDDScXwArhD5cPLw1O/w4MAR/ZF+AdMSDLD1kA3gJFESARmg6KHoAZ+w7nG/cViAWEDBschx09ExQcsxvdFKgeYhngFdIHsQ7GHBQWaSMpMGsyzCoIJTEiRyi0GZIWbRq+HtM0WxVSK6I9+SayNawd1RgILTwjASegLvoapCl+Mf0pUTsWMzUj8A+ZHI4nuicoPPg0XiQFHMwuySm3HhowZSZwK/0pUx0PLYostiqfMo4jgyBoKyYhgBsFJJ0fXhjfI6wd3BxKMx4tcB/jJt4zFyVaHYMgVBFME0gYBRyrJc0g9h05GjcF0RvyHvANYSGpEtEXHBBuENgfeQt5FTMKjvYf+Ffzmfu8DbkGrQmFANnyXAuK+9zxOffg9N3rteDY9PL1mufn8sPmcMfT0LXYm9dK07jjdetJ3eHknuDP1Y7Fd89HzKW348Di0H7Ta9pg1UDA/cXZtw/J/cO7u0DG4bHbyGXCE8xc2CXNBMY9s1iovK2Swvex2L2yz9TEoMSczzDO9r2gyqfK6sxOzhrKSteZxtfNo9kexT7a2tjp1JjUZM594fjWgeK76hjuW+hY5UnhHtEV3VjdfO2X5jH5nfJn3znvXNwn8J3wTOp24eTrkvVm73/6ZvPr96LnNfJT8OvvWvKi41b9rgPwC1wFwvy79ujoxu3J/v3+Nf61BVvwAwE3BTMEFQw8+mH8ZvMb96v+uQAb+XXnNui39SL9H/ohBYP5t/G77LTubPvG9YwA7/Ay59riRep/+GfhXNrp3LfvL+Qf+HYKH+6mCXHuYNER4AnuNfRx7FDvl+b29k/3ZAEB+q3esOvS4Bjmxu/DD2QB8+UGEHT5f/Tg9vvldeUG5+juPuYX9uju5PN1753ywxMOABIDgOwc45b2DPVRBuP9EPTf+h/ys/aTEkj3MfeFBm31+woi+cn6sQr0BrEIS/hS/hkBGQMm+h/6kAUF9b/t6/uMDH/4Q/6k/q3oUQIf+ogF4QuZ/3v/PuT+8gn0GQVA/cPm0gnZ8ifyHQRm78PoIvdcAYr9kf21AVEAKvUm9kD15Ou85hDwnupE8P343emK9yr79vwB+EjxAfQ19ALsSeF55uLSv+W3+zLxzu+A6O/onuBQ423vwvKA7mbpauS83BzrNubT3LDtQt9U4FTglNky8zrpYuy46y/ekOCB3CfoeeTH4dLoHd2q2Srvmu3H6bjffs0a0ObVAupb5EXgbuUV55jKr8rr9+DuOuGQ1r/lhdet3Kz0Y97e397dsO+n1MTeJvpf3wbhauS/7ebVBucB9gbjW+ZS/MgE+932+If0Ct5t+Rv1y+Qz3UoA+fvs66MAqP2QATX+awUE/Z7s1gwzCiwCkwzoDQYKIvdcBYEDGPQzDlMdww3SEZUhXhgrFOgRDCAGFHYKqBp2AGoNMhbzFDEgixI5HA0S9wuzG3EbmR5/Je4huxf3D1gMviATLGEn1C4MJtUUhx+kJQUcRzBoKcoXGyaKJBI0ITBlJKAumSDzGpkqAzTrFngdbCz+G50hQCL8ObonXhhlKusWCRuYMCU1dRZ/HVIr+xIFFoUzeUKOJzUloCLCH+MoFjdzNLgQeyj9I14eiED1MbU23y2PEe4jOzNgM+01EyRhITwtCR9DL8g3gigPM40rQCq3IOooXD7vH68oMC4fGyoizDAaNoMgrjT0Pesa3yVzNu4viiqyK9AxNSfGHA8vqzEyFOcnlzxLKzAuhjHxMo4hnC8AL0kQDCbUJDkcTyIlMWUgCCFVNPYbmhqsFWAzEjSpFjUjEyiRJiIgdCBxF5Ik3yvVIGEjwS2GKVsZsx3VGO4h5ikxKIcf1RqVJ040ejRtHrojpCMnE6kSqBq7HdgpCzZ3Kc0oViy9LAgjZhgUGG0g/ScMIpkoFyktLd4zMhieCxQeJidXGF8Osx+sITgmmSB7Iq8oBg7VHksdaRklLSYp7xUGDCcZsBS/GqkQJxtpG7AQ7TMeLcUk7x3VGmMRzwYqHocfAR3NKOMkYxG3IBMslw1xEaUbJApaI44lxhRZK2IXIA+0F4saNSNyCVgM7xm8D8oTnhMgDS8JAgvSE+wSVxKaGmYUmwLaCS8RaglNCxIFQP2PDTIaJAxBEK0TnwOJAU0HTQkzCjoM2/8SBc8IRgUVCoP3cgHACrf1UQBBEpcNKvkV6Wn4f/pQ713/t/nZ8qIIr/mp75X4BP8RDYfqGOpS+uXjivUoC/n9nfK6/hDytOw18vn9tQMx+83zLNlp8CL5kftP9frtEPhj4jLx1e0q90v6sO3+7JfaMuXS7Fzehdfo6l/lxuvc8bHb1uVb8BXfO9Xt2ULfLu4g4C/mnuJgz3bdluhJ5zrhSd9hy0LZlNmL6wnsRta05J/QWN9n1c7jVOiVzdfV8dJDy82+EezZ6Oncy9jb0NrY5dek9pTX7dGF0aDKP8rxysro3t8k5xbTEtbw2sjRiORk0krXCewc6U7Ogdpu3YTfyupz0D7YQ9PL4Ozf1tk632jTtOjL4HnowON94engf7u50eHoeeaL5+zjstWu1rzg09p30arZ7+4V4RLW3ttR2cDXx+HA48jZHs2u1H3hOuUt+jrhy9qw6W7dStVy3lvs4tjP25fYfOmO+EHrY+RdyqbcRPJj6EHli/E66/Dgfd8d31jZ+NLd4zfWvOD672nwt/Hg8F75w+C443ngTdpc3F/fT/lm7S7swvap6zrf8OIV58PoNwVnAqz0bfO85h/si+ep7wcADe2H7Nv/1fXV8QT91PtW+2bli/Oh9/fkBP9H+cn2ZfmxBDABW+5kAekBXvHu+A4CcuSS8V8IfQwwA0j3xwaK93IBoPvv8hf43Pc6DDMG+ANuEiALvOhb8Azz++NI9fAFEgMU89oBKAVP9YP39ABW+SfwAfgM+9Xr4/u3Gqj74PTR+Ef5kAP5/4wExvNW95sIsQbC+CAHQRo2EbUHePq1B2MFrgEU9xT5yhOqABkJDgYLAfsG9vxYBAH8OggsBGcCdQyxDCQE3PNI97Dtyf727mX5gBMb/8MJUQblCiQCxAVl9Xjw/wlyA7r+jvSPEy8NVQEq9Vb5DRAp/7gMu/Tz7aoI2RHABugL/wOl6sAA5/7q/d0OBhQM+0v2CPi+/6MC0wERDZrjIvdjCzMIuAhS/g4Azfm1BcAGCPyO+F8UnP4M+VgKuAorDpb0OP+o9WMNQRD0AlwJ9AZNDQzz4/819pAHFQpS/tYETPIGDEICVv+w9UICIAv69SALdgBcAfsEjAAM9zX27vhE+NIJqgInD3UMAf65BlECAfhvAlgKZuWP6sn+Zft2BJAFcgF7+Z8FXAGA7mn6QQwn7NXtixxL9l7tRQnLCZLzTOgRCXH0QeURDbQVf/T2+CEFVvtT9jcHqQ595ef4lwPJ+MQF0gtgBg3pBfGp7ZH7Ng0DA2sBI/X29r794gNA/d4A2P7g9tv/FQpUEeP/g/u+/Rjy9vTsCA4G0fQM/3ILNwda/igFNwXu+lAM3Qx48BvzOwTiARP7r/2O+nHyWvIKBYQKIv0nD30GdPX2+Ov1kAN6A/b8CPxA+aD/vAWd+FkA0hUi/zXymwRt+TbupgkGCmH8KvuTCMMJyfqXDc8CXu859w4A0fYJ8LgIkvm/6ccG4gEy8/X+D/4gCdYGAfrIAjz+QP0q71/j3PvhDSAL/wPY+FgG4QlL+HIFtv8j70Ty7vxe+TcJeRWUAAoHkvcQ/EoASPX0Apn7NwNJBvAHuQAsAr0Bzu3+8ED90RkzDkUJJw+xDmML4OxRAEIGVv3c80/1MAN2CrAYZAGXA9j8kvOC/9YEyw9cC0j12egHBEkEERcrDhvxvvWe6K/56/mAETIaMAFE+Pn9VQOo/awdEQmz/sgENfwzAqD7MhQRDVEIIAtL+E0HzhIrFM4S9Aj7DIQMjAzZFaYJ6v1JBK0NRRNTH8kf3RaJAX/6lwfpBXkVE//n+o8VWxE1G9IRjxGKHs8IRPjhEZ0bRQ19CMcGfQ5yCZ4JQRhQGOETAhX0CIgL8xZNBfAFpRPADKISUA6V/sMTrBW0E0wX6v8X+or/wAwVEBwMjxfhB9zzlASpDCARGQvPBNkNdQ5aIZAJePDiAfn92gF9DhQWVx6BA+D0QRLrGH8hzgymA+IDuvrNHmYOkwxqD94IjxNnCGcMzwSxCkEQZhQvCQMFvxwKCa//mgwVEk0D/AJ8Gq4BMAHnH3UYkwghBXUYFQR0/ScVqgaWEVAUuBCmA+0CwSnnHc8AMhKaFiQC0hPsEi8NbRrDE+wKlwdqC/AN7BDkEM4S1g67Fb8cmhpNDf4P0hWk+vgDOgx1Ej4PmgxbDewOzhiMDNgd7QTn+k0FlwW/GAwcjiMdBkICVQGz+DcHNwclAAMHTBUYDxwYSQzGFmkZU/blBqz6G/dBGqIMZwxmFDYLERP+EWIbMwQb+1wJ9vpbExEVvA/+ER0E7QR5DcML5BC/Enj2KAHU//QItBkDCSQIoe/U+aoEuQLVHF4aYf4u+JcJq/zAAA4Mog6IB4UAVxLr9xf+dRAx/1wBtA8ZDV7zuQZqDVsX3Bqn/58FFPci95cDRgdGBf4VrREM9z4Flva6/BkBogj4A0/xCRU3Abf7dRa1B83xvv+fA9nwUQJ4+i36k+XO6wkdp/9FDQ0WcexT7gcCVQFP8dYItv/v7If2Jvb0CmsFHQD9+uvv8+mT5wz1dgSGI7EMKvXj+7v0BfNI87fzUOkB9L/zeewJ9r8OtA9i8rDvJ+xU5oTfyvAU82ru8v1uCCL5UOemC57oetpa8ojc1ufk7Vr4CPjr+TX60fp4+CPxAwGS93/66/Xs6R/0rPpt7UnjXvUx9VryUvpYBDz+XvdjA5rx09wC5qXoUOle91b/EgP4B2cGBfX7527lSPOK9wnqF/xL9CL3nhNvAmMFAg279Pfo7Oto/mcINfry+7r4oum6/P8HI/V6AVb/RPCQAZn9mf30AsgAsPH/5NXtTPJe9Rzv1Pvy/XT1H/ao9RDy5O8F+SDoWOUf7sL0H/Cs7ufyKu9o/r77lvB53h/wWQBo/vb4PfBvAFPuS/gB+Cvtnfaz+NX3jvJA/5b04gGv9xjope4u9PQCt+1l9Xjys/Jh/pPpJ+pl+/PvnuL+8jXwuvqbCOv7H+6l6l/peO7S5sffNf6h8d3pI/FX7QLwi/OG/Lzay9yz9N3tAua/6ZX43O819MbzZutI6UXi3eep4zbqofUn7sPssO2I6N3pT/nY9BXf4OrG7/fiNuov6A7hn96a73D80fJs/cPs4dzv8MLyWOPY+jMKjN9F6MflqeOk+hvznfZf5yPzNuq05K3qyvSADRTvkvnG63nodPXD5DLnv+ndCob+yvTH6fvjqPsLAU0F4ejv9Ib8H/Bp9GnwUQDPAkT6OfPN8UT4g/368Q3rZfUb+6YBmfmD7xztt/m+/xDyFgJKAkHtGO5x8uf21ffu/ir5Cey05FTq/fqJA4UEx+nY9Mb5+vXACMLyQPdp/B/2UO8I+l3//ubz6XLgMfUOCDH/awHZ7rHlVvsdCu743PN87Und7Okm+vb2cP4q97jhce6a8RD2CgOE6zPhoPsQ9LPyMwio+b/rDetm6RHo3O9U6iDqKvHG8RDyVOD37Dj/2/859RDy6/n35BznOP/J9vL7tv3e25byOwLc/VgCH/ZS/uTtWvTsBjsCRQmxCKXuY+T2/G8CegXpCRUK0P7/Awj+qev+8J32PgfN9TsELwv5+0wREQtuCDcBofe/8Wruoe9792X7eQnvE8b1T/Gg+0wPR/mP7IgHXvcZBSsK3gLoC/QGxwbv8iTnYwt9DMAAnRvODrUFgQsZA1EEqQ5fDs3/4QXSD9IVBRipGNkNzwitB478NwnhBycPKiLkHDUn8iAAAOgPSBj0BPochiNPGkES2RNpJcYeeyL2GaoIYw0bHF0mJiF4IfYfkiB/ISkocCesIQghIA8UHhMuZCwbKHQa+iCSHDka7xUUHmQy/SUMIJUlnCt7Jl4cohDLC20eCCsJHYgNGyQ5Im0WBzElK2kbjhuHGb8YohLcJCUzZSYMJDEofByXB1MXzSbJIYoeixpxF4sUEyZeHE8c0R1jCSsSvBHgGSMcSyc1JycTzRxTF3EbXhr4A3IFBgwNEHgbTBlpGUQb5Bi/GOgZ0SFXGm0WQQzHCukJpRHgG3ID+wxJDGMNJiNpJawZYhtMG9YEUBAcEEUNOgjSFb8YlwXgFwMHWw0vDWoJWxk+Bav8wv65AKMCFQ5O/wz7Xf9d/5sKIvmV+D4B4/tT7If0jvQq8Uv2jOM661TqD/5yASPr9OPP3UD5V+lY3/fqhOuw6wrcHd/w4ib4vObT1M7lctiI4hHoxu+467TkU/LP2bnZmu1b6u3XzNTl5aLnVOa06mrqhdNN3rTu19Ek4TMAkvH75Wroy+RM7mL03O8v5hrWVN7+7KzwuvpJCNcAmf149oTh8/HQ/ir5PfY1/JX+lvbHCLAYJAhE/GcIDgD+9J8DVxCBB7gKGBf2/F75WAoFHGsHNfboEbP60wXnHdYOvAMwA7QNIAeBC0wb/hszDJkcPgng8NITzhZeHicZORheJFcc6xp8HLMdARvNIkQd+SagLlcaNR8qJpUh7iVLKWEh8iZgMcUsWimRLu01XDYWM6ozEywdNbYwhx9CObVCOVNuRfkukEApLqAwrjTpOhFO0VBqTMNIg1PrUctGWDsrQ89DbzfTOFREokfgUhNfpUrRUAlSvEYzOWA7/k7TPFdNh1Y3QPNNEFT4Ot47/lTsTXlCxk1iUp86dkENUzZGllYQXlBPI0txVtJOrjieTp1SZz0WOfpN4FQoQHVF4FR8Ty0tGURCPycZAkqETYw5ejxfQfQ3pCeUMRMuBRbsEgs4+TDjLGs2wSm7F7AUcCeLECcZOR6IC8QBKw5/Iz4FVAcvB4wCrQfj+94CCgNJBLEKafgj6ZH/FPXs6eD2TeRE7mbrCtoY5lvoCfY+5trYk+nx1v3JEtgZ4JHOXcxoza7Qkc7fzYzht75HxsTS/q+IrTXF/NNtvtHBFLQNsqjAg8Srw8uhbq7zuJavmrBavzzBYKLOqsOtIKXRtWnBgLVVo3qdP5tFq0WzUaYak0qYqbL0pDebyJyIp7WnMJm6lJWMXKHFi9uPgaH5lZelBJcakb2TSqC6jiyY5pb6gTefoI9hkpWMHaRYqmiYB5xZku2aKoNcm8SlRqN+mqCL3pzdqBi116ASpX6ev7C0q42YpqEHmvuwm6qatuyyArEBu4+vx7KDuDHEEbVnqvuoG7qstya7cMkAyzPZYc2JzJHIF8nT0CHaGszQyzfgUdUc5bziAuhm76LnVOoc7cr0UvyQCTH3t/kZAVEI/wdt7y8L2Q2xCo4lkh4QG5Uj3RaxDv4ZPCECF54RiiSdG4cV3jPPN1ol6yRlJJkc/h3SFUcktiobIgM2kTLuJQwoBCxEH6QjUTneNUcwiTJNOn8lJh0QJbcgoy0zPYw/1y0eLYIyVS7nI5UjiiICFU4uITI9G/kk3jMjHGYQEyRIFmz/Xf8cFEsd+hZEHVceTA99Dmz7I/GtCxf88vdw/AMHxwzg9J8Be//g7Nzx+vVU5m3t5/aw7X3nX+HS5oHgXu8V4yHc6OLe04HgBNBU5o76OuPUyjHIIdZHxLnVVc470zfaaM+a5RLS6dYs28HL4sz42sHJG8QZ4kPRo9Xfx7jh+vNc2vrrmMxDzQ/Ntswg3gbnafix333hjONB59bl5OsR6jTPy+Qd4Vvu+vV09zn5bttL9L713Pt0/RTxPPpE8p8FCP5cB+EJkvOZ/2H6vv3AAogNlARJBMcOxwrHEJcHZhKEDjMO2Q/6FK0TywewHKIQFRICFaQf/SNIFEsfCR8XJwElvioxLAwi/hsfI1odWh1yOo4bIiQPMzwtSjNTHzEm4yCgJBMk9iUWMyIsGjIPLb4mUieOIUQfhyHCGWUilStdLGQsRCFWJkgWDB75JEESQCDkGjkW+hyRKv0lbRZMG+EJ4QUyFBgdAhlmEIMe+hyiEHAjuieTEogNBgpVA+kDTBMfGxUGDP8YEU0HKwxbF779GQGo9yP1S/S6+nwgcgmo8cL0AfyS7y/iJ/BX76bkwACTBvTfDgKO+i/m3/yz+F7z6+1A83LaPew6BoED4PDW4ef6pezR9pcLbgad/AoFZww8/rwLwxEY9NrcFPnHBoAR7iMtI5YV0gkgE/ANwhkMJp0dlwfKF04u0zCPSHM0iiS+JJwxhTc/MBI8GTprPto6hE1EXKJJSUmEQ2M+1keDVRtTzk2ATvdEZkuLURBUOkliTHBgl0Q2RAZNj0z6TZs9CVDHS7w+/k4rTQ5DMk9qSAZDfEu5PalLRjhVNr9LdjvhSD5CWEGbNwgpLDG+KvQ7FjUaLrItfx+vJv0nBRzdCisWJxetE7QPww9hJSMULwsJ8n/2Lw0HACsM8QGK/W33nfak+PbyCezH4xjolNkY8jn3JvRp+oHaZNIez2DVhd2B1jfU5dsS1iHc8OYh0GTOkcRQtuu0yrv82Yjcb9d3y6W5pMVLwx+3Accex4ezxcKLumzC+NSwvF7CfaQnq9i95LApyr3MIsxJsCe3mb7oq7Szx6wrqGeqbMqowpqwj7fOtLu1BqwRre+zObhbt7u7KsIexaS9FLxQsICxNcMftZOyRa1EwebPJdGGy4uuCbmovPO2kr7JyVzUUdf1zQ/RP875xp/QabuhvA/PF8tN1pbqdete8UXsDuEv3nfH5tNx6Dbqi+9X9ejksOl3/ib4nwX69VDpBuUn5Cr7wABS/iQCixBGAygDOwKk9BT3+vda+pn9yw/7BGACqQqiCKYLTQf3FToKe/vaASAPtQtKApkczhrwB/b8jxF1EIr/YhUrCJMUixyIEWIXTx4nG1QPohBP9VAQsBIVCksjSRJ/IzwjsyFpHy0paRt6BXEdpQ9hI68o7ierMeMkXSbQJf0nCR/gHVsZsx+KLKY+3UMTMFkx1CjFKmwswiOrKTwn2y47NUspKD4KQtsyVEDQM6AkQCq1Ok4ufjWIRGww9D9kOOYzSykXIxY3dymUL2AxADXmN/A6nkDUJFYibzmqN2UqozfBM68onDONM3Y1rjjbNpgy7TdKMwAvjDlYOQAzxSriLjs1LD+NN6cw9S9sKBxDFjWZJNAlnCc/Nh8dsi8OOYMm+SgiJvUpzhq6IRMoxiIQGR4nlDvCGXgbuiWdI9YKkwgiKIAR5x80K38j6igUHBscERHDEfocGBeICVsRDCimDaoIwh8GCH0GRgde9R/6dgI2FYQSTQlXFtIJkvUx+/b2lu6P8K/5GQcKA54L0g/1/vrvzfuV/mroYvKg/30IWAzsDt/8t+/C9AXxI/G6+scGWOP6983/ouNA/Sn/g/0c44HcV+lI9W31WvhW+1HX8+Wb4afSTdjD5ODuL+Y19nHyqPGx4RLUVOLI1X3ZFd//2LzkivVh/HXpJOWl5izd09yj02va6dw25HLkRejN/zLzVOJZ0X7NIdI24ifwDt3T1Cvtw+KKyrXiM9s32hLQkcT42Fjdy+Qg5h3dJdep4zHG5skw1CXN0urA2YnW/Nc6427frtSq37nXQtmUz2fVL+JB6ZboHOPt1TDSPtwH09fTsd+e4KPVeeYn6B3ZmNZJ4YHihsdV2FTmn94Z3DPf1t3W2xnaVsg00ene6ORn3TDUOuV57EbSNNEu7IzXwNku7una5dfs48Pi09JU3gLwjOXS6rvs0uZ24bTsR/lR3wbjegFa/m7hTOio/b/lud2O+BT1K+V/+AnyH+w+A3IJegXj9x/4YvCM4evtBP9l9d3tsQYkBH/6OgZP/eP1Zfec/qz4be8+D6YJjvR1EHUUQPmd9jz+i/Pk76/9FQaH9i8HRRNjBSEFYfwT/1r0uQJjByn/7BSlF9cC1uXpBVEG8Oav+9oDQPNZAEQd4RGpEq0RvA1a9k/1IBEQ8vL7+waH9gcApg1cBwz9wAZD/sAGgQFyAewKOfdjDccSUv4m+nv9Tv90+77/jAZGB9j2Kf0m/iwGjw8hAdIJzwC5Am33FPd5B2MDJAyYAZoSbwTj91gMq/xuBlgMRgOR/4UIfQ4RC+ET3RSMDvQIKwimA1L+HQZBDDoGSQbACpcDqP1kAVwB6A9JDmz94gMx+f36nwNnDBUGjvTABFr++f+qBmMF9AqxBK0PwAoY8lb5iAvPBIEHBhJNB4EBhQD8AssJww9bFxkHrQmTEob6Kf/0BmcEzwptFO8VywefA7EObg5nCIoiQRin/0EY0SF1DqoGoRrhEVQJlhcdBFEIeBv2IVolHxerK0QfuvyaFioelARUB3EdYhVEJfwxux0oBWYOaSWwGOooERX+EwkV+w63INkPHiVpIbAUvAPUInMq8AWZKEwVyw3SE4QUSRIzCtEXWiVaIxUSNR+LEEEYpCHUImEhag/oFXoB8A1LJbMlaRuVJwwkxw57LP0hgBvvHaUVtBn3E9kT6xZ0IIoe4ygBIWIVPRn0BrsVQRr3FxAfYh+wHoQOQRa7FUwVYw0rDnkVTQsRF5cNUBSHFc4aoRaiBJMSKAm4CPcJSycUHrUFNR/ABjX6iA+FCML2Pgd2CrULdRAjEjIQqgDDFWoPkveS7xf+Uvwj69z9qQwGDowCbP8J6mn4Ogpl+2ACKvPJ+PL1dPEI+mX9Mwgi+3D41fVl+Rf2Muvz8XnmlvLr9/vjtOqz9CL31ekV6SfuMuel8tz1C9akxeTr2eQw1Kz0U/Zi8MviteC05N7V1uOt5m/R6dYC6gblDev9+Pvfuddt75LtmNZz1o/kA+D36B/4w+TL2PDcVNyQ2jrlzfkR7CDoku1I60HpGeJI9yXTf8m464DsG/0R7hvx9+aw57P0NuqS9Z7kw+ZQ6b79fQY8+IP1GOw7AvPx6Opi8mblGPSYAZz+ePoF+e76+u+45Zb2XvUZARv5Qek99oDwjvZZAAH4y+YHAM39TOwf+nv/8v858RT36Ob+7iQIbRTkGIr5Mff68XHwv/EX+BUIPgMQ+jH3YfpP9WoLYxEJ7A3rF/xI6YTrIAskCiwGTQmK+2nyT/MHAqz2NuJYBtoH2/9FCfsGDgLo6Ib++wgX/lr+EgUb/3jwFQYHAFwHUQgt+lvsnua9AZLvdPn3E+kBEPjTA6D9pe5L+KHtDe9m7frtagv/AZH9EgEU9ajxuOs25ivjcPy5AFvkNuyD/Tz8fO9a9l732ehq4IXRC9gr7br+vv2p7/foYuzo7BzjMudq5sHTXdDm1e3XXu2O9ALmSd2J2tbZ9NlV2o3VrtIlyb3YjOFJ3Wrg29TuyWm/CuIK4i3PJ+Ro05XJDt2p59rgVNzb0traN9if3CPpkdAn5Bjm29Tb0pfgvOi91g7d+NSM3SvnregD3jDYCe594yzd3tWM2R3ZaNG91pTRKNyL7UTuetye5LTkqtUk21/fQe3D6lDrpey45yPzQeu46bTwh/Lk8/LzdgRUCZcFnwdqFeELWvi8BYEFahEYDz0ZrCMBHdMykxKIEf4X2RceJdEdFjMxKEI/y0aFNVE5mzkgQK8iHT3/PCIsZ0UNT9FSGUDrV09Rpji1QjlPH1K0Tp9rYV4YVM1ZNVZ4UjpJ1VN5SrNUdF8UWX5kZ3gge7pcrFR8UQJQ2FxmT7tYTmlhYCxyG2FHYWBwhE++VUxUCF6RaSlp1F0pX/9/1F+vW7RQSEttV2pQ5XRSXvZSc2llWYdS2GJSXItH2UYcUYNZgUIFVSFr1U+4RzxYBU9YQVBJ3j2ISBBSlVyZWWNGvERgN8g5TTxCPbE/CUoWOyUzVTZvN4BMDy17KGgpryaDJAYU+Sr8MVEzBRZQDjEgIxTsCKkQJxfQ/CsIAhF5B2AEhQJA+2Po7/LC9l7zUO9H+c3z/9Zq6Of2XNrt057mVc6uzqnnIdqR0MDXjNl3xwXC9cVlvorCptaN1ZHIc8j5xNG5gLPnuQ2yobYJvQm5bb5Dx6bYLccBu6KqKJ1/u7S3YcHvu7ylBMTkvEy7ZMqVw6i4WKrwqfSowc/B0RPED8vdtE/EYr10wJK+R8A4yDK2WsV0wE3iC9gMyEu/xKe91rbGFs+U08/VLNmrw7LP1Mgo4nC/usPqzAW+eehg0X3jGOiq3cXMLcdj2pnI4Opj3CHW9N8O4bTw+N7665fYxcj8zYXZ++c97FvuOuWA6tbbFPmS72DVmutkymDVFeHW3XHy2fLD6rzaIdwg5LTkWNsU7RTtjN1C4R7NxN4k5zLrh+5z0uLYwN9t68vktO7675zPFOui5T7ex93L2HHovdjK7gn2lvZp9sDhZvFt61frXOAw0g7fFOvr8ZLvbwK/7wnyzf+P7hv3muli8kzwbfHn/hYC5Qg27uf+qPtP9c33peZT7tLsuQBH/64Flw2ADYgNSgCMCML0Wvz0AGn6jvwB/K0LqPXn8i74ywPVIBgVLwcGCMcQuA68BfsKZAHJ9ovzafqfASAJNClfFEICjxn0DDcBHA5bD/L/VxS3IKEU/ws2DwYUcgFcB2oPDPes9GYW2Q/zGB8fvA0RF0oARgWJA5n/pgutC9YQGBFbFfQK8xK6/tH2tQmECjYPywlmGvcV+haVKYgRRgGTDnkHowDlBEEM/hV5D5oQLwmXCbUBgQe1C9/++haiDmcMBgyYAZ8FdgAe/Ej1xvdS/t4G/faMBJoWQgaMDAcA8v8p/23vzft6Af8DWARCCnYKWv5qDQcCwvJP/XXvAuaD8eEPBgrLAQkVG/8F7wHyXf/f/HHu6/tw+AXtCPqiDjYN8AW39drcMulW+yr75/p2Cm4Ks/y1AekBpP6L6+f2SPe05kkKQgLu/lgGe/fN95X4wvyH9kP+U/gQ+k/7cPZQCpn/1PssAEjzcerj/Tj9nfjrFjoOH/JM5uEF7AgB8rwHNg2JA+D2WvwHBoUEPgPeBkICrPpJBAH+ngsNEG4IRgMq9bwDyf7y+88KFQjACBENS/iS9yAPSQqMADABbg4VCBYCSQSaEIAPMfdRANT9YwOpEIcZJAhnBscQcgEUGgkTzhrOEIQKORYOBIsQJASpFM4MrRPfIyMaHiUNDqUbgBccDAoLohJUE5cJxhzKGSMc6Bn5IqYN9Az2I78SJA7hEQEnVA30CGYUXwrWCpoOMSSxDLQVWiV1EkEQjxO3GvoUUxVNDUYFrgF9DhQaOhLZGV4cmhYcFoom5Qz4ARgZ1wC0GXQk8xh/JScTnhNjB8AGLw8NDm0UOhSvIoQQgxigKEES4BXKG7gSHQQ+DQYIPgVaGxEX+hRpGYcXQgiUALr+iAk5HrsVahWMDvcRPR8fFwYQMf3XABv9bwAqGAkTRyYXJfANQQwcFucbMhBXFNoHUQa/GM0kXiR1Fk8eAwkHAoAP7QD3DaEclhngGRQaixgFFjIUgBvoDyn9hBYqHKYHKw5fFFASUQhRBuUM7v5uDjwl7A5YDMIbrBlnCAMFMhjLBfsEIxKR+y8PbRqAESQM0gt8IIsQ1gYKB6IMFQpgAisOGQ2lGfsSdRL0BOkFQgai52oNVAfABEESfQIvDY8PLwv0AhwM3gSFBjH70P5qE94CqRC+/eD4HA7hC3f+E/t9Cnf+Zf1jBwMH6QHOFvQKJ/KuBQ4ELfyZ9QH+mf2z/BIHHAwt/Pb47xMx9evtvvdp9KD7aP7hES8Ff/pZAEv0vOLN85X8TPDlDDoM3PkE/a/54/90/23rzfdL+s7pRgUE/xf81hCbAHv3v/G+9aT4xu279u0CcPom9hf8S/b28Dnx8+1i8Gn4qekJ8Fb7HO1t9cvmPfII+s7j1fel8jXy8+8J6g3x7+ge/JMG7v7xAYwCi/MB+Nj+afDV7Ujrr/1A+0HvJAyADwz9t/Wr/ifyv+XC/m3xOe/ACNj8Pe5t9/AJzf1E7kT4CPx87dX3PgNS/BkFQPvxAd/82gFyB3/22gcJ9moJVBMM/+78dPGBAXv5tQsCDdz3ogYVEIsYZg58Ev8Le/fv9DMKVxodBKoCcgO6/sQBfQypEJX8jADeCJoW1RK5BP8Di/MzAKT47vyAD94IWAxkAef8+fuBCywCQgQODBIBww07ACb+kAWOIbgI2P7DDznxJAi1BQIRUAohAXoBYuyqBPADKxThD9IJ2Q/4A3IF7QR5EcgACP5bDeQQFBb3C4ANjAhL+DcDTQVCBs4O0g1JDLQPFB5JDIkDH/io90T84PIKDaj91PuC/88CvAUe/toFqe94+tHyfPFvAnj4/fgY9P70kve79Any6/cN7771xvPv8ib6HOUU86z0v+9x5pPrafjv6KHtaujS5iTfGO5i9GrmWv4F707ON9In7lHdA9pp8i/eDuG44b/rj+go4rHf8sKyy9PSDevh6JPdM90a0mrkEeCE56LbmNSF15fc0e4o4M7jz9+f2ubRjOGT6T7e1et93WblLupb6lDnRtzl4/7mPuKB3qzyKOI/0LDryfh86XzpCeze34PzH/rG+SPvBe0dAtnqH/TeBvL/OP2z9JsCbPuz+DoOohJ2AnkJyhnLB18SPgPY/FAMtA8uITYVrB0rFkgWKxArDpYZgQEmHUwPRgXvFQ0aKShXGi4hlhHHCngZVBOBCxQaCy4jHrgQqQzSE+scZhwMIl4kQRYmH5Ic8A35LuskXhj5Kn8lLhkJE1onsycrFiMauidmHCQQeB3oFUwTxh79JV4YhxdTIf8DSRCoIOwStQvABi8Lxf+iCu8VxwxYBiAL0g367yn97xWz/M3xPgPLDeUKHQR3/BjwAuYy71vuSOkZBaIKdPEm/OEHkfvG7SPtS/Rn4yTfAuYG6RDyJ/Lh6EzqJ+gD2sDhqt8r5YHiiN4+5BvE6dhF6h7NB89R0VXUstc30pfe+N7b0jvXjsV+0wrm5tNZ1bbGIdBZ1czOSd8+2DfUts5k0CXPtdQa1kPLf8cqwKfU18s8x0TDWc+U29G76tA1vZK68r6ZuizRS7/X0zXDG7iVvy6/38cly7XYT8DcxEfAnMlOztHBZ9fzuFO9P9R3xWHFAM9208nJlcPxzibHJsN62L3S18t+y+bVUs+owqPNlM/CxZa7c9JD0ZjSDtsEzNDNIc4o1DvRjOEV51HTC9YO1xLa3tMtzfTXO9Xt1Rvz/vAo4Bzpoeva4HLeluqe6ArmauyS+QH0W+4e/sbttdzp3HXpqPFE9vsM9AjwB4ARdQxnBnzx7vxd/c7pSQr/By8HNhOICfcJmwJiFeQQYALDC3UU9Ao3CTUfkxQXIf4ZixBiFZADBhQyFIsaRCFIINUgfCCGJYsQ7iPmMUEawh9HLpwpChFXGkcoyherJyEwBR6BBzIUmC5hI5wxCCm7H5kg3CIeJ58DEB22KCMa8iSGI4IqQChXHjkWqBpxHfYj7xe0E3AjZhwNFOQY3ykUHgEhmRyPDREP5/6XC9kN/hfDF1b98AcHBOERJxUhBakKwvodBkv6YfgDBVPwDgZa8qXwmwQj9aD5pPob9dXzG/2L7eTxfeeT5bvw3eNh/PPpxvFI87vsmfkazBniKvM638rsUOMK4BTrQenD5DbsPPjZ5LLVKOB949ri+u2W9ITjy+Dz6cn2y+Yr6yb4/+DV8anpHO9A86T0T/2a7br++u9162L2iQPG9VvwG/2k9BkBU+xrA4EBmwQ6DhHuTv9I86IG3/rLA7cYLAAUFHf+ogq5Ao8PLS/dEC4bEQtiEwwkwhmOHQQmsyP3D6Ql/SV/IfUxnC1AKOI2RjrNIrkxEjbTMEotzDDdRao5cjx+M9QsWDkhPF9J6TgdO9lO2jrTOhhIBkVaWDVWnDV2O6JJoke5O3lE8lsnTHFMsFOHTORRbVvcXRhIX0lXUcZRrE7rUQFgEFI5U1BLbU/cW51WTFQKQJZQwljKTrpahmRPVRxF3FH3SrtW314VSfdCFUmdWEBZ61c5UbhHBkFKO4RNxlGdUnhYl0KMP7REiTbdR9VP4jQ8LYU5AzqrKapBZk13M98tRyyYNoYloCj0PSUtdydpIUAkASWGK2wkGBsiJHQcMSTcHDIWMhTLDTkWgBf+Fxsc6xxNBfwAxw4rCFAQ+xIZDVQLSQRNCQoDGQsCC1r6iQPc+8n4d/zZDSEFqgRjCWbvlADc8bP+7vwY8hkH8vOA8kzs/ACk9sbvXu/g7iQMF/b/ASPtdt3k82rs6++i58b1wADk7+HmCfAr7cTeIObd7YDml+RT9If0K+Gp48r0feED3JbsM9uy17HjeeI+4FDpBuue5uXfvNoU6xbVHd/C8tTOBuOX5mve/+K05J7kANWP8A3x5eFg3bDp9N+F0XnsqtvD4CPpmudy5JvfLuyM3TPZSd+Y1ozbzfMC7oDo1uPd7Trd2Mel6unWdtXo6NnqC9aB2HTxKOLP4a3g3eloy57kOP9V1IDuU/jw4ubRmuVU6lzWUOVs+zrr0t5RAs7vbufZ6NnmDPNF6Ev0auQK3CvrK+uw52bzlvSm2gLs+u097qT2iOLZ6EnjEeIj84r9G/P+7JLx9+QQ+GX12e6l8g7f9OEx9bIA8vMKBewGoe9t+QT9lvSW7vLzlvYt/EIAhQI8+FvwLviD97711e0i/6YFh/Dr8fn5s/iZ/cn46O5097fvfOvc8dj8dgAJ9tzvtORe8TH96QEHBpb25/QQ8lvqivlYChkHKvFb6qHzJvRw/vAJtQV79476nP6383D+8Av5/xzl6Oa2/235AvDY/tX3g/eIDZsIyfZX6+znBuEg6p36WvyO/t4AcP5E+kv4Nu5b7kHp8vfy+frrxwxyAQXz8vPc+00LEepT7KT4lvIX/CwC1gRT9tX1d/xI9dj6pP54+EHv7QJyBeHmT/UM+5n9s/oy8br4uOfr8TH5TQWiBNH2Wv7P3bDpnfgF9xv3I/GFAnjyWQAQ/ED1/fzs43Tzi/P28rP22//f/CPpF/5883HqfPMB8vrtDeur/KT+xu818ir7XvUY8hXn/+L+9DH55/IU8ZX6FgD+8tnqNfht9fbus/xA8+TtG/1NAXT3QfEQ9mPoJ+wu+Ev63/5x7mz/DPet4jz6s/o27mbrTv8f9JbywvxI8VDpOt9A+dj8mfVx7hjyG/UU7ef+7/Ag6nzrkvfC8uTp8AMF+0/5kvdB6Wbvmffu+lL8V/X68Zn54gFE/AH4pPxt75L11wKMAEv4BP+5BqYD6v098Fb/4/cm/LECF/afAef2fgAzCmQBKveO+lEAyu5p/EUJ6A2xBBTxmwLV9fbueQ2MAAz3p//2/E/3wALdDLkAJAL0BhUIu/SZ+f8BnfLb/6YHWv5X6RIH0hEq+WcCS/pgBOkHEgeO/EzwawFKAEIA9ABUDRgPiAn7Bor1bgYrDtD8bffq/zAD7QJxE24OywF79x0IUBTn/qIKhvxT9JQCbwRmDiQEQgS6/Lv2cPw1+MQDPRkKC6Hx0wOQAXIDhQhkAWAAcfDY/h0AnwUjElcarQ026jYLS/54+v4X3/z2+hkD4RGG/k7/AhnaB28Ad/61Adj+Pg2eDWsDZvHy+bsdvvXY+AINFgAt/AMDLAY8+FsPcgkM9Y706QPn/rDzegFi9u0CYARjA9z9H/qTBpn9Xf+L7ajzJQAI/K/3EPgcDp8B8v0OBD4BbPtw+pAD4Oo57xUO2Q1//r79JxP1/rXgp/8RC9T9jARH/Xv5cPrGFOAZjvaFBJMO+fuh97gKdgJE9nIJZwSqABkJlSH4B4Tn1wAvB8MPNwmqBmn8PfL0DAcGKANjD/cRSQj69b7/sQj/DYgNmf92Cl8KqPu6/MQHVA9IFpYRafyXCToQVBNUC9YIuxPu/CQMXwgKC3UW/w0gE/L/2Q2WF2oXORZnCtMBXAmsIRIHE/8uGXwYSQq4DMMRRQnSDUUNT/1S+sYW1R4VDvsQCRXaC5sCuxOWH28EJv6TDFwJuA7vFT0b1SB5E5ABcgP7CicP7A5FCcsPeQ9tFMIfsQ7N/c4MqRYdBmH8vA3kGvwAkAVxGaYLZg5BFnYE1fF2ACsOUA55DTIavA/r8TYRJxE1+i8NkwxjA9H6zwZiF88Ilw2wGJcFPP4GCmAGTQHABmoL/ACFBHAhag8oAYEJWARQCvL3oe/LAdINcQ8CEZAHfQgrDhjywAZnBOD22RNKANXvV/UZCRUI4gG9AZ348ANW/+gLvvdj5pcD6v3hCdoHt/t6Ayb0W+rC9h7+1P9T+ETy5Qaz9BIBORjv8h/yivUT/fsEDPtl9Y78LfpA9/L3QfErDPn//fox9fbuJArpCWMHPPhCBsr0pfIi/T3yXxCXBQoFrOw96s8K1gZYAirzcP5l/WcEjAjy98Lyi/NjCfL10fhFDUT42gMM/xzv5PGMAH/83en/B3IF3/52ADz+ZwQ4+xIDMfm2/f8Hxw4P/tcACg9b8BkHjwvaCeUIBwSPD5MKzg6MCuEJFgB5C6T8kvkvD478Cg3rFtwadRIOCGQBgOx/9k/9+ft9CLgWPgfwB2kdNhdJBEjz4PZa9qMAiA+tD6YNng3RH8sJuQQVCh/2+w5fEvsMFgBcCXQgdgaBBRgTeBcZB8AABwJrB84W4BXWCnH0MwRJDCL94PBkAW0crQ1UDxwYkwxh+lL+LviA8jcBawM2DeETjhsNEML+bP0dBuwMhv7n+JX46/vABPgHRgMzCJsKRPzv9Mn28AN7/br8PP7Z5Kzw7v5A83Xp2PYi92PipPbu/OjsPuKd8uXlUdu6+EHlRO5i8Jnzmuk34Of0nuA+5p/cg+/W587lhQSA8Jn5zfF09f/ixN6x44vnEPhJ5WcEcPj67eD0XvN56gDT5O+P7OjwSPGh7ZnzDPMlAOTpt+/z7ZPjw+Km5GMF1PlB66Llk+dm68PqQPuE6RTvwv5S/L/x4PiFAlHfuOMU7dXxjviMBlr8pt7F/Sr7wvJ48lUBG/826gAAi++H9KHzLvBt60Xm1grC8MvgafLXAHT3yurj+azuHO8C8BTzt+1m81QJ/fqA8rTox+Xk50zyLvbS7LDxE/8E/xHgg/Oo89rg2e6a57DpGO4i/wXzbudM8Ev4afRU3nHwzuN55h/45eER5MX7FQrG82bv6/G/5YHizuMi+f7w5Odw+Hnk9NtB76T2/+Q32rjru/Ln9Lvw4PJu4ezhTPAN53zzauJi8pL1JOHv8uD2xvHE3qXsVOp16ZLxvvcX9hnixAPG79Xp4/2e7KzuV+fn9or1K+k26mn0jvyp75bwj+Yr5yL72gNI8dXxLAKl5uHirOys9g4AnfIy6zLl0fLu/v38wvop/6z4De3n/J38H/hw+DH53gKmBVEGFQpA/bTsF/4KA9H69vrU/bb/kwYzCk/9QgIZAUYF7QKV+mcE2PoU8536Pgt9DPQMywvY+uTz4gMqGuEJKAXkFnwSSQSfAxwSXh7LDbkGFBRl/ScXrB+5BpoWnhGpFv8HeRN8FCQO9iUYEcMXbgzsFFQN7vjwDUv68xIyHLsTQRrrFn0OLACmDToQqQ4X/H0ERRHC/DYNIxiaDgILpg2fBx7+RROSGOf8JAgyEK/7OwAQGfQE0fRQFrEITQf3CwYUdRAU888EUvxGAQ4KFQoKA60HSx/eAPL7RgVcCTj7Q/7zGm4GWARqFW0YhQj4A0UT9AgWAowC3gSpELQR5BhuENILERW8AzMGnwVYBscQSQq4DrcY6xaEFGoVUQKmBbQNzf+xDvoeDgpFC08aDRSlF2oLuBSlEx0CSQrDEwEh6BlMG/oUlhG8C7ULwxXEA4UEeQkCEVEIxhi+Ji8RSQ59CCAVqgJjBwkZ2/8RCYMc9h9gBhUGRQlX9fn/9wnKEZoYZhysG9UYVxjSEZcJpgcGCK4BKAlPGioeGBVmHKQhEQ2BC78QQQzKFbsTNg/rGAweJinvGwUWCROqAD0ZWh3sFBscLh20EygHpRXjIv4b6A+SGqwXPRMbHi4dNSO7HxEVMwocFBch+hrkEHUUKxb7DCYflhFgBMYUqRIGEg4MRBeDGj4H7BDkGMAMWAywFhUOJvSC/yMWVAlJCjYR/wf7DJkcNhFCAA0StQm6+v8JGQ0JE7gS3Q46BpcDWxFnCqD5jvxBEGAEBP//BWcAcgWTDqIMjvrwBVAQBgx17ejuxw4b/wMBEgXaB/L1dP0i+4/oVAfaBSMSoP+d9LUFtv8kDrgO6QXF/UoAhO0n7hUGF/6g/4UG7v6k9OUESBiqADbsnfjy99zxZfVP/TX8Uvot/uID5/zo8NT/6+3D5rDxAfZ3/OD2jvjf+nYGRPyd+GnwXvEQ8jrrT/149CL7mf99BifwgeL5/TLvsO3Y+CgBDPUx93IFAfijAmMN0P5f6ejozf/r9RXnLvT69QH04/cDA3D2hvpyAa/5s/YG53T33eew71fzX+l9Alr8pgHV8Xz1sO8N5XzxhOuO8lDvPgHeAirz/fgf8vrxivlm7wXvK+ee6Gj+KvUI+CsIDgaH7G3tvveH8IP5EQkHALDpjvQN7YPz+fuR++r/mfmMALP2qPWD9aYFawG/64PvvvU27ib0DRI8+pH/qgDZ8qD51fHlAOTxsPNi9oTtFgCfAc4MKwyd8AnocfCA8uv1/wPaAXD85/hA+ZAHZfebADYLyvTY9JX8cgc3A3IJh/iE5+f+Mf2w9bf7lwuQBXT16v3IAmX92/+mBcr0v+sSA3D8pPYwAQz5CPio+cAE5QDPBh0AAfrc/bf7sBJE+hf64/WL89oDHQBNB0v6mf9p+DH91fPV7x/65QaXB1fxPg9t96j5YATpAfsEePi8B0HtJvgb/6T+Q/7wBXILafK4CjoGagm4CkIE8Amc/jMGUvq/75n/RRW5BnD2cQ/ABDLttv2mARv5ZwgkEIr5MfczBJ38i++S76oCnfoJ8Kz2u/Sl7qT6Pgv2/K/7afoJ6ljflfrJ/g3v0wX+8ODsrPpw+g4AwvyC/+Dubuek/FgERPYI+Of6EPSd+s8IegHr8Yb+sPVX6zn5F/oi9wj8zf2A7l7vf/on8rP0ZwBL/tLq3O+qAHzt0ur4ARf+auQi+aMACe7n+lL6e/0f8HTz1PlF7AH25/7Q/rDvOwR2AFDvvAMdAmX7JvyD/Rjyv/Gs+t4E6Ql5Cb77h/IZAx/2EPYzAED7TQWR/8LyYABcA2X9Uvp49HD+OfUB/GsFYvIf7gz5EgcB/H/8QP3+9FEA4PhyATcF+f/SB1fv1fWG+m33Ivl081wJlfjeAlgIT/sLAX/4tQN7//AD8AOv/e/w+vfn/q/5eQkI/J4JF/wf8Cr7RPyBBbUBPgdL/uUGtv96AZ8B8+0b9wXzT/Gz+mcMiA0gDcb3FPFH/Wn2R/2Z9fL9WvyUAoUALvjwBX0CUvyl5lr8nfaa8T4PpPjtBKIK0wHWDDcDzf12AED3lvIX9nD8TQll+YkBPRPLAav8AfgF+V710fi+/30E9Ao8/noDS/ou8Bf8H/Rf5478kwgb9RkLdgifAdIPzwLj+R/y+f1M8nj2yf6r/AILCPoDAxT5EPT2/Aj84/9gAN0WOwBe+XD+vv+3+z30DQ7U/dH6T/vlANoFywnZDS7wbwSJA3v9KxJnBkf5KAGr/v34R/39/OET/wFH+Z8FPgPWCOEJPg10+YUIMw43BaYJVxaiEG3tsgBCCr8OOP/WCCcblvJ9BBEPKAkGDOUK1gik9Dz+EQsHBlEItQU1/G8A6QFA/7EC5BLYHVgKhQiLEPwAzff9+q/90P4+ATsEXw7rGrwLwAo+BXT1HQgF+Qj6EQsDA/AF1fXN+c4U3Qy6/J8BMfkM9b0BmwhfCqoC8QG9AZ342fD5+6MCQgAp/WH4+f9jBysOGPLK8E/9BfPPCokD0gczDGAAbwIB9EYDYwUP/ifuj+wrDhIBqgheIJcJYvLEAaIMjvYE/Wz71fNT+MrwgQsZCQT/mwgf8o/spez1/nv9CP5jB3Hs4/eW9Gn4kvUv5BjscfQ19mPowAZcBTcBAfp57AMBluyH9qz0nuIb8xkDi/O++2oJkvWbAN3rLuzR+Pb6Mfv67QH03/59Bm3z6/kf7OD2cPye7JsEh/i4DOkB3gKUAOzjVv8u9mn0J/CXDwgj5/oDA0T2nfC1Bx0INwOs+goHsBTN/UD3KhjdFjH9Yf4x+woD/hHWEEEQJw3WELEGnwNqCeP3Kvm4Eq0P1P2pFHgfSQiiBg0YOgZT+HkJ8AcYD+gRKh5fEhv/+hRNDccIpgtXFJ4VOSIFIB0G4BknEyQMLw36GiMafQoJG/MUVxygLj847xH7DDgktA91EuAXYSk5GPoeITAyHOMikiQ9GaIKKSrYJ0sf9S3NHnsilh/XL6QjbgyVI4MmFBbGHpgyKiCkI004KiSWFTgojS/ZD20aXDaOI14gmC44JlcQoCYHMUQh+iC4FLohaSMMJlol6x5iH7cgrCNFCRQg+hqiEPcXuAzNIiMcFBjhDVAYiiQJF3kVsQ5JBL776xhQGLwLtBdBFg0Y0hVUDXkHhArDFQIRkfv0BLAcpRFw/G4MfQa5AgoPLwdUE0kSIxiR++TvkxSeD2sFuQRKAE/3uQbn/nz19AS4CFr+SPPU/WsDRgOz+Ov5Zu9O/1gMjvIY8mX3ivl55G35Vvu08Cb4RO7d7d3hiAXJ+HHuF/ok5VPyeepT8JbqhN/O5eHoKOA34PPtkNaB4IHeHeHg8qLhh/SE5T7Y5O8h3IXX6Oz7503kYuqu1krTl+S84KrdRtzh4prvteJB5QH0De9W92veNMkc7d3pUsv02c7lkNrv6JLxgOacz6batPCN1WDdDuNg2S/gQef+6BXbMNiX2nrYWcna2N3jn9zL4Knj5Ovd56Hx1t0O21jjXN5T7HLkluwn6OD0wOFC3VL8wN+d7ifqcuLw4iThZukk5Yr3X+sJ8nHune678NLqJv7O7XHmL+Co83HobuHf+sL0zflB63YKFQZ86yQGywX2+uf+sQaD+8QFWv5E/Lv2mffdEBIFFQ5VA1EGlhccFisO5QD/B00DwAbPCjADBfdYDssJUOsHApoOcgtGAfsG8AduDLEKLAALAev5mhAkAgz3cgNvAg0OIxLhE7P++APpCcX9Kf/N/TYRsBR1EAsBHvzTBTz+mgxjBVEAQgaO/M8EVAWmBQoJ0fRt74kBegEkBOUCQP1/+k/1vv+R/XT72Pjc9cb5bPtO/wT9MfUu7An0mvEV59LqjvLy+/L7jvY4/dz5nuj+5mrmFO2/653u/uwG4+TxWvhp8OzjQe/L4g7Z7Of/5HXrNuy38cfd4tjG63nk8OBF5v/ab9Vi7DPjseGP5CTnhOsO1V3Qed6L6yTbnuJ16dLkuOso2EfMwNU+4IbP1t0g6EjtdPlV0unWfeGP4o7yHeGnytDPx+Gf3uHkFO+H8vfqDt/02SvfRPh88f/ghs9j3HD2+utI96XqXNy07JbyX98h3ETwSOmH8pn36/dq7HXvZwSm5Jrn6/HW49nknuYq994AtQEP/uvtlvSD/RHu9vBE8ITtU/Y4/wsBivlCBGn4buM65Xj4+f8G5wz9qgaw68AAlfi86Kz4Xvta+j3uOfneAkkGKAX2+pn5dPfWBHHsu/CV/Gn6IA8b/fQE9AQKBRUGPPokAur9LACk/Lf7WQACC54JMwqqAJ8DDB7n/mH8WALR9t4A9AymDQMJIxggDekBegPrGAITZfeBC5cD+f+lE78a7AwKCREXNwdnAscOryJMGUIKCRnsCOEL4BXzGFoftQNQDAINkwqOIT0XNRs2DZ4JQRJ9CEgYdCbNJPQKagtjD1AYVihxGzkYTQvZD1QJgQsUHo8Z+h7GFgkXxhqdG/0jMSLWDnILTBEnFRMsYh/lCiMYvh68C9US1hAGDJYZWw/JIwkfaSVhKU0L6AvwD84aQgjVFNkVEgc5Ijka5BaECk0JbRg5GJIgHx2oIsYg4BuiEH4AvxapEBEPHBjpB4gP1RhdJgkXaRvCIwYOeQ1cAXEb0RvSEXUQDPv7DIsWsBI2C2YScgmxBJcJ5QxfEqoAmgxGAzMAIA/dEFQLqgBRBiQEmAHaA9gdiAvu/pcJW/CD9yQGXhgZCeUG9xPsBlUDzfcoCUv8xf0cDALudP8NGHkVhv61BRgPRPIlALECD/65BiQMqRSg/SgH/h0ZCRf8tQWd9nj4IxggD+wUPRUT/9D+JBBFD30CHBTwAx781P0ZByoYawNtFKkSjviD9+kHPgkf+oEJYwMF+8sFuAxrBYr9Ywk4/azuR/9nBJQAKwixCkIIVv9CAhf2GOxL+kjt5/pBEBkHmwIsBOr/Jvw4/w3x7/QT+2H6HQIj85QCfBIB9nTzkAV7+UHxSgDiAWcCxAVUC+0As/qxBpn11P3tBA4GFQqQBWYSAf4M/RP9+wThCWACARsHAuP/lhXlDrECvxS7FRD6QQ5FCVEG3QwCFUURkxQtK6EceBmQCSANxhYuG4IqUyH+FWUe2CePGc0ieCOzJ1IlLSdTI3wSjTWgMI0rCC9zLBosdzNrNtQidzOnMmA9MDqFPbxGozexOw43bzn4OkRYrUokQ+U90zY8XuhEtEq0Sl9Jh1AYTkRSWEe6Yj5ISUUcUZpLLlTkS2VVFUE9TORV70rNU1dNJ1JeT2dFTEq0UvNHdj36TbtOA0KeSJg0lDPZSPtHQU0zRQ1PuEXBK9M0JEG2MGEpdjc1J7IxY0BQReooCRceM18UWxfFLL4iRB1HJDEswxGpENgpCR/TAVQLAhGTCEIIag8+C8X9jwuuAY8LERfABor/JvqBBR7+AwV5C+UAafTL5gH2vvcX/Hf8eeZf61wDu/bL4oPxafB55tbni++i38/XsO1n2RrQy94q8U/zBNDb0sDb7dfo5PPlq8tsyCDkttJg2ZbuReQk3aPLUdlAyGHL8+n8zxrSwdEo3IXbfdsO36THKNTUynbZudEeyZPhfs9R12/VN9iQ0kbSGdwAyYrEXcYH1cvYJOM713fLD9OjyzfYnM1n1VHb7stZ1zvZsdv80TPXCuLYyfXRUd3Qz5zR3tUA1XbZh+6W8kLZp8gE0vzZm9V93+XdkcwBx+bP+NTx0kLXy9iJ1OrQd8+GzfjSfduy0S3FGsgWzzDWKsKdwWTM8sIa0p3BRMFHymm/S8HnufrAt75Xuie3s71MsxyqbMSkwzaxoqx5sUKexKVpuWasVKVjrw2w7aQUsriwLKaIrfK+nrEhozOojKi8qaqaKrahtvGfOrLpo/yeBcAXw6muVKtmrCuq3qbRu7O9bqoCsbC2OrBMtZK6tLFtuHG1ZchXuMul+sANsEWrNrFPvHmzRMHNxA2y6LdEtePKDqbWrAW6yq8pyhu4isAYucqzGLNMrXmpU7n9xTm2/NFXttG5mMoJt4e7x7CasoCrjr+StpW/DtsayLbOQLz+tQy858UIyYe7NcOrzdvM18uB3B7P18vUynPKfs3uxfDaic4qxJXH6tCq3VvmU/Br2tjFZMzW3f/WzucC7DfacuQ+4tnmiOa448jZ9N0n5pDeXvlD/mbvQfHg6hjozukn5gno5OtP8yL7Ived+E/72Pid9ITtbfcf+Bjyvv9W+xf6YAaqCMAGxwag+9j+6Qm6+hkJrQnXAgsBjAwiIowGKxYxIEUNmhClHagc1gouFWkhfByEFpQzViDsCnctUi2zIUAoczSOG+cdBDCTP7VCvTJJPSomQCiuNlU4sjccRT1QgTY3Pg81XD4RRt453j+fPvNPZ0FfR6VQV0lITTpDrFSaSZs77EFjSGZNcUwFVRlCl0bkUd1JvEZEWAhmfUk1Vl5XG1PmZuBYU1SaRQ5F31wEYZFdumItZLBPfFOrZvxstmMMVSJfL0jgTsRrsE9pXhdgH05QS6JH81P6VSlfU07TPnI8A0AKQCg42j4eMRMweyyqNfw5OC7FMH8fmhbrGJkgiAtUD0AgKANbEbcgGB18GEkSUBJNA7gONhUdCCQI5BjJIe8V8iZmGrkEGBVEITQpxhw1GZYdxhznH883ejRSMUFHSx9WJBIyKSyMOastcjohOg49Nzz5MB035jWYOLY0fUEzQTc6pkI7O5NHzkWbP+FIgUBrPJ881kMCSJJRoU1TUsJU90LvUHVHGFS3T/hA4Ey1QEhVyVrGV+BOuEuLR4RHBkdvNwlKLz7HQW1R0VzzST5CQVMdN/g6si8ZQjNDEjjdSeI4qUkUT1RMWD/pNg8tEzADPPwv80scQ1U00zqUMcUyTjKzIXgdOy/4MmA7wS/nJf0fdBxwIxgVbRahFAIXTBVbDegXKiD6FIUG9wmo+X/8NgtnBjMGngl5C9MBiQGqBq4DbfVp/Mn6KvHC/MQBngtE+gH6AfyH9LIA0g1w/Arcq/7o5oXZ6QGC/8X7t/GFAujwDt1I6UjzuOeq31ft7N/o7i70e/uA6g7hhOvuzcDVCtrk55rpZu0d337T6OaU03rcWcuvyj/O7ssS2CjWIOQ/0PXRcL+zvUPJncNLxcq3VdKKwnPMetI5tkWxJKoyuM+icbGPsf+ng7y/tO+9I7ZXsHKfXZVGmUqefayYn8SjRqM3oxysQqiBoSKRHoxKkoilL6ksniyiP52Xo5enYJxKmHOViaESm+aauKhNnyCnEqXeniCnobJfrpyWN6cNtJeneauHtXWufp7wp/uqcqkVsM6qnqnwpceyob4yuMK5t7gRs4ymmrBQsqWth798tmq14750xJHGycO7v6y7aM+cyXi7BMZ3yQvM/M0aztjFisos1QHFPMN+z5jSp9Iezx7Np871zd/NHdPJx1jbceyCzpjQHddZ0SnKgs4A1brNjN026ELfReTo7vfiM92u2FDhreCF0yjgFd3v9CEDpPxW+d3rPeoo4nHmdevg9Bj0dPV4+P32bhCPC+v7FPFa9Cr5v/GFBvb81fMKB94IHQCH+JoMNwVe7wz5mf86Bt0KWxXSBz4DTQkB+ob62gGLEEYH7QL0Bj4LvxLhBbEKEQ9mEm0UKw6uBZ4LRQsDCbsdsx1iF1gMJAZcARUIXhYnFYAVIxY9HdUWWh+RJpkcBhQ6FEsfXhpLH9kVwwtqExskpypXGJkq5iuLHI4dvxpSJ0MnqyncHtkRZSZvMwUgBhJ0JngfdB4jFHwS4ya7G7ovLh8uG7MnFx9tIBERNRtTG2EpEBlFE2UgcRH1J3skBCoFHjwjGyh1EC0v7iuGLZ0fFBjcJFYgMztWJiE0XDjDE/kopCt3KzUhHyEjFNkTzC6VK4RDzC5zKqcqPRtEJcYWlSX+GQkXAhcrEq8u4yrnH38nfykuFxcjhi2ZHEQhSytQFqkU2yo1JQ0aqRY/LAUk6BGZIAssViqrK8Um6BEMHm0YDgp1EoMkzSBQGB8hNhfrIocdNR8CGeEHvxY6ClwH1CJzMHEdJxXkGBgZLxENGDkYVQH6FHwavxK/FMkfEB1BEH8hqQzZDRQccgs9EeETXiCpFAIPsBYhBW4OYAbDEesY6QlIFkkKHQJ9AqUP8A/+EZIeDQ6g/yEBNgt0/5sGNwmz/ssFAg95EZ8DxwjlBnoFbgbwA3ILlwXn/HkLgA0M+bEMpQ8b91L+3gaG/DMCxAdrBWMJRgHu/gMB1P9i7tHwe//PBLr6pfC++YDwRgdnCAz9Nfh56Prvv+3K9BD89AiZ/eTzxusf7BIDluqI6HHssO099hDyePJi9sQBpPr+6p7q5/jH52DRJOMf+Bvz+vGo+4PxMu2d7gH25OsG56zwX9/O5+P3vvWz9ob89vSe4kHv3PH662H8hvyO/hf8sPUt+gXv9u7V80/1pPg4/Uv+i/PJ/EkEoPkn7kXoBuXV8Qj8De39/GsBZfVw+h/w6+9f5y/mEPT/5HHqOgYM/zX+hQCw8Zn3auD/3hvxJ+gdAm8ALupT8qoEQP1x7hv5mfMc55rxMwT8AMsF8v9t7XnqYu7eAH/0peZ4+gj8Oe92CiQKkfsRDcn4dPNw9kT0fPXV9VgClALxAbUDQ/6p7Zb27vx7/VEAnP4vB2L2Zf1KABjy4gEwAbP2zfcdAPb8Auoc7wYIxxCfBfgBgQFL+oEDhvxA99j+p//PBvEBofVt7fX+E/8B/Fb/5/Q7BPL71fF4+L77/f6QAxIDsPMF86/7wvY97Dn5bP9w/oEHPgMn7gXzgQVi9qz4WvrtAGMFyAADCXD8qgLHBlr6lvB4+toJyf5cB4EHWAT2GaURpPah7U0FYxFI91b9KAv8AOr9yfpB64r1OhJ9AsPqpeqqAA4AuvgdAOvzJvwp/Uf7H/Dk77EGwvwt+mn8kAE8/nIDtQX36mL2DghrA0T8uQabCLf7qgbF+/bwrgG1B5X8Zffr+4b+0wNO/9oBnwF4+ovxNfKjAO7+VAta/EHrrPa07ib4lwcb/fLzrPaS7Sn9gQNcBYEHH+5t9Uj1s/50+6H16/nV75X+lfymB60J+fuw73z16/sb+b7/VOAx+6f/mutVA4r3egGS8+DsZu+4388CIAmk+Lr8uQJt+f7u+fkI+Gn6lfzaAS743eNCCHET3gS8BZL3fO3v6vL7XwwRCW4Iq/509RUG4gOg/SL7Xf/SDYPzr/veCEIE3gg8/ssJVv21A78ObfUSAdwYJxkWAq0JegEu8FQTjw9L/igFqRb3C5cD2RGg/c4MJAZL/mMHuvjlDgIP5Q4rCsAGdP/r91wBU/b3C0YFKw4cFib8DgyBBTsEYAAt/ssHSQS1BwoL3RYCF+QUVAtjCfMQWv5A+w4EIA2XDfsMkxTDE6wbjA4+CQIPkAehFFsNmwDLAw0O9xfRF3wSowJUD/oY8AMI/H0KFByLFmoT5BiEDtkNZg79+l73Ag2HGwIVwwl1EFcctA2iEvIcXAECD+Qc/wPoDQIZ2Q06EIQQ6QlvAqkOKxYVBOEPhBK1CZMIvxZQFJH9ZhDWCJABDP+iDnETDPPlBowG2/9jBx8fMR6BB9Edlw0q+2cACwEm9GL0OhLsDPn7DgpmED30G/c9F64FePYREXf+MukT/+kJLATR9p365POM3+/yXw5l94b6Mw6T6zntXAHU+wz5WvYR7ELhEPCtCzH9OucX+uf0v+vn/mcEgPKd+GsDh/L+7ib6ywda9mX/QgCE4Uv0E/v9/Gz9/wH3CT32RebZ7lr4EPK9AX/+pPRp+Ev0vvvIAN4AF/Z08S7wSPdL/Ov1Wvg8/GMHQP+XBSQGt/dGAc332PqFAkIIrgVp/KH3mukoB9oLr/koB9/+3/woB/3+/fru/B78YfrO7RjwNwd5CQn0OP0I/nztNfjJ+JX6Ce50+dz95O2V/CgBhQbk7fn7QPlc3Mn2PP7aBR/yqPUM/dLsg/2jAr0B/AAkAu743P0x+0TydPUV57UHGQn74w/+4PhX8aD9t/ssBujubfXk8w3tp//aAyAJGeTG9/L7cexYAh/2oPnk75n3Lfyo/Xf+jAIkBEHnYwPlBob8f/7k7TX4Wv5E+OP57/aw9YUCRPb1/hEJg/tyB7gIcPoF+3IJhv5A9Wj+kf2L7+76zwjf+msDWQDtAMb5dPN9CG8CIv0OAN4ClfiZ+3YGJval8sL4Bfll92sDGQWS95L5egFUCw4Atv1QFDX6pe7hCYEBZwhyCwH4zfE5+ekHuvpl/w0SZwqUAPAHcg2g/5ADdgLn/I/s4PJfDprvhQCeFX/6WvqMAEIKXvHv7gsBYu5X7UT6Ag2MBAMDuArO7xf+Nwf9+nD6RPjTBXHwH/j7DPn5xAdUC4UEDgC4CAoDdPeTCj4FwAiJAVwD7QJE8g4Czfv29Ef5RgF0/1QFJw9L/Kz6Zf+v/xv9F/6MAvb8V/VrAUEOhQaD/RIF2Q1I66Xq2gXR+E/5kxCXDeD4lABUC0oA6OwI/IP9De3j+cn63PWs9vQEG/eL77r6r/eH8gLs0P5a+M379wl/+M7ts/Kw8aT0pPrs6TH/Nf4F+c8GKvPy/QX50uyd+pMK8Am8A1sNTQG39bP+8AXn/Pb2vv/r8QX1ORgkCE/5ywdO/0D39vAt/lgI4/s6CJYRF/oX+isM3gQJ9ET6lASd7jX42gnWBIkD/f68A9D+5QpqC/L3hQInFfgDku9cCTsES/TJ+OP5mwbSDTIaCRMKA4QM1wL28nv97QIVBpcDbghqF28AdgLhDxIBHvzy+Xf+yfbY/m4GvAP3DUkQAhd+AAz5gQeBBZsCBP9gBG8C1ghgBnIFVA19Co8Pbg6PDV8ODgbEB7UHI/V6BbgMBhCLGpMGPgcwAZcNERGUBKoGwAAb+cX/NhEZAb8SLw8M/64BVvtxEWcG1gitCZH9pPwdArwFowDdDEYFt/st/NITrQ0e/M4MlAQ3Ab0BIv0Q/O0E9Ap6A/QATQ2/FB0Ezfdw+vL9g/szBowElADgFV8Mg/fpBSwEkf37BGX5wvwP/kT2CgXaCQnyYALLDwj8bwBP83IB+AGs+FQF3P2bBhIBnP7V9eP5zwRW+Rf8jv7iAaIEqQqO/ML8vQGA8mAEuAozBIkBiv21B0/96v2QCUj3LvKP8Ib87QTwAwITfQaZ/Sb67v65AqT6uvqW6IfqMfVX8cgCzg7SDVECLvTG+UzwafLC9jMAhBJe92H6yfaD87QPvQEF+ZX6Jv7Y/qD9GQOZ/18IZwp7+RjyowKpCr0B2gPJ9ukDmg4e/MoVTQdL9Bv3+uuO+m4GMw5yA3oDh/g59xv/T/dnCGH+2fAn6OTxh/LC+qIIHO0X9hf4jvKa7bjp9vIq9/L5mfO78Hj01gTc887t8/HS5rv2Qe+85sb1g/WA8v34SO8i/TcD9+xq7Pvl3eUC8KoCe/t86+vxnfIJ8JPlNfZP/eDyCfZm75bwqPN48ALwsO8q8x0Ee/t15UD3Mfel7nT5wvpd/dj2Yfyg+U/zPP4m/LkEqgKBAZn1s/reCHT3rQm8AwcEUQIU8SgD7QJYBOkJkxRnBJsCawcq+aUVVxCo/YUEGBWiDhkFNRmOHeAfNhHsEBwWnhUQH2YOCRVMF+gRsyEQH7ck4yCgIokuixb6GF0sQytAIIcdJh8rFPUryDNPJKMvby9OKmgpFyHCIcUsdChsKEAoqymUNZ0l8S6JMs0e2za6LRAZux23JLYy0SEPKQ49JiPSDaAqMDLvEaQnQy8fGyIinSFMD7QVRy6VJewU+hgLMD0bJw/UKF4k3QxUB+sczg7nHfUpyhnYHRwYORi8BeUKyhEzDPsGYAYOCg4MQRpRCMsJqRI+Cxj0nfr4A1DrqgAq983x1wKfB5X+g/Pf/AX1Q/4N8Ujz+AXD7KXo1e+77AzzXvcU7bf3GQXN/eDwTOil6kHvS/qK99H0XvkX+tH4I+3r8Sb2g/0DAcroYvAX/l395/6g/Tj/BwCK/+DsEepx7uD0jACBBekJIQPLC177afD+9Nj0AwkvB1ASdRBe+ZMGrQ3J/Lr4OgbwA6j5jAKbBJ8Fmgz3DfgD0fJyAQX57/Iy8yrvbgbg9Hz1vvkN8Qzz6+1c4LTwyATW42bvFeH/2Ivv9vIb8fDgoe1U3OHeDedX9TX26OxS/Lzmlure3ffs0e6434f22eiQ4CL30gcU7XYEcPY34ML6BuHs60D1kwa8D8n27+qp70v4nfDN+9HyS/gkAvL7EQkb9Rv52Q1H+bP4cP5gAIANTQEi/bEIsgB7/zcDJvoZB0EQsQhfCisKTBWBC9z9kwby/yQC2gv1/qYFJxWZ/yb4tQGUABTxsPE7AJH/lwnSB478U/i+/0D7+vOS+Qnynfih8UT2XAFe9V391et93dHuePSw73z1dgIU8VPsLvKA7nLkBuMF9YnWBuVa9B3ZmuX75SDqDtVr3HLgq8/O5dbl9+LL2Abpo9mkyU3cLc8wzOC7Wc3/2CbDn9i13K/MB9cPzdDP+NiOw8nJaMvnvynGRtbByU7SzNRSxYbNZb471QDJf8FWyr7IjdPNvtfRQMRaw3POO83uzSnG3tO5z13OVK+KwFLDjrub1QDJkNqj007QF8kQwVLHjct+1YrGKsRszO3bJctOzpjMH7cex07Kb9FWyNfNUd2x3WzKussG4R+/6shv02TUVOR20zrh09iZwszUhN/E0nbdu+7o4m7hK99q7GnwnuSZ89Xp/9iT47jnV+2D/UTyf/g8+DbkCPjV7YPvPgEX9gcA5/rG61kAaP4n7ir3Wvq5AuTx4PI+AfL/iA2aDOkBv+9vAGcCcgFS/v8FJh3XACARzwhnCp0ZogimCRELgBnHEhcf2RXkEvMQJxOkIyATHx/3E4Abxha/FK8gzRw0KTIYHBQrChAdBCiHGUQZUxfzFmoPnSFaHyYnZCx/Iy0pnSHyHpUhvijUIi0lYSkPK+YxkDTQLRoqFjcaNlw4XDgaLNsoXTJLKeI0uEOYLoRBDzVeIs87wTOCKvEsiixDMWs8Dj07M8gx6jK5OV0wbCopLF4cZSigMBI6PjzBL2M++SrnJ+YzZDKjM/UrPjybOQM6GUSmOmsyNDHXN1E3WEEOP8wuvTZyQEk/ITzsQ1g9cy5rOoIwQy+xP2s0SykpKi8+rjZwJUo39TO7GQUi9DfBL1Uw1ke1OkgYtizTOkcu7ieQNpgyjxNwKw8v4jKqNx0/gTwUFuYrsi8/LEcw0zzpOPkmtixmGl4iJinmM+QcwxFzKvcTCRvTNqMxxhq6Jesc2Q28CzYNJiUNFBUQ2RXHCqUTFBhqDd0OtQEvBxQYeQuDHpkcKxYKD2sHvAXj9+7+lAAcELwRORYvD4UIng+o+WcAyfpD/n0KqgSmCzYL6QmTBqj1seMQ+jsEQPszADH52P5RBDMKqgL28IPzSO0n7HHqXvOXA+UCagvN+TrplvSv+W35bfWs8r/vGPT27sPsh/iZ+3T5fPFE8Ovtv+3XAgX3n9r67WL0J+5E9Pr15PG44fjchONI7z3ukvez9oDo+vGO8gLubuVX7RHu/u4f7LHdI+ku9Dn1AuhP9Vry7N+46wX3H+wV6bkErPD35njyOe2x3Qbh9f5i8LHlt/cGCrvsQt8X+Ofy+u1L+OD2/Nes7BIFfO9j6EoAQP0C4ovxu/ZA9wnyUv4X/hf2xAUN77Dt6/Gz9vPt9vyhGAnwePg2D2z/mftBEJoQ6PBw+qD7fPXlBI8NLhNNCZoSXwz68dz5VBOTEoP3RBlpGVr6QQwKCbwDyASIEeUCWALsEv8LZhQ6EuQUegXpBzoQqgaPC2cExhYiIKkSLhcVElgIrREgC+P/Lw9QFjYPAhVMDygJog4AAMsH1gRNCY8V0wXeBP8DZhzkGCgDMwQAANT5Afp9CBIDNgtmECwCwAI+DVMXfQjg8gH+1gpH/6oACgUoAwcA9f6L83D+wxOK/xP7VQGtB7wD+f3c/eP/xw7TAdj4LvjC+sQFg/3n8tz7IA29AV75agl89QzzNwH+8lgCSgK1A4wEdPmG/M37XAFX8fL5Afw1+JgBp/+C/9j6PRGXA7r6MftQ60T2nfSh9QT9nwH9+J36Wva3+fsIivsI/kTyEeq+9U/78AP7BHT7dPWfATz+Wv5FCTMIEPwc5QLq2fLJ+qISvAtW/dT/U/Z/9tT7Mfe6/i/onuDn+jLxMwA2Dy3+Zuvl5ZL19+wb9ZH/cfBQ7Rv1KvsJ9qj9xvGM4+P5XAN/+kf7OP8j847y/fa38y70V+9P92317+yW9Nj2U/Qn8A3xk+WT6VvuftWf3nLgKNgD4ITlWOHP3yb2A9oxxmfhK+dzzl7AvN4W1xrQN9y14lzYpMOF29y8EL9f6QfdP9Skya3e/9rL2uHexcjBy4rKZNavwhbVhOeJ0FTcr8pJ3+3Zjc1U6q7W7N/H3aDO09hj3Afd8Npy3GfjBufx2B3hfOnh4vfo0fDo8JLt1esg4KLlUO1cA+kH+vOd+EDz2Pgf+GcGMf/n9lwHFO9e9X4A/hs6EtMBjxde+/QG4Q8GCmoN2gv7EG4QgQnpAf4duBYUFMYgJxGKIPIeWw3DC5IY8igXH3UYDCD5JmUikhjRHWoRQRZDJ48Z6xhtHl0mDBxbF3AfHBS7EwIZDRK8ER4rIiC/FgghZhpIGLgIzg7pBxwMeyJ8IK8kbhJ8HjUfcgkFHC4XfQw+C/cR6BleGjEeZSDwD7IA1RSiCm8ExwoCCzYLMwZiGUYDkftCCPgBOfkp/fQCHO04/zsCFPMZ4Mflhvzg7IPv1fP99nXnFO1I8aLjcep56vfsEtxJ4YfyoucZ4iPtW+Yy62LuJN/l4+Xb4thU3G7lWNua4+Tnbt8N6+bRptiB3HrWHtHA1y/gPMlg11vktdwS1LXWWclhyWjR3tMd1XfFo9Uh2AfX7dna4GDb5s872afUQ9Nk1JDWycs31rXWe8iX2qnlbt1N3s7r3tNoyzvVZ9fp4F/f+Nj42pvhVdJg1Vzg7dXT3L/pVOKl7IDmJdVF5szU19Xv6NLiteD04UXk9N/G8XHs6dqU24nY6OiX5KLhDfFX83D4v+1C4S/mHO0u6v7oMu+Z+d/+j+wC5kXq5/gf+vPvOfed9tzxxu12CtoFf/QzAIDsfee/8ZH9pgXhCSQQWAiS8bP2/fpp9E0HTQexBNoBOgjIBLUJawO2/Q4K/fa4EhUEawF5D6D/IAuZ/8sLZwANDhgR5/4dCEf9rQsSA/QKVAnU/wkbjA57/VQH2Q18Ehsa7QTR9rkAkwhCCjoIvxCWGdkTHQpjD24QpQ+4ChYCzf25AhwSOgitCRQWbgoGChkJgQM2D0EUOwLn+mYSww97/XkHIAs6Di4TogrN/0f9AwckDDMC7AqhICcRdgZFEYwKUQDdCmIbTBVPGkQfDgY3BRQWTBteGtgjxiBgAAYMhxeAGzgozhi7F0kO6A/WDLUJIiCZIKwVFRCOIYoexxIODN0S6Bc6Dl4gBgyMBi0jeyJ1FgEhdCLVFg0aDQ6KJm0YMhDRI1QPOR6sI+0xHx3kEm0eVAeHFwkXUBhqFXQkbSJbEY4hqQq3HIsSGQtPIIgL5xsvD48Rjxe0D/MS1P3OGrMbYhdaHd0Owh8FHuQWFgKtD6wX3giPGfsMBSDUIjIakh7hEeMi6xbpCQoP4RG/GtEbsx8tI3EZKxQJG78QKw5EG3wYUBQuGUgUfBg9E8AMOg61CYAZ7BAyFsoZtBlTIYwOtBPZD1sNSQ4cFiQKUA5SLXQemhh5E+chWAoF+ZYZ0g27E4chYhkcDlsPEBsFGJ8BHQTwA8352RFxGXINbgoJF9IHIQVFD84OCgkp/d0KEPR9BrsfhQjZDbQXpRPLAVgCKwxNDa0LCRmBCXf8rQ8zDFEE3ggRF5sEywNQDCANSRKiEHUSdPkF+TH5wvaBA6ISAhkNDvsMcg1RCH/+oRbzDhf2rgUb/0f7hBKzHT4PWAqMCG4ItQejAqkOGBXhCV8O3QozCNEZLwen/8L68v+IDaoIGBdnCGsDHBQgE8sHWArWCDj98v97/18KFQQZCRENIv0dBhELfQhw/NMFXw6D98gAixRmEqkMEQ1yCxP9XAV9DnIBafgDBREL1P8VEDoOogzDCYgFpgF89YARxf9e8QT9KAuEECEDahFh+uTzzf1o/jz+mwgqGO0CFQYDB4gJhAyXDfMS+fky8R0AzwZGA9kVbRqtC9YIWv56ASQI5QSUAJbyQfE2D6kWp//LA7EGh/TK8sn6Xf3C/uUEdPkJ8OUGmgwT/5H7BfdE9B7+1fNe918Kiv8ZCTz8au7ODFgEMu/aA4gFG/XIAkD7kvl6AQj8BwYx9bDzSQaZ9YfyMf2V/qT6PPgB/l/rQe1jA3T1MuvU+VEABfVi9sryrPQ99PDmF/aZ97jldPnlDPL1owD3CX/24PBm8az2MuUf8uUIf/6o83D4Xve449Xz7QAN70zuUQT28Ozf8QGIBTnz4/WK+QvWy9x7/7/rAuwi/woFreo+4nD+V+fp3BP7w+4d4UD7r/kk45bqS/bJ9qLnv+cJ8pfgGOzJ9gLuLfof9ujqoesJ9qD7DPMJ8hHseeSl8B7+R/ua7Yfq0uTW4RDwJ/K6+NXz8+UD4FDlQP2v/bfxgOi46x3fXNyd9G7p0e4j60HlcPjV6zLv0fj28jbugOi76t3nv+1b7EjtFPUq707/hvwr7c7tRPBq6LHb4O6l8o7yofd/9tj0qeuo8Y/sPeon6LTsde9N4gnqHO+a733nrPAi93LiPuBN4p3wXvNX8x/yJOG/6f7su/DV8fb4G/du5c7vYu7+8vfsW+z+7tbl/f6bCGACg/35/1ftyuon8OjkLvAY7jX+NfRT7gH0CfTu/jnvXvl17zXwNfzN9RTzV/Os9nXtxvfS6Fr8SgK457P+wvbJ+n/+pgW4DHT53/7eAiUAAvBH+/b4Mul5CT4JOwQOAnT7mffn8vcNYAR88xIDr/8N62LwYARH+ZX6iQGz8t3p8vUdBvL/kvmuA5QAH/QF92nyDPVGA7UFBP2H9kYBhQCw9Vb9XAkHAAj8lAKMANYGRgUzBgoJG/UB9KD90wOJA3kJ9hnK9GnyR/8n7BkBKw7OGrAQ5QKBBX0CZfkm+oQUlAAm+vsEhQIP/lgMLSdBDG8EXAfN/3/8lAAnFd0W7xPzGE0NLfxnBlAOeQsJ8tz9khaK/wUWqBxFEegRYAaUAjj7OgjsCpsCrQmaED4NVAm1Cfn9iAUCDVECSQYKD/MSywk1/lwJTx49F1gGVAXeBMAK6AtuBoUIRREVErwHp/+qAr8O1RalE8cS1R5iE88IXf8T+6kOmRxAHh0AXAnSEzcHVA86EEIK5/55DaIE1wBBDlMffBr9/rQVtQMJ8L7/wAbU+wcC2RGV+gcEVAlyCxEP+wiID474dPVnDMn+cgXvG2X/PgFJDFb90gnOENYO7BDDC4ANIBVUCfb6xf8gCWMR4BlbEZcN4Q2mB1L8ywkfHXT5pP52Au74xAPlCioeqQ4CC6MCegF4+J8B9xUu9HT95/5yA+EFqP3lBkD9afjF/dYG7QQ2D1gC4gFCCr71dPcZBbEGku859w4AHQjDDSEBmAFm76T4xAEb+csB0gczAkD5G/tM8qz2VQFw/n/2xuuD/dj4/ui++478fQTDCW3zpfLY/owCMwaIBRD68vmz/or7DPVE/EIKYfhP+ysKJAbOFJcH2/8zBI/uNf4rCGAAEgWaDJcHlvamA3T7PPiQAwn2KvmZ/+r/xfsVBkUJr/0b+1r2kvMN79H0cP4vBSL7xvWfA6H1G/Hb/7v0oeuK93oBogSeCScRIv+E5f/kUvorDOv73gB9CgcAxAPSC54NxAHIAr/tMudl/xYAfQwoCSQGsQjOEG4QdPmo+QH43gL9/sL8XAckAv8D6QFBDrEGNwMVCIb8JvxL/i8PIBEdCuIDVQNUCxIDTQscDnT95/oM/VQPfBJ5B6kSnguqBn/8pgHSETMKuBaqBKXydgbkEIgPGQ1JBHUOeQta9AoRngvhD3gj+wwGDvQKSRDoFdIVDgpjCZoazhZbEaYNSBjgGaEc4BUzDBwOYwvDETMKuxNQFuwQbg6QB78SvAeIEQkTyfgE/Xf+U/Y8+m4IbgblDnUOKAXSC+kB9vyW9Aj6BfXj+yb+UO20DyQMpgVvBEYDMf3f+nEZCPolAFAS3gQx+TX+8A/j/bECNfgoB34ARO7SDSL3WvKbCHkN8vk1+NX3OuEf7PPvofXR9Fr6s/YN5Rvzt+3V68Pow+aH7uHmfO098qXuj+Rq7N7fl9p87YbPKOCx4Ubeu/DH3wXtIdSB2rTmWsdOyB3TTdxD033j29LUzDrfTsz5zJnG8dQ7zay/TsxdysDbCuT108K3yb0eydjDNM2RzMHNF8mY0vDk+Nri1PzRWsVOyg/LqMRc2KLd3tWN00rTZNJkzoXXD9FOykrTk9+b2erMX+sF7eLWxNi505HQstPl4TrhLNuw54PvhOfW43j4T/O06iPtJ+QJ7ujunfJL/Ef/kwbWBPb6mvFP+UzyQPvOECb85QaeE88AegWaDi8PCgWr/nYG9wnhDdITwxXhEd0UmhKmBXkJ2RHGGp4TERHcGjIYKS71KwgjIiqSGOERkhh3KfkkxSzWPVktHilLJw8z5il0HrMprB9/KQ8pQyk0MXcxAzqYLh4nCRnYITEmqRK+ImkbJiNdKq8kgTigLNsogyZPJOsawiFROxsk5ikMJvkmwTUTJikypB8TJtAzIiCJMCk0oCwtLQc1ZShDJzs7iijOFhgXfyNsLG8zgjDYI9Qi+STmMUAmXSa9LrAaCCEbJNEhdyUBKXMqgBXoF7on+Sa+Kswq+SJHKDQxLSuKJO8dLh3OGtEj9THyHCcZFycXJ+MkKShLJZoQuxX9JzkiYhlpITIciAkVDIMYSBhmEEUVJA6uAVQHfBjdFLP+dgZmFvcRLAZMEUkQ4QXIAP36vAN6BbQP1gZGBSgJ1gr+EQMFJw+BBbkAkAmIBTj9WAhtFNHyRPokAvL9KAW8Df8NDPM4/xIFdPcOAH0O4//r7W3zCPqW9NH0vw7f/M7rsPXTA/X+pfDlBO/01fGV+sPuafCxCGAESOtp+pLvEgH/AYDyTQGD9fQE/f5w+PsE1gRw/sX7LAQF9/n/EgXJ/IUAbP/lCqj9jvj+E9ILMAGR/V73PPig/0IGzflfEBUMAfqYAbEChBTaB8cGs/hi8sL8lfr7Dq0HFRBuCGAC3QwrDMcKYASEEnoB0wWBCX0ECRVuDugPyAQvBUUTkwqMDkwbvAVvADIS3Q70BJH7ogjPBnYAUAo9FfcVqgbEB+UA/wUnESQEvvki964BRgflCs4ShBD3EVEGIvtKAPAFogqZ/1gOOhLABOELTQfxAS72iQPXALf10wPPBOkB1gpSJ/n9WOPG98r0QP9p9tT5S/jg7pb0Af5t+V7viQGw8VfnI/Mq+Tz+6/FI9frzxu1X77/t4PBm847+R/lb7PPv3e3G7Xzp4Ow97CvfZu1p9ovtlvIJ8gPc8dZy4FTopebd4y7sK9+Y1gra0uI640Lf1t+U1RLaiOBq4pTXeeRF5JHQZNaCzB3fm9253aLjwc/L3Ljhgdxo0bnbSs9kyq7Y6dKW8unadtOm3ubPVNyJzL3Up9D9yzPZudMh2qPXYNve05fYTdjfzwTSoMJV1lnTYNPS7Cvhb9OZyMXKQ9Mo3p/cN95r3kPPhdGb17jhvNy12u3TB9VU4Bng/uzl3VHfXN7M1jfeZ9W85HLiTeQy53LaX+e06Bzl2tjp3H3ngdia70XsEtw57driIOTo4qbknuTW4cfl/+Ch69ra7Oew67zcu+5Q4xHmNub28OD4SO1t7ZvdBt9b4nXlKvPN9Uzwv/Mm/Hj0Aur/4i7uF/Ze7w/+oPvD7Fr2afRX7Yvx6v2d+LXatOZgBp36Xf1NDbvszudh+m3rhOn9/P8DS/aS994EpPxM6qHzSPGE43T9+wwf+mnwvw7LCbP2kAmQAcryZfexBE/3F/xtHscODPun/x0ABP9NBYwKTv9s+54PixYKA8gAjxOXA6z6TBFCBJL5IA0VEAn0F/yLEgoJMhBtFMAKe/vWDiAVgQGxCuEFKAsZBVwLqRTEB+8VqRZFCRIBCROmB837gBXwC2cIxwhFEQYMogoxIPQCyf5bD4kBe/slALEMhBQoCekFVA+MAu0EpRMVBhv/yw3EBUf/kAeQBeUOXwj3D7kCT/scFo76UQQREyMU5BRCAK0HwAKxAlQJgBOFCHv/YwXj9eQSsx0ZBUkEwAbEAzH9G/9RBCEBqPt0+xD4Nfy4CAsBivUX/Fb//wVCBEv4ePhh/NMB2PpO/7D1ku1RAAMBBwJRAD4FJvyO+lUB5/gZA9YG+wha/Gj+eQlGBSn/wvqtDc39YvTHBmsHZwaxBuwKOwLY/DoKDgzaA0UNeQmv/VkABgpQErr8s/4zDmAAxwgYFxkJdgqTDNoBAhNQGLQXxhSbCuUMdgK4FE4qYhsuGwgn7xNP/WYUSCBpHYMkLSWCKJIaECP9IZ4TJTNSK+wOwAyDGpYdpRWCMOYxTxoXHxMkIA/3E9wmtx6SHvIgQB64ElIn3y8QGQAx8SwUGu8XDRhAHugR2yqCNJ0l+SpHLn8pZhBLKagmSBbqMJIksx3kFqAm1ChwKTgk9w9TIUwVUyPCG+sg2Ct8GN8lvxZmHPoYfBgzDgYQQCQyGu4ltxjGHKISTBGHHz4NgBEyFlobWxmSIocd5BTkFpIY7x3ZD1cWdRa7G38nkhi0EbAebCRmFFsX1RrcHAUigBVTF0gUQB63JNITbRitDzUb/h2ICxwW4ROhGLAczhJ9BiMUbRr7EH8hWxndFtwaRRWIEVgMpRNLHagg+hrzGosQhA5pG1MV0RkYF9oHHBBMFzEkAR3OFJEmSRIDAz4JzhC8C0EQ/hnsEpMUcRGzJxwUwAQUHGsHbwLrFhclqRQUFG0cjAw+DbceOhTlBNEZqQ4HAPsM8h5mGPsQ0RdyDfMOfgDoC3ERhQhwI78SfQICEyAPwAhAHuQYbwS4CBIFvAkSB54RNSEOCjoI4Q2FBg0OBhTSEzcJIQUJE90Q+waeCbb/LvLlBJ4TYASTDBwOS/ijAEkEMwauA/X+BwJW90j1AfRrAxv7ofMm+Ifqnfgn8mny6+2H+F8KYvIU80jvauwC6JbwvvWh8dz1g/MsAJ7mjN9b6rjlK+UG6Wn2Reil7qzsCt5M5m3tOfEg5BLeSeW53XDLjNd95zLpGeTe35Pd181q4sruPuJm6d3l/NXx1LHdWN3v6lfrxNrW233dReDA13fPgtC51QPcRtyw6QPYftOL6TvVp84H0VHdo9UxyPjYlcsW04TjReJHzFLHa9yY0OrQsdlr3EbUqteI4O3bJN8K3g7VusPYx0LXN9oA0xnc9NUtzcPoY+C83BXhC9Zz0BPMqtna3hneQtlR16LhvNok3zrjRtLfz2jNxdBu31DvNuoY8ODwVdBk0inQXOBj4jrf4eS20hngDuEY8DPd9+Af8s/Ztdxk0mPmyuiK9YvtP85U4qnppebE2ITpK+GT3y70BuFR35/cK+O84ljd+vE19ifywvKH6pPnTO5P8TrpuOfP37TmnfIJ9PgHf/QJ9OTtSd0+5G7f8vfC+Ir5H/DK8Cr3rO4q97/pj/DH4zDY9N0r6yQEvv+s+An0s/YF9x78jARI9STlcfKd9Cb2cgN5C1QLLvKZ817zXu9gApcJkvNT8nkJvvud/IQKCgVL/sX9nfT9+GX3H/Tj+0zybP9M8rvuzwS1A9z5Mf0ZCe7+gv8vB5AHGPKW9l39qPVt99v/qRR6AfgHXwgb/QMJlwvLBw/+DgDaAccOmwamCWYQXww+BYf4BwYSAcAARPzc+yQCLALIAH0GSQ4sAkwRCge391b/G//j+bb9QgqjAuUIXAOBA88GoP2ICToMKAupDF8IAwG5BKkMnP5A+b8SYwvHBl8UowKXCRkNXAlcBXIDyhNCAir73Q6HGT4PgxjCIX/4CwHWCo7+xwpyBYsUjA67E0gcnwVBFFQT8Av/A5YRwxfDEQwgJA6WGUESIxbYIcsLYhkKD+ENdRj5KskjTBVpH0kIWh3OEv4TOCiMDhsmZww3A1ccnR2KJFEGhBItI3wSbgYyFPIeuBJdJhQcNhUKDewUDytuDM4YZhA3BQUWaRsPJ4MaHx9mGFsRuxMuFyIirB1BFvcNyh17ItsodCC8DYsWohBxGzYV9w2KIIYj8xgRF/YhdRZEFxsc0hHWDiocixiXBf0f7iG4DiQQFQydF4QW4BUmIwIV4BdtHg0OgBlXHjkaMhp4F7sXog4xIu4nWxfFJEsnMhC8A84Q0g1mElYoEB0BGx8jNR8uG8YW0R/GGGj+IAknFWAEZhqdJYgN7xViGysQiAWuBbwPMhA+C1sPzgwZC9Ueog5yC74eQgprA8X/+AMzDm8EDRahFvsIoRqaEl8OuAwKCY8LHQIkED4Bzwi7F90MqRjwB777Zu/N/zcHjvoCEa0RgBUNDisIgv/29uf+3Plh+nf+7xGBA8gAzhKUBDcHkf3C+qHx5O/eCNT/ngnDD9cA4/2v+Z32Bfc+AZX4Nfav/aIGcgEY8mMFWvJ17Xf+Ee5a8owC8AfJ+Nz7UQII+prvS/Ye/prx5/7699nyh/h3/FwDCegF9ZcF7/Ax9Rvx/vJ6BYEFHQSZ99nyMvOw8SrzafBT+Prxu/K/8Y72rO4G6dMBxvG6/DsC/uxM8M3xPuYn5Jn98/Hr74fsk+W370zmU/Rf6Svj5/Lz7z3wqe/Z8rvql+IN70jz1t/04fPpsdn7287n++ns6wns4d7a4D3qsd0j6/Pr/+JJ5+3TEepI72DbBumW6FvkyNOI5BT1sOvC8p7kNuwj78Pm9+jV6TntAuyW8ifkjvbxAWLsLvAR4rDrvvlT9rv29vZ0/Uf5NfZT9BYAQPkY8JABZwCv/YEHsQ5a/tT5TQXpAXzzyfrzEFr4nfqaDisOnhVbDVgIbfnR+C8P7BSiBpcLyhviA+76SQiIEWMNrQtxE5oOKwpuCkgcWw8zCJoamhYkEF8MJh8yFBkNixRuDgUaAhOtEZ4PzhT7EBUSEyiDHIcZ5BjdFhETLhuHH+QQqByZIAwetBF5E34rbSLDFecdKiSgJM0iixywGnwYQCTbKF8S8A+wFh8jtigjFJ4TvxxiG3wWpR2oIM4Y7iPoFW4OywtxD3Qi3QoVErcgFBr3EWkbjhuqBl4cvA3ABFEE8AnjJHkNrRGlGQMHHQKMDuEJcP46Di8NZg4cDDMK+w7y/wMH2Q3sBj4PegOz9NT5Nwf7CN4AUAxnCnj2Xu07AsMJtQFvAMrw3PMJ8iUAxwjr847+1P899CL3iveL86D5EPZ09Rf25eVE9lr2hOmh81vuFPFt6+fyg/Xa4r/tfeHh4BXp6OoC7mveSOnO61To++GT5cfdQ9Ni7p7oFeOB4lfn+usK4kXiouFq5vfgOt1C2/jcteDZ5DPj6d7o7MbrauTl26LfWOUD2nbhXN7/1sPgFeUr593h9+Tw4uLaIOBJ4WPi5d/W35jWm9335hHm3eWcz3LeIOKu2PDe5duQ4CHc4tjL2P/crti92Fjl3eXa1sPgauQXycjVGeKJ2ubRSduf3MXMfdut6uXdhddY5dPc09Bdzs/dudPXz7ToseU25ozdhN+50aPZV+vs433jy9jl3/DeNuTh3CTnEeb42EjpCtqX5iDmEton6uzlO9E24hjoNM3H3VTqM+Hp0oXZ9N0S2HLeyuzv6iXXIOjL5OLWDt0+5FHXoM4n5A7fudsg5sr07+ij17ziTs7A2fr3OuH04VTkZ9UO2TvbPuaa587pj+JszLnR09Lw3nT3V+eQ1DfcN9xR1ULfX+vh6OXjc85g13Hogdrs5T7mXNzt1z7k2eys8hjy5dkO4SDkRexa8mbxouei5XHyouOm4hzp5/JQ5e/orPDW5YvxFPUq8/DmvvXtAJL38+Xg7vPvOuXJ/jbsDPVO/4EFJAL67WH6t/X7CoUG4/0Y8pQCZhyk/GIV5BZqC1QPJA42C+EJnRlcAYkBwwtLI9An4BmKKNILERHcHEQfGx4nG2EpPg3rGDAwySvVIC0jkSgkDKkYfi38LZUtqjeUNSIgqyvQLYoq4jYzQ8tCCy40Md47KTLTPrFDczAsM5Q590KwT1tOTEzzS9pEAko6R4U5zkcKPlw64FIrR9JG1VePTLU4GTh5Qqo/BkOpTTc+yzp4UDJH1zluRQpIeUQRQjdACj6XQgZH90JnQzs9PkTWQ3I8EFB5SnY3rUQRTBlCqUPdQVxAa0DaPgQwjTMuUNZHN0J2ObIz1zMAMyE06izmNX4vgTifNPg24UDxLI0tkiAFIkshkSbMMkcosycuIdAnQymnLFYonRklK6snWh9oL9suiib5IpUnqCDhCxEXTyadG7MbYS0xKrMnQy8mH8sFFgBtFIwO7xEMJJ4Rmg5XFjYVkwgRC8AMLfq1A6YLXhhTFakKVBEdAG4G6AsVBCwAqgLf/AnwKwzPCjYLWxXkFPQKjvT/AT3wi/OfB3YGXwhcBfsIYfoSBT4JawfU++/uMwTj93T5hQDR8qj3SQzdDBj0F/g99Mvk2ewm9l73GO5P+bP+9+q79D4Bj/AR5ALsZuuT6dj6vAmK9fThAfjY/gH6NfDd56nnNugf9gX3G/fy+7f1VOKt6gXtCuL29OjwTOwn8DXys/a/8Y/qV+d9403gpeqD71Psg/ts/7Hl6OpX7SDmPej67Rztct5B6X3jDe2S8Xj0t/MH1Tfg6eBC4U3kj+xF5ErXI+kz35/WHdfO6dbj7dWf2L3UOt9f36npZ9/T2FTkPtjt2WvUKNbA37nXXNpg2Wri6Oab4anhUdHl193rLvB15WbtUO/P2RXjqtsG35rvgPBH+crqdeU99Kjxku1a8q3mvODO62Ls1fUU91ft+vWL7bHjnuoC7v/i0uBp+DntHOUM85L5DfFY4T3yFPn+8EHvvvcB9rvsLviZ+63qYu5rATX4OP10/9j25/S78G35KANL+Cr7Ag1e7e74XAn/BycPU/D9/Bf+QgAhAdv/bg5s+9j+ofcDAWML9AZUCzsA9Aqn//8BYf427s8GLfqMBL8O3gC1CVEEhApH+c3/WxOQA3oFiQGD/Wz/LhMFGF8U8xi8DWoJKf9UCXUQ8AfpB4EHQQ7PCrwNHxe8DU0NsBS1B+f+CwGMBFwHOga1CX0IZwaxCE0F0P6mARkHyf75+ZH/jvzf+vQC4QmC/7r6jA6/DvX+s/xL/JLxzfsHBl752PiJAwcGgPCqAIgNZf82C5X+/fjg9Ib6KAcj89j2ZwbeBIf4Kf/U/wX3mAEq+fn7mwJYAiwAWvSz/tD+Yfwq+0/5Iv9rAekFMvNa9j4D8v16Afn9QP1d/aoCzf0M9aj7F/qz/NMBXAPTBeIDUQQQ+rvyIv3AAuv7GPSbAlUBHv57/7D1cP5P+3v9Ivla9gT/bgimCfb8jv4B9jH5IvnEAf38Kf0+BazyKAdnAs8KQgqo/V39DfGO/rr6XAuv+wX7ZwAy74wI3PvG+ZL5Vvdh+JX4bwSUACb+wviXBdz7IvuBCeD05POd+oP73gD8AjH/zwSJA/b68Ac6BtT/bPvv9ET2pPQ3B30GvAPaCaf/lwOk9owAMwDG9f8JmwIhAb7/UA5JDs35lf7j+aj13/pfCL77Qgb3EWj+3gSbAAYMtQkq9Y/uv/H4BXkJyhEnE7AQbg4t/nj4d/4OBLkALwXtBDMGxw4rEiMYiA0hA/QAJvZL/FL+t/Em/FAKTQsdBMsLDghA+2cGKvmO/EYDZfvj//34r/sm/NMBWAL4Be0A0fSQB2cAnwOPDaoEiv0HAMMLG/UB/n0K7voHAHv9Ywf0BKoEKxAZAWsB5QhgAlr6Vv03B2QB1fPq/TMMywkdBCQCYwMQ/MAAuv4Q+hf4JvgWAsX/8AszBAcGUQQf8rf74PTF+3f83Psq+e/0FgC6/CgBnP6d+ODwr/fj9dHyowIQ/AYKqgTo6Hjy1e2/6Wz9yvAR7NMDBgjJ9u/2NwdX9Rjwr/uK9frr9vRP+4DuzfE4+wcGv/NI94wEHOfZ7uf4H+7v8Fb50PxP8wnuNfiS8dnwIvl88cbx8++k+jH1GOxt8W3rj/Bw+LIA0PyO9i36NwO++3j4kveL6/34fPNP+eID1wCqAhj0pPhw+lL8+wbn/rf3/f4B+hf6Vv9I7UD1nfrn+gH6Y+gdAIwI+vNE+K0HWQAJ7v70s/Kw7/34iAWmCa//lwdH+bjhyu7b/4L/CgPEBwH2yvSR+9j6SgIvBekJ5/54+B0EGQFkASUAf/oP/vb8cP6IBVEEQgJRAkv6zgwnE6MChA4+AVL6OwTAAP38sQSDGLEG3PnLAXIJtQOXB14aRgE3AeERnwfPCoQWngm3+xUMrQe6/JMIOhB9CgoHcguICeP5xAWkIxkHWv5MFcgCFQQRE9IJVAvZFe8RT/mh76IQSQru/rol0RtKAisK2RGiBO78hBQSB+UAnRuhFFwDLwWWFygDMfUdBGn6BwbpB7gOohK4EEckAwMhAakQOwA59/bylwvsCIwOaR09ES8PhxUNDrf1og68EQAARgcdBrcYgxqPGToQLwndDB0IpgflAgkTpQ8CE2MRRQmeFWAEsBLSCfX+Lhv3ETYNAwmfB/QAZf8hA2AAwwtl/94GSQgM/0UJCgcrDE0JOwJ08ajzYADiAWH+EPwyEGcEsQTtALf1vAPq/R0CyweTBt4C/wUm/nj6q/4WAAMDhQDsDAn2Q/7LB6Xy0wU3A8n4+vOg+UD5RPqQBYwCmf/C9uv3U+zk8z4JT/e08Hv5YAT0BED3awPwA1vuVvf5/XHyHQLDC7v28QFKAkv8IAcE/x0KR/9w+DH7JvZo/jj7FQSg/+fy3O8oBf8LE/vc+0jxV/F56KT0WAYf9NX3WvK05Lzo7/Yu+GbpAurk7ejqeO7y9fvpw+IF8bPyUOua7RTzQeOj2V7ti+2X5rvwj+os3Vvkh+4c73ztH/J864zZluiA7grg8OJ24Tbk2ei/5+zrBe2P6DnvNurl5b/vjN+E6bP0l+Lo5qzuH/DO68r0T/e07PPtGPAY8GPkf/Yi/XzrJvpM8iPt3PMY9BjwMucp/T32/ur/Acb1AuLV78X7+vPK9CL7jvo18Nnmu/Lo7IvtBwKL7WLqCfS07Ov3ePT9+qD7Kvl2AO/05/ih87/zmu/S6pX4IQFcC9z7G/+mAef6Ivlw+M4MDPXc+UICtOrXAJn/DPvC/rb/WAa+99z5Tv/9/Ev+xAFnAAj46QcsBIr5DgpyCVwB4/WjArwH7v5uEHYAlAIcDNMDBgytCxQYogqXBXYK9vw+CWcMvA2xBqYJjAiUALgWIxSsF+sWIxT/DTnz4QtqF+UGyAQgC/sGmft1EvMUmhA2DzMIfQLJ+rQZcRNRAh0GYf7eAvX+FRINEnIFZwjPAJ4L4Q2wEBwQCgn7CE0DJAIgB9IRixLHDscKPgOTCh8dAhM+AbwJsBCEDsQFBgrdCmMLIBG8A4P7EgUVEpcFsQhcB0v8fRDpBSEF5Q7ABt0MZwaz/pAFFRJmGiQQmwDu/mcM9xUjEl4WSBiAGScRfQwII+siAhf3C1sRwAauBV0m5BiPGQ0Qjw/VFGcABhTPCrwDvAVCCkUPngnvF88KHQoKEaIK5QBZADsCEPbeBjMCrgGhFsMRtBWEFugR8AeUACQM4Q3SC4wMMwzdDjIayhdfCPoUfQas+OIDFgDGGD0bTBXsEPb6JAgJE4QQpgVrBdIJqgAkBrgIUQQRDdoLLvZO/9oLfQ6PFccIfQRqDT4L+AcMHo8TR/25ArEElw8gDVccEBtCBE0F8AVqC1gKyhvZG2cIVxAnFwINSgCBC54LZwBjC5MSMwqpDjoKr/nLB3kLhQL3C60LFQiaDugTHBSbAvADbhD5/+f4/wfDFYwKjA6LECEBsQonEQYKxf+4DJ8Hiv9NC54NmhbDCZoMUQiK+QYOywvY/qoElwcdBHYEPRHDFQoJXhb7EHT3+AHLDZsIrgNqD/AHXf8DB3UOOwAf+Bcf+wzV91EIKAfaCUIEmwrpBW35fQStB9X1hvzpCXv9uv6Z+ywGpgOz+oEH9vZP/dMBmfO+9Qj+r/1A9eP1OuswAfQEofUi/wH4wvim4sLyXvvo4t/+jvwy84vxdPXC+uDwKvFl93H06eBe77jnTeSk/DXyNfhw+tX1h+p146nn9ONu59XtJvp166HtFPOt5uDynuxE8Pfqptxu3bzeBfMN8UT0Yfz+6P/iPe6X5lzgnfSp6Z7ihOdn4TrrdemL8+Dudtul7hjynuaS82X57OsV5w3nl9hr2GX51P8K5LTmNfT682X3Bfd087/nSeOm5OXdoum+9WnyvOYY6sL2v/Mu8jbo5eXz6XHsUO3V7538U/KL77vureQG51DryvDD6BDyIQEQ+pb2BfNU6uvtCPyS8/Pvxvnj9SPvxu149pb2zfm6+KXyePKz8p380fpnBtj8SPWJAYDykft48Bj0FQTc9fQArQct/Pb2iA1CAtj0LAIOArwFRPpnCEUN0wHlCrEOWAxUBbEMvAUx/c8CDghYDEYHVxAUGDYVoRQ2EwIPOgZcC9YGzwC/DvcL2RURF0kQLxHLB4ATcguPE3gZMhLKG0kKvw7WDpMUqBwYFZIchxVjCSEFSByhGAIPzSIII2YUxAF9DPoW2RdTG3Eb8w5vBPsSkxKAEUgYqCAGFNYMYhdxEccOGQ0fGz0ToRjJK2kZpRWIEXUU5Bp8GCcXUBh4F/YZMSAnGdgnryqSFscS4RM6DuwSrB+SGhgdviTcGpMS1RYJGUQdtBn7EocTPguPCzYT1g46CGkb4B89EfcP6BGLFOQQdQ68CYgPZwSFAC8R6A02D88IvAVrB6IOYhPwCaYFoghFC8sH3gTsCLAQ+Af4AUT8jwvZDaMCtQvU/7QPlweD+xkHMwrZEQcGjvqP7DcBYwXU+ysIXAFl+4vv1ffF/0/7Uvq6+KjzhOn27pn7DgJA/az2rO799iwAne5M8jX8SPUE/RD0T/HY/lr6hvr676Xu5/SR/aj7yu7y+QH80P7Y+M3ze/cn8pPpfeeZ9SP17/Au9OvxTOoJ8p30K+3d7Rzri+uw61vw3e3s5/vh8+1/+CDqUOG45wXtXN7K6sroi+si+S7sBfFN4ALoZu+L6ejsOumZ9cPkcuST5eHoMvNj5ufyNuKj2Q3lGOi07hHkcfD+6nnmHOc63ezrEezS6NrY5dcG4WLqt/nH5RXfbuUv5vvhvOZQ7fLzce4s2ejkkOBn33TzW+4r33HuJ/Cb3dXpw+KA6sry9+ya58/dw+466UHpf/YN8fDkw+ZI9SDqIOJT8gH07OOe6CrvTObH57f1tOxY2+Tvf/y46dnse/1f5U3i7v4N7/PlyvTR8Knvyuo96kv2qe8b/fb0Fd9w/sb3l+bR9Nzz4O457/n9ofFq5Bv/afZY5VvuR/l89fL1WATo6LDnT/O/8YUAcPrg+AXvt+3Z7pQAvw6D9w3vw+j68xjyi+/j/e0CwOOy0/QEZwIq+1EIyfoy5ZbssgBE7tz9WAof9BTrIvdw/r71i+t4+hEVbfcM+0YH0fbLA94GogRH+34AMwD696jz5/jACq/3ZftVAbr+9wvlBLEE1Pvu/kwPgQEU9UoAlf41+FEEf/52AJsAFgBcBwz1vvuTChUK5QKz+h7+Wv5d/3/44/l6BScPlw2FAFQFiAXc+/QARgf/CX0MYwMDAaoIhQKqAk0NyADb//sG4PKmAZ4NdgR9DLwDjAQt/gXxNf5P+YfuKvuMDgoLyfZ//rgIPgP9+iEDXAnC8pgBPglnAIEHdgiIEcAAr/+BBxkLVxBYCAIRZAGiBPcV2gdmED0XcgvACDABOP3IAvAH/g8sBGj+HQaBCccKRQtQElwD4gFjDbkEVAUGDCgHIQH3C2AERgPZE48RERGQB30IsQ6WEUQX2RGeDQoPuxNnBHEPgBN2CpIcPROwFg4I6Qm3IssLpg2DGLAQRQu0ExQYAhWHE/QMhAq8A3YELw0JFZoWixBQFK0TwAgvD4gJnwVQEI4dfCDWCmIXuxP0CLwDGA85IJsCEQ3SDXUS6BfkFtgdag1iGYwOawGMCNITUQYrCEEUZwKwElQP9w2EDhwO2RMKC+gRfBRMEa0LjA4+D90Q2Q8gDYwGOgqoHGYScQ+/GgEb1RIFFqkS7A5METYPIBHADNEfqBzADOgXPRtXGi4dzhSbBg0WgBUGCoQWmRw1Gf4P/w1xEa0RXAvsDlcSKAO0EZ0biAkYDxUSvA2pCqYNKxASBWcIDQ4kDCgLuxWeFaIIlwVXEpoa4gEzDP4ZPgvhEeETDRDHClsPzhBQDBQaUx+pDGn66BF0Gl8OSx9pGVQNzwZxFXwYvAVIHugZIv0x9UEM6QfxAbAYvv3WCEgUIxIrDH0CkhgkAp38wAjTBbwDqQp5D/QCqQyeDwYKbg4RFW0UegFKABUQNwWaEFMZRQ8KEXIJ/hMKBxUQJh2mDUwPngtNC/n7Ww/VFq0LERNQDDMMAwlIGMoXWAjpA8AKrQdUBWYU4gEB/KYJtQng+CEFgBtuDFgOHA6BA9MBlwv7Cnf86QUYGcMVrQeFCDoGEgcVDIUIuvy3+8cMZwpuBukJhBBJEJQCVQG79qj5VAdh+uf8KAVs/94ABwSR++76jAKh8yrvQP1nBp8FZAHPCHoFWvhm8yQEKAeK+cQDE/1E/IEHlALlAKoCTQ3/BR78NwMDB+gLWArSBzcFMwAb/Zz+Af4f+g4AXAPq/YL/tQd6AaD5+f8HBuf+YADeAgH2kf+R/bf7Lvgy7+0ENfSL6xD6hv4p/V75XAPr7Zrrt/Od9FfxzfHlCHHs8ORU5pbobwDg8j30X+nP4YTn7/CZ96jzQgTV9xjyH+xB6RD08OZI7UTy+ve3+XTzne6T5wnuMvGL8zbusO9b8BTryvDz6anrofeD87/tzuv0463i7N+m4uv5Nfjo7EHv7OvO71fpfecU7ffq6O7V6xv5FO8Y6I7yjOUf9tz5U/b041jhne5B46T4EPa+/fPxSeXc8f/eCfDG9/b0V+d48mH49OOW8l/lUOv+5pfkDe/d4+/y4OzK6LTmx+eS7aLlFPNM6PTZYuo+5rjh8+207ujil+Lz6+HgMuWS8zLxQeuw6TXw4egn8MbrCuSl5vDgs/Rj5CvhkvVx7u/0LvIJ6MvaVOia7UnbUOP753XtU+6D8zLnOuXC8ozhI+u/5yPpOfVQ53XtbPuK+XjuV/N17dH05O/e3aD9PPh160T8kf2s8pPrs/aS793rmwD9/mX1dPn+8NblpewJ9NzvSO278tH4EPhCALUH6/cj7Uv0Nfix4VPuagm++cX7fQLJ+qz47AZl+bDrAvCs9BEJnfTlANkTAg3PBL/xLAZ0+VP25QAF9cb55/qFCC8J1Pn694wEMfuH8hIBsgAT/wz/AfzR9E/zMfdw+C70PPin/2z9QP1H+/gBaP43Aaf/6/eV/gH2Zf3oD3UWfQYHBj4LcPgq9Rv9wwkM/UP+kww2C6II8AfSD478e/3tBOr9FgBKACEFf/pVARkNegF3/Jz+f/qbAHUSAgsNEMYaFgKxAjYLtQMrCF8K1gz3DYsQIAnsEOwMYwOLFi8JuAzdCnkPwxf3DyYfVBN5D/gFrQl2BpH7KwyaEj0RpgsxJp4RzwKHGWoNywcrCiAVQgg3AQkVlhWiBFcUUx28BzMMqRAsBPb6RRFMFysKkxSWH+gLywNaGyAN+AdbF8MX2gcVCkAgixC8C+sghxXu+MgCsBJ5D9IVeBsOCvwCngm8C0wRWAq8D+UIkf+bBhkFjASpDNUUR/1o/rEOJAabAi8FXAEDATMM8AOqAlwF6QOXCWMJLwf9+rb/Qga++6T8Yf4wAVwHdgTu/sQDLf44+0IIu/bn+qYJqP0wAxkHdP9p+AcARPSL7aXyF/5GBV7tzfUi+64BYfru+J38peaW8vPv9+px8EkMbP+x4xv50fQi+9T9afjk6QLoVv8hAW3tPfQ2D+74IOrc9eP98++Z9XkHNfJi8MAAH/oR5rTwFPMN7Sr3R/t49JPpxvWo89Lss/Ii97fvLvJ//I/q/uqL8TH3fO9x6kv8SedX7UD9qeme6nT7IQGi55bqWvha/EP+3PWxAtHwRO418j7ireR08S8F+vN882X/jvqZ/VkAwvRf67f3zfUB9irx9vSZ/Zb2Bfkx+/34qPt0+93tNuof8sgCPP5jAzcF7/Bh+LP0wvyS9yb4EPwY7JX6H/rr73jw1wKO/Ff1QP3n9kYBYfpe9QnyI/NE9An2EPqa7e78I/V49jz+AfSuAXz1pPZp9uD0YvZW+c8Gh/KW9kT2Wvoi97Py1gY97iPvOPuZ/Wn4bfWR/Tn3rPRE9EoAnfJE+K4Bh/YX9rf3Jw/0As35mwCk9nT15/qIBfcLZwwoASb41feqAIwIwAa8CzoKEPz0AvgF+AUFFi8Pr/sI/usYohCpEOcd2Q1A/2j+Mho6DEwVxSr7DigHPgmhFnER9w9eGnwUuQDhBbsZSQieEz0bYwObAM8IiAdnBNoHoRYbGoUIxxBfFHkNag9qCWMJSQoVDB8f/R+AERcfhxnLCYgN7BSLHIAXXxJEF4cXBhR0JPkiBRaSHNEZmg7DDWYcgBvzFH8dWiN8FL8O6BPWCIcV4BvZFxAjvxaEEhoqtyLHEAkVGA8GCsAMbRbVFp4TNRvCIaEgmhDGFN0SRQkGEusa4x58Hskf4RFqC9IRqRKQCYATBRpYDkAc/g/EB6kK2gewEt0OxwiTCkUNzwYrFEwRFQonDyUAIQMDAygL5QqQAYELjAzdCsAKuAqpCqIIrQcyEhUQ5QpxEQ0UYASv+XYIww20FRkHjAJQEOEHLw/kEKIIrQvVFowMwv5FC7sXTQ21BXUO9Aa8BxUKg/2z/i8LogqPDXYGGQUrEq//7Abb/3XrJv5vBBP9t/s8/vn5Wv4sBogJ3PVl9Q/+fecb8QsBUQThBywG4PLs5/rvyf68BeP1XAFRAufyf/77BFr2MAHWCiP1NfC/7zH9FQpYCAsBePoq8Yf0yAKV+iL9U/JP+0IGOfk7ANnyafY8+g3x3/oX/vQGiQHN8RTv6/fSB+78dPMn7mL2ZwbU+94CcPyg+8n6NfLU+/LzyfjJ/k/56+0X/v8FU/jeAKoCf/5X7S36mwLv9CL7oP+V/vL5ywND/o72xf8i++P5nfp0+UD5Luy++dMFs/hyAYEHlfrk7Sb2X+nG7WAAG/d0++vx9vRP8wH6WAZl9xD00fio85PrYfpA9175yfqa75rxcPa3+9zzLvA18tMDG/tA9aj7AvAF8+/0r/+V+Kj3MAHG7+DqD/79/Hj2RPgB8l3/Kvli8rv2+vW+/0P+V/Uq8XD20fTy+U/9s/rC/Hj2Jv6V+rvunwHY+DLxawFB8QX5dgjlBuv5V/GjApH/EPwM/dH2DPXf+s3z+u3U+ZX+mAEHAjj7LvTj+Z383PsF8Uj1e/+d9LP0fPPQ/sL8Zfs1/rDvqPHu+v3+2PbC+hD6+fvY/tnwpfJp9gH6mf2Z+536tv/pAYP1qe/C+Pn9Xf188wz32PgI+NMFdP/LA1L8nfh//NT56/sM98MJNf7u+HD+qgK+/QXv5QaO/ED7MwbPBsAGBwaTBiwAOgYQ9Pb2DPla+rEI/ALeAp36S/6v/U7/NwHc+6T4S/Ye/tT7UQbC/m33LwUJ9mX1KAUT/ef2gv+k+IP5XAWxArwHQgCz/NMBu/Kc/s8G1Ps4+53yRPox+3Tz4/3j/c35NfbU+6YHnP5s/WAE4Pi/8fb8ywVL+hP9qgIb+aj9RgUnE1gES/p5C1L6ZvMb/9YKZwYp/bwHdgD9+D4DBgj9+mL2AABW/4r5/fjIAAMDLf75/Yb84/X1/mAC7/a6+ur95/5W+5X6E/9/+gT9zwCO9jnvoP/eBP36FgDb/4b6kfv/A5MGJvom/P8DNfpI9xIDPgV/+AX1lfpi9iL7awU+AXv7Xvls/Yb+t/dT+IP3G/lP/dXx5O3u/DcBMfta/k/3i/O1AZL3vvtnBvrz7vxkARv/owAhAcgENfKS9+D4T/1cBYb+kwYQ9tT5vv/j+e74s/bc/c3zhQISAdH2KAmuAVP0ePqiBLUBVvnv8Kj3tQE3CcAG0fauAVwFBfWK+5AFvANUC4UGyABe+y36tA2g/6/5xw7hDa//DP+4CJH/Kf+TDGAC2PZNA+gLOgZ//PQAJAqqArkC1gha/ET6xAdL/t/+BwQzClgK4PjIAGH+dgYcEssBQ/7TAz4L+wr4BZ4PvAl49C8HDQ54+kP+aheIDcLyUQibBpgBSQQyFjIU+vPkEogPyfha/iMSFQao88cQbP9p/HIJJxeLEgcA5Bz4BRvxNgsvD5sCOgbkElwBDP33E5oQmwDJ/h0IhAo1/MAM+hQVCFwLcgUHBrkEqQxQDgT/gQUgDVQJVAtuCE0Bywfc+dcAcRMnDQoRWw3hC4kDdgRjB8QHDQ7aB5sG5/gDAQMFr/0vC5sGuQIAANoDYwnIAmsFHQZ0/Vr+lf509ZL3DgSTCor/MAOEEDcDAfyQBzH/F/aeCaIKdgK4CJ4P7xEKB1wD/ABl+TcBZwpKAKH3CgMSByQEXAmFBIEJlwuZ+QXzKvXu/Jn1/fzsDIEDxAGv+UT2h/DN824I0wMF9SL9ogZ/9pX8ywcDAbf7mfkQ9mL0/ACQByAHF/Yx+doDZfkHAAsB1P+yADn5ePp2CkP+xvk3B2X1g/cM87f3VAmd9vb6bwTV8TX22gf9+qz0p/+k/ib4XvOz/u0ECfR/+nv7Yuqk/OEFcPz9+PL5HvwM88n2lAJ0+W31CwGg+Tn3PgH/BYEBVve79oPzmu+d8ukB/fqO9ukFd/5p+Aj6lf5I9QH6fgD68aT2T/vC/BD0SPUSA2MDNfoN8Vb9ywF0+0v8fPVe77r6vQGk/B0E8AfIAoP9QPeR+3D+DPvj+WX73P04/9oDDP2++c35Bff5+470Mf8sBHj6wvx7/fADzfnV9Vf1CPhh+O/u1Pkx9f8B5QZA+/b6afY+BZ34wvoDA7f7jAKK+x0Ejv6G/u0CMfuxAuUCjAKqAD4JnwMX/Fb9xANbD+78SQaBC3f+LwVp/O78zwjhB3j4nfIQ/KIEYweFAiAP7AY59zADbfla+u0CfQTeBAz7owI7Ain/kAUOBBf2jvhKAC72jvgx/egPuAwWAv8JNf5a+BD4nfxl9xf4Awez/pnzwvxJBPsEqPuS8478TPA59UICMf+fAWX96/UF8RUGzwDZ8n/+6QF4+kD11wDaAxUIYf7J+hD8Uvw+C1L80PwnD+UMqPn2+jADT/vwCeEH8vlh+ogLdQ4J9hIBGQdL/BkBWATHCjsC9ALABvrxcP5rB8L2gQGiCJn10fJgBpMIYwemCRYAhvwb+4b6nwFl/bwHeRPn+hIBuAg8/EkI/wcM98L+tBE3AbUBXAVjAyAJnP7LBf3+SQjsCCn/1P0P/ugVIQFkAdMFvvuZ/8373gL0BBEV0gsZBzYNUQAq+88AdgTn+KoIuBAZBcgAhQaJAzz8yAD0BAoDkvE7ALgK4/22/+wI1P/v9Kj7QPMU9RT1CPh0/X/+yARvAGX3DPUm+iP10fR082ACDgYp/aT+Afp7/2n2S/Tk7zLxofcq+1r+FPeADewO+f+o9XXrYvQb9eTzS/g+AYED2fJa9Of4PfaxAvL7XvlS/Cb6rPoI+tMDHQjlABD8qP0J8AX77QIzAtMBwvRfDGACCPrLC4EBLfpUCc8GXvmPDWMJs/zg9Pb2qPvF/TYR9AjLA/8D6v2+/zH/WQAVBkD/4PhcBekD+fnlBAIV5Q5RBNj2T/l5DVQLCgnsCAMDbgZNCfsEFgAZCf4RmwhNCZMITA9fCMAA+AW3+TISEQ2pDvQKPfT+EW4QEQke/EYDqgCK/VsVxwzKEToK9wsdBMX7Xw5qDyL9r/faCw/+MfvlCIgNrgN0+y8FbwTeAkf/BwR49ob8HBDaB/L/IvkhA9T7zftKAAX5ogrEB1r4NfaR/4EBhQQ6DvL59f5QCqYD6QNP+4UEEgGg++78s/zN/XT5Pg8X/lb33RIWAib69ARfCsL6qPdjBV3/Wv4zAE0LkAPN+YEDkvMe/iANFgCG+qD7hQS2/x0GzgwwA/n/iQGC/8b38AeUApX4Kf/N+WMF4QlbF60RDP3hB4UAsgDLD0EOUv4vB2oVZwDEBYsQeRV9CpL3VAssAGsBgx6/EvgFxw5mEuIBgQO8CxUGZAHN/bAQgBOECs4ajxNKAK//Bg55Ey8N0hH/BdYMoRRXEtgdVAkgB18O1ggcDG4O8xIJE8YUZg46DC4TeBepCur9uQbwCT4PUBYKESQOChEVCB0GXAlQDrgOtv1+AKIGHQokDIUIOgjAAgcEJAhs/UIGzhi9AQcCywPr9cQDiQPF/x0EPgfF/5AHWAYt/lAOnfr681gCmf3AAkD/3PVA/aMCbwIf+FftCfYm+FP0JvgkCJsG7vr2/AHy8vXeAjH/TOqL50v6f/gwATj/zfXY+lPyZfWd8qHv7/JI7/L1/vCZ93/2kvFe84vtePqS7TrrAfTr78vkHOUAAFfr2uLN8Vvsh+rK9HD8w+4c5w3vfO3W2w3x6/Xh5nz1V+9f5ezjJ+p87fbuSO/D7u/smut17Yfsj+pf60j3EeYv6KHtY94J6qnrAuRt7zX8zuPW48Pm2eQy60XkMusO3xjoiOiM4VvuMffC8Arex+dX6YTnvOjS6ojgJ+Rt8UzqNu7C8CL5SOvl5VfvuOmW6lP4Yfzs6wXzFPEV42rq6PCP5Dbs7/IC7gH0zu3+9HztfPE18t7dK+369XXrHOnO66nnCe6h657o0uyB4i/mX+sK4JLvNf6z8nv35Olj6LvyKvUY7prj6PDh4EXor/e3+TcFlfoN57jnMvOd8hUEt/Ww6+v3DPMQ8oPzfQKz/IvxGPJA+YDwxvFnAqv+kAFS/MX/RPoq+/sInfYy8zABkAHEBbkCbfUu9F39wApCAE0Dng2bBBv7UvyiCoUA4QeECs3/r/lRAF8Ujw1ME7UFT/0RCQILlwXn+nkLgQkkAigJEgXlAqIOHQou9pADahWqCFr+EQtuDAcC3gLDE1EI5/6AF1QJPgWLEOwQcgc5+RwQnhHPCGYQNhEyEPcJHBD3D90SIxZ5B+r/6/uXB5MO5BBqD18OUx8zDLb/pQ+WF+kHfQTKFQcAxAeWERUGcgcoB18Uww3HDC4XdRTN+fwCMSJgBCALrBtYDDcFdggyEMMJIxxaHYgNpQ8rEBgPkxBiGwYMXwzLD7wHmhhxEdkRTQtnAJoO/hcqHsMT7xXWEDoGZwxfCmML6A3gGaIKQgLNHrsXzhKaGvMStA/7DisOKAemB84ODRbVFrwNLhnKGVAOJA5UBU0B4Q0RF4UGrRO3IvAFiAmpDkkGLxGaDOkHlwWFBGoXcg0gCQkZZg4oB70B6QNGA1gGiA2xCigLAg3sEhUErQmlD9oJQgpYAvsKHQgUFnUWIAcCCyQGMwg+BX0MMhCEDtkZAhf3D00JMwBfCqYN/ALLCccKKwilE4QS+wTVFJMQ0wP7CpABDgzeCJMKqRK5Bj4HtA1fCpADogyQBTMCbwSpDM4MvAu7G5oSNg1KAN/+iAf/C+ENmwq4DJMIgQtyAx0KZwrwA+kHNwWfBSsQ/hsZBzMAMwAwAwMFqgAsAlr8VAX4BewIqgb3C+wQpgHq/UIAPgP2+hID3QzlBn0KXwrABOr/cP6MBN/+dgZYDFUBeQu1ATcFgQvIAlUB5QKIC8gEFQonDUUTTQNa/vsIuvox+3v7gA/oDZsKaweO/sL85QK4FH/4/f5yB9/+uvztArULR/kcDBIFYvb2+G8A7Ax//mMFzwa3+6D/EQ2FAqz4VA9yA3TxG/95CRkFR/+IDcAGU/ghBaIEIv1s/zYLhvpP9QYMDgqFBHf8nP768fr1awNP/TMCRPxW/f7uBfl9BFPyr/v5/ef2t+2D9ZgBtQH/AQz/p/+S90jzxfu3+6T2jv4lAPX+MwSqBC38VvmyABv5d/7wA7kCmwas+nv7s/he90IEoP35+RD6MvN094r7T/0e/tz1uvgB9kzsXvuO/Hj00fq+97TwG/ET/d4AF/i+97fzU+yK9zX6Oe2Z9ZH/5/rN8Vb3fQR49gH2+wTy85bwOgbq/VDtH/ao9+Du6/fr+7v26/Mb8xD2H/Sd/Kv8sOvO5S7sBe2P6kHxLuqe5srw9u496mL0Lfpu58PiU/QJ8uTxS/xP8eDw9vS38e/sh+4m+uf0lACqBpLzNfBP/aT4Ce5w/Lf5cfA59d4AJAK79Bv5E/3Z5ujqdPs26GbxjvTo7gz1QfHZ8o/q2PQ97CjiCeqp76zuPubJ/gnyHOmv993t1fH28Aj4DPfk74r7BfsU+fb8U/jk8RTt+vU4//LzwviMALr4+ftyAQz7jvSz8mbvePIM81f19vou9BT5dP909bP44PbO6cruDPUf9s31ivWO+If4s/IQ+JcHvvtP86/32fAp/VQFcPrq/R7+QPeO/kkGFQwwATX85Qha/owAeQk6BukFgQkkCkv4+wTkEnT7ofXIBKYDjvYzCpcPjvjIAD4H5QA8+l39IQVw+qv8F/yK/Q4C/wMCDXj2uvw3BSb4hQRnBpcFxfuTBn0M3gY6DtcA8An0BmH+5QgoCfwCR/3wB6//cP5uDlsPVAcp/YwEmwTb/ygFdgbtAp36r/9GA0/3Ywd1Fhv//fwzAH/0Uvqo/UkExwgoAZQAjAJ6BRIFNwMZBW8C5/5a/u765/xgBGcMqQyR/94EeQ8zBNj4sgCMDKYBJAQoCxv3F/70BjX0t/ll/8b5wv63++76e/uk+PEBmAFt76z0Uv7s68rurPjN9QAAwALU/SrzAfZNAY74dPuK/9z5RPqK/X/8dgJnBnj4kfte90zw1fUI/FEGhv7n/GsBrgWfA7ECYfx48pH9U/ZS+uP7HvzlBhf24/ufAWn2jARCBnzzq/xA/1738QG5ANz38vPv9AH4rPqD+e78jvZp8jj/1Pse/IUGlALk8bD1iv2v+Tj73/yG+qXw1Pud+sPumwb7CLfxafC+9Tj/YfzV9/sK4/us9CsIbwDK9GsDXAdf6aT0r/+V+M8KdgjpBSEFBwAVCi3+rPSmAUoAh/jc++kHqP1H/y8H7/Y1+GH8g/sB9Bv5NfiD+0UJPPxA85n3XAd//E7/EgHy8wz9SO+o89/+pPyZ+5QCQPvu+LkCuvrwCR7+oPuIBQX37vhl+3oDmf0t/iED0PwP/lb/R/9e+QsBmwRw/kf9VvkDAb7/q/xrA3v/FQQm/r77BwZa/F39SgAq95byJQDdCtYERQnDCWsFxAUzCj4FLADwB0kILwlUBXIFTQd1DqEYYw8YEcMRfQrF/3ILRBn7CNUaih59CI8LYhsQHV4YBR6hFoQQLAK8EUQfhBBHIgwePglBEPIi3B5PIpEoDRgREz0VUyGzIQUcfBJ2CuAX7x0FIg8rTyahIHEdPRncIuAhYSFtGi4ToSB3J1Il9iGnKuscVBEqGOsWixoXJy0nnRdPGioemSZLI/0nxiIZB0kQnRmHGREV5yGsFxUKxhoYF9wabSKRJn0QXwjzGHQcsx3sEO8TkxQNEM0coRg3CYgNDBxBFDcDywuIDWcM6BMvDe8RVA24CCcR8A12COUIywn0AukDPgsgDUURtBkoC8L+YALHCHUO6QdqCUkOVxCMBEkMTQ1CAr8QsQZA+9z3/wX/BTH5+wQt/Cr17vpKAv8BLfop/0P+vOh57OkD5/y38XD4ZvEr5X/4uv7k74fw2P6P8CThOP1S/B/uBfUu9N3lnurr9+jsL+hx8IP3nurZ6sn6RPBq5nzr8+X74VvwWvLO5S/mSPNi8IThx+VT7sveSd1M5k3iX+NB4/vh9NWX4H3n/+KE4Rnc8+nI19PWm98w2JfgK+H/3ljfK+cv3hbZHdtQ4dLefdmE3xbVk9/H3+nUZ9ky5wLsot033D7cCuAS3q3kUd840L/n7OXt203gjNcS3JvbB9t93bndgORy4mfjidiQ1CfkKOLp3NPagdhu26Lbetqj2ezfPepn47HlQt9n24vpduGL52bpJOW06FDp5d8r3y/oot987ezrbe018qnvSPW85NLqhOna4O/osOua4wLkU+y/79HuIOiv+aT2cuAv4ITp1elm7ZbwTOyp72bre/dI7SDo0fZi7l7xLvjc+0T22Pgb8fPtXvlw+gH+7vj2/K/3zfeJAZQC7QLQ/toF6/W08DcFe/uD+csB3gQm+gzz4QvIAhD67QRA/7r4cgHeCDH1HQLy+/b8Cg3n/DIQ3/6r/GcIOPsdCA4IDgwoA4wGiAWz/oQURgdT+OP9EgdjAy8FyhEhARUIhxdUDY78/f4NEt4A7v4nDVgKvAmPDZ4VCgNvBNEXQQxNAaYF0hXlDFEGWxdcBWMF3BoGDowEAwebCqkMGBXzDtoHmhR1ENIHnwFyB/8HXAk6BtoFPRmTDDIU+hRNA0UNahEkDPgB2Q/hESQM7xkCD1QLTBnZEXIJAg/DFUgUZhqdIZoWVxjZDccOlhOiCDUZog6IB30Q/hHDEfsQZSKdF5MKgBE+D24MhAxMD5YTIxapDlgKkwi1BdIV/hvoFcYUnhHRF78SeRNeHMoXfRAuE+gXgQWiEpYfVA24DEgUyhWEDp0bpB+TDl8KIxLzFuwIuAisF2MLqgLzED4HCgesFUESHQpjB+UOUBAcDAMJag8rCq0NIxZ6BXkPBRbWEOgR9wmEDiMWRBcnE8AK4QlJDuQSZhL3DxEPpglqC2MLhBIcGBgRQRDlAJ8DPg9mDu8T4Qci+bP+9ApQDtIR8A1uBnYK6QeO/JQEzg4KA2MJYwuJASgL3RD/CbEErgXHCJsIvQEzCn0M2gf0DIED9Aa0EV8StA15CRENIQXc9bP8mgwzAmsDfBKMCJABQRCSGGMHZf+FBowIMwqFAu0CvAdd/woLOhTlCNILHA6qAtT93gBNBwIT2gmBA5AHs/qqBC8JWAIkAtz9UQRrAcAKMww1/q4BLALEA/8BQgYzAAj64QX1/pH7r/1jBwcCdPFNAaoE7QKTCPgHT/328l77RPyo+YP9eQnwBYb+sgDG+Rv/PPpl+cACkf+o+ZH7ZwYSA2AATv8wAxf+5/R7/9z7YvbU/RkHjvoJ9DcDUv6W9NH2OwIp/7r8Ywk3B5n3qPVcAWL06O5VAzMGyfhL9Kv8mf9p+qoA9AI97ifwmf9e+0T8RgW1AYf0wvbf/NH01evn9o74be/tAKIIS/4M+x0CRgHj9dX1DP/g+Jb0JARw9s3zCwEB/msBdPl//AcA9AI+Be76xfu2/d4CE/u++9cCg/uFADX2AfKqAMAC1P9CAAT//faC/zj/yvKR+zH/pPqR++P7hvr5/Rv3kvnb/7v0f/xE+nD4wAQ+Ay38s/6xBmH4pPpA/U/xe/ll/QH8pPj5/24GD/4T/woHWATG+dT//ACd9M33E/8M/zX+IAcDB8b5FgCUBE/9tQHwBzADrgPeBIL/gv8oAZsIhQbU/ygDBwTU/6YHiAtqCXUWwAjpAUYBSQYRE2MDdgpGBz4F0wUZARkLKAmxDjMIHQTu/qYB/AIu9iEFRgfADH0OAABrAY744PhW/7797QTQ/s8AoP8b/WMRMwYLATcFDgR2Bgn2q/7WBGX9ZwZtFEEOmf06DOIDGPSXA9oF+AXeAhUEXwhd/wcCEgdl/3/4xAc3B4vxkf9yCZH9Kf+UAH/6Jv7pAbv0t/cVBsn8IQHWCrEINwPy+fQCoPtH+WAG7QRe++P1XANH/fEB9wtNA831F/b7DuUAD/6fBT32g/2yAGX5h/ha/IL/kf8I/LP6f/5nBPX++fmBA+P7U/Kv+zH7v/O3+Zz+SgDeAl3/mfmd+iL/AACZ+wH44/0x+W3rKu+R/VfzdPOr/HnsBfHU+X/4LvK+/Wz9v+eO+r71muVT8D30I+9m7/rx5O2O9Nj2Mfvg+DntCPj2+GPov/Pj/8PuDe81+uDstOQx9fr3hOmp6Sr1g/Vq7r/zxvHV6R/4xf/G77Tk9u4m/iPxsOky8XHuNfIm9hjubuWD9yL5peyW9Ef5E/239f7yVOo666j9dPXG74Dyg/Gh9fL5T/ud+FP25/yz/Pb02PZuBgz9uOdL/FL82PbPCJsENfju+vsINwcx+SL5gQnQ/I7yQga6/lP43gB0/8L8xwbdDE/9ofcSA2MDQP9vAs8As/K39ZsKzwB3/CQEe/+s9tXzPgWg/c31Jv5a+hD4BfszBDX+afxs+z3yxvmK+dD+egFE+q/5w+he+fALSPVi9qv81Plw9tj+XAev+8X90Pxe7anlzfUkAuf4HvyD+8r0f/jJ/Jn7zfOS8UjzSPM8+N4AXvsM+ZsEQPms8t/6Mffr78L22gXQ/Bv1Mf2FBqf/zfsKA+76+fvC/J8Dwv5/9NH6U/av9532Hv5vBP36gPCw8Rf67vrc+175e/uP7hvz4gGv9zz69f4lAMryW+xw+o76s/ZvAHoFpPpw/FgIIAct/kP+ZwY5+TnvywX8Aqf/+wZ3/iwAKvcdBJcNPgHaA+0AMfuR+xkD2P6QA7b/ivUb+1r2NfxKAE0JXAm397775/qs9t4E/wdKAqYBWQBL/mj+awNNBQoHcP7N/7r8WvrwD7gMwArLB3IF7QCbApcLKf2xBLULmwjj+28AtQn9/tIJMwiFBnv/DP8ODH4AIQH3DTYL/wGiBowIBfm6/JsILf4I/mcGiAdKAP8B2gXy/fEBiQGMApH7+f1CBJ8B7AowAYr54/mv+yL3vvtrB4UCT/fG94wGePY8/t0WIAes9mcEYwfk8U0DTQtw/sX9PgGn/zH1lwd5FQH+2PogDQoDuQCECiEDyfhCABkJUv4oAbkCVv0U+Yr/vv+O9BwMcgV87Z36kAGO/hP7JAaK/93p5/x2BAz16/cdBIP7But4+mAA8vVh+sQFRPyW9GMJ6QMU99/8vv/J/kf/pgOxBLUD/wEsBE/9KvuFBIb+9vxNCf8Df/grCKYJrPYDAyQKlvZI8aT2XvVM8msBDgqg/dz9CPyo80TwCPhS/tXzofPU/8AC2Pgx/QoFoPvXANz7Zu+6/uP/+f9nBpH/e/08/AMDTQEQ9h785QijAur/VA03CYwANf7lAE/9zf0ZA0f/3/63+Yr9Xf8m/q//0wFNBYr/MAFnANYGogpnAkYFnfom+kUN4gMx+8gEJAr0CE0BPgeMCowEKAVnBHYAMwhxF9YKPgNqCdYGAwckBJQEzwIsBlEGCPzY/hIF0gl2CKIKgQeK/0YHlAA8/gT/jABqCWACZwY3CTsClfgZAzcDWvT0CHoBwvju/JgBKwhd/5oM8Acm/ob6s/zeBK/5mwRYCBIB2P7pAzYNG/sx+/wCfgDPCEUJOgZrA8cKhQio/ekDWAaqBpsENwPeAFwB6QeXCdcC8vVCBg4K0fpnCAYKZwBnBPAFG/1a/iwGPgVL/kP+GQkzArkCwAp2AvAFJASO/psEmAEvBcQFE/v4A1gIkAOTBvAJnwWUAqYHVvtl+8sFtQHn/CwEBgwp/woDIv17+fwAoP/SB9z9egUoCaIEEgMsAnkN9AJJCAcC7vquBRIFuQYdAigLDgprBV8Kwwk2DzYNxwjhBzYNRQuiCqUVcglyA7kGWAKEDOEN9ArACkkOTA+5BiQIhApBDPsKtQdyAV8KvxADCaYJ0P5RBt0QgQnLB3ILQgjwBYELLAJUCY8X5Q64CvsQrQtyC4APYwtJCpcHuBKXCwcAUAxxD00JzgxIFogNQgi8C1EGr/vPCBQWmwKK+z4HqgbAAAILpgcU+Rf8rQmQB9cALweTBi8HDgTEB94GFQYrDg4E+f0ZA3kHJAiEDCgHogRqCbUFrgVYBukFRgczDm4MdghyA9oDzwb1/g4AdgSTCMQFUAqpCtcCawW8A8AGRgURCRkJ4/92BC8HDgr7CqIQOgxvAs4MWAbeBM8I+wZNC94IcRHACMAI9xHLB94GbwT7ErAQmwQSB177XvmMAGMHMfny/48TqP1W+fwAywMHADX6CwGz+sX7pgH8Ak7/CgNUDUoAzfc1+FL+uv7LAToKhQJGBeUKwwvDCTMMmwb1/iwE/AKeCU0DzwQgC2333PlnAGACFQhD/kv6dPvXAs8Gvvsb+dz7OPvV7TH1FQYT/64BBfe/70Ty7/C6/mz70fRx9Pr38vcu8g4GlAQI+nv7wvC/8znxMfd/+qnv2fKW8irzg/MT/4r9pe7r8+/0zute7zAB8vWL6SfyEeY65c33WvTr71vwMufh4vfm0fCd8ofsnubg6svmOuvY+qjznfT666Xm8+lQ74fytOa08JbwDeeW6hT3xvXS7Bv1SO9U6EzwS/aD8WbxI/GW7CfqTOjZ8mL0De90+UzsHddU6CvtU+6S9YDwk+vD5KXu9+yW6tj4cPw96uHgYuxM5kTwyfZx7o/qceYy8XztH+4B+n/2K+eH8Nz7J+qd+M3zgeC45/fomvFp8Mb5Lvg+5qXuQPWA7nXvu/bD6tLolu4J9kf5h/Cd+qz0HOnr7XjuLu419kv4+vVL/iL/5/5a+hv33Pcy6QLsDgCZ/Qj+CglYAsL2S/S+9bf5E/ta8jX2PPgj8xT54/8+AR78Uvoj7anv3P3F/Rv5kft7+7vqjvg4+6j5/f4m9uIB6/v699D8ZAH/BfL9Mfm38zH7fQLxAc8ISQpGBZQAE/sp/bECKAeTDKIKlwcoB4EHdgiID54TsBBnDDcD+xBBElEG4BUzDEkOtxgCDeER+hTGGuEPGQ1tHrcgxxIGEDIayAQkEP0h+hjOFHwUnR2eET0XySFAHnQcTBvkGNkTASGOI14c+hrgHSMY9xVeJOMe6xhtIDEgryJ4I38fsBqHGbMj+hwnGTkggyJBGhUSySGkI2UekiBlIJ4PvxI1I/cXbR7RGz0VTBcYG2EhlhfgFScZPRFBDNUUpRehGIMYNhGEDKUVsBpxGWYYEQ1UDy8N9w8JE7wNKxArEIgH+AcJFbwHQQ7WENoBVQHWCMoR3gJUCYUEd/z8ACL9DgjEAXIDBwb99lP45QCJA7wJkwZs++78dP/XAAsBBP31/pQCOP8LAfAD4QWqAtT7lfpl/ZAFuQJyA8AAAfru+NT5ZAEe/hf8MfWS9ZH7H/rN/xv9WvgY7tns2fLv7IPzG/0F+dHu1fNH/fr1lvZA+0v2+u1M7qH1lvTn+AT9T/Uc7cbxR/kJ9Hz1zfl47lDtmfle84DsxvMq+XXtmuvr9/7u2fDR9F/rx+Fm7Qj4EeTd61PuY+QG6aXqg/Ow8Y/ws/QG503kuvi3727nKvdF7CvjGPQM+1vwcPj2/IfsDetE/E/7t+2D+SPxhOlp8BT1UQCp71P2xvnd5bfxIvdi8AnwrPIR6MfnIvd88+/uu/IU8wnu5/TR9CDoQe368YfuX+ua71r41fUQ8FDtyuqH9Jn5HO9T7m3zRPgF8wHyvvla9tz1YvL28EjzrPZp9J7q0fCz9GnwMfWk/OP1mflnBCr7Lvbg9Bf4LvTz76z2ofOs9hP/RgHy+2H8PgMSA4P5PfDY9HD6MwBYAgT/1P2D/TH9dgCZ/yL7tQNRADH1uvgkApAFywHu/v34lfifAUkKUQZ+AFwDxAF0/zAD8AM+A4wCEPwp/xkJiBHODkUNvAs7AvsE8AOMCoEFYwVuEuEFOwTAClsPLwvhC5AHZf2qBvQEvAO8A2sHpgnABGsHqgb4BZsKrQnTA6IGhQaFCAH+d/yxCKYBfQxbDxkF+fvLAbgMNwPlCigDAwFnBm8AgQnLAX0E/we5BPEBs/quAc391wL8AEYBlwcE/f8LtQd2AFwHVQHTAQX5yf70BB0CYwuBCXf+ZwAKCzABD/6IC3YGcgHaB9IJDgKv/XIFBwI4+6YF4Qfq/4EFZwodAAz9LweICaj7OfflACn97v6ICdoJkAXXACgBhv5p+tT/wABp/HIBbwLj/b7/dgJkAaoA/ACs+p36BP8ZA8QFQgTTBQH81Ps7ACb4wv4HBur/JvyD/fb6q/z2/JQE2ges+CwEZwwkBAoDsQQdBL0BJAZA/8QBzwLtAsAKJAYVDogR8xArCA4CcguIDUkM5QTDDXILSQTkELEO6QfEBegL2gefA4QMoRRIFNoD3ggNDrwNmg59ArgI+wSmCZ4TpgU+CzYTWw12BOEHpQ8CFY8PAwVFFVAUhBC7FegR9wuQCcMX4QumCzkaCRVBEI8LORjgFysUAhcJEzYNcgPODFQNsQh5D1AMywWECo8T9AymC54NRgMZA0IGCglqEVAOrQutC4EFEQmtDToI8AOXBdoH3QwcEkwTIxJbFzIWBgxJCjsEzwrLD8cIhQiBCzoS7A4rEEIKBwboDW4MSgLlAJ4VsQyMAAcGKAMVBvgF0gdgBN4AfQjlDuUCZf8KD0kGGQFYBOIBHQhfCmcKwAJrA24KOwSbCjMI4gGjAmcAfgAX+FwLOhBE+jMACgOK/Qz73gS9Ac7rxvHQ/pX8Afz4AUv8lu4m9qz4fOku8Az/MfXg6sr02fLK7J32YfxT9r/tMfXC9J7q7/RW98btafQf8u/o4PCZ9YvthOUU7Yfy7/Lz8YDwpfCL6zLti+m07Lvy6+1957TkTeR86173/uxb6A3phOep6ZPrxu3+7r71wvB56s/hseHZ7gLs8OTO6VfpMucf8D3yyu7o7DXy/u517cDjiNzG61Tm9+QG6Xzv3emt3iDkvOKA5Mfjnuzg7DfgAuTK6l/npea/64/iwN/W52fjUd3e3Z7iLu5T7ifqdefg6kzsJOfk627p0uz+5sPuU/Kt5i7wvOjg7CDqCew1+MbvLvCZ9e/yaugM9zH7PfAF79XpW/DZ8qT2qP2s7s7tg/n37OjsAfTC+Fr0ceyZ93j2MfmuAYb8pe4n7s7v4O4t+jH52PiZ9aj5F/rZ7s3/kwaW9BjyMf0I/gz9gv/u/gT//wGxBqT8cPr7CLkC0frpASgHvAPEA8cIg/1+AGoTYw9YAt4GdgRA+7kG2gVcAyAHJAz0Csn6xwZmECQE/wMKC9MBKAVUE24G5QK8DYsQAwM6CNYODgQ+D8MNNwlqCfsQFBSiDFsVqRDPCj4JKxDwDW4IrBfoE2cMOgwGEMcIKwi7F7gMhQiTDoUIrQlmECcPTQvOFEwVowKbAg0QgBHhDbgQPg9jCXkR7BS4DJ4J/hEgEYQOCRV4F4sY3QylE5Ia8xKpGNUY7AzSCSMWBg6IEYcXUBTzFMsJUxfgF+wOlhV1FscSxwz0CiQMKw6iDlMZqRQrCnwWPRfDET0XDRQGFFAWFQ7VFkQbUxcjGp0XqRR1FPcVwxVTFUwR2RN5FfoUCRUkEAIR+xCiEscOKxAYFVAMmwrADKIE6QOEEKIQKAk3CegN5QZ6A8YU5BBUBy8NHQhZAOUE7A5XEI8LtA/sEpQE+AeaFowMjwvKEYwOTQuECmoJLAThB0EOuAy4ClcQ/wtNA7wLbgraBZ4JFQqmBZn/DgRNA7IAkwaTBjsC9ACpCiEFZfkWAvcJQgiqAKkK7Ajj//QImwiJA7ECgQsi+0v+DQ43AToGGQOTCA4K5QbDDUkI8v9P+zsCWvy8BbQNWQD8AGcAUQIOBIgF/wdD/t/6RgEAALEEXAt2CGQBKAWmBZH7rgMzBPsGiAkdAIUExwb7BP8DWAIzApMG9AT/BZMK6QEoAQILOgquBWAGtv90/R78Zf8VBgcEXwh2AC3+LAR3/jsC3gKZ/+kDqgSfA/gFwAJH/28EwABp+jMAWAIf+mn8jAiBA8AI2Q04/2ACyAJRAA4AOwC4CisIKAEM/28CFgJ0/W4ILwuK/U7/UApGA1kA2gmXAzcB6QOO/oEBIQEHAtMFKf/PAEUJ8AWqAs8IfQIx+UYBUQbSCbgOqQxVAU/1SgCxAmX/uAjtBOUAkAX4B00DLwsOCH4AAwed/JsCLAbU/58H3gAb+Z8D5Qao/QT/q/5d/R0E9ACo+cn8Wv6Z+6j3Lfw1+nTzsgCk9srskvcAAGH+bfHZ7HHsJ/J48hv7Jvi08BD85PHO6WL0vvul8ETwg++/54f0Mfes8qHv6/N08+/scfJ88crwxu8N8dnyrPCK9cruAuzH5UXsNfia4+/sI+8y6YPvdeuO9Lv0v+0+5MPq5eW/5XH0Qeu464/qnuyl6EjpSPFm6yDowONU4vfkH+737GLqDenH6ZLvouXW4Q3lDeW/5UXogOT03eHmYuo+4trix+MV51/lot+x4/ThzuNj5GPgfeGA5CTlPt652+HeeeAr4Sfmfecc4zPjfeFY38PmauZY3zrdbt1B47/n/uzH5wbhWN/l3fTha96Q3jbmfeUO4fvphOfP4frvVOqt3F/j6OTw4HbhiOKw6VDp/uo570Hp4d5B52Lw1uXg7Jnz2PQN67DnHO3z6xzvCehB6/bwu/Ac6crwj/Cw64749vIY6t3nAfid7lfrf/Sl8PPxIOj28pbwEeof7LPyFPVI7Rv1h/QC7uzrtO6A7rf3/fbv8Az3bfVq7sbxe/v28J32Lfoq8Wn2uvxT+ALwnfjC/Ej3afIF93/4Bfn/B/QKRPZM8toDMf019Dj9Mf3R9pX+vAO+/+f8/wk9EQsBWvz7BDoMcgWMBigB4/s6BkUPNgs1+psExAfwCccKeQdqCWsFeQf1/iQIrQkVDN0U3gi4CF8KUQj/CWcG1wCTClwLxwhXEmITZg46FFsV6A+pFIsQ3RCBC18OnhV8EjIaixRbDxwQixKxDrQTMSbgIQIXpRPwDd0KsBZ8HF8S/wtBFAkVkw6WF+MgkhxuDGMPlw/4BcYUJxtfFBUSHxkuG2MRLxFBFAITJBBMFdwa7xX+FYAXdRZXGL8UBhDKFV4aVBN1Eicblhl4HRQggxiAFSgL0hEyFs4SXiD6HjkYzhjcHAkXUBKDHl4exxL6FHEbERX6FEcijh9fFC4d9hk+D6IQ1RqOG+wQ0SHNHkkO+hjrHv4TXxR4GegNcg2sFXwctBN1EP4ZSBa8Df4RcRErCjUZbRQkDisSdRQ6En0KgBHzDhkNJxEcFuELjwvSEYwMUA7DC0EQIA99EJ4R7xPlDqkOfBa0DQkV2Q+iCBkNPg9uDMQHrRM5GkUTHAxnDEkKxxC4ErULmhj2Gf8J+wrpCfcJCRVJECAL8AvlDogRVxKmCUIKVxT/CVgM+w5bDdYO+w6mDccGDgwZCVwFGQnABkoCiAvsFJsGWAzzDqv80gebCqYFdgpcAxIH+whNBfcPEQ279ED9xw5yA28EfQ70DAMBwAIVCn0GywmpCv3+PgGJA/L9SQ68Ca/9nP66/K4ByASFBmoJXAdo/uwGJQDN98ACjvqo8/L1MwDlAOP/HQbeAEf5MfsLART1TO72+lL67/ak/iQCT/v29uP/CfZx7hvzyfpL+mbpzfnQ/qj3S/ob+7Dx/uYb/dD8I++78msBCPz67Qz3XvPv7FDtf/bC8p7qF/q+/+P1CfYI/KXyDek58Wn0xvFE9uD4+fsq8xf4Nf4f7qXuOfXv7ovrvv/Q/B/64gNt93j69vSs9GX3sOdb7mH6YvRt8/L5Bfcb8XHw8vPc8y7y2PSS75bwpP7k8wHyH/p48EHxZvEF9f7yGPSz+I7yH/YX+gj84/dE9C36BfmW8rr+5QQX/jcFMwSO9rP4vvuh8y38Lfyz9kD1EPgHBHoFLwftANv/3/xW93j0dPGs+JX6p//G9RTxdgB2BAAAafob+eP3fPNx8in9F/6d+owG/ABx8gj6gv8x93j2BP1T+OD4CgMdANT5qPnTA476LvT0BPL94Pgb+TX8Vv/5+XD+7/Y97jX2Mf1p+ED5UQBd/Yb+0PwM9eP3LAC3+wH0OPsi+RT3Mfv69773XvdgACEBSPUF89T/MwIF9ZH7r/2z+ib4WvpP+3jwq/zTAbfzNfDF/wcErPJT+NcAyvRt9Wj+afwb+Yr5Nf72+CPznfpa9vPtePge/IvzCPrtAEf7jvZ//sX9DPf9+hD2SO+h8V73e/kb+6T44/1l/6j1xvlE+Lf12PQY9ET2uviV/Gn8R/0m9gn02PxCAMb5T/kX+qXwDPV0+bP2NfzTAeUAEPZw9j4BKf1CBFUD2fIf9jH3f/pyAcgEfQT/A8QDcP7c+yr3HQSQAUjz+AGuA9D+1wCuAQsBCP5S/kv6t/uqAkf//fad+GcATv+n/wz9g/P699T5EPrN/c37D/50/zX+h/hE+OP5Jvwt/LPyIv0hAQH2BfcF+6H1I/PC/Gz75/p4+pX4DPOZ8w4Gmf8q+ZX4s/Tk81frAfZl+e/01wDy/3Tz3PWQAY74MvMm/hP7bPtL/s35pPpP/Xv/t/mH9KT4Zfn68xD6q/wU+Rf+5/ht+Uv8S/6O+E/zBP+o/bP4KvfJ+lftfOuD+wXzbfOh90f7EPZL9Hf8VvvG93D4Af7R9pn5Afi39ZX8LvhA9cb1OP/2/KT0yfZgAPgBdgA3BS36h/S3+SL7J/Ko96IGd/xi9lb/iv099kD/UvrV8YP3vvci+S70jAAGDEv84PZd/xf8GPRh/K/3afJL/Ov7nfg8+IUAEgH2+tT95/ry+Yr94/ta/K/75/qbArkAH/hh+r77wvpO/zX8rPQx9Zn7f/4f+IP95/4u+CP1MvOK95L3BP2g+aT2WvLc90oA7OnN8W31Yu5A9Ujz4/cQ9nD4VvdL9Bf4KvuZ9+/ySPfr9/34F/bR9jn3WvZ09/r1RPr2+ir7QP3Q/mn8tv+uAaz6Wv4x+474S/44/XYAxfsm+lb/Lf4vBYwCoP+g+2X9ogTV99v/qgbpA1EGbwLlABP7bwKQCf8DOfl7/RUI2/9NBaYJuQJ6A5cJvAX1/q0LkxAgCQT/vAP7DCEFHAxYDDMCHvzIAMsP2gsgD2oRLwsgC9kNFRDwCdoJgQeMCNYGlARqDwIVQRRqC30KGQ0NDjYNsQoKESQObhJeGuET6BNfFDYPEQ8cDpcPUBZIFicbhx8CFZ4VfB5pGbgWixzgGZoWAR+VIcIdHxsuHWkhpRVME7MhnSMFHKgeiiCdGYMi0SFtGBQYUxfZG9UW2RekITEiOR6ZHBAdJxnkHNghoRaeD50bfBp0Gm0iLh9HIiMcGx4xHlsVgxylHecd4Bk5HmUewxdLH2UeyhknFTwhaSHoE50dKiLCIWYaRCEMKOgTixZPIGYWKwyhHI0rUx36HJYf+hTWEOgZlh2oGmIdGBvoFX0OkhY5GpoWTBttFvMS4Q+EFl4YeRMYExwQ5BACGU8aiAlxD2IVcQ8CEcMTmhgjFKkU6xaeEfgH1RQmHRwOhBa/HOUOcgsFGFsZKxbzFsoR5Qp5DbsT2ROEFA0QRQ9fCGMLtBU9E4ARZwjLB0kKoggVBsQFGQneCD4JuAoNDiQIBwaQB6D7ZAENEJcHjv79/qIKzgzaCQILd/6xAiQGQgb4B9YEPgdUBw4GEgHaBW8ExANJBPn5YfzEBz4J+AXwBbkAzf8B+Of2ivtW+/b2qPfaBb0BtQNw/o74Jvqk9If2PfQt/Nj6f/rR+tH0Wvyo98LymfMX9h7+OflP9Sr5s/hH+R/49vox9173H/gv6CfswvgB+vb61Pv28gLwLvLG77vu4Ow59WLylupt7Qj46/fG63zrIOp55KLffO3K7LHlAfKS79noNuTV8YfyOuMk5bzoL+aI4M33GPTl2anrjvJN5Krfeeq76kXkv+cV5Y/kV+fK8mLubuN95bjj8+UO3yDgx9863YDs6OJy2jrlOuHE3EnhpehB42vc/+JG3OXXWNsZ4g3njN9y4m7fANVY2W7fiNza2GPeseVu3Q7hqelr2jPZ/9wk3aLbM93a3n3b5d/e1/Dc0t5G2sTaz9Vc3GTWsdlF4Gff2uC92CDegdyf1lza5dfE2BLY/9ow2CHYhOOi34TfM91Y2RncwN1u4ZvdMNqq3U3gm9kK3g7hQt244cviL+C82svkreJG2LXgAuYG4fDenuhU4rzcpuRf6bjlSd2l6LHlkOBE8uzp/+JQ5WLswvAn5P7u7OtU6PrreepM8Fvutv9X88/fx+nV63Hu0fJL9lfvePIQ/I705O3u+NT7X+ue5rDvsPNe9XT3Afbn+M3x4/Uf9l/rF/hp9hTx5/bj+yb+5/iV+GX5cfTr9+76/fry/wX5AwGQBTz8yACQAw/+8/FL+tcAUv6fBW4GqQqmB+EFOgi1ARf+WQBgBGn6egHWDg4EBggvCZ8B7QIVClwJGQG1CWMJDgb0CBkH9AZcBd4G1gZNBTMGSQjsBhUGwwvoDxUMgA0KC9cAlw2aDn0GuBDOEJcLGQdnBvsIhBDsFGMNvAkZCUwRtA2eCwUWBhCLEi8NAgsjFFASqRTsDF8IfQzDEaIQpRMnExkJKxaWFYcTMhjSFSMW0g82FZYTvxRaG6kWIxieFRwQeRH+F78SNhPcHBAdFyG0F3wS5BahFlcY3RYyHNUW5BSAFeELTBOaGocXERfgGcMRfRBiG5IYKxCaFiMcSRCID3UQvxQFFkUPrBW4FugXrRNuEKYN7xNIGFAKPRnrHBwYDRilDwIVjxHKFbsV2Q02D9kV9xVBDFMXpRcCFegTDRAnFxwSDRhfEpoMdRbdDFsNYhPzEiMU9w9mEDYT5BCiEtkXcROtD5IY5BAVDFAWzhIVEr8S5BjzDiQGaRncGLgQFQ7DE3UUTQupEBwScg2pEjYVqgifB84SBhRMEfMS4RG4DOEN0g+4DJoMXxK0EegNAg2iDj4P7xM9GToSCRWhFG4MWw9UEc8K8AMcDvMU9AxNCxERhAwVBnEPRQ+iCkEM5QpnBoUAAwkrDK4FlwUzBjz+nfgZAx0EbgpnDE0BTQcrCE0DAwFrB2MJr/3XAKMCzwAzCmcKEgfLBU0HNgtnAlb/uApBDg4CcgnoDef8xwhqC3f+TQHEAWACgQVCBq4Ds/70BKIGg/kb+6YBRgHf+n0CUQDV8ZsA0wWz/Azzwvz4AYP7IQOR/9H4AfRl/br8Ofev/e78pPxs+9z7Nfju/noFXf369wz5F/xd/34ADP0p/ef8f/q79l73zfki+wj8oPvY+mX7e/1d/d/+Uvrc94f4S/qS+e/2DPmk+qj15PEsApH/afY1/BD8ofcq+2sDwvYU928AZwBl9xDyq/z2+nv5ivvF+wH21fVP93jw+vdNBf8DNfQb8yPxeO4M+Yf2yfYX9u/0NfoJ8qXwXvmS9Rj0H/ZI7zLth+4f9P36t/vn/Az7TPLk6dz1V/Wh7f36mfuz+ML09vxW/zLzkftL+hTzOfdl//X+pPrn/Nv/IQHJ+mz77v6s+Dj7JQB7+3T/jAJA/zH7pPwHAMn+/f5W/3IFyf5a/t4CbP9e+0D5/wM4/4b8dgBJBKD/Iv2qBq/5T/tRBH/+vvvF+wsBxf88/B0CCwF3/gAAe/kM9eP9NwN0/W4GVQFl/Q4CR/s1/rr6qgBCAm8CrgWxCDME3/zhBdT7Yf7xAcgEzwYp/YUE4gPwA5QCjAA3BcsDJv5NAywGNf5CAowG9AZrBbUBGQFh/P36hQaJA5AD8AtUBbIAMAEvB0YDDgJVAdv/3gL0BAMJDP2C/ygF2/+G/lwDIAn0ADj9wvwp/wMDcgPXAlkAH/pw+vwC1Pvf/v8HF/oF8wH8YAJVAbUBNwEi/Xj05/T0BML+MfmFBNcAmfNA8yL7cPh//rkAyfyH+GX3rgEzAEf5r/cX/Dn5q/6G/Pb2SgBl/3f+LvYI/okDtv9p/HzzjvrN/SwChQCK+zH7mf8OAqz6oP35/Y765/xd/139lfrn/s8At/fc9xP//AB0+yr5xvm78GX1pPy++2n2cPxW/WnyIvde97f1qPE19pbwnuq+9474VvlL9or1V/Mc74f0T/cJ9EDzg/HH6WLubflh+gX5Mfcr7Yfsu/CK9cb3/fYi/dH2gPCH8IvvSPUX+lrycfBt8wz1Ofdw+Lr8f/SS79XxivVF7EHv4/mS7xT1ePT+9Lv26/OW8jnxxu9E7v32afR7+ef0yvKh97fxFPVb7nHu7/Dv9NH4rPQM9zX6Xvlx9K/5kfv29Pb2i/M58X/4h/h09wH4R/sq+xD4ePYQ9Gz7vvt/+tj6R/tl/az2bfP+9Nj8RPp88+v5F/qZ+1r6vvm+/S72bPtW+7v0LAA7AoP9q/z9/qYBoP9e9bf3QP9P+Xf8qgLaAz4BRgFW//gBvAV6A2z/R/uk/Fr4PgHiAWAAjATf/FL+oPmz+MQB7QBS+h0Azf3Y+noBjACg/4b8XAPy/YP1T/lp/HT9cPjF/bkElAJCAEoCmf2v++UClAIe/ogJBgrj/e0APPw7AFUDfQa4CGj+lAK8A5QAjAJQCh0KlAJGAcsDRgN7/3IFogj8AowGkAl2AJn/BP/EA1wH5QblCh0GjwtuDm4MqggKB88ILAbTBX0E+AfpB00HtQlqDSgLngs+D0IKegNZAPQE0gfzDvQImwQZCx0KgQUi/zsE3gIsBAILjwtrAcAAvA1+AJn5FQRrB5QCxANcCZABCwHlCsAIkAEOAvEB/fqK/+kJsQRCCtYIhQDn/lb/UAzpAVQFuArN+TcBkwyTDE0FIAnpA6z2pP4kBjMG3gKQB+wIjvyXBVcU8AchA5cLlwkDA88Iwwl2AugLKwzSB2cMUA5qCUYFHAyaDnIL7Ay/ElQHawViFQIPvAX7DO8RMwhUBSgJSQjtBF8OHBIoBXYGUQbWDFEIEgHsCvQM8AtrBVAKBwbY/sQDxAeiBNv/BhAZCWX5PP4RCWMJgQFjDf8N6QEWADMGUQR2AIQMNwntAEkMVA2UAib+xwb/C5QEDRDwD7kEdggGCFgGlwOEDowMtQEKBXkHRQsSB5AHYwNYAnIHjAa4DOwIMwiMCG8ERgWFBpcNGQeuA+gLfQbaA7wJEQ9UB4wC6A15DZsG4QXwCWMDWQD3DeEJ6QERCbUJmf/0AKII6QnhBaoEGQtkAXT9gQXU/7b9jALEBWACkf3/AVQHgQPj/U0BYwNrBVQLrgXAAED/fQKiBkIA4gOYAZcFfQis+hUEpgueCT4FkAMdCmsDZf0gB+UIbPu8A2cIVvsZAQoLuQT2+Fb//weG/qj7Qgj7BL77uv5vAAz9dPszBrIAS/h//qv+3P1L/CwA3/zJ/JAD9vzU+ZH/UQSZ/S38E/8M+Xf+LABW/TABf/5d/777Jvi6/kv+Vv0kAq4Bg/3b/zj/SgKqBLr6vvf9/sgAMftjBbgIuQCUAND+cPou+EkEMwK6/vwCDgDaAyL9LAIdCsQBjAD5/x78Xf3eAmj+R/0+A3IBp//f/hYC6v/J+pz+T/3Y+qv8PP7f+jX6CP6v/83/qPn1/q//e/nj/V3/Q/5l9fL1Uvru/H0GxAfLAf32e/vn/kDzOflkAbr6RPZw+l398v2mAQcAf/oM9c31oP01+qz4/fwf+rP4T/s4/x0A1P/N+xv3jvo4/dH6lfyUAHT5t/eUAk0BZf3XAIgFlATr+fn9egNl/YP77v4T/2H6CgWuAwX7kf+QATMA2PhcAXoBT/nU/xYCbwC+9f36CwG39Qj8xfvR9oL/lwXaAwz15/qBA7f3OfnN/ZQAAfwZATMIbPvJ+psEqgSk+N/86v/N9dT7pgFJBPwAegESBxv9XvuD+6H3+ft/+u76MfnF/3YCg/c1/Of4T/fr+fX+dgC+9Xv9wvzg+Az71P38AOr9QgI8/OP1AfwwA0f/NfwSA3f+yfpS/Jn/r/21AVQL0Pyg/VwFg/u3+9T9AADN/RIB6QM4/Yb+QgDu/vL1lfyfBZ384/vb/+0Af/yz/Mn4Mfm5BPgBPPoF+c39d/7aAX/+G/dCADH/EPqo+7b9MwL0ABkBBwCK+7r+OwQb/0/55QBCADH9bwLLA6MA9f7aA9j2CfY3BdcCJARvAFEASgCk/hYCxf/lAKoASgC++88CawfC/gz98vmbAFkAXAEvBa/9IQOK/9H4sQLdCuUCyfibAO0AAfrn/k0BdPt7/a4FF/yS97UF6QeG/h/4dP96A4UAPgNw/kP+F/pA/WcGRPo4/RkDt/uO+rUDxAObAAcEBfvEAYkBhv61BU7/qgCjAh0CwvqjAlwHJvpW/1wDPgPwA3YGhQDQ/ML+kf1GAZX+jAJYBBv/ePp0+wcCoP9h+uv3dPnc+Wn4EPyUBCb86/csAFP2mflNBYUA1fc99tT7mfmO+OUCowBS/HIBRPwi+Vr8uQY+B+0AEgMT/Uf/GQNNBfn/MwCeC+P7vvm1B4EBVvdGAcsLR/vj+yQIZwLu/Bv9qgYoAUD3MAOK/WL04/+FBsn8e/v7CEf/wvwWAhkBywFL+psEmf+K/WMF2gFNBRv9xwaXCZgBuv4B/toH0wXHCNT/9AKFBv38xwhrAyEB2gPAAur/ivuUBIEHywMWADsE+AFS/mj+AfxVARf+WAJnBBD8EgPPBsQB3P34AQ4EBwJRAjH/5QZyA1EC9ApA/yn/3gCjAIUC+APlCAoH0wV3/hkFXAU3BaYLyf5vAq//G/0kBEYBsQb/B5AB9f4M/TX8mwJrASQErQlZAIb+LAAT+xf+Qgb0Ain/MANCAB/6OwQKCZ8BDgD5/yEDsgDLA6IIogRKADoGFQSH+DoIsQgSAYUC6QEhA+P9vAVCCukDr/8ZAzz+Iv+xBowE7AZVAcX/egHWBlwB1P+MBAH6tQGjAg/+nwXLDbkEdPmUACgDGQO8A4kD2P7j/5H/YACfAR78FQaICS38yfyBB3/+yfbR+qf/5QIZA8gCtv3r+3T5G/26/mQBtQVKAuv75PNs/QMDIQEOApn/LfzN/bb9f/jXAOkFCgX8AMX/5QT7BKYDJv4x/5QELAJ//pn96v1gBtkN6QXlAEYFsQRRAt/8HQI+CUoAvAO5ALUBuAggCcsHcPjAAKMCU/jJ/kkG9ARVAfsGrgUWAAX3fQJgACb27AgsBK4DsQbLA4UEzfts/ZcD7v4t/iEFE/9UBZsIaP6MAt4EywXF/xv9kAdUBZ38bwLEAZsAdgY8/tz7jv7q/9j+6v1gACQEyASv/28EWvw1+KT+D/57//3+lAKG/Nz7hv4B/mX9h/gP/kf9pPw1/lr+nP50/+IDdgQ+A3v/hv48+LvyyfhRAGQBVQGR//38qP3F+0YF8ANL+pn7yfh/9o76fQI1/sb55/wB+v7yFPXc+yb6Mfug+Vb32PQm9C36yfiD9cn4q/y79HjypPwF+3j2h/ZX9TLz1fN7+QX5rPSW9uP5ofci+Sb81fPn8pn1KvUb+wj4yfh4+CvrcfJl+SPzXvmS+bjrZueA8D30G/V48qT0+vMn6ofyePbN9V7z2e676pfku+x/9OTzgOqa7Ujt0uzC9PrvdPNp8DLvDe/K7HHuFPOS8bzknuyA8GruOe0j753uEeaP7p7si+cu8D3ynuxm5XXlHO+06qXo7/Tz6drgpej75z7ik+cn7lTqBudM6qzs5Ouh9Yvzluq37R/szuvo7vfs0uyw8xj0Zu1q6gz3Vvsy64/uCPjr7zLrXvdE+sruOfM7AAH2sOvc9QHyI+/+8Ejv5/KS8eTxivVt95LzU/jR9Nzx7/YQ8v365/Qy8Y74nfik+Bv1T/2s+HD2jvQX9jADhv7tAND+mftVAfQE7AbY/Az54gPAAnv/CgnwBWsBr//C/qT+RPw6BnUMawfiAZ8HGQUWAmoLWALwAz4NlABW/eUIMwyxBIUI3RJVA0D/cRG4DiQG9AwbGkwPLASsFREX9AYnD+QYJAQDB+QawxHaCzIQDRQNFFsTcRNUDYEL4Q+hFKURYw+pFPcXcRPhCWoLjw9MEa0RdRDhEegR2RUFGJoYmhA2EbsZXw5FEScV9w+aGIcbuxOlD+gXyhvGGNUUUxVTFyQMNhOsGaUTyhkcGCMYKw5fEEgcTBNbF5MQ2gvoD6ISyhP3D4AXCg1jDf4PqQyPFcoRSRAzCNoHFRCEFHUU4Q89EfsInwVJCCsOPRG7F/4XZwDEA8sNDgyXDfANUAodAHUM2Q9UBZcLgA3eCFgIdQzACPcJ7AymBYUE0wV5C60LPgMsBmcKmwJRAh0K6QXPBm4MFQTc/UYHKwru/kf/6v2v/ZAFYAIsAlEG8AkWANz9lwWQAQoJ6QcZAx7+zf8kCGX/cgMGDMcMegMKA8sJBwI3BY8Nogq5BPcJRQmBBYgFYwemCR0EXwokDOwIUQblBPwC0P4vBy8Hogp9CjsCVAdqCVgK+AdrB+UE6v2uA4gFLAJyBbgOwAzpA9YGtQm/EG4OxwiiCFUDVAXHCNoJ4QUcDrAQ3gS5BOUGFQ6qCFEE1ghJBj4FhQK8BaoCpgFBDG4KNwGuAYwE0PyK/cgCmwKxBrIAQgJgBPL9GQmIC4UG+AdBDqkK0Py8AzoMvAcoAWoJbg6ICxgR0g1uDAYM6A2iCiwClwmaDGMFdgKQB9YKzwj3CYgJCgUDB5AFQgJrAU7/xAUhBTADEgVGBdcCVv1YAs8GbwIhAWMHZwKjAD4DQgLWBlwD5QYoA6YBMwg3B8sFlAAkBqYDbwCJA30GBwCd9koAe/9gBK0HzwRGAXv5KAGv+8b1G/st+jH1Vvci+0D3oP0x/zz6zfdM8tH2F/ZM8sL+MwBi9gz5HQDy90/3/fzy82n24Pbn+hP9hvrtADj73/oB/vb8Jvik/tT9mvFT+HD6F/xL/k/9H/iH8mnyyfi/8YTtxf/n+Bf2+vVA+0T8HO0f+Ir1h/K78uTzwvhP8SrzQPXn+E/3IvmV+ETw/faD+Xj6R/v9+hP/qPn69yr3RPTY/GX9OfOo8e74Mfk8+BD4DPd4+ED3q/7v9kXsnfbv9prtx+nc84b6RPQq80/zpeyw6zLvlu5174/u3PNE9ofsJ/B4+uvzU+x08wX3j/Dd7dj0qPUC8KT6PPwf8Bv18vsj9anp8/H5/Tj79voT++v5HO+s7sruyuhA9Qz55/qO9k/zafry9ZbwPez673HwxvMq+Yr1f/jn9Bv1QPUN8aH3F/ah77fz+vcm9m35DP9e+6z0vvkx+XzrS/S9AYP5ivdCAJn7SPOO9mX7kfuL77f1NwHC8rr4kAGz+ET0r/ew9Xzte/th/pnzFPe3+WX50fp4+Cr1pPyd+Bf4G/lA9RkD9AAx+6z6E/uo/Sb+UQAx++UEIAlE/Kj19f7IBEf5bwDtABD6owI3AdD8OP12AvEBYfxh+jn3G///AVb/uvoF9Vr+/fx//JX8RPxl/6D5ZwAm/PL50wGZ/xP7QPug/6D9EgGD/Wj+QgI7AKMAvvvy/bUB7AYoA6j9OwJnBjMCMf03AZcDzwhrA1b/qgAWACwGogRL/vn9Mwb/AQH6aP7lAGMFtQn/BTsCr/9yAQoD3/zy/9MDWATeAOIBaweO/rIAFQimB9oDjAT7Bs8ApgFjBSQIuQSjApoMqghCACAJuQYB/lgErgNkAUIIjwtJCvQEkf1KAIkDuQQGDAoJ+f9W+8X9kf+uAZcJawFCAuUGe/tP/bkAuQZ9Atz9WAT4AR0KhQZVA+0AKAFnCowAegMDB30GG/2O/lsNIAeEDCsM8Ac7AMX/ogoVBjYLrQ21B4b+awH3CeUCBwSBB5MG/AJVA6oIvAl5CeEFRgU3BbEIjAjb/28EDga1BxwQtA3pA70BQgj4A1wDpgcnD/APUQbDCVQHWAQOCOwI8AOFBOEJ0wUhAyEFJAY7AB0G7AifBYUEUQLLB1UDwAa1BcL+nwHPBIgFegH0AsX9VAUVDAMBFQT0CtoDlfrXAgoLQgh2Bn0KHQo+BdYKWAwm/Dj9Og7EA0f/5QqXDYwEcgVbEYUCbwBbDf8Hf/7PAHkJ4QVUBVQJsQR3/AoDhAwSAfb42gfDCc8AxAd9AoEDSQogB0IIvQGo+w4E7Arf/ssDxwru/GsB2gmUBE0BIQNNBTcHbwBgAN0KRgeg/0oA1P+n/y8F5QJE/Bv97QLj/83/GQVyATcD4gH5/cn+ZwSG/rr6tQUB/tT7PgFs/3YAmwaxAs374/8Q/DX+Uv65AmcIoP2K+/X+Jv7U+8AEhQSv+6//bPvc+/EBD/4x/yL/f/x0/4r/E/84+4b6Lf79/oL/OP+8A3/+R/kE/dz9kf12AOIBJvQB9msDSQTQ/BT3WQDQ/Ir5gQFnAF39yfyFAtoB2PhW+88E4/t0+doFp//u+HT3hv7XAmz/fQjwAyr3vvemAW8C4//IBOID8v+d+IkBe/948jX+YAK2/478YAB6BRIDWv5S/t4Cf/jF+0D7G/l7/4r7jAKr/g/+zwBE+u74vvk1/r73e/mFAvwA5/rC+Jn7RPiZ/ZH72fIe/K/97vwE/9H4T/v9+uP1Vvur/t/62Pru/r77mftGAXD8bP1L/qT0E/v5/5H7zf+5BAz/9vg3Abb/RPqr/pQCF/7V94L/3gDF/Sb+6QPy/R/yCP4x/zX+GQX7BigBH/TG94b8cPi6+EYFSQRW964BMAEm+mH+iv/Y/hT3ivlW/+7+wv6k/g4C4gF+AJH/nP4B+kT6Af5t+az6oP+1BT4JTv8i+777Kvez/CUAxf10+Tn5+ftw+Aj+QgIP/kT6cP5e9+v1vQEi+8L4u/ZL/r79QPssBjH9LvjG+cL8CPpP/S8FTQHy+1EAMwJm89j8HQTj/Z38hv7sCJX8lfwzCIP71PshBaIEmf2s+u0Agv9S/ML8IQW5AuP/CgVd/bUBHQCBBVEIdP0dAtoDPP5A+WsHZwimAy8F7QCg/wX76QX4B34A2/8DB4wGE/1+AHYAE/1s/U0BqP1//toD6v++/WH8mf2FAOv7cPjn+kD3yfpgAEf/QP+R+yb4Bfsq+w/+ZAG2/af/ePiz/AMBmAFyBZ341P2C/z4BiQHY/kIGlwNrBzX+rPqXA5ADQgIi+ZQAWApA/2z9rgO6/mX7NwV6AeDybP8+Bbr4r/v5/ywC3gA4/a4B3/r+9C3+8v+O+Cb49vxP+a/9e/9P/dMBawHj/472mf3f/qj1g/2g/wH8afxVAW35ivnTAeUCyAB7/cAA/fxL+HD6ogYZBRD8f/yK+VL+MwIAAB7+Iv2k/hYCOwJcA+IBlAC6/or7pgHWBMQBNf4KA34AYwN2Bgj8xAHAANT9JALJ/pn/tQXPAIb+MAPEAf8Bzf32+L77HQLN+xP/bwQT+wj+Nf4E/Sn97vxh/Or9oP01/or9qPUWACwAaP7tApn9xf9L+l77LABa/rwDrgGZ+Qz9BwTN+Vb95QqbAIUA+f97/bb/pP5jCxIDQPmxBvgFBfu3+QH+CwHAAv8FbwTJ+kD/UQQb/zsAqgL5/U0FBgjn9P38vAdJBGcC8vvj+fb4CgPHCgoDYfz4BdYEH/hCAD4DmAFjBUICNfxl+94GSQby+ygB1P94+pX8pgXeBvn5mwIoB2j+FQQKBTX4MffTAcgASgL7BHoBKf9p+p386QMoA3YGrgU4+xf4JvxnBOUCnwNyAYb8xf/Q/BkFmwZKAMgCDgQOALP4mAGfB2z/bwAdBF3/cPyMAnIDUv59Ak0HRgVW+7P8PgMm+ib+DgTlAIb8F/wX/qj7awFjAwj+OPur/Ev2F/59BHH0hQDHCED/5/wM+6D7F/rn+Kj7+f39/CQEhQKD92j+iAdCAH/4Hvw8+tH22/8dBlr+Q/5yAWH8cPwT+6j9Uvwx/SL/h/Rl/yQER/3EAfn5Vvcx+/38D/4B/L79mAEzAJ366QGfAa/3S/ot/jz+yABjBaoAVv//A7wDHQB9ApMG2Pyv+x7+r/+xBGsFDgiFAEf7gv/PAJX8Lf6MAib6G/2D/Z32Nf5vAMAC4/239ZX6g/Vt9e76RPgJ9q/5BwLU+wH23P3XAhT3RPbaAWn0PPgHBP36F/oOAv8HNwHR+mX/5QYi/6T+HQbg+Bv/iAdd/wz/3gCbAmcA+AFvAC36xvmz/noBvvnq/1EEnfxL+kf5zwAq+ef4IQOg+/L3bfksBIr5Ivc+BVr6UvwoAX0CcP66+hkDqgI4/8gAnwGR+3IBrgV4+u78+woDBxv/UQieCe7+3/x9BvEBMf8gCW4IHQDj+2MF2//2+g4GNwNl/+kDNwVE/JH7iQMDAY78IQGBCaIEpP7IADX6NfyxBGsB1P1NAe0EcgGxBp8HLwfSCbUB/AJKAowCYATaA+UCogT7ClwFXAk3CfADOwS3+4UCIA2FCEYHKwhjA3v/rgE7BLr8IQOxBoP9Q/5nAA4Iuv5W/+0ET/vF/00FUQb2+OP91gR3/PL/awNYAq/7EgFl/9z9rgPaB1gIHQKuBRf+d/6iBssHnwW1AwYI+wZGBaMCpgd2BgcESQrPCIr/1wJJDC8FnwMdAi8JPgmmATcJkAO1AToKTQ2xAu0C7AhS/kP+pgdfDHoFKAeiChIBfQL0CG4MwwmmCQYMFgByA0EM3ggsBpsAXAMDAekFCgnaAcAEcgcgCWX9PgPaB6v+mAHAAEkEkAGjAqYB4/+d/JX6uQaO/n/+TQVjA3oFKAUzCO7+e/uUBAoFNwM4/2MFdghvAIgFWAimBbUHJAjTBT4DcgXSBygHZwjiA2cAPgdcA9cCYwtYBlUBcgVyBcgCqgYDB0YDxf/AAj4FhQIrCtoLsQIzACL/2PwwA+kHfQiqBIUEHQqJA6YJ2Q8HBKD/BP8i/TH/vAdfDjMIcgNrA+r9Wv7IAtMF/AJRAGcC8v+6/t/8pP70AhIBYfh7+d/+e/t7/UD94/10/Qz7mwBD/or3fQLXAof2lADEAwT9q/4zAOP9H/iv+RIB4//0AEkIEgUb/Qz/5QQm+OD4xAMQ/KT6LALHCDj70fodBIr75/rAAJQE1PvJ+pX+PPgX+GAEkAeO+qz6pPyv+QH8VQHLA7b/mfswAfQABffEAdoJE//J/owAJvgdALwFdgLLAwj4QgDSB7f5OPswAzcDqgDpAaf/aP4HACb+F/yG+hv5Yf5s/xv5r/8WAE/9dgCfAVL+f/o7ANH6RPgM+4P9RPzG+RkFr/14+ib+mf3N/7r4bP97/+78UQQzAr79PPw4/yr5afav/70BWQA8/Nz9PP6v+aoGbwQB+Mn8lfwM9evzOwJ9AnD+OwJH+VP0wvgsBKYBqPV799T/UQLf/KoAzf2k9pQAG/39+JADQgIOAuIBPP5s/Q4C+Af8AHv5bfnAAEv+1P86DB0IoP8OAP8BVvd4+AMDS/wm+qoAd/7y/cgCoP/y+0DzivWMABf4Nfh//GL0g/naAdoBr/tA9bf5ivUU9ev54/sDBWAEafhp9uP9s/oLAZH/yfgM/Rv7OwSyAMn8nwPIBNz9mfn1/sn6BP8AAOP90Px0/y8L2P4j9ev5VvnY+sb5bP8zBC746/lGAcX76/nF/6MCZfmH+HYAe/14+IkBLAav/b75vvujAGX/vv+mBX0C7QD0CLkCpPzIBEYFjACg+Rf87v7j/bkElASc/kIC1ghO/6/5E/+C/3D+zf+FAuUA6v0p/7IAdP2g+ZH7Mf+z9nv3lARCAqv8BwAHBM39jv43AaD9tv3r+zz+wvjC9kD/nwFH/Vr8BwRH+8bz4/8OBEoAmAH4A779IvfC+Dn5T/vY/DH9Lf7Y+q4BlwMq+4r94/94+mn4jvx//F39RgGuBekDrgFJBmz7u/Q1/CL9Uvps+4UCDgjlCAcGowBP+7P+G/8F+83/4gHEAaj9e/+UBGj+ywEzBG33ofUb/5ABTQMdAhkBdgg3A833R/tH+1r6wv6++8gETQk+AfEBhvxe+Zn/ZwaC/9z5sQJCAssB1wAVBPsEyf5RAiL7ivvIBFECwADtAvgHywHn+mn6kfta/tT/7QQb/Rf+2gcb/fb6gQEe/u/23PfF+/b6WALpCUYDkvnb/zcFIv1l/cQB8v1p+GsBvAnN/7kA3gjIBOkB8QHj/Q/+zwQ+CcAG2gMVCIgHUQJh/toBeQkzCAMF8v3q/csDfQq8C1wBQgTHBk0HDgQdAE0L8AvABAT/ywGFBJQChQj/BRkHzgwkBuIDCgf8AjcBYAabBPwCFQaXByAJSgKfAf8D/f6jAsACPP4OAPQG2gXF/woF+AeUALIA+wZh+hf4nwfXAi3+ogq8C+UClwOJAYUAs/5GBXUOGQNuBgYOSgIt/KYHIAkOADMGuAjWBBUGRgdvAjMCZwbEASn9dP/XAtcCIQUOBGj+S/4+BQT/I/E4/8cKDP3y+wMFS/50+5QCAwHg+J38HQZe+znzR//sBkIArgPTA6j5Hv4P/uv3s/KC/5QE9vi+/1b9Yfgb95X6BfcB9mz/Yfhh+nT30fbg9rf1f/xE8gHy0fbc9UHx7/RL/Nzxkvda/i7wnfRl/frxUO81+Gn8yvL+9GX/v/P67b75QPul7mX1FPmo83/08vnU/frtofd/+Fvq8vd89Tnv4PBI78bvcfJa9LvwV/FB8XzxS/aP7l7xi/P+6rDvw+4J8pb0LvjK8OjqNfQY7Gnys/Tg8lr2g/d0+cL0EPbO77v0mfXV8aD7DPtt9wn2V/Vi9An08vc8/iL3RPQ8+B/0sPVw+lkAXf0f9tH0NfZT8gHyFPnu+PL/LADn9m35BfX+9J384/mv+0T6Yf47Ao76/fzlAnIBzfv4AcX9pPbN/e0CjAb1/vQApgXy/RkBgQlrAb79lwU7BF3/8v9fCrUFuvqv/94Ezf1w/msHMAFl/5QCRgci/wz9dQzwBUf72gGFCOr/BwIDBZcDZwSYAZAJOwLq/WcGwARcAZ8FVA0SB+EHng8KCTAB8QEDCZsG9AIsBnYCmwB9BowOgQNrAXUQWAiFBkkIwAiECrkGIAcHBMsHqQqtCfAFjAjSC/sIFRB9Dm4OIBG4DqkOpgsGDuwSOg6TDu8VVA8VDrAQ3RDKE1QR3RQCET4NIxJbEdoLeQ1FFd0QjxGtETMMpgs2CycP8A2EDrgOuAzSDYQKwwt1DF8IMwwvDZoMMhbZDfsG/hHODMcI7xPdEk0LgA/hDyQOWAqtD3gZmhJjEZYRVA1UC8MThxP0CoAPzhJUE30KKw45FtIRAg8KCSQIZwo9EcsP2gf0ClgMtQtbDT4J6QdqDeEJlAR9BPQKlwvlCEkSzgxVAzoI1ghjBRUG2gmbCFQFRgWeDQ0QywUGDkUNDgDwB2cKdggcDEkMwAjaAx7+KAMDCUYDIQOQAcQFOgZNBcAI9ALHBqYBfPV0994ArgFA/+IBGQHWBA4AE/uG+kf7kf17+9T93P25BE0DKf2XB7gIvv84/VL8bfXJ/tYID/7y+1L+cgXTA231PgGJAwH0oPtJBEf7Jvao/ev5I/N09dT5t/kb8YPzofNM8hD21fEF9b71V++38xv17+w98j32gO7v8Dn5cPYY7jntYvJl90Hxg/cLARvx2e6V/E/1SOsx9/38GPS08Aj+3Pdt69z5PPoj9YDuAfJm8ffoH/RE+ML0g/Ex+WruGOhm8Z3uFPEn8Mb3gPB57C72SPOW8CfuwvL28oDwGPKZ96Hzi+3G97f7I/U59fr13PGW8D3yq/4f+vPxyfgM87fvs/Sg+3H0OfGK+Yfyi+9W9233xvFb8KzypfBt8aD7Mffo8Lfz7/LD7gnyt/tE9Ej38vn+8l7zt/WK/0T4t/PR+H/6ePjr8SL7Kf2R+ygBMf/69zX4DP0B9iL7xf3Y/HYACfTG+TMC2Ph095cDCwEY9Fr8Yf7y+dH46v0HArf37vhuBgMD/vJl/8sF8/EI+FQH3gCo+5cDNwW2/Yb8kAEt/tj+jAaUBFb/awFYBMX/WQBJBDMGR/3r958FpP7n/OENegNRBDYL1PtA/fQC0wPXANj+wACQASQGTv9D/pH93gSEDjcDkf+QA94IqgBKAvALFgI+BV8IE/8M/60JgA2ECssJeQk3CdMBtQH7BtoDzwa8ByAJTQsKB+wKIAuIB0IAbP9rAcX/tQufB6IE6QG+/5AHF/7lCJoMmAEzABf+0wMHAl8MOgzj/4wC7v7eAlEAnwF1DKIGxAWbBjME0wUoB3oDFgC1BWcGogYoC3IDOPtvApAHywOmB0kKOwSK/07/zwDIAOEHzgxGA9/6sQSXC3T/PgEoCc8C3P2IBWMJowAZBWcIuQBW/+kFywlCAqYBJAq4CjcFJAYsBEIE8AdYAigF/wXpA28ElwN9BDABXAcDCQcAU/jEAfcJ0PyXB/ALwAAp/ZH/wv5e8VUB5Qgx+9j6eQnLBbP22gfpAWX3afo7AF39afLHBg4Ir/9kAToGrgG39fgF9AQ583v7UQhD/n4A/g+QBRP/4gPXAGn8dP2XB2cKzwSqAjADBwBH/QYOxwjn+lUDxAHU/aD9GQtnCgoHCgX5+x0CMfuXAw4E0PxgBFUD6QMb//QE+f9W/doBwvjLAToGyAIP/rkAuQZ3/n0CWAJd/5X+CP4KAxP9YwXABiwAMAM3ATMCR/0oAyEDLfyuAf8DawFS+toDpgUU+SEB9ARd/6MARgUsBuP7Mf/aA2X7oP0zAPgBvv+fAYwCywHhCfgDZf9kAUIAKf9vBGcGQgJ6AQ/+MAFNAaIEbgyMAkf5BP10/8gCYwU7AnIDYwXpA+f+hv4SBc8ER/1o/hf+3Pc7AhUGq/4zAHIH5QSv/TsEVQPj+xv9/wWBBxYAhQZNBTj7pPziARYCOfnj/UoCs/quAQ4IMwYoAfL9Q/6D+Uf5iv96AXD8Zfnu+nf85/ry+8X/oPsm9lb9egG++3T/NwE4/6/9g/sT/Uv6FPkI+r77zf/wA5cD1PsX+sL6G/fu+mcEVAV//HYApPrZ8MsDp/9/+OP74Pa++Y74OP1w/AH8Zf2O/rf5CfSbBND8NfZCAu76pPY+ARIBr/ff+oP9Vv1L/HT/AwVa/nf+Nwdl/YP37QSbAv363Pto/oEBPgUVBPb6+f0SARv97vxD/rUBS/5D/uf+mffJ/lEEUvxi9mz7f/7+8mn6wAIM+8n+OwJH+Rf2Nfw8+Jn5xf2o+2z7UvwSAZ36qPd3/uf8/fbj+Vb/Mfvn/M8ADgDg+H/8wAYB+lP4g/01+qv8+AHeALf5LAJO/1r46v+UAGH8KvuxAr77ZfvlBmsDr/3Y+Mn8afrN+doF2gNP/UD9ZwI3BS3+HQJJBP38xf13/mAA0wGIBVwDUQQSAx78zwIE/bP8zf9yARIBYAJyCWX93Pth+qT8vvvC+B0A7vxZAED5r/n5+177lAJS/PL3t/Os+MX9LAAM/zX+Oga6+F73RgFe+9j8S/4SA6oAT/ntBE0FcPyC/9oDIQFVAfAFMwC6/IL/1wIT/7792gXq/5n52P5rBYwCDP+fAe769vodACUARgOc/tH4AwFnBM3/AwV9BFL8zfvC+qv+Bgj4B6YFWAIe/BP9uQADAaMATQUoBWH+D/5ZAL0BVv9rATsCZf92BLIA/fgb+28ABwBl/XoBHQRL/jn5ivsdAtYEdgRjBa/7f/qyAK4DJAgzBFQHZwL2/Lb/RgF9BrUDGQOmAZQA2gErCCEFvv03ByQGvQFO/1wB9f4I+mQBmwDlAEf/5/5//ML4iQHlAmQBkf8SAcX/wvwZA3D80frwAzAD2P44/2sB9AIOBt4ALAAhAXYCgQXTAToG7QRRAgcCYwOJAyb+SQYZCWsBTQGiBn/89vabAhUECgPAAIr/Jv4t/HT9uQAdBHIBuQJ2AtT/yf5S/hIDYABS/BkD3gKjAL0BGQPlBPL9rgPhC/8HPgc6BiEBOP1cB+wMLwdFCYAPkwge/qoCegOUAlEIrQl9AtcAUQjHBpAF0gdGB9cCVQGIBUoAhvz7BM8I2//5/fQCYf6G+qf/jAQ+AYr/RgPhBzoGAf41/vgFKAWv+177tQEhA3T/qgIVBmQBzf+Z/0YBKvdl/bgKFgCQAzcBf/4+AY7+kf90+9/6WvR/+uP7Mfc7AmX9tv01+vb05/wzAFUBHQCxAiL5NfS6/EP+qPtL/KYBNfr2/JsEywGfAQ4EFQhKAI78UQCxBBIFuQT/Aa/7kAGbBGcIDgII/hYCpPo8/rUDMwL/A9MFcPjV9+UAEPz8ADMAe/0i/Sb6lfy3+xf68v9d/9z51P2+/SEDuQJ3/Bv94/vlBA4C8vmz/mX/q/zPAOkDdPmO+ukDHQBe+ygBCgl+AKT6S/wU9TX4VAXwBQH67vj5+xD2CPpCAoP93PUE/V39OfVe+1kAzf10+8X9Nfpl9W35vvvY+or7IQMWACr77QIX/rv0Kf0kBOD4lvZ7/8AAuQAwAeUCkf2O9in9kf/N+XoBCgV//K/7kvXj+TsCzf03AYP9R/9nBPL/lf6R/83/E/to/lL6bPtgAiwASQbn/Of+QghnAnYCE/+5AO78oPtJBFQFtQGv/wcEuvry9xkD5QCO/DH/KAe5Ahv90wEE/Rv53P1s/779mf8b/xv9H/oQ+hYCMf9a/OkBE/uZ+Z8DiQNKAh0CQP0I+JX+LATn+kYDNwcB/M37Mf+qBg4GYARYAsL+SgA7AH0G7QB3/k0JKAe5BAcAs/5cA9v/+f2z/sQF/wM3AYEJhvyZ+3UMUQjeALIAlwWuAwT9QP08/jMC5QafBY7+r/2fAc8GtQdvABUEEgcGCOkDDPtJBvsGAfj9+iQGSQQhA0kG7v44+4UCFQbj/7kAEgfaART5F/4SA1b/JALF/7r8cPq+/bEEr/cX+uUGG/t4+s8E6v3c/VwHrgOV+lL+LAIx/8X7UvxcA476EPodAjcDXAOC/58FRPx0+QMBVv/EA1kAd/wt/t4ETQHPAFUD3Pdw+u76s/ry/yn9iAUdBq/9QgRCABf4Iv26/o78/wFnAqD9hQA4++f+s/54+oUEKvuv+a4FMwJW+X/+3gLy+QH+MwKs+ib23P3aAdH6qPt0/3/+uvg4+1b/Ivcf+sgAT/uH9gT/fQa6+uf6bP3N95X6G/tvAs3/pP6mA5X8wvZe9eUCNwO+/ZQE4gN/+nH0egOyAKT42gGQAWH+H/ar/JAD+vdS+iEFNfwY8oUAkAEq9UT4zf+K+9H2CP7j+zH3ofXy+zsApPa++a4BD/549tT7yf5s+4L/BfsI+EIAJQDN+e7+R/8i+9z9OwB3/n/+cgEe/C36MfuuAWsFQP3G93/4R/2D/aMAS/4X/A4A8vfr8Y7+PgPy+zMEzf0f+Gn8U/ha/JH9KAOyABP9Hv5s/W8AbP0dBhIBU/iR/fn9RgMx/7kCiAejAHoBRgHb/5H7Jv65AAz9+AGfA58BDgB0+0/9rgEt+h/4GQGV/gz7QgJvAOr/GQPN/yEBwvYX+kYDoPsm/IwAwwnaA7kCzwabAg4C0wNjD8gE9ACxCPcJ6QnLBXkJAwOtCR0K9AJNB/8F8AskDLwLkwZRBtoH1wJyB8AE+wiQBR7+nwcKB538iv0VBkf90wG8C2sBZf//AyAJjv6S988CkwZ3/uf63gSFAIP9kAX/B7wF9ADTBTMER/+1AaYDsQYzBtoHfQp2BJABWATPBEIEegFJBN0KdgozAqMAYweiBN4GcgfXAFEGKAdnAPL9XAPWCpAF7v5RBtoHS/6jAqoEyAD4AW8C6As3BwT/bwQsAmj+YwMdCtYGJAZgAkD/Nfz9+oEHzwbACOkDyfyIBekFawV0/wj+CwEoARP/bPs7BKv+jvgKBc8Ee/8e/msB+f8U97P86QEM/4b+QgLlAB789AKUBE/7uQDhCWX/hQBuCMgENf4zAiAL1P9YAm4KwAqICdMFOgqXAx0CtA2tDWsBTQdBDHoB3gBJBuwIBwYkDFgK9AKFBJ8FJAKFArwJdgAAAOUGrQcDCQMFVAUvBSEBFQSTCA4A5QRxD4EHEgX0CGMHBgpqDcMJ9AgkCisKKwiXC5MKbgaqCMMLcg0HBtIJvAvACtYMngvPCgcG3Q7ACNcAlAKfAXILQQwKD48N+wjaB9oH6QWK/5oQhxNCCMcKIAdJBqYLsBIcDlgMyw1nCIEH5QSIDfcRbhIyEDMOAg0oA7EMXwozCMMN0glcCZ8F0gl2BA4GrQnlBmoNXAdUBcsJTQlyATsA7AjaB8AG6QMHAKYDAwNcCVsNxAOFCAoJ2gHb/0IGywl2ApoM0gkkBOUKZwh2BET6E/21AxkDegHPAOUCgQEDBxkD2Pyd+rr4aP57+S36xf2++2H6/faR+zj7MftP+VvwrO7y82n6DPdE+rP+Afj28ofyVvnG9+fyH/bN9XjwZvMb+e/0qPd7+eDyMvOO+G35MvOO8nT1PfAQ8iL54PDr7yr3WvJB7x/u2fBE8tXrTO5E7tLo+vPG9XnqFO327s7pSeea6zrp/ur+8IfsiOj34pbqcerS6ujwV+le71Dv0uii4Yzl/u4R6jrpxuu77uHiY+YC8PPpv+818m3rIOJB6d3pReDs4wLq+u8j6dnqH+5J56XmseXh6EHpNuzK7KXmVOQV4+Ho5OnS7CfyNu5b6uHkOuUc57vqne547tnyMvEq7/rtDeui6Yvtxu8C6OjuPfBB67PyKu/27j3uJ+5e82Lsv+0q8T3sSOvN8dXxtOrG70Tuluof8Any7/DR7n/0yfYY8KHv3PG/70XsyvI8+E/z4Pi6+njyAvBL9tz1qe1A+/n7AfLJ9q/7Lvi77or78v/C9OvvCPz9+t3ndP2FAnTxBfMi+2n4qe/n+rP69vas9gj8YfqP6tz7hQB48rP6gQFh/Lf1Mf9S/mn0Yfx0/wcAyfY1+qoGlfz8AMX/D/5VA9/+lwOJAXD+uv7PAOIDZwK8A7wFDgQ1/CL99ASQBz4JXAcOArIAQgJGBZcHIAmxDrEK+wRJBqYB1gQCC0IIOgZyBz4LywuTDicPlwvZDcMN9ApUB1AK/ws3CZcLMwx9DvMOMw55CVgIpg2pDA4KpgWpDAYQMwYZC5YTng0vCTYLgQXWBuUO2Q0RCSAJHBA6DBIHAg+eC/sG7BAvD00JdgqpDNkPEgUOCvcVOgwCD84OEgeBBXkNMhTwBy8NgBOEDDYNQQ7oC2sFDRKSGOUKvA3sEPcNjAwgCZcLTA+eD90QWw8kCqIMHBQGEhgRuxOIDzIQ8xCBC2MLwxMYGUESYhMuF2oLIAtQFKkQMhBBEs4UixjWDhUMERMgE7gO5BBIFC8JJw0gEaIK2Q2xCscQ3RTaCywGFQhYCnkLbg70CEURPRNjBxUEfQSXDa0NWA4cDFgI1gwGCpoONgu4COETFRKiCuwKKw4VDOwUfBStCcYWtBWiCrgI3Q6iEO0CkxBEFz4LsBJPGscOywGIDQIT7Ag3BZ4Pxw4X/j4LvxQVCtIL6QclAC8FtA2mC3IDfQj/CfsEtQM+B30QPgeJA3oDVv0oCQ0O3gaxAvgHJAq1BTcFlAJrAVgEBwaMBvgH/wtFCfb6vvv5/e7+BgpnCukHbP3U+doBbwTwB0kIjATJ+gj4kf2+/xYCqgRUCZMGZf8dAPQE0gci/6v+xAPtAKoEKwqpDOP/WvohAekFYwMB/OEHXAMDAbgInwHJ/gcAJAZCAAz9FgCZ/7r+mftL/B/4BwDwCRv9ePQ8+pH9dP3q/f8BQ/4Q/N4AUv7j+0T6TQFA/8L8jAJKAIr7Zfn4A8L8g/lyA0v8Af74B8QDS/jj/aoCf/zc9+74Uv7y/Qz5Afp0+c3zqgDeBBD6H/h3/Cb6J/J0+W35kvf2/ML8g/vc9zn3Af7eAHT5uvx3/rP2g/dW/er/mf08/Nj8p/8T+xD6uQLF/0D57v4m/qz0pPoM/yb4SPEF93D8wvIi+ZQCQP0y81ryqPk99uv1T/lT+Dbu6PB3/h/4OPu6/m33/vAj8f36Lvis9kv8Zf/n+rP8TQNa+sL67vom9r75RPZP9wj+ofVl9X/81fds+5X8Nfrj+WL0wvJp/Pn77/K++S72T/EM9Z32+vMf9Lf7lvaw9S74VvnY+DX6hvzJ9sb5jvxd//n7AfYi98n4G/1w/rf7uvoM/wT9d/xH/zj/uvw7ABIFdPle+ywC5/h084b8pgG++UT8G/0X+pL5EPh3/nT5RPr4AYfwBfGV/uP/Uvx4+Kv++fmV+LP61PnJ9sb5qgCz+vwApPwzAiwC5PMOAEv+t/ts/58FIv+V+E0BOP/F/Zn38AM7AhDymwBCBAj6CPhyBcAA/vJo/gT96/PG+SQC5/5H/d4CjvyH+OP3uvhp+u74Jv7R+vL30P75/VL8nwPy/bv0ywFcAZ32vvtRAgj+R/nIAGAElf5a/msBxvfC9sgClAIHAO0CHQLQ/Nz93gAdAHD8Uv7c/a/5bwTIALP2vv+JAaT8PP7y+1L+yAKk/noBoPsq+88IrgFp+Mn+tv3j98gEbgYX/oEDfQJnAGz7tv8gCaD9dP2QBWn8ZfnEA6YJawMI/Jn/7v4B/DoGhQge/F75+f83ARIBywGIBcAAEPjj/+f+S/x6BTsC8vvj/fADrgW9AdMDYAQzABf+3P3xAa4D5QRJCIEFCP6qBFgMD/4LAT4J/wM3A58BhQZjA5sC6QcKB28AMAGmCTj7Iv3ABq4BvANCBEIEAfyd/EoAAAAkBFgEQgZH/fb6oP87AIEFXAGc/v3+3/7/AU0D+wQwA1UDegNd/zMCPgOZ/7kCqgJvALIATv+UAlkA4/vlBPQKCwH5/WcCcPq3+RUEHQa5AET85/wlAO7+lAB6A/L/zf0F+5QAPgE4/w4GcgWbAN/+FQq9ATj73gSK+9T9ywFUBfgFDP/SB6IGkftD/igHegXU/c8EFQj9+mQBCgcm/k/9q/x7++D4HQA+A3v/Vv2z/n0EPPrc+zH/3PkQ/Nj6uv66/Ir7Xf/J/kv87vjq/4wEYf6G+ob+xAHPAt4IQgR7+cX9SgLU/7P83PsvBa4Fmf3y/4r/fgDPBAH8V/VW/wcE8vv5+1r+s/Y8+BkH7QAN76D55QLc+Yvz1fXq/6/5vvlYAir3IvfIANcCH/br87b/Nf6jAPL93/pE+Cr7fQR+ALr8lfgoAR0A8vUWAssFS/p79/AD2/9E9vEB8QFe8yrzzf9s/1b5jvx3/tj43PH2/DMAu/SbACgB/vDc9Qz/ofez+NcADPUf9iwAAwEB/HD62P6d9Jn1cgGyAJ32uvp9BML4+vW8A/wC2PaZ//n/HO9W93oBKvs1+GX/lAIQ+BT3r/9W/UT8+f1a/Nj41wDj/wH0h/YU994CbP05+T4DHvzF/wH85/wLAaMAyf6g+7f57/Cc/lgCT/k1+h7+e/8q9bP4WAJH/ef0f/p3/AX13/qc/i36RPqD+775qPVa9lL8r/9h+P7yCPqr/Jn/cP74AZH/kvNd/dz7mfkq+xP/fQJw+Of8Lf7pA/3+RPwWAuf0RPwwAfL/DgI3Acn+G/u+/474Uvzj/6D7VQHF/34AePrAADoIlfp/+kf9g/0E/fgD4Qeg+zj9+AEHAK/92gFqCc8E1wBGA7kCHQLhBwYID/63+b0BsQTPACQKiAv4AYkB4gPLBTz+lfwOBlEGbwAoAzMMVv/y+1gIuQTIAE0DMwgm/uUAFQiUAEYFbgocDlEElADpBeEFkAlFCXkLJASQBwIPxAOiCIwOkwhfCvAJLwmTCi8NIBGECkIK8w4gD8MN5QwGDKYJMw77DMcOZhCEDpoUMhLdDq0RSRBBDMMNPRG7FdUUYxGpFuAXpREnE9wYIxRJEpMU/hPzEJIYIiB4Ge8XPRU2F3wSLhXnH4cX3BgjGhEXWxVBGN0WfBYqIAkXpRMyEq0PuxedFyoceBsCFXUW6BG/DoQUbRiEFK0RlhOTEq0TpQ/oDysU2Q2XD+EPjw+TEgYOdgr7DGMPJBDZEfQGZwDEB18MRQkzBm4M9AhJBNoHiAfEBekHqQwOAsL+5QrwB0kErgFcAdcCowIkCvgBnfyMAvQEOwT/AQYIAAAT++0CKAEQ/HIBdgbG9wH0uvoM+0T8E/3Y/Ib6ZfUB9ib4sPF4+jz+pfA27h/05/Q570Ty1fUQ9lPyauxm6w3tcfD67azwzfX28DLtAfQY8uzpQfGW9mruzueW8CfwJOfg8NH4GPC06P7sQe3D6CfsYvaO9BzpYuwY7t3rfPOk9KHtAub34vPnx+nK8DXyv+s98nzrouMr7cL0sO9T7IDyHOsj7Rjy2e5m793tt++p61ry1fFI683xsO9p8h/wFPHJ+IDysO1X8YvvSO2z9pLzRexb8Mb1W/AV50j1CPhf6TLv0fRa8k/3h/Zm77DvlvK79o72Zu8F9XD4dPE99LfzOfEb8534lfwb+Wn2ivWG+qz6afq3+f32T/vN90T05/K39ZsA4//U+Rf4DPVe+b77S/hH+a/5R/u++1b77viz+LP61Ptw+rf1jvj9+tj8pPyz+i38CP5l/ZH9vv3c+X/8Wvw4+0T6Uvz5/+f8kf1//jX89vrtAAcAVv1t+fn5tQGk/CL/dgQdAL75UvwB/gz9kAFUBWAAFPdo/vwAqgLeAGz/lwOg/ZQAkAG9AfQAlAQ+Bf3+BwQZAUD/RgG2/bP+sgB2ArgI+AXAACwEtQEb/y8H2gfF/xv/CP5YAgsBF/6XBfQGnwOjAigFSgCbAjcHMwLQ/hYCNweiBukHqgJS/rkAAwNyAyAHwAY3ARkDIv+xAvsIGQXIBPQEvQHIACQCzwTlBNcCxAHy/YUCwAKJA/8Fzf9h/vADBgimAbwHegWk/okBCP4SAbb/0wNCBmX/0PzaA1EEF/yUAtj+yfqFALUBbwCr/KYD8AMt/Lb9MAMzCJX+H/j9+HT1oPug/0oAvv8SAf3+kf0wA/n9OP8LATH9lfpH+6D9Xvd/9or5G/vQ/GQBFgKZ/ev7+fl7+3/+RgEp/Tnz3Pdl/3D44/kx/fL36/v2/Hv3ivny+1b7qPu3+a/7uv5cA8sBdPmo+cn8nP5T9LD16QGR/eD4aP5d/1P2EgEKBxv9Zf+1ARkB/fx0+wAAIv8M+Uf99AJa+oP5iQN+ABP/OgY7ADj9WQCFAor/zfs7Aq4B3gAOAI7+ZAF6A2AAtv0M/wn2Af70BCwApgdGA3oBegXxAfgBvAUb/6T+YAL5+2QBawEvB7wHOP3iAwcG5QbIBA4EVAeFBgMBZwT3DysIwAK1B5cLfQR7/5cLagumA2cIXww3CfAHKAmeDyQMcgUNDlsNuQYGDPsO8AumDeENag3HCscIHAzDDXkPcg0vDS8PhA6ID/MSfRBjD/4TXxCpDhwO8w4UFCQQVA3ZFfoUzgypEI8RbhLzFJ4T5BaeFT0V9xXKEU0NUA6lE0UPQQ5bEbwRyhFxE20amhQCE2IVYw+XDccKIA8FGGoX9w+IEYgRsBAJFWYSVBEjEpYX3Ra4EDYPCRmHHc4OohBbF3wSLxEfF3EXAhVTGX8dYhmPDQIRgxgyEs4MRBm3HsoVIBWPEw0SMw6WE2YWdQ5mEP4RLhOIEYARrRHZDf8NGQ2ICRIH1gxQEssNwwkNDpMQ+wjwB6kK3ggVDIUIogQ3BXYG2Q0nDXYEyAJnCoUGvQH/B7wFTQOQB/sIwALpAZABPgGQAQH+TQcgB/n/q/6g+4r7f/w7ApH/7vwp/xP9q/5s/Zn9oPs8+o7+wvob9yL5nfYY9HD4T/ur/N/6OfnJ/BT3j/Dc9Xj4Nfry/dH2/vRT9Azz5/h4+FL8zfcu9Bf2H/TC9nHycPgM+wX1nfSO8n/0t/Xc9XTxpfK78lvuKvUb9Ujx+u/o7vPt++nd6xj0sPX67xTxt+1U6CPvjvJe7dnqK+0C7JrrW+6d8ODsde0j9cLwHO8Y8ofu0ugj61vs5O/j+Xztreqp7x/u3PGW7B/uv+1u6Zbs7/An7LjpnfBq7kHtrerg7C7wPero5gLiQeP759XtqPE97srsk+sR7KzsU+6S7/rtde1M6uzliOhi8LDxsO988fr1H/Ks7kv0sPU98jntFPnU+d3rBfFX89zvTPBW+XT1i+8M91b3+vMQ8DX0SPMY9HT1S/TJ9lP0+vWz8hD0jvSh9V71/vAU9zH17/bG+Qj4rPhp+q/7T/eO+gT9T/l096z45/j99oP7f/qK+RP/Uv7q/X/6Ivmg/e78VvlE+nD6H/Yb/VEAe/2s+jj7ZwSo+3j2qP2g+yL73gAAAAz9mwJcA8L+4/lL/BkBHQC+/ywAxf9//n0EbwLC+sQBhQIP/q//Hv4DAVECF/z9/FUBmwKfAUf5G/fiAc8CtQG1BdcCdgC2/9H6DPfQ/ogH4gEm/OP/iv8vBYEL+AX4A9oBwATEAx7+dgRuCMcG+AWTCN4GbwRqC+UIVQHpA90Kbg70CGMLYwlgBBUIzwLSB2ML1grlCqIEzwapCvcJdggRCy8HJAbWBvgH3QyxDnkPkAkVCp8FFQR5Cf8JhQiFCEkOEQszDJoOfQ4rCDMEmgx5C24IfQgvDewGNwNFD8AMQgatCYQKSgC2/1QLjAyTCiQMCguuAwcAlwdfCFwF9AYsBlUDmwIrCisKLAKQBToICgPPBMAEYAJJCF8MDgozAq4D0gfsBrUFgv90/wYIywvlBnYIgQeXA9YE6QEhAXkHwAiQBToGXAE3B30KGQfeBhP/CP7Q/EIEGQdCADcFOgibBukFmf9L/BUIqgJL/HIFIQEe/jcF8ANE/IEBmwTb/yb+4/vr+dj82P5ZAO0CmfslAP8BRPYQ+Cb+4/35+x7+xvdi9Nj0bfVs/az6g/3XAKH36PCs9DH7zffj9779pPwf9Kj5OP/g9jz45/zQ/FP4+vWO+DMArgFW+3v5dPnb/6D72PjU/SL78vur/uP/jvqO/J8BuQAQ/D30R/uv+zH39ABl/7r6tv8m/o76QPvY/Ir9mf+Z/ev55/xO/zMC6v23+wz9bPvLAX/+PPpS/mH+Mf1h/D4BywV2ADH/CgNE/Pb28v0dAhf8DP3N/6D7JvyO/nf+wvox/6YFhQL5+YP36v/y/Sb8gv87ALkACP44/xv9T/2IBUkGuQBP+3T9lwMT/4wAcgOR/T4DPgdrB7kEvQGjAuf+zwLxAWAA6v/IArwHe/v9/p8HXAGjAMgEzwC3+ygBPgG+/6f/PgEDA1EAwADU/yb+S/5cAQAAF/4HAvgBZAHaAWAAmwAoA0IGNwWMAokBjvwm/qv+6v+1BwMFYwPLAzMEFQSfBfgFEgPAAmX/ywMkAgz/QgZyBT4DLwVrA8gCjAbEBYEDR/8AAMACfgDLA9IHYwmiBFkAmwKqAh0CkwYkCFgCQgJjAzsAIQF2AGMFAguo/Rf+Bgj4AbkAkAFgAFEGXAnPAmAANfwT/TcDhQDwA1gEvQFYAuP9yfymA1EEBwSQA8n+jAY+Axv9HQKC/0YDxwh2AjH/awWC/5X6JAIx/94C9AzABvwAYf4HAjMIMwTaBR0AS/pd/dj6vv3xASwECgmBB/gBFQRl/0P+cgNH/XD8FgLLA6//NwPiAwz9R//tArb/LfyjACL9uvoLAdYIvAkDAz4DsgB//ib8Kf2qAFEAZwBW/9T9OP3hBQMDCP4zAvn9zf2qAGj+IvsI/i385/p//NH6pP4x+x/4mfnr+zX+tv1l/Y76afqo+6/72PZs+zMCH/qK98b3e/un/y3+4/3f/Az9UQDq/3j4PP5gAPb4vv10/Rf+dgAq+0v6vv0i/Sb+jv5t92n85QI8/hD8DP/Y/rv0cfTf+u78nfy+95n77v4M+/38YADN+/n5EgFL/Ov1E/2UANT7f/ge/L79+fuo/f38XvuO/ND+hQBE/GX7XAEdAF75Wvqr/Fb5AADN/+v3t/nY+Ov70PzJ+pn7xfu3+2H6g/1w/hf+qP3y+Rf2T/cB/GX9yfzR+q/5G/v2/K/9+AHy/8n61Pk59+v55/65AM371PkB+tT5yf6C/y36ivmJAaj7AfLN9xkBxf8X+tD80PyG/jX+RPrG+SL5owAoAYP18vfaAW8AKf13/kv6NfzWBsX/mfmR+837sgAQ/ML4jv5s/xP96v9D/kf9wAJVAyL/kvk1/Hf+qgDn/tD88QH4AQ4CVv3C/DsA1wBKABIBiQO2/fL7Xf8HAJgBdgbLA2X74/ls/VEAOP+bALUBCP6V/P36kvlKAhkDqP30AKT+EPjU+3IBHvxe+zz89ABD/mX3YALy/6j11Pn/AS38G/0hA4wAoP08+nIDpPyd/MgElf6R/cn8ywEX/jj/LAAZAZ8Dq/z/A7kCAADEAwMDlAK1A30Euv6K/br+6QMoBcsBsQbwBzMClAB2CLUJKf+O/rkCBP+UBNoJBwQSARIHxwgx/Rv9AACfA1wF9f5cBRIHMANGAbUBUQAWANoBe/9cBUoAUQD0BOP9bwC5BHYCS/xo/tcAWv5W+3IB4QkwAfwAjAIm+uf4oP2Z/Xv9UQLEA5n9CPi+/Zn/QP8+AWX/PP6r/l3/Uv7f/tv/tQP9/vb40P4M/c37ZAH8AmAEDgJw/okBS/7C/s8EbwTaAzsCnwOg/Tz85QTABFECAfx6AUkIowByAysI0geFBhUEKAXwBbEETQOmA0D9d/zhBeUG4gH9/uUEgQP2/AoFNgt9Bj4FMwZl/bP4+AH4Bdj+9f5CBgcGG/trAa0L8v30AOEL7QRh/HkHDQ5vANj+8AOICYkDuQQvC4kDwv5GAakKKAdCCIUIrgNCAt4Exw5nCHIFrgEkAoUC8vvEBXIJXAVyAdYE5QSbAA4GaweqAAT9ywMwA2QBKAefA4UAXAVvBK4DAwOv/8QDqgBcAREJ0wVYBGAEXAHEAYgHYwfLA64FrgNyATcBfQIdAFb/CgdnBA4C7QS5BmMJYAbIAjsAqgDq/1EClASjAkUJiAdcA1gGQgR2BlwH+wTaBa4FOggzBs8E+Ae1B2MHDgKmA2oJvAUb/zMG+wx2AJsCzwZvBE0HwAYDB+7+JQBCCkkIr/+YASgHq/4i/9MBjADEB3IHGQPtAF3/xAN2BM8A9AKQA0IAFgAkAj4BKf9GA00F/f57/0kEZwIhAY7+s/5KAuf+ywH0BsQBLADXAmsB2/9NAQT/jv6QAdj+kAF6A00B0wMZBUkGNwMHApQEzf9d//8DywWMBDMCMwiMAsb3KAHPBGX/G/9gBA4CWv7IBGMDNf4i/SEF3gKo+c8APgGD/cX91wA3Ac35Lf7EAZ38QgL7BBkBYALTBcsDd/7TAVgC7v7j+5H9AABh/DoG0gn1/sX9/AKqALr+ZwKR/0P+JAIHBOUAPPgi+aoCCPpP9+IBoP1l+wAAZAGZ+5X+hQTN/Xv59vrn/Kz6Zf29Ac8A9vw7AH0E4/1//ND84/d/+igDqgD9/v8BsQSMAmX9CwHC/hv/MwAB+l73Kf/iARv9LACg+538awOv/6T6JvyD/Sn/BP/J/GMDrgH9/Of85/wq97r4fQJw/sACHQZ0/2j+5QA1/jj7QgD8AAAApgHAAFL+DP+qAIkDCwEI/M39Hv7j/aoABwTtBCAHxAWqAEv+ZAH8ADH96v3f+rP+rgOfA2QBKAE4/235oP1E+L75HQS2/Wn6AfqG/DH95/aK+5381fXC9P34zfe+9dcAKf9e9wX1Kvsx/QnyKf3C/Dn1D/6r/vn5cPxrAWH6EPrY+sL63/pL+J8BqgKd+ob+nwEm+i38mf+d/AH+2gFH/0f7RPwt+tD8+fuz+ob+hQB2ADz8uvwE/er9uQCZ/wH6T/XJ+sn+5/yV/jH9Kvvn/P3+ZwCs+u76bP/C/Kj5q/6bAoP9LAJd/yb45/5ZAAH8CPyr/mj+g/10+zH/QP+O+Aj+KANd/6/74/+C/9j22Pho/u78CPwOAFkAuvoB9nT5Kf/j+Sb6e/099rv2jv4lAFb9d/z5+UD5Vv3Q/O76s/o8/HT76/WO+vn/r/2mATH/3Psb/9T/RgNyA9MBLf4x/Xv9Jv5nAJH9fgC5AE0DqgY3A9cAZAEhA6/9CPwp/WcAFgBNAYUG2/8WAssDe/uS+V39LACbADsAafwX/H0ChQaG/s39jAaMAED7Hv52AMQBrgEWAkT8mfksAOUCLf53/owKawWV/MAC1P3u+oUCAwWD+3T7awXeAG8AvAM3AQcATv/9/sL8lfqV/qIEdgJcAZ8DywEZAU0B3P10/QcCSgBo/sgA/wHTAd4C3gDn+rb/WATtAvwC9AKqAtMBLAAT/bIARgOMCJQEFPfb/yEB2PwSA7UB2//XAIwAR/+K/ywChQbwA3D8pPiz+L79fQKg//n99AIDAdT74/kX/hkB0P4zAgcAr/eV/kIGafw4/x0EYADXAAH8uv6g/4L/NwHJ/qMA6QEOBOr9AwGBB139nwESB4gFjALr+ywAr/1W+ywARgPAAHD8cgdGATX41P/iASUAuvx5B6IGVv0OAGz/Q/5E+FwBQgZP+eP7zf/1/oUALAR2BIr/FgDF/9z9g/2G/sgA3/53/K/7/fxs/+f8mfcQ+vn71Pn4AVUBOfnr+00B7v4m9t/8gv+z+Kj5pPpA/TX6DP83A6v8AfwM/6T+2Pjf/CEB8QGqAlUDMwIP/lwBqP2R/ZABE/3G+Wn8R/8+AQoDfQJrA8n8AACUAHD6jv6qAEICOPvj/WsDe/9s/Rv/4//n/FwBTQFd/TX8ywFnAnoBQgSqBJ8F3gAvBYkBmwDtBGsBjAJh+pX6xAFJBDME3gJvAo7+d/yz/rkAoP2qAEYFEPx/9o7+7v6+90v0mfuc/rf5hQCuAef+vvsp/WX9h/iZ+7P8Wv509+P3LABKAGz/AAC1ARP7EPxw/rf7jvp7/WsFYAKqAOUCe/+d/Ib+bP8B/Nj+LwUHAvL9dgKUBCEBrgFGBfL/S/yV/tcAcgMhASwCkAMdBPsGWAayAMn+LAB0/+0ECgNyASgBXf+YAVr8Hv4lAGACtQGYAT4BH/rEAUoADgBrAaf/CgPn+tT7+fst+gH8Tv/wA1UBzf8p/zMAHv75/4UA9f4DAwMD5QAX/E0BiAV+AGcABP17/+kBqP10/+0AtQEKA2cI1wKD/YgFBP9W+/b4UvwKA/L92gH0AI78g/07Auf+zf0sAob+Vv/N/aoCsQKC/+kBdP3y+7b/wADF/cQDnwPlAEYBUQA4/3j6tv+v/1L+RgO5Br0BD/43B34APPpCAnv/F/gI/BYCIv88/scGDgju/uP/XAM1/tz57QCQBSL9jAJcCdcAZf3xARkDNfwE//8F/wOjACL/RgVgBIwA/wWBBz4DUQL0BAcClAAhA8gEDgI+Adv/JvxjA+UETQP7BM8E7QDY/rECG/1D/t4AZwDtAO76Kf0i/aj9AwEWALb9Bfvy/xf+Vv9nBH/+mf+o/Qj8kf08/G8E5QRs/xf8OP1VAQT/YALAAjMApP7PAMsJlwMOAMQFXAFd/WQBzwYSAd/85QKMAKD9IQOIBRIDuQBgAM39Uv59BIEDd/53/uIBdgAm/u0ClwNW/av8pP6K+woDqQowAdz7p/9GA94EKAUsBgcCMfsT/ywEGQEdAscIOgZH/Vb/wAKQA9MDTQOfA3v/7QAZA00Bzf/5/5AFmwQhAVwB3P1nACwCvQEDA+f+vv8B/Jz+CgNA/+ID9AT/Bav+rPpkAR0CAAAB/qYB3P04/24GyALn/oEDYwcE/4P7jAJvAmz9OgaTCsAAlf7lApH/afyMBMgER/uo/VgI3gJh/igFlAJS/JH7TQWBA/L7+ANVAZL5/f7tApX8e/myAOP92PybArIAAwMI/nD+vv9l/Wj+BfvLA5n/Jv5nBLEEKANw+t4CgQE8+LUBXAubAIb6zwjXAp36LwVCCB7+afzhB3ID4Pb/Ac8KgQFD/qoCkf9P+fgB6QOd+hP7EgMwAYP7LAIsAob8mftKAAAAPP71/pn7nfzU+0/93/7IAFb/5/pW/ygBkf8sAIEBHQAt/mH8iv+bAJ38cgE+A+P7nfrxAU0BnfwX/sAAawFgAHYAowDy+6z4bwCK//n5F/4X/ib8CPxS/GH68vvtAKv+mf1S/GX71P/J/qT8f/y2/SL99vyR/5X6r/9NA+v7Iv0I/sAA3gLU/zj9xf8I/mX74QVrBRYCgQHu/Cr7/fgwAQcElAJRAgAAawEi/UoANwET/TH/VQE8/nv7ogQZAR78XAHeACwAd/zU++78e/2k/gsB5QLy/6MCawMzAGz/KAGyAE/5Jvop/yQCKAPJ/ob+QP01/BkBEgOo/Yb8dgBw/Gn4+f03AWX7QP+9ATX8zfmz/J8BFPnr9xP9vvu399/8tQVA/00BGQP/AVb9BftkAR/4e/u5BHv/nfoM+x0CZwQdAq4BywMzAuf+ZwI3AQcCRgUDAdj8IvtGAw4GMwKV/kD9+AHJ/k7/9f74Ae0Clfwx/dj6BP/wA5QEq/4f+L7/IQUM/Zn3S/zq/4UAAADEAYb6S/wSB/8FEgMLAVEGAwFA/Yr/DP1RAKMA+AUKAxf8XAMvCSgDyfyK//n9qP2JAe0EfQSK/w4E0wMe/Nz9bwJZAPL5zfvXAN/+lfymA94GR//LAYwEpP48/CwAogQ+AQz9uQKQBdT/OwCFAnIDlwMWAowArgOIBekF6AtjBWsBTQUhBQoF2gUVBjMClAQ3BQMHhQZGA0IG1wKuAxIHZwh2CPQGPgNvAHIHogjpB2oJMAFA/woFDgT7BlwJKAflBpAB6v/wBfsMmwodBs8G4gHIAPQEfQokCkIEHQLU/yQCvAUvB7wFmwA+A5sGg/3TAf8NDgL2/NIJjAiR/W8EWAiv+9j83giXB5L5Jv5UBzABBP9cBeEJZwS8A2AEfQLeAOUCNwWD/b7/IAdrBbECVQP0ApcD3gKBAcgE8AWuBSED/AIVBKIEHQbiA83/WAQkBu76CwEgBxIBiAd2CMAA2gGbBJ8DCgOfA8QHFQixAv8B6QP0ApADVAXABgoHFQSqAnYGXAfiA9IH1gh6BbIAzwRNCSb+pgMvB1b//f43BVgGlfzlAv8HyACg+/L/iAUB/n4AlARW+6v87QLb/xP7mftnANz7dP19AkT88v3n/rb9AABCAt4CBP08/L0B+f8U+Tj9/wGz/EIAs/7F+00BJv7C/vL91gRRBqD7wvxP+0D9Lf5KAHv/E/0HAPX+QP/2+I78MAMb+4f4xf/J/uP/UQLXAAMD7vyk/i3+kfud+g/+ywNi9lP4tQHc/RD8YwOxBC36Wvr5/ZL5nfaO/rwDH/il8lb93/rC9KD5s/wx+TH5Kf3v9qT0lvY8/Ev40fT2/Nz51PlW+Wn67vh/+Jn5/vT2+BvzofEQ+l75F/jF+0IAvvvv9p36ZfvR+L71xvcm9ifwt/v2/Jb07vqr/hD29vB4+HD6cPYX9lr6g/dM8jX2+ft49hTvxvXY9NHwg/NA+f70afAq+e/2LvS+9f32WvbV847yjvRt91ryzfVE+hf2fPVw9nj0KvN/9lr+dP0b+Yb8FPmO9tH0zfU1/Aj6VvmZ/ZX6G/XY+kD9Jvz5+2H4mftw9rP0Yf6d+iL5f/yo/X/+g/VE8gX7Afyh9Sb6r/nr9Q4AjABw+r71vvlD/lb3Xvcm+mH+r/1L+nv7LfqK+ef8tv0B9mX58v0t/Cb+2Ph4+o78t/cQ/N/6NfR4+mX/f/iO9jz6CPof+lr4AfpL/pn1EPbY/lr84/2n/3T95/h7+ef8t/mZ+fX+SQbY/jn53gKMAur/9ADN/Y7+6v/tAAMFq/7N/QMDrgGG/hD8jAIsBIEDbP1W++kBlACUBJQC6v/J/Fr6uQJgApH/HQQDB7r+H/q5Ai8F6QFGBdoDR/1W/TMEtQdyA3YGFQiqACn9xwYHBr7/HQp2Ahf8dgThBzMGzf83A2MFrgHAAE0JEgdA+Q4EsQhE/PX+0gk6BhD84/+1AWcAowJ6A2MFQgI+A5sGLwUZAR0C2gO++/n/xAUVBt4ETv/0AnoDcgXWBmMDvAXlBAcCzwKUBIgFHQqbBBP7iQMkCLEEpgPeAv8DQgRnBmMFwAT7BDMClwUHAr0B4Qn4B58DpgPtAhf+xAOFCGsD1wKxBFQHOgbLB8AIPgcVCGMFBwSqAokB8AeBC64FGQkzCu0ENwkKCR0KIA3lBqYD/wcvCQMH5QaFCD4HxAM3CdoJQgIdBrwLlwXIAm4GnwVgBJ8DkAUkBGAAWAYvBXD8cgMrCLkCegO1Aer/S/47AtoHKAXABrgIywUHAB0EzwTq/9YEYAR6ATMAwADXAq0HKwhGBa0LrQfLASwEWvxp/KMCAwPPBpsCdgLaA/QC6QXpASwA2P6iBLECOwCXCRkFbwCz/j4Fcgd2ANoJdgr2/IP9PgeqCKIEtQfpCUoCSgKtB+EHnweTCigLmwaMBDcD/AJRANoBtQUvB58HRgXlCMAECwGfAwcCRgNVA2sBoP9l/3oDnwdnBAAA6QHWBJn9/fqqBFwBqP0DBU0HSgC+/QoFWAQM/W8AUQYM/6D7MwQOAkD5NwF9BsX95/osAJMG+f/q/6IGOPvJ9ob+xAFH/0oADgJl+U/1S/5VAyL/Iv9s/Sb4EPgE/aoCZwA4/8L+S/6r/lb7dP3F/w4Ayfyz+Pn98v1/+rkCqgTf/sAAdgZuBlr8KAEgB9/64Phw/m8ChQCqAGoJQgS+++kBnwPC/oEBYASR/Uf72gHXAsgEfQKXA9oDH/oT//wAUvzN+7kApgO6/jz+BwI7BIb8XAFyBdz91P/0ALr+9vyYAe7+G/k1/G8CNwOK/UoAnwHtALkA7QD5+2H6EgWuAb79Jv79/gcAUvzY/gz9Xf1s/bP68v3C/k0BywFjAxYA+vdd/4EB3PlW/UoA3/yG/MgAtQXpATz82P7f/or7EgFNBcQBHQIoBXIBS/oSAcgEsgDxATMAzwBH/1kATQMZBTsCf/56AWj+wAKiBFgC6QOUAB78bwAoBzH/Mf9CAtT/Mf3AAJMIEgOjAkICgv81/O76GQWbBtcA1P9yAX/+FgBUBZsAKf8wA5cDwv6g/VUD7QBa/IL/ywOK/d/83gQt/Nj69ALHBhkBr/da/i3+G/ci+7UFEgHQ/LIAzfnG+XT7vv/j/5n7SgAWALr6zftcA6oAoP0AAND8R/lS+mz/PgF3/oP7nP65AI76Uv7lAnT7Jvpd/f8Br//N+5sAWQDJ+nj6HQBP+9j4DP3XALb/Zf0WAtT9aP6c/kf7Ofl//E0Dgv+2/cL+vQEB/Mn8cgEE/SwA1P/c+XT5cP7eABkFWATU/+v7Uvwp/Wz7dgB6AR0CCPoF+zAB6/vg+Ov77QJS+tz7yf4X+nD+f/4T/Vb9Zf9L/kv8/fg5+f36mfu3+xv/Lf4b+dD+s/pa/GACmwD5+6D5SgAB/H/8BP+6/Mn+hvry96D7Ivtl+2AADgBS/qj9t/n2+NT/uv5p/PL/5/rY9lL6BP0F+8n+AACv94f2g/uV/H/83/6R/UT6NfqO/GX99vyv+/L5T/ed+vQAYf6z+o74F/ox+1r+8v8q+yb8Hv57/dT5R/9jBd/8CPyc/gn22PozBAj+vv2V/in9Iv8lADMA7v7Q/J38Xf/Y/Bv/MAM4/83/owJw/kD5QP26/uD4g/0ZAZH97QCqAn4ApPiZ+RIBKvuZ+TMAOP/G9zj9ZwAX/JH7mf2g/4f2rPhs/eP53/zAAmMDuvwi/SL7mfeO/K/9afrN+zMCdgKo+/L7Uv5//ET8kf3f/pL5QPvaATMA3/w1/Kv8jvrn/jj/PPwM/Tj9qgDlAF77oPuJAUf7q/yjAhf83P19AkYBr/1O/8sDMAMM/SL7KAG+/cAARQsZBaT+yADLARP/yAAgB8sFlACYAXoFsgBS/oEF9AhcA6oA9AIoAR0CawPaBeIBe//tBJQCLf4t/tYE+AMDBUoA2Pr/AwcEbwJo/rEC2gOC/64DegEHAv8BrgNkAb79rgXpB5ABDP90/94AqgQ3B5ADf/zlACEDowBcB4EJHQI7ALb/8vtZAD4DkAWuAc39fQRNB/QEuQRjBwMBNwE+AxYCpgU3BQ4EPgHaA1QFogjDC6YHegMHApQEwASbBmcISQogCTcHiAdgBp8FsQTLBa0HkwoSBzMGvAXLAxkJqgimB/QGwAbaBzsE+AHABvQGiAeiCLkABwRYCEkGfQKMBN4IXAUSB00DcgNCBDcF3giqAIwC5QR9Am8CMAPwBcgC9AQzCK4D9ABjA7EClf6QA4UEJv4wASQC8v8SAfwCDgYoA0IAmwCQAaMAhQAKBcsB9ABcB0YDmf2V/oL/iQOuASb+owJnAqMAAAADBR0IywHXAkIChv7TAc8Ajv5d/dz5f/43AYUAAwNGA6//1Puv/8n+GQFRBI76JviZ++r9dPvf+psA3P2V/GcA9vwT/QcANfwm/HT9OP+UAjj9yfp6AcQBoP+FAJX+lf4dABf+oP2v/Rv/TQO5ABkDRgPPAHoDXvn5+Vb9jvwzBLEC/fxA+9T/+f/Q/pH93Pnf/Cn9yfp0+2H+UQKg/534e/sQ/NH6Zfu++yb6i/OFAHIFG/mD+b77Mfkb+5X8yfiK+5n9GQEx/zj9tv2++Uv+Ofm79or77v6Z+5X4fgBNAfwApPw8/qD7t/Pc+WH+/f6c/sAAF/qs+uP/kvmg+1b9cPzN+R78FgBa+l395QJd/9/8wvyk/tH6G/n4AYL/Iv0OAPX+f/ob+aMAE/vY+qIGuQR7+139gv/r9/b6G/8T/fb4YfwHACb6CPqG/JABivtA+YL/kfvj+d/6tv0q+Rv9ywPc+2z7H/oM+aj7EPwsAPADYAJP++v7owDC/MX/dgamAa//vQGv/YP9YAIoA8sBMf+R/c8AYAKn/30C8QHc+QMBwAR3/g/+Uvrj/bP+4/2bAFL8iv8q+0j31Pvc/SEDKAFKABv7MftkAf38XAHlAHYAqgJH/0f/Xf+YAbr+lAIOAn/+pgPb/wT/VQEKByQEFgC5Anv91P81/Lr61wCV/i3+2P7c/TX8qgB//nT5mwCc/n/81P0x+eP/kf+k+jMAJvwM/SwCNf5A+yUAgQPU/58BwAKmA9D+/f5vBI7+8QGxAgz/NwEhAWsDGQVkAbb/Tv9P+7b9NwGbAPL9QgCn/8L6qgBw/kv8zwCz/Jn5bP8i/yr7s/6G/H/+aP4T/xUEF/wp/SQGyALn/JsEgQOg+/gBkAPiAyQCRgXsCL7/G/8zArECIQHeAiEFjARRBHIBfQSfAZQAdgIsAH/++f1yA6T+0P56AQAAnwMoA1wBkf3C/qv++f9A/XD8zwZcAd/88QHXAAz/xAFcA8ACvQFGAzADYfy6/IkB6QPiA2cEcgFKAOP/d/xrA7UD3gBKAEv+8v3y/eUCGQPLA2QBWvyv/cX9d/79/iwAwv4B/JcDQgQ4/QcA6QE+ATX+dP/eAIb81P8oAWcAuvwdBLEM9AAP/iwCYATtAOIDcgdd/z4D3gTLA28AvQHWCGsFZwTwAysIlwWBA2MD9vzABCQI+AXTAzsEpgNo/iEBfQKMBA4GCgULAX/8PgHLBUkECgWFBEYBHQLlANoBSgLaAWMHXAV0/2cG9AYb/RkFhAqJAzMCxwYSB58BVQM6BnYGXAObBp8HoP2Z/3IFnwXlAlUDawWbAAcAXAX/AS3+vAfPBin9e/2V/m8AwABRAjoG5QLU/bP+FgDn/iEBqgS1BR0A+f2xBFEGKAVGBbEE1wCqAnIFsgDLAYEFLweIBbwF+AfaBRkFVAVVA58BvAUzCt4ISQQhA94E3gSQBQ4ECgVqCQcEhQCfBdYGUQZ9BFEIAwn8AvQGgQm8BVwFrQchBWsHawemAX0GZwg3CbgImwQhBa4FcgWIB30IzwJGA4EFXAPIAhUEwAoVCNcAzwBrA+kFSgKXA5cF4gGYAfgDpgHN+zsE1ghgAu0CVAUzBBP/f/62/+0ApgV2BmcC3/7U/wMFwALXACwG/wHN/2ACegNgAKMAGQdJBKf/rgHPBqYBjASEChID+f87ApsCLf6QA3YCMwA7AlwB/wUdAh0Gywdl/0D9yABs/6/9hQIB+q/7LwXTA/EBE/3F/Tz+wvxd/Y7+lf75+/wA+f0i+/QC7QDU/V75SPdl+Xf+8AP5/Yb8/fw1/O787vzQ/hP9uvrR+pn9BP9H/8X9CPoF93/2qPsx+534Lfpa/NT7SPfJ/Kj7SPfC+BT1+vVL9Pb4U/iZ95n74PgM+1fzAfbG9eTzVvci9yL9DPWd+Hj6pPZA+a/3Ivfv9Gn6ZflH+5L5RPCk+If4J/JH++v3h/I8+M33+fli9tH2jvjc9cLyXvOS9z3wRPjJ+v703PVL9pn7LvTc9TX8vvUF9Sb8zf0B/K/9nfrg9jH1R/lH/X/4KvmO/tH6S/pl/aD7qPtA/aD/T/c59UD9+fkx99z3h/ha9DX4oP1a9mX1bffy+XT5PPgQ+NX1bfdA98L25/Yb+Xv3zfXv9n/05/a6/l3/afgE/dj8u/aS+V39g/0f+kD/bwB0/VL8kAEwAdH2yABKAPL31P9VAVL8DP2MBGMDR/+FAnoBT/lX8+f6JARKAAz/7QJ//n/6+f9l/wH8FgKMAnf+jvyV/BkB2gNZACn/iv/f/lUB+AEDA7UDbgZGAywAegHQ/FEAr/9O/wcE1gY3CeEFPgd9AkD/egH9/gcCzwBKAukD1P2QA5AJBwZvArwDWQB//GcCgQMHBh0CzwBRBh0CCgNCBAcEYAB7/xkD5QQZBaYBJAYhAZ36WAKXAy8FWAjpBZQCvv12Av8FpP5w/rkCIv+g+VgEZwjxAQcEiQPpAdz9EgHABIb+/fqG/DsAcP5KAJAF3gC3++7+5QJvAEf95/4x/dH6+fvj/5ADr/9CAGcCe/vc+aoEzwZa/pH7Afzc+6/9BwSfA0oA2gEHBGsB2P70ApABq/50+6D9fgC5ADMGYAC6/n0CYf7IABkDowA8/kD99vyd+h7+ZAEoAaT+uvybAJ38hvwhAU/9ivl7/Q4AFPeZ+0kG6v2o94L/NwEi+5H7/wFGAUD5f/68A5X80fqYAWX/pPaz/AoD5/yD+9cAr/0Q+gj+E/8m+pX69f5a9mn2YAB3/or73/xA/4P38vN0/xv9f/R096v+Nfyk+MQDwADj9+r9G/1l+Yr9uQDJ/Of6Mf2O/L79bwSFBHT/RgFyAdD+aP5rAZcDZwDN/0oA9voX+h0ANwFnAt4E1P+g+/8BqgKg+x0Awv6o9RD4kf1rAXT/0wGQAwj6Lfp0/WH+zfth/Ev+afyXAxv/G/3xAWQB9f4I/EYDBwBh/pcDMwJd/8AA6QeUAJX6bwKuA1kAlAThBVECxAFvAiEBe/ta/t4AdPvJ/JAD0wGjAJMI8QFl+dz7tv0m/uf+UQKn/6D9YAASA+UChQD4A/wC1wAAAIwAnwPTA2oJmwgOBMAExAcRCT4DvAPWBt4GmwaQB8QHPgVnBK4F9AYOBHYEPgVRBj4HFQSFAur/bwDEAbUBmf+YAZQEs/7EAYwEXAE3A70BPgFd/6/92gPEBYwE0wMOBPgF4gPtBNIHdgRrA+kJ/wd9AqIIRQvHCOwGBwbEB60HjAbIBLkGBgqpCmcG3gBJBLwHdgbpA7UHMwgDBR0KowJL/kICawH/AzcDlwOUBOUE5QQDBbwDzwIkCCgH/AIdBNMDBwJUB7UJ3gbwB6IIIAmBBZAFogo6CJMI1gzTBQMFSQz0BtMFegVJBNYMRQljA60JAwVNAZcJ8AN0/8QFawMOAt4E7QTwBywGuv5+ALkAyf70AhkFPgc3Abr+hQZCBMQDHQYSBZ8DuQLhBVgGogQ+B4wK3gbLBYUIhQZ2BuUGOwQVBJMGBgpbDVwL2gfTAXYCeQm5BgoFAwftBCED4QVVA6oEgQXxAZsG+wTLA8ACBwSUAjABCgX4A0kIYAQoAwcCfgDaAzsEMwhNA4wGqgZRAj4HpgUwA94EIAnEBcQF9AT1/pgBPge4CKYBawMsBigBOwAoA94GkAEsAssDRPzf/FUD9AbIAOr/gQMoAQ4C5QKmA5H9wAB9Bnf+IQPeCAoHjAQVBmcIFQZ6BUIE6QeQBdMFTQdGAyQKRgc3BQ4GMAPsCAMH8APTA6YFdghjBQcC0P4hAYUCOP/LAWMD9AAOAJQAGQGg/Wz76v9nAKj7OP2MAAH+jvzeAEYDkf0Q/OP9bPvJ+tz7QP2+/fEBIQO+/8X/E//U/8n+zf04/XT74/8LAcL8oP0lAGcAJQAi//38kf2z/mH82PyFAEIEE/+V+lb9Nfy6/nIBgv8m+ob81P3N+3IFkAME/zH9jvoM/9T/pgGQAcX9PP4oA5QC5/xVAd4C6/mK+4wCdgD9/hIDzwLY/Cb8Zf92AKD9dP12AOr9OP0dAmj+yfZp/OP/F/5W+6D5uv5P/dT9AAB3/lr+Vv/y/3T7CPo8+hf8hQB7/837R/3xAav+2PxS/lr8DP2O/noB0P72+iL9Uv4I/Bv5lf7q/dj87vw5+bP8UvpH/cL8Lfr1/p36LfwM//n7/foT+3v5xfvf/Ej3wvpS/rf5+fl0/fn70fi6+vn/p/+Z+0T6F/qz+J36BwC2/fL5Bfte+5n1G/Xy/aT8hvxw/hT3/vSK+Rf8G/sQ+jz8pPo59TX41Puv9y72ePio95n1t/cx+2n6RPio+Xv7DPl/+nf+afyZ+8b5PPjN95L36/u2/XT7f/zU/1r6nfqg/Xj6Xf1//h0A1P14+jH76/s8/NH6Yfwq9xv1g/ms+Lr4PPxl/cn49vgt+ob6dPmD9QH4rPSh86H3wvgQ/BT3T/eO9lrymfV79xv7VvcT+wT/h/hx9PL1cP4B+P34WvzC+IP7/fj5+2X5PPzc/Wn4dPkX+vL9Kvc8+qT+T/t7+5L3+fvY+NH4s/wu+P70YfjC/Hj2r/eg+br86/vn8or3oPtW+/n7Wvxe+R/2oPnQ/Gn8Nf6V/lL8Mfth+ur9RPzF+3T9Iv/U/+f8iQGO/jH9tv9W/XT7EPztAFr8Jvqn/8X99vrb/5X8H/iv+5H7F/72+gz7UQBL/Pb6BP1//MX70Pwp/d/6JvqG/owAvvsx+z4B/f4B+uf6BP/eAjz+e/8sAKj9VQG2/2cAE//Q/B0CiQHj+f38MAMM/Y7+AwEB/Nv//wFl/wAA+f1S/Bv/6v81/s372Pw4/4b8cPwdAMn+0PwP/lL6QPsHAEf/qgJCADH9dgAM/1b9zf2v/wT/zf83AS3+Wvzn/mcEHQRs/64BpgMHAtMDfgDJ/p8BKAUzCDsCXf+UApQErgE7BFgGp/8zAgMDZf9H//ADvAeQBW8EWAIDAzADlwNnAEP+vQGz+j4BwAiC/7r+QgD4Aef+0wF6BXYAwAJd/w4A3/4T/QcC+f96AWcC9ABS/nID3gbu/g/+6QP7BMAAdgL8AE7//wEsBDcHRgWjAigBzwD2/ED94gPwA88C9AL/A5ABKf+TBowEXf2G/mH+owIhBeUEawGK/0IGeQflAmH+ogQ+BTMAYATaA2AEOgitBwMBiQHpCRkJ9AIOBFQHogZ9BEIGJApNA9oD+AXlACEDuQT0BtYEIQWxCFEGjAJkAQoF1wKFBPAHJAJYAgMFtQMSAWAE8AeMAg4CTQN9CMsHEgEOCm8EjvzDCT4NcgNrAfQGOwJW/yAH0gvHCC8FKAcVBJH/7QSmB7UDogQRCZMIRgFNAYgHZAEt/E0FuAg7BOEFawV6AXIBXAUOBqYDMwTEBcAGfQK9AYUGEgfeBFQHUAqxBCgFJAZJBHIFNwUzDF8KgQXwBwcGiAWmBWMJiAXTARIHxwbEBcQDzwiiBnoB/wdCCPgFtQOxBvsEbwDpA/8FpgWJAzcJKAm2/8gACgchBYEDgQckBkkEfQQgB4gHUQBRADcJTQcZAWsFuQYzBJQECgUoA+IBkAUvB8gCuv5RAm4I2gU3BfQGR/8HAJ8F5QKz/p8BjAaR/8X/nwPTASQEOwQwAQT/5QIdAiL/uQKQAekBQgLf/g4AUv41/u0Ahv5A/fQAtQN3/l3/vv/Q/P8BbwKv/cn8/wEi/br6r/2v+8X9bP0X/hT5jvxgAkP+Xf9H/V39lfxA/d/+e/st+l77kf0F+yb6tv1d/Uv6Zf04/+f6/fqk/tj+HvwF+xf6EPyz/CL3xvlA/4767vpA+4r15/ZA/ef+xve39+v7uvy6+sn4+fmL85n1g/kq89XzBfkx+Qn2Mfe++Yr1bfMU+WX3ofEU83/4jvTo7p32+vcM9UD1bfXR9jLzdPEx9WX3vvUQ9lP4H/KL75n5f/pW92H4u/bV9dz3Yfha9lL63Pc99s35ivfy+bf5oPls/Tn5g/Vh/Nj8G/d/+F773Pn99uP7q/wf+NH6DP0u9hT3Uv4t+pL5t/vc+1L6R/ls+6T64/ts/Qz98vf99or/EPyz9gz/5/4f+gT9bP/y+xP7EgMsAED5kfslAHf8qPlL/nf+egHC/g4AjAB4+qMCNwP9/Jn9SgCz/gj+rgGG/tj+rgHy//L/Wv7EATMGmwAi/3oBrgGbAK//4gNcA9v/kAOUAtMByAQVBGMJEgWUAG8CYAKXAwMBdgrWCm4Kngn/AYEHqgIzBIEH+wauBWcCfQjsBnIJgQuECtYIlAR9CIwGMwYoC2cIXAe4CiQIUQYVCEIIeQc3B/cJGQnpBzYL0gvEB7kETQdvBAoD+wj7BtYGDgq4CtMFZf+8A8QDgQFjBRkHAwMzAvAFAwXSB0kGVQEHAML8CwHABIUA3gBgBrUFVv0T/TcDnwPaBcsD6v93/h7+KAUHBHD++f2BBXoDYfr8AukBLABVA5H/iv+k/oUCMAHf/KT+7v4HAAcCWAIsAPL9pPyZ/x7+r/uyAEv+R/to/jj92Pge/EYBs/5l/dD8Wv5nAC388vsB/Ov7qgCV/sb5KvvpAZcDQ/4m/CL7pPq6/IwA5/wm/pQE5/6G/Hj6lfx6AU7/cP7U+8L4Xvf9/t/+Yfhs/a/9QPtL+oP7XvuH+ED7QP1p/Ov55/qg+Y7ye/c1/pH7EPoQ+jj7dPk1+M37afz2/Bv/CPzy+SL/hQK9AXv7DPce/uIBE/0P/hYAAfymAZ8DZwBrBa4BnwGbAuD4rPqqAiwC6QGJA+kB2/9O/8n+rPpP+dcAxwZVAzsAsQISAcn+JQCJAaD/WQDABpQAQPvpA0IGGQUzBB0A4/3/Ad4INwOv/0II3ggVBGACLwXaAzj/XAGZ/83/5QaXCUYFMAHpAzcFGQFs//8BdgKQAb0BxAOUAED/+AWQA8gAYAJvBIkDowKFBhUEegF2Am4G2gXaA1wF2gXlBM8CwwmTCK4F9AjXAnYAawPeBoEHuAgoCwYIawP8AA4EqgSiBPsIpgNs/yQGKAmQB5AHcgdrBZADDgTpBwcEvAP/CRIDowIRCdoJbgaiBIUGpgXwBygLMwwoBSwCKAckBCgDzwh9CuUErgP/Bx0IzwSBA7UBJALIBP8BhQR5B1UB+AEOBKMAWASfAWAAEgVL/lEALAQoAdYElATPAIUCLALIAokDZf+xAgMHVAXlBMAEJQD8AIwEQgQKBeUEwAhNBQT/ZwCJAyEFKANRAq4B9ATtBOkB7QKQAWsB5QRcAxv/AwEkAlkAMwDlAEIAzwLlAE7/UQSn/ywAqgTeAKD/LAKjAob+Tv8sBOkB7v6R/yEDZwJ7/UIEsQLq/XYCsgDb/3T/awNVA6T+nfyR/TABPP5YAoEBiv1CAk/9AfrAAM8Akfu+/R0Aiv/c/eP/3gIx/RD8dgAm/l75bwA+Azj7DP+n/4786v1O/5QC6v1W/V3/3/yYAbwFdgDc+Qz7yf7AAIwA9ABCAhYAUvyk/DX+7v43A+IB1P1h/CL9nwHxAd/+7v7eAOP/LfzN+f38Mfst+kIADgLiAdj+5/xa+Ov3E/1W/TsAnP5l/Wz92PpE+kf5mf0I/nv5PPhe+9D+qPtL/nf+afop/Sn/mf01+Dz8zftA98n8/fw8/kT8Kvuk/ML4ePo4+zz6q/we/vn79vgx/Qj8RPbu+tH6dP1s/br6E/2s+Jn90fry+XD8Ofl3/l775/wP/jMAegFO/1wBLfr9+gX7afztAIr99ADf/rP6d/x0/SL9S/5ZALr80Pxs/Vr+BP93/AT/6/t4+ib6FPlW+Uv4zf2r/Bv/OwIb/dD8QP2o+9j6mf8HADX8Mf3y/fn7Lf4sAob+t/nF+8gA0P5l/6MCFgAX/hP92//9/tD8egFW/zn5Uvy6/uv5+ftyAQz9bflp/PL/lfwU+b79WvwI/nT/zfur/pn5S/rc/dX3e/uUAO0A6v23+6D9s/52Ak7/YACmBWz9Hvz5/8X9jvwAAG8E6QF0/x0CcP72+rIAtQH5/ZX4vv3tBEP+6/v5/8gAe/tO/9v/u/YX+oUAIv2O+AH+qP1P+0D7zf2JAQX7KvtA/Wn8oPvU/eIBiv9H/7r+OPu6+Hj6dP1O/77/HQC9Aa//E/1e+4b+1P+V/BYAD/5a+s3/BwIT/5z+iv0b+eP7UvzC+nT9s/rU/VwBKf8zAGcCp/81/HT7offC+u7+uvwWAMsBT/2G/in/tv2o/fX+/wPlAKj9BP3b/34ACP7/A3IB6v9l/7P8e/01/IwAawNkAe78s/wzAE/9CP7pAfwAgv81/p8BD/4f+BYAGQFA+175yf6yAEf9qgCQAYL//fzEAcsB3/oP/sgAMf9w/HD+hQCZ/bP+UQBL/lr8nP6UAnT/6v3N//b8Kf3y/Vr8r/t7/SUAWQBl/Xf8bP9W/YP5dPuc/jz8RPwb/5n/aP6Z/Z8BJQCG+lb5CPxs++v5hv4dANT9kf9yAzcBQP1E/Ev80Pwb/0IAOP++/07/qP0T/Zn/DP+2/b7/mAHy/+78Xf0p/3IBTv/b/2X/cP4DAUIAIv/j+zcBkAWbAAz9pP65AHf8AfwWAOIDywPLA+UCQP/IAD4DIQH9/lb/g/2+/6MAVQHpA4EBmwKBAVgCFgLN/ekBXAEP/h7+AAD5/3/8CgNCAqT8Kf97/7b9KvskAlwBmftW/2X/pP5A+/n/XAH5+bkAEgMt/Jz+4QVrA4r7Tv8DAUT8YAADBU0FaP7lAE0H4//IADMEmwQsBA4C7QB3/mz/fQSmB/wCdgTsBtoBlf7f/ML+3gB2AiwE0wF//lEChQKk/E7/JAJCAPwAgQH/AXYCp/8LAcACVv/1/mQBvv9+AM8EtQNvBFQFNwPEAzcDkf8+AcgCvv96AcAEXAmfBZ8BXAUsApn9q/5cA1gCMAN2BowEGQH5/1UDsQJYAvEBdP9ZAKoCSgLaAzMExf8LAaMAqgA3Ab0BCgXaA6MCSgLABM8EbwKR/yn9JAIhBTsCAwHiA9MD5QCuA6YHzwDy/w4IpgFS/LUBMwSUAgcC2gEDAdMB5QKXAzMC5QIoA94AfgBGAYUCLASiBN4CJAJ6AZQErgWFAkYDxf9w/DAB5QTXAq4FKAcHAowETQUoAVECogQ7BHIBQgALASgBjAJGAzsEqgTABCEFzwBCAA4EJARA/+P/gQPb/00BUQLXAuUEsQSxBGsBQgSuA8X/lAKZ/8X9MwJ9BMQFvAczCDcDrgFrA4kBegPTAf8D+AU1/Bv/8AdJBj4HfQyJA/n7JASuA4L/3gAdAm8CMAHpAW8EkAPIAnYGtQPY/hkBDgL0AAz/CPxP/T4B3gYsBB785QKxBhkBHQBZAGj+3/7eALP8aP71/nv9VQN+AGcCKwg7BB0AVvs4+yL/mf3IAEYFuQBKABIBMf/IApsIhQYE/8L+PP5h/Lb9WASTBvEBYwm5Bs37r/92BKoCZf/AAmMDhQCBAb0BPgNrAfEBPgMB/toB7QJo/ukBCwGz/Hv9ZwKG/v38tQPEAb7/8v8KA5QC9ADpAc39Zf2g/wsB9AAsAsgCCgNnBGcEQgLU/8X/Q/50/0oA1gQHBJz+ZwIHAor/Tv9CALr8Af7U/779iv/c/fn/uv4m/vX+vv9KAE/97v48/Pn7hv78AGH+PPrN/U/9F/7U/1ECkAUzAkYBVQMLAef++ftH/SwCzwAdANcAnwM+AVb/JAL5/9T/1wCmAd/8MfvAAEIC1P+z/n4Ahvwt/F39oPu+/br+F/4b/a//wv7F/cX9+ftW/779JQBGA5H90P5VAWH+CPxH/94AUv6G/qD/XAHJ/jsCKAfXAEIAbwDJ/L79Lf5h/PX+mf88/nYCKf9h/gz/r/t6AWH+7vyYAa/7EPw1/t/8dP92AuIB3Pt7/Rv/q/zq/1kAMAPAAC3+QgLj/+r/jACQAUoAjAAwA00BhQJCAPL/Vv+C/4EDIQOK/2X76v+YAYwA5QBGAcgCf/6D/XD8dPlL/BYA7v5//l3/XAGQAUD9p//u/rP8xfuZ+wz9CPwlAPL9Iv9gAtcAsQTF/0f73/rN++r/hv4LAQ4EIv/c+xv/R//y/TsElAJW/Uf9PPoi/R0AIQGxBOkB9vyK+4b6mft7/+0AG/+6/qf/Kvnr+TMCiv9P/br+YADy/0oAYf5L/GX/mfv9+kv89vwsABYAfgDj/zMAxAHaAZX+Yfxh/vL/Nfzf+oEBTQGk/qMCTQO6/ED97v4B/Aj+aP5s/7P+sgDlAIP7WvwX/nT/8vtS/lkAQPvy+/n7E/tP+wcA4/9a/mH+2PwB/pX8G/+K/S3+2//R+vL5YfwlAMn8Nf6fAYL/Xf+MAHYAbPta/lwBaP6d+h78mAEoATsC2//C/hP/cP7u/vL7s/y1AdMDYfy6+jH/PP7U/ZH9Vv+O/ur9IQET/wH8E/9ZAPn9Mf1H//8Bvv3f+mX/kf/J/BYCvQGs+sX9QP9A/Vb9MwD4Ac8AFgLy/zj9oPsI/rb/+f3j/3f+cPxw/mAAJv71/jcBnP5l/RP9mAGbAND8vQGUAO78uvxd/zsAq/69AZQAjv5+ANcCxAH9/qoCiQMHArIAT/0AAN4CegFgAF3/Tv9gAv8Dxf8M/a//dgI7Agz9Kf3IBJcD0P7J/q/9xf2BAa4BVv/U/Zn9EgGc/hP9YwMkAmz9CwEDAxYAsQL0AlwBZAGFAFECSgBA/xkBUQC2/5ABpgMAAAMBLAR3/kD/SgKjAPL/Mf1H/ZH9QgL8Aqj9Tv8I/KT8Yf7Y/in/S/yYAcAA9vzy+0D/KAGc/m8EdgKz/q//GQEhAdz9/wHaAygBWALeBKYB3/65BlAKPgV2ApsADgKQA1gCUQS9AYwAkAEHAjsEzwD4AQcEfgCR/dv/iQOBASQENwP9/GH+kf/N//n/5/5d//X+e/+fAaoC8v92AOkBAf7AAK4BqgBd/9j8PgMwAxYAkANrA6/9jv74AWQBHQJcAQMFWAQx/+kBxAfTA9T74/+XAxYC0wFgBtYEUv5VAfAFjARCAN4CegFW/ZABkAM+A58DZwIp/9D+e///ASwEq/7F/z4BLfyjAEICLABRANT9vv8E/64B2gMzAC3+6/nc+5n//wH4AWsBzf88/OUAAABO/7UD5QBd/V39dP2z/vwC6QHxAfEBUv7n/uf+bwDC/ob+VQEHAt4Cvv/PAFkAF/5h/hkDqgR3/MgAcgHu/GcAZwALAekBvv/N/eIBbwDF/1gEhQAm/k7/F/63+Rv7OP17/zMCQP8E/0v6HvwM/1b9tv8m/LP+BP2K+Qz/DgC2/c37E//f+rP4Kf/C/mX9mf1cAT4BYf4zAGcAvvmZ94r/Kf88/DMAFgIT/xf8/fpd/Wz9pPwdAOr9uvxw/oUCFgDj+S38Mf/U/5X6xf0x/7r8xf2z/CgDQgL0APQAYfr2+q//tv/2/LkAUQKz/oL/YAA8/u78bP1gAPL/2PwT/5sA3P1L/koCdP/J+v38UQDF/RD89ACFAsn+kfuZ/5sC1P1s/cQB8v2s+pABvQFL/u0C+AV7/wX7uvzN/XD+tv+BBU0D6v21Ae0A2Pzu/owCR//u/M3/zf/Y/vQA1gSYAbr8bP9//vL7q/yO/hP/zf+iBIUCJQB6AQ4AD/7c+0oA5QAm/goDQgJh/iwCMwYdAjj9egEoA6MAOwQ3BYwCp/87AvQEoP1H/0YHQgQX/vQAYwWYAaMCGQWR/1b9MAG5AiEBfQIDA7ECCwH1/mQBkAFA/6T8TQE+BRkB0P4OAJsEuQCv/3IDpgEwAQMDywVh/nD+1gbaAzMAGQE7BCgBvv/hBXIFLAKIBdoHEgOMAHYErgNvAPADgQWfA88AEgEhA+0APgO5BLIAkAEHBDMErgHy/+UCgQHiAZADZwCBASwELAKv+x7+AwWbBJsA9ACjAmH8lAB6BaYBQP/LAXYGQP32+koCywET/br+owIm/v8BOwIM/1b/iv9nBrkA4/1CAL7/hQJA/7kAUQCjABID6v8E/aD/kwiFAmX98QGBA9oFNwPLA8gEkAEP/nf+/ADU/e0AtQXXABP/awV2BEf9Wv7lAukDzwDU/+0Atv22/WH+f/wx//EBMwDQ/ML83/6r/nD+8v8WAGj+kf2k/h7+d/y6/rP+JvyO+i3+Xf9092H6mwCjANj8+fsKA7UBvv2D/fX+mfu6+rIAmfvC+Jn/ZwIP/mX9zf0I/EP+3/6FACUA+f+K/6v8nP6R/0v89voLAfX+XvlW/ZH/bP9H/77/Vvug+TsASgDr+0v8G/8b/XD6e/8hAXT7cPyO/P32ivlCAAT/oP2JAQMB/fzC+gH+5/6O/Fr+3/4m/BP9ZwCr/AH+zf3j/QAA0frF/839wvwDAfL9Tv+c/mX/0P79/Ib6afrF/7b98v1RABP93P3b/wz/Afx4+tj+OP/N/4r/qP3N/9D+9f6Z/YP9wv50/+7+3Puk/tD+bP//Aa//hvxd/UIA3/4sAIr/Hvw4/yb+Mf1l/zX8F/zU++v7kf/y/wT9Kf+mAfn5DPsOAO7+e//N/3v93PsDA8sBivts/yEDXAF7/5ABVQFcAZADlwXaASb+GQWQByL/Vv3WBIwClf6uA1QFXAHlADsEgv97/cgCVQF2AGcCyABa/gz/rgHy/3v9OP90/XD6s/zb/6D/g/2UALIAvvsi/UIA7QDu/lr+bP/F/zX+Lf7XACEDMwJa+jH9RgHb/3YC1gTlBNj+EgF7/6j7xf1GAYUEg/2+//8BoP97/0oClAKz+mQB1wLy93T57QLAAur9LAAWALP+PPzQ/JgBJvyg+8QFyAC3+RP/+AH2/Cb6lf7N/7IAuQDU/0f/nP78ApsA+fu2/fX+f/5D/g4A8v8b/8gAJAJW/5X8xf+6/KT6bwAb/5n/zwQ+A6j91P2D/Uv8QP1s/aoCLAAX/JQAuQDF+6f/+wSv/UT8QgDq/xP9BwISB0IAq/wM/Uv+R/uz/A4ChQCbAlwF9AKv/RP/AwNa/t/60P4DAfX+FgDy/2cAyARcA9cA2P5S/jMAxf8p//3+pgMoBZsCuQB2AMAAf/7TASwCzf+k/oUA3gD1/noDDgTtAJABxAfq/536LAT0AkD/qgA3A0P+Kf+1AyQC9AJnBCAHywGqALUFUQT8AiQEUQQSARkDlwUOAoUG5QrsBnIFjAbaCdMFbwS1BxYC7QK4CF8KJAaXBbgKwApyB7wHxwpCBlgEOgiBB5MG+wjhC6kKIAeBB94IsQgGCpcLNwnACHIL5QgvB3IHrQtQCvAHJA6PC3kLXwpfCgINngnhC9YMKwqfBzYLHA4rDE0N6A/sDvsKKAmICfQK6Qm8DcMNRQ0zDoQM/g+eCS8LCg+QCXYKvw7oD5cHtQnLC4wIiA2mDS8N6QnACPcJcgnwCeUI8AsVCIUGOggzBtIJiAtyCxUGlwXHBtoDUQZ2BukHAwVGBZ8HdgQVBk0HfQgvBYkDEgNs/+IBGQWxBtoD7QThBRIBAwMZASwA6QMDAxUEYAJ7/fX+WQCg/YwARgF7/XD+G/2g+1b9T/2r/mAAkftL+tH6dPeo+ZL5r/sE/+v5RPq3+6j1zfO394r5Nfjn+Fr6KvdT9v34FPkF91r4vvm39dj2dPnc9cb1DPlL+r73ivUu+Jn1FPVl+UD3u/YI+FL6ePYf8jH3Ivfg9G33QPcy89j2f/iA8pLzcPbn9Jnzmff2+HH0I/W++Yf4G/Np9Dz4EPbg9mH4zfUb9Sr3UvwI+i72r/nG+QH4ePhA+QX55/zeAAz9lvYQ+Gz7ePj99pL3q/xl/TH74/1P+Rv1oPkb/9z5jvaD/Uv8DPtW+WX3PPx0+4b8S/xP+fn5yfrr+f34DP+z/u7+uQAb+yL5S/prAa//kfsSAUIC1wB0/aT88vvY/MAC1wDF/ywAnP56AZX+YfyZ/ZgBSgKd/MX9/fxA/fn7Iv22/xf8R/10+6D7Xvs1/M39qPuK/ev70fot/Hv9kfsx+yn9EPrY+q//Nf7C+Pb4pPox+1r8hv7N/ZX60Px0/f36OPv5/dD8EPqZ+fb4E/vN+xv9pPyz+Kz4ePih9534Afpe+cn4Jvgb92H4h/is+Gn4wvgX+Kj1Kvc1+Mb1MfWk+Pb0v/Mx+3v5mfXV9Wn4QPl79zn5Vvnj9XzzlvYq9zLzyfiD+6T0v/Os9of4qPeS91r29vLV9cn4DPeD88r0QPV084708vVe+fb2BfUb8xHuh/Lj9+f2S/R/9hT3h/SH9l71s/aD91ry6/NT9Hj0ePbY9vL3g/VP90D56/dp9tj0dPeV+AH4U/gx+/L5u/R49u74Nfot+tT5QP1W+Vf1/fru/K/5mfeV+JX4lfjf+or93P3j+wz/IvtI9QH4r/fY+sX9ivll+cn+HQD2/F77wvx7/br4Bfkt/qD5dPm5ADH95/iz/O7+9vwT/dD+AfzG93f8xAPj+5n5kAPN/x/6g/2n/3/8JvwwA30CdPsE/c8CcP54+jcBAAA4/3IDLAB3/msBJASFAPL/jALj/TX6mf1NAzAB4/+IBQMFHQDTA7kE8v1KAOUCkf9p/Ib+MwTtAgMB/wHy//n/vQHeAMgC9AKBAVb/PP4SAZABsQK5AlUDQgDN/8QD9ABcAygDcgFGAyQCiQGmA/AFJAQvB58HHQTIAnoFawfb/4EBQgZvAjADBgi5BokDbwTlBk0FDgAvB7UJUQAsAmsHXAOQAfgFKAUhBUYFpgUKB2AE1gZgBmQB1gR6BSQCFQb4B6oGKwh1DJAJkAOFBhkJCgcwAygJwAjTAR0ItQvDC/8Jkwr0CsAGAwcgCYgJkAlCCisKKAnwBwoJAwnLCewIKAcDB+wGEQ3wCZsG/wvSC2MJFQitCX0IxwblClgMkwiiCG4K7AiIB/sIVAt9DKkMTQuXC7gI+wrDD9ILzg7LDVgGvAkYD6kMXAvSDycNsQg6DKkO3Q5jD+wO/g/ODN4Ijw0gD1QPYxGXDa0JLw2pEvcN4QtxD3UOQQ6IDY8LkwroDycTJA59DFQPMhBNDakKCgvhDXUMhA77EJ4LFQ7vEXkLLwkgEXEPWApjCxwMJBDhD7gM9AovDa0PVAtQChUM7ArHDGoNYwe4CI8PeQ2PC8sL6QeBCXUMPgsrCvcJYwvSCTcHSQiXCWsH6Qk2DSAJgQfsCnUM7AgkCpsKBwY6CEkM/wemAyAL6A34BzoKpg03B9YE2gkVCmsFKAcvDfgHOwT3CSALxAW1ByQKrgPWBKIIeQdyB5MGIQUzBkkGbgiBB2cEogaxBGcEFQQSBZ8HGQcoBzoGHQZyBRUEBwK8BWMFTQURC4UGcgGUArUFUQKBAbEGOgajAgAAowKBA2cCsQQVBt4E0wEAAEoAzfs4/TMEVQNJBHoDxf8E/8n+OwCQAyQECgNNAS389voe/lUB7QBNA6YDdP8oAZH/+f/AAqD/F/4T/47+OwDPAlwB4/3b//gD1wCMAHT/qP2R/2j+dP9rAU0DbwLb/47+E/0zAAcCs/5h/l39QP3tAJQAdP+z/vn90fpW+wT/s/5H/3/+R/0M+9H6G/mg+0f/mfsX/HT78vsb+4b8Wv72+JL3ePox+2X3r/k8/Kj7bPu6/Bf+r/lp+vn7zfnJ+Gz7/fx//ML6DPl7+5X6oPnC+or9jvx/+uv7Lfx/+Cr1jvw1+sL2/fx4+or18vWk/Of8Xvde+dT91ffo8Ov1AfpP+xv9e/uO9mX1ePYJ9Kz0rPgM+/b2s/YB+qT2wvjf+m35Afiz9nv36/PY9lL6h/i39yL39vpP+U/3/fjc9831f/Z/+ED3E/vy/Y76vvfJ9jz4Wvik9kT4xvkB+Jb2ePjn+Kz29vyK/bD15/Sd+tT7mfV09xf4S/aO+Ov5Bfcu9Cb4s/ik9iL3KvsB+oP3Kvn2+Pb0jvRA+9z1zfPg+NX3t/dh+lb5T/Vh+FP4+fmK+Vf1nfZ/+L75kveG+sn8G/ud+HT3g/f69VL6Lfz2+JL3Uvp/+rr4Mftl+wH8oPuK+dz34PZa/IP79viz/Lf59vgi/ef+RPiv9+7++fny+TX+QP3C+jH7jv5s/Rv9YfxS+hv58vm3+6v+q/4i/Vb9WvpH+3/6hvqz/vn9nfru+Ib68vth/rb/s/wM+ev5t/sq+2X9vv39+nD8xf01/Ib8pP7N/yL7h/g4/WH+Vvs4/ygDkf2++zz8Zf10/2z/0P6r/Of8Vv0AAAAA2P41/mz9NwGR/e743Ptd/478hvq+/ZH/tv3R+Lr8oP3G+QH+jv4t/KD73Ps4/a//E/8B/Or9QP1a+vb8kf0x/QH+Uv7b/9z9CP5gAEoAzwB0/YP73P2Z/0D/3/zy+5H9ZwAb/2X/ZAHn/gMBvv/c+aj5Af75/yL7QPvr+3T7nP6R/5H/hv5L/vn7CPp7+R/6bP3f/ND8aP5a/sX9r//XAB7+Q/7Y/pz+Zf++/RP/yADF/TX+BwBgAM8A2gHaAfL/mwC2/yb+0P4b/V77Q/5w/in9dP+K//wAoP++/XD+Uvzy+Z34T/s4+9j8gv/u/Ib+nP5P/XT79vrq/TH99vzn/Ef9Nf4zAEIAoP3n/qT+sgA7AIP9pP4x/wMBOP8B/pX8kf9jA4L/iv+V/tT9lf57/WX7F/y+/13/4/1e+1772P6V/q/7Uv4m/sL6vv2k/GX7hv7F/47+Vv/b/xf8d/xA/9v/6v1//mMDuQLN/6T+WQBnAgAAFgJZAKj9egWiCMsBbP3TAWz/S/6fAZQA+AEi/zcBvQFa/jcBPgGqAMAAkf8T/aj9HQCZ/Yr7tv8hAW8AZf+Z/7UBR/3c/cn88v19AgcARgOBAfL/9f6Z/SwAwv7PAg4EdgAB/I78IQMzAqoCCgOJAdMBQP/c/c390P6R/34AZwK1A8sBS/6V/ib+dP2V/p8B3gJnAjADPgE7AEoAGQEkAiwCNwMKA9v/Zf+5AsAEqgaXB+UG5QLIBJ8FLADIBNIJLwu5Bu0CQgaqBIEDZwZnBmACyATsCs8I4gN2BPwCOwC5AqoAmwBcBSgF/AL4A4EFIQNrAXoB1P8E/3IBjARYBFgChQRnBHoBYwXWBvwCxAM3BQoD7QJcB3YKRgeXB2oJ0wPeArUHogg+BU0FsQiMCAMH1gQOBuwGwALLBfgHKAWfB1wFpgNGA1gC+wR2BKYD4/+MAK4BLAKXB+UEuQS1Be0CtQGxAhkFawNYBAMFlAKxAiEDGQUgB5sGzwiQB7kCJARgBrwHNwcKB4UI+wYoBWsFxAWbAtcCiAcoB+0EJAZjA0f9QgD0CPQGnwHPBiEFlf5kAcgERgP8AOIBNwNcA5X+PgFNB6MCYwXwBUIAQgSBCWcG+AFjA1EE+AVjBwYIjAiqBnkJRQlNA0oC9Ab/C7EIYwW8B30G4QXHCCAJUQaiBnIH+AU3Ba4BnwOxBqYBwARuBsQBCgV9BlQFzwCYAQoHnwO1A4wCFgI+ATj/nwMSBfQCDgJ5B1wFOwLPBIwCDgI7AnID1wJrAxUElwXABnIDMANrA2AGcgcdAkf91P8zAmQBlAJ6A5sETQEzAtMDhQLEA+0C3gDy/Zn/OwD8ANoDegGUADsCQP84/zoGAwW2/4P9s/61AwcCoP+MApcDTQO1AyEBLADpA/QC7v7q/z4BDgCMAD4BBwD5/ygFzwTJ/PL/RgNd/Uv8BwDtAL79Kf0M/0oAjAA7AhP/rPgB/qMCoP1/+l3/6v+R+9j8+f0B/r79JQCG/s37/AADA5H/0PwM/Vr8JvxP/dj+mwBkAWX/Uv4LAQsBYABd//38f/rc/a//1Pvu/IkBOwIm+nT7uQAx/538oPug/R/68v2v/3T7/fzN+1r+R/35+Tj/Kf/N+xD8d/xL/PL7uQBKABP9p/9L/v38Af4WAHv/zf1H/wAALADC/q/9hQA3A+UAxf/tAgoDjvxH+7kA8QF0/2sBkAPu/GX71P/0AgAALADABtcAXvsM/QT/Iv0T/U0DcgNl/+f+5QBs/Xv9cgOBAXD+HQKJAWj+BwDLAfEBMwCbAh0Cq/6yAHYCZwBW/x0EwAQ3A5gBLAA3AaD/lABcA1UDOwKXA/8DhQCc/m8CWATF/1EAlAT4AwcExAU7BH0C8QFJBMsFcgPwAywGlwPLAUkGUQZ6BWAGIQU3Ax0Elwf/A1UDuQaBB5ADgQEkBoUEFgLLAQcEPgPIAH0ESgJA/+P/FgIZAZH9ZAFyAYb8zf2yAFkA3gD0ADj/2P62/Zn9g/3c/W8ASgBvAGQBGQMKA4UCuQIX/psAFgJW/av+qgB2AgsB0wHABDsAEgHPAlr8yfrC/v8BQ/6G/LkC+f8T+538OP9W/Yr7oP/b/5n7G/lA+3/6R/ug/+7+cPoQ+DH/4/8Q/K/96v2R+9z5e/2R/aj78vur/C38F/ybAMgCiv2++Uv8wvqd+vn9Xf/C/r77cPqV+lb7tv3F/cb3RPgq+y36DPn2+Gn8g/uv+6/7OPuv+XT7+f8U+Wn2Xvfy9235QPdW+Qj8PPp4+tz7xvl0+Yb6S/z9+sb5e/nV9wz3RPYX+sn4QPes+tH6H/iw9c31BfdW+a/3s/jY+B/2e/dP9x/2DPVl9zn5Yfgq91b3Kvc99qj3zfmO/Pn5IvnY+Lv05/RE+Hv7H/pe+Uv6ePrY+HD4r/v9+Bv3Ivvn+sn49vjN+XD8Zfmh9aT4r/sF+wH4jvo1+ib6Iv39+sb5Zfnr+0v6uvg59yb2s/zc+wX50frf/Aj8yfxE/I767vxL+lL84/2O+ib4FPn2+vr3g/tA/bf7f/7y/Yr5H/q3+/b6+fsX+jz6rPhw+k/9QPvu+p34DPsi+Sr3Yfw4/UD72PiD+6z6Lfrq/779ivts+0D78vs1+mX9aP57+x78f/yD+f36BwCO/k7/zf/q/1b9G/sE/2H8dP2k/Ov7G/9KAJgBVv2O/or/SgAm/rP6Lf5P/aT+hv7j/wAAp/+uA3T/7v5h/hD80Pw4/TH9Vvun/1UBfQJYAhv/VQHY/vEBzwKO/m8ALf5H/+P/E//XAE0DqgJd/br+bP/8AMsB/AKBBYb8R/u5AAz/DP1RAmAGG//U/TH/0P6o/Wj+bwRRAJX8nP7f/pz+UQQzCFwB4gESA6//4//xAZgBwADaA1EE1wLaAekFMwZYAhIFyATTASgD4QVnBIkDYAQSBYEFYATEBZAFsQJGA6oG6QXeAjcDAwUKBZQEywdCCGcCWAJrBbUD0wFCAp8HgQVNAcQDOP+R/cAELwtJBj4B7QTwBTcFkAXwB/sE3gCxAgcCs/4kAogJIAnLBQMH1gaFBGMHGQn/Ayn/ZwJnBnoFLAa4CKYJjAR2BAoHjALy/wMHwwkdAvsG4QmFBPAD1gT7Bs8E+wTpB28EjAAoA1QFlwNNBbEIegXaAzsE3gLPBPsEPgk6BgMDWAa5ANMB2gO8BcQH2gUzBvgFWAZrAbIAogRRBJAFMwjeBqoCWAQDBfADIQUSBTcFGQMkAiEDYAIOAMsDJAg+AZAFJArAAK4BegXaA3YAAwMVCLkCHQALAfL/5QKTBjMG3gJ2BOEHYwMT/xkBqgRcA8gCzwb0Aq4B2gcKBQz/ywEOCMcGIQPAApH/3P3TAVEG9AaUBMQDnwOxAiwCtQOBAzMCegVgAmj+2gFjA30CgQG1AzMEUQKxBMQFuQIHAM8AZAFgAMgCGQWJAaT8/ABcBYkBjAIKA5n/hv4HAHv/bP1rATsCmwDU/8AClwMI/tv/r/81/ED7dP/IAkf9DP1W/8n8nP4VBNMBr/3N/Wz/QgC+//EBAwHQ/n4AXf9W+y3+GQMWAmsBp/8OABkBDgCMBN4CJvzN/zME2gEsAOUCJARNAdcALAAx/3YAKAGBAbkAZwCFAIkB5QKxAukBKAFnAhYA3P1h/gT/owAAABkDPgEi/VEArgHeAkICOwDC/rkADP/J/J8DawP5/1UBHQKz/jH9JQDxAUIAlfzf/nf+jv4HAvQC1wJA/2z/6v1p/Bv/D/5s/5sCVQHu+kv6nwFkAUP+Tv8hAYUAfgADBfn/rPp0/7UDSgKk/AcAWAKo/Zz+ywEoA+kB2gFRAs39DP0OAKf/JQDPAAMDdgBL/lgC/f4i/e7+Iv/5/TH/1wAT/WH+5/57/XT96v3tAO7+lf50/+78Afwp/UIAF/7f/rEC8v1p/Hv/jAAX/u782/84/yn93/4HADz+9f7tAMACDgDj/1wDcP4t/Pn9LAD9/v3+DgKc/qv+cgGqAEP+EgEKA7r6FPmO/sn+Vv3u/Dz+uv4M/dD+JQD2/DH77v4b/dj2EPy5APn9Jv4E/07/pP4m/uP/Vv0OAOkB9vrr+4r/JALb/4r/dgBP/XIBrgEzAvX+AfyBA3IBMf0WAMsBJv5//toBr/2V/NT/vQGn/1b7OP0P/v3+BwAX/jz80fozAiwCE/s1/s8CR/9A+6oAOP9p/NT/MwIDAef8owASA0oAVv8SA94CPP7lADcDdgDC/JQA5QLu/owALAD1/pABhQCo/Qj8bP3n/k/9jvxh/nT/XvvC+pn7KvuG/jj9vvla+Cr76/uv+6j97vyR/1r8uvgi+0D7bPtw/kYBCPyd/Nv/lfxO/6f/d/4x/yL/mf8I/Aj84//eAGH+PP70AFb/9f4sACb+cPom/rkCMf3r++P/Uv5s+779+f/j/Wj+UQC+/Rf+Yf5h/Ir9tv0WAmcCaP5o/gT9iv22/QAA1wCv/+kBZwD5/TH94/9jA28Ajv4wAekB4/9//mH+nP5RAOP/IQESA8L+nP7f/oP7PP56Aaf/uv79/Dj7Iv+V/pH7bP/0APX+r//2/GX7jv4t/qT8q/yMANMBBP8b/yn9Jvq+/fQAHv5s/TX+DgJ6ARD8oP1//gj+bP/AAGn6rPi2/xv7zfl6ARYC9f4DAR0CCP41/lb/Af5//J38Nf6z/kD/Iv8SAXD+cP4KA/n9UQCMAg/+QP1D/pQAzf1rAX0Cq/47AHD+bP/y/7P+5/wI/owA6v3j/Sn/MwDJ/kf/LABP/Wz/owCn/4P9R/vn/PL7QP1cAb79E/v/AUYDMfvN+7kCHv6s+jsCxAEQ/FL8WQDF/dz5awG5BO7+8vk1/jz+Nfg8/m8AcPzy+yUAmf9e+6D/Mf97/dT7afpH/Uv6H/r2/Cb8XvtL/pQCpP7N/XoBjv5E/NT9wABh/qj9qgDU/83/5/4zAJH/qP0SAR0C9AASAa4BXf84/aD/OwIoATcB1wLj/7b9zf/0ACn/Vv9nAOP9BP0E/5n9Nf7lAukDvAOMAM39s/6k/Hf8Hv6D/fn9xAESA77/+f92AP3+vv8AANcAEgGUAFEAXf8hAR0CWALpA30CQgA1/pH9MwBRAFb/wADlAMgABwIWAtoB1wD5/zsCWQDf/qf/mf+MAEv8hvyR/5n/E/+JAYgFOwCk/gz/Vv2Z/+0CjAK6/Pn9vQEsAFr+KAG5ADH/rgO1Af389vyuASUAVvtcAfQG/wM4/77/9f5l/z4DdgRcAZ386v9H/1L8mwDaAz4F5QLxAWQBPgHwA8gAmf/0AGcAywFnAKYBJASjAiwAMf+mA5ADywGfAUD/qgAAAIL/sQLlBEYDFgLLATH/vQGuBRIDmf0e/rkAKAEsADMAVQMsAmcCzwJRAHoDPgc7AJn7yAAx/28AWAaMBg4CMwAKA7UBFgAzAvgH+ANs/c8CbwLy/ygDuQTaA2cCqgTWBB0ARgHXAr7/1wC5BCgBMf9GA0oCRgOMAiQE9AYKAzcD8AOBAf38jAKbBAsBQgYKBU0F8AO8A+UEJQA+A+EFdgZYBB0Emwa1AR0C1gRvBFEG5QYvBVUBUQCjAu0CqgTEBfQCrgNYBLECSQR2Bj4H2gOxAgcEdgJnAKD/jATTA70BFQZRBkkGegXPBHoDfQK1A94CegM7APL/4gM7Aq4D5QQvBc8GEgXwA/EBMAGYAdcA0wESA8gCRgMwAyQCXAUhBZsCqgIhAaf/1P+UAPgBKAd2BpcDFQQHAqoCawHxAcsDSQQsBmsDegFKAlUDHQQhBYUEdgKmAxkFDgaBA7wDBgj4A/L/RgEsAoEBmwI+AxYCSQTWBtYGbwA4/8gClf4dAJ8DMAPTAaD/CwG6/rP8lATwBcL+lADIBMgCVQFYBEYD1P+jAnoDHQDn/jADpgWYAZgB/wWmA0YBlAIHAOIBxAUvBSQCXAG5Ap8BEgE7ACUApP41/q//dP9gAmMFQgSqAHf+T/1a/Aj+0wGUANz7tv3u/gH8dgB6BYwA+f/TATz+yfwT/U7/tQEOAlwBVQMWArP8vv9nAg/+MwAHBsgAiv0x/zz8Kf+jAur/Zf9VAzMCe/3N/ef+OwAOAKD9Af6z/vn7Afw4/UD5uvyBBeUAuvpo/uf84/c1/Cn/Vvs1/Mn+Q/6D+0D7g/14+rP6Jv62/Sb8T/17/1L8e/s1/or9iv3F/zj9H/io+fL9xfth+lL+t/u6+hv/0P6K+zH5Kvkb+RD6xfst/o78bfku+FP2QPnf/HT9+fuZ+6T4T/W3+WH8R/sI+ob6yfqS+cL8tv9p/KD5g/sX/Kz6E/2R/839T/tE+k/75/oi/bkAjv4x/Rf+OP23+Tz6q/xl+zX8Uvw8/CL7ePid/Pb8AfiG+jj9xvkm+BP9pPrc9/385/z9/Bv7oPny+XT53/rr+0v8LfrN/Y7+uvwAAHD+s/z2/Lr8lfyV/qMAdP2D/ZH/Zfkf+tj+qP3C/uf+Hv6o+Tj7DgBW/R/6EPjC+kf5cPiG/NT7cPqv++P9H/rr90T8Kvv697f5XvmS+UD9Nf7F/ZH7yfpD/rb9Ivvy++763Pm+/YwAjv5w/tD+3/yr/P38lf47ABkBxf8t/GH8Mf8LAbkAR//Q/sn+PP5s//L/kf3Y/lEAxf1l/zMCzf+c/jsAdP9W/U7/HQA1/rr8BP1D/pH77v6JA6D/Uv7EAZX+afymAa//jvzN/e0AfgCD/Qj+BP9yARkBPgG2/0D/3gAHAG8A3P1s/wcCWAIhA+UAOwAOAiwCE//j//gDkAHu/k0BwAD/AcgC4gFNA+0A8v+YAUICdP+z/nIB/AD9/lr+cgFyAfn/cgELAQAAZAHpAR0CwALn/rb/lAAb/X4AgQOqAtMDdgS1A1EE8QHEARkDmwBjA1EEuQJcA3IDBwTEAxkFuQQOBE0DwAIHBBIDbwT7BCEDPgGfA+EFiQGyAMsDLAR2AFUDPgUOAG8AAwPIAi3+NwFnBlwDDgLAAk0BNf7XAlgGCwFVAekFdgKg/zMCWAIdBNoFLAbiAf3+MAGUAm8EKAM6BjsE0P6bABYAmAHxAeUCowKg/w4AnP4M/yUAZf9KAO0AG//J/vn/JQAx/139E/9+AJABsgBD/mAAMwD5/5gBUQJCAu0AgQHPAgoD5QQKBUoC0wPwA9oBgQGBAQoDowIwAfwCawUwA/8DMwIb/Tj/fgCMArUBtv+R/77/Xf9d/QAAUv6v/cL80fpS/ur9oP93/uf6pP6K/1b9cP7q/aD9uv6r/hv/PP5H/3YAzwBd/8L+nwHlAIr/p/8ZAQcAe//lAHv/S/57/bP+mf+qAPL/Kf/N/6D9mf1H/aj77vrj/Qj+3PlH/b7/CPz5+3D+Zf2O/J38zf3f/Kj5/fxD/in9Nf75/f38DP1RAJsAWvyV+u7+FgAe/qMAs/7y/aYBnP41/Az/yADAAPX+Kf23+5n7mf3U/eP94/92AiUAbP3n/nf+3/7F/9T/g/0M+6v8F/4I/lr+PgF6AWAAHQDY/nv/OP+Z/ygBawF//in/GQMHAJgBzwKo/TH/EgHlAO7+e/87Av3+dP8wAd4AG/+6/g4Cg/3R+q//ZwDf/Or93gB//mn8F/6n/3v7vvvIAJQA5/79/kICCwGR/6MADP2G/N/+EgE3AWAA2gPiAaT+OwLiAfn/+AHLA/QA4/+MBJQE/AL8AlwDQgTeAEf/1wA4/6oAMwL/Ae0EQgT0Aq4BhQDTATMAXf9rAYEBe/8HANoBoP8T/88CHQLIADsALAD4AVb/vQE7AmH+1wALAQcATv8LAZsE1wJCAAsBqgAOAHoB7v5w/KD/JAJcAekBEgOJA5gBMf8SAUIAZwCJA5sAwvwP/vQCHQTeAFUD5QRrAWQB0wFvAH0CcgVvAhIB5QDj/2cC2gGFAhUE/AL0ApAB7v6K/9oBbwK9AWcAuQBKAJsCbwKr/okByAKbAnoD9AIWALr+WALEASwA3gJGBYwCr//lAsQDlwNcBTMEKAPlApQEgQOuAUIE7QJNAbECegV6AyEBiQMdAqD/Zf9gBP8F1gQ3A8L+NwELAW8AFgJNAYL/7v6fATMAhQCxAigFHQJE/A4CVQOfATsEYwNnAD4B1gTPAj4BBwAHADz+bP1yBSwELAKiBCgD8QHN/9MDfQRKAMQBwAC6/nYA/AK9Aaf/4/9vAGMDdgLiAekDkAHEATsCawFKAFwBDgR0/7P88QFrBRYCegEVBFEAOP2BAWACtv1A/zME6QPu/hkDcgfF/XD+iAVo/jX6/wGMAnT9BwC5ApQAIv83A7EE5/7f/g4EbwBs/QMD/AAp/fEBdgI4/8X/iQFKADz+4gFyAav84//LAfX+iv/eADcBnwF2AE7/g/1p/EP+9ABRANT9BP9l/8X/bwDAAFwB7QDF/0P+kAHb/9j8iQFVASb+2//PAsACbwISAQAAZAFNAdcAKAHlAEP+2P5NAX/+cP5CAn0CZwBH/3v/R/8m/tD8Zf2O/AX79f6r/tD8Kf93/hP9r/1KAHoBDP84/Sb+hvzj+w4ADgCK/aT+bwI3ATX+CwHpAZX+dP2K/6D/4/07AEkEGQFw/gMDFQQHAPn9CwFD/lL61P3U/ygBvv+MAh0Evv/LAWcAMf/y/Sb+EgOK/3D+1wCR/2H+bP/IAkIAvv0ZAyEDG//0AAMBoP8zADABGQFW/zsARgVUBU7/kAEzBOP/uQB6A5X+nP43A2z/uQBYBK4FogbaAa//ZwD8AEYBAwFZAHf+8v1vAHT/7vybAPEBaP6V/H4AwAILAbIAjv5a/n/+DP9ZAOf83P0SAUf93/zeAIkBAwFGAYkBdP+yADcBmf2FADcDTQMOAHT9TQGR/47+TQGQAQsBxAFCAg/+yf6bAND+NwGyAF39aP4LAYwAF/7u/j4BMf2Z+0IAcP54+ib8oP+K/cn6tv+9Ad/+CwH0AqT+kfsX/n4AYf6g/SL/q/79/EP+pgEHAOr/FQQwAU/9Tv/F//n9lf4wA70BOP1W/+r/9f6K/eP/egE1/AT9hQCv/fn7jABl/6v8XAF2ApX+vv1yATH/2Pot/PL72PqZ/VwBaP5L/PwAGQGV/uf+TQEDAa/9OP10+0v6pPzEAXYADP0SATH9xfs4/4L/gv8P/pn/Mf2G/Nj+xf9KAFr+7v6V/t/+1P81/jX+e//q/dz7mf0t/lr8mf87BKoAEPzn/rUBJv72/Lb/yf7c+837aP7f/L77zf+BAX/+PPz1/ur9OPvf/rb/E/0p/fn9+f1s/0oAKf8X/sn89vyd/CL99f4lAOf+2Px6AcQBQgBjA6MCIv8e/tcAkf04+0f98v9vAg/+cP7LAU7/8v10/+UAkf/Q/s3/Mf1E/N/+BP9s/VL8bP+n/zz8R/08/k/97vy6/nT/9f6R/6j9YfzQ/H/+rgGjAOf+qgBvAAj8Vvsm/o7+UQBA/7b9Zf9RAHYAkf9s/2j+Lf5h/qj9QP0T/br+/f4e/E/7yf5KAJH93PsT/br65/p3/gz9uvzQ/gcAs/yD+2z7H/oe/I78qP3F/Rf+p/8M/yn9Kf1o/h7+Yf7Q/k7/Mf/u/i3+tv/tAIwAgQFvAHD+s/xL/tj+Hv78AGMDQgC6/EP+Iv/J/l390P4dAKT+HQBrAfn72PgE/+783/pw/mH+Kf3C/IL/uv5O/yUAcP72/IP7aP7u/ob+nP6k/nD+Mf1yASwCQ/4lAGQBkf22/dMBvQHq/9v/JQDC/nD8tv1O/7P82PyV/tT9QP1a/IL/Af5L+sX9dPtE+gz9R/2++wz7Vv0M/Rf+3/x3/Hf+r/uC/0D/8vnC/tcAR//9/jsADgLn/gT/egEzALb/YwMzBPn/bP+R/zABowCZ/28C2//J/r0BOwILAQMBPgEAABIB+f8x/dD8d/y6/gz/aP5KAG8AVQFnAB0CLAIb/Tz+f/wT+zX+tv+5AFb/ZwBCAKv+UQK1A5gBtv+r/jj/Af5s/Z8B4gMLAcQBowIB/gH+PgH8AL7/NwFGATH/8v/PADMCpgF0/w4A8v+R/WH+IQEi/2X/AwHF/Xv91wDeAIUApgEsAHD+gv/TAWcAjv52AEoAYf4T/wsBVQFrARkD9AJKAN4AxAOJAUv8WQCBA0v+UQKiBIwADgKmBcsDzf0zAgMFzwAOAAsB6QNCAkYBEgMsAhIB4gMoBygBXf+FBGACbwDAAgcEFQTPAr0B8QEwAaoADgRCBGAA4gH0AuIB/ABZAGsBcgF9Am8CQgI+AUf/7QAzAu0CjAIWApsAdP8DA/EBG/+BAWACkAEOAsQDLAIHAGcCYALxAfEB9AIzAjz+dgALAXYARgGJA4gFqgDlAA4CKAHPAokD5QJd/xYCmwTN/w4AtQNvAg4AVQNGAzcB+AE7AAMDqgJGAc8EQgJd/2QBGQV6A4EBwALXAhYCBP9l/9v/ZAHaAzMCpgFkAXYEtQULAW8AmwKqAKT+jACn/3/+CwGFAqMCKAESATMC/AA4/34A1wJs/zMANwNnAJsAyAIZA2QBRgOxAnv/4gEhAU0B3gA7AJADwALEAbUDxANKAjMEfQTtAFwBpgF0/yn/Mf8p/07/vQGJA28AS/5KAN4CXAHPAM8Af/6z/gcAfQKMAAz/EgEHABkBfgBs/+IBYwObAlgCAwM7AiEDOwSXA4EBOwJ9BMQDkAMDA/ADyAJnACEBTQGFAokD2gOqAlgCpgWqBBYAegGbAjj/pP7b/zMAYf4SAX0C7v5vAD4D3gLJ/EP+BwL9/uP/JQD/AdoB/wGxAkf/6v8dAlECDP9ZABYC9f47ACQCegGuAaoEegNvAOIBIQN2As3/Q/4x/94AiQFRAGcAUQDF/z4BxAE3AaoAFgB+AEf/dP3y/4wCmf9D/koA2/+O/ur/egFo/kP+OwDb/28CQgLU/zH/iv+BAZQClAIKA2MFEgOz/iwAegF2ArwD4gP0AhIB9AASA94CiQEKA0oC3gCK/6//5QBw/jH/MAFvAIUA3gAM/2z9pPxo/tD+zfst/lL+OP0m/gz/Af5A+6oA+AHu/qT+Xf9yAXf+Afyo/c3/lAA7Av8D7QA4/zMCCwF3/kYBLARJBAcCR/9w/jABUQKuAZ8BRgG1AUP+DP0t/mz99vxW/8QBIv9h/pz+g/0X/N/+PgET/Xf8DP1//Bv7qPk4/Sn/s/7PAKoAd/6k/rb/Mf3Y/G8Ahv4b/9MBMAHF/7b/pgHXAO0Atv8T/13/f/6+/2X/f/5nAFwDmAGFAB0A2P4x/7r8HvzC/mz/OP1w/vX+e/2g/c394//Y/jj/9AD9/oP9cP7N/xf+F/5nAJQAKf8p/9j+F/we/kYBYACqACEBRgEM/zH/mwL1/qD9kf+C/wT/F/4+AeP/Iv2g/8AAzf1h+kD9oP/Q/gT/+f+Z/6v+G/8T/Tz8+f0WAJH9Jvq2/Uf/owBgADX+F/7Y/Nj+0P6k/Jn9/AA3AaT+UQAM/2z9jv7f/tj+nP7j/0f/aP6G/iUATQFs/4UAkAFa/or9XAEhAx0CiQEx/wj+DgAhAZABlAAAAGQBzwADAYEByAAHAnoDtQGjAMgC7QKmAWAABP9O/4UAwADy/9T/Jv4P/jMCMAPlAPQAQgJZAH/+3/4E/+f+Lf7q/c39yf62/8gAnwHn/pH/OP/q/VkAzf2z/MX/s/5L/G8ATQNa/n/+xAFH/3D81P2z/mX9cP4LAaYBkf8WAOkBDgDY/owAOwD1/msBp//Q/BP/aP6o/Tj/TQH8ABP/cgFNAUf/qgCC/9D8Yf62/2H+Iv8p/0f/CwEoAUYBXf/C/k0BKAEI/r79lADAADADTQNKAN4CuQIT/6/9Hv6g/wMBIQEHAu0CegHy/6MAXAHn/t4AjAJ7/6f/mf9O/9/+5/4ZARYCMf+g/VkAe/8M/Zz+gv+6/ukBjALU/8L+Yf6V/gT98v9NAaT+iv9l/9D+gv+MAJABOwI7ANcAOwIi/6MAhQIOAGj+tv++//X+JQBL/tj+BwBo/hkBRgGZ/bP+hQA1/AH4t/sm/gz9Vv8zAAj+7vzu/mz9F/q++5X8DP39/OP9vv9L/igBawWBAywAkAFVATX+uQB+AAz/iQESA9cCTQHlAk0D+AN2BIUC/ALxAcQBUQCK/Yb+kf8M/0f/7QD9/sL8d/6n/y3+OP3f/Kj7F/5//kf7uvwX/tT9q/6+/xP/tv3U/7P+wvzn/F39LAJrAeP9NwHAAj4BRgMkBAcCywH/AQcAhv7f/mj+bwDpAUYBWALlAj4BS/4T/c37Kf10/Rv9e/8m/o78Zf3C/mn8nfwI/pH7F/pH+Tj9Tv/F/c39q/7XAJH//f56AQcAbP+1ARkBDP8sAAoDMAEWAEoA1wCMAmMDSQZYBN4CgQNYAkIALAD8AqT+CP6fASwAyf7IAEoCoP84/6T+G/+R/5z+SgAM/fn7G/9l/UD9wv5o/i3+Kf8b/5n9Iv+G/uf8E/+fARYCmf/u/gAAUQK8A9oBLABl//X+cP4E/07/owCFAsQBsgCbAPQCYwNZAOP9Zf2Z/8n+f/4HAGX92Pyk/rr+Af57/4b+xfsX/lL80frU/64BbP8OAGQBDgCg/+r/AwH9/PL5OwB2Anf+BwAhBVEEnwNUBcAEhQJCAjMEbwIWAJQCNwNZAB0CZwTxAb0BegNcAbb/AABcAcQBFgBVA30Cr/3U/1wBR/3c+2z/Q/53/M39vv0B/K/7Uv79/uP9R/9NA8QBBP9ZAMX/Hv5l/QT/s/6V/pABZwB7/xkDPgUhA5gB4gO5Aq//yABVAa//BwCjApgB5QCJAX0C/wE4/Vb/cgG2/3YAmf/C/nD+7v6Z/zMAIQGBAZQAmf9nADsAr//q/9T9lfzY/pz+1P9RBK4DrgHxAfQA8QHpA4UCawHPACgB1P+6/g4C3gJgBGsFBwJ2AKYBEgPwA6YDlAAOALUBhv5h/ssBNwHAAhkDoP+jAMgAiv8LAQcAdP2k/lwBR/9w/k0DhQTpAeUAhQDtAFEAuv4WAKMAdP92AE0BgQEsAuUC7QKqAjMCpgGYAWAAnP5S/r7/dgBnAOUALAKxAh0AHQAWAkYBvv/n/pn/vv1a/Ef/JQCG/pX+HQA4/+f+wAA7AL7/Nf4t/H/8Vv2n/zsAkf8x/7r+e//AAHYCZAF+AMgAtv+z/lb9BwDaAf3+dgDXAg4C9AJgAoL/kf8HANcAXAPpAbb/mAHpAYUAZAG5AjADMwKn/xP/AAAlAMgA0wGMAqoCqgJ2AqMCUQKMAHv/jv6n/zABIQEwAe7+7v69AdoBYAIKA9MBqgAlAE7/Q/47AAMB9f4WAJQAzf9gAAAAzf9+ADcBzwBw/t/8Uv4p/zX8hvyFAB0AuQAOAnv/cP7b/zH/e/tL/Or9hvwp/dz9Vv9gAEICPgOqALb/OwDj/7b9Xf01/vL9PP4HABkBr/8HANcAcgFVAer/YADj//X+Zf9ZABkBlAAWAEf/LACjArUBdgBKADH/p//b//3+WQD/AX4AegHtAm8ALAL0ApH/f/4E/wsBwACc/kf/gQFCADX+OwJnAq//BwIzAoL/r/0OAN4Alf5W/3T/Uv5l/R7+kf8lAM8AWAK1Af3+egH0AMX9DgDeAHv/MwASAVEArgGQAXYAkAFKAHv/p/+R/+UA/ADb/28AHQBRADAB3/75/x0Ahv6Z/xf+HQD/AQAAE/+V/vn/BwBs/yb+4/1+ALUB4gHU/6D/Xf8M/Vr+f/4T/1EC0wF7/0D/4/8wASEBMf8b/9v/QP9CAH4A3/4kAvQEsQJNAfEBQgCg/Wz/MAEsAB0AiQEdAnoB2P4X/msBLAI3ATcBKAGZ/6MA2gEx/9z9e/35/wAAVv01/mz/4/9+AOkBFgBh/qf/DP8p/Yr9LAAzAN/+Vv9A/+r9oP8sANz9jv4dAB0AcP5w/o7+Xf04/8AA4/+v/00B3gCZ/cL8Iv8AAFr+OP3n+uD4NfxZALIASgDAAGcAdP/f/Ef5E/uG/vn9BP08/K/9LAAWAAsBGQEx/w4Af/4f+n/6DP1a/ur/OwKqAlUBowD0ANT/R/1a/mX96/kx+3v9s/yO/Of+rgEzAuf+iv0t/hf+f/zJ+kD7XvuD+9/6cPyZ/Sn9gv8e/mn6wvy+/0/9r/tH+3D8Mf1p/DH9kf3U/zMALf4t/N/8jv5p/Dz8E/0p/Vr8EPwp/xYAwv6K/4b+xf3n/in9PPxd/Uf9RPz2/HD8G/1ZAI7+R/04/zH/F/5D/iL9r/s8/Hv9aP7c/dD+zf9a/sn8d/5s/6v+Xf+O/r79f/5A/8L+HQBkAZABKAF2AJABTQF2AAT/BwAOACn/rgGUAMn+hQCfA2MD/wGbAv8BqgBd/47+9f4x/7P+gv9cAdoBAwHPAv8BBwCUAML+Xf90/5X+QP+R/77/owASA5sCnwEWAvgBzwDN/83/zwCbAiED3gLAAtoDkANvAjADawOMAjABvQHIAmcAbwByBcAEvv9kAT4DmwBCAkkELAKjAHv/OP9s/zX+G/+uAaf/CP5GARkDWAIDA6MCIv/J/v3+Vv1d/dz9Mf/iAa4DHQQKBaMCVv96AcsBd/7Y/t4A2gFKAn4AowD/A0kETQNrA2AABP8ZARkBDgCC/zABGQMdAm8A8QGbAmsBrgHxAeIBowD8AqoC8v35/70BWQDiAYUEOwIzAP8BCwF2AJ8BVQNcAyn/OwADA+r/owAzBBkDoP/eAAcErgG1AUYF1wIm/q//0wGZ/2z/OwIkBK4DEgOqBEIEvQH4AYEBS/7Y/r0BWQDN/5QCowIsAhIDdgKUAEoASgC2/13/aP5W/xIBiQGyANT/tv97/+r/3/7j/d/+uQDAAvEBOP8AALkCuQAE/0YByAKxArUBsgCc/uP/yAR6A34AYAKbAu0AtQGJA7EEywNVA58DmwB7//wCyAKv/0IC+ANNATMCCgUkBA4A3/56AaYByf4lAL0Byf4ZATsEZAHtADMEyAIP/n/+zf84/5sAuQAOAGQBsQK1A8ACywHtAjME9AI7AGQB+AFVAYUCrgP0BGAESgIwAx0EKAM3A5sCEgPPAvEBrgGbANcC/wP/Af8BRgMzABYAMANW/wj+UQDeALIAvv8ZAQ4Cmf/y/6oCEgHy/1ECDgIAAKYBAwP4AeIBXANRBE0DogRnBIwCMwSiBAcEBwTpAxUEOwRnBAoFsQSQA1EELAR9AjcDlAJW/2cACgOmAX4A6QEOAg4Axf+yACn/Uv52AJQA4/0b/aD/xf9W/Vb/MAF//v3+DgLlAP3+AwFYAj4B2/+V/vwAHQKqAMACywNyAaoAuQLEAUoAhQIWApQAKAFgAHv/IQGfAQ4A6v8i//n98v3C/Aj+R//y/YL/e/9h/JX8Jv6D+0T6f/y6/AH8r/vN+9j6Kvst/Nz7hvwm/k/9s/rU+0/70frC/hYARPzU+X/8RPxh+ob8d/79/Az9YACR/zX8r/3y/2z9Uvwm/ur9Uvxw/GX9uvx7/Zn/3/6Z/Wz9qPus+l77jvwe/tz90Py++zz6hvoQ/KD7+fuD/QH8+fsE/dH6AfzU/TX83PvR+nv7T/2g+5X6s/xH/83//f6v/Uv8T/tH+wj8Hvwe/Fr+9f4x+4r5Zfu2/Sn/F/7c+0/7g/ts+0/7f/qz+hD6Jvqz/Ef7EPo1/Pb6Ivnu+lr8Lfq++fL7RPrC+O76bP0M/XT7hvw8/IP7Mf3N/UD7kvkx/aT+Jvyk/g4AF/zJ/IwAtv9s/Rv/G/+O/O78R/2v/Sn91P2qAJn/mf1s//QALf5S/vX+0foi+2H+Nf6K/Yr/qgDJ/mX/BwLxAXT/nP44/0D/DP/u/mcAbwCjAGsD+APiA7EE1gRGA1wBmAH4AfQCvANGAeUAtQNvBIwEiAUdBowEKANcAYr/3gAzANcAOwKv/5n/JAKxAoEBZAESAYL/Kf+K/9j+Nf4x/28Axf+n/4kBCwG+/xYCwAIAALIA/wMwA3YA1wIHBGcCMwTtBCQEDgRrBQcGyARcAxIDgQM+AUYDLwWMAqIE0wVcAzMEkAX8AqD/r//q/+P9f/6bACEBIQHPAOUAUQJnAgMBbwJ2APL9JQAwAaYBbwLXAmAC1wKFAtoDmwbLA4wCLATXAs8CQgTPAnIB7QLEAz4BjAJCBiEDXAHlAnYC3gAT/yL/Vv8B/E/7uQAdApn/TQFGA2X/jv5rAc3/Vv2V/Of8e/1a/g/+iv+UAvEBvQFgAhIB+f+bAG8AyAA7AI7+OwAoATcB/wEsAoEBTQEdAgsBdP+5AHIB7v7j/WX/SgAOACUAuQDj//L9Xf8+Acn+Jv7F/779T/tW/UD/vv/U/5n/BwD9/oL/HQCR/94AKAE1/qT8Iv/b/yL/5/7b/2cABP/lAGcCTv9//rIAVv/f/A/+yAAT/zj7tv1+AGj+Af6yAM8AF/6Z/fn9G/2d/Nz92P6g/ef+IQH1/tj+pgEAALb9cP7Q/gT/p//1/q/9d/5kAR0CdP90/ygBZwCK/6j97vzN/Xv9Yf7n/h7+8v3j/Zn9jv53/mz9cP53/Pb6s/zj+yb6qPur/t/+Hv4B/jX+Yf6D/ZX8XvtS/Hf+wvxp/I7+f/4E/5sAvQELARYAPgFkAUD//f5RAJz+pP70AAMByABGAfQAbwDpAcgCiQH0ADcBZf+g/eP9aP5D/lb/AwHN/zsAEgESAZsAyf5S/or9hv7C/mz/uQBs/58BQgK+/5QAYAIsAqMATv/b/3oBiQFVATADuQK2/28AKAEWAIr/jACMAiEBp/8wAQcCjAAzAFkAIv9h/mj+FgBCAHf+BwAdApn/e/2C//EB3gDC/uP/+f/1/jcBnwGO/rr+9AKBA4r/9ADwA7IAmwC8A/8ByAD0BDcFowC5AHoD9AL0APwClwMZAdoBtQMwA83/QgB2ApsAjADAAt4CGQH0AB0As/75/zMA9AAzAg4AQP+MAMQBowLLAfQAfgDeAA4AcP5l/3oBFgLPAKoC9ARNA9cAqgA+AQAANwP/BZQCDgAwASgBE/8oAYEDWAJVAXoB3gCqAHID+AMhAVkAawElAKf/UQIhAzABjABKAiQCPgFcARYA/f7U/xIBegG5Ag4ETQPLAZABgQESAbUBbwJ6AR0AdgBYAk0D/AJvBKIEvQH8AAMDfQSJA28CqgKFAsQBSgLEA8gCDgLwAyEDpgE3A2sDBwIzAtcCWALiAWMDYAR2AkoAuQBCAhkD/wNGA8sBmAEHAowCAwHF/+IBKANnAs8CtQOuA7ECJAI+AyED4gEdAuIB0P5L/lgCnwOxArwDyARRAq//IQHxAX4ANwHeAjAB+f8dAkICQP8i/8AClwPLAcAAlAC5ADAB2gFcATMAjADAAKT+0P52ArkCzwD8AigDbP9d/3oBSgAT/2AAbwCbAM3/8v/pAdMBjAJ2ApQAZf9vAM3/F/4T/0f/6v+yAG8A2/8oAe0CdgLEAcgAzf9d/wz/6v1l/ygBWQD0AFUB3gA3AYEB7QDlAGcAR/9W/4UAZAEZAWAA8v8+AZsAtv/TAYUA9vyO/gcCUQB0/4kBZwAE/zMANwHtAH4AmAESAXD+jv5d/47+/f7AAH4Aiv+FAN4A4//N/z4Bxf9s/ZH/6v8P/kD/JQAb/7r++f2+/XD+Zf3Y/mQBTv9w/j4BegGk/pz++f9h/t/8Lf5O/5n96v2jAD4BSgCfAUICZf08/L7/kf+G/n4AAAAp/UP+Mf8P/vL9dP8AADz+Zf2D/dz7EPzu/lr+Uvyo+7b93P2v+xP9tv2v/S3+dP/1/kf9R/2k/ED90PzQ/HT/AAAp/yL/G/8sAPwA6v+n/4r/Kf+v/cn8Lf48/qD9/f6MAML+QP2K/QH8rPqO+hP7Jvw8/N/6mfl/+qj7s/qk+tH6FPnn+Gn67vq3+e741Pl/+tH6S/x7/aj7Bft3/Jn7bPuR/aD9g/uV/IP9vvuG/DX+pP75/b79tv0x/TH9WvwB/I78Mf10/V399vwT+xf6Vvta/GH8EPzy+5H7qPkf+tz7wvq6+or7Lfr2+Mn6+fsi+0v8xf2K/Z38Afyd/Or99vzy+2X9nfwx/UD/Zf2o/VkAwAAi/xv/wAD5/xP/wv7C/ib+Vv10/RP9e/1S/lkAdP/J/Ev+dP2O+Pb4mf2v/R7+3P0i+9j8PP5L/o7+g/3u/Kv85/qZ+c37Wv7N/xYA0P4b/5QAYAB7/0IATQGbAEIAFgBa/sL+2//q/WX9owBvAjABCwGMAJn/Iv+k/vn/FgCR/0D/dP0x+x78iv/f/jz+Mf9D/iL9RPwQ/Of8wv5+AK//Uv7Y/u7+e/9+ACgBGQG1Ae0CZwB7/wsBEgEAAKoAqgL8AkkEmwRvBFEE8ANgBBIDBwJCAkYBgv9CANMB8QHIAjAD0wESAwoF8QFd/00BLAIHADcBKAMLARIB1wKQAa//JAJNBaIElAJVAeUC5QJvApQETQOqAogFLwUoA3IDLASIBSQGAwN6AfEBnwFnAuUCTQPTA5cD4gPLA8gCEgO5AvgBMwLeAMgAywH/AUYD8APPAtcCEgNvAjsCHQLXAtMDjARJBKoEKAVnBA4EvAPlBCwEmwJ6A8gEtQVrBZcFXAXlBC8FogT/A64DxANRBDsEvAPaAwcEogQvBZQEtQOQA8QBWQBVA8QFXAXPBFEE4gMZA2sDlATwA9YEywU7BN4CbwLTA94EZwTLA4wEYATeAokD/AJCAqYDAwXpBZQElAKbApsCOwLAAjcDmAE7ABYCZwJVAXoDJAaFBAcCbwJRAmQBJALLA0oCOwCJATADkANVA4UEhQQOAssB0wMoA1UBjAJjAwMD/AL0AjcDfQLAAD4BiQGqACwC+AGn//L/5QALAXIBSgKbApQALADLAbkABwCuAbIAs/4oASQC4/8lAIkBpgHb/+r/TQOJAyEB9AA+ASEBvQHxAU0BTQGFAiEDAwGK/yEBPgHIADMAuv47AEoCwABH/x0ACwFyA3oDgQGUAI7+r/04/Zn9r//8AFkAHQDeANT/dP9RADcBqgCg/wAAR/+o/TX+kf9//qT+UQCC/7794/1d/+f+9f6MAIr/mf1l/U/9S/xE/P38R/1E/B78E//U/779CPwe/AH8Afxs/V39kf1l/Qz99vyk/Pb8r/08/mH8UvxS/F77afwt/C385/xp/AX72Ppl+538Afwm+hf8nfwF+4769vqz+hf6hvrG+ev5Jvq6+k/7LfqV+nD8CP6z/DH7dPte+1b79vrR+n/6yfqo+xP7PPrF+7b99vwe/N/87vyg+3v7bPs1+pL50foI/O76Lfp4+nj6vvn2+rP8Xvuv+br6KvtW+Uf5UvoQ/FL8pPrU+Xj6CPxW+4b6Jvrj+S36nfq++RT5zfvQ/Ov7qPsQ/Ev8Jvys+jX46/f9+Aj6xvlL+k/73Ps8/KT80PzC+ir5zflw+lr4h/hl+wX7/fop/SL9oPt//Gn8uvrU+c353Pkt+jj7Bftl+yb8QPsf+gz5BflH++P7H/q++bf5Vvms+Of4Lfqs+gH6Wvox++v5cPp7+2H6uvqv+xv7bPv5+xD8bP1s/Qj+Kf9s/bP8t/sI+n/8Uv5//Cb8g/2r/n/+6v0b/2H+4/st/ET8zfkt+l39pPxL+nT7dP2k/AH8T/3N/Tj9zfvY+uv5mflH+9D8Iv0B/s3/Jv4t/HD8E/2k/kP+iv2O/Pb6E/1KAN/+1P1nACUADP/u/kv+G/9s/7r+Zf9d/xP/PgGYAQ4AbwAZARIB4gGFAmsBDgCn/+0ASgJgArkCsQJKAjcD2gNJBJsE3gK1AVUBDgBgAL0BjAJKAssBzwLiAzsEOwRJBCED2gFrASUAsgBNASwCDgQsBA4EMwQsBPwCLAIdAm8C1wIsAigDQgSJA1UDbwTTA30CPgP0AukBjAIzAoUAegE+AzcDYAJNAZsCvAOxAukDGQXpAwcEEgWjAoL/AwH8AnYCQgIkBDMGkAczCPgH+wamAxkDyASJAygDCgXWBNcCtQMZBXoFkAUoBfQEpgNvAjADawOXA00F7QRrAwMDbwS5BJsCkAPlBEIEhQQ+BSQEYwNYBC8FVAU3BRkH3ghnCM8G+AeQCbwHCgcSB3YGMwYdBmAGRgfACJ4J+wh2CIwISQh5B4wG0wXaA/gDUQaBBU0DTQUdCKIGdgQzBAcEAwN2BCEFQgSUBKYDywMdBGcEfQRyBVQHfQYvBaYFuQbeBD4FdggDB30EFQYgBz4FsQb0CM8IcgnSCQYIYwWFBFgGqgaQBccGFQaxBBIFgQW1BZcFAwXeBK4FuQSFBAoFXAX/BcAE+APwA7wDFQR9BO0CKAMDBfQE+AVgBs8G6QdYBvQEPgXPBKYFJAa8BYEHsQZgBJQEVAX4BeUGxwamBRIFEgW8BWAEkAO8BQ4G3gR2BK4DwAJGA7kCnwFcA6oEXAPPAhkDIQPEA1gEFQQ3A00D/ALlAlwDcgNJBNoDNwP8AhUE9AQ7BEIEjARNBfsEqgQDBXoFIQVNA2MDawMOAiQCHQJyAYwCKAPeAowCegFkAU0BowCqAMgAiQGMAu0A4/9GAcgAGQG5AiEBSgDTAd4Avv+bAOkBawPIBFwFzwTeAkICOwSfA3YCJAQhBRUEcgMwAyEBKAGmA8QDfQLIAsACgQGBAdoBcgHpAUYDqgLU/yb+hv4i/WH8DP8p/9z9lf6c/rr8F/7eAHT/Kf8wAYwA8v17/dz9Q/4M/77/2/+r/rkA0wNCAnYAcgMkBAsBWAJnAjsA0wFnAnYAFgCJAb0B+f/J/kD/Tv8m/jz+q/7u/Nj8d/7Y/NT7d/6z/kD74/m6+qD5MfmD+177PPo1/N/8bPv5+9D+JQCG/s399f6+/Xv7Hv4ZATMA1P/F/wz/kf8SAQMB6v84/zj/Kf+2/TX+FgBl/yn93/zc/V39EPzF+478E/tP+W352Pg1+IP5r/uR+/36R/vc+0v6/fiv+/L7vvny+UD7nfrR+nf8OP1L/tT9G/0B/qT+OP/F/xP9zfvu/v3+dP1s/er9+f3Q/O78Wv5o/h7+Uv72/Fr6e/kq+2z7S/rf+q/7OPvN+6T8DPtS+pX6Zfng+HD62Pqs+qD7AfwQ/Fb78vuD/WX98vuV+v36g/t0+/n7qP0b/47+dP2K/Xf8pPpL/PL9Uvyo+5H9qP3R+kv6NfzU+0T6s/rF+777bPs8/Ev8Bfus+k/71PtW+2n6lfqD+8n6Nfqk/Gz9r/uv+478ivvN+XD6S/xW/Vr+aP4b/Rf8hvxE/Aj6dPkb+xD8WvwT/fn9CP41/kf/hv7J/Dj9S/4b/RP7RPrf+h78PPyR/QH+oPuR+6j9F/62/dz9wvwm/Cb8kftw+oP5LfoQ+hf6R/st/JH7kfsM/eP7S/qz+kf7QPte+y38RPy++xD8DP3U/br8R/ta/DH9d/wm/Lr8Kf3q/Wz/1P9h/h7+YABA/zX8S/we/kv+Q/4b/1L8f/qd/Ef9OPvy+1r+dP1a/H/8T/1E/GX7Yfxs+0T6MfsT+5n5VvuV/OP7Vv17/xP/pPzU+3/8Vv2G/gcAtv8B/sn+UQCK/47+4/+qAGz/lf71/oL/uQDiAcQBCwHN/1kAGQHj/2z/p/8M/xP/Xf/q/Tj9f/5//r79Jv6K/0oA/f6c/tD+zf2o/UD/kf/c/WH+Vv8m/jj9OP83AaMAOwA7AEIAQP/J/rb/ZwCMAHYAowD5/9T/uQBKAvgBYAA7AMX/+f+Z/0P+OP8OADj/mwB2AnIBegH4AX4AOP8X/pn9gv9GAWAAkf8hAeIBsgBRALUB8QFgAA4A8v90/2H+iv8SA4wCvQFjA1gCWQDPACEBvQFnArUBCwH5/7P+Nf5A/1EA9AD8AGAA7QAZAQMB+AEHAoL/zf2c/lr+YfyG/LP+3/5s/7kAgQEoAQAAhQCqAKD/nP7U/64BPgHIAAsBIQHTAQoDBwIhAUICDgKbAEoAnwEsAmACiQPXAjABMwI+A5AB5QAOAv8Bvv8t/l3/xf+6/iL/tv8M/4wAmwI3AU7/vv8hAbIAzf+v/wz/lf5O/0IA+f+yAFgCowLpAbUBVQMDA88AjAAdAs8CBwIWAtcCwAJ2AoEDGQNyAfEBDgIWAOf+7QBvAuP/uv4SAbIATv+fAaoCzwBnABIBBwAM/8AA8QFs/+P9kf9RANT/UQB6AfEBEgMsBFUD/wEzAvwCOwJ9AigD6QFNAcQB8QFGAa4B4gObBM8C0wFGAxUE8APpA2cCBwDb//8BNwNGA94C/wGuAe0AzwDlAm8EDgTXAlUB3gAkArkC9AI7BMAE4gPpA/gDyAIKA9YE5QSQA3IDmwKfAWsBWAIDBUYFxAV2BuUEfQSJA/gBQgJrA+UC/wH/Af8BGQM7BNMDNwPAArwDPgXXAlUBCgOFAukBgQOQAw4CIQMDBUkEFgIZA0YFpgMoA0IENwP4AZcDegXWBP8DzwRYBs8GWAYKBVUDwALiA0IE6QMVBA4ESQTwA3oDcgPwA8QF+wYHBKMAKAFYAjMCTQHxAdoBsgBcASwCbwKFAh0CywH4AVUB8QGjAtMB1wCmAdMDLARUBZcFlwMdAiQCSgIwA/QElATIBKIEdgSFBOIDzwQdBvQEqgLEA8ACe/8i/2AACwH8AKYBkAGbAED/DgD8AE7/Zf9CAA/+xfuZ+0v8Yf5H/+7+Vv9s/yL/BP8T/yn/4//N/7r+vv0P/nT/FgAWAJQAJQAM/2cAPgHtADMAiv8i/yL9afyg/TX+3P0i/2X/vv3c/dz9qP2R/UD9Uvyz+mH6yfqO+s37Jv5a/sn8HvzY/AH8G/vY+gH6cPr2+lr61Pn2+mX9s/7F/X/8vvsM+/b6wvob+XD4VvkF+eD4bfmv+bf5hvqR+zz6/fgB+jX6yfj9+AX5Mfe+9b714PaO9h/22Pj2+hv5FPm6+vL5R/mz+Lf34PZ/9ir38vcQ+Pb4Bflt9xf4G/kf+PL3vvnY+BT3bfl4+o74S/h7+fr3sPXR9hv5rPgq9+f42PqD+fb4Lfr9+Mn4OPvY+jz4yfig+zj7F/q6+qz6VvmZ+fb6t/l0+XT7yfyg+6T6nfzn/E/7JvxH/V773/q3+2n63PnY+kT8uvx3/Az9iv2r/Gz9Vv9w/hP9T/1P/br8dP3q/Tj9PP4WAED/zf0dAOkBgQFvAEf/JQBgAKMAxAHeAGcAMwKFAgcCMAPEA3oDwAKfATcBHQISA6MC1wKbBGsF+wR6BXoFlATpA4kDbwSXBXIFXAPXAlEE3gTwBU0H0gcvBy8H0gdUBxkHKwjWCCAHgQXeBrgI9AhyCToKbgpQCmcKBgz/C8sJNwlnClQLPgskDJ4N0g0nDWoNOgzaCdYKAg2IDWoLngkvC5oMtQu1C/sMLw1YDowO8AvACnkLLwtCCjcJKwh5CVQLRQtNC/ALBgy4DHkNBgwgC9oLTQtcCZsI1gpcC4wKwAyXDbUL7ArODKkMvAmpCnUMKAuMCp4LjAqICakKjArSCcsJNgsKC2MHtQW5BsAGFQhqCXkH4QfpCbUJ+whCCCgHsQZrBxkHVAWxBA4GsQZuBjcHMwhnCBEJQgibBs8GQgbhBeEFcgXtBIUECgVgBDcDnwNCBMsDWAT0BLwDUQJ9Aj4DpgHAAJ8BkAHb/zj/WQBvALkAegFCAFb/3gC1AcgAoP+g/0oAjAD5/1b/lADLAcQBlACK/yn/e/8OAED/5/7n/uP9kf08/rb9tv2V/jz+3P3F/Sn9r/tH+wj8S/z2+p369vqG+sL6Wvr5+R/6HvwM/cL6RPps+5H7ZfvF++P74/si+7r6RPot+rP6mfnY+DH5+fnc+TX6bPu++0D7/fru+i36kvmO+KH3s/bj94r54PjR+ML4dPmd+gz7+fm6+Hv54PiK93v5CPwi+7f5RPqd+gX5nfgm+gj6uvik+K/5Bfki+UD7R/sI+gj6BftW+/b6R/nc9xv54/lT+HT3yfgB+gX54/ci+Rf6VvlS+nT7bfms+Hj6G/vY+nD6KvnY+Hj6+fkU+TX6Lfo1+t/6wvqs+qj7Nfx7+zj7mfnC+Gn6g/vj+476e/kQ+hD6XvmD+dT54Pjc+Yr75/rG+fb6d/yz+ir54/m6+mX7Yfwm/Cr7bPvr+177Yfox+8X7DPtl+2n8s/z9/B7+Lf7C/KT8vv3Y/HD6ivkF+6D71Pu6/B78Lfz9/Hv9g/1H/fL9jv6R/Rf8f/wB/BP73/zF/Wn8G/0b/4r/QP9s/VL8t/tH++f8G/0Q/DX83/wx/Qj+aP7j/Uv++f2G/Lf7cPyZ/Qz9q/x0/RP9g/3U/3T/CP5O/8gADgAi/2AAxf/q/Yb+Kf9S/t/+rgFVAV3/SgALAYL/nP4b/0P++f1l/wMBsgB2AFgC0wGbAJgBKAFl/2cA3gAP/hf+/ABVAUoAPgHPArECJAIzBFEEMAFNAdMBDgB0/zsAsgB2AFkAlAA+AfEB4gMKBQcCmwAdAq4BvQEwA+0C2gG1AfgB/wHLAYwCLAQ3A2AAMwBRApsC4gHtAq4DsQLAAj4DjAKMAjsCywFyAQ4AOP+C/5H/jv5W/5sAxAEDA0ICxAHxAYEBzwDaAZ8Biv+FAHIBLADj/2QBVQPlBA4EhQIDAwMDlwMVBCEDBwLTAQMDFgKbABkBxAEkApgBhQC2/0oAAwFNAaoAwv5W/7b/aP4x/5H/PP4E/2cAG/8t/iL/1P+Z/6D/hQCqAIr/lABYAqYBrgE+AyQE5QJNARIB1wBNAfwCbwTAAr0BlwOQA+UCjALaAVwBHQBO/0oAiQG9AXIBmwBnAFwBGQGbAFkAwv6K/Yb+DgCqAK4BWAKUAEv+Iv/IAN4AvQGbAiQCIQGJAWcCIQGMAOkBBwKmAfwCZwQdBGMDUQRnBOUCzwJcA2cClACjAB0CEgMSAyQEKAVNA/8BCwGjAK4B+AGUAs8CtQFGAWACjAI3AZsACwH0ACwA6v9ZABkByADN/9T/JQBCAMgA/ADy/wAAMAFGAWAAyABVAQAAvv9+AFEA6v8LAWsB1P8SAbUDtQN9AqYDogQzAjAB6QFrAUoAlACyAH/+0P5RAgoDPgESAUYBmwBCAL7/uv6O/pX+Nf50/bP8iv3N/U/93P0P/tz9s/7U/0f/pP7Y/gT/Hv7j/eP/4/8I/sn+5QAZAX4A1wCUAN/+jv7F/77/QP9CAHIBuQDy/1EA1wBgAJn/4/+v/2X/e//9/kP+uv4zACEBegELAR0AXf+qAMsBjADeAB0C3gAM/2z/MAFGAQMBhQJnArIAjABrARkBAABGATsC5QB+AGAADgCn/77/ZwB0/07/SgAAAL7/FgDy/5H/jAC5ALb/6v8zANT/q/6O/n4AAwFRAMgAlABvANMBNwOmA94CxAFrAQMBjAAZASgBxAGFAhYCSgKbAiwCiQHLAXIBsgDtACgBCwGMAD4BawH0AAMBQgBs/1b/Kf8i//L/qgD0AA4AoP8sAIwA5QC5AAMBuQB+AM8AMwBW/yUAXAGJAaYBsgCbAA4CwAKjAlgC+AEHAukBbwB0/5sAbwKqAiwCrgFcASEBMAFNAX4AdgADAQMB+f9CAOIBnwG5ANcAiQF+AE7/7v41/qv+jAA+ATsAqgAhAXv/lf5vAPwA6v9gAAsB3gAdAJsAdgCn/0oAcgHaAaoAGQHiAYEBVQHtABkBIQEWACL/HQBrAUYBHQIhAywCCwGMACwAgv93/rP+QP/N/0YB/wGuARIBfgC+/3v/p//J/kv+Tv8sAGz/E/84/xP/DgDj/+7+/f4i/4r/HQBCAFkAyAA7ACwASgAb/6f/yABCAM3/iv+Z/x0AMf+g/wcC4gGMAGcAuQDtABkB5QAzADH/pP7C/kv+cP62/8gAQgAOAOUAjAAdAFkA2/+r/t/+Zf/J/uf+HQDU/5X+kf+bAGcAyAB2ALP++f2C/zsAp/8WADcB9ABgANcAyACv/6D/hQDU/zH/6v+K/47+cP4x//n/dgAZATcBLACk/vn94/3U/Q/+F/5l/X/8cPx0/S3+F/71/or/tv0b/eP9q/yZ+2H8OP2r/Bv9dP8b/8X9Vv8dAIb+1P3f/jj/q/6G/kP+Wv50/ywAr//y/7kAxf9o/uP9oP2D/SL9jvxs+xP7G/0P/l39tv0B/jj9CPzU+xf8Bfsf+i366/mz+nf80Pz2/Pn9PP4m/n/+PP6o/aD9+f2K/Sn9Yf7n/tD+0P7Q/jsAzwCjABIBEgHIAKD/PP48/ob+Af5L/qv+e/0M/aD9Kf3u/Pn9aP5W/Y78Nfx7+1b7qPu3+7f7AfyZ+wX7RPxW/Vb9g/3N/a/9d/wI/Kv8nfwb/VL+Q/7U/d/+8v+2//L/QgC2/3T/Kf9h/kP+Af4b/bb9wv66/nD+QP9W/wj+f/4x/6v+Vv0p/bb9lfw1/ML8jvxh/Kj9lf5o/sL+QP90/5X+r/1A/SL9Jv4E/3f+Hv5S/i3+p/8SAYL/Q/5O/zH/+f3j/Xf+G/9RAMsBAwHu/rr+8v/F//n96v3y/wsBjACg/zz+Kf0X/mz/gv+K/77/mwC5AN/+xf1h/tj+Hv5s/dD85/yZ/Uv+xf8WAM3/JQCyAK//QP39/Or9jv4b/28AVQGMAM8A9AAdAIL/+f/iAXoB6v/eAJ8B3gD8AP8BVQHIAEIC+AFCAN4AOwLiAd4AKAG9AdcAIQF2AoEBlABgAoUCMwDPABYCGQHlAMgCNwM+AWsBEgO5AvgBuQKFAp8B3gJ2BJ8DqgK1A+IDzwKbAgMDuQIhAyQE3gLLAd4CgQOUAgcCYALTAQMBvQH/AUYBXAGuAR0C8QGYAaYB5QBRABIBOwJGA64D3gL4AYEBMAEhAT4DhQTAAm8CRgOfAyEDMAOmAxIDsQIhA1wDxAGuATcDHQILAaMCJAQSAwMByADPAA4A/AA7Ap8BMwDAACwCJALLAdoBwAIZAwMDEgMHAu0AzwA+Af8B1wLtAnoDDgQhA6oC+APeBDMEiQMhA0oC8QF9AlgCawHTAWsDiQPeAvQCVQP0Ag4CUQI7AokBkAHEASgB1P/q/4EBZwIHAuIBfQLXAoUCVQEzAB0AQgCFALkAzwCJAbUBVQFVAcQBvQGuAbUBHQBl/4wA0wG9AbUBlAJCAuIBXAHlAKMAuQCuAf8BWAJ6AxUE1wIzAjcDIQMWAvgB1wIhA0oCywF9AvQCPgPLAw4E7QLaAWACMwIwAZABCgMkAgcAwAB9AiwCPgFyAa4BcgGQAekBZAH0AN4Ae//f/s8A/wH/Ac8CyAI7AiQC6QFGAcAAPgF6AVkAtv9ZAN4AAwFKAoUEawWbBO0C/AAWAPn/xf9KAGQB4gGYAVEA2//XADMCzwIOAmQBQgDF/0D/lf6R/w4AzwBVAdcAdgCjAG8ABwCyACgBZAFNAWcAIv+k/tj+2/+QAWcCLAISAQ4Aiv8HAEIA2//N/0IAdgDY/nf+iv/q/6//FgBnAED/Vv8AAK//aP6G/nv/DP+K/5H/xf3Y/Hf+G/+V/or/+f/5/0IA1wBZAL7/jAA7AAT/Wv4b/13/G/+2/wz/uv4HALUBEgHq/z4BhQCZ/Uf9gv87AJH/1P9d/3v9d/xs/QH+G/0M/br+hv5S/Ov7BP17/Zn9CP6+/ZH9iv3C/BD8Wvzq/X/+Af6g/Y78qPsE/S3+oP0t/tv/WQDY/h7+jv7c/Zn9/f6k/jj91P1a/jH9CPyg/ZX+8v3Y/vn/vv9L/lL+1P3Q/Of8Xf2v/Xf8UvzQ/I78jvx7/aT+aP6O/lr+iv0M/dD8bP0p/X/8q/zJ/ED91P2R/UD9D/5s/w4Ar/+G/ib+dP08/J38bP3c/Qz/lAD5/3f+lf4p//n9q/yK/dT9Jv66/jX+PP7C/kf/e/84/2j+e/10/V39Lfyo+839iv9W/xv/G/8e/rr8dP2o/bP8dP1w/ur9pPwe/AH82Pyr/mj+Kf17/Wj+Wv7N/aT+7v7N/VL+DP8I/mz9Nf5o/q/9D/4x/wT/Lf6V/qv+iv1l/Rf+5/4lAMgAtv9//jz+pP5D/gT9G/3U/Uv+hv53/gH+vv0b/7b/0P7C/mX/nP6z/J38T/2o/Zz+Kf8p/2j+Wv7C/tT9F/5d/0D/Lf5S/v3+D/4I/in/Tv9W/2z/OP+k/jX+nP6C/2cAPgGBAYwA+f8AALb/iv8T/6v+pP44/9T/6v8p/1b/GQFNAR0A5/7Y/vX+Wv4m/hf+Wv66/kD/Iv/C/iL/p/+Z/1b/2//N/13/bP/F/wcA4/8AAH4A/AC9AUICyADN/8AA/ABRAKf/DgBrATsCqgISAygD7QKqArUBQgDy/wT/aP5H/wT/pP7F/64BPgG2/1kAawGFAGz/r//Q/q/91P3n/sn+4/2K/7IAmf9l/1EAWQCMAJgBrgGyAGcA9ACqAGAAwABGAZ8BFgKMAmsBbwB6AVgC0wH0AM8AZwBs/77/QgBRAJsAyADPAM8AfgCZ/wz/jv71/lb/DP+2/+P/Vv+Z/7kAowB7/9v//AC5AJQATQFGAUYBTQHlALkAMAF2AhkDSgLlAEoAKAEDA0kE+AOjAq4BVQFnAEIArgGFAuIBAwEzAMX/dgDIAJQAqgCqADcBnwHAAPn/YACMAG8AZwAOAGcAUQDU/6f/jAAsApsChQJ2AsAChQKxAhIDmwJGAX4AgQEhAbUB/ALAAmcC3gL4AzADCgPEA94CqgDU/zMAiv8OAK4BQgL8ADABOwJ6ASgB9ADb/0D/oP8x/6T+QP8WAAAALABVAXIBNwG1AZgBAADY/in/QP/1/g4AywHEAZAB7QLLA00DPgP8AsQBKAEZAaMAQgB+AM8AegGMAu0CmwIZAzADwAJ2Ar0BiQEhAYUAOwDq/4L/4/+5AO0AVQGyAIUAmAFGAVkAhQCFAGz/r/+9AZQC7QBvACgBSgDb/4wAGQEDAQsBVQEwAcQBTQOQA7kCyAJgAlwBmAEWAsQBegG9AfwAp//q/4EBiQFRAIEB7QK9Ac8ApgHiAaMAbwBKANj+Wv5H/0D/F/4B/n/+7v6C/5H/BP/f/hP/5/7n/jH/zf+2/4r/r/8i/5X+/f4OAB0AbwDIAPL/Kf+z/qf/3gBGAZ8BywEkAnoBDgCbAJ8BVQH8AHYA2//Q/lr+3/4x/4r/fgBkAU0BcgEoAZQAUQC2/1b//f5D/tz9hv4E/yUA6QFgAgcCTQEwAbkAvv+R/9v/YACfATADfQI3AZQC4gNNAxYCRgFyAYEBXAF2AHv/dgCJAUYB1wD8AMgATQH8AsACpgGmAVwBp/8e/lr+aP7c/d/+HQCv/9T/CwFkAVkAzf8OAMX/2/8lABYAbwD8AMgA+f87AJQAR/+z/pn/8v/j/88AKAEOAEIATQGUAJX+zf1h/i3+Nf7u/pz+f/79/iL/s/5a/qT+jv41/mj+Tv8AAGAAYADF/6f/2/9CADsA2//N/9v/ZwAdAJH/vv8lAJsAWQCK/6///ACQAZQAHQAzAJH/e/+R/wH+LfzQ/Bf+S/7n/sX/LABO/0P+zf32/I785/w4/TH9Kf0x/SL9D/5s/8n+4/08/nf+Nf5a/lr+QP3c/bb/1P+z/o7+Zf8x/xf+Wv7y/7b/9f7u/lL+mf3y/d/+oP2O/L79aP7j/cX9PP7y/br8S/x7/UP+s/5a/pn9xf2O/gT/Hv62/ZH9OP35/dD+pP4M/7IAxAEDAer/YACMAIr/cP5L/nD+hv62/3YAUQBKAGcAbwCqAMX/nP71/nT/p//f/sn+Zf90/6D/gv8p/8L+p//XABYAG/8E/1b/oP+C/5H/tv9W/5H/AADy/5QAKAEDATABowCn/xP/q/4M/5H/jAAoAYwAwAASATsA5/4p/wAAKf/u/tv/oP/u/lb/4//5/xYAbwAAAKf/LAC2/wz/R/+Z/5H/Vv+K/1b/bP+UAGsB/ACqAK4BVQFs/+7+e/+r/vL9Uv7f/vL/YACqAJQAUQDAALIA4/8E/wAACwHIAEoAtv/N/w4AdgBRAOr/yACuAZgBEgFyATsCFgKmAUYB3gDPAOkBfQLeADsACwEwAXYAQgCMANv/4/+bAIUAbwD0ADcByADIAH4Amf8b/xP/E/8b/83/SgAWAGAAqgBRAKMANwEZAd4AuQDIAM8AbwDy/+r/SgB+AFEAmwBVARkBbwA7AIUA5QDtAG8A4/8AAB0AZf+G/mH+pP79/kf/r/8OAEIAAwESAUIAJQDN/wT/9f7u/rr+BP9H/ywAawGfAUYB5QCbAGAAoP9A/8X/p/9O/4L/tv9d/xP/Mf84/ywAtQGqAp8BdgCg/zz+aP5o/hf+Jv5W//QA1wDPALUBYALLAeIBNwHn/mH+3/6O/vn9BP8lAFkA3gBvAKf/4/9ZAO0AbwB0/+P/r/+z/nf+q/5L/pz+FgDIAHIBZAEDAaMALAAHAGX/Vv9d/6f/WQCMAIwAsgADAT4BpgFyAfQA/ACjAEIAAAAE/9/+bP84/8L+s/4b/5X+f/50/zj/f/53/qT+pP7C/rP+S/5L/hv/R/8e/qj9vv3c/br+LAAzADH/+f8oAQsBHQA7AAsBqgBvAG8A2/8E/3T/WQBKAGX/d/79/sX/JQB+APQAuQDN/5n/bP/u/pz+7v4T/47+aP79/kD/G//9/rP+kf/AABIBdgDN/x0AXf/Y/qf/Tv+z/kf/8v8HAGcAIQH8AFEA4//U/4L/E/84/2z/+f9ZAGcAKAFvAmACjAC+/34APgGjAJQAhQB0/6f/xf84/9/++f+YAaYBXAH/AcAC0wGyAGcA9f6D/cX9+f1a/mX/+f+n/3T/zwCfAZsAKf8T/2z/G/8x//3+2P4x/83/9f4B/in/MwBvAIUAqgCUAJQAhQAsAJH/QP/U/ywAhQCQAYUCZwIOAlwBOwBA/1L+Uv71/pn/2/9KABkBrgGQAbIAWQAHABP/zf0T/ZH91P0t/iL/e/+K/+r/lACyAOr/Tv90/6D/dP9H/3f+Mf0b/Y7+vv9RAGQBbwISA0ICuQDq/7b/Kf8m/jX+9f4i/77/IQGuAZgBiQFVAT4BwADPAN4Amf8M/2cATQHAAIUAmwCMACEBVQEDAd4A/ACyAIL/OP+Z/wcAWQCUAPQA7QDpAaYD6QNRAgMBdgCR/3T/vv8WAFkA3gDTAWACzwKJA0IEjATwA0ICNwFcAbkA/f6k/ur/wACbAPQA8QFCAnYCBwLeALIAVQEwAZn/Uv41/mX/fgAsAN/+yf5KABYAG/+R/2cAOwCg/13/Tv/q/9cANwG5AIUA3gBVAWsBwAB+AIr/d/7f/gT/gv8DAfgBFgK9ATcBCwGjAKf/Vv8M/0v+yf75/wAAR/+n/0IAzf+v/5QALAA1/lL+iv+r/r797v6+/yn/tv/XANcAEgHiAd4A9f6c/vX+cP5S/jj/AAADAfEB1wKfA+kDlwM7ApgBBwIoAaT+vv3f/q//kf+K/1kAzwD4AdcCJAKBAaYB4gEdAL79lfyO/Bv9Xf17/aD9pP4HAEIAAAAWAB0A+f+2/xP/F/6K/S3+2P7J/jj/mwAsAt4CdgJCAvgBMAH8AIwAoP/C/or/cgHaAekB7QLaA/ADIQNGAWz/Wv75/aD9lfwT/br+kf/N/+P/FgAdAKMA7QCC/3T9DP3N/Vb9Lfyr/Jn9zf0x/6MAIQEOAu0CZwKJARkBDgDf/lL+7v6v/wsBCgMHBCQEDgSuA/gBQgB7/0f/Xf8p/2z/xf8zACEBnwGYAT4Bzf/q/bP8q/z2/Ib8iv0T/07/OP+R/9T/QP/j/yEBhQAE/2j+S/7c/R7+G/+g/9T/mAGBAygDhQISA4wCZAHlAGz/CP7f/tcA9ADy/6oAdgIKA2cC2gHIAEf/Iv9O/8X97vxh/lb/BP/n/or/zf+R/6D/4//U/3v/Mf+V/h7+pP7n/kv+uv5CACEBlADb/w4Azf9l/4L//f75/eP9Iv8lAA4AqgAsApQCJALEARkBzf9H/2z/E/8T/83/MwAdALIAegFkAVUBYALxAb7/7v6r/g/++f2c/gz/BP9A/3T/G/+6/kD/Zf8b/xP/wv6v/RP9kf2R/QH+DP8OAAAAiv9s/zz+D/6Z/wsB9AB7/zj/oP+n/wAAwABrAZABgQEhAWcAe/8M/4r/2/9RAO0AMAH0AIwAlAAWAJn/bP9l/9D+D/4I/mX9qP3n/q//QgDeAB0CtQEsAFEAjADb/13/E/8X/lb96v3J/kf/+f9GAfEBOwKxAkICwAAlAKMA2/9H/2X/mf/U/0D/pP4m/jz+S/4X/nT9CP4AAGcAbwBRAKD//f5W/83/DP9D/qT+9f5W/av8Af4i/+P/yACfAVUBowCfAe0CWAKQAQsBFgAi/+7+Xf8HAKoAawFKAhYCLAIHAs8A6v+n/0f/s/5W/0IAlABnADsAtv9d/5H/oP9s/zz+zf0B/ur9r/2+/WH+5/50//n/JQDU/9v/1P/5/w4Axf/j/6//Iv9L/kP+gv/0AMQB8QH/AVwBsgCuAU0DEgOFAvQC5QKBAVEAlAB+AFb/uv4i/3v/HQDIAPwA1wD8AE0BGQFkAfwAtv9H/5n/Vv+z/qT+nP6k/v3+Vv9H/8X/7QCYAWsBTQEWAjMCXAEDAdcAjACJAfgB5QAlAMAA5QB7/6f/QgDy/9T/ZwBcARkB9ABNAWsBEgElAND+8v2z/in/f/41/rP+yf6O/nT/WQAzAHYAmwDeAA4CFgKyAJn/Tv84/4r/vv+C/ywAwABGAWsB5QB6ARYCiQFZAK//p/9gAA4CWALiAR0C6QE3AaMAJQAE/wj+PP7C/pX+uv6v/9T/BwDeALUB0wG9AfgBZAElAPX+jv75/bb9mf1d/Zz+LAD8AIkBowI+A58D4gPtAoEBmf8b/xv/Wv6k/g4AtQEkAjsCSgKUAlUDCgP4AaoAZwBCAOf++f0t/iL/+f9RADsAfgDtAMAAdP/N/YP9Wv7C/g/+1P0B/hf+cP53/kD/fgCuAfEBhQC2//L/2/8AAFkA1P/j/zcBQgIzAlgCRgPwA64DmwIDAXT/e/8dADMAMwAsAKMAlACFAPwAbwDF/28ALAB//mj+mf/N/zj/QP8T/xf+Q/4T/zj/QP/q/4UADgAAAGcALAAWAG8AsgDtAFwBvQFNAQsBIQFCABYAsgCbADMAmf+Z/77/uQD4AfgBtQESAVEAiv+V/qj9oP22/Uf9Kf2D/Xf+pP4M/wAAOwDb/4L/zf9O/6v+pP6O/nf+Kf8WABYAoP9d/13/Zf9vAO0AfgCyABkB7QCMAAsBNwFcAb0BTQEdAA4AKAFKAH/+8v0m/i3+/f5RACUAFgBVAZABHQDQ/tD+DP+G/mH+CP6v/Zz+QP+6/g/+Jv6z/u7+DP/n/pz+r/9yASQCMwJ2AvEBYABA/6T+7v6+/7kAegFyAfwAGQH/AWcCbwJ2At4ClALTAVwBEgGjAP3+yf4p/wz/DP9l/9T/r/9vAEYBVQE7ACUAOwC6/tT9F/4M/yn/Mf/n/h7+D/5w/lL+e/0e/jj/R/9d/yUA9ABcAYEB5QB7/9j+kf+C/8L+nP5H/3v/2/9KAIr/e//0ABYCIQHXANMBXAEWAK//oP8E/yn/2/+g/5X+3/4HAEIAfgDPAG8Ap//Y/jX+R/0b/WH+Xf9vAEYBMAHIAGcA4//C/mH+cP6O/gj+tv0m/sn+OwC9ATMCegGuAekBRgFnAJn/e/+v/1EAp/9a/hf+p//0AAMBgQEzAnIDgQNvAsgATv/u/kf/Mf8m/vL9pP5nAFUB9ADq/xv/vv8dAKf/5/50/1kAbwAOAOr/mwAZATABDgCz/jz+Uv6V/rr+9f57/0oAbwA7AFkAwAD8AOUA5QCjAIL/f/5o/jX+T/10/aT+2/+bAG8A8v9A/+P/MwBd/yL/E//9/jz+aP7Y/tD+xf9KAHT/3/7j/1kAkf97/4UA1wDXAN4AJQCZ/13/Xf+c/ib+f/6c/h7++f3n/r7/bwBRAJQA7QCMAA4AOP+V/gj+Wv4m/pn9xf1o/nv/MwD0ACgBYABRADcBCwHy/yn/OP9W/2z/jABgAHT/xf+FABYATv/q/6f/lf6r/jj/Xf9W/9T/bwBvAPL/vv+2/4L/dP/Q/qD9QP0P/sn+0P5d/77/MwALAXoBKAEzANT/gv/u/jX+Af7J/sL+jv57/xYAzf9gACgB1wAOAA4AFgAi/yL/+f8WAP3+s/57/xP/lf5O/6f/9f5A/7b/0P7Y/iwAOwA4/zH/4/9+AKoAhQDN/xv/E/9A/9/+hv5W/2X/Vv87ALIAowB2ALIAFgAp/yL/R/84/07/2//y/+r/LACjAPwAmwAOAL7/DgA7ADsAhQB2AG8AfgDIAMAAOwCyANMBQgJcAVkAWQBnAPL/bP8x/07/bP9ZAMsB+AGJAaYBywHtAOr/tv9W/1r+qP0X/sn+bP/y/4UAwAB2AJQAyACbADMAvv8i/5X+pP4E/3T/Tv8p/7b/OwASAekBVQGqAMAAsgAsAHT/r/9nAGAAbwCjAGcAMwDtANMBNwFgAFkAWQAzAPn/bP/1/kf/BwD8AHoBXAHXAGcAdgAsAK//Mf8p//X+Yf4X/jX+uv6n/5sAfgCUAM8A/AAwAXYAJQB+ANcAlAAOAK//Xf8x/77/EgGuAUIChQLpAVwBXAFVAbkAbwDXAHIBKAE7AK//gv/j/0oA+f/N/0oAQgBO/47+s/4E/1b/Tv+z/mj+OP+n//3+Kf8AAAAAiv9H/2j+Uv6R/9v/G/9H/zABMwL4AVwBlAB+ABIBvQEoAZsAxAHPAukBIQH0AM8ATQG9AZAB3gDtAOIBrgGMAH4ARgGuAe0A2/++/wAAjABKAAAA2//N/wcAVv/n/sn+R//N/77/tv9ZACgBawEZAfL/8v9CAEIAMwDj//n/DgDlALUBawFyAYUCXAP8AtoBGQFkAfEBnwG5ADsA1wD4AZQCjAI7As8C0wPTA28CCwHXAH4Ar/+z/nf+lf4E/9v/tv+K/+r/JQAHAG8AwAD5/5z+jv5A/3f+jv7U/9T/Mf8zAPwAAAAAAIEB8QGqAEoATQG9AWQB6QHIAoUCDgL/AekB2gF6ASwAxf9vAPwAowCFAGQBPgEoAdoBQgJGAbkANwGFAHT/R/+2/zH/wv50/wAAvv8dAHIB+AEzAukBegELARkBcgGbADsAdgASAXIBxAEdArUBVQHtAEIAmf/N/5QA1wDeAPwAZAHTAb0BcgFNAcgAoP/f/iL/p/8i/zX+7v5ZAOUAyAA3AekBQgLXAhYC5QCbAN4AYACc/h7+Iv+MADcBKAH8ADcBUQKqAuIBIQHPAPn/DP9H/5n/e//U/94A3gAHAMX/2/+jAFUBVQGyALb/MwDPADMA6v9ZAHYAhQByAZ8B3gADAWQBhQBZAMQB/wG5AAcAKAGYAcgAfgB+AOUANwE+ASwAlf66/rb/gv+c/mj+aP53/nD+d/7Q/vL/wAAzAIr/DP+G/pH9bP2o/RP93/y+/dD+2P50/88AGQHXAAsByAC+/9j+jv6c/o7+mf+UAG8AWQBKADsAYADPAH4A4/8dAEIAiv/J/nT/JQCK/0f/e/9l/07/mf8WAL7/R/+C/wT/3P1d/Zn96v0e/qT+9f4T/0D/9f5//g/+D/5D/gH+Lf6r/vX+DP+6/kv+3P2o/a/9T/0M/Vb9Nf6K/ywA+f/j/1EAWQBW/2j+S/4X/tT9nP7Q/qD9Vv08/qv+Nf6V/pn/AAAOAOP/2P62/Yr9OP3j+8n65/rj+/b8zf0P/g/+PP6c/kP+uvzF+7f73PvN++P7uvwp/Wz9tv0B/s39r/2O/pz+Wv6G/ib+Vv1d/QH+Lf4e/tD+8v9+AD4BrgEhAdT/BP/f/pn9q/yd/AT9mf1L/iL/AADXACEBUQDf/tz90PyV/Lr82PzY/CL9Q/5a/lr+DP+C/yL/2P5W/2X/Lf7f/Gz9kf2Z/Y7+Zf+C/13/OwCjAFEAbwCyANv/uv4X/oP9vv26/r7/p/+v/2cAOwBH/8L+Wv5d/Sn9F/5S/tT9+f2z/hv/2P7Y/jH/Vv/1/gH+8v1L/mH+hv6V/kv+D/7Q/rb/JQCMADABegEDAaoAFgAM/6v+G/8x/13/LAD0AMQBMwKUAqMC6QGJAcgAxf8b/7r+OP8lAKMASgBgAMgAmwAOAM3/LADq//n/FgBl/5X+0P62/77/+f8lAB0AbwDlAJQAzf8zAFEAr/8p/2X/e/97/6MA2gHPAj4DlwNrA30CpgGbAKf/dP/q/wcAWQD0ALUByAJrAxIDBwLpATMCvQGbAAAA8v+2/5n/Iv9//jX+E/+n/07/bP8WAN4AuQBgAB0Azf9H/yn/iv+Z/9v/YAADAQsBwADAALIAqgCMAHYAWQASAWcCVQNyA2MD/wP4A/wCUQIHAsQBmAEDAfn/Zf/N/1EAwAAhAUYBpgHxATsC+AHTAcQBwACg/xv/G/+O/nD+BP+Z/+r/YAALAYkBLAJvAqoC1wISA3IDRgMSA3YC8QFCAkoCegG5AKoAqgDeALUBlAKxAv8BmwJNA+0CwAJKAqYB5QBRAEf/+f1H/Xv90P7U/8X/mf8LAR0CtQH0AN4AgQESAe0AsgC+/2z/ZwCYAYEBXAEWApsCBwLaAQ4CvQEOAjADGQMzAs8CnwM3A6oCEgPlAukBpgFyAUIAZf9CAG8Ar//q/0YB0wEwARkBkAHLAYEBkAHIAOr/AAB7/0P+xf2k/kf/vv+MAGsBrgG9AWcCQgIhAaMAZAH8AJH/HQA+ARIBEgEkAkoCZAFyASwC8QHLATsC4gGuATMCmwIzAtMBrgFGAfgB7QJYAlwBegG9Ae0Avv90/2z/kf8lAHT/3/7j/zABawELAeUAOwAHAG8A4/8M/1b/tv8p/zj/SgADAZQASgDIADABnwHEAUYBIQF6ASEBqgDIAKMAjAAhAZABqgBgAJ8B8QFGAQMBAwGyAKMAPgHXAPn/lAByAZgBnwGBARkBzwBvAAcAgv8b/13/Zf9W/07/R/++/3YAsgCjAOUA1wAlAGz/R/+C/wAAHQCK/5n/AAAlAPn/BwBgAJQAmwB+AGcAWQDAAMsBDgKmAcsBpgF6AYEBIQGjAB0AAACR//X+Tv87AGAA7QAsAm8CDgLxAWACvQGFAAcAp/+6/h7+Wv7y/er9wv4dAMgAowAZASgB/ADIAHYAHQB0/xv/7v6O/ob+s/7u/qD/2/8HABYAiv+n/yUAJQAAAPL/QgDtAD4ByAAHAEIAbwCK/7r+wv71/nf+jv5O/5n/e/8WAPwA3gCyAH4ABwCK/3T/Xf+O/uP94/0I/q/91P1o/mX/jAC5AGcAQgBvACUAXf9a/nv9R/1W/aj9Q/5A/+P/DgAAAEIAAwFGAbkAe/+6/ob+pP7n/uf+Iv+K/1kA7QB6Aa4BawF6ASgBuQBgALb/nP7F/Zn9S/4M/13/QgD0ADcByADj/07/hv7c/SL9s/yG/JX81P0x/2z/OP+g/2cAFgBH/8n+Yf48/nf+9f4E/wz/6v+MADMAJQBvAPQAnwGyAF3/bP8dADMAkf/9/gT/mf+FAO0A8v9A/6f/QgB0/wj+S/79/u7+Wv6k/l3/1P9+AG8Avv/n/rr+7v4E/4b+cP4M//X+Tv/U/0IAsgCqAEIADgAOABv/Uv6V/rP+D/4X/nv/YADb/8X/jAAlADj/kf/N/5z+1P08/nD+6v3j/X/+uv71/r7/hQB+ACUADgAHAKf/BP+c/lL+nP7Q/nf+pP6g/4wAsgCMAEoABwCv/6f/vv/J/ib+jv4p/2z/OP8i/7r+q/5H/1b/OP/1/nf+Nf5//v3+d/4X/kf/QgDF/zH/BP/Q/nf+cP66/ib+Q/5A/8X/vv90/1kAPgFNAbIAbP8E/9j+nP4E/xv/3/5W/wcALAAWAA4AjAD8ACEB/ACUAH4Axf/n/gT/Xf/n/mH+e/9nABYAAACMAIUAtv9s/xv/Q/6g/Q/+Jv5H/dT9OP8dAGcAUQCg/yL/dP8M/5z+S/5h/uf+9f5O/5n/hQCfAQ4CWALaAZABmAFvANj+hv5l/7b/xf+yAJ8BHQKMAsACfQLEARkBOwA4/3f+S/4e/jX+e/8lAB0AWQDeALkAWQCUAPn/R//9/tD+nP75/S3+yf50/ywA/AC9AR0CJAIoAR0Ap/90/yn/9f4M/6v+BP8OAN4AegGmAbUBNwHPAKoAOwCC/7P+s/7J/gj+4/0b/wAAUQDPABIBZAHEAZ8BWQAp//X+nP5D/kv+jv4M/8X/1wCYAU0BcgFkAbIAjACMADMAKf9//kP+D/4t/rP+2/+FAPwAMAFNAVwByAAlAIL/Mf+O/tT9Af7C/lb/mf+5ALUBxAFGAd4AyAAzAB0A1P8T/+f+QP/N/77/xf9ZAGsBBwIWArUBmwCjAKoA2/+6/jX+uv7n/qD/fgALAekBbwLxAZQAOwAdAE7/pP5L/n/+2P79/hv/iv92AIkBywE3AUYBIQGjAEoAvv/N/8X/6v/N/3T/MwDeAAMBZAHpAdoBkAFcAfwAjAAWACUAqgC5AOr/iv/5/ywAxf90/1EA5QBnAAcA4/+R/xv/e/8sAL7/dP++/6//Iv+z/uf+Tv+Z/5H/mf/F/7b/p/+C/w4AqgDIAKoAqgAhASgBTQG9AZABwACjAOUAjAAzAM3/1P+FAD4BywEHArUBpgHLAWQBjAC2/0f/E//1/ob+1P0t/in/2//b/yUA7QAhATcBuQCC/8L+/f5W/+7+s/71/q//dgBVAcsBiQHiATsCHQJGAbIAQgCn/yUAwAASATABtQEzAhYCgQE7AIr/r/+g/xP/cP4I/mH+QP8dAMAANwGYAZABIQElAO7+D/75/Xv93/xl/TX+Mf/q//QASgLXArECfQKmAUIAgv/u/mH+zf13/mX/JQBrAfgBJAIzAowCWAJkAdcAdgDN/wz/lf5a/qT+DP97/6f/JQB+AEIAJQBs/wz//f4b/8n+Yf4p//n/UQC5AHIBZAHPAEoAdP93/ib+Lf4B/lL+q/62/94ApgEkAmACCgMZA4UCmAHXAAAAwv4I/or9g/01/mz/fgB6AbECtQPpA3IDbwL8AL7/uv7y/U/9DP3u/E/9Jv7f/tT/UQCqAMAA9ADeACUA4/++/yL/Uv4t/lL+Wv5w/iL/dgDAANcACwE+AUYBAwEDAbkAdgB+ALkAwAB2ABYA4//y/zMAZwCqAAMBmwAlAA4AWQAHALr+jv6c/kv++f3j/S3+aP4M//X+jv5L/ib+hv4t/tz9Lf4P/kP+jv5h/mj+Kf9KAIUAbwDtADcBAwGUAGAAMwAlAN4AtQG9AVUBiQFCAlECmAE+ARIBCwHPADsA8v++/2AAuQBCANv/bP+C/4r/Mf+G/gH+CP41/i3+r/1l/ZH9Lf7Y/kD/QP+n/yUAzf/N/6f/kf8AAH4AsgAsABYAjAALAe0AIQEHAoUCWAI7As8CdgJ6ASgBMAFvAL7/JQBZAAAAAADlABIBQgAAADsA4/9H/2z/Vv9l/0f/R/84/4b+Uv7y/er9PP6c/uf+gv9gAFEAHQBRAKMAhQCyAE0BkAHtAGAA/AASAbkAqgDeAJsAZwD0APwAlACjAIEBLAK1Ad4AqgCbAHYAZwCv/zH/p/9CACUAe//f/hP/DgCMAPn/kf8AAKoAEgGMADsAMwBKAKoAqgB2AJn/mf+FAIUAYADeAOIBWAIdAuIBawE+Aa4B4gGBAWQBkAEoAW8AdgB2ANv/p/8lAG8ALAA7AG8AJQAsAOUACwFvAB0AJQDb/6D/r//U/xYAMwAdAF3/Kf/U/83/6v9gAMAAqgBNAWACvQH8APQAZAE3AZsAfgAOAGX/Iv/b/x0ADgCqAIEB+AG9Ab0B/wEsAnoBWQBl/0P+mf17/aD9mf2+/cn+SgALATABRgGmAYkBqgAOAFb/aP7U/Tz+jv7f/pn/qgDxAQcC8QHiAdMBawHeAM8AlABgAPn/HQCMAKoAsgD0AGsBZAELARkBKAE7AEf/Zf+g/7r+Uv5d//L/mf9W/zsAowBRACwAe/9a/l39g/0B/s39Af7n/oL/8v8lAPn/JQAlAEoAfgCMAPwA9ADAAKoASgBZAG8AowCbAM3/mf+g/83/DgDj/yUAbwCMAGAAQgDPAOUAjABCAHT/aP6K/Qz9hvwX/GH8g/2k/nT/mwCfAR0C/wFrAbkA2/8b/wH+G/39/Pb8g/3Q/lEAVQHaAaoCYwNNA5QCmAFKAAT/9f4b/6v+Af4X/hP/r//F/5n/FgBvAJQAdgAx/3/+PP4m/jz+f/7f/l3/fgCyAOr/QP8i/1b/QP+6/tz9oP3F/UP+DP+2/7kAcgHEAUoC+AFVAfwALABA/9/+/f7J/ib+lf5l/xYA5QCBAcQB0wH4AU0B2/9w/gH+Hv6R/Sn9QP2g/fn9s/4T/8n+7v57/yUAtv8b/9j+jv5w/mj+Iv84/1b/zf/q/w4AHQAzAAcAAAD5//L/vv/q/zMAWQDlADABZAEwASEB5QAdAK//dP9d/9j+0P7f/lL+S/6G/sL+5/4T/07/Vv84/4r/e/8E//X+s/5h/lr+aP5L/nf+5/4p/yL/Kf90/9T/bwCjALIA1wA+AcQBgQH8AJsAYAAzAPn/r/9H/8n+7v6K/w4AhQCMAKMAYADU//n/vv9W/yn/BP/u/u7+E//n/n/+nP4E/9D+Wv5S/pz+wv4M/9T/DgAlAM8ATQHIABYALAB2AH4ABwDb/6D/Mf+n/x0AdgDeAFwBDgIdAssBkAGJAWQBuQAsAIr/7v7Q/t/+e//N/7b/6v8HAL7/Vv90/6f/vv8AAFEAbwAlAL7/Tv/Q/nD+S/4t/gH+Uv4M/4r/+f9nAN4APgGfAXoBuQCjALIAsgBKABYAdgBRAOUATQFrAXIBtQFKAq4BPgH8ALIAQgD5/zMAHQBnAKoAqgCqALkAhQAAAIr/9f6z/o7+d/5a/i3+S/7Q/k7/R/+g/wAA+f8AAKD/Xf8E//X+R/9A/8X/YADtAHoBtQFRAoUClAJCApAB/ABvAGcASgBnALIAEgEhAc8AKAGYAZABTQESAX4Axf90/zj/yf6G/pz+BP84/xv/Zf+n/9T/8v/j/9v/vv++/7b/xf/b/9v/DgBZAGcAYAALAa4B+AFnAsAC1wJYApgBGQHAAJQAYAAlADsA1wCuAfgBiQEZASgBGQGjACUAe/9O/1b/Kf8M/9/+5/5A/0f/Iv90/+P/SgCbAJsAWQAWABYADgAAANT/tv/5/w4AJQCUANcAEgESAQMBwABKAH4AYABCANcAEgH8AOUAsgCjAIUAfgBnAEIAmwCFAPL/iv+K/6f/r//j//L/OwBvAFkAHQDq/0oAWQD5/9T/2/97/1b/Mf8M/6//bwBNAU0BNwE3ARkBZAEZARIBPgGBAU0BZwAsAG8AyACFAH4ACwEhARIBEgG5AA4A+f9+AIwADgD5/yUA6v+2/77/1P/b/wAADgBl/9D+0P6k/ob+5/6Z/ywAuQAZAd4AUQBRALkAbwAlAEoAlAADAe0AlAC5AHIBOwI7AvEBvQFNAfwACwEoAZsAbwAwAZ8BMAF+AGAAQgBgAHYAMwDq/07/Vv9O/+7++f2Z/ZX+Iv8T/5z+wv6C/+r/QgB+ACwADgBCAOr/Iv+r/v3+Zf/y/x0AlABcAYkBDgJRAn0CUQIkAhYCxAGQAZQAiv/f/jH/tv/j/xYAZwAoAcQBBwLLAUYB5QDAAOP/pP6K/bP8s/wT/c39f/4b/zMAcgGfATABGQESAZQAp//9/jz+4/3q/UP+9f7y/4kBowIwAwMD1wJ2AqYByAD5/yUAJQDU/4r/4/+jALkAGQGJAYkB9ABRAOr/Mf/9/tD+d/6c/lr+jv4E/0D/bP90/wAASgAdAL7/e/9s/+f+cP6k/in/gv/q/28AwADXAN4A3gDXAFkAmf+C/6f/xf/U/wAAowAZAZABDgIWAq4BGQHAAGcA1P+2/8X/zf8WACwAZwCUAEIABwAlAPL/E/9L/jX+Q/5D/lr+0P5s/wcAAwEwAbkAQgDj/4L/wv5w/tz9dP3U/UP+5/7b/+0AmAE7ArkCLALlAOr/Vv/Q/lr+Lf5w/gz/DgD0AGsBtQEzAnYCDgI3ATMAe//f/mj+Jv4X/i3+hv5d/9v/LAAdAAcALAC2/4r/Iv9//i3++f0I/vL9cP4p/3v/1P8sAPn/R/8T//3+9f4p/yn/Iv9A/+P/mwDIAN4A9AAoAUYB1wAlAGX/R/9A/wz/QP9W/7b/FgA7AFEAbwDXABkB5QBKAKD/5/4t/sX9Mf26/BP9vv01/rP+Kf8HAM8A3gDAAB0ATv+O/tT9iv3n/P383P2c/or/OwD8AGQBgQGQAU0B1wDb/0f/wv48/h7+Hv7C/nT/6v9KAFkAOwAlAAcAR/9S/tT9e/10/a/9Af6V/mz/lADPAFkADgCR/xv/cP57/dj8q/zJ/Fb9F/7J/vL/MAEzAmcCywEZAVEAe//f/mj+4/2+/QH+aP7C/jj/HQDPAO0A7QDIAIUAJQCC/1b/R/8E//X+7v7u/tD+DP9s/07/dP++/wAADgDb/+r/HQD5//L/JQAOAA4ADgAWAKD/3/7n/jH/iv+v/+r/mwC5ALIAsgCjAN4A3gDIAHYAvv+C/6//vv+v/+r/ZwBvAPL/Zf8E/8n+pP7Q/kf/oP/b/x0AqgASAfQAGQFNARIBSgCC//X+S/48/rr+E/9d/x0A/ABGAXoBywEOAjMCOwLiAcAAe//n/mH++f0B/ob+e/9RAFUB6QEkAlECfQJgAokBowB0/8L+aP7q/Sb+yf7U/9cATQHTASQC4gHLAb0BKAFKAHT/DP+z/sn+dP8AAG8AKAEWAlgCvQH0AKMAYACR/yn/R/+R//n/UQB+AGcAEgGJAT4BwAAsACwASgBKAM3/e/8AAIwAzwCMAKMA5QDtAPwAqgBKABYAxf+C/07/7v44/+P/SgDIAD4BXAHlAG8AQgAHAM3/kf+R/3T/mf8zACUA6v8AAIUAGQEZAeUAZwBgADcBZAG5AEIAdgBvAOP/R//Q/vX+oP9CAGcA1P/q/0oAOwAOAEf/Mf+C/5n/gv/Y/rP+5/4b//3+/f5A/5H/JQB+AJsA3gCJASwCOwLTAVwB9ACbAGcA6v/q/x0ALAB2ANcAKAEDAc8AAwFNATcB7QDAADsAoP9O/7r+CP7j/UP+wv44/07/xf+bACgBKAFRANT/xf9s//X+hv5S/rP+xf8SAf8BHQJCAvwC9AJgApgBEgE3ATcBPgEDAZQAzwCuAUICSgI7AlECWALpAe0ALADj/0D/G/8M/6T+lf6c/u7+E/8b/6f/4/+R/2X/vv+n/zj//f5d/wcADgDU/7b/iv+n/zMAmwCbAKMAPgEWAkoC2gGfAfgBJALTARkBowBgACwAJQCZ/4L/mf/N/yUA8v8AAB0AYAB2ADMAOwBZAG8A2/9W/0f/uv4m/pn9iv3j/WH+/f4p/6f/YAALAU0BTQGJAVwBIQGjAAcAtv90/5n/xf/N/xYAjAALAXIBawFNAXoBPgHtAHYABwDN/3v/dP90/2X/tv9CAGcA2/+2/83/Tv+k/nD+E/9d/zH/Tv/j/3YAfgCjAH4AYAA7ANT/Zf9o/ur9PP6z/tj+wv5W/0IANwGfAdoBbwJ9AnYCJALlAFb/Lf7U/fn94/3y/br+mf92ACgBmAG1Aa4B/wH4ASgB2//9/ob+S/5L/i3+Jv41/sL+Vv97/4r/+f/tAGsBKAF+ALb/9f7Y/hv/s/5w/pz+R/+K/xv/DP9W/yUAlAC5AM8AUQAdAHYAowB2ADsAWQCUABYAkf9l/xP//f5s/2cAjADy/83/p//y/x0AMwB+AGcAhQBgALb/3/5w/n/+wv4b/xP/E/+K/ywAqgC5AM8A7QDAAJQAHQCK/5n/8v8sAEIAZwCqAKoAsgAdAL7/iv8p/5H/gv97/+r/2/8OACwAMwA7ACUAJQAOAOP/oP90/0D/Kf9W/0f/Kf97/w4AOwB+APwA/AA+AYkBRgGyACUAxf9s/2X/Zf90/6//4/9ZAGAAYACUAJQAdgAAAK//oP9d/1b/oP+v/83/FgA7AG8AYAAsAAcAtv9W/wT/yf6k/sn+BP9O/6D/BwC5AD4BcgGfAb0BZAH8AHYAp/8x/+f+3/7J/sL+bP8OAGAAhQCqAKMAowCbAFkALAD5/ywAJQDy/+P/r//y/wcAp/8p/wT/Tv97/8X/AABvADABpgHpAb0BRgH0AMgAfgAHAE7//f44/wT/yf7u/mz/HQCjAAMBXAE+AfQA7QB2AL7/QP8b/xP/G/8T//X+OP9A/07/+f9KAEoAYACUAKoAdgCyAM8AjADPADcBCwFgAMX/iv/F/x0ALABKAMgAawHEAXoBawHiATMCWAK1AaMAOwAAALb/Zf8p/6f/UQBgADMADgBKAJsAwAC5ALkAlAAdAMX/Tv8M/xv/OP9O/07/oP8OADsAOwBnAOUARgEoAW8A4/+v/77/vv+v/9T/BwB+AKoAdgAWACwAowCUAFEA1P+2/9v/dP8M/8L+3/5l/+P/FgBRAJQAlACbAGAAQgD5/6D/Kf9h/lL+cP5w/pz+dP+UAAMBKAELASEBVQEZAaMAr/8x/0D/Mf+k/ib+q/6Z/2cAEgFrAVwBIQELAcAAHQCv/7b/iv8i/+f+5/4M/zj/QP+C/9v/2/+2/3v/Kf9s/9v/HQAdANv/xf+g/2z/Mf/9/k7/vv8lAGAAhQDXADcBvQHaAfgBHQKuAfQAMwCg/07/Iv8i/5n/zf/y/3YAjADeAD4B/ABnAIr/yf41/rb9Xf17/fL9f/5H/3v/R/97/77/Zf/1/ob+Uv5S/jz+yf4x/1b/BwC5AFwBNwGFACUA4/+v/3v/Mf8E//X+Zf9CAKoAwAAhAcsBrgHPAFkA4/97/xP/wv6V/n/+/f5A/2X/tv9ZABkBPgESAX4ABwDq/6D/wv4I/g/+Jv5h/nD+5/6Z/zsAKAF6AZ8BTQHeALkADgBd/+f+7v7u/qT+jv71/mX/oP9KAPQATQFkAVwBPgEDAX4Atv9H/wz/5/71/v3+7v79/or/JQCFAFEAHQCUAPwAyAD5/3v/xf8zABYA8v/F/2z/e/9s/2z/bP++/34A7QAZAaMAdgCFACUA+f8OAB0Azf+g/5n/kf+g/3T/p//5/wcAkf/9/vX+E/8x/2X/p//q/xYAHQAsAPn/4/8OAOr/r/9H/1b/e//9/tD+Iv/b/4UAsgCbAPQAPgE3Ac8ABwC2/5H/vv+n/1b/xf8sANcA7QCFAGcAOwBvADsAr/8T/47+s/79/in/dP/U/xYAQgA7APn/vv9l/wz/wv7Q/vX+yf7Q/iL/p/8lAKoACwEZAfQAqgBRAK//QP9d/7b/LAD5/7b/1P/b//n/MwB2AKoAuQCFADsA8v+n/83/AAAHACwALAAOAOr/r//N/yUAUQAzAL7/Tv/9/sL+jv6O/lb/FgBZAG8ASgBRAFEAQgAzAKD/R/9l/zj/wv5S/pX+Tv/q/2cAyAASASgBKAHIAGcAOwDq/5H/Iv8E/8L+pP79/k7/1P9+ABIBXAFkAWQBMAHtAJsAQgAOAOr/gv/J/pX+uv7J/in/kf/b/1EAqgDtAAsB1wDXAAMBuQBCAHv/5/7f/sL+wv7u/l3/LADIAOUA5QDtABkBIQH0AN4AfgAlAOr/bP8p/13/mf/U/wAAAAA7AHYAlACyANcAzwBRAAAA+f+v/3v/Zf+K/9T/AAAWAAAAxf+2/+P/p/+g/77/zf8dACwAQgCbAO0A5QDAAH4ASgAlANT/r/+g/8X/vv+n/6f/4/9nAM8AEgHtADcBkAGJATAB1wBgAOr/iv+r/nf+Yf6G/kD/1P/IAIEB/wEzAh0C0wEwAWcAdP+r/nf+S/4m/nD+7v4lADABxAEdAhYC+AGmAfwALAB7/+7+0P6k/o7+q/5A/xYA5QCfAYEBcgEwAbIADgB0/wz/hv6c/u7+dP/q/2AA5QBkAWQB5QBRAJn/e/8b/8L+aP6G/jH/xf+bAMgACwE+AUYBKAEsAFb/3/6c/pz+Nf5w/mX/AAD0AIEB/wE7AtoBmAHAACwAVv/u/v3+wv4M/2z/4/9KAHYAwABGAVwBAwF+ACwAp/8E/9D+cP6V/iL/vv8lAH4AAwGuATMC+AGJAeUAOwCK/+f+f/5a/pz+E//5/7IAEgFyAdMBLAJvAgcCAwEzAK//dP/u/qT+nP79/vL/ZwC5APQAkAEWAvEBmAH8AIwAMwDN/0f/QP+v/9v/BwDj/ywAhQBCAPn/8v8HAOr/FgAHAAcAUQCqABkB7QDAAIwAUQAAAIL/R/9W/77/zf8lAKMANwHpAVgCUQL/Af8BywF6AcgAQgDU/2X/Xf/1/v3+DP9s/2cAyABGAZgBnwFkARkB1wA7AL7/DP+c/jX+mf3F/cX9D/7J/oL/SgCFAJsAwADlAPQACwHtAJsALADq/wAAp/+R/9T/FgBvAKoAzwDPAMAA1wBVAVUBPgESAaoAmwAdAOr/r/84/9D+yf4T/+f+/f6z/tD+kf/F/83/p/++/yUAWQAOANT/xf+n/6//oP+R/2X/tv9RAIwAYABgAO0ATQFrATAB/ADXANcACwHlAMgAfgBgAG8AFgCZ/xv/E/8b/xv/OP/n/qT+2P5O/5n/zf8OAA4ASgBRAPn/gv/J/qv+s/7Y/u7+s/4b/9v/lAD8AHIBtQHLAdMBegEDAUoAUQB+AG8AMwAOAFkAUQCMAKMAhQA7AK//Zf8E/8L+d/41/lL+nP7J/rP+f/7Y/kD/bP9W/+7+DP/1/ob+Uv5L/ob+3/6g/zsAfgD0AEYBZAGuAXIBIQGMAOP/r/9s/5n/1P8sAN4AxAEOAvgB/wFyASEBmwDb/+7+Af6+/a/9CP5S/uf+r/9gANcAmwAWAE7/G//9/mj+r/0T/Qz9Zf3N/TX+uv5W/0oAAwEwAe0AdgBZAEIADgDU/3v/iv/j/xYAQgC5ACEBiQEOAhYCrgEZAeUAsgBvAIUAOwDq/5n/r//U/8X/p/9O/4r/kf9H/8n+d/66/sn+9f7f/sL+DP9l/2X/Kf8T/9j+9f7Q/lr+Uv6G/tj+wv6c/u7+mf9ZAKMA3gBcAcsBHQL/AVwB9ADeALIAZwDq/6//AADPACgBAwFVAcsBZwJYAp8BAwHeAMgAOwCK//X+nP6G/nf+Nf48/qv+Iv9d/yn/OP9O/13/QP/9/rP+f/5w/kv+CP7y/Uv+Uv5w/sL+DP9s//L/jAADAWsBmAEOAukBnwGJATAB9AB2AB0A4//U/9v/MwCjAOUAegHiASQCxAE3AbIA8v9d/3D+tv1l/Tj9R/2v/dT9F/6z/kD/p/+R/3v/Xf9H/0D/0P6c/o7+q/79/tD+QP/5/28A/AAoAXoB2gHLAZgBkAGBAZ8BxAFcAe0AuQC5AKMAlABCADsAsgD0AOUAmwB+ACwA6v+R/zH/2P5h/nf+pP6z/nf+d/6O/rP+0P6c/rP+3/5A/6f/1P/y/w4AJQAHANv/vv+K/3v/tv/j/xYAHQB+AMgA9AA+AVUBgQFNAU0BPgHlAGAAHQAlAM3/r/+K/2X/oP+v/9v/HQAzAGcAYAAsADMA+f/5/9T/p/+C/07/kf8x//3+9f4T/2z/oP8OACwASgBKAFkAUQBCAEoAQgBRABYAJQDF/77/WQCUAPwACwEwAVwBegGJAYEBegFrAbUBpgEwAZQAqgDAAJsAbwAdAH4AqgCFACwAp/90/5n/kf84/wz/0P7f/gz/OP9H/6//BwDq//L/r/+C/0D/BP8T/zH/e//F/8X/zf9CAJsAEgFVAZABtQHLAcQBNwHPAJsA3gDIAGcAJQA7AHYAWQCjALIA5QAhAe0AjADq/07//f6r/kv+S/5o/qT+nP6z/hv/iv/U/8X/1P+Z/4r/dP/1/rP+lf7Q/mX/vv/j/0oACwHiAQcCBwL4AcsBrgE+AYwAxf+C/5n/+f/5//n/lAA+AcQB8QHpAa4BKAGbADsATv+O/kP+D/41/jX+lf4T/+r/dgCqABkBGQH0AIUADgBs/zH/7v6k/rP+uv50/9v/HQCUAPQAawFyAT4BAwHPAKMAYAAsAFEAowDXAN4A5QALAUYBRgH8ANcAqgCUACwA4/+Z/5H/MwBgAKMAwAADAU0BGQHIAA4Avv9d/+7+pP48/pz+BP9O/9v/ZwADAVwBXAEwAc8AhQAzAJn/3/6O/t/+/f6k/tj+oP/PALUBDgIzAmACdgLaARkB+f9A/0D/BP+6/mH+pP6C/2cAmwDIACgBiQHLASEBqgAWAL7/6v+n/0f/9f4p/2X/e/90/9T/LAB2AO0AyADAALIAzwCyAGcAbwB2AJQAdgA7APL/FgAsABYAHQAdABYAJQBCAPL/DgAdAGAAjAAsADMADgA7ADsAUQBCAAcADgCv/6//iv+n/8X/4/87AB0ADgAOACUADgAlABYABwDU/yn/Iv/J/sL+Kf9s/5H/Zf+n/w4AHQAdAAcAUQCyAHYALAC+/5n/8v8HAAcAzf/5/yUAZwCjAIwA9ACJAdoBiQEDAX4AZwB2ADMAJQBZALkA3gADAeUAuQBnAGcAfgAAAMX/dP+K/2X/Tv90/6//JQAAAA4Azf+2/4r/Kf8x/zH/R/9A/4L/e/++/5QAGQFrATcBIQFkAU0BwAAsANT/gv9s/77/2//q/1EAuQAhAXIBTQESAeUAlABRAJn//f6k/kP+Q/5//v3+OP/N/1EAYABnAA4Avv90/yn/DP/Y/pz+yf7u/kf/1P8lAIwAwADlAKMAJQD5/83/p/9l/1b/r/+2/xYAhQCMABkBkAHLAZgBKAGjAOP/Tv+z/jX+8v1L/qT+5/50/9T/LABCAGAAWQBKAAAAgv/1/ob+Nf4t/o7+d/7C/t/+Kf+K/5H/UQCqADcBrgH4AQcCgQFGARIB5QCbAEoA6v+R/07/Mf8M/yL/kf8lAOUA/AD0ABIB1wBRAK//9f5L/pn99vxh/PL7Uvyz/GX9PP7Y/r7/BwAWABYA6v/F/77/p/9H/xv//f4T/1b/mf/j/1kACwFyAZ8BrgHaASQCbwJCAvgBtQGBAYkBCwGMABYAAADj/yn/uv4t/g/+Jv5D/o7+q/71/iL/R/9A//X+uv5o/gj+e/0i/dj8uvwb/a/9jv44/9T/qgALAU0BkAHLAeIBmAFNAdcAdgBZAG8AjADlADcBnwEdAv8B/wEOAuIBrgFVAcAADgB0/wz/DP8M/xP/G/9A/zj/DP+z/ib+Af75/S3+4/3j/Qj+D/7Y/u7+7v5H/3T/kf8i/47+aP5o/sL+QP+R/xYAZwASAXIBegFVAWQBxAFNAd4AbwA7ACwABwAsAGcAowALAXIBNwH8AMgAmwBKAK//Kf9//kv+S/41/nf+0P44/9T/HQAOANT/bP8p/9/+nP48/vL98v0B/jz+d/71/qf/QgALAZ8B0wG9AXoBMAGjADsAvv9H/9/+q/7f/in/vv87AN4AgQG1AcsBnwEwARIB1wAzAOP/Xf/n/qT+nP7J/tD+Zf/y/0IAUQAWAOr/+f+2/07/QP8x/0f/Mf9A/zj/bP/F/+P/AACR/13/Kf/f/tD+2P4T/2z/6v9vABIBVQG9Ab0BawEhAYUA+f8p/+7+uv53/u7+Zf8WALIAVQGuARYCYALLAYEB7QAAAF3/q/4e/tT94/0t/rP+BP+g/zsAdgDIAIwAbwBRAKf/Mf/C/nf+wv7f/hP/Xf+2/1kAhQC5AO0AyAC5AMAAUQDU/6D/mf/j//L/SgCMAJsAsgDIAPQAowB2AA4Axf+K/yL/BP/n/sn+2P5H/5n/6v8AACUAlAC5AMgAowBZAB0A8v/N/+P/vv+n//L/UQDIABIBCwEwAXIBegF6ATABzwDAALIAdgD5/3T/R/+C/4r/dP++//n/SgCbAIwAbwBgADsA2/+C/07/5/7n/t/+BP9O/6D/LABvAN4A3gDXANcAsgC5AGAA6v+v/77/tv/y/w4AZwDIACEBXAELASgB1wDAAH4A4/++/2X/dP/b/w4AJQCMAPwAZAE3AQMBAwFvAGAAMwCv/0D/Kf9d/3T/mf8AAKoAAwESARIB/ADIAG8AJQDj/5n/Xf8i/yL/R/97/xYAfgCbAMgAAwEDAaoAQgAOAPn/xf+Z/zj/Mf+K/9T/OwCqABkBXAGBAXIB/ABgAEIAAACg/5H/Zf+R/77/xf/5/1EAfgDPAAsBAwH0AKoAjAAzAM3/zf8HAAcA1P/F/wAAhQDPAPQA3gDlADAB9AB+AB0AOwBvAGcAYAAOAAcAQgBKACUAAABgAM8AuQB+AEoAJQBCAGcAHQAHAB0AQgBvADsAJQBZAIwAsgCMADsA6v/N/+r/iv9H/4L/p/8HAAcALAB2AMAAEgHtAM8AfgAlALb/Iv/u/t/+9f4b/3T/2/9KAMAA/AAwATcBNwHlAA4Aiv9A/9/+aP4m/jX+f/79/nT/1P8zANcAVQFVAfQAmwCqAH4Axf9W/xv/G/90/7b/8v9gAO0AawHEAa4BiQGYAZ8BkAEZAe0A5QCqAGAAQgBRACUAdgBRAOr/zf+v/6//dP84/xv/R/9W/13/Xf90/7b/8v8zAPL/2//F/4r/Xf8p/+f+7v5W/4L/vv/y/3YACwFVAZ8B2gH/AfgBDgLaAVwBNwESAc8AuQCjAKoA1wDtAMgAyAALAQsBPgH8AN4AwABnACwAp/9l/xv/Iv/n/o7+Yf5S/mj+Yf6z/vX+QP9O/2X/iv97/4r/p//U/6f/1P+v/6f/tv+K//L/MwBZAHYAlADAALIA1wAZAU0BgQHEAdoBmAFrATAB/ADeAJQAQgDb/4L/Mf+z/n/+s/7u/lb/xf/j//L/4//b/6f/Vv8T/7r+lf5D/gH+Af4X/kP+wv4b/2X/oP+K/9v/OwBvAJsAzwD0ABIB/ACyAG8ASgB+AIUAhQCbAJQAmwDAAM8A1wADATcBawESAdcAmwAlANT/OP/u/rP+Wv5D/nD+lf7u/k7/dP/F/+r/JQAHAPL/4/+2/+P/tv+Z/0f/E/9s/3T/gv8WAG8AzwBkAWQBcgESAd4AAwGbAIwAYAAzAFkAQgAsAPn/8v/y/9v/vv97/2X/Vv9A/xP/R/+g/5H/p/+C/2z/gv9A/xP/E/8x/07/Xf9A/zH/gv/y/1kAsgADAWQB6QH/AR0CBwK9AZgBPgHtAHYAFgCg/5H/8v8OAFEAUQCFALIA5QCyAOP/iv84//X+Yf7U/YP9mf0P/kP+d/6r/in/Xf9W/1b/Tv9H/yL/G//n/gT/Vv+R/7b/JQDeADABTQFcAWsBegFcASEByABRACUALADy/+r/LACUAO0AEgHlAM8AyABKAOr/dP/Y/nD+F/7F/XT9Vv22/UP+q/7f/jH/p//b/83/vv97/0D/Mf8b/+f+uv71/jj/Vv9s/6//AABCAIUAQgBvAIwAsgDIAGcAzwADATcBegFGAT4BPgFNAfQAqgAzAOP/zf9O/1b/R/8i/13/tv/j//L/zf+C/3T/Iv/Q/sL+PP7q/fn91P22/bb96v2V/k7/xf8zAIUAuQDtAPwA7QDPAJQAlACbAH4AdgBvALkAPgGmAQcCJAL/AekBywG9AZgBVQE3ATcBRgGyACwA+f+v/6f/Mf+6/kv++f3q/aj9qP2+/QH+hv7C/o7+Yf5L/lL+jv5D/gj+Hv5h/n/+q/5H/8X/sgCJAfgBLAIOAhYCtQFGAdcAdgBnAA4ABwAzAIUAKAGBAcsB/wEOAsQBGQFgAF3/wv5S/gH+3P3F/UP+lf7u/jj/e/8OABYAiv8E/47+xf1l/UD9Mf3N/Wj+Iv/y/4wAEgHaAUICFgJ6AbkAYADF/zH/E/8p/8X/ZwAhAf8BMwKUAgoDCgO5AtMBEgFZAKf//f6O/lL+aP7u/mz/xf/5/1kAbwBvAFkA6v+Z/xv/uv5o/jz+Q/7C/kf/iv8OAGAAfgCjAJsAjABgAEIAQgAlAA4ADgBKANcAPgFkAVUBTQELAe0AfgDU/3T/3/7J/sn+2P79/lb/DgBnAJsAqgBgAOr/dP8E/8L+Jv7c/dz9xf01/ob+BP+g/1EA9ABGAT4BEgHPAEoABwCK/13/kf/b/zsAowA3AbUBBwIWAuIBXAEDAWAA4/+Z/xv/OP9d/6//4/8lAJsAsgDeAMgAjAAAAIr/9f5a/ib++f1S/qv+DP/F/2AAPgG9AdMBxAF6AQsBowDb/xv/7v7Q/vX+Mf/N/4UANwHxAUoCwALlAsgCWALEAe0AOwDN/yn/G/8b/0f/p/8HAGcAwAAhARIBMAE3AeUAdgBCAM3/R/8E/9/+0P6c/qT+q/4p/3T/tv87AFkAjABvAIUAhQAzADsALADq/77/r/90/zj/R/+K/83/JQB+AN4AKAFGAWsBgQFcATcBEgGbAGAAHQDF/83/p//F/w4ADgAsACwASgBvAGcAhQBvAGcAHQAHALb/OP9O/zH/Tv9s/2z/iv++/+r/BwAsADsAowDXAPwAwACyAKoAYABKANT/p/+n//L/8v8lAEIAfgD8APQA9ACyAPwAzwCFADMAvv++/0D/R//f/o7+q/7Q/gT/E/9l/6D/AAAOAAcAAADj/8X/e/97/13/Xf90/5n/1P8HAGcA3gAZAU0BiQFrAVwBEgG5AGcADgD5/83/4//5/ywAsgADAXIBrgF6AU0B5QBgAAAAe/8i/xP/3/4M/1b/Xf/j/1kAyAA3ASEB7QCyAEIA2/9l/9/+f/48/lr+lf4p/5H/AADAABkBgQGQARkBlAAzAK//Tv/J/jX+Jv4m/nf+2P44/wcAzwBrAcQBgQFGAeUASgDy/0f/7v7J/uf+7v4b/8X/WQD0AAsBmAHiAZABZAHPAGAAHQDF/0f//f66/u7+R/9s/6D/+f+UAN4AyABvACwADgDy/5H/bP90/3v/1P++/wAABwBCAMgAsgDlALIAowCbAFEAOwDy//L/QgAlACwAQgBgAIwAbwBZACwAMwAzAA4A6v+Z/8X/AADy/9T/p/+v/9T/tv+C/3T/dP9s/13/Vv9O/5n/tv/y/x0A8v8sAEoAMwDq/77/p/+Z/5H/iv+g/5n/1P8sAFkAYACbAKMAqgDIAGAALAD5/77/mf+C/1b/Mf+K/6f/zf8HABYAHQBCAEoAHQAWANv/oP97/yL/DP/Y/gT//f7n/lb/Vv+2/9T/r/8AAOr/DgCv/3v/Xf8p/2z/Kf8M/xP/bP/F/9v/HQAOAFkAqgCyAJsAjADAAN4A3gCUAGcAbwAzABYABwAAAPn/2/8AAAAAAAAzAEIAlACqAHYAdgAlAL7/gv8T/7r+Uv4P/jX+Q/5//u7+tv9ZALIA/AAhATAB3gB+APn/mf8i/7P+Q/7y/WH+uv50/+r/QgDeAEYBRgHeAMgAYAAsAPn/Zf8p/8L+uv6r/sL+E/9A/5n/2/8AAAAADgAAAKf/dP8x/zH/BP/Q/t/+7v5H/0D/Tv9s/1b/e/9l/2X/OP9O/4r/r/8WAEoAjADXAN4A1wC5AIwAowA7ANv/vv+R/6D/kf/U/ywAsgAZAWsBmAGfAcQBegFGAfwAzwCFAB0A1P+Z/9v/6v/b/+r/AABnAMAAjABgAH4AlACUADMAxf+g/7b/oP+n/3v/Zf/j/wAADgDq/w4AWQAlAB0ABwD5//L/4//b//n/HQAlAGAAfgB2AJQAqgCFAG8AZwAWAJn/G//1/l3/bP9W/6D/4/9nAMAAyADXANcA5QDAADsAp/8b/9D+lf6V/pz+s/5H/8X/bwAZAZ8B6QH4AekBnwFGAWAAtv9O/wz/Iv/u/sn+QP+2/x0AsgDAAAsBawGfAdMBegESAdcAowAWALb/QP8E//X+q/7u/v3+Iv9l/6f/AABCAIUAwAASATABKAH0AKoAJQC+/1b/0P5o/i3+Yf6k/v3+bP8lANcAmAEkAiQCQgL4AYEBIQGqANT/Mf/Y/o7+uv7C/jH/vv9+AFwB4gFYAmACUQIsAssB9AAHAGz/9f66/lr+S/5//sL+Xf/N/zsAhQCbANcAqgCMAIwAUQAdAM3/p/97/2X/QP84/13/iv/y/+P/JQB2AMAAEgE3AVUBTQFyAVwBVQEhASEBPgEhAQMBwADPAKMAlACbAHYAhQCqAM8A5QD0AO0ACwEZAfQAyACUABYAmf9A/wz/yf6G/qv+q/4p/2z/dP97/13/gv9W/13/9f7f/in/G/8b//X+Iv9O/8X/AADq//n/FgBgAH4AYABCAMAA1wD0AAsBwAAwAUYBegGYATABAwGUACwAr/9O/yn/DP8b/wz/G/9s/5n/zf8AAAAAAADb/3T/DP+z/kv+4/2g/bb9zf3q/Uv+yf5W//n/ZwDPACEBAwEZAc8AQgAAAJH/iv+v/8X/HQBRAJsA7QAwAYkBZAFyAUYB9ADIABYAzf+R/1b/Vv84/0D/OP8i/zj/G//J/rP+f/4t/g/+F/4e/jz+Wv6z/l3/r//y/yUADgD5/9T/iv8x/+7+3/4E/0f/mf8HAJQA/ACJASwCWAI7AvgBmAFGAdcAJQC2/2z/Xf+C/13/Tv+R/+r/QgBZAH4AmwCUAGAADgD5/6//gv9s/yn/R/84/yL/OP9W/6D/1P8AAAAAQgB2AJQA1wCjALIAzwDAAM8AdgA7ACUAFgAzABYAOwBRAIUA1wDtAAMBwACqAH4ASgAlAKf/r/97/4L/p/+R/6f/oP/U/+r/4//N/5H/gv9d/zj/OP8i/yn/Tv+K/7b/8v9RAFEASgAzAOr/mf8b/9j+pP6z/gz/dP/b/1EA5QBcAWQBTQFNARIBuQBZAOr/gv9H/2z/gv9d/5n/+f8dAFkAbwBnAIwAowCFADMAvv9O/xP/7v6k/qv+uv7u/kD/QP++/wAAMwCFAHYAsgCMADMABwDj/8X/p//F/6D/r//U/xYAYABnALkAzwDlAAMBjABZACUA1P++/5H/e/9d/2X/vv/q/yUAYABZAH4AOwDj/5n/BP/u/rP+q/7f/t/+Mf+g/xYAYACqALIA9ADtALIAhQD5/8X/kf97/0f/QP9l/77/FgBgAMgAzwASAc8AuQBgAL7/R//Q/rP+d/7J/v3+e//N/zMAzwCUAJQAOwDy/4L/G//f/o7+3/4T/xv/oP8zAKoAXAFkAVwBKAHPAHYAp/8b/6T+/f44/zj/p/8zAPQAnwHiAfEB4gGBARkBjADj/+7+uv6z/rP+Iv9W/0IAyACBARYCHQIOAnoBVQGjAOr/gv8b/9D+3/4p/2X/1P9RAMAA9AAoAfQAowAsAPn/tv8x/xv/9f44/0D/gv++/wcAmwC5ACEBCwEZARIBuQDAAG8ALABCACUAAAA7AH4AowC5AN4AEgEZAd4AqgCMACUAAADF/6D/p/+C/5H/e/+R/8X/r//b//n/4//y/9v/8v/N/6D/kf9l/1b/DP84/3T/e//F/+r/MwB+AN4ANwE3AVUBXAFGAT4B7QCqAH4AWQBKAFEAZwB+AIwAowDPAJsAlAB+ADsAHQC2/13/Mf8M/9/+yf7J/tD+uv66/uf+/f5s/6D/vv/q/w4AJQAsADMADgAWAOP/2/++/5n/vv++//n/LACFAN4AGQFyAXoBegFVAfwA3gCFAAcAp/9O/0D/G/8M/1b/gv/y/zMAQgBgAEIA6v97//X+aP75/XT9Zf17/Yr9Hv7C/mX/BwBRAJsAuQCqAIUAFgCg/0D/Iv8x/0D/kf8dAMAAcgH4AVECyALeAowCSgLEAU0ByAAAAMX/iv9l/6D/zf8OADsAuQDlALkAbwAWAKD//f5w/tT91P2K/YP9Af4e/pX+DP+C/8X/vv+2/6f/iv90/0D/Iv9A/3T/4//b/1kAyAAZAb0BxAEWAgcC+AHiAYEBMAHPAJsAjACMAFkAYAA7ADMASgAWACUA8v+R/83/kf8i/+f+nP7J/pX+s/7J/rr+7v7C/u7+9f4x/07/Zf+C/4r/1P/N/wAAFgBCAIUA1wD0AN4AzwC5ACgBEgEwAU0BNwFVAT4BKAH0AAsBGQEoARIB/ADtAO0A9ACUAFEALAAWAAAA1P97/xP/Kf8T/+7+3/7C/vX+Iv8b/yn/QP90/6D/tv+R/3T/bP9d/13/Tv+K/4r/tv8lAH4A5QALAUYBiQGJAZABawEhAfwAuQB2AFEA4//b/xYALABCAFkAmwCyALkA3gCbAFEAFgCR/zH/q/41/jz++f3c/S3+aP71/lb/Xf/F/9v/p/+K/0D/OP8i//X+DP/u/iL/e/+Z//n/ZwDeADcBVQFyAVUBXAFGAeUAowBnAIUAdgAzACwAMwA7AG8AfgCMAKMAZwBCABYAxf+R/2X/Vv8b//X+BP8x/yL/DP8x/13/Xf8p/0D/E//1/gz/7v4T/yn/Vv+C/3T/r//q/xYASgB2AJQAuQDlAN4AmwCbALkAsgB2AJQA3gDIAOUAyAC5AMgAzwC5AJQAYABnAJsAUQBCADMASgAlAPL/mf9l/6f/dP9d/wT/OP9d/2z/p/97/+P/BwBRADsABwAlAA4A8v+K/1b/Iv9W/07/QP+Z/+r/ZwDlADABVQGuAbUBtQFGAe0AuQAsAA4Ar/+v/+r/BwB+APQATQGfAa4BgQFNAdcAYADq/3T/E//Y/rr+2P79/mX/oP/N/0IALABnAFEA+f/j/2X/Mf8M/9j+0P4i/6D/+f9nAIUAsgDeAMgAqgAsAM3/kf9A/zH/Iv9d/8X/ZwAwAYkBtQHxAekBcgEDAUIAiv/9/mj+Jv4X/kv+uv50/zsA/ACfAf8BHQK9AVwByAD5/wT/Lf7U/YP9oP0B/pX+mf+MAHIBFgJvAnYCYAIHAiEBQgBs//X+hv4e/jX+Nf6O/jj/8v92AO0ARgFVAT4B7QB+AAcAiv/9/sn+uv7C/u7+DP+K//n/JQAzADMASgBRAB0AAAAAAB0AYAB2AGcAdgCjAKMAmwB+AEoAOwAzAAAAxf+g/6D/vv/b/yUAYACbAIwAlACyAGAAHQDN/4r/Tv8i/wT/5/7n/t/+Kf9l/77/4/8HADMAUQBCABYAFgDF/83/2//U/7b/r//F/+P/FgAzAIUAowDAAOUA7QADARkB/ADPAOUAwACUAJQAZwBKAGcAMwAWALb/Tv9W/zH/Iv8T/0D/p//N/+r/HQAsADMAJQAOAM3/bP+g/2z/Kf9H/07/kf/5/1EAuQAwAWQBxAHTAb0BcgESAdcAJQDj/5H/oP+n/+r/ZwCbAPwAEgEwAdcAbwDq/zH/0P5//kv+Lf5h/lr+s/71/v3+Vv+R/6//oP97/yn/9f66/nD+Uv5w/tj+gv/U/x0AqgADAWsBTQE+AQMBsgB2ACUABwDN/zMAZwCbAPwAKAFNAUYBRgH0ALIAHQCv/3T/yf6k/nD+Nf5h/mH+d/66/qv+0P6r/mH+cP48/jz+Hv4B/jz+nP7u/lb/xf8WAG8AjACMAGAAMwAAAOP/LABRAHYAuQDeAFUB6QEOAjsCMwLxAcQBRgGbABYAoP97/4L/dP+v/+P/JQBvAG8AhQBgAA4Aiv8x/7r+PP7y/a/98v1D/sL+Kf+v/w4AMwCUAGcAZwB2ACwAAADU/9v/+f8lAIUAwAAhAWQBkAG9AZgBnwGJAXIBNwELAcgAfgBZACwAOwAOAPn/LAAOAM3/2//U/77/tv9l/3v/dP9d/07/BP8M//3+9f7u/tj+s/6O/tD+BP84/4r/AAB+AKMA9AASAfwACwG5AKMAbwBKADsAAAAWAA4AMwBgALIAGQFrAZgBnwF6ASEB7QB2AOP/R//9/rP+f/6r/sL+Xf+n//L/ZwBnAFkASgAdANT/tv9O/+f+lf5w/sL+BP9H/6//BwCqABIB9AAhAQMB3gDlAKMAWQAsAAcAFgAzAPn/MwCMANcAEgHlAM8A1wCqAFkAAACK/07/E//1/v3+7v4b/3T/oP+R/77/zf++/77/vv/j//n/BwAOAA4A4//U/5H/gv++/6//4//j//n/QgBnAIwAhQCUAMAAwACyAGcABwDy/5H/Mf/u/tj+BP84/5H/xf8lAJsA9AALAcgAbwDy/5n/Mf+z/pz+uv7Q/gz/Vv+n/wcAhQDlAAsBRgELAbIAWQDU/77/gv9l/1b/bP/N/wAAMwBRAH4AmwCjAG8ABwC+/5H/Vv8E/+7+nP7Q/iL/Iv90/4r/xf/5//n/4/+2/6D/xf+Z/3T/p/+C/+r/6v/y/0IAFgBZAEoAYABCAFkAZwBKAFEAQgCUAG8AYAB2AJQAjABgAEoA2//j/6//mf+K/3T/tv/F/x0AJQAWADMAAADj/8X/iv9d/zH/Kf9l/4L/mf/j//n/DgAzABYAHQAOABYA6v/N/9T/oP/U/9v/AABRAH4A1wDXAAMB/ADlAMAAbwCUAHYAlACjAHYAsgC5AMAAwACbAJsAYAAzAA4Azf++/3v/iv+g/4L/mf+g/9v/1P+2/83/p/+C/3T/bP9s/2z/kf/N//L/MwCFALIAyADeAKMAdgCMAEIADgDy/wcAMwCFALkAAwFyAVwBegFGAe0AlAD5/7b/Vv8p/zj/Tv9l/8X/LACFAOUAwACyAH4ADgCn/2z/DP/u/t/+5/5l/6f/LAB+AMAAEgELAQMBzwBgACUA8v90/3T/kf/F/xYAZwDtAGQBnwF6AWQBKAHIAFkAvv9W/yn/Kf9s/4L/p/8HAHYA9ADtAPQAowBnACwAmf+C/wz/3/7J/tj+9f4M/4r/tv8lAEoAYAB+AEIAJQDU/4L/Vv8b/+7+BP/f/iL/bP97/9v/LABgAGcAmwC5ALkAuQDIAKoAfgBnAFEAJQAOABYA+f8WAAcA6v/j/w4ALAAWAEIAMwAlAB0A2/++/5n/Vv8x/+7+uv5//lL+cP6k/v3+Mf90/6//8v8lABYAMwAWABYA6v/F/9v/vv/b//L/FgBgAG8AwAD8AOUAKAEhAQsBGQH8AMAAbwBgABYA+f8AAOr/FgAzAFkASgAAANv/xf+R/3T/QP/9/vX+BP8M/xv/Iv9W/6//AABRAGcAhQBnAEoAUQAAANT/xf/N/+P/AAAsAIUA/ABcAZ8BvQHxAeIBywFrASEB/ACFAEIA6v/F/7b/zf8sAEIAZwCjALkA1wDIAIUAdgAsAMX/kf84/wT/3/7C/t/+/f4x/3v/r//j/x0ALAAsADsAQgBRAFEAMwBKAHYAlADIANcA7QALAfwAAwHeALIAuQCyAJsAfgB2AH4AsgCyAMgA5QC5AM8AmwAzAPL/iv9O/xP/uv6O/pX+pP7Y/iL/Zf+g/6f/p//F/5H/Zf9H/zH/3/7f/uf+yf4T/xv/kf++/+r/dgBnAHYAYABvAGAAWQBZAFkAZwBZAIwAjACMAIUAdgBgAFEAOwAdAPL/kf+n/4r/mf++/77/8v/N/83/2/++/5H/dP9W/yn//f7f/tj+0P7C/tD+5/4b/2X/e/+g/83/1P/5/x0AHQAdACUAHQAlAAAASgB2AHYAlACUAKoAlACjAG8AHQAsAFkAMwBZAG8AMwBRAAAABwDq/6f/r/9d/0f/DP/f/tj+q/6V/tj+5/79/nT/iv++/9v/4//5/7b/gv97/zj/Iv84/yn/Zf97/6//+f8lAGAAfgDPAPQAMAEoAfwACwHlAPQAsgAsAAAAr/+2/6//mf/F/+r/QgBnAIUAmwCqAMAAbwAzAM3/Xf8p/9/+pP5//o7+uv4b/2z/xf8sAG8AqgCUAIwAfgBRAEoA4/+g/5H/dP9s/2z/kf/j/yUAhQDIAM8AAwHlAM8AdgAWANT/gv+R/xv/G/84/zH/r/++/wcAUQBvALIAowBZAEIALADU/3v/Tv8p/wz/OP9s/7b/4/8sAIwAmwCjAH4ASgAWAPL/tv+R/3T/Xf+K/6f/tv/N/wAALAA7AG8AOwAlAB0Atv+2/3T/R/97/3T/oP/F/w4AQgCUANcA3gDPAMAAhQAdANT/iv+K/4r/p//q/ywAbwCjAOUA5QALASEB9ACFAEoABwCK/13//f79/gz/Mf9H/2z/zf8WAFEAQgBRAOr/1P+g/xP/BP/1/gz/Kf90/7b/HQB2AM8A9AALASgB5QCqAFEAMwAHAOP/6v/q/yUAZwDPAPwA9AADAfQAuQB2APn/r/9W/yn/Tv9O/2X/mf8WAB0AQgAzAPn/6v+K/13/DP/Q/qv+uv6z/rr+Iv9d/9v/YADAAPwANwEZAfwAqgAzAB0A6v/U/9T/DgBKALIAPgGfAa4BtQHLAYkBZAHIAGcALADb/83/oP/U//n/SgB+AJsAyAC5ALkAdgAWAMX/Xf9A/wz/DP8M/yn/p/+v/+r/SgCFAJQAjACFADsAMwD5//L/8v/q/yUAfgCjANcAGQH0AAsBwACUAJQAWQBgAFkAhQB2ALIAwACqALkAsgDPAJQAYAAdAM3/mf90/yn/Tv+K/5n/FgA7AG8AwADAAKoAYAAdALb/e/8E/9/+BP8x/6D/zf9gANcA/ABrAYEBZAEhAfwAmwAzAOr/p/+C/13/e/++/w4AQgCbAPQAGQESAfwA9AB2ACUAxf9l/yn/3/7n/gT/dP+v//L/LABZAJsAlAB+AEoAFgAAAOr/zf/y//L/6v8AACwAbwCUANcAzwDXAN4AzwDIAIUAMwAWACUA6v/5/wcADgA7ADMAMwAlAA4A6v/N/5H/Xf84/zj/OP8i/0D/Xf+Z/6//r/++/6//zf/F/7b/mf9d/4L/Xf9W/6D/oP/j/xYAUQBvAHYAowCbAJsAhQBnADsAJQAdAPL/AAAAAA4AOwBvAH4AowCyAGcAUQAlANv/bP8b/wT/3/7J/u7+E/84/6//r//y/zMAFgAzAAAA+f/F/5n/dP9d/1b/E/9O/4L/4/8WAEIAlACUAM8AowB+AIUAUQA7ABYA+f8HAAAAFgBRAGcAsgC5AJsAjACFAIUAYAAHAMX/vv+R/6D/dP9s/3v/dP+2/5H/p/+R/5n/iv9d/2z/R/8x/zH/Zf9O/3v/tv/b/xYADgBKACwAOwB2AGcAUQBgAGAAOwBnAHYAWQBgAHYAjACUAIUAjAB+AG8AhQBKABYAzf+Z/5n/Vv9O/07/Tv97/4r/iv97/3v/dP97/3T/Tv9s/zj/OP+K/07/bP+R/5n/1P/U/+r/4//j/xYALAAzAFEAYAB2AKoAmwCqAPQACwEwATcBMAEoAeUAyACjAFkAHQAHAOP/tv+n/7b/4/8AAAAAAAAOAOr/tv+R/0f/G/8i//X+0P7f/v3+G/9H/3v/xf8WAEoAZwBZAFkAYAAdAAcA+f/y/yUAWQBvAKMA/AAwAUYBegF6ATcBIQGjAG8ASgAdAEIADgAzAFEAfgCyAKoAsgCUAGcAFgDj/3T/Tv8p/9D+G/8i/zH/Tv9W/5n/vv/N/77/zf+n/3v/dP9H/zH/Xf+Z/9T/DgBRAJQAsgDtANcA1wDlAKMAsgBvAGAAWQAHAFkAZwCFAIUAdgCyAHYAdgA7AOr/4/+v/6D/Vv9H/07/R/9d/5H/e/+C/6D/Tv9H/xP/DP/9/hP/dP+C//L/AAAWADsAHQAHANT/vv+C/3T/Zf+Z/6D/zf8lAH4A7QDlAD4BIQEZAfQAZwBRAKf/Tv8M/7r+s/7Y/mX/xf8lAG8AlACFAGAAJQDN/07/7v53/h7+Jv41/nf+yf5A/5n/4/8zAGcAYABRACUAzf/j/6f/mf+v/3v/kf/y/xYAUQCqAKoA/ACbAHYAjAD5/+P/oP9s/0f/Mf9O/1b/e/+C/6D/oP+g/6f/bP9A/xP/2P7C/t/+2P7Y/v3+G/9H/2X/gv+v/9v/4//q/xYAxf+2/4r/Xf+n/3T/oP++/9T/OwBCAGcAbwB2AIUAdgAlAPn/1P+v/7b/oP+R/5n/e/+C/6D/gv+Z/5H/oP+R/07/R/8M//3+3/7n/vX+DP9A/1b/p//U/+r/FgD5/9v/2/+g/6f/gv+R/77/mf8dAEIAZwCyANcAEgEwAU0BVQEZAcgAlABCAAcAvv+v/77/p/+2/9T/HQBCAIwAlABvAEoADgDN/1b/OP/Y/pz+hv5a/nf+jv7f/jH/Zf+v//L/8v/y/9v/xf+g/13/Zf9H/wz/Mf9H/0f/iv+v/xYAdgCyACgBXAFrAU0BCwHIAKMAOwAlANv/bP+C/1b/Zf9s/6D/1P8lAHYAbwB+AEIADgC2/07//f7n/sL+f/6z/sn+/f5A/5H/2//N/+r/FgAOAPn/+f/U/6//tv+v/77/4/8HACwAbwCbALIAmwCUAIwAdgBnAFkAQgAzAEoAOwBKAEoAQgBKACUA8v+2/77/e/9W/1b/Kf9l/0D/R/9W/13/kf9s/6D/e/90/3T/Zf90/0D/gv+Z/6f/xf8OAEoAYACMAJQAsgCbALIAsgCqAIwASgBnACwAHQA7ACUAdgCbAH4AuQCqAKMAzwCUAH4ASgAsAAAAvv+2/3v/oP+n/83/+f8AAHYAdgB+AKoAmwCjAIUAUQAdAOr/r/+C/3v/tv/U/zMAhQCqAOUA/AALAQMBIQHeAMAAlABgAGAABwBRAEIAWQCjAIwAsgDAAPQAzwDXAKMAUQAzANv/xf+C/4r/p//N/wAAFgBCAFEAUQAsADMADgDj/+r/zf/F/+r/AAAlACwAWQBvAEoAjABgAG8AfgBnAKMAZwCMAG8AYACFAGcAhQCUAJQAuQDtAMgAzwADAQMBIQEwAU0BKAEZARIB9AD0AM8AwAC5ALIAlACMAKMAlACjANcA/ADtAAMBCwHIAKoAbwBZAEoALAA7ADMAQgBZAGcAqgDlABIBPgESAQsB7QCUAIwAbwB2AHYAYACFALIAuQDXAPwA5QADAfQA9ADlAIwAlACFAG8AbwB+AIUAlACbAKMAsgC5AMAAzwDXAMAAlABZAFEALAAAAPL/1P/F/+P/BwAHACwAMwA7ADsALAAlABYAAAC+/77/r/+2/9v/4/8HAA4AQgCMAIUAmwDeAN4AzwDPALkAqgB+AG8AYABgAGcAfgCjAKMA5QALASgBIQHlAMgAuQCqAFEAMwAzAA4AMwAzACwAWQBgAHYAdgBgAFEAZwBZAPL/8v/U/9T/2/+Z//L/FgAzAGAAYACMAJQAwAC5AIwAfgBgAFEAQgAOAAcAHQAAAOP/FgAzADsAYABgAH4AlACMAIUAQgB2AGcAWQBKAOr/BwDy/7b/tv+v/+P/HQBKAIUAsgDlAPwAAwEDAbIAlABKAPn/6v+R/13/Zf+K/6//8v9CAGAA3gASARIBEgGjAFkAAACR/zj/3/6r/qv+s/71/l3/vv8dAG8AsgDXALkAqgCFAPn/oP97/zj/DP/1/hP/Tv+g/xYAfgC5APwANwEZAe0AuQBgAOr/mf9H/xP/G/8p/13/oP/5/0oAlACUAJsAuQB+AGAAAACR/07/9f66/o7+f/6r/uf+QP+g/77/DgAzAB0AHQDj/6f/Vv8i/xP//f4b/13/kf/N/yUAUQCbAKoAmwCjAGAAZwAsAPL/+f/b//L/zf/b//L/6v8lAPn/2//F/6D/gv9W/zH/OP9H/zH/Mf9H/3v/iv+Z/5H/gv9s/wz//f7C/rP+pP6O/u7+9f44/5n/6v87AFEAdgBvADMABwD5/7b/oP++/6f/p/+2/77/tv/5/0oAUQCqAJsAhQCMAEoAAACR/13/BP/C/rr+Yf5o/nD+hv7Q/vX+Kf9l/4L/gv90/yL/5/7u/pX+Wv5o/kP+S/5L/ob+7v5H/77/+f87AH4AmwCbAG8AQgD5/7b/e/8x/xv/E/8T/2z/oP++/+P/+f8lABYAAAC+/4L/Vv8M/9D+hv5w/nD+jv6c/qv+3/79/in/Tv97/4L/gv90/1b/Zf9d/1b/QP9O/2X/Xf+R/5H/oP++/77/6v/q/wAALAAHAA4AFgDq/+r/+f/b/83/tv+g/5n/kf97/3v/dP9l/13/Vv9A/wz/E/8p/xv/Kf8b/yn/Mf8b/xP/Iv8M/xP/OP84/3v/dP+C/5n/iv+Z/4L/mf+g/6//1P/j//n/LABCAEoALAA7AFkAJQAdAPn/tv+n/83/tv++/9v/r//U/8X/vv/U/8X/r/+2/6f/bP90/13/Tv8x/yn/G/8E/wT/BP8p/yn/Tv+C/6D/p//U/77/zf+2/5H/tv+R/9v/xf/q/wAABwBvAG8AsgCjAKoAmwCMAJsAlADAAG8AhQB+AHYAhQB2AJQAdgBgADsAQgD5//L/BwDy/wcAxf/q/+P/xf/j/7b/tv+K/4r/bP8T/zH/2P7n/jH//f5O/5n/1P8sAEoAfgCUAJsAjABRAB0AAADb/9T/vv+n/+r/OwB+AMgACwFcAXoBgQGfAWQBEgHIAGAABwDF/6//p/+n/+r/LABRAKoAyADtANcAlAB+AAcAr/90/yL/7v7f/uf+7v5H/5n/2/8WAGcAhQDAAM8AowCyAHYAZwBRAEoAbwB+AKMAzwADAfQACwE+ATABRgE+ASEBKAH8AM8AwACUAIwAjACFAIUAmwB2AEoAMwD5/7b/bP97/3T/e/+2/+r/DgAWAEIAWQBZAEIALAAlAOP/oP+Z/2z/e/+g/6f/BwAzAH4A3gD8AGQBawFcAVUB/AC5AG8AJQDj/9v/1P/q/wAAHQBCAGcAlACFAJQAhQB2AGcASgAWANv/xf+Z/5H/gv97/4L/kf+v/+r/BwD5/0IAWQB2AJsAyADPALkA3gCqAKMAZwBKAEoA6v/5/wcAMwA7AIwAyADIAD4BPgE3AT4B/AC5AHYALADb/5n/iv9l/4L/vv+g/zMASgCFAOUAuQD0ALkAowCFAEoABwC+/9T/iv+g/77/8v8dAFkAmwC5AN4AAwEwAfwAAwHIAG8ASgDq/6//iv+g/3T/e/+g/6D/xf/j/wAAQgB+AHYAowBnADsAQgAHANT/tv/b/77/zf/y/x0AWQCbAOUAyAD8APwA1wDeAJsAUQAzABYAJQAWAAAAJQAdADMAQgA7AFkAWQBZACwABwD5/9v/2//q/83/1P/y//L/FgAWACwALAAsACUABwAlAOP/8v8lABYAOwBgAG8AjADAAM8A3gDIAMgAqgCUAH4ADgAHAAAA8v/5/xYASgBZAH4AdgCFAIUAWQBRACUA1P+g/3T/Mf8i/yn/R/9O/3T/p/+g/9v/4/8WACUADgAlAOr/+f8AAPn/DgAOACUAQgBCAGAAlAB2AJsAyAC5AMAAuQDeAPQAyADPALkAYABvAEIAHQAWANT/4//q/wAABwAHAA4A+f8WAAAA8v8HANT/oP+n/4L/Tv84//X+/f79/hP/Zf+R/+P/HQBZAGAAbwCUAIUAhQBRAEIASgAdAA4ADgAOAAAAJQBZAFEAmwCqAIUAzwDAAMAAqgBgAEIA6v+v/2X/bP8x/wT/QP8x/3v/mf/N/wAAJQA7ADMAZwAdAA4A6v+2/7b/kf+Z/5H/r/+v/83/+f8OAFkAdgCjAMAAwADXAM8AhQBZAEIA+f/b/6//vv/q/6//6v8HAOP/DgAAABYAHQD5//n/4//N/6f/gv9l/zj/Mf8M/+7+E//9/gT/bP+R/5H/zf/j/7b/6v/5/wAADgDy/xYADgDy/+P/xf/b/8X/1P8AAAAADgAsACwASgA7AEIASgAOAA4ABwDj/9T/oP+Z/5H/Tv90/4L/Zf+R/3T/gv+v/6//vv+2/6//xf+2/5n/kf97/5H/e/9s/4L/mf/U//n/SgB2AIwAowCFAKMAZwCFAJQAWQB2AEIAJQAOAAAABwDy/wcABwAdABYAHQAlAAAA+f/5/83/r/+n/4L/e/9O/1b/Vv9O/2X/Zf97/3T/p/+g/6f/6v/b//L/+f/b/83/1P+v/7b/vv+R/6//r/+v/9v/xf/y/yUAQgBnADsAUQAzACUABwC2/9v/r/+g/5H/r//U/8X/HQDy/+r/1P+n/6//e/9l/3T/Zf9s/6D/oP+v/+r/6v/y/zsALAAOAAAAxf++/4L/kf+v/7b/6v8zAHYAmwDlAN4AAwHlAIwAZwAAAK//Zf9A/xv/E/8x/3v/vv8WAGAAqgD0ALkAyACMADMA1P9l/zH/uv7Y/vX+E/9l/83/QgBvALIA9AAoAfQAwAB+AA4A1P+Z/2X/Xf9l/3v/xf8AAEoAhQCqAN4AuQCqAIUAYAAlAOP/4/+2/6f/r//q/wcAAAAzAB0ALAA7AB0A+f++//L/4//N//n/AABKAGAAbwCbAGcAbwBvADMAFgDb/7b/r/+Z/6//zf/j/zMAYABvAHYAWQBgAEoAAADj/4r/Kf8T//3+DP8x/2z/p//5/ywAMwBCADsAUQBRAA4Axf+v/77/mf+Z/6f/r//F/+P/BwAWAEoAbwB2AHYAZwBvAEIAQgAlAOr/8v/N/7b/xf/b/77/zf++/6D/2//b/+P/4/8lACwAJQAlAAcAJQDb/83/vv+Z/5H/kf+K/5n/4//b/zMAdgB+AIwAjACUAHYAdgBgAEoADgAdAB0A+f8lACUAMwBRAIUAlAB+AIUAfgAlABYAHQC+/6f/bP9H/13/QP9d/3T/iv+v/77/AADy/+P/+f/F/9v/tv+R/6f/tv/U/83/4//q/+P/+f8OABYADgAlADMASgAzADsAdgBRAH4AlABvAG8AMwAlAAcA8v/5//n/AAAWADsALABRAFEAZwBvAHYAhQA7ADsA8v+g/13/QP9W/zH/Xf+C/83/FgA7AJsAzwDXANcAwACMAFEADgC+/4r/kf9W/13/gv+Z/+r/OwCqALkAzwDXAM8AlAA7APn/oP9l/yL/Iv8M/xP/QP97/83/+f9CAEoAlACMAEIALAAHAL7/dP9W/xP/E/8p/13/mf+Z//L/FgAdADMAMwAsAPn/4/+2/4L/kf9l/4r/r//U/wAA6v/5//n/FgAHAAcAFgDq/wcAFgAdAA4AMwAlAAcA6v++/8X/mf+K/4L/e/+C/6D/vv/y/xYAMwBZAFEAWQAsAFEAWQAzADMA+f/b/9v/6v/y/ywAMwBKAIUAhQCqAKoAhQBRAB0ABwDy//n/zf/F/wcA8v8WAA4A+f8dAB0AMwAAAOr/4//F/+P/xf/U/9T/zf/j/+r/zf++/77/tv+K/1b/Zf9A/zH/Xf9d/3T/oP+n//L/DgDy/wAA1P/U/77/zf++/6D/vv+v/6D/r//U/77/6v8sACUAJQAOAAcA+f8AANT/2/+2/4L/vv+g/8X/+f8WADMAYABvAEoAOwAWABYAJQDy/wcA6v/b/77/r//y/9T/2/8HACUAOwAzADsAHQAdAPn/FgAWAAcALAAOADMALAA7AG8AhQCbAJQAhQB+AHYAMwAzAA4AHQA7ACUAdgCMALIA5QDIALIAuQB2AFkALADN/8X/oP+n/6//zf/y/xYASgBRAH4AjACjAG8AOwAdAAAA4/+R/6D/R/90/4L/gv/5/+r/OwBvAJQAowB2AH4AUQA7AAcAAADN/6f/tv+g/7b/1P8lACwAQgBnAEIAWQBKAEIAOwBCACUADgAHAM3/1P+v/4L/iv+R/6//tv/F//n/AAAWACwASgB+ADsASgBRAA4ADgDb/83/p/+R/4r/mf+n/4L/6v8WACUAYABvAIwAZwBZADsABwDj/6D/gv9O/zj/R/9O/3v/tv/b/yUAMwBgAJsAfgCMAGAAOwAzAAAA6v+2/83/8v/b/ywASgBKALIAyACyAO0AqgCUAIUAOwBCAAcAAAAlABYAFgAAADsAHQAdADMADgBgAFEAQgBRAB0ALAAdAAcAFgAOACwAMwAOAA4AFgAHAPn/DgDq/9v/AADq/x0AHQAHADsAHQAdAB0AOwAsAEIAUQAHACwAHQAWADMAJQAdAAAA8v/j/9v/4/8dAB0AJQBnAGAAUQBRAFEAOwAzADMA+f/y/+P/8v8OACUAZwBnAJQA5QDPAN4A7QDAAMAAjABnAEIADgAHANv/6v/y/+r/DgAWADsASgA7AFkAOwAdAB0A4//F/4r/p/+n/6f/1P++/wcA8v8HAB0ABwA7AAcAJQAWAB0AWQBRAGcAdgB+AGcAYABZADMADgA7ACwAAAAOAAAAJQBCAGcAWQB2AJQAjACjAFkALADq/77/kf9H/yL/9f4M/yL/QP9d/5n/2//y/zMAJQAsADMAFgD5/6f/gv8x/wT/DP/f/in/QP9s/+r/LACjANcA9AAZARkB7QCqAIUAFgDq/83/kf+Z/4r/kf+n/7b/8v8WADsASgBRAGcAFgAlACwA2//b/6//e/90/zH/OP84/wz/Xf+C/4L/vv++/+P/6v/5/yUA+f/y//n/4//y/6//kf+v/4r/e/9d/2X/Xf9W/5H/oP/U/w4ALABCAGAAYABCADMAAAD5/6//kf9s/xP/DP8M/1b/Vv+K/83/8v8lAEIAfgB+AEoAMwAHAL7/gv84/xv/BP/Q/gT/Kf9d/5n/6v8WAFkAfgBZAHYASgAWAOP/oP97/zj/9f71/hv/G/9O/5H/1P/j/ywAdgB2AJQAhQB+AGcASgAOANv/xf+R/5n/xf/U/+P/FgAsADMAWQB2AFkAYABvAFkAUQAsAAcAxf/U/7b/oP/F/3v/gv+n/6f/oP+Z/6f/p/+g/7b/vv+n/6//vv++/5n/r/+K/3v/e/9W/1b/Kf9O/13/dP/N//L/HQBKAH4AqgCMAJQAjABRADsAJQAHAOP/xf/U/77/tv/b/wcAQgCUAMgA5QDlAN4AyABZACwAzf+R/2X/Kf9H/yn/Xf+g/83/FgAzAFkAZwB2AGcAYAAsABYADgC+/7b/bP9d/4L/iv/q//L/HQBZAG8AmwCqAKMAmwCUAGcAfgBgAFkAdgBKAG8AdgBZAFkAhQB+AG8AdgB2AJsAdgB+AHYAZwBnAFkAYABKAEIABwD5/9v/kf+C/2z/dP+K/3v/p//b/9v/AAAlACwAQgAzACUABwDq/8X/mf+n/77/tv/b//L/6v8OAEoAfgCFAKoAwACqAJsAlABgADMAMwAWABYAJQAzAFEAQgBCAFEAdgBvAHYAWQAsADsA8v8WAB0A8v8HAAcAAADU/+r/1P/F/83/2//j/+r/FgAOACUASgBnAHYAsgCjALIAwAB2AKoAUQBZAG8AZwB+AFEAsgCqAO0A/AASASgB/AADAcgAzwB+AGAAMwDy/+P/tv++/+P/BwAOAEIAWQAzACwAQgAsAA4ABwDb/9T/tv+K/6D/vv+v//L/DgAlAEoASgCFAFEAYABRAEoAWQAsACwAJQAlACUAUQBCAGAAZwBRAFEASgBvAEoAYABZAHYAhQBCAFEAMwAdAPn/xf+2/4L/gv+K/3T/dP9d/6//2//y/ywAFgBRABYAAAAAAJn/iv9s/2X/Zf97/6D/vv/y/zMASgCUAKMAjACUAFkALADq/77/mf+K/5H/oP/U/wAAJQA7AH4ASgAsAEoADgDb/9T/xf+Z/4L/gv+g/5n/tv/U/83/6v/b/77/tv+K/1b/Zf8b/xP/BP/n/iL/OP90/4L/p/+2/77/2/+Z/4r/gv9H/1b/Tv9O/5H/vv8AACwAYABnAIwAhQBnAGcAFgAWAKf/mf+g/07/gv+C/83/AAAdAFkAlACUAJsAhQBgADsAzf+v/13/Kf/9/hv/Tv9A/4r/mf+2/6//zf/U/8X/1P++/8X/r/+n/5H/mf+g/77/1P/b/9v/4/8AAA4AJQAzAEoAOwAsAEoAWQBRAEIASgAlACUAOwBCAB0AFgAAAAAAAAD5/xYADgAAAAcAJQDq//L/2/++/83/mf++/4r/kf+K/4L/tv97/5H/iv+n/7b/vv/b/83/1P/j/9T/zf/j/9v/2//5//L/6v8HAPL/6v/q//L/DgDj/xYALAAdADsAMwAdADMAFgDy/9v/mf+g/4r/r//F/9v/8v8AAA4AAAAlAPn/1P++/5n/oP+Z/6D/r/++/77/8v8OABYAJQBZAGcAOwBnAEIABwAHAAcABwAsAEoAWQBvAFEAdgBvAG8AZwA7ACUABwAAAOr/4//y/x0ABwAAADMAHQAzAEIADgD5/9v/r/+n/3T/Vv90/4L/iv/N/9v/BwAWACUAQgAAAAcA6v/U/9v/vv/b/77/4/8OABYAOwBnAG8AbwCjAJQAlAB2AFEASgAlACUAFgAAACUAFgAHAB0AAAAAAOP/4//N/7b/oP+C/77/kf+K/7b/vv+2/8X/vv+g/4r/bP+C/3T/p/+g/77/+f/q/zsAYAB2AG8AbwBgAGAASgAdAEIAHQAdAA4AMwA7AEoAfgBnAKoAbwCMAJsAWQBZACwAFgDb/9v/tv+n/6f/kf/U/77/p//U/83/2/++/77/oP90/4r/bP90/4r/p//F/9T/2//F/wAA2//q/wcA4//5/x0AJQAlAGAAZwCMALIAzwD0APQA9AC5ALIAdgA7AFkAUQAlADMALAAlAEoAUQB+AIwAlACMAEoAOwAOANv/xf+g/5n/e/9s/5H/mf++//L/6v8dAEIAQgBvAGcAWQBRAEIALADj/9T/zf/b/9v/8v9KAFEAhQCjAMgA7QD8ACgBKAESAd4A/AC5AIwAhQAsAB0ADgDj//n/FgAHADMAOwBZAFEAOwAlANT/+f+Z/3v/bP8p/2z/QP9O/2X/gv97/5n/r/+K/77/p/++/7b/r/+Z/6D/2/+2/9v/2//q/wcADgAzADMAFgAOACUADgAlAFEAWQBvAHYAhQBRAEIAQgAdABYA6v8AAM3/r//F/6f/vv/N//n/6v/j/wcADgDq/+r/8v+n/5n/Zf9W/1b/Xf90/5H/zf+2//L/4//b/wAA1P8AAPL/4//y/wcAFgAsADsAFgAlABYADgAdABYALAAdAB0AMwAWABYAFgDy/wAA6v8HAAcAFgBZAB0AFgAzACwAAAAHAAAA1P/j/83/tv/F/9v/2//5/wAA+f8lAAcALABZAEoAYABRAEIASgAWAAcADgAAAPL/BwAdAAAAHQAOABYAMwA7AEoAQgBZACwALAAOAAcAHQD5//n/2//b/9v/+f/b//L/MwAWAEoAMwAzADMAAAAHAOr/2/+2/4L/e/+g/5n/vv/j//n/FgDy//L/1P/N/77/vv+g/3v/kf9W/3v/dP+C/9T/vv8HAAAABwAWAPL/HQD5/83/8v/U/83/2//b/w4AJQAsAFEALAAdADsAFgDj/83/xf/U/7b/zf/U/6//r/++/83/p//j/9v/tv/F/6D/p/+K/4r/gv+K/3T/gv+Z/4L/tv+R/77/6v/U//n/8v/5/wAA+f/5/yUAJQAWACUADgAsADMALABCADMAMwA7AEoAYABZAG8AbwBZAFkAOwAzAAAA2//q/9T/vv+2/77/kf9s/4r/iv90/4L/mf+K/3T/dP9d/1b/Tv9H/2z/e/+R/83/2/8WADsAHQBKADMABwAWAPL/+f/q//n/OwBKAEoAUQBnAIUAmwCjALkAmwCFAG8ALAAWAPn/2//5//n/DgBnAH4AsgCyAIwAmwBZAEoAHQDF/5n/kf9l/2X/p/+R/83/AAA7AGcAUQCMAHYAWQBRACUA8v/U/83/2//q//n/MwBnAJsA/AD0AO0AEgHeAKoAbwAzACUADgAlADsAOwBgAH4AjAC5APQA1wDeAO0AowBvAFEALAD5/+r/DgAOAAcAHQBCAFkAbwCqAJQAhQCMAG8AQgAOAOr/1P/j/8X/4/8dAAcAUQCFAJsAsgCyAM8AyACyAJQAfgA7AFEASgAlAEoALABZAHYAlAC5AJsAowCUAIwAfgBCACUADgDq/wAA2/++/+r/2//y/xYALAAOAA4AAADq/+r/2//b/6//oP+v/5H/iv+v/+r/8v8OAEoAMwAzADMAFgAWAPL/JQAOAOP/+f/y/w4AAAAdADMAUQBgAGAAmwBvAG8AbwBCAEIASgA7ADsAHQAHAB0ABwD5//L/zf+2/+r/1P/j//n/1P/q/9v/2/+n/4L/e/9W/0f/QP9O/0D/bP+C/6//6v8AAEoASgBvAG8AQgAzAAAA4/+g/3T/Zf9d/3T/oP/N//L/YAB2AIUAlABnAH4AJQDb/6//Zf9O/yL/QP8x/0f/iv97/7b/2/8AACwAJQAHAM3/oP9d/0f/QP8x/1b/QP90/6D/tv8sACwAQgBgAGcAOwAlADsAAAAsACwAFgBZAEIAWQB2AHYAbwBvAIUAYABCADsADgD5/9T/2//b/+P/+f/j/x0ABwAWAB0A+f/y/5n/kf9d/yn/OP84/1b/kf+2/wAALABRAGAAYABZACwAOwDy/8X/r/97/4r/kf+R/77/BwAHAEoAWQBnAG8AUQBgAA4AAADF/6D/gv90/2X/OP9O/zj/Vv9A/13/bP9s/6//iv90/5H/oP97/5H/e/9l/4r/e/+Z/5n/p/++/83/4//y/wAADgAzAEoASgBZAH4AdgCMAIwAZwA7ACUAJQAAAPn/AADj/9T/6v/j/+r/2//b/wAA6v8AAPn/2//N/6f/kf9d/0D/Tv84/zj/Tv97/5n/kf/N/+r/BwAzAEIAQgBRAFEAUQBRAFEAUQAsACwAHQAWAEIASgBRAJQAowCqAMgAqgCUAHYAWQAzAAcA2/++/6f/iv+R/5n/p/+n/6//xf/F/77/2//q/8X/zf+Z/3v/Xf9W/3T/mf/F/83/MwAzADMAUQAsADMAFgAlABYAFgAlACwAWQB2AIUAlACqALIAowCFAHYAQgA7ACUA+f/5/8X/r/+v/77/vv/b//n/LABvAFEAYAA7AAcA+f/N/7b/mf+R/7b/zf/j/zsAbwCFAMAAwADIAN4AqgC5AJsAbwBZACwAMwAWACUAQgBvAJQAuQDeAOUAuQCjAKoAYABZACwABwDj/83/6v/N/9T/1P/b/+r/HQAWACUAMwDq/wAAvv+g/5n/gv+R/5n/r//N/wAA+f9KAFEAbwCUAHYAowBvAIUAdgBZAHYAYABvAGcAWQB+AJsAhQCjAIwAjACbAGcAhQBgACUADgAOAB0A+f/q/+r/AAD5/+P/8v/N/9T/vv++/9v/p//F/83/xf+2/8X/zf+g/9T/vv+2/77/oP++/8X/zf/j/9T/zf/y/wAA+f8HABYAMwAWAB0AMwAlAB0ABwAdAAAA6v/b/6//xf+v/6//vv++/+P/tv+v/6//gv97/2X/OP8E//3+G//1/vX+/f5A/4L/dP+Z/7b/1P/b/9T/1P+n/6f/Zf9s/2X/Mf9l/2z/iv+2/wAABwAsAEoAJQAWANv/zf+g/6D/oP90/5n/gv+Z/7b/zf8AAA4AJQAWAAcABwDN/5H/iv9O/zH/QP9O/2X/mf+2/83/6v8OACUAHQAOAPL/1P+v/7b/xf/b/x0AMwA7AFkAfgB+AH4AhQBRACwAJQAHAPn/6v/F//n/8v/y/zMALAAlAB0AMwBCABYABwD5/8X/mf90/3v/kf9s/7b/8v8OAFkAfgCjALIAqgB+AFkAFgDN/5n/gv9l/07/iv+R/8X/JQA7AFEAowCUAIUAbwBCAEoAzf+v/5H/Kf9A/0D/Xf90/5n/vv/q/wcAFgAzABYA+f/U/7b/Xf8x/zH/BP8b/xv/Vv+C/3v/4/8OAB0ASgBKAFEADgAHANv/2//q/83/BwDq/+P/8v8AAAcA+f8AANT/zf+n/6f/xf/U//L/JQAsACwALAAHAB0Azf/N/7b/e/+Z/3v/p/+n/7b/2//5/2cAfgCjALIAqgCyAIwAfgBKAA4A+f/U/+P/6v8HACUAWQCMAJQAsgCqAKMAhQAlAA4A8v+R/6D/oP+n/9v/2/8WAB0AUQBvAGAAZwBCACwADgD5/8X/vv+2/6//1P/b/wAALAAsAEoASgAdAEIAAADq/+r/r//U/77/+f/y/w4AUQAOAEoAQgAlACwADgDy//n/4//b//L/4/8OABYASgA7ACUAQgAOAA4A+f/b/+P/1P/b/+P/2//y/w4ADgAdAB0AOwAdAB0ALADq/+r/2/++/8X/4/8HAA4AJQAdAB0AQgBRAEoAUQA7ACUAOwAlADMAMwBRAJQAlACjAIUAjACFAHYAZwBgAGcAOwBnAEoAYABnAIUAwACUAKoAlAB+AGAAYABCAAAAJQAHAA4AFgD5/x0AFgAWAFEAMwBCACwA+f8HANT/vv+n/6D/p/+g/6//1P/y/wAAOwA7AEoASgBKAGcASgAsACwAFgAHAB0AFgAzAFkAOwBnAH4AZwCMAH4AdgB2AFkAZwBKAB0AAAAHAAcA+f/q/+P/8v/N//n/4//q/wcA8v8lAAcA8v/y/9v/4//q/7b/r/+2/6//zf/F/wcAHQA7AGAAhQB+AGAAdgBgAGcALABCADsAHQBCABYASgBCAFEAZwBRAJQAfgBZAGcASgAWABYA6v/q//n/xf/q/+r/vv/U/+r/+f/5/+r/8v/b/9v/+f/b/+r/+f++/+P/+f/F/+P/2//N/7b/tv+v/6//1P+2/+P/6v8AACUADgAsACUAJQDy/wAA4/+v/8X/kf+K/6D/xf+n/6//+f/y/wcAHQAlAB0AMwAHANT/2/+n/4L/Tv+C/5H/tv8HAOP/FgAdACUAQgAlAB0A+f8dAAcA8v/5/8X/zf+2/6f/vv++/9v/4/8AACwAQgBKAFEAZwAdAB0A+f+v/83/iv/F/6D/iv/U/6f/4/8lADMAWQCjAJQAZwB+ADsAHQDb/6f/mf90/4L/r//N/wAAOwBRAIUAZwBvAEoAFgAAAK//vv+Z/4L/e/97/3v/kf/N/9v/BwA7AFkAYABvAGcAWQAzABYAAAC2/5H/dP+v/77/6v8zAFEAowCMAKoAowB2AIUASgAsADMA+f/b/+r/6v/q/9T/DgAHAPn/FgDq/w4A+f/q/wAA+f8AAPn/FgAWAPL/BwDb/9v/2/+Z/77/mf+C/6//xf8WAEIAYACMAKMAhQCjAIUAbwBnAB0AFgDq/+P/4//j/wcAHQAdAFkAfgB2AKMAfgCFAFEAFgDq/7b/p/9s/4r/Xf9s/6D/oP/F/9T/4/8AAAAA1P/b/6//r/+v/5H/oP+R/5n/p//N/9v/6v8HACUALAAsADsAOwBZAGcAZwCMAJsAbwCUAIUAbwBgAFEAWQAOACwADgAHAA4AAAAWAA4AMwAsACUADgAAANT/vv+n/3v/e/9O/2z/R/84/07/Zf9s/3T/kf+K/6D/e/+K/4L/kf+v/7b/zf/U/9T/tv/5/w4AMwBKAEIAZwAdACUALAAOABYAQgAzACwAMwA7AGcAUQBCACwAFgDj/8X/tv90/2X/R/9A/1b/Tv9s/5n/iv++/77/tv/F/5H/xf+n/3T/tv+R/5n/r/+2/wcADgBKAGAAYACbAG8AjABZAFkAbwAdAEIAMwAzAGcAYAB2AGAAUQBvAGcAWQAzADMAOwAOAB0AAAAOAPn/8v8lAA4A+f/q//n/xf++/6D/gv+Z/6f/vv/j/x0AMwBZAGAAlACFAFEAfgBZAEIAOwAzACwAQgBKAEoAdgCbAMAAzwDtAM8A1wCqAJsAdgAsACUA6v/q/8X/zf/y/+P/2/8OACUAFgBKAB0AFgD5/8X/vv+R/4r/e/97/5H/kf97/6//xf/j//n/DgBCADMASgBRAGAASgAlABYADgAlAB0AFgAdACwAOwBRAFkAdgBvAG8AdgBKAGcAOwAzAEIABwDy/9v/2/+n/6D/xf+v/9T/2//q/w4ABwAlAEoAOwAsAAcAxf/N/7b/iv+g/6D/vv/N/wAAHQAzAHYAdgCqAKoAqgCMAFkAMwAOAAAA4/8AAOr/BwAOADMAQgAlAHYAYABvAGAAQgAWAOP/xf++/8X/kf+2/6f/p/+v/6D/vv+v/83/xf+v/+r/+f/b/yUABwAOADMA4/8HAAAABwDy//L/AADb/wcALAA7AEoAbwBnAG8AbwBKADsADgDy/77/Zf9O/07/E/8b/0f/Vv84/2X/mf+n/8X/oP+n/2X/QP8i/+f+5/7J/tj+5/4T/yn/Tv+Z//L/AAAsAHYAOwBnAFkAMwAsAAcA8v/b/9v/1P8OAB0AMwBnAGcAhQCMAIwAZwBgADMA4//j/7b/kf97/0f/Zf9d/2X/mf+C/7b/p//U/9v/tv/N/5n/vv+C/2X/dP8p/0f/OP9d/4L/oP/5/wcAUQBvAHYAlABvAH4AZwBCAEoADgD5/w4A+f8HAAAAFgA7ADsASgAzAEIAJQAdAAcAxf/F/4r/oP+Z/5H/p/++/9T/vv/N/7b/1P++/83/6v/N/83/p//q/+r/4/8dAAcAFgAdAAAAFgAdABYAMwAsAGAAUQBgAIUAYAB+AGAAYABgAEIAOwAsADsAJQAlADMAMwBKADsAQgAsABYADgAAAAcA1P/5/+P/p//U/77/tv/F/+r/zf/b/wAA4/8HAAcALAAsAA4AFgAOAA4ABwD5/wAA4//y/w4ABwAsAB0AJQAlACwALAAOABYA8v8dAB0AHQAWANv/4//b//n/1P/j/w4A+f/5/x0AJQAWADMAFgAAAOr/tv+C/3T/gv84/0f/Zf9d/5H/mf/j//L/6v8AACUAOwAAABYA+f/b/8X/xf/y/83/AAAdAFEAjACMALIAsgCjAM8AsgB2AIwAWQBCADMAJQAHAPL/LAAWAEoAMwBnAIUAYACUAFkAbwBKACwABwDU/+r/p/+n/8X/4//U/wcAHQAHAEIAMwBZAGcAMwA7ACUAFgAOAOP/DgAAAA4AOwA7AGcAfgCbAIUAowCjAIwAqgBZAEIAUQAOAA4A+f/U//n/1P8AAA4A8v8sACUAHQAAAA4A2//F/8X/iv+n/3v/kf+K/4L/kf+R/8X/p//N//n/AADq/wAADgDj/wcADgAHAAcADgAAACUAFgD5/yUAHQA7AGAAmwCbAIUAqgCFAKMAjABRADsADgAAANv/tv+n/6//1P/q/x0ASgBvAIUAYABvADsA+f/y/6f/dP9H/yL/Mf8b/0f/dP+g//L/+f87AGcAOwBCAB0A4/++/6f/Zf9A/2X/dP+n/+r/LABKAGcAfgCMAKMASgBCAB0Azf/F/8X/vv/b/x0ALABKAFkAbwBZADsALAAOAPL/vv/b/6f/tv/U/83/8v/b//L/AAAHAOr/2/+g/4r/Vv8x/2X/R/9l/3v/p/+n/6f/vv/N/+r/vv/j/6//iv+R/3v/gv97/4r/oP+2//L/AAAlACUAAAAlABYADgD5//n/8v/y/wcA+f8WAAcAJQD5/w4A+f/N//L/r//U/83/1P/F/+P/+f8AACwA8v8lAA4AFgDb/9T/zf+R/5n/bP+Z/4r/1P8AACUAOwBCAG8AUQBvADMAOwAAAM3/4/++/7b/2/8HAPL/HQAdADsALABKAG8AbwCqAG8AfgBRAB0ABwAAAAcAxf/N/77/6v/j/9v/BwAHAEIAYAB2AH4AfgCbAG8AUQAsAAcA8v/F/8X/r//U//n/JQBvAIUAwADPAM8A3gDAAJQAdgA7APn/8v/q/9T/xf/U/+P/+f8WADsAWQBnAG8AZwBnADsADgAAAOP/p/+Z/3T/Tv97/4r/mf/F/xYAAAAWADsADgAdAA4ABwAWAA4A6v/q//L/2//y/+P/6v8lADsADgBCADsAMwBKAFEAbwA7AEoAJQAOAPn/2//y/83/4//U/+r/8v/b//n/8v8AACUAFgDq/xYA+f/b//n/4//y/wAAAADq/wAA+f8AACUALABRACUAQgAsABYAOwAdAHYAZwBRAJsAjACFAJsAowCUAIUAhQCMAFkAYABgACwAMwAsAEIASgBCADMALAAWAA4ADgDj/wAA1P+g/6D/bP9s/4r/mf+v/77/2/8HAPn/HQAlAAAAFgDF/6f/mf9l/2z/mf+g/9T/BwAWAFEAWQBnAG8AhQBCADMAMwDq/xYA4//y/wcA2/8OAB0AFgAlAEIAAAAAANv/vv+2/5H/kf9O/2X/Zf9W/2X/bP+Z/6D/tv+g/6D/mf+n/6//mf++/83/2//q/wcAFgA7AFEAjACbAHYAhQBZAH4AZwCbAMAAbwCqAJQAjAB2AFEAbwBCADMAUQAlABYAMwD5/wAABwDy/w4A8v/b/9v/1P/F/7b/r/+v/6//zf/b/+r/8v/y//L/4//b/8X/vv+v/6f/oP++/wAADgBRAHYAbwCMALIAowB+AEIALADy/8X/r/+g/8X/oP/F/+r/4/8dADMAQgAsADMAHQDU/8X/e/9d/2X/G/84/zj/bP+g/6//HQAAAEIASgAWADsA2//j/7b/gv+C/4r/oP/F//n/FgAsACUAYABCADsAUQAWAA4A+f/q/9v/+f8AAPn/zf/F/9T/vv+2/5n/p/+g/4L/gv+K/3v/dP97/3T/mf+Z/6f/p/+n/5n/kf+Z/4L/iv+R/13/gv+g/5n/4//j/+P/BwAsADsAMwBKAFEAMwAsACwABwAAAOP/6v/b/8X/AADN//n/FgDU/+r/2//N/8X/xf+v/5H/iv+C/3T/iv97/2z/bP97/4L/gv+R/4r/vv+2/83/6v/N/+P/+f8WAAcADgAdAAcADgAsAB0AOwBKAEoAhQBnAG8AZwBvAGAAdgB+AFkAfgBRAEoALAAHAPL/zf+n/4r/kf+C/6D/p//j/9T/2//5/+P/xf+K/77/kf9l/3T/e/9s/3T/r/+v/9v/AAAdAEIAfgBnAG8AfgAsADMAJQAHAB0AMwA7AGcAdgCUAJQAhQCMAGAASgBKAPn/vv/N/5n/tv/b/83/+f8OAAAADgAlAPn/BwDj/83/oP+Z/8X/kf+2/6D/1P/q/wcASgBCAIUAdgCUAHYAZwBRACUAMwAlACUALABKACwAQgA7ACwAZwBgAIwAmwCFAJsAhQBRAEoAHQAHAOr/zf/U/83/zf++/9v/vv/F/wAA+f8OAAAAJQAsAAcADgAdAPL/4//5/+P/FgAdACwAYABZAHYAmwDAALkAqgCqAJQAmwBnAGcAYABCAEoALABRAEoAOwA7ADsAUQBKAEIAMwA7AAAA8v/U/6D/xf++/7b/zf+2/77/1P+2/9T/4//j//L/BwAWAPn/BwAAAAcAAAAdACUADgAdADMAQgAdAG8AUQAlAFEALABZADsAOwBRADsAJQAdAB0A+f8WAAcA6v/q/9v/6v++/8X/4//F/77/1P/j/6//mf+Z/3v/gv+C/83/vv/F/wAA4/8WACUADgAzACwAHQAlABYAOwA7ACwAjACMAIUAqgCbAIwAYABZAFkAQgBKAEIAOwA7AEoAOwAsACwALAAzACwAJQAlAAcA8v/q/6//mf+n/6f/vv/U//L/6v/5/wcABwAsAB0AOwAWADsAMwAHADMAFgAzADMAZwCFAIwAwAC5AO0AzwDeAMgAqgDAAIUAbwB+AGAAYAB+AHYAbwB+AHYAfgBvACwA+f/j/8X/r/+K/4L/mf+Z/4r/tv/F/83/1P/F//n/6v/y/9T/r//F/77/1P/b/+P/1P/j/+P/AAAAAA4AQgAWAEIAUQA7AEIAOwBKACwAFgAHAPL/4//q//L/BwAHACUAJQAlACUAHQAdAA4AFgAOAOP/vv+n/2z/dP90/1b/dP9l/6f/r/++/9T/xf8AAOr/+f/5/+r/2//F/8X/tv+v/6D/kf+n/7b/tv/U/83/AAAdAAcAFgDq/+r/+f8HAOP/1P/U/6//2/+n/5H/p/90/6D/tv+R/8X/6v/y/w4AFgAAAPn/6v/U/9T/tv+Z/6//dP+K/6D/gv/F/83/+f8HAAcABwAOAPn/vv+2/4L/e/90/4r/p/+n/9v/vv/b/9v/zf/5/wAAOwBKACwAQgBRAEoAQgBRADsAHQAOAPn/JQAHAB0ASgAzAGAAUQCMAJQAjACbAIwAjAAzADsADgDb/77/mf+Z/6f/zf/j/xYADgAzADsAJQAsAOr/4/+n/3T/e/9W/3T/oP+g/83/6v8sAFEAWQCMAHYAdgBRAFEALAAlAB0A8v8lAB0ASgBgAEIAdgBnADsAUQA7ACUADgDq//L/mf+Z/3v/Tv9W/07/Xf9l/2z/R/9l/zj/Mf8p/yn/QP84/2z/dP+n/6//zf++/9T/2//U//n/2//5//n/DgAHAEoAZwCMAMAAsgDeALIA5QCjAIwAhQBZAEoABwAsABYAUQA7AFkAhQBRAGcAUQBCAAcA+f++/6D/dP9A/07/QP84/zj/Vv9d/5H/iv+2/6D/iv/N/6D/tv/F/9v/4/8OABYALAA7ADsAZwBgAJsAsgC5AJQAowCFAGAAlABnAJQAYAAzAEoADgAlABYA+f/5/+r/zf++/8X/tv/N/83/vv/j/83/zf/j/9T/1P+2/77/r/+K/6//r/+v/9v/DgAsAEoAmwCjAIwAuQC5AIwAdgB2AFkAbwBCACUAYABKAH4AlAC5AMAAuQD0AMgA3gDPAH4AOwAOAOr/r/+n/4r/mf+v/8X/6v/q/wAA6v/j//L/zf/q/83/vv+n/5H/xf+v/9T/vv/U/w4AAABKAG8AbwBgAGAAYAA7ACwAQgAzADMAZwBRAGcAhQB2AGcAWQAlAB0ADgDy/w4AAAAWAAcALABZAEoAUQBKAFkAHQDj/8X/mf9A/0D/Vv9H/3v/gv+2/6//4/8lAB0AOwAsAOr/2/+v/1b/Zf9d/2X/gv+v//n/DgBKAJQAuQDAAMgAsgCbAHYASgAdAAAAHQAlAB0ALABRAEIAWQBZAEIAUQAHACUAFgDy/w4Axf+v/6//kf90/5H/oP9d/3v/Zf9O/13/QP9H/13/bP+Z/6//r//F/83/vv/N/8X/tv+2/7b/p//b/+P/6v8WAA4AMwAdAEoASgAsADsA+f8dAAAAAAD5/9T/DgDy//n/DgAWAPL/AAAHAM3/tv+C/3T/Tv8i/zj/G/84/0f/QP9s/13/e/+K/2X/gv+K/3T/mf+K/3T/r/+Z/8X/AAAHADsAJQAlABYAAAAWAPn/AAAWAOr/BwAHAAAAJQAlADsAMwAdAA4AFgD5/8X/zf/N/6D/oP/F/6D/p/+g/6//oP+C/6f/e/+C/4r/bP9l/1b/dP90/4r/vv/N/9T/6v8AAA4ABwAHAA4A+f/5//L/6v/q//L/AAAWAAcAHQAzACUAYABRAH4AhQBnAGcALAAsAPn/6v/y/+r/AADj/9v/2/++/8X/zf+v/77/p/+Z/77/oP+R/6D/mf+g/77/zf/F/+r/6v/j/9T/2//y/8X/+f8WAB0ASgBnAH4AfgDXAMAAhQCjAHYAbwBgAFkAbwBZAGcAYABKAHYAbwBnAG8AYAB2ACUAJQAHANv/zf+n/6D/e/+v/6f/tv/b/9T/+f8HACUABwD5/6//p/+v/5H/zf+2/wAAOwAlAGcAdgBZAFkAWQBKAA4ABwD5/9v/6v/j/xYA8v8WACUAJQCUAG8AowCMAEoAWQAHAOr/vv+2/77/r//j/+r/BwAWADMAWQAlAFkAJQDq/+r/oP/F/7b/xf/U/9T/AAAOADsAOwBRAFkAYABKADsAMwAWABYABwAzACwASgCMAJsAsgCyAMAAjAB+AHYAUQAzACUAJQAHAEIASgBCAFkAQgBnAEoAQgBCAAcALAD5/9v/2/+2/9T/6v8WAB0ALABRAFkAWQBKACwADgDq/9T/tv/N/9v/8v8dACwAWQBKAGcAZwBZAHYASgBRADMAHQAOANT/xf/F/83/xf/5/+r/BwD5/+r/FgAOAAAADgAsAOP/BwDb/6f/1P++//n/1P/q//L/zf8AABYAFgAlAEIAJQBKAFEAQgBCAEoAUQAzAFkALAAlACUA+f8WAAcAJQBCAEoAWQBZAHYAZwBvAH4AdgBvADMALAAOAPL/6v/y//L/8v8HAAAAOwA7ADMAUQBnAGAAMwAlAPn/+f8AAPn/+f/y/9v/4/8OAPL/FgAdAB0AWQBRAEIAUQBKADMAOwAsAB0AAADy/+r/6v/5//L/AAAAABYAFgAdACwAAAAlAB0A8v/b/+P/zf+g/8X/oP+g/6//iv++/9T/8v8OABYALAAdAAcAAADy/77/zf/b/8X/+f/j//L/BwDU/wcA8v/j/yUA6v8OAOr/xf8AANv/BwAWADMAOwBKAFkAMwA7AB0ADgD5/+r/AADq/+r/BwAWAAcAMwAsAA4ADgAAAAAA1P/F/6f/kf+g/5H/p//F/9v/AAAlAEoAQgAzABYA+f/N/6//mf90/5H/dP+v/9v/2/8OAAAALAAzADMAMwAHAA4A4//U/83/kf+K/6D/r//N/9T/2//y//L/2//q/+r/4//b/8X/1P+n/6D/oP+R/6f/r/+2/83/zf++//L/zf/N//L/xf/b/6f/vv/N/8X/8v/5/wAA+f8lAAAAAAAHAOP/6v/j/wAA6v/5/xYADgAWAAAADgAOAAcABwAdAA4A6v8HANv/1P/b/9T/4//N/+P/1P++/83/r//N/9T/1P8AAPL/zf/U/+r/1P/U//L/2//5/9v/zf/y/9T/2//N/9T/vv/F/83/r//F/9v/2//j//L/1P/j/77/zf/N/5n/4//U/9v/zf/N/83/kf+n/6f/oP+n/6D/mf++/6//p/+n/5H/r/+Z/6f/kf+2/8X/oP/j/77/zf/U/83/2//N//L/2//q//n/HQBZAEIAfgB+AIwAmwCUAMAAjAB+AJsAhQB2AIUAfgCMALkAwADlAN4A3gDXAKMAlAB+AFEASgAzAB0AFgDy/w4AFgAHACUAJQAzAB0AFgAHAPL/AADy/9v/1P++/9T/8v/y/xYAFgAdAEIAQgBnAFkAMwBCADMALABRAEIAbwB+AHYAjABZAGAAUQAzABYALAAOAPL/HQDF/9T/8v+2/9v/zf/U/9v/xf+v/5n/mf+C/4L/iv+C/3v/e/+n/8X/zf/j/83/tv/F/77/1P/N/9v/6v/q/wcA4/8WAB0AAABZADsASgBnAFEAWQBZACwAHQAlABYAJQAlADMASgBKAEoASgBKAEoALAAHAAcA1P+2/6f/tv++/8X/AADq/wAA6v/5/w4Avv/F/77/vv+v/6f/1P++//L/DgAOADsAUQBvAJQAsgCUAH4AZwAlAAAADgDq/9v/FgDy/ywAQgBKAJQAUQBnAFEADgAAAOr/1P/F/9T/xf/N/83/1P/b/wAAAAD5/x0AJQAOAOr/AAD5//L/4//j//n/1P8WADMAQgBnAFkAfgB+AFkAWQA7AEoAQgAsAEoAOwA7AFEAYAB2AHYAZwBvAG8AWQBnADMAFgAlAOr/DgDj/9T/HQDq/xYADgAWACwADgBgAEoAQgAsADsALADb//L/r/+g/4r/bP+g/6//2//y/xYAJQAdADMAQgDy//n/4/+v/83/mf+n/6//xf/b/9v/+f/5/x0AJQAlAEIAUQBKAEIAFgAHAPL/xf/F/83/2//b//L/+f8OABYAHQAlAOr/AADN/83/zf+2/9v/vv/y/+r/8v8AAPL/FgDq//L/AADy//n/4//U/+P/2//U/+r/BwAOABYALAAdAOP/tv+v/6//gv+K/6f/mf/U/+r/+f87AEIAYAB2AG8AOwAHANv/mf+Z/3v/bP+C/4L/r//q/wAAFgA7AFEASgAlAPn/2/+v/5n/Zf9A/2z/bP+C/6f/zf/y/wcALAAzADsAMwAOAAcAFgC+/77/2/++//L/4/8HAAcABwAWAAAAFgDq//L/AAAHAPL/zf/y/83/xf/j/+r/8v/b/+r/6v/F/6//zf+n/5H/p/++/83/1P8WACUAHQAsAB0ALAAlAB0AAADb/8X/r/+2/+P/AAAAACwAQgBvAIwAlACqAMAAfgBZAEoA4/8OANv/2//5/9T/BwD5/zsAJQAzAGAAUQBgACwAQgAdAOr/2/+2/6f/mf+K/4r/zf+g/7b/zf++/+P/4/8OAAAADgAWAPL/BwD5/9v/8v/5//L/AAAAAA4A6v8HACUA6v8OAAcADgD5//L/OwAWACUAMwAWAAcA6v/b/8X/xf++/83/xf+g/6D/kf+n/83/vv/N/83/zf+n/6D/p/9s/3T/e/9s/07/Zf9s/2z/kf+Z/9v/AAAAACwAMwAsACUABwAHAAcA4//5/+r/AAAWACwAWQBZAIwAhQB2AH4AhQB2AGcASgAsACUA2//y/9T/vv++/6f/zf+n/83/xf/q/+r/zf/j/77/tv/F/7b/oP+g/5H/p/+v/6//2//F/wcADgAHABYAHQAzAB0AOwAdACwASgBRAHYAYACFAFkAYACFAEoAdgB2AHYASgBgAG8ASgCFAGcAhQB+AEoAbwAzAA4A8v/y/+P/xf/q/7b/zf/y/+P/BwAzAFEAMwA7ACwABwAAAOr/1P/j/wcABwAsAGAAdgCUALkAuQDAAKMAmwCyAEIAUQBRAEIAdgBKAH4AfgB+AHYAdgCFAFEAZwAzACUAHQDy/wAAAAAdACwAMwBCAEoADgDy/w4A4//N/6//iv+C/2z/mf/F/+r/8v8WAEoAUQBKAFkASgAlADMAAADj//n/1P/y/x0AMwBCAGcAZwB2AIwAdgB2AEIALAAlAAAA+f8dABYALABgAEIAYABKAFkAUQAOAA4Axf/j/9v/oP/U/+r/2//U//n/AADU//L/4//N/7b/mf/F/5H/iv+g/5H/xf/N//n/FgAdABYAQgAlAAAABwC+/wAA6v/q/wcA8v87ACUAQgBKADMAOwAOAA4A1P++/9T/p/+v/77/r//N/8X/xf+2/6//r/+R/3T/Tv9H/07/Vv9H/13/bP+C/6D/p/++/77/1P/U/83/vv/F/9T/1P/y/+r/FgAsADsAUQBKAFkAQgA7ADMAWQBKADsASgA7AFEALAA7AB0ALAAdAOr/8v+n/7b/mf+n/6//iv/5/wAAAAAdACUAFgAAAAAA4//b/9T/tv+n/6f/tv/U//L/FgAzAGcAlACFAKMAdgBRAGcAHQDb/+r/1P++/77/xf/y/83/8v8zAPn/DgAHAPL/8v/F/83/mf9l/0f/R/9O/0f/dP97/4r/kf+n/77/r/+2/83/2//U//L/+f/5//n/BwAWAAAAJQAHAAcADgAWADMAFgAzACwAWQB2AH4AlAB2AH4AZwBnAFkAWQBRAB0AHQAOAAAABwAAAAcAAAAAAB0ALABRAFEALAAzADMADgAOAAAAxf/N/8X/1P/b/9T/+f8HABYAQgBvAH4AlACMAIwAdgBCAEIAHQAAAPL/8v8OAB0AMwBgAIwAlACjAIwAfgBnABYADgDF/6f/vv+C/6f/kf+v/+r/xf8OAAcA6v/q/8X/r/+n/3T/gv+n/1b/gv+R/6f/6v/U/xYABwD5//L/2//F/6D/iv+Z/7b/r//j/+r/AAAsAEIAYAA7AFEAWQAdAAcA8v+2/8X/tv/F//L/6v9KAEoAUQBvAEoAUQAzADMAAADN/8X/mf+Z/5H/kf+v/6D/zf/U/83/zf/U/wAA1P/j/77/tv/F/5H/tv+n/7b/1P/b/+r/6v/q/9T/AAAlAB0AOwBKAEoAbwBgAH4AjABvAIwAdgBnAFEAUQA7AEIAOwAlADsAJQBCADMAZwBRAG8AjABCAGAAMwAzAB0ABwAAAAAADgDy/x0A+f8dABYAHQAdAAAALAAHADMAJQAWAEIAOwAlACUAHQAWACwAAADy//n/+f8zACwAJQBgAFkAfgBnAGcAlAA7AFkAFgAOAAAA1P8OAOr/DgDy/yUAFgAHADsABwBKAAcADgAHAMX/zf+R/5H/e/90/6D/mf+Z/83/p//j/9T/p//q/6f/1P+2/5n/vv+v/83/1P8OAPn/DgAOAAAAMwAOAB0ALAAWACwAHQAdAB0AAAAOAAAA+f8dAAcAJQAsACwAFgD5/+r/1P++/6f/1P+2/77/4//q/9v/4/8AAOr/6v/j/+r/zf/U/9v/zf/q/+P/AAAHACUASgBCAHYAbwB2AJQAWQBgAGAASgAlAB0AZwBCAEoAbwA7AGAAZwBgAFEAMwAdACUA+f/b/9T/r/+2/5H/tv+n/6D/xf+v/9T/vv+2/6//r/+Z/6D/iv9l/3v/gv+K/3T/r/+R/4L/tv+Z/77/vv/b/wcAAAAHAA4AFgAHAA4A8v/q/wAA4//j/w4ADgAlACwAMwAlAAcAHQDy/wcA+f/U//L/tv+Z/3v/Vv9d/0D/QP9s/13/dP+R/3v/kf9s/4r/e/9l/6D/dP+n/83/2//j/+P/AAD5/xYAAAAlAB0ADgAzAB0ASgA7AFkAYABnAIUAZwBvAHYAWQAsAB0A4//F/6f/tv+g/5n/vv+g/9v/xf/F/+r/2/+2/5n/oP9W/1b/Tv9d/2X/gv/F/77/DgAlADsAYABKAEIAOwAOAA4ALAAWADsAYABKAG8AdgBgAJsAlAB+AJQAfgB2AGAAWQAsADMAUQAlAEIAMwAdAFkABwAWACwAxf/q/+P/zf/j/8X/1P/b/83/8v/5//L/FgD5/xYAFgD5/wcA+f8AAPL/8v/5/w4AFgAzAEIAYAB+ADsASgBKACwAHQAWABYA8v/j/wAADgAAACwAHQAHAA4A+f8AANv/zf/F/5H/kf90/2z/iv9s/4L/e/90/5H/mf+v/6D/mf+K/3v/bP+C/3T/e/+n/77/8v8HAEIALABCAEIAOwBZACwAUQAsADsAZwBZAGAAjACUAJsAqgCMAIUAZwBvADsAJQDy/8X/1P+2//L/4//j/+r/4//b//n/DgAAAPL/2//N/5n/zf+Z/5n/zf+n/+r/6v8OADsAZwBnAHYAjAB2AH4AjACMAJQAsgCyAMAAsgCjALkAsgCyAMgAowCqAKMAfgDAAHYAhQBvAG8AmwBCAG8AMwAlAAAAAAD5/6//+f+2/9T/2/++/+r/4/8HAB0AJQAWABYAFgAOAPL/4//y/9T/8v/5//L/MwAsAFkAWQBZAG8AMwBZACUAHQDy/9T/4/+2/9T/oP++/5n/r//F/5n/xf+g/9v/tv+g/6D/e/+C/3v/iv97/4L/Zf+C/3T/dP+R/5H/p/+2/9v/2/8HAPL/AAAsAA4AJQAlABYA+f8HAA4AHQA7AFEAZwBnAIUAdgCFAG8AUQAzADMAJQDq/wAA1P/q/+r/zf/y//L/FgDq/w4A+f/U/xYA6v/y/8X/tv++/77/4//b/wAA4//5/x0ALAAsACUASgAdACUALAAOACUADgD5/wAADgAOACwAJQBCAEIAHQA7ABYAAADy/+r/4//N/83/tv/N/6//vv+v/5H/xf+g/8X/tv+R/5n/iv+R/4r/dP97/6f/kf+v/77/xf/U/+P/6v8HAB0Azf/y/9v/6v/5/9T/FgDy/wcABwAWABYAJQA7AB0AFgAHAA4A6v8OAPn/BwDj/+r/+f/U/zsA6v9KAGcAQgCUAG8AjABgAEoALAAdACUALAAlACwAUQBKAGAAZwCFAGcAhQCFAHYAhQBnAHYAMwAlACUABwAWAB0AFgAzADsAMwBKAFEAYAAsAB0ADgDU/77/p/++/6//vv/U/+P/AAD5/zMAHQAOAA4A+f8AAOr/DgAAAB0AMwBCAHYASgCFAGAAbwB2AFkAhQAzAFkAFgAlABYA+f8dAOP/HQAAACwAFgDy/xYA+f/q/83/r/+Z/7b/bP+K/5n/iv+2/6D/xf+v/6f/xf/U/7b/xf/U/7b/4//N/8X/zf++//n/JQAdADMAJQAzAB0A8v8OAPn/+f/q/w4AAAD5/x0A+f8AAAAA8v/y/9v/p/+v/4r/Vv9s/zj/Tv+C/3v/kf+R/6D/mf+R/77/p/+C/4r/bP9l/4L/iv+v/83/8v8sACUAUQB2AGAAWQBnAHYASgBZAEIALABCAEIAWQBvAH4AhQCUAHYAhQBZAGAAQgAdACwAvv/q/9T/tv/F/+P/6v/q/ywA6v8OAAAA+f/j/83/2/+K/6//mf+n/7b/xf/y/wAAHQA7AFEAQgBgAFEAYABRAFkAbwBgAG8AbwBnAFEAdgBvAJsAlAB2AJQAYAB2AFkAOwAzADsAMwAlACwABwAdABYA+f8HAAAA4//q//L/zf/j/+P/4//y//L/+f/j//n/4//j//n/zf/y/wcADgAdAA4AQgA7AEIAbwBKAFEASgBKAEIALABCAB0AMwAlACUASgAsAFEAWQBvAFkAOwBgACUABwDj/wAAzf+n//L/oP+v/9v/xf/q/9v/vv++/83/2//b/83/xf++/6//xf+n/77/4//U//n/AAD5/+r/AAAHAPL/8v8OAA4A+f8zAB0AUQBgADsAbwBCAFEAMwAlADMADgAHAA4ABwD5/xYADgAHAAAAJQAzABYAQgBCADsAJQD5/+P/tv+g/7b/p/+R/7b/vv+2/77/2/8AAAcALAAzABYABwDq/7b/tv+2/6//xf++/9T/4//y/w4AAAAAAAcADgAHAAcAFgDq/9v/1P+2/6//oP+K/3v/dP97/4r/p//b/9v/BwAOANv/tv+n/2z/e/97/0f/dP84/13/dP90/6f/mf/F/77/1P++/77/tv+n/77/oP+2/6D/oP+2/83/xf/N/+r/8v/5/+P/DgDj//L/+f/q//L/8v8WAB0AUQAzAFkAUQBRAGcAMwBCAA4ALAAWAA4AQgA7AEIAYABgAEIAUQBKAGcAWQBKADMALAAOAPn/AADU//n/2//y/9v/xf/j/77/6v/j/+r/4//q/9v/zf/q/9T/4//N/9v/xf/F/6//p//F/7b/2//U//n/6v/b//L/1P/q/+P/4//U/83/vv/N/8X/1P8HAPL/+f8AAAAAFgAHAAAAAAD5/wcABwDy//L/4//q/w4ABwAAABYA+f8OAA4A4/8OAAAABwAlAAAADgAdABYADgAHAB0AHQDy/+r/4//F/77/vv/F/6f/vv8AABYADgAdADsASgBKAEoAOwDy/+r/r/+C/4r/bP+Z/6//6v8AAAcAQgBZADsASgBKAPn/6v+2/77/r/9s/3v/gv+K/7b/4//b/ywASgBRAIUAUQBZADsAJQAWAOr/4//F/+P/AAAWADsAYABZAHYAlABnAHYAUQA7AB0AAAAWAOP/BwD5/wcAHQAHAEoADgAsABYA4/8AAMX/4//b/7b/6v/y/wAAMwBCAGcAUQBCAGcAOwBCADMAJQAAAOr/DgAAAEoAWQCjAKoAqgDlALIAuQB2AFkAOwAHAAcA4//q/wcABwAsAFEASgBnAGcAQgA7ADMABwDj//L/tv+v/7b/kf+v/9T/6v8AACwAFgAzAEIAHQAlAAcABwDU/83/+f/j//n/FgA7ACwAWQB+AHYAlAB+AIUAfgBgAEoAOwAWAAcAHQAdADMAHQBRAGAAQgBgAFkAYAAsACUAFgDj//n/4//N/+P/zf/F/83/vv/U/+r/AAAOAEIAQgAsAFEAFgAdACwAAAAHAPL/AAAlACUASgBRAGAAWQBRAGcAUQBgAEoAWQBKAB0AFgAWACwA8v8WAA4Azf/y//n/8v8WAA4A+f8lAPn/4//y/+P/1P/F/83/zf/F/83/8v/U/+r/4//j//n/BwAzACUAYAAsACUAMwAWAEIALABKABYAMwBKADMAYABCADsAOwA7ADMASgBKAFEASgA7ACwAAAAAAPL/2//F/9T/r/+Z/9T/r/+n/7b/r/+n/77/vv+Z/7b/r/+Z/6D/iv97/3T/Zf97/2z/dP+K/5H/r//b/9T/vv++/8X/vv+Z/6f/r/+n/7b/1P/U/83/6v++/+P/FgAAAAcABwAOAOr/DgAHAPL/AADq/+P/zf+v/6//oP+R/6//r/++/9v/+f8AAOr/BwDq/wAA+f/y//n/tv/F/6f/oP+g/6f/zf+2/9v/8v8AAB0ABwAAAAAAAADy/8X/r/+n/4L/p/+2/83/8v8AAAcAFgAlAPL/FgAWAOr/8v/j/9T/xf/F/77/2//q/wAAFgAAACUALAAlACUAHQAdAAAAzf/U/9v/tv/U/6//tv/N/+r/JQAOAAcADgAAAMX/xf+R/0f/e/9s/3T/gv+R/77/tv++/9v/4//U//L/8v8HAPL/DgA7AB0ALAAWADsAFgAWADMAHQBRAEoAhQBnAGAAYAA7AEIAFgAdAAAABwAHAA4ADgAWACwAAAAOAAAA+f/b/8X/vv/N/9v/p//U/7b/vv/j/+r/+f8AAAAA+f/5/9v/8v/F/77/2//b/+r/8v8lAA4ALABZAGAAUQBCAEoAOwA7ACUABwAHAPn/LAAzAB0ASgAzACUAJQAdAFEAOwAsADMAHQDy//L/4//b/wcA4//y/yUABwAWAB0AFgAlAAcALAAlAPL/FgAHAAcAAAAOAPn/+f8AANv/BwDN/83/6v/y/+P/6v8lAAcAUQBKAEIAQgAdACUABwAOAAcAAADj/+P/BwAAADMAMwA7AGcAUQBnAGcAMwBCACUAMwAzAAAA+f/y/wAA4/8HAB0ABwAHAAcADgAHAAAA8v/y/83/4//y/8X/BwDy/xYAJQAAACUA4/8AAAAA2//b//n/4//q/0IADgA7AEoASgBCAEIASgAWAEoAJQAsAPL/6v/q/9T/JQAOAEoAWQBgAGAAQgBRAEIAOwAdAAcA1P/j/9T/4/8OABYAJQAzAGAAWQBKAEoAQgAdACUAHQDy/wAA4//b/+r/6v8HAA4AHQBCAEoASgA7AEIALAAWACwAFgAlAB0AJQAzAEoAOwBKAEoALABKACUAQgAlADsALAAlAEIAFgAlAAAAMwAOACUASgAdAEIASgAlAPn/HQDq/w4AAADq//n/+f8dAAAAOwAHADMAFgAAAAcAzf/b/6//1P+2/83/4//5/wAA6v8OAOP/+f/y//L/8v/5/w4AFgDy/wcAFgDN/wAA6v8HAPL/DgAlAA4AOwD5/x0ABwDy/wcA8v/5/wAAAAAAACUADgAzAEIALAAdAA4AJQAWAOr/+f8AAM3/8v/j/83/2//j//L/8v8WABYABwAWAPL/1P/j/7b/r/+v/6f/oP+Z/83/tv/b/+r/AAAsAA4A8v8AAAcA1P/q/8X/mf+R/5n/p/+Z/9T/6v8HACUAUQBCAFkAWQAlADMA8v/j/83/4//y/+P/DgAWACUAHQA7ADsASgBnAEoAWQA7ABYA8v/q/77/vv/F/8X/vv/F/+r/6v8OAA4AFgAsAA4A+f/N/83/p/+2/6f/gv+Z/5H/p//N/9v/AAAWAPn/MwAzAPn/LAAOACUADgAAAAcA4//5/wAALAAsADMAZwBgAEoAWQA7AA4ADgDy/9T/xf/N/83/xf/F/83/+f/b/83/4//N/6//p/++/6f/e/+Z/6//oP+2/6//r/+v/6f/r/+v/77/vv+v/6//tv+n/77/2//j/+P/1P8HAA4AAAAlACUAHQAlAAcAAADq/9T/xf++/+P/r//b/+r/tv8AAMX/xf/b/77/xf+n/77/oP+C/5H/iv+R/6//oP++/8X/r//U/7b/zf/b/+P/8v/j//n/6v8AAAcABwAAAA4AJQAlAEIAHQA7ADMAFgAdAA4AJQAdACwAMwA7ACUAOwAdAPL/AADy/w4A4/8HAPL/1P8HANv/8v/q//n/6v/y//L/8v8WANT/8v/q//n/4/++/+r/xf/j/w4AHQAzAFEAWQBRAEoASgBKACwAOwBRADsAUQBZADsAbwBnAFkAsgCMAKMAwAB2AJsAYABZAEIADgAsAOr/BwAdABYAQgA7AEIAdgCFAFkAZwA7ACwAAADy/wAA4/8WAOr/DgAzAB0AUQBCAFkAUQBRADMAHQAAAOr/8v/N//L/6v8dACUAJQBZADMAdgBvAHYAhQBgAHYAQgBKACwAAAAdAAcAHQAlABYAHQAzADMALABnAFEAWQBZAB0AHQAAAAAA8v/b/9v/xf/b/83/zf/q//n/8v8HAA4ABwAWAA4ABwAHAA4A+f/y/wAAAAAOAAAADgAlACwASgA7AEoAUQBCAGAAMwA7AFEADgAdAPn/AAAsAAAALAAlAAcAFgDq/wAABwD5/wcA+f/q//L/1P/N//L/vv+v/9T/vv/U/+r/6v/j/wAAHQA7AEoAMwBnADMALABZACUAMwBCACUAQgAzAB0AWQBCAEIAbwCFAGcAYABgACwAOwAdAAcA+f/j/8X/tv/j/6f/vv/y/9v/8v/y/wAA8v/U/83/xf+Z/4r/e/9s/07/QP9l/13/kf+n/7b/1P/N//L/6v/b//L/4//q/9T/vv/F/6//4//j/+P/BwAHAPn/8v8WAOP/6v/5/83/2//U/83/tv++/6f/p/+R/5H/vv+g/6//p/+n/6f/r/+v/5H/iv97/4L/e/+K/5H/mf+n/5n/r/+n/7b/vv+2/8X/p/+v/77/p//U/+P/8v/5/w4AJQAHAB0AMwA7AB0ADgAOAPn/BwDN/9T/1P+v/83/xf/j/9T/4//j/9T/1P+2//n/tv+v/9T/oP+n/3T/gv+n/83/6v8AAAcAFgAlAA4AHQDy//n/8v/F/83/zf/b//n/FgAsAFEAQgBgAGAASgBZADMAFgD5//L/tv/N/7b/tv/b/9v/AADy/x0AAAAAAPL/xf/F/5n/e/9d/2X/Vv9s/4L/kf/F/+P/AAD5//n/AAAAAOr/AADb/8X/2//N/+P/+f8HABYAOwA7AGcAdgB+AHYAUQBRAAcAFgDy/+r/AADy/wcA+f8WACUAJQD5/yUADgDj/+r/r/+n/6D/p/+g/5H/p/++/77/AADy/9T/FgDq//n/4//j/9v/zf/y/+P/AAAHABYAJQBZAEoAZwB+AGAAfgBZAGcAUQBZAEIAOwA7AA4ASgBKAEoASgBKAGAAZwBRAFkAQgAHACUA2/+2/7b/kf+Z/6D/vv/N/9T/+f8WANT/FgAAAOr/FgDN/9v/vv/F/6D/p/+n/5H/8v/y/zsAMwBRAJQAYACMAG8AUQBvAFEAWQBRACwAQgBKAFEAYABZAGcAZwCFAH4AhQCbAIwAjABvAHYAWQBZAEIALAA7APL/JQAWAB0ALAAWACwADgAsAB0AAAAdAA4A+f8AAAAA+f8AAOr/DgAAAPL/AAAHABYAHQAlADsASgAWAEoAQgAWAEIAOwBgADsAYACFAH4AdgBvAG8ALABRADMAJQAzACUAMwAlADsAUQBnAFEAMwAsACUAFgAdABYA4//q/83/vv/j/83/8v8OAOr/DgAlAA4ADgAdAB0A+f8HAAcA+f/5/xYAMwBCAGcAZwCMAIUAhQCjAJQAlAB+AG8ASgAdAEoAOwAsAFkASgBnAHYAfgCFAHYAdgBRAEoAHQAlAB0ADgAOAPL/DgD5/x0AHQAdACwAFgAlAB0AJQDN//n/8v++/9T/vv/y/+r/+f8OABYALAAlACUAFgAAABYADgDb/9v/1P/N/9v/4//U/+r/8v/q//L/4//q/9v/2/++/77/vv+Z/6//r/+2/6//kf+g/6//iv+Z/77/kf+2/6//kf+2/6//xf/U/77/tv/F/9T/zf/N/+P/zf/q/wcA8v8OAB0A+f8AAA4ADgAHAPn/HQDy/+P/8v/q//L/4//q/7b/tv/F/5H/vv+n/4L/oP+R/4r/iv+g/5n/e/+K/4r/kf+g/5n/iv+g/6D/mf++/8X/zf/N//L/8v/q//L/zf/y//n/+f/y/+r/+f/q/wcAFgAWACUAJQDy//L/6v/N/83/vv+2/5H/mf+K/3T/iv97/3T/mf+Z/4r/oP+v/6//mf+n/5H/e/+g/4L/mf+K/3v/xf++/9T/8v8OAAAA2/8OAPL/BwAlABYAHQAOABYAAAD5/xYAFgAsAEIAUQB2AGAAUQBZAAcAHQAAAPn/DgDq/w4A8v8AAPn/8v/5/+r/DgDb/9T/zf++/9T/oP+v/7b/p//F/6f/xf/U/6f/2/++/83/r/++//L/mf/b/9T/1P/y/wAAFgAOAB0AHQA7AB0ALABKADMAMwA7ABYADgAsAB0ALAAAAB0ALAAdAFkAQgBRADsAJQAlAB0AJQAsACwAHQAzAEIAOwBZAH4AYABgAHYAUQBZAFkASgBZAEoAMwBZAEIAMwA7ADsAUQBCAFkAUQA7AEoALABCADsAFgAWAA4A8v/y//n/AAAAAAAAHQD5/wcAHQAHACwAMwAzABYA8v8HAPn/1P8AAAAA8v8sADMAMwA7ADsASgA7ADMAJQAWAPL/4/8OAAAA8v8AAAAAAAAdACUAHQAWAAAA4//q/+P/4//5/+P/6v/b/9v/+f/y//L/8v8AAOr/4//q/+r/BwAAAPn/DgAdAAcALAAsAPn/JQAHAAAAHQDy/xYADgDj/wcA6v/b//L/AAAOAPn/DgDq/77/zf+v/6D/p/+2/77/vv/U/83/zf/j//L/8v/5/w4A6v/q/wAA2//j/+P/6v/y//L/BwAWAPL/+f8WAPn/DgAWAAAA8v/q//n/BwAAAB0AQgAdAFEAUQAzACwABwAlAPn/AAAAAAAAFgD5/yUAMwAlADsAUQBRAEoAMwAdAA4A6v/j/8X/6v/q//L/LABCAHYAdgCUAIwAbwBnAGAAWQBCADsABwAOABYABwA7ADsAUQB2AGAAfgCMAGcAZwA7ACwAFgDq/+r/6v/y/83/8v/y/9v/DgDy/wcAHQAOAOr/6v/b/6//zf/U/8X/vv/N/9v/zf/b/xYAJQAlAEIAMwAAABYAAADb//n/4//y/wcA+f/5//n/BwAWACwAMwBKACwAJQAOAPn/AADU/+r/tv/U/8X/p/++/6//xf/N/+P/zf/U//L/AADy/wAA+f/F/9T/tv/U/6D/zf/j/6f/2/++//n/+f8AAAAADgAHANv/DgDy/wAAAAAOAB0AAAD5/+r/4//j/9v/xf/j/77/vv/F/9T/AAD5/yUAFgAWACUALAAdAA4ADgAHANv/2//q/83/1P/U/w4A+f8HAB0ADgA7AA4ADgAOAPn/+f/b/7b/zf/N/6//+f/y/w4AQgAlAEoAUQAzACwALAAAAPn/4//F/+P/oP+C/7b/r/+2/9v/4//5//L/AAAOABYAAADy//L/2//q/+r/1P++/+P/zf+v/+r/AAAHACUAFgAWACUABwAzABYA+f8sABYAAADb/w4AAAD5/wAAAAAAAPn/HQAAAB0A+f8OAA4A2/8AAOr/4//b/wcA6v/5/w4ABwAlAPL/DgDy/w4AHQAOACUABwAsACUAMwAzADsAYABCACwASgBKAAcAMwA7ACUADgBKADMABwAzAAcAHQAHABYAMwAdACUAJQBKACwAOwBKAB0ADgD5//n/8v/b//L/+f/j/xYABwAsADMAFgAzAAcASgAdAAAAHQAOAA4ABwAlAB0ALAAWACwAFgAHAB0A+f8lABYABwAOAB0AHQAHAA4A2//5/wAA4//q/+P/zf/U/+P/zf/U/9T/4//y/+P/4//N/+r/AAC2//L/2/+2//L/2//b/+r/2//N/wcAFgAHAB0AHQAdAAcABwAAACUA6v/U/9v/p//F/8X/zf/U/+r/1P/U//n/1P/5/wAAzf/U/9v/1P/b/+P/4//N/8X/p//N/9T/tv/5/9T/xf/j/9T/2//b/9T/4//N/7b/1P+v/9v/8v/b/w4A8v/j//n/+f/y//L/6v/y/8X/6v/y/83/DgDN//n/4//N/wcAxf8OAPn/+f8sAOr/8v8WABYADgDy/xYAJQDq/ywAJQAzACUAFgAsAA4AQgAOAB0AMwAHAB0AFgAWACwASgAdADMAQgAsAEoAOwBCAEoAMwA7AFEAUQBKADMASgAlACUAOwAsACwAFgAzAB0AMwA7ACwAMwBKAGcASgBvAFEAQgA7AA4AJQAdAB0AHQAlAB0AFgAOACUAQgA7AFEAQgBRADMALAAzAB0ALAAlACUABwAlAB0ADgAzACUALABCAEIAJQBCACwABwAdAA4A+f/5/wAADgD5//L/+f8AAAcAAAAOAOr/8v8AAPL/8v/j/wAA4//j//L/6v/q//n/FgD5/wcA6v/U/9v/vv/N/77/xf/b/+P/2//j//L/6v/q//L/2//U/9v/1P++/8X/vv+Z/6//tv+n/7b/zf/U/9T/2//N/+r/6v/U/+P/xf/F/6//p/+2/6D/zf/U/+r/DgDy/yUADgDb//n/1P/y/9v/1P/U/7b/4//b//n/AAAOAA4AHQAlAA4A+f/y//L/vv/j/77/xf/j/7b/6v/b//L/8v/q/x0A8v/q//L/zf/N/77/vv+n/5H/p/+K/7b/vv/F/9v/vv/5/+P/4//5//L/2//b/9v/vv/N/7b/4//U/8X/8v/U/+r/AADq/+r/AADy//L/zf/b/9T/xf8AAMX/8v8AAPL/+f/j/wcA6v8dAB0AAAAAAPL/+f/U//L/4//N/+r/8v8AAOr/8v8HAPn/+f/y/+P/+f/U/9v/4//b/wcA+f/y//n/AAAOAAcAAAAOAPL/DgAOAAAAJQAHAAAABwAOAPn/JQBCACUAYABCAFEAQgAsAEoALABZAFEAUQBgADsAWQBRAEoAYABRAFEASgAsADMAMwAlABYAJQAdABYADgAOACUADgAOACUAHQAOACUAJQAdACwAJQAsAB0ALABCAEIAWQBKAEIAQgAzAEIAOwA7AEoALABCAA4ALAA7AB0AWQAlAEIAQgAOAAcA+f/j/+P/8v/N//L/1P/j//L/6v/5//n/FgDb/wcA8v/N/+r/xf/F/8X/tv/F/+P/xf/5//n/BwAdAPL/FgAHAAAABwAAAAcAAADq/xYADgAAADsADgBCAEoAOwBKABYAJQAOAAAA+f/y/9v/xf/N/+P/1P/U/9v/1P/U/77/4//b/9v/1P/F/9v/r//F/+P/1P/y/w4A4/8OAAAA1P8lAAAADgAOAPn/JQAlAA4AHQAsACUASgAsAFEAWQAsAEoASgAzACwASgAdAB0AMwAOABYAFgAAAB0AMwAHAB0ALAAdAB0ABwD5//L/4//q/+r/2//j/+r/AAD5/xYABwAHAB0ADgAlAA4ADgAHAAcA+f8AAA4ABwAzAAcAMwA7ACUAYABgAEoASgBCADMAUQBnAEoALAA7ADsALABCAFkAYABRAFEAMwBRAEoASgA7ACwAOwD5/w4ABwD5/wAAHQAsAA4ADgD5//n/8v/5/9v/6v/q/7b/1P++/6//zf/b/9v/2//b//L/+f/q/+r/xf/b/8X/oP++/8X/r//b/+P/zf/j//L/+f/y//n/2//q/9T/r/+2/4L/oP+v/6f/tv+n/6D/vv/F/9v/4//b//n/zf/q/8X/vv/b/6D/r/+v/8X/oP++/77/r//U/6D/2//b/77/8v/y/wAABwAAACwABwDy/x0A+f/5/+P/8v8AAPL/HQAOAB0AOwBCAFEAUQA7AEoAUQAsACUAAAAAAA4A+f8HABYAJQAlADsAMwAdABYAFgAOANv/2//F/6f/r/+v/8X/tv/j/9T/2//y/9v/AADF/9v/zf/N//L/xf/U/+P/4//U/9v/zf/q//L/6v8OAOr/+f/5/wAA6v/q/w4A4//q//n/8v/j/9v/1P/j//L/+f/5//n/BwDj/9v/2/++/83/2//b/83/r//N/77/xf/5/9v/2//y/8X/vv/N/8X/1P/F/83/2//b//L/6v8OAAcA8v8WADMAOwA7AFEAQgAsACwAQgAdAB0ASgA7AFEASgBKAEIALAAlACUAHQAOABYABwAHAAcABwAHAA4ALAAzAB0AJQAHAPn/AAAHAB0AAAAdAB0A+f8sAB0AAAAdAB0AJQA7AEIAWQBRAEoAWQBKAEoAZwBgAEoAZwBnAEIAUQBRACwAOwAzACUAHQAOACwALAAlACwAJQAOAAAA8v/j//L/4/+2/7b/vv/F/8X/vv/q/+r/zf/j/9v/2/++/9T/2/++/83/2//5/+P/8v/y//n/FgAOABYAFgAAAA4AHQD5/yUAHQAWACwABwAdAAAAAAAAAAcAJQAdADsAJQAWACwABwD5/wcAFgAWAA4AFgAWAB0ADgAsABYAFgAdAPL/JQAAAB0AJQAlADMAFgBZACUAUQBCADMAQgA7AFEALABKAB0AQgAsAAAAHQAOACUAFgAOAOP/BwDU/9T/8v/F/wAA1P/b/+r/1P/U/7b/xf++/7b/zf/F/7b/vv/F/7b/2//U/83/6v/y//L/6v8OAAcA8v/5/+r/8v/j//n/DgD5/wAAJQAsADsAYAA7AEIAUQBKAEIAOwBCADMAMwA7AEIAHQAOADMAHQAAAA4ADgDy/wcABwDq/wAA4/8AAPn/6v/5/9v/8v/N/9T/4//y/wAA2/8HAOP/+f8HAPL/AAD5/wAA4//y//L/AAAHAAAAQgAAABYAHQD5/yUADgAsAB0AAAAWAPn/+f8AAPn/FgAWAPn/DgAlAPn/DgD5/+r/8v/j/9T/vv/U/9T/6v/j/+r/BwDy/+r/BwAHAOP/8v/b/8X/2/++/9T/4//F//L/DgD5//L/AAAOABYAFgAdABYA6v8AANv/vv/q/83/zf/N//n/AAAWACUALABCAAcAJQAAAOr/xf++/7b/e/++/6f/zf++/9v/4//F//n/+f8HAOr/FgDj/9T/6v++/+r/xf/U/9v/1P/j/9T/6v/U/8X/6v/5/wcA8v8OAB0A2/8lAA4ADgAsAA4ABwDj//L/+f8OAOr/DgAHAPn/LAAAABYABwAOAA4A+f8WAA4ADgD5/8X/zf/b/8X/2//b/+r/2//U/9v/4//y/+r/BwDj/+r/8v/5/wcA8v8HAMX/xf/j/7b/xf/b/8X/2//q/+r/FgAWABYAMwAlACUABwDb/9v/2//b/+r/6v/j/9v/4//5/wAAFgAsADMAHQAWADsADgAWAB0AAAAOAPn/HQD5/wcAJQAHACUAFgAlACUAHQAOAAcABwAHAB0A+f8HAPn/6v/y/+r/DgAHAA4ALAAlAB0AJQAdACwAHQAWACwAFgAdACUAHQAdABYAJQAsAB0ADgAWAPn/2//5/+P/4/8HAPn/6v/5//L/6v8dAAAADgAsAOr/8v/j/+P/1P/b/+P/6v/5/9T/DgAOAPL/BwDy//n/AADy/wcAFgD5/wAAFgAWAA4AAAAAAPn/4/8HAPn/6v/y//L/+f/q/wcA4//b/wAA6v/N//n/6v/j/xYADgAdAB0AMwAOAB0AHQAOAA4ABwAdAAAAJQD5/x0AOwAsAFkASgBnADsAQgBKAFEAOwBKADsADgBCAPn/FgAAAPn/FgDj/wcA4//5//L/4/8HAAAABwD5//L/8v/U/9T/1P/N/9T/zf/b/9v/4//U/9v/+f/q/+r/BwAHAPL/AADN/9T/2//U/+r/1P8AAPL/+f8HAPn/8v/5//n/6v/5/9T/AADy/+P/DgAAAPn/6v8OAPn/+f8dAB0AFgAHACUAAADj/wAA+f/5/wcAFgAWAA4AHQAlAA4ADgAWAA4AJQAOAAcAFgAWADMALAA7ADMAHQAAAPn/AADy/wAA6v/b/9T/4//b//L/HQAHAB0AMwAzADsALAAdACUABwAWACwAFgAzADMASgBvAFEAYABgAEIASgBKAGAAWQA7AFEAJQAzADMADgAsAA4ADgAsACUALABKAEIAUQBgAFEAYABgAEoAUQBKAB0ADgAOAPn/BwAHAA4AJQAWADMAJQAsADsAJQBKAA4AAAAHAOr/4//b//n/2//U/+P/6v/5/9v/4//j/9T/2/++/8X/vv+n/9T/oP+v/6//r//U/6f/tv++/8X/oP/N/7b/r//b/8X/4//F/+P/1P+v/9v/2//b/9v/2//U/9T/zf/U/83/zf/q/wAA+f8HAAcABwAHAOP/8v/N//n/1P/N/+r/vv8AANv/8v/5/wAA8v/5/ywA+f8OAA4AFgAWAAAAAAAOAPL/DgAAAOr/DgDU/wcA1P/F//L/xf8WAOr/4/8WAOP/+f8AAPn/8v/j/9v/1P/U/8X/tv/U/9T/4//U/9v/6v/N//n/6v/U/9v/vv+2/77/4//5//L/AAD5/+P/6v/U//n/AADy/xYABwAAAB0A8v/j/wcA4//b/9v/1P/q/+P/8v/y/+P/8v/y/+r/2//b/+r/1P++/7b/xf++/83/8v8AAB0ADgDy/wAAAAD5/yUADgAHACUA+f8lACUAMwBnAEIAWQBRAFEAUQBCAG8AQgA7AEoAOwBKAEIAOwBCAEIAOwAzADMAJQAlABYAHQAAAOP/AADj/9v/+f/b//L/DgDj/9T/+f/5/8X/1P/q/8X/xf/b//n/+f/y//n/6v/U/+r/DgAdAAcAMwAzAA4AFgAAAB0AFgAdABYABwAlACUADgAOABYA8v/5/9v/BwDq/8X/DgC+/8X/tv/N/+P/1P8HAOP/AADy/+r/8v/q/9T/1P/b/8X/6v/q/w4ABwDy//n/+f/j/+P/4//b//L/4/8lAOr/+f/y/8X/+f/F//L/8v/y//L/6v/y/9v/8v/y/+r/4/8AANv/4//q/+P/AADy/+r/2//5/wAAFgAdAAcADgAHAA4AJQAdABYAQgAlAA4AMwAsADsAMwAdAEIALAAsADMAHQAlABYALAAdABYAJQAOAAAADgAdAA4AFgAWAAAA+f8AAAcADgAsADMAJQAWACUAHQAOAA4ABwD5/wAABwAHAB0AFgAzABYALABCACwAYABRAGAAbwBRAGcASgBCAEoAQgBCAEIASgAzAEIAQgAsAFEAMwBKAFkAWQBvADMASgBCABYAAADy/+r/4//y/wcABwAOADMALAA7ADsAJQAzAA4AHQAdAPL/AAAAAPn/DgAAACwALAAHADsAOwAzADsAQgA7AB0AMwAlACUAJQAWACUAFgAWAAcAHQAOAAcAAADq/wcA+f/5//n/AAD5//L/1P/j//n/xf8HAAAA+f8HAOr/AAAAAPL/6v/b/77/8v/j/9T/6v/N/+P/2//5/wcA+f/y//L/4//q/w4ABwAdAA4AHQAOABYAJQAHAAAABwAHAPn/LAAAAAAABwDy//L/1P/5/9v/zf/j/9T/2//b/9T/vv+Z/6D/mf97/6D/r/+2/77/p//N/8X/vv/b/83/xf+v/7b/p/+Z/8X/vv/N/8X/4//y/+r/8v8AAA4A+f8dAAAA+f/j/+r/4//F/wcA2/8HAAcABwAWAOP/AADy/+P/2//y//L/2//j/9v/xf/b/9v/tv/b/6D/tv/N/6D/xf/q/83/1P/q/8X/2//b/9v/2//q/+P/2//q/6f/6v/U/83/BwD5/x0ABwAOAB0AAAAAAAAAAAAOAPL/6v/j/+P/6v/j//L/AAAOAAcAMwAWABYAJQAOADMA8v8AAPL/+f/5/8X/6v/F/83/xf/F/9v/xf/q/+P/4/8HAAcADgDy//L/2//F/+P/zf/q/9v/2//q/83/AAAHAPn/AAAdAA4A4//y//L/+f/b/+P/8v/b/+r/8v8AAPn/AAAlABYADgAsAB0ADgAAAOr/BwDy//L/JQAOACUAQgAsAFEAWQBKADMALABCACwAJQAsAA4AFgAWAB0AFgAOABYAHQAzACwAJQBCADMAFgAzAB0AHQAdAOP/+f/j/+P/8v/y/wAADgA7ADMAYABKAEIAUQAsACUAJQAdAAcALAAdAB0AOwAWAAAABwAAAOP/HQAWABYALAAWACUADgAWABYADgAHAAcADgDq//n/DgDq//L/8v/U/8X/2//q/9T/8v/b//L/DgD5/xYA+f/5/+P/4//j//L/DgD5/xYA+f8HACUADgAdACUAAAAOAA4A+f8WAPL/DgAdAAcALAAlABYAAAAOAAAA4//5/wcAAADq/w4ADgD5/xYADgAdAA4A+f8dAB0AOwAlACUAJQAAACUAAAAAAA4AHQBCAFEAWQBCAEoAMwBCAEoALABKACwA+f8WAAcA+f8OACwASgBRAGAAUQBZAEIAQgBRAEoAQgBKAEoALAAzAA4AFgAsAAcAJQAOAAcABwAAAPL/AAAOAOP/6v/5/9T/4/8AAOr/FgAHANT/BwDj/9T/+f/j/+P/6v/j/+r/2//q/+r/4//y/wcAAAAHAA4A2//j/9T/2//q/+r/BwAdABYADgAWAAcADgAdABYABwAWABYAJQAdAAcAOwAsACwAMwAdAAcADgAWAPn/JQAWAB0AJQAlACwAFgAWAAcAFgAAABYA+f8HAA4ABwAdAOr/DgD5/wAAAADj//n/6v8OAAAAAAAHAPL/6v/j/wcABwAHAAcADgAsAAcAFgAWAPn/FgDq/+r/AADy//n/DgAWAPL/AAAAAAcABwD5/wcABwAlAPL/+f8AAOP/FgDy//n/AADy/xYA6v8AAPn/4//j/+P/8v/U//L/zf/F/8X/xf/q/8X/2//N/77/zf/U/9v/1P/N/83/zf/N/9T/xf++/8X/zf+v/83/vv+2/8X/kf/F/77/zf/U/9v/+f/F/9T/6v8HAPL/DgDq/+r/DgDN//n/zf/j/wAA1P8HAAAAAADj/8X/2/+v/8X/AADU/+P/4//j/9v/zf/U/77/tv+Z/+P/xf++/+r/p//q/9T/tv/q/83/zf/b//L/AADq/wAA6v/q//L/8v8lAOP/DgAOAOr/JQAWADsALAAlABYAFgAlAA4AFgAOACUABwAHAA4ADgAHABYAQgAzADsAMwBgAEoAOwBCACUAMwAHAB0ABwDq/xYA+f/5/w4ADgAdADMALAAlACUABwAWAA4AHQAHAOr/8v/F/83/xf/N/9T/4/8AAOr/DgD5/w4AAAD5/xYA2/8OAOr/zf/U/83/2//N/+P/4//b/9v/1P/b/9T/2//b/9T/6v/5/+r/zf+2/8X/zf/U/9T/4//b/83/xf/N/9T/vv/N/83/2//N/9T/4//b/9v/tv/y/9T/2//5/9T/BwDy/+P/4//5/wcAAAAWAAcADgAHADMAHQAdAEoAJQBKACwAFgAsACwALAAOAA4AAAAlABYAAAAlAAAAFgAOABYAOwAlABYAFgAHAAAAJQAdABYAFgD5/wAABwAHAAAAHQAdABYAMwAdAB0ALAAWAA4AMwAdAB0AJQAAABYAAAAOACwADgAdAA4AOwAAAA4AMwD5/xYA1P/j//n/2//U/9v/4//j/wcA2//5//L/8v8OAAAAMwAWAB0AHQAWAB0ABwAAAOP/DgAAAPL/BwAAAB0ALAAOACUAJQAdADMALAAlAB0AFgAHAB0AFgDy/w4A+f/q/w4ABwD5/w4A8v8AAAAA8v8OAOr/2//b/9v/6v/5/xYALAAOAA4A+f/U//L/zf/j/9v/2//j/9T/8v/N//L/BwAAAPn/+f/y/+P/AADy//n/2//5/+r/+f8lAPn/MwAWAA4AHQAAAA4ABwAOAPL/AAAHAOr/AAAOAB0AJQAzACUAHQBCACUALAAdABYAHQAOACUABwAHAB0AFgAsADMAMwBgAHYASgBRADsAQgAsADMAbwAsAEoAQgA7AFEAMwBZADsASgBgAGcAYABCADsAMwAsAPL/HQAOAPL/DgAAAA4A8v8lAB0AMwAzAAcADgDy/wAAxf/q/9T/p//y/77/6v/q/8X/2//F/9v/+f/q/+r/8v8AAPn/AAD5//n/AADN//n/AADq/wcAAAAdABYAMwAsAA4AMwBCACwAMwAsAAcABwDN/9v/1P/N/w4A6v8dAAAAAAAdABYAMwAsACwAHQAsAB0A+f/5/+P/4//b/+P/+f8OAAcAAAAdAAAADgAlAA4AFgAHAAcA4//F/+P/zf/U/77/xf/j/9T/6v/y/+r/6v/q/9v/8v/N/7b/xf+g/6f/iv+R/6f/oP+2/8X/xf/N/9v/+f/q/9T/+f++/9v/2//F/+P/xf/y/9T/1P/y/9v/1P/5/+P/zf8AANT/6v/j/9v/8v/b/9T/zf/q/7b/vv++/77/tv+R/83/r/++/+P/4//j//L/6v/b/+P/2//5/9T/4//q/7b/1P/N/83/6v/U/8X/6v/y//n/FgAsACwAJQAsAAcAFgAHAPL/+f/j/wAA8v8HAA4ADgAzAA4ABwAzABYA+f8dADMABwAHAB0A6v/j/83/vv/U/9T/2//y/wcA2//5//n/2//y/9T/4//N/9v/AADq/+r/6v/y/9v/6v8AAOP/4//y/wcABwD5/0IAHQAOADsAAAAWAAAA+f8HAPL/8v/j/+r/2//5/+r/BwAAAA4AMwAHACwAHQAlAPn/+f8sAAAAJQAlAAAADgAWAA4ALAA7ADsAMwAsACUALAAHAA4ALAAAADMAAAAdADsABwA7AB0AJQDy//L/8v/N//L/1P/y/+r/AAD5/wAAFgAOADMAFgAsAB0ADgAHAOr/+f/5//n/8v8HACUAJQBCAFkAOwBCAEIAQgAzAA4AMwAWABYAFgAlAEIAMwBKAEoAMwAlAEIAOwAsACwAHQAlAPL/6v8WAAcA+f8lAB0ADgAdADsAJQAOAB0AFgAHAAAADgAHAAcA6v/y/wcA1P/y//L/6v8dADsAFgAAAAcAAAAOAPn/HQAOAAAAAAAWACUAAAAlACUASgAdAA4AJQD5/wcA6v8HAAcA8v/q/w4ABwDq/wcA2//U/83/2//q//L/4//b//n/8v8HAAAAJQAWAA4AMwBCAEIALAAzAAAADgDy//n/FgAHACUAJQA7ACwAQgBKAFEAZwBKAEoAOwAlAAAABwAdAB0ADgAOAPn/+f8AAPn/+f/5/yUA8v8WAB0AAAAsAA4ALAAWADsASgAlADMAFgAlAAcAHQAsAB0AUQA7ADsAMwAzAFEAOwBRAEoALAA7ACwAJQAOADMAFgAdAFkAHQAzACwAFgAdACwAJQAHAB0A+f8WAA4ABwAzAA4AAAAsAAAA8v8OAPn/HQD5/w4AFgAHACUABwAsAA4AJQAlACUAWQAsACwAFgAOAOr/HQAdAPL/DgDy/wcABwDq//L/DgDy/wcA+f/b//n/6v8AAOr/+f/5/9T/2//j/8X/tv/q/77/xf/b/83/2//j/+P/2//j/8X/1P/q//L/4//y/+r/xf/j/9v/4//U/9T/xf+2/9T/4//y//L/JQDy/wAABwDb/wcA6v/j/9v/4//q/+r/4//y//L/8v8AANT/+f/q/+P/AADb/+r/+f/b/8X/zf/F/7b/zf/N/77/2//j//L/8v/j/wcADgAAABYA+f/F/wAAxf/F/9v/r//b/9T/+f/b/9v/4//5/wAAvv8HAM3/2//b/9v/BwDb/+r/vv/j/8X/6v/y/8X/6v++/9T/xf/q/wcA6v8HAA4A8v/q/wAA6v/q/+P/BwDy/+P/AADj//n/AADy/+P/2//b/9v/vv/N/9T/xf/j/77/4//U/8X/4//N/+P/zf/F/83/vv/F/+P/xf/q/+r/zf/q/77/1P/F/77/zf+2/83/p/+v/7b/r//F/77/2//b/9v/FgAAAOP/AAD5//n/6v/y/9T/zf/N/9T/6v/F/+r/6v/y/xYAHQAOAPn/8v/q//L/+f/5/+r/BwD5/+P/4//N/9v/4//j/+P/+f/N/9T/zf+n/83/tv/F/7b/vv/N/8X/2//b//L/4//5//n/4//5/9v/2/8AAAAA6v8AAOP/6v/y/wAA4//5/x0ABwAWAAAABwAOAA4ABwAdABYA+f8OAPL/BwAOAAcAHQAHAA4AFgAOAA4ADgD5/xYA+f8OAPn/6v8WAPL/MwAlACUASgAlAFEAMwAdACUAHQAOACUA+f/5/xYA+f8OAOP/6v8HAPL/DgAWAPn/AAAHAPL/+f/5//L/8v8AAPn/AAAWAPL/AAAWAPn/BwAHAAAAJQAlAB0ALABCADMAJQA7ADMALAAzADMAOwAsACUAJQAsAAcAFgAWACUAQgA7ADsALAAdACUAJQAsACwAMwA7AAcADgAWABYAQgAzAEIAQgAsAEIAUQBZAEIAQgBZAEoAHQBZACwABwBKACwALAAlAEIAUQA7AEoAUQBCADMAUQBZAEIAOwAzADMAFgAdACwAFgAOABYAHQAdAA4ADgAdAAcA+f8sAB0AAAAdADMAMwAdACwADgAHAEIABwAlACUADgAlAAcAMwAlAA4AOwAHACwALAAOADsAFgAWACUAAAAWABYAFgAdAAAA+f8AAAAAAAAHAOr/4//F/8X/zf/F/77/vv/q/77/zf/q/83/zf+2/9T/+f/b/+P/4/++/+r/1P/b/wcAvv/j/+r/+f/y/+r/DgAOAA4ADgAlAAAAFgAdAAcAAAAAABYA8v/5/+P/BwDq//L/HQDj/x0A8v/q/+P/zf/b/9v/6v/F//L/8v/b/+r/6v8AAOr/4//y/+r/6v8WAOP/+f/y/8X/AADN//n/6v/U/wAA6v/y/9v/8v8AAPL/BwAWAPL/+f8WAOP/8v/j/9T/4//5/9T/8v8WAMX/HQDb/77/AADb//n/2//q/9T/zf/j/83/6v/q//L/8v8AAAcAAADy/+P/+f/y/wcABwDy/wAAFgAlACUADgAOAAcADgAOABYABwAHAA4Azf8HAA4A+f8lAAAAAAAAAPn/+f/y/+P/1P/b/9v/2//y/wAA1P8AAOr/zf/y/83/2//N/9T/zf/F/9v/zf/y/+r/+f/q/wAAJQD5/ywAMwAHAA4AJQAWAAAALAAlABYAMwAzADsAJQA7AEoASgBKAG8AYAA7AFkAUQBKACwAMwAsAB0AHQAWACUABwAsAA4A8v8lAB0ALAAsACUALAAsACwAFgAOAA4ADgAOAA4ABwAHAAAAAAD5/ywALAAlAEIAQgAsACUAWQAlADsAOwAdADMA8v8dAAAAFgAdAPn/MwD5/x0ABwAHABYAxf/j/83/tv/q/9v/xf/j/9T/zf/U/8X/tv+2/8X/tv/b/77/xf/y//L/+f/U/+r/6v/b//L/6v/5//L/6v8OAPL/zf8AAPn/6v8AABYA+f/5/w4ADgAOACUAOwA7AEIALABCADsAJQAzADsAHQAWADsALAAlACUALAAdACUAHQAOAB0A8v8WABYADgAOAA4A6v/b//n/2/8AAOP/BwAAAPn/DgAdACwABwAzAAcAJQAdABYAJQDq/xYABwAHACwAHQAAAA4A8v/5//L/4/8OAPn/BwAHAB0AAAAHAAAA4//y/9v/AADq/wAAAAD5//n/+f8AAAcALAD5/x0A8v/5/xYA+f8AAPL/DgDy//n/+f/y/9v/4//j/83/2//N/wcA1P/b//n/1P/j/9v/2//j/wAA1P/q/+P/zf/b/83/BwAHAAAA8v8WADMADgAzAB0A+f8OAAcAFgAAAPn/+f8HAA4ABwAlACUAHQAAAA4A8v/y/wAABwAzAOr/BwDy/+P/AADj//n/1P/5//L/8v/q/wcAHQAAABYA6v8HAPn/8v8WAPL/BwAOAPL/8v/q/83/+f/y//n/BwDy//L/6v/y/wcAJQDj//n/8v/b//n/2//y/83/2//q/+P/8v8HAPn/zf8HANv/1P/y/8X/1P/N/9T/2//U/9T/+f/j/wcADgDj/wAA4/8HAOr/4/8HAOr/FgDq/+r/8v/b//L/6v8HAA4AFgAlAB0AAAAOADsALAAHAAcAAAD5/+r/+f8OAPL/BwAHAA4AHQD5//L/+f/y/+r/4//U/83/xf/U/8X/1P/q/83/4//F/9v/1P/U/9T/zf8OAOr/+f/j//L/6v/q/xYA6v8OAOP/DgAOAAAAMwAAAB0A+f8HABYA+f8lAA4ABwAHABYADgAlAPL/8v/y/8X/6v/N/9T/1P/U/+r/8v/y//n/BwDq/+r/1P/y/9v/zf/j/9T/6v/N//L/AAAHABYALAA7AB0AOwA7AEIAHQAdAB0ADgAWABYAJQD5/0oAFgAOAFkALABKACUAMwBCADMAQgA7ACwAJQAsAAcAAAD5//L/DgAlAA4ADgA7AB0ABwAdABYAAAAHAOr/AAD5/83/DgAOAAAADgD5/wAA8v/5/x0ADgAOABYADgAAAA4ABwAOAB0AAAAOABYAHQAWABYAJQDj/9v/DgAAAOr/HQAWAA4ABwAWAB0A+f8dAAcAFgAAAPL/AAAAANv/2/8HAMX/FgDy/+P/FgD5/ywAFgAzAB0AFgAAAPn/8v/U//n/1P/U/7b/r/++/+P/AAAOAB0AAAAAAPL/8v+2/9v/xf+n/8X/r//U/7b/2//j/+P/AAAHAAAA+f8lAAAAHQAWAAcALAAdAAcABwAAAPn/DgAHAB0ADgAWAA4AFgAsAAcAHQAOAPn/6v/5/wcABwAWAAcADgAHAAAAAADy/9v/8v/j/+r/AADy/wAA4//5/wAAAAAAAOr/DgDy/wAAAAAOAA4AFgAlAPn/JQAAAB0AOwAWADsAHQA7ACwAMwBRAB0ALAAWAB0AJQAOACUALAAzACwAQgBKAB0AOwAlACUAOwAsADsAOwAzAA4AMwAOAAAAHQD5/ywADgAOACUA8v8lAAAA+f8WAAcABwDy/wcA2//N/+r/xf/j//n/8v8OABYAHQAsAAcA8v/y/9T/4//b/83/6v/F/8X/2//F/8X/4//U/+P/6v/b/+P/xf/N/+P/xf/b/9v/p//U/9v/vv8HAM3/zf/y/8X/4//j/+P/1P/q/+r/2//q/9T/+f/y/9v/AADy//n/AAD5/wAA+f8AAAcA8v/5/yUA8v8AAA4A8v8WAAAAJQAOAA4A+f8HAB0A8v8lAPL/JQAWAPL/MwD5/wAADgAHAAAA8v/y//n/4//j//L/4//5/9v/AAAAAAAADgAWAAAA8v8OANv/+f/b/+P/+f/F/9v/1P/F/77/2//F/9v/4//y/xYA4//j/+r/6v/q/+r/4//U/77/zf/U/77/1P/b/9v/2//b/+r/+f/q/+P/HQAWAAcALAAdAB0ADgAdAB0A6v8OAPn/FgAOAAcASgAOACUAHQAWAA4AJQAlAA4AOwA7ADMALAAzAB0AFgAOAAcADgAOAB0AFgAsABYAHQAWAAcAFgAlABYADgAdAOr/8v8AAPn/+f87ACUABwBgABYALAA7ABYAFgAAAAcADgAsAAcALAAWACUAOwAzADMAFgAdAAAAJQAAAPL/+f8AAPn/4/8AAMX/+f/j/83/+f/j/w4A6v/y/+P/vv/U/+P/BwDj/w4A+f/b/+r/1P/q/9T/8v/q//n/+f/b/wcABwAWAAAADgAAAPn/DgDy//n/+f8dAOP/6v8HAOr/AAD5/w4ABwD5/wAABwDy/xYADgDy/ywA6v/b/wcA4//y/wAA+f/q/9v/BwDy//n/JQAHAB0AFgAOACwAHQAdAAAAJQAOAOr/MwAHAA4AJQAAAA4AAAAWAAAADgAHAAAAFgDq/w4ABwAHAAAAAAAOANv/6v/F/83/6v/j//L/4//5/wAA8v/5/+r/2//U/9T/2//U//L/+f8AAPn/8v8HABYAJQAAACwAHQAAADsALAAlACwAJQAWABYAFgAOACUAMwAlADMALAAdADsAHQAzACwAJQA7AAcAMwAzACUALAAWACwAFgAOAA4ADgAOANv/6v8HAPL/BwAHAA4ALAD5/wcALAAAAB0AAAAOACwAAAAlAA4ABwAOABYABwAOAA4ABwA7AAcASgAWAAcAMwAOADMABwA7AB0AFgA7ABYALAAdABYADgAWAAAAJQAOACwAMwAWAB0AAAAOAA4AHQDy/x0ABwAHADsAHQA7ACUAJQAWAB0ABwAdACUABwAlAB0ADgAWACwA+f8HAPL/6v/j/+r/8v++/w4A6v/5/wAABwAAAPL/HQDj/w4A+f/5//n/AAAAAPn/JQDb/wAA8v/b/9v/xf/F/7b/zf+2/9T/xf+2/83/xf+2/7b/8v++/+P/HQDq/wcA8v/U/+r/xf/b/wAA6v/q//L/6v/U/9T/1P/U/9v/4//q/wcA4//y/+r/p/++/7b/1P/q/+r/8v8AAA4A+f8AAPn/DgAAAPL/8v/b/wAA8v8AAOr/+f/q/+P/HQAAABYADgDy/w4A4//j//L/1P/y/wAA+f/5/+r/BwDy/83/+f/b/77/AADq/77/6v/b/8X/4//U//L/AADN/+r/1P/F/8X/p//N/6//xf/N/6D/xf+2/83/2//N/9T/8v/y/9v/8v/b/wAA8v/y//L/1P/j/9T/6v/y/+r/AAAHAAAAFgAAAPn/BwDy/xYABwAlAAcABwD5/83/BwDq/xYA8v/y/wcA4/8OAAAAFgD5//n/+f/5/wcA+f/5/9v/4/8AAPL/8v8AAPn/DgDj//L/+f/q/xYA8v8WACUAFgAWABYAJQAWACwAHQAHAA4AHQAlACwADgAzADMALAAsACwAQgAHABYAAAAHACUA+f8WAA4A+f/q//L/6v/5/wAAHQAlAAcALAAdACUAHQA7AB0ABwAdAOr/4//5/+r/1P8WAPL/+f8OAOr/HQAAAAcA+f8AABYA+f8OAA4A+f/y/wAA+f/j/+r/DgAAAB0ALADy//n/+f8AAOP/6v8HAOP/+f8WAAcAAAAOABYA+f/j//n/FgAOABYAHQAHAAAADgAOAAcADgAAAPn/HQAOAA4AFgAdACUAFgAOAAcAHQAAAB0AMwAWACUADgAdAAcABwAWAAAABwAHAAAA+f8WAPL/+f/q/+P/1P/F/wAAxf/q/+P/2//y/8X/6v/N/+P/xf/j/9v/mf/U/83/zf/U//L/xf/N//n/4/8OAPn/AADj/+P/2//b//L/4/8HAPn/DgAAAAcAHQAWACUAAAAAAPL/BwAOAAAADgAOAPn/4//U/83/6v/y/w4AHQAHAA4AHQAOAAcAFgAAAB0AMwAzAEIAOwAzADsAQgBKAFEAYABgAEIASgBCADsAMwA7ADMALABCABYAHQAsADMALAA7ADMAMwBZAB0AFgAlAAcAOwAsABYAMwDy/zMALAAOAFkABwAdAB0ABwAOAPL/DgAAAAcADgAHACUAMwAlADsAOwAzAEIAJQBCADMAHQAdAEIALAAdAEIAFgAlAA4AMwAsAA4ALAAHABYABwAOABYABwAOAA4ADgD5/xYADgDq/wAAFgDq//L/LAAHAA4AFgAHACwABwAOABYADgAWAAAAFgDy//n/AADq/wAA+f8OAAAAFgDy//n/DgDj/wAA8v/5//n/DgAsAA4ALAAlAB0AHQAOAB0ADgAHACUAFgAHAAAA8v8OAPn/8v8WAPL/6v/5//n/+f8AAAAA+f/5/+P/6v/N/9T/8v/U/9v/8v/q/83/6v+2/8X/AADF/9T/1P/b/83/tv/U/9T/2//U/+r/1P/U/+r/4//q/+r/AADj//L/+f/q//n/8v8AAOP/8v8AAPn/DgDq/wAAAAC+//n/BwDq/xYAHQAAAPL/4//j/+r/xf+v/9T/6v+2/83/AADU/8X/4//q/9T/6v/j/9v/1P+v/83/1P/N/+P/2/++/77/vv/b/+P/2//j/83/1P/N/83/1P8AAM3/vv/q/6//8v/b/9T/+f/F/+P/1P/q//n/1P/y/+P/6v8OAOr/BwAAAPL/DgAHAAcA+f8WAAAADgAdAPn/AADy/xYA4/8dACUABwAzANv/HQAHAOP/HQAHAAcADgAOAAcAAAAAAAAA8v/5/wcA8v/y/w4A+f/5/wAA+f/q/83/8v/j/+r/BwAOAA4AFgAsAAcAAAAHAAAA+f8HAA4A4/8AAAcADgAWAPn/+f8dAAAAJQAlAA4AQgAWADsAJQAWACUAFgAlAA4AFgD5/wcA8v/q/wcA4//5/+r/AAAOAA4AAADy/wcAAAAdAAcAFgAdAPn/BwAHAPn/+f8dAA4ABwAOAAAA+f8OABYA6v8dABYA+f8sABYA+f/y/w4AHQAAAAAAHQAOAPn/BwDy/+r/AAD5//n/FgAHAAAA8v8HAAAA6v8WAAAA+f8AAPn/6v/y/+P/6v8AAOr/LAAHAPL/AADj//L/4//q/+P/1P/N/9v/zf/F/9v/1P/y//L/DgD5/wAADgDq//L/8v8HAPL/6v/5//L/8v8HAPn/8v8AAOP/AAAHAAAA+f8HABYAFgAzACUAHQAWAB0ABwD5//n/BwAAAAcALAD5/x0ADgAWAEoAJQA7AB0AJQAlAB0AMwAdAEoALAAlADMALAA7ABYALAAlAB0ALAAHACwAFgAWADMADgAlACwADgAOACwAJQAlACwAFgAlACwAHQAdAAAADgAOAAAALAAWAA4ABwAWACwA8v8HAB0A8v8OABYA6v/5//n/8v8sAB0AFgAdAA4ADgAHAAAADgAAAAAAAAD5/w4A6v8WAA4A8v8AAOr/BwDj/+r/6v/b/wAA2//j//n/zf/U/wAA4//q/wcA2/8OAAcA8v/5/+P/AADy/wcADgDb/xYADgAHACUAFgDj//L/6v/U//L/vv8AAPL/4/8WANv/BwDy/wcALAAOABYAHQAlAB0AHQAHACUAAAD5/xYA+f8HAPn/FgAlAAcAJQAdAOr/FgAOAOr/DgDy/wAA8v/b/ywAAAAOADsAFgAdAAcA6v8AAA4ABwAOABYAAADy/+r/6v8AAAAADgAOAA4A8v/y//L/6v/b/+P/4//U/+P/4//q/+r/AADy/9v/8v/b/9T/zf/F/77/vv/N/77/zf++//L/4//U//n/zf/5/8X/8v8AAK//+f/U/9T/xf++/9T/oP/N/9T/2//q/wcAAADq/+P/+f8HAPL/DgDy/wAAHQAdADsAFgAlAB0AAAAlACUABwAHAB0AFgAHAA4AFgAWAA4AFgAdAAcAFgAWABYAJQAOAB0AAAD5/x0ABwD5/w4ABwAHAPn/6v8AAOP/4/8HAB0A8v/y//n/2//y//L/BwDj/+P/6v/q/wAA6v8HAAAAAADj/+P/4//j/wAA2/8AANv/zf/5//L/AAD5/w4AAAAAACUA8v/y/w4A8v8HAAcA4//y//L/4//5/wcA6v/U/+r/vv/F/+P/r//j/9T/zf/j/83/4//N/+P/6v/q//n/4//y/+r/2//q/w4A8v8WABYA6v8OAAAADgDy/wAABwDj/wAA+f/5/wcA+f8AAA4ABwAAAAAAAAD5/+r/4//j/wAA8v8OABYAAAAlAA4ADgAWAPn/DgAHAOP/+f8AAMX/+f/q/8X/AADN/9v/+f/b/+P/4//b/+P/AADj/wAAAAD5/wcAHQAdAOP/LAD5/+P/FgDj//n/AAD5//n/FgAAAA4AHQAWADMADgAsACUABwAHAAcADgAAAAcA+f8HAA4ABwAWABYAHQAlAB0AHQAOAPn/DgAWACUAFgAOADsAJQAOADMAMwAdACUAJQAsABYAHQAlABYALAAlAB0ALAAsADMALAAlAEIAMwAdACUAMwAsABYALAAWACUADgAAACwA8v8zAEIAHQBRACUALAAsACwAJQDy/yUAHQAAACwAOwAdACwAHQAHAB0A+f8WACwAFgBCACUAHQAsABYAMwAsACUALAAsABYALAAzAAAAFgAHABYALAAOADsADgAlACUAFgAzADMAOwAdADsAJQAOAPn/4/8WAOP/AAAWABYABwD5/x0AFgAOABYALAAdACUAFgAHABYADgAlADMAFgAHAB0A8v8WABYADgA7ACUALAAAAAAA8v/j/w4ABwD5/+r/6v/j/wAA+f/q//n/4//q//n/4//q/9v/8v8AAOr/BwDq/+r/4//y//L/2//q/9T/+f/j/wAA4//F/wcAr//U/+P/zf8AANv/2//b/9T/vv+v/8X/vv+v/77/r/+g/83/r/+v/9v/zf/F/8X/1P/F/7b/vv+g/8X/iv+n/8X/dP/N/77/r//U/83/4//y/+P/8v/q/9v/+f/b//n/AADb//n/8v8OAB0AFgAOABYAAAD5/xYA+f8WACwAFgAdABYADgD5//L/FgDy/wAAHQAHAB0ABwD5/w4AAAAOAAAA2//y/+P/2/8HAOr/6v/j/9T/6v/j/9v/8v/y/+P/8v/y/9T/1P/U/+r/6v++//L/4//F/wAA6v/q/83/+f8HAOr/AAD5/wcA1P8OAPn/1P8AANv/8v/y//L/2/8AAAAA8v8AAPL/DgDj//n/AADb/+r/6v/j/+r/+f/q//L/8v8WAAcAFgAsAB0AHQAAAAcAFgD5/x0AJQAHADsADgAWADsADgAsAA4ADgAAAPn/DgDy//n/8v8AAOr/1P/b/+P/1P/b/wAA+f/5/+P/6v/y/9v/8v/b/83/zf/N//n/2//q/wcA8v/q/9v/AAAAAAcA1P/j//n/r//q/+r/2//q/wAADgAHAA4A8v/y/+P/6v/q/+P/DgAAAA4AFgD5/wcAHQAOAPn/BwAWAPL/HQAWAPn/JQAWAB0A+f8WAA4ADgA7AB0AMwAlADMAFgAHACwALAAsADsAHQD5/ywAFgAdACUAHQAHAA4AOwAHADsADgAOABYADgAlAPL/HQAAACUADgDy/ywAAAD5/wAADgAOACUAHQAlABYA+f8WAAAA8v8OABYA+f8lAA4ADgAlAPn/DgAHAAAA8v8HAPn/DgAdAPn/FgAHACUADgAdAA4ABwAzAPn/JQAHAA4AHQAHAA4A4/8AANT/1P/q/9T/8v/5/w4A6v8HAA4A2/8OAOr/6v8WAAAADgAWAB0AAAAAAAcA+f8HANv/DgAlAA4AMwAWABYADgAdABYADgAdAAcAJQAWAB0AFgAAAAAABwAWAAAAAAAOACUAHQAlACUADgAdAB0ALAAzAEIAUQA7ADsALAAzADsAMwAlADMAOwAdACUALAAdAAAAJQD5//L/FgD5/xYABwAdACUAFgAHABYAJQAHADsAHQAOAPL/6v/5/9v/DgDy/w4AJQAHACwAFgAdAAAAHQAsABYAJQA7ACwAHQBCADMAQgAzAEIASgAdAEoASgAsACUAJQAWAB0ABwAlACwA+f8zAB0ADgAOAA4ALAAdACUADgAOAPL/BwAOAOr/AAAHAA4A+f8HAAcA+f8AAA4A+f/5//n/8v8OANv/6v/j/9T/8v/j//L/4//N/7b/vv++/8X/4//j//L/zf/U/9v/xf/b/83/1P/U/8X/1P/F/9v/4//y/wAA6v8HAOP/+f/y/83/zf+v/83/r//j/+P/1P8HAPL/AAAAAB0AAADj//n/AADj/+P/8v/b/xYA+f8OAPn/1P/y/83/AADq/wAAFgAHABYAHQAzAA4ADgAHABYAFgAAAAcA+f/q/+P/HQAOAPL/AADy//L/4//y/xYA+f/y/w4AFgDy/9v/+f8AAPn/+f8WAPL/4/8dAPn/+f8HAAcA6v/j/+P/+f8HAOr/HQD5//n/DgDq/wAADgAAAPL/DgDq//n/BwDj/wAA+f/5//n/8v/j/wcAAADy/+r/2//F/83/8v/F//n/+f/q//L/4//5/+P/BwDU/wAADgDq/xYA4//j//L/6v/b//n/8v/y/wcABwA7APn/+f8HANv/8v/5/wcABwAOAAAA+f/5/wAA8v/q/wcA6v/b//n/HQD5/wAAAADb/9v/1P8OANT/2//j/77/8v/F//n/8v/b//L/zf8AANT/xf/U/83/1P/b/+r/xf/q/9v/1P/5/8X/8v/b/+P/AADU/+r/8v/U//n/AADj//L/+f8HAPL/4//q/9v/2//q//L/2//q//L/4//N//L/6v/q/wcA2/8WAPL/2/8AAMX/1P++/8X/zf/F/9T/1P/q/wcA+f8HAAAA6v8OAOr/2//q//L/6v/q//L/4//5/+r/AADy/+P/6v/j/+r/8v8OAAAAOwAWACUALAAWADsA+f8OAPn/AAAdABYADgAWAB0A8v8sAPn/8v8WAAAA8v/q//n/6v8HAPL/BwDq/wcAFgDq/zsADgDy/wcADgAAAAcAAAD5//n/4//y/8X/8v/b/+r/AADq/xYA4//5/+r/AAD5/wAAJQAOADMABwAHAA4ADgAHAA4AHQAdAB0ADgAlAPn/8v/y/wcA+f/q/w4A6v8HAAAADgAHAPL/DgD5/w4ADgAlACwAQgAsACwAUQAsADsAOwBKADMAOwAsAAcAOwAWACwAOwAsACwAFgA7AEIAQgBKAFEAOwAsADsAMwAzAB0AJQA7AEIAQgAzAEoAMwAdAEIAHQAWACUABwAWAAcAFgAdAA4AHQAWAEIAJQAWADMAHQBCACUAMwAzAAcAHQAOACUAFgAzACwAOwBCAB0AUQA7ADsAHQAlACUABwAzAPn/BwAOAAAAMwAAAPn/DgDq/wcADgAHACUABwAdAA4A+f8HAAcAJQAHAPn/+f8AAPL/AAAOAA4ABwDy/x0AFgAWACwAFgAsAAAA6v8sAPn/2/8HAOP/8v/y//L/8v/5//L/6v8HANT/4//j/83/4//q//L/xf/N/9T/2//N/9T/+f/F/77/2//N/6D/1P/N/8X/zf/U/+P/xf/5/9v/6v/q/+P/6v/U/+P/2//b/8X/8v/b/+r/4//F//n/xf/q/+P/4//5/83/8v/j/+r/2//q/wAA6v/5//L/DgD5/+P/AADy//n/BwD5/wAA2//b//L/zf/U/+P/zf/j//L/vv++/77/vv/U/9v/8v/j/+P/8v/b//L/BwDy/w4ABwDj//L/+f8HAAcA+f8AAPn/1P/j/+P/4//5/+r/DgAAAPn/BwAlAB0A6v8HAPn/BwDy/wAABwAWACUAAAA7AOr/FgAsAPL/JQDy/xYAAAD5/xYA8v/5/+r/8v/q/wcABwAdACUAFgAzADMAHQAsAEIAFgAOAB0AFgAAAAcABwD5/ywA+f8zADMAJQBCAB0ALAAdADsAQgAlACwAOwBKADMAWQAlABYALAAAABYAHQAOACUAHQAzADMADgAsADMAJQAdAB0ABwAHAAcA6v8dAPL/AAAsAOr/DgAAAPL/+f/b//n/6v/j//n/4//y/+P/+f/q/83/FgAHAAcA6v/j//L/p//N/83/xf/b/77/6v/j//L/DgDb/+P/2/++/7b/tv++/8X/4//U/83/+f/y/+P/BwDb//n/+f/F//n/2//5/+P/1P/5/8X/AAAAAPL/+f/5/wcA+f8OABYADgAOAAAAAAAlAOr/FgAsAAcAJQAAAPn/8v8HAOr/AAAHAPn/JQAWACwADgAlAB0AFgAlAA4ABwAOAB0A+f8AAOP/DgDq//n/DgDN/x0A1P8dAA4A6v8sANv/2//F//L/1P/q//n/4/8OAM3/BwD5//n/+f/q/w4AAAAOAAAAJQAAAAAAAADj//L/1P/b/+P/8v/y/wcABwAHABYA+f8OAPn/AAD5/wAADgAOACwA8v8AAPn/6v/5//L/AADj/xYA8v8AAB0A8v8zAA4AAAAHACUAHQDy/yUA+f/5/x0AFgAOABYAHQAAAA4ADgAAAA4ADgAAAB0AJQAWAEIALAAdACwAHQAzACUAMwAzAEIAOwAdADMAFgAdACwAQgAzADMAWQAzAEIAQgA7ADsASgA7AFEASgAdAEoAMwAlAAAAHQAdAAAAOwAWACwAHQAsACwAHQA7AAcALAAsACUAOwAlACwAMwAlAB0AJQAsAA4ABwAsABYA+f/y/wcA8v/y/wcADgAHAPn/+f/U//L/AADj/+r/4/8AAAAA8v8AAAAA4//5/+P/2//5//L/AAAAAPn/AAD5/+P/4//j/+r/8v/j/+P/4//q/83/6v/b/7b/6v/j/7b/vv/b/+P/8v/5/xYABwDq//L/8v/b//n/4//F//n/1P/y/+P/4//j/6//AADN/9v/8v/j/+P/2//j/8X/2//b/+r/zf/y//n/6v/5/83/AADb//n/FgD5/wcA8v8AACwAFgAWADMA6v8AAPn/6v/5/+r/BwAOABYABwAdAAAABwAdAAAAMwAHAPn/HQAAAA4AFgDb//n/6v/N/+r/2/8HANv/8v8AAOP/8v/j/wcA6v/5/wAA4//b/9v/4//b//n/8v8AAOr/+f8AAAcAFgDy/w4ADgDy/9v/8v/5/+r/6v/q//n/2//j//L/8v8WAA4A+f8AAPn/6v8AAPL/zf/U/+P/1P/b/+r/6v/5//L/8v8HAOP/8v/5/9v/FgD5/+r/FgDj/+r/4//b//L/2//q//L/6v/j//n/4//j//n/2//q//L/6v8dAPn/BwAlAOr/AAAHAPL/AAAlAAcA+f8WAOP/FgAHABYALAAAADsAFgAdAEoAMwAzADsAAAAdADMABwBRACUAJQAlABYAJQAHAAAA4/8AANv/AAAOANv/6v/j/+P/xf/5/9T/xf/N/8X/2//U/xYA2//y/wAA8v8AANv/AADN/+r/6v/b//n/4/8AANv/6v/q/+P/+f/5//n/8v/5/w4AJQAAAPn/xf/F/9T/r//j/9v/xf/b//L/zf/j/wAAvv/y/wAA+f8OAPL/8v8OAAcA4/8HAOr/2//q/wAABwDq//n/8v/j/wcADgAOAB0ABwAHAAAA4/8AAAcA6v8WAAAA2/8HAOP/8v/y/+P/BwD5//L/+f8dAAcAHQAWAAAAHQAHAAAA8v8HAOP/+f8OAAAABwD5/w4AAAAdACUAHQAWAA4ABwDy/w4A8v8AABYA8v/5/wcA8v/q/wcA+f8dAB0ADgAlAPn/HQAlAAcAJQAOABYAJQAOACUALAAOAB0AFgDq/w4AAADq/wcA+f8AACUAJQAWAA4AFgAsAA4ADgAWAAcAAAD5//L/4/8AAOP/+f8AANv/+f/y//L/BwAHAPL/8v/j/+r/6v8AAPn/8v8HANv/HQAOAPn/DgDU//L/AAAAAA4ABwAAACUADgAAABYA2//5/w4A4/8HABYADgAdAB0ALAAOABYALAAzACwADgAzACUAFgAdACUAFgAlACwADgAlAAcAQgA7ABYAOwAlABYALAAdAPn/MwDy/zMAQgD5/0oAHQAlABYAJQAdAA4ALAAdACUAFgAzAA4ADgAzACUADgAOAA4A+f8AAPL/DgDq//L/DgDy/wAADgAlAA4AMwAdAB0AJQD5/x0AFgAzACwABwAzAA4AFgAdAAAADgAOAPn/AAD5/+r/BwD5/+P/AADF/8X/4//j//n/+f/q//L/2//q//L/8v8HAOr/FgAWAOP/+f8AAM3/6v8AANv/+f/b/wcAAADy/yUA4/8AAAAA6v8OAAAA+f/y//n/AAAAAAAA6v/b/9v/+f/5/9T/BwAWAAcAJQAHAA4AHQAWAAcABwAOAA4AAAAAAPn/AAAlABYA+f8dAPn/+f87APn/FgAWANv/FgD5/w4A+f/5/w4A6v/q/+r/AADq/wcAFgD5/wcA8v8HAAAA6v8OAAAABwAWAOP/+f/b/+P/BwDy/w4ADgAsAB0ALAAOAPn/HQD5/zMAHQAHAB0AAAAWAAAAFgAWACwAQgAsADsAJQAdAAAA8v/5/wcADgDq/wAABwAOAPn/AAAAAAAAFgAAADMABwAHADMADgAOAPL/BwAAAOr/BwAWAAcADgD5/w4ALAAWADMAAAAdABYA+f8HAPn/+f/5/w4A1P/y/+r/4/8HAAAAFgDq/wcA+f/q//L/1P/j/+P/1P8WAAAA4/8WAPL/+f/b/+P/+f/y//n/6v8OAOP/AAD5/9v/4//U/+P/6v/j/77/6v/j/+r/AAD5/+r/4/8AAPL/BwDq//L/2//U//L/vv/y/9v/xf/j/7b/xf/F/6//1P/N/83/6v/U/8X/tv/N/77/xf/U/9T/zf/N//L/1P/5/+r/4//q/83/8v/j//n/AADq/w4AFgDj/xYABwDq/x0A4/8lACUADgAzAAcADgAHAAAA6v8OAAAADgAHAAAAFgDq/w4A8v8WAAcA+f/5/9T/FgDj/w4ABwDj/+r/6v/5/+r/BwDy/w4AAAAHAAcABwAdAA4AMwAAACUAJQAAAB0ADgAlAB0AJQDy//L/+f/U/xYA8v8dACUA6v/5/+P/8v8AABYAAAAOAB0A8v8OAAcADgAHAAcABwAAACwADgAsADMAJQAHAA4ALAAlADsAMwBCADsAQgAzACwALAAsACwAAAAlAA4AHQAHAB0AOwD5/x0ADgAlAB0AFgAdAPL/8v/5/wcA+f/5//L/+f/q//n/HQDj/wcADgAOABYADgAOAAAABwD5/yUAFgDq/xYA4//q/xYA+f8dAA4AFgAOAA4AQgAlAB0ADgAHAAAAAAAAAPn/AAAHAAAA6v8AAPL/BwAOAOP/AADq//L/8v/y/+r/2//b/77/zf/F/+P/4//j/+r/xf/N/8X/xf/j/wAA6v/j/9T/2//5//L/BwD5//n/4//q//L/4/8AAPL/8v/q//n/1P/b/wcA6v8WAAAA6v/U/9v/+f/q//L/+f8dAOP/6v8OAOP/AAAAAPL/BwAOAOP/6v/q/9v/4//U/9v/zf/F/8X/1P/N/77/1P/b/+P/zf/q/+P/8v8AAOP/+f/b/+r/4//U/wcA8v/y//L/+f8OAPn/DgAWAA4ABwAOACwABwAOAPn/+f8WAMX/AAAHANv/BwDq/+r/+f/y/wAA+f/q//L/6v/j//n/+f8AAAAA+f/y//L/8v8OAPL/AAAHAPn/FgD5//n/BwDy/wAADgDy/xYAHQAHADsAJQAsAEoAFgAlAFEADgAWAEoAFgAlACwAQgAAAAAAOwAWADMABwBCAB0ADgAdAPL/HQDq/yUAHQAAACUADgAOAAcAHQAOACwAFgAOAA4ABwAOAPn/FgDy//n/AADq//L/6v/y/wcABwAOADMAAAAOACwABwAdABYAHQAOAAcAFgD5/xYAAAAdAA4A6v8OAAAADgAOACwAJQD5/xYA+f/5/wAA2/8AAA4A8v8HAA4A+f8sAAcAAAAdAAAA8v/5/wAA4//5/+r/AADy/w4ADgDb/w4A6v/q//L/8v/y/wAA8v/5//L/2/8dAPL/BwAHAPL/+f/y/wcA8v8HAAcADgD5/wcADgAAACwABwAOAAAABwAWAAcAFgAAANv/+f/5//L/HQAHAAcA8v8AAPn/8v8AAPL/OwAOABYAHQAWACwADgAdACUAHQAAACUAFgAAAAAAFgAHAPn/LAAWAB0AFgAdAAcAHQBCAAAAMwAWABYAFgAdADsAFgAsACUAHQAsACwAJQAOAAcAFgDy//L/JQAHAAcA+f/U/+P/8v/q/+r/FgAHAA4ABwDy/wcABwAHAAcAFgD5/9v/AADy//n/DgAAABYA+f8HAA4A+f8OAAAALAAOAA4AMwD5/xYAFgAWACUA+f8zAA4A8v8sAB0AHQAdAB0ADgAHAAcA6v8AAAAAAAAHAAAABwD5/wcA8v/q/wcA1P/5//L/4/8WAOr/BwDy/9v/8v/b/+r/2//j/9T/8v/q/9v/DgDj/+r/2//y/+r/zf/5/+P/4//b//L/6v/F/9T/vv/j/83/4/8HAMX/+f/q/7b/zf/F/+r/4//y/9v/xf/b/8X/zf/N/8X/vv/F/7b/2//j/8X/8v/N/9T/2/++/+P/6v/N/+r/2/++/+P/2//j/9T/6v/b/+P/8v/j/w4A8v8WAAcAAAAsAPn/+f8AAOr/8v8WAAAABwAAAPn/DgDb/w4ADgAWABYAAAAlAA4ABwAdACwAJQAlABYAMwAlAAcAQgAOABYAMwAWACwAMwAzAB0AMwAWAAAAAADy/xYABwAWAAcAAAAOAPL/HQAAAPn/FgAdAB0AFgAlACUALAAdACUA6v8AAA4A2/8dAOP/AAAAAAAAJQAOAB0A8v8sAA4AFgAzAA4AHQAOACUALAAlABYAJQAAAAAADgD5/wcAAAAlAA4AFgAAAAAAAADq//n/8v/5/9v/HQAWAAcA+f/b//n/zf8HAA4AFgD5/wcAFgDj/xYADgAHABYAFgAOABYAFgAWAAcABwAOANT/DgAHAPn/FgAHAB0ABwDj//L/+f/b//n/2//U//L/2//q//L/2//q//L/1P/y//n/6v/j/83/2//N/83/zf/y//n/1P/q/xYAAAAAAEoAFgAsACUA6v8dAPn/DgAdAAAAHQAWABYADgAlACwAHQAzABYADgAWAAcAHQAOAAcADgAOAAcA4/8AAAcA8v8HAPn/+f/q/9T/8v/b/9v/4//b/83/vv/y/9v/zf/q/+r/+f8AAOP/4//q/8X/+f/q/83/6v/j//n/+f/q/+r/6v/5/+P/6v/5/+P/FgAWAPL/BwAdABYA6v/y//L/6v8WAA4AAAAOAAcA+f8OAAcABwD5/+P/+f/y/wAABwAHAPn/AAAOAAAAAAAAAAcABwDy/wAAFgAOAA4ADgD5/+P/+f8WAAcAAAAHAA4ADgAlAA4A6v8OAAcADgAsAAcAAAAOAPn/AAAHAAAABwAHAOr/BwAdAAAAHQAHAPn/+f/y/wAA8v/5/+P/1P/j//n/6v/5//L/4/8HANv/DgAAAPL/JQD5/zMAAAAAACwADgAsABYALAAWAPn/FgAWAAcA6v/y//L/AAAHAA4ALAD5//L/AADy/wcAHQAzABYA8v8lAOr/8v8AAPn/DgDq/wcAAAAHAA4AHQAdAOr/DgD5/w4AHQAdAB0AHQAsAAcAAADj/+r/8v8HAAAAAAAWAAAAHQAAAAAA+f/5/wcA8v8OAPL/2//j/+P/8v/q//n/+f8AAOr/BwAdAPn/AAD5/wAA4//q//n/4//j/9T/BwDb//L/6v++//n/zf/b/9v/1P/N//L/2/++//L/tv/q/83/xf/F/6D/1P+2/7b/vv/N/8X/xf/F/9T/xf++/9T/tv/5/9T/6v/y/+r/1P++//L/zf/j/9v/+f/U//n/FgDU/xYA8v/y/+r/JQAWAPL/HQDb/wAA+f/q/wcAAAD5/xYAFgAlAB0AAAAOAAAADgAOADMABwAWACUAAAAWAAcALAAOADMAJQAWAFEABwAWABYABwAAAAAAFgAOAA4A+f8WAAcA8v8OAAcA8v8AAA4A+f8dABYA+f/5/wAA6v/q/w4AAAAWABYA6v8WAPL/8v8HANv/8v/y//n/HQAOAPn/BwD5/+r/+f8HAAcADgD5/w4AMwAWADsAFgAlACwADgAlAAcAMwAlACwAOwAdABYALAAWAAAAQgAHAAAAJQAAAPn/+f8OAAAA+f8WAA4A8v8WAB0ABwAWADsALAAlADMAHQAdABYALAAWABYAHQAWAB0ALABCACUALAAdABYAQgAdACUAJQAWACwALAAWACUAHQAOAA4AFgAHAAcA+f/q/wcAAAAAABYAFgAAABYADgD5/wAA8v/5/9T/4//N/+P/4//U//L/zf8HANv/+f/q//L/FgDj/w4A+f8WAAcA+f8HAAAA+f/j//n/+f8OAA4ALAAOABYABwD5/wAA2/8HAPL/xf/j/+P/xf/q//n/AAAAAOr/AADU//L/2//y/wAA2/8AANv/4//y/9T/4/8AAOr/6v/j/+r/4//U/+r/+f8AANT/+f/j/9v/1P/F//n/tv/U/83/vv+2/9T/+f/U//L/8v/5/+r/+f8AAAcAHQAWACwABwAdAAAABwAlAA4AMwAsADsAOwAsAEIASgA7ADMAMwA7AEIALABRAFEAQgBZAFEAUQBgAEIASgBnADsAUQBZACwAWQAzACUALAAlADsAHQAdAB0AFgAOACUAFgAAACUADgAlABYAJQAlAAAAJQAOAAAADgAlACwADgAWAB0AAAAHAPL/FgAWAPL/JQAHAB0AHQAdAEIABwAOACUABwAWACwADgAWAPn/+f8OAPL/FgAOAAAAAAAOAPL/BwAOAOr/FgDy/+P/AADj/+r/+f/j/wAA+f/y/yUA8v/b/x0A2//U/yUAAAD5//n/6v8AAAcAFgAHAAAA4//U//n/AADy/wAADgDy//n/AAAOAPn/DgAAAAcAFgAHABYABwAlAAcAMwAlAAAABwAAACUA4/8OAA4A8v/b/+P/xf++//n/zf/y/9T/2//N/83/2//U/9v/r//j/6f/zf++/77/1P++/+P/oP/y/9v/4/8HAOP/8v/U/+P/2//b/9v/+f/j//L/4//b/+r/p//j/+r/8v8AAB0AFgDj/wAA1P/U/9v/1P/b/+r/2//F/+P/oP/b/8X/oP/j/83/AAAAAPn/8v/b/wAA2/8HAOr/8v/j/83/AADj//L/8v8AAPn/FgAWAPL/JQAdAB0AAAAdAAcA+f8AAOP/BwDU/wcADgD5/xYADgAdAPL/6v/y/83/1P/q/+r/zf/q/wcA8v/5/wcAFgAAAOr/8v/5//n/6v8HAAAAAAAdAB0AMwAzADMAJQAzADMAJQBZACUALABCAAcAAADy/w4ADgAlACwALAAzAPL/AADj/wAABwAAACUA6v8WAPn/8v8HANT/+f/j/9v/4//j/9v/2//N/+P/zf+2/+P/zf/y/83/zf/j/9v/1P/b/9v/p/8AAM3/xf/5/8X/8v/b/9T/AAD5//L/DgDU/+P/4//U//L/1P/y/+r/8v/j//L/6v/q/+P/4//5/77/8v/N/9v/BwDj/+P/6v/F/83/FgDj/xYADgDq//n/1P8AAAAAAADy/wAA1P/N/+P/zf/j/9v/1P/j//n/1P/b//L/2//j//L/HQAdAAcAFgAdAAAAAAAdAA4AFgAsABYAQgAsAB0AZwAsACwAUQAzACwAOwAlACwAJQAOAB0A+f8dAAcALAA7AA4AUQAOACwADgDq/wAA8v8OANv/DgAdAAAAFgAAAPL/DgAOABYASgAlACwAMwAWACUAFgAdADMAFgAOADsAQgAzACwAJQAWACUAOwAdAB0AOwAsADMALAAsADsAFgAzACUAAAAzAPn/DgAlANv/JQAOAPL/BwDj/wcABwAdAB0AFgAWAAcAMwAAACwAMwD5/xYAAAAHAAcAHQAOAPn/DgAHAAAAAAAAAPn/BwAdAAAA+f/y//L/8v/j//L/4//y//n/8v/5//L/6v/j/xYA4/8AABYA4/8HANv/2//5//n/4/8OAPL/xf/5/9v/+f/5/wAAAADq/9v/6v/5/wAAAAD5/wcA+f8AAM3/+f/y/+P/6v/j/yUA6v8sAB0AJQAzAAAAOwAOAA4ABwAHAAAAFgAWACUAOwAdABYAAAAdAPn/FgAHAAAA4//j/yUA2//5/wAABwD5//L/6v/U//L/4/8HAOr/DgAHAAAADgD5/xYA6v/5/wcADgAHAA4AJQAHAA4AJQAzADMALAAlAB0AHQAdAB0AFgAsAEIAJQAdAB0AAADy//n/BwDq//L/AAD5//n/+f8HAOP/AAAAAPL/BwAWAA4A+f8OANT/2//5/+P/6v/j/+r/AADb/wAAAADN/xYA6v/5/wcAAAAlAPL/FgAAAPn/AAD5/wAAAAD5/+P/AADq/wAAJQDy/+r/+f/b//n/DgDy/w4A8v/q//n/+f/y/9v/+f/q/+r/8v/j/+r/AADy/wAADgDy/wcAFgAlABYAFgAdAAcADgAOAB0ABwAdACUAHQAzAB0AOwAzADMAMwAdAB0AFgAdAAcAMwAdAAcAFgAAACwADgAWAA4AAAAHAPn/AADy/w4A+f/5/wcA+f8AAPn/DgAdAA4AAAAAAPn/FgAHABYADgDq/wcA8v/y/+P/6v/q/+r/2//b//L/zf/5/8X/zf/F/6//6v/F/9T/zf/j/9T/xf/j/83/4//j/9v/2//U/8X/2//N/8X/1P/U/9v/vv/b/9T/1P/b//L/+f/b/wAA4/8AAPn/8v8OAAAA8v++/83/zf/N/+r/2//U/83/6v/N/+P/zf/U//L/vv/q/83/xf/b/8X/6v/F/8X/4//N/+P/AAD5/+r/4//F/+r/6v/j//n/2//y/+P/8v/y/+r/BwDq/wAA2//b/wAA2//j/83/6v/q/8X/8v/y/+P/DgAHAPL/DgD5//n/AADq//L/BwDj/+r/AADj//n/AAAHAB0AFgAAAAcA+f/q/+r/4//j/83/8v8AAOr/AAAOAOr/8v8WAOr/BwD5/yUAFgAHACwA+f8dAAAAJQAHAOr/DgDy/w4AAAAAAOr/6v/b/+r/AADy/wcA+f8WAAAADgAWAPL/BwAAAPn/BwAOAAAADgAWADMABwAOADMAHQA7ACwALAAOADMAJQAHADMABwAsACUALAA7AAcAMwA7AA4AFgAOAAcAAAAOABYADgAsAA4ABwAOAPn/BwAHAAAA8v8WABYABwAdAAcAFgD5/+r/DgD5//n/BwD5/+r/+f8lACUAMwAzAAcAFgAOACwAOwBCAFEALABRAEIAJQBCADsASgBCAEIAWQAsADsAWQA7ADMAOwAzAEoAYABKAGAAbwBKAEoALAAsACUAMwA7ACUAMwAWACUADgAHAB0ADgAWABYAFgAsACwALABRADsADgAsAA4ABwAdAB0ALAAlACUAOwAWACwAMwAOABYA+f8AAAAABwAWAA4ALAAOABYAFgAHAA4A8v8dAA4A+f8HAOr/AAAAADMAJQAlADMABwAzAB0AJQAlAPn/FgAAABYALAAHAB0ADgAAAA4AFgAWAPn/FgDy/xYADgDq/x0A1P8HAPn/AAAAAMX/FgDy/wAADgAWAOP/4/8lAOP/HQAdABYALAAdAB0AHQAWAB0ADgAAAB0A8v8HAPL/4/8WAOr/BwAAAPn/BwDy/wAAFgD5/+r/AADy//L/AAAHAOr/6v/5/wAAAAAOAAAA+f8AAOP/BwAAANv/+f/5/+P/+f8AAPL/HQAWABYADgDy//n/8v/y/+P/4//N/9T/2//U/+P/1P+2/8X/zf+2/83/xf/j/9v/6v/y/+P/BwDq//n/1P/F/8X/r//N/9v/2//q/+r/8v8OANT/8v/b/83/BwDy/+r/4//y/9T/4/8AAPL/8v/j/wAA8v8AAAcABwAAABYAAAAWAB0A1P8dAOP/1P/b/83/8v/U/9T/4//b/7b/2//b/9v/zf/j/wAAzf8AANv/6v/b/77/2/+2/7b/tv/N/8X/vv/U/9T/xf/F/9T/1P/y/wAABwDy/9v/2//U/77/zf/N/77/2//U/83/vv/U/+P/1P8AAOr/1P/j/+r/8v/5/wcA+f/N/+P/1P/N/+P/4//q/9T/2//b/+P/6v/b/wcAAAAAAPn/8v/5/+r/AAAAAPL/+f/b/9T/+f/y//L/+f/y//n/6v/5/w4Azf/b//n/vv/j/9v/2/8AANv/DgAWAAAAFgAWAB0ABwAHAB0A+f8OACUA6v8HAA4A+f8dABYAJQAWAPn/HQAOAOr/FgAHAA4AHQAOACwAAAAdAB0AAAAWAAAADgDq/+r/BwDy//n/+f8AAAcA+f8OABYA+f8dAAcA4//y/+P/8v/j//n/8v/q/xYA8v8OAPL/AAAWAA4ADgAAAAcA2/8dAAAA6v8WANv/8v/y/wcA2/8AAB0A6v8OAOr/+f/q/+r/BwD5/wcABwDy/wAA8v/y/wcA6v8HAPL/AAAHAOP/FgD5//L/8v/j/+P/4//5/+r/8v8HAA4A+f8OAAcA4/8HAPn/8v/5/+P/6v/b/9T/AADb/wcAHQDy/xYA6v8AAB0AFgAHAPn/AADb//n/DgDy/wcADgAOAA4AHQAWAA4ADgAOAB0AAAD5/wAAAAAlAPn/FgAlAPL/QgAlAAcAHQAHABYAFgAHABYAAAAAAA4AAAAWAAcADgAWADMAOwAWACwAFgAsABYALAAlAA4AOwAsAFkAJQBKAEIABwBKADMAMwAzACUADgAsABYABwAlAPn/HQAAAAcAFgAHAB0AJQAdAPn/DgAWAB0AJQAsAEIAQgA7ACwAMwAdAAAAHQAHAAAAJQAHACwALAAWADsAHQBCADsAMwA7AEoASgBKAEoALABRACUALAA7ABYAJQAlACwAHQAzACwALABCADsAJQAsACUAAAAlAAAA+f8dABYAHQAWAA4AHQAsAPL/6v/5/wcA6v/5/x0A2/8OAPn/AAAWANT/AADb/w4A8v/y/xYA2/8HANv/8v/j/+P/AADj//L/2/8HANv/8v8HAAcADgAHADsAAAAdAB0A+f/5//L/BwDq//n/6v/5//L/8v/5//n/DgDy/wcAFgAHAOP/6v/y/+P/1P/y/w4A4/8AABYA+f/b/wAABwDq/xYA6v/q/+r/4//5//n/FgAAACUABwDy/yUA8v8AAPn/6v/q//L/HQAOACUADgAlACwAFgA7ABYAMwAsAB0AFgAHABYABwAdABYAAAD5/wAA8v8AAAcADgAlADMAJQDy/wAA6v/5//L/DgAdAOr/DgAAAAcADgAdAAcA8v/y/+P/AAAHACUAHQAlAA4A+f8WAAcAAAAWABYA6v/j/+r/4//b//L/8v/q//L/8v8AANv/BwD5/wAA4//F/+P/tv/y//L/BwD5/wcADgDq/wAA1P/j/9T/AADb/9T/2/+n/83/4/8HANT/BwD5/9T/DgDy/wcA8v8WAPn/+f8HAPL/DgDy//L/8v8OAPn/+f8AAAcA6v/j/yUA6v8OAAcADgAHANT/8v/y//L/2/8AAAAAAAD5/wAA+f/5/wAA6v8OANT/+f8AANv/AADj/9v/2//j/9v/8v8AAOr/BwAOAPL/+f8AAOr/BwAAAAAA+f/q/+r/2//U/83/zf/b/+r/4//5/9T/6v/b/7b/1P+2//n/2//j/+P/zf/j/+P/4//N/9v/vv/j/9T/1P/j/83/1P++/8X/p//b/6//tv/b/77/6v/N/+P/1P++/8X/zf++/7b/zf+2/6f/vv+2/83/4//b/+P/1P/U/8X/xf/b/8X/vv++/9v/4//q/wAA+f/b/+r/8v/U/9T/1P/j/8X/4//j//L/AAAHADMADgAWAAAA+f8AAPL/+f8WAA4ABwAdAA4AFgDy/xYADgD5/w4AAAAOAA4AFgAdAB0A8v8HAAAA+f8OAPn/BwDq/w4AFgAAAA4ALAAAABYAMwAWAA4A4/8HAOr/BwAWABYALAAAABYABwAOAAAABwAOAA4ADgAHABYAAAA7ABYAJQAdAAcAMwAAAA4AHQAdACUAHQAWAAcA+f8WABYABwAOAAAAHQAdAB0AHQAOAA4AFgAsAB0AFgAWAAAAFgAWAAAAJQD5//n/HQAOAA4ALAAzAAAALAAdADMAJQD5/zMA8v/j/w4AHQAOACwAHQAHADsAFgA7ACwALAA7ABYASgBCACwALABRAEoAMwBRACwALAAdAA4AOwAHABYALAAdABYABwAWAA4AJQAsADMADgAAABYADgAOAOr/BwD5/wcAFgAHACUADgAlABYABwAOAPn/8v8WAAcA+f8dAOP/DgAOAAAAHQAHAB0ADgAOAA4ADgAsABYAFgAHABYALAAWAEIADgAHACUA8v8OAAcABwD5/wcAMwAAABYAHQAdACUADgAdAAAA8v8AAPL/+f8AAAcABwAHAB0ABwAOAB0A8v8AAPn/+f8AAAcAAADy/x0AAAAOABYA6v8dAAAABwAlAAAAFgAHAAcABwDy/wcABwAOAA4AAAAWAB0AJQAWAA4AFgAHABYA+f/q/w4ABwD5//L/AADq//L/1P/q/w4A1P8OAAcA6v8OAPL/AADy//L/DgDj/9T/4//5//L/8v8AAOr/6v/b/83/6v/U/9v/DgDb/9T/8v/F/9T/BwDq/9v/6v/N/9v/xf/U/+P/tv/j/+P/6v/j/+P/AADF//n/+f/j/xYA+f8OAB0ADgD5//n/6v/j/9v/zf/b/9v/BwAAAPL/AADj//n/AADy/wcAAADy/wcA+f/5/wAA6v8WAB0AAAAWAAAA8v8AABYADgAHABYA6v/5/+r/8v8HAPn/MwAOACUAMwAdACwAAAAlABYABwAOABYAFgAAACwABwDy/wcADgAWABYAFgAHAAAAAADq//n/BwDj/+r/1P/j/+P/xf/5//L/BwAAANT/4//U/9T/4//5//L/xf/j/+r/tv++/9v/zf+2/83/vv+v/83/6v/y/83/2//j/+r/AAAWABYA8v8HAOr/8v/j/9v/+f8AAAcAFgAlAAcABwD5/wcA8v8AAAcA2/8WAPn/BwD5/wAADgDy/x0A+f8lAA4AHQAsAAAALAAOABYADgAHAB0AJQAlAB0AHQAOAA4A+f8OABYAFgAdAB0ALAAdADMAMwAdABYAFgAOABYAHQAdACUAAAAAAA4ABwAzADMAJQAsAAcAFgAdAA4AFgAHAAcAFgAWAB0ADgAdAA4AAABCAAcABwBCAA4AJQAsAA4AFgAAANv/6v/5/w4AFgAAABYA8v8AAOP/4/8OAMX/AADj/9v/AADU//L/2//j/9T/zf/b/9v/4//y/wAA+f/5/wAA+f/y/+r/8v/y/+P/6v/y/83/1P/q//L/4//q//L/+f/5/+r/HQDy//L/DgDj/wAA8v/5/x0AAAAOABYABwAdABYAJQAOAB0AJQAAABYAHQAHAOr/DgAAAPL/MwAWABYAJQD5/x0ADgDq/wcAFgD5/wAALAAdABYADgDq/wAA8v/5/wcAAAAOABYAHQAlABYA+f8dABYAFgAdACUAJQAHAA4ADgAsABYAFgAOAAAABwAAAB0ABwAHAA4ABwD5/xYA4//b/w4A4/8OAPL/+f/5//L/DgDq/+r/2//y/+P/+f8HAPL/+f/q/+P/8v8AAOP/DgAOAAcAFgAWACUA+f8WAA4ABwAlABYAHQAOAA4ALAAzAB0AJQBCABYADgAlACwAJQAdADMA6v8OACUA8v9CADMAFgAdACUADgAAAAcAHQAWAAAALAAOAAcAFgD5//L/4//5/wAAAAAHAAAAAAAWAA4AFgAlACwAHQAOAB0AAAAHAAcADgD5/wAA6v/j/wAA6v/5/+r/8v/j//n/AADy/wcA1P/j/+P/2//F/83/4//q/9T/2//y/77/4//U//L/AADj/+r/6v/5/83/4//j/9T/xf/F/9v/vv/F/83/1P/F/+P/2//q//L/xf/b/9T/1P/U/+r/4//b//n/8v/b/9v/zf/j//n/6v8HAOr/2//y/9T/6v/5/8X/6v/q/83/4//b/+r/6v8AAM3/xf/j/6//xf++/77/4//N/9v/BwDj/9v/8v8HANT/4/8lAMX/6v/j/+r/6v/b//n/8v8OAOP/DgDq/9v/8v/q/wcA2/8OANv/2/8AAPL/6v8AAAcA+f8WANv/BwD5/+P/AAD5/w4ABwAHAAcAHQAHAPn/AAAOAPL/AAAHAOP/AAD5/wcAAADy/+r/6v/y/wcADgAWACUABwBCAB0AJQAzAAAAHQAWAAAA8v8dAAcADgAdABYAJQAAACwAMwAlAFEAJQA7AEoADgA7ACUAHQA7ACwAMwAlACwAJQA7AB0AHQAdAAcAFgDq/wcADgAOABYADgAWABYAFgAHAA4AAAD5/w4AHQAWACUABwAWADMABwAWABYAFgAOACUAFgAWAB0AAAAOAPn/DgAlAOr/FgAWAPL/LAAOAAAAQgAOAA4AAADy/x0A+f8WABYADgAWAAAAFgAOAAcAHQAWABYADgAdAA4AFgAHAPL/AADy/wcA8v/U/+P/2//F/+P/2//b//L/4//q/77/2//j/9T/zf++/83/xf/j/9T/6v/b/9v/AAAHAPL/AAAAAL7/DgDb/wAADgDq/xYA1P8OAPn/2//q//L/6v/q/9v/4/8HAOr/FgDq/wAA4//N/w4A4//5/83/8v8HAPL/FgAOAAAAHQD5/+P/HQDj//n/HQD5/wAAAAAHAAAA8v8AAPL/8v8OAPL/BwAAAPn/DgAWAAAA+f/5/83/+f/N/9T/BwDj/wAA+f8AAOr/6v8WAPn/6v8HANv/6v8HAOr/BwAHAA4AAAAAAOP/+f8OAPL/BwDy/wAA+f8WABYAHQAWAAAAHQAOACUA+f8sAA4AHQBKAAcAQgAOABYALAAzADsASgBCAEIASgAWAEoAOwBnADsALABnAAcALABRADMAMwBRADsAQgBCACwAQgAWADMAJQAzADMAHQAsACUAOwAsADMALAAsAB0AOwAzAB0AQgAdAFEAQgAsACwADgAdAA4ABwAWABYABwAzAB0AFgAsAB0AHQAWABYA8v8OAPn/8v8OAOP/BwD5//n/8v/5//L/4/8AAPn/4//q/wAAzf/q/+P/4//j/77/6v/F/+P/2//N//n/vv/j/+P/xf/b/83/zf/b/9T/xf/j/9T/zf/5/9v/zf/b/+P/2//j/9v/xf/y/+P/8v/j/8X/8v/b/9T/1P/j/9v/2/8AAL7/4//y/9v/BwAHAPn/AADj//L/4//j/xYA+f8HAA4ABwDy/w4AJQAdADMADgAdAPL/FgAAAOr/JQDy/wcAHQAdAAcABwDq/wAAAADj/xYAzf8AAOr/4/8dAPn/BwDy/wcA6v/q//n/AADq//L/4//U/+P/vv8AANT/xf/j/9v/+f/U//L/vv++/+r/zf/j/9T/zf/j/+P/4/8OAOP/BwD5/9T/4//N/+r/xf/F/6f/p/++/7b/2//N/83/tv/N/77/tv/b/8X/8v/j/83/4//N/9v/+f/q/w4A8v/5/ywA8v8lAPL/BwAzAPn/HQDy/w4A6v/j/w4A2/8AAPn/BwAOAA4ADgAHAB0ADgAOAA4ADgAWAAcALAAHAA4AHQDU/w4ABwDb/wAABwAdAAcAHQAHAAcALAAdACwAFgAdADMAHQBKAB0A+f8dAPL/BwD5/w4AMwDy/xYABwAOAAcAHQAdAAcAHQD5/yUA+f/q//n/AAAAAAAABwDb/+r/6v/5//n/BwAAAAcAFgD5/xYA8v8HAAAADgAAAAcAHQAHAB0ADgAWAAcA8v/q/xYA8v8OAA4A1P8WAPL/BwDb/wcAAAAAADMA1P8OAOP/FgAAAPn/LADy/ywABwAHAPL/4//5/wcAHQAOAAcADgAHAOP/FgD5//L/JQAHAA4AJQAAABYAQgAHABYABwAHAB0AAAA7ABYA8v8dAA4ALAAsACUAUQAdAEIAQgAlABYADgA7AAcAJQAWABYAHQAHAEIABwAOABYA+f8HANv/8v/q/+r/+f8AAB0AHQBKAEoABwAlAAcAAAAHABYAAADq/wcAAAAAAOP/AAD5/9v/8v/5/+P/1P/y/9T/+f/j//L/DgD5/wAA6v8OAOP/+f/5/+r/+f/j//n/6v8HAOP/4//y/+P/+f/U/w4ADgAOAAcA4/8WANv/FgAlAOP/BwDq//L/6v8OAAcA8v8lAOr/FgAlAPL/AAAHAPn/+f8HAAAAAADy/wAA4/8AAOP/4//y/8X/+f/U//L/AADj/wAA6v8HAAcA4//5//L/xf/b/+P/4//5/wAAFgAAAPL/FgD5/9T/FgDy/xYABwDb/wcA8v8AAOr/JQAAAPn/BwDj/wcA2//j/wAABwDj/w4A8v/5/w4A6v8lAPL/FgAWAAcALAAOAA4ADgAdAAAAFgAHAPn/FgDy/xYAHQAOACwAFgAWAB0AFgAHAPn/FgAHACwADgAsACUA6v8sAPL/DgAWABYAFgDj/w4AAAAHAPn/AAAHAPL/AAAHAOr/BwAAAPn/HQDj/xYA+f/y/w4ABwAHAPn/DgDq/wAA4/8AAAAAzf8AAPn/AADq/+r/4//q//n/6v/q/+P/AADq/wAAAADU/+P/6v/b/+r/+f/y/+P/8v8WAPn/+f/q/wAABwAAABYA6v8AAA4A8v8WAA4A8v8OAOr/FgAOAOr/LAAHACwALAAsAEIAJQBRACUAMwAsAAcAOwAOAAcAHQAOADMAMwAWACwAHQDq/wAAAADq/wcA8v/5/wcA4//q//L/BwDj/+r/6v/U/+r/8v/U/9v/2//U/+P/2//b/+r/6v/N/+r/4//b//L/vv/q/+r/6v8HAAAA6v/j/wcAAAAdAB0AFgAHAAAA+f/5/ywAMwBCACUAMwAsABYAMwAdADsALAAsACwADgBCAB0AFgBKAA4AHQAdAPL/DgAHACwAJQAdAB0ABwAzACwALAAdABYABwAAABYAFgAWAA4AMwAlAAcABwAAAB0AAAAWABYA+f8AAOr/BwDj/83/BwDb/+r/AADb/9T/6v/j/+r/8v/q/wAA6v/y/+r/6v8AAOP/AAD5/w4A+f/j/w4A4//y/83/4/8AAOP/AAD5/w4AAAAHAPn/2//5/wAAFgAdABYAAAAlACUAFgA7ACwADgAHACwAFgAlAB0AFgAlAB0AOwAdAEIAMwAOABYA8v8dAAcAMwBRACwAUQAzACUAMwAzADMAMwAsACwAFgAOACUAJQAWAAAAHQAHAAAAHQDy/wAA+f/j/w4A8v/5/w4A8v8AAOP/AAAAANv/HQD5//L/AADy/wAA2//q//n/2//5/+r/zf/5/9v/2//y/+P/8v/5//n/2//b/9T/2//b/9T/2//F/9T/2//q/9v/2//y//L/AADq/+r/8v/j/+r/1P/U/77/1P/b/7b/4//N/83/2//j//L/1P/5/+P/6v/j/83/1P/U/83/zf/j/8X/+f/q//n/DgDF/wAA6v/5/w4ADgAWAA4ADgD5/x0AFgA7AA4ABwAdAAAAJQD5/xYAHQAlACUABwAHAOP/BwDj/wcAFgDF//L/zf/b//n/2/8AAPL/+f/5//n/6v/F/83/4/++/83/4//F/+P/xf/b//L/1P/q/9T/1P/b/+P/4//q/+r/8v/b/9T/HQDU/9v/BwDq//n/6v8OAA4A6v8OAB0ABwAHAAAABwDy/wAAAADy//L/+f8HAOP/AADj/+P/4//F/+r/4/8AAPL/BwDj/+P/8v/N//L/1P/5//L/4//5//L/BwDq/wAABwDU/+r/4//y/ywAAAAAAAAA2//q//L/DgAHAAAABwAdABYAFgAdABYAHQAsADsAHQAdACUAJQAlABYAJQAsAAAAJQAWAPL/MwAWADMAFgAdADMABwAlABYAHQAHACwAHQAOABYAAAAsAB0AMwAWABYAFgAAAPn/BwAHAPn/HQAHAAAA+f/j/9v/8v++//L/DgDF//n/4//5//L/AAAAAPL/BwDq/wAA+f8dAPn/FgAHAAcAMwAOADMA+f8WACUADgAsAEIADgAAAB0A4/8sAB0ADgAlAB0AJQBCADMABwAsACUAHQAlACwA+f8sACwA+f87AAcADgAWABYABwDy/wAA6v/y//n/BwDq/+r/BwD5/wAAAADq/wAA+f/U/+r/8v/j/+P/6v/q//n/BwAHAPL/2//y/9v/8v8HAOP/+f/5//L/DgDq/wcABwDq/w4A8v8HAPL/6v8HAOP/2//5//n/+f8AAAAAHQDq/wAAFgD5/wcA+f8HANT/+f/U/9T/DgDq/wcA8v8HAPL/AAAOAOP/AAD5/+r/6v8AAPL/8v/5/wcA+f/b/w4ABwAWACUADgAOAAAAJQAdABYALAAOAA4AHQAOAAAAJQAOAB0ALADy/w4AAAAAACUAJQAlABYAJQAdACUALAAdAPn/LAA7AAAAHQAOAAAADgAHABYADgAAAAAABwAWACUAFgAsACwALAAdABYABwDy//n/AAD5//n/BwDq/+r/1P/j//n/4//5/+r/6v/j//n/4//y//n/4//5/+P/6v/j/9v/2//j/9v/4//y/+r/8v/j//n/8v/5/wcA6v/y/9T/vv/j/+r/6v/5/+P/2//b/9T/6v/j/+r/AAAOAAcAAAD5/+P/+f8WAOr/JQAWAAAAHQDq/zsABwAAACUAFgAdAPn/HQAAAAAADgAAAB0ADgD5/wcAHQAHABYAHQAHAAAAFgD5//n/DgDy/wAA+f/5/9v/6v8AAAAAAAAAACUA+f/5/w4AHQAWAAAAAADq/+P/DgAsAA4ADgAOAPL/+f8dAAAAHQAlAOr/DgDy//L/6v8AAB0ADgAdAB0AHQAAAB0A8v8HAAAAzf8HANv/1P/b/9v/zf++//L/zf/b/+P/1P/j/8X/6v/y/83/4//U/8X/1P++/9v/2//F/+P/+f/q/8X/xf/b/9v/2//q/+r/8v/y//L/DgD5//n/+f/5/wAA8v8OAA4ABwAAABYAAAAHAB0ABwAlABYAAAD5/wcA+f/q//L/6v8AAOP/DgAHABYAMwAHABYAAAAHAAcAFgAHAAcABwAAABYABwAsAA4AJQAdABYAFgAAACwA4/8dABYA4/8dAOP/DgAAAOP/+f/5/x0AHQAHAOr/BwAOAPL/AADy//L/+f/y//L/2//y/9T/4/8OAOP/8v/y/9v/2//q/wcA+f8HAB0A4//q/wcA6v/5//n/DgAWAPn/FgAAAPn/+f8HANv/1P8AAOP/LAAOAAAADgDy/w4AAAAlAB0AFgAdAAcADgAdACUABwAdAPL/DgAWAAcAJQD5/w4ADgAHAAcABwAWAPL/DgAWAPn/AAAWAPL/DgAdAPL/LAAHACUAHQDq/x0A+f8WAB0AJQAsAAcADgAOAB0AFgAdABYAFgAOAAAABwAAAA4A4/8OAA4A8v8WAAAAFgAAABYAFgAWAB0AFgAlAAcAFgAWAB0ABwAOADMAAAAOAB0ADgAlACUA2/8AAA4ABwAOAAcALAAAACUAJQAHAAAA6v8AAAAA+f/y/xYA+f8WACwAAAAsAA4ADgAWAA4ALAAWAPn/DgAHAAAAJQAWACUAMwAOAB0ADgDq/yUAAAAAAB0A4/8lAPL/+f8zAOr/DgAzABYALAAsAAcABwAWABYAHQAlAPn/FgAOAOP/HQAHAAAAJQAHAB0A+f/q/w4AHQAdABYAHQAlABYAJQAsAPn/DgAOAPL/AADq/wcABwAdABYA8v8dAPn/AAAAAPL/+f/b/x0AAADy/x0A2/8HAAAA2/8HAAAAFgAWAA4AJQD5/+P/8v/j//L/8v8AABYA8v8HAAcABwAOAA4AJQAAAAAAAADj/9T/8v/y/9v/AADq//n/+f/5/xYA+f8AAPn/6v/j/+P/+f8HAAcABwAAAAcA8v/5/yUABwAOAAAADgAHAPn/FgD5/wcA6v/y/9v/4//5/8X/8v/q/wAABwAOAAAA4//q/9v/6v/b//n/6v/U/+r/4//j/+P/1P++/9v/vv/U/+r/4/8HAOr/DgDq//L/FgDb//n/4//q/83/2/8AAM3/AADy/wAABwDj//L/6v8AAOr/AAD5/+r/8v/j/w4A1P/q/wcA1P/j/9T/AAD5/9v/4//F/9T/zf/j/9v/6v/5/9T/8v/b/8X/1P/j/9T/2//y/7b/tv/N/83/zf/j/wAA+f/b/9T/BwDq/wAA+f/j//n/2//y/wAA8v/y/w4ABwAOAAAADgAWAPL/DgAAABYA+f/5/wAA6v8HAA4AFgAWAB0AFgAlAPL/DgAHAM3/8v/F/+r/8v/b/9v/4//N/83/6v/F/9T/zf8AAOP/xf/5/77/4//b/8X/zf/N/9v/zf/N/+P/4//y/wAA+f/j/+r/+f/j/wcA+f/y/wAA6v8HANT/BwAOAPL/FgDq/w4A+f8HAA4A6v/5/9T/4//U//L/4//F//n/2//N/83/4//b/+P/4//b/+r/4/8AAOr/8v/y//L/AAD5/wAA2/8HAAAA+f8lABYADgAOACUAAABCADMAMwA7ABYAQgAlAFEAOwAOADMALAAsACwAMwAdABYALAAzADMAJQAAABYABwAHADsAAAAOACUABwAlAAcA6v8WAAcA6v8dAAcAJQAsAPn/JQD5//n/FgAHAB0ADgAWACwABwAdAB0A+f8dAAAA+f8lAA4ALABZAB0ALAA7ACUAOwAdABYABwAWABYAAAAzAAAAJQAWAA4AJQDq/w4A+f8HABYAHQAWABYALAAAACUAAAAHAB0AAAAOAPL/DgAAAOr/AAAAAAcAHQAOAB0ADgD5/x0A2/8AAA4ABwAdAPn/JQAAAB0AMwAOACUA8v/5/wAABwAOAB0AMwAAAA4ABwAAAPn/6v8AAPn/+f8HAAcABwAlAAAAJQAsAAcALAAHAA4AFgAWAB0ADgAlAB0ABwAHAAcA+f8dAA4AAAAHAAcADgAOADMA+f/5/wcA6v8HAPn/BwAHAAcABwAHAA4AAAAHAPn/BwAWAPn/JQAsAAcADgAWAA4ABwAAANT/8v/q//L/DgAHACUA4/8WAAcA8v8WAOP/JQAOABYAHQD5/xYA+f/y/xYAAADj/w4ADgDy/wcABwD5//n/FgAAAPL/HQDy/+r/BwDU/wcABwAHAB0ADgAdAAcADgAHAB0ABwAAABYAFgAsAAAAMwAlABYAOwAlABYADgA7ABYADgAWAA4AHQAAACUABwAOACUAFgAzAAcALAA7AB0ALAAOACUA+f/5/xYAFgAWACUAFgAWAAAAAAAsAOr/HQAHAOP/JQAHAB0AFgAWAAcAFgAdABYAFgAAAB0ADgAHAB0AHQD5/x0AFgAOABYA+f8WAOP/AADy/wcAFgAAAB0A8v8WAPL/FgAHAOr/HQDy/w4ABwAHAPn/2//5/+r/4//5/9v/1P/5/+P/6v/y/9v/4//j/+P/4/++/7b/zf/U/+P/1P/q/8X/xf/y/77/1P/q/8X/1P/N/7b/xf/N/83/tv/F/83/p//U/+r/vv/N/9v/p//F/6//tv/5/77/4//j/83/8v++/9v/zf/F//L/zf/5/wcA+f/y//L/2//b/w4A4/8OAPn/2//5/+r/+f/j//n/AADy/9T/+f/5//n/LAD5/w4AAAD5//n/+f8HAAcADgAAAPL/1P/5//n/DgAWAAAADgDy//n/6v/y/+r/8v/5/9T/zf/q/+r/xf/q/+r/1P/j//L/2//j/+P/r//b//L/p//N//L/zf/b/77/xf++/7b/4//F/+P/zf+2/9v/zf++/77/4/+v/8X/4/+v/9T/zf/N/8X/xf/q/9v/4/8AAPn/1P/U//n/8v/y/wcA+f8AABYA6v8AAA4AAAAWAAAAHQAlACwAHQAWADMABwAWAAAA+f8HAB0ADgD5/xYAAAAzAAcADgAdAPn/HQD5/wAAFgAWABYALAAlAPL/BwAHAA4ALAAOADMAHQDy/zsABwAWADMAHQAlABYALAAWABYADgAAAAAAHQAsACUAOwAdADMAJQAAAB0AMwAdACUAMwAdACUADgA7AB0ADgAWAA4AMwAHACUAJQAWAA4AFgAsADMAQgAdACwAJQAlAB0ABwAlACUALAAsAB0AHQAzAEIAJQAzADsAFgAOADMAMwAOAB0AFgAOABYAAABKADMAJQAdABYAHQD5/zMAHQAWABYA+f8OAAcAHQAdACwADgAOABYAAAAlAPn/6v8HAPn/AAD5/+r/8v/q/wcA6v/y/xYAzf8OAPL/+f8sAPL/BwAAAA4A6v8HAB0A+f8OAPn/DgD5/wAABwDy/wAAAADy//n/DgDy/wcABwDq/wAA4//y//L/zf8AANv/2//q/83/+f/j//n/HQDy/+P/+f8AAAcADgD5/wcABwAAAAcA4//y//n/8v/y/wcADgAHAAAABwD5/+r/HQAWAPL/+f8AAAcADgAAAA4ABwDb//L/4//q/+r/AAAAANT/AADU/77/AADj//L/8v/N/9v/2//b/9v/8v/q/9T/8v8HABYA4//5//L/2/8AAPL/AADq/wcAAADb/wcA4/8OAAcA8v8dAPn/FgAHABYAFgD5/w4A8v8AAAAAAAAAAPn/AADb/wcABwDb/+P/6v/j/+r/8v/y/+P/1P8HAPL/AAAsAPn/DgAHAAcAAADq/wcAAAAHAAcAFgAHAOP/FgDy/+r/FgAHABYABwAOAPn/DgAlABYASgAlACUALAA7AB0ADgAsAAAADgAdACwAHQAdACUAFgBCAA4ALAAlAAcAQgAdADMAMwAlACwALAAOACUAFgAAADMA8v8OAAAADgA7APn/JQAOAOP/BwAHANT/4//U/83/4/++/9v/2//j/+r/6v/j/8X/xf++/9T/zf/j/83/2//b/7b/2//U/+P/8v/N/77/xf+v/83/2//F/9T/xf/U/+P/1P/q//n/zf/5/9v/1P/q/7b/6v/U/9v/4/++/83/1P++/+P/AACn/+r/2//F//n/2//y/+P/8v/j/wAAFgD5/wAA4/8AABYA6v8dAA4A2/8dAPn/+f/y/+r/BwDq/w4A+f8AAAcABwAOAPn/DgDy/xYABwD5/ywA8v8AADMABwAAAB0ADgAAACwADgAAACUAFgAWABYAFgAWACwAMwAHACwALAAWAA4ALAAdAAcAHQAWADMAJQAzADMAFgAzAB0AFgAzAB0AJQAlAAcAHQAOAPn/AAAOAA4AHQAWAPn/HQAlABYAHQAOABYALAD5/w4AHQDq/wAA+f8lABYAMwAsABYALAAOABYADgAlABYALAAlABYAMwAlAB0AFgAWAA4ABwDy/0IAHQAHAEoAHQBCABYAFgAlABYADgAdACwADgAzAA4ALAAdABYAFgD5/zMA+f8OABYAAAAHAB0ALAAWABYADgAWAAcADgAdACUAAAAsACUA+f87AAAABwAHAB0AHQAWACUA+f87AB0AOwAsAB0AJQAOADMA8v8sAA4AHQBKAAAAHQAHABYABwAHAA4AAAAOAAcAHQAWABYAJQAWAAcALAAAAA4ADgDj/yUABwD5/wcADgDj/+P/BwDU//L/4//5//n/+f8OAPn/DgDq/wAAAADj/wAABwAAAAcA+f8WAA4A+f8dAPn/+f8HAPn/6v8AAA4A4//5//L/4/8AAOr/4//q//L/2//j/wAA2//y//L/xf8WAPL/2/8HAOP/6v/b/9T/1P/q/9T/xf/j/7b/zf/U/77/8v/j/+P/AADU/9T/xf/N/9v/1P/j/83/1P/U/9T/1P/q/9v/2/8OAOP/6v/5/9v/1P/q/8X/1P/y/8X/6v/b/7b/zf/j/8X/8v/y/7b/8v/N/8X/4//N/83/4//b/9T/2//U/+P/xf/j/+P/1P/y//n/+f/y/ywA+f/5/wAA2//q/83/2//U//L/1P/b/+r/6v/q/+r/HQDy/w4A+f/5/wAAAAAOAPn/HQDy/w4ADgAHABYA8v8dAAcABwAdAAcABwD5//n/DgAAAA4ADgDj/x0A4//N/wAA4/8AANT/DgAAAM3/HQAAAOP/8v/y/9T/4//5/+P/8v/q//n/AAAOAAAA2/8AAOr/6v/y/w4AFgDj//n/BwAHAAcAAADy/+P/AAAAAAAAFgAWAAcADgAWACUABwAOADMAFgAOAB0AFgD5/wcADgAAAA4ADgAWAA4AFgAAAPn/AAD5/wAAHQAOAPL/DgAAAAcAAADy/wAABwAAAOr/4//j//n/4/8AAA4AAAAHAAcAFgDj/x0AFgAWACwAAAAlAPn/DgAOAOr/HQD5//n/BwDq/9v/+f/y/9v/8v/q/wAABwDq//n/AAAAAAcAHQAHAA4ABwAWADMAHQAzAAAAFgAlAAcAMwAlADsAJQAdAA4AAAAWAA4AFgAHAAcADgAOABYAFgAOAB0AJQAWACwAFgAWAB0ABwAlADsADgAHACwAHQAHAPn/AADq//n/HQAOAAcAAAAAAPn/8v8HAAAA+f8lAAcA+f8WAPn/8v8OAAAA+f8dAAcABwDq/+P/4//q/wcA6v8AAAcA+f8AAA4A+f8AAAcA+f8HAOr/8v/5/+r/zf/y/wcAzf/b/+r/4//F/+P/1P/F//L/4//q//L/8v/U/wAADgDy/wcADgDq/9T/6v/q/+r/+f/5//L/8v/U//n/2//j/w4Axf/y/9T/6v8AANT/8v8OAB0AAAAdAPn/+f8lAPL/BwAAAPL/FgAOAAcAHQAOAB0AMwAHAAcAFgAHACUAJQAWADMAFgAlACwADgAlACwAHQAOABYALAAOAAAABwDy//n/AADq/w4AAADq//L/AAAHABYAJQAWAOr/AAAAAOr/HQAWAA4ABwAAACwAAAAHACUA6v/5/w4AAAAWAPn/+f/5/+r/AAD5/wAADgAOAA4AHQDj/wAABwDj/x0ADgAlAA4AAAAHAPL/FgAAAA4ADgAAAB0ADgAOACUAJQAWACwAMwAdAPn/FgAdAAcAFgAlACUABwAlACUA+f8lABYAHQAlAA4AOwAHABYAFgAHADMALABCADMAQgAWAB0ASgAHAB0AAAAdACwAAAAOAPn/HQAsAAcALAAlACUAQgAsADMAHQA7ACUABwAdAOr/HQAAAPn/FgDy//n/4//5/wAADgAOAAcABwAOABYAFgAlABYAJQAAAPn/BwDy/wAADgAdAA4AHQAOAB0AHQDy/x0AAADq//n/6v8AAOP/6v8HAPn/DgDb/9v/1P+2/+P/xf/y//L/2//5//n/AADU/+r/2//U//n/xf/q/+r/zf/q/+P/6v/N/9T/4//b/+P/r//q/8X/r//y/83/AADj/+P/1P/N/w4Avv/U/9v/vv/y/9v/4//b/6D/xf/b/77/xf/U/83/r//F/9T/tv/q/8X/1P/q/77/zf+n/6//zf/F/77/zf+2/6f/xf/N/+P/vv++/9T/oP+n/77/xf++/8X/1P/F/83/2//b/77/xf/b/9v/zf/b/83/xf/F/83/6v++/77/8v/N/83/4//F/9v/1P/U/+P/2//q/+P/BwD5/+r/8v/b/+r/2//j/+r/6v8AAPn/FgAWAOP/FgAHAAAAMwAOADMA8v8WACwABwAdAPn/HQAAAAAAFgAlAB0AMwBKACwAWQAzAEIAMwAOACwABwAOACUAHQAWACwAFgAlAB0AFgAlACUAHQAdACUADgAWACUAJQAlAB0ADgAdAB0AJQAsAA4AJQAlAB0A8v8OAB0AHQAsABYAOwAAAFEASgAzAEIAFgBKADsAQgBCAGAALABRAEoADgBgAB0AOwAzACwASgBCAGAAMwAsABYABwAsACUAHQA7AA4ADgAAABYAJQAdAFkAFgAlABYAHQAlAA4ALAAOACUAAAD5/wcADgAdADsALAA7ADMAJQBCAA4ALAAdACwABwD5/wcA4/8WAPn/BwAOAA4ADgAOAAcABwAdAAAAJQAAAAcAJQAOACUADgAdAA4A8v/5/zMAFgAHABYABwAAAA4AAADy/wAA1P/5/9v/6v8OAOP/HQAHAPn/AAD5//n/8v/q//L/+f/y//n/AADy/wcAJQDq/wcAFgDy/w4A+f/5/wcA+f8HAA4A8v8dAPn/AAAWAOr/QgDy/x0ALADj/0oAFgAsABYADgAWAAAALAAAACUAJQAsACUABwAsAAAAJQAsABYAHQAWACUAJQBKAB0AFgAlAAAAJQAAACUAJQDy/zMA+f8WACwAFgBRAB0ALAAlABYAOwAdABYABwAHAAcABwAAACwAFgAHACwABwAlACwADgAlADsABwAOACUAFgAsABYAFgD5/wAADgAAABYABwAAAA4ABwAOAA4A6v8dAAcAAAAdANv/BwAAANT/+f8AAOP/BwAOAPn/+f/y//L/4/8AAOr/BwDq/83/8v/j/wcAzf/q/83/2/8OAM3/DgDq/9v/BwDy/9T/4//U/77/tv+v/+P/vv/F//L/vv/F//L/xf/y//n/zf/y/9T/zf/U/+r/xf/j/83/vv/y/83/2/+Z/7b/r/+2//L/vv/b/9T/tv/F/9v/r//U/9T/xf/b/6f/6v/q/9T/4//b/9T/4//N/9T/+f/N/9v/zf/b//L/xf/j//L/2//y/+P/1P/5/9v/BwAHAOP/2//N/+P/1P/y/9v/2//b//n/6v/y/wAA4/8HAPL/DgDy//n/8v/5/zMAAAAOAAAAAAD5//n/6v/j/9v/tv/b/9T/xf+2/8X/tv+v/8X/6v/N/8X/6v++/83/vv/b//L/zf/y//L/+f/y/wAA+f/5/+r/2//5/9v/8v/q/+r/6v/j/+r/xf/y/wAA8v8lAAAADgAAAOP/BwD5/wAA4//5//n/6v/5/+P/AADq//n/8v8HAA4A+f8WAAcADgDy/xYADgDb//L/2//q/83/2//y/wAAFgDy/xYADgAHADsAOwAdACUAJQAHACUAFgAWACUA8v8dADMAOwAdAA4AMwAWAA4ADgAdABYADgA7ACUABwAlAB0ALAAsAPL/JQD5/wAAJQAAACUA6v/y/wcAAAAHAPn/FgAHAAAA+f/5/wcA+f8AAPL/FgD5/xYAFgDN/w4A4//q//L/2/8HAOP/+f8HAPL/8v8OAPn/FgAWAOP/FgDU/9T/+f/U/9T/4//y//L/+f8HAPn/6v8HAAAAFgAWAAAAHQD5/+r/2//y//L/+f8OAAAA+f8WACUAAAAHAA4AJQAOAAcAHQAHAPL/DgAOAPL/HQAOACwAHQAWAEoAFgAsACwALAA7ADMAHQA7ADsAOwBKADsAOwAHADsAHQAWACwA8v8lAB0AAAAWAAAADgAdAPL/DgAAAAcABwAAAA4AAAAOAA4ADgDy/ywAHQAOADMA+f8lAB0AHQD5/+r/HQAHAAcAAAAOAPn/4/8AAAAA8v8HAB0ABwD5/w4A+f8AACwADgAdAAAAFgAWAA4ABwD5/zMA+f8dAA4A4/8AAB0AHQAOAB0ADgBCAA4AHQAdAPn/JQAWACUABwAOAAAA4//5/+P/6v8HANv/6v8AAOr/HQAAAPn/+f/5/+P/+f8WAOr/DgAOAA4AFgAWACUAAAAAABYA6v/q/x0A6v8OACUA6v8AAPn/AAAWAAcADgAlAB0AAAAdAAAAzf8HAPn/+f/5/xYABwAHACUA4/8WAPL/1P/5//L/FgDy/9v/+f/q/+r/AADF/yUADgD5/yUA8v8lAPL/LAAdADMAOwDy/0IA8v8OAA4A+f8OAOP/FgAOAPL/HQAOANv/AAD5//n/HQAOAA4AJQAAAAcAHQAlAB0A+f8lAAAABwAOAAAA+f/U//n/+f8HAAAADgD5/wcAJQAAABYAAAAAAAAAFgDy//L/DgDy/w4A6v/y//L/AAAHAPL/BwDy/9v/+f/q//L/+f/U/+r/4//y//n/BwDy/9T/6v/U//L/zf/j/wAA2//j//n/8v/b/+r/+f/y/9v/DgD5/yUADgDy/ywA8v8WAOP/AADj/8X/DgDN/wcA+f/5/wAAzf8AAPn/6v8WAAcADgAAAAcAJQAHADsADgAdABYADgAsAPL/HQDj/x0AFgDq/zMABwA7APL/FgAOANv/HQDb/w4A4//b/9T/zf/y/77/8v/j/wAA8v/5/xYA1P8AAOP/8v/b/77/1P/U//n/6v/y/9T/4/8OAPL/8v8HAPn/6v/j//n/AADj//L/1P/q/+r/4//q/8X/AADq/+r/2//U//n/2//q/+r/8v/b/+P/8v/q//L/6v/b/+r/4//j/w4A8v8HAAAAAAAdAPL/BwAAAPn/8v8AAAcAFgD5/xYAMwDq/zMA+f/5/x0A+f8WAAAAHQAlAAcAAAAdAPL/FgAsAPn/JQAAAB0ABwAOAB0ADgAWAAcALAAHAA4ADgAAACUADgAOACwABwAAABYA8v9RACwADgA7APL/HQAAAAcAFgAHAA4AAAAWAAAAAAAAACUABwAHADMA8v8WAAcABwAHAAAASgAOAPL/FgAHAPn/DgAHABYAJQAdADsALAAsACwADgAsACUAAAAdACUAJQAdABYAHQAOAA4ADgAsABYAAAAlAA4AFgAWAA4AHQAWAAcA+f8HAPL/AAAWAAcAHQAWACUAAAAAAA4A4/8OAA4AFgAHAAcAFgAOACwA+f8OAAAAAAAdANv/BwAAAOr/+f/y/wcA6v8WABYABwAlABYA8v/y//n/6v8OAPn/AAAdAOP/AAAHANT/zf/j//n/2//j//L/zf/j/83/4//q/9T/BwDj/wAA6v/y/w4A2//5/+P/+f/5/9v/+f/q/+r/1P/b/+P/6v/5/wcABwDy/w4A6v8AAPn/6v8lABYAJQAsABYAAADq//n/8v/j//L/BwAHAPn/BwDj/+r/JQD5/+P/+f/q/x0AJQAAAA4A+f/y/w4AFgAOAA4AAAD5/+r/BwDq/wAAHQDj/wcA8v/y//n/+f8OAAcAHQD5/xYAAAD5/wcA2/8AAAAADgAHAAcA+f/q/9v/1P/j/77/zf++//L/1P/F/+r/oP/b/9v/zf/N/6f/4/+2/77/1P/U/+r/2//j/+P/1P++/9v/2//F/9T/vv/j/+r/AAAWAOr/AADj/83/1P/j/+r/zf/y/+P/6v/b/8X/vv++/83/1P/U/83/+f/U/83/4//U/83/zf/U/9T/8v/N/+r/DgDq/+r/6v8AAPL/AAAOAPn/BwAOACUABwDj/wAA+f/5/wcA1P/b/+P/zf/5//L/6v/5/wAAAAAWAA4A+f8AANv/AADy//n/HQD5/ywAAADq/x0A+f/y/wcABwDb//L/+f/y/wcA8v8OAAcA8v/y//L/BwAHAA4AFgAsAB0AFgBCAAcABwA7ACwAMwAdACwAJQAOAB0ADgAlACwADgAdACwAFgD5/x0ALAAOACUAJQAWACwADgAAAA4AHQAsAA4ABwAlAB0AFgBCAB0AJQAWABYAMwAHADMAHQAdADMAFgAlACUAJQAlACUAFgAdACwAHQAWADsALAAzAEIAFgA7AB0ALABKACUASgA7AAcALAAlAAcALAAlACwAFgAWADMADgA7AB0ABwA7AAcADgAlAA4AOwAdACUAOwAOACUA8v8WAAcAAAAHAA4AHQDq/0IAAAAOACwABwAdAA4AUQAdABYADgAlACwA+f8lAAcABwAHACwAFgD5/yUA8v/5/wcA8v/5//n/+f/5/+r/BwAWAA4ADgAHAAAADgD5/+P/HQAWAA4ADgAdAAcA8v8dANT/4//b/9v/AADN//L/6v/y/wAA+f/b/9T/BwD5//n/AADq/wcADgDy/wAA+f/y/xYAAAAAAPn/6v/y/+P/8v/b/9T/+f/b//L/DgDj//n/vv/N/+r/vv/j/83/2//U/9T/6v/j/9v/1P/q/83/2//j/+r/AADq//L/DgDy/wcALAD5/w4A+f8AAB0A8v8OAPn/+f/y/+r/AADy/w4AFgDy/w4AFgAHACUA2//5/yUAAAAOAAAABwAOAB0AAAAAABYA8v8WAPn/AAAWAPL/FgD5//L/FgAHAAAADgAAAPL/AADq/wAAAADj/wAABwAOAPn/6v/5/wcA8v8AABYA+f8dABYAMwAWAAAAHQAOACUABwAOAAcABwAOABYAHQAWADMABwAdAAcAHQAAANT/FgDq/+r/AAAAAAAADgAdAB0AHQAOACUABwDy//L/6v/q/9T/1P8HAAAA6v8AAOP/8v8OAA4A+f8OAAcA+f8sAA4ADgAdAA4AFgAlABYAFgAOABYAFgAWABYABwD5//n/BwDq//n/8v/U/wcA+f/y//L/1P/5//n/6v8WAA4AJQAAAOP/HQDj/wAABwDj/9v/tv/U/83/4//F/83/4//F/83/6v/y/9v/AADy/83/8v/F/8X/1P/N/+P/xf/N/77/vv/N/77/+f/N/9v/4/+v/9T/4//b/9T/2//5//n/4//5//L/AAD5/+P/4//q/+r/6v/5//L/BwDq/+r/4//F/9v/1P/U/83/6v/U/wcA8v/y/x0A1P8OANv/+f/b/83/DgDb//n/6v/y/9v/8v/j/w4AHQDy/x0A+f8sAPn/HQAdAOP/HQD5/w4ABwAAAAAA6v/F/+P/8v/b/wAAAAAdAAAADgD5/+r/+f8HAA4A+f8WAOP/6v8HANv/4//5//L/2//U/+P/8v/j//L/8v/5/wAAAAAOAAAAAAD5/w4ADgAAAAAA4//N//n/6v/b/wAABwAzAA4AJQAdAPL/HQAHAAcADgAOABYABwD5/wAADgAdAAcAJQAsACwAQgAWADMAMwAsACwAOwA7AB0ASgAWACwAJQAlADMAHQAzABYAHQAWACwAJQBCAB0AHQBnABYALAAzADsAMwBCAEIAHQBKADsAQgBKAFkAQgBCADsAOwBCAAAAMwAlAFEAUQBCAFEAJQBRACUAUQAlACUAOwAHADsABwAdAAcAAAAdABYAFgAAACwA6v8lAB0ADgAzAAcAQgAHAB0AHQAAACUAJQAlAAAALAAHACwALAAAABYA+f8HAOP/AADy/wAABwDU/wcA6v8AAAcABwAOAPn/8v/5/wAA4/8OAOP/8v8AAPn/HQAOAAcADgAzAAcAHQAdAAcAFgAWAB0A+f8OAAAADgAOAB0AJQAlABYAAAA7AAcAHQDy//L/HQDq/w4A8v/5/w4ADgAOACUA8v8HACUA4/8OAOr/DgAOAOr/DgDy//n/BwAOAPL/+f/b/wAA8v/q/w4A1P8WAAAA+f8dAPL/AAD5//n/DgD5//L/8v/N/+P/4//U/8X/vv/b/+r/BwAHAPL/8v/q/wAA+f/y//L/2/8HAPL/6v8HAPL/DgDj//L/AADb//L/+f/q/9v/AADb/9v/zf/y/+r/xf8OAMX/+f/j//n/DgDN/xYAzf8HABYA2//q/83/8v/q/+P/4//5/+r/zf/y/+r/6v/5/+r/2//b//L/6v/q/wcADgAdABYAAAAWAAcADgAAAAAAAAAAAAcAAADq/+r/DgD5//L/AADy//n/4/8AANv/xf/y/+r/6v/j/wcA6v/j/+r/vv/y/83/4//b/+r/BwDF/w4A2//b/wcA6v8lAA4A+f/j/+P/2//b//L/4//q/9v/2//5/+P/vv/j/83/zf/j/83/6v/U/9v/8v/N//L/AADb/9v/1P/N//L/2//N/9v/1P/q/wAA6v/q/9T/xf/b/83/1P/N/77/1P/y/+r/6v/U/8X/zf/N/wAA2//j/wAA2//q/+r/8v/b//n/BwDy/+P/+f/5/wAAAADy/w4A8v/j//L/BwDb//L/BwC+//L/2//b/9v/2//b/83/8v/U/wAA4//q/+P/6v/5/83/6v++/+P/8v/j//n/4//b//L/6v/y//L/zf8AAM3/8v/q/+r/AAC+/yUAvv/j//n/1P8WANT/AADb/+P/8v/b/wAA+f8HAB0A+f/5/wAA6v8WAPn/AAAOAAAALAAOAAAA6v/5//n/DgAlAOP/4//y//L/8v/q/+r/+f/N//L/6v/b/wcA4/8AAPL/8v8AAPL/+f/j/w4A8v/j//L/6v/5/9T/8v/q/x0AFgD5/x0A8v8lAA4ADgBZADMALABRADMAHQBCAAcAQgAzAAcAMwAHAGAASgA7AFEAQgBKADsAWQA7AFkAQgBRAGAAQgBRAEoAWQA7AHYAZwBCAGAAUQBRAEoAdgBZAFkAZwBRAFkASgBRAFkASgA7AFEALABnAG8ASgBgAEoAUQBRAFkAOwBKAFEAQgBZAB0AOwBCACUASgBKAEIAMwBgADsAJQBvADsALAA7ACwAOwA7ADsAFgAzAGAAOwAdACUAFgAHACwAAAAAAB0AHQAOAB0ALAAAAAcADgAOABYAHQAAAA4ALAAHAAAABwAzAOr/JQAsAOP/OwAlAEoAJQAdAB0A6v8HAPn/FgAWADMAJQAdAAcAHQAWAPn/LAAAABYABwAOAB0AFgAlABYADgAAACUADgAWAPL/6v8dABYAHQAAABYA+f/y/w4AAAAAAA4ABwAAAOP/1P/b/83/DgDj//L/8v/b/wcAzf/y//L/8v/y//L/6v8OANv/2/8dAL7/BwDb/9T/BwDq/w4A1P/b/77/8v/5/+r/6v/b/wAA1P8HAOr/4/8HAPn/BwAHABYA6v/j/+P/8v/y/83/4//j/9v/6v/y//L/4//U/9T/1P/F//L/4//j//n/2//b/6D/xf/N/9v/AADF//n/xf/j//L/zf/y/83/+f/U/+r/+f/y/wAA6v/y/+P/6v/b/w4A8v/q/w4ABwAAAOP/JQAHAOr/FgDy/wcAHQDb/wAA4//N//n/1P8AAAAA6v/b/8X/1P/q/9v/vv/U/+P/8v/b/wcA8v8WACwA+f8AAOP/6v/N//n/4//N/9v/1P8HAMX/6v/5/wAA8v/5/wAA2//U/9T/2/+n/83/xf/y//L/zf/U/8X/1P+v/9T/2//b/8X/2/++/6//AADF//L/zf/y/wcA2/8HANT/+f/y/9v/+f/q/9T/4/8AAPL/4/8HABYA6v8dAB0A6v/y//L/6v/q/83/xf/N/9v/2//N/9v/vv/U/+r/4//5//n/4//U/83/zf/j/83/1P++/+r/2/+2/+r/r//y/9v/xf/U/7b/4/++/9v/8v/b/+r/8v/j//L/1P/q/w4A2//y//n/DgDq//n/6v++/wAA+f8HAPL/DgAAAOP/BwAAABYAAAD5/w4A6v8AABYA8v/y/9v/1P8HAPn/6v/5/wcAOwAlAAAAHQD5//n/6v/y//L/4/8lAA4A6v/b/xYADgDy/yUAAAAHACUAJQAAAB0AJQAsADsAFgAdAEIAMwD5/x0AFgAzACwAMwA7AAcAOwAOACUAHQAlADsAUQBKABYAMwAAADMALAAsAEoAHQA7ADsASgAzADsAJQAlADsADgA7ADsAHQBCADsAMwAzAB0AOwBCACwALAAdAA4ABwAWABYAJQBKABYABwAzAAAAMwAsACUAQgAlAFEAAAAzADsADgAsAA4AMwAsAEoAOwA7AEIAMwAlACUAMwAOACwAHQAWACUAJQAWAOr/JQAlAAcAFgAOACUAMwAlACwAAAD5/x0AJQAdAB0AFgAAAB0AAAAAACUAAAAHAAcABwAWAAAA8v8AAPL/BwA7AB0A6v8HACUA8v8AAPL/xf++/77/1P/U/+P/1P/b/+r/4//b/+P/6v/y/wAA2//U/9T/2//q/8X/4/8AAOr/FgAOAOr/HQDj//L/JQAdACUA+f8WAPn/8v8dAAcAFgD5/wcA8v/q/wcA4//5/wcA6v/y//n/AAAHAPn/BwAHABYALAAHAA4ADgAlAA4AJQAzAA4ALAAOACwAJQAsACwAHQAlAA4ADgAAAA4AAAAWAB0AJQAlAPL/AAAAAPn/DgAsAAAAHQAOAPn/DgD5/yUA8v8AAAAA4/8HAAAABwAAAA4AHQAHAB0ALAAdABYAAAAHAOr/AAAAAM3/FgDb//L/FgD5/wcA2//b/+P/+f8AAAcA6v8WAPL/vv8HAOP/8v/y/83/8v/y//n/FgAOAOr/JQD5/wAABwDb/wcA4/8AAOr/2/8AAM3/+f8AAPn/BwDq//L/8v/y//L/+f8HAAcADgAAANv/DgAWAA4AMwAAAAcADgAAACwAFgDU/wAAAADU/w4A4/8OAAcA6v8HAOP/BwDb/wAAAAAAAAAAxf8WAOP/4//y/+P/8v8AAPn/4//5/83/zf/b/8X/1P/U/7b/xf/U/8X/1P++/+P/6v/b/9v/4//F/8X/8v+2/+P/+f++/77/4//j/+P/6v/U//n/1P++/wAAxf/U/wAA2/8AANT/2//q/83/6v/j/+r/4//q/6//4/8AALb/FgDF/9T/6v/U/wAAtv/b/9v/1P/j/9v/6v/q/9T/1P/5/9T/8v/y//L/DgDq//n/AAAOAPn/6v/q//L/HQAAAAcAFgDq/+P/6v/b//n/BwAOACUA8v8AABYA+f8AAOr/FgAAAPn/DgAHAAAA+f8AAOr/DgAOAPL/LAAOAOP/JQAWACUAQgAHADsAMwAWADMADgAlACwAAAAlACUABwAsACwAHQAlAAAAFgAsAOP/HQAHANv/JQDU/wcAFgAAAA4A8v8lAAcAJQAWAPn/AADq/wAABwAlAAcAAAAWANv/6v8zAPL/8v/y/+r/FgD5/w4A8v8OAOr/+f8HANv/BwDj/ywA+f/q/w4A6v8lAAcAFgAdAPL/FgAOAAAAFgAHACwALADy/yUADgAlACwAFgBRADMALAAsAAcAMwAlAAcAJQAWABYAFgAAAA4AFgAHACUAJQAWADMAJQAAAB0AFgAHAA4A4/8OAPn/6v8lAAcAJQAAABYAMwDq/wAA+f8AAAcAAAAHAOP/1P8AAPn/BwAAAPn/8v/N//n/6v/j/xYA+f/q//L/4//b/9v/vv/q//L/4/8dAB0ABwAAAA4AAADb/wAAAADq//n/+f8WAOP/8v8lAAAAHQAWAAcAJQAWADMAFgAAACwAFgAlADsAJQA7ADsAOwAsAB0AJQAdAPn/BwAOAPn/FgAAACUAAAD5/zsAFgAdAB0AAAAAAA4A6v/q/wcALAAsAAcAOwAWAB0AOwAHAA4A+f8HAAcADgAlAAcAFgAHAA4AAADy/wcA6v8WAAAABwAOAOP/DgAHAA4A+f8WACUA6v8dAAcAAAAdAA4ALAAHAAAAHQAWAA4AFgAOABYAFgAAACwAFgAWABYABwAzAA4AJQAWAPL/OwAlADMALAAdACUAAAAWAB0AFgAdAPn/HQAdAAAALAD5/yUAJQAOADsABwAzADsAFgAsABYADgAlADsADgAOAA4A4/8WAA4ABwAlAAAAFgDq/+P/+f/q/+r/2/8OAOr/AAAAAM3/+f/j/+P/8v/q/83/2//U/77/vv+2/77/tv+2/6f/1P/N/9v/2//N/6//mf/U/6f/zf/U/9T/+f+v/83/6v+2/+P/8v/U/wcA4//q/+P/1P/j/8X/8v/N/9v/6v/y//L/6v/q/8X/xf/b/+r/tv/N/9v/zf/N/9v/4//N/9T/4//j/8X/6v/N/9v/8v/y//n/1P8OAOP/2//5//L/8v8AACUA+f8WAAAADgAsAOP/AADj/8X/4//y//n/4//q//n/8v8AANv/4/8OANT/2//q/83/8v/j/wAABwDF//L/6v++/wAA1P++//L/2//j/83/vv/q/9v/4//U/+P/2//j/wAA+f/y/77/4//j/9v/2//q/wcADgAHABYADgDU//n/4/8OABYA8v8WAPL/AAAWADMADgAHAA4ALAAzACUAOwAOACwABwAsADMAHQBKADsAWQA7AGcAMwAdADsALAA7ADsAUQAWACwAMwAlAB0AJQAsAA4ALAAHACUAHQAHACUAFgAlACwALAAOAA4AAAAAACUAHQA7ABYA+f8WAOr/+f8WABYAAADy/wAA1P/b//L/4//b/+P/+f8HAA4A+f8AAOr/8v/j//L/2/+2//L/1P8HAPn/6v/q/9T/+f/q/x0AAAAOAAAA2/8HANv/6v8AAAAABwAWAPn/AAAWAPL/MwAdAAAAFgAOAB0ADgAWABYA+f/5//n/8v8HAAcAFgAOABYABwDy/ywAFgAAAAAAAADq/+r/8v/b//n/2//5/wAA4/8OAA4A2//q/xYADgAzAB0AAADy/9v/BwDy/+P/8v/y/w4AFgD5/wcABwAOABYADgAHAAcAFgAOACUA6v/5//L/2/8WAAAAJQAHAAAABwAAACUAHQAOAAcADgAOABYA8v8AAAcA+f8HAAAABwAWAA4ADgAWAPL/LAAHAAAAHQDy/yUA4/8OAA4A8v8zABYALAAlAB0AOwAlAAcAHQDq/wAALAAAAA4ADgDy//L/FgD5/wcABwDy/zsAAADj/x0AAADq/w4ABwAAAPn/AAAHAOr/AAAWAB0ABwAdAAAA4/8dABYAAADy/+r/1P/b//L/BwAWAAAAHQAOAAcAFgAHAPn/4/8WAAAA+f8HANv/AAD5/xYABwD5/wAA+f/y/wAAHQAHABYAAADy/wAA4//U/wcA+f/j/ywA+f8HAAAA+f8dAA4AAADq/x0Azf/q/yUA8v8WAB0AFgAHAAcA6v/j/9v/+f/y/9T/BwD5/+P/8v8AANT/6v8AAAAA8v8AAB0A6v8AAAcABwDq/wAAFgDb/wcADgDq/wAADgAdAAcA8v8WAA4ADgAOAAAABwAHACUAMwAdAA4AFgAAAA4ADgAHAA4AAAAOAAAAFgDq/wAADgC2/wcABwDq//L/FgDj/+P/BwDq/wAA6v8AAPn/DgD5//L/DgAAAA4A+f8OAAAAAAAHAPn/BwAWAAcA4//y/8X/6v/q/77/6v/F/+P/AADq/x0AAADq/wcAAAAHAAcAFgAOANv/8v/y//L/DgDj/xYAFgDy/x0AHQAHAOP/FgDy/9v/BwDq/wAA8v/y/+r/AAAzAAcABwDq/9T/2//y//L/6v/5/+P/AADb/+P/8v/b/wAA6v/5/xYADgD5/xYAAADF/wcABwAHAAcABwD5/+r/BwDq/yUAFgAdACwADgAWABYAJQD5/yUAFgAsAEIAFgAlAAAAFgAWAEoAFgAzACUABwAzAOr/JQAAAPL/+f8AAPn/6v8HAOr/JQAAAA4ADgAdADMABwAlAPL/FgAlAA4AJQAzAB0AHQAdAA4AHQAlABYADgAsAPL/HQAHAAcADgDj/yUA8v8WAB0A8v8lACwABwAHAB0ABwAAAA4AJQD5//n/DgAAAPL/2/8AANv/2//y/9v/4/8AAOr/AAAWAPL/+f/5//n/AAAOAA4AJQAlABYA+f/5//n/2/8HANv/DgDy/9v/AADj/wAAxf8OAAcA6v8HAOP/2//F//L/8v/5/wcADgDy/+r/2//U/+P/r//q/83/r//q/+r/1P/q//L/2/8HANv/8v/y/9T/AADy/+r/6v8AAOP/+f8HAOr/8v8AAA4ABwAlAA4ABwDy//n/BwDj/wcA8v8WAA4A+f8WAOr/AAAWAA4A+f/y/wcA2//y/wcA+f/5/+r/8v/b/+P/6v/U//n/6v/q/wcAFgAWAOr/8v8AAOr/BwAOAOr/8v8AAAAAFgAdAB0AMwAOABYAHQDy/xYABwDy/w4AAAAHAOr/BwAWAA4ABwAAAA4AAAAOAAAAAAAWAB0AHQAOACUALAAWACUALAAHAAAADgAlAAAA6v8lAA4ALAA7ADMAOwDy/yUAHQDq/zsALAAWADMAHQAOAA4ADgAdAAAADgAOAA4AMwAdADMADgAOAAcABwA7AA4AHQAlABYADgAdAAcA+f8dAAcAHQAHAPn/BwD5//n/AADy/+r/DgDy/wcA+f/q/x0A2//j/wAA8v/y/wcA+f/5/wAA8v8HAPL/6v8AAAcAFgAAAAcABwDj/wcA4//U//L/xf/j/+P/zf/q/+r/4//b/8X/zf/q/9v/6v/q/9v/6v/y/9T/8v/y/7b/6v/y//n/2/8AAOr/xf8WAMX/6v/j/83/+f++//L/4//q//L/1P/j/+r/8v/N/83/vv+n/9v/1P+g/6//xf/N/6//r/+n/6f/r/++/+r/4//j/+P/2//F/9T/zf/b//L/xf8HAPL/2/8AANv/8v8dAAAA8v/y/+r/HQAAAAAA+f/y/xYA6v8OAA4A+f8AABYAFgAAAA4AAAAWABYAAAAHACwAHQAHAEIADgAOADMAJQAlADMAMwAsADMAJQAWAAcAJQAlAAAALAAsADsASgBCADMAHQAzACUAMwAdAB0ALAAdAAAADgAlAOP/JQAlACUAUQAOADsADgAWACwADgAdAA4AFgAOACwAMwAlAEIALAAdABYAOwBKAPL/HQAlAPL/JQAWAPn/DgAOABYADgAOAA4ABwBCACwABwAWAAAAFgAOAA4AHQAAABYABwD5/ywABwAOABYA8v8AAOr/FgD5/+r/LAAHABYABwDy/w4AAAD5/wAAAAAAAPn/AAAHAB0ADgDy/ywA8v8AAB0ABwAdANv/AADq/+P/BwD5//n/BwAsAAcADgAAAAcAAAAAAAcA8v8HAPL/4//q/+r/8v8HAOr/6v/5/+P/6v/5/w4A+f8OAPL/8v/b/6D/4/+2/7b/xf/F/+P/1P/q/9T/r/+n/83/r//U/9v/xf/q/9T/4//q/+P/2//b/83/+f8AAMX/+f/5/+P/6v/y//L/2/8WAAcA8v/y/8X/AAAHAA4ABwAlADMADgA7AA4AHQAdAAAAHQAdABYAFgAOAAAAJQAHAAAA+f/y/yUAAAAWAAAA4/8OAPL/DgAOAPL/AAAHAAcA+f/5/w4ABwAWAAAABwAOAPL/HQAAAA4ADgAAACUAAAA7AA4A8v8HAOr/FgDy/wAAAAD5/wcA+f8AAPn/BwD5/wcA+f8HADMAAAAlACwABwAOAA4ABwAHABYAJQAdAB0AOwAOAPn/BwAAAPn/FgAHAA4AFgDb/wAADgD5//n/+f/y/+P/+f/y/+r/8v8OAB0A+f8lACUAAAAdAPL/FgAHANT/DgDq/w4AAAAAAB0A+f/5/wcAJQDy/w4A8v/q/xYA4/8AAOP/1P8AAAcA6v/5//n/8v8AAOP/2/++/8X/1P/q//L/8v/5/+r/1P8HAPL/zf8lAOr/+f8HAPn/BwDy/wAAzf8AAMX/2//y/8X/6v/N/wAA1P/y/wAA6v/j/8X/xf/N/+r/zf/y/+P/1P/b/9T/6v/b/83/tv/j/7b/1P/y/8X/BwDb/9T/AADj/9T/zf/U/9v/4//y//n/AAAAAOr/AAD5//n/AAD5/xYA4//U//L/zf/U/8X/6v/j/83/1P/b/+r/xf/j/+r/1P/j/wcA+f/U/wcA+f/q/9T/6v/y/+P/AADb/wcA6v8AAA4AAAAlAA4ABwAOAA4ADgAzABYAFgAHAOr/DgAHAAcA+f8WAOr/FgAlAOr/HQAWACUAAAAHAB0AHQAlADMASgAdAEIAQgAHAA4AJQAdAB0AQgAWAB0AJQAzACwA+f8lAB0ADgAWAA4AAAAlACwABwA7AAcAHQBCACwAWQAdADMAMwAOACwAMwBKACwAHQAlADMAFgAlAEIAFgAlACwAJQAsACwAHQA7AB0AOwAzADMAUQAAAEIAAAAHADsAAAAzADMAHQAlABYAFgA7APn/HQAzAA4AMwD5/yUABwAdAA4ADgAzAOr/OwAOAPn/DgAWACUAFgA7AB0AFgAdADMAMwAWACUAHQAWACUAOwAlACUAJQAlABYALAAHAAcALAD5/wAA1P8HABYA2/8dAAcAFgAOAA4AJQD5/wAAAAAAAPn/BwAWAOP/+f8AAPL/+f/5/wcA6v8AAAAA8v8OAAcADgDq/9T/8v/b//L/8v/F/83/1P/U/wcADgDq/w4A+f/j//L/4/8WAA4AAAAOAPn/AADj//L/+f++//L/6v/q/wcA6v8WAPL/6v8OANv/6v8AABYAJQAWACUAJQAHAAcALAAHABYAOwAHACwA+f/j/xYA8v8OAAcA6v/q/wcADgAOABYABwD5/+P/FgD5//L/DgD5/x0A+f/5/+r/8v8AAPn/JQAHACUAMwA7ABYABwAsAAAAFgAlAA4AFgAzAPn/+f8AAPL/LAD5/xYAHQDy//n/BwAAAAAADgDq/yUA4//j/wcAxf/5/+r/8v/U/+P/vv+2//n/vv/q/9v/zf/5/+P/vv/q/8X/vv8AAM3/BwDU//L/+f+2//L/vv/q/+P/vv/q/8X/1P/q/83/2/+v/83/2/+Z/+P/tv++/7b/oP/U/6//zf+v/7b/r/+v/9T/1P/U/9T/AADN/9T/2//U/9v/zf/y/9T/4//y//L/BwDy//L/+f/j/+P/6v/b/9v/+f8WANv/8v/y/83/BwAWAAcA+f8AAOr/AAAWAOP/6v/5/+r/8v/y/+r/+f/j/wAA2//b/xYAzf/b/+r/2//j//L/8v/b//L/6v/N/8X/zf/N/+P/AAAHAPL/AAAHAPL/6v/j/wAA8v8lACUADgAWAPn/AAD5//L/4/8OAB0A8v8HAPn/4//U//L/4//5//n/2/8AAOP/DgAOAAcABwAWABYA4/8WANT/+f8AANv/HQDj/x0ADgDj/wcADgAHAOr/LAAOAPL/AADU/+P/BwAOABYABwD5/yUAHQDy/yUAHQDy/x0A+f8OAB0A+f8OAPn/4//q/wAADgAOAPL/AAAOAOr/HQAHANT/+f8HAA4AFgAWACwAJQAOADMAJQAWAA4ADgAOAAAADgAHAAAAAAAdAB0A+f8dAB0ADgAzAA4AHQAsAAcAHQAHAB0ALAAzABYALAA7APn/HQAOAAAABwAAAAAADgD5/wcAJQAAAB0AFgAlACUAFgAzAA4AAAAOAA4AAAAdAAcAHQAWAPn/LAAAABYAFgAHABYABwAlAA4AAAAdAAcA8v/5/wAADgDq//L/DgD5/wAALAD5/wcALAD5/ywAHQAdABYADgAlAA4ADgAHACwA6v8AAB0A+f8AAPn/FgDq//L/+f8AAA4A+f8dAAcAAAAdABYABwAHAAcADgAAAOr/AADq/wAALAAAAPL/+f8OAA4A6v8WAPL/8v8HAA4AAADU/x0ALAAdAPL/AAAOAPL/BwDj/wcABwAAABYAHQAHABYALADy/wAA8v8WAA4AHQAzAPn/FgAHABYADgAlACwAHQA7ADMAMwAHACwABwAdADsA+f8zACwALAAzABYALAAzABYAHQBCABYAOwBCADMAUQAzADMAHQAsADsALAAzAA4AJQAWACUAMwD5/ywAJQAWACwAFgAHAA4AFgDy/x0ABwD5/0IAAAAAAAAA8v8WANv/DgAHAOr/HQAAABYAFgAAAPn/HQAAANv/JQDj//L/DgAAAB0ABwAWAPn/OwAlAA4AMwAAACwAMwAsABYAMwAzACUAOwAAABYAAAAAABYAAAAlAB0AAAD5/x0AFgAOAA4ABwAHAOP/8v8OAOr/8v/5//n/8v/y/x0A4//q//L/+f/y/+r/+f/b/w4A1P8HAPn/zf/j/77/+f/F/w4A8v/b/wcA2/8AANv/4/++/+P/6v/U/wAA1P/q/83/6v8OAPL/+f/5//L/1P/N//n/xf+2/+r/2//j/9T/2//j/+P/6v/y//L/1P/y/+P/AADq/9T/4//b/+r/zf/F/8X/vv/F/83/zf/N/wAA6v/q/+r/2/8HANv/4//5//n/6v/q/w4A8v/5/+P/2//q/77/4//b/+P/6v/b//n/4//j/w4A8v/y/wAA+f8OAPL/DgAHAPn/AADy/wAA6v8AAOr/+f8OAOr/+f/j/83/2/8HAOP/1P/N/9T/zf+2/83/xf/F/8X/1P/F/83/zf/N/9v/xf/U/77/6v/U/9v/8v/j//n/r//N/77/xf/5/8X/r/++/9v/6v/q/+P/4//q/+r/AADy/8X/2//b/8X/1P/F/83/1P++/83/xf/b/+r/6v/y/9T/2//b//n/4//N/wcA2//y/wcA8v8AAOP/4//b/9v/+f/U/+P/8v/N/wcAAAAAAAcABwAHANv/DgDy//L/BwDy/xYA6v8AABYAAAAAAA4ADgAOAA4AFgAOAAAADgDq/x0AJQAHABYAFgAAAAcAFgAAAA4ABwAzAB0ADgAzAAcADgD5/wAA+f8OACUAHQBRADMAHQAOABYALAAsACwABwAWACUAHQAlADMAQgAzADsASgBKAB0AFgA7AB0AOwA7AA4AMwAsABYAJQAzADsAJQA7AB0A+f8zAAcAFgAdAA4AJQAAAB0AFgAAAA4AFgAsACwAHQDq/wAAJQAdACUABwAAABYADgAWAPn/BwAzAAcAFgAHABYAMwAlACUAHQAWAAcAHQAlAAcADgAlAPn/DgAOAOr/BwAHAA4A8v8WAPL/AAAWAPn/DgD5/w4A8v8AAOr/AADq/+r/FgDF/wcA2//q/wcA4/8OAOr/8v8OABYA+f8lABYA8v8OAAAABwAHAB0ADgAOAA4AJQAOACwAMwAWADMADgAWAB0AMwAdADsAQgAWACUAJQBCACUALAAWABYAQgBCACUALABCAAcAOwAlACUALAAHAB0AAAAlAA4A+f8dAAAAFgAOAAcAOwAzADMAOwAdACwAFgAlADMAJQA7ABYAFgAWAAcALAAdAAcA+f8HACUA8v8OAB0ABwAOAPL/FgAOAOr/DgAWAAAABwAdAPL/6v/F/83/4//U//n/2//y/+r/r//y/9v/xf/j/9v/vv/U/wAA2//N//n/8v/U/wcA8v/y/w4A6v/y/9v/8v/j/9v/AADj/+r/6v/5//L/2/8AAPL/6v8AAAAA8v/5//n/1P/b//n/2//b/w4A+f8AACUAAAAHAA4ABwD5/wcADgDy/wcADgAWAAcA+f8HAAcADgDy/wAA8v/q//n/BwAHAPn/DgAHAB0ABwAHAPn/8v/y/9v/DgAOAAAABwAsAPL/+f8WAOP/BwDU/w4ADgDq/xYA8v8dAPn/DgAAANT/8v/j//n/+f/5//L/AAAOAAcABwDb//n/8v/b/+P/6v/5/9T/4//q/9v/BwAOAPn/4/8dAAAA6v/5/9T/8v/j//n/+f/y//n/4/8AAAcAFgDy/xYA8v/N/yUA8v8OAA4ADgAHAOr/LAAOAAcABwAWAAcAFgAdAOr/HQAAABYAJQDy/x0AFgAHAAcAFgD5/9v/BwAHAPn/AAAOAPn/+f8OAAcA8v/q/wAADgAOAPL/DgAOAPn/8v/y/+P/tv/b/9v/2//j/+P/1P/F/+r/1P/q//L/2//j/9v/+f/b/+r/4//j/+r/zf/q/+P/8v/5/+P/+f/q/9v/6v/j/+P/8v/j/wcA6v/U/w4A6v8AAA4A4/8HAAcA+f8sAA4AAAAlAA4AAAAdAA4AAAAOAAcABwAHAAAA+f8HAA4AAAAWAB0AJQAsACUABwAWABYAAAAHAAAAAAAAAPn/8v/5/9v/AAAHANv/8v/j/wAA+f/y/wAAAAAOAOr/8v/q/wcA+f8OACUA8v8dAA4ADgD5/+P/HQAOAB0AJQD5//n/4//5/wAA+f8WABYAJQD5/x0AMwAlADMAFgAWAB0AJQAAAB0AHQAHACUA6v8WAPn/4//j/+P/DgDy/xYADgDj//n/AADj/9v/AADU/+P/DgDU/+P/8v/b//n/4//U//L/6v/j/xYADgDq/+r/6v8HANv/6v/5/9v/8v/U/wAA8v/y//n/2//q/+P/BwDq/+r/FgDq/w4AFgDy//L/AAAAAPn/DgD5//n/1P/y/+r/6v8lANT/BwAdAPn/AADy/wAA2/8AAPn/BwAAAOP/DgAAAAcAHQAdAAAAOwAdACUALADy/zsAHQAsACUAHQAsAA4AMwAsAAcADgAsAAcAOwAWAPn/OwAOACwAFgAOAB0A8v8dABYA+f8zACwAFgAsABYAQgAzACUASgAOADMAHQAOADMAAAAOAA4AHQAAAAcAHQDy/x0ABwD5/wcA8v8AAOr/6v8AAOP/2//q/+r/6v/j/wAA6v/N/83/zf/b/+P/AADU//L/+f/j/wAAzf/j/8X/4//y/7b/6v8AAPL/8v8AAOr/8v8OAPL/6v/y//L/AADy/wcALAAHABYAHQAAAAcA8v/q/xYAAADq/+P/8v8HAOr/DgAHAPL/+f/q//L/AAAOANT/6v/5//L/AAAHAB0A6v/5//n/6v/U/+r/+f/b/9v/2//5//L/8v/q/+r/4//q/x0AHQAOAB0AFgDj/wAA+f/y/xYA8v8AABYA+f8HACwABwAOAAcADgAdAPn/BwAHAAcAFgAdAOP/DgAHANT/DgD5//L/+f8HAAAADgAlAB0AFgAsADsADgAWAAcAFgAAAPL/8v8AAA4A2/8HAAAAAAD5/w4AAAAHAB0A8v8dAAAAFgDj/8X/+f/F/9v/1P/y/+r/6v/q/+r/BwDU/+r/4//N/9v/zf8AAOr/1P8HAPL/AAAHAOr/6v/j//n/8v8HAAcAFgAOAPn/JQD5/wcABwDy//n/2/8AAPL/8v8HAAcAFgAdACUADgAAAPL/AAAHAPn/BwAHABYAAAAOACUA+f8WANv/6v8WAOP/FgAHABYADgAOABYADgAHAPL/HQD5/wcABwAHAAcA+f8dAPn/BwAdAAcABwAOAOr/BwD5/+P/BwDq/w4A4/8AABYA8v8WAAcALAAsABYAFgAsABYAHQAHAAcAQgAAADsALAAdADsAHQAlAAcADgAAABYAFgAzAB0A4/8WAAAAAAAlAB0AFgAOAAcAHQD5/9v/8v/y/wAA2//5//n/AAAWAAAALAAAAOr/BwDy/+r/FgAWAA4AFgAdAB0AHQAsAPn/AAAAAAAAFgAAANv/1P8HAAcADgAHACUAFgD5/x0ABwAOAB0ALAAOABYAHQAOACwA+f8OABYA8v8HACUAHQAHADMAJQD5/wcAHQAWAAAADgAAAPL/AAD5/wAA8v8AAPn/AAAAAOr/BwAOAA4ADgAWAAAAHQAOAAAAMwAOACwABwAHACwAAAAHAOP/4//j/83/6v8AAPn/2//U/6//zf/b/9v/6v/q/wAA2/8HABYA6v8WAAAAAAA7AB0ADgAHAOP/AAD5//L/+f/b//n/6v/b/+r/+f8OAPn/BwAOAOr/+f8WAA4ADgAdAA4ADgDq/wAADgD5/xYA+f8HABYADgAzAAAADgAlAAcA+f/y//n/+f/5/xYABwDq/wAAHQAAAPn/HQAzAAcADgAzAA4A+f8HABYA+f/5/xYABwAHAB0AHQAsACUAFgAsAAAAHQAWAPn/LAAOAB0ALAAlAA4ALABKACwAUQBKACwAJQAsADMAJQAsAEoAOwAzADsALAAsAAcAOwAdACwAMwD5/xYAAAAdAPn/6v/5/+P/zf/b/w4A2//q/+P/6v/y/9v/BwDj/9v/6v+2/+P/2//F/+P/xf/F/8X/1P/N/+P/BwDU/+P/xf/F/8X/vv/F/77/1P/j/+r/6v8AAOP/4//b/9v/xf/U/wcA1P8AAAAA+f8AANT/AADy/9v/DgAAAPn/4//b//L/vv/y//n/2//q/+r/4/++/+r/4//F/83/AADN/8X/8v++/83/p//b/8X/tv/b/6//2//F/9v/1P+v/9v/zf+2/8X/p//F/83/vv/U/6//r/+g/83/r/++/83/vv/y/8X/1P++/+P/8v8AAAcA6v/5/+P/BwDy//n/6v/5/wcAAAAOAAAADgAOAB0A+f8WAAcALAAdABYAUQD5/xYAHQAOAAAAAADy/wAAFgAOAAcA+f8OAAAAJQAHAA4ABwDj//L/+f8HAMX/FgAAAOr/HQAAAPn/AAAWAAAABwDy//L/4//b/9T/8v8OAPL/+f8HAA4A8v8OAA4ABwAdABYADgAsAB0A6v87AAcABwA7ACUALAAlADsAOwAOABYAQgAHACUAJQAAACUABwAsAB0AHQAlAB0AHQAdABYALAAsAAcALAAHAAcAHQAlABYADgAdAB0ADgAOABYA4/8AAAcAHQAdAAcALAD5/wAAHQAdAAcAFgAdAA4ABwAWAAcAFgAAAAcAOwD5/zMAHQAlADsABwBKABYABwAOAB0ADgAOABYABwAOAAcAFgDy/x0AAAD5/xYA4/8AAAcA8v/q/+P/4/8AAPn/+f/y//L/+f/q/wcA4//j//n/AAAAAPn/2/8HAAAAr//5/8X/tv/j/7b/4//5/+P/6v/q/+r/6v/U//n/4//U/9v/vv/F/8X/2/+2/6//tv+n/9T/4//b/83/+f/q/8X/4//N/9T/4//j/+r/xf/N/83/xf/q/+P/4//U/wAA6v/q/zMA2/8AABYA+f8OAPL/AADj//n/AADN/wAAJQAlADsALAAWADMAMwAdADMAFgAlACUAFgBKAA4AHQAlAAAAHQAOACwALAAdAEIAFgAOAB0ABwAdAAcADgDy/+P/HQDy/wcAFgAlADsAQgBKACUAMwAzACwAJQAzADMAJQBCACwADgAOADMAOwAWACUAOwAdAAAAMwAdACUALAAWADMAHQAlABYAHQAsAA4AMwAdAB0AJQAOADMAHQAlAEIAHQAdACUAJQAlAEIALAAlAEIADgA7AB0AFgBCACUAMwAWAAcADgAWABYAJQA7AB0ASgBKADMAJQAOACwABwAWACUADgAHAPL/AAAdAB0ADgBCACUA8v8WAA4A+f8HAAAABwAdAAAALAAWAPn/JQDq/wcA8v8OACUA4/8sABYABwAOAB0ABwAAAA4ABwAlAPL/JQAdAAAAOwAOADMADgDN/9v/1P/U//L/8v/5//L/4//y/w4AJQDq//L/6v/F/83/2//j/9v/+f8AAOP/1P/q/9T/2//j/9v/zf+2//L/4//5/9v/2//b/7b/6v/b//n/8v/q/8X/8v/b/7b/6v+2/9T/zf/N/5H/tv/j/4L/2//y/9T/1P/j/77/p/+2/6//zf++/+P/8v/q/9v/xf/N/8X/1P/F/9T/1P/q/+P/tv/j/9v/2//U/7b/1P++/9v/+f/y/+P/8v/q/8X/8v/F/9T/4//b/w4A+f/5/wAABwD5/wAA1P/U/wAA8v8OAOr/+f/y//n/FgD5/yUAHQAHAA4ABwD5/w4A+f/5/+r/8v8HAOr/+f8WAPL/8v8dAOP/BwAWAA4AFgAOAAcA+f8sAAcAMwAsAAcADgDy/x0AAAAOAAcAMwAHAAAADgDq/wcA2/8OAPn/+f/5/wAADgDN/x0ABwAHABYADgAlABYAOwAlAPn/HQAOAPL/LAD5//n/AADq/w4A8v8HAOr/BwAdACUAQgAOADMAFgD5/x0AAAAsAB0AFgAlAA4AFgAOAAcAAAAzACUADgAHAA4AJQAHACUA8v/y/w4AHQAHAPL/FgAHAB0AFgAdAOP/1P/N/7b/+f/j/xYABwAHAAAA8v8AAAcABwDb/xYA+f/q/+r/BwAOAOr/LAAAAAcAHQAsABYA6v8dABYAAAAOADMAHQAOAB0A+f8AAOr/DgAWANT/HQAWAAAABwDb/x0AFgDq//n/+f/j//L/AAAOAPn/xf8HANT/2//5/+P/+f/q/wcA2//5/+P/2/8HAPL/AADq/wcA+f8OAPn/4/8dAPL/BwAAAOr/+f/b/+r/2//j/+P/1P/y/+r/8v8OANv/1P8AANv/6v8AAPn/DgDq/wcAFgD5//L/2//y//n/AAAHAA4A6v/j/9T/xf/5/+P/6v8AAPn/DgAHABYAAADy/xYADgAWAA4AAAAAAAcA+f/y/zMAFgAsADsAFgAlAAAAMwD5/+r/OwAWAA4AAAAWAB0ADgAOABYADgD5/w4ABwAAAPn/FgAOAPn/+f/q/9v/BwAlAPL/AAAAAPn/AAAlAPL/FgA7AAAAMwD5/w4A8v/q//n/4/8HAPn/DgAAACUADgAlAA4A8v8dAPn/FgDy/w4A+f/b/wcAAADy/yUALAAHACwAAAAHAAAA2//j/9v/zf/b/+r/zf8HAPL/+f/b/+P/8v/q/w4A1P8OAPL/4//5/+r/6v/y/x0A4/8AAPL/AAD5//n/DgDq/wcA2/8AANT/6v8OAPL/FgAAABYADgAdAB0ABwAHAPn/AAAHAAcA6v8OAOr/zf8HAPn/AAD5/wAA+f/q/wAAFgD5/w4AMwDy/wcAHQAOAA4ABwAWAPL/LAAOABYAHQAAACUA2/8sABYA+f8OAPn/JQAHADMAJQAdAB0AFgAWADMAZwAdACUABwAOAB0AMwAzACUASgAlADsAFgAdAAAAHQAWAOr/LAAOACwAHQAlAB0AJQAOAPn/MwAAACUAFgAWAEoALAAsACUADgAWACwAMwA7AB0ALAAHAA4ALAD5/wcABwD5/+r/DgAWAB0ADgAHAPn/1P/5/wcAJQD5/wcADgDU//L/2//b//L/2//q//L/1P/q/+r/1P/q/+r/AAD5/+r/1P/j/9v/6v8OAOP/+f/j/9v/1P/b//L/tv/b/9v/xf/j/+P/4//q/+r/4//q/+r/6v/b/9v/6v/5//L/6v8WAOr/+f/5/9v/8v/F/9v/+f/5//L/+f/y/83/+f/b//L/4/+2//L/zf/y//L/4/8dAOr/BwAAAPn/JQDq/wcABwD5/w4ADgAHAAcAHQDy/+r/8v/5/+r/+f/5/9v/6v/j/wAA1P/q/9v/tv/j/8X/1P++//L/BwDU/+r/zf/b/9v/8v8HANv/6v/q/+P/6v/5//n/8v/q//L/6v/j//n/4//q/w4ADgAsABYADgAWAAAAFgDy/x0AJQD5/yUADgAOACwAHQAdAB0AFgAlABYAHQAWABYAHQD5/xYA+f8WAAAA4/8WAOP/DgAOAAAAFgAHAA4AFgAlAAcADgAWACUAJQAsADsAJQAzACwALABCACUAFgAdABYAAAD5/xYAMwAHAAcAHQAHAAcAFgAlACUAFgAHAOr/DgAAAAAAFgAAABYA6v8AAAAA1P/b/+P/8v/b/+r/8v/j/+r/8v/y/xYA4/++//L/1P/j/+P/+f8AAOr/+f/y/+P/6v/q/83/AADj//L/LAD5/w4ADgAHAA4AHQAlACUALAAHAB0AHQAOADsALAAdAB0AHQAdAA4AJQAWAB0AJQAOAA4AHQAlABYABwAWACUADgAsADMALAAWAA4AOwD5//n/8v/q/wAA8v8OAPL/HQAOAA4AHQD5/x0AFgAOABYA+f/5/w4A4//5/9v/4//y/83/BwDF/+P/6v/N/9T/r//N/6f/tv+n/6//r/+g/77/p/+g/5n/mf+n/6f/r//N/8X/zf++/83/6v++/9T/xf/F/77/xf++/83/6v/U//n/2/8AAOr/2/8WAMX/1P/q/+P/+f/q/wAA+f/q//n/FgAOAPn/BwAHAAAA4//5/ywA6v/q/x0AAAAHAA4A+f8HAPL/4/8AAPL/AAAWAPn/4/8WAOr/1P8dANv/DgAOAB0AJQAAADsABwD5/w4AAAAsACwADgAzACUAFgAOAAcABwDy/xYADgAlAB0AJQAdANv/AAD5/wAADgAsAAcAAAA7ACwALAAsACwADgAlACUADgBRADsALABCACwAQgAzABYAMwDy/wcALAAHADMAJQAlAB0A+f8WACUAHQBCABYALABCAPn/AAAHACwAHQAzADsADgAlAA4AJQAdACUAJQAHABYAFgAlACUAFgAlAA4ABwAlABYAFgAWAEIAMwAWAEIAJQA7AEIAOwAdAB0ABwAWACwADgAzAA4AFgAOABYAAAD5/ywA4/8HAAcABwAdACUAOwAWAEIAJQAOAAcADgAdAA4AHQAlAB0AFgAlABYA+f8AABYAFgAdAPn/BwAWAPL/BwD5//L/AAAAAPL/8v8HAAcA2//5/wAA+f8AAPL/FgD5//L/6v/q/+P/8v8WAOr/AADq//L/+f/j/wAADgAlAB0AFgAOAB0A+f8OAB0A4/8WAA4AFgAOAB0ADgAHAB0AAAAdAPn/BwDj/+P/JQDj//n/AADq//n/2/8AACwAAAAHAAcAAADy/9v/DgAAAB0AHQAWABYA6v8AAPn/AAAAAPL/DgAOAA4ABwAOAAAA6v8HAOr/AAAdANT/BwDj/9v/8v/U/w4A4//q/9T/6v8HANv/FgDy/9T/4//5/9v/4/8AAMX/+f/N/83/8v/F//n/6v/q/wcA4//q//n/4//y/+P/4//5/9T/2/++/+r/2//b/wAAvv/q//L/4//y/+P/2//N/+P/vv++/+P/8v/j//L/AADq/+P/+f/y/8X/AADj/wcAHQDb//n/6v8OAOP/+f8OAM3/AADq//L/+f/5/x0ABwDy//n/AADU/wAAFgAHAAcA+f8OAAAA8v8AAOP/8v8OAAcAFgAlABYABwAAANT/+f/j/9v/BwDb//n/+f/5/wAA+f/y/+P/+f/y/wcAAAAOAA4AFgAlAAAABwD5/wcA+f8AAAAA2//q/+P/4//j/9v/4//5//L/4//j/9v/2//b/+P/6v/j/9v/4//U/+r/1P++/83/oP+2/8X/tv++/7b/r//b/+P/vv/U/77/xf++/9T/8v/U/wAA4//U/+P/4/++/8X/xf+v/9v/vv+v/9T/vv++/9v/xf/F/+P/4//5/7b/1P/b/83/AADj/9v/1P/j/+r/6v/5/+r/6v/b/9T/4/8HANT/zf/y/+P/6v/y/+r/xf/U/8X/1P/j/+r/4//j//n/1P/j/6//6v/q/8X/HQDb//n/+f/b//n/4//U/+P/+f/5/w4AFgAOAAAAAAD5/wcABwAOAA4A+f8dAPn/HQAsAAcAFgAlAA4A+f8dAPn/DgAHAOr/FgAdAA4ALAA7ABYADgAOAA4A4/8WAAcAAAAsAAAAMwAzACUABwAlADMADgAdADMAWQAsACwAQgBgACUAJQBRAB0AOwAzADsAbwBnAGAAUQBZAEoAOwBgAFEAQgAzACUAMwBKAFEALABZAEIAJQBCAFEAOwBCAEoAMwBnACwAWQBKABYASgAlAGcALAAzAFEAQgA7ADMAZwAsAFEAMwA7AEoAHQBCAEoALAAsADsALABRADsAQgBKAEoAUQBCAFEAQgBnAEoAWQBRAFEAfgBgAFEASgBZAEIAUQBRAFEAMwAzADsASgBvAEoAWQA7AB0AJQAsABYAHQA7AA4ALAAHAB0AMwAOACwALAA7ABYAJQAdABYALAAdACwADgD5/w4AFgAWAAcAHQAdAA4AJQAlADMAJQAsACwADgAHACUAMwAHAAcA+f8AAPL/AAAWAAcAJQAAABYA+f8OACUA8v8HAAAADgA7ADMADgAsABYAAAAdAAAAMwAWAAAAJQD5//n/6v8HAA4A+f8OAB0AHQAHAAAAAADj//L/BwDy/w4AFgD5/w4ABwAAAPn/AAAHAPL/BwDq//L/8v/y/+r/zf/j/+r/BwDb//L/AADU/wAAzf/q//L/1P8AAAAA6v/N/+r/8v/j/9T/2//j/9T/6v/q/9v/vv++/77/zf/U/9v/6v+v/77/zf+v/5H/p/+v/4r/tv++/9T/vv/F/+P/tv/F/9v/2//N/8X/p//U/9T/1P/j/83/6v/F/wAA8v/j/w4A2//y/+P/4//U/+r/AADj/+P/6v/y//L/8v/j/w4A8v/5//n/2/8AANT/2//q/+P/+f8HAA4AFgDy//L/AADy//n/AAAHAOr/+f/5/+P/BwAAAOP/8v/j/83/+f/j//n/8v/b//L/1P8HAPL/1P/y/9v/1P/N/wAA6v/b/wAA6v8AAOr/+f8OAMX/2/8AAAAAAAAHAPn/+f8AAA4A+f8HAB0A2//y//L/+f8OAAcABwDq//n/BwAOAAAALAAWAPn/+f/b/w4A8v/y/+P/6v/b//n/AADF/wcA2//y/+r/zf/q/83/2//N/+P/zf/b/83/4//q/5n/zf/F/5H/tv+2/9T/1P+v/9v/tv/b/+r/xf/5/77/zf/5//n/6v/b/9T/1P/N/9T/+f/F/+r/2//N/83/xf/j/83/4//q/+P/6v/j/+P/8v/y/77/2//N/77/zf++/9T/1P/N/+r/1P/U/+P/1P/U/6//vv/j/83/2//F/6f/4//F/83/4//F/9v/1P/j/83/2//y/8X/8v8AAPn/AADy/wAABwAOAAAABwD5/+P/DgAOAPn/BwD5/wcAAADb/+P/6v/y/9v/8v8HAPn/BwAHAAAA+f8WAPn/AAAOAPn/AADj/wAA6v8AAB0ABwAOAAAAHQAWAB0AHQAlACUAFgAdABYADgAOAB0A8v8WAAAAAAAlAOr/MwAOAA4ADgAOACUA8v8dAA4ALAAWAB0AOwD5/zMAJQAlAEIADgAWAA4ADgD5/xYAJQD5/zsAAAD5/yUAFgAzABYAOwAlAB0AMwAlADMAHQBKAEIAHQAdADMAWQBRAEIAUQBZADMAOwAsACwAJQAsACwAMwAsABYAJQAdAB0AJQAOAB0ALAAlADMAJQAsAA4AAAA7AB0AHQAlADsALAAdADsAQgAlACUAQgD5/ywAJQAdAEoABwBCACUAJQBRACUAMwBCADMAOwAsADMALAAdAEIALAA7ACUAJQBRACwADgAOABYADgAWAB0ABwD5/w4ADgAdACUAAAAdAB0ADgAOADMADgAHAA4A+f/5/+r/FgAHAA4AAAAsAA4A+f9CAPn/JQAzAB0AMwAWACwALAAOABYAOwAAACwAOwAOAEIAHQAsACwABwA7ACUABwAWACUAHQAWABYAAAD5/wcADgAAABYA8v/b/xYA6v/q/+P/2//b/9v/AADy//L/4//F/+P/6v/N/+r/1P/b/x0A2//q//L/zf/N/9v/4//y/9v/1P8AANT/2//q/+r/1P/y/wcAzf/5//L/6v/y/9T/8v/y/+P/AAD5/9v/BwDy//L/8v8AAAcA+f8OAAAADgDb/+P/AADb//n/+f/5/wAA+f/y//n/AAAOAA4ABwAAAPL/BwAlAB0AHQAlACUAFgDy/wAA8v8OABYABwAsACUAHQAdACUAAAD5/xYAAAD5/x0AHQD5/zMAFgAOABYA+f8OAM3/+f8WAPn/BwDj/9v/2//j/9T/+f/b/77/AADU/+r/4//U/9T/p//j/83/zf/j/77/vv/F/77/vv/5/77/2//y/7b/4//q//L/zf/N//n/8v/U/+r/AADj//L/2//q/9v/4//y/+P/+f/q/yUAAAD5/xYA8v8OAPn/+f8WAPn/+f8sAA4ABwAdAA4ABwDy/wcA8v8HAAAABwAAANv/FgDb/wAAAADy/x0A4/8WAA4A1P8HAAAA8v8lAA4A+f8HAOr/DgD5/+r/BwAOAOP/+f8HAOr/AAD5/x0AJQD5/wcAAAD5//n/+f8WABYA+f8HAAcA4/8OAB0AAAAdAA4AFgAHAPL/JQDq//L/+f8WADsAFgBKAB0AHQAdAA4AFgDy/zMAMwAdAAcAFgAOAPn/HQAAAPn/8v8HAAAA8v8dAAAA+f8HAAcA6v/q/xYAAAAAAA4AFgAAAAcAHQAWAB0ABwAWAOr/+f8WAOP/AAD5/w4AAADy//L/1P8HAPL/4/8AANv/2//b//n/+f8HAB0AAAAlAB0AOwA7AAAALAAdACwALAAdABYAJQAlAOr/FgDy/wcAAADq/wAAAAAHAOr/FgDy//L/DgD5/wcA6v8WACUAAAAdACUABwD5/xYAHQD5/xYABwDy/wcA6v/5/+r/AADy/83/+f/j/+P/1P/b//n/4//q/wAA+f8WACUAFgAOAA4AFgAAACUALAAWADMADgAWACwAFgAzACwAFgAlABYAOwAdAAAAJQAdACUAJQA7AB0AHQAzAB0AFgDy/wcAFgAOAB0AJQAWACUAJQAlACwA+f8AAAcADgAWAPL/+f8AAPL/DgAOAAAABwDj//L/+f/j/+r/+f/q/+P/DgDy//n/FgDj/+r/6v/j/+r/2//5/wAAAAD5/wcA8v/U//n/1P8AAAAA2/8HAOr/8v8AAAAA8v8HAPn/6v/y/+r/8v/b//n/+f/j/wAABwDq//n/HQAdAOr/6v8HAOr/+f/5/+P/4/8HAAcABwAAANv/BwDq/wAA8v/5/wcA8v87APL/BwAAAOP/BwDq//L/6v/j/+P/8v/b//n/+f/y//L/4//y//n/AADy/wAA4//j//n/+f8WAPL/8v8AAAAABwAOAB0A2/8AABYA6v8OAPL/+f/y/+r/8v/y/wcA4/8OAOP/6v/q/9T/BwDj/w4Avv/j/w4Axf/5/+P/8v/U/83/6v/U/83/2//j/8X/p//b/+r/1P8AAPn/AAAOAAcAHQAOAAAA+f/y//L/FgAHAPn/BwD5/wcAJQAlAAcAFgAHABYAMwAlAAcAAAAAAPn/BwAOACwADgAOAA4AAAAWAAAADgAHAAcAFgAAAAcAFgD5/+P/+f/j//L/DgAOABYABwD5/wcADgAWAAcADgAAAOr/FgDU/+P/8v/U/+r/2//q/8X/2//q/9v/6v/F/+P/zf/F/9T/tv+2/83/2//U/+P/2//b/8X/vv/N/6f/r/++/6//r/++/83/xf/F/9v/2//b/9T/r//F/8X/xf/b/83/zf+v/+P/4//b/+P/tv/j/77/r//F/77/zf/q/+r/tv/F/8X/vv/F/6f/r//U/7b/vv/5/7b/1P/q/77/6v/q//n/6v/y/wAABwA7AB0ADgAdACUA+f8WADsA8v8lADsABwAHAB0ABwAAACUABwAsAB0ADgAdAPn/DgDq//n/BwDy/w4ABwDq/+r/+f8OAA4ABwAdAA4AFgAsABYAHQAzADsAMwAzACwAFgAWACwAHQA7AEoAHQBKADMAHQAzAB0AOwAsAEIAUQBRAFEAOwBvAEIAOwBRAB0AQgAsAB0AQgAdADMALAAlACUAFgAsABYAOwBKAB0AMwAlAEIAMwA7AEIAMwAzADsAOwAlAEIAOwA7ADMALABCADMAQgAsACwAUQAsABYAMwAHACUAQgAWAFEAJQAzACwADgAdAAcAMwAlADsAHQAOACUAFgAOAAcAOwAsAB0AHQAOAA4AFgAsACwAJQAWAAcAJQA7AAAAHQAsAAAAOwAWACUAQgAdACwAMwA7ABYAHQAsACUAJQAlAFEAFgAlAEIAFgAzAB0ALAAsAEIAQgA7ADsAJQBKACUAFgAlAB0AHQAlADMALAAlAA4AJQAOAAAAHQAHAA4A+f8HACwAHQAsACUAFgAWABYABwAWACwABwAOAAcABwAlABYAHQAHAA4ABwD5/wAAAADq//L/+f/U//n/8v/j//n/+f/5//L/DgAHAOP/6v/y/77/4//q/+P/2/+v/9v/zf/b//L/4/++/83/2/+v/9v/2//b/83/zf+g/6D/xf+g/7b/mf+n/83/xf+v/77/r/+Z/9T/vv/N/9v/2//N/7b/6v/y/+r/+f/U/8X/4//j/wAABwDb//n/+f/j//L/8v/y/9v/1P8OAPL/BwAdABYAFgAAABYAAAAHACUALAD5/wAAFgAHAA4A+f8HAPL/AAAHABYAHQDy/w4ADgAWAB0AQgAlADMALAAHADsAAAAsAB0A8v8sAAcAJQBCAEIAJQA7ACUADgAsAA4AHQAOACwAAAAOACUA2/8zAPL/AAAHAPn/MwAOADsAAAD5/wcAFgAHAOP/JQD5/x0AJQDy/xYAFgDy/wAADgDF/+P/4//N/83/vv/F/83/2/+2/+P/vv+2/+P/2//b/83/AADN/8X/6v++/+P/8v/y/+r/tv/N//L/zf/N/+r/tv+v/9T/1P/y/+r/1P/b/8X/1P/y/wAA4//j//L/6v/5/+r/BwD5//n/HQAdABYAAAAOAAcA8v8AACUAHQD5/x0ABwDq/+P/zf/j/9v/zf/N/83/vv/U//n/+f/5/wAAAAAAAAAAAAAOABYAJQAHAA4ALAAzACwA+f8WAA4A6v8HAOr/AAAHAOP/BwDb/9v/AAD5//n/6v8lAPn/AAAdAPL/AADy/xYA4/8HAPL/xf/5/83/AADq/+P/2//5/w4A6v8AAPL/+f/N/wAAzf+2/yUA6v/b/wAA6v/b//L/1P8AAOP/6v8HAOr/DgC+/wAA+f/y/xYAFgBCANv/HQAdAAAAQgAdABYAFgAOAPn/8v8AAPn/+f8dAB0A+f8HAPn/BwAOAPL/HQAWAA4AOwAdAB0AHQAWABYAHQAdAA4AFgAdACUABwAlAAcADgBRABYADgAWABYAHQAOAAAA4//j/wcA4//U//n/4//5/+r/+f/5/+r/8v/5/wAA6v8AAOP/6v8AAOP/AADq/+P/6v/j//n/+f8AAAcA+f/5//L/AAD5/9v/AADq/8X/1P++/+P/4//U/+P/xf/y/+r/2//q/77/4//U/8X/zf/b/9T/zf8WAPn/8v8AAPn/1P/j/+r/zf/5/9v/4//q/+P/2//b//L/6v/5/+P/6v/j/+P/1P/y/wAAAAAlAAAADgDq/+r/8v8AAA4A4/8dAPn/DgA7AAcAFgAOAA4AFgAAAAcAJQAOAB0AJQAOAAcADgAHAOr/BwAWABYAHQAHAA4ADgAlAB0A8v8WAAAA2/8AAL7/2/8OAOr/AADq/9v/2//b//n/6v/y//L/BwDj//n/FgDb/wAA6v8AAPL/8v8lAOr/FgAAAPL/AADq/w4AAAD5/+r/6v/y/wAA8v/5/+r/2//5/+r/AADy/wAA+f/y/yUABwAWAA4AFgAOAM3/DgAAAM3/FgDj//n/JQDj/yUA8v/q/w4A2/8AAOP/AAAAAOr/8v/b/+r/BwAHAPL/+f/j//L/4//U/+r/zf/U//n/AADN/+P/8v/q//L/DgAsAAAADgDy/w4ABwAdAEIAAABKACwADgAWAAAADgD5/wAAAAAHAA4AHQAOACwAMwAWACUAFgA7AB0ADgAsAAcAFgAdAAcADgAOAA4AJQAWAA4AFgAHAAcAJQD5/wAAHQAHAAcA6v8dAPn/BwAlAPL/DgAHACUABwAOAA4A+f8dAAAAFgAOAAcA+f/y//L/AAAAAAAAFgD5/wcA8v/q//n/DgD5/wAAJQDb/xYABwAAAAAAzf8OAOr/AAAHAOP/AADj/wAA+f/j/wAA2//5/wAA2/8HAPn/FgAWAA4AJQD5//n/+f/y/x0AJQAdADMAFgAWACUAHQAdAA4AFgAsACwAJQAzADsAOwAzAEIAUQAzADMAMwA7AB0AMwBCACwAYAA7AFEAQgAdAGAAQgBKAEoAMwBKADsAUQBgAEoAQgBgAFkAUQBgAEIAWQA7AEoAYABKAG8AZwCMAGcAZwB+AFkAdgBgAHYAbwBnAH4ASgBKAEoAQgBKAEoAUQBnACwAJQA7AB0ALAAzAEIAMwBCAEoALAAWAPn/DgAWAAcAAAAWABYADgD5/wAAFgDU//n/AAD5//L/8v8OAAcAAAAHAB0A6v8HAPL/8v8OAPL/MwAWAB0AFgDy//L/1P8AAPn/+f8WAPn/8v/y/9v/8v/b/+P/8v/q//n/4//q/9T/4//j/+P/8v/F//L/2//F/83/4//q/9T/+f/q/83/2//5/9T/2//U/77/4//F/+P/2//U/9v/xf/N/9T/4//N/9v/1P/U/9v/zf/b/wAA2//U/w4A4//q/wcA8v8AANv/zf/q/83/1P/q/8X/4//b/9v/4/++/8X/vv/U/8X/2//y//L/6v/j/wAA1P/q/+P/4//5/+P/BwDq//n/BwD5/wcAAADq/9v/1P/5/+r/xf8OAOP/2//y/9v/2/8AAOr/p//y/7b/vv/U/+P/DgDF/wcA+f/5//n/8v/5/+P/8v/b/yUA4//j/w4Azf/q//L/BwDy/+r/8v/5/+r/6v/j/8X/BwDy/8X/8v8AAPL/4//q/wAA8v/b//n/AADq/wAABwDy//n/6v/j//n/4//5/+r/2//5//L/BwAHAAAAAAD5/x0A+f8AAB0ADgAdAA4ADgAAAAcA+f8HAA4A4//y/+r/FgDq/w4ALADj/wcA+f/y/9v/+f++/9T/+f/F/w4A6v/5/wcADgAOAPn/FgDN/wAA8v/q/wcA+f8HAOP/6v/q/wAA8v8WAA4A1P8OAAAABwD5//n/8v/5/xYA+f8WAAAA+f/y/wAA+f/q/xYA+f8WAA4AFgAdAAAAAADN//L/1P/U//n/2//y//L/2//N/9v/xf/j/+r/vv8AAOP/6v/q/77/6v/F/77/2//q//L/8v8AAPn/+f8WAAcA4/8OAPn/4/8OAAcA4//5/wAA4/8HAPL/4//N//L/BwDN/w4A2/+2/9T/zf/b/9T/4//U/+r/2//b//L/4//5/+r/2//b/9T/xf/j/83/vv+2/77/1P++/83/zf/F/6//1P/U/8X/zf++/9v/vv/N/8X/xf/F/8X/4//N/8X/r/++/77/xf/U/8X/zf/b/+P/zf/5//L/4//5//n/BwDj//L/AADy/wcADgD5//n/8v/q//L/8v/y/w4AFgAAAB0ABwDq/wAADgAOAB0AAAAAACwA8v8OAB0ABwAdABYAHQAHACUAFgAHAA4A+f8OAAAALAAdAPL/FgAHAAcADgAlAB0AHQAHAA4ALAAHAB0AMwAOADsASgAdADsAUQAdADMAWQAzADMASgA7AEoAQgAsAFkAQgA7AFEAOwA7ACwALAAsAPn/LAAdAAAAOwD5/w4AHQAOABYA+f8dAAAABwAWAOr/AADq/83/+f/q/+P/DgD5/+r/8v/y/+r/8v/b/8X/8v/N/83/AAD5/9v/+f/5/77/8v/5/9v/8v8HAA4A+f8AAAAA+f/5/9v/AAAWANv/DgDy/wcAHQAHADsA+f8sAA4A4/8zAOr/AAAWAAcAFgAAAAAAFgAAABYAMwD5/wcABwAdAB0AFgAlAOr/AAD5/wAADgAlAA4AAAAsAAcABwD5//L/AAD5/w4A+f/q/xYAHQDy/xYAHQAOACUABwAHAA4ADgAzABYADgAzAAAALAAsABYALAAWAEIAFgAWACUAFgAOACwAOwAlAFEAFgAsACUADgA7AB0AOwAzACwAJQBCACUALABKACUASgAlAB0ABwAOAAcABwAsAA4AMwAlAB0A8v8OABYA4/8lABYADgAWAB0ALAAWAPn/BwAHAOP/BwAWAPn/DgAsAB0AFgAdAA4ADgAlACUAAAAOABYADgAAAB0AOwAdADMAUQAsAB0AHQAzAFEAFgBCACUAHQBCABYAMwAsAEIAOwA7ADsAJQAsACUAOwAsACwAJQAdACUABwAWABYA+f8HABYA6v8lABYAFgA7APn/FgAHAAcADgAOAA4ABwAzAAcALAAOAAAAFgDy/ywAFgAsACwABwBCAB0ADgAsABYADgAlAAcAAAAAAPL/+f/q/+r/1P/b/+P/4//q/+P/4//U/9v/4//U/+r/FgDy//n/AAD5/x0ABwAWABYAFgAlAB0AHQAsAA4ABwAzAPL/FgAWACUAJQAOACwAAAAdAA4ALAAlAA4AJQAHAA4A+f8dAA4AFgAzAA4ABwAOAPn/4//y//n/BwDU/9T/6v/y/+r/AAD5/83/AAD5//n/AAAAAAAABwAHAAAADgDy/+r/6v/5/+r/AADq/9v/+f/N/+P/2//U/77/1P/F/77/1P/F/9v/p//N/77/mf/F/83/xf/N/9T/zf+n/6//zf+g/+P/zf+2//L/tv/U/9T/tv++/9T/xf/U/+r/xf/q/83/2//y/8X/8v/q/9v/8v/U/+r/8v/U//n/+f/y/+r/AAAWAPn/BwAHAAAAAAAAAPn/+f8OAPn/BwAOAAAAAAAWAAcAAAAWAPL/FgAlAB0AQgAdACUADgAWACwAAAAzAA4ABwAzABYAAAAOACwA8v8sADsAAAAzACUAJQAzAB0AJQAHAAcAMwAdADsAOwAdACUAMwAzABYAJQAdACUAHQAOADMAMwAzADsAMwAlAB0A+f/y/+P/+f/5/+r/HQDy//L/BwDb/9v/2//b/+r/6v/N//n/8v/N//n/4//b/8X/1P/j/77/1P/y/9v/zf/j//L/2//j/+r/zf/N/9T/1P/y/+P/xf/b//L/4//U//n/6v/U/77/1P/b/9T/6v8AACUA8v8WABYA8v8lAAcAFgD5/wAABwAdAA4A8v8AAOr/BwDy/wAA6v/q/9v/xf8AAM3/6v/y/+P/4//5/w4A8v8AAPn/DgDj/+P/8v8AAPn/4/8WAOr/6v/y/wAABwDq/+P/8v8AAOP/DgAAAOr/8v/y//L/8v/y/9T/4//N/+P/4//j/+P/2//q/83/6v++/9T/zf+2/9T/r//U/83/xf/N/9T/tv+v/8X/r//U/77/zf/U/+P/2//j//L/6v8HAOr/BwDy/+r/4//j/wAA4//y/9T/1P++/9T/BwDN//L/6v/F/+r/1P/b/83/zf/q/83/4//b//L/8v/y/w4Azf/q/+r/+f8HAPn/JQAlABYADgAWAAcAAADy//n/+f/5/wcABwAdAAAAAADj/wAA4//y/wcAxf8WAPL/6v8AAOr/6v/b/9T/zf/U/8X/6v/y/+P/2//j/8X/tv/N/83/1P++/9T/tv+n/7b/xf/b/8X/zf/U/+r/zf8HANv/xf/5/9v/8v/U/9v/xf/b/+r/4//q/9v/DgDq/9v/AADq/8X/6v/j/+P/AADq/wAAAAAAAPL/HQAWAAAAFgAHAB0AFgAlACUAFgAOADsAMwAlAB0AFgBCAAAAOwAzAPn/MwAAADsAMwAWAEIADgAWACUADgAWABYABwAdAAcAAAAsAA4AQgA7AB0ASgAOAB0AMwAAACwALAAWACwAAADj/x0AHQAOACwAJQAdACUABwAAAAcADgAWACUALAAWAA4AAAAHABYA+f8WAA4AAAAAAPn/BwDb//n/JQAWABYABwAHAAcADgAHAB0AHQDq/x0AFgAdADsAJQBKAEIAJQAdABYAJQAdAB0AJQAlAB0ASgAsADsAQgAOAEIAHQAlACUABwA7ACwAQgA7AEoAQgAzAGAAQgBRAFEAMwAzADsASgAsADsAOwAsADsASgBZADsAOwBKAEoAQgBZAGAAWQBnAFkAYABCAEoAQgBZAFkAMwBvAEoAQgBZAFkAWQBKAGcAOwBCAEIAUQBgACUAOwA7ACwAOwA7AEIAUQBKAGcAbwBZAFkAMwA7ADsALAAsABYAJQAdAB0ABwAAABYADgA7AA4AAAAHAPL/DgDq//L/8v/j/9v/+f/q/9v/HQDU/9T/8v/U//L/zf/q/9v/xf/y/+P/2//U/9v/xf++/77/1P/F/77/6v+v/83/zf+2/+P/p/+2/83/tv/U/77/vv/b/9T/4//q/83/8v/y//L/AADb//L/6v/5//L/6v/y/9T/8v/b//L/4//N//n/xf/b/77/vv/q/7b/8v/b/9v/AADU/wcA8v/q/xYAAAAAACUA8v/5/xYA6v8OAAAABwAlACUAMwAsAEIAJQA7ADMAHQBCADMAMwA7AB0ADgBCAA4ADgA7AAAAMwAOAAcAFgAOADsAHQAsACwABwAdADMAHQD5/w4AHQAAABYAJQDy/wAAHQAdAA4A+f8dAA4A8v8HAAcAHQAdAAcADgAAAPn/+f8OAB0ADgAWAAcA+f8HAAcABwAHAPn/BwAdAA4AHQAsAB0AFgAOACwAJQAWADMAMwAdACUAMwAlACwAJQAWABYAAAAdACwAFgAHABYAHQD5/wcAFgAAAA4ADgAAAA4A+f8HACwAAAAOAAAA8v/b/9v/8v/N//L/zf/N/9T/vv/U/83/AADN/9T/2/+v/9v/vv/F/8X/1P/q/+P/1P/U/77/xf/q/9T/6v/U/77/4//F/9v/6v/U//L/4//q/+r/xf/y/8X/xf/j/7b/4//y/9T/4//N/9T/4//F/83/1P/b//L/4//5/+P/xf/5/9v/zf/b/83/6v/N/83/zf+n/9T/4//U/77/4//N/77/BwC+/83/4//b/+P/tv+g/7b/vv+2/9v/zf/N/7b/6v/5/8X/2//N/+P/xf/b/+r/zf/y//n/8v/y/+r/8v8HAOr/+f/y/9T/8v/q//n/2//q/+r/4//b/9T/6v/U/+r/+f/q/wAAAAD5/x0ABwAAAAcA8v8AAOr/BwAAAAcA8v/U//L/2//y/+r/AADb/9T/1P++//L/8v/y//n/+f/y/wAAAAAHABYAHQAlABYAMwD5/xYABwAHAB0ABwAWAPL/AADq//n/1P/y/w4A4/8dAAAABwAHAB0ADgAWABYABwBCAB0ASgAzAB0AMwBCADMAMwA7AA4ASgAdADsAQgAdAFEAJQA7ACwAOwAzAAAAOwAdAA4AOwAdACUAJQAdACwAFgAWADMAJQD5/wAA8v8OAAAA6v/5/+P/AADb/w4AHQDy/xYAAAAdAB0AFgAWACwAFgAWADsA8v8WACUAFgAdACUAFgAdAB0ABwAsABYAHQAWAAcABwDj//n/4//b/+P/2//q//L/BwD5/+r/BwAAAAAA4//q/wAAzf/y/83/zf/5/+P/+f/N/9T/1P+2/8X/vv/q/+P/xf/U/8X/1P/N/83/8v/b//L/1P/U/9T/tv8AANT/6v/5/83/AAD5/wAADgAlAPn/6v8HAOr/4//b/wcA+f/q/wAAzf/b/9T/zf/q/83/2//y/+r/1P/U/+P/xf/U/8X/tv/F/6//xf/N/83/1P/q//L/1P/y/+r/1P/F/83/xf/N/+P/zf/j/7b/zf/N/8X/2//b/+r/xf/5/9T/tv++/77/zf+2/+r/xf/y//n/4/8OAOP/8v/q/xYADgAAACwAMwAOAA4ALAD5/zMALAAWADMAAAAAAAAAFgAOAPn/JQAdAAcAMwAzACwALAA7ADMAHQAlACUAHQAlAEoAJQAlACUA+f8lABYAFgAzADsAJQAWAA4AFgAWAAAADgAsAAcABwAdAPL/BwAHAAcAFgDj/wcAHQAdAB0AJQBCACUAUQBgADMAWQBgAEIASgA7AEIASgBKAEIAOwBgADsAMwAzAB0AOwA7ACUAHQAdADsAQgAsADsAOwA7ADsALAAsACwAJQAdAFEAJQAHACwAJQAWACwAOwAWAB0ADgAsAEoAFgA7ADMAFgAzAFEAMwBKAEIALABRADMAHQAsAAcAAAAHAPn/AAAOAA4AJQAlAPn/LAAHAOr/HQDq/wAA4//q/xYA6v8OAOr/AAD5/9v/DgAAABYADgAdABYAFgAWAA4ADgAOADsA+f8sADsA+f8dAPn/BwDy/+r/FgD5/wAA8v/5/xYA+f/y/xYABwD5/xYA+f8OAA4AFgAlAAAALAAdADMAJQD5/xYA+f8WAAcAFgAdAPn/FgAOABYAFgAdADMAHQAdACwAHQAWACwA8v/5/wAA+f8WAAAAAAAAAPL/8v/q/+r/8v/U/8X/6v/b/9v/2//y/w4AFgAOAPL/BwDb/+P/AADN/+r/6v/b/9v/vv/N/+P/2//b/83/xf/q/9T/1P/b/8X/BwAAAAAADgAAAA4A8v8AAPn/+f8OAPn/FgDy/wAA+f/y//n/4/8HAAAA+f/y/w4A8v/b/+r/1P/N/9v/AADN/wAABwDy/x0AAAAlANv/8v8AANT/HQDj/wAABwDN//L/8v8AAPL/AAAOAAcA+f/j//n/6v8WAAcAAAAHANv/+f/q/wAAAAAdAB0AAAAdAPn/BwAOABYA8v8WADsA4/8sABYA+f8dAAAAFgAdAAcAFgAWAAAAHQAOAA4AFgAWAAcAAAAAAPL/FgDq/x0AHQAOAFEABwAOAA4A8v/5/wcA+f8WAAcA4/8OAPL/AAAAAPL/+f/q//n/8v/q//n/8v8AAB0A8v8OAAcA2//y//L/AAD5/wcAAAD5/wcA+f8AANT/8v/q/9v/AADj/wAAFgAOADMAFgD5/w4ABwAHABYAAAAdACwA8v8AABYADgDy//L/8v/F/+P/+f8AAA4AFgDy/wcAFgD5/zMAJQAWAAAAHQBCAAcALAAlAAcABwAdAAcABwAOAPn/BwAAABYADgAlAA4ADgAdAB0AOwAAAEIAJQAHABYA6v8AAOr/6v/b/+P/+f/y/+P/6v/j/9v/1P++/9v/vv++/9v/1P/U/9T/2//j/wAA1P8AAPn/xf/y/9T/AADj//L/BwDN//L/8v/b/+P/AAAHABYAHQAAAB0AFgAOAA4AAAAOAAcAAADb/wAAFgAOAA4A4/8OAPn/zf8HANT/xf/j/+P/BwDy/wAAFgDq/w4A4//j//L/xf8dANv/xf/U/8X/vv+v/+P/p/++/83/p/+2/77/tv+2/83/tv/b/6f/p/+2/5H/vv+v/8X/r//U/9v/xf/b/8X/8v+2/8X/4/++/9T/2//N/83/xf/F/9T/vv/b/+P/2//y/+r/2//b/+r/4//j//n/+f/b//L/2//U//n/zf/j/+P/+f8HAAAABwDj/wAA4//5//n/6v8lAAAADgAAAPn/AADj//L/+f8HAPn/FgAAAPL/DgDU/wAAAAAHABYAAAAlAPn/JQAdAPn/BwAHAB0ADgAdAAAA+f/q//n/BwDy/ywAAAD5/zMADgAAADsAOwAlACUAFgAzAAcAJQBCABYAFgAdACwAHQAdACwALAA7AB0ABwA7ACUAHQAsAB0AJQAHACwAHQAWAB0AHQAzABYAQgAsACwAJQAlACUAFgA7ABYAHQAHAB0AOwD5/x0ABwDq/w4AFgDb/+P/8v/y/wcA8v/5/+r/8v/5/wcAFgAWABYA+f/5/+r/6v/y/wAADgDy/xYAFgAWACUAHQAlACUAOwAlACwAFgAAACUAAAAOAAcABwAlABYABwAOAA4A4/8sAB0AHQBRAAAAHQAsABYAMwBCACwAQgBCAB0ALAAsACUAFgAWAAAAFgAOAPL/FgDy/wcAAAAdABYAAAAlAAAADgD5/yUABwAOAAcABwAlAOr/MwAdAAcAJQAWAAAA8v8OAPL/HQAHAA4AFgDj/w4A+f8OABYA6v8OAA4A+f8sACwADgAlAA4A+f8OAA4ABwAdAAAAAAAOAOP/6v8AAA4ABwD5/w4A8v8AABYABwAlAA4ABwAWAA4ABwAdABYA6v8dAA4AAAAdABYADgAHABYA+f8WAAcABwAWAA4ABwDy//n/+f8AAOP/FgAAAPL/LADy/xYABwDy/+r/AADy/9v/FgDq/x0A+f/q/wcAzf/y//L/+f8HAPn/+f8AAPL/BwAHAA4AFgDq/w4ADgAAABYAHQAOACUAJQAWAB0A+f/y/w4ABwAAACwAJQAAAPL/AAAHAPn/8v/j/+P/AAAOAPL/AAAHAOr/8v/5/+r/2/8HAOr/+f/j/7b/+f++//L/6v/F/wAAtv/q/xYA4/8dABYA+f8WAA4A+f/5//n/6v8AAPn/BwAOAOr/+f/b//n/2//q/x0ABwAlAA4ABwD5/w4ADgDj//n/+f8AAOr/+f8AAAAA8v/q/wcA6v/q/+P/6v/y//L/AAAHAAcAAADy/+r/6v/j/+r/8v8AAAAAAAAAAA4AHQDy/w4AAAAWAA4AFgA7AOP/BwD5/+P/FgDU//L/AADy/w4A+f8WAAcA1P8AAOr/6v8HAM3/zf/j/+r/6v/q/w4ABwAAAPn/2//q/9T/zf/y/+P/6v8OAOr/xf/5/wAA8v8AAOr/FgD5//n/JQDq/w4ALAAWABYAJQAdAAAADgAOAA4ABwAdABYAJQAlAPn/LAAOAB0AJQAWAB0ABwAWAAAAHQAdAB0AMwAHACUAHQAWAEIALAA7AEIAFgAOAB0ADgAWAB0AJQAsAA4AHQAsACUAMwA7AEoAQgBgAEIAMwBKADMALAAlADsAJQA7ADMALAA7ABYAMwAHAB0AMwAlADsAMwBKADsALAAlACUADgAOABYAFgAdAAcAFgDy//L/6v/y/+r/6v8WAOP/FgAWAOr/+f/y/x0ADgAOAB0A4//5//n/8v/b/77/4//N/+r/4//F//n/2//b//L/2//b/wAA6v8AAA4A+f8AAOr/DgAAAAAABwAWAAcA+f8AANv/BwD5//n/6v8WAAcA6v8lAOP/+f/y//n/DgDU/+r/6v/U/+P/+f/U/+r/+f/q//n/2//j/+P/zf/b/+P/6v/U//L/8v/b//L/4//y/77/xf/N/6//1P/N/+P/zf/q/9v/vv/U/83/4//U/9T/vv/q/+r/1P/y/+P/zf/F/+P/zf/b/9T/6v/y/9v/4//N//n/2//b/+P/4//b/+P/4//N//L/vv/F/8X/vv/j/9v/8v/b/+P/AADU/+r/+f/q//n/4//q//L/8v/y//L/4//b//n/2//5/9T/6v/N/7b/4/++/+P/1P/q/9T/1P/U/77/4/+2/+r/zf/U/9v/4//q/9T/AADN/+P/8v/j/wAA8v/q//L/1P/U/+r/4//y/wAA8v/b//n/4/8OAA4A+f8zAA4ADgDy/wAA2//j/wAA2//5//n/HQDq/+r/+f/j/+P/1P/5/9v/2//5//L/BwAAAOP/+f/y/9v/BwD5/+r/AADU/+P/6v/q/xYA+f8WAA4A2/8AAOP/8v/5/wcA6v/5/x0A4/8OAA4A+f8AACUA+f8AAAcAzf8HANv/8v/q/9T/2//y/w4A8v8dAPn/+f/q/+P/BwDy/x0ADgAAABYADgAsAEIAFgAlADsAHQAlAB0AMwAWAA4AJQAzADsAFgBRACUAHQA7AAAAOwAdAAcABwAOACUA+f8dAB0ALAAzABYAJQAOABYAFgAOACUA8v8HAA4A8v8sAA4A+f/y/+P/BwDq/w4AJQAAAAAAFgAOAB0AOwAdACwABwAHACwAAAAlAA4ABwAzAAAAHQAlAAAALAAHABYAMwAdACwAHQAzABYALAA7ABYAJQAWACUA8v8OACwA8v8WAA4ABwAHAAAAAADj//n/AADy/w4AAADq/wcADgD5/wcA4/8AAA4AAAAdAAAAFgAHAAcAJQAHACwAQgAzACUAJQAlABYAFgAlACwALAAzACUADgAlACwABwAHADMABwAAAB0AAAAdACwAMwAdAAAAMwDq/xYAJQAAACUADgAzABYAJQAHAAcALAAdACwAHQBCAAcALAAzAAAALAAAACwALAAOAAcAFgAlAPn/LAAOAAAALAAHAAcADgAAAOP/6v/y/9T/AADb/9T/BwDb/wAABwAHAPn/8v/y/+P/BwDb//n/BwD5/xYA+f8HAAcA6v8OAAAAAAAWAPn/DgD5/+r/4//y/wAA2//5//L/1P/5//n/8v/5//n/+f8HAAAAAAAHAAcA+f8WAAAAFgAAAOP/DgDU//L/4//j//n/4/8AAAcAHQAHAAcAAAAHAA4A+f8dAOP/+f/5/9v/AADy/+P/DgDj/9v/AADN//L/8v/5/+r/8v/j/77/BwDb//L/8v/j//L/xf/U/8X/zf/F/9T/zf/U/+P/tv/b/9T/2//U/83/BwD5/9T/6v/b/+P/6v/5//n/4//q/83/4//U/9T/6v/j//L/zf/j/+r/6v/j/+r/8v/N/+r/AADj/+r/1P/N/+r/+f8HAAAAAAAHAPL/DgAHAPn/BwAAABYABwDq/wcADgAAAA4ABwAAAAAA8v/5/+r/4//y//L/+f/5//n/BwD5/wAAHQAsAAcADgAdAAcAHQDy/wAA+f8AAB0AAAAzAB0ABwAlACUAFgAdABYABwAdAAcABwAOAPn/AAAOABYADgAAAA4ADgAAAPL/BwAHAOr/AAAAAA4AAAAWACUADgAdAB0ALAAOADsALAAlADMADgAsAB0ALAAWADsAFgAOADMADgAAAPL/HQD5/zMASgAOACwAHQAOABYADgAWAA4AHQBCAPL/DgAOAPL/DgAHADMA4/8OAPn/6v8HAM3/FgDq/wcAFgAAAB0AAAAHAA4AFgAOAAAADgAWAAcAAAAOACUA8v8lADsAFgAzABYAMwD5/ywAOwAWADMADgA7ACUAHQAHABYAFgAAACwA+f8WAAcA+f8dAAcA+f8OAAAA6v8HAOP/4//y/+r/6v/y/wcA+f/y/+r/+f8OAPL/BwAOAOP/AAAAAPn/8v/U//L/4//b/+r/+f/y/9v/8v/j//n/4//q/wcA6v/b/9v/xf/j/+r/1P/q/9T/4//y/+r/6v/U/9v/8v/5/+P/AADU/83/8v/U//n/1P/j//n/4/8WAAcA1P/y//L/zf/y//n/AAAOACUADgAOADsAAAAWAAAAAAAWAAAAFgAdAA4ADgA7AAAAHQAdAA4AFgAWACwABwA7AAcALAA7AB0AHQAlAB0A6v8zAPn/BwD5//n/JQD5/ywAFgAAAPn/HQD5/ywADgAOAEIA6v87AAAA+f8OABYADgDq/x0AAAAsAAcABwAAAPn/DgAAACUADgAdAA4AFgD5/xYAHQDq/wcA8v/5/9T/8v/y/9v/4//F/+P/6v/5/wAA+f/j//n/AADb/wcA6v/b/+r/6v/q/8X/6v/j/8X/4//b/+r/4/8HAOP/zf8AAMX/4//U/9T/8v/N/+r/2/8AAPn/+f8WAPL/+f/b//L/2//q/xYA1P/5//L/DgAWAPn/FgDq/wcADgAWAB0ADgAAAPL/BwDq/wcAHQAsAAcAAAAOAOP/HQD5//n/JQDq/xYADgD5/ywAHQAHABYA+f8OAAcABwAWAAAAOwAHAA4AJQAOADsAHQAdAA4A+f8WAPn/DgAdAPL/AADj/+r/4//N//n/+f/5//n/+f/q/+r/4//q/wcA4/8OAA4A6v8HAAcAAAAOAA4AAAAHAPL/DgAWAPn/BwDy/wcADgDy//L/BwD5/w4A4//q/wAA2/8HAM3/4//y/+P/6v/b//L/1P/j/83/2//F/+P/4//F//L/1P8AAOr/4//5/+r/4//j/+P/zf/y/+r/2//y/+r/2/8AAPL/AAAAAPn/JQAAADMA+f8OAA4A4/8lANT/+f/b/+P/+f/b/wAA+f8dAB0ABwD5/w4A4/8HAA4A8v8OAOr/DgAHAB0AHQAlAAAA+f8dAOr/JQAWAB0ABwAWAB0A6v8OAOr/+f/b/+r/4//U/wAA1P/q/+r/1P/5/9T/4/8OANT/4//j/wAA+f/j/yUA8v/y/w4ABwAHAAAADgAHAPL/AAAAAAAAFgD5/w4A+f8AAOr/4//y/9T/AAD5/wAA4//y/+r/xf8OAOr/6v/j//L/6v/j/wAA4//q/9v/1P/q//n/AADy/+P/+f/y//n/8v/j/wAA4/8HAAAA8v8AABYA+f8AAA4A1P8dAPL/AAAdABYAHQAHABYA4/8HANv/+f/y/9v/8v/N/wcAzf8AAOP/2//y/+P/+f++/xYA2//y//n/zf8AANv/6v/U/+P/4//j/+r/AADj//L/BwDb/x0A6v8OAOP/+f8sAOP/LAD5/xYABwD5/xYAAAAHAPL/DgDy//n/8v/5/wAA4//y/+P/2//b/+r/1P/5//L/2/8WAPn/2//j//L/2//q//L/8v/y//n/+f/q/wAABwAsAAcAHQAlABYAJQD5/xYABwAOABYAJQAdABYAMwAOADsAFgAdABYAFgAHAPn/OwDy/yUAJQAHAAcABwAsAPL/LAAOAPn/DgD5/wcABwAHABYABwDy/ywAFgAOADMAHQAWAAAABwAHABYAFgA7ADMAMwBCACwASgAsAEIAQgAzACwAQgA7ACUAMwAWADsAJQBCAEIALAA7ACUAQgAWACUAOwAdAB0AFgA7ACwALABCAEoAMwAOACUAHQAlADMAHQA7ACwAUQBZADsAWQAsADsALAAlADsAHQAWAAAADgAHAAcAAAAWAA4AAAAlAAcAJQAsACwALAAzADMALABCACUALAAzACwALAAlABYAJQAsABYAJQAlACwAQgAsACwAJQAHACUABwAAAB0ABwAlAPn/HQAOAA4ALAAWACwA+f8zABYAHQAsAAAALADq/w4AFgAOACUAHQA7AB0AHQAdAB0ABwDq/w4A8v/j/w4AAAAOAAcA+f/5/9v/8v/U/+P/BwDy/+r/DgD5/9v/AAD5/+r/2/8OAPL/4//q/8X/1P/N/9T/r//U/83/zf/U/8X/xf+n/9v/tv/q/9T/xf/F/6//2/+K/+r/4/+2/wAA2//b/8X/zf/q/8X/1P8HAOP/DgAHAAAABwDy/wcA8v8dAAcAHQAlACUALAA7AEoAJQBCACUASgAlACwAOwAOACwAAAAsACUAJQAdACwAFgAdACwA8v8OAOP/BwDq//n/DgAAAPn/8v8HAMX/8v++/9T/1P++/9T/zf/y/83/+f/N/83/4//N/83/1P/j/77/6v/N/83/1P/U/8X/zf/N/6D/2/++/9v/4//q/77/1P/q/77/AADN/+P/xf/N/9v/tv/q/7b/4//N/8X/4/+2/83/8v/U/9T/6v+n/+P/4//F/9v/2//b/83/4//b/77/1P/b/9T/2//F/9v/1P/j/+P/zf/j/+P/4//b/+r/1P/F/8X/6v/N/8X/BwDN/wAA8v/q//L/2//y/8X/zf++/9T/tv/N/7b/tv++/6//4//F//n/1P/j/9v/xf++/8X/2/+n/wcAvv8AAAAA1P8sAPL/+f/b/wAAxf/b/wcA2//5/+r/+f/5//n/1P8AAPL/6v8OAA4ADgD5/yUA8v8HAAAABwAAAOr/FgDy/w4ABwAAAOP/BwAWAAcADgAWAA4A+f8WANv/MwAAACUASgDy/0IAAAAzAB0AFgAzAA4AJQAWADsAFgBKAEIAMwAsADsAMwAOAFEAAABCADMAFgBCADMAMwAzAGcAMwBgAEoAOwBKAEoASgAlAEoAFgBZACUAMwBKAAAAMwAdADsALAAzACUAQgAsACUAQgD5/0IADgAWAB0AAAAdAA4ALAAOAB0AOwAlABYALAAdAAcAMwAHAAAAAAAAAA4ABwAOAAcABwAdABYADgAWAA4AAAD5//L/4//j/wAAAADb/+P/4//b/+r/6v8AAOr/8v8AAPn/8v8AAAAAzf/q/wAA+f8sAA4ADgAlAPL/BwDy/wAABwDy/zMABwAWAA4A8v8lAPn/AAAWAA4A8v8OAB0ADgAlAAAAAAAAAOP/8v/5/+P/4//q/9T/8v8HAPL/HQAWAAcABwDj/wcA4/8AAAAAAABCABYAJQAsAAAAAAAOAAcABwDq/wcA+f/U/xYA+f8OAA4AAAAdANv/+f/5/wAAFgAAACwABwAsADMADgAsAAcAFgAAAAcAFgAOACwAFgA7AAAAFgAdAOr/DgAHAB0A8v8dAPn/6v8HAPL/FgD5/xYA6v8HABYABwAOAPL/DgDq/w4ABwAAAA4AFgAWAPL/HQD5//L/8v/q//n/8v8AAA4ADgAdAAcAFgAdAPn/AADy/wcA6v/q//n/+f8AAOr/HQDj/+r/+f/b/+P/1P8OAOP/AADq/9v/FgDy/w4A6v/q/+P/2//5/+r/AAAAAPn/AAAOAOr/BwD5//L/AADy//L/xf8HAAAA6v8AAAcADgDq/x0A6v/b/wAA1P/j/+r/6v/q/wAABwDq/9v/+f/5//n/HQAWAPn/FgAOABYAHQDq/x0A6v/5/xYABwAlAPL/DgAAAB0A6v8OACwA+f8dAOr/HQDj/wAAAADq/wAA4/8HAPL/DgDq/wAA8v/q//n/8v8lAOr/+f/b//n/6v/j//L/vv/b/9T/6v/j/9v/4//F/+r/8v/U/9v/zf/j/9T/zf/y/9v/8v/q/wAA2//y/w4A6v8OAPL/BwDj/+r/8v8OACUA6v8dAPL/4//q/wAAAAAHAB0A8v8HAAcAAAAHAAAAAAAWAAcA+f8AAPL/AAAAAA4ADgD5/xYAAAAWAA4A4/8HAOP/HQAAAAcAOwAHACUA+f8dAOr/AAAWANv/HQDq/x0A+f/q//L/zf/5//L/FgDy/wcABwD5/wAA6v/y/wcAAAAHAA4A+f8sAA4AAAD5/wcADgAOACUAAAAOAPn/AAAWACUAHQAWAA4ABwAAAPL/8v/q/w4A1P/j//L/vv/U//L/4//j/wcABwAdAAAAHQAWAAAADgDq/wAA4/8AANv/zf/5/77/zf/q/+r/4//j/w4A8v/j/xYA4/8AAAAA6v8OAMX/6v/q//n/6v/b/wAAzf/j/wAA4/8OABYA+f8OAPL/+f8HAAAAFgAHAA4AAAAHAAcABwAAAA4AOwAHAB0AHQAOABYAJQAsABYAJQAlAAcABwAAAOP/8v/q//n/AADj/wAA8v8AAOr/AAAdAAcAHQAWABYADgAlAA4AAAD5//n/BwD5/zMAFgAsACUAFgAHAPL/BwDU//n/2//N/+r/4//b/83/+f/N/+r/4//q/+P/6v/5/9v/8v/N/wAA+f/q/+r/+f8OAOP/FgAWAAcA+f8dAA4ABwAWABYAJQAAACUAHQAlAAcAOwBKAB0AUQAzAEIAFgAWACwABwAdABYABwAdAOr/+f87APL/OwAlAAcAMwAHADMAJQAOAB0AHQAWACUAHQAdADMAHQAsACUAMwAlABYALAAWAB0AHQD5/yUAHQAWAFEALAAzAEIAMwAzAB0ADgAOAAAA+f8dAA4ADgAdAA4AFgAHAAcAJQAWAB0ADgAAAAcA8v8HAAAAFgAOAAcADgD5/wcABwAdACUAJQAlADMAAAAOAAAA8v8lAPn/HQAOACUADgAOAA4A2//q/+P/8v++/wAA8v8AAAcAAAAlAOP/FgDy//n/4/8HAAcA4/8dAOr/BwDb/wAABwAOADsA+f8AAPL/+f8AAPn/AAAdAAcADgAlACUABwAAABYA+f8HAB0AJQAOADMAFgAOACwABwAOAA4AFgDy/wAA8v8HAA4AAAAOAPL/FgDj/w4ADgAHACUABwAOAAAADgAHAB0A+f/5/wcA1P/b/+P/4//j/wAA1P8HAA4A2/8AANv/xf/N/9T/1P/b/9T/zf/N/+P/6v/j//n/AADj/wcAAADj//L/6v/y/9T/6v/y/9v/4//q//n/1P8HAPL/8v/5/+P/+f/U/w4A+f/q/wAA4//5/+P/6v/y//L/8v/b/+r/8v/q/+P/6v/5/+r/zf/5/+P/zf/q/+P/8v/q//L/BwDq/+r/BwD5/wAAFgD5/wAA+f/b/+P/8v/y/+P/+f/j/+r/BwD5/w4AAADy//n/+f/5/w4A6v/b/wAA2/8OAOr/BwAdAPL/FgDq/wAABwDq/yUAFgAOABYA8v8WAB0AHQAlAAcAHQAHAAcAAADy/wcA8v/y/wAAAAD5//n/BwAWAOr/DgAWAOP/BwDb//n/+f/q/w4A4//y/83/xf/U/77/4//j/9v/4//j/8X/2//j/83/6v/U/+r/AADy//n/4//b/8X/6v/y/+r/8v/5/+r/6v8AANv/6v8AAPL/8v8OAOr/+f8dAA4A+f8HABYA1P8AAPL/AAD5/+r/DgDj//n/2//5//n/AAD5/+r/6v/N//L/1P/y/+r/2/+v/9T/2/+v//L/r//U/8X/xf/F/8X/tv/F/wAAzf8HAPn/AAAHAAcA6v/y//n/xf/y/9v/AADj/w4ABwDj/wcA1P/5/9v/8v/y//n/+f8AAA4A8v8WAPL/AAD5/+r/8v/5//n/+f8OAAAA+f/y/xYA+f8HABYA6v/5/wcADgD5/wAAAAAOABYAAAD5/wcAAAD5/w4AFgAAAPn/DgAdABYADgAAAAcAAADy/wcA6v/5/wAA2/8AAOr/AAAHAPn/AAAHAAcA8v8HAPL/AAAOAPL/BwAOAA4ALAD5/xYAQgAHACwAMwAzABYALAAsAAcAJQAWADMAFgAsAB0AFgBKAFEASgBKAFkAMwBKADMAHQAzAEoALAAzAEoAFgBZACwAMwAzAB0AMwAHACwAJQAlACUAJQAOADMAFgAWAEIA6v8OABYA+f8AACUAFgAAAB0A8v8OAA4AFgAsADMAJQAOADMAHQAlAB0AHQAzAB0AMwAdABYAJQAHAA4AHQAOAA4AAADy/9v/BwAAANT/+f/j/+r/8v/y/xYA+f/5//L/+f/5/9v/6v/q//n/8v/5//n/1P/U/9T/6v/b/9T/2//b/9v/vv/j/9T/zf/y/9v/2//F/77/zf/N/9T/xf/U/83/zf/N/7b/xf/N/9T/1P8AAAcA8v/5/+r/6v/N/+P/zf/q//n/1P/y/9T/4//y//L/4//5/wAA2//q/+r/AADy/wAADgDy/x0AFgAOAA4AFgAsADsAMwAsAEIAMwA7ADsADgAWABYABwAWACUADgAzADMAHQBCACUAUQA7ADMASgAlAEoADgAdACUABwA7ABYABwAOAB0AFgAHAA4ALAAOAB0ALAAdAB0AJQAzAAcAHQAOAAcALAAWACwADgAOACUABwAWAAcABwAOAAAAJQAdAAcADgAOADMAFgAWADsAFgAsADsAMwBKADMALABCAB0ASgBKAEoAOwAzADsAFgAzACwALAAlACUADgD5/yUABwAOAB0AMwA7ACwAMwBCAEoAMwBZAGAAUQA7ADsAQgAlADsAQgAlADsAQgBKAFEAOwBKAEIAMwA7ADsAQgBCAGAASgA7AGcALAAlADsAJQAWACwALAAHAB0ADgAAABYA8v8OABYAAADy/+r/BwDb/9T/8v/j/83/4//q/9T/4//F/83/2//b//L/8v/y/+P/6v/j/83/6v/j/+P/1P/U/+P/xf/j/83/xf/N/8X/1P+2/8X/xf/F/9T/4//U/7b/6v/N/9v/4/+2/83/zf/b/9v/4//j/+P/xf/y//n/1P/q/+P/2//U/+P/4//b/+P/2//b/+P/6v/b/+P/4//N/8X/6v/q/83/+f/j/9v/2//N//n/2//F/9T/vv/q/+P/4/8WAPL/6v8AAOr/8v8OAAAA+f8WAAAAJQAHAAcAHQDj/wAA6v/q//L/6v/j/+P/AADq//n/4//b/9T/zf/5/9v/4//N/9v/6v/F/+r/1P/N/9T/xf/j/9T/4//j/7b/4//N/9T/6v++/+P/xf+2/8X/r//F/7b/1P/b/83/4//q/9v/zf/q/wAA+f/5//n/AAAOAOP/6v/q//L/+f/F/+r/1P/F//L/4//q//n/4//j/9v/2//y/9v/8v/5//n/6v++/9T/xf/b/+P/2//5/83/2//q/wAAAAAAAAcA8v/5/+r/+f/U/9v/DgDy//L/+f/q//n/BwAHACUADgAlACwABwAdAAcAAAAdACUABwAOACwA6v8HAB0A+f8lAA4A+f8OAAcA4//q/xYABwAOAA4ABwAAANv/+f/q//n/6v/j/w4Azf/j//L/4//q/+P/8v/q//L/vv/b/9v/1P/U/7b/4//N/+P/8v/5//L/6v8dAOr/+f8AAOr/AAAAAPL/6v/5/8X/2//j/83/BwAHAAcAJQAAAAcAAAD5/wcA4//N/9T/8v/y/wAAHQAAAB0ADgAHAAcA8v8OAPn/8v/b/9T/2//y/+r/BwAsAAcAJQAHAB0AFgAOAFEAAAAlACUA4/8lAAcADgAzAA4ADgAHAPL/BwAOAAcAAAAHAPn/6v/5/w4A+f8AADMABwAOAB0ADgAlABYALAAlAA4AHQAlABYABwAHAAAAAAAHAB0AJQAlACUAMwAdAA4AMwAOAA4AJQAWAA4AMwBCABYAMwAsACUALAAsACwAHQAdACUAJQAOAA4A+f/5//L/6v8AAOr/AAD5/wcA+f/q/wcA4/8OAA4AFgAHAAAAJQAHAAcABwAdACUALABCAEoAbwBCADsASgAHAA4AJQAOACUABwAHACUAHQAdAB0AQgAsAA4AJQAlADMADgAWACUABwAsACwAFgAHAAAAHQAHAB0AJQDy/wcABwAAAOr/HQAOAOr/FgD5/xYAFgAlAB0ABwAsAAcADgAHAB0A8v/q/x0AAAAdACUAJQAWAB0ALAAOAB0ABwAdACUADgAHAA4ABwAHACUADgAdABYABwAHAOr/BwAWAPL/8v/5/9v/4//b/+P/vv+g/+r/2//j//L/+f8OAPn/FgDy/9T/8v/b/+r/BwDq//L/6v/F/9T/1P/b/+r/zf/y//n/4/8dAOP/8v8WANv/AAD5//n/BwD5/+r/6v/y/+P/HQAAAAcAJQAAABYA+f8HAAcA6v8dAA4ABwAWABYAFgAdAA4AJQAWABYAJQAAABYAAAD5/w4ADgAOABYALAA7ADsAMwBCADMAJQAzAFEASgAlAEIAMwAWAB0AQgA7ACUAOwBKADsAOwBCACwAMwAlACwAQgA7ACUAJQBKAB0AJQAzACwALAAlAEIAJQA7ADsAHQAlAA4ADgAdACwAJQAOACUALAAAACwAJQAWADMAJQA7ABYAHQAWABYAJQAWABYA6v8AAB0ABwAWAAcAAAAHAA4ADgAlACwAFgAHAB0A8v/j/wcA4/8HAPn/1P/y/9v/6v/b/8X/6v++/9v/zf+v/9T/mf/U/9v/r//y/83/xf/F/9v/zf/U//n/6v/5/+r/6v8AAOr/1P/b/+P/+f/q/9T/AADF/9T/6v/F/9v/vv/U/8X/oP++/8X/tv++/83/tv/U/7b/tv/b/77/zf/b/9v/tv/N/8X/vv/j/6f/4//y/8X/AADj/83/+f/U/83/8v/U/9v/8v/q/+P/4/8HAPL/6v8AAPL/6v/U//L/8v/b/+P/4//y/9T/4/8AANv/6v/q//n/4//b/wcA6v8AAPn/6v8AAOP/DgAOAAcABwAHABYA8v8dAAAA4/8AAM3/4//y/+P/8v/q/wAA4//U/w4A1P/j//n/1P/5//n/1P/j/+r/1P/j/9v/tv/j/+P/xf/N/9T/4//b/+r/DgAHAAAA+f/5//L/8v8WAPn/6v/q//n/FgD5/+r/AAAHAPn/HQAsABYAJQAsAA4ABwAsACUAJQAdADMAJQAOADMAHQA7AA4AQgBCAAcAHQAOACUA4/8dABYA8v8sABYASgAdACUAFgAOAB0AAAAdABYAHQAOAB0ADgAsACwAAAAsAA4AFgAAAA4AJQAOABYAFgAdAAAAHQAzAPn/HQAWAPL/DgAHAAcABwAAAAAA6v/q/+r/BwAHAAAAHQAWACUAJQAzACUADgA7ABYAAAAHAPL/AAAAABYADgDj/+r/AAAHAAAAAADq/+r/AADq//n/6v/5/w4ADgAHAPn/DgDy/wAA+f/j/9T/2//q/8X/6v/j/+P/8v/j//n/1P8AAAAA4//y/+P/1P/F/9T/xf+v/9T/1P/b/+r/2//b/6//vv/N/7b/6v/F/77/1P+n/9T/vv++/9v/zf/j/9T/6v/F/9v/6v+v/+P/zf/b/+P/4/8OAPL/+f/q/9v/8v/j/w4ABwDy/yUAFgAOAAcABwAlAAcALAAWAA4AFgD5/zsAJQA7AEoAHQAlAB0AFgAWAB0ADgAlACwALAAWAA4AHQAWACwAFgAsAB0AAAAlAB0A+f8dAB0AJQAWAOr/MwAAAAcAJQAAAAcA8v8OABYAMwAWACwAMwAHACUAAAAdAA4AHQAlAAcAJQAOAPn/HQAlAAAAFgAlAA4AAAAdAAcAAAAlAPL/HQAHAAAAJQAWAA4ADgA7AA4AHQBCAB0AOwAlACUAWQBKAEoAWQBCADMALAAzADMAMwAOAA4AAAAAABYAHQAlAAAAHQAWAA4AQgAOABYADgAHAAAA6v/y/wcADgD5/x0ADgD5/wAA+f/y//L/8v/y/+P/2//y/9v/4//N/6//4/++/77/1P+n/7b/vv+v/83/4//U/+r/4//b/9T/1P/q/77/1P/N/6//4/++/6f/1P/F/6//xf+2/77/vv+v/6//p/+g/5n/vv+g/77/tv+n/83/tv/j/8X/vv++/9T/xf/F/+P/r//j/8X/2//U/9T/8v/F//n/4/8HAPn/6v8AANv/AADU//L/+f/j//n/2//j//L/+f/y/+r/AADq/+P/DgDq/wAAFgAHAAcA+f/y//L/BwDy/yUA+f8AACUA6v8WAAAAAAAdACUAHQAdACwAFgAWACUALAAsAFEAQgAzAFEAFgAdAEIAJQBCAEoAOwBCADsAMwAdACwALAAlADMAJQAdACUAJQAzAB0AAAAlAAcADgAlACUAQgAWAFEADgDy/zMADgAHABYAHQD5/w4A8v/y//n/4/8WANv/8v/q/8X/2//F/9T/6v+2/9T/BwC+/wAA+f/j/wAA8v8WAOr/JQAzAAAADgAdAB0AFgAsAA4AFgAlAAcAFgAzAB0AHQAWAB0ALAAsAEoALAAzADMAMwAzAEIASgBKADsAMwBZACUAQgA7ADsAOwAzAFkAOwBCACwAYAA7ADsAZwAsAFEAOwBRAGAAbwBKAFEAWQAdAHYAOwBCAGAASgBZADsAWQBZAEoASgBCAFkAQgBKAFEAMwBRAEoAQgBCACUAJQAlADsALABKACUAJQAzAAAALAAsABYAAAAOAB0AJQAdAAcALAD5/x0ADgDb/wAA8v8HAPn/BwAAAPn/HQAWAB0ADgD5/wcABwAOAAAA8v8OAPn/BwAWAPL/HQAOAAcAHQDy/wcABwDy/wcAAADq//L/+f8OABYA+f8HAOr/1P8AAOP/8v8AANv/+f/y//L/AADy/wAA6v/j/wAA4//b/wAAzf/U/wAA4//y/9v/1P/q/9T/1P/U/+r/1P/j//n/4//q/+r/2//U/+r/2//y/8X/2//q/77/+f+2/9v/2//F/+P/zf/U/7b/vv/N/8X/p//U/9v/p//q/+P/zf/j/+P/4//y/+r/8v/b/9T/6v/N/+P/xf/N/9v/tv/j/9T/vv/U/83/4//j/9v/6v/U/9v/2/++/7b/2//j/9v/+f8AAPn/4//j/9T/2//b/8X/4//N//L/1P/F//L/zf8AAOP/2//5/8X/zf/q/83/1P/y/+P/6v/N/+P/6v/j/wcA4//y//L/6v8HAPL/BwD5/+r/6v/q/+r/xf/U/83/xf/N/9T/2//N/77/1P/F/7b/+f/j/9T/1P/F/77/xf/j/9T/6v/b//L/6v/F//L/zf/j//L/6v/q/8X/4//U/9v/AADj//L/AADj/wAA4//y/w4A2//5/+P/vv/j/9v/6v/b/77/zf/F/8X/2//U/9v/6v/b/83/2/+n/83/4//F//n/6v/q/+P/1P/U/8X/4//U/+P/4//b/wcAzf/U/+r/tv/N/+P/4//U/+r/zf/N/83/vv/q/77/zf/q//L/4//U/+r/r//U/83/zf++/6//1P+g/9v/xf+2/+r/r//b/+r/1P8WAPL/2/8HANT/+f8AAOr/JQDy//n/FgDq/wAAAAD5//n/+f8AAAAAFgAOAA4ADgAWAAcA6v/5//L/FgAAAAcAJQD5/yUAHQAHAA4AAAAdABYAJQAlAB0AJQAOACUAFgAsACUAJQA7AA4AMwAOAB0ADgD5/x0AFgAsAB0AJQAOACUAFgAWADMAHQAlABYAMwAHAB0ALAD5/yUAMwAdACUAQgAdADsAMwAlACwA8v8sABYAHQAzABYASgAzAB0AQgAsADsAHQAlADsAAAAlACUADgAOABYAHQAdADMALAAzAB0AMwAdACUAMwAlACUADgAsABYAMwAsADMAHQAOAEoAHQA7AEIAQgBCAB0AOwAlACUAJQAzAEoAMwA7AEoAJQAdACwAJQA7ACUAMwAlABYASgAdACUALAAAAEIAHQAWACwAHQAsADsAJQAlADMAHQAsACUAQgAdACwAJQAsAEoAAABKAA4ABwAlAOP/BwAlAB0A6v8sAPL/BwAWAOP/MwAHAPL/8v/5/9v/+f8AAPL/JQAWAAcA+f8OAAcABwAsACUAAAAlACUABwAzABYAMwAAAAcALAAdAEIAMwBZADsAJQA7AEIAOwBZAFkAQgBgAEIAQgBRAFEAUQA7AEoAQgBKAGAASgBRAGcAQgBZAGAAWQBgADsAQgA7ADsAZwBgADMAQgA7ADMAMwAsACwADgAdAAcAAAAWAB0AHQAOABYADgAdAB0AHQAWACwA+f/5/x0AAAAlABYADgAOAAcABwAWAFEABwAHAB0A+f8lABYAFgA7ABYALAAdAA4AHQDy/wAA+f8HAAcA8v/y/9v/8v/b//n/6v/U/+P/vv/q/83/zf/j/+P/6v++/83/tv+n/77/xf/F/6//p/+2/7b/vv/N/7b/1P/U/83/1P/b/+P/xf/b/+P/2//q//L/8v/b/wAAAAAHAOr/8v8dAOP/AAAHAPL/DgDj/wcA6v/q/w4A4/8HAOP/6v/y/9v/BwAAAAAA8v/y/+r/8v/j/+r/DgDj//L/+f8AAAAA6v8AAPL/6v/5/wcADgD5/wcABwDU/+r/vv/b/+P/2/8WAOP/FgDy/9v/2//U/9v/zf8AANT/1P/N/83/2/+2/8X/1P+2/6f/1P+v/77/xf++/8X/oP+v/8X/xf+2/+P/p//U/9v/xf/U/6f/8v/F/7b/vv/F/77/oP/j/9v/1P/N/8X/xf/U/8X/r//U/6f/tv/U/6f/p/++/6f/oP+v/77/xf/N/83/tv+2/7b/1P/b/7b/1P/N/8X/zf/F/+r/4//U/+P/4//j//L/FgD5/wAADgDj/xYA+f/5/wAA2/8dAPn/FgBCAOr/6v8zADsA6v/j/zMAJQAHAB0A+f/y//n/LAAsAPL/4/8HAA4A+f8AAPL/BwAWABYABwDj//L/AADy/+P/FgAHAAAAFgAOABYA6v/q/wAADgAAAAAABwDU/xYALAAOAA4A+f8HAAAAHQAsAA4AFgAWABYAHQAsADMAJQBCAB0ALAAzABYALAAlAEoAFgAOAA4A8v8OAPL/FgAdAAcAHQAAABYAHQAHAAcADgAOAAcAFgAdAPL/+f8HAAcAFgAOACUAFgAHAA4AAAAAAA4ABwAWAAcADgAWAPn/LAAdABYADgD5/wAA4/8WAAAAAAAHAAcADgDq//L/4//b/+P/8v/q/wcABwD5/xYA4//y/+r/4/8HAOr/DgD5/+P/8v/5//n/8v8AANv/6v8AAAAADgAHAAcA+f8dACUADgAWABYADgDq//n/DgDy/xYAFgD5/wcADgAHAAcABwAOAB0AFgAOAA4AAAAHACUAHQAlAAcA8v8dAPn/8v8WAAcABwAOAPL/+f/y//L/BwAWAB0A8v8dAAcABwAWANv/JQAAAA4AHQDy/ywAAAD5/yUAFgAAABYAJQAWAA4ALAAOAPn/FgD5/wcA4/8HAA4AAAAAAAcABwDU/yUA4//y//L/1P8dANv/DgDy//L/AAD5/xYA6v8zABYAFgAlAA4AFgAOAAAADgAWAOr/HQAOAOr/AAD5/wAA8v/q//L/6v/5/wcA+f/5//L/+f/q/+r/+f/b//L/BwAAAOP/8v/y/9v/JQAWAPn/AADy//L/4//N/+r/4//b/xYA+f8AAAcA4/8AAPn/+f8HAPL/4//q/wAABwAOAA4AHQAdAAcA+f8AAPn/DgAWABYADgDj/yUAHQAOAB0AFgAlAOr/HQAHAAcAHQAAADMA4/8dABYAAAAOAOr/HQDj/wcABwAAAPn/4/8OANT/+f/5/+P/1P/U/+P/vv+2/83/1P/F/+P/2//j/8X/6v/q/77/AADb/+r/2//b//L/1P/y/77/6v/y/8X/AADy/+P/6v8AAPn/+f8WAAAA8v8HAPL/DgDy//n/HQDj/yUA+f/q/xYA6v8WAA4A+f/5//L/BwD5/wAABwD5//L/8v/y/+P/4//b/+P/6v+2/83/4/++/83/+f/y/9v/BwDb/+P/8v/b/xYA+f8AAPn/6v/q//n/AAAAAAcA4/8OAPn/2/8HAAAA8v/q/wAA2//j/9v/zf/j/+P/+f/q/+r/+f/5//n/FgD5/w4ADgAHABYA+f8WAAAABwAOAPn/DgAWAAAA8v8AAPn/BwAHABYA6v/b/xYA4//b/w4ADgDy/wcA8v8AAOr/+f8zAPL/FgAAAAcAJQAHABYAHQAlAB0AMwAOAA4ADgD5/yUAAAD5/xYABwAdAEIAOwAsADMAMwAsAB0AJQAsACUAMwBRACwASgBKACwAJQAlAFEAJQBKADsAHQA7AB0ALABCAEoAHQBKACUAFgBRACwAQgBKAEoAOwAzADMALAAsACwAMwAlAEIAFgAWAB0ADgAsAA4AMwAdAB0AJQAOACUADgAAAAcAJQAHABYAHQAHAAcA8v8HAAcAHQAdAPL/+f/q/+r/AADq/+P/8v8AAA4A8v8AAA4A4//5//L/2//5/wAA6v/5/wAA+f8AAB0AJQAdACUAHQAOAPn/FgAWAPL/AAAOAAAABwAOAOr/+f/q//L/6v/U/wAA4/8AAAAA8v/5/9T/BwAAAPL/DgAOACUABwAAABYAAAAOAA4AOwAHAAAAJQDy/ywA+f8OACUAHQBRAA4ALAAWAB0AOwAOACUAFgAOAA4A8v8HABYABwA7ACUAHQAlAAcAFgAHAAcAFgAlAAcAAAD5/+r/6v8AAAAA8v/y/9T/4//5/wcAAAAAAOr/8v8AAOP/AADq/w4A+f8AADsAAAAdABYA8v8OAAcA8v/q/+P/+f8AAPL/AAD5/wcADgAOAA4AAADq//n/8v/q/wcA8v/y/+P/BwDy/wAAAADq/yUAAAAdACUAHQAOABYAJQAHABYAAAAWAAAAFgAHAAAAFgAAAAcAFgAOAAAAHQD5/yUALAAOACUABwAAAAAABwDq/x0AHQD5/x0ABwD5//n/+f/q/+r/BwAAAOP/8v/5/+P/+f8AAA4A8v/y/xYA8v8AABYA6v/5/+P/6v/5/83/8v/y/wcAAAD5/w4A4//j/+r/2//j//L/1P8AAOr/1P/y/9T/+f/j/+P/8v/N/77/zf/F/9T/AADj/+P/4//j/+r/6v8AANv/4//5/+P/+f/j/83/4//F/9v/4//5//L/2//y/9v/8v8HAPL/8v/5/+P/6v/y/+P/+f8dAAcAFgAHANv/HQDy/wcADgDy/wcA4/8AAOr/+f/j/+r/+f/j//L/zf/5/9v/8v8HAOr/6v/y/+r/vv/y/83/xf/F/77/1P/N/+r/+f/j/+P/6v+2/8X/vv/N/8X/vv/j/9T/1P/q//L/2/8HAPL/6v/5/wAADgAAAOr/1P/y/8X/+f8AAOr/AADy/wcA8v8OAPL/+f/U/9T/+f/j//n/4/8HAOr/AAD5/9v/BwDU//n/6v/5//n/1P/5/9v/4//j/7b/6v+2/8X/1P+g/9v/xf/q/9v/xf/F/8X/vv+g/9v/vv/j/+r/2//j/9v/zf/b/+r/vv/j/83/8v/y/9T/8v/y//L/4/8AAOr/DgDU//n/BwDb/ywA8v8OACwADgAAAB0ADgAHADMADgAsAA4ADgAzAAcAHQAzAAcAFgAWAA4ALAAlACwAMwA7ADsAQgBCAFEAYABRADsALABRAEIAUQA7ACUAQgAsAFEAMwBCADMAFgBCADMAQgBRACwAQgAzADMAOwAAAA4AAAAOAA4AMwBKAB0AQgAlABYAFgAdAA4ABwAOAPL/HQAHAB0AJQAWACUAMwA7ABYAMwAWAAcAJQAHAA4ABwAAAOP/8v8HAPL/JQAAAAcAHQDj/xYA+f/5/wAAAAAOAPn/JQAHAA4AFgDj//L/8v/N//L/BwDq//n/6v/5/+r/DgAAANv/AADN//n/8v/q/w4AAAAHAPn/BwAHAA4AAAD5/wcA+f8OAAcAAAAHAAAADgAWACwAAAAAAB0A2//5/+r/4/8HANv/DgDq//L/AADq//n/BwAsABYALAAHAPn/+f8AACwADgAlAAcAAAAdAPn/BwAlABYAJQAdAAAADgDq/wAABwDj/wAA+f8AAPL/+f8AAOr/+f/y//L/6v/q/+r/+f/5//n/AAAAAAcA6v/q/+r/1P/j/+P/+f/5//n/DgAAACUABwDq/x0A+f8OABYA+f8AAOP/AAAHAPn/FgAOAOr/4//q/+r/4//y//n/8v/y//n/FgAAAPL/AADq/wAAAAD5/wcA+f8AAAcAAAAAAA4A8v8OABYADgAlAB0AFgDy/w4AAAD5//n/+f8WAPn/LAAAAA4ABwDj/wcA8v8AAPn/JQAAAPL/BwDq/wAA6v8WAOP/DgAOAOP/JQDy//L/6v/j//L/6v/N/+r/BwDq/x0AAAAOAA4AFgAsAPn/DgAAAPn/DgAsABYAFgAlACwAQgAlADsAHQAsACwABwAdAAAAFgAlAA4ALAAsAPL/8v8AAPn/+f/5/w4ABwAAAAcADgDy/+r/JQDy/+r/FgDb/wAA8v/b/w4A1P/j/+r/6v/j/9v/+f/y/w4A+f/5/wcA+f8AAPn/BwDb/+r/+f/y//n/+f8OAOr/4//j/+r/6v/j//L/6v/j/+P/8v/j/+r/4//b//L/+f/5/+r/6v/5/xYADgAdADMAAAAWAA4A8v8lAAAAJQBCAAcADgAOACUADgAlADMAFgAlADMAOwAlACwADgAWABYAJQAzAAcAJQAlABYAHQBCAB0AFgAzAAcAFgAHAA4AFgAOADsAHQAOAB0ADgD5/wcABwAHAAAAJQAdAB0AHQAdACUADgAdAB0AJQAdACwAAAAOACwA6v8HAA4ADgD5/x0AHQDq/w4A8v8HAAAA8v/q//n/6v/j/w4AAADy/wAA6v/y/w4A6v8HAAAAzf/5/9v/8v8AAOP/+f/j/+r/+f/q/+r/4//j/+r/zf/N/9T/8v/y/wAA8v/y/wAA1P8HAAAA+f8AAPn/AADj//n/4/8HAPn/2/8HANT/2//q//n/AAD5//L/AAAWAPL/BwAAABYABwDq/x0A+f/y/x0AAAD5/+r/6v/5/+P/+f/q/9v/4//N//L/zf/y/wAA8v8OAOr/AADq//L/6v/y//n/2/8HAOP/8v/y/wAAAADy//n/4/8WANv/zf8HANv/AAAdAAcABwAAABYADgDq/xYAHQAOAB0A+f/5/wcA8v8HAA4ABwAlAAcABwAlAAAA6v/q/9v/6v/5/9v/AAD5/+r/6v/U/+P/6v/j/+r/+f/U/9v/+f/U//n/8v/b//n/BwAHAA4ADgAOAA4A+f8dAB0A8v8HAB0A+f/5/x0ABwAHACwALAAlAAcA6v8WAPn/8v8lAA4ADgAHAB0ADgAAACUA+f/y/wcAAADy//n/AADy//L/1P/j/yUA6v8OACUA6v8WAA4AJQAAAAcAHQAAACwA+f8HAPn/+f8OAPL/AAD5/wcA8v8lAB0ADgAHAOP/6v/F/wAA+f/5/wcABwAHAOr/HQAOACUAAAAHAB0A6v8WAPL/AAAHAPL/AAD5//L/AAAOAPn/AAAHAAAA8v8AAPL/+f8AAAAADgDN/+r/4//b//n/zf/y/9T/vv/q/7b/tv/U/77/2//j//L/8v8AAA4A+f8AAOP/8v/y/wAA8v/j/w4A4/8OAPn/4/8lAPn/DgAOAPL/FgAWAPn/FgAOAA4ADgAHAPn/6v8AAOP/+f/b/9v/AADq//n/4//y/77/2/8AANT/4//N//L/8v/j/wcA+f/U/8X/zf++/8X/zf/U/9v/1P/N/+P/vv/j//n/2/8AAMX/2//q/8X/8v/U//n/BwDb/9v/2//b//n/2//N//n/6v/j/+P/6v/U/8X/xf/b/9v/1P/5/9v/+f8AAOr/+f/U/9v/4//b/+r/6v/y/wcAAAAOAA4A8v8HAPn/6v8AAPL/6v8dANT/8v8dAM3/AADb/+r/6v/b/w4A+f8dAPn/FgAWAPn/LAAWABYADgDy/9v/8v/q//n/8v/y//L/4/8AAOr/6v/5/wAA4/8dAB0A2/8OAPn/6v/5/wAA+f8HAA4A8v8HAAAADgAWAAcADgAlACUAMwAdAB0AJQAAADMAHQAlAEIAHQAzACwAOwA7ABYALAA7ACwAJQAdAB0AAAAWACwALAA7AEIAUQAWACwAMwAsACwAHQBCAA4AQgAdAAAAMwAlAFkAOwA7ACwAMwA7AB0AOwAsADMAJQAlACUALABCADsAOwAsADMAHQA7AFkAMwBKAEoAOwA7ADsAUQBKAEIAOwAzADMAHQAsAEoAHQAsADsAJQAzACUALAAzAB0AHQA7ADMAHQA7AEIAMwAlAB0AJQAzACwAHQAlAAcAAAAOAA4ABwAHAOr/FgAWAPn/QgAAAAcAHQAAABYA+f8HAAcAAADy/wcA+f/y/xYAAAAzACUAHQAlABYAHQAOAAcA6v8AAPL/+f8OAOr/+f/5//L/+f/q//n/FgD5/xYAHQD5/xYA+f8AAAAA8v/y//L/AADq/x0A8v8AAA4A4//5/9T/6v/F/+P/6v/F/wcAzf/y/wcA2//j/8X/4//N/83/8v/y/+P/+f/5/83/4//j/9v/6v/U/+r/6v/j//n/4/8HAAAA8v8HAAcA4//5/xYA1P/q/9T/xf/b/8X/4//N/+r/zf/y/wcAxf/5/+P/zf/U/+r/4//U/83/zf/q/9T/8v/y/+r/6v/q/9v/2//q/9T/AADy/w4AAAAOADsAHQAlABYALAAOABYAFgAHACwABwAOAAAADgAAABYADgAAACwA6v8WABYAAAAdAAAADgAHAAcAFgAOAA4ABwAHAAAABwD5/+r/BwDy/wAADgDy/xYA+f8AAA4A+f8OAAAA6v8AAPn/8v8AAPL/DgDy/+P/8v/N/9T/4//q/9v/+f/j/+r/6v/N/wAA2//q/+P/8v8AAPn/BwDy/9v/2//5/9v/6v/y/9v/1P/y/9T/4//5/+P/+f++//n/4//U/wcAzf/j/+P/8v/N/+r/1P/U//n/2//q/9T/+f/j/+r/2//N/9T/xf/q/83/4//q/+r/6v/5/9v/zf/N/6//1P/N//L/2//b/9v/zf8AAOr/8v8AAAAA2//q/9v/1P/y/+P/AADy/wAA8v/5/wAA6v8AAOr/BwDy/wAAAAD5/wcA4//5/+P/4//y//L/4//y/wAA6v8HAOr/6v8AAOP/+f8AABYA+f/j//n/BwAHAAcAMwAlAA4AMwAOAA4AJQAHADsAJQAHADsALAAdACUAQgAsAB0AQgAWAB0AMwAsACUAHQAzAB0ALAA7AA4AJQAOAOr/DgAAABYABwAOAB0AAAAHAOr/BwAHAA4AOwAsACUAJQAsAB0AJQAzACUAHQBCACwAMwBKACUASgAsADsASgAWACUAJQAWACUAOwAsAEoALAAzAFEALABCABYAFgAzACUAFgAsAEoALAAlADsADgAHACUAFgAdAB0ADgAWAAcAFgD5/wcABwDy/x0ADgAdAB0AJQAWAA4ALAAAABYAFgAHADMAFgA7AEIAFgAdADMABwAHAA4ABwDy/wAAAADj/w4A6v/q//n/4/8OAAAAHQAOAA4AFgAOAA4A+f8OAPL/+f8WAA4A+f8AAA4AAAAOAAAA+f/y//L/2//y//n/2//5/+P/4//5//n/DgAOAAcADgDy//L/BwDy/w4AAAAOAPn/8v8OAPn/DgAOAB0AHQAAAPn/+f/y/+r/8v/y/+r/+f/5//n/BwAHAA4A2//y//L/2//y/9v/6v/U/wcA8v/b/wAA1P/y/77/2//b//L/+f/U//L/1P/y/+P/4//b/9v/8v/U//n/BwDj/83/8v/j/9T/4//b/+r/1P/j//L/2/8AAPn/8v/q/+P/+f/j/w4A6v/y/wcA4//y/83/+f/U/+r/FgDb/w4A4/8HAAcA8v8HAOP/8v/j//n/4//y//L/8v/b/9v/8v/F/9T/6v/5/+P/4//j/9v/1P+2/9T/zf/j/+r/4//b/9v/4//j/+r/6v8dAAcAAAAdABYA+f/y/+P/4//j/9T/+f/y//L/2//5/wcA6v8OAOr/8v/5/+r/8v/q/wAA+f8WAA4A+f8WAAAADgAWAPL/MwAOAPn/AADq/wAA2/8AANv/4/8HAPL/AAAHAAcA6v8AAPn/+f8AAPL/FgAWAAcADgAAAPn/BwDb/w4ADgAHAAcA6v8HAOP/FgAOAA4ALAAdADsAHQAsAB0ABwAWAB0ABwAHAAcAAAD5/+P/8v/N//L/2//U//L/vv/y/+P/2//j/+P/+f/q//n/8v8AAOr/4/8lAOr/6v8WAAcAAADq/w4AAADy//n/8v8AAOP/DgAdABYAOwAOAPn/FgAOAPn/BwAAABYABwAAAA4ABwDy/+P/BwAAAAcA+f8AAPL/2/8HAPn/8v8HAA4AAAD5/+r/AAAHAPn/BwD5/wcA6v8WAB0A4/8WABYA+f8OAA4A8v8dABYADgAsAAcAAADq/9T/BwDy//n/BwDq//n/4/8OAPL/6v8sAPn/JQAzABYAJQAHABYAOwAsADMAUQBZAEoALAA7ACwALAAsAEIAOwAOADMALAAdADMAMwAlADMAJQAsADMADgAzADMAMwAlADsAHQAHACwADgAlAB0AFgDq/w4AHQDq/ywAJQAlACwA+f8WABYA4/8OAA4ADgAWAAAAFgAAABYAAAAHAAcA+f8dAA4AHQAWABYABwAWAPn/+f8dAPn/JQAOACwADgDy/xYA4//y/+r/4//5/9v/6v8AAAcADgAAAAcABwD5/w4AAADy/w4A8v/5/wAA4/8lAOr/8v8sAAAABwAHAAcA4/8OAPL/DgAlANT/OwDj//L/LADq/ywAFgAOAA4ADgAHAPL/HQAHAPL/+f8HAPn/+f8lAAcAHQAzAAAALAAWADMAMwAOAB0A8v8WAAAABwAAAOP/8v/N//L/6v/b/wAA2//U//L/1P/5//L/4//y/9T/+f/j/wAA2//F/wAAzf/5/+r/+f8AAOP/4//N/9T/zf/U/83/zf/N/9T/2//N/83/zf/N/+P/2//b/+P/1P/j//L/AADq/+r/6v/q/+r/6v8HAAAADgAAANv/4//5/9v/+f8WAAAAMwAAAAAABwAOAAAA6v8HAOP/DgDq//L/AADj//n/BwAWABYAUQAsACwAJQD5/w4A8v8sADsAFgAzADsAAAAWABYAFgAWAAcAJQAAABYADgAsADsAFgAsAB0AHQAlADMAJQAlADMAJQAlAB0AJQAlACUADgA7ACwAFgBCACwALAAdAAAAJQAOABYAJQAlAEoAJQAzACwAFgAWAA4AFgAAAA4A+f8AAPn/BwAHAAAAFgDb//L/6v/5//L/6v/q//L/6v/F//n/zf/q/+r/6v/j/6//4//N/83/vv/N/7b/xf/j/7b/4/++/8X/vv++/9v/tv/F/83/2//b/83/2//U/8X/xf/F/83/tv++/6//xf++/8X/8v/U//L/6v/q/9T/zf/q/+P/AADy//n/8v8HAPn/8v8OANv/4//b/9T/4//j/83/6v/U/77/1P/F/83/1P8AANv/AAAWANv/DgD5//L/4//y//L/1P/y/+r/xf/F/9v/zf/F/+P/xf/N/+r/tv/j/7b/p//U/77/zf++//L/1P/N/+P/vv/U/83/xf/U/9T/zf/y/9T/1P/U/8X/4//N/+P/zf/F/8X/zf/N/8X/2/+2/77/vv/N/7b/1P/b/9T/8v++/+P/4//q/+r/1P8dAPL/6v8OAOr/+f8WAPn/BwAHAA4AFgAAAA4AAADy/xYAHQAsACUABwDy//L/HQAHADMAQgAdAEIAOwAzACwAJQAdADMAFgAsAEoAHQBKABYAJQAzABYAUQAzADMAMwAzADsAQgA7AEIAQgAlACwALAAzAB0AQgAzACwAUQBKAFkAMwAzAEIAMwBCADsAMwAzADsALAAWAEIAOwAlAFEAJQAzAFkALAA7AEoAOwAWAEIAJQAOACwAJQBRABYAMwA7AA4ASgA7ADsAQgAsAEoAMwAsAEoAMwAWAEIALAAWAB0ABwAzACwAJQBCAB0AJQAlACUAJQBCACUAJQA7AAAAHQAsACUADgAlABYADgAdAAcAHQAHACwADgAWABYA6v8OAPL/AADj/+r/BwDq/wAA+f/5/+r/4//5//n/DgAdAA4AHQAHAPL/BwDy//L/6v8AAPL/zf/5/+r/2//q/+r/FgAdAAcAOwAHAAAAQgAOAA4AHQAHACUADgDq/wAA8v8HAAcABwAdAAcAHQAlABYADgAOAB0ABwAWACUAAAAAAAcAAAAAAAcAHQAAAB0ADgAOAAcA6v8dAPL/+f/5/+r/8v/y//n/2//y/wAAHQAAACUAHQDy/w4A8v8dAA4AJQAsAB0AQgAWAEIALAAdACwAAAAsAB0ADgAzAPL/BwAdAPL/8v/y/wcA8v/5/w4A4//5//L/8v/q//L/DgDb/wAAAADU/wAA8v/j//L/+f/5//L/+f/q//n/2//y/wcA6v/5/wAA4//j/wcA6v8AAPn/FgAWAPL/JQAOAAAABwAOAAcAFgAWAAcADgDU/wcA6v/U//L/vv/q/83/8v/q/83/6v/N/83/4//5/+P/6v/U/+P/+f/b/wcA6v/y/wcABwDq/9v/+f/N/+r/8v/q//n/4//q/8X/4//b/83/DgDU/+r/+f/U/9v/2//q/+r/+f/5//n/4//j/+r/1P/U/77/2//b/9T/4//N/83/zf/F/8X/4//U/+r/1P+v/9v/tv++/9T/zf/N/9v/4/++/+P/1P++/9T/vv+2/9T/1P/j/+r/1P/j/9v/zf/U/77/zf/U/9T/6v/j/+r/1P/y/+r/zf/y/8X/2//q/9v/4//F//n/1P/N/+P/1P/j/83/4//y//n/FgAOAA4AAADy//n/4//b//L/AADy/+r/8v/q//n/4//y/wAAxf/5/+P/vv/U/+P/+f/j//n/BwD5/wAA+f/5//n/8v/q/+r/6v/j/+r/4//y/wAA6v/y/+P/1P/U/+r/AADb/wAA8v/q//n/6v8HAAcABwDy/wAAAADj//n/6v/y/wAABwAOAAAABwDy/+r/AAD5/w4ABwAAAAcAFgAOAPn/DgDy//n/BwAOABYA8v8HAPn/+f/y//n/6v/y/w4A4/8HAAAABwAHABYAMwAOABYADgAlAA4AJQAzAAcAMwAWADsASgAzADsAHQAsAB0AFgAlACwALAAsADsAMwAsACwALAAzAEIAMwAsADMAHQAzADMAHQAdAA4AJQAHAB0ADgD5/zMADgAlAA4ADgAsAAcAHQD5/wAAFgAlABYAJQBKACwASgA7AB0ALAA7AEIAQgA7ADMALAAsABYABwAWAA4ABwAAAB0ABwAlABYA+f8zAPn/JQAdAA4AMwAdACwA+f8OAAAAAAAdAA4AJQAHAB0AJQAOACUAJQAlACwAJQAAAAcABwAHABYABwAWAPn/BwAWAPn/JQAHAB0AJQAOADMAHQAlACUALAAsACUAMwA7AEoAJQBCADMADgAzAB0ADgAOAA4ALAA7ACwAQgAlADMAOwAdAFkAOwA7ADsAHQAzADMALABCADMAFgAHAPn/AADy/w4A8v/q/xYA8v8HAAcAAAAHAOr/AAAdAAAAFgAOANv/+f/y/xYAAAAHAA4A+f8sAAAALAA7AA4ALAAWAB0AMwAlAA4AJQAlABYAOwAlAB0AMwAzAB0ALAAzAA4AFgAdABYADgAAAAcA4//b/+r/zf/q/9v/4//b/9T/6v/b/+P/8v/j//L/6v/F/9v/6v/y/+r/zf/U/+P/+f/5/w4A+f/j//n/6v8AABYADgD5/x0ADgD5/wcA+f/q/+r/+f/5/w4A8v8lAB0A8v8lAA4ADgDy/w4A+f/b//n/2//y/9T/4//j/+P/1P/F/+r/xf/j/+r/4//q/83/2//y//n/6v/y/83/vv/q/77/zf/j/9T/6v/F/9T/AADN/9v/2/+v/9v/xf+2/9v/tv/U/+P/4//y/+P/6v/b/+r/2//j//L/4//b/9v/zf+Z/7b/tv+g/7b/zf/b/7b/1P/b/83/xf/F/77/tv/N/8X/zf++/9T/2//F/+P/1P/y//L/4//j/+P/zf/U/+P/vv/5/wcA8v/5/+r/+f/q/9v/AADq/wAADgD5//L/4/8OANv/4/8WANT/BwAAAOr/8v/q//L/8v8AANv/6v/q/+P/BwDj//L/8v/q/wcA6v8lACUALAAzAAcAFgDy/wcAFgAHAAcAAAAWAOr/+f/5/x0ADgD5/x0A6v8HAAcABwAlABYADgAAAAcA6v/y//L/6v8OAOr/8v/5/9v/8v/y//n/8v/q/+r/4//y/+r/6v/j/+r/4//q/+r/1P/5/9v/BwAHANv/8v/q/wcAAAAWAAcAFgAdAAcAFgDb//n/AADy/wcA+f8AAPn/BwAOAB0AFgAlACwAHQBCACwAFgA7ACwAJQAzABYAHQAOAA4AHQAHABYADgAHACUAHQAdAA4AFgAAAPn/DgD5/w4AHQAAABYABwDq/w4AHQD5/ywABwD5/wcA2/8dAAAAAAAsAPL/BwD5/+r/+f8AAAAABwDq//n/6v/U/w4A8v8OAPn/8v8HANv/DgAHAPn/DgAAAAcABwAOABYAAAAOACUABwAdACwALAAdAAcA+f/q//n/DgAdAA4AJQAHAPn/BwAAAPn/AAAdAOP/+f/5/83/HQAOAPn/DgAOABYAFgAWAAAAAAAAAPn/FgAOABYABwAWAA4A1P8lAA4A+f8HAAcADgD5/yUABwAOAAcAHQAdAAAAOwAAAAAABwAOACwAHQBKACwAFgBCAEIAMwAsABYADgAdADMAHQAlADMADgAsACUADgAlABYADgAsAB0AJQAlAB0AMwAHADMAOwD5/wcAFgAWAAcAFgAdACUADgAOAAcA+f8dAAcAFgAWAPn/LAAdAAAAJQAHAAAAJQAHABYAFgAOAAAA+f8lAAAADgAzABYAFgAlACUA+f/5/xYAAADj//n/4//j/w4ADgAHAAAADgAHAAcAHQAHAPn/+f8WAOr/AAAHAPn/FgDy/wcA+f/j//n/2//U/9T/+f/U/+P/8v/y/w4A2/8HAPn/6v8HAAAABwDN/w4ABwDb/wAA2//5//L/4//q/9T/4/8AAPn/8v/5/+P/+f/b/9T/2//U//L/+f8HAOr/AADq/9v/2//N/+r/2//b/8X/8v++/8X/4/+n//L/zf/q//n/xf/y/8X/zf/b/9T/8v/q/83/4//q/+P/6v/q/wcA1P/q//L/2//y/83/6v/j/9T/+f/b//L/+f/5//L/6v/y/9T/+f/5/+r/8v/q/wAA+f/y/+P/+f/q/83/8v/q/9T/6v/q//L/+f/U//L/1P/U/9v/2/8WAPL/JQAHAPL/FgDy/yUABwAOAAcA8v/q//n/+f/q//n/6v8AAOr/AAD5/wAA+f++/wAA8v/y/wcADgAOAPn/DgAHAAAA8v8HAPL/zf8AANv/6v/j/9T/BwDy/wcABwDU/+P/6v/j/+P/AAD5/+r/DgAlACUAFgAOAPn/+f/5/wAABwD5//L/DgAdAOP/JQAdABYAMwAOAEoAMwAsACwAQgAzAB0AWQAsADMAJQAlAEoALAAlADsAHQD5/ywALAAOABYAFgAAAAAAAAAWAAAABwAlAAAADgDq/wAAFgAHAA4AFgAHAPn/JQD5/w4ABwDj//n/4//5//n/DgAlAA4AFgDy/wcADgDy/wcA+f8HAPn/AAAWAPn/LAAdAA4AHQAlAA4ABwAlAOr/+f/5/w4ABwDq/w4A6v/5/+P/6v/j/+P/AADj/w4A+f/5/xYA+f8HAA4A+f/5//n/+f/5/9v/BwDy/+P/DgDq//n/DgAOAAcA8v8AAAcAFgAdABYAHQAsADMAJQAlAA4AFgAHACwAMwAzAEoAFgBKADMAJQAzACUASgAdAEIAMwAsACwAJQA7AA4ALAAzADMAMwAHAAcA8v/U/wcAAADq/xYA8v/y/w4A8v8AABYA6v8lABYAAAAsAAAAHQAAAAAADgAHACwADgD5/w4AFgD5/xYA+f8OACwA6v8AAA4A6v/j//n/6v/q/+r/DgAAANv/8v/5/wAA8v8lAA4AAAAAAPL/DgD5//n/zf/b//n/4/8AAAAA8v/5//L/4/8AAPL/DgAOAAAADgD5/w4ABwAWABYAJQAdAPn/BwAAAAAA6v/q/xYA+f8AACUABwD5/+P/8v8AAAAADgDy/wAAAAD5/zsABwAWABYA8v8dAAAAAAAWAAAA+f8AAOr/+f8HAOr/FgDy/wAADgAAAAcABwAWAAcALAAAAAAAAADj/wcAAAAOAA4ABwAHAA4AAAAOACwADgAdACUAJQAlAA4ABwAWAPn/FgAAAPn/MwDq/yUABwDy/wcA+f8WAOr/HQDy/+r/8v/b//L/4/8HAAAA8v/j/w4A1P/b/wAAzf8AAL7/vv/U/6//zf/b/83/xf/j/+P/2//U/+r/1P/q//L/+f8HANv/BwD5//n/8v8HAA4A4/8HAOr/BwAAAAcADgDb/+r/xf8AAA4A4//y/9T/zf/b/+r/8v/q/9v/2//y//L/1P/j/9v/2//q/9T/AAAHANv/AADj/9T/+f/j//L/AADy//L/6v/b/+P/2//N/9T/1P8AAPL/8v/5/+P/+f/b//n/8v/j/+P/zf/5/+P/8v/5/+r/1P/q/+r/AAD5/+P/DgDN//L/8v/b/+P/4//N/6//2//F/wAA6v/b//L/2//y/+r/+f/q//n/2//q//n/+f8OAPL/FgD5/wcAJQAAACUAHQAHAAAA+f8AAOr/FgAlAAcAQgAsAB0ABwDq/wAA+f/q/w4AFgDb/wcA8v/j//n/8v/y/+P/AADy//n/BwD5/wcA+f/q/xYA8v/5/yUA+f8AAAAAFgAHAAcAAAAHABYA+f8WAPn/AADj/w4ABwD5/wAA4//q/7b/DgAOABYA8v/F/+r/8v9CAAAABwD5/wAAJQA7ACUA8v8dAA4AOwD5/+r/HQAOACwAHQDq//L/FgAOABYA2//q/w4AAAAOAAAABwD5/x0ALAAlACUAJQAsACUAOwAsAA4ABwDq//L/4/+2/8X/tv/U/83/p//U/9T/zf/U/9v/tv/N//L/+f8AAOr/AAD5/w4AHQAWAA4ABwAdACUAAAAOACwALAAsACUAOwAsADMAMwBCAEoAMwBKACwALAAOACUALAAlAEoALAA7ABYAHQAsAB0AFgAWABYAAAAHAA4AAAAAAAAA+f8HAB0ADgAHAAcA+f8OAOr/8v8WAPn/+f/5/w4A4//y/xYA8v8dAAcADgAWAAAAAAAHAAAA+f8WAPL/8v/5/9v/6v/5/+P/4//j/9v/6v8HAAAA8v8HAAAA8v8HACUADgAOABYA+f8sAA4ABwAsAPL/+f8OAPn/AAD5/w4A+f8HAAcA2/8HAAcAHQAlAAAABwAAAA4AJQAAAPn/DgDy/xYAFgAlABYAAAAdAPn/+f/q/yUADgAWADsAHQAsAAAABwD5/w4AAAAOACUAHQAsAPn/HQAAAPL/BwAdAAAAFgAsABYAUQAAACUADgD5/yUABwAWAAcADgDy/w4ABwDy/wcABwAOABYAFgAAAA4ABwD5/xYAAAAAAA4A+f8AABYA+f/y//n/+f/5/wAADgAOABYAJQAAABYABwDj/yUADgAHAA4AAAAAABYADgAzADsAJQAsABYALAD5/x0AJQAHADMA6v8HAAcA+f/y/+P/1P/U/+P/zf/5/9T/4//N/9v/BwD5/wAA2//q/+r/AADb/+r/+f/U/wAA2//j//L/8v8AAA4A+f/5/xYA+f8AABYABwDq//L/8v/5//L/AAD5/9v/6v/N/9v/4//q//L/zf/y/+r/zf/5//L/8v/y/9T/1P/N/9v/6v8AAOr/4//j/83/4//5/yUA+f/5/wAA1P8AAPn/BwAOAAAAAADy/wAA+f/q/+r/8v/b/+r/2//F/83/1P++/8X/zf+n/9T/tv+2/83/r//F/5H/1P/U/8X/8v/b/wAA2//j/+P/zf/q/9v/6v/y/9v/8v8HAAAAFgAHAA4AHQAOACUAHQAdACUAFgAdACwAHQAOAB0ABwAHAAAA8v8OAB0AJQAWACwAJQAWACwAAADy/9v/4//5/w4AHQAHACUAAAAHAAAA8v8WABYALAAHADMAJQAOADMABwAdACUAFgAdAB0AHQAWABYAFgAlAB0ABwAdADMABwAsAB0ADgAlAB0AJQAWADsAJQAdABYABwAWAAcAJQAWABYALAAdAB0AMwAdACwAOwAdACUAFgAdACwAQgBCADMAJQAdACwAOwAsADMAMwAlACwAFgAdABYADgAOAA4AJQAHAA4AHQAdACwAHQAdABYABwAOAAAABwAdAAAABwAAAAAADgDy/wAAFgAHAB0AFgAHAAAADgAlAAAADgD5/+P/8v/y/wcA4/8HAPn/+f8HAPL/JQDq/w4AHQDq/wcA+f/y/+P/6v/U/+P/2//j//L/xf/b/+r/AADj/+r/BwD5/wcAFgAOAAAADgD5/wAAAADq/wAA4/8AANv/zf8HANv/AADy/wcA6v/q/xYA2/8HAOP/BwAHAPL/FgDb/wcA+f8HAPn/BwAOAPL/DgDq/wcA6v8AAAcA+f8AANv/1P/U/9T/xf/U/77/zf/b/+P/4//F/9v/r/++/+P/4//F/83/6v/N/9v/2//y/8X/vv/q/83/8v/q/9v/6v/b//L/+f/q/+r/6v8HAOr/+f8AAOr/BwDy/wAA+f/q//L/+f/5//L/BwDq//L/+f8AAAAADgAWAAAAAAAAAA4A+f/b/9v/8v/F/9v/8v/N/wAA4//y/+r/+f/y/+P/AAD5/w4A6v8OAOr/1P/5//L/+f/j/+r/zf/N/83/2//j/+r/BwDq/wcA+f8HAAcABwAdAAAAAAAHAA4A+f8dAAcABwAlAAAAHQAOAOP/4/8AAAAA+f8AAAAA2//q/ywAAAAWAB0ABwAWAPn/+f8HAAcA8v8WAPn/4/8lAAcAAAAdAB0ABwD5/wAADgAOAB0AFgAHAAAABwAHAAAADgDy/wcALAAHAB0AFgAHAAcA6v8AAAAA6v/y/wAAAAD5/+P/4//y/77/2//q/9T/4//j/+P/2//j/+P/4//j/9v/+f/y/9v/zf/U/9v/2/8AAOr/1P/j/83/BwAHAPL/AADq/w4A+f8AAAAA4//5/wAABwD5/w4ABwAHAA4AMwAsAA4ALAAsAB0AAAAWAAcAJQAWACUASgAWADMAHQAlADsADgAsADMAMwA7AB0ASgBRAB0AUQAsACUAMwAsADMAOwA7AB0AWQAdACwAMwAdAEIAFgA7ABYAMwAWAB0ALAAdADMABwA7ACUAOwAlABYAHQDy/x0A+f8HAAAAFgAWAPn/JQAHAPn/+f8HAAAA+f8HAAAA+f/5/+r/8v/q/+r/8v/y/+r/4/8HAAAABwD5/wAAFgDb/yUAFgAAAA4A8v8HAPn/6v/b//L/1P/U/+r/1P/b/8X/6v/5/+P/+f/j/9v/4//j/+P/1P/j//L/4/8AAAAA+f8WAA4AAAAHAAcAHQAHAA4AHQDy/xYAFgAHAB0AHQAzAA4ADgAWAPn/DgAlACwAHQAlACwAMwAlACwAOwAOAEIAMwAOAB0ABwAdACwAJQAlACUAFgAsAB0ADgAdAA4AJQAzADsAQgBZAEoAUQBRACwAMwAzADMAJQAzAB0AFgAdACUAMwAAACUABwAWABYADgAzAAAAOwAHAAAABwAOABYA8v8zAPL/+f8WACwAMwAlADMABwAdAA4ADgAHAPn/AADy/+r/8v8AAOr/8v/y//L/AADy//L/AADb/xYAFgDy/ywA8v8AAPL/8v8HAPL/MwAOAA4AAADq/w4A8v8HABYA8v8HABYA+f8dACUABwDy//n/DgDq//n/6v/b/wAA8v/5/wcA4//y/9v/zf/y/+P/BwDj/+r/BwDy/wAABwDy/9v/BwDN/+r/6v/N//n/2//q//L/+f/y//L/+f/y//L/8v/5/+r/6v/j/+P/4//q/+P/1P++/77/4//N/83/1P/b/7b/xf/b/83/8v/F/83/zf+v/7b/tv/U/77/xf/U/7b/zf/q/9v/xf++/83/xf/F/83/r/+n/6//tv++/7b/xf+n/77/tv+n/6//p//U/7b/zf/U/6D/6v/N/+P/BwDb//L/6v/U/83/2//U/9T/8v/q/+P/AADj/9v/BwDy//L/8v/y//n/4//y//L/+f8HAPn/+f/q/+P/8v/y/wAA8v/j/+r/6v/y/+r/DgD5//n/JQAWAA4ADgAHAOP/+f/5//L/+f/5//L/+f8OAB0AFgAOACwA+f8dAB0A8v8lAOr/BwD5//L/+f/q/w4A8v8AAPn/BwAHAA4AFgAAAB0ABwD5//L/2//q/9v/6v8AAOr/8v/q//L/8v/b//L/4/8OAAAABwAlAAAAFgDy//L/6v/q//L/1P/j/wAA8v/y//n/6v8AAA4AHQD5/wAAAADj/xYA+f8dABYAFgAsAAAAJQAAAB0AUQAsAEIAOwAWADMAMwAdAEoAOwAlADMALAAsACwAMwAlACwAOwAOADMAQgAdAEoAOwA7AEIAOwBRAEoAOwBCADsADgAsADMAHQAlAB0ADgAlACwAFgA7ACwAJQAzAB0AHQAlACUALAAsAB0ALAAHAA4AJQAAAB0ADgAsACwAFgAWAB0AMwAOADMABwDq//L/2/8WAPL/+f8AAOP/4//U/+r/6v8AAPn/AAAOAOr/HQD5//n/DgDy//n/4//q/9v/6v8AAOr/zf/F/7b/xf/U/6D/xf/F/77/zf+2/7b/p//F/9T/zf/q/9v/6v8OAOr/8v8AAAAAAAD5//n/+f8HAOr/AAAHAAAAAADq/xYA8v8OABYA+f8WANv/8v8OAOP/AAAAAAAAFgAdAB0AHQAsADMALAA7AB0ALAAzAB0AMwAsAA4AJQAWAOr/8v/y/wcAFgAOAB0AHQAWAAcAFgAAAPn/DgD5/wAAHQAOAOr/BwD5/+P/AADq/+r/6v8OAAAA6v8OAOP/BwAAAPL/BwDb/+r/6v/U/+P/6v/5/+r/6v/y/wAAAAAWAAcA6v8HAAAA+f/5//L/4/8HAPn/6v8OAAAAAAAAAAAADgAdAAcADgAWAAAAHQDy/wcABwDq/xYA+f/5//L/AAAAANv/8v/y//L/8v/y//n/+f8HAA4AAAAdAB0AFgAlAB0AFgAHAA4AOwAdACUAJQAOAAcA8v8lAB0AFgAdACwALAAlAEoAFgAlAA4AAAAlAAAAHQAHAAAA+f/j/+P/8v8HAOr/AAAHAAAABwDj/+r/zf/j//L/vv/q/9T/vv/U/83/6v/U/+P/1P+2/+P/1P+2/77/zf/F/9v/4//j/+P/6v/q/9v/DgD5//L/8v/b/9T/4/8OAOr/4//j//L/6v/b//n/8v/q/+P/8v/N/83/1P/j/+r/vv/y/8X/4//5/+P/DgDq/83/AAAHANv/BwDq/wAAAAD5/zMA2/8HAAcA4//5//L/+f/U/+r/2//y//L/AAAWANv/+f/q/wAA+f/q/wAA8v8HAAAAAAAAAAAA4//y/+P/AAAdAOr/BwD5/wcA+f8WAB0AAAAzAAAAHQAdAB0AHQAOAA4AHQAdAAcAMwDq/wcABwDb/wcA2//5/+r/1P/5//n/AADy//n/+f/y//L/6v/j//L/6v/5//n/+f8OAAAAHQDy//L/DgDy/xYAJQAsACwAJQAdAA4ABwAdAAcADgAHAOr/FgDy//L/BwAOAAAABwAlAAAAFgAHACUALAAAACUALAAdABYAHQAWAEoAQgBRAGcAOwBZADMAQgBKAEIASgBCACwAOwBgAB0AWQBKADsAYABKAGcAQgBvAFEAQgBRAEoASgAlAFkAMwAsACwALAAlACwAUQAWADsAMwAzADsAFgBKACwAJQAzADMAOwA7ABYAHQAHAPL/DgAOAA4AAAAdAPn/+f8dAAAAJQAOABYAHQAOACUABwAlAAcADgAzACUAHQAOAA4ADgAOABYAJQAOAAAAFgAWAA4AJQD5/+r/AADj/+r/+f/b//L/BwD5/w4A+f/5/+r/AAAdAM3/FgAAANv/AADU//L/8v/y//n/BwAHAPn/DgDy//L/HQAlABYAJQDy//n/DgDF/wAA8v/j//L/8v8AAAcABwDb/wcA6v/U//L/8v8AAPn/FgAAAAcAHQAWAA4AAAAdAPL/AAAdAAAAAAAHAPL/+f8WAAcAAAAOAOr/2//5/9T/+f/5/9v/FgAAAPL/8v/5/+r/4/8OANv/6v8HAOr/4//j/+P/2//y//n/6v/y/+r/+f8AAOP/AADq/wAABwDq//L/6v/y/+P/BwAHAPL/6v/j/9T/vv/q/8X/1P/U/83/+f/U/+r/zf/b//L/2//j/+r/6v/F/+P/1P/q/+r/4//5/6//4/8AAOP/BwAOAPn/8v/b/9v/AADq/w4A8v/b/+P/2/8WAPL/FgAWAOr/+f/y//L/AADj/+r/DgAAAAcA8v8WAAAAAAAlAPL/JQD5/w4AJQAAAB0ABwAdAPn/AAD5/+P/6v/q/wcA2//y/+r/4/8AAAcADgD5/wcAAAD5/+r/8v/U/83/8v/U/+P/+f/j/+r/+f/b//L/2//b/+P/xf/q/8X/2//b/9T/6v++/9T/zf/F/83/zf/U/9T/vv/b/9T/xf/y/9T/4//j/+r/2/+2/9v/tv/F/+r/6v/b/+r/8v/b/+r/zf/b/77/6v8AANT/AADj/9v/1P/F/9T/6v/N/83/8v/U/+r/8v8AAAAAFgAOAAcAFgDy//n/AAAlAA4AAAAOAAAAAAD5/xYA6v8HABYA4//q/+r/DgDj//L/AADy//n/1P/y//n/4//j//L/2//j/+P/vv/N/83/4//j/+r/2//b/+r/6v8AAOr/+f/j/+r/6v/j//L/4//5//L/BwD5//n/BwDj//L/6v/q/+r/8v/q/9T/2/8AANv/2/8AANv/AAAAABYAFgD5//L/+f8lAAAAJQAWAAcADgDy/yUA+f8HAAcA+f8WAAAADgD5/w4A8v8AAAcA8v8WAAAAFgAdAB0ABwAAAB0AAAAdAAcA6v/5/+r/DgAHAAAADgDq/w4AMwAHABYALAAHABYALAAdABYABwAdAAcABwAOAPn/DgDy/x0AJQD5/zMAHQAWABYADgAHAAAABwD5/xYABwAHAA4A+f8dAA4AHQAdAAcAJQAWABYALAAdACUAFgAlAAcADgAdACUAHQAOACwABwAdACUA+f8AAPn/DgAHAA4AFgAOACUADgAHAA4A+f8HAAAA+f8HAPL/DgAHAAAADgD5/w4A+f8AABYAAAAWABYABwAsADMAMwBZAB0AHQAWAA4AJQAWADsADgAOADMA+f8AABYABwAsACUAHQBKAAcAJQAdAPn/OwAHACwAOwAsADMABwAWABYADgAlADsAMwA7ADMAMwAsAB0ALAAzAEIALAAsAEIAMwBCAEoAUQBgAEoAMwBKADMAQgBZADsAWQAzADsAMwAWADMAFgAsACwAHQAWACUASgAWADsAJQD5/x0AAAAOAB0AFgAHAAcAAADj/zsAJQAdADMAFgAdAAAAOwAOAAAAFgDj/w4AAAAHAB0AHQAsAA4AFgAWABYAMwAOAA4ALAAlADMAMwAsAPn/AAAOAOr/BwAAAAAAAAD5//L/6v/5//L/+f8HAPn/+f/b//n/FgDj/x0AHQAOADMA+f/5//n/8v/y//n/DgAlACwABwBCACUAAAAlABYALAAAAA4AFgAAAA4AAAD5/wcAAAAHACUAAADq/+r/6v/j/83/6v/q/9v/2//j/9v/2//j/+r/+f/j//n/AAAAAAcA6v/y/wAAAAAAAPL/8v/y/9v/2//U/9v/8v/U/+P/6v/F/9T/6v/y/wAA2//b/+P/tv/q//n/2/8AAOr/4//q/83/1P/q//L/4/8AAPL/6v/b/7b/zf+v/6//vv+n/6//xf/U/6D/xf/F/6D/r/+n/77/mf/F/7b/vv++/4r/xf+2/7b/tv++/77/zf/j/77/4/++/83/zf++/+P/2//5/+P/8v/j/+P/6v/U/+r/AAAAAAcAAADq/wcAAADj/wcADgDy//n/DgDy//L/BwAAAAAAFgAWABYAFgAOACUADgAlABYAFgAlAAAAQgAlABYAMwAOAB0ADgAOAAcAAAD5/+r/AAAOAAAABwAOAOr/2//5/+r/BwAHAAcALAAHAAcABwD5/wcABwAdABYAAAAHAAAA+f8OAPn/6v/5/+P/8v/j/+P/+f8AAAcA8v/y//L/AADy/wAA8v/b//n/8v8AAAAA8v8AACUA8v/q/w4A1P8HAPn/4/8AANv/6v8OAOP/6v8AAOP/8v8AAPn/4/8AAAcA6v/5/+P/AAD5//n/DgAAAPn/+f8WAPL/BwAWAAcA+f8HAAAA+f8lAPn/BwAOAPL/+f8AABYABwAHAA4ALAAsACwAJQAdAAAABwAsAPn/FgAHAOr/FgAAAPn/DgAOABYABwD5/ywAFgAWAFkAOwAlAB0ADgDq/wcADgDy/wAAHQAdAA4AMwD5/xYAOwDy/ywAFgAOABYA6v8OAPn/HQAdAPn/FgD5/+r/+f/y/9v/2//j//L/+f/q/wAA4//q/wcA+f8HAPn/+f/j/9v/4//j/+P/8v/5/9v/8v++/77/xf+2//n/2//b/9v/4//F/6f/2//b/8X/zf/j/77/zf/b/83/4//U/+r/2//U/9v/6v/q/9v/6v/q/9T/6v/q/9v/BwDy/9v/+f/q/wAA+f/5/x0AJQAHAOr/+f/5/+r/AAD5/wcABwDy/wcA6v/5//n/8v8HAPL/DgAWABYADgAdAAcAJQAzAAAAJQD5//L/AAAOACwABwAOAPn/BwDq//n/BwDq//n/6v/y/+P/BwDq/9v/FgDy/wcAHQAHAPn/BwD5//L/HQD5//n/+f/q//L/8v8AAAcA8v/y//L/4//5/xYAAAAHACUADgAOACUA8v/q/wcAAAAAAPn/AAAAAOr/DgAdAAcAFgAlAA4ABwAHABYADgDy/ywADgAOABYADgBKAA4AHQAdAPn/FgAdADMAMwAlAAcAJQAWACUAJQAAACUAHQAlADMAOwAlADsAMwAsACUAFgAzAA4AMwAWAA4AOwD5/zsAFgAWADsAHQAzADMAFgAdAB0ABwAlAAAAHQAlAOr/OwAWAPn/MwAOAAAAHQAOAA4ABwAHAPL/6v8AAPL/BwAHAPL/8v8OAAcA2//5/9v/2//b/+r/8v/U/w4A4//5/w4ABwAlAOP/6v/j/+P/+f/j/wcA6v/j/wcABwD5//n/BwAHAAAAAADy//L/AADy//L/6v/b/+r/1P/q/9v/6v/5/7b/zf+n/83/8v/b//L/8v8OAPn/DgAAAPL/AADb/wAAzf/q/xYA8v8dAAcA+f/5/+r/6v8AAOr/BwAHAPL/+f/y/wcA8v8WABYADgA7ACUAJQAOACUAJQAWACwAFgAlAA4AHQAlAA4AHQAdADsAHQAdADsA+f8WAB0AAAAsAAcADgAdAPn/BwAdABYABwAzABYA6v8AAA4A+f8AAA4A8v8AANT/8v8HAPL/HQAsACwADgAHAAAABwDy/wAA6v/b//n/xf8AAPn/8v8HAPL/AADq/w4A+f/5/x0AAAAsAB0AAAAHAPL/6v/q//n/4//b/w4A+f/y/wAA6v/5//L/DgDy/9v/8v/U/83/4//y/9T/6v/5/9T/4//5/+r/4//j/+P/AAD5/wcAFgAHAAcABwAHAAcADgAdAAcAAAAOAA4AMwAWAB0ALAAWADsABwAzADMAFgAsABYAMwAOADMAMwAWAA4AHQAsAAcAMwAdABYAHQAdADMAHQAsACwAJQA7ADMAMwA7AAAADgAWAA4AJQAlADsAAAAWABYABwAzACUALAAdACUAHQAlAB0ADgAdAPn/BwAWACUAJQAlACwADgAdABYAFgAAAPL/AAD5/wAABwAOAA4AFgAHAAAADgAAAAcABwAHAPn/AADj//n/AADU/+P/2//q//L/4//U/+P/6v/b/wcAAAD5/+r/2//N/83/1P/U//L/zf/q//L/4//5//L/8v8AAAAA+f/5/+P/+f/y/9v/BwD5/+r/6v/y/+P/2//j/83/8v/y//L/DgD5/wAA8v/q/wcA1P/y/wAA2//q/wAA4//b/+r/6v/5/wAABwD5//L/8v/j/wAA+f/q//n/JQAdACUAJQAOAA4A+f8dAAAA8v8HAAAABwAOAAAA8v/5/+P/8v/y/+P/1P/5/9v/6v8HAMX/AADy/+P/BwDy//n/BwD5/+r/+f/j//n/+f8AAPL/2//q/+P/6v/N/wAAzf/q//L/vv/5/8X/+f8AAM3/4//F/83/zf+v/+P/4/++/wAA1P/b//L/+f8HANv/+f/5/9T/+f/y/83/BwDj//n/FgDq/w4A8v8AAAcAAAAOAAAA+f8OAAAA8v8lAPn/HQAlAPL/AADq/+r/4//5/+P/8v/q/9v/BwDy//n/BwD5/+r/AADj/+r/8v/j/+P/zf/y/+P/1P/j/83/xf/F/+r/zf/N/+r/1P/q/+P/8v/q/9v/4//U/+P/2//b/wcA6v/q/wAA4//q/+r/4//y/wcADgDj/wcAFgAOABYADgAOAA4AFgAHAAcABwAWAPn/8v8dABYAFgAlADMAFgAdAA4AAAAHAAAADgAHAB0ADgAOAAcAHQAWAPL/DgDq/x0AFgAlACwADgA7AB0AQgAdAA4AFgAHAB0AAAAHAAcAAAAAAAcADgAHAAcAFgAHAPn/AAAAACwADgAWAA4ABwAWABYA8v/5/wAAzf8OAOP/1P/q/77/+f/y/+r/6v/y//n/4/8AAA4A2/8AAAAA1P8lAA4ADgAOAAcABwAHAA4A4/8HAPL/4//5/+P/6v8AAA4AAAAAAAAA+f8dAAcABwAWAAcAJQAOAB0ABwDy/yUA8v8WAA4ABwAAAAAAHQAWACUAHQAdAOr/BwAOAA4ALAAHACUAAAAHAAcABwBCAB0AJQAzAA4ADgAHAAAABwAAADMAFgAsACUALAA7AA4ASgAHACwALAAdADsAFgA7ABYAHQAdACwADgAWADsAAAAdACUAJQDy/w4ADgD5/ywAAAAHAPn/6v/y//L/6v/j/+r/6v8HAAAABwAHAAcADgAAAPL/BwAWAA4AJQAdABYADgAWAB0ABwD5/yUAHQDq/wcAFgAWABYADgAlAPn/6v8dAAcA8v8HAA4AFgAAABYAAADy/wcA4//5/wcA+f/q/w4AFgD5/xYABwAHAPn/+f8OAOr/DgDy/wAABwAHACwAFgAsABYAFgAOACwAFgAAACUA6v8WAOP/BwAOAOr/HQDq/xYAHQAsACUAJQAlAA4AFgAOAA4AAAAWAAAALAAdAAcAMwAWADMAHQA7ACUALAAzAB0ASgAOACUALAAlACwABwAdAA4A+f8lAAAAAAAdAOP/AAAHAA4ADgAOAB0A8v/5/+r/6v8HAPL/4/8OAOr/8v8OAPn/AAAAAAAA4/8HAOP/AAAdAOP/HQD5//n/+f/y/+r/6v8OAPL/BwAWAPL/BwAOAAcAHQD5/xYAAADy/xYA2/8HAOr/+f/y/9T/DgDy/+P/6v/q/83/4//b/83/8v/U/+P/8v/U/+P/6v/b/+r/8v/U/+r/+f+2/+r/6v++//L/zf/j//L/+f8AAPn/+f/j//L/1P/5//L/1P++/+P/6v/N/+r/4//5/9T/8v/N/77/+f/N//n/1P/U/9v/1P/F/8X/xf+n/+r/2//U/83/zf/N/83/xf+2/9T/tv/U/9T/tv+v/77/tv++/8X/p/++/6f/xf++/8X/1P++/+P/vv/N/8X/vv/N/7b/zf/F/6//tv/b/8X/oP++/77/oP+2/8X/vv+v/77/2/++/8X/6v/b/83/2//F/77/2//N/+r/6v/b/wAA6v/5//L/8v/y/+r/FgAWAB0AHQAsAB0AAAAlAAcAFgAdACUAMwAlAB0ADgAHAAAA+f8AAB0AHQA7ACUAFgA7ABYAHQA7ADMAMwBKACUAOwBZAEoAUQAzACUALABCAB0AOwAzAB0AQgAWAEIAOwBnAGAAUQBZADsAQgAsAEoAJQAsAB0AHQAlAAcAHQAHACwAFgAzADsALAAzACwAUQAzAEIAUQAlACwAQgAdACwASgA7AEoAUQBZADMAOwBZAFkAQgBCAFEALABRAFkAQgBgAFEAFgBRAEIAJQBZACwASgBKADMAWQBRAEoALAA7ADMAHQBCADMALAAzAB0AOwAlACUAQgAzACwAOwA7AA4AHQAHABYADgDy/x0A8v8HAB0AAADU/+r/AADb/wAA+f8OAAcA+f8HAAcAAAAHAAAA8v/q/wcADgDq/xYA+f8WAAcA8v8WAOP/DgDq/wAA8v/q//L/2/8WAOP/BwDq/9v/6v/U/wAA1P8WAPn/2/8WANv/8v/y/+P/4//N/9v/xf/b/+r/6v/5/9v/8v+2/83/6v/U//L/8v8OAOP/6v/q/9v/4//b/w4A8v8AAPL/AADj/83/+f/b//n/2/8AAOr/4/8WAOP/+f/y/wAAAAD5/wcADgAdAA4AMwAAANv/2//U/9v/zf/j/8X/6v/y/+r/+f/U//n/4//b/+P/6v/U/9T/8v/U/+r/4//U/9v/zf/F/9T/2//N/+P/1P++/9v/1P/N//L/1P/N/83/1P/j/6//6v/j/83/8v/N/9v/4//b/9v/4//j/8X/6v/y/8X/6v8AANT/6v/j/9v/1P/b/+r/zf/q//n/6v/5/wAA1P/q/+P/2//U/83/1P/N//L/zf/j/9v/2/8OAOP/4//5/wAA2/8HAPn/BwAWANv/DgD5/wAAAAAAAPn/BwAlAB0ALAAHAB0ADgAsACUADgAlAAAABwD5/x0ALAAOAB0AHQAlAB0AFgAWAAcA+f8WAPn/2/8AAPL/6v8HAPL/6v/5/+r/BwD5/+P/8v/b/+P/6v/y//L/2//y/+r/6v/y/+P/+f/q//L/6v/q/+P/tv/q/83/zf/N/83/xf+v/+r/4//q/9T/2//U/83/8v/U/+P/1P/N/9T/1P/y//n/2//U//n/zf/q/w4A+f8AAPL/BwAHAPL/AAAAAAcADgAOAAcAAAAOAAcADgAAAA4AHQAAAEIAJQA7ACUAAAAOAOP/BwDq/wAADgAAAB0AFgAlACUALAAWAAcADgAWAAcADgAdAAAAAAD5/xYA+f8dADMAAAAsAAcADgAlABYAHQAOAPn/BwAdAAcAJQAHAA4AHQD5/zMADgAAAAcA8v/q/wcAHQAsACUABwAdAAcAFgAdABYAMwAOACwAMwAdAB0ALAAsACwAMwAsACwADgAzACUAHQAdAAcADgDq/yUAJQAdACwABwAdAPn/AAAWAAAABwD5/wAAAAAHAAAA+f8HAAcA+f8WAB0AFgAlACwALAAWADsAOwAWADsAOwAWADMAMwAWACwAJQAdACUAMwAzACUAMwAsAEIAJQAzAEIAHQBKACwAOwBCAEIASgAWACwAJQAsACUAHQAzABYAMwAzACwAJQAsADMAJQA7AA4AJQAWAAcAJQAAAB0AFgD5/w4A+f/5/wAA6v/q//n/1P/q//L/4/8HAOr/6v/5/+r/DgAHAOr/4//F/9T/6v/q/+r/BwDy/+P/8v/q//L/4//y/+P/zf/5/9v/+f/b/+r/+f/j//n/zf/j/9T/8v/5/+r/8v++//L/zf/b//n/2/8OAAcADgDy/wAADgDq/wcA6v/q/wcABwAAAAAA+f/5//L/4/8HAAAABwAdABYAAADy//n/8v/q//n/AADj/9v/AADj/wcAHQAAAAcAAAD5/wcAAADy/x0A8v/j//n/4/8AAM3/zf/j/9T/8v/y/+r/6v8OAPn/2/8WAPn/4/8HAPn/+f8AAAcAFgAOAPn/+f/q//n/DgAAAA4A6v/y/wAA+f8dAAAA8v/5//L/FgAOAAcAFgD5//L/DgDy//n/+f/y/w4A2//y/wcA6v8AAAcAAAAHAA4A8v8HABYA+f8AAAAAAAAHAA4ABwAdAA4A6v8WAPn/8v8AAAAABwD5/wcA+f/q/+r/6v/q/+P/2//q/+r/4//y/wAAAAAAAPL/4/8HAAAAAAAWAAcADgAAAAcADgAOAB0ADgAHAAcAAAAHAB0A2//j/+P/mf/U/83/2//q//L/DgDN/+P/1P/j//L/DgBKAFEAfgBRAG8AWQA7AEIADgAsABYAHQAHAAAABwDj/9v/tv+2/6f/p/+v/5n/iv+g/6D/kf++/6//r/++/6//vv++/8X/vv+2/6//xf+2/83/2//F/+P/p/+2/8X/tv/b/9T/2//b//n/zf/N/+r/zf/q/83/2//U/83/4//N/9v/4//q/8X/vv/U/6f/1P/b/83/8v/N/6//1P++/8X/4//b/9v/1P/F/8X/vv+v/+r/2//U/9v/xf/j/83/6v/5/9T/2//N/9T/1P/b/+r/4//U/9v/6v/b//L/+f8AAAcAHQAzACUAQgBZACwAQgBKAB0AJQAzACUALAAzAEoAOwAzADMALABKAEoAUQBKADsAOwA7ADsAMwAzADMAQgBKADMAQgAsABYALAAsADsALAAsAEoASgBRADsAQgAlAAcALAAWACwAMwAlAA4ADgAOABYALAAsADsAHQAdAB0A+f8WAPL/BwAdAPn/FgAHAPn/HQAsAB0AFgAWAB0AFgAlADMAFgA7ADMAOwAsADMAQgAdAEIALAAlACwAHQAzAB0AOwAzAA4AOwAsAB0AUQA7ADsAQgA7AFEALABCAFEALABCAFEAQgAzADsAHQAzAEoALABCADMAOwBCAEoAQgA7AEoALAAzAEoAQgBCAEoAQgAzACwAJQAlACUAMwAzADMAOwAlABYAHQAzACwAMwAsADMALAAsAFkASgAlADsALAAWACwAJQAlAB0ABwAdABYAFgAAAA4ABwDy/ywADgAWACUABwAlACUALAA7ACUAFgAdAA4ALAAzACwAOwAlACUAHQAHABYABwAOAA4AFgAsACUAMwA7ACwAOwAWACwAMwAAADsALAAWACwAJQAWAAcAFgAHABYABwAWACwABwAdAAAADgAHAAAAAADq/w4A8v/y/w4A6v/b//L/6v/q/w4ADgAHAA4A+f8WAAAA2/8WAOP/8v8dANv/DgAAAB0AHQD5/xYA4/8HANv/6v8HAM3/+f8AAAAA2//j//n/4//b/9T/6v/j/+P/8v/j/77/1P/U/77/4/+v/83/zf+R/8X/r/+n/7b/p/+v/77/r/+2/9v/1P/j/83/vv/U/6//r//b/9T/4//5/83/1P+n/7b/xf+v/83/mf/F/6f/r//b/77/xf+v/83/r/+v/77/xf+2/77/6v+n/77/xf/F/77/tv/N/83/xf+n/+r/1P/j/xYA1P/5/9T/xf/b/6//1P/b/8X/zf++/83/1P/U/8X/xf/b/8X/vv/F/83/zf/b/83/tv/N/77/vv/b/9T/1P/N/83/xf/N/77/vv/F/6//xf/N/9T/2//U/9T/xf/j/9T/6v/j/9v/8v/j//n/xf/q/8X/1P/j/77/+f++/+P/zf/F//L/r//b/83/1P/q/83/2//U/83/vv+2/77/r//F/6f/vv/q/6//4/+2/77/zf+g/9T/r/+v/6//tv+v/7b/vv+2/77/vv/N/6//zf/F/83/xf/N/+P/zf/5/9T/2//b/83/2//j/9T/zf++/7b/6v++/9T/1P/b//n/zf/5/+P/6v/y/+r/BwDU/+r/AADq/wAA6v/5/wAA4//q/9v/+f8OAAcAFgAWAOr/6v/y//L/BwDy/wcAHQD5//n/AAD5//n/8v/q/+r/2//b/+P/4//j//n/4//U/wAA6v/j/+r/+f/j/wAABwD5/wAA8v/5//L/HQAOABYAFgAWADMAFgA7ACUAOwBgAB0AOwAlAA4AOwAsAFEAOwAzAGAALAAsAB0AMwA7ADMAWQBKAFEASgBnAGAAWQBgAFkASgAsAEoAFgAsAEoAHQBgADMAHQBgADMALAAsAB0ALAD5/wcAFgAOAB0AHQAlACwALAAOACwADgAdADMADgAWAB0ABwD5/ywADgAOAB0AAAAlAB0AFgBCACUAMwAlAB0AHQDb/ywADgAAADMABwAdAPL/JQAlAAAADgAOACUABwAsACwAJQAWABYAFgAHACwAFgAlADsAJQAWAB0AHQAWABYABwAdAA4AJQAOAB0AOwAOACUAJQAdACwAMwBCACwAMwBCADMAMwBRADMAHQAlAAcAHQAAAAcABwD5/x0ADgAWABYALAAlAPL/HQAWAAAABwAWAAcAHQAAAOr/JQD5/xYAFgAHAAcA2//q//L/4//y/+r/4//5/+r/8v8AAPL/8v/y//L/+f8AAAAA+f/U/+P/2//b/wAA8v8AAPn/8v8HAPn/6v/5/wAA+f8WAAcAFgAdAA4ALAAWAPL/DgAWACwAMwAsADsAJQAlAEoAWQBKAFEAWQAzAB0AQgBKAB0AOwAlABYAMwAlAA4AHQAdAPn/LAAWAPn/FgAWACUAHQAlACUALAAlADMASgAOACwAOwAWADsAQgAlABYADgAHAAcAOwAsACUAMwAAABYALAAsADsAJQAdAB0A+f8OAB0AFgAsADMALAAsAB0AFgAHABYAJQAsADMAJQAdABYAHQAlABYAFgAsACUAJQAdAB0ALAAOACUADgAAADsAHQAlABYADgDq/wAADgDy/xYA6v8HAOP/2//y/+r/AADq//L/vv/y/+r/4//5/77/8v/N/+P/8v/y/+P/6v8HANv/+f/5/+r/1P/y/+r/8v/5/9v/AADU//L/6v/b//n/8v/y//L/8v+2//L/6v/b/w4A8v8lAA4AAAAsAAAADgAHAA4AHQAHAB0ADgAAAAAADgDj//L/FgDU/wcABwDy/xYA6v/q//L/2//U//n/6v/b/+P/6v/N/9v/+f/U//n/8v/b//L/2//y/+r/zf/5/wAA2/8AAPL/4//j/9T/" type="audio/wav" />
Your browser does not support the audio element.
</audio>
fs, hs =compute_fft(audiosignal, sr, n = None, scale_amplitudes = True)
fig,ax=plt.subplots(figsize=(5,4))
ax.plot(fs,hs)
ax.set_xlabel('Frequency')
ax.set_ylabel('Normalised Amplitude')
ax.set_title('Frequency Response of the combined signal');
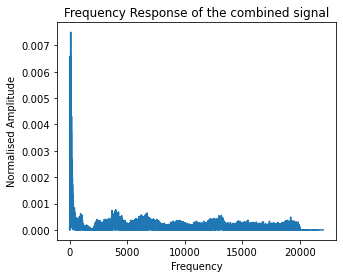
As mentioned before, we will filter all frequency less than 1024 Hz. It will also remove the large DC component that appears in the plot above.
def butter_highpass(cutoff, fs, order=5):
nyq = 0.5 * fs
normal_cutoff = cutoff / nyq
b, a = butter(order, normal_cutoff, btype='highpass', analog=False)
return b, a
def butter_highpass_filter(data, cutoff, fs, order=5):
b, a = butter_highpass(cutoff, fs, order=order)
y = lfilter(b, a, data)
return y;
cutoff = 1500 # desired cutoff frequency of the filter, Hz
order = 1
audiosignalFil = butter_highpass_filter(audiosignal, cutoff, sr, order)
fig, ax = plt.subplots(2,2, figsize=(14,10))
ax[0,0].plot(time, audiosignal)
ax[0,0].set_xlabel('Time [s]')
ax[0,0].set_title('Audio Signal')
ax[0,0].set_ylim([-1,1])
ax[0,1].plot(time, audiosignalFil)
ax[0,1].set_xlabel('Time [s]')
ax[0,1].set_title('Filtered Audio Signal [Hz]')
ax[0,1].set_ylim([-1,1])
fs, hs =compute_fft(audiosignal, sr, n = None, scale_amplitudes = True)
ax[1,0].plot(fs,hs)
ax[1,0].set_xlabel('Frequency')
ax[1,0].set_ylabel('Normalised Amplitude')
ax[1,0].set_title('Spectrum of the Audio Signal')
ax[1,0].set_ylim([0,0.009])
Fs, Hs =compute_fft(audiosignalFil, sr, n = None, scale_amplitudes = True)
ax[1,1].plot(Fs,Hs)
ax[1,1].set_title('Spectrum of the Filtered Audio Signal')
ax[1,1].set_xlabel('Frequency [Hz]');
ax[1,1].set_ylim([0,0.009]);
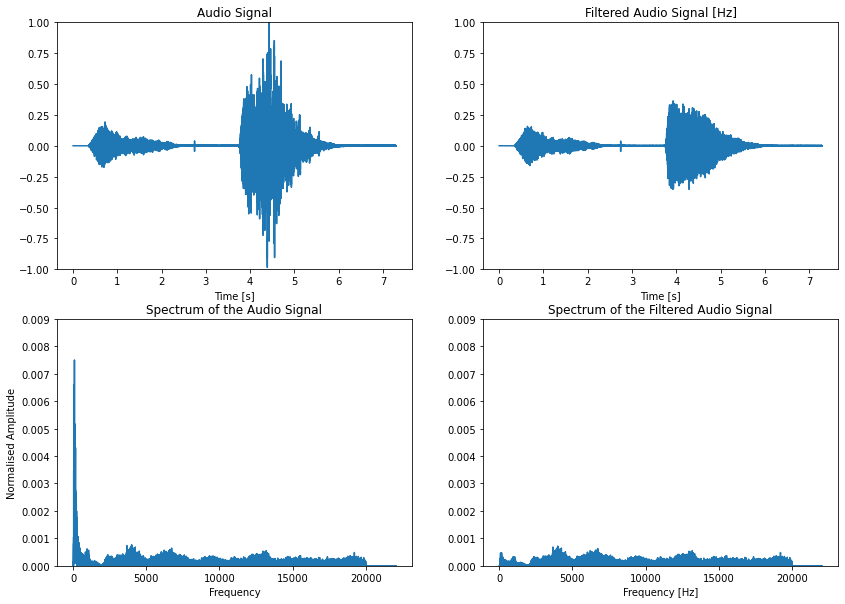
Listen to the audio signal filtered using order 1 filter.
audio = Audio(data=audiosignalFil, rate=sr)
audio
<audio controls="controls" >
<source src="data:audio/wav;base64,UklGRiTQCQBXQVZFZm10IBAAAAABAAEARKwAAIhYAQACABAAZGF0YQDQCQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAASAP3/6/8BAAEAAAATAP3//v8QAOn/AADu/wMA8f8FAAQAAwACAPD/BQAEAAMAAgACAAEA8P8EAAMAAwACABQA////////7f8VAP////8AABEA/P/9//7//v8QAPz//P/9//7/7P8BAAEA7/8EAAMAAgACABQA/v//////7f8VAP/////t/wIAAgABABMA7P/w/wQAFgAAAAAAAADu/wMAAgAUABAA+//8//3//v/s/xQAEAD7/w4A5/8QAPv//P/r/wAAAAAAAAAA7v8oAPz/DwDo////EQD8//3/6/8TAOv/EwAQAB8ABgC8/wAAEgAPANX/AgABAAEA3f/R/yMA+P8LAOX/6v/v/ykADgDV/zkAGwAoAA4AHgAFAOD/CgAbAAMAzP8fAPX/0v8AACQACwDS/xEA6v8AANz/BwA9APv//P8OAB4A9P8IAPX/5f/q/+7/KADq/wAAAAAAAAAAyf/5//r/HwAHABgA7//g/y8A8P8XACUACwDA/17/tf/W//H/hgA1AJj/9v9BAMgAMgAEAAMA3P6D/y3/Q//8/48A4gAjANQAmQCf/1X/ZP+C/3b/pACEAMb/GgCDADMATgAsABD/LP/W/6gAYwCHALYAkv8CAHEA7f9d//7/RwDM/+j/7f/NAJMAiQCk/4/+IgD4ANsAr//2/1MA1f9LAOH/1f8BAIIAxP9h/wAAJQCfAIAAMABv/7D/iQAAAJL/KABXADQABQCp/wIAp//v/xcAyf9nAJwAbABEACQACv85/wUA8v8ZALoAcQBs/+P++P+xAMX/4//5/iz/1v8CAF4AXgCoAL3/JP+E/hkASwCY/+P/iv5C/9X/cAC3ALgAbwBY/x3/yP7i/7IAtABaAGz/CQBRAMH/u/9bALgAOAAs/0L/aQANAesAFwCA/ywAEQB7/8z/VgB9ANL/7f/M/44APQF+AGX/J//3/x0AcwA4AK4AsQDZAEAAxv8KAVUAxP88/z8AjwBhAGAAlv89AAwAwgAuAG8AowCn/4H/df+RABkAXgAl/4X+dP9+AMIA0v8UAYH/O/6T/kj/bQBrAHsA4P6q/iP/KwDIAHwAiP+v/rz/2//j/9b/lgCwAMT/YgB0AAEAgf/2/8D/FgABAXMAggD7/7L/wf9yADoB+/97/wMA3v/l/zMAlv8+ADIATP/d/y0AOQFWAB//cP95/8v/QwA2AAYAdACT/5b/Bf8kAOoBv/8CAKb/Ev+v/4gAgwHuAJsARP8M/2H/SQDy/+P/DwEPALIAWACTAY8Bdf8h/0r+ff+7/9v/YgCF/y//IQDBAK4AeQCW/hP/Cv+o/wQBYwCsAPb+TP5s/8EAZAAY/9b+pP+AAFQAJAJdAdAAb/9k/hEAH/88AewA9P8bADf+f/9SAX8BVwDZ/5f/4v93/jL/KQLgACEAB/+B/yv/Uv5yAAQCeQDt/PT9gf+vAe0Amf9CAW//L/+f/h4BDgIAAAAAff6m/6X/bgDcAREBEP8X/kIAOAEyAb7/qAD2AAz/KgBcAQYBPv+b/xwAOv+W/t7/QwE7ATMAuf4PASQBs/8+/r3/8gEd/ur+ogAEAXT/sv6/AGH/kv/y/64BtQDq/tb+6/6TAXoArACLAKb/fv4Q/j8BEwFNAYsAFAD8/hr+/P81ATABTP6Q/wMBhwDG/iX+4wHNACP/cf4JAEEB7f62/7MAWQDs//D/BQDy/xj/av/SAM4AlABSAA0BRQC4/+v/t/8y/0X+1gCvAaMAJv+bANsB5v1O/iUAMgGIAKT///81/6cAqv+7/3ABKAHJ/2P+Rv8O/xoAFwHhANoAnP95ABgAfv5v/40AlgAKAC0AAgEqAFX+3/6sAAwB6f9//xgAgf/f/af/BgJ8AaEB4P+//n//F/+O/+7/TQDj/4z/fwAKAJr/HgHEAcX/hP6r/2EAhP/B/2IBCwF6/+7+Ef8wAS8CGf/V/Wj/YgBN/ygAOQPd/1795f8PAHoArACc/2P+xP3Z/rj/3AGCAgEA2/4m/63/vf86AcoC8v9f/tgAQgF//tz+YgEwAU8Amv8eAcQB/gDL//b94ADsABf/jwBRAQ0AB/4jAIoAyP7i/zEAp/9//gH/pQHEAigCFQBX/nT/Mf6b/ToA1QD1ADH/SgEMAjT/cAD//2z/8/0h/hMAyAA3AjMAlv/i/9P++f3M/lMAQwA1/+3+bgDY/2IB6QH1/2H+m/z+/mf/PwE4AcP/UQF5/jH+fACyAoQAd/0a/jH/7gD3ALkCDQJbADb/ff00/yUARQFNAAkB6ACA/oP/MAFUAt3/iQClAMn98P7t/iQA6AAXASsBXP+h/2n/GQBgAeUAgQCc/qz/KgDn/dQAYwH5ABAALv6fAEkAhAB9AK3/rAD4/53/C/8GAQkA8/4EAF7/WgCR/14AzQBuAKIASwCrAGT/OP/w/mAB+wI+AHj+Vf6Y/6r+yv9pAZIB1QAX/47/I/+ZANcABv8mAJ7/eP7W/uv+xf6o/ykBcAGU/zr/vgBiAF7+1P7tACsAIwBQ/sj++AGCAIz/1v3GAMYB1/5MAQsBaQCv/xoAKABo/3cB0f81AFAA9/9CABAASQLm/zP/8gHY/0r+s/9VALMAowCYAYICuP+y/rv++v6J/6D/2QCxAZUBdf3h/QkCWADE/ib/1QHB//78GADd/5sA7ABO/xUApP8N/t3+hwFxADX/pwAIAdP/H/3A/REBEQAzAEACXwC4/hz/uwFVAjkAGv95/UP/5v6//cgBqwMqAhX/MP+1/3r/cABaACYB+v1s/EsB6AFz/+b90v8mAWj+Af+1AG8BlAC+/tsARgJR/3/8sP5hAIUAgAGkAVcDBwCT/VkAEwFeAQT/SP8jAGL+D/9DAuwEgwCI/d79qABz/wv+4wLQAF3/Zv0M/nUCrwCM/38AMwKb/l394v7mAAMBOv5zAQYB9/8H/rX/7gLq/27/nP/rAb3+Ufw//RcB+AJt/YYBcgGD/wj/f/4sAr4AqwCb/8MArv+6/dP/AgF2AYT+YgAqAJMBjADI/T4CSwAE/7b/SwOBAYr9Y/+VAKECXv07/bT+rf/RAPH/MQN8AJr/T/4oAV0Bbv2T/g/+YQA2/df/hgHxAH8Dpf4zAM7/jv/u/7j+QwBZ/8UAJAOIAnH+UP47AXMEbQGf/U//pv7aAK//BwD4AZYBfACm/Hb/3AD6/x7/uQDNAHr9sv9T/xwBz/4F/Z8ANf8l/6z/CgKAAR//o/2Z/uIANQD0/4kAGwSlAHH/IgFoAKABN/7c//X/Bv7U/Y8BgASvAUkBdQCtArH9efusAGgBjgC3/VEAwgCr/kf+MgBPAUL/K/2n/ioDZQGfAP7+MwHS/z77bgLlAhj/dvxy/gwBxP/1/+YAiQNA/4b9A/+1//wAlADGAu//XP5B/y//tQB6/b38nADG/938bACTAvEC8gLH/k8ALP9h/GP/AQCm/1n+LP8PAX4ArwBWAIv+C/9zAM4B5QL2/8IArwCw/zz+I/3uAAoBtAEBAAAAbwCP/5YBEAGpAlcA2gCdAEb/EQGk/xgD2AGH/ZP9fgAuAGn9yf/XAVcBbgCAAbH+cf5k/wMAgwAv/rQB3gDn/r38yft9ANMAhP9j/iUBlALvAaIBYwGLAMT8rv2A/2MAKwBuAc0BN/5r/k4AjQLqAdH/V/4Y/w7/Pf99A6kBeP/q/eX+jAAT/7EAnv52/xD/PP6qAHYAiQLRAHEASQD+/Lj9QQEHA7X/Cf4j/08A8v3H/gwDOwEN/2/9A/+1/3r/gwAPAZMBL///AHYCQQCt/Hf9sQB8AFQBRwC8AXP+XfsWAbIE7gNeAXYBPgBD/0D+h/8DBLgBo/y4/XcAqQDEArwCMgEo/m38sv3lAiQFsAA2Aov+YPwW/gf+pACn/+z9KfwVAZoCzQBgAp4A//96/Qn+SQA7ANL+if1jAK4BkAAKAkgBqf6w/OP72f4DAS8CHQGMAdAASwCbAcn/5v+Z+7v7kf2y/20DUgHNAx8B8fxp/8EBVP9v/CT/4v8d/zgAngEGAtkBZf5E/dD/RwBL/0T9hP5VAr8CRAACARcA//5o/9D/WwGpAOUAW/+y/2sCvAHz/gD+dP3g/UEDDgMoAMX/UP+qABn/sP2sAvUDqwA//4f+wP9MAHUA3P4n/+YA7/8pAG0BYgMUArr+q/wOAYABs//cA/MAjP/F/v78z/8jAZEB0//T+9f7HAEPA6oAiwFBAsv+qf2e/vkAywEVAbX9MPqh/kH/1gDEAqUAPQH+/3v+NwBYA7ABe/7C/An+7v/f/xv/jP1mAJ4BBgKfACP/0wE9/8v8of3k/xICvgELAQn+pP+pAlgA3QH+/yH/qgAG/6cATP7a/zMEqAFS/5f+Of9zAAEAuP9q/60AwwBS/wsCowDM/4j9lP1HAAD/EwKm/n4AUwDz/DP/If7LABAA6gDiAEcAugAsAlIBmfx+/17+nP66/bz9owJWAV8CpAO0AJD/qQFCAMX+hQBYALX/MQDt/dX+//9Z/yMCxv4WANz/3v07AWf+BAGKAZcAEAKP/Sn87v8cA0YAJf8HAM3+wf/w/oIA6gC7/zkBMQBPAWoBXQJGA/j+J/2P/eT94P6E/gP+2AB5AQ0C3wHJAG0BWv8u/ob9cP4V/c3+xQGSARMEWwPDAPH89fxs/4oAKAHuAPwCIAPdALIAgQLd/6j9wP2H/Nr9uQFRAWj/UADA/wcCFAPqAnj/0frS+/78J/48AH8CkgBi/xD+YP9NAu0BpwS5AGv92/4k/mEBVgLK/qr+2v7J/k//uf7JAjEEtgASAA4AxAAu/7QAYQN6/uT7GvtL/5kCOAB2/8T9pwGKAN4AJgOW/1/+OvtR/nAAyQCCAksAS/4a/O78nwA2ADAC6gLz/Ov/TQGSA+MDLgCDAVf+z/7z/DP/BAJIA5UDNf5F/vn/7gJ8/83/NAGcAEkB3v04/6b+a//CAWj/MvsA/sMAVACSArYBcQD7/Tb8Kv1NAOcBMAPOBEgBXP0p/gcA9QBEAMD7F/7sAkkCsADFAMQAjgEcAeP/tQFE/K/6cf3O/scCUgNRApIAvv8h/Rn8uv7GANkBjQBM/98AIgGf/zQB0v9W/e/+t//Y/5wCCAKDA+UBy/4IAMf7VwDsABf/7gHi/af+tgDPAjEC1AB2AVAAFv19+978SAB0AXMAqQE+/kz+QPyJ++8ARAIbAb7/8wHp/nn+jv6PAJ8DUv8q/878kf3ZAGkCvAJqAQgFUwId/Kv+FgHiAWQDpP+f/cn8SQDDA7oAPAF6/o7+Vf7I/BYCnAE6AY3/Rf6eAMb+u//r/o3+H//e/9YBnQAnAuz9jP9xAuD+1gJm/o/9IAFpAaYCUv6XAP0BKP/4/xz/JQANAQv+FQEZAon/lQOoAFr8R/0//1UBtwB9/sj+hwCj/7kBcP4a/5EAOv7M/3P8vQDPABgC1wLR/M7+rf7SAp4Aaf7QAeMAEwHs/tr/0wH2/8H/GAGE/5IDmQOV/qT+/P84AiQBIgHn/i3+zfwC/xQCl/+aAOf+B/0F/FgDOgbZAQ8BLPx3+kD7Hv7a/4X/eQAKAlkAAgK4BNj/TP/+/RT8EP4XAAwFJARK/Wb/mACZ/SX/iABeASoAWP+xABAB//8TAST/Tv8V//T86v5YAHUENP9u/53/Lf4xASH7Y/9iAiEBnv9WAKEAlwFzBKIAgv9/+/b+q/+YAM0E3QJ2A7v7QfoxAHMBoQQDA8371fzl/0gBjAIiA84BWPxn/HL7M/4BAgwCKgOH/zz86//OART/1wDAAIf/df1AAIICYAHGA3cC+gDb/xkAEP7SARkA6vys//37b/+w/34DWAYHAzkCCv2E+rv8dgDf/8IAdP66+zj/8P6m/93/v/8ZAg8D9ADU/rcBYADJ/SgAP/1MAGUB9/5AAX7+tv6V/Pf9VgTXAaMCygSJ/pj9ivua+n8DigN8AYn+E/u//L39jP9ABfQEc/7S/vj9uf6G/G7/hwaWAUT/sv99ApMBegD2AIv+0f1e/Bf/lAIBAp4BcgFe/6P/8AETA+kCZwAT/EX9Bv/t/u3/8f+yA+D+uv0uANr+KwLiABMBNv9J/h//zQCXAikCBQE+/y0Ah/rS/ccCuf9wAkECnAL4ApT+ivuUAB0Bqf1E/778Lf+PANf7c/6RAksDqgP8/R75xv67/yYBXgKJ//z/8Pnu/vYDHwMxBgUAyf0w+1n9egMqA2wEEANu/Sz5ZgArBxMH0gL++QP7C/sW/X4EYQC1Bb8E9fmi+6f/fQaTA+z+TvrC+r3/gP9uBcsCigIZ/135q/zD/2sEoALg/qr+1/3B/TsDzgCBAHwBgvud/hoApf63AdUD/P6w/y0A3P+G/zEAEAbC/ef9CwHE/x8DxP2b+0D93f6KAmYB9v1xACYBVP0N/Q7+zf/hBP0BS/4q+z/8ugE9AH8Cav6sAYACBAImBL//2AVTAdn/OP7a/gIA2/5DBG4CiQLi/9cAUwEWAx4B0//q/Wv5mQCOAOMBTADd/Zv63vv5/mUADgNgAOUC7/zx+8n6Zv8rAdD5lvsz+dr/IwXMBbYAkf+i/Z74KP7jAGYFsgI6AC8A2P3s/74CbwN9A4QBe/1Q/K/+MgT6Ba8FHQDz/938Cv2nAhL6Cv+aAer+JAElAvQCpf+l/439UP5//jb+OwIrA/wCCgE//ggBrf6n//gD5ABQA6cAZgKlAXP+owL7AY8FE/5H+/IAEQP1AMr5Y/8j/oD+UQIQ/7ABSADx/5sBAgEsATwBF/tV9DL6Qvwg/V0CwwEBAxIDCQF4/y37Ef/1/h76Nv7n/Ev+2v9kAZIDygA0AP/8dwHSAN//IQJX/7EAe/8FAdIAcgBgAhYFo//j+xQBPQI+A4H9LftY/n4DBQLYAccBUvxqAPT8aP5OAZ7/C/+3/VMBvAN6B6kEvQEZ/4P5NfwzAmoBfP9GBRkDeP7sAC0B1wT5A1QBfwDt+t//wf/+/Ez+Bvtw/lIAsP8IACAD3wFbAKL+hfxKAPQAxwF5/bj6hfrl/m4D1gIEBEsBAPyd+toBcgToB6gFg/5J/bL41/te/VL/rAhTBKP7o/3z/bsBWQQJB9EF0vow/Df9TPqw+4ACTgKe/tP/7wDYAo//OgEH/d76Tf0L/joBNwIFBLD8TfqU/nIBUQKh/uP9Tv/L/tL/TQKPAGcDnANP/+D/sAA7BIAF/gJTAHL8bv6H/5//RAASAHf9gvs/Bq8F8QR9BIL+3P2M/Mv9HfqDAOn/AAD5/NP6qwKp+qwBSwOAAc4D+gCh/rz8jQKtB4oFgwFNAgj1sfIr+pcEZQn9BZ8F8/rl/48AmACu/hgBDQQa+Af+AAFM/+EBOABo+Yb4Dft4/yT/uf1sA50CPgE0/ywD2wNoBE7/wfp3+d75dQBv/ycEHQEs//f98wAOAScD9wlaA0cDQv/XAIf/MQDr/D7/MAGf+hAB5PtgAhz/7wDeBYz/rwVXAdX8FPz+/TABfwVk/13/6f4i+EX+Qf8K/wgC2ACG/tAHogNWADIABgE7Bkz74v9rARz9zvzz95n7ggMMA0QFuwIs/t0EeAEKAekAFf81+WH62f0O/ywA6/79B6v/5wKxATT/BQLF+Er/kP7X/gYDaQeyBigCDPxN+x/6gf7OCM383P4A/gr/CALdAogD/fmx/4X9N/5y+fP8KAPJ/BQB2f1KAd/9uv8HBAv8IQGx/6f8vP3V/6cA2/y4AhgHEASW/Zv7VP40/ND+1wBRAFsD2QJsAHj+Q/5xBUAFEAEL/Vv4rgBnANP/2f6U/xEGmwRHA+L8KwLBAvn9/fuVAKEKvgNaAFz4efhB/vL9BgNT/er94gXKAbD8R/8wBksH5/9/APb+Xf3w/DX51/1/ASkEaAFC/q3/hP7g/lcDmgjPCOb/u/qg/f/7//3DAF381Pkh/70AVwRrAoIAfQE1+dL71/sABU0KRQRn/hf5jQD1AWn+IPwSA9EAlf+6/tL9sACOAIIH2P3i+6P/gwLyAB0AcP6t//0DKv2cAhj4ufzd/Z/82wanA2cGpfpV/BD/QAB/AVAFBgdh/T39v/rTAmsCOwEQAT77Lv7A/nj8NANCBhcCQQGz/RsCXvy2/BUAPwSDBav8Pv0B90n9Y/6CAR0G2QP8BbD8rvwO/4gAwAS7AKH8JP0H+1AA5gDnBEAFEgLjAaL1FAGpAef/WgDW/TcC+/7HAqb/dgOv/lABNAEx+R//k/7vAHkBOQUIAB/60vlz++j8+wLjCPcItwWZ+ln6rvXS/1IEc/+QADf9Qv6n/F4FTwK8A6kD6/4z/1n+oAIgA+ECVPoLAS7+bfrHAqgAUgFaAYYBKAGiBxAE4v4M+fT4XgCIArID0/hO/J8AJAAmBCADa/7Y++375PeFAKAHgganAjf6hPeM/NEAFwGU/g39EP+p/Q4AqASXCcsGQvxR+rz+wf1B/YwDqQRDBPv/m/3jAdMDeQZ/BIH9Df3p/Zv+vwDBAQADN/vf/ScA6wBFBP3/0ATR+z35Dvs//i0BXP4kAxv6SgBv/k7+kwD8+d0DtfyDAP8BoQMPCh4Bl/2h9eT7PwQeAQwBvAQGA8b/LwFAApkJkwW4/HT4o/pyAiIE1gPuAJj+nAIDAGX65gLI+zn6qP6U+FEEQQINBIsCMfkE+536JgOsAef+sf+H/hj+IgIlAcH94QMW/t/8ZvxvAywICgGDBDICi//IAEcBqP5s/3/7ufve/9UB6wpBA/b/df4A+uwAsALw/+387/ucAEcA+furA8j+cf7EATMA/QQu/dIA4QC9+0v+Vv6Z/00G4QZm/Cn88ADIA5/6Z/5EBdb9af8GACwBcwHqBGACKv3Q+Fr6EAG4AeYChv4IACsAUwVbA739gQNc/sf5UvhJ//UDSAWVAGz6XvyF/1kCjwQJDC3+Vfi4/iv9GwIRA3kCjP///z77kPjw+uoDlArmARP+Y/f1/UYG6APp/zH9agJz+dH16v1MBNoGSALT/wb6Gvo7AoAA/wLeBPT++voN94ABaAf9B2cKQQGc+/730/hj/foHTAdS/mn8lvqzA8AAEAR3CHj+Dv9f/ssCRQQgAO/8Dvgl943+8gN2AvwBwvrY+0QCKQesCkEBg/g1/fn+kvtsBHAFQf3V+mn83/qG/RQHDwVXAVL7Kv1JBoQH3wgpAFz5TvzM+3P64/sHBHcDyvkX/rgDNAIqBaIAOvj4+2r/qwceByUDAQew+Vb6Ffzw/90GHP1h/Uv7cf70BgILiwM1Av8BlfWz+p7/ywPTACP9V/5b/AL/gwLfAPP7v/3M+hj87v1mBhgGWPxs/pj/2wRGBEkB1fm0/n/7/PgKAdH9ZwlCA0IBpv/Y/RgEmvxgAjEBVQLRAmUAhf7W+cf+qwC6BRQA+PyGAuj6gAAvCGAFgQfABFn9EPzm/C/6o/8v/bT6wv69+cQGxQhAA1MBuPkhAZf8vfuGAIv9RALj/8/85vlz/DIE4wO/B38CyP+dAL77ewMdBbUF/P7A9pT8HwArADcBbAKN/Hv66fuJAu0EVQRCAQf6XwDkAk//6vvg/5r+Qfnw/NwCIAYzAvIEfQTz/1MB4QPz/nH/RwHv/c8D/QGtAZMCev7iA/EF6wLV/zj3LP2R/DD4U/90/98K0QaGAMD8l/zeAjH8pv1Z+Yr/Cf0e9ib9TAG2AyECJgIg/UL+RPn3/hQG+QSFDSEEhPfG9aH5K/2q/7wAHQO6AvsBiwO9BaUGVwNSAWz41vt1AIz77P3A/RT6TPvQ/5EAlP0h/ysBWv7A/2r8hwR/Agv9gwIG+Yn8i/qc/DAFfQbmB0kFuwB//YAAQgBhA7kC3ATCAcH+3P8sAAEBmgH3BG/7NABO/1ECdAPh/DwCNP7/AP38YQBOAFD/0AB4+7r+7wIOCBH+WvwXAegDWQGG+af80f5T/kAClf/G+xcFkv8h/Qz+QANQCBcCLgFk+Xv9ef6c/Mf+j/vT+V4CdwijAfwDxgFdAjz+LPm9/d/7Jvq8/Q0BfwEtBq8DhwFeADH8m/iA/VIEHwPhAqb+cAJc/Rj/kAhrAHr/zADQA2P9a/gPBoEKhgZC/Kv50wOCAmICv/0v/ncH6QFZ+63zjPw0BB386AHcBef/hPqE/Db/pP6s/Ar+hQJ1AU7/XwCD/4n/Qf5B+BL9sAPNB38FuATXB6v8/gF5Aqv0qvjtAE4HBARtAOwAvgDXA+MDDgJo/Qf7j/sL+v37ogZqBPX/6AFN9jH5FQM7BpUDLQONAT/4gvbK8SP/RQS7AysFOPnX/HH8AwDoBCMI2wfr/lj3BvnfAsID4AHX/XQESQEo/l/+hvwtA5z/1wmlD4gLuwEy+rH0APR6/0b9kgSbAln9Of6N/NwFoAHu/eT8XPbJ/owCAASvBq79lADy/SQA6gG4/PQA3frtA4sFPAJHB/b/OfyzAO8BQf8XBdMEYALg/MD7NQRpBR8Bz/1X+g342P3p/mEEywBo/g/95/MJ/+cDVgjkCYID/vxU8XHys/to/g/9W/8CAzwFWwMqBnUDVgDGAKj7vv+ZAkEEtAFF/Sn+pPyV/XoGXgVj+gH/wv0h/+oEdQPsCez+hfqq/O/yoQBrBo//TAGl+3/9OQGk+U77Pv+U/CUD0wLS/iEAY//p/H77TAVvBrMGKwMs97v3Y//oBLsClARlAk8ETQD9+s0C/wQZDCIElP44AMn78QJ2BBcDtwNm/5360vXy+FME8AU0A4j8Jv/TALL7QQb2A7n9bfsr/IL33fgEAbf8JgeKBDUBKf0l9oX8YPkCAigG9wR/AyH9ygGWAfH6ovvJ/k//3P2++h37hgBEB7UErQa8BJMAwgFt+Q363v0kB/kFGwUdBK36HgKQAUkEav7p+239d/qA/8f7pQII/gcE4wpdAiEDyv/C/4X3Pvp/+o76qgJF/6kDzgKBBUsEuQBrBgMD8QO6ANb7PgBrAZD/Sv/DBZUF6AHX+ovyOf3a/5H8BP2kAykMCgS8ANX6D/UJ99v58v+Y/+T/VwC2+C74PwCg/8kBdQOSAsX/p/3/Acf7wv5KCCIJ8wDl/lkCmvif+wQCwAcvB0AB6waF/oX+dQi2AlIBSAEX/yD/k/6y/Xj6VfwBAb8BcPwB/3YF3wBQ/Of2NP37/yAAjQJn+B79RAA0/uX8wALdCi8AMfxR+Pj76gdhBusDxwh6A9H7CPqS9doFfAp2AWMALwJIBOn9MwLc+ggA7QSe+20Aofe6/mIF0wKfAEH8MwasAKP6wPtX+p7/fQEOAY0HuASv/YX50/fDAXj+FALIBUH+Av2386D5ywMRBN8FvgVn+oj4tgQiAYIDiAEP/WX7/vocBXoEqgkHAnj22fs//wIFjPyd+dYBDAGRAQAEQgckBmwBaf4H+X/3G/0BBLT/IflK/+z+LASyCHYBp/30/JgDlwDfBPQGc/vP+cT3sP2JA4IEPAdq/mnzcvhi/xMIswuBCe8FZfj1++X9bgVMC8IBHwCL+Wb+G/sz/MQKTQYXBvIADPjc/6v/YP+JBPr+8/3Y/b37sfqr/VsBgf6++HL7t/9Q/Mv6/vjeBPMG5AVBBZX6cv6v/377uvy8BxADz//Q+wP4u/zBAUsM5/9lBdMB8Py//f/4rAa+/Y3/cfkA+4YCGPh4ABkBQQKQBRP+tvug/YD8J/rk9ukFvAnjA8QBnPUhAVoCbQXcCtP/XADY/Vr4vfZiAOQJvQ3hDPD/5vkMAJACRgF3AmwCLPpQ9Dr3IwFGCZQCgwIbA7MAe/5x+cMAlgXA/5/7WPaR/wMJxf5PASD4YftFBFf/iwgIB3MNNAvBAfb1MviDBMgDF/87+4MEhv4qBz8C7P3xA9r9mAMj/U8DqQEJ/+L4T/fS/Zr+4wD0+tr6yvS4BNIFsgSMCYT6Jfsg+J/+jQFN/kP9zf59ApUCfAf8/yn7IQBR91/ylPwHBmMQDwzZ/mX7hv5x/XkCxwFZ9/v74/qS+dP77wb/Cp0EsQB892r4xv0l/6X8PwBR/WACVgF//6cG6fk1+K/1VfivAx0LmQjBAiYC8AB3/yr6lAPUBDEFTQHE+Lj/5QVKCawDb/98AWT++fze/y8BGwoRBwoEIfxq8Ab+QAWvBrYBUwO5BxMFF/u8+dn/Dfv6AAAA7wBj/4wEyADo9sv+Uf86B9EENP/p/OkCVAAc9ln8cACbBFf5Q/ltA6wASANrAZn7FAMjBJkASAI8/Qz9APgA/LUFWQAi/2MBC/g19y7/cwSNBwkA5QAa+7H7vvzh/SQG/QAOBoP6V/ks/xf8pP24+38H3gHRBMkI/fvzAR0G4gf4AsT7ngD0+nv5Cft++2EG1AGEBucFZfsvAQH+vv2iAY0Dif0T/XUBy/0U/m/88AAt/yYDRwUJ+9kDnQR5//EAgfs9/WgFBAZrBB0Bf/sZ/gf9hvwDAeoDKAO99w/6MAF4AgkHLP0C/uoA1fowBCsEagG0/5H58PgJ/KgEZwQQBYn+2fnPAR4DcArgA9IAiAIG96z2EfrsAmIFsQMVB2MBxfkf+zT7ZfnMAFoAygAq+036/gU9AqQH7wQdA34A+/BD9br60wRLCUIFtQCHA+UIcQU6AqP3Af2S+2T4IP/8BHELCQTv/uH54/52/5H/8P8N+7n7vvkg/jcA8gYkAsn/jwI1AkkCv/7zAg39q/qG964D0AmfBysRbAag/lj5Ifqg+zT+0wXlAqr+DQawB6kBKAWt/RP4G/lX/+L9jPpgAgf+BvtH/NAAeQS9+XP67QBb9Fr5xQF/AXMEAwOW+7v0EABJAvMFCf+v+hr/lflxAPMCSQjPBJIBhv3e/kUEEwKFALb4EPv3/eMB7QaZD7EJggVS/vvzffqh+9kGCwjhCjsEfgS7B7X6hfMO8/IAzfwqAVf9k/4cBJMAVgI598gBiPu39/H+i/td/34AuAQeB20CD/3E/Bb7XACaA00H1QdVCHQJavdj61r0KwZMCSAG3gSOAjkErAE0+AD6DwB6/2r9V/34AiYHqgrn+RX7Hv1K+pYJFwDa/s74i/iF/eUCdxEvCZEBsfj889X4DgALCMoIOv6h9D/1sQB4Bu8FKQdfAGEB0vfG+qEC9wC8Aw3/kvwo9Ef7JwDX/xT/rv7nA0r6ivuXAZ8HLAnPBRQBT/mi/cv8ZPpc/nL8UQJoBtwCfAY0Avj+wgEDBMQGYgVNCFUGt/ho+akAFP3o+oD3m/zV/Hb/Sgk0B4IEGwBc/mj4uwF3CQ3+9vnd9Hnx+/m1CuwItwFQAY0Ar/pd9Or/Fgo9DNUF1AIL/8D5sfzL+F/+LQalB4X9p+5A9HH9OQa6DCQN3gjjAT/6Qffo+6P92AL3/Ab6PPn4+TkF7AMrDKgIov+w/Wr9SAdNBiAClAIz/yb4a/1H/voHoQwlBvz/YfPNA60HXAFa/ZL8tQJPAE/+7/eG/DX+ZPwD/N4GQgad88HwA/ak/WX/4glLDKb7s/OZ94j7JACd/3AEkgLD9oL7JfoqB18I0f3EAZX6DPoJAa4HPAvJCjgD3gAc/vn9nvoc/hULt/8O9/r1Rf/LCjsUfRRzCIH7qPMF+7f9wgEqBRUDX/2P+Wz3WP6xCkwM3AMdA6H/p/FBAd4ArAUhA8LzcAHu/soATfry9wX7fARqDSP+lP/PCJ3/sPeZ+l700AT4Bc36mvxx+cUBIwEUA1IA2gI0//f6sP/y/bwCzPtO+qX9YgYABYn7TAFTAGoBlPnH9XIFsAXiBUgBl/5jCp4DbAMMAyYAffjf8a78Q/7EAXwAiP//AZ4C2PtN/WIF4f+TA+z+e/5cAGL6E/9m/8D5Mv0X/YX+NQTZ/YEBkgEoBewJcwpMCoD1O/Xg/Yr6NwGVBMEKlwfS+xoCHfhr+DAEbgEJBKsBQQfOAEkANgYo/Qb5dfvmA0oDYQR+/vf6wv9FBGgHhPq8/JYG4Pvf+lQAWQHQAi4AhgIA/h0AfPsu+PD8j/iqBK0CcgIo/vP2kfmz9Wj/TwDmAFEDGwNQBSYFuAP6/+n/yP+H/pD6D/V3/x8OEAdZ/rv9eQDI/KT/HAUoCDQNKwUGBM/5N/rJ/VP6XPx+9Hr7T/97+/H97giWCpsIGADk+lMGH/+YAf7/If+qAL32Pfdx+cYKFQ39+ln3fPy4A+gIFwU1/5cBtP+H/Xr64fi7B/8LSwdt+urwB/mw9PH9NQCJAUoPpv8J+6X8bQQLEVoKKwTY+O33hv1n+vD9a//d/Mr4ZfnK/4wIOw3nBKMAhAAnA6r/xvwc/Tn7O/3Z9q//xAJgAmAFCPpo+xEDtwVq/kX82vxI+aQBtw32ByYAOgQ+CfwC0fc89l3yA/5j/eX9FweCBjEPIf6T9+j/9/sr/JoCM/21+Rf9aAIxBgj5a/79+zgARAKcAb0K6vzy/Y39iv+7+jH9tAJg/6cJZwWnBVoFaQcBAYn5EAIrArf95Pe2/fkBOgEwB1EIUQMpAdr+dvrT+2MB+wkw/4729ACE82718wQ+COgDffgX+gXzwv7uB0QIjAHV+fkFe/6bBNcJQgSx91v/OvtS7nwF+AmtB5P4kQjKCWT/uwDy9z378vMfBa/52PsvCUD90vG/+JYLGf3oAab9zfu++qD83f5e9kv/iwQBCtwAYAXEBOwEUgOt+dDw1PNSDrMEkALeA5kAdgbiCCcO3wbNAsMCmPpo+SL9tf+UA4/9tgIM+pT9SwpvB1sGw/Mf/fz/of9WB1IDw/ur7ejtgPP2AgIICAdZAUr36PgvAEYGuwjsCa/7F/SN93r5ugFKBtIAqQD9+kb/1wcEBPgEiv9I+Lnz6gGGByEFAAWy/br/EADKAlsGdQJQ9jX6h/lmAF8OrQ1xCaX6iPoG/G8N4wi79av5FfiA/K38gAoGD00JTQG16YHrw/+WB04L3QQ/AGcHxfZ69w8CMv0oBYIDCQIb/cn67Ao0BegD/P8Q+KMGhgDF/if3VPwDC34FtQO89Rb4//P09Cb9C/yyCH0MUAXnAT0AuPrn/UD3EPav9WYAEw2fA6YEPAIsA0T5X/wF/6P28wACBDYJ2gac/pf+/vyf+rQAnv0qAIIKpwQ++i7/zwSy/jACqf27A1wCBwDcBcUBCQYr/lcCLQLJ/Nn+ff0YBHcF1fs9ANkJ+gOX/XT6XQHD+q74Y/opAdoH2v+D/sv1O/tM/K//Kf7UAfcILQG9AWv6cPyE+LADsgOHACUJYf+3/5P5UQPoDOwDZPyeAAUDMv99/pgCgf/r8qL5QfbY/icJYwhLCtj8TPsGAL749PP//VYBP/vW9kEBuQAWAekEHPzeBQ4BKgSN+HrnffkPBh4PvQFd/HoD3gHoBtIBhf60A3EGj/0C80/9pQHiB4AGwv6SByIBEArqCXr97PiA+XUBbfRa+wYDTQNtCJ8DUv+J+J/5Cv9Y/Ff9EweyBNP/t/+GBO76i/ogB5MCogjV/wX5tffr9E0C6wibBTIAPQFJAWgC8wJuCNAICwC5/Av6IPv0/kcF4wKm9Xz0LQNBCHIHq//Y8175s/+xAJcEFAZVBa39RfZk+un70wILAOX/k/l28twEdgD5C28R8wkTBgX69/py9PT8S/mO/r8NKAPe/T/6U/9uBXgG7QR5+xD0qvaNAa4JBgCE/2P+ZfxCANH7KQk//4j2afU79S8JTgwZDo4I3Pkk9cf6P/+GBjIGJAXc+9TuSvm4AUsPowa8/80ByP1t/pwBrwwHBD0CjfTI71H/Ogf6DjYDHv3j9OH0agJsB3MK+ASr/Qr14e7h/ikHuwDXBAwECQLuAbwFEP1f+IwAzPcF+Lj68QLXBrr87QTxCFgG9gPS+LbxOO8j9Xz66wRjC2gCMv7m9Y31Evc1B/kPnAaSAPvxqAD4AX0GRgqN/RUFwfR5+78Rkgs9B5cKdwjrAAn56v1gBT8CaQXFATX4G/U6AZYDBgKo+y3wyvgqAKIIhQXRDXkIquqF58b1c/0m/cwINQSL+5L+ewZUEa4VtQqv/Rv7Ffep9zLw4/laC24QrATJBSgMjv2FBST5a/RJ9KP32gSK+e4CTwQyBCL//fMS+6kDXgF4+TH+Q/8WBFkBP/qE9Jv3fQaXBXYH4P2b+RIF4ftR/AsHeAY8B8cHVfx5/RUMgAYkAqoCZgYkA7r3Qvkg+RH/pgQ7EkYPTQIUAxHzs/Nm8aT6AglO+/kBlQC28sj0BP5vAlABwv7G9Vr6zwSEAy8K5QR8/6YHVPfZ9kMBqvgM/vEIQQyTB4ML2wle9gP3//tBA1MJnAECAUX7nvzNADP+fP8hBZ0BKvGy9Uf5oQCGCi4GowZp+x33Lvcm9soCYwGE/aAEsP4U9gX6IwdJCXUEaf6l/q0NiwSXAyb/0vd+AwL4HPdrA7ELewcYBaYAfvzcAvz9mwBz+0L85fq58Yv6bQBHAbUELAZJ/7f3CPmDAaL2wfppDGUFUADZAnID0vY2/cQHbglHCyD8vv0l+j7/iRDCBDYGagKF+b//vwIBC+39Vvcb+z/5dQB6BAgLfwSi+/z05fUQAKIJ1A40//XxL/WAAHYHMwLX+Cj6H/Cz+20JufwzDKEK9QOh+0f2j/yJALgIiwA3/xf4DwOABgP7WAVF/xj87/31+2IFlA+CDoIGqfqY+JX3cvsuBGwBmPp/+/8CO/28CkgPjAU3/2Txo/IX9t3/twTkBWz/pPsl/pcAcATyBL7/ZPLf+5P5k/9pBGUB/gpFBi4L8QCyATkBhPvo/rfxG/qHA8oEwP4d9JIAPAeQB7EIYwFlCCX4P+pB9zkA7wxGAbH6OPMb/GwE3fMSB8QEHwMsBAz3XwNyBCQKuARq9zv6OfWQ++X4k/xKA8v50QdrAxL9UQKyBi4NugWLBDj5HPtAAs3/zANw/Ev3d/+XCrYD4gauDJ0Fwgba+enz9/Un8+EA+AUSCgcOOAmdAy3v8/NI/qn7AgYo/2X3Qv8MAOkBfAPyARkF2/5DBIQE7gMj/1PxzQNn+Jv7tgnU/rcBZPnyASIB3AItDIYAwv32+7YB2wYtBg8GJ/r595YA/AHE+xTzE/2H+PX3Ewn3B0kPkQfy8+jr3PYqBVgAx/9lAJsADf8T/VQDhQhZBJ8IkgSO/Cf1ffm6CCv1wf14Dv8QOAdF93MA+ftxAg77jwHSCBP68gRi9wXtafB0/hkO3wPe/X/+mgKoCGkHqQJqAK7+kvUC5tTy1QB4+RAA4QTHClkKXAIxAhT8dvoY+rr5DP8XCOsK8v++APL+g/dI/zMHLv+z9wgD3gEaBIUDFv5aCy4Env459K3xSwP/AEEDMwPeAgMJZv3s93j/RP3rAwMD0PxMB+sJkAcZBl0P//+Z8gr81veXBdwD/AStBc/1bwFUBGEH1Qg/BakETvgv/Yb+FfXt+Hr2EvyYAqX/hwuiD28Jj/lM8VrzUfd/CSwBxfR6+pQH9wX9AHQKpwGkAx324+/f+/33NgUTBq4ErwGqA3kFNPQq+jz8mPugAC/8jwSxBa/+jfvF81b8Rf7GAQcN/gACCLwFTviqA/AAgvyH+8j3pgCFCCIEp/47A9sGGAW2BwUAWv04/XDxzPheBpUHRghpCZH8bvtB/fz7YQJX+L8Bif/R/KADPP00/pD3eAjgA4L9OgnK/Tj2IvJF/4X77viZBAYHiwjdA4cJBAVd/10CMgIfAfUGxwhB+nj2lvZN/NMHsxLXFJwCwvo1/Dv1bfvWBwUFzf+i+EX5zfN98ucGOQdRBa7/8fX39xv74wFt/gkBc/1Y+qr8v/W+Acj6Ofz/CeL7Hf1C/yULFQzOAJP/ZPFnAfMErwHQDNQBRAJL9ZjwKPxz+kAFMRCrESoF2fen+hH2kO/W/JsHYgKo+575Uv/kAEkAXxBXDcb7uvvp84j9qQdCB9ULNvwQ+iz2rgQqGAkJMQ0QAuv9C/8i9NkF+/nR9cz4uPS1CcUJAw9U/Jz0qgZB93/+4/mY/ST/2+vXAU8Okg9bBsz3SPVQ+h0CegDTCScKKQWaBToE6foI++8FZ/kw89HtafmXEJgFSvsr+Ef8pv1l/nkFygaeBbP2jvb8A7MBVQWpBIP3/vaJ8fgD3RX1/coH+QsrA1kDdf85CjcFigGYAI74wuYX7er6RfWDEmgdpA+IA3f3bfMn9hICEwd9BXP2RPSq/IwAmAk/CawHsv5n8bz0cfk2A7YICwFhBdwG3QJK9x342gGU+vn5nPc7ARQLDwelCIUEeQC9/7b2fgeiEGb76wKl+j76uvxU+VwOmQVL+6vvifn6COD97/4oAVr3Ee3T8uT+2Qql/Bf2MPzI/EIFKgT6CEcDUP0u9An2GAcSBWwJLhHAEp0Gx/6JAe/+Sf9yArz+Svnz+h75xv4iBXgJmRNMB7YCigGH8J/+DgJw+Hv6ZgPiAgT3ZAhMAg4Jhwhl+HkGpPPE9xf7c/kzAev6Mfx5+VMFQgC1/3P8efqC/wrwLgEhBWgCKgPY+gwD7v4j/1z9vv9zAe79nA7xBbEB1wYG/rUI5P+w/u0FlP1OA9f13/4WB3L/mAQz8mwDRAPi9TYKEAX3BsT9/vZRAmX8Uv52AmX/fwZWAML1VPnx/sgOfwQcAikFNQGHB5P1DfvF+EP0i/9W/ir/VAB/CrAJlgZEACH+CfP57HX6iwXyEbsDRwE++Gz1mf0a+kMO+AcuA3T9WfLv/joBIgFD96nvBPiXBcsU5RdnCpj+pPV77CL6jALvBG0G8PjU/K3/VwN5CpQHHAbs+zj9r/1RA2sOm/gI8XD8b/9FAU0A1gqsCZf3PfswCJoGs/4f+lbzQPHy+dgE7AWxCxEJb/T39gr9/hCSD03/Iga/7Wb2Lf/B/ekHmPXGCjkN8fjPAtkDmwsIBZ35p/xS9ysEnv+k8Wf6gf2bC/ML0QXQAin1TvTQ+XL7cvlZ+ecAdQIv+HgA7waLCHMFIP7iAtby++/e+n0CUgUn/Df4T/uLCfsPwA2ACbz/IPUp91f9RgUrC2v+zP5Y+q7twvz+Cb0MMQFk+N4CD/UX9cX+iQJ5Ch77eQLJAnH3hPcy/QgHDAAuCOP+Z/i5CdIF7QYVBWIMogr4864BV/9LBJ0EBvU1Bvn4pwYKCY0EDxC+BZwKPfSA/KIAZvsWBsn+E/3J/UEDWwQpBMH3cANAAMb/9witCZwSG/Ft7Ebu9/5cBfHw7vvL9FX4GgJZC74TYBOBCjPx0ueO8rLwlvvXCcoH0gq7+AHzI/qY/9b5pQhLE+r+EwLh7/rvjP9cCdMGZ/mu+njwLPEw/LIDMAJ7CkUMtAydA278igTU/ckCjvwX9hjx9wr4F2/+CgG7BDcJ+Po7/F76iesIBIAPMws/CWkClQHn9kX0gwPk+J0B4AFp/foNrwFPDH8BZv6aC0Ds2fabB/gLXwop+Z4B5/to/Ob1oO3w/dLz1v80Bv36ofYR9uMEiP1kAcL/Fvfj+JL0Q/wv+2kFNQseAkgKogZv/gD8Ff9KAwv+vgKkCgsV8Q1JCMQQl/wz793vWfOmBcUMpgHHA3D+I/ts+sfxIhElE+QBj/Qv7Iv6fv8fFP0NWgOK95/qBvRH7i4H1wvA93oIRwiJB70QXQY9AZD/1vz595X/sfrC9+gH//KG/iALZQDuBG/20/zZC0oMPAYB+g32NPn7/cgE6/Fb9EUJXAKhC4MIjgSl91b5BAca/y4NqgYS+3v2gfw5AtYGzgaB/rcG0vGb8JICCQaYBmX9OPFd8yoGgAjA+gH+6hHeBQALewU996YB4/ZlBEzv0PF0EYYIdQhd+3cD9Psc7jMAaQRAAZYBsv9q+fQIhwH68/36Z/Ug+pD00QPZERoGOAaL96n2nfhSAawVLQjA/1D5ze8WBPMESfxYA2bwCPh6/lwBzhABAJMIYfog/fUEDfHJAtn04ACwBiD/lxlLBr329/ig+/39DwNUC6gDkgC69aD9/RP0DZUIg/gM85/0cPMwCmcNogcl9B/yR/n/8K0LoREdC9QBSPMe95b8RAjBEC0IVvnm8O3uiATeC4QDbgVcAvb/AfzPAOoFKAAN9xf7Nv+D923/kBORCJ71Q/bo9Nv41PvZBHcCpwRBBLoEbAhG/EUE4PIt8jv3av/CCZsCXA90+0H7YAOFDNwHlQEdB+rwBPi6+wMRUhGQAIgBOffl/VEAXQRY/x0AV/su/Y0CsfjlAskEBQaZ/336r/GI7AcCkgL6/kIJ5gdE+iD3ef8BCLAAPPwKBvL8u/oK9Onz2wLS+6UG2gQ/AfYUAQTA9Fr+JwX7CDT6DPwkAr7y9Q4+CMv+TQaD9LYEz+uK81UJ4Aa6AfD1aQuiAXgKlgB1/mIFzv/l/cnrlAJ9954HgAbq9/8LvQD0CLIE1glGBlYEBwdE+FD/6wQp+TQDCAV984cDEfuTAgz2Cu/AAv33nQrZAPgIBf888cwDl/0f/VvxA/hy9LIAjv9u70gLwBJ6B2z5vAfHApUA+P988BMO4wcCD/gVDPal6rnv0ARCBsEMxwlWAoYBn/Ti7G8A7BjkBEgK6/1b6XnnUe5KECT9Nf+8CQT6fv4aA4n9cvaf/DAEXgrYBiEKhwCB+Af6qvgw9XH5ohI4DcIF0v979af2qAbODs0EAgNsCqwGofhnCfgCvgnbBwL5jf/s7kj4rv4CCNsCHA1hDZv9FQgT9Oj4GPUn+cD4LPxzCSbydPpJ+DL4OQyaBWb2MQFt9NzrDQnfB4kDiP45/GH8xQLYBnAEjwkL/Vf+i/le8in+9gAyCDz8lfHyBA8E6wuiDHv6YABy947zkvGh8QUBPAdSBG30WvsYA0AHvBE6/bP+/QvG/EcALQvOAV32CvuI/zQBQgnVCHYNegi8A2wJYQdgBeH4mvhB+l77MQ0mDKcJNwhO+pD0WfbnBdwHFgLP/x/2Fv6o/OUHQRJv/l/1RfX99sb0iQH1CZsI8/8H7xXwOPnVBBQAP/wAAKoCqPp78z0ETQZl90zzvAMgCO4I9QPR+HIFMP0o/c8JrwZQDSQIZwTBAvD5Vw3EA9nsZ/c38SkGmQtg+5QHdAR9CLj3iPh+DJH4T+Po3GX5ogbhCD8RawfBBLn2Xe4R8ir5eQl5BbX8I/4+8X4AHho4F0EO9vZV9gzuE++iCvMSGwxB+HH2oe2/CDga/BNSF5Twq+7H5Y3wdArn/DEL7v0O74v5Hv9EDVEIggBhDXr/+PKa+d79TgFeBMkRFwoIDe4JjvyT/Bb8GQoZA60GlwQ79n75VQQaEEoHPA4jBf/ya/IZ6u33cvyj/SL6b+1//SvyAv8AGn4YFhrL+Hnpd9uO9HcVywdEDHL/fgHf6kD3bA95ABAV4AQJ/4H2JAK4GYoGAwgS+j3tb+/KAzECn/AkCRcIQP/+ApwIIw3Y9Vb69P286ID6NQywCFABhvxhAvIETP7G/gH+MfhC96HspP3VCPMDHgwdCCcLuwOO98fylAB3CLf5o/Hy7qoBmgaeBocCxvvLAyn+8f0g9q8ApQv2ALwMswKn9sn8nvxjAp3+Bv/6BMkCsfs3+csAvvsPBHoSugu0/NXzhAOuCfMH/gfX+Qr8mPxr7w76fwSmDhsVJ/909hXnjeMgAbwNIBFcA5cFHAjN6iLwkfu9/6b/UvshCj/4BfhrAR/+zQo4+eoF4Ai9/4oE4PKS/jkBBQW2BtMLThAD/R34O+vc8jn5MgW4D3EC6AI79Rj20/qEAQkVKxCPB1/8Te5y8RX4EATTCHb9ggQZ93X34wj6ASQPUwGr+xkHiwE+CbYM4QDI7+zyYezd/EYQHwUzBFrupfO3AggRGyCODCACv/Td91EEIwUEBgf4au8B/WMIkwnsDsMFGPYs6d/8ywnVCAcVnfFf+QAKc/qlCYoFVPww9QPxKfceBXMIyQsbBebydPcR/LsKyf7lCQoPG/mLDvD6FfZQC5ILa/LZ5fD11ukm+IQJ8Q2PBvP+N/6qAskJpfvDA7Psy++k+nbqrQyEC6X4AOoo8oIAG/6aDUATAhaYAJr9ff1T7KQBKA/fBP/yGO5j7Xj2UREoFPINHg32DRX/sO4t+UnyNvtnCpn/lA0rA8/+zQQx9wIOuAq7+WP8FPyB/1YCCBMeDpoDbQWe7kTpUfZ5/3MKxwe6CUcAjvRMAkkCWPmcALoCV+kU5AT1Wgc3DtsHoQ8f/g7+PPji+cUSjv3kBmT6YfhzFcEEGAEZCZ8Ptvh05nD31fto+tcT2BbODb4HQ++B+ofuI/vGCpIDxQah7ykE3vulAhgO1PZE+pbyse0E8JQIUhRjIW0Lgvk3/bbf5+a07BMAB/wyCg4Opu0LEJ4Row5zDMb7iO0U5Rr1UwTYE2oOlxi4B7TiiPkiEyoSkQUKAgUEn+z48pP+uvg5FYwJwvUI8JH83w2HAVYV1gd3/lj3geZv8v7stATAD8YEjwvOBw775AZkC9wEJA2M/PH1V/qw/3v5ifsb+/rqcAOG/jX7HAqaCvMNff0L7WDyW/st82cBoAAP/q8CPfobCJABwBCUBb7ukgm1/T8BXBF3CiYQ9waI+wf7tPsuBboBdviI5RDwfRqmDWYHIwGX81v+qeyd74n+df5o/yr3wvsrD/ATRAUq8qvos/aJ/HsE1hT6DAYJygB9/3IIMgL5/2P1mfCc9g//PgjK/fYBbwlYAj0JMQKPAmkJjurZ5d7t1/Q0BicGhQNS+IEI0AnD/hcBJfZIAngIjAfy/ZMIJRHp/m75sPCb/l4GnwPhDkYLqP9nBIcJ/wq8AesDZAWi86n8fvG6BBkEsv50EF/f1u2N9wwCBBuGCCsIpvTE9cn7d/28BfMABv1X8BvtyQtZEKH2nvtw+ekJUAwqBLcDoPBoBgn+t/8qFaL/A/r69FnxvvrIDowSLAfR+A7xowGJAW8HrgpR/+X4f/Ms+pwGJRGsDLb48u1h8k/tff8zFUoXxfgR3ub5cvPsA5wVLA03BYnwCvQW+I4L9xFuEKT4S/Pi8+r6yxDNAgwbfAFsAg0FL+cU9hX5XwWO9DAGdhLaCokAyfe4/+rucPp7/+H4DPIRAVsAkv+HEv4EifzM9n3+RQbSCrkIqgVO9urx5/nR9GMN1hfODJj3GfPl9m32fwk2FlwUGgU98ZbqyOsY/PMQkgI0CY79I/qr/8br7wt7ATYD4Ao/7TfuAQHXFMkOjBJqCvL8//gM+I39kgNB/PT5/gSK9NL9sgnnEU0PjgSL/BroTPTR8o/6lwlDC/IBIwHw+pbduPCJ8+YIdRehAiEDqvnS+tPzmgXECPoEvfzE6A7++QsfFhIMrwz89XXr7+4l7w4UFA64FBf7bPZtAX32PAbm/UoNxwF+91X2APE597cKgRHp/icDfPveBeT98P0ZBDQI+Q6GBg8HivMZD7kJIPexCMsGnwXo/W8EnAfK/lD3CwebBUH+JgWS+lTypfcY9sHq3wcJFBIP9A1l8tHsi+kt7XYJvwQoESEP1elD9VH0Ff/ECCQHaQ/L/Fb08Pyd/mj5tAWN/mn3ZvWOA4H5Ke9aCzT+qxSyA1DvpfUI8vMVPQYY8/UG0wWJ6dPuUPy7DM4OBA0iChv4kBJWCDsQBAXm8u0EM+Q+6+n/WA9FGcwLXgH8A3wBW/IJ+SAG6xLCD+cCUf8e+unzo/lQ/LDuYPe+Bwr/UgIEAl8FghBuAukEIfYX7TH6m/tA/UbsrPBNBtoT+hT/CfYEAASs/LXwieyZARkEgvE/BU0MaxKiDgz/rfgz7Yb9ygauBJ75q/Wu+Lr47PkkAJsPXfu17bP7pQnRDB4K4QBt+Oz8s/lx/Qj4XvqrA0z4IvgBAcwPHQ/oBPYMxwbs99n5f/52ArsFnANKBVYER/oZ+x0EhAGcBJz/Lfa5AJXvNPyrDxgAYwsPA/wEAwOC8kvwdPgw+Bv3LwF88yAPMgTuCMQWqfvLBcv5rhBe+4D26P/y8foHkv1DD14DhPvR/F/2q/jhAnEQbfda9sj2TAuWBrcCfAPy8NYJof3d/IAJXw9uABLgRO99+PYM0RNlBkgLkvU791EN+QRw+5sEogKy8ZvzoPtbENb8t+Ij9HkD6A62CcEPTA9eCM/0YPNUB7wKMARe8RbvGeQ0+IkG+hRiDfz/ugvv7U8EnAI9CVMBH+ZL/fv/Ug5f/5H/FABk/Nz6ovKMAgEV6A0i8RACbQfaBo0A1QOJ/Cj3lwpS91AE/QT8ByX9iPJU+hvviQROBPkDxQILBRUGsAzQE+kIT/yX24vvx/dc+JMEBfh6CIsOLw8HBOT6Twx6/5bnXvIV9bL2zgOzAQ/+t/UQCHYKZvs4BTECVfh/7T7zsQOFEPMLjghXAEP25fsU+F8HLRAuHXMGpO0FBt/17/K8+5v5gfzRBDIPBgt+DIASwxXtA3LpD+nN7nDj8P1yE9oKvQe89O33ggwOF3QLwfpF87z9O/Q850IGdQuyDKQHUvfM+Z0AFQIU/pf1+gGHEiMFLQje/AUD4gS9BUoPcvBaCN4Fm/XZAV777QZd/HoDNQhy8oP+IPv9+gcE9wsxH2oGs/cU79joretj7qEHgv0z/bYCnAE3CHEKbwqDA00HMfea78X5T/hm9Kr4OPm8AToG6/gNAJACC/9+BVQJWftl9KPtve3xBNAI7hO3GBn+pPHA8Fbqiv/cAcwCJhcUETENaABaA+sK7QbbA6H82vQa8Szw0PvoDLYEJgsf9wDq6e5O83kOqgKEA2AHuAS7E5EJQPs8++j3CfhG70X3mglUCa4RMwjvCoAFiv+SAUj6Bfpc/2AMwQglEZfyN/AkBckDDwQV9XEDluzP87QKLQZQApgD2RXs+vDuMAUsC7kADA2S/7btovto/HPz3OI0/7UXIwV5ATkNEP+lBPUTLQEB5sXsw/797GAAPQkPFBMNyv2FALfwtwB8Bv0SkfKl+vAAkfL/CsT8+Bbm83P1TwM+8sQFnQARETz6dwhdA8HdEOh7/GoSdArMAdQDHAaq7o71bfZE9j4DmwGeDWcCvwyfALn4Bv4x9i/ydQDHFov9XAQY/FgEDwJm82ELzPVVB1ATzhGVB+X8kgZZ+uX9Nvwu/yn7ePWT7oPokP1SJ5UiSQjLCw/u5ulI8fP/Dwxs/8X5j/NN88r4FhBiC4cQZAR1+fX87O5JCcEFJw4YEFr+jgryALT5W/vf+Av7NvsuCa0O/QQfB5Lp5vP4/+P9WhWj/78MsBDR9EHtwuHv4tT+2f8l9RH7sP41DVgAkglQAlD7if8J5a3w6gKcD/sIgPuq9MPzVOMT/yUUCgHVEHT/LQVNAmQOGQsQ9ef/L/X4BGYI8hqoDYQDQAH69Iv/7vg9DCP/DgzGB2b0sAPx/joRNwrQACH1gvXJCyr7ke+7+KEBBAhY+AL2rQoqBxAG/wj1BVoCVgtGEIvz9uVA7hP1FgQtBp4EIQkFAaoHfP8e+9wFLwAu+4jqJenH9DAKURxWF5MH4fPe9dD1JedM+moNjgVwEFYGOfkh/R0GVflo4ejvnPQ5DekOEABICiD9LOzf58D7qwe/DcoBIvbG+UX7oQatCgYH1P8VAabuHvYfE5sUnxGDCJ76d+0D/EH5nADrEIQP2AnG9OoDbwLRCbwLc/dO/8Xj8t/AAdsTGxORES8AGOmP+GX+YgssGToERvON8OrsXPwVEFQNwQtaA+LtgO13BEkAIwaAAiD+Tgp48er6Svfs+mUDgwECEqMDfACi6iDuJfhNASoOEgQnBWr4yQfBA4gDBwfUB2IGaOnU+pkCwwQeC7YEvfye+PjwS/o2D9wGtgkEBW4PKQ3W+nH3VOoh8v33F/85ExMIA/7+CYv9oAo+BAz5iALs834AW/v2A/8Ewfxg/Ev9DRFtAQ/23PG6AwMEhAKOFSMGvfTP6fv3nvIu+k8M2QAKCWn8c/ujD34HGhU4EALsB+gw3tLtgQw5EpcTzAfu/Y//gwHb998Cuf/57DrwZO9t/g8MWAdrBWv5MfLk/0371AGNChgKVAXz9FIBZu316yMKahOPHTgTYQoQ9TjzWv9yBA4ZSw7eAXD5jfC3B40LyAVfDIb+TeWk3OL37wehEOISUQFp/4T2rvQU/rkNEwxm8zPlruIU+XIO4xZGFiMO6gQk9zHuWAmMGVL8//jf88jkkfugCyMHxQ9bBEf4Ku2u6aIFhAlmEXYGPPcH64no5vg/91wIpgyQExv8w/nL9i3rlgplAIQfLQ8z/yP/GvBYDlXwVwmsD9Hv7e/34fr92xVAEDYRVRlm+Cfxngbd91oAOgpE8RvqYfrO+PL9OhKdFQ7/yPsSAhL+RPpGAFsgxAV25rDyCfMe7dvxrw8JCG4JIhMbA53+cvULBv753elO918EpgmJBIITB/jQ/PAOIv2s87TtggfgAYoEtgGT/tH6XQGnF3P8DQT5+bIBcvnO9NwK7/tOFxkN3gSQ8mL17QbgBccRvfrb/oX48f4x/AH9dgidB60KGPY2/rD0lfW/ACr/CP6a+/0ACAPgCo/4Futq9l36w/2JFdUNUwYXBOznuvxfB2HtffkEAR/ylAOGAs4Qsxb5BGT+G+te96z3sQdWBWT9TgSx+7gCehLHEbL1TAQF+U/7LffFBNMZdvPCB10CAQXKAO8JowZI5O742gDECSv4de+j77n51/cAC04a4A+eGK7nfucI9YD97wABBdf9JunDC+8DuP+3AcYNpf6I9CAJKAnGG0oCrPV46I/wtA0oD3YP9AIw/GnqW/TABkkM3wXu+S7zlfzLEycWDxjn+uzuBvMP+OMK3gKVAMvzmfdY9vv9AifpEsX4sOsT6rX5JfuBAwgCw/Y484v0Ce0nC24SWPzK/6jrlP0v/acFZwvK6j31N/sQFIQO+xIyEw7v++kd38juSg79MDMm6RLeBH7yEPgc8koEUvM8+V4H/PlZCqcCthKEF4APGAcV5Urhx/Pz7x7pQPwXAkQL8wmtCQoCr/VMDSEAEfPM7gX+GgVU8/QJgwZp/nf6UQMDEXcJyQgU/if9mgoRC3LyHgOjEK0Cw/SF58r/hPSjA/sQmvqNCZcLVAfU60zek/B5+YX65gf3IesW5wFW6ujn0wm/FPkLDA4bE2HzfOfsAVsU+R8JBs303/tA/dv9GgxsDOgFfRZ++a3pZOlm9OAAQ/7/A2nvewvC+B3sqA6hBu/+Zuu5/Fn8m/pfDYMMI/9o+iv3r/Il+EHz7g3282f6bw7A/9IKzvgMApH3TQ0dBvDsXgycCSf8QewJBHMBEf0bA8P+xQUh8egAkwemAmgZYBi7A+Hr2O76BUD8hQKlBkb7zRHHBSztA+bZ9AUJw/05EnsfR/zA8LXr2+/wBqoN4QvzAln+L/CJ+4gD7/tr8gTpagBoCMUeuA7E/4f3eOq7CY4P3RgdAxbqneVd8o8DWRkxIR0SCf6W2BH3Rv4FFi0hvAB5A6ry2O8n/6cN8upD6d/09QfIF+ARFBHl+hgEIudP7JTqNA1hHZTh8vzyAxUheyVMBtzzVevQ9HEDUAcd9dEKagZRBRP88ACQEwcMfQKm4AbYM/C6EBQQuwquA6/6R+o+87b9uf3hBsjm4+vX5SIF8R65D1kYvAZc7DTcn/lEAfYS/ASK/Z8Ca/NqFdgBIAngEVAL/vlE3vjvtfFuCLEj5RlmD7ILqOkE4fLuBwLABgb+3grP9JXybPgO9Nn7PQd8DiMPAw9tEGP8vt2s/eIL/wfOBtH5EPDb8Wf/dgFmElQWNCHZCof3Of9z9w3zN+bP/qX6ZgQqESP2UfYZ7SH6swzjCmsAC/9BAqwBJQub/ZT2eAD7A68Qjwlq/vz7PPESAvkDtQs3CBT5YP1S7gIIVQDE//MPLhHOGJXjFeBQ43LpaQGY+68PLiGpGKL2GOCl5/QPvw+IClYPgvtx+5rqA/0QC4wPBRMUAm71EelL7ZP6Qgv4844DyAmxAWYFuvVGF/oBoPQJ/tPz+O3E4un+gQqdCLwHogrTDLgEUQWXBroLQQvcAIruNeEu8PMCMxdvHIEPgAS/7/D3xO4B92MJ6Q2AE0j12fV38O4XUSbxCwv3CNSW2H7eyhjVGnQJSAE49XT/8PkiDvz81gO98tHt2PFW8Comsx6z+WbwXPyw8pAPZRMwBagR+f9AB0n+MAd9C7sFcBBhA5nzu+/r/igLZvX48KgDGvOO+N0LAQtH/fD8H/dc6rXnbva3EbEDTv8c8iMDyQ/0BQr/geVv/Gj0FPamCcwR8QiI+hwGp/3sAcgDOgf7BicAie3N7UUM7RXXCzTy7+on7kcF9htWDwX9vPy99r/nBe3DAO8UWQ2O6m7WgunnAlYSBBk5Eub8F++46Vn5jBGADTYYMQZo6inuTv+ABvUN8SCOCaj5eQUNDPUMjA0q7e3sQAj7E6YUJffPC//9P+bi89oMESr3Dmnx6OYj7cX+gQ9CCYUFevZl8FDv5vFeEIQZiyF/9PrhauUb78sJmQa3CWH8mP627DH8DwynGnkTieOLARwCFgVz+r77CgJn5Yf3zfdbBqcI2RisE4HuPwLc/gH2le8L8nvmevmmGW3/dgfz9agFo/yU3GMXWBFV/E3pWPZdAXMIzy/YBkYClewg1zP5lwugKW0argYf//Ln3OgzBkgNbAqLEIAHaAY8/LAGZg4k9vj+ofrW7VzpJ+sHBjIC+/gtAEwS6hD7A2rxcNly9TsLqg1TBXoR/wJU35jm5e0oDx4hLjGoF7jpJPr9CwUBG/ijEscbHAY+9/EBdPyJEvwCT95E9fj0cA3/+zcHcBNi9nH+zuzZ7B3mGfjyBZj9RP2X/i8DMvjK+uvwQupq8JIL/guXAKAJDwEeF68XoP1qA6b+WfevA8T7VwGeDdEQ4Ajv5HLwAhJqG/ILIPjg+mT2qfVAAmb6nfHa9h743/rJ+h8J/v3++uoGU+iI6o73Jg3JD7vrYfiPAZ4BnRQIF74NDghwCE72q+Vg/3kNnv6cCIYQ+A3gB9r9fwB29gz7aAHBBkMRNw+uEoP4BfD5A73+UvQ7/1TxP+xaCFYCCROjB4YPiA7y44kDi++p6iP1z/60Gun+RAi6BWTy++bJ3nLmwfPEDiUfDBr/A1IGQ/f8+/8P3wFs/xXsMuTt73gUrhztCLQHufYQ7TLk6Ab1IYERswe6/9flj+ONEDEM4v5y7TLq+vS0AaUYxgBDCIQG8Ph/94ICLgwn/iYPIBJoB9X9HP6n6XTqI/ilCPsg9wtTHgf4D9+C9R/wXRcOE2cD0vqg9VEEhf/l9pL2kAMI/EX5lgQa8OPxJwFC/UMLswY7+fX45vp3/EQLqQnY7NgBfQFe84n+cgVpH04XIwGC+tP3nAj1CI77hPeh9T8EK/Z//6whmg3SCh/s5+cK+eztXBPtApL5zQke9w/xjwB9Fcf6n/AL9fjoG/kyGAoPY/jNC9cFoPqm8RH8Zg0X+ioMhQnd8+L4EwZwAV/4wBfaCYT/fBrsBHT5jfcF9kMDWfp0BTwCe+Q68MUCKwN4EbYckhbFCdXpq+pk6PT7Tx5s9fHzo/529UX93Q3MEGQEwwxzDJn3YuK38mYCUB04GYcBw/Nl0pj0AwemHXwhIfin+TvpWOzy+Cv6MRCGCZLyeO6E8j8Lew8pANvwX+Ti+7D9efObBVYIAg/RFHIChA8G/Qv3cvvo9DkjVBRDEmUBufsdBPDnvPsB9nIJEPlt/O0guw6fD3ID+e/z2wblifpfAyQCLQx9FRMNmvh56pH+bP9I+//kFuoP+CH9iw6lCp4l7RAZ94oBl/cV+mn31/Yp7ZX39BSQA4wGQAo89KDyKfcAEKoaawxmBSgGt/hGA4MECecH7Y/wWvXV7bEQPCWxEBoeJxPOB9oEMAs++eDlzeMH/yUIc/gkBHH+YA5Y/7r7IOxp6PkE1f9WDRz63gC68sT5wgtO5BUBGBLX+bnvW+g+7z8IcQcnByL+5wTuEcQA/gpX/XYCv/7C9IgCKP7qA57+igCf9Dn7kAvLBcoBYPHX+ksHUgdqB0kICAbL/ATwjuw79hn9bRRqCtnx0/aa8E/sUwdnHh4MSwxGApnuvPf6CaIaEgh/9FXyhgJuBoMSGQq6+BALwAWEDzIJvAvg/qDy3f31CvcXv/muBFHnM+dW8Wru/xZdBlMTxfto5/Dx5fbz+HHwlwtB/hD7e/eq9D8T8Q64D1cPaO8M6nP/DAdY/xoP9RPS+Jf8JfnPAIcCnwNrEw0UPRhC6tvYqfEk8zz58/+xCpEKG/Ee+s0AtQfQGQECSgUf87HtmfEs9A0JfAxMFN8AWgGf4yX0tAwgDZ8f9QwUCXXl8wJ8BrT52Aq87hXyD/TQEIcK5wauErTtr+l5AxIBgPep+qv4Jfh99UwXgiQJCFzwPeq04XXigQX+EpcOKQgODEjv9us0+MYATR2ZDKwLxfC587AIn/uOBtMBGf+q6hTuuwY9IYApgg5oC4/4E/LK9pH3zvyY+OEJlg3KCDACa/oY/l7zmOxM8kMAXwp6/GngtuIK+vYJ5xF0CBP7yfgSBrj4o/qNBqDypf1MBC77tgdEHNccjCBWDEjuAwSjCFcJmv5I7KT0BAP0BMzsZgSpEFEIVRW782Tt1f66+YzuAeoq+5wFoP+z9+ULzgnz+1v6cvIk9cUCIAYF7bcLWhfrDDf7+N/LBPwA9gssDQ4DeBPJCQj/FO+KBwMPVwZkBKPtN+u2BAUNxwlJDWH8ufSq89T0ufigAS4LTRE1+iPl7/Rf733/chCEAZ/9igGqAKb8ffqDD84FHv1cEy72M/WS9m/8kxD+G/QhKAKu8tPrDPMe9C8NSx0fEOYJyQH06S/ZPAUmBDkOMhUwFNUOnOse9kXRv9ln/TAGqxlyCEn7pe3d+2cY3AeGA5cGweUj0yfYOvgSCDkPMBvaBbYDwgBE8b7xFQYKBHL3rvkiBb3+6u6DC30IjgbjEMsRYAm4+NgC0vwJAUsECxU1FK8D1/vA3ynwpQIlFEf7SP7lFor6Mgf15c38dRK4BEUQNu5H/9Hz0/72/M75ViF9/hPvmfW586LxhBDyEyoBu/DxAKYMEvOGCHP2Awko+uzxyQz0+a4BLOwh9dwNEiC+BN3/IQNX9SX63+TCAUIQQBVaATT9c/R859b3V/BXAOT85AqDCgYGNwXaDLQQ0AOYBXnvX/Dx55jzrQIwDmcXHBZdFvoTqwZq4IH76wGp/S393/W2AocAFAp9AAH0W/Ea+qL2pvYS/aINdgeb97QGge9u9IwJQxcdC9/1hfRD6H3zGwSBEaoL8Q3FFlMG5+1/82gF6fDY9I8Wch+nEun/yOb51FfpOf3H/2QQYQcb/6X3lPysDhUQRCe0FCr0V9AS4fYEEvP//BIFhhUO/xIF2BDM9C8QtR8YBK7scPpP9L34B/02AlcIpwbvHZYK4/bI7kMDMvmR+DcSYfN3/X4Cswd99Nns+Qcz9K37U/+HECoLQ+0n/jX0PvJE/RT1bvGU8PT2AQtNGdUUjw67Aq32U+7r/HIG7/aH/mQIywEBAEAUqxY3Cw/659/J6D/5dxHhH3MdUhDv+l7uA+tp/JP55PrlBY/+PwUZFjUF/gQKFt77RPev4XHq5Q6V++L1XvJ2CIwQXv9l9F33fw0uBM8MxwRG8nf4U/Yl8ivic/hVIqUXmw8xGQQLIASr8BnvYfvyB38I6uRF9hn6jwc0CpQHliQ+CFkFz+pa34zvqAIiIg4HePxi9jvm2eAS/CkbxyB5F2f/lfZE+C4BzAcwA+zw4/A2+G8KPx7vHaYJpffJ+4Tyb/eg/MAKp/4S+G39ePKNCdUWthTk9Dfyr+Vb82L+1OSbBJz3+vvA873q3ffuCE4TFejF8jD9vv5JAU7+IfbK+7wDfef89xQPdx8lIIgOl/Sk9B0GyPOTBq8QxQjoBKH2Pfk8EMgraxjcDloFQPQf+aHtz/Z0+QQEIv+n/roKEwCaHZn4+uKi9AH6qgto8KXrm/EACYT7iOyVCMIEwQKm+QMCNwTWDAgXNfnV/AsJV/zeAPn+aQKHA27zGgFPEAUPMQUXAbnuZP4KDQ32kfmw/CcC0enL6UfimvfWHpEP+BtlBO39kfDW6srllOquGkcLxg0pESUZmAds/wYPl/BT76Lq4/N48AMIpix7Cd4IbRamCfP54u/k7SPsYvSLBdsH+fx9Dqz50dhlAIYPMxFhD54EFwV87eflMuUp8YH4ZvuVBYb+vxDNDu4L4CYJHVEEuPVr5rPnzvCk9zQUpSDtDYsGS/4GBMMV7BMJ/DDfKOol89j8Gw/6DcYLRQBe8Pbha/cHDOUPe/YU5K325uZNCVgWVQXrEfgISQ0w79juGvub6aoHVxAMDxcYUQ/w7HrOEfAAC6QX/BrDHncKntL34fvtVPmAFv4hYhA69mAFHusj7G0S9AlDAqQFl/iJ8jjtrQWfIvL9zvmfAIAAjO9L8YMGff8qGdEGvPf29n/4i/y57VIAc/11/wESUf/i/+YH4f5ZFBPyBegI/rv55wahBEYZBft99D75Zvl1AtvqQgryA+v8hAbkDDv3ZvX7G8MMPAQ+92Tzd+xC+b8HnQdRCv0CBP6O3l3yOheHFHj+zApnF777pAWVEJTrOtya/RDlovHLF1wXiRlW/6cVk/034Bv5hPoWBcsBkRcKB+zfMPRF/zn6avtzDZ74F/+MD3L5vhZPD0sXwQ+u4KTqEN7M7nIOqiavKHMAVfS85SvhhvoeCLEG/wgfAHv6yfWm+koQ5RIV/fHljvKU6yoH5yw8Bx8G7QM68Qf1GfkfCJMJH/xY8Ub+RBFaFskPn++44c3vpPkFBCEXLA1V6d7tI/ZU97QH3g9M/CPiSvmsDGwJIhSvCv755f3v/Gf3V/cMDRoMhPVm/7UNZiIl8ErrAQ+Z+xQkMRBPAcEHG/1Q3XvNDQDo52AHnBAXFHUVG+pUDUrus/ddCCb7Ivnc9gATIQqkFSANl/oK6F7xu/8A+MIR4BRPDpL+KApaAlr8sQTk9hcC+/Fu7kTyeAoGErH/Ywcg8NHvDt4h5GUcYx7uIAMG8d044ATucgQUA6cNBARL8O4GIwNtD6ARfgVfBvjgse75Et0O1BL+CUEGw/Tz780Gdvoc/On5U/1T8470aQ9h/pcDo/1y/b/3F/0bEbb7Y/uQ87b4LvjE+XQJRRAFAv75MRjlDqcUXxEZ9+TnteyYCvMFZginCQIBxPoU/TQNGwZyBxEF4OsK5U3m/QtpHbkIhw7kBygHvvFz9uP55++f/kLnx/1tB5sLdQQn6dsVgh1EBC3tzd2n7fLr6vC4/l37AhmdFsX9qvk9AkQeqAQU7yHge/rKF0wQURku8aQGBhkj/2kDJwDqELX8n+Mq9lQOTxAF/nP7HvzpAQkBF/1w/W308v2b+374f/8KAo3+bulh/tsJ1QKDDFv/uPmWBAUIJPEp6+YGLAqb/FQNChx5D8r2AvF/DpgA0f2OCpbnivVFD5sVowkT+f4TMP/Z5mPuNwGOCd/5+Phc3Ibo2/SQ/M8GxQSoH7f9de/B9Bb4Z/mK+on01t6VCggZkRczGX0Hlvpe7Zbk8/caFekV2Q2w9FPw+/hxDpUEvP8tBPbsu/mJBRAQHP5D/sf6ePer/vD30QVLCJccbhGoCVYNiwtDBPD6OvYU8zkG+P45/bX3gBfEHrMEJvso6yz9qwiMBWTyc/zs/Kz2QObh6vADQPsqDCsCoBSEC0gJaQ9L7JsAwf2++5/6oP/E9tbnzgUWCoIKewnhAR38GN186lcEfekf9JQA0P6I/aQFdws9ALwVuQdD8VfkE/SKEGQD7RCTDSnyJO6u+nYQNCbjKCsPzPLV8vv3zvepEN8WcvFc5tT7vPcW/SgPFQ0HCIYEtgLg/qX0au508P/+4BSdELj4ht0Y6KD50w9YN9IaR/VM4Fzd5O+Y/I8YCB7d91neP+/CEQ8qRhrIBx/sNuKc9qf5hApuG6AXOfWj6+byZwIZDAsCGBR59cnlS/vhGAAuyxMRDKPdCs8m7y/ou/2wCFgNMxTmDIsKHw68EjAI0w888Vbe3/5v9QntG+0l+xoPqRIOEBv2YO8v9FcI+iNPBgf+nPyw4zLTa9gBCFgK1xAF/tXlN/ZB+PYZnRnXGZD9S+qp6G3wxhnGA9oNyhCiCN/zGvneAnbyOh7ZFYkICwGYFWgh7gmc8s3nNQ5P+s32YPn/ACkJm+aV4Rnlev2hAEn/lAkqCY8KHvPR42fvyf22/cr0lQU9/pfvrAgi9nT1wg3rF1sTb/tUDp8TmBbED/T2dwaCBtD77e2+7NMIvAysD6D6vOI18lD1TBfcI3URyw5R9hLirOEq/TkHFgP37v7a/e6B6moLCyj1AocKTAOY8sINKhMeEiIBFesz9mwNIBUIEZb8zuKa8Mv6Lv7C/3QZaChE/Mb8sP3s/asNIwCW/LH2LAWzB1TiaNQl7kMMcAc7CEEMcP8C8434mAXn/50WgxG09ofqkuniApn4uA/MGpT5e/TJ9nn9IQE2E2YVfQsW/RkAcADl6xgLVBwWCi/1LeuB+L75jfUL9GbycQOOCrwJyQg2BaoQE/wl9yQBy/EC8ID/UAC77Jb+hgFDBc8L6+z19noHUQbeA68K4xd0CAgH+wgR+8T2WfFF9TzqnPjGBEP59hc8Go8KxvR8A5UBJOmPDYACAQmPAKX1xw7o8QH+FPuG4h372vxgDEccWAtxCgf8nwEL+7r06f7g6gHzH+D48VQFwxAkHMP1zw9z+uPzP+8j2uQJcgTeE04QnO9z/TkOVQyP7Rb0i/8m8VUPQQjR77EOlQ7GFXAMSQ8nGQX2beyB13vuF/L4AQweKQC6EysN4hj0D7r04Pq06Lr2yOTL7IMR7hCQHF0M0e/r9sUDQwRaEqsYowc9B7MG2f6b+tzy8hKFCtPt8QSR9Bny3/0E+BAClAjf+PL/nAE+8ggMZ/fpB1oc4/gl7JHX8OMf7dUPtCZiI0UX2+t/8kfvSAmOD273svzj2Yv4ZhlMIAYpJfdR46zZue+5Cg39iw1FAhX1au+u+IEQDwGuBaABDPO35lrmYwN3/DYVfi06AW7xTeE+3lv9OA53C43ynADaAOL1JwPXFNYkFQgoBqf5CPND9q/rQv+W80UOexlsBugG0gnCHiIWpxw0ArXoOAYYBnbxk9x572v+4gi5Fm71xQBuCzT3ivf/47wFqBjc+BH2/+du9EsFZwPa5SreNwXqCy0aeRYKERcFqfET4y7QbQCLF1AY3CA6DNj/YPdW8RH43va48Qf5j/a0DMYNQRw1H1bzY/g841Xrn/cLA1kX5AnyDAH5mA3H/YLv9P6P43L7lwqpHu8glQ2LDTTp9vNy//r2Mg5E9or76Pz6+fwijRKLCF37HvyI9s/xmBHhAxINKP8s7rr0Vf70EBMD4geVB+wAvvfM62748/8i+8YCPvpV8Cfzufa/Eur/H/07+6HgBfp69LoJXxvx9pf81PV95BL2Wwk6DKII2Qq//wMJZg6YCfwLO/hKAJjn5OPi/vMOYDFIFDwTxQSD7Xn7xPKTATXxevk7Ag7+aBT8+uT8dvGl5GT0d+roDckLBAsmD1rylQch97QJMADu9g4b2Oep6+7jG+zDCtQRxSvfE9gk+BLIDXIIouGM+1/nRPLU8d309xmaD/Mm/Ad58av2w9dw6rPnSveNEr39IAlk+tL59Qy++kb9muZg87T4AuUE+nXyAhYqGRYFGQza+5ELXwbECwEUYANKAmb/Mfvy7xH0Y/8M/DgLoxvxB90JFgdj+IEKTg7LEJ794PaMBsvlceKR/T8Wchst+g73BvOO/3IKXfmeB7ED+gIp3ongLg1R97YREP0o8IQMlvjaD/P+yf22Bszv7gKr64j/WBGwBBwZlAlnFMMC3QG3+FvrTxOI+tkAh+5w9Ecbxw1AC6j5nfzI5dP2+QoG9E0CHgfl/prtggDQDX/6p/Va9f/vRAdYFBsHrwiT9rX6/ffd9fwB2vQVCCIcsQ/jDoEM7gAKAYjlfe/+DQMFhAnD+FLzugDiARwEjgZkERz/6+0n85vxRxBpDYvz9fWz6IL24/xMAOn69vqQCuzsZvjiAwEFdfpD7UMTxxNHHWQPyOxM8W3r5f22+2T7XAWnCV8a8wnCElAEFwAuDD7w/gGu6B7sBgeX7IMLqQuKAGUMmwY6CiXsgODt8l77G/Js8iMg7hNUDZYAM9hv+8YHChV8+gDt1Qqz6xUDjRolIFgi4wBp5fHswAbSB9wUkQxLBOkFXvftBNYEzQCOBkj0sP38BY71a/Uv53PvoP+aDcEjxg67/hICHgQc+9HwAe8h56Txjvs9+N/3/QZlE8H7kgQyFQIQWw8R6MrlOAPqDj4Mx/bk9L/1w/I6+swGQgQxGWEcdgfvBIL+Vhw8EsYGEwow5ibea9xQ600GDCJUJu8JQQNoAsL8U/ZR9Znuq9dj3JftrgxcGjr5lAek+IbksQnn8HDf4fSn/FgCE/aH+2ce2h4PBTDvOPmWCUASxByOB4oQVgWN91D/6Pp9D5AERQ6kCmj00/ldCkwiDP827H/yse2p+Orux+d69VbzIvzeAxcIHiIACqH2CPIP2EHzdRlmFrz8hf6LAYYAUB2aC20JrAep8mQGY+7PA1sToAGU/mbr/gNI+S8XBQfm3vcHGQJoGscLqQNkBPHev9FhzaH5ABM5JZQV3evx8x78zv05DmoN4wpKCtnscvyXAF4EHQYu8Cr6suex/KMQfw78DIr5TAzoAIf5KgYW+dgBLf7x/C0OiQ8K/Y/WCOC/6H8B+A4N8asNjP2HD+UeFgR9ESz12e9Z7LzwW/6UDIIT0ACB/w7ydgRFD14CvhfaEuz24faP7qQBjAoIFKsqjPnUBvL1G9/W/VfnBQJsAuHwXAIuAQoLzh7LC2L6BQqV96PXx+t/EgARSA6eBjUHAvMF3G30kwQ5GL0KNwdJCiQHHxewB5D+n+1X4pfo3ObICosYofjc+2v5Of5ID8UWCQ5c74fjusw37dAVWyj8Mhj2BOj696vwMvow/KIEUgUd+MD1r/FWKNolE/Ne/lvp7QIrBT3zevNS7NwSfA41DwMI2PgXA3T1TPkrA9AH/COIDqXqk++SBokYmvbLCjgCq/MdBcz2fxBECSIaWPL+y7jvdOs1D2ULxvGD+mbn6/iqBKH8oBT37PLoVezK+NkdW/cvC/DuSu/6/BnxhRmwCAIgZwzrCO8adQC7GZkDDuN+5fH90RQO/s8RPRlkALAK0e1b+xsEpP9xCvj07QuiA/IEbASu9/TqB95P88L8IBEtB9sNDAUG9v4Eifwe+wgB8AT78jf17fSdDEgfXglo/n3cW9mr7eL7jA6+HdUfKRlKDAkAXAUK/Jvl4uSl+8EKGSFhGHz/HAt/9Njrn/nDAMsMevM76qn+zxvACo3y/vqn4PzzVfAM7+z8RQLDGsDvCQsqD2T1svsp4jrwwPcGDnUU2A+PDPAErwJZ/vwKPBPxB27ov/AD5iroQArLCxgLnwQ6+7T5Ow4vC9bzfOY9B0cHme4D/7vpZ/ZbA10E/wAN9KUO+wYT/7IR8xJCFSYSsvxz4XHn6ByvEXD5LAfkARkKcQE5CEL8MQXBJFMCqwL2BCYNPxOo7XftXeve58L89v3f92gFiQgr9vMKIgsY7ffvWPGt+1H26AhCGNv7SwQZ8pXcGu0r9qcBGAeFF7kgRQ2EDtUJ6PTH71H/9hE+A8v17QG6FU0Rvg4BCYD5+vqV+ov5l+t0BrcOkwu8FgkJzAhr6jLxSu0b5j4Bsf2qCVD5o+0m/MoBIwf4BdkAdfZB8hv6JPdr76/4zwEdAz/8wPuhA2MGqP0a/bH4zAchFUwGrhBJ+oUCDg219Vf/9w+yGTwGNwrP9z/4fBUcAe/8Ivmo73fqoNQQ6QsbqBWYGF//T+qR7DPh1QJ59qD68vrP9ooDuAPvJP0UDhh6DLTg3umB9T3+nBJwILsaLQudBFL+Su48BMEJ2v389Wv3tQe39UkJCQ3l/Bz6gObk9Sf6Lv+aBXLzefji/DQGbAzPAvL9tOUd7mH7uvaSBksVchgr/g76DwMQHl0eC+4H6svebeOT9aT0Lw47JQQe5Q1w/NPy1AAC9g7snP0h9C7yjfot8w8LPQ0gBRoRXfWg9Rb6XPGhBR0FBAgjCg769v9X+X3y9wU5C8IIAADDBdQA5vnFAJf8GgW+Al0LAve9/+0wQxpyC2bzY+KZ/TgAwP8OBX8DxARk+CPwsgoUHFke2Qqu32DmFf8lCzUSA/vk+dbvMNuS7koJuBm/FbkGuO3nATsQugRH/0HkyPIh5YTm7gna/YoF2g9AAfIBGw7lBcr3Heun9iv30/qiBlb7jAegAocQuBFzCKMTVPai5wL2VgR3CAUdPhZ3/JP8t/roBjYOgQiO/P7yGufO9vMRDAd3BXQBbPTy9RL8FBESIIQTRQPq8PzjDekKA34HcvIZ+Gb3/vg8BhgVQh2nDjX/ReSu3dPz7PhqAOgIN/o/+RoAP/rh9J74S/1A/tgLhQ44DSL3beC08McAnxhoGpz3TvnHBvrtHAK5FFsRdAnw6eQCAP1195AMEwzc/k3vLwyp/u4IHA3X750DqA5EDpTqGehw/K76mwC/BT4R9QteE3sIE+B47VoTZRjABKnvJvff+S4B1QsB/dcKawS77aDo6fGgA84FlAlf90fzO/Rh7zEGDAtECTEABehm5ofu2gPHFkoSIwK98qv9RP5XEg0lPBYQCf36//eL6OYIXBRv+bEBr/wSAVADiwTxChkIQAePBfPn/e7f89r0YRl2+3QBZ/qp7h/1iulmEHcI7QGLAKcA+gquBUEAqvLX96QCFBWQCLD9pRiOEEb8yBVdA7fpp/PD5Sv3+Pq0CbERefxUCQYIr/3AA+n96ddV0NXnlvyw/kAKgRsrBbgB1gOj96/wm/47BxL4rvm9AAMQjh1kDoD/FPWQ+GcHxP5eECghowf17vfwowEcAikNYhE7/SjxCeR36igSAxm/DGb/1fq6/yLvMgQ2CIf7EwEU+HT3bfSOAoYOLgD4+3v+hPnM/UYEZA0aDQcX0g5y6tfu+uwK+yYFaQH2/BH3TRK1Ef38sQMiFQj/KPja7C3llQKcBQkG9e3n864Hlvmk/X8LdQ4lApn6eABu9YLy1Q2mApH5VAWCDBH3ofU+DHv1bAVKAwn9KRQBBKYKuhipBPb5ROFW5HsCVfYp+5vsNf8/A6ft1hAjHT0bbQHF9ZjlCvhgC5YHEAhQ8OUABvLQ9X4HjxAdGwoSe/5d8A0GVv9uDLUGW+5V6DDz2go6Bn0BAwSDAvrz5wlGAAMBpwYB7Fv1NedYAgoTVQ0gFeEH/gV4+8r9KviY9xcDP+7p+sgH1/QdBFwIsxKyHLkQIgZt4TrZfvWp/iH2oBJiIJAEieoo4jD0nfV9EckK2vD3CAgBfwsbB90EWRz1+Bnxcd543zoKdf/LAQPwCgRlG/QOtSWTESAJTABI9IDocNfO+A76e/HxDU4KLAFSE8QMLPyV9xkFSv+x7Fzwi/ysEeEMXf/89rAMIwiF6AHu7Pk6EtcOZw3uENoDa/UH/nYVvBHEGv4TbfmI7/PraOf6/gIF7fZpAqoCtwEC/5sNzwj59ygAohEDB93j6+xO3TraOf4OFvQMav4s+VHddPsVEQEY3x37CzgIWe6d8H8BqANe+TT4//DQ2Jb9uiICHaoWHxHu+szuzvV3/LsGXg/IBxD2Mv+sAzgAxfl18JH29veWAS8PiAxEBNEN9f2+8TgFXv1i9isALgWg9aX4rwcj/9zsEvFyAhX+jgqaCvsACwUQDLIOLP8g+E36hvjS+ML/R/xDC1cGzAGQ/U3jvAu8/9nttwkcDwMqtw/O+kP+RuFo62gBNwJFAID/nAknDSUHQQVHEfwLRvWa6u/aku0OAMoD6BrcIEEPqfOz7gL1pP/18uDoRfw09DoKOA0Z+2QLzPQq/TYGIPlVBeUG0RIz8QvpKgr2Bbv7A++19932FAuAIWsYgg/DCfbw3NBn6KT3eAkvBXv9LAWo6YAAURcRGdoLU+7O57XsRAWFEy8JTQzN++/nIPj2BAwi1h4WEk4Heu7q9v4EixaVD/gJyfLG5Kb1rQInGtAeBg2c7QXw1ep38i0QbRhNB1bnz/GI+YsAygdJDxv7/+TO8sDwDvOaCkEYsgIdDOcIHgAx8hjm/v1V6DT91hCoDj8UEPq77PbvtfooBDYUYQlNArEHf/459wYFmRGj/4HwTeQe9Oj8pQV+DtUDGQT49Ab+KANXA/UQ/wmn+RHnBPE3/d35s/v6/dT5s/7IFMgTdgnjDJcALO3N7l4F6RV8DfQD/fsD8FX8V/7f9T0OshMrCPQHxgbJCYb+5ue+3/DnXfpQDD4NYQFt+yj7EPg+Ar4K3gcS/77laOum+zT8awP5AlMKUAcf9p8CNg2vFkIfMv/lBI8A0+Bt9sXuOvdRHiUf7hRpBBP9rvle7iT65glX/8v7QAWlClMD5wMPAYDwiO4z6X33RREhHUcQPPhF/c3tdeeaAKMBEwaoAZb06ANECEAALg75Dy0GM/1d4pT1lQZxBOINgPyKDoIDzwAcDNX4IBAKATT52Pav748Dx/eb+1D84vRd+1/4qw47Can2/ROGBQgFuP2c31/sQfFSDCP4KPm1FJv9Gwt1CS0NMBL27ir3rgsT8oPvvPXb/vsMWQ0OHEUPZg6hBYHnzeHR4R3ySPoO/uQSGhlpF4wWuQbqBA7tw+yQ8HXHoespEqYX0w9K93IGPgqFBVUHr/Nc9sf90PkEBMYHUx2cCw3l8OTx5nEFZB3eElECbQDR/Nf6dPi28mIJ7BcFBefypfxHFBYbPwNN7knfOOin8X/zq/nz+OISIAzmDwAJi/7j/dHngv3Z9WL/ZQwcB4b9V/OwAjYHjxHhBiMQewmtCzcTOfib81z1rBS7B0T5+wB2+1UM+QQVBCoFhfv/AFrlM9acApQPDAt592jwOwZdA/QNHfM74lnvTOsF9/X+zA9LE4EJlQaWBGwNTQjL8CjqPPWjCxEn8CDXCboADuwf5kT62QjFFuEM1gw+Bt7x3vlB+fYHmwMU9TTwKe9VCb0P+gwl9knpBvz/8vPtEggZCe8BJPqU5DwBvh15H+cDfNe+3BjuW/Jl+TsaUykGELr+Ifiq+hAFEAI29l79CwlaBg790/sP/CsEchUmCUL5KQYp+tjw8f2B+K0bDxp7+KH/q/s5BSD6SfXeAA0A7gsJAH/rgfOt8Rz2KQgQ/FIVNxQH+SgCwAL0BP76Zfyl8mHtk/JQBVcTvQcDDZAK2gXK610CHBFSANMH3fOdA/MG6P5+AeUGkw+i6wjimf1o/KYCVQDM+g0IhPB8AJj+uf74F536bPkY99v8/f+WC24TiAAs+y3zPe7y5n4CMA5pEK0XOhKoEuEMSQeR8sDlcebo7KXs7fPa9+QNSB3TFwUWXf3GAvfiZtp+5Ffj5gpq/oIH+h2DFvgVTQOw7Jz0cPwfBcT6F+57AYnudfZhCSMYIyjWJZshkP7j+1P8t/B369ztWP7f/fkDVAnNBv4O4AML6aXutgE3Bzv7DQE5A0r3Gv/JCFoFAeAV2KrewOusCKsKKBdvELsCIwNG/VYKXAue+3n9nO0L8w8H/P3lCK8IOgh5FZ8LevwHB0YawR2kEOgDCf6O7c70ZPXO934VIxyAAZ7lx/hXDYMHDPz0433kcvi389oDhwouBooL8O6j/gD6x+9GC9ns1+ck8qgCVyFmDHcG/Poj+LkRAP0pB/EQqQVEC5P/qgBTAcoByPZN8iD4nf2xC/wH6AJC+Ar5Jf94ASv/MPcm/RoDU/7M7pDyZv/FBPkJWfFc70cJC/48Cq8IdgrzGoj+Avxa7En2dwqzBfYNBgGb94P4kf0SAnoMOvxd+t7wcPMCDiAADCMzHswBMfx+6wH0dfRD7ojmMOQ88yQHxAZHGscfnxG2/UXqXPH18AADCgBj/5T/GwKUDDv7wwAVBcf/CwGRChYIAw5tCTQDCgZw69b1Rvwp79kCFhNVEZAHK/XKApoB6fVo/Bv17/+C9qwFKwf8BGUWQf8u/2P8Pf5g/3YMMBIQC5YD8uey7o36+vxA+hz/o/Y1/TEIqPtkCf4OjA/s9sfaFu0cCtQDkwGL94rorf+m/QIMOQbM84gIRQLo+fT7/gHdDkMTuwVFBY0Gnfm06ZrmSfm2ESYosAsJ/S39+fAHDRgVNBdCEGEDn/6S6iPt2P4aFFIE3vXw+zXqJ++wAdgHC/4XCocUgAIrAxz4gurk5uDo4vjX+uEIXQ5N8x0GqQYSBCQUyPMuAgv51fPJEUoAJgeHC+QDQP+W/I8AjgQN9c31Q/60Ao8dZ/7a7S7sX+9G/8f3Hwbe/OL6Hv9LAP4EWP8JBxX7seQQ6zD3S/2kCvkE5Ab/BpkIHAuZCC0brwMP9I/7yez387ILWxE/I18fFfim/cb4EfZx+or1ghqJDxTxE/jU+eQEGv1D8OHyqPdECYX8IP32Fd8D8e0p8gj6uvcCBi8TlgQaAb4I+AUU+kvqHPsRDqELJhgeDMUJogTv8Mz9lv7j+ZTz6PQTAl0HFP3vDjMepO8V6a/3yQC4Ch/1fuyI9eL7uvlX9wv8gxRxDfvxkv7b/4UHiAL17xrvTvJGEegL4gA3CfoEOAMoAbYQqfnt9s39yOvRBYYSeRtnEssJ/Pgj2u7kWv4mFVL+7fUE76bwtwbW+9USJRPVC9/1k9FX8aH+/woGG/0DVwlFAhrvjAYoEEIfyRqN//EBcvM49CwC3Q5LBrH5+BHbB/4Hiwkr/E8Kxfrs6mfznvwqCr4NUv1p/ZMAN/Sn/7j/sf5QAG4E9QZT7Aj9IwGE80D5A+1Z+gHy8e2hB/X/YA54Fm78XACv+zfyG+3Q5S0ESwNS/AkGG/+lACb2r/75AmIRtxRV9iwFJwIzDroKWu7z/Wr1vwfiBbX39grSBiYGqPJM89MFyA5zD//3mvcUCcAPtQUR+Dvns+ag/ngIVP41BfQIq/Db83b6vAqlKGshJgG17y7uhv1NEMj7Agtx9yfejfsY6BUOPSevFEgM0PbYBVz0+O2m/izjSuRS/HEDzBVGGJUMVQe59wbvvel39JMBYwaXBsX/sQq1EhcYFQUU8az6le0t9FwLtw9hFOsOywlB94PntP6SBBD1CAdhBXQBLxu0BTz7IPjj6xfyNOskBoIT+Qp5D2EB1fCc8fL5a/Q0BJ0MjvTr9mAHuAyvEo8OJ/kE3uvfkwADBugTlhyL/WDtUOUb6E3sXQSYHD4M+QQd94j2Pfra8hYDePe67Jj/Gf9S9Db96wAQDc0Q5AMmFUMAKAIf/OLcIvZj9owKJwlBCQkQZ/kbC6sABgdfDQQFnwSE81EBrAUI9wsAeQnoDYQN9Pc7+ngBVgoxAPTw7hNiE14KVPw38ML5Nv6EChv2PvgUEHMLQftR60n7zxEBH1AUJfW1+sf4be0J6uzsygz3Ez4IZQLiBFX3pP8z/p7lHxCcCeb3n/qn6VP0EPwbBf4F0gNvArIMfQ4a+m/4LAlJ+kjmgu6J8aoB1gjOE7gD6vg/BjT3EPrq+QoOjRUMBAD1XOiG7tT4swD+9w0DhADp7jnqlf7HFvASKgvE7XTyzwcSBSQCBQtkCVDpK/FG9qD8jx21EccOwQFC944VrAGi+FMAZP6pCjUF2hXXGugCFv1r+z3sffe4At30vv8XCsoR8BBZGwQjwwYx50HguvK16nsAgBUV9M/s7/WC7cb98jIbNXcKTfCE7t/lJeJS/FoBFP919e3u0Orl/IUpphxS/83l7efX+IABbhrXEDoOIA0r87DY7e2dD4j9mf/FAhgLThF+CrICmPhq/RzrQuox724J4CbeGUARbvfM70Pvb+qE6wPicfWo+rj+JRwnEigZnCFPEg7//dmf7wHq3+nRAL/xTQ6ODkYQE/8P8ZwOlwaoA2UNFhOE9Kv2EPqU424AwQ6ABxYCzgeABQ4C/QaIEkMCzN2U7VTth/oeGDgSYwSC9zUQ8w/j9kH8bPZI8FP7hgVMC5EUdwsv6azUqef/CnMSFh83IqIQUgsQ+X371/nb7n3ke9O86gIBzB+FNaokDQwV6fTtqwJ181T3hfpM8/8AqvgtDd8WrftR9jrb3uNe92kLKB1RAbX4Tu5T9LT7vvt0CPwJghPx/lz2XQA0BoMO6vq/+t3+oQTBDg8OoRRKCvv7T/rY+4v4OQ2KFbgI7AIi6Bzsmu9c64MB0gxIDGwMWf5N7aEApAeyEr4JQ+zI7azpoQVyEh4C5P1VAnAAAvGF74bt3v7P/z782wjTC08hIRFv8pr5fvOB7xb+IPkb85kFwBc+DWYD0QtJBvYAVv+dCPwTbgMi+9H2DPNmBJT+Ev9VERn7rPFvA7ICbv6YB8cHPwNrBLb7O/Fp53b0jvap/xMgOxtFEaz4H/WH+MXqnwp5Di78/vwV9t/w9/UUDKgQYP7oB30TKAnE+XfpEfAq7H/uePsu8Xn7DANbD8sKqPqjDoICSvfaA9/38fj4BLL4CwPBFHAP0A1B/2v5LPhX8o38PgirCR4U5BvQEnUP9fKW8Pz5eeY/8CfzngMICPv1pBH6Etr7Tv0jARsGJf0w7Grref/lA0b58vtB/ysGNe666WoATASNFcUVWwu4//n1VfbGCOcLavzu+Mf3bQjsBIkDywTbAhH3/e2Y/msF5gcr/7gLDfT4+ToWwAb3B0bcCdmI4oXnrwxMCkYNwxkQBRL6sAgT/r//jvTd8JD5lvnPEXMQtA5JDJkH8viF8ff76fb2AZAHmAV0DiMS/A7NBOP0YvXW+0MCUQFp/773/+HX4uDzrBETGzwTTgDM/Y36z/HMEGcFWQNv9A3Y6PSAAaoUNx+SFsQRM/dr+usCafgHA4r0Ffs2AAX/bRhMF8EXjP5N67js0Pih+cb4PgKL+6cA0PeEBx0E5wTz+iLiyvnc+w8KEwQGBpn/Ze9NEUYSGAc+AOnm0PDlA1P/TyClFK0Dxfz73X78KAwIFNsOhwEq+Xrgc+8JBgYPjRXNEH3+juRa35Hxl+2u89UUPhtD/mT/5Apr91T0QvGVAWIFVBPFFJHzifzS+fIT8Aee5dj3F/xRGqgWZxGVLHETPP0e5NLibfuM9igInPnVAUkUsPz7BpT/p/4Z89HtMAH5+Rj+xREfDxgBL/qf7c7udOXL+Dr+wvs7DpIOsB1a/eD2Xfn895X+w/Mp+Vjy6PtW68T/HxO3CCILNfoVAFP89wUVAxQFKgRQ9YT+HfGh+jsDFQAsDNMCb/tZCHb3DfrZA8T8qgwF9FX1ffn08NAGsQvWD3/9NO5z4nLmEgAOCM8Rjx1gFCP/TP4y9jADXwz5AZYRYQS/+ioBPALJGNQaFgjBAB/xb/SE9Jb1thTwG70miQiM8EYGXv+6Cln+NPqL89vZ/fQw9tcElBgaA18MOf1O8hP6KOMa+UgBVvKi9Y31q/nj8SwDFA2iDMEB2uDT34H4UxT3EC4ONwue+HX31gLdAvj7dPvS+jQPshVcCrsCGvY29en7+vodDyAWHP8yBhH0lvUr/7kDUBb855jnify1BV0S1gEABA3/8/ZU7nDuXPyuChEUNQOK/CkA4vtuCcr7bvD6B03/NQaWDiQGHv+U9/vuiOZMAVUJhRcpETcArwmE/jYNngah/V79c+1t6zbxMAn8IOsWxQIpAhP2JAnCAjb40PtM39TzP+RH+08S7QhnJ6b4VO5X66HvLA3m+Lv9VvBy89oDOQD1/tn79xAtDfwCsQoWFTkaQQEc89D0mPMJ8iYDdQns7wwFpw3TDusoSBFcBQjz6u5cClTs4fKcA7zlQ/R7+JwFZheQCBIS0fBd748I4gTGATb4HRfI8bbvShOt/KMRrgHZ93DyXfZpDTX+8gqCDWwGQPRt8wkC4PKg/DUGuARR9DP8sAlO7kvw1foP/e7umfIP/uD32xeKFfYLrQ3lA977Oeo39Tb9fQCgApoQIAg88mH68vh/B30QaxMHCf8PUAsh+akJZANfCj/yyubL6H70bBahD8gQIO/tBs8Oru1mBZLzzQKkDZX70fbq85D4Keso4qTmmQmTFbz+Df+Z/xD7e/eT+j0JkQxm9/jtCAJzBOsIEQFj+3IHcO1HBfkEqvwGFi8BaQzdAT0EuwbN/jf7oPF3A6z8Lw/LATwKuAxO/zf+NN27/BT1KQxtB7f20gvs44MDM/v4AqkY+fS5+874wAgHBGTqlv/AAff+lQ42F98kjgEZ96f99ex3DUIQkRipE677Cwj4+zH+mw5j9zz9xg7H69D0QAbU/Jf16PB4DDcUKvhu9QL7cef58rv3CxIaJekEk99j0HIAA/mrBBYIa/pWElHxGga9CD8WziMp9DvtCdv56HYB/QM7BdIHbx3AGc0AfO207ybzWvUF82j30hVWHZ0bGvs69+gPCesJ8IXmhtoJ7gMCQyKKAQ0ESg5MAtwKlQ1IEH/96/Zh5hrgsvSKES4K8xPLHzMAZBK9BPYTMgNm3Tzzx+RfB24MHAzBCPX6Bg/z+Er3Ke3V6oD2wfal+5D0yf9oETYSz/uP/ZwH7fX072zzfAR3E+IUjBAJ8tD0WPdl4oQE6QkXC/IZlg80DPn3evtZBFUA0w7WBqbr1fKO+EUBsQOV/o0VYQGEDmYB0OTD/gD/2wnS8KD8yP3G9PL+o+TJAZIQCiL9B7LhHu0V8+cB5PjRGB0YWhHhEZDtSAIm/Fb+e/qu6RsCEPogCtkMVwhzEB78sgHK70rz5AWs+9371e61AAkNYwQq+XLtNvRC6472vBCiHRcWQPpR7fP6uQ1j/iT4pf/R+nb7xPP1AkEUOQxO+8v01wmHCooOVRArBXv+hPE5+WEBJwaTCYMItfQ08a8Bzvrp/i4GCBOXCrwGJwYK9cv14us1ADMEUAOBEKv0/Ouz7c3/zgxHDT4X8wkYAOn0Xehg5f4GuyBLD5wD/uow9arxLu//EZAMqw6t8e7pCwXVCc4STQaEDtUByeoM8CDhaun/BcQV9Q57+lH5B/mpAooOtRrhC4jzWgwE773y1QhfA3MEId+6/3z+4wvyKrwW7w2+6vz0PuTb6+sKWv1g/wr8GQZd/iT6Y/dr8dv4VfQsANUFZQIVA0Dv/AGpEP0TDxr88Brz/Oeq52MOtSiRLBASqgFd4rrtq/70Eu4PYQB0+CrlaQBW+E4RQQe09F8FYPDx91HskPiS+SfwBPxCCooOfwI/BPXtB/LR/cz87w+YCJYADPhS8/cLv/v4CZETTwOxDaL8ghc6Cej6yfcm3zf0kf7mHbMSDfsH9lD3kBH/E/0ImP3g8OHr9uts6KcQMCMGBePwNO+c+7wDJ/r9CnoWw/ixBRPyqAADD9PzzvuD8I0IxQDYCbQeFxY3D2f6BgBQ+AD4eQG+D7QF6/dj9hDrXPquDUQe7CK4Evfvy9pe6wvr4NzE9VYCCQs8/pL9kxJo9jj7/elg4+vwvgFlCLv5JBLPAgD8E/7kCELwmOKc/P/+WhIQBJIl6BquAysSWeNJ9Aj8JutcA7wFbheLHNgTXyIi8SXiIf+MA5cETP7pDuwIMf6L7qTxBQATB4LuDNpJDo4PUwxOC6kWgBxE5evWftva6ugC4Q4mDTAM5xJEEtj6B/DIBcn5QfBp9wj8zQ1GHFEhSgrY9ELzdN6E27Pn0ApjHFwLBxt1EE8iJhK/4WLumeuG9Nnx+v+mEzgKXgbKBv7+Vf84Ddfts/f0ATj5pQcOAssZzPvz8d8DU9hj6nL4F/7U/0r3qw+zA7EC5AKsAA75Ef3V+0vt7BLLAoX3n/RT9sIHdPO+BhoA9PDA/jYQ/iSqE3jzjPbt9bb0pgOpA7UHWPwN7Lbo0BAcHKoO3wh3+RwONP9OCnYJl/oF9kzurPOd67sTpRIlJJgPiOal993jVQRP/ubz1BBcDnEMLQoEC1cETPz7+Cn26+6o+tUDa/99A0YGjfOY/I4HO/0tDFsGdhtIBaXuSfkG4+vvrvMqEu0NcgMcAADtnAn1/kECkwbZCq8BjvZOCLb3GwJz/U7+zQF46gnzkP/1Cg0JCQo5DwEGSPU66Dr5qAjs/7EE3wWBCz0NvejA7XD6fADpCrD7twLI8zrmdvbqBNgGLhDoHXf2T++I+Vj5/ApaCG8N3vWC86H83e0CCQkOpRj2DQjxeQlzAi8BDw3J/i4BB/kv9CcDqPZs80IDjgLwDEcRLAnWCK78pvkk+JLuqgtaA5j1Jg1+/S/9kPKs9SUFBP2kC0IL4QLkAYgKNAA39cDoE/EfBsz0fgpcDdEH8g5O98Tnx/ekEEQEjf/+B7sOr/2E8G/61Pbp+iT/sAoIB6AAAgEv6QvvIAQi9Tb8TBXiCIj3jfvyCGsG3PhR8n33bvFP8pgERQPnELwRB//eAGAExw9gDgz+3v/M9O3pZAQtE38LpApmBPz7a/6h+7YPbhoV+ynpouKZ984KYAuIEa8DGPhE+cH2Mfm9DOcI++ci5HX5PfzY9oUGOgrQ9mP5FQpRDe8IdwTX/R3lJ9+D9VUApQp3CxAFBA0CBBbyq+8V9/AP2gTt9NQM2BLcES0FLPvgAlz+KPSZ9nwIYxS6CI0A2A2FEzYEa/UDBYIIKACR+Gn/lhcQ/+X3FP4x+XEDwfcH9bsIRAg0+sn2PfvmD+4AmveJDH78UvVS71H4jAVF9c35fAHA/rv5Qf1wB4cJ/QEN82P6rQqtGM4J1fZZ867fP/A0AR4SIQmb8QABgf7cBlwKVBbnFrr+judt64f8xfSkBXf6Xgmy/qPrNg/qBLEe9Q+A4u/w+/HO8LoBGxKkGx4LDfJh8jPxrvjP+Yj9lweaDB8WWxQCE7sEF/om+YH1rPbw+xUFOAqDBuP7r/QYCMAHUvVnAZT6z/dt9Nvzf/7CA28IHfkP99L7UQJq9h/3YvW57mcAN/voEmAeSQlg+oH3w/Ul9JH8TwZ6ERP7b/nMDXsTjA2G/Qjx3PuHBmHx5ADMCV4MrhG+BEwRCgi9CwgJO/BZ+iP5f/Vh9gL+6QiW++n4+Qf1CeAG9Qsw9sXj5uJ78rUB0PlgDC0IrghrFiQJqPYl9M//rOtH6pQBNhsEBiz40Qgg+AwPYA8P/vYJ4P2g68/p4OvPBFsJF/TU/k36ufZxAO4QNQTM9y76ove+CPUE/BJxBvX5TfZp6RgBmgmxEjUOSQBH/QsBMgALDHAb8xKpARjtPO5W87UNBA8b++UCbvQu79z5oQRNHHUWtvR07NXydQa8EFMCPgORBTPzquu08rj+NBLlBkv/ggDLC5QRcvOC9Bj3i/Hp+5IGFwZHDuoQD/wpA6ED4/UN5vvfq/RJ/vIDNhdTHysPqgS29RLoQfIs8db0KAH5/Bz75fntCtMaQwRl/nAJef9H9uD3TPgnA2cLeP9e+Dz9BAo8CrT5NvvmAWMBdQfqAvr35/qY8mXr3/WDBFMZxxThBsn/mP1M+Gjuuf9K+TzyiPM1+9QaYxo/EmgM/f8I9Ov1jevT+hcSDvLy+dsOOQ88CKj/Ef4A/evyB/bxDtwGGA0CDXgIxggL++TujuDA+mQCHfbkAMkISAX2CsURzAIp/2H9afjN+Nb5PgMuAnL+fgKMBooKxP3hAtL5cvIqABbyrwJuEOUVrAMN9CL0RuzcBnwIQQ0sCUPvbtnw5O0GsRH9F8UbKhUD+gf7i/nU/jQA5vm3+Y74oQHz9wYMCgjZD4kBHeK79CbxxAfxEl0JRwnU/Y7nB+/g+F3+MADV+18HLf/X//L3ff9g7175Mgj++CsXcAejBZ37o/f295PvqP/V+/wLHw2NBwQG5BGkDqkDW/fs27TrlPmVCIQiGyNeE6f68ufs77L0B/9v/6n8Tfyq/c0bog6eBxsKrfpL9ab+u/ow9L8F2QS8GPIDBPDx/xwCygMQ+9D8gP0iBzH2kPTr/nD5FPwc8877RQYuC6b/0PHZ9IH+HQMoAwgBXPs39yr02QJW/mH35gjMBBMD1hJ3BjACjAGL8ZH9rv3e+P0NUv8JATseJfXD+GIDp/mfFncDQPUc7hv9/gqHC1wIQQA2CdPyN+tq8tUFkw4RBwrzbPdrDzwGnwcU/uAO6wv4+Bfv7ugs/DP9IAkDCcQftSQ780Lr/+/H5trwSPOgANYeyA8kA1MDIQXfDgUH3fOI+R74PeOj7Yn3BAhRDkELDgce/W4CXv9G//z+wv8j/eL67AEN+c7vuvJh9tMBeAGcADoLSBNFCK/3pADQ8IoEGQ1x/HoMwPbu++37tvP4AAUUzAm99LQP4QQxCS8W3gfdEIsH0O4F7Ory3fsqBZIB3gQKCbQFJgKdBO/6QPmP+uXy7gVZBDUCP/3841nyePp06U78XxWsGkgMrP/e7dHh5flY6NIB9xkCDRQdAf3JBD4PnfcM/D4Fuvt89G3+JgYlErMOZhFPBfT+jvOC8jQH4/3EE27+MenD7lXj1/M0/3Qb5xMjAsb+h/BP+w3xN/o2/YHpJvbC/j0CtAYPD3f/av5QCYH+lwieBGMO4gIw6rkBgwdq/VT8gQE0AN/+nvEJ81UGHQZ9Awv04ABCFw0Mkvhb8Hr1v+g+7Pr94Af4C7T+AA33ECEQhA4D9T36XfxnC7MJ3Qx1HFgDIvtz9f0PZw5sBm8Bfe0MBw7/QAkk+5b8AgsB5i3yo/RPDHEURBDDDebzQP/f26Tgk/+W9/MDtv2FB/38YvjcCnf/ygCGDPkLleg46Jz0KfU5FNgUZQIL9m0Dlv4p8AIDoxJxBTPuQwdpDIwGwQoI+FPtSfekDFsEBgWxA5/6LvVT7Kr7Y/8MDTUHNfEC/TYEHgTW/JsHjAQQAGj/cub5BLwVcgiTBBEGegZu6/7vCvXN/qQLJgdr/u/9NRnrDrkJPvQF5tb6b+a07or4Aw44I+wG8/3l+3gEEf8w+JH6rfG5C+QK3Pg/A0UUsA7CCpEMNvI+/XXpfd+R9VkF6ig1Ec8O+Abe+CD8t/KK+UjxG/kv5TD1iRTLCucXA/0u75Xyw+XF+rISUxOSDjUHLu7g9HAFcvoXDLr+8/M4/4oC5hE7/7ASuRB7/ND17eZX+nf+WBl5EMIKbASP4VPg+9fD+zkVzRY9GukZ7xETCxf66OXh+crr5/UNBoP7zwR9EF0V4AnRBwz59+nj5pT4ivzO92MiLx8D8ZjvbPMh7Jz+4QfZ/Hj2Av5J+qLt/vqQIJohyf8H/m/om+gcA5IBX/yeCjcKOO35/eH/whg6IlcGZg2a+9z55vHk+T0OHhPpBrL6vv3y8zENJAvXAGD+8AIBCrf3D/xOA538z+gF/tP93/trCSXsTeq77/ICxf2mAPoLbvdK99H2qwnACs0P8wP44Y/25fjy/Y4GzgcsEfQJYhgQEUsBxwNcBhf4nuidCrkChv5WCmEFlggj9j/29OoV/TX8puvB8Wj44hNw/AMJ3QFu8G35OOQb8tYBFQXo9XwGaPhp9ToOe/twDir1UfWaEO4Bqw6FETwCD/6n/p/t6fpUFdEOIAgzB1EH0gQvBegNDQG28FAEjwQpAsYVfwK09gAAheEd3Lr9egkLDaUAuf5HChDujvN2Dt4CSxAzBE7pGfKl/Er84u6cABwOZw6YATgK9RgT/vkRqgH75437Tvgd9TL8cA46BVL/qf5YB20G6+7xAl/xBPctGdMONhHU/z762fGa7dD5i/4SC9sALwgX/ZMNsB568dT4PPx+78n94wHT+iwLkwiNBkgFs+zMEagIbO9dBXD4XOQ6830G3AMsEoIOagw196Dw8gq3+5MI7hCP+pzq8wU/D6L59gWn8m3yUfoP+04NJAk3FlMQKfyC+BUAUQRO95DwDNpM9g0DQ/MrEI8HBRaoBjv1jQr89N76AATkBVz4kvsW/nrwswxAA4gAqQKk8HT5YfwHEG4eHQkx/ev5w+Sg4w3x6fceCqoA0f91FH4QiA+NBxLryPAz+OXl7QDxBpsOGiEkDSgJ0PZx9yz53fsF7BDrCAb4ABIichApEpsCw9o/8G3pVQpPFjYLP+9z9REREf9iD8YFBgaa9+vlvPgu9nkEtRdJDu/4BPpr/q0BCA7uGJsU4v057hPvPe15/M8OZPVA8bkBRBQVJLYaig0r9snvc/Xp9Z/0MvgiCjv+yPVL+4r5gwyl/zvxNPBk6Yf6A/t5+xwCKwboDeP9cd2G51j9hP+IBzn+yQftBqz+Sv+oAdgSDxCx/1fx+w5kF8AOcxJwBef94/ak/xH3KwOrDw4MywGS7tkHQgba/sUF+gAZ+/H/0Ah0/Z0JEQNd/dcCx+ca88X4Ju/h/vH9hALEDIsORwEe8lv67vje+Xj5s/5ACZf9kv8b+q770QYk/fYDLwKuAAYGmveu+9D9J/RZBKYDLPxjAl/7bA74EUwRHAho5hjtgOOd804HaxETIn4N1QU+8ALzL/dg/zEONgGSAyryR/1HA9cAVgKl/qr7N9sr767+LBJkIj4V+RcK+rj9rufU3MsFYgRuEBwOCQ0pA3T/FRPLBB33f+rF8hPw8/u8FU8RThXjEPMCFPhWA6T8IvOz9c37fvbC76AUKw16Ar0NfhENAE30EwD+9zQMAwWpASz+N/MAAV7mIvX1EKEAJu8c6DjiPewIDQ0YpxgAGgISPfZB5QXsc+7676Xpsu7V+Z0NLyOxGEwP3f67/0P9nuk59N72kwIDAz0N7w+DB2kedglR/GP0wuPN4PbrTgQPFt8jMRsAH28BaeQL8jzzZvvlEJ0MG/r8DlH1Hehc+r7zqhQKC0z07/fe8tIDExt/EGsKHAgb7TH4f/KD8ZUCbQDDB+Pz1/kFAi8IYw9BA4QGC/VLBm8FPesLCGoGUPSJAg/7J/slG3wZ6w1C9k7heN8Z6tsA1wmhHp4Prg5sBabydAbt7APkt+if+Wj4gvi6EKsBuwQV+TX6NQY1DBELdPOb/tgD8gGoC4MOQwKq/7Prtd8P+aH7mBLIFwMRPxEwBaX/BPEX9/7rCfuTDSPva/yx/Ub16gaG//34h/67/Qn/XhDwB8kBqgrc7GHzpQL6/9b/Fvjf/asBGxcBFcoQ5vzs9Gv+m+g5/xn4EgyKHCoQUg2bAyUWm/QH927q3eL9/pP6YAgjEpUaSvxv9G3qc/0ZEAsEnBJg75DuMe7g+6T4i/9zFF7pmQVvA+vyGv6U+pgIJxBUDyv+zPQg6DrylwPiEUYnLxHQAE/5c+h++8EQ0xAJAs/zy/NZ+zkK5gmhEE8KNg3GEIXrGfTUBvL1VPBi9Tn3kBGFDsD/g/917nz47e95+2AQRg0n/B7tl+tu4goE9RHDHuQSnfDu6M7qbQmZB6oKlP3C/WwI4/iuCRwSeRDVAn4BT/T//R4J5PLnAkIB+xWLFZvyufdUAl0AzvitCAj6rPl+/QztIf+a8OvwifH97D0JsQrRBkIT8RWM8PXxt/j66I4DN/ksA74Ppf5aCUcKBguE/sYDX/9V/aAFGPKeCvwHmP92CDgDVQVM+5b22eiq+p0CFAcJE+sGJhaXC4X8//5cAjXrnOiW/0r1fgbT/ob7+v2W9usJEwnnCMD+FAEV+MX6NQxE8DUIbRHT82L05fu2BwwDlhF8EO8EX/eN6b8FgfUFBvwTgPrtDIP7leqn5Z3yNfUl9uINGP8ZDWP+T/JcAjrtQv0LA53ztftjFKoJa/2LBPLpCQOlCHT8UhLFDpYHR/er98rxFRIQFWH00wSq8QsJPhpgDScMkwh289jfz/g368oNtx4WBGkAkvrwD9oECQoO85bnCe1X1pr8TwtLHdwahvUI7RLpXf3oAQ8ElAW9BwoQxfHH+BkKTgKwBrUAaAYn+zbxsfCw7nAHHBPMI0USAPwS/gno6//rDm8BHvzf9NnyB/QkCGIKWg6lA8/zCvci+dsGNAGY/n7sZvZ3/zr5BBEJCYsUjv5j7IHzXvekDf0RNB0nAyT9+vRJ8kkE3QBEEU8JmBHz+u7ztghSANwTxPu3+jL/D+7jAbf+awpOHoIQF/xm+hD0EPPhAHv28gZgDOT/jAeB/O/4jvbv9azvDfvjBtj9txHnC5v5yPuV+mT4v/wV9OD8bAfi8YP4GfmsBWYRXAt+/X/nSfnA9D3xv/T3AwQP0fK+9pjm7unrBt0NPgqk+lcOLvj98cQEf/x1DdUA1QJE7xHxNBAQDfMZmAfnDdgBCP7EDvgCPBEpCw7/nehM9kcEOQKsFGcTowbU8Y8DVf6R/M0FovYp8BDgGv7sCfsNZyK5CdT1lud77kz5bQDCBof9nQKq9ywGXwk//HQLtvUY87kEuxMAAvcAegck6Yj50O008m36LPatA9gFCBEdCF4T8vt37g33RO5Q/hwMrhBk/nYMEQy2B50CuvbnC8IDFwpV/fz8CAKK9SIIz/lrAXMDMgENA+v0WwiE/dv9twBQ+tf6ZPk5CSrwavei/wj8pgxIAyULl/t/+gAFsA3DDMD0pv8e7NH2jQxd9Jv9YQkTCU8Guw3pCIYF1Qb68Hv2tPpD/2kAT/1uAXv97QkWAcP7tPGF+XEGS/efAQ70zfYqArcGd/oJ++IH8vcfD5cA5f69/W/ynPonBDoWxQBUGLf1u+noD7EFGx8RGFYLVPWW9NPxrvgsA8bp7fz657b1kgl+BqoNWgC7Cjvwvv4LBnD7JQnH8yr4rPizBi8FlfizBqcBd/cv+N4NWgZbB6sIWu788SD0O+jB830PvxE+F1MMCfwI9vT2jgiL/uP9Hvr0CZ4SBwnNCZv1RPjw9CUHAQGg+xsMfOEw8BUBAf/dEoYKw/4Q7ev1qwEJ/qoCLv0cAUMK4Asf/lf+cwcJAeUHjfqQ9hb+mPXb8tgHKBy4ECQgEwMz6oH34OHN8aAFvgNg+tgOhAm1+k8NGfvPAdsFjQHj90EDMwOC8SQS3/h4AxkVmfk0BA39t++x9tYHCO1L8sUJeQJeDFUCoQXmBD4N+QtJ91D/qwCJ/zLvseT294IRZQ2PB30Ktfs5ClcLofYM/DcCtO9v4pPuUft0BgMIpAJT/78IvgyU+/z5Y/Ui7MkCqAg1AHUZWBDS84X8evT28uMCePkJ9J/8BQFDAgoKqQeEDIgLPPEB+nwHxf9u9LEJ/ALC8FkUOfv+ArMKYuyU/MQIaw5v/TADcPt+/5/6AeEd+0L6swA/DVESdAOYBbwFbt037iH+cQGuC7sUpQg7BIsSrPZv+10KAgHI/FP86f4f/ycIrgKOBg0LCv/RAdX5hPHf8e/4HfXzAEgbxgQnDpMFz+bsBmIPuf9Z9/zjIdny8G375A2nHrENvAB0+AsJMwXqBHT6eOwO+rj8GQkUE8sVoe6b9kAFwfVMD3oElwlkAcT4iANDAcMUkxazCWHtv+UE58fiIfbWCaAFRf6uD5r/MwJxFQAROA/u7N3i4+La7AD6b/kTFV0K4QLoAzD/IAcaDrQILvDb93Ly3gYOEFz6NAAd+q4LKgVODOwJQ/Qa/v/o4ewgBjQTrg1dEGkFnwHfEAXzCvbc+40ANQY8/tL5VvatFUkMgARnCjUE6/3Z8BUGCfu6/dv69+c+A7sHmRfUDJvuqubj7oIFuPqqA/IBzQOKCHTtogOVFOcCqPSx9HLtHfFgB2EGQAlTAGMGQgGB92gGYfSLBaEGNu389x4DswcJC8oEs/B/AQ/4SPYvE64PwBAX9lb0Qfh+/PMEBwDCEowGjAtkCuH3bf5yB3r6i/JUCiX7+fZkBDkA5PY9+hcG/fwNBPr5u/Q3AVkCwgLx+cYNUApD6dLuEfkD/qoETBDlEdgM5wcV9Uz6ivL193cEDP3oFmwVjgAr8J/uzuRg/MMaAPwAD34I9Pml/dP+FhQw/qjzdfPc8qj5YApSA1ECYwwy8JL2seiB7pYQnRDWDhkDig/vCTL8JfTC6QH3iehW4T/8rRRKHsUffguA8sP9+/U98wwE7gUxC3oDe/7482b5nAOdAeQLzfgL+VMDj/wFD9EbLRKqDwYRMfkD6untPP0wBXIBnQsKBaoPnBJw7vD0lv9x9jMGZAkD+CYEZgED61LyJeiUABgPRv/ADUL1XPEe6xzxdwFFA98ldQ0q/dz1Ueb67zUCahF1BKYBGu8jALYD6/k/FcMPKwiY7gHuBvVI/uoIFPr+CbcJ0wb6+Sf8Gw3B/hH/k/Ma8+P9F/+O/zj4R/+sDDcKAwc0HFsLE/eg9AveYvo0BgIGpQ42+D4NMBRn/aQAqP/m6gvtIgBrA1QT4gj5Aef7k+6wDRMHMvzmAe308vD9+a/+Z+rE+toMHg8XCSjziAGj9Vn2SwGs9sIIhgKOBHkFx/yrC+4DLPso+YX2rvRf9un7LQKdEjkPXw9lDGYHqAuR+6ED7vpU+jkFrfdo/vjyJv9bBHcGmBghDbEGwfyqBSME5hLuDPPjc+jG4S31uQodDbIY1ws57A/gh+0E98weshllAE8HzuKd6e77FP0SDvD8tQGX+BDuiAGrAeENaBOHEnH+jvliBOMCDgxu+Jz5Ff2iBCsEBPR2/IjvHAfdFMgURBoHBE/5o+2n9AH4QREcDLLoSv5T9Tb72gxGADP9ygMnDoD8lAL5/aDqXvIV9RULwQwGBfn6TfMU8QLwqAll+8QK1BkU+HkCWAG7+Af+uQHK/ez8l/1w8CsEEgNLBnMPXvnqEC/6Y+v8A1T3gQkbCeELGgQb/FAA1efI+koERA78AHfzSvqT5r//JvdtALoT+vZuALzyivcdE7gJ4/xU+/z3xuswCOMOLA+mI6P/NQBWA0TyIQTI/Uz3IPke9M/x7/7LADgB4w6MACj43f5VAxT+JfzKARb5sPek/6b4nf6KETQVSQ4SAYkMBAB76/X/KweABvUN3gfI9kEOAQ3G+aX9gvOy+xjrOOex/0UCPAcEE/wHSPz6Crb4V/ogAe3xq/72+pn91Pte/uIV0AyhCz0K0P2KAG7/F/0O8uLyNfW5/uYHBv9UFbsMOv0C+Q3v4wBg+gD3IPMAAaQOFfpf+2H4+QcpCJH8IwM9+Vn8QvMsAGoPpwU3Bsvz8fUV9Q7vewudGRUdxRtZCU/1ifCW+Xb5G/3cA28H9Qk/AP8J3QEM/ocKRu+R8PUAYAQZ+ykBDwfo9GH7V/OsAGD15uo8DFj2Wf/2DnMHlw8yApr+evrE8xD+iAkcBwwBKARq8Zz1DwFk9McGIP+yBLQSAf7jDscKcPP09vf9/Pua+l78VfpNBWIAivniBdoAnQCDCiQLiAbp/C740PYm/6/4+vvkDGcL7gtw/PoMsgx7BUgNk/J+Afn+DQKmEfYH3Af18qjwF/ci9Ir6awh5Cz/4QfqgAEL0Gf7XAGP3Yf1U/2b4V/bF/gryTfua9yDlBvge/6MX7xTX++T3ZPlI/wEBgAaO9yz3m/nH6m37Bg00CawLZwAO6a7x/QjUEJgQgwxgEtkSYfrv/4cJ9/4f+uzstur0BB4S0A0GF2T+wfPd+ObywwpHFJoMMAW7+P/pKfveAoYKbAn88bP8++zp84sHkQyWFXgI4/wzBREXAgBLAJX+LuLH8yrwpvEPDGr2gvoLAePkyALjEsv9dwrcFxoESABz8DffwQOmAC4CzQYk7jT9Bv0E/DkOFhFxELD8tfeLA4UNrBFTBgYNC+7e50r4ffDmCQQMUxGACaQFKwr+AAgLCgEn8wPvc/Lg9uoPVxbc/6X8u/Wv8+kEA/li9PMKLPb9BooTPQ7mGk4C2/D6583vPfT4AScJV/qQ+QP5jAcoDiwAbP9399Xoxu9Z83oKgAbWB6gUifr6BvoEWPgg88/6WP88BVwU7REJGK379f2d+2XsLQc2BRgAFwqfBujrTOeJ7qbzTQz+CZQCAwt6AwESqBbeBJH7eOhZ4HTjCgBdBcoQthnZ+Hz+3/igBPgO1ABxB/Lu8u89ABzuhftfExYM0/m3+NL/qQIiEW8LJgmG/5z2bvDA5GoG5A3NDgkHFAOiC6TtE+sr/JT/KwHuF6oE3vaMD5D26PHq+/vyUgqwGToGDgmwAh/03/gD9xQGUBOzBXf1uu9e6TH/YhTZDvQJuPSh74jssetoEMYafxMXEX304+By6lX2xvd/CNwHcgIxE4wHbw2WD5H78/bl7UfzVAAo82v8xgdQ8q8GUQ2YAgYLUAC28ur7QAIn94EA5vY4/7cGCfpWDIUKE/o89Az6XP1jEDQMuvwtCWX+lgEpBIHzefu+AMn8GgyYB0j/3ADs+ff7xP6ICjEH8PzH+J/zpvTe+EoHXPtU40znAPNlCAcUWhcTH44IYfxE8YnqQP34AuEAvvvND0EO7AvBGRn5rvU0+qPtdwB2CqMX2RuaBlL0VOEW8x/53P9uDSkAwAVb9BL6lQQaAT0IbPWf57nuVQieC7AV/xqHArj1h+ox71755/a8AEgGVgMSFk8LiP4ZB0YDRwK1+mj/OP2x/voCKPZ1/Mn8HPx3AA8FjRkREbMGNwD09sL+sOuY/KMA1PJqEmYEE/YTAf/+H/e8BUELRfbXBdEIvPwfAgH6Gvzs8y7kSgNoB0AFtxpQFNYLrf8z+0Dxv/Mt/P38+QJO91cJ5Aeh+/sNIQOK+yD9CfUI+ZL/8wDe+xj8/w0mDPT6k+tr6vD8J/t+AWQONwic/HnrBvB3ArgUSBlOA+f8PPcX8voC1QIRAgkDjf3U9xv3BQ+tE4wUGw1A/sf7rOwZ/fP9S/jl/VD3d/1VAAALJvds9578S+9eCWYGNwMBAYPu3f2fDRcHGAgvAGbzLvz9BEEG4QpnBybpG/miAPr7PSQyCpUAwQjA880KiQ0O+sv89fmj6xLuT/fX92oJNQ0V8prw6/i3AogIrgASAxr4+vd2+ZH4qAtaDKAEmPOP5H/3nQ7JFEMR/RWBEPT8pgG/91D1rgmCBtcHHwjLAcT0u+4Y9Db5ZAwnDBQB/Py794QGRwgAA0wVAAbk8VntzuaIA0kUShEaEEEL1Pza8pT5C+urB5QKUO9yEHX6yP9AEDX4s/+g+FH3rfSlBngBxvodAejoHvg9/GUF7w1KCVEMzQtK/4Xxkf9G9dzvbvScADkCEQkvEXD+UAfl9CHwNvSx/H0POgdIGVb+auqUBSv/QwDb/wX3yPK4928OBg8zFroOr/0TAPf0aQrGCnz5ZgSk/Qf2igH6CxMAqfKC8h30ifNUCeUZCg/CAvICL+wY10T7Rv7iBfITg/c5+DwD4wFlA8MNjAX6BMcBzuHa9doU6gPY/7X0d+b3AW0ItAQUDMELKAXZ+KsDXwlUBiYCpO7r53zp5QN1F4kQ/xdHA4P71/+D/00OyQfYBQH9tPqi+FwEyBG+AzcJdPkZ7MP64/ca8eEIVQIz/bwNjff8AtH/fO4S72/rQ/ZxAQIIpPqhBnH/5/Y+Cin0QfjN9uTy9P+m9NwIARgcCNT1HfsL+jf9oQiu7tr9PAt5B7gL7A4iB7L2HP1z5DP4KQ3WC5wZRAkd/zgAZgm29ZMBZP7S8yYDyOR6+XQLnQO7DlEVXAST+f4GXf7CB30AjPCv+8T37gFyDWIHaBHGED79y/+/BrP5b/RB92r9UwwwBsQD/QUR/zEBSPxE8p76ywKT9Sb+IASdC5gT5gKnBZ76vPPU/o3+WgEeBM4BI/W79dv2MO/PAw0JBAidD6XxhPa+DNL+owFv/V7u+/cB9j3xUwaqDNMGGwnNAob/Yg4h9q/vMApN+cQFzwZd9sP7rP6VCJoLHwd8+Oz/rgPQAfT/OvWtAFH+++vh8TMHtApQDRQBgveq+lXy5vPX+JkE7wTzAPv3ufZqBWYIjA3FAZLw5fDr/goG6AhSF14SSgTR+o7tOfxoELoEGQRdCsMNxQYk+e71bewJ/JD58PDnCcQHqwOWCVULbwK39ent4OxU9C3wof7RBkMDXgVLACAEJwgvC3QBiAFjAjIA7AUd+uMCXw/MCf4Bg/bg6hntLwGxCxcM4hBpD4b+F/b8/OgDZgdTBnHy9+gx++IBeQTuB2QGRfmU6m3kaur3/xQVACJxDkQBdgI69PH2awK6AMj1R/HK7Z36nxAjEAcXwgfy8hAAYfxf/WMHuQMW/H/9zAGr+aoBG/7a8PX+l/+v+E8C0/Qw9QEJMwClDiMZaAPz+H/++vOy+dQJvvJaAkwHAwSWGwALBgJWAOTs/uyBBpgERwwtGSYDRvwW/74Fpf2w/7MC3vZZ+Dr2KQVuCqYLOQbD97/8/fmAAkT1d/SgD8oBAACmCHf92fn3Aor64/vmDTgEAP4h+cPrmO0LBYsJHxAKGhH8dPLi7kXyDQMkBwcE1fvZ8zzh+f6LGRwGaQsb/rLuWPse/psEIAqV/s/wrfuTA7EFOgzR/Nz8of/p/mcH5xZCCwbqwvsSBBMETw7HDt0F/PhU+Jn5PwF9/sEMVwA76g0DAgj7AGILpwbB54b0lARN7yH9ogif75Ty1PUd+74hthOLAHIB/+y57Yj//P/wArcJ4/RG+VYQCQ4QD4UWefyl87v7f/WkDF8G4PaZ+/n+3AS2BMv6JvKi/rz8Svx/DFEN/fUF8vT11+jO+oQLe/73BAkYhALE88n2LPx6DMUJzAZtB9ECrwAG/SD4Dwh6DAIEU/18/ecGyvVo/3QAAffwBlL+o/X08fXzTwHUB5MDkv98/Fv6FfKA9RH7d/VEBeID5gCRB4sHjArpDe8LBwdAB63xj/AV99n07gYiEywLEwCbBUnx9feXArrwnQQOAXj9sQi8CGcHPwXz+y7mRfUoAuMKbBk2BJD94Psm6fjxjgaUFnElMxd4/0X1Pfu//Sr8lgnP95DrEPQr7xIDexuRHFEGu/Or9Cfvcf0ICcwAYQPA9NHpw/bYAdgJEge++WACogpU/OEDMwN49aX2Fe4L6HMDJx0qEUoIH/+j/R8KagQL+ejzlfOf9Iz3Ifs4De8ZjQxmATn70fZQASUDjfu2/fgBVw7WAUv8BA6P/7P1dvXl6gf0ZPuT/JcN1AyLCOwKfgVP9gH8WgXY9msLmg0j/cj/V/GX6Ur++f1xB9klFg6iEqoOWvbSAyQCa/bY930Bu+u4/tgRnP7GAxj4he1B8q35xPt9AjkCdQRDBp/09v3I/Wv13fsa7W3qevD3AY8XRQlyDNoFQPe495P9rAQuCu4ZLvqN9uf6QfRMBW798PY77IMDQArnD3oWMAFIBarwUfjNCe4CaAcWC1P7YewJAVUASQJWCQX+lgMOBTMKhQkEBjQEHfxsA7r2xPusBpbzAvgi+sn8Mga0DIUJkgOUCQD+Cu9W87L7ogBwALvxPPf8/qPx8//cDSsCGwobA6zsCAZXAtDwTgoHCfv0OANDBdTsZACQDMQRPyZ4Ddf39PwJ5IfhXAjx/I7/4hMN+bj+Fg3N/YANihRW9r7rVOni5xQAYAtUAgcLQwIF77v5fwnBCrcNRwMF7A/7/AAR/7r8AfV0A0MADAbyBKL74woMB2X0GvquBEUDpgwoBdn4AAmgCAH8PACPAQUH8vws7GfzTgKpA/MC4wuM/GQJbxB89vsBIgZV9wYDKAsJ/QUMgAQb+LEAEfm/ALgF4/pS9coEt/rd+WgD9vmjBK8Fcvzy9y/9/vLr8ij8gADsAgz39Pvy+w0BQAbDBbcENwK7A4n9AAWbDCoC9fgE+LjywPhiBJsLowDY9HUCCP+3/i4QwgwJBjcMT/Tv7nX6fe4L/KEJjAdj/+YDHf/gAf4PDP0ACbIIkPMQ+ObyEfx9B7cBVgTBCBkDif73/gj4SPgcCFMGNPiL/usB3vwVCkkSQggN+q0AjgEL+R0MAAR3/Xv4mtvO86QU+RXJGZMMZ+6I8qr/hPeXCq0Hz+rF9rnyKfa0GKgOtf5P/hPnCuukDKQEcAE4ENf5PvLtB4UEfQqbEeLpneem90X57BJoGDQOlgpW+fLlvfZf9vjxCgW8/tL8HwufEv0DtAH3+lXvRfpC9b78JwXj/YT+0P8dBrICKgEwBeT6/vf48En5AQoLDuERxQVGAij1GPWU+EgAaRUMCdYDhAJmA3D4CPjT/VgBoBZCFAMMJv1z+eX1aP4+AuP5LgjG+Xz7vgexAOQF0AM680Dz5QHHBXgHTw4LBLru4Ot979n81P7C/U4DRwfgBkf/2ghdAOL5k/Ol54j3xQzdAVkAziOlE6YKCwzg6m7qbOms357yBRGRHBEbchPp+DLwBPg99cgTVhP98n37v+567cAGrwgzDRQURACs8kz6yQYgD9EBXf3l9yL0F/g6/dkHDwBeBMkASfmCCssMiwPD95r8OAHE99wB5QVbAMoAOAp+BJz5IgON9Aj05wS4AXUBwgKz9j7zxPt/+nUIQwCU+IEJL/mN77X/Cf5y+TsFrP42/jMPhAlv/BoLawW6++0GIPH4/1QIwPFg/aABx/yRCMAV5gkyCEkCtPFN+R4FOP6v+276r+7p++f6RfaS/vUD/gQCAhoQmAnoAscCl/DJ6lr6jv9T/NAMmAeXArUHcPYs+4j7/P2oDlb9R/0PC2T9sfbpB0AITv9mAygBhPmB9KIEHP0D/DELqgByBugMHgpF/HcCDQmn/oP5VPGd9bD2avcW+nYFdQJ2/0f/UvS2BVEMKgR+AqQAZ/s1+iT2XvMt9mf8oglxE84W+ALDA6b/GfKpBgAEUv2ZAwf43PHWB9EW8A6TB6rz1uR3++oEhQqMGJQDKflD+efvtffyCBsDcvt7/aj6+wT2DXII7/svAVL5h/CE+v75RwnuCeP5eABBAjsAxwo6/PH62APdCGwOMvonAcj/O/10A0L/KfwXAqUFZPEV/SX93QB9AUryo/pt/xkHyPvF/zv2DvDVAHbwTfDC+TH8kPuLAg4LBw4XG7EMlfjl+0n3N/zdA3wEaRVvFGL9ePZM/sYHkhCRDIf9m/Dp9yz3hvggFNUDpfjt+cvnOvjvCDIGfQRnA1/4LfbNAWf7eACqEHb/ivysAQr2CQh/CNv2GQYLC4r/RRAlCNTyFQXmBbb27/feA4H9MAVhClL6+QmeAOLyp/aO8v0CxQJn9DH7zQgvEf8N5gdQ92/pOvVM9XDum/dzAqb8gAQKEvUEX/1j9sfqfuofA48HMQkFFB/9Hf4UAmoE2gzjBI0AxwWjCtr+rAoEDwUCIQqaALD+nAqgCJ8JOgSY9/nsL+sj7lH6iQkWBGb+U/vB9tryhvs3Aa7+8v938HzsI/oPDBcLlwl2AQH1vAJU98kAphLECK4DJ/9a+0H85QP3/qMEsweT/vkEsQjq+2UCRgjl7nj3egH9+YsHug54Bt388Pn4+kf5xf9eBh4DYANa+F39Ov2I8x8CMgBT+v76UQQ9AHf+5wa5/skCbQZ4BYQAwAWnBqcF4wm6+8r+qP0/9eT1ev6rC24URRokCIIAMgCG8EHt5fFO8M72bwiRBKkJ3QcY+jsDgu7N5nv1Xf5CECAPvP+++u8HmPtp+C8EMP54Bxf9R/t3C0AKugMs/Sf+8f5TA/L/rACfCZYEmwkUBS/1g/nq+hf5ef+YCrcDmP27Aa74GAKyAh77pvVc9o38HfG+/zIFjvwm/ZsDgwYB+c37f/+gA0QBY/mU+MkA1weTAu4BQf+XBT7+lvZ0/Y4ChQUy99/9cQjZC6sOYPix90j/m/Pt/KYEXQDsBl0FTAGFDpcORPNV6EXsm/E4ASIKrAixFfUNiPlKDCT70+7B/f/nnPCeDx8YnhZtD7n76vyWBkP3ffSD93Dwm/TIAy4K0x0nHJ78d/oi9vDzRP3L/bACqQHH+Yv5sf/uA9wI9gq//cz6ygIpAOb9ngEYApn26O5E7+n/2xBDGfIMZfT4A7H5Euyn+Db5cQFlA6YAUAFoEHYHNvvq+pLuC/0JBav/UwIkCAYCMwFPB176dAPrAXT2GQqnCaEOFxWJ+yLuUfJR/E/8PAX4BwT4GP3zBhYMwQqMAtzzv/EW9cfvj/ruB4UEF/1a87zlSvf7ASL9Vw8TFCIK9ghQ+KfwdwLT9uj6ygh1APYCYwpAAkn+PRW4C0ADpgV0+FL/bgUiARUEY/3D7iH1U/lBAuEIeQpGBfH4//Za9Tb46/dJ+8XzDv1sBxcKeA2yCK0JsvJI9s73MvtmC1EHGwXNANUFRQRQDfoNgQVE+Fz0aQibC44HlAQV/6fqe/SiBhQH0BGmBm/0vfWc+mL9PwZU/Zb4Df0M9VX5Bgh5/iTwjPi+9UX0AQOaBgr9IQijB7ICOAds+An6JfYQ+eoDPw3EDK8FixC6ABn5+f7Z+ncBswupAtQGDRPd/qwBNwKl+df+h/oX/L74uvqlAHIArAPl+ob7Z/1Q8zn4tvcD/58GbfbJ+L8B7/u9/gz+WfWPANIBP/iJAo4LegtGA7D/E/w392sBRgg/B5AGPwiODDcEivpd+dfvn/vFBl36vwzjDl/8GQAj/oL/HQEs98Pqj/OhAC8ElhMrEuIA3fjP8DTufP8oCNgUTBgt/Jr5kPv3+HwERw5lDskHfv078gL59gXzBPkBPAqB+1rx0PEa8fIH3woOCWIAdfh9+QHve+5+9+kHRQJRAJID4/KA7cT9cAn5/zEAmvk2/FYJXwY4Bl0EngZV/Kb4IQHpCLgTIAl8BSAD1/2NBzYEsfPO9yoAowCJE9cRFASTC+kBPO40/aQCXPv3A2zzNf2gENgG7QJJAiz2xOxwA5f9m/u4Eqb8Ke2j/fb2nfVeC20GqwO5AOPxRf1RAJ334wqP/4rzgQyx/a76PAdY/o35QP18/Nj44gMjDG0JXQXyAXr2c/bc7tfzw/1PAwoVB/9o/BABIf9AAlYEbgxdCO8D4vGq8ZTzB/ssCRwHd/+i/nn/MfSJBakKNwZhDoX6DOdp9zH+5QZuF3UKfwd3/Lr1Hfw5BV8Gkfy2A/AEyAW5C4YJeQBh9+vpcvo1CfUCdAptCIj4xvL5/GLxr/h5BP39HQEaEAcKA/dVCnj/U/NO8BP1Rvi+9sUTNA2qBP4NCRAXB3cBcP019GzuUPiFAi8DjgnW/fH6cPXjDVcTgfS5Btz9keYZANUMufskBx71tewl/xH8zAmpDYEBe/as/4/zZP27A2Xt/QjeFFkDigBqBv33qv/RAUj04Ppd+5L+lQGmC0kNSwyrBloCE/XH8D39U/v7APQCMwbBAS//P/zt/3D/6/jJ+WjxK/2oBwcOUQzcCc3+c/Us+6r62PPe8HoAzv5BED8N+wMUDVUCnAM59cz15/Wy/Yz7qvg/FacL3w54CRrzd/5p/4zxIfxXCaz+WwfZBAnxFv1N/hEANgqo/pP4ef1IApr2EwIUByr4QQJ99Cv5HglOCoEW3RLqBVn9svJC69z48P/IBccJeAFNBrgEIQClBG3/df7GCYoBOfYvAJP3Tetv/aD7jQXnFNj+dQOSAjv72AHT/uX0IPjQ+6jvzADwAZv95wOiAdsFsQmdCdL+ywKK6bLnOgHq9zwPPB85DSL/6vvx9nT9DwtBDygEZe+77yXwJfuvBxoMJwZaAHECbfSr/tsPaAoH/4r7nfsK/Y32LfGk/pEBvwerDT0DafsqBgQCWQJQEZL5pffS/57s8/h/D2AHHglQ+n7r3wUOCVoNUwkm9ZHyfPhd+cAGwCC+D1v+Ffwk9or2GPnm9kLzC/nc/l8IDAg8AiIHM/8G8lQAlPpe9sACiPSe93oMdhePCjcHdPytAWMFi+nU/tT9CQfaCY7z4QRwBLEIkwaxAF3yjek9/Jf67AM3Cez9Gf0//0n7P/mjDEwG1fjq93X2QhTNDFD4GfsUAGMEdwM+DWf72wMkD8MBogGK+aT5Nfib/RgB1gPZB4oOCAaZ9h4HJAtfBKH2TvDg9o72tvRQ9RkIZhgWElIJTvf17DT/3gD+CTYBkOl18/Dq0vBgCRkE+AWREbTxJviSF9gAlv1r9nn23wZ3Bc4AG/vuBpQE3wegBXP6Ug3G/ffyWv6M+CX7Tfze+6v8LgcDD24I3/7O/q//kvMZ69jsdv5qAOEFRQgM+MoAIQiwDSsSEg5iB/P0NOs8AHD7tvczDYT7MvfeBTkMhgQiAiAHjgA7AMoDJPwT6av2lfy1AU0R+RhREH/67vyx7//yNfuKAREGZQVZDBT/DgEjCVYMR/7Z+IjzRvIB/fwCERVsAbnw7e4r+z4M2AZyBff7UfQK+poBrQzNG7wJCfQ15eXpffkx/MsWDRbHEdME9uon9Pn4yPwjEA4SoP1s+yv0eO9b/ykEngBX/vz6+v2CBiMBbAE0/yn5kgRoBDD6GAM2+uXx2AVDAukLwQoa+NL+YfM28doDCQPu/ywKxv+dASoKjPat+Tf+6PQX+wUC8PumBEMFuvl9Ed4Tg/4p/5T7wvhbAGv+UwLDBXb/kAfrAbv9yQteChvzQe73AOj+ygrHCdn6Kf/i9Zz1WPhmAvcNcA+kAaL7rApX+mX29/d/9qEJmw7ODsYJCwJwAkoGs/pj9dMC9f0R9gn9Mv+ZA0cNgAMB/8wC+gJj+I3mYO/i+pAB/QL/A4YNSwZ3+FP2/O+M7r/92wEd/t75pv2//Y4AewyIBrUGOADM9FL2S/tL/l4C+wGI+ZIDLQx3Cn0Oaw4f+sb8aQeh9uz98wRw/Tf9IQDd/M0Clwc4CawK+/m+9fXwG/ZN/zUGkAP6/XsDNff7ACEHFwT3Be8Ccvo1+FwC6QL6CD7/ZQDECmYRgROOBBH/+QD08oXpwAA7/jwBsgetAl8COgUrB0b0yAGr8grtuvqL9MkBX/kg//kDdP6F/NYFMwz4/779N/qZ+O39ggvbCeQJjQgC+2XyL/a1BvoEQwgfCnv7l/7sBWX5SgBN//Dug/hs9dgB3BPxB+H6G/ah8zn84wUiAH4D/v3R9hYAsA1uDwsI4AGJ86Xz5fUN/v4FKgLaBZn+cAcIEnoHUweFAhf4Ifq4Bg4FffnV8x/uZ/Xa+xL7HAY2DR8HEQo5BEL6cAPu+6vuqvkvBMkBAgHw9S/xqQBqCz0NqgmzBQn9EAHd8HHrZw7dB90AMQiiAb8B4v2S/eL7pfh5/xjxA+9P+8MBmxbYF4wXigCP7ULvSuqGAtEJtwlGCYf81fsVB2EA3P1FBh37MQOZBfcG2wiP/Uf50QU0Bhf2YgIG/WP9dA2PCn4GEPli71D6ePlxApgQSPlS/d0A0vX//mcHrgWrBkcC2vrTAWvqLe+gADL90AYRDt/96+yVBTQDkgn8DQH8S/ZN7m334gKJEqgOvQKa9eH0ZffE9xEBSwHCCSsBjQUZCiQIOwEc7Wnws/kyArT5EfsLB/v+5P5RB8f/vgffDHf7A/+0ByANlwtwA+rxS+3o9yf9TQHAD18YEQLmAyD4UfQSBkD80gN5Bx4ASPSp8mb2AvwXCK8ICwwFBIj7AAB9/rH8Rf7S/mn/efmtBAEGiPkyAdz8X/qN/Yb1deyV/poC8gCID9kAFAWn+d7od/Jp+Qb4j/juEgILbQbiC3j8X/0VBVIFk/v8Aj7/7PrWBFUEaQL6/K8DX/8XA2oSAQiWBWT/yPU1ArH/kfLN+yD+ov4OEd4K8/xhBDD01+7QAy7+2AHIAt/3bgD8/iX7fAkiDiAFwwI5+WD4BvUC/0oSPgYPEBgFIO0B+uIDRgMSCy8WUAEJ9pD6X/ihAeEAR+8W8ln8EP6LAnH97AzbE9cEEvZw8RT4Iutb67X2ewbzFlMOfwVXCiQCTPnq9Q/tN/e9BacP7wfOA7YLQw0IETYDP+su7aL78e8p/1oTxRIVCVnx2PWr/+MJRwJ390Lw6fYbCkQFYBNICS30k/IN7z/43/+WBWcRZA7NAfII4/lk7pr74ftNA8INKAqH/SD7CgEeAAT/4wNw/Mn+hwgKAXMFWP6k82X+hfmf+YsIOPugAqcWxgKQ/rP+sOj767/75vBS+/EEPwEMDloG4hLZDG7xLPub81Xy2v6L+8UFLA/7B6kHtwLrA7wLwgLV/boDFQTu+fIBWADx+YMI6vtk+ZYJLQqaDO8IIfa28v/8hvcd++j6SPegAlkEQwj6Aa76PwA58ivrkPd3/0IFXQrBBDf+Yvpg8A/9Sf/V/OwTrQQD/o8JdPqK/I4EBfpfAQYIEvmkBPwGUwtcE2L9gfqy+WH2qPbf/ZEGQgnU/2H5nAWO92n5rAGt/VkHOv9M9ukCwf/o8uX3dfifCaQKSf+JBGcHSwpV+zT4Uf3uCNcG+P/n/3z2PwgeCzcF2gT5Ck4MI/n58lHxeP4KBjQC1wDj99f76wM6+uz7ugZJ/RX0r+5y77L/ZRBiB6T6Wf7J+wf8jvlf+nIKUAxw+m/6jQgVDAoLRwPm/jEAt/7L+x39IQHpAAv7nQBpD38MCgYvAA79Vv11+fb8fP439zT5fv+T/fAKsRL0CWwEl/Wq5Ynocv50BnQJrw52AYL9vAEE/tj3Ovus/iH1P/hNAFcDMAp8Bh8BhgYyBqv/GQEaAewERgbi+OX4Zvh1+1kONxRKB838HANGAOf7CPpJ9iL8R/lu8Wr2swjgD8P/MPq0BwMAw/sM8D7mUgZ7CEwCYfwt9zP8Zfjq/pkEhg8VDGYLOgWA+4j+tAIuAuLuxPm8AIoCzwcLAoMCARDSEyT5nAJ3AgD7YQIt9q36agOB9ir87xAiA1gGlgEU8j/xa/eJBB//rAoXBy/5Kfwh/mbzvfrjApL0lPdW9zIGZgoLCroGjQP4Bib4TfgH/MgL3gqAC3YGUQFsCQL10fLX8fL0uf46BDoHhBNpE/L/RgQh9+XtZfjz+nH9aQNb/nsBGAY2BtgCQfXX/yzx4vG3/5IBFw41Avz/3QIcBFD6Q/qjAaIEVQZsAA8B7vjvAbH/AgWAEHoAb/02/eb9qQZnEaoE+fq2+XPsivroBtT5JQHp/nX0dgWn/yz6SPma/N4JWANWAr0BVvlE+rsD7fhYAGcGcfMJ+OX8lwiQDrcITAUJAvLy3fg9Cvb+BAfz/c/5EwPCAQcGLP/lBrsAb+6U9HoEaQX9EvkZsQjtDWP8rubN6/fz5QFPCTEEw/3o/YH74fzrBukK0QJS/3T3GviCBNv7a/lM/pH3E/Pl+OAGqBpUG5EJtP0d+kj+gvoP+ncAj/yp9Uf8+gJzEIgT9/Yj+KX3ie+eB8EKiwJ1BwD09uyx/RcBEQYiAIf+afla/foCavtzBSkCPwJn+xj+TgUYCFsLIP1YAJrzt/VzA53/uvvUA24BDfV4CZUB3wPGDMb+KQAPAPADoAVq/tXyWfG98RIFwhdhFCMHKvuZ+7nyUPc9/GUFCAl6/GrxQvZrD5UNYgMr+wDwRe5M/I/50fsGEgALYAHY+pD8QPdC/OEBjPwzDA0SXQm//BL71/ZR/279nfqd/gX2pAVXBcwLIA5QC4cOz/0o9Q34VPyH+/cE1P8XAukChv18BAUBCgH7AL8DXvklAn4H+/4YBvv7LfMM+RgB3v6dAvr6vvwS+8vxCPuQ+7ILKwSyAOkHRwNICvsFqPnD/KAIN/Ns7zbz5PMKCZAObxGmELILMAaU/jzx5vWv/JL4dPt8/VsJ/xJRD+H+gfQ06370KACo+jwJ0AiBA2gMqwziBCICRPZP6YLvQficCrkTRgn+AJv6YPSN/jL/pPfI+2P0hfGHA40SLAeBBnYFRv0o9XzwoAuSB8L+KgKH8Jv0GAfZA18J1BaOApIDlQHF93IDrvbU7o32Xf59ARsHqwbKA8QKiQBe+L31vPiNADn/yv2S/UcJDAelAZYG0v08/VPz8fcy/5/9Ng3n9cf2qQPcAAEMOP3L+XzxLPajBw4Lvg2WA44N9wZY9iT4Ofgj97T3a/28Aa0IzgnODMMLvBXmE5H5NPZ+6w3pHPql/+0HfBmRDsEEXwgc9qr/YgHM9Hj/AwHL9cr5zAUCAhUO0QZ887T2rfN2A6MJRf8eB1f4kfSg/dbxCwlOEZECGAX0ArwBSATD/Wruy/a19k3xAfwyBGgO0hLzBe764P889Xr4ZP2t9E33VQDYACEDORGwB50MGwNg83DyGvGj/Nv04gA7C84EJQIJBJgB1QYxCgXx0PeG/7QB5BN2B//6fQeG83Pu1P/k+qoMTQwpBfsHigpYBxL+t/xf9/7yu+0N+aL8nwtiE1oAkgAQBNf5OfgM/YH4ZgyOAEr+6Q8Q/pX2IfHT7oD5jx0cF/EEwwLD9X77ePcD/Sv+hv5kAHL++fdS+qkGywTGCR0CnwDfAb/7qf5t/4z4MgGfAtjqufYaAib8sA5EEzoFYA6y/nzyaP8893X7FwEl/rDysfR8+p4LxQ71AAoHEvFH//QDm/m2DEUE5AU8C8T/+vkJ/2XyVe5b/f0D1AerFjYTwQSyDKb3OfSf+1/5xgg5/2XxEPrGAqkBsgnZArv6UPpY89XxPP7GFcEPJP09+hsAevuJ+JLzcvJkAVsDLf8uBjQWfwzOC9f8W/JsBbT4ewOLBQcD+QVM+uT5EfrOBZIIuwJ493f3avqCBWkRVgdkC5IE7u127J35yPLLAPQDXvb5C7cIJwWdB0f9cPzzCQX3fvIpFPD7TvV4AlT/xwM5/v79zAUJBWUBeQCm9V4IxRFLAnQFMv3g9HT2qPewCIQQDwDV/6fv6OOhATsIvAG/EKYFgvbe+iXrsPc5AfD6iwLeDTAMD/vw+p3xZfPC7Bn1PwSrBjgMUv3oBVgGyA8/B0r/TAE36/LtBfIHB6ARKhFWDdAJ5Pxl+hQHxfuEDXcKPfmR/OT+uPvQCtAL4PcTCAYAz/cp/woAHwIGBVb7ePX+/TICxwpB/zAAWP1Z/Lb+DvkR/Ub9rgiDCFIKNvv4+Or7PO+MAmkKugU9Co8KcffI/dQDVvYe/koB1Pjq9xQFpQH7+RP73AHeAhP/m/5b/CT+KACL/jz0Rftl+z8AJQLq/YcG3fc1/8b9OvBy/XYRaAIs8wwCdvPwA5IHjP8tFc4S2As18i7ucfRs+ZwBov7nB2EHuxWXEWsIoAyc+Rz4UfWB9E7/zf9ZAYUJBAYFCIQUNAIi8XP0Qe4O8g0P2wymATwHnfwV+D339/OG9w0FeAD/Bf0FofXiC8MF1fiRARkHAwbx/t7/bfs5+vD9BgTeAKUC9Q6HCPb/uwXW82n2oQHG87oI0/68A+gPAvBQ8igDYf/G9VUBzvHD8xII+AGmAM0HvRDR+MXwQ/BS9Dn+CgQwFCsMHAND/jT6YfmRCPwPSQGN8Rn4FQU5AmIUAwkm8VP1w/gD8YD9WQ+AAtgGF/2T9PIAiv+wBpkMcflb8t39svTDATMRVgpxBG/6aviCAIQMkQ+bCkYB+vo38c3s7fU4/sYGPg2gBIUEmw8N+D/70gVX9Hn4KfP074sBwRIeD+wFSf3g/Oz+reud7wP8WQRcC/gLgQnO/lsD9v4o/mgLOQSe+mL0gPfl/BMHRRVABCn9AP5P9TH62f5RA0UFeQWIAd8ISQZb/Hr75fCe9O7y+PX3/SMGwAas/t4IRwU/Azr+/PxiAYL8pgGB/IfzPvcX+oAB2xF6B/n+PP558sn67ApZDSMNhwuO9df0nAO6/YL83Qm8B1QA9PwS8GT9YASlCD0Nqgl3C0gFiQPU/5QALfen9nL2iPphBGv+tgVhA0D9IQUGEDf96P4P+P3kKvyJ6gv25hDTAwoGhA3mAgT+VQcs+o73lPxi/en/3ABoAMQJ4ghw/S4Cs/ruAnMEyfgo93MCmgguAq0AQfd8BSr3ivIdApXzMPzSAT4ApwPKET0CNfb5AV3vave9AxX62QCSDDMBAQWSCHr1cwDY/RX61gfm/mn44gL0/28F2Bi1B1UDQQJp8/D3Hf5iBNUEggDw+lgEVP94+GsB4fo3A34H8QJXD0wEQOqZ9UTwj+6hCFkCvwHVCOv/hgIVGAoJMvyh8ozpnAYxBrQM2A1hC+UBavwSATb3KA0l/iH8ef/y+HgEQvxmBEAKxwno+Y/3cPTu8oUEDQF3BjIDPvRz9jf/FwmpDDD/Bvs79+j16vUr+YEEaQsCFFwB8QcSAczwH/YF9uQBrfFP/KYDPwWkEt0Ucg4I9lr7SO9V7XAAhgOyAmoFYA1hBUgGbPyN9Xr0Du14/McDbg5oGpALHfmN7a/vn/EDAXQQDv3h+Tr9B/tPCHESXAVd+M/t09+N9WgNQRWuDbAE9/8C/O38pvPj/PIAdvbo+q4EhQfYDYEJwwosCCL7ZgCS89r/qwiVAe0BsQneDQX4bvrP9FIGSwM7+t8OS/16/4cC/vPs8cIJqfdX8BIKo/lhBBkDU/bS/R8BiwDRApX8LPWN/uf+HwBJBRIH3wAQAYz9p/y+/l4KIg/i/wQFsfMt+X4Cs/5MBg0C2f67+OENVQsjCaAMxPLb50H1rf1JAPYayQrZ+Pn0Hecy+XgGfQMUCWkJyfTB70X0GAWHExEUFQX283nyq+T788cD1gvSEMcFogFhABAF8ftx9Ev7ewPcAOoJsA35C+AKb/r+AeUBsPJu73j38vTaBaQkUx2iFtgM4+y94Lb1+PRJ+8cNXgjP/OX57/r7+k4MqPvo8Xjx8e2hB7EKuAsRD0gLl/cw9f72Ee2B/3YIxwFE/goItwCM/GgDSfYJAq8OxwT/Awz/Dfug+IH0t/yR/TsEIft29zwH0QPZCUMMWv1k8On6k/dEAOUMG/mpA44G4wg6DnQJ2P8q8I3uNumS/ygZtRMvEUUMSf3F+C77yP6uASMBa/iz9C3/0/3qCTcRDgEQ+DL03uhJ7pgEUwHcCX8NWf4dAdgCUfzu+Tz55vFT+m8FpwL+CZQKbfwWAuEHXAeJCaIJxP6a8Wv/ePiQAfQGu/L9AmoLzwQ4AsMGHfdl99cA6/o9AoIARgF+/A0Agfuc/uUAvPHs+1AAIgPVBIYKO/sK7/MAh/XN8vkCsgMoB0EMlgDk/qsGJwQ6/Y311+wJ940INQIqDcYUAv0d+JQLY/56/QATq/2H+4P5PfepAqP45/fM9fT7/gknC5sFsP5RAWkAp/M1+JoF8wQ+AKwFF/4Y9bcIvv5Z/2ANxP/lAT8KxAhF/fkJLQ/HAOn35e/h+zgKOA5ZBuAJ7wSl9ZL2EfPX+w4LcgRm/s34ueyz+ywNwREgCTkAUvdj4yXxZv5vAN0J2ft27nP84/gk/P8RxQsWBEr6u/gf+FkA9Au2AfkDQgGg9H/xV/jQAOwOGgzVAUj7OvfLAnwM8hTIBLoFRv004nbuKvxPAqAHBQjq/24IdwHM/WD/ifMr/vD8xvhI/tAViQvp/B8LJAR4+eb0fPcO8A35SP0TBCwPCh98HPj1mPxC9QH6dw3cAlT8+Pyt8mT0/g5vAsoGJgFE9ioCcwCqAggFuwdV8CXy0vOr9NQLJAWu/0IKDf938KoB2Pjo/YsANfayAgkDPwxADOoFlwCwCBX/Rvir/jH0DP7w/0n9Zf89CRIFGA3DCfvyagQd+Yr0VAdjAwcEmwvj81bpmvfH/owL1/ux+Wn6yvyWCT4J9wiWBwYMaPgN9VH3mvTC+Dn5mAlWE6UNWgKXB5H3i/e+CDYBMwp1Alzzo/qbBEQBxg2cC5f6XPyl7djwzv5UCB4Mqw7iCY/5Gfvi+Wf4efQa++IB3wCeBz0JmwD29Ib+xvo6/a/8k/CU/XT7vAEFB2MHwgewBs4DcvRw+9v3Lv1MBrv91P++AvADhwJTCu0Dsv3P+BT0RAH7BA0IFgH58jz44QHm+x8FYwnf+PjxaPUvAZUHmgSl87T4IftSAG0Ljf51Bf4GjwSmAF4H8v2Z8vb6svhrBVMH1A3MC7oR4QfY/CcE8/WhAi8BJgceBYYAbgHT+9wGrwZDB378AQMk+vr5wv9Z/JsDp/1oCE8Cm/yJ8xj+uvu49h8FL/EX8Bf66geWBWUQz/4e71n+Afx7DJICAgNq+Kb3bvu5+eEEM/k1ABEFRgmO/00CrPz/AXIHzvYVAfj6Uv4T9sr4vfeE/WgEj/vyB9kHvQxQ/roA++uO7WYA8/VeBb4CbxM8B5UBygIF+J//6gisDaL+YwaeAaoBAfurCswOY/78BjDzB/5fAp0I/QuqCTsJ5/mX8zT1OwmHAHEC7fzF+BL/IwOXCab9cQSJ9Z7tHPEF/7ANfA1TBez5hAId+8L5hvkY/s/0i/7gBDD4+RD7BiwCAv4+/ZwDzQaOBTD7TgFL81T+4gDtANQBgvxr/xr3kw3PC/EIcQnP/Anx8uyL/gv/1gMhB2n/tftl/B3vBPnXB7UBOQiF+dL/XwLC94T7h/xL9z/uqv9mA8QFRwvFBP3yZ/FVAIv27QYSDPUCQgR4B28M3wDh+yny6vS9AysEmAXCEHwK+gpfC+bxSfZV+koE5QzCChENrwJhAj/+HvoA7rnryu4m9csE0RYRJjUQGwGA9Knu/u4b/pEBxPAzAob9WfxrBiUSAglC/moC3/hhATj88gQq/1b4lv9o+q8BWQgGECoAgvmLAsAIIP5LAZT8ZO2J/Sb9LgyoD14QKgEL9GP5Yuod81D8qQSGAeYMrAj+BmIBbOop9R7vXQBbB9QKNQb/AysFdvQrBCb7Rfii+tb9//h7ARoPfgeACc//Hv797pn9WP0Y+O8EBgEKCToA7AKW+7UCYQhjBS35TfTeAPb0/gPNDFYU9P29+TT/iepOBI0M3ASH//4BsfqD/BQBKgINBHAGNA+f8/D0cf8qBQf8E/xkA0H0h/5LBfMYuhAsAtL4MO/z8iQAAg2//vEB/e/G99IM+xK/EB0Civ6j8c7/qPqc+oD6pPNH+TkDGgtpBNcT+vzG9I36kvcC+3j7l//U8P4F3AcjAAwJ7wY+/qLzI/K68UAChwGOBe8HYQQwBUr3/Pm3Air/MgHYC8IAPf7J/VP6OPyj+ZMCmwW4AnsCRQhg/bAI8Qe48IUCsAOvAjEFxwYBAmT3OPtN9VD4nQVvCisFdQTbAAL8wvmg/OwFqf+d8rT0WwPN/Ef9lQUl/BYDVwoF/C744QYIBKT+ogA7ARkF/gYYCcsC/fvy+KP2HPreAKUK+gx3Apj9R/Yj9ZEEBAlABez4Z/78Bef8ggZ9AJn+sQvjBOb+AAMyAQr5FgGl/lD8HwgCAoIFWAEC+B4BWgNXAmQCOgM9+Tz3Tfpq/PwH7wU0+9fqJfYfACT80w5eCkAEqQUV/iT7pPrO+f34uPuF+dUB9wdB+/TyCvzdA70ANAU7CFcFAgMU+7jwmfp1B4kAnvwB/176dPIh+6ECbwVxCxcCg/3L/1oCDwQG/ygB6QY0BBL/oAEaAon/eAZqA6/6RQKQ+7T7jA7oB8oEbgMY/0YI5Qer/8r1zPKe8sf0VPk4BtAO9ARfBiD79PZOBKH8jfs9AYD4d/s9Ceb44fXjBRcDnQjUCY39b/sc/XL0kfmACAEQFRGoCMz5wO4Y8nL2bv90BsgFaAiLDLECT/l//sH6fvQD7175qfszA0MPyAG7CnkEtvYr+qXxD/MiBvIESwaVDvD+rgPI/Xf6UQN3AwUEcgIeAn/5XwgMCI8G8AUIAN79UvLD/RAA2AiiB8sFQf1gAJsKdOz4+bn8JfXrAlAG1gg+DAgErPmEAA336f5KAhP7oPbJ9gP6HPx1EJ8MmgFt7+/ztv9NBCkJ/gIYBy341vl+9nj/BwNJ+IUFQv5CAb4CBfzL9Kj8bwQoDU8RUf1H9z/4OwC1AmwNtQWJBTYIY/PJ+Kn/6AzGC68GfwEt/Zv43P1uCBYHnBIB/hH6HPfl92EAFPbr/r772/T98y0H/ftT+0MIy/zAAxQJsgm69AcFg/596/X2bPCa9Wn47Q8qEQMJSgpaBpH+Vf1QAo72l/+M+U37VPkrAKwM2P9uBuAC0AGK+Rf0XfoEC+oMcQVk/A3wLwm//EP4dQCc8nD3TQD7AqIMbQ0N8+n8rPfJAc4Sbvzv/wz7r/cW+hAJuQVfAWQJrgOeA3QHJBXQBu8G9f0R7rf0mPT4AXgE2g8WDzz7AvOy+GT5OQHLCxQBU/te8yH5sPMT9s/67/imAbT6yQJKB4sQtQ78ARr5nPW7+6T9TAVF+48GfgTI/JsMYQLwA1MM7gBH+54E4vy8Ad8OYQcl+6D4hPUH9QcKVAP2CdcSvgQV+LjsbfXo/wAJ8PoA/aj1RvTxC5YEgw/gDZj3Tupw9kr4bPlgB9H+AQPz/C8GwwOVAO8U1Qt1/5X51vPI50H8DAWb/3cY3hOwAsT8z/tmBB8MK/0u8cr2uvmj+KkFLhL1D6gVIPtp6cXraejG9d37RQlNDOb+JvsXBfYDEQWJBiTuce9f80D2M/8d/P8DpQoDCbwD0gWpAOj5D/jT8sIIoA5S/nQB7/XS+F4M3QVm/3MAIv4T94/1cPf+BQYTrg1JB+3yQe6m9FX16wEjDGEMJQR++x349gXsASb8pwr+/EX7UwQA9Jr9IxemCcb+NwbL+0b3uf2uAFUI7A2RCfUC1/yqBY4L1Pkd/Z8Ii/iD9OcBhgjcFewSCf6c+9n3rPTX+3D9J/6Y96zz/f0oBg8QDhFwAuLvpury8Efy5QBqBkAGNxHECPz8r/rR9hX3rfn887H4lgAmBBwJxwcQBxAHvwPn/JX+4PjK/W31x+jTA5/+5wBbD/MDPPjE/J7+fvJPBCIF/AICBpv51PiG/DsBIADf/dv1J/3O+AX2iAmVFM8YHhFhBiDyO/Pn82T24v5SACoO/QIPA/oLFgpHCFkKk/l28jABEvV6CNEMbQTBED8InwM8BtH8sPHS9Fjmk/CHCDcNnhbLEOr+8Plp/KvrHfA++VL4/fWB+KUHWAqZDcELewH17Y38WPv08mYNSglfClgGgwFIAEcO9ATQ7nD7i+y1/DoRrA1OCjUFMvt7+0sGYfYs+J7xR/by/1b6kgtkENIAQ/uR99bv5QPQ/Qj3/PjV+Hn+OPm5/036qhG7DDr9Z/3k87MCBABmA9r+pP4i+FP8wgbWCNUW+wFOCWoFf/pQAAb2EfxfAssEzQyXEFoCLwJV+fj4hf+n85by3PjVBMkPEBtY/8zz8vU77Vz4NAO8C18Hzg5C/8/8Tf9b/hMExfjI/l3tu/V5BAQSbhwYGhMRDvUb93TmFvCv/NT9wgeXAy4DoQH8DBgAywglBW/zsfGF6lfwKPv2DfUJvQ+5/8P1O/5l+h363O48+CX37QBwBmEKFwlfBHQDj/BJ/g4AMADa/f//Pvuk+TP/HPwnFncFEwdp/KLnvf+tAxsLjBMoDPLwG/f5+Pn53w2XEHwJ3+8W9SIAGwiqFfEWCgfB/QD5IPAD/o3/Qv3p+h8GegHN/JwLPANlAlz5r/YkAoQKDACj+v72gO37/QP+UvWN+UoCp/uZCHsM4AT5CGzzkvU39bz/JAgv+4vzB/aH/z4GURWF/b4BUwDk7Vj7uAEYETQNWQnx+yT7GPX59BYFk/i6Cj4DvfcI/yAFBgh+CS0S/Poq+zUAR/zp+o798QQ9ACoFjwBlAmgHEAB/+ZT+DAUiA0f+Gf3A/wcCPwb38yn3Rf1J/BwBr/hyATP8F/4F/Xb+hQyWCZ8DRfkI/tX0HPyOAjH41QB//O0B/vkm+okIzQXYD68KeP+1/gb2NvSA/ykHVvxp9Vz8ovwhBBkSrhCGBZ/+Gfad8hT3gP6wA4gBbg/0BbP4D/w4+Y4F8AcXDAAGpf5O+7v1Z/xQBfANrgRdDu0BlvSqAJL7mggTD2gIOPfn9mr0vO4lAuUMPBAd/+T6TPqs+Vv+ZPaB9Jv4qgDk/74NRxHSCe4APO5766Przvh3ABYIqQ6ZAnP56P+CAej15ANdBAX75/ob/MIBpALyFWYIHfTw+Nnu/OwQ/c4ROhAeEYUOUwCA+k729/9t+rn7xQWU+wf/KAllAO378QZT/iP9YwRf+F/8XgZw9gX6fA5v/yABzASi+Pj/2An0CbD5E/Ud7jryfgi1F3cS6Pep/ooEigZHFjIUbff14brp9uxaCEUbYhLQBeb7zAAmAegGjQN7/y7ynumQ+tECfApGBM4D1wmc+lzyBgAh/EL/WRLc9OLvdP1r8pD+kwnrBfMASfoi9lP/sQKoCPEK8PzC9if06PkDA6YLKwgiBCwBs/Sx+HIAEgBE/+sAJP2JBMoKZv4A/1gAOvqw+df6pP1pAQUECASi/YwBEQVj/Tr7PAZvCm4CEA7oAp33fAXTCbkBNfwq/gzxuvsi/R0GAg5eA6IJfPcL/78BBP0f+Fz5vQUB9sv/CQc4C/AE6PqU+On1r/sjAjcJLfqkAZn/NfsoB7MFXAJO9sH3UfUi+/YHwgwhANn6qP5j8z/8ZgVoClr7PvsnA8H5UwxKCeT7+ARrCij0Z+jN+UH/UAavB1j+jPlYANgHw/5OAfUGp/mi7jfywvbu+s4IrwgTB5EOPQuO/6v6wAEo/IAAIgIf/u4Ah/+yCKkH8wxCBvAAKP1x9+EAy/n/C+EInvkk+9f4Vv7b/EX/UPyNCHH7WvfKBgX6agbZCM8CFf0W/+b1A+nx+hgI4BVABuT7Iva97QQF3wjnAh0J2AYO8Wn36f5g+x0LwQEy+Jn9BgIt9ob5lA22EFkPUAV3AFj0bfIg9XX4ewGW/Fn43PSUBpwH/gVhCqf/bv8h+bD7lvN28sgDEwak/xMBbwD8/pILS/zVAVkL7v9BA/76iATVD1kOG//+9qj/CQPMAer8fwRWA00HUf0j9/sH3gaqA6gB7QtAAA7vIfPO+eYHyg0ABsv26fXJ9o3+oQhzDvcGj/aE9uPzywUcDj4Em/cN/XAB//W3EI0Nh/2D/in/9fWR+lMLk/GV/AMMwgmgBFb/ZgCQ8j/+bPxa/+D79vwj/xzxOwd3/O3zYPqH+lv5jACuC5L5tf4f+eH5dv/N+bn71fPn/Q0C5wWuAw4FVgG4AKgJv/qwAwwDxPx/AcX/LABvCcsMgv/cBGL/PPnv/bwD8gMQDgwTcwE+AXz2egHBCAgEsQSM+On4yvoSA5oIxxVGAfnxcPhB8c8CRgMQAgoEAQcD/hj8UAHE92H76/MVA/MGZQYDBfH34/zq/PoJKPyy/SAFP/hXBED/EPqY/RkDC//3ARgDCfa5/Kj2D/vQBccG5QWO9WbzwPs9/9oDoA06BnIEQAbA83f0PfvU/iIATgav/2X4OQKKBdwIUwNoDHIDiPam9zL5cgNX+Z34M/Oy/w8C9PnLDrEJDQIJ/Dj70Pbm+mwAcPph/AD8vAAm9mIFpQ4f/q0ExwwwBaj4UQVb+yQAGRdVAWL7EQUDBFz4xQJnDQMCvweVA8wAKAIBCPMFXfPp+Pj+0gAGAUYDd/7ZACEL9v6Z/+77h/fZ9Jb3av/t+24FcwS/BXsLpwVt/Yz7Bvlq9gX8g/0nAMT3JAEuBgv7vA5pD7T61P5+AKj0kv8qAaz6NwWE/gX31vA59u4D4fl2//kNCgoNA8EDuvhS7jwB2P93+fD5uPYd84X7mhVmD80XXg9i+sz38u9fBzsGrv3+/mX+fv4RB28I8/7eD2P+yvil/Zz2KQMSBSkEF/0QBEQCuf3IA40DpgJu+tP+k/kl98sB7f5j+xX+ZwkiBbICEAai9/r5KgZ0C3IAtP5I+yjn5OpQ9AsMyBFUDY4FM/QoApMH4QSH/eQB7f0N97v6s/2YEUIGxv0Q9sH1Yf8AAGAKQAO6BtkE4P/w+1T46vxh/ioE/PgD9UT9QgocBm384QI9+CT2KPxJAFsGzAh9AzL9XgQdBuAGev2w9hj8hfdF/W780/s+AXECnQo1CesGBP7h+638sfbU/fL7VvjE+5UEjAO6A2YHmPsG/cr6C/+l/Rj1eAUC/w//BA92Ayr8dgM6+zPxnPgP/P7/6Ab7C6AFpP8jCMYGOgP5A8MBdPSA+cECWwHEDNwJawSf+YwAXAdI/OwEDPxp9w7/Yv+j/soCHwRC+x39rP1IAK/6xPnoA877QARaC8P8LQY5CPv0NPlqBysDq/5zClQFt/oDA5cE5ADaB1AEt/1FAyH5Ufrz/pH9sv9Y+Z4B6ARQ++T2+PuX+qb86gKS+n/9AwLM/F73+vm9/WX2+PdyAbL7+P3dBiEAXPzPAHIBjvxFC1ACIPbqAhz/jv2zAUQOcQRSBo3/LPMeCj0BSQnGB+z+lgIw/WoCUAOpCY38fwRw/j7ucv9E/4AKbgSb/l/+Cv6zBrn4/AEvA7X5F/3f/e0G7QsjDBMCtPw/+gf+ywFa/lcKXwSUAQEDH/gzAP8FzwE6/zr+FvjD+YP/+wGDCE3/bv66/dryZPywAF364/soAsP7XPsXAiLzH/V1AfEGNwt5CUwByPrB///0/vdr+5/3twYU/8z7ogeEBhMB3QgXCe8CIwn8+4/1UPkd8/b8EQBe+hUCXwddDekJ9AMB/pL6Ifzi9Cf8ZfyeCOoC/vlLCyH7EgTLBHL8+fol+sD/Tvg2CQwFdQdyBjsBFwS6+vULAQLG+nwCOALr/4H/MAIh+jn+1/xD+Pb3zQk3Cw35+gOhAnr5OPhg+hb54fSD/Cv7q/J3/TsFZP/pBFMNlQh2A2cHgfkN+5ACYfwBBagBsgHJ/6ICAQV6BaEEQfX9ACgBiQSqBO71Z/oe+lMDQgMRBG4EU/+T/KPxPgECCrgAk/8M+6/3ifx5A78EUgMcA7P//Pgq/oYHRgVHBwUH8vQA9TH+3vq5BOALrwVy/MIDxwbQ+/D/UQHV/on8+ALPAJP/sAuaBZ//Lv6OAZb1/vpmBevyJ/zo/ZH6QQMuES8LAf/lBSP3BPve9hn0jP7p/0UPTgPx+BQBvgJ/+WQC6AeC9Bj/IP/e9mcHtwlrAYgEoADa9qf7Q/qV8tz4/f2pBjULR/tzAc3/0PyGCKr+pP82CJgDd/EvAoENQfv4/IX5x/qz+UQKPw2eA+EGt/cC9kT86w0SCjMBhv7n8Nj1/vt5DCoGgQCH/Z3x8QHyAx4EOglwB5f/Kveb+mb/BgH/A08NiQQ9/Mf/f/uVBG4ORgP/+YP69/aU+f8Gtg19C3YHPfa48XYCtAIT/lEADQFb+S3+ywQwAHEAtP67Br73q/XhB5j4Q/weBH7+ZwS9CCv8jfxACcD/9vkw8bPzZgLYB24Srgos/6v8M/j9+IsAUQsd/4/1oPwJ+soGqQqV/i36uPma/dj86QDp+5cARwKg+c8FP/vy+lv82/UmBYwAPAGgB5sBZvx7AEkFafx8//f5wPfcCz8OLAj2/6r9f/gw9Ir9Av0RBJME8wj/DvECrwWn+1Hwxflb/VT5TwBlAN/1lAMCCesIMwjO+6j4hvMj/NMGGQDtBj0H7/cc/jMAbvXt+V8BLwLSCGINGwbAAW36DwIsA+36MQSj92D2xANeCEAHxgXPBTv5WPzOAaIFJQDWAOsDnvVDB+EIUgHLAvD19feP/swCg/43/Sr7cfr2/Iv8owWOBUwILQVh+or7xvVK8/j1X/umBzkEuf7OBDwEFAZqBjf5sfQS/Nz39vu4CtcGBwdHCgsF/gMmA5b/yfRM7EnzF/yuAmQMrwdCBTsLagFB/V3+7/qj/A7zze+gAFcG8wKl/wr8yvqM/0oB1wLmDokGQPo/9lr46wPaCGoGYPuFALT/7flEBokLXQgUBFwDGv4YBeYEygF3DBgH5AjdBBb+1wF39v3zLv9S/QgEJwj8BPcFyvmb/5z3efN/AZn8Kfp39nL//P+bBcL+7PXW+930BQjX/5b/OAYW9Hf2fvx3BhoJUQ0L/Pf1C//u/XACO/+HCJr/Ifo+AbcANwDVAQ0CUANIB3v5EgBj/D3+QwOi+qQItQGX+Gz2mAR9A2r9e/1z81D+6fzNBh0EqAloDT364f25/s/8w/LzA+D/r/d2BC78bQaEAkoHwRDmCPT9pPba9CP9XBG1BYz9nwEh/Uj4yAIECWoH+Q23/PD2WQJlAun27Pzm/5IB3AtpAOwClPr7+vT7pvol//j40gGs95QCQAWMB+4M5/YI+jj2igCj/mDzv/1MA+sHXQQrBGoBDwDm9mL5wARRAhgDU/+R+wsCcgtSAzT9mv0j/tj83QNbBgT4cPv99u7+7QfqAHH/kvmW8FTwNApxCNEHHwJL8qUDBQRSBEb7e/R99W/1HP5mBoYWFQmp/A8CxQXHAqH9iP+y94/96QC2/TsHkwlHBpMGpQP2/Cj5dPew+SX9pf9eAQsLGgfUAE4I3ADoAN3+rvEk8cT/xQN8/DwFwAeOCMcJBQe6/PrxY/p8/LEIOxAYBqoA3fS49IT7CQYMCZv53fS+90YCVgrhDW0F2vCc72jwjvkYBCUKMwJ+8U4FzwdSAckJAfxu7VHxxPcc/ZILawtFCD3+0fjAB8UI5gujDsAF6vLb8pn7jffgBh4WmQeV+AgEEf4yA+wRmweoAMfzHPLU948CcQTTBtoE2/Sx+nP1XPi7/eT+HwEKAPcIaQNuByAFWfus+yT7VPf2+4EC4vm4BOcGrPim+CIBewBMBlgLn/1pA/UBK/s7+pr/ZP8Z+eT9efl4BbMEQQgNC7YCDwTt+5EENPW49s8BUvlPCbEM5wQv/UoFsvtq98MGbPnj/6IJbQEn+RT1rvUD/TcMJwyACAIIBf1W+Hv7cv5IC3IIJvza9yz0CPadAbQOjQGzA78I8fki/Q3+Dfwd/ugGJv4E91oEeP5M+gv7A/20AkkGrwGE+rT5cPTX+Hv+dANXCTUDSAD2CkUJVPaq8/Lx6u8v/KMFBQr9DZUNcAGU//0M7gXf9Vb4VvM19CsL7hAyE1AVuAQE+0H6je9D9TwEPgCZDQAPLv33ACMBi/6s/YQCuv8N9rH3pu+5+FMIZgOmAHD+X/11/kP/svdj8vH7c/0cAbkF1vyNAZoAKPssBZEAf/x3/bf6gfkXAF4JvgRrBqUBQPiy+yoE+v+o+74IZPzZ+VkGKAFKAdcCDf9m+eYDyAJ5+6IEHwf3/cLyIPcZ/T0HLQyVB+YFkwCD/az5AveG/+UPUwUX/bz+A/Jh9rIDIQyzCNkMvQQL/B4ISwIzCZsMWf6A8x/0Zfuv+FT78AN9DswQcgoGBO//6PKy8cj/HgHRB2sDePHH85IG/AHy/3cJHf3v+pkAMwEO+tUBbvtP8ywM0goIC7ICz/i/9nbvCPyLALn/vvv1AEsDZwbYCZkBJwIX+b/1IvSK+m4BUPpx/owJOgtVAMgBU/yb/BgDQve29Q7/JAUKADYE+gwkBs37dwS/A3j0Rf5Y+R34zANf/bAAKgUsBQUDFvt9/ogL0AII97gDHP/F9Yf+OPyNAAkLLwn9/xf75wSW+tH3Hgo2BrMC9gEQ/+YAoAUxBiAEsAPm+Xr3bfpf/OgKvwuY/qwBn//YABgH6QIp/SX2Mfev8Hj3agLWBQMHwP94Axz9Kwb2Azb0CvOY8hD/sQHZBzsDeAMDA4r+BAVE/Dn/O/f/903+j/5kBfMHZg3I/071oftNAYb1sv9IA8P2TQWF//r3fPx4Byv+q/7AAwj7kwUT/VcE1P9E/YEFT/3A/Kj8bQOy+t8EUAdyA2kB7gExCd75kASU/z0BywEH+k4B+wB5BVT6FAVpBywE1wCuANwDZvpe/q/2rgaWA/YCnQNc/GAIpPnJAX3+N/85/7r2i/pZ/1EG6/gIBtsDwQPwCCP/5Pj390L8yO2i/cgDHAoSByIGsQjR8Ib5uvSI/Fv+dgcLCWz9rwPj8H4Ag/xtAMr5XuzNB30E9AAFBc0QZPvD+dT6LfL2Cf8DHwC1+48HdAZgADsAeQh6D7H7nQYo+U3+SwHc+34CkgB8C7P5NgQXAUEDxQJD/ZkIrvGw/pD8R/ow/f0CbQQQ+pwIRvsi/g79AgE9ADf6TQhjBAYCSAKsB3XzCv+pCH7/4AcUABv8PfeoCu/9GgVtD1kCOgc98x4EXff+81cBSP8tBD79ygcl9pABcAW7+hMAlQI3AfbtSv9Q+kH5fAIOAAT8RvtrBgD5YQVqBTsFDAHO++IClfalA8sCNv0Q8DL4XANyBeYVOgkKC+368vc9+5P6ygZy+Qj2AvWBAAr/+gs6GhQF5/1S92/xafVJBML8TPuzAywAY/uD/iUOfQToAx8AcP2O+1j8VgVK+rwBiwEeA/X7Lf2jBF357Al4DAkA9P53CgX5a/e0B4b4y/0m/rz/gwEpC2oHU/w7A70BNANI+LgD+wA1/5oC1fshBNf7CQmU/4n5qfxy/D0BUfzfCyP4HPzuBGP5aP04AaQC/vHc/Xv9Lf0JAcn6ZwCz+VcCiwMb/sP+SwDN9ur97wuV/DL3EvztBz79cAD1A4P25PyrATMJ2P6aC2QFgPRuBlYGGAPX+Hn9o/lu+bsGTwj2A3H+KQbJ98r/ZwjwAOX/vPtXBOT+Qwm4CykBEvcN9ZwA8vq5BSkK+geRBUUEIQAs/0UR5AFo8yL2Svso/9EHPxDcAcP+i/uS9l301f7rBwH7EwA9BJH7uf2lBMf+Sf18AQf+EPe292UCIvjQ+gcEQfsY+9kGJgzn/PcBVv209D7+g/75AlP5A/+x/fvzuQVKCEUAnvze/7z1VPtQDv4FQQQ9BiYCj/Xh+JEF1wOJBBsG2AMW+cMA+gDU/C0IKg+2Ej4AUAWSBJP2Uf9F+y77D/6hBDz7JvsEDasFgfwO/w0LzftI9z3/ZPeC+6j7A/769icBgQlB+Xv56PzO9lTzoQ2QE70DkwFp+HHwt/gqB7j+Gv6jAQL+Gf1CCewSYfy5/KX9PfV8+WYEgweA/7EKfwJ8/n4HFgOd9w/18fy077z0kQjXD9gEYADlAoj3wvrt/GYAwwErBbcBq/htAEkK+wSE8zMEAgEL+kMLJwlDCqsEagSx+b73IQIhCIQKg/vv+YTwxfcmCskLYAP9/2sAL+7A9k/+lABlAAoBiQcIAWQH5P0Y91H4XABe+FjxvAJ7+P8ADgVFCtYOdgMu/gvvWPzv/3/97vdo994C+/xRCnYIsf8eAWUA1Pgq/EgHswJRChsAdAGMA2H82AIE+z8CnwRyBOj+/QBIB6D5Lf4p/WQCOQNkA6QIn/89BR4ABgBp+y/3KgDc+GQDFQppB4YDwgHqAGnzrAKPB6//pAQQ/xX96frBBM8Au/hNBSsA9vvD/u7+ovYw+0kH5wBF/dL39P6aATL+bQEJ/Aj+2v+f+jD2xwXl/r/tc/yC/h4DFgtsD6UDj/dP/hn6EQCVAz0CDPw2+YAAef+iBs4I6QnLAWH5OwPnA7cCKwhxBpv6dP2///T4ugAiBpf8APnNBHUFagbUBh8Cn/82+Yn7UPps/O3/MAQ3AUb53AJuAHID6Ql4BVsGwwR8+1bxYvuyA77/MPxO/0EDtwTICZsIJwdH/iH4J/FT9WMH1f9W/Lv5DwATAwT+4w1VAnL4tPrE9wr1pv1LDLn7e/zd+/X0cP0zBPgMNv4Z+1T7dvUO9V/9hQ6FBqIHEQQ79dL3ygSlA9/6cgVKAd38nv2dAqgH+wiADAb7bv3FBKMEcQKd+eP+o/rp/doCTAJLAx0GQAlH+mr+HQN/+JX4rfut/g38KgTOBdwAsQjCApT5/PwZAST9WwBlBJcAIgIO/5MF6wP/9+P/F/yz81r8ZQODAQ4HyQhO/z0BXgLS/8f2//jDAFf5EPvc+Rb/0QWbC/EKLQA1/yH10vi8/H8EGgnM+Uf6pvhB/noCIgnkCsf/cv0U9Wf23/wbBHQDuAPdAzwA+AchBd8G4gM1+5352vo0+4gBgwgk/dUFBglY/lYC2v0V+br85gGfA04GiP5E+dz6B/fHAuwGKv5X+ln5MvnX/iYJbgUAAsEBUv6o/2//FwXABG727fdR/icAYgVAAoQA6v+rAtf+Rv4LCL8DAAluAoz7OgA3+8T5X/fpArIB4gJVA5j3yQDHAIQEuQQoA8gEE/yW+L76yAZC/WP4tgEy/M7+i/8UAmcDugDa/XH5YQZsDEQG//3E+Bj6fPYq/kYDPQb4BUT/ywIbAswEaADw++X/QP1c/q3+lgBtAyIEXf4m+zIAbP3c/gL/DP4JA6T/av7w/ocC0ABo/L786Pid/yT68f2yBnQDQgiUBTMDHPXl+kX/Cf14Bjb8aQFfA24CSf4N/2kDEv5sBMMBcAOqBnYH1gEu/xABz/o2+Hb8nAFt/+IGVQXOBFMGgQKg/SD6BgE1+5v4D/zJCWwDoftRA1L67/yT+v/8yfzyAfsHR/xz/18D0v1y9Hn/AP8G/IIFPf09AlgGvQIt/kf6Ffm/9hz41v8GClgFXAJoAiYBbgFE/QH94v6JAKL+Hf95BEoI+v5J+5sCuv9/ALb6xvfUBbkPuQneAq4DxPs/9sD0evzcA2oFDQEw9h37ewMlCQP+lPqq/x77NgWSBfD9kP8DAXb4cvzZBeAGOwII81356gB1AQAGrQJI/4gEvAQx/UwFPAjyAKT6PfpX+bv1+/wKAxIIBwlaBwQAF/hd/Mz+q/6nAJIFDwSLAa8C+fun+Xr9H/9xAN4BmgQMAUz7X/4ZBcQF4gYSCEz+UvxvAgYBq/5u/2T+mvtU/ngCFATkBkIE0f3j/gL8jvtG/BH9IAVZBEYBSv7/AEf9XfwXAKH1WvcL+yv+xQLtB3YGOf56/I34ZP7r/o3+9AR/BIkBj/xT+ET0tvng/JgCJwl9AyoCxvwM/h4EuP/W/lr/BfzG+iz/7wIzCMQH3wKl/iX5sPoY/kAH3wjSCegGYffJ+/oG2Qa2AkkF6vz7+Yn+EPoLCWgM6/8C+Pf2vvsX/8kBLQR5B2UHbgLS+QP60vvzAJn9ifqe/lf54v4oBs0KhQNeBkUEVfb0+9H9nQB7/owFGgOU+uMAxv6U9gf23QXrAQ0C+gWN/sYA4vyP/a7+rAFmB3QEvfu991n6cft4/JADzwNU/+UAhflK/MwF8Qp0Byv/qvwp9Aj31/gM/m4HHQRdAMn+mgCzAF8L9gmKAIMBX/mD+ukBAAX1AxAFMP/69VX+fQQrCS8I7AIu/sn6VP/k/1kBYgLqAI37KvhS+bX8XgAWAasB1v95+y75xgGmAaACjAK/9kfzh/W8++H/pwwxCSkDOwclAbH+SPwh+5DycfxmA2oGDxEwDq4OaAN9/cf3ffYE/XsBpQNKAkIImv84/HEEkAnwAOz6rvo49Oz9dQWGApX+6AQ8A7343Pmu+YX3mvovAOv9nv+AAjkBUP0lAWYG/QELAzX+yvh8+w8DX/9x+VP/Yv/3A1wFqgLgAw0DYQFO/iUAOQTEAw38Mvda+wn8jgFRCFQE8AVtBKH5dvW8+aD++f+DBKYEmAK5AGT61vvs+zAC5QjXAbcD5/+e9b/0JP+sCCwDXgV5BDgAiwHSAQIGeQNOA4MBqPlG/vr/EPlG+6wCZwZPBbYEyAFn/bH9lP+IARsD3gIc85Xy5Pyh/F4HzgZaBuAB4/o7+zH4HP9y+Q/5LAE1BhAMxga0CKEDcPO97iz0o/lS/UQGqgnIBowG3Qb6BqQH8gUw+MTwefg9/A7/9whYDIcCtPuV+RUAwAQLBEMDNvsbAVoEI/mY+Nv+Jv91/4z9sfgk/s4ANwC3BOQF//9z+nv2xPmHAewGpQwUBfn9Dfsl+wT8QAECCSEAPv8JAHT/YgRRCyIKsQL3Ajn3rPQD/+YFVQXqAOEAtQDCBZr/iPYD+aH/yQGe/NL6CPtL/b/9/wE/CUAIQQIR9SnsWfbr/hr82gSxC74E8wHKAcIEDwWw/8v89fnl+Ln8DAM9ChsQwQrd/RX47vxXAXv9Uv2VAen/sv3OANYFiwp7BvT9F/lr+bv+wP29+xb/NAH8+c/8uAb8BEcJIQgkAG36PfXm94P+eQLiBZUCl/oC/Sj9Ef5SAbkC0wBb/c7+dPWm+MgBAQFSAjsCOQEj+S36g/r0/akJeQRH/lr54v2hBLwDuwMSAnYChf3DA1ACVv6jBGD6h/p7/1oGXQgqBjkJTQBC+br0lPknAKUCkgMUAXAAAAGsAVYAjQeQA/b7kPhp9w7/HAGPA5kEjQr2AnL4EPt9+N4BXwIcAP8FgAc1CLL+9f8mBTUCFft28wv30/2qBY4DtAgUDq0Ha/9E8Uj2Xf6+/Z32ovaaApUIfQaC+4z/tf8x93zy2Pe5A3oIWQj/+0f9FAXRBMf/GP7GAWwA4Pum+cQGDgkfA3ICbfyu+7MBywCM/f0CcgYgBQgBB/5E/iv+HPiy96z6bfzfAWYFKgccA10CF/4V/LoAHAPk/BD12/pTAcwCVALLCMYDPgH0A8r96fsO/Ij8EPUNAdwKqwbKA+kCWQLq+xsCb/us+6gFewO3APAAuAQ4AqH/EQHTBKUAdQG9/3f75gIhAxH/vP1m/13+fQG2AvX/7vvg9bH3BPlp/4oBIfyyAAUEKwM+/6v+qQER+hX07fFM/doJrAnoA9f/bwd+/eL6jgAhBQsKJPwJ9Wf6YQggCD8EkQM+BEUCnPjM/lcCEQacBZr8avZt+Wz7JfovAaoIhAppAIr/q/tB+Nv83/rZ+UH73QHIADcCrQWhAr3+JAFhBJD+DP6U/zb9xgBTB1QFDAAzAlkCMPqO/v4AzP+rBSgGzQJY+6f5TvrpA9EF0wOK/bTyuP7GAeEDDgPw/tD5APoBAvL9eQWRBRT+oPmp/J4AHv1D/8H+5wRWB0AD9gC8++j6f//t/K3+FAiyAhD9OwE3An8Baf80+9IBRAv1CnwBpfrm+0P86PtZ/eQBiwMeAKL79gK1BvoERACJ83v56Pxo+qX85P/l/aP7hgHY/doAYwcqBUgBhP4j/BH5SfxMBokIRwPgBKABjfsXAd4HuQCVABcGW/6W/FMGRwkoA2kDXwC8+Gb2O/20/qv+fweIBNL93fvE/0P64fuXA/n6/vjm/54GJQA7/A333/GU+c0AQgW5AgYHxgGr+2cB9fxl/Hj/Hfxv/AYCUwdYB5P+rvtFAUACUQJ0AzMBfwSGCA4DoAR1BZH+qPmC+PQBiQ3DCXUBpv1C//sAsv0fBIwEff/T+Qv1Ff68BmwM1gWbAVb9uPZt9ur28gdBBdH8vf+I+nf9TPxg/bUCXQYtAsX6yvx4+ysBWv7G+TMEmAKu+0v7S/55/TD/AgJAAGEEkwhpBgH6K/MW9s/5r/5+BWQISgEcAeT/Vv9cBHgGh/8c9kL6lPo7/5MFAgbqBKoCOwM4/wP/R/83AZT7xfl1AXP/hgSFBSv8aPxxA0/+n/wU/y3+Bv63+GP/MgWTBz4FpAL8ATsAkAKf9yj36PzoAtEHSQQVCtcHJwO8/273QPsPAA4BLwaNBHQDaAB6+Ef4oAGPBab+7QAR/GP7/QM1ArMAVf4aAdMBUP9jAUwFFP529xf+CgDYAjQA0fhU9zUACAmJAyMDxQU+/oj4QvmA+/0BwgJk/L39EALw/8j8+/0W/qz+XgDhAdID/P/B/TP/gQAjArkBFv+X++768fbi/c0HWATvAzf/XwBmA5gCdgNEAMn/hv0N+wf+7wlvB5P+ov4u/rMBW/97/ygAqAOPB5r+/vusAjYA7vy5+zb+MQYjBRgHxgO9AA/8MfY794H5ZgJ9/9UDZQV2AMr+aAIMBtcAbwXt+Cz0A/yC/f39iP/MA1L/GQCqAQQFGwNzBOj++PV6/zAE+AUDAxECtf3W+pj4nvvkBOsAjQNW/7j7nwX+B+H+dwCUBwv+xv0A/wH6l/oc+Iz3C/n8/LMEewneCBIG8gIF+if4yP1G/YL8CPwp/RT//gFvBpoDWvwh/Yn8GAFnC6sGTgUyA90ClAAv+JP7APwl/lYEGwicBn8IeQT5+zUASPyN+gj7VPkp/woAwQBrA4UAeP2Z/dn9S/lj+yX9yvdgAWoDOwALADz+7AVzCFsDuPtD/Nf8jgFjCOYF6AWaApL+iPs7AsoIwwKh/on+Gf7D/30E1gOz/kn8gfwX+479IgIAAbb9F//o/tgAqQYQA0MD2Pnl8rL6+vfB+o0D3wOq/6MFWAb5BP0J4ftb+KP7xPPk+scAMgCECPkKIAAOAxMHPPjC+2/89fn8A7UC9Qg7CHUCGv9C/aP82fu+/rj45gAQ/kf8fwVXAnYKRAVC/cr9jfs49s/1iPtX/mEHawJJ/1IEYwArADcB1gCp/tn+Rf0y+pgCLgSh/wMDNAERBPsBuP56AFj75/2+/q8FvAWpABT9vPfg/aj/JAcTAWn9Vv3y99wB0ATYB9P9qfyA+lz0yAH3BA4KywSn+4j4Of1xAvUA6gjyAxcBFgBt99r+kwecBvoFTgO1/jj8w/+JAecDBQVv9oz1xf1JCOcPWwhsAyL8u/PF7yP8NwKz/4wA5frs/6kJ2Q4B/2b1+vkA85Pzfv/CCnIHpQXkArr1bve0Bq8EpvyuAOD8RP3Q/14CywTC/x4DXgLy9JD86Alk/NoCugoBAKsCZwayACv0J/xNAsL+ggA4A2ECNvq1BXUEkP/eCMwH2vyE8+/9av9g/hcEqwRW+8r5dwCp9/j+wAjWBt/8G/xoAs354/3HBAgAJv3UBEX9OfUuAZ4DsQFs/44C4wZ0AuYAdAIn/YUBEgjp+jv5bQZvAYr7LwTaAAH8NPzi/pwAYAOMB+D91vsJAWcAhfUT+koDiPx+/QABWwam/+3+1v2T+Vz/EAHI/y331gP3BPL8DghXBSv8Ffhr+yf7DQDxBNAAZQNgAvoAJAA+/rIDjAJ0/r38HPjP/MECPwXfA0QDUwBQ/QQDNQGPAlL+jvwQ+235/QtVDBYKKQMI+Bn8XP3+Az79P/ph/ez5I//+BJ4OEwwyBcz3ZvLR/NL4tAHAA4v8PgEDAtz7TfxiBqP74viY/9j6zv86A3wFSQVPAXD7n/Ux9l/3df+e/V7+fwqMARoBsArDCNz//fqa+136PAOuAqAGRQUrA+EGp/jIAYkEswDzAxMH3Aag/0AGdvtZ/SoAA/rfAYz9iwCm/9j92gBsAxL9ovTY/2P5X/k4Aqv7nAC4Aab+GPsBAPkEJ/sM/4P+tvwB/yEA0QeOAsMAaAENANoC1AUpAIX75gXKCCEMbgK2/R0CdfVS+6v9af7JBqYBJfyQAHgKxATQ/xj7pvdw/H31PfdvASgBLvxK/or98PxdA5D5j/acARIAZ/5OATAAgf/y/e7/RwZaBdQFxQRp+tj6KgBo/iIGbguhB2cCxf6E/4sAiwTBBd0Frf5Q+Vn9uv4rBY0HVQEy/mX9mPPR+WMFwAFfBfIAYf0zARb+f/qZ/00GTAX3AWj9FfnO9EP3GAGwCx4P3wj5+cjyj/11Bu0F/AM7Baz+E/ch9bn9ngEB/xEBPvvtAToFHQHj/sEAjgKb9iH3EfnM/WgDqAClBZsC3/eH+pMCBQSzBjsCRvas+akAEfwtBDoMhwQn+6D3b/6OAlYBbgCUAs8DXgTR+3D3MQQQCC8Dmf0UAO0AyPvX/1wHhQe2BuMCaPpAAQsFLP+9/I4CaQEZ/MICff8T/j7/5f/gA9MBc/4LAI4Cgvtc+gX7KP86BZT8xvju/pMAxvpP/vcD1gIEBEf/s/68/g8AUv6T9qQDvgWh+1f93/9aAxcGowZmAjQAoftT+1v69/w7Cv0CM/pH/nX9QviHADEG5vmG9ML3WQH4A2L/LQN9Anb8sPkx8tD2yQbABKH8YAABBzIDs//cA4AGGwbLBln+e/lzArQDxQKaA6kHVwCf/m4E5/9gA1oBAAeQBJP/IQUxAgb+tPeX+GTyev8kB5X5LgOHBr0Cdf3vBOQBbvZ3/M31dPvhAUcHggWe/+kI7AFmAGcBAQPT9sLx9QZSBdwDVgT0Bm0BGwRmBZ/xDPxm/u/3e/ftAnUFCfsOA3r7Kv8t/pX8WwJ8+iX+Wv2S/CECKAuy/u78vAW09Nn5x/2m/4YCzv9OBOwF+wu9CqYH9/4r/4L7KPNjAY0Bq/9f/20AH//yAKULjAt5C0//wPkH8iT6Fwcc+Ub/FgNqAsX9PAKMBTH8kvzE+Ff9UflFBTkJQ/v6BVAExfvf++0BLPZU9P0D8AOkB4oIKgbQ+sb2bfmD9dYASw65CQv+4wJDA9P/FAF//l3/3vlf/lb/afkbAnIF6f3U/7sJUvwU+hMDAPwvA1AGNwOe/O72zPzH/ZT/BgFK/Mz03vugAKX/ggkyC80Hbv33+TX7dPfw/aQAUQK+A9sAR/rL+GsE4AYYAycEaQJB/Fn+owO1CdAOfwHj9BLylvjv/1z+SQPRDcoLK/uc/Hr8NvvNBoL/IPrs/DMCL/88+2wCSP5b+XoAOgcd/ZQD0Qsh/CD4nf3QAOn8AgYRBs/6gwJnBKsAF/5CCBAEO/UIALcF7wC9/sf/T/ah+ZICagDICmwK8QSW9pj0DwTnATf9Sfn5/TL78v8BBg0EIQzKAlH5ZPGN+TL/yvcaA7wE1/3R/JUGSgO3AYQAn/bq/UMAWAcFAe37NQQw/LT7nwYIA175RQhFCtIEIQeRAX/6dPckBRIEIwOaApP2lfQA/n0KOQYdCMcIf/2Z8i3zCvjf+ZcH+gVQBLYFPANv/kXy4fbm9PTzivr8/nQGPwpFCbMAzAJM/kT+wwBq8Zr0U/gVAUQNPwiDBxUJUv6T9qEC+AD4BQ4Ih/nrAnoImQw7Aoz04fsv/c39cAYcDAkAfANxASL1b/0FAC0Ccf51/rUB/v1lAMkEY/5j+3sDlPgE+i4E+v6a/nYBvv/r/ckCSf6s/F/7Jf6ZAf/3BwDoArr8LQHpBAYDFgOF/ffxhvI1/eUG5AKqB3cG//vyADYD8wLkAx4Jpf+19p38OQAyAsoDRwQB+WX+swZ1A8wDwwlyCFT4V/wf/e/5j/3V//z82fxNBGT62/0yBuAHIf2w9Yj+evj6/vcHuAe/AOQAePx09pEGfgNH/jD/jwflB6n+dAPm/gr/2AQaCv/+ufrnBWz+qv/6A9kCygH9/YH84/th+hgCegpd/skCpgdo+A/25vVx+fAEtATs+fD4LPts/34Dy/86BJkAAPoh92r4FACi/90BJAGM/mP91f7+/28BQQR4/18B5fhB+JEFxwQhCwQOHv6z9jn5U/Jj+3IHBQhyDKoIVgbQA38CeQWeA/H8ZP0D+4Tv/fneA8QDMg07DU8Chvsm+XH2tvZt/0D/Q/iV/Q3+xfyVAowGyv3M9hP42/QR/SAFdwkiCK0D6QQaBGoHrAO2/tT3uPMi+r4Auw+XElwIoAG/+Q/+EQbiA8MB/QD9/RH79fzW/d0C3gDH+Bn5Mff3AAUESP86AiwE6gB3+bn5dv0qBrb/sP5y/xb7VwYL/fT6tQPbAzcHygrtAVn6kvmx9A8DDwU9BqcKn/u5+IEEFwdQAOYA8e/76nPzQPdGBiENyhGECX/76fiJ/uf3cPUW+1T09f9CAagAiwoBCSsFwPwa/tUHuAtlAxsEzAHV+9MB/fpfArEJdv81AKUFwgP8BZcKygQrBpD+Xvly+7zxkvQo+IYBQQwSB1ACmAPX+2ry0vN9+JMJ5wML94L6wfdV/zICowIpBoz94u0S9XgH8g1VDW/+8v1H/+v2Gvh2/iIBVgAr/OL53w02DkoABgHl/0T/EAHwAeoA6APl9cH07P0M/6sIKQJhCckQMQeI/778yvsv9Xj0jfWEAWkGYAQmAT0EaAos91j0vf01Al8E2wgJA6n54gKu+aD7TAEnBeIFSvl4BYQIDgQSBXUFF/nG+I4F5vqi/9EEoQdXA2D+SAGL+av8df1d/Fn8XgjMBH/5N/5L+P0AePt3+UkBkPtkAdUAiwLcBAcAKPZz86b7eALTB1P/Mvo9+v35ywNkCMsJwghp/YL4Wf1u/SD8hQUXBHn+CQVh/14BwAHWAFUCtfUf/4wEYwT1CjAIowJz9dHzDfj4+7YAGgR1++jzWgrOC0YGxAwkAYP6ufP88Hb7ZAIIBowJyAC5+iMI0gMjAfEDQfsUAmEAH/sT/aL8iwLhBtMELQTkBasDfP0o8sn27ABt/MT9lQHABlgKCAbUAA37IflV/NL7xPvDAGT/FQD1A9cDrAN9/cL9NQBc/cIBbQK1/cb7awE3AWkBXwNP/I0AlwDYAXwBQf+s/X73oP8d/k4D6gYsAKH+RQFbBqT+i/6T+gn52PWP+44MdwjvCuwEP/rX+E/70wCaAakCOgOqAdYAoAvzCXH+3fvP9NP1gwArBQEKuwqHAu38o/qX+fD+kAYG/y77Uvt599b4Hv5FB9UCHv/5+4H4j/0ZBlIK6AGy+pr1Yf0xAAcChgWY+x8AewPj+sP2r/9vBTz7bvr7CLkN2ws8BXb2NPQ9+mH+m/wUAbAEsAHyArUHSQ7ABaX8vfZG89/8CgWPCwwLVP8r//b9+/N/+zz9CftOB6oEtPz1AuP5c/X2+6r7xArMBYn8jAML/4L+yAWhABD2dPyq98v6ngcmBykKTQQJA/f75fTB/lEDHw3rELIDBf+++hT3XwAm/5P8gwTWAaABywfPAGz+IvwO+C8EbwrWB1YANfAU7rj8uv6UA84JZf5u/yf8D/8VDtwD5/pV9bfyXP0MAn0HRBBJEOYCKvbT/IsB7fzI+n356fw7/iT+vgF5CbMGrPqP+4z6PQNbBmD4ZP78/XH1ofdEAy4ILgC/+pT2if9Q/Lv7ogW9AkoD4PpR/roI8gTe/YT4svslAkn/8Pha/+f+qPvoArYLmgulAev6WP3WA8QGeQeL/z/8tPYh9jkFyQywDKwDof0C/a7/vP4HBRsKPQIKBF7/XAFrBQUF9QHx+b/5Wfa5+IsA3AchBzwEVwNr+0r6pv8nAZ790Pfe/T8L5QVo/S/0XvKtACz+jPhtAy0JJQMaAuT+VQn8CqH25fKQ87sDrwbN+qD/s/84+73+XgIh+moEgwag/hz/afWp/ZYDD/2ZAq4DDfzuAQP8E/W+BTsIQAP2AIEC9wNy/t37DAAb//7+AQOI/kYCfwTMBiEGIQLr/7L0p/Su+2cAxgLSCwkK8//sA6z7RPlxBK39Ifbe/FsAjgYxC44MBgcO+b/4EPiq8JX1QwKLAgoJKRHNCRACoPxt9TfyewAMAqD+HP/iAiEN/gcVBq/7+/ff9uLzXf2E/V8I1AdbAzgE2/3NAQ/9av0uBKIAOvgm+Er/C/ykAoIEMPkB+pYC8gqSDG8LyP9c87r0LPxxAFX9x/31+Qr5PwM9CAMIeghHAJf4fv4WAUX8wPlU/JX5yP2YAdwBnw/CDhkCFf1v/Y77Mfv//W8EjgH5+AL+k/qKAgoJ3v83BNsG2ADL9Jv2hPrc+uwDkQC/AOYB9AA4A5QAogMn+/r2f/98A/EJCgvJA+X4kPp//lv+LP6PAu0CWfh0AKD8J/+7Dt8Cifr7/vf+kPsU/v76Iv/f/vn52wMgBawIRQbd9pX6XQbTAjIJwQXN9W345fnD/80Hbwa6AbMDLAAu/Nv9Vv1qBbMBJwGM/Rv3mwBNA4EJdwl8/lLz5fLL/eQBnQPFAmMDD//k/9wKnQBi+9b6wPEN+WQCKQS1An0E3AafB1UDQQK/AWrxbPjnA/b9egQGAlD99gTyBVoDTAX7A6r9cvr59f/4+wA1/1ACTALxA+YDQgAVAn/8dv109ab4B/3p99MIZg8TDksFbf3y7230wQDb81z/EQGLBQIJrQV3EKMFQ/wZ8TTs5e8zADYO2AYaDwYLlP0q+5v8Rv6V+4f+QABF/wsH8QpRCKIGj/xI+6j3RPiDBp8GkAZFC9ECN/sOA833sPojAwEAAQgq9SX61wLk/AL/Zv1HAP79OQWB/HL6v/w3+7//xfy0CLz+pvk0//71hvrJAtwGXAKX/uv8X/3HAgEAnfsv/bkF4AHY9QgBOfyw9hABqAJrCZgH4wPI+jn8HwC8/m0BJADqAQX2XgcaEPkDkgxvA5j2MfdH++P5fwN2AqH5VgB8CAwOdAE2/c0DfPnn8/P8av+IAAMCeACX/24FuwPT9eX6JAFeA74FwQoFCA4AQf9E+Cf9Wv5IAygM8gHv+X397wF4B3YHrv91AOj7w/vnACkBrAMCAFj1mfzEBkP/C/8n9oHxO/On92oCjwYHCDgCwv3s99f4w/VQ/5UHhPoY/fv5Cvcx/+0ISwpNCB0GJfwA+SICowj8ANQEagZS/TsCWwjNBUEFSAGk/IL9XP81CdcFmP/iBw8FzvwvA48BOv0FA8b3n/XW/hgDgQOFAP4AHgSGAlL5Vvuo8mH0ev1W97gI5A8cBjn9Iffl9QL5MQgTA6X8eQFP/qz60PdAAUIFggo6DTAF9QICAJ4EDvgn+DUGv/8k/of5z/1nAXEEUgbFCDAMrwHZ/3PvlfLZ/5P1G/mp+lICewYMAaMB7fxK893x6/fa+sEBP/5U+e38zgUFC4AFPgfzAUP2MvVa/uH9J//4CC8KWA/1DaQG0AAgBcoFaf+sAGEGqgeH/D4CHvyt9v8CHAAwA98MYwuf+fP0SvUW+AkBpQMqBLD3+fy3/h/wyv2lBv77zQBLAYf2Ovk6AN4ErAcIBbQEef/i+RcG8f/v/XcFLvqm+Vf+PgjFDOEL5QRC/rD48feUAt8CSQ9KCEv6pfbw7Q/3mAN0CdQG2fry7jT9fwI9Ay8LcP/2/UX0K+zd/3MHyvz6/OT5awK+Chz6v/qj/YD7sP8RBPQGggoBBFX+AAYcA/ACEviH8A7/1AGQAzsLRQmTAsIGsQgZAbr+P/3j+Wj4SP+8Ahn+wAamBOQDkQv0/jDyGu9D/vkIKQd4A8kBXgEO+0/90fMo/FYGF/p2BVcNXAaA/pj4o/W++t8AjwAFAHH/Tw2/DHMFrANZ9ZD4rPwe/9ECRwPQBVr+xAGTAkgB0P89+4/4x/h4A+T8cgD4BNf4jPUR91L7Y/4/BHoBHACqAFj6Sfo0/gICX/2o9ID/mgjbBXwKJf3H/qIEB/x8AnQEDQemAS8BkQXLBln+xfkEADL8wglYBYX7tQAg/nL5RQG5DwwGMP+e9SfyevSQ/rwLCgLjBBv+xvev/H4AFwaRBqcF+PmL+FL/cAYeBRT+pPuI+VQAHAebByQHIAen+uP5Lv/HAEMIiP9i9KD1vwRrBmsI0QFd9dT88fT5+tf/ZAIpBMT4Z/yM/1EExwTS/0H01Pe8/QT0jf7mBsQMhQuoAugHwQBF+roC3/wZ+ysKYwVJ/cUJOAbDAIQFcAP1/rr2ZAI8BIwCXg28BWz9I/Zp+LT1HP4OCK0Ckf+C9yP/iPj/+88J6v8lAC3+Y/ba+38DyAYrDJP+3/A/9f/xmviSBgAErg5HDXX+PwZl/Cz+wgBC8In0h/3190P9agxoBpgN6QS09sn3PPFk/QsHxQe7An4CFPlA95D+VP06CXgCvv1x+2T74whNDl4J5Pw3/sD7Dfo5/SH/QAJJ/kUIAASBAq8MZ/2Y+pL7WgQACy0DQQg4/UT2W/+WA7L81ARQCxP7hwTsAXoBwQge/Yn9S/Xp82r4dvodBVYMhgIS9XD74PGd9MQBnPVR/fEBFfsmAcUH5wVs/vv6APl1/QsBOANcACT/eQq5BwgArAC6/CP8DwE1ACMFSw21CR3/EwAqBDv0Au5O9JL2UgAPCuIG5wRF/5T5zwGXALD/qf0I/bQAa/8Z/1oA/AYVANb9lfr5+cgLRAfWCwIW/gRy+tT1NfXp+1gFjwhMAwUDiv2a/9j5pwBFDAT/KgsRAPHy0Ps4/0QEqgRRCsT5Uflq/FH8GQU0/pEArvjk+mn/kPtUAgcD2v8U/gMGpAUnAAX8Y/fQ/bUD2wMR/oQHYAma89X68f/L/WIJBAqwBLv9y/tX9gb7XgdmCRv6G/PU/vHxhfyTCNf9DgCE/Gv+CwNaB4sCpvyk+8f0jvJh9TIFgAey/RIHyAZKAU7+ZfMm+XH+JPuG/agHfwqCBUwEpP5wA/X+9vhd9tP6UwydBcUHZQ2xBtYGdQea//35TvyF/OsGgQU/B3QKEgAHBeH/LP4dCS4E4fvH/336tPPQ/0v5bP9CCRX8QgSyAAv+HARZ/tL/AQFk+Z/0ZP7H9rP36/1Y+LsH5giSA5wEoAH+/LH66/l1+ycADP/eBg7/FvYDAUQDWgPIAyX9/fVB9GP2jQLTEBsSZAcx///3nfgYAGn9wfsr/8cBW/jDAUgK2/4m/xf+EQPd/bb+/AFs/c8JPQ0sAkr1Sv+H+h329wlIA1H99vuY+2T+vgM+DMMFufwg+zMDdAQjCWcLSPIE7cvzhe76+SEK2xV8EpcDevvT+Dn7W/u1/o75q/vtA37/sQuPEDoHwPzh9M/1uPhaA4wJsgftBtEP7A9oBLb8q/Dw7CXyG/xDApYHKxTGCaz/dgHl+Cr2MPUW+YT8YgNrCPQANwNOArQAOfHN818GRfvWBf4MxAKSAB4Cq/zb+Vz+YPS/85v8Hw5CBSj6SwQ19trz+/yMDDML1QIQ+cHo2gBjD5sKMwFRANcBvPRA/P0GAwgCBLgBP/l1/1YPMgm9A0cAnAMB/UX6wv2W8Tz0j/spAMcIKAimBu0EMPOV8zT+Zv0WA1MAHvfp+N8EaAHhBHkI1P0H9SD0NAZIBPABuQPyBFUCxQUnDT0BwA0x/rHuC/q6/nv/AgAfDWYGoAkgAKz33flM9rgFyf/DAFMIVPva8G/80AJbBPELnwDs9n7zFvli/dP+0AwKEgX7qvfuApP5iwQIDdUG9v/K+6PvyO9HA9kJegzZAeQGpf6k8AEAMPw1/H8D+APZA94IpQZr+3r3NvqXABX8rwNLBwH7zgEtAjP7agTrA7f4Of3yApUBWQFiArsEggE9+3r/zQAv9Mf4fPxy/PwEywIdC0AJQgGL+/H3h/x7/P8Ck/tSAF/8NPP8/3EDsQmKAJL/mQEh/338o/nsACL8YgURBuQESQqZAt7/Q/mb9hX6vPu/AesKUQqpBhIEvf1z/GcDDAViB1L+aPMG+kv39v4IAeIGQwUY+4QBbfft/twATgWjBNf+5AMq7a7x3gNYBJ8Akgi5AQvyFPp791UAlQviDioGs/X+ASMFEfutBQ8L4/yO/D8A5vWCAcgI2vyzADH+xQAzARwB3w4VBnr8O/3s9mjxbPlo+k//SQ5mBhz/7P6B+Ln3MgNMAzkCLgWCAWgGhgWiALL8Xfhl9837S/iVA9cNTfp7BK4L2ACgAur61/SN/P0DfAEgAXT9jfmK9RfyMgMyCCEJ5hOqBTv+cgD5/Er/W/+L/tb/zQCy/bADfgXcDO8R1P7n9U7xZfeNAGoFGg9pDhsCWPl392/0bvu9+4b3P/pZAhwC0P0bCEUJXAJn+TL8uv0Q8rH0vP7E/kn+w/6++YsFCw2LBdr+oPwtAgP+Ovu5BA0HJvm/+ML9WP82EzwT3P0y9SH1U/lqBDILBwnjC+QDc/0p/qD6oAdO/yX2DQCo/AEEEAmPA/YEHwqc+U318/9RAFwM9wGz/Qf5t+8K/oEAtgJEA/T9aPSl/ZkG/P5NBUj8CvlD/G72tgDTBKgBnP+I/nP9IPpY/FP7QwDzAu0HWAnk/oQF1P50+7b+df6t/Vb9NA4mAZv8vwMi/7P70PtiAq31gAQaCfX7hwVCBnf79O9C+ej4hv1HBZkCSgjHAF8EXPht8zALdAGR/EoESQB1AdsF4AWsBaAK2v8i/Jv9UvpRCJcBJwOhDNoE0glY/9nwfPrGBJn/YAYn/oLtN//0+Jv6pwz8Cf0Ivf3b8aDvwPVRAWcHQf1N9xT79PL+9i0C6AI5Ba4Iyf7D+dkF3gX4/kgEGgQ094r3ivmo+zQElgmhDEoGMAq8CsgG+wZwAMv4avMg/Fr6jv/hAtz90wwrB5oBnv2y+gH7+fM2/M38CgOKBED9wvoi/NwKZQiM/WzySu9I9ywATwvCCPYLhAu8+l741wHTB9wDWv0O+z/+5QlSBo3/ZAT5Ayn+d/jR/WL+PgQMCjYEDPwG/LUDgvSl/HMH2vul+w375/cD/tANnQhCCl8DsPa/9Mftyv8bB+EGOQmFAGP08vj0AhYB4Qm3A9n5b/9y/Mn1fQEzAXX/6QY8/wP+cvvhAqMFRAVcCTsE2ftu8yD7j/oTCNIRqv5c9wv6O/9t/DX/Af9896j79f98AmgHbhHIByb39PKo6EfwSgBXDAIRfQyzCAr5svQo/WcELAGYAaMA/PygDBcIvP0t/nf/DP0Q/2/82/ZU/4H8uAFeBxUG6fwm9an0mvp2B7oFRgaS/cX/3PxB9VH9of6w/wQGRRTJATH9FwZPAc8FVQXpCJ3+APzu/WoA/Ql1DZwHr/LL+McEngGRBiYFhv1g//7+5PVd+SYDmgEp+tb3wP4mAb77M/uO+/gCWQUv9XTyE/3e/rj9wgG+Be0FjQtCA6XzVvec+yEASvxR/wUIhwXhA6b8OAVcDR0JX/lk7Pnv/fihAsUC0AvVC7oG3f32+sMAMPgs9vjzLPibAIUMTBE1C2YJDASj9G3w8Pol/dQEMwa6BlMCzQG6/678iQV5BRoKOvh7/RQD5/jnAFT7c/yQ/GAGM/sR/XwNAAGsAW35sfllAYUF6wD78iL8/Aj0Bjj5xv1NAYr33AUlBK8BARKbCOT4F/anADX8Cfez+E73xwFjBB4N5QX7/aME1v3q9yH6bv1M9wf+7f8bA2AMggVKA2P8z/WP/lkA4/s/BEAI0AgZBrUFCQUm9ZbsUPR6+2/9fg2XCo4C8QQ++OL4PQBfBGEDQ/61+ij7+fXx+ksOqQIU+sUAl/zLAkUMrwr1BqUBMvqK87P5JASJAfn6KPujAeYBCgtnEQQEhvpj9a7xw/bOBfEJhwlSB4X63frL/Nf8aQH7/nsB1QD4Ad0ISAayA2/9QPnp+csC8//Y+s0HHAID/Gv71P7n/af8cv0I+JAA1ALsAVn6gAKLDVD+0vqo+Lbwl/ozCwMHZgnSCnAATvo6/0YExv/XAgb8Bf5NAwARwhMoAboBn/ob9eXyB/i1+NYCfgmu+e8GVAjgANoAZP9J/jX4Z/Zt8sDykvk5ATQBeQEQA4YALPzUAy8G5/oQ/1r7nvRF+UoDlwMuA6IKuAC/+l7/VwekBtIBigHu/Z/+agKDCX8MMxDUApHxW/vn/ML5AP9S/X3+CAO7AvwJ8wzpBtAAmvHc8L39mv1SAxkKgP/4AQoE4Pdx+KX88AVWCuAEJwVYAff6egBPAGD1GAJvBT/0o/snCF4HjQq0Bjn4XPiA+8v74frqAHYKEQdH/r38JATJ/MoAT/vd66P5nv5t++r/PgsOAD39y/+M9+YBhP8xAbD5UfjF/Sj5S/2AAl0JAAJCCnYF2vW6/Zr+0vhHAvMOegPlBPIDrQIoAg38Z/6u8lf2cQLHBE0GJBSUDk74+f3N/q/3yQBVB4b5RPk//mj6HflIADsJNgW7B4oIFQUf/oAAYvXu7ScDfARYBUYIwghk+9r7lwUr/ugB4wBmBbH51vkRCHYBSQWzBckB7/e0+Pf4XfYnCC8LIAW/AP77IvUk9N7+vgAxA3H7xfU0A3cFpgcxCZ795vl2/XX2PvnWAgP7Gfld+pX5wgPZBlcBAgEk/e7/qwHE/8UDFP/4/mP/3wCJ9Un4HQhbAdIKzRHuBgL82QROAA4Dfw5x/9f/+/uMBfMB6/+fBX7/jvsf8ykDffvBCD8MQPtRBUUCiAD+9qj/T/m8+HP8T/CY9iH4CQU/CZ0Riwx6Ahz+7O9o9B3ynf+gCaD/XAKkBEX+eQBrBM/+tgLL/dH4lPsB/JUHFgv5BOkAy/Zt9+ICWgWsBHYBgPyH/PIAWwNdBP8AGPnw+sMCRwiIBjf/LvqAARMCyf2YCXT/kviQAGP43fnVAgcGEftm/psD/vtnBNkEgwclAN/7tABf+qX/BAJYArX86ARfAmn52ASm/tL8uv2fAQwE5wKJAID/HQIp/Jf5QvJK9s//gAFz+27/wv/T+XsHmgWmA90Bi/198gD5hwa+AmoJI/yn+u31ufZBAzgFuA0RDFcOLP/U/jP/BvohBiICEgHT+7f9LAA+BBsI0AWyBcD9ogDzAVIFWgOO+ez3U/fY9uj4fgIuBWcF3gUt/jX6//3598j1GP0A/KH89Pev/JIJJgjpBOECtPwH+ioBywDq/uv/of2M+Tv7DQnKDkQK2wA8/X7+hQHhChQD9/do/Hn+FfpaAaoJqwGiARIGivwT/pYGiP0q/+0CCv4SAKv7/PmT+t7+xwQWBqT+fvi3ALH8af7TAtL+rQV+C1sDlvwSAh774PZe8cXzUAKvBRoPHQ1GCUwDbP9U+Hv0FgGK+l4COwYs/TX8pANQBXT2CvtY+rv7J/+nBQQI1P7qB9T/iPrF/xb+OfTJ9XEEi/4v/1QGKgyjBlcEqQVk+AD5G/4M//L+EAb2BD//AAQ6AzkA3vySAOb4R/L2/2MHEAKw+4j99gDkBc4CkPsq9wYCNwt7+Qr8dgb1ADH3DfoeAh8AlwcKBRwBzQaGEkwHNfnQAwX0xu7o8p34AwfnEagXHAfDADf7v/el8pn+QAqb9a/+EQZOAyAGoQo1/+Hw/QDS+oX5EQTx/Pj1wP0CCwUBJfwzAGv8SfhU//oJYv309BH8DPVV+T8Rwg19/gMBTwA/9834gwa9A2X9DAeKBWb81v/VDHUGNPwq/qj1FvepAOkK4QH6/BUIPvfj+kAG3gFxAhEFWQGG+S3/4vwa+qD1jf54BmUBFAz0AaP32vvnAFr+iv8pDEIEbALRAhD6EftqAPr/3PmX98L9gQloC1IPzQ7h/L/6U/qw8Av3FgSXBHD9HAKd/48BzQ5OBQX/YPnZ9xT6CfbUAJUH+v0O84wEoQcT/aUGbfx+9gn/Jv/G+jUDzQIv8XvzUATREZwJYv4nApj51fGa/9YBywRVEEAGKfor/ZEFdfhY+dwEUQC7BSkJKA6kBAn8WPkt98v+WwQnAyn30AIs/9D0IQCUBV0F4fl3AG39v/mOBggBQ/gB/RUGyfaL9VwAVPxzA2cIHgVZ/GAB8gaB+hr3FP3pA+0BxAnUCrH76wDQACYApQI/B0gHh/bH9rH+6QNVB18JaP6g/PgKugNv+oH67vvw7IHyYAK9/T4GdQSe/dAAoAVB/AD3Nv05A1QEavoUBVgAFPkgAjUBVQFUBX4K4//CB5kMVf0k/tIC8AQ2/er/MAV+/g79qPji8/r5pwRJ/zP+fwnrBOT6fPfHAW8B8vjQAiP74PT1/kD5Q/EFAoIMcAGsCmEHtvp3/Xj/UwQ/ANsBgQIL/MP/MQsFCUX+sP8s97f1XgI0C2cKAAXyCh4BCPfV/8b9Y/ql/q38xfcv/T0HdwTl+zb/W/5I8oT1v/3E/00HggteA6n7t/wM+/v4/fqIBHQFpwDLBkoABgHKBH4CpgF1/9QFOv+B/QcDMAZCA6UEygga+NUA/wQ++yX6Q/ne+/X0z/5qAQUEEggMA4cCbPQg+uEAdvyC/XcDoP/N8v37gf+H/5kFFwXZ/k0B0AaxAwoCMP4aBo8E//6OACr4PPe1/6kEPAEjCSsJSPoM/WYFpASvBR0I9vyL9M/72/7T+qkB0wdjB3EEMgAS/lT5yfxeAYYAEABmB9AEGPsWATj/ZPmV+Pn8rvrd/LUIdAdcBRH/A/3m9+70ePuM+o/+wAX2CLz/NwDEArX29fpQ/o/9Hf8TAGsAzftEBlwH7vxP/bD9IP0X+wAAvwOJBIAC7P5O+uH3mQLu/q37ygOkBCf5P/iCB2UEeQO+BIUBH/2X+1cBTAEQA4X/mv4KAoAJNQ1C/sv8qQmeBK39wgVWAs/4Tf0VA0cDcw2nDb/81Pen/Jf9bPaPAJMG5P5mADICxQGD+ugAS/9H9jP8FP0t+XD7bgkFBpoAhQSY/Sf4K/mR+k74+f31AJ3+VgKPBRYAcvl6APcJMgpv/3z4HfX28ez/OAj9BuIJoQF5+sX8iwZPCTL8wfhJ+LX5wf8tCp4OyQNQAKf8D/ot92D3ofoa/E0HCAbtAyEH9ATL/HP51wDY+uj61/0b/QgHlgSJAf4FrAJhA74EsfwT+FEBIAAB/QoJDgUcAF//V/5jAL7/5wRaALkB7gXHBIoAqvnZ/UH9D/zz+nX/uQFN/x4ErALPA5gFDwKt+hH8wvzn9nf6nPud/U4AMwOh/737eAJ9AUwE6gVPAYn+H/jN+lD8FfunAfsBEv5v/ZEFcwhNBTMECvwE/IL9OwE3Ar37LgIxAlcCrgIj/ysAO/qz+mT+6AXxCKcANPwm/NEEKgO+/yYAv/2e/mT3xfg3/xoC6QHWAuIEDgEuBib/CvjA/Gv52/x9AFIARAGpCOELWwAc/DP6gfej/2oHFgKB/dIDzQPgBbURpQ8L/OXtuOwv8uP/Lwe2BGAEWAe0DcULZ//k+Mby3+j58k0AbgXRDYwIIgL9/hH6pPoG+gn7O/7TAuwC5/4FBfUJqgeEA5H8I/qy+lT/5P9JAh8JPQIL/JP6Xf5z/E33MABgCQkNDQdABYn9V/JH9UnvDvYHBrABMP2cAFQGMwizCCkHBAEm/aH1evVr/DcBBAVnBFcEi/8z/1T8UvziBK7+ZALtCecE4gOiA2f/KgBbAbn2bvZr/2/8EwDuCSQH5QSYBKr+W/cr+Ov7dfgc/3UDQv/FALoEFwMc/3MCxvq59Ez6bf4CBoIHjwa0A4H8T/sC/aYEfgfvAYEDGwIvADoB5/7n/oz/e/7C/EP/rgZZCX4C2wDHAkb9lvVG8gb3S/w0A3UE8gL4BCYEsgLY/B3/AwH8+iz0xvBq+d/+kgX4CYgHzQd/BcQB5f3ZA/MBHvaD9ej3UQAbCEsLYggFBJgCrPqw+RD8bwHeCAMIKgX0BHsCFPpT9of0sviU/pQA5f8N/4cIegqTBvT90vqk/xr7R/WM9Gf+Sv9hApoGFAK9CIoGIPyg+Ib+lf0BASYH9AKYCqcEnPuX+sb6wwEBAwsIFAnjBi0DMvnJ+CP9Y/v6+Tn8eP4J/cT+NQa5BakB7Pl69fP3h/u3ACkClAeUAsX2T/TT+qP+DwEiCM0BFQA0/00BdAbDA4kDZf8vAxID0gCV/7j9ngFY/X/9bf9vBKoFJAXECUcFaQVk/xf43vSs96IAA/he/B8DggHoBnYBGwGRBA8GbQGI+xj6l/KI80/+2AYdCOcGX/9+/7z/K/rC/mz+YQAB/jn7CP8BCPoICgGhAdX6sfvF96z7+QjBCTwJRftM+B3+KwTdAwYBbANH/PT/HAE+/zkFNgROAZ4AEP+E/QMAE//e+1b/Uv+S/CP66vpaBzwIigN8AUb5E/om+3r/owYZAVz9GgBE/Ov8Xfzm+R3/EwApA7ECZQOxBVEGSgN2/Pz6DPYo/F0BegP1A5EFuwdZ+nwAnwIo/j8BF/qN/s8E0AReAkcD7gLB/TYBv/7u9wT8vP79/54GfwcpAz4AfgGI/eP3ofwXAMsAkwGVBMICFALCAvH5+/sAAPz93/1d/+MEwAapBQT/8/n8+2f8m/0qARL/df4NAJ/4tfs9A44EvwOQ/6T+W/nM+8kAIQBnAar8Kfz+/pr9gv80A7oCiAc3Bm77wPwq/Yv60fvyAKcEOwEQAQABGAEABnAI5wG6/o3/y/iL+dwCxgZDB9EJsQYI/GD9xgFm/bL+Tf4e/fL75/9QDHwI4QKy+xv1Q/zq/IH8zvow/pICmvzW/SkESAMB+rD1+vel/jEHFAXr/2z+xvtg/Jr/vP2xADIIGgaX/ywAWf8H/W8D9v+Y/W4IfAPj+iQCtwhRB88D/QFQ+On13gCd/h8CGQV+/qT+fwGzCMMCtwCVAWDzyfEA+PT+IASyBDcEOwBO/TD+aQBUAOwBjwLj/fv65/2t/1AAugXTAwMDewCI9x77TP7iA8wFWgDLAZT/y/5f/az+wQOGArL7Q/Z0+ub8qwDKBOEFGwajBFAEcwCpAZIDJAAJ/4H+YgGvAPH71P+GAlMCZQR/BpcEVQIdBH7+HvxS/9QBUgCr/eX8dvnk/D75H/p4AzEHKwcoAB3+xP4FAXP+WPkW/eoDkgEA++r9Qv8t/t37gfqP+nsFWAxxALb/7QH5/zMBMQI7/QP5JvqD9HX3WQRKC9IJPAON+wn6hP+c/+oBxQLq/bf6y/nA/wMAQwTeA6z4zPi1+0MG7AaiA/kHMAPXAHX/EAAJ/ocDygSi+Rz+8wObAkEDlAV2ADX9NAEIABP9HQOJBVsA9AIN/Wn1i/gk+/r3q/i/BN0HCwU6Bpj86va8/8f+9P/eBaQClfxw+tgAfwRdBgEHp/0v9pL+cgLmAd0GlgPyALoEwQUaACwCXP2q9k39h/wB/3YF/QWWAbMAnf1Q+MT9GgTLAeMCEwYc/Df8fAGX/F76jf0p/RD9MgWlB8kDegJEAET19fto/2j6IgRnA44FeAOJBZsEAvza/Lr6ev2d/owBZAF0Bu4GmP2c+9D7Jf/9+uACjwUGAQ0ClPiv9IT2Mf75/mkCkAeJ/kP4w/mz/HP5Hf8eBZsB5QTnBmAAzwBoBfr4K/cXAaj/Af/uAVAGIgLkBPoHl/+TBesDq/td/Ef8Ivxj/QYFeQPH/+X/KfvZAJ4JZwhu/838Ffca8fYBOgpdBQkEmQGb/Nr+WQZ8/eL7bgFi+rP8xgZDB1UDHAJR/h37R/wYAF8B5gFqBND/4/sRAFoBEf7y/qX+y/nf/IIB3wJgCXsGl/0m+ArzOvlH/XT+EwOyAp0DwgEZ/WUA1QFg/ev5avZI+ej+zANaAxIE0AY7AGH9z/y/AfwBcgA5AQX8iAB+BwgF0gGICPwCHAF7AqX5+f33AfIBXPlC/z4GbgGACEkHXASpA33+RfXd+E0Bhv1Z/KkBkQIe/woEUAFWAC4GTwGx97f3o/y79kb8jwTLAJMBVQCe9nv1OP46AbL/B/7l/FT61ACVB90BdQRyC/YCWfXm9Z/9hv8UBMIHPgUzCYkEcPqv/usEdgMc/lD8q/xD/1P+TQA5BskCcwET/m78iAO4BEkB0P+w/aD8qP+9AUYDmAWVBGEATf8ZAtYBCf8VANr/aPoR/BEAVP75AhcIwgA//3oBZ/in+Pf9+frE/5UGjQC4/oMETf02+aX/AgHSAa0AUv9y/jEBMALc+6v9BAMQAR39aAAJ/5P+BAKi+W/6zgRaAbD7hwUpAzj9wAWMAmT/OgBZ+pPxU/f2BCwHpQa8B1YBp/hpADUC3/vD/tr9qPm4AAIJYQSaA6wABv6QAHP/IQB2//3+AAObByQHSglmBf36kfe5+5UAEAMrCYMET/6K+/v0DvgaAwgGB//p/JH71/oZAbYFOgJX/uj5dfQA+fQFNArjAbwBYf7Z94n9qf6r+k8A8wbQBKcKvgkx/QL83/4M+nn5nv19+y0A4wNaAwAEVwiGCKP7Vvyy/Xb5UPxf+0T8aQTQCJYEmP9jAGH/Pvor/jz+zf+HBRIBmAIQB/0GmgEG+w37Ovwd/ocEUQYXBd8BhPl8+l//YQN+AC3/IgGa/bf+lPsY/u0CEgIN/Pn1JvqS+5f+8wBKAwUEGQNWAAP7KAAkAroBlP2S+HT75/usAqQIiAb2Ah4ECAO9+tACzwZx/6UCiv9K+bz6JP/u/ND99AZDB2oEagPN/0n53fm0+4L5Av5dA3f++P2qCIQCjPsi/bX3mPjzAWYGXgQECwIHbvxcAKX/xf1E/VT5iPjCAb0NlAsaB2QItf/b+Wj7ovnU/ooFYgM1AK4BcQPUAKj+/f6l+nr8h/4a/3MLjAyMAv35n/ch9PvzGv8N/oD+dgLR/kcBuQY4ByoEdv7h+876tvhq+kP5aQEuBsr+//sC/zIHmgdYBpgCW/+g/w4AugQJBRIFX/tN72bzbf/dBJQF4geuAn7+3f+//3X5xff8/jb6MPtpBb/+X/le+mj16/qeBOwBUv89AB7/HAQrC/0GSf7R/Ej8L/kRAhsL7QU0BIoEHv7IAB4Hw/+1/AcCogHpA34JXgdRAGYAX/0F9Tj3J/tP/FgBfQZEATf+1gXnAi4ABwPl/ML6ZAHaAqD+hv0D/zT/2/77BOQF7gBi/xn6yP+hCnEK7wEU+777t/y4/g4BOgPM/8j5RPo+/Hr9fAD2/1L/tQSlAq3+Af+9+0z2qvaC/HD51vjsADED5gaBB5v77vgO/3D9ofu5ANUEFgEKA9ED9fx/ACECT/tM/eEE7wOoAa0HWAd0AekD+v5395v/fwNt/mMAHwMRADUBXgXeALn63gEnAsL7pgRqBnv/vQEiAx783vySANH3dfckBdkKhQdgCfMCUvsq/cf80/zi/uwDV/53+MQAnQhYA07+BgO0/+b+wP5R+2P+vQM5Alv4tvvFBgQEEQAZBQEADvUB9Fb3MPwCB0oNWQF4+03/v/ng+XcAN/53+9f7Nvy5+6oBsQicAtMCbgPv/Cb7lPrW+ioBbwijBH8AaAGRAYf+tgNeBWABYAfEAQj9/P/HANf/qQA3BQ8EmQelCLD++/r9/+L7UvySAXX+/P/LAvkCzwD4Ay4BJPUq9pX50fnq/4gDGv8s+zD94P3w/sADTgJaAXEAHv0A+pn7kgLm/YH8JAFQBQYHBgZsBNYBNgMu/An6xfvh/OICZQIFBOgFLQNl/wYBg/07+M0BfQXf/aD8Ov9F+5P/XwimA6wEAgd8+m71Vf8wAZr4xvwXA2P+GQQ9DKcBqf3QBF/6bvfK/038qPz1BmsINf0yANMCu/zM/dv8Yvzz/aYA5AEFAakGqgaL9xj3uP1u/Fv/G/1Q/hP/swGYAkf+GAVUBeb+2Pjm9BX7BgNRBQcHuAMq/Uv+dvwD/nIEOQNeAMv/5v55/7AEgAQbAa0A3/wx/cIAxgL3A5MFiQlkBkD/UP5W/OD5df+4ATAD7gq9CMP+svyBAKX66/1KA5j7MQBd/8z5nP/AB70EHfyk+6b2KPYw/l8EFQJO/5P+gfdaAJsM5QPDAMgDj/uf+h3+kvii9/L+CgOi/sH+BQJT/0gERwhKA0gBbfwz9gD1jv6rBCP9Kfps+XP/QQYZA7QBcgGpANQB0wAXAJoDdACy/D/7YPum/lsBCgMCAfAG/QmoA9j+EP6V/jsB+weNAzMAygZ7BlL/PgCgABT4/PrHAEP/r/6IAf/9Avw5B9UGRgNKA7/82fnl+iz8rvry/W3/bvt6/vwGoQWl/3kF1AJC/8YBwPyO+NH9qgboAL0BRgO//R7/ugCfBJ//KPsy9zr1Av2ABEQLKAmiA0D+fvso/d//cv2u+Jj5hvd0+VX/3QRmCbYGTgE8/VX8Lfy4/tsCBgOx/kj8RAMjA6L9ufxh9336awTcBMEB5Ab/BpH8Gf5n/7P7Vv7r+3j56v4VA5EDqwPOAU8BHgDjAGX8xvhkA9UFwgJOA8n/5P6LAMb9xv2LBP4I7gII/dsB2QALARUEbQKWAAX9U/8+/wsBHAepBQwDyf4N+oD88ALPA+sBZP+DAI3/ZvwQAswAAQHkAZr56vqx/D77dv3FAR4HlAMi/m7/Gv46+0EArgUPAtb8U/dM8Y35CQZfBWkFdAZmA5H+/f7pADD7bf7H+/PzS//bB68F/wJ7ARn+v/3IAdn+of3XAo7/Tfn//v0A2/4iBhkGzP7g/U0Axfqf+UcCGwBY/Gz+KgBY/1wD9weYAXcFigsZAlT4cPcS9tr35AWrC9AGCwMBAL/6Of8ZCdAESQFy/v75yvnXAjMI+P30ABACaPwjAc4EbQE2AOEHcP9s+WcCgQEiACAClAIiAPEFvwcp/MD7FP0n9qH3Fv/n/g8B4QNi/6H90wBf/8b2kPgy98nz5AG5B8QCf/+P+xD0QvEw/KsAif9nB3kGrP8RBbsEAADABOUCV/oT+9sAngB2BNkHXwMSAuIBewU4BikFgwMi/DD/lgJbAOEC2gXDAYD59fgoAHwAcf3TATf8y/snArX9z/9RBTkFSvx/+8/95feV/mkFh/6A+2kBav9d/WkC3wFdAS4KWgjP/ikFywJg96330vyIALAF5gdBARUBQgT8ANr+9gJxAIT5Bv/NAcH6g/5IBTkACP/3+jv0VfrNBfkFXgIdCYEA4/UV+j38FAJcBn79sfWF/CcBWgDlBM0L+QS2+W36x/le/iYDhQAs/In6fP/J/QMA6QQQ/1T4rvqPA98CugD5AxsA0vnS/Jn/hP14A40HcAVABVAF0P6m+nIBXP5j/lMFDQG4AgUHAwU/A/0D2AEC+zX+xv6i9IX78wO2/dQBeAnjA/b+z/+C+cL5dwPF//v5wP6VAb/9pgJCCFD/pf3C/6757/3nBuYCxwOKCt4BK/tvAZQAffpz/8cAf/lgABEGNQCNAwQE8Pii9nn7DPqo/n8IugBs9Vr6rv07+cD5d/tb/XcBxAKVAewB/AFz+Cn1ef8dBMQFywTPBTkJMwUKA1wA5vsJ+4H8EQGOBkEKdwaKAVcEqQUjBcsEdv5X90r3jvmE+soDFA7kB5j/8f2m+G/6xQCr/Zn70Pyq/9f7qv4tDLYFWgBq/hP27feS+hr5zfr0BMAIoQf2CEUEQv6U/Df6+PnqAt0DTgDlAPIBpgLwA1ED8/j3+moBiPwDAEsIjQehAvT+qvcA8ob3AgCqAdEGuAby/5oADP+x+t77aP9a/J77yQA8BDcFSQVoBKsAQAD7/jX6bPVd+30GGweaB9cFX/6H/IIA7AFQ/hQA5ARR/fT6HgH1/hT+tQOjAzH/oQdnAub0zvtfAUz+Q/0cAlL+FQCWCpQFzf1AAcX9XvDN+FUC/PwGAYcHWQUIBWMJ8QB8+ZcBfwHe+jn8Ovt8+Tf/uQd2CEwEjAQf/oj77f+6//ABU/48+EH73QEfB/MEGP+P//39Ivuq/Xz/vgHWAQn/7f3V/qYBHQH4AEIGRwe//yn4ZPno/O788PuV/A8BnAVzBOwA5wIABMsCOwCu/kv/Iv5m+8z0qfybBz4ClP/mAuwD8gLBBBgBsvtD/jj8z/Ss/AwIvAGbAMEGkAIc/mf+Gvpt9yL+EwB7/j8EgwVj/TIAKAhzACL+UgML+0H43f1J/6UAswThBb/8nP/RBnMA4AH7BdwAcvyB/vD+av0nAZ0FKAPDAqsDsfx2+5D9rf3r/u0AMgNl/WX9TQPOAhsBFP0P/Mz56/nB/CD4eP3NBN8D3AXzBdH+FvtD/dv8xv9IBJYCdvsqAboJ1ga8BoL9aPRU+g4C3wH6BfYMvwMX+vf8yf+eAHgFf/1T9A77jQA8Af8AmwLV+8X6iQBuAH8JMgxk/2z1TfSK87b6VQdUBIf/2gFdAx4A3v2nAOL/AgRwAlP5s/shAAgAhP5VAjQGNwUsANT89//ZAgsG2wJbAKYAcwCj/pT63/5CAjUFlQc7A4z75PkF/Ur7YP80B1sDmP12A1cAJ/rCACIDzAAoAvQBzPlc+3EBrPlq/JYLjwm8AlsDqv3c+LT9zP4x+ToDpwiG+8z5nP+u/joATQXr+3H23P+X/iD8cgW1B8v+yfsF+4n54/2wApkCAQBPAtEEo//IAPQErgAdAKr/cf9EAAQC4AU5Ay0DDAEs/Yb/VwE2/4n6iv3TAO79Df+5/bL5y/xSA0MEfwIDAlf53PPV+8//Vf69/37+m/oK/3sEyAZsCCYHaf2O9a36UvjW/HsJKgpSBhQDiP9K+k0BKgZ//xf/2P9I/WgBDwkkBWsC8wEu/YD86/+CAL/96f9I/9r/ngJ2AWUBjADM/wT8jPm6+kX+ugRABTUB5f9A/ff5LQDxAYACUwS5/eH9YADDA2ABhP5AAeH53vwVAt/+owQBCj0DD/zl/D/5qPWk/V0Ej/+IAy4Iif8lAlUFK/2996D5R/kT+mYH7wrYA3gEbgDX9j/3/f0IAEAB+ASH/Sn3bwDNAvoCaAsuB337kvu1+5H33PoIAOQAGAPBB4oGHAO8A+ADRAOgAVz+Afts9p31xf+FB2oF0wdhBu/8ZP6TANv7hv0EAPv7+PtiBHYDBfyuACIC0fvF/Hj95f79Ab8B5wDM/5YEXP0X9tv+3f7e/nYBMALqAtsCqwO2/oX9+gNYAlz+HgD9+7D77AGmBIYCTgCdAU0BOAQKA/AAHgEB/In5XftI/iAALgFgAGIBSwWjBVz/9Pv3/Xr7gf06AdgAfAIlApoD2gQsAdr9Gfsa+uD5mP5ZBfoGPArJA0b7U/tz/Lb9X/5QBcoE0v5E/679e/1cApIEE//l/nj/qvnU+8kFCwe5AmcBxPdw8Zn6sgG4APUC+AN++4D76wET/CD9fwG6+jX34PyzBg0GCgceBzb6dvnW/vb7d/2oBOgEQAVzBH8BjwC3/SwA6f17AcAH4wVMAnb92wOrAcv6+f5z/pf82QBzBscF9gahB3T/NPdA9933Y/sICTwKxgKEAaUAH/sY9wL+Zf40/hgEYgR6BX8FigCR9nb3zP3G+0QAZAQXAeEAcAIp/7/+lAHB/qb3w/iqAgMDKARaAwP9zfyz/FX85vweAz4EHQFR/6b9sgD8/0YAzgGFAMb/CAA8/3YACQP+/ob83f9BAf/+7QE6BdsDIgaTA578e/z3/uH+iAB0A9cA6/oJ+zf8mf34A7QDv//kArcF/v4l+iX89PtO/GwCsQT3/44Bbvy6+McCDQWPAtYAagNiAYT9aATnAsEAbQTh/Xn6bf5d/eT/dwbzB5cCQvyv+xX7Df4gBSIEVQPCApv89fqB+7z8F/6//mj90vuD/3L9Af0aAJD9Q//5/kH4WvxHBooCJv1wAMj/KP1DBDoEQ/oM/9cDaP0RADII3AKEAZIIXwJJ+/78o/yd+aYExQ7QCKoFKwAw9YnzT/6ZAv39Ov3m/O/9pwJICiwLEAfSA1n4VvIa+l8CTQWbAUkA8v/X+lb7WABQBGIJAgmmAiEB0/7f+g75gP2FAuD/SAOzAPn9xAMaAuH9QfoC+5D1PvnOB6oH0wYCBgP/vPqEAXABovVb91r9HPlk/LAIgAbhBPYGQPw7+Tn/2vzF91n/1AdyBYsFvQIU+9/5kPub+HL3OwABBD0EOgbFANX/9QLkAvD9FPml+wP/FQLpA8kBpP+0/pv3uvjvA/8H4QbNAasBjwHTAMECbQHs/jT3QPfG/YsE8wuQCQ0GlwQY/xD4NP1BB8ACqvsV/RT+B//uB3wIYgN0BAP6zvEp+GUCLgaRBoAMbgHW9BX48fUN+hsJhQtdAW39r/py9df+iQxKBmMA9QBC9un1vAESBYECqwKRAPz6xP7NAFL7dv6FBNoCEwGDAQ7+MvzUAcYCXwEWB8YEVflL9Rf4ofolAQ4IugiyCLsH3vzC9Gn87AC2/Hj6of3t+4L9Ngf3BkYHWgQH/Wr48feH/K76Pv8YB58C0QChBQkEJwDrACj/V/lc/Dj+y/cnAFQHSP+SAMsFxv9j/3cDIAC6/SMDAgBo9Fn8AQCN/A0DNwfPBI7/PAKb+0z6egQWAcj9cQCP/nH61v6rA4sE4QNi/xD2rfSn/uQExwnkCDICY/6v/B7+KgPbBAsCaP5Z/Rb/WQGAB8IF6gIgASf81PwZ/2MEVgXhBO0Cvvy1+vX8uQHUAiEB+v8Z/R/5G/vQAUYE8AJIAIX4XvYk/l8Auv+rA5kClvhw+BgAlP+HAS0D+fdO+C0FGgS9Ax8HEQJS+m78bwBB/bMEZghr/uz8RQJBAUMFgQnN/q/3ePwtALcAUwTEAsT9+fx//uAABQSgBnD/R/na+Gb80AUACMYC6/0Z/bv9MgErAED8a/6V/o/9BPxnArQH5wO7BG4AvftU+kD3kfZq+qUEAQnRBVIDg/8M+fT4Wf2C/sABKAVdA0L//gFaBTcBcPvv+Iz1yvf2AvsELwc3DR8HU/4n/48ChPw4+Nj+2v5I/t0CyP7P/9cHQge5/jMBJQXi/WEAYwGT+6T70gJ7AWcA+AizAzX7pPzRAHz8Uf4CAD35GAAQB4gDeAB/BVUBLfypAPH9u/ll/eT8lvdq//sCMAK4BGEEJwHD/dwAZP4i/0UEJQIN/f72ufaj/WcBzAN+A/YCOQg+A7b8H/zS/sD9APnc+n/7HwEHB88FQARLBJH+MPVn9Bv6gQD3BkgIoAAUAQgDIwB4AAUAavzc+JH+EQB8AIgIpQSZ+s/9MwPsAPYAagAy+Dj7qgYfAWL+YQOCAu//dQG+AGH3XfzlAZ36r/6FCFsFAAHoA2sBkQCcAbH8gfi0/cYEAAVrB/0GOv+j/MEBWgJO/1ECGgQAARsCVgEkAKUD6wAg+wT22Ps6Bv8BYf8EAoj+if/uAbn7gve9+nv8n/jM/XsDggGGA3P+tfkuAK0Dfv0p+tX/OwG4AqQEev0m+q3/8/5c/mIGhAYRAHwAQQF8/SYC1ASF+Z74X/7E/1kEYwbGAhH/QQAs/Dv4k/90ASoAaQeRCFwB4P8zAlL+6Puo/5v6Ovy9BFMEpgW5BzgFV/qM98z9PwF5BWsFHgDU+bj4afko//gI7w0FA+LzYve6/IoBWwZCBDv8TPpb/kD/oAk6DA7/O/Yb9g37HwGtB2UFW/zb/Wb8yvo+BvsGAP9g+wr6O/fA/JwHagV4/3v9Avob/FAIWgf0ADEA5vqQ9wf+jAZhAJT+AQDzAbYJeAcu/2H7lv9E+rb4bASXBpoFiQbe/+z6qAAo/kP6bAHzAkT9T/9rBd0DsQPFA6/6d/cj+xj+PAW8BRL+ufW3913+xQDzBYIEHQGp/eH7WQBxApj/aPmm9lj70QQCCtwIEAYpA8n89fqF/Ub8BwGFBkYHTgcyCEYBDfss/rX6Rvgt/wYFUgJgAtwDGgIjAzb+APhF+tX98vur/ZMBpgPCBicEKP0/+gX9mf2nAN4GfgBN/YECo/7g+5z90QEbAWL/BwPB/Ar/CgN3+2j7CwA2BM8Bzv8u/a74r/sp/Jn6uvyaAOEEhQWe/qD5Bv3pABoCIwNAA/X/MAFg/z360P7m/s784QBUBtwJTwizBroBz/+CAqb/Wf71/o77L/pvAbYHmAgVCMkEsADJ+Vz0RPeqAK8JeQqcAlj8s/1W+679+wX//1j2iPM89vL7dwe6DbYCc//p/ub1EvhsBeQGgP4N/Ef4avko//b+OP10BJAIWQCg/nsBgANRArcAov5WAB4HbAId+0T7SP+AAIcG0gsLC/MFkfqq+Av9PQSSBHQB8//7+Tj7ngH9BQYDQ/5V+O31JPXl91UDmAiICo//CfOM9WT7UP9jAYMFAwRaAGz/aflk+XgEJgkiBPcBKwNO/jcAKgePBSoJhAVN+7737vqeA98F1Qc+BrT/KfyE+e/8QwAj/wwD9gJG/Vj6EvqE/Nz/VwOQ+3H2jPx//EH+AQWHA8r7nf02/RH5uPzPADgARAKABc38MvzGA3wEIQUEBzMC1ff39jj5OQDaC6oNDQdvAcr/Qf/EAJ4AyP/mAHAAIv+aATgB6P8HBC0DnP+B+9b36PcsAKgK8geIBPv/evY59bz2WfxVBKwHlwNs/agAOv5I/oECbf8r/jb7I/zV/iAHvAz0Bl8D0v3Z+dH5Hf6AAe4BJAN0ATj+Rf0HAEECRQTrAOIAkP9m++YA5vsu+94AbfmD9Tz9pActCOEG0QPn9nb5AAJ++5P7aAK8Agn/dAE+AWX85AaHAkPy9fibAtsGogk4Cm0F7QFmADj0/fRKAoMEdwDb/QAA5gTsCE8ESP0b/5UB6f9H/5EA4//qAMECfP9//Wz/cv1y/iECDv8HAGQBZgBk/yb/+gG/ArgChf79+nf88/7u/Xf9owLCAMMBrAVj/9P6Hvwm/K78IwFwA7MC+gOfAUz3ofnW/2X6oPslAPMFlwUjA2MCY/30BLQDkfs4/Y//bwBY/8sD5wFRAWMF8/9i/1IDcwGE/7/+kfec9hr8Ov6DABkFJwmtAPL8B/xu8xn4HADO/1T+HALC/0D5PwCTAokFTAqsAcr5evlwAUIEWgLTAdH/qwN2A7wEqgL1+6AA8gEQAREA5f3j/0QA+ARnCCIHvAOV+rz2Z/p1AHAAsf0pAYwFWwc1BZX+AfdT+Rb/zwQnC7QINQQ1/mL7WPuE+hr+MgDU+lH6EgWlCkcGBAAz/Nj6vQD0/wn4rfzJAc0Bgv9f/Y/5Jvm0+4L5Ff7KBDIBdgBMCLwD6P78/3P70frJ/y8AufdI/FAAW/t8Bj4PDAmHAXf6K/o0AREEUv/199P7t/2C/R0EegXpA1T+5Phw9VD8lwTIBO8ECwPzAVgAgQHsAC0BdAHz/yn+x/tpACYEGgj3BgMCLgBTBMMKcgZt/k/3oPel/dgBgQNpBDQEaf2w/C4FDwfdAJr1RfBj+2AHowvTCnkEm/qu9sT3Ffpm/i77yvdU+wkHHQ9pDToJ2fzz85rxKvNS+LH8FQIjBVAHVAZLAtkBK/3L9R/3yvo9/c4BhAipB34B5v4E/Mf7e/86ACD5S/gI/ScDUgqhCtkHr/0X+Uf5zvuGAuEAjf5i/PsBRwYOBDQEEP4W/6MBBgDGBMcD9wE3ADT72PtnAXYGbQUtBjQGnQGR/kX+U//b+zz9VPyh9hP/1wmuC7AHTAEC/Ab4oPe++NX+PAuQCaD9e/qE/2gBYPtD+/EBlwRTAeb9PP7VA7QHEv4p9pT5W/7VAFEBMwBI/Rb99f+X/Yn71/3E/qgABgDUAq0GUAWiA4P76veS+//7nPpl/l4JKQwhBvX9dPmL/o0Ao/2T+/b/dgfKBEH/hv1g/0kAbP2z/Nj9kABmAtwBzgMMCY8Ejv1B/+oBZAA2/Ib9bf3AAvkGtf4B/E3/LgMNASIBbQJfAAUBEvxi+sL7dP4oBDcErQJq/tP5dPsQ/nQAAwH4AT8DF//ZAFsEMwAR/Vb8vPlP+3kBigAHA/8IBwYX/rn7mfl099UCmQXtAhUDlv1t/zMCDwKP/Un6fv5PApcDVgQnBdkBhvzL98X8FgOhAhoAD/1PArEG0wWD/6P6u/m09+r81wLrCCUKnQDx+T75bfzjA14F+/x/9dT41/+rASwGNgfgBFQAj/gx97f8PQFg+vb6yQORBJcBHv7Y/q0DRwa5/tv5OwC5BIMCCwS1BTkCNwH/+Wr3Cv10BOwIBgSEAQAAPwQsBxAFYwYPA0T7mfKx9AL9VwLwB4cEZ/+/AccCOQB2/wUD7gFf/C/5tPhW+nj/5gSVAqD+lPsV/QYAl//j//v/FAPVAbIBzgJtBN8F0v1c+6/7qvwK/xP+uv2u/2gC8AGlAvEEtgVA/N/4pP3N/MACjwCl9fbxfvdHASUGYQTF/Yn7s/1M/6T+XgMxCGsBsP1o/IT7iv0A/ML6mP+OC6IMoAMDBV4Aw/vbA48FPwKKA+8DFQH7BHkHbgMaADb+Yfrg+BsC/AGHASsKpQoyBXD/Bv0X/IcBWv4X9aD2Cfuo/Z3+PQcwBWX7evko+ZX9bwHOAR77tPt9/zj+qQHvA88CgfwT+VL3JfkD/58G+gxGBTb/yP05AEoElwLNAbH7dPx7AxD/B/8/Azz/tfsM/W0Aaf+aAIMDBwHPBhUIufyq99T+7wFC//j+ZfhN+jEE+QXxAmIDKwS+/Z//BARdAYL+zP53/00C/wmFAxL8jf1I+mj9sAWBA0b8x/zR+zD7eQTJB2MCU/6B/uz8yPrJ+nT1rfs7BZ0Aff8JAkUAc/lc+lkAEwHq/Vf4PfhwAEMO2QrkACP/B/jd8WX1HAIUBFUIkA2TAsoBEAeWASv8LQOPAmz5hwDGB90I2A3yCir+ePjd+kL48P0iCNIDoQDiAm8GSwn9Btn8ufJA+CP9r/zaAOoBbvzj+nf9eP/5BIgGzACD+eb4t/sK/LH/MAHv/fX7qfsC/ewDyAgABkwAsvrX+F/6I/9GBDgCbAB4/qv77wTxB6gCRAD4+6L3E/Uo+2n/1gJSBkcBc/9hBMMFcv0h+5v3svSE/ST+8f/XAw8HAQljBVMCrPoD/o3/GfvNAGIDCAWgAzoFpgTWBQMHgfwe/nECcf4i+rIDHQpaBoAH8AHW/0v/xv3b9oX8vAoHApr9E//6/zD/kP+EAR/9bAFMAmH8dv86Aq37LPbK96n45/3xBUUCS/3+AXkC5P0q/yj8SPdH+4MAxP86/owEAAG4/icEZwHuAtoAKf0d+5H8IwN8BfMHBALU9475Mf7rAOQJjwmVASf7rPTO9xkBmgn4CLMDFv7Z+S36oP+YBAwCRP4O+XX4Pv7wBkkLyQUs/ZH89v63/Hr7dPfV+ev+ugJhBikHkAY8/sL6UQFeCyMOZgOR9m70afmsAa4GvQSjBzsGev8R/j0IMAy0A4j/M/hB9jL+xgCv/qwBkwIZ/MT6Ifsh+uQB9wIM+y3/kQFS/+sDCAWx+j/2YfuV9kH3hwJtBQ8BgwLVBLwBawNOAL/3ZPZv/C8EuwODA3sDQ/24/eUAW//q/2MDrPse+BQDOwawB4oEVf6B/aP+oAASAIABC/4V+PD9egYBBaoCUfz29DP6mQJ/B+0IxAao+1T5dwEJAQ0BtAAc/UUBjAOa/QcCpApTDMQGawEZ+5L2Tv5r/pX+XQhrCgf+uPh2/7b/aP/y/v38Ef1+/br5U/U2+6oHvQTD/Nf/ivqg9p/8cP8d/74CEQL6+zz6PP7lAiUFTQUz+2n7Cf+I+Rz/pQhGCUwDlgJj+3n5ZgUlBVYBcgLv/DT5OgLCBcUC2gf9B78AjAIpBhgDxgGi/1v4bvz9BkQEswA3AYr/UfyL/or+HP8bBFsAaf1Y/skEewFM/AL8EPRu9CH65wLKBIAD1QMM/mT6yf1TA0YFxga0/zj7MAHuBcMCUPuz+aL6BvuO+xcAvAoGEjMJpwF2/yn60/YD9qL0bvkDBioApvkQAPEDKwKbAVAD+fvB/Dv8jPaN+0UFNAcK/yX+b/4p/kICqv/5+p3+5QC4/wwHLw7MCyQIcgFP+Mz5wf/L/lv79AJ4BLf/nQZyClwJnAYYA/r3kPRm/Bv+pAEDByYFIvkO/UoAgvYY/B4DqgOYAi4EpAFVAmkFqPxe/AT/9/ut/LP/ZwAkBB0KGgK6/IP+6/vm+Xj+dwWaAjUGxwPf9n/4ov4fAMX6EPvF9/z2hQHPApADUATmAhn/6v5h+8r1LP2q//z70fpLAcMB0/2hAS0CJAWtB6L/5vQF/DoGsf9S/1kE1v9I/ksD2v8B/q0GGgbP/4kF2Qf5/UD55/iR+jcHshBpB/L5hvhe/l0D1gj9B9IASv7+92/1owHeBrgBbf0E+O35LQRwC6wLpwTX/Ar30vVT+4v/JwJEBT8E8/0G+hYB2QW2+0T1wPy8BScIPQkABZ/9Xf3G+lL32fc//fH/avt5/9oGxgm/CNoAOvS67un3ogMiCpMNnA0aAe70oPTS9Z37NQBx/l38HgNzC6cICgZEAQn65/qd/MH7ZwHlBjwBGfxv/X/9GvuC/9gCWQCACUoOhgN2AG0GbwEC+Lr8tPvE9c/+iAaLBM8DaQEQ+EL79QNy/4n9LgHjAdz+J/9CAbwB5QDF/Vv/IgEX/CH0uPYnAGgIphCfC7sBlf0Z+wr7Xv3T/1v/Fvui9nX5DgBnCI4OHwe9/KL6JfhH9oQAmAw6Cm8FlwNO+Hv2c/6A+vL9DwfPAr//oQUNBqMBtAQSA5D7R/xT+bb0xABoCcICbgHPArj8rvmn/vj8tv5OBtcBvv2K/gsAa/rq+QkFDQOi/bz9Qf+b/rECkQbL/C/7pwDt/E79tAi/CJYCKAJQ+Wv1v/7TBHABZQPaBykDbAQmBdD9LgCBAAT0s/YLBtEGvgAjBSsHCgN4BMf+ovPw86n5wftCAdwHdAOa/cn+YP4m+lT4qviQ9yL6tQSIDrcLUAJ0+0v3EvtS/bgAgQigBAz/lv51AkAI2QwiCZH9vPub+WX4AgLFCikGdgRWBrz6M/Wn98j6dP0mBQgHsgAoA1z9JfQX9/P/ZAANAzMF+/vh+TP6fP0KBqQL/gTA/D/+Jf2S/6QGAAZj+cX1Ov3t/8oHyQ6fCkAF1f5C9RLxUPudCIAFIQKXA17/rvwRAdUFuf5/+Uz3YvVl+qn/IgbYCdsGbAG1/6/+pP0+/rb8HfuD/mD/l/lAAq8LqgQ7ACYEtANz/lT/yftw+kkCcgWbBG0DiQHn+sv41vqr+JP4dfsCANMDdgWzBaMJ6gd/+rz2Tvem8sfxFfrDB24JGQddBXv9d/0wAH39/P4KCHsG+/h8+ugDPQVQBkAHS/9O+X/+BAFXA1IJJgZO+6H6Dv/R/2gGDgmgA+gAgP6I+Y/5mvsR+ZL8OwUCBRgCKgcMBDL7ovwf+4/yvfUXAVQD2gWQC+AGrPta+k37V/r9AcQD+PqT+vIHbAgbAhwIdwZG+2v1IvqW/vkDKAZ/AKICFgaDALf5i/+qA5D+Hf3a+eD3JP/7AvgBTAl/B4X6Dfis+lT5BP9fCtcFyfye/Gb7Cvie/bIDp/3+AXEHlf4j/o4FoAQa/TX6kPUj9QwCkQg0CP4IugSx/Uj+6v8I+zj9RwAl/8YDQgsqC1QFgwTH+iLydfyeAm79qP8yBeb63/mlBTEE9QOVByQBavcI/FD+Ovjq/Y8BAPxH/agFrgF5/vICcgICBlsGyv77+fX97P1l/sQFAATR/CD7yPvv+TIFcglB/rr9CP8U/6MC1gmSB5v9V/yu+yn0FvVV/qr/eQO6CogL1gU8/9H3lfVZ+yv7EvjO/9gIwQRUAy4C3v0o+L7wfPNtAMoKuALAAFMJxAuyCI0DA/uv8qT3OvVT+MsIqg/UCrsIxwkG/8X9a/4i/OD7k/l4+xH9jQTLCV0MZAmN/L/vRu1l+DUAOAb6CLMCWv2W/oL/Svzu+wn44PI0/cEHcQONAdwFZwBG+vICrgTO/soDkQTu/vQC/gbJ/UX8IAQwBBsFcwm+Bar/iwORAof8ov31/pf/IgSmBpoARwE5/vjy0fnGAGX+XgGJAWj7XPs4AN38KPrC/68CQvxd/+UFwPvk92b6z/cJ+QMBxQNu/vIGLw+PB+L9RPul9yHyVP45B2sIHAsMA1b8ZvxGARsCkAKyAKj6KgFjAzYARAMMCbME3Ppg/sb/lf1aAI/+yfjo+uf8Z/rTAdQJ1gWZAGEFfgXy/Tj4Avns+C31aP4iBsQIag52CRAARABcAMr3a/VO/SD/3f5gCG8LIwgBCC8A7va0+mP9+PVa+Q0BDf+iBIsORAifAXD/PPR28Gb7QgGVANYJ3gjs/L7+XAGr+Nf1HAL5/+n3qP1+AS0G+AuLBe/30PSj+ML3KPvkBUYHAgb6Ayb8O/q6/UMBoPw3/vkEyAKEANsBFwQXBOgH7QOm+B73KPxs/24ESgwsB/gCQArgBIj2wftIBJ38evxA/4H7RQGeC/gE4fxABPf+WfNg9ln8y//gBFEHgQF8/x0DLv0+9yr6Ofuq/UsCpgMmAt4AowFiAIL+//yG/8P/J/4ZAaj+bQBYALv60foQ/x0B7vtQ//sDEQNdBscFhfxM+Br9Avyh+zwCWge2BWMEGAKU/NkBFQTy+wz4ugHzB8n/Zf9DBOgH9QenANj71fgD+/H/Ov5zASoJsAhbBlkGCQTAAmL8uPOq9ZH8AQTQBFsBAv/C/UwCGgZRAcP+pwCE9nTzSvtw/lcC3QcyBp35Z/g++2n3U/3JB3kEkf7jAw8DKQCGBGAF+fr19An4ev7ABLEEkQP9/vr/+f6Q+vr7tP6t/yn/DgrtC8EAVflg9lv12Pa8/eX+6gFPBxUD2AIjCeYC8PxwAy8Bkv2bBZwGf/8YADgA2/tm/4wDz/yX/z4IhwFt/jYFggaSAT7+MPre+DoAhgZOAin73fmE9kX3BP/FBn4JOAfABeL/C//4Arf9o/ve/zr9Xfh2/+MDi/gO+Qr6jPIxAvgQ9gxaB60BJPFs6O/2vv62APgE0v6v9dP/2g+MCvQCo/6Z9MbySP+TCVUMlxINDt7+afu3+jj5av3iAooCjQLSB6YEEf+LAIkDeP/R+jr54vjTAfIGkAHh/RkBo/y08+/0rvri/kYDMgk/BND+yQKT/mz29vynAcj6kfq6/28BVgVTDz0HL/xb/RH8wPsE/k4EkQbcDDwLxP9//Pj98/9y/p3/sQBgBHICGQAdBD8Dhv+Q+ZP4K/vwAUYB/Ptq/Zz78vor/8P/+/rU/X0BsP9VAS4Fx/5E+0b+k/oXAHcE/v4F/EEBPgN2AYcIoguBB7gA9vr19dn5ZQORB2wKhQUjAcL+iPor/AEAvAFRAIX9svs2AY8K3QeTAOT/X/uy84H1gPvQ/e8EmQl6AnT8xvu2+SP65gGfA2gB4wXyAtf9EwK7/0z50Ppn/fj8uQAiBhQEAAMIB68HugGG/yb7dvVu/00FoAMBBE8Egf5g96H6UvyH/O7+UAOFAQAA7wg4CeAAmPux99HyHvluAPn91gP5DU4Hb/qI/SP87vk6AY3/HPydAYQJ3wUWBIcFt/ig8bf2PPmX/w0LCQeu/dEDSArVBKP+P/1g+Hr3c/1GAwkHdwagA2/77vhJAWL/B/oZAggIPAPZBQ4LaQA/9qD2jfSL9QYDOAqcAcQF9g/jBsj+q/+e+nv3nv9A/ur63AcZDEUDfAGeAF75N/lX/ZX/GgG1BLII2wVoAUT/dv0X9aryfvga+xH+DwTHAwH+sQhnCwX9E/ug/pTzCvTpBFsAsv2kBk8AXfRW/zwGlfoq/2kBqvvS/94JYwhzA8wEXvt89In6Cf3y+p0BhgoPCSj+cf4eAZn+1wPoBT8Dlv4VAAv9TfoYAWD/Q/V79n0D5QO+Bp0JlwUfARv/jf0b95b97wCY/rME1QgoA0ABgwGs+838wAIHBQ0EsAr6CHP+Lf6gAc4A3QDJAi76sPVx/FoGggjwB1IFuPss+qv80v1K+/z7Rf2h+l35C/92AUP6Hf5OA0j/hfrt+Yfy0/GcAcYGmARPBxkFpPY9+PIAtPlp+VICcAFMACkQIRAUBdUG4v5d9AH6mgTpAbMDFA75CNsE7wXx/f72C/vBAFH/UQE3AhUDegEp/SoB2P2k+F37/v15+Dv7WwN5AGgDcwFL9uryegEABAj9JwumChn5m/XR/T7+1gMoCtH9WfqAAvIBL/4eCJIJZvtr+vgASQEeAk8F/gOK/pD5wfzo/zgBbAJ9/fj8dgMfCNsA/vkK/tr+a/17BSwJvPwi+zEB6/sn/m8GEgDK+Rr/wfyC+9cI9wy4/737BwFC+KLz9f26AAsEIg2SCNj+6Py3/DD7I/4SB34G+P6Y/hkBIASPBR8Ep/9R+g/7hfzj+nf9WQLSAdz8C/4WARf4pvSE+Wf57/75BOkAMPtJ/kT/e/dg/PsCafr7+ZECSQKkAyQK8QWJ/6QBdwE7/nQBbAW0AbwBIwRqBAUHhAWlAtgBCwCZ/oP+cP7IA0UMPwk/AIz+QP6F9hb6uwPV/g3+jwU9AfP63gVmB+34/vdt/Mf27/l7BTIDoQDeCBMHlPax+E8B9Pzs/xoDpQJCAJIAp/2m+nIB8wDV/4kDdAYfBDT93/v+AKL9GveQ+238y/jX+qoAewLWBzUKx/wy9sj8Zfzq+BECvwIF/LUDKwfb/SH+CwXk/778igAVAXUCPgfZBqEB0QE0BF8BOP1o/ogCoAM8/Qr8sgDY/3sE8Acw/n34NQC9/2P6kwfDD2MA5fh/++X2Rf3WCmoEMPmOAKb+TfLE/zMM1ABc/bICz/j/8j7/OwaaBfsI/gLv8y70qfsd+eT7ewamBLX+VQEHBIkDpwTwCK8Eevkz9iz4tfvlBD0NTAjS/Ev9U/50+EAAyQnYApb6wgHOBHwAzgaYAUL1mfxjBPX5q/cAAvP+WPxKCIAKP/+8/T39LvvK/+0CfgFm/n7+LPoW+5cCLANAAGf+dwMeBy//yfiYAPADkf6UAb0FXf7f+1b/xPjX/ccIUgJT/PYEEgSy+JkBjQYe+iv5QwHT+iv6/Ai7Bdr9w/12+yv5cv1eBpMGSwQ8ArP9j/xx/RP9X/9dAdIB2APdAHsAKQfGBUr7DfsvANf8wwBFCp8GzwHUAjv8+/ZH/qQCb/vp/lUH5vty+CED5gQMBzkKT//T8ST0Hfpm+0QCnAnbA9b7hP5VAvD/O//BAQX9R/nQ/IkB0gLaAtsIxwYM/pD9IvnG9JT9EAAO+BD+pQ5UDrcFsQW6++Lw5/VU/Bz9egDOBzYF1QLHCXEGHPty94D1zPTWAGsM0AsBB+0EmAHJ+HD2hPna+2YAkwRxCGIHhQW/BeMAbvgS9cT3J/ptA7cNlA3+B+4E2PyN75H3oAE3/gIBuQYvA+P9DwSq/tr2+wASAGf2A/x9BK0BWQFpBXf/3Pdk/Dz9ivtPAqMAVvxJAJkBAgKoBbIDKwCi/1wBZwNRAz4CMfwT/Uz/h/nK+2IEQwVlBYUHVQS2A0MBQvuM9Wn1rvep+mIBMgJtA6EDpwTw/6X1pfan/rsCiP5g/Xj/XgG+ACMFKQaAAFcBi/w++A/9yQeABygC+QN3AOn7qP8UCGMI7Ag2CfD/Afau+lQBkP/lAzYDU/yt/PcFBARLAZIE5vpn9ez7rADR/goHUwaA+Tv3ffel+WP8DgLdACz9Sf1N/B8BXwWeBMsDfAJM+pP2zPyU/+gDVwh0AFj95gJ2ADD7CwREDOIACPxz/Uf7ov2DBU8FiAAKBXX/NPf9+Wj/kfzpAVcLPAM3/lv/oQD9/SX8qfqy+/ACvQN+AFkDgwVQ/Xf8yvyA/04HcwSs/ND8GABz+Qv/wQooBw79nvxr/fv8Ggp1Cy8D+P4Z98PxYPz0B9IDswClAXX/+v0hBP0EXQJe/d3zjfMG/YQEDgJiA3ECFf4LAZYEYgCf+tH8m/h0+P4CDwOsAWcHYANu+UX6Dv9N/uMDHQkd/M71/v/bAC7/fwkSBp/9VAJa/g/65gBEBWv/q/6XAR//hACaBQMEAgIICH8Arfau9uv4jf89Az4Bsf2sAnECj/tc/dIAo/2q/REBsv0S/nUAp/8z/f0BQwNd/OIA//+o+aL+2QkQDj0ImQEZ++D4Af4I/vv9BAdgBgYAcv9YAAQDKQQxAW38SwHxBd78mvtJAl/8Rvt3AzUBcPwBALj/cfqz/8gC5fp2/EkFUQLI/9sDzP9x+2b87/ou+T397/+YAPIEggZmBncHxwJ4+/H+ugCe+1P8wPw4+zECQwlVAFH9iwXgAU35rPrg/nD9nQKhBN355PiH/z79jfw3BbECbvaO9tj7nABoB/8IXwQjAOoBz/6b/hIFIgEMAMsESAKu/0kFpAa5BrALLgaM+4z7DQXrAsH+7/8s+eD8cAmlCw4ECQFv+1Dzhfkl/Fz5w/9WA/D9ywFIBxj+VPdf+Sb6kPoCACP+YPgeALkG+wNIA7H/ofmI/RgAnftS/KQBKwAN/nwFyASs/sEDywBX9mb9oAdGBMwCsgOg+m345QKbALz7vwF5ACL8/gFtBSIBsgAAAjn9YvssAb8C4QQGBin+Qvl0/l8EuQHrBLAEf/sr/usCpgNSBbgEY/we+P0A4wJx/hADdgGu+AMB7gWJ+Gb4yQCu/ScB6QaD/qv3q/ws/T74AwALBJ0CSwe6BBT5r/d+//37N/8QBlj/A/yxAgkDyf+YBp0GEgAL/vEAnP98AdUI/wDB+mv8CPzr+dj+2wcnCvgHGAGN+8T7Pv4i/KAALgTf+g75SP3w+8D/qAglAab5If8z/DH5Vwi3DZb9b/j9+4b5OfxFCcgJogMcB1QA9/UU+0b/zvrKAWoGIwGpBE4JeAMw/lgB1Psp97kAKQEI+6EDHwFR9i//GgUh/dD7rgMe+9D3AQZUA5f/LQlrAdrv+fmvADD3SPy4BaUAzP7PBl7/kP9hCmUDKfn2/+IGbf/HAscG9/zR+lr/8PpM/pYKHAnzAh4FjgRE/WcCGwWs+Z/78QGX++D8fgdQBDT8Kv49/wD85gInBlb+YgCF/9X39P3aBvr/ufp8/tP7h/h5AogG2f1/AAoAnfhF+yUA0f1Q/iMHYAPf+i7/tADf+cz9jQPn/vf9iQKhA3j/9wOjBET+aQEv/pP65AHbBnIEbgKSBscCwPq2/QH9WvuXAqoCxP6KAzsFJPu3+s4DWQJy/+sAgP0r+iQCwgWJAJYBxgBz/Fz+agFD/ij9zQC3/48ATAdAB/IAHP/j+lv5MgHUAW/8/f2eAaD8tv1bBdwAvPzCAWP9xffTBeAI7fws/q7/GPeI+GoDFf+M/58G3v9r+toD8Qgi/m//QwCf9b7zvfsZAW0F6RAaCq/7g/sq/JT3LP1NB+wBsgEjCHIB9/mNAp0ARfam/wcDL/0bALQFYAPIAWkGDQCG9Rb7pQBa/Q8ExwPR+Cj8wATEBEQDAASv/Rb52AHSBp4CRwUA/w7vEfTZA3kE4AH0CsAHhPst/QcAzf5YAqn/xPPi+aoGfgKO/vkGuAgvADgAOv3N+f8CNQN1++QCwAmS/rn4QQCHBFYA3QL1Ah/8IQI/BXb9xPjc/zACKv7HA4oCOf0jABwAmfgL+1sEKQRWAaoCKAOY/z3/avrR9mj7QP95AHYBgwbxAhMBHAR9/qP+gAJr/o77FgDKAOX8Ev7SALT8Q/yg/GP5gQChCZ4HhQArBA4BePWV9037pfybALQA3/k4/bMHjwXu/Y8ATgBh9vT/4wcJAjkDwwSvAjX+IwB0/mr4SP40AfX+UQESApH9xP+LCvoNfAvrAob0jfDe94/+FgNlCJkDDfuW/HEDAAQAApMFAf1R93X8Sv01AqYL/wxz/mb3lPrN9jn4UgSABfwBTQh6BsEAngF7Bdv8Y/QG+pn5vf/9DqYTAgo1/xb4re8u8Q/9PwNrBCoHGgKX/QIBdgFg9mnzt/4C/Nv8eAY0BN3/Xv0b97fzNPoA/wT7rgKeDUcEIf8dAwECPwAzAN7+5vma/VMDnAKmB5AKJ//A90L/WgJh/6EG9Qn/+6v4IwBDAc8BzwBj+tv1VAH7Bn39mgQfCqX9W/od/gr9wPxyBTMHc/1mAW0CnvupAmwJDgPOAGMD9PpU+CAFwAmaAlIDk/6a8iP25P7HAqkJkg/g/6n06fyg+nb8bgXIAS78Jf7u/cj4ePoBABn6XPjYAncFVwX3BTH/bPf3+6H/lPlI/i0GYAHh/gwCxv5//SgCjQTI/7EBPwRu+4ICrQv1BY0Auv8r+2X0ov3zBqH/7AAqCND/WQDEBkQAoP0EBwkIqvrc/ZQA1/m5AB8Fc//r/48G5wFZ/PQB1/6n+O8CzALb/PACd/zb8yz6+AYrAwD8hQC5+Qj1x/xHAPz8MgSUCU0AJv3G/Zj5cP55Cd8B2fb++aEAUwT/DI8TLwbu/Tf5lvDq+aMIBA0NCaYGTv6u8/X5PP91/7MHIwZX+N/2NgHeBMgDjQNG+BPrtO9p+Nb8iwiNEXMHX/4v/qz1hfbUBU0IpgHoAeL/jvgu/tUIMQfxBagF5vmU+ooKyQjTAcAAt/zZ/IcFEwpU/iP9hwOP+lH6EgXtAQz4q/p+/Gb+iAuFCvH68/b++Jj1s/kYB/IGiP02/K32GfX+/l0DJAN4A0sCbPnh9sP93gFFB+UJAQO6+zoAVgG3APkEOQSl/RP7ff/H/G8BPgtMC/4Dn/8J/lLz3vfhAncC6gFdBRcCG/iE/AQCI/oo9mP8K/4BBY4O+waw+xX7n/2P+wcBfALE/hcBlwCMAJgBzwPYAZ8AGAN0/Uj71QN3BQcCwAbJA1b6ovmt/X3+qQHpCYQCJ/dT/Fb+lv79BWwHU/vB9pEDXwLj/n8DugB6+zz3cPkX/agGkAvSANL5qvtt+zn6aAODCO8GFgUg/tz3m/xSBHwD4QL8+5/0xviQBicOjguhDGkDtvUa9OD6CP4/BJwI3Pzd+dUCaAg0BrsG5QEv8lLwQPfE/JEBhgahBgcCJALt/yv57/tR/0/3Cvbx/DYCAgMFBaQG0wGkBJQBrfVm+MsBlwEy/7AFnQcC/0cA0wNT/YEAlgQX/7H+uQYoCLz/Wf5W+djylfqVBg8KCAcVBLv7F/jS/xYCWvyz/Av8tPij/FAAtAJ+BT0HkP518yP6hv+0AbQGuQD5+7/7bfyP/kb/sgeAB6/8h/tX/tQBiwnwCtD/GPtc/7P/q/11BDsL3gNg/yH+/P3+AwoHoQA6+Cz7wPuV/eQEigZMCBsFNv528xLyJv9kAOYBgQb+AIn6iv1aBFsCNAQMBSj1tvGZAgwFuAQFDHIGefsq93v8tPlZ+igErP5o/M0D4AW2AdICIQI/9GvykwAQBCACrQUwAdv82P/X+3zy7/m5CD0GXwPPBEP+A/25BL4Etv5z/RD7lPKY+6ULYQhHCXkGtvsa+3YC4AV2/Zj9uP+B+YD9jAWAB9kHrQWs/o701PSf/WIAigpIEFgFYfu39Xz2D/rO/Sr/OfvYAhEJ/wM7BNUCr/7T+fH5N/7MAW4H4ABg+wsDRQbjAX/+/fwR/VMDpwfKA/oBVwVsARv82vtK+9n8NAFJBDsCYgP4Bb/8APP497L8/v5bAoT+/Pqw/fMByACMBy4JbfnZ8nPzLPau+2QHOgwRAacBtAJI/TMCkwOz/Y37lwCMAMP7JwVODY4HAQRIAYn4YfZ+/Gb+C/wVBG0KxwElAU0DkgCtALIBCvyW8wL4Ivr5+ToF1wqgA2YAvv5L+S78ogVmBHj6Zvs4/JECXQt9Bf/7wfr5Asr95/qNBrsHd/9LAX4DVvwz/s4DsgGL/EYEFQPW+K79bwBeAtoD2AXM/dz0qv97BDoAXvwu+bb50P2XBgELCwRTAoz8j/Nu+cv8AQB2A+8CXgJCAWsGQQZKAM7/O/t594D70f37AeAINw6ECfP9Rv6T+v/01/5uAGX96//UBNsHbP9lAHP+YvVC+yMACgDqAlQITQAr96768Pwb/qQB6wMX+5z7zwNXAYEAuAMCBJn72/nn+uD5MwOPCFEFoQJWAgH/KfsPAEoD+/7wBOYKEgBQ/On/f/9UAp8FUQSh+2z+pwYr/2X++AR8AZn9lwHMAjf9nv6dAEj42vmpAGv7OPpqBEIKRgA3/4kC8/bA9af+e/4D+f3/LAX//2YFPAdT/HT7TQGo/O36J/93ANEBeQqxDPv8DfyGBHwB5f75//j+lPwxAGUDFQHmA1AGfvmA9iEBsP8Y/rMBEwC9+2EA6QNg+8L6iQEy/C74Y/+5//X7NwJDBzADlAN2A+75gfdfAicF0/4mAo0FhQGS/7QFhQNL/ckCkf349ef+jQidBxEGxgd///P23/uu/cj+hAcYAkX6L/2UBXgJOwKXAh/9YPNI+fT7uPqaBBYO6gkg/vr81fs29G7/bQMM+uz7PP8Y/yQBigbf//n3/PzhAHv+3ABuA0f7wPr7A/QGUfwY9Nr4H/24AgUHtgNBAPECKgMp/j3/2QOf/IP3t//dAnYDQgcDCEYBSP0xAZb+s/xoBe0DKfqu/tUDqgNTBLgFEgCf9uT6/f+nAn0JAgip/Ej6i/wH+PP70QaYCAgC3AKUAPX2bvmwAYQCfv34/IH/CQEWBfMCifvo/N39TPg3+T8DGgmHBOQGqAgo+m/zafop/lIB0ATxAuL6tvkNAdb+3ABkB/z/S/rfAF4Dr/6C/hcAYPn18wP/EgGQ/u8JmAlQAHL9qf4/+xn8IwU0Aw8AjwnsByn8JQA0AnH79/v+APIADQErDckN3P36/L0BWvvV/HAFKQO/AFkEVP/l9w/8/v9O+vr6JAJwAfQB6gc/BzP9gPoZ/3b8ovsj/vr7SvjL+r/9xf+qB04MlgRW+vL8UPx9+LH9tf37+h7+9gSmBMr/JAMB/xjzrfYK/6b+tP8SA8IBDgFoB14KAABw+Hv6mPgj/ncDrfyX+5UE2w2RB3EEoAj2/lP5BP/b/1/+2AB1/5D/WwekDR0IawBn/xv5SPjqAZIEcwF3AgQFUgMS/isAyQAZ/AoCzgP5/3oAdQDa/Vz4svlc/EH6MwGZBxsE4QKcAqkAY/e581/8dP++BPoE2/m59hL+QAE2/14A8gDb+kX6xQdRDAAKeAXu9f7r8e/W+n0FtgyQDbEHyP7RAHEAzvkwAMv/xviC9xMBtgc1BTcOqwqQ++D25fR79w4B0gX0ATcBWwNWATH9bAMTBo/+Ufzx+rn9hP27ADQFf/1Y/vkBOP/N/5MCKAMfA6QAn/ve+L/5yf/U/1EDhQkOAnn8mf51AeD+D/sZ/YT9evth/z4DegMACSsFPPu6+wH/Hv7v+B/+hwNP/rsBKQejBs8Isgnz/Qfy6vhU/3H93AX6CHH9N/1PBMUEfwTgBwkDDvbe+sQBnP09AXUEqfqV9kQBeANo/oMAKwXX/nj8FgaoAIj4Nfvw/e8Bvwb7ATr3Rfe9AK0B/P9zDNcLX/1H+tb9oP/q/88Cj/oR9n0AxgIXAnMHZAkh/avzrPqk/Cb9DAUWBhYBqwGiARn4DfmOBHkFcP6m/OL+Rvq1/3gHNgOnARADQAJm+uj6kv+Q/RECjAR5/dD82wVqAk75sfwtBPn+yft4BhUGnQT+AVfzDPJm/S0FGgQlAS8GmwKf+4kEKQQ5/NT+5/2h+cr63gNeB20Eigi1Akr18/gIA6YBAwYUD9EFi/v8/CP9hfo1Ah0Hcfwd+74Ac/+z/4sIGQZL9tX5C/2A+O//2gVwBcoB2v5w93bxuv4IBgX+/gB8BZoAi/4xAKP9k/sMArcAFPgeA2UNYwQUAET+MvmQ99/8YgNzA5QMqgxz/A/8fgBJ++L44P6vAYv9VgKDCDcG8wXnAJP2vPWP/Wf/afsK/y0CrABKBJ4FZPxU90X+RgI6/UL94f/o99j6bAX3Bj8M4QqH/C3yBPdj/7L8efyMAXP/AwPODLEL+ga0BqX/pe/K77j7Ev8tB/8NcQR2/TEBmP9o+TT99QUb/ln4jgPJAcf+kwbYAcj5Af2a/zv9I/9KBhkAD/U3+5r/wP9WBEwFQAKwA/QICAJt+cH4U/QX9/kCpgYrCFcLyQiD/iL8dgbN/vDzXfiD/BwF6Qx9C8cCHvwE/fv48PyUC60HS/lt9y379/v7/pkGLQXN+X35SwCiBAUMsQk6/ef05PSY9BX2mAIUCfMFNAKY/Bz1MfyzCxsNcwXj+pz1IfCq9swFLAQqBfkGjv0M+HMCLglbAnoCOQOB98H0UQK9A14CDwsPCRH8OvlfAG7++QGECYwBkfzXAYUFbAFV/RYBxPvC97gCbQQeAfgInAmF/c73RvziADUARgRPBGb6fvwa/Zr2dfxbBdADewB+BHEHKgB4/bIAo/h9+aL9KvYl+OkF+wxHBSwDsQFt93r0Cvz+ATgGWgtfAU/3A/s6AIn/0fyHAKH+E/sx/sYASAK0Ag8FVwFH9mP5Nf/J/hYHOgdW/pL8dv5EAFn+ewLGCE0AafqX/r4BowvZDYUCpP3t+jn/QwPpAawIKAFc+MMBeQdFCRoGwAEc/5L3uPr8/qv9KwQ1AkH+0f80/zX+bvhS+Vb7l/sSA0UDb/uX+of/rf1h+ir5B/fS9kf8agRFAxIDpQWB/gf58vkR/ZoC6wWnB58AlPipAgcFp/7yAqwDb/9t+mT+SgkYC+wOSwlP+vv6zfoE+6wBEQIpAVn+ngF8Bbf8k/7IBzYHqwWU/LvzIPho/hsDGQVoBVcCb/aG8vL/0AjtCmUKhgBw+YX1RPdx/9oBUAXeBSEB1gArAEf/EACgAD/78PE99bAA9wbQCyUPcAXA9MXs7vBN9vT+dwoRB2cEowVeABj5tvmjAr7+hfqe/0L/mv0iBncHMQGQBAEAgfcw9X3+QAzACy0I6QH/84r2JgAE/IsBTgjpBqv/VPobALv/gAC1Aif+C/qR/Kb7lP6pCWQLcgZC+0f3l/ad9qYBzgZBA30DUwSvAQQDtgFu/sf7GPwx+wL34v9FCeoIDQh+BrQBePtk+Un/EQD2/EX+Ovx5/lAEKQiUBp8AggFKASD6tPwGAsQAlQRDA0AAmPsC++gEuwKLABsD3vrS9u79RgDVBC4MnQolAtz3cvqd/dP5Q/5q+cbzcQAxBkwH5we5BR4FRPv/9rv3AfQo+80DfQIvBjYGnADl/FH5tv3e/TkA6wKH/RL96QSuDCAH/QBV/Mb2/PeGADsDhgElCP4FN/9J/joDwwRs/Nr/dAAT99n9Rv/V/ekIGA2jC4T/Evvt+JDvs/0tCvECfv+gA+b/9/yBAAIElQJtACcDwfkD+MUB7gFpAVEFZP+j9Tv5hP97AcIAOwY+BZH5gvh2+ur9lQT3AUT93Pzi+z37SvooAc4CjPk2+SH+hAE9AycHAAhi/ib5IvyP+K/+pQafAi8C8v2DATgBrv65B0oFhwEoAbD8zPkKAPcI1QpiARP88ADT/9EDwQYzAlUAKvzy+Fn+BAZqDGoHMf2X/XX6vfpa/g4CAQnEB1wBVvsi+Pv9owRaAO8Ak/zR9Qb6lQCKCJkGqwTe/t71aPi1/q3/WvwoANf/Tvhd+f0AFQGWAIQF2gHx+of3JvdO+poB1QX0AAv/LgJmAWT+gACxAPP7FPuQ9+763gfgCfoJiAa5/6MAoPwQ/cEDcwIhA6gBCgBGAzAAjATiA/v5T/1cAdcEPAm8B/j/2vnW+2UBQf/e++0B4v2V/sUFOASwA9IBCwJW/ur6FwKJAFb11veb/tQBQwreCsoDFP3t/OT+2Pl2+pD+L/3d/CcC7AYRBEwFnwMu95r4D/0M/CIBYQXnAwn+Ef8a/8/6/P6TA8D7B/dmAJv/Zf+yBJACewBb/Ez/XP+q+x8CEAEI/HsBogK3+8f+IQREBOn/Vv33Asb8YftTAkoAXgfZC4IEBP6H/MX8y/m6/CMFfgNY/Uj93/yP/vYETgaK/7j5PPxtAScBpgHoARf/Qv78+X75cQC5CdAMwQFH+RX7n/0dAuIF5QXYBvT9zvhe/TAB1ApWBFn6ufo3+DH+6f/s/kAFKQTeBEsFD/zu+IT6if4hAh7+rvxB/Y/8Uf8KAq4FlAz2BVr5ffmJ+lP9gwFfAvAEdgGU/Vb+y/1KBvgJjQG/AKn+BfqU9yr86QWKA2b/yf3r/O0D4gMX/r79B/2M/+b8nvoSArsAOwAvAKH9CgHB/sP8sP5zAOUDqQV0/1H80/2S+hX/fQFYAZkCLQPWCeMCDvvg/Kr5OAAcCRQBof0KAWwCuAdVApH+0vs49sD/qwH+ARMGSP9V/boALAKgAy8Aivvm+2T6ofxTAsEEuQegAr7/AQCo+M36xv+PA00DPvuL/qQCTQUXCCMD7P0+/dH5yvn3/54AhALo+yT+dgK6/CEEyf2K+mwA/P/9/z78C/01APL+s/xfAdf6Lfm9/e/64Ad3CyAEwvrr8wj9cwTUBoYHXv//9+H+CgFMBHIJ2QGK/qX62P0xBzsGswigA5L6Ff+NACwCuQYuApn/3vz2+4YERAE1/boDeP56/sAE5ALkABj6KPo+/okBCQvKBAz4W/eu+RcAUAPhAbEFJgNN/4YBsfw8+nH9XP0aALsAevsF/04CTwS+CbX+wffU9rXzCQF5CBUL8gmc+Wj5Iv3r9vD9kQBQAHEFOQJaAH//QQIUBxgBoPsW+bz0mvsIBvYHGAquBGv7b/q6+6f/oAW8Aj395PqF+xgErgW5BBgEowB1AgH8R/Tb+Eb+TgWjDJoIRwWN/Kv3RQCl/wYDUATj+HD1Vf5HBXgMyAv/AOv8dPY9+S75lfvZCroGl/84/YL5XP2s/0f89gA3Aub9Ff3U+cj/pQRY/sv8kf5s/4wB/vsnAJkFZP6+A///jP3dBBwB6gLvA1wAav0U+Kb9nwjQB0EJLggKAIP9nPoY/Q8DjAPgBJ4Aqvr5AiUGcANcBHf9x/lF+7/6Xv8HBPoE6QgJ/rP1OPoK+r0AR/xM/qEHO/5E/JH93vo+/r0AqwD/A1cAqPr3+QD8jQQ4Abz8dwAQ/Xv85v/tAI4DtAAp+rv83/3M/xMDv/8GAloCSPzE+jn9Rv8oA3IHuwePAt/7m/20/P39jAFkAZ0IxgNlAvcF6P6SArP/b/tW/uX4j/rfALoDTw2WCjr9WwB9/r/6qwFA/u37GwELAhAAmPzn/YUGRAbIBn4I8vjt9gn4xfYaBisJCAef/8f4cQARAOr/5gRB/W31o/lw+lkBngQ6BBoJDP5W/Cr6ZfavAPADsARCAfn73/kP+738/AI6BqYDYgTL90f16f1HAv4LpQY8/xj/SvkI/K//PwD5Br0CXvuuA4IHDQaHBWj+//0Q+sP4qgLQBLwLZgrjANv/ifgL+TwB9Ps8/LT/Pf17BfcJ6wogBeH21PTj8hH1Zv8+AagCWQmXBVYBe/2M9sL6D/zJALEHYAFd/SX8Qf2OBJ4F5AQPAbP2L/3FAvQCpAfj/qX7sPpZ+qwFTwe0CCUFBfUV+Jn/F/7tAt0CbwDF/tL5B/zc+yj8jAUeBWwFjQiI/Rr4xPim9wj/9gI1Bj0Ha/5w/lQB///wAdoBeP5f+k/6xAO/CgYJCwUA/DP8/frr9s//GgX4CzcJ7/4P/rD6o/o1//795gB7BW/9e/uV/fABfQnVA/7/KfpL81n4zv5fBfQJ+AG4/0YA3PaY/DgChwStBvX8OfkI+if/OwaHBRsFxgX1/Rj5wf52A4kGUwMC/3D5qvXw/VAECwvECRgA3f+V/Zz8pf+S/70BrwBZ+Vf5qv6IA0kMhwc4/qr5O/Ax+eIEFwVbCGUAy/xJ/xP4Dfu5+2T69QEN/iT+/gUS/6r9hQPe/W//BPzK9JP7NftEA+sKfQXLBSIAaPn8+0oABAB0Aa8CyP6R/HH8xgUTDMELiAes+Eb2d/rv/94HmwNrBFcCePpdAD8DHQICBMgAagBoALAAWwIM+k3+WAe6/6P/+/3l+PgATQO+A+QECP25+t/5Af0/CLsHXAQ8BNX57vdn/7r+gALJ/xL7WQAx/iAAywXxAuQEbAGR963+k/4f/W4CIfz4/pf+AP6QAtL9hf3w/tn9uwLpAdb5gADWANz87gHpAIkCgv0l99X96gB1AW8GOgFf+0D6W/q+BLkI5Qc3Bf77Qvsf/vf7pAFcBcn/Uv9++0/+zgGuArANOgjv/yP9CvQo+KoAaAKrA5sDwwJ+/xL9ZgNvCLEC8gAp/f703fm2/HQBHQuMCo4G3v2Z+ab9UP3q/v8Aafxj/Dn8y/p0BYEIwgPOAWP58/n6+v/4ZwD7AdkFEwWm+Rj7gf8G/5YBNwKUApMBXfse/BT8yf6uCbsHtAJw/jP6IP2QAGgDygeZAWD6UvuZ9WP+kQj9B/YIPABQ/XT7VPtEANn+Vfyf/eD+8/4hBY8DOwOGAYz8M/sw8vH9agf7BVAMZgad/1n50fbQ+Cn98v/BAaYD9wWSEpAI1P3B/sb1mPVe9K/9YwswCqoKBQi0AA7/Y/eA8jT/wgTYBKwB0Pz+BM0CevoQ/eX6Vf6uAQv+rgO7AAD+HwFe/G38Ovny9zQAaAP/BvUIrgKw/Nb1p/a3/KT9ngAAAeMBnAMHAL4ApQV8BTMDh/w/+i7/nP3BAkEGVwapCnoDIP7+/s37SP9YBzUGDwOk/d777AGfAaYHGAbw9lH2VPfi+lEGPQVFASf/u/29/f347fpV+3n2H/rv/sADgAh+Bo8Bqv4P/ub5lvN/9oT8x/6iBDwMoQ+lCff7R/hI+jkB1AeE/In71/06+rcFVg5gD9wHxvaD8tH6Dv57BMgGBwSuAwf5LPslAT0EfQtDAaD8EP1J9jb9iAVFB/EGlfsQ+iv+e/nBBLALQAbfAWz36vVW/CQALQe9CEoCQf8d90L4aQPSAoQFuAJH+wj6nfrcAlQFZ/9E+yT31/ar/m8AugJ4CG4C7v3C9ZL0DPwX/GsFBQUDAIUBKfkg+gD+Cv/MB8MLTQXs+3T3mPf9/rYCtQSbBtj+mAKEASP/aAusBjEAofwk9X/7IQJvCg8R1AWFAHz/TffH+S0BbQZMCugD+f4q/jv+ogVzAr//ugD4+uD7lfqr/2UCWAAJBQYA5vmF/LsBVQLhAZP/EP2p+K70tvz3ArsI1Qe+/Sr8Lfs5+L/7CQGpBcgEtfpN+6v/FP7cBLMDUP9g/wz1APT++Kr9cQuIC+ICFP529wD8oAQUAzgFwACa9zj4IvfNAz4P6wqSBkv8Yvbn+eP8tgZmDDIA1/ux+bf8mwo1CgYJ3wHZ9sL3kPjj/BQIdQi9BSgIuv4H/bUBigOCBJj+ZwMYAnr5efw2+wP+swgTBs8CsAHm/Dj+wfth/kEGWP6b9wn7k/yhAUIDNANkBbT7Tvr+/MT6Bv+/+lX72gGlAicEF/7s+UsBrgB0/dMAsPqD/MwBzwHqBPz93fwI/Nj5BAFCAiMF/gueA138YQAI+TP+ugI//y4IQQDE/ioBYPmTAboEgQGZBNn6QflnAQn+jgb6CoUDJv2y9AP14/pm/mYEswQLAKwHNABF+zwCov65AwwA9P1KAOj6uABMCUwJxgaf/rjz1viP/2oGjgggAIgAygDTBbkHcv7S/of8a/V496D5uQN+CnsCOwTkABz8dgBj+Wr+0wID/NYCVv+J/90C0Pke/z0C7f4mAbT/K/2IAWwGuAkpBHj3nvib+NX60AGGAGADzQPFAZYDUwMYAdr8gvoR+8r5E/zK/zAA9gJjAqv8QP5XA9QBdv9A/MH7/vqK/HUBSf3YAVAGC//z/4gAtv/n/iX6BP7rANsFfApSAUwD0gRB/FX8xf5QAdwCbf/5ACUB9/zaB3cFyv6wAaX4Y/39AHIBHgQ3/0ED+gEv+xf5c/x5A2ADywJoA+7+Nv+qARACZAMQ/6n9V//m/5wFJwM7/3UAw/t1/vwANv+n/4H/vQctB9v8BPsp+P3z8PvBAMMB2gkiBTv+tPxF/ar+MvXZ9Zf+iPkQ+kEAff9bBtsG/AAoAQn8gvtx+9L7zgCO/dYAJgbS/ID87ABoA/YKMwn1Axb/L/4LAKf8QwHvB18DpwMrBPb9zP/p/+MDqAVg/1r/WPhM9hj/hQMfCy4RQwN5+Hn28fW//8f9AQBLAJz5ngFt/sEBYA3nBxwBk/xE+A76APxPAfUFVP+wARUCBP9WBnoGgARN/sX1ZPdg/GMASwaoBg4CcwLx/WH6hvng/U8BtvnQ/VH/fftCAboAafxn/tv+uwCpAEL5rv8aAKL9IgP5+1wBHQN7/ocD3vx7/lIEcv7nAJ4EQ/8w/0b/RgBNCZQINwgqA5X12/tGArMC8AeAAdv4dfq/+8YDRg22C6EGOvfn9Qz9LfzFBMMCtwDc//r55P4PAssAJwK5//f88gHB/bwDOQsWBV8CyfKL83P99v+9BsIBHwDO/k79ZgbqCV0Bfvyr9O7tqPqT/mcFogvpBEsJjf2E9Bz4Y/UWAMEE0AHlAWj7lPuQA8f/T/4+Azf9iv3I+xv9hgZABKcEMPzL9eX9qP3A/akDMQb5AvcBmAKmAFv9vv+wBGcB4ASQApr9YwI8/IIC4woaBZkCA/js+bAF9AWHBmQDof53/oX74vvgArr/vwTPCan7ivhg9ZL2HAGwAa8FsP+Z9mb+Mv1VABoORgDJ9uD6k/JN+1kE8gSJCZkF1wDk95L1TgCyAggCmQUOAWX9GATSBUoHwgisAxr6vPFU+ar/4wHaBhECuwCwA3UBPQAOAfv+g/wJ/NP+IQCB/DYBVgFa/1QHJQBG+XT8UvkA/uEFHgc3CyIDv/pe/1T9Rga3Bv/90/8i9jn8zgTLAg8NigsUAJf6ovKj8wwAyANyB8AB/PixAf3+g/ulArn7Tfg6+gX3CwHOBGEE4QLO98b7xvg6+AQCLv86A1cFNQFlADP67/ey/0gDHQdJA037vwBt/OX7HgX9BOgGKgAs9Oj3MQImDaUPwgSX/zn1sfHBBXUInAdqDd8ANvmT95H5UgS+CJcLZgdU/vkC+wOt/oEHDAY1+SH2pfMT+m8DVQqDDFADAQC/+hP2Pfs3+vz78wFIAcEBRQHN/778/fnaAYAC3P8wAh34x/jmAzUCPQWVBCoAtQBj+78AkgVf/tgA9f6D9lf/CgDy/YwFBQI3A0P9H/q6/3D5iv+7A176RP4c/7f3UQF8AC8B7wZa+gj9d/0j+t79oPyB/s3/IACBBdoK7gTnA8H+kfb7+Vr6hAPXC8wNMgts/AL5wv5PAhEJPwhPAPz5afgHAwsOARBrDuv7hO7F8vLxSQI3DBYESwPj+3P60Pt9/fsG/QXa/lj9fvSk9Q39dPoCCj8MhAFF/lL2Vff3+/v+/AEPBaUDLAVaANn+SgjX/wD+Yf1l9un5q/tXApsK/gkQCWP/XfeF/+X+Qf/V/5b4ifvdAH0B1v+9AVsEIACT/Pz45u/59bYBkQY0CzQEPALY/SX52PuI93MACwWQA+0ISQHP/qUDggLXBSYG6/8i/lX86/6eBvwFWwiABNr7IQLOA/wBhP8S+2X9jP54/vMDgAa4Anz6D/QD/ov+mf13A3f9jgHCAej/bwFH/jr7lvQh/KgEzwHh/6v9WgCpAtH82fsI/ysCkwb9Abf92vvW+E0DsgbU/HH9IfuB/EIG3QjgCHQAtP1PAI/67f7BBFf8of2yAu/+tf4Y/hIDigHz/xsJcQJq+276G/Zw/qcFiAELBL8BqPxj/iMAfQJV/nP/jv+L/IkBHgQIC7YMHQPe+fH1EvwW+VT3TAKnAzAGugc4BRwJVgae/TX0iPLl+ZP6cv8EDOcJZAU8///zlvPE/BQLXwr6BDoExvvZ+Iz9jQGgAxEDkvzu+rL7Df+8B+IGQwUrBAn2lex9+K8FAw1eBDb4Bfs9+LL8FAFiAuQGrvrs8gj2YP75BvMB6P5D/9gA7ANxAuMAV/4JAef/TfqP/Ln8qv/gCKQFjwXdD5oHggDZ+LT2KgOI/w0AewHXAVIHcgJEAzcMmwYL/cr4Ku/p+FwDTQX8C7MFMwAq+Jr4+gNnAYUE0gfU91PvvPbiAAAJAAs2B2v4CvMa+577ZgXYC50AK/tQ+3L96vr9/awHlwOLA2f/TvcC+x780f7xA+gEdgRF/lr6RQC1/mwDoAOy+GIB1ACl/TYDpwHrAon+1/id/ar/LQI2BSn/zgVyAujxcfZb/2cH/gjV/+72rPbb+gcAvAejCzIEZPPB9Oz95QbbDioJbwT9+Bj2JP7v/tID5AWNBmoExPlx92sFjhGYD/sBKfgo91Hy3vmr/8gFRRGsAQH6+Pxl+/cAPQRlCZ8E0/V589T1qPeZBswKqwSjBfP4+fPSAG0GLARe+5H1BfgO+F8BSg54DYQMhAG+8ibzAvep/r4DbAisCU3/uf+RAAYAFQd8BPUB/f5b+iz8mAG1CLQDu/Vo9Br5RgAsCxAHdgPA/ev3Nvuh+gQDwv6i9TP+BwVYBGAFfwas/bT2svW//ZwGrQwGDEEA/v9P+5zvLveUBhwQrBEfCDT/R/bg79D1Rf4LCOwHHf/K/8gCGQLrAhUEEQKs+bHzGPga/40GXQYzBdUDKfom87v3tAN2CGEF0wLaAjD9l/0t+2/4bwZCBe0Al/5z+Mf6mv5YBAgH6gA6/x0C3/s1AaMDwP3dAv39efgV+x79OwSgC5YJ9Agn/5zvTPQ++skD7Az9AZgA8AOh/Qf/tv41A0wCH/ch+UX9SAQMBtkB8AMfBTf9r/XU99j52/7AAmUGlASaAcwBoPzE+w75GPg7/aT/nfzm+ysCtw4FDYr+Gv44+oz6ivw9+OYDWwvYBUUDeP/yAdsJBQC3/W38ZPuzCxAIMgTMAaX27fzi/Vn8rgvJCpICtgHv9hb9wQGX/Ff/Rvmf/20KdAUJBDoAMPj2/l398/V0/p7/IwI/BLYDeglu/3L0hvTm99kEzQel/V37ZPqb+b8A7QQgBUYEm/wD+bb4x/usBf0Cmv8E/VP3ef2QAaECogNHApv/sPc++woHwgbxBGYCsP2f/Jr5rvjC+yQEogz2CKn/PQEz/5z78wMaAjgECgPM+PT2efb/BMMOzghMBZX+RvWY+tL/cAGnCDP/oP0B/Wj5EQYEAxICogVC/CH9GAS1AH8ALP7M/C0DtPnj/kIJngAOBxYCKPbp/rL/Tv07A0UFaQbtAST70P23+28Atwn3/WP5ufhI8mr6VAH9BxAM+AR6AMT6d/gw/wz+m/pU/+n5ovfRAMYFAw2iCpgCefzv8736AgBwAEkJhAIXAVQLugP9ACX/Z/knAKv83fpZA2UA/gNqCeUJuguf+6rxyfLH9ZQEbgYfBuYImv6N+sf+gP0v/Oj66vXp/EUDqAToBNr/1wNB/CD10gGRBLwBMQI3+0D47/XJ9NgCAwNrCUARWf7k/0T/ovjCALr8IPvI+/b8lAmpCOACCQuZ/tjzU/xN+hUAwASwA2IJ6QVAA3oCOPq8/4cDkvt4Aav+Y/pRAo0G2w1HB336wfni+Uv8RQJHBOID1wLy+g368f20/qACiADb/yP80fR69gL1sv0sCkYI7gOw/Bf6J/rv+8wFyAhqBE3+xfW69LH+WwWWChwJyf9++ir3qADlCbUJeQib/CTvTPa2BH4JJQ+lBAX6lPd29fEA8/0i/lgGMf2q/UIGQAQ6BV4Fk/9K/tX1UPk+An39MAb2CXcAn/t79f3z1P9ADKIOdwZI/Kf9v/09/DIHYwf8AA/+mvAZ9dEDCAZ5Ca0Dsvzx+HD43AVmCDsC6AWP/WH0bPea8pP3JgNrBegIvgWp/5r5jvJF+aQCYQZ3CX7/ZfmnAEgFfgYiAjT/evzU9978/AZgCUMGoAUM/ZP41/4SAFwKLg3/A8YASfqe/EL7SfhoAFgC/wWXAcv51gHxBJ8DQAjQ/6X4UP2199T6PQLd/20EogIX/kH/uftOASQDFvim/L//7/7GBpkEawPw/lTzpvbp+vIB9g3YBDf+SgBI/csElgSR/Ab+3PiE+D0Bjf6GBFkK0ARmBuX+ffnT+rb2AABeCc4DbQNE+s3ytfyO/PcIUBEkAhH3XvBD9CICJgrFCZ0KuvrX9TT8yfutDR4Fzfb6/Gf7Yv5OAx0FsAtcCpQB8APu9v3xR/0bAMILmweJ+gL6QPwTABoFwQM3AC74efAEAFEKJQ1RCxj9L/hy9eb0BfypBiQMNgnZ/fv18/qP+sADRA5OBXH+dfZf9yMEqwjsB4r+WPkN+b34KwW7C4EGywKu+RD0E/1SAqcJMA3aAln/5vaA9o0ACAJnB74EZfuG9lj2yP+eCcEH9AQmBfr3e/Ps98v7mAs0CVb9Zfrq86v8JgO5/uQGBAFU+QX/kveT+ooCHgJICu4HYvzp+ZnzA/fIBJMETwnSAoT0mP6RBQAGUAruBGv9rfpc9Kn76wOgBzgOKQEc/Fz8yvV6//YK5gczAy39TvYbAJkBuAELA9n1NPsMAysCYgmcBCz+NwTk+fHzuvjJ+uYHhQdFBaUIjgDs/AkApfyY/tgEHPro/PX/ufzEC7gLxAQ6/vbxjPUO/mQCHxBcDbz92fm27anuMP3mCI8S8gyTAfP8DPZZ8eX7xv37BW0IZfmh/SMEWAw9Ch0AG/m38PLx7vm2BzcOYxMTCYHzqO857972hgQWDRINxAMB/6/9evzpAaED1fdI8u77nQGkB80NaAojBNv82P+B/kP78wKrAksCTQTC+xv3mP5zAGwH9wswBqz4GOrM+SMDcwFIBk7/0PiZ/rQEHgDDArX/wPUB9jn3sP4cAkcCoApjBKL9VwJ1+Qb8Awa+AL4Ag/4u+XD7jP0nBdQH8/yQAJkAIPii/14C9gccDDABvgCZAFP+YgFI++L4Tv9a/ev7vwn+Du0J7ge+/Cv29/Oi8739TgUPDAwOnQMIACb9q/FW+DsAeQDeBvMDPwI+Aib/JwYtBUX+LP4C9AL6MA7cCqEK5QRm7fzuKPSV/esP/QWdBCABq/WU/QABUQKEAmf7j/F3+FgBDgbaCeIAtf+a9UfxKP+DBdsK5QhK+4f41fnr9jIDUwZQBYQGy/iR/FgCt/1FA+oBNfuJ+KH6XgJQB+wIngblA0D/qfwQ+kz8dwjYCLUHswQ8/WP6gPbE94kFEwnm/30Am/+WBT4HbQeAB9DyiO9x8xP0SgS6CR0GvQe//mP7hP4F//gETfxh9Vn9rQGFBMUJrgGt/DUBl/2BAAj+r/wz//z9DgPjATT9+P7R/5IAnAlPBgf+2PZH8uT/YgVJBrMD9vcB+BH7V//XCXsNMgco/X71EvRd/PIHBAsJAtT9mf0Y+TMBjgJnAHwCtwFBA63/SgZKBcT72fnx9yn75QUhB8/7vgKrBVYCyv729zD8MPqIBE0M1wAsANb9aff/AL0JLwW1/hb1efXiAZcJdRFgB7/2yPu4+Rb8iQIZANgFdgCF+MP6SPz2AL0Ebv9EAQ38tvDB/IMEDQqJCAP9EPq69CP4UgS8B5sH3wDk7DT1tAUtBbMPEApHAvsBqviO/hUDbfvB/c76F/swBU8CdAydEuwEEP7N9rH0cfXp9rYFyBCRCdACJvw4+RsDhPvL+cQBD/hJ9rz3eQE2DFMHXQn0BMv0JvNl+pT+7gd8AL322fu3+5EH1whDBrsJAvko85f3RvcvAloMfAR0AYL+Nv1KAqf77ASABy38mPj28Zn78AupDUkJZQVX+jb6Xv/NAiMNW/8P+KL9gPs7Bf8LZwueCNj6+fF1+or8BgG6BR0Ekwh4/PD07f3wAj4E0wB9/AT8Gfep9oAEvgiOB67/yvQC/Jf/Af1EAsUD7v2F+8D8DwIHA9P85P/YAOT/tgFE/Gz9gP5V+w8BmgQnBe0Cuvou/LUFFAKtARkFHvyE/QD+0v7LArn+awHs/0H7xP5DBNUHcAzzAHP0EPmu+DwCiAu9CpEGL/iH9pMAIwQDB3gJAABP+qX9ZwDiBr0C4/1+BFUDZAHU/4r7PgNDA5r2nfVm/mQDOAEt/q0HGQwW/vH8bvlt804AGgBE/GYDhgJw/qv+6fwY//L6tvM6/fv9jAIbEBUI0P4S+sbwufO9/SEB8gTlATsA1P/b9i//SAlTBREDBP+G+msBiATaAdcIAQEx+8b87PezAQ0GmQW2CvgF4vsW+vb8ZAQlB8T9qQKe/nP1s/4r/5oGcgse/GP2hfaD+XkCSwOUCroOc/tM+Or/CPt3ARMFnv6A+335Nv6rA30GawrTB/j/Bv3o9/T2fACyAnYCjQEZADAEDwA+/VcFMgCG+Br4FfSb/tEIoQkuBlT7M/i4+r77u/6BAvj7m/zZ/lP7cQRdA8cBugLd+zv8qvvp+dT9XwTNCqIQnwSN9+37lf2WAkEFvgT1Amj8AAKFBx4EugDe/zb73PzABegCagJPAnr+/f5y/CgAtABJ+MD+PgPc/RL/BP3++Sb6UgA0Co8NQQf+/Ef0Qe3x9gsAEQTYChIFGv1u+5UC1gbrAmoBcfr57QT3VQqsBokGNgew9gv2j/kU+QIF6QVzCWsJ6vpq/db8SfvaBQEFw/w//VD5HfvbBeQHgw9yBXv1OPYH9nUAwQuRC5IEx/2597D5c/+VAhQKlALE/pX/JfU6/Y0GpAVcBzACWPp69z/2r/1TDOILMQYX95TtSAGnBmsDuv6S8fT1uvxSAdYPuxCXCHAAtO7S77H93P70AK0G2gGhAOcEWwG0BVAEVQOF/1LuiPE0/iQJ1BKhCb78CQBg/lr41/rDA/YKYv2E81f7TvtQ//sL7gdQBYAEE/X/8Kb3h/55Cc0JIQH/+ajynwDADIAC7wDN/fb3/P2dAXAA+QXTBXYCFv0y+o4GOwfcAIwA1fu+9zz9Mf1A/6YMywwOBRn2WPT5AOr+of/G/xz4Lf57ARX8Dwb3Bf3/IQBk99z6kfuw+d4GTgM3AIEFiP4xASQFEAN4Amb/6PpI9+T3DQS2DSgGXgpTBJr37P6u/DQARwUBANv+GfnH+PsEmgWGBbcJYfyr9of+8/2S/1MDA//Y/h38f/sNAdsBygqOCCH4evWL+rD9ZwRxB6MFRf3N9QX7mfhTA7cOfwJs/68Ag/tm/lME4f4p/iT83/qT+7L5PAcjCIkDSAOC+sr7vANPBLwAJf7H/Jf6TPVt/WoFhwZlDNAFqQHDAEf63fjz+Pf6m/5lAbUKjxBMB4EDBgG59IbztPtn/b0DrASYAJsGWf8G/fb9afwYBC79V/q2AuwE4wIoB7AEhP249tHxPgGGAzoG5wdx/dEARv3e/OACWgbXBYL9TPj+AGUD3vgk/mf7jPgH/kn46QCYCbgFugHZ+8YCTwJy8nH2sPxE/hwIwwe2ADP+XPl/+V8ABwI/Bn7/UvkwA4f9PQCYDWwGjf6l+fz2aPzR/FIBTAsHCBUDpftp874C8AtbA0QB7f15/lkAev26AzoEPQAFBTf+Ef/kBzf99vwDAs38Jv8fAjkDwgRRAQEDIAFb+qQBZwLt/ysCDfuu9jv88ALmBbQGrwQzAwD5AvMO+Zn4gP7sBZ0CGwLxBCD7Tvb1/iAEHwT/9eLxTfn6/GAJag/ODsgKhfzJ7ofvHP87CisH0wLPBVv/hPviBIYFjwixB+f7SfaX95v8AAAbBMsJMgmJ/MD5QPuh9y0BNwcrBU/7u/UX+UX4UgDQBngCi/9+AMz8wfqYAL8GEgTW+DX4BPu0/HMK+Q3KBVgI9f9b8zb7HQLzBD3//fpqB5AHigfsDH4CnPxi+j7xCvWo/pH/2AXRCNQHYAXr9Lf3+QLu/d4CcwGn9rL6GP1GA6cMjgEy+j7y2e1D/rgEhAtWF2YMWfht9GvyS/heA9IGOg9JBfv7+vze91QFPg4rAL77WPtG934EvwnuB0sLX/559tjy++5BADMIKQS0Cnn+7/jq/l/yH/kkANz6sAEAAYQACQa1AusEIQaP+XXzJPJw+WUIMQ5HEakHL/Yp+DX9hPtjBfAGnv8xACcAhQTAB98DSv1r+TH6MP3t+jL8xArVCa8EDALI98/5DACfAZX/4wDyAon7hfmJAPIB6v9MAXD8yfa++9MBVgK7AGYDDgZ7/0v/k/8u+o3+AAIbAVMBugJi/q78WgGRBlYKlANdACz6jveG/goB8AO4/4b7UfxFAPIBKgSlA7j5tPjS+Oz5TQJZCdYIBANsASUByAAs/aT84f7B+FT91wXGA7wIEQptAjb+9/sE+3384fym/x4F+QKtAfX8F/o2AS8ATwIIBe385/fj9zX9dga3BcoAjQe4BCn7/wA2/v7+Cgfq/+r9u/xb/BoCfQIEA78FBP/E/WsH8gEHBboHsvnw9Nv1f/voAFAC9QPmAkb6T/ss/xP6aABbA2gBIgE8/Af8Nvt5+dADTQQ/+jr8nvap+XcM2gtgBR4Ehvkd+EH+bQT0DssG+Pus+6/3h/szB0MJigeMAuj4DPhY/ukKEQ9JAwH6W/ha89f51ARPAgoGHwGB+yv9sfp3/ysDmQeFChj80/Gy+nf+xAcfD6AE3/oo9FrztPolCyERNQru/Vf3HPsM+1oDlgULAQv/Yvg99Hn5wAT0CTILwgJ39Frv9vUpBWAMUAf/AJP2EvNX+2sAzgTkBSUBTPpq/GYGogr5BJz+MAIq/kr8J/35+xoEVQYEAxz+HP2b/ij+BgDpA6wFowNtAjT9rf1H/w3+yP3v9ur5Vv7i//IEXgaABkkChv2c+Wr6Ff3RAFkGpwAFANEBSv3D/1MCyP5//GT9TftFA+UHJAULCT8CuwBx/1b3Sfd9+psBDwejB1gDCgHV/4MAev99/ez/5/vu/gIBN/39//wHUgmX/7f8HPqW+Ev4Qf7UCYoEjwA7/5D7ewP3BIb91/sE/tkAowP6B+8G0v5j9Ff1zfsI+xQGBArXBQEGUgK2/yj7JvqA+4L7FfvcAEkDjAf3ELUIcf1/9PTv5/DR+igKFg3OBjn/OP5C/Pz8BAAk/pH9U/65/uT99gCKBkgGLAFhAcb6C/BE+rIHFgk3C6wHVP2B9w72bvq0AcsIYQf0/Y38hwAi/3D+zgZaBoj6rfQf85f6jwtmEnsPbAUy+AT08fGW++sKhglpAXP7WfZ9/oEIgQfmBFj3GPEj9bP6rQaCC1IOFgjo+CHxBfUf/FYBFgI8/58CKwBr/8wFNAjABTr+O/gN9RP8rQN6BIcKJwvCBvr/IPjo9RL3kP6KBSIHGATcAW8CbAWYBdP+9vzz+ZX2HPf3/wMN9Q7RCDD/kvjj8zz2xvjX/KoFRwT8/kIA+QXKAXEB5gOM/7z6iPJX86H7MwYUDhIM3gD19EPxNf6SEW0TRwzQ/3Py8e2q8lL9/AZBC/kF2gDFAY7/L/xzAIYC6vuO89D06P76BwYRTw+JAW/2vfLc8uj93QwHDP8Cfvrl+Er8pQSCCRAEUf/Q9/rxEPbwAr4MYg4KBVL4HvRl80T+UQf7BjYHswAO96H2uf91BEQHYQjwAhj7x/Xr+fkFwA0YDMwGTvnc7uTxdPl3BkcVDhZPBDP0PPIj9xn8nwNBCCIEb/6t/1YDfgRXBDj7ZPeb/ob/NPkL/Y4HOgXUAKf+Kfr19fX9JAdJCeAKoABr9svxlPgjAKr9OQL4Bd4C4wJNB8wDyftK+S/9f/uD/F8K5At9BiQDmPgv82j4e/0AAnwD6wbiB/MAIwLV/cD1MPr5/N737vc3Az0LSQq8CSoD4vbE9bD4Z/snBd8MxAU7/ff7pvno/W8ELwiVBDT8SPs6ADYDegZpClcCY/li8sryTgHWCF0K+gXk+4T5QPgK+lwGUQptBGT/v/ld+OcAsAQJACb9N/dV98D7HgKJDh8RrAYb9lHoiesM/SMIJBAkE8YFxfhk8qTx5vkkAj0Du//8/f0D3QNFBL0MnwnR/UrzOPJ++O7/jQTuCAsO3QcUATP9o/n4/Tj+Z/zOBBkFOgHPBLkCMAG6/uL88P+1/KL9WQPmAPMBcAJp+3oA7ASCAK/+Tf+rAXD7bPduANcHugMM/6P81fl6/VcATwRLB00FJf1q9U31v/jeAl0IkArsBe79MP5l/oz8nfne/G8BZAPgAkYFLAOC/B/+Cfxh/RACJgA6+wb+3wK9AcEA9P5t/Zz6twLmCQQExP0H+/f4bvVv+icE+AizA3gBpQQKBZoI+wPp+NX3aPjr9dj8hwYuDDMMUggB/4v1pvhT/oUAOgPrBZwC/ATrCOIEjQDm+jT3hvUf95f8BwW0BFAGswkqBtMElfjl88X57Pwp/d3+iAFr/X/+qAB5ArcCk/xk9n/7DwLgAYcDXgUDCdwBVf6HADv6r/je93T67QC0AwoB3QP6C7gI6ACz/EL8Dv0d/L3+KQMLAj/8dPp7/lwABAKzARH/if9C/uT/pAG3/C76u/p7/RUDUAcMBwIC4P3Z/M/8xfsr/RkBtASjCjAN6QkqA2z7bfkY/8EFYAd9Aoj8OgBPBtMHTAVBArv/9fqI9r/yyvpRBkEH1AMz/3n8KP1L/yYAMQBZ/Qv6X/a59qX+GgUoCUEJ4AV0/IH1jPhI+o/+4QO2BPQE5wHr+0n9OARUAxwCswHj+i71QPTc+wsIaw/KDAQBvPZt9AX2o/zCClUKegCP+3X4AvyV/qwCagecBDr8HfZP98cBXgoJBOUCPgBK+kH7dvx+BD4JFQblAzIBRPrb+Iz8WgXWDiQI8gDN/Kv4z/qoAvgGhQI6/0n9tQKWB50F1P3y8xH2APnM+2EDawjFBCr/+wDs/pX5ivo0AHYB0P+y/oL9OQCOAnIFeQUEAND4MPCk9hgJRBA5CZT+d/tE+wP59vyXAjcAAf0IANEAeAN2BScAPPyp+jr/PwGf/SH7jfkg/1MLPw5DAnz7P/d89e38kgPVBfcBbf9O/VL9ov7HAXgFBQHi/kr8M/rd/4YHBQmWAvf7pPht+vX9yAZQDM8ErfzK+fD8fgE/Bg4HdAMAA3X+NvmH+lkBEQenCAoGPv6r98zyvPdpAtUFAAYuA0H/OvzR/D8BRgfLBTr6CvGu7nH3UQJ9B5YLjAifAOf8y/0W/037ZvlI/gr+W//kBaEHvwgtBWr+7v2s/Kn7UP+rAA0CZAT3AvUBTAI0AfgAoP5x/F8AZQOYArkApv/K/6n8SPos+9f9TANoBl0DMwGs/7/4b/l0/rD/DQKlAPYBGANB/x4A9P+q/rX+fPle+O4DsQVGAQQIDAgS/3H87/7wAKMDtwIS/Ej3Evx1A00ERwYBBwAFhwMl/GT0f/aA+rj8HQPICDcGrP7z+Br6R//bAMUBlvra8174g/w/BKMLiQonAoT4afM/+rUCpgZzBxj/BfvQ+Jj9IgddCuwHtAFq/ej8KwBG/3kGZgn5A54Bff1B/V//0wTmBJ0GjAWXATD+tPiR/HsBJgS//6v5o/Uo+ecBBwnRC0ACQ/sj99H0RvesAN8FkAHA/1z+U/8vAUQE1AaDBjH+YvSJ85f9rAu3C2ICOfv596z50AESBh8GjgLs+dPzQ/dmAxMIlweWAuX7OfgM9Q/74gVLCtkF8v1Z9tX0CPu3BakKpgZYA8/+Rvnc+awBUAVbBGwBBPp59Nr2bgMtEVUUJAwD+tPrqu/P+GwDzQ+mEp8ISvxb81nyDvzzA10HXga/AfD7KP1u/kICrQmbAeL6wPVs9IX+rwmSDcwKygFZ9mLyjO/l/MAKQwsQB8f+sfrN/BwDmQRyBjH8NvS9+Qv90QRcCVQHt/8p+2H7Xf6M/4UDrQjAAz0DCQKkAbECt/5M/I/5sfVv+1UGWwnZCUYFXAAlAHn/Nf5S/Ij8E/9i/RD5iPix+VUCTQnDBJ0CmgGY+j32rvVZ+soCwAIjAagD1AX6A77+9vus/GT9hPvL+ST7fgJ1DHQQqAho/vT4x/WS+rADNwaK/yf6uvyeApoJdwiN/zn5LvLs83z/PAnuDcQG1v9+/UD8Qfww/Mv9MAP1Beb+tfl8+TgAiQjaC3UGefpC87bzKf70B94RQw5P/Qz2cvSB+uwDMAZAAnkDzwN5/5j59vjoA2sJZQl1AtP3BPXN+HL+ygM8B0MG2/5x9zD7S//gAf7+J/sc/rT/QwD9/tkBOAP7BecFlADQ/kX4Zvif/S0B6wWXCAsE2vyJ/XcBcwdiCBYDg/zZ9uj4OvwzAHkDOQJKAZ0BwwT5AhT+X/2x+OT5Yv3r+Ij9lwfeCbsGtvyx8931fvo9AEMIqQZO/bb4N/wiAg0HtAfgAO746vaV/jgIBgt3Cb0Du/r48575OgWeCQEMWQQJ9hX1dfywAksI1wet/RX5avmx+qABFwnxC3n/8vCv75b1UQBmCCEH7ADw/Uv5qvqIAbEEVwqZBSL5QvM39J/8WAWPCLoLxQxvAQL4DfmS/YwHbQxqBkT/S/od+zwAJwRoCmsLpgIi+bHzyfWv/rUFfAcPCYwCs/kM+Qv7eACjBTEFb///+en2QfprAeYF2gdcARkBiAGq+Jz0nvh1AP0FbghEA4sAVvwn+XwDkAf+AVP5FvcF+DD/yAioB+QG8f9e9mv0Kv+3C9ML+gLE+kD47PQf/WMFwgI0ANv8L/4XBR8GeADe/g37oPjE+dn8pAJNBTwIHAMC+mz3S/g//UkH7wx+Cd7+APVt+Fr9mgCcBtwIEgd1Ak39G/13/wAAYwNQBGEAJP35/Nf8+f/nB3wLmAZj/Cn1c/TQ/IIGfQhgAsv7SfjW91UAVgj7C6AFKvpe86z1h//eA2wF3gM3BqICL/ic9xL/nQitCFIDNP0S+h33tfodB4IMugm//Ib1ZfV3+SsEnAewAw379fVq+WD/hwM9B1cGAwK8/fb15PX5/e0FVgt1BF/6Uvt/+pP8TgXDCjcNhQNO9gb2bv34Am4GTQIv/gj+TPmN/aICPwiPDJMEU/oT9An3CP5tCHUJygF3+6n3Avtt/l8HZwkrAfn7dfvV+1z9awNXBEsEyv82+vv7OQEBA9X/KgIZAe/91f1A/nYAMwWNBGz/wQC7/Vr6lfoIAeUH/AO+/c37a/5N/6EFHwaH/rL5nfjy/k8BbAIXAWQC1Aa2BGj/Q/ra+OH5ZwEoBDUDzwNDAEX+dP1CAfMB/f9q/6j9Uf22/3ADaQInAeP7SPd6+c75GP02BBYJHAfR/uz4Kfs4AqAHvgjOAwD7HvSJ80/+7gcdB8wE1v9L/1gG4QqiCfMD4vh58Sf1OPtrA6oIBwzKC6YBdPa/8Qr4uAE3BoYGNghzA5L6ZvqIAZEG6wJi/Y/46fcx+esArwpqCkMBFPcy/IgA8QFNBHYCQP+N+Jn1hvU//WoFZAcdB3sBFfwU9+/2Tf0gCJoMdgOn+qf38Pt+AyEGBAWVAIP85Psx/Qj/fwaUC0YC+/ln9w33mPu7BM4KcAoxByr+ivjM9Oj3MAIEBiMF9/8V/FD5DPzbAXcGvgh9/5X2Qfcx/GQBmweRBtL/n/0M+nf4nP5JBbADp/41ANcDigQsBZwFTgQDAPj6Vffh+WkCHQV7BOsFbgYDAmr5K/jf/sUDdAEw+gL5eP7fAhAGngZ2Azz8x/fH9tr4gwF6BlwEMv81/14AFABcAVQD/QSy/nv6Ff+pBK0CcAFgAV39u/2U+9z7jwFPBwAKDQflBFcAH/Zl8M72gf8xAp0AfwCkAxsG/AOt/sP74v0U/rb7j/6TASQD0AHlAXYCHwG//uv2efn3BP4K3wlwBQ7/PffJ994ADAhoBdYBVABC/8H+Iv64/wECQQHo/Gv77vno/P8EkwllC7YD9PXl7g7xMf+YC1cI0AA7+LP1qftoAusHBgaq/gb61fuj/EICFQexA+cCLgCz/Xr71/rPAOAJbgyyBWb+rfqM+WD7VgQJCBwFGAFk+ZD2kvyAA9kFygSW/Pv2c/kv/9MFbQYnAp376/Z4+ez/QgT0BW4D9wAhAEr8f/t9AksKfwbN+0T1d/Rb+KACtw2XDu0FfPsh+pD84f3s/CT7hv3u/fv+YQbUCQoF2wQPBJj+hPc+8r35VwfIDpEMmQYY+5bwMPBe+JYF7wzjDTcFt/xW+8z6Xfor+6789fv3/RT/8ANvCEAJDQrDAf/4bfID8DP1t/6iChEQ8gslA2r87vgB+YH6A/3mABYBBQExAuX/twGiBXgEbf+v97L1zPtkBDAMyg3bBdr6ofKi80H/iQfACZAGrgA7/Df5UPr4ATUHgwQuADf3F/Q1+d4B0gy7DvgF6/cz8Ubz3fssBqIOGA0I/0v3LPYv/O8GkgtCCYAD8vc079r2OQTaDVQNdQrSA7H2ZfWm/TwF0geBBJ/5A/TE9jf6wwOwDEgQEwe/+Ub2fPQN9Pr6nAaXCs0Fqvra9MP6CAFTCEoHGf739abyu/yXB5QJ9wpkBiL6xvMz9OL6/gGSBYkJrgZ7/+b64/vSBNUNbAle/eH13/Ib+5IGpgy2C94AiPXx8c/8ZwvSD3gMjAEB9RfyOvbQ/SsHPwq9BYH+VPr/+kH8o/4yACf/dwBnAy8E8QKEAs8B7Pyd91n1efbV+TX/2AV8CxQNgAU1+gvzGvPb+T8CoQVnBR8CKPvK+RsAyQYhB14DA/tn8x30qflzAiMMDRDoCAn+W/fA+YQBaweoCfUCA/jH8cT2cwXgEsITdArs/gbzAvKh+r8ELQu7CfYE0f5b+fz4F/7PBeEKFgQh+D7z1fIG/RQMAhC6CAH7CPLN84H8NgnuD3IIbvtv8bjvS/qhBU8LaAmF/yz2nPMM+lkEdQ6cDu0D/vbC8rj5G/64AigG4gNx/av3CvYi+tUCWAmDDXAHavxW9hr0WPcm/zoGeAfoAO/2rPY9/VgGrgyOB4j+Zfet9bb7RAZnDJcM5wVn/BP6O/xYAC0FjweTA9n+Wv7XAYIEQgE4AGcBC//W+rH7VwBLAhACJf94AdwE8f1D9R72YP62AfIAfgKaBAkAs/pO/In++gCh/pX7cv35AUQFQQVDBzADcfui9rz4w//VAn4B+f4s/8T/6AI5BaMDHv8g/Yr9uPze/mQBlATDA1v+IPnR+qD9X/5gBKAGOQjAA+D5B/fX+FP9rwSYB6EGJQcAAAX6Ffj8+nIDcgXgAgL/oP4MAboDmQXPBYQBlvnc9Xn4Qf6BBX4KKQfiAcL7nvjl+AD83Ab/Cb0DPPsr9ZH4uwNZCSsGBwMc/S32IPUS/X8GJQuQCYMB0Pok+Cv66f9EBu8HkQF6+Iz22/2jB7sOhgwZAtX4FfI/8Yf7QwYqCtYHjwGY/oD9mfot94v68AEoBCACn/6c/zQCtAETACH/RfwU9rb3hP/0Bq0NiAvyAYP6Y/Y39K762wSuCSoIwwJ/AE/9PPtn/9IBLgHW+x/6QQN6ClAJCAKp+/v5gPpb/HIAZQSNBFEEdwFL/Tv8g/rZ+df86ACbAg4FggR1/8/6AfkJ/kkApv4g/yoBQwUeBrABo/+mAc39rvgZ+kX+TQUMC3wJMgWGAUD7avcp+vsAswYaBJ/9Q/p3/VIHNwmvA97+QPnm+KX7YACABggGbAOLAjz+Rfyi/Pf4DPuLAIkDmQaEA2v77vlu/6sGUgcRAPH6K/fz+N8AlwQCBh8EVPud9pv7AAIpB6MGCQIZ/M/3U/nB+ev9Pwb5BUX/Bvzq+VH8tgHAAicD9QD3/fT4gPbU/lgI+wppB9v/iPhV+Sj+iwJCCfAM+QbB+yr2o/fc/I4HrA/tDHUGkPyR8lf4DQRdBoIHeAQx/Xz5u/jj/TYFnQp8CO3/hfjt9DD0/vcfA00KhwnYASf7FfuP/l8DbAEN/pz61Pb19yP/4giRDPoI9f6R9GXzC/1+CAcLNwX++9r1r/jF/CMBlwRFAzQCUP0r+0T+DAGVA/YC4ADm/Uf7Pfkj/LcCuAUJBLj+yvqF/E4Cjwh/CXUBmfem8OrzU/6CB9QMNwx7CFb+p/Wk9Wr9VwakCD8GlAGc/ln7OflC+/IChApBBygAm/1c/ov/RwDL/wwAmv5F+xn6Qv3ZBL4JuAhGArD4r/Iv9G/6hAQ1C7sGpv0N+M/51P5kBQwL9gZA/H72Zvem+j0CJQjrBTADewDs+9f6Sv68A3wIxwemAB365foPAJYE8QZ4BwEEiPyR9bv3UgD1BsMGsgDk/FP6Kf5XA0cE1AVyAMr3yfZS/J7+fAKJBRoEmAO0/Nr19vdvANcHyAk4BXX/h/tg+jT+1/4pAgwEYQBJ/ab7l/9oApgD1AJFAZcAJvvi9On4lgSdCv0IngAX+sT2rfVz/rAIdwpkAzz6TfUo98H7+gGHCoEKVgGE+WP3hv3/BaoJTgmFAYD33fD88Ov+ww5VFFAP0QCs8UfxRPvoBUQNvQfO/DHzIvHx+/kIgw6aCG39pPWm97z9uAP2BgQDDgAt/kv8cPyFAaMH9QfnBCIAa/pe9Ef4DAEGBSgISAU5AKn9C/4TACIAKv7t+1EAtAKC/hb/tgH3ArIENQNH/777Y/gS+SwAjQaGCLYEif0v+Yv2YPiNAAAHAwcPA03/Z/v9+a398QFNBHYCFPzL9x/8NgPFBtgIeQW1/Oz1b/aP/kMHVQsFDAQGivnw8vf07vsTBUcJsAZeAj//yvth++H/zwXFBrgCufzh9wIAzAgTBcX/kfuC9VzzOfyeB5IO5gygA8f5i/El9lcAdgXTCywJw//U+SvzU/Cd99ECRQoACe8CxwAe/xYBUwOp/7r/ef149m/1T/wnBMUKHgn0Al0AcfgJ+CEABgdIC1sGEf5k+Pz2vfm5AVwGMQRE/vv4Wvv9/gMEoQcmBrcBrfm39XT7GQKnBQIHWAOwAS/9dvds+wID0gbyB+kGjgMjAU/8EPnE+gcASAWxBOsCIAHl/tL+NQFsAxoBQ/ps+NT6EP43BhALoAcaAQX3w/DF+ZwCxwUeCBgEHP0a9pL1rvk8AIMEowP9APn7Uvz9/9oAwf/N/3b9Jfup/Hj/ZgTFBFEAPf75AtkEYAD+/Nv8yQGJBM0DIQKSASz+3PsSAysIEAQD/Xr4yvmb/30C5QURCAcB/flV9875xAAGBnEG+APc/D/08/Wb/xUFWwmnC+kC+/hf9fH4AgHEA18A3P47AOgADgX1BuoH9QYo+o3wJPbh/Db/SgdMDQAKcwMD/J35zPyQ/Yj9UgE4Avv+k/v++rb/3wMcAlUADQBt+pL6CALBBlMInwTM+qz0XfY09Wn8EwoqDekLTAf+ATn+y/eT9lH/5gEWABQBAQAvBIsGRAQSAhL+1fmE+Tb8Y/6bBKEK8An6AxT8H/Sx9BT9zf4zAhsHfALg+rD3X/ldAtQJ2geaBN78HPRA9Db76wPXB0wDmfvs+Kr7xQLfCXgJUgQrABb6V/fE/KgDSglyCuEDJfxO+5H7zP0cArgDqgVnAmP7xPp2AH0F5gnrCCEAP/eo8EXzbfu1AOYFdQuCB8H7Vfm5/Z8BMASjAAn6dPgh+l7+6Qj1DbQFzvrA9Fr2gQAAC6QPBgtd/eX3RPsK/LIA5AX5BWIEJf8f+rT8Jf9d/XkBJARSAQv+ePsm/hkBqv9c/rEARQDh+WD1TPhYAMUHngWt/E77evnZ9sn61f+3BwwLOQQk/Xj88Pz0/Hn9eP4TAuYCrgAiAkAFdwYGCPIDIv0o+ov3/vv7BCEJzQhwBSH/Zvoy+yD8GP3JBOMGBwOIBEYBFv/F/wH9zf3BAX8CyP/A/0z/XP8RAasDeQRKAKD7ifsXAt0FGwekA778tfpZ+Af4Mf/CBWkCf/+B/Rv7uP7B/tr+eQTVBOn8d/h++e39SwNzAx8BYf02+nb50/1KA9QGiAgPAzb93/q0+dr6KwCqA9QECQT9/DL7tPwA//YFVghUAtH6lPhx+ef/1QbMBagCCv6a+lD+dAKQA1UGMgeTBEz/8fcg9+b+dQaFCP8EkP/Z/Wb9xf76A6oG2gL6/TX86/k7+mD+pAGhAwIEfgAR+935WfwrAvAGyALH/Wj8kfgm+kUClgYhCRAG0vyc+L/4Lf2BBbIJ9gcBALb2IPV+/AQEfQdDBxkBofsp+Rz4Bv1TB2ILJAVl/833DfOI+s0D0gcbCLcC2PoG+Eb4O/1UBdYINgn6BDj6XvZl+nMAOQlyCFoDq/5K96z2r/+JCOMH/gQWA9H+Tfvu/PsACwU1BGj8lfp//GD7gf6vAqsCvgQmADP4lftO/UD9GgIhAiEAngE/+mb3kAH9AkIBFgGn/+7+XAC4AMj+9f93AJb/ZAG1AiwBQwR0BRcC4f4Z9xb20fqt+0sEnw12CLYCJv1X9df3lftu+8oBfgdSBe4DOQF4/tb+tP4S/GT7dgBTAzgHWAgbAbX7ev1pALUC/gSBAQECSAT//4AAxQGK/RL8mfqj+lIEzAb3A3wDnvwY+Ur6C/yQAb4H4gVq/yL7yvP/8yv9RQQyCGQG+QCH+736Qfug/ioGeQUpAFP9Z/x+AVoK5QX8/X776Ph4/z8D+gITBh8GMAFO/5X/o/xx/mL+tgCiB2EHPv7y9jD3+PiF/7cDpQM6A13/Jfll+QAAaAVWCosHUwHA/Gj43/iP/M/+uwRxCtEEpADf/3L9cv4BBJYDFQCnAez6O/jgATQHuAMI/jn5BvlU/YH/MwMDA3r//v2T+8v8KAF0A38CSwED/UL4ePl3/K0AlQQkBrgCEvzj+jv7q/0O/2D+PASTBfcAs/94/1n+ZQDR/2z/ugV3Aw4A1gCp/nv9/P/uAcL/Jv6l/bcD0wepBVkEVP+L+Fny6vN0/JYHjg/SCzIE5ftV9Ab3Uv9+BAIHKAYXA30CBAO6A88EbQH5/ML7yPpg/Q8CMQUYCqsLNAL29Tv0DftLBN4ILQLV+WH6dvqU+Ob8LAHBA50EQf/v+o77VvuZ/DUAKwB/AJz/Xftq/eABCQQ1BnkB+vhU+ZH8Kf10ASAEagW+BlIAI/o0+4L+9QDMAyQEwQF3/ln4LfgG/70C2wJSBDQEIv4H+jL8nwJkCV0I2gKe/Tz3ofZLAFUL9w1MB8z7kvcm++b+hQU1CVgGgwGc/Jz7owArAgUArgKDAcT9F/qS+Of9tQO4BDYBoAE9Aef9zv2V/UT+oAE/ApX/mwFbANH6r/ye/ZX+dwN/AY3/OwLvANL/FgL4Adr+Wf18+/v5LP6RAzMHBwct/tL2Hfqm/yAG5wh6ALb8yP1z+B75WP69/mAD1AbUAQgAmf9I+/38hgC1ANwAmf20/fcBYgOaBFwEe/8w+4n6lvqC/WkFnwl4BzoFhf1I9W73wvsbABEGsQbLAVz/QP3+/DED4QQdAFv9NPuz+3ACIQQfBGkFZgDZ+sD4qfry//EG/AgEBrACxfwA+e/6uv7HAYYDiwEXAJP/j/yD/XUC+wEYAUIDm/9O/Yr9Of2BAdMF1wSWAJj9HvwW/XT/pwIHBm4E3/xy+ZT7ZP8OBbcD7AIIBh0B+vgd+UT++gBkBGcE7/0D+r36wPplAsgJFAVLAmT+kPaC9Ur7dwJJC9EJWP87/BT6TPsbAegCIwNgAX77gPsQAvwFkgh7BuX/Evnk98D5Df0vBcgHIQajAlv7Pfqu/2MATP4i/zwA6AAU/1n5mPWF/VsGfAXmAf/8xPpw/YP+vf8ZA+wBLgDv/6L8V/tR/K39KQJIBiIF+gHPAXgCVQDqAL0AXf5GAQQAn/sz/u4BKQUPCbgFkv8i/bz6AAAOBhQD9f61/H79//+UAY8BQgHMACMACgDlANr+Qvvo/dYB2gLyAhQB7f6k/5/9/vteAKf/8P9OAH77v/50AycEtQN6AYn/nP1o+yP6yfwZAxkGagRqA8v+I/uo/Gz6uPvgAdz/S/1EANn+qQEmBF79K/6//1L6nPhF+//+PQVnCIoEof+5+fz3xfvGAfgFvgTAA1sAsPzG/qwBzAORAzT/EP6GAH4A2QIbBa0CgABR/jj/LQIuAUz/uf+nAhYEFgQkAtT8jvmU+TP9XAOLCE4FXf3X+az69gDiBBIDiAAQ/xH7Wfio/psEmwdbB5j/UPfW9p/5RAHkClsJ0QVPAt753PQu+f4BhghzBwYA2vzM+v/4lPuxAdUFjgQnAa78dvw9ALUBJf+q/sP8pPku/T3/aQJCBe8BQf8a/vH6+Php+z/+SAULDIAKEgS2+l7yWPJ6+7UEjQiLB+kCdf6hAPIBjP4hASEB9/4JAVH+kP2XBHIHbQW6A6/+afsj+lT53f3CBL8JNQdGASP9BfqM/HQAzwGHAWv9qPg6+ocAnwZwCH0Dfv7X/Kf7VfpH+lP8xwDPBBoFPQKT/yf/igAsAyAC5v1/+zf7Xv0eAVoDNwTrBaEEjv8x/d/8Q/09AKkELgMH/sH8OftN/VoB3wBqAJ7/MP/bAGYAYf5wAg4EzP1q+xT7Z/1hA3EDif/ZALEB1Pwq/kMCc/+//CECeQZvBZkE0v9j+7f8f/37/UICjQOlAlkCiQFPAa7+zgDQAkIBgf9J/BL8SQAhBSUFWwNA/3P9Of1O+o37Jf6pALQD3AQLAmv/tvu8+bT/RwI1Ay4FAwKR+qj3/vnn/nQFsgWjAZb+NP0E/Cj+6gOtBVwEkADo+hb57PlR+8QB1gf4Btv/rPf49dD8ewMFA1sBS/9a/sD/TQBy/mP+AgKMAav/7v08+5f8EQGGA+wDrQTDAmv/J/3o+//9IQLMAsQD6QQTAdj9ifxNABQGMgbDAqQAGgIMATIALAKuAZcDkQaABGUB9f1p/OwAIwUiAxL/3fuP+F/7UQLEBjEIbwNq+ij1nPbM+WH9fgKbBLQC8/9p+r/3Yv23AiIEnAKP/OP22vaU+4UGLAwmB7gAg/h78//3LgEkBggGtQPl/4r9bPuC+k39lAIWA+cA8P/9+5v6Uf5OAbUCEwYGA0H9e/v290L8iwQLBqcEYgJx+wz1VfmeAg4MoA+MBg37xvkO+7z8tgQvB0oFdgLf/Pf7IQAUBVgIlwcDArr8Vvpf/EQD0gdjBxMDFP1k+br43vv/ARMGDwe9AnT9a/rm98r9NwZjB4ED3P2T9/n2C/1r/0AAIwF7/7X9ofvk+pr8pQAhBcsFygGx/N34uvez+v0BgwfcBwoFYP4y9xr3OP2i/98C7wf5BjAFOwHf+sv7XAGaAcsB9gKS/hr76Pun/5AGjwsBBun7Sva79qf+VQaiCAsIdwTX/ZP5hPjp+x0DcgPi/cX7KfzF/TsCjgb1CE4I///l80v0L/wZAQIHFQbMAOv+Qf3T+Rj7JgCPAdcC5QXHB+QDhv2892T3Uv7CA0MFJQE6+nb4MAB+BnMFbf8N+VT6Afxy/x0HVAhCA2QA7Pus9//4RvlA/gIGgAbfAx8DJgGw/Tf/9QGSAL7/YAFRANP/SgDL/o4C9gYbBZYAlvy8+1ABMwncCC4DLv+F+737FP7g/ZsCbwdoBHcBvP5x+hj88f4R/mQBxwJt/kr94fwd/GT/xASnBmsDxfuH9f33Ov51An4DZANJABL+Of0a/JwBTgLY/7EDpAVd/7D1ovHM9q4E1graBVH/lP38/kH/ygPXAsH9wv2N/sD9Hv4N/s0A7Ad4B6cE7f5W9XDzo/vdB+YMAwcX/ij8fP5vABQCZQKh/3P7ePvg/wEELwbpBOz+sP3L/6IBjwQZAx8APP/f/Ub9QgFiAmsBJAEL/rb+ogLFAhQBhQGl//z9S/3L+kD+RQOAAyoBDf2E+SD68v+4BVADEP56+oP30PoFA3YFzQB9/kf+Lv57AZ4A6/6qA/QCEP6C/gT/6f0KACME7gWABQ8Ctf5i/vz+ZwCNAWUB1P/9/V/9rP4+AhoDxf+E/qn+6f2t/pP++vxZ/ZX+yf77AtgDa/7I/Av9jv4hAK4ALP6X/agBFQXYB3EDlfy5+p79GgH1/4oABQKQAgUFxwXLA1QB+Pz0+RL9hADuAd8E7wS/AVMAif4X/V79Fv1//Pz/j/91+qH+SQMVA34DAQDG/SYAUP03+H/4LftuAEEGbAccBMoA1/7l++j8ngLXA+MDfAJD/mgBFgRpABz/SgCi/BD8x/+fAcQEVAIk//YAV/9M/GD9iv9GAHQCNgQFATL6fvYc98z8hwL6AjMErwSIAFb9xfxP+/L9KwPaA/EAc/3r+vz81QOMBmYCLv1H+w/9QQTlB8gEXARMA7kBeAKMAIf5n/jx/dwAGQY4BxMClwDEAFP/UQBl/yL9ef1h/GD+GgXJBzIFiAKk/Lj0KPN1+PoAAAk0Cc8CUQCt/kT83//+AnT+cvzN/1b/Gf7P/JD8HgGjAzD/nPyl/1wAywA5AkoB8v37/b7/2/5e/wr9q/vj/gkAwgEDBGADjv8K/JP6bf08AWsA7wKJBU8DJQAwALoAo/2V/Af9Zv6A/3T/1/6HA9UJ2wcuBbT+LPeZ+Ej+EgKNBBoEyQBqALIADgCb/vP+cgCaA+wExv0F+eD6+v9UB3AJDwIg/ar7Q/l2/gYFxQR6AtT+8fkN/Nj/FgApAo0EKAIf/Ir33vXu+lYE1AjQBA8ASvqf9P349f7sBF8JjAa6/sv6F/x//RYC6AKvANkBlAPhARIADv/z/vUBAQHmAk8HuwOp+1D3g/oeAaoGKAWOAH/9DP3a/9cDeQWp/5/7m/vk/K0CLQRpANX/3f8Z/zkCWf+A+jz+YADlAkoFQQMsALL9RPwO/KH/2gAb/+4AfwSLAkIBBgKs/TD9q/7W/D7+TwCt/8EBgwTrAsP/o/w4/dwBAwN8AGD+z/ut+lT5/vs+Ah8FAwcTBSMBdv2f+GP39P2pAfsA0QMyACT+KACJ/cr8W/98AEQCcAabA0z+Df7W+0T66P79AN3/DAJNAmwBFwOhAUb8jvs3/l4BewMIBLMFdgVlA4AATfx6+H/45/zHBCMMTAtGAzn7P/eD+Mr+WgTTBroGMAMs/Wj6X/7X/xUAggFsANX+D/+H/44AZgNPAmr/rP+GAEb/6/9fAUABzwKbAAT7LPlM/EEAvgRrBigDnAFt/178tvwg/Dj7c/6fABYCJAVFAtj6F/fz94f79wRICyQGDQCR+t72O/vHAlcFPgV/Ak76rPj8/WUBlQTJBZUDhQFb///45/cq/zsFwAeVA4b5FPSf+HYAYwoRDlwFm/vi837zaf2OBqoHCQZaA5f9Bvqd+xAAxwG5AdAA3wDNA6QDRwGbAZMAFP2V/pcBfP8g/Nz6Pv9nCcQMIAdD/wr2//LX+dQEzwr/B6v+cfiO+uj8wQGqBVUC3P4l/kf9qf3Y/2AAYACo/xUAIwB3/yYBXAHjAeAAiv3v/NP+IP+pAPAFggU3A14ByPyr+hv5BftVA78JYQrZBb3+lvp3+JH5f/9GBK4FpAP8/5/+4/5L/O774v4IAO0EMAQx/q395/w1/HgACwNyAYP/2vrn+cL+LQMnBV8E7f+s+YX4yPwoArEEEgT8ASkAUPzX91D9UwWZBvMDlv9K/fP83vlm+SsCgQbfA2sE1QG8/Sr9tfyC//oBS/8y/Yr/SwKfAO7/TwHD/wUA+ALPAGz+k/2m+Qv9PgT9Aq4AngBF/qv9bABpAOgAeAOAAVf/1P8k/xkAvAEKAVcBGQNtAt//vv4N/tz+HQNWB4IIMgRj+971M/k3AT0G5waIAXL4Yfa2/P4FTgruBcz9LPgY9xr4eP+2B88I4QXV/iX4WPUx9yv/CQeiCeUFn/1W+mH92QHyBI4Dw/6O/Dn9ef0hAbsEMQbbBa8Atvn19ZD5OAEwCMEHcQOMAQD9xvqS+377l/1r/kb8mQDzBNEA2Pzf+9X+PAMMBCoAnf0U/iX8YfvH/Ef/9AO1BaYBz/4gAQ0BjwD7A0gDQ/+U+iz4CQE1CxoIef+2/vj/if7y/M/7Iv4oASYBRwBSA/oDT/56/AkAVAGi/xz9Sfro/AYAhP+LAPEAfQKMBlwG8gDz/Lb4DfrlAIUCwQKnAkQAQ/0V/owB7ATHBuME1v9S+rT6Bv0lAxgJmATK/Kr5DPxZAccGoAddBsEC8vqo9fH2q/0ZBB8H1QcGBqr+FPhP9976DAEBA6UDAQKD/fz8b/5EAk0H9QWgALr4WPEx9cr/+AcsCvoGKgLw/sf9svxo/aH+UP0G+3n6efurAM8GbQbyAn//pPzY+sH5TPiF+6UBNQQPBlMG2P8q+OT4pfzCAdAFCAOz/hD7lPrt/CECkAiRCewGRAJ9+0L4Dvt6AOwEOAhHB3sCVv91/mj/BP8AAJkDpgYSBfr+YP0yAV4GfAS6/3r9/vit9kn6uACQBrEKdgZe/nr3YvWx++0B4wbbB/UDbPw199n5Af9tAaUA8v9N/rb/6wDSAUkFjQTyAs0Bfv0g9pb16/rs/YIDhQjhB30FS/1j9fr6oQDK/4wAXf8c/T39j/3A/mUE3geYAnr8d/dJ82j3bwIvC0sQlA7x/33zhvIj9aj9iQZMCMcIAQc9/6T7yv5BAVMEpARIANj83/vX/zgHNQn5BGT+hPl19z33Vf1XBYMLqAs/ABD4D/Ul81T74wW1CKsHSAHM9b3z//jS/kEGewZFAt/9sftk/fr++wH3AlICvgMQAIT71v62/2b+JwElAQECoAIF/37+hwLEA50DEwUzAIf4dPd//DwEKwiRBP79ofnU9ob3vQFoCokISQRJABL+JPz/+KL5e/9nBCMFugVNAUz8O/3J/w8CGQOQAWT/PgKJA/0B/QQYBEX/s//i/VD4U/wIBZYHnwaoAAr5+ftzA3AEzgRgBB/9E/rh/EX9hf7z/tv9xf1cAJ0EhQXwAtP8iPdv9sv4FP5sA5YH5gUk/436dPpH/7YAivxn+gz6qP6pAo8A9wHDBSAChfsA+Xz4nv19BDIEmQPWA6/8/PZm+9gC/AcDB0UCdP+d/Q37E/u0/3MFbghNByYDAP5P/TQA9wHNARL+RPqg/3YFNAb1BxkD1P56/iD+SP/I/+cAKQFiA2ADOAK0/0v7nPmQ+t8AZQbUCOUFj/4s/C/74vmwAKcD/P6w/7n8Nv1xA2gBCv5t/5z/GP2o/dP9wP5wAVACgQFF/3P7Evfi+QkA0gDOAL0CgQMLA1n+xflr/Iv9NvsT/RkBPwEoAvkDjgJIA6gD8AEjAiL/5vnw+qr/CAKDAzgGUQf0AwQAEP3+/TABiwKOAor/U/34+8P9AgI3BCMGWgLn+VL1svn5AaUHFQUM/n39af6V/4X/Yf0t/kMBiAIvApwAZf3n/dD+1wAOA/wEuQKi+qP3/foEA3wIaAYfALz+wf1f+sT9JwE5AqgCEgKj/Uv8Tf1k/W0BBQNyA/wBJ/8j+0r7QALqBOMDsQHU/Hv5jPysAAIFSgiFBBz/Vv3m+gb71ALUB7wFmQFHAJT/qf+4/hj90wAtAlAA1gHcA84Apf+BADAAcQBC/TL7yf2rAdwC9AJfAZT98/r++p/94wAoAjb+Rf6jAmoCt/8Z/HX4g/xNAjcCKAOLAh0BUf9c/TX79/js/JEDbQjiCHwDZPsg+rn+kQKcBmIDX/oB+PP9LgR2BaoB9/68/or9Xv3l/0YAcAArBIYFFQNJ+0j17fbr+gD/lgNaBvUCI/7o+23+VQINBd8FIgE5+9P3JPuiAm4ExQFKAkcCigC5AM0A8wJHB9AH/gOf/8f4SfbF+6gELwzVCkIDIfoE99j6vP/RAz0FxgF7/kf/RP5UAHr/ov3FAqX/x/bS9HL6XwNICpQIhQKi/Fr08fPU++sENwj3BIADuwBD+5b5r/o6/XQDOgT3AXEBgP7v/nEBcwErAd8AjwCKAl79nvgo/ggBAAQFBDP+zfrR/BkALQOEBXr/GPmB+tMA1gMHBM8BI/0jAKICwP+M+zv4N/dS/hUI1QnxCXwEofzf9mb1N/1oB6gK7QW4/cL4nPziArgGAQf7ApD7NfTm8/T9hgo9Db0JLQQNADr8Z/bk9nr8sACiAasAqf3D/gsEWQX2BDMCPP0Z+l75OfoE/3kFkwZtA/L+r/pW+e37hv/dA0kG1QKy/5r+3f0l/3UAzQCAAOsB+gEXAWQC5v0g+pT+KgLWA+ACfv0d/SYDWwavA0IDNAOt/Gr3MvZk+fIBfwlSCiYFS/vJ9NX4IABcBcEEFgBf+cT2CP78BpgJjAJ++vn5Fv1I/Ib/pgM5AggFQQLq+9f7cf1UAlEL6Ahj/dv5Uflo+x8BSgT2A2kDhgG2/ucACAO3AN0AbQLc/rf9kvwm+0MAGAORAv8BmP85/Wv/ZwEfAAX/D/7w/gQBlv5V++X90f+Q/2ABIgTpA6MBhP4c+Tj5kv5//8ABUAZ+ArP+J/2P/csDggXEAPT9R/7S/WX/dwKUBC4Co/tg+Hz45/3rAuQGlwkmBoz+e/dk9iX89QRgBsEBYPz292L6lQDgBewJAglwAnL/ef7n/WUAwAAaAJL+5/wp/xEDXQaSBpED7f/m+qz7VwLVAxMBkv83/o39LwADAVAAvv5i+8v9MAMDBAABIv2X+iD6Nv05AwwFswKFAOf9hP3o+6/6LP8BA6MCCP+J+uL7XwLJA8EBNQLaAY4Apv4//H3+ZQTFBBkA+vsn+ef5RP8tBhYJ+QcGAWb4vfo/A4QHrwOL+przqffHAeYFxgatBUUCYP4b/Tr8Gv35ADgBEAIdBAkE0AF2AXUAEf5c/db5vvpd/zkCPgTxBXAFBgT3A9D/qfpP+E76Ov97A9ED6f8i/8//AQLJBP4COPz79338xwH0A/kCFv/Q/O38q/0kASoE/wIxAYP+xvtM+/77E/9uAxAErgD1/e7+3QD+AdUCC/+M+iz7CfyG/ZgANQKTAnEDDgLa/tf8ffk/+tUA3gbFB3ICOP0I/Kb7RPvs/oEBWP+b/ob/NQL4BsoIoAM8/fb6SvsT/hwBwwGgAIMBgADS/rgCWQPAAAoB2wKZA/kCmADh/A79M/5o/vH/BwHCANMA+QJVAywB3v8F/lX+LQGoAIb/G/4//ZYAawKsAqgCoP+X+236vv25AywGvgL5/rv9LP65/Mv9CQITApcAnf+s/R39rf2a+778rwCSAkAG1wb4/zT5TPlV/ZgBYANaAcf9Cvuf+U383AM1BrgESgJ3/lL92//GA0ID0wC3/W78Zvxe+1n9+wPlB2sEsAHq/r/8Lv+0AFn/MwEzA0YAOADz/az67vwdAGMBfQLPAzIBl/4l/if/5gDQAuYAsfxq/jr/Tv9WBCUE0P/a/yT9dPow/Yj/kwJoB/sGBgIw/+P7vfpa/rIBgADS/moAC/8EABwDygFvACIAkvs0+74AiQF4A00D+/3F+lr7sv1fAHoE6ARMAusAE/4i+6r91v4AANMEZwWOAuf//P4s/pX8lvvy/KIADQW9BnwDt/9O+/367P8rAnMA/f2p/Yz+U/4S/lEAQQBq/0MCwwLI/7f7O/l7+3YAHAM1AQoAVgIcA9sBfP8e+5H8aAHX/17/JwIdBI8GkwWtADr8ufqa+2oAmAWZBqoDD/54+tX7+gI4BoIE5QDW/Bn+v/2b/WIBswI6/0v+kQA+ADQBMgKwAPf9IPxd+wEAogYfBMz/1wAKAeP93/7kACQAHP8v/A/8owCdA9sEUAjoBbf+E/u7+sP8T/w5+6z+vAFRAEEAhwSpBLr/6P2o/JH6ivpI+N77jgiXDGIE5/tW9A/y0Po6AuIDkwSrAb38Uf8lBuYGIQWdAXb6E/jG++H8N/8vA5ECAwTGB2wH/AX1A+/9Bfu3/XX/JAEhAEf7afyEA8oFLAV3BfUBw/2q+gv6zf5/A/YCPAHKAez+0fuR/bL/rP6S/n3+5vs3/+UCMwPQBIMCI/59/Qz+Cvu3+3EBVwVABtMEJAAj+rD5J/7+BA8I/AT9//n97/2Z+xn9q/5K/3EB5AJ8A6T/0Pq8+lr+jAFZBGwCMfz6+eD8AAAWAiIEvwF1/t760fb5+nIEsQeiBtgE3f5U+mv6O/0CAbYFeAXOAFwAXP/9/00DqwOVAMEAnAB2/Gv7lvsfARwItQnyBAX/i/z4+af8rwCNAEv/KAEBAc7/AAKtANT/8ADT/yP/dgG/AE3+JADDANH+xP91ACP+3wC4AtL/C/2a+2H8CAAuARL+aAIQCFkF/v/l/K758/ds94319Pk9APUFcAzlCpIA1fnO+Sb7qvys/aQAFgBF/uD82v4yBa8Du/8O/hL+dP9uATwChQKeA0IBE/+Y/cb9uwECBn4FngFd/8T+Of+X/z4AtwJOB8MHLQWJBKD/OfrW+sT7Gf5dA5gF7wM8AvAA0P57AC4Bg//j/hL7o/jy/CoEUAZQBvIEkvwK98j5k/wLAB4BXfyT/RMC+ALkAdr9PPoS/IEAMQBZ/Vf7BPvu/ewArgH9/9L8+vl/+hkAZwRHBdUEcAAb/Db8u/xb/N3+YADRAbcFUANKABwCswGj/p//NAFk/xP/Qf8yAQ4DDATsBP4GEgac/H/2ovnYALkFOAgBCRkFJP9B+R/5EgCGBFAGGwePAuH8z/mU+hb/zwRPBDX9kPg4+q0B1AZeBgkCjP4+/Qj69PiL+xP/6wEBBXUD+f44/G76ZP49AzADWAHv/8n9Wv3d/dn9ov+4AQsD4gLx/qr4bfjH/DUA6AJxBWUFUwGx/rn9ufxJ/ef/fgD2/iP8NvmS/6gIpwqjBVz/uvpd+BT8cgFDBAMEQQUHBWEAt/1p+iT8ogAWAYYBPQIFAtYAxQOnB3UGhgCr+zb7D/vP/JgAPAXQBowDeP7S/N79Nv6SAI0CJwWUA1z/CP3x+kv9w//h//r/JAI2AKX8Tf41/w79+Puw/RP/SQPLAlv9Efyb+wb8Bf61ADD96vmw/ZsDmggUB84ABvom97j4OPwlA8kGUgR7A0sBx/or9oT5MwMnC+sIEwKFAGb9Jfmc+Zb9ggHyAnkFcAdNCJgDxftJ+vj7Q/4QA7QEMwGvAVAELgK+/6b/uQAGAsQAiv9tAVIE2gTjAMP9ivxZ/D0C7Aa3BJYDCQPJ/0n7hvjE+vP+ZQI6AzAE3wJI/vX80vud+oX8KAHQA6YDov+7+kL8Jf9P/zr/Kf9K+wb4cftyAvYIcwhBAN751/pb/Tb88vzV/hEAygJ1Aab9BPzM/eH/RwI5BfoB2v3h+vL7fAEoBRYEbAGj/4X6Wfn0/cADawduCF0GwQKP/wb6i/vd/54BQgStBoQELf81ARIEjQHs+5v4kv0yCCoNZAk/A9f6OPb7+BoAeAMg/3z8wP74BLUKoggdAGH3kPKH9Z7+XgXcBwwG1v8a+ln2APjS//gETwbfBGgBPfw4+Zv6dP3S/wMCEANy/0L+4P1M/7AE7wTRAbj92frS+GD8+wK4BUAEmv7r+5/64/y3/mH9egBEA94EAQVMASb8K/sY+0P8qAB1AP/98fxXAGYGRAnlBicAmfxN+gf50vuXAE4FiQnuCmsEOf1e+bX4dP8xBy8JrQXB/1P6x/rEATAHPAeuBEABe/1g+8L63f34A2wExgLwAAH8CvqA/b0CTgWMAk39BPuN+0T8N/6FAjQFhQBT/bH8ZfzA/gz9vfrZ/QQD4gT0BVwDJftZ+Vn6A/s6ALkEAQKt/8ABVwG6Ab8A2fv9+Sz9BP+2/yYDVQPlAUEDZgFg/P36l/qR+2cCoQfdBSQDAf+7+kT9X/7D/i0DAwXjAnYBLgEQ/a76lf3gAqIFmALG/Q398QHfA2sEKAYVAnf5/Pbn+zwBPwU/BkMGZANj+yj2qPqLA7EI8gcAAfX4+fKU9tkC3woCDP0D7Pmy9Wj3iPyoAOoD0wWkBkECMfvN94v67gCvAWv/lv1A/H7+vgKrBXIGQgR3/pj77/pX+/v+DAH/AbUE9QWmA6D+bPoX/Q4DsgRYAs7/if2Q+0r9jwEBBbMGewbGArH8ffYE9TH8MQOqBLcGAghpAe34ffdh/EYD8ANa/m374vti+07/bQZXB50D8v3s9sr0EPouAHwGaAkiBa4Arv4w+zv46PyKAVICTQIQAaYBawONAyIB/gEaAez7f/zq/6UAdwI9BgoGuQReAoT9ZfpW+3r+hAKTB4wHSQSR/xj5Zvb/+qgBbAM2BaYGSARU/Tr4cPiR/FgC0gEF/7D8G/wZAJAGmwiNAz38a/cl+FP7agH2BN0E/gPXACn+NPux+sv7oP6QAuIF9gSu/1n7XPj++uv+JgLEBToF8/1b9/b4bP2KAxgGxQTkAFT8KPqm+2YCGgWqAVL+W/70/ab/qwLfAi4Dmv6m/bIARP9U/pf/0gDlAl4GOQepAx/9Ovvk/msCrQMFAdH/o/+M/UAAsgeFCSkGGAMgAbn7ovWi9tr9xQZXCPwDZv+S/VL9nfyU/4UAHv5k/F/88/4aAu4DOQFn/8z+o/qS96P51f4EA1UH2wdxArf88PbS9n78kAGlBFIE6ALnAMn+p/0c/sH9Lv3h/tUBNwT3Apb/Ev3L/g8DDwXKA0v9DPeA+cQDPQodCFwCtvuC+Hn75QGABmQG2wPM/5b7avm/+NT9TARZBjIGkAQUAIL5evq7AB0DkAAU/uL+9/8yAb8A9gCBAuABRv47/Ab8bfv9/84D3AMIAv8BwQEd/6P+Y/3j/Fb81/1qALkDvQX0AC//FAILAzsBagA7/Nb2U/jd/2EHQgjfBt4BUvxu+Yv4KP0MBPAGtgIIAeT+kfp6+3P//wAEAWgCWwABAUMDjgJ8AUH/qfw4+1/9CgBEAtgDdwRSBMYDhQDw+Tv40/vkAX8GVAdQA7L8pPc89vX8HAU6CI0Fkv6p+Rj6EAByBDwEHgLR/Tf7R/uL+xP/pwS1BlgGUAMQ/o77sPq4+2z+vP9+/qH9c/55/xwEJAiSB7YBVPvH+Lj2OvhW/cQEvAeBBFEALv9IAawA0/9JAPQAsf/3//0BBgEF/pj7Lf59AsMGZgcXBA3/6fqs+vz6ff98BKYHvgYbAEP7ivyFACIAvf78/mb/TP/c/igA3QLEBREDSf19+b75av6E//T9W/8TAggCwP1A/RgBoQRMA3z++vw9+U/3pvqVAL0GzwffBgcEI/5v9//1sfyGAzgFXAWsA6f/Rf1s+xr9sgHRA2kAhv3//Dj9zAIDBzoGkgLD/tD5VPaT+ZP/WwbfCEUEwf0w/p3+k/weAOUBYgH7Ac4A+Pur+1UBZgXyBigE+P/h/Bv74vi2/EoHEQv6Blz/7/kY+aj7LgFtBhAIRgW5AIj61vZH+3MBRAROBJkB/v8N/kL7wfxoAMQBH/8R/ggB6ACA/rr/NQAj/F369vs//SL9+PwaA4QMrwzSBC78T/iB+E34nP1+BRoImAUiAsgAxf+p/v7+NAHYAgMDkAEbAEr+dfzu/Of/FAIHAfj/hv1d/oEDEgZhA2X9X/pK+Nf3tvku/7EHFgmWBC0B7f399+vzMPZ+/a0EBQiMB0kE1v3K+bn8YP/+/sH+zgF2Aub/2f+vAsQFSgRb/5n8Rv8z/33+OwFMA/YEagL9/W/8tv75ABkEigWsAyYAlvvr+W742PtpAg8HpQhzBAv+UPpU+fv6WgEgBRIFAQMd/479VP/lAID/KP6W/s8BbAVNBDsB3gJCBGgAKf1u/iv/0f2LAHkEDAXBANv7I/qi+7f+aQH5Bt0IsAPF+8H2K/Zv+F7+SAKgAakA9wDcAXEDHACe+uz48fql/D3/XQVXBvEBT/yF/P/+Vv+c/y8AsASSBJX/Of7OAWsFLgcPBNv7GvbO9/QA0gZyB9cDXgGGAEb/JAHtATQCrv5Y/N3/QQGh/bT6Yfw/AMsCvQAXAHEBrwOeA4oAV/1j+Sj5//vM/34BfQFbAv8ExAYoBPb+P/im9jX8IQL1BM4GRQU3ACn+dP85AtsAEPr29nT7OwECAycEJATRAEn++P0R/fr70vtq/Mf/kAMpA8MCTQKE+531kPiw/g4EbgVhBBsEAQHq+/j5c/41AksDYAOBAnMCdgAS/l390v+AAI4BOAUiBD4BqQJTBqoEYAAM+6H5QP5QAH0C0wW0BVj/gvtz/BH9o/3UAPsDWwMhAvn91vrk+ZL6X//iA0kEn/2J+Ff6d/4qBBgG5QKD/eP5N/tw/cABYAWMBMkAc/v0+RL98wBqAYABFQNsAxwCZv9f/4/+9PsA+gn9OgPIBgsGEgMNA9ABz/+I/L/50vvN//ID5gPpAN3+GQFoA2MCkgJdAjz+LvpP+2P/9gLQAU3/lgB9ApEAFf5S/2IAZAFWAX//tPsr+yH/TgAxAoEE2QOUACj9L/vC+y4AOgF+AdoB9fwp+tD9owNPBckEyQPQ/wj86/n2+3z/dAGKArQDFgZkA8f+Ef3G/LL+QAHkA48Cuvvx9xf7SgAwAxkGOwieBFP+LvpP++D9ofzY+wf/TwJZAJD/eQSiBuYCY/+P/cz70Prk+0sBKQadBYICFgE6ADv9HPws/1YAjP5GAUcFMQUEASb9o/6f/y/+uvui/Q0CAABo/ZUBKAQwAbr+5f1w/R76FPes+ZgBEwpLC7oGXv5R9enxGfiNAbwHjwptBuz/dvq++qf/GAKiAzUC9/1B+vH7pwRVDVoO4QX0+y72ovXw+Fr/TwWpBnEFBAOkAQYA8f6C/5v/nP/S/vz/kABc/cP5C/sJAIsBmACx/8EALQB7/ej+ygLBAoj8cvid+J/6Vf7nAlIIpwjlBYMBYPq09T30afpKBVEKwAjgAiD8xfgL/JICrQWBBJsAvPtU+j3+rwJDBW4BPfp++r4AWQQiArgB1AKiAXL/9vw1/ysC0QErAEgAzP/S/WYAIAK0APz+i//xAj8E6wLHASUBU/3T++D/7AIRAl3/M/+BAG0CzQAM/cP9EwEeBd0G3AEV+rf5P/7WAtEFHQTs/vD4M/YN++EFbAmSBJX/xvsm+9D8PAA1Ag8BUfwm+vP9FQHkAqADfgKL/dX4EvmV/ToCFQK+AIkB4ADk/CL9EgFeAQT/SP9fAusC6P+f/Tz/BwCR/BT8BgIXBQgEngQIBlsEwP0j+Bf6zAImBgUEhwNJBHQD1v+Q/fT8RwCvA8MDCAOCAer+wf2QALACCgTVA8sBj/1w+wn8zvxNAAsCmAMtAjz/k/xL+/UA8wQQBBr/Sfiq9Aj61QPICEwHsgCT+bT1D/hY/egDCwe7A38BIABJ/Av58/id+w//0f/JAHEDfQJW/g77O/z4/Ub8xfvl/v8CJQT5AQEAbP6B/cb9bv9WAd0A0/59ANoDMAThA30DcQEP/ff6vPxjAJMF0QgOCREFxP9F+2X75P+hAEoAZQIaBY4FiAJx/of+1AA8AFT/dwB0Abz/t/81AbQC1AKL/8D8Ffzo++j7XP5uA+EHOggvBOT8cffg98H7QAAnA8ICbABW/6z+/Pwh/B3/OgHGADEAp/8l/yT8FvvT+87/ywIbAtUA7vwo/Ff+4/+t/eX7Vv0oAGAEVwYxBo0Di/4y+Iz3Iftf/S8A5QMqBsYGQwf7A50A9vtb+Zf8Rf9p//X/ygQrBvcDhwCO/rH+lv7M/9oBPQWjAhj+G/5p/+L/w//1AJUD0wMN/9n78fy0AGADmAR/BPUAdv2D/I/+WQDbAHkAPwEDAtP/Vv3r/FH/ZAFWAZMAdf+e/ZP97ABGBLwD+/7t+uL4mfdc+E/+xgakCY4HbwTz/Ar1pPRf+hcCfgSZAB7/vAGfAh0CFQSUA4z8A/be9nf9gAPrBXwEHAOEAxsB4f5L/Zr9cQClAGIB+wFjAqUCVwGA/5n/+AB+AJ8B9QH//8P9/f7ZAYIDjgQEAgn/Wf3N/nf/2/8F/3v9IQCgAhIFOwQLAsX+wfow+nr9JgNpBDACGP47/Oj+RwFjAWoC3gBf+zD7tP0FAKoACgESAzIDogAH+jf2IfqKAvUHtgdBAtD4XPPi9R3+ZAW8BxMEq/1y+t35y/3rBJEHqQRL//T52/R88y78KAh+De8IWwBW/bb9u/6g/1wCjwP+/3v+gABXAaD9NvwvAMME2wWUBA0ECAGF/dv90QN0BSL+pvez+egBbQVABuwHFwXk+zb3uvtzAWcDFgHgANkATf1N+7z+XwOVA3IB4QAPAN/7uPk+/c8BrAGN/9n+o/7U/ur+RgCnAKj+mvvj/LsAhgE6AaMBZwJE/rT5Mfmt/AAC/QN1BjwIZQPz+RT20PruAGgChALXBFUEUwCr/bX/7AF6AXgAYP+R/yb/mP53AocGUwQ+AB//2f2/+xH8s/78AkoFLwP6/6/+3P2g/WMAswOkBEgAMPuZ+cL51/xCAAUDaAc2CfgD2/su9+b5ev+5/y/9LP/iBUYI7wMk/zr+WP2e+l36sf1lA78DAwL9AsUCkwDL/Bz7aftx/O39DQARA+oDKgS6BEoBIvtV+L/5rft2/gYFUgp7CmwFvfx290P5iP4SBIQFbAGc/Gf82ACCBYwIzwXc/yT8Avp1+0j+gQKcBO0CVwCv/ST/igGJAtYCEAGe/bb8BQG5BZ8FNQAz+9X6Ef4wAmsDeAJDANT88PxWAF8DXgPo/2X8lfsY/kL/rv5e/yUBpwKgAHn8ovqv/GwAWwKKAeD/df52/fL8Mv9LAXb/wfw9/ZT/hwGaAl4Akv6L/Ff7iv3P/noAVwOqB3UF6/1/+R77wAEUBBAC6fzD+eb6kP/+Bi0KZwZ5/0H7hPrS/ioEXwVAAzv+nPrf+2n/QAFOAnMEGgVNASz+GP7D/5kAewCfArMDCQED/MT6Tf5kBJYIyQcbA0D91Pp4+6f+tgBzAg4D0AGrAJv/wgD4/8L/YwEzAkIAQv2j/HH++QAlAZQCNwFy/Bn5X/ubApQHrQUJAIH8ovfe9Vj5nAAdBu0E4gGR/gv9Fvo3+Yz8iQFEBFsCvwAF/4D/5ACVAVcAg/qG9Ub4QQAhCBoMVQorBiL+cfgL+UT87/42/70BawPEA78CoP8gAHgB0wAD/+T7CvyxAAkGmgcrAqD7Jvhy+Nv7aQF6BzEI2wJD/fD9IwAI/2v9Wv5oATQBLP9XAAMDWwIZAPEAjQF1AMz/WwI0BIQBNf9t/jz/O/4Q/YcCAgfuBCb/ufza/Ab8qP1XAHIDkgM5ATD/1f3N+/H49frCACQEaQNRAtn+ZfsE/vAC5gW7Aez7Q/pi/Cz/1//kAlwFdAOyAEYAuwEHAPv6APmX/McA2gH/AVUCKAH8/dz81/6lAJgALf7y/OP8s/zF/Tb/FwGqANIACgNhAvsAkwCI/639+fyk/tsBTAPLAboAFwHhAKIAmgKMBHUEpAAy/Cb9zgF9BTgFnwJQAM79fvtu+1X+QQLtBX8FsgHG/qP8IPu4/NQC+QfaBYL8rvQq98v/4gVUBpkEawO9AB/7d/jv+nD+ZwGlAtoC8AEe//z8N/4CAXYBPP8C/ab8SvxR/6ADAQQnAwUA1/tq+jX7b/2qACEDBwMCAlcCPQF2/FL4cPhL/YEDWwZnBHQA2f2Z+xn91gEVBRsFuwCh/KD7fv5UBAUH8AT1AFH95Pt4/NL/ZAQQBisEjQBL/+//hP/R/tX+EADqAE4ABv9H/tcAtAN7Anv/JP6B/hYAzAEsAlMCbwCw/TX+SgGiA0YBEf0h/RIB4QKaAdwARQHhAHz/OP5E/cr8jPwn/vUARACw/Jr7vvw9/hsCkgOAAE/91f1EAMf++/rd+bj96gKnBKwCSACl/ub99v/LBD4G2wBc+4j6RQCxBRoGMQOf/z/9d/rD/MoCpwdVCA0EvgA6/uX6/vfq+r4CMQi/BuX/F/uH+iz9nAFCBS0F3ACE/In7H/2g//4AFgEm/0r8Jfw0AP0EZAVpAzwBev6I+7n46/m1/+MFbglCCW4D7Pub+FT6Kv4IAOMA4QJCA64A1gDoAjMC0P1E+bf6RgC+Ap//i/56AGUBZv9r/LL+RQMmBBoA+vu++i/7tP1QAWIFpwf0BbEAl/u3+mT8v/6UAX8CKwPHA4gBNv7G/q8CCQSbAjn/IvyD+877R/7eA5gIEAaP/6/7bvrK+hv+NwKGBMoDBv8g/dT9vv1B/hwBIQNcAKP+aP9h/6L+rP1V/TP9Yv0L/50C/QS8AzUBif+c/aL8FP4tAPEBSQJEAQgC3AKDATX/6/2t/UP9qv/6AykGZATiAd3/g/2u+jP6XP8ZBWsGlAKN/mD7hvgc+Rz9kwN6BWoE6QLS/qn76/qy/JD+1/5G/vr/kgJKAp8AFAGEAZMA0f8i/xcAlABEAqMEUwWQApb7MPgA+04C2QgZC8kGaf6v+m37QP2T/rj/2QBqAoYCGQEXAI79hPxo/bT+v/+A/kn+Mv9bAIEAif6o/AD7w/zaAXAD/QLHA+cCP/+j+iX4UfoY/wUEswYhB84DTPzo+N77oQAXAogA/v4L/3UBiwIdARr/MP0B/CP9bP9FAt0F9gZxAmr7Rfhq+qv+AwEKAvECGgQ8A5cACv9v/vT+pP0a/uwB4AUYBaYAJv7s/Ob/3AE2AdcBgANoBB8DuwINAbL/Y/7U/IP9cQBPA74CxwHLAT0CXwHO/iX7NvoQ/Tj/4QDZ/6P86foh/hoDTQTiAUf+lvuy+Kv4LvxiAYMFdAU+A2D/B/tW+qj80v60AG4BBAJbA0gD2gENAHT9SPsy/OP/kgK0AB/+R/8VAjEDgAJ//5T95/0Y/gsAMAHh/xr+Qf5j/3IBVgRcBOADZwIAAXH/Y/3Q/Mj8Nf/0AeMELQZGBqAEagB3/kD9f/2j/wABGwITBDsFbAPQADkAUwDR/Vn6Jfqp/QQEAQlpCPsEU/6E9+32EPt7/4MAVwCAAd4CGAJh/vL6Mvod/E/+pf+mANEBHQLpAF//0/w1+7f8Ev7e/RP/jgHVAfkAbACy/xv/M/4e/iMAaAFFAFv/IgFLAxYDUwAE/DL6sv2wA98H7AYfAsH98vrI+zH/uwIWBS4FrgSdAUf+YfxJ/Bb+U/92AF8AmAEWA9wDQQN2AP/9b/vO+pj76P+NBk8IwwVEAnT/9fuS+Yf6DP8fAz4EugXHBi0FR/9y+k77z/56ACsAXAGYAOX+9f20/YP+3f2j/m4CjQSCAb77m/hU+pb9Nf9K/8j+vf9MAbIBSwF2/0D8h/oF/PL9gACjAvAE7waCBAgAWfun+VX9cwFUA50CdwKTA1IEfgQ8ALr7jPsR/okB1QNlBQ0DFP91/Sr+0wBSAvEB1/+2/e78PP3r/a7+TQCKAawB2ADoAUQDjQHx/WP7IPvI+5r8IP68AisGZQQoABj86vtg/wgERAUBAUT7cPhs/E8DfQbvA7X+7vtH+7P8pf+oASMD0QJ8AswC9QA//UL7L/3Q/mX+xf3u/3kDKwQnBLMClwBk/sL8mv1t/gX/NwDHA+0FxQPv/mf8ZP3l/eUATgLZAFL/KP5PAMgD1wMR/xP8r/t1/dQAMAOEBA4C2v7C+1v7NP5+ALQCZwMrAgQAu/8RAGoAxAA+/n78q/ya/Tn/zwCrAjwDnQPYAuv/s/1Y/I/96QBiAc79RPop+34AzwZfCEwEtP1A+UP5u/zBAZYEIwVJBPEBDP8Q/GD6wfsaAC4DNAIjAgcEDQUABMX/Efx0+pf6bvyUAJUF0AeGBw8FMgE0+6j25Pe3/VcDkQTBA1MEqAZLBdEBA/7H+Mr2AvlD/8wDSQRiAycCvAEr/9/7Tfvc/Hr+7f+9AUIBJf9d/V/9mv6o/mr+N/6i/h8AYwDP/w7/Kv8eAAgBMwLGAYABAQKJALL9+fqU+mz8fv/rBAIJEQkRBDj8IvlU+4r++v97AA4D1wQ/Arf+8vx1/JH8Kf2B/qwBYgXKBlcGmQOA/cf2wfUh++gB3gYNB5oEagK7AUAB7v9u/oP93P50AQ4EWwUdBa4CEf/f/NT8F/5VAO8CTQM9A4oCmwAb/Vr6hfuf/lgC0wK2Ai8CY/+d+0n4/fgB/OH/bgO4BQsFwAC4/Hn64/ls+gL88f4+Ah8FgAWiApj+sPoP+jb7cP0FAEAC6QTRA6IBz/94/Sb7u/sC/5UCQAXyAwcCMP95/XP81frF/Gr/6QKEBZoFlAO5AH/+fPw9/bkAFgGl/h7+fv9DAzkF7gTnA+oAu//G/tz92P0z/wQCRgKt/xX+9/9bAwUG7QQ7Afb88/nq+4T/+P8v/+v/lwGWA3wFEgVsAXf8j/qx/EP9Wvy1/b4AHwM8AysB8QDnAI/97/ro+qD9vwBsBGIHlwUNAaf6BPiC+3r/zQDeASwEqQR4A5AAN/2q+yX8rfyu/d0AqQQgBa8BeP2V+/T9bwB+AOP+OfzN++z+YQMMBwoG9/7B+MX2ufoFA+sIkQmNBaf/hvnB9276+v+6A00EigPWAHcBsgLkAgkBT/2t/I7/GQNKA6kDPwTrAsH+Cfvq+lX8fv8sAZ0DWgTvApIBMACU/7T8dvre+K/6Yf5uAXcEUgSxApD9f/ni+I/7LAHTAxgEXQKa/4X96/zM/Fj93v4IAYEE8AU2BMz/c/xG/Fv9hv+iAZ8DJQSxAmEB4f62+xr7gP4vA4MERQL1/xsAGAFhAEr+4Pqj+Yf8qgH0BVAGTARgAdz82/i6+HH8dAH9BB0GkQRwAD77W/lh/UgCyAP4AZP/hACrBG4GKgNx/Qn5z/kL/yAEjwW1BawEBwEY/gT8pfyX/jsAMgEuAeEA6/8TACIALP8H/QX8hf5jABsBeAFUATQASf0D/Lv+RP8q/Hr8HgEVBYcEIQEK/7n+Yv31/CH/CwMzBsgEagLc//H9V/66/fP9JQBaAlYDnAGS/9//eADO/y396PlL+rX9QwOYBvQE9/98+ab3tvoN/xgAEv9CAD4E8wZzBLP/3Poc+H75yv5aBHcGWQTrAXwCxwAc/vT7lvv0/acA3AV2B6cFIAQaAp8BW/4Q+nz5Rf2yAn8GRgmKBkn+xvdu+AP/PwRHAwv/yv27/00CEgIWAAz9XvmS+TD8YQBFBIoGEQYCAoT9rPll+lv9BwAOBCUFSAOzAEcAhQHu/5H90Pwp/6ICkwR9BUYDLf6z+Qz5Dfzr/2MDWAfbBjIAGvmz9/v8YgFZA2kCIf55/Br/qwN7BUEC1/u/97P4o/wvAs4G3QeaA0z+UPt++iD7gfz+/4UDEAT6Aaf/XP/9/wz+xfxC/vf/VAB9AfMEAgbDA5T/a/yZ+5b7F/2//7wBMwOEA/sCQAFo/Qn8Kv08AEkDAAKbAB//OP8GAaEC1AHO/SL7t/vv/1gFawgAB1IBcfpr+LP8qwIvBpAFnAI4/hn6Fvp6/qYBVwJTAx0DbgFt/6z+b//4/oH8dPu2/moCqwJLAvwAywDuAGL/pv/s/qH+Cv87AA8CXwF1ANz+Ev4q/w4BAALnAasAmf6C/sz+Uv+aAFkBAgDG/Y38y/1hAHUBGwHi/5z+qP2f/6MB4wDr/h/+7f8pAW4A0vxE+lH8RwHZBA0EUgH9/7UAFQJmAvz+yfpp+Bv7vgGFBv8HzgZTA1j8XviP+R/+mQPtBZIFwQFP/eP7V/7AAGL/xPys/NgApwWTBskDl/4s+db4g/oX/XgBOAWaCPAG5/8m+Sr3HPsGAe8EIwaXBDACwQAr/7/98/sE/PX/bgQqBkIFpwKd/lz8Ef0k/pD9lvu7/OYBkQVaBScCWv7d+375VfsyAFICggFaAO4ACgF5/3r8zfyWAMcCGwPtARwAEf0y/GL/vgJdA+f/rvxB/QQA8wALADABLAEnAGkAaQFvAogBgv9f/XP9cv6d/3oALQEcAzoDQAMeAn0BawHF/jL8Dfrd/MoBmwNnAkkBDALeARAAF/wz/FH/0gH5AXAAIwCu/77/3v8tAAAASP/G/vL/CwJMApABdv/E/Wj9Mv4d/p79PACWBDYF9QB0/Iz6r/x+AMQB6v/q/T39ggCGBS8G+AKk/dv6EvwO/oP/wgCeAT4CYgIhAWb/Dftq+f37FACaBE4GpgTLAPr9EPwu/Nn8Y/1D/9wCIgdrCMsHeQPl/Cr4U/ld/kgC4AX4BmkGgQIx/Uf60PrF/okCfwQOBPkBNf6s+4P81PzL/KL99f6bAVAD0gMCAzEAVfsO+D/6Pv4xA4cFGwV3A8b/lf3m/KX9zvxq/J/+fwOjBm0FWQEe/CL6xPqaAPACRv9j/Kj8tALYBAYByfsl+Xf5Qf39BEgJLwbb/XD4ePky/gIDYQVmA1n+I/tK+3L/OQOwBAEFrQP0AdsAHQDh/54AEwGUAOX/oQC+As4EeAYUBpoDqP7g+en55PypAAsCywEIA3QDAAPR/kn5+/by+BL/ogINAhD/APxm+rP7EACAAksBcv21+/v9rAB9AoICpwBM/jD9T/46AXADbAMJAjMAp/7B/D39cgGyBJQEigIsAI/+jP6f/5EBxAHD/uX68PnK/tcCPgWGBQECYP5j/NH+DQD0/fn7r/xF/zMAPgFvAcwAa//S/2ACEQNh/776jPteAGoF4AXJAQ7+kf2g/wACnwIp/8782/1bANED4QQmBHsC+v68/fX9gv/4ADQABQAEAO/+tv5mADECyQNpA1ECEwFs/uv7evr9/D4B1AUBB48D2P/H/Pj8/f1SACABQP9h/T39FgFTA2QCagDm/vX9w/ul+4UAdAT0A+D/gfs7/EX/NwK7A4MD9QAa/W77q/vz/VwAPgNIBVIDXv9S/NH8T/+E/3L9uPzc/QAAKQKJAh0CMwE+/6n9Pfyc/Gv+BQAtAmkDGgKH/gH8bf3AAlEFfAIw/in8NP5uAWUEQwTsAWX/N/7+/un/pwHrAkwE0QLUAIX/PP1p/aL+IQFcA+8DKQJe/2n+7/5KAOQBGgKc/5j9Nf41APUAIAC+/wQB+AEVAXD/rv4A/mH9egDqA00DWv8s/Rf/fADS/zX/N/8S/sz9vgDcBQcHxgG8+oP4ePqf/EwAfANSBOQAev1S/aL+ef8z/V/8cP3O/20BJgHIADMAcf/S/XT9g/04/2MBaAFsAdsAsQChADf/2v1q/gQA5QIOA00AOv4h/SH/4wEdBHQCcf1q+1L+eQOsBK0BCv4g/Vf/CgDTAL8BjQF1AKX++P2X/zACoQKbAHn+s/5BAdIDJwOX/xH8q/rt/EIAYwSOBb8CtADIAEkCZwC8/QX9rP39/h4AiQH3ArADrwLwAOH91/s1+zf9gAFMA94Bjv7j/P38gP36/JD9RADvAJr/df6x/58BTwEK/0j9cPyQ/TEAiAIUBkUGBwJj/SX6I/uv/yADigS5Aq4AVP+9/lkAtgBJALn+Qv9FAWUCNQFQ/u3+pQAbAnkAN/2F+0P+NwSBB0QGAgD6+9T80wB6A5QBvv2C+kj7FP9MBCQHeAXjAUj+8/tw+wb7R/yD/nQA0QKkA7gCrP8U/oT92v1q/if/VQEAAeD/c/1u/Fn+0wDRAXUAt/4F/Yn+awKLBDgCMf4m+vr4hP5JBUwIzAIe+rr3S/3yBHIHFgdaBZMBK/1Z/KT+xgBtAiwCqv9c/kH/IgJnBiwGOgFU/oD96v14/9z/h/9pAGkB2QBTAHn/6/2K/sMAxAHW/s/6Bvu6/twCnwVRBLz/ifsI+3UA+wS4Ain+WfsZ++n8mf98AnQETQNH/y/9u/14/1v/wP16/rX/NgI5A7oA2v1Q+zb7zP2LAjYE0gKLACP+I/5d/7cB5gKdAcn+lP3H/2sD1gNLARr/wfy6+0T8XwDpBOoGEgWjAZkAQ/9B/qX8J/3u/jX/OQBXAkIDoAKvATQAKgBD/m77OvqE/v8ENQghCKoCv/z7+EX6Vv4KAk0DNgDM/aj+4AJrBYMErf+g+rb4Rfpo/gcC8AMIA8kAdfx4+T37xP9EAyMDcADo/Zb8YvyZ/s8ACgSOBHIC0P8t/Mb8NACwAigB7f8DAPH/TwDTAOQBFwFM/8f9WP0D/0wC8wQCBugD+f5G+n73o/jS/g0IiwyJCUcB0fiH9dr4t/+aBY0ImQVn/wr6V/s2AaQD6wDG+8j5Wfs1ANwFHAguBmEBavpy9Ub33/72CFcMogbe/nX49fWN+L79EwPJBLcDbQMfA4IB+Pxx+C/5Gf09/t7+LAFXBTIILQaDAJD4LfVt+M8A3QjQCXYFyf7q+p377P/BAzAFPwP0/5b9Y/uk/CwA4gPvBAoDpf+L/KH72P3dASgDVAJv/0/9dvwB/QwCegbfBdoBm/3o+0f9Kv6I/7cCtAMfAnv/Rv10/sgCMwXCA93/Jfyq+6n9e/+EAA4AZP6f/VAAEgTLBNkBiP3H+936kvs7/qkAoQM5BHgC+P4C/an9oQCZAt4Awv62/mgBWgGn/27/HQAqAEX/RgBPAj0ExQI3ANH/bP+G/t380/waAFgFoQgYBpP+XPe69uf67gAXB5kIMgSa+1X2kfhp/2wEDwMpAK/9xv02/3EApQAA/oL7g/ue/q3/rADJA7gF4wMY/qf7x/ub/fIASwRDBdsA3vuE+5EBFwb8BKEA+fuc/O//4wHyAFP/UQAhAnIDMwJFAU0A7fsK+Yj6jwCRBREFbwNWAgUBz/7e+/H6bfy2/8oCMgR0A+b+uvsN/OX9Pv90/kMAFQJUAmICogFhAKT9c/0+//f/Pv5M/l8CPAZ1BXAAd/z9+h391wAOA2QCfABmAcsDswLE+672R/lqAAQFoQXRAyAAS/1g/PL9f/8GALz/t/+4AlsEygKqAPL9jf2c/2cAUwCu/hD9Dv1+/vMBYgR2Aw0AYf3j/dMBSAS7AmP+TvoK+rr+4AQ9BuADdQDx/6sA9//DAFYBzAE4/0r+/wDiATgASPt1+XL7s/07AJID0wQ3AMH4+/Vf+lwAdQPxA/gD0wDX+0X6m/xJAJcA5/+2AIUCZgMaA5QD8wGf/vH80/2u/t//DgL2A9oEZgKN/tP9U/+a/5v/eP+oAc0FHgajAzD/Pftv+vT8FAISBvoFSQGV/dj+4gKfA5z/y/vj+4/+NADiAIEBzAKeAogBgv9d/KD7sfzJAPMDeQOAAZ/+S/xt+0X/bwLRAXP/j/+GArwA7Pza+qX8rP+ZADEAqQDmAXD+3PvM+637Svs0/C0ALQT0BKz/M/sx+6P9wgCQA+ID5P/j/LP8pf87AnICsQLkAtQB0wBQASEBogH3AQIB7/3y+qP74AAxB1IIjgVw/0f5H/db+pAAIwXzBqsEPgEf/or83P0SALUAIwCLAM4B5gKLASj/vP1k/oIB9wRxBRUC3/6p/l0BnQIpABv9y/sf/mACmwe4B68BeP0t/ucAzP9M+x766vz3/2sCZAMVAjz/JPxQ/Cz9R/x//J7+ZQA9/wX+Rf81AWYA5P9FAH7+r/sQ+SP82gFOBNcE+wRzBKH/hfs//Mb+mgGEApsCBwL7/679af3xAfQEEwXgA87+6fic9vj8nwWkCIYFev6a+wb8Yf4kAXwAPv+Z/sz+dv/t/80AqgKpA9EDugOgAPb6+fdZ/SAEjwUNBOUBhQCf/t/8Vf2n/4QB3QDZAToERgQ4Atn/S/5R/Lz7xfuV+4X9KgExBVYFyAGh/j/+uf0T/A39xP38/T3/RAIPBFQBm/zv92r4aPyPAHwEkgZMBSj/JPsD/Cr//wLuAxsEuQE3/T78jv4lAtID3wOiBKoDJQAa/gr+/P1Q/1MCnQTvAyUAwP4EAlsDwf+N+/f5Mvp3+04AAAWyBqAGnAM/AKz8kvko+bb7SQDQAdIBDgOdA7AB/f4E/Br4WPnl/8IGDQkOBIL9rfoB/S0AGAOBA7v/U/wH/OX/8wPZBQEFcwK8/vL6w/ke+5kArAUYBzIDv/yh+W76CP4AAPEBOQPOAWr8E/m7/cUBuQJlALz+aP6y/I797ALaCeEIigGw+q733PiL+5P/QgM7BpsG9QMW/4f8e/zg/G3/DAE5Ay4E3AEg/x37ePkq++r+vgQACDwGpAFd/dv7q/22APEBswCI/EL7///jA+0Dtv8H/Xb9K/4bAD8CxASOAzUBLgBZ/m/8rfoo/rMDkwVYA9QBIgNhAh3/VfwL/ZD/0ALxBU4GpAMd/uD68ftg/Qf+2v/AASYEkgQ+AvD/tfz4+hT7ZfxP/Xj90/7KAa0DdQL5ADL+uvqB+FH6dP87A30FpAQVAsv9+vqJ/Z0BTwKi/8b/VAEAAXIAEgD7/tH+aQDKA5IE8f8Q/D37wv7OAdUDwQWvAYf77/gw/Z4BGQIfAn8B/P/0+/D6cP41A/gFCAUeA9sA4v3r+2793f48AEUB8wChATAD0AVDBYEBeP0W/KH8ovwQ/LP+pgViCQEJOQOd+9r3M/e0+h7/4wK1BJQDAwEn/jf9Z/4l/1D/qf9c/rv8Efxo/aUAsAPnApv/wf8pAB//Af/G/z8Ae/83/g7+8v8NA2oFSwQXAs39ovta/j//iwByAQgC6gAW/+f+df3f/Of8KgCJBZAHJgSY/uf6WPbE9V79zwYaCsYG/wDa/TL+jP4NAHkAYQA8AJ8A4QKeA8MBaP+W/u/+FQEZAokAEgABAu4EiwPT/gT7evup/k4CvQSbA54CKgCG+2D6nvwnAAEDWQI/AXICHQLk/R/6Cfpo+5j97//TAm4DGQB9/eP7ivw2/T/9cP/JAgwELAE2/nj8lPzT/pAABQBd/i//AQImBc8F9ALI/rL6aPjB+4sBWATjBl0IdAYEAOD3kfZc/NMCqgXdBcoDUP/D+tX5Rf4kA58EgALZ/tf8T/1o/mEBxwNVA74AtvzB+tX6FP/gBGEGSQUJA5UBMf+K/CP9ggFVBtEEov9P+1n60v3aAvcEfQLX/sX9xf2y/cv+GgDiASkBf/9iAN/+6fqD+CD8xQGVAsf/8/1KANMCpgMBAj7/PP4V/5ABCwEX/AX4N/qHATYHoAhxBdf+Tfm499v8KwWQCIkFNf92+vX6mP2UAJADKQMbAb7/tv6eAGME2AVXAwb/Df1T/MD8QgCoArgC/AKvAer+G/1h/Zz+rP+YAH8CsAU+BqUBM/ol9876WwGSBk4GMwLO/NX6Wf3SATQEKgID/5r7Kvzv/78BsAAw/7X/ewAZAP79hf2m/un+IADEAh0FUgL1+hv31/nF/b0C1gjtCKgC7vkT94/98ANBBIwAx/3q/Cf9gf9WAh4ECgQ/AnD/qPug+p39VQNsBRECzP96/4H/uv0p/YP/IAIqBDYD2/+0+7z6V/1iATkFzAUWAzv9gvh3+hUBrAJIAHEAvALrAUz9Tfui+0j+xf/BAbsELAQ4A3QCVgJb/qL53vrCAFsEowH1/3T+Zv/2AXkFGQnQBJn7m/VF+OL+ygRiBv4DjQDE+8n6u/xi/4cCfAQaAhb9/Po//JUBrAXaA7b+Svsd+lX8YgMhCCEHfQAx+RD4jvydAZkCCAN2BAoFnwJv/UH6lvvk/mYA+gHUA6oDpgDu/bH+YgD1AEP/5P1P/9EBhwBl/E/97wHLA3kBKP1E/HIAYAKxAEH+3fyH+6j51fx+A+wG3AQeAiEBnv/g+xL57ftTAT0EWgQGBS0C7vwD/ND/4QPpAtUABf8z/mP83/xeAfwD3APOAMj+2/y8+/78dwHtBHUCYv6V+XX59/0PBZ4IJQWMAI38Sfw7/k8BTASuAxUAsv24/uf/EAAPAUsC7AEuAFn+Ff1//MP+GALqArEAVP4m/jj+fP3S/Jf+8wChAZb/bfz3+y79iwENBHkCWQFdAMn+Jv0S/40BUAAY/p7/qQSPBU8Bdf2H/rEB//8w/U39nv7mAI0FAgjhBZQC5/3/+uD5+/nz/FsBfQXNBu8HHAY+ACX6m/ea+sH/DQTJBb8FHAK8/DL6nvwXAS8D7QLX/8v+v/+FASwDVwLhAH3/f/0X+vD5Wf2dAgQIjQhPBZsAXvq09jz66AFvBtIDPfzq9r/45v2uANsCawcSCBoBZPgc9Rr6kwDpAiQD8gCU++j4qPzeBGkKGAeZ/673d/Qm+a4BVQdKCK0F+P+U+4v4tvrY/5wCVgQ3BAwEUwJKAJf/rAAMAY3/Rf4F/S//7gEUBHEEgAJcAEb+z/xp+/D7zPzx/2gDRQWLBcwAv/u+94344v1BAhsCiP51/rIAbwJAAj8CegRSA/38vPeg+Zn98QDMBI0IIwrHA3v7d/io+/gBZAMoAgIAMfxY++z/DwaNBxIEqv3s9830MPdjAEEKrA1+B2sAu/u9+Oz49vx0A3MFqgKx/t79pv8qAvoDxAGw/kf8tPtS/MX/EAS6BUEE+v/3/Wr8Y/xS/8YDxQRjACX96Pxf/mb+lAB+A8EDmgOSBQUIzQM0+pzysfMz/LcEkQlxCbYC6vqs+mMAEQVfBHr95fVC9bj5WwIfC6ILMQTh+kX4SPuA/pkBcwMBBJcDKAC+/PH8sv/wBMsG5AMW/XL2gffD/R4GMQqSB/8Byfwo+VX5Sv20AfUCXP/y+or4SvwPA/EHygm7BbX9XPXU9K37DQFaAez9dPwD/5YCUgTqA30AS/zs+kj+NwLHAOT9cP3O/08EuQeEBrcA0PoA+BD7RwFaBZ8GxwYLBl4EEgEt+xP4jvtjAQAEXAIsALH9Ef5UAlQEaAJF/jr8d/3k/r/+nfzm+5T/RARlBqICXfyw+vT9vgIoBEUCqv6b+6j6Nf0WBAwIkAZoAo/+B/zK+wf8cPwEAcgElgXtA///n/2S/BX8ff1sABIC4ADW/m0A8gNDBI4Ax/y8+qr5evx7Ab4GPAfxAdP9E/ti+17+7AGTBPUBQv0S/QMAvwIEBKcBGP4D/Dr+iALnAlMAm/7O/mT+Q/0U/jICOgUlBKwAuPsX+ZP6cv8rBYsGigI3/Nf4zvpV/qwAZQA5/TD9igDUBNsHjQZkAQD77faq9k39QwdCCwEJKQRl/6/6nvhr++oAEQaxBogElQMIA20Az/vP+Tr74f2/AWsCvgI6BLIDHQLXAIgAxP0s+/D4qfkSANAE+AVfA8YA5v6X/Jb66Pk//YQANwI2ARwA0QENA3YC5v9q/wcAOf7n+8P7d/+sA2cECwPeAAr+Qvzr/X8CwwUTBV0CLQB2+4H2Vvd8/ZYD2QXyBrwEW///+Jv2m/xLAfsBcQAj/yoA/wDOAIEAegDi/0MAjf1u+5/+/gIWBiIGzQQfAKD6X/okAIUFGQVPAvv+4v1+/Ij9wwJ2BCgC3wBvAgYBE/xi+pL+ugH0/9D+RgHoA9gAufxu/eEAlQLa/279pP1O/WX9+/4PAvkEywNSAFH+Xf96/uT7Cvxn/8YEJwY+BD7/fvoe+sj9HQRYBj4Da/zt9zT5Iv/MB9QKjwVq/Nf2QfiT/SgDkgX9Ay//lvr9+gz+4gGuAxoCVQHI//H8l/vQ/Q0CaQboBzYEt/7H+Zv4jfvjARIHJggzBUz/oPyT/r0CEgMeAuoAOP53+8X7QgAnAooDSwT1ApH+Kvrd+tD+jwGcAG0BNwBb/Hj61/xJA/gGsQWM/5X5k/Yw+Mz80AG2BYoFUwRTAXr+Hf3y+wP8Ev27/+ACoASYBJ8CT//u/bP/CwCG/nH9J/6q/xYABAK5BIkFpwGC/C383f6YAIn+dP1v/Pn7If93AroEYwRkA8oAi/2k+zL8v/8rAiwBzP8zAa4AMgFVAhkCRAL2AFoBigODBC0AP/sE+5P+GQOGBVIF1ABH/Gr7hfzF/bf/kgGQAvwA0/v2+MT7sADKAi0CKP7S+ED2pfhoAGMHsggOBD3/BP5U/qX9mf2CACYDLQKX/qP9QQBQBBQH3AYUA879efmo+aT/1wYOCqYEa/4k/Wj9MP1P/nAA2wC1AtUCRgED/6/8HP2L//ECmQMeAzT/0fqt+4wALgNEAaj/2f0N/icAEgIsAj0Aef8l/3L+Y/7I/9kCUATkASb/Svzp+cn4MfsJA+0HmwbOAnT/5fw/+Tv2nPaF+iABiQctCYQEz/3t+9z8eP3z/Pf8nvwK+yf9hQGjBwoJnwTE/w/73fph/oABpwIDBGMETQHy/NH8+AGwBJAD/wAFAbABjv5l/aH/KAN/BQQGSQUXAZ/7lPi/+1cD5AjjB4T/ePcZ9sX81QaQC1IJ5wK5/Kv3HPa/+Bn8hf/tAlIGGwZpA/IAB/5Q+5z3f/Zb+kX/YQRHB7sGewPC/AD6hvvT/Kj94/yn/9AC7QN0Awr/wvou+ZP6uf6CA0sHnwhrA7D6ePfJ+z0EiAjOBp0Drf/u/F/8u/4FBCMIRgbhAA7/8/7N/xIC9wL6A6ECzf0x+gz9AwLtA5kD9AAe/4/9d/4QAV0BvQApADgCpQEC/cX5VPq+/hcDFQVABTcCmPtq+Pf6MADBA6oC6f5w+qL4kfpxANUFOQc9BJj+xfui+ZL5w/yOAPsDNQMQAK39/P0G/xMAXQIwAVv9oPo//O8A2QM/A2IAvgD1AIn9Efz5/Nv+zgCYAtIDgwMYAIr7U/t5//oEiAYdBDoBm/2h/N7+5QFpBJAEcgGj/QL87fzsAgwIfQYfAYP8wPuj+zb+hwPQB4QGNP9O+fL4fP2iAGUDQgU9BIsBfPvm+HD8vAERBGcBrf1T/Pf8kP4CAqECrP9u/fz7nPs+/On9ZgAgAqQBPP9g/tH8/Prl/E8B3gP1AIr+wP6BAH8CSgHAAFYCBwJV/9D++/+4AhEERwNtAqgAYwDL/RH9KAC6A+EE2AHT/sH9IP8V/0L/Qv+c/mD++/4eAdcBJAOaAl4AIf2++2798P4EAaEDAwVzAQ78gfki/MUAkwMJBHMBX/+j/94BTAKy/4P8ePxO/hH/igA/A4AFIwOS/kH8RP1P/70AmgGnAS4A6v2s/TL+fACOAmcA7vtD+WH9SwREBVwBJv5t/SL9Zv1JAe4EDgVGAi0AOQHsAUAAc/v0+Sf+nwP3B+0GnwF+/fb79vyj/wUDBwV2AYH99vrM+zT/uP+P/9r+Jf/P/h4AiQHOANz/uv21+mv4+vu6AW8GxAVXApwCGAE2/RH5w/nr/IkA5gRYCL0H6gFu/An7Bv/iAiAEPAHl/Pn6iP3oAqYEMAXOAVz+m/6+//UCHQSWAcH9B/wB/JX+iQPgBeIEuAPdAzr/dvh59yf8ywGHAq8C5wQpA1/+T/x1/az+bf5f/qEAmAIaA5ICDgBP/S38FP8xAAH/xv/AAPcAV/+I/i3/jv9q/pD8bfs+/H8A8ATIBZABgvzx+eT5TfzC/wsDGgPn/l77oPyqAKID3QMsAUb9I/vd+2f/aANpBZYFVgGY+vr4cv4zApECuAKfAq8BLv3I+1b/ywRVCN0G4APg/mv7hPue/noBSgSQB1MH4QLp+/f5cf2sACACPAQnBt8CJP4k/gkDdwRt/9j5u/g7/P4Aowb0CI0EZfyc9v325fpHAIoDEQOsAAj/lf+8/6D9NvwV/NH5yvlM/cYAEgN4ASn+S/1n/1MCwgQwA+/62/R1+MIABAbOBxMGXAAZ+v/3bPtsAWYFWgTqAIT/+QBMApMCpwJaAkAB5/yd+bz93AMNBE7/gf6uAmcF7wR5A98CBAG6/U39RP+hADoByAGCASUB3gIfBbACWv7x/Hn+JAF/AW4CnALhAI3+9/28ACsB4QEZA3sAyvxA+2P8Kf2B/pwCpwfRBlv9uvXa9gP8KwApA2wEaQIj/436ufgC/IYAgwLc/h77+fkp/Z0D3gVhBWIBSPum9qb1evvXA34HiQVJAJ/7iPuN/eT+5wCvA64C1/2m+XL6cAIZCQ4IRQUKBR4ChvxO+bH8BgP1BP8DyAEBAc8AhAE9A2oEVwM+AGb+xv2l/4UCxQTGA6oAPP6P/AD8IfzA/rgAeATGBgUEAgH//Gn6D/uv/kQE2AhkBKz5MfOa9T/+IQRLBz0GWQCX+iD6OP7wAJEDCQUbAUL5vfVi+Wz/NwQOBQEExwC5+l75+v4kBCIEGQE3/Tn6r/nG++j/0gTsB5gFU/9l+Hf0WfdNAFIJjwxnCfP/UPfT9fj6SALdBNwEngK9/1v/EAEZBC4FdgQYAzAAP/qL9zX8AgVTDAcMqQXJ/LP1LPWd/WAIlAsaB0AA9PvG+E34Lv2yAmoFgAO6/0T+J/yY+hX90QDNABD/dv9V/Yv7Xf8IBYEG3AEn+oHz1vNk/AcHFw2NCs4BT/iY8kT1WP8IB2QGoQKuAB0ABP+d/Pv8Xv9/ANT/Nv8CAIUB+QS9BZkB5vxE+6D9qf5I/7sC9QYNB4EB+f1e/kD+K/+2AksGFQarArP+k/yr/UoB2wS1BG8DfQMaA7L/2/qg+p394gCIBD0FwwBO/SD/qwH7/976xPhN+Sv60v3cA/MIEgdMAHz71fhE9/H2oPgC/bUDighzBgYBXv2l+437nfpM+5oAmQUXBVsA2v65/zQAdABLAE8ALP+f/zQBVwLSAjYDGAPpAIP/8fwY/Lf9QwLOB3IH9QB79x33Fv18A7UHNQVTAjb/VvxS+1P//gPeA5oB2f6B/60AogJJBE0Cjv/H/tAACANyAr8AYf/9/b3+bgH2Ax0CLf4C/JH8iv8TAtUDtgAc/Hr53vjD+/n/TgUZCP8CV/mk88D1kv08BAcIZgbV/735EPe9+kr/hgJSAo/+0PtW/DcAoQOaBnwH8gPo+/30RPeFAA8ICQusBzH+i/bf990AnQdPCcsHkAUrAXT5CvYP+vsB1gRFBbAFpAIZ/qb6DPzYANwEfAOi/lz6l/r3APkG1wUZAML7Vvll+Ab7nwPrCuIJ2gJ1+3L4IPpt/eAAhgT0BTsFDAGp+wv5ZPrd/h4D9gSBBJ8CKP4x+kz5wPuH/xECzwFN/7r/XAEIAnwAz/6M/zT/Vfz0+mH+4wTnB8UCVPzc+IT4jft0AWwFLgeVBn8CSAA1/QL7Zvvg/RYA3QCmA9MFbQbiA9MAOv/L/cf8D/9pAr4DcQIrAN8C5wOiAdz9Zfuf+Z/4J/0/A2IIsgd3A9H8hPYh9xf8CwNaBwIHDgMg/Kz1mPbS/SYETAZgBqIEx/9v/Hz97wGmA0YAn/yR/R8AagMmBw0GkAEo/Y78Tv63/+r/PAJ3BIMBfP7H/nL/QP18/Gb/nwOPAmb/hP/k/rj7TPhz+wAA9AJPAiH/Wv3H+2H8c/7n/0L9D/wv/WQAtgQ9BbQBVfwX+oP6Tv37/i8A8QC0AqMFogYiBXX/nPzW/L/+EP+eAdUELwSCAkr/If6e/O/+PgPuBREFswBD/iv+9v+c/9gBjwH3/zEBVAIKBNMCfgLbAFQAMP/T/Jb9NgDdBR8JAwkIBe38P/bn9av65QFfCKAIuAR6/hT5sfiP/GYBMwHN/RX+eAA+AUgAyP0v+xX4UPdi/DYEEgcHAiv9fPsM+U74q/sa/9r/rABqAgUCWQLnAi8B7fxV+Ib4WfxQAiAHswgYCJACcfvN+VH+0gJvBPIEaQPc/tX6efuGAAsG5AZAA6v/gP0K/Hf+EwKHAQEA8P+X/2/9Jv4JAhsGOAYLAKX70vnQ+7wBXwZMBxUEIQGw/5v/QP8p/S76mfu3ApgHEQgOBJoAwP1z+w39kv9OAa7+o/0MAQEDVwH9/Rf+Lv/7/vL8Fvt5/L7+ov/IAFwCiwHv/U77gfwPAG8D/AJ1/777jfoK/C//SwKiAXQAKgLYBC8D0f1r+sz8PAHuAXwB6QBe/7D9Wv4hAvMDYgG9/rL+Yv/t/un9QP+gAWcDKAH5/EH7ifwn/0IBVAR7AlL9Tfk9+q7/VwNJBckG5AQd/gX7oPvu/4sDuQNRBvIEQAGQ/sX+mQEHBEEE7wOYAmn9i/yZADoERAOs/nv8AvzG+2X+QASdCIMGRP5F+eb2yvb2+1oBxAQ2BdkEGQGx+mj40/sV/1P+UAHgBEgDMf91+7X9mwG4AGz+uP3P/j/+9f/YAiYCk/9a/bv+sv/DAEUC6wPPAwsAzv2n/ff9IPxy/PL/DQOIAocAfwBT/2L/AQAoAToCggE0/9j9Lv3d/Pz+IgJABZUDFgGpAFEA5v9rAJICTgRoBGcCzQL4AQMBc/8J/fj9YQAwA48B4v6p/SMBKgWGBNkBvfwg+j340/oDAbcFewahAoP9cvgu+AH89ACSAv0Apv8k/xP9Vvsd/kkBQQHD/AP7Wf0p/9T/FQF3A5IBBP0R+lz7RP3z/sECTQO3AGv+gv73AawDzwH0AB8AhP6r/8ECFgMuAAv8u/tL/1IDlQhtB5UA//rO+R3/wgSABgQEcAFc/5/+QQAUAvYBFAFPAksCxQCt/oD+TP+6ALEE4gYwBY/9Z/ej+Dn8i/5n/ykAawDp//3+RgF1AYP+k/1R/E/8z/wU/okAhQJ7BOkE3gHW/eH7T/tz/mwCQgRhBeoE9ALv//z7zfjF+tMAowVUBCv/c/xt/eIBdwM3ArUAjP2j+lH7+P+0AW7/Cf8oAEcBZAFmAIn/Mf+2/43/s/47/if/IgNDBRcDr/+m/Mv8AP9E/9kANAMYBGIEmQI6AXv/7f3V/skAkQGNAUcE6AbZBAH+7Pmr+gL+SgN7Bx8IuAFY/NT7JP3H/t/+YgDP/6r7Qfhq+7YCDwTR/yD+/P0k/N/64PyBAGb/Af6xABcE3wPL/UL6dPxhAMMDZQOQ/ib59vjRAWYKZwq6BtIBo/vI9Zn1zvwzBTgH4AN3ARwBmv8I/14AFAB8/rL9BQHHA+QBEv5d/QgAmf+r/qP+nf4q/iwAmwRMBeUBf/1o/SD+U/wq+0P+xAElAuQDdgdSCAYC3/sE+9b7kvyL/7oCOQWXBikEIQLG/3H9Nfzx/Gn/wwIHBLoAE/8v/2sAVgB8/zX9yfmz+sH+PgMKAg3/3v3F/Cn7J/oZ/icE8QVXArn+zPvw+HH5rf4zBe4GJQSaANX+2P5r/qX9dv6y/6IC3QQ1BBsD/wG/AIT+AP1e/T//UwCfAHUDzgRMA0cA7v6l/439gfv4/twE3QWzAdz/hf42/JT7hP12AkgDNAEbAAMA7f3e+pj9OgGAAhcC6AJYAjj+Zftx/dAAb//j/c//GAQYBDQAYQDPAEf+J/sI/fED2galAkIAgQG1AGf9wfyM/2v/Ff2m/UUBjgScBLAAUf1T/OT8zf+RATMCtQIvAvT+RPup+Rn6G/wsAGYFuwZGBGr/Xv3g/Tf+kP5W/nH+8vyJ/WMAwwIjAAT9Lv/+APIAnf9CAHECMgMQAcX+N/6g/WL/rgPJBvUDS/4q+y/9CAA+AKAAUQN+BvADbwAh/97+2vze+oX9GQFBAoUANAAuAo0Cdf5f+9j8fQErBtcFxQMV/7j63/lI/CsAqwNaByUG7QHi/Un9LP6b/1YBJgHvAej//f55/0f+v/3X/6AE8gPK/lf6fvnV+87+IQKVAmwAYvxE+QP8iQH+BVgGcQE/+jv0fvTp+2sF+wg7Bv0Aq/km94r86gSjB/8Dwv5D/LD7F/xzANIDOwRAAbf/jwDh/8L/vQCPBOQDYv68+un8rwGnApQDZANdAQH+Pf24/0sCpAIxAeYBqgB5AdgChANCAib+Jv7M/gsBggMkBj0F6P9l/F/8VQKZAm3+XP2a/8YC4AEUAV4AJwCM/9j+OAA+/0b6Wfex+xABvQNiBIYCl//s+5v4X/cQ+1cANgHCAFUBOAHn/+b8jvsz/JP8vPw+/5MERgX0AhUBOP84/pD+EADFAHwBWgJWA5wBNP5o/gQB2QNhAuX+Uf7x/y8CiwEaAQoCxv9M/VP+vwHZAuz/WP02/Yn9l/6bAlgFKAOZACEB2QHW/8n+rQBrAhYBJwA5AwwFwQDu+5f+wAIlAssANwFFAc3/1f6RAIwCZwFXAOwAPwHE/XL5b/va/5sBx/79+3/+zQDu//IA/QE7/337e/lC/Ej+nf4+/4b+hP3T+p/8uwCbAqsBjP/9/s78kPz3/5QE+wM7/Sj5IvufAdgFgwaYAxX/qPsP++j/+QUkCaYGQQGM/CL8MgBGBf8HXARC/un5F/tc/7sDQgdtBrsCv/6N/Zr+dgHoAucA7P29/Kv+GAJdBXoFxAPM/837CPvs+6b9+P5UAd8CnQP+A/ADBAGk/Mr8jv2X/Ab89f6tAVwCWAPCARv+J/pp+cn9vgG0AmUCfwFW/5P7/Pk7/GX9PvwZ+/z8UAGCA+YCv/+e+yf50vjP/AsDnwWGA+T/5f2A/OL7L/3BAKIDbwP+A2EFNgZ8Agn9hfss/JD9xQCsBukIZAb5AGf9NP9dAMj+AP3h/o0CcgVmBQkBu/zW+eP61/9qBXIF3wGCAZMB6QAU/wv/TgD2/67/UP+qAHcAgf46/5sBdQM4A+ICZQKiAKD8Qfqq/HoAngKbAQAAIf5X/ZP+7/8oAB3+0vwp/hsBmgBm/tn95fzn+in64fwlAI8Bmv8G/jH+nf5kAEMCeQK//cn5SvyyAusFnwMJAHL+wv/0AKcDdwVmAwAAs/3y/5AEewUvAvT+7fxz/XX/ugLyBYEEHAGt/+L/VP9h/p/+4/6X/Vb9TwGIBrUGpwAk/Xb7cffu9Q37OQQtCn4IBQJP/QX76Pr3+4z+owEcAmwCmgJnBIEGuwNm/lD6m/jA+aH9DgNLB2IGogONAEf9kvsy+mL6RPyB/oUAgAHF/5X9ef2d/qr+nvwx/Dr+UQJPA28ADv/h/kv94PvB/dwBYgSyBYcFTgPZ/lH6/vuIAl8H5Ae2BQUD7ABh/0j/7gAsAO3/LAKSBQUImgVYAcT8Ofr7+iD/5wMXBQYDDv8U/X784vxY/fD+Sv/D/GT9RQC7AYb/if4u/1f/dv4a/Zf9Vv1s/bX9YQBAAhgBYQA+AfICpQDc/Xf7avx+AGgBIgGiATEDggOtAej+T/yA+tn6lf4bAxkFGgN6/+r8Evyg/VMBFgMMAXb9N/t++838cP9YAeABcwIxAjMC/wJaAwwBCf6y/RgBbAVfBCUB7wE5BLEDq/9I/Yf+sQHVBfIHegZXApH9lPo1/OX/lAK/BGUD2f7n++n8v/87AREBbP8Y/nT9b/xX/an/Jv+4/LX8ugDCA6kBhv1Z/CD9Y/xu+zz7Yv1WABMC+AK+AS4AJP8rAEoBBv8e/PH8RQCFAh8EZQM5Aff9n/uy/asBuQOSAloBzQABAan/2v3E/X3+pgA/ARMBJQCL/6D+B/7s/yYA+//8/0gB+AG5APD/PACRAiQCff5A+/T7aP/pA1UHWgdYBBr+APqE+pv+VQKJA7cDogLGAmMDTAIc/in7Bfvc/TsCGQMCBN8CS/+c+6n6Ff8RAr0Bmv8I/+/+6v31/W//fQFn/239R/3O/Yf/5v6s/R39r/6HAWcEIgUIAB/6YfhO/MYB8wPVA0wCVwBT/dP7gv7kAVECNgCG/w4B3AERAev+nf0U/s/+wf6Q/v//lAHbAsoAQ/6s/iP+bf7RANQDzwOxAJn8qvoB/rYCOAaXBSECMf6p+7f8zf/iBK8HsAXEAE/96f4AAukC+gDI/8H/Of+X/1MBBQRlBD0BZv0a/AD9cv7FAXQEFgOLAEX9V/pb+p395AGyBO4Dkf+M+/X5WfuO/rkC3ASKAbf9JPyx/vcBuADZ/Xb8uv34/34CgwI4/4v6FPk7/RIAfwEiAUQAygB+AC3/vvwm/OX8Wv2m/cP/mwEnAbgBZQKAAej+0v2xAN8D+AGj/nsAkQS1BtMDDgAK/5T+JP9SAb0EIQZdBJUCgwLRAlYBEP86/Z/9mP95AbMCdwK1AgoCj/80/kH9bf2R/a39SP/LAQwFuATG/0f7Qvue/fL+k/7Z/nIBiwPJAsz/Cf57/dH8gf1u/w0BJQK6AYcAAAEbArIB/P1++5X8L/4wACkBSQA6/17+v/1W/x8B1ADP/zL/WP7d/Jv8w/z1/DL+agDGAe8BaACt/hH+OP1B/TX9Mf8VAtcDLQSlAtYAGP9X/0H/nf+yAFoBBAGIACgCLgO3A6MCGwCU/jT+If9OAFMBygGIAwIFeARMAXL9kPtI/E//0QGgAxMEpQMDA7UBJwAJ/tX8uvyD/qwA1ACrAOYAFgGDADH/Mv4d/vz+Qf8s/oX9b/4IAOYBeQMEA1b/7fpB+lD9o/9G/0kBEAREAkr9k/oP/GT8u/zz/vUBBQPcAbkCDwPO/8r5rvcY+4H/DAJOA68EjQKLAAMBdwHz/qD7+PsiAEsFEAVqAdb+f/8/AUsBUf8S/dv9EP/BACED1AQKBGIB5gBc/xv9pvts/FoAZAS0Bd4C3wD9AKkBRAE7APn/Z/8D/3z+8ACRA/ICBAJoAUcBYf+Q/mv/GgBxAJH/cP/EAPoAIv+6/g0AHwF5ACn/vf1y/Mn9zP+SAioERAGM+z75I/wx/zUAmgDvAqcCev8h/Xb8y/0k/Vb9XwB2AsIAqf0d/uz/ugCC/wX+Qv6r/pP/8v8JAbMBkv+4/i//av8HAFIBpgKkAkMB//3x/Or/dQPzBDUEzgEl/lr9rADbA68DOwAY/d38ff/mAksFawUQAkj+Uf1X/k7+DP3U/Dz+KwHlA5cFFQU3AYT8p/gB+qD+IQK8A28CBwFlAD8AjwD0AIz/C/31++P88gATBF4EKQPj/8/8sfqR+jL8Fv5BAHACIQRBAz8Adfxl+Qf6Rv36AYwEJwKS/sL8c/z+/PD9ov85At8CYQGa/879lf1X/j3/v/88AXIDuQRiBIQBVv1A+k386gHeBZoGTgOTAGQABwCrAFUBIwDk/q7/QwL8AxEDBgBd/pr9I/4VALkBnQL0ALH/Gv8i/03/Af/Z/1//2f64/1sBKgFb/9X+NP+UAB4BwQCI/8L+o/7S/eL9g/6ZADYCEgKpAJf+bP00/S3+Cf+6/5IA0P9Y/8P/vgDjAA//8v0x/QT9v/4TAcADmQNzAKP+0v0X/Uv9n//cAtID6wBJ/U/9xv/nAbAChwJRAcL+EP48AGwCrwPjAZL+Mf32/p4C/AO1AnQAuP/IAOsAmAC0AYcCmAAL/yj/5v/r/8j+c/+5AiYFJAPN/2b+Iv4Q/gT/WwAj/yT91/3uAd8EtALJ/SD8CP5H/7YASQBc/ij8nfwBAJkCdgMgALX7mPoo/QIAXgDa/S38bP0CAFIDMQQ8Azn/QvrH+Hf6W/+GBAYGfQOBALH/5gC6ABQARv+y/lAAjQFnAgABqP/e/8EAeQFlAKz/4f8OAdkAZQA/AMX/YwB3AVUCBgLsAVUBfwAdAOH/CwBlAEEBuwHBAdcAPgA0AY4CRwLQ/t/7G/1CAN0BFAJjAfj/wv8FADr/F/9C/jr9ivzs/Br/NgDUAYsB9P+s/5X+t/4+/lr8P/qk+jT+FAIyBKoC2QAcAN7+7fy6/F398v3s/mwAAgOBA1ICbf+q/Yz+nf5z/sD+3P8uAawBkgIFBM8CYv8z/Qj+tf8PATkCJwJyAV8AhgGsAgQDNwJ8/8v+cf2U/cgA3wM2BTMEBQJT/5X9G/y6/Z0A3wJlA14BGABJ/xH/8/0i/kn/FAGpAbEARQA2/9z+bf3F/FX+4wBvAcv/MAAEATACCQA7/rj+rv64/hr+xP93AXsCXAIuAQQA//2Y/bP9b/48/m/+ZADRACgA/P9YADQA4f+u/iL9ef33/U0AnwLnAmcBq/xv+hn9fAJmBswE+/9P/PT81/4UATkAqf0L/oIAXwT1AxoB3f3n+0b94v5mAZICpgJsAk4B5f4q/aT9r/94AcMBJAKVAbUBCAMqAwoBh/1X+wv+QgQZBmcDlP/u/Wf+Xf+iAPIAoAHzAGgAZgB3ACsBcgHzALD/vf6N/jMAKQBrAMcBEABj/c77Wf7oAQsCIgCr/n/+kv5a//z/e/+z/Pb6zvxyAOECKwF//v/9Lf9qANkBSAIKAPL9CfyE/CH+a/50ANACkwRmA94A1v8k/iL9vvvZ+5n+LAH4A20EDgJG/pf8wv0iALEBuQFBAvQADACu/87+Qf8v/9oAogIfAsgBcAHMALb/r/4W/7MAXQJ8AhEB/f5Q/UT+DAFeA8kC8v8F/+z++v1x/r7+/f5FAYkCeAH2/1L/GQBLAE7/Sf6x/s//7QDTAbABNwEv/8L9jf5W/y3/ef7F/qkA1AFVAez/7P33/V7/WgBLAWQAl/7r/AH8Af7tAggGEgT5/wb94fzY/bL+vv/eALgC/AL7Ap8Cqv8R/R/8K/6xAU0CIgEhAY8BsAECAmcBjgApACEA5P95/hz9rP2RAKED3wTrArH/Tf1Q/L38cf1M/n7/5QGeA9gC7ACU/fH5c/hY+mf//ANLBOICLAFt/v77CvsV/c//kABiAIgBnQPZA98AZP3l/fT+p/4f/qH+Qf/o/90BKwRhBcACnv5N/UL+Bf4J/bH+9wEuBPIDmwLyAOX+B/6z/tH///9aAGACJgRqAysBtv7P/b3+6/8FAhIDCwKjAAIAXf99/6oALwGIAXEAfP6Q/mwAgQLiAhcAoP2C/e7+NwCbAFgAjf6w/pkAewDh/k3+/v56/ycAMP+z/qz/0ADRAhADcv87+xH6TPwJAB4C7wJLAlgBuQBv/0/9vPr4+6L/cAJmAkkBmf+W/Y39Pv4sAVACbwEBAEn/JADn/6L/sv6Z/54BrgPFBOgCiv9g+8L6u/5zBLEH2gYjAuj98vxn/s4BdQHh/8L/4f8gAUYCMgKeAP3+GP0V/Zj/aALQA9wCbgCt/AH6z/r8/pMDZwU0A+v/2P2d/YL+qP5H/zUAmQCOAEz/f/6C/y0A3QBDAOv+xf5c/nj/FQHNALT+4P1u/j3/CgEgAegAXwAXAfQArP1l/GL9VgBuAvQArv7w/oH/iACnAQwBDQD0/aH9hv6I/8T/hv+MAAUBZgHo/w3+Ef5iAGYCEgHJ/y7/DgCPAcIBNAHBAD8A/P+z/9X/pwAaAWUBoQEYAan/FP9WALgC/gO1Acn+t/yi/Dn+cADyAj8EkQMBASj/h/6+/pD/lAB3AAQAAv+N/jUB1gGLAKT+Uv3X/Z7+ZP/M/7MAWQCRAFAAmf5b/QH9vf6RAD8BSQA7AA0BWgHNAJH/SP5P/HP8b/5UAaoDmAKmALz/D/4R/RH+qP62/9f/qP8CACX/qf42/6gAhwD7/YD8iv0sADgBaAAvAAEApwBRAcYAVgAf/wH/j/+BACABjADgAO4B/QFgAIT/if/HAAEDJAMaAooAtv5A/9cBEgPDApIAqf7+/vn+UgAkA9YEwQMVAbX92/x5/hAA2gEPAX4A0/+3/0gB9P+Y/sn9k/5vACQBagCx/1MACwAt/3b9u/wo/tEA5gPwA/AAuvx6+tb7l/6GAXQCZwHFALEAIAAp/gH9Av2G/ggAYf/I/rj9u/1l/2IBwwHn/gf9B/2d/uL+F/6b/hkAKwLSAWMAAv7y+/D7qv3HABQD/gNtAgcCtwIcAWD+mPtw+0f/vAObBT0FbwNBASUA1f9eAAQBZQFqAUYAzADgAh8EVAQvAQP/fP7a/oMAtQGtAt4BtgBcADoBDwEQALH/h/5i/vn9J/5g/xYCtQTeAyoAdvza+3L9LADuAMAAK/8G/WX+t//ZAFIAeP9u/xz/Ef/h/Y/8lPx6/8wAbP8F/tT9MP9r/73+eP3P/Oz8hf3y/0ABSQCm/rD92f3X/kj/xv5N/14AGQKjA20CSf7R/IT+vf+pAVsDhAVSBkkCGf4H/Z3+1QFcBGMFSAViAjD/M/8nAQUDSgJoANP/OgGAAvQCmQIBADT+1f2f/90CHAThAjr/WvxW/I395v8mAoYCiAE4/yP9aP3b/+MA/f6H/QD9GP+3AQYBrf88/z4A6f99/kf+QP6F/k3+tP7S/+3/S////qD/Vv+9/U38zvyD/2gBRwGq/wD+Uf4m/2D+Z/5v/0MAfwDm/34AnQDZ//P/LAATARUBuf99/wQAOwBCADcBJAOvA4gBJv8p/nT/8QIKBVoEkgK0AMf/0wBjAa8A1wCdAZkCdAIwAWD/xv5y/1b/HwGiAg0C3ADC/03/bv5L/fT8af5xABYC+AElAAj+jf2a/rr+Zv5X/SX+BgH6AfIAm/4l/cj+vgBkAR0Ayv3H/Jz8Ef+yAboB0wHAAOP/xP9f/nb99P3b/jwBFgPZAkkBdf9p/m7+dP99//P/iAClADsAZv+8AD4B2v8W/0T/1//OAN0AewDh/kv99v26/18CEAP3AcsAIgAa/1n/RABbAPIBpAEbAVAAG//t/3MBmgHJANj/FgCDAacBswKXAGL9Pv2R/s4CIgRRAYn9bfxG/jMBaAIoApgBsv6S/Lf6z/uU/4kCfAPwAAX+Zf2f/hwAqgCG/rb7m/tp//0DKQVsAWX8FPvl/PQAbwPpArEAwv5a/uH9pv40AGQBMwLrAZv/mv6D/oP+KwASAVwANv+n/7oAGQLoAav/3v6o/g//UgCgAVICKAIXAXIASP98/qX/f/+9/+//FgA5AdoBowH0/+D9tv1h/90AWwLVAsgBkf+0/YP+9P/TACsBXwH1/6v+Sv9JAL4B+wEqAcr/0/6M/sL+ggDo/4/+5v0F/iEA+AA2AQ0B2AD1/tj7x/oU/Mv/RwKjAwED1f+y/L76Cvso/QIAFgHOANz/4//YAHkBwQC9/mb9dvwm/cj+UgGqBDQFLQJN/vn8AP9aAWEBZgF7AGL/3f/lABkDOAPgATkBRgH0AHr/AP8hAIsBdgGcAYMB7gBmAUYBGwKOARj/sv7Q/zcBaQF9AK3/vf9dAE0BewGv/3P+ZP5s/wkAYwB3AdQBngHM/4r+dv5m/tv+cP9DAEkAhABYADQAGAA3/1z+rf4VAG0AMwDM/oT92v3Z/iYAL//8/p3/ef+4/1X+XP3K/LH8fP5MASMDhwJhAHD+Ov3k+z/7G/1mAEcDXQP9ASoAsv5x/of+9f69/7sBIAMGA+wAXf2m/OL+xQKvBFgDwABg/nv/dgKUBHkDEADk/fP+QgNLBUIDLQCy/SL9NP/1AiEG4QVdAvT+6vtE+zH9nQBABQcF9gFa/6v8Bv0u/sL/cwAk/wX/kv/NAEwB1ADz/wT+GPwf+0n8vv9SAzAEgwLJ/mn6QPiz+wECfwRnAtf+1/35/Tv/0P8iANQA8/8HAM//fgBVAe4AUQBl/6b+Hv4P/y0ATQJKAkIAjv6c/fD+FACTASICywEWAcr+uPzF+2L91wAgAysDMgJBAEb/+/5A/+f/EgFzAnoCbAFG/1b+8v4qAWMD4AKEAJ7+ZQCQA5oEoQIaALf+rf6n//EAsgGDAQABBACD/5n+3/4qAFwB9gHI/5X8FfsL/VoAzgJTAQn9J/qj+kX+RQErARD+NPzc+4f9mQBbAlQCggCd/t38ifzJ/YYBiwThA8AAp/2K/sQAEQMxA+0BLwDI/k7/PQFQBJEFaANL//j7mfv3/akAnwLDAqcBCQDO/vn/6gBQAWf/R/xa/Nz+TwFYASYA0/4L/hD+c/99AMEAUgCa/qj+tP4H/7kABgI1ArUBugDx/83+Kf01/fn+HQH9ApIEHgTOAcv+E/xn/D79yf5RAAwBygLRAav/lv8GAPP/Kf63/Mb8Df4CAM8BnAJiAQkAO/42/qT/Nf9v/53/aAAhAqcCNgLYAJv/d/9JAM4AhAE4AUMANgB4AbICHAPcAUX/H/8nAP8BwQFB/y//6/+nAHQAggBGAQcBdv/Z/m7/5f4Z/uT90P83AVUAHP72/On9r/9kAKz/FwC3/9b+sf1Z/cz+5wB1AsEA8v1B/DD8qP7gAiEFWgSQAV/9cfy1/br+xP/RAM4ApgCIARkC2AI4An3/ffzL+vL7Qf8PAhoDEQIVAPv97PsT/c3/7QE0AnwBxABl/4H+E/4aAFMDRATKAhYAe/2J/T3/5QCrAu8BRQEZAfUAkAHUAJf/3v19/bL+4//XAIsBeAJJA28Cgv5U+pD67/7SAwgGlgX7AbP8G/vG/P//hAK/AqMBYgDP/1f/MACFAQcDlQKQ/8T8UPxo/+cCSQR1A9cAXv0B/JL9/gAJA00CfAAV/Uf82/xU/nYBVwPDAiL/afv/+Rj8YP+VAWsB7P8A/1X+S/6O/sP+t/54/7X+0P57AJoAoQDMACUBWQDF/kj9Bv5HAPEAeQC8/+7/hAB9AAkAvv8BAO//cv+y/+b/WQBvAYYCigIaACT+Wf3x/vIAjgHnAYgBqwHpAJcAQgC1/3r/TADlAdEB9gChAE0BxQEjASAAGQAUABAAVwAPAEMAIwCwADYC7wIUAqn/o/1g/Xj/8ACvAJ8AJAB5ABoBq/+U/o38SPzO/kIAgQFbAQUBeQEdAT//8fwW+z/7Cv5xAeQCLgGo/2//Cv9I/fL81f6BAXMDawIBAOn8tfvo/SEC4QN6Auf+J/tP/AwAtgMlBIoBhP9A/9UAwAENAWoAQv/h/A39Nv+HAhEFhASNAXL+TPwU/AD/tgEMBMICEABn/yn/eP/H/gT/yP97AfwBmQE4Aef/Wf93/rH+BgAHAXoBZQCG/pj+8P43/3IASQAEAIP/rv/RALsAAv8//FH7v/6rA9UEmQJc/4r9Tv4j/07/FgAkAB8B1wGeACMACf8k/l7/pgExAp0A+v03/Y//3QDqAJb/Bf8CAYgBlgCv/6r+Iv5+/sn+GP+0/2gAnwGtArwCVwF9/nz9of/KAasCFAKFACIAZQCa/wkAmwAQAagCywJjAdP/AABuABEBgACt/lz+wv/mAjQD/wD//e/7X/3VAEECrAENAGP+Iv+8/yQAUf7D+wL8pf1U/1D/hf9T/77/Sv///uf+Zf6i/gn+EP/S/7f/xf8ZABQAaf7b/dv/1QKVA+EBJP+U/TH+DQD6AEsBCACE/tD/bADrAAUApv78/or/NgFEAbsA8v8q/7EANAHA/zn/hgAEAycDPACZ/TX+twBOAgMDEQKWAGX/AwB2AkgDowGD/lz99P4ZAXgCpAL8AbwAhP9Q/n/+gv/TAPYBFgKcAToBVwD9/zP/H/0I/Wb+bwDdAdoA+f+e/x3/bv/S/nf9lvyc/SkAbQHcAPX9afyu/bf/AAIMAuz/ff1U/QD/IAAaAKf/FABwAnsDzAE4/xD9a/2j/tf/KABqAMYBKQPWArMAMf6G/DX+NQCuAQEC5QC4AN4AIgFV/1/9cfzH/aoBSQM4AqIAcADeAW8Bkf5l/Ev7Of5PAnIDEQMtARUAEQCPAM7/VP4B/kL/RQFlAhMCqgA/AI8AvwHnALf+Gf5V/w0C8QHYAPf/Lv/D/m3+u/4N/ysANQCHAJEAT/+5/or+1f/L/9P++f0B/rEAXAIxAngAcv9W/4f+GP53/qIAPwMkBX8DJf/I+/P7Z/94Al4EcwOzARH/8fwK/hL/HACYANkBAAPFAUX/r/3//hABpAD//d37mPxY/9gBbALNAOv+1f3A/cH9MP5D/wwA1QC+ABf/G/30/d3//AIQBC0Anvyd+8X+4wFTA50D6AE/Acn/9v6p/kj/2wBpAckBXABb/3wAMQI1AxMBZ/xv+j79PQL6BCYDJ/8T/K/70f2LADsBagAMAGYAngEEAan+sv22/av/9gHfAcwBlwHJAZMAlv1D/Zb+mAFQBOgDkwJtARIAxf8JASICqAIPAaL/RwBMAIX/rf5e/1wBvgEMAWkA1P8TAGr/7/yo+8f7HP6SAeoBeQFSAC7/C/5o/D38VP0TAJUChgPnASn/c/0C/S0A3wEAAOn9F/1kAEQD2gKBAX3/gv7u/Z39Jv7w/jsBuwPPBLkCmf7Y+yX8MP7E/z0AC/+X/2UBSQNfA/v/ZP1i/HL9hP50/0cAKQGFAvUBJgFq/8/+5f73/qz/4f9FAUED3gVhBb4Bh/5d/KX9+wBgAg8C4AGVAbgCfQOWAUT/9/06//UAxgCL/wz+gP7OAGAC2AFDAMT91Pyr/jf/kf1P/Aj+pwESBNwD4ABT/WX7N/xR/oMA2ACt/5j/CACaAMYAQwARALL/4v3I/Hr9DP/lAfgCPQGy/nD9Kf9UAJ7/nf5e/Sj9Av/MAhEFXQNn/w/80PuQ/Z//swD/AIYBFQEVAA//UP90AF0AE/9z/U7+TAE3BDUGNgSEAPb8q/rI/LcAigQ/BaUCMgHkABQBuP9o/sz//gH6AlEB1/8WAIAAngARAHv/gP5s/dr9fv9RARAB/P71/V3/JgJ0AuT/dv2o/Ib9Sv56/lsAKQIaAlUB7f/c/vD+Iv6i/VH/GgGcAQIBGgE/AW3/cv1J/Mz9rAAgAiUClgGPAAH+TfwX/Zn/1gHpAa0ALP7e/Ff+PgBHAZkAZf7F/Vn+UgAPAk0BZf+j/c/95P/9AHAAfwB5AFEB/wHkANwAsgAgAGQABwAqAO0AdwGNAuwC/gEtAZYA+gBdAasAwP8U/x4ALwLqAiABHP/H/t/+c/9F/0T/fABCASoChwHc/uv8JvzC/UoBMQLnAPD/PADrATABFv/1/B39ev/0AbwDuQKcAMT+Of9d/hn9cf2p/qoC4gRvAxn/mfs6+y3/gQLyAY7/ifvA+yv/SgMYBEYAxPxQ/Pf97/6T/7j+VP8/AKD/s/94/8r/QgC2ADcABP68+3/93wF4BaIFdAJR/+/9wv0y/o7/AQEwAygEowP/ARgA8P+p/3IASP/W/Xv/0AF6A7sC5v+w/Xz9IP/jAeEBEv8X/Sj+LQEaAj//mP3//iIBkgLrAN/+f/zR/HP/yQFjAxUCGgFiACoA1f1x+9L7y/4hA/kEFQSyADD+rf3G/hX/Zv5H/lX/HQENAhYCBgDc/cP8rv3Z/vD/GQH3ASkCOwCt/pD9MP8VAlYDwAHS/tH8Xf0IAIoBnALzAI0AKgFfAS0Bg/8//9H+Vf+u/4f/1v8GAm8DMQLB/3r7D/tA/nwDfAZvBJ8AxP3X/TL/AACR/6f/XQAoAbgAuP/o/nv/BwKAAoAACP5S/Av+vAExAkEA5Py0/EsAMAOnAwAByP1p/FP9xf2l/+8AMgI2AyUBWP8o/Jv7C/7eANoBswBq/z7/5gDeAFcAw/6A/qj/KQG6AfT/Y/8CAFACqAJZAXAAfwCLAG//i/9r/9MAGwKiAlcCqP9t/pb+qQDBAeb+qfzj/eMAiASXBPYAnP0x+/j6qvyM/wQDcwTgA4oB/vzE+pD7Ov51AqMDoADY/Z/+jwK9Ba4C+vwb+qz6F/8VAzQD3QH+/yH/FgDvABsA2/2f/RkAqgHEAC7/+P06/+UBnAIIAuf+hvwN/Q7+cf+OAOMBLAJRAXv/R/3w/ML+KAHeAW8BggBWAP4AGQIvAe/9q/uU/H0BYQX8BNwBV/94/4EAegAZAFz/1v6k/yMAQQC0/wv/TgDCAUYBuf4p/Hv9bQGsA3QCBf4E+5/7SQBEBIMD4gCe/TX8p/yZ/oYAFAIeA6gCEgKEAIz+B/2//R//3v/S/yQAfgIrBEoDav+A/Bn8Sf0LAFUBgQEBAkQC0wE/AHf9A/zr+zv/agPnA1sCBf+Q/hAAaQB5ALr+rv19/oIANgL/AZoA/P/9/7T/ZP6y/bj+QwAVAtMB9v9k/7r/fwB7AegAkv7V/HL9ZQHdA7EDZgLr/9v+Wf1H/En9egCgA8wEEwMY/539JP01/3IBqQD2/6z+y//8AAIBGABH/pz+UQAMAXv/Jv+t/74AdAB9/Sz81vsF/5gCLANnAWb+sfz5/BQAJAFYAOz/y//7AG4Aev5n/Q3+8wC4A2wCOQAI/3/+zP+N/9r/4wAVAugC6QFjACf+AP1N/iYB7wEgAcL/O/+/AIcAfv+o/iL/qgAfApEBZgAKAVgB4AFeAWIAlf4j/l4AvQE0AwMDfgEyAF7/s/6Z/+YA8wHzA/gCBACh/Mf8EAAkAqcBvv4L/bD9XgArAp8DIwPL/3X9zPyQ/XX9cv1P//YBYAJCAPr9y/2F/1QA/AC3/4z+wP1A/Tn/9ADaAY4A3v63/Tn9RP7B/2IBjAEYAOn8yPsM/4sC7ANvAfv81Poe/GX/dgJ/A70BLQDZ/n/+zP/W/8z/sf+J/yAAVAGDAlACgQHp/qr7tvt9/pkCHgVYBA0BQv4q/qz/vgAqAMf/m//m/7UAfwD5/1UAjwA+AfAB/ACl/5L/8gCeAEX+B/4i/wkC9ASSBCoBjPxq+xv+kQE1A3ECrABTACABjgFUAY//tf6J/zMABgEwAXQAlAB6AWYAGf/6/fD9ff9hAM8AbwCQ/xL/Cf+V/5f/Bv/I/hf/Vv/R/gr+6v15/yYA1f+m/yL+kf5s/4n/jwCYAI0AXwCn/7b+rf5L/4IAkAGeAYMAHv+C//b/VADEALEA2AB5AcEAdv8P/yz/HwA+APv/Mf8RAJEB6QGKAcz+Ov2K/PH+0QKBBMcDl/8T/dn8wv5LALz/kv+WACECggI9AqcA9P/R/9v/hv8c/xIAEQGUARECmgLfAKD/V/94/5L/7/5u/2cARQJDAgUAOv+9/94AfgGM/5r7cPrQ/BwCGAZWBB4Bdf5j/TH/bQD8/8H95fy7/5cCYgMUAnMAk/8C/2b9GvyU/SUBPAS0A9UBvv7R+zL8Tf7cAI0Ayv5O/pMA1wITAoUAev77/Zb+yv7h/s/+DAALASEBEAIpAbf/sP6T/R7+nv1w/sEARAIdAnr/SP7C/hMAx/9h/sL96v5/Ae0BfgI3Ab79vfxz/hACeQRRA98A6v/a/v79cv1y/mkBYQSxBacD/v8K/T/8MP10/jEAvQEPA0IDRAIZAFj9IfwZ/eX/gQL1AqkBVQCzALUA2P5E/QH9rf/VAtwCmAK7AU//pP3y/Pv+oAHAAqYCegBN/p38Df1a/6MB0wEsAEf/e/4j/2D/6v10/dD+jwEPAy0C0gAoAB//I/7X/Ab9Cv+HAfgD2QMrAmEAFf9T/t7+Jv5I/Rv/lQErBSoEnwAy/ub9CgG0Acv/T/1U/SYAAAMTBDUCjP8f/kX+ZP7Z/pH+fv/CAr8ELwRsABf8efoM/Pr+VQGBARIBgwG5Aa0BDgBR/ln9Ev3t/Y3/SwH9AhEEswLO/z38h/tE/rAAgAKoAXgABQAEAM4ApgCGANn/zP50/gn+xP2N/T7+z//aAIsApv8k/yr/Zv9f/w3+o/1Q/hL/DQEiAY4AYACD/9H+iP06/mABEARJBPEBMf98/uz+IwCiAn0DmQKCAIz/2v9iAK0BpAFnArgBO/+5/dD+kgKFBDYDof4m+7v7N/5OAkwDkgDx/VX9y/9/ApcC7wAF/uT8Wf0n/rz/cQFSAwwEsALt/kH8VfzD/TYAVQJ5BBwEqgKQAPD9L/06/Q//QgFiAkUB8/91AM0AgADQ/bf7efzl/6cCEQLNADP+iPx+/UT+iP7j/uX/yQGVAbD+fPvr+sn+DQMMBD4BC/1Q+3L9YwB3Ab8AYv+nABwCoQGW/9v8iPw2/gEB5AG9AcUC5AMlBIoBgP10+lL8pAFMBuMHIARw/6r8FvyR/fn+IAL0BMkE7AKN/wn8b/ue/RoBHwMVApkADQB7AfwBBADv/mz+TP5+/3YBDQNlAykC8v/L/Tb9nv6vAFwD7wMqAoP/8fx0/CT9kv9jAroDbQJJ/oX7wPwdAHgCfwJ8/r765vrV/f8BewOVAZv9+Prg+3f9ZP5X/vT+cwAFArMBW/8K/jT+Dv+F/hL8dvu4/iUD/AQVA8D/Wf1J/Yv/NgFEAakAvv+nADEDFgQkAqT/6/7IAMsC5gJUAZD/Sf9t/2YARgMHBoQGOgLD/a37u/wJAe8D+QRHAmL+ef3T/iYCLAPCABf+if7m/yQBgQLyAdkAKv5K/G78fP2QAFMCPALc/xL8q/rb/LYBnwTKAkz/RPz5+l/7jvys/7AC0wPwAmwAZv7E/IX7Kfsc/R0AwAEhAu8BDgH7/k79G/10/Rf+iP6//iUBlwNBA8AA//tT+s39MAIUBeADCQFT//T+FwDLAIEBygEVAfQBzAKwAgYCxgGFA0UD+f8Z/V/9jQH/BCwEIQH4/vT+GQHpA7sDMgCf+wX66fwZAKoB/QEZAQYAFv9B/rr9UP6R/qH+if69/cH+lACeARYB3f5I/c38NP14/rP/egBAATkB6gBzAMr/HP9Y/jz+2/3X/cP+cwFEBBYEpgLV/yD9v/yW/Br9K/6KAPcDyATYAqL/Lv3v/NT+/v9HAJUA1QCwAi0DVgFH/3n9Cf5cAKgBQwGoAJwBvQI1AnwAc/7Q/a3/ZwIsBBMDLABq/pT+7/8WADb/p/+EAbwC1gDe/Wv9fv6VAFYBAADZ/lf9AP6v/xoAAwAB/w7/UADnAIMADQCv/xoATACr/zwAjABhARwBhf5z/nj/JQB6AND/IgB4ADsA6ABPAcQAU/+C/RH+PQCNAN3+SP3y/Av+//58AGsD1gPeATL+qvu6/QoA+gE+AswANgC+/00B7ALHAcj/K/5h/iEA6AH6AjEDpQKxADH/fv8qANoALwDt/jX/AQBdAPEAMQEGABb/+v5k/zoAZP///Tz96v1CAIIBov/C/Q//dgByACP/y/23/af9wv4DAcMCOgLI/2L+oP6K/6H/Dv8q/2b/4P8vAHIBwAI4AjYBZf9s/X39sv5jAOMA7wAfAmwBNQAIAR8B+P+b/tz8r/3v/88A4AHiAp8D6wL7/2T9vvxg/Yr/cAJ8BPwEpgIxAAH/n/6//tj+bwDvAaIB9ADHAZYCcAGm/6H9S/35/lQBmAOJAgcAXP3v/EL/sgDsAE7/Sf6f/nf/NgCZ/1H/8v7K/gb/7f7G/hP+lf3o/Qn/Xv99//P/BwDi/2T+1fy5/HH+1AD3ASkCdAHh/xr+wP0N/3UAqgGjAtkCFgPqAZr/0P5V//kA3QHvAVoCPwEkAJ3/+v9GAdIBHQJYAe//Tf/J/of/bQL5A0YDaAAr/j//+P/5/9T+sP1K/6gBbQMMAwQBO/4P/aH9mP7O/1b/HABQATQBUf/G+6j7A/7qAL8B5v/7/q3+3P6m/vn9gf3I/ocAlAFYAcX9Lfsa+//9MwK4A9sCtwC3//v+9P0Q/jv/ZQENAX0A+AClAR4CaQCb/sz97/2RAA8EywW8AzL/i/yl/XoA0wFBAd4AkgKWA5oCmAEPAB3/7f7r/n3/PADEAKABwgMcBJYBHP5P+yX8+f2F/+gA4gGHAhoBc/8w/s/8D/z4/Lf/yQGFAuEAaP7a/TD9gvyL/dL/lwLRA0kCHQCA/eP6t/nK+pz+sgLpBNUFkQWyA5n/svmF9kn4df1ZA88G8AcKBvoAnfxl+zr9kP9gAVMBowAEAXgBxwNsBUoDev4p+oD6vf4DAysFLQW7Aub/DP6P/a7+cf+N/9v/9gBsAW0Axf/h/t/9jvw3/OL9qwCRA/QDLgI9/+77afoQ+z/9JwDKArAD1AJ7AM7+hv0R/e/+JQAyAR4CSQK1AvUA+f6E/X79a/+cADgC8QJyApwB3P9i/7j/IP9u/vT+hQA4AvECKAI8Aev/Wf5h/mr/5QACAQUAzv/GAOwBMAHP/+n+Qv6r/pP/GAGvArsBPf88/kz/cABIAKgA5gFjAeP+Tf3T/fj+9v/m/w8AEAL2AqoBd/5z+6z6SPwGAJ8DywTrAfP9w/x4/iIAvv6u/Ij8S//1AtUEVAQdAV/9/flI+Zz9wwPaBkwElP+O+2j79v6xAqEF5gTsAIH9C/yI/Zj/iQCoAekBwgH+AWQBMQGr/9r8LP0p//oAKgNaBNwCRv43+sD5sfxdAaEE4wTLA1QBsP15+1f75/1VAUwC7AEzAjcDBALB/9v9wvxT/oUAbwIeA4MCFwEU/9P+Dv8F/+z+D//3/y8AJgDo/8kA/gDx/4P+7fyI/i4AXwHBAcL/FP5O/qYAvwF7AQoAmP4V/x7/AP+O/80BvwL9ACX/Of1W/qwAnwGWAK3+NP29/OT/AgNxBKcDyAAv/oX8w/zA/ccA3AKYAuABbgBF//j9Fv+1AfYC0AGn/gv9Vv72AKMB0wGwAdr/3f39/fgAugJ8ArH+IfuB/Gr/VgJjAqMB0ACk/gj9BvzN/Yf/w/8qAJEA0QBxAJIABwBh/w/+kPyG/kQCfgSyA2IA2/wr/Ef+VwBKAhIDCwI3AegAuwAn/5T8K/3P/+4BJAObAqsB1wDj/+f+Cf7p/WP+gAARA6IEmgSxAQ3+avxR/Pr+oQJIBAcEvAEY/wz+/v0q/uL+LwEJAqQBQAFcAKX/ff7G/dj9sv49/5r/egFYAocBWv6T+zr9SgEzAzYBPv7b/Gf+uQCFAQIBuv4s/ZT96f4hAGP/svwc/L3+JgKuA+IBXP94/c78yf3L/psAfwFsAckAMv+i/tP+NADSAa8BgAFIAUABugH2ADH/Mv5X/44B/QMFBa8DzwCh/SX8v/xj/loAmQMnBxAHCQST/nX64vr0/Nr/hgA1ABoB0wHqAsUBM//V/JP7uPwB/tX/vAGPA5kEMgJ1/hf8M/wX/q//LQBuAEYAcADLAdACQgH+/Uv8zPze/8UCKQIYAZf/8P2M/eP+agKtA98AUv2J+x/91/8YAT4ByQBp/4T+Kv/WAGUB5f7y/Hj9Qf+hAeQBmwJRAg//J/3X/J8AUQQ0BFEDqAAX/1X+Of5c/8cASQLsAoIDPgFp/oH+qf9OAYwA7/5J/10BrwJyART/df2E/Uz/3wDGAI0AcP8w/7YAWwBY/qT7V/wR/58BCgNxAQIAtP1+/Af9+f7WAQ4CqAHT/37+I/6P/fj+mwD+AF4AuwAaAsYCTQFl/yf/5f8QAVn/nP6IAN8BTwMqAisBFgFMADz/Kf7g/lEAQQB9/6n/cQBLAQsBxQBEAU0Al/4g/JT7Ov1bAD4D5wLFAoYCmgHG/tf7WftA/KX/OwLRA5cEMgPGAKz9Cfw6/OX90f+5ATADAQP7ADP+iv0p/k//Tf8m/z8AjwCGAEX/n/6a/rr+aP+9/6YAdADv/6n/uv+Q/3/+W/5T/+YBrwLgAfAAvv4f/v3+jQBPAfsA3QDpAEACYwJXAFf/VADFAJ7/C/+FADkCXgKxAcj/9P2O/WT+AQH7A8kDhwAw/Vv7Mf0KALABuQE7/4H9yP5UAggD7f/q/Ef7s/zc/+kCtwPXAVH+1vtx/mgBNwLZABr/EP8H/5P/lwBaAhwCQf/j/Zb+zP8fAFAAMAFRAVcARgBwAEgAFQB8/lv/2ACb/079PvxZ/0gCWgOPAmgA4/4W/d79SwA/ATYAcP2A/W3/nQDbAIwAzwFjAWT/3//mAPEAd//Z/igB4QJSAlwASP/b//X/QAAjAe0B5wBI/tP9wwCSA3QDogHz/z3/q/5+/qb/8AAwAQYAAf4Y/Rf+CwD9Av4DkAH1/oH9RP25/Xb/3ACxACAAK//6/+oAqgCuAHoAUACr/nr8cfwCALEEJgXrAZn+tfxE/O39oQAqAooCPgBk/T/9Ev6G/48BRAKHAHr9hvxs/mQBNAKe/5r9Rv27/Yr/3AE6A+IBxv33+nL8Xv+RANEA0AGvArsB9f8///kAlAGx/67/dQCqAesBZQDAAPkBzgEGAZwARgDMACgC9AFcAU0Ah//XAGYBQwCSANIAg//z/Vf9TP8WATwBgAHeAtMDs/9d+0H7Q/6fARUAIv/0AJIC2wEd/j/89/vk/HD/7AG2AzMCdv72/Ff+h/8d/zX+2P4R/y3/MgC8ANEBQAH+/lH9C/0M/rn/8gJiA+z/6fwB/VIAkAI4A/IBRP+q+3r5DP2pAgkGNwQU/1D9H/5s/0MBBgL7/xr9XvwYAPkE4ATqAdH/WgBJAG7+BP4x/zgB2QFrAe8BEAKqAesBHwLGAHf+4vtm/e8BpAIzAvsAt/8zAKn/FP/4/gcAZAFXASkCg/+1+t76mv6NA70EgwHr/hz9cvxq/Pn9TwBSAB0ABwE1AxUClf78/LT8I/63/tL+WgH2AhkC5f8y/5H/3P5//eb8Of6m/6YAUwI+A+UBSv4p+5j7Uv49AbwDmQQMAmf9iPto/UgABwJ+AYz/of6L/zYBcAROBeQAwPsN+pX9uwKWBasGYAWYAWT8EPpz/cQC1QXbBe0DpQCi/Ff7sf7FA+oE7wA8/rv/zAG8AT7/X/08/fz9ZABFA0gDoQBs/kz+If9d/k384PymAMQDrwP0AD39Q/wh/aD+DAH9ACYAw/8qAMf/X/26/F39LP/8AIQBlQFo/7j9uPy1/Nz+OwBpAaQB9f9y/aD6TvvS/6sDwgQuApn/mf7a/OP8y/+UA/cDmgAM/4X/IAHVACr/wv/z/3YAvQGzAjEEzAGP/c/8cv+BAnMCQQFdAHAAAAE9AUsCoAAP/tn8eP5yAxUFrQSLAob+7vvG+jz+LwMnBPsBPAH/ABUASgF7AlwCz/7s+cn3QPuVAtYGeQlaB04A+fi59Tz6LP//AYkBTQCaALL/iwApATb/Zvv6+Or6JgBfBE4DywBW/kj8jfpS+/f+igHkAV8ATAD1/1H/KgBZAMj/Bv54/UL/ogH5AkACYABM/9v+pf59AA0CcgKaAET/WQG/AkkCQgB9/zv/8v4DAKsBuwTjA8D/fv3W/aEA8wFtAYIBpgH4AO0AvwCr/5T+/v3S/yYBgQHcAYICGgMiAWf/BP8AAH//cf6vAI8BwQDP/on+wwB6AcH/7v3m/Zb9Qfwd/IoAigQ6Ayb/R/v6+1X9x/05APsBdAEU/gD8SP0b/5H/y/+NALr/V/47/l8ALgO1Ajz/Xf06/Wf9kf91AhIEWgPnAKb/uP/9/zQAPwHgAnkDEgGP/lj/MgGyAtICIQJJAQX/efwo/eAAcQPuA7wCQgAy/uP8Wf08ADcDOwK3/zH/Rf4s/p0AJwKZApcBV//3/qv/p/4K/Y3+WgEpAUj/of7EAMkDEAT6AQIA7P0C+/b5OP2TAZMDzwKLARcAWf48/jj+kP6x/VT7lvu//vEB3AKDATP+UPwa/dH++//V/q78Pvwi/1MCiAPZAgICdwCU/jT+Vv6HAJQBjP9E/pz/pQNmBgYGaALG/m39fv1Z/yMC9wRbAy3/1f5IAOIBlwGz//n/RgHh/0/9jf62AUMEbwOa//P92v6oAD4AaP+F/2T+2P4DAXsDLQRbAgcATP4f/rT+mv/l/+j+RP/GAGwCdQIcALn+rv4V/5r9jPvo+23+mgA3AmEE4gKS/Xz3i/Yv+zkAWQPqAo8BiP88/HH69vyAANX/av2e/Nz+mQHgAiwCu/7M+lv5vPx6AvQERQOzAZYBbAGAAEIAkQB0/43+wv6XAYYEFwVRBPoCrABN/Yn9UwE9BDYEcwHN/zUBagKTAND+1v+FARcCaAJfAkEAMf4//ez9IACIADgBbwP+A20CEv4h+yX8xP7AAvIDYwKN/5/9zf7m/w8Ar/6U/sr/VQDE/6n+tv9XAEYAAQCm/xH/XvyP+6f+ywE9AqX/+vz//WYAGwAS/tz89/wR/58BHAMAAqf9u/vZ/Hr/TgHoAMz/wv7//tgAfgO8ASv/sf8uAEoAy/7i/ooAPAKGAnUB5QGFAFP9wfvi/lkDEwUqBMUB6//G/fv87/6WAaYCWgJkAUIA/v/9/lUAbAEjAPj/m/6Z/0IBcgEaAlUBfv9s/Bv8hf6/AMEBfQGyAMX/GgDM/+oAYgE//wT9qPxQ/m//IAG1AmsEMwMg/2r8q/un/PP93QDwAy8E/v+++6H7xv04AMEA5QDc/3L+Y/5/AOwCDQDd+4b8bv98AXwBVQCgAAIBdABLAGEAp/6c/KD9rQDaAvIChwORA90Bw/2Y+vD8jgB3AjQCWAEDAWQBsAB8AGYBQv+X/Ij8uwDlAlMBJAHIAT0DBwG7/Sr9pv7/AIYBOwGhAPEA1AD1ANoBIgFEAKT/7f+WALAAxQCfABQBqwLNAlIBxf87/oD+y/70/ij/iv9GAJP/uP4b/mn/UgERAY7+Pvx3/HH9mP8KAVUA0Pzm+c37Nv+/ArgCeAGI/9D82PuU/B8A9gAx/0f/7P9K/37+Sv+6AVcDYwBK/Yf9vP8nAagC4QSlA9oA4f0R/bn/7QA+ANgAWwRgBLoBPwFJAHIAuAADAeUBZQJtAaT/pwF+AxoDswBo/jT9vPyq/vIBCQZxBW8Bav1S+/D7qv23AWYDTQHw+zH55Pz5Az0HCQQm/1X5rPcC+uz/1gQLBGAASP32/lIBlALaABv/Hv2m+lb8pP+GA5ADzQKJAbj+3/u3+WD8LACUAa/+pP14/28A/wAVAG0ARP+c/X/9Wv9rARIBAgEaAZkALv6r/f7/XwIABBUDjgLoAO/+W//+AD0C8P+A/dn+CAPSBL4DywHMAJIAuf0Y/jAAKQHvAMD/qwHZAVYAZf1A/bv/tv/YAGQA0f/Y/ln+nABbAYQAMP4t/goA5gBdAAEA8ADl/wv+6/2NACwCYgDf/q4BTwTBAuv/Z/wF/AL9zv0sADgBagEiAMEA6gKhATj+C/wU+yv7+PzeAGAEhwMvATn+1vwX/aP7D/0VAVMD4wGC/7//YQGLAZf/Fv7h/cz+Yf7E/tAB/AO3A2kBWACi/9X99Pwx/n4BhQRyBfUD0AAz/XD7Qv12AXwDzQGV/3D+wP+9AcMBIgExACb/PwDuAWkB6P71/EX++f97AGL/7//mAscD1ALXAD4Awv4g/WX91v47AnABAQBiAgIEhQMJAcD+oP1I/Mf79/2+Af0CaQJzAtQB9/+W/BT6pvr+/cEA+gF1AgwBsf/j/i3/0/1y/Gz9Xf+VAvABsf8G/tT95v7l/tX/y/+fAIUCMQQHBLj/Yfv4+V38Tf9hAXsC8AJzA34CuAGYAPb9d/rh+fP9iAOYBpoFYAQ9A7wAI/2Y+l38Fv/tAUoEjAVnBOD/lvyu/agB2QJcARYApP/b/2H/pf82/1j9tfyk/iMBkAGfAdIC7gNwAVT7wvaf+HD95QEhBc0GjgW6/2L7I/yf//z/nP0l/s3/RwGrAOkBbARpAtn+HvwW/bv+MP4L/70AnQKsAWb+fv5LAIX/B/76/bv+w/7u/pUBcAMdAXH93v3PAUACuP7K+rr7p/8rAiAEHgSsAg//bvza/hcBPQGi/6D+QQC2AO8ARAKxAk4BY/6h/usBkAOoAiAA4f6q/g/+t/2Z/2kChwNsA/kCYQCQ/Db7uv39AhQFXwMf/9X7SPwC/kYBUwI5AR8Al/5w/44AzgA4AGH+C/41/g3+Xf/dAaoDBAL3/v77+PoZ/eYAVARDAjr+ZvuA+53/3QNHBWQD7f9n++r5CPyc/1kCiwLTADr/vf8CAUECvwEKAPL9ev1FAKsCPQTHA5sBWv8J/pL/GgLGApQAZP+DAMYAjP9G/9oA/gLoAQX/+vxW/I39Y/65AWwFAQPx+/n3s/yaA1gE+v9z/LX8OP+sATkDvgJl/ij5MvqUAMoEKAWjAUz+C/0v/aj9HP5q/9H/gQFwArAC4QGS//H/qP4c/KH6wPx8AUsELwQBAkEBSgDe/jf90fw4/S79v//2AsQE6AKc/xn+5P1P/ysB+AOmBUIDBf5O+zn9pABBA8kE3gRnAXr/SwAcAicEHwIf/6L9LP/IAQUD3gIoAboBGgEF/7D8O/qj+17/mgRQB5kEq/5O+b35af7jAfEAhf3V+gr7wP/pBEEFfQBG+rX3HPq1/qECDwNyAGv+OP6T/7wAy/7u+zf8sP9EAnoCNgIkAhQBWv7h/ZT+Nf5n/Vb+swPNBmkFVACs/RD/Y/9K/9r+JwD7/+r/XgHFA6AEowEq/wf+//8jANUAsAIYAvgAav8/AJEBIAJIAXUApf4G/Mv8KQGzBmkGkAFd/Pn5FPxu/6UDCQbuAyP/bPxD/e/95/1i/lj/xACLAIMA2gFJAgsA7vsQ+6v8iv4LALEB8wJOAtj/bf2O/AD8Rfx9/EL/EQIZAvgAWP8wAHEAV/5++6P69/uP/wkEIgaYBcYB5/0B/LX8pP7rAI0DBASXAhQBSwDO/0gBGwFi/1z/jv8UAZsDbgXiBJ8AwPuj+ycATQTmA2oBQ/5w/H/+TwGoBGsG3wKi/dz7qfyJ/osAKwLSAVAAnP+//hD/mf6n/rX//ADyASEAdf/a/08AY/82/tj+yv/C/87/7gFsAl4A/Px9/NP+2f9y/2b+yv/V/zf/lv/i/zMBZABv/dj7APzZ/FX/swLoA/0A+/yP/PT+cwD//tP9L//+AOIB8wGAAWn/bfxB/BMA9ANAAn79PvvS/SEC8wOMA9wChQK7/1P84vtX/owCEgQjA70BnADr/xMA7wF/AigCmAHaAPwBUgK3ADb/Sf7D/nAAhgOCBV4EowD9/CH8YPz0/poBmQNnA/D/7/2v/Un/I/+F/7EA2AAdAT7/dv+R/+7+6v0I/jT/Sf/KAKMAuwCl/i794f4aAL0BnAD9/43+ZP11/BL9zf8gAHgB+ADvAVcB6PzX+jP8rgB8AQsALf/p/6T/fP4TAIABDgAB+/X5lv5DBNAFUQPfAC/+hfzB+1795v/+ACkBzQEJA04C2QDl/2n/A/4//RT/jwH8AvsCjALXAQ8CcQGWAKABPwJOAQr/uf76/7MA7wFKA9AElQI0/zf/lgD/AukBl/4i/Yz9Gv+3AHUDdAUuBH0AFf37+uD6OvxB/h0B+gGDAAz/z/+3AWIB4/5L/Nn6xPq1+zP+XwPPBH0AA/1e/JP9of9rANcAv/9W/D/7d/0fAdcB1gDkADYAqf6u+8z7bQDNA/4CwQCY/v78Ff5CAWkFKgZQA5P/Wv0n/sv9OP6WASwF+AU8BGgC7gAaADn/p/7V/Yj9YgCiBOgG2QQGAU/+NP7Z/xoBHALbAgMCZf9J/sX/nwIfA10BPACL/7L+Af08/gYB0wC3/f/7Nv5bALgAo/7S/T7+cf7R/i7+L//W/q/8vvvG+6r85v6PAbQDSQTuADf8x/mg+lD8Cv5vAG4BAgEFACsBwAPhAl//U/yt/Hv/vgHIA+oDJwNRAQr+/f1Q/1EBFAPaA3cDtACz/uH+DAJzA2oBtP/n/5EAmf8tAIMBSgEZ/w7/+QEIAxYClv5G/WP/3wD+AN8AkQEeAa7/GP+h//7/6f4t/eH+WAMQBPsBzP9T/lj8ePsT/kEBhgL2AUsB0v/5/PX5VPlM/qsDnQTGAVb+bfzA+xT9KQABAnYAtv1t/CD+I/+Y/4kAgwFfAi4Aof2D/ScAkgIlArgApP6G/BL/FgUQCCEFcP1T+TL7lv97Ay8FegWNA7L/J/wL/ez/BgJ/AjoC4ALOACL+of0+/3kB1gGyAb0C2wLeAcj/YP31/Tf/PQEWA4IEEQRnAR7/6fzM/Tr+SP78/38BywIrAZT/Tf+C/+L+3vwI/Dz9Nv+YAfECOAH2/cP7N/ul/L//YQHAAFD/S/7E/oH+Ev5N/rT+iP/E/4b/xADHAuMCUACS+w367fvQ/wYE+QRvA2P/IP14/Wb/5AHiAQQBUACdACQBtAA0/7X+nP9EAUEDMwOnAmgAiP4W/Tb8vf36/6kEyQYxBsQDNv4q+mz57PtO/2QC3QKrAgQDpgJaAggB+P8I/gv9+Pzt/l0BiAE+AlACuAGE/z7+Fv8M/5b+Rv3N/QcALAGGAd4AVwAN/139Av0F/jQA5AFkAqEANf7V/Qn+SP/JAF0CfgMFAhz/xf3s/hEA6f+AAOsBewJIAfL+pf5X/9YAwQG0AasCEAB2/fH8Hf6jAL0B+gGaAlMDmQFsAB//tf0i/Fz65fzhAPMD6AMmAy4C8/6y+zf5rfqU/aYB7gTnA9cApfwj+xb9GQAYArAByP89/gP/IwD5ACUBkACHAEb/e/4kAI0BxAJyAogAbP8I/3AAuQEJAiUC3P9y/kH/QgDbAI4BMQLZAt8CTAAC/q391v0v/lT/GwADAN7/GwDRAXkCjQB+/VP8Y/wn/MX+9gHzAgYDgwJgAYf/8vsR+gL8Tv+tAj0DZQITAmIBwQDS/2r+7Pwm/NP8K//HAagCEgK7APL/PQAfAPP+AP71/cn+hv+w/3oBkQOpAvz/9vxk+6X8Kf4+AH4BtQF1AlcC9QEjAHP9Nfsz+5T+zgFEBLwEBAJmAAkAGP/7/vf+q/+IAVMDHwThAe3+Dv6B/vL/UgHwAjwDKAD2/K37F/3j/8oCsAPiAMP90vsg/D/+dACXAVkA/P7S/sX/CQHn/+r+V/8J//L/4wDeAYQCzP/0/EL9PABKAwMDIQF6AL7/bv/n/2wA/QBdAAEAggCQAWcBRgEHAZv/QgC2AHAB8QDk/qr9+f1hAHUBwwKoAmn/y/24/ar+t/+h/6H/Rf/6/tH+wv5u/wsALQAAAMn/eP+Q/mn+Of8XABUBKQEnAVwBqf9G/fD8i/41Al8EPQOYAE/90/zf/YL/MAHUArkDIAEa/gf9HP4y/+z+/P52/uj+aQBXAU4CAAJ1//j8V/1M/4H/mv/l/9j/OwBm/6n/hgFPAnACYwG//tT8y/yi/VIAtQIhBLIEIwPNAOv+H/5n/Z/9zf76ABgD3QNGBY0FmgLH/ff6Jvvf+zD+awGqA8EECAIc/lP9of07/pX/PwFtANb+n/0n/uMAywEYAvgAj/80/o3+fwEWBKoEYAD9/O38r/8OA8MDiQPoANr9Cfy9/ckC1wSKA7EA+v6s/sn+vwCvAREBj/7y+tv75/+XA/oDCwEs/ev7W/28/kYAbP5u/SP9ev2OAGAAcf/3/f78Tv8sAg8E/AKs/xL9IPy7/M7+wwATBLwF6QSFAt3+/vzr+7r+/wHoAo8CDgFtAZUBawF/AFL/UQBmAAgAvv9//oD+XwCbAmMCMgAV/1X/9//S/gj9dv33/ogASwH6AdQDugI//079Uv3H/jv/PgCSAnEDnwFu/pf+GAFQAWj/lv7e/x0BUgAI/uj9+P/ZAbYCLgFK/hf7Yvo2/gMCxgITAOf94P1v/pj+f/3X/Z7+rwDZAcUAnf+s/SD+2//mAa0Bxf90/4//7/8WAAAAXgH6AvoCwgLIAGf++/xK/n8BqANTBboEhgOdAQMB0P8c/bz8uv0cAJwCkAXtBfoClf7l+sz57fpu/jECXATeAqcAb/38+7H8Hv0e/xQAygGZAoQB/v6r/Kr89v0nAMgB8wJxAd7/dP4t/sH/cgBMAWYAPwD6/nX+sgCUAhYDewGt/lf8oP33AAUEnASOAbr9Wfoo+2n/DwRvBW8C4f+7/Eb7VPt1/TABCgJdAq4AHP9b/8X/rQD5/8H+RP0m/ST/VQJCBG4DCQGu/ln9Sf0LAGkC4QJgADj+2v4UAO4AGP9o/pT/mAAzAa4AQgAjAED/rf65/wABhgFK/zT+jf5W/+b/j/9MATMCaQGM/mP91f5/ANcB1gAGALz/yf8yAbEC0QJTAM/8jvta/dMBAAUdBYwD1wDP/ir9JP0O/qj/PgLTA6cCVf/g/aT99v6aAKMBVAKnALz/yv8vAKb/D/6V/roAzQC2/x//7v4lAIwAgwCy/53/nf8d/zgAmv9i/tX99/0DACoBAgEaAQgBLv++/Bb94P73AMkBSQC5/r/9L/74/ngB/wNLA1sBuP7O/DH7+/vJ/yMDIAWzA+cB4gCO/tH8fftv/Mv/JQN9BbYEgQLu/yP95vzc/bX+CQD5AYkDNAKM/9P8o/tb/sUBqQPPAhoAW/5O/Z/+nQACArMCmQE1AAL+Pv3+/fb+ZAGAA2gEsgMJAYj+c/3/+9b7cv7qAdsEyATGAvAAP/+8/d77l/sF/bD/DwPIBfUFpAIZ/vD6/fsl/+cBCQKQACoAQ/5L/JT8MP/NAugCQwHNAFsA7P7D/fv9Pf/0/oT/DAG1AdICMwJnAAj/tf2j/AH9dgBBA/wCvwAo/hP9Jf6qAHsCyAG2//f9yf1c/kH/QgB/ALAA6f/+/gn+6f0c/3//9f/A/4L/GwDzAPsAAABa/0P/1/+pAAkBsQChAJYBtgFxAJH/FQDgAukE4wPEAcP+j/13/nz/BQGwAToC0AOmA4ICuP+b/Hv9sP4qAEkBLgGZAUgAJwAyAJb/Tv+m/nr+IP57/Zz9lwAUBN0DvQDH/GP7lP0iAFUBJQFF/9T9wf6mAOQBBwL9AIH/cv6//pH/lP+8/yQAHQBy/+b9lv3I/30CAwMPAdX9F/wz/Cf9uf/fAsEDXwHN/mH9GP3L/FX86f3DAFoDbAN4AsQAhv1W+6r79P6bAU0C7QGzAaoCgAEg/379NP/eAA8BJwIGAtsCdAP+AdAAgv/i/j8A3gJUBKID/ACi/uT9zv5nACACKgTKA50BSf8x/WD9Cv+XACABLwCB/7//zQC6AYkBOf/t/Cf8rvxV/vT/QgGnAHQAXQBv/x4AF/+u/UL8r/tj/bL/tAIeA4EBsv6k/G78Hfwq/gcAhwDbAB0ATwDlADgA4P3W+9r7vP3WAOgCtwMjAxQAQPyH+vL7L/86A48FxQSvAQz+1/zQ/XcA+AIdA4MCqABh/9z/5ACYAmMDqAKPACj/4/4a/0gAhgHOAfMA+wAnASUBWQDq/jL/Nf9v/zAA9AG8A/MDGgK8/ez5T/qV/ggD5QRcApr/Yv4v/Sf9/v1lAFYC4gHL/+X+CP4w/QX+RgDAA4cDnwE4/6T94v1H/Df9MwDUAkwEvgJD/8/8D/x3/Mz9Av5l/iUAMgFBAbkAkf4L/WT8u/xP/7z/7v9fABUAEwGUACz/Lv4v/10CxwOLAmP/x/3u/ksBowMoBP4CQgHfABABuAE+Af//fwD6ACgCUQJMAoMDegOEAkv/Dv36/BP/EALQAtgCkwHC/6f+oP7A/tf9ef4QAA8BRwBr/cT8H/9hAUEBEv8r/hr/tf+v/uz8yvvA/NT/9QLVBFIDcQAO/qL8Sf1O/cL9IgBsA7QEWAGO/d77dv35/1gBuQC4/1kAtgBeASoAaP7//Zr+PQDo/6P/tf+gAEwBLgCQ/ub8OP5xAR4E9QIB//T7hvwBAHQCtQMNAgAAbP9S/zz/YP5X/44BjwMqBA8CSf+i/vj+5P/GAPwAOQGQAf0CDwP0AGX+Vv1w/5AB+gEqAd0AkAGeAV4Aa/1V/Iz9iv8DA8wDQgGR/o39QP8vAN3/Gf+N/o7/Wv9W//j/CwBSAFUAVwBX/2P+/f7+AZ8DQwH//e/7Kv4cAWYBQwC0/ob+Gf9sAKMBHAJoAM/9qP2u/fz9Tv7+/sUAMgGH/9H9Gf5l/hH/CQD2/9P/I/9O/wMAOgCLAMwAtwCS/+/+Nv8VAJQBfwKpApIBwf+U/oH/rwFOAykC7/4y/dD9nADhA0wGEwWiALL8rvsF/VT/5QDeAOwBoQJmAXr/I/63/goAZAA7/o787/wu/voAzgKdAYH/cP3b/Oj+xP+HAEoBZgHHAdr/7/2L/WH+FAKOBFIErwGd/Tb9jv87AisDiwG8/6L++/+jAWQBeQDy/kn+6P7X/wMAlP+GALgBBgEa/1L8K/xa/vwB1QPLAUn/DP0L/UT+nP9XASkCPwKGAQEAD/6S/fj9hgDMAi8C0v/7/eD+0gAvA7gDkQJ6/w/9IP15/rYA3QCfANv/UACdALYAXQG8/+z+V/68/mn/9f/BAB0BiQDH/u/91f2x/wwBWQFyAfL/hP5v/Sb+lv+/AEABcAHhARUBzP/7/1cADwAd/zT+/P5nAMQBNwLuASABQf8c/wAAbgCh/9b+SP9tAO0BoAGXAOf/WP8//gH9O/66/zgBEAKXAX0AB//s/dL9iv+QAL4AGADK//sAFAGEAaUA8f5//rr/AAHN//r+Yv60/6QCWgMOAkj/Hv2//Y8ABwGJ/5v9Wv2sAKMDugPYAEz9F/yU/igBpwHUAIT/1P84ABoA3f5a/d79JgATAzUE4QF+/un8g/3J/of/jP81AHkCywMfArD+jvu1/HAAYwQfBZ4CTv9q/K/9gf9TAf8Alf8HAbQCjAPqACX+Nf1B/hoAJwCy/5z/6AB0AZoBWwBD/cf7c/yGAM8DJAOpAE3+M/77/nX+Zf7//vz/jwAFAKb+HP0Y/Tz+GAGvApYBDf/b/Hf9HP+4ACYAUv7b/REAEgIaAkMBXf9Y/4v/1/7s/iH/qgDXAl8DpQL6/738J/23/mkBXwO3AosBzv8hAC8BYwH5ABMBlgHYAOT//P/JAVAD4wIaAbv+L/6NAJsCCQPfARD/lv0h/gAAzQEaAowBYgAqAFj/q/1S/Bn8Xv5rAYMCzwHz/5f+2/3U/AP9hf2U/gAAJwGEAuIBuP/l/Fj8o/4fAC4BlwDn/xAA1v8B/wz+tv75/2wCCQMmAfz+qfzy/Hr+AAHTAtoCuQHP/+n+Hf6L/XH9c/+SAVsD7AJWAJ7+KP0B/yIArwBVAA0A/QHBAl0C9/9R/lj9cP7TAEACmwJfAAMA4ADbARABNP+R/jT/XwHmAWMBrv+H/7IAtwGrAVX/cv3e/fQB5gVEBr0BTP0F/BT9z/9ZAGwAjgCsAV4DOAMlAJX7Wfo//XMBnAKHAcv/5v6e//v/DP+j/Nv8IP+GAWICMQAk/sj9FADLAYIALv6p/L39HwDBAWoBtP+J/vf+9gC2Ad//Yv4x/jH/JQEkAWoA1gAuARoCwgBy/RH8r/wiABIEuQS6Aon/vvzM/En+Df9z/8b/0f+2/w0Anf+d/zEAOgD4/+X+dv5m/kn/3QCPAYkAkP5p/gUB/gM6BEECA/9C/Sb+PABHAjUD8gLOAjUEUgNMACX90fqw/JMBKwZqBgMDQ/+a/Vv+rf6Q/b38hv6eAWQDYgMkAbH+8P15/T79xPz2/Mf+dgGzA8QCIv+O+1b75v1SAA0BVv91/rH/egGgAV8AN/7V/Cr+ZAAeAkYBKP/h/cz+wQCeAUsAOf4Q/s//pwL+AXP/1P1Q/bX/kAF5AdP/ov5n/60B3QLOAYP/qv0L/pP/0QHBAbD/c/55/3IBmQGjAEv/gf8sAJIA9v+s/lz/2gB/A+gEYQMhAMv8Dv03AFgD/gOiAbz/SP9bAAQCHwEKAD8AkQFGAmQAO/5r/ZT/ZQLLAqsAb/yt+hT9GQHVAg8BQ/4W/an+pQCqAKr+V/2T/ssA8AH8AGv+Wfxr/YH/YwCr/0v+DwBtAucDAAPn/4v97vs5/aP/uAEJAmoAjQBfABUAAAAQ/z//igBNAfoANP+R/u3/mAEWA6IC0v+v/Jv8ov7FAA8C8QDT/23/DAHaAVcAHv6e/QUAGwJrAvD/8f5d/+v/ggAMAOb/j//c/60AswECAU7/uP7V/7wB9wCz/+X+Zv+FAP3/1f30/Nj+FQHBA2MDpABs/Qz8rv0SADgCgAHZAB4BnwEEAfP+I/3k+zP+AQIjBFYD9gAgACwAyP8G/iz8efvL/dQCBwZvBSQBzvtO+XX61v1IAQwD+QNbBEsDNQC0+4L5e/pu/g4D+gNqArf/jP4w/zT/kP4d/XX90/+8AsoDHwJD/+L8WP3M/hsAFgBuAG0BKAKtAqUA8P7+/eP+ZwEmA8EC/v/n/an9ogA/A0ICPABS/oD+qP85AIoAJgD6/w8BkwGMAHD/Uv6m/rUApwH4AA7/lf2h/lUAyAG5Aar/AP69/Xn/8wG6AiACjwA7/zz/hf4E/i/+CwAgApQC3wKYAbUAfv8C/iv9Sf0LAMUCMAXCBD4BVf2b+pT7vv7dARYDDwKBADEAOgDB/zf+6Pym/R3/zgHVA/QDUwKA/7n9Ff1v/Tj+7/9AAp8EvgX7Axv/9fq2+kD9qQDpAiMDGQKMAXQA7v59/iL+R/4w/yMAZgA/AA4AsQASAqsBr/4f+9f6pP1EAcACIAAn/Vb86f36ACoDoAL1/8z8i/to/Gf+JgCyANsBqQNSBFQCtv7N/DT9jP/LASoC9gGVAf8B+AHwAC3/LP0C/lYA8AL0A0ACvADN/+r/AAD+/tT+/v/dAWADgQK4/5z9I/0i/5sB3gG3ABH/Bv7p/lgARwBv/+X+Qf96AC0BOf8h/IP7dv0vAIcC5wLTAJT+Dv1E/Sj+zf7m/9oAxwIaAxICAwCi/V/9vf34/lD/KgClATMDFQOdAPr9ofuM/HT/JgK+AvwAJP/L/RT+0P4d/2z+J/4FAGQCTAPwAQv/2vyr/Pf9AwCWAFQAMQBfABcBYgHmABMAWP9m/6n/uv///9r/UgGDA+oDFQNDAZT/cv98AK4AjADx/yoAgwKeBAMEgQEO/2D+jv9uAKIAXf9o/m//WAHQAh0Bqf3x+jb8U/9lAaEBOv+4/Rf+eP8AANr+If12/F/+2ABUAckAWACQAK4BfwHV/hv8k/wLAP8DYgX5AnL/sP5hAGMB1ADx/qX+DgBKA6sE9gFs/4L8Z/1/AH0CSwKM/6H+Lv8RAbkBTwCG/qj9+v5lAGQAPgAgAHT/j////nv/hAA1AY8CEAI5AIT9+/sh/hcCtgSXBPkBy/8d/zb/S/8k/4b/DADEAW8CKwGk/j/97f0f/0wAc/8d/kH9t/0aAGEBiQDX/Zj7cvyo/4YBywCx/fr7wvxV/4wBCgLvAbD/9f6n/ub8a/zm/M7/gwNbBeIDdwDb/fr8kv5JAAMAp/8WAZ0DJgW4A4v/Y/wX/YgA0QMoBGoCSgCp/wUBQwLTAc/+GP29/twB4QMxAtP/2f7d/+YASgAW/0H+z/7V/ykBOQHD/5b+7v64ADsBVv/y/HX8F/9KArUCCAEb/7T+iQBeAYX/cvzB+jf97gHfBJMEqQAB/cn7QP3N//0AYAFQAHgALAFeAAH/U/2O/VP/rQCMAJT/qf9PAf4B4gAy/in7mPsK/3kDrQTlAdv9vvqg/LwAwQImAjgA9P6YAJICyAEQ/yX8wPz5/8sDggVxBLUByf4Y/4//7/8WAG3/1AB4AmwCugDv/iT/9gASAhgB8P7+/Yf+QADuAeoBGgC1/bn9LP/qABkBvP+1/pn+4f8wAN7/Uf9O/zoA1QD1AKD/w/7u/hIAtgFPAdcAiADJ/4sA8QAeAUEA6f5E/7QAXgKxAQAA6/5r/woBtAEoAbb/+f5h/p/+G/8O/sb8DP7fAKgDwASYAQz+Vvwe/VP+uf5V/0AAbwLoAwIDHgDL/YD9Nv+FAYYCYwFTAEMAkgDUAZwAIP8A/tL+WgEGAjUC/P8N/4T+Bf/u/zn/vP9//5j/dwAWADX/kv5F/vf+vP7D/l3/ov/aAMIAwP/t/T/9//3m/5UCTAIfAHD9yPyj/zwDRAQ3ArP/Gv5m/qYAwgI5AhIBJACMABkC+ACQ/yT/0P8CAnwCyQHu/zf+tP6I/0UA7v85//H+3v8wAYYANP/q/S3+d/9cAKYAcv+w/oX/ngBKAXcAN/6y/Zb/VALlA/wBuf4+/RD+0AB1AvsB3//h/Sj/rwD8AJL/yP1u/j4AgAK6Ac3+J/xA/CP/LQGGAZP/2/3p/ff+4/9D/1P+AP52/o4AQAKGATgAY/+C/+T/sv/S/ov+MQA+AuYDXANpAaH/Z/4T/0IAtgDvAK4AVQD9ABYBlgAKAGP/b/9DAAEBqgAZ/zH+HP4O/6v/qf9yAEkAcgBcAO3+of5k/v7+oADvAHcATQA+AH4BpQIiArT/UP2c/KD9mwATAq4CmAJMAYoAuP8z/0b+CP4y/nz/zgDwAOYA8P9y/wz/lv5b/vT9kf7I/x4B1gEfAQn/Iv1B/cz+igAXAhwBrP/f/nT/awAfACsANP/d/+cBaANAA1EABv5W/ocAKgMQBEIBkf77/T3/aAJiA1sBFf93/sb/nQFyAd//mv5e/lX/eADPAKcAqwD5ANsAZf9//Zr7rPxEAL0CpgOlAc/+4/07/1AAnP92/uX9zv7rAdoD0QLl/638dPzv/TQAwAHoAF8AcQA4AY8B5gCT/2/+mv8wAfcBOQEfAD4ARADvAGcB6f+0/s/+6P9KAbABWgDr/vz+U/8/ANf/XP7Q/T3+hQBdAmcB1P5m/UP+if/F/8/+4/1g/98BvgOYA9EBF/8I/cH9+/55AE8ArgDrAVYCZALp/4/+DP65/wICjgJ+AtsA5/+i/6MATACY/73+U/1Z/sD/OgAKAJr/mf4W/2oADgGiABP/9f3Z/aD+5P6K/4//SP/I/7AAawFaACL/3v6F/zIBCwLwAaIBqwBlAD8ADgB4/0n/AQFTAgYDgwK6ALf+Gv4M/4YAkwEOAUYA7/+FAOwAhwAP/839b/3f/uMASgHoAT0AC/8D/9j+bv+I/j3+Xf7W/70BHwI0AfX+Xv5V/67/T/9d/nT9T/6UALMCnAJNAE3+xP01/4MA6f+i/nf+/f84ApUC7gCn/Sr8NP6RAGcCNwHl/oj+UwDZATMBrf9K/az9bAC2AasBnwA1/6f/pwC+AD0AMP/p/iEADAKWAgQCVAAL/3L/IABmAVgBuQCnAD0AsgBGAIH/Bv9Z/gkALgFQAUYBzv+e/mL+x/+JADcABv9s/vT/mwD+AMz/9v00/UD+4/8hAaIBPAB5/6b/gQCfAAAAEP9P/oD/dgDNAEkAcf+N/6UAmQEVAtAA3P6B/vD+zACUAaIBmwGlAE4A9v9BADQAFwDc/wcAGgGsAEEANAAYAMsA2wDn/8X+JP5e/8kAbQHcAEH/Lf4t/9kAnADZ/4L+gP21/kAAkgH8AZgAw/+X/0//l/+E/nL+d/8CAZ0CdQEGAJX+f/44/3MAXAAQ/gH++P5mASUDiQJ1AEb9yftj/Pb+UgETArwAhP93/zX/b//4/gT+wP1V/mEAQQK+AcIACQCs/xcAt//D/sn+9v+xAYQCPwIEAXT/7P/fAEcBdAAl/5n/VAGYAy8D6QCT/jT+WQDeAXECvgC7/vr++QAEA4ECEwDn/Zb9I/8sAb0BwQBRAHkA4wBKAeT/if1I/Kf9DwFyA4ADFwHw/tn91/4SALP/VP+9/sb/wwHvAtwBj/+g/bj8yf1M/8wAEwHwAPkA7gAZAID+fv3B/Aj+AADcAHoAvf83/6X+j/+BAOj//f6c/hj/NADQABQA6v7W/rb/DwEkAX0AUf+D/s//owA5AGT/lf/h/44BsgJPAdX/2f15/Wf/wAE0Ag4BV/8c/8sApQHCAdb///0G/sf/VAFuAYEArv65/nn/XQDfAA0Anf9n/2D/yP8t/2b+bP6Y//kBCANfAosAyf4V/qz+Xf/G/y0A/v7D/5sBcwJoAskAMv8j/4X/5//+/+r++/7B/04A0gDy/0z+Mv6g/48A9QCN/2n+3f4XAJMACACp/rL9Of+GAG4BXAAP/hP+0f8DAjMC5/9m/Rz9Hf/QAhEEfQIPAC3+5v9bAZkB7gBP/4T/RAEHAjYCxgDT/nz/BgFnAfv/Zv7r/TEAHAOWA6oBCP6d/EX9h/+QAXcAOP7o/HH+VgFyAogAav5c/p7/WAGnAKj+C/0c/bIA4APqAxEBn/2m/Xr/qgH9Aan/2/3W/Y8AwgKVAjcBCv8C////pACpANH/kQBAAZUBRwHx/mv9ov1AAMsC5wKcANT9Pv1//pYAVgGAAGb/OP5+/vD/vP8j/5b+3P6XACIC3QFY/+P9Ev2m/toAaAE3AqQBQgJTAt4AZf4L/HP88P6ZAtgFOQZcA2cAT/7Y/TH+nf71/jwAbALUA/MD4wEB/2P8S/y+/oEBpwKiAZkAZ/8p/2X/8P6h/QL9dP59AQAD/AE7AJn9fP2f/sH/zf/V/kT+mv6+AIkBdAHz/3P+m/7Q/7YAJADU/7X+4/5TAFcBqAH6AMkAIQDS/1r/wv7a/hP/MAA7ATgCSQE9/3P+Uf6V/5gA+/97/wH/fP+8ALwAKQCx/vD9kP8DAWQBngA0/27/jADPAS4CdgDc/jr/qwCMARsBBgBg/0kAPwLkAvYARP9m/gD/IgFGARcAkP6z/kEBmALzAUX/v/xe/Kj+lAHHAZD/WP3H/DT/PAIFAjAAav16/PT9uQCsAqYBQADB/cL9M//v/2AAJ/+t/9EAhgHgAScByP/1/r3/7/8WAJL/OP/O/48AiAHNALf/ef7F/uEAEwKsAXv/gP6m/qH/NgEMAWoA1f/u/uv+x//A/3D/DAAxAS8CMgLnAO7+NP6f/sH/PQGmAbABpgFCAU0BngCz/t/97P0x/28BZAOZA+QBlf+4/aj9L/4K/zr/YgD1AEYBmwGAAIv/Zv1m/en+jwCtAesA4f+L//8AmQGjAO/+s/2S/SAAjQJ9Au0AX/4c/lj/xgEmAm8AMf4a/Yf+ZQDnAZkADQDB/2AAYgF3APD+Rf0n/QD/bQFLAR0Brf9h/0oAOwAdACf+pf2G/QP/twCoAdcBngC3AAIBUQH9ABQA6v77/or/WAD/AD0BgAHJARkDEAKDAFP+yf2D/wsBgAImAaL/Dv/j/44AKwHd/+D9//3k/qABiQJlAff+zP0E/23/rv9N/uf8pf0LAEUC1AFj/zT9l/zE/pYA1QCY/7r9df6OAAgCfgFo/8v9A/9dAUACvgGJ/8P+gf8KAbQBAwG9/27/sACQAdYB+f+H/YH9NwDFAk4CDgAr/Vn86/0xALsAXv8f/iD+gQBqATQAS/4//On9VAD/Aa4Bxv8Z/2v/LwGIARUAaf43/m4AggItA7QCGQE9APwA3QBYAW8A1/4R/8H/9QEVAnYBvwDQ/0cAgwANAD/+Sv3j/U7/cgDKAJEATv83/kb+ZP6y/Wz97P0e/98A7QGNAT4AZv5p/Xv91v42AD4ANAGeAQYCWgLTAa0AU//h/r//vQHqAtoCpwH4AMgAoQCUANP/7P5G/6MAqgHrAa8Aw//M/kD/HABy/9X+H/6P/n3/BgGMAXQA7f7p/Xb+oP/rAHQAXP8N/6v/KwHhAXEBFQDG/t7+FwC7AZwB7/+E/5z/VwHPAh8CswBF/7H+Yf9cAEoAzv/o/tf/hAC0AEcAkv59/iL+bv8wAMv/0/4u/cz98v6WAAsA4v48/hP+UP8FAPL/8/5v/nX/2wBpAf4Ab//A/kj/JgEmAgUCoQG7/9v/rAAxAXcBZQEzAUEBPALyARABR/9W/uD+vwBVArwBUQBA/3j/gQAzAXYAuP5P/bL+GwEMAt0B/v/6/bn9Uf+sAEMB3v+Z/s7/7ADAAY4BiACS/3D/sf/3/53/5f4c/wAAXgFSAX0AY/8T/9X/uQDfALP/v/7p/VH+XgBgAZsAV//P/bv9Lv/Y/xYAI/8n/kv+7P9yAakAPf+7/XP9Pv/mAMwAIwAb/yL/dADzATgCEgE2AJn/nADsAHcBwgF7APYAIwEiAR8AKv+w/y8B5gLqAmoB6f74/Ur+tP/GAZMBnwCR/5T/GQGJAZYA5P7g/DH9d//fAfMCXgHN/mD94/0X/0UAXQATAP7/yABaAScAnf6U/PT8j//zATgCkgFCAHz+ov55/5UAwgBlABoA3v9k/5L+a/7e/hgAbwDbAPoApQCW/wT/tP48/nH/Vv/UAIgBvQEfAiAAzf2k/BP9lP7OAfgC0wIgAQn/pv4w/h7/Ev/C/87/fQCeAd8AagCw/wf/y/9WAA4AjABMAKwAigAmAOj/2P61/j//sgHfATgBnv9A/uH+BwDlAYcBzQBI/1f+Pf+JAAIBPADD/4X/ngCUAccBAAFe/0T+r//AAJ0BzgGW/5j/UP/h/1UAev+S/tf9RP8QARUCdgE+AGb+fP0w/vn+rf9z/4//Ef8///j/QwDb/+L/QwBH/7X/jP+j/xIB8AALAej/s/7P/p7/DgEBAkQC9gDX/3H/6f9tAH0AUgAv/3z/zf98AIkA7v9NAND//v/s/xQAtf8u/uL9uv6gABcCMAKdAA7/vP7r/zoBRwG8/+r9ZP6lAIkCjwMTAgP/+v06/gIATQFXAZMA5P8NAEIAEgGmACkAV/92/h//OP+7/xEAfACJAFwApf8h/o79dP0H/zsBgQJhAnoAqf7E/Q7+Ov9z/2n/9f+vAH8CGAPGAbT/4/0n/nP/7ADlAb4BnwFhAfgAtP8t/oX9AP6w/x0B6AFSAY7/Nf9v//r/MgAU/wj+sv0B/+0AdwFBAe//Av80/wAAbwBG/yD/FP/EAMgC0QLXAYr/6f78/+wAZAHoAF3/ov/tAGcCqALGALH/vv4jADAB0AACALb+Zf8oAFoBTgELAAj/I/4R/oP+qP7Z/t3/UQBCAKL/If+5/nf+jP6d/r3+ff/hAJEAvgCY/wb/pf+3/yEAPv+b/8IAnwEZAvkAa/9O/pD+owAaAsQB2QDA/6f/lP+7/3//hv8wAF4A8gB5ALz/gP9h/4D/rP9N/5X/qwD4ABIBNwBi/wD/RP/8/30AwQDlABUBTgHWAIcAAQHPADoBswB9/3H/VwA4AnACwAEKAAf/y/8zAZ0BOACZ/u/9fP/PAJYBDgA//vD9ef0L/4T/Zf8V/wv/4f9nAOX/+P0R/Q/9kf6SAGUB1gCr/yj/Uv9QANP/I/+D/oP+PQBYAWICSAJ4ADwAHgDh/x4APP+H/8QA6gFpAswBlQD2/s3+iv+QAHYBigGFACEAQADq/28A7P9v/1P/Y/8BAN3/rf+Y/xoAuwDOAFwA7f7p/VD+lP+qAMAAYv/J/hj/MwDSAfYAVv9Q/tn9x/9nAcgBJQEiAHb/bP8uANz/Pf8Z/6L/XAGJAvkBOAC+/jH+Q//p/yQAZf8C/+z/zABdAdAAgf+o/cD9w/4CAM8BdQFRAfz/IP9L/1r+rP5K/9z/0gAqARUB8gBCAKL/Rv/G/y0ASQAoAOr/t/97/6kAeAGeAZUAP/9j/tj+3P8+AP0AAQCT/5b/9P+uAFT/9P6C/oL+hf/5/zEAJwBEADcArP+o/vv9KP4X/xABhAI8Acb/z/4K/5cARQGXAAr/XP5B/1cBBwO6AkEAxP5c/uf/AgJUAdsAeP+l/zkBNgK2AZX/p/4y/vz/3AE4An4AUv8X/47/FAGnAPT/Gf8P/9H/fwD5/+b+VP8aAJgBpQGuAEH/if4u/9j/hQD9/2r/9v8eAQ4CugEYAFr+4f0o/9QAmwGVAbMA2P9N/13/DwBEADYArQAvAKb/AACS/zn/YP+k/6P/kP/d/y0ANwBRAEEAtP/m/lL+yv4sADgBIQFnAFL/Bf+S/84AzQGWANL+wP2M/mkAIgInAqcAc//E/nD/w/+Y/2D++P2E/zEBLwINAiQAvf2a/Tb+7f9xAG0AogAmAH0BawEkAY7/xf0z/g7/rwEEA1wCdgCl/oz+DP8qAH4AHADN/w4AVwFMAWUA5P9U/m/+Y//e/5wADwCgABQBlQAuACT/Yf9KAIcBGQKKAID/qf5//xsBdwGwAVoAR/9G/8b/UgDn/7T/1f+m/8r/sQDrANAAOQAs/xz+Vf5z/30A5gBu/2b/u/8BAdEBKwB7/vr8/v3l/9wB7gEwAO7+2f5wAMkA/f+N/i/+wP6BANkBDgEhAOL+m/8vAMr/m/6U/er+NADSAUABkv8B/7L+BgDQAHAAWf9S/t3+PACOAWYBMQC3/vX9AP8zAGMB5wAUAEcAzP97APcAjwAE/+v+IgBCAXUCCwHW/9z+cf80AVcCUQJIAEv/7f5JAHQBBwHUAKr/uv/uAEEBOADP/r/9L/7V/5cBfwGPAOH/Cf+6/2z/4/49/ib+8v9lATQCMwG//9z+y/5j//D/cv/6/i3/sv8xAS0BTQBP/5b/9f+KACcBfv9L/ov9B/9OATQCtAGm/7X+Yv5G/+v/JgD6//v/EAETAfAAGwCT/pD+Wf/W/7oA8gDn/6L/7P+VAJ0ARwBd/0P+CP+oADACRAKIADL+1P0v/zYB/wJoAen//v6d/lEAsABpANX/pv8VAbwBwACH/1P+gf4pADUBnwGWANT/3f+//7n/sv6p/kj/pADQAYkB8wCw/+L+4v6+/qD+9/5QAGgBtgE8AVf/wP7Z/jf/qP+C/2QAmgB/AesAO/+7/kL+CABAARQBAQCR/v3+VgAiAeoAhP+s/l3/kABBAisB3v+Y/tz9t//rAGYCAQJ3ADn/g/5g/+7/hAAzAOD/VAAfAJoA/QCm/27/5P4J/xUAEQAOANL+af8JAdgBxgH+//r9uP0+/9QAvwFmAIn/xf+tAMUBbQEkAFH+t/6eAMsBvAF4AeT/1/8FAYkAuADv/6n/AwBxAJIA0f8h/8z+ZP+C/0AA6v9b/0T/5/75/gf/uP/G/7//zP+x/3f/2f7t/lr/sv+u/ywAWwCAALEARQCA/7z+H/8DADwB3AF/AY8AhP8b/zX/gv8/ACMB2gHIAW0ADf9f/lP+4P9nAGUAUQB4/xIA7ACZAPn+lv3n/Lj90v/uAGYBMQBw//j+Pv9SAB0AvgB0ALoA8gBCACIArv91ABcBmQElAX0AeADhAEkBmwC0ADUATwDTAGMBnwFfAHD/d/4d/o3+jv9uAOwACAEvAKb///6w/kv+1f0J/uz+kQD4Ac4BAwDI/Wn8iv2//wQBGwEZAN7/dwCsASQCkwCF/pX9s/6bAEoCkQIPAWwA1/9fALsA8v8rAH7/O/91AJUAQQB+ABwAOv/f/nH+df5D/+n/pQBgADn/qv+7/xEAjwCE/y7/jP75/j8AEAFdAWMBrwBV/63/GQAUAKMAuwAoAI8AzwAoAQMCaAFHASoADv+X/vD+JgD8AE4CbQGlAKn/Jv+I/9f/cQDu/7r/Rv/H/xsAOgDB/5T+bP7f/qv/l//1//f/wv86/wT/Nf9K/wAANwBkAND/WP/T/lf/ZwALATQBrgALAD//5v9GAJUACQBQ/87/IQCeAc8BdQFPAD7/vv6z/iv/i/9aADYA9gChADf/JP7b/f7+aAB7AXsB+gDJ/0D/CgBSADAA8P+X/77/3gDaAaMBrACu//P+BADOADkBIQFoAEEAx/8IAAcAmP/h/j7/rgChAfYBNgCX/v38N/2g/8kBzwIfAqEA//7n/mf/z/8y/6L+Z/9hACwBOwFqAGf/Xv4b/tX+//9vAakBfAH7AEj/of7A/tn+b/+fACYBowApAQIBl//R/yH/3v6F/0H/CwDS/+7/qP+5/yIAif/F/87+9/4Y/3z/cgAlADAAb/8v/4//AABcAMsAfwDm/6L/WP+MAM0AJgHbAIr/Mv9I/5IAeAF5AR0BUgBB/5v+mf8/ABAB3ABm/4T/Zf+V/2IAPADD/8z+Lf+N/4AARAGXAEIAfv+F/4r/av89//T+4f+eAN4BbwGl/5D+af45/3MATQHCAK7/Pf+s/6sA5gDd/wf/pP78/5IBIQI2AYr/Mv9t/0EAtQCSAOP/MgCpAOQAcQGVAAoAUP9O/0v/8P/iAEkB+QGVAK7/cv5j/n7/TwDlAMr/Cv+m/mr/ZAAuAfL/KP7L/Uv+IgDUADwAQf95/5P/8v8GAM//s/9U//b/rv9jAOL/w/9PAFIARAEYAVABRADJ/+T+0f6y/9T/zQHjAZcB2gCu/9H/tf/E/+L/+v+N/1n/6P+AAOgATwELAPX+Tv8n/8D/XwC7AOAANAAqALUAfwAdAM7/xv92APMAegAGAIYAtgBdARkBKgBr/yn+mf/mAIQBlQFXAA4AsP9k/13/M/+3/zMAhQBGAEr/x/5w/lH/PQCx/2T/3f4V/2j/9P8aALr/NP9H/sH+uP/HACEBVgBFACT/T/9NAFEA1QD0/z7/5f/rAIkBuwCo/8n+h//pANEBGgEq/yz+GP7o/xMBpgCX/5f+qP9MAJkAHwBy/hn+nP7k/zQBCwGNAKj/Sv+A/xj/V//U/+//OwANAesAGADK/1T/mv+KAAMB4wBtAMX/4/98AJsAxwDo/1r/Z//P/9oA5wAEAXUA3v9TAPr/6f9H/0b/tP9VAGwBEwFKAM7/2P/g/6//vv9d/3z/YACHAU0BLwAA/1T+uv56/7oA8gAgAUIAbADGAB4A0P+f/lP/YwD2ACIBRABt//b+0P+QAPUARQC3/w3/Yf9KAHMAAgEYAMr/Qf9B/+j/NQB1ADj/Av9p/kv/zAC3AJMA9v93/23/5v/r/+//X//t/80AgAAwANz+7/6T/2AArAFZAfD/zP6+/pD/EwBHAIMAMgAWACQA5/+P/1v/s//5/x4APQDFACABDQHrACoAWP9B/9X/OQDUAL0A9ADqABYApP+0/s/+nv/XAOcBrgE1ARwAKQBYAGv/df/q/tb+7f86ADEBUgEOAHn/bP5M/qD+eP+3/+r/bwB9/4T/0f76/j//4/72/vL+AwAnAOoAqgCa/1L/Yf8TACEAdwCo//H/PQBoAHsB1QCsAGT/pf7p/nv/hABHAUECmgHJAFkA///I/+P+dP6K/i7/NgGPAhAC8QD2/rn9GP5m/zwAnwDuAAoBRQHPAO//y/5h/tf+JADYAUcCxAGhAN3/mv+J/9f/Xv80/5P/TQBDAvcBJQDl/tD9mf7O/20BlQHE/xf/nv4t/yAALAARAKD/af+G/8P/hgA1AJj/df/8/vr/HwA+AA0AQP9m/5b/KwAQAB8A9f8bAE8B/ADc/+H+Kf4q//sAzQHiAd3/mP46/z0AxwFvAbkApv9J/8n/wgBnAaEAuQCnAL4APQCe/5//sv8cAL0APgE4AekAFgAkAHj/Ef+c/2X/8v8ZAPD/zv9YALYA2//g/oT+Ov63/ov//v9+AC4AOABkAHYAFQAi/5X+SP5o/3QA8QCNAWUB+wBuALT/Zv8o/1L/KwCRABsBZQFXAZQAY/8B//v+Lv9E/8X/4/8xAKkAUQBTAOb+ZP41/6b/SgCp/8r+PP4n/0AAEQGnAdL/6/5W/qn+AABbACcBfwCLAMwA3AB8AUUBqgA/ANf/Xv+2ACYBgQHcAewAPQDU/g7/9v+dAP8A4AB8/xL+l/5J/uj+sv94/23/QP/3/nT/tP/V/5T/lP5c/w4AegB1AJUAHACE//j/nv+gAMoAowAFAeQA7wCcADQA8/8HABgAKAGVASQCXQHO/9b+Mv7o/sT/5ABbAAAA3P90/4//Ev/k/pr+YP/c/60AngCj/2n+Sf4f/wH/DwCx/4n/MwBf/5H/uf9q/4f/n/+f/8YARQFQAdgAmv/1/hf/RQBfAZwBywCi/0b/of8PAAwALgCmAPUAyAFdAeD/iv/W/lr/n//E/ysAWgDcAMQAVADm/ub+m/6r/ywBBAEuAYP/rv+s/4X/CgD3/9T/pf+mAL0AdQE/Abb/H/8m/+T/xgCPAXkBwQCa/1L/BgDiACUB7ABQAHb/JACLAIMA6f9t/4n/xf8ZAF3/xP7v/qX/pgA+AW0ARP+w/gT/yP9S/5b+2v1q/jsAaQFtAbcAkv/v/jf/Of9N/4L/QACiAHIBhwHfADIAOv+F/2b/4P+LAPEAewFEAeAA/f/G/9L/EQCy/+b/ov/H//gAWQA1ADz/4f6Y/qb+WQDt/14ATAAGADwAef+l/0j//f4L/yj/0//u/3IAFAGCAB8Aq/+F/+b/IgB3AIUA6//K/9X/SwAHAVUBggF+AFL/GP9q/+P/aQDWAPX/Uf+q/04AYwCHALb/wv5J/yQAjABMAD0Aev+m/5P/3f46//L+qP+6ACoBywDa/zv/Yf8AAJQACwGyAI7//v7p/5IAUwHIAOn/Nf84/88ApwC+AOH/m/49/2QAUwFIAdD/Vv7g/nT/tQATAQEANv8B/yIAZwFGAWD/of6Z/QD/2QAeAYwBq/86/6r/BACEAMX/h/9V/8D/qQD3AI8ABQCW/0//lv/0/wgAmgDrAPUAIQF6AHT/6f5E/7L/MQHUAYkA7v9x/5//RACTAGQA9f+J/yAAiQCAAB4AYP82/yb/BwA9AGkA1P9c/9j/8v91AKgA0QA6AMH/qP/M/wwAHADPABMAIgCKABUB9AGmAa4AwP78/ar+AAA5ATQBrgBVAHwAiQAAADb/kv59/pH+Iv/O/0UAOAA/AOr/JP8X/9b+EP+I/2j/z/9HAKcArAD4/wr/Ff96/8v/nwAAAO7/lwCeAF0BzwCm/5L/TP/d/9L/R/9+/7z/kwBmAWsBIgA//6z+t/4dAE4ALQCk/zX/Jf+H/2gAVACx/77+af6m/rT/MgFTAVkAs/4E/h//ugAsApsBXAA3APb/1QDSAWYBnwC2/8X/iADcAA0BSAGJAfUB8AEPAf7/ff+8/7f/sv9A/1P/dgAYAZoBpAC6/9j+6v2u/nH/6f/t/6f/Sv/K/+f/j/+A/9/9SP5E/9f/TwHEAOf/Dv87/oP/UgBCADUAT/9x/9f/XwDgAGsAjQAWANv/KwDJANkA+QDIAI7/Nf8A/yEA0wArAacAKf9T/wb/7/+8AOD/QP+d/wwAZQBkAL7/lP8o/5v/wf9x/9f/hABIAWQBHwGK//v+Zf8oABABXAEGAUAAIQDk/1cAkAAYAO//cf/E//X/ZQDlAMsANQCF/0H/1f+6AIMAsv/2/rv+xf92AIYBAwHi/+j//f7D/2D//v5D/+b+nwDdALIA6v9+/gD/Mv9a/9b/Xf+0/yEBMgEJAbD/vf78/or/EQGVASEBegAZACYAjgBNAL7/Sv9I/7b/aQBpAbUASADM/x7/b//V/7kAugAVAFn/U/64/vr/swA2AdUAYf+S/8z/sv8cAOD/nf+e/zEA4ADsAJkAjP/9/q7+y/7k/+sAPgFdAXUBYgDP/w7/hP6Z/5wA7ABiAAUAu/8RAOsALAFMALv+i/56/8wAEwG5ALn/6f5p/ysA2wBCAFn/MP9G/+v/JQBn/yj/Zf+o/97/ZQAsALb/sv+K/6H/DwBVAMX/4//o/8j/nP94/8r/1P8mADD/M/+3/zMAPgE3AVUA5/5A/oX+Kv8eAJkA1v/x/6r/4P+wAFX/ZP8B/7T/+v8NAC8Abv/oAM4AAgFhAJT+ff2N/kUAXwGeAnYBmgCg/9f/KAAgACwAAADKAMcANwLJASYBfwAt/zH//f4eAAgBRgIfAqMBUgGg/8P+W/5j/kb/7P+nAC0BKgEnAZD/yf5y/hn++/9XAH0A9/9B/+f//v+kAN//rP6k/h//uwAqAZQACAAF/yT/GADeANgAdwA6/wT/f/9z/w4A6P+1/2j/hf/U/+//lv+r/1//V/7h/vT+PACMAIMAagDl/i//Rf+PAFEB2AD3/0D/+f+NANABLAHe/4n/H//e/0IBTQEyAa0AHADiANsA1QBQAOX/oP/Y/3IApgA+AVoAJADC/7v/WwAAACUAeP8k/2H/OAAvAeIAbADV/mn+Xv8iAAsBoACl/wAApP+k/5IAPgANAPn/6P9/AGcAigAlAOj/yP+u/ysAyP+u/3UAFQBaAO8AGgADAF3/Dv/R/7X/+/8f/+7+gP9h/6X/kv+V/5f/PgAyAM3/1f57/tn+Jf9jAGIATwDk/+r/SQAWADcAdf+i/0cA8gB7AWkBogBLAAUAOwCeACMAiwBeAMwA7wCJAFwApf82/6T+1f6j/zUA9P8IAPX/ZP+5/zUAYgCq/93+Jv5v/hn/7P/xAAoA0v8AAFr/xP/i/+j/bQC0AMgANQFoAVcA6/+T//D+Ev8dAIgBmAFuAd0ADAD4/2cAiwDd/z7/P/8uADoBkQEeAQkAGP9Y/0IAtwAnARIBNwDR/yMAwf/g/4r/+/6K/3z/TQCIAFsANwDj/3wAPwB8AK3/PP+s/6r/OwAKAOT/6v8AAJMAmwAzAOH/HP82//H/4f8LABsATQAZAN7/9/9l//D+7f4Q/4n//P9rAOkAzwAlAB3/Ev8b/3//qv8D/0T+rf4VAH8AMQE+AML+7f7G/jr/9P8bABUAEwG7AZ0B3gBV/2L+Q/5A/54ATAKAAvIBIgEfAD4AaQB6ACsAIgAbACsBKgK/AbIBJAAJ/7j+wP4AAEkAqgDTACkA6v9t/3f/pP/b/xkAuf9F//v+9v69/28AIgCc/wn/7/7I/uD+q/8D/0f/EAD7/47/bP8a/8b+KQBYAMgAfACa/wkAh//W/8z/Vf92/2z/wP/OACcBAAGXAML/qf8U//j+Y/8UABAAaQAdABb/RP8x/xEARQDu/9//G/9a/5//DQCxAKEASgAXACUAegAYAEsAmADXAGYBagE2AWcAZQBRAEEAEgHvAEAAfQCMAfgBPALNAfH/PP89/5r/igCCAKAASgC7/8n/d/9a/8T/PgDW/7r/tf9V/9L/kv+V/5X+/v31/uH/IAHDAIr/Vf5e/nr/qADRALn/Rv9F/0YA3gDp/7T+mP5N/5YAVgGlALv/xv65/tb/3v8JAOP/aP+9/yUAsP8s/0P/sf93/3//YgCrAAsBoACk//7+d/6P/6YAYwFVAYAALwA5AHcAcwBKALv/pP/I/3gAiAHiAbwBiADu/4P/9//DALAAVgAOADAAOwEAAuUAyf+I/lD+pv8CAYkBuwCXAFUAfADSADsAv/4O/pP+JP+/AHcBCQF6AAYAqf/v/ln+hv4H/10AugBMANEAOgAuANz/Pf8H/9v+3/+KAKcAmQCgABIAIQCa/9H+Hv9K/xIAIQDS/0f/If+7/8n/d/9I/9j+yP6G/0H/ef+B/1D/X/8AAJIAmwDHANb/3v9R/07/qQAKASABZwCKAF0AOACcACEA0v9a/5//xgDEAIwAOQA//y8AJQDV/xQAkP8BABMAWQA1AKv/Ff/n/h3/yv9DAGz/wP9w/zD/EAAyALsAzgBKAM7/V//m/8gAoQBdADgAUgAyAdQB1QHCAMD/zP9XALQASgH3AP3/WQA4AcYBkwGMABT/m/7z/nH/RADvANMATgAIAKv/Tf8m/xn/Dv+8/kX/IQA/AKEAggCx/0D/iP6+/iH/lv/kAF0BGgErAKL/a/+I/0QANwCZ/8D/zP/E/1AAeABOAFEALwC4/6H/tP+w/5v/5P4t/47/WwCTAGQAUQDj/nX+eP56/jT/y/8wALoABQF2ADoAUv+p/mv+S/5q/2QAwQFsAqoBxABT/yv/jP9sAMYADABmAC0AcAErAmMBwgDj/tD+sf+KAN4A6gBzAKX/bgDsAEABAgE8AIv/M/8R/67/GQDe/8EArgCfAJIA9v+J/+j+wv7t/lr/1v+oAC4B4QD+/w7/z/7T/g3/T/+E/5z/eQC+AOMAkgCZ/5v/rv8HAAYATgDk/+n/NwA+ABAB2wBUAOj/o/9Z/0L/1v/e/+X/RQDeAP0AuQBv/4n+rf4U/wsAigBKAOH/eP+3/0YAXQA4AIj/H/+C/2QAZQH7AKUAhP/k/q7/BwC+AD0A6P9+/zv/9f9lAPcAkAA9ALH/Uf8X/w3/KwD/////tv9V/y4ApgDQAF4AJf+q/sf+Fv+0AFkAyP/A/xT/aACwAKAAt//7/lL/GQBgAfcARgCm/5L/OgCwAKAA3P90/5D/zACmAZ4BXgCC/63/9P9SAOf/ov8z/5L/uwBPAfwApgAFAIT/wf+D/67/mf/A/zoAnQCRAD4AjgDy/6v/Tf8B/3z/TQCbAPz/Rf+e/sD/AwAVAP//j/7p/o7/WwBMAZ0AWP/l/tL+jv8AACQA6AA6AIsAcAC1/9b/p/9LACoAIgBAAFgAEgHvAC0ApP/J/y8AzAAlAX4ALgDc/wcAvgB0AIIAfACbACMBfAA/ALL/r/8IACsA2wCeAAAB4QDIAI8AzP7Q/tT+6/9fAZoAVwD9/yH/cf/E/3T/of8z/3//4v8MAAoAK/+e/7H/nP8c/xH/0/8SANkAeABy/7D+p/6Q/5UAnQDZ/03/k/4j/4b/nf8xAN7/CQCIACQAZwDT/0j/tf9D/7H/d/9uAOwArADnAJT/hP9l/3IAygDH/4kAXABdAAMB4wAkAJz/Cv+7/yMAHQBzAID/GQC6AGEBiwF0ACYAsf8bAGAATQDj/5//1/86ALAAxQBnAGT/cP+f/2j/vf8lAOf/tgCAAPr/1v+S/jb/OP86/+L/+v8fAIb/Z/8W/43/EQDq/23/Pv5e/jD/NQD1ACAAl/5c/tL+WAAkAVgAj/+R/ur+WQDtAFEArv8r/7D/ZQBRALAAVwCz/zAAJgAxAJYA+f/o/yMAHAA8AFUANAFVAQABKABp/+P/ewAbAUEBXADd//b/ZgCuAIwAhACPAJgAIAFFAakAZADQ/yH/qf/e/+X/2P8WALgA3gCgAMr/Qf8c/0j/yP9TAJ8ApQCp/+/+2v7J/j4AoQCUAAkAT/+E/8H/cgCl/zX/kv6i/oz/IgB4AIT/d/82/4L/CAB1AHEAtv+y/y7/Vv+c/0IA2wDDAOcAlQAKABoAcQA2ACwAbP92/+4AHAGLAb0AYP+S/97/eACFAEYA3f9j/xQAIwCdAEcAXf+0/4v/EABWADMABAA7AEIAx/9lAFEAQQCjABUAbP+J/1b/nP/DALAAHwDQ/9n/8/+JAAAAx/4o/0D/eQD1APv/6v+l/5H/8f8FAPP/BwB0ABYBlgDU/6X/W//F/1AAZgCcANoAHgEwAfUADQAu/zL/Nf9d/zQAhgB+AJ0AIgBS/xf/6P6N/4AADQG0AGv/Pv8H/xQAyQBFAIIAVf+b/wwBNAHUAOH/5P7k/or/6/+5ADkAm/+dAMkAagBDAH//mP+a/67/BgAE/5H/cQATAQMBPQCx/wj/gv+I/1X/0f7n/uj/IwCdALX/MP9r/2P/pv+l/0j/bP/3/zAAggBEAO7/g/8bABYAAACAAB4AqwAJAD4A2ADBAIkAkv/M/2j/GAC5ALoAqAAZADkACQA+APz/jv9a/0P/RADvANMAPAB5/4D/GQBxAEgAAwBw//j+0f9tAI8AFwDc/wcABgC9AGEABACW/3P/awAOASQB/gC6AAIAXgDM/2f/z/9X/+f/RwCVAPkAyQAzADr/qP79/h3/EwD/AIQADgD3/hj/2f8pAKIA3v9R/73/EwC1ALcAEgDG/3X/EABpAFUAVwAOAPr/ev/e/63/4v9WAOr/gQAwAPH/z//G/6z/hf/C/4T/LwCVAFMA+v9V/9D+Vf8JABkATADi/2f/8f6n/yYAw//0/xn/1/5b/7L/VAAxAMz/+/8OAAsAUwDV/7b+mv4p//n/egCaABABkQA+AB8Avv+B/4X+UP+8/6UAvwH5AG0AMf+R/4MAfACJAMn/nP9U/5sANgFTAEMAf/+q/xYA2/8HAM//tP/V/0sAqwCKAMsAEACy/2X/Of+F/8L/mACNAF8AOgBBALUApQDN/57+Kv6q/m8AkwF8ATAAyf6p/lr/jgBgAPL/Kv9U/3YAvACFAKH/+/5A/0IARwBxADYAYf+l/+7/8v/1/wgA9f+vAOkATQDj/+b+5v5m/xcAOQGjAYkBYQFkAHT/WP+c/ir/6P8QAMUA6QBPAfwANwAsAH//zf6s/gH/IQBCAXIBqQA+ADH/2P64/2n/mf92/5H/qAD2ANgALQDu/6j/b/9DABEA/P8OAAwAUwAeAHQA8P/O/w4AsP/l/+r/NwBRAFQAVgDq/+7/3//4/zAAFAC1/wwA5v/G/9L/7f/M/9b/AgBv/+j/o//a/4YANQBPAMD/p//L/3oAvwDkAO8AGgAoAPz/awAeAAYAFwBcAAMB9QB+AY4Azf+g/zL/kf8UAFoA2//1/y0ANwCtALAADQB4///+Hv8UAJEACAGLAJT/3v4E/xEAWADG/7//Xf/8/gsAnACQAPT/K/8d/9v+Xf+0/7H/CQA+ANgA5gBvANn/YP/J/y8AOAAtAO7/lf9z/6H/jv+k/yQAjAAnALH/nP/S/nv/3//4/7D/mP6p/zoA5wDyAFP/qv4j/z0A/ABMAXgAvP/u/7sA8wAMAMD/Xv81APYAyAGCATUA9P+//3EAkgB2ABUAfv8FACkAkADiAH8AQQB9/wP/bP/A/6kA0gDf/2T/Jv8Z/1oAAQHg/6//df9r/5wAfgAJAIf/Hf+4//3/x/+I//n+B/+m/zgAPwDY/2AAcgBcAFwAuP/r/yUAMABMAHP/Rf8OAFUA6wCGALT/nv+f/2kAwwB4APP/UP9g/xEAWADr/1z/1v7Y/rj/fQDmAJQAif/8/yEACAAZAG//nv/7/8YADgHHANgA9v9S/4f/ef+4/2sAaQDoAM0AkwAKAXoAUADA/xT/Z/8qADYBaQFqANX/pv+l/6YAhgDs/1z/1v7t/18AgwB8AHX/Iv+X/6v/vP/b/xj/V//C/5f/YwDP/w8ADACK/1f/rf6C/y0A7wCcANn/cv97/ycARQBcAO3+Iv/h/3kAPwGAAPr/n//W/18AzQDc/+P/6f9H/+z/8P8qAP7/IgBTAEMAEQCg//z/V/+v//b/sAD8ALkApwAGAGD/fP6l/9z/mgAQAaQAYQFkAGMA0P8h/yf/P/9mAPgANgHDAEEAxv9R/07/FP/6/44A4QC1AMj/d/+k/8j/d/9I/8b+TP8UADUAhwBZ/9P+IP+6/8kAtQDs/yX/Bv+l/0oAFgDu/6j/lP8XAFwAuQCVAHgAKQDr/+//OwAwAPD/TgAIAPYA2QBSALEARP/C/vD/TgCuAMMACgDR/zX/k/8EALr/bQDq/7f/MwDO/w4AHgDP//3/M/+A/xkA8P88ADAAFABr/1H/hf+w/1IACwDl/48AKQC0/0MA//8AAAAA2//1/xsAlwCv/5r/0//J/0IARwDx/2D/pP+k/+4AHAFRAGYAZP9L/+//4QAkAQ4AQf+L/zUA0AAEAXUA8f+9/1wASgCGACIArv/1/3b/WwAkAPn/xQD5/9b/FACj/8f/9//5/wwAif9p/5n/9/+LAAEAFADH/yz/HwA+AEQANwCa/5v/HAAZAdAAXgC5/w7/rP90APEAeABOANH/7f+DANkA0wCp/17/2v88AFUAxgBWALL/iv9q//b/CQAaAKf/AQA4AEAARgAmADEA3P5M/13/M/+3/9f/AwCV/8//IP/f/2YAUgBnAOX/s/+d/+j/7f/e//X+hf8LAAgA0gCEAOr/7P5s/wf/E/8LAAkAYwArAFoAyP9k/zn/gv5N/6f/uf9ZAP//NgA+AMT/GACCAI4ABAC6/37/8//AAFMBgAHHAI4ATQAHABgAXQBdAIIARACTAPgA2gCfASoBSgCX/7v+e/+EALQAEgGTAHX/7f/M/+j/yP8b/zX/y/+fAG4AogDL//j+UP+X/77/lP9x/8T/mgBqAFUAsv8u/3v/cP+x/8D/AwAnAEUASgApALP/U//R////IwAKAPf/5v+h/8b/LQB//yn/iv9F/w4AQwA2AAYA8f4B/0X/WACRAOL/MQDe/67/GQBeABQAo//H/+X/WADaANUA0ABeAMz/1v+5/+z/zAABAZgAw/87/2H/bwD/AIQADgD4/mL/EwDbAMMA0/9//wX/uACWAesAYQAD/47+Rf9qALIAjwAFALv/EQB8AD8ARQC4/yD/cP/E/4cAkQAJAWcAP/+u/6z/FwC5AIIA+//q/+7/cgCmAE4APwDF/6z/cv8gAMAAiACAAIv/M/+l/8n/iwBLAKr/cf/U/n3/YADhAMgAVwAPAOj/WgASAP3/Rf9p/5n/5P+0AH4AiwATAP7////t/97/m/+c/9T/cAB/AFQAnv+x/8H/cf/7/7P/Zf+o/97/CQA+AA0A1P+m/+7/qP9w/x3/N//x/8//yAB8AOT/oP9p/xkAAQBdAIH/Pv/S/6UAGAGrAFIAi//+/9n/z//Y/7v/JABCAJEAKwDa/7z/JQCxAFcAtP9C/4v//v+RANEAOgCK/+r/JQAwAAIAgf/k/w0AeQAqAEb/V/9m/xYAgQAwAEwABgAXAIEAegDQ/2v/rf8YAN4AIgHFAFUA6f/t//H/vf9u/+b/yAA1AR4BQABq/3L+v/6R/xQAtgCAADAAJwDE/wYAKgCP/+z+6/7G/5wA7AD2AHwAPv9R/5j/rP8qAFj/CwCdAA8AVgCO/1r/RABuAGsADQBT/9H/7P85AGUAdf9r/63/UADUAGEAzv8f/xT/w/9PAGQABwBz//3/RgCnAJkAxP+9/0n/t/9XALUAkgC+/5T/lv8GAIYA/wByAMn/wf/O/8X/4/+x/5z/QgBHAEwABgDh/x0ABQApAGn/dP9q/2QAQAGmAIYA/P5m/2AA8wDGAX4AZf8C/9n/BwH5ALYA2/8q/8L/8/8aAAIAJf8G/4D/PgChAEoABADN/+n/pP/t/ycAaQAeAPT/CAB0/8b/iP/E/z0AMQBfAN//5f/r/10AXQDd/4j/Q//7/w4AZwBBAKH/of/G/z8A6v/c/4f/Qv9n/4X/VAD7/9f/3/9A/6//K/8d/+//8/8ZABQAIwB4AE4AZACaAA4A1P8mALIAjwBPAHcAKAAOAEIAIwAcAHMAOAD2/9P/3P92ADoAiwCVAAkALAAkAFQAMQDx/5j/h/+x/y4AlABlACwAtv9o/yn/iv/G/wgAKwAQAOn/f/+9/+//lwALAOX/MwDg/8MAsAAxALr/tf9pAHkA0ACDAKD/xf91AIMARQC3/7P/wv+YAJ8AEgAhAGP/y/8xADoA+P95/4D/rP8qAOv/3f/R/xEAsv+K//3/If9M/5T/qf9fACcAsv+v/4f/jP///yMAnP+d/57/MQAqARUBBAHj/0P/ev9v/x4ATwBAAI7/NwB2AN//LgA2/3D/jP+1/zEA3//4//r/MQAVAO3/gv/S/yQAQgBaANv/4v9n/87/WABHAJUAQQDZ//P/rP/P/0YAk/+W/xgAXQDMAIAAQgDa/8//DwBDAIAA+f+e/8T/9f9SAEIASADe/67/iABtAGoADAB3/0kAzgCUAAgAmf+I/7L/QQCRAOL/jP+1/zEA8gDDANT/Nv8U/y//RgCnAM//6/8TAA8AVgCPABcAgP++//D/vP9JAM3/jf/b/6v/PAD6/x8A9f92/5H/b//V/xQAWgARAA4Awv+p/5X/hf+v/3X/IwD4/3oAUADl/w4AegCHADT/pv8R/1L/0QC7AKkAGgDe//f/eQBiADwADAAJACwAbQDHADEA3//B/xYASQCXADAAy//6/1cA2QDl/9j/Ov8X/w4AjACoAGMAYgCX/9H/2v8YABMAov8PAHr/OQCKACUA6P9+/4X/U/+Z/9L/WwA3AGQAvwA+ADIATP8l/6z/KgCQACoAWP9U/xoAhACPAIT/Lv+g/9j/lwBDADT/Ev9T/5n/LQDu/17/If86/08AdwApAHz/7/7t/tv/hwA2ACsAkP/L/+j/EACzAA8A+/8gAGMAKwA1AFAA9/+eALcAywBsALL/r/8HAPYA2ACcAA8AHgCsAMIAZwFXAA3/Yf/c/9IATwHpAAQAqP/L/40AuwAWAG3/G/+j/1oApQApANj/X/9s/0AAWAAQAIz/fv9g/23/if/9/6H/of80AHL//P80AAUAu/9s/8D/g//l/w4ACwD4/x0AYQA8AAsA0/+3//z/RgBdAJUAnP/m/zQATwCJABIAxv8r//v/fADAAMAABwCF/9T/ggBpAIwAuf+Q/8r/VQDGAB4Avf+A/+P/MQDzALEAxf9P/xX/ev85AOcAugDx/xb/e/9MAOQA7wBkAKz/YP9JAKkAwAD1/z//0f75/i4AkwCcACEA0v+R/97/rf/Q/+z/Sv8lANX/gf/j/x8A9wCiAEsAYP8j/2D/pP/vAGQA0P9G/w7/GQCoAEABSQBM/7f+Lv9qAGgAeQCq//D+N/8DAKgArQBUAB3/o/5o/5kA/QDwAAkAh/8w/9r/YQBhAL0AvP8SAA4AegAIAYsApwC9/27/U//j/1cAfQDTAAQA4P+c/4v//v9+APj/sP9j/9z+KAC0AAABzgCS/wL/If8DAAUBrQCv/xn//P5T//b/wgDS/zX/gv9j/0sAPQBoAFQAev+5/7T/+v9XANkA1AAqAMb/rf8GAOH/ngBtAKD/of+O/zcAPwAOANT/k/9x/43/NgC+/wEA7/+W/4cAWgASAP3/2P+W/9D/2f+q/00AiABbAEkA4P+K/47/AADu/7r/tv+N/7b/HwBRAGYAZADR/8j/GwByAMsANQC9/yT/Yf/c/8AA9wBqAHsAvv84AEAAMwDPAPD/l/+r/wQAlwDWAJoAagCw/wgAiABIAHIA7v/N/3r/TAD2ALMAkQD0/63/c//Y/wQATQDQ/+z/OQD3/0IAov+Q/0n/t//X/9//ZgD3/4sASwD0/y0AbP/j/sD/qQDAAAkB+f8w//z+HP8AAMsAbAB7/5X/O/9h/0oAvQA8AHn///7n/h8A0QC7AE0AKv/l/ov/fgDnAF4AXf/p/kT//P+PAKsA0v81/7n/NADjAJIAdP8z/7X+Uf+sAIoAcAD//yL/hP9UAI0AKgGUAFH/Tv+7/yMAsADYAFD/8f7M/3sAUwERAW0AIP8B/zQA9QAPAbYAEQBW//j/HgA9ADEAOf/z/wcAPQDFAAsA0v+2/w0AZwB4AE4Av/+n/27/5/+RAJoARADJ/y8Ay/8eAIcA///I/z//iv8hAIkAXAATANn/u/8kAB0AKgAiAPf/eP/u/+D/nP/U/+//KQAzAM8AcAA1AKv/uf74/lH/vP8AAEoABADf/0EAfgBTAIv//P6J/lL/vv9dAMwAJADU/zb/XwCWAFQAxQCw/+T//P/Y/5cAVQDp/23/G/9//4YAEgEUAV4ASv+A/1AAZgDAACwAR//H/xsATQB2AMz/Hv83/zsAngCkAJcACwD3/6//9v9BAEcA8P/z/z8ARQDdAKAAJQCw/9L/EQBYANoAQQAPAIz///+SAHYAFQCR/xQA//+RAGMABgBy/7D+vP+3/+r/7//N/43/R/8QAB8ABwC9/1v/Mf9Z/x8AhwCAAML/Tf/c/hX/jQCpAFEA5v/p/mn/KwDuAMAA0P80/zf/AwBxAAEBqgDk/2j/hv/6/zEAhAAOAMP/vP/c/4gASQADAPH/YP8SAEYAXQDMAO3/3v/A/wMAuwCEACEAGf/8/uf/bADGAHoAT/86/xgAlAD5AMgAaf+7/o7/2/9TAaQBPgDE/xj/xv92AJcAZwB2/2z/ZP8VANwAsQB8AK3/c/+O/xH/CQA/AHv/lf9g/5L/XgCDACAA4/8e/0r/3P8HAOL/ef+m/4D/0P9HABQAo//H/9L/JABnAC4ANwCa/+X/xv/R/zUAUACKAID/9f/A/zoAiwAmAI4Alv8GAGEAOwAwAPD/qf+o/0wAdACCAPv/jv+2/yAAdgCEAI8A4f9m/+D/ZgBSAHoAvf9u/+f/av9RALAARAA3AJr/CQAHAAYAmADD/2D/f//1/9MAcwCUAFIAZv/g/x0APABoAFMAHgD0/y0AEgBYAH4AUwDV/4H/iP/7/2oA6P///2z/Uf+9/0oABwEuAID/4P49/3X/SABxAAAASQA5/yoAfgAuAJQAUgBVAB8A9f8uAFwASf9JACgAe/8DAHD/MQACAJUAwgCb/9T/AAAlAEMA7f+5//7/x/8JAKz/YP8kAEIARwDx/6r/cf/E/1AA1ACYANb/b/8d/8r/ZwB4ACkARf8f/zn/qf8oAPz/6v+3/6H//f9GADkACQBjAND/x/8tAO7/OgDDAMIACAAZAG//VP/3/3kAYQC8/zcA4/8yABUAAAARAMX/dgBMAKwALgA3/3D/w/+HAMkADgCe//j+LP9WAOsAqwAbAIP/mf6X/4gAEQBFAO//cf9W/y4AOABkAAcAF/9p/xj/xv9kAOQAAQGrAEAAjv/u/83/IAAsAP//EQB7/0wAKwAQAHwA4/8fAPX/rv8HAE8ALQCk/+3/uv9IAIMAVwCQAPT/v/+U/04A9v/m/zQABQBOAAcAPQCNAF8A3/94APP/9v8uAID/GQBK/6X/3P9jAIcA7f8UANr/GACl/wAAt/9X//n/6P+RAIgAEQAOAGb/8P7w/xcAXAA4AD8AWABG/7T/wv/h/0IAbQCz/6//v/+n/6cAGABKALz/t//8/47/EgCh/w8ADAAcAM7/oP/Y/+D/iwA5ABsAzf97/4L/GwC8ABYANwA+ALL/CgB3ABYANgCIANv/UAAuAKX/XACBAJ8AgADn/xAAVwAhAD8AagDo/xEARQAAANz/BwD0/y0AJAD5/x4Ac/+0/8P/YQBOAPb/5v9F/1gA2f9OAD8AVv/5/9X/FADH/wkAvv9eAEsAKgBZANj+AACS/ygAfAA+/y4Ayf95AL4APQDW/2//6P/a/08AUgD5/wwAHADg/53/w//h/zAAgwANAHj/bf+v/wcAGADw/ykA6/+l/8n/QgA1AOL/egAZAIH/rP+F//n/aAD5/zEA3v8t/0P/n/8yAAMAOgAvAN3/UQCv/2QAiADb/+L/ef/w/3MAggCNAIQAMwC7/8n/LwABABMADwD7/6EASgBzAF0Apv+S/83/sv/B/3IA7v+7/37/4f9DAFoASQBe/37/Tf+V/zwAaABmAOX/jv+2/8X/9f8JAOP/MgAVAJIAYwArAOz/Jf+s/6r/FgAAACQALwDw/5gAw/+9/xIAtP+L/8f/0v+k/5IAmgAgANH/Wf9V/5v/0/9KAAQAlv+Y/1D/FwCBAEMANgCZ/2P/y/+e/w0AZgBlABoAuv/a/4X/QgCRAFAAeAC8/8n/wf8EADoAngBaABEA1//f/8IAGwBNAFEAwf/g/+b/WQAjAHgAPAAeAJkAHwArAEgA3//4/0IA7P9eAHEAtv8NAEIAWgCkADsA+f8MAJz/r//R/yMAeQAqADQAFwCA/+P/VgDq/1wA3f8r/3n/gf8aACcA/P97/3D/n/8NAB0ABQByAG3/QP94/7f/s/+v/9L/Iv9y/3v/XwBNAOL/DABl//L/GABdAJUALgAlAJ7/DAAKAJr/LgDv/1//fv8qAJAAmQCzAP3/Dv8Y/zQAdADMAFoAtv/8/zL/JAB5AAUABACD/+X/DgAwAN8AtADs/yYAsf+c//n/6P9tAA4A5/+i//7/pACpAIgAJAAdALz/AACmAJgAaAD4/8P/qv+W//T/CAAGAOH/ef8TANn/BAA7AEIANQCY/5r/ZP8VAP//IwBBAGv/iP+y/xwAqgAtALb/DgBm/+D/ZgDl/+r/t//q/+//OwD5/0MAJACd/x4AGABKABcAJQCw/9L/bgAzAHMAOAAtANv/KwBIAN7/5f+z/4wAgwBXAJAAGABdABMA7P/d/9L/WwBcACUAQwD//7b/aQAdAJf/mf+b/+b/xv92ABYA7f9e/1j/QwD//xMBJQDo////tf8yAM3/fADR/yMAVAB5/xQARwCDAKEAOACt/8//tP+w/5wA2gBUAOj/tf+f/yAALAARAOr/7v8oALL/r/+a/+X//f/Z/2EAhP+c/8L/KQCiACcAMQA5/6n/zf/8/1gA2f8pAGr/9v8uANz/LAA2ACsA//+SAND/x//3/0IAfwAcABcAt/+z/+f/kQBQAFMAwv8E/37/4f/EAOcATACG/4v/Rv/9/yQBjwBhALv/tv8gAOP/jgCXAPr/+/+g/7P/5//H/3cATQAZAJT/X/+R//D/YQA8APr/Vf+u/0//lv9iACoAEACf/1X/Lf+N/7b/RQCTAHcAFgBt/5z/iv/G/y0ANgAZALn/ov8QAEQAWwCBAEMANgBh/8r/HQC8/4EAegAGALz/kv9w/zEAcQAAAEkAu/+R/xQARwCWAGYAGwDf/8H/8v+r/87/fQD3/y8AAQCT/+D/iv9YAGwA1//x/73/JQDo/8j/QADG/9H////t/97/5f/q/wAASgDO/7P/HQCq//L/KwBHAHEAJAD5/4z/ov9HAF4ATAB0ADkAdv9s/0AA/f8iAHcAzv/Y/wMATAA9ADEAKADX/xYAyP/B/xYApP+2/w0Awv/O/yAA0f+R/xQAkP8BAF0Apv83APb/+P8wAPD/9P/2/woA0f82AAYAFwAAAO//zf/8/5AA8/8aAPH/qv/g/1QAewCaALQARwCDAI4AOwALAC4Akv8DABQA7f+oAPX/LQASACEA0v/b/z0An//E/wYAdAAmAEMANgAsAP////8jAFP/rP9g/9v/UAAJAFEAnP8K/zn/qv+7/yMAHAAEAIP/if8zAAQAFgAAALb/jf/t/0wAhwA2AND/2f9g/8n/VAD7/43/kf/L/7H/CQAaAPH/GADK/9X/FABHADkA0//u/7r/EQAgABoAAgDe/xsAzf+y/5z/MAAUACIAQQDZ//P/GQBeACcAoAATAFf/wv+E/woAdwCEAEYAJgDW/xQAEADp/0kAFgAkAAoAm/+u/wcAGABwABAAVwAhAFD/KgC0/2gAHAA6/xgAy//6/zIA3//B/83/xf8rADUAPQCgADcAGgDe/9P/pP/t/18AFQD//xEAsv+v/2QAPgANAFQAHwAZAEsATwAtAH//0P/s/93/mwDY/87/xf/R/6QAqQC/AAcAhf+L/0YAXgAmADEA3/8uAAAAgQB7APX/UgALAOX//f/G/wgAPgAxACgAxf/1/5v/wf9OANH/EAAyABYAAACR/8z/DADm//7/x/9j/8z/HwBQAJ0AIgCu/4b/sP/l/yEALQDb/wYAvP8SADMA8/8+APz/WAD+/6L/fgAKANH/NgCG/8P/TwD3/9T/k//f/9P/NwDlADcA0f/I/67/4/9pAOf/IgAuAAAAgQBVAFcA6/+4//3/NAAYAAAAAAC3/+r/AAAAAMr/5//s/93/CACZ/1IALwA5AFIA1f9dAAEAAQDv/4T/wf/N/zIAYADg/woA5P+g/9f/zf9o/4b/5/81AGIABQDz/4f/sf/3/9T/bwBHAF4AOQCu/wcAYP9//+L/sf8bAM3/IACbAEUAJQDo////tf+y/1MADADT/yUAHQAqADQAPQAxACcAVwAzAE4A5P+y/y8A7/87AOf/7P+5/4//EwC0/wsAHADy/+P/+/9FABIAof/Y/87/af8rACMALgA4ANL/WwAAANv/dQA6AOb//f/Z/3L/1/8oAPz/DwD6/0QAgQDo/0gA8f8YAF0A8P+YADEAJwD7/+r/JQDn/1oA2//i/+j/o/81APT/5P9XAGsA+/8OAB0A9P9RANT/7//y/3T//v9/AMIAeADz/5n/dv+j/1oAJACd/x4Aqv/N/zIAhP/4//r/xP9iAM//j//K/3j/t/+O/7f/RQA4AFIAHQC8/6T/tv/p/zcA4//E/73/uP8PAAwAeAAEAPL/4v/W/14AFQAQAPz//f9q/6z/GADd/3YAKABFAO//4P8vAN3/ZADQ/5D/EwDZ/wUAKQDF/ywApQAoAEUAEwCh/zQATwDk//z/s/+d/+j/tf9pAB0Az/+QAPT/GgDx/wUABADf/y8Ak//g/9P/AAA3AL//uf/H/wgAq//O/zMA4f94/8r/5/+i/9n/KgA0AJf/BwC9/9z/LADI/1MA1f/w//P/9v+dABAAMQDN/2j/4v/6/x8AdQAnAOn/JACv/2P/pv+A/77/OQD3/+f/DwDp/+3/FQA2AND/IgCcANn/8//j/8T/PQD7/6EAzAARAOn/NwCbAOr/EgDY/5b/BgDh/4wAlgD4/0MA7f/M/x8AKwC2AFwAkv/f/+X/6/8TAFkAEACN/5H/AgA5AEAAfQAuAO7/g/8cAGAA4P8cALv/yf+c/+f/RwC5/zUAKgAiAJwA/v8iAC4A3P9RAMH/8v9jACsAfgB4ADwACwAJAAcAKwAQAB8ABwDh/x4ABQBOAOT/6f8SAMX/vv+m/yUA1f+m/8r/1f9dAPD/KQBGAG//5/8iAOX/2P/g/x0Acv+y/0IAkP/v/zwA+v/7/w0AQgA1ABgAOAB3APL/4/9WACAALADt/xUAEQDF/z4AHwAHABgASgAXANz/GgC5/9n/z//Y/ykAWABZADYAKwDs/8v/w/8YAN3/v//M/9b/JwAyAJcAjAAUAOz/uf+Q/wEAEwBGAHAA//9IALr/o/8jAOX/6/+4/2n/Yv+4/+v/AQCl/5L/8f/i/9X/JgAMABwAYQAEADoA5v+P/9z/4/8NANT/AQDv/+D/CgDS/wAANgAHAM//2f/O//3/IQD3/+b/2f+8/8n/HQApAFkANQBPABsAqP9eALn/EAANAGX/FgB//+L/aAD4/2gAHAAEAAMAzP/7/zMAu/+R/wIA8P8FAE0ALADt//H/TwBSADAAcAD//7b/HwAHABgA3f8aADoA0/8lAGcA+P/n/yIACQAHAOL/HgAGAPP/9v/l/zMAPABVANf/AwA5AJz/QgBHAPH/PQDo/7X/HwCr/87//f/r/wEA7/87ANT/EwAPAOj/AAAAAEkA8v8rAP//tf8fAOP/6P8RAA4Awv+8/wAAyf8vACYA+/8gAL7/8P8FAE0APgAgAIgAEQAOADAAXgDw/xcAJQDo/yMA0/9cAF0AJgAxAPH/GAC4/6H/xv+//6f/7//z/77/JgBEACQAnf95/6X/SP+2/0QAEgBGACYAMQBMAD0A+//X/zoA1P/c/+P/1/9xADYAPgBEAAAAAAASADMABAADAPH/9P8IAOP/DAD4/+f/EAAyAM3/xP8ZAJT/TgD2/3f/yf93/zcAPwBqADAA8f8FAAQA8v/Q/1kAfv+8/8n/1P8TAI//7/9f////NgArAEgAuv/s/8v/+v/E/ysA/////20A/f80ABcA7/8oADMAFwASAOv/7/+7/5H/p/9u//n/+//8/yEAv//x//T/5P9XAP3/j//v/6n/3v8JAL7/FADa/yoAbAAfABkA8P/z/7//uf/s/6b/7/8WADcAdgDf/+X/6//K/wsA5f8OAOf//////9r/BgDO//3//v80AIYANQBPAIoASgDg/wsAUgBCAOz/cAA2AJn/dwBgAE0AdQDx/yoADwAfAD4AxP+9/93/rP+9/yUAHgAqAEcAy/8MABwAu/8RAOr/AAA3ABoAFQCj/37/4f8dAOH/HgA9AIz/EADp/yQAVADE/xgAk//g/y8AEwCRAGIA4f/C/4X/iv8hAPf/VABEAMn/1P8AABIA6/9KAM7/MwAXAKX/JADn//7/IgB4ADwACwAbAPL/GQA5AAkAGQAUAH7/qv+o/7n/7P/d/+T/sv/5/57/xP8GAPP/rP+X/6z/cv8OAOf/IwBTAOj/SAAVAEgAXwBfAHEAEQDq/9z/BwD0/+T/6v8kAEIAtf8fAFAAQQAhAPf/CgCb/y4AOAA/AEUA7/9OAGMAYwD0/wgAYwD0/+T/DQDU/wEAOADk//z/fP8DAF8AJwChABMA6/+4/4//yv+d/8P/z//G/+T/IAAsACMAiwAUAOz/OQCJ/6D/s/94/0n/2//Q/33/8/++/zkAQAB9AMEAUgAdALz/AADc//X/LgASANj/BAAWAEkAhAD9/w8AMQA6APj/MADe/4j/IACs//T/GgAVABEAIAAsAMj/HAAEAIP/0/+k/1r/DQAdACkA6//v/2AABABfADoACgAtACQACgAbAAMAzP9EAAAAEgAhAD8AagBDABEA1/+6/8j/rv8ZACcAxP8rANr/GADv/83/fAC//wIAuf+0/0MAtv/8/+r/t//q/wAAEgA0AOH/1P+T/7v/7f8CAF4AJwANAIr//f9ZAP//kgBRANP/SgAWANz/GQC5/yIACQDj/x8AdP8iANL/yf9UAOj/IwDm/+v/7//O/w4AHgAqAOz/AQCm/7f/IQDk/+n/2//Q/xAADQAdADwAZwBBANn/cwDd/5r/QADZ/ykARgDd/7//zP/7//z/WAAQAOn/JABBACIALgAlAIv/RwAnAJ//1/9w/x8AGQDw/zwA5//s/zkAnQB+AMH/3/+u/3X/tf+e/8T/hv/n/yMAHAApAOr/XAC4/+v/EwC0//r/ev8CAPD/FwBKAPP/4/+x/y4AXQCCAB8AGQAmAIz/7f/e/0AAMwDz/2MAvf9LAAUAu/+AAFP/df8QAI3///+2/5//xf/Q/yIAHAAWABIADgCe/+j/2v+G/x4AGADK/9X/FADs/zkALgDc//X/+P/U/wEASgDO/zMAzv+z/2cAwP9yAG4A2f9OABoAAgACAEsABQC7/1sANwBRAEEA/v//////SADx/z0AaACv/5r/rv++//D/YQAWAFwAXAATAJAA4v/6//v/jv9JAAMA8f89ANb/JwANANT/AAATAFkAWgCAADAAOQD3/0IAbADq/0kABAADAPH/BQAXACUAQgAQANf/zP9EAO7/OgDU/6X/AAAAAKYA8//1/9P/EgDq/5P/TQC+//D/BAADALr/o/+1/9b/FQDI/9P/3P/1/8D/8f8GAAUABAADADkA+P8wAN7/9//B/6n/JwB7/wIA8P/z/4kAJAAdAOH/1f+4/+v/SwAFAAQAAwAnAEQASQBOAPb/rv/Q////2v/0/y0AWwBKAAQAqP/L//v/DQAvAPD/BAAEAN//5f8zAPP/4/8fAND/EAAfAPX/9/9nAC4AAABKALv/7v/f/wkALAAAADYA9f8bAKj/8f9PAFIAjAAUACMAQQD+/yIA5f+z/+f/kP/K/x4A9P8tADYAUQAcAPP/9f/l/6H/af/Q/1n/Z//h/7D/CAAZACYADACv/ywAEQAgAIgAEgAhAD8A/P/r/+//FgAkAB0AFwDv/wQAzf/p/+7/zP/7/+r/EgDY/wQAFgARAA4AHQBPAAgAPgAyAPL/BgBPABoAKAB8APb/+P/n/xAAHwBRAEEA/v81AJj/h/+f/9f/3/+u/wcAqv+W/wYAYQApAOv/yv+w//f/1P8TAA8AjP/s/6b/k//N/w0AZwBTAEMA2v8rAMf/wP/x/6r/4P+v/xoAAgBeAJYACgA/ACAA5P8gABkAlP+8/9v/0P/a/zwADAAuAJQAGwC8ABYAAAASAMX/PwB7/0wA9f+b/xwA4P8KAAgAGQA5AEAANAAFAOD/CgDk/8X/9f/3/wsA5f8gAPb/+P8LAC4Ayv/n/xAAxP9iAM//2P8XAO7/OwBCAGwAMgBNABkAXgDx/5f/LADI/9P/XAAlANX/JgDE/z0A+//p/zcAUP8EAOD/d//c/xkAAgC5/1kA//8jAGYALQASAHz/3/8KAL//AgA5AOX/2P+o/3D/+v/p/+7/8f/P/w8Aw/8YACYAsf/l//3/of+0//r/6f8kANT/EwDr/+//YACp/9//wP+o/7n/tP+NADoALwBdAF0AJgBWACAA5P/X//H/GAC4/0YAAQAmAAwArv8ZAN7/QADG/7//uf/s//D/cv/X/83/6f8AADcAYwB1ALn/x//l/2n/9f+b/woALQDu/ygA/P+z/3j/SgAXAEoATgA/AGoAHgDi/57/+//E/77/7/+p/ygADQD5/1YAIABRAAoAGgADALn/2v+X/xkAuf/+/1oAyP+wAEQAAAA3AOP/1v/x/yoANABiACoADwAxAPH/4v/6/+n/7f/M/zIAzf/X/xUAyP94AOH/nf8eABgAXQBdAIMADQAKABsAFQAkAC8AOAD3/8H/zv8zACkAWABHABQA2v/0//b/rv/j/5//xP/j//v//P/F/wcAqv/g/x0AYQBgAPL/PgD7//z//f+0/2gA1P8AACUAsP8bABYASQBNAFAA+P8LAAkA9v8cAKj/uv+1//v//P8hAIkAgQBoAC8AEwDZ/87/jv8AAAAASQCqAPb/QQAiAMD/8f8rAP7/o//a/7z/AAAAALf//f+P/0j/tv/8/w4A1f9LACoAj/+l/5L/8f/0/xoAcQAkAFQADQAKAOT/e/86AAoAPwBqAOj/WgARAPz/WAAQALH/QQBZALX/DQAcACkAIQDS/wAAAAAAABIAxf/2/xwA8v8+AEQAJADV/7j/tP/D/+H/5/+1/3r/FAC1/1YAjwA8AHoA4v/6//z/IADR/0gAAwDx/3QAk/8pAOr/3P8sAO3/AgDw/7z/t/8OAML/vP+k/8n/d/8SAGsAMQBfAN//HADN/8X/vv/d//f/+P/6/9b/FQDI/wkALAA2APX/QAA0AM7/DgDV/wEA3f93AAMAOgBTAJ7/RAASAP3/DwAeAPT/CAC+/6b/EwD9/zQABQAEAPL/hwA2APX/LQDc/xkAAgA5ABsAOwBnAC4AAADJ/+f/tP8MAPj/ZwBmAC0ApQC7/8n/CgC///H/9P/2/8H/FgBJAGAAOwAKAPf/iv/9//7//v8jANP/NwCa/2T/uv+1/+j/WwDb/6v/FwCA//X/GwBNAGMAKwAiAPj/CwAbADsALwCCAI3/7f8CAN7/iQCA/wYA4f/V/wEAAQABADgAUgDn/5EAq/8EABYANgB1AAIAlQD4/+f/2v9hAOH/sP9kAKz/4f+L/4//3f/2/wkA9v/m/8b/9v/4/wsALgBKALv/yf/T/6X/EgBGAF0AEwAQANb/FQARAOn/AADu/ygAsv/U/6X/7v87AMH/KQDr/7f/DgAeAAYA4f8LAMD/p/+U/6n/8f/i/40AqQDQ/7X/+/+y/6//PwAgAL//y//o/37/vP8AADcAdgCo/97/m/+c//n/+/+OAOD/+f/6/9f/uv///5IArP/O/w4AMADM/zEAcQDu//H/c/9q/+P/6f+2/6EA3f+a/1MAsP/3/woAdwAWADYAUQBBAFkASABxAKT/WwA3ACwAWwASAGoAVgBFABMAIQCI//z/IQDk/w0Ar/8aABUAEQDF/77/JgBDANv/9f/l/6D/IQAIACsA/////xEARQAlAIwAXwCC/5wAxv+t/8//2f9OAIf/HwDQ/+z/8P/h/0IAIwAcABYAbgDZ//P/BwAqAP7/2v9hAOH/i/8iAHcAlv+9/wEA3P8/AHv/8f/0/2P/JgD7/8X/0P/s/xQAkP/v//P/mf8IAPX/QAAhAK3/GAAUAMf/LQBuAA8ADAAcAOD/QgBHABQANQC9/wEAOAC//7n//v9tAA4A5/9HAN7/ZQA/AA4AZwCJ/8X/0f+j/0cAOQBTAB4ABgApAOv/pf/u/2AAFgDJ/67/h/+x/y4A7//N/yAAvv+U/+D/5/9sAEQAEgAzAPP/BwDP/2sADQDB/wQAzf9EACUA1gBQAOX/RgCm/8r/r/8IACsAEAAfAPX/m/+v/xoA3v9AAFkARwDx/8//6/8TALUASAA6ANT/yv9CAOz/cABbAMn/5v+h/2r/9v8cAPL/dQACAMv/sf+J/w4A+v9EADYA4/+x/67/PgBFAEoAqf8DAEwAmP/2/y4AlABSAPn/RAC2/x//8P88AB4A4v/D/6r/cf8fAAcAKgA0AAUA4P94/wAA7v87AGcA9//C/87/oP9qALIA/f9ZAEb/x/+//13/bADp/yQAQgD//+3/8P/P/zQABQDy/1AAif/Y/5b/qv87AFUARAAkANT/XP8OAB4AYgBhAPP/4/+f/8T/YwBPAC0A3P+Z//f/Lv8OAHoA4v9WAPz/MwAEAPL/GQABAF0AFAD+/7X/jP8QAPz//f9ZANr/9P/2/xwAzv+z/y8Ay/9VAFcANAAFAOD/QQDZ/wUATgAHAAYAPAD6/zEAXwAVAFsAAADb/+P/HwAZAAEAEwDH/+T//P/9/1kAIwD4/x4A4f8LANP/pP9bADcAZAA+AJ//1/+o/wIA3f9j/7n/x/+///H/PQDD/wUAYQC7/7b/sv8dAGEAKQDr/7f/of+O/9z/BwAqAOz/y//o////EQDp/9v/GQA5ANP/XADv/5b/YgA8AB4ABgBy/47/AACk/xEAVwBGAHAA2v/P//7/2f8qADQA4f/n/7X/1v8nAEQAyf8KAHcAu/+j////WwASAEUAJQCM//7/7P+VABwAqf86AJz/wv8EABYAkwBRAAoACAC+/wEASgBzAG8AEAAyADoALwABACUAVQBFABIAIQDS/6T/2v/i/2gA5v9+AC4Ayv8wAKb/JQDo/0gATAC9/8r/MAAnADEAhACg/8X/vv+m/6X/pf83ABkAFADI/5v/wf8EACgAfAAIAPX/5f+O/1sASgBOAFEAQQDZ/zv/9f9AAP3/DwAMANP/pf+k/yQAHQAXAIEAHgC9/8r/5/+1/wwAUwCNACgAsv/U/wAAAABKAOEAov/Z//P/rP89AEMAygC0/zAAAgC5/1kAyP+vAPr/DQDU/4D/LAC2/x8A9f/l/47/3P8HALz/XAATAOv/yv/V/6b/pf8SANj/zv9W/5z/5/99/87/RQABANz/GgCn//D/zv/q/zcAGgBMAOL/1v85AC4AJQCMADoAHAAWAMn/QgC1/1YAIAC//14Ap/84AMD/uv8jAJz/LwDL/7D/GwAWADYAGQA5ABwABAAVACQAQQAQADIAFQC2/7L/1P8TAOv/ggB7APX/GwAEADoAiwBLAM///f/r/4H/4/8fAOP/aQB5AM//NAAqANn/FwDK/9T/pf/c/z4A1//f/y4AJQCe/+j/7f9L/4IAHwArAH8AUv/j/7H/HACqAGQA5AA3AOP/xP/1//f/iv/9/33/lv90/3z/TQAZACcA+/8OAHj/bv8dAJf/YwA9AJ//6f/u/9//CQBkABkAJgAfABkAOQAuAFwAXQA4ANL/tv+N/3//KgBHABQAbADF/9D/7P9v/3oAGAAUAEcAXf/r/+//zv8zACkA6//v/5b/4v+x/9L/XAC3/yEArP+9/7f/jv+TAPb/wf8pAMX/rP9hAAUAOwBnAJv/HQCE/5z/jABeAJYAVACe/8T/4v8MAEEA6/+CANb/zP9pAAsAigCBAMQACwCb/67/Yv84AFIAMAA5APf/wv+X/77/SwAqAKH/RgC5/0X/fP87AEIAov9+AOb/2P/z/6z/KgC0/x4ATwBAAMb/5P8gAPX/igDv/+D/5v/Z/+H/5/8iAK7/UAAJANH/o/+j/0cA3v8uAO7/u//b/xgASwBPAHcA3/8cABcAAAAAAO7/TQAZABQAEADX/xUAkf+U/6oALQAAADcAUP8o/8H/TQDj/x8AGQDL/9b/y/8eABgA8P+p/xUAyP/m/0YAuP9GAMv/HgA9AOj/SAAVAIAAHQDh//r/1v+n/8v/CwDA/7r/7f8VAKP/2v8YAO//BADf/67/vv8BAAEA3f8tADYA4/8fAOP/w//0/z8AWAAPAEQAtv/q/zcALABIAKj/3v8tAMn/5v8iAEAAkAA8ADEAXgDe/wkA9v9TAHoABgAXADgA0f8jAGYAZQAHAPT/ZACs/08AZADj/9b/8f90AFz/6/8TADQAdAATAJEAmP8aAEwAGAAUAOz/OQCJ/7L/wf/O/zMATgCtANT/7//z/5n/dwBgAE0A9f+u/+P/jP/t//D/z/+h/yEA0v8AABQB3f8tAAAAf/8rANn/KgBHAIMARADJ//n/+v8fAD4AVwA0AAUA4P+c/8L/KQAhAC0AJACd/7D/rf/1/y0AbgBZAFn/sf+b/6//PwD8/+v/t/98/4P/5f8zAE4AiQDc/4b/nv96/wIAOQBlAHYAlf+F/53/sP8JAOP/xP/0/+T/xf/1/wkAGgDx/yoANAC8/8r/5/80AJkARAAAAJMAPwDq/9z/mf+cAGsAVgBqANb/AgA5ABsAOwBCAKL/x/+b/4r/xv/2/4oAOAAIAD4Asv9l/ygAIAA/AGoA6P8jAPj/HgCZAEQAyf/5/7D/rf8GAPT/LAAAAAAANgD1/y4AbwAiABsA3//T/8r/5/9HAPD/BQDy/xkAuf+i/yIALgBKADsAZwDA/83/xP/Q/9n/z/8zALz/XACl/9v/PgDp/24Aof/G/+T/RAAAADcAZAD1/y4Abf/4/8P/z/80ABcAgQCe/2f/4f95/5P/KADY/xYAyf/U/zcA0f8RAOr/yf/U/wAAyv/U/3AAWgCAADAA3f8IAD4AjgDy/wYATwC//18ATADQ/yIAif/q/zcA4/9EAO7/uv/I/5z/1P/K/8L/zv8OAPr/RABJAAQAOgD4//r/HwArALX/xP/0/1H/z//+/+z/8P8EAPL/vf/K/wsALgDK/1QAsf/4/0IAo/+kABUA7f8VAMj/CQA/AKEAggBEANv/q/+8/zcAUQAcACkA/f/+/2v/mv8uALf/DgALAJv/r/+I/8T/9P93AGAAAwDx/5j/BwArAP7/7P85AC4AAABvADQAGAAAADgAPwAOAOf/7P9eABQAIwAuALj/fP+6/yMALwATADQATwAIAL7/AQATAA8AVgDY/6j/lP+p/xUAEQBFABMA6/+l/7f/xf+H/x8ABgDP/6H/of/G/wgABgDh/wsAwP85/5f/PgDp/0kAKADF//X/if+O/+7/cQBbAFwAJQCw/63/BgBPAOT/VwDG/63/mP+//4MA/P9qAAwA+P8eALz/EgB9ANQAKQBZAOz/Xf8hAAgAGQA5AOX/s//C/3L/oP/F/1EAZgAIABkAlP+7/+7/KAAyACgA6v+l/zcAPgChAF0AlABTAHn/pf/K/1QA1v+DADMAzf9XANn/cwDv/5cAMACn/28Aov9HABQAIwBmAOT//P/G/+T/HwB2AEwAKwDs/4H/v/+C/4j/jgApAOr/JQBm/+D/LwAUAH4A5v+P/8r/5//Z/xcAbwDs//D/KQD9/zQAdAA4AHcATgC+//D/BQDg/9T/yv9CAOz/AgBLAPT/LQAkAEIAx/8bADsA5v9HAMv/HgArAGwAoQCCAFYAIAAaAKf/JgDo////2/+G//r/Q/+x/y4A7/8WABIAof/G/wcA9P9SAPn/VgAzAAQAAwDe/xsAKADq/+7/KACg/1gANAAqAGwAjf9bAAAAtv8gAOP/xP/i/7IADgD6/3sA9v9lABoAzP/W/7r/IwAJAL//3v/l/7P/1P/K/+f///+1//v/oP/F//X/m/8dAM7//f/+/8f/iP9W/5z/nf/n////7f+5/+z/AQAmAB4A9f8tALf/6v8lAEIANQD1/y0At//F/wcABQBOABoAJwAyAJb/qv8EABUAWwAkAPn/DADT/0oATgAsAJIAUQAcAOD/LwBwAEgAFQARALL/eP8lALD/QAD9/9n/mACw/wkArP+8/wAAt/8OANX/uP/G/+T/1/+6/7X/DQAvAN3/rf+9/9z/0f9/AAoAPwAzAKn/3//T/yUAVQB8AOP/6f/u/xUAIwAKAC0Akf/M/9b/OgBBACIArwBVAOn/7v+6/+3/gwAgAL7/y/+x/3b/2//1/y0ANwB1/+z/uf/Z/wUA8v8GAKr/3/8t/+r/EgDr/4EAw/9PAC0A7v8WAFsAbgD+/34ALgDc/+P/6f8SACAAPwBFAEoABAADABUA2//i/8P/z//Y/3L/xf/Q/xAAewBRAEEAIgDl/9j/BAAVAFsAJAAdAPP/5P/8/+r/gQBDAEgA8f/Q//7/2v88AOj/SAACAMz/6P+2/w0A1P9KADwA5/+1/3r/8P8qAOv/EwAiAK3/9f/S/+7/3//l/yEAv//M/8T/hwBaABEARQCT/wMAAgDe/1IAVQBEADcALAA2APX/0v+S/97/CQCs//T/5P/8/w4ACwAJAKz/vP/u/9//CgBkAAcA9P9kABkA8P+8/9z/9f/4/zAAOQAuABIA/f8iAOX/xf/R/9r/BQDz/ywANgAZABQANQAGAPP/4/+x//j/1f85ABsA8v8GAAUAOwALAFIA1f8BAF0AEwD+/8f/wP+6/1oAAADJ//j/1f/L/4z/RwCn/zgAQADG/1EAd//u/9//rv8+AEUANwAaAF8AFQAjAAoACAD1/+X/DgDC/zwAVQAgACwANgArAEgAJwAyAE0Aq//h/zAA8P+F/+b/RwAmAAwALwBLAIX/HQC8/23/ZgCI/7L/+P+e/wwACgAaAPH/vf8AAMr/5//s/93/PwAhAAgA4v8MANP/t/+0AGwADQAdAPT/rP/h/wsALgA3AL//8P/h//r/MQAVADYA9f/S/1sASgDO/zMA8v+Z/7//8f/0/9H/7f8nADIAFgBbADcALADt/9//+P/U/+//zv/9//3/DwDo/0gATQCZ/z8A6v/c/2MAvf8mANX/y/+NAAMAzP/p/6P/EQANANT/7/+p/xUAIwCc/zAAFADa/8//6/+4/yEAdwA7AHkABQDg/9T/XQBdAAEAXQDw/3MA7/9zAEoAlv8ZAPD/FwCl/+7/uv8jAAoAmv8uAJL/AwDM/8T/4v/D//T/9v8cAPP/YwD1/wgAPgDX/xUAIwDU/8r/MAAmADEAOgAvADgA0v8AANv/4v/D/3P/2P8EAN//HAApAOr/AAATANj/qf/f/xwA8v8rACMA5v/9/w8AHwAGADwAHgBiADwA6P9IAKf/OQAuAAAA7v/N//z/xf8aAHEANgD1/xsAlv/i/zAA3v/l/7P/1P/d/wgA0P8QAB8Avv/v/87//f/9/1kAIwAcADsAQgBIACcARAAAABIA/f/+/1oAIwDB/+D/iv/G/2QA0P8iAPj/wv+8/+7/FQC2//z/2P+W/8//6/9u//n/HwB0/8b/CADi//v/DQD5/2gACgAbACgA1/9NABkAOQD3/8L/4P8LABsA3/9TADEA3v9AANj/qf/M/7L/5v8PAOj/tf8fAKv/4f+eAO3/TAAGAPP/4//X/wMAFAB/AOb/WQA1AND/owAnAMT/GQDd/wgABgCX//b/+P8LAPf/1P/K/wsALgDu/ygA/P8PADEA3v/l/yEA9v8vADgACAAGAM//NADh/0IASADe/y4A7/8DAKf/3v9SADAAJgAfACsA//81ABkAAQBdAHAANQBQABsAAwADAPH/PADD/+H/1f+U/2AAFgDu/ygAjf8AAAAAyf/4/8P/FwCl/6T/2/+G/+j/IwB4APP/mf/A/xUANgAGAGEABQAWAEkA8v+r/7z/2/8ZADkA0/8SADMAzv/Y/83/e/+n/yYA+//8/+r/kv8DAPH/KgC2AEgAOgAvACYA6P9IABUAIwBUAJ7/aQAdAM//DwDV/wIAy//6/3r/uf/s/8v/QwAAANv/4v/W/97/CQAHAAUAu/9//+L/sP8JAFEA5v8hAC0A3P8sAEgA3/9TAAsAm/9CANr/4f8LAK7/0P8QAFYA6v/c/xoAOQAcABYAbgB+AHgABAADADoAnP+L//7/kP+T//L/4v/o/7b/+//Y/9//HAApADMAvP/u/7r/yP+b/6//LAAAADYA9f8bADsAwv+X/+L/+/8NAEIAIwD4/0IAbQAzAAQAOgB5AAUAFgAkAML/8/8HAD0A6P8jAEEA7P85AOX/RQBvALT/1v8CALn/NADP/9j/KQDG/2QABgAqAEcA8P8XAAAANwDR/9r/4v/D/3QA8P8pAOv/bv/5/57/jP/a//T/v/+5/9r/BQDy/6v/KgD+/xAAMQDx/73/EwBZAEgAOgAcAHMA7/8WAAAAkv9MAOL/VgBFAAAAlAAtAMn/CgBkAKz/4f/n/+z/OQAbAE0A9f/T/wAANwAHABgA7//O//3/2P/z/xkA3v92////7f+6/0cAuf/H/y4A7v8oAGoA6P8QADIA8v/1/63/9f8IAD4AVwAhAD8A6v8lAB4Aqv9NAFEA5v8hAPf/+f9DADYAYwArANn/KgAiAAkAYwA9AMT/4v/o/6P/IwAuANz/9v+J/47/7v8DABUANgBQAEAANADO/w4A1f9v/wsAif/F/+P/1v9xANv/BgDh/3j/uP+z/wsA9/8dABcAAAA3APb/5v80AE8ACACHAEgAOgBUAOj/WgDb/9D/IgCu/9D/IgD4/8L/KQA0ADwACwDl//3/xv8IAAYA4f/n/7X/sf/T/xIADgCNAHEA7v9MAOL/DAAcAKn/8f/i/4v/kP/d/z8ADgCd/1YAMgDg/0EAx//S/7b//P/9//7/NAAYAIIA6P8jAAoACABQAOX/awDW/wIAFAAiABwAqf9MAND/tP/6/5//RQAAAKX/NwAHAE8A9//C/xcAt/8zABYA7v9fABUA2//i/+j/2v/0/9L/7f+6/7X/+/+y/5z/wv8qAA8A+//E/+L/+//E/+P/MQAVAMj/UwAxAAIAJwAxAAMAFQBIAMz/aQAwACYAHwDQ/zUABQAEACgAfQA/AFgADwCf/8T/vf8mADEAOgAcAM7/oP+z/x0AvP/u/zsAnf/C/wUA4P/U/4D/vv/d/9L/7f8nAEQApf+2/w0A1P/L/wsACQDR/+3/AgDd/+T/agD6/9b/AgACAF4AFAA1AD0An/8NAAoA9//B/7v/JAD5/1YA/P/G/9H/2v+ZAOn/EQDq/5L/8f/P/w8AZ/8XAEoAl/8rAP//EQAyACgAWAD+/9r/TwA/ACEAGgCV/8///f8iAC4A7v87AEIA/v8jANP/AADc/6z/FwAAALf/6v8AANz/LAA2ACsAIwAJAPb/+P8eAOH/1f+m/xMA/v9HAM0AgAAwAPD/KgD+/+z/JgAfAL3/gf8sANv/9P8tACQAVADp/wAANgDQ/xAAxP+9/28A7P85AEAADwCNABUAEQDq/9z/GQACAN3/9/8vACYAQwC3ACUA5//s/97/ZQBRAAoA5P8yAAQA3/8JAAcAYgAYAG8A/v+1/zEA3/+u//X/wP9e/7X/+/9FAAAAXABvANn/FwDK/wsA5f/9/+v/bv/n//7///8QACAABwAYAN3/0f+j/7X/+//q/xIA6//v/83/sv8KAEAA/f80ACoAxv/2/9T/AACl/9v/vv/w/04Amv8uANz/9v/l/47/bgCh/w8AaACd/x4A4f/6/x8AGQAmAPv/MgCE//j/HgDP/zQABQApAP3/RgDw//P/PgCy//n/w//h/wsAGwDN/0UANwD2/2YAv//f/8D/uv8RANf/lf8FAHMAAABKACkA6//K/+f/bAANAFQAHwAGACoA6/9wANr/mP/j/3r/lP/h//n/nv/E/9D/x/8IAAYATwB3AE0APgBFAAAASgApALP/wv+p/wMAp/8BAO//zv8zALv/NgDQ/zUAYgA8AAwAd/9JAM3/VwAPAHn/XQDL/1YAMgDg/0EAov99/+D/+f/W/zkA+P9VAFcA6v9cABMAtP/o/9r/qv87AOf/IgAuAFv/MgDg//n/DADl//3/xv8IABkAOQBTAFUAHwBRAAoACAA9ADEAKACg/zMA8v8HAGEABQApANj/8v/1/wkAGQAUAOz/8P/z/9H/SAA6AFMADACc/wsAGwBNAHUA8f89AB4AmP8/APz//f9HABQAIgD4/x0AGADd/1EA+f/6/3sAh//W/ycA1//M/3r/8P+X//X/LgASADQAvP/c/77/3f/S/yMAQQDZ//P/9v+u/yv/sP/A/9//QQDr/10AcABaAIAAHQD0/9H/o//a/xgAJgDo/+3/3v8JAOP/DQAvAO//KQAhAGQA4//p/9v/q//O/9j/8v+G/x4AGADL/9X/3f8bAPH/UADl//3//f8PAEQAyf8cAAQAg/+c//n/6P///9r/q/+7/3//BgAXAKX/pP/b/5j/iP8yAF8AFQAkAEEA/v/a/xgAOAAtADcABwDi/zAAzP8MAFQA+/8NAB0A8/8HAD0AaQB5AE8A0v/b/+L/1v8nAB8ABwDh/7D/GwC6/6P/SAC6/xAAVwDr/wAAEwCiAEwAz/8hAAgALABaACQACgAIAOP/RAAkAOf/RwAnADEATQBjABgAOAAtAMn/LwABACYAMQDx/wUAOwALAPf/LwC4/+v/EwCP/6X/JQDn//7/NQDQ/8f/mv/4//r/xP8YAPD/FwDc//X/GwDN/yAAPwAyAPL/mf/k/w4AsP8aADoA5v/Z/6n/zP/p/+7/uv8jABwAu/8RANj/8v/i//v//P/q/8r/HQAXAKX/SQDg//n/HgD0/2QAPgANAAsALQA3ACwA7f8CAEwAPQD7/8T/9f+t/+L/VgAzAOD/LwA4ANL/JAAvACYA6P8RAMX/vv8mAOj/EQCy/9T/yv/C/zwA+v9WADMA4P8dAM7/s/9CAP//2v9PAPf/1P8TAFkA7P8nADIAlf9PAAgAGQA5AAkAUQCv/9H/IwBBAP7/2v9hAKn/FQBIALr/yP/A//L/vf84AC0AAAAAAKT/AAC2//z//f9X/9T/y//V/yYADAAKAPb/+P/n/+z/8P/h/+f/tf/7/2kAsP/k/1gAj//v/wQAKAAgABoAAgDe/1IA1P8BACYA+v9EAO7/zf+f/yAABwDi//r/MgBNABkASwD0/1IA+f/6/x8AYv9KABcAyv9CAFoAAADt/18AAwBeAKf/y/+fANv/UAAuALf/6v/v/wQAOgCv/9H/WgAAACQAZwAuADcAUQAvAO//qf/x/z0A6P8RAPz//f/Z/+D/CwCb/woACAAZAEsA9P/2/woA0f/t/14AJwB8AD8A6v/u/4P/0//c//X/QACz/4v/NACq/83//P/q/1wAk//N/8X/q/8FALv/JADm/+v/SwAqAA8AaABmABsAFgAAACQACgD3/8H/BAAWAO3/lgBmAPf/+f8MAAoA5P8NAAsA0v/J/woAv//x/zwA6P8RADIA4P/m/2sADQD5/0MA2//P/9n/BQA7AAoA0v8AADYA0f/a/z0A+v/E//X/5f8gAL//JwD7/7L/HQBy/+r/EgDr/yUA6P8jAOb/xv8sADYA9f/l//3/6/+4/0YAJgD7/+n/kv8nAMT/9f/3/4r/2P8EACgA/P8PAMP/9P8tAMn/+P8eAOL/w/8FAJb/mP8IAND/tP8xACcA6f8kAAsAGwAoAEUA7/8WANv/0P9sAMT/BgDh/9X/JgAMAAoACAA9ALH/HABgAOD/+f/D/xgAEwBGAHAAIwBTAAwAUwBDAMj/HADg/woA9//5/x4Aqv87AAsAGwAoALP/+f/o/yMA5v/r/yYA+v/X/6f/FADa/+H/ZwAuALj/RgABALj/ogDw//P/UQDm/w8A6P9bACQACgAIAPX/LgASAGsAMQAoACAABwArAOz/AQAmAB4ABgAqALT/w/8FACkAIQCt/+L/w/+q/6j/cQAAANv/UAB2/9v/mP8IAD4AHwBQAOX/IQAIAND/2f8qAMb/GgCEALP/1P/v/7v/AAASAKD/2P/y/+P/w//i/9X/b/9nAFMAw//0/wgA0P+P/zgAZAAZABQAEADp/23/HAA7APn/aADm/zQAKgDr/0sAzv8zAPP/4/+f/43/2//1/0AAs/8dAPT/9v8cAM7/xf8sAP//2/89AMT/UAAJAPX/ZQAIABkAy/8xABUAfwBUAB8AGQC5/+v/7/88AOf///8jABwA4P9UAB8AKwA1AL3/lACb//j/6P+j////Wf9DAMj/wf/N/7L/+f/6/x8A9f8JAJn/CQDj/5//xP/1/3b/tv8yAIP/LgATAEYA8P8EABYAf/9iAJf/YwAGAJf/PgANAHkAmP9jAOL/+/+hAN3/dgDf/y4A3P/j/x8Ah/8xAPH/KgD+/9r/TwBSAFQAMgA6APn/w/+q/+D/+P/V/zkAQADG/9H/2v/P/8b/0v8AAMj/0/8AAO7/FgA2AOP/6f9JAPL/KwA1AOL/MADM//v/agAwAF4AAgDL/2gAHAApACEAGwCEAP3/kABiAKr/FgAAAO7/8f/P/+v/3f/k/+n/2//Q//7/7P/e/xsA3//B/+D/HABhAAQAAwAnANf/zP8yAAMATAA9AAwAiwC5/8f/9/+v/xoA3v8JAAcAGAA4ANL/tv/p/yQAMADw//P/9v8JABoAuf/s/wIAFABHABQAEAD8/yAAUQBmABsA3/+v//b/CQDj/1cA6/8AAEoABAAoADMAKQD9/yEA5f8OAAsArv/j/9b/AgDw/7z/7v+6/8j/rv++/zkArf8GADwAZ//h/+f/7P8UAP7/EAD8/zMABABNAPX/if8yAPL/GQAUACIAZQAtABIAMwBzAMr/+f/7/w0AHQAFAAQAuv8jAOb/NAAqAP7/WQARAMX/vv/w/5f/GQCm/4D/9f/4/zAAAQDw/5f/GQDe/9L/JADm/zQABQAEAN//LgAAAMr/MAACAN3/5P8NANT/3f8aABUAtv/7/47/pP8RAOr/EgDG/xoAzP/W/xUAyP9AACEACAAZAEwAz/8PAB4Ahv8wAAIA3v9SAB0AvP8lAAsACQAZAMz/DAD4/zAAgwAgAPb/UwD6/+n/JADm/w8A+//p/7f/1//y/xkAOQAuACUAMABLAPT/CAArACMA+P/6/wwACgAtACQAVABEACQALwBLACoAbAB8AD8AoQAmAB4AGADw/wQAAwAVANv/9P/S/8j/QQDr//D/4P/C//P/4/9WAOr/JQBDALX/MgCV/+H/w/+q/wMAp/8BAKb/NwAIAIb/CwB3/3//BgCp/7r/IwB3/7f/IACa/67/9f/S/5L/AgDw/xcAEwAhAGUABwAYABMAWQDI/0AAWQDa/6sA0v+3/+r/7v/y/9D/NAC8/+//u//I/xwA4P8vAF0AJgAMAJ0ARwC7AF8A8f90ALn/NAAqAFkAIwDm/+v/gP8HAM//6/+4/9j/zv/Y/2AA8v89AJ//xP+r/6n/FQARAFcAof80AAUAKQBGAAEAXQDv/xcAt//Y/7v/o////8j/5f9X//n/nv96/wIAlP+7/+3/JwDX/zoAHADO/2oADAAJABoAFQBbADYABwAYAAEAEwAiABsAAwDx/wYAvP8kAPn/DAB4APP/GgDx/wUA8//Q/8f/wP8DADkAUwAMABwA4P8vABMANABhAAUABADf/+X/xv8sAEkAKAD8/9j/BADN/zIAOwDU/7j/6//K//n/VgAzADsAVQAfAOP/DAAKAPb/QQAiANP/SQAoAMX/LAD//yQACgAbAMz/HwD1/1H/BgCX/xkAOQDl/1gA/v///9r/GAA4APf/VABEANv/9f/S/xEADgCe/9b/8P8XANz/BwD0/+T/RQDK/0IAWgC2/w0ACwDS/+7/8f/0/63/z//Z/7z/2//1/0AAs/8wAEwA9P9kANH/IwD4/x0ABQDO/+r/AABKALv/JADU/+//KQBX/y8AuP+P/yUA5/8jAAkALABtAOr/OAAtAO7/KADX/9//+P/6/8T/hv+d/7H/0//J/+b/tP+e/wwAwf8WACQA5/8iAMD/OgAvABMARwA5AK8A+v9EAO7/8v+HALX/aQAwAPD/4f/U/zgAm/8cADsAHQC8/7f/RQDK/8L/BQDy/wYABQCW//X/0v9s/0EARgAUABAAMgBfAM3/+/8gAJr/wP8VAJH/p/8TALT/DADB/7v/SAC6/yMAUwDo////SAA6AC8AOADS/wAA7f8DACcADQBUANb/AgDw/+H/VQAyADoAHQApAOv/3f8IABgAAQDd/+T/1/8DAN7/CQA+AOn/NwAsAP//AAARAH0AUgAvADkAGwAoAPz//f8PAPv/1//f/y4AAADc//b/5f/9/6L/xv8IAAYAFwDv/ykADgALAFMACwAuACUAwv8FAAQA3/8uAAAA7/8WACQALwDw/4T/5v/G/+T/RQDv/xYA2/8ZAAEAy/8eACsAfgDm/0YAcAD//1oA7v/f/+X/6/8AAAAAEgB9AAkA0f81APT/GwA6AOb/DwD7/+n/AADJ/x0ATgDR/yMACgAIACsA7P8CAN3/0v/t/ycAIAD1/9P/pP+R/8z/6P/I/+b//f80AM//fP+o/7n/EAANAEIAWgC2//v/jwDz/9H/EADE/9D/IgAuADcAPwDq/9z/h/+e/0QApP/I/woA5P8yAPL/9f/A/8z/+/+z/y8AFAAiAEAA/f8iAIn/6v9cAKX/SQAoALP/QgC1/zEAOgDB/2AAzf/8/+r/7//g/+b/IgB2/zYAGQDw/wUA8v/Q/5D/EwD+/1oANgA+AEQAAAAkAB0ATwAbAF8AFQA2ABkAy/9oANT/SgBOAKz/KgDZ//P/LAC2/+n/2/+r/zwAQwDa/z0AMQADAAIAAQDd/+T/fAC//wIAAgBK/wAAyf/m/8f/LQAkAK//v/9d/yIA5f/F/+P/6f8RACAAZAAZAHAAIwDm/zQAFwDv/wQAKADX/xUAAACR/xQA///a/ysAov8iAAkAGgBxACMAHAC8/8n/+f/o/+3/XgAUADUAKwDa/yoA6//v/87/IADk/9f/AwDx/xgApf9KAPL/vv+4/w8AMQDM/0QAAABcAAAAEgD9//7/IgD4/zAAFADIAA4AQgARALL/ZgCt//X/5f/q/zcAv/8nAA0A1P8AALf/MwAEAE0AiADt/18AJwAyAPL/9f/3//n/HgDQ/0cAAgDw/87/6v+3/9j/FgB//6v/X/+2/7L/5v8hAPf/5v/H/xsA8f/0/9L/JADU/+//OwCd/0MANgBQAC4A7//y/6v/zv8OAJ7/nv/7/+r/7v+6/8j/0/+3/9j/zf/F/1AAUwAMAC4AEwAhANL/NgAHAPT/UgAvAF0AAQAmAPv/6f8kAPn/+/8yAJcAMABwAEgAJwANAJ3/+v8NAPn/sP8JAFEA5v8hAEAADgALANP/EgD9/8b/PwAzAM7/2P8DAJX/BQApAP3/IgDS/wAAyf/m/8b/rf9z/7P/MABv/3oAUADT/1wAyv9CACMA0/8lAAsAUwALANP/AABt/+b/6//K/1UAxP8+AMT/vf9dAO//8/8sAG0A/f80AGEAFwAlAB0ATwC//ycAaQDn/0cAOQDl/yEAPwD9/w8A+v8gACwAEQDX/83/1/+6/yMAQQA0AJf/4/8NAHj/EgCz/7D/9//U/+//8v8+AA0A5v/r/wEAAQAAABMAIQDl/9j/qP/M/+j/yP8cADsAjACDAA0A5//Z/5f/4//p/wAANgDj/1YAxf/R/zUA4v9oAAoA5P8NALD/df/a/4X/sP/k/43/AADJ/+b/2f/z/wcAKgD+/yMAUwCw/3cAzv/q/zcA0f9tAPz/DwAMAEEADwAMAC8A7/8WANz/9f8JANH/IwAuAF0AbwAQAFcA6v/v/zsA1P/v/87/agAxAAIAAgAUADUAqv8pACEAUgAdAPP/PwDF/+P/DACv/5r/QAAPAAwAQQAPAEMASQDy//X/CAC+/xQANQA9AEMASQDN/7L/CgCt/wYA8//j//v/DgDn/9r/9P+s//T/0f8jAC8A7/8EALr/yP/l//3/DwAxABUAWwAAAAAAAADu/ygAoP+PAGEA8/8+ANf/8f+G/+f/RwDe/9L/NwAHAM//WQD//9r/vf+3/+r/pf/J/+b/DwDo/8j/+P/n/0cAJwANAC8Ay//6/9b/AgA5AEAAIQAIAFAA5v99AHcA4P/5/9X/8P8FAE4A9v8cAE4A9v/4/zAAOQDT/xIAs//5/1YAjv/J/woACADi/wwAHADz/9D/7P/w/6r/zf+y/+b/6/+m/yUA+v/W/ycA/P8OAB4ABQDz/wcA9P+t/8//2f/h//n/w/+F/7D/v/+5/yIA0/+3/w4AsP8IAFAA0/8lADAAFAA1AE8AQAAhAD8AIQBkAD4A1/8oAOn/EgAzADwA+v/7/+r/EgAOANX/AQC4/+v/7/9gABYAt/8gAIf/RAA3ABkAAgDL/2gAr/8sAEgAFQA2AAcABQDg/x0A4f/n/9n/z//G/7//JwD7/+r/3P+s//P/GgDx/wUA4P/n/yIA5f/9/zQA4f/5/zEAFQDt/97/CQC+//D/8/8aAEwAvf8TALT/1f8BAPD/YQDz/2MA4v8MABwAu/+SAAcABgA8AOf/NQBiAAUAKQAzAM7/RgBKADwAMABMAM//2f/z/5n/rf+Z/z8A6v8lADAAy/9DAO3/cQDb/9D/IgBAAFkAtf9EADYAYwAGACoANAAXAJQAwP8nAPz/6v8lAOf///8QAPz/MwA7AML/TgCa/4n/2P9e/9r/z/98/6j/TAAYADgACAAZADkACQAsAKP/bQD8/7P/HgC9/9z/9v/l/9j/KQCh/8b/PwDX/83/1/+V/+H/wv/O/+v/pf8SAP3/DwDW/8z/MQDf/0AA/v/s/wEAAQA4ABsAg//S/xIAs/8dAJf/mf/A/zoALwABAF0AuP/r/+//YAAWANv/PgD7/yAAPwBXACIA9/9nAC4Ayv8dAPP/9v9TAFUAIAAsAEgAOgBBAOz/XQDe/9L/EQAOAAsACQBRANP/NwAIAPX/5P/q/5MA9/8vAAEA7/+E/xwAFwBb/zIA4P9mAPf/+f9DAKP/EQD8/w4A+v8NANT/pf8SANj/qf8CALn/a/8aAPH/KgAQALH/HADO//z/DwDV/97/CAD1/9L/2/8rADUAGABLAE8AZABRAAoA0f8jAC8ASwBhAM7/IAAaAKf/y/+e/3r/pv9u/+f/2f/O/2sA1v9MABgA3f+bAI7/NwB2ALr/IwAKABoAAwC5/xAAVgBGAG8A/v/H/8D/zf8fAAcAvf83AAgAhv96ABkAAQBdAPD/TgDR/yMAQQBHAHAA2v8YABMA2f8XAEoA8/8ZAPD/9P8sAGz/CQAHAL3/EwAPADEAlf/h//r/jP8jANP/AAA3AOT/fAD2/1MADADl/0YAy//n/5D/8P+8/7b/DgDV/xMA/v9sAA0A5/8QAIz/tf9EAKT/EQBYAOv/OADS/xEAe/+V/yoARwDe/5v/HACE//j/nv+e/w0Ar/8aAMz/1v9MACsAx/9lANH/IwB4AM7/WAD+/9r/YQAqAMb/dgAoAA4ACwD3/3kAqv9NAPb/HAAWAJL/3v+J/2oA1f/L//r/sv/T/+//4P/U/zgArf/0/+T/sv+K/3z/AwDf/xwAcgAlADAAgwBFADcAPwDX/9//HAAXACUAHQD0/ywAJABCACIAwP/y/wYABQBOAFEACgAIAOL/QwARAPz/awDo/wAA7f8VAO3/p/8mADEA8f8qAFkA///b/wYA8/++/yYA+//8/yEA5P8gAPb/5f/9/zQAPAAxACcADQAdAE4AdgAWAO3/AwAUANr/9P/2/8H/BAADAAIAy//W/6f/EwAiAK7/KwCQ/93/PwDq/yUA5//a/8///f9ZANr/qv9NAL7/uf8PAEL/n//W/4L/5f/8/+v/7//N/8X/GQAUAOz/AgC4//7//v8QAPv/xf+tAPn/MQCWAPn/aADB/wQATQDi/wwA+P/6//v/RQAAABIA6/8BAEoA8/9jABkAXQAmAMT/KwDZ/7z/7v+EANj/4P8dAM7/RgDd/ywANgAHABgAAQDd/7//JwCx/+b/2P/z/2MA0P8PAOj/tv9XAP3/j/+l/xIAof/r/0oAl/8GAPT/9v8uAKX/XAAAANz/YwAGAAUAOwAdAAUA8v+Z/9L/AADu/ygAMgC7/+3/FQDa/xgA7/9OAJsADgAeABgA7//g/8L/KQDr/7j/6//v/zsA+f8eACsAtf/D/8//j//K/1UAMgByACQA+f8MAC8AXQABAIIA+/+N/9v/GQDw/5f/PgDp/7b/MgAEAPH/GAAmANb/y//7/9f/8f/P/33/zv/X/83/MgDy/z4AMgCo//D/8/+s//T/9v8cAE4A5P9EAFwAEwA0AGEATgAaAIQA6v8AAAAAf/8+AEQANwAHAM///v8QAB8A9f+cAMb/5P9FAFv/jwApAHz/TQDj/2kA+f8MAHgAhf8dADwA1f/w/04A5P9D/x8ArP/O/zMAzv8hAOT/xf/Q/2wARQAAAG4ADwAfACsAEAD7/8X/4/8NAOb//v8iAOX/DgDV/8v/MQDe/wkAGQDM/x8ABgC8/xIAIQDS/wAANgAZACcA6f82AIf/sf9AAHz/BADx/xgA3f/2/8H/lv89AMT/PQAfAAYAqv/y/3UAFABaAJH/JwBEANz/UABTADAAFQAQAA0AeQA9ADEAJwCf/+r/AADc/wcAhf+d/8P/qv8DAJX/KgDr/6b/yv+L/w8A1v85AOX//f9GACYAjQBfAHIAJAAwADkA9//U/wEAJQAeABgAuP80APP/4//8/7P/eP/v//L/Yf/v/5b/vf/d/+T/DQAdAHMAuP/G//b/rv8HAAYABAADACgAIADR/xAADQCd/zAAAgDe/0AAIQBSAB0A8//j/w0ACgD3/x0AKQA0AE4APwAOADAAy//o/1sAEgAzADsAQgAjAHgAFwAAAG8Ax/+a/9P/JQDC/+H/1P+T/7v/yP8KAOT/MgCo/97/QADG/7//3v/A/4P/GwAWACQALwDd/9L/EQAzAOD/HQApAFkA2v8qAFkA7P8CAPD/KQC0//r/DQCv/9H/SAAVAMj/UwBDABEAMgA7AJ3/sP+t/4b/QwDt/8z/xP/P/8b/dv9Z/3r/3f8bABUAJAAdAPP/iABJAN//HAApANj/KQAzAHL/xf/j//v/DQALAC0AEgAhAL//JwB8ABoAAgA5APj/HQAqAA8AewCs/3L/RQDK/7D/LQC3/yAABwDP/zQA9P8/ANf/KACPALz/XACUAOT/IABkABkAAQAmAFYA1/8DAN//0/9cANz/UQBmAPf/LwDL/8P/9P+s/xgA7/8EACgADgBVAOn/7v8VABEAxf/j//v/xf8+AB8A0P/s/zkAGwAEAE0A9f/A/wMA3v8bAN//HABzAKX/gQDV/7n/yADq/8n/5v8iAMD/AwDe//f/+f+x/xsAlv8rABAA+/9FAO//KQAOADAAAgA5AGUACADQ/w8AxP8YAEsAcwA4AIj/6f+S/ycA6f8SAEUAk//y/2H/3P/R/+3/FAD//+3/uf8iAPj/ZwD4/9X/OAAIAD4A/P/F/+P/xP/1/2UA4//7/9f/g/9k/7r/EADX/18AFQD//+3/p/9LADwADABBAFkANQC9/xMAawCx/xwABADN/zIA8v9iAPT/5P/F/5n/CACG/zEAAgCC/z8As//5/0MApP9bABIAxf9RABwABABgACgAs/9CAOz/uf80APT/9v/4/7D/CAA+AMT/KwAQAMT/KwAQAFcAMwDz/2MA4v+x/y4AJQDn/xAADQAdALz/pP9JAIQADgCw/2UArP/h/0MANP8mAMP/qv8WAH//vf+4/+v/AADc/+P/+//F//X/LgAAAAAAEgBYADUAYgA8AAwAZgBkAD4ARQBKAJb/KwA1AAYATgDk/yAAvv/e/y0At/+g/3v/qP+5/9n/FwDc/6z/9P/2/8H/AwAoACAALABbADcArP88AEMA7f9MAND/x//k//z/s//V/93/rf8YAO//KQAPAOj////t/14AFQAjAC8A7/87AEIA//8jAFQAHgAGALz/3P/1/9P/XAASANj/OwAdADwAHgAGAHMAEwDZ/wQA4P/4//r/HwCIANv/GACCAJ//RABuAKH/DwDW/ycAMgCo/0wAmP/R/zUAYf8lAOf/2v/h/wsAigDK/+f/////////IwB5AAUABAADAMz/DQAvAN3/UQAdALz/SQAWAFsA7v+o/wIAb/9DAEgAuv9tAPz/s//C/wUAKQD9/0YA3f8tABIA2P87APn/HgD1//f/ZgAJACwA7f+U/xcAbf/B/xYAkv9fALr/2v/P/3z/FgDJ/0EARwACAF4A8P8FAOD/1P8TAMb/PwAOADAAOQD4/zAA3v/3/9T/JQDo/7X/DACK/w4A+v/E//X/CAC+/7j/6/+4/0YAuP80ACoAj/9KABcAAAAAABIA2P8WAAAAt/8OANX/y//6//v/xf8HAM//j/8AALf//f80ALz/JQBnABwA8v9jABgAAQBvACIALgAAAEoAzv/Y/wMAcP8xAAMAAgAmAGkAQgBr/z8A2P+7/+3/3/9lAPb/0/8SAOv/7/87AOf/kP8mAMP/qv87AML/FwBKAOD/LwDL/x4A4v+e//v/xP/Q/9n/PADV//D/BQCo/97/rv/j/9b/8f8FAKn/KAANAAsAGwBNAFAA0/9cAFwA3f/2/woA9v8cABcAJQB6AGIABQA7AFUA+//F/9H/IwDT/wAAbgDG/3X/tf+x/5z/5/8QAB8A0P99/6n/S/+m/+//YAADAAMAOQCJ/2oAVQBXAA8A6P/JACEALQA3ACwASAAVAEgAKABFAKYATgAaADoA+P9VACAALAA2AOL/HwArADUABgDh//n/VgAzADsAZwDT/7f//P/r/+//KQAOAPr/1v8VAP//2/8GAM7/DgAeAKr/qf8VAH7/BQApAI7/NwCa/+X/IQDk//z//f80AOH/QgDt/wIAy//D/3QAy//6/w0A1P9KAPP/4/8fAPX/QAD9/9n/8/++/yYA+/+g/6D/s//U/wEAJQAwAPH/9P/R/+3/XgDM/x8A0P+Q/yYA6P81ACsAx/8bADsAwv8EAF8AAwAVAP//EQCy/+b/2f+8/wAAkv9MAOL/1v85AMD/AwAVABEA6f9cAO//AwBxAO7/8f9z/2r/0f8jAMH/FgA2AKz/TwC//xUAtf8w////tf8xABUAEQBXANn/zv8OAMP/4f+MAEwAdAAmAAwAZgAbACgA1/+7/+3/zP/W/ycAMgDN/7L/ZgD3/9T/JQCL/+z/AQATAGwARABuADQA8//R/xEARQAAAEoAzv+g//3/6/84AOT/xf8HAPT/GgDx/08ALQDJ/woAUgDn/+z/SwCF/wsA9//U/wAAt/+QAE8APwAOAEMASACn/0sAGACCADEAAwCWAK//4/9EABIA2P+W/z0AHwCr/zwAVQCy/0EA7P/L/1UAjf8RACAArP/0/9H/EQDq/xIAawBDADYALADa/xgAEwAiAIoA7/8pAH0AQABGADgAQADY/ykARgAmAB4APQBWANj/FgDu/wMA3v92/0gAzf+y/9P/gP/j/8T/GAC4/9n/FwDc/+P/xP+HALX/jf8RAI3/AADt/ygAIACH/9b/cQBIADoALwDv/zsAwv/O//3/tP/D/+H/CwDS/yQA5//H//f/VAD7/8X/YwCr/wQA8v+9/xMAtP/V//D/vP/u/xYASQA6AMH/OwD5//v/VwDG/z8As//U/wEAJQBVAMX/GQCU/wQAAwC6/0gAp//d/7//AgBwAH7/PABVAFb/CgDR/6P///8RAA0Ar/+//6f/3f+I/+n/NgDQ/5EAmf/S/zYABwBhAJf/0P+1/wwAQQC0/wwA+P/V/xQA7P8UAEcATACHAMf/9/9CAP//7f8UABAA/P9qAPr/RAAAAAAASQDN/8YADAAcAJgA+v+y/5z/1P+4/yEACAD1/9L/2//j/+j/yP+J/zMA8/8+AMT/q//z/6z/PAAeAPT/rf/i//r/xP8GAM//of+h//3//v8QAFYAMwAXABIAIQA/AMX/9v8JAOP/VwD9/1kAfwDU/9z/4/8yAF8A8v89AGkAwv88AGcA+P9CAG0A/P/Y/wQAg/8JAAcAz/80ABcAAAAlAB4Aqv8EAN//+P9CAO3/XgAUAO3/gwANAAsA5f97//H/mP8IAFAA0/9JAOD/LwATAMf/rf8GABcApf9JAAQA8f/0/xsAAwDx/yoA7P9LABcAJQALAC4ASgDz/1EALgDK/4v/DwD7/43/yP8cALv/tv8yAPL/0P/+/yMA+P8dAGEA4f/V/8v/1f8mAOj/AAAkAOb/NAA8AAwA+P8LAAkA0f/a/wUAFwDc/wcABQA8ADAAy/8xALr/IwBBAP7/IgD4/8L/4f8dAAUA4P94/yUAnf/V/5UALf+y/woAm/+c/wsAUgALAAkA4//7/+r/JACw/xsAFQB//4YA2v+q/xYAAAASAA4AQwA2ACsASADe/wkA9v/l/6IAFADs//D/qf8DAAIATADP//7/2f9y/yAAGgACAAIA8P/O//3/tP/o/yMA5v/9/9n/KQA0AE8AUgBCAP//2v90ABQAWgBbAAAAAAAkAB0A4f8LANL/EgDq/wAASgDz/ywAEQDp/+7/8f/0/y0A7v/N/44ABADy/xgAuP/r/wEA3f8/ACAA0f9tADMAFgBJABYAAADu/9//5v/9/9n/4f8LABsAuv/t/7n/7P9eAMv/HgCG/+f/IwDl/1gAa//S/xEARQAlAOf/EAANAEIA//81AAYAFwATACEAGwCV/xgAAQC4//3/RwAUAP7/IwD4/8L/vP8SANj/4P/5/3oAUADA/00AUABBAEYA8P8XAO//zf/X/7r/2v9z//3/IgDA/0wA0P/+/xAAn/9XAP3/WP96AD0A6P9bAMn/VADD/xgAJgDD/2IAzv9rAOj/7f8VAO3/zP+f/w0Aiv80AGEAYABOAGMAKwAjAAkAv/+VAOb/NAAFAAQAKABp/ysAEAD7/3v/3//T/9z/vv+4/zQAcv9YACIArv8+AA0ACgDk/w4A1f8TADQAvP/c/z4A6f9JAGAAAwAVAMj/LgDv/+D/VAAfAND/2f9PAL//Xf9HADkAGwAoADMAYADy/xkAFADa/8//DwBWALL/5v80AAUAu//u/7r/a/8bAAMAAgDe/y0AJQBCADUAhv8eAL3/SgApAMb/LAC2/w0A+f/W/8z/6P82AOL/+/8NAAsA5f8OAPr/+//8/6H/IQAtALb/MgAEAKj/3v/S/+3/zP/7/1gAff8EAPL/4v+NAN//+P/V/xMAEAAfAD4A6f9uAKH//f8iAC0AEgDY/xYAf/9QAMD/AwBxANv/UAD3/0IANQDQ//7/IgCu//X/GwDg/woA5P8gAIf/1v8CAPD/8/++/0sA9P/R/7b//P/F//b/LgDK/0IAIwBBAP7//v9aAJIAGgAVADUA4v97ACsA///t/ycAHwDj/x8Avv/d/9H///+j/37/vP+l/6T/o/8RAMX/0P/a/wUAKQBrADEAzP/7/+r/XAATAA8A+v8NAPn/sf8JANH/EAANAOf/ov/Z/+H/i/80ACoA/v8QAB8A4//7/w0A+f8MAPj/1f8mAB8ABgCGAOz/8P8XAAAA7v/f/woArf89AIz/kP/w/5f/9f+b/y8Apv82/7n///9IAMz/MQA6AAoALQAkAC8AOQAbAAMAJwDp/xIAxwBWAP3/6/8lADEA3v9AALP/QwARANf/qQDj/2kA+f8MAPj/wv90AIH/BwDi/57/DAD4/wsAHAAEAM3/MgADACcAMgBgAF8AFgA2AD4AVwAzAHMAEwDZ/ykAIQDS/xEA1/+o//H/l//2/8D/uv+R/97/v//x/2IAhf8vAMv/HgArAP7/NQBO/2AAKADX/3IASQDg/2YA0v+2/3wA5P+OAPP/9f/3/x0AqwCt/3UA8f+F/8L/u/+2/1b/QQBHAN7/wP/x/xgA3f/k//z/IQD2/y8AJQAMAHgAPAAwADkA+P9nAIoAAQAAABMA6//d/+T/6f/b/77/k//g/y8Ayv96ABgA3f/3/3f/NwDR////EQDX/3IAt/8OAB0APABDANv/PQDW/6f/AQABAN3/v//L//v/sv/m/0YA8P/h/+f//v/s/7n//v/a/8//DwDo/1oA7f+6/xAAsv9mAC0A7v/y//X/GwCD/0AAxv/R/zYA9f9AANj/BADy//T/5P/F/xkA3v/A/6f/SwAqAOz/OADl/w4ACwAJACwA7f9xAIAAHQAFAOD/QgAQANb/FQA2AD4ADQB5AOH/QgCSAIf/aAAKANL/NgDQ/xAADQDm/8b/CAAGAE8AdwDN/w0A+f8fAL3/yv/6/7H/eADO/yEACADQ/+z/y/8wALn/bADF/5n/CAC+/yYA6P8jAPj/VQAgAKz/FwAAAAAANwCbAOr/yv/n//7/IwD4//r/HwDi/57/HwCZ/y0ANwDj/0QAyf/m//7/IgD4/2cACQAsADYAYv8AANz/LADt/wIAy/9C/wwA0/8AAO7/FgDb//X/UgDn/0cATAD0/2QAdgDx/xgAOABSAEIAfwBUAOj/bQD9/+v/EwDZ/+H/CwAIAIf/+v8NAAoALQB//xgAFADs/zkAwP/f/wkAGgAVAP//IwDB/wQAAwC5/6L/2f+8/6X/7v9w/9b/JwANAAoA0v9//yoA/v9r/5wAtP/C/yoAj/8lANX/8P/O/8b/4//X/8z/6f8kAMH/KQAOAPr/RABcAFwAAQAAADgAGgC6/+z/3v/A/6f/8P8pAKH/RgAUAKL/7P8UAOz/3f8/ALP/sP/3/xwABACD/y4ASgDz/ywA2v+q/87/RQBdAAEAOADk/w4AHQCX/4gApP9s/2UAmv/T/+7/zf/8/1gAWQD//zYA9f8bADsAHQC8/wAAJACw/z8ARQAlAAwAHAApALP/5/9HAMz/ev9LAPT/0f8jAOb//v/s/wEAAQCCAB8A0P9HAAIA3f8tACQAwv/z/wcAKgBHALn/7P8BAEsAhgDZ/08Av/9w/zEAzP9EAEkAAwDM/x8ABwAFABcAkv8DAKf/EwDZ/wUAhQCP/+7/Xv/a/wUA8/92ABUASADM/zIAOgD5/1UARQAlAOf/NQArALX/DABTAOj/NQArAH8AwgAcADsALwAUACIACQD2/9P/AAAAACUAsP8bAIQAs/8LABsATQA+APz/MwAWADcABwAYAMv/HgAqAOz/cADI/xsATQA+AA0A5/80APT/GgADAPH/hf9CANr/vP9KAM7/WABHAJT/8/8ZAF3/6//K/+f/WgBIAF8Auv///7b/DQCv/6z/KgCP/0oA8//R/6P/tf/o/9v/GAAmAGgAwf+FADQAl/8HAM//6//d/9H/o/81APX/dv+2/7L/wf8WACQA1P/v/wQAuv+2//v/oP/q/0oAu/9//73/gP8ZAAIAuf+QACsA/v8QAFcADgDo/yMAif/q/5L/AwA6AAkAPwDq/8n/nf/n////NQDQ/0cA8P/z/2QAvv9LAE8APwD9/9j/u/8kAOf//v///37/cwDv/4UA/v/H/1IAeP/v/xYAEgAOAIwA8f/0/y0A2/8rAP/////b/2IATwAtAH//KwAiABr/IwDB/wQAzf/X/xUAkf/e/8D/8f/i/9X/AQAmAGgA+f+w/2UAGgDM/3sABwD0/2QAPgBFAEoAzv8gAFEA1P8lAFUA6f9//ysAEABV/3gATgDk/1cAs/8LAC4AEgAPAOj/fwD5/0MAEQAOADAA3v8IAHT/IgD3/9T/bwD+/8f/5f8OAMP/4f/V/zgAGwADAMz/xP/Q/6L/WQDt/97/UgDC//P/BwCY//b/+P8eACoA/v9aAMj/HAApAI8APAD6/zIAuv9aAAAAJADU/wEAAAAAAG8A/v/bAOb/6/8BAKX/EgD9/0cA8P8FAM3/sv8dAAUA4P/U/8r/MADw/87/IQCt/+L/1f9eALn/7P9LALz/pgAEAPL/9f/l/8X/h/8xAF8AFQAjABwAqf8oAI3/yf9TALH/LgASAP3/WQAjAOb/2P+7/wAAAADb/77/pv8lAB4APQBDACQACgAtANv/vv8BAMr/+v/W//H/PQD6/8T/PgANAK//5P/E/z4AMgAVANv/UAAbAHH/+//8/w8ADAAJABoAFQBs/63/4v+e/1YA2P8EAN//LgAlAJ7/HwCr/4UANAC8/5MA0v8RAGoADADT/7f/IADk/w0ACgCt/wYAKgBZAP/////a/4b/+v/p/8j/5v/9/w8AHwAZAAEA3f/2//j/MAACAAEAggCx/xwAFgAAABIAof9GALj/IQBlABoAcQAAAO3/AwDw/08ALQDJ//n/HgDi/7D/5gBLAHL/agDV/8v/1v8CAPD/BQDy/6v/KQD9/0cA3v8IAAcA9P9RAOb/IgDS/9v/4//o/9v/4v9oAOb//v/+/8f/5f8OAPr/6f9JACgAIABRAAoACAArACMAHAAEALr///8RALL/LwCCAOn/AABbANz/9f/3/9T/EwAPAEQAWwASAP3/xv8/AFgA7P84AAgA4//7/9f/TQBQAOX/MwApAOv/7/87AEIANQAGAAUAYACW/z0A+/+g/1cAtP/o/6P/tf/o/6P/2v/P/+v/uP/9/6L/6/8BAN3/CACr//P/rP88AEMA//8RANf/OwDU/8r/+v/W//H/KgAPANb/8f/P/+v/gP/j/+n/pP8RAOr/SQA7AB0AFwDc/+P/1//x/wYAFwA3ACwAJAAKANL/7f/M/x8APgD7/9j/u/8RAMX/4//7//z//f+0//r/HwD1/wkAGQBMAD0AHwB1AKf/7/9zAMr/HQAYAN3/df/a/zwADADT/7f/xf+H//v/6f8SADMA8/+s/8//RgBdAIIA+/8gAL//uf/s/wEAXQDw/xcA7v9NACwA7f8CAEsABQAEAKkA0f9tACAAPwBXANn/cwATACIArf9QABsAzf9XAOv/SgDO/yEA9v/T/yUA1f8UAOz/JgAxADoA5v/G/+T/xf/Q/+z/AQDL/+j/yP92/6T/fv+F/8L/vP+2/7L/+f/o//////+j/8j/CQAHAAYATgAtAFsAAAASAJAAvP/c/9H/fv+X/9D/7P+m/wEA3P+///D/zv/9/1kA2v8FAE4AUQBUAAwAnQA1AKr/cwDLAOz/AQAmAGf/vP/c/xkAFAD//+3/3v/S/9v/4v8fAD0Asf94ABcAEgBrAPv/IACs/+H/sP8IAD4A/P8zALv/NgDj/+n/JAAdAE4A5P8gAD4A1/8VAEgAuv+Q/7n/ov/+/xAAHwBQAPj/QgD//xEA/P/9/34ACQA+APz/DgBDAKP/EAAgACwA//8jAB0Azv8OAOf///81AOL/1v8UANr/YP/u/6j/AgABAFz/IQCI/x8A9f/A/18Auv9aACQAVAAfAOL/QwDJ/woAGgA6AC8AEwBq/ywANgCZ/5wAIQAbADoAQQAQAB8ABgD0/wgA9f+cADQAKgDr/10Ak/+W/3UAgv/2/+b//v/+/9r/GAA4APf/LwCCAPv/MgDg/2YACQCZ//f/nf+d/+j/WgDJ/y8AOAAIAPX/5f+z/x0A8/+H/8UAwv/h/x0AvP/K/6//9v+v/wcABgCGANn/BQCFAP3/NAA7/wYAGADK/4wAFQC1/zIATQD1/0AA6//K/zAAAgDL/zAA8f8FADsA5//+/6P/7P8CAPD/zv/F/1EA0//c/2MA0P/s/0sABQApACEAdwBgAM3/MgAWALb/DQAwALn/IgAJABkAJwCy/4sAAQATAEcA8P8XAMr/+f/W//H/9P8sABEA6v+mAAQA8v8rABAADQBCAH8Ar/8aACcA/P9YANn/zv+z/zAA3v+I/3wABwC9/+//8v/1/xsAAwAVACMAr//2/9P/3P8HAPT/CADQ/5D/yv8eAOH/egAYACYADACK/yEAv/8VAO3/8P/0/4f/1v+5/+z/pv9KAPP/4/9pAB0AYQAFAOD/nP/5//v/MgBgAN//1QAFAKn/KADX/wMAuv8iAEEAxv8/AEUA7/8pANj/FgDb/77/JgAMAOb/of9GABQA2f8qACIAGwDf/woAv//w//T/9v8KAOT/6f9//+L/MQAVABEA1//f/+X/xv8aAN//+P9nANP/NwCa/3b/EQCy/+b//v9aAP//AABJAN//wf+7/yMA+f8MABwABAADACcARACk/9v/YwAqAMf/CAAHAIX/sP8IACsA7P8CAMv/sP9TAOf/7P8UAP//WgDt/8z/VgAzALv/2//i/5//6f82APX/rv/1/9L/AAC2/8X/LADI/8D/FgAkAB0APABVAA0A+f8xACcA/P8zADsAQgDt/xQANQDi/0MANgArAEgAAgDM//v/DQALAEAADgBVAHwALQAkAPn/+v8yABYAtv8gANH/yP9AAKH/6//d/4f/RAAAALf/MwDg//n/6P+1/w0Ar/8HABgAAQA4AAgABwD0/2QA9f/l/yEACAD1/63/0P+0/x4A4v/o/+3/3v8bAN//CgDR/zYAPgD7/yAAGgAnANf/KABFACUAMAACACYA6P/I/1MADADl//3/xv/3/3f/t/8OAJ3/DAAcAAQAKAD8//3/xv+//xUA//8RAOr/NwDj/+n/JACd/zAA8P8qAEcA8P8FABYApP/t/0wAc/9rAOn/yP9mAPf/HQDh/1QAMgAoAPz//f/r/wEASgDz/9H/kP85AMD/3/8cALv/SQDN/8T/KwD//yMAQQAPAFYA/f8PAOj/IwBBANn/FwDc/xoA8f88APr/DQBUAMT/KwDs/0sA9P8IABkAuP/+/9n/vP/J/y8AuP/r/xMA7P+4/zQAYQDh//n/1v85AK7/BwA9ANb/OQAuAAAA7/9gAKj/OQAuANz/9v+J/1gADwD7/w0Ar//2/7AAMQDx/1AAGwA7AOb/DwD7//z/2P8pACEAv/9MAIb/1f+4/8b/LQCk/wAAEQD8/+v/7//N//z/2P+7/wAApP/t/6f/pv+3/6H/MwCE/9T/3P+//xQA7P8mAMT/UABAALP/QgA2AFAAUwAwABQA7P/e//f/LwDd/1IAVACf/+n/EQDq/28AawANAPn/6P/a/wUAFwA3ANH/2v9PAC0ANwBRALAA6f/b/4cANgAGAE8AnABq/xkAgwDF/1AA0/8AAO7/AwBMAOL/+v/8/8X/rP8FAAQAFgDb/73/AQATAOv/3f8aAPH/4v/D/+H/5////yMA+P/n/1oAIwDm/0YApv+l/9z/rP/h/x0ABQCp/wMA8f/P/+v/AADv/+D/wf/g/x0ABQAoAFgADwBWAOr/kv+WAJ3/1f9wAKP/EADX/8z/6f8RAMX/LAAjAOb/IQDS/24Aof/G/xoAgv8IACwA2v8GACkADwBWAPz/MwDz/+P/+/8OAIwAFQBIABUAkgAZACcARADu/4QAof8hAL//p/8BAMr/CwCb/woACADj/9b/AgDL/57/1v+V/wUA8v/1/wkArP+8/yUA+v+x/wkAPwBFACUACwAuABIAIQAbAPL/GADw/7z/bgAPAJ7/+/9W/8H/4P/U/xMAj//c/+P/HwAZAN7/GwDy/ysANQArACIALgAAANz/4//7/+r/NwBkAJn/CAC+/4H/UQDU/5L/zf+f/8X/iADt/0wAPQD7/2oA5/8QANf/OgAcABcAJQDV/xMA/v8jAPj/ZwAuANz/BwD0/y0Ayf8dADwAMAAnAEQAgAALAC4AbwD+/xAAoAASAP3//v/s/xQAIgBAAOv/EwDZ/xcAJQDV/xQA7P/w/5f/9f+b/4r/IQDS/zYABwDP/30AnADZ/04ALQDJ/y8A3f+//5T/FwDK/6//ZAAZACcAxP8YALj//v9HAMv/QwDJ/9P/AAC3/+r/7//N//z/DgAwADkAUwAeAL3/JQCw/5v/+P/D//P/0f/I/+X/IQAtADcABwAGAE4Av//e/63/0P81AM//6//K/8L/zv8OALD/if9XALT/HgAqAMf/CAC+/wEA7/8pAEYAJgAMAPj/5/+1/x8A9f8bAE0AUADl/0YASwAFAHIA3P/2//j/HQAqAMf/v/+V/+H/wv8FABYAJAAdAE8APwD9/0YA8P9OAPb/CgAaAN//UwCL//7////I/0AADwDD/xgAOAA/ACEA5P8NAJ3/CwD4/wsAGwC7/zYA0P9HACcA+/9YAOv/AQATADQA9P8IAOL/6P///9v/9P/k/w4AHQDh//r/MQADADoAUwBDAO3/8f/0/wgAKwDa/yoAx/+//8z/n//8/w4A+v8MAEEANQAqABAA1v/e/+X/6v9KABcAJQB6AOL/+v8yAE0AGQBeAIMARQBKAM7/RQDv/ykAMwDg/0IANQAYAN3/0f+R/wIA3f/S/5H/y/9DABEAMwDO/9f/zf8NANT/7/9gABYANwAsADYAGQDw/wUATQDR/zUA9P/3/0EAov9sAA0A5/+0/+j/2v89AFYA/P+QAIX/LwDL/8P/GAAAABMAtP/D/6r/lwCL/+v/JgDD//T/v/85AIn/WAA0AAUAYAAWANv/0P/H/8D/FQCR/ycAjP///1sApP8kAMH/4P/B/wQAzf+f//z/6v8TAOv/EwDZ//P/0f/s/8v/+//8/47/AADc//X/m/8KABoAcP9oAB0AFwAlAGgAQQDr/10A8P8FABYA7v/x/wYAKQDZ/wQAlv+9/1wAuP/9/yIA0v8AABIAxf/2/y4Ayv/n/8f/5f8gAOT/DQAdAOH/MAACAAEAJgCx/xsA8v/i/x8AGQDw/+H/MADL/x4AGADw/wQA8v/i/7H/wP/N//z/oP/q/1wAJQAMAMD/3//B/+D/5v/r/7j/tP8eAOL/6P8QADIAOwAvAN3/CABQAMD/AwA6ANP/bwBrAI3/NgD1/y0AbgDr/28A2v/P/+v/EwDr/wEAJQDV/wIAy/9DAAAAAAA2AAcA9P+a/5v/wf9OAOP//P9FACUAaABUAOj/2v8YAFz//f/Z/4T/HADg//n/w/+q/4T/5v/G/6z/PQAeACsA7P+DAEQAyf9nABsAAwADACcADQD5/x4APQAMAOb/NADh/+f/EABEAEkAOwALAOT/fAAaAPH/YgD0//b/+P8LAPj/CwDS/xEA/f8hAL//8f8qAKL/RwDe/0AADgAeAOL/DABTAB4AYgBy/zMA4P+v/y0AJADC/ykADwDo/0gAOgBmAIj/VwCO/+7/KADq/8n/Zf/N/8X/BwA7/60Ar/8HAPT/rf8GADv/KwCi/yIAHAApAHz/cgDJ/0EAfgCK/6IAXP99AGT/JwDp/zYAdgDM/3sA4/9pAFP/rQCK/w8AHgD1/y0AEgCPAKr/YADN/+oAqf+pACwAWwC4AMr/wwCc/7EAoP9FAJP/zf97/wIAy/+M/38ACf86ANH+xgCw/3cAFgA3AIgAWv+zAFj/sQAx/9wAQf/pADoA+f+fAOv+7QDh/i4By/7TAHL//P/q/7f/2QCs/pcBHv5cAfD+ggBpALD/LQD+/uoApv4CAtD+6QDd/iwBOP9gALv/fv9iANz9hAFY/rABxf49AUb/kACGAMX+mQHV/X4Bnf6wAf3++wB//73/AwHw/ZYCQv2LAoT94gHb/rr/yQBC/qEC3/2/AsD98AId/VoCdAC3/voA+fx5BJ/81gSi/QQGSPTVBrUDvPVEDcDvaQ1K9yQEjAJC+CgHXfdsDYvyYQcu/2L8ighz9YEJifg2BBQAL/3IAyT9YAKI/tcBB/7NAk3+OAEMAGL+PANq/KcCjP9+/xcAuP+0ALP+mwB7//H/mP8/AHv/OgCv/+P/aQBm/xkBzP6KAEsAO/91AJT/hQDZ/xcAJQDn/9r/z/9GAKb/gQCx/0AA6/+T/00AKv9DAJH/3v/3/8H/FgDc/ywAbP8JAIf/6P/I//j/wv+8/5MAiP9pAB0AKgAiAFIAQgD//20Axf8sADYAPgAyAF8AKAAOAAsA5f/9/w8Aw//h/zAAuf81AHP/awCe/9b/FQBH/9sAiv+iAMv/HgB1AAIAcAB+/4YAa/+JAJL/FQAjAGX/KAAx/5IAdP9sANf/3/9BAH3/YAC7/yMA+f9VAOr/7v+V/z0Anv/W/wIAOP9gAEz/XgBv/+j/2v/P/yEAiP9pANX/ggDE/1AAm/8dAE4AGgBfALr/bAAf/5YALwDK/wsA5f8OANX/SwCq/zsAnf96AKv/PABCAGv/0wAo/1MAMQDe/1MA+v/W//H/4f/6/x8AdP9HAIH/0f8jAOb/IQDl/+r/JQCw/+T/VwBq/xoAzP9pAIr/tP+MAKf/ggDX/3EA2//Q/9n/KgAiAOX/xgD7/7MADwAfAOL/6P/I/wkAiQDJ/9UA9P8/ACEAdgDy//X/dwA6/xgAyv/6/+j/AACR//D/l/90/2wAQ/9EAKT/JADU/93/iQB//1AAwP8oAOr/EgDq/8r/wv+p/4QAfP9fABUAEQBXAA8AMQCV/2EATgCI/8T/KwCQ/3AAx//3/+f/j/+5AJT/FwA3AIf/MQAoAOr/gQAeAGIABQDg/+b/tP8eAHP/NAC8/7f/6v+4ADf/3/8MAa/+GQGF/4wAAgC5//8A7/46AWj/PQAfAIb/sgBE/yAA0f///1sAAACAAFUAev/NAO7/uv9tAMX/dgCn/3AAIwCu/ywA7f8VADUA0P/s/yYA1v85AJz/eQD0/4j/xQB5/0oAYQAEAKkAmv+KAMr/eP9vACH/zwBJ/+7/FQAi/+IAWf/XAOP/+//8/3z/AwCV/3QAN/9NAOP/HwAGAJkAHwA8/+UApf9JAAMAlgDC/zsAVQBo/5kAn/+hAG7/iwCDANf/cQB//ysAa/8IAKv/zv8y/6T/EQCg/48AvP9cAJL/KABqANX/FAD+/zUAvf8AAID/YwAYAMv/nv+M/0gAlf+YAIz/bAAyAF//bQBE/1cA/f/s/zgA5f8gAKz/9P8IAAYAqv9NABkATADi/wsAZQCI/8UAw/9PAD8ADgCxAKD/MwDO/2oA6P8QADIAFgAkAML/KQBq/z4AxP91ACcADQBnAGT/qADz/mAAKABW/8IAZP8nAFb/5f9rADD/2f/P//3/tP/o////EQBXAOv/SgC8/zcAmwDq/zcA0f/a/3P/MwCX/ysA//9Z//wAEf94AKn/3//T/zb/FwHd/s8AAQDK/1UA1f7IAPz/fP87AAoACAA+AFX/eAAEAPL/9f+t/ysAIf+9ACj/QQA0AHL/6wCF/3kAhf/6/wwAwf+FAFf/CwB3AIT/wgAbAIP/rwAL/70A4f/5/+kAX/9tALP/ZwAJAOP/aQDU/6b/bwC0/8P/dABv/58AR/9sAEUApf8SAI7/7wAs/6AA7/+7/9v/vf+CAJ7/xQDV/6cAGADd/3YAg/9lAL//FADI/xsAcgCS/zoA+P/6//v/jv9JAN//5v9ZAH3/vP9JAOD/HABOAPb/QQAPAAwA+P9VAA0ACwBSAFP/LADb/2IAz//r/zgAdv9IADn/FwBb/+r/yf8dADwAZv8HAVH/4wARAMX/rQAb/4AA5//s/4MAQ/8NAAoAY/8pAW3/+P9DAJH/JgDW/3EAIv8HAYn/MwAEAHD/DwH8/jIBT/+8ACkAj/8VAUr/uAA3/5cACwAJAHUAAgACAN3/wQAG/0sAl/91AEwAKv+xAI3/JAAKAC0AAAC3/3wAUgBUAJ//6f/u/6f/3v+b//j/L/+h/yEAY/8EAU//KQDHAEP/swBX/0IAIwBS/1AAHACW/9D/RwA4/xYAtv8OAGcACQCtAJ3/QwDt/6f/lQDA//L/GACT/zsAeP+3/5AAl/8+ADIAzf8NAB0AYQCp/wMAAgBd/zQA4f+w/y0A7v8DAPH/dAAUABAAHwArAFoApP9tAOr/AAAAAJL/XwCD/68A+v+N/20Aaf91AJT/zv8zAE3/gwD8/zMA4P/C/wQAAwBMAGH/SgCW/xkAXgDL/58ApP8kAK//mv+u/z4AMgADAEwAT/9yABIA2P9gACkADgALABsA4P9mAK3/PgBpAHj/lABSANL+jwAFALv/3ABm/70AvP9JAJcAZv+FALT/aAD4/x4AYgCGALT/MQBfACb/0wBM/wIAy/9n/04A5P98AIj/ewBi/wEASgBy/48AhP9UANb/JwAfAJn/LQDc/3UA8f/P/yEArf/i/x4A0P+0/wwAQQA0ADwAQwA2APX/UgAwAPD/hgB9/ykAof+z/1UAev/fAFf/+f+w/+X/2QCJ/xABkP9LAPP/v/+6ADn/qgDS/8j/QQDH/63/BgDh/9T/lAB2/xEA/P/G/ywAJACv/9H/bQDY/00ABwCq/ykAMwDg/1QAewAZAJYACgD2/woA9v+c/1UAxP+G/1UAoP8OALD/CACG/3n/8P+p/wMAgv+cADQA4f9VAOn/yf/B//L/BgDh/7D/5P9E/3wAv//e/0AAfP8rAW7/sQD8/0T/jwAo/y4AJP8GAAUAu/9uAOv/bwAiAEAAj/9KAOD/CgDk/+r/gQB5/5QAif+PAHL/6v/KAPz+6ACV/yoA/v+0/x4A4v/6/9f/8wBm/zsA5//s/5T/Tf+DALL/QQCi/yIAm/9mAEAA2P9gAEz/8QBT/wcAKgB9/88Ay/8LANP/JAAdAOH/+v/E/wYAzv+PAOH/nf96AOL/DAAcADwACwBk/80A7v/f/3gA4f9nAGT/TAB1AIL/rgDC/wUAlwCd/8QAr//k/8YAQv9oAK//GgDx/8//NABg/1sAEgAzAAQAu/9s/8EALP8NAOcAkv4mAQ//ZACaAB//lQBl/ygA1/8DAEwAUACb/2YAdv+j/38ALv/HALH/eACp/xUA7f+V/08AB/+nAHP/kADP/8b/dgBw/44AqP/x//T/GgDM/0QAkv8VACMA0//dAB7/zADa/wYAYQCE/2YAUf89ANb/OQAuAJL/XwAVAH//YP9uACEA0v8kANT/yv8dABgAOAAbAAMAJwAyAPL/GQAUAKL/WQDt/ycA6f+2/yAArP+GACIAwP86AJz/+v8fAE//FgC3/+r/XAAk/z0AMQCV/5kADABmAJwARf+QAKr/Xv+2AH//4wC2/7L/nQBZ/40AFQARALQA7P8BAKcAmP9RABwA4P9nAJv/eQD0/ywApP///7b/IAB2ADn/zwAS/1QA+/9o/6wAQP8KANL/EQCg/w4Awv/z/6z/9P8/ADH/JgGi/1kA2v/P/0YAb//WABj/ogCB/6z/hwB+/2EA8/8+AMT/mgCN/yQAiv9q/2MAF//sAJj/iADu/4P/1ACE/7AAsv8cAPP/BwCZAPv/VwD+/2wAsv8cACkA/f8PAAwAVACM////7f8CACYA6P/t/7r/7P+5//7/NQDi/1UAxf/Q/0cAb/9oAK//PwBFAFv/2QAs/2kACwB2/+4Ah/8NAJz/+v+f/5//IADR/+z/Sv/wANP/t/98AJr/eADO/48ATwD2/8IArv9QAK7/rP/QAKb/SgBhAHH/6f9uAP3/tP9oAK//9v94AM7/6v/v/ygAWAA0ACoARwDw//P/4//p/9v/4v97AAcATwAbACgAxf++/yYAVf8bALr/EQD8/9j/lwCw/xsA8v+9/wEAEwDG/y0A7v+V/74Ahf+xACAArP/iAA//0wDy/0//YACW/z0A1v9xAEgAFQDI/xwABAC6/0gAXv9+AK7/BwCHAH7/PACL/6L/2f9PAK3/YgBPAHb/IwDT/yUAwv+rANL/WwDu/3H/RgHx/jkA+P9B/3oA4v8xABUANQD1/8D/cP8fAD0A1v+oABkAFABsACAAPgANAML/FwC3/0UA7/8EABUAR//JAMX/vv8CAIH/dgC6/+3/JwAw/9r/9P+s/5kAsf/m/6H/6/9vACH/TgC+/8v/+v+f/zIAcf/7/yAA9v8cAPP/BwAYAAEASgDg/y8AFADH/2UA4/9pAFP/LAAkAIr/kACY/1EAiv+z//n/sf/l/w4AMAC5/zUA4v/EAAoAGwCEALP/1gAGABcAEwC0/1UA1/86AEEAff/O/7P/HQAXALf/WADH/xsA3/+c/x0Az//Y/87/xf8HAAUA8/9RANP/7//y/xkAJgAMALAAsf+LAF0Ay/9VAGoAQwDt/wIAuf8iAHb/7f/x/8//6//d/2QAGP/9//7/tf+M////EQBW/50AWP8MAAkAh//FAIv/bACzAI//XAABANz/iAAkAB0AhgDZ/wUATgB1/1oA7f+n/xMAa/8aAF7/IgAbACgAWAAPAGkAeP9cAMr/CwAJANH/EADX/9//Uv8+AMT/BgCp/7r/SAC6/yMA5v/r/93/iQBa/w0AHQCF/1QAev85AAkAmwDY/00APgDE/4cAWf+NAIP/rv8ZAJT/cwC4/5AAPAAeAKwA+P8dACoA6/9LAPP/0f/a/z0A1v+n/4IAVf8uABIA2P9OANH/WgB//wYA4f+d/+j/IwBTAOj/EAChABMAof+jAMz/jQDf/9P/ywD8/rEA/P8OAEMAyP9mAHX/7gBRAAoAZACs/wUABAAVANv/hwDI/xwAu/+R/zkAGv+SAL7/pv9KAOD/wwAcABcANwD2/67/PgD8//3/DwAMAAkA5P+zAFj/egAGAHL/2QCt/5oADQD5/x4A9f9lAJr/ZQB2AHD/MQDx/5j/dgBw/1YAs//C/6oALP9pAML/cv8gAPb/CQBRANT/EwBrAHr/FADH/+X/2P/N/9f/g//4//n/1v/e/wkArP+GAKL/RwAUAGv/iQCA/3UA8f+GADUAz/+jAEv/OAD2/+b/DwDD/z0AQwDJ/5z/i//r/zgA9/9mAOX/MwDg/+b//v/s/yYA1v/e/+X/MwDg/0IA7P8mANb/AgCDADH/EACg/6D/IABRAJz/VQDp/xD/CwEL/2EAOwBB/8QAnP+w/+T/MwBM/wIAy/+M/1oAbP8uABIA6/8TAP7/IgAbAGAA8v8+ADEAuv9/AK//CADi/8P/dABv/x0AGADv/xYAXAAAABIAawCx/68Aev+nAPT/rf8bAYb/sgDq/zcAPwD8/+v/3P+IAKT/bQCh/w4AsP/l/1gAj/84AGP/cADt/6f/SwBg/1sA7v8DABUAbP9TAAsACQAZAF3/tP8xAMz/6P8RAPz/IQC//0wABgCE/54Ao/81ACsA2v+GANn/dADv/+D/ngDI/9P/gQB5/93/LQDb/ysARv9sANf/zP9pAFP/GgBw/zEAzP/E/74ATv+pAFEAiv99AMD/3/8JACwAbQDY//L/GQBLAM//tP/6/5//xP+r/2EA4P/5/2gAZf+EADMAKQBGALj/kAAqALT/DAD4/+f/bADX/83/MgDf/woA0f///5H/uf81AM///f/+/8f/LgCBAGf/8//j/7L/iwCT/3IAAADc/78A4/+OAN//wf+FANj/KQD9/zQAFwDK/54AEQD8/yEA0v/b/2H/EgDG/+T/jgDO/1gADwBV//f/nf/V/wEAEwBHAAIAggCy/8H/8v++/zgAwP9xANv/0P/s/7j/tP/V/zkAdv9IAKj/FACRAJn/nADr/6X/EgAzAAQATQDR/6L/7P+5/5AAvf8TAEYAgf/2/2YA0v/b/3UAy/8xAMz/RACTAIj/VgCO/7f//P+P/yUA5/8QAMT/4v97AOP/+//F/wcAKgDH/wgAvv+T/00ALACR/5UALgAAADgA0f9tAKD/6v83AGQAUADT/xIADwBDALb/VwAPAPr/+/8gAFEAZf+XAIv/DwAfAHT/IQB2/0gAlf+q/83/sv8KAHb/SAA6AK7/BwAGAOH/5/9ZAH8A+f/6/1cA/f9ZAEgAgwB8AL//XgACABQAbACN/xEAMwBf/20AMwCW/4cAWf8fAL3/yv/7AEj/twBb/43/gAAu/6IAAgCnAPT/5P9qANX/OQCJ/0UAAADu/+D/QQDH/9L/EQB7/6kAYv+CAEQAtv8gAKz/PAB5/0sABQCqAAgAGQC6AIL/5gC4/yEAGwAoAFcAof/aAOb/fQDS/wAAkwCa/50AEAAMABwA4P/C//P/BwCq/6n/cP+M/+z/JgB6/5UA0/8SAJAAhf+MAEr/SgAXAMn/HQBN/7sAuv8jABwABABgAHH/6f8RAHv/zP+OAHH/RADJ/9T/8AB3/0kAzf97/xUAkf9eAF4AFABIAMz/HwD1/wkAGQDe/2UArP/0/9H/kgAZAKf/XQBc/zMABQAEAF7/2v+q/zn/YQBy/1cADwAxAAIAAgA5AIn/1/9M/xQA2f8FAKn/3//A/3D/ewDj/0QAEgAOAEMA///b/wYAYP8RAI8A8/9RAFL/GQCU/wQAOwB4/1wA3f9kAOP/aAAvAF0ASwCq/2AAFgBJAPL/BgC8/yUAVQCf/9f/uv///zYAvv+T/wQAXv9sADIA4P8cALv/NwCs/+H/eP9dAKb/kv+7AJb/hwDs/ycAMgDN//z/jv83ANH////I/wkAZAAGADwA1f8mAB8Avv8TABAA+/9qAB4ABQDz/+P/aQB4/zgAPwCg/8cADAAKANL/2//0//f/+f9U/4kAW//8/yEA9P6GAI//7/9zANz/GgDe/wkALAARAFcAIQD3/4sASwCGANr/GADv/6n/qADj/wwAHADz/wcAGADv/zsAHQCF/1QAMgAVADYAKwDt/wIAFAD+/zUA9P9SAPn/1v9eAEwAqv/y/+P/jP///9r/z/9Y//r/DAD4/0MAyP/l/+v/k/+W/yoAj/8TAEcAy/9DANv/BgDz//b/ZP/M/2kAnf9oABwAPABVAGj/hwD//5H/XgAUALX/+/9qAC//IQAbAF7/kQArAJEA0P/a/wUAFgAkAPn/oADu/3IASQC7/9v/9f/S/7b/agALAMD/KAAyAKj/AgDw//P/9v/4/2cA0/+mACkAIQBkAL7/lP8XAFwAk/8oAKD/2P87ANT/ggCf/+n/EQB7/3EApP8AACQAeP9KAHH/oP/X/ygAVwAPAFYA6v9uAMb/5P97/5X/4f/V/3AAtf9pAAoAdwDN/+r/pgCE/y8Abv8wAAEAk/9gAOD/5v/Z/+D/1P/v/87/fQAtABIAjwA8AB4Aqv8pANj/YAAoAI7/NwCs/yoAawD7/0UAEwD+//7/ov+jAAMAzP9oAIr/NAAqAP7/EAD7/0UAEwD9//7//v/a/yoAj//K/zAAuf80ABgAbwDH/3b/EQD8/w4AHgAGAKn/OgD5/zAA8f/h/x4Aqv+qANH/EQBqAJ7/DADm/zQA4f/5/0QAAAAAABIAoP/Y/00Avv9LACoANACX/9H/NQC9/wEAk/9fAN//nP/n//7/RwDM/1YA6v9I/6P/EQBXADQABQBNABkAFABtAMX/9f/l/zMAPAAwAN7/GwBNAJn/rgD6/7H/HADO/0UAgP8sABEAsv9BAH3/8//j/+n/bQD9/0YAAQDL/9X/AQA4AK3/q/8EADsA5v8PAAwA+P+w//f/CgCb/woAmv/T/5L/FQC2/9f/lgCd/8QAHAApAOv/yv8dAJj/LACj/zUAYf8lAAsAUv+HAGz/9/8KAOT/WAD+/+z/OQBSAB0AdAAmAAwALwABANz/0f8jAAoACAB1AMv/MQAVAMj/QQDZ/2EAOwAdAGEAPAALAPj/wv+p/zoA5v80AM//6/+4/8b/BwBO/5cAnf8xAJYAr/9kAAYAPADD//T/CABh/9z/YwDQ//7/NQDP/+v/7/9gACkAMwCFAP7/NQA9APv/IAAZAAIA3v/3//n/Z//h/+f/2f8FAAQAKACy//n/+v/p/zYA4/8NAEEAkP/d/xoAAgAUAKP/NQDP/+v/AQCT/zsAU//R/1oAbP9lAC0AAACAAOf/EAAyACgA6v/u/xYAyf8vAN3/PwAzAKn/zP8fAAYAqv+FAA8A+v/p/7b/DQDC//P/BwAGAKn/AwDe/1MAQwAjAHgA4f9CANr/GAC4/3z/8v/i/wwA5v80AOH/HQB0AIIAsf/T/zcAmv9TAJ7/MQDx/4X/VQBV//j/CwDA//H/4v+NAAMA3v9AALP/VQBXAGr/LACR/xQA7QDj/0QAyf/B/ykAIQA/AHv/g//A/83/DQAKANL/AAAAADYAYwDi/zEAAgAnALH/rv8sANv/UAAuADcABwD0/wgA4/8fAFAAHACo/wIAlP/O/w4AMAAnAPv//P+O/xIAof/r/yUADABTALD/CQA+AOn/2/91AN7/5f9FABMAawCy/woAZACZ/5v/ZgAbABUAbQD9/34A5f/q/wAA3P8sACMAZgAbADsA5v+P/+//zf97/wMAuf+i/1kA//8jAMH/zf98ABoAcQBuAEYAuP+0/40AJwAgAFEA5v/r/wEA7//y/ysAkgDj/zEAlgCd/2gA+P8LAFMAef8mALH/0v+S/5X/TwB1/37/FwDv/xYAAADb/xkAAgBdAN7/v//e/5v/QQAQAGkAHQAFABYAbf9TAJ7/MP9/AGX/zf9XAHz/YABx/+n/kgCs/wUAu/8kAML/KQBGAO//PADC/wUATQAsAP//bQAhAIkAXAAAADcAGgBxAKT/2//0/z8A2P/y/ysAfv88AIv/2f+q/wMA8f+F/3oAGAAmAOj/NgAZADkArf++/zgAiP/X/5X/hgDa/6r/YACW/xgAOAAtAO7/TQAZAEsAKgD+/38A5v9ZAP//o/8QAFcAWAC0/zEAAgACABQAx/8JAOP/sf+u//X/+P8LAK3/0P+0/7H/CQCs/+H/Zv/z/77/b/8wAMv/QwARACAAUQAKABoAFQDI/+b/NADO/1gA2f/h/2cA0/9cACUA1f+CADIAAwBxAKT/bQAhAOT/jgCW/1AA+P8wAAEApv/c/4f/VgCg/+r/JQDC/wUAzf8gAOP/sv/m/9n/KQBYAP7/IwD4/8L/zv+h/6H/6/9KABcAEgDY/wQATQD1/0AAIQDS/xEAIAD2/xwAOwD5//v/6f/J/x0AKQDG/+T//P98//L/KwCQ/xMARwDe/0AAs//C/xcAyv8wADkA5f8OAB4A9P8tAMn/5v/Z/+D/eQDP/6MAcADa/1AAif8NAML/cwBvAJD/OADS/+3/JwANAOf/bAAfABkAFACQ/3AA7P/w//P/9v9BANn/mABDAMj/0/+l/7b/DgCw/y0Ayf+v/1EAr/8/ALL/+f9DAAAAAAAAAAAA7v+WAOf//v8QAOn/EQAgAIkAt/9XANn/PAAwAKf/SwCF/y8AOAAtAO7/FgBbALf/6v/u/7r///9tAOr/EwDG/7//8f9O/zoACgD2/y8A3f+//5T/zv9GAEoAzv8OANX/XgA5AMD/XwDx//T/v//x/+H/ef/v/ykAMwCp/wMA8f8YAG8Aff+8/wAAAABJAM3/IAAsADX/y//o/+z/XgACAHAA7f+5/0cA8P+q/xYApQC7/8n/0//c/xkAzP8fAKv/4P8LAK3/BgAFAGAAKADY//L/GQBeAAIA8P9OAOT/MgAWALb/sv/B/04A4//X/zoAHADz/6z/BQByACUA+v/7/yAA4/+f/yAA4/8fAAcAPQCNAAMAcQDI/9P/EgAPAHoAGQA5APf/LwBwAEgAJwAyAAMAAwBMAIb/HQAFAHL/DQDU/6b/yv8LAJv/LwAlAB4AdAC5/w8AHwAZABQA2v8XAO//zf/8//3/DwAMAK7/BwC9/7j/2P8WAG4ANACYAOj///8AALb/VwAPAPr/HwAHAL3/SgDg//n/QwBa/2kA5/9r/+T//P8OAPr/HwArAG0AIACJABIA2P9NABkAOQDA//L/4v/W/xQANQAYAAEAbwDa//T/PwDF//X/igATAA8AHwCr/ykA/f8PAPv/IAAsAMj/HACp/9//m/8KAGQAdP9ZABEAjf8kAPn/+v/X//H/4v95/xMAIgCb/6//h//p/8j/5v99ANL/EgBGADgALQBcAFwAAABKAM7//f9ZADUAdADL/wwACQDR/1oANgD1/+X/MwAEABYAgADV/93/CAC9/wEAAQDc/+P/xP/Q/33/l//1/5v/wf+o/wIA8P+q/18A3/8cADsACwBAAKH/2P/z/+P/+/8OAML/qf9NACsA///I/0EAWQDs/zkA5f8OAEMA//8RAEUASgApAP3/tP/V/8v/DAAJABoAJwAyAAMAzP8yAPL/4v/o/9r/hwD/////SACD/8D/3//l/yEAY//e/+X/xf9RAMH/u//I/9P/3P/1/wkA9v8JANH/IwCu/3X/7P+m/8r/QgAjANP/SgDz/+P/DADm/0YAAQATAFkA///I/+X/DwDV/yYAMQDM/1cA6//K/2cA+P8wADkAQAAPAAwAUwDD/08A5P/F/ywAkf+DAMT/dP9GAJT/zv/8/+v/pf/J/6//9v8KAIj/HwD1/+X/IQAaAPH/z/9GAIIAMgDN/2kAMAA5AFMAHgBPAGP/8f8YABMARgAmAB8AGQCVAPj/MAAUABAA+/97/18Alf8FACkAfP/f/8H/FgC2/0UA3P/j/0QApP8kAPn/6P///xEA6v/J/x0A8//j/x8A9f/A//H/mP92ACgAIACtANT/lAD3/0IAbADq/7gAAQBKABcAyv8dAPP/h//E/1AAif/8/30AQADY/wQAFQC2//z/2P+W/4b/5//H/9L/2/9h/+//8v/Q/+z/3f8bAN//+P9CAMj/5f/q/zgAZAC+/10ASwD0/y0A7v+6/37/8/+//97/rf+Y/xoA3/8cAAQA8f8GALz/yf/5/wwAwf8DABUA//9bACQA1P/d/9H/IwBBAOz/SwAXANz/4//E/xkAFABaAEgA8f+q/87/6v+k/xIAxf/2/wkA0f+SABkAFABaAJH/AgAUACIAZQC//xUAIwCu/9H/SAAnACAAdgAVAH8AZwBAAJAAYQBOAC0AEgAOANX/y/9DANv/vf8TANn/FwASAOv/AADc/xoAXgAVAEgAOgBBAFkAtf9EACQAMAAUADUAmQCf//z/IQD2/xwATgDR/9r/TwCb/3gABQCW/+L/ef8UAEcA3v8bAIQAs//5/x8A4v9oAEIAIgAuAJQA5P8zABYA3P8+APv/MwC7/yQA5v+i/8f/dv/I/+X//f+0/wsAif/F//X/m//5/zEAXgDe/1MACwDl/9j/FgCTAJr/QAAPAAwArv/2/4oA7/9OAKz/z//9/yIALgBKAIUADwAMABwABACV/yoA/v8iABwA8v9jAKv/FgDc/xkAJwDW/7sAFQAkAC8Ay//V/wEA8P/z/wcAGADv/+D/CgC//xUA7f/e/9L/tv/X/5X/BQCp/8z/6f8RAA4Ai//+/6L/IgDl/7P/ZwCJ/8X/BwAGABcAyv9UAA0Awf87AOf/EABEAMn/5v/r/93/LQA2ABkAAgDw/xcAEgAhAFIA1P8TADQA4f8eAAUATgC//xQAWgCR/97/9//C/7v/2/8GAM//fP/y/z4AHwBQAC4AAADK/zAAy//6//z/xf9RAK7/0f/a//T/5P/X/zoAd//c/z4A1/9xABIARP/q/23/nP8wABQAWgD//wAA2/89AOn/EQAOAJ3/MQCV/yoA2f8EAN//iv/9/9n/BADf/woAdf///9r/vf/c/z3/ZAD2/wkAGgDe/67/GQAmAAwAVACM/xAAaP/P/34A0/8kADAAJgDW/wIA8P8FAM3/IAAsANv/KwDa/wUAFgASAP3/NADz/+T/6f+k/zYA4//o/1sANwA+ADIAFgAAANv/0P9HABQA//9IAPH/KgAQAB8AKwDa/xgAyv/n/yMA5f8PAOj/7f85AAkAGgACABQAWgDI//j/VQAyAE0AUAAJAL//JwDp/wAAyf/T/zcAmv8cAM3/DgALAOX/MwC7/xEAMwBgABYAJADn/+z/3f91/+3/p//d/wgAPgD7/w4AQgD//xEAIAAaAMz/MQADACcAVwD9/0YAFAD+////2v+9/9z/4//7/8X/9f+KABMADwAxAN//+P9CAOz/OQAcAE0AUQDT/yUAi/8QALH/rv8ZAG//MAACAAIASwBPAGQA9v/4/4wAOQAuAEoA8/8ZABQASADx/wUAFwDJ/woArf8YAJT/4P9UAJ//RAASAP3/DwAMAC4A3f+//97/9//5/wwA+P8eACoAx/8IAPX/5f8hAOT/DQAdAM//MwCp/6j/OQDT/4EA+v/p/20AIQB3AAMAAwDM/7H/rv90/+z/uP/+//7/2v8FALv/7v/f//j/MAACABQAIgD4/9T/EwBHAN7/UgBnAEEAawD7/0UAJQCw/y0ANwDj/2kAHQDh/x4A4f8eAPT/CAA+ANb/AgAnAFYA/f80ADwA6P8jAAoA5P8gAAcA4v8wALn/7P9LAKr/zf/X/ygAMwDN/2oAVQAgAD4AoP/8/+v/pf/c/5n/9//5/wwA+P/V/xMA2f8XAO//FgBJAAMAAwDx/+H/sP+t/9D/EAD7/9f/AwDx/wUAl/8GACoAxv8/AEUApwA8ANX/JwAxAPH/UABSALD/5P/8/9j/lv/1/+T/1/87APn/+v/E/+L/1v8CACYAHwDi/8P/BgCp//H/z/8iAGUABwA9ALH/if/q/yUAMAAnAPv/1/8oAPz/s/8LAOX//f8PANb/TADi/+j/o/+1//v/xf8rAMj/+P+d/57/1v+U/zwA+v9pAHkAGAAmAOj/IwAKAAgAKwCQ//D/KQD9/zQAz/80AM7/xv/R/7X/MgCo/ycA+/8gAD8A/P/q/9z/YwD1/xsA8v/1/+T/6v8SANj/OwD5/x8AKwBHADoA+P/6/9b/TADP/yIACQC+/93/0v8RAFb/CgAaAKf/OQDS/24A6/+4/yEA5P9qAOj/kQB1APH/YQCF/y8A8P/O/1gAj//d/7//AgAmAPv/IADj/zIA3//4/wsACQAHAPT/dwC7/6P/7f/e/xsAlv8GAOD/HQB0AMr/+v/W/8z/1v/e//f/wv/z//b/wP/f//j/HgBiAPP/9v/T/8n/HQDh/wsACQBRAEEANAAFABcAt//F/ywAIwBBAOz/XQAUAP7/SADe/xsABAA6ABwA8/8sABEA6v/c/xkA3v/3/x0A4f/C/+H/MAABAPD/YAAEALr/2v/0/z8A/f8hAEAAIQDk/w0AMADL/x4A4v8MAOX/IQAtALb/agDD/xcAbwDs/0sAKgDZ/zwAQwD//zYAhv+w/y4AAABKAOD/+f8xAN7/LgAAAAAANwCa/xsA4P+c/0IA7P8UACMA5v+z/x4A9P+//zkAnP8vACYAw/8YALj/tP+e/7H/0//u/ygAIADR/7X/6f8AAFsANwB2AE0Avv8BAN3/0f8RAMX/BwAFAOD/ZwAbAM3/1/+D/0AA2P/z/1EArv8ZABQAWgAkAMH/KQAOAAwALgBKAM7/DgBDALX/+/8gANH/2v+9/9z/9v+u/ywA2v/P/zQAFwAlAOj/NQAGADwACwAcAHIAEgBYAOz/AQABAAEAOADk/yAALABIABUASADf/8H/TQDj/zEAKADq/zcAvv/w/xcAyv8wAMv/+v8fAPX/QAAPAAwA+P9CAP//tv+f/w0ACwCb/y8A3f/R/xEAIABjAD4ARAAkAAsAQAD9/9n/KQAPAAwA+P8LAPf/CwD3/x0AFwCS/18AqP+5/0cAuf8iAOX/6v/c/+P/sv/B/+D/5v/r/7j/IQCb//j/wv+F/y8AAQDd/y0AEQDY/zsA1P+l/yUA1f/w/87/6v9KACkAIQAtACQAVABEADcAPgAgAOP/1v8CAPD/4f/n////2v8YACYAHgBQAC4Ayf/n/34A+P9VAPz/s/8dAAUAFgCk/wAAyf+v/5r/0v/J/5z/VQDX/ycARQASAEYAEwDH/+T/MwDy/z4AHwA+AOn/tv/X/9//+P/n/0cAAgDw/wUAKQCz/wsA5f/Y/84A3P8sAAAAAAAkAB0A8/++/yYAxP9QANL/kv/x/8///f/Z//P/9v8uAMr/+f/7/zIAOwDn/0cAAgA5APf/LwAUACIALgDv/2AAFgBJAM3/6f8SAOr/7//y/wYAqv87APn/w//h/+f/7P/w/yoAof/+/6L/x/9kAJn/9/9nAOX/IQAtAO7/XwAoADIAFgAAABIARQAlAPr/+/+z/x0AvP8AAAAA3P8+AOn/7v/f/+X/xv8aAJX/4f/n/2v/dwDN/+n/2/90/+v/gf/j/+n/2/8GAOH/+v/W/5T/FwDK/4v/IgAIABkAXgAnAMT/GADw/87/6v8SAOv/3f8sAAAAbgAhAOT/DgDC/87/DgDn/+z/XgDw/2EAcwAlADEA8f/h//r/+/+y/y8AEwD+/yMA+P8wABQANQArAP7/SADx//T/LQDb/z4AMgDy/wYAqf/y/ysAIgD4/0IA2v+9/yUAsP8bAM3/xP8ZALn//v/a//T/BwCY/wgAKwDs/zkAGwAWAG4A2P9OAHYA8f9iAPT/dgAoAHv/JwD8/yEAv/8UAO3/gv8aAKj/JgAMAAoAGgC6/0gA3v+u/xkAy//o/20ADgBCAMj/+P8dAIX/QgDa/+H/CwDA/83/DQBnAPf/wv8XAO7/lv/0/9L/AADt/wIAOQAcAAQAzf/8/w4AVQANAFQAMQDx/1AA5f8zAOD/+f8MAPj/MADe/xsAFgDI//j/QwDt/xUANQArAOz/AgAUANn/8/+s/z0ADAAuAG8A/v81AM//6//L/0MA2v/0/1IAnf/V/8v/QwAAAAAAJAAdACoA6/8BAN3/ZAAGABgAXQCT/xYAEgAOAPr/DQBUAB8A9f/l/w4AsP9kABoAJwB8AKz/YQC8/0kAcgAAAJMAY//w/wUAhP8uADgA9//m/w8Aw//P//7/7P8BAAEAk/+o//H/l/8+ACAAmf8JAAcAKgD+/7X/HwD1//f/ZwAbAOD/HAAEAN//LwAlAAwAwf8DAPH/qv8pALP/sP8tABIAIQBSAJ3/+v/7/43/EQDq/1wAAAATAA8ADAD4//r/MQBw/x8Aq//g//n/sf+dAOz/XQAmAOj/SADx/2IAYQA8AEMA7f/M/+j/AABJAE0ABwA8AJ7/ev8UANr/PABWAEUASgDz/xkAy/9DABEADgD6/0P/+//F/4b/sf8JAL7/AQDw/87/MwC7/+7/qP/e/9L/7f8VAO3/OgD4/wsAwP/f/67/GQDw/5f/GQDe//f/CgCJAKX/EgBYANn/cwAmADEA8f/h/wsAGwDN//z//f/Z/ykA2P+p/8z/jgAEADoAZgDS/xEAs//5/9b/8P90ACYAMQBfAPH/YgBhAOD/QgDH/+X/s//n/1kA2v/0/+T/xf8ZACcA6f9JAPL/GABLAAUAFgCk/+3/3//l//3/2f/g/9T/AQATAFkAIwAuACUAVQANAOf/NQAqABAA+/8yAPL/GQBLAM//2f/g/woAQAD9//7/IgDT/23/+P/n/2v/GwADACcAMgBx/8T/0P8PAB8A4v/o/9r/q//O/1gA/v+0//v/xP/1//f/+f9DAO3/zP8NAPn/DAAuAO//KQAOAOf/bAD8//3/2f+8/0kAAwAVADYAKwD//+3/8f/P/8b/5P8NANT/yv/V/7j/2f8EALv/EQBFABMA/f8PADEAlf8YAO//u//t/4L/GwADADoAQQAPAB8ABgA8AAwA5f/Y/wQA8v/0/+T/IAAHAIb/1f+4/8b/CAA+AB8A9f/S/8n/r//R/+3/p/8BAAEAAABcAAEASgBhAKn/JwAyAAMAOgAcADwAHQDP/7T/HgCY/wcAGAC4/yEAm/9TAOj////t/7n///+j/xAAsv8cAM7/xf/j/w0ALwATAEcApv9dALj/DwBoAOb/WQD//1oAyf8cAHMAEwAiABsA8v8rAGwADQBCANr/BQA8ANX/EwBHAPD/z/8zALz/JAAdAAUAOwDU/wEAEwDZ/7z/AAAAAAAANwC+/yYA6f+j/1oAEQBFAAAA7/8EAJX/BQC7/zYALADt/3EA2/8YACYAHwDi/wwAQQDr/xMA2f8XAO//cgCBAOj/SAAnACAA9f9AAGsA6f9IACgAIABRAPn/QwA2APX/UgDV/wEAXQDd/z8AIADk/zIA4P94AAUA4P9mAC4AEgDr/zgAdf+1/zEAuv8jABwA4P9CANr/z/9GAFz/6//K/8L/4f9T/xoAcP/6/w0A1P9vAMf/5f8OAOf/7P85APf/QgB/AOb/xv8IAPX/5f8gAKz/4v8LAK7/vv8UAP7/fwBBAOz/cACj/yMACQAaADoA+P+MAPH/KgD+/yIAQQCh/zQAKgD+/xAA6f9JAN//nP8dAM7/DwDo////IwDT/yUA+v8NAPn/6P+1/+n/7f/x/z0AHgBiAPT/0f/I/5z/5/+0/9X/pv+B//b/wP8oAOr/pP9JAF7//////2z/rv+Z//f/nP8dAIX/wv/z/4f/HwDQ/0cAAgC4/8b/rf+r/7v/WwAlAAsAGwAoACAAUQAKAIkAXAA4AAgAmf8IAND/NQBPAFIAVQCy/9P/3P++//D/KgDG/2QALAA2AKwA0/83AAgA9f9AAA4AHgDi/zAAJwCy//j/CwDl/+r/kv+o/ycAxP9iAD0Asf9AAMb/CADQ/+z/FACi/9n/zv/Y/83/DgDn/7X/1v/e/0AADwAMABwAKQD9/9n/u/9JACgAIACJAO7/FQAAAEkA3/8KAOT/aP8YAJP/KQDq/xMANADO/yEA9/9mAC0ANwAsABEA6v8SANj/qf8nAI3/7f/e/67/GQAUABAAMgAWAO3/XwAnAA0AQgA1APT/LQASADMAKQCO/yUAsP+t/xgA3f8IAND/2f88AAwAQQD+/yIAUwCw/0AA/f80AOH/5/9sAKD/agALAK7/GQAnADEAKAAyAOD/LwDd/7//FAD//+3/TAAYABMAbADX/xUAEQDq/+7/uv+j/zUA4v+e/9b/lf8qAOv/OAAbAN//+P/C/yoA/v9sADIAFgAkAB0ATgAtADYABwA9ALH/5f/9/9n/8/+Z/2UA9v8cACkA/f9rAOn/WwAAACQAQgDI/1MAHgD0/z8A6v+l/wAAyf/5/wwArv8HAM//DwDW//D/YQCX//X/LgDJ/+f/DwD7//z/MwDO/w4A1f8mADEA3/9TAMP/l/+s/6r/FgA2AFEAHAApAP3/6/8mAAwA+P8LAC4AEgAhAGQAPgAgAOP/HwDQ/6L/IgAbACkA6v8AAAAApf/b/xkA3v/S/7b/6f/u/7r/EQD8/w4A1f/L/7D/m/8KAJr/HADN/+r/bgAPALH/m/8dALz/NwBRABwAKQAPAPr/sv8vACUAHgD0/7//TABQAMD/TQC+/4H/UQDB/00AGQDe/y4AAAAAAO7/FgDb/1AAQAAPAOj////b/+L/aADm/1kAEAD8/yAA9v9BAA8A+/8NAAsAwP9MAOL/+/8gANH/WgARAPz/of/9/+v/EwAiAK7/GQDL/wwACQAaABUAyP8uAAAAAADv/xYAJABCADUAGAA4AAgA4/8MAEEA7P/w/ykAxv/2/1MA+v9pADAAAgABAMv/1f+B/7//y//D/wYABADg/woAPwAOAPr/sf/l/6H//f/+/xAAaQDn/1kA/////9v/9f8bAM3/fADR/xEA6f/J/woA5P9XANn/YADy/xkAJwCx/2YAv/8nAOn/tv/q/8n/CgCI/zIA8v/1//f/1P8TAMb/GgDf/wkAv//L/zEAzP/E/6v/KQDr/yUAHgAYAF0Ay/9VADIAqP8nAB8ArP8XABMA6/8mAOj/WgAAAMn/VAAMAAoALQAkANT/uP/9/+v/k//N/w4AsP/S/yQA1P/v//L/9f8JANH/IwD4/0IA//+j/xAAsv8cACkA2P8pAA4Anv/o/0gAzP/X/ycA/P/9/+v/7/8WABIA/f/+/0cA3v/3//n/w/8qALT/+v9EABIA/f+h/zQAFwDc/z8A6v8AANz/4/8fAL7/3f8aAAMAzP/D//T/9/9BADUAGAAmAB4AKwAiAAkAvv+m/93/GgC6/xAADQDm/yIACQBjAPX/QADq/9z/GgCn//D/zv8hAPb/LwAlAPr/MgCV/yoA7P8UAGwA6f83AD4ADQALAPf/HQBOAD8A6v/c/z4A6f83AOP/xP8GAHL/IADR/7X/+/8OAFUADQAdAPP/PwBqAFUARQDc/77/AQC4/9n/TgAHAD0AMQDf/5z/r/+//97/CQDR/zUAvf8lAEMA7f+DALL/LwBLAOH/VQANAOb/IgAbAJb/BgApAOv/EwDr/wEA7/+7/xEADgDV/xQA7P8UABAADQCv/6z/BQCp/xUAEQAOAFUADQAKAAgABgCq/83/xf8ZAAIAAQBLAAUATgAsAO3/uf8QANb/3/8JAL7/cAARAHwAZADj/zEAzP+f/6D/xf/Q/xAA6f82ACwAIwAvALj/NADh//n/VgAgAAgAYgAYABMANACq/ygA6v/c/9H/EAAyABYANgD1/2UA0f9IAAMAzP8fAND/IgCb/1QA6P9IACgADQB5AJj/dgC6/8j/eAAEABYAJAAvAJP/KQDY/5b/vf+4//3/2f/h/x0APADV/14AAgDL/wwAif/9/4//yv/5/+j////t/0wA9P8IAOP/6P8AABEAMwBOAMAABwAqAMf/9/9UANb/JwD7//z/2P+7/wAAEgAOAPr/6f/b/xgAFAD+/xAA1/8DACcADQAvAN3/5P/p/6T/tv+y/woACAArAEgAOgBBAA8ADAAcAOD/HQCGANn/TwBkAJn/CAAHAOH/HgAqANn/TwAIAKv/cwAlAB4APQAMAK7/rP/h/+f/7P/e/9L/7f+6/9r/YgAXADcACAD1/9L/yf9BAMf/GwDf/67/9v/A/9//0/8lAPr/DABUAB4A0P/H//f/1P8AAMr/5//+/9r/GAABAO//BADN/8T/q/+8/9v/vv9dAF0Ay/8xAHEAJABmAEAAIQDk/8X/9f/l/0YAAQAlAAwAwP9NAD4A/P8OAPr/sf8cABYAEgAOAIv/RwAUADUAYgAqAP7/2v8FAOD/HQDz/wcATwD3//n/6P+1/9b/3//T/xIAxv/j/zIAAwBxAAAAAAA2AL7/AQDL//r/DQDU/9z/9v8JAL//8P9y/47/yf/B/ykAs/8dAKr/8v9QAAkAGgAVACMAwf8oANj/FgDu/7r/SACn/8v/HgAYAN3/LQDb/9D/NQDi/x4ABgAXABIA/f+0/57/+//X/ygADgALAEAA2P8WAAAA3P8+AOn/AAAkAPn/QwARACAAUQAKAD8AMwCW/ysA//+Q/yYA1v8CAMv/DAAKAKz/KgBHABQAEABXAA4A6P81APX/0v8AACQAwv/g//n/nv9EAFsAAACBAAwAZQA/AOr/SgDz/2MAKwAiAEEAxv/S/8j/5v/r/93/BwDi/57/DAD4/+j/tf/E/xgAEwA0APT/GgDx/8//6/9LAAUA4P9BAMf/QABGAO//FwDu/7r/tv/E/6v/KQDr/xMADwCx//j/5//Z//P/9v8JAOT//P/Y/+D/CgCt/z0A1v+U/zwAsP8bADoAHQAXAO//8v8ZABQARwA5AK7/LAD/////7f8CAAIAAQBwAOz/SwAYAMr/wv/h/8L/vP8AALf/DgDV/xMA7P8BABMAx/8tAO7/FQA2APX/CQA+ALL/5v9GAMv/MQDM/+n/2//i/2gAHACGADQAz/9GABQA7P9LAAUAFgAkAML/cwABANz/ZADi/wwA+P/6/w0A5v9HACYA6P8RAOr/AADc/5n/CAD1/+X//f/Z/ykA/f80ABcAEwBGAAEAEwDZ/7z/AADu/7r////I//j/+v/W/4MAIAAsAFsAbgA0ABcAJQDn/yMAHABzABIARgAmAPv/IAD2/4oAAQBKAAQA4P+LABQAfgBmAEAARgABABMAIgAtAFwA7//y/+P/1v8UAMj/GwDy/77/y//D/7z/yf8KAOT/6v8lAAsA9/9UAOn/7f8nAJ//DgCw/xoAKADF/xkAAgDd//f/5v/G/1IA1P/d/ywA7f8nAOn/SQADACgAIAD2/wkAv/8UAKL/x//A/7r/EACy/8H/zf8OANX/8P/O/6D//f8PADEA3//4/9T/7/+7/xIAagD6/3wAGgDx/73/3P8sANv/UAAJACwA///t//H/z//Z/5f/GQDw/wUAFgDJ/9T/3P+s/6r/8v/i/x8ABgAXADgA9v8cADwACwAJANH/o/8QAB8A0P/s/wEA8P8XANz/UQDT/9z/rQDC/3MAyv+L//7/ff/O/47/SQDy/77/7/8EADsACgAbAAMAzP+M/yMA5v/Y/wQA8v/i/9b/8P+8/yUAeP8AANz/0f9aAJH/OQDl//3/DwD7/zIAFgASAEUAbwCQ/wEAuP+z/zAA3v9AAP3//v/Z//P/PwAgAPb/CQA/AMX/9f9AACEA5P/F/wcAz/+P/zcAGgBMAD0A+/9FAO//TQAZACcADQDB//P/vv8UAOz/AQABADgAGwAoACAA4/8yAPL/UADT/+7/KADF/1AA5v/r/yUA6P///zYAGQABAPD/u/9//6v/8/++/wEAEwAiAFMAHgB0AF0AFAD+/xAA6f8SAEUA3f+//8v/DAAvABMADwAMAAoAPwBFAEoAKQD9/zQA4f8wAEwABQAXACUACwDl/2oADAD4/1UA/P9YAMf/5P8gAL//FADs/8v/6P/I/9P/t/+O/9v/q/+X/xkA3v8IAD4A6f8SAP3/RgAmAB8AGQCU/xYA7v/f/+b/2P/z/9D/RwDx//T/CADQ/xAAxP8GABcAt//F//b/CQAsAAAAEQAgAJr/QAD9/w8AMQDM/0QA7v/y//X/GwBw/5//RACA/ysA7P/L/1YA6v+3/8X/rP+X/wcAqv8WABIAs/9CAMj/GwAWABIAMwAEACgA6v8SALP/HgAqAMf/CACG//r/+/+g/yEA0f8RAFcANADz/xoAcQDt/9//LgDc/9H///8RAPz//f80AHMASwAqAA8ADAAuACUAMAAVAO3/JwANAPn/DAAJABoA8f8YAEoAPAALANP/JADn/xAADQDB/7v/tv9FANz/0f81AOL/DADl/+v/SgDz/wcAYgDh/+f/EADW/xUA//8AAAAAtv9FAEoA4P8dACkADwDW/wIAy//o/1oAAAAkAAoA9//5//r/RAAkAGcAHABOANIAFgAkAGcA0v/b/xkAJgAfAOL/DAAKAD8AIAA/APz/s/9nAOX/6/+CAOj///+AAML/8/8ZAMz/HwDi/wwACgDk/0UAJQDn/zUABgDO/0YAEwAiABsA8v/1/wgAPgAfABkA3v8bAAMAp/8mAEQAEgDY//L/vv+m/0oA4P/m/0cAy/8xAAIAFAB/AJz/1f/w/7z/EgDY/6j/FQARAMT/PgCf/zIAFgBa/x8Ah//W/xQA2v/0/4j/6f+k////EQAOAFUAn//X/xUAyP8KABoAzP/7/8X/9f8JAPb/eAAEACgA/P+h//3/2f88AJ8AWwBcAG8A2f8FAPL/vv9LAAUAYABgALv/tv/p/+7/uv/I/wkAGgDe//f/1P/v/7v/2/8ZAN3/GwAVACQACgAtABIA6v8AAAAA7v8WADYArP/z/wcABgAFAAQAAwCn/8v/i/+1/wwAHAAEAPL/BgDO/zMAzv9p/+P/6P9bAFwAyv9CAOz/uf/+/5D/pv8TAOv/AQBdAMr/+v/p/7b/6f9//+L/6P+j/xAARAASAOv/JQDV/97/CAD1/+X/DgDn/xAARAAAABIAMwA8APr/DABBABAA6f8kANT/uP/9/8b/5P/X/xUA2//1/y0AAABJAPL/PgDW/9//CQDj/0QAyf8KAOT/xf8sANr/vf/v/zsAHQAFAAQAOgAvACYADAAJAOT/DQBCALX/MQAoAPz/WAD+/zUAGADd/xoAFQD//wAANgD1/+X/DgDD//P/9v8cAHMAAACl/wAAyf/5/zEAzP9WALP/+f9WAKD/RQAAAAAASgApAFgANQAFALz/EgDY/wQAcQAAADcA4//p/yQA+f8xAMz/1v/x/7z/JQDC/wUAFgCk/xEA/P/G/wgA4v/W/wIAFAD+/zUA0P/r/xMAj//v//L/BwAqAA8A+//q/xIADgDo/9r/z//G/9H/2//0/9L/AADt/5X/KgC0/+j/NQCr/xcAEgAPAAwA0/9cAEoAFwCBAAwAHAA7AOf/RwBv/8P/vP+l/9v/vv9LAM7//f8iAAkA4//p/+3/zP8xALr/NQAZAPD/PAD6/2kALwDd/xsAAwACABQAEAD7//z/DwAeAAYABQAoADMABABNAFAAeAApACEAGwDf/wkAv/8CAAEAuP8PANb/uf+0/9b/AgDw/xcA7/8EACgAsv9BAP7/2v9PAPf/ZgBSADAAXgAnAB8APgBXADMAYQDO/+r/SgDO/0UASgApAH0ACQAZAPD/9P8/APz//f/r/8v/sP/3/6//df9Z/y//WP9m/ykAMwA8AIwAhAC0AP7/a/9j/2//ef8BAEoAqwDTAAQAFgDb//X/wP+C/2T/p/+nAD0AVgAgANH/fv87/6v/qf8VAFsAygDtAD4AaQDU/8v/Zv9N/wIA3v9lAIgAgABVAOn/f/88/5n/rf/1/1IAsQB8AHYAOgDU/7j/s/9CAP//WwCAAEIANQD1//f/nf/V/93/0v/t/18AJwAgAD4AoP+g/47/tv/8/zMATgB2AE0ABgD0/+T/xP90/w8A+/8yADsAHQBzAJP/u/9+/5j/BwAGAGEAKQAhAIj/HwAsAFn/DAAcAOD/ZwBAADQATgA/AI8ATgD2/9P/EgD9//7/WgAjAAoAZAA+AJ//1//y/73/SgBhAM7/DgDC/5f/LADI/9P/JADn/xAA+/8OAAsA0v8SAMX/mf8bAN//CgAaAKf/AQDL/8P/FwA4AC0A7v8DADkA0//J/0IA///s/ycA6f82ACwA7f/e/8D/AwDx/+H/VQAgAPX/QADZ/wQAFgDJ/woAv//x/zwADAD4/x0APQCM/yIACQDR/1oA2//1/9L/AADb/6v/zv9p/9D/kP+T/7v/7f/x/wUAPAALAAkA0f8jAOb/s//6/wwAQQDZ/+H/+f/E//T/LQASACEACAAGAE8ACAA+ADIAOgAdABcAbwDr/wEA7//g/woArf/Q/9n/FwASAOv/JQD6/w0ALwAmAPv/xP/i//v/6f8kAB0A4f8LANL/AAAAAO7/OgAvAEsAKgD+/zQA9P/2/+b/NAAqAOv/OADk//z/DwDV/yYA+//X/9//5v/G/z8AWADr/wEAuP/9//7/2f8qACIAGwDy//X/CADQ/+z/3v/k/8X/4/8fAKv/FwCl/7f//P+O/yUAwv/z//b/wP87AK//9v+J/9j/OwD5/2gA5v+i/7T/sP/3/woA5P8OAAsA9/8LABsAFgDb/xkAAQDd/y0A7v8VACMAr/+//7n/2f8FAOD/HAAXAAAAEgBGACYA1v8CAN7/5P/q/zcABwArAH8AQQBZACMAHAAXAO7/8v8GAGEAKQAhAC0Ayf8dADwA5/9aABEA/P/9/9n/FwC3/yEAUQDU/wAAJQD6/9b/OgD4/57/MQAVACMACgAIACsA2v/h//r/1v8CAF4AOQBAADQAz//9//7//v8jAC4AEwAhABsAAwBfACcAMgA7AC8A8P8pAEYA8P8XADcA0f/I/wkA0f/t/xQAEADp/4AAjADe/1MACwDA/wMAzP8MAAoA5P/8/w4Aef/d/xoAp/85APf/HQA8ALD/GwADAAMAFAAjAC4AuP8hAPf/+f8MANP/JAAdAOH/CwDBAPf/LwCUAK7/GQDw/87//f+0//r/DQDm/zQABQApACEA0v9IAPH/dQBLACoAWQCQ/yYAxP8GAAQA8v8rAMj/CQAHABgAuP8PANb/p/+UAOX//f9ZAKL/2v8FAJb/q//g/2X/g/+c/9T/uP+P/xIAxv+//xQAEADp/9v/BgCF/+f/EADW//H/vP/K/+f/7P/d/wgA4v8MAOb/tP/V/8v/HgDP/0cAOQAbAHIAAABJAAQAFQARANf/FgDb/xkA8P8XABIA/f8iAMD/FQDt/xUAIwDB/00A0f/s/xQA7P9LAE8AdwApACEAGgC6/+z/JwDp/zYAUAAJAFEACgAtACQAwv8pAA8AsP8bAHIA7v9NAAcA9P8IAL3/JgAMAAkABwD0/9L/yP+c/9T/yv95/+//4P/U/93/PwAOAPn/MQADADkA0//u//L/KwBHABUASAAVAP//7f86AOb/s/9nAAkAGgAnAPz/RQABAO//4P/B/3H//P8zAM7/MwDz//X/5f8hAAgA4v/7/1b/+P+d/8P/KgDs/zgA9//5/wwA0/+l/+7/g//l/1gAIgBlABoAFQARAOn/7v8VABEAMwApAOr/XADv/zsAMADw/zwA+v9pAEIA//8jAPj/+v8fABkAXgBwABEARQAAALf/DgDC//P/9v/T/zcAUQAKAPf/VAD7//z/MwCW/wYA4f+w/y0A7v/N/+n/2/+r/87/2P/g/woAmv/l//3/xv8IAL7/7//g/6//PwDq/8n/+f/6/+n/EgDF//b/5f/G/2QA4/8xALr//////5H/cAC1/3sABwAGAAUAg/9TALD/GwA7AFQA+//q/yQA1P9LAPP/4//p/8n/+P8LAK7/vv/w/87/6v/K/6//v/+U/7z/3P++/yYADAD4//r/HwArADUAmgAfABkAJwAfAAcA4f8LAOX/IQAIAAYABQAEAAMAOgDm/w8AMQDM/x8Aq/8EAM3/oP/8/9j/8v/Q/zUAz//r/yYAVgAgAAcAdADe//f/CgDS/7b/6f/b/wYATwC//zoAHACp/9//+P/U/5P/FgASALP/ZwBAAOv/OAAIAPX/CQAZADkAUwAwAEwAGAA4AC0AAABcALf/MwDz/5n/5f/F/z4A6f9bABIAxv8aAAIAzP/W/wIApv/v/ykAWAD+/zUAYgD0/ywAyf/4/+f/EAAfAND/bAAgAAcAGADv/+D/wv88AEIAIwBmAPf/1P/v/xYAEgDY/ykAjv/J//n/nv8MABwAFwASADMAYQAEAAMAJwCy/+b/DwAMAEEAIgAuAO7/KACz/9T/JgDo/5IAUAAcAM7//P/Y/6n/p//w/zwA+v9WAA4A5//s//D/4f/V/wEA3f8tABEAWAA0AOH/VQDp/zYAPgDE/ysAIwD4/zAA3v/A/xUAyP/4/zAA3v8IAFAAQQB+ABwAFgASAA4AVQANAFQAMQAoAGoA1f8BABMAov8PAAwA+P8eAOL/QwDt/8z/MQDf/9P/AAAAANz/BwDh/9X/y//6/w0A+f8eAL3/OAAaABUANgDj/x8Amf/S/wAA7f9MABgApv/K/x0Ahf8dAAUAhP/T/8r/1P+T/+D/5v/+/xAA1v8VAKP///8RANf/8f+9/wAA3P8HAM///v81APT/CAArADUA9P8tAAAANwD2/5z/CgCt//X/GwAoAA4ACwD3/woAQAD9/7UAbQBFACUADADl/3z/OwDm/yIAGwDf/y8AAQAlAB4AKwC1/+j/tv+y/xwA8/9RAEEADwD7//z/of/9/yIAwP/f/67/4/+f/+n/2//Q/zUA9P9kACwAEQBXAP3/IgAbAPL/PgD7/8X/4/+x/9P/t//F//b/wP+6/yMA5v/+/0cAy/9DANv/0P/s/wEAOADk/0UA7/+o/7r/IgDT/8n/HQCX/ywA7f8UANr/4f8eAKr/FgAkADAAAQA4AMD/8f8GALz/SQBx/x8ALADa/xgASwBOAPb/iwDw/ykAIQDk/2oA+v9XAA4A+v8NAAoAUgALAPf/LwDL//r/+//8/0YAuP80ACoA6/8BALj/6/+T/9//CgA/AA4AMABwAP//gAALAK3/4v8eAAYAKgDr/6X/EgCz/wsA9//C/6n/lf+Y/6z/YQDh/2cAHAC7/wAAyf/T/8r/CwCb/9P/AAAAACUAwv8qAA8A+/8gACwAEQAyADsA+f/7/+n/AAAAAMn/wf+7/6T/tv8fACwA2v8GAM7/2P/y//X/GwDf/y8Ayv/V/zgAQAAzAPP/GgAUAEgAJwBEACUAHQAYACUAMQCU//P/vv/e/0AAMwA8AB4AGADv/04A9v8JAAcA9P8bACgAagDo/0gAFQBIACcAxf8rAKP/IwAuABMADwAeABgAJgAMANP/yv+d/wsA0/8AAO7/8v8YAMv/VQAgAOP/HwA+APz/DgAeAOH/HgAFAAQA8v/Q/8f/GwDf/woAZADQ/yIAQQD+/8f/5P/8/8b/9v/m//3/DwAMAC8A3f/k//z/xf/R/7X/xP+r/87/DgDV/0sAFwDc/9H/7f+5/9n/TwC//wIAFAAjABwATgA+ANf/OgCc//r/6P8RACAABwBiAAUAcwAlADAAOQAcACkA6v8SACEAGwAVAFsAt/8gABoAuv9sAMX/GQAnALH/wf8DAAMA8f/0/wgABgC8/xIAjv/c/9D/tf/o/8j/QQDG/z8A6v/v/wMAAwBMAM//RwABAEsATwAaABUA7f9MAPT/9/8dAE4A0f9IAF8A3/8cAM3/1/+6/9r/z//r/xMARwBLAL3/yv/n/9n/vP9uAMb/v//e/5v/LwDK/3oA0P8PAEQA7v+7AN//ZgDS/+3/FQCR/0sAqv/g/+b/2f/z/xkA3v/S/zYAvv9eAPD/8/8sAO3/TADQ/zQA9P/k/44ABAADAEwA0P/+/0cA3v9lABoAAgBMAOL/QwDb/+L/MQACAPD/vP9uANn/8/9RAPj/CwD4/x0A4f/C//P/4//E/9D/2f+q/9//5v/r/xMA6//L/7D/wP/M/w0Awf/g/woA0v8AANv/9f/S/wAA7v/M/w0Anf8eAPT/0f8jAJz/1f8TAP7/IgD4//n/MQAoAFcAawAxADoACgD2/+b/of/Z/xcA3P8ZAPD/9P8/AGn/PgAfAIb/VgCy/x0ABQAWACQAwv8pALP/HgAqACIAQAD9/w8AMQAoAPz/RgDv/wQA3/8KANH/2v90APD/FwDv/xYAkv/M/zEAcP8MANP/AADc/z4A/P/q/zcA5P9XAMb/UQDm/w8AMQDx/2IAz/9YANr/KgD+//7/IwCu/z4A1/8VAKP/WgAAAKT/bQBp/ywAIwDT/yUA+v/E/wYA4f/5/1YAxf8ZAJT/vP/u/4P/QAA0APP/UQD4/+j/SACC//f/wf/O/1gAtP9VANf/zf9XAOv/7//g/woA5P/8/zMAFwASAEYAOAD3/woAQADY/wQAKACy/0IA7P/L/1YA/P8zADwA+v/7/zIABADx/ysAIgAcAAQA3/8JAAcAGABdAF4AcADt/8z/sf/T/+7/qP85AC4AbwA0AGEATgAIAFAAwP86AK//v//w/8//IQCa//j/wv8qADQAPABVAPz/WAAQAAwACgDk//z/IQD2/0EAEADW/ycA/P/q/+7/FgDJ/xwA4P/U/+//lv/1/8D/FQD//0gAFQAAAEkAqP8nALH/rv+s/+H/CwDA/zoA1P8lAOf////t/6f/ggD7/w4ACwCt//X/CQAsADYAGQABAAEAEwBHADkA5f9GADgAiP8yAAMAuv/s/97/5f/Y/00AGQAnAOn/JABUAMT/BgCp/83/6f/u/wMATAB0ADkAeADz//X/GwCo/xUAIwD4/1UARAAlADAA3v/S/9v/0P8QAGkACwAbAPL/BgAqALT/6P/H/+X/fP/f/xwAhP8vABMA6//L/8P/cv+g/+r/kv8DAKf/y/8MAEEARgBeAAIAAQA4AK3/GADw/zwAHgAqABAA6f+AAK//LQAAAMn/wf+7/xEAjv8AACQAZwDl/w4AHgA8/9D/ov/a/wUA4P8vABMA/v9/APj/CwBTAJ7/MQACABQASAAVABEA1//f/wkAPwD8//3//v/+/8f/0v8SANj/FgDu/xUAo////xEAsv95APT/9v8cALv/EgDq/9z/LAD//+3/OgDm/6H/NAAXAAAANwDk/+n/yf/5/zAAFQBtAA4A5//s/7n/6//L/zAATAD0//f/+P8LAOX//f80AOH/+v8xAAMAAgACADkAwP+6/yMACgBRAB0ABQAWABIAMwA7AAsA9/95AOL/1f8mAJ//MgDy/6v/KQDY//L/BwDP//3/IgDA//H/BgDO/9j/BAAVAKP////t/97/QAAPAEMAJAAKAPf/CgD3/8H/4P/m/w8A+/8gABkAJwAyAAMAzP+x/0EA6/8TAGwADQDC//P/0P/H/3cABAA6AB0AvP/J/3j/yf+d//r/DQAvAAEAyv9CAO3/FAAjANP/3P8ZAAIAOQDl/7P/HQDh/wsACQD2/xwA4P/5/wwALgAAAMr/CwD3/woACAAZADkA5f9GABMA6/9LAAUA8v8ZAEsAz/9rAEQAAADb/77/XQBv/zAAFADH/1MA5/81AKr/8v/Q/6L/x//l/yAAv/8UAKP/IgAuAO//KQAhAPb/rv8sANv/9P9AACEA0f8jAAoA5P9XAI//EgA0AOH/MABLAPT/0f8RALL/CgAIAPX/UgDn/8f/GwAWABEAagDo/xEAIADj/zIAAwDM/9b/3v+u/+P/n/8fAD4AMgByAAAAEgCz//n/+//p/yQAHQAXAMr/MAAmAMT/GAAmAIz/EABEAAAANwCa/+X/oP98/6j/p//K/7D/CADQ//////8jAC8A7/9OAL7/AgAUAOz/FACQ/93/9v/4/zAAXgA5ABwAKQBGAG8A/v9tAEUA3P8/APz/DgDo////NQD1//f/HQAFAAQAOgD4/0MAEQAOAFUA6f9JABYANgDj/+n/SADN/+n/EgAzACkARgAmAAwAQQAPADEAAwACAHAAbQBYAH4AQQA0APP/BwArABAARADJ/woA5P/F/z4A6f+2/9f/zf97/zkA5f/r/zgAmv/4/+f/x/8JAAcABQA8AML/8//j/3r/FADI/xsAzf/q/9z/mf+t/zz/vv9v/zAAAgDL/40AzP8yAAMAAgACAMv/+v8fAL7/3f/3/6//UQAKAPf/5v/+/9n/8/+IAMn/iwAUACIAZQCI/zIAzf/X/wMA8f9PAAgAKwBIADoAHABOAHYAFQDt/ycA6f+k/wAAAADb/6v/vP8AAMn/CgBkAAcAKgA1AKr/8v/Q//7/EAANAFQA+/8yAAQAuv/I//j/MAAUAEcAAgAUABAAxP/Q/6L/x/+t/73/yv/n////2v8FAM7/IAD2/+b/WQAiABwAFgBJABYA7v8VACMAnP/V/0sAz//9/8b/0v/t/6f/AQAmAPr/IAD1/xsATQCs/zwAMQACABQA2v8qAI//3f+//xQAfwAvAEsAFwA3AKz/vf+3/9j/BACD/+X/s/+L/+v/7//O/w4A1f8BACYAw/9iAPP/GgAnAPz/IADk//z/WAB+AC4AOADS/zYA0P8iAHgA8/+IANv/PQBEANv/PgAfAKv/qv9yADcAPwAgAD4AMgC7/yQA1P/v/+D/r/+//ycAsf/4/1UAsv8vAKX/yv/5/9b/AgDw/zwA1f8UAP7/IwBBANn/BADg/+b/of/Z/wQA8v8+APv/6v+k/8n/5v/G/wgAvf8mADEA8f8qAA8ADADm/9n/zv/q/9z/9v8cABYAJADn/yIA5f/Y/xYA7v9NAAYAPAAMANP/EgDG/xoAzP/p/zYA9f/3/8L/BAADAN//HAC7/yQA+f/D/3QAFABHAAIAFABHALn/IgD4/+f/7P/d/y0AJAALAPf/+f8MAMH/OwBUANb/TAC9/wAAEwCh/zQAqv87AB0AKQB+AOX/IQAtABEA6v83ABoA8f/0//b/LwC4/zQAKgDr/93/0f///+3/8f/h//r/xP/i/wwA+P/V/xQANQC9/+//OwAdAPP/PwAOANT/3f8aACcAoP/8/w4AsP/S/wAAAAASAEYAXQBLAOH/5//s/97/5P/q/wAA7v/f/woAPwDq/wAAJQAdAAUA4P/5/zEAFQBIAHEAEQBYAA8A+//8/7P/CwDl/yAA0f///zYABgAYAN3/0f/I/0AA/v8QAAwA+P8eAAYAPAD6/0QAEgAhAC0A7v8DALn/EAD7/+r/NwD2/67/4/9EABIADgD6/7H/wf+o//H/TwAtAO7/8v8GAKn/zf8gABkA3v/3/woAv/8CAN7/QAAzALz/NwD2/wkAGgBeAF8AAgBeALn/x//l//z/RgABACYAQwAAABEAIADR/+3/p//d//b/+P9DAO3/XgAnAPz//P/Y//P/vv8UANn/8/8HAPT/LQC3//z/6/+l/+7/qP/w/yoAIgAtAFwA3P++/0sAz//9/2wAHwA+AEQAEgAhAAgA9f8uAAAAEgAhAAgA9f+t//X/LQDc/6z/BQDN/7L/eQAFACkAIQAIABkA8P8qANn/8/+s/7z/AAASAOv/7/9yANz/BwAYAAEAEwAiABsA8v/1//f/LwDd/9L/kf/L/9b/p/8BAMr/HgDP/yEArf+Y/xoAgv8tAO7/TQA+ADIATQAZAEsAqv8WABIA6v8AABIANADh/wsAGwDf//j/CwDl/w4A6P///+3/AgDw/87/MwCp//H/9P/3/woAv/8VAO3/zP/D/yoAEADW/wIAy/8xALr/x/8bABYANgAZAPD/z/8hAPf/CgBkAPX/5f/9/9n/zv8OAB4ABQDz/xkAuf+i/+z/y/9DAAAANgArAKP/WgBIABUAEQB8AGQA4/9WAA4AHgA9AB8AKwDH/63/GQCU/87/RQDd/z8AagBVACAAUQDT/wAAbwDG//f/r//R/9r/9P8tAMn/5v8iABsA3/8KAPb/+P/6/5//1//M/+n/yf8KAPb/wf+7/8j/HACp/8z/xP8GAPP/v//w//P/9v8JAPb/nP8LANL/AAA2AOP/RADu/zoAr/8aACcA1/9fAKf/XgDw/+H/HQDP/9j/cv/8/9j/4P8cAE4AGgACABQAyP9AAA8AQwAAABEAIAC//xQA//9aADYABwD0/+T/xf++/93/LQCTACwANgA+ADIAzf8gAD4A6f8SAA4AHgD0/y0AAAAAAO7/FQDt/6f/AQC4/+v/3f+//ycAHwDQ/xAAMgDN/1cAWABHAPD/z/80AAUA8v8ZACYAxP/0/+T/sv/m/w8A+/8NAPn/HwD1/9L/bgDr/xMANAAXABMAof/r/7j/2P8EAAMAuv/s/wIAgf+s/wUAPADV/xQA/v/s/zkAUwAwAPD/PAAMAFMAHgArAP7/kP8BABMA6/+4/zQAz//r/yUAsP9AANj/KQBGAAEAggBWAGoAVQBqADAAFABIAPH/BQAEAGAAFgDJ//j/w//z/wcAKwBHAN7/CQC+/wEA8P/O/1gA6/8BABMADwAMAC8AbwDs//D/8/8sANv/BgAqAA8AQwDb//X/rf89AJ//xP91AMz/ewAHAAUAKQAzAAUAKAAzAJb/GQDd/1IAwv8EAGAAuv9IAN//UwAeAM///v8QANb/uv9sAPz//f9GACYARAAAAAAASQDN/8X/4//E//T/0v8kAEEAtf+e//v/e/+C//f/5/8iAC4ANwCs/73/yv/C/87/s//n/9n/4f+w/+T//P/r/yUA+v8fABkAJwDp/+3/OgDB/+D/HADz//X/wP9NAAcA4f9nAOb/DwBDANv/9f8tAAAAAADc//X/9//n/zQAvf/v/6j/8f+Y/6z/KgCP/0oAFwASADQAzv/G/xoAOgAuAG8A/v8jANP/t//F/+P/+/+g/zMATgD2/9P/JQDn/xAA1v8nAFcA2P87APn/HwDQ/+z/3f8aAPH/GABwABAAMgDf/y4AuP/r/wAAyv8wAMv/DADT/xIADwDo/6P/2v+q/5b/9P/S/zYAq/8XADcACAC9/wEAbwDs/3AAIwAKAL//zP/7/+n/AAAkAAsAiP8NAHj/t//9/+v/SwAqAMb/rf/0/4j/6f8kAOf/DwBEABIAWAAiABsAYADy/z0ARACTABoAcQBuAA4AVQD8/0YAk/8DAAMAp/84AOX/WAD+/7X/MQACAKf/OAAtANz/4/8xAAMA3v8JAAcA9P/S/0gAFQBIABUAWwBJAPL/YwC9/0oAvP/b/z4A+/9qAMP/PAAeAL3/7/8EAPL/9P8bAPL/9P8tAAAAt/+g/1b/1P+l/wAAEgCz/x0Aqv+o//H/9P+s/wYA4P/n/yIAGwDg/8H/BACD/+X/xf/R/8j/+P9CANr/hgD//yMAHADO/yAAPwAzABYAJAAwACYAxP89ADEA3/8JABoAzP/p/20A6v9cAO//4P9CANr/KgAPAMP/BgAXALf/IQDk/+n/AADJ//n/1f8CAAEAyv/V/xQAtf/7/w0A1P9dABMA7P85AAkA0P9HAAIAOQAbAPL/KwDs/ycAxP8rAOz/uf/s//D/TgD2/y4AJQAeAPT/9//5//r/RAAAADcAh/+M/+z/p/8TACIAGwA7AC8ASwAFADsAQgDs/0wA4v/6/+n/yf/m/9n/BAADAF8AJwANANT/AQATAMb/GgCV/xgAAADv/xYA7v8VAMj/+P+e/57/+/8gAAcAdAA5AOX/agCe/w0AVAD7/3wAGgAnADIA8v8+AA0A+f8MAOX/DwDV/8v/HgD0/1IAVAD7/yAABwDi//r/xP/i/+j/EQBqAJ7/HgArAMf/igBKAAQAYADy/xkAJgCM/20AMwDg/y8AAQABAID/LAARAMX/9f+t/9D/2f8qACIACQDj/9b/8f/0//b/5v80AOH/QgBIAAIAOQDT/xIADgDo/xAAVwAhAPf/ZgAJAOP/HwAZABQA//+Q/6b/JQDo/6P/7P/e/8D/3/8JANH/yP/T/9z/9f/l/+r/3P8ZAKf/3f8/AOr/SgDy/wcABQC7/9v/9f/l//3/NADz/ywAWwDb/xkAJgDp/zYA0P/a/yoAj/8lADAA3v8uAG4ANADh/zAA3v/l/zMAOwALAJv/nP/U/8v/QwA2AND/RwACAMv/+v9EAMn/1P8TAOv/JgD6/x8A4/8fAAYA4f8eAM//2f/z/z4AMgBNACwANgCr/wQAAwC6/38A5v9+AOX/IQA/ALP/MADw/2EABABNAAcAKgDs/xQANQBz/1gAtP/W/7n/ov/+/7X/MQC6/8j/5f/F//b/5f+z/9X/y//o////2v/0/9L/yP+J//3/2f/g//n/1v8CAN3/GwDx//T/v/8CAN7/wP8VAO3/OgAJAFEACgDk/yAAGgDx/8///f/Z//P/GgBeABUASADx/xgAOAB2/zYAvf+m/zcA0f///zYABgA8APr/1/9MAKv/TgCJANv/PgAyAPL/9f/S/+3/JwDp/0kAYAADAN//d//u/9//rv/1/y4AAADu/4QA/f8PAFYAxf92AN//LgAlANX/XQCm/xMA/v8QADEAFQDt/wIAAgDL/2gAwf8WANv/vv8BAKb/EgCh//3/x/+///H/BQAEAPL/UAD4/1UAaQD5/wwAZgAbAE0ABgDP/2sAn//7//z/j//c/ywAEQCg//z/s//V/93/GgAVADYArABUAKAASQDy/9D/tf/7/7L/+f/6/43/IwAKAL//zP+M/37/KP+K/7P/5/9HAN7/GwA7AMH/KQBYAFkAyQBGACYAHgDi/+j/7f8nAPv//P/9/9n/vP+S/97/5f8OAOj/2v89AB4AUADl/+r/AACl/8n/CgD3/6//GgBMAPT/CACIABEAxf9jAND/WQAjAOb/DwDD/2IABQApAFgA2f+p/ygA1//N/0UA7v9yABIARgATANn/BQDN/2oAMACoAFAAZQAtAMn/+P+e//v/xP8rABAAIAAHAM//DwDW/8z/jP/a/8//2f9OAFEAwf8EABUAkf/w/7z/t/8OAB4A4f9oAEEA7P84AHb////t/7r/RwAnADIAFgDt/8z/DQAKAAgAPgBXAOr/SgAXANz/UQDB/zsAHQAqAJAAGAA4AOT/6v83APb/5f/Y//P/UAAcAAQAKAAOAOf/7P/L/8P/KgDZ/+H/MABLAAUA4P/C/7v/AAAAACQACwBSAB0A9P8sAMn/CgAtAG4AMwA8ADAA3v8bAM3/MgA7APn/+v/X/xUAyP/4/wsA9/9CABAA+/8OAPr/HwAGAAUAFgAAADcAPwAgAD8A/P8hABoAAwAUALX/xP/i/9X/3v/A/8z/1v/M/+n/7f8CAKf/uP80APP/9v9TAPr/+//q/7f/2P8DAPH/4v/o/+3/uf/s/wEA7/8pALP/wv+8/3//PQAfAGMATwAJAGMABgDz/7//3v/3/9T/JQD6/w0ACgA/ACEACAA+ALH/5v/9/+v/EwC0/wwAwf+D/wkA4/8yAAMAFQBbANv/YwAqAOz/OQAJAAcABQDg/wsAZQC+/8v/MQC6/yMAHADy/1AACQAsAAAApP///wAAyP/T/+//g/8JANH/o/9sANf/KAD8/9j/8v+r/zwACwAcAHIAXAAAAMr/wv+8/9v/9f8bAM3/1//f/5z/5//+////yP8JAAcAvf8TAA8ADAD4/0MAkgDj/zEAFQDt/xUA//8jABwA8//2/0AA/v8iAPf/wv+8/7b/IADj/zIATQDj/+j/2/+9/6X/kv+n/yYAjP/t/xQA2v8YAMr/sP+b/8H/u//b/+L/+v8fACwAEQANAAsArf91ACcAMgCXAB0AFwAlADAAzP8fAOL/6P/t/7n/NQAGADwAMAAUAGwADgDn/xAAsf8KAPb/rv/2/xwAKQDF/1EA5v8PAB4A4v8eAIb/QwDI/67/BwDP/+v/7/9gADsAMADd/+T/IAAHACsAIgBAALT/sP8bABYAAAA2AD4AIADR/+z/JwDW/97/5f8hAOT/xf8rAP//2v/0//f/1P/v/+D/HADO/6D/MwCp/7r/bQAzABYAAAAAAMn/+f8xAKf/XQAUADUAdADw/4YADwAfAPX/9/8KAPf/LwDL/zAA8P8XAEoA8/9jABkAAQA4APf/nf/V/xQA2f/z/z8ADgALABsAOwBCACIAUwDV//D/FwCl/+7/8v8GAM7/xv/j/5//6f8AANz/9f9AAEYAOAAtAAAAXADc/77/FADs/wIAAQABAN3/5P/p/6T/AAAkAMH/KQAhABoA3//T/xIAs//V/93/CAArAP//fwDU/wAAJQCw/wkA4/9EAAAA7v8DAMz/+//8//3/6//d/9H/bQAzAAQATQAHAM//2f9gACkAWABsANf/FQA2AOP/6P8jAMH/BAADABUAWgDb/wYA4f/n/zUAPQAMAEEANAD0/y0AAAAAABIAxf8HAPT/5P8OAOf/7P8BACYA+//p/xIAoP8hAOT/1/8VAMj/+P+w/+T/oP+z/1QAHwD1/9L/AAAAAMn/QQAQALH/CQDk//z/DgALAC4A3P9RAPj/+v9EABIARgATAA8A+/8NAB0ABQAWABIAWADZ/wUAOwALAPf/LwCVANP/EgAOALD/GwCD//j/5/99/wQA3//4/9X/uf8PAMP/KgBHAPD/TwAbAN//wf/y//X/rf8GAOH/MAACADkAUgDV/xMA/v9HALn/7P/e/9L/SQC6/0gAOgAvACYAHgD0/y0ANwD2/1MAsP9AAOv/yv96AM//2f/h/wsA9/9CADUAKgD+/7X/6P/I//j/5//s/4H/CADQ/9n/TgC//ycAsv/T/9z/0f/s/6f/yv/n/xAAxP8rAP//IwAvABMADwCe/2kAwv8pAH0ACQA+ACAAGQCU/zwAHgAYACYA+v8yAM3/MgDg//j/5/+j/zUAmP+//ycADQAdABcAEgBGAF0AFAAQAPv/MwAWADcAUQDB/+D/HADh/9T/SwAXAAAAEgDY/wQAFgDb/+L/6P8RAPz/2P8pANj/zf/X/7r/2v/P/yIA0v/u/wMAAgDe/9L/WwAkADAAXgA5ANP/AADu/9//HAC7/xEA/P8PAAwAHAAWALf/MwDy/wcA9P/2/67/0f8QAHv/AgACAPD/8/++/wEAAQDK/+f////a/xgAyv/V//D/4f9CABAAHwBRAAoAv//e/wkA9f8uAAAANwDk/w0AVACf/x8A9f/4/wsAGwCXAAsALQA3ABoAzP/p/yQA5v9HAAEAOAAtABIAIQAaAMz/jf/t/4L/0v/I/xwAzv/9/1kAov8iAMD/3//m/9j/FgDJ/0IARwAnAFcAIQAIAFAACQBRAPj/nv8xAMz/DQAdABcAJQDn/1oAtv/p/xIA6v8lAB4AGAABADgAGgAVAAAAyP/4/3n/EwDZ/4T/VACM/yMA+P+d/+j/tf8yAN//QQBZAMj/wP+o/7n/7P/d/9L/AADb/xkA8P8EAHIAyf/U/yUA6P///0gAKAANAFQAMgAoADIAFgASAA4A+v8yAE0A9f8bAN//5v8PAMP/GADv/87//P/r/xMADwBDALb/IAD2/5z/ZwDA/8z/+/+z/y8Ay//D//T/9v8vABMARwBeABQAov8QANb/zP9EAAAAJADC/wQAAwDf/2UALQA2APX/5f8hAAgABgAXAAAAt//G/+P/HwAZABQAEAAyAAMAFQC3ADcALAAkANT/AADK/x0AFwDc/ywAyP/T/8r/wv9gAPL/LAD//8j/QQDZ//P/9v/4/wsAGwByAAAAAAAkAML/PADn/+z/OQCb/3kA4f8wAIMAjf+lACgAIAAaAPH/BQCp/xUAyP/4/0IA2v8qAEcA3v8bAPL/BgDz/6z/KgDZ//P/9v/A//L/q/8EAAMAuv8QAA0Ar/8IAAYA4f8dAPT/9v9TAMP/hf/n/7T/+//p/8n/wf8WACQAMABLACoAIgDA/3EASQAoADMA8/8ZAMv/HgA9AGkAHQDO//3/6//v//P/LADt/xUA7f/e/y0A3P/Q/zUAGAABAMr/+v8xAJX/BQDz/9D/7P/e/+T/6v8SAMb/UQAvADgAQADq/wAA3P8HAL3/t//r/xMA2f8pAFgA2v8FALv/yf+v/9H/2v/P/9n/hP8cAPP/4/8yAN//UwAxACcAMgC6/9r/vf/v/83/6v8AAO7/FgC2/yAA9v9AACEA9/9CAH3/BADg/9T/3P+Z/+X/xf/j//v/1/8WAG4AawB7AFEAeAApALT/5/+Q/5P/u/8AAO3/FQBIACgA/P/Y/6j/cP+M/5D/8P/O/1gAWQD//6QAFgAAAAAANgA+APz/6v/K/+f/j//v/xYAJAAdACoARwDw/yoAIQD3/x0A4f/n/9n/z//9/w8AMQBMACsA//8QAEUAJQAeAE8ACACr/+H/5/8QAFYA/f/9/yIA0/8AANv/4/8fAPX/ZQAaAPH/9P/2//j/nv8MAPj/HgAFAAQAFgC2/yAA9v8uABMADwBDAFsANwA/AEUA7/8EAKj/OQAbALv/gAAwAAEAOABSAB0A4f8eAL3/kv/x/wYA8//j/+n/7v/x/xgAJgAMAOb/6/+4/8b/BwAGAGEAKQAhABsAAwAVACMACgD2/2YALQAkAB0APAAeAM//6/+m/9z/9v/T/wAAEgD9//7/2f/h/1UA6f8AACQAr//k/7L/wf9OANH///8RAHv/8f+q/7v/NgAHAAUAKQAhAPf/CgD2//j/CwD4//n/VgAOAPr/ewCZ//f/CgC//ycAIABRANP/NwD2/67/PgDX/00ABgCq/xYAyf+v/+P/DQAKANL/AAAAAMn/+P/6//v/1/8DAAMAJwBpAPn/DAAKABoAAwAUACMA+P8LAOX/IQC///H/l/+s/wUAqf9MAPX/0v/b/wYA4f/V/yYAHgA9ANb/JwANAB0AFwDc/wcABgApAP3/bAAyABYAWwDJ/woACADQ/yIArv++/wEAuP80APP/BwArAMf/LQC3/+r/JQCw/y0A7v/f/y4AAAATAP7/EADW/8z/HwDQ/zUA4v/V/xQAov/+/xAA6f/b/ysA7P/e//f/+f9WAA4AHQAqANn/4f/U/93/iQBcACUAQwDI/y4AAADK/+f/2f/z/6z/z//r/93/GgBMAPX/UgBVAA0AHQDh/1QAxP/i/40AqP/e/+X/s/8dALz/SQCFACEAGwADAPH/vf/c//b/QQDr/wEAOAC//xUA7f+5/6L//v/s/zkACQDj/x8Aq/88AMP/TwAtALb/VwDr/10ASwAXACUACwDl/0YAJgDo////2/89ALH/CQDj/9f/FQCR/3AA///b/wYAqf8DAN7/m/8KAOT/6v8SAMb/GgDx/xgAAQDc/xoAzP/7/9f/8v8YAPD/BADg/6//9v/4/9X/EwBHADkA5f/9//7/IgDA/xUASAADADoA0/8lAFUARABuADQAKgAPAEMAJAAvABQAx/8bAPL/q//z//X/5f8OADAAFADs/xQAIwD4/8L/BQDg/8H/zf+y//n/1v/w/wUAzf8OAPr/n/8NAOb/2f8pAOv/OAD3//n/6P8jAHgAqf8VANv/9f8IAKv/YQAEAAMATAArANr/GAATAMb/CAAGAOH/CwBTAPr/MQAoAPz/MwAXAMn/+f8eAND/WQC1/+n/WwCS/0wAUAAJANH/NQD0/+T/IADj/1cA2P8EADoACgAIAPX/wP/M/w0Awf/z/6v/KgAPADEAOgDT/zcA0f8jAPj/HgAYACYAQwDt/zoA0/8AABIA2P/O/9f/AwA6AC8AAQBKAPP/BwD0/5r/+P/C/5f/YwD0/wgAUACc/9T/uP8PAOj/EAANAAsAUgAwACYAjP///8j/wP/y/5j/5P/X/xUAo/8jAPj/1f9wABAAIAAHAAYA8//R/xAAHwDj/zEAzf/7/zMAKQB9AAkALAD//8j/rv8HAAUAhP9UAPv/oP/q/8n/1P8TALT/QwBIAMz/RADc/+P/xP/0/wgAKwBIAPH/dADw/xcASgDO//z/DwAeAOL/MQBMAPT/0v/t/zoALwBdAEsAzv8zAE4ALQAAADYAGQAnAA0Awf9OAOP/MgAoAPz/WADZ/yoAIgBSAJ3/6P///0f/7P/L/wwArv/1/y4Akv8VAFsAJADn//7/EAANAOb/IgDl//3/6/+4/w8A6P/t/wIAOQAbACgA/f/r/93/0f9aAMn/LwAmANX/FADs/yYA6f9tACEA0v8AAO3/AgDM/+j/o//a/+L/+v8yACgAIADR/8j/0/8AAMn/1P8TAP7/2f+F/6//v/+5/8f/CADQ/8f/9//U/zgA9/8cAE4APwAgACwANgC+/0sABQAEAE0ABgBPABsAFQA2APX/CQBRAFMAMQDe/xsAFgAAABIA2P8WALb/1/8WAMn/5v8PAOj/2v8YAIH/0f8jANP/JQALAC4ANwCa//j/MADe/wgA9f8uADcAv//w/7z/t/8OANX/FAAiAPj/+f/7//z/xf8HAL3/yv8dAAUAFgDu/zoA1P8AAAAAAAASANj/TgDj/0QA7v8DACcA1/86AOb//v/s/8v/w//P//3/IgAbAPL/KwBaANv/4v8xAJX/FwAAAO//4P/m/yEA0v9JAAMAFQARAPz/xv/j/1cA2P/y/ysAyP/l/yEArf8rANn/vP/u/wMAFQD//1sAEgBYAMf/5P/q/9z/dQDe/2UA0f8RADIAqP/e/9P/2/++/yYAHgA9ADEAAwA6AAkA5P9EACUA5/8iAOX/RgDd/+T/DQDn/9n/4f8dAM//RgDd/xoA3//4/2cAwf9fAN//CgAIAL3/7/+E/xwAzv/q/0oA4P8vAN3/0v+2/9f/KADF/4gAbQAOAHoAKwAQAB8A9f/T/zcA0f/a/xgA3f/k/yAAGQDe/xsATQAZABQAEACf//z/s//5/0QAyf9BALT/MQACAAIAXgDL/0MAAAA2AOP/6f/I/+b/awDo/1sANwDj/zIAKADq/yUA5//Z/xcA7/8WAO7/FQDt/wIAAgABAAEAyv8LAJv/CgAbAN//HADg/y8Ay/+w//f/5v+0//r/HwDQ/7X/6P/b/4b/nv/W/wIAFAA1AD0A+/8gAOP/6f82ABkAAgDd//f/r/+a/xsA8v/i/40AKAAOAAsA5f8zAM7/MwAEAM3/IAD1/0AAtP8eAPT/5P8gAHX//v//////EQDq/9z/9f8bAAMA3/8JAAcA4v/o/+3/FADa/xgAEwDr/yYADAAKAOT//P/9/+v/SgA8ADAAXgAnAKAANwA/ALQAx/8bAN//5v/r/8r/CwCu/wYAl//R/+z/AgAmAGgAVADE/1AA9/8KAEAAxv/j/9f/AwDe/9L/EgDq/yUAQwD//0gA8f8GAOH/nf8wALn/2v9hAGEA8/8sAO3/3v8JAAcAPQD7/1cADwAMAEEA6/9dAAEAJgBDANv/YgDP/+v/XQDw/ykADwBWANf/FgAAALb/RQCl/zcAGQA5ANP/kv8DAKf/AQDv/zsAsP8IAPX/0v8SAP3/IQD3/1QAw/8YAN3/rf8YAAEA3f/k/zIAzf8gAPb/LgAAAAAANwD2/y4A3f92ADoAVAAxAAMAAgCm/93/5P8yAPL/UABTAAsA+P8wAPD/qf8VAKT///8AANv/0P/+/xAA+/8OAML/KgDG/+T/IADR/xAADQAdAOH/+f8fAJn/0v9IAM3/DQBCAP//IwD4/zAA8P/z/xoAgv/A/8z/1v/e/+X/RgCT/83/6v+3//z/of80APP/4/9XAP3//v/s/wEA3f/k/+n/7v/f//j/+v8MAC8A3f/k/9f/3//l/0YAy/+e/x8A4v9DAO3/OgBmAL//OgAKAPb/HAAXAAAA7v8DAPH/9P/2//j/1f/d/wgAq/8FADsA+f/7/1cANADh/0IAEAD8/9j/8v/1/63/BgDh/wsA0v83AHYA3/9AAOv/EwD+/8f/QADr/xMANADP/+v/AADc/xoAFQAjANP/pf/b/77/AQATAP7/NQAYAEsA4f8wACYAxP9iABgAyv8LANL/pP/I/67/0f+1/wwAZgDA/ygA/P/Y//L/GQDe/63/KwC1/zEAAwAUACMA+P8wALn/NQAYABMANAAYAMr/+v+x/67/PgCy/0EA2f/O/w4A1f/w/yoA6//v/zsAwv8XAJL/3/+u/+P/HwC+/10Ay/9DAO3/FQARAMX/UADT/xIAMwApAA8A6P/a/08A0v+2/3wA5P8gAAcAz/8PAOj/7f9MAOL/VgAyAOD/ngDa/xgA7/+p/zoA+P8wADkA+P8wAAEAAQBLACoAWQD/////7f/e/0AA2P87AAsA5f9FAAEAOACbADMAYQAXAAAAXACA/z4AHwDQ/xAA1//f/8D/8v8GAOH/nf+w/5v/wf+p/zoA5v/Y/2AAcf8NAOf/DwAfAPX/QADr/yUAsP/3/9T/3f/k/yAAGQACACYAsf8cAPL/PgANAC8AXQCU/3MAEwDG/3YAOgAvAPD/KQAPAMP/TwDk/yAAUQD5/2gAHAAXABIAIQA/ACEAGgDx/8//2f8pAOv/SgApACEAZAAHAPT/5P8OAPn/+//F/xkAy/+e/x8A4v8fAND/2f/O//3//v/+/xAAsv9BANn/FwAlAML/YQDO/yEAv/+C/9L/tv/p/8n/QQD+/xAAHwD1/y4AAAAAAAAAAAASAA8A6P81AD0AMQDx/8//xv+a/wkA5P8NAAoAUgBCACMAQQCi/1kA7P/e/1IA+f8MAPj/QwC2/+n/NgAsAEgAAwBeABUA7f8UAP//7f8UADUA0P+0/+j/tf/W//H/GAATAI//EwAPAJ7/1v/x//T/9v8vAF0AEwAiABsAAwAVAMj/+P8LANP/EgAzADwACwAbAGAAAwDf/1MAw//h/zAApv/d//b/5v/9/+v/8P8EAKj/AgDL/4z////I/4n/sv8dAHL//P/r/xMAkAD0/2QA4/8fAOP/w/8GAOH/+f/7/yAA0f8QANf/FQDt/0wAKwDa/08Av/9MAKv/zv/8/7P/QwD/////yP8cAOD/HQAFABYANwDj/zIAKAAzAAQAAwDx/8//2f8XABIA2P8EAAMA8f/0/y0A7v/M/9b/zP8NAAoA5P/8/yEACAAZAAEA8P/g/wsAGwDy/9D//v/a/5f/GQDw/+H/CwAuAAAANwBkACsA//+j/zUABgAFAOD/+f8wALn/IgAuAMr/CwBSAML/FwDv/wMAAwC5//7/o//s/97/9//U/wAAXADv/04A9v/l/w8ADAAJAPb/0//J/y8AFAD+/xAAxP8rACMA+P8dAM///f/H//f/1P/v/xYAyf9mAAkAPgANAML/8//R////2v8YAMr/CwD4//n/MQC6////7f8CALn/IgAJANH/EACf/9f/KABFANz/LABtAP3/IQDk/w4AMAAUAJEAYwDi/x4AGAABAAEAAAAlANX/3f8IAAYAGAC4/w8A+v/7//z/j/8lAHn/uP80AM7/DgDV/93/CAD1/5v/HAApANj/KQAzAOH/+f9WAPz/IQA/ACEA9v/m/1kA7P8CABQA2f8FAPL/BwDh/57/DAD4/+f/IwBTAHoAKwCRAOP/1v85AK7/PgD8/w4ACwAuADcA0f/t/97/wP+6/xAA/P/q/xIANADO/zMAPADn/1oAo////8j/0/8lALD/LQC3/9f/OwAdACkADwDD/8//6/8TANn/8/9jAPX/GwDy//X/LQAAAAAApP/t/xUASAAVAMj/0/8AAAAAt/8gAPb/wf8DADoA+P/6/1YAMwBOAL//3v9AAMb/BwArACIAHAAEADoALwDK/wsALgASAA8A+v8fAAcA9P8IAD4ADQAKAPf/+f8eAOL/egA+AEQASQDN/w0ACwBAAA8ADADl/+v/7/8pAOr/pf8AAKT/EQDq/wAA7v+6/0gAFQA2ABkAOQD3/wsAQADr/+//8v8ZAPD/FwBKAM7/DgD6//v/agDo/zUAGAC4/9n/qf8VAO3/3v/l/w4AHgCq/wQA3/8JAPb/5v9GAN3/GgBfACgA/P9YADQA9P+//7n/7P8BAMv/+v8yAKj/8P8FAM3/RQAlANX/FAD+////WgDu/xUANgDQ/yIALgDK/x0APAAwACcA6f8AAEkA8v+r/xcAyf8KAC0AJAALAK3/GQCB//b/CgCa/0AAxv/k/zIA4P/U/5L/Xv/H//f/nf/n/xAAxP8GAPP/9v8cAOD/5v8PAAwAwf+o/6f/uP+h/8b/5P/q/0kA4P/m/+v/yv8eAOH/QwARAOr/XABKADsAZwAcADsAMADL/1YADgD5/zEAXwA6AEEAfgBBACIAGwBfAM3/6f/J/6//v//e/wgAh/8xAMz/1v8CAN7/9/+v/y0Ayf/m/yEA0v+k/+3/JwCy/0EAEAAfACsAIwBmAAgABgA8AGgAQQAiAEAA/f80ABgAyv9nABwAFgAkAEIAWgAAADYA9f+u/xkAJgDp/wAA7f/x/wYAvP8SAA4ACwD4/0IANQAYABQA2f9hAPP/LAARAI3/yf/m/+v/pf/c/77/AQATAMf/0v+2/8X/dP/+/yIAwP8oACAAGgAVANr/9P/k/+r/NwAHACsAIgAuAEoAOwAdAPT/GgDf/wkALADb/+L/MQAVAP//EQDF/6v/4f8wAPD/8//2/8H/OwB4/8r/CwBj/xQAkP+m/+//qP8CAPD/FwDc/+P/1//M//v/xf/Q/6L/tf/o/xEADQD5/+j///9bAMn/5v8iAJv/CgDR/5H/FADa/xgAEwDZ/ykAIQAbAM3/MgA7AAoALQCk/xEA6v8lAHoAz/9HABQAEAAfAD4AaQDV/3AANQAGAGEAqf86AAoA9v+LAPD/8//2/+X/2P/g/0EAtf/W/zkA5f8hAAgA9f/S/23/0/+3/6D/RQDK//r/+//F/ywA2v8YAAEAEwAiAMD/FQDt//H/BQApAOv/7/8EAM3/VwCh/+v/EwDG/y0A2/8GABcAJQAMAOX/xv/k/9f/8f90AAEAFABHACcAMgAoAEUAXAA4AC0AEgDq/yUAQwBIACgADQD5//v//P/9/yEA5P8gAOT//P8zAAQAcgAAABIAIQCa/wkABwArABAAn/8yACgA2P8WACQA5//H/7//8f8FAPP/GQDw/yoA/v/Z/+H/1f/w/4T/CgDk/zIA8v+Z/2QAh//o/zYAKwA1ACsAWgARAEUAAACmABcAEgBrALH/QQDG/xoATQDi//v/xP8+ANb/FQBtAGn/9f/3/9T/OADk/0UAJQDn/yMAHAApANj/zf/X/wMAJwANAC8Ay/+e/8P/BgDh/x0APACe//v/DQDU/wEAyv8dAPT/9v8vAAEAOAAaAF8AAwACACYA6f8RACAALAAkAEEAIgAcACkADgALANP/yf8KABsAAwAVANr/9P/k/8X/KwDt/xQA///t/ycA6f/b/wYAFwATAMb/9v8vAIH/4//W/6f/FAC1/1YADgDn/1oAEQAgAPb/HAAEAN//HAAEAAMA8f/0/9L/7f8CAPD/BQAEAN//CQAaAN//LgAAAO7/cgBJABYAJADU/7j/2f87ANX/y/8wAN7/CQDR/xAADQDC//P/rP8XAMr/CwAbAN//5v/r/yUAw//0/7//3v/S/9v/GQDe/wgAdP/H/+T/oP/q/24A/v/H/1IA5/8iAMD/FgAAAMn/VADW/ycA6f/t/ycA6f9JADsAQgAiANP/EgAOAPr/VwAhAOT/1/8DAAIAp/8mAB4A9P/3/+b/WQDa/wUAFwDu/zsA1P8TACIAwP8DACcADQDB/zsAHQAqACIACQA+ANf/KAD8//3/RgA5AC4A7v8WAO7/KADp/yQAVAB6/97/9//U/wEA7//y/+P/MQAVANv/9P/S/8j/5v/r/5P/lv8GAAQAFgA2ACwAo//t/xQA2v8YACUAHgD0/xsA8f8GABcAEgBGADgAGwAWACQA+f/V/ycADQAKAGQABwD0/xoAzP/7/8X/9f9TAB4A9P8tAO7/3/8cAKn/FQARAOn/JAAdAOH/wv88APr/DQAvABMA2f+8/8n/1P8AANz/LADt/xUANgDQ/yIA9//5/8P/4v/6/w0A1P/c/1EAr/8aAAIAAgA5AOX/DgAeAPT/5P8yAOD/QQDZ/7z/NwC//xQA2v8FAPP/vv8BAO//zv/F//b/wP/f/8H/KAAgAAgAPQAfAD4AxP8rABAA6f8kAPn/MQAnAOn/2/9jAOL/DAAcAJb/4v+x//f/5/8QAB8A9f8bAPL/GQA5AAkA4/8NAOb/DwAMAPj/HgAqABAADAAvAN3/CAA9AB8APgD7//z//f+0/zEAJwANAEIA2v8FABYA7v/f/xwABADN/w0A5/80AOH/5/8jAJz/CgAIAAcAGADK//r/1v/M//v/1/+o/8v/+//E//X/9/8KAC0A3P/1//f/HQAFAAQA8v8YAF0A8P9hABcA7v/y/wYAFwDv/zsACwAtAEkAKQDq/xIA/f/s/yYA1v8UALX/HwBQAMD/KAAgANH/7f8UABAA/P/9/zQA8//2/+X/DwAMAMH/OwDB/xYAyf/m/yIArf8rAMj/5f/q/wAAEgC0/zAA3v9j/6f/pv83AOT/IABjAL3/OADS/zYAYwDi/wwACQDk/7L/CgDS/yMAHABOAFEA1P8lAOj/WgDt/9//QADr/zgALQAkAOf/RwBMAAUAvP8kAOf/tP8eAJj/9v/m/w8AMQDx/8//6/8BAO//TgD2/y4AXAATAA8ADADm/8b/CADi/57/MQDx/73/SgAXADcACAArADUAc//r/93/rP/P/1kAfwDU/wAAAADK/9T/7/8EABYASQAWABEAIAAIAND/7P/w/87/DgAeAPT/9v8KAOT//P9GAO//KQBGAO//BADf/woA5P8NAPn/6P9IAMz/MgAWAO3/8f+Y/+P/sv/4/+f///9IAN//UwALAOX/MwCp/xUASAADADoAHAAWAAAAAAA3ACwAIwBBADUAPQAxAPH/vf+3/w4A6P8jAC4Ayv/5/7H/wP/N/9f/3//T/wAAt//8/+v/yv8wAPD/vP8AABIADgAeABgAJgDo/6P/NQAGAOH/HQAFAPP/9f8JANH/2v8FADwA5//+/yMArv/j//v//P/G/xoAp/+m/xMAj/8TALT/5/8jAC4AgQAMAFMAMQDx//T/0f/t/zoA+P8wACcAHwBQAC4AAAC3/0YAyv8LAFMAwv88APr/MgADADoAZgAbAAMA3v8bABYAAAAAAFsA7v8WACQA+f8xALr/7P+5/7T/nv/E/xgAJgAeAND/RwDL//v/6f9//wYAvP8AAEkABABfAE0AKwA1AND/NAAFAOD/CgDS/yQACgAtAEkAFgBJAPL/BgAFAPL/4//W/xUAyP/T/+7/zf/8/9j/AwDx/+L/1f+5/w8An//E/+L/w//i/8P/KgDG/wgAPgDW/zoA+P9DABEA/P8OALD/GwAWAO3/JwBFADcA9v/m/9j/KQDr/+//OwDC/wQATQAZACcADQAKAC0AAAAkAAsAGwAoAPz/RgABAEoAYQA8AIwAFQARAA0ALwAUAOz/AQABAN3/5P8NAK//GgDx//T/LQCS//H/vf/v/ygAxf9RAOb/IQCJAKX/JAAdAKr/KAAOAOf/NQA9APv/DQCd/9X/y//D/xgA3f8aAPH/9P/k/+n/2//j/zEA3/8JANH/EQANAK//CADQ/+z/y//V//D/8/8aAAIAFAAQAPv/2P8WANv/0P8iAAkAPgBFABIARgBdACYA1v/e/xsAu//I/+X/s//C/87/xv8aADoAwf/N/8X/q//h/8L/zv/9/+v/AQCCAPv/DQBCALX/HwAGABcAAADv/xYAEgAzADwAMAACAEsA9P8aAPH/vf9KALv/SQAoANj/FgDJ/3kAPADo////NgDQ/xAAHwCG/x4Az/9ZACMA5v9rAPv/MgAEADoALwBLAAUAKQBFAJP/KAAOAML/zv8OAMP/4f8wAJT/FwDJ/9T/7//z/ywAyP8JAAcA4v/D/yoA6/+4/1kANQBQABsA3/8vAKX/3P8HAL3/EwD9//7////a/wUA4P/n//7/EAD7/9f/AwAVAO3/8f8YABMA6/+4/zQABQDN/zMAzf/8/zMAFwA3AAgAPQDp/wAAJADB/ykA2P/N/+r/yf8dAPP/GgA6AOX/IQAtANv/9f9AAOv/3f8sADYA4//7/yAA0f81AD0AHwA+AA0AHQDh/8L/FwAAAMn/wv/O/9j/g//4//r/sf8cALv/JADU/93/GgACACcAsf9TAIz//v81AIb/egC9/8r/+v/E/73/7/8EADoALwDv/04AGgBMACsARwAnAPv/6v+l/yQAiv80ACoAof/r/93/9v/B/xYAAADu/wMA8f/0/xoA3/+J//z/xv/2/xwATgBRABwAPAAwAAIAy/8eAPT/rf8GAGEAl/++/0sAl/8+AB8Avv9LAM//xv/2//j/ZwD4/wsAZQD2/y8AXQAmANb/OQBAAOv/JgD6/7L/d/+3/9f/8v/1/0AARgDK/wsACQD2/8D/TQAHAKr/KAD9/w8A1v/e/1IAQgDI/1MAQwAjAAoACAAZALn//v+i/+z/OQAbABYAAAASALP/MADw/+H/+f/W/ycAHwBQABwA8v8HAAUAFwBJAKn/AgAUAJD/OACt/xkA8P8FACgADgD6/7H/QQB9//L/9f/S/xIAxf8/APz/2P/y/xkApv/d/9H/7f9MAM//DwAfACsAIwB4ACkARgA4AMD/FQDb/ysA2v/0//b/5v9ZAEcAXgAnAEQAAAASAEYASwAqAOv/OAAbACgADgALAOX/s//5/x4A9f8bAAMAAgDe//f/+f+x/0AA/f8PAB8A0P8QALH/5v/Y/zsA+f/D/xgAuP8hAOT/6v8lAOf/IgAJAAcA9P8IABkAAgAUANn/FwATAMb/UgAvABQAx//3/1QA+/8NAML/8/+Z//f/QgAQAA0Awf8WAMn/5v/r/8v/+v+N/8j/5f/Y/+D/5v8PAPv/DQAwAPD/PAAeAAUATgDR/0gAFQC2/w0AHQAFAE0ALADb/z0AMQBfABUAWwASALP/HQC8/0oAqf/M/zEAzf8fAOP/DQD5/9X/AQDd/9L/AAAAADYALAD//xEADgAwAAEAcADs/97/GwCo/0wABgBhAE4ABwBQAHb/AAARAMX/BwC9/xMANAAXABMADwAeAOL/HgAYAMv/6P+Q/xQAEADW/xUAEQB8APb/eABhAOD/QgC1/+j/EQDq/+7/KAAgAAcAdQACAMv/w/8FAM7/xf8+AOn/7v/x/8//tP+w/xsAFgC2//z/xv+s/+H/1f8mAPv/IADj//v/MwCp/9//rv+r//P/vv/e/wgAGQC5/7T/VgBFANz/dgA6AOb/DwDW//D/BQDy/xkA8P/h//n/xP/P/+v/JgAxAPH/z//Z/wQAzf8NAFQA+//8/9j/4P8KAL//JwD8/7P/QgDs//D/TwC//97/UwDn/xAA6f/J/y8A7/9OAAcA9P8IAND/EAANAB0A8/8sAO3/3v8bAM3/DQDn/xAAMQDx/ysAIgD4/+f/x//3/53/1f/d/2P/OQD4/1QARADJ/x0Azv8hAL//FQAQANf/TQD1/+X//f/Y/wQAAwDf/2UA0f/t/zoArv8+ADIAAwA6AAoA9v94APP/GgBeAKf/8P+8/9v/4//7/w0AHQA8ANX/AgDL/wwAQQAPAB4ABgAXACUAVQB8AD8AMwBOACwAyP8cAE4A9v/B//L/4v95/yYAHwAGADwA6P8QALL/CgCt/6r/cwDc/ywA7f/e/+X//f8PANb/TAAYAN3/LQBJAM3/MgA7ANT/AQC4/9j/zv/q/7f/2P87ANT/AQAlAPr/DQDm/+v/SwDO/zMATgDR/8j/+P9VAPv/IAAaABUA///t/3EAAADb//X/5f/q/+7/8v/i/9b/FAD//7X/6f/t/7r/tf/p/+3/8f/h/wsA+P+w/z8ADgDV/yYADADm/w8ADAAcAE4AGgBMACsAIgBAACEALQAAABIA2P+p/xUAyP/l/0YA7//z//X/5f/Y/wQA8f/0//f/wf8WAMn/LwATAMf/LQDJ//n/+v8fABkA3v9AAA4A+v8fABkASwBiAOH/CwAbAAMAKADX/00A4/+f/0QA3P/1//f/5//+/6L/IgAJANH/IwAcAPP/4/8xABUA7f8VAMj/rv8sAEgAJwAyAM3//P8OANX/JgAfACsA7P8nAB8A4//o/9v/GADd/y0AWwDc/ywAEQDq/+7/3//4/8L/4f8dAAUA4P8KAAgAvv8TACIACQA+AA0AHQDh/wsALgASAFgANQA9AAwACgDk/8T/BgDh/+f///8jAPj/+v8xALr/tf/W/97/GwDy/ysAIwDB/xYASQAoACAAPwDF/xkAcADt/3EAAAARALP/nf9DALb/HwDj/zEAKACy/0IA2f/h//r/DADU/9z/LADt/zoAHADz/+P/6f+2//z/2P+7/zYA4//7/+n/yf8KANL/EQCO/5H/AgCU//P/4//W/wIA8P9PABoA3/9BADQAz/8hAC0A2//j//v/1//y/wYAFwBKACkARgBwAEcAAgAUADUAz/8PAB8A9f/l//z/IQD3/9T/3P/2/4n/MwAWANz/9f+J/9f/3/8cABcASQDy/6v/YQAEALr/7f/x/8///f8PAB8ABgD0//b/0/8SAMb/CAArAP//IwBBAA8A6P///+3/FQD//9v/dQDe/8D/FQDt/zkALgAlAAsA5f9GABMA7P8BAO//4P/U/8r/CwAJAPb/CQD2/wkALAARAMX/GQBMAM//WQAjANP/7v/N/w0A1P/d/+T/1//f/wkAGgDM/wwA+f/o/9r/9P8/ANj/4P8vAO//u/9JADsA+f8MAOX/awDD//T/LQC2/1cAxv8IAOL/nv9EALf/DgAdAOH/VQDp/8n/5v+0/9X/JgDW/xUAIwDB/wQA3//4//n/xP9iABcAEwAiAPf/LwAUABAADQDm/+v/EwDs/wEAEwDr/xMARwACACYAVgAOAPr/1v8CAKb/JgAxAAIAXgDw/xcA3P9RAPn/w/9PAOT/MgAWABIAof/q/yUA5////8j/CQC+/97/CAAZACcADQDB/wQAKADF/wcAz//9/9n/PAB6ABkAAQDd/z8As/8LAC0Ayf8KAD8ARgABAO//KQBGAO//FgASAOv/JQD6/8T/9f8bABUANgAZAAIAuP/r/+//lv/1/8D/8f/i/+j/NQD1/y0AAADJ/+b/tP8eAAYA8/8sAO3/OgAJAAgAPQCf/+n/JAAKABsA8v8GAM7/2P/g/+b//v/s/zkA5f8OAPr/1v/e/8D/OgD5/1UAVwAPAEMA2//i//r//P8gAPb/5v8hAL//OgAuAO//KQDq/0oAzv8gANH///8RAMX/iADt/3EA7f86AHgAvP+BADAAAgDe/xsAFQARAPz/DwDo/xAAVwCP/5MALQDJ//n/w//0/3X/2v/P/8b/iP+N/xEAoP/q/+7/8v9QAEAA/f8iABsAzf/p/9v/vv8BADgAQAAhAD8ARQDv/6n/8f/i//r/6f/I/xwA8//Q////NQDQ/7T/+v/p/yQACgAbABYAyP8KAPb/rv8aAN7/5f8hAOT/jgAWAFwANwAIAD0AjP///9v/PQAMAAoAUgDC/+D/wv/g/8L/FwASADMAPADn/zUAGAABAN3/CAArAEcAFQBaACQAwv9OAOP/DQDC/87/IAC//ycAHwDQ//7/NQAGAAUABAADAN7/5f8hAOT/IAAHAOL/HgD0//f/LwDd/wgAGQDw/zwAHgAYAAEAEwBZANr/KgAPANb/JwDX/zoAHADz/+P/n//E/4b/w//h/wsAm//U/yUAi/8iAC4AgQAeACsAIgCJ//z/of/G/wgA4v8xAPH/vf9KAPP/4//p/8j/UwCe//v/RQCS//H/4v/D/8//xv/k/yAALAAjAPj/QwDb/xgAcADs/14A3v8bADsA1P8lAPr/+//X/83/DQAdAOH/QgD//8j/HADN/zMAKQDq/xMA6/9KABcA7/9NAOP/6f8kANT/3P+//ycADQCc/wsA0v/u/xUAAABJAM3/sv8cAAQAu////yQAr/8/AA4AsP+//8z/+//F/ywA//9IADoACgAaABUAWwDJ/y8AEwBHAIMA/P8gAAgAKwDH//f/CwD3/woACAArACMAHAAEAN//0/8lAOf/2v/0//b/5v/9/w8Asf8JAL//3v9AAOv/7/8EAN//rv8HACoAEADp/+3/JwAgAD4ARQAlAB4AKgA0AAUAFwBcAAAAAAAAAO7/3/8KAD8A6v8lAML/vP/c/77/AQABABMA/v8QAOn/AADb/+L/MQC6////IwD4/zAA8P8XAAAAyv/5/9b/8f8YACUA6P/a/+H/sP8IAJn/wP+C/4j/6f/J/0EAx//S/yQAr//k/0UAEgA0AAUAFgAkAHj/NwD2//j/HgDi/wsAif8OADAA3v/3/0IAEADp/xEAIAAaAAIAOQDl/+r/SgC7/xIAIQDk/1cA/f8iAAkAvv9LAPT/9v8cAOD/5v/+/xAAaQBVAB8AiAA2AD4ADQDU/wAA7/8EAN//CQD2/+b/2P8WADcA0f9IADoACgAaABUAEQAyAE0Avv/w/ykADwAeAAYAKgDr/8r/MADe/+X//P9GABMAx//3/53/1f9v//r/VgDq/1wAOAAtAFsAEgBGAHAA2v/0/+T/xP8GAAUAFgCk/8n/CgAtAAAAEgAhAPb/+P8LAC4AAAAlADAA8P88ADAAFQBIABUA7f8CALn//v/a/7z/yf+v/+T/1//x/ysAEAD7/9f/uv/a/3P/2P8EAN//5v+0/x4AGAA4AAgAGQACAMv/HgAYAEsAFwBcACYADAD4/+f/NQDi/wwACQD2/wkAZAAHAAUAOwDC/xcA7/8DABUAIwBUANb/XgBMAOL/QwDt/6f/uP/Z/87/DgAeAOL/QwD//wAASQAWABEARQAAAMr/HQDP/yEALQASACEACAAZAN3/GwDx//T/GwDN/+n/AAAAAAAAEgAhAAgAq/+p//H/BgC8/xIAMwCp/8z/sv/T/+//AwDx/8///v/s/xQA/v/a/8//2f/g/y8AuP+0//r/sv8cAAQAKADq/+7/TQAHAOH/w//z/7//pv/v/xYAt/+z//n/w//0/wgABgA8APr/DQBUAPv/MgA7AOf/x/+b/xwAzv/F/ywA7f8VACMA5v8PAEMA7f8VAFsAyf8vADgA0v82AAcA4f9VADIAAwBxADYA4/8NABwAFwDc/z4A/P/F/wcAvf/v//L/GQDL/wwACQDk/zIAqP8CAN7/iP/E/wYA4f8eAGIA4f8LAMD/OgAKAPb/CgDk/8X/4/9pAOf/NAAFAM7//P/r/xMAIgAbABYAWwDu/xYA7f/M/x8A4/8xAAMAOQAcAM3/DgDV/wEA7/8pAOv/t//9/9n/zv8zABcA7v87AC8AEwAQAPv/IAD2//j/CwAJABkAFAAjAFMAaADU/yUACwDT/wAApP/J//j/1f/L/0MA2//Q/zQABQBOANH/IwD4/+f////I/0AAtP+w/9L/pP+2/x8A9f8bADsA+f8eAOL/+v/p/+7/KABXANn/4P/U/8r/MADe/3cAKQBYAJEA9P9AADMAFwDu//L/4v8MAC4ASgApAP3/NAAYABMADwD7/7L/wf+7/xEADgDC/yoA/v/+/8f/0v/b/9D/2f/h/2cAnP8KAC0AEgAhAJr/QQBq/6z/GACl/zcA5P/E/73/AQDK/9X/FAD+/zUAvf8TAEYAJgAMABwAFwAAAEkA4P9UAB8A9f8IAOP/+/8gAD8AoP8OAML/4f8dAAUAKQDq/1wAyv/V//D/PABDAO3/cQA2AD4AHwAZAN7/CADj/wwAQQC0/0MApP/a//T/9/9BAOz/OQDl/+r/pf+S//H/z/8hABsAFgARALP/5//+/9r/TwAbABUAAADI/woA9v/4/9X/JgAMANP/XAATAA8AHwA9AEQA7v9fAAMAFQD//9r/KwDZ/wUAu//t/xUA2/8rAOz/OQAbADsAVADW//H/vP+3/+r/3P/2/+X/jv/J/9T/yv8eABgAXQATAMf/UgDn//7/NQC9/+//u//b/wYAvP8AANz/BwAYACYAMQDM/x8AYwAqAGwARAASAGsA+/8NAEIAx//3/y8AFAAiANP/7v8oAHv/3//T/7f/IADk/yAAUQAcAPP/GQDw/8//DwAMAPj/CwDS/8n/CgD3/8H/4P/m//7/IgDl//3/NAAFAOD/1P8lAOj///9/AAoA5P/q/wAAAADc//X/LgASAA8AQwAkAAoACAAZAAEAAQDd/xoAFQAjAEEAEABEABIADgDV//D/vP+k/1sApP/u/ygAxf8HALz/7v/N/9f/8v+Y/7//3v/3/+f/DwD7/7L/CgAbAAMAXgAVALX/HwAHAKr/BADx/xgASwDz/xoA3v/A/wMAuf8iAC4AAAA3APb/HAAEAAMAFQD//yMA1P/K/x0A4f/V/0sAKgA0ABcAJQBDAO3/AgC5/yIA5f/Y/zsA5/8iAMD/KAAyAAQAAwCn/xQA2f+8/yUAQgD//xEAMgAWAAAAAAAAABIAMwAEADsAr//k/zIAu/8RANf/AwDf/9P/NwDj//v//P8hAC0Ayf/U/xMA6//d/y0AAACk/8j/ZgAtACQAZwAuABIA/f8iAC4AJQAeABgAOAAbACgADQALAC0AEgD9/w8A6P///xEAsv8KAC0A7v8oACAAGgAnALL/CgAaAF7/2f/z/4f/MQDx//T/CACr/xcA7//y/1AAHAAWACQA+f8xACcA1//x/73/uP/9//7/EADp/7b/xP/i//v//P/Y//L/BgD0/ywAEQAgABoAOgBBANn/FwAlAB4A9P/2/woAiP/p/9v/vf/d/+T/DQDU/+//4P/C/7v/EQDq/+7/8v+r/xcAEgAPANX/y//W/7n/7P8UAP7///9IABUASADM//v/RQC4/6IA8P8XAEoA4P9nAOX/DgALAMD/zf/8/9j/4P9BABAA+//8/w4A6P9IAEwABgAqAP7/NAC9/yUA+v96/97/CAAZAMv/HgAYACYA+//p/zcA9v9BACEAGwBNAPX/GwAWACQAQgAQANf/3/+u/+P/6f8AAEkA8v/1/+T/1//y/xkAJgAfACsA//+1/8T/GAAUAP7/IwDT/+7/OwDU/+//BADf/+b/xv8IAND/DwAxAN//+P/n//7/tf9EADcABwAGAOD/CwCI/w0ALwABADgACAA+AA0AHQAqAA8AQwA2AOP/HwAZADkAQAAhAIkAAADu/83/DQALAK3/dQDw/yoAIgAJAHYAzP8xAPH/hv/V/xQA2f8FABYA7v86ANT/AAAAAMr/wv8pADQAvP8kAML/vP/u/7r/7f/M/9b/AgAmAAwAQQA1ABgA3f/2/1MA+v8yACgA6v/u/9//rv+Z//f/wv8XABIAIQBSAOf/WQBIAMz/xP/i//r/1/8VAG0A6v8AADcAmv/4/zAAuf/r/93/CADi/57/HwAHALz/EgDr/8r/HQD0/z8ADgALABsAu/82APX/GwByACQAQgD/////yP/4/wsAGwBgAN//QQAiANL/EgDY//L/PgBEAAAAJAD5/9b/3v/l/9j/8v8rANr/BQAEAPL/9f/l/zMAqf8nAPz/2P8oAMX/YwA+AB8AKwDa/xgAyv/V/93/Y//L/8P/qv8EAN//HADy/wcAGADK/9X/y//D/5f/0f+1/8T/4v/6/2kA+f9WAOr/t//9/6H//f8PAPv/DQBCAP//7f8CAPD/8/8HAFAAGwBgADsAHQApAOv/SgDO/6H/s//V/wEA7//z//X/GwAWAO7/8f8GAPP/LAAjAEEANQDi//r/DQBBAOz/OQAbALv/EQDF/ywA7f8UACMAwf8WALb/xf/j//v/1/8DAAIAy//7/9f/KAD8/9j/8v8rABAA6f83AOP/VgD9/0YAXQDL/0MAEQAzAPL/9f8uAAAAJQALAAkA4//7/1cAIgAtACUAQgBaABEAMwC7/9v/PgCf/yAA0f/s/14A3v/l/9j/lv+9/9z/BwAGALz/JAD5/57/6f/b//X/5f8OAOf/7P/e/+T/IADR/xEA/P/9/6H//f/+/5D/AQCl/xIA2P/O/0UAJQAeAOL/+v/E/1AALgA3AD8A1/9NAL7/3f/S/9v/BgDz/xoA3v8bAKj/FQAjAMH/FgAAAAAA7v8oAOr/7v8oAOr/NwDR/7X/xP+9/93/GgDx//T/GgDM/w0A+f8eACsA/v8QAOn/NgAZACcAVwAhABoAFQA2APX/GwAWAO7/TAAZAPD/KQD9/w8AHwAGABcAOAAtACQACwDA/xUASAADAEwAKwDZ/wUABAAoAEUAOAAaABUASACV/+H/+v+x/y4AOAAaADoAVADD/+L/+v+x/0EAIgBSAGcACQA/ADMA4P8dABcA7v8oACAA9v/B/ygA/f/Y/zsACwD3//n/DAD4/wsAwP+6/+3/AgA5AK7/9f/3/8L/BAADAEwAGQDw/ykADwCe/x8A9f/S/yQA1P8TALT/MQBMAPT/dwDN/8X/9f/A/7r/7f8UAP//EQDF/wYAKgC0/wwAHAAWAFwAEgAhAAgABwDh/+f//////zYA4v8fAOL/1v85AMD/OgDm/+v/3f+t/wYAl/8ZAAIAFABHAAIAAQDw//P/vv8UABAAxP/i/wwA+P/6/x8A9f8JAPX/LgDv/+D/CgCt//T/5P/8/w4AMAACAMv/QwAAADYAGQDe/9L/2//1/y0AgQAwABQANQD1//f/HQApACEA5P/8//3//v9HALn//v8jAK7/4//W//H/KgDZ//P/9v+u/2MAPQAxAHEA7v/x/73/yv/C/zwA5/+1//v/e//f//j/QgAQAPz/DgD6/wwAr/8/AA4AHQAFAOD/HQCE//n/6P/t/0wAPQDD/5j/9v+J//3/6/+4/0YAJgDW/xQAEADp/xIA/f/Y/+D/HQDz/xoAJwANAC8AuP+h/7T/6P/a/5j/GgDM/+j/7f/e/wkA0f9/AAoA0v82AOP/MQAoAFcANABOAC0A7v8oAPz/IQBSAOb/DwBpAB0ATwBSAC8AJgDo/20A6v8SAEYA3f8tAO7/XwDx//T/GgDx/ysA2f/z/9H/yP+u/6v/KgDZ/ykADwDD/wUAzv/8/zQABQDN/1cAxv91////o//a/wUABAAWAO7/8f/0/+T/DgAdAAUAcwDv/+D/+P8LAAkAmv9TAB4AKgD+/yIAUwCe/zEA8f8YADgArf8GAM7/6//v//L/KwCj////NQDi/0MApP+2/x8Ah//6//z/2P8DALr/7P/L/wwAZgAtAG4AIQAtAAAA7v8DAJX/8//j/zIAFgAAADYA4/8NAAoA9/+c/9X/8P8EADsAQgBHAN7/0v8SAMX/rP88AMP/9P8aAAMAAgABAHAA//9aAMn/5v9GAMv/HgDP/yIA5f/q/wAApf/J/8H/8v/Q/9r/BQDy/6v/PADo////fwAKAIkAEgA0ADwAHgBiACoAIgDl/0UAJQDo/zUABgBhACkA/f80ACoA/v/H/0AAIQDS/xEA6v/J//n/w/8FADsA1f/w/+D/1P8BABMANADh/wsA5f+z/9T/3f8IACsANQD0/+T/1//f/woA0f+R/yYARADu/ygAxf+r/87//f80ABcAJQALAAkA4//7/zMAu/8AACQAiv/9/9n/vP8kANT/EwBZAEgA3//4/wsACQAHAAUAPADV/wEA7/8EAM3/DQBUANb/OgDm/yEAQAAhAOT//P8OALD/LQASACEALQAAACQACwAbAPL/9f8IAND/2v8qAA8A1v8CAAIApv+l/8n/5v+0/+j/IwDm/w8A6P/a/xgAEwDs/93/LQDu/xUA7f8VABEA6f8kAPn/DAD4/+f/EADp/xEAIADR/+3/8f89AOj/7f85APj/HQDP/w8A+v8yACgA/P9YAOz/cAD//zYABgAFABYAyf9CALX/MQAVAP//AACk/+3/zP8fAFAAHAAEAAMAuf/s//D/8/8HAL3/7/8EAN//wf8DAJX/z/+P/9z/PgAgAGMA0P80APT/PwDq/xIAawD7/0UAkv8VANv/0P80APT/9v/m/w8A1v8CABQAIgAuACUAQwA2ACsA/////+3/3v/l/9j/FgAkAOf/IgDl//3/6/+4/w8Anv8MABwA8//2/+X/DgDD//T/0f///xEAoP8OAAsArv8rABAADQAvAPD/PAALAC4Ayv8LAAgA0P8iAPj/HQAFADsA+f8xABUA7f8nALL/CgD2/xwABAADALr/EABEALf/DgDC//P/mv/3/wsAwP8VANr/KwD+/zUA4v9WACAA4/9XAKH/MwAEAAQAKAAgAOP/1v86AOb/WQD//yMAHACW/wYA4f/C//P/GgDe/wkABwAqABAADQAKANL/WwDJ/woACACr/zwA5/8QAOn/JAD5/wwA+P+L/w8AxP8GAPP/0f9IAN7/LgAlAML/cwA4AAgAPgCy/xwABADf/3gAFwAAADcAGgACAHEANgArAJEA4//7/yAABwD0//f/HADz/xkAFAAQAA0A1P8mAOj/a//3/woAv//x/z0ADAAcACkA/f8PANb/zP8xAMz/xP8YAPD/8//2/xwAKQAhAAgA0P8QAAwALwBdADgAGwAoADMA4P8KAL//p//w/+H/5/8iAC4AgP++/+//l//i/57/sf/4/7D/LQDu/wMATADi/x4A0P8PAB8ABgAXALj/IQCt/73/OADS/+3/FQD/////SADy/wYAcwDK//r/MQAVABEAMwAWAAAAAADc/xkAuf8QAFYAagAxAPH/mQAMABwAPAD6/zEAqP8UACMA5f8zAOH/1P/d/7//8P8FAM7/6v/J/9T/uP+z/9X/y//V/97/GwDN/zIAKADX/ygA6v/c/+P/DQCv/5r/LgASAA8AMQAnAOn/EgAzADsAQgDa/wUAKQDY/wQAXwAoACAABwDP//7/2f/z//b/5v8hANL/yP+u/xoAOQDT/wAAAAAAAMn/wv8EAAMAAgDe/xsAAwDM/w0A1P/K/53/sP8bAM3/IAAsAO3/OgAJAAgA9f/k/+r/yf/U/wEAJQAeAD0A+//p/zcALAD//xEADgALAPf/VAB7AD4AVwDY//P/BwDP/1kAEAD7/zMA8v8ZAAIA8P8EAOD/5v+h/+v/7//g/1QADAAvAF0AFABHABQAx//A/wMA8f/P/w8A6P8RACAABwAqAMf/LQDc/9D////s/xQAEABEAMn/5v8iANL/yf8KAPf/CgA/AOr/JQDV/xQAEADW/xUA//82APX/LgDc/ywAEQDF/2MAKwBHAAIAOQDl/6D/2P+7/9v/4v8MAPj/sP/3/woA0v/t/7r/2v/0/xoAFQDt/0wAvf/v/xYAAADc//X/GwDg/+b/IQAtAJL/8f/0//b/CgDk/9f/3/8cAJb/KwD//+3/OQAcAE0AGQAUAOz/OQAuAO//BAAVANv/KwAiAMD/FgDt//H/BgAXANz/9f8JAFEAQQD+/1oA7f/e/+X/IQDk/w0ACwAIACwAEQBXANj/KQBGALj/6/9dAPD/8/8HAKr/OwDU/zgAUgALANL/AAA2AAcAKgCi/0cA8P+X/+P/6f8RANf/TQAsAP//7f+5/33/zv/Y/ykAfQDS/zYAPgDE/xkAFADs//D/8/8sANv/GADd/5r/QQDZ/87/IQA/AOr/EgAhAC0AJADn/34A+P/V/yYAHwAGAAUABADy/xgAFAAiAAkA4/8yADoA5v9HACYAMQA6ABwAFwCS/wMAzP/7/7L/wf/y/9D/EADp/yQAeP8lAB4A9P8tAG4AMwDh/0IAtf8xAJX/KgAiANL/NwDj/1YAaf++/8v/1f/e/xsAOgDm/1kA7P8nAA0A5v/G//f/wf/y/wYAKgAiAJv/QQBr/+T//P/q/xMAxv/2/67/LADb/wYA4f/U/yYA+v8NAK//0f+2/+n/JADn/+z/SwDh//r/DAAKABoA3/8JAL//FAC1//v//P+O/zcA0f8jAFMA6P8jAOb/2f8XANz/9f8uACUAZwBTADEAOgBBAFkANQAGACoADwAeAAYA4f/V/+//4P94/yUA5/8jAFMAHgB0APD/8/++/yYAsf8cADsAwv8pAP3/NADP/w8AVgDX/zoAZgD3/0IA2v/0/1EA+f9DAAAAbQDq/xMAIQDS/zYArP88APr/1v/f/+X/of98/9//wf9gACgA/P8PAPr/DQDU/+//KQDY/83/IADR/+3/AgDL/9X/8P/P/yEA9//U/7f/6v/v/6j/gwAOAB0APAAeACsAIgCdAP7////a/wUAzv8hABoA8f9PAK3/YgCY//b/UwCw/y4AEgAhAC0ASQAoADMA8/8HABgAuP/Y/wQAzf/p/xIAIQD2/2X/KADX/zsALwDL/1UAxP8rADUAKwC1/wwA+P/V/xQAov/+/5D/EwD+/+z/JgDE/8//x/8IAND/EADW/8z/+//q/+7/zf/8/+r/3P/j/x8ABwDh/8L/hf94/8r/5//Z/zwAHgAqAFkA7f8CABQAEAAyABYA7f8nAPz/6v9KAOD/CgAtAO7/KADq/yQA1f8mAAwA0/8lAJ3/+v/X/ygA/P8OAB4Avf9KAM7//f+0/9X/AQDv//P/0f9aACQACgAaACgA1//y//T/CAAHAOH/CwDA/xUAtv+y/+b/tP+w/+X/6v8lAB4A4f9oAMH/OwD5/1YAVwDG/4kAt/8OAOf////t/8v/QwDJ/+b//f/+/7X/VgDq/wAASgDy/z4A1/8VAP//NgA+AOn/JADn//7/RwAnADIA8v/i/+j/2v9iAM//DwDo/2v/5f+z/x0APAAeACoARwACACYAVgD9/0YA8P/z/9H/7P8UAMf/LgDc//X/UwDn/xAAHwDQ/5D/uP/+//7/IgAJAD8A1//y/ysA2v88AAwAUwAxAAIAOQAbAPL/9f/3/+b/DwD7/2oA+v/p/yQAwf8WAMn/+f8eACsAIgAJAFEALwATAEcAJgAxADoAr/8sACQA+f9oAAoAGgAoANf/8f8rAOz/8P8FAPL/BgDh/53/+v/p/xIAagAxADoAwf87AC8A8P9OANH/yP/A/9//HAA7AB0APAAMAOb/DwDV//D/zv/Y/87/6v8lAAsAGwA7ANT/AQA4APb/VAD7/yAAGQCU//P/9v+b/53/i/99/wQAqP8nAEQA3P/1/+X/IQDk/1cA6/8lAPr/xP8rAOz/XgACAAEAJgBWACAAGgDx/8//2f/O/zMAzv8zALv/7f8oAI3/NgAHAPT/9v8vACUA6P8QAEUAyf/n/1kAyP9AADQA8//2/+b/IQA/AOr/yv/5/57/RAAkAPn/HwAGACoA2f9OAPb/0/8SANj/4P/m//7/EAAfAND//v///yMAZgDk/1gA2f/h//n/jP8jAJz/5/8PAOj/AADI/9P/yv8dADwAHgBiABcAAAA4AOT/IAD2/67/BwC9/zcACACr/wQAzf+g/9f/8v/Q/yIA5f8zABcA3P8ZAAIAOQAJACwA2v8GAM7/of/r/wAANwC//xQAkP/L/zAAp/8mALH/wP/y/9D/NAAYAEoAPAALAEAA2f8pAEYA3f/k/43/2/8ZABQAEAAfAD4AMgADALr///9+/8//6//v/wQAuv81AAYAFwAlAGgAeADh/+f//v8QAOn/gADn/9r/hgCi/+z/FADZ/yoANAAqAA8ARADJ//j/CwCJ/zMAlv/Q/+z/uP/Z/87/IQDR/yMAQQD+/yMAHAA7AOf//v/H//f/5//+/2wA/P8OAB4ABgAXACUAMAAnAFYADgD6/x8AKwD//+3/AgACAEsA4f/6/wwAwf8EAM3/6f/u/6f/AgABABMA/v9HABQAEABEABIADwDo/xAADQALAC0AEgAOAPr/1v+V/+H/+v/W/97/LgA3APb/5v+h/9j/4P/U/yUA6P8jAC4AEwA0AAUAKQDG/xoAJwD8/0UA3f8aAAIA3v/3/woAQADq/xMA6//d/+T/6f8AAKT/o////+3/zP8fAFAALgDK/zAAy//V/wIAFAAQAHr/8P+q/xYAJAAKAIkAt/8hAOT/1/+o/7n/7P/L/x4ABgBzAO//OwALAMD/KACg/yAABwAYACYADAAKAAgA0P/H/9L/kf85AOX/6/8AAMr/CwDS/yQAHQAXABMA/f/+/xAAHwAZACcAMQA6AEEAWQD//+3/zP9EABIA/f9rAMT/YgCX/xoATABz/2sA1v/x/xgA7/8WACQAQgD//xEAIAAHAOL/HgAGABcA7v8DADoA0//c//b/+P/C/wUA8v/1/+X/DgBDAJH/SwDh/4v/IgDT/xIAMwDg/8L/FwDu/wMA8f/i/wsA5f8OAAwA0//u/zoACgBSAB0A8/8HAD0ARADJ/y8AAQAlAPr/n/8gANH/2v/0/wgA4v8eAFAALgAlANX/OQAbAPL/YgAFACkADwCe//v//P/Y//L/4/8fAPX/GwAWALb/DQD5/9b/OQDl//3/DwCx/0AARgDL/zEATAAYABMA7P/w//P/9v8uAAAAEgD9/8f/GwADAAIA8P/h/+f/7P8BACYAVgDF//X/GwDN/w4A+f8xAAMAAgBLAM///f9sAPz/2P/g//j/5//a/xgAEwAiABsA8v/1//f/r//R////AAA2AAcAGADK/7D/9//U/27/r//k/7L/HADO/zMAzv/q/0oAlv9QAPj/+f/o////IwDU/xMA2f88APr/6f9IABUA2/89AB8Avv9dAN3/LQASAA4AVQDp/xIAs/9CAP//7f9MAPT/0v82AFAAQQBGAAEAEwC0/9b/3v8IAAcAvf9KAM7/2P/y/ysA7P/e/0AAs//5/wwACgD2/xwABAADAAMAzP8MAJz/5//Z/+H/MADw/xcAAAA3ABoATACHAMj/HADg//n/VQD8/2sAHgDi/8P/GADd/+T/IACs/yoA6/8mAOj/EQBFAMr/HQDz/z8A1/86AB0Azv9GALj/DwDD/5j/0f/s/wIAFAA1ABgAXQDL/9X/JgDW/wIA8P/z/xoA3v/l/+r/t//q/9z/LAAjAOb/RgDw/+H/QgA1AD0ADAAcAAQAzf/X//H/BgDO//3/RgAmAAwA5v/9//7///8QADIAqP/x//T/rP8FAPP/UQAKAPb/HADg/8L/4P/m/6L//v8QAB8A4//o/+3/uv/H/xsAFgDb/2IA9P8aADoA+P/V//D/FwAAABIAj/9KAPP/4/8fABkAFADH/y0Ayf8KAL//3//l/+r/SgDz/z4AIAAZAPD/FwATAKH/6//v/7v/AAASAP3//f8PAPv//P8hAJr/0/+k/6T/yP+u/z4AoP8OAB0A4f8wAPD/BQDy/9D/tf8MAOb/DwBWAPz/IQD3/woACAAGAHQA7//g/x0A4f8LABsAYAADAAIA3v/l/w4A5/9aAAAAbQAzABcAEgDr/zgA5P8gAIf/+//8/w4AQwC2/+n/yf/T/5L/3//T/xIA/f8PAFYA/P8hAC0ASQDg/3kABQBOAGMA4v+yAMb/GgAVALX/+//X/ygAMwAWAAAA7v8VABEA/P8zALz/t//q/wAAJQAwABQA7P8UALX/RAAAAO7/cQASADMA4P8dACoA2f/z/ywA2v/i/+j/EAANAC8AJgDD//T/df/a/5j/0f/a/+L/aADm/w8A1v8nANb/FQDt//H/KgCP/5QAGwAoAFgAIgD3/8L/KQD9/w8AVgDY/83/1/9w/1YA/f8PAEMAAABbANz/UAAJACwA2//Q/xAAn//X/7r////a/yoARwAUABAA1/8oAA0AMAAUAOz/FADs/97/5P8zAE4ABwCHABAAIAAsANr/KwDH/y0A7v8WAAAA7v9MAND//v+i/+z/FADa//T/PwAOAML/8/+s//T/v/8nAB8A4/8xAAMAJwAfACwAIwDB/6j/TACr/7v/7v+6/xAA/P8gAD8AIADk/2kA5//a//T/0f9aAO7/XwAoAOn/7v/f/9P/yf8KAMD/8f8YABMA/v/+/zUAUADl/0UAEwDG/3cA3//4/wsACQC+//D/zv/Y/ykAxv8sAAAASQC6/+3/8f/P/1kAtf8xAKf/3v/k/9f/KACO/zYAGQDM/0QAEQDY/zsACgAIAPX/5f/q/yUAMAACADkACQA+ACAAPgANAAsAQAD9/zQA8/9RAPn/+v9EABIAIQAtADYABwAqACIA5f+h/7P/sP8bAPH/GAA4ANL/WwC3/9j/FgBJACgA6v8lAML/8/++/xQANQDi/zEAFQD/////2/+r/xcAAADc/9D/x//l/7P/CwD3/4r/2P/z/9D///8jAAoALQARAPz/IQD3/x0ABAADAKf/pv+4/3z/TQDQ/+z/FADH/xsAu////wAAtv/8/1gAx//S/yQAr//k/7L/CgDS/7b//P8OAPr/+/9XAOv/OAB3AOD/5v8hAMD/3//4/+f/IgD4/0IAIwDT/9z/9f/A/7r/7f/M/9b/zP/W/8z/HwArABAAHwAHAPT/9v/m/yEAGwDy/2IAqv8WAFsAyv95AAUAKQAhAPf/QQDZ//P/9v8JAFEA+f/o/yMA0/8lADAAJwBEACQAMADd//f/+f+w/wkA4/+f/+n/EgD9/w8AQwBJAAMAFQDt/97/0v/u//H/KwD+/xAA/P/q/1wAyv9CACMA0/9KAKn/FQA2ACsANQA9AEQA7v/f//j/HQDh/x4A9P8aAEwA9f8IAD4A/P/q/zcA9v/T/xIA6/8TAP7//v8jANP/3P/1/wkA9v/T/+7/zf/8/9j/FgASAP3/awAMAFQAMQDM/w0Awf/y/xkApv/d//b/CgAtANv/GQABAAEA3f+s/+L/CwBlAC0AJADn/8f/CAD1/xsAFgA2ABkAJwBEAO7/8v/Q/+v/AQABACUAHgArABAARAA3AOP/DQAdABcA7//g/+b/6/+4/9j/BAC6/8j/5f/Y//L/GQDe/xsAFgAAAO7/lf8FALv/yf8cAOD/CgAbABUAAADt/8z/HwAHABgAyv9CAH8A+f+fANv/0P/+///////t/0wAGADw/+D/CwCb//j/5//s/14A3v8IAPX/9//n/1kAEQANAEIAEAD8/+r/JQCd/zEAzP/W/14AzP8xAMz/MgDN//z/agCe/wwA5v/Z/xcAAAAlAPr/6P9IAAMATABQAOX/RQDv/87/s//C//P/vv85AAkALAD//+3/AgCn/yYAsf/3//n/nv8NANT/SgDO//3/NAC8/xIAxv8aAMz/DABBAOz/3f91/8j/wP/f/9P/7v/y/73/bwBsAHwAUQAKAAgA0P/s/8v/1f8UAMf/5f/q/8r/5/8QAFYAWAAPAB8AGQCB/xoAOgCu/4gAEQCg/yEA9v8KABoAAwACAN7/CABQAMH/zf8gAOP/HwA+ADIA8v89AEQAyf/m/w8Asf/T/yQA5/8QAPv/6v8AAAAAEgAhAAgAGQAUADUATwDS/zYALAD//xEADgAdAAUAYADN/w4AQgDI//j/1P/v/ykARgABAO//BAC6////EQAgAD8AIAAsAO3/AgA5APj/CwD3/x0AFwAlAB4Ac/8zALz/pP8AALb/DQB4/+//BADf/y4AEwA0AM///f8PADEAAwC5/+z/AQDL/8P/TwDk/yAAGgACABQAtf9EAO7/8f/P/9n/FwDu/zsAQgAiAOX/IQD3/y8AAQABACUAnv9DACQA1P/v/87/xf++/xQA7P8BABMAov8PAAwA5v9GALn/6//v/+D/LwDd/z8ADgDC/xcApf/J/woA0v8kAAoACAArAMj/5f/q/yUAMAACAEsAqv/g/xwAzv/q/+//AwDf//j/MAAmAPv/DgDn/+z/8P/z/wcA9P8IABkA8P+p/83/jf8RANf/zf9FAJL/8f/0/63/9P8tAAAA2/8rAO3/JwBXAP3/DwBWAPz/IQCcANj/OwB6APT/PwD9/9n/8/++//D/4f8wAEsAGAATAOv/7//z//X/UwBoAAoALQDt/wMA8f8FAHMAyv/U/xMA2f+8/+7/3/8KAD8AIAAsAEkAOgDU/wAANwAIABkAFAA1ABgAJgAMAAkAUQD5/wwALgATAEYAy//V/97/rf8YALj/2f/h/+f/EAAMABwAFwBKAM7/DgD6/8T/9P/S/1sAAAAkAGcA+P8dAAUAlv8rACMA0/8SADMAYQDz/ywA2v/P/7T/1f8UAOz/JgDW/wIA8P/h/x0ABQBOACwAJAD5/1UA1//N/zIA3//4/8P/BQApAA4AQwDa//T/LQDJ/+b/2f8XAKX/yf/U/27/QgD+/zUA9P8IAPX/rv8ZAMv/QwDt//H/BQDg/y8A8P8XANz/PgAyALv/2/8rANr/BQDg/9T/SgAEADsACgDS/+3/AwAUADUAPQDp/wAAyP/4//r/DQAvACYADACu/9H/EADp/xIAWAAPAAwA5v/+/9n/8/8/AMX/GQDw/7z/AAASAA4ADAD4/wsA9/+v/xoAzP8yAN//0/9cAKX/AADc/wcABQAEAPL/0P80AOH/QwAjANT/AADK/53/w/8qAP7/EABEAO7/8v8GALz/EgAhAL//AgDe/9L/2//1/3cAu/8RACAAh/97AOP/1v86AMH/8v+9/7j/DwAeACsARwC5/+z/AQDd/y0ASQA7AAoAUgALAFIA+f/o/yMA5v9ZAP//IwDT/8r/HQCF/woALQDu/wMAAgDw/+H/HQDh/8L/8//R/+3/zP8fABkAlP87AAsA0v8AAAAAAAAkAB0A8/8aAMz/DADm/9n/PADn////NQD1/9L/7f/x/wYABAAWAAAAEgDY//L/9f/A/wMAzP/o/7b/6f82ABkAOQBAAGsA1v86ABwA8/8HABgAXQDL/zAA8f/P/9j/8//j/7H/HAAEAN//LgBvAKL/2f/z/6z/KgD+/xAAVgAzADwAMAC5//7/IgDl/+v/JQALAOX/MwAEACgADgDn/+z/8P/O/8b/GgC6/xAAxP+9/wEAyv8dAPT/9v+u/+P/sv+c/x0A4f/6/0QAWwASAFgA7P/L/+j/fv/z/9H/EQAgAAcAYgAFABYAEgDq/xMADwDo////SAAVAMj/+P8wAAIA8P8FAE0A0f/a/3QAFAAiAAkAGgDM/5//+//X/9//+P8wALn/2f90AMr/HgB0ABQANQAGAAQAKADY/ygAMwAEAAMAAgACAN7/CAA+ADIAFgAAABEA6v8AAEoAzv8OAAsA9/9UAPv/fAA/ADMAhQD+/0cAAgAmAB8A4v8xABUANgA+AA0ALwDv/6n/OgDT/xMANADO/w4Aw//P/+v/7//g//n/HgD0/wgABgDh/9X/3f+I/w0AHQAXAEoABADf/8H/BAC6///////I//j/1f8BAN3/CAArANr/PQAMAPj/MAC5/zQAz//r/xMAov9rANb/FQAjAAoA9v/m/yEAiP8yAM3/DQDn/5D/AQCl/9z/BwAYABMAIgDl/zMAu/8AAIAAwv8XACUAMADw/yoADwD7/8X/q/88AMP/KgA0AAUAzv/8//3/2f9zAAAAAAATAOv/yv8wABQAx//3/+f/EACf/w0ALwA4AC0AJQBCACMAUwDV/ycADQDB/04ABwArADUA9P/2/9P/3P8sACMA1P8TAA8Aw/89ANb/8P8FACkAIQCa/1MA1f/w//P/4/8fAKv/4f8LAAkA9f8bALv/AADI/4r/DgCL/yIAGwAWACQAHQDh/9X/JgDD/xgA3f/2/woA9v8KAD8ADgBCAEgAuv8jAOb/RgAmADEAJwB7/97/rv/1/+X/WAAPAMT/KwDH/9L/yf8vAAEAEwAPAEMANgCs//P/0f81AAYAFwAlAMP/KgDr/7j//f/Z/wUAFgAAAFwAAAA3AD8A6v8lANX/8P8EADsAQgDs/wEAAQDd/9H///+j/yMALwCl/zcABwC9/+//u//b/+L/6P82APX/GwAWAO3/OgCu/xoA8f+X//b/0/9cAO//TQA+AMT/UADT/wAA7v9NABkAuf9HAMv/DADm//3//v/H/xsA8v8ZAAEAy//n/xAAsv8vAN3/v/8UAKP////I/1MA1f+4/w8An/8fAAcAKgDs/zgA5f/q/xIAof9rAPv//P8zABcAEgDr/yUA+v/E//X/9//5/wwAHACFADQABQA7AOf/tP8eAAYABQBNAOP/RADu/wMAFQAjAEEAj/9dAN3/CAAGAJf/PgDE/ysAyP8JABoA3v8uAMn/+f8xADoA0/9KACkA/f9ZALX/1v/x//T/GgADACcADQAKAFIA+f/W/zkA5f/r/0oAKQDG/+T/DQD5//r/MgDy/+L/MQAVACMA+P8eACoA/v81APT/v//M/7H/HADg/6//PwCy/8L/KQDr/yUAsP/A/9//if/q/9z/mf/S/6T/yP/m/+v/AACA/wcAKgDH/xsAKADq/9z/PgBEABIAIQAtABIA/f8PAB4AGAA4AGUALADt/7r/2v8qADQAKgBZADUAGABLAAUAKQDq/9z/4//p/yQAwv8EAAMAgv/l/zMAzv8zAIUANABhADwAHgA9AAwAwf8oAA4AsP8bAN//+P/n/yIALgC3/zMAPAALABsAOwAKAPf/CgDS/+3/3/8JAD8A/P/9/w8Aw/+q/+D/wf8EALr/2v8GAKn/KACg/+r/3P8HAHQA3f8IAND/x//S/wAA2//1/xsAAwAVAO3/TADP/1kANQC9/zgA0v/b/73/JQDV/8v/DADm/1gA/v8jAGYALQAAABIAIQC//ycAHwDQ/xAAsv/4/+f/tf8MAJz/CwAbAM3/RQAAAMn/CgDS/xEADgCL/zQA9P8/AHwAGgCWAML/BAAWAO7/AwACAF4AAgA5APf/HQA8ALD/LQASAKH/MwAXAMr/jAAnAA0AQQDH/+X//P8PAEMAEQAzADsAwv8EAPL/vf8BAAEA7//g/+b/IgAbAKj/OQD4/+f/7P+U/2AA4P/B/wQAlf/0/wgAq/8EABYAtv8gANH/2v89AAwA0//u/ygA6v9KAE4A9v9TAEMAIwAvAO//KQAPAPr/+/+z//n/w//P/+v/3f8aAAIAJwBpAB0AFwAAAG7/wf8EAKj/8P/h/8L/zv/q/wAApf8SAP3/6/84AAgAYwAGAPP/PgDX/xUAEQDX/wMAFQAjAOb/6/8mALH/9/8dAOH/5//a/xcAOAAIACsAWgAAADYAGQACADkACQBjAOL/HgAYAMv/QwAjAAoAGgBNAOL/+//X//H/BgCX/+P/6P/I/67/LAD//7b//P/q/wAA3P8+ANf/AwBMAM//NAA8APr/MgA7AAoALQDJ/+b/DwDD/+L/DADl/9j/8v/Q//7////t/xQAEAD8/yEA5P/p/xIA/f9ZANr/GAAAAMr/HQDP/zQAvP/u/6j/lP8XAMn/HQDh/zAAAgDd/z8ADgCw//f/HQDh/x0AKgAPAAwA+P8eAD0Asf/T/+7/cP/p/7b/6f83ANH/2v/0/7//8f8YAMr/1f+4/w8A1v8CADkA0v83ANH/SAACAMv/DADm/zQA8/8aABUAIwAcAPP/BwAYAG8ARwACACYA1v/M/3sALAA2AHUAAgDw/+H/QgAQAA0ALwDw/xcAJQALANP/NwDR/xAAaQDV/zgAwP8VAP//tv8yAM3/IAA+AOn/7v/N//z/6v8AACUA5/8QAA0A5v8PANb/8f/0/7//lP+8/6T/yP8cALv/AACk/7b/6f+2/zIA8v8GAAUABABNAND/EAAyAPL/UACvAFYAIABjACsA2v8FACkAIQAbAAMAJwAfAL7/FADZ/8//DwDo/38A1P/v/2AAqP8nAA0A1P8TADQABQDg/0IA7P8BABMAtP/D/xgAJgAMAEEANAAXACUACwAuADcACAAGAAUA4P9BAFoANgBQAAkABwDi/9X/8P8XAEoA8/8sABEA6v8AAAAAJACw/7//uf8QAFcADgDD//T/5P+N/20A6v8AACUAwv/h/9X/AQDv/zsA5/8QADIAzf/E/5n/9v+v/wcA4v/V//D/zv8hAOT/DgAdAOH/CwD3/8L/KQBGADgALQAAAO7/zf/X/8z/DQDm/yIAGwDN/9f/AwDx/+H/+v/E/2IA4f8LAEAA2f9zANz/LAAkAAoACAA+AFcAs/9VADIAFgARALP/+f/W/8v/+/8NAML/FwAlAOf//v8QAMT/0P8QANb/OgDm/8b/CAD1/wgALABIAN//LgDv/83/1//f/woA5P9pAAsAGwAoADMAOwCw/2QA9v+u/wcABQApAA8AHgAGABcA3P8+AA0Ar/8IAKv/KQDr/+//BAC6/9r/z//+/6L/WQA1AL3/bwD+/+z/AgAmAB8A4v9DANv/0P/s//D/TgDk/w0A1P/d//b/rv8+AI3/tv/E/4b/+v/E/xkAAQDv/wQAAwAVAMj/UwAeAPT/LQASAP3//f9HACcADQBBABAA+//q/8n/1P8AANz/9v9BALT/6P8QAOn/WwBKACkADgALAAkAvv8CACYA1v8CAAIAuP8PAPv/RQBvALT/HgAGAKn/8f/0/wgAvv/w/xcA3P/R/8f/5f/q/+//8v/1//f/LwAUAOz/OQCt//X/CQDQ/2wA/P8hAC0A2/8+APv//P8zAGEATgAaABUAyP8JAPb/+P9CAEgAOgAvACUAsP8bAAMA3/8JAKz/4f/n////NQAYAN3/5P8OANT/AQATANn/4f/U/+//4P/C//P/vv+4//7//v8QANf/OgD4//r/MQDx/wYAvP/J/53/nf/6/8T/0P8QAFYA2P8oAA4AsP9SAML/vP8kAOf/x/8IACwAtf/p/yQA1P84AC0AEgAzAOD/VAAMAEEAbACf/2oAQwARAHwACAB1ACcAHwBQANP/SQDy/9D//v+j/xAA+//X/xYApP/I/67/h//o/6P/7f8CAAEA8P+X//X/LgAAABIARgDd//b/LwBKABcApf8AANv/4/9EABIA/f8PAPr/1/9MACsA7P85AC4AAAASAP3/DwBEABIAWAA0AE8AUgAwABQA7P9LAAUA4P/5/x4A0P/+/1oA7f8VAMj/LgBcAO//BAAoAOr/t/9FANz/GgDx/73/EgDG/y0Ayf/B/7v/2/8YAMv/HgAGAOH/CwAIAPX/CQAaAN7/5f/9/9j/FwASAFgAWgD//20A6v/K/1QAjf/a/wYA4f9UAOn/AAARAPz/DwAeAFAAwP86AEEA7P+nACoAEAAfAAYAz//G//b/CgAaADoAUwDD/xgAJQCM/+z/AQAmAPv/IAAsANr/BgDz/+P/sv8KAOT/1/8oAMX/9f8JANH////a/wYA8//R/9r/qv8oAOr/3P/2/+X/DgD6/zIAOgAKAPf/QQDZ/wUAKQDY/zsAwv9OABoAlf8FAOD/5v80ABcA7/9yAAAAJQALANP/JADn/1kAIwAKAC0ANgAHAM//IQCI/8T/0P+1/8P/vf8TANn/BAAoAOr/t//9//3/2f8XACUAHgBPAEAAIQD2/8H/8v/j/9b/FQDI/67/KwD//xEAMgAWACQA+f8eAPX/9/8vAN3/9v/4/+f/2v8qANn/zv8OALD/5f/9/w8A6P/t/ycAMgADAAIATAAGAOD/VAANAPn/+v/W/8z/sf8uAAAA3P8/ANf/8v/Q/+z/pv/K/3j/bv8dAGD/7f86AAoACAArAEcA3v8JAAcAGADd/y0A2//1/1IAnf8xAN7/CQAZAMz/RAAAANv/KwA1AOL/1f8CACYA+//8/w4AQwD//yMAZgD3/woA5P8gAJr/0/83AKz/PAAMAPj/5/8iAEEA6//v/wQAKACz/+f/2f/z/ywAEQAgABoA8f/h/wsAGwAEAN//HAAEAN//QQDZ/+H/CwDl/zMATgD2/0EA/v/Z/yoA2f/z/wcABgAEABYAAAAAABIAs//n/+z/3f8IAPX/GwAoAA4AHgAYAEoAvP/c/1AAnP9CABAA1v8nANf/FQC2/+n/JADn//7/EAANAB0AFwA3AC0A7f86APj/MAACAN7/CAD1/wkA9f8JAL7/8P/z/wcAq//g/x0Al/8+AOn/EgAgAAgAYgAFACkADwBDAAAAJAAKAOT/6v8kAPn/6P9IALr/SAA6AOb/DwAMAPj/+v9WAOr/JQDV/8v/+v+y/xwA8/8ZABQAx//l/+r/t/8hABoAzP/p/8n/HADg/9T/7//g/woACADj/8P/vf+4/w4Aw//P/zQABQAEABUAIwAKAK3/4v8eAOL/+v/7//z/xv8IACsAEABXAKH/s//C/+H/CwAJACwA2v8rABAA1v8CAPD/BQAWANz/LAARAPz/WADs/wEAAQATAA8AHwAZAAEAEwDs/yYA6P8jAPj/CwBAANn/8/++/xQAx/8JABkAuf9sACAA9f9TADAA3v8tABIAIQAIABkASwAYADgALQAkAHj/AAAAAO7/KADF/1EA5v/G/y0AAADb/+L/sf/4/8L/qf86AOb/WQAQAFcARgATAFkAyP9lAK3/GAA4AMD/OgAcAHMAEwBGAN3/GgBNAAYAdAAmAAwA0/8SANj/4P/m/7T/+v8NAIsAJwDW/ycA/P/q/xIADwAMAPj/wv/z/9H/tf8NAAoA0v/t//H/9P+//ycA6f8RAGoAsP8JAL7/y//o/+3/TAD0/xoAzP/X/ycA/P8OAB4A9P8IABkAAQDL//r/DQCv/2QAGQDw/+H/1f9dALj/IgAtALf/6v/c/9H/7P/e//f/HQDO/+r/yv9VAB8A4//o/7b/MgC6////SAAoANf/KAAzAIT/+P/6/x8A0P/Z//P/BwArAOz/gwD8/+r/EgD9//7/EAD7/w4AVQD7/0UA3P/R/xEA6f8SANj/FgAAAO7/qP/w//P/4/8yAPL/KwD//xAARQAAACUAwv/h/wsAwP86AAoA0f/t/xUANQArACMA+P96AAYABQAoAOr/JQDn/0cA8f/h//r/+/9FANz/YwDQ/8f/CACr/xcAJQB6ACsAEAANAPn/DADB/xYAAADb/1AA+P/C/+H/CwD3/+b/2f/z/wcA4v8eAL3/3P/2/+b/DwDD/xgAAQATAOv/3f/k/9f/8f/i/2gAHABzAO//u/8RANf/OwD5/zEAzP8MAAoAv/8VALX/+//X/xYAtv8gAAcAz/9GALn/WQDa/8//DwBDAAAApP82AL7/EwDs/wEAOABAAEYA7/8pALP/sP8IAKv/8/9jAOL/aABmAOX/2P9x/8T/4v/o/+3/FQDI/+X/IQDk/1cA/f/+/xAA+//q/zcA9v/T/0oAu/82ACwA2v8qAP7///8QAA0Awv/O/3v/zf8yAPL/9f9SAOf/kP/d/9H/IwDm/w8AHgAGALz/3P8ZAJT/FwDc/+P/RAC3/8X/PgAgANH/IwD4/wsACQD2/wkA9v8uAO//BADf//j/CwAuABIADwBoAPj/CwBAAA8ADADm//3//v/a/yoAxv/3/1QA6P8jABwAKQD9//7/NQDP/+v/OADk/8X/GQDe/+X/RQAAABMADwDo/yMA5v/9/0cAuf/+/8f/GwADAIL/QADG/7//OQDT/wAASQBgADsA5v/Z/xcA3P/2/8D/3//4/9X/SwAXACUAQwBtADMATgBRANT/7/+7/wAA7f/M/w0A5v/Z/+H/5//+/+z/3v8bAN//0/8AAMn/5//+/yIA+P/n/+z/8P8XAO//AwAVAO3/AgAnAA0A1P8AABMA/f80AE8AQAAhAPb/QQA0AL3/AADu/wMATAA+AEQA7v/y/9D//v/a/xcASgDg//n/DABBANn/8/8sANv/KwAQAB8A9f8bABYAbgA0AAUAOwDC//P/vv/L//r/MgAWAEkATQDQ/1oA//9bAEkABAA6ANT/AADK/zAAy//V/14Auf/+/yMA0/8SADMA4f8wAPD/BQAWAMn/CgCt/+L/DADl/9j/4P/5/zEAOgCu/xkAp/9u/0IA2v8YABMA2f8XAMr/CwAbAN//CgD2/woArP+Y/wcAvf+4//3/DwDW/wIAAgDd/xoAAwACAPD/4f/V/93/v//x/yoA/v9aAP//AADb/5j/9v/B/wQA8f/i/+j/2v8YABMA/v9HAAIAFAAiANP/JAAwAHAANQD1/0AA/f8iABsA8v/i/wwALgDd/wcAPQDo/zYAPgCy//j/QwD//+3/TAA9ANb/AgAnAA0A5v/+/zUAPQAMAAoA0f+2//v/6v8lANX/y//D/+H/5//H/0AA6//v/+D/QQDH/8D/XwC6/38ALwABAG8AIgAJANH//////xEAjf/b/ysA2v89ANb/8P8XAAAANwAtAO7/3/8JAOP//P8OAPr/6f/t//H/9P8/AA4AHgAFAIT/HAAXALf/IADR/9r/TwD3/0IA///t/wIAgf/k//z/xf/j/9b/uv8QADIA8v9QAOX/6v/v/7v/JAAdAAQABAAoAPz/6v/c//b/QQAiAGUA9v/l/w8A+v/p/1sASQDN/zMA8v/1/xsAAwAoAFcAIQD3/0EA2f9PAFIAwv8EALv/2/8GALz/EgD9/9n/FwCl/5H/zP/E//T/GwAoACAAGgA5AAkABwD0/7//AgACAPD/8//R/yMA+P8LAFMA+v9EABIADgAwAPD/TwDk/9f/FgDJ/woAv//M/wwACgAIAOL/+//X//H/9P8IAAYAqv/y/9D/2f8FAKn/8f/h/7D/0v8kAPn/w/+9/8r/5/+0//v/1/8oADIAzf8yAOD/CgAtACQAVAANAAoACAD1/xsAXwBfABUAAAA2ACwA2v8qADUAvf/v/wQAuv///8j/0/8lAPn/MQBfADoAHABOACwAWwBJADsAVAD7/w4AsP/3/xwA8//2/+X/2P/y//X/0v8kANT/EwBHABQAEAD7/yAAv/8CACYA6P8AACQAHQAFAPL/vv/L/8P/BQAEAAMAJwD8//3/2P/z//X/9//5/zEAOgAcACkAs/8dAPT/5P98AAgAGAAUANn/KgB9//L/GQDL/0MAAAAkAPn/+v8NAML/8//Q/+z/FADs/zkALgC3//3/2f+7/zYAYwAYAN3/CADi/+j///8kAC8A3f/k/8X/BgDh/57/HgDi/zEAJwANAAoAm/9BAP7/NQBPAPf/VACf/x8ALACj/+z/AgA5AOX/IQAtAO3/8f8GALz/NwAsAMj/eAAXAAAAJQALANL/yf/m/6H//v8QAA0AVAD7/yAALACR/wIAuP/+/6L/j/8BAJP/FgCR/xQAyP+u/2MA4v+fACQACwD3/6//CAD1/xsAOgAvAO//FwDJ/woAGwAVADYA4//7/9f/zf+y//j/w//0/xoAAgACAPD/BQDg//n/1f/e/9L/7f/M//v/1//N/+n/bf8JAOT/VwDY/87/RQDK/x0AGAAlAAwAUwDD/wUAKQDG/z8A1/8oAPz/IQAaAN//+P/V/zgALQA3ACwAWwDu/xUAWwDu/ygAIAA/APz/MwAXALf/WADs//D/BABNAPX/rv8HAKr/4P/m//7/RwACAEsAGADv/7v/7f8nANf/OgAKABoAKADp/7f/xf8HAKr/8v8rADUAKwD//0gAOgAKAAgAGAA5AC0ANwAsAO3/3/8JAAcAGADd/+T/1/+o/3AANgA+AGkAHQAFAAQAOgD5/wwAQQD+/9n/8/+//ycAaQCv/z8AMwDz/z4AHwDj//v/sv/U/93/mv9lAIj/1v/e/5v/QQC1/zEAJwAyAOD/HAAEAJb/YgC8/+7/zf8NAFQA6f8RAA4AMADw/zwAMADx/yoADwAfAAYAvP/c//X/wP8VAAAANgA+AA0ALwDd/+T//P/q/+//4P/U/yUA5/8QAPz/xf8sAP//AAAAAO3/zP/E/wYA8//R/+3/AgDe/wgA0P/H/xsAAwDf/67/4//E/73/bwD+/9r/KgDH//f/+f8eAOL/sP8JAKz/8//k/9f/FQC2/8T/9f/S/zYAUQAKAC0AEQD8//3/IgAuACUACwAbAIUA6/84AD8A2P9gAPL/GQAmAB8AKwAQADIA8v8GAKr/8v8YACYARADJ/woACAArADUAPQAMABwAYADg/y8A3f/k/zIA4P/4/+j/IwDm/+v/EwDZ//P/4//p/0kA8v/1/xsAzf/p/+7/AwDe/9L/yf/m/8b/0v8RAKD/xf8HABgA3f8aAPH/BgAXAO7/TQDj/1YARQBdAEsAFwA4AL//AgC5/zQAz/8hAGUA0f9IAN//5f/q/xMA6/8TAP7/EAD7/+r/NwCs/2EAFwAAABIAof/9/7T/1f+m/wEAOAAaACgAIAAsABEADgAwAAIA3f8tAO7/8f8GALz/pP8AABEA2P8oADMAKQD9//7//v///+3/lP8EACgAMwAWACQA+f/7/+n/pP8AANv/BgAXAAAAJQDD/+H/CwAbAPL/BgAFAOD/QgCi/+z/XQC5//7/EADW/9//m//U/zgA0v82ABkA3v8tAO7/OgDm/w8AHwD1/xsA8v8rAMf/LgAlAB0AGADv/ykA/f/+/7T/w//h/57/1v8UANr/BQAEAN//+P/6//v/oP8OAIv/ov80APT/GgACADkAwP/y/+L/6P+1/+n/NgBi/28A2f9hAGEA8/+IAGz/eACp/7r/IwB3/zcA9v8cAAQAcgAAADcAUQDT/0oAqf8DAMz/sf8uAO//u//b/xgAuP80ACoADwAfABkAXQDw/zwACwAcAE0AGQAUABAA/P8gAOT/6f9JAOD/HADO/0UAggD7/1cAxv8IACsAEAAyAM3//P/F/9H/yP8JAD4Axf/j/zEA3/8JACwASAAVANv/KwDH//f/CgAIAAcAGAA4AOT/RQAlAB4AKgA0AOH/1f9eAN7/ZQAsANv/KwDa//T/UQDU/9z/GgC5/zUABgDh/0IAo/+i/xAA1v/M/9b/3v/l/6H/DgBDACMALwATACIA0v8AAO7/FQAAAO3/AwC5//7/7P8UAKL//v8jAJz/LwDL/x4Az/+i/zQAvP8SAA8A+v8NAAoAQAB9AC0AAABJAOD/CgAIABkA3v/S/yQAwf8EAM3/1/+6/8j/GwDg/xwA4P8vAJT/zv8gAJr/UwCw/xsAOgCv/xoAp//L/7D/0v/b/wYATwAIAD4AxP89AA0Ar/8HAKv/KQD9/9n/FwDu/xYAAAASAFgANADh/zAAAgDw/ykADwAeAPT/CAAHABgAEwBHADkA0v8kAK//v/8VAMj/LgAlAML/FwATAP3/NAD0/xoA3//A/xYA7f/M//v//P/r/7j/2P/g/6//UQDU/xMANAC8/8n/5v/H/3b/2v+q//L/BwAYAAEAyv9nAMD/TQA+ANf/TAArACMACQAsAAAAkgBRAC8AAQDd/xoA3v8JABoA8f/0/y0A7f/x/wYA8//R/9r/BQCp/7r/2v/P/9n/BAADABUAyP8cADsA+f8fAAYAPADV/wEAJgDW/4MADQAwAHAA/////wAAJADU/+//cgASAP3/bAAyAPL/PQD7/w4ACwDl/0UAAAAlAAsA5f8OAB4AGAAmAHsAvv8mAPv/sv9UAAwALwATAOv/7//g//n/6P/a/xgAJgAMAHgA4f8LAPf/5v8iANL/SQADAF8ATADi/wwA0//K/+f/EAD7/yAA9v8cACkAxv/R/9r/9P/S/wAASQDy//T/CAAZADkA5f/9/+v/7/8WABIAIQAtABIAIQA/AKD//f/9/7T/DADB/9//0/+l/+7/AwAVAEgA3/8cAHIAJQBCAMj/5f/Y/7v/tv/p/xIA2P8WAKT/AAAAAO7/OgD4/zAAzP/o/8j/HAAWAJL/XwACAKf/EwDZ/6n/FgA2ABkAJwD7/9f/FgAAAAAAEgAgAC0A2/8GAAUAcf/X//H/z/8PAPv/MgDy/+L/+//X/xUAAAAkAC8AEwD+///////a//T/GgBfAN//LgA4AAgAGQDL/wwA+P/V/93/CADi/9b/FADs/8v/6P8jAOb//v/Z/5f/GQDw/xcAAADc/z4A1/9NAD4ADQBUALH/QQDr/+//OwDn/zUAqv8WALf/1//f/67/PgCN/9v/0P+i/yIAwP+6/xAA/P9FACUA+v8yAAMAXwAnAA0A+f/W/97/wP+6/+z/3v/3/1QAn//p/0kAqP9eAF4AzP97AIgAEQBYADQABQAEAAMAFQD//zYAKwD/////yP/m//3/2f8pACEA9/8KAOT/DgDn//7/EAAyAE0ABwAYABMADwAMAC8AJQAMAPj/HQD0/6z/z/+h/9n/4P/5/9b/8P/0/9H/2v/0//f/CgA/ADMAYAAWABIADgD6/zIAcP/7/+r/kv/f/wkA9v/l/zMAvP8AACQA+f8xABUA7f/e/xsAAwAVADYA4/8fAGIAKgBHAAIA8P8pADQATwAIAPX/5f/Y/+D/r//j/9f/uv8QAPz//f8hAAgAKwD//xEARQAlAAsAGwAEALr/yP/A/6j/FAAjABwAKQAhAL//p/8TANn/8/8aAAIAJwD7/yAAGgDe/9P/EgDY/wQAFQAAAG0ADgAeAPT/0v/t/8z/6f+2/yAA9f/T/yQA5//+/0gAFQD//+3/zP8fABkAAQDw/zwA+v/E/1AA0v8AADcABwD0/+T//P/Y/83/1/8DAMz/1v/x/6r/8v/1/+X//f8hAC0A7v/y/+L/+v8NAB0ABQBNAJsAIAAsADYABwDP//3//v/H/0AA/f8PAPv/6f8AALf/MwAEAAMAAgACACYAw//0//f/wf/g/y8A7/9OAGQABgA8ALH/LgAlANX/JgDo////yP/B//L/BgDz//b/+P/n/+z/AgA4ABsA8v/i/+j/o//s/wIA3f9kAD4A6f9cABIA2P8WAAAASQApACEALQAAAAAAEgBqAPr//P/9/+v/XQDv/2AABADy/ysA//9tAOr/AADu//L/PQD7/zIABAAVABEADgAdAAUATgAHAPT/5P8zABYAyf/5//r/DQAKAPf/HQDh/9T/JgDV/wIAFAAQAPv/oP/q/wAA7v8WAO7/3/8cAAQA3//T/9z/BwDi/57/6P82APX/LQDu/9//QQC0/7H/CQC+/5T/BADy/9D/NAAFACkAMwAXACUA+v/W/wIAAgDL/4z/RwCDAOn/pQA7AML/BQC7/+3/zP+x/xwABAC6/8j/HAAEADoACgDk/zIAqP/M/9b/3v/3/+f/NADP//3/RwDe/+X/1/+o/ycA+//F/wcAYP/u//L/9f8tANz/UADB/9//CgD2/woA5P9XAA8AMQACAN7/GwDN/0QAXAATAA8A1v+5/xAADQDU/+//BAAVALb/MgBNAND////a/+L/sP/3/x0Al//j/+n/AAAkAAoAUgAwACYAewAZAN7/wP+V/5f/mf/3/woAGwAVAAAAAADb/wYAFwDv/83/MwDy/77/OAAIAND/2v8FALv/AAASAP3/IQAbADoA5v80AOH/nf/o/7X/6f8kAAoAv/8nANf/8f8YAO//YADy//X/QAD9/8f/ZAAsAP//kgAsABEA/P8OALD/9/9CABAAHwDQ/+z/8P/z/+P/aQDn/7X/VgD8/0YA3f8IAAYA4f8wAJT/PAAwAPD/FwCl/7f/1//y/wYA8/8HAND/2f8pAMb/CAC9/7j/RgDL/+j/NQAYAMv/QwAjAOb/WQDs/xQAIwDT/wAA7v/y/z0A+/8OADAAAQA4ABsAKAAzABYAEgBGAEsA8/8/AA0AQgAQANf/OgAKAAgAGQBeAPD/BQApADMATgDR/yMA0//v/wMAAwAVAP//EQDF/xkA8P8XADgAGgAnAOn/EgAzAAQA8v8ZAAEAOAD3/woAPwCz/9T/y/+L/9n/BQDN/1cA/v8QADEAAwCWAC8AOAD3/woA5P/F/wcA9P8aABUANgCZ/z8AWADH/0AAxf++/97/5P+g/yAA9v/B/2AAOwAdAPP/GgACAPD/BQAEAAMAzP/7/w4Anf8eAPT/v/86AMH/FgDb/xkAJgCf/zIA8v/1/0AAIQAIAD4ADQAKABsA3/9TAPr/1v/M/9b/zP/W/ycAVwAzAAUAYAAWAAAANgAsAP//AAARAPz/DwDV/yYA1v/e/y4AEgDY//P/BwCY/77/3v/3/9T/AADc/+P/DQB4/9z/vv+m/7j/2P/O/8X/9f+J/8X/rP+q/83/6f83APb/+P/5/zEAOgAcAE4ALAARADMA4P8vAAEApf+3/9j/8v/Q/yIA+P8dADwA6P9aACQA+f8xAF4AFQD//20Axf/j/0QAEgBYAP7/7P/e/63/BgAFAOD/r//2/67/0f///8j/ZQAIACsAIwAJACwAEQD8/w8AQwDt/0wA9P/3/woAiP8NAPn/DAAJAPb/wf+o/8z/Z/8FAPP/BwAFALv/7v+6/7X/sf/B//L/4v8MABwAOwBCADUABgDO/zMABAAWABIAxf9jAOL/1v9xALb/+//Y/6j/FQDt/wIAJgAfAKv/FwAlAPr/MQDx/2IATwD3/y8AEwDZ/xcAJQDn/1oAyP8cADsAwv8XAO//KADY/wMAKAD8/zMAzv8gAOT/xP8ZACYADAAvAEsAFwAlAOf/tf/o/xEA/P/9/w8AVgAgAAcAGADL/x4A9P8/ACEACAA9AMT/0P8PAGkAVAAfAD4ARAA3ABoATAAYABMA/v8iAAkA9v9mAC0AEgBGAAEA3f8aAPH/4f/6/+n/2//Q//7/7P/w/wUABAAVAAAAyP8KAOT//P8OAAsAQADZ/wQAKADY/9//CgCt/wYABAC7/zYAvv/d/+T/sv/B/xYASQC7/zYAGQDw//P/LAAAAAAANgC+/93/iP/E/5n/v/8CAIH/0f/b/73/k/8WAMn/0/8AANz/0f/s/zkA0/9JAM3/6v8AAMn/CgCa/wkA5P9EAFwAAAAlAPr/+//X/9//CgA/APz/RgABAMr/QwARAPz//f8PAB4AGACm/9z/9v/B/5b/z//+/1j/CwAuABMAWQAiAFMAVQD8/w4AQwC2/9f/3/8JACwAtv9EABIAxv8sACQACgAbAAMAFQD//8j/CQBRABwAvP8SAMX/rP/h/wsALgDc/wcA4v/6/x8ABwAqAFkAWgA2AD4ARAA3ABoAJwAfABkAAgAUANr/KgDr/8v/QwDa/ysA7P/w/wUABAAVAO3/OgDT/wAA3P8sABEAxf8ZAPD/FwDv/ykA2P8EACgA6v9cABIA/f/s//D/qf+6/9r/KgBHABQAbAD8//3//v/Z//P/GgAnANf/3/9BAP7/IgBAAP3/NAD0/2QAYwA9AEQAyf8cAM7//f8hABsAcgASAFgA2f/h/wsA5f8OAML/BQA7AOf/IgAJAAcATwD3/x0AvP/c/xkAlP8pAOv/pf/u/9//+P/V/xQA7P/w//P/0f8QAOn/7v/f//j/5/+1/zEATADi//v//P/9/zQA4f9CAEgA8f9PAOX/DgDC/wUA8v+r/04A5P8yAPL/9f8JAHT/7P8BAJP/8v8+AOn/SQAWAO3/JwDX//H/BgDh/x0AFwBKADwACwB4AOD/CgAIAL7/JgAxABUA7f85AAkABwCG/+f///+1/1YAjv83AAcAqv8pANj/BADx//T/CAA+ANf/AwDe/8D/KAD8/1gAx//3/y8Ay//V/7n/6//L/8P/8/8HAL3/JQD6//v/IAC//14AFAD//xEAIAD2/8D/TQA+ANf/AwBeALn/7P8BAN3/rf/P/0cAuf8iANL/yf8cAPP/YwAZAEsAqv8oAGoAw/90AAEAEwD+/xAARAAAAG4AIQAtABIA/f/+/7T/1v/w/yoAawAfABkAOQDl/+r/yv/C/7z/bf8cAOD/r//2/woA5P/X/7r/2v8FAJf/GQDw/6n/AwDe/xsAzf8OAPn/+//8/8X/LACj/7X/1v9MABgAFACRAPX/iQA3AAgAGQDd/1IA1P8mAPr/HwAZAMv/QwC2/+n/7v/y/xgAAQA4AAgABwDh/wsArv+r/xcA7//y//X/GwDy/wYAKgDr/93/CAArADUABgAXANz/4//7/47/EgDY//L/UAD4/x0ABQAWAO7/FgARAA4ACwDl/0YAAQAlAAwA+P/5/wwA0//v/zsAwv8XAID/4v/7/3v/JwDE//X/GwADAAIA8P/0/6z/vf/K/wsA5f8gAFEA1P8lAPr/n//8//3/6//v/+D/5v8PAOj/7f/e/wkAYwDQ//7/2v8FADsAnf9DANv/vf9dAN3/GgAVANv/UAD3/9T/AQAAABMA2f8pADQAzv8OAAsALgAlAEMAIwAcADwAHQAYAN3/BwAYALj//v81AL3/EwBZAOz/AgCm/+//8v+G/wwACQCs/xgAOADS/+3/AgDM/8P/vf/K/+f/kP/v/zsA1f8TAOz/y/8MANP/JQALAJv/HAAEAKj/AgDw/87/RgAmAOj/EQDF//X/0v9//z0AxP/0/3cAFgBbABIA6/9KACkANACGADQAKgA0AOH/QwDt//H/YQAFAPL/4//o////AAAAAAAAJADn/34AZgD3/2YAGwByACQA1P8mALH/9//U/93/CAAZADkAGwAWAO7/OgAKABoATABQAGUA5P8gAPb/0/83ANH/2v9PAC0A7v/f/xwAKQDr/28AIgDT/zcA9v/l/+v/EwDr/zgAUgDn/xAAHwCr/+H/5//H/1IACwAbABYAAAASAOr/7v8WADYA9f8JAKz/9P8aAMz/DQCc/zAA3v/A/0wA4v8eAL3/7/8WAAAAAADJ/x0A4f9VAGkA+f9DAAAA2/8GALz/t/8zAKn/zP/7/6D/DgALAEAA6//v/ykADgALAPj/+f/W/ycA6f8kANT/7/8WAEj/EQDF/+P/+/8NAPn/1v9eAN7/GwDy/9D/7P8UACIAUwB6AND/RwACAAEAAQDv/xYA3P8+ANf/AwAnAMT/4v/W/97/9//5/zEAOgAcACkA/f8PANb/3v/3/woALQAAADcABwArADUA4v8LAC4AAAC3/yEAGgDx/z0A+//8/8X/9v8JABoAJwDX/18A8f/i/x4A4v/6/8T/PQDp/xEADgCw/xsAlf/h/+f/EADX//H/BgCp/xUAo////9v/q/8EAM3/6f8SAP3/6/8BAO//KQD9/yEAGwAoAFcANAB0AMv/1f8BAN3/5P9FANz/4/9WAA4AegD1/xsAAwDM/w0AnP/V/0sATwD3/0EAx//k/yAAv/8nAMT/q//O/9j/4P8KAAgABgDz/+T/HwCs/7z/AADc/+P/6f8AAEkAKAAOAHoAPQDo/yMAQQDH/wgAGQDw/xcAyv95AM//DwBWAPz/WAC1/x8ABgDh/x0A4f/n/+z/AgABADgALQDu/9//5v/9/w8A+//8/w4A1f/w/xcAAAAlANX/SwA8AOj/SADx/+L/w/+q/9//nP8LAPf/1P8TAOv/SwDO/zMATgCs/z0A+//8/+r/AAAAALf/RQABAO//8v/j/+j/yP8cAAQA8v8YAAEA3f/2/woACAA9AB8ABgAYAN3/9v/m/8b/GgDx/2IAKgDG/3cAAwDx/wYAl/8GALz/3P9jACsANQD0/1IA5//H/2UArP/0/+T/xP/Q/9n/PADo/xAAaQAwAN7/CAAZAN7/CAAsADUAGQAUABAA+//F//X/GwAoAA4Awv/z/wcAKwD+/+z/8P/h/8L/l//j/7H/5f8hANL/7f/M/+n/NgAsAO3/OQAcAKn/JwAyAJb/9P/k/7L/CgD3/xwABAAWACQA+f/o////EQCy/woALQDb/+P/xP+9/wAAyv8wAEsABQAXAAAAEgDr/9z/9v8JAAcAKwDs/4H/9v/m/+v/AQAAAAAAAAAlAEIAkgAZADkACQDj/0QAAADu/xYAAADb/xkAAQABACYAsf/3/9T/3f8/ALP/5/8PAPv//P8zACkANAA8AJ7/6P///8j/HADy/9D/tf8xACcAMgCXAAsA9//5//v//P/9/+v/yv/6/zEA8f/P/9n/vP/J/+b/DwDo/+3/8f8FACkAxv8sANv/BgBPANL/kgAsAO3/AgDe/xsAzf8yACgADgAeAPT/9v/T/7f//f/G/63/TwDl/+r/SgDy/wcAKgAiAOX/MwAEAN//LwDd/wcAGADd/+T/1/+6/xEAsv/m/yIAwP86AAoALQA2APX/CQAHAPT/CAAGAAUAOwDn/0cATAAGACkADwAMAMH/AwDf/67/PgD8/9j/FgDJ/woAPwAgAHYATQAHABgAJQCe/wwA+P8LAEAAfP9gALv/2/9QAK7/YwDi/wwACQD2/xwA4P9CABAARABuAEYA8P8EABYA2//Q/8f/CAAHAM//xv/k//z/2P/g/xwA8/++/xQAEACN/8j/HACW/wYAPADV/wEAOAD3/x0AKgAPAGgACgAaACgADQAwAAEASwBPAAgAKwAjABwAOwALAAkABwDP/w8ADADB//L/KwDs/xQAEAAfABkA8P/z/9H/7f/x/+H/+v8fAKv/FwA3APb/UwCx/+X/jv+S//H/qv8pAA4AMAACABQAtf+f/w0A+f9VACAA9v/l/9j/u//J/woAGgAnACAAPgDX/xUA7f/M/+n/EQBFAO//OwAvABQA7P/L/4z/2v88AMP/TwAtABIADgDD//T/v/8CAPD/4f9nAOX/DgBVAMX/4//7//z/2P/y/z4AHwD1/+X//f/Z/xcAJQD6/zEAFQA2AAYAKgD+/8f/LQDJ/y8AFADs/10Auf/r/8v/w/8FAOD/HQAXACUAwv+8/+7/uv/I/wkABwCY/9H/NgD1/xsA8v8GABcA3P9RAFQADAAKAAgABgCX/wcABQDz/ywA///t/6f/8P/O//3/2f/z/ywAyP94AOD/CwAbAKj/AgABABMANAA9APr/RAAAAAAASQAWABIA6v83AAgAGQBwAFoAEQAgAPb/rv8ZAAIAAQABAN3/0f///xEAIAB2APH/q//O/9f/KAAgAD8AfAAIAD4A+/8OAPr/sf9BAOv/EwDH/+T//P+z/9X/uP/+/+z/FADZ/zwA6P/I/xsAzf8yAAQA3//B/83/jf8RAEUA7/87AB0Az/8PAOj/2v8YAIH/GQCn/7j/NACq/18A3//T/9z/LAD//yMAZgDA/0wABgBPABoATQA+AA0AQQDs/xQAx/8tANz/mf8IAD4A/P/8/zQAvP/u/wMA8f8FAE4A9v8cABYAAAA3AKz/hgD//yMAQQDZ/ykA2P/O/+r/JQD6/0QA7v8VABEAxf8HAM//6//v/2AA4P/5/wwAif/8/8b/5P/X//H/KwD+//////+2//v/IAAsABEA6v/J/9T/AQCl/xIADgDD/wUABAAoANf/AwBMACsAEAANAML/qf+V/6r/FgDb/ysA7P/e/y0AAAAAABIAIQAaACgAsv8dACkA6/8lAAwA0/8SAFgA7P8BACYA+//X//H/z//+/xAA1v/x/wUAKQD9/zQA4f8wAPD/qv8DAIL/LQDc/9D/IwDl/+v/7/8WAO7/FQAAAEkAFgAkAGcA0v8SAOr/AAAlAOf/IgAcAOD/HQDh/+f/RwACAAEAEwDs//D/8//2/0AA/v80AE8ACAD1/5v/CgAIABkAXgACAPD/zv/q/+//OwBUAPv/RQDv/+D/QQAQAA0A1P8lAPr/6f9JAM3/MgDN/zIAKADF/xkAuf/Z/6r/8v+9/8r/1f/w/87/2P9NAL7/SwAYABMAIgAJABkAuf/Z/7z/AADJ/+b/2f+8/8n/wf8EAN//QQAiANL/tv8OALD/5P/q/8n/ZgAbAGAAOwAdAOH/5//s/8v/+v/p/yQA+f9oAAoA0v82APX/GwByADcAGgA6AC4AgQD7/zIA8v8ZADkALgC4AKb/NwAIAKv/8//R/xAA6f8kAML/BADN/w0ALwC5//7/kP+4/w8A6P9IAPH/BgBhAHH/DQDC/+D/eQCF/1UA+/97//H/vf8AAAAAyv9CANr/4f+MAPH/GADv/wQATQBQAGYA9//U/+//KQDY/ygADgD6/x8A9f/S/8n/eQDz/+T/DQDn/8f/LQAkAML/KQDG/y0A2/+9/xMADwAxABUAWwAAAO7/8f89ANb/3v/3/4r/DwCx/8D/3//T/8n/HQDz/1EAVADo/0gA8f8rAOz/JgAMAOb/awDE/wYAvP8SACEAv/8VAP//7f+n/zgACADQ/0cA8f+8/wAASgA7ADAAOQAuABIANAA8AB4ABQApAP3/x/8bABUA7f/x/xgAggBEAFsAJQCd/8P/z/8hAPf/QgA1AL3/JQDV/8v/1f8CADkA9/8dAPP/0f+1/x8ABwDP/w8Asf/T/7f/sv/m/9n/FwDK/+f/RwDw//P/9v/m/6H/6/+4/7P/HgDh/3oA9f8bAIQA/f+QAAUA8/8+AOn/yf8vAMr/5/8jANP/kwD3/8H/KQDq/9z/vv8UANr/BQApAP3/DwDD/wUAKQAPAAwA+P8dABgAAQBdABMA/v9aANv/vf/v/6n/zP+f//z/MwDg/0IA2v/0/ywA7f8DAAIAJgAfAPX/GwBNAOP/HwA+AB8A9f/S/1wApf8SADMA4P8KAAgAKwDI/wkA4//X//H/4v9DAP//EQAzAAQAKAAyAAQAKAAyAAQAuv+1//v//P8OADAAAgDL/+j/fv/P//3/WP/6/8T/q/87ADAAAQDw//P/BwC9/7f/RgDv/+D/HQDz/77/FAA1AM///v/+/7X/1v85AOX/MwAXANz/GQC5/zUAz/8PAGgAHQAFACgARQDK/x0A9P/2//j/1f/w/87/6v8AABIA6/8TAP7//v///xAAMgDg/woA0f///+3/3/9AACEAZQAaAAIA3v/3/8H/zv8gAGL/8P88ANX/OQAJAFEA5v/9/zQAvP8lANX/8P8EABYAAAA3AFEA0/+mAAUAKQB9ANL/gADn/xAAMgDN/x8A4/8NAC8AAQDd/xoAzP8NAC8A3f8/APz/NAA8AOf/WgDI/+b//f/H/xsA3//4//r/6P8RACAA0f+j/+z/y//o/9r/BgC8/5L/FQC1//v//P/r/7j/6/8AAJL/KACg/w4A5//a/08A0v9JAM3/IAAsAO3/JwANAB0AFwBKACkARgDd//b/HAApACEA9/+LAKb/OAA/AMX/dgDM/0QAJAALAC0A3P8HAOH/5/8jAOb/2P9gACkAMwApAA8A+v/p/wAAtv8NALD/GgAVALb/MgCo/97/5f+z/0IAWgARAA4A5//H/y0A3P8ZAAIAy//6/+n/JAAdACoAIQD3/53/HgA9AAwAZgAbABUAAAAkAAoAGwAVANv/GADd/y0Ayf/U/yUAi//+/7X/xP/0/7//3v+b/9T/t/+z/8L/FwDv/7v/EQCy/9T/7//y/ysA2v8GAM7/2P/y/+L/RAA2AD4AIAAsAEgA3//T/wAAEgAOANX/AQDw/87/RQATAA8AMQAVADYA4v8fAAYAFwBcAN3/GgDM//v/1//f/1MAw/89AOj/2v8qAOz/JgDo////AAARAPz/6/8TAOv/JgBDAAAANgBQAC4AEwDG/z8Axf/R/yMArv9jAOL/+//8/8X/9v/4/x0Az/8PALH/9/8LAOX/2P+o/xQA2v/0/z8AMwDz/2MAKwBHAJYAr/9RAAoAiP/X/ycARQAAAFwAJQAeAM//tP8wAN7/GwCEACEA9/8cAM7/DgCMABUA7f/x/6r/8v/Q/xAARAC3/w4ACwAJACwA7f/e/wkA4//W/wIA3v/3/x0AKgAPAB4AGAABAMr/1f/w/xcASgDO/yAA5P/X/ygA6v8AACQAVQD7/zMAu//J/y8A7//y/6v/8/+s/xgAOAAIAD4AxP/i/x4AGAAUACIA+P8LANL/JABCAP//EADX//H/z//Z/4T/+f/V/5T/zv+O/yQA5/81APT/CAArAOz/SwDh/+j/o////zUA4v8eAHUAOQAJACwAyP8JABoA8f/P/zQA8//2/1MA+v9pAAsA0v8AACQAr/8/ACAAv/9xANv/KwC1/8P/KgDH/8D/p/8BABMA/v/s//D/vP+k/5H/AgBLAOH/MAAnAOn/7f8VAP//JAD5/+j////I/y4A7/8EAAMA3v/l/+r/yv+v/wgAGQBLAHQAAQAmAAwAwf8WABEAIADk//z/IQCI/w0A+f/6/+n/7v9MAD4ARAA3ACwAIwBmAAkAiADt/5X/FwDK/zAAy/9oAPn/w/90AAEAAQA4APf/5v8iAK3/BgDP/9j/FgDc/ywAtf8fAND/EAAfAL7/OAD3//n/6P8jAEEA7P84APf/iv8PAOj/yP8JAPb/HADy/+P/+/8NAAsA0v8AACQAwv/z//X/5f8hAAgABgAFACkA6v9vACIA0v9uANj/TgD2/9P/NwDR/9r/4v/6/+n/AAAAAAAA7v/x/8//xv8IAKv/4f8LAOX/RQAlAEMAIwDB/04ArP/h/0IAyP8uAMr/5/8iAPj/5/8QAB8A0P81APT/CAAZAF4ASwAYAEoA4f8dAPT/rP89APv/n//q/9z/GQACAAEAAQC4/w8Anv/o/9v/0P8iANL/7v/N/+n/AAAAACQAHQDh/wsA0v8AANv/4/8xAJX/TwD3//n/HgCG//r/ev/w/yoAtP8eACoAEAAfAND//v8QAOn/JADn/w8A+//q/zcALAAjAPn/HgAYAMv/CwDl/9j/zf+y/x0A4f9CANr/9P8tAMn/ZgD3/4sAFADs/wIApv8AAMr/ZwDA/ygAagAeAD0AMQCEAPz/IQAtACQACwAtAEkABAADAMz/DAAKANL/o////9v/vf8lAOj/2v/0/wgABgAXAEoAKQDY/ykA2P/N/w4A5/8QAMT/4v/o/+3/AgACAAEA3f+//wIAgwDp/xIAMwDO/7P/+f/o/8j/LgAlAFUA6f83ACwA7f9eADoAQQDZ//P/9v+c/8L/4P/U/xMADwAfAIcAIwAvAEoAFwAAABIAxv+//xQAo//H/y4At/+z/+f/IgAbABYAJAD5//v//P8hABoAFQAjAMH/KQDq/8r/VADp/xEARQBKAAQA8v8ZABQARwACAMv/1f/w/xcAJQALAOX/6v/c/+P/1//M/x8ABwDP//3/RwAnAEQAWwAAAO7/FgDb/+L/HwDQ/+z/8P8EAAMAuv81AL3/AQAAALf/IQDk/0UAEgAhAEAADgBVADIAKAAgABoA8f8FACkARgABACYA1f/e/0AAxv8HAND/6/84AOX/DgALANL/JAALAOX/MwCE/xwAOwD5/wwA+P8wAJT/8/8HAJj/0f8RANf/8f8rAMf/UgALAFMAQgARADIAAwDf/67/4/+M/5D/8P+X/6v/KgDr/+//KQAzAOD/CwBAAMb/LADb/xgA3f/k/zIAqP8CAMv/QwDJ/xwATgC//zkArv8HALz/AABKAAQAOgAvABMAIgAJAL7/AQDd/xoAFQARAA4A+f8fACsAbADX/zoACgDk/yAABwBQAPf/HQAFAPL/0P8iAEAAfP87ANT/uP9GAN3/LQAAAMn/wf/N//z/of8hAD8AIQAIAPX/5f+g/9j/4P/m/9n/8/8HAAUAFwASACEA5P/q/8n/+f/V//D/TwD2/woA0v8AAJH/AgA5AMD/XwCD/wkAGQCC/1IA5//s/xQA7P8UABAARAAkANT/EwC0/7H/5f/q/xIAxv+//ycADQDm/yIA5f8OAB4Az//+/8f/CAAZAEsATwDk/3wALQDu/zoA1P8lAMP/qv8oAOr/XABvACIACQDj/3r/uf81AKr/KQD9/4//JQCe/wwAQQAPAGgALwAmANb/zP8fABkA8P8FABYAEgDY/83/DQDU/wEAAQDK//n/1v8CADkALgASADQAKgC0//r/MgAVAIAAQgD//1oAAADu/wMA8f+8/8r/5//+/+z/3v/S/6T///8kAK//0f8RAMX/0P/s/yYAMQDf/wkAGgDM/9b/XgACAAIAFACQ/wEA3f8/ADMAzf8OAOf/EAANAHkAPABDACQAwf8WANz/PgDX/8z/DQCv/wgA4v/D/wUA8//j/x8AKwAjAOb/NADh/9T/OAD3/x0A8//j/w0A1P/d/ywA2/8GAGEA4P/n/yIACQAHAHQAFAD+/zUABgDz/+P/MgADAAIAJwAyAAMA8f8YAMr/+v8MAAoALQASAP3/NAA8ADAATAArAP7/tf/o/xEAIAA/AA4AHQAXAO//BAADAN7/9//n/1kANgAZAEsAGADv/wQAKACy//n/1f8nAMT/mP9RAMH/OwALAFIA5//a/zwA1f8mALH/+P/V/93/GgAoADIAFgBJAAMAOgD4/x4AGAAmAEMAo//a/+L/6P/I/0AARgDw/xcAJQBVAB8APgBXANj/4P8vAPD/FwDc/+P/DQCv/wcA9P/k//z/6//c/+P/HwC+/8v/DAAJAPb/HADy/77/3f/k/+r/3P8HAD0A+v8NAC8AuP/G/wgA0P/Z//P/mv+u/wYABQA7AML/4f8LAMD/TAAZADkALgASAOv/AAAAAAAAbwCP/wAAJQDn/zUAUABAAKH/6/8TAP7/7P/w//P/vv/L/9X/pv/v/ykAof8PAAwAwf/f/9P/EgDG//b/CgD2/woA0f8RANf/8v8rAMf/9//5/7H/5f/F/xoAuf/s/wEAy/9DAMj/CQC//xQAEACN/0gAFQA2AND/NQAGAPP/UQD4/0MAtv8fAD4A6f8kAB0AKgAPAB4AKwBaAO3/AgAnANb/8f/h/x4ABgApAP3/DwAMAK//GgDx/xgAOAD3/xwABAAWABIADgAwAN7/9//U/7j//f/Z/ykAIQCt//X/wP/f/1MAHgBiAE8APwAzALv/AAC2/8X/BwDP/9n/lv8ZAPD/BQA7ANT/7//z/77/FAD+/9r/BQDg/woA9/8dAGEA4P8KABsAAwACAEwATwAbAE0AGQAnANb/FQDt/8z/sf+c/+b/j/8lAAwAHAAWANv/4/9n/yoA/v/+/zUA9P8IAL7/AQABACUAHgCq/xYA3P/Q/xAA6f8RANj/AwAoAPz/2P87AFQA1v9fACcADQAvAN3/5P/F/xkAlP/z/wcABQApAKH/IQDS/zYAGQDe/wgA0P9HAAIASwDh//r/HwDj/x8Aq/8pAA8AMQACAN7/ZQAHAD0ARAAAANv/4v+x/+X/DgDo/zUA4v8MABwAFgBuAEYAXQAUADUAKwCi/8f/wP/M/+n/pP///+3/zP8fAPX/9/8vADkAGwDf/+b/2f/O/8X/0f///9r/4v8MAOX//f/G//f/5v9GAAEAk/9gAAMAFQA2ACsAbQDq/xIAIQCt/8//tP/V//D/hf/m/+v/y/8wAN7/9//5/+j/yP/l/+v/EwD+/zQAhgDa/4YAfwBBAA8AHwA+ALH/UwAxACcA/P9FAEoA4f9nANP/AADu//L/GADd//f/wf/g//n/MAAnAGkAQgDt/zkALgDc//b/LgDc/wcA4v/V/xQA7P8mAB8ABgAqAA8ADAAKAL//AgBeACcAMQBfAMz/+/9FAJP/FgAAAEkAOwAdADwA1f85AAkAPgBFAO7/OwAdAM7//f80AKr/OwDB/+D/QgC1/zEA3//4/x0A9P/2/8H/FgAAAO7/FQAAAO3/OgAvABMA/v8iAFMA5//s/wIAy//6/x8ABwDh/9X/FAC1/8P/PQCe/w0AQQCQ/wEAAAC4//3/2f8EAPL/BgB0AN3/ZAAZAAIASwAFAE4A4//X/5X/9P/R/0gAOgCK/0YApv8lAB4AKgDs/6b/XAC4/zQAFwATAOv/pf8SANj/lv/i/wwA+P/6/+n/JACc/+f/IgCc/+b/j/+4/6H/RgATAP7/NQDP//7/x/8bAN//HADz/77/AQBu//n/+//E/+P/6P/I/9P/3P+s/+H/1f/w/xcAt//F//b/wP/f/woA9v/4/wsA5f8OAB4ABgBhAPP/BwAqAFkASAADACcA+/8OAOf/NQDi/wwAUwD6//v/1/87ANT/AAAlAPr/ewAaAEwAUAAuAEoA4P/m/8b/5P/8//3/RgDw/wUA8v/Q/+z/lP9OAOP/MgBNAND/kQDi/zEAJwDp/yQACwBSAAsAGwAWAAAA7v+6/+3/AgDL/0MAJAAKAD8A2P8WAMn/wf8EACgAxf/1/2UACAArACMAZgD3/+b/NADh/x0AmP++/8v/nv/7/+r/3P/1/xsAzf9FABIAxv8tALb/IADj/+n/SQDN/0UA7v/f/xwAzv8zAOD/wv8XAO7/3//m/8b/v/8UAOz/AgBeAAIA3f8tANv/q//z/wcAGADd/wgAPQAxABUAEQD8/9j/8v8HACoADwBEAO7/zP98APb/LgCBAPv/VwB9APf/HQA8AAwALgA3AAgA9f/A/6f/FAAiAAkA4//p/zYArP8FAPL/Yv/d/7//p//v/+D/CgAtANv/PgD7/+r/AAAAAG4Axv8IAPX/rf8GADwAHgCq/ykA2P+p//H/z/+0/9X/AQA4AEAAs/8LAAkAmf8JAAcAqv8EABUAyP8KAOT/6f9JABYAAAASAP3/6/8BACUA6P/a/wUA4P8KANL/2//1/xsAKAAgAD8A6v9JABYAEgBGAAEAJQAeAAYABAAoANj/AwDf//j/MADL//r/1/8DADkAHABgAHIAJQBCAFoANgBjACsA7P/w/6n/qP9eAN7/wP8VAMj/LgDK/wsAQADY/ykAIQD3/0EAIgDl//3/tP/V/93/0v8AANv/4v8MAEEA/v/+/1oANgAHACoA/v/a/08AGwAVAAAAtv/p/xIA6v8AAAAAyv8LAOT/6v/J/8L/4P+v/+T/6f83ACwAIwAcAAQA8v+9/zgArf8GAOH/nf9VAHv/8f/0//b/HACp/00A4v/o////yP8cAPP/4//W/wIAOQDl/1gAWQARAFcADwAxAPH/GADv/6n/OgDT/wAAyv8dACoA/v9ZANr/GADv/ykAIQAIAAYAGAAlAB4A9P/3/y8Apv8AAMr/+f/o/zYAKwDs/6gAq/9gABYA7v86ANT/SgC7/yQAwv/g/x0Azv+z/9X/EwAQAFYA/f/9/9n/zv/Y/xYAAAC3/0UAAAAAACUAZwAcADsAHQC8/xIA6//v/83//P/G/+T/1/+V//T/v/8CABQA2v/0/ywAJADU/wAAEwD+/7T/+v9XAMb/0f8jAMH/8v8GAOH/QgAjAAoAGgC6/+z/JwAfAAYAGAATANn/4f/U/yYA+v8yACgADgCMAPH/BQAEAN//0//K//n/DAAuACUA+v+f/yAAh/+x/xwAqP8CAPD/FwDc//b/5f8PANX/8P+8/7f/MwCp/wIA8P8qADQAKgBHADkAUwALABsAlv8rAMf/CQAsAJH/XgDe/wgA9f/l/8X/rP+8/+7/OwDU/zgAGgDx/ysA2v/P/zQABQA7APn/w/8qAOz/AQDK/wsACQD2/xwAFgAAACQAMADw/3MA3f8aADoA0/9KADsA5//+/+z/pv84ANL/2/8GAOH/MAAUADUAGAAmAEMAEQCz/x0ABQDN/yAABwD0/wgA9f8JAD4Asv9UAPv/1/9fAAMAcQAkAB0AYQApAA4A6P/t//D/qv8WAAAA2/9jAAYABADy/wYAz/8PAEMA7f8VAMj/UwCw/xsATQB0/yIA9//n/8f/5P+z/6//5P+y/xwA4f8LAFIA1f8mAOj/yP8JANH////I/0EA/v/Z/08A0v8jAPn/QwAjAOb/DwD7//z/2P/g/8H/4P+v//b/HAAWAEkABAAVADYA4/8xACgAxf9jABgAEwD+/xAADQDU/yUAw/8YAAAAAAAlAEMA7f/x/zwAef/L/8P/z/+h/8b/v//M/x8A4v9DAMn/CgD2/9P/AAASAOv/3f8sAKT/EQAgAIf/6P///5H/OQAJAPb/QQAPAEMA2/91APD/9P8IAKv/YADN/zMAOwDn/zUA4f/6/w0ACgAtAO7/TQAGAPT/UQD5/1UA6v8kAOf//v9sALL/VAAfAOL/DABmAGQALAARAOr/NwC+/3AA//+2/zIAqP+5/8f/0v/u//H/vf+l/8n/+f+x//f/+f/W/xQAEAD8/w4AegAYAIIAMgDf/xwAlv/Q/+z/AQA4AGUA9v9lAD8ADgAwAPD/hgDs//D/KQDr/8r/+v8MAPj/CwDl/zMA8/8HAPT/9/9BABAAHwDj/8P/z//+/+z/8P8pAKH/2f8pANj/4P/m//7//v+1/7H/HACp/6f/OQDS/yQAHQAFAPL/0P8QAMT/4v8MABwA8/8ZADkACQDj/x8ALACQ/3AAyP/T/yQA5//+/7X/MQDf/4oAEwAPAI0A3/9mAAgA9f8bABYAEgBFABMA/v81AAUABADy//X/0v/u/9//HACp/xUAEQCg/0UA7/9NACwAWwAAAAAAJACd//r/DQD5/8P/KgCi//7/WgA2AHUAJwAyAKj/AgDL/9X/AgAmAB8Aq/8XAMn/QgDs/yYAaQD5//v//P9FALj/DwDo/9r/4v+w/3cA8v8HACoA6//w//P/9f/l/+r/3P8HABgAJgBDADYA0P/a/8//of9GAMv/6P8QACAAPgCy/woA0v8jAAoA0v8RAA4AZwCu/2MA9f/A/18Ap/9LAOH/MAAUAGv/QACh/w4AQwCR/8v/nv/p/+3/FQCSAOP/+/+y/8L/8//j/0QAJAALANL/SQADABUAbQDY/ygARQA4ANL/7f/x/+L/6P+Q/93/v/+5/9r/KgAPAMP/PQBWAOr/yf/5/9b/3v/S/7b/xf/j/8T/4v8eACsA7P/w/zwAnv+x//j/wv+8/5L/8f/P/9n/8//R/0gA8f8qAEcAAgDd/3X/EQAgAAcAPQAMAAoA9v8cADsACwAuADcA0f/t/8z/1v9xAAAAWwBuAEYAOQDl/w4Awv8FAPL/9f8bAN//LwDd/9H/NgD1/8D/JwAgAOP/RADc/77/y//D//T/9v8uACUAHgD0/9L/2//Q/+z/3f/S/wAAAADb/1AAZQAIABkAOQAuAMn/wv8XANz/BwAYAO//BAADAPH/9P8IAD4AaQBCABAAMgDy//X/UgD5//v/MgDy/wYAFwDv/zsAQgDs/wIA8P/z/xoAAgDe/wgAGQA5AAkA0f8jAAoALAAAANv/BgDh/zAAAgABAO//FwASAMb/dgADABUA7f+5/zUA9P/S/9v/4v/V/xQA7P8CAHAAyP8JAD4A1/86ABwA8//2/9P/yf/m/zQAGADv/wQA3//m//3/2f/z/77/y/8eAKv/8/8+APz/IAD2/y8AXQABAAEAJQAwAN7/CQA+ALL/+f8MANP/7v8DACcAsv/m/1kAx/9AAGsADAAvAMr/+v/p/+3/OgD4/zAAy/8MAEEA6/9LACoAIgAtAEkA8v/Q/yIAHAApANj/8v8ZAMv/+v9EADcABwAYABMAtP8MAOb/2P8EAJX/4v/D//T/9v8cAPP/vv84APf/CgDk/8X/GQDe/8D/FQDb/xgAEwB9//P/vv8BAMv/w/8XAG7/+f9DAAAAEQAzAPL/0P+i//7////I/0AAxv/2/5z/+f8xABUAEQDF//X/0v9uACEAUgBUADIAcgA3AFEA+P9VAA0AHQAXAAAAJQAeAGIAKgAiAOX/DgDV/7j/6//d/7//zP8MANP/SgAXABIADgDo/yMA+P9VAB8AGQDM/8P/GADd/y0AEQAOAOf/ov8iAOX/6v9KAM7/2P/g/9T/JQCw/wgAPgCf/+r/JAAdACoA/v8QAA0ACgAIAAYA9P/k/yAA4//p/wAA2//1/63/hv/V/97/0v/t/ycA/P/9/w8A+v8yALv/EQBFAO//OwAvABQA/v8jAMH/AwBMAAYABQApAGoA6P/t/xUAtf+f/1cADwDD/zwAw/8qANn/PABDANr/dAACAPD/BADy/xkAAQDd/wgABgAFADsAMAAmAPv/xf+Z/9L/f//i//r/xP8YAN3/LQAkAOf/7P8BAN3/ZAAsAMj/LgDv/xYAEgAzAAQAKAAOAAsAQADr/10AAQATACIAQABGAO//BADy/ysAtf/o/7b/1/8DAAIA8P/h/wsAm/8KAOT/DQAwAN3/9/8KAL//p/8mAOj/yP+u/wcAz//G/2QA0P/s/8v/6P8RAPz/DgCe/0MAEQDq/xIAj//c/6z/8/8aAN7/ZQAIABkA8P8EAPL/0P9HAG//6P/s/97/GwAoAEUAyv9VANb/3/9TAOf/WgAkAAoACADj/zEAFQA2ACsA//+kAM3//P8zAKn/TAC9/xMAIgDS/yQACwBAAOv/EwC0/+f/NQAGAE4ACABQAPj/+f8xAKf/JgD7/w0AMADe/0AA/f/r/93/9v8cAOD/QgAQAOn/kf8CADkAZP8VAO3/3v8bAM3/6f/J//n/1f/e//f/1P9dAN3/LQARALP/QgDa/wUABADN/0UAJQALAHcAYAAEABUAEQAOAOf//v/s/xQAIwDl/zMA4f/n//7/RwBeABUA7f/e/8D/3/9TAOj/WgBbAAAAAADu/ygAsv8vABQA7P9LAOH/wv8FAAQAuv/t//D/9P8sADYABwAYAMr/wv88AMP/FwBdAN3/CAA9AMT/0P/r/6b/NwAIAPX/ZQDR/zUAUADA/18AFQARACAAdf/H/63/BgD0//b/LgC4/w8ADAD4/9X/AQDd//b/UwBWAGoAMABMAPT/5P/F//X/0/+k/yQAnf/V/8v/DAAcALv/EQAOAAsAwP/x/8///v/s/93/GwBw/x8AGQABAEsAz/8zALz/7v86AJz/CwDA/7r/yP+u/1AA0/83ABoAzP8fAAYABQCE/xwABAC6/zYABgA8ADEATAArAP7/NQD0/xsAKAD8/1gA/v8jAEEAtP8eAPT/5P8OAAsAQADY/xYAJAD5/zEAAwAnAA0A1P8AALf/s//C/xcAEgDG/y0Ayf8KAD8As/8vAMv/6P81AOL/VgAgAHYATQD1/y0AEgAzALz/7v/N/43/EQD8/8b/BwDi/+j/IwDB/zsA5//Z/zwAsP9AAOv/EwDr/+//KQDr/28Ax/9AAEYA7/9OAAcA9P/S/+3/8f+9/5L/8v+r/6n/OgAcAPP/9f9AAMb/5P8gAOP/1v/M/w0AHQA8ADAAqAAGAAUAFgDJ//n/w/9PAPf/+f/o/7X/+/8OAAsAwP9fALr/2v/0/9H/NgDj/0QAyf8KANH/2/8GAOH/MADe/y0AAABcACUA1f8mAOj///+2/0QANwDR/9r/9P/3/6//PwAyABYAAADJ/+b/2f/h//n/6P8RAA0AHQAqANn/4f/C/+D/r//2/+b/tP8eAOL/HgDP/yIA5f/F/xkAzP9WANj/OwAvAPD/BAADAHEAtv9qAAsArv/j/9b/XgA6AC4AJQAeABgAEwC0/9X/uf+0/+j/2v9iAPT/PwAOAML/PAD6/3sAUQBBAFkA2v/0/9L/yP/4/+f/RwBeABUASAAVAO3/uf/a/wUAqf8VABEA1/8DACcADQAKABsAKAAgAFEALwDv/04A0f///9r/c/80APP/4/+y/8H/8v/1/+X//f80AAUAFgDb/wYABQDz/xkAFABaAMj/HAApAA4AegDi/wwAHAC7/+7/KAD8/w4A1f+m/8r/wv8FAM3//P8OAOj/7P/e//f/r/8/ACAABwCHAO3/XgCDAPz/MwApAP3/IgAbAPL/PQDE/6v/BACo/zkACQDR/zUA0P8QAPv/6v8SAMb/4/8NAOb/NACGABAADQDm/+v/OAAbAAMAJwAyALv/2/8GAPP/9v8JAFEACgAIACsA7P8CAMv/sP/l/6D/DgBVAPz/IQDR/xEA1//N/0QA3P/j/+n/2//Q//7/2v8qAEcAAQBdABQA2v/0/xoA3v/l/yEA9v/m//7/NACY/xoA3v/3/4wA8P9hAPP/9v8JAKz/KgDs/wEA7//g//n/DAAJABoAJwDX/xUA2/+r/xcAEgDr/9z/4//X/9//if/F//X/wP8oADMAOwALAJv/LwDv/7v/JAAKAC0A3P8HAOH/sP8tADcAPwDX/3IAAADb/ysAkP8mAMP/KwA1AL3/EwD9/0cA3v/l/yAA9v/m//3/DwD7/w0AMAA5APf/VAANAIr/DwDD/+H/MAAUAOz/AgABALj/NAAFAM3/DgALABsAzf/8/yEAGgAoAPz/IQDk/+n/EgCz/+f/EAANAB0ABABgABYAAAAkAB0AFwDK/x0AFwAAACUAMAAnANb/OgBBACIALgBcACUA+v8yAJX/9P8IAOL/HgDQ/w8A+//F/3T/2f8pAA8ADABmAD8As//5/+j/2//i/wwAHADg/x0AvP/c/z4AHwAHAAUAqf/M/w0Awf8pAP3/2f/g/x0APAD6//v/s//n/9n/FwAlAAsAigA4AD8AMwAXAAAA3P8HAPT/v//M/wwALwAmAB4AKwDs//D/BQDy/ysA7P/L//v/DQDC/87/IQCI/zIAAwCn/yYAw//i/+j/SADM/8T/PQDW/zkACQAHAOL/1f85AAkALAAAAAAAEQCg/w4AMACU/xcA7v/N/yAAvv8BABQA2f8FACkAxf++/yYA6f/t/xUA7f/x/wUA8/8sAO3/8f8YAEoAPABVAEQA7v87AMH/BAAoANf/FgARAMX/vv8mAOj/bQD9/9n/KQDY/xYAAAAkAML/8//R/9r/GADv/wQAFgBbAH//BgDz/6z/z/+h/8b/v/8nALL/LwDd/+T/RADJ/y8AJgAxAN//UwBVACAAPgD8/yEA9v8cAAQA3//m/8b/LQARAP3/IQAIABkAy/8xAEwAq/8EALr/tv/p/yQAVAAfAHUAFAAQAEQAEgAzAPP/9v8uABMA6/9KACkA6/84APf/LwABALj/NAC8/7f/6v/J/woAGwBNAPX/9/8KAK3/BgAFAPL/BwDh/wsAif/X/xYAAABuAOv/AADc/+P/MgAWAG4A/f8iAPf/+f8MANP/3P/j/w0ACgDS/7b/RADJ/9T/EwDG/xoAAwACADkA+P+v/xoAzP/7//z/DwAxAKf/SwBy/+r/AAC3/2oA1f9eAAIAAQABAMr/wv/h/53/jP8QANb/TABQAAkA0f9IABUAo////7X/6f/J/woA5P/8/yEAv/9MACsA/v8QANf/zP/p/xEADgAeACoA/v81AGIAPAAMAPj/MADe/0AA/f/Z//P/vv/L/8P/9P/2/y8AEwB+AC4ANwB2AAMAFQA2ABkAgf9kAL7/JgBWALP/VACM/yMAwf8EAN//wP8WAJH/FAC1/zEAlf/P//3//v8iAMD/8v9z/zQA8//2/0EAxv/3/xwA8/8HABgAJgBDABEADgD6/wwA+P8eAPT/5P8gANH/IwAcAAQAFgAkAPn/DACc/+f/WQCQ/0sA9P/k//z/xf/2/9P/EgD9/yIAGwA7APn/HgArAOz/gwAfAAcAYgAFABYA7v/f/2YA0v9IAAMAzP8xAKj/SwDP/w8ADADT/8r/iv8PANb/FAAjABwABADf/+b//f8PAOj/AAAAADYALABIABUANgDQ/+z/JgCx/2UA0v8AAAAAAADu/7r/WgDI/xwA8/8sAFoAEQBFACUA+v/W/wMAAgC5/+v/AQCl/+7/u/8RAMX/9f9lAJr/LgCS/wMAFQDI/3gAu/8AAO7/FQC2/43/NgC+/xMAIgAbAPL/9f9AAOv/EwDr/wEA3f/R/1oAtv/X/xUAf/8FABcA7v8oACAA9v+c/wsAQAAhAC0AJABUANb/3v9AADQAFwCS//L/4v/o/zUA9f/3/8H/cwA3AFIAngDt/wIA8P8XANz/GgAnAA0ACgDS/0kAzf/X/xUAtv/p/7b/6v8AANz/9f/3/wsA5f/Y/ygA6v+l/wAAyf/m/yIA9/+eACMALwBdAMv/HgAFAAQAu/8jAC8Ayv8eAOL/CwAcACkAMwDO/7P/CwD3/8L/OwALABsAzf8gABoA3v9SAOf/7P8BABQA7P8BABMA7P/L//r/RADu/xUA7f/x/73/EwA0ALz/NwD2/xwAOwAwAN7/5P9FALf/DgAeABgAAQA4AD8As/8LAPf/1P8TANn/KQBZAOz/XgDe/63/KwC1/wwA1P8lAGgACgB2AAMAJwANAOf/IgAJACwA//8kAOb/xv8IAGMAPQDW/0wABgDO/7P/1P/L/7D/9/8KABsAlf/P/+v/AQDc//b/UwDV/wIAJgAfAPX/9//m/9n/TgDk/9f/OgAKAC0AJADU/wEAAAATAA8ADAAuAF0AXQAmAPv/sv8cAPP/rP/0/5r/wP/y/+L/6P81AD0A1v86AEEAxv/S/xEAIAAHAND/6//d//b/HAAEAAMA8f/0/wgAYwDi/+j/SAC6/9r/KgDZ/7z/JAD5//v//P8OAPr/sf/m//3/DwDo/zYAGQACAPD/vP8AAKT/yP/m/zQAFwATADQA8/8sAO3/JwANAPn/MQAVAP//EQAOAPn/+/+y//n/6P///20ADgDV/yYA1v/M/zEA3//4/7D/v/8nAMT/9f8bAAMAAgAUAP/////I/wkABwC9/wEA7/8pANj/BAAoAPz/DgDV/wEA8P/O/8X/0f/I//j/MAAmADEA3/8cAAQAFQARAOr/SQDy/77/JgAMAMH/KAAgAL//AgABABQAIgD3/wsAUgD5/9b/FQD//yMAHABOACwAJAAvAAEAuP+P/9z/vv/w/wUAFgAkANT/EwDr/8v/CwD4/+f/NQAYACYAQwDI/woALQDt/zoAHACp/8z/xP/i/+j/yP9TAAsA+P8wAPD/PAD6//v/IAD2/y4A7/8EADoAr/8aAAIA8P88ANX/FADs/8v/DADm/w8A1f+5/xAA1v/e/0AAWQAQADIATQCZ/wgA9f/l//3/tP9VAPz/DgBDACMALwATAA8A1v8CAAIAAQDv/87/xf/2//j/1f8mAB4AUAAJAOP/xP/i/wwACQAsAO3/hADX/wMAJwCy/1QAw//0/xoAFQAjAPn/DADT/9z/vv/d/9L/7f8VABEAIABRAEEA/v8QANb/FQA2AD4AMgA6AC8A3f/2/+b//f8iAAkAGQAnAOn/AAAkANT/3f/R/7X/ev/M/9b/p/8BAN3/CAArAEcAFQAQAEUAAADu/83//P/Y/+D/LwATAOz/8P8XABIAxv8IAGIAz//r/6X/kv8DAPH/KgAiAEAAs//6/+n/o/82AIb/MAACAN7/QAD9/7T/sP9AAMb/GgBMAND/RwDe/5v/LwDd/+T/DQDU/xMA2f/z/+P/6f/b/xkAFADZ/yoAov9GABQANQCZALH/+P/V/93/rf+9/8r/1f8TABAAMQAVAAAAEQAgANH/SAAVADYABgCF/1QAsf/4/2cALgBKACkAWAAQAA0ALwBdAMv/1f/w/+H/CwDl/zMAFwBJACkA/f8PAPv/IAA+APz/s/8dADwA1f8mAAwA5v/G//b/LwCl/wAAAADu/ygAs//5//r/DQDn/1kAbQDF/3YA3//4/1UA6f8RANj/8v8GABcAyv8dACoA6/84AAgAGQAUALX/+/8gAKz/GAAlAMP/KgA0ACoAIgD3/+f//v/a/yoANAD0/1EA+f8MAOX/2P8WAAAAEgBGABMAx/8/AOr/NwAtANv/UAAJAOP/1//f/67/0P/a/8//IQC//ycA1/+6/0gA3//4/zAAJgDo/9v/KwDa/wUAYAC7/+3/AgDe/0AADwAxAPH/KgDZ/5f/KwDI/xwATQAsAEgAFQAAAO3/FQD//9v/GADL/57/+//8/yEA9v8KABoAzP8yAHIANwDj/+n/tv/F/9D/tf/D/+L/1f/e/+T/oP8zAAQA8v8YAPD/YQDg/+b/NAAFAPP/vv/L/wwALgAAAAAA7/8WANv/9f8bAPL/9f/3/woA9/8vABMA/v/a/7z/kv/f/xwAFgASADMABADf/1QAw/8qAFkAyP9lAC0AJAAdAAUA4P/m/w8AMQADAN7/dwDO/9f/FgDu/xUA2/8YADgA9//B/wQAFgAAACQACgD3/woAdwDg/y8AOADk/zMA8v91AN7/LgBvAKL/NADh/wsA0v/b/wYAvP/u/7v/SADM/+n/AADJ/xwAhP8vAMr/1f8mAAwACgCa/0AA2f/g/wsA5P/q/+7/FgCk/+3/3v8JAAcAPQAfAOL/DACc//n/sf/T/9z/4/9WAOr/AAAlAEIANQBiABgAEwD+/7X/VgD8/zMAKQDG/+T/xP/Q/9n/KgBHACYAHwBQAPj/MABeAAIAJgDo/xEA/P8OADAA3v8JAJn/CAD1/+X/fQDk/zMA8v/j/0QAyf8vAMr/HgA9ALH/UwALAPj/+f8MABwA4P/5//r/1//M//v/oP+g/+r/3P/j/w0ALwC4/+v/AQDd/+T/6f/u/9//UwBVACAABwA9AAwArv/2/9P/JQBCAP////+j////EQDq/wAAyf8vAAEAAQA4AOT/IADR/+3/8P+8/yUAMAAnAPv/MgCo/8z/1v/M/x8A0P/s/6b/3P/2/+b/6//K/7D/9/8vAAEAbwD+/zUAUADl/+r/NwAtAKT/NgDi/+j///8kAC8Ay/8eAM//xv/2//j/sP8JAAcA9P/k/8X/UADT/zcAGgAnAA0Awv9OAKz/BQA8AML/8//R/+3/AgDe/wgAGQDw/xcA7/8EAAMA3v8JAL7/y/8xAN7/GwA7APn/VgDF/+P/1v+n/wEA3f8IACsAEADX/0wABgAFAGAAFgBuAOv/AABdAEoAKgD9//7/x/8uAO7/uv///xEA1/8WABEA6v83AOT/MgAWADYAUQD4/0MAyP8cACkA6v8lAOf/EAANAOb/IgAJAAcATwD3/+b//v+Q/8r/CwD4//n/MQAnAOn/2/8+AA0A1P8lAPr/MgAWACQALwDd/wgA9f8bAM3/1/8DAPH/BQAEAAMAuv8jABwAu//b//X/CAAHAPT/LQBJADsAVAAfABkAy//V/97/0v82AOP/RAC2/+r/XADv/zsAwv8pAP3/RwAmANb/qADi/x8AhwDa/wYAKQAPAEMAyP/4/0MAfv8qACIA0v8SAA4A+v/7/8X/q//z/7//3v/A/8z/+//X/ygADgALAMD/zP/p/wAAyf/U/zgA9v8cACkA6/+A/+P/HwD1/0AAMwAXABIA6/8TAEcA8P8FACkAxf/j/w0AHQAFABYA2/8GAAUAzv8zABYA7v/f/xwA4P8KAPf/5v9HAN7/CAD1//f/CwDS/xEAMwDz//X/CQD2/wkA9v8cALv/EQAgAKz/4f/D/8//s//V/6b/EwAhABsAXwCo/ycADQAKAD8A2P87AOf/2f8FAPL/4//D//T/5P8OAB0A4f9nAMH/3/8KAJr/eADg/x0AYQCp/83/HwAZAPD/dADd/z8AMwDg/1QAsf8JANH///8RALL/CgDk/w4AHQC8/8r/+f+e/9b/8f/0/xoAAwBMABgAEwA0AD0A+v8NAAoArf8GAM7//f/Z/wQAAwDM/+n/tv8gAOP/MgAoAMX/9f/l//3/6/9KAAUAYABgAM3/MgDg/+b/DwDo/1oANgAsACMACgAtAAAAWwASACEAUgAdAAUABABNAJn/PwDq/8r/QgDH/4oAuP9YAGwAxP9jAPT/UgD5//v/6f/b/+P/sf8cALv/AAAkAB0ATgA/ADMAhQAhAOX/RQDK/wsA9/8dADwACwD4/9X/7/+X//X/5f/9/6H/2P8XAKT/2/+9/yYAw/8FABcA7v8oAMX/YwDi/wwA5v+z/wsA0//u/7r/IwDB/xYAJABnAEAAxv8/AKD/DgALAAkA9v8JAGQAq/8XAMr/wv+8/9v/GQC5//7/EADp/+3/zP/p/zYAvv8BAAEApf8SAOv/7/8EAAMA8f/P/9n/8//R//////+2/x8Amf/3/0IAkP8TAA8AxP8YABMA/v9HALn/tf/7/9f/8f+9/yUAHgD0/y0ANwAHAPT/0v82ACsA//9IAPH/KwAiAEAAawAMAAoA5P8NAML/8/8sAO3/AgCU/87/6v/K/x0Az//9/+v/7/88ANX/SwDh/53/MQDe/+X/6v8lANX/8P8XAMr/+f/o/xEADQAdAM//DwBDAO3/OgAKAGQA9f/3//n/DABmAPf/ZgD3//n/+v/p/xIAxf8HAPT/0v/b/+L/sf8uAAAAyf8dAOH/QgA1AFAALgAlAAsACQAsACMA+f/D/xcAyv/n/xAA+//8/w8AMQAVAJIABwA9AFYADgAwAAIAXQDe/y0AJADn/zUAGAABAN3/GgACADkAGwAEACgA1//f/+b//f8iABsA8v/1//f/r//k/+n/2/8ZAN7/5P/F/6z/dAC4/zQAKgCh/1kAx/9AADQA8//R/9r/GAA4AEAA6v8lAOf///8QAOn/2/8rADUA9f9AAOr/NwD2/1QAMQC6/xAAsv8KAL//OQAcABYAJADU/zgAm//m/6H/DwDo/zUAGQDL/3oAq/+qABsAKABFAMr/QgC1/2kAwv88APr/xP9iAJf/LAB+//T/CAC9/zgA9//m//7/IgDA/wMAzP/W/xUA//9IAN//LgDv/7v/7f+6/9r/9P8IAPX/CADj/+n/EQAOAPn/MQBMAPX/GwA6APn/6P///6P/tf/W/8z/HwAGAM//NADh/8L/zv/9/w8Anv8fAPX/wP/x/6r/4P/m/zQAGAATAP7//v///8j/CQC+/97/CADj/0QANgAsADYABgA8AAwArv/j//v/DgALAC4AEgAzAAQAFgAkANT/SgDO/1gA7P+4/2sAaP89ANb/zP8fAIb/CwDT/xIA2P8pADMA8/8HAOL/CwB3/xEA/P/r/0oAhP8cADwAsP8tACQAwv88AFUADQAKAAgABwDP/7T/CwDl/8b/9v/B/00ABwAqAFkA//9bAO7/FQAAABEA/P/G/xoAzP8NABwA8//R/0gAFQDI/1MAHgAGAOD/HQAFAKn/8f89APv//P8OAOf/NQCY/xoAOgDm/yEA5P8zALv/JAB5AD0AaADm/w8A6P+2/w0ACgC//97/5f/q/wAAEgDG/7//8P+q/ygAoP/q/xIAof9ZALX/DAD4/7D/GwC6/zYA4v/7//z/2P8oALP/5//Z/+H/MADL/zEAFQC1/3sA9v8cACkA2P8WAAAASQAEABUA2/9QAAkArP90AO//FwC3//3/DwDo/20Axf8ZAMz/sf9TAAsAHAAWAAAANwAsAP//WwDc/9D/IgDT/xIA/f/Z/wQA4P+v/+P/6f/b/xkAJgBEAAAAEgAhAAgAKwA1AD0ARAAkAPn/MQCn/8v/1f+B/wgAmP8aABUA2/8rAMf/GwAWADYAYwArAEcA3v/3/x0ABQAWADcA9v/T/xIADgBDAO3/p//d/9L/7f8nAA0AHQBPAK3/GAA4ABsATQD1/xsA3//T/wAA7/8DAAMAp//L/x4AmP8sAMj/0/9cAJP/KADq/9z/BwDi/2gA5v8PADEAzP/p/+3/3/8uABIADwBDACQAHQDO/9j/KQAhABoAXwDx/73/OAAtAEkAFgAkAC8AAQA4ABsAXwAoAMX/9f/l/47/3P8+ANf/8f/i/x4A9P/3/y8Ayv/V/xQAx//l/yAAv//e/+X/6v/J//n/HgC9/10AuP9GAHAAtf9WAMX/GgA5ANP/3P/1/wkA9v9BAMb/CAC9/93/CAC9/10A3f8/ADMAhP8KABoA3//4//n/DAAKAAgAUAAbADsAQgAjAGYAdwBNAFEAUwDo/xAA/P/Y/2AA3/8cAE4A0f8RALL/wf/g/3j/yf8dABcAyv/n//7/2v89AB4ABgDh//n/MQDM/w0A+f/V/97/5P/8/7P/MADw//P/UQDm//7//v///yMA+P/V/wEAJgAMABwABAAWADYA9f9AAFkA/////7X/sv8KAAgABgAqAKH/xv8aAN//HADg/0EA7P/d/2QA0f/s/5T/BAADALr/EADE/ysAx//3/wsArf9QAMD/8v+9/6X/EgDr/wAA7/87ANT/7/8WAH//4v8eAAYAzv/Y/xYA3P+r/wUABADM/8T/BgA8AJ7/DAAcAOD/LwC4/yIA9//C/ykA6/8TAA8Asf/l/w4A1f8mAOj/EQBXADQAdAATAP7/RwBMACsAkQA9AA0ALwAmAFYA/P9YADUA9P9SAB0ATgAIAAYAFwA4ANL/o/8jAIr//f8PANb/uf/s/wEAuP9rADEATQBQAAkA4/+f/9f/qP8UAEcAFQARADIAAwDx/ysA/v8jAMH/AwDx/8//tP+L/+z/b/8wABQA7P9eAAIAOQDA/9//5f/r/8r/wv9OAAgAKwDa/wUABAC6/0gAKADp/9z/BwC8/9z/LADt/xUAEQD8//3//f/Z//P/9v/T/+7/3/8KAJr/rv8sAMj/0//c/9D/EADp/xEAMwDg/1QA6P/b/xgApv8lAPr/6f8RAA4ACwDA//H/4v8MABwA4P8KABsA3//l/yEALQDb/ysASABMAHUAJwD7//z/6/8AAMr/MAAUACIAUwDD/zwA6P+1/zEA8f8GABcASgAXADcABwD0//f/nP8LANL/WwBvAA8AjQBNACwAyP/A/9//+P+w/8D/FQCj/xAA/P/q/wAAAADc/4f/MQC6/xAAfADR/1oA7f/M//v/6v/u/wMAcQAkAB0AKgD+//7/2v/h/+f/EACy/y8AEwDZ/zwA1f8mAAwA5v8PANb/FAD//9r/mP/R/9r/z//r/xMA6//L/1UA6f8AACQAr//S/9v/GAAmAPv/MgAoALP/VAAfAOP/+/+N/7b/xP8GACoAbAANAB0AYQAEAE0A9f8bAM3/oP8OAML/4f8LABsAcgBcAAAAJQDV/5T/BADf/xwAOwAdAAUAKQBGACYAVgAOAB0ABQC7/yQAQgAQANb/AwACAPD/4f/U/8v/w//z/xoAJwBEAEoAFgA3AFEA5v8PAOj/2v9PAOX/DgDV/7j/2f+8/zcA9v/4/+f//v///6P/2v/P//3/x/+t/wYABQDg/xwABADN/8X/4//7/6D/MwDg/+b//v/H/0AAxv/k/w0AHQAXAEoABADN/zIAlv89AB8A4v8xAN//GwAWAO7/AwAnAMT/GQBLAKr/4P8vAN3/CABiAD0AQwDt/0wAPQDp/20ADgDo/0gAJwD8/w4A+v/7/w4A5/8QAFYARgBKABcAAAAAALf/xf/2/y4AEwDr/93/9v/B/+D/VAD7//z//f8PAAwA0/8lANX/8P/g/y8AFADH/xsAzf/8/9j/KADq/6X/7v/N/x8ABwDh/8P/qv9NAHUA3v/3//n/1v8nAA0AZgBAACEAPwAOAAsALgAlAPr/HwCr//P/BwArACIA5f8OAMP/BQAWANz/GQBeAMz/6P8jAIr/2P+W/xgAJgAMAFMAHgAYAKb/AAAAAAAAEgAhAGQA0f///yMA5v/9/yIALgASADQATgAIABkASwAFAOD/HQBhADwA+v9EABIAIQBRAAoAUgDC//P/LADI/0EA2f/z/9H/EAD8/47/XAC3/+r/yv+v//b/wf8pAP3/NADh/7D/v/+6/9r/vP8AANz/rP/h/+f/2v8FAM7/xf+Z/5v/wf/g/+b/tP+NAAMAAgBLAPT/PwDq/yUA5//a/8///f8PAMP/4v/6/x8A4/9WAOr/NwAsAKT/NgDQ/xAAxP8YACYAjP8jABwABAAoAGoA6P/a/wUAhP/m/+v/7//z/6z/8//2/+X/6//c/1EA1P/c/z8A1/8VACQACgAbALr/7f/w/+H/+v+f/+n/tv+y/x0Azv8zAPP/rP8XAAAAt//q/+//8v8rABAAoQBKADwAVQBXADMAKQDHAB8APgAgAPX/0//c/z4A1/8DAKf/8P/g/x0APAAwAIMA6v83AL7/y//o////NgArAEgAp/8mAMP/BgDh/6//LQDu/ygAMgBNAAcAGAATADQATwAIAGMA4v/o/+3/8P/0/+T/sv/U/zcACAA9AA0A1P/c/77/3v8IACwAEQAgABkAJwAfAPX/CQAHAM//xv/k/9f/3//4/x4ATwAtACQACwAJAND/x/+KAAAASgBzAKX/SQDN/0UA3P/R/1oApP///9v/0P/+/+z/FAD+/7X/6f82ABkAAgDw/zwA5/81AOL/w/8qANn/KQCh/yEA5P/F/xkA3v/l/+r/EgCh/2sAxP8GADwAef/d/3X/bADX/xYAgABCAH8A1P9vAOz/FAAiAOX/DgD6/zIAFQBbAMn/wf8EAN//HABOAD8A/P/9/yIAGwDN//z/DgB5/93/rP9z//3/xv/S/37/z//r/7j/WADs/97/iP/X/8z/Q/9EAMn/5v9HACYADAD4/wsA0/8kAB0AKgAPAAwAHAApANj/KQCz/9X/OACt/5oA6f8SADMAqf+EAPz//f8PAB8A4v8xAMz/1v86AMH/YADf/8H/FgA3AOP/MgBNAOP/RADJ//j/6P+j///////a/xgASwCq/xYAAAARAP3/xv+///D/z//Y//P/h/9DAMj/wf8oAMX/GgACACYA+//F/+P/DAD4/zAATAAYAEsATwAaABUASAC6/xAAsv+v/z8Asv9UAB8A0P9HAEwABgDg/9T/JgAMAOX/RgATACIAQABrAGkACgD3/y8AJgAxAF8AJwBFAO7/AwDf/9P/7v/N/yAArP9PAAgA4v8fACsAEAD7/1gA2f8EAAQAAwDe//f/5//H/y0A3P8ZAPD/FwAlAPr/RADu/9//+P8LAMD/uv/a/xgAEwA0AE8AGwAVANv/GAABACYAHgDi//r/HwAZAPD/z/+z/x4Avf8AADcA5P8NAAsA9//B/+D/wf/g//n/1f/w/+H/1f/L/9X/y//o/8j/CQD2/wkALADb/xgAy/8MAC4A3P/2/+X/2P/y/wcAKgDH/9L/NgDj/wwACgAaACgADQALAAkA9f8JAFEA+P9VAA0A+f9DAKT/2//i/zEAFQD/////7f8CAMv/HwD1/y0AgQAwAAIAFAD//9r/z//G//b/r//R////7f/e/xsAKAAOAGcAHAA7APn/HwAZAMv/MQDe//f/1P8BACUA6P81AAYAKgAPADEAhAAgAD8AIAAHAD0A6P/t/zoAHAAWABIA/f/G/wgAPgD7/zMA4P/5/+j/7f9xAO3/AgDe/8D/FQDI//j/HQAFAAQAKADF/6z/8/+//97/CADQ/9r/GAC4/8b/0f8RAA0Awv88ANX/8P8pANj/8//j/+n/yP/m//3/6/8BAN3/9v8KANH/NgD1/wkAUQCu/ywA7f/M/9b/3v8JAPb/ZQAaAAMA3v+t/9D/EAAxAN//QQAPAMP/KgDZ/wUAFgDu/zoACgAtABIA2P8EAPH/GAABABMARwBLALz/EgAPAMP/KgCi/w8ADAD4/zAAOQAuADgALQC2/0UA3P8sACMAwf/y/6v/8/91/0cA8P/P/zQAqf/f/8H/KADF/xkAzP/7/2oAwv9zAO//KQAhABoAhABFAJQAQAAhAPf/+f8eAAYA8/8aABQAkP/L/wwAHAAWAO7/3/+u/+P/+//F//X/GwDy/1AAwP/y/ysAov9aAO3/JwDp/8n/ZgCt/+L/6P/t/8z/6P9IAPH/GAATAEcAAgDd/xsAAwDM/8T/GAABAAEA7/8EAAMA8f8YAAEAAADv/wQA8f/0//f/CgD3/xwAKQAPAOj/fv+q/6j/AgDw/wUATQDR/xAA1//M/+n/EQAOAPr/aQALAEAAawD7/yAABwD0/+T/DQAdAPT/GgACACcA+//8/9j/4P8dAKn/OgCK/7P/HgCY/xoAzP9EAH//9P8bAIP/LgCA//X/m/8cADwAVQCOAOD/QQCi/xAADADU/0oAKQAPAFUA/P+h/w4Anv/o/8j/LgAlAPr/jgDy/xkAOQAbAAMAOgD4//r/HwD1/xsAFgBuAA8AHgDP/yIAwP+V/wUAqf8DAJT/KQAPANb/FADs//D/vP8lAOf/EAANAFQADADB/ykAoP8zAOD/+f8eAAYAKgDr/yYA1f8UADUA9P8IAFAAHACp/97/5f/q/yUACwAbACgA2P/y/wYABQAEAPL/BgCp//L/KwDH/y4ANwC//wIAAQC4/zQAFwAAADcA0f8RAPz/DgB6AND/WQA2AKv/4P+d//r/n/8NAB0A4f9VAOn/2//Q/+z/3f8aACgAIAAsAEgAKADq/4EA1f85AC4Akv9fAJX/BQApAP3/DwDD/2IAz/8PADEAOQBBAA8Aw/+q//L/q/8FAAQAOgD4//r/MgA5/xcAEwD9/w8A+/9XAMb/LQAAADYALAD//1sASQBNAL7/3f+//7n/IgD4/9X/OAAtABIADgDo/20A/P8zADwA1f/d/+T/DgD5/x8Aq/8XANz/4/9EAAAASQC7/1sA7v/y/z0AxP9PAOX//f/9/w8ADAD4/1UA/P+z/wsA9//m/zQAKgA0AAUAKQAOAOj/EADX/xUAIwDm/+v/JgDW//D/vP/u//L/dP80ALz/3P8ZAKf/AQDK//r/MQDx/8//6/8BAKX/SgAWAMn/ZgDS/zcABwD0/xoAp/85AMD/OgBUAPv/IACZ//f/HQDz//b/LgAAAEoA4P/5/1YAoP9FANz/4/8NAOb//v/+/1oApP///wAAtv8gAPb/5f/Y/xYAJADn//7/7P/e/wgAmf/3//n/ef8TABAA1v/M/wwA1P+3/+r/pf/J/woACAAZACYA1v86ABwA8v9QAEEARwAUAEcAAgDe/0AAs/8LAPf/nf8wABQA2v/0/+T/sv/U/8r/wv8FALv/EQDq/wAA7v/y/xgAuP9GAKb/yv8dALz/EgD9//7/tf8fAL3/3f8IAAYAPAD6/2kAwv8pAH0ACQBRABwABADf/0EARwBLABgA7/8EADoALwABAIIADAAvAAEAuP/G/9H/IwAKAFIAHQAqAP7/7P84ANL/AAASAOr/AADu//L/4v/W//D/z/8PAAwA0/8SAMb/0f/t/wIAFABaAJIABwAqADUA4v9DAP//7f86AOb/6//v//L/BwD0/2QALAD//0gAKAD8//3/IQAbAAMAFQDI/+X/xv+//wIAlP8pAP3/2f88ANX/SwAqACIAQACz/wsA9//U/zgAQAD9/+v/XQATAOz/XQABAPD/FwASAP3//v/+////EQDE/ysANQC9/yUADADl/w8A+v/p/+7/AwAUANr/z/8PAEMA7f8VAP//tv/8/7P/CwDA/7r/IwAcAGAABABfACgAMgAoAP3/IQDA/9//5f8OAB4ABgCp//H/vf/K/wsAwP/x//T/5P/X/18Azf8fACwAfv9hAOH/CwBAAA8Anv/7/yAA0f81AL3/JQD6/8T/GQABAMv/CwAJAJr/5f+O/+7/uv8RAPz/IQBSAPn/aACc/x0ABQAXAEkAFgA3AL7/FADH//f/CgD3/woA5P8gAOP/sv/m/7T/VP8IAND//v8QALL/QQDH//f/LwC4//3/IgDl/zMAKQD9/0cAuf/r/wEA7/8WABIAfQD3/+b/WQD/////EQD8/+v/3P/2/xwA8v/1/+X/2P+7/+3/JwANAEIAtf/W/ycAev8nADIA8v9QABsAKAAOAOf/EAANAC8AEwAQAB8A4//D//T/PwAOANX/AQATALT/1f8UAMf/GwAWADYALAD//0gAzf8NAB0Azv/9/w8A+//X/zoACgAaADoA5v/r/yYAw//h/4wAzP/p/xEA1/8DAPH/GAATAOz/AQCCAB8APgAyAAMA8f/0/xoA3/9TAAsA+P8LAPf/5/+0//r/xP9iAAUABAByALf/2P+7/zYAGQDw/yoADwAeAJj/LQDu/8z/DQDU/+//8v/1/9L/EgD9/8b/LQDb/+L/+/8gAAcA9P8IAND/bAAyAN//LwAmADEA3v/3/wsArf8ZAN3/LQA3AL7/OQAbABYAWwDu/9//HACp/8z/+//8/+v/AABKALv/EgDq/7f/DgCe//v/IACZ/wkAYwArAFoAWwBJAPL/4v9DAAAAJAAdACoADwDo////o//I/wkALAAAACQACgDk/9f/lf8qAOz/3f8aAMz/+//8/yEA5P/8/w4A+v9EAKT/yf/T/7f//f/Z/xcA3P/1//j/5/+0/9b/8P/P/0YAuP80AAUA8v8rAMj/QAC0/wsAQAD9/xAARABbABIADwDo/yMAnP8dAGEA8/8+APz/MwBzANz/GgAVAH7/PAD6//v/MwDy/xkA3v8tAAAAJAAwABQAIgAuADgA9v8KAAgA9f/A/0wA4v/o/zYAq/8XAO7/3//B/+D/wf/g/y8A7//O/7P/MADd/9L/7f/x/+L/w/9hAOH/5//+/xAADQDm//7/tf/7/8T/0P9sAPz/RQAlAOj/SADM/8T/BgAqAP7/2f88AMP/vP/c//X/0/8AACQA+f8fABkAFADZ/08APwDq/yUAsP/A//H/z//Z/zwACwDA/zoAwf/g/x0Azv8OAAsA5f/q/wAA3P/j/x8A9f8uABIAxv8/APz/DwBDAMj/+P/V/xQARwACABQAEAD7/9f/8v/1/xsAOgBmAC4AEgBGAO//TgDk/yAA9f/4/2cAwP8WANv/9f8bABYASQAWADYAGQDw/zwADADA/zsAr//2/xwA4P8vAMv/VQDp/7f/IAD2/67/0f/a/3P/RgDd/9H/NgDQ//7/EAD7/w4ACwD3/y8A3f8bAM3/xP+Z/4j/1v/f/xwAzf8gAOP/DQD5/7H/0v8AAO7/qP9LAL3/JQAeAPT/UgDC/04ABwArAFoA//9IABUAkf8UABAA1/9MABkAAQABABMAx/8tADcAGgAnAPv//P/r/yUAsP8bAM3//P8hAOT/agDV/yYADAAcAM7/xf/2/8D/8v+r/04A9v8cAE4AGgBeAPH/GAAlAPr/DQBUAPv/6v8kAML/BADg/6//UQDm/+v/SwBhADwAHQBhAM7/DgAwALn/7P/w//P/GgA5AAkAUQCc/+f//v/I/2UA5P8NAAsAGwAWADYA4/+x/y4A3P8HAOL/+v/X//H/BgC8/1wAJQALABsAAwDx/+L/DAD4/8L/4f8LAMD/3/8JANH/2v8YAMr/1f8UABAA6f/t/xUA///t/ycARADJ/x0A4f8dAAUAqf86AK7/UQAvACYAaADB/zsACwAbACgAIAD2/9P/EgDY/+D/5v/+/zUABgAXAMn/+f9DACQAQgDs/xQAEADW/wIAuf/s/wEA3f/2/woA5P98ABoAFQAjAK//PwDq/24A/f/Z/6sA9/8vADgALQDu/wMAFQDt/ycADQBCABAAMgAoANf/OwD5/9X/FAD//+3/zP/o/7b/sv/m/8b/9v8KAPb/0/8AALf/s//U/wEASgDz/2MAUAAuACUAMADL/57/HwCG/wwACQDk/zIAAwA6ANP/7/8oAMX/9v8cAM3/IAAsAKP/2v+q/+D/+f/D/wUA8//1/y4AEgDY//P/9f/A/9//CQAIACsA2v8qAOv/gf8sAMj/5v/G/4f/RADb/9D/EADE/+L/ef/d/wgAq/9hAPP/9f9AAA8AQwARAOr/3P8HABgAAQDv/wQAAwDx/+H/+v/7//z/IQCt/ysA/v/a/3QAy/8eAE8A5f8OAOf/7P+m/wEAJQDD/7z/t/8gAAgABgAqAA8A6P///zYA0P/+/7X/6f8RAPz/IQAaADoA5v9ZAP//EQBXALP/+v/W//H/z/8PAPr/6f/b/77/OADS/4AAVQAyADoACgAbAKj/XgACABQAEACx/woAh//p/yQAQgBaACMAQQBsAA0AHQBPANL/EQD8/9j/FgDJ//n/HgAYAPD/BAAWAJH/AgACAPD/KQD9/zQABQDz/wcA4f8LAC4AJQAeAGIAFwDv/wQA8f/i/x4AGABLADwAw/8FAAQAFgDt/ycAaQDC/yoAIQCI/+n/2//Q/xAAjf8jAEEAov9+AFMA6P8QANf/qP/L/wwACQAIACsAIgDl/9j/zv/q/wAASQAWACQAQgAQAB8ABwD0/wgAKwDs/8v/+//p/9v/BgAFAOD/HQC8/+7/FQC2//z/6v8SANj/qf/f/xwA8v8rACMA+P96AKv/BAAWAJH/FAD//9r/BgAXANz/LADt/97/CQAsABEADQAdAAUAOwCL//7/x/+b/0EA/v+jACcADQD5/9b/AgDL/zEAzP/E/wYA4f/5/0MAEQAOAB4A9P8IAAYAKgD+/0cAJwDE/xgAOADl//z/s//6/7H/ZP86AJz/CwAuANz/LACR//D/PADV/wEAXQAmAEQAAADu/wMAp/8mAB8ABgDO/1gAWgDa/z0AVgAOAAsAQAC0/7D/0v/J//j/MADM//v/RQDc/4gA7v8oAOn/AAA3AIf/DADB/wQAuv/t/xQA2v/0/7//TAD0/wgAPgANAB0APADD//P/LAC2//z/s//5/9b/8P9hABcAAAASAMb/v//e/63/GQDd/y0AAADu/6j/uf8QAOn/SADy/wYAzv/9/7T/w//0//b/+P/V/4IA1v9fAN//CQDj/5//aQCL/1kAyP/4/x0ABQBzANz/PgD8/0YAEwDr/wEAAQDK//r/6P/t/3EA7f9fABUAIwAKAFIAVADW/0wAz//Z/xcAEgC0/zAAJwAyADoA5v9ZACMAHAAEAE0A0P8QADIA8v+HAP//WwDb/wYAFwDK/0IA2v/0//b/CgC//xUA///a/ysA7P/w/wUAzf+N/0kAzf/E/ysA7P/w//P/GgDe/xsAFgAkAAsAUgBCANr/KgCP/+//zv8OAAsA9/8LAJv/LwDK/zAA3v+I/+n/yf8KAAgAKwDa/wUAKQAPAPr/DQD5/x4AdADe/xsAFgDt/xUANgDi/8P/BgDO//3/xv9SAB0A8/8HAPT/PwDF/1EA0/+l/5L/zP/p/6T/IwDU/xMA2f/g//n/sf9AADQAKgAhAJv/rv/j/7L/CgD2/4sA8P+E/1QAnv8yAPL/BgAFAAQAFQDI//j/ef/d/5r/5f8hANL/yP/B/zsAVAAxAN//eAAEAAMAlgAKAOT/IAA/AFcAWQDa/yoA2f+8/xIAIQD2//j/VQAgAD4ADQAdALz/pP8kAAoA5P8OADAApv9KAPP/9v8JANH///+2/1cA2P/y/1AAHAAEALr////t/wIAFABaAAAAyP8KAC0ANgAHABgA7//z/ywAbQAzADsAVQDp/9v/BgAFAAQAFQA2AAcAvP/c/9H/IwDT/yUAMAC5//7/tf/7/7L/CgDk/+r/XADv/00ABwAYAN3/LQAkAPn/MQCn/yYA+/8gAPb/0/8kANT/AQABALj/6/8lAJ7/6P8RANf/KAAgAL//8P/O/47/7v+6/yMA5v+h/9n/4P9CAEcAJwD7/0UAOAAIAAYAFwDc/6z/qv/N/9f/3/9BAMf/GwAoACAALADI/4sAy//o/yMA5v80APP/PgAgAIf/6P82AHT/DwAxAMz/DQD5/0MA7f8CAF4A3v/A/zoAVAD6/0QA7v+6/xEA/P8OANX/JgAfAND/NQAFAOD/5//Z/+H/5/8QAMT/c/8PAPr/HwA+ANf/XwCV/5f/GQCU/ykARgAmAPv/IABRAFMAewArABAA/P8hAPb/LwBdAO//8//R/xAAHwC+//D/FwC3/yEAGgAVABEADQBCAMj/GwDy//X/GwAoAEUAyv8LAC4A3P/j/w0Ad//c//X/5f8zAAQAAwCn/xQAx/8tADcA4//X/6f/8P+F/0IA7P/w/yoAof+0/9X/AQC4//7/7P9wABAADQAdALz/7v+o/4MARQASAA8AQwBIACgAfABSAGcAif/X/ygA/P/G/7//JwCN/2z/wP/x//T/CAA+AHsAGgDx/xgAOADS/2z/LgDc/xkAzP/7/0UAt/99AOT//P8hAPf/wf/N/0UAyv/U/93/LQCk/9v/YgAqADQABQBOAPb/wf8DABUA7f8nADIA8v+HAFoAAACTAAgAq//z/6z/KgAiAMD/FQDt/97/9/9CACMA0//u/ygAxf/R/+z/y//o/1n/RABuAOv/bwD+/yMA+P/6/wwAHABgAM7/RQDK/7D/rgAwAKgAUACJ//z/2P9OAIgANgAHAPT/9v/m/1kAEADX/xUAo//I/wkAvv8mAB8AKwD//6P/NQC9/8r/MADL/zEA3/8JAD4AoP/q/8n/5v9HABQA//+j/7X/+/8gAPb/5f/Y/4T/wf9gAHIASQBgABYAAADu/8z/VwBrAB8A0P/Z/wUA4P/5/wwA5f+z/+f/WgD//+3/OgD4/9X/8P/z/9H/7P/L/zEAJwDX/00APgANANT/OAAIAOL/+/+y/1QAw/+9/0oAzv+z/wsAwP+6/9r/BQCFAKH//v8QAOn/AAARAA4Anf8MAAkAPwD8/1gAEAB6/97/dv/b/+L/MQDe/8D/KADX/7r/7f8nALL/+P/n/zUABgAFADsAr//R/+3/JwDX/9//5f/G//b/ZgBkAJsAfQDS/1sAf/+9/+//8/9QAAkALACk////2//0/xsAcgA3AAcAGADv/zsAVP/2//j/5//a//T/LQC2/zIA8v8rAMf/igAlAMP/PADV/ycA+/8OAML/zv+O/wAAyf+K/2sAsf9BACIAdwBgAM3/RQDv/+D/1P8lAOf/EACOAGAA4P/4/x4Avf8TADQA8/+s/wUAzv+z//n/+//p/wAASQADAAMAp/8TABAA6f9tAA4Anv/W/ycA1v+6/9r/PQDW/wIASwD0/z8Ajv+2/43/yf9UAB4AKwC1/8P/GAABAN3/LAARANf/8v8GAHQAEwAPAPv/xf8ZADkAQAAhAC0ANwAaAN7/9/9UADEAOgAcACkAIQAIABkAlP8pAFgA2f8XADgALQCk/xEAMwDg/+b/6//v/6n/FQBtAEUAAQA4ABoAlf+8/yUAMAACAPD/4f/n/+z/XQAUAGv/0v8kAB0A8/+IAFsAkv+V/yoAbADE/+L/w//P/yEACACIAO3/Xf8iAEAAtP9VACAArP9PABoAOgDm/2r/9v8JAFEACgD3/9T/3P8aAN7/wP+o//D/BQDy/9D/WP/D/zwAMQA6ABwA8v8HAPT/CAAZAMv/1f/w/wUAFgDb/wcA4f/C/08A9v/m//7/NAAFAF//7f/x/yoANAAFAM7/2P9NACwA7f8nAFcAof/r/yUA6P8jAPj/1f/L/zAAp/8BAIIAaQBUAAwAQQDs/wEApv83AD8A6v9cACUA+v/E/ysAtf8xAHEAAADb/ysAbQD8/yEA5P/X/17/tf9pAC8A3f9j/8v/sf8JAHYA8f/0/wgAvv/L/wsA+P+L/8b/GgCo/wIAy/8wAEwAvf/K/wsAdwDg/1QADADm/8b/v/9xADYAPgDE/ysAEACN/zYAUAAJAOP/HwD1//f/HQA8AEMAIwCc/9X/JgDD/wUAFwAlAB0ABQC7/xIA2P+7/yMAiv9YACIAHABNAPb/LgATANn/u/8kAOf/EABpAAoA0v/J/woAZAB1ABUA//8RAGoAMAA5AAkArP/0//b/LwDd/xoA3v/l/zMA8/8ZALn/x//A/xUANgD1/+X//f8PAB4AKwDs/wEAy/+NAHEAJAAvAKb/EwD+/9n/qf+V//T/PwAgACwAEQDF/ywAWwA2AIf/1v9MACoARwC5/5D/uP/9/1kAWgCk/6P/EAANAC8AOQDS/5H/uf/a/08ACAC+//D/YADPAO//8//Q/33/FwAlADAA3v+I/w0A5/+0/0MA7f+n//D/BQBgALv/o/81AL3/OABSAJ3/6P9Z/3n/JgAxADoAHAAXADcAPwCy/4r/fP+o/xUANQCHABEAxf8HABgAEwD+/9n/vP8lAFUAMgByACQAwv8EAKj/8f9PAOT/fABSAK//5P9XANj/zv9YAMb/mv9mAGQArP+8/wAApP+k/8j/QQDG/3b/twAkAIv/IgDA/3D/sf+KAG8Ax/8bACgAMwCFAH4AGwAEAKj/8P+GAGwADQAvAF0ASwAYACT/GQCB/4f/swC0//r/6f82ACsAyP8JAOP/6f+k/9v/PQBpAEIAIgAJAKz/c/+h/yEACAAGALz/NwAHAL3/XQDv//P/vv/d/wgAT//g/3kAhgAiAK7/YwD0/+T/RQDv/yf/if98AL//JwAfAD4AjgDy/+QAWwBb/+r/gQBm/7z/gACw/2UA0f81AFAAUf8YAMv/1f+m/yUAnwAAAKUAYADg/+b/tP+e/wwAHACE/woAUgDm/33/BAAoAMX/GQC5/yIAGwDg/8H/hP/m/0YAcACj////NQCG/+f/WgCSAAcA4v8eAAYAzv8zAGAAzv+z/x0AKgB8/ykADgDD/08ACAArAOz/8P9PAGQA4//p/+3/lf88AAwAUv/Q/1kAWf+f/1cA2P+W/5j/GgDM/43/SABMAND/EACOAOEA6//b/joACgB1/5EAPgAyAE0AKwAjANP/Nv9L/93/5P/YAGcBHwBP/83/DgB6APT/v/8CAF3/owA7AZAATwC//wIAuf8h/wQAcQCk/5H/y/8MAEEA7P+B/4f/+/+g/w4A+v8MAFQA1v8nAFYAMwDO/yEA5P/8/yEAdgCXAOf/fgB4AJf/h/9oAC8ASwDQAAEAAQDK/+f/NQArAFj/1f8mAOj/yQAPAOj/tf/7/7L/U//j//v/jv9t/68ADAD4//r/xP/i/wwAHAC7/5IAPwCPAIUAxv91/6P/IwCc/1QA6f8kAEEAWgDa/5j/dgCV//T/5P+OALv/Nf+VAK7/mf/l/6EASwDz/1EACgCt/yn/r//2/9P/EwAPANb/FAB+/03/XwC7ABYAxv68/yQAHQCYAEMAkf8m/4kAAgEqAGr/rP+ZAOn/IwAdAF//tv/p/zcAUQAKAPb/rv9jAAgBLwABAF0AAQDv/2AAu//+/uj/yQBGALj/Dv+r/70AKgCQAKwAP/8t/1cA2gBBAEcAAgAA/+r/kwCcANj/y/4a/6P/tgDdAI0AXv/F/hYAbgBrAPv/Vv9A//oANgCZ/5wAMv/J/9T/SgDPAHAAkQDQ//7/a//TAKoArf8YABL/VADFAIwAzP/7/zIA8P64/0YAlQCc//f+mgChAJP/qP9eABUAWf97AL8AGP98/+EAbgFt/9H+fACs/5j/LABtAHz/Av+jAPIAVABpAHkAc/98/00A0gByAMn/wf/N/6D/MwD0AAwA5v/p/o7/3ADV/5UAQQD+//7/Wf8MAMIAif9o/wYAYP+TABoA8f8FAJf/KwCj////fv9y/1b/1P8AAO//cgBI/9v/Kv/5/0MAR/81AOL/sgCPAGEAl/+G/40A8f/0/2QACQHC/4T/5v8PAOj/R/9aANv/c/8PAFgBXQDt/qUABACV/+H/nwABAbn+ev9wAH8AiwCm/wEA7f7I/2gB+v6J/zUBwgDBAAgAPP+8/mr/mwAOADAAcADa//T/v/+DAI8AlP43/84A7//y/9EAJwDp/zcAmwCz/0H/QgA1ACr/ZwAyAgsALP96/7n/tf9DACYBM/8R/+b/awB7AFEALgCj/gn+bgDvAR4APQBV/yz/DQDU/zoB/P8N/5j/dgDgAOwA4v/4/r//zP97AGL/2v6V/9AAUAKRABgA8P+p/zn/3/71ANf/3f4rAacABgDPAHAAMv5m/swAkf9c/9j/rAHdAlv/RP98AOL+z/76/2kA5//H/5wANAA8AHn/uQCVAOH9hP8J/6kA9wAOAMQAv/42APP+8v/4ASYAC/9N/6oB1f+U/xkBqv/d/vP/mwCg/0T/2QAwAd/+Tv/y/73/k//y/0ABkwAaAIP/QADsAIb/Qf/T/ur/qAFUAAwALwATAH4AHAA6/17+xQD6/x7/lQDl/9kAZP/yAKEBy/69/gz+FACmAcMBswD+/xAAeP7Z/+EAowBJ/mT92wEAAuQAAADc/77//v2cAMgA/P8y/xEAEAGO/loBlgBj/rX/MgC7AIH+YADRARgAuQCoAIb/9f2l/jUBrwAL/zwAHgC9/6X/3P8rAKP/SgF2AO/+3f/2/9P/AADfAW4AQv50/lL+YQHFAjkBsv+a/ioA2f9hAGMBZP8k/jn/QAJSAm4Aev40/+//gv7kAb0Bvv4x/o3/8QH9AMv/Cv+E/+P+9v5SAaQBmgDC/qb/gQDD/2IATwA+/wj/OQAwAb4AdABv/wr/hQAN/5oAxf86/qgAYwCbAUkABAAU/67+cf8NAI4Bcv7DAAwBewCa/+P+GwCo/4MA4/xxACYBNACrAAf/lwHr/0n/ff5NAWX/kf1ZAfQBkwEI/loAbP/j/gkAUQAvABD+mAAhAZ8ApP8mAbT/G/7n/kP/jgCU/ioCPQFsAMYA+P7R/9b9tAA0AKb9ef+8AWgCIwAcADwAvv0Z/RsA9gFvAV0AlQCvAEMAggF+/xH9pf58/7wA9gGnAVMAsP+cALT/Cv+3/SwAAwKJ/zMA8v8LAkcAbf51AMz/d/4J/TUBjwJqAY//t/8hAF79VQE6AgAAC/01AC8C0P78AN0ADwFB/SX+PQH+/9sA+gADAgj/gwAiAXr/t/73/h0C9v3d/vYB8QEgAJf+8v9P//L/0P8kAbP/rf67AE0A5AC3/6D/VP7x/vQB2wCLAPD/hf8KAD8A2QAt/0H+UP8aARoBPQA0AdD+9v1fAJgBkQAV/j//QQDG/4kAAgEE/9b91/8/AuAA+P28/3//YgB4AmgAhf0A/vsAtv/YANMAyf1a/dMBEAQa/zT/Sf8z/lkAFwPKA3L+SvuYAIEDgf5f/yYBMf5W/1cCiQLj/4r+Qf9XAfIBQv5x/dEA8gAc//AAnAD3/Pz9VAEmApP/Ff+yAOv/N/+V/4gByv6m/IsBsgPg/jj9gwLfALL/jgG8/mX9+/6gAasBDABA//oAkf8R/mQBZwCr/oH/df+TAdkBC/+FAA8AnP70/oUAAQKY/oL+GQGIATn/mADrAQkAKP65/WkCgQAv/2sA6f8UATgA0v+0/i0A7v8DAL0BnABV/lr8zwFVA3L/H/8i/Zv8pgCfA9YBrf6j/S4ARv6c/mwELf89/CIARwP+Abj9rgDV/6H9B/+sAnEC2fu+/k4D8gHo/uf+C//e/mEA0ACCANb/Xf97/oUCKgFF/Zf+y/4vAXUBKwAiAOYA6/17AA4DV/zH/tUCjgCEABEBtv98AE7+pP9NAsD9RgC+AkYBcP7BAMMBhvxNAX0CH/7W/ZMC7gGJ/hEDZAEs/vP9//7X/4YBdAIF/qH/xwBGAbz/sv2JAogAn/1z/zgC2f+C/mMBCP/I/QIAzwF//QAAwQQoABr9qv1+AFMAtAHt/un9ewFCACcCcABH//f8nvxnBEEC2fyd/lgDrf+k/KMEkwGA+hD77QHyBb39xABrAv39dP41AhoGfvxK+pUAaAEx/xUC1wPb/yj+7vylAyEAuPyaASL/7/3IACcDvP9G/r79xQDWAJn/iQAN/X3+BwOaBK7/UwFYAJf6WvtiA/gFmPsY/UQC6wMO//YAqAOE+Yz5/P/ABeMA2P5hAp8AIf4nAT4E8fyG/I38UADfBSQCxP2P/gQDHP5l/SYCpwBL/pMBcQQPAVH8Qv5rA7X8UvoeAswDp/zBAC8JRwEg+xL8JQBk/jYAyAQD/d/8OQGmAzsDyP2M+x/8YP2fAC0EbgJNAKn+7P62AMoA2gAC/BL9PAEiAFcCxQRCAqH72P2CAvz8avwPAO4ClgO7AM4AJwH//+v+Q/7M/ID+mwJxAKwD7AYo/fj6w/8FAE3/SP7ZAIoAAADBBIwD0v3G+bT7ov83AfMFeQCd+TABIQRyANn+ggCI/TH6cgIXB/YAvvyKAJYBif3x/T0DOv/3+AkCiAUAAfL/UgF3/ZD5xv6eAzUD0/zP/rgDNQLk/fH94gMZ/wj8Pv6LAlYC7f3rABAFjwGG9rcAiAOT+0MC0P8pA139qP3oB+D9ffzh/K0DCQMq+v4BiwJ2/x793AI+A2z8kP/d/8cDhgCL/Zv/Kf1M/wYCNwNG/nX95f/bARMCYAAKA578m/rWANoEPwGI+wYDtP9y/GYDYQKyAPr+sAB7AOb4xfndBo8IEAEf/nr9KvzZ/VQGXQKZ/h/7+PiZALIIvwl6/PD7Gve//5cJ8P2y/kT6/f8aBaEF3QAI/sj/s/l8ApAAFwADAbr+DQDU/48GZgFe+0H75fx8BIsDqvx5/5YBcwSc/Wj7kAJpAFQAufp/AJACVgBFANz/9P57+/0D/gHN/q7/BAfM/FT7qQQi/UcAWf1lAvT7zAP0Bg73P/zxAbcKCfx9+RsDxf84/VAEXgdf9c34kwXyBgf9OPoZCSUCvfEiBLgGmPjC+8IAPwg3/Q4AbgMS9Cb8DA94Aa336/9u/+8DKfmWBi8H8fWM+X0AQQlWAWQE1vun/T79Nf7UBQH+Zwgd/Bz4Q/9hBeMBzPdkAkoCPP3eAPEDpP7NA50AdPt9/Xb8Bv/0AigBxv41BZoBhgPJ+wn9Gwb2AGD7aPtvBB4AiwIs/4sHDgNM94j+v/5WBiv7a/+t/+YBsQOZAFoKGvzV+TX3AQQg/2H4GgYJAqEI+fcoADsMS/m8+p0EhfxX9ekIev9m+1AHgAGiAPf6m/7Q/yv7P/xuCMsGy/cbA5YDuf+e/QH+jwG79eL5PgcZC8b87P8NBe/zHQXQCUP28fjJ/4r/TQMnCk4F5fj393sFxQOK+rMHlAcp8/n5JQSBBQ8Cs/3/BSr5L/g2DHEMlvd79skEzfx6++L/oQnLAsH5TQHuA7f/l/tJA6H3IvwDBA4HqwM8+UUE9vwj//377f66AUP6rv3l+zoJ5QqWAvn8Jf/+8o76Fwp5/TH39wBcEtn6RQTLAqr3iv689BUKYfsJAhYM7/1Y9+7+dBOt9bns/gRpB6b4lAvWEWnwyPL5DLQFhPKP/aQCKAWq/BQMHgwK78v2F/oz/xsEpBAV/xbraAZcE5f8U/WxCVj6sO5x/54PLQa8+F0D7Qpk+bH01Akf/Yn1w/1zCy4DsPeoCsQDKfiE/1D+H+xDASQP0gDG/JEAmRCy/87so/13EGT5G/OZBa0GLAbG/SX/igGvAu/3Qf5FA4T8OwI5ATEIMvhg/NQJYgPc+EP8Hw2g9lX8dfuA/koPJ/hZ/cb7Qwg1DDj78/UC9N0K2fnJ/owKYwMt/EPzMws/+GIB5Qjb+r7/GvImBVIHFwMH/mX8dwc7/bgA0vqTAIENh/FC/AgLDPniAXr8rwhKB1/0PftfBGwIkfTrBo8LsvrH8TP/+g0S9M79WQzeBy7zVwJBC1Hzcfi6BhcIjfAhBtoKQQHD/ATzqwXSAEj94f34Avz7bwDcCegCNQME+jn4mPrzBngG4//y+yICZQVX8i0D+QjY+jwASfoACKoOdvK+/poECP8GAh73iwDV+08AYgeDBEkESPcP+4/48wRSCSz4QAHh+dL/EQh6A0EFr/UY/sj5mgAuBvT4eQyh+WH8Zgni+C8CLwFZ9MwEcQS1+KIMsPliAPUAVvc9E/H+3+/z/Y4O4fL1AawUTPaZ/yv2tAfH/Hz2Sw17/50DOvVACfYHjuyDBkAFc/PM/F4I0/7XBzgLmP2H+vPzPAEL/gf6dQrWBY/78Ab6EOjssvI6Efb82faF/acHnPba94IjXQaD5qn73/07+N3/IhQsCbrr6PsuCywL/f2+9iH7tfJ7BEcGVwTOBRH3PAJeAWz8PQPg/zH4X/xnApoEugXfACr8PPlwB3wElPZ/8twJPhHK74YG2wcE+vYDe/qLAz4GcPnc+xcF7O7yApMZGAE/+TXzTQOR/+7+4QpZCdD9uuwcAiIC3fhUDP4HRvI2Ba4J6fpI/0r4ggPYBJD0HPxxDiH5eQSsGxzuYetWBJj9AvjSBxQFkgGr/Qb7+wuLBIj8wvJn/gYCSfr8/XYIiAb+/T0PMPiT+9cCofcIAQwBVvcy/cQRfP/AAqIAwPq+AboFDfS47WwMifsSAOwAjQsB/pPyEQqK9jAECv1DBxcAgfeqCxQF9gSW7Kv8SAIVBeEDBv+bCy30Z//EAzoAywSqBWz7cfv8DjP4qvxe+y3y/xVZBofpnwH/Do0HMAE5/hD+vfe/7h393BsQAdbtDxFpB4LwCwBCCXj3Ge6K9oQZShUD3loCrCFl9d31JQRz7hHymApPDtUMF/0N+t/96vwhA+IKs/cL408DRf1+FNkl9O286FT/4gcEAGoFK+1E+w8HBvJqGosALPpcCl8CzfRX+CYPHN8++xwXgANvDyX61QGVBRHzsQMxA2rnSfD+FlsWfPQeBJIHGf3YAo7uWADi+9P8xAp3ANMKx/3J/g/7IvlZ/cb7YQUg/ML/xANzARsCAQS9+/373fcc/GwU+PcmANUHZfbw/FH9ehYY/gDquvpLCe4QGf80EP37V+QdATICUwhzCaz81//7+8EEMQS5ATkHC+3S9MH8yApKHI3w7vbjD2L8v+5IAKX+B/TfCVIAxQH7/m0DIxX1/uPvlutx/GD42BGOGTzyYALu+nkD5vS+/CYV8uOo+HsHtAkWBSD+AQmT+VEDMPMB8yD5oQbWHCn0OfSjDvXraPfFIF/7Uvpj//wFqRJm7dwB8ApO7mDxvRAEEPX4+fpvC4IJSfQSCbgEU/Vi9ugKlgHt8KAc+gLa6xv3lg5kAuv3lBXW6KjyagE/DWEZReXH96UIdv06BYUOMgKO4FzuGxAECO35rBOeDHPfsPapHAn+AfBb/90CagZv6an1/iVWDWnznfuQ/xzztfDjFEcSZu/Q+NYR8wWR+hwDRfec+af0mfrKDDQGPA9t+24KMQjz6137TfCtCb8JAwFI9ND71xVr+2oROfkpAaHtI+MXI0fx0Qm3CS/2yAZS9IP+b/WeB8r1yQpUB7jnKBjeBkkBK//F+JXvFu99ETgDgP/0B84SvP4N5pUEW/0y8t8NJ/8GB4EUGO6AA4T3j+VID5oLfe9mC84mROvlBHELQ+ylB57fw+//FYwMbgUZDf4KzPju/IX8VPQH77buswqKJ3EG5/u/8QwKXPwl5RElHOWZ8YEK7gtJJcDxbQOW9rjycvbY/Tj5ZvuEDokAJyJzCSnziPBl9Gj8C/Ya7rIAxCgQ/UMNFQZA4p37hepECdQP4gH+Djvz/AUdBef69/v85okDc/1DCqcKbv5uDXL/Ug6x+vrnJPas/Sv73xo+9UzjPR2h9CERhg047Qz2B/7FD2D1PAoE/ef3vf8O9dUJqwrIBFnyiQISBV7qgwofETv0rvn0CEz/svzcCPb5HQqk7XvwhRBHAOMKnu0PFVgBpgA0DffkVgqL7q4H3AC1+bQKmAzD/Uf/jRev1gQFbA6+/2r98ABFAu3ztRDM8EMXLgKP6hn6hgPACOIDzgb+9McZS+yR++8F8vVpAszwUASGAJ39Z/oxLB34LNzpBZ8EXfq48DEW6urvCMUGywJmE5PemwwA97DhqAuxEsoX/g2w53r9swD69UMPvPtl8evxJA2R/v4g4wGY6JQx5dwU980ImOW4BHQEMwiE6h4BIgs/DwwRrv0Z8q3ntvhg/s0DqwbVCBr8uRZ7DLvrEQa33+HjmSG+C4zxIR2vDYD2hg3r+7Lyy/e29Zrjc/jIJFIoNQ5B/Ez4Gezi7zIBrwFW9jQA+QJ6E9H7Av8qFIHiVvXNBNL9SvPUBhkIovmrFYINAObW284g4Ph74uP9+BqLH/7duA2nHVgACtxoCeTwh+IhJqz1Nw3V9RUQUx1G/R/xQ/l7AW/aphwQ+q7/qA5wCZXzSe9UJjHdVwJ7BJMPaw3z35n/df+j/4z1HBViATL5tQCHFO3oI+j/GNHsSx8wBAIKR+58+HUdJtr9GwD2D+3H/lgE0h/pBeAAn/Y9Ex/i2PgLJ87hcOcPDmH/S/hTF0oZWP4r5vb7J/r7+HEGff3tAN3kEQUTLFz+yOEvBkv2FOW7FNcO+gRS5ToGBS7s5tjyK/yn5+/7bfuoCz4QwQ7gCQINdgfJ4k4KbQVn7goESPVt5tnvJjAzGWL6KhIG+IPiBeEuCtwhcQKJ8PcEUwh/BvHqzf6U8+XKABueDF8Q7xdBDhj+mdzgE//7bv6R69fySyRkEwIBQvomCwHyw/El6ooRWRXs90AgqCNJ5zbK2h9V+dvjivvBDBMbG+PBD9/+awSyCg7wrQ/o+XPzodjy9RMu0gcq7aH8XgdfBi4KjA4FBPDfOM0k+Z8UOwwwH44OmOpe/ZAL4vZ69VTyyghI/ArQ1yzXOSfezPZlJdHm4s/hFvYL0fME7DYFRCQs9NbvLBtpDm/lxffeCsf5D/O/8U8PJh+yAVn2NgBeBtr03v5XDGj82+gl59IVLRuhFsr1HvcIBzrrzQ3ECnL1NteTDPcWt/fwF37vIAT0CXwD9PFPBJ0L4elx/ccEVyMn/QYKkuW51fgddAB+Br4O0wSW6N74/w7vGiwAz+Gv6gPttxxlClAZnemzwL0NDSHnDmL8uvQE4tIQuQ/eAZ79K98K96sF+REjF6kb/Oil20UFW//p3nQN+iH58uEhRgYo/9P/0tq392b6yewIBMow8hKnEZbsFutOI1jthd9K64EXACHR+IoY7SOb4iDcFR6E/AzkagUs/gkIzBKbEdMU2+4Y0MPsCxCKCNT/lRFQBdfxQPdX/dn8PfRIBacQNeOL5VUObR3c/fPYowerD8z1AApDJxr4vdwIEWgRuenp1jsZ/Pq9+3I5YQQf/ZbqSwbOBtTqIP1GAMoYkev05j0mUPO4zhkw/i456b7pVw+G9FvidBnu+Pf8zvnBF/0QhN+KIWjySfBpBYH7bvrX39c2DirHyHnjTx0CEkPoSwbPDx7Me+lpL1Q68usWw1Qz+wJR38ov6u9rzaTmlSBMDRnjziYdAxr0SwKFDc//vbkTE+cy9uXU5sclpBKy1wz9YwR+9Qzh7wsnT8MgPcyc9REK5tXdGpMDxfUcGdf9jxCa+GjrkuqL8vMXMRahDMDw0yKjIgjFmxNu/ELTiegb38oyoiU1F/ALWwvQyPfWWxqS74ksuf3K82LvXAhEGuLyMQQy3WUAkOpLKfIq1N72DVYMmemm9bIVtvCK9CIBwB8X75sWMRbzxfYIoOL+HTj7JeMRSdgBPsSI+BkQb94N+mQZahagzTXsEz66HUzrf/ycDpWiL95USqk1Vfk+ADcTFN96178HuiS92bwDMjlm/MfwCwgJ44bi3Bdy8dP6PyQwERkAbQfI5fQFMuimwQsTAwHjCMcDwBrhKKntf+Ck+yzxu/jiHjz9lRH970D9tA2r//MI3QdHB9nZ+S0lBU3sUBfK+FISbAdwEegUR/ecz2zy+w0q7snjtx6YDf/tMjs9CLIEDPiuwijywgTP74AB7CFO/TzzmgKFCY8CHd4l6WQSsfZJGs4yC/hb36Pgow/s/n7/WxYWEQu5IO2zUrjTyw3oKwXv4+pABiIYZOqV95Xh5Q8G89XV9DIMFSQMmiV25A3m5f796GDt6ddJBfMRlhtdLLICR/0E5ZP/qfff6+j2PPh9FsAX5xdvDQj4cOEa++oVWezv5ukaWQ5RBw4g6Qjo5t/e/w29Jsv8KeDhBF/8EBW3+ezYZjAG3bgDMzMK5Eb9BfY6B+jtBPVzCkr4KfysC1hD1/CYtZEEmwv79cAF9gA7+6QT4AOnBmkK+teSB7cKbecfDgv8zRTNA/nnYAnm/AT3VvH1DFb9MAzZHH3vhwmV6zjjNffsAh4Y7gnGJpf6yNoSDKIG4/Dg4fYExRJR6soFtCGYCbcFQw6B6uD1LPVT7Ug5O/Ef79YdGPuTGDj4CQ0B8ecDawE42IsnBf7eAvz80hoT/xbLaxh2EuUH8t3NEgwbPdzHziL9oiDY/NYAOfVZJWXTuvmlKxrfhwSJ7W/93NwIBnMvJDoLxl+jxCo02WEcK/6nDT8W6cxCPEYVXQgh8WEGhdUuxQUtcwR3/T3t9hMTFsr/jgGdAfoERdcxLRIb7t92E63sOPpSEmzuuv78EInif/QiHqL0KzYNJqfp6g+l5i35wP6F0L7svCca9gH27g9zCItKVtuA6UX8W8yGEhn4cB16Avz3gw/Z+UYO9fwJBUAJo/JaBMPuTNdMDfn1MyECHiAIzvFTwc9P9wOr5iIDtrwwBen00QzSUjsEnsi+EeAFVt4FxtsObifezclJPS8/7jPzxgAUFPu1Defi++nlyQf7PqMiwe6lMTAB2tsm2+jnoy1j9T7Yfx/xFvve0Q8yJz/uut307RQy/PpB3NkPpwaBHVbjMQxsFLnCb+35E5n+LvmvKG31APpDB/gaRBC25lkP7c/cGDUOCtMvDuoA8xhgGVgHdgJQFwPZYdsfJboG/fs4CETt/eJcHjYKowXc7hXvyBJhz+b8ByITG9YWp+vv/Sfh8cC0HJUQBu0CJQQaVvyD8CkmZ/zmxH7YmusUJA4RKgzc/osLRfwqEYkkUsOo6OXc0fmyIHzuZATgAMP+FQD0C+oQxRQT7NHyLQjM9AgHyNg+AlAj6fNc8p0a2SGEHNMkMtxOxULaQhi9MPAWiv6DBHAFw9RYFnwOpPYC7gb9GB7hDJAnlvsE5OfU5/7/GrL82O2mElgiMvuCB7rXtg323rb0njmv/lwG6uM0GkTKGvUcBKjoHVHe2rjrwh1T63a8oyZAIobXkyD98UgfvwtA5xEQeeXCwcwNSzdLAysEzPu0D6nSR/F4E9btwDdME3ECAe105uMStvyN65PV4iEoGUbR8zIfFXHd1PF68ckMJ/jJJ6UXVAhe/zzJOxEK9VnjRvMSFPIVZebpM/wXh/eO2/XH2yGMH2MDyxoTEuvCXfT3JinpHvFs4iIgyBtP4hUUYxbMFVTcVu5tBY3eOfuoDdkIbveaG+jtifcW94joQEMN8cUI+RwTzfnqEQKaAh4dkztC9zzwY/YZ92oc+/1nyCnJxwyOL35I+BOe6KLaGPMQC+n2PRGkxq0CUBwU2R0BmxBMEyzr4vre6sUS8Aip4DUumyS683G6+fYu9H8SxkBf6lADJfdY/90DsfKrAggF8PUjHUggDNqFUjgWHL378GjE0gL4GB8bSvxWCmIeNO7FKInIpv0pNre9LPD89j8D4faQMb4Op64/BhLw+AZQJAYh//r62xO3lfDkWnbq7f9l+gsDjBXMCLESdPD9H0HTcv/GMUMGbdWJBxwzOdBCCify6PQv9X7/BQhN8+EL/96VHAf8+wFT+l3sjvtb9U4kdtjTGIoONOhKA4ICFCGF8P33Od3PHPEO4O8qSMTok+eV+2QYBy0P78ktFubUwo4CqOtoE+EJawJcMd0/wPYz2W8Kbsir8FYjHdjYEYkfuOgNI3IIht0R7RjYfeqg4uwVvTnMITIVWOzNEVjL+6xbGMYrbhKD7kgeJxPs0l78ABZG5KDWMAWo+Ob9ZAB+FEwwh+bo5BrsGOe8ELb0+vcx86vsbCO47OHvl0eBGPjAKATgNzfMqAVoJJvnNAdw+yQJjhzjD6j6QSQZ/VXHtgAbJegUidKMA9QPHhUm7aP+HlII0zkTeBQJ0iwGF9h/44EImyMgE14iL++5yEwWm/dv9zoRQP0J8gQd+Q/75lkXOPY464/RnuGLPu0ZVAzrD3MB7eSO/aL5QOW/DobpE/zmDDwYY/kAGVQPPbRz70fo2QLV3IQvn1LWz3rsodAVIwsZleYTBCrco83tDG9NQSKCH4vvYdJWvyn21B59/oUKP/2jWLga++QF/Wro9tktz1Q5swpD96EdtRNfHoPxsA5g5gTvTSPw56D3fARyGWDzR9hHJIIBDdWEF59GE/4a7yIAfvpD+njlauRu/QcSW/GvPebp9cuNW3r5StdKDZoWWtYr+zAOTtLq+FP28y1HDsnHv/uoBqXrgijSIgv3t9h1znsytgB2DFIhUbok5WQpj+SH6u0aJNykM/0gpOUCKkn/J+jnFFL8IM6t6yfbs/gbOxIm5gQ5ND3/Ls8fIXP0X9p6Btc7GOW07pkgot+qHInMEO20J1gEYB4s0nYCqC6c6ij81Pz+4SD0AffSKmomzNDp7jEQPfAwIfwTAdo9FTvjCfv3QpjeZsmTCOAriy6EA9HvZR77wrnVBjUHz23/6xIfABcgBfGpD2UC/u9VHxkXrMUjBUY88Kr86/MSBBKzIi3YOA5g8IgCjfJuDC41YbdC8WEbRPID7vhAHwYave8V3/1V82QCyyNMBbfkAAMCFfHvPAiZM+Pe8swf7y81cvBx+WLtGv4BVbnFPz7B70OpLO/K4ZBB9936HHv7zv6JMPna6SEI7yTNNteMOj8T4c2vTQgKKgAUPKDifcKB8tPrbh83ExQJ8hXh5GVKYf5Y1t3oM8yzJJDgCgNQNAUQZ/ox+l8SQ89r2HsFCRK5AtgjuTE5Bq/21+/64j6/vvfvFJcx7xH59nM84f5bwrbUsPeL04goZjqx8OAlrfzxCxXjINEC3En1sB1L9g5eHAnQ6pQaEtPkGhfye+oKJADtOuXu/OUXq/9L3fEl6gGB9AP2juM6Vt3g8ttQByXYRh8x7R0qkSZh7avk3+9P/r7huA2F/QosMO6tBntS/dWb47r2Wtzu7pcjsPpBIcwI8tTPSpXffds1BJPmcu1i7xocJRWEPvbujOk/J+QShP48vRHfj/q7GbHUVenlS2LwWhbrJnYQevuqzX7wB9b52FgViB23BBQL9gN8FHUBX8396ar0dBIbCI/4WyMpT8XmX7oAO1rUCd6K/LD6Lkp548U5VDvh2Rn3QMfG1XL9hxD0E+Qi5P9O634URw30FscIW9RA5nYVOOb6AboQpAaLI2LsnyLUAf76eR7C2wsaKQ+99OzmW9tX9u0Axxz5JR8PG8Dw5xMbZPN65SwK6/8g1E8CEBn4IRrZVvelCHDZoET5DR7hn+lP7YLp7B3mR37Zn/Tf0oYbd06e9Lsdr7QRqwwJ+gseDVoqFPl25nkkgA+nR/QMyL1uxsTuOffK+aRWbOICAfsTsPf1JKLIYB/GFn7fadK9HLckIr52NT4a1d561RIPkhtm1wIU9Rz4+8MGhVcn3dv2xirst3/7r96tK0sDCPS7U5P4a/9j3vHp8ObuwTHQ/Q78CC8AmFxhCrr/ver+/b/uGsL5M5Xj9eEWHJZJOB6H0E8EbfWf7y/m9zTUMCH7Zvj6FnL4IsFmGc+2a/70MZHW1RJ9EU0EJ+euHc/PaQBPN+j1LEXv1tzr6d/L6LsosN3z6MHS3iTmGLUzf00zBdDwA7/dClzaJPlBG0vwfQ3D3PQNxz/UMNPPWdYB4BEAxTEM7RIqCSdM+qC6/REc+bmOkRwo/EcY6Dka+wkDHex3xmX67v0g/0ALC/VEXWAmpx407hrTvdw7tCgRneM9Sm4bqOBjO0YbFgB+5rr8iOfkCiXgsBmzIwa9LPZyM/b9QerkH7ieJgVr8Y/3C3SS81AUB/BRGtMAgNSM6rDDIu2V6VMcmSyBMYEJcAZB6zvimgT7z1AGU/Z/+d0PyCyPHtXkOhow4JXw0wAhFUMrfdQQOCsht+WLDiQCL/Rf2uoX0+7SBUjdn798bDMoVQ9HGyfe5OjzD4PsVt24IKXVtvYxP27uUvCOCgfhohyv+AAQl0ud1JsYgdyL3UEBKqcE2eLr+T+7C6X9gSQtCD85jPgu1sXkQtlO5aD7RDeQNdLnZQFMBFz/1AZN7bL35LihBD4+P/f/9pUH2TF9AFLvngKyyQTm/vzwJ6Eo6eeRNdz8j9YUB4nxzPdss9IbGTKy8JAyDRBaGwoELNgd2cvo6+uqCFUejNhgBrFEuT1k5czNqgCcESgiHPrrL3/92Qe6I6fZpiIBySC3T+1BDhoQ8yEnTOWX6uxcR1/9fuHf62nWpaAuHXzxWxylFmD2ikxUx5390ips9e/JT7id5a0WNCoQBVVK0BV16XoYe/6y3Hr9SRsh8/MjZBpnE0Xs4NZnD6u1XdX0C1T2QyAUU/1sMhrL/z4GaJvcsjXwgasz+uc1Liy/Qon8W0jNBI2UJ/OW1vDzI//OKEJC9hjFJITtnAszzXm+bfkA7J8U7yPtJ14LVx1kGofngcVcDeP2aLsOLPwWmAnK9GYZpP0Wu4Xq/9jqEm3pOSevLlAIMRbu06cjK+LI1HTeeBjvO0Du3UdCBFUIQeFbnesuK9HIxeU5YRTeOoUEZgitFCvWjg9RqFfmcgO2C+JUKdr8IhH7J/KV+Jj6pU4m3yj2Fupf4mr6+gEQSMLgfvNGOITSBAqkB//RwvoS3Dr5nAt2TsEViPe59i2fcw6d7pYOBgGY3cohiSwuQ8jo+QNI0t2y+dwREHH6KQTyXwHrhENxFt/3mROwyP39RtETGDID0xakJU8iBDRrxMj0Sdvo+yghigTNC4LnUfM8K7Ewptie1kCy/81mESc1M0IbBrn1+7sv/Zb9hemhCxvJ/PeYUrYW9gKyRmqrbcHh2mYQnHNVxhgeKQSI1QAC8f16Fh7of/m8ANhORgWXEqo7pcmOrQ/J9/Gr+gNB/vovHqgkSxiVK0fQvAr4sFPFxxwVIhAEbuONHJbs1Qf7StYF883wAY3OsiEeLvO/pAUL4/cMtUgWJoHNxv4Q5GS21jRo+wpKxgIBvmAv3v9Q7mPR1AEm7IPhWjrjHAj5H/XeDzHweNLW+JDfvwMACazsNzR3EjsFTwbN2xPomgFj+27s8ysFLcI4wBNU2/3wqsjZ54Hpf/1eIowZIxGfKORyVAiD3vrRC6qK6r7ztyrcIYIS5fqhIP43abcr9K7Fwc80JwLadyYRHaX9SPrA+/AmcMGw9EAia+OUGMbMKOo+Ubb+Gf7g86Pb4AHvCNooxw4FxUEN6xRW9NQyevaM+c77pOalzOjICDEHH+YbxPu7NmIQ0LWRQvz+nO6m5D/jfzdF5RbymwGJ+xjy4fa5GpDlB+mG6tH95jGlDaP5RzI4LTzpOyGd/f2x1euL4cACbBF9B2w6pyxjH0QMqOYz4imz8sYbQS8Ry+0wLGkbKAwn8DkEYwHrpwHUGQ4J9eVDgET/CyYHzuA+82gULwp/zr7pMNRY3zpPcg7NDDT0bOYGBRHUkyaSPH/wV8g94Mksk/bC118t6ffL23gG7QzPLortn9hv9fzeqg4498HdSiOgD2QNvAuzFMgrN8+t2UD6pOGmvB8DcEPMBBJd2y0Y+Wr42bszFMH7/8m863QJoBi7R9NZYAkp+i8Ia9DWrpjz7uV032go6T4/JTsUuCYFAGPgHphO3H0CpceCN2sOBRjGIXsGvC9M7/71aLvQrHAIgw7fBuUdNjXqG8MKrP9pwejG3N3t3qBZzDuZAhcSA8zv1NofDkXjqhDhNDpy3tU60yLPFU8bENm49cjW171VEEobN+Q0BmA4WSH1v7ncpQbsBPwVJPcpHGLxWuuE6W/DTxk3OHc1/h3X317nAyiDHG4YYPY6vYrcGdCC+MowYkVKHtjdmgXtEvYNCvqtx0fHauuwEMUQ+e76IqU27RQWISLkWuUL3ZrbvQ3QFXweZ/NFJxwBzfXKIuiw4NAaBl4PM/YJCoMX7eWMJF4a7iAM4DDQPxQOyCH+BiyoBP3sQRseDhjyNUYQE8MCNedywzT7qPbktR8AUls34Gsd6y6cLWsUjY5yFrPbRsYwJskNYhF17pgNIOzcA3o1OORz4K37lPMD+avr5Bg+Bw7MTutk+HsoWN2P/Bs6juuYCQT25AGL6ov1BETFBePlNhrc5CQOAzGb1voPLNOA7IkWNxekIn4C1TdA1BAEQO/Pq6H+Yi8dHAzXbRKTD60BYPuoIPkJfsgY0lYkqzfNAoFgNO/G1Gz0qbzyw+8AlFcaLSwnSeygC6T2yv3H9Oy5J+FyuaAzkzQlUNUnj89j+7bjdAfz1dX4idxr9bsuVw8yU6374LIv9HIMbbvR/WRJVutuCrMpi9Z34ggQfAMW+brKKPIXElEAfiMoQqsZi9miGqEGdM95B+/6qs6TEU9H6P3N/P30NQFNPxvglefM8qvXRTI/5szZEAMAxC8IJV6oN6X5wNuKvz8f/irFoiHfny3A1voSEEZuAD4NdOjmMYvx/8N2Byi78h3FDfpGox7rjEEjTP3tx14uyELl4AjjpvnU7CsYCAj3Hf/8Ys5I8MgXtw+vFrEn4/FW9DLZrNt8Ap7lAzXpDOzRAifIAwgi4x1FExTzB5X99ZgLHBfsK0wm2/Je0KQIyun0F7sBaxRdNqTsiBETD+4CkN8xw475xfaJ7dQS5Q6dB0jt6wIMKeb5pvoU5w79JeeO1ZAwegq02xXhAwptIEQPqhRbDv3w6NOd/0IQFAqnIw4oLBrp3dPWEOQa31EVxgpRIF4Mid8IJ8IX8yzT6zuteO0B2r7rBwF+TccWKdE1ESfbrwelCH3fNw9GDfb+Qum7Hn4IadTzCCXFuNvwW+sh9BZBDlfp7RQ/6QYATAdC/2Iejf0H7gbSPgdDJr0qw+rJ05AmqOx6CWovcxa1uzSd8fQ0BQEHsxPZRSvlqvPORL0DV+5F4qDiTeZDI9T/XClePO3yZ/+v0PH0gPU8F98J/Pn6EATxCTNs/ioAiuQwvcz95+mS+WcNsyeMA4Tr6eYltOPw6ijEF5wd3h/I8UvxAvXP6eb21uvSEbcdEgQBHaAqI/eRz2PR2OrZHU4CVznnWmgESv2h6E3U1uxVAQHH1fLEGS8Cki0lIn4nSbZPtyf8Ywyw/yvuA2n7DZn2ceovzb7/YdjGASUaaivP0uUJyzzKBskYocHJKDknsatvFPdIIOE5w2QdmQwLBXgyptk6C1NRYMDz6Cf4gLR48rYLdRsOHa8cpQAo/xT0AuOtzfnDuAag8x8zIWHaCH3Ma8C62/71WTCcBDTxIgwpBChHJxi75oL2iuWz9lMFT/0M9rwFDvRx9lv/ZQb3MNQmCglK9i4C3sO8prEMry2AH3rgPfiuTfUJROk06UHksehx7zotkAYxKwlUzQ8kx+Sajvio634lGkG9/jobwiBvLdXYROdJzNzDOQEWJQo20gbCK8W+v/rcH0XpERsK3PXtfxfLAQS3ZCJqEDP4dx9o0yUZQvEVQ50Yt6ld9B3++/4RyfIohjJ/9PskQt1Qz5Dk0+MPKnsR6CkkGf3aDhht5coDsOAzty0JGAU4GaYHHhlvCIzxIASYAf8IbApeDIT+LgEn3ufRue45DEL+hA6jHEX6YByKCBn+WPhV8svvnwBkLZz8NzH8AMOyEhsp2eP//ku226oLJ08kI1QDpu3pvmbmXfzxF4Mz7cpRC0cSd/8zD5kCCCRjt/X2ujTV9JXf6AOE+8GrtyZsHqgGeksa7nX92wNaxEToxdE52msVRwokGDImzhcU9T0Vfeh4u9wXp/iLF/MnVPzvMkvgrbcxCG7ycP8XLpn0y+xFL/v199vEB2bcSy02Ijvq/yVtzLLlOyYCNFUehdU2C8Hn7vG3HFDfMw373nDLJxtrId4y/+TE9jEZtOY5+XbhpQ7g4aS+NUzNPVrREN6ZCfkBE//9IoIdXAfTCd3X5E7CF3OYeAK3n7zsixomEURhb9SRySTXUCa4I9uvXv/OND0U/NAUK7w7VdiOBVjk5+ec4D307U6z/AYL9imGJ9ougNSa6K4ThN6qrfoYJhXT3ZgvyuoBDPUAk/FXO9Li3gXdCyERlAPH9UcTXqCC+YgZ3zVhTifPjywl+0uxf/TvBkbxxNp28NASDkzUHX4ZQfqSp7Of0M1P5iETWWH2+Ootkyvc0ScEJASbz9mXXi6nAlPd6EfqMkw9wtwd1lsWq/B0vTLiehpCNOQm0AknC67kOQcF+6L8agy78VrsyO3PAWDvehZl9wf1WAViHfQtIuSMDHvpugG87kHE4jAy7TLgBzTUC+HNR+21C5UqGSjmF9U7luQ5zW/pv+Zb9NXm5vD1CxU0DgB/6S4DSBN7ENcCJBLT83sQVshiyEokm9HJ+EE0a/DXGcdgP+Oh4+kiutpZ79LtMQE4L9Mq0QGl7IvYLNbr/hr8ygUG/HVBihnb8HhKaQxnzCKvveAn9+T72yh+DjoIOvDFCv0rRPOW/fEJH9Lh7LkAaBVoGu8EZBK07yLpxNth7QP8OyhNQicjhQe+2HIEwNw/IMAuzs/n9vTXRO4n/J0eAS2B+0inntGzSMbAgvTFXRr53Ohl89ADKiZW7EMGFirY1YcZ4/VUxCvfU/frUYkP2Chr/mgDlGJJvRu+9cOI4aMwQgOlLaD3Kfe55/v6VkkpBVwCC4Z7yYF02DrhH1LtJuh623Tv6/c447fv1/8rO20HQfPTMngw/vvP8MvfnO6C9crBthlNLWzv6tgPAjQXDO9MSbYO67c8B3XqlAFqKqbi+ueII88mnNBD1n8A3ftXGZntABBADD76vid4D+Yc0gA/8W7oD/RL9aPUowG/AAP2kxdiJeAH2vWICN4NueYR5UP4DfIq6sURcETS7O8Nqxyr85kTt5LvrLQjdzElRi4//hfw0/rkhBVQy+v6LDTqvQj/1h1DQGo3vOCEGZir3wXhHdfRmxAg3rUgDv4HM0kh7PI7FQCIJ95F60MWhzPEth8Ksj26DnbkYw2GBJHQM9N8+CkLw/VUEtUt4hy15KMCc+3h9lYnWw/18z3X1Q5b76ol8SY9y/bEPe+1JLPvJiVT9pkFMgk/41Y1Df+r/37L7PJ3D578XRBR6bEE0OUD6VAFkk7gAPzNujh7/yoiGEqO7APVwvwd3ovtTP2FBBc3TA7PGycYFeZvz07UcwoV8V8BMTQnzxMO6lSiBWf0/ZkB42f4vOGkNsIiVgYktlQySB8QzWg/Ze/C6m7U2OEOKwTzN/oD92gCORJc+Cj95vK89mEITvPLAbEV/Sl4L1U1SkwAyXrP6wYk2/kIFNy3/8Tux9SZKQ8siByJ4LrxZcjT3AH94+70H2XONgABL3YMdPb0AXf089mJAuEH30H704r4IkW/xOHpjhNBL/kGRe2J+D0HUCyrDFghSv9Fq4ba3y3aFQb+aBfMGmsI3gcFAgUWfyVt0XLJEgTvFD0ZVBJ5+30ERPNj3msIQuJdzdf6Dy6+MWDsB+8+C6H3LhIsCM3cVPPL9hoEbSGJPZET8eic4wPmtyf6GhX60uxS6OjTq/0GJWnqaBtgFbHiJhFSDbfuJBwZ6/af78sjFR0ydhZ1ALLj+hN03b321kSjy1X0AA1Z4kBEQUkW66Iw18pCsas9s7vg0mIT8FPUNEQdSE5r9tIeONBPrUGsH9W+IuT02FvXSuUAfwffAhXnt7woz/DLDvIgMNAfERDmDqD3Ef3EBBHsQrt3s0bp8SRcP9oHJPDHGy4OLeWnI45AjskLpAnrrhlv/cEKtld1KIDhIaY71eAXetqSMHwjG9osLfcQ0ts0DmDhK43c7gIQ3yF8Ny8GFTl4F0/UOe+A9djpfhevJowffA7J1ZLRhAYIFXDt9wFg8ZM3VGBa51jkqgah4KO9tvPxBT0H8xqSPSMxjf5R5D2/BgCx8ikShSmG9arrj/J/LGj1qheg/6WWiuKVOEA0PC6rEFPvnAH64wUgAO3Y+psSvsdwLswMBzNrB2LhXRby3h0Ed8Fo+z4w0g3R/THozQ21wVnm1BUiBYgIJPPQ+dz5iwtq9HkKZAKqypfn6xgqDAH3Gxq0HvEdyLSrzqgSbeB/AtsQq2DJAgrqpu311AZKKMX/4ZwC+gP1D870C1r5/0nZaL1f0eQSJA1XHtZLyDTwuV/gWeXQFeEB+OKNFezkLyaiJTwzfet+qMbOAM16NKMeUPytHpzxbNae9h0FBAAD51cDxvKApUQcKCBY9x4dcxQXDAnY2BA1HHMF7P7w4IAd9QpoGckuVM+/IU8/2eJc+Rrd7+ueIk9amigb4AwNgN6++UTtQ/L2KhPZQ+lhBib9lFIlITmO+OScCJ75Ag3uAwEqedsD/w0wMQi08DHNguz5/Vfi7f4AW4jwFeF0XfcvExM2HQzdZpIDJoIvmMOOHtUWNgy9BV4YsRif0T0LTgQA9grKAM1aVxwJncu+42D7VAty+/gUn+cV7/PKR8IHEaUM/yxPOAD/NujfA+D+Dwy/4tC7k+cNEcUg5wfTIaoG2xMl7nvCIBrjCHr509K+B/0qq9AJGvMgMudxBnsmrAaKrPMJoCRN8tYxE+paG6MXh/abNZLXQ9cc4hEMigTyCytoshEj5qrcptqjD2/43Mt1B6cNvPOyOQI+ShLOytDbqej1yussYwagCo0faszKEu7cvweRErLmHUAQqXsELxwc2DgUH9q/G3D0ayN1557pwnNG43YgvAigtXQN4NOXCN5a6QeA8034zALk+CkXJyELywD0j89xCmko6uPVMHjwkQbTEInYfAsIEHvZlq9U8po9/z7cIXUlKxJJu/WGhOz9F3P2LkUhL78AOg8l7BrshgiKxxLdixxf5bUPlSxsKZ0ZJNHD1tYBhCaX8UjYdTBXBBME+yFlyG0afBnw7rEVNPABB4XFDNeCC5IBby0aGZk1gAoh2TsSYPme7QYJk+948hPzGgnCDvQJZDoVxE/V2/RczDZZki/ACeTpI9Hi3Ef2P0SRyGDr7xf183IIW9piBZ769dNj8fkRrgu8Jcgm+ATS/vzebtqX5CL8Vfc0KBUb6fQf/kENfyaO1vfYndGlIX00Bue/QU4NzOB9CLXumOVt+8DLqNUw8ycd9mTEIEn6QdseB9P+avedBYTqrgfJ74Jn2h6tvx/zIdYy4fEPBWpsFZ7m9OkYEVomRPzSM0XmrNmDxvUNHncA6Ejreuvy1QAF3vgIE+wHHO757RP+KgekBqLzOsun9Nf9e+ZyF+A4oQuv+rLY+8okAlvGvRPqOP3uYi87GaMdCynj30/ch+3uw7/8xjvHKWMgxgMoGAAGI+22xuTScu9I4G0o9zp+OswumRYh5ta/hul29+vJ9fPYJUr8ckBzIvgITO17vsANbd8t784EnhfbJh8gOD/gBnH5gMFlzdkJEQazD10DwQ+DDwk5hirW5fL/pOP1mtvbiyECD7oiFgVm7OAdigp83db2Pta42dAWCOC3DtMXYg73JfbKrs5R+rEju+2t9lE4Mw2BCwj9/QAn3/nPe+hTDjIUzxvBRGTwP+hMMTcc59Xz8ZjbD9i29izifzeTITUSlPrNF7UdB+/gEdjM3APJq3u+gVxa/t0lAhQB4FP0gvU1E4PxcPlhzO/sl3B9/xMPDSEPvoEHpt9o9SwQZRVVK5nafhz/75/l/hB8qn8XLCW15qZjIznQ3vz4yx2a7xK65gjsAjzbDAl5LBUlJN+R2/zio9vIH3UG0RFKFljyyjCbytvJdhOi5wrp7Q/NOQf0UgQcEvzn/tvs9W8o7gTd9k0MnkHrFewVgxd/vIm0iwCUKcPR0QZHBdv2qybECNIb6uIU00wHNSt3CKAIixmg7tfPaPTSIvq1MQBMCGTTUDYfCDojYQkoCqUTBal5xRgClgZIChk8jQp//vjZ/MCRGUb1YgPJ+Kr3WvnrM8cwEthY7ASvKQx42kDrZRYAuSsoJAQNRWwrK/Nt62fNvw0g3vgVwA0wBmv8iB2ORJL+KAL20FfXHdNtI+09uth1KH06WgzlEtny+Lu6wUTrdeKCFn8RevbwLgD2FzuvG5K/i9vnqYshIz7zGBHtj+R3FTf+4BKXANgBSgOqNdXfS890E08FDSzI/2s8ku54shPkdxCpMSXZffSX+DIeXRr3HPkc9r9w1O/7iRDkA/YwpiIfAKXTtbfGBrDteAyq/bUAcSti+fICH/UDMbABt74C3CvoNVccDsMGtysSzaL1fOVp+5Q9xicl3vPfczGj69v+gzH20Vj37P258rRF8xJI5if3ffYWw5XtQyfO7nlCsCc4zpIAPwA9/AkeafRD6nwAqcSlAGcLB/4KHiDs6fhdNelGJOPQ0ODYH7ptKM0XB9fSKEAOOid+Qen+g/og0C35WOB59pwq1g8NJZQEZhOf403+bue92NIf2B78PnUF9Br07FXlxPgzxCDecNhMD5UY5wwV5XwAWRzH9A/7WPiuEnvkmPlQEe/xmA6ME2zoxPORD+oE6C6qA4cLphkAAKMP8N8tAiEMCgeAQzATxtfR6zfNQBcEOhHlVAiSzIjFxxGVEt3X2u+qMczygjDu8MjrLygVwkHiaOs2HGLk3d95Kzr1hyDvAGH+tBBHCP/5zuqIBUvYofjhDrAR8PgaqYjd2AyxKK8a1t+dDEXsxwUCNULz3BVC72zI0cDnFa5FcPJ4LA/xdOOt9oT8TAFi1QotS/jx6u4VixLAIN8WGftMxj7wEelTEnxYKhoT4Svir/LF9WsLLB5S/hT3PjPr6ursjApuEHwYo4MMI4s9x6Zf2+X6siiRyubiPBBmIG8luPj3MYrBx6so5IX+A+Vk8zVCXukaL70zlvkFKmj75cW3xyb/5e+x9nEL/fUzD1gv7jt5MY8SINe+1KfordSIEswvyfjh9znn/BCjOIf8rurR1mK/Wgh6QxgbzRA86ZLtMSBw7gjvwRzo7gTj5A5j7ZM0TCiGyb32bQWx5hQLNjHw6lglywEhzJMMWhJKHmMERAVdxyoRggj66g8qiOVbImAXXfM2JOUrItT6+/3+Q8Z8FyD3rweuDMEmteDeyD0CD91mPmg1URdOLKoEf7u85X0G1BgPCMTSSkxH2Ljj5Hp/9g3PCSMT5z3IAzsF92LuBi2s49bsWDzeFyDUvfls71bYD/Vo+GEbClSw2E/Q2CSg2jkL0e2szdYX4AzJF1k3MhwBDXky98swxV/6BcD5Lc84mC7/f2QKPO87B4uaoecxFF3HaS3CPbRYqFcK1Hm6YZ/p1XrsGBc7D3cArkTQ3YAlgCym1ynlrMx6CBjzkvIpXxAygsUO+qsPR/wjDQMaDOyZ9B0zI+/cFmj2z8sQEHcOUi4cCrzPieOH5iDdi/aO49cAnAkFBn4tyynPDVux4a+H3rPpiwH3Q8X5qAedcmsskEBF2WSkpbZ0x6gYaxh9PlIrL/5k/oYsx/yPByXzZLgf71TrVBgoEEBgih2mkL3pdPM+5Wbn5D9MTPvmSucv+NMIZBbZClv0as/KBUAOj/rrP8HhGr1W8WXkhegmKERe0gXJ5RH6uQwBN0v0ua7vDHQN/vHs9LDbqC3H3u3k2A5s7VMUN9MD8q86mjdy38rhbQjOtXj1Ri8ZA6HwuOdnC2UoLuua6lY70wxZ6l0ksOzq7mUWqsPFIM1mut323nYBQAGoKrQMcPfF45jY/Mv+KPhAAr//EVTxe+7YF9Hbj9x60FQDz8anGdACW9LOKdzo8CkGCZjp6cFi8JIvXt3bDFwaWSAV2PbfsSIqCTLYlPsEJ9bfIweX+r8I2+f0+5Y1cOuT+GKx1CNYUVnkAx6GFOPckdVLGD/0JOuI9rvooPi7Dkgy6vjUD4DVGgBiElbObB4zsF0hdTrMzkIaW+iUHnYrpvVMzpb6LxKM6E8nahBQFtb/RtzuBmgJIvxD9+v8WQOG/g7RnuaLBasCrOtv64gNKAZHKaEHZwLPA5SgmL6pGQ0FxPArMFMVLxgmJTD/SQmN5eXq6c3CEdoiVNsRPE0RK0h6KkmaXSuKG8bT/wbwBtsCLAzUEyfpjOHuBqwfSRXv1c8INRuH5lcPu+vmGypDOB27GnfJYtP6D5cUaslqBeJg3Rg/KzhD5yRX5VnYb8Tv29sEUdd2Fv/zXAO8R3sAWxWw09OHTtZrHHY9it0G1rQdsdB15RD/DBq9F2yGQe80ZTj0GhugPbDvr8/8qIQHniWL7MYlnQ+W0qnRyhWr86vh5UkLJ2T81/DF+p0B3gCNEEq0oL180lvp3E3PQixRS/5Y3rr1bb18/VHsv8vB0BANyC8jI7Q2cdek5QUr1RJ21LnxXxDX66tJXSeXzBf8H/N6xJUSDWkpF/jpxem25IQVDda85MwK5sMHELUt5SkuDpncnPRuqdLPDhBZ+aIrSe0B43c5l/nf9gECTtWM4rkFCS0YTWEm6L9++DffJt4LLW/vrOXs2rIN7fRZF50j087KI2QIVsTM1PAEIQ1KKm8XmQk/GR7HvPXeCLT8LBOH5f3GPRuSQ5YZZmXbTJXP1cmf1W/xcRqo4c71S/mqC01HthlvJHYG5/EUzQUJhGXMAU34Avqo2EUZmAyk5+FANuftwEM9miDCBrX5Cgir8pnj8DBAGIzpa/iIAmYCx95//W7nMeTHQjIErw23F2okFQ5yw9EQGflpzlDARgwPTnH9+9ntE1IM7wELEIfNzhB4yrnXQURu+c39fBxSULfgdOIuGnbKret13VH3fhlSKywerA5tJ8H6bAXy0lrfSTTp7MjzfQ2y/ekMCiphB+b/UfxQopMLy/Md8b1RUQ+wImUDrcGf329N9faj1zcOue+1AArLzjiJOIkwciKou1/WTs9EDYQGxg8PE9gEfh7XDAn+YfrHBgnD88FH+Qowe0OcRa8NJd7F/LrhVgym1jj+vEMo4VxDR0tg//Iiq+kWvwrebQhjCWYEgC8JIT0ewhp94nndiiA5KfPWhuSZF8T8PvQ2Nv4SObKb7bdA+AtwGthBaq1+zowuEBkfG63m+9+Z7BMSXyCcAi3x/OxF4xshpE7RA6AI2cga0533ztdP+LD9azdiAnkg6TxUADX5/cSKB6EDNRMUIsfzMw0xCHUWGuDR4XUB/uv95FcADiktGTwVjAA1BoTtjPutAlDBp9MF26LsVBtiNt/8f/dUL2Mw7gyyAIX7O6DHuTvndi6TKkUDmh9Y2BP+dOZCBLIIwump+JvTDC35+9YvSRY8tfb3QtNXFOf/yNb9AMIEYecj+65JA+3t0Vfy6cIa5w0kGQhw2qLgVQVT7rXkAyYF1hvxkgVTr00YmgymAK8jlv4ZwNbDtBka3Xfn0+/q5bDzl+8WKFUJ0v+GycO/utZx5+VEnBVh8877JueV8dbvYM924z7lM/FREdPcyRU5EwYC9+1vzfslmupe22r9nPuw7UjVJxKxBNLuee5u6MQUzVBMITrTlfCD/ffpB+9DJucD3dEX/P78qBeOKRIhjwaU5DUGpg3uGpcgufIo/hHTW+WSS/cXuSAlMGPkbL3+3bVNLkI+9qX59vN74pwPLigiAtz4fQZ++Z77YBuwAjcQgCUyMjUC1dVuKC34d+dBKrw9POtG4M9dvQ2QEUQze99S8gnsnu/aEmX8agFNJPosWh51Dg3/bdMCGLgLz/D/BxLKJC1ZDrEJEBxW3EwCbQraZKMLpe2D/GHRNxZW8KklySUTCoILCw8A9ZzT5CLt4g/5ljCFNuY9Bgaa/63eweJ+z6DK9uRMBko+Bz0+JSIqLCkY093Czcjk1+Pozf5SGMUV/0xq+YEGDxHXxFT0ouJ78qjiEOnTGp0kWFMmLZL1S/ZjviHG0gBJ3bAZQTK79qMmJC4iDeECyuX45V3RD9TnAk8PljAdEIMX+PL42fkBFseAFyskZ//lAb7wngO75GvGZiBpZHLD87wnFOgJUeNLESceVL9vBv0Odg5GIfJZ2gP6sfT6w67F5Wb4oB/r7vf0xzwQ1cE5KAit+D4c/sTCtEPs9isZ8zweKfeEzxcPUPMF4Vz1ZQ3wAd7yjeTtOoE/oPBc+Drk2uQH2B0g8ScjrYbjqTCIIBcjjSE39Cq/ysq7DRb8GgK95bLjRDX99co6MQ+g3KgInsyA3pm3hTXKEWEKpVF41pgpvTCOLL/2HvHr+s2luvuxDJr6sxJ0EZH89ygnJwH37+RMEasGOdKCLJ7bhur0RxYZDQBZ6Z74Av53FzkdoQbx5oADgwitATDmMvxAKqC9GQmrJcbppvX1Et/31broDXXllQH1LvgZEz0J8GvrliWgAUbswuk7xygUPyB5H5wbEtehH8/hntLtDs0BWAWB0FEgvydRFlQHZ7IJOLs7Cejq7l3hpf7WFytHMuIXvGsOrN88AIL7cusFEzXXd/91HKH6lBq77T72LOxw70s1tfNe9RsEdvPR3Evd4zdXPeskqxJ3/PnwJvGgGAIVl8d/6F8r6AJS3kbMTwnX62708SaVuEEGFzyX/vkLrPJf0STM5A4oFeHzMwyyAafwFwDuEHH9FB+RCdzeiRttF4wMsOAK740MB/coJqnxJ/TxFhwPVPMS9kUgmNhoDYsVMPyrMeLjwQFoSs7smN/yQAX8i79z6xEYByotGgEzpQL13FDChevoHwb6aA3n46kFFvYb2q4l0P3eFbYSYNUG0bfsJt7P3/g3cjmhEGb7M/rZzHbV6g7CJiMj6bE88KtQsQji74kHtw3z7efj4NPoA6QzQu03BhT85sF/FwDoHM/6P+YFJM42B4/4e8bu/M0EhBT6QoP9Mvw7B6q48dGJDyXYLQz9Jdgmr1HmJX8P9tZx6g6dYbGC9pXyBmefDyBSV0gRygj3jMalpAyc0/fm99b6WHhXQ4EEiABvz1/0YOJCxw71KLs7y0n7ED/lOFQYfgVFuI4DCP2b5IjWM80RHOYccyBRPNgXbq9mri8OkPhR5Nwfk9IYHmt0yBqoLbnor51FvRwjwOOr4p9JKfuaNrIOvOXHDlHX6veCFRITPgAw3q/2Uw/7Qzs+cMTb6ovgSvisP9n6rRlq0ozMyTd9/GXdeBdcHN4OUPfB7d0SbBf/BjTb+vKDB18BbOu92xoKoB5/K2IuSypT6aHzSuMa3Dkwehmf/L34ihefK+NMVguPxS+yKueINJ7+zyfB5/ALyzVFBwYxDAF17Km9+P794YQAPVc6AGUxfgEV+7H96cKx+YAVIQJ0+zc5lDhDFfcE7up50fnYr/FYAIMCEBfzUz3vGf8xMFG/P+kp7mTwdwHpGyNPHiql/Z7WvOEBxLjyPDk1LSvzxvLkNZr6Fh4Y3AOlfggsJGQ3AhNEQtH2Aayh3NfSPw9iBmIH5xBRGwwpeeGvAUb//O5nIWIN0OODsmjtYBMMB+oHOMrW+6gnaCAeIYcXNuS8r3XCP/BqOuEFLAUoPJ8EYfxtBHDjHfFb/JTugTHE9e4E2zdz6cQAGs2pxKPuWRq2EbUFqizN6qgDWPZ3DRECdLeb8T77mSbtCBwmNj5r5BzxystSBh4YYtLZAjAGTue/7Woh5g3T3lvx/fQFDUwcWyyBFp3U3/Qi4nn29Cgy6zoQjQnvASoe6SoVKafqCPLCzeftfQtl99szQz1IHEvsA+3yBSMDmun3CZUVkgyoDBLylBjLId7/P9Yd/oQTWxULFhn1Mf1j7iocEA4/+ITOYtcVNxvwo+2jAzPXhvbhG+n9Bw/VJJvhhfL4Cwrsif418qC+xuGCC6nqBQn+IF7eZwj//qvbkOJvuRAVSguF7k0PTQBgB9fwK77QrZAMg/xC5CoGmBOI8JbAYwh9CPgUswE4vqzi9R3sFZHLibev6tLeyL8K+Wj8ef7fCvIlRxu67vn+6uk34HTGgRBCGK/XfCAGD0YONCLL4bTdx/RZBN7yqsjBDmsvyiyWAMvaPgamt7zVvunt1i0BoxZ/VwAxOTCzIuQRVvPRplLqwQEB+9v+NA4NH/UwgTtk7JsHLQuQxN3PGRHIHfDE8P8NLe0G3T5eHj7TxOsD7L0IXjTv7zr3QNz38/ojMfB8FhgGqiEUFOL0UQ9dHtgAMdCzNwEPssRm4A0DcwHg/7ckcCOlPa8GXhObN8cFmtT05t/qG/dOOAPopAuc+RjufVQ+KUQSde+j79r3fQA2DGYY7Bc26Tzhw+7DHR4usB2x4l0R9SHE5GQKsdmDD5AjXuBS8+z9TyYlCzUSVymQKzAaA+g/GBf/sdUGF7EIDuu9N5kmpREWH0Pdbv3b/TEOUhbR27gYlh2iJ8MqMfnV5XGtbv4jJbPg6CDTKwsrMvD8wss4ZSFY+A7rxgGaHWrCe/ZLJnv5+QQCDKUFx+zD7ZIZ8CgACNXfZOp68z/0GOZh4GxQ/znTwi/PwPUVIIsVf/ZAB5zyl9/wDtgNtu++0w7Xy/nI+igmBzVdDvnli/brDV4kWAcqpj/UKOUb7kIolydHMKQO5/XqBln7V/Zk02G59AQmHooiYRcOEn4XGcpB9Y8Rrs7L3h4CfgEvBw8U8vWG/t4FEtEDCwkjh+Fd+FXwYewCBkUEXvq0DxMDdd4//gX3yRTEGWsdffSSxKD1+vX6UPVM4AAs7E3PgOZp+E3op8AG2PX9CSSnMM8PxO05+YwUrPtL21zMNeUz7GbwDiSrKHLHp/+CMYTxSRntCH73k9jg8pkrRChlGCr6KiaCAHrWlNzc+jMk6Q2nHPAUmecOD+8dbe/+6QnlUgKXAhQJBxf2FuI0SwsW7tvy7Na8rPjYqhmjPzQf8PbwJcgTSAWzJkQW9JW0uaf1dPB7Ny8GBBGKCdoRmuzD5C0TfsBe7VcCmyvUDcH1lgeW8aQrouvF9Knud/w3DYMK0S+Ny3T5nxhjIPNAo/gc91IAQO48/2PvQ9MKGkIjWCuBIZP4exe68n0D0ALW4OcC0v9Y/vgZ0g9DDWMAv9/18aH/ehes7K31VRob7o4IFvt16iDuRO3oAuH9RAyrISTx6feSLecFJN5642sZ6Qoo8G/6PA1PEi3syPWR0OEA1D+ZCWfxrwcRCEcFJgCU6uAoaQM31Zv5LyJFKwv76PAjzSLvZhNF9a8NU15kEHrIjSlI1qrXFx561qzvqgjp/c02D09C96zQmO4gusTb6hJlF3xKfiTsNcz1jc1rC5jjtw+O7v3OYsSM7bYkDgAVHfIO5fnZz4XwoiEeC/q/pNFAK8DzWRBa77fxtw//747+9etHEpnldiDiITv48TpIyQve3e/v2yoYIgx5/jXvPiw6EUAGcfmip/UBDu4u0Ros3C0XAS35SCy/9pTDEADcAqEGe+sj22wcTBEIGIMKeO67C3II8ePh0CUL3gtc+QX0xCcdJpHqzAiH5pIIk/gY+9kOFPeODenWtydXCyLOECBS/XjCX9T5J2UzMh5wEkHQY9SnCZ3rzxw4N0Tducwv6tkxsRedDO03GfSZwi2yxi4NVXvn1RgP7wHkaPe1339Mjf0k2i3wCfSQSMUGtxpG5hOt3Acv7Cj/JQQf+iwKjBe3PZvu2gQ5/nCdGen7/3whwR9NB24ToRN4IM7Nut1e5M3qSulw6WsTAAbfMdYVKRh44IXPW9JS2Pk+MvCx6wntYvS3CDct4jQoubzWkMvn+hIRT+ktFDoDWh/uAagdpSp20A/VstjX86URDRtVMZYBnPW/Fq0HUNoY14I4gzAzEF0XcdTE173CceRtNLExXxrd3sn1C/dw8skWMf0g8dnIp+lKMgooYUznIKTEkfCT1HjSTB6TCHYMdAfvDUHs9vrDIRLQ0x/2I8vsrwzNCqX477A59sD24NSl/AcIo0Liw8TZa2CuBTsFoflqz1/u4fPND+0ZcPf36Yz5R+jbC/BFKPwH+4gJFdJ4A9coDw8X5cAVPzp++MbdTum7GmTh1/klQujaV/6JOvH4Zvyk8YHMLic+CEPiuxDr27Icaye0DjMjVv4YtbautQx5A0gZwQ1OA1AstSE6MZsF6s6uzGT1jtpb58k/oClqCJsjQytr9WD9tfHwzsz4jdmA2AIiPjAUGxwdYi6l96/fEOv71oLwcBQPGuzxUxHhAwfvphAQ9CADaOQ8+DLk4eqVFOYaiU7M2V38KxGO04rulNq+Cd4ZDBKk954S0Qju6d8JFfWi74sGjgSi1YISe/xr8UIXjeICP13fAMjhMOfTZiHGQjEEd9P005IPAdVxEyQU5+ALDfn0tStDNjMmpg0dxSrQmOOS/u0Y+BWzB1MDtBXhAyPrmf6l/ebuYtS56Pgpvy8dE2Xkpe7f+qzlUd926DD4y/tNE1spsBeJ8mPwlMRq1CQO4BDdGp0YRup16w5YaANh6BPqVZ1N8W0M1ybHMyQ21v7UFWUC2N56Py/Z6e9e+UHdzucoEPcmQtNJR0YSR+pE/if8NzJz0ULjqfaPE3EjO+w8FUwEG+K3DCUGjgjKAhXexAoLAT8Gjg8g9Sn3ue8TCnsYxgdO0HzrIyVR9ov3oDQeF6nzsfUo9G3zcNU4E8b1+fd7HY728EAg8AkSDDCt5aQlVvM5D1by6OvfCMDYoEnZCLTlmxbM8G4aSOBTBAAm19Is7bMUOy4WGHQn6xP3uibb0NwPy3gYPx6x6BY6G1/4I+YhhtaBvyzHQdobKJoNoiblAS0CfCQt2BP1aedvCi/++QcqOlvoRQsRD0P4GNaU9zr7CdbVIk0U+BsoCkzzy/En8JLZmQMpOR/wERbC/OLTUceSCj06jP/LKpPoh+uAGRIWRvZZzJvibN3rDpo1yjO4828E+ykP8O/RJPMSOQ/51eGVFictM+tq0wwVEOozG5MFle3UJoDrmB4gNTXanbm+/3klEexl29711QgR+HExizyEBqH26tMk+h7x/+Il/OX0EwvNAoANozihMX3rnL635FUQH//99FAFUxFHIUoe+B28B67eUNi++xHDVfMIdcLvu94AE8L/uyBy/4n9RepjDeALzuGN/IKzhgKHMj/XngWsBBn4gutT9gQdrA5xEBzjTvx2F/L0mAiG6Ij4VBLl0cn2+gY1F684UvmjHgP6e8xt+/wgrCtlzR7eP/SL178Byy3gBk8DlREr7O3+POFmB+HiTc9dACnoCiSLI/8i7PlM+VkHHepUBGYBhAQE1KLvXwOPGd8yh/CeJ2YjO/At96PsiQGx4ivyrQqq7YcdBSA5D6b9Hf/IF7T9LvEW+OzitOgMJJDz1CfeTRbm4adGrGH5mPKJRi0zKfzHF+kFDh4iwkfgp/h3s9/bbxPQD6w9hUNl/68TNcMgttrKRwUCW34E4fd4FPv8nfpcE80E8fIX4n/k7v3pMIgJPeSdAhXFiSeeCo/ekytVGUYL6tvgMavx7NC+AbrTdihV9loBoDY85+LicQA1GOn+H//UC4XNCtIJF/MUbePJ/ZwbRf4K/5IGlvRA6f/7BN80984eQP5WG6caXf4726EKyiE07bEpyAMF3iHXytmNI+vvjg5+/yLLDiRfDgcNyvlXAqUXSwxwHeLumA+f4LvhByJsAVfdbPUnHS8D8TWgKrcIurI0wo752u+RT0cNUvat7W8JyBPmASYPb7reBKcNyxtBRhbwN89D/M0hXiCYGV0Ox9+DsyEGGCcBDXMG3xDI15Xo+BUg3kANosKk7IYYLABLQ8QW5PSj8Wv8F6gk3BEKixiANMfyYjT5C0kp0SRv1xn6qrCWvbQQdx2UJDYmqwbZ6KsDOxK+C4r497Xj5TFB5zI4DO8j3AfS2p4mRvXvxii8/vdpLJ8OeVr7I7YTb/O89q34c8Do/ZGoFATQR5/wCD57Ty/5W6dt1UbpHtYk/TIGPDmhPCYObxbUBPXpavPc5eCz5el/E/vzrSB8Khsy0RYy2m/P4tRFG/stjPhj/hYbdAIo/XMiJgWR0LDyswaX+dPxNxb5IML0UBrtDAIt6+iFugINgMFrMwRBFtSq5LHrcCTjBcTtuQFl+ZLmRurbAO4k8xAa7bjrdgObL3zndwcE/cbgBv71udQbHhuA8xYBw/uFN5P1bwYTER78chaXvjrwHQHx7C4fUvSEKB/qgN3NMwreehacEK703f3gx6kSRwlfE2bdab3JMtDn1wPFDm3sNQgbw3AlGh0I3ZcEl9UB3HwdCkeTAQr/Ew8828L3Ze066lj7jd1S93kvRRVYF7ftJcPHF/PwVvBKLIcG3t9z9pwLe92bDjwHmdGq0urfJBnoI74+1AxX2BLdON73FJ0QsB50GOjWlud8CP0fySlF4NLrgu67tdYvDTUO4GX3vw5HD7XmZAybHyMCL+SgxqMH2RN7BSgPovlmBxX65gYw+zrfZQJd6XMNDwsr/JciUfryH4oRtfxUNZPpmeHtCTbVLgNZ0KvC/EL9EgENjxsU9e3w9BjsDZjSfu+N4oQOmA9+8igkJ/w80dPtQQh+60EAMB8FE1gpOiVq0MfhQhf1+IYJq/XC+d4YqyHmJw8cBPGm7YgGU7l46pA46hcm8wkTNUkeJXwUQtFVu/L8IBBlEQPrQbl2+LBaQR9f2pLnBAVb9hD2FAuN3B8D4xxG/MMTwSTeJznnS9ET9a3UdgqAIKnjSTJUQaf4ZwfA9JjoRfUM5SLr9dXeBBk5j+5aEfwdbeLCDIncff3hA+S1XQtXDSUnQhUuFm0v88rD8bbxrROTDzn2Yxep880CogSoK+D9iPkR8sXLuvz/60T8pRdnSjD4Rsjx/VsheBvusvjulvU47OMO7vouE2Hsms4o/+4c+vYn6AkDgCkQ6yEBWCJ+2/ghefMK5aUWY/c12UPlszktDxAZFQ7c8t4BLOs+Ldz1Ftw07Q/58C//NVg28NbE6OvltsQsKDIr8h8gE1IUMALdBDgmZP7j8mPovNKvEftYLQ+/FRU4ofGcuK7AaRsoNQdPTxlr9MIa/Bt2Gz3f0d4Ey+rTzfsQEAJFCnaFXqnjNtd558bpZNgS0GP14QBdCujsWwULL40rweBgvQ8Dbf1o80kxYA7W7bwlwenK5lj/2egN9uP9fQQK4bouV1FHBokS+iJ7+gfYyuHcAC8YhwYY4Vz2hisSCNsVxPhkwZnW2devD88GM/xi5sIKrRlkAUIADr3NAjnle9ke/TwNfgaP6EskHwXcHoDskuAe8n4KoBNs0BMEAdI8AAoYFDLdHhbuPRcYuPP+HhSFCVMAVN6v2RbvhT535qAUtxqSAOYyQec6+IjqBdMB6sT2SQvlAag5AyEB3I7ratNS6lD3Ug5v/pLzcDPsAsgaHAdI6u3esMPmJDwkOAUMAtflQ+qzIY8OI/ew3VHJOBCm/AcYRDgzEqHHXMSpBW0Nah3e5iQCfxi45hviQs9C36v1VhMcGpUYXkKOIhXzDvJ282XuTdDX+yMEWyajFqjdGQ6g3tYJYQJFAS3xgd7SI3b8FTiVHRkkHMsbsN0hyudvAAX7vSkFApAC+igJAKvuc8ifAqruDA4kF6cJTQolBr4d4OpbybnKHO1O5PEhciQvH1AUdeciFfH89iZpH1zjT91mBsYSXfcS/eX5dOT9358HkuwqJzMdt/mZDqwIOAC02X4UVdmt8HoiBAzJ+8LUMS7bKQjwA97J6UHw9gUrBewh8y6nBigGQvUSK/f7DSAl6lafEQ3ezUfuUjhoNV4EGwXR+Vvg4BtxAh0CVTExFkC/gOOg9HP08fKw9VP/o9K/COr2GEqsRHjoJgOg0oHl3NpX8h0E5vuIEy4QdCOEDJYJ8/+D1IjfnP7cFfwyMyNJCWATMA8Q3jHa0dq48OD5bsKPJ4pRsyyW967LIvLQ6zTtac9s9AcpfkjfOcT4f+bQ3CLksuNr/KQAQ/Pg9RVGxy4QNYRW889qsQ2u7/d29T0baUHy6dYcgiSlDJbDs+3jGnfsYc3K0ncDPAQnJyMPWBwe8+PK09Xr9QUiXy1DSrTlfuBb60EFcBtR6nbXg+WrN0cpOCINMPL7Qp0k7nsVNRVzQSTknPmh4cUNoRZf/87pob+cH7wEORqvMjUvefKG3N0IjwW5D2TrngI8CJorDB80FD3x39Ha5+DiGiyMCX8Ref5xAn4dx/4OTukrstG44LAm4AIe8+UFefQF+ukNlx0M/F4DtwIi68/lOQoy+lsQvxPV7IcH9d+v8GjXrvXmCFsDDTOJ+Y4RCCEJIAENU+cC6Yb0HgkQMDAwzPYIBDMeKSw39qTiatFW1qcLY++59wQoW1SC6A7cjhC87233lsc08FH5Jf5VDFUFBjfgFLYbqfD6n9/TFBhzOMEPmSF+/zOxrxs+JjD9Ud5U6/v3qOZkWzNDVgZt563iQOR/2snsLh0pJ8OobhLoLBA9lB/xq+H+eq9O+p4sRQRqzqK7Thtj7iQZ8ReL5HWiucQOCXwUbD+6FMv4390w69LRAfbsDsgHtg+x5ZwYcv7g/AIBrtjNx9DYchZzKvIaDgrK85TU9gLGBRvm4raZ+6YsC+e2IoL9Y8Dpysfm3uEy/3QLWfWZJa0O0/kn2XTvc/Ms7hvGTd+jJxrmfBV17+TrPNG30I9BgxW+DYfb88lIBuUaOPAL+XfyguNQK/ftyNT2EKr77MH8C5QgY+5wEo0kvAoN0w7l6ulHAIjpUv/rJFPizhv/L5Uh0uT6sxPE9tZ/KiIsugKcAO8ikTGEFTn6y/0rCWjfZ+p3AZ/xGRNQFn8KIuJ55a8c/e279QMBkgXCClcT3w5k54cfYh1d6US+iRmWHLbObwVTBk4txQZI4F3vKzb4LKfuahjH9IcQlAG+HvIJls0G6zO6JQkYMUEryjk5DNj3u/MiEpYKxNiXAm8RQOo6FW0UsABPLrBN0gER20zajsOx92ce70BmGI71b/eU/+Yr9RG92Xz/nCOOwNzueRzAB5UL3eqvESH/kAVz73n+tiGODGMgJvXiBjf/cyriRD4F9v1DyvrmIBdlJ7UA6Q6HTuT95fg5P+giWNhM3qjpMBYHCdjtqzWY7XIS8Tfd5wbz8OlMxpjv1EsULgsZaQQ+ADEIXertCKf5Xtg1wRP9dyNmDpcyATHh7lsNHytj5iAD0cn7tb7sOSaGV6jt6RCbOxrrJt6yLT0Ze8CI6NkMqgwUA0IiOAYU60P+zuRODY0fxg5s/ETlVd0Q9g8Rrvy0EJkkNgyfCMAQHyOgN/rogsy+69/VYBb1GAIoejG+/agUnfLtDmwPHwE24o7XjyR3A38qPgdj0SvvceNKy5z6yUS6HEgtNgKS+XDf9u0NRywLRv6l4enqSt9MOzVmuPpq5uSr99OcAloWEQ9aE/bdsvTDKiXCiSYRBoDXdAQaBfcTVa8X9+fpA9LvDQ//Vzw699sBvDU6II4Rz90YEDPc3NsuCETgOBKF+g34mxQFFmAH/PB/ECYdjwU7xt7rYS47AoTgIth4N+coMLXYKAv0+7EfDqL+BBWxFJ46Kwwl7sQUI9vcBP4cZAAbATfsQu9JC5r4BjuFJ7T8U/uCuYj57vqC/gvqBQgSAqbVYiNlBUQ0hRxTyTzPxwR62GPsEk6a/sb7Ds/V4aAjLiA8+TXT2+hH7iAi+A1mAmsQwPVw1Qjts+eh/cs2sevmzPriJ/dk8+BEEStj8wgeWeVk9b3nfPEX9WXsgAukIyUzrde96yj3V8zWDlAT7e2rBd0Vzw0kNfUe2cnw37Tbwsyg+FAg0yBmAugfsfQY7v/QncL2G8EFOBaA4ZHx1ksF9YkDnEHg58LCOeJFAPYbsP2LDJblIOrIFqkjNzmY+KLcRNJy7/z3aRwVI/3YjfmE8l/wjARMyEe37eSpGp5MMQMYBWg/IPEf4NC+Irh898/j1gFsPG4gPCSb75r2q/Mmrm0oPiFb7679+AwoEU35IQ/C8cL/YM5s2PgT3iZKSwLcT9cNEdPsxBvjJoP3kcUDzwsfrAiaE/D9kt878ArfNQY8/s4AVuyE8WsQMTHoIhXbReYMwz7i8hraCyTyje0i+tUjsRbf+VcTrN43ziDVsCzAHLf5MClQ0iv0ZiGs9Hr74P5+0ib6cx/vEWX+MgZoE1PyRgcgA4wFM9Q5G+MWA8+SKtYb5CguEF/or7WW7RD3bbWF7V32JUEQOfsq6BYhDAnddaqq817g4RKSN3j9cvSFFbn5uBuhNgrp5+MO+XQR+BpyHFP58gcL7bu4guMYEqY+sB2u6WIBUyEZ84cGTRK84sbpMwSF6ZDiKgYW8W8YiAAeFn0TTugs9NvIJ/FB9WYPz+YMDc8rKseMLmAkntsS8DrajeqqGxn+4g3uNqjz8fGUHAT7OeYyM0Mf5PwOLlLwaOinCVreONse8bAi8gg1F59atOW/u9vsFANt8ysR6xYe4JAFOA+BN84J2fhtxiG+ry5IDcRCxDbDJ3z2wLUf4/Mk/yQ82RUYZO9GFkAbifP4IQ3TW/c799ne4ukaEMMcYQwSNeALDu7K9sv4ZeB96xn/ng52/kXf/SlRDavpJu88xfzpzPP8I9szWfS4+1z/eAZRxp0AdjZD0O/5Cgx6IDArERZ8F/ntyOxR67Hfzw9tIYD/vDirDIbrpQFwDjYDxKv19jnR0+ZOKQX49R6yAksQhvc59z0FedaS7LT5zwYDCIz3OzDfPRPtFQhe5IvlNBid9cAWb9oT2nlKzjCp+AEK2OUWEPMar/8sIS/JWwuZ6by9QioWCwjq5smq7N3qMSvLJ4PVgByx/bneMgF2GRnS2sr/9O3njgFcBaA3QAlnCWckV+L95P/44jdSGhIElhUe8LgGeAsTBrkRVRvG/2TvpBdODpziVetYAT3pVQNlEkffVO2/CywQMu1X2NT67+5nDWAbkvSB97LtVw2m9dP6rSTg5X/xEwMlBbMaezmfNRb5080lysMCtve1LjE63/ckCAXYlQQ+W1o53+pN5Hipu7mBNAnv4hoMWYL9SveSFLXD9c5NIb/tZ+526n32MQHlCa4OZBIOKcjaR/JaBFwTezJp/irwlxRwDub/vRTL1njsAvXOCgIrKSlTGCDT1zAG9hnnGfgDwwAMENOM6+UTJDR4MqD3FRju+zrtyeeSvXneTjX5OsIeZeEs3icO9Af5HfP+GBFwB6fVk+7uGC9HyRx02P/BKAjGLfUi8DACNsMK3apl4JIFP/BpADb64+gz2uYEAwNLJFwg4egy80viLe4F7enwDxZ0LX4CaMzw6hEW2Q90ANwP0tYOy90MJioeGaoapD5W7XmxJfVpK9z5jeo198785yz6Ih4jav7/7B/R68lOHB4QQgpqAPkoniogzdIOGT674QzazxCm5iPknOnL7I8OO9nr/KUl6RSZCzLW6/ylLbs9Cv7dzvcKXNHX9LcwRwZk8Qq+F/LSKtUUbxj+LDwHEc6L+mkfePg14LfUVedjDEocnVKeGs7yogzQtR7duST2FLr8juq4AGz+yj/KZKniROc0Hi3rIxD3B1DQqMxjEOwUyO1zGr767v5M6If0MzPG/nn6LhQBAogQOSpUx3vV6Bzu+8Lwm+dP+gL+2SI/LcQDt+VfC0MDjtCN9B3tGBas+AD46CpT+4EDs/PA8I7iVejQAdH4EkV4P+7MxvlrHdfrsxOHEOD59NXI6lbwdPRYQgP+TQRHBsbzifp63Ysg9PAN+MoQveKP+SPf1RMyDzP1DSYk2FbUQCKhDG7cCC2IRvnZK+7U+CvkBOQ6+kgVEubuCdUclBQqIeXy7+zS/oz2+gNNDvgUgy0YGXMMvfct3kPgd+R65dHoBBZ4Gm4400JdCy3pTPQR3tOWTuBP96L4NwQDCLA55f8wD9LaJLbwJXsaVOGPADYetg8vF7/e2eYS6wnUHQ1qGaELcPdiGojgn+VFKXj1yd1q5AIPOAHYMuE8swRZ8YXx+/1R3+Yrgvbt8FMrJQoIGODpJhbHADjZ1fwIGCrqnLQMEwUahvCb7C8mGfguxi3zugXcUfHwv8Wi/aMDxe8T1MUr4xUq4r7gKglmKdoNvguXD3oiqdpe1pD9vQ1wLHcCwv8p7w4KtQvN8EQXme8ADeIfvePFCLnm59o+RvgET+QmCG/Ve98e47Qh8TFW9v/nntB3DnQU+eT+CqUIZPUr+CP0Pwpy63DwWgm06G4Oq/6b8qPt/ArVR9vwNPIa9mbZqgrXE578DNvJDJcJY9es/jUPKgGT9zj6w9F17eUxpR4UEksPgiB021a7r80X2SQkcv4V9FUIeBt9FPQpISxGxkwBTRZR9vjFhOP6Cw4G01h+9y/dqtXfrOADlzBXOmIdB9OU2a49HAu5BjUeLqmCsn0xYQSMy30fX/4GJmv6kNmVTKDMMdM/MPvdhhAzKCfy8CGhCML3NPCt4C0A5RSHHR7xaAKq4evxlkBGCa30GRoQ/qHrCEW6P2bz9NnWyXbjTR1DF5kh7u9xzqc/RhV9Bv8KyQcEAYUH8THyEzQeervR+D3tYcjeLXoDpAAS9kQ4uxWYIvIAws54HUXnfgUp5SsOUxD7ACQQE/vTLvbByvlmEQvedPr1A8U10vWB96kbU+cexN8KnxCy9T0mEgHv70rVou0MCrABJQE74tL8P+cq+lsj0jh4BtLO3QPH27jyJyeGGlHsEODs+eHhCOMcDvVF8AKa80v28PW8/s3yLRoq4msO3yc5CNfkwiVzL7iN9sd83QMMfyVZAjAD6RAmKJPtOTS+/5LF8eZt0ZnrMzJoUrTkEdqc/zgEQOlf5ZIQmuYQ8PwZjCjFIfUcDh8u72zo+/sJ26LiKPby+lYbcQLgzTIFVQzc945RNiSW9wf8aumo7pP4Cx/09nbchf8/D3PDJexIAcDfWC86A3gULx0cEHkTQAUl8YnUOPNHxZzTHxRGN9LmSNx9HfgMHyag+Nriv9t9BCsBNxgWRHzNl+vV1q/QrhjS8SxL3zE+0SoEoyMG/BbEeBBcDqklvDgI06QamCoR+sq5t9NNBq4Qbxxi6IQlGATeApsLqurS4F7n/Auz7CkKfBFaTAD9JdOGArbLt/gT9EHvguubJ90P8uyeD1cIhUEU9xPeAQ4d5tzDgN7q/L8IkwmFCVEg7umeDY5NleEQ4aYz/+Zq00AUOwX15R8BxPhF7akXLgbkAnsLdA8w1LjpHRjcAT0l1AdTIH3XMK2PFEQeUP34/HgEuNYH6msviGmXLFTkir9b4eY9DBmRDWf+CvN77cTmmxfnHAPlLfsa+/bxTxxuM8xPIs5N2NX2S9xTCdQSuTSR/zAEJAGmK+kjZAUK+d+2ddxs9HEvbDr1PvIOWQVQ80XEZwAe8ET7hPkQBGwDQQIH+UAlegeKvAgDTuE08qD4aALxASUTFRgS6xAiCOGtzrfuRxMNIVENpfcy8SwJm+UpBX4BbQoT6uOzqwjqLxMgVBbTDUcSbAsf7mrNrsIl+YP2Lu35AcwAPjVWGCzPZ85P+rcmf/3FHyY29toQJPrnH7I9F9cFVvoZ5dEc0hAkBl8E5wVtIKD2HhVf5qn35O3xHwQ4W7+26aICcPRT3h/8Xw2dGMIB6ucV/dT5IP5q5c8XPe4m5qY8siED4Dn44fFu3+Qwcugh6rIU2fHa+QUBjwu5/Wv6zAWnGgoT5yUO5EXrkwiY4U0EmeALGdUTEeek9336Chu/D+rSCddrK5zsvPnnLzANmNzE9jMaqM5SLs0HHPkBK3/cvCW5DwL5Fvup+d8JxwvaGd8PhjcHAcToluiV6NXkeNsqCUD/Cxmu8dgIhhMV/TwI1eKEDdPYWwvlA1npfCMz3OBAPRzg4NIGKebCDpH1ViXbEXvm7xUW5asMCAbU5wQOnQ54IdYJhvliD8oHaPMhH773wu/lCrzAagYVLKMmMvJm3z8bs/Y+BOcRD+vpxrIEJBz4LnsqzO1YyjXZ6UDs834ANBOH0moFFTYzR3LzPe7q+y7pv+0j+WAZUy5l8GIAUDqv78falezMA17LBApqFuDq1zq1FDUaRwVvABnrut/q9lUsZAv1zaUxMAHU+erljw5gG94GyTKA/W86qvJu8SD+Ocf57ob2gRFLAoknFgfR54hCHCq917Px/PX/1qrwPCiEKTEBahS0EwD8CMiu9U4figpFF6oHlBtT/xfumwfQEkPwcAIj9PXPfANa5rEF8hRiECEEa/R8A/r0cx6sBcoMZRxY35/PjO//COsJFhKs91bmKw0DD3HoqO1f81cRFhIe6WMMDBGtJlcpic3V6YHPL6drHtUKuf6zGdwDfycDCizRNu+FAWXK6/zyHg8VjSG8/gz2ovFd1XS5UQ9sDGfsVRDRDSBDoPwn1lMXDQ6n9pINpfDh14gLnesH/I0iNyzYAEvLmhLDHKkLSQQ25yLxyuq688skEQo+7R3rcwDcIB7v6fR8zW7IU/L59Fw9Xka+MTfBBsVTBKndNgo65t3idAOHDvn/0OzNB80PfhH57bX0s/CA+er7b93J7UMtuQ2qkuLULgAE+b8uglImKOrihv5GyQnFNBbs+kT08Ass9ngEJvDgFW0af9hGKF/rlN6RIP4DGQ5zDPUALNyQ7Rj9+Rko/IrbH/0x3gft8T0ZTIDSR+fgB/LnHhdZEqb95cQ34m80NiOOBsYkI/sKxonn6fvaHqD7KQJvME4blgXZ6YH/y/Rr8Qb8ZcaB5CwRkv58HwhDqSKn8YfmXPjy5GDO4g0LG+Lk29Hp34kVzyMWJYPo5OmwEBfb9wzQCrgIiQfWE8A1IfJdCw7siv0M8fazJhB9+DkKlxdbCGcy8SL1G975Pt/QnEXDHCrBG8MZlgcKDl0QCQNi6gHvDAf55L7+ZQ3iJOxTpikJ89j2suhF/GLw7culFhv4OQTnG1gViy9QyXfarfvG4Gz6kixmMK3dhQvXH37TqwvgLsb5AO0f2YzcG/nmDmo6aCmT/S0mjQTksbT+1iKsHVkov+Zg1cT0dhJVOgI9xNZQk7+6XwFPUjpDlTDKJLnR7Nyj6sYPnSGvwTHnQvGa+rQzhzDiChnL0fJ86S3afgEOEW/5dQedCTvs9i7q+fTiGdot9G762NdTSfrwtu+xGNT5hhx/DhQYM7Dm0gMgdvl4DhgUJAHIES0lTOhaGhgUN7d1tHnuADuCIDBRTv7zv2cs9xW5G8/n7dsP2yfjBhpFFUBOjO8F2iP/W8O4BUv4xdbRH/UbR+9JAXgaTyov4CHNIAhC3HrLgPXbRYsg8fdpICzEnt/+Qwv+LeJ3Cibv9NVv/FYmMAWM27rn3A20Fq4UJQ2o31nd6vMbBnbwbB+/JyDnKS6zCuTk6caIp3QjRiIHB9chGwfI8q36nju+KxDiGeKn3MT5kxdEQR0bRNnrClW5v+gHJof+ZyK58C0ULu0J6OUNPrXt8uImTQEHD78ryBM57b/b8Nz5vYTn4fkY1RouaTAHN/oPWgHhEQHnBAjQsn7byQw25usDUCVACLzmPgkS2zH3IrlI/5cbxsZeTnYdGzD7+gbbwAo/8NsS7t4kEQoGLPYjxT62XiVENvcauROaN8Pir/WM+GbOFxNE+JvnyhA+JYHpUfmrCffYzsYc0x8AUxpzN84vqgsOApkbxwATA2QAKcXIwFfozhAZA2Yw+xHM5iYJMuofFuQwMhaqByzsrfoy+p0EOQQI2LwMFRZ79OHoreDUGdQM2PkCIbD5RMlWEucLOCDeHQ/syEKi4zHwxg4J2NEdsSniQDYg/xQAGS/2FefmNKgrz+2CJhr8JA27S29HDeIB0AjbdqaTGEkpxwd/D90Fhv2aERwuI//V6aTn+fh6+qENICM9AjzxWgEG8draAR9bGU0MZhhj8kocXBQp+yIAm/c4IYAC4ukD9Zjx3SOQHaH/oAfhGOYy7vLL0ejsJ83JKOwtJAGAQycHXNZr3RksBe5stjkMs7UjyS0kSRqyHWQ7rfYO6CkKxwlF+jOtwwHc+YTeAyDsJi73Ke+T+7baPB1J7kMYD/rN5GEWZ+gRQk8RUB7wzaKlhMnXyb8cF+wYKlwAEgg/Ivf5VRpB5oTZr8es2yb8zCv0EiMP7w2dy03qVOJs1jL31yMGE3MLaOP/7jcbfPmoEaHg29amufLqclGED2wKAw3B9mHlD+X7AWsere911xzx+tDuIjkj4s8qBq8Vne4z8ifsJejYFpoGzNCY804q0QjS7ZntsOPyMeM1reIF2hH3SSldCZ7lsBemCKb5XOgH9+UowPasB5DvO+CyM1QJJv3A8hMD8idM4LXTmu9VGj8foQGEEFYHufde5T3yXiKrBjkE8f5m4hEKlOJM6voMnAK5BzMDLwZfzpoORSQW8usE6Nsa8rEBk/h89iMcRzoWCYj1JgKdBO7h++it500cejmh9IMDBt/h6YIua/tX53Ia//955EEuRCIj64j2PAL4BAj+PvtUB6MPswa1KJA0WvXa31fr9Pt8GesN2viT5+3YKi5dTt0BD++75S/rV/0qAYYKWgGn9+v5fhjLMXz8nNU16Xz+iRQsBSM6WxQyvacecSIrCB4CVvdD7FzF2SHGKXvpSBjwC4zvRAdJ/fAcRCB8Dvz0J/s2M2nk1gMJBYLcYBRK5ygGohjPDWD9gdrG8ggESQfAIBU3v+cqzEj3C/mv4j0DGhoE4MQN5yUoGXwbr9bZ6Hr9FvOpDgUCrQ9XNIRG8O/UwL4Kn8GswbQSSfXlLNA5//8nEsIclBtb+vfT89bg/M0iahNOIfwpbvlqsLjbixVVFZMjc9hb2xniGgnxK3EM+QJn0coUNhuV9Pa/gcseMrj5K+RkIFcbAwKoJqT6lN/78/AVVho26VAcKPK+At8cUuJ67fD6LPiD7U4aMzVBK9X0AvDM37Hnwy6I6Nrr0CeaQdcuGelO2/jPJtt734307P/U+6w6LCjxFXEeq+RWmSC6uxkuBaobXQRwAgsTfheAGe+7xBPn+nPRbf5xD7UhHgywSuH7/s6y3+3qIvUyA/Tz2QWRVqfqqfDy/jYXPOtcwTcpifHgEWYEIfQvFLwDxwgT7kf7qdeJ7p1K3gGj94kZ89JKEhf8yNwsBCgEhB7SMUsu3teW6ezkkeYeAq8PdQeZ7ngbRvvDLSAGqewmBJnezO5+8sQPJ/W662LQldZv688cyk9tIp4DzhZ28caxSxTwCPMaoxv0ACkNZunOItPvqwsR8mbr5/h47w8wxOaRAp//bgIh9AXo3QNu7SbmbuHIKQPsagwjAKbKBCtB8VH7/PARCBAmiduCAQv9BgS2B6DiZhtjH2rbhPTA91bn1iYNGjIC2flr/aYQjwwOCpHqeRQ/8uuzzfMeGokrvQkK9Lk5tSDQ2RT7Iebm7xjCfcJ2J07cXya8KNblavSK4Joc2eVP98YAbem/QmUm7tn40tjkiup37F7tGgjwAz8LFROlFPUTBgBq87Oy0PqoEmDz6CCo5kLxlxL1AtTameGB+TDytRScBnAanCYUMpYXddrF3YXAkdCE97oqJhDNDBE3xPMEGjQ3jucspSbahxgbACsa0T68G/z6rCUa3telYPiuDwfe8elsJ8gG0/yICC0QAiKo/Hf/WBf+06HYdRgZBokKmwSZ3cjVFh6cF7nuDfieDUcEO9mXOkEQW9e29UsCie1h3h0oG/S1CE31AOXu+AP67gjO6UIxVQzyIuIrGxTCNoILZdT8ojHjCAcD+6rwBCjrSusUjuS7Ew4xz8mW46rxOARzGf/f5uyoIK0AWtlaA0rjqQRpFejn7euwCoA0wRkl9hz2bhZN+TTVp/d7GrACzee37e8mwzlGDDkXyd+l84rtL9i7Lz/6lvzYKcz2R+a1/Y/7K/g209q+H/Uy80scrUBII3c3OiWA6ni/M+YNFHfwo/VUDYEo1ROPBzseIATy92/5KQZf+UcqhRoB+iwdaCsdKCjRudCtsTThnAlGG2EqENxzPRj9vfb2AJHPD/5i8DcXe+ZzBz4pyBwO9ffeKv8w57Tzy+QVBeoP5zXnHEkNgwww08cCH+zBCI0OWhlx+9jlTyGbBioDL6bQsK/0kib6MVoWPyzO+B4SJvq04dLajbPgu30JUENMEDg3eS/6JErxzMzY9fzRatzy8opHjjMFHKlHiB049JLdit1RtkLPPQYwOAYeoR/NKwT4+ilQ7Ly6rNoFAFfzouOqFk4FsCsiIQDpZBfoIPrRQKlr48hIHzx+CbogOv9UwDPh4A+RyOX1zySRAFji+AOTNv74HTro8s275/2G5U/09CqTNObx/POEu+EdDyViw8kr5w3a6YUBCy7/7Af4wS++1in/MSIZBhHtItTX9JQQyQPFCyULCxjoFQEYeQiD4Z7d9+CT6d7fbC1xKCsPZwe5EoMFguqSDDaXhxjNFlzNCEOrCnYhNSVbDZzfb/N58W7bowmND9Abud2U5GjjxvVjMEou7AcHxJTHy+LrBU4p8v901s7PcNo3EzgRbSvyClHeBfEc4GQLEQx5HYPyd8H26AQJ7xGRM30fFgd3OxfmfBZD1z/A0hecrVsgiSQ1EZgO6fKpPx3pff/OEFvFUMss71U5iCDk8in/+/iUy9LGo/196a4kEAyg9R1YoAba3GoBRu9XvTgILwXy8NYq+QqtLsjbl8qi6wn7pvSL9HQdic1vH+1D4AmXFpwvDLUTm6T55MssBDXxlSbiNuQCqzH3BWT9TvOC6La8jtRZIT4rLCXWFkn7ltZI8kwW2wPl2eX+1xG1+b4f6S2BG1wKOvGe3ljq+xDxCQH+KA2vAsQuLflU1hUEmuRwDk8GAfOY9XMOkiOe25Pw+RLCEu8JtPS9Dtzn5dMZ/yXopiknKhLhPBzw+LQHPhrdydULOu1y2WkihunhBlj2w+ykKwoKU9jIzWQDtt7KJQ8pffJLNLT03w2y+5AABDkoCqTpfwGQETDwDR4TD+PsSPaDIEYAUOGGNzI1liAgAfnWHdxYAyTbs/mXJ8gHEzGK8v3qYQyE5ETptvqr89EDmfSi+/8nNuqkBiYXwPJS5TEC0Q8F2bMgoQdz5gIRV+qe58P7bSSGN/gaNBmoARPjyfwcDfn+EuOU5V/2Ih4rOywLIMzP9fsOWbeQ1YMILzSx9Rzm+FxLFy4HHApU4m3G3uEb/UYKWyl7/78C8fqVJ6/8UARt/ZSkRPUB+d4sMjdaG9wgaBDe8xLdqd835g8Dg8U5Lv4ucRMgOzr8YTYwASAUlhBG0P3d+/GtNAc5/eyBvBgFsfRT8HYHixFB8UzgjT1qIRMaW+AUyPLeadNkHHwZ6hVH7LrVdCzlGWP0gPcj3w4V2AkpCSIkqdW1HoAsh+I1Dv7+sO5j8BbO4/YtBPQdD0d89IPf3AREC3vsLSgUNkDRxc13264biB6qDTkraADQq4rTlQ1f+ZhOZxo/74Hrre2eFr7x0iln7GbNzeJJDthJTf+tI6AMg9Wv1tP+0g2dxcjxSgHSAJwjpR1o/z0AMe/T24r6zcDiDHgkf9X/DIT1EuoL78HhTeTRCwkjIAZ1OLMxJ+cDAl/ku8lbEnLd0O8w5XzdGy80BvgRLhS7C6DaueFR+RrpX/sS/o4Lme+AHfUSfx/t+9PXsvExvJ7yHvvL/aYnfFPGFXDzRQNU7970Ft0k9UrjXyXrFT4BHx/YBDnmiObEHiu27+CxAk8KgR5yB+s9zOk65NjrDcCw2DgQnRG11GjP8SBaGxMAAhvB6ebaIt+JCtP0bwn3D8EHegem8gNH3NGZy4v3R+udDLIlhVZmFLQEwxCPEuHbCe1g+9/ugP0x5P8ZIRgVIt0eTu431yn0WBOYF+z+BPrs/jcJjR0p2/oHze4r3Ub0xQhzKuX70Ru/8GYbFx7L8hUIffK6+kH89tmP4phQ/iG8F7ERtual1mnrWyRy6hIzhR8KB/33kAT4PQHcThlPATfRiQCLHSMDsNq9FyjbV+eaA9YTcCpF3r0OBQOd1Br/njey2S+vzBS/7BspzDLJFYvllMdbE67u5ArKEfMaLtbQ6cYyUvrlIdb65Pny694ERz02AmDzhRWFHPr79uok+wUO39iRJ9kR3cipM8065h0zCqH0sM2o6BkNpPoK2/P+2/0Q5s0c5vk2I3kVDfsYzOTQLUd1/wv1tRS0Ebf24vkOI1T6Z8+dA18vqfhj/MnqE/tqGKHj6PBBLZ0iy/0S7ejaFhO4HN3kYc5j7DXq1uPzLHEaNRkJPcPsPct610HOrQmrITYKQvrjBSpFwxY+3AgNvsrhr6ILAwAZM8ZKpgtd/VcbajB5/qL3WtsAz80MMx3Q/Dk4LxRN0S4RuO2jDArohtrZ6OXbwR1F/pILW/MSBJ7nEfb+EAfp9yXz6hMFDu/Z+2AvIf3d6GLp+R755iMhLAW4+FksduCkB3zx4xfXAy0EJRMf2l8R0RDQ8JW2Tv4x/cTXeQdcA6YcsvgKC/0KDQY28X/ittfj4DYi/ggkE0ndZwnmAnjwa0fM/zIAPeCJ7l4Vfw/lAAvT9AueMLM3Nx8p/0jRY+AW797RYR1SBnDZ5QhpEkQ3FSe9//sNAtTVzZzumyG2MCAGu/ReyC0IaBJLCRJC3xd38tLmIuRF9Mvh2fZ/NL3uoOaf9NgR+kE8AIUulvRMvYjdGuCgBf//7yFr8IT8BxRzAXQyJ/yc/HPQU8PQAjLpUhbkJsb8zvpeG3DuTOTkFETmK/KI+YftRh0/IHXr4wrABX/jHh5j8gsA/hPf6p0I5glhBJ4FPRSOI7AGLezG/NvfruiwDWQCFPLOADhC/yD07+rZ5cvN2BnfMhgVPeoS1RB9HLgCFBZrBiz0D9DNy9gHGCXUDL394TbS8gzoihXd76/wqw41H48VXu73xHf4EtFDH2pSOMWMA+YfFfF4ymb8Ki6NAYwCPsV4ADwZmd4/KzgBNvrrHbry9uYJ1CT/YxmxFbv7DPua/ibtauXM08sWwCQeFNXilvT1Ga8Z7BzH2C3q4dre+8rp0+cGKGQuwCwQ6IXw8bgl2G4QGgUGAlbnmgNzENg3hCNcBTvpOebJwYHY+S0/AFHcIfD4EUIVRDgoDUH6Wdj86o4Yr/WmJZ3xmhz+7fHLnxL/DFD/C/rwDjuuaQ6jBWj8/VK8DT/txLoXCFfxJuhIB2nxX/sF+KQbwgKfJ60ZW+z0x/nkd/fW4HUyXfMZH20xXBBuOWLUOvFt6ZjF8dwI5SwSWPu1ELAmNSnNGa7tbdYyCID57bv1IU/yrNub/0gDDUKgBaMgWv1P1uUIRfEGEgQNpgMz/73p9x01Lmn9YPFK3DvuIg6p5/4au0Pd+BDdGRO7LQjt8tprFJwAm/ThBi8FG/sS3bAUGwiE0kIFJvGYBNMhVejH/ZEXDPe2+FkUB/WW93/42bxu6hM1jjBUApwcYRqkDvsXDAO4B+jQK/oR8UL17BFFCro7oAu2/pTKMBzR/zWt/gLP7TgeHfuU5XkKND+39ZK24++EwjgRTwVnErw8MvAC59rrudvf3xUOa/Fc0JX5nyUvLssz/OBM0FwXjAI+7mHvJABG8c0YGSCLC4Ig8hyGA9IpMidY2FvtgMuDBaXpuek1O5jtIyBvFDwFwik+ARG+VPINJ6UAQ+IP7GIEps7dAjT+IyGF8/Dciijm7jBKJA9q6sL4ad1R++sSuhy7DqocvbrxCXAw/P0TBY3m/PtV9DMceAiR+O8Kph79HyP3e//9FWTqEtXO/Efc3A6r75DTRzvROlkODeghDyYX8vjDFUcDruW3DJP1oOLK5NPvkTmvE8z+Axby9tno1A2+BZ3xCvxJ+pgCBAq7OkoHZgjRA/LaFvZ32kf/gfBpGlwUmwVCUToQQu8H5UXTMtnUBqUV6xXnI8wkagD/2LEJNOrhAX3lT87SNWXp//5DWkQvORLo/bbyLL+2wFEeVwR9CjBMLQhd2+sOwB1X9sXdQsPn4ZsKEhMRHT/5DxSaORfcQcHPHI7yvt2w5tXVwwQC/vgXnz1yNxHKOMsPLYvyVNgX4EwCZ+6N7PFIOFHi+4ThXfnc0Gj5CxxO84PgL/+6E7Ew2ElFBBLQ37kn7ssXCSO/E7XmaheSGODxyQisETkD3wAR0NnH7fHKLTpAivbD63EFau6B1dQyMhBwxeMFb9jyzeEs+kU1B2L9vOP++FX4FQg+OQDK1QdcAwzfKBDg8pMgngmlE6UiU+5G7KwJFgDjA7oN2PA37M7sPAlYDF0gRQX67KfW+LdJKZwdPhn6KorTLc4x0PAZYDHe/F4KO+DB51jo/doOMYEJKtYkAfTzjPvw7p4V0EUhy23bYiaJ/9XVEva+NWLnzQUjISHvItz57pkoedktBY4XI/oMG8vi3/cwBQP4RgLd29jPCAtf7ULfIBLRJfkLtNXRHnETBLvy8BAseePG57IneAMjEYUlLSYm7ov6DQeLy2v+pQ6WG34abQzKEI3dAAQ3I37dvvNY96PEq9PO6U0NLyeUFSD67PxZ+hLhRNViHb0MKOQZEJjH+u2qEPkRFgmFwinxyhHNOvs3gw4a30rgIgYpBboLFRCZLEoI//CWEaw+CxPP4BvjmeQC/pcE7T6+EuEEifaWz+30PdllCrwgqAdk7cMH0hVv7vT23Ng/uVvUphynBPQz4jnR5Hr+reuCHc8ZI/De9A7yQA277v742htZEoH9of1MBmcqUf/N/vE+yNMZ+aYCYNOOMmEFQgNmMtsQPfXm95AE9/KE+BrYvcx3KkU23/Y6C98lWO/U92cRM+cM8ej3mA9fDl0KAVOlM9zXHt1k1WDGUSN0Ac/3QQJEDOhVFPZ7H+cbpOS64dnbyw2C9ZkGdvTp/pzc1B1GOn3tsygR4+fZ/gEIIloiWfss63br/uR97zA9qwXizS3plx663ZnuZhPR8b9D4AmXFrcaCONq3lHpDfTm2FwVqTMMBUsFLTPdA+ToWdIH8RbdNqLlGMAoVx+VPSYx9dGy3uD2XMeB9vveYeXL/7otREIfK2rxGha6F+q3Iw2W8IbVEuGoI9NOivuYM98PIum/AlvxDv0y3BPMtSCHNPMMM/Ya6OL1cQOOKwLtX9R++BHWjO7gRrZZAwvM9q3BqtzAD6UGtS1n6OfsJPW7/WM4pP+EAqoR0OyI8IoFSvgC+6LkdtQnE+D2EwrtIovt6/rN76sFd+d13q0f1ejj/EIMpvZ/Df8P20l4KmjaRdpc8bPbRwkHLk3oFPpY8EYA4PiLLLQ0/K0A7ZAMRCLcBKQdgSzYxMTT59tBBPXc4/tq9iXZ/g3yFZgvVCllMtjVZOiPzkfgSiFf5N0zBO7e2fQhNTFkD6neAPCK/JUHjO3ZE509hyBxErk3jwJC90T8BLZgz/LxDvhlDIphZxp76b8kT+jr5u701uM/DbgXe/F8Ao0HMRqk9uDWrfSTzAzHLyjNTqgsmC6L2KHh899B8RUS4++qFTLh9ipw+kvJ+xcNAx/0+dof15zeNEaAJHMP9TUPGQXudOP7CXLKTfPO8rcFi/Ti8w93GyO78j4gADN96AHgTywHBa8KCN4Y0mUa7R2fJ535jeDg8JrsBPrNIqlIcwrB4zDMj+Ml+jz2twroDrUZ/d/9Kcf3Ec4+ImjK+tlX2N//wTGzAOcOYDUWELvYRAHC6ha1csr55czyHSTzMh0lo+ODwibgE8pjD4Afrd6YGoFeZO+Q3EX6Q9X85gTQN/+V5o4aqyIg7pUq1/nZL4Kz8pWlLzXtxBB+I7cXhOWa7Xckm8nH63zfAL2A5E8Z30Gj/ugHRROH/VoFTyQh47b31SRVyqYdvg2wHwf+BvP0TrPIXwAOBbDvyfuWC4tBYv+RF1ffM+lLAoATXTCs4DPqMPQH9GXzOkTdFc8Fei6izHgsovnP45IkEwe8GcfudRF8HP0pHAZfF3cQjNHY/MPWeSHHIzceZgza+LUoYwcMQm/nv+HKBHXdMRJX+VoM7QUu8boQQwx6FNsGYdPqAMsXh/A+6/AsvE183kHLKw1DG2j0NeSl70b2keVxMSBGAer2JXn+i9Th8zoPkh2e9XX0HwcK7s/x/y/jyNzDNPb/8/HaGvCvLZb3JCKY8T7sOOCn9cgWNLWRzT3D99Ge9dtLA0W7EMITZNFNxC4V9TxkA2Xrhawr6xIiaiXnIETj1eh37f7Qs8x7SP8X2eHR5Xnbuua15HwaYwBgGOX9XBXi6Uq6cBpgA865DL9c9v7UtkOTPHwIXxKHvJvihOi9+DXg7PQaFHPhYAkfF9T+geg8r/bw7iso7Mb+wNAO880h8wDhFRULACnB/aq5P8r0BsTuRwa0HaDZ1wkPDl8HYf5/GblIyRKXxq28ygOM+fkn2SXV34wuaiDdE3wEvdflEGj0EQb4Devi4zh9bUItF92QBIEIU/JNCsH5NiBFEysObCyFIpky/x428D/HtO5TEX7vafvqIg0hpBFvR9weoOpYAHjkfeYeGj4q8+N79GwXkCdPBVoEzjWxqjvlvDiy/ispFj6KH3/nhOqBFML4WsbU9Ar8CP4YA74vWS4D9Jsu1seCuln7LR0DDlfWxjmQ8vblsSm10QHXKviV3cEFSB1/G+MFk+ij73rlkxfv+VHZD9yMB2w9o/xBEoMout2bte36MwUfBMYmuRII96n8NCNs/zfzQtQSyufvTwSQBWz0Tg8B/pzuV/rDCJsDKe5N7mz/mO2eDY0bY8823h0G2DzDHwzpD9wYwkntNxQ9KrMRSO7CDyrWU7uzMy0A3/hQ4LK4mAET0EQhuAZIzDEUWv+2v7XpjDqQ1PbSsQWd9hz0RiDEBP7KthmU+urBU+GxKE0HDO/5RBXyy+UGBfrqoSGc2Frcpt7ky9gwiSBPI6n4nu0K4a7migfRzlTWpdn2HY770hLONsUEUwHH9+T7ibmpDjUHI+n3AnP4Nx3SBB8ffR1J53O0Q/il9MPk3B8TNtofYfZgIMj0pAyG7vi+S91aApImvu1TB8Ed1B1F70Dtyv7AAHwLQwHqFebhSB+vLZDkAQEoGLgWZ+LG94klMQ7CN0kJitN+A2gNchoM7ZcTXA+zB4JJfySGICbgaM9q45MH6vcG7lcgr+xjFRghqzH8GHHb3/FX9tr3n/aQ/i/UmA0FGhnxBzttHAvjjuXo27f2hRrMC84a+B0sEV4YFybvH5Dzq+s79bfrRvaxLfLuvwrZPi3YOP3O8tQSbhM8BwpPy/xrBhkNLhg6BePVd9SJy3n9qQyERoA55DFwD5YkmTkR2n8cufmjx0rMDhRQMRv9gyXAFhogvRl1A/Lag+2aEzkGUO3E5QYYoinOC3kEnD301ZPKyPVb2YEMNQht+HDF5v5qIhfowACqMNrhYOwYMfMHA/lfyZP62LF05i81uf8gSQP3ZgG8FVgNHyQqCezpp+gs/dDvrTaoPJ3+hv7qGxfmrNmMBCv7kN4D8ssuHhkDAfT/4P3J7VYlrBXK88AJeQS/4ZnmLkik6SfyBRubEQTxjOEgV7gJRe9J+Z/dGr+EA10vGgw9GHbgzxK3+1kHODDu8unWW+04BtTuVBdvKV4E3/GxJ3My0Qdo+eD/T+2Y+7QJrLxD35cV+gAz/gAKMA4DHPHsFBR9CXbpbhLetNER6xSrEjQYc9p/CcMLzy4e7o0Xq+1d6UwUfAVKP3EI/yQr0Q/eqe8v4mot1eoL64kQ3SkjBEcVOgkJ6e7mYMQ46R7s0zlZOIzwAhEU3SPc2QHQy8zXGQIFDyYImPh8HnY8HgmDAWLiOqqF54fhuRH1MQkluDaI6Ijn6Qx2EGrb2fleKbIXVQxJAF8Q3/8YF0TpI9Ff2+729xBr/+09KROt52YGlBQT/m3rVe5/y8mxpuniJJ8QoyidFwQAJB9D+czjWAPo2LrTs/Df8h4NzwSnI1wZ6SAABh/83xXI6AX4XMlb8invutvvKG4QUgU6BZgXjhYWB8sOcBXJ32i/lM1BzFEMwicd/aYLdhEE9jAc5Nafu2MVvgAsz+kAMhUx68oHseLBDIAjIx4SF6fFxeSI8CkLa/c+FKzd4tqSXd8JkhT2M40CO8NI/2kfLe+GFdv4v9HewwslyRxM31ve8/2j9gHNwUMWMmkCJ+Bn73rqbs0PL2sCP/IV8NUOpBBS8dsa5gA+4Rjj4h/rAD8B+w6oLZYbZMx+LGYGQvcrCqzjd8qv20oMSut/P3Au7wuoDU/Cy9m9/mUWqiZ25aK81AvZFMgu3PMq4GT90MJPCLPEjBJoIjidwQ8LNNodsRVmD0brRdSa7foUVtbA5OkmoNlj/mH6JxGdBfgF0w79rPzbSAhoMcfv9fbNLPrIhbXXASAav+fSOEUIpNF78zzqQSLQCNLlzthsBA7hjxnJYlfy4wL8+rrprtSTHy8raNLNE93ak9sdAnshyyR85xb05eXf6fP2PSaJFTMPbOWvvQ0P2hR7C+Te3ttL4rAp/Apvz447wN9V6xAztOrc4dkRk+GXu+D9ZOnI9hcEsB/GGi/3UhIn8GTdUu0h7qffke5OA+kWshPiKFkkAOEL6ybkstkT9TnydOPHI6ItxvCt/oL/lBXHC2XU/f3ACDi/afT5K4vrGfr/IKfuPfvtCjXsFRYvDHwk0wojvPz4Ud7Xw3oXGxex39cK5SL88fEY0Aq96RMaPMrG4gYU4Ncf9Zf3NhGN+H8bHvfs6W46ruwvH6kCqgTj+Ijfjhk4AcgSmvFsCK4CySCSEUr7GhruD1AJNsS2/wr+PxS/Hw4N3hBC7ogQ/NyL6lT9DAVEAksGrf/Z0rYi/z03E1rusBF/CMznZBuJ94XvsCmjAyrs7xBKFUsHOQy1Ms8HO92+FNASZe+eHGIqzwjm3t3ifhhdIaQVntoe70P0iB8pHOnjJy3o6jXe9ut/EqAOpAIOM0XzaAF9CfoDYtX2AioagQLrL/kTahs5LKIxZ/G54v3yGAjDANkCaShfEG4PxSGYTb4JFPhV4RHHhOlW+lfoD9OnKYYSeiw9FggFMQON3or2DcuGF5gZ6/Jn75rwCxDfJg4PlBWrD+K1wfbL65gUt2/3LELzb+xa7l4eJCJcxrnn6MAO1cEZajYjOnMOlRT4pmL0KhMe0OUKE+Cg/3EkCw/7E1/8Y98Vz8DNp9FA6OcTCxjKGGAoSiviB3r7BtYIr0354BJCJEMYkx14/HDkuw131aYAsQuw9QP06iCBL4IEkiVJ21/fOfl+zHnW2/TAGloV8PDS90wGNtIj4Vob1AwG5R/0yfZw8UkQ+CMWBvrzLhm3+Y0AHRz0DkHgJPG1InbfwQXqNBEH/+1K6zf+gSFhJDoRRwn53P7EofjSGAQE1DYbEBbGvgP8D2n+Bwq0FbL2Mbxd9hAfEfrQJwP9a+Gl2PDaZflG5ZlFLRa8CQMCBwdjJ0LN3/9TzlT7bAqeGGw9C/LlJm4GZxaA4UURYyqL6VsjYPRHKUQHZwKw/TLL+dqC4ncdN+GQ+okTrgd7Bu4cqxWcxiz06d+eDt8dbRa6IkToZ/EP2OsGOgamC+skcO+W61k8Dkbl/J8kD9cjvj8EYhfuGzAJWyJNBmjgHfBeOeYNG/8w/UXIFAYRIIQs8/j5+2MlWwWL9DkDPekZzw4AOfuj8owSoiOo4hsHmAY66ucKk9Y1DKT6qRrbLhEFDRkrADH+IO9ZBhzrOAdsCbkNijlLI1goR9rG5kXftujACUf1DR9G+kIOd/9N+fwOwd242MPYr/zo9RYS4hg0A20qJwMc4THyBQ9622n7zPto1HpWdzid9Zf7zevjyVrzTygDCeYe5f1E4UIVmCwyBooaP+vO2k7zWOZ3PkMO8fNh6Zn7Ewv361X2TPrWDKXyMDJt8t7vPA931qv4FwNC5+bR6R1b4ccGPDVQHjQW7eLyBJHjfP+S9X4FKv5Z++MkCg8M8tbdGx9hAqP549MpB/IhqfoRL/zfN+HTGJEBGd2nHqT/GvuIApy/7x20/iPak/VF+5vyyBcgHs/wHg5r3UHjPPexBocU8eJjFToPMeH5E1f5f/ND9Bjc8Rj7HU7tJgtLG8Dn4S4s9p7TjurZxGQkmBmHOXv3FPMzFFjEefDT8cUDN7SMyxMZ4S6lFOLx0hya7vkrTvn4ufPNsdwnI7L6uAMo/PjrWBDFDxgPkBAEIILd7fbmMtTvnwWi7pDxHwJo/2gTVwUjIpPvpf7c8J8BzRAh/lwARsS5JA//mPbJEs8AWAZY1XvOv8KNCVf2ZexB9zoy6y/7DKUW4LwP/5jVcf07KBXv6wmN/dAOKNKGI+IX68LaC+gIpPkPGS5TcgzM3egDIuhe+dwSYQql9m7UHNdpE2suUBAsB4D1dP4QCtUAt/TD5mP2MQKKACS9Shr/N8jAeecZ7i4PlwPrDQ4Zz+4H/t3wAw09DloN5wGbAXfzY9RGD9NXRhHq4jclXwZZFb8EW/bK/6MCfQIP73kaOO6r4Yv3ovtLAJwayPCj+ScsVuyjELv38OzE/7b8Od7fz/fvAPPzFvn1dS6nI2ELggbB7H8bD+hY9Vbvsfh7BJP2nviq5t0d1DSPHmTzkPemBKnwJt0A7zsM3vl2+Gn4eASBCGEBMwvlAQf5VeTixZvlQvdDHcUr+g84AiPPtw5dHBT1l/Nb/s38dumTCjX89SdRC30BCP5/1nz5lvi+NOApzxZK5aPlNOan7bksbeOCD/n38u9fB77+IilHBQ3k5AFgOtABpxea5B3xaRu/5KAOXcGE+P0EnhdBRN0Kmg8V24DXBeup9zUCUkhvDxr11x5n62UAyeurJQT1zc8p9KjDL/6LOR03Fh3H+tDEMuc9EDoMXukRAr8CJKd833QaSDmBGVUC/PxS0IzgyAfG/RjQ1vUoEFcYxwzvKX/9c+HpFXPXxfODAP0Iuw0n6/L7+xkw5qe91hFEAYP/4BZ9F0oSKQVu+e7zpOcE1SIomQI1D+MiOcynBBwM4/735izTIx3P8WHw+z31H9QYDeY620PgJ+GpJJkBNwlULQwMpegAJI7uO7HGCnj/lABNBo076ix5AOcCxAGuDvXfwgmo3pDO1My4BfFbd/2dGGbwzt2w+XkCbBKx60MYWOG70JTvxhXbI4L2nP120CPuwPLz87L8PfpnKkb6RhAYK4L+cebf8K7dIuYcGZQRCxjeCOwmIPkVAaYg9c7qBDAFfPVK/T8PVCm5DQoI4Ao06F3JP/4q/6b7+QoSEv/kkd/VPldH+BJs5B3g/Lpt0BAjDVWtDksHjRlXrBUTYjhaKeIdY+fZ0DvNLy8HPWs5HBk9JI/p3NfqGMPdr+zi2rEAyxvJGOQZl/vqCUr4d/75Bi8EYfOa7Nflfx4dNGT6Zgum82/hTwsY7b3mRx0A++QLqhJHACIGNPEmFu0AgvXUELAKBf3SF3P9Ft0xAyj7c+vB87chDxWsFqwW4Aw78PzgDB/CAWH0tgjiH5LgofOXFlrPAuOB+00dKPpkBzwVhh7tC/UH4gon0ZMrfQpuBa/twRT2Q6vVGxq599D/3BEq2qHolgYcD3kEKCrj9K//URCg8Ef/cvoc7RTr+ezq5O8RSQsk3PELMCE35LL0gg1xAP/muQ+FPC/qWP8rDpjtNP7cEa38e//jAUXcXAdU+f0cxQvdwHLUm/42FeUBbh8u/t/rM9/1C3vmUr73JKHPnOWyAGr3/B9CDh8aFfabDOf75dlNy5vHUSXCMeQF2iBwJd7oNeUz9BL4FhBs5tjOBup0G/Q6fhq4NkAaGOxO5+bV7NYz0jQkghihHRY/khlS+u3SsQA38TXqeMEX74EjfwXiSF4Nmw9y9IbTtPNx3fTW7+FLNt0lqh2NJ30KDfKf5d35bNtS3TsT4SEH2cQGAUUpCQYPfQ6O9Bf6LeTbyEjvkwl8DXsXNxvEEX4RvPOC0cX/puzlGdg5u+ZBC3wPvhnGLwju8+lB0U7ZiwUlEPE1WySSAd3q/gP7/1b/JBz55OnwOhk/GnsIwRXL9G3qvf0i+bkYfthAJnhGUv9L7Rv+Ug6mxBse7hl28dnrtPoSE/fO2C3rJ9/auMpOBEP7VOw5RGD+ng8MIFYJ++hN1ZIGTsx5318amxM79uMOqCWi8xr2Sv5xCxjp2uB+FJLsqv1sGVzr67w83vII1/x+K8P/QBLRKpIHXgNT1XkBZNYA3D3g/AEePR31rhNK5TX+xxhC+ra3krQYRTkILAOYH6cdlvL81UH1TsrmC7MFcsly3GwfxiqhGowmxPqK8C/TdubW+2TX6RG6P5/Tt9uJLbfigfWdAE3yZ/8u2C34MhPWFwATcgU2AF4GeOlewNTbiuGXCYMf7QI/DlwFYwM7+nLld+xoE+cDvOOv9h7/kg9C6nYGySYnAX731+Z4EWkKEQxWFlP8NO8S74ox/hR02t7xsR+NGUIOKg7n+Jb8XRtQM7Xkcuxm8kziKwZaBwE4o/ngA7AScO84HD4F1A+05K/v6Rv3+OEQTwxd+sMerBrFyAvkGgKQ+jcoAipNO7sF3e4+IgYS9fScCf4j/NaL6yUp1wJA/cT7n9+H/UAz9xipMLIa/PcV7pXLUQiFGlsSYe7x+s8HaQvhHd/lHP/fCYsRqgjKCEj01/7MKjL+UC4ZIt0Mgs9V4W47Lw28HjPuvts857rxGwrvGKJI6iFJDL0Xmg54ATECd/d3CPnlGbuTAI352QjFWHsk5/o46CanWdeT5uka4QFN4GpOWAN2CEscYgaEzCvKD/H+xmgVxdi4CNkrJQMYIpf9efy12dcKwgL6/dUCcAN7+fTQYP3qz+3v/v206V387PxjD/D2Nwx69w/Yd9IBy3nsJcK58W4fWeitKp8JARwICVO5QNFfuAQXQ88in8zvfjOGEbXl10lP+NQNsPbL6fDCArEAOfEbRiLI8vn7HdQc7C7wNs6NOIASm+I9pyccVEbmFUP0l8tL2yzg/ykq6rEIIARN50/9z+KQ64bvKPzn7Dcv7AQDEf0cRept8Kv0IPztyPT8x+b895saSBL1BvTqF/4tzS7p4Q3sHUbW2OQBKcD0sgXlFg4Ncs+V0soK5x987fLJMOsJFHEYuuyDD0T46uE8CGn8t8dq7OwIUfQBF/L1rRAX/SDyqgTK3c8RGxI6/Or/4QpUB8/5nBfj8BXRhBJx98z2ECAt/Tv2s/jxF1D79AZB9brJLgeeCn0hFAvc72H/2P0PAAEc4QeN88QhM/9FBlAKpCXmE9fOkQDfJ+0n0uxs68foDONoFnEcovzz7jUGnxK6L/kMbAaa81Xi9PFu0JsvCTi474HxARMSNEwEXfdoCx4Aj/u27L3wAjEDHwcD1RadGU8WS/My9+z6aw639AED2yN58kEQliOJG5vpSw7WDsr3biBM0PnyDBRmK8YBCvXuJrzb/w52DTUjXBFf3u0Si+Xs7pIZBCpbDxUL0RMfCNsAXxVELuMFNBD+82nwA+Ty8kVJ8xOEEEwT+rs26H8qWupsKiBbzQSu9YzHdgFlQxUAxRePF7PPKuXo/wYUbzlU/woBzh0p9R0QEw5AAEX//u90BLX3MwW0BeT8kgbU7+P6z/NQF4UkguL06agH3QsgIdIOOgu0IvvZlOs0A1P9FSLP7unfJuC0CpglzS1lMU/05PHd/+wLYver7b7SfdAjBSwg6T/JH80ENeDczNrXzRyaMjvnRTH4ATbe9CR++gUI8AJq5v7PXvrfEqP9BDdjQB4zpgCJ4In0uOE51mUhFy73/UIkWwJXAxsRsxMzA+zOKuv/5xoZ8DsKKKjw7OOH/Obq3NcK7XE0BuP1DZUYEe67KFf/bhy+0HXguvCOy78bAQ3mKXYNtgoGLRLx1PxZHK7Qw+iYNDzEcd4kLWgV+Qji7ussCfbZ2ZE4A+mI5L4OmfrfBZ//RyKoFTLql+m938zXahYjKiXr+f8XLsIPystx4ugL/PsV8Oz3FBVjHTAnaBr74DcBxSou5jbelvH37VzVpQH9NIYLRBeXDwUH18cg4KcfYhoPBf/QDu1f0P8PODqaIFH0ydQr1sDjPk6u7xfmMPzQAIgjSvPxE7MFLgYr+Zj9lOdz/E8ZHtI6y34sLS4y32QVqd3j7KgA4hDwKg8Dki+o/inhoKwsA08XMN1OD2LfA+A5EYQtANzdB601nhDS2uTajRDay7QTa/LY7WgPfPJ+IoTQmA2BGNbBrAia+knBAfbbF87pDxIjKEPj4AZMCm399QGwu7jiYf/L3137CAMz9vcisQtx0Z0ESBsEKaH+s/gMA2nDbAejD1vOVeANCQ8V4uzAA5sUQP+mHJXj/cysEnUczQZD6zXnlgUC9JzcdyUh/PnmKfoR2U8IkAfIK58OUO2RAPcRzSJ07gfl9+kgA83wxf7t5LwK2ydcvl4eThTL1ckSxQTG4mb8SfrH/vsL3u8F/gjkJhEjACHh3fuG9FURu/EmF1EDnvuvLhvwSdWu+48aHAOl4KHLnfybC6wMiR7g65ERCxEM9yEAbuMw+nP6xQeN9R3jGi/GDszE6fBBHCQHEP+T62Xw1Oj2DhoIEbjIH1kCtvRGGmUExhWj0MYfJQQRugrwCvlfCeYmwzwsBFzy5/m8837oUfN69N4Afwq46yEXTyUEH4zjqdNvCof0Le5/Cy32D+XjD2wBOgpIBCPvtgWV+cj93A/6+NnqLRKB7M7qiyfc8wriGAWN3CLb5QCWKuchzv55IQHrp98QB0MeI+lFw6sHBtv11ykLdU7fEkPr3gm40ynlFwVARif4fA10HKC4LBEd+0XztfqF0vv82SbODEILphlS+7Axugm+0nH0owJcDB/qhQkSBCP6XBYq+ItE5RQd3UH/Qb108fwEIDFEKcjPORYoHfjxntPr+yf+ePEHGanoVu7p2YL6NyUEF6dGg/zr3fLbxtgEEqAJAwQK5C8EJxtYKbM6NQmDCYPk+8ho2bMm+Bx8/FciPfjm+n4IdxQb6+DvTg4T7+jn9vfNQ3QmXg8DChDV4NzU207fQAOjNTY4LgS4AqsH4PpHAs3khQXkBbAF4CU18ATvWxmNOer99uWF7BvK7uc4JPYy+vq8+yoRCfsOC3Yv79795Qf7htYmAtv+whxJ6EPfS/s25HXyeyPdKQDTxelSAnwf4wBhC14XFeRlEFH/w+k23X8rADSH+xUKTwQe+5sJRSsg/M70+gegFJMKLBFEHRTsitK/8Mn0sejsN4cVK/Md+Q72DRm7ByHZYuHrA1356kogJf36GPv32TrlauJ/MaIQNAa/EEDwz/NqCpsgHQaAHdcNFPHH1Zz3kAbLFXg3PtQw6fgf0fTk/AAHVPmq97DVs/llGQYaWC7T5ongXvFG/Mf8meLY9TbsPPVNBtsLfQG7BK0MNvBX2lTvujev1rW35yWb4Rsu7EEyz3n15BJi/0HKOg0EI9n/ZOCB7awsmftCIBYKDN2uy5LqR/2Q8rxPXiCdCwbqNwhyK0HiUgPM5sn3vgJj/YjciOFJWmYbRAH5CxwNyiv73Hvj4epKJGFMlfvX6K7sARt28dDnIfP3BB0h1ACrKfoTPUDtCUPbJ+mDvMfvHAEJOiLzCAzDMVLsm+So1FIt+OqZ3P4QcQhKDe8bkjSH8NoIUerp4QYJgQAnLREOBe7C5Qzydg2LGALzEQP+FIbicBi2DEj95hCv6qjUhQIPJknwmOgIwXkatSY01Hc2OgbA9X4F8w5YJYn8nNmvzyHzBOGLI6kM1+d6APAOLUSWE/gbKeHNyEH5sQEE+krvzitq9Csh0zwjE24wLMK838QOIuT1Acr47B1ZGYX8Igfe8dHj0P1MBd/Vz/3i9qUh0DjxyYsExwhJ7Xj3Qs9/+ussJgTK4zATsSDOA+MGbA/A7pT4gfi88LQF2xH2FYn1VeUi6bsR8gZ/Ei8uQQbm48oUyRvZzaYrY/fayKHuo8jUEVD+SwDR+PL8WClYGjscjAbBCqLa9MHv2T/iOglZBQke3ghn8q8vCgAb79H7jR3bKyQKzAV+7/obodwHAlEOFOYiCLLLsCA3EosnCAg+40MUjOYZElXHFPlVAcL0lRit8mMlK+9Z8QvTROVfJMQmVP7pwbwppP8t83kqd/HXAx8OkuaR0g4STSJhDLMSsSQkHK7bQwnk9ZLwcEAbHO0D6dQj6NwAKfykGMHtJSvrKVX8DCeD+aDZ9dQ060Dx2e4mGWoLMQgiEoglQgWC2MnuNeMK5ZoRIEAS++vvxRZ4DqMxjQIMCa75I9Tw7jz5X/9HGDYb0N2C7NDzDSogM/sVSgl7zErrU9npDIYPMOZC+xzLJv/PD0sStDLY8qz85fU0tSQIvRp843bjs/CJFt0XrQMk7l4IMgnl64vb8+BV+GMKUfkB7pwoTgd2FtMB/dlaI18FEO1F/VwFfgeBGjMSTfxr8dT9FAyk7WUI3vgQ7cADQxZ8JiIC7/g86irF7PmzJ6QW+xuQ7ZTqY/i05zTtvexe/XX2qQClDfcOixE9GfHkF8+1AQwNYhO8+vQKyxQ1ErcK6g/t7detnwBD/evapvcTHa8zqiBPH4j4Vwvt907L+djLzF7omgeG8Wzm/TFKN7T4E/WC6hHaQd+G9YDQ4/b7P1oIxSMJTDoDoNtR2o/S1N8D4A8Xiz4GBKwTyB/G+Hb6sy/MA2qnquvCIi8FghlvJqL1KRMvGt/PQc/wHej0GcIQNtkHDO7YBcbyqBocAvwJRe/+3ybpYAg3AjbgegMA8M/hafS5SKsVTdQAGaoMxwEa62b7WwT0DHgNQ/+iMr/dR9gKCQHmkCdiJjICffn89IT7QPU76/n3ChzoBxUOP/ay/q8i3imn/FenJPh527bLWzrOKxPmWu+J/n/Z8xn7Am7sMw84/6jelOC6BnvacfdhEUIBzxKBHTXtvuz1B4ocsTyR5WLwa+z1+/P7sdZbK0EceAN/+N0AbelMBh0idPQbDv4IdfUryV/tJAxaADoClwJ5Bcvl0BXvGFsY7fKn4oQVysiNFG8JIa9uMR4d9wV8EEULJjHy4CnE0OZwCGAXlC3iAsECa0rh8y/IuPR0FZ7rivR55uTnqDEaF+E3ZQJ0BHj9crLZ0x/dl/NvEEE/IAg1CI0X6PiC84bPu/Ru8KMJ8gtRBgcWGSDSK97tDeSD7nrqVtuRATgVEQQJCCYaWhvJxX3Y+RYF+Y7FgvhTJFocIxbg84MPYu0eCCEAK80AB6cGWwRR5BwLHwPD3BwoSCqqCcgGgyv0A93MmPMlGKfFgd5LQf7YnAhNMD7/4wem9dI8jiJ94HrpBurv5n0LCRBf7eMX5wqf3B/b8gdgGzPz2AjwEUbwNA+fJaLulvPJBx3SBd2MGXQUlfFR5SgXchFY28oaRSmF2krSqRahEkvspvyJCA/6IQufOivimeCFBSbZmADLA/ghPSNk+PwHmwlh3a3+fwZH4P0vpSlPNK0RMNW2CB3Pn9QuGEEIpfz+HDovxSvzFP7yOuUB3J/a3tHBBjw3IBZrAhwEFeCW2b0Bsvml/HEGGwMcHy0kIhmtEoz0Z/41/oHXfdZ86doPMRsaGsEccPK65qcg0ffo0JYikhgL5Bb45BCH8rruIwIKHhb4dM1k8FbJoRRSJv4I9i9U/9gCHO1k/qUhSwW73oze4Q2k/H7SBPOfEKkKbyeu+eQJRhr83DDz0/7RDZsX7/ZVCQMflddK+hMIV+o4FEv2xfpy3YLUbQX9GUsb+BFxEQosxf83y+IQD97x7rL8ltgHPTcaA92S800LNCTYBXPVyCGZNEwFqwCOCiIfINH92Xf2c9bm8xALUQ0dBUHhNCBJP9fK7NwdAckEgftYAeUcMBvcDtPg5upe8X4eKBD/CXwHiu2M8RvxuScPC7YqhxQz+CLYB8puEEEOq0jCFH788/vvA2j02Mp95Cjfgi4fG7QbkAcLCOJMxgR13nvfb9Yt034MfhkgJb4gNASyBZLgghf8BeKwDecIHpUZNyc2IlcQa9b4vBjibQU/N6H8I9wq9JHqExhJPl4aaQ6YAFjoA+Yy08EHvuMbDpdF/d+NIE0xhiaAIKPYyeqK5jr4jfXqw/7oh/6UDSkj1wJnB1v4fNE7Bir839dNCtXhvt7I58X1nxqR7xEorgkvApMV2/O4/2jdPw2D7o/rk/UG1xoQYzMoO9MVx/wMxCT2cwWI2uEEK+1TI+USsPBHCvQCnQTlvCjHF/oFFN0A0f0UV7r9uNJZDRXd7uxh/ZDxlvXoAYT2dvS4Ijku8whu1d4M9xzK1ZXzKwuF8VMF8hXTIAoravm2/FDxNchqCU//pNyGKUUi1/npBcb0Te4N5Yr4hA6B/ML9CBWfGxAPpAPe4fntYhFxBaH2dBLMBZv8vCuAFYQN1/t68bcEj/enDQILVw2bAdvm/AmE++DyFCl4KILxPeNX/Gv2owkFFJ4VVP0r6dUJj/U2D58cMRyA4xryX1AwGyoJN/u+B6rTGwXVVnoA6vJlEO8lW8ogEXI+lQsa9g/LMhqYAc0blDEx/6vJhfndFR/fxDa0ED7Sps9hC0oOb/DvM2AJ4dmU9DwBQORc25T4AjMgABP0py4+8kqlYxxvXkuguP/aAIisFCL5O3oVMrk0Ab0fExC96nnjuQJ8wETzOh6OHf0AbBef2/2s4holEvfqt/Kj6x7j+zCfLnDqQxARIX7VOcQL2wTltReTDjAdJfsf3xz7H/sm1CLbRiRE3Svfmv7mIjUkTxK5GpvBu/og5UvVYgJtCgsQT+VXFPLb/vHhITkIeB2m6azrPva/DXb0y9jCAoba/Nd58gr3nu6JAN0pkQxp+Jj5uv5e4obmnBWY+yIS6SddBKLWwPI6LSH1V+K25b8NviXfFycpOPQWEakATbwV9WMVg/6G90QFVu29AaIskgQ03EwGPv885VgTgARHBKoD4htuECzb7e+u+oYHaeO29qUY+zCWCd31LjFj8DMd7/l34gIFlseN/+McHiRU+28T4yAn8NwLQ//a6GYFrxlJ0zT58AFO23UAP/rnEEooSxtL/UQhYedm1wj+QNvhFAfltOTbNHEvMxiHDaYFDPOC57kBvhE4808kjeoTCdpEhu5dHtgIMOTf0e4JVUZNM8QFhMO4D0rw6w2wME0DbhkZ3br11AT5BGYgmyhnAoPQ18/24SAgWAvVBWQSoAf8A5j9igxPCOr9JvOq+C/9JCUO+SDKeOo8Au8QW/ONGmYMZe0FBKAOMxoAD0r5+A3/He23M9lPBALeXvO0Eow0Yvq5EIQZsuANGWUSidPE+UX8KedUFUX4X/U8CsbxohmEE27T+eF59H8QeSmXIkwJ8vjeGa7v+wIv+cXn7hEIB28LGvM7LvkKhANuHpj1zewJybwCiP4qHxgNuR3oKdTTMyp4+lvFmtNB8vPf/+PoUhoGUQEPKunn5Na0DwoHYetJJ7n7NvYIAGzr6RBoDFQnzgHx7gwNUeIa9HUdQxlrAWItqxRc5Xf8TPUoAPXj2waAAjPlcRHJH4UVhPLhAVTbrcTG/CgDI9P89XRF1gQ/wLzs5gkf/zYXsAfr/ZPZmOkGAbDXzyQYPYcGmuEL/rn3HBJ6IcD+GgyO6RsOk/Cp9rT6ewj1JOXefwNN1+3hZRHaEk8LLeas+nrZxeWMGkoQHOGD3VIDt/6g+NkLc/2NAgcH5+5e810MxBtz/EPqi9X49PINRieQJDkI6AVe55gY6eIP6pH7WOKV98P27ywSEvkLIs1s+KQfUuIi72HnBf658dgdBfpw+L8AceXKErnljt11/m80GR6k8JgS/i892TzGiQdi7wsNYBtoE9wXBz2nEu754gJG6yTe3q3P+kghUyo+H+kR9+/j3b0AVNlG/KnmH+mZ8rcYXi75FnUbwdCm9T/hKANLBpzXQyZRAj0UXz8qMxnuqtMG80jg3ffOI0Q6nATLFOwiXOmH/Rrw6w7NCjzqyh0HCQL41O+2BzwApfpzEhvfEAAV+z775B4jI/0V9+qy36HAJ/FQFXMnnBnc4mPzYRS6MkUBhgmVHZryQdIc8wE0jP1V8HwJYgoEIRIN8O1MEyAPnuF0+nD5KdwsDJo7NucVDfsrpuZvDpzvqw748gjh7RSj3NYkBiLvAvz2cQnpKbXNjAP7CM7c7fWWGHsdNwF7MgIjQgcC1hDlMuAdyok1KCIF+DQS3Ewo6GDXcC9+3xEOU/DJ0YLxr/1pHqcXOCSj9Kbge7qR3dH9N9q2DngYmhVPBUwGiQgQ8pryzgEc+vHfPQlKJuL+kvNWD9EGIg2iD332j/ERFQsg+wkaL0cXJ9z81YXJz+bGHkwPqhlm8inSbwC4AUkndPV2+2nbX9PFIrnvJiOMG+YC+sev4gn8/reVINw0LDm1AQYKzRD2A2MRk+JeFFDiUx+PCvzj2iTq+ob50c2GB2byeO01XcohZcGX7Zw+H/Bg3rMATtqF318FpA80/tUOpBhdCxPuht707rLadf4/J5bvAe3W+XQTeAfY4Dceuf9F3hf98+U95o3/uQGo9isQnQUL5bHpkuxMFdAAnANDRPjsOLbF4Uzidd1dDe0LZ8cyCTQgv998Dk8SwfS4B9jqOuZLwrnjVkMb7zgBshkr1fPKAsTw8jkbtStf+JzFru5XNlELw85VDePo4rU661cCb/6UJvEcIOa4srjE4Q027PH8sB9A/6gVaDR3EbTZFczc3pm/Gb4oHmAfExAwJ48TbO9SCIEYDeNG5VLjsduexUHuNUaYP/wRwwuXBQjFZNlu56zhHhlxCaMKei6CCOQahxSE6zsMqeFX4Rfy6/vy/gYKei1eAnoiDAeu05MI5By99+3yoRFDHB4cwQf7D6cCz/yP61L5Y/n543Uhuv1z9Q0whx4dCAcF9O8MAobymvFvGh7uBPLmKX8yaPQICtX6uNXOA50QthCu8xBAnzgpFjgRlgS1883UeyJS7BUDeiKDC8b3vfovThsFcDGSJ2bEld+aATwDb/asJJkIHhSwFAr4hRMS9BYO8/TU2N8Uh+WyvbX+njI2FdMy0T+i9V7om8XrCgIY7QIdMDTS0d21A1Qq4ib/BtwWG9xN9s0OIxvuG7MSFAei/G0WoPUB+T/t0OBt9+kNtAG/2bv5FhQJL4kiWgRLA2HaTtDc3GHrahWYHhoZtxHf7mP4fedn5o8KNeVc/oYOAyZoVQIUJvkP4yfG+/cqEZfw+wGNLZcdcRmtDkIDdv9Z5j7Sx9WSFOQ76DWtKzTwY+BM/1zu1N6r4+v+fAcZJug0yA+e76TpWgFmwQX+MhBJzOsUyQdtF+ccySVmH+ryAePgy0j53ukW/1IGPfRaJd9DyhVDD346WuLq0hPTjerTBLT+ojRXFxD15fbrFt3bQtbvCX/tJfDj7WMimR3WFDINjNZQ+RIHY+lO2aPuvQ3oB6gWFh5r+YT+3v0F+TP/GhTkFCHflgC9FlUKoQG2BfTyFOi4Fr74HQ+lB6nsheS73BAFyuGzF/4utwk9BR7fmPk1BV/mHeJR9l7rkf5YD6r8PRZxG3ER1+PR0u3zrvxVB6YI5yelDP7hlgge4+j+y/qNtWEDQQbFFl4DdOybIhvpnv42FGAR69GkuoEiV+QN4WMv2AQR1GXHx8io+AITDvib+kkDEPBL854X+Bob9QzL4+bL3/L8aDAAA40Jc+oG6/XfgewTK2L62+VSEcIv+Qk6LjEcBd2u3tC3EMOG2CEdZi7aHrAsNe6g1QPymQd7/Rzt9fVn793tzho3Mt8Sbwf8BKvjIe7K91kGxu1PApw/KdozAswtawPe/ngzMC+Cvi0LD+3q/SIjZBuNGoW/RAIICSUYWxdyKGfvkexiOH8AxUOgA+cIL9ZfzypWKyuxFZrs8xMdC2ksDUDkHsz7ScawFIf+lBXLLlkr6S6lOh41ceWGDFkO/gJn6NwAyArZx1NJvGk7EcgZauk8ttnYXfkTLIE4WiajJ9nxBvWKLGsUrdZj1STVfPopSs00hRyrGlsdGA+A+IHeNNynHvoNqii7ItP+fyrY+efa3NcvH68VmdzS/ELYBgkROSNFaCE18MHx1N7R077Uchta/v7xzf/k7K8kQREv8+becfRM65kIbS/rCb40eeJBzucSr+d+1qD5fhI88pYS/SdbHXT+Wum7066DO/r8RPfzXPXR++fqrtuN+PoQ0PK61MXeN82p0r4WOg4o9w3tya0SrQ7t1fyIKNEwK/hU8cLtB9suyBTtaQQzucbOHy4f/IP8WyF46eMEqSWIAM2/3tqyCpXieO0tD+PrU+zJCXn4VwC3zxL6eQjVxGTrjPFt/R/jkuif3aMFoSaF76jTjcXOKw/c3L81BR4DZBXz/q0Kg8Nx518IrOTOADAeoxnZ3iXnuAFp6335AkIht8S27j266DPx/wx+FOvzf6ZO5W4GBbA1IPQPjZYFK2EgTvfC7iHt3AEp0uLQfACmDWTUOQmf+xLvaQrI+mrxXtEiFvoYYu5uCXcxwQgp2dr7CxmZ8E/c+gjQ9s0INAtLBvkJDQkcI9MNJOkQ7YsMVtl28GwfXfut+rkmCBJk7H0bCwAq3S3hAQAwFfn75+xCE6sPDBOoSuYJ0fS0/5ECst5QEV89CAYMGkTxdApG7kD2OAo6/lkOIPl0I1UYUjv9CHgQkOO3tyYYYvD6JPYViQYeBLcHMBPx8tMmnQlf9DobNSvT70oRNCwf8LUdqC9K7TDfYRRwGWcp8Cf7Dqrs89tv800HmPyzB+QzYwb4AHEblDEt9QX7BhGSqSPf+AoWBIECYDMtLo8JnPNfzeUI6QEsKQIUZ+2z/gUgaAt5zvVG/v4L5k8fxuK6+V0Cjjy0M5/4UhGuHsfKW+sMN/fz/iVZDufvPy7pGqkZt91NzcLuIvZMFQsT6Q08BTMzPjVz61f1D+DU3u34uPkqLsoU6/gw/38hLx985VwGBvnIECsVRykfMAf/GApGzS8S5/gABMUYu8ZMKeMS9RCOAHn64wquBY/xSdPsEh/34S6/DwUJAytA2DDaUOtxFpAOxB4SHzUKzA/kR1JCFAjZJB76hugh28zk4v1uJ0w5dBqYI3oTayD77kvThBSbB77xwDE3CxH7vQzC52AELes98gjStNAUA6wodDN5D/AY0vIY/ufm9PBY+abrOebG8TtFdBZeKKXpi9SSAh3dXBTL2LTj9gDZAFstbx2GGKELXAdJw1DExOMTxqLvIe/c7RbpLA+3Inj43COX91fu6vqb6mrgmd2kIBnwjv36EDsjOPZptyYkP96W5ugIzft6Fj//QSmZ/Tr4DuWH5kjviOtiJJojuEcW/XnxKu7OvJLV29QeDOHsBQL6CLwGekQVOdwCkdU45oSrLuYDCcUHyBjs61YD0cZ1AsIZMfusEh4OnC1WA6UFchleA3PbH+2C+lDuNxD7Gv8QfuTuBiAzNfb+6gHg0Mn7CGHd4PSoHgQSTxY7y1D21NbG8wXo+ebHKCHCqhWzE4/yCRgRIbgIitbN18XjORmjBeEqGQVo9CoZyOHPwarg5Bmgzungrgt8Gb8Kuu5iJlrqu7k24ajk8uhsB3Hw3Qlm+WXqSR8h9XbPNMZs9GrqRfo0MQoA3RWFDYbGs+4rCJj20v270/zfcftt94QBfxC4JBbywOj5/fHdwPS5/3HhRw/C/GLcdf/l6z/74/xg+NkBq/SG8Hn+0iW29QvlUgFd4Zvphf5qHGIkz/jz1B0D1zDhFiMg8QQe8n3orvQIIs0L4gopDPP4DdxR/YoVgwl8E075Pel3CrkY3epXApsCsw2N8lbYIA0v9REAvR0kMyzHMOMWP/sGd/Ju+1sib9PjIfocHfKrUM/0/dZ2yeMF9z5TEEkTrfyx7lse5A5q6Df/Of9X+7DtbA9UIfMjjPrQ8qUV9/loKwoHmOvo92f51gwBFN4rEvDI6GQbFR73/r7/cRFZHl8NF+ybAlXzlP7G9fHrgR3kCt0igymt5mnoNfY4/aMhrBjU834ZrwK84CchKxxvDxMDS+RC3FTrwQfNLIQwDwAH9bHiGuKExPEGSjQh9X4dTvEE9Y8WtRTVD5rQ+99c4avY7wnMOewRyepaE/XtBdgY7XYAZBvJ6m0LL/V8D0hHB+XyCPjy49gwuDbCAPt+DzE06g7vMqTvRxitBgfU9wTS1Y71r9q1JP4RNxYAHM7NtvyU5pMMuQtP6IbqUAYE/HYZhiy7EEr+WM7iEB79tQEIA7DswPzJ4bYAlBFsGjMB8gYv/uf/aRc1/5IHIgHXAIr4y9to9tQHLQd+FaHpgOEiEug3XQyV5Tn1bvRS95Lw6gOxD7ZEphJ15DIIQQf3Cl3RjPPDCPAACffj/X4VAPP9AuYRPQBU5rT4juJuBC0oOfz9GWIdTvvx7PXTm9nuHWkXTBKeBwvydw6IJfwOSfp4LVwCJewu/akX+wdkImo5RbC171Yh2wc1AHTvDRhF9JIC+BaK89TvrwSiAy72cfi2BKkMTetw5YgFuAmVC7HveNf68GgXOxON2tADUv4A9hIQIxFGOpfgfQKsBPTOez7tJ+nmwsCM4QwErgEHLu8QnRkDFfvrPwwg9XboUxAF9F/hXAbP8B0N4h3l3zvrSNGm/lLsvev/Lh/V6fvXBGwOHiPqJwwRlslv9y3RlAh4HQ8BTgMe3L8YKCMvGnv9NwJa+PDcPu3/7UAIjhy+F7LvEgwsEzv9GAMO8MH35t160GvsJgKFIqs6DQqZzY/d+vepANEY7iN69A/lQvgh82r+PwJRAsQGHv8G8WoDSv7g8qQXQP/YGlEZJOSqANny1P19Af34swpC7qn1ECbNAtPweAMK1G8A1xff+mX/2fRmA9gO7hfBDisCQelr6sHnmtRqJKkvl/8IGdT74O4oB5AGTP1b8bQWYfEv2Hr5Hh6zLyERDxoaD0nv0tKhE4kP1u0HFuoCNuGD1NlFZxmx8vwmCdmL26j4UhYKF/QUBBfrCqb2GAg5FSntXv+Q92/zbuyjB+wk0vGtAe0q5xJr+ikGUusrxJT0Lgs3GAJDZ/7x9wIDnOUAA6sGDfj583fwCeoYIis4aSvS7I4DbAnawbj7j/XpJS76Wt8UDMQEjgMA6VQQ8dHIE5cP+Mbs5zEi8D0Evyrr0Ax8A04CayGNDqb5JUtC7WzkouolEpciodxIBprwLv79GsUWTgxo944YZw8a+LYT2gLO6ZHhydJD7ND5FdpN8x8PMOIqGOE4eQGx8Kj7ZwLW9ZcI8gAz+RH44vhxF7b8+/tuKTH4T+3OCyj4P/Em8XYmMAJc4+gR4v/57skU6xLb2HgNzerD1YP+9/giBfzpQA/k7T8BZjaNCAzvjuK89XnzN/kq4ez21RI/BlYnNg/980Tgjd2/7uXr4BKU/mPZJRpKLfYVxRB3D6vp48jlAekMoemX/N4j6gtt9H36g+4b4BDdUBP+Div0TBUUH7wEMOxe/pYEEfxFB1IR4PJR4ej31AHEGjMb0/iY7ELtSP3mGMgbVh80CvXozwle+v3VIu9CA9oLkQKIFroAAO6YDrvNdN0zPVcgkO8EEh4hMQGC9ZLqpPWu6gnwwgrK9LQC2g2xBaAALgQwB0ThyuYr8zPq4ulrC8U5/gumD3b6tN0CIFX7otcN+3gYy+l7+SobIf5QEzoRXiwf6YXxeRYh2TwCGAtlC+LtRvxzAL35Ug1fCav7ZN4aRoz5KdKWQ80ob/PKy7EHdNCo+aNJtfYDEgQOHwdp3y0B/w4b3BX+odAkCQwLpwyhEvjvABTv2HYNJPpjALwHS+MtDmTVKirPHH0UKwny2z0XjOP2F0YO2ADvBLv3GggK/yIes+Ot+K3qTfYpOGscLQx+0+4AAAXZ/jU44PF4y9nsEApj7bwVrlSh8TP0qRvW+CPwNPIVBd3wpSTpLm8BWAYwBfAAdt5fDJcXCtsd2EMhRB0eGmxPJfr0/iXlXuSH/MPKkhYfAY8K5gtmA98qpunF7vTXIMWiBZoLeweoHD4OgR5qDKvJ5wSL9SHVtgUy1WzuTyE7BJkAzAN9E0wR1QBiABjfD9+wCnIFVx//GqwCTAoc2eQFwvzW1ocQegZu803uNfeb7qkouCG201HnhvMT/d/myQG5Efbnzb+G3IoEVfaFDPH3vfN++BYjSBMl6fvqiOzK7rfbPSSvCG8gGAM8w4gDv/YW/m/zWwXF5bMCOvcH/IEdytVaApDrzxA78OsCkxNi2dAUJLbSxUbuIxNKINwF8hVHC2odCep+HjP8vbS+4+jd+AjWI31Apy197ykAYeuwC/Ej3dUQ4k0KiRKG9vj8kTgtLfzYatFx8+rx+CKk7JMFvCjcImYtT9ku+5nhjt7++CX7KPwkAHgQwOjpOAEbaASyCyDuZvRQ+QExtQzULPIdo+XC24rfIAA7/toWi+54IHAfQv5kMaYLKRhM7XrWN+Sm73omAvzmCjcZCfIsFqwrmPwW6kPmae0tLW8dxSxdKuABtQ9wCwQrteNd3Fr9otItCdIG9ffzTBVTJert+w8UVvHtAAcAC/qv2AEAIC8yFEUf+h4y8NrMCN2dB8cFZf5VJl4SqPT9FsMDLtrg8i4cQBqX+2oS6Q03+rATwgKC+dLXr/CqFqEBdSJ8O5Q1QBg2BSX90wwa5lbjefLV/8Q26N0gG2lDAf7+InzgjtoIFMz3wAIrFTjg1QpCHB8EaS70EDDmRrsU6PIH1gZQOIgb6uzc240RrwHW5SIWtvl3B2oCduJPDwsLXQQwFzvtTunKCJXtGuPi/VjzyOPaBU31W/UvL7IWS/DaBf8kFvkw59nzctCP3m/xjf0EFqUFfv2v9KPCugY0DVrg1BbO7Sj+Wesk8IsZ8uGfAHrk9bidyhHJP+j0GXwDKQpt8T3SDxgQ7NzX9+zR6oPYbMQKAmIE398xApXjMpsTxuXkaedw4TYQTyDR9nkLqf4L5ArB4eUE41S1yNrDCVsOzByuChbU3OrLy7UA9/PD4cUBx85zEQH+dBanMFgLbPdlyrC5t9TnEFjkPgc5MnkNWwqpIzgZ/OtZD3IMqA8UEIQC0CKR8i4HHSNN6TkiIhioCf4GOfaZJ8UFVCFWL4UuPhc+C/v++dau/Pn9fybjDXU5+B1l6E4UeOGYGPsUNQEA6wEJUx/pCZYjCQsjFL/nvgbAAJr/ugUE4B8mhC4KOnAeJAOM85fTTegvFzITiA2SHb7i1xHUGH8RtCHL7nb3x+Kq8T4H9Qrj9ffL7NdCAXYTMgj9IYP+a+sD44jtvRBy/1saau6d2T7Wx/AaFzTZNs8B3ygUlPOOJ4BNBfgEPljuf6nJ3vMHwRU8/rUF6u7vGpQWRyuFEGDJUPSO27vv8gpfWIMjZtixSHoCrvWW/QzURNtG5tz+ielMFU7/1QuE/qgGzFfKFQ8ZFNyxyz4GNwHsK3IOOfOhBpbvJ/7TQ9DyJvVeHSvtbCaY8k35JyI9EgcTkOZ7+nYC9QZZ74HykxEI5SzYHgPgK4TxqAIUA97LvBUi/RMaziQg/wL/eLts7Z7zdCCjBnHNay5K7GHudx4M5cXZ6QRlHTAOgwuVE1UMNO4a9C30Md+52In3oeuh/cYTVeqJEFcWehbNBffzEv0k/hzqsdMt6eS8zfjPMDINLgei8x33KORA8GsRVBZpB0z5NO6O3sYI5vqL5MsTFOyb8jP1geYjK/4J6Q8rC1znC/Kp6sILVACR+VIM0+z35xUilxeCCarutMSt1hjtwiL5DRsBuA0rD2fF+dCOSqElaPyW4goO8edu+Vw2bPRX+nf2nyRO2sH63D/p8PH37gHCGKrY3goDLuj1JQC8NitBEdSoH38Ox9NvIGoP3eNw1r81mCBe8oYoQBkWHuYPwh7nA17axzGUIR0Hmh/LHI8N9dtQBnsAD9pTIklB8g1UFWU4jha8B54AqSPa/kznXBRIz+74IRDnCfEjC/sRFOT2hukAFUkQ+xQRIpoSo/VW5LDgehm3MJobxigKCxveQ/+aDtvzkiiiD8zgbwqGBEQqRxhl9rARZOtV4S4O2iLC057sjBWG6A37mP0SOZ4AUNpuDjfbk+zyJecpfNU779kUSdRS5AgzU043/Bz3bPLr7R4I2SkvGxS9IAX4+FrsG0V5E4QbNQDGuRD1OR3sF6EZSOgt5qUIq+OBEUwjffaOEk38x/lH4zz9FjOJ3fn51Ai21wbxTxjJIMLkLhzHLczNw/KKHmkIYvmM/TkNS/Bl2VcOCxJGxaUBxjSJ/9QGyg2mDpXgnQk8Bqe4l/w6+vLlIPonIEfw6fQLJ+LiJOUY3oQuOyeA1r39SAqKBKvz2vY34p8IHBnM+IcAORqfClzgTPEL6E4DexbfDaX1+uuPDy0sDCQ85mr4q/nl0ZrZ7vS3/hQdxzUWDBYIUA9aDaLyx9oy4ev7gw+9/XUO4QyLFDUh99XXvl35MxEN6bbULwh/C5UUnQLLBuUUj87tAb39hvTQJycWGOI/z1X5h+/HAVzoBQdPBm7qOUavJz4LEPjk8SPdl8k1DtcOsgXrIZ4Rt915CrAkyNFS5AsD8NaTHVId7e2OKdzvdN5I+nIChBfo0triSgrv7lT8nPwg7fzmX/BNCUMFzQLLFvUCJtZF8IsFKvG5+KTqU9v+CkcoiP09CCUPTOR65Cb4pP4iAfUFCuYK+OACiPm+BkDX3feQEAzZ9/qKKBYVNN7DvOjvN/jp3W4M+fut68wlTPmq4bz9Kw5eLoDP0dfzB6TOFQQLOTUNaO7uD1ztpOPU9tsV4x+GBEfx6rHU+oQRLRS0AFfu1QrX0mgA+fe6EEQVzvHU8qDH7OyQA+zeU9T9DLf8RQ3VGbXdkv0yGJHonNSw6Hf6pCBg9xoIrP1Izu76lBfFD6j9SfkWyT327Pj3JqQgNeR5De7YGgVn6zMTuBoK00nwIOzi3LTEvUAyLPIFkfrg528A+v3QShXvT+Sq6ArcEuKZ6Sc4FBexJLrrE/foBDHtcx9B7EL8kjDiHw/XU/0eBVAJiiMp2671SevyEIALJfqtCJrp5iJ3COsZJwnCAfv/9qJB7KYpmRvrGBULj+Ui7coJMvk+4zT9oTJhBsTpfPzT9rb01A+pEXT1A9iR8gMVPBo/SQX9mu0zFmzzneFF/jAhV+rR9crv7xzMPPIPyPvlu472Iy6gDGYCfCB7CuDul+4H8Zfl29oODMnnoQY/K/IjOSDkF2AoYuNH8EHr7d9B68X2CzlgEC0KgSI5AEXhc/DE/WACrEiaM3MH6ALK4tr1b+xlBEEsffRs9Ycn8Aan+04YpBAxDErTHf9xCTfZgCG+DBQExgn7I0oUh+HEFqcTteZq/moVoccx82Auny9ED7PumBjv7RMKpPlC5UT3YviCLOYUTQsRLS0SIbnQ2ennHMcm/SEnahjq640UyBiS7ND1Rg9e+c/jzfz7BDHeqAzfVs34VumH91L6/xT+B9QRqeTS8lAgTBWE7qQVAEHtHX8Aed+zBqT/ffb23YfpUDBm9wgOvwOP9igH1+zsApztkw94Apr9EBcsEzT61dIW5KXRIwXN3JD99D4HAIoa0gy5FcL7lQXL24/WER70B6z6auI+NRMbXPiU2wPtLSky954aztlY0AIcbC0GCRoUivwqvuUB6/wR+ysmmisM5XPeRunXAOIHVgR0H0Gy4vH7JoAXPxR19qH8uO3fDpYOGvFY64M0O/St6DUYdBQRGZfUcvdT4UcixSL2+twLlQOrEsbNbfcF4S4S7RSf8zoG6dbaHpcANPmH4oEHGRwP4nUcbvxb/3wI0vv/5CToifNL9Dkiywn0JrQY9+/CCB38N+O6At8VxLX60GAMjAHNF+0Vcgcx8g4TxQTx1Ob6RSij0P7dulhu6M7WLCR1HkzhN8vvJhfsMcqeN1BC5eKh80kUAfgX7cIaFyjwucr39xM59ZcXFCLuDVDCFeKF32UIpjJ5D4MIUehy8R8FZxMm/1EIqQGH7XEHbx9bK5X3Ve5O9wbcIeoCIKwSMOQCA0MhTBAY98AJAQjh7NAbyxeTzBjdcA7OBcDznPx89Vnjr+isG+4jr/tVKcgLIt847hnqRxDoDDP6BPl087sF0xNZ788FEzpo9iHYmw0p74rWziL/HHL1d/QOGFkWxexCH2b+Xc6C63MFae0n4LYjHPd+0bMizA816BIK4gVFIFMUePBPCTL8fPqJ2NvClQsoNtIk9gvo7fwSGRiy5x0NT/zP0yfkEARq+uginzpR+0oMb+Mj9PQAZOWNDNL3WgyZEUsS0PwHAcH/Os7M34MEr0pSHwANHBkXEy0H67nY9zEIavDg23rm7w1RHQQ7p/Ui/efsi9mv/jEMESXcEk7YFsHbED0OLDrIGLbLX+Gqxjf8hv2nOEtDE/hr4yf3MQbg9kJIBwfg6+j+yukC/Tvt9y1WE8YDCApB2RUGgiFnHiAVivj/AxECvQGIGHL1T9p38Z8LRxe+MHMobApf04PKcfVP83UcQN8426IkFhPjJ9AIdQZ8JS/oqMMKD1Ykovn67gburAQ79135CB8qGUQJRwpR6u70dhPQ49zqCRGX/N8L1/7x118ULhUtDMAS+dTUzufl0AvPEXwEFCDj8qPD6PhiDrEWTwMJ8wYMNQsEOALyUrbn70vpWfdwGJQmpDPr5mTHaxutJoM05fbk4U3oINbxN1IE8v41Brr0fhFe8vT+R+y6/s4MoBTA9I7sVCvx8WTdOwQHEfzop+zVKtzk5ei+OQocIO/S6SwereVH2oYc+fKoEDQUWwdw5cjo1E1IIX7SigY5EDfafA2jCLP4Chs6BT7uZulK9z//zwZrBSAJff0fD6EdjhLk7Rr4HAj1wvzlkP8iDzQE1vxT/1cDRBuC9yokMt+fzHHwLvQYJu0mDDIl3+7bneA50WL+s/5f7Q0CLSWODiUiIv6TGF8aAr4C9O3X1NY0NtYJWgfRGfr95BHCC9Mg0+A+0PL8utnPHUkcjAlRDTro2u5tB7wBJw4FEJjGTuzP7DgHeC/F/Dz7NL8f5UYFbf90QNgtXN9E1qcJpueH9nYU6RbRADnvyR4c12HueR9v7j73mhyTEGLNUgeMFuQqTStB33H0g9J424cBYgpmA1As/hjw0Sv+ENqx8In+jRGNAqjTFjWF+RbtQTOlBEfNw/mfBArVzwiU80T1HcQ23/tfUgRZJfIzasII07wMiggL3+8fDAPF0zH0i/VNKyYV3QNd9rXctNQv15gA0CaIbLoeRd6F9cHll+Yp7BbxHNoK/Cj80eqyBtxCSTh35Bnj6N+l14jODgMoCPr6kiL0NXUFF9gtOsvXbLziBK/NifMBBQwebxeTF7oTaxE1CGT0Hx7MAOsHAfsk3hH+uA7x6s7V8ApjCLT/kxO2KJ8RIv2WGwHqmrrk3t3rbPEwF4MmWCi0LCcgse6f0UTUL//uCW/mRhgwADYHpUwRE7gWRSWr4UvKDNz7EI0mx/vqAL74nNR/DBsm0e+lEeUIteGXEh0FIASnEAYI7+Bkx1boBfgzAWjx3RNGFQv8eP6d/ST11/FHCxffjN7d+lsMcP4j+5gGB/yxIlgVePV6yrkA7ygtHCsJtfHAHCfqKwcPBSLpDQVCCU4FKvdvGDD5lBvg/LfWAO8NAMok2ehtABL5/fr+GGvg++eBF372MNfOB2H/phkyN/EMJOge5FnmAPiH5vTZ+yz+BLjwwwU2+8MCBQs4HynFrdVRGWgDOe/F+3ohTQUVDxQLHfQo8ZjiM/an7X0Blh1EBckA8AKM9eP6RyKKEDrXdPxQCarnZf6p+Srpied/Fg8ycBCgJ4X239DcCxoOCuWyJMZDlcw87N7p5eiCJlAMpRIj6dEKiPJz5w37JxWETqfzIBC16p7m0AsG4Ebsb/alSnwdkf9F5DvbOB32JGQo4tk+/0QS5O+t/S/0Bx5oHkIDH/F58IwD5w8l8P/hiAFuD7kcIANz6dfn3AuMGMnxYhxjF4zeH+fA9qIDPAXgFUwDBeKa1cvrIxmGKe0jd9pD/QoKqP6bLRXuufwuCpP4FekuCNoTadNm40/R8Q0mOtUYkhlv5p7U2BLxMyf/tfJu5U3CrO2SGbAM0hwmBdbO/vdlATkMIip355HSFR2kBFsAwDUqBzHjDOfG5yfp9QAE8wf1qAh+CJEHAtrIAAYusSbABPv7SBAJ2evl6yZpCjgVgBUuvZ0CBCkwFg8dBvnDDg3ju/hSKNYUTyI4Gl7UUMMrDG4XdRpbIIQaW/mJBzz3Qcu74mH2mSG378AWoyPo9rItWhWoCqf2nuAS2IXXZOKn+zgGCChKOv3jUt5//rYvte880/weyPDhFUAeOwaBG9oJgwe01MS/WSaoIfX9JUGsFAz6mwnb8m34nRMYD+7nuftEFQ8gUx/XGsT6Pu+u7yzXkv6J+3sO8TppImU1fBs9xGD33g0f2/8deCi3Cc7zIvruJuMOORXv+7TRa+b6D2Mm+xFKD5QIbggaCekXehHB/zj+CdIeAN4n9xviC6XnlPxK8hzvuOeqAAwzUQqN+Y8I4xXlBM3qutGpzowGnyS6+jPVnxW/DPTsyTJSGhnu7fGc79fwk+Q1Fzw2BQzbA2kNte1NvVnxqRoICTf/bPXD77TrOhvR/Rj+NQL8zlHuqfDgB/gLZCXuHUbmQAMB9V0BcP4Lx8HVS+6++/QYtw4mDGgOtQU+BE0GwBhdAWD3wt9U4uvlNv79F5rWVPZ59g/7IDIILu8HpQpeCOjO9PSX9lrxp+cpDrISc984E5Dld/ob+7Dy5BxL5STVouI57Z71FhRz69fk1/QA97MUPuUP6QsDIfWL0CHuqvED7KP8rM5T6xjt0yGzI07lnNj30E8e4vD02gf/lADmANLZ2+ja9l0tRvkMzvIBW+CQ/2gN+R0UDuv59Rxl2nfhzhjuC8vbB9uzDJAOfwi7EZMNB9K99YEgctJQAU1Ovhq++DMAKPeAEG8crwtc8TTMtOpJE7MY6yzvRd4ldhZiADjMG/9EHygLuAE6EP4SbvuQKRFJxBHJ8OwRs/lm3xkKxicXCiIQxitO4h/ftg+fOGz6tNDAHhTfHwHIPIkLte3i7ykNQvo/Bk4scyXu9nch2upaskoYARuUKL8TnQ0rKTsNIwelCc0KAgIAFSsDsRqLKEHuzP2EDx8BtwvNEa/6jAmjIakPIARLEHAfbhoqDQ4M2PYZDzgBQtZTHvEvuU/6HVXgMxLs4BLt0/pRC8A4mjR1H0gQ3CcsHA37jN9K+S38Jt4r6GMJyA+uKCI/GgBuD3cPX/DA0R7gEhdt5aQTrSa155AO8hpU13Hh1SXrDPXtjQ1iFvfW7O/FHuT4+iLKLgwBefZqFIP98saLCNQQ1Niv1dQRhh/n5SX4/x9lDK+0Rfz28CCVUCMwJVfsbfdDBdTs+seM68rm36+wt/8h1AnE/ecVLfIJyFDLIwRqyjPqCPuFzQW/c+qnI4bRt9+d5TLfTvKi19LwMvSU+b4KM9tcvDsB6eYI0In5msxZ73HrQ8TQ7fX2txpG7mvQNgND1Ie8nuxUBOfXMtod5KnxLu+18Jgk5sbE5BgJ37AUun4CwSak6Wf2HNYv2QQFoA3lCPKySuFkAdrpqvBPGEgY2Mbj5hrzIeDOD5Ap5QP31Y7PZdPhAwQXWvI5xYLdwiVd/NzkAu45DEkKM+R93rzQjQ1A1bHnRxjn9n8fKPWP6KjzPxV45RgChf7JyssdQ/H2+oftnCunMj78+QXB7M4FmslNEAMnQRmJ/tvZHQyZJ1U+5P9uCg74/CblEpzfg/w96oQnAhC9Kk4ZpQ95JcABaQnaFaguAQB+5RnngRYXDGUSWjJ9LCxH/Bt5FKMGpQaZGPYqxP8X//0xNg3sMVcizShFMwYWdRijGpIocTNnSk4OzRG6IFQs8iIU33sq4SgbGQlXzjTbIXswdAey8ZAQXh/c/3zyJyT0Bnv2w0NuQAwGzAPDAQvu+/TM4mgMABqR/yYxDR+f+R0A9wlV6Mz3SC+MHeoJnQ1JHrDkOtUv8UDpyg3PMf8tEPmb+HAHoPuI4nPnnelNzDgVnhqL3J/7gSEB4AXJmARp4XyuI759/p4VuQEGEWQQ0+d96j+/N7JIA+PblNhj660JJBZp1iz+MvlBzKzilvJHzpHpeAWA7arhV9iS7W/hUQxi6xbehPUn0nP6h9LREndByPofvyPFM/NLyUX/Cu3k/NsOGvEuK0Hy8gBbC9PiSutREvjjWtsGLXH6ZQbv4tUoUU5z/10r7tTv3tbkPOnyGDwqSE3ZACYFRAmyEO4JEBcODovI9wgU/mAfPyxZJx8kDtOVGToYvCL4HwP7vhJN+1cs3xDOJPEjgOWICOr5cgM/DxgnQQm+BoUfeA9jGz7/QxqFC34I9AqWFSkO4e1WJSEAtQNECrgizSY8+B0VYBA8IZsVsB8mHUn+j+93BET1WfddQeTn4wGhJqkQfhxV5ZP7P+/K+zz71wBRIZEJjxamBdr0dPiT69fpwfPR4vL9LhUFE2gPwvBRAFfYVvMCBxvX1AEm9Njqu/+TIa8P9eUb94fNXc3F+uYRRQQM7p0UzQyh61YeHyO45+PfZN1004bddgrkGy3ictZiC9Tw3/+1G6XWBOde1I7Wf9xf87NTMwoSzabeIPfv2QXAJe9l8NXYTyZeLYnE3CQOC0PWxBb6By359Ozn/aHAJvkbO+IoovLUz3wXfe/5C1E9nCQXBRIZhCbS+zUeVyfw1U2kQPwOH7IzgleuRJQVJvSSDQz+0hv7NL8Vx9pDCkNAFDrWaVMj7fSU9zMZBCMlCpQlZRk2H00QjDuvVPIV1BA8/6HytAxBLLMdwgpnCq/wpQM3EvQU8/XA/6gxzOKE5ykClwABBIbamw/+AS/hkw8ECFLtIA9X+9fuMweV474LRdny2y0YAOttEL/8Jfvg4xXFv+QI2i8MwPjK6Efsy8yV6F3wo9UwsyzeLedX4wXfjuVuIEfvQdyjpG/B+QUb5LIHxuyM5XjbiOCs633hLta/yf/eSsFlCiIVZwklF1XD6boowBfcS/eL55fmnP5l8HoC3xyT3rrgXM6HtLG/O90LL0UsAxfM9KjK0vKK73fUYgTSA2DSHQFw7NMDMjFJ62z9orMB0zEKA+h9K3op7R+A1AHuAgTC1IXwTOKZ3AHpFD3vHT/rjwCb+Sf9keVI7fsBQwy5BxsRyh1eH7MGggH341rsLhy187/vtuWFHGE7+TIeG9DNn/Fq/bnv0gWUIJE0uzHSEEYVKQoc9gQQLNjr4mAWKwh4IjtOPEFLQ5MpogVp/WzFr+/uJfkidSnWL7f9CwrDO3kgsDs2CfLn8eGa5e0j3yqDHIAgAz7/EGoNgggS5VfwnPWI/RMGJjKODXIEMRh2DicTogQyKDkD7d1i9KEXjAoX8Wc1liY18PXX8hKJDAjgjRwq9ugWSCZ8A10ROB9REZHwzfajtGMGDwuF8580IQDoKvEhjBdLDQAj//mdxLULJecGHZYkoBt7LrMFRQhMBa0JivF28QnpRP22Hf1EmEQXBhQIVfEB+Xf+OOlV/P72rwtFGbH2XyxuLeD+mCAo+1bWZOwdGWn1VAnrLDbygBteA4330d7T1bYPzuod/vICYQthEMYU3x7L0ynWsRe1Dtzq4Q8mAwTnBQeEBTMJag/kB8b72Qlq/HLyTA/UC8L5geat9XQHuR7SBYzzO/TH45srSAA71yjiaOyWFCHSMwmxHqLq5vT975r8lNeh8GIDjPVv37AI4DmU2hTmmwR1/ibBtccUIWbi8Qu6JUALjBZD8v/0rdtx5KoF8fUs1rvx6SyS4uHbTRzP2wHfV+eXv+PXafRGJVkX6vshHVz4esdo4ALcKM633ED6uBwRDd0fIyQ0827QDPez/6PIJuzsELEjXCZXJTjxX9OO6M3jjunABZwiycPAAqwVcctRFfEVlQ1QyXvDIO8UEFMNBRLzFSO4c+rR4xnEwd1eA90b2QCHKE8X2RDi5RTJLPev2VTqb/z/7akOnTU7PIIBfPYT/EbllukX1+DvM/mrDMoKNhIxSaobYOz0xZ7HEt6hDNcsrPRo4qkksQO+xu0NkfiP9/rfk8nYBmYQvR/nHOUA4fG9E6TG+tq7+wzr4zhtA8T6Yv91G7MMgu8CDo73A/2G5SP5PRq8JpMdOgp25+zijgFY6o/wBBEGEJ3xQx6UHKbxKe40DN0MS8cS/KIfVgbY/sYGEwK0/AX5NM7m7XwToB4HBvPt0BtwKHjfG+PIKwDwlPjPLDf0Ae8zEC0KlOBFA5YujQttFtYWtgOr9Z8TFy9p5cnz4UFVLaTckvTjK/Hnpdj9IpATOOjiHDgHIPdXMgE4SCOo+kX8weksyZDyrR+eAZLusi8dIOYBth6RAqHvjPZRCo350eNjOI4f/eScL1QwT+NQ4gP7ZOE+3hQHmhrC7ocbPTSbB3sFqu65+HnfgwlFExP7JDIyL1Ly2Ky4DEMLDLsA/BcRf+RkCklQaiROH8oWkwjFzBrUxiH+zUDwwQ754joADCLQC+HvIwvf81QLGPy1/OcU3N81HfMk7Oqi5Djybvkf8av+2w+WDujiQfg0/OUQ9yTt+bcQEveP/e7h5OaJFGYG6xp6+6Um7fuE3REXnuvZBwYVZ/pE8jAL3Re8Co8eFxsiBgr31fZe7bjjlfyEDBz7M/wHCK70GugH9uP3oR3aExPmKvuE4ePrQQURGk8FsdiVCAD3x/wLDicIaBTjAAYcWAoHy07nVhm2A7EJ+CG6AC7yaPIq+wgNWRlRJ0j3Yv+fFaHVXukiAZP6jAs7IYoed/Uh7U4MRgl++PA68BWE1B0a1SwE9PXiOhpj/0Dq6REG3g7v9iGGK4Urtv/aMikKTrKzAS0UptCr4LYd7AOmKgRC3AI1xZbnhiWg/j0nSO4N7+30BOjBGAfqKyMiE8zvycjLIGQtz8l8KkTyROIE93z6AvbX4ygLpSppHcXsIhFc6egAFBheFm4O996B9b7ENe+ILOokLgSiIVMS5NkgK7AI3vax/lbqn/jJ62rvRPoUE6AKSiIMCJnphvezy5X63gbZ/4cR7A5NChvghvl7+ar5Oef47Z4Doek2C3vxAgUQB88SygQe17IB9Okl7eXzKD8BHPzZwSCZ3RHFgwUD81zJ8vyIBY8H6RGeEi8KmOHwG74GJMqwwA7xju8DyGgB9CX8Id/+T/fRwzfzASKH9rkJBOLO9bjwg+hjAkgKKiPc+/b1bPEc/XX1aNwX9N7ZYP/ADLbYCvHLDF4QIOwa7i7+Pu1VDb8SAcCfo6AUIP/d1cwu1in2En/t5eu8+Q7W6QDLB3nRG+g3HFsKVhd5Ne/sF9z8HZATo9ZL3ukHEftJEm00JPqE3YHuYfAD79EMfj1sD6MCrA/xBo0Ap+6uJlfFtridGzYYzjyhC/EQcfR8+EoaHvtOGHLpJvP7+44vGjwBDbYDlOuVJp327eZg/mnecgkxKcoZfQraBKsIwess1jUIlwMUIPkFaN1jBEb1aAaFHQwDqdc7HtQSqeOFC54WYxMI66b95tUp8mEz+kcgRcbpP+jh30jiSesU/wcnbxPU+BbzhP1j8TErqzEry/XSDAYe1sjj2zeVKnYYgRv085ffGuhVEbzxocGPJ6Qj2QiNHvESBQPlw0oFRx5S/X3+fw+n/bnZ4xZkA/cUSBNj7NHNRslRF6DlTQOXRGkK5u9FELP95dh3+GnfQemO6VjvxzvHGPQI7w8F78/pVt/61yrYth5tIwbWr/F4HzQWM/LyBVEHzuGw0m625tTGEf45Tyy0AO3vi/u0/czlCPU29ebIJcsm48jtoSYDMVkDA+3Z6WnsfvBv9MrqxOfB1OUDCxmaCYUPxe/A12TF2SZSH1nqtSJX8o/c2BNfKjoRpgKU6p0CjftdBxAlyeCJF84XU+jw58AOJCAs7YYAUux2BVMclRrr+mztWSd/Bbr0weQv85b0ouNj9mzrtQkPM/cqZ/aCDE0K6eIq9pYCmiRQFyoUkhOIAzwflQWvAOoR/BKxEjcPVjUcNyMjXyE0PaQZHOTNCiEIKyRmFxUsez3/INxQAPFQ8TkECwN0I20KSz1TFltLfU8lFXwaExYCIjfSzBzuFo7o7StoO0Q5oP/sOhQfvtvF+7cbjR1SD0NUAiOlAlQQOwQe+kbkAwT360cJNiK7C9klBFBJR+XtX90n3G3fpwUh4+z/Jin8Chk1XgC7ACEmCc1n5sLnqQRwICQZGvjy/CxP2++u6OTRWs1b9fvlvEUYANXjMyHb8lPkQBKB/iLLpdO/9aAM+dAfCIc9vO0Z3e0Mg/Ps00fw3dZa+VcS8SiXGd3kA+bVyU/a4efu7kr4gRON6vbaEeoO8VQoV9LNz3Lbwttg3Ra7gAGlElkS88UIvkX3/dpGxrLkIfrFuZ/jGf+R55fkSuVh2CaxqNpn6/bmuuFgALDypa3o6GgREMcZwpH82sDzzcEV5e892zv0+vr9zvHKBd+b0rTlzRx7FD3wAfPg7NfUf80053vYhutq/5b1AAUCGjRAUAhy6EzEXK6dCVH+tRbCBKbM5CGZCcYDlSjKD5HxxdDp2AneGEWuPOkOYx2B4AINRfk1Ahr96QFIFVjkYg86AFdUfip9+szlXrCXNI4C4haeHW0dFSBo5KcHGfUuNl7VSui5A/jdHk6OBYMxYDN7D3riS9peEcTh3DwKDfT6WxQmE1k2uf8gILPprsbC3t8BdyXMKCcmEAidE1zrDjiQFUDQxBDyuqLjPAb2/McwVihrDCviaOtIAxYEBuz9G5EWk+vC+BXIzP7aExgaUx3T0cTq9f8AHeIGMR6DG7PFTRWgA47wZfKj6BIUIelkJFsvjCd0H/3l7xGe/3r/ReRpxo/xQhK5H74T0z4tBA8Jhymd9q8NdumoA8P9AQFQIpcjoS1u4qgRKwYy9Xz9UdMS75rueSP/GBQkwjAYJ5cfjPiGDoDapfRMApLxs/mN+ccheuT34rT1lxTMWGkqnf/GATAXlQ2e9NwDROvp1DHVkO7hA8oVVWGqGnjo9SYQAODilAgDCr7hVBr/M+ALG/Ro/qwKbNpn8HQHaskVzp8r4xLaJd0twPkoEgLWiupg6sTkAwiIBhcSPA/gFpT45g3r2NLMtgWfBgMRPgB7KWsWmRTdPuL2OtCP+vXpOd2O7jwEnxsPBrIHw/Mk90Ll2viuBNzjQSVJCfABoACR5oP1uOoJ5HPYT+aS+64RxuZhDa03QAQQEz/wFfOk8+nOMPcEB+wLegolFyoTVvGlGVz43tOm9gXWqsZh7k093iKmBwM2AfUlzwjgcQfO//bbcgTx+ojfLAY1OMkpmg885MqrzdocD8AL0wjPLdwkkvvkCKwHDP7xzrH00vcx0O8xTBQUCPYYKu8486T3ogNx8xwJlPhX/sEBUPXPKD4Gq/tQB9bl7tSeDVMJEPwxSJYknNcKwpQcmx6v3/wbLiQaBaHkjfdAESkKBgUODRP/YOwYCOX2hRpoIC0H9/g912ADZ/Y08QcZaA13DMkUGd0P4nAiuw969Ez4txrCBbv1Mv1cHCAUx9ML81vvagBVIewwN/yg+NkT4+lqK34RaiEVAgzy2xE54T0GMeZDFND8gQ75M7ERkikq6JMOcgHa5HLnFf/8AJfo0hzRD5YScAkpHkrjH+cmJSjzMOq299ctH+Vz3zcC3Oh/7kH72jHC7bMHHi1m9frx6fxNDxP+UP9964HbpNnrAI8dTgRsFlgYSgUKA04rJuOTzdcQRtElGDMupAgrJirxMfXh2ODeQ/qQ+NoJcAf0Kab0uwq3MKfv1PtVC5by39Cz8LLmruTzIOYPoQctESoJa+FA1B7YuPowL+8Q3AxL+RgDfiNxCCj1bMhF3ObZkensKD0UKUDHMMLtHe1ECeIVifQPAc3h1eMdF5wwHCYl/GoQR9iczq/5qtYZ/7sjPhXYEeQOMAhVALv7tg4L77bDbw6wGbPhyffLCPkBvOhF6Dr9CNu+CME/7PtN9oIeaRO15JHhKRfs5Cfoew2+0koM3SVWCGX54vlwLtD9Guaf63r9oPcV5m0IIQSHIkQLyQe05F/sCvHHp9MWRQM6/IgebPHVDt4RhgNi7o8I5PQn++vfJO+iJTT1lxmV5Zne4hlRD/7qoubhEYTw2fCkDEEJyPq+LwUJmcmzBML/Neyv39j61fqa+aIULB3l7wTrKTL/2+PQcfLI7HIC4wiWN0ENGvC8AW3jTL2q9LAMr+u8NnkqkPSi/p322Qc/BXLSCvpjAR/YJySVDa0DjTaiAzzszOGY8Zf7beGd/WgcywHJ9lYHgvfl63HwUOtg9WMLguSw+QIXLe8dB1rhvwNnFs3ayxMPA2MBgPut7agC+e0pIb80gRdyGtUWF+3Z+6gNIeeJ5VPkcBfYDIfsIjieNVX9n+vVBZTl3MskFBnv5ewTMCUJEOOC/6UtnAa23gX+xAcY4pwBsB22Bj8bef2aDiv/uAtbF67oWxhU508cdy/W8+/wUtcdB8jx2yGKHgbkMA7uIjMxcw7PFXEBJ8540V8PhzQW8/zxpva37AT4OBSuGpTj9fIpClgqxhjj8ATyzMtm9abknfQAJVUNZRNn9HzrJ+1sF7D7tQHCFG71CRft8KnudgQzSUX9O+V+FJXEFglFASAd1gat7uby+8CSCeoFHi22GawFjxM78pP4t/hTGevqKOjkEgUYQyDeAIQEU/eV0O/0RPxe/74URg6wB7QOly8i+oLlQc691jHqEtcQIJjzdfFt/SMGOQzp9ugLadIe9gPl7ebvFeb4k/tB8Ir1+/1P90vykgPW7DABEPy8+rINvNZ0ASMF5fdW4tb06xYB7I37cu+w7vPehwogGLnwMi/w/5quGshjGM3p5OWdJ6btV/h7+0kVPAmG9wvzE6610wTuvC14H0b93vzg4T8VUwadF4D1B+ZW8pcBmi4dAfoJG/6T8a7eCwyrHcD7XR7R9KcKehTxEBgGd+nHAFYI6PqZ8lcnp/bvy0EavDVHBUEExgmf6c4eRCloILD/ffoCMNrsnQfCNFAZow3Q9V8aZAP3+0cyfTNPAX4SeTf8/0kale/X4vYOfhT5O5gSCCRjCqoIyfdo9AkTetPXIAr4puAnEEEX1zUJCUoY0+yb32kKH/kA5xUQnT7sCnPnHuK1+YwR2gxpGHIZbvFeCvIBL90SNpcSy+8wISQN+euU4CwZKRV55Xz0gRiW973aGQOy71/stAwvHNz07vRtD4bDyu0HGtXyceOo3IfuhtXG+EYWMfsh7N77XQOAuCTnjynA4lPNhAJCHJQPs/uD6RrPgL/X4mbmwN5dKusvBehABwcjn/3J2zjh+/hV0PrOjell9e0Ncgss8mL4h/SX02/vdO29/lv49+9DAR2xIvSXIZnSJ+AE7GH3aAGF87MUoBEZ8A/+e9L1/Xcsv/Yl/IHYk/csBrL04h8yCJj8ke/u9pf1cAXXB2HrAubQ2FgTsvl278voVQuLJ+rQfQ6w2lzbV+0m5kkj/u8tJm314dt39YD29A1kE1sxIOt8+ivwbwoWFCTxsinl1e7oZCY2+h77+xM1G9/93e5tDkH4z+/6J/cRVv39/HAXigKQ4pIDtQfK7QfYnxjlEPAQsiKU9t/8Rf6XDa4DiCvcMEL26/6lAdIIsvep6PwHq/91AbxJMDbTAbwXaBmv+e30QhU9DHUDoxK9L6gY1AXlK8H6VdHh2kQBahW4HKVPMzYtKfo4ZiHeC43VPPpv/H3MPSfxGeYSJC1UDAULlvYZJ1sUUex4B6Qbp/6X+lMyIQ6FKqEQ7PXnA9bWvAerBigVxiHIGFkVWRC3GZLg3BYpNRHw2ADHJA0SdNGa8QwXlulpFU0m2vGbvDnpRi87CqAr2A0J9IT4lv9BCgGwxf74G1Dy1g89CdAYYg718k/hSPLb+94Meuy95fMR9/zN6FX52CRhAJUHKvu11nTi+b/w63L1tRDkDK/Ixu2U58AOCBRP6Kn6I9Ti+N3c6969BGDQpA+e22rekBa469H6WP7n8Kjwrwrt4Y/yTNun3QwADOAxI43uYgUWCD32HhhToirroxka42sK1/Cj6wgLWwRY+FgM2ifu71zNL/FX/Hf7AhjJI2ryRu56CMEmefcBBIIjD+OHEp/6NQm6EcAR2yPc9WciEfeP7UoMnyojAKTy7hTX+6AbneK7IXAWzRm5LBXUdgce6N8cB/pgEQhCNvg4KxjtBA9x+NIZbmPMBIUdve+RB4gvvgy2E+8kAxhL4vEdARn+CC0wCRxGCd0ryyvz6IUSvRm2B279pAa9OTcQ/hPb+XrqxQ0FEnUvV/1UA8AzA/h9+b8buw7wO/4qm9Em6c8QlAhO6XYDJz0JCtAIHhl0Ak8PDCQdIzTmX+6ZBZgFzvx9BXInJv2UAM3swPqtGncIEAF+zjkBThVl+I0XWCsf/WbVXP257LUNTB8O43XZIfDSGWcWwA5A+4nkN9l20poIhxE5EKIb4t+K3tnxW9F6BTsYiNC0xlvwnfQuzn4T5Sy240rbcN6Y/m3UlOTrHiTvSeSZ2ujoQe+1AojwVNy5+djnw/+U7ZPgseGk12701/lD/DYH1QeYywPLlPfI6IYB2we29+z0j+Um903pugEtAYXXNPYC5Zric/F/H7UD1gE5DQjKOP/E2uUBI/2+4qYceeef6Lzd0Rd7+avp/Oxy7207FfkIGIDf0b42AwHw0vsG6NQPEihg9tXhcv6d927V+u9RBszymfC0GgkWo+G37dcbdubL3aENw99K3dcBdv42+RQRBRKTAyvyBuhOFX7asPqRLJfKKAeiDnv3gwTkByUGH940KXIiF/bF7B4P+/Nt0kMene6q/r4TGQzmAYH1zhYA7q7muPog5nb3bDWpHGsJ//uzFSPolrcmHKHlI+dNHKUbjuJj7tUvhQCP/9b8SRShxNEOF05T1NkdfjDs8UjKrwVUEIbbxAc9PRgJf+hQRdcJHfMk+YD13RXU9oEWqer52fMGmgXg+8gZvReo0pkGOArjCA8cn+Si+Qntr+2rGy0w5ww0+4MHt+YYGzcP/fszBkvU+OM9GfQwxAfGMAIsjelBBvoNTvZE6QD7hgLxDwMXLBjq+X/ns/8Z/hP6jedNF/8isefd7wQHfAIuDnr/AucaAaftsOZy+6IXDxyw/PvtvNVp/U4bwyFzJcv3NPU88CDgDQyCM3Uhb+TY2H33b/oXFZstQBrK8S78AQeP6l8JIilnA/S/1NClF20DWes9FOL+T/5lNcwehuzW0+TTSssg7PkYdRgyGRQa+Q6yAXj8FOTa6Xbh6AuSDgXpCT+mFmHuGvQTCocu3tI84dAFovVFD3EbwRwX8130Hgff8w0EtQzm+vrkIhslHK3K5PiICDgNdAMn6+wBQteE+AwM1Sd1HjD20grQt1fj/w1SBx4GGPY+I4D0PRmvCeH24QtByxn8Ev0y/DoGyhv7DgPbRRaX973i4/5u+03yre0IHU8c3fGn+vQREADp9xnegtqEDiYWOQJB/WsV9R5l+J/l8gu3AiDy9hYH+6nu2BesHW7/H/Ap/1DdZu3nDkYRUBmP670Z7v9KzbERaw9h7f/pwh/M/Wf6xxQ49LDiS89uGXAduAXS8nT+PgYU8UcgTPcN6BTwNRHpAX/rPjC0EDcJGwPq3pn0MgtQEWsRrvz39A0KthwrCc788whd5pv6phxnEYD5eQtqHEYPDf5r3NkIn/RqAWwRte67Djnx7gvCIVAF2uph92MHXdqFA9QinCcFCX/WIApk6OTbwS6PBdrs9gUb/mzw5g/3JWsA3gMUD/gO8NsI7zYHjt/FBtcY5vxDycsdwDKb64oGGfEPDVETfA248DTVEwizA+kCEwQNItof2As1AzfXHwmXGkjqF+Ex/BEFcAPXK+IWCfPm2z8MNSgs62MM5+Zf17ECyAZBHuP+ZP/H7JbhrPUo7Y0NUUCNECjODwV2/nEDYg+u+jH54dJv/7YC4A/tK843gg2zsr4Tye9q6TY3E+nD6IIB9iV77tLzFjb0AFPu2uyi+O3yRBlPFdL3lszO67NIL9fN5tUd6/fC7+gDAQs35rUk5Q5K2ZDfCAw9/eThBQp87HYPERCBCrb6cfIMFNT5bP840xrrNA44AS32BPkzMZ0IzP1sDdUDnPRe9FENWc354YY0xSl++376zjAh9QOsPAnWI/f7dg3F+LzwEvZ9OQg7w9dJAtgaY+dZ4cUW0/3p39MVDwXK+sMQZkpL/E+sgPsmDB8fzwjDABznpNLcHdoGZf4cHeIdBwB90pbzQQwRF3ERaetqCi4I/+F66hgK8hoEJ8kTSNsuAxATFBe5/sb4QxVx2O4Fa/vuAsEewQPIDwfdYgZcHT0XyA9U7zvdtPb0NI3oNdmkIWUZLPEZ+sYHKfFZ/xv+xdZX1/glpTIw/4wGXg+N9ZfgQhFiK3ffItYgArj5QwiaGAYhiCh3/wrTb+BJ+fUEbAO29BsH8ARNEFEp4Pajzob9gBYA6T/VsAi3J5zfRfGMJfv7mgNuFtjllbwI7pcTKBDwCnMomQYuu1QW3BFW1csMzQhC8PvdZgImK43+two8JLzt+d6yAhn50+3l/rQKsu7X+r9DzQl15Iv+APKOAzDVzcisAHEelBzvGjr+4ADUDiPGuAT5/bfcmiuG8jXM7+OCGtoSyP93/9/ohgk5/DkcnOTCvgYUBQJjH0MUJvIkCHPgNc6y9swK9QzJ91Lq0iEF7kQQsEZD3Cvhpe+LBSQYwfq47Q4Dj/zz9aD5N+pfMXgJP/vC7c3hPCtIIl8VjOtiEmDjl+MtA3jnKDeqEd8Myc120XcrLBkgCZvhhQM+AKIRhRh86sLhkOk8JN/stvcvLGPvbA95AMHYR+eGEDwDSNSvJ6cZVARzB3UAuA/W9VQLkfDM/psYsyQE9EL9FyFhzo0QcRh0DxUKB/x4GSQIFREuA+gAYehFCZbipuB5HKHoJxZuKgIslg7l8Q7khbXP3I/0dvMEFVI0tQO4BDI5sh6z6brDV9i63sH+ByRoHaoS+g5TOXb3geyd/W7MPhTAGI0GOeV3AZs6n+6d75QUeBtx7ULhYur6+wMj7Blz+QbDCfYRDAzk/MpU/uBBbxBcEdQjNQDs0nTlU9tO1F8BlQapHXwovDMbDY7fh+La/TMPcugI36HkOPLcCsEQ1gG6DQwRFeoZ3KvnFw19+q/5qP7Mv6LpahEC8Y/b5wPeA4jPSQu8GBnscNVkBoflW9C4IpPr8AUMChkQIPQU3+cYpOGB9Z3f3hS7/SH51UZSB4ccngP+C8bbRtg47KP58CNJ7ho/HhUE9+cJPQRN7Y+2nwzkAVUM4Qqy/5gOZgrzKK/pffzG+GHgfeSB7lBDhRlW8GTlYO8c/Ef7MCXk8XQC9ij4GnP7DQ5TI/DEVdu2+b4GJxaqNBkR7sP0HNwQs/hl+aIf9RMk3EUZdOvU+2f66vKi6SThDEJo9PPOQgRRJ1oIQOeVEUvyCPYy+vUCDvVMBdA6wAte9ETeht136bIH3A+E9aYDOyQRHXzKMwWNBOnUDwAJ7rT2dAMnLUkGQOjlAjkWQwjCzyMGieVL8QUgjuKq7ScsMUfrAav2v/664LfeaOgCIiwHKe+QG5TkttQVDewccOuf1IsIUxgEGcsJOg1K39rmdg989W4WpucQFBoYo+D0EhQZigfQ1k4BSvsL+l4PvRtBEgHdgjcK+zvtuiIO8RH5Luh8E1MMLOvN8eoNdx9P+en8lORo6wkhUzDH+Iz7CyVr2YfXufcvEgEmNv1O62fgYwjhJOgYiA6rFiMC1eSBEWUNov9+AEUC5hnMGxEYxRxI99TPZATcD1T4LfpvAqUGbxYYG8n1FQRoALQKywKB7YMJ5e+037L4dyOxH7QaphLj5NnYNAgGPoMJ7fvPKPMVZe4m8D4XODF5/jDtDBIi1kwenS295h4TBQP4Dp3n3gisCQb4yzSw9hAJI+tJBJXw2MBRATbQyRZbKU0MIRrIDFf10NPh/bME5/+80ZjvjBLx29oLuCTmBdP7MAOW81zeeRm5IWHWZ/qED3/ZRezXLfXyWc10Kl0A1vwMCVMbKw2PwcH52uU998QO+gsn+DIF6j4S56ffH/3WByjjUPCvOk381ffaI2Yky/V17EkWUvi76GTukveGFsEUmiLcBhP6NRKY4znvCPG89akRGv59CYIgvhWNC4wL1NmD6eUB8t5iCt0wYfPa+KEf8AnyEELvoQkZBYXYffRHDnAsLRIdEub+r/bv6SPumQrN27DkTfbpCi/zlx5lO0j6L/QQ6B0M39ue7t0dd9nY98UpQCpy4nPnIvTcxMPquwewGaUlyidHHloRwwwV+sTm1Oak7J3gSfk9JZsnYQm4GcchFOjT6Fv6SPAHC8cDz/eHEeMaRjHfBtj2MvFixqUOChbO/EoP/g6I9I7XagOuI54LU+vYCbsAkfWbErIMORmwC+nuNNfA96AZdQVU6zL49v2E528ZyvJ+1LMFV//i/XPvig7KEwvgTf5xEq/wpPLzDqj2+7cu4jogI/qn/VMPcvXhA/cphAVN2tgNafYF07QBFQkYFgURIwTe7dPqJhGK/H3TZOPtGV33tesAAejy+gFKGMEO8N6oASIbNgsGvZvNoCYq+HD+0wgIDsne4vex8+THSB+LFewvmfin3p8Pr/0DIt0cXgHb7Nb27Mn81aMZyABzBLwU2P2v5GUSCT8a+MPGsfAA8pXlfvOVCf0EV/8MCX0V9/8k4ggN+93G0rT2PAOtEicBGwXiCcokTARk+hbnSu508+HkFxel/N0NRhYbI8HkGcg7F/ztu+0CDSsfA/tPAYEkAfw4F3MtZwACyx/UixXN+E7VJf74An/9ogfTIQH87wbPFhX/1/dx0h4Ej9zh9rkBm+ibK+ITNx038Fv8pu6R11D+zO9xBIT7+ygUJdj2GQem9H32IgvD7/nxKuG+6gol4QauDFsyVyME3QfmtQTc8e4Kgi/SDzTVhPhO5yn88BF0DagVwAG0Epb20fVu9zghRBA4133oifx56mr9RkgL/3wMzgz153r9leoyFPfqgvOh/DznNxr0GO8vDyVc2YXLlerZ87X++SEPFk8EsPqV/NYgRfLXC+sjMeWI6u0BkhyEDJUZjeppxBoK5AN78HgCeil0EtLmvACyDNf8kgNKEQLk89KuFfoAYvI/Dwz4EffV/AoZmwpAFxkCfvKx/p35/TMt7WTw+OiY5+MUiwf0F/byrAJK8Dn/GejJ4gYCaCGqHMbfYDDH6z71/BFgCGQOeuw7FhLQc/T6B0cFUQPFFT4f8NqRHnoNyhJkEsT+Hw1p7rEEP+bw0HcBFDc8CCbe4yKKAarG2PqkBUvvkhgNJ0nnPeaUC3b20Nes32oVPf1544D57/XB6BULOTL4BNYAgv1I1fjChRJhGVftlim67QnnKw7YCrkWGwr+Drvi49XJElAipvh4/uUFwPNoBngoZg7s5IIJsfG+2ngExAVN/QAKdQwA5JfrNQtK9Ob8mxoxEKPcB/DpHJ3nteVfJKsTBdDVDAIdIumNDXwJgA9J65X3EAmX5eoCeBiDEx/qciGZEYnj2BtqEiL+XQCuA5XmpOr4BF8dNyQeHIX01d9HDwrsw+8gDHX98xY8BJLj8Qo+EEH+9fYn6isH3+4MA+AZhuUQ4GkBAySCAXEC1wOR7h0O3fiSD+wVogRDF9/VLe5N/R32SPzh7qsoEvdhEm8cgfabBhPwCw+bAWQM/gl/+D/aEvPLBoP4OiFc+XAcSPWa2X786f/pFggJCxW1+iER8fsfAUQBGdAm8A/pQekBBQ8wjyl/IBrlq9lu/3fu7wJG70MH5QEEEZsIMPIWFwoKwPhCxMwFafbO6205GvaRFmMgNQTGHuMAP/NZ/CTmjd+P7rYBXyFa8wwKIDSn/inyPuks8Cnq+PbvCdQTDiA3+mAI6u/i2eL+SeuYz6QN5yiP8D0qfxsqBXgnef9i6XTaM/9R4nLyvwmZAsMlOvTXDKTx9ee8Auf/gAniCBQ/lvqP6lL7ef+P9f7kbCrb+Y3zMffNBs4RJxiPHQ7OGArnBbT1JCuHBdLj4fxK99rqnfki+jA0n/1l6KkLfgO5EBMQUhX736YLgxeg/E0IQCalEOG1KPQ5DqMWout/B5Uzt8S7/KkXYQSqCskFjv9rzRLvRBIwAnUHiP/95yn3jPyX9vwAEilZPCoAmftoEInmodT15Obwo/aB/jYGOh6SNwwHOwPr9MzPiQeK4Cjp8hdH/7EGVt3t7ZQ0phYh6ov6ouY/4cMGhxaPFgb/af1p/Tfntdj9+1YN2AQz/Azx0QbxFyokV9f62xQCGujiJxIOAhagHK/5BQAj3A4Jjwzm9+nR4dZtMhYIZhlrT2UHQMyK/DoYodyN8wDy1uHZ8qrixyqCHOr9Khb22X/TVtzIENoJUAnIHtDVcvpP80j/XPibztnrgAQGCBrkBDVJJ18VS//I3X4XJuAI/5z6xM5NAdIoOfq7D7EuS/QCEu/a6OL1B78LDAo/5wj7AxeAJdTuSwKO35EASw4v5Dsl+v8zMpgNVw0QBdO8AA6F9FryZ+rDPFdhsOr9ArXiVdoOG9IWOQbE76wRMDDu7Sbh+jiyKpbiPetW56T/4yTcGjcUlggTEL7ze+5IAKPUNuDrJQEXK+byI9w3ZfO78cwfVO1czqECTv5tEDwUyy5mCNzWOhUG/ivzyfwGE4ISRC7THz/Z5BG2/bjsDPPaFyQR6ubqFLsBxRNnPW5J89ud1msYreCX7aL+aiqL9/gJsTJN96AJ8Qt17bzMDyUdGDH+/yKJ9oQBBfqZI1/++MT6CVIPgOOj/i8wB/kFA881T/ld1sIMhBwryEntXjYT/bf1FRsDAWvKNQy1I5j15PYt2tsBrQUiCz8H2fX4+KX9cwXBwlMHOvnR4Bf5eN7eG+UFq/pX4gYCCSBC+N71+Ob00Z7FfBkJExTw6xAJCo8MlASV7mfjgvB3D6cANcvI7IQroQdp0TUCA/Mq7KAORfj0F7gQCRyPz+i7UST2EFD02fT864fZTwdx8qfdyAoPEsX0a9u8/EULugi97H/zxNtXCsMoveCl5fD31f6tyhkJFwxP7w4Fgut57grUQDU7C1Xvhg9t2OAALu1i/zzxktjZ7536+OUo61kR19Md9UDyZvt1KMD1tibk+RPaNxyc5UTfyBpYCWP+1A0n2g/ZnQvJ/zD4P/aPCIgmAv+JBSMp2RRqJTTgn7EUGvQMgb6V7zsQIfG/F54oOQVLy/XwtCrr3sj4TQih7uwC8BNmFN3tLOpi9GDxmM64/lgaOgP6DJgRpiLrEbsmBO6V6lYDTfboGhgC7xWpBgAlSO6M5rc4r+aNED8Cpu488z7xoghf/NMqRAQDFDMHPAZKCpn55Srz+dLowN3NFOT0m+X7KaQSkRsP8lxCnyo54Koo7B/L/tIIfxqN+U4U7v0k+bXsnPIINKAMliCL/w0HoTCII+cIL+bW/MfxHP3BB07zgNdZGSAJj7tOAVMgNRJk9aMF7AbAEC4JQO0L89TjtCE591Pd4QLO/7scUyExH3vk7fZ0B9Ln9++v7x4j9iRIEzfpYeF0/67sKRRR/gjyggOx6loDAAQEBKsLHtej0aYHBgZ8CykG7PbW8a/nVAa0/4D6FfXH76b8ZgHJCgAD+O7c22T2M/K42j3rfwJbGXEUFAMOEwEHx9r13RzjSPlF9xcAC/wG5GcOrhuTAgbjzwTl5PDR1P+V+BYKAQrBFfjfANpWEAX7MfPuAlbmed06HbkA1/yVBBsKBxOB163TW//5HwDxfgY9FmcGTxZb4cDJ0+vQCVfedAhlIPEmqT1y0AvlkARYBuMs0fhewiPb8w4yBPMSpChXKYYOGe7j5Bz3OjerG0/tfMXQ8Ic0VxBGKd0B+901DUcZnOTZ4cMZaAO7GVshrxu4+X8CHDao3NvqmQjr4+LrLfSbH58xGCrcGOrrYAB+Frzr3vbo9tPxeQqQHi4d3QSVHjH79MdI1wMPxB7F2r0Y3itK4NAaTAGj2bIItg2ICMTokgjoHmshIhgZ+tv3GvSxF3DWJ+kMC4ADVzYA/7cSFw9iDJQMrOwWBMf4zP8M93r22QOeHWsU5xG89uH/nUFy5+/l1PlZ3t/9UxyRGEcISSxTCNXq0/KxKrkTPct2B1ny/evJIBYsLQFM99obDO9f5hkKpTkhF0HtohVi6R31FBCaFIggftUh81r3+vKjLvMLgRPt7LDn3gE66egUFzTkJUfe9+Xi9DoNgjKoCPz+DN+/8H3ja+4CIJEONxnx/5kAxwn5Cd0czhII3/3cVPKP/tU3dA3o15oA6hBf3or2Z/Pi6eMPYPOeKO4UuiBCJHHSydyf7TMMutsFAicEmt6WKNYMEALm4oPlQBCZDOkeWBDxGgkRjwFO5VfCnwVo9X/zZQy44Yn6uRK+MC8B1QtLHmPiweaHzScYaRSZ99f1kMIR+8wTYQaO8gcHZ+/O5t33pgHzDgjg6AP06zPo6hHEEl4Bl+aR+Wj1H/Gg+X07bAKd4tIChcMJ4WsLhzb9BVv/+R9c+bbxzde/Cq3o3/B3Fw/IRv7HO8kpoOgG/44Wf8pg92P/+vPZCwcXwCfF5lwDfDsD/G/cP/uh1kHjlDdmFngg+Rqh3nLk3hSqDg3suRsm7ife9uh7BA0ui/GjHk4UdM9E1iEHEAmz4dQN8/vp52EHKxeGANPsAg4J7YrMzP+WDKMAZBPnFZsLK/Pv/ETfwMz8+cza3gM5OI8WBQeNCR39TvQ1/lLbFew4/6T9VRG66KMTZDfV5ZDk6RZt9DXiXw2+Di8N/RIkHaL9me7MDzvidvzMDr0O5hVqBhclL+vX7KDwRQcKEuP77TmY8D/upydTDwbuZR70GuzQQwx//aL2ughJG7QMdRIVRyMVMAnb3/LuPQo1E5o1YBRC9G0LsyDZ9poPPA7/FdQLJQ7SAZzXnjbJHwQNJBMFCWgGeBdFGnnkKhNvDX0lTRZEGhcsA/57CFD7IAKIBU5NiRxGBGj2r+aUTZT/EQ5XC9QFfxYWDB4UD/VEO+7tFeq5C8T76RHW+akSitwn/04Xj/c9Dzn86QhEAG/nX/i9Dijx89ljCkAKouiX/UXMxdM5EbkLkRYr/gQXXPuzu3zfZwSz2rLPE/xq1PH2Oh3QI0PW5bHYBhK5PM4fDafx0OYi/VsRSMyR08kaufoes6XZM+993WLjufpf8bPSx/2j5VADRh+n8K/hKNq8/c3r3ADDEDfzo9bKvKPvIveoA+IDcsyc4vYjlf16zBD7SPnf4RjrTwJO2ijONg4G2XLJjPirJ1ElVMaQ2FP2sO5SEl0RpsyHzv8cE+yBACc1MxEl/F/Ra/ys0jzj0zQI6ozzGfUTES4Mvwm5EETTD/vR5HgObvh/5KMmMfJRCAYCjAjY+IP5MRP+3xnbyuYhEF8WwiuqBVHn+v677LsPUfJZCG4VBet4C+4NWxHc9coEzx6u3LP3jBXN72j3qQPKALsL1z3yO1zx6cp47BEEZ/hxEucKtd2E1q30egPD/e4IBAtL/p71B/SF8d4BsRbx+f3bPurT/4IRVdzf4YMCiupgFG/nVOu9BZzpovLZ4hT6m/W97IzoYP0E5JnS0RxJFVfjgt058ILD5OGTGHfzUOStAtADaefiDAAHa+u1Aa4s4QJM3nDxH/Uv+tjVYyLhHN7ewBKH6z7j9DorN6/5n/Li9+jzCe6cJQEjT+x6AIIOovsWCXAUb/o5DG8CFjGp/53RLx5C7s/lp/l6Fib8MB/wIb/sCP+q+NUv/cof5uoLLfDPNLH9GhPj/E7wnvH+5YXh1g5zK9b7q0E18Or7bCZY7u/8zOL/7AbfRRdu/IcTDVSkFBIhxezu4AP2cRAJFWPvsgWbHqgWvw8gNlkKNACl/Sr9RwVz8YEo0QGt5+T0Pg4vK284SUYyAp3OeOhmGKsC8SvgLcD4lhNRCsYTJg85BYDr2fluD5D5dT26Pc4M7w4x/AP2M/zc8+X6dwXaFuElmBRHFA0XdgyH//jtGgrfCfr4RRzXC3MGwCOEIhIXrBJR88b9uhn97gUWMhN5/k76AhgJSUv2Ah/uMTb5zwKwIoQZQ+iVBrcjixCA/g9Hcglf0hkxOSe7AnwSPS2V5ljxNyF5QZE8IQmXIZbhq+xLFHgU6g5jLUNA1fNaCcbw2grqGy34mgjWAy4uEAGzD7cjowpgEtH1KSPTAN7dMPSKBr0R7AvxHubpWfm8FmD+6fZCJHY/MuypD4IP6QHBMgwGkfk11vDc9R5DI9sT1RzZGrXi0/FEJPIsLg0s5j8EXMpm5WMyz+IQDbYOMd+P3uPbgQFBBuIbn+zUyWrO4+D85jzYlfBr0dnXstaK9UwCmuRA8FzIBb3DzzTsqLtW0kIF57tn7GIWCgnW+znt7/CHzoH03gb55EjqIhiUKQ0EkC2JBZLO2gDzHrIsIAVG+xEHrgO/ChxEoC69HYVO89t579MUFwL5Iqn+sR70F5caWROl81AFQQG2B5H8AR2qFugAsxUN/+0dvBN9AHQXF/5N9BL3vQoJEyAnvhU0HZkdoOtNEjL3UBi5CFzitwVZ5nkeQiZaF7b8f/Un7bzwePJTzjQGiec29TUerDSQ+0Lp9BdazcDgxsrXAgcFY+gzGRnqDhjfIKgTku/J3evLgd3eAZzjoy6gD9rnrPxV5kLui/BByiXKvwDlCeAcZPr74ufZftiD8afQJN1u36brV+ua2+L8BBK48lbR9OIEwHnTswCb9E/2sAAqBSzsS+9J/wH4GtaW77vuKNpP/hkLciHP70zy7fmD6FMLxSly9r6n8Q740Mq4Byu2HNoNK/KjHuXsPb8y6kYHHumF2fwCDOFLDAYXuSRj81fe4P6GtWnX8OmnEK0RsReV797VTg5626z4gs8/1wLo5ObxCUMDXCWy7LD01sg0z2j1aen38RvTzh3D8FsM8xjdzULLwMNf8ta/qPDr83ve/BcHAN0WDv/U8MLJMrtB0pXnng+I7K76fPpp+2sSRAV28y7Nj8pD5HoZnx2B/B8Hf/mICm8S+/JY60no7Aq++Lf5TR01AJ8TtAo2+Q8PvyhDFt7WHwh3JggArgnOIN4IdN8//VgFfQDlEIIAdf3N9OMW7C+kFiUWQw9C/njfxv5CAwj3OSWHB2cDThoLI4MhGhQfBtr66izNFWvuDAxKEigV4xXvEe35xgbnH4Xx7u+FEdYVvxGFBXv/ZgMCAZkAhg287rYif0Zp7gL39Qjj+GXox/eCCZX18R52MzoT9xv+MNAJk/mV7zsIDQVd41MIFP+NOoRSYzJpIKH4Bvba4/jzwwKlGbsSfRJmFmIO3EpAMP//DeVq8gEBXu5xJWkGee6jIakfxAMp8CkllgsE08zzcQayFQUdezE+Bqf58An54Rbpwv9VJDwGOfpbBfsOvR7M+CYG1g8OFQUWMAKo7C3/ef4m+f4tAiUhDvHvouM+3bH0ZxpDEpYPJw4QHYIHPRvnJ2IHofAc9PARNgIIDtTzHN3l9igi0yvM9SolNSGW9FL5oPNLFQYRtBME9crW3BHSLnr1t9TlD3T70Plc4THjfxtu+jktUvtJ8hEUyPoc/xjZ2vlV+y0fk/An5f4Kr+MnIRUSVxwG+VcHBhK907AovBjoF7Hw7OC3Bi76GT4x/tYg/iTTwmsDYgkiBz/s3O+10sPa/CTSFRxNpgrI/bf+otgx+XzWWAPh5ZfjBulx4UMu3Bso+/gOChE04PoDJR1s7Z/8NBa93UXgmx3SCS7sl+f/IfIGkti9BEggxhXfFKYE389j9xTrZct76oob+wxb9VINGfLmEQcBAgWf9D7MPPsI3azc0if5QewFLPCI/Lb9fOq7/zYAQMcYAy8Q0Pn8/3AbWQ+I7CwbGuLa6lMSa+X7+OUAxh+D/CPvfwXF2ID3HuWkBiYXWO25D9nu2t1o5UULzgkFDcUpnPgp1gPi5QB448z6SQKx5w7+VxVVF1/wOQCA+9f4m/wR93ULr/oZ5lsPbREv2yoTzRZb1ZDvAAi77Jb+sQxlBGoNpfaf8mf6iPiazjreOgmyFJ33KuD1/JDmHyTvH4H99fGNzf3ptei6/g4R0S2xCODuBd535awj4d/84LnwyPbSDcQAoAEKCzclSAz/4q7n6Q8/4lCw7Ov6I4oQhgqNIAYBGPaL+8cOxfI76aIFh9nz9eIfYBTOEqUdGAWA1vX91QRG9SIgRBo4GgQPL/wXCMnqwO4z/jgCEwqCE2USGvRjDXUdPf094ZLYJNi2/yEZA+/uGe4f2PsvCcLtyfB73gXiVwrf4hD2FT1hHzYXehjZ7t0AD8ePzisF6O34MRwkx+Ub/+MsvhF96V0IDvlZ24j8disKG8Mhqgws3MTbg+xBHqH5bNhfEeYRlu6wNX4qBf7sKV3vVOXr8T7vhPVq+AIZvRQiD5kQ1/+V1s30vwbPBo0M3gUPGjnrrgDBB/Pi2A8LC9Pu5PS4C5gBKtK652Uq8TdcEesE0AJU8EYK7PaR62cC9AP8FNAEQ+UN1sQJKgjy/m8HD+wJFin9keRi+pwD+wo8FBcP6eVP6T8DX/YV3u4EZRMwDS8hKRCU2FLsGh6p8vD6GABvEFgYLAgNG4v23QeSEHTuktmW+RYhKP+lFAER2wV5OncaL9KnxAQL7iZ43gb0thij+gr0k+5Uyx3vtzloB/fK9NQNFKcOlvkzDVDslgQ4BlQAh+RG6WImOwad/m0EZRDuBPIQSBMLzU7ztyGnD9T61hVKFunx4A+18ZrZnQqLF1H3Guwz+5wCSg8WATcHPgVv8t7e8uauD2QImiUS+ebPnPXP48IABCdfBZHt6ffa4kMPFhxBG04b5tYF8ZDzYw25ArfzwgCK5/MQsgiJIuMgcPha293wygMS/FQNpLx8DCkVNN+RIO/8PRZZ7+7hBu6HyiQsTDNcAHMKVxex+5bilwMS/lkE6QhMFE34ScfFLOg/SA98DnLo79Mi1okIvS9GHtIWH/pZ5BAT5Alq+LDzlwBuJPPbQfe7GUoJ8hLV9L4T8PC0A3Aektn7/Yc5Gi+g7EEDPO6pxisp0xdF6PH93CkpB/TwUReC4F0MZvkn55YCod1oG2IWwhGTApP5quhz2jf5FN9HG1kFbxoOKYvgMQ4p++74t/A07pEJAP+xB30OFCl7IbwVv/ki9tkKfdoM2k73ig+uDYQJjRpkE04j0/tz7/4ASe42Epr8jt0o7IEJTiCvGXMHmd6gBLkbC+It1J4APCznFeAJlRWc95T3lPpay4zMVgwMLukU6PSyB78jcPgmBpweFtSI/lQh+9xo/LIYLfiZ/2UA5e9t4PIEphZN5cwH2Ax09OLzdhl5DhzTpArH9azlgeSYEFcZ4MPhANn/PO82BTc/qTDR7qApN/m0zK/jwerPzurYsyo+Ffrm1w6/G1bQtOCsNmoAgtrqI7TuKr2DAFwbywcS5brzY+X2tyD2RTx19+QApDHs0fXebxchBTn9D/c337HK1/myP1QPv9XWDHT9LuedG/QjdvCsAggdZ+036I8I1yiO9Q4Ofg1vvtT54QtWDqMMkxU1Je/s7cjt6AcFbPSkHdQPRPTo/7L1NArEFPUQ3/Lj6QDruAAMDav6wAERC6okUAlKFyUUXezxB9juvPkKDpYZNw5o9MTqAcySHyAlwvA3FYD8NfhLEz37OPK3+ev49/Wk2PXlgCQMI/HmogIkBDPaL/xd/iUDV+NHBTUPkORoDgAX4B913FsGW/7WtrkG8BdAJsbtGPqcDaDi0REeG6ET9A0iDnz09gLD+2TmR/MB0gws+CYfw8MP0P8e7VMPmQcjIA7gdfZ99LflEBmnHtQla8JG/8kJWOHBHZb5iwOm6vMB9QwfDmcN9xTdFP3InBldHeL9MQNK2XH6ygqS+dr+uvc79goY6PSrDFwjy/p8GbcXmu849GIaHPoy5FkAMv6r2wf/uiGJ+DwPpQQwBWPyUeXLHsUJsvr/AmcJAu79+F0Vqeh35AH5Avvx92cXDBfv8NP44g2xI78Axfr7M/7os9CYHQkDmBNdF37iytjV8uoZHPQDAgYwshN192kL5BYX8Pn80vr97dfIPeMvLerXwQlSPDLtevDnAnoadddC2cwNudz34BwHWjQrFT8N2R0h1fQAdxeE9F/1B/J0Fu7c0vZ5LJj0GRkZHYcGK/rXEHX/vuL2FxAGmw0I+ez+Df7/1JgEJfRw5VL1RguMBEsSLSev8J3vif6K/zf5+/ypCBT5eOdECjIoKw029EwJVB2xwS3M4Blx9Oj3VDP2Id7ntv9/Gun548rK+nr/p9aV/hYBofTa+MEdjfXF5NsFKf3i8Jrj3RcsAyELNSwz+B/fq/Ht8QD8sAva3/caShOoAnAkh+waC7X8At+yB+gtbSMkDYUi3P104bX9KhCO9p3pyAOu4HXuZkkwE5XqwRID+iTnU9wXBJYcEvhMGN0qIOjA7HAdlAWj2l7x2g2O1NL03SKlD18JP/zJCNf64hkqFnThqwGtL7f70clxFLoDYduk7fDz5xWaI3g7Jh6K8BcL4fBTzH7wCgGxCNAAsAx7LyXt2PUrGXrvW+bs5Tf2BOVH/nwRZQdmHxQfximy6YDbhgZKAAj5cvGYAXb8EQ1pBEABmxSNCU8UkQ3GCBcJp/J++Zz6eM3m/+0RqxZuLC7yhPZL6YcMvxIQ8Ff4IOsm3KvzbiHl8lAh/hFg5ubx2uQWITr/bQV3BhjnnumS+28FtPe3Fz0Aa+gk7mUshBTh5KITX/vp8433u+2b7gUIdBW2/rH4zRiDJrL1Etkr57P01vBcDngHJ/zbMZAQetnABIL/Le/hBB3nS/TO+aDnFxG9GYfZngkdKQPwEP7M3ZUHaQfZ7qgRpvtAEvMApfra5QH1TBI58r37rwJzCkUPTBvs8vb1TASR3bEQPR1cB0//gPXSELPzmPcwFm3kFt3R384D9xffEBIzDAr88SDs3vsaBtLw+vM0yabYyvo38kIg6TehKsMFfeFO9dHfUOsh+sESqDxl7X74A/HG68w1pQhJ8Qf4bgKwA/T/kw06AqEXGBhZ6V3bmgtQHXEBbAav5J0KJSNe7p8x+wPy03jjVM1k+9IZISifBZsEe+jL6bEB/O38G6L9cty4zavva/QfC3srnN5q+0YBRPNq6SLkhADdCq0P3fxW9oAB7CmU9yfqsPhw3n4Mfff048cORAuXAWwR6fVOGlck9+Wk6frdSOTeArcwaBV96dn9/v+V+dDgNhC5Htb+6QYT9Sb66gJt+lv6qPpWBKUtVA+a1Q4K9gcr8eoORA/LEvH+6AyPAyvz0BBeCBMchRE+C3TrHvwZIJTuRh9xCiQJHgOl12wMcAkkC9EW6SwC/FD4wwUy4f4t5RfL5CT7SyUADpbz/icNK3ooLfwz/NQJswbkHN3t4AEiB1r4GSEhFEge5w5WEMkq1+bE8bok3xpK+p/03fqN4MwhtC4u/4IbrRW5BJIBl+wC8hkQPgK8AfcATwQXIfvyswwsE2XetSCsA5fPkuRA+/ge9+5GBCo1c+qYudsOyB6gyFIJdxpD40T6FfqxzV3nPCmhC/PfP/CmLETwRdVjHZgMuc9QyzML8eWHEE0rtfrRBW32kvgKzO/it/kH7bzjsueO9Y38hiCg7dz0EA0X+A3Ap9zH+ni+RACW6MvfZhAcGcT9reKh/y3sAAfK5JzvQiEh3NnYTvI/7ZYANQt27xsN2yszEbzt8tvF6Lr4lhWPCr0BtwwNDIwGPui8+KkEDxaBGiLZi/MJGJMR/RFVCxoNlAzrCMrYZtnC663/xhyFI5cnDw+vIU/yudmG7PDvMiVzGTAwPSIv4tAIwhj16STkHQtEAw/pnwMJCAAJnxg8F+H5adAF/m/prd7I5djgvSC87pjzlgDc6u3zg+kmzNX+/TCT1Yz6Atiny9oNqxM/C93gdAYx2tvn2gA1JFsfJgIRKKDqWvg02hAHTgrF4iMhtviE5cYiikWQ9bsxOAXyzNYYC9Sn93gQXjg3RPb429xp7xgIb/OuEev3Ggc5HvII2yd+7tT7OTC586r0HwX1CN0nzgEV944Vf/31+jkFqu1sEdAk4AryDO8JrSNpBJ/hMv097Vr2WxAg7WwBsidm6hHcz/oB+dDT492qCFQFOh0rE27zWOvKAUf2E+YB+aDntfz762P74Bds9VsLkd2SwPP3jgc1+rwJISgg9Wvr9v009UveS+H8E1HE6PNdHCTT4/rR/LwH29EZ7cf6EtIEEpgOogRz6vkWQ+xQyIEBk+A+3wa9c/V0FCva4xacHDrvMgwN8cv6kRK52aLwpfep3BLzoh3F+GwPoRKM6HsBldtqG7P3peaIAUb9rRhP4MkVxu+v8D8PRAkzCRz0fhhxCToEPrZV73v5b+f3LOkEny8tFckIJfVK42v4ZwRDHJzxfu5qBrkrifmjAuH95shZ+ywEFxVi+igJ3C3pJafuQvVLLGrPLvE0DtQNyDIC/2whDQaezaAEZB7N+MgUszu8Em4LmAPTI9Qm+gHZJgoH0Nsg/fwHahSqOLsRyR1eFw3hVBhC+o3/uyuEB8YeDwwd5KwcShJT5rUBTQlSHPnsHPNYGTERpy8dJIcC3dS5BlIK8QUD/a4QBUfe8ucdbgO6BkArp/iZ/MkAhCS5DOEo+QmxALz7CAKjKk/5bxj290AMI/50+WcYBQrrJhb1Cu0A2LoOHCeC+7v7u/dl+CPnMxmyDjsfOSayCCIVPP7z9xAA2RGy/5YF9A48EBge5B4eCFP9Hx7VFTkXuRKf8IjrIAcy70UPNDEl868kmf5l0OEYBwAK6Yrz8vTUAgYeyhlf/Hn5jP30Dsn0MOgg8b3MkvQ/C44gpx94+uwfd+ky5gUJhwPxBbPx9hzLEIwOziQvBobwf/D/A+0BfBqpDzXkVv38FdgOHQSzFvIBidwpAUzoy+nyFnn2p9yq5Y0cWwSl2KcM6gFWwEjhxh2dA1sE8j1OEVu4Cfl4HZD4OurUEk8FHbebAH4JKhG6GUMnKxnBtJf5RATe+uAF8CM/E+vi0vYQyyLpbf51GVLbwsY8D1/UaO7pNmAfc+DLAYzrC8o8z1zcxx5O7t3n4fpZ4If8OQge7JLzRdUq6zUZ/PR0Jj8aKgVx8h/iu+PExl3jBe1RF9UWlB1WBor0aQgr0Dnqd+A57+AQIP+oEFkMtwYh/ZvTia/A9tURC/jnBVPz1AO0EBgc6wMj12XlD9to33jhlP1lJjodvyxG+I7Q/vWcBBEDifgj81rulPx98AXuwQ6IE2oKlvTF807w6vLnKWIE7bwO+iALe/nyCUUMvP+V15jTfOyEDU0I5R3xFWPuXAn8CO/7ZefV/6oBpgPP+73Yz/zgGKYWaPFOFdQJGtrF/hsbxPo39Dw75v0r5sYHO/ns08DkdTQNBkvqUBuPQ6Dtrs/KFnoFK/hWEw8M6rxc/Yo6hfkf6f8ofRnS0JQAXQ0SDMT88RvzFdD9NyWF5UPnk/ZKBLPtkRYBVzThI/xyNdIDk/kwLhsm5s/t8M32T+kIFLIlXyw0CykgcArHxnfl8CnwH3TWcjIIKdjT7Agz/yvycvfNGJ3va/F1HYcGKBqvD0YTNumu874K4/D+/zLuUx+HMJ8Fxg8JANLntAO18lPZ3AZBFxgBSw8k/jrvFwCw2xv2rfC+/nYdofA78e7xUzEMH//iNuvK5LfaX+IjDFD8RhHTGkDyW/ZOEtUnOvtmxjvtyBDJ8DH3xgNd/ub2//WM27T9LTP49qDtvgBhEGgDafRe9kf91yLi+1jmqeln9AYSAPrL4Br9myhsBL7uABpl4+Liwgsb5k4Rzw2qDukNoO9v+rb5wwg53/n6DwFr92wQaghsBpX5hTLLBm/vzPOtznjzyvER9ysLdhQH+wYAbvXW/9YlFP3WA9jlhdaY+0cKwh2WGrz9Qu/DEBUFYwSzHhYWn/P0vB/WNvQ8Co1DUCVH+pQBpelo7hP/uvPWCBHPvsVhEq/2zx1cPRoHCtdJ0VABquvZAx0d3fHS7OoDNxLvAYIU//Ij0pMSiSYFCTgJOxHZ74rxXf9Z9y36Ru9TBmoAOutFAnMHvv9r9bP5Y97Y7g/+ncCX46Ltltz59mkGzPr89xcxnuE4tisI7RRp0wi5SxK7+zHrVw3lGvf7Osk1DwjA59EHRCcYpf2744QdpQ5OC0YTkNig51PpLwsG2IUNujia9CIUW+TwHAAKTek+NRT6NRJZCdvhDgG3CWsJZwKvBeAVpRp38mgJaBx5BloU7yMwHT8P+AdR6Wf7Yw89Q4ZBQQMnDhX+XAwpCBoqARBM+LcinN+G9TgT4FNXKyr6VTGr4V0EthksBmgN6wZVEmkNmPn1528ykxalC/MoLvqRIRkX5ObL51QMpjJWEK38MhBHHgcNFPLRAaHiWvTnIHP4VPiAB8oZJftq8IgH5+lA7f/9F+327zAyJw1D804P2Ptk913SV+pj3YvujCmGHHIhk+0eD/0NK9WnC139SePB5Y77KBAtDvEUXBYb6aTHogRg6ibfS/Xy9wL6te7BIT3kdNYQ/s3uYNwU7Sf//ciuAAoIzeCnt8vT6hT16cn0sQE4CdDg1vRxATvfg/Zs+BUAENYp6xEa7flX7WgMJfmBBisNuOTT9ejj3OFG8PEJ8u7IBiEQ+PdqFojT8Ow3+lns0+L7+E4PRtMa/44fawa172z5etkE4fr6EgLFBPDc7wvRDwQKSA+KHTMKsevTBh/6zfcz/FYCFufZBfAFauFfFPMr+A47Dg0tz+hD2GP4RP8KF8IO+vu5AeQRdeiV9BoSqPQACJYmqgzcI6MN19+mEPvhZOoPHggJBQK6BJMJ/fzhKYIU8uTY6y/ogRWaBvr9syRIIyApkgY/5nz3WgoRAen9uw3wJOUqDfXj5lj2mRwWGr77pg5MCn38A/PbPJwlKvPCEiHeOthx+RsYiidmKr8xuhQU2JHs//qc64kenxhdDbcD2BKfBpYRjP6i8E0SWd+gKvz9v/dKHGbvNw+Y7xsRevE5FnwZTef/AnjnCBCH98QMQgZq7aw0aQvD3rP9Ww4aF5Mloenfys/t2wQYCHsBYRYFKP8RTvZLBdwGlgOl9vzi8t3L8P8ZZPyxAGUfWvwN/IL6q+1TDhYYm+ZM2TobZQ/z3jb+ogfdDYAXsv0x44HibQAZDdnxRgpBPrcL3O4ODdD5k+GyAXAqFRPaG8ciW9364boRQxusE2wnJhjqwrfrQAy/E40vAQBY/V7mX+/06kDn0CMHHgz9t+9QHvIQavC34lP5Jwe07Voe5OVV3TwrISHQ/KcXrBZk9XL/ueF4JFH69eaWHBzkiw5GGdM3R/kl4cwDo8lz/Or74P+y+IEfWxT65UsTo9aJCwPwmOBrG3Li4RD77WL39gfm8oH9dskUHN8YUQlbFgDufhvXEar8k8nq9cALqOR1E2vwxiIGI8QGVhCd7XgbZPiE2bntVPjcD3QPHRZ6GiP9lPCkBCrq/Oc0DboDovgpBsv4ogSz9lzonvBb6DQU9/oNCTsQ3wxUHfXoP/rH8VfuEfTUCSzqx/hFR38U+AHX9OEaGdsot0IWsvSUBcwmCAve7K3zKxPkB6rObN5/5JvQlxVJJG3/DPjtGEbuAutKCIgFIPZ/2tcDZMqaAttAlPriCKkfcA8R4J/nxQSnBlQBSiIH9bvWfg4KA9vuff1HIfDsne4pB8sHGxNMC6YN08yp1Uzext7pBJIpXjGRDHcHLAcI+fXhyyPECQ7KRfvV6zrmASWmOYYKUPyP+Lb5Ifna7UQPThzw+hYH//zz9oIkHO+m373ZDe5RE3gDriao+k3vCRwnFBT0u/ye+fbdVOsu7rkMoPohCG0QnuUQAS0NNgRs5eoBzRaJ2Qz4uSodHTUJbgjDAn7el/mHEbbtxtpTASEQDfFdHEISwgqKAbn23u7s0yMibu/UzlL1jRq8Irj6Qx/t3wDWyPYV+sz6mBUbOGz4vgG1A0IJ4w6rDigZLdZyyFH4cgqj/+QtYjBVAtP6vuFj7y0DfvrT8PfQw9ZBKcczivDX/XUFOtfO2ub1Rf4PAu8QMvGm3FgcDCU5/D30NOtj6HUF0+q495YoxgVvHPD2U9b7Kc4MutVKER4SwuXZDKH3EvXbCjb7/hQR5yboBxtK7HnoiweKCeX9U/glCD3YoeT6IO/3/d+TCqoYyvfE/Hb0Yfsy+w3b5AccCrLbzBNPQMn6YRY/KdbwzOUs7CH9PNI9+8s0shCE8gQBKP6pzXr/JCB27S7vMikW8ZzJvCjHKSb0E/23Biet/s3tLffz8vZAKCcvc+TS1EsjCOO0zkMjz/1M3DQkTBlX3MX12xQKEt3oo+3FCk/dogAZGwQARh5SDqrvovSzEF4bvQAU/pvv6N9iBAolzRZg8MTrfuH7348J5QzBGmQJEOWD28TvbS6DJkoBIepe9uTYn9ldHd77EQr4/orwPCMR/f0FwBygCCT74+3y9pHx/QL0/nUBjxTgAaUpqRpP7yH0jvyy6WPOsgeSD1YMjhZgD0oI2O/jAdj0PvHq7on92wQ14wb8ZgnOCO3yTAz7GYHh8OHh7C0UHBePEvALaN8f+yIEoAzrDCQcExKg4hwCLP77CRD55fjTAObpuCz6O90gZA66Efff1d9l8+HZTP2i+B4ipgKD8w0EVgPIHfbwFw3r8YX2Lxb2AdD6d/xvBXjttQp144wZXiNy2twa6QGOC4oSvyD7K4zzbgO2DHkDq9rv/ZL40NLVK8MikA8kB1X10e2r5REuSg224IkNewK0zoPlXBxF+27/1BCu6DnXLP3sJToPbfxDFj0KR+ni9JXrGPZkGyMcEQG58GkOvwnq7KED1CBEA7L4ZApVA1MS4goUC/4PU9ux3+D9tA1UChkXnzug01HWYv4kz7MMvCrfQfYbQPQD/Rn2ZOEy6S4vePS15o0GKf869AcatVfGA5jvDfpm6MLkMvSjKdIlNxcvHy78VtKe9H4KZQHewU3rxSzR6tUmzy86CtUJQevV5ZrYlQAsBxvxkgW2FSUJpv0L/wziqPpHDu3wuP3rE8kZBv6W4TcDsDaDGl/r2Oxn7z4B4gOE9bz8IBNwEVf0f+K17+gQvCFFE2ANwihmBEDpK9ac0+oMEi1yKK3V3fQHEWTu+QUMB9j2X9yEBxbwu+lnD9w2MiCV1UoWOuV9uTTuFgNU54f7uyP04hEAPQ3vD9oVfQJKEpzVHdZLF+vwaQR4O/roDfI0EOPnnAu6GqYQnBItAhQG2hfo9SDUluhlBBQYhih9C+b/owAG8cHXDQHoML3OLuXj84fe9v+xES4+lQtCAGTrgOzf2Qf4JyyWzwbwufbUAyMJ6PJtDAfytOiM+icS4QmLIQ/73fqtEG/a9+XyDGYOHdIH7nsHEBoQI9z8n/6j0ZvxFwtm83QLORiNBTfuRfZA4uXy8w+nBdHwGdm7DKv+g9f5DUgNcx6qJdHmwOllDDcTkhgnEhvygvSNAjT6MOsoAbwjXPCr+qkgURCdMSUHhvLy/yLKevsjFar9yQmfGgAJ99w/BAnvU+qxCvrmm/MABqEFPfoBFdwYOfeD8k/pyuZv4OP09g7ZHEP+RfGQFmTvXufQEOTxAN4zAnwaNR3xI7Yvp/kwuznHQQc7MhQAYgzoIVMBXQpjHFoblviM/OfIS8M4C8YKhieVF4ULoA/GIH0ZatsC44Tk3ARE+tT1KxKuAfcFoP9jHrIF8/vWCGDqoe2G9l0iiCDLCJr33PdSDTX2kAweEWDkY+ND7ikf+iA2/ywbZgQ796PfvPKCHdcEByNb78PFVALRGwoTTAmY8a0NmgNpyVEbjQh8Ec4+uvpY/gf3BQbVEvcO0e598Eoe+w6J/pn1DhKFEsYVxACO6Nvx0u0xASnuUQntDdT9DviE6OAIx+sMCDwK+caL3ATnnNcq6eQQpQgDHIEVNvrnC/Xwjed3193sG+SX+kEBJ9eXNIoh5grDBcMBS/Iv73U+QeTV+GUnVf6e4fjzZSLY7iH+aeTuDnj7B8/6JgPn99+BHeUjYezb69Pu87md4tLxsAImAOINHQLT1fEAXPMg8V/sNOuKAgfvvgIHDmAC2OjaAH7hStqSENzCEfhs/Wv1XSX68zsX19QO7Q4PLr5QzQLyjwvX8r0dn+4A418W/eJE6qDewQjl84XUXPw9+PkkajKoAG265NYI++HudwkMBtQHt/pfEzo9lBivBJP8093E8Jf1r+dkHc8kXgqYAnEB7/4y9fwNNvtZ668FIiN7DVDrDDu3M6by6/mP7hbqHfZVG2EUXwE7IHEtwBBaBNA2Xh/kAzAJE/GIDEQMHRN6Jz8nzTHUI1EENuw1AyfxSgrnPYr+jRk7NFr72gcHHdgY0Pr46zoDUgvbEvkd/hy4DXwSSAlH55T1aww0ICsIPgCNGCoNO0EeL8sPYx7X7OjfxfaQIrIQ2CDsRJEOOgF0/GQag/5X4goEVOrzBoYEJwQXF0MTySRFAXDu0s5B7oD8nsyQ/pzsmgPYFK8CczPwC0IAYPr99ZXgrffWOB300wRP+rj95yIq9U4VJOO6+Ekc4uW5E+kYWQF1AoIV7fHY8TsmWvBJx//SjvrMEckfWhJQ7wbwc/gMGgr43vngD/Ha5/FG/E33EAJ0CggMnNXN45sQgwumEi4PyvheByIcsge19UbnMeqC6HcD9SVe6h7l+wx3CvYCiApbAabNKeTyFikEYe3yBAX3W8oX2yYBWgCw7In8e+t50LznFhebCaHQHu1nGKYIp+mlCUEFX+ri4U/ZkPa3/MkWU/wl+SAEgQfZF/Pysg7b81LqfwSd+Szm1waQIxfJQObW/p30wghkHIkX+M+K97sHX+Qg/ywjDPjqzIHkQvrT7ezxIzVj/kPUTvWJGkoJ5uO1G6TuS+pCBAnmLe/QLgIbYdfcBPno8xhsFojrUBQO8/cbtAfu9RQXPxLK/mX4ww4x63wFGhEw+cwDUwDLHEr2feuyM1wVyPaQ71TjC+t5AbARSO+mKrgXK+YN/ioBQC3/BFwBFd7y1BX3aPOSKI0OoSBJB9H2rRJUDUkH9PUPG3TrPvqBBCz3BSIAC4sMc+7c8msYE/5RCGgmXemQ4NIS4wbq7ETZQwF8/GPtfQnQIt4dCvJ89w/oYflmFrbxndpf27L8PQsREj0i6RVFFS/0qdq57h4AxAsK7jEWjBu19J4IkfsY7x7Vpf41+AzetgerCMn/BBaUWJrgd6QA6QnmEwUe7hb6avep4bz1Iw/SAKnnjRkx7R3XXPwNDFMWYfMv/kv7yexm9K/yDP3iA98exwtd6a/2TfOM9ejsCvnN+LPZfwQIGvL+rwsNCLzPeswY7igF+/8S+RYP0etm2kLqTQR6BL75ZfyW40P0mQYBCh/t1xASDYzZe+8c2rUP6wh6B7oUSd8LBh8R1gAU5fEDRuR43a0H2/cvSFX/8uxyDF3lbglX4N36s/Hf6DQO1/0tDjwFhA09+HwFswMF7tb2WtIwDGgCAwLiQFkXrPCy2Lfl6/8GG/gRcxJhD7jmPfE6A78b+gkAA5DxGffsFEoQMy3n/qUCwv8A7R8Dnux8FnAMow4CE6Dv7hKTEgsGZeZy9ckRF+n0Jh8XXuo2GYn6w/76+xQBzAC6+b0E7/fwE1zm0gvmEg/qDRtt+YoBmgEGHEQqQQWYBF7czeb48wP+eiC9ILUM0RIRJPwJC+4W4BQCWBV+AO4kuRcq7ncJzgKv8Bn+Ox1iCgO+oejpOwwTNBaIOWbd2tfRDfblQOaoG7wn9f2FAUwiMQcx2Bv3/vJK028cjD23Ag7qvjk8Ih/s4B4CBUvfFvEMFa/vvP5cVBsdZ+bR9sD5OfhdCZcUpvQx7Q4jfC0v9NrweSIZ9DbgpB5I+DHfLhY7GZnONOzgJ4QIqhhnHnIAZNrOEf4dZ+cCA3j2bQVR9fMGuxwa9w8cbBho8qbgZRNS80/Y6B/yAcj4HvssEc4AMf1XM7LgYtx/DLbnW92r7wgS/iEq/0H3XRBs7e72SR3l9X3m9Q/p+CXq/AJw/SIV0wCLE9Xutt+dKDrccPv/IEUdeBk94aX5oO7Z8RYFZB1k/JzmO/rM1Esl8Ti98K7xlPo19CPm5+/+/xH4/etc7yjqsfg7GT8BZ+QJ+kIDMxMoCz3rsu+V/MkKVvcbBGTrNtv0EGYP8A7KB4gSUvjY9asIBvIYDqgU/BVQ8hX6wBblByr37e15ILPy3N06EkcQmgpFCf4R5fje7NwR8RLi+koTHQab5/byjQ2IH7/jH+4hGBfx3wi/Kqr/HQPFB5zrNhpRIigazw3Z8Uj6c+HDFGtGqxNaD9kpQvKmvB8DDyC2Er0gDhznHkP2Qg0GCLziyza5GFPNvdHt/CgFa/A6Ni4vZOtG+5QI09Kc51AbxgESAcUGw/5T4k0bRCsu6uwpthc35ETk7emg/WTfviPQNIsFzBGQFk4GsMavDxYGM9xaJWz/de7t4BEO0RASDy//+swFArvjFAzv9oMFnB9b6QcPguaA+ULysvOA3Ovn4B7l/xgdmvaCAs7o/OmgEcDgZfHm/70MTQUwG2EJGPLD+Sb/pAwt5yD8Kv3TCvslhfmz6UwOyxn07P73MALPBlASpO9a93bxEA2ZGnHr4vod5s0HNQ3B3OL9v/j3BeUOcfNB1xUBghDT9d0gPwbY/gIJXPla8UvnPf6SFo4aSQfNBdDq4Ok5Dlf8Nwja//vZ4vW2CeQnSw4j9wUlautuyX7j0/sG8Fz+4hbeAM8EGfwwNF/5eNTnFhjfE9mOEwAzRADH/sMTc+i+7ogdu/0O2NATPfQh0jr70iigEPb68Qyk8F33FdXK+cAI3vC8NqACstkwCo/+/e6/J7cSOdzR7UPodvhL8/sPpjMT8J/uCQC77QAEERIQDvjwuemfEP8H4e3z997gQMUu//AjFPcyDXUOZ9Vo8h/+PQNY/E/xy/sF4rfiOOW8ENH4n+eV91nXPQK+8Sf1FuxQCrM01e7j88zsYunQ4sz9DAut/nMJyAHtIP/altCm9FLr9e0J+0kddPSKBl8A6ttx99IKKhIU7n7iJ/p76JK/LOoHFgMWEAWR+R/1G9CKDOAowgE3E7MG693u4YT9Iv16H2MaEOyY8kz5gwEJ7EzbAeU094oIiQdvJ9jz9ureJQbsit+86zYOXvhp2MwJneYy/mUnqhxt4Dna/hVW9GT34w7HEuX6TwSGGR8JWg+kCXDxLMkH3vAKKxAZ+6sSyP/+6dkyLBQvB5oQ7/HB5sTgmwjWEx8OW/+n+lYVDgD/CgYTMeVn5KDjfPHAGHE7PiMKK6Ykosy02zDdNQzjDiYEZRHZ4CwI9wigLAD1fwAOK0TmdfJu2zsUShatMSoUccJMAHgSZgd046ESRfpr908sGfQn8iPu4QFvAPPyxyhmK+cYlxXy/DD2zgiXDqr3iPXk43z6KhnSF8dECAeEBF70Vs1y6AzhACQLH/kaVf5PABoQ4PeODmHqgP/S3zzJL+LRCDhF2yyVEnQDagliCHATpCSS9xLRPfuPARQFKiXsMeQnn+EK64bu9+fjG20o1ukI66koov4OAXAj9A5F++T6HeU09VXzpe2CBMrrVxCK7HLnGyORGR78JwXFIe8BAAODFUgSWtkC7L0Ab+1t9XAMwz0ZAtQRYg9h8AQRIhTLBkXt3/VN/CYdLwMiCvUYGwpt9qbY2QEs9Xr2J+3M75ICJQJG/swMsx3V+aMgzgCJ2r/0WfZA68j4YBmCAcgQxf8sAFoI5e+hEBsUiw2rDikBo+46++QP3unU4EUmjgyr/rcgSe4BAyQLsf/P9QfzLR697NLePhZzLEIKUx8+MEvA5eEUAITh0wVx96MeyQnJFAQmTuarD1QK9fUp5FgLfhjVBGsnQfMvEm/8xwaTIgvlDwwA8Djwkw38OBMcnfJZDhPSWg8n8sr3rCtg438jtty1zB0VMRSAIdzPhveYImTyDtc2AbUb7/dZKpAI1fV745v8TzQE3l0D0u2I1YwHfBOtLNIEWA+o+/3q+PSu//oapwol9nPjURDUGN8jBgjt15j16uhCCCz33ubsGVIcifyG+BAVYfSm+BoGWOvt57sNEAKL0v0cMxz45lnvfei4CRkFhgIJIxb5jwGKEW/lCge1EQsEMAPN+0T9K+edHFYl5PRnGPEZftuVw8nvgevc+mYymwwMBT4Y0Qnn/VzzSQxm+E642+DKBCXaPRhtL13qcwNTEEjxsNl54WMAdwHd9EABq/p09ywquvkE84QlT+tQ3sPbO+1NCgbw7R5gGlXzqiEuB0b7Ffh38L/5eOPeC4nkqvxqIroA6R2L7pfTgL0r8xkIC+e4I3QeECLyCJf4e+SP1LjwJOdB7Qz7bCzw/y35UCdS/JYD5+oA6PTVx9lKH78CkRqyJHv4l/K96jnnCO0jCqLyUe8iBWcaZAiU4KcW7eJi3JMNK+Kc8nsdLCVK+GoBNhFF+aPgW/d8DPHqFxDB+9PvFAGrCsAZ0dA9+pEkHOry+Cfw6PdxJ98fPRbO8ozpw+5b7nP1pvBKBxr25fmg+AMGQfEP5sMo8/iMFRAfO+TU8VL4D92k3l0kWgA++7zz0uRNAz/rJBJk82rmfhKQB9EGDgQyC9v0xOJpB34Q9NwB6VgBqtj65WoIMAynDhoMDOll8mAMyOpSEC0P+fWUAvPR6xFqG5vk2Qt5CFD80NMFBv8tvQ2oHPLzKAmpDgD3OP65AAMJPQTGExDsrR0+NIT0LQAO3cD7hB/oEKQOYQwfGq8K+gAb/BwaDAR/7LkbeBPsCJ8fXStT+i/wxw9LBJXfBfivMBXq8/P/JysfpSunDlr/X9om4PEdaCZy+6YIQC+n6obYYwEaGCEJHAPRFY4Fdflg+6copAC57tIftg+a/OXz7SSJAmXw7wWV9WsUCP/n+5X3GwZr+wv/6jW4DnIE/wGS/MzzVQojEwzrWwzDE5cJC+nj8VkwbhDD7YoFBxRNEWkJB/j29KDxqRGyGc7ckt0I9RAWsh9m5hDqAgWmAFr0ZwhEDvv3MxU57hPf5t5k7hEhA+An+A4euwcQ8kAMPApO1LwSueqC2BTfcPPhOKTzewA0FPbhm9uQAar1NNuaCSUFLQcXAFL7HQgm4bX4HwvA9wYODu7JzHbjRwquDA32cBS5C+LXCMmOB9MY/f/S/IfWM+ap5qgOSiH35kEGNwjO6U/1ZPjs7yoC4/jA+L77StR3BZ8Ez+NqAtb0xv0o8NAFKwub2vL8D9/t48L9ugLpCTrhNQIMCNj9fO7Q+m/o2NIJH64K2vpp+oYHmBF59Rf4Cvh3Bd32V++r7Xn1zgDzCrkEJflGHcoUd/6U6Tj3HAeQ6W0Ao/jD570Ejg7sEHUAFAh4ASjt2v0lAakDwvw+/cvmHf3xFKcOTwvI0aH/2Qim72ACW/oMB6n6oPPO9ToCEPfw+KUZ+RVl7NUIMxAeyVDzZBSj/Z/ofgTwBi/eVglILbwE+POqGLX+IOH84GUNuvHX6sIslxxZGBf+WwNp4DT6WSdHDaAJLe15Ap7/zgwZ+CITwgy56ZoWU+xVDzULEescFxwIGdMEBnoT18z4/ywfbwJx3mD1dAJb86cFOSjSGzjloRRYCCXk5PgiDKbpXdiUFbcEhftAFmY2Yw6W4EQCCM/79ERC3vxH/1IFMN+f7mX3cBTdE34VUf9nyFzgOunBC29GuhDM3kH4wfnR6dMGnyOGFsQFVc/07rEce/QZEzAQfPSx6z8O4yD/KJ0fU93X9XP/zBMYH7EWBPo09vIXfu5v77UCihqb8wT/cRLs814TaBjsDqHtARaNLXQNC9+f+yP/peR+KUXztQvyIpgryhp049IHtfqeMBocLwGi4yAS0E6T8BgxVCtmBuMODAkEALT8dyQY4YTnsQUYPxw+aw/kMATgQfMME1YVUg4yBMMmStnU/Rs4SCJnACkGXhIhyBXylSjyIVwaUy4pIJ3kmAamCnEADR+oN90rx+/H+k0W2PmGGn0hKev49dYHqR2MN3gpUhz3FQ8A3wx2A7bgSwoF8PfpMCu2Bb0DTy2BCIDVOdzz/I32vQAKG2bvHeo/JCoGwuMMBlwLTABD+sP2JvPzAMoLbP+cACbxdQVkA13wLCRCDwndqgQiFhD5TP4p+oz3VPm79qLTBeVvMRsTbQFk6wzhZ+cV6iPxE+I2/qLuZwgg/YQDehuV5GjrHs8x3FThY/QKFdD2Jven6K39ugHSCTD9IdlADDsBUewLGAQS2fku8k8ACO+oviHn2RHO82L2MiRCFfEKoRs37p2yarPW9F/oYfV4JJTvROuFAjr/9t9d7Fn0a8jl6rkC1CG1E2D1AQio22jyqAKw7lHoGvMx5xTMGRxFE4sQjibvHWz/1scn9EfK59yiFY8OfhDOBa8NueY0BmEP3AeF6c/Nawxl60fzUgfT41H1ryrbI07flu8v6TPHPOZaAuwE6ux/DHoX3eH8/xwfle+20wnwnfHd7+4dKz0Z/5DO+Q4THWkL2fAI3+rkiOsVEtAQxQ0iFykDWdLy7+T49t5pFF4Grvl8BLsINRJcAgnwIuuX5cjiKgLZDT0DXihGKhri3fQT/bPr5fRPBR4CQd3c/r7weQt+FLoXQRGcwYPpme+k85r9mRJk+jPbtg4m81DgrefcGtAG6eI/79foaAdVBq8ePP8H7+sO/O2o9fjpkPIDDYn27f6v/M4TIxuxCCcHId0+9CooHisaCEca8Rl039H8/epr90si4h3tLQABjfO1Gh8PCAKGDd/tneLUA4cEJBv7GO/7MBKz+WziYPkWAxznh+YdJuoCLu5JFJEgEwUK3dENJRyXAsT9TxM+CwPyLhFaFvLn1PUjJ6QIbhM3FbX7tvfx7twHjB6d/TQFlTB92OX8WSaIG/4nldOt+0H/zAQIBrEBmyUO79f65umGBUAeXQ2nFd71fBLO8jP7H/NpzWIUBvG3DWwk2/rTEfgAMxAx4i74VCrd+pwAsvZ87qL2limQLacbriFG/670Xd1e/ZkPZff++Ff5awuhAMkHnx2JAFv/2hEe7q3bDOho9XP+8PteBU0B3vtbAnn5merO9VMFnu/U5p35XPOh8YMIFRig+fnujSMrHUDwr+058J/Yr/lXFOrwi/K8D+ISsdlRCYEnsfy6GiP2JOol5Jj3ohgT4hnxrBqwEZHvQANHBIztaws+9IL9fQ4IC34Da+VKBL8D+fyI+vv2NQeBC3EU8OGe79oSAwJqCq7/8f2h/hQMo/1V6Fn9+fmfAQ8OJw9YEvYJHAnY7SLfXv93Ddv5l+dqEBEKHgB7A3TqYwTC+/sBy/ap8foJdh9kHFb3+vxP6NP02fYXDnn/AQAbFAfixhrFCcUc1BVC8jP03dc3AXn3eyLS9FX1zAQS2agf+Pnz9WT3g/OH+Hv6BBmWCnsCmvS6Fh76dfl1HkLl/edc/RoAaQ0SEIUD0RBjCg3z1hVaDdj65PCu43vsO+w+HpUWXAtdGEj6MAX64wwCyQCy5uQduQXxAE39ESJkGyXjoPQo663k8fZFGsT15xGLK3nyKQWS+TQX8Qxa183OQuCzGKIcwyusJg4ZlA5W47La1/CuARL5ggXKAzoGWRqsHcQm4gQT6uvohNKa6svz0da8+F8dIhozA6wVLgjA5mEHBuWu8voFOfFB/0DuZPgF+xoKcQmeENwAlOLlFqkAiAiYH1oD+/AW+mkYV9uQ+A4Zg+3H/d73FRKGCCcGkSGZ9Wj4dwzX+RPnVPNZDhf979v/+0ogDhQMAsH8egAo7kr9xfiS7gzt3fCCDFIEvyH4B/cKlgR01lr2OOcr/XL/Cv64987u4A3UAk4NYgSg9JfjB/q49uHwJRuIBTAnRBK0yQDsWeSM38EW7/K56R4pmStJ+CT6xCNi8F7mJwhN9zXhg/3FDULrfveOEDko9/JI/p0fSdDF7H4J2uyN9xUOABR/+Nbs1glv90v3lQ3v9zf6zPYqE+gB6upC/BLuTP45EjojvxKO/6UIcx0nBQT8jvq13cgF+fY0BxsgUhJPE1TrpfomAM0EYx5lBK7xiQbh+Hr6lggJ2jX1oARzBFoBSdWSGMcoue3t+wwjBwqM2hnz6O+I658GiiSxJzcHfRn18Eu5feetFmoR1RYnHiXs9+yDAWz/DBLBFUkdPPz47J4NfAOIA8D/wPFg/SX7w/91EQwLywMzA6DuCCCbKXr4eRft8W/jmwGn+Lbw1gbMNt7/+t/s+R4OH/1UB5o0BOy+71IcVP3FBcMhKfuD2a0J2vw64nYFbRefBCf7CwfsANbZxv5MSSD0quDNH5rrzPKaGnf+ggItHP0MO80Av6kdIghR6v9ODCcB4M75GA6D6oLbOh0i9rPopS8MFQfmmu+HIG/ndskj+VTi+ASwCPAXBx2mEqw/n+AE4nEOy+IL0lvQ1BbHC3kX5DfMDtAGRhWR/lHCOwySERPi9fk/+AEouCQ6G8H+fe06+ofvkfGM6DkVrghbD1gIjvLaEyPl7w0w9UPcXSlwCpr80PLp8RHkl+UA9Hvv/w5U7YgDYQYp7gwLXAN2D1UFufKTyzXb9wFVBZX7rfaOKvwEvQR1+qXfyQib+HsEvBFGC97/rAeq8hnsZ/oE/3sGCP8OHlDfHPr0Eq/anBG3B0nsJeSX90n4TfweGcEM7wJl7BPzwtgr88Eq3/Vo5wACtByVGL7xxBJtEJHXvfU5CPXpNBUXKdLsawzgCtz5/hWP/aAZt/nu6Q31o+pOA776zxFDAwDjDuEBHJYn1/XB+arg4eaz1Sj87Cit80r/z/Gf0m7l4Q1KDsfmLe17+iH0Sv8EEsXwyOEVCx0NNPho/yMNQePn0BcLYAlF9l8Rqf6i3Sn2WxFvD2gIThJD/gDSTgDyDhno7/OZ8gr8VQj7A5UNsQ3y/4YQ2wD19WYQ8uT5AjUeU+sR+oYOUA+cAaIXUxkM+k3+9QMxA3floxePI8rwMhj8/ynzXQa1Ban6k+VPIaIJ0OvvKJgC9NBw/NAaPALSA9wSww1g8fDcRQGL8r32eCsc8FbrVAev8/MR5gX4FH0SyAg9Ga33KANv9cX3EO905qANPiBuM+oCbAq+Dhr7qPeL99UrQujS+BoPmtGjER8LqP1VB0oILxdh7g73VAZY/7UC1ApYBX3vLBrOCxTvbBuZFIL8puBtBtwRgPh4JYP2nP3HFfT87hGYDcwpRACu8ysCLeDjBMsL0wzV+JEBiP4A6x0mURhlHAUVCArR+KG39wIRH/vv0+0fAZv2HNzpG7McVAx7Bsvz9+d02c0tXRWl5v/05OOB9AHtPSDrGY/17v5D7PUKdA6kEpcNYfmF+nXtK+4E/vwY8hVUCMb8quoGAfEuswwT3sL5Qgx6BNrt9vvV/loAjQ5y6inaRfnsGqf2LADU/Ovh9xmj+rv5ORNC+2ALG/lH5yX90hzrK+YJXeEf4zgKBCBNEKoX1Rc+Fi/9IfLfLOQjU/8B5NX2PN4d4i05mAzPC+TxZvP0ApbPvgny8EjiA+3u+y4JW/k8Hr33nPd0CoL4wOE+5uvvxdTvBv753PkkL+cZrx7BGh0KX+9L4C4D4wZwACcC3wBVBxUigBUB62oOmef0yVDw6umUK0IpfhIIBKPMX/ciFPcJBO0e8Cb+vecP+p4BW/b7DT8IwdCb8MkStBUUI4L8hvJTC7kD3frDMtgOj9SG6pbzFBGlB/4rTCBW4d/pv++CAL/9jymmIcnqogIOEyb2bdj7+wz9vOHnAjYUeftyB/v60NKo/hAIPvDICvgHf/0wDqAYXBTm5HbtGxAQ5OXXNAVrJhcDbwz/DsPlnwIuEvD8BuSmCRr78ufcCbYNZCEB+wgDyfeh1PgPVAe05Uj52wHb+Bv70xusIYX7iB1oCurIvu2tDvD+5fKdEmv8yeeA/xwSOusU2yRDGQm90oEEwABOB/z3UQnX+5jdyf+/B93Z5vHrFcPybfgd8hkP6AWA7rwRKeUk+oMG4OEL7VIFbQPM7eny7tq6GE0dg/HzC+n3WvtHxbf4hg+1z5ge5hL492v1MQElDtfyHPaEB7b+Zs73+7npiuUwJ6gFeRNAFa0Feuh02/zscufZ9O4GNiSr+H7/Ig3B6wIOvPujBVz3cdWi3yXpAiDoFNsYNyg58F3krAWO8d3kexy7+w3rSfv/7BoJ8QJyG4cKN9ifDysVifT2Fv8gGvlo7r7xjdBQ2c0y9DjT6PHz2heoEosXCxKvBXrnIuGA6uHdqwF2HxQRvfAN/E0cUw93CAruwuvE+SsBGgPFCNkmvQW3/ST84+Mr7xj9Rgsi9V0ODTH3FRAJcv4i6X/2bRsSAdz33BG/BArzKvJ1CrgIBw9zCX74hPlZ++MUYAzMJoEHP/MxFOPqhwXd6Fr2/h9r9t4TvCDK/UDxPCyiB8zkNgvACDQQifCxFmYeDfxeEw0ZXQ4l+pQNqPmi5bj4KwdxEKYAExfYJWAXaBGBCgb+k+je+dHv9+MNDMwC0xqoGAQDqgRr7FINtvavDO0YAgJ4GQTpkfg5+psJ2RulA4cV2v+x4fncUx2RDtPzZSdWILD1W8ma7g4M4Qs5EvsOB+2M1r8CNQFP/n4PUSFz+3bq3Ahg+DnzhfEyFxv/rgzZOfUAaffY7nL5tQqnAtT+7wF5/8UFJBS8/oIjsCPG6nLlVO3l4jX0MRY2BXgKdxuT/XDpZ/ha//4JM/+j7l/zNuH456b/1vSS5jIbBSE99vb07ftFA5D5wvQx66L9bOKA3msOewMNBvX0de/Y9o4KVBTn+J3vNvrjAeH4+/KX//oSnvnw66Hhjg2fEIXx4Ao767wWKf544GUDcwpyG7z4nN14wfUAJQs28cUSNP6172XVQvKpCOT7PPpk93PsBdeB7LIPuRwyC6z4Nebi/74Wrea89I4PU/t3DzX2Q/HDFWAGkwVF6irrxP6MFM8LiOmfCeAMXhEq/8rygP6I8QLfNuB1CXkGxvraA339B+tTAkkIK/Qw+NzyfPaw+LQFaP7x70nkaQczIDr2N+Lp96kG6uDYBb7/owYlJ1v/ggu13yH51QzL+/cE2/qeGpnrwu7p9Eb/EBld9L4VB+hY1537BgSsE2z1PBZhBEv4X/uz47YNagsiATfZWt6S+7IT/zX3+X7qcP6cAAz2ygNpEycgOwz61H/6wfDT8KAlpxF76AETkxOs4fMFOPPuCM8b8AcT+RDiAhLCAK8AeyFyDbrsAPU6Gzf6c+d7FLEUsuji+IsKdfLB+NAc0gCB1dIQ6CyF9VX/0Sj25JDidC/H/mTo2hGFBMMAg/Rf9WcVwQAKIjMHaM/IJrIOH+F7ChIGgfjS+n8ggvuG2/MkLAgn3IL57RU9CMwHGCq13VPhKQR3/1AkJQ6EB5Dt5e029JciHz8c+Wfl7Nr+/bL5lPR0Gt4hx82Xr6k5JShbDkksDgL7y2/oAB8s6/gVxDAP8KrcewFaE/35y+HADG1M6fNC/84dHO+oEq4WvQwA83wCSAGT7Jrlwve9JQXviPsqC4QC9SKaCgsIcfAq+88kYvte3fb/uPuy7I0OQf2uAoYCvACuEobhE/iAHl0X+ABk7LL4sPo9/oHtjPSVE9snPhxH9h4E0wMF68T7SwyvEKYTOPmg9NkJq/hz+vcVlvLh8iUHwtMTAaAe7AGCFZX7df7n7oHRTPsI8FLYbf+9L8UdpOXq/cAXiAXt70kHXRUH2XcFbhfr/CoPmg5UIvbxBPItCIcPjxm4ACAWAesk9/Ej5PlUECseAPtF9Yvk/t8H9CsDlhbR9KXoVQCzCC8KbwkdGRPvru6jDkL2qfmICzL9wO4KDaP3hfaRIV8VARBG9an5TgqDD6Ea/wfu+z8A3wt143AEqg2K9MojpwUiDTTm0O+gMDbuRfYsEwL8T++BB+4QAwYsAZjwh+0/4DPofwKKFUEVFAILC1EHverb/gfxM+oCCTEorics6pkN4gG45qbeWgGsK5PZCPve/c4JdBXGDjQdsu7ND8zx6NMt7qgNcOlr8hgTA+MfEXIFAQEtAr8A3g4W9hUJvA0lA5D06f0LABIEwgDX+a7q9vdXJzYGqf02GsgVP/20BT78rfP5+5H39f15808lOhZd6ksKlhAjCwoQHfhW1s8EggJ+5a4J7xYQCjTxGe/y+oH8ee3t+ZoDJ90SCCYfKOzW/awFxflX8zf9BQSm56f05gQy/+f8zRfmEvbusuqGDj8gitwQ/e0fEfWvByoLf/978nsA/QMN+NAbdyMy7kDEQwqHHcP5DCU+Dz/ueeHGCw8RI9+IIvYQIcaZvdEDRfjt6pEn5dxL/+MbJxH9/h/n2CJT5O3bGgGd+ar14gggE0vweQuZEHv/hwr9GJAS2N8f4/wP3/HsEFUjewM0B+/ysA9y7LYG6CUE+Kz9+fRR9hPSLQuZG4T68w12+j/7PvR9HL4VIesm5I36+PN38PAYEeZ33EkFZwSx2Zj/SzcdB30K4Qf866/r5gfbBNLfi/23LZIcBvRv+DX0lfh7Bl78v99543ATwwkB/ggHGRY9EdLrouwE1m3llQzw6Xv0PwvO+mr/YQfp8EDy3Ac84RncEgapG1sU5AUyF2oKw+cj4PQPWxSN7l0Lhfj093cVDgXn/1AE7B33BT7suAHTCugU9wwvBOT8B/E47M3zpvQy7Zz/5QfT+C3+6xLE/0ns4v/2Dlf6Hf96BW7kiwFH/GP4EvGh3VMap+sN2oAFiA8iCe79Lxdg3VLeBvmc/CD1YvhIM5jiodVM4d7s3yumAbcEyeh62vHveAoDGV4KpTEdCRb5leto6NkHseWS+gMIpxT5FFkBDvWr5df6sAPPCNn5t/6eAGPzBgQ+8in5PRhQCSz5q/Ul5F/mfuSY8G8tYSAC/joEIPu5BY30KPK+AvT8VwdJ/p0fjwAW718MoOksF/obxA1s3aPdSgUG6Nch3xTsI6T/OeCmBabVOAjdGd0NUelgCUIWJ9/mCSHnuPoC8e7tcQtq7XsWEQNR+J70ffkoCaXzeBcf+PvV+QZS+/3wTRKhEBXwYPJJDGLuiPzxIKYU4AGg/UsOTPmuDFn/POyN9jDqjR/g8M/rcSILCj0YsgwF8f/SXf38ClLbY/bZA7gQpA+CGfL1//IpF+DnZgQe+4b/qR1U9asGGyinG8b64we896MLI/3f0PkoohMO8O8ckhpV+sfpwAkj9tPuviVlGm/9BAht8YLYGPFaBsD6W/X2BCETjQ1RH8QrBfz94Zr5kASyyz/1sjpYCMULNRr2AVP8fCCL+OjXauoy+gsuQfJ3E9E+pCG7BgXW8xAJ7rzpWAgx6W35g/3bH1cb3O9g7g8Re/bI4pwMOwloA60CmPrG6VXqMPjM/NTyeP8DEvkIzgaWAB4R8AT4CvQEwvBIBCDu9gM8Mfs3bgU6A5IPy91I3PL2Lxje8z/5JR7rFHQKswYAGT7k7etUAnLw3fjA+swH2evBANwdL/un7yf4ce/ZAeAteBJuG8Yw8Om67w8I1/NKAYQGYAv7CxMQhPr1Dh4CAerkHeP2cAGN/KwImhvfAhIo6ALE+Ijid/FJ7APVoAZWFdENPP3FP0EAZNv4GqH3Rusz9YYS8u6+4BQYyBSc5pQSUSVo6BP4tAS+5BzTSROJHvv3ZhMFK8TxWeAPIUf3JOw/FvISuOf58c8rRfwI8ZooawRyvAniZQ9qBFYTpB2Z7Mfet/X4/GML5PfcBoj0jd9Z90f1/PUZDBMeq90i53EUOvtd8zn8cvMD9fQSv/qY+LoA/fyxC+wItwEN42j07wZw66jxwvgmAUYQ6gUC98gE9PWN8PcTguQ29CobE/hfB6sPnflY6a4ATOMk2IzsxgwrHEXbW/dJBloVD/+k+6IF7c1R9dTwYOfE+TdAyBP/yoIK0P3xDfER/QC03NzeSB+wHfHmu/xxQI38ZthB/b4Rpuul/Y4qbe187PkYogMS0Zz0ufxf7u4KCxNt/qPjdwfCAJzvaQEpDF33Kf/5GInnW+1AAQ8P+vjN7bUduONC+FAhJ+rD8JMd+CU13+ns1RIgGQMZRv9VH8/sL+o2+AXS++DDBoU2KAG2/2Edpwv2EIUUuvPC3uQDYv40/1PzOP/XFF7/igXfCXsCoQh0Bmrj39/F+WckChJeG5saBOMm+/DyfwnD+jj9ewdV3uEIAgZ869TwciFUCzL3kgxc+j4V+/+F86ft8vMX+dP+EQlU6AcT9vsOAFsTLPYVGrP2Yvu0+7f44P2iBQwmPewo+n/6uAWe/D/y/SZD4kLqhAz/DwAAlfhDDrn7NvYZ97kWUPBnAYwYDviD+AD+rThcD571jwge7qHuiv8SGgQl7B77/CjnLesvBccXtA4/GM0Pg+kE/7IGZgVFLLASlN7k6tgxlBPbD7ct8fw42aXeNCpN//wVHkc+9BHj3O2pEiYCD/5NGPcE3dJw6FseGu3vDGAdY9xf3Kr3HPY/8N/7ayGXI/bwaAi2D4b7NwER8rL0Hvns/ncuoCfs+4EewgqN4b/wEgbYF7AGpPg+Bq4F3fuEJZMaOPWXB0f/iOP15jIQ0wpy+CkPxxqh8FflVfd93bsDyhIiBQYgM/uc8QwvjhMr41nzB+dC32DsPQinBy3+ZxFRHqIVmelQ+Az1Ut9q+2sSuRjsEoASVewT4C/2Lfqu5K8CYBLI8R4XKvT/4QPvUetFCsX+4e9499P/yu8lFBwJaPUQBPXd+euR7/4G/QTT7EAJDQrtA+ACPwKrAU78pPrVFVgMD/3oDbMRSud+0UD/lAziHcjz1uopEd/4aAxBDvb2RgD2G/j8QtuAATEgBAAj7Y0Gn/Ip97b+sN/n6G4MpwhBDtf5pvfCGc3ms/2Q7Jq98fjxCbj1U/Tb/N/ySwCxEzwYnuIo54MBF8mn6zkX3RqFHlsUbeBPy43ptxJiILPyzhG8ECnnywg6F1jutgw+IqTlgN7W47kKtiiAHNIEiPPS3pvtnhQ8/E0DyufQAoEdXvd5Cinn1vSBAJLpVwYcDZ4g0ww34wXizv3JJV8DKesD4kn82SRpA0IUVgBC/oH82+d0BP7vIf81Dtf98eH4D4wgPPj+Do4Q+AK+13b/iBSM7lgBQQxJB1n68BNQArPu9giz+3D5gvxO+uf6Zds0BHAhUvouEekcLfdT2Vv1pNdq6tocNAD5CiXxl/tW+HYKISdf+i3zeQFe9IXiDA28AncHjQnk68L09wKBD/r4MPEa+T4mJQnS+CIKNeu79kj9ihghAmr/Oxdu5wPg6BX/DuL7JQFd8WkV2AGh8Gr+2fy9FdoN+/S97Jb9BfrtB8AOaAV5CQL4pQxVAZzjFhiX/Qnrchez6iICICh1HKv2JuPAE0kI9/3OACnxpO9KAXbvL+QKB34RmRV+Evv93ezE/sYFyAJM56322BFe8wj28PRAE2gKAAUGC8rk9u5RCZkR8vnYBC0CggZhDC/ndvDW/GIGFA5hBrEC2g5zETzv7uP+//YM7wij7t36UwA//uEgqApnEw79Z/RNAJ75CgDu89Ak7gCk87kDhQ2o/lDa/Bym/d36FxchFBYQKwtfCnH49ggN2pzoVPI5+GQdgAlfB2nxZP1i/B0BpwU79+/wBO70BE7+thgeAa3uQRSm6jPtChhI/xPwjgjT9fX5mBgzDS4XGQA496wFCd/2AscWD/dI95LjGvwp/xbs4Qn3B0T8DvRYBOcgCwROAIoRivGe4jEEWxnX91YALQ6o81sBCxSsMgkEQeoxGanpxNyzAL8d9Qx38zEQ+fpb6T8HuxHg7e7l5gKuACTydfNECQUNeP5D/v/6d+v+BVUNS+4q+wYEsQW7+6/64QYq+pABswof7yngHA85GcX7RAnlBk74ZPwOEvgU//Gv+W4OSfN47jAPphGI7kXpgvvu8XgA9RmNCiz6C/YOAmUEnfK59oD2Tvx3B33pDeTcDqUWRQN9CvT2Vu/MFVz4NgTpHUvqwgTvDlkG8AhuCOAPnt5q8kr4zgTnF0QC3BWO6Hf2AgcZ93L2wPIcB7zsERViDUnxviGdCLzlGfqHFEYJqPJZ4DL35xEYIY8U8+huCPMPOeTR+fETigsuHMIKafoF7o3ufiLL+Gvr3COtGjXyS/PRDWD0nvX9GMn6H994BAEZCQap7IH7NhPn/Kb9Tg2t623qLhB89ff4JgcdFWIRkuLx+8D2pAwoJwL39u/mACsTzg56/5EXYASkzsAGhRZz4c/wSzL6D07KUAoQBNH2TP/1K3gecsgWIIMRj9We68cgdPxRzykhlO9E67QPvi47GhznsjOw8Ma/Iw12FDvxGf0lHenrEeVHIxUUbOhz6DYEYAn444oSaSN9/E8FlfUL+Sb3mgxFDnblv/q2DmwC7AZh/vjsywD83fH1JSYeD9gVdgglA8rtn/NN/cL+og5i/Pz5EtnJ9OYAgO53E08E0vk/9BoA2A29+k8CmANb7TTzQvZz4aHsbw+oHKf7kgWjJUb93euDDET1ueBYF1cV5PwODawbExyM+0Lz0u8U4Lf5xhEv9b3h/AM7DWMDsw+gAOYMlg/T37TVO+Md/KPqJgGOKEcJKANy7ljpeN/q7bgkJRLQ6UkCehlp7Fb/WRswBQD3fPMe7Znssg8DHU8Wn+cO9OIQm/OBBsQHPAPFBELxNvewIAb8oPHXFUzlu+/K5xT4bCWg75v9oRUv46bz6yFc+43soAvZBmP1juuvC+kYFepl/icBbNbeC44gwgKn+UL9MQMG7DD51ReF/C7zjhKE/Db31xEzGvUJve6S8JDrzOVe8g0blgSt+EggggcA98f8tgjm78P+JA8c6Ff4bAX5B9HwyfbdGnQWRPtq5R0JcRIY/1sBKvAH5LAFBhYTBa4WzBuWCZ76Geyx+tkC3/kt+HD9DgSoBuUQsfwf9V/3IPIiAXnuTwxRFtz5vQBlAgASTPWA7dzvsPnH+xvlaAXV+BEaMSHN/YH9rfIlGqv1Af0dEnT8JA74+XYQcf96/4cKQfX+CZAICgYvAHoVVgP27yr2EAhTI6juSQl1FBLw3wNL7TfybRKMDMrjs9pr+QQQwhPTA20iXQfj3g8DMOq48AEJJwvtCZXvowWJAzf7EAz7BRjiA+68BKzqt/RtAoEwLh+z/p4SsPHo5T7qxfkC7jnzzhruACjlIAGkE5AR9vac5EAAuuHX854WmQqZDkABbO6m5SIf/Qvw5sIIkA8I+jjufA4rE/oZz/x+9OT5uvuoIQj2MPkdKLkatOUL7vsFOvF5GJ4OIemk7qgcYh7C2zv+jw0P8Bz/WQfsFWz86v6QCD7T5vo4EkPlLAXlFVHiJ+HDF6IY6BBAE7/3fPD276DxEAZf+i4VQi4z6Cj87A/J7UkPmgs137r4QSlE+P76CQUq/5cNzvCdBZnzIA0rDIjxBfGA9AYyrPSE9y4ETeoW+C/w0wQUCWEvNw+GAKAPiex74w/33gHC5DsR7CF2/gb0mwRM/NvqRPrABeL/ddRaASwb/vV4/BAUjvm236/2mOOj7TLxavvGCXkKFBibCHbwo+3g/dLxx/PC8m4adR5wAqQFBfn9B+Tvwe1W5o3u7QFXCkMQCPvDM0MtUf/M5YPRtvB69X30qwGcF6gYc+pf8lIAovnZGQ0E2/zQBHv+EQB5/h4XTh2vBY749v193K7+mhIyDbQJVOfVJnMGc/ChH+3/tu3vFjkMbeg2H8oOXuy33L7o7PiN//wvJxLPAfYBdPKe+Xz5of1aDPX4eeqyDXAHSe0TDMwx8hjR+YLZF+cQHugSjQlpB0j3eAFRCPn7lPD4CSke+ACDAjkA5RBo/CfqW/vH3UohFg5SDyEDCcp9HrAUYv593sf2FfL/7OcrEg7PF2MAowQ38IbeQxMgEifhldksEyrtrukVEH8YQfu256AE2wGb/SP1DgO/4Nz1iCgkDB/2GufIBLTxZvTQAWHvaB5hEa/nEOcqA2EHcQ36IsTpivrXF6YCyALZ7HgHc/1m8Kr25fc0/CLyACsE+MbouTFg/vLq5gl0FXfq7ebvDUD8dfojALUbGgM56pMGrd2O/igku/yH73X1ng0G/yIP2BxW/3j3A/2M+MHm2ROsAk3pDv4a8c4QuBhvNfUcDORpBELxjPRNHAATsedyAlol4el/+ysX7h6i/QrPqgkO7ATz3z2hFNzwsgnTEH/k3O3WBaj2y+yV50ob/RwJAVQpTw9u3M/hUgusFqUCqQ2f7S8CJBVaC8Ilb+vx6ToAbPIy/YADEA6OC6MNJvuv9scJjBIc767SXfEz/B4KvRmjB/X+XAbe7knt/PipBmEG2tr36LT8/AXfCfT+cP4f8S33HQPa54ECIjB17cXx7PjI1wMCCwF79+8D9Ao/9oQLQga78NEbb+UV2ioFWvinBqb89OVg/UgLlwhH7RrW1vN0+9Py4/7gJoYbKPmH/2LkiPMVFqcIB9Pl1N0LGQW6GdcPXPX0AwLuIvmM84ruI/ox8nAFEfgHClkFEfgS/vbvNBNs78zsWQb2+kXgNufgLmzy8d9UC5f76Pf6ElMiq/nf50kAWPws0fwOMBgb7uMVXwIh6fXpuP1yBt8I8gcbBZX/WfyqAQr/VPpy/Y0bauuq9GcEp91FAQ8FD/FXEPMsk+dh7HX3XPRkBu/zfQfa5wIDgQN38SAUNCbODmTdT/zpADP89v8nBZTqvfdWGoIDjgx2EBkiDfn/7CoInPg0/BYfJyNr84EHOQEw3vj22whz6AgAvhA/AewPa/3JDxL6KAX2BTrSIwHSFj/46vP1/D7zkAWC/k73bwMf6bT2ZgUv6GoTCjRaDacWevC875sMNxB/+0niHQmB3y34BSDcHnw1rhDj3FnlCwc8BN0uCwK56KILR/1b+9z/IyWHD8jwGvUCCYHxfPd9IoMSIRbNBHIMWfxK/8shke2j6PYPzg2UFdUJ2+ah6P8DgyRaA0UK7iHyBFzsMfNDGTr7cw41Egb0JOd1/AAv9hQrH1f3H+TGBkoK0/o94WkQVQhr9BkIX/ys93cW3wb408r9miqkAnvoqwyZDRrxFPYBIvX+vuedKVL+fPTQEhsQbfUZ1IYVGRUc++8ODg7QCJ73gwiBBnMMLRIz6p7budhf/T4PDhLhCi4GIi9z9j7ZYQiAGmPuTOm1GNDdrfe2Ea3x1/ez+PgaUAXWAVkbRg8HylTr7jz85p/8aibc+IXoI/V6CnT4mCfzItf0Q/xJ/vP7aAA0G7/vw/Oj/t/q5RhGAtgCA/Kh2V4E3hoCJfgDmwhC+gDhW/Yu8zD4+P+7HRPy898hLc0S6QK6FYD+ufa49oD25+b+7HgCARQTEvP3+BU5E/jyEPVH4TfdOQNwGV/rFBBcMg7h/O/Y/w3rMwrX/Mjxxe5y76EhUwIk92ogsf+97c7jrO5x8Bj76Q0oBIEEPghYFVLsCv5CDUj8A/666lEEWvzJH5AaTu8y/NTw4vjq8nUHPA8bCLUi7BRd/+rumdvx+94Eaum5/moBqfo5GLgQ1usnFxMIz+Z9/Y/mkQWR/HsBTBV98zX3+gj0/jnuOAgM9dDusffDDXQLkgYSLaQNmf3u3QDhjfxQCGILCQEYBp367gJW7lQCmQIH8pz+Lfi0+vQVGS8G8pXjF+nz9KL7q/Ey+DnrlQUWBkEMQwSfELkZxe7Q6CTzDv0F6aUBrhncBakNuQqs+qzvKe+fATDzjAiEFfn1IRGI9UYA2w8a9zn1NPuaEWj9FwuUEJIcVu8+5q0FIeFD6JXt8CI0GE0LLwHp6ofq9/2rKjrcTPPLCmHzfvDqAi4YrOWbGSIDAN4A66gBZCA89kYJAgtI7aP6Gx0+/UflzCKE/g/S5vxKF+YH4/foHHIGUeEbB4EE+fCU+SUY9+lE4bUfqhTmAk/uEvdi2c/qWBD6/YsKvPmd/WnaoPoyGFXmkwLFB7D0CuCd+eUYXBQiEXcGugZS8YHp+AJAAjX19wrODF4H/BJ1ECn4nvKCBy7z/QIHEOUJohGJ8I31qPBR8GoTKP8+9ln4weja95YDSQfkB9XxtvvF9Z3fWgsbDKn1cQdd/izt1PFVEjgYsv1H/crzyOMiBcQKZ+jMATwajQkU8boBGyKg+Of4hx8O7/vpESRmCH3dFPoM/2bpQQRgDeP9T/f69hIAO/tEERAOHuF62PzvLvUn8asEMPIA7CoJ2QKO9poRmhxy6Gjh/xKfCWYH1R9c/pn9OAiP/vPycfmaF/0F3SFvKrzy8uw0EUUCducGECUG5u1M/cgawxic8hQA7wm/0P7jjxIf31X85QTm9SEHUPz8ADHsmwlZ8uvbgvZSBqYCK+3YLUIFDe7EFSH5VARUAaYSlgxb+MwWFRHyCN4QEgKt8X7oKgOJGZD49gUwGAwAGwgoFFMAIPCX7sDps/Uj+SgAGg6D+sAHGhb3+GUCZf1n3YDwEAMjBVkDDQIlCU0HaPdmBsgr1AW878T9Mu11D8ggV/8dCAsHm/T4CHgawCO7AQL1sRYS+Bb/cxU5CaUGSw4bDTDeSwQMJmPkQdsOCK8DaOL9GIwhxeEX/OkMovoa6+/2/wsW7+r3Cvgv/fgIDwwhINrhQfcPDtfqtA27D6sKLfAeDhQaDAf8Fw3yYAvAARbsGQrKCL73JuuzCUrzp/IDHbIZwgBT53r+6/5Q8/QCnwW/++TnLPltAwLlORIpNPvv1O1Z+YfdsPKO/YYO4RaA/yj+aQMHChMHFwGQBdz9fPUn9o/vpffaC4MdcRgk89ECpBwR+8ffjPlEGHn4IACKEUjckfTUDLrbcvCUAUzzJgIs+lv5A/y59dcOGgvG29bv9QoV21/pUgb4/bgX+BmwCH7sVfccFUP7YgPjDEX8Af6HBqsC/xCAF0vwDPuP8cfiM/aEB6MfIAbnAPgLPhQ0C7oGuPUS3wsB1e4a/L4ALQHAG5bswv5DDdDuTRVtFZbiIP+1BQHxNQ5tCMDw+umy8Ez71gJo/wUInvYi7nARoQVCBRseeQ4s4mTxvgeq/CABBAU2/vzl1gZ8AonkKCXdIw/jbeXV9/kQnwYI+tAq+/yg6xAgnAZe6FQRxReYyFzvCA6q+TYolRoXDzkKkPtsFanza94zBc4AWO0/+YYYRfpq/zITD+cQ77j8Mvt36YP6V/nYAoQkBf1D59321B+l/uQFJQm95kECmN/B8JcPBQcRA9YTxP1w+EAS1fqpIb79/PctEo/qePMG/OQQ//6hANQMo/rG/i4CnQGb8koIjA8x/dr6DfLYBycD6fquDGwAzAu/+sj1VxHr9WT6wQKH6xzkOwu3I88NKBYWE5UEjwSzDoj/BPPWCP0HrQhq/TT+KQNYFLIpoQrSDP4Ll/eP3hICCiSR9CojkyV359vzjB0AHOcK1xYKANXwG9ATALUhgfaDJOsShdsH9NEkhhNRGCsjSfNb6SbzrhPOEG7/1ueP2I8BURBQF0cpdhUuA6T6PPEDDDwHnARt8gvjFQoiGe4OrgOVGKvxoNd08F7wZ/xMHAgX4et69ucBgBbtCa0T5QKGvT/haP6A/rLz/xVN+ADYQAlP/gAIQhmrHtPhf9NUBQQNlw0w67b2GfoA8M0SyASH3fHuWBai/ojUSPJD+cL3BAz5+CYGgflO74EHDv7R8Nf0PPmL6UXwiwUnCa8ROSM7+ObaGOsS/14Nf/pQ/4wLbQ5P7vgEhwbR6SMSoPUs2+HZbASRAwjj9wXp7sngLPWRCf4GMPJBAcj+e8lX3VgeBwfb6d3+k+290pAL0Rge7/rz5Rlc8d3NZR13FQHuowIJAHDcJe97E1T02Op6A2IUYPD68+8d+/3g5Yz3bOuK5WcOlRAs7pDyuxVRClvjgPMsC2TiYuQjACz2vvp5+y75mdzn/XQPSwFf/Wjw3hV05GrnAgIt71QHWQeFAEkBfRQw+qLuCvcxCGkAE/OQBL7pIwgQB63q+vlwHbIjC/nd9rT4jgP4/coOmf5U2VMbfhE/9TUCBuwi++36ePqpAeoBZxK5CTcKOO395pgSBQoK+9D21PKp/ND9W/sq+u0KdiLHCmIOm/vf8pMYt//mDp8QzwIhC3wKCvEj8joLzfOaGPIPmhBGGQkOSxlB62j+efvO5sr/rAZI8ST17AsdEkwMRvk9JkQXkdv64f/+/P/ZCA8PegGMCRz9thv8/L7wOhiS/kQG/BXgGsMHqwz79uDwMRC4D4kVwQTZDQ7+uP4tF0cVBRJMBPkUSOm34MoZlvxZ+G8ORhPi9GLlSijbCUPy8Q+8/sTuyge6GATjwwi599n7oyRp9XInuPRu8W4RRu32EIgN2hSy+iYE0wCq7xUpMQD72v3v7Qnb/osDMyIl8h4GViuUCQLepeoxHp7tWuyJE8IIjAX8DU4fD+uT8mAlYgHi5cD18R+PA4Tyfh+m7Hnw3igIAUbpzfMZ/2MEgRh7BPbxYhQhBnnvQuNP91361/5J9wn4yCkyArkUpxIX43kBfgso/JzjnwtpDlv9KiDF/tz1jRrjAnDt3v7fDx8JjxYhJL8BuwWL6gHx3/+p5CsTKfWb5fsAigQVA4oAvSt2CGbmlfyg90LyI/Up/i0JvQ1++DbvEe5p6qcWnCH3C9YGqf2IDU7+bgB4FrsGRfNw/N8IZ9mEAW4hkO2f75kFQgiU9FsX2BzS7BfmbP6vCr7lVOq0E1bxfd6ACLjukPG/GHML/PRZ8AoGZghU/FT1UQfc+PYCbRd26a4GrBWTBFsGYvGH/5ESxxEaBGruqe/H/aoJkQY//yj9PPCv9zn5QgzKF74BUv9D2YvnLAlOBQoSk/Djzj3mtAkuEMQV5Ae08xkAvvm23h/54hPI8h4FGQnX7hUKUxbsAJDzbPiZAdsAne/TBwAMJ/4wC4nx6fw9GDMVfgXp+QYEge+6zKvn7xM19iL7iiFUAoTwCxgQKJT1tuPr+vEA3gTV8Mj06QKH7SQOPiJw/9IGMQuR7EzkO/EWBGcgWwPu8o3/pd+z/jEKN/dq+DjviQLX+goT9BJ77On4gvtXAOL7RQfO9j3pHQu+9+rwGfmSEqQBHdhABzQOIQfME3MOI/FL2n/2kvoj9dIAbB68Dz/6wwBl79//y/MR9KYNFAPJ8+n61xYhCncBhf51CCT6b+QSBEj6xe3RAyIa4PWg5xoSagK+6ZrzZBIwB7//SB/REyTpvuhbChPoF99DGLIaKvRK6x8Emgqn+w4MaQ/p2D3l0xAMA7AEMBpADBnpFfPJBNXvodwB/00D+OteGzsphQf//fYPxwpg7AnwCgrA+H7vYRli8nfuyhKVB50O+fcXAasJEw/YEb30A/kx/ywMb/by+cUMEfgRBj7r0eSKDukQWwY1BucBlO1UBmIEoOTD/9AIzPvq/uv/jPzKBZjzH/yBDGvuIgWY/lP6CxpAEVX8TwOOFpjulvez/xPiMfynBugBLvm6DFQaaADZAhwWIAus7hYBwgNE5JHxcgYgBQoC1hfuElbudwFZDOD3ZgQJE4gDEgQ8BrT3T/m3/noR5wiJ9qcAsAK598cM9RPUCigpG/9G7h/wqv+BH2zyoQZs/eH4s/vK8JcMUwUOEmv+kfTi6fH0Zvqj29wHqwsGF+MWbu5d9WDhGujN/HX5mAz0+uYAxv3w9+8rnAdQ+fsEIgHlBrXcBPm3CVH1yw3/LbwVGegdEQz5INNeAocHWwZr/fEAbAvO8v77TQlo9IHlnBAFDMzTPf/0F8b1uPsTAO/w7vzkBsbkePEFGD78xgdoHi8T2QFv6gUF0vG77qQSbQtw8aTmDw1m++MHSh+vA2XhDOiUKlD/Y/iqDPTjeftGBErx+/E1/mgGTwV++w351QPKEcwAQfQ7Dof4MuI//yv+Aey5/iULKg0GEQIFtPU4+pQGdwcS+xfzNwS79xvXU+i4EAz0p/ZgDx/k1vTmDBYHAvaxFOMP69ajDQn/F9et+aAEDfdv+R4BvvYbCQkNURVsCz/s8gohC8PfQAIBIDnvMvNqEebsSNwyDMAQjulD7k0OZQxY+BUHzwDq7CEUQSOn9FPb8Pt7InP70OnFAMj5WQRODbP29eKLFWcVNPKeCJ8ScxhpAV766uU07aseVgRg9TX+G/wXB3MQphC5Brv/IxCBDNn2Tv2XJCcG789nDBIKgfo9KP8V5vI2/OMfUBVQ7pnxGB3n9/ffKhfy/wjwYQg5A+f7oBWRIJHz2uf9CAoIL/zYBOD/z9wf6x0j9QNi+PMM2P4q6YfmxBZo/xHsrQRW+r71FP8YFuYC3/3W+83lnf2A/RgLkw+e+jj6Q9GaAxcxPO859fEGiv5k9iUNyB+X/G8Cl/9E2ZrNgf9KHnABKAneBQX0kP9PClsF8PBP7v317vfPBSgaZgczAOkcEfur6/8DE/oj6ZL+YiTbBl3yGwmLHowHgfwxDxT4Nfzj/i0Q8ABA58H7afGg95X2EAuhGF/8/eKR62sEpgXcBlf/uQSt43r0dBvG/L0Dwg7aDsPq4d5QCP0GDvwHFX0d1fzpAScfFxaN+6H8hhFZ7RvY9hdUDKcBkBOX+uT/gekRDucic/1tBEv8v+4G80UIFPyUCFf9kOS394HtpP/eCV0eoBj656b2X/a37ZAUXBhyBc4CBv8Z+of72wjTC9sNxvUl+3L0x/BnKWIZkQ8zBVz+cPMN+okRQuo0AWgSIQcf5nL2Wg+58W8PaAiZApfwf/J2FY70XPjCGewNUPQaAnMGld5I7kEPXfKl9KoLNwzW96z9tAeL8hj/Q/4eAYrvtfjBCU4BLxhK+y7peO5V9uXsDfzaGaoIG+tO8BcYcOu6AnI/BwzG4PkIqA5b1roJuhte9pT2DAHi/HrjwRbcNELwdOvmHDr+zviNEpb8huOi+3QSE/Rz/dQBFPTM68f/UgBz5F0kvwyxzuP4jgvSAdP4vRUZAf7KmQSDFtLr3fb3Fh/9rtR5A4ARLPR8AYQdKQAK7XIkxA/L7O3+RAasAmEDmw2QDXwIlwJ+B/f0xvHNC5r6wvcMGDMGZujzE8ITveB8BSYWOeEA2rLu4O6P6lIU2yWd/0MArfuw5/jjtvz7DGPw6PLGEzgXFfoJBmQYQPzyCaH7ft1KCi4LOwlwF+QBV/zz+fsLaAVo6Ar8lBx6B0L/wiAuEIH3UfN5/Dn0u/eEBr/7kPuY70n8iwE4/mECQAd+Dln99wGl/7QPGhZc/QAFhem57AIgdgJf7AUIzBMCDXj34weTDtf89/5L/QX0kwmfLXAFgvGpA4v8pf349s35m/bIAP0AOecD8wQF3A9nCfwMsAJb7gIFZvMB8Az1/foBEgP9mgceDTf5ieJmAjgC1NzfFtr/MurL+MoFBhUM++8cugsa8fzqdvQDCxLt5gvjEiX9J/hHBjEcs+k87g4F4v34EnIQsgWb/V4QkwcX67X+AgXUBMj+j/uV9qL5JgsrDdX59tqzChESq+j7Dh0QEvUhAbsE1+119CUK3wVy8871uhL0/ab/rBNB+9EEbP+g8XgDTvslBZcF7OlRBFwOsf8+BzIOtgAD+fgGAOf967sJsP0t8vAGHhlD9DAAdfEy6+MBI/7jEnL2Pgs3EnID5P7f/JMZePrLCIj3hef9Bh8EbgeK+hMS1QsE/rgKIQdLE5UKg/3D+9YJGgPqAB4cV/jp6iP3+u3BCg8McQJ3AfkJkAox8zT5bQCqBJcAVvhC6qkEnBOT/NP+G+Qs/CMXWgAJ/OEF0fys9x4Hiu63A2AmZQk0/U4Ni/1y/QYIPvw7+qb0gxI0/f/gjQVCDJz6XwQWGxMA8/Ig/gTxetmUAUUiN+up3WwBtf8R8XYNfwLG3ebrlRHqCHr2GQgEBY4Fs/yPBg4DhACFFGf38On3+tEGJwemEBcAz/nlBlf8+vw4/0r+AQLWEssK1f6Y8jP2c/8I7KPyLQBfCmABawzhClL1zf0M+rECgP46CLQGf+5F/ZIE0QoHC/EWiwe77RAL2/iR9jACO/2ACMwA+RUa/Nz8YBQk9432VfIlGZUOt+1i9/Hb9d1s9kcJLuRc+josMe0Z5iT+fAUP+4ntHQLt8VL3oAd2CXv+EQgVIHL5m+W669z+FgC1By4bvwIPCUgVUhObCpoO3/1D60D8BvqtC7b5rf6jDs/aEej9/HgCLxCg9PXsiPNRCJQQ2PEI7lv4Qfh32G3yEB+bB54Mqe++4BHtbO1QE1wHgvWb9jYB6ABl8nUmVBvP+zkAhuUT8oHuvADOCCjs7ffY+Kz7YP2hGqcRM+m7+kb+6edx9cwj5wDl4SD9o9/R43YXVwpR/ev+XOg04iPyUQ00DyH9/e7g/FLzzQB7J/YNog2G9Uzqt/bXBbUM2uxqCU4HMO5u+o8aLBJk+HgOL/1w7AoELBLDAvAB6gBt9Wzxo+8IDVMOTP59GAnz4MDo94EFUgfqF6wGIvmI6XQGBgHr+lofNiJW7nzaXP6M74QLfxnP/zH23O0bDIkABAIrH2kQHuc1A8Iex+x0FIgEq9Mz7r/0ZQwKB/McYBMG44n9cA7b+jv+qBCs7wLu1v9hEuQWs/xpFkwD6eXt9g76fPqDD7ERgAiIG0kYARMCBCv7+v3p2UfovB6nEh8QYCjpDwLw/OxF9GkAuANQ7YT6nwDS8/ME7BRBFJQDa/7x3c/qOBJ5DhEALgbEBDPa4wPDCfsDeBBO9ysWBwOl+BoGTRCaGM7/B/S76NT/BBIoDa8b/hl+CC37bO4E94QGWRCoGqoQ3gWmA88DcgX5FeAbMg+WAXHq1xDAENLvpRmd/HQC6xtn+cgGLQ0JGRj5hPMFIVAgZvc48i4OMNaJ+vkn0gmM/Tv9dhSr8joD1Bx0Di8H6QJe/InwPhSpFmYA3vytBIL1I/KhGD0GMfbAChcIuAwzDPj/BPR08ywPhfvh8v8GVQub9H/iQw/qEJkA4gVQBMPZ9OhXFg/2DQgBAKfv7/fvAgASKfbR81L++uqo4qv9GwWRBgIF4vHy6BsE2Q+uCTUFCOhL8p7vtvmQAuL0F/2o/aPoP+4uEpbtXQGDB8/gjuVX/R4UHes7/2vz0+Hq8t7r7Qou+a7+WAXr3qTofgKRCFMWJQpx7PvzlPyyABEB2fZz/fIGP/1RAhIJJAzKAXHwXPBh+skPqgVeBnD+8+3I7lr0aQlz/4P6beqL76UBuv1JDDQDxfYN31biAPcM6qj+wxYxCD/tWP1YFQ7/wAA0DIX9U+mC7iAEuwBTC10Tc/y/6Nr45Qxc/XgB7Atx7SjuKRCK/fHstwKXD3fvD+4nENb2Of2hB6ruLNpl/iYZouK1+6kCb+lW+an+9xRdDCgHExD06kLopx8cA+jtiBix+HvjFROuIMP/6RNLGyftIe2VG9wTOe79DkT3AuYx/IcI1SKo8s8FQg0x2S7+AQzl+Gj5PQGh5tPqHRXxBxj7ewVIBbr3ZwosCAjnn/jLBRr8AfWmARcXWQyf+6D1XvFoDJ0WJ/i69wIG4BCRAPD9khG9BWYDGfq29xX/sAeUAB3oKfyPBqD6jgebGA0DrwtLJEcGrPjZ9p4AxvYL7jwCPfrrAj8XOBhFBiIGBhZTETH2CeF+8gMDxBDaEukGngJRAUUAXAiUBJn4Ww/zA4XnDvWXDkQU+AZ9/gPwGvJGC6Ie0w55/RgFJABb+r0EsgXcApQAVPAT+74UsCWdFzgPdAgv70r5//f4CYH7FvxEHWb4xPX1B98RCAT7BEj5S+FN/mH6cfjo+TwE9ggN+6MCQAB6/kwK/wVI9ij/CP8wBDnp0emFDJf4+BQKGOH5XuQ0+OAUM/mcDb33AvS7Ayv0Ag1T97X/ewiz/gn4kOeq/Xb0OwP//Rv//A7J8ckZIAoo9jUJcfgh+yvmg/kdChgB8BeeDlbwM/gmFMD3kfHeFQUFlvcjCUQMlfaH7WoED/sW6xMJ3QyP9ksGQBFV9PTueQsWD6fp9eKmADv3U/02GFAUtwXd+Ar7cvVC7V3+/AD99XYEDAaR+W3/TgZrAiYA6QAI8cnzGgEMC4kPxwj4CmzwAvN5AEjshwCDErn/afao+yj2UfzA/SIR9RXz628MfR4MBIYAhwQ2AuD7oAcA9Wf9fwCwAAIUrQSDF4gbwRTo+rDsxgd0CyMGlPI5C0kD2/AhE/IJKfeL8zoFIvrA8NIJGBzJFbbosfnPB4AFmQY054D7FPMuAbwZBvKiAvAVIgNp7LX4bQ0oGO4FjuohF0UQrgPvD1YD7PNI8KEWtfRS9m8cBwoz/EPxmhPxDtICVgmp/aHvhdoO+bP7AfHEBP77j+wS/E8TJP8R/LoBrOf067H3NwD/FDgJ4AC0ADnx8/z+CLX5RPBs97T+aws/FuQU9g05GKYQI/Qc8r7lMPuCCG311PYGALwQRwVaBzz3ae5qBbEAV+ep6LMgKwQt5f73afJS/L/8/AEH+anxYwfhFdDzde30F479IvEV/Lj2AQgTDM4J4/Sz+IwL5fntCtQCk/IN9zzz7fX74oQY3x8V43X3LABz8uHunwrIABbKYONYCfwBKQD4DvP9RNz/9TT+zNgJ8eUYlPvJ4hUBDfzB7bcJKxbRAvLsJwN2AfbnRAYICx/xgATx/X/n/f+7C271hePY+zEKOgn9BGsAswDi81f6XPLb/HMMFP517vDqA+5dA0EgNQCk9JP4MfZt/a0CogcuCTEYHAca9nni6OdJDaYDXfFNABj/8PlNETUT6gbkAOcNNgPG/t/mzdkZBy74T/ZFAuYRdACO5Gv3oPUI/P/68REdD7Ps4fnsCxwBGf/zC8zyXu7iBbn5z+sX8cz/lRxnF34IJQCfCHsKoftKCI8A4Qiu+GgNrBPm8hENBfjeA0f8wAGsH5EEsQRCEUkHuOsIFHUaGfo3+NPswADNBuwOeB2C8vbymBLM78vyAAd2ESAD2u7pDWgIjQ0JIAEN+edn64HznvMdEigM7wgj/2MJpggF6zwZNCVB8ertAw2VDLEHVAx/CBEHHg1AFvD41fQqG1YGcfHpBc8R2wXLBFQQJPFx+18r9Biz81EBFvsg5d0GXwOG/JAGwRFcC/XgzATKG+73Ivn4C77ymf1LIcj6AfN3EEQUse4E/6IPzfFdEIQJXfyT/dkQSxWn/pkU7wRt9ZbzNQdDAIbyCBttDF33mvh5A8rwOfKVG9z6afFLA5nz4vj6CsAFDvulExARXN+c5ScMZw3MAYMIMAME9HAK/RBP+ebyQgobBnH+9A4cEkQR4/CsBP0U+f2PDI4K5+pH57AKcvRn/24OowOEBOfnOA7VDBb09gbGBx/9xO6Q7Rf0cft7/Y0YMgiH7OsO5w2Y/a0LfAEgAZkG3PCNCbkSTAVCC88C6/pm+wkAh/+K/s70Uf3eAUgAXwAg9Jb49Pk7/8z1PPtnCPLwne8e+Hnlz+ilDHsK3fX59zIFwvLS7I0bjgxZ8owDQfbV5Gj1YxC+EJwBmgtaEVPq9fYYHXX+TvyCDAQCj/nd+IL3HOww+VsKiASv/uoMnP8R6kgDaP8j9M7//gDH9bPoUPjt9wLzJgRYA+T3S/ZPEGT/U+Kx/bwRDAo69SsQtgiM8BcKRQdB+Xn41Q8P5FPxXRsl9oQE3ftHCvYLygGFElABT+yZ5CH7cu1iCJMaNvQV+C34cv4RAyYGFQu68ELrM/8v/JgIgBe+C+T30wKAA8DpPAIZA2oJ7g3R8yABhwbMADL+cPoo+/kGlgHfA4EOKPYw9pYQbQvn/QkAdu8L7WftJvkeC9kD6Q2M937z1AS09Q8BcQLU+cIFhAaoAvsHcP4Y9tYEwPr960f+8QO37sL3ixdxBjwSYhuy8VL8C/5M+CT55/r5FV8LvPcU9NH+L/4C89QQahSG7k72kBNE/lP3oxDa/Vz4igAb8/X8nPyA/wgJt/af/FASegYV/ewMtvqc5AX+8AqJEVEaGhDQ8NrVVPmZAEX49xA9BGj5SAYLC0/9bRFEBkDyHwVE6mT9wgas9Q0LIPhX5ncFjAwi8wT5gfmF9/MJKwD77UH5dP7o963vFP6N+QPqMw9B8zrdxf75ExEMhul/4jTnNPoe/FcScAd78yYSWPVO4ykD2hQ49V/2Xfbs5PAJpA6QAOX47gTSAhHydAKa//T91PvO/08EE/6MCrj3aPKN5dD6gBlV4Xr+PwSo9I8GNPvBEo0PLft65Ab6FO//8T0Zgv0l/278PALv9xX76w82/mr2ZO147Z73ARAGCqsBCP42AJUODPMe7Pj3hvmC/HMDa/lp6sgEkwzl9V759fzCBWQADfLY/r76XwC9AXb32/smBO4E1PId7z36Uf8tAVcNEg53AJcAOvyh97ELkAhT9SLyU/XfBecP3RniB5L1afNA8gD/Z/ag+BINvQgG/PwSLgk2+cId8QkV5r/7YwBy9pj5gP3HD8kLrg2NFYgCQOisAQsYKfn+C2IaXxhM+9rzrQMVAOsHz/T5/l0NMwpG9XIK2Ac5+lUbIQiC8PbtlhlK/az1cA4PAucEh+txCoIC0PGu+UIL/A6z+JENfwlz9+vzLf04/asU3Q7t/LkMOQaV81n+zRY7+MkHIw/N9dAElxPXBDrv4AenEM//vvOSAfEESAWCKdEod+0v56cXgAKu6wYGyQQC9KQJmRSqBlD+NR8sK4j66++BCN8YMQNPBeL2ies4CeodCA4F4eMAkQhQDAQMeQEEBun6AgGi62sG/gg7DYAgYPy4/HUBEPwAAeD3nuvGBzYINQDyF+YVQwW6EugR5ACJDOH/sQA789f8dg+vBPEWcgSx9l76ggGj97gFlTILHjX9ZPVA6QXmcwg5Ffj3rOmIAvwDJvMLDNcgvg+P5DrxmPTi3h0KAhh/AlL8ig7XEDr1z/Y5ABb9hPYtBQISRQL5AVYFtQEQBvX7//A9AjANIflM+GcPhwiIENATLP069mXee/VlAoH5exyBE/H+lQCPCgj6cu/8EFUN7u3o9rwIMvev+CwbIg9k8FEJhP/z5KftkQpSCuHtZRuYDrPi9gIoEazyMfbFBBnnxepYA6ET//kX80sNfwH06276JPox6QETbgMi86X/ZwXP/s3rJgGX+gf32QKeDlvyNfQNBsX3wv3a95kE5QAcBB8GswoY/Eb8chBu91ELO/wF6y76owCH+S/vDRA6HUUGQ/Nz9grzsAVqCSj2IBjWFrfqSvF58W/0MhLaAnr1ifkiAkcIsQhl8b31zBDT8wX8WAOq/pgCdAKq/tnte/5t98vvOvwf97/tRAgCHpr0EwWTChDb9v1FBe73dAW/8or+kwO8+XYVGQqey/TqnhpL+Qv9nRZqDvDtw/X5CRz/fgc0CJTpi/Om+5bumBohCjLquvAB757+lwajCfoO9QZZ78EHZfWz4pwDhu7C4IHsyQmeCTwFthPZAmzvZPecB2HoGdyJAnYA8verDO4SQ/7L81kMdfFm4e7yjQirBZHamQoDFSX/3QW/Bgbu69baFeYQnuuB+HweLQsR5qQBLfiy6fTuGAkK/izq4BTiHmYArwB3DyD1Yt8G+hoD8/vmB9oMEhKr+FYGUBRk6EPuDQIF8k3sViJoFMAJJSDv+nsDHvWC9h7/PdiD8GoRIf/r/LoNygNc9PX00f+j/4f7BQNT9er5CR59/Uv5ww7q8zP4Evo5BF3+awGZDOP6vASwDd0PfAIA+Q4JawSR8yoUmx+MCJ4YUxEJ7Dz14/7t6kMEcAMo9ajzCf1eG6oZ8hiMBAABY/no7HnpWOZC/YoCqA5A8wzqjxSFGkkKY/o8+Lb2j+2K7pQMcgxjAc4eAQu05N/8FwtE9L30NAcj+qT8lRbtCi75EfqBFHr55OqyGHkCY/UF+EYBzwjG+RMGPfJK33H5EwzZ/VoA3REOB5IIqALW7jn5JA8cAbvtNgNn/cr4agSR+9n7t/v0EicRXfDG7SYRvBMh764CaweQ/oD4bv/qAZrm2gnFFKjtfui9E4EaNup8/FkS0vBZ9b8NHAa3/G/+VQpL+7nt2gOE+BLlcQSpDOL0LAfuFnAE1vcoDc4IY/YMAmf1meZb8XUCPQffCdUBhQ50D0H0wgDe/CL3sfaf9tj9YgQeDSQKVwqd9izzjwvSETv+bP3e/2fo7vdxBL38DwvlFicQFPK29ZQS0gSKFQ8PJePh8Hr2iAC5EZMWexHeDMwJpfpF9a3r0g9qBqfhDwz5DSr/XgScBfAC4fqX/D3zPvnXCx0BTOwm9NMJLwULBZX9WeZq9uL8EP67B0MBowbPCAEEHPWS9m/8vgJIAkjqbQi8ENTxGffDAtT0zPCpCxYGnAPUAcv8p+8x9GAkQg2y+kn6vPF88tnflwDnCBb8dRoYE1jwXPnAF7/8DPBfDvMDDARlCjf92f+ABqUKP/p37hj8uv6A8XADQQmI/kcLM/w7/rQFkgl0+a7tVg4sCEX6kPczAljg3uGMD233GfqvBakNDP4I+oEPsQn0/s8AfQ7Q+e0BmP1e+OwK2/3+9gn6rhJwCe/yzPqnE88TOQysFQb26OkW+5H/Ueln+4ohwAFJ8jQLkASH8bwKafz+58X6XPyFABr0KxWaLaX9oPC3COP+N+vZA2/3++ttCNsFg/xA/JURiw9V/foEvfz/+uUE2P8GASz/Y/0OEREJ6vFE+sP+jfyICCz/meyn8VsEtwrK+JYHkwkC9y/xOu9J/eL91gsdAXv5FPDaAKcV1tnU9AAAfu71An39bgkQA2AIBASt+/MFbwwpAVf1NgJeA2EFI/1+/5kAUv5iAXH9mQipCH0HOQvxDHQEzgtqDjD6dgS/+wT2NgZYAvUJXPwI+UYH/ALXE3EJVQBU9pn8RA937DUEUxSKCawNXgFJ/VTv3ASkFZ0DHehV92ITK/ulCZYSxP0SAEIPuAJW8c4TJRwsBDnqMPpLEjr7gw15Cwjw/+MG9XgcJw2/Es8USQHkAH4HlgsS+gH7I/ak+m73ePPYEHwbSRRi+ir5+QApA3UAG/oGC64BBQxvHZcHMQYlBiL4TPk4+Gf9ng62C4wVQRyg/Mv+ExVhBNX87Qv9AkX6RhCIEzwGef7iA6YNwe106z4TRRR4/YMEUgh+9aUNRQki8FjyHvPZADn0B/m7EngQaAO3/h0AXvaGAY0NC+/k4L8EBAG/AGsUZAh5Dmb8/gHSAX/rQwHUA7wDAPkpBZgENfNqCI0EN/gy7rAPFQ356JIFzQ+7Cyn38gnhGPzhXO4OCnjvPNmrCecs0wDO/1MGu+qM5GoAfAlfABIHAgAd8yrj2/yKBkX8qQji+jrzEO4JAkEG3vhQ+TDznvdpDQ4OnuE09t4GxfZz/PsDPg8xAUICcQfR+Dfi+QccG3fwXgg8Fn3vHeqfDUwOmgPZBBb3qufL8uoEQAQVBQH5avi86L30kRA7B4IBmOo77RD3sPSK8L7ymf19/en+ywKKCs35vvWN+7reg/NjGjwAtukc71gPxxH7BoMIq+fn9jwBSQFJBXz8JAPAAg3/1/JHAYD9VPxW/gLlOPCXDz4Q9ATsAzL2yvVj5ADnX/eK+BvvHPS3GYAKXg2q/X7vp/bG6pLzSfASB2MCDwGlAWryxwea+nnvw/Qj/aYRDQLu9xMDUwGCAiX/XgbF+wb9ef/y15TpQw3KDX8NCw149Fvv/PeP82DzNvHTCA0Aqux5934TbQ9A7vjwf/Bz5ZDeegdNBNHxLxNqCeH2Hu2jEsEQeOf68NP8GffG6r4ooBfq0QIHzRbv7rbmfAbgBaz0hP/7+Av5TgGDHdgMH++C98L0fPwE7I7yTPQ58EAZg/wm6JIHKvzP8c3/IxI5AfzvcAMP8uHpvvZSCdYTVf0NBZX8TuOt8zEF/Pxr9GsEuRX7/JIGshqg78bvW/xs/S36Mv90A276dQZA8bcAQgXv+If7E/BwA+/zfP4iDwoKsgtC9b0Eyv808V39wPeD+6f69gJn+yb8NhmrClAI8AAt97v/4wNJDGUA0fcMAjUI+vXwAt0JhP7lCaUKGQIm9HIPMQfv68kECxFZAef7whQaAfzyLAkkE1oGKPB4Dx8FYfcSJSMJJvbT/dIPoxe48wsRGgb9+9cF9gBCD3kHMDHjCJvWavcx/gYF7g6vFGP/SQe5HU0FtfOJEVgVSegQ4Zz9AwikCsQNfwdADQj5igQ8BLDo1QwqBrf3zQevEq8UogMjAr0DsvYlAWoI7gboETj9pBGJGWT9NAlXDuD9K+AW+1IMqgMcFQoT3hldDWEG+gql+BDxlPnVBB3rvQDQIXUAPQojCy32U/sGDoEJIfMFCxgIPv7JBQ0Ar//J+1gANABa/Er/nQRVAC/+pwyBFAUHMQlJAa3nFwxFDLj1JREKDlr+gfMy9OX8OhAJGKUAcveE94wN/QFr/PoWnAMuCRP60fV8DiMHlwsc9rfsr/rTCE4E9wqdByTtSRF/DPUEmQ+rBisGRfW/BMz/twKeElYDXQbe/mXxnfdyCZT6yPxlFcERVBhG/AfwE/7N/XkCU/7nC0X8Kvgy+zXkCfz1DmwEagLvCAjzYPIaEP4F8e8LAzcQnO/p8CT2tgJbBYjz3gVTB9wIofw29WLwCwNDDffnuhFxF/AGcwWA7wYAc/efA8cCpe5l9fIHsQZD7WoMzQonAgD/nPVGCfH6sQqA+jrtXAmz7xX0YAVBA5QFIPpY/AoEf/1NAtMOAAFx9zgPLvmK7lsLbwCO/n0Aqw/s81vgZxaxEDf5+fNsBEsFge1r/lMCR/YgBXkKP+kQ6+4K1gvFAlcGcgIm9SL6GABf+JD5JQm3BSz74PkZ/8gATQwbFzEB8wdmBffvWvpXABHwFOIpAfERlfqG94EHvfrD6/QGLQWl+Bv+Fvvf8C3lfP9vB9z1m/e/+vPnot4u/9wBNRHFEorz3gQWBs74gvSnBkQKK+sP90L9QPnnEfAOwgPd/6IDqAxN9O7ujQ6GFDfyQgfyEF/jdQbDC0fpvvQU+CD72QP6BJr9rfECBGkHV+V47iUCywC48KAG8f/t26kHJRO++CjiEgAHDXD6dw7MAnjxU+hBBMYBvvMuBhwDyQFr/s7/xPZECcEX+/7H8TP3dwCFCK0JO/+r/xb/SPk48av1uf15AWwDwAF4//AA8QWBBGEHpPqO9Tz58f5Y/U73QP6MAqr1Te44GqgODfWUBSMEUfiXAqAWwvIe9k0PQwx786boiwfUAc79VwNFA030I/a5+4zrKwLkIuQYzezI7WrslOk4CFwA8AAI/1b8KArf88TyAwty/+H7twFi8Dnu+/QFBR8V1RIjEgMKUPIS4AME8AFm7gYT2hBhBln7oxBSE2TxCwkeBGLxhf4fE1YO0gBIBmoMLg3Z+m/9pQbM9R7+ugoN/X0HwA3fAjv4V/1IBvcBFwKMAkIRWP3H/KQIZf6e9JDxFw9HAIf5kwQzDQz/CfkWEk7uxfUoDu/8r/aQ+B0HkAJI+TUJwQRt/b0BMvEK6XYDDBCa/jUVawTE+ZIGcfT1/bX1eAYuCdUHYg4XEzkELvF1Cm7v+/gzA6QJ0QxY8koHSgSaA4b/kvo4B0oCzfP8AooJ4fNQAOoKzwkXBBT6tvkw7/zu9Q6jBM8D5RfWAsP2x/nlCUH+kfug+v73CAEFBvEOS+7Z93kH2Pjr9rUEIhJO+h3yp/MG/GAGOAaAA6H8y+0d8g4KUPbC/38Wju8p4Xn90A2KCNMHFQXx+ZLlxuubF50DFfVeE3cGSeTL6OIABPo7CswNUwF69oP1HxEhCvP2vfTfAWH6AwnvAbrzTQ1+CIoEDu/dBWsSVgUY/KjmJv3FBYgPaghl+p76nAZ0C932/P/ZAC/4if+/Bar/0PjwBL0IbPDN8xoISgtY+4325vmZ5IL1jQl3BSf32geQCL7ravvh/GD5k/Dg/h3xKOX+CuIKuAoTAf/+t/lq8OcApQcH/nf80/j65kj3bBTXEs4L+gQW647tk/tkCFAM+we2FcwBvvGU9Ff03QTiD5L5D/Zo/44DRQixCXsScPpE7yH44AJD67T28hKg9VMFxwKJAy0HzP64+yn54vbn9L0M2wO4D0oByPuhCEP4HgL+8B70nvw2B3gPKwKoBwcOOAkw+ygJEQxO+ZP/J/cb868HRAZjAksDzAprCBT/TPs69msKMQlQBFcElQT0CIH2RvA393AMngMP8sAEQwQvB7ECqAB5CqT1sASQA3LyiBFAE8YD9ACIBuULjAQq6jv0Pgmv+PMB/hCnEPEGqwW//1kGfA4PBs36gfGz96XuIAgjCNACpAwa9278c/H28TsL9wYx9bEF1P61988JmwU2AhT6Ogxj/B/oL/bM/20Cf/XJBCYVuAuvAwQIy/oM97gK2Qc8+4sYAxXB8uP80fGC/oEGGQ0cEFfzKgAEA5T6hwC8E2gPsfms947/WP469ScG4wxY/OkFQgxD85LzifSSAgILuQcrECUBeA7NEi8K2f4J+2QAw/kb+u/3JAKVAcT/ygXjDZQFpgWQDYv+9+2u6Xb52wE5E5UAqvXOB9cDpfdp6Xj6KPjr/IQOEw1T8YPyZxVU8DjiEQL0Cf/7uv+uDaf3+fcGEjMJjfXN+Oj5zOlp+XsUigOwEO0JU/O/8Zf14hdk+SwD9Q/K4uX6IBh0E5r9kwck+YrZz/SiCekHGf4iCo8LjuowBdsoGgK99cMMUQXv864EJgbO8tkMAgsS/tMJrQwM/h/0bQcvDPgBQwW5ErbyiPA6GxkG3e1jAw0P7vMi7+r7i/o+8zMN8BPf7z32xfeTCXv8JuuvBz0LigYQ9VsDDPi456z4CAR5+3bwrRsXBQ7d3O/uDQYMGfaOFeQSMPGF7+oB3fzj8zQUEwjo8eEQNBBW8vXpswPzD2v6CBgWE4LzOf9L/nL6rfQIEqMJ0+zU+EQApwlX/RT/4vRx9FwDegC7Dz4D0ACFAf/21fru/rcQV/1b9eALG/xO9s4GvxLh+8rw+g/NC3H4G/i4A7jyuu0hE0MFbvA+BdAFi+vk8oYICwoV/m77TwzK8b7q5AI29DzxIAAZCBr+gvIlAGANRQEN8xD+nwP3Bx4V+gIn9lH0pv42CZT3NwIY/MsGrgzc5/MD/RWvDFr/TPt9DG75t+vaB7oKJeejAB0MRukE/IAVoAEP5FP5KRB49WHwvxL4BqPubPnz/rn2j/SBEWwAc+vZ/oH/lf0p+vIEx/th/PAN0PoJ9J4Eig/R+xn5owFW8nQCOwb3/fAHtP/rAYv4DvFNBGMCjf+YCzIIPPzMAqwALQiADF7xyOyEAn8GVfdfEhkXvf6g/n/6r/AI7qEPaQdV/XAIh/8OCZf28gS7F2L+rPsS+3HyK/hfB9r6Cvk6CfkC7/1j/BUFsv4y8mL+dPs29qb8LwGa+GD4XAPRBskFZPWhBIgFDPUeAmEFmgE/66Pwfv5EBQYcxBnuBejpW/kkA5LlifkbD5z7XfGT/iAGYQZeDowHU/hE7PfxIggP/p76ZQYG/uD6WgKfC5sLogjz/N7xLv1aBIj9ZwLhC9v3HfU9EokLk/86CE4SYgx478P8EwvN+VL2sgDrABL1tBHjCjzzBAHLBUgBvO5DByQGo/DSA7MI6ALD54D50Am+62D/2f7A8u4K8hf7DkPnnPoNEW3wMfdHBF4K+vw+CukZHvWk9RIQGg2q7O76egOo6fn8CgxEEOYELAUUEsv1cvM99nrurvym+fb7bPg+CvUO1PBx/1b3DfWo/aUKVAxJ78IF1wKj+Hj/fAYVDekCJw2f+7Hso/+SEXEE8vvODa3/l/Y7/BoFXP9/CZQfXfVx+fMNwPLT9Q79BwP4/LEFpwvB+Gb9OQJ7/nDogf13FBj6cPmUBFsGG/rA+9nyaPbwFAkK2/T98zQCbwMyC6sAK+5kCBkEjvZZ/CsC6gxQB0IGYQLB9ngAEQ6X/nTwVwaHAzX7LQnJCtcAgPxaCTHn++kAFDcKewsIAL7/uP+r+xQFVf52AZoAjf9U9CsIChIB+Rz2UfDsA4QCjQQuDff3EQfE/K3s/QiRG2kCzOi/AGUB6O80/1UFwPXH/MoRf/YZ7esTiRUF+kLrgAE6C7MBJQic+jn7xvFi/NkT0fHq+1QLxPas9XAOyQumAdQJhfEcBYsDXvshDnn7vf+vBHsCs+90BvMQ0Oxt/fAHHAaoBqILnfpv8uT5H/jeAp37VQaSCa76LvCy9QwIggBf87HvrPZ9+Sb38AG/FmD9XfNYCtjvHvsrGWcIKvET8BABUPuh+ZUU+Qod/jsLKfwf9Tr/KxmXFbMBswZ+9s/9vge4CzH8gv1gGiXuRuzSEsL/hOYqBIMduu6W83gUPAIw9On2chCS/wPniQmk+RvkHQZtFRL5LPd0GjL9ePdgBrEC5gN88CMNIv5h+S8OpQK1Cj/0lg6/Ejv7BvVZ9egPyAefDbn0sP7NB5fuSQ///oD5hwF//rr3c+5UCP4NDwJx+DQExv0g9XP3IPPgAkD69AXqCT/zJwcPD5z/9fUiAugGhgAkASX5og1rAiX/xxSl89P1DPw9/KUB7gQ5EHgIzQPE8DcEDATnAlYSy+41+0r19PBgBTT9NwtJDOn5m/QP8qzyLQU4AcEHAxTw+MT12/v775T68Q+kBE76bAUZ/WLu8QrIFFD+wPqN+0MEY/2aBYwQZgPv90QIVQFU5L0Qpg7d+Nn9wfxoAErzRgm4ElH/7vST/47zM/iDDMIEvgn0+Tz3L/0OC037ZPibBUzqqgGmA4/3/wv+HaEBSeUw/FYDjAKjA20CSvbE+vz6+v12AX7zsw5tFEHvA/T+EEv30eXn9BUDjgoECXoGnfiU9XnxXv3pASsIUhF2BY700OIsAAsOpAapBw0Aivc3/Yr9DPGxCJ4Tpw3sALj96QoDCfQDgPUh+qoIAQGq9wv3k/nbD18fjQUD+HAEIwLR+xXvZ/89EaP31AH8+Zr9gA+BDZMH7N/R+oAAwea3+zQP8Qg1/poM6wat97zi7wS5/onlWhmfCLoFHAyPAt0Dbu0Q9YcGqvkF+akLWfoACwMRW/TqAIAGjAca9zLy4Q5yBoPvMAFO/478xgsJ9UDxz/o0/7H8B/sdAhILggrM+2wIsfL36gr/yf2+AS4AFAlD+Bv4QwDr/p39+fFzAgcAcf6hAnsCpgI5BG4OEw2EB7L89fpN7G3iN/emCw8MlAlTA0b8p/47+voS/Aus8bH3UPJG75r8ABELA2733wCA+VLp5/JMBtQAQwO+/kv5ZfTq9AwGawEB+X8Cqwur9Q3yCg5JB5D6w/uh+Yj1JfmFCLcFzvnD/wUI2ABtBBALPvQ39DP9qvwUDBkCkQMVApzgx/h3C6/5ZQrjCLrkRt8+/EMGNQdC/80ENwJd6ZIC3wvqB1QAB/Xs7FjhiPu0DyYLpfEj/Bj8s/tFEDsBowk0ACT9Vv07+Nj9ygklBG3jj/zhBlsAVv2bAs4AZet/BM3+bPKGCpkN/fyi67nv3grQ/R/5ABna+J3jf/yF+x/u2P5rD+wCJfprA6oICgVGHJsR7/dGARL92PwpBVb/G/9aEDEOzfpj9A0WcRzN7n76HhM++2vwshF5Fcj0+gHyIe8B6efeBSb79fS1+0r4yQLv/u//Bgn1Cw8A3QvYAFb5PAe7+SIRsP649QIKNwiyBpz8qBG0AqP8m/jb/dYeQw2sEC4Imv4jDZkTsxSe987v4w1jCJ/+qhaQCkf9fPlx+J758vTfD0kcRQqF+tgJqwHb+T4SKfik/ToVofFY7OYMnRJZ/JAGBB9j8t7qNRz4D433HgreKBMGO+kpGb4XFuuGAw0bOeIg79IjLwZK9voC+wupCQ8GGgXq9IbyAgDTCx0CFvz0CT0Q2gG46dvx5v5vA7QD9/9/A+QCIQwvD68NJvdg+qYQLvFC+9QFzvfcDkITJvy88tYJlhGvBpj7rP0YA6/mLP3IDSH8JwyeBZoE7ep89FQUDvpLBWnzG+pv+KsAbANA+UoNtfCJ9D79ffWlDaIBk/3x6VrtbAVmD0UMg/4vAjrtguiw87IEbQtaGRYVWtbI5pgEYv9SA4oD2vmu4T8Gdw208DoDXAdo+jL6jAVB+zP/swZS8/jyvPgxCBsHxPD/+nsG2fHe85kJS/0MAAQOjvbk6MkEEAv37IXx8PBI81cJnP8u/6QJxxAI9Zzxogck/HoPqwnW+0Dwe/fhDW/1kQGXFhYUEflV+WgL5PXH/5EUTgnO+D0HGwTy+TH7uwA2Bj/3gQhACxMBYvrx97/0jewkBSUE6gs/CezyIgLpBuAHcQD9/uv47ei8+ysBlvgqAs0YGA8z9mD/oAbaFqkMKfyL/AfwGPgyAnAEtvljD9ISx/Et9N/7iQ5A/sjzYwHI+jL5vvMe/tj2GfZiEkgKYfFe9Y/+mutb8TsBjwCcCqX5xP5DBHHznRFBFN0DuAYNFQoIC+Su+tIQZAKT8ecIpBOiCMsUnwh+A84BJAbQ/GToaf8EB7jz0u7V/jIHwgB+A7wBPPYH/QD68/Jj85LwoANWAUH8qQHYAXD7oe52/toJEf1l+goLg/zL+KwAGP7YCUv/OAhW/Rv6hwvYBv0Bo/SrBJL9C/av/xcHp/U94Hb+vvyMCekPsgXO+zzpvAD78s7m8fgB+CntJfZ9AYz3CQktC7H8SPdI64n6y/mP8VYTMRMN92r/GxF6+Sj5mgh18Jj5/fvHBt4KbALgETgAUP86BzsDpvaZCOoEj+Vm+4wBWgXLCXIFf/c96/nuHwI08L/opBpnBJD88fylChoLReM3BP38FPaB+Nf8jgkw9eX74AGXCpMEOghEBZHvdwMQCa8J0wkzB/cPZ/9X+zn6I/TDC9oKdu/G7jIECATfAEUAs/2sAVP+GBGM+hbhzABvAfXpuOQTAw0Tzf8a/Qb+1u367v76c/qw/ef74QnyDQnzjv58GHQD6e/ABLEMK/qZ9CsImgjk+LUUqBSK8ooBPxLI/a3hKfzOGsQOQQtdCaoE5OhJ7GXwgeTPCIsQ8xGqA+P6hw3Q/4XyU+rS94/65QOLEFQE1wrP/1kApAAS9lkI6QJI8hr/3QlqA+UKwxYzCcf2KwXMAi7gQPxoHg0EX/5fFNIENu+b+q4HoAZx54z7Axk38B0CrhcM/Zjysv0s+Rrm6w1tEg70BP/DBdoDowaE/2b3pgti/zT+EgFJ92kbxBAv/wz+b//0BQYGQwqG+4YUERvW9WDnRgMfETTx3QX0BbrzbguvBaL54Pu3CYkGcPcg9JLuiwWtC8kCy/Zi6sQFQwHM/w0AQP8tB3P39gly/Xf4hQ1aBRT52vq6BnMA8AhZ/uYATgpEA6QDw/YH/sYHPRMkBkT3VwTgDb0AIvRyAEQGBRIhAcH23Ps5+0YLRQV59Or1VAx//7Xrl/rVAaUM7hSnB878Fvc1/bUBCPJh/LsGuQbH/O3/sw0A9Xb8hQ9uC8j/jAFNB4v2d/rUBL0KKADx+rQU5Qaq8K4J0wHJ63z/7f2j+CMLMRGxCl375Ony9Cn/RgL9E7IIdvDx56jytvkvANITqvuY/mQK/utp9Cj/Ow70AD/1dwccAFYUdgcY/nv4hPqPEnj2mP92CIYFHO1g9HEbogbAEkEO+ACf7QfwJA4WANMMdxBv/uXnxvNlC5z3DPx0BRcCwfgG+z4JHgqCBx/9K/zE/AkGgQQF7uP8hgFWBTIZVQ4180jwiQMx+DH4XQQuFtQTEfgtArT7HvVyAIUCpPUX+cEHK/w29hT9KgBw8eICUAlM/7L83PcNB5j6JAS+AE/vrfnTAhQENPky/qbxOweeFrf2JgAyETf85OV8//kTMAnwAmIMDAkx+wcK1QtE4ePpdhi3+cTvzQ9xEzL5wPz9Gt/wnu4eEkcBZumL838LVQDn/g4Jx/si6B39OxWp9K7iZQ2OD0j2dAmD+hn+Uw+ABHAG+/T854gBTxLL8P3/WhGN66/6rRBVACH4Mv7yA+8HivVs9yoThAY88o/2PfeB+LcHhwDt7yL1twUM/Wf9Fwvd/0gEIwBj9kX6Wwnr+NrwFw8B+fX0kQQl/+cBzxDTA/Dx0/6K9eb8yv0qCYMVi/Yw8yz+g/xs90YPvQt989z/S/Vz+AoJo/3nAJUA6vlxAi8CmwDp9vH2xgFyAxMEkQJPDbH9K/FX/fL/PP+WBtcI+uTT7oIT5BHX+2Hu2QhY/ob2LAwTByT+EP3lC+8H/e9K+SYScfjb8wsVjAGJ8NvvkARqDh4DERnmCGfnnO3QCdsJmwF4DaAIKf1766UFcP8y37sClAyDA/v6dgUVEcsHi/qH+7QHa+xb+Ir4p/SzBpv75A2LAbz/oQYQ9d7zPfjVBNXzg/oOEr0Kh/lz9Y7+jfajBYH/6ek/BR8IrAT0CM73l//g/mrylwJfCu3+EP9nCaj/Xf+bDfH+mAFyA8nq5f5ICyb+BgmGE54BLfJjCdIDivWDAsELUP4T73IFxweQ/sf/KA6T/NffrwPaBUQC+hL8E6EB5OD/7+r+9/TT95sYYxHQ7Q8LsQey9GcBAwSBAejtifeVBxsFrwOuAqoKKgggAzYAzP3F8vv1NwGZ9bb6DgigFToab/zA8tT2Oe2f/nYHGwBa9df2dv/G9ncGuw88Al74OATT8fjwRhGB/RT4kvSWCVwG7/5NGt/+oPIu+ewBx/ruA8QWswiw+coFWQm54uL//REE/wn8jgEfGy334/gnFx3zZ/ZjDy4Lgvfg8SwE1v/y95b6dBBJB9H+3gt69iEDkP49DNsQk/LGAPIEA/aO678SkBFYArUFBPru9wrunAxID7z5XflxDOEImu9I+yD8cvSM99YCNvme/JkKwP6X+XL3IfwnBOX30vDj+f7xf/3iC9gGcgU++6rzMP0Y/qoF2gw2Ac4F0PLj/6UKBQqqEVPuuP4lA9sGQAZX/hsRKQdJD2r1re44CI4GCwL06owBhxn9+M/1WAea+Y7ylQ2oAQbd/wLmEIDuPvk2Ba0JjwSa+r0GgfQb6JMDRgd/8+n0BANb+YUF6wjJAa4MNwmcA7brJgEZBGXstwNBCKf9Hv+IC6L17vcZDggODQar/HQFCPtT8LH4cRjjD1X2Sfk985gB8QpYAwT+9Pt7APYIlgftCIUDmf8R+xn0mgVxDGUCEvlxBtv+SAazDE7wnAHH/r33EgTu+u79iA28/kr5MAZ1AcAB9/av7Fj33why9z4BVQ5J9Oj9vv4I/Cr9I/1S/NoA+P9pAXz//OvNCR4IJgL5DDT9JgPs9Lz56AYHATsOXAYH8YH8iw5L8r395R8jAOb/jP6i+Jz/Bf1MHfEC8+mmD9EKfe3V7QT8WgTCB1MOqQcv7rz8+QkT+9f+HQV0+CQMkBDN3Yj4tRQfCN0BcPEl7xvwQQweHT0E2fI+Dd4Ht+bc/04HyAHgCv0AvfF88qIRxwyV8IkAH/1Z8KT4nhBsEC7tTAZjEHX3Owc1CLPmFen2B9MD1QY1DCABJftF8Mv4WAwUCLoO7gn/7bTpHPgsDq4H/gcKAZj03/6+9/IN/g5i/EcD0AW/+nbp8gMrEkP65f1zBzH6C/SPBbcGqvh1BI4PfwdV7Vb04Qbs7i38nQuCAVf2IffS/TH4CghiC9n7qvVF+1bshgPEEjfnDwqlHGX/rflK9p35CPfR9aL+qQROAdoSKguf7VQCkxi6ARbukPrv9jDwuwloF5H/b/93B2r51vpz+FIA8/y0/5UEVOm9CNwSIv6pCWn0GfDD/NsBKQQ+/ucC7AsnBg/38gobCNPt1PcQA50CcwhFEvwCGP/eCh0Iiv3rA1INiPJC8vr61/9VDL8LBhAx+kbuO/wzAKX1nftXBwfxR/sz/ZjsOwMnCFYM2P3x6VL60O7t8VcCQ/ui9oYB+xVNAmDzWAntE9HyWvOfEpXtqvoFGbL96fuDEBUcyAW+9E4ChRQ9/Yz8zQ/R6zj/VhQU/Az8WQFpBeT+/gKZ/k7viPGVAGMHuPKjBLEOrvhW9BP0HQlU9PH1UxFP+xHzP/lJFbj2ivI8GHP40P4SCz4Myf+b9j8NmQkr/zcDrwS49IcF+g4y8GL5mx0ADp73JxBEEIfyBvAKC5f9NvegEXsMY/Xs7EAI5fgY7igNjANa+eAF+wcs8IPxIQhJACP1nwLwFmMGPfZ2/ZntI/YoDXcCDvkLA3YLmACFDTUNkQlFDlX3L/wy+8b87wFDANb9kwLbEWsASArtB0j5TvsI5838yhe5ByEDwQTz98jvZvg2AIPtAwGuCffwwfUS/agQO/aj+cYIKO+E/cELAAx26EX53Qu/9JP/TAgGBK3yqAL3/Yv6FAqAEiQQh/3dBqnyLvZmDOEM+wRD/yMKlAU/AKX5Vwf2Alf8nAx+Bi7u2fmGEkn97Pla95sKsggj9D0JZvkR9iwNQhJa9DD3zgft66zvLQrzE/D+UgNTC1vxufdkCTgQcgbpBN4JRurX9oQORgPx++XuDvmQ9PQCKQpU9mj/OAYxCTzqAv0KCXPwvvqs+a8DM/ya/zv9X/mE8hXwWxGt+cL6tAx8BZwJ9QYsDZHzZ+2gB00HWQEl9zUIQQ6J99sFtQu9AlMH/Abf/3z5OAAWBj8DtwVf+QPyuQX2+qT67xAdAXD06AC7APb5yQS5BIT63PLU/KMDKfztDwQR9PaD8nXyZO9jAqsNdgyJABIA9g3o+hcLXRg/9i/tUe/e7X/2lw11G8oGqfnR+iLurfJHAMoHOf+++Ff/WPmb95/0OfvhBt0AFevg8QICMvl8/wL/yACO/6n5uAgxAUDwiQ6VDIbrfgjGDiD7LAD1A279l++p9tcKyQVUByQYdwtu9U/8kwui6cTvAA4g+B/2xAocGYbyIfSODZr1CPaEBsQOJfZ29fAA+/CI838Ucxhd8xr26/wr9tb9gwtnD0ICmPcgBysFdesqCkwcBPwR/DgBGOzDAwMRkgXOBwvp8wFhFFjttfS1CrQIrQCkA1L9vvrM/yf7+vbV9HjzAQMEBVf09AadBmv+kwYvCGP+MPWMBQD3aPL1+9wCNv8r+akW1P/d95YCuAAOBk7zZwZPBfH9thA2CIf7pvh+ASXy/O2ICP4LNgbH+tP/ywBV9a0Xig0C7MX7Fvwc6ovrGRMMENkCvAsz81zpxfiPFusLyOs99EQLRw/H/nMIr//y7SgKjP9n9cAREgtrCFsGDfzM+lUHnBRB/73sU/CXBWP+gwLdIEQQAfij+oAA5OXC7YULk/iu9BUHPADl/iMLIAHD977j6e6ZDe31K/hYBFXvUf8yFEgQyf047sL8A/Ng9KgCCwdgHEsVafPh8GUGPP2MDT8H/PS1AY786hNEByL84g0TDiL6rfD5AGn2yQKyBIf+JvxzA/YfFPvl4zr14PWV+8b5BwkrE47xrfhlDE78afhvCO4NQPRe9FwK7gBK9BsNGBa1/Izz7voWCGwDnwOfEVoGOwHzFGYBAPL1CHIIEfvO6gn1Of75+8ENugrP+RYEphMk+K/rBv2u/kX8YAAUB6sB7vk0/l4C1/mG8Sj5fAO07THzPRYqDOj7DgUFDtD7gP5qBW/7ify9+On/UPL+7zQIhQxK/x/9xRDE97Pmtwk1ElAFhwf6Cyv63+oA86z2q/3vAWwCZwRF+zANYw9x9wL/CAWW9kzzDwDo/xUCaAsmFNkLAQSvDtPwHuNO+4X+0vck/IoOfBmjFh4LkPsr79z63fxQ86gBhgb4BMf5hv9LDJH6DAQ+Ca7n7ecmBHgJ9QuwBt4CnRSUA4DmFvRl9vP12QLO+koS/BnrAHgChfTk7rIBTBKc/QXwFwk/BuIDwQCtCDsJBvhbAgnwI/RrDbEE5f9RBdMQOP5r7cvv0fW1/qECzQ57+GP8XhWA9gLzzgVB/Bzrd/EC/mD8cw9DH7QI4u7VAc4O1/cR+hgGaPuJ7lMIZBtf/S8AZRRJBvD9af6h9ET3vgnhEgYJEgCTCigHzvhm8BL8xw+NCcf/Pe6c8QUDFBN7Ehz1bf7/BFMFOvwo83URqQ/C+oLtAvhTAHD7FwusAuQEJBIO/tD4DgKT99D0zQOs/uX6lwOkBiwJZfaZ9lT+MPLx/aH+qPOW+sgMkQf59tUF+wtK90T5NArj6KznARNvAyv33Bf6Fb/7TP6D+UD4NvWnBwMdJvtfBGcW4vTW5wwJ+ApL8jkErAkl/poBPgRk93z4YgQD+BruQ/diAR0BlwamAhb0G/ZQCQX4DtcAAl0eVPZ39Q4On/qa9IgI/QIq7ur6iBMF9ebiggZFGP8C6wopCRnuqvwr/XHu4OT5CaYUwvP9Bqj/Z/Os8uf9cvX49IUONPpLAPb4vvhL+oT40wpL7+LxkwAX/gHzrP46EfTzewR5FEbt7fuMEpHyiu4KCO4Qu/Uz/ZsXEvao6TwLzgz86tj/BgnO+Rj9MwuvEqjnXQSuBWvhIgk9AXDxXvji9RL5CgGXBYH75P0V/gj/LQvH9b/+ZARJ7mT9mPuWBAkKBxFb+6HtUQiI8tkEmQkzAzoL7wtzDvv/OQMK88sBnAOM+SYT/w1HAmH+9/wt+z/75AVjFMn+4/dUA3T4z/0MCswW9grT9lz14vo48hn0+wcTBlUWlRLu98P/2/Tx9qULnQKTBsUBqQv8Ejf8/wIdETIKLPqlCiT+xuxLApoOyBTh/UIDTQ5e+LIBQxbZ/R71vwpHBSf4Hvv/FSMGpOlL+ksIHPXO+IgQ1/3L+esCBg4Q95zzVxyjBtbqS/8AEIH3af4jBmsBKQOQ+zwQ3Pof8R0JPQMv+uYF7Be5AwUFSRdrAm3utPOqBzMAFvfOAG73e/RWBVUYK/iA9B8cfwJ6/VsCDgPbBhj83P2Q9sEBjAhxBEr64QGoCbkAPBK9CoQIkQ31BNoDnftfAhYOsP+cAMsSuv7g+ygD+gKtCa0BJAqZ/oH1tgMMASjzrvlJDpAALwIMAgn0/PQK9sQBZv4mAKAAifsj/xf36vtw/pX0TQCxArsAcBj0/hXu7gyI/f7zDxLkC8n2BANeA2X+RPWaBBAcjQVzAawBwvaU8/MKQAhU8Xz/yweVByTwXfwYEdUCTPtd7b7utfdRCrcEEPDc+lD/3f1hArH3/fWdBb37Ye9i8hYFrwXj/aMV1AOH66z7Bv7V9Yj5JgQ/AA/4dPl5D4cSb/XxC8EHZuUn/qEE6f4yCAoH5PxR8eXlffexB/D3JPmU9tkCcwN5APUI0Pi3Az7239kp5pQCGQRB/VcEjgGMCp784fBx8vH2ZP6E+ZsAjwCHEZoKRvmDFFkTRPlO9Fb0cuXdAYEakfpc9iP+OBALCXzjZwbbCiLi3/poEaH3f+zvAhP5jumr8+8AdwD66gj1cvfK9SIBZfYuAPIBpvFP/+YCBe6x/uII7vNS/KMRTQck8dvxawGcDbP7GAx1IVnzLvBlFSv/Zub4CKQVVfvO808XcgPf4zMNlAuo/M7sPvkK+WzlTwZkD7AD6Pr8DkjxbeTlAM/5IQGb/tMRSvz+8qYNzANd/AT3NgTmAwb9jwHyDi4CofKnDp0VEQEUAb4C+/de9lf89Rs6C7z06wcf+F3xlwCyEWf8GvXjCyf4QPJLCOcGhfei9Wj93fgx/EoW8gb49ef+K/1Y8/D9ZhaM/yAHXwyv+Ar71QHoGc0C8/ZhBYQI0gEw8fgK4w08B70TAwvx9kb5mwbS8+4C6wjjBPIMh+vD/SkTLvg89lAWpgsw6SQCxQZw+rT4zAa2DwXzkPiTG7sNOuOjBxUWc+Cy9bsd5wdo+WwOqg/4+S/4PAaZ/Or+ShLYCeb6EgEkCC/7j/3UBxELu/L557UOf/o99ygjegIWBHIUOur68eICfAQz/Pf3R/6gAOMLlfht91z3MAsDIYX+uvWoAYYOUvcK/ZoV7PglAoMJi/B381UQrhbdCvUG0QQ8Az3wAfOiAlj6yQKNBCEHJgtn/l0IPwfp/G3rUu3q9cPz0RPRBUX9B/dd80MJ6e/mDW4UGPXA893wDwIy/XYXjhJE8PL5HfKa/oj4Of21GG8FOALhAyf9vAG2BKf6QvO0A7cEYATFDr/4sOW6/BwKyv6aCH4N0/v28Ezzgvmx+l8NBxfd+vfmPQSRFGXyf/ltDtv7VvB2BssOK/YrA8QKl/Um9MwGIw95+Tn5pQ8ODqX9ZwBu+4j8WgY49+n/AwJw/G3+pPyH/2f3agjkCnLy6OE6/8QTOu9HDYMVifWh7vr3g/fe11gHuhjb8bzzfho2DE/kUxSeASbndfNeBGT82+FZGmkY3f5UA7gOjgCx4soQAwvJ3CX4lRmh+wUCLSh0BhH1JAP5+uzwcPaBERoVGwMt/QX/W/cw8oIejgvO5qcAo/x982n19xhmEnkGPwCm6UL9kew5BV0FUfLFB6sDZgSX98UH4PmB9PgB9+qFBXkP5wNn97P/qw5L9/4CDgI9+mn5UfkTB932Tw0eDgf7ewPp/cMAXvQ/BSgEEPJzAr0H1f827lwJAwxr6qACoQt5+4X/Iws3C3fv4vp5B/3wcvkgAU0Fu/6oA0EFXQICFgsDE/fG/WX7jfnpB0cLy/4V/SX1CP+C/+MHvRkv/N7lOvSP/IIF7Qr1AMwD4wevArT1w/bVCHkGffLq97H4neqNCHoQ2Pqp/7wR9Qd79P4GZwM78FD2Tg5ID+H5DgvjBa3rJfOsAqkCGeyO+14HEPPvBnEVrQyv/SP21/hp7j7xqQPIB735Y/Om+bP+EPud/mMId/yI75YEAA4H/dIG5QkBA5z+efmh/vr3gva5+v//FQpvEv8N+vc19fX4PvGd/aIVwBPz+f0Ei/U337AUYAZZ8zr+G/Lv+8T5kgZaA58BxAS5BmT5jeyIGTMBi/CCEeT7BvIZD74LIPK9/O0DuwKd/4oH6RN8/9//pxUJ+cLrChH5B3vzEvjy/6oHeQ+YCQrxb/sGBGD5Ovqp/n4Hi/3y/e7/ye0uA1QQSPnQ60P8nwQf52P+cxOF/HwGzQ3e9BnvkwFm93T8gwfMABEASQKpDfP6lPS4B1UCMPPg/AYLlv4cAzwM/QeT9Mz/Vxm79LzyMwKQ+e4A8A1/CA/1Nwy3AubwoAYABzP7GvksDVT5wvmSF1sKFvoz70H8EvdK9/MWiA2h+ob7NwlrDh76DgV6CX31ePl3/OcBIwVdDV8FtQZPApLwNAT79FP26f8IBFACGwWzFYbzH/Ij8aP5o/ik8ocHJv4BB//zaPfD/n396g9F/evy7+pW++sILA3PBzUEWRdA8bnwUgw9+9b/eAOvDtwFbfLyEWgPYPbh/7UK3AEBAhINRvxa9Ib9Sga1+zn5tQ4X/fLtff4iDxEFX/utAoTxZfR3A94CGAqK/M3uhQawDZX/oQzjCNnyGfTQ8+f/MReNEjEJNP/d71/1gQAgAfr/lAv5CGH2c/fN/n0CB/z7AZ0D2/tECRv+T+uU9AsEQAJD+1YGqgvt+k3vTfglCvQOHgtFC/Pw6vBBAwsKMhOtBVsMuP2d8HH6af99DCcDBwE7/Rr7OP8TD5cEVPG7C8sGh/qJ9a78WPfF7MsCTwD4AMD8cfwn95LvlQhOCpAEJP8NAzn/4fc7Cd/2m/SCDQQJd/wW/u4D/QZYDd39jPyY//wC+Qnk/g4K3QRx/Tf9JAFHAaLzRgpFDzn5P/qeCLvtguP+BYEIQwS//Sn7o/gq9W/6pwNgC4sCOAWPA1H8cPpd+kQHKf899S4IBQZP/y0CJAWdCKf17AUqGaIKswbhAqX17O2kCmoWzgNBCCUWogCB5sL2kfpi+e4Ilgqr9l/0NgmbA+L/hgUWA3f3X/XgAXn0V+3+BVgOTfWx8qkB9fVS7oD+9wqgAEL8RgaEEDUJ9/L+9T0LCwcf7svwhANdBvz7wgRWDEf+pvou+0oAF+dp+3EdTP12BmH/uvj6ABf6wv3289r0zeb1+mX/1/OlETECjwJZ+Znt5wQqDJ4MJgctDAvyf+g7Ap4FDP4CAFYNPfiVAH4TugiaBmALMBMX/I7zVf9XCkYJnAaP/iLvBgFkCDQQSv3M8z8Ar+0r+uoIcAM9B2AKFOdl6iEFG/jiBcwCfPt/+/L0JP2J+134ZQhUBZz2TAKiAbgO3Aoy+Rn81PluEf4Gd/EYAM4BsPoEBo8MHvDv9ScPxwJt9rAG/hjm/o7wqPdV5+Xz4Bb1E2jyYPKV/IvuzPsTEfMBje66A94D4O53AZMNmgTh/Q0EaPqI7738IQNKAPYBdhTuCPT6PQ9BAO/oXgJGE4PzPvBpCcIKmggWCMUKbvvh6mb/fgUY9hsL0REc+W74seqP+Y4PhAG5CZ/+SANmD1EBrv2TAAoBGfV//2/1OPqhDLUE/xL594D+EBY7A8ACyvka/9b1kPRSDIcMGAHX+3MH4u5I6wgLawP09xEA3hP+BA32uAML9w3vJ/5mAsL9zQIIAd37PvUv99kMJwN8+zEKN/c+9UEQ4wxLB3IFSvjQ7NAAkA6w9LMLOxOg84T1+/+SEnUNrAZWAFf31vxO/WMN9vxt9wgU0gqsAnz2A/W9An75EvbM+ZMMvgW4/cMS2u7e7+0cBA379xr5nQaTAOXvmPNy+McDuA6yCG/1UvUvAdoNZw25+DUDAgpyCjL+f+gBCf0I/+E87zgO2gakAvwJwPWE7g4EIgxe+oz9zQ0p/q/oq/lJB5X8OwSB/Wz2lvJm/TEP5+vH9ZoXtfUe9sARKv2S/awVUggX8Hf8uwYC/uT1OPkKDM7z8vQdC7MLywlR/tcN5PM/70wFFwAZC3IAtfbC/AcOcgK/AN8GAunh83T3iPgEB77+zxNpERP5xQq+/qvqVvszAMP6UgmGCPz6KQNd9ZMA9v9z9X4QB/ZJ9GIUyQc78BwA+Aqn8lT/5wlB9RjsHQN0DIn4EvxFBq0C0vNh/E8HgfG8+yEN+fyr8Y4JSxrz9/H5YQEj84z8g/4HESwH5gLNDlv6+Owy7XwSsg8K/zoQWwvQ8YHlBxABBtDwqwrhB27+M+q1/hoQKvAS+UkV+frN4lYMigxG6wD3eguq/i3zmgfMAPn0OPNmBQQPQ/Q//lMSxAXG8dwB2QjH/iwJO/yK9QYMaAnP9yUG0gVk+j8CuAfUAYwBmAit+RP2hfq4C74SzPow7nDzwgH+AWQJvAHt+5UGI/EH5asJdxOK/YwSCf8Z8af+wfTyAMkD9hCMBxX9PQB3/kEGjf2kE0wD5+yl/Rz/dwzl/7MI+hIn/pkA+/90/Hryg/vKAhr5rwZ/Ca8CR/4n80H6PwZg8ubvWglGAT34rgvhBKMCDQrk/zkDz+iW9XEOoPha+zMHuBx1CAIEZA1ZAOr+hAOWHxn/w/X7CgYMjAl4/RwHq/U9CLkHb/R6AfT9Hg0UC+wHkfkq+h3/0vLUAPj5qAUP/E7qJAaCA+Xore8XCJ/w6v7EF4P5uvUrA08PDPJj4+IETg2O9obvfwt3/kX3/QyGELQHU/qHBwgCZfWA/c8C1QmzBoIJOQ58/Pb10/4zAMz+HfigANwQlgyd9bzz5ga4/oMEFAWr86wDDQVK86DvRQDOEgwCKPFnBvsId+96/QIDxvgh/db+nxaRBujwTQFu+/Py3gE5Eo0GjQOA+fry7+1p7vEQ7gtyDp7/9+04B8EGOQSQ9EDzN/0L/jz5d/EvCmH6ROwkD6ELH/x9+fYCyv7n6Fv7OQlNAPP+cghsA+D2pQnPC3jyjwLVGPH57f3/EW4FBvRJAGwW+/Ux/qQS0g+7CaD+1wlw92z1ShRJEKjupADWDIzvOfGPAdAHGf95DjMHb/PD+bX9gfV6+N8LhfL683QH9Ae6Cef9Gv/q/gr1g/73CdvybgFiG1UC1ftKBi4Bggd8DpkCFAAEA4ECDf0fBmoCpffQ/sAGnwlQ9dIAawXrAbwGZwLs/wz0Vgy/+hjoDfGS8coMVAzbEOoJnfx2+oj7kvda6S0YxRqP+RIByvdK904GlxbUBhwBfwQ69uP1XfGrCdESUxCdByoB/f3i5aUCX/ys9x0H8fuT+yPzEwC88kT5kwP4+/UMZPs+9wgEBgIc7o3uiwdqAwQA9Piq8KX8tftRDOATLfiBBbwFwvJa8E4DdAsC9/cRkQf891IKIALr9x/gSe1pAaD/qvvZ+ggBYP2SC5v/HvCm7YXsa/568tP2iQEy/Iz5XvJkAHT/ff/n+qDlj+aa+BkKyv/TB1URVf1Q8RTzgwZcAf70IP+A/onxnfuoCjj+VQXXCLT2TPnsB4wIZ/d891YATvNO+vwM8PWD9Y0Jvvvc9DX0RP1TARPxF/oq+47urA1+D2Tw5/nE//3yPe85/dr31P0pDYT/q/XW6RQBggBYATcQRfpdCjYIfPZ25iP1ug6h/5z9aQToClPrDfiCERD/pg0hEfT8auYZ/Sz/fOdQ9YMGGBQz/5oDDAvn9+P3Ffe8AIcBlQhcCHj3W/O18rEDfwW2C7MWgAhG/S/wHfQa+w4Fuw21CoMToAtUBIkAKPn09m4Cgge/8nUGhgh7+hEOjAKNAXT/WP9wDKr4ef12Bvf48/e4CegHp/R1Awv/FPbDBWYJ1wSl/gcNMhBr/PX7SQKW/Jr0BQc0EzwDcRDeEeD58PS2BlUEG+8rFBASx/WlAx0PeANP6yoPLRfh9p3sfA4VCcXXPhW8HYrtAvVPC1gCIuzvCx4JD/63/XwLJwXR3KUOaRfu74EH+xbHBRb09A0XCbDu2wVbDGcLNvJj/d8cNf6BCaMEff+zDCX/DQvLA1r7+fy/AtoJRATBBmsKOATh70/11Qo4D3MQlAi8+ZD3Fv0kBekJzwtbF+MI+fiU/YXyD/35DJ0D3/1PAX4K1AnXDmgN8gEwB5QFg/399Iv+AAOC+0gCWgNlCOwHgwTm96j2pgUbAjf7MfF+BcoM4/HLAMEVsgIn9+n9H/CD9mEMYwcS+l37nw1UAUD0RArZ/1r0UQ8HCNn3T/x/AvAJNu0//WQb4f00BbEDve8A7xsGoxX48ogCwBHz/EX/AALI+3XsqA/WHD71Y/6gBv792vpZ8+377wWTBZgHYALz9En9ZhAJCCwE6wmO/a//ngHD89j1ogxxF+UBVgTwDC7tG/AGCgH/DP6JAzEJtRBW9Y7w6QQaBFz4Pv/RB7bqtfj9AxTzlP0y9jkH/A979jTqL/NJ+wP/jAaq9/UNJxCO74fqsu96CdsH/gflAFz3MgRm/HoIaP6F+LUVCQ3+90T6cQOY/QgUEg9H8bIUBQ7I7yvu5QAeBQziyQmIGOH1WwpNG1b5WdrT/qsMJPHM6sUI+wSE2n0CpBkp+p3/9vWZ5HL2eg3ABT/w1v+dA3P2IfUGAAEXkfs084r1SuhHCncUov6G9NsDgwjY+2z7wfXb9Ev+zQKOA2UGLA91Bc/gzOjY8sX39RTVES4IhOxb5xYAfAbyDRsMdwAZ6OLltfiG/3MFzgpQFIgJ0vWY+d0Gqwya9Kj1VwRx/GwG3hJoFX3xiuZV/O4I7gBh7lUPHwES+zAPmfqV9OX5Rwqp+eTy//xb/Ob6G/Qk+ErvMQajHfr3D+TQ964BEQEDAsgLNACx+q4H2v/U+f32PgokA1f8dQueAxr3f/M3ECL7AvQLD1X6r/+HGFQJ/er4/HEJRPg97lj0AARKAqz1DfrW+fvspxDgF2D4B/X1AdH7vuho/3P/8vpTCQMHjgL8+ML4BQsEEHn6rgNKB5LyMfdhB1wMMwQAAIMBNQg9+6P5aRDiBYn04AT8AQvqJP2kCNP1uObi+YoI0u4AAhoZ+wah7Evu4AOg+uD6TAQDAaznF/NPFwMDIwrkEHf7WeyE8AMMsgJu/rUM9RFPAyIHLhaf+3v9Zv7S8k/+/vWG+kwMBvWT9g0KgfwdBtAHZACG/+3xnvCXC0MIL/AuBIL6eO/3+6MA9vl9+z0Pif9l/RcELgbCA2oG8AqO+gcDXAmJDkkDz/P8+HP+fAn2ChACN/8aChoDIQHmBzoG0/7FB0wS3PFb+ZMLR/Jk57UC8A5g+B4ALwJF+hb6fPcOCdf62/1vEa/il+mmD9wP7AOV+T4Kl/zL+UAAC/7c9gwAMBEE/9cOKAHEDtULBeZQCR0DGvwTBlEUPgDq77cI1wHi/fLu8RBoCWLf3wkJEU70mfG/FdwFgeKaBEEAlel7/PwRbgYmAdUOQfz38ujzV/gB/rf6tQi8/tn3gApgBgkB/hIwAQzqyw7ZCgTuQf7yDmMBTvUJCgYRUv/g/roGb+2C7swPOwyFAwsKFAa49+v7MwSDARL4S/54/ZbzuBBmBHrqIAWZCML6vf8Z+iUBBQxk/5EGvvZi9/0aCAQz7OP/Pv1L75gSGROm+igJ3AS8/pby2f9LFy72pvdwDRL04+7/C0wYGQTv8Lf8svtB9cQQNhOn8Mjs7gDZA74CAwSHDDf+8ujdAED+G/h5EDYFkfSc+4QLnA0sASIGUAa4+nv2wPeBAyYHygiED5gF7PEmBT4XOe/l+XcPbv+Y/Rn6agcz/pv8cgpCBp/0s/gnD1borfFfDF79/QK1A/0C4e3n8pf+Jf7OCJoH4gpx8k7vJP4DAB8NRwBh+Zr7KvywBAUH1wl3AycD5wId+LMAKAN4+YMC4gH5+2f9cvqpA2j90PLGC40YKPt19LcBku1X71wMAg+0/tzzzPd0ASb+nAJPCbj+o/n08x4E+gT5/iwQhgtD/Xj5nhZ9/cPtSQlK8Af5PwQ2DG4LAPhhD3IJGOyn9pQOkwcX8/QGvw2F6pv+7AxN9Hv0IPVH9BHwKgXyC0MA4vpD/9ANovF0+DIChPQ4/O35wQTd/iH8Ywa1A8z8D/WKCGoSgf8E9uQBmAlUCmMXZgcq6975Swbz/l/39fboDwwOOvfD/v/9wgBZCz/zJeU0A0EOZfci+V4AR+269N8bHwdK2Rf7GBPr+JXqbfS9DzP94/2yExL0T/YtECgSA+/U7N0NbgcLDAIDy/pR9Zj+EBbYB/b8P/MLC08GzOvmDW4U3vM773YR6wNQ61sM9gnK48HoqwxHCVr41AE7Bgz3a+fGB1YOB+/bDycONePk9OINwPjS/K4R7/CF9lsRFRCAAIT8JAgh7T3zLROWDeLx2v5aF6b1vfDrFcwPje6wByIH0ttL9zIS9/7R90ULAxGQ84bzVgtOAwAAQARl/8v2dgyrB6XocPM+90MWZwQb+V4T5f1gB5X8e//iCfUG/wD0+JD1weGfCQ0RRfcy+9oFGgjj7GH5pxJuAiPts/7ZA5bwIAICC9v9ff7gAR/9hfOr9x8I6A7d+afttgK+CFMOqwjHD74GnOevBAgAaPpi/zoJ8Q/a800BOASrEf4B1/pRCornlP4aC9oF+gn0BcD+2PVWA9PwIv2MBrH66QkZBBsFIvXfBiEYhfEc9FX9bf6B/UcPDBZM87n5wQaeAKr6EgazF6cHTfwRAxoBYf/WDYQLgPCy6CsBSggI/c4UOxSK+Of4HADYBBrx4u+QCioJxPjwADwXv/Li7GwPbQP4+JgAqAw18ev6xQ1x+JMFUhEeF0n6GfIMApQBbAqvB6sLL/dkAaMT4fNUApQQh/5GA48BY//2At8I9BA+/SH9Wwn5BwsDSgAU/or4TAU+AXgFcgggAtgQmQfY/T8FxgCc9i38jwWnD2IKzf/zDHgNX/sDADQOtv8o+8gBAABv+NkMKh3xBscBvPqnAMn0qP3FGCb/oAJJBaH8CPmVAdL9T/3kFfX6gfNT8rTuFQaeBAkPZApQ+Gj9mfJX7Uv/KAmo/Q33iv1/+xv/RPX+9yIEofNZ+ir8HvxcBDT42vAP+i8B1AKIBi3qH9799jAEq/vf9IQGnPyr8U79Cf03+d3/tAsR7yLqjwzGAin5AfSJ9T37qPsoD+f3JezD/vsENgI9/PQLrvVu6/AC+v2w8dwB9w275kPivfjw+vL+KgFdAIj61u6t82X7OOziBRwOlung50D7Hv5c8PX6ywRwBEr6suzq7Yf1/P/d+cABKg5k/yT2+wh8ArDtdgMNEKD4oOnKA/kBMOttB7sZD//e7D370PxD8lr9TBc+DgfvdfrI/0f6VQ5wDjX6Yehk5fH2PP00D8oPqvxzDQ/6r+cZBC4WRgXm+wkMVfcP/sAKmQDaAa39vAIf+EoK/wZc9aIH5AB+B1kAqAJPFYsBSvVwAOT7Efc2EEoFHPL2/qIMt/xL5pQOmRKK6i79tAtPA/0OJAp09gb5lAGTC+YIYvVqBd4MA/lIAb3/mPmF/0wNmBT1B7j/nP13CswIcQZ3Awb8hwdb/RP1zvMp/cwYMRKc/137svSfATcHP/06ADEB7AQfBR8Divyi/EECoARFAHr0xv1BBAoI+gX//6sDkQeEBBMEtwNY+TABmQCt/b/7rwFwCscASAIlBKf9A/vRCn0GiP4X9ZP4Pw0T/qQEABHmAn3yhfuQABT+sAkuEYcBG+qTAOAGuQlfAx7/qQnz+KkBygN9A94AtAl7CRX4Jwaw/Yb50v//9jD7FwFGBdETIQll+vsDFv0r9/oMHwys9QT2SfUYAnP+Z/e6C9cMEQI4/6MFcfis/zALj/zM9Bz/CAxCCNQJ4/oS8fH5zgC7AYwKkQdX+IL+7fTv/5QP6AKNAa4BXPlF+Cj9VQS1A+H9n/v28t4ARwH5AoYIdPeU9W4FiQ7f+80L5QMj8gf8FfT1/ff6KwYHC9H3/fIEB88GCPERBP35EfE5Ar8EqAAq9z0K+gju8xb62QiZE+L3Y+nu70Hq0f0uCEAISAWTB+sANv26C338RADBBED64vTE+AAAcfBL8bX7bQCYBBcP5Q0JANr71Pcp/TMFHAu6/kPmx/ZLC9H3Af3MBaL3IAMdBYL2dv3uA6gBIQLk/GQCfgkuE5MLlfRN98QAKAWV6h7yNhOuBBv4ZQdWCD/wBw4nGmD8xAL+B+4Ev/kk9yoEMgHW8Rr/ZQ1n9V71WxCfBQABmhIVAJT4ywHaBhv+LfVEB30EmgFH/6z7kQMQCMz+Zvgw/VPn7P86EQACMxRoBeX/2wkp/2X/4Aip9lH3SgLt8SACyQHHDxcONfGkBBMJeglhAh4APQifBAr2ZgASHQ4EzPUYBPQMy/i67WIP+AtY9gcEHg25Agf/PQLfEcMFAfS6C7kHu/XnBE0LjAF/BQIF4wLG+5/3hwFWBY4I2gHYAKcF5gLcBGwM4wNmAMcLfQAl/Ib7e/6GC3//m/g4DxwK1fPG/wwC0ANYCTgEiwsjBgIECQWw+b7vavW4BO74x/cUAc4BmQFlBbcVBgN7/q4E3PSN8ivub/w9EwAOxvgQ/nD+p/wbCPv/Uv3b/20NBgkB+M71NBA8GPDuyfZICWL7CfknCSwIiQArC2ETZAX05mH0SgnJ9/rr1g6CGWD+Cf24+TD3UO/z//IG3PFt+ar+4AFo/db9sP5v9df3MPcI8AHtBv/UDBv/Q/UBAuIHe/NQ84z8v/gmAt/4mfAG9UD6vA1YCezxePBtBof7gvARA9v8aveqA3wGvvWk9cj2x/cq+m7yMAxkCcf1hPQt7zjyRfc5BzP/zPi+/5v6nf+X/K/9PPkW94wDbPme8XP5c/Rr8D/+twX/B/oBfv3WBlL3yuh5+gcC9QUZDqX5VvaN9jb12wWjA4QM2/4S9sD8e/h+AKr1lAbKC4X6k/qC9i39vwD2ANT1wfr8++LxjAVUBPv56PfP9jb2Pe5d9rEMMg5B/YUAEPgz7PcASAmX+l71Mf3b+tj6rwLJB/z8A/9LEt4DBP+gBnv8+O4J+Jr8DAa8HSP5e/NLAgn+tQca+UL+qf1h86397whR+yz2OQn1AbP+ivh2/8cHgffd8J7nce9l/kINMxTIB6wCIv+FAO8BqgWqBzgCfQCL+Bzv3vjGDVkOmAbJCQ4TyAUX/NIKLwxAAYv0OxQvEu/rpvwPA9P5GvxVE+8FFvarClIJKf+Y9ekBPf9mAYQEwgDPBl7/mAPC+in/jAAbA9sBnvaQB2oBdwV3C+wEjQXNCEQKZv34BfAKmf8R+wz/z/8X+0cHWQNSAAUObgmYBtH8DPpeBmcD0PlR/UX+3/OVBxwOUQR+/Iv+qRW1+6TvrQS7/sH9cwzgBwH/Bw1hDIf+tfJD+yMIHQRhAv8CaAH4/UYNlgVq8awFcgYb+kj/iPuZAyUGd/W9+cIF0AfZA1vuX+z5CicLQQb8DvMEFv6V/BHxmOoMAlcXxASU9eQA2//uDfEa9QdyAej75wOyAITy5wTTDQoHqANvCVsDqPyqDo4FrfHd+iYNdxMTArkHQQGN9P7/4fLiAWIKAAfKBRv1n/zbBswDUv/vBSL7e/l5/Pj/JgxVDoANMfw6/nnzFfItAg0Dyv4G/4wN7QIrBSYK5Aep9pnu3Qa5AqL60ftMCCH3oO/FEEAHtvU0AEECYuiF62EMAQ2WBWUIBwTz8MrqswFRAy/7EwAf/mz3SffGC34JxfOS/nkFhfeP/eP9Y/iPCA8R/Qfr8iH5wwSbAUX+MO9N8kcKpxEOAowFGAL395/8APb+9bUHYgml/14BAPWvBbkM1AHmAFjtXe7B7pwExwqw954FBgyoBdUClPL37PoNzP1f7o4IKvxq9R0JLgRH8F0AAAij+m33ePP/8C77FQGfBCMK8vU0AzIHn+ie8YgDMwIF/e0ClfLB7KPx3PW1C5gCJwmqD7j1/+Y19YIHoP1N/i8N5Acu8dABSw+V95r82wjtBmv6qvUU/ngRwhGL/jf6Q/saDD7/ePhSBmb+uQBbB/UI9/kaALEMAAja+mXoev7I/6j0Ig9PCBr7cQjqAmv5bPwTAZkCNQfXAIj3lwB0BmkMWP//+Xn+vPqaCyQBVfZcAgwCs/7v/KEJFBMfAov+aAjs9bDqLgCFCn/5I/2IBEj54fuoAu0BVfjXBPgTUQh08SbugAZXAM/7+gTQBekFEv5lAd77LP0uEogQf/8f8iT6jQpF/XgBZAgk+MgHOBCCDTAE9vv6/uH1kQEa/2P7Ifs0A+cOiu3W+YAQvv1h/GEHFfwp8MYA1wDv/FD9ywHXBQP+ev9G/Z/5OPvIA6r/+fq+BX0ELQLoAqz+gv/wBX8Mewdo/wD9MPEG+N369f6KEj8InQIdA4UDjQLgBZoFUP0L/UL1SQK+/Xj2QQpABpH/eQQ3/8j9kwcpBL39qPPa90UAmvrcAyANeQ7b/zj17vyr/cD8eQi5Cj36I/vk/kH3Lvt1+scHQBQd73fzmw64/EL6dv0A+7wKOBDM/F73qu4v9L8F7/3VBoUGxv6FAFT1qPTuBw0IxQV/A+/2/wt1AefxGQFn+toEmhF9/qP28Qe19xDtiQOB+4YFhx1jCG34afPu/nsOuwGABSz2mOmT9VPxYPu3BvYK8RQRDcf8qAJ59oL1cAQ79Gz0twQNCEP8xgVQBhb08vvOBbD8ivTaAcf4MvQwBl8Y4hXtAFMBu/pG9lPyf/fcAaIAugDs/ZT6HvrMEGkGx/iNBCf5DPpUAkP82PQ2/vL58/d5/cn5fwQO+2D0TforAaIGHwSIAvz6mPuM/7X/u/N9ARASdvof9c/3nQJ8DGQGbgQNAUcBLAljBqLyjwM0CCv0WQIsAYgC8wc6+WD4bQJxAOECVAP28EQAWhCVAeD7GATMAhzp0+yIAIwFrQPd9jcCEgp4/pcDUwvA/aX5hww3/rXu2gPTC7j94PXXALYEaP+zA1MBCf2QABIGJQnJ/D/7AgvHBd/zrPjb/5n3zAllB13yefmU+KYBkAPV/UQApgBhAP78WwWfBnkEhwLR+KDwovYeBMcG8wNK/s/7JgC7BJ4FMQ80B/z4+PcK80D8XgkYDIH9Fvnc+mz7oQjCCM75bPmUDiL9suU0+aUR6Qqu+nsCAALdBe8DYPlv+R/5HQ3eC5vsa/bqEBsKAQA/Az/4gf48GcMC4vJT+gD88wix+1D0/AQuBib/XwYIAWL+UAxeC7j+IvGS+j0BegbTAHv7GwlqBzEGQfke+RgDAgTdAXID5wiz+Lj1NgDTAV0FbhCeBnHwtu+o+7MDPwCoA68FcPu4+Cv2i/RyDA0MLfwgBV/+Ve4f+wsK2Pr4+U39kAkCAb7vMg5kBcbqQ/niDoX9TQA7D94Fdf2F9XYOu/qu+9UQJ/7++9L6Sgh2/cMA/gK3BBIK1fbVCpAFt/2GBzEETAKqBLQFQ/Yy9T76QQjBCYL/xwuYDOT7p/isDR8OKfGG8oP/YvYUBgMSCgCw+AQJhQt47ArwVvpwBOYHc/Y4COEKHv+J+q383Pl5+vH/C/rSCVD7S/yJCE71uP3SCH4B3PHc+RkBsfo69LUFkhkB/7H+1QJk7ebtJ/2i/c39QgrfCzr6g+1K/wkEYwLmBvMA4/1h/zkBZf4TAIICmwud/Rfv6wBZ/PX5CAk/C4YMVQR9+kQDkfrF/HQMGgnmBbgACgRY9CXzLQumCOwACvGNAS8SpPt5A4sO3AqEBWX+XwENA13/B/yq/THus+9FCs0KP/zF9XIGvQEf8RsI4RXlBagBtgMX7RXlWgEICyz3LPmmDJ8JmewPAI4ZdPKT/GYYYQKq7AEMCRoh86nxHgHODgf9jQCDEEz6g+/6+K4RiQUzB3QGLPn39jT//xd+A3n7+/Ko9mj5VOrzBsEOvAGt97cBhwGS9vEFLQjO9bTu6QLVADX8RwtNAIr4AwaLAi0Aff5/9n4CTvoj/dsQhQXGALIAEvls+6UKOQiz/dMCT/1I+DT5sP07+Mr3iwyOAwn9vQRKCE8NPQOu+ZD03PeQ9y7/9QQs/9QPcAhu/IoEev4/BKgFqP4TAW8AsAZZANT8SwWeAyACdfSo+gcK8P6l7qgDzxPZ8B355QQK/o0FGwMnA3Hu3/QrECMIKvHL+AUIXPFZ9R3+T/soDp8Kwv3K+Ez2IAM/BFn6xgAjAoP5VvqMADb+X/niBPsIifdn+nEHUQHl/eT30/nzA8L6+gI5D2H/ivsHA+r+PPvD/x36Gvq8AnD7FwM/B3AAnwaCCNAJRgBF/SMEc/cH+BkFkwjRAz79sAwv/B/iQf95CF357vk3CNwAefceCeQDPvZ49WQLkAP366QBZwKl+Lj6YAOpA4LwZP6iB1X5rAjDDXEBVQQRDK8Ehva3AN8BA/nN8on51gCs98gRRRe/92T2OAVy/uz5PwRd/NT5rQR0CAn/ruk98P4KZfMR76QMm/8i+rkG4QjA+JMBChA4/DfykPjV/oL5iQEMDGgHZPw7Bc8OhPvt+Bf7y+9r+TwQ5AZgAZoIow2qBb73awJD/Nr9AAFk8artmQR7CpD83QSd+H78Gg4TAiT1/vpZ/5QDhgJ+/JgNtga++b36wvtQ7qL16w+/AvMMzRKW/kX8LwPf+0D13gPrBIQBVAUQAp37RP6iAkEJRAGP9Cz75vzt/G8E7wvbCwgPvAhd+oz1SP9q/kj1Kfns8vf+jgssCdkB6gDp+0vuLPyW73H2FRKp/rX2f/dq/y4BUvGy/2oCF/FQ8a7++/ul99sUowzP9sHymAS/CFDr/QrZB5nz+QsrC1X9+QOYDxH7O/sa/kH+4f6v+E0RixBP+VQEMwty9lf9Wwa0/ZsB4ApbAvb3+PuQ98H/tv38+ncFYQlqB3b7kf3C/jsB+wegAwX1eesS/ZQHbQFUBdYAovvNANUFPAhg+ID6uwbN/lP3eAU1Dsf+nAqRAVPvVwNMBkX6dPvjAq4BIP8u+pkE2gN38rMC7g6ZAvP4wgTmAszsffVbBaUASv6iCK4HOPj77Qz6ZAl2+i/8NQUw8hf2dgs0DagDyQBw+rf5FwXOApX9ev3IAX7/1PEaAI4NPAUYDj0F8fvLBKoFJA0HC9sE1/pk+WT78f31AyL8KATtA5QJFRBkBKL9dv/jA5f1gPO8+DUC/QDSAw0QX/yfAl0GdPC27oD7XAPKAx4CM/jr+DYKPxLU+gj68RDA/s7xsftcAiUF7gMtBOP0avDJA9MJLvyk/SQc7wkJ8hYEDfeU8T8HCgwU8qH0ng9HAfT/LAhSAE/9B/wB/Dv3h/Pj//cOqQaiAr4HtAGm/zcAmvc5+BwFzf8o+wACowROA0IFRv+S8IX/JAtzBYoElgMsAqr/n/vD9PL/XgY/EtcEVOLp/XsBifbbB/ICxf2mAM7/rPz3/eoExQ5/BcXxF+tJ7xD/DwvIAVX9PQptA971AfP4/3cHVACyCJsBjOx2AUUU2fdqAIMMywDKAWr1Pf7PAF0AiwSd/a8CVgWiCX/4qAF5EeD0ngHaDicIKP/S7r78LfcN85cB/Qj7AA/2XBNDAKnp8ADfBWkA1fckFCYOSPRU/UL8GvpV7MMGoREC7uj3MwN9AEkEiQzTCnv8iP4G/qf5Bfqz/cMDSP6i+B744/yKA5b8EPBH+Vb/IvqDD+wKovSK/WoLSwPT7EEBkQcs9ab5VP1UBO37vwhtEcX9i/zHBNgC4vM+AMoKtwpxChMKUAX7+VwDffmJ+okFTPli8pT7kAPGB7wKSQcuCBn2AwBzAeXx3P5XBHYHgvRd/aILlv+N+sn/xQEC+kMG5wQo+mj4yAfJB/kDHworCcUJEPyPBwX9SvvwBuD8SgDr61DwOAV6CjsIUgOYAaL3EfTu+8IBtvl+AncN8vNz6AoBxgGQ7y3qjwDxBzv6RwzIDGMD4fpn/xcA+fPx/RMB+QTd8n728Ay4CnsGqgagCUP3aPszAgH7F/m0AR4VdQlgA0UIK/5k99D9eADh94IAMRAzBQn6bgZxCtn/PgHwCcL6svL3+o8BvQd6APoC3AUYBgsMIAiB+DT1wfr4+cAIXwL0/aH9n/lnAEnzJfpSAM4FBgMmAt4A+u5LBZgA6P9PA0b+CQdu8Y/2v/iw9Tn8KwWyDysGJwFZ/xECe/zFAcwCXv7ECBEHcABl9JwDbg1L/mn+SvZL/qwELvn4/tcCPAS6BsESSQHI8xsK8Pda8HntbPlpC4X86wZYA7/3uvtLCGj++vuiBxT9qv/p+84IKwfc/UAEVfgT9lwBsQOP+1QLxghNAC4Bk/4d/A3x/AC5ADP9DwqvEA8BtfcUEED8au34BBj9SOsZ+X0JTQAD/qYTAxOj+HH8xgXV95vujgNlDqT27QW2FVP8dvQBAoAEe/IX/DYOfAbg/Lz5OAoBBlX7yAmiC8r+uPzoA+H7E/nBALcECP2X+/z4H/EEBpgI+AKSBt0ERfox9qwBcvPD+KUAX//JALnxCfof+139Owa3Akn8TvZuBPb+QgJuDvD8RABk+0D4kv26+iMQKg7O/fH1tPr1BQv/lQcNB1n/lfvXAdIXyQNE+pEJxPxz8+X/Yw2I/MHyTgSj/dL2SQYMC8gCafw+/I/2r/lACtEFKPit+WYDN/+a+boGFQcm9mb2Kf0A9pkKfhuc/p/x2f1EB9IJowh9CVn93Ow5+gUI1f6UAdgRCwg68Gb4XwLtA9EDxwE6An/3v/zHAsb9dvr3+6YKNQZd/KX9YvXI/ZoCBAH9A/34cPzV8638VwhK/VcJMgrQCn72ZO6EAtQD1f1I+agDg/ko/nQQLwS5+WQGzw4e9x/wtASBA132Ig4zFnr5VvUjAnD52/KmCVsIG+9K+F4UzQIY960JYwGP8XzyTw1DBj/y3giYACztS/5rCAP3C/HhBcH9mfvJCvAD8QjR+tX8rwC4+kT+LPbnDcMABP0nDVMLUAWZ7u8GNAK56mcGKB3H/EbuOhVFAl/tRwu7EEb0S/J7EREDNeNzBH4Zbf3b9cUCh/oG7G8FNglN8H/0mwreAwD1swc1BvX2aPbvA3MClf3a/4b3sPuU+k7/VANwB2UC6faxA4QHGAI0A+UFSwE4/Hz4ywEcBGD5sAbcCab1fPTxCKAF3vjs/fMEpgX2AcwB4QHZ9azvJAa4Alz02ACuALn7RPy2/VP5g/4wC2YDEwDl/DH7JQcqAzn9Z/3tAE//A/+vBTL4YgYnDgr5av0mAOQG0QonAXP63QEu/Sz39hIiDhwDEQF69R/zN/CpBz0NEgcNBVD+KgIW96oA1wL9983+XQTQ+8f1hg7rAvf18gTDAn8AL/dO97v77f01AfQGNwrjAGoH7Qdl/sP8tQE5AM/tbfNTAksJBAoz/Rj9fPr2+IAGIwq0+uz4FgRJ+ZLwZAExCe744QNTCcL5/fRU/uYKifMR82UCn/7f9NoDFRknBHcISgtdBon5BvUAB5fuUvpnEswBWfV++IYL/A5jBhIEigjsAiX6/wNEADsC3gle/YHzrPGxCO0NpQFS+H/2FARe+5D9K/01BZQGh/US+ZP0KQEvDTcMJ/vP66sCjQ9w+Fzs1vumBREGmANLB97znfp2FnEPLAUh/2kM0vwS9BP8pPaXAEUBSA48BCDy5QYLFCwBGfHU+vH3tvjGA3kLKwhF+p4GwgSs8Pf35wTF/hXv+fZCBVf/x/mQDCASvfvUAiAJqvgb9DQAQwumABT2Hwb/C2j7T/2EAyQFgQTk/xj8oQRYCKkHGBXLAMb2NgJaAd8AuALFApX47f+GAbIFXgOm+hoDAfpB/TcGUwjbBsgBN/i88r0GYwj2BL8HyfG270YBlf4hBtoKRgP9AVn0gPIZBNAU3wqa/cz/lvNB8xgA1w1LCq35kvXm8WX6aQQpBysCAPWw/X4Gne64/J0blPhW7fEQfQon7eABPQuU6c7wphEPCwvmdfYlD/D8IfhuCdgSkwGd/0UBWPwF+Wr/SgUa8Yn5KQ1cBlv+QgBG//8AAf/Q+8MEuQbFBIL9ov3TAAkCUAW9/tP0TQJSBjfp1fyTDBX7GgwQDJD2IfvqAuf/e/43AHoKPQkN+nn5fv83/UX/zQOYBgoGhv15+voEPwZl/OMGEwgo/qDyc/+4CujsTP5qB3TyN/T8BaMH4e0YAZAN//iH7dj7jQrH9fT9ggjh71H2wQee/v/y0PaNBFz4zv3DCjD5sP5RARz+KgT6CMAIgfgD+D8HcgEF8Gz9zgm5+psE0/+V+McHbP49AC3+rQ9QEJHy+/fv9bb8p//6BP8BovvTA2sADgE48QX9GA5D94vyKQdTA2sFawq6BDcJTfgL/kX9Ufef9gIBFA/N6rzzdA1DAY78cw+zD4HyjfWUAIX1M/AAB4sSD/Ik54sGJ/8d8Ez/EQf8/JL96Afj9vbyUfp3Cdb9nPXdC9sBbQHt/5oCbf6n/dcAOvUuAWfyXPEpCagFZAFFCnMTcQSf92UC4AO3/Lf1wPxY+bjrZQwXDbz1gAdXD/n2CuyRAvgGrvun+xUHp/7y8WX+Cw3U/BLrxf+C/frzAv3aC/f+yPPoCw0EbfwBAegDkQH/+sz4Kv91Bpn4mwIyDUMAtP5UAS38rPkvAxgWlA/AAeoJbP9E+T/2lvqOC+oDbQG+C/kB+vORBKoJDQWkAwH6KQO69WXz5g3XAdD9lwYyCLIIrvCU60oFtwaR9dMCIAGL92YSDxC//YPyEf98Cj33AvlGAYwLlQev/RYBo/2C/IoFfAYR8jL9DAnmAj0Hp/gc/qkD7PZ8A9z/Ue8cAvMNGvpr9mwBpAC7ADP8CgGAC6nzNPe9Dq8FZwgrC4cDifee+ikEbvsH/CAKZBrDAkD0hA7pCj4CZgSy+2j+GQI2BI4NJ/vu+RMIMgO5+p/1xQdNCqUGO/bw8tIFYQEOC/EDjfxw9W/xEwl0Bjf+3wkqD5/3yu23BokLKQFLCfYD1/KJ9aMIrg8NAiUJaQvC9tTv4QrmBu71rBE7+03s8AR8DOMF0/R+//4EzvqC+QQQXQeS4/QDtw717Fn3ChQ5B4ns0vmO/2b8pAI4BCgIzP56AY0JKwQ0+Qv98AFk7YT7ywp+CaEE5vXvAAwCjQa9CHr+mwSfAS36QP0tAiIEtw4t/tPmvQANDCQBVf61/CcAxgD0BUcCQADHALf5XAPZ+VL6qg/gB4v7e/xc+zrwZwHyDMP9wfz+ASkI1wP9BgMItgJHBMD8/vnF9472TgiPDxH+8AZVCJz5ggUCBOUFPwxj+mfzpgB6A2f9nv0cAon+LPafBR4GDvJX/qMM6/rq9CMAGf5e+2T6TQC3/PzzJwVGAUXruABTDGX89/7G+lH39/TmALQOJwUeCHIL8wE8897/nwEi9XwDqAEi+hr4APsnAfYMrQs1ArQRVATe9O/8E+p37loBBwISC3z+a/4uAof/9wat+zH4ZPapBooAUfqwEuYDi/fc9E0HXAvM97sQAA+F6g3wWQuuDDUAzgfFC4v2YPhAB1kGeAT0CkYK+fxy+Jj21/fL8iz5EwT1BrEGkP+mCKz8GPTR/Hj51f1m/vT5qPbk954DOQ2pAjL3qf1jBVXyf+7zCdD/oPa9CloOI/rv9DsJtgV08oL9nQwW+B7xVAkwAt3rkwP/Dzb3yPGmAUARfP3U/fYOre/R577/2wcjAKIChAa377bojgNnD/kBlwEJ/X/wSPMRArcPDQe7AgwBsv+wAEX4B//6BLwErvtb8hwCoQG++JwOmxD7/twDThHhDR/yxAB2D/3tguwe/mwICQIAAmAXBQas7y4CAga++P4A7gd39dHx6gRqBv8JXgKmBGUEVuup+0EBavUr9lIEwgpu/OX7IQZqCjz1WgPcDH73C/46AXL77/cFBWz9ce9c+vEKxAqP+nUCSwWKAosBvwEX9T7zTBC2BAD6LPwB/8oBOfj//4j7Mf3h/YT3OgECA8QISgimCl8AIOxZAjkHzvIC/r4FIfwE/GAHMhI7BRn2gP7d/sz2VwaiD9AD8AO9CnH/wO0lAvQKrP4GAlD9Wf+o+yr/rAbZCc4AW/dzALr48QSrCEwB7wSy+2/x/v7nDwL5XfoXA3H8k/ZDAXgU0AIwAQUALflJ8sXx0Q3jDqr9mft7AAv5Wv62C7P9i/qdBYkFb/gX9wIHrP9a9Hb+bAkJ+Oz3Xw0r9fTzdQrxEVgA3ejr/eT9uOx4+tYVFAZQ+hEF8PJm9aL7IwcdBkX6DQcuBdn2SvsBD2UFyvxRA8D6+vIY+E4GnwnXAFX5VAIjB2n2ogGzDLr3FvYAAIgLiAMy+XkGkgTa9Qf30AaJ+ar0TgF9CqYFy/6yCgn+2/9jAAf4dfTW/v4PdANS/jwBawiG+Ov7Tgit+10EpwJN88H0UgO7CI8RSAyq/jP1Tfji+1v4XwapB8IHKPJK91IImflG8079Qw/o9n38cQTq90kEmQNg/yQAOgV6ATn8vvSA94v9iP/p/1sIbgT39ugGV/tZAEQP6gfb+gT2hQg1/Cv+ygQs/qMDWPhq8wH/+f0E/5gLjgiTAmsAi/aA9moJ2gQn/kwHWfmN8DH8oAP1/bcHPwnH8nXyeQHaA+QCPQhmA4j6cvspAtUDAgJ0/m769PRP/zgP2wWT+xr3pfwHAOAHUApu/JL/jQQVApv4lAdQFQH8sPohAmTsJ/wrFOkABAAaAiv+awNHBWYEYAAM+4H7NwNU/KgCTQwMAHoBQAg1/AzwFf1RAYPypgB1Cdf+awdOCucC0e6G9FYJ1fhU9qEIgQQe8YsBLAmp/AP80wGEBqHuVPfSBBr7eANsEaIPCfzQ/UT5x/HaAH8Drvos/0AP8gyC+Xz7RAJK/T39AwEPBBf2MfxaDakGFv3+++z9Efk3Bf8EnPxJ/9v/dAhlBzT4XfomCp/4g/3VDBH6nP82CwMG6/u9AMQL+Qco9x30ZgXb+yYEgB1wCL323f3MAN/5UP85D/UIQfrk/fMHhvqu9YsJRRA3/6r4x/9b+6L+IwLGB2f8HvdiBlD/fvS59hcJKwXCBrX5Yu3BB1MGIwHn9lMDkAWu+UcFyP5iAD0AXwTW/S31AwttDtv7ZPZD+Rn+5we2DCsBXe+K/ZADrvwJDqYQDftU97b38+8D/pkFRwqj/j/1+AdqDfsEcANmCbv31vkSAC79lgY6BIcAcPkxAaIE8wtrEc8Ds/iD9rH+Yf8bBMcH9ArzBQoA0wDJ/Vj8v/qB/nkDAQpa/1H9r/yA+CIHrAQ+AUf/6v7cAX/4VPR6AoACdQOGBcnw8/t3B+cAS/cZ/jMJs/4zAzf55Prm/a4AoQlg84H6ZwEn+/P7m/64BcP8ygJRChX94Pay/jj9h/NVAkIElvOO/WcA2vqp/qwDmQpXAeH57vsZ//f8RP0ICTf/R/26DegAnfKo95T7cwaWALD3dgQFAwv+1vzqCbMP9PwjAKz+ovXb/139QfjN9t7vhf6UBcQCbQhxBxL9DvT0/7r97gMqC7nwtO3T+cgAgvoi+ogJ1wCD/YAHev1B/vAFSPsN/A4AcATwC0z89vZbCUMIVAFOA9f9Qv5pAuj8Wvw0/UYBeQvWAjIICgeO/0QG6etR8YX8QPswD38IqfjC9SAD4QJx/3T86/PB/en+Nvkv/DMELw3uA7zxovvr/Tn7l/3s/iv7revkDxAZhPWO+Iz/S/lZ/yUDGvlIASYGrQ1FBicAWQE49zsEzvZk8vwAOQkn/9P3Ew2PDFUJuPxRAZT69efl++0H5wdvBbcJQ/dm+nMIG/fy/ZgC3P9V+WIALgry+ZwC3Q8ABAj9Uv2FAob4ufXCDfgEGv6+BeQBb/bU9LkJAvqY+vcYXw9p9SX8OQLr7sv5TAU7/yb1wf/gCIj4sfkbAW4N2Pv19kUI3/xM+Qz9rQR2+LgDpBMZ/Mb7Wvn59wIABAENC0cS2Aoq92T6OAcr/GcEMRRSBJb++QMe+QX6SAfRB+oC3vui+CECmwXA/T4F3AI07nIDEwwa+j36D/Kf/RkAEP42BYr5yQJf92Pv6/1dA9MP3AcsBHn2ifhlCaH8KAhsBUsDIQgh/n7+AP+9BLH86QZGBJb6dQhi/c37YAIcEMgFlPovArn0vvxe9PLyrQQn/oH9pf9D/bD5AQZw/wPzUgfuAH77r/839CQH9wTC9y8HtfvG/sMLnf9X+P8FMg18AaoFYQcuCJH6DfxcCrv5XwOXBKD6EQGlADYGMAkw/lz6cvqU8Vr6KQTYAdz6ngHL/6jzvgRI/kj50gV3+tTzqgQKA5X4zwLd/F4CsQEFA+cOIfhS/F4TQgc69xcMAgcO8okEngfvBkQBzggtEDT2hPYQAEYBJP0DAj4HZgT4AkT7vgPk+xf67P8++i73mPfWBo75PPvJApP+2gcuBbb/VPYo++H77P8q+Xn4uRNbArz2IgVnAar8FQRBB1YE+QCaBH8D4/F99XsDtwj0BucGOP6v+4P74fOEB8gGaf5H/dX4W/ml+gAI9AZWB/D/avMr+bX6dv1A/1kCXf7W90sMkQvS92QAAAVfAlr6i/5aAhj3BwElBHgBCfjzC/Yeyftl9a4B1Abv/OAEyww39sMBdQW7AQv5ov2+DzAE2wCK/yUKxAE9/K78VO1TBOsLNAQQ/nL/Hf5w8Qj7Yv+dBHcHfwPh+PLuEf7ACR0EMQXjAkP6d/3u+kr+tP+u/rIMMQV99dEIeghX7qUFBhIs/Wj63wZCBoH3Z/0bBbIEFPznBHoGXuwS9b0FDwVP/en+TwSE97j3lAbz/Af0Hw4VCVXvWvOL+Jn+qv+eA6QM6AHu9D35Av5w+94BTArlCuH6i/YWCVwLRwZZBd8CvPiv/toF6PgE/dEGrAmxA3sDWwh6AVL/BgAN+8L3lgP8DfYHCvse+cb+A//uAAL9CADoCmX7kvOoAisF3gLH/bcH8wdt9/QCuQir/S/9fgN6/NkCTAKE8/cBVwYhB4YEa/n9+yP+7P2CAzUFFPYn+QYAsfpI+qH+dw/XBbPyNPXI/WcEjPrZ/goECfp5+nMBaPu+7T4GfRA7/SP/SAVyAWv0OPVW+nb+gAp7Cl7+5fU7+j4IBgET/BcKw/24+IoALAPa+oD8Pg2wA3L3Jv5CC0H8LgQ3Eiz8NPXq/HP+uvOBAxYAdPqRAE3+JwqJ/sIIPgss9CLxzvwJ+t72qwSV7iP2rg9BCccCI/bH+SP8NvkK/MP/4f9r+SgHR/6N96QMJgVx/Anyju8A+CgGlRIjAIP8V/64/Cj/Uv8iBAP/Xvne+scCxQVNBYYAIvdb8ebyQgKrACH6KP+5BIICt/YzBjAC4/ZU/OTzePjA9VUDGgEX/zUJpgDtBZ7xCPtr+6D30QH2ALAPjfjaAukGEPxPA8j+pv2h+KwHqgOjB+gBaepqA3cCI/KEC+0AWfP+AyMCIAfQ/IP+HwPS++v0lPh2BF/xKQjZDPT75v4wAFYNUPj7/SYOWPty+j4NyA50BzAKkwAs97T0DAHKCtD8Fv+qDOoAcv9CB3UBPwH3BOoJUfOW8IcH7v1q97z6av2K84n/GQ16+I/3Pf7YBK4CI//g/ov5wv6R/p/9cf43BF7/UPsI/yv5eADVE5MR4fzwCMYGQ/Y2/8wIdAeV/c0KqQv7Acr+EAzKCEvttAmZBpLwKAeECTb78f3/ENIKf/7bBu8CDO6v4iz7FhPOBZUB7grL/Uf0KgTqAR75lAngCAD90/hK+qIGMQwcAfL9SP/D/VEEEQWtBh0Hggw7Ahf6e/4s82H+G/27/BsJVQ52EcsFDgiv+qXzlvs/9rP/vPwJAd8EzfQ8BSITowZr/FoA2/fa760BFwSRCf39I/vECW79OwA2AwMCjPjC91wCXgajBfr76wfs+eTqNwLiBOYHOQ5qBRX8z/B//2IIdvQx9sECSvnm7EILKhNj/7AEjgIH/lP0lf4BCPf27e/c9toBB/02AuYOVgBz8+H9KQh0AIT4AP4j+l31T/oiBUoNDwFMAi8Hk/TB8jEQYxLK+RP0d/fC+LT+uw7eCnoARgTZCKYAHfp8BfYAk/nS8sf67ALuAvsPaP6b+gQF0fn+AJAGLP9a+TH4/PiC9HT/sgehBUb+2vmyBNj50vpHB1z8s/Pi/1AGwu5X/XAY4v6J70AGSgld+Oz65gvLB1TyBAKqDgj6y/ZvCSEC9uvn/uQOvPzp+VgI4P4W9uABGwQR9+H58QVl78HyGw6eBg/+vwFRB6ryY+zKDHkENu4C+U0MywMz+v0WCgvb8mMEhQEB+NsDCAsZ/5f6VAF9/4oCsRJJD7j/TwToA5j8P/x3BAEJVv/0/ZP/ZvLf8mYESQYFCJcMnv2i8+AFZQam8zUBl/1v5yzyigKhC3oEhAn/C/jxDPVQ/8ABAPtp/aoCeP3TD5cBUPwPCe8FvP6091ILDgHA/FgK4gTh/PAAjhK7/HPuYAVuB7X9qwg7CmT/JP4nAOP8cO/I+UABivNE+W4L5AT9AIoUDwDM6gf1xPur/f7/fgg4ACP77AIOCd4Gov9GCDkEE/5c/G/+XwakBXQS3AwP//gARgjqCYP5//t6BK4DUgI/BO4D5/xq+3n/vgIC+/z8hP9FAiMEfPt4+HLzLPcz/Mv8J/il/lQGevb2/+IGoP2yAoD+kf1b+Xf2qAftCskF3ALiAhQHhQADA6IJav/v/KoNQwZc904IQQ19BAP/+PzgAUwBPf4v+iMAUwhMCBr8GO/f+nAEaAD9+ZcE7QQM/H4JEfVh7A36HfncAMD+7v9kArgCMQIOAn3+evxqCvIFbPpQ/uv92/k7CIsMDQMgBdwF8wXL+8H8/QkTAokCowzB+CT4vws3/CT6afqK+D0PbAMj9BEGS/lf8c8IDvk87zAC7vtV+ZwBcQGoCJUCke8m93D54vU3Ah4HEgvx+ev0cgrNAggBqwbIAqX+rPwrBVIFCgCEBncNtQG2/rsFp/+U/7wA+PnH+vsBLAp9EFII/v1l7zP06weL/3T7OwHP+yf4hAAU+or+6QDg9wwFCAAT/Qz7Lv+8+xr5BQSTADMLTv9q/E36lveSATQCpgs3/dMF+wQ2+cYGfwEW+zcAxApSAEIAMv6h71z5sQivCgn3K/2PBDf3nPa1//wID/q6/GQBZO5R89cFtw22+2L6ZwS3/WMAZwLPA/LzNf7RDGH21wNdEXUJbgH4BMUJHQIxACH9wwae/1YA8gMs+ZELMQKo/GX/YfgeCMoBz/m4+kcANwcv/i32FfDu+ML9+/VW/p4CD/yX+vD81P5o9sryhACkAYL1b/uaBF/9R/ofBuoKnPro9wT+Rvgw+F78hwCmAccLcwybAV4BYP9eAYP+Wvye+xL4oQSdBqz63v2LBFAE1ALD/3r6/fxhAIv6wfyIBo8O2P7n8xf92PocAnkIAQJK9Hf8ZABG+y4UlgsI/uD5gfTmAXkDVwe0BSn7Qf0ICqUGPff1AwIHZO+l9uQJyQKT/gIJnQZ+9pv2fgAQA2n73vspBAT93fvXCOj9XetX/YAGxgDI+bz2NQWrANYB4ga7ARsBVwM1BDr4NPab+Kb+7wlqBTj70v90CxcBWPy5ALD7Qf5WAikJwQAH9yz+egGA+xn10wQ7AiP/hf9k9uUA0forA0IBm/qJB0X7EwAxByr+EvwM/aj5kwA0A670hf95CGD77PwpBksBMflE/3IMPgle/ZD6L/up+Nb+iQxXBCP68P00/wXxsvI/C9MFaARPCGf0dvGX/wIGZQJX/94E9/+A8on8Nga1+vz3O/9d/cL4bP8tCKYEa/4uAkwGB//RAiQMrATAAeD8qfnP+W/6UQaPCRYCRwS8C9j7Tf1QBW/8UwRMBh0JpwH7+CT8sf69/0L83wC88//w2/79/Lf94AZsCFf7rfxXACQBQv7M9Cr9bfXi9PoAmQMdC5L80P1d/J/ySP19AgMLhP/nCPoQjf3e8/f5PhAa/RwAcgjh/SIF3/20BTD+mQWMCFn5O/1b/w8Jcvbv/+YKgADWAPP2pwMq+wj8dAb3+TXzHv5cCer3gvwCAlQJgQUI7gv9xQeLBQ4G0QVG/bv1cABHCKoFCQk4CAIBAf5g/N0FnwBH/5gDFAdvB7j+fgoKAXT9NgR+/Uv5G/z2CNj7LfeSBp0AgvnxBnX92/JE/lD+6AQt/CL9zQqy/qL7mAH9/zH+IgHHAb77xPqoBmkKcPzC+6MLwwOk9rH68gVhDhAAJgNEBC393waBAfECD/+f+QoICwUM8af76QtV+i3/dQXw9xQD0QfS/10BD/y3+AsB2wIO/nT4gvwXA8v7Zfw9BrcBffxDAOz2/PrYB3MEBAy1A1v7ZQQDAMP7vP3bAqUAdwKEBeP88/inADcOvgr+/DEDeQf9ARIGnfwE+W4B8QmVD7n9CPfDAJYFTf0qBJ4ITvaG/tMAqff9+PIFOw4SBhUCf/zV/n7/mACP+Kv0g/8Z7tkBJhRE+aD43/2IAmj6xAJPC6j8/gL8+eH8iPog9ykFDf/6ArUEMQCa+ZcHnw4N+G73pAfTCJn8ggGL/df5uwHNBgwNsQUJ/r765fpN8q31LQi8Bp4CeQKWBKb9IPgYDLUE7fGJ99H4zAQQCokHb/0/+UULHQxi/nXzcwXoBTr4GwQDAusC8AtBCBb2TvlsD2oKIPky/eEFAgMZ/Q0CTwse+AP7PAFk9DD84wBDBsv/jQBOCZgB7Peb9oABvfu9ABkJ7fjN+m8Cuf5q+BgCjQoc+9X67/4IDPkHt/UKDlj9Q+pUDwEVlfj69N8EMPh/8n4IhRJdBwL9ewJe+jjwmgBCBw78IP9RChgHkPMM9nYHv/aS6zkGhA28/+QD+wHN91L5VgQ6BTz+8//YA40F4/kz+WcGiAbL//QFOQzh+9T9sgD0+5//Hv+mEOIIEPsRAur8SvxM/RwHJ/yt8xoDyAHr/ij60gfnAOjzdQbbBQj/mflCApL9u/Lz/YgD+wFX/CsL3Aio7371Fgf1AL78UAeCAmr9bP5IBUQFT/L29DcN5gVX9SMC9wS9/R3/bwCs+1f5xwMVB8L6sPFl/RoNJgTCAb4FivE39gMGFP4B9Jv9UQr09jb5GwTZ/tUEHATB+yz3iQIZAKn4AwON/4AARAGY+Pz8P/lE+iYCwfto+ecD/gkF+zj+gP9S+LQGfAZq+XX44gZz+b30Rf6i+Q0ALv/+AFf0P//fDfMAgQOk/VH+svz+/jgDK/oP+I38sQLV+3v6aASwAon6TQMzBxL7PvwMBmEFkf1N++j5/f+SAXDzbfy8Cvz8gv6X/3nxrfcRCWoLe/f9+MsE4QXG//366v4h74T34gKM8tD2fAXbBBD8tv8aBnr6SfY3BtUAVvKW+H4HP/zs7mUFvAf2/qv/KQCXA+T5wPbWAfQGgAEAAjwHavbc8ZkNMw3JAtcEzP+b/RwDzgMH/kcIjABp/PcFMf9TBbgDyAKuC/n+8/X4CGIIf/hp/QsFUQAg+aIGSweS+lICawfo9Er5mgzc/2D+BASZAxb/q/ylAi8APwNwBkEEwPYq9lMNGAJd9F4LzQg2+1cDrQha/oL8EhGOBhH0JfxGCIb9A/dIBOIDoArLAbAEAQXo9F8LnAoR+ez7aQPK/l799AbB/fz+PQa1AJIAgPytBZoPrf5C+wICIAIN/+78+AcgBWv7hwUBAr//JAcHBG8QgwLc9j79ov0dAX36CxNKECAMwgdP83QDwfZe/EgF9gIm/yz3AgiRAlYI1gsYB4oBp/YwAvH8q/yiCewAJ/7dBiD/wfoqAJAAg/4n/loFJwLJ/jsHWAfW+xT1m/3w9jz1Fwbx/5j/qgfWByX6Sesb+lL7m/YUAu0Fn/qm+SsEDgHXB4ACs/V09IzumPx5BrT6mPzxCioH9fA58/gEBAWXCZ4CdfhR9lT3hAqrBar2Uve8C2sE8OwHBjICc/3LBU/7Jfyp+lgF/wAS9mT8z/34AMEFbgX6/qH5n/eXAM78X/eBBXb+RPe9AKX9OPPX/RQLhQLL/pb93gGfBtP6QPtR/ND8PglEAt71Svv9DKYOj/6U+U34kfgy/9wIEf6JATwRx//p+fr1Lv3mCZQC6/9z+RXzIPLDB/gFrfRnA2QDsPzz+vX+zP7490wANgUcAoL71P7j+xrrZ/sBDe4DbP+J/4ECof39+uQEdQXFBfsJaQAl+/sIrA+wCg/5Ye8tBLwMT/4VAesFnfq0CbkMQwJKDjkCpgHHA9fqaPO7CZ8GsATRB0QCt/z7+3f7HfJr8fkGZBTeB6P+BQUDAFL6z/5/AkL9mP+XDzr9gvANCSINtAf6Aw352vQ9ARMShgCi95QORA3Q/sr6yQLv/p3zWPva9/D5wwz9EPYCO/iBAKYDt/jz9U/+yv+Z/X/+1AMq+8n45grOAln7NQBJBQcCZ/8sCVcBmvoZ/lUIRwVJ/ysDxwOrAFv7iw33Bzj/gwfb9rjypPzdBVAGHQiYDF8CdvZC8o/8vf7p/u0JwPo/8dEEYQs2BTMEGQN1/Vf52/s9BmH7jvv6C3D40vg1CiwKtP9L++MAjv6GBKUL/Aso+EHyTwGQ+V344weKCpj6nvjHBCQEIfvU+MH10vjDALT5MAFOCG33rPrkADj48gKb+1z5UAY89I/7AAZZ/QIHAAWr+vT/Gf/IAIECuPeJAfkLeQVVA1MCbPZe+lEEwwIsBAADAQwaAULxk/f8AMEE8P4O/Qr88gTqA6v7B//V+0f8pAW7AAD2svwkAKb7Ivyd/kz9KASZ/un6Wwgk+2H9DQnd/S77cwIhA0v4vPupCF0Brvl+/AgGDwM59vkIWAPP9uYDwf7o/H/8Cwd2Bbz4GfWX+dYDv/vMBmQD3vj9BYP4wPFLBWoEhfbD/RkE3QFU/eMCvwm9+SX4nQT2/XfyqgZdDAP2dQGwAnb66/6WAjoKpvzb+7MBLfvaB6IQTADR7+j1JwHUBTIEZATIBhAAsPZJ+Xr+kgAgC6cFefrx92H7cAfKBtf9Z/6JA2cAG/fr8mH9bPkt+NEIlAvnCJ3/3fqM8Hby6AEvAvcIMQON/7b/W/k0+RL4VwSUBGL4w/ZUANcIR//4BT8FJfofAq4GfwHP8y4AEv/w8wkEwQMgBgoATP1+AY33cf3P/2b98wPKBiQAn/iSBM0AT/KPACoAsAZSBZf95AMw+PMF4v0h/BMDfPqXCDj/MANzBboJAwt5A+sHhPTC+Dz60P5HCtz/YwiTAeX2Dv0SAEX/SgL2Bpz8fP18/+MBLQM6/EsD8/pT+AX5tff2+Yr4rAdgA8YI2w46/6j+//8J/Mn6nAc3B0/8ev9yAUX8dwLuC4oAevTU+xkJbwJnA9AKYQLz/AX75gItAL36WweZAEjx2PugAin2L/1YCzL+ivX9/vkHE/669VEDOP+LA2MGE/z3A5f2JfojBFr0sP9tDOIKSAGP+ywBnANHDAsCUASYEOv4DPddAm78GfrQAxkOGQX9/QEF4/o78/gDuQVS+9Pu+/4LESz94veKA98Ev/YMAgUDvesG+JAJSP8K9OYDRwIB/KL8oAM3DKT5PPtXAf/+P/1AA7UMaQToAvkAEvhp8yz6uALOBpEGOwYPCTACSPvy91sBVgRu+wgFBP/89XcF9QmtAGX/2fxv8vv71/1e+igC5vqqA78L/gPQBSoKWQGE+Bj4HfD5+lIGn/8NCL4Kf/0BAWUCVf6D/goCLg65A+/6Vfp9ApcDxvw9DIcDB//r/Z/3Mfv0+B8FQwsJBCn4G/koA1j7DP4UCDUEuP+I/LQFvfvL7SIFqQbR9urzugPCB8L9ngaSB/0AiPp6BxkGs/MC/ioFMwBS+Zb/2gSj/AYADgQ6/r75kwBVCowAofz2AYb6F/zL/hD7Xfrs/5AGzAVU/Yr7wAPX/b/0wftuBKr9Mf6ZBb0FrAFV/3oJ9wM59Vv0UP1S/Er5CgbVCG4BegUSDssFzvpd+bj6Cv1NA4sF4AHPAi8B2vwF/A4DGAGS/RUDGQedAdD5F/xQAcAGHAB1AQYApf2CBMMBnf7Q9tkFhg8xAEz38vy5Apv3FfjFA3sM2AnwByoESPo2/3wFKv//+Qb8QfhO/6sBEwPkCDABsgM+AEkCMQFN9mgCkgBA+Ob5w/+9/yT3JAlsBWb2h/6b/0n73PUwCXYFEfZIAS4BFP/U9lkE9gY+84AGFAvJ927/nxEVCOzy0/5MA9n22QLTDd4LbPgVAP4Pc/rC/bEGZwYVBAn+m/tV9pb6PQh/DhYAvwMlCcT6o/PI8Tn5y//LA08HDwDD994C0QKl86v8XwTY/t4A/wHVAnADyfsPAEwE9/oB+wUCh/3h/6MK1gWCBnsHxQD9ATwAHfcE/WkBk/kk/3IHdhHIBOr5YwSd+xTxo/YfBM0AvAJZCpYDUvqc+GYCWQBr/4b+nfhH/MMCSgHuBNcE4fhu/ev8l/1t/9UA4gg1BF4Ab/+qBbYE5f0r9+by1AHlCPj/8/ysBJ8DpftnA50MK/lV+P0NXPsA77L/8wXDAD//9v4T/an/YwKnA37/UQG1AbD7lvtj/swBjgWhBSUAUf79/EcF/gbK/RYAW/e+8IT/1AgBAq0Iqwra++wCOgQc+VT9mwPmAZ76tfgR/B79IQG2ApAEwwQOBDQEqPi2+I8DFgNQ9sf5/AMj+uD+nQGZAjYHTwVHBFD7RwMzAT/37v+G+G/1gAK1B2IJdww0C6X8evkQ/5D6cABA/GEC0QY37RD4kw9zCDAJcxQ6+oroZwH7/5z1AvsT/wsA8fxW/7sFdQIJAC4JjgBY9Dn8Vv+6/Jv4i/JS+JsD4xDqBozxNAWiDRf9NPu2/IX4H/sJAXb2kPyZ/jL7rQqMAQEGLhOqBVb6jO9y8s3+N/sQBHIOVQAx/0oBXPz/BVETYwq39Q/3f/eI9BL6twv+Do8A+BKqCNPrZPmOBtEAhfhTAnUDqfvz/rv/hwNP/u//LwOH9SMBlQOn9/wBcf++9N74fwaW+5/4xAraAxH+8v7bBmAEf//4AVz3Bvge/9ECDgKvBEoF6QRZB+wFcv+A+Z766vdv/Df/rQqXBtj33AJeAen6Uvub/hb2LfumAFb7tABk/FkCzP6X/RIAAQL8Av36/v9L+fL5dQFMB2f/N/UqAOn+EAEuBV8KbxDkBKMBbwaA/0T6GfSm+Q0HTAIgAOcBcwjnAPr7vgOe/bj9rgCQAi/26PMUBAkHoP/j/PQBtfdz+N78J/m9/zwCOAC6/ZQEYwGs/u7+q/oOBFD/bAUnDJv7j//oBWv9FfivAVIF9P3a/s8ByAVB/ikHBhLU/p39gv649Rf6UfyQ+GoA6wEq/gkJE/9P/X3/O/dWBzX+9PqHB2D3+/l6ABP9DQTCCjwH2fao/FYBB/sPBFoEkgp4ApX7mAZp/5n/QgGJA6//ZADfBtsAtwNh/Rj9JfxT/cgHVgVf+/fx7f8eBLkAcwEbAnEFuvl++Ej3jfFp+7wFvgFTAGwC7QYWBi36SAE8/9b5ufi0+Yb+Svw9B1wAPgOvCssEcw2Z/rPzE/WA+fwEkAC5BukMKv5h9k8ArgA9/WgNswZd+LP5W/MD/QIFjwYnDn4ETvd19fv0yPmjBFcHYQEtAHIC1vF09ugMxwOA/YMBUwU2A3QDCf46+T8CYPhX+BH9S/9tB8UFqQUNA0ADgwZ3BUX8hPci/mICofi+9ggJxwbX/gEJ6wjW9un5Rf8i+LT+5P9uAigAGQWdBFL2Sfq4/ygD1PnuAMsF/vdG+0P8wfpZ/MwIuwabAV4BSv2xAAj93wM8//cA9QR29/T2w/5dCGP+OgJMCgsDGAKkBIYDT/Z3/w8HWP469RD7ogmvBg4IlgC9/fj+lv1H///3bPvFCFUMbff79DUCaP+D/if+5wJlAL3++gaCAMb4zwGhBNT9Tvw0Ao0ITvzj9RUD6wJw+4EJzAbn8/X9BgKq/If9IwWJCAAEZQbU/xf5d/ZL/s0C8P0XA/f+H/o6AAMFf/7NAEQGkv7S+9f74gfoA7b5LQfnAkT5EfrFAZYDAf/VBqACFP14AtMHpQMG/PEF9AbbATD+HPa6/hoGdgFy/jn80PwQBR4IB/wG9oT+twUIBFv2g/jpDHQHIPox+2P54vorBZkE4P2K+gX7oQSc/UH6EwvUBfX4UwOVB9f+iwUeBSoANAAB/tsCQ/0z+70Ap/5n/YMCNwe+/OX/xAcS+I37+gMa/4z9Lfca+Sn7xAcQCD/5qv7I9hT6jf/JAG0BBfpdCKcEUfrl+HsCwgYc/8MNMgai++7+qgI4Aqb5LgXKCGIAQwPmCC7/bPhqDcATUAPC+/j3If1tASH+YwNS/BX6wP1X//EEfPs+/4AE1/qQ9Hn8TgYKAJYGAQPv8u34QP1c/hz/nvxt/rn9dv/lBIoGgf4WAKwDPflkAW0DPQD0/Ef34wgFB/T9/gZHBf71GPq8A5IBEQOZAJAJDQYP+F4A2Q4sAt7tePuRBb4A9P9FC0UFCvTa/bgJYQTe+LsAI/1j81kAQAVxA7YD+P/o95z4s/vMAqkHffiv/P8AMvSUAU4FGP+h/4H5hf/Q/dwEUwlx/rP5VPAx+P8CZgizBggEOP+C9vID8gAJ/ywKNgEx+LT5JPsu/wAKZQVsBJED3/mA/C79igER/Q/9nQRzBXwGc/2bAFf/2fnD+1MImgop9DABnQLf9kgBCAFrAhwE6v1++egEWwCi/kcKx/4b+VP90frx8FL3Q/43BCwK2gAcAFn0JftcA3b+qgTn+joCn/1v9SsFsAaP/+T6BQTM+Mr0BgeoBF4AzQADCsgHJf/ZA5sDVvKn748GWgQ8/NUGMQq5ACr5wPdC/4z/sP3IBv7/C/3dAakLWQNJ83H70AOpBLj2cADiAwP9LgB8/QkOFQkUBEoDTPJl9v8DSwPQ+/0FywgW/ngAigK4/B36e/yCBI0CWvr+AJ4E4vyR/skIBQBr9CT8LAXV/QD6VgfOCZ3+4/aqAqQJ4/ut+1EHZfzz9DwIEwci/TYJ/g70+6TxrPjC/Pn+VwJMEKoHx/idA/gAoPah/RcHlP02+NoAsAAu/soDtQwtAqf1XP5f/Lz2VfocAGMB6wJjDlYGNP+rAqD+7Pmf9acCpwMa/AgJVgWn+h8FJQ4/AdT0lQF0BSL+bQdwCCwA8Pi3AFkHs/Mx+jMPwwR+9Nv9SwkP/gYB8wbY9+Dzz/+pA/7+kgJfA+wBc/3B+DUAmQC5+kP18AIrDIP/6vkx/toJSv4H/CkGgABB/+8DFwqx9dX3Tw4dBD76l/3WBRL9HPqGCmcH1P2bBhcLDv1b98ECRwAo+GQC0QUCAAX5BfsZAWr7EAJWBUv6j/0nBMgDyPwV+cUB+f1N/50DEPvC/qAFkf+D78L4TgsbCJn8H/6pApbyov/hCxAAE/qPAdwMdfMy8HwFMgPW9rj8FAeL+i4FwATp+2z9bf7OD6D+1PdS/yj+bQU9/KMAgv9lAF4GSf2b9un+YhUuAgL1cgLdBZAK9gEFA+IE8vsD9Fj3Sv+T9+oAoAwU/g76/Ap6Blvzefg9Bb8GvP25+0r/bvcX+Rb8KfhhACYHcQG8+AD6awDW/0v/LAPrAi3+cfzM/4r+t/pbAQUBfPqX9zkCvwQp8IL6Dwv9CND9E/xqDk4I1Pze/BMBg/jN9zoI9fkR9GEH8Ayh/wv+bv8l+6IB1AJjBjYE9wJPAe357v9RArv5ofdhCJEBXfOv/0oF5wPJAmYDy/ci9akHUgY4+kf8/AM+/vX3DAb8CCD56PzL/WPwwfmtC1EGogELC5sHH/xT9xIBGQOq/MYBugJu+5/+LAd9/HsA4/8fAFwFbfdoBXb/+fwmCO/+hgJOADECUwC6+272//fgBm0A6wCmBkv9xP/HBNYB6/lH99gDCQSyBCMD2f2YA3IAuAAz/Yb9GQGeAtAABflJAXgBsgKWCCkBFfmD/GQEFQBPAxUBX/iPAZj+ffykAjX6C/tb+3n8Owb2BYj9VgPjCBP0DfncBrgCkAOqAzH9tPm3DDoHRPbOAa0KNgS3/iYExQJOAlUH9QqL/2j2jgnUDS/2n/OtCE4BL/eSBZkIEP17/HIFpvgI9VYE5v/C/QQDZv6o+M/7LQM9/nX4Pv4w+tLzzft3BAYDLv1cBZwEZveG/PoEqwWa/z3+PgHeAZ79Av4FBb0JjAXz8O36EQZcAZUHBQzWCeD4zf/h+yvz6vqdBMoLEvgo//AEE/4X/nIFHAWG8CoE9gaG6m7yngy+CdP7QAKZAdX9IfgY++4H2vjx+IYTWQMf8VUBRwg2+lj0oAFWBLoFsQSMAeL/P/53CbkB3fUn/P//2P5+/j8DVALL/wIEngZa/tP3VQGD+ZX1AgaHAXUC8w4qCK74h/rM+sf4jvyo/SYLywIY+MsEOQQW93cCPw8j+r73SAPIAWH6yQfQEj3+pfWX+CD9MPaf+8wJFAR6CK4NDAX19iv8tQbQ+V3yzv6CBIb+ngHxAOoBbAx8Bvb+MfoF+t3/z/6H/ZP9pAmFC/ICsv1//bP+VfnoAjUDrvxx+jMABgET/BII8weh/noAzg84+VntvAgEBAX6tf5MBfT3v/vhB3YCAATUBkcMpfx8+hYIEAMo/zMCNQK2+fn/LAYw/AUIWREdBKX/cwIwCjT+GPsvBGb1ivkzCYYLxv6l/doK0gjm/tb/bgfB+gT3aAIjAM/9NgSaCoUFqvtx/VIBogDTA/kGuP+f/pYFKv5F+gf8UQeDAh/8Sgx+A5oCXf98/yQGhvzQAqUEH/1W9/IBxgg/Ap8ENgrIBd76Uvfx+aX+UPyJBlcFFQPKBLD/ZAjq9pH80Abh96/7LwesCFHyOvqIAFz4OwZQBSEDYvqX+A79VPxE/gL8WATs+TX3Kv2r+BgDvwY5BeL2bfcL/Ij1r/1+/mICufpk/O0Cgvqb/7UCIwXu+5345Pgx8S/6TgOhBkn+SAFpA8v2Z/0n+Sz4+wIrAM0CA/448pH4d/0v9yoA7wEg+Af8fPkS9w79jf1pAWMFY/ix9sv5o/K0+oP7pAGbCRH74/wXAdPx9u/L/PQBQ/5TAN0DMfsJ+tEBrgE+/EgArwP2+CL9LARu+kv7WASaBvz+tfl7Acj6f/pMBr//gP4IAlQHVPw78oEBEgE/+4EClgEy9/oBswWv9Vn6kwJC/lv7MgZhCIX7Hv7vCfwEjPaf+/oFa/+MAf4Env1Z/CsCkw4PBk777gQxBPz+VQA2AjUBoQpxElsFQfQ0+q8Dn/vM+KL7KAkvCe4BQQhG+77xv/9pDcb9/vU4CWgEdAAe/Av4nQWVAr8EQAM0+8r9OwAH/hv86gu+CKAHnQqV+rz2afsGDvsGZ/v7CQALVgXg+6j69/le/ZMMYgWsAVsCA/6HBUH9UPjU/GIHrgcT+H78OvvN/ED6P/7/BAb78f6c+hb8MvwG/ywDO/1yAvH9mvvX/xwDwv1B/a8Cdfp6/f8JYgT+9W/4Ff7S/7wCnAdVBID76gEhA2f8rf34BB8BEPoQ+qH5HgDlAcUEsQJg+Mj5e/p2+S79LgFf/w3+2Pzd+gf/lP8EAF7/WgCh/tj4+v32ALn6Tvr7AxD6MPg3DJkF3Ppv/IkD8ASX//0DgQNB+mP1J//BAL72cAb3C5L4x/elACIF+gFgARb+B/YY/50GAgEH+L78h/5Y+i7+/QEbCioC7PzD+KHtSfxVCuEFQv4SBLkEeP3tAnv/5QJaBK/2YvwX/tL+BQQtBBsG3/6OA7IH4wKW/vj6bQLEBGYCugJVCW0Emva//H8D/QXCBPgC5goQ/031bAUzCVn/SvrY/UP+mf6PBE4KGglwAtIJMf797935Q/o5A+AJcv2V/XMLiwxCAt39uwEyA8T2RvlmB6j6Q/tDDrUChveaAqUHQwFOAWAFWf1Y83cBVxP/+xT3lxHRBMP1LAB5BZD8XfyTDgUKk/ZK/GsLVP7I9L0HNwOlAAoLwgBd/GoEVQpU/wT+4gRX+KzwE/wGC6EDsP/LDdMJv/vKBecGtfS7/NkD0vr484/7igpUBYv/FAKQ/E39NwKh/3QEBgSl/0/6rPgnAScCjAS8A4YEBPyi+1kGIv55BBoDQP4gA7f/Qv7aA8wIoAKuCeMIc/5w+wQDQwcN86v5tQbm+5L+4AqHBYj8cP+rBZsAc/ObB2YMqPLa+RUIb/yo+AcFCQKSAaABPwJFBZ/9NAQ9Amr1CQCdAQX5KwQLCD4DXAbLD4cFi/Xr/ooFWv/l9bEGYwRS8poEpQxXCvEDngSpBFD5QvtvASoC0QExA1wCYv96/Ob/2P/RAU//DPul+0b8RQwcAmv5FwgXBt3+1/ubAIr9xPkzBcwH7Pyq/ZQCVv4z+7z/ngVpB2gGxwEoApv6RQHpDJwA6gfcA5nwA/wcChkCdP7YCU8B9vWyAJ0G1gUABq8DowWf/HrzkwEpBaoE4Ai4/W/0Zf8gDer+8Pn5A8AAGgBJ/rj5fPgyB98Nuf7d+uoCgwRw/JL2VvmvAdX9XQPWCMz5HwF8CmT4LPQ0CgwElvYB+8b9Nwj6Bfj8KfkIADgGNvrQ+Jn+/ftgAbECMPP8+FgL9QNx/lL/zPW8++kDIABw/W79dQFJ/VT3rfvB/2b6rQGRCY79//moA8QGq/xWAG0BxPU6/dkHq/uz8Q4Hmwxl++gBCgoa+LnzkAKlAon2sfxRDPf8QvTMBMAGHfh4/tEE0fMQ+dcDNwAaAOz9ufpp/vD+eARMAVf5LQBR+4H7lfvk/nEFFwOjAtP/kv///f/62vbYAZ8ASQCRDm8AvvPu+BQCP/mK+OEGZASc+hn1xP1cAI79uAN0Bi0CMvrI9kn5a+8q9m4JcQXEBnADjfnt+Ln5i/4bBywHCwMi/r7xevEl/OME7gJFCIgHofu5AKD8Sv6IBa/8gvk3/XX8UgF6B20CUPmC/9UJJQBm/8f87/gP/1z8qf+fBGkIngRQ/Zj69/dNAZYFOfwq/GL6L/tEBWED6/8Q/qP8b/XH+FMD4wH2AnEAVv1O+Dj5SPZv/tAHJ/3u/o39QP9P/VsBogUk92b1qf64ACX3jf4rBboCnwGNBA4HvfqP/esBJvxf+gQChAU5A0f+XPqBAfv+zfw6ABoHRgOH/YkB4gFf+JDxuwaY/xn3UAhvABr0a/e5CXwIFfll/5sKo/mn6XL6rgXSB8YKpgSB90X20vrF9Vf5kgSYCZT9Zv0dBpP8fwJFB0ICS/5i+zn+tPX6/tIH1gF3/yH+AAhYAuv8sQGP/rn5q/xIAr/+fwj8DdgCTvvX+aP+MP8Y+xQAzwOu/mj7+gDeAfb7YAxrC6/1vfXrBcwHzPYx/VL//PqTAagEjfwp9u8B7QI//QL/NgmLBHj9EAIpAf/2u/f5CaX6kfYABXAB3wBUB1EDqfi4AT0BGwUJAwH4ufwKAr4EbP4TBoQKTQRG/ez6DPz/+CgFxQgT/8z7dAM3AzP+rARFBPUEDwNI/aH5aviAB/UD2vzBBgf+ifyUB4IK+fcX+KILD/2P/Z8IkgR+/Q//mQdQA+EBuP+o+qr4LfxPAWgIxwalAdQBD/qE/Q384/zdB4oETvsJ+Iv9jAFMBzMJ7f/d9sv6RADZ/p4ElgTb/BEBLAR6/14AjgVcB1b68/TDAhsFjvzgBlcPd/45+pL8HQA1BSAE0AEi/HX9CP/YBbYE6wAo/2D9UgfU/Orx7PttBWP92vg7AlYGfwA69DsAbAJf+F4E5AQJ/gz9Mv7uAa4HrgQj/KMBq/+H+HUA4QGUAHwCywISBu3/XwAiBrsEHAXE+8L3Mf+rAxgCyPtL+m//mgYVAmYC5wZg/8AEqQDp8SP0PQHmBbr4bPop/Y/8EwV4BjcFnAG5ANL6//Zg96H64gPDAUYB/QThA7ABHQbQB4f/+/9sAZIAZwLW/ZEBgwX0/KD+bgOhAwEE0wWyBAj/4AB5/uH6h/3C+aX2qv8oAPb8PQPTAuEFWwFp/Nb+zfkY9eXz8fxR/d4BIwglABUEgQOW/w77yvolA7wABADf/9QA+QJfBxYGWv7XAdUAygWDAxD8o/8SAWcF5f/j/Pb5jAKRC6z/z/94/Rb8uP47/Mb3GfsfBTED5/7Z+Dz6/gOSAt/6awKEAcz4nAGQ/r77WQSaBkwCzANcBCb6OPzeA6EE6f6PAKAMhgiZ/8v8qgF1Bjr/kARc/8j4og3YEjH+qvMAAdX6BvmoAo3/GANw+4EBgwKZ+fgBqAHm/yIAKP2D95n6xAEo+/v2GgMIBiID7/9zAJ8Fg/k2/Ef6Rf7qCd4BkwlTA8v+lPzb+XQBpf0wCLMJ4/4C9LP3qQl8BZMFbgWhADsBlfos+Iz5Uv22/xICbQZsCAkC7fgE++f6Kfoa/ggG9gdEBTEGKgCd/Tj+lAAPA4oCpARPA7/6nPrwAzgIYgt7C4cHIfyPAVkDKPW2ArkOQQ80AYn3dQE3/eD6EgN5Avv3hP/iDr0GMPnz+w/5j/Mr/Mv3PfldBqAEVP4ZAbQE4/0M+lj7JPil91H/KAdEBUf/0QSYA6D7MgaZCFr90P9yA2H9mf0WCQkPMgQtBOgHePiN9zgFgwbT/JX9ewbdBBoArvq9/iQBjPby/1sFVf34A5b9zfkR+un41gBi/3z9m/R4+L38mf5XDD8DLwI2BHv8I/q5/SQEKv+hAfgCWPxX/fD+CgRNCGUF0wnTBNz3+PwaA+MFcwNZApEFqwAB/G39yv4s93X5ZQY4BNv9SwE0+h/sZfetDtwGR/irBjIBr/Ck+hsEkf/2+V39LwFRAS315/1dDS3/LgZaBgD3rwI1D40Epvia/V8AaAQVB0sHLQcaAeEH2QXg9VH1+wLxDtUD4fq0AUf+Gv3dBMkE3/xG/p8A1PyS+6Pz3fp+A0j24P8TBLD3cAHDBPUAifWC+U8IM/7E/h/8uft2+n72SANABsj/l/2HCwkEefvDApz8C/w+/cwAIv+9AEECkAVeB7v9hf2U/jMGqgft+EPuCvh+/5P9/gAJA0IFB/wI/0ADYv+ZAgEA5Pqa9Ov6ff3Z/wIHv/+Q/SMCTvpW+60N/wdE+Rj1KvrBBxMCsvvNA6kF2AMbBOf8IPtcBfIBjvek+83/4/y3/rAAiP3e/S0LJQic8g/96QUS9lT1sADKAlP6/PnV//YCCQOgBn79Du7K/o0KC/wH9UED/gNq+A79bwBsALL/uwWWALT50QdYC5MAn/lv+5f6Ivv1/voCywZsBwMBJ/5IBUIExgHq/jf5VfT0/rEDZvlq/V4JSAli8xL5hgc/Amf72PkBAEr3fAJTBpX6dP+b/JoDPAD795IGJwXN+0P9zf6a/gL+SAo1B9H9pgRcAA39JABNBcMCDf4ZAn4DQAMY/5r8UgQvCnICKv8tBxMGw/TF864D/gWk/s0DZQhF9lb0ngEWCfv/agCwEML+YvFl+MT+U/pH+68LxwnN/QD9jQJq+db6rQrHA2r7cwX0Apr6r/8jBLIDqf7lBLkCoPnn/1AEXv4E/K0IlAgZA3f+O/vA/gj7X/6aBXEE2AARBEkE0PoQ900CnQbz+X78wge+BPgDhgc/An79nPwZAz8GNP+UAAMGcP5G+owGWgU6AgcEJgBe+4D+bwcQ/fn7LgUfBiT79/Y+BGP/dPkB+rYAof7F+GQDQ/069rX5ZgDg/X/1CgH7AIz07/lQAgABGgLpATn90/yh+mL7EPyw/YwETgMGA9EEIghqBuADoANm91b/IgO39tT7mwHDBR0B2AKSCXr8QP+3A+7yk/E9/qYGEfyC+GAJtgBn9Hj6BQLz/BP5kgRDBNn4CvSw+6b6ov3lCHEFOfmh9I4IoAhy/fkBKwLq+3T46wKSAlL9j/6jAEv/N/+aCvQNNv4e9ZH9Ofr7+k8E7gYTBMz7XvkD+9r9LQSCA+vzfPdWANP9cPsb/G4FJQIpAr4BQABj/HsBbwzh+KHzaPhR++b/hPrDAFEHbgG7AdoEuv4v/jIBXAUUAdn9i/3q+Sb5iPh8A5L/1vskBYEE7/x692v5uP3sAw//wgHHAar6Fv/V/hr8MfonAXcFUQLZ/oH/K/8G/SABPQbgCykDdgCn/3319fffAYIJRwSTAZMDUAOk/uX9XwZw/g/6OQWiA6z9jv7sAE0HU/5I9dr+owaxA337swJQAeoAKAg/Afv9b/0zBFr/lvuy+HL3Ygl6BVv9VQL/Bo0DvASFAsn9HgTE/G8C2gVw/Cb3K/vJADf5UQP/BtIBYwhkBWb5HvzVAM3+jQGS/Jj9LPqy/+IGbwCQ/+L5HgEm/P/3gwZXBwUB2Pp4Auf/s/43DUAFwv62/oj+igAe/MoEYgbg/d//1ABA+Tz+HAtIBSIGKwZDBdX9tPjXA4v84f/j/X/8GQUQB/AInvxLALACCgTu/cH1YgAn/tIBLgFWBMkDMALHC/v+4f3s/MH3Ovsp/aT9fPl7BZkI0AmNBwb+8wP+/EgFawaW+lEAo/pq/jsALP7rAnoIQAUN9yz8pP7LAkUEZQZtC+HyU/KEAtr9TPm1B00QD/vZ+J/9Jf3R+rL9IA1aAP72yP3c/m/+7QwUFDD/owB4A1769/vcAaIAbf5wBlcGcAG3/gwJBAji/EEEtgLX+if/FgY8Adb+JgGnAjgDyv9JAyUCmfoW/RQGBwPh+rz81QGMARgAEwiqB6D3G/kTAm39Pvmi+84JpQKw92z/OfRm8uYGjxU0Ban3bQJ6BM8BUgLIB+3+5/SY+8r6g/OC/isR1QwPArAEWAPw/KkEAgjH+fPuU/pdBQUCWwMMCZkJEPvN+wYDRvd78q0GOgzX9rcEAguM+/j6Lv7cA7b9lv4jBk78XfNM/GoCof1WAlAKUQA5/OT96vq5AAQBaQu1AWH58gJm9GP5tv9zBKEINAKkAo0BMAKE9b/1iAFxAHQDVwk3BPT4gP5yALL9GAG9APQAg/sB+p79Nfwt9y0CkAz8+BMFeg8j9Yz5PARi/xL3JP/qC0j8hPap+vX4qwF/CoYHyf0sAkEKGv3u8oH6bgRUANT+EQm7/QD7UAsiAs7yNfyBDOkGf/w9/Av16vJS/54KJQpFAtH/fv9J/YT8AQFOAAL9ugXp/KPznP6xAvH/gf12AwQEjv6+BH0Gq/1r9wf7b/1p+0YCmQdE/Z/xN/8+CsD+gwFxAmb5A/hP/Xb8CPiEA9oE4f/1/aEFoAaD97L9tv2C9Sr1tQGqCRr6q/pkAcn6VQDiDZMFMvqb+30AfAK1AAsGkQKZ/G8BWf6n9Or9kAr/BS0DK/6I/zcCMv+ECkwEwfJm/qgJ8wFl/awE3QZ6/p79bPyr+t/+0QCGAUn/ov4v/9wB4wRvA9MAy/4fAvP7MPcx+uf8iQGo/24HYQHi9pIA2QMOBl4Drf10+mwAKvxK9/oJigeC/WABDQP2+WP3ZwDKBLD/mfYc/nj9Lf4sBxcIOwYY/Ej9EPp499L/Q/0tAeAI/ANL8yv0sAhtBmf9fwDxBHgC6wHJDMf9BfHQ/3AK4gTk9UcA/QUo+d38ZAW8ByMDYgITAz73EfdJADr/mQAjAjMHeP8r+mIF/Psn+CT+Af9R/A0AJgT7+WT+AAB4/BX9zf6GBkkAX/+nARH7t/nR/fIFZf90Aa8Kzfya+XoCqQSj/Tb7agMrAdT74gCYA2/+iQBVBdYIbADq/5MIq/oU9nj8oAIr/1T/GAcm/dj9LQU6AtL7nQPQB6DxTfD1AFkBff33/MsA3QFU/T0CHgU0/Iv4SAMc/unuMf/yCvsBBwLMA8gDZAHm/z0EFf1qBCwITPXA+fcDrgkdAukACgOa+vIFXwWgBXj8zvVwCk0DEvjPAOcE4fq8/LkFPvqf+B4CdgYFAEn1C/zn/msBvAMw/u35k/eUC0MJ0fWT/xwLKgAf9oEF1gCw+WkDqAgHBAT5qQMBCVgA5/2aB58FAvn9AJAGc/6H9RABnwZ4+2EAX/94/KIDVgAk+W/2v/s+ADz8GPuUACIDX/hW+On7n/vTBKYA4ff/9ez+AAE7ABYFTAJpCMn+BPbu/Z/+Uv/xBqgMK/0o/2MH0f0DBecEAAGbAvUBuwJY+aL6QQWvBjL//v71BcQAr//FAjH9hPT2/1oLZfse+VEEmP94+LH/TAUW/44ANAXJ/RT/+/8D+9z+hP98Cj8JhP3//e36Nf0u/jkEfgWMAcsGuwFZ+076GwJqCgwBKvx2A5cEqf52+w78Zf0mAqYAnwO/B4T7Bvxx/ZX1X/7BBugAbv5p+hn3jAKvABD5/AMIB7IAXQIj+zD4jQFQAHD8M/1lByIJXwCEAJj79PQGAAQIaP/L/SkAtwlkBq73L/3k/8P+dQJLBX70ZvKKBtL5xvd2DI8LiQFbBtwHL/xb/awAO/0G+nj7TgB5AY4CxQFBBn3+yP55Ctb7egKLB+v64/mY/dIDKvzpBW8HfPwOAWP8if/rAKX9o/mu/WUE/fyA/ScBhgNQ/6sAxQIb+08BFQTXAFn7tPaK/NX6FP98CaX+R/j+CggMmvUh+a4L9v3I9ZEKXQe/9//5LAXC/Xf0gQngD2X+UPKO/7f/yPC3AqoHPfy++wMHSQTw+OUE3QIQ/lX65veZABH5+vkzAsP/3f2NBSMPaALb/wcJAQBQ+k7/twaC/879uAWFAvYBWv+3ApoAvPsPBawGfwJNAl4D9Pw3+LT/PgZeAg0CsAU+/V/4Cv8aAjv9M/42Abb6k/nL/038iP58CvoKawjd/j34+vuk99T4U/4j/dj+gQgZCtz/dgCYAZ398/+bAJQCpwLqABcAsv2JAn4EMwRHB1YCV/zv9+n3CABQAM79wgHHASUBBQRjAycCOP81/V4DCf69+rT9Av7EAAj2iviMAVEBxf/vBboOsf78+vf8Tfk3AHYI4gVE9kD7iQWSAOz7swPnAbj9UwmeAl/2KvhsBY4AffS0BYESkgc4+qP8V/tT/WwHAwmP/9TzZ/4g/VX23gJiCtQLswObAB//7/7WBdv8g/r2/sv9rQHm/WYBUwcoAp77BfpFBtcEgv8s/235O/7q/Er87gRzCZYD8P87/+X4nABKCtAB2PN/96H/xwAv/pv+qAZ8ApQCFgNM/N0ESg1I+Q7vPP9s+2j/OA73C3z+KvpbApb+0/oWATcPUgKX8cgBgAA2+lMDkgYjA+7+wQREBLL3MPzQAPP4Dv1HBwL9sPhDBPwAPgPQAJ4Etgrq/o7/cQEd+9LwlwFmBk38/AkGBbIEZgDS/7wCZPb3/4YGswYkAIv/0wWG+Pv6uQIvAaQF/QWTAOL2IfbO/fT+egOKBXv9xf94ARX9mwGzBlgHf/0Z+13/mftV9xH3CwVEAqT8GQgbB6gFiwJkAAH9I/sb/zD9P/9T90n4kwPH/p0CIgXcBPQHFwLh/iD6ZPmu+6X6Iv6XAY8ArQEiAVP+pQbIBJf9M/67+hT4C/oT/RgByA1hCW4AkgEn/Hz+rvvR/dkChQOFBzn/jPqf/awAfQKHBCMCnPw4AMcDbAUJ/v7+2Qnb/UL02flG/SX8of9IASj+/AOOCbQHSvYl9RsApPV4+xAFAAMJ/7/5ff4F+VT1/go/DAL4Gf7pCDYCL/4HBjECMvmAAUwDTvpi+IUExAnK/Tj+gwnVAZP7rP9l+Ur/FAnhBS39x/v8/0D9avwF+8X71/gm+Sf+7/2cBQQM4Aad/Mv3gPb39Rf8SAb3Adj1bPwkANf4UgXBEEIBlP9EBIL6+Pc/+ugAtgZGBlQDlQcEAwj1uf6ZBbX5QQCwDs7+9/bT/Bf2Sv8SCLz/fv6UCBsEkvf/+eb9ngHfAKf6oPwC/274+Pkq/qb0f/9sFdAFWPWOALT84fCL/iwGePuC/jUF5wJ/+7n7KwIv+uP7QgUoA6j+zAHaBq39CfyTAzkB/ABYBsf+VfLN+NsEhP5Y+wsGZP5B/NsHnQVj/ED34Pgc+qH9VgLdB04CFfoh+Av1cv7AB7AHhgIZAYr5gfIRAK8GpgIL/3MAAwHL/SQGTQy0AXb6NwCdAcb9LgSRCVEDe/yS+jf+jv2TA9ELHwTx/y4Cmv/29gL6OAHR/UEAfgAuAGn9SfdGA4EDgvad/pUF7vuv+FkGEf9V+JEGFAVPBMz+W/sM/WX8nwAYA24Dgv3/BoMHhQFeCakDof6L/w//4f4RBGUI2P42/3oERPRX+JEFiQH5A5AD7QCo9Y37cQgIAAj4dvRm/Tr6Qvm4BBMCOP6oAdAGIfxn9+ADYgBj+DD+rP2h/gsI3AgQBmr/lf2yBgcE1/x4/w399fqWBX4LSwQsA38D/v3h/RX/OAO0BpEHyQJQ+R37DAMRB+gEWgAi/zv/A/5ZAWICBPz1/6MDmfxJAQcIfgBy/fkBpv91+m0AXAIn/Qf66PvM/yP50gK7DVgB2P3VBpb9pvgdB9YA5fhf/agFewNj+5T9fwBzBlYE2wNL/0f+pQIKAAsBbvpn/wAGoQV8Bq//Fv7+ArQCefqQ/TAInwDz+QcBdv+pAhcEEAFjBKL9pPuXACICvPri+egBYwBY+6n6ZwO+Aor+fgIAATf+BALsAtwC5AOP+dP8mv8I9zIBdQi7BLIG/AbCA4oEwv3C/YEBBfvmAqQEyf9oAVoBhwJkAW8EpAJ4AIL+bv0YAYL+LgIgA+r9ovnGAD4GOvpC+UUCxAID+X8B9gXp92r66AH2AFL19f4ODCcCf/6DAND8ufU9A1QL9Pt1/VUJ9P4Y+AkAYwC1BB4IVwdB+/j0lfyzAC0FAQFyCNYBA/TN+oP6U/9RAKICeQGy+QD8LPmU+yz/dv0vALsB3Pyt/EUApgAm/vj5ZP8JAx0F9gGI+6cB5gAmACgEJwUCBOz/YAFaBBUE5we7Bpb+rQJyAsn8jPw3/ZIBQgCc/LsBcgd0AGICdf1F8WL51v1eA6AAifsL/D791/x7+H4AOPxe+/b5TfbmALj/BQRcAG73YgInBOD9BgGI/+f+2QFZASoCl/9CAsYEtwQzAKb+CwYSAxf/jv8+A/P/l/5kAmf+wvuQ+qT+IwGVAxYB7/65AC77C/wF/MH4W/gvAVEBsPb+AOwGXfzs/KQDVwAw/q/+5AE5/2D3VAE+BK4AJQP1ASL/cv+xB+wG/vqR9wEEHAYHAEoGPgBU/t8HyP4K+XIBfQVaBAz/w/ot+Gf5p/9LAGEARwWrCtYChPsPAPj+LABgAg8C5vuS9m78pgBhABkBFwgZB/wCwgFA/iwAfv+GAFAEIAQN/Hr+kQhG/00DsAXD9y79aAKCAVH8Z/6NBWn8Qv7qAo8B3fyJ/H0FHvnA8zoCmAMc+tn9nAWe/rP5Gf8pAy34V/r5B+wFmACyALQI/QOM/0wC7Pj/+C8AoAXlBNsBJQpHA5T6jwTPAoP99wLuBof+Jvx+COsGnQFNAfwB1QOq+rz3Ov27+Yz+pQKhAZcIRQUBAaX9OPtj/3n7Qvp8AJsAc/uz/a4Cnvzn+/0FGQMw//r9Ov4IA+T7qgJfAyT5lwD7AEX+zvy+AUUK4gO5/E3/gP5H/VUBvfqQ9YP/3wXJAp4DzAXUBeD/6/nI/879l/6lBhX+3/RF+o4H+Qgr/3MFSQgJ/lj+v/9W/CkCFwnX/3z8vPzY+hwCVQDsAXEFpgFCAY/9evek+nABmgJeAPz8Xf6Z/dMDpwLG+E4BJgTqAoIEVwLB+mP43QLeAL38EgRDCbEAbvmyAlYEEAPdBqcCjP/9/lwDCwB/+8gC7v4a+4P/hQZJAGX6dQGm/ej35viqBmkJtATD/7b0Bv0r/TT8CwHm/qX6PvoOAiH+Sf/TBAQKggDc8QEDmAVCALEGTgM/+0L+hwcGAfD8gfqS+/b3gfcbDWUH/QDsBugBhP54+b8EfAX6+dL+h/wo+AD+pwSnAFf70vzO/mIG1wLZALoFyf6G/8QAm/4R/H7/Sgae+QL0XwNdC+AAMv/VBVf7iPRqAU0DEfee/JcJAwdD+fEEyg7d89/3GQs593ruQAWaBdf31f+QBvf/Xvw6B4AJQfl9+nMIz/2+9nAGJgCc9lEExwTJ+/j9wQIg/y76YgR0Ahj2AgDDBMj82P5hAskCQQO+/+n8C/mn9+L9/QRwAsb7jP+RAGUByAIJA/UDHALT/k77bQRS//X3MAWtAwv7QACNB/EFAATX/zX9NAHBAHX/WgCk/yf57PvVAkz7EfxWBq8FZv+0/Nn9w/1j+/f4xfuA+r/3JAPQAdr8TAPtAEv9Vf/xBb8HMQCe+8b++vpd+tQFswSG/b0ACQoQBZj8TwSjBUP8Lfp9AJwALPy/Ak0M/gH7+lYHlAjV/FX4cwFC+pLxFv2eAm0F2ACrBxMKP/3kAuD+Efy7+XP7lAgh/sH7jgLk/if8fv/yByMA2PldCNEGfPv3AOwASv1B/9kBRgGi/IX/JgzwCQf5AACOBo36sv38BNj3f/k2BpL7rP+9CFwKuwrE/P33WPuw/dv+bv4U/fb4B/mSAAT+IfjOApMFtfsA+EYDQghoAhMBivvm+w79//5uAmP5DP2dBRf7CPvvBXEG5gPKA7QDzf1TAV0C5/iNAfMHoAZH/VL3lQLD/az7WgNaA2gB7wKXA3P4t/sVAWj8FQMwAaz4sPziA+gBavtl/ncEhPnP9jAE1/4y9Xj7/QTW/jj4+QXcCdAADwakCQr9+vUw/oQEYv7T/C8Bzv+q+63/KgiMAsQBzAtPAjX4sf4YAJz7+v3SCVEEPvgB/6MAI/74+scBZQU99/T6pgSw/BT5zQXLAa36YQewCFr9x/vQBRL/cfT/+ZX65fgdAUQK7QB9+wgIxAYw/yMAFwYwBBj75Pp990H2+/0fC7kFHvzhBuX7KfkOAy8DkQJ4/pUCG/w0++UB1QNjBLb+ZgB2/0gAmwIS/nH+6QGn/f74rf5eAMP7pgRHD3QDVfcSAAsH0vx8+mUCof9s+L/5cQFY/Q37GAYqCeb/TPosAin/n/ghA5wEKv3u/VgARwDUAz8FawF7/on71fyV/Iv+XAOqBXcBEvxbCHUHRAKcCd8FBfxF+iYCmPkA9T/8mQMZCXb8Ff7PBkz/DPyOAA0E9P8X/ugAQPoP+eIAEwHo/MX6fQNjAzz68v24AEf+rP2XAuMD6QENA7X9/PoJ/ckBXgn1BK3/IgTBAkb3PPfs//EAKAV9AWP9EQL5A5ADowAnAJv9fv18/vr8jvzK/IQB3wFh+nP5XQN1BnD+ffqV/gb5zvqsBDwAZ/+0BNEGN/3N+pf7NPl+/6sARwPuAicDbwasA0j+nf76AeAAWgEsAvoCHAINAfv+/gJwBXMDKAV+ATz8pPgI/sj/Bv6JBXEKowC69yb93f8H/6/7HwBXAwX/4gKRBfL26/AvA2L9xvgJA00C1f4N/kUFTgJMA78Elf/9+yr5sAGpAiIBIQH8AEoAI/1ICHoIHP1aAv4Ehfrx+/UGZAXQ/7T/egDu/MP3h/wpAXT65PsBAfH+tf3r+48E7/+59ioBLfso+WYBtAGP/U38tQJ2AcYDBAAC/ysEcvykBrUEnfZjBLoIJQPQAY8ENwjG/k3/jgVPAdb/AwlJCfj8MPxJ/dgBHgCB/QwFqf1y+60DMARsAEQAywCL/a8A0f1S9xH4vfjE/5oA5/7MA2wD/gS4AaMFsAQs97L7Nfgv9t7/owN0BfAAbANmAvn9cQd1CV4COv0s+3r98Pp7+v4FdApdAecCgAQa+KL57wK3AUr+SwL+AWz8/f5YAYoESwJg/Jf+k/7y+FT84gMp/iv/XAOk+vb6SwSIA/sBaATi/5X7G/8KBYgA0vtiAa8AzPtX/o8DlwMcA7AGCAVu/V//sgba/9fyev9uBwb5YwRNCVj9mgE6CqIDBPRKAQcIB/zt+lz+zgWTAAT+3QITAFP91AQJDMv6VvfWBWD/q/p3AVoEpwPH/yf9Nv6v/Aj8OgW4BCf6CP/iAdv+2Pzf+1b/iv84AqUB5AAz/qb5/f5aArIDCwJ+ALr8e/poBOMAqPndANwCSQB1AW0FaQAA++ABcAEUABAAkwIzAEv2uf2b/z7+mQAaBuQJ3/tA/akATf68AgIEpQGK+MEA4AaW+Xr7bgU1ARH7KgQ2A3r91/+M+1MD0QEC/i4HdP9b+OH+UQirAkL94gDtAOH+dfcN+lv84QDVBmcBw/8p//UGtQhs+8z6NQEm/Nr3MP5O/CP6nAH5BEwEy/+e/4AC/v7L+vn+AQWJ+1n+KAb6/eD+fgRqBFD/IATiAYb5wgC9/mv/c/4q/f8F0QLT/68E6wN9/1cEOASL+q78DP7z+Jj56PrT+/78oANkB0D+QvmJ/wkGHwGJ/6D/7/md+8j/8QX4/zr8AAIF/+ABAABW/fkD8waoA00CgwPjAPICHQWKAtz8Rf8HBUECUAGx/w4Cx/4b+T78Z/3uAEUDbgPQ/w//dAePA333mPwQAJ/3zvdr/Pr91fm5AewEHPvO/9QGkQSO9HL64wRh/FD/FwCvBGsDHQM9BOv6ff1zA0kDgvrR/l0D7/oW/wQElQHHAdsILwTQ+zkARwP8ACv6e/dw+38ADwKj/h7/Ev/i/fcB4QL0AGf/FP52/4r8q/hJALYGEf4g+xwB0v+d/KcAagTt+1v89QGkAO4GJwUb/uP8W/6SA4sFeATCBKwJCALD9jr8MgCcAkYFnARpAXX82/y5ArEBDf4sAuL/YPzD+VX7Q/9I+XX8HQLV/xQA7QA2/On4V/g4/pP/KviX/wcASf0dAFMCSf+U+H0HRwnr/zf/KgEgBoX94feP/VwDpwTcB7sKBAGS/KcE3gBK+mICIAmlB4sAmfnA+P8AnQNUAe0A4v/8ADn4tPZR+1r6S/pOARoHLP92/Yf+FPxO+YQBIgdh+8P6N/1j/KH5Q/fQAUoG6wNrCG0Gtf8yANICA/zr+6QFzP9GAc0HtARDABEA4QTrAcMBZv4f/Wf+jfxQAGT/R/2OAmkJMQPp/+v+9fub/fL3/vcZALwB7fu+/xYBNP0b/uj+TQTgAKQBpQWo/wz8H/+sAuj9UP5nBPsDr/++/wD/Wvjg/vIGXQNvA+wDhQNL/S7+CAeY/PD58f/P/5/+lfwYBbkAvfklAbwDqvsB9Hb93AMYAWIBfgPhATf/cQBR+yP6mP/uBLb9p/WEAE4E3AbhBIn+iP64+4QBJgGH+8X+cAeSBuT+SAN6/4v7OP8pAA4Aef++ArIAZ/4A/zoDfAW+/4cCoQS9+4z6HAWECFgEDwLU+8H5AQCrAjwDKACw/mYCfgDnAPMBxv/qAvMFZwCp/XIDIwNd/1H8pfmY+3r/JgAb/jD+XPo8+3YGqAd7AIgArAM1/vL5Dvwu/XD9Ivw8/K38xf8eAl8EnQXC/dn/BP/3+8sC6vv4+cYCk/+t+TMFUwvQ/Mv9XAbv/hT4E/3N/5n82v9dBqQGKwBuAbEF+//2/MwBqABd/f4D1P7/9yr/rP1A/N0A4gXzA2/+pARiA7D9lwFn/gP4c/1BAbT9BAAWAFsArwQQBJADH/75/OUDyAJ3+tH64QLBAkUI9QYe/uQElQPQ+Y73Rvoh/8ECggJBBKoF9wD2/Ej/OAHc+sEAyQQ5/GP9wP13/eD8jv2AA0YFDP27+bcBOf9S+YL+BwHj/gYHPwcT/5f8UPyI/R/6iAJuBcD9awD7/4v+jQAKA/gEqgWZ/zABagTa+2YAAQXq/Tb6k/7t/jD9rwDx+xn+awEd/V4E9AMK+u/93wKV98TuVPtIAhv/+AQrBpL/6/x7AkL+T/ZL/Br/bQAzAGUCigasAXsIbhFMCTb/0gKyAZf5GQFPAKb8fgOiBsUEBwD8AzkEDwVOBXT/tQD7/fH9vfrX9HT5Uf2K/Mn9UgIM/RL43P05AVH9dft5+1P5qwCMAUH5Kv7nAeIAzQLtBFACe/4IBHEAiPvC/Ir+yArRBrb8oQVbCP4CdAcsCFQBfgDnANX75Pgi++368wBwBP4BRgTQBMf/efjn9n/16/qg/Gr8AwMe/1T7Uv4IAs77H/01Adr6Lfis9xUDrAdeAvsBwgNvCKEDfAFlB1wCYwABBlQDkv3ZANEHsQGh/mb/4QD2BBcGHQzwBE8A1QGZ/q/5sfq1AmD3ifcbAhn+AvvyAIIEAv2U/M37xf1b/xr91wFr+Qf4WQHX/Bj9ZgFDAKT/KAKYAYv91QH4//H7IQIOCKYH+f9S/k8B0gYHCZgC6/1g/P/7evvL/fH+dQKqBoADKADq/8MFugUO/YD37Pf3/ib9+/xhAY/6P/rU/xMAQ/5FAnX/t/jk/4X7pPiHBuAJVwJ5Ax0GnQE4AOYAdgPH+J3y1wRzCa79BAJODoQJ8QULCdkFLP+v/sMDpP4S+ZsAEwKL+v//rwV2/kL+6gIY/Y35hfvG/9MAffw8BSICw/UU/XUBBfc79S0AQ/1T+e/9Mf44+oz6KAJlAwAAdQPODIEGZ/4GAjAADPwD+wMAOP8V/64GgQK3/8YIaAy+BAEAsgW1AdH5wf2P/4n7RP1HBNsA9v6/APoCLQEQ9XH8YwKb/fH/y/0i/Bf8Ev4ZAJgBlwPVA8gAL/6NAAMApf58/2X6Yvh7/wH/OAL1DN0ILAJmAn3/CQKKBtABuv52/dH+vPvS+U0DrgSFB6gIjf7x+uD+nwJGBLoCkPpS+of/svfx+M8C0wB8BHoE+Pp3/h//MvytAAf+//eA/PMDAP5M/B4JYArhAf/+Qf6a/yv+j/oA/48AgP2BAH8ChAKvA8YE6wODAt8AVv9S/238ufhq+Tn+XQAmAFgBQQS6BGf96P01A5EApPw0+939qvlv914AdQLz/X7+mQLe/xn/4gPVAUEAY/wL+GH6j/3LA38E+AGmAGD/XgFFBLIHigOeADgBUv4g/H35cwG1BXn9ogE5B+EDXAXhAjH7Rfwl/oUAsAbKAfj7bgHyAR3+owDUAz0E+ABx+hT6iP1f/kUAzwIRBJED4ALQAeUBvAAz/EX6E/ko/YYBFQEEATT7IvzeA2gDCwTrBPAA4f3+/Hz7xPng/9cBX/zj/yEB+P6bAI7/I/8IAaICHQH++hL4Nv3X/4b4xPq4BZoDawTgBiL/tfzfAA3/A/b3+Sv/3/tC/lIA7wPEBVUJ+QmhAfD+cAB+/zD6c/qd/W79pv5gA2MF0ACFAT4DIAQKA+z+SAAB/+T8k/46AdwCAgGY/6j9VwBmBtoCNP/t/mb8QP4Y/xv9DQH0BD8ApgK9BW/+DgNpBCH7aPn7+80BuwBD+9b9zQP4/9z63gUqBWX9uwNxAxP8TPiz/8UBvftw/gj/aPzM+pz9rAHKAugD9wYIBHv8WwNoATb5NwAxAlD+cACDAicAggOKAlD/LgKY/tn85P0V/sQBpAGE/j4AaP8FAC4C//uC//f/Avxz/8/7qQEGBuP/m/3Y/OkA4QAz/y/8Rvx6A9QFIgUH/7b+UP7g+ID9WP4aACcIWQV6/jL+IQBYA40CPP2O/ef/aP48AZIBPP3pBcEL2wOn/00B4Pzs9ib9GAIr/zD/3wLCA3EBnPrI+UUDggRCAQMBrACo/Ob/8QK/+0H5oPkOAewAHvpr/fEA6QEOA/4FSwD9+/D/b/4O+iX8cgPZAvz+VQANALv8nQGrAmT80v7vAl4Cu/0s/tH+F/x1Af4E3QH/ANcE0gIj+i/5aAB+Auf9gPuc9mLzHv7ICPIHZQWBBZIDgAD/+TnyXPk4AzoBnf7w/CEBGweDBdMGpQXN//8Buf1J86/21f5MAr4FZQp2CVAEvwEzAvj+1Pji/Bz7afMF+RAAHP4d/lAEZQqtCZf/SfyX/qb+8vqt93H6z/v7/Pv7pQBnA6oBLQdUAqj46/9aB+H/3vup+2L/XwEq/0UB9QEzB74GZABZ+/r9jAK5/O38nf/n/+j9l/3EBfQGSgLLA4kAkP6mAQL9SPsC//z+qfwJ/+39/P8OCAcCeP6XA9ICiv8PAD39LPqs/GkAowLCAP0C3ARQAF78PwFiA9oAawLv/+79MwAJAmoAuQMsBmgFWgP5AIUDMQKu/yT8af+Z/3H9NASmAA/8JQGiCGIGsAHfAs0AVv2c+qP54ftB/ZD8P/8ABHMEfwGtBY8CKv0W/7n6Qv0C/jv8nv6u/ywAXwL3B0QFzAGaAs8BlP5V/Av9IwCTBPwEXwNuArIEEQOq/5oB3gFZ/xb8N/4nAQb7D/xJCcIFLvjN/dYCvPuqAJQFPv+S+4z5JvrJ+5T5Dv0JBDf+hvqnA3wHKQQDBRoDyfkg+sX7e/gD+mb8aAAHByIKQAnDCeQBUPnx/74AUfi++s0AGAOTA2v+Fv+eB90GFQPGAqz6Uvj//jH/wfwE/PYAiAUCAnL9rwEDA3v/OgDUAIYAVP2uAywCA/b9/PcBIf5PAmsIGAHX+xwBhf5e/cEA3AT+A8b41/xeBND7bf6XB2IDFfpU/oEGaf+Z/4kI1AD/9PP6QgF4++r7sQO7BxUFlQILBt0D2vwK/kT9zPUl+a0B5f3v/HEEugPaAboDfQGF/Hr8Kf1F/CD8gPrf/ZsCQAOIAEX+Uf4R/ob/Bv0m+4r+bgPPB0cErvxF/y4GAwDD+zMChQU8BPcAQv5o+dv9cgouBcL8EQI+AqL9CACRBJAGDwNQAccB8flP+IMChQGF+S8BNQWS/UYASAejA8b4Ofdo//T/1fib/QgCSvooAbcI+P/S/jAHRAIW9hb5q/2u/McA6gAW/5MCUQXPBhwDIQDqAoUFWgFS+k7+EgB5/rgBRQSdBuQD9P2UAMYC3P8HAIP+9P9R/0n9Kv0M+40BIgRd/q7+GwIQ+u36nQNW+WL3v/5bANv/gv1gAXwDsPwy/lAFUgB0/doDdQLe/JQBqQQpAbgAQQTPBSkCDgWAAzf+qgI6AxcB4QBrAMUA+wA5AZICNQEr/mQA9v/K+2j+If2e9Uv69AEf/pr7/P9YAE/7gPut/h37+fl4AKoA1/kW+bEA6wCx+rAAKgV4/S//+ga+AnX9/gK6BeEBD/5E+ykCjQQRAD4F0gaq/8n9VANOAJP8yAIpATL9Lv9l/ar7nAC3AX/9n/0j/AH6GPsX+Zr9KQGg/fkBhAGE+Uf7FQCD+az31f6j/+j9hf1K/j78w/23AMr/fAE7BSACPPv4/t/9D/1tB00J/v1U+HEAyP8k+2kB9wUiAQ8BJAlaBfX7agD0BYn+FfxgAYgAePxx/VAAmf69ANsF6wIw/+r+uvpN+VT8/v/iA3sCaf/c/Ln5qftRAC3/MwD6A3f/f/8vAkr89v+BBJr/0P5z/Mz+kQOz/lv8UgJICPkHaQRQAMz8+Prf+4z+C/87/+wEewUO++j3Fv44BAEH+wLc/Bn8XP2o/dL9Ovx2/V/8Sv0nBNL/1PzGAiT/xfo/ALoDm/39/AsDR/7e+kMBNwfhBPn/pAJpAVf/pANzBED9m/nZA7QGNv+PBQMIl/z7/osIzAQu/rUCLwJs+z/9pf7r/6P+jgCCB2MDw/27AgUG8f2z/okAIfbW+EoCagF8/44EewaLAPMBIQhWBuv+Cf0g/17//P7l/sgCUAJeAtQIfAigBlwHSwYvATP8hP3v/pYBOQN6/Dn88QP7BE0E6wU2Bh4Bcv15+TP2avul+kX9QQGs+n37swKMA+j/o//q/jz7S/sl/fj7KvuN/u0B5v+i/2IETwKf/rkEdwWQ/cT/BghzBNH8VwOlBYQA4gS9Ba4C8gH0BIIFVwGO/U/96f6B+c7/mAQn/eMCSAUj/pYA2wOz/Pv0Q/eI+b71PvnQ/yQB7AD0/y0ArAMtAxv/zgJe/Zz3tv6NAWcC4gMjBC8C6gKOAZEEhwqAAR3+gwK3/uT+tAKV/nj7BQAbAm/7j//dCF7/Gfve/9D+FPuR91j5I/vL8270JATMBjf/ngPQB6b8NftEA5r+wPhI+JL6EP3L/x3/9QLzCXAGrwRdBRQBI/4UAKP/kQAX/xf7NwB7AiUCrANlAxQBXQBQAjP/Zft1/1wB1fo9+Uz+2wAdAE8AsAFG/5f6K/8CBB39FvzgAKr7dPZZ/Z0CVQPnAsMBgAJt/9UALwJkAI8DlwOM+4X4KQDuAcL/O//BAcgCyv60A7sGuf0l/F0Chv6w+A/9ZgRM/9r1BP5QBRn/RP5MBY8E6PxI/PD9Lfyx+6D/JQK1/iACQwdzABMADAeTAZX7Pf6E/x0ArQGg/4f8Jf+WBhwHG/9I/6sDFQG3/kj6l/n+/Mj8pP8BAd7+qP7G/kr+/wCWAOL90ADC+9X4jP7P/Bv5MP4IBl0FdAKwAd0B8AFn/zf9uvog/tED1f4x/t8D+gKyA/EGaAgNBbEBPwTJA7n9hP1PAc/8f/2+AykD+QHRAnoB5v+XAw4F+gBZ/x8AkPsH+Dj6o/zu/DAAVAR3AHQBQwOhAvcAPvzS+6/6Kv4Z/+0A/QP6/3QF+wWP/uwANgWyAyr/A/wo/osCMgJEAaEFYwM++/f9KAB3/Zb8xf/IBFMAl/wRAfMCtf4Y/tP+Bvzs+vv77wAvAX78DwEKBpv+nvnm//cFJQJ5/Pf/LwCi/bUD/wOX++D8/wfRB2/8pwDyB1f+cv6HBvAAvP2LCIoHsvrx+5IDlAFO/BACLQNe/PL+wgO7Afj4fPvVAd/8Vf1SA/cCAP4H/lL8gfnv/en+/gDmA9D9OPwxAC4DugS4AU3/Sf6O/5/9DPqU/TwDHwQnALwEggmPA7/88vz7/hT81QTQCjcA6fnm/Tz+ZPnc/7gFugHg/nT/DP7s/T0FhQVk/fT7Z/9Z/NX7RAOmBO3+jP1YAocBAf98/2r8X/qN/R8B6QGkBA4H0ANV/+P+9f4U/ggA1AEZ/+P7jf20Ao8E4gLtBUgFDv3B+54B+gSjAZX+b/8v/3j9Qv8TAwcAOf4/A5oA0PxRAZEBz/2q/oEAMP8x/kkCSwS1/o754/t/AH4CPgSeAaL9lv0j/5kAqvw3+pcApgMRAd4BvQPxAu3/kv6VAf0AtP25/mX+EveB9zwDxwVaAn0ENwbj/oz4mP0TAHb88/5BA3P+ufvhAeABBvrl+uMEBwZkALr9vP2J/vn/oQEXADL9mv5h/z36yvuuBToFdv/4BHAESfpA+20BM/6G+6L/2f9OADz+8P4KBAoDQAQ2A+n9XPvb/n79uvlk/Wf+SwAuAhwBdf/NAqcGNgSqAeb+qfw6/Cv8Gfrr/oUD0gAsArACBAGvARQCPAAdAN/+SPwl/aYArwJyAV7/af71Af//w/10A4v/xfaG/NcFdQA2/r4DNQC2/EwAwwKCASIA2AL/AED6p/uD/sn8ff4sA+kBKv/GAUsCZ/9O/woDx/4u+dX/ugD6+7b//wEF/0b+vPzL/CX/t/zzABsHiwBH/pkFFwUM/Yz9aAEs/fn5Yv6BAff8Wf5wBeUFYAI7Bc0Fk/gi95EB1AAU/lkDeQEh+gH+sgDB/ef9DQIGAwv+VvxV/b75dvt4A1sBDvwp+zYBVgGt+/n/jwEvAS4C7gS/Agr+bP4k/TX/SP6d/nAFwQWMAvsBhgHlAygFfgGOACgAMv+t+0j62f43/9v9pwE5Bb//DfyJ/TL6AfhE+d77Vv+u/1v85PlP/bYAM/5n/iX//fqH+yMAaAEd/oj8cP8zAcMBGAUQBycBWf8TA1EA0/8wBVQEO/49AU0DRf6MAJ8EzgQ4AjYB5wBv/4z/i/0o/RP/1gBTAdoArv8P+5H56f3WAL8A0P+P/7b+NPp7/HsBdv6w/vUAY/3e+mYARgONAFMDWwaMBFwBlv8tATEEAAFK/jgC2f9QAS0GXgDyAHYHBgehAT0BGwUsAoX/0v4N/7n9Jfwu/cr8bP7QALMFXAJH+/H/3f0a8s31TgPhAmcDGALr+icAlAMIAxcD5/97/iD+GPr/9wb/jQUUCDsHqQLdAvwFUgRAAfQC+QRIAvkAWgD3+8H97QDs+2r7XwT+B1gDVgKoACj+XP2m/JwAxwBV/6z+dvrq9S36zQNoAY7/BAJS/6X8IvuS+4X+agMTB7ADl//2AP4AKwJFBBkF+AO2BNMGPf8U/YgBTwFk/lsAQgUIBU0HrQbzBLQDDAK7Avf+kvzQ/cn7NfiX+1UAjgCKAg4DFP9aAswGxv3L9zb+twBA+yD/HgQQ/oP+MQNo/9f69gFvCfMFr/+m/C8B9ACf/wYF4QAg/20GUQRw/nb/XQF8BCEFXPw/+bX7v/uE/gYABwEgAiMBowEaAV/+aP+o/gz9Mv47+/D7P//m/xYDJQSIAIAA+wA1/9v+yv7TAB0DUATUAjcD0QM0ARsATP9QAhAAKvwR/30CUATBAqcCkAEbAM4ASf/X/Xf9LP7l/7P/if4b/7b/RwFmAmwALv4s/g/6rve2AKAGVQQgAn0AUf+B/cj+5QHy/zACJARz/yz81fsYAKwCAAFM/00BngDB/Ar/3P15/JwA4QNcBQIB2Pu5/Fv97/zT/jQAIvx/+V7/RwCQ/V0DVwl/A6D8Sv5V/ln87v4+A9/++fli/s0CMgMAApEErgPZ/M/8eAJVALv7lv/AAXoAUAAuAMsA1/6++vz8S/52/OQANgBp+jf8U//R/9wAyAIJA2j95vyIAZP+H/3IAf7+N/p1AaADTv16/joCFQI3/eb9vAYBBt3+p/6i/2v/CgFYAYD/mf+zArADuP18+oT/5v/E/pH9Xfo0/3gEyv8n/P3+fQEuB9wF1P+O/f34L/iM+O36GAEgBL0B0wCKAnX/oP4NARQDHQFP/pP/2/08+rn8vQDv/bL+IAOAAAP8Jf1fAfT/GwAMBL4AxvsW/KH8w/q0+1f+Yv/7/DT9GAX7BaP/dfuO/O/8h/2JARgBYgGvALH/if/V/tr/rgG5Apb96f1R/kT8lf8W/0T/NAHA/1f8nvyk/u4BCgBt+yMBNgLT/Rj9qv5H/hn9vv4d/Qj+/f6gAPEBw/4BAJ4ErwfhApT+gf9i/27/m/6E/gP+Hv9yAbv/sf30AWcGSgOQAFMCBQJk/lf+hf7I+wP7FP9HAhr/Z/2h/uX+T/3aAAIFuQBp/LP/1gAj/L78+P9LBBwEI/9K/Wb/ZwMEAc7+Gf7S/fb+PgAJ/sL8KATgBYACXgEcAkcCegGF/eD3u/jO/AQAXv/IACcD6QMXBE4E5wMJ/nT6Hf1C/zf6xfu4Aw8ClwGvBlEFigCZAuABVv2f+2b8Pf2R/m8BpwB2AQ0DOgBg/Tj7E/xzAn0DbP7K/Sb+kv1i/Kn9SAFCAioA/wDkAir/nwAYA8L/qwDqAukAhgGZAlACQAU7BO0EyAYlASD/2PxH+bMAGwWU/8z+agLUBHYDWQEKBHUB+/qt/In94/dm+mgD8gDu+sv+/wM0AWP/vwJwA1UBjP2l+y/6hPrC/58DtgMnBZ8I2AJm/Y3+agA5BHgCMAC1/TD6kgB1CEoDDgB1Bo8E8AB3AMv+CwGiAZf/UwH/ABUAeAVGBW8ASQGxAhkCtgOTBPMAYv3i/KcA6gNfA5UD0QJDAVIDQwSEBG8EQf+F/EL80PnO+wAABAL6AJH/KwJqBGwEkQMFA47/efwT/Kr5Q/yA/vMAcwWuBHwDKwN8Ag3/OP2d/d7+GABs/iwBrwMrAXAAFwP6AHr91/8n/7n88f5I/nD65f2xAhkCm/8E/dUAewM3ADMDiAWBAYABzgMF/dD1iftMAcD/TP8dBG4ILwrMCVIHdAOA+jP6gP+A/D78pgHTALP7sf5nAt8CiAIIAVQABv2T+oD9kP5G/6kDBALi/Un9VgHMATH8T//BAqIAKQG8Ann/s/2FAIICYgKiAQAGOwlKBhwBxgMCBxwBK/9n/wH+vv33/QL/bgHUBA4GTANcAVABaQBR/lb8P/tE9z/5ZABN/if5dP+LBpoB5PsK/GD8jvo3/wUBqv63/3f9Uf5w/0MAbQC5AuEGdQOM/8kATAMN/l7/fAduArL7fQD9Arr9xAELB1IF4AWsBRsAiPmg+Jj+qP/9/JgAwf6J+1f97/6l/23/Gf4b/n0ABf7m/Zr/eAD2AX3+1vxh/WL9wf4AAB38cf2MAukBDwRIBIgEZAZDAZD9wv7r/WgAjQE+AJcErwGZ+/T8a/8dATQDSwIL/8r9N/43AMr8ZfuwAScCyf4D/nT81voi/VL8S/q5/wQDMf/7/Rj/V/8NAUoCMgHO/kH/m/6p/hIARgBPAsgADP+o/qcBfgMEAeQAcAEIA6cBigBMATMC6AAy/Cb9xv3S+gr8vPy2+0j/7gAHADz/t/wj/Xr9T/wZ/fL9NwCyAiT+6PsoAOf+6f/1Azv/S/2iAfH+Vvw1/5oC2AUZCPgHDgVB/+L9MQMPAfr9iwKABAkBQP/A/uD5IvtFAh4Ci/6L/5D/jPw4/Z/+4f1y/+8C2gCh+a/2bfk+9xH3bf/T/578E/9U/8b6LP8/BoEBfgBxBc0Cx/tx+0P9zf76AIQCUQLr/j0EIQsUBaL/Hwd4B1H+4gGpAfD7rwD+Acj8ePzBABwBgfw6+oD8Uv32+if8+/0M+vz6/v/2+zj65QEaAiD5Evfk+iX5ZPlvAP7/L/2gAsYDcf/rAM0Hmgm1AzAB1wMSAHD6EgIXCRgFLANpAiUAaQHiBMsDUgCI/tH+5/6D+5z9wAJ9ANn6IPuF/pX9z/oY+/79tfpW9075Kfnn+IX9ZgN0AokAJwFfAgb+KvvMAugC3/z7/ZwBuP9GAFQEXAX9BnsE0AGyA5AEHwV/Bbz9AfvAAysDvf7p/lgAbAB2/T7+HALYAcQAHwGF/YT3APfs/Cv+t/v8/WQAKv/EALUCOf7E/Ar+d/sM++b/7ABQAKECDgOcAk0AwQFOBf0Dnv9O/Aj+tv+f//0A+gSdB8UEGwEcATv+CfpM/4oD0v5k/aYCWgLX+ov6WgBa/5b7hv2qAHcAlv+uAX8BCv6O/Z3//ACS/1n9TP7uAPP+tv00BFYF+//8/yYCNv8L+5f9qgK+BFgGQgX/AEn+s/8c/7z5gvnf/ncB5wFWA+wEHQS/A7AFtgLe/Vz/JgLI/vn5IPn4+9n/KgByA9wDNf2b/UEDtAMMAgMC4/6X/Q/+/vzE+nn5ZfzP/H/97wD8AuUAuABBBIwAfPws/vj/5/81AC8C+gFMAAgBSAOXBPYALf1jAGcCIgBS/+MAzAFSA20GMAZjAXgA/wUGAhL6cPvbAB8B1QDDAlD7rveO/n0ASPv//V0ESAFN/v3+MwFg/oj8p/9Y/fr6Qf5O/vb6QQBOA+8AWwTYCB8G4/4W/U//hwEvBB8H8wS+/7wBNwVDAmD/zwI1BEsAJ/5y/+sAxAPrBXwE0AFe/g0A6gGF/qf9r/5t/f/9G/+t+8n6+P4r/3X99f6dAvsD+f8K/7v/Q/1v/eQBUQKe/WH/3wGP/oj8LAK5BvsDMwLGAYABsf7L/YYAJgIYAnkBngGn/1z/twFGBXUD1P6y/sz9uv4K/hv7bv7SAJP+TwJ5BrICPwIJA8b+2PvX+c/5w/8zBCcB6v4DA00EhAB7/wkDBgON/gr+Iv5F/SL79f7yBxwFGgLNBRUCtvyA/pb/LQGbAl8Apf4+/M35x/mU/bUAKALPAfP/UwGAAf4ALgO1Auv7dfjw+xP88Pfc+XMAywACAt0E3QXdAzwAfAGOAar+Z/wfALYEtwIJAXwBaQHeAlYFyAE1/ysCPgFn/R39/AApAj8CsQQOAo39jAAIA0X+8/xrADEAivq190X8AP7L+579hf/1/RkCzgYHAuL8kf5NAsYAZf5r/iT9ivwD/5QBjQA/AusFfgWgAp0BVgWCA1v9OP2lAQ4DhQCQAFMCqQGeABcDfAEX/eH+Y/+b+rL4KP8QAyL8APr/AN//cPzjAuwEXP96/m0Awf29+9AAnAOl/Hr56/4AAZX/4wCZAw0EFAajBxEE+P96AFQCAQCnAC4Cqv5p/RH/rv8W/nf/CgXeBUMAxP3MAXcDbwLkAcj9Tfhd+fv/AgORAhABs/4o/qT8Af3FAg0G8QMnAGH87vvj/1kBqQGDBO8E0QGJAWIBKv4r/8sDNANF/yD/NP1M+7T72P6xBT0FcgUfBgsB1v9+/Rb69Puf/2b+efwo/bX94wCGA9UB+P/S/n8B9AQE/qf68f+o/mf93gGmAZb9twBDBXECf/yy/ygFHwDg/tQB4v4B/M8AVgW3AhkAGQKCBZgFWwN4/1L7yfqb/tD//P6d/57/RABa/1P+lP4TAJkEvAYV/gb2QfmE/aP93ftA/l/+zvtH/qAAJwElAev/JP+9/zX+EADIAWz/Ff2r/yIFAAXqBjkGDABd/CT9Dv6qAO4ECgP0AgUCMgEcAVD/vwGnBN4AA/u3/nH8/vRC9j/70/0a/iAA4/+I/aD6r/1vAC38Iv3a/2f6zPVX98D68wAAA44BQwIKAuwAdQCDAKEATwKlAar+efzz/c0BCQNzAjMDfwF5/icC0wNKAgsAYv6w/Sr5sPgi/SH/b/7nAS8CqP1m/rb+df6K/gj+G/zT+Gz5tfv2+9j/tQUbBToAh/6cAGj+e/yE/Br7Iv38/qv90/w/AEAGSAhfBFoAav7+/Fz9Xv3F+VL52fyr/PT86v7G/+T/7QElBAcA7fwKAIkA6PwD/nj+Ovq+91j5cf0l/Z78CwSFCEICvwGEBYACXADa/qD8Mfsv+8f9JgBoAJACNgLS/ef/cAKF/y7/zgPVAEj81QLhBC7/sf7lAcn9hvjI/BgDagFl/TgCngYFAkIAPAOo/zj/bAVvA0n8YP6/BaADHQCtATUBqf3D/mMC1P5o/q8DSQYvAlH/WAQ5BHL/owEhBJT+of0tAOf8IvxV//0CkAM5AjwD1QPtAJ8C3gZOA0j//////4/+ogCqAZ7/NQJkBhAD3/7aBGEIvwX3AbX+HQF6AdYBSwQ6Adf/VQRJBDsCrgQ3BXwDAgEB/mL9HwB5AuoAPgFlBV4GDQR+BJ8DrwDm/i3+wgB+A3UCzPwf/IsAzgEfBLYGtQbSAxUDEgQOAhQBiQOCBGP/efu8/2UEHwSMBJwFBwXEA0ADqAZLBcz+l/0CAR4DTAIWBPgGHwZHA0oDtP/a+X79YQMGBPz96fn7/rUC8//2/yMDCANUBcwEY/3x+rn9cf2i++P5evgt/VUCvAF5AcUCcwK0A9wEUQAG/jQAzf40+nT5RACDATX/1QT8BSQALP41AzkChfrj/cMC/f6s/ckA+P3X+3X/Rv+d/QH+6wEdAdP3O/XW+Rv7Xv/NAm/98f4wBN8CgwCe/iX8vfte/uT96PmA+Sb+FgBt/3sBpANxA24EjgEm/TX+L/3L/Gr91vwn/OT7/P24/Hn6jfzO/uL9qv89Afr91vpF/N7+IPvW+TH9mP3P+Wz5gv01/kb/SQEE/hj8qgCgAtH/+PyO/bD/ZQDh/oP9FwHnAxMDh/8H/av8G/7q/+r9dP3y/dP71/tO/lb92v1tAHz/pv6x/m/9Qvpc+lT9fv55+3z7Of2v/Of9Tf3j/Nr9PAPqBEb+Yv3FAPsAWwA5AUYBBwH1/if+XP2n/Wj/yPyJ+0T9vf+B/3YAZgOIA58BqQBjAHH+O/0/+935v/gb/cUBxv+s/5j/ZgECBFAEzwCP/ej/af5o+x8BPgebA2H/3gCQAU390fw/AbgAV/2k/bAA5v5n/8YE7AMQAA0AfQLNAlIB5Pz2+Tv+hACH/Ar7Uf94Aoz/0/yJAM8CZADEAgoFBv9X/VECdAMjArYAaP0e/bUBJwDk/RsB0gC8AD8ChgEDAUQDAARtAYAAX/z8+g8AyQIvA0H/vPzP/gr/f/1Y/nX/L/0tAFIE5gG5/uwBTAXh/xX8pf7+AHUCbgT/Avj/nwC5AQUAkv0OAHwBZv9hANMCAAMjA1cFcwQOAMP/iwLS/+D51Pjk/dD/WgCEAoQAjwB4AjcDqgKSAewC3wOrAN78fP6O/bn7BAENAxT/+wDDBboF5QOb/iP8YPsx+ycAoQDq/a7+lwBEARwDcgN7ATQC+wAx/bj7Wv6MAeL/+P4cAfb/DAGcBmQEAgAtAzwGOgNMAFYDLQFX/JD+bABB/vb/9Qa+BO7+cAEIA6H+qfyJ/rv8pPzSALIE/gLWASoGrAPw/2UC2gBL/In/xgCj+fH6IANiAyIAfALlBXcEOwLqBt0F8/zU/Yz/Pfum+qL9Pv/Q/sL+k/9PAckCEweWCG7/A/yHAFn/nv9LAwEC9P7M/q7/0P9Y/1gBHgW/AVr6A/s8AbcBlv9CArEDhwCSAK8Bov+0//j+Fv6Y/Zr6j/mH+4r8sPqq/UgB6gNBBisDVAGBASIAYf5JAXUAMPuS/iYBwv15/bUBNAbkCBQFRwByASoBYQIlAygAZP1l/dkAYv4F+zb9af91AAH/iPwv+4/91v+VAOT+Wfrj/G3+fftP/pP/WPz//qUC5f7O/M3/kQGvAKAAvQKRAkP//wEBBhwDlAL4BQwHlQIg/un9vf1V/6MDiQYXAVz+SQOTAmsAev/Z/Qv9hPqQ+UL94wA4AUMAIP78/cAA9f++/lb+svqz+JD8CwFbAmwEOQXR/yn6Yv3+AdMBoQMXBfMC3P/kAOECKP/h/awBowFiAJ8DcwZ7BM8BxANAA+H+4f52AAD+2fkv+8v/NQLHARoE1AUWANX8EfsE+5P+kv8qAYQBff6z/eEAJAGc/Y/8T/5r/sj8wvx3/qIAuf9T/ev9Hf+T//MARQFv/uL+DALeAUf/bAC1ARH+y/0XAKX/tP7DAVsC8f1vAbcHOAb9AXwEEQbX/ov8BP/7/ZD7Jf38/eb4Evu9BJ8FEQCg/zMAgf7u/Qn9F/uc+4j8RPwe+zH6aP2P/p39cv8OAIv/twEyBAMCCQCJAN0Ad/4w/oED1AKs/f//QQW9BE8CugKMAQD9yvxvAEcAAf+3AVYEsgFt/3gArQEyADf+SP/r/mj+7/7q/YX8Wf5WAjEEPgRXApX/y/11AfwDHQDiANAD+v9x+0P9LwL6AfIAggRZA3P+ZP7cAOj/MP3mABoDMP9X/l/+5f1L/Qn+EgCv/cX9pgDO/zL/NgDR/+r+kgGzAdr+lP9hAF//nPz7/GQCOQPeANoB/QBwAM8DiAZYBiwD0v/+/i7+Yf1C/4v/JQHLAiwBcwH2AYAA0v6z/+T+PP1Z/j7/Gv8N/igAjwBN/5T/yv0h/Kn84Pxp/e7/vgEgAnv/gf4oABABuQH1AH4BewDR/6QAAv8K/aH/uQKhAmgCkf9v/yUDQwQmA9EBhwCSACwAd/y0+pz+agNUA3YB9f8s/8L+JP+Z/6j9Cv7K/9X/Rf2F/tYCpAEX/47/XgGD/tn7t/u/+ur8MgJ/A0wAUgE4Aq/95vtNAWsCSv+TAB8CRwEp/4sAFAAM/gIA4wJWA73/3gClAjIBiABs//j/CwBy/ZD73/5UAoQBUAMxBc8Bp/6w/TP9FvxA+vH7Gf7W/4oDpwT2At8ARP+J/V39T/55/O/7Pv+MAWH/ov5C/wv/rQHrAF7+1P5q/4kA3wHeAbkBeAKfAFsAkwCD/V3/SwKNAEz/yf4q/58AM/6h/60FNwQWALb/jgD0ADMBdgCm/mP8uPvW/Ez8YP0NAYMDiQG8AK4CTAH4/4wAOP9r/J79YP/8/ar+8gHZAJf9gAD/AuoBegI0AZT8cfskAOoBGgAqAb8DXwJ5AIgBFwEl/lz+6QAC/5394f/3/rf8Ef2C/4sBeAKUAywD9/8o/D778/uX/NT9Uv7r/Ej7DfxX/0QBzgDPArUDdP49/bj/wPy2+q/9OADP/h4A7gXrA9n/xAP7BA0AUf48AdwBIQC//yb/iP9bArMDwgERApwDiAAM/VL8Y/zM/Hz8ufu++Rf6RwCaAl4AKQGoAWT/jvy4/AH+uvtS+pH7x/uK/jcDdQMmAw8FugSYA8MDYgJ7AFEAHgHT/+z+JwIIAzsCzAFzAbMEOgXIAyEEVAP3AbT+f/tf/Mv97fw+/oX/qfw6/Gb+jv10/YoAhAGP/uT8ofx7+//7kf0v/on+iv+f/nL9CQGAA9MCtQLnAg0Cov7R/dP/t//+ANMD8QJKAaIDmAXvA78D0AO1AboA3v/z/Q/+yf37+0b+MwHlAAAABALYAT/+vf+EAe7/ofzZ/NT+P/wK/C3+Bv76/YkBiwNsAtECfwNTA4QAMP51/ar9ogCsAskAxv9RAOb/lwNtBkoB8v3vAHcAWv2m/Yz/NwEBBOcGnwO8/av9JQF9AO77k/xHApMEdwKv/0n8V/q+/X4BawE3AXwBXAP/As/9fvvh/XL/wP11/KL7svwR//kAdQRjBNECIgPlA54Ac/rh+i3+HAB1AX0E2gXGAuICrwITAI3+/P+9BNACYf4RAbwCVQCOAPgCvAA6/wwDvQEn/Tj/wQJbAZP+kv8XAab+ov8EAw0Avf2kAn0CP/x9/vIBIP/K/rQDEQRi/iH/ZwPhAaX/lQHFAGT+zAFqBUYCdf8nAisCFv/C/gEASf9uAN4CJf+l/Pb/jQHz/sn9FP/j/Uj8zf6v//L9j/6i/8gAMgBM/5T/yf3G/Eb/SwJxBJcErwEg/yX+tv0D/qcDHQaJAKT/zAFQAqQAqQCvAez/AP9FAMsArvwc/XwBdv4Y/M8AZgTiAJn74Pu//IH7rv4IAiAAk/yb/mcC3gGkAKkAxAIYA0cC+wEB/3b83PyM/rMApwJbAkQDEwT7AKT/8wKcBA8CAQD//hr9zfzK/qr+nvxI/pMCXQI/AGoARQEXANf96P7n/mP99/3d/pL9uvr3+7UAzgJTAbUAFQKLAkIBEP6h+0L8WP2C/k3/p/+FAagBZgBSAFcBAgGrAJwAiPxn+y3/gQLNAWEBRgPZAY0AJ/8q/t/9gP4qAbsBQwKiBD8FIgFV//sBYQGF/oX+9wCAAR//Ef4rAEoBwgHJAuUCh//0/Nf+ov5g/AT+EgJx/0r6Mv0PAt4AZv42//H/Yf/J/7AAQ/9T/m/+R/uu+okAYwO7AjgEVANQAdgAGgCA/n/9Nf/w/yT9HPxz/gsAZQB9A1wI+Qg4BQcAM/vl+cr6TPuB/bkAzwG8AG39xvzZ/0MDJAR3AYf/z/w0/KT71PpI/tf/vgGzAvQA1v9MAL3/yP6rALEB8QFZAdv+6ft6+9z8/f89BIIF3QNgAMn96/y9/pD/o/7C/iYAoAB5/Dj8nv+gAO7/8wCPAWH+6P7GANb/svyg/XYAS/+nAJkABPx8+pf/QAG3/yUCzwJEAowCfgOXAcb/1QGvAIf9Wvzu/sr/Lv/ZAAj/bf74AcQFEAOY//sCmgA2+bz5fgAzAh0AvgBz/9/6WPkD/Qj//Pxt/RoCMAF8+1r7/v5WAI8AiAGDAPz/6//9/ab8Bf5KAkkDbQE2AIL9wvv3/9oC7gAeAuMF+AURARD/UgCI/iv++wG7ABD9Jf+bAJz9MfsVAHECYgCLAtwEVwMY/1j/P/4Q/Av9xf7N/9D8Ev3d/nD+vf5JAesDlQJxAncBK/8a/uX90f80/7P9lP4l/3UAzwHQAN3/6AHsBI4FigP6/wv/gP31+t/8f/+sAH8DowbWA1r/xP8/AQ7+MftJ/lb/QQClAQgAGQBgAWcCcQJSAQ3/7vx0/bv9N/vZ+iwBRQW+A3EC+AEk/9n7dP5C/wb9ev8GAlUAGv1e/Mj8f/8hBK4CEf8JAFYCvQEIAB0CbQIm/5sASgJU//L9SQC8AMv+9//HAs8BX/+AAJ4Asf3H/fD/9wGvBFwFqAFQ/v79ZP+S/sD7yvw3/4QA/gCoAGH/2v51An4DlQBTANkBjP/h+qj7Ov5w/+sB6wJaAgYA4P/oAG7+Yv+rAt0B1/5t/zEBqP7Z/uAB3wGVAX4BsgAg/zf+kv/iAcADHQXFBHgBv//e/yz/5/72/Vn9yv2p/zwBNgEb/7f/KQTcAygAGv2F/Ur+HP0q/ZL9sf7h/zMBrQCd/58AzAFOAWcAnwEqAdz/BwDjAF0BvQDiAPAByQIfBJ4EDACY/W8A7QAY/5z9Ff+lAiYEbQSUBOgDkgJtAcb+afuC+xL6tfkX/QH9pvwbANcE0gJ1/lcA8AIjAGD9iP6o/H767Pth/zb/If3KAVMEwAAZAGMC/wEdAkwErgOEALP/IAEvAG//egCuATgC8QKGAwgAlP2jAK0C3ACJ/nb+wP28+1v9Kv95/0oAqwCcAH4Am/9z/ZP8BPzM/Sn/mv6HANsAU/8aAOQCHQLT/v7/zQKcAfAAjgL9AZoBXQEXAKX/3QDdA7MExgH5/dv8oP9OBKQGkARdAOv9df2l+yH8aABrAl0AIv57/BX8kv6k/zX/k/+p/xcB4wFd/4v9B/+m/27/eP+1/tL/pP98/ln+5gDCBOsEvwPhAgoD4AHxAYEC3QBj/fP7Qf93/jMAVAMcAtYA0wE2BHMBzwB0Ar//UvpV+Y/7w/oT/awBygIV/8T/ZwIQAEP/5v5g/JH7Xf3L/Az8U/68AGAAvAB6AxcD6gHFAvEBm/0w++r8uv1z/a0A3gTaA5oCfAWVBhUEJgPjAYD+R/2p/fb8nfzZ/Q//5QBjA6sDKgL4ApwCBgEaAEn+Hf55/XP8a/xR/Ab8u/1CALYAlQGy/1L/HQLqAG/+K/9V/7n8Av6BA+oE3P+p/rgAbP6m/dX/OwHHALIASAGsAPwBawUEBfQBuAFhAMn9y/4/AGn/zv6v/9/9+fqY/DcBDQHT/TIBfwSrAD3+qgAdAc39uf3O/aH6cvrU/S3+pvtG/Dn+pv8nARMBgP89/+T/e/+V/2EA0QFAAZMA0wBM/xH+c/84Au8BWgLCAiIAK/5f/UEAOwOdA8cDegOrA00Bhf1f/wMC5gDd/5j+W/1G+wn7TP2d/r//KwL8A/8CxgKEAcn/Lv/T/U/99/zB+5H7Fv6u/40CcwZaBkIEoQEHAa7/Sv1i/Z3+LQA9A4AGgwOq/x0DwAUyA47/oP2E/vP+y/7L/Pf6ZP5dAXQASf/J/1P/vwDIBEcD6f/t/zn/H/s/+FT6kvsP+4r+6wF3ALwAngPIA3QAAP/Y/yf/if9XACEA+AAnAjsB+v7T/7gAV/1q/Fj/VQAgAGgCzgKH/x4AsAJeAFT7SvrW/PL8nP3g/xv//v5pALAAev+3/q//iP/C/oH/1AE0A4UD1gLGAFYAxgCiAT4BEQDq/xIAbQFuAPv+nP+xALYBuwCT/jb/mgKKA2cALf+N/w7+N/7H/iD7iPfC+vH+p/87AScDjQOzAPn9N/2q+3/7PP2Q/sX+8P43/zn/rQG9BDwCkv+EAP4AJwB7AGMAlP2Q/0EEuAMwAMv/6wELARv+H/9AAwsCx//A/0n+0fxM/u4AqP1y+0j/EwGT/17/pADM/9D8WfwCAPMBpwJGASj/wf++AY8C1f/b/rj+Gv5XAF0CeQEyAuAFZwcYBJAAmwG6AeD+W/y0/LP9Xf6hATADNgK2AaoBagG3ASf/cPz+/Zv/LwA1/lb+KwBIAKgAPgBV/3T+/AC/AyYBe/6P/qH/awANAC8AggB6/ycANAHTAEACQQNDAkICcwDr/eH8evwY/sP/QQJVAywBcwH2AX//R/ym/TEAEf7e/ZUA5f8w/oz/AAEGAR0BwwFXAGn/0gCD//P97P7t/97/Uf/0/3b/yP+0AkQEXAIcAWoD5AHF/Cz8SP6Z/HX7Rv0s//8BsALjAh0CDgHuAWkBIP8i/SIAtAKIAQIAkv4Q/+X/6wBhAE3/mAGFA58C0QCYATsDPgK6AKf/tv7R/sgB4QJK/gn9of8OAD/+Ff4t/5v9JP5NAAcAz/8jAZEBLgAlAGf/Sf2W/C39uf09/k4AeAGuAEUBvgGKADoBbgKsAcUAQwBbAFsAW/9B/ob+v/9MAM//kABBAj4BWf/4/uT/2ADBAGP/I/7J/k//pP3w+138uP0G/+//9AC0AeEBYwPgAk0A9f8a/1X9tP0U/vL9Ef/l/yUC1ARlBK4COQFEAKT/1v1S/SP/BP9Y/iv/1v8B/3r+D/9Q/9IBSQWkBsICWf9i/W/68vu7/JL8Yf3XALYEggPCAnUEQAXLAncCVQCB+kb6nPx5/Lf7JP8dAjUCFANmATD/7P8WAVECpAAS/of/Hf/W/OD8/P1w/br+pQLdA8UEtAMMArcAbf8t/8D9C/5//oL/VAGTAUUBYgHoAR0CtwKvASIALQBI/3z+If4L/HP8gv5L/nj90f1A/xn+QP73ADMAXf6c/lD/cv/X/7r/xv4D/zcBagFD/nL9KP7N/jEBkATAA4EAWgLZBJ8DnQDIAKYCMwFkAFAA0f71/KD+HwHDAGL+ZPxj/qQAdAEJAssCrQEN/7v+i/6a/Ub9mP46/xX+GP7n/5EAGQDL/x3/cQEeBB0EzQHN/6AAo/6a/RUANP/Z/bT/agFbAQgCcANpAkkAJ/8t/4v+vv2L/lT/0wCaAW8BCAOdBWEE//4s/Zj/iwG8/6T/kf/8/BP+vP6d/Tb9fABtBLYDRgJrA6EEbQFY/vL9vfoo+FP67vuo/bMAAQLTACkAhAPaBGMBhf3J/RT/d/77/qz+kv62/0cB8v7F/EcA0QLZAoMCYgK1AWAB9wDr/2v+7/3G/64AagG8A2MFDgRnAjUAXf1s+wH6K/uw/bn/bABrASkD/QPuAjMATf+l/of8CPpj+eX7Vv24/lcB8gG2AVEChgMhA5QA9f6F/woAm/9A/2H9t/qG+/7/8gLRA74FOQdpB/UDYP96/Xb9lvy6+uT7kP5G/+wANATCBJ4DxgK7AS4Bu//t/xUA5vwh/EMAcgKaAOr/JAD5/2sBpQGJABIAWACQ/7H8nfw1/qP/fwD6ALkBUQGDAycHagY2Abz9zvwx+9b7Xf29/qL//wAuA+8DQAQ7BQQGkgX6Ajr++vse/Rf8hvgc+Z39KgDG/64A/wI1AxcDaQFC/ir+GgC6/9H7dflw+nj+gAFrABn9cv2vAdoAPf68/98BFAFc/9b+6/6jANECNQNdAZgAWAE8AgUC+f9V/xX9+/r3/Or9i/9gAxkFZgSuAt0ARAA1/+n8uPyi/Gr7h/31ANgA4v4IAIoBFgDJ/w8CpgCh+8P8agAt/jn86f/xASAAeAH+AzgDLAOTBCoBMPwQ/LH91/wq/fP/5wEOBJMFugZeB6kGlAROAKr+AADX/f73T/fO+6P+nf7P/g4BAQJ/BMkF7wLIAP0AYAG3/HL3OPYL+PT6lfyI/V/+NAFuBCYEsgJjAv8BQAFcALX+gvzR+zb+NgAHABoBWQRlB7EHMQWuAz8C3/9k/27+bfz1+uL9CwN2A+8C4wQ/BkEFNwIu/R35yPdw+Ar5y/ec+sP/5QEaAukBCwK4Aa8C4gLM/ur5Fvob/YT8T/qj/Jj/LACZA4EGeAaFBzkIVQUjAqUA7f1g++f6Z/3I/zUDjgeLCC0HkQWNA57+ovq6+XD6vPsO/Hj90/4hAGkCKwN7AiMBUf0n+XT3Cvkc+/r6ef6VAqkC7QFrApkCpwAcAs0EWwIo/gD9S/29/AX+2QD7ARoCFwaqCe0GAASYBGgCEP8F/rr6S/jg+5IBjgG8/scAGAWMBeMC9QAc/rv6ZPu3/In5s/i3/YgApP9s/x4BjAGsAK8AMwHTAM3/H//H/Q797f7I/1D+uP+XAw4FtQJhAM8AAQAA/3v/Sf4Z/KP8YgDVAhECLgNPBhgG1QMnAhQA0/wl/ED96/yE/c3/2AB3ANABaAOIAuUBHwQ+Alb8B/tY+7z6ivv9/XX/fv8qAKMAp//I/lAAnQDH/7//Af+I/LH7wP0w/p//SQJdBF8DkQH5ANb90/0PAkMFBwST/wL/NQA9AA4BugLbA3gDpwIzASv/Bv2F/Gz+hf/DACECXQJUARAAHwDg/t/92v0y/hv9y/uJ/J/7H/3GAJECgwNYBJoGUASp/xUApQDL/s39gv2L+4j6CP3F/wkBkAJPBfAFggWYBW4DBf+z/V7/jP2V/Ij9hP5h/w/+7PxL/Dv96f3Q/ab8vv7iAyMEaAN1AkEAn/7B//MA5v4q/af+tf+6++b6NP8qAp4DJgU+BlAEvwHbA1oGrgMFAYj/Pv1m+8r7r/3K/2oBAwOXBDIDywLkAYD+j/yU/E78lPsG/rUAXQGqABsAyv4p/gb/W//6/jn83/st/YL9av0P/gUAUAFtAkEDDgOrAWsBEgE5ATQBQAB9AOT/i/69/Ez96wBXBIQF4QQUBLQBuP84AtMFHgT0AacC/wEn/o/7Ef1r/Qr7ffqQ/Bj+DACyAd8BJgFJAdQB+ACAATQA//x//Pj9t/2S/Bj9lv0g/lr/VwAhAFQB9APYBHkDgwL4A30DuQC5/1j/wP5wAT4CJf9w/XL/6v9n/Ij9hv/T/sP+cQC8Ao4B5ACVAZEBZgAE/hb74fnw/K/+SP0X/eH+UP/f/lIBTANMAoACYAKQAgUFHwTe/yj9/Pxb/an+bf/2/tEAGQL9AsUC7wAyAkgDRwEU/sv8WP2p/+cD3gP3ASkCPAFF//n9JP3i+m35NPtu/X/9WP4KATIBeAFGA7oEGgQXAxEDCAG9/Tn7JPuk+gj7tfv2+9j/wwMNBXAFIAdCB8kGHwaOAon+EPr9+Sf7OPoP/FoAZASfBPEDUgNmA50E/wLB/4/8lPzi/Bn68PjP+jL+oQBfAeQAXgEuAlMB1f0l+o/6tP0o/5f9e/1n/u7+AAASAAACtgTBBhgGYQEZ/9r/qv8WAO8Adv+1/xMDEwXyA4sDKQXRBQsEmACF/E35rPpK/Qj+av6m/g8A6P/I//kAa//g/fL/T/9D+/f7s/9DAMb+Ff/U/pv8sv0oAHwAdwAIAiYDYwH5AMsB3gB8AEEBqQHqAaACDQNhAXcAlwBR/jb+EQDX/93+kv0L/sj+dwFHBHMDIgIiAD3+ovzp+pf5w/r++7D7PPzU/aAA8ADDAcwDpAP/Ab8AUgHY/0r+jP6d/qv+pwDVAkgCsADp/+3/AgCaAlIDmQHLAXQCiwFPAHkBnwGqAUgCwgCp/fj9GQG6/oL6NPrV+7b8Xv/NAtMBVAErBPADk/9q/Bz9P/5K/XT9Ff3J/Lf/WgHM/y7+v/5bAN0A/ABvAKL/XgJNBs8GogUxBeMCcf7v+zX73Px8/wgCgwPCAhIBJwEpA48D8QJxAvoCrgF8/27+BP5S/bv5cfp1/Nv8d/3S/iAAv/+qAW4D6QKd/3n/yv8W/Jz6Tvxm/87/6v82/2v9xv0l/wX/H/1E/yQC3wG5AVYDtQTNBDsE5gEB/s78Ov87/4L9ov2//0wALQEHAsT/q/9nA44FGQL5ADwDdAEB/mL9v/2s/K392/9P/9n8Lv5pAbcB9QFfAvkA2P4N/Qr8gPoi+z//1wEmBG8FKgRZAvUAev/F/HX8Sv0a/i397vyb/nUA+QPzBsEGpQNxA1oDHgG+/vj8Rf1N/jYAhf6Q+8b7ewChAxIDswO2BOYGtAXvAXT9Rvpy+mP83/zi+l/7//3HAosEugKc/6v9tP+yAGn/p/16/88BrAFqAPr/tQGaAlACD//b+4H7mPzn/av+gf/lAL0CkQKRAY0BQgJlArcBYgF3AJL9hfss/Gn83/o6/On/9AJBBP8CMQE8//cAkgEu/8P+3P7d/jb9L/6e/5//EQL3Ak0Azv6OAWgC///I/2oCvQI1AtoBsv9j/h/+ff7o/Fv87f2e/qn9wf1+AHwCuwO4AtcCKAObARIA+P3H/An8mP2P/an8vv3E/3kCywPvBHsEqwEzATMDJgL//j/97f2d/hr/FQI/AbT+v/+qAUMARf4dAHL/4/y1/YX/+v/o/yYBcAL3AVwAyv/C/03/S//Y/U/7SPs3/lsAXACpAUYC/AJ/BLUEAAMLABr/e/5W/Q38UPz5/hr/xf5QAZICWgGIAvwDawIBAAEAEwCw/SL+lQDCAOD9kf38//v+9P0mAPwAEf/4/yABrf4B/4ICKwI6/07/KwF0AmkClQF6/9r9Mv76/j3+t/0sAEgAFQBNAgIDSAJoAbYB3v+X/fz9vP7W/kf/yQDZAJwAJAETAokCGwGH/9T+2f9OAD8A6wCZAGgAeQAaAdEAXf+jAFMDwgPMACD+ff7t/vv9E/0R/ez9nf4vAY8EGwQ7AhYCCwJ9/xH9If3A/O76L/pk/NL+oQDOAeUC6QKgAZkBywEDAdD/sv5v/ZD8YP3S/iAAv/9v/+kACAK6AxgFqgJ+AJ0AWQD9/mL9d/6QAGEAcwDeAB8Amf95AWwDPwHr/g7/Pf8H/6T+if3c/EP+eADBAnIDfQK2AH//vf8R/wb+L/2o/Zv9ofyQ/IT9TP+8AccDwQJwAosCewKBAjgAY/9eACkBSQDw/jX+w/3D/ZH/9gLmA5YEWAT9ATwAMAAUAI7+Hf59/xkBKgDU/eL8Dv2Q/tr/Fv/V/kgAJwDA/VD8Y/2w/rz/t/9C/uD9TQBTAWr/9f8OAqgBLgCA/3D9uP1BAbsBh/8MAMsEYwaSBCwCz/+h/yQBkwKjACb/MQJcBEgBF//W/rP+LQA5AY0AuP4d/6gB1QDd/SL+cABcATr/tvwQ/Uf++/9W/7/+of7A/pL/7f0//X79NP+nAGEAPADGAXIDbQP4Abb+9v70//f/1P8S/3f/yf/qAY8DJgLOAR8EaQVtA/X/F/4v/7UAyP+X/dX89v74ARkDbQIqAWECcASUA27/FfxW/C/86Ppx+SP6kPuB/RMAtP9U/2QA5ABuAFsB4wGU/0b82vwx/2f9H/6nAVUBfv8cAqUDfQBlABAEWwRYAFj//QGvAkwBWAINBJ4C9QCgAEoAFwAj/xD80ftJ/v3/IP8C/1wBvABgAAgCpQKw/2H+6/81/uP7QfwP/iT9nfwA/48Azv/HAPEDeQQvBKcCDgHG//b/1QCV/uz95/6gAHAB9AFwAvUA1//d/m39RPx//e3/lgCLALoAmAFeArEBpAAoANX+LfwM+6f8mf6T/b37Xv42AicDQALlAhAEJATHBPsBpf4w/jD/H/4X+gP6sf2rAQADRgJnAbUBHQQuBG0BR/+g/s78Hvuk/Bb+K/5j/xkCsQFH/8X+Of9RAcoCQAI6AL39Z/8HAVH/u/4OAFUAaQCjAo8CMACDAFkB7v60/nwClALp/mX9tQCmAVH/uv76/i4A8ADUAAH+bvre+x7/yf7K/Oj8gv0i/mz+zf7m/7oCNwQHAvv/w/60/cb7O/yK/ZP8vPyH/0gC6QEOA9kFcAW8A4QDLwIs/xn98fyt/fz99wA6Az4ClwEjAcYA/ADgAbgAEv/T/zcAYP7R/Bj//gBL/8j+hv9m/03/JwBZATkAB//L/5z+//uM+/38Xf4w/6MATgFXAYMBgABB/1H+pf5p/+H+h//XAGYBWAFKACj/Pf4U/ob+3/2j/dH+NAFJBAoFjwOnAjgDqwKi/2b9nf2S/WX92P9gAFr9Jf3v/wYBrf+sABADegPzAvIB+v5e/KP8f/zd+VD4F/qw/cwAuwLaAkwCSQLHAmABS/1x+y78SP2q/VX+vgCuAQACVQKaApgB/wD3AokCZQGOAVEAPv6o/n8A1QCHACcCjAQJBe8F3QVcA3j/jv2r/fP6n/m3+r/80v7GALcCWQSYBTsFMwIt/gL8MPq9+h78Kf22/eD+5gG/AWgB3QJ2A9sBxgDZAaIBS/5i+6b9d/7V/m8BPwPoAvsBwgMKBHcCRgJ7Aur/H/0Y/Gn74Pzv/3cCxQGAAQID/gE8/xb+c/1++937+P6//5L+Nf8pAfEB6wC9AHYBigFNAN/9JP5d/7T/HgA9AHr/AP8RARcDkwPkA7gEhwR/AiYBff/+/KT8X/7n/o3/pgFHA6gE1gTWBAsEdQE9AFL+IPw4+zb7Xf0tAF4BPQBoAFYBpQAn/6z+3f8+/4n/6v8z/oj8yP1xAG0A7AAtAeAAfwFcAhwB9P4pAGsAwf6z/bn+MP9Y/1oC7ARYBjIG3AVLBCcB2P56/Mj6Svtb/Sj+Tv/zAKQCywRzBYcDQADr/6YAYP+w/NH7fPyX/Pb8ZvyD+6n7qv5cAG7/1P+EASsDMQLnABQARv8e/jL+e/+6/20ApAHoAmoCOgH9AKcAdAAUANn/l/94AX8E7gUSBfEDsQS2A4sAyP5M/vv98P3m/Oj6dPqJ/IH+4P/VAAgBxQElAnMCVAG1AG0A0/1w+wb7/ftm+wD8OP4AAMsAywEaA7oDlwRZBBUEuQOUA9IDpgKhAc7/jP6f/8T/y/1Z/Or8g/2A/uAA3gKZAl4AzwEwA6IB4gCQ/xD+kfzK+wP67vfE9935Xv40AdMAPADKA7kFmwMIAZ4AFQKZAB8Ahv89/fv8AwD3AiwCZAHsAqcDgQHIACIBHwDkAIcDoALj/2sBKQOKAeD/6ABMAMv9k/2K/RD72/k2/S/+qfzj/a4BuQKcAEYAYAGvAaMAqACW/rP8jv28/Ff6Nvp//ZH/zQCpAk8EHwR3A3QEOgPM/5z+wACa/yb8Q/5oAbMAkQAfA+ACFgA2APkBAwF1AHMBTQC+/xYB4gGDAHr/OP9d/mgAtAK9ACb+zP6u/7n9Nvtr+zz8U/1J/7L9s/zd/yEDGQOPAeYAEv+//gAAof7O/CX+cf8u/q7+mQEXA2kBagCPAUQC6AK0AvQAaQAyARkA7v5t/y3/H/+6AKsBHf+R/vABWwI+AI3/o//q/vv+sACN/3r9ev+9AcMBfgHqALv/EP9P/qH9yvxn/MD9Qv50/q7+3f48AP0BLgKdAfMBbQFt/7z90P3Q/kQAgAD4/lD/cwC5ACYARAAUAV8BLgGpAFEAHAAZAXsDdAPGAcoBFQFxAG0Aaf9N/lX9kP30/Aj8qv1rALMA7wGoBGcEnQLRAYwCdwBb/aT8W/zC+kP68/u6+3v8Qf/IAuYDyAJlA+IC5AEFAQcAKv+r/UH9W/3u/HT9Yf5F/yMBfgGjAXYB0P8iAFUBEwGBAEMAAQF3AsgCFwEC/8f/QAD4/Vn8IP0w/lH9Df5NAPYAfQDoAcUDwALJAe8Am/91/or+m/7c/ND7n/yj/Tv9If7v/2QCzwRPBK8CzQHiAcwAtP5v/Pb6b/t3/PH92/9UAnYDOQN0AqAC/gPeA78BUP7F/OT8yP3c/hX/1v/fALkCogNNBPgDjQI0AvsAt//o/nb9N/sO+sb6hP3f/68AyQL6A9oDBgJn/xT+gfyG+5f6j/ou+0L8FABzA1sDNALJAjEElgIRANX+Df4R/gX/bgB+AHgAigKiAxAChQHyAd0C9wPkAGj9Dv4oAFgAsv6C/RD+4f80AskCzf8c/nz/GAHe/o/7Ef1d/1j/CP4i/xkBCgJNA4QCTQAo/hX+9f5g/0b+ZP42APX/1AD3AaoCOgOIAggBVABDANb9UPyt/Wr+I/3E/acBkQOUAQ4BzAI/AbT+0f9tAGX99Pu//bD+pf0I/u3/gwD9AL4CKARHA8cBOAHpAM3/Qf6V/VX9kv5a/53+UP/lAdUDcwNsAk0BZwB2/3//z/94/WD8Fv74/58AAADJ/9H+5/6gAKYAPACL/2j+Ef4q/4wAJv9g/qQBxgPRAQYAl/8q/3b+sP6q/0r+6f6RAY8C/gHiAPICnATcA5kBH/56/Yn9cP3x/l3/6f5FAPMB7gFXAQIBCQK5Ao4CswFcABMAQ/5w/Gv9yP7e/fz8TQCMAkMBzQAEAo0BPf+q/iL+Z/yE+3f9LP5e/HH+MgIBBPMD+AKqAFD/PAAv/0P+zv1z/gsALQACAYgBigOYBZcFOgX9ArABbwFH/qb65foL/jf/g//pAdgDUwSRBDAEugJlAKr+w/ze+v35ufpQ+3D8SwDlAXQBwAG1AtIBiAABAU3/tf1u/X/9ev1i/Jb9kv9OAdsCUQRbBUEFTwQGATz+bP1r/TP9Pf39/XH9zv6gAVQDMgTRAzgDXwEYALj/sv4l/a/7hfxp/Qr8cvwoAFwCsgJmA2MDhgPHA68C//49/Hb8Sfwk/Pb8M/7G/50B+AMSBV4DEwNWAicAxP/Q//z+lvyY+9/7K/wz/Qr/GgJaA9sDnQMzA7kCwQAH/6H9TP08/Cr7ifwU/7IANQHJA4AFlAR3AvsAkwAG///+ef7l/BD9gP4oAPz/DgB8Ad0DoQTgAzACB/9K/4D/lP09+936KP0k/kwAZwJOA9MEMAX1AgD/Vf5e/qr8qPui+/z8b/4Z/5D/uQDjAv8ErQRUAgUCRQHN//r+zv1g/p7+P/8b/2r+lwAiAhQCnQJnA5oCYAGbAI7/j/6w/Uf+6f8RAAr+fP0N/77/yP46/roABwJpAGb/J/+H/qn9Df/2ALL/Cf/x/8//ev6x/aX+6/+mAHQAbwDIAH0APwDY/z0BgwJQApQBRQEtAtQB1QGPAqEBTf8m//b/G/9q/rf9Ov5MAAoCBAMCA6EBLAFOAQsA8/1C/Of7Mfyk/Db8N/sC/QkAwgFqAd0BcgNIA90CFQHa/WX8q/38/i3+9P3//v0AvgJfBK4EHwNiA5cDmwIDAJL+xf2w/I7+WAASAScBOQIFAyUCSgAR/ej7D/18/Zv8rfuC+z798P8cAkkDzQMABCcDdgG7/vT7k/pp+xP7hPrg/ID/CwJzA2AFpQeJB7cFGgQ4AYf9Ivxx+/X6fvo4/Q8A7AG4BCwFmgTbA/kDswLN/3j+1f2Y/GL7IPt++xb9qf4AAG4AkgEhAiQBogC2/gb+Q/7j/lD+of0IAAsCgwIIAz8ERwM0Aa3/pv2o+7T7nPzW/D7+cv8lApwEqgXKBT8F4wXjBIACt//l/Tf82vk++VP5jPpV/d8AXwMqBTEHUgg2B6kEPAFm/c76Svml+Hz4S/lO+lj8Jf8bAUUD3AP6A2wDQwNqAiUAef83/9v9Qfye/KL9Kv69/rUA4gPaA1IDLwMSA4wCZwEiATEAgv+t/1AAUwCL/7L+cv7k/sH/TgDkAJUBRQAR/wj/8f8p/xX8aPxA/f38yPww/XT+Vf8LAaAAf//y/sr+9v8b/33+k/9e////tgAkADAABgJxBCgEIgPAA78DhALyAEIAyP+u/4oBVAPCAjcBewH/Ao8CQwBa/wv/KP+//oz9Tf1S/W3/ZgAs/1P+kf1B/qv+D/7H/Bv87/z2/Un+ZP0t/Sj+BgCtAVwC5wGLAkYDxgFuAcsAbABsAV8CagKmAE8AZgFbApwBzQGvAzIE8wIXAiADqAHj/lD+tv4W/ez7uf2r/hD+cP74ADcB9/6F/mL/o/5j/UH+Yf7W/sb+A/8P/4P9fv0K/Yv90P77/7MAFALWA/MC3wEDAmoCqQHFAfACBQPZAFH/9gD9APD/zv9YAKL/M/+4AKcAhf/C//cBPQN1ARf/w/7c/rj+0/5A/Y/8Yf40AOH/P/4T/SX+8wD+ASoAIP9gAPUBlgLKANn/zv8OAPsAygAiAPP9Wf74AMgARQBxAa8DHwS/AqMBKwC1/9cALgEEALr/NgAq/4b9FP5z/j39Rf0G/+//TP+U/ykAav+Z/3kBjAG9///+RP+w/l3+1P5q/ywAbQAhADz+Ev4ZAAIASwBkAQ4CcQG/AuEEWQIFAPP/CQFnANH+wv7r/ar8qfwc/+7/zf9ZAS0DtwNrAvMBOAI5AhAAPv1m+3v5Fvkk+qP7afx3/YwAMARABZgE6wMYBAMDRAC1/ij9Z/va+tz8Q/5k/04BuAMrBjAF+AMOA1EC3ABU/1D/3/6W/tr9of76/0QASQDhANwBbQFJAGAAcgAP/g78HP0//lr8Dfxp//YA6v9I/6cBVwIYAYUAsv4j/HD64Pvm/c39vP41AX0CFgP+AvsBBwKiAa4B2wGkAWcC3QEAAZcAi//G/wgAhwBbAEb+Gv6L/kL/DACc/1QA/AAVAXEAEQBsAV0BPAB5/479cPsp+hH66/kE+ub7gf9oAvUDEgZrBzQHhQUCA7IAZ/7X/Lf6gfl6+nn7uP1nAeAEdAaABkIHpwf0Bf8C+P+8/DL6Lft5/BP8LvtU/H7/GQEaAXUAmAEmAhcCZgH2/aD8ovwS/dr96/4QAEYB1gOZA/QAHv8A/7P/iv9V/n/8mfye/U7/YgHFAsEEowVWBZkFuANqAUYANf5A/Ar8Gf0o/R/89P1dAAYCpgN0BD0EkAM7A/MAKv0v+jv6o/sd+w37Ovzl/Sv/IQHYAcQA+gAoAmUDqAHU/zb/pf6f/tH+2ADlAAIB9wHgAd8BpwGMAdEAlgBmAEAAs/8wAN8AEAE6AoQCiAKJARgBTgBO/o39c/27/d/8aP0O/hD9j/2c/nX/7P9eAN8AxgBWABABtgBt/2T/3f5K/o3++v7j/on/tAA3AegAzQBeAQoCKAMNA5oCdQL9ArUDVwKXAIv/Dv/O/nb+Cv5p/bD8sf2n/wMB+AGpAY4BmgAf/6f/Jf9N/jP+MP5T/qb+Rf/7/iv+0P4MAIr/ev6z/qz/GADLAJYCqQJcAo8DGAQBAuT/IADSALwAcf8e/7b+4v1y/7QAbgEpAvgCHwR3AwECCgHEAEEAjf53/V/8kPsi/Af9Hv8UANn/YQCYAMP/zf5S//X/LgDLAG4BcQFxAFr/Zf57/Qn9QP1+/Yz90f7YAOcBngIwA7kD8AMdBPQCggAxAE0APgAw/9j+AACl/yYB7wHZAZAB6AH6AuMAo/8P/4b+uv1z/YX+l/6W/08AQAAzAE4Av/+A/qP9p/yn/PH8Uv2N/Zj9Wf73/zIB5ACVATYCtgFzATwAi//E/t3+4P/U/ygBcgJXAxAE2gOeBDoEjQMSAvH/g/5v/dz9/P2q/qX/pQCqAL//qACcAToBVwCz/1H+2Pyq/Lz8Sfxb/Ej90f6N/1n/MQDOABQBKQHKAJAAKwAiAAkALABbAEkAvABQATQB5QBhAoEDiwPwAwoEeQOTAWb/S/7C/cP9sf2Q/UD+GQArAngC6QCo/97/wP+l/q/9evy6/G/9gP2y/bb9Ov5v/57/Vf9AAEgBCwJwAvcB8AAbABYAAADb/3T/Rf8PAEMAbQBtAcwBBgKiASwBTAAX/8X/h/9V/+YATQHVAHQA3f+//4L/iP9o/yn/LwDw/4L+yv04/tr+Jv/R////twAUAacA9P92/38AiwCC/z7/dv+h/on+df5m/koAGwLcAx0DSwLZATMBsAGkAHIAygBJAYgAM/75/QP/EQBo/3P/7AD2AKEAggCM//r9KP7P//7/xf7K/nX//f6u/gL/a/+a/wkALAB8/lf92/3X/fj9Tf8pAWACSQOWA1ACfwBmAFUBWgCR/wIAugCqASABCwBlAB8CpwPyAqcB1ACX/+H+Pf+t/1/+Qf52AHQBFwBZ/mH+aP4B/2r/4f5g/i39zP0n/pP9q/uS++H+dgA6AAn/lf+IAT4CrAK7AmkB2QAwARgAIv5Y/ab+7P9NAXsBWQLWA4cDJAT8A6UDggKXASMBHwCZ/zr9LPtz+lH8VP4W/8T/mgBcAmoDZwMqAnMAbv8u/y39oPru+Db4uPng+3r+fwDqAUgEjAa2BYYDoAILAmwACv7D/IT7hft2/AP+HwCMAgQGlwd9B5sFFgRbAuP/v/0r/Fj92/17/UD9pf7HANgAngFiAuwBHACB/sn9avyb/NX8lfyb/Wv9bf7i/3sA0QC7APUBTQJsATUAhv95/0f+df11/gwA5wC9AbIC9wKcAi0CwQFXAdz/A/4v/uX+Zv+p/ycAtQGIAjEDzAMiA4UByf/3/k3+MP1y/Rb+h/6J/9f/cgDKANn/Tf+6/0b/Qf3X+278RP3M/XH+5f9tAakCmQQjBC8CmwCO/7X+Ff3b/Ab8yfuK/Rn/2wARAyMFzQVDBkYGsAPO/2X9dfzZ+4D78ftg/Wb/CALfA0YEKwSVBFgEfgLt/2v9Hvxb+xr7Z/sn/B39iv7oAPUBXgLEATUBVQHt/4L/mP5I/QT9F/3M/QL+n/9+Af8BeQLcAs0Buv9G/zP/SP/t//H/4f8wAL0BNAMDA6UCWQJmAjkCtgDZ/jL9dP3g/cj9t/4u/0YAKAFLAUIBTQEPAk8CWwGV/wL+mPx0+1P7yvqm+o384P4+AGwBTAIDBC4FUgQyA/4Ayf4m/eb7+fsr+1L8Mv85AUoDYgRoBV4FnQTdA3gC1gA6/iH9ZPzL+1L8Cf0y/xMBBQKRAjYCfwH9AIIAiv5y/On71vuT/ND9CP+oAJ4C/gSaBI4CVwHc/7z+U/13+8L6V/uI/JP+uABPAr4E7AYaCAkHKQSgAV7/Z/1k/PD7bvv0+2P95/77/yIBJgNEBLoDAQMQAgQB4v9S/jf+a/4T/k7+kP7X/sf+l/+aADMAhQAkAZEBaAGhAKcABwF4AE4AwABjAFAAQABGABL/Yf32/RP/HgB0APEAfQJLAscBbwEDAWQBHwGwAMT/Av7S/a3+E/8c/9z/HAH3AI//Rv6s/Yz9qv2M/vz/2QBCAaoBtgIxA0kCNAJIAkMBE/9P/Xb8fvs4/C7+Zf87AA8C0gPNA5IDqwObA0UDtQJRAUH+bPvf+pH6nPq6+9r9pQCcAqAEKwW+BEIE3QPUAjAA7P1f+4r6vPqH+ir8fv5gAaIDFASWBH0E+QIuAp0B3f+6/RT81fvG+8/8Fv+hAJYBFQPKBIIEHwLF/wX/kP7T/G78af2i/uj/yQARAaUALQLoAp8BFQCh/uX+Zv+E/2L+6P2c/w0BfwGOAKoALwEHAfkA/v8P/73+Mf7k/cz9Sv2J/nkAYwFYAgsDvgIOAbT/VP/i/ob+PP6T/pD+NP/eAI4A4P8cAGMBjwIQAigBtv+y/9cB6wHk/8P+gf+H/0D+FP1+/Ij9q/9QAWsBtf/7/+sAmAAMABn+QP5i/7j/jv/8/QT+6P6f/2j/hv9DAAABQAKtAnICnwLFA6AE3wMdAo0AcP+v/m/+g/3//eP+QP8cAAcBnwHyAEIAtgBLAdQA8/+H/1L+Iv3m/A/8GPuv+3X9Lf98AJsApAFqAx8EUgOWAEH/Qf+J/qr9Cv0b/Zv+igF7BOsFDwVwBGEFRAT/Aav/cP4a/0b/ff8D/x/+EP9nAZICJQKWAX4BRwH0/4P9H/wn/FD73PuF/C/8yPx6/cL+XP+O/wIBYwFUANb/ugBfADn/zP73/6ABYgGKACUAsP8JAGUBIgK4AXUBsAJCBPADGAIcAcIB2gGzAMT+2v2f/ZT9+v0A/V39F/73/gcAhf/C/xcAuQDMAP//EQBXAH4A9f7d/SL+IP0+/Jr7T/zk/Yb/IAFXAU4CqQObBF0EhANpA1ECSwHS/1j+3/2j/XT+MP9r/z8AWgFQAuACPwKFAakBwwDT/7X+4P22/V39zf06/m3+hv/8ACcBkP9K/6X/ff4g/S39T/8pALP/CwB6AaECMQIhAlsBzgBKADr/TP4t/LH7Uv3+/oz/bP/4ABYD3gTvBI0EHAVEBF4D7AF0/t36+vh5+Rn71fvJ/Fr/owF7A4kEvQQbBD0DZwOsAiMA3/xR+xL7c/tV/MH8UP36/b3/OgFZATsBEwINBH0E+AK9AKf+Cv1T/X7+x/2P/Xf+awD8ALf/of9rAFoC+gLDAnECvgAYAPEAMQGHANr/KgC2AFr/Lv4a/q396f1m//YB8QENAK//Y/85AJwAtQBKAdMA9ABoAK3+2Pxg/Dn9aP6V/5f/rP/iAEwCFAOgAlUCKwJRAaEAW/8K/pH+tf9WAH0AwQBBAQMB4wBH/3v+Rv6s/SH/KP8//3gAPACxANkAwQCuAFUARAAAAJL/Af/E/oD+k/5J/0j/Iv8XAIMBpwH7AdICRgJ7ArgCiwHP/3r+1v1k/dP9P/67/o7/JABEARgB4QA3AfoAgABB/5v+vP5U/pX+lP/O/yAA0gAGAVQB7QA+ANf/FP9S/tr9sf3I/ZL+bf9BAP8A0AExA94DnwNaA/4CjAE9AOb+GP2B/Hb8E/1t/dr97f+GAQUC/QH3AYMBOAHpABYApP80/93/0v9a/1X/9f7P/w8AHf8Q/hT+LP/D/4cAAAHjAWUD5APJA54C9QD8/47/7P76/ZH8cfy1/ab9h/1e/un/pwGhAg4DVANlAjYB5wCU/9z9Df1D/bj9PP6B/oL+cv+g/9j/hwEGAqEBiAG9AZ4BzQA4AUYBYAD0AMcBAAEn/879p/2v/s7//f9GAHIBwAIVA8MBRwEvAo0CawJdAKH9Ff0S/ev8ufzI/KH+jQCWAAoArf9QAAsBNAHlALkAOQAH/1r+hf1a/QL+r/4o/1L/PgBGAXYBLQFhAVYC0gL8Ac7/ef5E/r/+/f4K/5b/KwBKAXgBrgCe/+j/EwG5APD/uf6v/k3/bf65/XL9Ov7e/x4BZwG1AQYCogFjAYsAJgBn/6f+w/1A/NX8vP0t/vb+QAHRAygEtgO0AmUCcAJjAfj/mf3X/Jj96/30/FH8VP70AMkC5wMDBBcD6gFUAVkAs/7f/Vv+Pv6T/Xj99v23/mb/lv9QAB4B5gBdALj//P7U//AAaAEiAUQAAACk/zX/yf6E/pn/wACdAeEB4AFOAssCjAMmA9QCpAIMAQz/XP1u/FT8nPxE/fP+qP8VAFwBUAHaAW4CTwGe/4j9I/xy+xr7MPto/EL+9//qAQwCJQFtAc0BlgBl/27+O/6T/qP+RAA5AVgB0AL/A88EhAMbAfX/Uf/y/qX+MP4b/lX+vP/yAZMCSwLJAucD3AIkAPf+A/5k/eP8s/zo/Er9Cv/g/0EAAAFkAs0DbANUAm8ANP8R/4f+p/yA+3L8Wv1x/uP+QADvASQD1wSyBCUEjAL5AG0AsP43/Zr8Vf3Z/Yz9zv09/3cA8wBsApwDxgNCA44CxgHaAGX/kf31/Pj8M/3j/V7+iv74/ogA8QGBAoMBtwC7AWcCbwEk/xX+Lf9qAAsArv9P/5T+AP8M/zz/Yv9LABwCyAKsAgEBYAByAG3/G/9//73///7C/u3+EP9k/xP/wv+YAKAAW/8K/ln+9f5y/w4AsQA1AWgBNAEdAWUAGgCDAA4AeP+Q/v3+i/9o/kn+af9SAbkCoQLnAWYCpwIRAqgAlv4S/hX+4/7j/lD+uP/HAEkCDwKmADwAw/9PAL//bv44/Xb8gv22/mX/OgAfAY0BrwFJAWMAvf/t/kX+4v1w/hr/2P4k/xkAYAFVAi0DfwP3AgcC6gDg/1H+kP1T/oP/wgAbAHH/1v/x/z0AxABEAYYBYAGaAMX/GP+N/jH/2v/0/1IAQgDs/5T/Ff+N/38A1QBiACn/Pv7K/aT9mP0Q/mEALgJoAigCYAEuAfQAoABcANr+Nv7Y/qP+wP0b/VD+cADeAbsCIwNAA9YCSQLoAMz/aP+6/hz+Zf2d/W39o/32/vT/QgGsApgDngP9AmkCcAGDAJ//1f6O/nn+w/1l/Jf8nP04/oD/mgA1ASAClAK6AnwCgAE1AWgBagAv/2b9dvwT/Vr93v22/goADQIqA9cCSgLrAfoBqwHpAIUAfP+4/mT+e/1S/Vj+Pv/3/2cAUwDWAEABTAFVAW8BFQGn/+3+EP+G/k/+a/4W//z/agCNADoAnP+L/w8Aev+B/+T/DQDVANEA4ACSAQ8ClgHrABcAk/9M/6T+i/6v/kz/Xf9F/2n/GQBgAR4CWwKKAfYBcgLmAaoArf+W/rX9N/2Y+/L7g/yN/dT/TAFsA5AE5wR1BGADAAIHABX+E/zk+mD71/tJ/Lr9ZP+IAqMELgUKBf4D7gKRAZz/q/1k/Ln7Q/yO/AL94P26/94BhgOkBHQDpAJ7Afn/ZP4x/br8EPwL/Wn+AwApARcC+wKhA+0CIgF6/8f96/1j/Qf9vfyp/cX/QQEZA+4CAwPvAm8CrQHn/gf9c/x+/Cz9tvzt/bMAFAIOBKME9gSUBMECkgEu/+b9N/zx+9/85/w5/oH/wACdAbsBHgIBA6MCQwG5//z+4/22/Nj8hfyO/Wb/BgHVAVgCLwM6BLQENwODAaP/Df6z/MH7kfsR/Hr9H/+FAQcDYAOpA+MD/wPfAx0CL/9T/Yz8pPz/+w38vvxQ/gMB+AFhAn8ChgMjBPoCiQG6/7P+Fv5z/ab8Ov3Y/oD/BwCq/3IAOQFXAI7/kv/f/5v/HQDz//b/rwBrATkCXAGqAAgAc//E/sj9ov09/pb/0P+2AMwB5AIPBFoEcAP6AZgByADX/yT+Nf2r/Dv85Px8/D396/1C/9kBbQIuA1sDxwKqAZ8A2/9f/nb9Ofzg+6v7/vpl/Bj9Yf5+ADICtwOSAxkD2wKqAkoCEAJgAVEALf+w/in/df6K/nn/OAALAWoBgAE2AdUA4wDwAZABCwFpAFP/UP84/hD+3P0f/az8P/2A/lz+5f5j/v3+DgFbASoBlACuAI8BwwGzAP3/2f+X/77/pv+T/zn/KgClAecBGgHjABUCngJmAlsBlwAdABcAlAAbAM3/Hv8A/1f/mv6m/eH8av39/WH++/5j/g3+7/5KAPQARgGtAVkBqgFqAUYAEv9z/aj9L/7l/lT/4f4aAPUBYQO7AykEAQRyA9kCbgEAADT+oP5T/0//3v66/rL/r/9RAHkAFwBb/x3+wv1C/ST9+fzp/Mz98v6V/3P/Df8ZABYBTwHWAKz/BQDN/8P+f/63/ov/fgBFAlgDWAPZA+UDbgN8AzsCAgFg/9f9wf2K/XP+VP9SAPwB1gPQA9sCYAKMAKf/bP7b/Cn7y/lZ+kz7E/1d/h4ACgJfA98DjALBAKv+bP5w/k39BvxI+yD8vf0w/1kAlAHJAp8EhwXkBEsDgAHsAIcA7f9d/5/+Cf8VAJIA5ADfAYQCCgO/AxcDfAHC/03/7/5+/gD/ef76/ZT9Q/72/gX/7P5E/i7/af/O/tD9cf2W/gH/ov99/0z/JwD8AMsAEADX/0v/uP9q/2D+nv5k/0wABgCq/4QAEwKLA5QDdgMEBFEERgQoA/YAxf+Z/z7/q/60/ZL91v4TAbsBCQGgAXcCgAOtAlsAx/6o/rP+lf1T/Jj7lfs5/ND8yPx6/Qz/YgDiADUAUAB3AIUAIQB2/9j+kf6z/pf+N/5Z/oj/sv8KANMAYgENAvMC5ANKBHgECQRoBDED2gFHASoAj/9s/t39s/0B/nb+oP/GAEYBeAL/AhEDiQHf/5n+//wk/JX61fk8+uv6DPzT/Zv+hv8gAUcC2AIUAnUB4wCAAFQAMP/X/uz+a/9SANX/8QCPAjcD9gOgA7cD7wMHA+8BfQEOASMBRwEFAPH+pP7o/uf++P5h/p/+CQCuAGcAm/9l/7j+Uv7I/Ub98Pxh/Ez9Qf69/mj+t/4u/7P/CwCJ/9f/TQAuAfUBAwLpAdQBsAETAW8ADwCM/37/KgCQAPUA2ACeAQYCEAJiAiMCKAI8Af4AqACr/3D+F/6J/vT9EP4U/hf+Cf9e/+z/lQCwAA8ByAAgACwAkf+m/1z/Df/g/pf+g/+r/mz+qP41/zkArwChAZoBlAFGASwB3wCPAIUAWQBtAMX/9f8I/yX/0gA9AQICwwHIAd4BywGXATYB5wCVADEB0QCC/xf+rf4m//T+uv4u/nj/AACl/9n+xv20/YL+uv4c/gv+2f1o/ib/v//x//UAowEIAecAFACi/w//qv4R/4n/WAD/AM4AuAC8AUMC+gIMAwgDzgJ6Au0BLwAk/87+r/+I/6/+S/7X/qT/bP9AAFkAyQA1AXgAcv/4/dn8q/yF/EL8/Pzb/dn+AP9p/4gAggHwAWsBSQF2ADoA+P/A/lj+Yf5F/9kAjAGcAU4CuwMZBXgEmgPDAssBKAHb/yj+kfyW/Hb95P4b/0j/7gBoAj0DCwNhAlcByv92/tP98Pva+iH7kvvK/Gn92v5LAFQCPwMfA5gD5gL6AYMARP/S/av9ef0+/ez9Zf6BAGoBygGYAgcDmAP4AuQB8gBCAMj/Lf/V/mv/UgDDALAAoADdAEYBBgEbALr/Wf9C/2X+/P2o/Qr+AABvAP8AFwGHAfQBEgESAEL+zv1L/b38pvxK/PL9Wv8yAIcBmQKcA8YDCwMFArEA1/8U/7/9YfxK/M39hP7w/dj+AgHFA0UFHQV8BAwEegNKASz/hvxl+0r8bvxn/Dz8nf08AGwCdQJqAuICQgNHA/wApf9G/r79nf48/qT9Tv1V/jv/mf+a/50AXAHRAZ4CwAFWAe8ACgGNALr/2v/0/z8A6v9b/8P+XP+z/4v/tP/D/73/7/87AGX/zf/8/6IA8QDU/+//lv8YABMARwAUAH7/qf/K/gf/2/5d/8f/GwDzAHoAPQAxAF8AFQBIABUA7f9w/+T9Ov61/RT+dv82AIcA//+lAIcBYAEcAa0ARAH1AQABFgD+/tT+6/8mAB4Ahv8LAHgABgFnAeoAvwHZAhcDsgESAMT+yv4r/67+y/6I/44AzwADAYcA//80/1z/s/+J/j7+yv1v/mH+ev4i/+H/DQF8AIkAyf+d/0H/d/7V/g//df9+/zwAHgC+ALACdwOWA2MCtQEGAmoBx/9h/tT9df28/ff+dP+0/8QAoQFSAqoCyQHdAEMAbP/j/k39UPwp/Pj7wPz1/ZT/PAChAZwCPwLiAacAvf8S/4f+h/5P/g/+3v5z/2sAtAErAsECugKPAmoB6/+A/yv/+P6F/qr+yf/n/9oAxQF/AZMCOwMuAw8ClAAs/3b9g/yt+0r7jvtI/az+lP8GAcMBSQIPAvMBfwEQASMA4/68/Rj93fxm/df+2v7L/x4A0QCYAVsB+AJCA/4DXwQ/BJEDlAGyAA4Anv/4/mH+wf1U/TL9dP2W/UX+sP8vAdQCfwLxAdoB6wBy//j9kPyS+7P6JPrW+fP5D/zC/ez/BgIlA8UEkQTTAxUDDgJLAfkAkQCG/y//Dv90/zQA0ABgAUMCjQPfA44DAgPcAgYDKQMdAvwAJQCe/8P/lf6i/fH8Uf2M/Tn84PtO++377/zR/fb+c/9GAKcA4wCkAM3/Q/+d/vL9+vyy/J78/PyB/jwAWQKNA2AEngV3BQ4FuQRiBMADTgIjAcT/4P7O/kH/sP+cAEgBCwLfAgcCogF2Ab8AGQA3/+39mvy/+5D7bPwe/b/9Qv70/hb/1f4x/i39Xf3N/bv+Qv6Y/jr/c/+AAW0BJgHKAeABzQFfANz+uf74/ggAQAHNAb8CAgMVBDoEewNyAh0CpAL6ALb/sP5w/pj+gv4o/+b/fgBnASQCJgFZAMj/ZP+4/nT9pvyk+/v7w/ws/V/+jf+lAAgCXALCAdcArP8W/4v+Lv6Y/Vf92/1q/k3/AgA7AbkCtQPvBGsF3wS2A1gCKwGU/6f+sP38/I/8ufzd/f/+oQC7AfsC/QO4AzcDKQKpAD4AoP8d/q/91vxM/F78AP0D/nj+NACJAQcCxwHcAEIAWgCk/7P+z/7l/lT/Pv+I/43/JAD6ABMBKAHb/2H///54/p/+9v69/6cAwAG1AsQDsAP7AzUDywG6ABP/4/1H/Gz8nfyf/G7+4/+iAdUC3gP7AzgEHwTiAcwANP8O/Qr8FPuq+vr6GPyS/Vf/QgC4AeYC6gIkA/UBSgHAAPP+AP5P/Rz9ZP7+/rH/eAA+AZYChAKJAowCsQE4AQ4Bxv+Y/l3+m/6Z/9L/twA6ASIBIQEgAVcBSQDN/9X+V/4W/nL9p/3S/fT9f/7e/68AWAFMAWgBNwIlAuABJgE1AJj/Pf8H/2//L/8g/wMA8gDqAUQCwQHGARQCvwFoAWoAZ/9g/1r/5/7k/QD9J/1I/q/+uf6x/1MADgGkAS4BqgBkAPX/B/9a/iv+hP3//VD+AP/q/7gA8wE4At8CUALLAXIBzgC4ALj/n/5Q/sn+8/67/xEA6wCtATcCXQIdAS8BKQDr/0n/6f31/X39Hv5+/xcASgA+ARUCsAK8AeUAuAAk/yr/5f7Q/Sj9fv17/v7+jP+kACwCngJBAtEBQAGAAIv/6f55/g3+2v2x/ST+3P6W/y0B9QHdAfABIwK5AYYAa/8H/wD/sP6D/t39Nf5r/z8ANQEOAr0C2wKpAgACdgDd/sv+Yf7C/Qz+//3R/nr/p/84AAsBRgHRAQsCkwEgAS8A3f8H/zX+jv5p/4f/Hf8k/+P/MwGwAbkBLAEEAYoBqgBj/5L+Iv/P/8b/v/8B/yD/3//4/53/VP9kAGYB6QAoAKD/V//B/ykAaf9P/6n/FQCAAOf/tP9DALcA8ABlAIf/1P7E/kv/f/4j/hP/nv+gAIEAxABWAcwBPgJyAeEA6/8S/yv+Ff0l/Y79P/7y/gMABAHnAa8CvgK3AkIC0gGtAHX+dv08/dX8S/xd/Db9ef7//yUB3AFwAowDFgRLA7gBhQCQAAUAOP58/WX95/0s//v/jwCIAZoCUwOLA6QCxQGSAVYB7wCa/0D/Uv/h/mD+Z/7b/qX+s/9m/4L+gv6C/sz+df4u/j7+BP9a/43/o//t/5UADAF+AY4AOwD5/2f/Fv/C/lr+vv7//20A6wA/AU0CTANhA3EDWgMQA2YCJgI6AcX/dP8z/7X+vv7F/hX/sf/4/53/sP9lAFEAwwD4/7D/dv+z/mD+Zf1A/RD9tP2T/S79S/2t/Vf+l/6o/14ABAH3AP4AKQHLAMgA6wAsAYMA2ABSADAASwDP/9oAVQFvAXIBdAGaASYBSQGvAd0BAQJEAgsC/wBfALr/R/8h/5T+D/5u/RD91/w6/HT8pf2u/vL/CAEfAQwBswB+AOX/IP+l/gv+EP6l/XT98/2Q/kb/owBgAdQBDQJwAfMBggKHAngCfwJfAjMCjwGJAMn/eP8SACEAGwBNACsANQCHAJIAiADcADIBeAFSAK//K/8u/r39qvyX/K38dPzt/PT9tv7T/8sAAAGZAaYB6AE/AcoAfgD4/2cA5f+h/+j+nv7A/9//CQB4AQ0ClwKHA9gCcAIHAVMAnwB//3P/IP/d/nH/Vv9A/+T+Cf85/yj/CP+S/qL+wf7H/pX+Xf9ZACMAUwDo/7X/+/9W/wn/Of+p/wMAJwDX/7r/kQCKAUACrQLzAlED+ANrAwsDPAIVAYMAjf/Z/uv9Yv29/Dr9tP4+/wkABwCHANsAMgF1AFv+z/1x/Ur9YPy1+7/7yvyQ/ln/+v98AJ0BzgFiAR0B1ACYAB4ABgCE/+b/tQAmAUkBHgKCA58DNQO7AlgCCQJaAYMAjf98/ln+vf5p/qX+jv+mAGMBegHCAGUAPwD6/j3+bf1q/Br8/vv6+/f7dfwV/tL/3QAzAcIBkgKUAu8BagF+ANP/t/+O/yP/3/6r/2AAlwCxADUBxAESAlECOAFqAW4BgwFvATgAMAF2Aa4BAQIcAdMAqgCuALD/B/8Q/qX94/0S/bb9A/4J/v7+DQB5AIYAEABV/1L/qf4g/lj+X/0W/cz93f39/WH+M/8CAZ0CQgO1A8gDjgNeA9wCKQJ0AZgAewB1ABUA///t/6gA1AF7AvACqALIATgBsgBqAPr/Vv8t/1b/nP8+/kr9T/0c/Zn96fxb/Pz7+Pub/J78Rv0E/g3/hwAAAU0A0f+j/8f/ZQCa/xr/fv88AHoA0QAsAvoCtATiBdMFMwXnAzgDqAFBACH/XP6J/vT9R/4M/wUAmgEoAnUCfAImAgMBKf+G/Xv72PrD+vz6mfs8/DD+Vf9TAPsAcAGaAisCYQAD/w3+fPw7/Jn8Hf0w/9sAfQIGBMIEIgUVBuoFVgT7Abr/6v6d/aP8AP3M/b3/XwHoAoEEIwRFBJgEtAMyAor/wf1k/Fz7mvqR+gv7OPxA/tH/tgAUAc4BrAFZAd8AoP/o/uT9Xf0V/Tf91P15/98AWQFiArcCegJbAtQBVAGkADoALwDd/6z/vf9cAKkBWQJAAqwBRgFhAAQA8P58/Qn9K/yy/Fb9//2//tv/rgE4AksC/gHjAJH/f/61/YH9efxw/CH9eP0K/wQAPQGDAsEDnASCBJADcQJSAcX/K/8a/gr+7P7a/9EAqgHJAngDlwMKA/IBRQBb/+X9FP3t/Ez8Tf0w/lX/9/+eAKYBjAGuASMBVwDp/vj97PwB/Eb8kPwY/lT/ZAAeAjgDwgQPBUwEUgP0AX8AZf+R/Sr8evzf/Nb91f6SAEMCjQOqBKAE4gRMBC0DegHB/7b9bfwK/Dn7AfzH/Nb9Mf9IACoBzQFkAsgBuQF2AWMAPP/h/vH9DP34/DL9mf2P/Rr+i/4MAMIAQgFQAicCPQKEAXABKQEkADAAAQBc/w3/F/+x/l7+1P61/2gAMQHTAWkCqQJvAlMCFwJTAbUANQAF/6L+QP65/T3+OP7a/sz/1v8nAB8AYwCsAHgAqgBSADAAb/9U/6r+s/1d/mT+/v56/5T/8/91AM0A7wAdAQsB2QH+AfgBAgGrAHgAqf+D/3T+Uv6l/qH/tP9DAH8A+gADAo0BQAFcAAIBYgCX/+H+8f1X/nD9Av5i/Rn98/21/nb/tv+OAAYBwwGRATAB4wBtAA4AVP91/0b/av+//ycAswARAcwBmgKsAqkCuALoAWQBZwB2/8b+Jv5K/jH+wv43/9//MQHAAX4ClgKUAdcArP9x/s797/yq/Cv9Nv0v/kL/ef/eANoBkwIoA1QCXwGIAFr/eP6d/cf8d/yB/Hj9if5CADcBEAKJA7cDAQRfA5EB+P8K/+39Zf2a/NL7fPwr/YL+vP+4AJkCCgTFBLYEJgP2AaUAA/9W/gH9uPz//N79Wv4b/+4AMQJIA9wCrQOvAy0CUgGh/5/+Pf63/e/8z/zH/Oj9Lf+z/0IAEgFgAqMC6QGtAOb/of9q/5f+gf7e/in/LwDv/5gAjQAFAR4CfgG1Ad8AjwBhAJb/dP/W/hD/CQC+/93/GwBfALsATQAHAJj/vv/L/3n/N/+T/kn/AADb/5n/Pv92/+3/p/83/zn/YP9t/2T/cP96/0sAhgAAAT0BkQAIAR8BsADW/3D/VP9R/2D/bf/B/7v/WwAnAVwBKwGEAUwBHgEwAfT/df8P/6r+kP6g/nb+Zv6T//L/UADUANAAugDyANUAPQAfAIb/Cv/e/jn+Wv4r/vT+Fv8M/08AQAAjATQBnABJAdIABQHk/2j/PP/h/r//Jf8G/0n/SQAYARkBiAEXAZoBFQLAATIB0gAqAToB/QATAKL/x/8+/xr/Iv87/07/J/+u/77/y/9VAGkAIAEfAWYAUgB4/5H+RP6G/SP9r/yu/K/9R/4w/2wASQJtA6EDpQNMA84CeAE/AOj+Lv5h/c/8WfxD/BH+Tv89AScCmQKcA+sDKAOJAQYB0v9a//n+u/2Y/Q39jf3i/YL+l/8ZAPIAaQF/ATUBHgHBAL//S//I/gX/x/6C/vH+S/9KACkARgCCADIAhAAzACkAs//6/44AzgCoAdcBIgJwAgoCkgH6AFsAgQBm/5T+kf5q/t3+8f7M/7IA3AGCAtACswJAAiwCCAFUAIz/NP+j/uT9lf15/Z3+Bv8S/2X/u//JAIABtAAiAGUAiQBuAGr/c/5j/uv+6f4y/+v+6v5YAJEAmgAfAHUAFwFgADsA+f/V/8v/sf+u/wcAYQBhAOIAAAG8AOEA7QBiABgAAQA3/yT+R/1y/fP+TP84/xYAuADgAWAC/QG/AWgBRwGsAD//9P37/Nj84fx8/Qv+pP5XAIAB3gL4A38EWASmA8wCiAFfABL+yfxn/HP8W/1d/YT9Jv93AGIBjgI0An8C8wLiAtQCagEiAIj/H//s/WP9vvzM/Eb9Ff1M/sX+X/8jAMIAegHWASECSwKkAmsC4AECARgAyP4C/mP9mfw//Gb8mv23/tT/8ACPAssD7gRYBU8EwwNQArYApP+P/r/8y/u++9n7Fv25/T//wgB8AioEpwTnBAcEGgMkAsoAjf6G/K/7Xvux+5f7TfyF/af+bABsAToChAI+AmICfQHqALwABACD/9D+r/6C/pX+f/63/lP/4//qAJgAIAGzARcCegJcAjACsQG5ASwB4AAzACkAawAMAMH/J/92/yL/Kf9l/yf/dv/t/0wAdACDAFcAkACZAB8Aq/86/yf+Sf3z/An99vzn/N39R/7W/4MAfAB3ABYAbgDr/wAA//75/uX/xf/R/37/BQByAIMBzAE7ASMBNAGxAacBCwGNAKsBkAGMAXcBdQBzAWMBnwGYAUcAy//B/v39J/3F/An9Uv38/Tv+uP7C/zwAsgAQAdsAsQAyACf/T/7G/TL9u/y3/JL9Qv7i/ggAQAFgAoAD5wMoBCQEDQOtAnABy/8v/0P+h/4s/43/gADoAHMB9gE7AqkCyQGVAdgA5P97/9r9jP1y/V794P0A/nb+sP66/jD/D/9z/on+UP7Z/fr9cf7R/lX/wP+pADECjwK2ArAC9AFbAbwA4P8J/5P+tf5R/xgA3gDIAc4CRQMBBNAEUAQwA+wBnQC0/67+Nf2r/Jj8HP0I/g3+Sf5E/0UAFQEXAT0BSQH3AEYAbv9T/7z+jP6d/jz+3f7x/u7+W//F/4gA7gAvAfQAawGlAZ0B8wERAQEBGQG+AL4AvP82/yb/K/+e/2j/4v8eAJkARgE+ATgBVQANAJ3/L//7/vT9bP46/qT+RP8x/5H/lP8pAFgANQD0/2P/Xf8g/+/+JP8Y/1f/1P9vAMgANQHpAYoBKwG6AN7/Gv8N/sj9tf1M/n7/mAB9AVoCVgPYAywDVwLjAfIA5v/8/hn+dv1g/T/+zf6s/oL/iQDLADcBMgHkABQBFgGWAK//mP7J/aP9vP10/QX+jP5W/0EANABjAcQB7gFZAsAB/AE9ASMArv9i/zf/FP+M/0b/j/8AAKYAPgETAakBjgF4AXkBCACH/x3/fv6S/mr+gv6C/t/+9P9kAOQASwH5ACUBRgBc/8P+kP3S/ar9DP7u/iP/GAAoARYCZwKoAjYCbwLjAfIAVADn/pz+YP55/kT+iP4t/zIABgGLAUEC5AEsAhoBrACu/yj+Xf24/BH9D/1s/jz/mgBHAQoCKAP4AZYBagCe/5z+3/21/Vz9qv5u/5z/+wA7AvMCHARiA6gCowF0AIH/lf2v/Cz8yP3J/gb/SgCaASoDNQQKBGcDmQIoAe7/k/4x/Vz7wfuB/C/9z/6M/+8B2wIbBMAE5wMAA/oAbgCf/hb9pPxJ/En8Jv1s/k7/hACkAWcCcQJ5An0BaAAu/9b+af5s/bX9yv3e/in/+f+NACoBYQI1AskCCALIAV0BPABDAGz/4/5R/yn/9/6+/3AAtgDKAP8ATwEgAVUAxP+G/5z+hP47/jb+of6J/vf+8/5f////yP9BAH4ALgBKAAQAOwDU/27/Zf8V/x7/kf5H//7/EADFAPsAgwHwAYAC4QJSAikC0AE/Ae4A9v9S/wX/2v7u/jb/lP/h/wsAQACiAAEA8P+8/yP/BP8z/q/9s/3J/cj9//1j/sX+y/4H/6b/7/8GAVQBXAGHAZcBgAFIARsBiACAAOf/2f+X/0//zv/Y/3IA3QCPAR8CSgK1AkEC0QEbAQcAvP/s/uj9YP0F/XT9lv3p/Qn/qP/NAEsBMAE/AbcAt/+x/qb9vPxJ/Lb7ZvxQ/fr9z/9uAb0CywPHA8QDUwOJAq8BRwAT/1H+W/7R/jH/IwB7AccC+AN/BH0ExgQQBHwCWgHM/6/+pP0n/FP8dvzJ/Pz9z/6w/y0AXgGJAc4A7v8V/xv+4/wf/Fz7Q/xE/Ov8vf5G/5AAmwFzAp8CCgKTASABngBIALr/fv/h/2cAaAEPARQCwgIEAwQETwN2A6UC/QFjAS4AW/+M/lP+gf7L/ob+4v69/un+V//3/k//8P41/iL/uf7k/bn9cv1f/i/+0/5F/0T/6v+A/wYAFwCmANAA3wD9AN8AbAETAV8BUgF/AdsBSgIiAoEBEQGlAJkBEwEnATgBxADoAIMAMgCo//H/GAA4APf/wf+p/7r/2v/y/oD+bv6F/pf+bv7f/Ub9Bf4w/i7+Y/5q/jr/z//G//b/LwCnAPUA/QBvABAA+//X/9//wf9gAE0ArQCgAS0CwwKWAqkCywJBAuMBKQE3ANH/NP+2/pr+yv0m/hX/ev/M/wwAsADFALEA6wAXAFv/6P7S/U79iPwN/OT82Pwr/YL+YP/dAKEBYwEgAu4BDQGPALz/t/+O/zX/lP9f/wAA3AD7ALoBeQIlA2cDCAO7AuoBnQEWAfH/Tv/d/l//Wv/U/vz+Qf94/xMANABPAHcAzf97/yb/hf5O/jP+aP4j/iT+pf5X/1P/Pf+//zoALgCl/+7/g/9S/6v/cv/q/yQAjADfAI8ABwFnAZABxAHbAckBzAHiAXIBhABqAJ8AbgDG/xoAzQBuAKMAOQAJACwANgD1/5v/Lv9p/wYATv9L/0r/pP9a//n+T/4i/iT/zv7S/i/+C/+W/9D/bADp/+8AHQGeARYBXwCWAEIA7P/u/qL+Zf42/0v/Sf9JAAYBDALgAgoDzwIhA5gCGAKbAKH/Mv/8/Rb+hf0A/vf+dP+2ALkBQQKcAj8CYQGcAFf/Uf59/dP8gfyb/Pn82f2g/uf/fgDUANIBQQGWARAB///I/5n+Xv5T/iX+bv6H/9cAiwFTAikCLQIvAowB9QCN/7T+YP7m/Sr+YP5E/2oA6wF+A64DZgNRA5oC8gCv/9/9fPzM+yv7dfsy/HD9BP8BAcECGATjBOAEOAR3Ag0Baf+C/Z37X/qZ+tr6JPzT/bD/RAI0BKAFHgbMBb8EnAMMAmv/X/3K+3T7Qfsq+1L8CP15/mwAJAIGA5cDwgMtA1gCGAHO/7H+uP3L/On8Xv3z/cf+Tv+pAJ0BuwGKAT4BNwENAVgA/v///0gA4ADsAJkAoADwAMEAiQAlAJ3/jP+Q/yX/vP6e/uP+ZP/M/44ABgFnAfwA3gD8AAAAW/+w/kv+Df7//Rn+Lf6I/r7+tf9WACMBRwFkAY0BigEZAXMAXQCB/6z/4f/V/5T/lv/i/zEAqADRAHQBdQF3AYoBUAFGAT4BtwAlAFUA6f9//5j/Pv8a/5D/Jf8G/0b+mv0j/iT+W/6I/j//ZgCuANYALgEYAfQAoABKAJb/u/57/xT/nP4r/2f/KQAjAcgBcgIgAwYDYAPdAhgC9wDY/03/tf2B/TL94v1d/lX/rwAOAckBqAGfAXEAWv8u/rz8bvxU/In86/wF/lX+hf9CAEgAFwF0AXYBCQF5AJj/K//B/kb+Uv7v/iUAxgE5AoMCZQOaA+kD3QIqAisBJgCM/9j+yP5x/sD/TQC/AIoBrAG1AU4BDQEOAGb/E/5e/U39K/yN/Lf8xvzV/UH+z/6w/5v/CgCs/wT/Wv/5/iz/DP/x/rn/tgBdARwCyAIJA1AD9QJiAn0BxQAdAM//kADQAAQBdwGLAWUCXwMUA+oCRwIwAYYANP+z/dn8Tvyq/GL9v/3C/oH/PwDrAL0A0ABLAHP/Qv67/QX9X/xb/Gr8wv38/mcAVQFfAtkCqAIUAw0CpwF6AXgA8/+H/7H/CQB2AE8BoQFAAnYCawJiAo8BVAHbAHkAz/9q/+H+YP5V/jn+tv6H/pn+YP81/7f+G/81/yX/Pf+Y/hX/Mf8h/yj/mf7x/gH/IP85/yj/9v7N/q//PwC0AFwBPwIJA88CDgPBAgECwgGgAEkAu/9s/2T/7/5b/2n/4v9WABAB3QFMAkgC6gEuARYAkv+A/lr9WvxW/FT8ifyk/VD+JgDXAGYBSALWAVYB7wBSAIr/WP92/sD9Zf2K/c/+sP9lAFMB7wElA4sDkQKBArsBCQHoABUAWf8L/97+O/+r/yj/5v/HAFkBqgHoAIQAfQD3/y7/ef6e/YH9af2g/Sj+X/4e/ycAjgBNAK0AsABpAFUARACTAK4AsQChAIIA+//X/zn/O//1/9L/WwBJAHIAFQE7AVoBBQH3ADYB+gCkAM3/5/7m/i3+mP1p/bL9k/5b/1gAyACRAWoC0AJ7AloBOgD2/kz+nv3b/ED9Ev6p/n//UAALAccBqAIUA9gC3gK8AYkAkv9b/nb+Lv4//nH+9v4YAJUA+QASAUwBVQElAWsAVf++/o7+Qv7O/QP+m/2T/qX/t/+PAKoAHQFnASEBsgAgAOT/RQDJ/3j/EgC0/8QAngCSAEABkwAdAcEA0gBgAIQAkAAqADQABQDPAEoAFwBKAIUAWQDa/6r/pv78/q3+t/7S/tb+tf/p/8oAtQBtAKIAAQC4/3z/Av/F/pP+yP6Y//b/LgDeAOoA9AAhAZ8AkgBRAFQA1v+U/7z/SP/t/wIAXgAWAU8B6wGMAa4BSAHRAEwAc//r/6X/AAAlALD/UgBUAFYARgDd/+T/Vv8I/9z+b/6Y/jj+tf4t/wz/c/+h/0YAJgDV/xQAtf9n/2D/bf+J/6D/DgCfANwAWAHgAfEByAGnAcEALQBcAJL/J/8H/2//+v/FACABoAFkArYBqwHXANH//f6s/Xn9B/0s/d39f/4B/yEAHQHDAVsCigEZAWEAOv9f/hz+iv26/Qb+e/4AAKUA0QFCAngCyAIsAq0B2QCb/xv/x/7K/Tj+2v6U/3MAKAE6AvMC9AIFAmoBkACF/4j+Tv3R/AH9lf2z/iv/sf+vAKIBigL6AaoBjQDf/1L/A/4u/mH9df28/VH+7v5b/7QA/wDiAeEBuwGvAcgAVwB8/8v+mP5L/jH+wv6j/o3/WwBuAEgB1AH6AaoB2QHHAW8BJwETAZQACADQ/6L/Rv8z/23/QP+v/5r/ZP9w//v/RAAAAG4ANAAFAPL/T/8o//b+g/5x/hj+9v3H/cf9f/5L/0oAvQA+AZQB7AEOAoMBgQHtAL8AKwDH/wkAvv8UAEcAlgAxARsBrwHvAVcBuwFSAdkA1ABhALz//v4L/4L+g/7f/uD+hv/o/0gAFQBZ/x3/Ev+//rT+c/4a/mb+2v4m/3X/ov81AAgBoAEaAukB1AEvAasAnAC0/1T/UP+F/9T/JgCNAE8BNQK3AtYCkwKVAvABWAEmAGf/KP8r/uD9bP2Q/eT9hP6+/wEAXQDeAOoABwGvAOj/yP8a/0X+Gv6b/ZD9rf3X/Yz+Hv/L/40A8gBEAZkBbwEnARMB8ADmALoATAB0AMwA7gBBASgBJgE3AdUAvgA9AMT/4v/V/6b/bv94/6X/NwAsAFsAkwAIAD0Asf++/lf+p/2I/W/9Ef00/dH9Yv40/xMAtQAmAf8AzgDvAEAAxv+H/2f/uv75/j//G/8AABEANQFoAZEBoQL6Ab0BLwEZAb4AhgBsAFcAawAxAKkAiABuAEYAEwDZ/7z/kv9d/w7/Tf7Z/sn+Kv+w/7//TADi/+j/EQDE/2H/Nv8U/9P+n/6a/s3+9v4F/1r/sv9BAO0A9gAjAVkBKAFLAWcBIQHpAM4AlACKABMAxwAPAdsA+gDJANoAeACGAOv/Jf90//7/ov8QAEQApP8AADX/b/9B/8D+Ef90/or+P/4n/nH+T/5s/mD/pP/t/xcBGAFjAWgBNQEwAU8Av/+6/yH/Ff96/2//HgBPAMEAVAGBAcoBuwEwAh8CSgLGAf8A8gBnAHgAvP99/ln+4P1c/pv+qf5a/9f/uwDzAA4BEQEBAQYBCAB0/43+wP2v/Wn9Vv1+/SD+6/4QANgAiwFBAncCkALaAWsBAAFgADoALv+x/s3+v/7r/iD/qP+DABABywEYAsIB7AFDAc0Ayf/k/nX+9/2B/qT9Gf7B/u3+WwBuABEBlAGQAegBZQFnABwA4P8J/1v+Pv45/kj+DP+8/4EA1wBlARACzgGHAd8AMwCp/13/6f7D/rf+v/5s/9P/AAA3AK0A+gDvAEEBggAxABUAEP8+/77+jv5X/2X/8v9QAPkASgHVASACyQFLAeYAJgAd/5H+IP59/sj+Tv8WALcAOgF+AdoBfgGQAXoBwgCJ/wz/lv6i/an9Lf25/U/+//5p/+L/1wBmAbQBOgEiAen/tv9D/wn+Rv53/vr+d/9JAOEAtwFAAq0ChQI/AhkCCwFEAFr/Mf/q/sT+FP9C//r/oACDAacBQgEpAcoADwBn/0v+6P1y/YL9Wv6s/iX/0f8TAfAAHgHBAAgA4//5/r3+Mf73/QD+iP6//g//PwDHANoBygIvAyUDHAM4AoABawAw/yH/y/7Q/gv/zv9qAFgBdALqAn4CFQLlAeEAWQDF/hL+3/19/dX90v2//lr/RAC4AN4AIgHEAJ4A2//y/lz+q/3V/b/9L/6J/hz/gQB6APYAtgH1AbgBUQH9ABMA/v9r/3X/kP+U/zsADQE1AXoB1wEfAR8BLwC4/8b/Pv92/37/BQDg/3kAhgA1AE8ALgBuAMb/UP/N/j3+FP4X/r39iv5m/6n/8gAgAWkB7gGOAQkBHQBz/4z+Qf5w/ZP9aP4m/2QAvwALAs0CngIxA8oC9gHuAGQAYv9+/hD+y/3c/er9m/6H/2gA1QCJARoCDgKWARAByABp/7v+C/58/WX9Lv3N/YT+4v97AAkBaQGSAeoBeAH4AEcAuf+P/27/Qf/C/87/xf8HAHQABAEuAZkBNwENAesAmQBpAK//9P7e/jv/zv4u/3z/qP8nAA0ACgDk/7L/Zf86/83+h/50/sH+//75/nb/2/91AJUAeACGAEcAgwBXACEA0v9H/8f/dv9//08AQADZADABiQGGAU0BewEfAecAgwAgAKz/hf+K/zP/f/+Y/9H/SAC7ALwA9ADpAAMAzP9o/83+9P2P/dD94f0T/s/+Zv/g/w0B2QBUAbgBGQEsAXEASQC6/1n/Hf8S/y7/sf6F/x0ABwFVAYIBAgKeAeEBFQGDAHwA5P+y/2X/Of+F/4r/2f9zAJQAMAEHAYoASgAqACEAwP/v/n7+tv6I/vb+u/7n/kP/Vf8bALv/AADI/+b/xv9j/6b/W/9E/2n/BgDP/0YAzAAAAWIBCwFrAdsA1QA/AdwAegCHAG0A/f9rAHsAGQAnAFcAfQB3ADsAQgAQAOn/JACK/yD/k/5Z/qv+R/6K/tP+Df+r/+D/5//H/9L/yf/m/9n/hP/m/2r/h/9pAML/FwBuAGsA6gC9AM8AlQB4AOIA7QDRAPMA6ADzAEUB4QDaAGgBWgFzAT0B7QCtAOb/of9Y/8D+av6C/nD+T/5+/u7+kv/x//T/9v8cALv/SP8P/4b+YP7D/pL+ff7t/mz/0/9JALwAUAHaAf8B5gFjAR4B+QAiAOX/xv+//0wAvgDQACkBzQH0AcsB8wGSAZ4ASAAB/7L+lv5u/hj/xP5e/8f/QAC0AH8AeQAXAKX/7P6g/tD94P3u/Xf9rf4B/1j/wv/h/4wAzQDKAH4AigATAKL/ov9F/zL/yf9mAOYATQGyAQQC6gEeAn4BNAEdAUAAWACi/4//k//d/uH/CwBSAEIAEAChAO//8v9h/7X+4/6Z/rr+Qf5z/tL++v5k/wMAzP/o/zYAYf9u/wn/J/8s/4z/kgCaAJEBaAFaAXMB4QB+AOX/s/8v/zL/Nf/e//f/ZwAwAdIBjQL8AXYCsgFMAa8AMP8h/6T9PP0f/eP8a/1H/vv/6wCtARICCAJ+AdgAGgA5/yb+kv3k/KH8Wv0D/gv/BQArAc4BLQKMAo8C/QF2Ab4Avf8BAG7/Zf+7/0f/ov+jAOAASAHmAYcBBgKyADMAYQDe/t/+cf49/jj+Wf71/jv/vv/d/y0AJAAdACoAj/82/+/+kP6g/i7/Rf9p/+P/MQCWAMMA5wApAV4BLAEEAUEBNwAIAJj/Pv8bAJb/GABdAIIAawE3AVcBJwEAAfMAnwC2/1b/G//r/jP/JP8q/2b/Ov9z/9j/lv/i/9b/AgDd/z7/Uf/g/vP+3f4o/3f/yf9UAHsALgFiAVUBgQHtAHUAXgC5/9r/hf/C/zwA1f8oAUsBZwHaAdoBEgL1Ad0BkwGxAMX/T/+n/lb+8P0y/rD+uv4e/5T/YACqAEEBFQGDAA4AeP/t/vv9Ff6F/Wz9tf24/XP+9/72/8IAHQGeAfQBkwFFAc4AbwD+/1n/jP9Y/+X+ef/K/9X/ggDFAKEBQAJkAhQD/QKNAsUBxwD7/6D/sf66/kH+g/02/iD+ov74/q3/PQD8AJYBNQEeAVMAwv/x/iP+tf3v/fr9uP2r/iT/0P9+ADEBrgE2AUMBcwEZAasAigATALT/1f/L//r/VwCiAN8AWgGFAXEB8gCxAHwALAAAANv/q/+X/+P/w//0//f/5v/+/6L/M//H/hb/nv6G/tD+nP51/zP/bv+v/9H/WwDu/3EAAADu//H/z//+/33/PABnAHgAqwBCAZcBfwGkAWUBaQHsAPUAxgCNACgAe//f/1L/T/+7/5H/cQC3AEoAzwCCAFYAtAD+/8f/Uf8q/+X+dv6w/l3+C/9N/8z/RABJAGIBHQH4ADcB1gC/AFAAwP9L/+3+j/5o/qX+fP/f/9QAdgGKAdEBrgGAASMBNAFSAPn/jP8i/03/kv6S/4L/0v+SAD8AjwCYAPsAbgBrANb/FP/4/k7+a/4T/oX+GP+i/zQAYQC9AL0AmAAfACsAx/9k/5X/YP9s/+X/IQB3AHIAywDbAFQA6gBOAGMAdQAnALMA/f9ZAP//2v89AOj/NgBQAEEAkAD1AGkAZwDUAKsA1ADPAPEAZgAtABIAxv/R/37/cv97/4P/Uf9h/7f/oP/Y/2AAqQBkAIgAgADC/4T/Cf8B/w7/8/5M/13/of/r/xMAtQAmAVsBhwHMAJIALABH/1j/L/9q/4f/Z//h/1UAVwCQANAAcACkAF8ATQAZADj/cf9o/07/cf+x/9P/AAASACEAPwBGAEoAYQBgABYApP8j/zv/Bf/H/t/+zf7k/mX/3//m/0YASwBPAD8ADgD6/9b/p/8S/0H/Qf94/+//BABfAF8AzgBeAQgBDAF+ATQB0wCqAFIAHQCq/5b/hf+d/8P/BQBgAE4A5AAUASgB3AAeAM//tP+e/9T+xP4B/9f+bf+J/47/EgAhAFIAQgD//9r/GADv//D+Jf8G/zb/cP/m/vr/VwCPAOIAtgACAeIAJQHaAEEADwDD/6r/lv8q/0H/nf9n/zv/4v8xADoAiwBwAKQAuwCEAFgAov80AAUA4P/C/97+YP9I/9j+Ef8t/9f/cgDKADcBaQGkAYoBUAEPAQ8Aw/8X/3n+oP4H/uj9Yv4P/5r/UwAOASMBJAI7AswBcwEWAFr/nf7N/V39A/0W/af9Lv4u/1gANwHqAVYCiAJnAqYBLwGYAB3/bP5e/gn+/P0p/s7+nf96AIkBPwJjApMCpwLZAQ8BWQBr/2H+5/2E/X79Df6T/lv/IAD3AJIB/AGaAV0BYwGKACYAMP9D/vT9fP1l/Xj90f2s/oH/dgBPAVgB4AHfAUsBCwFDAKT/6/6f/r/+xv5N/xUAkgAJAbMBzQEsAuUBYgEwAU8AUgCv/yz/Z/87/5n/Uf+Y/+P/1v9xAO3/p/+B/z7/Gv/Y/rX+CP9d/0X/af++/0sAYQBzAEoAFwDc//P+A/+g/sD+2f7b/gMAFAC2AIMBAwJqAikCGgKfAbsAKAD8/1f/Qf+w/4j/n//X//L/4v+NADwBEQG6AT8BygC1AO3/OP9K/h7+nv1u/dz9af38/XL+9/7j/0QAuAAnATgB+wCmALz/Nf9v/67+XP7S/rH+BP81//D/9ACiAXgCkQK4AtcClAIUAj4BkgC+/yX/vP5C/mH+n/7k/vj/egCsAOcA8QAxAdEAcQC2/zH/6v5o/iP+x/3+/WL+/P5T/5r/LgBvAMgA/QA7ARAB2wCMACcARAAkAAsA0v8AADcAGQCWAHgAhgC2AJIA5QC4AMwAEwGBAHsAdQDx//T/GgDM/7H/if9p/3T/ff9f/37/hf94/4D/h/9n/wP/R/+i/5D/yv+w/+T//P/G/7//8P+8/9z/PgAyAM4AlACcALUAbQB9AC0AXABcAG8AtgC3AMsAJQEjAf0AggCOALwAFgAAAKT/EP8a/6P/fv+p/wMAlf8FAOD/1P8TAOv/uP/Y/7v/Nf9v/1T/UP8p/0D/QP8u/1f/eP/v//L/UADCAOYAzAATAaYAqwBSAOf/RwDe/5wARgCVAK8AoACDATgBoQErAQQBrABmAHcATQCtAML/BADy/+L/DADm/zQA4f+w/2P/lP/x/hP/eP9b/7P/HP+k/6T/bP/S/23/if8y/1r/MP97/hD/Yv7X/sn/U/8+AOsAUQHtAdcB/QHRAYoBGAFOAL//gv8+/1H/PP8r//r/xQBFAb4BDgJzAkMC5QHRAeMA7f84/13+0f2X/dj9MP6K/nn/OACJAEwBVQFvAfEAHADg/7/+IP7q/Yb9gP3X/VX+uv7X/6kALgGHAQYC6wEgAtsBEAEAATsACwDS/8n/LwBKAJgA6QA9AdsA6AA8AdoA5wCnAD0ARADJ/2X/Xv8P/yv/Vf9j/4L/0v9//yn/G/+0/k/+6v13/rH+BP/J/1MAnwCTAOUA8ADBAGQAGgACAF3/1v7+/sH+JP+r/87/xgAPAZMBNAIRAqwCOgKnAUIBJgB6/9v+XP4H/lf+l/4U/3n/3f8/AI8A4gCRAJoAVwAhAPf/r/8+/9D+0/6f/tH+5/4L/03/lf/z/4kAuABvABIBFAEoAUsBeQFDAc0AAQFOACwAkf9d/33/pv4O/2L/8P8EAM4AOgH9APMBkgEyAQkBLwCB//T+b/7y/bL9AP4H/rP+h/9V/+YA8QBVAQMCMAGJAakAUQD4/2b/3v5e/ub+Zf7s/mv/CAB1APIAaQFtAYIBlAG0Ad4AxgAMAC3/+v49/gH+CP6h/nb+1f5r/4j//P9FAIIADgFuARQBTQF5APT/CAB0/w7/8/6D/1L/mf8IAHUA8gBpAdsBNQF6ATEBmgCOAM7/H/8B/+n+RP9D/zH/tf+x//j/HgAFAE4APwAyALv/bP9k/zn/X/+j/2z/m//4//r/VgBGAG8AWgBIACgA1/8oAHv/uv9IABUAbQC0ALYA3AAzARwBCgGfAIAAHQDh/7D/q/7b/gH/Dv9P/7v/SQBgAKkAdgCEAGoA6P/a/3P/w/6A/lz+B/5E/q3+OP9y/+n/bgBGAMwAtwAUAQQBmgCzAP7/IgAuABMARgA5AGUAmwB9AK4ADgGPANAAFgG7AKkAdgC7AM4ANwA/APz/IP9w/x7/7f4Q/5n+A/9H/6L/x//S/+3/uv8QANf/uv///37/Fv9W/xv/xv7M/mL+xP4C/2r/UQCwAFkBqgHrAZ4BcgGHARYB4AAzAAUAFgCk/5H/p/+4/6H/DwCNAF8ABQH3AGsADwG1AJIAPgB7/0v/kf5E/uL9Xv4b/gr+//4M//T/PwC0ABIBOQE0AeYAOgFFABIAtP9B/2b/KP9k/3D/1v/e/y4AkwCuAEUBTwF9AX0BMwEvAeIA/v+Q/2//0v7D/pL+/v6f/x7/3f8tAMn/QQAQAEQASQDg/+b/tP+L/0b/Dv/z/rn+5v7A/rT+Uf88/3T/kQDRAKgAGwEbAXYA4ADZAMIAwQBSAJ4AbQAOAOf/ov/s/7n/6/9dAEsAYQCYAHsArABmAGUAYwC+/8v/w/9y/2n/Bf8j/zz/vP5X/53/Zv/z/6z/4f9VAEQAXAA4ABoATAAZAMv/w/+X/+P/sv+c/+f/IgCvAOkAhwGqAY4BeAHmAAMBPQB7AIgA2/8rAKL/a/9R/07/g/9k/7r/x/8JAPX/CQAaALn/tf/D/2H/Nv9L/xL/Lf/o/jH/Wf9n/7z/yf8KAPf/eQBPAFIA6ACWALAAoAA3AAgAGQC4/9n/8/+H/+j/7f/x/2EAFwCBAOkABgEvAYYAowA6AAkAv/8B/47/Nv84/zr/qv8WAO7/zgA3ABoA3/92/6T/NP8l/3T/av+a/y4AJQBDAMkAogCVADEB0QBeACcAjf+R/xP/Zv/O/+r/bgARAYIBlAH+AYgBmQEAAfL/mP+q/iL+xv3Y/ef9Pf7e/s//fQBCAbwBHwJuAmIBQgFwAH7/p/7V/cD9CP3m/Zj+J/8bABgBCQITAlIChQKJAooBvADz/+H+hf47/hL+X/7C/jf/FgClAD0BkwGhAdIBGwG/AD4A1/9L/8j+Bf/H/t/+Kf/n/zQAGACUAEAAWABsAA0Ar/8s/9b/uf+Q/xMAIgDUAOIA2wAfAWYAZQBRAK//df/8/tL++/72/mH/yv8LANMAGQEHAecAcABtACAAYv83/4H+2/0O/jj+tf5R/wYAmABGAYgBTgEyAeQA7wDBAPb/QP8u/3z/Of9g/6T/yP8JAFEAngCkAAUBLwEGAdMAhgB+APj/+f+x/y3/aP8q/xz/bf/B/4P/wf+o/2//HgAYACYAHgC+AKwAeABhAAQATQCH/3n/b/8v/0X/af90/7T/egBQAB4BjAFSATUB+QDbAGcAUwALANP/SP+R/6b/XP/q/+//FgBbAMsAyABqAGgAQQBY/1T/iP+v/rn+Zf5Z/uL+0P5V/63/9f9SAGcA+QCkAF8AhADq/yUAwv9y/8X/9f9AACEAUgBVADIAXwCEAH0AUgB5AIcApABNAFAA1ABPAK4AxABBADUAmP+H/1X/P/93/5H/uf///1oAJAB5AGEAhgB+AHgAhgC0/8P/Fv95/h/+Mv7D/qT+V//U/5QAMAFRAf8BHQLHAW8B8ABAAKH/Dv9y/j7+qP5X/rz+V/+v/4kAOQERAs8BrQFsARMBSgBf/9j+NP76/bj9Kv5O/rT+Y/8UANsAHwGgAWIB1gFoAWoAHgC9/xH/h/6H/ir+hf4G/7j/WABHABcBPQESARQB3gChAAAAyv9m/wP/Wf8L/5b/BgBhAL0AYQBzAF0AlABTAEIAWgDb/ysASABMABgAcAA1AOL/nv9C/3r/Jf8r/0L/VP+I/+n/NgCtAOgABAEuAeEAyAAyAIUAfQAJAAcAc/9F/2n/q//O/2sAaACLAAQB0QAFAdIATQC+/0r/Nv8m/2P/E/8u//3/xv8tABIA2P87AC8AXQDL/57/n/9o/8//j//K/9T/y/8LABsAzf+y/8H/u/9a//n+Uf8X/x//uv/H/wkAdgBxABQBKAGlAKoAGgAVANr/BgDh/53/+v/W/7r/7P9LAAUAcwADAb4AmQBEACQA+f8MAJz/wv9y/wz/z/+P/wAAgQCyANkAHgELAXsAPgDX/9//CQCH/9b/lf+F/1P/UP8XAMr/5/9ZAJIArQB5AHQAEwAQALH/CQAHAOL/QwDt/0wAKwBHALsAzgDdAKAAXAA3ABoAcP+M/0b/j//v/7v/kgCtAOgAPAG1AFoAWwCk/2z/Gv9X/pf+gf7e/in/nP8LAGUA0gC8AAYB+AD/AE0Avv+B/1D/KP+H/vX+TP4P/2P/gf/AAHYAKgFxAYYBXwGsAJ0AEADW/13/a/8H/9v+Of8o/4n/6v+4AKcAvgD1AGkAjABMACsAEAAfAND/ov+i/yH/X/8i/97+Kf9l/83/6f8SAI8AhgCjALsA4AA2AVQAaABmAK3/vv9J/0j/EP8H/yX/dP+0/2f/hgDbANUAPwEmATcBngBbAAAAf/88/7z+sf5x/of+9f47/9D/bACzAEkBLgFiAbEBEwEDAWIA8//k/2j/Tv/w/lz/2P+p/4MAtACRAHcBZQHpAE8BaAAdAPP/Pf91//3+Hf+l/5L/p/+B/ywA2//i/x4Avf+UAFIAHgA9ALH/5f/F/5r/0v/J/xwAKQDG/9H/7f/M/7H/+P+d/4z//v/I/1MAQwD//4AAHQAXABMAWQAjAFMAaACc/wsA5f/Y/ygA/f/r/6X/kv+D/4n/sv9UAEQASQDhAKMAXgBMAD0A+//p/+7/Xv9r/2P/pv8BADgA0wCqAPgAkgENAf4A8QBUAEMAtv9o/yr/0v76/r7+Iv9f/2z/5f/9/1kAbAAyAHIAEgDG/9H/R/8h/7n+Qv9n/4X/CgDS/5IAPwBqAIwAOgCwAAwAVAAeACsAtgCAAJ8ApQCXAEIAIwAKAKz/Yf/u/83/aP+r/5b/BgBPAJwAWACRAL8AhwCkAM3/aP/g/qn+ff4P/hT+BP6e/hr/kf/w/4YAEgEUAYQBFAHxANUAYgAFADr/BP9q/kr+sv6E/ob/1f9LAHYB1AGgAp8CZwJMAtoBDwE0AM//xP6T/pD+RP6s/sn+GP98/7v/WwClAOIA2wDDANQA4f8LABsATP9v/xz/yP7y/oD+3f4W/9T+2f88ADAAuwCWANUAvgC+AAgBZgBAAEYAAQAlAHn/Sv+3/2n/Yf82/3D/ev+B/ywASQC8ACsBOwE1AUMBBAGIAEgAuv+1/wv/8f7K/ij+cf6//rb/xP9QAOYAFgFhAWYBtAFgAZoARQDK/xz/tf49/kr+aP42/hD/m/8vALkAYAGKAeQB4gEoATkBjQDy/3P/6f7D/lr+Bv5o/hT/Qf/o/5EAGwEJAY4B+QGXAZIBHwHVAHQAFAB9/xb/DP+6/gz/qv/g/woAiQCmAJgA1wD3AH0AdwCFADQAFwC3/2n/4f49/xn/D/+a//X+O/++/8v/w/+8/+7/8v/i/x4AKwDs/wIAJgAfAL3/AQCl/5L/p/9c/3z/J/+u/+L/HwD2ACIBWQGFAboB0wEvAQYBwQAIAND/ov9r/yv/C/9f/0f/Wf/V/0sA0ABzAawBowFRAf4AlQBk/xT/Uv4S/gP+0v2I/of+Uf8YAIIAIQEzAVQBNwEfAcMAigDv/7v/tv/6/hr/jv6x/k7/g/+KAIIA1wBBAToBbAFKAfgAtQB/APn/MQDe/9P/JACv/xoAKADX/9//UwAxAAIAFAAQAGkA+f8MAPj/1f/d/7//3v+u/6v/KP8t/wz/g/6o/rT+B/9u/2b/8v91AF4AqADkAMoA2gCLAEsA9P+s/2D/Ef9k/7r/tf8fAFAALgCBAPwATAEeAUMBOwHHAHsAUQDB/1//fv9O/3D/sf/l/zMABAADACgAfABRAFQA+/+N/8n/G/+k/8j/ZP+6/8j/wP9e/7X/jP9+/6r/3//4/wsAeABOAHYAuwDhANoAQwHgANkA1ADz/3YAg/+t//X/5f8gAKz/qwB4AAYB+AD/AAUBZABjAL3/3f8Z//z+wP5Y/oX+YP7D/l3/2f/z/3YAlgAdAAUAOwD5/7H/rv9P/1//Nf/t/lr/xP+r/2AAlwCxAOsAvQAsAXEAgABCACMAQQDG/9L/yP/T/9z/UQAcAGAAYAAWABIA/f9ZAOz/JgAMAFQAaACv/+T/n/97/zn/3v7y/qX+6P4x/yL/Tf84/ykAkACrAB0BrwAgAVUADQAKAAf/Ev/3/hj/Rf+h/w4AVQDGAEUBPgG4AYgBBQHkACQAsP8Z/9f+tf7Q/h7/bv8LAHcAvADPAE0BiwAmAGkAwv9N/13/WP8K/wL/NP+l/6T/AABJACgAagAxAN7/0v9t/wj/Xf/E/u/+//7n/rH/+P+MAJYA1QDQALoA4AAOAOj/2v9O/5X/mP+s/2EAvQA+AW8BqQFpAX8BIgGgAIEAnv+x/6z+yf4Y/3r+R/9r/z8AtADbAEQBmQFJARwBrQAwAMv/wf61/ir+BP74/af+a/9j/zkAUwCMAF8AlgCLAEsAYQAXACUA5//a/6r/zf/q/zcAYwBjAE8AUgCMAJYAsACzAMcAfAA/AHwAiQBcACUAMADM/9b/FAAjAMH/u/+R/6b/uP+0/wsA+P/U/+//OwCd/8P/mP9i/6b/Nv+6/0b/ff+E/4r/IQCI/9b/zP8fAD4ARACBAEMASABfACgADQBCACMAHABgADsAHQBhABcAAAAAABIAWADZ/2EAhgBHAIMAVwAPAEMA7f+V/3L/6P4x/yL/qf/x/ysAWgBtAH0AQACPAAUAqf+C/z7/d/9//6r/4P8KAAgAiAC3AKYAqwALAfwAXAC5ADkAm/+v/7//y/8xAHEAgACeADYAiABbAEkAKACz/4r/WP9m/0z/Xf+i/yIA5f/Y/2AAFgBJAF8Azf+f/2j/F/8y/9n+yP5P/5b/vf9vAH4A1ADQAM0A7wAaACgA1/+o/8v/jP/s/6b/EwB+AHgAvQAHAeYAugAXAbwAlwAwAMv/w/9z/47/gP9h/9z/vv+m/+//qf+6/37/l/90/1j/Qf8d/9z/df99/wQAFgAAACQACwDA/5X/YP+2/6D/MwAWAFwA3QCOAD0BXAFQAfwAywB/AGYAGwCo/xQAtf/E/6v/FgAkAEIAtgBcAPAALgBuAH4AwP/N/2j/Tv/d/hb/5/75/iz/Hv/w/7z/kv8VAP//IwDU/9z/mv8//5z/Zf+W/+L/MQBxAIAAeQAqALYANgBQAIsAEwBHAJUAiwBwAO4A0gAFAS8BPgFcARkB4gAjAAoAdf/8/nn/gf8r/3n/gf+H//v/DQB5AIcAfwBUAJ7/jf80/9v+3P65/ub+0/7o/nv/p/8UAJEAYgDQAAQB0gAYAc8AggBWACAA5P8x/zT/Sf+S/6f/8P/PALoAFwEqAU0BaAFHAXYBLgG8ABYAXACl/0j/Wf+c/rz+1v6h/h3/k/+D/wkAGgBeADoA+P/C/wP/kf+3/q3+yv5g/lf/Cf9e/7X/DAD4/0MAbQD8/30ALgBcADgAGgDf//j/jAAVAG0AWABrAKAAlADTAKoAPwAgAFEACgA/AKIAlQCvAKAApQAEAN//5v+P/5L/Of+X/yr/Cv9x/0P/n//X/00AGQABAF0AXgDw//P/BwBO/0z/7v7+/jD/a/+//xUApABNANEAhABYAKMAFQB/AEIAEAAyAF8AcgCTAJsAIQA/AA4A+v8fAAYAPAAMAAkAPwDq/+7/8v+Y/9H/o///////IwDDAAkA9v9BACIArf/Q/8f/Y/+n/4H/Yv+m/+//8v8+AEQAJACMACcAewDSAIQAogBeACcAMQCo/5T/u/+k/5H/3v8bAM3/IAD2/wkAUQBUAGgAQgBsAOn/7v+o/6b/7/+W/6v/cv+N/6T///+2//z/ogA4AK8AVQBFADcArP/P/4//gP89/+H+B/+T/5b/BgBhAIUAtQA2ACsA2v/P/7T/w/+F/0H/nf8d/6X/pP/b/6wAUwD8ALgApwCrAC4AlAAbAKj/FADH/8D/8f/0/3cAlwCMAM0ASQAWAFsA7v9x/1X/ZP+n/2//wv/h/4v/ov/Z/wQAqP9MACsAx//3/53/wv+F/53/nv/D/5j/0f8QANf/XwDx/2IAvgBhAKsAdwByAG8ARwA5AJwAfgBBAFkAEABXAFgANQBiACoAIgAtAEkAcgBKAHMAXAATAA8Aw/+9/0n/EP9k/0v/N/9L/4H/K//4/nX/kP9v/7D/9//U/6X/t/+O/5L/lf+X/wcAKgBZANsA1gBAAV4B0AAWAakAGgA5ANP/7v/N//z/ogCnAIcAfwCeAMkA2QDBANMAYAAWANz/Pf8r/wv/8f5v/4v/2f+9ANAAKQHvAGQAdgC6/6P/Rv+N/mb+o/54/sT+qP+B/y0ApQAZAVEB2ABCAcwAWwA2AL7/Sv8j/zz/h//D//T/iQDwAEIB8wGAASMBRwGGAOz/XP/p/vr+9v5h/7f/xf8sAG0AfQDTAD4BtgClAKoA0v9a/zD//P6u/sr+Y/+B/4f/1v86AGYAiQACAZkAVgBYAP7/kP8k//P+8P5J/yP/mP8/APz/tAASARUBFgHgAP4AuwBfAAMAzP8w/5D/k/9M/8v/jP8QAFcAkADQAF4AXgAnAA0A5v9Y/y//IP/v/lz/H/8B/6H/j//c/z4AagALAAkA4/+y/8H/qP+5/1j/VP+a/2T/cP/o/4AAeQCrAB4BrwCNAHIAEgAOALD/QAD9/4//3P/R/yMA+P9DAG0AoQCnAIcAAAFgAE0APgDE/9D/7P/L/9X/lP9y/8X/mf+I/43/R/80/9z/rP/h/x4Avf8AANz/4/9o/yn/QP8J/xT/MP99/3L//P8zAJgADgERAZQBRgFjAR4BeAA8ALD/dv/r/rL+zv73/mL/7/9gAKoAnQGEAV4BPwGSAK0Ar/8H/8j+TP5p/kr+6P76/mT/JwD8/48A0AAEAUAB7wB3AM3/af/g/uH+Bv8S/5z/eP8TAH4AnQClAVQBSQFTASQBfAAtAFsAt/8zACkA6/+UAEAAawCgAIEAVQBFAG8A/v+1/7H/Uv88/wb/Sf9s/5z/5/+0/1YADgAwADkA0v/J//b+F//E/oD+7/4k/5n/PwCPACwBYAF4AVQBEgHKADQATwCI/zH/Iv/M/iz/aP+G/wsAwQCcACMBEAEAAeEAawB7AJn/iP8M/9/+zv7k/vb+u/4y/yL/l/90/9n/BQAEAKkALADt/zkAUwDo/yMA5v+0/x4A9P8/ADMATgB2AIQAogCnAKsArwDpAPMAxADDAPkAtgDKAKMAJwCy/4r/of9X/2X/lv9h/1v/sv+v/9H/tf/E/ysA7P8mAAwAwf+p/13/Rv/p/tX+NP8k/0//qf8nAGkAQgDJAOwACAFDASkB8ADmALkAlQB4AGEATgDk/+n/yf/B/zsAQgBIAOAA2QDBAOYAbwAiANP/kv9L/wD/w/62/r/+tP4G/0n/kv+n/8v/DAAJAPb/QQBZAOz/AgCB/1D/KP9A/6//GgCEAHwAZgEhAekABQF2AHIAEgAzAAQAAwAoADIAlwDDAMIAwgDTAL0AcwATAOv/bv94/1v/Df88/+H+4f4Z/2v/iP/p/zYArQAxAawAsAAxAKj/lP86/yn/Cf8n/63/9f8tAAIBUQFHAZsBSwEdAR0BZQB2ABUAo/9+/yn/Zf85/4X/5/9ZAKQA4AARAe8AUgAKABsAXv9r/xn/6v7E/sr+UP8o/2X/g/+u/+P/aABCAFoAbQCg/+r/Sf8i/zv/Kv94/6X/7v87ALAAfAAuAQYBHQFCAboABAFRAHgAPADn/zUA9P8bAAMA3v9AAH0ALgBvACIAGwA7AK//CACr/yj/Gv9H/5D/Sf9I/2z/wP+6/5D/y/95/6b/gP+Z//f/eP/c//X/5f/G//b/CQCa/y4A7v/g//j/sP8JABkAJwBWACEACABiAHQASwBhAHMApwA8AEMAbQAzABcA3P8ZAMz/nv+N/zT/k/9x/43/yP/T/zcAv/+5/8f/Y/9v/1T/B/+2/uT+Zf8n/1H/hf9CANsAjADNAO8ACgHpAKkAiAAAAAAAWv+N/5H/Jf/R/+3/OQCdADcBDQE1AUMBqABiAL3/pf9I/2z/if8x/7b/jf/a/ysAWgDJAMcA2ACJAEkAOwCd/x3/Nv/K/rz+IP9w/8T/UACKAKYA0AAEAQkBwwB4ABcAyv94/6X/3P8ZALoAzQC4AN4ADwHaALAAoAAAAKX/pP9s/2T/Xf8h/83/xf/Q/38AVAAxABUASABfAN//wP+o/zj/8P7J/hj/fP85/xcApgDQAGABeAGLAWMBDAFpAPr/Vf++/nv+j/6N/p7+dv+j/zUAGwEbARwBrwE3AdYAdQDw/wUAy/69/rL+8f2O/tb+Wv+x/xwAcwDLAO0A5AACAYYAIgDA/4P/vv6O/tb+of4c/0j/AABuAEYAOgFsAUoBeQEwAQcBLgATAKH/tP/n/6P/RwDx/+H/CwAuADcACAAYAKb/pf9b/3v/3v8JAFEAwgCvAI0AcgAAADcAYv+B/2L/7f5s/z//0//c/wcAYgCZAJABeQGMAWQBDQHrAGEAKQCh/yD/FP/m/kH/ef/d/y0ApQAGAeYAAwG+AIcAIwAt/x//Af9C/r7+/P5B/+f/7P+DAHwA5QACAasAnAAiAOX/oP98/xT/MP9G/1f/1P/v/04ArQCMALoAlgAKAGQArP+F/53/Hf+l/3//KwAQAFcA7AAYAKcAdAAUACIA0/+S/7r/kP+T/+D/wf87AEIAtgBuACEAZADR/9r/qv9x/5//jf+2/9f/zf8NAFQARABbAEoAhQAhABsAOgCK/6H/j/9b/43/7f9MAFAAeABOAD8AjwCYAGgAZgAbAN//HADg/woACABQAOcAugC7AE0AUAAuAAAA3P/R/+z/gv8IAL3/AQATAFkA2wBCAGwAIADj/5//sv93/+z+fv9N/4P/rf90/+v/3f/k/3wAGgA6APj/ef+4/0X/Mv8j/zv/dP99/7v/JABnAHcA9ADEAMMAnQB/ALAARADu//H/vf+l/+7/3/8vAIIAHwCHAKQATQCaAFcANAAqANn/BAC7/1r/MP9r/4j/ev9v/3n/uP9q//b/wf/f/y8A7/9zABMA2f/g/6//0f/t/3D/ef+m/6X/AADu/5cAsQDYAAoBMwHlAG8AkAA9AEQApP/t/97/m/8KAJr/LgATADQAYQAXALgAXQDw/xcAyv9T/3X/If9M/5T/KP+u/77/XP+z//r/HwAZAPD/BQDN/9f/KADX/wMAJwCN/wAANgCr/wUA8v/Q/6L/tP+x/8D/KADX/00AUAB4AL0AYQCYAGgAVADD//T/rf88/5n/LP9D/5//DQDC/+D/ngBtAI8AqwCcAGsAjgADAIP/rf88/wb/tv53/7b/IADlAFwAywC2AKUAzwBdADgA0v82APX/wP/f/2T/lf9z/2n/vv/L/x4AKwBsAMYA1wC/AK0AwgDl/+r/k//v/m7/5P6v/2P/Sv8lALD/UgDoAOAAEQGUASEBegCaANf/lf8E/7T+z/6u/hX/sf8JAIgAAQEHAVUByQC0ADUAq/+E/9H+Mf/9/vj+Gf9G/2r/vv9eAHAAyQAjATQBCwH8ALkAcAD//7X/jf/r/sT+uP6L/8f/QADsAAgBnwEXASsB3wBFAFwAuP98/6j/Jv8G/1z/fP+V/3P/IQAIAOL/MQC6/yMA5v/G/wgA9f8IAPX/QAA0AM7/DgCe/7H/wP8n/63/Yf9J/9v/GQDfACIBNAFnAVgBzADuAHYAKAANAFP/Yv8S/y7/V/94/+7/KAAgAK4A6ACpAPYAagBoANT/Sf/+/q/+y/50/gr/y/4s/9b/3/9AAFkAbAChAIIA+/8NAJ3/sP/A/4P/wP+n/8v/+v9XAGsAewCtANUAvgCZAKAAgQCyALQAkQDRAM0ANwCIAEkAAwDf/8D/3/8t/6D/af90/6L/j//c/9H/NQAYAAEAy/+w/1H/PP8q/+X+HP/a/l3/IP8n/4j/1//x/wYATgAtAFsA7v8WAAAAJABnAGUAiQCBAGgACgCuAMMA+gAAAbwA9AAMABwAKQDY//L/YwArABAAHwArAJIAPgANANT/pf82/xP/HP+j/sH+tv7j/lL/Yf/K/0IAEACOAHMASgBgAM3/VwD+/33/PADV//D/KQA0APQA1wBBAToB/QBgAa0A1QAqACIAUwB5/+//zv/Y/2AAOwBmABsA8v8+AB8A9f+b/6//0f9s/63/dP+0/4v/kP8mAOj/tf+f/9f/Xv9r/z7/Gv9+/7z/AABcAN4A6gAZAfUARgHiADUAmQAfAOP/1v/M/8T/BgAXABIAfQDBAPgA7QAJAYsAgwD8/9j/g//j/gj/pf7o/sL+Ev+d/4v/j/8lAFUAIACbAA4A+v+x/z//Uv8F/yT/Kv9T/6z/vP+S/ygAVwCQAKsAwQAdAcEA0wC8AL0AYQDz/9D/x/8JAPX/5f/9/yEAQABrAGgAngBtAFgAWQDa/yoAtP+x/+X/V/9A/y7/V//3/hj/of98//L/BgAqAH4AUwCNAM0AgQBDANr/PP90/1j/Cv9x/43/7f8VAJIAvwDRAE8BDgFbARcB4QBsANf/gv8//z//G/+R/2//1f/w/08AZAAHANAAcQCAAEIA7P+B/xn//P4c/1v/+v6J/3v/lf+8/6X/AADb/ysAEADX/3EAgAAeANAAXgBeAKgAvf8mAAwAHADg/+b/DwCx/y4AgQCNAJcA1QCaAI4AcwAAANz/dP9G/+n+Qv5h/rH+X/7C/m//sP92////gACMALoAOgBBAI//Sf8j/7r++f7j/j//if8OAEMAkgAuAdEBmwG6AR0CIAFXAfAAZQA/ANf/qP+C/5r/nP9CAFoAgADoALsA4ADHAKEAJQALAJv/5P4b/9n+tv6//nz+Ef8t/2j/BgDO/1gAIgCKAIIADABBALT/HgCG/1T/mv/1/nP/av/j/0QAgABFASsBqQGgAWIBZwHFAMQAZgD3/wsAdv9Z/7H/if/F/77/AQBdAEsAYQAXADcA5P/X/6j/E/9B/9L+RP9W/2X/uv///zYA9f8bAN//LwDv/xYAXAAAAAAApf9bAEoAKQC0AFoAbQBrAAwAQQBHACYAaQBCALYAbgB9AMEAPwB9ABsAFQARAMX/vv+m/9z/rP+8/+//8v8rAP//EQDX/6j/pv+T/7v/R//H/5v/G/+2/43/kf/M/zEA3/8JAGMABgBhAE4AmwB9ABsAKAAOAAsA9//U/+//qf/f/y4AEwBrADEAOgAvADgALQDb//X/m/8cABcAEgD9/2r/mv+b//n/nv/W/0wABgAFAGAAYAAoAGoADADT/6T/Nf/b/u/+Sf+0/hn/kP+T/ykAMwDiANsAngC2AO8A+AA0AGEABQC7/5H/p/8mAMP/TwCJAPAAVQETAToB/QCnAPUAfADR/xEAjf9s/2T/Xf8z/yT/4v+x/0AA/f9+AK8AMQCpAPX/LgDK/4r/Rf/o/lb/0f4M/4X/5//H/1IAeQAqALYAbgC0ALYAEgAhAOT/xf++/1z/6//K//n/aABUALIAxwDqAIUAtQCSAD4AfACa/3b/tv8e/0r/Nv8B/4//Sf/b/wYAvP9cADgAGgDM//v/e/9e/33/A/9+/yn/iv+O/5L/zP/W/18AAgBeALoAqQBRAHgAhgD+/1oAWwA3ACwANgAGAGEAKQDZ/04ALABtALQAJQHsAIcAyQBGAIIAMQCV/3P/H/8m//T+zP7j/i3/sv/4/3oA0QAFAQkBegCHAO3/Sv9b/8P+f/5b/lH+yf7O/nj/AABvACQB/gBzAZkB2wDDAEEAov9Y/0H/wP6i/kL/jP8jAMIAQgFNAVcBSwEwASwBFQD//6P/6v4O/z3/UP+8/24AfgCvALIAxwBpAAsA5f+g/2n/Bf+A/xj/av/R/8f/LgDu/ygARQBKAPP/0f9G/zP/2v63/nj/SP+2//z/agBWAEUAbwB+AK8AHwB1AN7/iP+y/4r/s/+w/+T/IABRANUA0AAEAdIATQCaAFcANADz//b/5f/r/yUA+v9EABIAWADZ/xcA3P91/+z/Sv/K/8L/4P/C/xcASQBOAK0A+f97ACsANQCY/5r/m/8b/1r/DP+q/5b/YgC+APUA/QDeACIBoADKABAAHwCG/x3/gP89/1D/z/9GAAEAbwBaAJIAUQCLAMwApAAYAU4AZADj/2f/Tv9e/5D/AP9E/0T/1//M/8T/PQAxALsA4QDsANEAqADRADoA5v+P/0n/Nf/u/iP/F/+g/w4AegAbARsBeAFUARIBAgGGAP7/tf8w/7L+4f4G///+DP9g/6T/7f86AIsAugC6AKkAdQBfAN//dv9s/z//0f7n/sH+o/5V/5v/1P9KAAcBnAC1AO4AUQBmAC4AEgAzABcAt//F/+P/sv/4/9X/8P+GAKMAFQCSAGMAPQBpAGcAnAD+/yIAwP+V/3P/Rf+g/1f/r/+a/+X//f/G/xoAAwAnAHwAPwDF/z4A6f+k/wAAyP/4/x4AGADd/xoAAgAUAG0AagCxACAAZAAZAN7/QADq/8sAfwAvAN4AjgBgAIUAfQBAAA8ADAAcAJb/vf/K/1T/iP+N/9r/9P/k/8X/vv+T/5b/q/9N/7n/WP/4/iv/0/4O/4f/w/8FACkAawDFAHoAvgCsAC4AXACA/1D/Tf/v/jb/zP/p/20A2QDUAD4BEwEDAeMA7gAaAPH/9P8+/9L/Wv+f/+n/f/8YADgAGwA7AHkAvP/K/3j/Sf9a/x7/Sv/H/jv/Yf9b/6D/xf8+AEUAbwAiABsAAwAnADIA8v9QAGUAdwCEALQAtgDvAPgAWwE9AaMAqAAZAHAAIwCdANsA5/9+AC4AEwDZ/4T/5v98/3H/1/9w/2f/z/9F/3z/qP+C/+T/oP97/5X/l/+H/3r/gf+a/67/BwAqAEcASwA9ADEAAgDw/7z/t/+g/6H/of/9/6MAqAAtAU8B/AAVATsB2QBTALD/iP8M/83+0f7n/nr/OP+7/yMACgCcALUAtgBcAFwAEwBY/1T/vf6y/gX/ff4S/0D/5/9sAHwAeAHmAF8BLQFyALgApf/J/2X/Av80/27/wv8pAKIAzADcAJ8AFAGUAGUAiQDc/9D/ov+Q/4H/4//7/+r/gP+G/8P/l/+Z/2P/p/+m/27/iv+z/53/nv/E/73/JQAeAD0AMQAnAPz/6v8AAMr/5//+/33/8/8+ACAA0gCpAIgAygD/APIAsQDGALIARgAmAB4Avf+4/3z/qP+U/3L/IACa/xsAYACo//H/z/+z/7D/wP+V/2D/bf93/23/wf+o/5T/qf/f//j/+v8fAAYAhgBaAH8AsABEAG4AkAC+AHQAcAB/AC8AOAB3ADsAeQCHAGwA6wBzAG8ARwBMABgASwBPAOT/RQDK/8L/hP9A/y7/+/7R/sL+Ev8b/5L/uv9aACMALwBwACIA0/9I/+3/gv8s/3r/p/+T/7v/WwBJAKoA5QACASwBhgEDAeMA3ADn////2v+Y/+P/HwAsAJIAmgDGAKAAXABcAN3/rP+9///+nf4H/7b+QP/B/6n/JwBXACEAQABqAOj/EQCy/4r/Mv9I/9r/Yf/c/6z/PABoAJ0AJQHZAFUB7gAKAYwATAAGAJf/0P+1/8P/4v8wAN7/GwADAN//eABOAK4AsQBXAH0ALgCl/6T/R/80/xL/9v48/1D/cv9p/9D/kP+4/1kANQBiACoAfgB4AAQAFgA2AL7/pv/v/7v/SQBNAGMA0QCWAMIA+QAlAdkAigBvACIALgCl/7f/s/94/6X/bf/m/9j/u//J/9P/EwD9/+z/y//o/1n/VP8s/9T+av91/37/zv+h/8b/BwC9/xMANAAqAEcAcAB/AB0APAAeACoAEABWAFgADwAxAF8AcQAAAMoAWQDa/08A5P9YAP7//v81APT/v/+6/8f/dv/b/73/gP+Z/4j/xf9h/5P/8v+r/6n/8f8YAJP/cf+N/1n/jP+j/2wAMgA7AMMAUwDEAMMAZgCuAHoAPQBEABIAagBWACAACgHWAJoA2ACJAEoAzv/F/9H/o//H/8D/uv/I//j/1P+4/8b/0f/t/97/0v/b/5n/dv9+/wT//f5U/3b/yP8JAFEALwBLAGEATgCbAFgAkQAYAHAASADM/0QA7v86AC8ApwDQALoAFwHOACgBpACpAFEA+P8wAJT/cv+y/3j/kv/x/+L/1f8CAPD/BADg/0D/5P7k/tH+1f6z/uH+UP9y/2n/9f8bACgAMwAEAIQARgBKAPP/mf/l/9j/FgAkAC8AAQAmAB4AYgBPAGUA0gA7AJ4ApABNAFAALgBKAPP/vv+m/4D/dP+i/8f/CAAHAE8AQAAzACkADwAMAOX//f/r/4H/Pf8s/8H+Ev9A/xv/kv+C/0AARgBdAIIARADKAGwAfABkACsA///I/9P/t/+z/53/i//Z/wUABABNACsApADOAG8AfgD4//n/HwA+ANb/uv/H/3b/AAB//2H/t/9E/9f/FgC2/0UAkwCJALgApwBPAC0AAADJ/9T/k/9e/7X/MP+Q/93/mv9TAFUAswC1AJIAdgBxACQAiv+P/yT/PP9Q/6n/AwACAIMAIABjAFAAGwCFAH0A+QDtAHUAlgCeAG0ARQBcABMAxv+t/4b/CwDA/wMAcQAkAIsASwDQALoAhACPAE4APwBW/4r/Mv/Z/sj+qf7r/kb/xv8IAIcAWwClAJgAQwBIAJX/l/8Y/8T+FP/l/mb/8//1/2UAmwAjAUcBGgFkAegAuwA6AC8Ayv/D/7z/W//8/+r/XACCAB8AmgBXANj/FgDc/6v/hf9A/3j/tf71/t/+qf7+/h3/bv+d/8P/c//Y/3H/ev+C/5r/5v/Y/2AAYADOALkA3wCPAKoAnABrALIARgCCAGkAjABeAPIADQE1AXoBDAFGAZgA/AAlAOf/2v9z/2n/4f51/1j/CwDT/yQAjADx/yoA6//L/0L/Qv/T/sT+kv5Y/s/+5v4K/zr/qv/N/1cANACYAEMAAAClABYASQBgAIQAfQDTAL0A0ADMAKQA8wCyACMBIgH8AG8AfgAcALv/SQDN/0QAt/9X/6//K/+M/33/Tf9w/2f/O/88/3X/a/+//8z/sf8cAOD/5v8iAPf/+f+x/9P/t/9p/+L/6P/t/14AzQDvAAoBogFjAecAKQHvAFIACwAJAL7/AQCT/1//EQDX/18AhADGALIAfQD4AFoAfwBCAGv/4v6r/pH+RP6I/of+9f5g/7f/IAAaAEwABgDz/xoAuf8QAMT/q/+E/2X/AwDM/zEA8f8rALYAbgARATgB/ACmAIYAbAD7/9j/FgDu//H/dAAmAFYAjwBOABoA8f9z/3z/cf9D/7H/nP/n/8f/LQCTAFIAVAAxAE0Aq/8o/wj/yv4o/oT+Bf8R/8D/3/9mAEAAtAA3AegABQGtAOf/x/9j/6T+Df8q/2b/zf9FAPAA+QBcAdEB0wGLAVEB2AB3AAMAlf87/xj/j/+3/7P/5/9HABQASAA6APj/HgBg/8n/r/9j/8v/Hf8S/0D/G//+/nr/uf8h/5b/c/9X/53/Zv+X/+P/DAB4AJgAewCaAI8ATgBkAD4ADQAKAAgA4/9pAGcAZQDAAIgAygBrAMUAnwA2AFEAnP8LAMD/zP/E/3P/IQDS/+3/JwAyAM3//P8OAHn/XP/7/gj/3P6m/iH/Av99/7z/t/8zAAQATQBjAPT/PwBFAAEAXQAmAOj/fwAvAJUACwHqAD4ByQCiAF0AFABHAPH/BQA7AML/FwASAP3/WQBIAHEASQADAN//+P+w/z7/dv+R/zj/X//a/4b/sP+t/+L/w/+F//n/jP+1/9b/lf+X/4f/6P/t/ycAoACmAJgAsgDHAMUAjABxAG0AIQAaAAMA8f/0/wgAKwBaACMAVAB7AD4AxQB6ANEAuwBNAD4An/+y/0D/Qf94/4D/0P+Q/5P/qP9w/57/xP+G/8L/l/+H//r/sv+c/9X/y//n/zUAUAAuAIEAaABBABAAHwBQANP/XACUAIkA3QD8AAMB0ACFAQIBPQB7APX/5f/F/77/AQDL//r/6f+2/zIAFgAAABIA6v8lAFT/df9G//z+Cf/d/gP/2P6T/5X/z/80ABcAbwB+AK8ARAARAFf/Zf+W/2H/EgDY/5cADgGiACgBFAGUAHgAYAApAI7/kv+C/1H/mP+a/y4Ayv8vAEsAPABFAaoACgGfANv/BgA7/xj/1v79/kL/Qv/o////SABfAJYA1QArAKQAAwBv/4z/6v58/3H/sv/m/+v/XQBwAMkAogC6AKgAmgBFABIA/f+0/8P/qv8oAA4AVQDqAOIA7QC/AL8AGQDw/+H/i/9Y/1T/df9G//7/EAD7/zMA8v9QAPj/5//s/1z/2P9f/zX/XP8g/5X/4f9VAFcAawCyAKIAgwBEAO7/qP9d/0X/IP+D/8D/AwBxAIAA1gCHALcAkwBSAIwAAgAUAMf/m/+K/w3/F/9F/3v/g/8bAPL/PgANAOb/WQA1AAYAKgBrAJ//DQCd/y//xv+a/0EA2f8XACUAwv9OAHYAXwByAKUAOwCMAIMARQA3AD8ARQDv/04A0f/I/9P/bf/T/7f/DgBVAFcAawBWAI8ATgBSAGcAQAAhAIj/jf9a/zD/Rv99/5b/q//z/+P/ewBjAD0AewCbAGoA6P/I/2T/gv+t/6v/u/+2/43/tv8yAOD/QQBHADkAwgCJAEoAYAA7APn/DADm/8b/iP96/4L/mv/T/8n/+f/6/zIAKAAzAE4A0f81ABgApv+A/6v/hf8u/7P/Zv+E/8H/cf8NAEIAfwCwAKAAuABwACMACQDk/2j/qv/g/6//PwD8/yEAUgDC/04ABwDi/40A3/9BANn/hP8vAMv/QwBbAJMAiQCTAJsAIQAtANv/vv+T/4P/0/+l/7b/DQAwAAEAcABIAPH/9P/R/9v/c/9q/z3/LP96/2//w/8XAEoAmADXAAkBwwB4ABcAyv9m/zr/Kf/3/nT/Rf/9/2sAVwDHAHsA0gC8AJcAegD0/wgAmf+I/43/EP8s/4z/yP8cACkAMwBgAE4ABwArACIACQD2/8H/8v+G/4v/ov+P/93/9v8KAD8AMwAEAIQADgALAGUA5P8gAJn/5f8OAPr/aQBnAGUAPwChACYAHgArAMf/5f/Y/ygA6v8SAFgANQA9APv/IAAZAAIAAgA4AAkArP8FAJb/mP+//7n/7P+5//7/2f+q/9//nP/5/wwACgB2ADoA1P/v/ykA6v/v/zsA+f9DAO3/zP8yAN//+P/V//D/vP/b//X/rf/1/y0AJQAwAEsA9P8aALr/7P/w/3L/RQATACIA9//5//r/aP+9/8r/wv/h/9T/yv8wAAIA8P/z/77/FADa/wUAzv8zAE4A4/+OABYANwA+ACAAPgANAGcAHAA7AFQAoAAVAagAGwHkANwA1gCaAOsAPAAMAFMADADl/w4A+v8fAIgAgADDAIsAcABIALr/ov99/yj/QP8u/x//OP8D/37/qv+W//T/9v8cAOD/1P+4/4//yv+v/4j/jf9s/8D/FQARAGoAVQBXAKIAgwDGAHoABgAqAP7/7P9LABgAggCNAF8AhADq/wAA3P+Z/2T/uf99/03/3v8I/13/xv8+/8D/qP/L/+j/tf+N/2z/if9o/4b/sP+t/6v/vP83AHYAcQCTAD8A/P8hAAgAPgAfAD4AVwBGAIIADACLAIIAHwD3AH0AiQC5AF0AXgBLAM//tP/V/7n/6//v/xcASgA7ADAAJgAfABkAy/95/5P/J/8I/xP/Zv+W/73/XQATAEcAAgAmAFYAe/+o/6b/uP+h/6H/IQDk/2oAnwCAANYA5AABASwBOwG0AFoAEQBp/yr/eP82/zn/8/+Z/0AAawBoAA0BMgBgABYAbf9k/0v/N/85/4X/eP+l/7b/1//y/1AAQAAhAHcAcgAlAML/BQDy/+P/w//P/w8Asf9lAJsAogDfAI8AzwCnACoAIgDT/wAA7v+6/xEA6f/u/ygARQBvAFkAIwAvACUA6P8QAI3/Wv+f/x7/pv9J/0j/IwCc/x0ABQAWAEkA8v+/AGIAPQD7/yAA9v8t/43//f4L/wP/6v6h/9n/TgB2ALsAvACFAKIAqAC9/93/rP88/6v/O/+G/7D/9/8vACYAaABUAKAAkwB3AKkArQB5AE8A0v+2/43/Nf9c/4//yv/U/xMAIgBSAFUAVwBYALX/+/97/5X/qf+D//j/r/8/ACAALQBJABYAbgDr/wAAJQD6/w0A1P+3/+v/3P/R/xAAVwBYAFoAgABCAKL/Rv9Y/3j/JP9h/8r/sP9SAHkAhwASAfAACwEOAccAIACZ/z//vv79/uX+9/5i/4H/BwCZALMAxwD9AAMBvgA9AMT/hv8v/yD/yv6q/lv/e//M/zIAhADHANcACgHpAM4AlAAbAAMAJwBD/2j/z/+P/yUA+v9WAEYAOABSAAsAQADG/+T/DQAdAOH/i//+/6L/ov/+/xAAHwDj/wwACgCt/4b/5/+Q/27/wv8EACgAMwDPAMwAkgCaAFcAawBEACQA1P+B/2L/Sf9//wYATwA/AKIAugAEARsB9wD+AAQBLADI/67/vP5p/wb/Nv+n/1z//f/Z/4YANABPAK4AZwB4AOH/HQC8/0j/R/8P/xn/If8n/1H/GACm/+//KAD9/1kARwCoAGMAdABwAP//NgAGALz/AAASAP3/IgAbADsA1P8lAGgAwf8pAA4AHgDi/9X/lQAcADsAVQD7/9f/lv+F/2b/hP+K/8X/vv9v/4v/ff/O/zMABAAoACAAGgC6/7X/1v9L/4D/rP+X/2L/uP/Y/+D/QgBHAN8AEAHbAB8B+gC3AIEAHgAYABMAtP/6/9f/FQBIAHIAygCjAAQBvwB1AHEAbQAzAAQAu/9+/4X/5f5T/yv/Hf9J/zX/uf9q/+T/1/86AC8A3f8aALr/tf/p/8j/nP+v/5r/5f/9//7/bAAgAL8ArQB5AIYAfgCdAEcAgwAgAD4AfAB2ALwAYACpABoAJwB8ANH/SAA6AC8AuP/9/yIAwP9fAAMATAArAKL/EAB6/zj/Ff9D/0L/Hf+m/zb/lf8FAOD/QQCjAM0AXABcACUAw/+8/5L/cP+x/xwAFgBuANoA5wAEAS4B8wDWAGMAPQBpAEH/i/+h/4//JQCw/0AAMwApAA8ADAAuAKX/7v9x/2j/c/8g/3D/jP/s/xQAIwBBAEcApv9u/9T/bv9T/yv/+P4Z/w7/rP8qAH4AeAC9ABkB9QCzALUAbQD9/yEAm/9l/7r/bP/S/0kAcgCBAMQAngCkALwAYABNAL7/k/+W/0//X//a/8//DwCNACgAagAeAD0AHwB0/4//7P5s/3b//f6x//f/1P/K/zAAOQDA/xYA7f+6/5D/XP/r/27/eP/K/6//PwBFAKYA0AC6AIMA2QBlAPb/CQBQ/xcA3P/j/zIA8v+sAFMAjQCEADMAOwDC/87/RP8x/5H/OP9x/7L/nP/5/+j/7f/M/8T/z/+P/1v/H/84/3L/oP+O/9v/BgA8AHoAdQCWAHgAmAB7AFAAHAApAEYAOAB3AE0ArQDDAMIA0wCYAJ8ASQAoAA4AZwAuAAAAJQD6/zIAzf/8/7P/5//H/1H/hf/l/kH/HP9t/5z/U/+JAIAAZwCdAJEAUAAJAAcAvf+4/7P/eP9u/4r/xv8aAF8AqQDSACoBXwH2ABABbAD8/zMAcv/n/kP/MP8h/0z/gv8IAKv/FwC4AAEAOAAbAN//5v98/6j/OP/e/sz+CP9L/1v/6v8AACUAMABeAIMARQBKAHMAgQBWAI8AhQBrAFcAawB7ACwAfwAdABcAJQAwAHAAEQBXADQAmADFALEAxgBWAFcADwAMAOb/6//d/2L/gf91/2v/mv+c/8L/u//J/xwAPACMAHEAAAARAA4AsP+//6f/Jf9i/27/r//S/8j/LgBKAGEAvAAHAfgAAAG8AJcAQgC1/8T/c/9F/0T/af/Q//7/NQCZAOoAzwDMAG0AMwDz/yr/Qf+u/qb+IP+4/lT/Pv+u/1AA5f+iAHAAEQANAK//iP+N/yL/cv/q/yP/vf/v/ykAxwBpAPoApQBgADsA+f/D/3P/V/+d//r/6f9tAGsAjQDgAOwACAF5AJgAjQDf/67/h/8L/1//Wv+f/x8ABwD1AMYAsgDZAFMAVQD8//3/fP8V/zD/6v4g/zn/X//I/67/LAA2ABkAFAAiAIoAAQAlAMP/vP/u/3H/6f/J//j/QwBIAF8ATAA+APv/agCyAH0ArgCxAI8AzwCCALMAtQBIAIQAMwAEAM3/1/+n/8v/w/+Y/+P/sv8KAOT/aQAeAGIAmADD/xgApv+3/47/bf93/5L/zP+M/xEAsv8cAAQAFgASAMX/PgDX/00AGQDw/2EAPAD6//v/6v/c/xkApv+T/7v/yP9mAD8AIQCuAHoAvgBiAE8ArgCw/wgAYv9u/2X/Ff/W/4L/9/+v/z8ADgDn/2wA1/+EAMX/4//W/zn/cv/6/i3/Hv84/83/xf/Q/1oA7f+DAEUAyv95AL3/OADk/6D/DgDn/zUAPQDFAGcAigBvADUArAAuAEoAYAAWAEkAFgASAA4Aw//z/9H/yP8uAO//OwBCADUA9P+t/5j/df9Z/0L/1v+U/7z/JAAvAAEAEwBZABEADQD5/wwAwf/g//j/1f8mAAwAVABWAI8AzwCVAPkAtgClAM8AEwAiABsA3/+K/47/XADv/wQAXwDM/zIAOgAdAPP/rP+F/6//UP8p/0D/Cf9M/xL/nf+L/4//AQDK/zAA8P/h/9X/3f+t/8//of9Y/7D/0v/t/7r/WgAAANv/YgAFAGAATgCIANwAnwCTAIkAgQBDAEgA8f/i/x4Az//Z/04APwBqAGgAZgAtANz/GQCm/+//zv97/9//Uv8q/wr/3f4o/wj/OP/O/7P/+f9DAAAANgDQ/yMA+P/C/2EA4P9nAK8AsgCiAIIAswB+AK8AVgChAG8ANQCHADUAmQBXAJAAhgB+ALAARABJAE0A9f+J/3v/Af/p/tX+NP8k/z3/v/+C/y0A7v/x/1AAGwC7/37/qv8C/zT/Sf+R/7n/EACzAH4AMAEsASkBTAHUAJkAaADm/+v/OAD3/1QAoABJAJcAjAA6AMIAigA4AGQAGQACAMv/w/9g/5L/8f+F/+f/x/+b/0EAav+s//T/9P6E/4r/av++/4H/v//e/8D/KAAyABYAbgAPAFYARQDv/xYA7v8DAN7/5f/9/zQAPAB6AIcAtwDdAAwALwAlANX/uf+0/8P/c/9p/9D////a/08AGwDf//j/wv/h/4v/ff+E/xv/R/8h/zr/qv9x/8T/vv+4/w8AHgBQABsAAwDf/8D/qP/w/8//6/9dAIIA6gD0AFgB3gDqAL0AhgC1ACMAeQAFACkAkABPAFIAsQChAJQAnAA0ABcAyv/n/2v/UP/x/rf+HP/+/sT/q/+7/9v/0P/H/xsATQAZAPD/vP+k/zX/3v9j/4L/GgC6/20AWACjAPIAMQH2AOsA9QCOAIUAkAB0AHAApACEAI8ATgAaAEwAKwAjAFMA6P///+3/lP9OAIj/xP+Y/63/KgBG/9n/Tf9L/xL/QP9T/7z+s/8c/5L/uv9+/wUA8v9QAHgAcwA4AC0AJAALAMD/p//d/5r/+P8LAPf/ngBtAMYAoACBAJ8A7v9NAL3/uP9X/y7/fP8n/5v/Lf+g/1f/r//2/4n/DgCw/1IA5/+1/8P/c/+h/6H/2P+7/9v/mf/2/9T/3P8sACMAVABoALAAjgDhAH4AigDeAGkAjABxADYA4/8MABwAPAB6AJkAswCQAL4AdACCADIA3/+c/6//mv8a/37/Kf+K/6H/av/j/+n/SQDN/zIA8v+Z/1IA1P/v/4T/d/+k/7b/IAAHAGIABQA7AIwAlgB5AE8AnAAPAB4AKwDa/xcA3P+s/8///f/+/0cAJwBpAFUA6f82AND/ov+Q/5P/lv9z/4//bf/B/4T/wf+o/3D/DACu/xkA8P+X/77/pv/K/8L/l/++/zgA9/9CAFoAWwBuAH0AdwCqAMAA0f81APX/GwA6ANT/gQAMAEEANABPAEAAWAB+ABwABADf//j/nf8MANP/AACl/8n/+P+e/7IAxv/AAOQAXAAVAYMAswAiAOX/oP+O/7f/1//N/+n/SQAoAFgAWQCSACsAbQBYACIAQADr/xMAav9i/4H/UP+X/77/uP8PAB8ABgA8AEMAWwDJ/6//mv8a/w//B/9u/2b/qf/x/xgAXQA4AMEAZAAsACMA5v/+/8f/LQAAAEkAcgCBAOkATQDSAE0AYwBiAAUAcwCS/wMAXf+i/4//W//Y/0z/AgC4/zQA8/+a/wkAvv+m/27/Qf8u/6H/+/53/7f/oP8hAOT/RQAAAO7/OwBUAPv/IAA/AOr/XAASAP3/DwDo/4AA1gCaALMAawB7ACwAtv8NANT/3f+//ycA+//q/0kA4P/5//r/1v/f/67/Pf91/zT/2v5L/+3+Wv/7/+r/JAAdADwAHgAGAHMAJQDD/+H/nv+e//v/DgBnAJ0A2wBEAfIAMgFTAdoAnQCjAKkAGQA5APj/wv8EAAMAOgBmAHcAcgCBAB4APQDD/+L/nv9V/5v/mv5O/zn/Fv9o/9D/7P/w/5gA1f85AAkA9v/A/5X/z/8O/5n/dv+2/+n/EQB9AIkAuADeAOoAmADEAHkAhwBIAEwAdQA5AFMAQwAjAOb/RgAmAI0AXwADAEwAvf8BALj/fP+D/67/q/+X/77/b//C/7z/f/+9/7j/fP+o/8z/ev/L/9b/3v8IAAcAGADd/xoA3//l/yEArf8YAEsATwBkACwApAByAG4AxwBEAEoAKQAhAAgA0P8QALH/+P/V/93/PwDq/0oATgB2ACgA1/86AJz/Zv8o/5v/Lv/7/ub/IP9w//v/xf8sAP//tv/E//X/GwAWAO3/3//T/7f//P+z//r/VgAhAHYAcgBJABYASQBNAAcABQBOAD8A/P+QADwAsgC0ADUArAAcADsA5//H//f/nf+d/8P/vf+l/wAA7v/f/9P/NwBRAPn/aABUADEA8f+F/2b/Ff8L/3L/af9P/87/6v/c//X/QACQAIYAyQC0AEcAFADI/1L/c/+P/5L/3//T/xIAMwBOAIkASQA7AEIASAAnAB8APgDE/6v/qf9w/3r/b/9U/1D/YP+S/8z/HwCaAHwA0wC8ABYAt/+g/x//cP+M/yH/u/81/7n//v/+/38AQQCjAHEAkgA/ADIAFgDu/ygA1/8WANv/4v8eAFAALgA3AHYAcgBuACEAiQAAACUAMAACABQAEABpAGcA1ABhAKoAdwBgAIQA6/8TAI//7/+7/7b/RAAlADAAcABaAAAAJAAKAFIAHQD0/7//uf99/1//kf84/7v/f//P/6H/fP/g/4r/DwD6/w0A+f8MAOX/xv8aAN//CQDR////yP/T/6T/pP8AANv/PQAfAHUAOQAJAD8A6v8kAAsACQDj/9b/uv/s/97/CACIADYAPgBEADcAZAArABAADQD5/x4AGADd/+T/xf/j/0QAJAALAEAA6v8lAB4Aqv8pAP3/DwBWAOr/EgAzABcAAADu/ygAIACs/6r/qP9w/3n/lP+7/3//z/9+AJ0AbAB8AK0AsQCOAHMANwB1/37/A//G/hX/+f6b/+b/fgCcAJAACAEMAY4AlwB6AJj/iP8e/1z/V//S/jL/bP+b/x0AhgBZABMBJwEAAVABjQCEACEA5P/F/2L/bv9B/7D/CAA+AI4AzwCUAMEA5QBKAGEA8v++/4H/UP+p/zn/vP+k/9v/GQDe/4kA3P8sAO3/cP/V/0r/t/+z/2b/BAAWADYArQCwAOoAhQBGAJUACQAaAPH/z/98/1//2v+9/4EAjQAqAQMB0AA8AX0AdwC7/3//Tv/w/iT/8/46/6r/u/8jAHkATwCJAG8A/v/s/93/dv80/4H/Bv8k/2H/JP+Y/wgAPQBpAMMAZgCcAKIAJwAxAN//5v9q/3T//v/H/wkAUQCdAFoAtwDwAK8A1wB2AHEASQDy/73/pf9b/1b/rv++/wEAy/9VAGoACwBTADAAOQCu/6v/l/8q/4v/a/9Q/6r/g/+J/7P/nf/n/yMAUwBoANUAqwBTAJ8A7f8DACcAsv/T/6X/2/8+ADIAhAB9AIoAXAA4AGQAGQA5APj/HQD0/4f/jP+j/+z/Xf/Z/87/Mv+2/9f/zf8yABYA2/9QANP/pP/b/73/pf+S/7r/yP/A/9//QQDr/yYADAAKAD8AWAC1AG0A6wA9AB4APQDo/1sAEgBYAMf/GwBNAAYAdAATAP7//////+3/JwAfACwAEQDp/8n/Zf+D/3f/Wv9D/43/R/8z/+//lv+Y/9H/yP/A/wMAAgCn/wEA7/+7/9v/q/+X/5n/iP/X/7r/2v8YACYAaADCAIoAOAAtADcAGgC5/+z/AQDw/xcAXABKACkAawDo/0gAuwBgAF8ATQBQAOX/RgAmAOj/EQDX/83/n/9o/4b/ef9u/9T/3f8IAFAAigCCADEAcQARAEUAJQAMABwAcf+y/3f/f/+Y/7//JwDp/0kAcgCBALEAWAA0ACoAIgD3/4r/av91/zP/t//q/yUAegCHAH8AiwCVAPj/VQBEAMn/5//H/63/mP+s/6r/BAAoAFcAfgAuAIEAegBQAEEAIgAbAM3/Vv+J/7P/Zv/N/3v/p//w/zwAxABmAEAARgATAH3/lv8q/5v+Yf9b/47/yf/5/2gAQQBHAIMAfAA/AHwAZACIADYAdQDNAFwAbwAiAHcABAADAEwABgCGAFkA3ABnAEEANADP/+v/gP+s/3L/oP+z/9T/3f/2/y8AuP/r/8r/wv+E/2X/cf+y/+b/av/2/67/0P81AD0AVgBYAEcAJgAfAND/EACf/5///P/9/yEALQCmAE4AiQDdAMQAeQA9AEMAEQAOANX/k/+p/5X/KgA0APP/ZAAZAPD/8//j/2kAHQD0/wgA0P9q/4j/ev+C/wgAq//h/2cACQAsADYAGQA5AOX/RgAmAJ7/DADm/+v/3f8IAND/2f/z/5r/GwCD/5z/+f8MAOb//f+QACsA2wCeAG0AVwDr/wEAuP/Y/87/xf+H/57/DQD5/3oAYgBiAL0AYQCGAGwA1/8DALn/7P/w/3L/e/+D/8D/g//3/y8A8P/z//b/CQD2/+X/xv/R/37/z//9/4//SgAEAGAAcgAAAFwApf8AAAAApP+2/w0A1P/v/88AJgCNAJYAeQBPAEAARgC4/0YA3f/3/2X/cf+M/2z/UgALAJwAowCWAHkAFwA4AAgA9f+t/4b/Hf9u/2X/qP8nADIATQBjAL4AhwBIADoAHAC7/9v/0P9r/63/c/98/7v/yP8cACkARgCUAIoAbwA1AD0A+//E/wYAz//9/+v/AQAmAFYAIAA/ADIA4P8vAMr/HgDP/w8A6P/a/ysAtf/o/5H/JgDE/wYAYQDg/0IARwDe/3b/7f9w/+j/yP+c/9T/3f8/AOr/gQDo/1oAAADJ/+b/V/+d/0L/w/+F/9T/EwBHAEsABQBgAOD/HQAFAAQAAwAVAEgATADi/x4APQB6/xQA2v8qAOv/OABlABoAgwDF/ywA7f+5//7/x//l//3//f/+/1oAEQBqAHoAKwD//9r/GADv/4T/wf/g/2X/3//B/5b/z//r/xMAEABpAFQAHwA+ANb/lf/P/2r/dP+Q/5P/lv+Y/ywA7f9MAGIAhgDbAGcACQAsADYAq//z/5n/P/9S/4b/w/+q/00AdQCoANEAFwG8AM8ApwAFACkAfP9x/1X/rv/j/8T/PQBEAFsANwB2AF8AcQClADsAVQD7/6D/V/9l/xT/Qv96/5T/lv+9/yYAHgB0AF4AXgCDACAA4/96/5T/Tf+V/4X/QP+d/57/6P9IAF8AqQC/AFAA1ACrAPf/eQAYAEoABQDg//j/nv/o////bQBYAFkAyQCQADwAVQD8/47/pP9s/z//QP94/5L/lf+q/83/RQDv/83/DQDU/5P/lv/i/7D/Uf+9/wAA3P8aAAIAAgABAO//BAADACcAIAD2//j/CwDl/yAAZABjAFAAGwCXAIwATACZAHwAUQBUAPv/6f+2/43/f/+G//r/ev8CACYAnv9pAML/zv8OAMP/4f+d/+j/o/9r/63/q//O/yAA9v9BAEcAAgBdAAEAOABSAFUAaQAwAF4AJwBWAFgARwAnAEQAbgBZAJEAGQBeADkA5f/9/9n/FwAAACUAMAA5APf/MADd/3b/tf+f//z/jv8AAMn/iv8hAK3/9P/k/w4A5//+//////9bAKT/AADt/xUA2v+G/wsArv8GAHQAggCgAMsAtgCAAFUARAA3AOP/DQBCAP//NQA9AOn/bQBGABMA7QBiAIcAtgDb/z4An/+g/3v/FP+L//z+eP/K/8L/PAAeACoAowCoABkAOQDA/6j/Sv9J/5H/Xf/+/5D/AQBdABMAkQBQAHcATgA/AOr/t/97/17/kP9J/8n/wf9OAFEAQQC2ADYA0gCWAIwAlQAcAE4Av//e/5v/QP+v/4f/1v/x/8//6/8mAB4ABgCYAEMASQA6AJz/sP92/5H/gf9j/4H/Y/+4/6L/tP8MAC4AEwBGAEsAKgBHACYADAAKABoA3//T/wAAAAAkAPn/HwBQAFMAjABMAGIAYgAqAGsA6f8AADYAh//D/3P/of8hAK3/KwAQAMT/9f+I/9f/8f/P//7/2f+8/9z/mf+b/woAiP96//D/vP8AADcALAARAFgAkAC+AL4AYgDQACYADAB5AOH/CwAuANz/LAD//8j/ZgAbABUAgACeADYAGQAUAJD/y/+L/2v/Y/9K/yT/Kf/C/zr/mP8sAO3/JwAgAD4ADQDC/7z/tv9W/1L/T/9N/yb/K/+x/67/PgBpAHoArAB4AL0AhgBHAHAANgA+APv/xf/j/7H/QQA0ACoAfgBlAC0AEgBqANX/8P8XAKX/3P/Q/8f/m//B/5b/q/+E/5z/HQDP//3/6//v//P/BwAFALz/tv+g/8X/vv/w/wUAFgA3AAcAPQAfAD0ARAAkAEIA7P8CACYA6P9bAG4AfQB3AJgAsQBFAG8AkQCHACMA+P/6/8T/9P9j/5T/qf9e/8f/wP8VAO3/FQARAOn/7v+o/14Ap/+m/xIAj/+3/0T/jv8AAFsAkwCuAJ8ApQCqAFEAZgDl//3/6/+A/6z/vP/u/zsAeQCZANcAiQC4AJQAQABYAOz/pv9u/3j///5o/07/cf/p/+3/TAAZAIIAHwAZAPD/hf+d/0H/Hf///kP/Q/+f/+n/EgCPAL0A4gCkAIQAfQBlABoATADi/7D/9//U/xMARwBeAHAAtwCTAOUA3gDFAIwAFQARAFb/nP9T/2L/uP+h/+v/yv8eAD0AMQC6/zUA9P+I/7L/Lf9E/1b/if+O/3//0P8QAAwAsABpAAsArwAeAD0A+//8/+r/yv8wAAEASwBPAGQAdgDgAI8AvQDQAF4AlQAcADsA+f8MANP/yv/U/27/HQAXABMADwAMAEEARwACABQA2f9N/7r/D//i/hn/6v4y/23/0/8AABIAawCgANz/iAA2APX/ZQCa/9P/kv+6/2v/m/+u/4f/jQByABQBzADuAGYBnwDvAHcAFgBbAAAAEgD9/6L/6/8BABMANAAXADgALQBuAEYASwB0ADgALQDc//X/rv++/5P/cf+y/wn/uv+j/8f/9//C/wQAuv8RAOr/pP8AANv/q//O/9j/zf/q/7f/IAD2/9P/AAASADMAPABDAG0AfQDk/2oAQwDI/0EAIgB3AAQAXwCpAHYATAArACMAd//u/6j/lP/O/7P/5//H/wgAPgBpAB0Az//G/7//p//L/8P/Tf+D/1H/Tv/N/6D/DgBVAOn/SQByACQAHQA8ADEAzP/7//z/2P/g/y8AcAB/AMIAnQDaAJ4AfwCwAGkAVAANAOb/j/82/8z/sf+c/x0A8/8/AFcAWQBaACQAHQC8/7f/Vv+K/47/f/+Y/2P/y/+e/wwACgAIACsA7P8UAP//EQAx/8j/wP9M/6b/gP8ZAAIAJgBWAFgAfgBTAEMAEQDX/xYAAAB//5j/mv+b/9T/7//N/w4AHQAFABYA7v8DAN//5f+h/7P/wv9y/8X/0f/s/97/m//T/wAApf/b/z4AxP8rABAAxP8rABAARABcABMA/f8iAEAAIQAbAE0ABgBPAIkANwB2AIQADgAeAD0AMQAVAO3/TADP/7T/6P/a//T/0v/t/3D/jP/H/1H/4v+w/2T/zP+x/67/vv8BAO//qf/f/+X//f8iAAkA4/8fABkAAgBdAF4AXgBMAJkAewBRAFQA6P9IAEwAPgAfAAYAKgD+/0cAXgBMAGIATwC//8z/xP+G/57/jP+Q/0r/f/90/1j/sP+a/5z/CgAIAOP/HwA+ADIA8v8YAN3/rf8YAMv/CwDl/8b/iABbAIEAsgDZAIoAEwCQACoAWQCSAFEAUwAeACsA7P/e/y0AJABUAHsAiADKAGsAMgA6AGX/uv9+/4X/1P+B//b/rv/j/9b/zP/p/8j/LgCl/6T/pP+R/97/Y/+n/8v/sP8JAL7/FAA1AL3/SgDz/xkAzP/7/3wAh/9EACQAHQBhAHMAlABlAHYAXwCWAC8ASwCGADUAKgA1AM//xv8aAPH/GACm/wAAJQD6/44AOwBUAAwA1P/c/9H/7f8CAAEA3f8aADoAHABgAKoAPwAzAGAA8v8GAAUA4P8KAOT/sv8dAOH/wv/h/+f/IgD3/zAAFADa/wUAu/8AAO7/lf+q/6j/cP+M/7X/1v/e/+X/MwDO//z/NADz/1EAVABDAO3/lf/h/8L/cv/8//3/2f9zAG8AWgBbAEkAYAAoAA4A5//H/3b/bP/3/9T/uP/r/+//8v8+AEQAJQALANL/kv+5/7X/w/8GAM7/6v/K/9T/JgAMAAkACAArAOz/3v/3//n/QwAjAAoAPwBYAA8AaQBUAMT/PQDo/9v/KwC1/x8ABgCX/wcAvf+l/+7/FQA2APX/LgDK/2X/qP9w/2f/l//Q/+z/8P8qAA8ADABBAFkASABMAHUAAgABADgA0v/u//H/BgAXABIARgBdAPD/BQBNAPX/LgA3APb/0//K//n/HgAGAE8AmwAhAJwAfQAbAAMAp/8BAJP/u//I/9P/EgDG/z8AWAAiAFIAegBiADwA+v/E/6v/X/9s/z//wf/N/+r/gQCfAAEBzwDxALAARAAkAAoA9//B/7v/SP9+/6r/lv8qACIAUwCfAEkAhACPABcAEwCh/4//bv8b/0j/bP+b/1L/0P/a/6r/OwDm/yIAUwAeAL3/yv+v/1D/vP/c/77/uf/r/xMA7P8UAKMAqACIALcAbwDZ/xcA3P+H/+j/tv/p/yQA+f/6//z/IAA/AGoAaACLACYADADT/6X/yf9l/7v/R/+1/57/aP+9/6X/7v8DADoA+P8LAFMAZwAuAEoAKQCh/9j/lv/1/3b///82AJn/LQDb/3UAXgBeAEwAYgA9AMP/TwD3/x0AFwA3AFEA+f/o/8j/wP/N/8T/mf/3/5z/sP/S/wAAbgBGAKcAYgBPAGQAYwArAP/////t/4L/mv/T/5L/uv/I/2UAGgA6AGYALQCTAAgABgAFAM3/1/+W/07/qP+5/33/TgAsAG0A2QBlAK4AngA2ABkAFACi/6L/ff9N/7n/If8D/7X/sf/T/zcAPwBqAEMAWwBuAGsAHwD1//f/wv/z//X/wP+V/wUAzv+O/zcAYwBiAJkAVgBGAF0AAQBvABAAxP9QAAkA0f9+/xcA7//g//n/+v/7/+r/SQDy/z4A1/8VABEAjf8AAMn/wf+7/zYA4/8MAEEAIgBlANH/IwDU/yUAQwARAEUA7/9NACwASAA6AEEAkQArAOz/OQAuAID/BgAXANz/rP9PAAgAmf8bAKj/8P+8/+7/OwD5/wwACQBkAAYAKgBHAMv/sf+J/6D/oP98/83/6f+2/0UAEgBrAGkACgBSANT/ggD7/7L/CgDk/+r/3P8sABEAMgDy/ysA7P/L/wwArv8sAP//2//1/xsAFQDb//X/dv/a//T/rf/Q/8f/mv/B//L/vf/d/+T/DQAvAAEAAQDK/x4ATwCI/zIA8v+Z/z8A/f/9/yIA9//U/28AfwBBAGwAVwBGAAEAAQDv/04ArP+F/6//Pv+t/77/3f/2/y8A7//y/1AA5v9GAEsAvP/c//X/5f/9/w8ADADT/8r/iv/+/xAAxP90AAIA3f8tAAAAEgAOAPr/HwDj/7H/CQCs/yoAWQAQAI4AKQD9/zQAKgAPAAwA+P8LAJv/CgAbALr/bQCz/y8A8P+8/1wApf9uACEAGwCXANT/7/9OAD8AIADR/zUAUACu/2MAPQBWACAA9v8uAN3/ZADQ//7/NQC9/wAA7//y/ysAbQDq/yUAQgD//0gAFQAjAC8A7/8EADsALwATANn/FwC3/8b/BwDi/+j/tf8NANT/EwAhAPf/CgBAAH0AGwByABIA6v/c/3X/x//A/8z/1v/x/+L/1f/L/wwAUwAxAF4AJwBEAO7/3//4/8L/8//j/+n/pP8AAO3/zP8yAAMAFQBIADoA5v80APP/mv/l/8X/mf+t/9D//v/H/8D/3//4/wsA9/8dALz/3P8HAOH/5//H/xsAzf/X/wMA8f/0/xoAXwADACcA1v+n/8v/jP/H/63/0P8QAB8ABgAYADgAGgAVACMA5v/Z//P/4/+x/9P/yv94/8r/5//H//f/LwA4AC0ANwAHAFAAQAD9/yIA0v/b/6v/qf/f/67/LAA2AGMArABAALUAWgDJ/xwAvP8SANj/zf/X/5X/GAABAEoATgBkAFAAZgBkABkA3v/S/9v/Yf/c/4f/sf8JAJr/LgAAADcALAARAI8ABADy/wYAqv+7/6P/tf+N/2z/wP+D/wkAGQAnAFYA/f+QAD0AMQBfADoA+P/6//v/sv/m/7T/MQACAN7/UgD5/zEAXwAVABEARQASAA8Asf/l/9j/u/9bALf/MwBOABoAJwDp/0kA8v91AF4AAgABAN3/9v+c//n/1v+n/wEAEwA0APT/CAA9AAwACgD2/9T/EwC0/9X/8P/h/1QAHwAHABgAJQBDACMACgAtANv/KwAjAPj/VQD8/+r/AAASANj/TgCIACQAsQBEAFwAJQDo/zUA4v9WADIAKQBGAN3/LAARAPz/NAAFAAQA8f+q/87/1/+7/6P/2v/P/8b/v//M/wwA1P/c/xoAAgDe/xsAFQAAACQACgAbAPL/GABLADwAaAAvABMADwDo/xEA/P/9/yIA0v8RAI7/7v8VAMj/ZgDS/yQAHQCX/5n/iP9o/4b/wv9y/+r/pf/b/wYA9P8aABUAWgC2/zIA8v+Z//f/nP+w/7//p//d/y0A2/9jAE8AZQCJAAAAXAAlAAsAGwAEABUAAADI/0EAIgD3/4wAAgCCAHwAPwBXAMb/9v/B/6j/p/+m/4D/Yv+T/9//wf/N/+r/3P/j/7H/HAAEAAMA8f/P/w8Anv/p/zYABwBPAIkAAABvADQAvP+TABsAOgAvAO//YABOAAcAKwBHACcAewAaAHEAbQDq/zcALQDu/9//LgC3/8b/BwCr/87/2P+o/wIAOQDA/wMAJwD8//3/xv+s/6r/lv+9/8r/sP/S/+3/JwANAFQAHwAZAEsAGABKAAUABADx//T/0v/t/xUA//9tAOr/XABdABMAowCDADIAKQAOAOf/NQBiAAUAu//u//H/z/8PAEMASQAWABEAxf8ZAAIAAQDd/7//8f9O/6j/pv+T/7v/EQAyAOD/5v+0/8P/vP/c/5n/0v/b/2H/yv+d/4v/7P8UABAADQAKAD8ARQATAA8Asf/4/8L/cv/X//L/vf84AD8A/f80AE8AUgAvADkA5f8OANX/gf+s/zv/q//h/9T/AQDd/9H/IwAvAF0AXQA5AHcA8v8+ANf/zP8fAIb/w//P/w8Asf8JAAcA4v9DALb/VwBGAO//cwBdAG8AbABFAKYAKQDr/10A8P/z/77/8P8XAO//YAAoAEUAgQB7AIgAbQAhAD8ARQDd/9H/fv+X/9H/o//a/wUAKQAhAFIALwDw/+H/5//Z/2D/f/9h/zb/cP+M/9r/vP83AAcAGABLAAUAYAC7/wAA2//i/0MAyf/4/x4AGADv/wQA3/8uADgAGgBxAAAAJAAdACoA6//v/04A0f/t/xQA///a/8//xv/3/xwAKQAhABsAOgDU/8r/1P+T/83//P/9/9n/l//1/9L/7v9xABIADgBDAMj/wP/y/+L/DADm//3/IgAbAE0ALAB/AFQADABmAJwAkAB0AJUAUwAMAAkAPwDX/9//UwAeAFAALgAlAAsA0v/J/9T/yv+w/9L/tv/E/9D/2f/h//r/RABJAAMAFQDI/67/0f/s/ycA1v8nAB8Avv9LABgAyv8dABgAJQBVAFcAfgBTADAATAAYABMAWQA1APX/QAAzAM7//f/9/6L/2f/O/7P/sP+a//j/+v/p/wAA7f+6/6P/kP+B/77/pv9J/23/nP/C/87/xf8+ADIA4P8cAAQAAwC6////EQDF//X/GwBgABYANgAsADYAdQBMAE8AQAD9/yIAQADY/04ALAARAEUA3P8aAMz/1v/e//f/QgAjAGYAGgDx/ysAx/+t/+L/DAAKAPb/CgAIABkA8P88APr/+/8OAJ3/MQDM/x8AKwAjAEEA6/+UAPf/ZwAuAAAAJQALAEAA2P8pALP/HQDh/3n/3f+//wIA3v/S/2z/5f9p/4f/6P9+/yoAtP/V/wIAy//V/5T/zv/F/77/AQDw/87/6v8AANz/PgAgAAcATwBSAEIAIwB4AE4ACAAZAPD/BQDg/xwATgAIABgAcABtAHwAwAA/AEUAXAA4ABsAAwAVAO3/8f8FABYAt/+g/w4A1f+U/87/1/+W/+L/6P+j/+z/pv8BAO//zf/8/7P/+v+f/8T/9f8bADoA1P9KAOD/HQA8APr/HwAHABgAyv/6//v/IAAsABEAtADs/yYAMQDM/0QAAABJABYAyf8KAL//zP/o/9v/KwAiANP/EgBGAMr/CwDT/7f/1/+6/6P/fv/P/9j/FgAAABIAWAAQAPv/RQA3ANH////I/5z/5/+i/+z/FADH/0AAfQAtABIAMwBOAFEAQgBHACcAsv/4/57/Z//z/6z/vP/K/0IASABxAIAAeQCZAOn/NgDQ/6L/WP9m/3L/+v7T/6T/EQDq/zcAPwDq/24AWQBsAA4AeQDi/8P/BQCW/xkAuP/r/wEA7/8WAO7/KADq/8n/LwBLAGEAFwBcAG8AtP97ACsAIwBmAAgA9f+b/9T/7/8pAMX/LAARAOr/bgDr/yYA+v8NAAoA0v8kAAoACADQ/1j/i//H/5v/5v/r/xMA6//d//b/CgAtABEAWADr/wEAEwAiAEAA/f80AIX/nf/6/43/yP8JANH/EQAyACgAjwBzAF0AlQBTAEMA7f+C/5r/rv++//D/8//j/9b/8f8qADUAYgCGAH4ALgATAGsA6f8AABEAxf/2/8D/KADF//X/QADr/zgACAArACMACgDk/9f/3//l/yEAv//x/8//tP/V/8v/MQAVACMAZgBAACEALQASADMABADy/ysA7P8CABQA/v///+3/FAAjAPj/1f/w/6n/cP/W/6f/uP8hAPf/1P8AAO//4P9mAAkALABtALP/1P+4/8b/rP/P/+v/AQAlAMP/YQBOAPb/LwDv/wQAFgDt/ycARQDu/wMAOgAvABMA6//v/+D/r/8aAPH/z//r/+//BADf/y8Ayv/C/yoA6/+l/yUA+v/p/20ARgBdAEsAdAABACUAHgD0//f/5v8iANL/NgC+/yYAaAAvAJUAUwCNAAMAFAAjAC4A7/8WAO7/g/8bAF7/yP+b/5z/+v96//D/l//j/9b/uf8iAAkAGgDx/+H/5/+j/7X/w/+9/9z/0f//////EQDq/wAASQAWABIAWABHAAIAJgCf/8T/4v/W/xQA2v9PABsAKABFABMA/f8QAAwA5v8PALH/LgAAANz/UQAcAAQA3/9BAP7//v9aAEkAKAD8/0YA3f+a//j/5//s/xQANQAqABAAMQA6APj/+v8NAPn/MQDx/+H/CwAJAFEALwBKACkA6/+l/6X/yf+v/+P/sv+c/53/1f/L/wwAeAApAFkAfwBmAGUALAAAABEAxf/1/y4A7/87AC8AXQCnAD0AVgBFAO//BAADADoAHADO/w4Anf/V/97/iP/p/6T/tv8NAPn/DABTADEATABiACoARwA5APf/CwD3/4r/fP+W/3P/s//C/+H/HQD0/z8ADgAdAD0A+v9XALP/nf/D/4X/i/+P/+//qP+n/93/9/8cAM7/6v/v/83/6v+k/8n/wf+W/xgAk//N/9f/3/9BAMf/9/8KABoAuv81APX/5P9YAA8AVgD8/0YAEwC0/zEAJwAgABkAFAD/////7f8CAPD/8/8/AGoAQwBbAEkAOwAvAMv/+v+f/yAAvv+5/w8An/9XAOr/JQAwADkACQAaAJYA+f8wACcAMgAoAOr/7v8WAMn/HADz/77/JgCM/yMAnP+K/w8Anv97APb/5f9rANb/FAAjAAoA9v/T/8r/wv/O/7P/nf/6//v/IAD2/wkALADb/1AAGwDg//j/sP+t/9D/NQBiADwAVQAyAPL/BgDP/zQAPAALAGUALQARAFgA2f+8/yQAwv+8/8n/wf8EAPL/GAAUAOz/FAAQAPv/1//f/woA0f+j/6P/2v/P//3/WQBtAKEAXQABACYAHgAGAHMAJgAMAFMA1f9LAD0AVgDGAEMAbgBGADgALQAAAG4A6//d/wgA4v8MAPj/5///////7f/e/+X/xf/R/7X/1v+V/2D/yf+K/47/7v+o//D/PADD/6r/FgASAI7/yf8KAK3/vf8AAEoAPAAeACoA/v/H/wkAYwB1ACcAjgByAAAAEgDY/ykADgAeAAYA4P8vACYA6P/t/wIApv/K/4v/EADE/3P/RgBu/53/jP/a/xcA7/9yAAAASgAWAAAAEgD9/8b/0v/t/7r/IwAcAHIASgAEABYAEQDY/9//5v/Z/xcA7v+XAOf/EAD7/47/JACd/x4AGAATAA8A+/8NANT/EwAPAPv/6v83ANH/7f8CAPD/PAALAPj/1P8mADEAXwBfABUAIwAKABoATAArABAAfAAaAN7/QAAhAEAAIQDk/0UAAAAAABIA2P/z/9D/EADp/9v/BgDP/7P/5/8QAOn/AAAAAMn/wf/g//n/DABTAFUAIAD2/xwABADf/+b/2P+7/9v/9f/3/y8AFABZAP//NgBjABgAlABTAGcAeAAXAEoA8//j//v/6v/u//L/BgDO//3//v/H/y0A3P8ZADkALgBcALj//f/r/4H/Yv9c/2n/dP+0//r//P8OAGcAQQBZAEgAAgAnAMT/9f/3/4r/xv/R/8j/CQDj/1cARgDd/2QAUQAuADgAPwAgANH/EQDq/+7/8v/Q//7/2v/h/8L/BQDg/9T/yv+d//r/1//f/+X//f/r/93/mv/T/xIAjv9JACkADgAwAN7/GwAWAO7/3//A/4P/GwDy/9D/EADE/wYA8/8/AFcAIQAIAAcA4f/6/1YAMwBgACkARgATACIAQADr/93/9v/4/9X/XQDd/+T//P/G/9H/kP8BALj/of/r/8r/5//s/97/rf9h/5L/lf9g/9z/BwAYACUA6P9IACcADQBUAB8ABgDP/+v/yv+w/y0AEgAzABcAXABvAEcATABiAHQAJgB7ABkAAgDL/+j/2v+Y/1EA1P9KADwAMABLAL3/EwDr/8r/wv8FAAQAzf/p/9v/q//z//b/m/8KAHb/yP8JAJr/CQBjAAYAFwBKAOD/HQAXABMADwAxABUA//8jAHf/NwD2/+b/fQBAAJAAPABDAFsAAAAAAAAAAAAkANT/y//D/8//6//c/wcAKwBHACcAjgApACEAPwD8/1gAov/Z/7z/3P/j/2f/4f+L/7T/sf/A/wMAzP8xABUAEQBqAFUAVwD9//7/x/+b//j/w/8XAO//8v8ZAMv/VgBXACEALQBuADQAvP/u//L/BgC8/9z/BwDP//3/EAAxABUAIwB5ADwAHgBiACoA/v/Z/6r/AwDM/9b/XwAVAEgAhAAzAIUAfgBAAP3/7P8mAOj/2v/0/63/0P/Z//P/4//W//H/BQA8AB4ABQBOABoAzP8fAOP/6P/t/13/tP+M/6L/2f/h/wsALgCTAGQAvwBjAD0AVgDq/9z/4//W/6f/FADs//D/PADV/6b/yv/C/4T/LwATABAARAAAACQA5//+////7f/e/+X//P+h/9j/FwC3/9j/3/+c/4v/2f8EAM3/IADj/x8AYwAYAF0AAQABAMr/1f/d/wgAUAAJAFEA+P8eAGIAFwA4AD8A2P8DAAMAzP8fAL3/EwA0APT/UQAvAAEAyv/6/9b/lf/h/wsA9//C/ykAIQDk/zIAFgA3AAcAz/80ACoAawAfABkAFAC1/x8Avf/K//r/HwB1AIMAfAAtADYA9f8bACgA2P8oANj/Xv/I/67/mf/k/zMAcgBvAH4AQQBGAAEAAQAmAAwA+P8LAAkAvv/e/4j/sv/4/57/+//E/77/y//D/6r/3/8KAJr/wP/y/5j/0f8jAOb/WQAjAJz/LwDL/7D/GwDf/+b//f/s/wEA3f8IAAYA8/8aAEwAKwA1AD0Asf/T/7f/1/8DAAMATAB0AEsAKgA0AAUAFwA3ABoA8f8YABMANAAXAN3/ZAArACMALgDv/7v/2//1/63/KwD//xAAIAAZACcA6f/t/8z/+//F/wcAvf/v/wQA8f8rAKL/EADW//H/9P+t//T/0v82AAcABQAXANz/0P/H/y4AJQAdABgAJQBoAPj/HgAYAMr/HgCq/7v/AADb//X/LQA3ANH//////xEADgDn/xAADQBUAMP/4v/6/7L/QQDZ//P/BwDi/0MAyP8JAPb/wf/N/9f/AwC6/xAAsv+u/77/y/8xAMz/DADm/8b/9v8KABoAAwDx//T/9v/4/wsA5f/Y//L/BgC8/xIA6//d/wcAhv8eAAUAKQA0ADwAegDi/wwAQQB+AC4AbwD+////WgCk/yMAr//2/0EAxv9SAC8AJgDW/5T/4f94/8r/ZwDl/w4ADAAJAPb/0//u/7r/tv96/0wA9P/k/1cAof9ZABAAxP9QAPj/+f8fAFAAZQAaAEwABgAFABYAEgCPAM//RgA4ANL/bgAzAIYARwAmAPv//P8hAOT//P/q/yUA1f/d//f/+f/o/xAAfAA/AEUAJQCMADoACgAaAMz/+/+O/9v/q/9y//z/s//C/wUABAAoAFcANAAXABMAxv/2/+b/DwDW/5T/vP9a/43/kf+5/9n/BQBOAAcAYgAXAEoAFwAAAEoAqf86ANP/kv+6/7X/6f/I/woACAD1//f/5v/+/+z/AQABAO//KQBGABMAx/+b/9P/7v8DAAMAJwANAOb/2f/z/wcAz//+//7/IwD4/wsALgASAA8AsP9TAPr/DABUAOj/bQAgAPb/+P8wAEwAKgBZACMALwATAH4ALgAlAIwAFQBtAA4A1f8UABAADQDB/87/s/8dAPP/vv8nAMT/BgDz/wcAYgAYAO//8v/Q/8f/LQASAP3//v+0/9b/8P/0/+T/MgAoAA4AVQANAAoALQDu/9//QQD+//7/EACy//j/w//z/z8A6v8SAOv/XAC4/+v/SgCp/wMAXf+i/+v/pv+l/8n/5v/r/0sAzv8hAAgABgBPABsAlgAvADkALgASACEA5P/X/5X/GADv/87/DgD6/0QAWwAAADcALAARAEUAJQALAPj/5//H/wgA9f+b//n/w/+q/xYAAADb/xkAy//6//z/2P8oAMX/rP+8/8n/+f8eAGIAhgAiABwA4P+K/+v/k//f/9P/3P/2/9P/JADC/ykAWQA1ABgAEwD+/9r/KgD+/xAAxP8YAPD/FwCBAPr/jgApAA4AMADe/wkA9f8JAL7/8P8FALv/AAAkAEIARwBeACcADQBnAAkAGQDx/+H/+v/W/xUAyP/T/xIA/f80ADwAMACWALAAHwArAO3/AgDL/+j/fwDB/xYAAADu/ygA1/87AOb/DwBEAEkAKADY/83/xf++/zf/zf+y/3f/3P++//D/qf86ABwATgA/AMX/4/+f/9f/S//L/57/Qv8eAJj/GgAVALb/+//F/wcATwAbABYAJABCACIALgATAA8AHgCY/xoAJwDp/zcAGQBeADkAeABOAPb/UwBoABwAKQAPALH/wP85/4X/iv+P/0oA4P9mAAkABwBPAC0AbgBGADkACQAsAP//o/+1/43/o/+j/8f/CQA+ACAABwBPAPf/HQBOAAgAGQDw//P/mf9k/8z/n//E/5j/v/8VAO3/JwAyABUAEQAOAOf/IgDA/5X/z/98/6j/cP+e/+n/2/8YADgALQA3AFEAiwBLAAUAYAC7/xEADgDV/yYA1v9MAPT/9/9BAP7/7P9LAAUAzv9YANn/FwAAAO7/KADq/9z/0f8jAJz/wv/O/9j/zf97/ycA1/8DAF4ATAA9AFYAMwAEABYAAABJAN//CgAaAJX/8//k/+n/NgD1/9P/NwA/AEUAgQCfAIAAVQBXAOv/EwDr/7j/2P+p/wMA3v8bACgAIAB2AAMA8f9iAAUAu/8kAFQA1v/e/xsAlv+Y/3X/a/+//8z/6f8kAFQA1v8nAB8A0P8QAMT/9f/A//H/TwAIAAcABQAXANz/BwA9AOj/7f8VAEgAOgAKAMAAPwANAHkAz/8PANb/zP/7/8X/0P+1/9b/uf8QAOn/NgAZADkAigABAF0AJgAxALr/x/9SANX/OAAtAMn/+f8MAPj/QgBaAEkAKAAOAPr/DACv/9H/IwCu/z4Asv8KAFIAwv9OAPb/CgCH/5//sv9l/9//nP/5/+j/IwAKABoATAArAH8AHABOABoA8f/i/57/1v/e/+X/2P8WAFsASgCFAKIAOQBAADQAKgD+/6L/DwDE/8//2f8EAE0AGQBMAD0A+//X/ygADgDn/+z/y//o/2v/dv///9v/vf84ABsA8f8YAF0AFADZ/wUA8v/Q/8f/9//n/+z/pv/K/wsAiP/q/+7/3/9mAJwAIQDk//z/6/8TANn/PAALAOX/6v8lAEMA2v89ADEAhAD8/9j/FgCk/9v/mf/2//j/w/+8/yUACwDA/xUAo/+j/6P/2v8FABYA7v/f/y4AEwBHACYAewA+ACAAdgCEAGoAHgArAKL/2f+X/77/FADs/zkALgBcACUAVQBXAFkAfwAcABcA7v+6/2z/m//m/+v/yv/V/6b/uP/Y/83/1//f/1MAw/8qADQA4f9VAPz/RQABAF0AbwD//yMA0/8AALf//f8hAPf/eQAqACIACQAHAE8ACAA+AB8A0f///9r/z/+h/w8Aw//i/3oA0P8QAPv/xf/j/wwA+P+w//f/nf/6/+n/2/9QAOX/xf8/AMX/q/8FAM3/MgDN/w4AHQD0/z8A6v9JAPL/KwAjABwAmAALAAkA0f/I/3b/EQAOAJ3/+v+y//j/+v+x/9P/JQDV/xQA7P+m/wAA3P8aAN7/CQAHAKr/zf/q/6T/kf8nALL/0/8SAOv/EwAiABsAAwAVAMj/+P8wADkACQAsABEAsv8KAPf/CgDk/+r/yf+v/wgAKwBHADkArwAMAC8AOAC//zoA5v/Y/87/6v8AAAAA7v8WABEADgAwALn/IgD3/+f/NQDP//7/IgDT/6T/yP/B/6j/8f/0/9H/IwAvAEsAPAALAGUAZAAsAFoAAAB//ysAkP+m/+//g/8JAPb/UwD6//v/DgBCAEgAlf9hALz/7v/y//T/ZADj/w0Anf8LAMD/KAAyALv/JACv//b/0/83AHYAFQBbAFwAAADu/ygA6v/u/9//QQD+/9r/KgDZ/xcAJQD6/9b/zP/W/97/m//U/+//zf8gAL//JwD7/9f/KADq/yUA5//a//T/0f/t/zkA5f9GADgA5P8zALv/AADb/9D//v/H/wkArP/P/+v/3P8aAAIATAA9ADEAuwBfAAMATAArACIA+P8LAMD/uv/I/+X/IQC//ycAHwAsAH8AeQA9APr/6f/b//X/CQAHAOL/MAACAMv/1f+m/93/9v/4//r/MQC6/9r/z/98//L/vv/w/87/6v8SAP3/NAAqAFkAIwBTAEMAAAA2AOP/6f9IADoA+f8wAN7/9/8LAC0A3P8ZAHAAIwBBAP7/EAAfABkAAgA5ABsAzf8NAML/BAAWAAAANgD1/wkAGgACAAIAAQDL/x4Az/8PANb/uf81AM//fgBAADQAhgAQAHsAGQDe//f/5//H/wgAmf+t/wYAvP8AAJL/uv8QANf/KAAyAOD/+P8LANP/7v/y/+L/6P8RAPz/DgBDANr/BgA8AOf/EAANAPn/VgBFACUAQwBtADMABAA6AB0ABQAWABIAIQD2/+b/6/8BAKX/3P/j/wwAVAAxACcA/P/Y//L/9f8JAAcAGAAmAJ7/xP/i/+j/WgAkAEIANQD0/y0ASQBNAAcABQA8AAsAm/9BAMf/dv82AOL/6P/b/ysARwACACYAMQADAN7/LgA3APb/5v/Y/+D/nf/C//P/v/+5/9n/8//2/9P/3P8HAM//tP9DABEAxf8ZAEsAPQD7/yAA0f/H/2UAv/8UABAA1/8VAMj/QQAPANb/TAC9/yUAHgDP/0YA3f/k/w4AsP/3//n/+v8NAMH/u//b/+L/6P///7b/sv93/5L/uv+1/7H/wf87AMH/8/8+AOn/7v+6/xAAaQALABsAFgC2/zIA8v8GAHQApv8TACEAQAAhAAgAYgBPAEAAMwBhAPP/LAA2APX/5f/q/yUAwv/h/7D/GgDM/+n/WwC3/1gA2f/O/8X/mv/S/9v/BgCq/ygAIADk/w0ACwBAAP3/6/8TAP7//v9tANf/FgAAAJH/OQCu/ywA///I/0EA/v8QANb/FQA2AAYAPABVAOn/AABJALv/7f/M/7H/5v8hAL//FQBtAI7/gADC/4X/QgDa/yoA2f8EAM3/xf8HAM//IQAbACgAIAA/AEUAJQD6/9b/FQD//zYAKwDs/xQASABeAEwABgAFAPL/BgAFABYA7v/y/wYAYP8RACAA5P9XAOv/7//y/+P/6P/b/73/pf/J/9T/3f8aADoAwf87APn/sf8bALv/7f/M/+n/2//Q/w8A6P9IACgARQATAEYAlQAJAIgAgAD6/wwAQQAQANb/TAArAP7/SAA6AEEA/v81AE8AQAAzAIYARwDe/y0AEgD9/7T/1f/L/7H/wP+6/+3/p/8TAMf/iP8gAAcAKgAiAAkAGgAUABAA1//M/9f/3//l/+v/3P/j/9f/3//T/1wASgApAGsAVgAOAPr/ewDj/x8AGQDL/wwAZP/x/6v/8/8HAKr/TQCs/xcA3P/j/w0AQP+v/4j/aP8GAOD/r/8IAOL/1v/w/8//s//C//P/0f81AOL/+v9pAFUAVwDr/yUAHgD0/y0AEgAzABcAAABcAAAApf83ABoA8f8qAFkA/////zYAKwAjAFMAegBjAGIAFwBKACkA6/8TACIA0v/J/y8AAQDv//L/BwDh//r/6f/I//j/i//+////7P/w//P/mv+J/+r/pP8RAMX/LAARAPz/MwBOAGQA9f9lAOT/MgAWAAAAJACK/w8A6P/t/0wAGADL//r/sf/T/8r/r/8tAO7/FQARAEUA7/8EAPH/qv/g/6//GgDf/xsAFgAAAAAAAAASACEAdgDf/0EAx//k/zMA4P/5/9X/JgDW//H/9P/k/7L/1P/c/6z/4f/C/2EAzv/q/zcA0f///+3/8f8FAE4A0f8RAPz/xf/2/9P/bgBZADUABgBhAJgAHgB0ACYAxP8GAPP/GgDe/9L/2/8GABgAAABKADwAHgDP//3/tP/D//T/CAB1AKf/AQDK/7D/CAC+/wEApv8SAP3//v/s/zkAZQAIAD0AxP8YAPD/4P9CANr/GAAlANX/3v/S/5H/FAD//xEAMgDy//X/5f/9/zQAcwC4//3/6/+4/w8Aw/8FAKn/3/8JAPb/HABOABoAp/9LAM//xv8aAKf/3f/S/+3/AgDw//T/UQAKAGQAYwDi/zEA3/9AAOv/3f8/AOr/XADc/+P/+//F/wcA9P8/AEUASgBhADsA5/8QAHsAPgDX/9//0//J/6//5P8gANH/EAANAB0APADV/8v/6P/a/8//xv+t/6r/qf/f/8D/8v8rANr/GADK/wsA9//5//v/6f+TABoAOgD4/x4ABQAEAHIA7v9NAND/RwA5AAkAiADu/zoA1P8AACUA1f9LAAUA8//1/xsAAwA6AK//vv/L/2f/4f+d/8P/z//Y/xcAJQAdACoARwDw//P/v/8UANr/vP8AANz/GQDM/zEATABQAGUAiQCTAC0AbgBYAFoA7f/x//T/0f/t//H/GACl/4EA6P/a/5kADQBUAOj/EQAyAAQAKAANAOf/2f/z/5r/m/+c/53/+v8yAPL/9f9lAAcAz/8PAPv/xf/j/5//6f/b/3T/NAAqAP7/IgDl//3/2f/z/1EAHAAXACUACwDl/w4A+v8NAC8A3f8IABkAJgAMAAoALQB//4b/HgD0/7//TAArABAA+/8gACwAyP8uAO//FgDc/77/8P/z/5n/rf8rAH7/YQDz/9H/WgAAAIAAMABwACMACgDR/8j/wf+D//j/nf+w/3b/fv+9/yUAZwB4AIYAIgAbAPL/9f9k/97/rf90/9n/qf8VAMj/LgA4AC0AbgBrAEQAJACMABQAWgA2AAcAYQAqAOv/7//g/9T/EwD+/zUABQAXAAAAEgBGAN3/GgDx/73/pf/c/wcABQApAP3/DwD7/+n/7v/N/5//6f/J/+b/IgD3/x0Azv8OAB4AGAATANn/PADn/xAADQAvACYAMQBMAND/RwDe/y0AbgD+/1kA//9IABUAIwBmANL/AADJ/+b//v/H/wgAGQAnAA0AQQBHAMz/HwDi/+j/IwD4/x4AGAABAKX/EgCz/53/+v+f/zIA4P/m/yEAm/8vAMr/wv8XAO//8v++/wEAk/+D/+X/jv/u/ygADgBVAFcAWABsAPz/xf/R/5D/y//D/6r/AwCn/7n//v/H/9L/JAD5/x4AKwD//xAAxP/i/x8A0P8QAAwAiv8OAB4Az/+QAOL/6P9IAMz/HwAZABQA7P8mAB8A9f8bAN//QQAiAOX/RQATACIALgASACEACAAZACYA6f8AAG0A2P8EACgA1/86APn/VQANAAsA0v8AADcAvv9LALz/SgAWALf/agDD/+H/CwD3/+f/x//S/+3/uv/I//f/1P8TAMf/LQAkAB0APABDAAAA2/8rAKL//v+1/9b/FQCQ/93/0v+2/7L/CgDS/xEAIAA/AI8A8//1/wkABwAGAAQA8v/Q/6L/2f/z/7//AgAUABAADQAKAC0ASQAWAAAAkwBkACsAfwBCADUABgApACEAm/8KANH/IwAKAPb/nQDs/yYADAD5/+j/IwAcAOD/VABEACQACgAbAN//0//K/8L/4P/n/w8A+/8yAPL/BgD0/9H///8jAPn/6P8QAI3/tv/p/9v/4v+NADoA5v/IAOn/JABCANr/4f+w/9L/7v86ANP/NwD2/xwATgAsACQA1P/v/6n/FQC1/5//xP/j/9b/p/8BAG7/CwDS/6T/IwDm/1kA7P8CAN3/iP/X/wMAXgDx/2EAFwDK//n/w/8GAM7/IQAIACsAIwDT/0kAOwBUAA0ALwABAO//KQDY//L/9f9TALD/0v8kANT/EwD+/zUAGADv/wQAFgDb/z0AHwDQ/2wAsv+c/x0AvP/u/xYAAADb/77/OAD3/woAdwAWAEkAKAAOAFUAHwAZAMv/MQDx/5j/ZADj//v/MgDN//z/2P8WANv/BwD0/+T/IACs/xcAAAAAAO//8v8ZAJT/zv97/6j/AgDw/xcA7v8oADMABAAWAO3/zP/E/9D/7P/d/y0ANgA+ACAABwA9AFYAagD6/2kAMADe/3cAOwAdACoADwDo/+3/8f/h/x4APQAMAC4AEwDr/zgA5P8gAAcA9P8tAKT/JAAdAPP/BwDP/w8A1v/M/9b/3v/l/2n/q/8FAM3/DgALABsAYADN//z/WADZ/ykA2f8EAE0A0P81APT/5P/8/w4A6P//////7f9xANv/hwDt/8z/RADb/z4AxP9QAPf/5/9HAN7/GwDy/+L/1v/w/7z/JQDn/zUAPQDo////tv/p/+7/FQCj/yMA5v/r/28AEABWAA4ACwDl//3/xv8IABkAy/8eAAYA4f/5/zEAp//d/63/q/+p/8z/6f9s/1MA6P8QAB8ALAARAOn/XAC3/zMA8//1//j/CwAJAPX/ZQCa/wkA4/+y/8H/lv+r/5b/4v+x/wkA4//E/wYA8//R/9r/dADd/z8AxwAfAGMAGADL/wsArv/1/1MACwAJABoAAgDL/9b/3v/l//z/DwAeAGIA9P8aAAIAXf+0/7D/CQA+ADIAOwBUAGkAHQAqAA8AQwARAOr/7v+7/yMA+P8eAOL/DADl/9j/cwASAEYAJgDW/ycAsv/B//L/q/8EACgADgALAOX/MwDz/5n/GwDN/43/SAADAJX/FwDv/7v/EQDq/zcAUQDB/xYA2/++/8v/i//+/7X/+/8NAJ3/DADl/yEAPwAOAB4AYgBPAAgAPgD7/1gAIgAbABYAyf/4/9X/FAAiAAkAPwBFACUAVQANAPn/HgDi/0MAEQBYAP7//v/a/3P/IQDR/0gA3//l/yEAv/86AAkAPwDq/+7/8v/1/xsA8v/1/63/0P8iAPf/+f8eAAYAPADD//T/BwDi/1YA6v9JAGAAKAAgABoAOgAKAD8ADgDV//D/FwAlADAA3v9AADMAFwASAA8AQwCj/9r/qv/O/yAArP8FAPP/vv+m/8r/wv/z/wcATwBSAPr/VgAgAC0AEQBYAP7/x/8IAIf/jP/a/7z/kv9NAOL/+/8yAM3/VwD9/w8A6P8AADYA4/8fABkA3v/S/wAA7f+6/9r/PQAMAFMAaADB/+D/5v/+/7T/1v8nAMT/BgBPABoAAwAnADIA3/+u//b/QAAhAC0ANwD2/+X/DwAMAPj/CwDl/9j/OwAKAAgAGQAnADEAAwDx/+H/HgDP/yEAUgD5/x8A4v8MANP/3P8HAM//6//v/+D/1P8lAMP/4f/C/7z/pP+R/zkAnP8KAPf/5v8iAK3/GQDL/wwAwf8WAAAAWv8NAPn/+v8NAFQA1v/x/2EAFwCBADEAOgDm/+v/3f/k/x8A9f9TAB4ATwAbACgAWAA0AE8A5P/q/8n/CgAbAPH/GAATANn/qv+V/5j/9v8JAFEAZgAbACgARQATAP7/IgDl/zMAYABOAGMAPgAfACsANQA9AEQAWwBKAPP/BwD0/+T/1//x/+L/1f8UAKL/x//3/woA9/8dAAUABABfALr/tf/p/6P/NgAGAM//IQB2/zUAGQDL/40Ap//w//P/vv/e/5v/+P/V//D/BADy/z4AVgAhAFIAQgAiAEEA6/84AAgA0P/a/zwA+v/X/zoAwf/y/77/JgAMAMH/FgC2/+r/yf/m//7/2f/z//b/+P/C/xcAAACl/+7/KACy/9T/bwD+/xAAHwD1/1MA5////xAA/P8OANX/FAC1/9b/8P+8/wAA7v8oAPz/NADO/+r/JQCw/wgA4//7//z/MwBzABMAWQA1ABgAEwDs/xQA7P/d/y0AAADb/9D/tf8MANP/yv8wAMv/w//0//b/+P8LAAkA9v/4/8L/4f+d/8P/GADK/+f/IgAJAL7/FACQ/8v/aADB//L/9f8JAOP/sf8JAAgAGAABADgA9//5/zEAFQAjABwATgD2/xwAKQD9/yIACAAsANr/BgApAA8AQwDb/xgAFABr/xoAOgDm/1kAWgAAANv/vf/K/+f/kP9u/+f/IgCb/+b/awDp/8n/HAApAOv/JQALAPj/5/+Q/+//BADy/ysAEADE/9D/2f8qADQAFwAlAOj////t//H/BQBzANz/vv85AJv/VAAMAPj/VQDE/xkA8P8qAEYA3f8tAAAAEgBqAPr/RAAlAPr/RAAkAB0A8/8/APz/IQA/ANj/8v/Q/zUAqv9NAFEA+P9oAHf/NwD2/5z/QgD/////EQANAPn/6P/t//H/z//r/xMA2f/h/zAA8P/z/wcA9P/S/5H/AgDd//f/QQBHADkAQABrAPv/6v8AAO7/3/8KABoAp/8BABMAIgAuANz/4/9EAO7/TQA+APv/fQD3/1QADADm/w8A6P8RANf/8f+r/+D/r/+s/wUAqf/x/8//DwAxACcA/P/Y/xYAAABJAAMAKAAyAM3//P/9/9n/4P9CABAA+/8OAOf/2v8YACUAsP9AACEA0v9bABIAxv+//xQANQDi/+j/NQAGAM7//f/G/7//AgDw//P/PwAOAPn/1v8UAP//yP9BAP7/7P8BAO//zv/q/8r/5/8iAOX/jwAXANz/BwC9/+//zf/q/9z/vv+4/+v/yv/D/wUA8v8+ADIAcgAkADAASwDh//r/+/8yAPL/4/8MAPj/+v8yAAMA8f8YAMr/HgAqAA8A+/8gAD8AMgByADcAGgACABQA2v+8/8r/+f/o////WwDJ/y8AAQATAJAAGABLAPP/BwAGAPP/LADt/18AAgDw/xcAAAAlAMP/BQDy/+P/DACv/xoA3v/l/zMAzv8OAB4Az//Z/ykADwAMABwA4P8KABsA8f/0/63/4v/o/8j/QAD+/+z/3f8IAD4An//p/yQAr/8IABkApv/d/+P/1/9xADYAGQAnAPv//P/r/9z/BwDi/+j/7f/e/xsAuv82ABkAy//6/8T/GQC5/9n/4f/C/ykAxv/k/yAArP/P/0YA8P8EAE0A0P9aADYA9f8JANH/IwD4/zAAOQCu/1AALgATAFkAIwCc/9T/yv+d//r/ev85AAkA5P9pAML/PAD6/zIAhAAhAC0ANgA+ACAAGQDe/y0Ayf/C/xcAyf/5/9X/JwBEAO7/OgAcAJf/GQACAKb/EwDG//b/0/+l/4AA+v8fAIgAEQAgAOP/n//p/xIA/f8PAB4A4v/D/73/yv8LAAgALAAjABwAzv/Y/+D/1P+3/9j/4P/B//L/9f8JAAcAPQAMANP/EgDY/87/xf++/7n/x//3/9T/AADc/2MAKwD//1oA2/9QAMD/OgBUAHr/SwDh/+f/x//A/wMAgv8IABkAJgBEAIAAVQANAPn/MQBMAAYATgD2/xwAYABOAIgAEgAzABcAyf8vACYA1v/e/xsAAwDf//j/CwAJAPX/CQAaAN7/CQAHAAYAKQDr/xMAxv+//ycA6f/J/woA9v/4/9X/uf/+/7X/w/8qAFkA2v/i//r/sv/4//r/MQDN/9f/8f/0/y0A7v86ABwAFwDJ/9T/3f/k/zIAzf8yAM3/sv8vABMANAAYAEoAFwASAGsA1v/e/y4A3P8ZABQAtf/p/+3/zP8NAC8A3f+t//T/iP+y/woAiP8fAPX/5f8hAOT/IADj/x8AKwAjAEEA/v8iAAkA4/8NAGcACQBjAFAA0/83AAcAKwDZ/wUAFgC3/w4A+v/7/yAA9v8JACwAEQD8//3//v/s/8v/w//P/yEA9/9BAEcAAgBeABQAEAAfAND/EAD7/6D/6v8AAG3/CgDk/43/NgCr/+H/MADe//f/+f/o////SADx/z0AMQAVADYAYwBPAK3/dQDe/63/PgCx//j/CwD3//n/QwAAACQAQgAiAGUA9v9BACIA0//b/+P/+//X//L/0P/+/xAA+/8gABoAJwAyABYAEQDq/7f//f8PADEAAgDw/2EAFwDc/z4AMgDy/wYABQAWANz/9f8JAOP/HwAHAPT/GgAVACMACgD2/0EAEADW//H/GAABAMr/CwDS/wAAyf+v/ywAkf9MAGIA9P92APH/BgAFAAQA8f9z/w8A+v+y/y8ASgDz/xoA8f+8/wAApf8AADcA9v9lAAgA9f8bAN//LwATAP7/EAANANT/EwAhAJv/5v/G//b/LwDd/1EA1P8TAA8A6P82ACsANQDi/zEA8f+9/5L/cP8MAIr/6/8lAB4A9P/S/zYAGQACABQARwAUACMA+P/V/wEA7/8pAEYA7//O/w4Anv8MAAoA9v9mABsAKACy/8H/qf+V/xcAAADc/77/y//D/xgAAQDd/wcA0P/r/xMA2f/z/9H/EAAyAPL/PgDp/+3/3/8JAAcAz//+/8f/LQDu/zoA5v+i/1kAa//k/w4A1f9dAPD/8//2/+X/s/+d/+j/2v+9/+//zf+y/y8A3f/k/1cAIQAIAAcAKgD+/9r/9P+s/xgAgf/j/zIAXv9aACMA+f9VADIAYAByADcAUQAvAAEASgDz/z4ARQDc/ywAEQBXAGsARAAkADAA8P/h/zAA3f8tAFwAEgAhAAgA9f/A/7r/IwDB//L/PgD7/zMA8v/Q/xAA6f8RAOr/kv/f/8D/uv82AOL/6P/a/73/AADv/+D/HAAXAO7/FgARAMX/0f/a/xgAEwCi/zQABQC7/1sAEgAOAMP/PABWAPz/MwAXADcArP9PAAgAq/8qAMb/CAAGAAUAzv8zACkA/f8hAPf/QgDH/wkAGQC5/+z/8P/h//n/HwD1/wgABwBhACoARgBwADUAKwDa//T/GgDM/zEAOgDm/2sA6f8AAFsA3P8sANr/4v/D/7z/AAC3/9j/zf/8/8b/mv/A/9//wf/f/0EAIgAbAOD/+P8LANP/EgDY/7v/yP/T/0oA8/8ZAF4AFAD//9r/PQAxADoArv/j/x8AYv8TAA8A6P8RAEUAXAA4AD8A6v/v/83/6v/u/9//UwAeAD0ARADu/xUASAAVANv/BgAqAMb/PwAgANH/SAAVACMAwf8WAAAAAABuAA8AQwARADMA4P/B/ykAIQAaADoA5v+P/yUA5////xAA/P/F/+P/VwDG/1EA1P/c//b/5f8hAJr/HADO/zMA8v+r/04A0f/I/+X/DwAMAEEAIgAtAAAAt/8OANX/uP8PAB8A0P9HAAIAAQA4AMD/AwDw/+H/wv8FAOD/HAA8ANX/JgD7/0UAAAAlAPr/6P9bALf/MwDg//n/HgDi//r/jf/t/4L/m//m/7T/CwAbAE0A4/8yADoAr/8/ANf/3/9TAAwALgA4AD8A6v/u/wMA3/8JAJr/LgBcABMAawANAAoA9/8cAAQA8v8ZAN3/LQAAABIA/f/G/9H/7f8VANr/4v8MAEEAIQAtACQA5/8QAA0ALwA4AFIAZwAcABYA7v8DABUA///b/wYAFwDK/+f//v/a/5f/BwCY/5r/CQC+/xQA7P8mADEAAwDe/wkALADa/2IABQDg/53/nv/W/5T/KQDY/ykAWAD+/1oAEQAgANH/IwBBAP7/IgBTAB4A9P9SAB0APAALAC4ANwC//zkALgDc/9H/2v+9/9z/rP8FABYAkv86APj/1f/d/+T/MgAEABUA2//i/57/6f8AAKT/7f8CABQA2v8FAAQA3//4/x4A4f/n/+z/3v8tAKT/2//Q/7T/DADm/w8A6P+1/43/tf/E/+L/MQAnAEQA3P/1/wkA0f8QAOn/AAAAANv/BgDh/x4AKgBHAF4AFABaAO3/JwANAK//v/+C/+T/oP8zACkA/f9+AC4ASgA7AHoAGADL/wsAHADN/9f/AwDM/2kACwBAAP3/of/+/6L/NAD0/y0AWwAlAEIASABxAAAAAADu/xUAEQDX//L/0P+0/7H/UwAeAM///f/Z/+H/wv/z/1EA+P/n/zUAPQDW/6f/AQATAP7//v9IAN7/wP9fAPH/9P8bABUAyP/B/83/DQAwAN3/ZAD2//j/MADL/wwALgAAANz/LADI//j/HgC9/xIA/f/+//7/7P/L/zEAFQDt/97/wP+V/7z/JQCw/0AAMwAEABYA7v8oAOn/SQC7/zYAUADl/1gAx//S/wAA7v/M/x8ABwAFADwAMACoAOL/6P8RAKD/6v8AACQAHQAqAP7/7P/w/wUA4P/U/yUA1f+5/w8AaAD5/wwACQCs/73/t/9YALT/1v/w/5f/LAC1/0QAJADn/yIAwP9NAND/tf/o/9r/9P8IACsAyP8uAAAA7v9NAL7/OQD3/woAUgDU/xMAIgDS/zcAPgDp/xIAIQA/APz/2P/z/9D/2v8FABYA3P8HABgA7/+7/yQACgAIAFAA0/9uAP7/x/8tAJL/zP+f/8T/4v/W/wIAAQA4AHcAOwBUADIA8v9QAOX/xf/2/wkA9v/4/wsA5f8hAPb/LwABANz/9v/m//3/DwBWACAArgAwAEsATwAIAGMAq//z/77/3f8tABIA/f8PAB4Aq/9OAL//uf8iAOX/xf++//D/zv8hAOT/IADR/yMAQQDH/5wADwDD/wUAFwDu/wMA8f/i/+j/tf/p/3//BQDO//3/NADz/2MA0P8QAOn/JAAKABsAcgAkAHkA9P/2/woACAD1/wgALAAjABwA8/8sALX/sv/B/wQA3//A/ygAxf8ZAAIAJgAMANT/JQDn/yMAHABOAFEAeQAqACIAdwAEACgAIAA/APz/DgDo/5D/JgDD/wYAKQD9//7/x/8tADcALAA2AD4A+//Y/wMA8f/0/7//3v8bACgAIAD2/y4A7/+7/yQAwv+7/+7/p//e/7//8f8FAOD/CgD3/2YACQDj/zIA8v9QAPf/HQAXAKX/7v/N/w0A5/80ABgAOAA/ANj/YAAWABEAxf/j/+n/pP8jAIr/xv/k/8T/UADA/7r///+j////EQD8/0YA7/8pAP3/xv/3//j/QwDt/8z/1v/x/8///f8iABsAAwDM/0QAJAAdAE8ACAA+AMT/mP9SAML/hP8KAK3/4v/o/+z/8P8FAPL/4/8xAKj/3v/k/7P/+f8MABwAqf/M/+n/AADb//X/UgDC/7z/EgDq/4D/GQACAPD/BAAWADYA4/9pAAsALQAlAAsAGwDf/woA9v/4/8P/PAD6/x8ABwC8/0oAu/8kAAoACAA+AMT/KwD//xEA6f8SAEYAAQAlAAwAUwALANP/JAD5/wwALwABABMAtP/D/wUAqf/M//v/xf8HACoAov+0/8P/z/8PAB4AUAAbABYANgD1/y4AXAATAFkANQDQ//7/EAAyACgA/P8OAPr/n//X/9//5f8hAPf/VAAfAAYAKgBrAEQAt/8OAOf/EADW/wIAFAA1AFAA5f99AJv/HABOAKz/PQCx/xsA4P/U/yUAw//h/8L/4f/U/yYAHgBQAFMAHgBiAE8ACAArAFoA2//Q//7/7P+5/9n/4f/C/04Av/9eAEwAGABdAPD/FwDu/zsAQgDs/wEAJgBDAAAAWwDJ/6//9v+K/9j/8v/Q/xAA+/8zACkAxf8aACcA/P/q/+7/u//I/9P/kv8oALL/5v9ZAKP/EADp/8n/5v+h//3/2f/O/w4A1f8BAN3/GgDx/6r/cwA3AC0A2//Q//7/Rv/G/9L/yP8KAL//OQAcADsAeQDi//r/6f+k/6P/tf/W//H/PQAMAPj/ZwBBAA8AaADm/zQAKgCi/zQA4f8wAPD/z/8zAKn/TQA+AA0AHQAXADcACAA9AEQAJAAdAPP/9v9TALD/LgBcAO//OwDU/8r/wv8FALv/AAARAOr/XAAlAFUA/P8zABcAAAAlAOf/2v/0/xoAuv/a/5f/GgC5/+z/JgB6/14AlP9hACkAxv92AJX/qv+D/wkAv/8CACYA6P9bAKT/SQAVABEADgDn/0cAFAA1AAYAYQDz//X/+P+w/+T/oP/F/+P/DQAKAD8AMwApAEYA7/8pAOv/AADv/wQAKAAgAGMAvv/v/+D/wv/z/+P/DQDB/04A4/8NAFQA1v+DAA0A5//+/0cAJwCy/0EAx//S/zYAGQACABQAIgDT/wAAAADc/wcABQDg/y8AOAAJAHUAJwD8/yEA9v8vAAEAJQAeAD0AHwDQ/xAAxP/i/wwAQQAPAAwAZgD3/x0AFwAAAAAAJQD6/zEAFQCj/yMA5v/G/3X/2v/h/57/QwDb/xkA8P8XABIA6/84AK3/GAATAP7/NQD0/wgAGQDw/+H/+f8MAMH/u/8kAOb/ov+h/+v/uP/G/wgAGQABAN3/5P+N/+3/FQDI/+X/2P8pACEA9v8cABcAyf8KANL/yf8cAAQAKAAgAAcAGAABAMr/1f/d//f/CgDk/+r/7v8DALr/EADp/5H/JwANAJ3/wv8XACUAQwBIAIQARQDv/wQAAwDM/x8A4/+f/zIAzf8gAPX/+P/5/3r/XgDL//r/MgADAAMA8f8FALv/AAAAACQA1P84AD8ADgAwALn/RwDe/y0AbgAPADEA8f8YAIIAMQAoAGoAnv/o/9r/vf/v/83/IAAsADYABwA9AOj///82AOL/aADm/8f/LQDb/wYAGACA/+P/xP+G/+f/x/9AAMb/CAArANr/BQDg/0IA7P8UACIA0//J/9T/7//g/y8AEwA0APT/GgAnADIATQDj/zEAKADX/6j/8P8FAOD/5v/r/xMAx//k/w4ACwBlAD8A/P8PAPr/1v8VAO3/lP+8/+7/zf/p/xIADgAwABQAEABEANz/BwAYAMr/ZwAJAOT/VwDG/+T/1//M/w0A1P8AABMA/v/s/yYA6P/t/ycA1/8DABQA//9/AAoALQBuAMb/CAAZAN3/CABjAAYA4f8wAKb/OAAIACsAWgDb/3UAAgAUAH8ALwAlADEAlP/z/ywAtv98APb/+P/6/9b/AgC5/7T/ef/d/4j/+/8gAJr/0//J/9T/k/8oAMX/rP/P/8b/BwD0/5wA6/8lAEMAEQAzAM3/MwCp/wIAAgDd/y0A7v86ANT/AAAAAO//KAAgABoAAgAUAEgAcQAAAO3/cP+M/8f/dv8RAPz/xv8IAD0A1v8VAFoApP82AFAALgBcAAEAAABKACkAxv8sANv/vf/v/ykAMwDh/wsA9//U/zgAPwAzAE4ABwAGAPP/rP8FABYAyf9CAP7/o/8jAMD/8v/1/9L/NgAHAPT/CABiABgASwAqAOv/OAD3/+b/xv8IAKv/8/8sAP//EQDq/yUA+f9EAEkAKAAOAPr/6f+2/w0Awv/z/ywAyP/l/w4A1f/L/x4A9P9SAEIAEABEAMn/LwA4AOX/MwDz/wcAKgDs/yYAMQDf/wkA9v+J//3/2P+p/wMA3v/3/1QARAASAP3/DwBDAO3/8f8FAOD/1P/K/8L/qv8DALr///8RALL/CgD3//j/MAAnAOn/7f/M/+n/7f8nAA0A+f8xALr/bAAyAPL/KwCQ//D/FwASADQAFwAAAFwAEwDr/yYAjP/s/yYAsf8cADsAHQA8ADEATAD0/wgAPgBEACQA1P84AAgA4//7/w0A5/8QAB8A0P8QAMT/YgA9ANb/OQD4/9T/EwDs/5P/OwCL/0YAXgCU/3MA7/8EAN//CQD2/9P/JQD6/wwA5v80AM//2P87AAsA0v/b/+L/sf/T/7f/DgCw/9L/JADU/wAAJQBVAA0AZwAbABYAJACv/xoAAwBMACsAx/9AANj/8v8HALz/7//y/73/3f/R/7b/DQDm/7T/DAB3/5H/8f/0/y0AJAD5/wwA0/8AABIADwBDAO3/XwBMAL3/AQATAI//7/8pAMX/GgDM/0QAJAD5/3sAvv8TABAA1v86AAkA9v/m//3/DwAMAAoA0f+2/8T/GQAUALX/QwBbACUAZwAJABoAOgAcAPP/9f8JAAcA4v/o/9r/9P9SAB0Azv8zAM7/2P+FAMb/GgAVAH7/KgDZ/xcA3P/j/x8Avv/L/9X/FADa/yoARwDw/xcA3P8aAAIAy/8xAAIAFAA1AKv/8/+r/87/MwDz/z4AMgByADcAUQD5/8P/KgDH/2QAGQDe/xsAzf8NANT/EwAPAEQAbgAhAD8A/f/r/6X/kv+6/+3/AgCm/+//BAAVANv/9f/3//n/MQDx/3QA8P/z/2MA9f/3/6//9v/m/7T/CwAuAAAAEgDY/xYAXAATAFkAx/8bAAMAuv/s/8v/1v/e/xsAg//l/9j/zf8zABYASQDN/yAA9v/T/+7/qP/e/+X/xf92ACcA1/9fAPH/BgC8/9z/GQACABQA7P9LAM//IQAIAL7/3f+///H/BQDz/5n/GwADABUASAAoAPz/6v83AAgAPQDp/wAAyf/B/xYAkv8nAOn/tv8NAJ3/1f/e/63/GAABAAEASgAFAOD/wf8EAN//+P8eABgAAQAAAFwAAQBdACYADAAcAM7/MwAEADoAQQD+/1oAWwDJ/1QAHwDQ/1kAtf9pAFUADQBmAOX//f/r/93/rP8YAO//FgAAAO7/KACy/x0Azv8zAAQA4P/m/4//SgC7/zYAGQC5/9n/4f8LAOX/MwDz/z4ADQAdABcAEwBGABQAbADX/zoALwDK/x4A9P8tABEAIACa/67/0P99/zwA1f9LAE8Arf/i/7H/5f8OAEMA//8jAEEAx/8bAAMAFQD//wAAAADt/18AAwBMAE8AGwDN/+n/NwAZAEwAKwBHACcAMgADAPH/9P/2//j/i//+/8f/9//C/wQATQCZ/wgA4/8fAAYA9P8IAJj/rP/P//7/2f/h/9X/8P/O//3/WQC1/x8AKwAjAC4AEwAPAOj////b/1AAGwCo/ycAn//E/z4A6f9JABYAJAAKAAgAiAAjAAoA5P/X/83/1//f/9P/7v8DAPH/vf8AANz/GgAnALL/CgDR/+3/8f/0/+T/xP/Q/5D/yv/C/xcAEwAPAB4Avf/d/9H/2v8rAGwAIAAHAOL/+v9EACQAVQAfABkA3v/3/woA5P8zAAQAAwDx/xgAuP/Y/04A9v9mABoA3/+u/9D/IwD4/wsAGwByAMn/5v9HAMv/HgAYAPD/KQA0ALz/3P/j/8T/4v/D/+H/wv+8/8n/+f/o/8j/CQAaACcA6f82ABkAOQBTAPr/MgDf/wkA9v/T/1wAEwAPAAwAHABOAAcAPQBEACQACgAbAF8A8v8GAM7/2P8pAFf/CgAbAKj/JwDW/97/CQD2/xwABADf//j/5//a/xcAEwAiABsAAwDx//T/9v9BAOz/FAAiAPj/QgDs//D/FwDc/wcAKwDa/zwAQwAAAIAAMAA5AHcA4P8KAHcAu//b/2IAz//9/w8ARACR/6f/SwDh/zAAuf9ZAO3/zP/7/43/EQCO/zYAGQDM/zEA8f/0/+T/IAD2/0EA/v/s//D/4f/5/8P/GAC4/9j/8/++/93/0v/t/ycAIAAsAH8A5/8PAFYA6v8lAAsAGwDy/+L/DADB/xYA2/8rAP//o/8QAOn/EgAOAFUAMgC7/xEAxf/Q/+z/lP8EACgA1/8WACQA5v9sAPv/6v83AOT/xP/i//v/sv/5/9X/FADs/zkALgCl/zcA0f/a//T/9v/4/x4A9P8IAPX/wP9xAO7/KAAgAOP/+//q/yUA5/8iABwAKQDq/xIAIQD3/2YA9/8KAOT//P8hAPf/HADg/4r/6//v/+D/VAAMAAoA0v8AAO3/3/8JAOP/oAATACEALQASAEYA7/8XACUACwDA/ygA/P/G/9H/EADp/8n/VAAMABwABAAWANv/GQBwALX/RADu//H/9P8IAFAA5f8hAAgA9f8bABYAAADJ/8H/8v+Z/63/PQDo/+3/zP96/7n/7P/d/+T/VwAhAC0AEgDY/xYAEgAOAAsALgDc/5n/CQDj//v/MwAEADoA5v8PAB8A4v8eAPX/ZQAHAAYAYQC7/xEADgALAC4At/9YAOz/pv9KABcAEgAPAAwA5f/Y/+D/nf/n/+z/8P8FAPL/BgDh/wsA0//J/x0Al/8HAPT/0f9bANv/KwDs/7n//v/H//f/1P/v/87/IAAHAOL/aADm//7/2f8XAAAAt/8zAPP/9f/l/yEACACr/+D/r/8aAN//HAByALf/RQATAI//3P/R/zUAGQA5APf/wv8EAM3/6f/u/9//0//u/83/MgA7AOf/WQDt/wIAFADH/y0ANwDj/zIAAwC6/yMACQAaAPH/KgD+/xAAMgADAHEAEQBqADEAFQB/AOb/6/8BAMr/5/9HAAIAFAD//+3/JwCf/zIAKAAzACkA6/9KAAQA8v8rAEcAJwAfAPX/QAAPAMP/YgDO/+v/OADk/yAALAAjAOb/IgDS/6T/tv+f/w0A5/8QAOn/2/8GALz/NwDj/9f/JwAyACgADgAwACcAMgADABUAfv/P//3/ff87AJ3/+v/7//z/WAAQADIAuv9aAAAAEgBYAOv/EwDs/yYAMQAVAO3/FQC1/8T/9f+///H/4v9DAP//EQDX/9//5v+0/+f/2v/0/6z/YgA8AAwA5f+h//3/j/84AD8ARQDv/xYANwCs/zwAHgAGACkAIQAIABkAFAAQAOn/7v8DAG//HgAGAOH/MAABADgA9/+d/9X/8P+p/wMAuf+1/wwA0/8AABIA2P8EABYAyf8cACkA/f/r/7j/6//K/9X/3f8/AEUA3f8aAIMAMwApANkALgBcADgAmv8uAMr/CwAuANz/LAARAA0A+f8xADoACgA/AOr/3P/1/9P/EgDq/9z/9v/4/+f/kP/v/wQAzf8NAOf/7P/L/57/+//F/9D/7P/e/7//p/85APf/1P8lAB4APQBEAO7/8f8GAKn/OgAKAL//FQD//zYAKwD///////8kAOb//v8iAOX/awBWAOr/JQBVADIAuv/a/+L/1f9LACoA/v8iAAkA4/8fAAcABQDg/6//9v/m/w8AHgAYAPD/BAAoAP3//f/+/xAADQDU/wAAOAAaABUAEQDX/6j/8P88AAwA+P8LABsAFgBJAAMAp/8UAP7/EABXAOv/3P8HAM//6/8BAO//BAADALr/EABEAO7/OgD5/9X/3v/S/wAA2//1/8D/p//e/xsA8v8YAAEA3f8/AMX/UQAcAPP/dQDx/4YA7P/w/2EABABNAAcAPQD7/7L/CgAIAOL/nv/E/9D//v8QAB8AYwDP/8f/9//U/xMARgBwABAAsv9BAKL/x//3/+b/IgDA/xUA//8RACAAPwAyAKj/FQDa/xgAOAAtACQAHQA8ANX/y/+M/7X/1v8VAP////82APX/QADr/+//4P/m/w8A1v8nANb/p//L/9X/AgDw/xcAEgAhAOT/MwBgAPL/BgD0/wgAvf/d/wcA0P/Z/7z/SQDN/w4A+f+M/zUAvf/v//L/4//W/zoA+P+w/0AAof8zAOD/1P/d/4f/HwDQ/9r/9P8aAAIAAgABACYA+//p/yQA1P+CAAwAQQBHACcA6f+2/0UA3P8ZAAIASwDh/0MAfwDC/3MAAAAAAO//hQBGAN3/UgCd/wsA+P/U/yYADAD4/0IANQBQAC4A3P8HAOL/DAAJAGQA4/8MAC8Ayv8LAOX/RgDv/04AGgDx/4YAtf/o/+3/zP/E/8//DwD7//z/xf8aAPH/vP8SAP3/x//3/xwA4f9CACMA0//c//X/wP/N/zIAAwA6AC8AuP80AM7/2P8WAKT/7f/x/wUAYQApAOv/EwDr/8r/+v8fABkAJgDo/yMAeQAXAG8A/v8jAC4A3P8aAMz/RAASACEAPwDq/9z/GQDe/63/YgC9/7f/IQC//7n/x/8JAOP/1v8nAA0Awv8pADMA8/8aAHEANgAZADkA9//5/+j/IwDm/+v/AQDv/wQAKABXAP7/EADp/9v/UADl//3//f/Z/xcAEwDZ/wQA8v/Q/9n/8//R/9r/vf+l/wAA7v/y/ysAIgDl/yEACADQ/+z/y//o/5D/y/+e/+j/7f/M/x8Avv9dAN3/LQAAABIAagDW/0wABQBOABoA8f8YAAEA7/+7/wAAAAA2ACwAbQAOAB4A9P/R/+3/lf8XANz/df/Z/+H/nf8MAC4AOAAtAO7/KACy/woA0v8RADMAzf8zAM3/6v8SAMb/9v9BAP7//v/s/wIA8P/O/w4AMAA5AMD/KADq/9z/0P+1/0QAkf/x/+H/wv+8/xIAawD7/0UANwA/AA4AMAA5AEAAawBEAG4A/f80AOH/+v9EAAAAXAA3AFEAQQAQAEQASQAWAAAAAAASACEA5P9FADcACAA9AB8AGQA5AOX//f9GAMv/DAAcAKn/JwDE/6v/zv/F/wcAvf/K/9X/y//D/wUA4P+v/xoA3/8bAPL/GQAUALX/HwDi/8P/9P8tADYA4//7/w4Awv/h/6//GgAVALb/RADu/ygAIAAaAHEAyP/m/yEA0v8AADYA4//7/7L/wf8EALr/IwAKAOT/6f8SAMX/BwAYALj/NADO/7P/CwDA/9//CQDR/yMACgD2/3gA4f+w/2QArP+q/4QADgD6//v/1/8WACQAQgAQAPv/s/+d/wsAGwDy/xkAOQDl//3/DwAxAPH/KgD+/xAAMgADACcA/P9FAO//YAApAMX/4//W/zoAiv8OAAsAwP+V/73/gP+G/zEAuf8iANP/7v/N/9f/AwDx/wUAlv8rAJD/AQDd/+T/IADj/0QAkv9xACQALwCCAA0ALwDd/wgA9f/3//n/QwAAACQA+f/o/xEAaP8YACYAMQBMAIcAWgDJ/xwAqf+6/9r/z//r/xMA6/+4/w8AZ/8XANz/h/9EAAAAgABnAEEAIgDl/0UA3f9RAPn/DADl/7P/QgDt/xQAEAAyABYAWwBJAOD/ZgBAADMA4f8wAPD/zv/q/6X/EgCO/yQAMADw/zwAHgA9AMP/vf/c/4f/sf/4//n/sf8JAFEACgAaADoAVAAMANP/7v8DAAMA3v8uABIADwBVAEUAbwBZAEgAFQA2ACsA//9/AOb//v81AJj/mv+J/+r/7v8oADMAKQAzAIT/wf+E/+b//f/r/0sAqv8oANf/zf8NAIr//v/H/8D/3//l/9j/4P/B/wQAzf+f/yAA4/9EANz/4/8fAAYA9P8IAAYAhf95AOH/1f9dAMv/QwAAAO3/XwA6ABwAYAC7/+3/8f/P/yIA0v8kAAoAGwDy/xgAAQABAO//8v8sAJD/JgDE//T/ZAD2//j/CwCt/9D/kQD1/3cATQDj/w0Ar/8sACQAHQDz/xoAp/+m/+//u/8AAO3/3/8JAD8A1//y/ysA7P8BACYAjQByACQAQgBIAPH/9P8/AA4AHgBPAAgAdQAnAPz/tAD+////WgAAAO7/FQDb//T/5P+y/+b/j/8AAMr/MABLAM//fgDA/xUAyP93/8n/r/8HAIb/HgA9AOj/IwDm/8b/GgAVACMAngAjAC4AOADk/w0A5//+/zUA4v/V/0sATwAbAAMA8f/P//7/NADh/+f/NQAGABcAAAAAACUAwv8XAO//lv8rAJD/3f8aAF7/NQD0/63/9P+a/wkABwA9ADEAFQARAOr/XADK/0IASACn/wEAy//n/+z/JwD7/8X/BwD0/+T/6f/u/9//CQA/AOr/3P/Q/9r/4f/C//P/0f///xEA/P8OAPr/6f/b/2IAz/8hAFIAwv8pALT/wv8XABMA2f9OAPb/if8hANH/IwAcACkAIQDk/8X/9f8bACgAIAAIACsA//8QAI3/EQD8/9j/8v/j/40A3/+LAEsATwBkANH/bADq/+7/3//m/9j/FwASADMAYQAEAPL/vf8TALT/DADl/9j/lv+r/2AAlv/1/wgAGQDw/+H/1f+m/wAA3P8+AOn/SQAoAA4AMADw/zwAw//0/xoAJwANAB0ATwD2/woAPwBYAEcAJgAMAPj/+v/7//z/6/8lAFUA/P/q/+//qP+U/7z/7v+o/8v/+//p/+7/8f8YALj/DwAMAOb/IQBAACEA5P8gAIf/sf8JANH/7f/e//f/LwDL/zAAJwCf/2oA5/8QADIAFgBuANj/OwD5/+j////t/wIAAgDw/7z/EgDY/xYAbgDY/87//f+z/wsAQADr/zgA5P/X/wMAAgDw/7z/EgDr/+//BADf//j/MAACACYARADu/ygARQBcACUAHgArAOz/AQABACYA6P8jAC8AEwBHAAEASwAqACIAGwDf/+b/2P/z/77/OQD3/8L/8/++/zkA5f/9/+v/yv/n/8f/5f/F/xkA3v/l/w4A5////+3/JwBEABIA6v/v/+D/LwABACUADACu/wcAz//Z/7v/2//i/+j/yP/T/xIAs/8wAKb/yv/C/5f/PgDX/wMA8f8qAP7/2v8qAOv/JgAeAAYABQDy/9D/EADp/9v/BgAFABYAyf8dAAQABAAVAEgATQD1/1IA+v9EACQACwBSAB0A9P91/7X/xP/P/yIA9//n/9n/KgDZ/xcA3P/1/0AAtP8wAN7/0v8SANj/OwDU/93/LADt/ycAaQBCABEA/P+z/x0AFwAAADgA5P8gAPb/HAAWAAAASQDy/ysAyP/T/zcA0f/s/7n/EAANAK//LAAkAPn/aABBAP7/RwACAAIAFADZ//P/LADI/+b/IQDS/xEAIAAsAFsANwD2/wkA5P/E/9D/x//S/6T/EQAyAPL/KwBIAN//+P9VANb/JwD8/2oAMQACAF4AzP8xAN//QADr/6X/EgDG/xoA8f/0/7//zP+x/+X/IQD3/y8AAQBKAAQAKAAzAM7/DgD6/+n/EQAgAPb/HAApAGsA6P///1sAEgBYACIAGwDN/zIABAC6/zUAvf8lAAwAHAA7AK//LQA3AL7/3f/S/8j/wf/y/wYA9P8/AOr/3P/1/8D/8f/0/+T/xf8sACMA+P8wAPD/FwDK/7D/GwDf/+X/DwDo/8j/+P9nAFMAaABTANb/AgDw/zwAVQBXAGsA+/9XACEA0v8kAAoALQASAA4AQwDI//j/QgDt/97/9//n/yIAUwALAEAAWQDs//D/qf+6/7X/6f8AAMn/+P+w/+X/s/+v//b/0//v//L/9f8tACUAHQB0ACYAsf8JAL7/uf/+//7/IwAJAAgAPQDW/xUAIwDB/+D/nP/C/87/6v8TAP3/RwDw/wUABADf//j/sP8tAAAAyf/5/7D/9//5/3sAPgAyAE0A0P9HAAIAFAAQAJ///P/F/wcAPQDW/xQA7f/L//v/DQALAMD/FQC2/x8ABwCq/zsAeP8TAOv/AQAAAG7/VADo/xEAMgA7AK//v/9xALb/VwBGACYAVgAgABoAFQD//xEA6v/J/x0Aqf/y/73/pf83AL//FAD//+3/FADa/wUAPADn/8f/CQDj/+n/EQAgANH/2v8GABcAEgA0AAUA8v8GALz/JQALAK7/BgAFAM7/DgAeAPT/ZAA+ADIAFgDJ/+b/2f/g/8L/zv+g/8X/4//X/wMA3v+b/9T/7/+7/wAA7f86ABwAOwBCABAAaQALAC4Ayv+v/7//lP/z/xoAFQA1ACsANQB0AMv/HgDi/8P/YQAXAAAA7/8WAMn/+P9DABEADgDn/zUABQApADQAKQAPAEMAAAA2AD4Ae/9MAKv/lv+9/6X/EgDG/9H////t/5X/BQAEAAMA3v8bAGAAzf9XAOv/EwDr/6b/AACl/7b/xf8HAPT/5P8gABoA8f/0/xoAFQBbAG4AawAfAOL/6P/a/6r/4P/m/8f/GwADAPH/z/8PADEAAgBwACMA5v8PAB4AKwA1AE8AGwCo//H/z//G/wgABgAXANz/9v/4/wsAGwDy/2IAPQAxABUA//8RAOr/JAAdAPT/CAC9/7j/IQAIAAYAGAAAABMA6/8TAEcAlP/O/yAAh//7/+r/7v9NAOP/aQBnABsATQA+AEUAAAAAADcA0f8RAEUApf8AABIA2P87AB0APAAMAMD/KAD8/6H/IQD3/woALQAAAEkAzf8gABoAzP8MANP/AACl/7f/DgDV//D/8/8HABgA7/8pADMA4f9CAP//o//a/7z/7//N/w0A+f/o/1sA7v86AOb/DwBDACQAHQDz/wcAmP9RAPn/w/88AJ7/6P/t/ycAsv8cAGEAzv8zAM7//P/Y/+D/LwABACYAHgDi/wwA5f/r/yUA1f8mAOj/EQAgAL//SwD0/+T/6f/J/9T/3P8aAPH/BQA7AEIA//82ABkAuf8iAPf/5//+/8f/5f/F/77/OQDS/0kAcgDu/00A0P8QAFcAMwAEAOD/+P+e//v/MgDg/xwAKQAhABsAOgAcAAQAAwADACcA1//M/+n/7f9MAND/IgBAALT/jAAnANf/FQDb/wYABQDg/woA0v/b/wYA4f8dAPT/CAAYAF0AXgDw/yoA6/8mAOj/IwAKANH/SAAVAIAA5/9HACcAjf9IAAMAAgACAN3/rf8GAM7/s/8LAJv/CgC//97/CQDj/x8AKwAQALL/+f8MABwAKQAzAGAATgAsAAAAEQDX/5b/9P+//7n/IgDT/zcALADt/0wA9f9SADAAFAAiAEAANAAqACIA0v82AL7/3f8IAKv/4f/n//7/2v8YAAAAAAA3ABoA3//4/+f/kP8BAKX/pf8SAP3/DwD6/+n/EgAzAJb/mf/S/wAAtv/p/0kAlv8rAOz/AQA4AIj/DQCv/z8A6v/u/00ArP8qALT/+v/W/9//LgDc/wcAz/9GAMv/DABBADQAPAAeAJkA6f82ACwAyP/T/8n/CgC///H/z//+/+z/8P8EAAMAOgDm/yEAQAAOALD/0v/u/8z/sv8KAFEA1P8lAFUA/P+z/x0AKgDZ/04A0f/a/+L/1f8UABAAVwAOAGgACgDR/1sAyf/5/+j/yP/T/+7/XwAoAFcADwBDAEkAAwBfAPH/PQAeAPX/5P/F//X/0/8SAP3/xv+//97/wP/x/wYAFwBKAGAAKQCh/9j/qf/e/9P/JABCALX/HwD1/wkAGQA5APj/wv/O/7P/CwAbAGAAOgBBAP7/x/8bAPL/4v8fABkApv+l/8n/wv+7/wAAAADu/wMAAgAnAMT/PQAMABwAzv+O/+7/g/8uACUAVQAfAD4ARADc/xkAp//d/7//OQDT/8n/5v9q/+T/IAB2AN//ZQAtAMn/ZgAIAD4A/P9YAP7//v8jAOb/NADh/+f/7P85APf/+f8MABwAzv/F/3YAzP8yABUAJAAKAIj/6f/u//H/vf8lAB4AGAABABMA/v/+/xAA1/86AJz/CwAbALr/IwDU/8r/1P/v/+D/HQA8APr/RABJAPL/BgAXANz/LAARAA4A+v/W/97/wP+6/7X/xP/0/xsAAwA6ANP/EgDr/5P/8v+r/2AABAAVABEA1/8WABEADgDV/wEAuP8hAPf/+f8eAOL/+v/E/+L/nv8xALr/2v89AOj/WwAAADcABwDP/+v/AQDd/9H/EQDX/7r////t/ycAVwAzADwACwAJAOP/6f8kAOb/2f/h/zAAOQBAAGsARADu/xUAIwDU/9z/4/8NAML/FwASADMATgBRALAAMgA6APn/6P///9r/9P8/ACEACAA9AA0AHAC8/yQACwDS/xEA6v8SAA8AHgArACIArv/1/+X/2P8WANv/BgC8/yUAMADw/xcAXADd/xoAXwACAPD/hf/5/7H/CQAsACMAVADW/xQA7P8CAN3/9/8KAAgABgD0/xoA3/94AAQAKAAOANX/SwC8/+7/FgARACAACAD1/9L/tv8NAAsA5f/8/9j/KQAhABoAFQDt//H/BQA8AAsA9//5/8P/BQAEAM3/MgC7/8j/LgAAAAAASgBOAL//OQAJAD4ADQCd/0MAkf+C/wgAKwD//0gAFQDa/2IA9P9RAB0AFwA3ANH/WwA2APX/+P9VADIA8v89ANb/3v/A/6j/JwCf/9f/FQDt/97/wP/x/+L/HgArADUAz/+0//r/6f/t/5X/9P/R////IwD5/0MA//82AAcA4f/6/8T/vf8lAPr/1v86AJz/HQAXAO//OwD5/zEAAgACAAEAAQBLAAUABADf/wkAPwD8/2sA1v/M/x8Amf/2/+b/6//K//r/aQDU/xMAIgAbACgA6v8SAMb/rP/i/8P/4f/6/wwACgAIAD4A+/8OADAAuf/s/93/5P/8/w4A+v/W/0wA9f8bACgAsv9CAOz/AQBLAOH/HQD0//b/+P/C/wUABAAVABEA6v8lADAAOQAJAPb/CQDj/w0Awv+p/xUA///b/9D//v/H/+X/oP/q/0oAqf9MACsA2v89AOj/EQDp/+7/OgDB/6n/3v8bAAQAAwAnAOn/7v/M/7L/CgDR/+3/cQDb/9D/IgCu/+P/aAAKAOT/DgDC//P/vv/w/xcApf8kAB0AKgAPAAwAVACx/0AANADz/3YAFQBIAF8AKADq/+7/zf/E/77/pv/c/+P/VwAzAAQAKADY/xYAJAD5/zEAFQDt/ycA+//8/w8A1f9LAE8A9/8vAPD/zv/9/zQAFwAAACUAsP/k/8X/4/8fAPX/igATAEYAXgAUADUAvf8lAPr/1v/x/wUABADN/0UA3P+s//T/BwAYABQAEADp/9v/4v+x/+X/DgCw/9L/pP/b/+L/nv8xABUASAAoALL/5v/H/9L/AAA2ABkAp/8BABMAj/+3/w4A6P+1//v/1/+6/xEAVwBZAOz/FAAiAC4AXACCAGkA+f8xAN7/9//U/8r/HgAqADQATwBlAAcABgDh/wsA0v8AABIAoP9GAO//FgDu/wMAJwDX/00A4v9WAA4AMABLAM//RgDw/wQA8v/i/x8AKwAjAAkABwDi/+j/tf/7/w4ACwAbABYANgAHAD0AMQDx/+L/6P/a//T/CAAGABcAt//G//b/5v9YAEcAFAAjAMH/8v8GAOH/+v/W/97/CQAHABgA7/8XAO7/zf98ANH/2v90AN7/GwAoANf/8v+9/27/r//k/yAALADt/ycAxP/1/63/vf84AHb/IwDT/8r/MAC5/w8A1v/x/8//xv/2//j/CwAuAEoAKQAhAC0AEgD9/+v/AQAAANz/9v8JAKz/z/8PAB4A9P8IABkAJwAfAPX/dwDy//X/QADG/xoA8f8FAGEABAAoADMABAA6ABwAPAD6/x8AKwDI/wkAGgDe/5v/CgDk/8X/dQAVABEAMgC7/yMA+f+e//v/IADR/+z/XgAnAA0A+f+e/+j/yP/m/w8A+v8fACwANgA+AA0Awf8pAA4ACwAcACkAIQDR/+3/8f89APr//P/q/8r/5//Z/yoA6//v/wQA8v/Q/yIAm/+c/zAAuf80AOH/+v/7/+r/NwDR/9r/vf8AANz/GgA5APj/CwDl/9j/BAAoANf/TQA+AB8APgAyAE0A0P8iAAkA9v9BAA8AHwD1//f/QgBHAAIAFABaANv/0P8PAB8ABgDz/ywAbP/l/yEAmv94ADwA5////xAA1/+6/9r/GAABAMr/QgDt/97/CQC+/7j/ov/r/wEAAQATAP7//v81ABgAJgBDAEkAFgDt/xUAyP/l/+v/AADK/+f/tf+x/wkA0f///9r/9P/S/xEAIAD2/y4Apf/c/+P/1v+n/8v/DAAcAOD/+f8wAKf/EwDs/zkAUgD6/wwACgAtALb//P/9/9n/vP/J/woAv//e//f/CwDl/zMAFgA3AD8Axf8HAPT/9v/4/zAAFAD//0gAJwDp/+7/zf8NAEIAEABXAP3/2f8XAMn/CgAtAKT/EQAOAML/BQDy/xkAFABHALn/tf8MAIr/2P/N/9f/OgD5/x4AhwAQAPz/MwBgAM3//P+iAJT/BADy/wYABQDg/y8AEwBZANr/TwDl/8X/BwD0/z8Axf9RAMH/zf8yAAQA8f8rADUABgBOAKz/KgD+/8f/GwADADoAHAAXABIARgABAN3/9v8cAM7//P8PALH/CQD2/xwABADf/9P/3P/1/y4ANwA/AFgA/v+RABgAJgBDALb/DQD5/8P/qv8pAOr/AAAlAAsALgDK/0IARwAVAH8A+f8xAEwAq/8pAOv/3P8sAAAAEQDq/wAA7v8oANf/3//m/7T/5/9+/+H/+f/7/w0A+f8MAAoACADi//v/1//M/w0ALwATADQA4f8LAFMA1f8BAAEAAQDv/ykA/f/+/xAAxP/0/7//AgA5AJv/HQAXALf/WAD+/9r/hgDs//D/zv+z/zAAy/8eABgAAQATANn/FwAAAO7/KAAOAAsA9/8dAPP/BwDi/7H/5f/F/wcAz/+P/8r/wv+X//X/5f/q/yUA+v8MAJz/+f8MAOb/2f+7/+7/3/8uAAAANwAIAAYAYQBhABYANwAsAH//YgDO/zMATgDk/1cAof9GAAEAuP/r/wEA7//y/9D/7P9LAPT/ZADj/x8A0P+i/1kA2v8YAKb/EgBGAAEAXQA4AAkAUQDm/7P/VQCy//j/VQDp/wAAAAASAP3/2f8EAN//5v80AOH/HQAFAPP/LAA2APX/5f/q/4D/BgCX/77/SwDh/zAAFAAjAOb/6/9dAAEA3f8sALb/6f83AOP/MgAoADMABAADALn///81AOL/HgDi/wwA+P9CADUAPQAfAOP/MQADADkAwP9NAPX/GwCFAMb/ZADQ/+z/JgAxADoAVAAxACcAMgCo/zkACQB2APH/z/9sAGj/4v9DAO3/8f89APr/DQAKANL/EQCg//3/2P8EAAMAzP/7/+r/JQD5/wwA+P/6/9b/JwANANT/OADS/1sAJADn/+z/pv/c/7//uf/s//D/zv9GAAEA7/8pAP3//v/s//D/l//1/8D/uv8QAJ//DQDn/+z/3f/3/+b/xv8aAAMAzP/o/yMAnP/6/+j/7f/x/5j/GgC5/xAA+//X/00Aq/8XABMAxv8IAOL/6P8RAPz/2P8pAP3/6/9dAAEA3f8IABgAAQATAP7/x/9AAA8AMQACALn/NAD0/+T/6f8SAP3//f9ZAKP/EAAyAPL/YgBPABsAKADX/wMA3//l/2sADAAvADgAGgDf/y4AXAA4AGQA9v8cAKn/FQDa/6r/TgC+/wIAOAAtAO7/8v+r//P/9f+u/z4Aev8UANr/z/9rAPv/IADj/x8A0P/a/wUAFgDc//X/0/+3/+r/kv9MAND/tP8MAPj/QgDa/yoAov+0/zEA3v8bAPL/4v8fABkAFAB+APj/VQAgAL7/8P+8/xIAs//C/4T/nP/n/9r/PAAMAAkA0f8RAOn/2/8+APv/agAxAPH/KgDs/xMAWQAjAHgAFwAlAJ8A7f9xANv/GQCCANf/OgDB/xYAtv+y/y8Apv8TAP3/IgAuACUAHgAFADsACwAJAAcABgAXAO7/TQDj//v/IABi/xMA/v+Q/wEAEwBHAAIAOAD3//n/VgAgAD8A/P8OAEMA//9tAOr/kv8DAJX/4f/C/wUAYACo/xQA7f8CAPD/KQAhAOT/IAC//zkAwP+o/97/9//5//r/DQCd/9X/3f8IAAYAKgAPAB8APgDp/zYA0P8QAPv/IAD2/wkAPwD8/zMABAAWAO7/uv+1/zEAzf8fABkAgv8/ANj/FgCk/yQACgAIAIgAfv8qALT/QwAAAO3/cQDJ/2YA9//5/8P/qv/y/xkASwAYAAEAEwD+/6L/NADh/9X/XQACABQARwDe/xsAhADY/wQA3//m/yEA0v9tAP3/of8hAPf/QgA1ABgAggDp/0gAOgDm/8b/v/85AK7/BwDi/+j////I/2UAv//e//f/r//k/3v/zP/E/9D//v8QAFYARgCnAIYAx/8bAM3/xP/j/wwA0/+l/wAA7v/y/6v/BADy/6v/8/8HAM//tP8LAMD/KADq/xIAWAAQAB8A4/9EAMn/CgAIAOL/DADT/xIA6/84ANL/2/8GAOH/HQC8/1wASgA8AB4Avf9KAKn/TABiAKr/FgDJ/+b/2f88AB4A4f9oAMH/OwBUAMT/9P8IAOP/6P8RAPz//f/Z/wQAu/8RAMX/0P///5D/JgDD/xgAOADk/zMA8v8+ADIAzf8NAPn/jP/a//T/9v8vADgAZAAZAPH/TwD3/5z/VQDp/0kAFgCk/yMA5v8PANb/cQD//+3/FQC1/x8Aq//O/yEALQDJ/0EA7P8BADgA0v9uANj/OwAwAAEAXQABAAEAAQAlANX/FADs/8v/HgC9/yUAMAACAEsABQAEABYAAADb/77/EwDs/0sA8/8/ACAAh/9EAKT/AAARAA4ACwCJ/w4A5//+/9r/9P8IAND//v8QAMT/GQABAO//TgCs/z0A6P/a/ysAEAANAOb/IgDA/wMAuf8QAA0Aiv8hAAgAGQDe/+T/1//y/xkA8P/z/+P/MgDy/ysAIgCu/+P/+//X/wMAJwANAOf/EABpAAoACADj/x8AKwAQAEQAyf8KAC0A3P8+AB8A0P8jAMH/OwAdALz/bgD9/1kASAA6AGYACAB1APH/GAABAKX/NwC//7n//v/a/zwAMQDe/xsA8v90/8b/0v+j////yP/l/w8AsP/S/+7/KADF/+P/6f+2//z/DgDC/+H/5//a/wUA8v/1/xsAFgDJ/xwABADy/ysAo/8iABwAFgBcADcA9v/m/0YAJgBoAFQAMQADAPH/4f/n/2wAagB6ABgAOQAbAN//LwDv/zsACwAJAAcAvf9KAOD/1P9dALj/6//v/4T/5v/Z/zwAHQAFAAQAzf9FACUAHgD0/+T/xP++/wEAAQAAAO//TQAZAMz/1v/M/x8A0P8QAA0Awf/g/6//BwCr/4T/LwC4/+v/JQDD/7z/AADu/wMAFQD//zYA9f8JAPX/+P8wAN7/LQASAEYAAQDK/0IAyP/4/53/6P81AOL/MQAVAEgAFQAjAPj/sP8JABkATABPAC0A7v9NAD4ADQBnAC4A3P/R/zUA9P8bAAMA8f8YAAEASgDz/1EAHAC7/9v/hv8MANP/SQCFAA8AaAAKAOT/DQALAAkABwD0//b/wf+7/wAAAADb/6v/BADN/8X/GQCm/93/0f+j/yMA0//u/ygA2P8DALr/EAANAK//ZAD1/+X/DgDn/xAAsv/m/w8Aw/8YAO//qf8nANf/3/8cAPL/GQAnAB8A0P/Z/8//6//v/+D/+f/D//T/CAArAP////82ACsASAACAAIAFADs/wEAy//V/6b/7/8EAKj/JwDp/+3/FQAjAEEA7P9LAAUAFgAAAMn/5v/r/93/5P8gANH/WgAkAEIAbACg/0UAAAAlAFUARABKACkAIQDk/0UAJQB6APT/5P8gANH/NQC9/xMAIgAuACUA1f/d/4j/+/+g/w4AMABd/+v/k//N/yAA0f81AAYAFwATAA8A6P+R/7n//v+i/9n/FwDK/x0Az/8PAEMA7f8nAOn/7v8DABUAEQAgABkAJwDp/9v/mgDE/+L/VgD8/yEA9/9UAEMA2/8+AFYADgALAPj/CwDS/wAAAADb/+P/+/8gAL7/FADH/9L/2/+Z/wgA9f9AAA8AQwDb/+L/DACu/xkAzP8xABUA7f8nAA0AQgDs/yYAMQCo//D/4f8LAJwADwAMAAoArP/i//r/RAAkAAsAGwBNACwAIwAvABMAIgBAAFgA/v///xEADQALAOX/DgAeAKr/FgDu/5X/TwD3/0EA7P8BADgAwP8VAO3/AgDL/zEAAgDe//f/wv87AAsAQADr/+//8v++/7j/6//v/87/MwDz/+P/1v+n/6b/7/9x/w0AVACM/yMA5v8hAAgAKwAjAPj/MADe/xsAAwBfAPH/PQAMAAoAdgADAF8Auv8QADIA8v89AGkA1P+4/w8Aef9LABcA7/8pAA4AHgBiACoAtP8eAAYA8/8HABgAk/8oACEAmv9TAMP/4f/6//v/1/+o/97/rf/Q/+z/FADH/9L/JAD5/wwACQDR/xEA/P+h/+r/AADc/+P/+//8/yEAPwAzAPP/vv8BAMv/CwBAANn/FwASAP3/RwDe/y0AJADU/zgA5P8gAOT/1/8oAMX/vv8TABAADAAcABcAXADK/wsAQADr/xMA6/8TAI//AACl/7f/WADr/zgA9/8vAPD/FwA3AL//FAD//9r/4v8eAPT/9/8KAC0AAAC2/0UAJQBDAFsAEgAOAOf/RwAnAA0AQgDs//D/FwDv/83/MgDy/xkAOQCb//n/1f/e/0AAMwApAP3/IgAJABkAJwD7/6D/MwBOAKz/BQDg/8L/8//j/w0A+f/V/97/9/8dADwACwBAADQAKgD+/+z/y/+e/8P/4v/V/97/CAC+/8v/nv/W/xQA2v8YAO//8//j/x8A4v8MABwA4P8dAOH/+f/o/9v/4v/6/+n/AAAkAAoAGwDy/ysAEAAfAD4A6f8AALb/jf8AABEADgAwAPD/4f/n/9r/FwAAABMARgBdADkAGwADAMz/DQBUANb/cQA2APX/QACz/4wA8f/h/0MAEQAgAL7/JgDW/97/CQDj/zIAAwDM//v/MgDy/xkAJgDp/9v/GADL/9X/FADH//f/5//s/6b/3P8aABUAEAANAGcA5f/q/yUAQwAjAOb/6/+4/7T/MABwABEADQALAMD/3/9BAOv/OABAAKH/DgDD/8//xv8IAFAAGwA7AC8AJgDW/ycAsv/4/+f/a/8bAKj/pv/K/9X/uP+h/zQAz//9/w8A6P8RAMX/LAA1AND/EADp/8j/+P/C/xcAEwDZ/ykAWAAiAMD/zf8NAAoACAAsACMALwAlAB4AYgAYABMADwAMABwA8/8+ADIAFgAAADYA9f8JAD8A/P9GABMA2f/O//3/2f+7/9v/0P8QAMT/PQAfAD4AewD2/xwA4P/5//r/HwD1//f/+f/o/yMA+P9VAPz/MwAXAAAAAADJ/0IAff8pAA8AjP81AJj/GgDx/6r/8v/1/1IAQgD//7b/DQAdAM7//f/Z/+D/+f/o/+3/uf/+/7X/6f9bANv/BwAFAM7/2P8DAEwAGQA5AGUAv//e/y0A3P8HAAUAPABCAO3/OQD4/+f/7P8UAKL/ov8iANP/kwAtAAAAJADU/yUA+v9XADMAFwAlAOf///8jAC4A3f8aAKf/AQATAOz/OADA/wMAAgDw//P/9v8cALv/EQAgANH/7f8nAMT/GQA5AMD/XwDx/z0AHwCY/y0Ayf8cACkANAA8ANX/8P/z/xoAAgAUAP/////t/8z/6P/b/wYAl/8ZABQAx/8uAO7/KADq/yUAHQAYACUADAAuANz/BwAGABcA3P/2/1MAw//0/xoA8f8qACIAZP/e/wkA9v8JAPb/UwDV/zkALgDc/9H/o//s//D/4f/U/zgA5P8zAGAA4P9UAPv//P8OAPr/RAAAALf//P/r/9z/PwAOADAASwDh/wsA5f+O/zcA0f/a/yoAj/9KALz/3P91AKf/FABsAA0AQgA1AM//2f8EAAMAFQAjAK//BwD0/4j/MgDy/+L/QwDt/ycAxP+r/xcANwAtABEAIAAsAAAAJAAvAKb/7//y/6v/4f+v/wgABgA8AB4Avf84ANL/7f/x/8//6/+l/1wAAADc/1EAnP8dAAUAqf8nAA0AQgA1ABgASwDP/6H/2P+7/+7/8f8YAEsA4f8dABgAEwAiABsATQDj/+n/7f+n/5T/8v/1/8D/KADq/xIADgALAFMA+v8NAPn/1f/L/9b/FAA1ACsAIgAJABoA3v/3/2cACQAaAPH/GAABANz/LADb/wYAvP/c/6v/zv8OAIv/EAD7/zMAOwBCABAAxP/i/8P/9P/S/yMA+f/D/wUA8//1//f/1P+m/wAAt//9/zQAFwBvAA8AaQD5/wwAZgC//xUA2v/0/63/4v9DALb/RAASADMAPADV/wEA7/8pAOv/JQAMAOX//f/Z/04ArP/0/z8As//n/8f/QAAhANL/7f+n/93/0v8RAPz/IQA/ANj/KADq/7f/6v8SAOv/AQA4AJr/rv/1//j/+f8xAHEASQDy/+L/aAAKAD8AIQDk/yAA0f8QADIAAwADAEwAKwA1AAUAKQA0AM7/IQD2/y8A3f/k//z/xf8aACcAMgAoADMAFgA3AKz/BQDz/2L/3f91/+z/AgDL/9X/8P+8/8n/HQC8/+7/3/9mAAgAvv9LAKr/FgAAAMn/5v/r/xMA6//w/ykAIQA/AFgANAD0/wgAKwDs/0sAGAABACUA6P81AKv/OwBCAO3/TADP/zQA8/8aACcAxP/1/5v/0/+3/w4A6P+j/zUA4v/D/8//DwD6/w0ACgD3/x0ABQBNAAcAGAATAA8AMQAVACMAwf87AB0ABQBzADcAGgAVAEgA3/+KAEsAPABDANr/UAD3/2cAGwCo/xUA/////wAAEQDX/83/DQAdABcA7/+W/+L/w//P/1kAtf/o/yMA1P8lANX/lP8WAO7/qP85APj/QgBIALr/NQC9/8r/HQD0/y0AAAARAEUA3f8aABUAtf8fAND/x/9AAP3/RwCnAPT/GwA6APn/MADe/9L/tv/q/+7/uv9IALr/IwD4/+f/IgCJ//z/xv/2/xwAKQAOAAwAQQDG/y0Ayf/m/yIA0v8AALb/DQDn/7X/+//8/w4AQwARADIABADM/zIAg//4/x0ABQA7ANT/SwDh/zAAXgDw/yoAof/G/+T//P8OADAAXgDM//v/6v/c/9D/tf/7/+n/7v8VABEADgBVAOn/SQBNAOP/RADb//X/CQAHABgA7/8pAA4A1f/e/+T/xf8sAP//2//0//f/CgAIAGMAvf/K//n/sf8JAOP/DQAKAAgABwAFABcA7v8DAN//CQAsANv/UABTAOf///8QAPz/6v/c/3T/2f/O/+v/OAAaAF8Ap/85AAkA0f81AKv/YAAWACQAMADL/x4Az//H/y0A7v+o/ycAHwDQ/xAADQDm/+v/OAD3/9T/SgDO/8X/GgCU/ykAIQAbAE0AGQA5APf/CwD3/y8A8P/g/x0AFwBKAM7/WAAiAPf/VAANAOb/2f9OAOT/1//x/+L/DADB/ygA1//y/ysA//9IAMz/MgBNAPX/GwDN/w0Anf+w/wkABwAFACkA/f/+/8f/0v9JAJb/KgDs/5T/TgD2/y4AEwAPAOj/EQAgAAcABgDO/yEA9v/m/yEAGwC6/yMACgD2/woAv/8UAJD/8P/O/w4AMADw/zwAw/8qAMf/LQAAALf/RQDK/x0ABQAEAN//nP/5/9b/zP8MAMH/u/8kAOb//v8QANb/8f/0//b/+P+e/57/6f8AACQA+f8xAMz/1v9MAL3/AAA4ANL/AADt/7r/7P8CAAEAy//6/w0Ar/8sAFsA3P8HACoAov/+/8f/5f+PAOH/QgA1APT/UgDC/xcA7v/f/1QA6P9aAG4AMwAXABIA2P/g/2cA5f9YAA8AxP8YAPD/FwDc/xkAJwD7/7L/HQAXABMAkAD0/y0AAADu//H/9P8bABUAJAD5/9X/lP8EAAMAOgBBAP7/IgDT/+7/zf/p/9v/9f8JAKz/qv8DAAMAp/8TAA8A1v8CACcA6f8AAAAAf/8GADwAef/v/04A4/8NAML/4P/U/8r/QgDt/zkA+P/C/ykA/f/Z/+H/QgC1//v/RQC3/yEACAAGAPP/9v9TAB4AKwBsAEUA3P/j/0QAJAAdAE8AGgAoAFcA2f8XADcABwA9APv/RQBKAE4AGgACAEsAz//+/8f/wP/x/yoA/v/H/xsA3/9mAOT//P8hAL//JwDE/+L/HwAZABQARwAnAJ//6f/u/wMATAD0/1IACwCb/2YA0v8AAEkAAwAVAO3/JwDp/+7/3//A/83/IAA+ACAAUQD4/zAAAgCm/wAAOAD2/woALQDu/wMAzP9EAO7/zP/p/9v/PgDE/xgAFADs/93/9/8vADgAUgDn/xAA+//8/+v/t/8OAAwAHAAWAO7/8f8rAEcA8f8YACUAw/+8/yUAHgC8/+//4P/U/+//u/+AADAAAQDw/+D/+f+e/0QAAADu//H/q//z/+P/HwAZADkA5f/q/wAAyv8vALj/ov/+/9n/8//j/8T/4v/W/ycA1v/x/08AiP9FAO7/AwCEANj/FgAAACQAwv8XAEoA4P8dAOH/HQDh//r/DADU/wAAAADc//b/LgDc/xoAFQDI/wkAvv/w//P/mv8uAMn/1P8BALj/MwDz/ywAgAD5/9b/FAAjAC4AOAD2/xwAFwAAABIAs//n////7P/w/yoANAAXAAAAEwDr/8r/VQAyAM3/6f8AABIAIQD2/xwABACW/+L/w//h/+f/IgAcAKn/JwCy/4r/RgDv/xcAEgCz/+f/7P/w//P/LAARANf/KABYAGsA1v8VAP//yP8uAAAAJQDn/zUAGAC4/zQAz/9GACYA6P9aAO7/OgAKAC0AJADU/xMAxv/3//n/+v/7/+r/AACk/yQAHQCq/83/6f/b//X/CQAHAOL/w/9PAAgAKwCRAPX/LgASAA8A+v/E/xkAAQATABAAMQADAKf/OADS/8n/QQAQADEAAwAVANr/GABLABcAlAAbABUAJABCAOz/y/8eAKv/4P8KAC0AAAAAABIA6v9cAMr/HgAFALv/WwDu/ygAIAD2/woACAC9/wEA3P+s/z0AjP/s/8v/+v9pALD/LQDu/4P/9//5/3n/uf+i/6L/6/+T//L/9f8JABkAFAD//7X/xP+9/wEA7/8pAOr/EwAPALH/GwAEACgARQDc/77/3v+t/wYAKgDr/xMA6/8TADQABQA8AFUA1/9MAPX/5f8gAJr/LgDv/wMAFQC2/+n/AADJ/y8AbwB9/zwACwDT/1wAAAA3AAgAKwD//0gAcQARACAA0f8jAFQA1v9eACcAn/9XAOv/7//g/9T/JQDV/zkA9/8LABsAFgAkAOb/IgDS/zcABwDi/2gAwf/y/3UA8f/h/zAAAgDd/1IA+f/W/zkACQAHAAYABQAEADoAQQDH/y0AJADn/9n/KgD+/8f/CAD1/0AADwAxACcA1/8oAOn/2/8rAO3/AgABALj//v/Z/6r/zf/8//3/IQAIAL7/JgAxAAIAFADs/wIAOQCt//X/GwCW/+L/1f9LABgAXQA4APf/LwDd//b/5v8hAPf/LwATAOz/OQAJAPX/5f/q/9z/0f+j/38ACgDS/4AA+f9WANf/3/8KAOT/1/8DACcA1/86ANP/JQD6/+n/7f+n/0sAqv/y/wYAz//r/yUAQwD//wAA7f8DAN7/9/8dACoAxv8/ACAArP9iALz/3P/j/x8AGQACACYAsf9lAAgAUAAbAPL/BgDP/zQAhP8vAN3/CAB1AKf/AQDK//r/1v/e//f/1P8BAO//KQAOAAsALgAAANz/PgDF//X/9/+K/0YA8P/O//3/DwCe/7H/HACW//X/0v8RAA4ACwBAAP3/NADP/w8ADADB/xYAJAAKABsA8v89AB8A4v9DANv/4v8MAOb/xv8IACsAtf/7/+r/yf8dAOH/1P/v/wQAzf/p/zcA0f8QAA0Anf96AAYAzv9GAN3/9v/T/8r/1P8TANn/vP8SAKH/6/8AAMr/VAAfABkAXgDe/+X/xf/j/w0A+f8eAOL/+v/7//z//f80AAUABACEAP3/DwAxAN//0/8SALP/5/81AL3/JQD6/5//6f8kANT/SgA8AJ7/QwDb/9D/IgDl/+r/JQALAPj/CwD3/x0Azv8hABoA8f89AEQANgAZAKgABgAFABYAt//q/6T/2//Q/yIA0//u/xUAEQAOAAsAigAAAEoABAADABUAEQAyAPL/UADT/yUAHQAFACkAxv8/APz//f80APP/9v/T/9z/GQDw/xcAEwCh/0YApv+A/xkAy/8fAKv/TgAaAJX/cwATAMf/9//5/7D/5f8gAOT/DQD5/x4AKwBHABUAtf8fAOP/6P8AAEgATQC+/wEAJgAeABgAAQDd/7//FAAQAA0AQgA1AAYAFwAlAEIA7f8CAF4AAgDw/xcAAAC3/+r/AADc/wcABgAXAAAAEgDY/87/6v/c//X/QAAPAMP/GADv/wQA8v/Q//7/EAD7/8X/vv/L/wwA0/8lAEIAEAAgABkAOQCu/1EALgAlAFUA1/86AMH/BAADAKf/OQDS/9v/BgC8/6X/AADu/7r////t/ycAMgDf/woAGgAVACMAVAAMABwABAAoAGoAHgBPAMD/AwAnANf/TAAZAEsABQDz/9D/tf/7/+n/AADc/+P/+//8/w4ACwD4/x0AKgD+/zUA9P/2/woA0v8jAFQA1v/M/zEAAwDM/7H/0/+k/9v/PgANAPn/6P/t/97/0v8SAP3/6/9dAAEA3f8sANv/0P8iAPf/5/9HAAIAAQC4/7T/w//h/zAA3v8bACgA/P8PADEA8f8FABcA7v8WAMn/5v/9/9n/l/8HAD0Anv/W/wIA8P+q/wMA3//A/zoACgAaACgAIADR/0gAXwACADkAQADZ/6n/8f/0//f/HAAXAAAAAAC3/yAA0f/t/14Alf8XAMr/CwBAAMb/GgBfAHEAEQBYAOv/7/9gAM3/DgD6/9b/OQAcAAQAOgAKAC0AWwDc/+P/DQDm/zQAKgD+/0cA8P8XACUA1f8UACIA+P/V//D/KQDY/7v/2/+r/87/6v+3/yEA9v/B/+D/CgAaADoAVAAeAKv/8//1/8D/TQArABAA/P/q/1wA3f/2/0EAov/Z/xcA7v8oANj/4P/m/8b/CAD1/wgALAAjABwAPACd//r/DQCv/1EAHQBOAAgA4v/7/8T/KwDs/xQAEADp/zYABwAFADwAMAACADkAQAD9/6L//v8QANb/AgAnAB8A0P8iABwAqP8nAPz/DgAeAOH/VQDE//X/9//U/0oAKQBZACIAQQDG/+T/VwCh/+v/pf8AACUAsP/k/7L/HQA8ANX/OQAbABYAWwASACEA5P8yAPL/q//z/3X/EADE/73/EwC0/9X/pv/v/wQAKAAgAAcABgAXACUAHgA9AAwALgDK/8L/8/++//D/FwA3AAgAKwD//yMAHACp/ygA1/+o/97/wP8DALn/2f8qAP7/NQCq/7v/tv97/wIAuf80ACoA7P84AC0ANwC//wIA3f/S/zYAq/8XABIAxv8aAAMAFADI/+X/DgD6/w0Aiv80AM7/of9YAOz/cAAQAA0A5//Z/4YAov/s/wEAuP9GAAEAEwD+/2v/5P8gANH/7f8UAP//tf/7/yAA0f9aAO7/FQBIAMz/+/+g/8X/GgACAPD/FwDc/77/FAAiAFMA6P/s/ycAn//E/wYAFwAAABMANAAFABYANwAsANv/9P8tACQA+f8fAPX/5P/q/wAASQDN/9f/XwDy//X/LQDc/xkAAgABACYADAAuABMAawAyAAMAFQDa/wYA4f/5/wwACgA/ACAAZABQAMD/TQAZAAIAggANAGYArf8ZAEsA4f8eAL3/JQDV/93/GwA6ABwATgB2ABUAgAALAC0AAACk/wAApP/I/woA9v/m/yEA5P8OAPr/6P8RAA4A+f/7/w0A1P/v/xcAEgAOAPr/1v8DAAIAFAAiANP/EgAOAPr/jf/t/xUAEAAyAPL/UACu/4gAWwASADMAvP9JABYAJAAdAGEAzv8zABcAgP9iAKr/BADx/+L/MQAVAFoA2//Q/6L/j/8BAO//4P8vALj/xv+t//T/GgADAJYA1P8AANz/9v8JANH/IwDT/xIAtP+w/+T//P8hAGQALABIACgA/P9GALj/DwDo/xEAsv+c/9X/gf8aAMz/+/8NAAsACQAHAPT/9v8vAN3/PwDX//L/PQD7/zIA8v8ZAPD/qf/N/2kACwDl/w4A5//a/wUA4P/C//P/h//7/7L/5v9GAMv/aAAcAPP/BwD0//b/5v/Z//P/BwD0/wgAGQDw/ykAawDE/xgAOADS/yQA5//s/xMA7P8UACIA0/9JAOD/+f8wALn/owC6/zUAUACJ/6EAAQA4APf/5v/+/8f/QADG/ywAJAAvABMAx/8tALf/IAAsAO3/AgDw/xcAEwBrAOn/2/8GAKr/FgC2/yAAGgCU/04ArP8GADwA+v+OAPL/GQABAN3/PwDq/9z/vv/L/9X/3v/S/0kAAwDf/0AA2f8pADMA4f8dAE8Av//e/xsA8v8rAOz/8P+q/83//P/Y/xYA7v/f/wkA9v8JAAgAq/87APr/6P82AIb/DAD4/4v//v8QAMT/KwA1APT/9//m/+v/yv8eAOL/MADe/5v/CgDk/0UApf8AALf/6v9uALT/aAD4/9X/SwAFALv/7v/M/5//oP+g/zMAzv/q/1wAyv/n/1oA2v9PAFIA1f84AOX/2P/y/ysAx/8bAOD/wf9NAOP/DQBl/83/xf/j/3sA4/8xABUAyP/4/zAAuf8iABsA8v8rAKP/WgBIAAMAJwANAPn/HgDi//r/VwDY/wQA3/8JAD8Axf8ZADkA+P8wAAEA3f8/AOr/XABKAOD/1P+4//3/2f8pAOv/7//z/z4ADQAdADwA6P9IAAIATAD0/wgA9f8JAJoA/P8hAPf/+P/o/+z/y//D/73/bv/m/9n/vP+k/9v/vf+4//3/WQD//+3/TADP//7/2f8qAFkA7P9MAD0AQwAkAEIAIgAcAPL/0P8iANP/EgD9//7//v/s/wIApv8lAEMAEQCPABcANwAHAL3/JQD6/w0Awf8EAAMA3/8JANH/IwDm/w8A+v8yADsA+f9DABEAIADR/zUAGQCU/+D/r//k/5//1/8WADYAYwD0/1IAMAAUAJEAdQAUACMAHADO/yAA9v/4/x4AmP8aAEwAUAD3/9T/OADk/9f/3/8KAPb/5v9ZABAAxP8ZAAEAJgAeAIb/HgCq/83/MgDN/zMAlv+9/wEA7/8EAN//LgAAAO//4P/m/w8A6P///9v/PQDo/zYAKwBr/y0At//X//L/vf84ANL/EQAzAPL/9f9AAP3/RwA5AK7/PgCN/6P/EACy/8H/8v8ZABQAIwBBAA8A6P82ABkASwA9APr/RADc/77/pv/v//L/BgA8AAwA+P9CAFoA7f8DABQASAACAPD/KgDr/7j/DwAMAMH/OwAKAFIAHQAFAIUA6/8mAB4AGAA4ABsA3/8uACUAHgA9AAwACgCI/x8A0P/H/wkAdP8QAPv/sv/5/8P/9P8aAKf/AQDd//b/+P/n/xAA6f8SAA4ACwDA/18AKAD8/1gAtP8xABUAEQCy/5z/MADw//P/4/8NANT/pf8AAAAA3P8ZAEwABgDg/x0A4f/6/2kACgAtANz/GQAUAP//7f/M/2gAwf8pAP3/j//v/zsALwABACYA+/98AOT/DQAKAK3/KwD//yMA0//u/83/jf/b/6v/zv8gAKz/4v8eAOL/aAAKAPb/+P/6/8T/BgBOANH/NgArACMALgAlAEMA2//i/x4Aq/+7/0kAuv8jAFQAsf/4/+f//v81AAYAFwBKACkA2P8pANj/X/8RAOn/7v/x/z0ADAAKAFIAnf8wAMz/jP///+3/TADi/7D/CQDj/+n/JACK/5AAPQD6/2kA1f9dAMv/aAAvAF0AXQCU/3MAkv/y//T/v/8CAJT/KQAPAMP/PQAMAIn//f/r/+//TgAaABUASADf//j/MAA5ABsAu/82AND/7P8BAN3/0v9+//T/9v8cAAQAKADq/xIAWADs/yYA6P/t//H/KgDH/9L/JADU/yUAw//h/+f/EAAfAOP/HwDi/7H/CQDj//v/DgCw//f/5v8PAB8APQD7/7L/+f/D/xgAuP/9/0cA3v/3/y8AEwDZ/wUAKQAOANX/XgAUAH8ALwDd/3YAzf8yAKj/AgC5/33/TgCa/0AADwAMABwAlv8rABAA6f9bACUAMAACABQAWQD//4AA+f8eAAYA8/8/AKD/IACH/zEAFQCj/20A6v9uAKL/DwD7/3v/OgCJ/yEArP+q/6n/p/8UAJD/JgD6/0QAEgAhAGQArP8qANn/BADN/43/2//i/0MAEQAgANH///9tAA4ACwBAAA8A6P/a/xgAJgDW/wIAuf/+//7/7P8CAKb/SgAEAAMA3//T/zcA4/8NAAoAGwDf//j/HgAFABcAAADc/wcA9P/2/2YACAA+AB8AGQBeAN7/GwADAPH/4v8MABwAOwDn/zUAdACm/28Ax//S/zYA0P8jAOX/MwA8AOf/2v8qALT/HgBQAMD/OgDU/yUA5////yMA+P8LAOX/RgDd//b/+P/V/zkA9//5/0MA2//Q/xAAsf+vADEA3/9TAIv/EADE/+L/DADm//3/2f8XANz/4//p/0kA8v/1/2UArP8YAO//8v/1/+X/ogDw/6n/FQDt/8z/DQD5/x4APQAfAGIAKgAiABsAzf8gAAcAqv8EABYAEQD8/+v/AADc/+P/6f82APX/wP8oAOr/AAAAAO7/FgAAANv/vf/v/7v/7v8oAPz/MwAXADcA0f/a/wYAl/8ZABQAIgD4//n/HwAGAE8Av/8CAN7/5f8zAIT/CgD2/8H/8v/i/x8A0P9HADkACQBRABwAu//J/+b/xv8tAO7/AwBMAKv/BAAWAJH/lP/h/x0Az//r/xMAtP/6/8T/BgAXANz/YwD1/0AA/f8PAFYAxf8ZAN7/GwAWAMn/HADz//X/wP/f//j/CwAuAEoAOwD5/0QA2/8ZAAEA3f93ADsAVABWAA4A1f+m/9z/0f+1/+n/JAAdAPP/GgC5/9r/dADv/7v/AADb/2MAYgD0/xoA3//T/yQAMAAUABAA6f/b/73/EwDH/wgAUACu/xkA3v/l//z//f80ABgASgDh/zAA8P/h/wsAm/8KAAgAKwAQAA0A5v/H/63/q//g/4r/xv+s/z0A6P/I/y4Abv8dABcA7//y/5n/PwDF/+P/HwAZAEsAGAAmAB4A9P+//xUAEQDX/wMAzP8xADoAZgCKAAAANwDk/7L/1P8AABMAxv8tAAAAEgDq/7f/s//C//P/BwAGAPP/YwD1/+X/IAD2/+b/6/8AAAAASgDg/y8AggANAAoACAA+AA0ALwBLAAUAKQAzAGAABACo/wIA8P/z/xoAlP+8/9z/q/8qAA8A+/8gACwAIwBUADEA8f8FAKn/FQDt/wIAXgDw/3QA8P+7/0kA3//T/xMADwCe/+n/AADt/ycA6f83ABkA3v/l/+r/JQAeACoANABhACoADwB7AND/2v9hACkANADz/xoAAgDL//v/1/8VACMA1P8AACUA5/+i/xAAMgDf/xwAFgDu/ygA1/+6/+3/FQA1AOL/1v8nAA0A+f9oAPj/CwDl/+v/OAC//zkA+P/6/zEA3/8JAAcABgAFAAQA3//4/x0A9P/k/0UAEgAhAD8Axf8sANv/BgBOAOT/RQASAI//AADu/6j/FAD//xEA1//f/y4Ayv9CAO3/uf9HALn/2f8XANz/UQD4/wsAQADG/wgAhv/6/9b/zP/p/wAAJACd/4wAzP/7/0UA3P8aAPH/mQD7/+r/3P8ZACcAn/8fAND/2v/h/0MA//+2/zIAqP/M//v/xf/j/+j/7f/x/8//IQBAACEAGgADAPH/GADd/6z/TwAtABIADgAwAPH/vP83AHX/tf+x/8D/KACg/w4A+v8NAC8AEwDH/7//TAAYABQAIgDl/zMAPADn/xAA+//q/0oABAADAPH/z//r/8r/+v/E/73/JQDV/xQAWgDb/xgAgf+//xQAov8QANb/AgDw//T/LAARAPz/6/8lANX/AQAUACIAUwALABsAYAADADoAiwDw/ykA6/8BAEoAzv8hAOT/6f/b/9D/EADp/zYAPgDX/ygAMgAEAE0Ahv/o/1oA7f8VAO3/AgAUADUA4v/o/yMAwf8oANj/8v8rAMf/LgDc/9H/NQAGAPP/GgDx/8///f/H/wgABwC8/xIAIQAtAO7/zf/8/yAA5P8NAEIA7P9LACoAbAANANT/JQD6/zIA3//4/+f/7P8CABQAIgAJAFEA0/8TANn/FwDJ/2X/KACz/8L/BAADAAMAJwBEADcALAAAADYA4/+x/8H/uv/I/5z/r/8/ACAA5P8gANH///9IADoA+P8wABQA7P9wABEADQAwAAEAEwA0AAUABADy/wYABQAEAAMA3v/A/83//P+z/+f/2f+X/ywA///t//H/qv8WABIA6v9cADgAZAD1/67/UACu/wcAGAC4/7T/Zv/O/8X/BwC9/9z/GgDM/+n/NgA+APv/WAAiAMD/KACy/8H/8v/j/x8A0P/s/8v/1f8CAN3/dwDy/xkAJgCf/w0ALwATAP7/EABXAEYAAQA4ABsAOgAcAOD/5//+//////8jAAoAPwDq/+7/3/+c/+f/2f/h/9X/JgDo/20AIAAaAIQAs/9UAMT/GADL/7D/ZQDR/yMA+P8LANP/EgDq/1wAbwDs/14A8P9zAN3/PwAzAJb/PQDW/xUA///t//H/vP9t/9T/AADK/zAAJgBpAAoALQDu/83//P8gAC0A7f86AK7/0f8jAK7/0f8QAPz/xf++//D/FwDv/xYAEgAhAC0AJABCABAADQD5/zEAJwD8//z/s/+L/w8A6f/I/y4AOACcACEAUgAvALn/NAD0//b/CgAIABgA8P/O/+r/EwA0APP/PwBFADcAZADj/zEAKAANAAsALQAlANX/SwC8/wAA7v/y/xgA3f8aAMz/6f/b/xkAAQBLAOH/5/+jALr///8RACAABwAqACIAwP86AAoAGgAoAEUAAAAAAO7/8v8GAGD/AADb/1AAQQAPADEAuv81AL3/OAC//8z/DACK/yEAmv/l/7P/sP8IAPX/9//C/zwAi/80ABgA7/9OANH/bQDF/wcABQC7/yQAHQAXALf/MwDO/zMAKQCz//r/sf/l/47/7v/N//z/DgCL/yIA0/8SACEAGgAoAOn/2//1/wkAvv85AMD/8f8YAAEAXQAmAAwAHABzAO//KQAhAOT/DQALABsAuv///9v/BgAFACkAMwApAP3/xv9kANH/EACf/7L/LwCm/xIAxv/k/yAAGQAUAEgAuv///0gAlf8XALf/IQAaALr/IwDT/+7/FgAkANT/7/+p/xUA7f/e/0AAof9ZABAA+/9YANn/BADy//X/LQDu/9//5v+P/9z/4//E/6v/qf8DACcAaQBVAA0ACgD3/y8AEwD+//7/yP9AAP3/7P84APf/QgDH//f/HQC8/wAAEgDr/8r/MADL/9X/uf8iAAkArP90AKb/NwD2/y8AXQCm/28Aov9HAF4Auf/s/6b/EwD+/+z/8P8pAP3/tP8eAAYABQAoAP3/2P/g/x0ABQAEAE0AUABlAD8A/f80AAUAFgDu//H/9P/3/woA9//B/83/MwDy/+P/DADm//7/x/8bALr/kf8UAP7////t/0wA9P/k//z/jv8lAML/BQDy/xkAXgCm/28A2v/h/1UA/P+PADwA+v/E/9D/x//S/xEA6v8AANz/4/8xAPH/mP8IAND/2f8XANz/LADt/wIAOQDT/zcAUQDm/+v/3f/R/zYA9f/S/wAA7v8oAFcADwAMANP/t//9/9j/8//j/8T/BgBOAC0AJADn/8f/5P/q/24A/v8QAFYA6v8SAA8AHgDi/zEATAAGAOH/HQAXACUAHgD0/z8A6v/K//n/MQC6////NQB0/w8A1v/e/+X/6v/u/83/MgDg/1QA+/8NAPn/DAAuALj/DwCe/wwALwABADgA9//m/yEACAAZABQAtf9EALb/IAAHAAYAPACL/6MAgv/3/y8Ay/96AL3/OADS/+3/FQDa/z0AHwA+AGkA+f/7/w0A1P9KAPP/BwArAP7/bAAOAOf/tf/o/+3/JwBXAKH/s//n/+z/8P/h/+f/EACf/w0A+f/W/0wA4v8wAAIAAgAmAPv/DQDU/0oA8//R////7f8VALX/DQD5/3oAUAD4/1UA1v9fABUAEQDGAEMAJAB5ABgA3f8/AKD/RQATAKH/IQCt/5oARQASAEYAEwAiAPf/QgDs/zkA+P8dADwA6P8QAPz/IQDR/20AMwDO/yAA9v/4/+f/WgAAAAAAJADm//7/2v/0/wcA4v/D/wUAqf9MAFAA5f8hAOT//P/9/w8Aw//0/wgA4v8fAIb/5////7X/HwAZAAIA3f9SAOf/tP97AOP/w//0/9L/AAAAAAAApP8AAG0A/f+0/9X/uf+i/w8An/+y/woACADi/wwALgC4/9j/8v/1/wkAGQDM//v/RQDc/9H/7P9eAJT/PABDAH7/dAAmAHsABwD0//b/d//b/77/EwAQAFYAIQAIAND/EAD7/7L/QgDH/wkA4//7/yAABwArAP7/7P/L/zEA8f8FAKn/qP85ABsAKADY/xYAyf/B/xYA7v/y/xgAAQDv/6n/lf+8/6X/WwDc/wcABQDO/0UApf8SAA8ADAAJAAcA9P9SAML/zv99AHb/SADM/8T/UAD3/1QAsf/T/5L/KAAyAAQAAwDe/0AAxv9RAPn/6P9IABUANgArAEgAzP/E/8///v/+/6P/7P/w/+H/CwAbABYA7v/M/9b/3//A/zoACgAIAD4A6f/t/17/2f/z/xoAcQDI/1MAw/8YADgA0v82AND/RwDe/xsAOwAdADwA+v8NAOb//v/Z/2EABADy/1AALgATAMb/dgAWAMn/QQDZ/xcASgCW/wYAvP+S/xUAtv8yACgA6v/J/53/1f8UAOz/pv/v/xYANwD2/2UAGgBxAJMA9v8KAL//3v+b/xwA4P+v/+T/1/9fAKj/FAA1AD0ADAAcACkAxv+//8v/6P9s/+X/2P9NAD4A1//x/8///v+i/xAAHwAZAN7/GwDN/7L/iwDd/1IA5/9HAHAA7f9eAMz/MQAVANv/KwD+/8j/9/9CABAA6f9JAGAA3/9mAFIAwv/g/+f/2f/h/53/nv/E//T/9//U/wAAt//9/zQAFwBKADwA+v/W/8z/1v8VANr/9P+//zkACQCs/z0Anv9WAA4A1f8BALj/NADO/yEAUgALAC0ANwAHACsA2f8XAG8A2f8XACUAVQDp/xIA6v+A/z4AHwA+APz/RQATAMb/LQASAEUAAQDv/ykAxf8HAD0A1v/e/63/q/88AAsA5f8OADAAqABQAOX/MwDO/9j/u//b/+L/w/90ACYAw/+q/04ALADb/2IA9P8IAFAAQADZ/ykAMwA8AFUA6f8AAFsAJQCL//7/7P85ABsAKAAzAKn/OgDB/wQA8f8GADwAZwBBALT/DACJ/yAACAAGAE8A0v8jABwAPAD6/wwA1P/c/xoAp/8mAB8A0P80ABgAAQAAAMr/HQAqAOv/7//O/7P/r//k/+r/EgBrANb/uf81AKr/OwAdAAUATgD2/2UAiP8fACwAtf8NAMH/KQAOAFUAIAAaACcA+//X/9//CgCt/wYA4f/U/wEAAADc/3X/IgAcAM3//P/r/yUAQwARACAArP+q/xYAJAAKAAgA9f/A/xUAyP/T/zcA0f/t//H/9P8aAN//wP/y/9D/DwCNACgAoP/9/0YAuP/r/8r/Zv9y/43/2//i/wwA5v/9/yIACQD2/wkAGgAnAEQA3P/Q/9r/9P8aALr/EABXAA4AegBQAOX/awDD//T/dwBNAFAA0/8lANX/y/9DAP//JADU/wAAyv/C/xcAt//9/yEA0v/t/wMAFAAjAPj/HgAYADgAZAD2/wkABwA9APv/MgBNAOP/MgDf/y4AEwAhABsA8v8GAM7/2P+7/+3/zP8NAB0AKQAhAJv/0//c/9H/EABXANj/KQD9/8b/CADQ/0cAuf/s//D/qf8VAAAAEQD8/yEAPwD9/zQATwAaAAMAzP/o/6P/7f/x/3P/RQCl/+7/TQD1/xsAqP+5/9r/FwAlADAA3v9SAOf/a/8/ANj/BAADAKf/EwAQAB8AYwA9ANb/cQDt/wIAFACj/yIAwP8WANv/vf8mAJ7/HwArABAAMgDf//j/+v/7//z/DgAwACcAMgADAKf/OQBAACEAdwDg//j/CwDl/1gAEABo//T/9v+K/zMAvP83ABkAzP8fAL3/JgCx/xsAFgASAA4Aef9dAMv/1f8BAN3/CAArABAA1/8VAKP/tf/p/7b/6f/u/6j/3v8IAOP/DADU/zgAPwAOAAsAGwDN/9f/TQCr/ykAWQC1/8P/KwAiABsAKADq/0oA4P+v/2QAvv/w/2EA8/9QANP/7v8WAMn/HAAEABYAAAASAHv/FQBbAJL/lgCv/+T/IADj/1YAjv8AAAAA7v8WAAAAJAAdAOH/5/9HAN7/LQAlAB0AYQDz/xoAJwBEAAAA3P/j//v/agALABwAOwDC/7v/2/++/xMANAA9AGgA1P8AADcA5P/8/8X/PwD8/+r/JQALAPj/5//+/8f/LgAlANX/cAAQAJ//VwAhAEAAfQDS/1sANwDj/zIAzf8NAB0Aqv8WABEAxf8sACMA+P8LAK7/9f8uAG3/HADg/3j/SgBy/w0AMADw/xcAyv9UAPv/RQATAMb/5P+y//n/DABTAPr/6f8kAIr/xv+JAMn/1P/d/9H/SADx/yoA2f8qAMb/9v8cAKn/KADF/4gA7f/M/zEAzf9pAAsALgA3AL//JwANAOb/IgD3/1QARACk/zYA9f8uADcA9v+LACYADAAKAKz/KgD+/7X/DADm/+v/7/+7/+7/AwDe/y4AJQD6/0QAEgCz/wsA9//U/+//hP8KANH/tv9XAP3/RgDd/xsAXwCV/+H/1f/w/wQA8v8GAKr/lv8YAAEAJQAMAPj/5/+Q/xMA7P/d/2QABwDi//r/1v/M/9b/lf8XACUA+v+OAHIAJQALAC4AAACl/xIADgDV/wEAAQBKALz/7v9yAAAASQAoAP3/RgAUAFkA///I/0EA/v8iAFMACwBAADQAKgD+/9n/8//j/43/yP/m/7P/CwDT/zcA0f/I/3gABAAWABEAxf/R////o/+1/wwAZgBSAOf/bAD8/w4AVQDE/+L/sf/l/+v/AAA3AOT/DQDn//7/2v+8/wAAt/8zAPP/BwAYAKX/JQALABsA4P8vAEoAqf86APn/6P81AAYATwDk/9f/KAAOAPn/DAD4/wsACQDR/0gAAgACAAEA3f9SAOf/IgD3/53/aAAcADsAHQD0/wgAq//z/wcA9P8IAKv/FwASAMb/PwCy/y8AJgDo/1sAyf9BAEcA3v8bAN//0/8SAEYAy//V/97/dv8RAPz/6v83ANH/EQCg/6D/6v/K/9T/uP9GAN3/GgAVAJH/FADa/+H/CwD4/6//5P/X/6j/uf+0/9b/y//W/7n/NQAYADgALQAAALf/jv82AL7/JgAxACgAfACs/wUATgC//zkAUwD6/3sABwAYAAEA3f8IAL3/OADS/wAAJAAvACYADAAKAKz/vf8AACUAnv/o/xEA6f/u/xUAJADm//7/IgAbAM3/MgDg/woAPwAzADsA1f9wAOz/3v8tABIADgAwAIMA/P9GAAEAJQBoAJz/+f+x/3f/2/8GABcA3P/2/xwABAAoAMX/4/9WALP/1P8BALj/IQD3/0EARwCU/xcAAACS/00A0P+i/zQA9P8IAND/tP8xAAIAFADs/xQA//8QAFcANAAXAJL/AwACAPD/8/8aAF8AXwA6AFMAMQCV/wUAzf9FAEoA4P9CANr/BQA7AHoABgDz/wcATwBSAB0ATwDS/yQAwf8pADMA8/9jACsAbAAOAHkA4v+w/wkA4/8NAAoAPwCg/+r/AADc/9H/7P8CALn/DwCx/wkA9v/B/xYA7v8VACMAHADO/9j/u//I/y4AEwBZAOz/pv8BAJP/zf8gABkA3v/A//H/hv+w//f/1P/K/+f/IgBAAEYAAQATANn/8//R////yP93/yQA1P9dACYA+//8/8X/LAD//4AAHQA8AAwArv8sALX/6f8kAB0AKgBGAPD/BAA7ANT/ggAxAN//HAAEACgA/P8OAAwAwP/N/9f/zP8NAAoALQASACEA9v/B/2AAFgDb/+L/6P+2/8T/4v+x/wkAvv8UACIA0/9JADsAr//k/1cANACGADUA4f/D/5f/GQDe/8D/8f/0/z8ARQDv/xYAEgAhAC0AEgD9//3/IgAJAD4AoP/X/83/n/9FAAAAXAAAAO//BADx/1AALgAAAO7/AwADABQAtf/p/wAA2/8GAPP/BwArABAADQAdALz/XADv/+D/LwC4/0YAk/8WABIAxf92ABUASAAoAA4AVQANAMH/BACD/9P/SQDN//z//f+0/8P/KgDZ/wQABADM/44A4P+c/0IA7f+5/yIACQD2/+X//f8PAMP/BgA8AEIA//82AOL/n/9EACQA5//H/8D/lf+8/wAANwBRAAoAUgAdAAUAKQD9/9n/qf86APj/6P8QAJ//DQD5/0MAEQDq/wAA7v/f/woAUgAKAC0A7v/N//z/s/+d/zAAAgDL/40A8f8YAAEA7/9OABoA8f+8/0oAcf/X/3IA2/8+AEQAJAD5//v/sv+v/6z/BQDz/6z/PAAMANP/AAAkALD/9/8vACYA+v8fAGMA0P8PAB8AGQDL/wwAQQCi/yIALQDJ/woALQBJAAQAzP8yABYAEQAOAOf//////0gAXwAVAO3/AgDL//v//P/q/wAA3P8HAOL/HgCq//L/GQA4/ykAIQDR/+3/TAC9/8r/MADe/xsA3/8cAAQAOgD5/+j/NQAGACoA6/8mAPr//P8OAOf/EAAyAAMAp//d/3b/7f/x/4X/CwCt/wYATwAIAIcAIwDm/zQAFwAlAB4APQAfAJj/5P/p/+7/OgDB/04APgDX/00APgD7/6D/MwDO/6D/IQDR/xEA6v/u/9//HACYAAsACQC+/5T/u/8AAAAA7v8VANv/KwDH/+X/DgDV/zkA9/8dAGEAPAD6/0QAAABt/y4AJQAeABgAEwDs/8v/HgDP/2sAMgA6AFQA+/8NAAsALQC3/zMABAA6AGYA5f8OALD/9//5/3oA4v8xAAMAuf81AHP/IQC//6f/y//o/9r/vf8TAMb/ZAD1/xsAFgA2AGMA4v8xAKf/FAA1APT/LQBJAAMAAwACAN7/CAAZAPD/4f8wAJT/FwDc/+P/+/+N/0kAuv8jAC8AuP9GAEsA4f/n/yIA5f/Y/wQAOgDB/87/DgDn/8f/m/8KAK3/vf8AAMr/5/81APT/LQBbAO7/AwADAAIAFAA1ACsAWgBIABUAyP/T/9z/mf8bAKj/OQDl/7P/HQDP/yEAiP9XADQA4f8wAMv/w/+Y/xoAFQAjAEEARwDw/+H/wv+8/+7/cP8fAND/kP84AC0A7v8oADIA8v9jAOL/HgAYAMv/QwARAPz//f80AOH/HQA9AOj///8jAEEAIgBlABoAAwDM/+j/EQCy/x0A4f9CACMA5v80ALz/AAA3ABoA3v/S/xIAoP/q/yUA+v/7/9f/8v+9/93/9v/B/ygA/f/9/0cAXgBMAM//6/8TANn/KQA0AM7/6/8TAA8AQwBJADoAZgD3/woAGwCo/xQA7P+5/xAA6f8AALb/DQAvABQA/v/s/xQA7P8UAOz/8P8qADQAKgD+/zUAPQD7/yAALADI/8D/8v8rAMf/m/9BAP7/RwBeADoAQQB9/xYAAAB//2IAKgDs/zgA9//U/93/5P8NAML/8//1//j/VQANAEEA2f/h/9X/3f9kAOP/DQAcAPP/4/8NANT/uP8hAOT/IADj/8T/9f/S/9v/9f/S/8n/LwDd/xoA8f/P/1kAov/H/xsA8v/1/y0AAAAAABIA6v8lAOf/2v8YACUAQwAAABEADgCw/xsAuv+j////kP/w//P/vv8UABAA+//q/7f/2P8oAP3/IQAbAPL/GAAmANb/JwAfAIb/HgArADUA4v9DAP//o/9/AJ3/CwD4/8L/PACd/zEAAgAUACMA0/8AABIAIQC//8z/sf+J/yAACACG/8P/BQAWAMn/1P/K/9X/8P8XAIEAVQBFADcAGgDf/wkA9v8cAE4A0f9/AC8A7/9OAOT/HwCIACQA+f/6/+n/bgAPAAwA+P/n/0cAzP8xACgA6f8AADcALADt/xUA7f8nAB8A4//7/1cAIQDk/3wA5P/q/0kAFgASADMAKQAPAB4A9P/S/7b/DQALAK3/KwAjAEEAWQA1AAYAzv8OAOj/EADX/9//CQDj/5//1/8VAGz/LgAlAB4AhgDH/0AAxv/k/yAA0f///9r/9P/k/zIAOwALAFIACwDl/9j/OwBUAGf/9P8IAIb/HgD0/63/9P/3/woA9//4//r/6f+AADAAy//6/8T/BgDz//b/HADO/w4A5//H/1IA5//+/xAAsv/m/7T/MADe/8D/cQAAACQA+f/D/xgA7//g//n/+v/8/+r/AAASAEYAEwDH/2UAvv/w/zwA+v8yAIP/9//C/7z/JAD5//v/IAB2AAMAFADs/wIA8P/z/wcAz/8PANb/uf/Z/+H/+v8xAN//5f8PANX/8P8XAEoABAA7AOb/6/+4/zP/AACS/6f/3f/k/zMABAA6APn/nv+f/w0Awf8pADMA8/9RAAoALQA2ABkAAgABAN3/UgBUALH/QQA0APT/BwAYABQA2f9zADgA9//5/4z/NQA9AEMAJABnAHcABAByAO7/FQARAMX/GQAUAP/////t/8z/MQDf/9P/yf/C/04A4/8fAOP/n/8fAND/IwAcAM7//P8PAAwA5f/r/yUACwAuAO//BAAVAMj/QQDr/xMAEADp/0gA3/94APP/rP/0/6z/KgDH//f/+f/o/xAA6f8AAO7/FQDt/xUA7f8VAH8A5v9HAEsA4f/6//v/6v/u/xYANgAZABQAWgDb/6v/4P/U/8r/HgD0/wgAGQCB//b/HADg/+b/6//d/7//AgDw/+H/+f9EAFsA7v9fAE0A4/8xALr/IwD4/3n/JQDD/yoA/v/+/0gA3v/l/w4AVQDE/xkAy//D/z0Asf8JAL7/pv8lADEA3v8JAAcA9P8aAMz/xP+G/7D/5f8gACwAJAAvAAEAyv9VAA0Ar/+bAOv/EwA0AAUAKQDq/xMAj/8lAIv/2f8XAKX/EgDG/1EA1P8lAEMA///t/6f/uP/Z/ykA2P87AAsA5f/9/+v/JQD6/9f/p/8mALH/CQBRANT/gQD7/+n/WwAAANz/0f/s/wIAFAA1AD0AQwA2APX/LgASAA8AHgAGAE4Av/+n/wEApf/K/6//GgADAMz/6P///yQAwf8WACQA5/8QAGkAMADL/1UAIAD2/8H/AwAVAO3/OQDT/0oA8v8rAEgAFQBtACAACAAYABQAEABpAAsACADj/5//DQD5//r/1/8oALL/LwBLAKr/OwAdADwA1f/w/ykAIQAtAEkAcgDu/00APgCf/8X/BwD0//b/UwDW//D/BQApAA4Ai/8QAPv/1//y/+L/w/8qADQAz/9ZAMf/CQBjABgAggDW/xUAEQCy/woAGwBNAPX/0v/u/xUAyP/4/0IAyP/4/wsA9/8KAAgA4/8xAN//LgATAA8AVgB7/zoAiv+z/0IAo/81ACsA7P8BAN3/5P9FAJL/AwA6ANP/NwCa/xsAzf8NAOf/7P9LAIX/ZwDl/7P/+f8MAC8AAQBdAAEA7/8EADoALwDd/wgA9f/l/w4AQgD/////AAAAANv/GQC5/8b/LQCk/8j/Zf8DACcAjf9IAAMAJwANAAoAQADG/+P/6f/u/9//CQAsAKP/7f8CAN7/9//5/x4Az/8PAAwA5v80ABcAJQDD/5f/9f/A/wMAAgCU/7z/2//j/2gAZwD3/1QADQDU/wAA3P9jAD4ADQAvAO//BAC7/+3/AgBv/wsA+P/5/0QA7v9fAPH/4v9DALb/6f8kAFQAaQAvAEsAPADo/+3/TADi/wwAZQDS/zYAq/+E/x0AvP8SAP3/tP/D/xcAJQAeACoA/v/a/6r/OwDn/9n/KgDr/0oA4f/n/8f/5f8OAPr/aQAKAFIAZwBlAPb/0/83AL//AgAmAOn/AABJAKj/uf/Z/7z/XADK/x0AKgC0/9X/AgDw//P/GQC5/1oAo/+1/x8AdP8PAOj///+2/+n/kv+V/04Arf8rAP7/2v9PAAgAq/8qAMb/v/9xANv/dQDe/y0ANwCH/zEAp/8mAAwAr/8sAMj/+P8wAN7/CACZ//f/HQBy/0UAyv/n/9n/qv87ANT/JQDV//D/4f/n/0cAOQAuACUAjADx/wUAFwAAABIA6/9KAPP/GQA5AC4AXAATAA8AHwDi/+j////b/+L/MQBxAMj/CgAIAKv/TgBkACsA//8RANf/FQBJALr/2v8GAOH/+f/7/+n/EgDY/ygAxf/R/20AoP/Y/wMA3//4/x0AGADd/xoAAgC5/7T/1v/e/xsAXwBfABUANgA+APv/6v/c/ywA//+AAGcAGwApANj/8v/i/9b/uf81AE8A0v8RAOr/t/+g//3/2f8XABIAxv8sANv/UABAACEAGwA6AC8Apv83AIj/+/8OALD/ZAC+/14AJwCx/xwAKQAOAMP/dAATAMf/9/+K/8b/LAA2AD4ADQDn/1kANQC9/0oAKQC0/zAAzP8MAC8Ayv8LANP/pP/I/woALQAkANT/AQAlAMP/TwAIAIb/+v8fACwANQArAFoANgD1/1MAHgD0/+T/6f/u/83//P/q/9z/4/8yACgAxf8sACMA+P9VAOn/EgAzAM7/DgDV/xQANQA9AOj/IwBBAI//AQDc/7//3v/S/9v/BgDP//3/RwDe/y0AEgAzACkA/f9HAN7/v//x//T/0v8jAOb/IgAJAL7/SwDP/w8ADADl/w8A6P81APX/0v8kAOb/tP/V//D/FwC3/9j/KQDq/wAAbwDZ/wUAYADN/1cAIQAbAAMA8f8qAOz/8P/g/0IAkP/d/y0Ayf/m/9n/KQCz/9X/8P8EACgA6v9KAAQA8v89AB8A9f/3//n/DADm/7P/+v/E/wYAcwDv/87/6v8lAB0AvP83ANH/2v8YACYA+v+N/1sAbgA0ALz/7v8WAMj/CgCs/xgAEwD+/zUAPQD7/yAAUQCu/+P/xP8rABAAMgBfALr/EQDp/xIA/f80ADwADABTADAAJwCy/xwAu/8AAEkAlv89AB8AGQAmANb/FAAjANP/7v9NAND/NQA9AAwAVAD6//z/xf/2/xwA8v8GAKr/8v/Q//7/IwCJ/yAACADi/x4A4v/D/+H/+v+f/yAA4//E/4cAyP/T/9z/vv8mAIz/IwAJAL//TAD0/y0AJADn/9n/PADo/5D/XQCm/93/LAAAAEkAAwAnANf/hAAzAPP/UQDB/zsAQgAiAOX/MwApAP3/NACX/+P/sv/B/wMAzP8yABYAyP/B/ygADgD6//v/6v/u/5X/z/8hAMD/3//4//n/6P/t/14Auf/a//T/CAD1/+T/DgDC/04Arf89AAwAnP/n/5D/OACt/3UAFADa/08A0v82AND/7P+U/wQAFgDb/1AA0/8SAMb/GgBxABEAIAAaAAIAuf+0/zEAp/+U/ykA/f8PAOj///8RAA4AHQAqACIA0v8kAPn/QwAAAMn/+P/n/xAAxP+9/8r/wv/h//n/+//8/30ALQAkAB0A9P9kAOP/+/8yACgA/f/9/1kA//8RANf/zf/8/47/AADu/wMAFQDt/zkA+P/5/2kACgAIACsAEQBFAO7/OwAdAPP/BwDi/wwA0/8SANj/BAA6ANT/AADK/53/1f9LAOH/w/+8/9z/0P+i/+z/3v/k/+r/EgDr/wAAAAAAACUA5/8QANb/TAAGABcASgAXAEoAhP/m/8b/5P9pANX/pv/c/ywASAA6ABwAFwAlAB4ATwAbAKj/8P/z/7//8P/P/+v/AADK//n/6P8jAEEANQA9AOj//////0gAAwDM/2kA5/8iAFMACwAuANz/4//W/9//LgDK//n/HwC9/10AOAAtADcALAAkAK//PwDq/+7/KADq/0kAzf8OAEIA/////yMAHAAXABIAIQAIAOP/DACv/z8ARQDv/xYAEgDY//L/GQDe/wgA9f9lABoA8f9PANL/7v+6/9r/z/8PAEMAJACeADUA9f/S/+3/JwAgABkAuf/s/xQA/v8QADIATQAZACcARAA3AL7/uf8iANL/JAAdAKr/FgAAAMn/+P8eACoA7P8mANb/gv8tALf/6v8AANz/GQC5/xAA+//F//X/CQA+ADIAAwCD/9L/NgAZACcA1v/M/w0A+f8MAMD/8v9iAOH/CwDl/w4AVQAgABoAAgDw/87/DgAeAM//6/8mALH/9//5/57/+//8/w4Aw/8qAMf/9/8vAN3/GgDf/xwAzf/8/8b/BwDQ/9n/TgB1/zUAvf/v/zsA1P9LAOH/+f9EAEkA8v9iACoAx/8bAPL/BgAFADsACwAIAAcAPQD6/0QASgDy/z4A1//x/wYAPAD6/0QASQDN//z//f9GAPD/BQDN/9f/TQA+AOn/AAA2AJn/LQDu//L/BgCq//L/q/8XANz/rP8XAMr/CwD3/+f/bABEADcAPwDq/xIA2P8EACgA/P8zAM7/2P/g/8H/KQD9/8b/rf/i/zAAp/8BACYA6P///7b/HwAHAKr/FgAkAOf//v81AL3/uP9p/5n/5f/F/ywA2v8YAAEAbv8vAPD/vP8SAP3/tP/6/2kA+f/W/0wAKwDZ/2EAFwASAFgA7P8BAMv/CwDl/9j/OwDn//7///8jAAoA0f82AAYA9P8sACQA+f8MAAkArP/P/yEA0v/b/2IAGAAmAHoABgAYACUADADl/w4AHgDP/w8AHwArAP//2v8FAAQAFgDJ//j/1f/L//r/HwAZAPD/KgAPAEMAAAAAANv/0P/Z/6r/OwAvAAEAEwBsAMT/4v8xAKf/FACQ/zgALQDJ/0EA2f9PAOT/IAD2/4n/6v/K/wsACAAHAPT/GgA6ABwAFwCk/wAA7v+6/9r/9P8aALr/7P8CAN3/UgBUAA0A1P9vABAA1v8CAKb/AQDd/xoAFQD//xEA1/8oADMATgDj/0QA3P+H/3sA4/8xACgAIAAHAL3/bwAQAPv//P8hAPb/HAApAKH/NADh/x0APACw/y4AEgDr/+//FgDJ/4r/DwAMAOX//f8iAOX/6v8lAAsA0//J/woALQAkANT/JgAeAOL/1f/e/8D/Xf/Z/+H/5//+////2v+9/yUA5/8jAC4A7/8EAPH/PQDo/xEA/P/9/w8Aw/8YAAEAJQAxAPH/KgD+/9r/BQDy//X/GwDy/1AA+P/C/2EA8/8sAEgAzP8yACgA/P99ABsA8v9QAAkA4/8yAAMA3v8JAPb/+P/5/+j/2/8GABcA7/8oADMAOwBCACMA0/8AAAAAyf/n/9n/4f/n/9n/z//r/6X/EgAhAK3/9P/S/yQACgD3/xwAFwA3ANH/7f/e/y4AAAA3AGQA0P9HABQAEADX/6f/SwAYADgAPwDF/9H/o//s/wIA8P88ADAATADP/zQAYQApAEYA8P/z/wcAGAC4/w8ADADT/yUAi/8PAMT/mP+s/73/NwDk/0UAJQCw//f/CgC//7n/IgCu/+P/VgCz/+f/EADW/ycA6f/J/xwABADy/3UATADi/+j/7P85AMD/8v8YAMv/DADA/zsACgAIABkAy//6/+n/SQDy//X/ZQDj/0QASQDg/+b/DwAMAPj/MADw//T/mv/3/+f/7P+CAJ//MgBgAPL/BgDh/wsArf8ZAAEAJgAMAMH/OwAKABsATQA+AOn/gAAdACoANACX/2MABgAqAA8A+/8gANH/NQAYALj/2f8pAMb/UQDm/6L/WQDa/yoA7P/d/wgAmf8aAAMAuf9aADYA9f8uAO7/XwAoAPz/WAC1/x4A4v/D/yoAov/Z/+H/CwDA/9//HACp/ycA6f/J//n/w//0/7//y/8MAMH/u//t//H/9P/k/zIA8v+r/7z/yf/5/wwAUwDV/yYAMQDx/z0Asf/4/7D/CAArAJD/JgBWACAAGgA6APj/CwBTAPr/6f8AAAAAJAD5/zEAgwAOADAAOQDl//3/xv+//zkA+P/C/7z/7v8oANf/OwAdAOH/+f/W//H/FwA4AJr/5f8PAPr/HwAsAFoAyf/4//r/1v+n//D/FwDK/9T/3f8tABEADgD6//v/6v8AAIEAaAAvAEoAKQCh//3/7P/d/z8A2P8DADoA5v8PAGgA+f8MAPj/CwAuAMn/+f/6//z/IAAtAJH/FAD//37/KgDr/93/9v8cAAQAKABYADQAFwBKAGEA4P/5/9X/AgDL/7D/wP/x/xgAk/8WAAAAAADu/ygA/P8OAEMAyP9BAOv/JgCe/2f/BQCE/9P/yv8dAAUABAADAAIATAC9/wAA7/+7/+3/zP9WAA4A1f9eABQANQA9AOj/7f/e/xsAAwA6AC8ASgApAOv/XQDd/wgABgDP/+v/pf8SAOv/7/8pACEAPwBFAEoABADg/8H/8v8GAOH/CwAJACwA7f8VAEgAzP8fAIb/w/89ALH/QAAPADEAFQARACAABwD0/7//OgDT/wAAAAAAAAAA3P8+ANf/AwA5APj/+v8MAK//BwDi/7D/GwDN/zIAu/8RAEUA3P8/AA0AZwBTAAsACQA/APz/DgDV/97/dwC7/1sAJAD5/0MA7f8DALn/2f+8/wAAAABJAAQAcP8MANT/3P8/ACAABwD0/+T/IAC+/4H/0f/b/wYAqf8DAAIAFABIAAIAcADt/7n/EADW/8z/RAA3ABoAJwAyACgAIAA/ALL/1P/d/+T/HwDj/4z/kP8mAB8AKwAQAFcAIQDS/zYA9f8JACwASADx/wYAFwDv/zsAr//2/woArP/0/z8AIADk/1cAIQCt/+L/HgAGAM7//f/Z/7z/7v/f//j/1f8BAO//BAADAMz/HwArACMAHAApAOv/OAAIAOL/aAD5/0MA2//i/0MAyP/m/4//pf+3/47/7v8oAA0Awv+8/23/0/8AAAAAJQAdAE8A5P9XAGsA6f9bABIADgCfADYABwD0/5r/+P/n/9r/9P+s/wUA4P/C//P/GQBMAAYAKQA0AM7//f9GACYAHwA+AA0ACgCt//T/GwDf/y4A3P8HACsAEABpANT/AQA4AOT/xf++/93/5P/q/zcABwC9/wAASgDz/+P/RABuAOv/AQBdAO//u//u/xUAyP/T/yUA+v/7/zIAKABFACUA+v8yALr/EQD8/7P/QgDs/xQANQAYAN3/LQBuAA8AaABBAOz/3f/3/woA5P/8/0YAEwD+/xAA6f/t/5X/KgDZ/wQAFgB//+L/sP8JAKz/l//R/6P/ff+8/0kAu//t/97/9/8LANL/SQDf/9P/AACA/wYA9P+//xQAx//T/9v/BwD0/y0AgADn/xAAxP/Q/9n/zv/q/9z/GgA5AEEANABhAAQABADx//T/v//x/3QA3f9SAEIAIwAuALf/MwAEAM3/VwAhAAgA0P/H/wkAh/8eACsA2v8FAAQA8v+Y/xoAAwC5/9n/YQDO/8X/PwCy/+b/j/8lAOj/yP8uALf/MwDz/ywAEQCy/y8AAQDK//r/sf8JABoA8f8qAMf/0v+2/zIA4P8KAC0AAACAAPr/HwDi/0QAWwBuAGsADQAvAO//TgAHABgA8P8XADcAGgA6AAoALAAkAEIA2v8qAP7/WgAjAAoAmwCh//3/DwDo/8j/0/+3/+r/JQALAPf/1P8TAOv/SwDz/wcA9P+b/9P/7v8WAGz/UwAMANP/XAAAAO//AwA6APj/CwDT/9z/vv+4/7T/DABTAPr/DQAvADgA5P8zACkADgBDACMACgBSAB0Al/91AN7/5f9qAB4AKwAQAEQANwC+/97/UgCw/wgABgCq/xYAyf8vAAEAAAATAP7//v///+3/JwAfAL7/JgDD/8//DwAeAPX/5P8OAAsA5f/q/wAAgP/i//v/MgAoAOr/SgC7/9v/KwAjAOb/DwAeAPT/5P8OAOf/EADW//H/dAC4/1kAEAAgAFEAwf9yANz/vv/d/wgA4//o////2//1/+T/DgCw/y0A2//Q/yIAm//5/wwA0//J/8L/zv8gAAgABgDz//b/CQDk/zIAzf/X/xUAJAAdAAQAu/82ABkASv8lAJ7/jP8QAJ//IABRAAoAGgAVABEADQDU/zgA9//U/+//qf/M/9b/FQC1/7L/0/+3/zMATgAsAAAAbgAzAM7/IQDk//z/IQAaACcAxf/j/+j/2/89AB8AGQDw/2EAFwASAMcAxP8rAFoAAAA2AOP/DADB/wQAFQCR/ycAewBjAIcASAADAEwAPQD7/zIA4P8KAAgA4v9oAMH/8/8HAKr/BADf/y4AJQD6/1YA2P/N//z/xv8HAND/6/+m/5L/OgDB/wQAKABFAG8AbABpAPn/HwAZAAEA8P8XABIA6/84APb/r/+//ycAMQDN//v/MwDg/53/MADw/wUAFgDc/ysA7f8CAN7/9/8dAM7/MwDz//X/CQDR/zUA9f8IAFAA5f/r/wAAAAAAAEoABADy/z0Asf8uANz/0f9IAPH/GADK/7D/0v/t//H/GABLAPP/ZABQAAkA4/+y/woArf/i/wwA0//J/53/1f8mAB8A9f93ABYAkv8CAPD/vP/u/9//+P8wAN7/UgALAMD/OgCc//n/w/8YAEsAl/9jABgA8P8EACgA6v/c/wcA9P8/ALP/QgAjANP/bgDr/0sA4f9B/4v/j/+l/wAAAAASAP3/2f8EAE0AdgDM/+n/2/+G/7D/5f/8/+v/OAA/AOr/yv8LANL/7v8DAPH/z/+h/0YAFABHAPD/8//2/5z/LwABAEsAKgAPALH/LgDv/5b/KwCi//7/7P/w/2D/2/9QAFL/UAB4ABcAEgAzAM7/of/Y/83/IAD2/1MAaABBABAA1v/x/+H/CwDl/w4ACwBAACEArf8rABAADQD5/7H/CQDR/yMAZgA/AA4AMAAUALX/MQC6/+3/FAD//38ALwAmADEAOgAKABoAp/+5/zQABQBOAOP/DQD5/wwAUwD6/2kAQgD//xEA/P/Y/xYA2//j/8P/4v8eAM///v9HAN7/5f9YALT/HgA9AB8AKwAQAPz/2P9gAPL/YgA9ANb/8P+q/ygA2P8DAPH/YgDh/9X/AQCm/wAAkv8oAOr/7v/y/wYAKgB8/2AAFgASADMAFwBJABYAbgAhAK3/GADw/6n/TQC+/8v/5/+1/x8A0P8QAMT/GABLAE8AiQDu/00A9f+u/xkAy/9DABEA/P8hAOT//P/r/9z/0f9aACQA5v/Z//P/LADb/ysAov+1/wwALgDv/7v/JAD5/zEAFQAjAIr/fP+D/2T/JwDp/24ANAAqAA8A6P8RACAAGgCn/0sA8//R/9r/KgA1AM//fgD4/wsAQABYABAAn/8yABYA2/8GAGEAFwDu/xYAtv/X/6j/FAAjAHf/SQAoAOr/AACS/00AKwC1/+n/7f+6/+z/FAA1APT/dv81AKv/zv8gAOT/IAD2/0AAxv8aAN//0/9JAAQAKADq/zcABwA9APv/xf9jAOL/HgAGAM7//f+0/+j/x//l/+r/yv8dAAUAFgBcAMr/wv88ANX/AQA4ABsATQDj/zEATAD1/+X/s//5/wwAHAApADMAzv/F/6z/l/8sAO3/AgA5ABsATQAsAEgAAwDe/0AAIQAtABIA6v/v/wQA3//T/4EAHgBPAGUA9v8cALv/SQCo/5T/cwAAAO//zf8OAB0A9P/2/woA9v/B/wQA8f/i/9X/JgAMANT/3P++/6b/JQBoANT/AAAAAO7/AwBfAMz/MgCEANj/YAC7/wAAtv+y/+b/tP8eAPT/LQAAAFsAEgBGAAEAuP80AM7/IQC//xUA2v+Y/xoAAgDe/2UAZAD1/1IA1f/w/+D/iv+0/7D/m//T/wAAt/9YAA8AHwDQ/+z/FAD+/1oAtv9XAP3/2f8XAO//8v8GAHQAy/8eAPT/GgADAAIAOQDT/yQAr/8aAKf/8P9OAPb/VAAMAEEAIgBAADQA8//2/9P/7v8DAAIAuf8iAMD/g/8uAAAAEgD9/w8A+//X/xUASADy/ysAfwDB/wQAOgAKAAgA9f8bALr/WwAAABIAIQDR/zYAdP9ZABAAxP8GAM//RgDw/2AAKQAOAAsA+P/5/0QAuADc//b/rv/R////NQArAP//WgDt/ycAxP/j/5//+//q/4D/PgDp/zYABwAYAAEAEwDZ/6n/TQC+/yYA+v/8/30AGwAVAAAAyf/m/yEALQA3AOP/DQCv/9H/IwCc/9T/3f+//6f/EwAiAC4AAADu/83/e//x/xgAXQDd/wgAGQCB/+T/sv/B/wQAzf/8/w4Awv8FAAQAzf8NAAoAQAAhAPb/wf/y/+P/DABmAOT/IADk/9f/zP/p/yQAiv/9//7/x/8bABYAEQAgABoAAgAUABAADQDn/+z/EwA1ABgAAQBvAOz/FAAQAMT/BgCX/+P/MQAoAA0AHQAFAKn/JwDX/xUA7f+C/y0Ayf8vACYA+/+OAPL/PgAfAAcAdADL/x4AGADv/ykAIQAIAAYAPADD/7z/3P/2/9P/AAAAALf/6v/c/ywAtf/7/9f/g/8JAL7/8P+8/0kAcgDc/xkAzP/7//z/MwBgAOD/CgAIAPX/CQAsACMACgD2/woA9v/m/yEA5P/8/1gARwCDADIAFgAkAOf/IgDA/zoAQQDH/0AA/f/+/0cAFAAQAA0A+f8eAPT/CAD1//f/CwCt/wYAvP8SANj/lv8rAKL/IgAcAPL/KwD//xEAIAA+AOn/AAASADMAKQA0AE4ACAArABAADQBCAOz/y//o/9r/qv+p/wIATADP/9n/FwDc/+P/DQAvACYA+v/X/5X/BQDg/+b/IgDl/yEArP/0//b/iv+z/9X/AQDK//r/DQDm//7/EAANAGYA0v9//xgAy//6//v/MwA7APn/HwAGAOH/+f/7/7L/QQDs/xQAowADADkALgATACEAQABGADgAQADY/xYAEgDq/1wAJQD6//v//P/9/9n/FwDv/wMAFQDb/+L/DAAcAPL/0P///yMA5v80ADwAHgDi/9X/SwCY/6z/qv+o//H/z/8hANL/SQAWABEAMwDO/zMAFgAAABIAxv/R/xEAoP/q/6T/yf/4/57/QwCR//H/BQC7/9v/hv/o/5D/y/+w/9L/2/++/xMA2f/O/8b/0f//////EQBXADQAPAAMAC4AbwDs/yYA+//8/+r/AADu/xYAWwASAGsADABmABsA8v+HAKP/2v8YAAEAOAAIAD4AHwD1/xsAYAA7APn/HgAYAAEAuP/9/34Awf/N/1cA/f8PAB8A4v8MANP/t/8OAOf/EABEAO7/uv9IAMz/n/9pALD/QAAzAE4AUQDm/34A5f/G/wcA4v9WAEUA7/9NABkA8P/h/9X/3f+t/xgAAQA4ABsAKAAOAGb/4P/U/+//FgBcAO//4P95ADwAMAAnAB8A0P8QAA0A1P+CADEAAwA5APj/MAACALj/DwBn/7z/JQDC/zwACwAJAPb/nP/5/x4ABgBhAOD/HQBPAIj/sv/T/zcACAA9AEQAyf8KANL/EQD8/w4ADADA//L/9f8bABYA7f8VANr/z/8iAPf/+f/6/2kAMADe/1IA+f8xADoAHADO/9j/qP/e/xsAzf8yAM3/6v/c//X/wP+6/0gAgv/3//n/+v8yADsAZgD3/2cACQDR/8j/5f8OAOj/EAAfAAcA9P8aAPH/qv/O/w4ACwAbALv/7f8VALX/+//X/83//P/9/9n/4P8dABcApf8AABIA/f8PAOj/SADx/+L/1f/e/9L/AABbANz/GQDe//f/CgDS/yQAQgBsAEUAJQALAC4Ayv8LAC0Akv8nAA0AHQAFACkA/f/r/yYA1f8nAMT/9P+b/67/YwCr//P/BwDP//7/tP8eAIcA//8RAA0A+f/W/6f/OAAIAFAAQQAiABsAqP/x/+H/+v/7/9f/KAAgABoAAgAUAOz/uf8QAMT/BgBOAIj/HwC+/7j//v+0/1YA1//y/73/AQBKAM7/agD6/7L/5v8hANL/7v86AJz/MAC5/8f/LQC3/0UAEwAPAFYA6v8AACQA5/8QAOn/7f8nAMT/4/+f/x8A9f/3/1QAn/8fACwA//8jAPn/6P/I/wkArP+8/yUAQgARADIATQAHAPT/LQASAKD/RgDv/04AdgC6/xAA6f9JAM3/DQBCAJD/JgDo////EQAOAGcAHADg//n/DACc/x0ATgAaABUA7f8nAPz/2P8DALr/7P85ABwAOwBUAB8A9f/l/3v/8f+9/7j/MwC8/xIADgALABwABADx/8//DwD7/zIAFgA2ACwANgBQAOX//f/Z/wQA4P/4//r/n//X/8z/1v/f/9P/7v8oAA4A5//s/97/5P/q/wAAEgD9/+v/AQDd/xoA3v+u/+P/ev/L//r/1//x/+L/1f9LAE8A5P8gAOT//P/q/yUAZwAJAHYAFQDt/xUAEQCy/9T/3P+s/yoA2f+8/yQA5//s/zkA9//5/0MANgBjAKv/BAAWAO3/cQARAP3/6/8TACIAGwA7AAoACADj/9b/AgBeAMv/w/8qAP7/EAAfAAcAqv/g/8H/8v8ZACYADAAKAD8A2P8DAIP/LgAlAML/qwDk/zMAKQDY/ykA6v/K//n/MQAnAFcAWAA1AAYABADy/xkAFAAiABwA4P9BANn/PABVAOn/EgAzAPP/vv8mAMP/BgDz/6z/KgA0AAUATgBjAPX/5f/q/+7/g/8cAPL/4/9WANj/YABNABkAy/8eAD0A1v8CADkAigABAAAAOAB2AM3/1/9NAL7/EwD+/xAAjgBgADsACgAbAPL/0P80AAUA4P/C/6n/3/8cACkAxf8/APz/s/8LAC4A7v8DABUA2v9iALz/NwAIAIb/HgC9/28Ax//k/zMABADy/+L/aADB/ykA2P/y/xkApv8TACIA0v/b/wYA4f9CAP//EQAgABoAJwD7/yAA9v9TAPr/HwAHAAUAcwATAOv/3f8IAND//v//////tf/E/+L/DABmAPf/HADO/47/t//X/6j/zP8fAKv/BACo//H/KgDH/xsAFQA2AND//v/s/97/GwDy/xgAy/+e/+j///8AANv/GQAUAOz/JgAfAD4ADQAdABcAyv/C/xcANwC//8v/sf/T/7f/6v8lAPr/RADb/xkAy/8MAEEAtP/6/+n/EQB9AFIA5/80APT/v/8UAMj/UwD6/8T/KwC1/8P/qv8EABUA2/8YADkALQDu/9//5v+h/9n/FwDc/ywANgDi/x4ABgDz/+P//P8OANX/FADH/+X/6v/u/9//nP/n//7/RwDM/wwALwC4/zQAqf8DABUAyP9BADQA8/+s/wUAFwDu/83/6f8AANv/GQAUAOz/pv+4/8b/9v8KABoAOgCc/9T/AQC4/3z/zf/p/5L/FQAjAFQADAAcAGAA4P8KAD8AMwAEAPL/q/8pACEAGwA6APj/QwDb/3QAOQAJAHYA3/8cAPL/9f/S/xIARQDv//L/BwAYABMADwDo/1sAAAASAA4Aw/8qALT/1f8BAPD/KQBGAEsATwDk/+r/EgDq/wAAEwAhANL/AAAAAMn/LwATAMf/9//U/6X/JADn/yIACQDR/xAAxP9QAAkAv/8UANr/z//G/1EACgDk/0UAAAA3APb/HABOAIf/1v86AC4AJQAwAAIAAgAUADUA9P8aAEwAmf/k/+r/AAA3ABoAFQDI//j/HQAqAP7/bAAgANH/2v+Y/ywA2//i/8P/4f/C/xcAJQCL/0cAy/8MAPj/sP8IAL7/8P/O/w4A1f8BAN3/GgAoAFb/+P/n/2v/5P/q/zcALADI/0EA2f88AFUA6f9uAMb/9v9mAFIAHQDz/+T/6f/b//X/UgDC/yoA/f/Z/+H/1P8mAOj/IwAvABMAIgAJAAcAKgAiAJv/+f/V/7n/7P/L/wsACQD2/0EA/v/+/yMA+P/6/5//1/86APj/HgDi/57/QwDu/wMAOQDl/yEACAArAOz/FABIAMz/RABbADcAPwAOADAAOQBAAA8AHgD0/7//OgAuAO//FgDu/xUAAACk/8j/5f/9/8b/CAA+AA0ALwAmAAwA+P9DAO3/AgAmAOn/AAC2/w0A1P8TAFkAEAAgAPX/QAAhAC0AJAAwACYA+/8NAPn/6P/t/xUAo/8QANf/3/9BAKH/awD7//z//f/+/zUAqv8pAP3/RgABABMAWQCj/0gAFQARAFcAxv/k/9f/3/+u/wcAKgC0/2gAwf+7/zYABwBPAPf/VAAMAPj/MAACACYA6P9bADcA0f/a/xgAbwBHABQANQA9ANb/8f/P/9n/zv/q/+7/AwDx/73/7//g/+b//v/H//f/HQAFACgA/f8PAMP/qv9NAPb/+P8LAEAADwDo/zUAPQDp/+3/OgB3/xIA/f/r/10Apv9KAPP/9f9lAOT/DQAwAAEAEwDs/wEA7//O/zMA8/8ZAN7/5f9YAOv/pv+3/9j/zf/q/wAAyf+v//b/+P8eACoAx/8bABUA7f/x/08A5f/Y//L/vf/K/7D/LQAAABIA6v9cAAEAyv+MALn/NQBPAAkAPgDp/yQAHQDO/+v/SgCp/ygARQDK/1QA6f8RAA4AsP9AAP3/tP/o/xAA/P/q/+7/u/+2/+n/AADb/xkAuf+P/zgAv//M/8T/vf/K/9X/OAAIAAcA4f+e//v/DQDC/xcA3P/1/50A2f8FABYAtv/F//X/CQAsAO3/3v9TANX/8P8XABIA2P8pAFgAtP8xABUA//8RAMX/GQAUAOz/OQAbAM3/RQAAAAAAAAAlADAAAgA5AAkALACj/8j/GwC7/xEADgALABsAAwDx/wYAFwA3ACwAEQD8/9j/FgBcADcALQA2ACwA//+j/9r/vf8TACEA9/9UADEAFQARACAAvv+5/w8A1v/M/zEAKADF/2MABgDz/wcAvf8AAFv/6v83AOP/DQCv/6z/vf/c/77/JgDW/5X/TgDS/xEA/P/Y/+D/eP8lAOf/7P8mAMT/z//r/93/5P98ANH/IwBUALH/LgA3AD8A1//f/1MAMQDe/xsATQD1/xsA4P8KAOT//P8hAPb/LwABAJQAGwADAEwA4v8xAPH/9P8/AOr/7v9yABIA/f80AAUA8v++/wEAyv8LAPj/CwD3/53/QwCj/xAADQDn/1kAtf9EACQAi/8iAAkA4/9pAB0A4f8LAMD/KADq/8n/HQApALT/+v8fAND/EAD7/1cAWQDa/wUA8//j/+n/7f86AC4A3f8HAAYAqf8oAEUA7/87AAsAGwDy/73/SgCp/83/6f82AIgAEQCPAAUABAADAN7/9/+d/1UARQAAAMn/+f/o/7X/HwDQ/8f/wP8DAPH/z/9GAPD/4P8LAAgAvv/L/0MA//8AACQALwDw/wQAOwAdACoA6/8TAKL/2f8pAKH//f/s/yYA+//X/9//nP8vAPD/zv8hAL//zP/W/ycAHwA+AGkACwBlAD8AfABkAL7/OQAJACwAIwD4/+j/EAANAHj/AACl/+7/3/+u//X/+P8LAMD/OgDT/9z/LADt/xUAyP9AAFkA7P85AEAA6//K/x4AKgDH/xsA8f+9/wAAt//r/8r/CwDl/47/EgDY/+D/wf/g/y8A7/8EADsAHQBhAHMAOAAaABUAIwDm/0YASwAFAE4A4//8/zMA8/8+AB8A4/8NAOb/RgDw/6n/FQAAABEADgBCAO3/8f8qAOv/3f+I/9b/AgDw/xcAJQD6/x8AGQAUACMAnP/C/+D/+f8MAK7/0f/s/8v/HgAYAPD/BACo/97/9//C/+D/CgDk/9f/TQD1/wkAUQDB/+D/5v/Z//P/0f8jAC4AJQALAC4A7/+o/xUAtf8yACgAxf8+AOn/AAAkAB0A8/8sAAAA2//1/+X//P/G/xoAFQDa/ysANQDi/wsAZQBSAML/zv8gANH///8AAMj/0/83ACwAJAAKAK3/KwDa/xgA7/8EACgA6v+mAM7/DgD6/7H/HADO/+r/3P/Q/9r/BQDO/yAAGgACAAIA3v8IABkAJgD7/yAA0f/a/xgAEwBZAO3/8P8XABMAIQAtAEkAlv8GADwAw/8qANn/8//j/9b/8f/0/y0Ayf9BAMf/5P/q/7f/RQDd/1EAd//u/18Alf8qAOz/FADH/8D/FQDa/8///v8QAMT/hv8eAD0A+/9pAEIASABfADoAZgAtAAAA7v/f/+b/RgATAOz/FADs/xQAWgBIAPH/GADv/xcAXAAlANX/y//V/8v/+/8NAFQA+//8//3/2f8XANz/BwD0//b/HADg//n/HgDQ/6L/6/+4/+v/OAAtADcABwDi/wwAHAApAP3/DwDo/7X/MgCD/8D/8v+r//P/0P///6P/7P8UAOz/FAC1/wwA0//K//n/sf/A/wMAJwANAC8AFAAQANb/zP/7/6D/xf/1/9P/3P8HACoADwAMAEEANAAqAA8Asf/4//r/+/8yAAQAAwC5/0cAOQAcACkAs/8wAMv/sf/3/+f/EABWAEUAuP/r/+//4P/5/7D/0v83AOP/+/+PAM7/IQBSANT/SgA8AFUAIAAsAEgATAC/AFAAGwA7AEIAx/8bAHIApP82AGMA0P/Z/xcA3P/R/zUA4v9DABEA6v8SALP/+v+f/9f/AwDM/x8ABgC8/8n/+f8xACcADQBCABAAHwBQAAkAGgBMAFAALgAlAAsA0//b/xkA8P88AFUA1/9NAAYAz/8PANX/JwD7/zIATQA+ADIA8v91APH/4f8eAJj/BwDP/7T/HgC9/wAA7//g/+b/xv8IAND/NQBPANL/EQDq/zcACAAYACYA+//8/w4ACwDT/yQACwAJAPX/5f8hAPb/HADg/+f/RwDe/63/BgCX//X/QADG/2QA4/8MAPj/sP/l/7P/LwABADgA5f/F/wcA4v/V/8v/VgAgAPb/+P/V/93/9v8vACYADADl/8b/GgBMAKv/BAAoALP/VADp/xEAVwDr/xMAIgAuAMn/5/8PAPv//P/9/2sAxP/0/0AAxf8aAN7/CQAHAD0AMQAVABEA1/86ANT/uP/r/9z/4//7/yAACAD1/7//AgDM/7H/CQDR/+3/uf/s/0sAGAA4ABoA8f/0//f/1P8AADcA0f/t/97/5f8zAAQAFgDb//X/5f/F/+P/6f+2/9f/8f+Y/wgA9f/S/xEADgALAPf/QgAjAMH/3//4/3n/7/8EAPL/4v95/wEA3f8IAD0ADQCv/+T/DQCd/x4AGAATAOv/8P+E/5z/CwCt//X/rf/i/0MAJADm/w8A6P+2/1cADwAxAEwAPQAMANP/XABdADgAUgDn/8f/GwAWAFsAXADc/ywAIwDm/w8ADAAKANH/yP9mAAgAPgBpAEIANQD0/y0A7v8DAEwAUADA/9//HADy/wcAz//9/8f/9/8KAC0ANwC+/xQAEAAfACsAfwAdADwAHgC9/0oAqf8oAPz/jv83ANH/IwBmAFIA+f8xAPH/vf8TAMb/9v/T/yUAsP/k/yAAYv9dAKb/3f/2/9P/bgD+/2wAxP++/+//FwDu/5b/TwDS/zYAPgCy/xwAFwC3/+r/EgBX/8L/zv+g/7P/nf/D/+H/CwCu/ysAyP/A/zoAHQAXAO7/cgDc/9D/NQC9/yUAQwA2ABkAlP/g/0IA2v/h/zAApv+l/xIADwBWADIA8v8GAM///f9HAF4AAgABACYADAAuAAAASgAXABIAawBWADMA8/8ZAAIAy//6/1cAMwDO/zMA8/+s/6r/g//T/8n/r/+//8z/sf/4/1UARAA3AD8AMgAoACEAGgA6AEEAWQD//xEAVwBZADUAqv8EAPL/mP/2/67/9v8JAKz/GACl/7f/IAAIAAYA4f96APT/CABQANP/AADc/z4Asv8cAOD/eP8TAKH/NADz/+P/1/8nAFcA6/8lAPr/DQCd/zAAp/+B/60A+f/V/zkA+P/U/xMAx/9AAOr/AABKAPP/UQB3/zcAGQACAF4ASwCrAIn/RQA4AOT/jgAXAAAAAADu/7r/tv/p/9v/4v9DADYA0P///9r/BQAXAMn/QgAiAAkAdgAVABEADgD5//v/DQALAOX//P8PAB4Az/8iANL/7v+WAOf/2f/z//b/CQDk/8T/hv+e/wwArv+Z/wkA0f8QAOn/EQAOAOf///8QACAA4/8fAND/7P8mANb/JwDp/9v/9f/l/yAAGgAnADIAAwADAPH/GAAAALf/IQDk/43/yf+c/wsACQDj/w0Awf87AB0A9P8aAKf/FADs/8v/6P8QAPz/6v+mADwAHgA9AB4Avf/v/wQAuv82AOL/+/8NAPn/6P/t/ycADQAvAPD/BADy//X/0v8kAEIANQCHABAAMgDN/9f/8f8YADgAwP9fAPH/KgCRAPX/GwADAAIAFADa//T/PwD8/yEALQDu/9//+P/n/6L//v8jABwAKQDq/wAAAAA3ABoAp/8UANn/hf/5/1T/wP9MAOL/HgDi/8P/z//Z/ykA/f8PAAwAQQDZ/xcAXAC4/yEA5P8gAPb/+P96AM//RwACAN3/CADQ/zUABQDz/9H/2v/0/xoA8f8GAOD/wv8XAO7/KAD8/yEACAD1/3cAFgA3ABoAJwANAGX/KAD9/3z/TQC+/wEAcAC1/2kA1P/K/zAApv8TAMf/GwAVANv/9f+///H/PQAxAPH/BQDO//3/2P+7/wAAtv/X/zoAQQC1//v/IAAHABgAXQCVAAkALADb/ysAEABEAJMA0f+SACwA2v/0/7//8f+9/9z/4//7/w4AMAACAEsATwD3/xwA8/9RAPj/1f8mAMP/9P8IAND/7P/w//P/LAAAAO3/AgDe/+X/MwC7/9v/KwDs//D/qv87ANT/AABKALv/EgD9/0YA8P8EAAMAzP8yAN//HAAEAPL/0P/H/9L/AAAAAAAANgDj/w0A1P/K//n/MQDx/wYAYQCW/z0ADQD5//r/ev85ANP/EgAhAL//FQDI/xwABADN/x8Avv8UACIAwP86AAoAUgBCACMAUwDV/97/5P/X/00AUAAuAF0AAQABACUACwAJAOP/+/8zACkADgAwADkALgATADQATwD2//j/+v8NAMH/BAAoAOr/bgD+/zUABQCp/18AAwAVABAA1/8VAO3/JwBEAAAA7v87AB0ABQAoANj/FgDJ//n/MADx/08ALQCAAAsACQA+ANf/KADq/yQACwD3/y8Apv+3/8b/v//e/+X//P80AJf/mf/k/6D/2P/y/xkA8P8XACUA1f+m/27/wv/g/8L/u/8AAAAA7v+6/9r/GABu/+f//v/s/97/5P8zABYAAAASAEYAuP8PANX/3v8tANz/iAAkAC8AEwC0/8P/hf8LAPf/+f9DAO3/3//l/7P/+f/D/+L/DAD4/x0A4f/6/8T/9P/3//n/HgCq/ykA6v+3/9j/FgAkAOf/RwAUAMf/9/9CANr/9P/k/7L/HADO/yEACAD1/wgA0P/s/wIAJgDo/xEA/P/9/w8A6P8RAGoA+v/p/4AA+f8MAFMADAAuAMr/sP8IAL7/3f8aALr/EAD8//3/DwCx/9P/yf8KAOT/IABRAEEAIgAJAFEA0/8SAP3//v81APT/UgD5/x4APQAMAC8AEwDZ/7z/t/8gAPb/nP9nAOX/2P8WANv/4/9EAAAAWv8yAJb/vf8AACUAjAC6/2wAMgApACEACAAZAN3/CADQ/5EA0P/Z/04Amv/4/wsAQAD9/+v/AQATAOv/7//g/53/VQANAJ3/HgA9AAwA5v/9/zQABQDO/yAALADt/ycAMgDy/wYA4f/V/xQA2f8XAO//zf8gAAcAPQAxABUAEQD8/1gA7P8BAEsAFwA4AAgABgDh//r/1v8CABQAov/a/8//RgDL/zAAcQCj/xEA6f/b/6v/BQBx/8T/KwCj/2wA/P8hAD8ARQA4APf/QQB9/xcA7v/f/y8AAQAlAMP/4f/n/yIA+P9VADIAlf89AAwAHADz//X/5f/9/0YA8P88APr/6f/b/wYA8//R/0gA8f89AB8AKwA1AOL/6P9r/+X/oP+z/x0Az/8PAAwA0/+3/+r/t/8OAB4Aqv9gAAMAFQARAKD/IAC//7n/EAAxADoALwBLACoAIQBlACwAyP9BAP7/x/9AACEAv/8CABQAx/8uAO7/zf+g/w4AQgCj/1oAyP93/9v/0P/+/+z/FADs/ycA+//8/zMABAA7AAoA5P/q/9z/vv8UANn/vP+3/9j/FgDb/wYABQDy/77/JgAfAPX/CADj/zEA3/8JAPb/+P/6//v/RQAAAO//u//t//H/BQApAP3/DwAxADoA+P9oAEEADwBEADYAUQDm/w8AMQACADkAQAD9//7/7P/e//f/+f/6/0QASQAEAE0ABgC8/wAAJQAdAD0A6P/t/14Auf8QADIA8v8rABAAHwDj/zEAAwDe//f/wv8EAN//VAAeAKv/FwDu//L/BgA8AB4AGADd//b/QQDZ/xcASgDg/1QAaQDn/zQAYQDO/w4AaAD4//r/MgADACcADQDU/0oABQDy/ysA7P/w/8//2P/g/2X/AwDf/5z/QgCQ/93/CADi//v/sv8cAM7/6v8SAKH/6/+4/3z/AwDf/9P/SQAEAN//+P/6/+j/AADI/5z/HQC8/8n/VAAxAN//LgAlAIv/IgAuANz/GQBMAE8ACQAZABQA/////7b/HwBRAK7/PgDp/yQAVAANAIsAy/9WAPz/jv9uAKH/6/8mAPr/HwDj/+n/JADm/yIAZQC///D/8/8sACQACgAtAJL/3v/T/+7/FQBJAAMA3v9TAOf/7P/L/8P/9P/k/yAA4//E/z0ARADJ/y8AOAAIAD4A6f/u/wMAAgBeAAIA8P9OAL//OQAuAO//KQDq/1wA3f/k/w0A5//Z/yoARgABAHAAx/8JAPX/wP86AOb/NAAXAAAA7/87AOf//v9HAN7/QADY/87/oP/F/77/y/8xAN7/QAAPAPr/jf/t/wIAgv8/AA4A+v8MABwAPAD6/7H/5f/r/5P/AwAnANf/FQBbACQACwAbAPL/9f8tACQAwv/z/wcA9P/S/yQAZgAJAD4AfAAIAOL/6P8jAGYAwP86AOb/2P87AML/FwAAADcAGgAVABEA1//y/+L/HgD0//f/5v/Z//P/rP/h/+f/ov/Z/wUAlv89AAwACgBkAKz/BQDg/+b//v/+////7f9eAN7/QADr/8r/CwCu/1AACQA/ADIAzf9qAPr/1v8nAOn/2/8ZAMv/w//P/7T/1f+5/8b/mv/B/9//5v/9/+z/8P/O/+r/AADc/xkAgwANAB0AKgAPAGgAHQA8ADAAJwBEACQAHQA8AOj/2v9PAJv/CgAIACsAIwDl/zMAvP8SAOr/NwAaAN//HADN/+r/t/8gAPb/CgBRAOb/2f/z/77/lP/O/+r/EgCP/6X/7v8DAPH/KgAPAJ//MgAWABEAIAAaABUAIwAcAAQAKADY/83/1/8DAN7/GwDg/8H/FgCk/+3/3//T/6T/7f/M/8T/BgDh/x0Al/8HAOL/i/8QAB8ABwAYACUADACu/9D/IwCu/2MAGADd/3cAzf8gABoAzP/o/yMA+f8eAE8A5f9FAO//FgBJAM3/RQAlAPr/MQDf/xwAKQDY/zsAMAAUAP7/NQBiAAUAKQAhAAgABgAFAPP/9f8uAO7/FgAkAPn/+v8yAAMA8f8qAMf/LQBJACkAfQAIABkA3v/3/y8AuP9GAN3/0v9IAPL/vf/v/zsAnf9DAFsAtv9FABMADwAxAPH/BQC7/8n/QQD+/0cAOgDl//3/IgAbAM3//P/q/wAA7v/N/zIAKAAhAC0AEQDq/9z/h/+M/37/zv/Y/7v/SQDN/9f/FQCj/7X/xP/Q//7//v+1/zEAFQC2/zIA8v/i/7H/5f8OALD/9/9CAP//2v8YADgA9/8KABoAzP/X//H/9P8/AA4Awv8FADsACwDl/0UAEwDZ/6n/8f8GAPP/LABbAKUABABfAE0A4/9pAAoALQDc//X/CQA+AA0Awv/z/77/FADa/wUAzv/X/7v/kf85AK7/BwAYAO//8v8rAFoAAAAkAAoAQADG/9H///8jAAoA0v9bANv/4//7/yAALADb/8///v8iANP/SQAWANv/9f/3//n/+v/8/7P/5/+0//r//P/9//3/7P8TAMf/GwCo//D/4f+w/wgAq/8XAAAA7v8DABUAyP/B/wMAzP8yAPL/GAAmAEMAJAAvAEsAKgBrAA0AVAAMAPj/5//s/zkA5f8OAMP/z/+h/+v/bwDH/y0AEgCz/x0A4f/6/9b/3v8uANz/GQACADkALgAlAGcArv8HAAUAKQBGABMAfgBmAC0AEgAhAPb/5v/G/+T/6f/u/xUAEQBFAO//8v+r/wUAu//t/ycAe/9eAPH/4f8eAOL/6P/H/8D/uv/a/73/JQAwAAIA8P8FALv/o//t//H/BQDO/w4Awv+p/9//CgA/APz/DwAeAFAA9/+MAAIAy/9VAPz/MwDg//n/w/8FACkADwAeAPT/dwADAN//QQD+/6L/DwD7//z/RgABADgALQAkAPn/aABBAP7/NQAGADwAHgA9ADEAAgDw/2EAPAALAPj/5/9ZAKP/SAAnAI3/NgCr/04ALQDb/1AAwP/f/woA0f/t//H/z/8PANX/y/9DAO3/cQBJAPL/YgC9/+//KACg/yEAGgDf/xwAqP9w/x4AGADw/zwAHgAFABcAyf/C/+D/+f8MAC4AOAD2/+b/xv/k/w0Awv8XAAAA3P/j/9b/AgCU//P/YwArACMA+P/6//v/DQD5/zEAJwCg/zIAFgAkAGcAHAByAEoA8v/j/9b/AgDw//P/BwAGAPP/YwAGACoANACq/zsA1P/v//L/q/88AAsAQAAhAEAAIQD2/2YACAAsACMA0//c//b/HADN//z//f/Z/wQAKABFAO//8v8ZABQA//81AD0AHwA+AA0AHQDO/+r/3P8aABUAtf9WAOr/3P8aABUAEADp/zcAvv/d/+T/DgAwAJT/4P/n/8f/9//5/wwALgATAFkAWgARAA4AsP/S/9v/vf/K/53/1v/L/9b/p/+m/+//4P9UANb/uf/Z/6r/AwCn/8v/1f+5/7T/DADm/8b/dgCo/7n/EADE/xgAuP8PAOj/tv8yAAMA8f/i//r/xP+9/8r/CwDl/9j/TQCs/wUABADN/0QApP/b/xkA3v8tAO7/8v89AB8APgBEAO7/TQA+ADIATQDj/x8ABgAqAA8A+/8NAML/FwDc/xkA8P+8/zcArP/0/63/vf84AK3/TwAJAAcAYgDh/2cAHAAEAHIAJAAdAHQA3f/2/0EAx/8tAAAAEgBYAEcAXgA5AGUACAA+AB8A4/9EABIADgAeAM//tP9DALb/xP89AJ//MgDN/8T/9f/l/1gA/v8iABwAu/8AADYA9f+b/+b/DwDD/wYAKQCh/9j/KQAhAPf/wf8pAP3/tP/6//v/MwApAOr/AADc/9H/2v8YADgACAAZAPD/zv/9//7//v///9r/BQA8AAsALgBKABYAAADu/zoAHQDz/z4AMgDy/wYAKgD+/xAA+//X/9//rv8HACoA7P/L//r/DQCv/+T/DQDU/wEAAADc/wcAz//+/1oA2v8GAOH/wv+X/6v/8/+Z/wkArP+8/9z/rP/z/+P/aQDV//D/BACW/xgAy//n/+z/FABHACcA+//8/8b/5P9FAAAANwD2/8H/KADY/xYANgD1/0AADwAeABgAuP80ALz/yf8dAKn/KABFAO//FgDb//X/GwDN/+n/AAASAEYAEwBHAAIAuP9GAPD/zv/9/9n/KQDY/+D/5v+P/xMANAAFAM7/MwDy/9D/kQC9/+//KQAOAB4Aqv+E/9P/7v/g/0EAEAAMANT/XABvANr/FwDv/ykA2P8WADcA4/9EAEkAKAAhAAgAGQBLAPT/GgACALn/EAD7/yAA0f//////7f/e/9P/EgDY/xYANwAHAD0AMQAVAG0AIAAIABkA3f8IAND/IgAJABoA3v+b//n/w/8FAPP/LADI/8D/zf+f/zIAKQAhAC0AJAAKAC0AJAAwAEsATwBSAB0AYQC8/xIA6v/v/ygA6v8SALT/5/+1/+j/kf/w/zwAw/9hAAUAFgASAEUAEwAiABsA8v+HABEAfAAtAO7/KABFABIADwAeAKv/TgDR/yMALwDK/1UA1/8VAO3/FQD//37/KgDZ/7z/NwDj//v//P/r/xMA2f/g/y8AAQCT/7v/o////9v/q//g/6//CACr/zwAVQDX/zoA+P9DADYAGQAUAEcAAgACAF0AlP8EACgA/P8PAB4A9P8IAAYAz/80APP/BwD0/9L/2/+G/9X/pv+l/8n/wv/z/wcAPQAMAOb/NAAXABMAxv/k/yAAmf8JAKz/vP83APb/LgC4/9j/4P+c/9X/y/9DACMA1P8AANz/BwD0//f/VAAMAEEA7P/w//P/rP90AO//KQBGAMv/VQAyADsAVAB7APX/0/8kANT/y//D/zwADADl/yEAmv/T/8n/wv8XAMn/+f8xABUA2v/i/wwAwP/y/9D/tP/o/7X/+/8OAAsAGwBNAFEA+P9CACMA5v/G/+T/1//x/ysA7P8mALH/+P/6/+j/IwAcADwA1f9dAPD/qf/N/9f/AwDM/1YA6v9cAF0AEwB+APj/HQAFAHMASgAXAIEAegAGAAUATgC+/14AOQD4/0IAtf/E/8//DwD7/8X/PgAfAOP/VgBFACUAHgA9AB8A4v/7//z/6v8AAFwA7//y//X/if8OAOf/7P85AEAA/f/Z/87/6v/v/7v/7f86ANP/3P8ZAKf/7//z//X/GwCW/wYAPAAwACcAMgByABIAfQCKAAAAXABdAAEAEwDr/wEAEwAPAPv/6f9JAOD/1P/c/6z/BQAEAM3/xP/Q/yIALgDv/xYAEgAOAAsA5f/q/+//4P/U/1wA3f+a/wkA9v/T/xIAMwDO/+r/yv8dAGEAzv8zABcAyf8dAGEABAA7AB0A4f9CAOz/uf/s/5T/lv+9/6X/yf/5//r/MgAoALP/QgDa/5f/LACj/+3/p//L/0MAyP8uAMr/CwD3/6//PwAOAEIAIwBBACIAGwAWAAAAAAAAAG4AtP9DAFoApP8RALL/5v+0/7D/LgDc//X/0//u/zoA5v/Z/zwACwDl/zMA4P8dABcAJQBDANr/TwAbAE0AGQCn/wEAuP8PAOj/EAAgAL7/FAD+/xAADQAdAE4ACAAGACoA/v/s/yYAjP+1/9b/zP8fAOL/6P/t/8z/1v/M/9b/8f+q/5b/BgDh/+f/7P8mAGgAZwBAAOv/JQCw/9L/JACd//r/+//X/9//nP/U/xMA/v/+/9r/z/80APP/9v8JANH/fwBUAEQAWwAlAEIA7f8UAP////82APX/QADY/wQA8v/i//r/xP8rABAA/P/q/zcA5P+y/+b/tP+w/+X/RQC4/0YASwAFAHIAEgBrAJ//6f8RAKD/agDD/xgAJgCM//7///8jAPj/HgA9AB4A9f/A/wIA3v9SAB0ABQAXAKT/AADb/xkAFABaAEgA8f89ANb/AgAUACIAwP8oAHwAiP9XAA4Aw/8qANn/FwAlAOf/EAANANT/JQD6//v/DgALAOX/2P/g/8H/KQCz/0IANQAGAKsA0v/u//H/qv/O//z/2P8pAP3/of8hANL/AAAAANv/9f/S/wAA7v/f/wkA9v8cAGAA4P8vABMAov/r//D/FwAAACUACwD3/x0A8/8HAJj/9v/m/8b/LQDb/ysAWgA2AIgAJADU/xMA/v/+/yIA5f8zAE4ArP/i/x4ABgC8/8n/1P9u/9T/EwAiAEAARgDd/xoAOgDm/34AQAAPANb/JwB7ANH/NQAYAMv/1f8UANr/4f/6/8T/9P/k/yAABwA9APv//P8hABoAXwC6/20ADgDC//P/h//W/6f/uP+h/8b/CAD1/9L/7v/f/9P/yf+d//r/sf/B/xYAAAAAAAAAEgAhAGQA4/9WADMAqf8oANf/TQD1/xsATQCr/xcAEwDZ//P/PgBEAFwAXQABAEoAKQAPAAwA5v8PAPr/6f+R/wIAOQAbABYApP8kAOb/ff8pAKH/jv/u//L/UAAJACwAWwDb/z4AxP/Q//7/kP+CAMT/mP/R/7b/sv+c/zAAlP/g/woArf/i//r/6f/u/ygA6v9JALv/yP/4/53/HgD0/y0A7v9NAFAACQA/APz/awDD//T/PwDY/xYAJAD5//r/6f/u/xUA2/8rADUAGABLACoA/v/+/yMACQAHAD0AMQDf/xwA4P/U/zgAv/8CAAIAOQBSADAAOQDT/yQA1P8TAA8A6P+AAAsALQAAAO7/AwC6/+z/AgAmAPv/RQAAANz/LACR/xQAEAAfAD4A/P9YANn/TgAtAMn/+P/6/zIAAwAnANf/zP+y/+b/DwDW/3AA7f/e/3cABADf/3gAYQAXABIA6/84AL//FQBaANv/4v/7/yAA9f/4/x0AFwA4AOT/sv9CAP7/7P8UAOz/AgC4/yIA9//m//7//v81AOL/VgAOAAsA9//5//r/1/86ANP/7/+7/wAASQCV/wUAzv+O/wAAEgB8/6j/3v/l/yAA5P/8/9j/8v8GACoARwA5AC4A3P/j/8T/0P/s/xMANQDh/0MANgArAEgAJwAyACgAWAAPAB8A4v+x/xsAu//t/97/5f8zAAQA3//4//r/jP9aACQAHQCYALH/CQAsAO3/OgBTAAwAQQA0AM///f/+/+z/y//V/6b/7//g/53/CwCu//X/5f8zABcA3P8+ANf/AwDM/0QA7v8DAPH/9P8/AKD/agAeAOL/MQACAMv/sf8JAL7/OQD3/wsAGwCV/xgA3f8aACcAsv8cABcA3P9jAFAA9/8wAPD/vP8AAAAA7v8oANf/3/8KAJr/wP8DACcADQDn/yIA0v8AADcABwBPAAkA9f8bAAQA8f8rABAAn/8yAAMA3/8uABMA/f/s/xQAx/8bAPL/9f8bAAMA8f+9/9z/4//7/7P/QgD//9r/dADL/zEAAgDL/8P/BQDg/6//UgDU/10A7//O/yAAh//7//z/DgAwAAIAAgAUAOz/JgAfACsANQC9/yUAHgD0/y0ANwAHAD0AMQADABQAtf+x/wkA9v/m/1kANQDP/7T/6P///9r/z/+0/8P/GAA4AOT/DQAdAM//6/8AANz/vv85AOX/DgDV/2//MACU/ykADwCx/1MAi/8iAIoA7/+FAFkA//9IACcA6f/u//H/z/8PAPv/IAAsAMj/+P+w/wgAvv/w/3MAJQBoABwABADf/xwAFwCk/+7/8f8GAM7//f8PAAwA5v/Y/ykA2P/g/9T/7/8EAAMAJwAyACgADgDn/9r/4f/V//D/BAAoACAAGgAVADYAUADT/yQA+f8xABUAIwB5AIX/+f/W/6f/OACI/+n/EgDq/zcA9v9BAA8AjP8QANf/3/8uAJP/qP/w/wUABAADAF8AOgAcAAQAuv/t/7n/tf8fAPX/CABjAPT/m/8uADgACAArAOz/XgACAAEAcADH/y4AbwAiABsAOwAdAM7//f/+//7/7P8mAAwALwAmALH/QADr/xMAIgD3/woA0v8AAMn/HAAXABIARgDL/x4ABQDz/2MAGQA5AEAAxv+///D/z//r/wAAEwAhANL/AAAkAAoALQA3AFEALwBvABAA6f8kAOb/2f/O/w4A1f8UAP7/7P8UALX/DACc/+f/IgD4/zAAFABHABQA7f/e/+X/s//C/+D/5//+/8f/9/+d/7D/rf/Q/8f/0v9JALr/SAA6AMH/8v/j/1YAIAAaADoAnP/n/+z/3f+t/3P/6/+4/w8A+v+y/0EA7P/w/ykA6//v/04ABwA9AFYADgAeAOH/QwARAA0AHQA8AAwA5f/9/6L/IgD3//n/1f9MABgAyv9nAK7/9v/l//3/NACX/+P/6f+2/+n/JADC/wQAKAD8/yEA0v/t//H/vf/v/wQAFQDb/ysAIgDl/yEA9/8cAJf/vv/d/5r/CQD2/y4A7/87AAsAwP8DAPH/KgD+//7/x/9AADQA8/8/AA0A1P/L/x4A4v8LAPj/MAA5APf/CwDS/0kA8v/1/wgABwD0/wgABgDP/zMAqf/N/9f/zP8yABUASQADABUAWgDb/xkAOQAJACwA7f8CABQAEAANAAoA5P/X/ygA1/8oAMX/BwC9/5L/FQC2/yAA9v8uAO//8v/1/8D/KACy/0EA7P8BABMAIgAuAO7/YADN/w0ALwABAEsAFwAAABMAxv/R/xEA/P8hAD8ADgDV/yYA6P9bAEkAAwCWAB0AFwDK//n/nv/E/xgAuP8PAAwAZgDS/9v/BgDO/9j/u/8kANT/3f8sABEARQAlANX/FAD+/8j/QAAPAOj/IwCu/+P/+//8/2sADABUADEAp/8UAMf/9/8KAC0A2/8HAGEAvP83ACwA7f8CAF4A3v/3/woAdv8jAK//9v/l/7P/1f8UAFkA//9tAP3//f/Z/87/MwDz/2MAKwD//zUAGABdAIMA+/8gAFEA+f8MAPj/MADe/9L/EQAzADsA1P9wAOz/3v8tAJL/OgDm/7T/wv/h/x0Aqv8WABIAMwA7AOf/EADW//H/9P/k/yAAmf/l//3/tP9VAPz/xf++/6b/EwDG/y0AWwDu//L/KwAQADIAcgASADMAzv/Y/zsAwv8pAOv/3P9RAMH/FgAkAML/PADV/wEASwAFACkA/f80AOH/HQA8ANX/AgDd/wgAhv/o/zUAmP8IAPX/5f/q/9z/4/+f/+n/AADb/ysA///I/xwAKQDq/xMAtP8LAC4AAABKAPP/LAD/////SADx/1AAdwA7AAsACQAHAOL/6P8QAB8AGQAnAPv/xf8HABgAuP/G/z8Axf++/xQAx/8bADsAQgD+/7X/RAB//wYAKQDG/y0A7v9MAPX/GwDN/9f/OgAKAC0AAABbALf/IQAtAKT/IwCv/ywAJADU/8r/+f8fAKv/PADn/8f/QADY/+D/+f/V/5T/u//b/5n/GgC6/7X/RADJ/y8AOAAtAAAA7v/y/9D/NAC8/xIANAAFAE0A9v8cABYAyf8vAAEAAQA4AOT/IADj/8T/vf/v/xYAt/8OAPr/sf8cABYAAAASAA4ACwAuABMADwAeABgA8P88APr/MQDx/6v/KQCO/+7/zf/X/xUA2/8rADUAYgAXABMA/v8QAB8A4/9EAKT/7f/x/6r/FgDu/83/RADJ/8L/KQCh/w8ADAAcAPL/BwDh/4v/WQDa/xgAEwDs/xMAov/Z/7z/3P/Q////7P8CACYAsf8cAAQAFQAAAO3/hABFANz/GgDx/wUAFwA3ACwA7f8CALn//v/a/+H/HgAFACkAxv8IABgAFAD+/xAAHwC+/xQARwDw/wUAzv/F/xkAOQBTADAAJwAyAPL/PQAfAPX/GwADADoACgC//xQAIwD4/x4ABQDz//X/0//u/83/xP/1//f/CgAIAAcAKgD+/xAAVgBrAPv/DQAvAPD/KQC0/+f/2v/0/z8A6v9uACIA5f8zACkA/f8PAPv/1/8VANv/4v/6/8T/4v8MABwABADf/woACADi/8P/BQAEALv///8AACQA+f8xAEwABgAqACEAQADq/1wAJgAMAC4Ayv8dAPT/GgDf/0AA2f/O/zMAzv+z/53/HgC9/1wAggDW/ycA+//Y//L/4v/7/+n/EgBqAIz/7P/w/6r/AwDx/2IAhf8KANL/tv8NAHj/SgDO/yAAPwD8/0YA7/8EABYAJAAKAOT/DgAdAPT/5P8NAEIAtf9EAG4A/f9HAPD/PACe/zEATADi/zEAzP9EAAAA7v+6/+3/8f+8/zcArP8FAOD/wv8pAOv/yv8LAOX/s/8LAK3/vf/v/+D/5v/+/zUABgDz/+P/DQBBAOz/JgAxALr/EAANAPn/6P+j////2v/P//7/IgAJANH/EADp/yQA5//+/0cA8f/P/9j/qf8DABQA2v8YAN3/CAArABAADQDU/+//KQAzAPP/PgDE/77/JgDW/zkA0/8AADcA9v94ADwAsP8IAAcAqv8WACQALwBLAHQAJgAeAIcA2v8YAN3/5P8gAOP/HwArAP////9tAMX/GgAVAO3/AgABADgA0v9bAMn/LwBLAPT/9v8KAPb/d/9JAKj/3v/A/83/RADJ/1QADADU/8r/MADL/1YA/P/9/34Aif9qAMP/vP8AABIA/f+i/zQA4f9VAOn/7v/f/9P/EgDr/0oABAAoAPz/DwDD/xgAJQCe//v/xf/j/4z/7f/w/7z/3P+Z//f/CgAtADcAGgDe/xsAKADF/z4A6f/J//n/+v/7/6D/DgD6/7H/CQD2/xwABABfAPL/vf9KAKn/AwDe/+X/MwDO/yAA9v9TADEAJwBpAPr/DADB/wQAzf/8/2oAsP8bAAMATABQAPj/QgDI/xsAKAAzADsACwDl/8X/BwC9/xMARgBeAPD/4f8LAJv/QQDZ/+H/VQCy/y8AEwDZ/2EAKQDr/xMAxv8IAPX/9/8dAOH/eQDi//r/MgDy/2IABQAEAN//rv8HAL3/AAAlALD/5f+g/8X/vv+U/xcAEgAOAAwACQDj/+n/2//1/0AA2P9OAD8A1/8oACAABwArACIA+P8LANL/JAAvAN3/CADQ/xAAHwDQ/9r/FwDv/ykAs//U/xMAtP8xAJX/4f8LAOX//f/Y/xcAyf/5/8P/9P+//xQAEADE/z4A6f9bABIA/f80AAUA8v/1//f/wv8pAA8A6P8jAAoA5P9FABIANAApAA8AewAHAIYA2v8XABMAof9ZAH7/8/+s/8//DwDD/yoADwBpAFQADADm/yIArf8ZACYA1v8nAMT/KwAQAEQANwA/ANf/zf8yAKj/TAAYACYA6P8RACAAmf8JAKz/4f+d/9X/y/+x/y4At//9//3/x/8tAMn/+f9oAMH/8v/1/0AAIQDk/48A8//2/0AAIQAbAAMAJwANANT/AQAAAAAANwDk/yAA4//7/8X/vv/w/6n/KAAOAB0Az//9/+v/k/9gAPL/9f/l/w4A+v/p/zYA4//7/9f/zf8NAC8AOAAJAOP/HwAGABgAAADc/ywA2/89AB8A9f8bAE0A9f8JACwAkf9eAN7/CQBRAC4AOAD3/xwAl/8GAJf/9v/l/7P/+f+f/0QApP82AOP/1v8VAO3/JwCN/38A1P8TACIArf8+ANb/AgDM//v//P/9/w8AQwDt/xUASADM/3sA4/9EAMn/CgCJALf/fQDk/zMABADf/y4A7/8EAM3/HwDQ/+z/3v/3/woAv//x/8//xv/R////yP8uABMA2f9zABMAxv/k/w0A1P8BABMADwAMABwAFwDu/ygAMwCFAA8AQwBJABYANgC+/xQA7P8BABMANAAYAAEASgDg/1QA6f8AAO3/8f/P/7T/aACc/zAAJgDW/97/5f9FAKX/SgDy/77/AQDK//r/+//8/yEA9//B/2AAFgAAAFsAEgD9/8f/5P/q/xIADgBoAEEANABPAAgAUAD4/zAAJwD7/+r/JAALANL/AAC2/yAA4/8yACgA6v8SANj/KQCz/+f/IgDT/9z/0P81AAYABAA7AEIA//+j/+z/3v/3/x0A4f8wAAEAXQBeAAIASwDP//3/2f/O/w4Aw/+8/5L/zP/E/9D/x/8IAPX/0v83AOP/MgA6AC8AJgAxACcADQBCAOz/AgAUAP7////t/8z/+/8NANT/AQAAABMARgABAAEA7/+p/wMAuf+1/wwA0/8lALD/GwDy//T/QAD9/zQAqv9NAPX/CQAsALb/MgCD//j/CwD3/y8AFABZAP////8AAAAAyf+K//3/tP+e/x8A9f8bAAMA3//l/6H/6/+l/9z/PgD8/+r/SgAEALr/IwAKAOT/xf9QAPj/1f/w/5f/0P/H/+X/jv8AAO7/8f8GAOH/5/+i/zQAz/9ZABAA6f/u/7r/NQBh/28ARwDL/40AFQARANf/8v89ANb/AgCDAA0AeQBPAC0ANwD2/y4A7/9gABYASQBNAD4ARABcAG8A/v9HAPH/TwDk//z/IQCt/wYAl/8ZAAIAAQDv/xcA3P/1/xsAg//l/3z/8v+r/+D/HQDz/+P/1/8VAGz/9/94/8r/1P+m/+//4P9BANn/TwDS/9v/GADd/+T//P8hAL//OQDl/+v/AAAAANz/9v/4/4v/NADh/zAAOQBAAMb/CAA+AMT/dQDe/xsAzf/p/xIAs/9CALX/MQDx/+L/MQC5//7/WgAAAAAANgCH/zEAJwDX/xUAEQAOAOf/IgAJAL7/AgAUAP7/EADX/xUA//8kAB0A4f8dABcAEwD+/yIA5f/F/9H/NQDi/9b/gwDX/18AKAANAB0A4f8eAKr/zf+y//n/sP/3/8L/zv/q/8r/VAD7/3wACAArABAA1//M/+n/JACd/58AyP94AGEA4P/DAAoAGgDM/zEAlf/h/1UA1/8oAPz/IQAaABUAtv8yAAMA8f9PAEAAMwDz/2MA0P8QAPv/DgD5/8P/PQDW/ycADQD5/7D/GwA7AAoAGwAoAA4A1f8mAIz/fwDm/0YAlQCc/3kAvP9KAAQA8v89ANb/FQDt/0wA4v9oAEEAEAD7/yAABwCq/2AAhP9BAA8Aw/89AAwACgAIAIcA7f9eABUA7f8UABAADQCv/xoAlf9PAL//8f8qAGr/CADQ/yIA9/8LAOX/MwDy/+P/MQBw/0QAtv/X//L/q/8EAN//LwDd/wcAUAAJAOP/HwD1/8D/OgDB/7v/yP/T/wAA7v8DAPH/9P8tABIA/f8PAPr/1//M/8T/q/+7/xIADgCw/9L/2//Q//7///81APX/CAAsABEA/P8hABoAlf/0/ywAEQCPACkAIQBSAML/BADN//z/DgDV/4MA+/8gAAgAvf9KAM7/6v8lAAsAwP8VADYABwA9ANb/3v/l/6D/2P/y/77/y//n/7X/DABBAP7/bABFABIADwCx/xsAu/8RAA4ACwCvAB4APQBEAMn/1P8AAO//8v+r/wQA4P+K/0YA7/8pACEA9/9BAJD/7//z/wcAPQD6/2kA+v9WAFgA6/84ANL/AADJ/+b/DwD7/0QAAABcALf//f8PAIz////t/ycAsv8vAMr/sP8IAND/NQDi/zAAuf8QADIAAwAVAMj/HAC7/yQACgD3/xwAKQAhAL//OgDT/8r/1P/K//r/6f8RADMAKQBGAAEAJQAwAMz/6P/I/wkAv//L//v//P8OANX/XgC5/9n/BQC7/9v/vf9dAN3/LQDu/8z/aQD5/0QA2//i/9b/zP8fAPX/LQAkAAsAGwA7ANT/JQD6/+n/EQDq/+7/g/9BACEA5f8gACwANgDQ/1oAyP+u/xkAp//d//b/+P/6/zEAOgDm/8b/GgAVABEAagBDAO3/OgAcACkAMwCp/zoAr//j/zIAAwBMAL3/EwDr/zgArf8ZAF0Ay/8xAKf/OQCb//j/+v/E/wYAvP8kAOf/NQDP/w8A6P/a/wYA8/92AMz/+/+z/woA5P/X/wMAgv/l/9j/FgAAAO7/AwC5/yIALgDc//b/0/8SAOv/3P8/APz/MwAXAEoA4P8dAGEA8/9RAPj/MADL/+j///9IAHIAyf9UANb/uf/Z/xcAEwAhAFIA1f8TABAA+/8NAPn/+/8yAAMA3//4/9X/AQABACUAHgDi/zEA8f8qAA8An/8NAK//UQD5/wwAigDv/zsAwv8pAKH/6/8mAIz/RwC5/0cA3v/A/9//if8OAPr/VgDq/yUAHgD0/wgA0P/s/yYADAAcACkA6/9vABAA6f/b/wYAFwATAEYA3f8IAND/7P8mAEQAJAAKAPf/5v/Z/7z/yf/B/ykAjv/J//n/ef/L/x4A9P/3/1QAQwBuAA4AVQAyAPL/GQC5//7/tf8MAK7/mf8bAIP/wP8WABEA/P/9/2wADQDm/2wA1v8nACAA4/9EAH//9f/3/x0A8//R/zUAq//z/z4A6f9bAFwAAAA4AOT//P8hAAgAPgANAB0A8/8HAAYABADy/xkAgwDp/yQAHQDz/wcAKwA1APT/GgAVAMj/0//J/4r/xv+///H/BQC7/xEA6v8SANj/FgBcABMARgAmAB8ABgA8APr/1v/M/9b/AgDe/3cAFgBJACgA/f/Y/6n/8f9z/+v/pf+S//H/4v/V/7n/NAC8/xIA/f8PAPv/DQAwAN3/GwC6/0gAJwD8//3/IQBSANT/XQBLABcA7/9OABoAAgAmAB8APgDW/zoAHAApANj/YAByAO7/cgASADMAvP/J/woArf/0/+T/xf8HAIX/wv9zAKX/bgAiANL/SQDN/0UAEgDY/wQAAwDx/xgAAQAAADgA9v8cAAQAKAD8/9j/FgDc//X/9/+d/x4ABgDz/4gAEQAgAD8ADgALANL/tv/F/6v/qv8WAO3/8f8YAO//BADf/+b/NAAFABYA7v/N/+n/tv/8/+r/JQALAPj/CwDS/wAAAAA3AD4AMgAoAEUAuP/r/8r/sP8/AMX/LAAAADYA9f/3//n/ef+4/7T/6P9r/y0AAAAkADAAFABsALL/QQDZ//P/v/8nAB8Avv9dAMv/HgCq/xYAJAAwAJUA0//u/83/6f8AAO7/AwBMAAYAFwBKADsA5//a/xcAyv/5/zEAOgD4/1UA/P/q/zcA0f/t//H/BQCp/9//wP8DABUA7f8VAMj/LgCl/yQAHQAFAE4A9v8JAOP/DQD5/zEAzP/W/wIAgv+t/8//2f/h/zAAuf9HAEsAvP8lAML/l/++/93/5P/8/+r/3P/j/x8ALAARAEUASgDz/1AALgDc/wcA9P8IAL7/AQATANn/8/8HACsAx/9SAAsACQAZAN7/GwC6/1sAEgDq/yUA1f8UANn/8/8HAAYABQDN//z/DgD6/+n/AAAkAPn/sf8uAO7/u/8RAPz/IQAIABkASwD0//b/QQAPAB8AUAD4/wsA9/+v/9H///8AANv/GQDd//f/QQAQAEQAEgDq/wAAAAAAADcA0f+1/x8Avv9LAOH/MABeAN7/QADG/wcAGADL/2gALwATACIAwP8oADIAKAAzAOD/HQDh/+f/2f+8/wAAyf/U/wEAAADv//L/GQA5AMD/KAAyAKj/FQCj///////b/z0AxP/0/5r/nP/U/6X/EgAPAPr/DQAKAL//AgAUANr/KgDs/yYAVgAgACwA7f/f/67/GQAnAA0AHAApAP3//v81AM///v81AAUABABNAOP/DABmAC0A7v8WADYAh/8MAOb/DwD6/9f/OgDB/wQAuv8QAA0AHQAFAOD/5v+i/w8Aw/8YAAEA3f91/+z/AgCT/04Amf8JAOP/6f/t//H/z//+/5EA9P+JAEoATgBRAEEA7P8BABMAj/8TANn/PADn/1oANgDQ/zUAqv8WAMn/CgAIABkAFAAiAEEA6/9LAOH/CwD3/9T/7/8EAAMAAgA5AAkA9v/l/0YA7/8XADcAv//w/xcAJQDo//////8jAC8A7//g/woA9//m/yIALQDu/9//HAA7AB0ABQDg//n/6P/I/wkAvv/w/wUAqf8VANr/GAAmAPr/DQAdABcA3P8aAN7/CQAsANr/GAAmAB4AYgDP/yEAiQDc/z4ARQA3AOT/IAAZALn/EADp/zYA4/8fAPX/5f9qAGgAQQA1AE8A5P8gAOT/sv/4/zAA3v/3/y8Apv9dAN3/9v/4/8L/BQCW/wYA8//2//j/+v/E/ysA2f/h/1UAaP/i//r/sv/T/zcACADQ/yIArv8GAAUAFgBJAE0AGQDe/0AA/f8PAPv//P8zAPP/LADt/97/CQC+/93/CADj/+j/yP+u/4f/DAD4/4v//v/H/+X//f/9/1kA/////+3/AgACALn/6//v/xcAAAASAA8AsP/A/8z/DQDm/9n/8//2//j/sP8bAPH/4v9DAAAAAADJ/8H/8v/1/wkA4/8NAPn/+v/7/8X/9f8JABoAFQB/AHkAKgA0AAUABAC6////yP8cADsA1P8mANb/AgAmAB8A9f8tADcA0f//////NgAGACoARwDw/2EAPAAeABgAJQBVAGoAQwAjAFQAHgArACIArv/Q/9r/vP/u/xYA2/8+ADIA8v9QAPf/ZwAbAAQAOgDU/zcAmv/T/+7/qP85ANP/t//X/wMA8f/P/+v/OADk/w4AMAACAAEAEwA0ALz/AADc/9H/NQD0/y0A2//j/x8A0P/+/9r/4f/6/9b/OgAcAOD/+f/6/1cA/f/+/1kA7f8nAEQAJABVAA0A+f8xAMz/RAA3ACwA///t/wIAp/8BAO//8v/j/+j/tv+N/xEAxf/j/wwAQQBHABQAIwBBAEcAAQBdAF4AJgDp/+3/AgC5//7/EADE/wYAFwAlADAA8f8XAAAA3P/2//j/CwAJAFEACgDk/1cAtP+w//f/wf+p//H/9P+a/+X/xv+s//T/mv/4/wsA0v+2/7L/CgCa/5z/+f/W/6f/7/8EAM3//P+z/9T/AQABADgALQAkAPn/DAD4/8L/FwAAAAAA3P/j/w0Awf8WANz/0P/s/97/CAC+//D/8//2/xwAOwALAMD/TAD1/xsAKACy//n/+v8fABkAJwAfABkAy/9DAEkA3/8cAAQA8v/i/wwACQD2/woA9v/4/wsAGwDy/wYABQDO/8X/LAAjANP/SgAEAPL/9f/S/0kA8v+9/+//u/82ABkAFACRABkAAgA4APf/CgBSAB0ABQBOAAcAYgAFAAQAOgCc//r/xP/P/+v/3f/R/9v/KwDs/xQA2v/P/8b/v/85AOX//f/G//b/HAC7/yQA5//Z//P/0f8jAPj/HgAYAKX/JQDn////NQC9/yUA1f+5/+z/uP/+/9n/KgA0AAUAOwBCABAA6f82AGMAPQAxACgAMgBNANH/7P/w/wUAFgCS/wIAzP+x/y4AAAASADQA8//2/+X/6/8lAOj/IwAuACUA+v+N/9r/vf8AABMA/f9HAMv/+/8gAFEAQQA0AD0A+v8NAOb/DwCx/9P/XAAAAAAAEgDr/xMANAAqAGsAHwBQAFMA6P8jAOb/2P8pADMA4f/5/0MAkf/x/yoAx/8/AP3/xv8IAPX/m//B/zsACwAbABYAAADu/5X/9P/R////2//P/0cAlP/g/woA5P/8/+v/EwD+/xAAjP/t//D/4f/n/6L/IgDl/yEAPwBFACUADACKAO//FwAlAOf/IgAcAPL/4/8MAIr/2P/y/77/XQBLADwAegAGABcAAADv/xYAtv+N/7b/DQALAC0AbgAPAFYAIAAHAAYAzv8hAOT/1/+o/6f/yv8LAPj/QgCRABkAXgACADkAGwADAKkAvv8mAB8AdP80AOH/+f9WAOr/7v/f/6//9v8JAPb/5v/9/9n/vP/u/ygA6v8AAIEA+v8NAC8AAQA4AAgAPgAfAOP/DAAcAPP/0f/a/8//2f/z/ywANgArACMAQQD+/9n/PADV/97/GwDy/+L/QwBbANz/KwARAPz/DgALAAkA4//p/wAAAADJ/9T/pf+3/7P/r//2/8H/BADx/xgA8P/O/yAAv/85AC4ANwAIAPX/UgD5//v//P8zADwAQgBtAGoAsgAgAAgAKwB+/6n/8v+9/wEAuP/G/xoAAgACAAEAXQAUAMf/CAAHACoAx//k/w4Awv8pACEA5P/F/77/FADZ/xcAJQCe/+j/7f/e/67/PgANAK//LADb/ysAIwBBACIA5f9FAN3/9v/m/yEArf+r/zsA5/81AD0AMQADABQANQDi/wwA0/8SACEA5P/X//L/4v/o/zYA9f8bAAMA3//l/6H//f8iAMD/zP/p/6T/yP/B/9//iv9X/y8AAQATADQAPABoABwAYQDz/6v/BQDN//z/RgDv/wQA8v+Y/9H/2//0/xsAzf8yADsA+f+NAN//CQBkAL7/JgAMAAoALAAAANv/4v/7/9f/cgASACEAZAD1/y4A3P8HAAYAvP9JABYAAAAkAB0AFwAlAPr/MgADAAIAJwDE/wYAzv/G/wcABgAFABYASQBgAE0ALABIABUA7f8VAFoANgDQ/yMA+P+w/9L/NgAZAN7/GwA6AAoACAAZAN7/9//U/+//KQAOANX/3f8/AMX/4/8NAPn/+v/p/zYA4/8fABkAy//o/7X/xP/1/xsAAwDM/w0AHACp/ygADgDn/zUABQA8ANX/8P/g/+f/EADp/+3/gv/S/yQA5v8PAOj/2//0/wgABwA9AEMAAADb/xkApv+T/wMAp/8UAOz/lP/z/77/8P/O/6H/DgCe//v/1/+V/wUAcv8gACwAtv9pAPn/6P/t/ycA/P8OAGcALgBKABcAEgBGAAEAyv/n////NQAGAM7/RgCm/9z/GQC5//7/tf/7/9f/g//l//3/2f/z/xkA3v8tANz/4/9EAO7/FQA2ACsAyP8JAPb/5f9GAKb/SgBgAOD/eQAXAN3/UQDm/9n/PADn////NQAYAAEAAQBdABMA/v81AAYA8/++/xQAEADW//H/9P8aAMz/+/9FANz/BwAGACkA6//d/1EA+f8xABUA7f8nANb/TAA9AB8AGQAUADUAz/9HAPD/qf8DAIL/0v8AANv/BgD0/ywA2/+9/10AuP/r/yYAw/8qACIAwP/x/wYAzv/9/+v/k/8WABIAxf/j//v/IAAHACsAfwBUADEAFQARAPz//f9ZAP//2v/i/wsAUwD6/9b/FQAjAPj/VQBpAB4APQBDAO3/3/9AACEAGwADADoACgDR/zYA9f9AAMb/UQBBAKL/7P/L/wwAZP8VAP//o/9IAAMAgwD8/w4A6P/a/wUAu/8SAP3/DwDo/xEA6f83ACwAtv8yAN//+P/C//P/LADt/wIAAgAUAMf/GwBNAKv/FwAAAKX/AADu//L/9P/k/+r/t//F/9H/IwAcAAQATQArAEgAOgBTAB4A4v9WAOr/t//X/6j/3v/l/yAACACY/7//AgAUAP/////I/9P/EgDY/wQA3/8JAD8AMwAWAO7/KADX/wMA8f+9/6X/yf/5/57/DAD4//r/HwD1/y4Ayf9CADUA4v8MAOX/xv+s/+H/w/+X/wcABQAXADcABwAGAJf/0P///8j/UwDn/9r/GACl/yUA5//s/zkACQA+AA0AQgDa/xgAOACa/y4A7/8WACQAHQCGACIALgAAANz/GQDx/2EAPAD6/3sAPgAgAAcABgBOAPb/UwAMAPj/CwDA/3IAJABUAGkA5//+/+z/3v/k//z/2P8WACQAHQDh/9X/AQDv/ykA6/8lAPr/sf8cAAQAqP8UABAAHwD1/4n/WADG/+T/MgDN/+r/t/8OAB0AYQAFADsAQgDH/xsAu/8RAOr/EgAhANL/IwDm/7T/HgArAMf/CAAsAO3/zP8fAOL/1v85AK7/LADt/97/QAAPAPr/+/9qAOj/EABpAPr/RAAAAAAAgABDADYAUAAJAOP/1//x//T/9v+c/7D/mv+u//X/CQAaALn/EAD7/+r/bgDZ//P/4//W/8z/n//E/wYAFwDc/z8ADgDU/+//4P/U/93/5P/p/8n/wf8EAM3/6f+2/3v/FQC2/8T/BgCX/9D/7P/L/x4AUAAbAE0ALAARAPz//f80ALz/AADu/6j/OQDT/6T/JAD5/8P/BQDg//n/+v/X/9//0//J/8L/KQDY/ykADgDo/0gAAgBwABEA/P/9/zQABQAEAE0Avv9LAPP/LAARAA4AVQDX/18AFQBtADMABAA7ANT/OAC//xUAIwDm/yEA0v/t/xUAIwAKAPb/LwDv/+D/VADo/yMAVAAfABkA8P/h/+f/IgDl/2sA6P///1sAtv8zAPL/9f9AAEYAJgAeAD0A+//8/yEALQAkAHkAPQAMAFMAsf/S/zcA4/8yADoACgAaAAMA8f+8/+//8v/i/wwA5v/Y//P/9f8bAOD/nP8LAMD/3/8cABYAXADc/3YAuv9+/zwA1f/L//r/DQCv//b/rv++/97/rf89AJ//6f/b/4b/1f+m/93/GgCV//P/dgCo/14AOQD4/0IAEABpAOf/fwCLAPD/FwA3ACwAEQBFAO//BAAoANf/AwBMAAYABQDy/wYAKgAiAGUABwAYABQAEAANAC8AOAAtAAAA7v9NAL7/EwD+///////t/0wA9P8IAND/WgDt//H/YQC8/yQA5/8iAEAAWQDs/wIAFAB9/3MAyv/n/zUA9P8aAMz/HwAZAPD/8//j/x8A4//7/w4Awv8XAAAA7v/y/6v/vP/J/woA5P8yAM3/1/8DAIL/CAAHAM//of/Z/wQAFgAAAMn/LwCl/xIA6/9u/+f/x/8IAOP/DAD4/+j/SAAnADIAAwDM//v//P8PAOj/yP8bAOD/CgAtAMn/QQAQAPv/MgC7/wAAAADJ/woA9v/B/+D/+f8wADkA5f8PAMP/l/8ZAMz/+/8gAL7/FAD/////IwD4/x4A4v/V/yYA1v/M/zEAp//L/0MA7f8VANr/z/8PANb/3v/l/yAA5P8NAEIA//8QAA0A5//Z/xcA7/8oALP/+f8fAKv/TgCa/wkABwDP/yIA5f/8/7P/1f8BAO//qf8oADIAqP9eADoA+P8wACcAHwA+AB8ALADt/97/GwDN/w0Awv/g/wsArf8rAP//yP8JAPb/LgAlAAsALgDv/wQAAwC5/7X/HwArABAAVwBYADUA9P/2/9P/7//y/77/EwDZ/zwA5//H/0AA2P9gAAQA8f89ALH/0/8lANX/8P88AAsAGwDN/w0AHQAFAGAA8v8ZABQA//9IAAIAOQAJAOP/6f/u//H/mP/R/8j/wP/f//j/CwDl/8X/BwDi/8P/dAAmAPv//P/Y/83/6v83AAcAPQAMAEEAIgDA/zoA1P8TADQAFwATALT/CwDl//3/WQD//yMAQQDs/zgA5f8OAFUAxP8ZAN3/iP/8/+r/EgDr/6X/3P/Q/9r/GAAAABMANAAFAOD/CgCI//z/MwDg/2cALgAlAAsA5f/q/8r/HQDz/xoAFQD//20Axf/j/x8Amf/k/yAAGgDx/yoA2f/h/+f/x/9AAMb/9v9BAEcAFADs/yYAjP///+3/8f/P/7T/HgCY/z8A/P/Y/2AAu/82AFAACQCtAC8A8P9hAM7/MwA7APn/jQDy/wYATwDS/xEADgD5//v//P8OAAsAQAAhABsAFgAkAPn/sf/l/9j/OwD5/wwAUwDV/0sAKgDs/wEA3f8tABEAMwApAA4AHgDi/x4A9P8tABIADgBDAMj/LgDK//n/1v+n/xMA/v81AAYAFwDc/xkA8f/0/z8A/P8PAOj/NQC9/wEAJQCe/x8APQD7/w4AVQDp/zYAGQDw/wUAcf8gAOP/+/8zAOD/ZgAbAN//QQD+/yIA0//u/ygAjv8AAAAAyf/U/+//BAADADoAHAApAOr/JQDn////IwD4//r/xP8YAN3/LQASACEA5P/E/2MA4v8xADkALgAlAMP/FwDc/+P/6f8RAEUAAAATADQAz//G//b/5v8hAOT/DgDn/8f/UgDV//D/BACW/08A5f/Y/xYA7v8VADYA9f/3/x0A4f8LAPf/QgDa/wUA8/8HAE8AiP9XALP/sP8IAGL/3f8sABEAjv9JAKj/8f8YAJP/cgDu/7r/yP/l/6H//f8PAOj/bQAzAAQA3/8cAAQAAwBfADoA0/83ACwA2/9QAPj/QgC1/9b/OgAJAGQAKwB/AB0A4f8dACoADwBWAEUAAABKAPP/9f8bABYAEgDY/wQA8f8GADwA+v8NAEEA2f8XACUACwAcALv/2//Q/9n/TgAtALb/6v/c/9D/2v/P/9j/lv/Q/6L/ov/r/wEAAQDd//b/5v8PAAwACQD2/y4Apf+3/yAA0f82AAYA8//2/+b/6/8TAKMAzP/W/xQAtf8xAAMAAgBeAPD/KgD+/9n/BQCW/9D/x//3//n/w//P/6H/6/+4/w8A6P+1/+n/kf8UAMj/0/8SAA4AHgCq/+D/r/+a/+X//f/+/8f/v//x//T/CAArAOz/OQAuABIAIQAtADcA4/8fACwAEQAyADsALwDw/04APwBFAO//BAByAMn/HAApAOv/OAC//ycA1//f/0EAxv8tAMn/5v/+/8f/QAAhABoA8f/0/+T//P/Y//L/UADT/wAAEgAhABoA3/8cAPL/4/8MAC8AOAD3/x0AFwCS/9//d//b//X/5f99AOT/agD6/8T/0P/H/+T/xf9RANP/3P/R/9r/BQCp/9//CQC//6b/JgDD//T/CAD1/wgAq//h/x0AGADv/2AAu/82AD4A+/8gAKz/dADw/87/6v8AAO//qP9eADoAHAAEAPL/9P8bAPL/vf8lALD/5f8zALv/yf8KANL/yP/4/x4AKgA0ACoA7P/w//P/PgBFANz/LAARAPz/DgD6/1YAMwAEACgAIAAaADoAiwAmADEATADQ/1kA/////xEAsv9nAPf/QgCkAKj/uf9+AHgAl/+Z/3cAOwDn/yIAwP+6/9r/YgBPAK3/mP8IABgA3f/3/9T/EwA0ACoA/v+i/9n/BQDg/8H/TgAaAAIAOQAbACgAs//C/wQAKAD8//3/DwCM/0gAcQARAA4A1f8BAO//OwBVAPv/DgALAAkAGQA5AEEADwBWAOr/EgAhANL/EQD8/1gAx//A/8z/jf/t/6f/EwAiAOX/IQDR/xEAIADj/+n/AAAAAO7/FQAjAK//0f//////JAAKAD8ADgDn////2v/i/wsA+P8dAPT/CAAYAMv/VQAgAAcA9P+//97/m/8vAO//8/8HAAUAFwC3/9j/u/+2/9f/AwDx/zwAMQACAEwAvf/v/+D/1P84AOT/RQAAAMr/+f8MAAoA9v8cALv/7v8oACAAPgAgABoA8f9PAFIACwAbABYAAACk/9v/GADL/zAAJwDW/wMAFAD///////8RADMAFgAAAAAA3P/1/0AAIQAtANv/q/8pAMb/v/8nAPv//P8PAMP/4f/V/93/GgA6AEEAx/9AAP3//v8iAIn/VwDr/xMANAC8/1wA3f/R/0gAFQDa/xgAOAAIAPX/QADr/7j/DwDD//T/mv8JABoA8f/0/wgABgCF/2cArv/j/+j/o/9tALP/QgDs//D/FwAAAEoAzv+PACkAIQBAAP3/DwD7/9f/AwAVAKP/NQAGAKn/8v/i//r/1//M/+n/2/8GACoA/v/+/+z/AgDd/+T/DgDC/wQAOwAdAM7//f/+/8f/igBKAPP/BwDi/+j/x/+b//n/6P/a/3QAFAAiAC4Ayv8dAAUABAAoAOr/yf/m/yIALgA3ACwASQA6APn/1f/w/+H/HQAqACIACQCZ/1IAMAACACYADAAvAJP/KADq/+7/KADY/2AAg/8uABIA2P8EAKj/OQCc/woACAD1/+X/s/8wAJT/BAADAMz/sf/B//L/mf+a/+X//f/Z/ykADwAeAND/NAAqALT/aAD4/x4A9P/3/y8A3f8tAKT/IwAvALj/WQAiAPj/CwBAACEAGwBfABUA7f8nAOn/NgDj//v/VwC0/2gA5v/G/z8Axf8+ACAA4//p/9v/GQDw/wQAFgDu/9//5f/r/8r/1f/L/+j///9+/8//DwCw/+X/WAA0APT/ZADj//v/IADj/3wAGgAnAA0A5v/s/xMAIgAbACgAxf8+APz/s/8wABQA7P/e/xsAuv/a/8//tP/6//v/MwAEAAMAJwAgABkAXgACADkALgASADQA4f8wAPD/BQAWANv/GQAmAOn/yP/4/+f/EAANAC8AuP+h/0YAuf+0/0MANgDj/x8A4v8MANP/AACTANL/NgD1/wkAUQD4/x4AKgA0ABgASgDh/+f/7P+4/zQAz//G/xoA8f8qAH4AUwAeACsAIgAJAOP/+/8OAPr/HwBjAPT/PwAzAOD/1P/d/1EA1P84AAgAvf8TAMf/9/8vADgAwP86ANP/t/9YAOz/JgAxACcA/P/q/+//4P/m/+v/AQDd/ywAtv/E/+L/w/8YAMr/MADw//T/BwDQ/w8A1v+5/9r/KgDZ/wQAFgDb/+L/sf/4//n/MQAoALL/1P+4/8b/BwDQ/8f/9/8cADwA5/8QADIAuv///+3/uf8QAB8A4/8MABwABAAWAFsAXAA4AD8AIAD2/8H/FgASALP/5/8QAOn/AAARALP/5//H/+T/1/+o/ycA1v8nACAA9v8JAKz/PAAeAPT/QAAzAGAABADy/ysA7P8UABAAewDj/9f/OgCu/1EAwf8EADoAHACYANX/JwDp/wAASQDN/w0A5//Z/+H/nf/o/xAA6f9uACEACAAZAMv/+v/X/9//CQAsANv/0P/H/63/vf8BAAAA3P/j/5//1/8VADYAGQAUANr/9P8aAMz/HwDj/0QAAAASAKIA8P88AB4Avf8SAP3/x/+//7r///8QAOn/EgD9/yEALQAkAB0A9P+///D/4f/V/yYA6P/t/8z/MQDx/xgAEwDZ/3MAAQBKAE4ALQAAABEAMwDg/woA0v8RANf/FgDu/9//HADg//n/HgAGAOH/MADL/0MASADy/ysA2v/P/9j/8/+r/zwAMADM/zEA8f/P/9n/4P/C/87/IQAIAL3/7/8EAM3/DQAdADwA6P/s/0wA4v8LAEAAxv/2/8H/4P8KAJr/CQAHAD0AHwAGADwAw//P/+v/yv/n/xAAxP89APv/xf8ZAMv/MQDx//T/GgC6/6P/2v/P//3/bAANAAoACAAHABgAEwBHAN7/9/8vAO//KQDr/7j//f+0//r/DQBCACIA5f8hAOT/IABRAAoACAAZAN3/9/8KAOT/IAB2ACgARQASAKH/WQDa/xgAJQDV/xQAtf8MANP/AADK/+f/EADW/wIApv8mANX/FABHAPH/9P8IAPX/iP8gAL7/uf/H/7//AgDw/zwAVQANAAsAGwCW/8//xv/2/+b/2f88AAsACQA+AEUAAABuACIACQAsADYAUAAcAOD/r/8HAJj/LQA2APX/LgAAADcA9v9BAOv/AQCl/7f/IQDk/yAA4/9EAO7/KAAOAML/PACw/xsA8v8YABQAtP8eAND/7P/w/4T/HACX/9D//v9+/yoA6/9KABcA3P/j/+n/2/+Y/z8A6v9KAE4AGgAnAA0A5v8PADEAuv8jAOb/RgA4AOX/MwApACEA9v9BAP7/WgC2/x8APgDE/5oA6f83AHYAFQDt/zoACQD2/2YA9/9BAOz/8P9OANH/EQBFAMr/+f/7/+n/NwAZACcAMgA6AC8AOAAtAEkAYAAoAOr/yv8vAAEAJgDo/7X/DQDU/zgA5P8NAOf/ov8iAPf/HQA8ANX/FADs//D/BQBx/7L/nP/U/93/PwBqAOj/SADx/8//2f/z/9H/x//l/6D/IQDk/yAALAAAACQAQQBHAN7/LQDc/77/FADH/+X/2P/N/43/yP8KANH/WwDu/wMAOgCc/y8A3f/k//z//f8iAOX/WAD+/xAAHwCZ/9L/2/+G//r/MgDf/wkA5P8NAOf/RwAUALX/HwCZ/xoAAwDx/08AGwAoAPz/IQAaACgA/P/q/xMA6/8lAAwA+P8LAPf/HQAqAFkA2v/h/zAAgv/k/8X/vv8mALH/QADZ//P/GQDe/wkALAB/AC8AXQDw/87/2P/y/2MABgA8AOf/2v8qAMf/9/9BABAAMQAVAMj/+P+e/+j///+j////7f8CAN7/9/8KANL/AADt//H/4v/o/+z/FAAQAA0AHQAXACUA1f/d/+T/sv/m/+v/JgAeABgASwAXAG8AEADE/1AA5f8hAC0A2//1/63/BgAXAO//OwAdALz/t//Y/+D/0/8AABIA/f/+/xAAVgAOAOj/EADX/xUAEQD8/yEA9v8KABoAAwACACYA1v8nADIAFgBJACgADgCw/wgA4//W/97/5f8zAOD/ZwDl/w4A+v+f/w0A1P8BAO//YADy/9D/EADE/wYAzv9GALj/NAAqALT/aADT/9z/0f/I//f/5/+i//7/RwDx/3QAEwA1ACoANABhAM7/DgDo/9r/GABdABMAEAAxADoAZgAIAD4A6f8SAA4AsP/3/6//9v8cAOD/LwAmAIz/o//a/8//2P/g/x0ABQDy/wYAGADK/8L/YQDO/8X/PgCg/w4A5/+1/0MApP/b//T/9//m/9n/KQAPAFYADgALAC4AAAASAP3/IgCt/+L/DAD4/wsACQA+ANf/zf/X//H/9P/k/w4A+f/o/+3/FQDt/wIA8P/h/x0AKgAiAPf/+f8eAGIAPQBWAHwA5P8gAAcAvf9KAOD/QgB/ANT/7//y/ysA7P8nAEQA7v8VADYAPgD8/w4Awv/h/+f/EAAyALr/EQANAOf//v9aAO3/3v8uALf/6v/K/+f//v/s/14AAgDd/wgA4/+x/+X/6//v/+D/QQAiABsAFgASACEA5P8NAAsAGwADACcAsv/m/zQAhf/n//7//v/I/y4AJQCd/wwAwf8DAPH/z//G//f/1P/K/0IAEADp/xIA2P/y/z4A1v8nAA0Aiv8PAMP/BQApANj/FgDc//X/GwDy//X/5f/q/wAAt//F/+P/MgAoAEUAEwAPADEAuv9HACcADQAdAAUAFgDJ/woA0v82AAcAvP83AKz/z//+/yIALgASAP3/IgBSAOf/IgAJAD8ADgDC/04A5P/X/00A9f/l/8X/0f///8j/CQDj/8T/4v+x/xsAu/8kAEEAEABWAOr/JQDn////7f8CABQAx/9AANj/BAADACcAIAD1/wkA0f9aALb/oP9FAMr/MABwACMAHAAEADsAHQC8/zcAPwANADAAy//V/wIAy/8MABwABABNAPX/9/9CANr/qv+7/6P/2v8GALz/JAALAOX/6v+3/+r/AADu/wMAJwDF/+P/MQDM/zIAFQDb/ysARwA5AEEANAAqACIA5f9FADgAv/8CADkA0//c/z4A+//8/1gARwAnANb/lf8XAMr/wv9OAAgABgDz/ywAAADb/z0AxP+9/wAA7//N/+r/AADc/+P/n//X/4QA2P87AGcAwP86ABwATgDk//z/MwDg/1QAxP/0/9L/2/8YAMv/+v/p/xEA2P9gADsACgD3/5z/wv9y/yAABwAGACoAIQAbAM3/VwAhAFIA5//+/zUAqv8pAMb/9v8JANH////t/97/CQAsAO3/AgAUAP//2v8FAOD/+f8MAAoALAB//+L/1f/L/x4Aq/8WAMn/nf8eAJj/rP8FAM7/IAAsAEkAOgBUAGgAHQAqANn/BAADACcA/P/Y/00A0f9IAAIAy/97APX/LgAlANX/OAAtANz/LAARAA0ACwD3/9T/uP/9/7T/+v+y/8H/KADq/xIA2P8EAIP/5f9GAMr/+v/E/ysAIgD4/1UAHwC+/6b/yv+w/9L/7f8CABQA///t/ycAxP8rAFoAAABbALf//P8hAL//OgDm/0YAXQDd/+T/6v/u/zoA5v/G/z8ADgD6//v/DgDV/7j/xv8IAAYA8/9RAPn/QwBIAAMAJwDE/+L/+//p/xIADgAeAE8ALQBJADsA5/8iAPf/1P8TAOz/3f9kAJn/9/9mAIn/IAC+//D/8//R/1oAEQBqAPr/RAA3AOP/aQAdABgAAAC3/47/3P/Q////7f/w//T/0f8jAOb/6/8TACIA0v9uAFgAov81APT/0v8AABEA/P8hAC0A2/8ZAAIAJgAxAAMAFABIADoAUwAMAAkAGgC6/0cAAgAUAFoA7f8nAA0ALwAmAMP/BgApAP3/6//d/+T/oP/q/yUAHQA8AEMAWwC3//z/DwD6//v/1/87AK//PwDX/5b/KgD+/38AHAAXAO7/AwAVAMj/HADy/wcA4f/n/+z/AgA5ABsAFgDu/wMAzP8fAGIA9P8tACQA+f/6//z/MwAXAAAA7v/f/+b/tP/n/zUAvf/v/xYA2/8HAOH/+v8NANT/3P8sABEA1/8oADMABADf/9P/7v8WAAAA2//1/63/q//g/+f/2f/h/53/HgAYAMv/jQDM/+n/JADU/xMAxv/3//j/6P/H/wkA4//W/zoA+P96AD0AHwArAP//EQDp/9v/mf/k/8X/4/8fAL7/7//z/+P/+//X/wMATAD1/0AARgDd/y0A2//1//f/1P/d/+T/DQDU/10A3f8IACsAtf/7/6D/6v+S//H/BgCp/18Auv8jAFMA1f/w/6r/AwDM/9b/OgAuAAAAOAAtALb//P/9/+v/EwDZ/xcAEgD9/zQA9P9RAC8AAQA4AC0Ayf8KAFIAnf/o/7X/n//p/7b/DQDU/yYA1v85AGUArf89APv/xP/j/x8ABgDh/9X/3f8tAO7/OgAvABMADwAMAOb/6/8TANn/TgAaAF8AJwBFAKYAPABDABEARQDv/wMAAwDe/0AA2P/z/9D////a/xgAAQDd/1EAnP8dABgA3f8sANv/BgDz//b/HAAEAAMA8f/0/+T//P/Y/7v/EQDX/wMAJwDX/zoA5v/+/yIA5f8hAPb/wf8EAPH/4v8MAOX/MwDh/8L/8/+Z/8D/8f8GAOH/MADw/wUABAC6/0gA3/8JAPb/HAA7AB0APAD6/8T/0P8iANP/AAASANj/zf8gANH///82APX/LQCS/zoA+P/V/14Auf/+//7/IwDB/xYA2//i/0MA7v8VANv/PQD7/w0A5//H/+X/xf8sANr/GAAmAB4AGAA4AOX/xf/R/5D/AQDv/04ABwAGAAUA4P9mABsAKABFADgA0v8AANv/0P8iAPf/QgAQADIAAwAVACMA5v8hAOX/MwDy/xkAFAD//yMAwf8EAMz/1v8DAAIA3v8IACsA7f85AOX/6/8lANX/FAAiAFMA+v/E/wYAKgAhABsAhABGAAEAXQDv//P/LADa/2IAFwDK/1UAHwD1/wkAUQAKAOT/RQDK/+f/IgAJAPb/5f8hAOT/DQAwALn//v/H/3b/7f/M/wwA5v/+/yIA0//u/6j/AgABABMAfgBBACIAGwAoAPz/DwAxAAIA8P9PAAgAGQBLAOH/QwDt/xUANQCr/+D/5//H//f/LwABAEoA8/8HAE8A5f8gAKz/vf8TAOv/yv8LAFMA+v/p/yQAr/+s/wUA4P/5//r/1//x/8///v+1/+j/7f+5/zUABgApACEALQAAAO7/OgDB/wQAAwDe/1MA+v9WAFgA2f/z/ywAtv/E/+L/1v+n/93/5P+g/yAAv//L//v/xP8+AA0AVAAfABkAJgAMAAoA0f8RAMX/4/8xABUA2//0/xsA8v8YAPD/4P/U/93/rP/0/wgAvf8TANn/4f8dABcASgA8AB4AKgDZ/+H/HQDh/zAAAgAmAOj/2/8rAOz/JgAfAD4AMgDf/9P/3P/R/8f/5f/q/9z/BwAGAAQAKAAgAC0ApP/t//H/vP8AAMr/+f/D/08ACADQ/zUAvf8TAI//7//y/ysANQDQ/yIA0v8kAPn/+//p/+7/KADX/zoAVADo/7b/HwD1/9P/AADu/xUA2/8GACoA6/9LACoADwD7/+n/JADn/1kA7f8CADkA0v8AAKT/JADB/wQAcgDJ/1QA1v85AC4A7/8pAMX/9v/T/xIA2P8EAAMAAgDL/9b/FACj/9r/GAA4APf/+P/6/+n/2/+Y//b/5v8hAC0AEgD9//7/EAANABwAFwCTAD8AIQBkAD4A6f/b/77/y//V/7n/IgAJAAcAz/8hAEAA6/9KAOD/+f8MAOb//f/r/yYADABTADEA8f89APr/IAAsAMj/eAAEAM3/6f+3//z/of8PALD/0v83APb/HAApACEA0f8RAPz//f8PAOj/SAA6AAoAGgDx/+L/DACc/y8AJgAMAAoAv/8UALX/RAAkAB0AYQApAGsADAAvAAEAyv/6/wwA1P/c/+P/1v/M/5//1/+D//f/wv+7/xIAjv8kAPn/6P///wAANgAHACoADwAxAPH/4v+NAN//5f9YACIACQDR/zUABgDh//n/6P8RAMX/PgBXADMAhgD+/8f/GwADAMz/+//q/yUA+f/o/xEA/P/G/6z/GAABABMA6/8BAN3/rP8qAP7/7P8mADEAAwDx/8//DwAeAPT/GwDy/xgAy/9DAEgAqP85AC4A3P8ZABQAyP9AACEACABQAOX/2P+p/4L/GwDf//j/HgDP//7/x/9AAOr/3P+IAO7/XwBxABIAMwDg/woAZAAsADYAdQBxADYA4/8MAOb/6//v/ykADgCe/wwA+P/V/xQAEADp/xEA6v8AABIAs/8dABgAEwDr/yYA1v+n/xMAx/8IAPX/5f98//H/GACT/04ALAAjAC8Apv8AAAAAgP8GAAUABAAWANv/GQDd/xoA3//4//r/1v85AAkALAARAA4A5/8QAMT/0P80AM//RgABAEsA8/+s/xgAk//N/8X/vv8BALj/6/8lADAAOQAJABoAFQDt/ycA+//X/ygA2P/y/wYAvP9uAMb/5P98APb/CgAIAAYAqv8oANf/KABYAH3/lwCe/9b/cQC2/2kAHQAFAAQAAwDx/73/NwD2/8H/4P8KAOT/6v9cAAAANwBkAND/RwACAEsAPQDW/wIAlP8EAM3/6f/b/5n/0v9///T/5P/F/ysAyP/A/xUAyP8vABMA6/8TAMf/LQDu/zoA1P+l/0kAu/82AAcAKgA0AOH/5/+1/9b/zP/o/9v/4v/o////EQDq/+7/8v/0/y0AEgAOAB4A9P8aADoAVAAMAAoACAAGAAUABABNACsASAAVALX/1v8VAMj/HABgABYAkwD2//j/CwAbAPL/vv8TALT/MQDM/+n/EQDF/wcAKgBHADkAwQBAADMAFwCl/+7/qP9LAGIA8/8/AEUApf/u//L/9P/3/9T/JQDD/wUA8v8+AFcA6/8lAPr/+/8OADAAAgABACYA+v/8/+r/AAAAAAAAyf9CABAA1v9MAAYABQDg/5z/CwDS/+7/FQARAGoA+v8fAAcAz//Z/87/6v+3/+r/t//Y/83//P/9/+v/JgCM/9r/z//9/+v/3f/k//z/6v+S/ygAsv8KAAgABwD0/3X/EADX/9//wP/y/73/7/87AML/PADV//D/4f/n/zUAz//+/xAAMQAoAPz/IQAIAOL/6P/t/wIAy//o/8j/CQD2/wkAdgAVAFsANwAsAO3/3v8uABIAWQAiAC4AEwBGABQA/v9HALn/2v/P/8b/9v/4/8L/FwDc/6z/9P/R/+3/AgBwAP//WwCAANX/XQAUAP7/2v8FAAQAu/8RAPz/of+z//r/1v/M/x8A0P/s/zkArf8rALX/n/8fAOP/DQDm/2sADQD5/zEAzP8MAPj/6P8QAA0A+f9WAPz//f/+/9n/KgDr/yYA6P/a/+L/+v/7/+r/JQDC/+H/5/8QANb/JwAyABYAWwDJ/y8AJgAxACcA6f+lABYAAABcAO//FgBbAAAAJQAdACoANAD0/xoA8f/P/zQAPABVADIA4P+v/7//OQD4/2cAeAAEAGAAOwAdAAUA8v/i/x8A0P8QAFYA2P9NAL7/8P8XAMr/ZwAJAAcABgAFABYAJAALABsAFgDI/+b/6/8BAMr/MAACAPD/TgAtAEkA3//m/w8A6P8RAPz/6v/v/wQA3/+u/ywAEQDX/00A0P/+/1oA2/8GACoA/v+i/yIA0v+k/wAA7f9fALr/EAAfAKz/TwAaABUAIwDm/zQA9P/k/zIA8v+r/ykA6/+4/9j/qf8nAA0A+f9DANv/9f/3//n/+v9EAO7/8v8rAJD/8P8XAAAAyf8KAOT/1/8DAMz/DQDU/zgA5P/8//3/j/8AALf/6v+l/8n/HQDO/w4A+v/7/9f/zf8NAAsAQABYACIAQAD9/8f/CADQ/9r/z/8PAOj/kP8UAOz/y//6//v/agBoABwAmAD6/+n/kwD2//j/HgDh/zAA8P+X/+P/xP8GAAUABAA6APj/MAA5AAkA9v/4/x4A4f8LAC4Ayv/U/+//4P/m//7/NQDi/zAAAgACAPD/qf86AMH/4P/m/8b/5P/q/wAAt//8/yEAZAAHAGIAPADD/xgAyv9CABAARQBKABYAbgDr/10AEwDs/xQAov8iAPf/1P84AIj/1/8VAKP/tf/E/wYAzv/r/yUAsP/3/+b/7P/d//b/QQC0/x4AGACm/yUA+v/W/wIAFAAQAPz/DgDn/xAAxP8GADwA6P8QACAA0f/a/z0A6P8jAAoAUgBCANr/YQAXAO//AwAVAP//JAAdAPP/BwBz/w8Aw/+X//b/d/8AALb/IAAHAL3/EwDG/9L/EQBFAAAAEgDY/wQAOwDm/1kA//8RAEUANwDk/8T/GQCm/wEAEwD+/yIA5f/9/6H//v/s/8v/egDQ/xAAMQDM/+n/7v8VABEAMgApACEA5P/p/wAAyf/U/6X/AAAAAO7/FgDb/+L/6P/a/+L/MQACADkA9/+d/x4Avf/c/xoAAgACACYAMQDM/zIAAwDM/w0A1P/K/x0AFwA4AD8A/f8hAAgA4//7/8X/9f8JAAcAPQAfACsA7P85ABsAzf8yALv/AAAkAPn/DADB/00A4//W/xUA7f8UANr/GAA4AD8AfQBSAEIAEADp/wAAyf/B/wQAKAD8/+v/AADv/xYA2/8GACoAj/8lAOj/kP/d/wgAPgD7/zMATgAaACcADQAKAAgA9f/l/+r/7//g//j/6P8QADIA8v8GAOH/wv/O/w4AQwDb/z0ADAD4/x4A9P8/ADMAKQDr/xMADwDD/wUA4P/5/x4AKwA1AAYAFwDc/9H/EAD8/zMAFgAAABIAMwAXANz/GQDM/+j/EQAgACwAyP8JAOT/6f/b//X/0v/u/zoAwf8pAA4AHgAYADgAdwAEABUAAAA2APX/LgBKAM7/RQDv/04AYwAZACYA1v8CAN7/0v8AABEADgALAC4AEgD9//7//v8QADIAAwDx/wYAzv8OAAsA0//c/77/AQC4//3/2f+p/00A4/8fAOL/6P82AND/EACx/9P/EgA0AAUAKAB9ABsAXwAoANf/AwAnADIAKAAOAPr/6f/t/7r/ov/a/8//xv+//xQA2v8qAP7/tf9WALP/LwAUAOz/SwAFACkAof/r/8r/1f8mAPv/MgDf/xwAKQDr/yUAHgAYACYADACu/9H/2v/h/wsA5f8OAMP/9P8aAMz/RADu/ygAMgDy/1AACQAaABUAIwAcAAQAKAAzAE4A4/8yAAMAp/8UANn/vP/J/9T/JQBDABEARQDv/xYAJADU/28AEAANAAoAv/8CAAIA8P8pAP3/tP+e/4z/tf+f//z/s/+v/y0Ayf8KAAgA9f8JAL7/AQBLAPP/LAARAI7/7v/f/0EA/v8QAB8A4/9oAOb/WQBtAOr/NwD2/wkAPwAOANX/EwAQAOn/SAADAPH/KgAiAOX/DgAeAL3/3P/2/+X/2P+7/9v/hv+L/8f/iP/p/8n/5v/Z/87/DgDn////IwD4/x4ABQCp//H/GAAmAAwAwf/g/woAPwAzAGAAFgDb/xkA8P8qAFkANQD0/1IAHQDh/wsA5f/F/9H//////zYA4/9oAEIAx/9SAAsACQC+/xQA2v+X//X/rv/1/67/4//o/+3/zP+x/xwAu/8RACAACAAYAMv/+v8yADoACgAaALr/o/8jAK7/4/8fAPX/LgDJ//n/aADU/wAAAACS/xUA2/+9/yUAw/8YADgALQBJABYAJAD5/x4A9P8IACsA///t//H/z/9X/8L/zv+g/+r/JQBDANr/KwA1AAUA8//2/+X/2P8WAAAAEgDq/yUAMADw/zwADABTAEMAEQAOAAsA0v/u/xUAtv9XAGsAHwArAP//IwD4/9X/OQD3/y8ASwAFAPL/0P9HALn/2v9hAKn/OgAcAOH/+f/o////AAAkAMH/8//1/+X/RgDd/wgABgDz/z8A6v+BAGgAZgBkAOP/DQCv//b/HADz//X/5f8hAK3/4v/o/0gAFQDa/z0Asf8JAAcABgBOABoAAwDe//f/r//R/9v/z/80AM//6/8AALj//f/+/xAA+//q/+7/3/8KAPb/+P/n////7f8CAAEAy/8wAN7/UgBCAMj/CQD2/0EAIgBSAB0APABDAAAAJACK/+v/AADc/xoA8f8FAPP/GQAnAEQAJABCAEgAFQBtACAA5P9EABIA/f8iANL/7v/M/9f/AwDM//v/6f/b/ysAEAANAOf//v/H/8D/AwDM/wwALwDd/xoA8f+q/xYANwDR/1oA7f/M//v/jv9JAPL/9f9lAL7/AgDd/7//8f8FAAQAFgDJ//j/1f+m/0oA8/8+APz/6v8lALD/QAAhAPb/LwABABMADwAfACsA7P8UAEcA8f8qAEcAOQAJANH/tf+f/9f/FQA2AAYAPADo/8j/+P/n/9n/8/8/AKD/6v/u/4P/ZQAtAO7/KAAgACwAIwAcAOH/5//s/93/LQASACEA9v8cAAQAcf9WAA4A1f8BAAEAEwDZ/04A9v8KAPb/LwAlANX/cADI/9P/7v8DAEwAGACCAB8A4/9WAEUAEwD+/8f/wP/x/yoA7P8BACYAw/8YAAEAyv8LAOX/2P8oAP3/DwAMAPj/MAC5/zQAPQCM/8f/9//5/9b/AgAUACIA5f/r/9z/vv8mAOn/EQAOAML/TgAaAMz/MgDf/9P/NwDk/w0ACgD3/9T/yv9CANr/BQBhAAQAAwAnACAArP+8/xIA2P+W/+L/sf/A/zoALwATAP7/IgAJAAcAPQD7/9f/3/8uALj//f8PAOj/NgDQ/xAA6f+2//z/s/+v/7//JwDE//X/GwAWAFsAyf9CABAA6f82ABkAJwCM/0gAJwCy/xwAvP8SAP3/2f/z/77/8P88AB4ABQAXANz/GQDM/8P/4v/V/yYAMQBNAPX/LQDu/83/1/+6/xAA6f/u/7r/NQCr/87/IACI/1YA6v83AFEAwf87AML/4f8LAPf/QgAiANP/EgAhAAgAGQAUAFoAyP8JABoA3v8bALv/EQD8/9j/OwDn/yIALgAlAAsA9/8LAMD/KAAgAPb/CQD2/y4AEwD+/9n/FwDv/6j/FQD//8j/CQAHABgAJgDD/xgAyv/V//D/8/+IABEAjwAqAOv/SgDh/2cACQAaAAIAy//D//T/9v/T/wAA3P8ZAN7/GwADABUA//9s/y4AAAAAADcAPwAzAPL/KwAQAPz/2P8WANv/hv8eAL3/7//g/8H/TgAHAD0AMQCn/97/9//m/+v/OAAbAPL/UAB4AGAAKQAOANX/3f/k//z/DgDo/9r/KgBHAKb/XQA4ABsAXwDy/4cANQAZABQARwAUANr/dADw/wQA4P/m/0YA8P/h/x0Az/98/xYAEgDF/+P/6f+2/8X/0P8QANb/8f89ANb/AgCm/+//KQD9/w8AHgD1/9L/SQDN/w0A+f+e/+n/tv/8//3/NABhABcAJQDC/wUAFgDJ/woA5P8NAOf//v81AOL/aAAvAAEAJQAxAPH/4f8wAJT/zv/Y/xYAAAC2/yAAv//w/7z/3P/Q/9r/KgDZ/04ACAAGAE8A9/8cACkA6//v//L/9f/3/6//LQDu/8z/RADc/wcAPQAxABUA2v8GABcANwA/ACAALABIAE0AGQAUANr/9P/R/zYAPgAyAF8Azf9XAA4A6P8QAOn/SQDN/zIABADx//T/5P8gAKz/BQAXABIADgCe/7H/if9W//j/6P+1/zEAzP/X/ycA1/8DADoAwf9gACgA6v9cANz/LADb/+L/DAD4/1UA/P/F/wcAGADK/x4Az/8PAFYAoP/q/xIAs/+w//f/1P/c/+P/RAASALP/+v8MABwA8/92ACcA/P/9/9n/KQDr/+//hP/B/xYA2/8rACMA+P8LAPf/1P8mAPr/RAA3AAcAKwDs/yYADAAvACYAQwAkAMH/8v/j/+n/tv/E/z4A6f8AAFsAAADc/6z/4f8LAAkALADa/wYABADy/5oA/P8hABoAuv81AOL/6P8jAOb/2f/z/77/8P8XAMr/QgDa/wUAKQD9/w8ADAAvAAEAXQDd/+T/6f+k/xEA/P8hABsAAwACABQA7P8UAFoAAAAkAC8AJgAeAOL/1v8CALn/DwDW/8z/aACd/0MA7f+5//7/2v8qALT/QwDI/8H/4P+v//b/0/83ABoA8f/P/0YApv/K/zAApv84AIj/n//p/5L/8f8YAO//4P8vACYADAD4/zAA8P8qADQAPABVANf/TQAZABQA//81AD0AxP8rANr/KgAPAB8AKwCi/9r/hf8vAEsAz//9/7T/sP/l/w4AHgAFAOD/5/8iABsAzf/8/+r/7/8WANv/UABTANX/OQDl/8X/LADt/xUANgAGAAUA8v/Q/+z/3v+//97/5f9YACIAGwAoAOr/JQDV/yYADADm/+v/uP80APP/GgAnAPv/xf8HAAYAPAAeAOH/VQCg/w4ACwDS/+7/8f+9/4D/BwDP/2sAHwD1/y4A7v8oAA4AMAACACYA1v8CACYAHwBQAPj/VQD7/yAAZAD1/1MAMADw/+H/1f/w/7z/NwBRAPj/jAA6AAoA0f+R/97/0v+2/yAALACR/xQA2v+8/wAA7v/y/9D/IgD3/wsALQAAACQA+f/W/0wA4v/6/2kA5//+////NQAGAAUA8v8HACoA2f8pANn/8/+s/yoADwDo////tv/X/17/WgBIAE0A4v96//D/BQDOAAAAEwDr/wEAXQCCADEAqP8mAPv/agCw/5v/LwABAEoAFwCS/7r/IwAKABoAgv/A/ycA/P8hAPb/CgDk/0UAXAA4AC0AJAAvABQARwAUAMj/wP+D/67/mf8+/4n/e//f/9P/f/8GAAUA8v8HABgAuP/9/1kAWgBbABIARgAmAFYAagBDACMACgA/AEUA3f8HAFAAQAA0ABcASgAXACUAHQA8AEMAAAA2AOP/6f+j/+3/AgDw/08A9v8cALv/2/8GAOH/1f/d/+T/sv/U/+//zf/X/9//0/8AADcACAD1//f/1P8TALT/1f85AOX/6v/v/ygAs//n/0cA3v9SAAsAGwAoAOr/7v8DAPH/4v8wAMz/1v/x/6r/4P8KANL/2//i/9X/AgBLACoA/v81ABgA7/8pAGsAHwAZACYA1v9eAAIA8P9PAK3/z/8PANb/8f/h/x4A4f8LAAkAmv8bABYASQBNAOP/+//q/xIARgDd/9H/EQDF/ysAIwBBAA8A1v8nAMT/0P+0/1YADgAdAHQAEwA1AL3/3P++/wEA3f8IAD4AHwA+ALL/HADO/7P/+f8xAN//GwBNAAcAmQCx/xwA4P+v/y0A2/8GAOH/+v+x/wkA9v/B/wMAAwAUACMAHADg/woA9//U/yUA6P/s/xQA2v/0/y0A2//Q/+z/8P/z/wcAKgAiAC4ASgDg/x0A8/+a/1MACwD3/wsA5f/q/yUACwBlAGQAGQAnAOn/JACc/wsAGwDN/0UAgP/j/+j/yP/B/6j/lP+p/9//rv8sAMj/+P/C//P/YwArADUA0P/+//7/NQDQ//7/IgDA/zoA1P/v/xYAEgAzAE4ABwAGAE4A9v8KAD8ADgDC/+H/5//+/+z/FAD//7X/6f+k/9r/9P8IABkAuf8iAAkAvv85ABsAFgARAMX/0f/I//f/HQBPAAgA9f/3/8L/BAA7AJ4AEAANAB0Aqv8oAA4AMAA5AAkABwDi/wwA+P/V/93/9v/B//L/0P+i/8f/5P+z/9T/7/+W/xkAy//V/xQAx/8JAIf/QwA2AAcAdAAmAHsABwAYABMA2f8pAP3/IgAuAO7/KABYADQAYQApADQATwAaAEwAKwAjAC4AAAATADQABQDg/woA0v/b/9D/tP8MAC4AOAAIAD4AHwD1/y4At/+g/3z/qP/w/yoARwABAEsA4f/6/+j/yP8uACUAVQDp/1wAJQDn/0cAzP8MABwA8/8HAAUABADy//X/9/8dAAUAzf8OAEIAyP8uAAAA3P8ZAAIAFADs/0sABQDz/+P/xP/0/9L/JAD5//r/MgADAAIAOQD4/x0APADo////2v/0/xsATQA+AA0A5v/Z/wQAKAD9/w8ADADm//3/x//k/9f/zf/X/9//HADN/+r/EgAOADAAAgACAPD/zv/q/8r/5/8iANP/7v/f/+b/DwDD//T/LQAAADYAGQDw/+H/CwBAANj/BADN/6D/1//f/xwAu/8kAPn/+v8fAOP/aQDC/ykARgC4/w8A6P/a/73/3P+s/+H/1f/w/xcApf/u/xUASADy/wYATgAaADoAVAAxAAIAJwDp/wAAAADJ/woAv/8VALX/n/9EAMn/LwABADgA5P/q/1wAt/8zAM7/MwApAOv/SgCp/ygA/P8hAPb/HAApANj/KQDG/xoAzP8MABwA8/8HAKr/qf+6/8f/rv/i/7H/5f8OAB4AGADL/wsAm//U/zgALQDb//X/QADr/xMADwBDAMn/wf87AOf/RwAnAPv/IAD2/y4AOAAIAAYABQBOAPb/HAApAOr/NwD2/xwABADf//j/CwAJAPb/LgDc//b/CQAaABUANgA9APv//P/9/yIA5f+g/7P/+f+M/9r/GAC4/0YA8P8XAAAAJQALAOX/MwAXAEkA4P9BANn/qv8WAAAAEgDY//L/q/+8/8n/+f8MABwAYAAEAE0AGQA5AC4AJQBVAPz//P8PAB4A4v9DAAAAAABJAN//LwABAJP/qP8CAAEA8P8EAAMAp//e/4kAAAA3AD8A/P8hANL/2/8GAAUAzf8zAOD/r/9kAAYA9P8/ADMA8v/Q/+z/FAAQADIAFQDt/9//+P/5/+j/EQDF/wcAYQDz/ywAEQDq/+7/qP/w//T/v//e/wkABwD0/7//zP/7/3v/3v8JANH/////////7f8CAAIAAQABAO//OwAdAOH/wv/h//n/+/9XAA8A1v8CAMv/aABUAAwALgDv/04ABwAYABMAx/8IABkAJwD7/zIAFgASACEAdgBNAPX/QAA0AAUAu/8AANv/KwD//yMAeADh/zAA8P8FADsAwv8XACUAHQAqANn/TgBSAML/TgDj/9f/AwDx/wUAFgASAMb/ZAC+/+//BADN/zIAu/8jAMH/FgDJ/+b/DwDo/yMAr/8/APz/MwDz/9H/7P+C/wgAq//g/9T/EwAPAMP/PQDo/8j/0/8AAO7/3/8KAPb/5v/r/8r/5//a/+H/+v/7/+r/3P8+AB8ALAD//xEARQCl/24ANADz/xoAzP8MAOb/xv+t//T/rf+9/wAAyv/n/7X/HwA9APv/MgDy/+P/+//8//3/2f8EACgA/P9GADgAGwBfADoACgAaABUASAADABUANQC9/yYAHgD0/y0AJABUAOn/7f8DALn//v81AD0ADAAcACkANAAFABYANwC+/0sAGAC4/+v/uP/9/yIACQAHAAUA4P8dAPP/0f///9r/GAA4AEAARgBvADUAPQAxAMz/6f/t//H/z//+/8f/wP/f//j/HQCX/wcAvf/v//L/4/9EALb/VwDG/7//3v/3/woArf9iAKr/zf8gAFEAVAAeAD0AxP8GAOH/5//Z/7z/3P++/7j/2f8EAM3/6v/u//L/GADw//P/GQC5/1oASADf/3gAzv/9/9n/4P8dAOH/jAAVABAA6f+2/yAA0f8QADIAzf8NADAA3f8/AEYA7/+7/9v/GQC5/+v/y/+w/xsA8v8GACoAxv/2/8H/qP8VAO3/TADi//r/RAAAACQAMADw/7z/NwCa//f/+f+x/y4A3P8HABgAJgAMAAkAGgACAAIAAQATAOz/8P/h/+f/7P8BAO//zv+g/7P/HQDh/+f///8QALL/5v8hAPf/VADW//H/9P+s/8//2f8pAOv/AAAlANX/FABaACMA5v/Z/wQA8v/1/wgAvv+4/9n/8/8HAPT/GgDM/w0A+f/V//D/4f9VAPv/MwA7ALD/dwAWAEkAlwALAEAAIQDk/9f/AwDx//T/PwAgAAgAUAD3/+f/WQARAA0ACwAIABkA3v8IAAcAGAA4AAgABgDh/9X/AQABACUA+v/X//H/9P8IAPX/UgALAAkAdgA6ABwAFwAAAKT/7v/x/+L/+v/7/+r/AAA3AFEALwATAFkAyP8uACUAsP9AAKH//f/Z/87/6v/K/zAA3f8IAPX/GwAWACQALwDw/zwA+v/W/8z/n//X/7r/7P8nAOn/AADt/wMAAgDL/wwA5v9YACIALgBvAP7/NQDP/9n/zv/Y//L/q//h/zAAAQABABMA6/8mAEMAWwDu/wMAAgC5/0cA8P9PAC0AJABUANb/OgDT/yUAnwAkAFQAMQDM/x8AGQDe/1IAHQDh/wsA9//5//v/DQDn//7/IgCu/xkAOQDT/0kAFgASACEACAA+AB8A9f8JAPX/if/q/wAAyf/m/9n/vP8AABIA2P87AAsA9/8dAOH/5//+////EQANAOf/EACx/9P/EgCz/wsA5f8zACkA6//v/wQAOgDU/zgAv/+C/63/hv8wAMv/6P///7b/xP+r//P/9v8uABMAIQBAANj/YADy//X/LQDc//X/wP/f/8H/8v8rAOz/pv+l/5L/zP/7/3v/8f/0/+T/DgDV/93/v/8UADUAGABdACYARACTABoAJwBEADcALAARAA4ACwAuANz/GQAnAA0ACgDS/0gA3/8uADgA5P8yAJb/4v8xALn/EAANAAoAPwBGADgALQBJAE0ALABIAPH/GAAmAOj/IwAKAL//AgDe/3b/o/+1//v/IAAHACsAIgAJAOP/DQDU/8r/CwDS/+7/OgAKAK3/BgDh/6//CADQ/9n/4f9CABAA1/86AMH/KQAOAOf/IwCu/+P/6f+2/+n/AAAkAPn/+/8NAC8AJgBWACAA0f8jAAoA9v/4/+f/x/8uAAAA3P8+AA0ACwAIAAcAKgBHAAIAFAAiAOX/MwC8/wAAAAC3/zMA4P/m/9n/BAADAKf/8P/z//b/+P/6/wwACgAtADYABwBPAEAAIQA/ACEACADi//v/aQALABsAFgDb/9D/ov80ABgAAQATADQAKgAPAGgA1P8AAMr/sP8bALr/EADX/8z/xP+Y/63/4v8eAM//DwAfAAYAFwC3/9j/lv/i/wwAif8OANX/pv/v/+D/LwDv/xcA7v+o/ycA+/+z/9T/AQDv/ykAMwApACEALQAkAPn/ewAsABEADQDU/8r/+v9pAPn/6P/t/xUA///a/ysAEAD7/+r/EgCz/8L/4f8LABsAqP85AMD/FgBJAAMAcQAAALb/RQBKAM7/RQDv/ykAIQAIAJoAoP8gABoAuf///+z/AgCm/+//zf8OAAsALgBcALj/DgDo/yMACgDk/yAA9f8uABMADwAMAAkAv//w/8//IQBkANH/IwD4/x4A9P8/AEUA7/9yANz/LAAjABwAFwDu//L/GQAUANn/TwCI/+n/7v+D/wkAmf/3/9T/pf8SAA8AHgD0/wgABgD0//b/5v/Y/wQA8v8ZABQAEABEABIAWADZ/+H/MADe/0AAWABZAEgAJwANAOf/2f8XANz/9v/l/6H/IQC//8z/DAAcAPP/BwBPAOX/IAD2/0EARwDL/zEAOgAKAPb/CgD2/3gATgBkAIgAAABJAN//CgAaAAMAFAD//8j/+P9VAJ//RQASAOv/SgAEAE0A4/9WAP3/2f8EAPL/9f+b/y8Ayv/C/87/2P/N/+r/SQCp/xUA/////xEAsv9CAOz/3v8IAAcAGAATALT/1f+m/4D/4//p/+3/zP8fAL7/y/8wAN7/QAD9/w8AHwD1/y0A3P8sANr/9P9SAB0ABQDg/+b/6//v/wQAKADq/8n/CgAIAPX/LgC3/6D/6v+l/8n/+f+w//f/LwABADgA9//5/9X/FABaAH7/TwAIAKv/FwCl/wAAAAAAABIAMwApAP3/NADh/+f/WgBbACQAQgC1/9b/FQBZ/wwA5v/G//b/+P8eACoAIgCu/ysA2v+q/wQAAwAnAA0AVAAMABwATgAsABEA6v83AL//8P88AOj/7P8CAMv/6P81AAYA8/8aALn/ov/+/6P/EAANAMH/YAAWAO7/8f8GAOH/1P9LALz/7v86AOb/2f/h/+f/2f8XACUA+v8NAPn/HgArANn/KgDr/yYAMQDe//f/5//+/9r/PAAxAPH/4f/V/7n/j/8TALT/6P/s/97/UgDn/yIA0/8AADcA9v8JABoAFQC1/w0A5v8iABsAAwA6AHf/EgBYAP7/WgBbABIA/f/G/9H/NgD1/1IA+v/E/+L/1f9wAP//WwBJAM3//P/q/+//FgDJ/+b/RgAUACIA5f9GAAEAAQBdAMr/VQDX/xUASADf/y4A7/8pAMX/4//X/6f/y//V/ycAsf/4/+f/2v8qADQAPAD6/x8ABwD0/9H/7f+n/6b/EwDG//b/LwDv/wQAKADX/xYA2//i//v/sv8cALz/AAAAAO7/KACy//n/6P/a//T/9v8KAAgA0P8iAAkA4/9XAP3/IgAbACgA/P+h/w8AsP/l/0UAOAAIACsANQD1/xsAzf/8/7P/MABeAN7/UgD5/+j/2v+9/+//KQDY/+D/QQDs/yYAMQBMAD0AaQBCACMAQQDZ//P/BwBiABcA7/8WAO7/8v/i/zEAuf8QADIAqP/L/9b/OQDA//L/GADw/wQAqP8CABQA2v/h/wsA0//u//L/mP/R/9r/GAATACIA9//5/x4AGABLAAUAKQDq/wAAAADv/xYA7v8oAA0AQgAQAA0ALwDL//r/6f/t//H/BgDz/77/3v9AANj/4P9BANn/PAAwAF4ATAD0/+T//P9rAPv/VwAhAPf/CgC//0wA0P/+//7/2v8qAOz/FADZ/xcAyv/5/wwA0/83APb/LwA4AC0A7v/f/y4A3P8sAO3/p//d/7//JwANAPn/HgC9/yUAegD1/xsATQDj/wwAQQAQAPv/1/8WANv/4v/7/8T/BgC8/zcAPwDF/2MAGAABAAEA7//g/9T/7//N/yAA9v/4/wsA0v83AAcAKgAiAOX/MwAEAAMAOgAKABoA8f8YAMr/5/8QAB8ABwDh/zAAzP8MABwAqf/M/8T/BgDz/wcAGAABADgA9//m//7/x//3/+b/2f8FAM3/IAAHAPT/GwDf/xwA4P/5/zEA8f8qACIA9/9UAFYARgCUAOX/6v/c/9H/EADp/0kAzf/X/zoAnP/C/wUA4P9BACIACQB2ALr/EAD8/6D/WADH/y0ASQAWACQAr//k/+n/2/8ZAEsAKgA0ABgAEwD+/9n/BQAWADcA9v/4/zAAAgAmADEAOgBTAAwA0/8SANj/BAA6AOb/NADP/+v/3f+a//f/r//2//j/1f/L//r/VwDG/ywA7f+C//f/r//k/w0A+f/W/97/0v+R/4MAMgAWAEkA8v8GALz/XADc/77/AgCB/wcA4v/6/zIAKABFAO//BAADAAIATADi/+j/NQAYADgALQASAI7/t//q/5L/8f/i/+j/7f/e/9L/yf/4/+j///8jAPj/+v+x/wkAUQDB/2AATQAZAHEAyP/T/9z/0f/a//T/LQBbAFwA7/+FACEAv/8nAPz/MwC7/+7/AwDM//v/1//N//z/6v8AAEoA4P+v/7//y//D/5j/9v/4/9X/3f/2/+b/6/8BABMANAD0/ywANgAsADUA4v/7/yAAGQAUAOz/8P/z/7//y//D/+L/HgDP//7/EACx/+b/IQAtAEkA4P/m//7/j/8lAEMA7f9MAAYA8/8HAL3/3f8aACcA/P9FABMA/v/Z/4X/1P+T/6j/3v+t/9D/EAAxAKj/FAAQALL/5v/Z/xcAt/8zAAQAFgARAI7/NwAHAAYABAAWABIAMwBgAPL/UADl/w8ADADl/0YAJgBoAB0APAALAAkAGgDe/xsATQA+AEQAJQDn/zUAGADK/zAAOQDl//3/NADh/+f/IgAJAAcAPQAxACgAIAAHAD0A+/8yAAMAAwAnAMT/dQAUAOz/OQDT/wAA3P/j/9b/zP/E/6r/8v8ZAPD/BQAWALf/oP/9/9j/KQAhABoAcQAAAAAAAADb/wYABQA7AB0A4f/6/+n/2/8YAN3/v//x/7z/7//N/9f/FQAkAC8A8P/z//X/GwDy/xkA8P+8/xIA/f8iABsA8v8YAHAA2v/P/zQAl/8sAP//yP8cALv/7f9MAND/7P8mANb/AgAmAAwA1P8lADAA3v8JAND/IwAJAAcAPQAMAPj/+v9EANz/GQA5AAkA4/8NAPn/6P9aANv/BgAXAMr/5//+/zUABgAFABYAWwBKADsAHQAFALv/2/8+ALH/CgDk/5//IADj/9f/FQARACAA9v/T/1wAEwAPALIARgABAO//zv97/9//+P+w/+T/MgApAP3/WQC1/wwAZgCb/0EA/v/s/wEAk/8EAM3/MgAoAMX/GQDM/7H/5f/Y/6n/uv/a/wUAFwDu/ygA1//y/z0ADQAvAAEAAQDK/8L/4f/n/+z/FAAiANP/EgCO/6T/yf+v/2MABgAFAAQAFgDI/4r/IQAaAN//+P8wAMv/+v8fAPX/LgAAADcACAD1/wgAKwAjAPj/HgAYAN3/GgAVAO3/XgAVANr/KgD+/zUAGAATAGwAaQALAMD/8f/0/9L/EQD8/yEAGwDf/xwAzv/8//3/6/8mAOj/NgA+ADEAFQA2APX/QABYAMf/LQC3/7P/5/8QAFYA6v8AAMr/+f+x/+X/DgDD//T/0f/t/8z/MQDf/8D/XwDy/ysAWgARAOr/EgDr/9z/UQDm/+v/7//O/+r/7v8WACQA5//s//D/zv8OAFUADQAdAGEAFwASAEYAuP+0/wsA+P/5/+j///8AAMj/LwBKAAQAKABFAAEA7//y/xkAAgC4/1kA/////xEA/P+PAOH/CwAJAKz/BQAWAEkAOwALAMD/FQDt/xUAEQCy/xwABAAWADYAPgD8/zMAFwAAAO7/zf8gAL7/JgDW/8z/RACR/0wA4v/o/0gA8f8qACIA0//u//L/vf8TALT/DAAcAIT/ZgD3/6//UQDm/8b/GgDx//T/5P/q/7f/s//5/9b/FAAQANf/3/8uABMAof/9/7T/w//P//3/DwDE/2IA4f8eAE8ALQBuALT/1f/L/9X/FADa/zwA6P/a/z0AMQACAAIAJgAfAAYABQDg/+b/DwDo/+3/3v/A//H/vf8AANz/BwArAH3/zv98//L/UAAJAD4AMgByACUAVQAfAPX/GwC7/yMAnP/6/2kA+f9oAB0A8//2/9P/3P8ZAN7/LQAkAOf//v/s/ycA6f9JADoAHQCGADQAKgDr/yYAHgD1/y0A7v8VANv/BgAXANz/BwAGAE4A9v/4/0MAkf/w/wUAu/82AND/7P8UALX/6P8jAAoA5P9XAP3/j//d/wcA0P/s/xMAx//3/4r/6/8lAOj/WgBtAFgA/v/s/97/9//B//P/vv+m/wAAgP8rABAA/P8zAPP/GQDe/0AA/f/+/1kA//9tADMA4P/5/8P/vf/K//n/w/+9/0oABADy/xkA3f8IAPX/QADr/7j//f+0/7D/9/8dAM7/DgAwAMz/+/8yAAQA8f/0//f/QQAiAEAAWQAiABwAFgASAA4AHgA9APv/6f8SAA4AaAAKABoAOgD4/1UAxP8+ADIA3/8cAOD/LwDL/zAAJwDW/8z/+/8gAL//OQD4/+f//v///zUA9f8bABYAAAA2ABkAFAAjAIn/xf/j/9b/FQARAEUApf/u//H/0P9HABQAIgD4/wsA9/8LAPf/1P8AAKX/3P8HACoAIgAbACgA2P8DAPH/9P+//6f/3f/S/+3/AgAUABAAHwD1/+X/DgDo/////////9v/9P+t//X/CACZ/9L/yP/4/wsA5f/G//b/CQDk/1cAMwAXAO//zf+y/8H/4P/m/zQAz/8hAC0AAAA3ABoAFQA1ACsAEAANANT/EwD+/8f/QAAOAOj/7P8CAN3/0v/t/7r/IwAcABYAXAASACEA9//m/zQAqv8DACgAxf/1/y4A3P/R//////8jAC8AOAAIAPX/9//U/yYADADl/w8AegBQAFMAQwD//wAAyP8vAN3/v/8CAPD/BQAWAO7/zf/p/7b/6v/u/83/sv8cAM7//f9GAJP/OwALAOX/RQAAABMANAAFAOD/CgDS/xEADgAdAPT/v//w/+H/+v+x/0EAtP8MABwAlv89ALH/QQBGALn//v+1/9b/3v+b/y8AJgDD/3QA8P8EADsAQgBaANv/KwAiAMD/KAAOALD/UgDn/yIAZQDk/0UA7v8WACQACgAtAAAA7v8oAPz/2P9gAOD/QQBHALn/7P+4/8b/v/8CAMv/+//p/8n/QQD+/xAAMgADAN//GwDN/+r/AADc/+P/sf8cAPL/0P/+/8j/wP/N/zIA3//m/zQA8/8sABEAMwAWAO7/AwDe/wkA9v/4/2cACQAHAD0A6P8AAAAA7f8VAEgATQDQ/zUATwAtADcAGgAVABEAIAD2//j/+f8fAND/x/9AACEAGgA6AFQA+/8NAOf/x//k/9f/AwDx/yoA/v///+3/JwANAK//CACr/zsAHQA8AEMA7f9fAAIAXgDx/8//6//K/wsAwP/f/+X/2P/g//n/DAD4//r/HwD1/9L/7v/x/2IABQAWAAAA7v8WABEAs//U/+//cf8yALv/o//t/4L/LQASAP3//f8PAB8A4v8xAEwAvf8mAB4Aq/+FADQAKgAiAAkABwAFABcApf8SANj/u/8AAMj/5v8hAEAADgALAAkA9v9TAAwACQAsAAAASQADACcA6f+2/0UAt/8hAAgA9f/l/+r/NwAaADoAHAAWAJL/8f8GAAQATQDj/zEAzf/p/+7/8f+HABAAIAA+ANf/3//T/8n/5v/Z/2EABAA7AB0AKgBGAMv/aACv/xoAFQDt/zkA0/83ANH/7f/w/xcAyv/n/0cAp/8BABMADwCM/+z/8P+8/0kAzf/q/8n/r//R/9r/z//G/+T/6v83ABoAJwAfABkAJwD7/9f/FgA2ABkATAAqABAA+/8OAB0A4f/C/zwAHgCY//b/HAAWABIA/f80ALz/pP82APX/wP8DABUAIwDm/yEA5P/F/wcAqv/y/xkA8P/O/zMAPADn/zUABgAEAOD/5v8hAMD/JwDX/wMAFQARAGkAHgBPAAgABwD0/z8A/P/G/ywAkf8UAJD/AQATALT/QwC2/zIAOwBUADEAKAAgAOP/+//q/+7/zf8NANT/SwAXANz/UQD4/0MA//9IAAMAFQAjAOb/WQC1//v/DQD5/wwArv/2/9P/pP8kAML/zv8gAIf/6f8AABEADgALAC4At//Y/7v/yP8cAOD/wf87ANX/8P88APr/DAAKAAgAvf8mAMP/GABdALj/WQDs//D/8//j/9f/3/9BAOv/JgBDANv/GAAmAAwAQQDZ/yoA6//K/zAAlP8XAMn/+f/o/6P/SADx/8//6//v/6n/8f/i/8P/KgDZ/wQAKADY/wMAFQDt/xUAIwDT/xIANACF/x0AFwCl/zcA0f8QADIAOwBCACIAHADg/woAv/8nAA0Awv+W/wYAFwDK/x0ABQA7ANX/JgDD/6r/TQDR/0gA3v/l//3/6//K/9X/3f+a/1MAHgAGAPP/9v/4//n/6P/I/xwAzv8gABoAzP/E//T/5P/8/w4Aw/8FAM7/IAAHABgAOAD3/1QA6f8RAPz/6/8TANn/FwAAAMn/5/9HAAIApv8AAAAAt//9/yEACADj/wwAVAD7/w0AZwAuAAAAJQDn/9r/KgD+/0cAOQAJAGQAGQA5ABsAFgASAP3/awBWAFgARwBeACcA1v86AOb/DwAeACsARwAUAP//2v/P/8b/v//e/y4AJQBnABwA8v9QAOb//f9HACYAHwBQAOX/IQBkACwANgDi/8P/4v8eAL3/EwD+/8f/LQC3/zMAFgCBAFUAIAAsANr/9P+//xUAtf/W/7r/x//l/6D/6v+3/yEA5P8yADsACgAbAAMAXwACACcARADJ/+b/IgDA//H/PQAMAC8AOAA/ANj/8v8+ADIA8v/0/xsAuv8jAC8A7/87AAsAdv8jAPn/sP9AAMb/GgAVANr/PQAfAAYAvP/u/9//rv8aAPH/4f/6/8T/GADd/+T/MgAEAPH/GAATAKL/2f+p/9//0/+S/xUAo//t/ycA1v9w/8P/BQCp/xUAAAA2ABkA8P8XABMA/v8QAPv/1//N/yAALADI/0EA6/84AAgA0P81AKr/KQDG/wcA4v/V//D/vP9cAMr/MADe/7//8f+9/zcAv/9xABEAxf9jAL3/AAAAANz/4/+y/+b/tP/6/x8AGQA5AOX/IQCI/9b/JwDp/zcALABtAOr/AAAAANz/9f/l/2sADAAuAAAAJQDV/6b/JQDV/yYA1v86APj/5/9sANf/FQAAACQAHQAFACkAMwBOABoAcQDb/4b/nv+e/8T/q//z/6z/FwAlAAsALgDK/zAA8P/h//n/DADT/9z/LADb/xgAAQDd//b/0//K//n/DADm/yEA9//B/xYAAADu/00A9f/l/+r/AAAlAJ3/QwAkAOb/RwDe/wgAGQACAAEAEwAPAMT/KwA1AL3/JQBVANf/FQAAAO3/3//4/x0Az/8hAD8ADgAwADkAwP8DAPH/4v/V/8v/6P/a/z0A1v8UAP////+AAPn/+/8yADsA1P9KABcANwBRAK//PwD8/w8ADAAJAPb/HABgADsAVADp/yQA+f9DACMA5v8iAMD/3//A/ygARQDv/xYAEgAhAAgA9f/3/9T/uP8PAMP/hf/5/9b/zP8fAOL/1v8CAN3/LQAAAMn/+f/D/+H/+v8MAAoA0v8RAPz//f8PAOj/IwD4/wsA+P/5/+j/fv8YAMr/1f/d/+T/1/+o/0wAKgA1APT/CAD1/+X/RQDv/xYA7v/f//j/+v9EAEkA8v/i/0MAyf8cAHMAJQAwAAIAOQAuAO7/FgARACAALQAkAAoA9/8dAAQAFgDu/xUANgDj/40AKABYAA8Asf/l/3z/8v+r//P/GQDw/zwAHgA9ADEAOgD4/9X/8P8FAOD/+P8eAM//2f/O/yEA0f82AGMAz/9GAN3/9/8vAAEAEwDr/7j/6/8mAOj/NQDi//r/IAC+/14A8P/O/+v/t/+z/wsAQABYADUA4v8eAOL/DAAcAAQATQDj/zEAOgD4//r/HwAZABQAIgAJAAcAvf8lAPr/6f/t/7r/2v+F/zAAJgAMAC8Ayv8LAK7/0P8QANb/8f/P/+v/7/8EAPL/4v8MAAoA5P8yADsAHQA8AEMANgD1/1IAQgDa/z0AMQDM/x8AGQDL/wwA+P/n////IwAcAPP/GQACADkA5f8OADAAy/9DAO3/FQAjABwAKQCh/+v/3f/2/+b/2P8WAMn/HQAXAAAA7/8DABUA7f8nALL/+P/V/7n/DwCx/wkA9v+u//X/wP/N/+n/tv/F//X/m//m//7/2f88AOj/7P8UAOz/SwAqANn/zv+O/8n/CgAIAAcATwAIAOP/DAD4/wsA5f8OAOj/tf8xAN//LgDc/wcAKwDs/yYAsf/4/9X/JgAxAAIAFACQ/yYAw//0/z8A6v9vAEcASwD0/xoAOgDT/yUA1f/d/y0AJAALAAgA9f/3/+f/x/8tABIAIQBSAC8A8P/O/+r/3P/R////EQDF/77/JgDW/zkAZQAIABkAAQDw/xcAAADc/1EA0/+3//3/xv8aAJX/qv/y/9D/IgAbAAQAAwBeABUAyP9lAAgA0P81AAUABAAWACQAQgAiAOX/6//K//n/MQADACcAxP/i/wwA+P9VAPz/2P/y/+L/QwAkAAoALQDc/9D/IgDT/+7/8v/i/zEAp//w/ykA2P8XACUACwAbACgA2P8WADYA4//7//z//f8PAB8ABgA8AAwArv8sANr/z//+//7/EADp/xEA6v/K/9T/3f/k/9f/zP/7//z/6/8TADQAKgAiAPf/1P84ABsAFQBIABUAJAD5/wwAHAAWADcABwD0//f/5v/+/zUAhf+w/7//E//V/8v/+v8fACwAbQCz//n/1v8CACYAaQDoAM0AFAFwAKQATQD1/wkAh//o/7X/1v+n/6b/yv94/4D/Pf9j/1z/fP+o/4L/dv/I/9P/t/8zAAQAAwAnAPz/IQAaACcADQD5/+j/IwD4/zAATAAGAE4ArP/i/wsA5f9GACYAMQAnAGkA5//s/zkA5f8zAOD/CgD3/+b/IgDl/w4AHgAqAMf/v/8CAJT/FwAlAPr/VgDq/6X/EgDY//L/PgAfABkAAgDd/+T/1/+6/1oAJAAKABsA3/8uAO//OwBUAOn/AADb//X/9/8KAC0AEgDq/wAAJQD6/zEAOgBBAEcAcACSAFEAiwCnABgASwBOANH/7f8VAO3/AgAUAEcAFQD/////7f86AC4AOAAaAPH/9P/3//n/6P/s//D/FwAlAOj/EADX/6f/8P/z/xoA8f/0/z8AMwA7APn/DADB/4P/+P/C/wUAFgDu/7r/yP/T/+7/KAAgAD8A6v/u//L/mP/2/5z/5/8iAMD/FQDt/8z/MgBNABkAAQABABMA/v8iAEAA6/9KACoANAAFABYANwDR/zUA9f/k//z/2P8WANz/LAARALL/LwABAN3/ZAAZABQAIwAJAD8A1/8WADYA0P8QADIAAwDf//j/r//3/y8A3f8aAPH/BQAXACUACwD3/x0Az//r/yUACwAJABoAAgDe/9L/yf/T/9z/BwAGAAQAFgDb/77/3f8aAAMAFAD//xEA/P/9/2sAMQDN/w0A5v+0//r/6f/u/9//rv/1/+X/6v+3/+r/3P+s/08A9/8KAC0A2/8rACMALgBKAAQA4P/4/9X/JgAxABUANgD1//f/5/+0/+j/yP/l/+v/AAA3ABoAOgBBAA8AMQDM/w0AHQCX/z4ADQDU/xMA/v/Z/7z/7v/N//z/2P8EADoA1P8TAMb/9v/m/9n/4P+v/xoAzP/W/ycAxP+r//P/4//p/0kAOgAdACkA6/84APf/nP9CALX/6f9bAKT/NgAHAE8AQADY/ykAof8OAJ7/1v8nAI3/EQAgABoAuf/a/xcA3P/R/8j/CQD2//j/HQD0/5r/5f/q/7f/IQCa//j/+v9n/wUAzv/F//X/0//u/xYA7f8DAF4AOQBTAAwA5f8hAL//zP9EACQAQgBsAOr/AACS/8z/+//F/xkAlP8XAMn/5/9ZAP//EQDX/ygA1//f/woAGgDx/wUAcwC4//3/DwAMAPj/5/8jABwABAC6/20AIAA/ALQA7P9LAOH/wv8FAJb/BgAXANz/9v/T/wAAEgAOAOj/7P8nAOn/2//1/wgABwAqAP7/x/8JAOP/6f82ABkAFAD/////7f8CAN7/5P/8/8b/CAAYACYAMQAVABEA6v83AAcAPQAfAAYAPAAMAEEAtP8eAL3/7/8WALf/VwC0/x4A4v/V/0sAmP8aAPH/BQA7AOf/EAD7/+r/yf/C/+D/wv8EALr///9tAMX/UQDU/+//FgCk/zYA0P/a/+H/+v/p/wAAEQD8/w8ADAAuANz/LAARACAABwAYAEsABQBzAAAAEgAPAOj/EQAgAPb/5f/G/7//SwDP/w8ADAAcAGAA4P9UAAwAHAApAA8AVQDF/wcAPQD6/zIA8v8ZACYA1v/x/8//IQBSADAASwA8AMP/z//r/+//KQDq/yUAVQDp/+7/AwDx//T/5P/X/9//wf/N/+n/7v/x/ysA7P/L/0MAAADt/wMAJwDp/zYAPgANAB0A8/8HAPT/ZAAsADYAKwAjAGYACABjABgASwCYANb/JwDp/7b/MgADAF8AFQD//20A2P/g/8H/BAAVAAAAWwAkADAAFABaADYAGQAmAAwA5v+h//7/ff/O/yAArP9iAOH/sP9kAOP/1v/f/8D/8v9z/7T/5//a/wUABAAWACQAHQDO/yEA0v8AADYA0P/s/wEAy/+w/0AA6//v/xYAyf8vABMA/v9sAA0AMAABAPD/8/9P/zwA5//H/1IA1f8UAKL/NAAqAMf/9//5/zEA3v9AADQAFwDv//L/9f/S/zYA9f8bAE0ABwDi//r/+//q/+7/zf8NAOf/IgDl/w4AVQDX/xUAEQD8/yEALQBJAAMAFQA2AAYABQBOAPb/wf/f/5z/5/+i/8f/0v+2/yAA9v8JAAcAPQAfAJn/GgADAMz/6P8RAOr/JADV/6b/SgDO/yAAGgDx//T/iP/E/+L/w//0/+T/1/8VAO3/AgAnAPv//P/9//7/EAAfABkAAgCm/9z/0f/a/z0ADAAuABMA/v81AAUA4P8KABsAAwBMABgAOABAAA8AVQANAK//CAAZAEsATwAtAEkABAADAF4AcQA2AD4ARADc/6z/FwAlALD/CADQ/7X/DADm/7T/5//s/5T/KQDr/6X/AAAAACQACwAbABYAJAAKAC0AXAC3/w4AMADM/zEAOgDm/8b/v/+5/8f/UgAdAAUAKQCh/+v/JQAeAD0A+//p/+7/lf/h/wsA+P8wADkAGwAWAO7/3//A//L/GQAmADEAAwDx/+H/+v8MAOb/6/8mAAwACQD2//j/HgDP/w8A1v+5/1kA//8RAOr/3P+H/9b/AgC5/yIArf8GAKr/qP/x/+H/HgDh//r/ev8UAP//7f8nAI3/IwDB/wQAKAAgAPb/CQBRANT/JQAeAPT/v/8VAP//EQAgANH/NQC9/xMA/v/Z/yoADwAMAAoACAB0/yEACADj/2kACwCJADcACAB1APD/FwAAABMANADz/ywAAADb/+L/DACc/9T/OACI/yAAGQDe/0AAxv/R/+3/uf+1/x8A9f/S/+3/AwC5/+z/OQDS/zcAGQDe/xsA3/8cAAQAuv82AD4A1v86AAoA5P/p/8n/" type="audio/wav" />
Your browser does not support the audio element.
</audio>
Now we try with order 5
cutoff = 1500 # desired cutoff frequency of the filter, Hz
order = 5
audiosignalFil = butter_highpass_filter(audiosignal, cutoff, sr, order)
fig, ax = plt.subplots(2,2, figsize=(14,10))
ax[0,0].plot(time, audiosignal)
ax[0,0].set_xlabel('Time [s]')
ax[0,0].set_title('Audio Signal')
ax[0,0].set_ylim([-1,1])
ax[0,1].plot(time, audiosignalFil)
ax[0,1].set_xlabel('Time [s]')
ax[0,1].set_title('Filtered Audio Signal')
ax[0,1].set_ylim([-1,1])
fs, hs =compute_fft(audiosignal, sr, n = None, scale_amplitudes = True)
ax[1,0].plot(fs,hs)
ax[1,0].set_xlabel('Frequency [Hz]')
ax[1,0].set_ylabel('Normalised Amplitude')
ax[1,0].set_title('Spectrum of the Audio Signal')
ax[1,0].set_ylim([0,0.009])
Fs, Hs =compute_fft(audiosignalFil, sr, n = None, scale_amplitudes = True)
ax[1,1].plot(Fs,Hs)
ax[1,1].set_title('Spectrum of the Filtered Audio Signal')
ax[1,1].set_xlabel('Frequency [Hz]');
ax[1,1].set_ylim([0,0.009]);
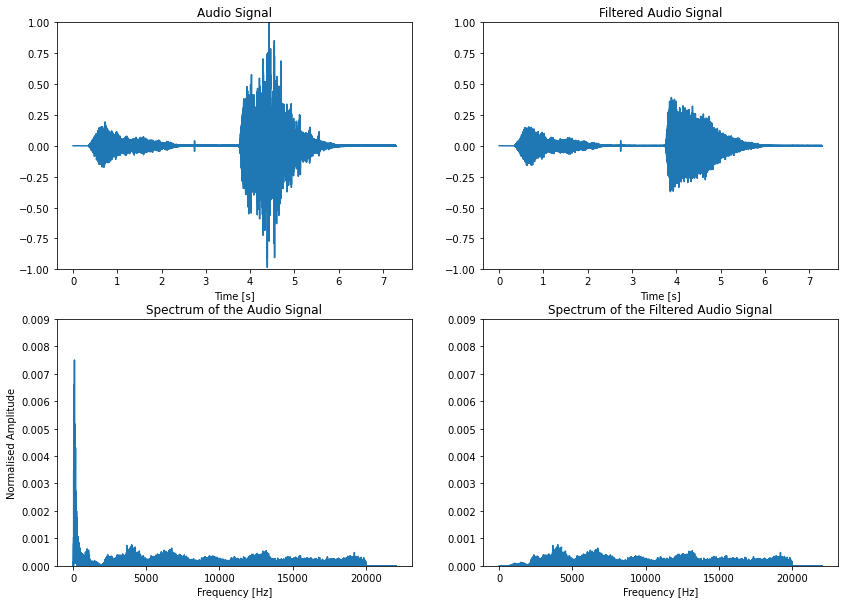
Listen to the audio signal filtered using order 5 filter.
audio = Audio(data=audiosignalFil, rate=sr)
audio
<audio controls="controls" >
<source src="data:audio/wav;base64,UklGRiTQCQBXQVZFZm10IBAAAAABAAEARKwAAIhYAQACABAAZGF0YQDQCQAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAANAPf/7f8FAAQAAwAPAPn/+/8KAOj/AgD2/wsA+/8OAAkABAABAPL/BgACAAAA/v/9//3/7/8FAAMAAQAAAA0A9//6//3/8f8WAP7/AAAAAA4A+f/8////AAAOAPn//P///wAA9P8KAAcA+P8LAAYAAgAAAAsA9P/3//n/7v8SAPv//f/x/wgABgAEABAA7P/4/wwAFQD8//3//v/x/wcABAAPAAUA8f/2//r//f/y/xcADAD3/wgA6P8QAPv////z/wsACAAGAAQA9f8lAPT/AwDj////DAD3//v/8P8VAPD/FQAKAA8A9f/A/w4AGQAOAN//DwALAAgA6//u/zYAAQAOAOv/9v/9/ykAAgDS/ysAAAABAOb/9f/i/8//AwARAP3/2f8uAAMA8P8gADYAEADh/x4A9v8KAOv/EwAxAOf/6//8/wIA3P/1/+j/5f/3/wIAMgDz/wsACQAHAAUA3f8RAA8AJwAEAAwA5P/h/yYA5f8KAA0A8P+7/5H/CwAxAEIAoQAhAJb/AAAzAHcAw/+h/7X/8f7o/9D/GgDCAAEB3QDl/1UA3/8H/xj/e//U//T/9ACIAMP/FgBXAO7/+v/V/wn/i/9SAOgAYgBRAEQAOf/P/ywAsf9l/yQAWwDm/w8AGAC9AEAACwBI/7z+eQD7AH8AXv/I/x8Asv8oAMr/2/8TAHQAu/+U/0QAUwCTADoA1/9I/77/fQDl/5z/NwBIAA0A3/+j/w0Ayv8fADsA8f9xAGgACgDT/7j/9f6K/2kASQBcALgAMgBP/y3/XQDRAM//9v9O/8n/dAB6AJMATgBNAF7/Ef/0/psAkwDY/yEAG/8SAJQA3gC2AFMA0f/n/hD/MP9oAO4AkwAHAEH/+v8vAK//zf9gAIIA6f8k/5j/tAD2AHQAlP87/wQA8f+N/wUAfQBzAMj/9P/l/4QAygDS//X+Jv8hAEEAcwAdAGQAMQAjAIj/Rv91ALb/X/9D/2oAmQBOADsAl/9MABgAngDx/x8ALQBR/3X/rv+0AB4ARwBD/yX/UAAaAesA0v+9ACb/c/5b/0QAJAG6AHEA/P4x/+j/xgDuAEEATv/a/hEAJQAdAAcAjgBZAGz/BgD9/5b/Vv/2/+L/QgDoACYAGwCk/5L/1P97AOgAmf9e/wsA+v8RAFQAy/9oADwAe/8iAFcA9QDS/97+gP++/yEAegBDAAAARwB2/6j/ZP+JAKsBUf+w/3z/Qf8RAMIANAE1AL3/t/4H/7z/pgBBADQAEQHp/2EA6P/BAEYAZ/6u/qD+PwCTAKoA+gAPAOH/uQDvAHEA+f9r/lf/mP9GADcBNwA3ALf+rP4YACMBcABF/2L/TADkAGsAhAEgAF//VP4W/iIAgf9tAboAwP/+/6v+UgC+AUEB2P9w/2n/2//m/v//UwJtAJP/zv6Y/4n/MP89Af4B+f88/Sn/2QBMAs8AXP+sANn+9f7n/jcBYwEo/1X/aP71/xoAygCfAVkAoP51/tIAWQHUAF7/PQBOALD+BgDpAD8Avv6B/yQAhv9j/8wAswEMAcv/r/7mAIcAG/9L/h0AxAE0/o7/IQEGAW7/FP8CAZ3/7P9BAG4BAwCD/vn+ff/BAT8ANwDu/y//nf7z/u8BKgHaANj/bP/A/p/+uQCBAe4AYP7+/yMBUQDX/t7+MwKFAPz+1f6JAEQB//70/7QAGwCp/7r/1//O/z3/1P8FAaAAJwDR/1QAgP8x/6L/q/+C/zH/qgHNAVEACP95ACkBpv3l/tcAaAFcAH7/6f9V/6sAp//S/yIBXwAJ/0b+p//D/8wAVwGrAE0AJP8HAKr/k/7q/+cApgAAABgApQCy/2f+gf8uARIByf+I/ygAqf+i/qQARQLrAHEArf4j/lr/V/8OAHQArQAuAOz/twAcALz/8wD1AOn+Rv7P/3gAsv8PAE4BgQAM//v+jf9rAZ0BlP4p/iwAAAHt/68AswL2/lf9RABYAIwAcgBp/7X+2f5UABkBaQLgAQL/RP4E/77/4/8HAa0Bqv7U/X0AmQBM/lj/rAH9APv/e//aAP0A7P/x/vn9EAHOADP/tQAPAbL/UP6oANEAQv90AJQA+v8l/+///AHuAWAAPf5G/QX/e/7V/o8BqwE9AXj/PgE6AXD+0f91/zD/dv5n/2IBmgEdAq//M/+g/+7+w/4HAFoB5ADJ/7D/9AAbABoB1AC4/sX9Qv1IALwABgJDAZr/ywA5/q3+/ABEAp3/WP3o/loAugEtAfcBcQCo/gv+b/3Z/9kAjAFQAMMAVABb/sz/NgGTAf7+w//X/7r9mP/8/ykBeAEYAacA6f5v/3T/LQAIAScApP88/rT/PQCO/ncBagGHAIz/Q/7NAEcAWAAnAHH/XgCr/4T/Uv8lAQAAOv9mANr/ugDq/5IApgAGAAgAnf/k/9n+IP9R/4IBHQIX//z9tv5XAMT/9wADAmQBMACp/nH/Vf+1AJgA8/4tALb/Af/L/x0AKQD0AM8BPwEs/wj/YADI/zL+M/8bARoA/v+e/pn/QAJJAGX/W/5JAZMBt/7/AFMAlP8T/7D/1v9e/zQBh/8HACMA3/8yAAcAsQEu/+z+YwE8/2D+LwDAANgAgQD6AB0BWP4M/tf+of9qAI4AcAGRAcYAP/2l/mMCNQDn/qL/zQF6/5T97wCBAOgAvAAh//T/j/+G/sv/+gFlAEH/kQCJAEr/fP0T/ygCugCZANoBjf9M/i3/bQEyAe7+Uv7B/SYAHACM/xUDawPFANf9h/5l/3L/aQA2ALQAC/7L/ZcCOwKL/5L+pgB0AdP+vf8jASoB4f9V/mYAHQE3/q/8wP9dASIBfwH0AKEBLv7R/B0ArQCpAKn+fP+EAD3/VQDfAsIDuv64/Df+IwHy/xX/NwNoAAz/6f1V/w0DiABZ/y0AMgHN/Z39xf+FARQBlP6PAZYAcf8j/ikAjAI0/wr/hv9tAXb+WP1q//UCdQMA/tYB9wDw/s/+zP76AQEAvv/a/gQAGv/+/X0AXQFAAZT+lgBDADoB7P/W/QoCxv/d/t3/nAIcAPD8hP+3AAUCSv1i/nMAYAH5Aa0AzAJx/67+Af7JAHwANP0p/0b/hgHM/n0BWQL6AEcCZP1A/wX/Ev+n/+b+kwDL/w4BbwLaADX9G/4aARYDb/+f/D7/SP+FAVYAtgAPAv4Ar//i/FIAawFLAJX/+QCaAND9VQD6/1MBCP8S/psB/P/3/2AA7QGIADn+lv05/00BTwD5/2AAwQLL/g/+6P9N/2oAtf38/1MAFP+9/x0DWgR2ALf/6v6zAHL8LfzaAfwBugBs/iMBJQEv/0n/HAGLAVH/9f3s/1wDigBn/xL+NQDd/s/78wI0AmX+Df3t/zsCpACvADUBogIq/mj9jf9fAEkBfgDVAcb+5P1c/6b/DAFd/rj+ewIrAb/+GgLyAtEBlQCb/JH+7/2J/EgA5QCCAJT/oQAKAu4AsgARAJr+f//EAG8BewFg/kr/RP+i/g7+MP4XAqoBqgHI/97/PwCD/zgBSAAxAb/+Yv9G/3f+awBB/y8CWwDw/Fb+hwENAef+eQG6AlsBCgCdAAf+dP69/1EAjQCQ/rwBVQCU/nv99/2pAikCbwBz/7gB9gFWAHj/8v46/sn7Jf6EAFUB9AC/AW4BNf4r/x4BfwL7ANn+Ev5p/77/KQBkA5gAfv7H/Wn//gCc/w0BJv8xAO3/eP+gAeEA9gGg/yH/Bf+8/Jf++QGcAgP/E/66/90A7v4zAIMDxQCz/vD9BACwAF8AEQEGAdcAev4yAPQAnP5D/GP+tAEhAXMBIAAeASb+pvyIAmsE6wHL/tb++P3J/eP94P+EA4AAjPz9/uQBtAHWAq4Bp/9J/Qj9Zv/XAw4E1f79/9z8Tfww/9P/QALxAIX/sv47Az8DdgATAdb+Tf60/Eb+rQBvAET/vP6XARkCcgBAAfj/xv0c/eT9aAHyAukC8QCuAI3///4JAFv+3f4T/Aj+yQC8AuYEfQGFAg//1PsP/w8Bsv4E/WUAEQFPADQB3AFWAWkAWv1l/WIAtQDL/4P+SwBIA1ICWP/b//H+UP4w/9H/EQEbACsA5f6Z/9QBigAk/jD+vP77/3AEtQJc/yT/BP9ZAAD/YP7VApoCz/7h/QL+uP9WAGwAK//i/24BSABtADoBFQL7/x/9kPxKAT8Bdv/DAlv/X/5j/tz9KAEQAskB2v8G/Yr+hQPcA3sAqQCBADv9Hf3Y/g8BNAEJAFf92vs5Ab0BpAI0Az8AUgDw/vT95f8cAsD/Iv3h/EX/WQEjAWwAaf8YAmICtgHD/3T+zQBL/vv84v5BAZMCSwERAJT9ov/6AVP/gwC1/nH+MgD5/rsA4f69AOYDbgBb/mb+mf/YAFUAGwD2/wYBuABU/40Bvf8C/5n9qf5tAR8AfgL2/rQAOwCP/UAAgP/SAZoA6wBYAID/wP+dAF7/zfuT/xP/6f+w/04ATQTYAdMBvQFe/qz9zP+N/tj9AAD5/6T/VgDF/koAdQHDAMsCSP+TAC0Anv6uAeD+MQH0AJb/egCS/Lz89wAZA7f/3v7u/xD/OgCs/x8BFAHJ//MAu/+LAD0AnAC1ANj8kfxo/rz/KQEJAdMAHAOgAgACyQA3/3v/o/1W/cf9cv/u/gMBKwPkAdkCugDh/Vz7Dv08AEQBdAHWAAkCKQG1/s/+agAd/jX9qv7W/gcBQgTFAnoADgE1ALEBegE1AOX8Mvo9/Zf/KgHGAqcDwQBg/3P+7v8DAqYA7AGU/YD7Hv5m/q0B7gGj/kX/BgBgAA4BngC4A1IDHv+Y/tH+kP9e/gwA6gFV/XL8oP1VAnUENgE+AO/+SgJ3AEkAggHG/VT95vsAAOgBogFOApn/Ff4z/S7/pAKTAX4C3wFa/Mj/wQDmAe8AO/3V/qL8Sf7b/eYAOANEA0UCRP1n/n8AsgId/7n/7AAbAH8Ar/2m/4b/fQA1Ap3/r/xWAJUCYgFsAn8A3v4G/ab8wv7UAXQCWwI8Ahr+XPuQ/f7/3AAtAP/8aABnBH0CWQAxAP7/agC1/7L+ZQAa/K78oQAaAsgEdQMaAeb+Of6f/B39aAAGAiACOQAE/2gAPgDL/kAA8/5y/cf/tADHALMCLgGVAV3/6fzb/jD8aQGtAfb/WAKW/u//wAG7Ag0BTv+t/5b+fvzB/Hv/ywL9AjwBnQFH/uH+1f1n/mwDPQPwADP/vAC3/er9nP6WAIUCEv6C/lj9Of9hAugCDAIVAGoC8/5I+l7+BQFvARcCdP6j/Un+HQJTBIYArQBN/g//av/B/n8D3gGwAOL+HP5vAL/+2f8+/0T/CwCqAOABFwDyACP9Uv+rAT3+xgGp/fz9pgFoAdMB1/1nAFYBs/7c/2b/lQAwAZn+kQHGARj/UgL0/uv7Rf62AEoCEwEJ/7X/OAEaAI8BW/5j/6sAmv5OAMP9/gFbAbEBSwHq+8/+Mv+mAuX/Lv5lARgAFQBb/rf/XgF5/5P/1ABq/7cCiwHx/BX+8//LAVoANQB4/qv+f/45AXwDfwAkAW3/Rv5f/rEE3QQT/w3+h/ou+/H9ewHMAuIBFwJxAv7/2gD8Adr8Dv3l/K/8zv/kATIFdQIi/CL/cAAu/lEAjgHKAUgAl//JALgAif9jAKf+Ov9h/yn+mgC3ATEEb/74/lj/c/5LAVD8JgEoA/kATf/w/wAAfQAXAvH9ev1X+///9ACxAWsELQHZAHL6m/tFAtkCWgRTAS773P1CAQ4CPwKbAZT/RvsZ/dP9SQElBMcCZgJi/j/8XgCTAcb+ZwAAAOf+tf3EADcCaQDMAbv/S/7O/br+zf29ARIABv5fAbb+ewJUAp8E2QTj/4H+evpr+m/+QQJMAa8Bbv/L/ZIBCQFVAQIBbgDJAVoBnP7u/M3/ef7d/NP/3/1KAe0Bm/+wASv/5/+2/roAmwWXAUgB3QHL+0D8F/xC/YYFrwOeAPX9IPwr/7UAQALaBQ8DYPyF/Yv99/7R/RcBGgbK/7v9qf4VAcL/z/59/9v9WP5e/rMBQgR/AkkBiACV/jL/HgFRAUwA2/0w+xL+hwC6AKUBYAHRA6z+Qv7NAIr/LQIzAPv/TP4T/mr/7gDbAZgAMv/n/Uv/cfscAFAEsQCbAmgB4ABlAIj8cvspAVoBdf6MANb+jwFiAjv+MgEKBOICgwH4+3H5NAD7ALUB0gG0/kL/7PrVAIEECgIYA5z8uvtb+yP/lATaAqUCTgCq+z76aQL9Bh0EzP4z+Bn8S/5wAUoH0wEdBfcBhPhx/PQAuQXsAHr8CfrZ/EoCtgG3BVcBJwD9/KD50P4WAh0FxQEM/n3+ef4v/80DhQD3/4YAufvQ/zwB3/9cAvYC6f39/pb/ZP9S/xMAVAQo/J79+QDD/3ECgv0P/e7/yQFXBPsBn/73AP8Akv1A/sn/TwGLBDQAz/xi+wz+JwPyADUCHv4ZAQoB5v8MAdX8JwJ0/fz87Pzu/sgASwDcBP0BcQH0/iUAiQCmAW7/kv65/ZT7SgOLAtoCmQB8/rL8Pf9GArcCkwPC/xUBfPsB/Jj8iwFsAhP8PP9T/p0EHgeEBB7+EP0I/IL5VwCUAgsFxgAq/nb+H/3V/yECzwH1ANf+IPz8/IIADQWwBHMC5vyn/Tr8KP6XA1L8JALfA8IAVAIkApcB+f0+/v78kf5C/23/vQJAAtgAhv6M/Lj/9/2M/wsDiv9pAbv+ZwCX/1z9rAGyACADP/zP+zoCfgPhAIH7AQLsAGIBFAQmAO8B0/81/0UAJv/9/tP+P/qO9xMAxgJ1A9MG+gMWAzsBRP7I/Bf68v4o//L78wAeAKcBogICA2MDnP/T/n38+QDq/wb/5QBH/tn/+/6VAEgA9/94AdUCav2M+2gBBwIfAgz9ufzwAP4ENAIpAWwA7/uAAMT95P9LAjIArP/R/v8B3AL/A17/Ufzi+lX4pf26A00CbgDtBG0BTv0xAGEA8gLpADT+/P2a+sgA8AAZ/xkB/f7AAsUDMQKuAR4DZgBV/uz8+PsGADsAaACx/Nn7rP19AnAFAQNyAu7+6frH+xgD+wO8BHUAEvr5+qP5PP/MAbMDBgryAgT7XP5i/54CfgOmA18AAvcN+9j9Av0QAA4GIQT9//kAZwEPAmT+0f9f/BH8qv/BADIDywLQAs77cvuRALQCTgJ4/l3+CgCv/6AANwLg/70BvACu/AH+Nv8IAuoB2/7s/Cv78v7hAGYBHALSAcj/Fv8VCJgEtwHO/236bvv9+6L+4/yRA1UC4AEm/zT+HwVX/bgDVAMoAAUBkf3i+4P7WgFRBFsAZfzD/Zv0Ovi/An0L2QvnBDUCqvjK/pL/mv82/q0AhQKB+B0AvwK5AIoCTAAY+7n8pgCABAUD/gDIBMsBMP/+/CwAl/8G/4T6n/ih+tL9wgQ6A0cG8gHh/yn/4gFIATYC7AWw/Wr9gfpJ/S395f5I/cUAuQKT/UAEnP9dBVIBZAIGBdP9hAJg/Sz6cfuj/roBSwTT/W/+qv5e+ssBlwIIAuADkwEg/xwG5f+J/P78N/5NAsr48/65AJH94/6n/AICcAiQBScF0ABs/CUCAf6p/c79z/yP+Wr94wH5AmIDnwHpB0L+wQDj/s38of+V+H0AJQC5AOsDqQVfAiz9/PgA+4n8DAK4CUX9GQDD/wABIQOKArwBh/krAIn+xf+a/BIBxwXw/o4CAv+3ASf+6f+6Aij7awDZ/s384f4TAXIBMv5zA0gFagDB+gX7Lf9m/qUBMAMIArwDzwH6/pv9Pv4yBAkCe/3z+mn5tAIHAj8BZQAcAaoFDwKc/1D6EQAtAEf8S/yMAbAI3P/e/PP3t/vNAqYCWQYyAPkAvAbBABz8If8qBH4C0fpA/OL7Avxm/Tz8KQIYBcgFtAGy/koAX//6/1kDoAWjAqz5V/ej/Av9XAAWA13/mP4eBIwE1gX1AUD/of8I+Yz9u/5KBnoHCf/S+YT3QwBNAT3+gP0gBC8BBgCh/3H/MgKKASUGNPz9+28AiQJTAG7/Sv7h/x4DqvztAVv50P9jAZQAcgijAv0CLPj3+3z/nABMAXID0wLF+an7mvvRA28CzAB6ACT8TQA5AbD/aQW+BQYAyv4Q/IQAyvu3/WUBJQRLA/36Lf3l+bgBwwKxBIMG5QHnATb5LfuY/jgANgO4/vr7F/7H/VMDHQM0BUgDGv+u/rH1ewJRAk0ApgCn/pkCPP9XAvX+/AFb/R0Ay//X+fwArQCbAj0CHQRI/j/6b/yn/6sBNAZECFIEyP5+9Zv4GviIA04GnwBtAY/+KQBC/1gGfgGFAS8A0fsf/WD9jwFAAWAAvPlxAS3/Tv1fBUgCMwJ3Ae8AEQBwBEL/zPoC+FL7dgNzBO8Dcvqh/5MDMwJiBI4B1vyz+1j9qftgBEYIygN3/tP3q/il/5ADywIHAA//KgHm/+oBkwTtBVoAA/dL+Ij+tP5n//oEOgQ9Aur90vxYAVUCNQMAAEb6Evyc/lAAgwLiAgkDQPwPADICNgLcA9j+ZAIn+kH6Iv7PAcgDcADZA3P7xAGg/4//SQG6+7cEXv0IAXsBpwH+BDP7bPm+9QH/lAZgAtYBHQQvARn+xP+TAJMFv/+G+CT4h/1oBWwFfQMGAEP++QE8/2L7yQM+/Yn9ZwKU/eAHZAP3AtX/AvgG/Ev95gTQAbf+eP+I/p7+FAJWAHT93AI8/WD9Vf6qBH0GRP4AAVL+h/yc/oj/7v2y/4T9lf/uA8cECgr+/8r8U/w0+soBkgJ8/2j93/2MApEB6f2aBBf/CP+7AZ3/5wJg+3b/aP+f+17//v9XARIG5gMD+uv7NgECAxX7JwCcBQb+FwCzAGcBDgEGA33/UPvP+d/9gQTWA24Dv/44ABMAlAMaACj7zwA6/Cv62PubA4gGSgWP/+36fv7KAXQDqgMpB974bfbM/mT+HQPjAlQBhP5i/zf8OvxyAPwHNwpJ//f7Jfg/AJEG+wGm/Q38NwHw+fz5UgOsB9YGWgC4/cv5RfwdBGgBqAKnAp/8kvrq+bgEtwfhBNMDKvoq96z3N/xbAooKawYi/c38Bv2EBXcBWQPlBLn6i/wN/V8BwAGt/Q78RfrK/PMEOAh1BF8C2Ps8/sYDpgURBYT6zvQg/Pf+If1SBTUEYvwh/GH/VP+QAngJWgRo/5v63f1lBbIDMgKE+Qr2Bfy7/Zb+fwE+CFoFZvxuAWkFFQL2Apn9jPd4/TcB7wZHAwj+hgBc9av55v1wAmUHov0y/6P+XgJ1CB0Ih/4E/Q79ZPQI/bEChQWOAW/+QAAU/94BDwQ6AeT8YP+D/bj/igFYB7UDAvoX/ZH+jQJrADP9LPjf/l39XP2IBfsBfQrEAR3/w/31/J8C1PuzARoAyACfAFD+bv0h+1AB6AL6BXb/S/2LAu/75QHuBpwBmAGv/fD3lvne/MT8KwM/ARIARQT3/40K/Qfu/1T9qPfT/yP86PzVARL/FwMWALP9l/xNAHEGuwOgBO39rPs0/T36NQKCAq4BovtC99f/ugNkA7EDsQMv/r/9UgC8BWkFXQJC/q74xf9XAaX9q/s9AEL/yfu7AHYF7wVTAJMBvf+E+5f98f/v+9n9UAAk/tEDcgH+AIwBIv4vA5IDtf8+/fb3NQCqAEb+gAVuBIwLXAMM/IL5E/soAU37C/7H+4UCMwCc+4EDEwbQBRQCmADL+6H9ffroANkFRgK7Boj7gPIy9sL9twIEBRsFuQWOA5EBygEbAgAB+PyO+wf2o/wZAnj+1gEKAoz/vwF1BYQEtQCEAR8Cmf56/3v8MwOC/5r69v9Q+Nf9kP26AIEHsAUBBID/M/vm+Uj+3/7kAecASwIn/2j9rf+mAK0BEAIrBKn7SQGNAOwCtQKe/NQB+/26AFr95ABxAGn/mwBD/DQAVgOQBUD7Rvt2ADoCKP96+ar+bwEwATsE7gD9/fcFev+2/Uj/cgOHBef9HP3N9wT+5f8U/7cBW/8o/7wGBAkBAPQA+P02/vr6vvgp/6T+sf7hAiEF+QPuBTYBQ/4x/YT60vlEAL8FvQJDAUL93QCH/Cz/jgab/X79V//MAUX8V/ppByIIjAGe+Gb57APBASABWP0C/6UG4v/s+pf3lwJtCMf/kASvBXH+Yfq6/YAAw/9D/uv/NAPRAGD+Tv98/r3+Ef5u+rkA/wXgBvwBv/8WAUH3Bf7n/jX1d/0/BuoJPQQTAHIAIABGAhYBxv5T+0n76v1e/ngBtQlyBAH/SAAO98v81wXxBREBa/9p/bb2Bfkk+VUHoAkABokESvlH/pz+2AGbBIoETAGf+Nv0bfqNBPUDPAHl/dwDEwDG/Q//iP6lBJQAEgiUCI0AFPeP8yL0afmRBmsEzwmGBe3/7ACV/8MGigDZ/K380fgMAiwEUAM0Axv6l/3h+7r+TwAz/PcAY/wSBZoERACeA0b8rvpIAHMBQP88BHoCiP+A+7H81wQrBE//C/3Y+3f8PQPMAwYHrAH1/gr+6ve+AyUGmAbiA7n7t/ao8Nz3WAOgBbcD9ARHBmUFLgGwAZv90PoR/CH5v/6MAVMCjv+Q/Az/Ff8oAUoIpQS0+nYAw/9LAVoF/QFYBff5K/iV/BH3xwWwCGYAdAGG/EX/agLd+/v+uAL8/wQFjQL3/Rf/S/6l/LX8SQW5A6QBSP2V9Iz5pAKnBvUCWANOAFoBhf1u+rYCigNCB7/9tvkR/Q773QJpA1kBaAGz/VT7cPprAFQKZwgiA438ev+NABn8EQWdALv6YPro/OX6q/5BBloB9wg3A6n+Tft398L/Fv7wBf4G+wLd/zv6SP/l/gv6C/0eAb8BogDH/msANAWtCBoDegLI/sj6kfz99gL7dwDuBzQEpwHC/2L46wBZAGQCLv2+/Nj/qv4MBLoAaAbuACYFwQcl/V39jfqf+6z2l/z0/pEAkgfdAl4FhAL6Avf/NPzcAOX8yf14+0P5df8lAQIAnQABBvkDyP+++lv3LAQNBmwCuQIpB3cKEv9I+0D3l/VF+wAAcwWpA6cC1QEu+7P8SAQ3ArACQAK+/6n8ePvY/9j6Av+IBjMErfs/+4f/sfiv/j0FfAgdBZT+FQNE+//8pQX9/hb+sf6k/eb+cP+u/0H+YwFcBXgECP9zAZUFYv9x+7r4TABlAoIBZQJy+Vz/9AGM/6L+bQOkB6P7Xvmy+Jn+lQghBDoADgMA/cL3rvm9+dAJfgry/zH/6QAbAm78CwFV+28B7AQ8/IYBwvq+AigHZwJa/9T7aQTm/ZP5uPw1/b4CfQPtAccFrAA7+tf4i/rFBBkB0gM4BVT9QP2m9zwA0QgZBtoEBwK39/T4rQT4/1UBz/57++/7of22BuUD9gUy/Rf1kv3EAQsGxf31/AAF+wJiAiADxQNsAHz79/nZ9z36sAFDB+sB0/xZA2ACpQWABqL9rvqM+9UBeP7JAf0B6/et+T37tAI5B9oFtAWL/JT1Gv4jBVwKzQh7AgP9YvKH+Xb9UgTzBpj8OvzQ+OX/jv5HAd0M7wSKAhj9LveaAJ0AhABpBIn+T/4C/xv+jf75AXoEyQBF/AIAfAOs/6r+8v2pB6sFWQGQ/mf1Pvtm/RD7Kf6HBzoBQv4e/Hj78wE5BmUMOv6UAlP+zfpH/RP7uwdd/o0AHvxr//YFX/yHBH4DzwKJA5L7p/qo/YP9yfwQ/HIJpwgZAFX9cPRcAcgBOQN4BTT6K/yR+5X5Cfx3BmsMyQofBQ34nvUK/t0A0P8JAdUAsPpF+bP/FQnXDAUDUAFsAHH9yvsC+fQA7gOF/ff6EflDA4YJEv5wAEv5qv5XBmoA/gZ1AgAFgP+d9jDwHfhtBdsDyP8S/v8G3AC+B14BsP0qA2H9pQKz/IICGQDP/f35mvsOA0oDPgRl/ir/ZPuXCZIGNwJiA/b0V/h8+FIAowJc/xH/8gCsA2oC4wTT/Az6GwDl+aT5cwXqC3APLAV+97325/tv/JwBhAC4+Lj/FQBTADoDTAsACmEA6/uB9en5iQC+AYv/tAKn/5wDOAH1/iIEUfjF+cn64/+bCeALuQQp/Vv8nvtN+8X4ugLCAuIBEf6M+E4BNwavBrf/YvxI/3D92f2TAbECtQjHArH+mPjE8hoDcwi9BkQA6wAjA+P+1fYA+YwAUv2GAxMCbQKdAFQEpf9E+HMBsQESBxcCUPxr+1UBlP5t9/L/zwP2BXb7nf2/BlcCPQMfAC/7PQKjAaT9Hf8i+7T8iPp7AHQIpAFIAPcBW/p6/LIEcQfGBsr9Yf7u+WH8nP47AHIG1f8dA6H4aPpAAfj+IgHw/0YJbQGWAqgDj/d5/osBeAFO/L73mf50+zr9FAHcAocLmwSUBiwDXPm1/wz9wv1rAQ4CYfw5/Y4BNv40/4b+yAKYAF0DWQPl+XwCpwGU/Iv+3fpk/ocF7QPlAKH9I/qe/vr+2/8zBGsF+QJd+R/+2wRPBN8FlvtT/RoAMfvZA/ABdv4e/U75r/tyAIgHwQQvA5L8G/prAoICqQZU/sD7/P3r9TD6ZgB3CB8IGQTZBBX+j/hl/EX+Uv5YBYEDogJc/cr9awdIAdsD7v5i/GL6NvAK+t8BMApbCjMD+P01AFoDZv6F+8D0af1G/vP9cgUkCQYL5QAQ/Gj5v/9/AJQAwwD1/Pr+dP79AuADYQdCAGr9ff9i/gf+P/uX/+76Kfth+1oHywlCBNgIyvsO9kf1a/rv/uoCCQljBC4AFQbpBPz9tAAy+g74bfxsA+0Bg/9FBvUAg/44AJ8DogQk+nL8YQLf9/3+DwZ8A8oDPgB7+UX2kQJbA48EFP2R+v//N/xmA3QEwgYGAXH90fqm/agC/f/S/rb5uf6OApYFzQf8CgIBrvtf9qfxjvz5/6kJgQeTBkz+Of5mAL/1cvTt+b0ILQRSB6kCOgNdBvAAKAGa9zICLvyF+hQC0P4kAgAC4wMwAxH94/ii+kX7TgGNA/oECwNyAaoAD/Lk7lb+BQ91DaEGFAOz/2cAmP3v9vD7pQLCAQAAYQDCBOMFWQV19Zj5af2I/J4Jrv7+/UX62Py5AocG8g7RAbP5LvT39LL9TwU7CgIH+vsy9iX7ygZRCVMFdQPo+yT9X/ZF/PUDcAH5Ai3++/xH+J8BzQUgBGECTwGRBDT7uv38AtoFmAP//Xr58vQQ/Df9Ov1fAkIBUgalByQCrwNo/vP7Lf/TABQCjf8PATj+EPR5+X0CJwDz/y7/QgUqBXsG6gs8BdX/7PoL+tb20QCyBQz6q/ja95r5TQTHEGIJyP+k/qv9dvkr98QDSwpkB2r+RvsW+U33LP1P/E0DLQlkBxf9k/MM/qUHuAzpDAwH4v6I9wHzwPSS/MX/cwTu/t79Kf9ZAWoK4wVcCcUBkviN+Gj6fAPRAK38yP3r+5n4eABaAvIJEQryAFD7jfNCBaoGbv+n/KT9lwO6ACr/HPsmAcAC9gDRANUIbATi80X2vv76BaYFMAthBwf2VvL++XD/cwPlAakE+gBK90T+b/5PCYcGffub/w/6HvxkA2gH4QbMApr6tflx+er7q/srAZwLR//B+av8nQbrDXkP3gfn+Dnvau7W+tz/MQQsBuAC9P2R/Gz9AQVLDTEJLP7a/CH6QPHVAuEB6QTpAPH04gMNAW8C/fwB/WQBvwgGDAL78vz8A1T6tPXH+2/5YAlOB1H8W//E/XkFNgNUA5D/BQE1/Zv6DQC7/s8Cgvz0/CUBpweFA5/6tAB6/z0AK/r++dMI9gV/AwP+F/zKBZT9Y/1S/a77qff19ncEAgYECBoFEQP7A7gCJPxV/pkE9/2YAOr7Xfyg/mb6JgCUAIH8DwFQAZACQgYg/w4CAAG5AjwEcgHP/gHuV/QnAAT//QWJB+cJigPe+BgAufh7/LEHXgNDBLUAIATp/O381AGo+cT4zv2oBWwD7wI2/af7PQFuBPEEAPlL/dQFifuy/IgCuALnArX/VQEm/ab/Tvyd+5wBov4OCVsENAKQ/bX4l/0y/LcFsQRRA10D+gD2AOX+kvyY+fr6Svy3/Hn7RfoGBhgQ9gRO/DX9iQDp/VQBSQVpBUYGafxz+430Lfku/w7+yAHx/FkF9gdSA70EUQs8B/AAvvfr9DEAaPnM/DX8yfxN/7b4NP3YAeQPLQyz+WH5UgA4BsIHPQFj+x3+xvwC/E77fvy1CT4JXAE29rDy2/6y/WUHywenBkgO6fuz+NH7kQLdCQn/cvgk8bD1e/7//Q4DsgSOAhcAMgK3By8MqArd/kn6w/pj/aT60flG/KH8KgBn/LwF7waBBAAFRPpp/TYETgSQ/MX7qP0Q/DsEmQvbAer5HP53AQ777vPV97X5OgdRBjkGDgxXB0gKAfjg9M/+F/zS/a4DUv6Q/OIA8wTYBV75xP8P/g8CuwLYAJ8Gpfht+478X/9M/C8A8QQIAXkIlgFRAPb+0f8S+kn2rAAMAf39d/sXA50GogTiB4cF4v7C/IH7lvk//eoCXwi0/Ez3vgJC+OH9tAtACqYCU/gW/Hz4ywQfCtkFPf0497oCKvvOAH0DzPzK80P+hfyk9RoNBA3LBuH4pAc3BZD68fxM94r9GfqaCg3/+wHSCzr+Pvar/0UOd/0sAY/8o/v7+7X+xQAn+mMDJAZSB4H87v8t/rH9PfzR9ZHzbfzUE0IGvQLSAkD/vgOTAwgFDfwA+aL6Pva6+VwA5QPlBgUBjgXR/TQCcwuQBOQAgfGx/boAKACcBcL/bPlZ8XD41wEHD0EO3Ads/8v2tvq6AfAEmgM4ARb02fEJ+tX+0AaZCJ8BDAGf/I4BqQedARkB7Pu89wb43wZICQME5gEM+wf+0P4hAQgDY/6X9fT8qf6NBZAO6AclAFjzQPfD+68K2AL58lv7N/1KA+UDBQ4ZDAAClPlt6Ur0/AmgDYgLfgEz/KgBUfNC+FsDs/5VBeUBpv+4+6H7iQk/AR//5/tn9/wFcP+r/iv6egH9DB8E2QDD9dn7fvud/7gHVwVjDWYKI/+P+ir55/UZ+5z3X/p0/fsHUg8uAlQBB/5//vP2sfxdALX6jQWYBjEIxAKz+iP8QPwv/MsCBQB+An8J/gAq+J/+RQM6/bwA+vywAoYAaf4wA5D+4AHZ+sf/uP/w+4f/bv9dBcEE4/sPAfoHGwC4+j364QGi/Bj9kwCFBooJqP9J/iP4bv/bAFwD+AAcA4cG5fwY/Zj3yPuD+mMFhwO6//oFzfs//b355APHCeD+OvkF/3YBXv76/hYDKgCG90cBGABMCO0N1wfyBBj3xfdq/Uz4s/cVAw8F8P6F/EQGuwNjAr0D2fpCA2X9p/9B9nftwQOXDecPTf/D+oIBHP94AtH81vpOAOMBMvrc9BsCCQZuCRQFMP2aBIv9gwSfAYX2Q/bs+uQD9PkxA2YJBwdeCPkAdPwJ+Mf7sQFM/5IAqwdaAtT8Cv3wAKr49fpmBmEATgRo+8n3ffri+0IJ6AsmBdj+rP9t/wgA6v9YA0cBBvl6+Gf5if2QAnIHegPR+N/79gnMCt0F8PyY9C/9awMPA5QEKAMeAPT4RfV7/Ib/hQWvARUBI/z3+HsKwwPKCnkJ6f0z+bbwYvaP9VYB/v8DBqoQ4ALf/TT88wEbBlAEvQCC+JH1K/zYBtgKMf+X/s/92fzPABv9DQj+/Dr3H/pe/YcOewtKB0v+4/HA8kD82gFcB5IE2QH1+QHzYQH7CLQQigMd/Ej+Pvss/XwANAin/TL87vIe9awGmwt3De3+/vnt9YH69wdnCdsHt/8m+a705fSGBl8LhgJmBGwBYf7h/XsA0fik9zUBzfoT/lkCBgk1CSf+xQQ8Bff/m/xH9DLzXvdMAUwHSA5cDo0BsfzW9tj5uf0RC8MMBP+p+Pru///cAKsDfQRv+HsAF/Sb/t8Q1gWu/2cBP/5u+F71Df7KBYIC/AQsAXr6xPtWCFYIqQRV/sn2uAF5BwALXgM3Bun8IOVg7Lv/QAeTBcgMEAQc+3P+JQQ9CWkGZ/ic7snxSPS7+u/5NQf/FL4SOwOYAqUFevfY/xz2qPZ0+7AB1wyvADMIHQbqAsH8k/TR/c4EmACv+Sf/6v8TAx//ffmq9/P92wpaBuUECfs7+UsEr/va/QEHwgNGAtoAB/cA+9sHUwB6/AT+kAGR/vz21vzh/4kG/wkOEX0HKvmw+rrvt/YO+nIF9g96AKcFVALO9in8IAWjBrgCwv6I96398QXEAZcE5vwV+KP/aPIw9zwDzfyiA9QLVgqGApoDsP8j8M/2R/+KBrgJuwBKAEX8Zf+MA90A+AGcBYUAwvNj/IUBZQcfDD0DlQAF9kr1CPlV+1YH5AOU//EEOf5A+Iv+ZQkvB+H/UPru+xkIHf1w/Mr5u/bQA+T63v3mCaYNhwUqAbX8YfokAQD9MQB+/PX+F/+x+UgEdAiQBoUGNAT2+332YvqIAin5+v6WDKkB7/sx/kD+v/Ts/QAHhQUmBGn2G/ve+s4BDA+cADgBoP3u91kAVwPJCLf7yPhd/5T/iQb0B9IJPABN+Jr1d/rdBGgKdQlx+CTwlfiaBIYIKgFy+SL9jvftBH8OuP8OC1kEuvtQ9XX0nv39AaoHg/76/bH5/wQhBl37GwW0/v/89f8a/w4H0wssBSf7VfJH9Qz53//tB+0DMv6WAPUGlwCfChgJgfwz9yTv4fZy/jAIBgqEB4z/g/x+/00BPAOKAQD86vJL/5f+fATwBgkC6wcnAB0C1Pcc+in7gvhm/lz2cALWCkQJJgJB+uYG4wkGBl4D7PpTAGvyxOz+/roHQg+YAAj7afcNAiEI9PhbCl8EiADd/+70vAFAARcEL/1R80j6rfmDAoEBrQUmCjQAOgtuA6f8FQHpAggFWvsQ+j7yYfjlAD7/JgMg/Xz75gSjDBoDLAQ7Bk790f3z8x/0dvtA/RELfQxzC2YJeADt+V3rwvb3AvYANQngAPP6NgPkAiYDsgK8/y4B8Prw/yz/Df5o+ijyLAZp/JgB2AxoALsCv/szBDcCkwL6Bwr7zvlJ+qgAGwSHARcAgvam+MACpgNr/q/5PwWFASQCWg+oCIMJtP1+7YvtXv0SChADfgEzAYsAuv5f/cUCAgXx/kgBZPy19pn0OP0XC2755QMqENELw/4R8t79evuFAp/8iQMaCA/6nwTk+L30k/1jCycUlQRF/ZX9TwAeA+X+fPlV+Jv4IPQI7jcBbA78BZsKPwtAC0IFI/uw+lX2u/dU+pv8qgICCYQHrPtF/Z/8gPjtAdoHLv9W+r4FNwPRA7YBnfxbBz7+xfkL9Ij3gglgBasFlgOoAeIEQ/kU9xsAo/5ZBPIBW/xnBaoE9P+A/eADS/Ww7i/91/xqCsgGGAbRBHz3NARiBakF+AOk/m79LPQk/PT+Cvny/+P/9gX8CZkEhAu1CCL+PfB+7rX2U/7SDdECw/iPAN4KcAX0/moFX/tI/VHzzfPeAqsA+wvsCHYE+f+tAMYAsvI6/Mj/JwCdBBQApAa4BP38Nfsp94sBGgP0BDgL0PzbAc/9LPPi/4P9Fvu4/ED8zAWiCrMDOv5ZAvIDhgBqASz62Pkh/JD1wABxDJIJaQb3A6P3N/n//Gv9lQMc+5cElwE3/8QEEv5u/8T6lgkTAsX7WwW7+d/1G/eHBc8BUwDqCSYIcgV4/pQBqPtY97r7hvy7/EwCqwLE9lH4Pf0RBQUO3hH5C/H3nPPb+L32IQCvCiEFY/9w+qn9jvvn/ZoPYQpHBAv9lfVs+sD+LQSS/xMBRv10+7r+LvrWBbr+ogDLCp/7xf38/3EIugTT+FP52vBQA48FkQGFCV79Z/549Tf3YQVMBI8MmBBSCs76tvCO9z33pPbjBSgNugTc/TD9rwLGAt4AnQvfAivyu/VD89//RggTBTYGgvcW+aj5VQhmFIEA9gFS95D26/qF9WMI9P2T/SEDcQHOEnoM2Qrp9hvzpQR59gb/uPshAEQBqfIoCVMPRAmW/NLwsvNM/DEE7gFvCAoFdP5i/h39z/bV+u4FVvsY+ur6yAhTGSwIDf2G+zEA9gC9APUEmQK2/g7yNPaiAx8AMQIKAIz1YPkM+UwLTxXa+nMDNASb+pn7ofnBAy3+4vv1/O74WPC+/uoNQgivHYgaXwMn9dLsEe/89o0D+AX/AW71HPh3Ao0FxgoLBnAB2Pj98N75QAGsCfUKCAFwA18CTf2+9Jr53wOO/dz+qv6XB5wMPQR6ArL8PPkB+vv03AU0CqT14P5H+WP8CgHQ/yQRhQQR+8H0zwH7DcYATQFAArj5p/R1/nIJQw8Q/uz4g/+B/yIF6QA4AtP6S/YJ8uv4OQmsBBsG2ggDBef3kvPq+b76Pf7+Av0AwP4SA0oD5wg7DJ0LFA5q/Xb4OPgC7ZT+3wE4+qD+nwYUBMz5YAnvANYEQwFS8+ABsPJ0+wIB/gD8B3YB5wKyAPIJSwJ3ACn9Mfz/ANz0QAbLBnUBXQDZ+NYApPx5/cv8xv83AT/+YAvZ/9b7kgBC+akDlfuq/PsD5/xAAwz5DQQcCmIBLgXW9VwH1QQP+foKQgJ/AX74OPVmATT8E/+VAj//pwTS/Yr2Zf2TA6EO6gDy/SgAUPy2ASTzkvxR/bT8fAgZBqMFGAXCCvsE5P6H+Br4+PFQ8/QDagx3EUv/cPwS9qL3kgE5/zQPQQT1/Wn5SPMmAs8DzQLV+jP4PgPSDTYUCA2g+m3wbO0+7er/CAggCNgGfPojAP4CJAV7CEAC/v6D9nz67PyTAtcJS/UJ9IUCYwX1BcIDaQrTBE/09/pbBhYCefqk+K32BfrdBP4Mqgn2CcYCmPCa92T/aw6KBtz1KP0a6z76oAR5AxgLFvoPDeEJMPbaAOUAoQVj/df0Mfuf+bsGpwGZ9wED5QVAD2gJ2f/l+9PxQ/a5/msBcgBSAW4HHgb/+5UDfwblAyf+Y/en/Prw9PTWAhoJxggE//H8NAH0C6sLuAOS/Bn0O+8u90MAbgfTCcv8rf6U/NX1OQc7EJQMdf6k9zICuPad+rAEMwZ5CV35ZgBu/zf2xPnAAB8Imf9OBYL73PfOB20B5AA7/lcDdv/E7UT/uf4VBNgD6Pd6CXz9HQrMCAUCIgly/LT/o+2N+jAA8fz5Bnf//v6mACkFQQRAAsf3ogO//0T/BgZIA/8GW+kz7gn4NApODYn6igZNAFUEBguWDdgMHARb97HjseVt+Ab8bgglEqAKkAjh9sf1mP+lBDz/AQsVDqr3fPuW7sD1xAarDBYGYfnf/A/3g/wMCAoMvgbJCaUFEwG09jHyufsn97z9/PlO+Hj50xEMFlP6K/6JAQsEevfg+938jPSMDWoSAggyAn76XPp48072Mwaz/FsFGQR3//ULUP3/BGX5SfgsBJLqmPtmCzYLoQUk9j8APfzH/of77fhLCgwBjQvcDGr/7vvL/LsI2v64AHv9TvZH+s34ZAE/AMkHYwjh/GsCy/wf9iT3zvyrAdj9MQPCCEQN4wGL+z4CL/Eh7Sv39gBlEqITQwV2BX7/M/3V/Zf4NRMgDPT3oe787QIAcQQyEikF6fji8JTsZfzz++QSvhC1++kJSQVCAZUFDvl79af2jPeJ98ABJP9k/+UNvfpJB1QPvgEmBDD3Kv9oCnoFxfzY8t/z7/ojAX0Gh/ZL/XsPAQW8CXYC0fzb8pP4qQV9/bUItf9Z9qj2uv9oBcMHIQXw/DUEEfM4+HYKVgoaByX9/PSE+0cMaQnE+mr+zwzT/Fz/3vjs7mf8x/WcBGX0Hv2LGL0JCgaQ+eEBcvtV8wsHnAhaAz0CmP+u+v8HkP449PT9FPtrAd39MAtwEYMAQP7p8ZP1APvqA5wRhf/T9z31lPJMCA0Hyf5mBSb2SQF7BycI6xDx/BIDrfWN+rYBqvGgBOn4ZgUpCEf/jBL7+kXvkfZ3/HEACwXaCTsAjf2B9uUA9BH1BS3+hfHX8lb65/0oEtUOpwSy8xv37gDW+70S4g8SA1L4NO729oX+8QeaCon+aPLl8Gz2agy1DkwDXANh/2f9SvvhAIYEaf5V+Aj/fgNt/W8F1RJbAs7xHvfk+TwAmQPZCWUExgPsAHX/sACT9UH+PPHw9ub/Gwg4DucDkQss96X53gF8BwIABPpk/4buV/uYAWwSxgvi+TX8yfVR/10CVQUYABsBnv2UAP8EI/yrBegEUQM1/PX44/Q/9r4LxwgIAy8JXAMq9mr22v/SBUr9QvpXA9n6Jvu2+Pz8Rws5AxELogVDALsNpPm77rv7MwLSA9T23fuoAhr33BDFBUX8FQOK9IYFp/HO/qcR/wkuAiD40wpd/hcESfml+G7/dfqN+mrvRQh0/pwMsAcL+nkLOf4+BEz+cQG0/Br73P0F8539lwN7+okFFQbb95AIZgAVB/v7ofl2DL4AyA4UASsFmfnl7+UCLfxv/Kj0ff53/dEIVQXE91UQAA+t/kbyawDw+vD5DvuB8SoOoAT/Bx0JY+yR6475JQ8kDXkO8AYs/pf9jfTm89MIoRhL/9MB7PVY6Yrx0P5cG7QDEATrCSr57/0BASv7xPaY/p0E0AZDAO8AqvfO87T5Jfzb/K0DMBfBClcAzfqZ9F76gAlFDGf/SP3NAqD9/PIlBHX9LgMTAKz0dP4E9BMC2wihDkgGqAtQBlD2MwDZ71z5t/l8AJsBHwUYDon3agHL/1MAQg9XAwX19v9m9e7yXQ7PB34AO/tJ+gr8GgL7A///9AKT93T7BvpD+CgG+gfFCwn/QfjdCp0GlAn8BITzNPuB9bP27/lU/rsM4Q1/BqX30P9sBZQFcAne82b33gK59Kf6SQQU+2/0gP2dA1kF0goYB8QHSgCo+7cADf6H/EL0XPni/l0CxhBcCioEdgDN9I70IvvrCT8IqwBV/o73FAEPAKkIWwwb92nyXffE/Mn90AlCDd4GsfyF8Kv3CgPJCx8Ekf87AsIC4PoB9/cGaAVl92j3VQe5B3UElv3k9OgBkPqa/JIHKAKsBZf+Svs4+4H2TQkO/zfv3f9+/hISYhFx/wYJtQJ0Aw/0TPiICfv1xul/76UOxxUNEBcPNf8P+qjuLO3y9pMAaw1IBS38VP5x9bAF5BZJCpj8nemF8ADxFfpDFNgUIQje9bz4VfZPEN4XnAi/BKPiCetv7Zf/dxbsBXgPrv+e9GUBoAXZDVYD/fl5Axf1/O1P+Wj/zgJ/BLUMCAFGAbb8l/J89z/79AiBAakEMwKr9xb/oAkPEGIDfgbO+8LuMPXT9D0G+gkSCTkEFPpaCdv9bggxGBwKrQHZ4ZfdSt+VAHEbpAfdB5f6xf0c7hIAPhRqAhcRj/0R+fn0WAIxE2b8dv0B87HuCvniDcQJzPruEFwKY/+YAeYDygOj7kX3zPx37v0DKREoCM7+3PqdAKUBT/v//HT9ZPrG/Mb3AwpeEP4G3AmAAe8Aefg08PvxLALcBy76S/ee+j4Nsw0SCS8ClvuQAob87Pzb9+0Cxwke/b4FZfpF8uD7yv2xAy4ALwHcBU8CVPxu/FIErv+oBr4OnAJ19CLxfAIYBuYBSgDO9MT68f1Z9lIEyQy2EKwO5fZy8iPsHPNYEUsWVxAn/k3+X/4D5zj0OAKVBR0ExP8SCxH5bftpBEwAVgnS98ADlQMi+un+jfE8AO0CSAXDBHIGRgYD9FL0BvBV/vgGKBBgE/4B0wCD9Qz6SgCTBYoRDwWR+b7weOph9RQA9wqUCx3/7AQi+Z78swslAokKzfpL91sChfzTAkUD6/fO7Vz4D/mJC20YzgcXBP7x/PvUCdcQuBOh+Q3wG+kA810BzwESAlT3ufVmBu0OgAtGC0b/+fKq7sQF0w7aCKoNOuzD+LIHo/hgBhQATPi69Xn3OwEtDakLfgmv//3w7PkwAHgL2v1UBmsG0vHsBb3zavQsCfAF1fCp7ncElP1kDYoYoRO7BfH73foa/tsBFfSn/F/r2vVPA/H3zxYHDir6dvFN/jEL8wUZD80L8QVz7xnw+vMr6yQE3g1TAQb0wvb5/OUI3hz6FB0HRQE3/oLwIOjt+Jj3eANgD2YCNQws/237AAH89bQKWwNN9Gr6sfxNAb8DEQ+0BHr5+/vp6+TwZgM3DCISHApeB1/8BPSCAiABhvk1AQkCPe6T8jQHqRSgEpgF0gbu87L1XfOL+HcNZffHAJ72CvkjEpz+KPyeA98GvfIm67gCeAhoB+oZaBK/Am769ufR+B/zAwP+DkgErwQe8UsGxf2nAz8Ky/Nu+gf3BPgC/wAUvxVPFbf4/+l68tDgHPTtAGYTVwxIFKIPffA6D4UIo/8i+jbsE+fB6ocBgg85F3cKswy9+B/eyvx6EskKVvxA+on9Ze1E+6QIwQOuGWQHL/Uj9ZQDsQ/W/yUNWftN8+vw0+nn/NT81BKeFQwF+wZ2/+3zqv9rARj6vgCD8lfy5vtSA5L/uQOEBID5VhE9CYkEag5VCFoF9PPu6af1rAAE+3YIEAUWAasDQPuoBgf+gAij+tPp2gWF+mD/vwt6AQ8EUvot8y34RP2IBxMEmf0n8wAE1iXKDoEDu/uj8VD+dPEB+sMIJAaOBED8rQD6DcMJavcm6WzpMv0XBMYJlhJsBMz9k/YB+DoB0fvz+5X21vhiA+8L/xBJBLEG3QkCAMsDPft5+34AzOcA7kz9xAbtE4UNLgaF+pAHuQOK9zv6jvLm/84DlgAc+GMCBweX9Sn14fNJBYsL7gbIDdMFXPqu/zwDWAKV+Qv98P408mX/MvmKDAgJiQIfD4nkTPu2BuENaxvtAAH9Uuyl8lv7Cv60BM/+3Psf9KX3xhNfEHj2t/1K/foKEAiP/bP8yO6+BYX9FAAnEBL5+fYa91v5SwVCFLAPAwDX8zTyZQQnA28GyAX0+a32V/YPAHoKig54BDTy2u69+Yb66gzeGd0QZvHb4R8Dsv7+DHYVNgV++rjqk/RW/OwMZgzUBCTvvfDJ9woCYhMvAioTRff4+Wn9IuhJ/v4DUQ5S/uENRBJjBPf4YvMr/WfxTADrBOP+LPttCecF/wIhDxf9fPWM81H9tAPgBCMAVvxM8RL0XwDi/iEUMhXwAyzxJfPf+9z+Wg97EzgJuff76ULtLvezCeQXpQRuB936Y/mO/9bwQQ+AAZABmwUn7Kv0TgiOFA4HyQTL+VTvUvFX9nD/4QXk/y4AbAry+2YGWQ4kD/QFTPm780Xoevsv/hoHfRFwDNP/8P3K+FHleP8yBHsUiBfc/LL7uvOA96X0HAawBbP/rfiM7F0FLg8YEa4Bev/x7Ebsbfjs/mge3g9aDif0JvS5AHb4mgev/ooKE/299dv4mPjWAU0R4w+o+mX++PfNATP61vu3AasDXQYh/JD8fe75CR8CdfMxBjQDtAH4+2IDXQVp/dn5XwmqBX7+kgQb+2z3AAB7AMP56hO+FckHgwAC6NrqZfCu+uoTpgm2DowFNOVD93j6xwWdC9cFxgjm9X/yRf7fAJL9uwi5AM37FP0pCrv/K/kFEnYB0xCI++Hrhvdl+KEWWwFK8S0FoAFk61P4dweMEiANbAX4/rHvHQiD+yMBZPaa64oBXurP+80ReRplGfAEoPl0/JX6lfDY+wkIkw5PBZ33cPZh9R71/v5OAxX6mQUgEucFawZTA4ADlggI+DD6Me8l7p3/PAIPBHP3aQDfEqsWcA0H/e/2mPZi8q3tfvKuCfcJDfoIDXMOIw2BAzT0XvLe7usCMAqCBZD7HPuSAPEBmgMNCLYQH/o/8VABEgvvB4UArPa/8XL5SfkS/0j81gDxCDT+FwAQCJ4Q1AjY+y4Bp/kI71j2/v2nAvgEIAIFA20BuPml/XwG/AK6BHD/+/hSBNH2NQW2Eob//gZK/Cb90PoP7+Tz4/97AQIChwqT/QYUtgNeBJgKC+9q+qnxBgdF81f02QDY98ENrAJCEJEBPPuF/iz7HwAiCUsQzfY4+X38hw0zBFX+9v2d7/MHH/vr+5QGgQf291ji6PrWBjUWuxNDAb8Ct+939osKtf8M+LwBef9C8+r6+QREFGr+OeztAoQP/BLgBm0GMwD69m3oyO4gBPwEyf2q8G/2LPXfDLYW5xqcCtn6iwPu6RsCPP9wA+n69OeEA5cF9Q7h/Xj+Mf+l/AL9w/ilCJQTkwU37K3/UgPVAO36sv50+Vv4vAr9+F4GMAWrBUj7f/WOALv5NQ7WCQIGOgLyAWIAFgNqBCf3Ju6W24b6XgYeCF4RmwMKEIkO4gfn+eDy5QI49hzntflgABgEvw74CGUDJfx3CwgIDPjLAIP8/fSm8MH7JAsRETkGdv+H9/DxYvv++mwJ2AyqEAH3O+ZhAkb2tPl+Bb8E2wc7DdAQiwZAA7cDDAFJ7znfo+tR+i/4BhQ5ILcOLAZb9HH6UgsIDRz8vO0R7aH7r/ZP8o0RtRCxC7MCdvRy+vQBkQK6/j753AUwEPv+JAAt9pf9Qf+V/x0GB+zfBTsC0PUmBD3/pwkt/8IFkweW9KcC7v+pAMQHfwoPE8z1dOtN6yLvOforAt4XcQnJBqsI+QP9BQsDyP6y9v350O0+7nr9E//J/igFVgaXDHYMKP5VBEcEPv9CAz8DmfUV8/XyZ/k9D1QNAhAYC4Hv/+ky8WPznAqaCsMI+RT4Bsf+7PIY+Ff/Y/sI+tf2o/VQ+e/+Xgz3F4cKwwvd9zrxz/uUAjkXEgUhAs4BJPxTBYP3M+xN8YHz2vjK9jUDsxI6DeoOYQGTAWX7fve7+xD46PsRAxAN6QWWCV7u0/OpCSsGnAQN+H0Gs/NY/z4SGAg5AUgArgsl8C/rFgO2Ban62ATE90rtHACTAiH98PRTElkgWQYxAEgHqffS/BYHd/Ml4kjzygcS+rANIhEDEwcFZvWa+SzvnQGEBUUMUe4K+0kCpvdpDgf/GBPS8Lz39AW895EKRgMgDpf2wwNJ/bPh0PaxDHEaewrB/hf/Rf9q7MD43vwt/3oK4AVVDPn9twTB92XzjPuQ9/P4MQjzFhz7oAF7+qUCxv//9LULdvdcCPYN+wW6+R3yh/3f9D/8of1pAlgAIf5w/ND8oxEiLNoVQfX89gjgW+fs9iAH3Q4zADf80/mG/YoEoxWXCQcIOvk08Qz4SfCrCksEmQiUBZj07gCM+N/18Ptv/WwCOgRWD6kOnAHJAXTqRvupB2AEghRB+xwFogOz6vbrCezT9xoUgxBKBIAIkgiAD9v9tQLg+Cnzv/he5n75KwsvERUF8Pdq9Wb5ivHYDhAbpgKHDO34CP7k+igECP6J7J374PX0BiAILxPKAGb3F/gX8q8Af/0GD/kAQgv4A/jzjATO/6QNNgLd+OfxyfdYDIX7OPW3AVIJVwtL+3b7xAxtBEIAPwCB+0j4AACgAbrpR+g3+pIFtBICEEUKHQqq/8QD3/pt+IwCd/xo+bDvqvbaBTIWxBsxC0b3WOj/8GT2QfAdB/kU7gemDMn+2fOW+gIDDvgM6gAABgefGfYRH/96BXX3juzz8AkHaQ46DcH9UPSm+oj9wwZmBrr/0/hQ+/juJPy8FPEN5gQR+kDwVuxsALAAmwiGE34LGQKk8LcBBwBmBRgEhfJz/crqBPN6Facd7BHVB6T0OeVQ+vgANQpTD0H3xesI8Wb1hweMFcwLTwWQ+0jsR/TDC5oFpQi+AjT+jgd78Tr+3/zCAUAI5AMTDi/8UPle6tb1CQOYChARiAI1Afr1YwSc/sj9EgBm/0f9IOh6/14HuQdmCr8BDPtA+u739AO5Ey0GIQUz/sYEwf4L77Xxzu3V/JAFywtDGLcGufsyBXv4vQPq+77z6/5r9AkDFv/uBrEFn/2i/mwASA8M/fv0VvZlCAkGpQIkD/f7ue7p7EAAVv4YB8wTIgQzCH761frQCrT+zgY5/UrgBOnt7KEEqh75GUURPACr9sb5YvzG9cUBvP6o8Uf7I/+ZDW8ULwkMA0L3DvRsArD9/gJzB4QCvvs77w7++e+d9jATBBQSEz8BrPaZ5+Punv9JBeETIASt+EX1JvRuDHsMYQTvB136NOq+7g4OYxgRF+oOTvlc92/xC/To/jAKSwOU7YLpEvKCC90Z2BbJC7z95fNL63zrNQhsEUH0TvaJ92Hy2gyzF1kNKA/t/7b1+PAs9QQQkA1iDcX9s/AQ7FDylQUeBKUQWQ2RC6zyk/PB9Ffwxg77AfcXUwCE8TX1tO0rDDHy7gtiDT3x2fiH9D4STCBBEBIJVAhe6CLpqQC19GP/Jgff8ULz5gbKBboJYxaAD1D2T/V9/Jz5hPjC/0gXg/iA4rn3fv1H/cYFSR3DDTMJKgv+99H0O/CgAUv30u4hAXQMvAwLBMEMqPGk+ekILPcY85b0Lg71BWsGFQLv/qH8EwM1Em/1y/0u9mT/jvlY+Y4N4f08E/kCuvkP7Yz2WAgmBSMMsvWW/K/5/QF1AD0CCQtqBp8FHvPC/bz3h/yCB18EUwLa//oDlwMFBxf1a+42/voCYQU2FbMFO/uq+Kfkx/7tB0HyRQIACTP8fwwECJYPVwxi9+3y/ee3+m3+owz0BrH+kARt/CYDVA0UBqvs0P3G9c/7gfv5CAkWhvCNBVP/WgFz/f0EBgBA5i8B3QiuDQP8/Pf3/NUHPAV6EscVQQIZA3TYJeXa+ekDXgboB/z/UvFLEhwGjACIAT0JFflE81gHDgQBD9PzVe3a6mb7DBaAEJkKZfz/9xDuLf7cDoAOBQTn+Gb2nAF6Ep8LWQWp6ePmdfN//WYOGASZAWD4wv/4AGUIoSSNBbzsdOiP8AIEpAVaC6gG4/s9++/+AfuhFK8RQPhw+17soQDF/6kFogZp6oD6/AFdFHwHxQWnAIzieulI7CUE6x4nLwYTvfhG7OzifvHi86sIkPsUBfgQ4gK7D5MEVw5cCuT86fNq3HfnfQHIASkAoxLmEqATKAp/AwD5Ku+OBCT27+0G8dkC7AdQ+BENvQU4/Uj7/AOTDA0BoP7N9Xf4dgWWA9DvfwNNDRv++PQs8SIMKgJWD8wU4PvKB6IEJP1h52jm1P8lCYoIZRCvHMIF3+7q3x7p1wuUD+IB7wA9Atfnf+jCBxcVhxa2+cLuovtCAOsCjQ5MCpoBwAzl8JvqYvRHBDIPpglaC/H3CRD6+oby2RCUAjb5DOsU/6X+d/3oCzIFHvdp9YX2dfeBAPX+iRU8+zcD8RHt/2IH2/W7/2n3kQovAHjshAu1BBr4Tu+uCIoEUQBeBW4AnAUR9P0EZggiAYMQpgYB8V3i2u/nCO3/UgZVCJj9AhCXALPtsfCLBLQU4gUsE+cTXu6V6WrtfPgtDmQOvQbW+2f49u8L/z0G1f4Z+Zb2Sg6YEM0aAQKm8vHutOqpCvcKdww39U3lVe1VAYARiR3WF8IAL+6G11H/jwdKGAIXvvNk+J7tEfNFBbwP5PCb98IGUBXjGewJIALO7OH3ceOV8qj4JhgDHAzkuANLCGMafhAF7ibjZ+Zr+JwIYgqs+uYOJAcXBN/7gwHoDngCxPiY4e3oYQjKISgWDAlV/vj1DuxU+ugEWwOlCNPspvjX+DcVviBABt4FHfG13vLdgQKVCbMUjQLT+04B6vXwE5H9dwPLB1z+pvAs4tH9OgS2FwQlRQ6e/dH3Zt5x5M37Ag9RD00Exwwu9w351QA0/qwFWAz+C08FeP9e/I/qpNnYAI4MmAXRAlf4OPU7/ZgLZQszFZUPMg+M9MvmPvR+8nL1ovIrDnIJHRD+FMf4tPsR914FvhF/CCL7fPkS/Pb6zQHJ9Grysf7nAX8KTAD29oT4bvSZB0EIXQyaBWL4N/+Z9aYOjAQFA+0NIAjmBw7ai+We9NwBiBdEDYoY3xrjBbrkotr67ecT8Av0AZkCgvAn9QztCwQyD+IN+goT+b3xBu+d+xELghZn/gwMcgy/AKkBj/OgDwv3DO6u+rb0c/Vq86MQbBV4DDkGKASIAcf3gPjp+QL+gfyY9CjrgOs9A1IVGiDGGDoEDPjc6Vn4nPXxARsRwg5lDDDv8/RF9VEXmhcY9zrnadXy69v9WzA+IrMHxPwV82H+4/lKCvb3qv5Y8Xjz1/xR/5op0BK17NXqQ/tK9oAQ6AwT/EoFTPQJ/ev2MQE+BH/+LweZ+nbxTva4CJsR1fwm/cgOsv75BHgSAQrd+br53PUj7/7zCQVeGJUD+/xx8h4DxQkz/Pb1YuVRAU78BwFUEZIRfwM19tQBOvpl//UABwNSAVD7iO/z93UUJRXvBNDuLvCE+lgQDhx6BtDzPPZc9M7tm/oJDjYZOwk86tPjpf8GFpwaIRSfA6btxeYB6zT/RxKuB+cKifaC48HxSQafC0gO/Bb5+lLv9v2AA3oCVgF36CHzsQ/gFAIONfLdBs35FeuW//YUPiMH/0HmGOd19pUJDxS5B+AACPSv82/4Df/RFy4VHxD340veTO4L/3UWOw3PChz8mf6S8V0DdQ7UElcDLtuw/nb/0AE9+XP9MwS/7rEF0wadEbgN5ROsBVnkmvtt+aj0svSd/A34zwxjIqsB6gUF9ZsDBfq14xQbWQsw9b7pWvwDBzAKliIx8xnxmOT834gJqhfpJk4LRfUx8avkgfE3ENkR9gmRCp7+4fxK9ZsAfgWL8D/99fui9Tf5QQH3GAsPbgO2B0URqwY99jzop92SAOYRwAwzAA0H0vb/3Y/xw/8oHA8gnB0N+vHUfe/NAqz5afaZD0ERHvpf8VgAK/54EXMAn+YYBRoHGBrGBNgLcQ948eL6H+639Ar1jgjoEBAERwFSAMABvPZ2+hb0svNF/pkU8QwW/rsDyvlWCo0DK+ss9db0LfTBA9D+QwanD5oN8wK05zT83hk5GF8CCfEG+NT3UfvJB+P/VvrGAWkDMgWnA7EMIP7R+tADrOl/890CehJZDMbqdPvDA98BPQ4fCIv64/Sv9i/rhOdBB3sS/QKeC5QOZAeK/8L3BP1r96v/WgZFCeQN+QUSBGrsV+wNA5D+PfjXBEz6CfuHFIkJMhLiAJwD5P2v2woACvF69GkDOAwHHl39PgQv/6bva+2R8DkAtA6qIMAgRQ2a8lj0SunF8v4ExfZU92PsZvCKA/UhJR3CAmT/q/Hq70fx1xP1IVUHbfra86zj0+3XGEANI/7i8TD2ZgR/DtEaVv2/ASX9hfFd9E8AqgaL+BIHBAUL+QLz0vfL7PT33gnDFo8iPAXcDoXpB94T/bj8ux1/D4z8/PU79VEEAf/7+A78MQj8/2T+2we59cv79QnPA5UM+QLf9SX42ftB/o0JgANf69QCogHI9poDTQhRGLAGX/Ak7/PyBwX4Aw35EvpG/QcMbv8NCWsg3QPp/anleux4ApX7bxsrBc/75whs9vD00AQMEmT1fPCb+Qf0ogapHPgJLfO5BGD8efPI8PT+IA0A+hoKBAT18cH7egizAr/7exUxAmP4GQ589uTvaPTd+HkH8/8rCjkFau6aAC0RqgygEs0REgJc8k/bW+jG8O4HtiD/9Uf5EwWZ/cUFzBDfCxz8fwH8/arsheNq/EIMYB1eDv30V+1J3CMHKhalIPoVpOtG8o/qV/boBQcHYxaqCCTzr/TG/EoRNg28+nfvF+xrBnsGM/14DGkJMAkUB+LyIv7s7azum/jl9z4fCAgVAkvzn/Oc/9TstgYvBCcV0ANPBwAhZgULAQ70Wudg4UL2yQ0nEs4LxA43DuP+AOx65nv+iv+l/BjuOPvfCnQN8BbjCnEY7vqb5ITz++4H92/5i/06+gwIMR4CB8EGUgZ08kj2Nf41Ek4S6P009qr3yu52/JP+yelt+aoCvQnGBJkgMCRGBPwHxvbO63nsOvXf6THkv/BqEB4W9AXID+sHJhL8/9X8TvLW9bsQJQfXDVH4Qf6A8sb7xQle5zkGLBBt9pXxJvKj/iYU1wxWB6X8rgH8CEn2Wf9r8+n6r/ku9SUFqwESB+0BCwQT+8MDGhAGBlAAivO0/3cJYQUWAhEALfy79ILuUfN+AXwIOxgzBxXxVvqV+Nv5YBLvHAwCE/7X807n/PZsCE0RPvsm7SLz6AVgCEUPHAOx9AEHewBgBxr/ZQDT9cbwjADzC+YRMPTpAGXrwfU6BVIF9iQdCyMP4PR45+f3yf4EAY76DxGX/+j7h/ki+d0RuAXiAHv8s+IF6SkDeQmoARMOlQwU8zT7vvvxBCAGAwYoEKQJ3wZ33xTfagEzBnIM5Q9+E6MLtvJh/UoC6wS+DZvyQfZv6e7sEPg5/5ARvg67Djj56fp05l/+rROHDXQVwfwX+JLesAGhBEn6fAqx8oT8aQLCGTMMUQTpCW3o2+3iCEIEsvsWABL/of9//ooY4xZ39BvjzOeT61D3NRl4HJ8O1AJnArfpFu+m/4cHUhojAgn+begf82MIHPyMBhgBK/9R8fL75hLPIIgYgPYB8x3mjOlM9rr8zwT3AqgRVw8pBmX+v/hE/mD3+fb/AG4NFBH2/9DqBvaNDXkVIRLxAJzykvLa/tTyove1Ahby5P+DBSj9QQhIFPkK+gVW8AHdefpAAegCvfu/8rcCkRGPEKT7SRJfFmgHeQy669PsigAc/Cz1y/avCBIO2gNz++wKyAJj9DL1APIz+X0GuAaC8a4OfhEzAWrxHOK0CpYF5gwgCZH95wlf/eT08+ylB0oLtAD9/u3uzvXwD1oSnQn6B/r22/Po9/P8hgKCCVYNnQuk8ynnzvwn+6IK3xMqALD7zv4o/fL51PlCC2v+NfcdCkDv5vSO+9QDYhPcFHwPnO6P5wbshvu1AXcXXhwSB939ovZs58LlPBSJDskRkg9ZBjD85N+w8k7dMfXQGf8a/CBQBpD3du6n/g4Tefwx98f5keEk4Gv05hb0HtUa8xh3/IP4sfVy67HyHQfVAjv4Yf3CB4oARPX5D/wH8wJQCKcDOfkh7f/6bvhI/ysDUQ+HCOf3sPRH5Wn/5xFTG6P/ywImFPT1yAE05woCoBF7/1oGWeg4/aj1fQL3AB3/RB2Z9oDtyPkl/Cv++xeeEXX7n++tAWcJ8fENB5r2FAi++Vr2+g5/+0EDfvLe/+sTkhnk+D31s/l+8Oz5l+3MDMEUtxAr+gf4FfTj76QEFAC+DmMIWRDxCAgAtfykAL7/ePLl9Wzn3PFz8w4FuBI4FyUWYQs4BNf8CfAr1637IASSAfsC+/6yC78HNQ1FAYT3fPnAA+kAngGOBjYQnQPe83UBde079/QJBw9x/cTrOvFZ7vD/Wg9qFRMJUAZ/CDf2x+U39K8HV/dPAAQcYhiMA3rxz+Is4kgB4hTXEh4aIQnI/Rj3gvx1CeADOQ9q9XLbV8z+7h4VQARZDmMScRnS/gYDTQnn7m0IeQ7P8Jzi5/e394wAWQZiCswMZgdqFYL8uOwo7UgEFvx2/nATVvWZAXIFZwf29ZX0Xg7H+ggDEwWeD9ADzOnP/dT2S/kjBSH+c/2Q/3EGMxReFkIHHftN7/zo7+mu/c0G0vmYA1ULPAOTAZYQKAtG/Pru4eHE9twKeByKHZ4OcvtW6XXmAe75A9sCQQWQDRkECwjyEMn7zfrnBsTtde/Y5RL5gxpPBD8Ajf8QEocRuvxc9FX6egxR//gD8vlk7Oj38fma+l7zoQzMKUYRwgExBEnzz+5N5Lzt/f8TDAcKwe0rBewJVhOED6QHuRhf9uLz1eGY5Jr9/g8WI4kAvPaq9DDtlfKQDykjChm5BBXsVulU8Q79CgNb/srxEvkrBBYT0huVD2L3d+qg9GfyDP2QBKgPCQKE/c8DlPvcD6ITXQhM6rbu9uuf/0EKafWkE+8DcwYd/nz45AVsEBUQm+Zb9r8AgQDaAMH8nfbR/TgEce0NAsMT6hdIDOj1eOI/7EcBevRFCWMPxQTXAOz2UP5KEkQgHgNN92jw6ucx9fPygwLHB5EQaQlgB4cOuAACFWLu6eJE+/kB6w6Q9LX1Zf9TEkcBWPVWDvsEr//p9t/+Ov/7A2QHOusT9B8BGved/hr/zAMKBSL5lwjSEl4LSf/m+8PvzwK/DbL3Lf4qAisGR/Io+fD45w5DKM0LWAw58O7rq+XL6UXvCPyDJN8LVwi7BYkGUPMu74//QOjL8Vf3tQY9B0sb8y7WAV7+Mgah9jrrFuqP8TD45gRNE7gPSwJSDh34IeJtDKsTHQwlAyL2tfYU5g3qJfR+BQANoA1EEskGRxHzBpj+mg5h+yfkYN8t3wHvLgG+C+Qh9SBVBjr9CPcy/n8LFwSw7nLfrPY5Bd8OBRo4EHAHBPqt7k7qDQQlEzsOBfTM6a4A5vUAFZYW//6EBb34p/rd4qvsNP4L9DkSARQADE4NiP8Z5OHYRAVAHKwdvRT4DJj0Icw97EcA0Qy9IOAc1QH66RL7uecU8lcVDgfx/XUA7PWO9Sz3KQ8AIC/3O/aM/sb+yPJ/+lYOxwQ1Fm3+3vHD9ev6kQBs9rMJOwWTBUIRYfsF/AUC4PjtCZrq7+rvBL8BoQwDB4cT//PF8qD7Yf7uBuTzoxHtBv/+NQaGB9ryofXPFRYAGffm7jPyqfOoBHUQvAvDCSkAyvsq5gUBXx6kEPj3LQIaCB7tUfkdAkLkg+SeCzb5RQokJyEZdA+W8swEM+033O38tADwCbwEWhNi/t7gK/2tCHYDoARHEfj6agFqDJb1pw0HAEoClfeK1OTsH+77BoQhryk2GpDuOelE5p/u8wvhFJENVgrq/gb6F/iP/twOTgml8qTk0/gR+PgRyCf3+Uz45fa06sj1NP76C68Ji/zb9tEFMRNkD7ACgedb5vv8uQjsD0gZIQfj5zn04/8cAm4Ogg6F+Ibm4QH9D3sGxAml+5HtePXd9/j2m/svD4kJZ/XcAd8MGhcs5wPtaxDC/KQcVAGO85n7efTp4aHlABxNBdsfKB0RFC0KhuH8AxfoT/Y1Be73iPh4+fQQwQJPCAP8M+3o5cL4gQlwA0MYeBLfBZH2zAFV+oP3HgHq9uYD3vet+sMCvhbNFGH+PwMC77D0quxQ+9cpyxp4DuvuqNJf5OD6IhCuCg0PdQFo8dgHuwFsCbQFFPiu+Vbf6vcDGeoNjwt7/5f7gu8S8xsLjv/lAiECwQXR/XUBYRb1AH4DOvzy+933/f18DLL1rPcl9Kn8TP46AWQNJA0h/FH2eQ+BANEBgfv+5u7khfXvEz8M1AvCCWIAWvySAFAN4AITAm7+fes974T5kRtEH0MCyAIk+Y735Od+8yL70vZ0B6j1lQ0SEiYPaAPd7DsV3RDk8zXk0+IP/Oj/yQfiEqsLIB7PDsPyMfGK+rQOH/JN5GHjSAT4GrYLDQ2Q6DYBQQ6Y9Nb7bPtsCuL34+nLAzQYjBJj/m/9cP9wBCECFf65/kf4fQLa/5H9rAO2A8L+xe5ABcUL9gASBqf3xvQNAJEBIO/i8QUOjwxA/rwLahEA/37qqO1mC0L9Cv2+CIrsDgG7FusTpwIO9LYLKPYB54T3MgveDin+vv4Z6w7/EgzUD2oS5QidFp/vneZf8eT3Ofus/VX6oe3FF24apA0gBi3yQOo252TrRgWsHAIULQZv8Mjz6QCmEhIFxf89A9rwSgHLCqAOgvqA+7j5QPlGAfb7GQhsBn0RL//O9ej4N/fZ8vzvfPOe+IYNigYeBv4CYBxxF2P5EvOb6+sB9wrMBLH0IAHGARr9IfPN/dET7ga+ECIBiAsE/Az3SfpB3ob4yviJ+jL9EARM/gf31BT/ElINWAfr/Wj5yORd+1YTEPp/BggPWwhzA4YGkwVY95cGzvQf5FXj4fq3EwwD+gv/Aw7t+vH7AnUUaB3ZEZfzpN8165H4Sv7dFIwTD/Gd8B4KwgYzCz8W+gvBAc37MflH9mvwHPEo+S0IJhZZCcnxAuIE94MKVRmOLLgBhN8x2YHmnwHJDiMh3xgf8f3iS/yRGbchnwXp8FXeD+Nn//IEcRI6GaYLYutm6/r5/QntDh8CXg7P8MvqhgQjGo0eDPs58mfREtmYBJ0DUxihG34WbRIvA0/8BPxF/BDxU/hi4dXesQbkALL+dgSVEl8ezBYFCxXxHvBg+ekK6Rk89gzwb/IE5Ffk9PfPJJAcsxeR/2Ls5/+BAUcZJwxiAmvmnd1q6Lj4lRwMAuEIDwcS/fPtkPkdBRf5mh7kDNP8O/f8CIUMVfPO5MvneRAD/iL/1QQDDO0PsfEb9nYAdBZ5Ep4KqgwaBMf+iehZ4tb0bwOSAcH5SQjV/rvzJgvW+FX7xg+WEHIEA+71AJsChAFg+dLnCP2o//z5YvW3/WIZCxfWEtb8aO2WArAGIB8eG2j+J/em4l3b8uhfCKkO3wa89XDsQgZXBGUeXyj9+Z39nfSw6E4DWgP9/eruhuPg98EOnxDAB6/17edW/xsMiQ68DakdfRwe7YzxqPWA+CkGd/jV94v2qwXcBVro4em2CuYhpBPDDCwJKfml7yH4agMm/HIMmADh6PvmwfALDFAC0BSVFXbzAPQa+3gDXAYrEvULvf2A8d/3qPrI7aUNDxYU/8zuce5dAZUEjQJaA70DfBEHEfIIbgKg+ysCAe5B7uL6tfD+9T0H3QZY9z8KYAohCvcK6u4K/eQKbgVaAKwDsQkb90L25fiK74LyRvV5/6r7DQ2ZFd0Hgh0GE+z8aOpI+9D54ugeDaz/EwRl+5306AvS8Q8BrP9W7ycLDQsjFOoXb/9g++vuIvcN9IfzrQAG89YANfYQDB4aphoDGBHvvQUX8JbuoPCL5/sWlQuLEuEGT+n/+pQIZQIZ6QP3eQTi+c4UcQhM8+cPdQmaCUv84PxGAjfk8OZY4+gEJQw7GTUoKAOaDzUCUgZl+GzitO/O5xr9yfPRAnkhNRa7FXT+muYV9M0BGAFeCi4JH/Ya91v4jvQp9vz1dRQmCCfxjArW/C3/ggt1BesMpQ1G/CwCVwHj83UKMPXLA/IOBOv/5lzhgPmVB9wi3idzE5X9lti16XTvTwrQC4f1Zf4758ALeiPVGz8VluMY3SLkAgMgGoYI2hL+AjX3HvZOAbESsv6qAB37J/B77Br1YRE3B1UXWh707FbkXOF07OMO9RieDpP2EQWGAwX6agafELQTXvIE8iXrOu3h97/1HAyfAvsYSxm3AFv/DQBEDQr+Mv9c53XbGgCkAezzG+3ECCsXMxuwHbX5TASgCfr01/es6/IMTRXf8oTzvezX/QkM9AVV7QbwxxWjE60VJQdu+yvvVONe4iDi6BbiI1oYSxQG+uLv2e1D8P784f9Q/6UI6gZrF/MPKBMmCong+exT48P1wgXoDsYZKgWQAxTxaAQw9dnt7QC47X0J2RMAHPcQB/jQ9hPcdPENAYH8khHQ+s8C+QT0ApohGwci+ubvE/W09F32ORMcAuwHw/lN79L7hwZLE4oB1QPvACv6ifQw8DwBQQj7Ap4Ie//f+N/+ZgPDF57/BvyN+vvn2wTi/2sQPxbA78v3YfS46yECahFLDZMEuAJS98r/EQKn+zT9Ou4q+yjsz/SUEvUboCzSA/L9IfBW4uT3y/UIB6n65QUCDeMGxxXD+aj83fQX8LgDBf1mGnMOFwY7A2/oK/4D8CwCmviK89YSteQ487n1vgTOHiEb1SO2ANYHJvH97KnrStTJ+dXwcAT6CG0O/SmEFHod1ffC5oTyw+BV/TMAyg+kII4EtQlQ+A34jwYe8wH3red++oMBv/OGCioD+h3hEzb6Hv5V79/+Mfn0/R0DzfPw9sD4F/r79vABnw4EC6oVKhtHAW8AAvyO8KgC6gJ2ATzw/e/TAYzpmPJ5EBwgchjb9JX1UfbWA6MKP/nUBZ//6/2c4m7xZht3Av4Vcf3j8ygNHvgiCzv4fPiZAEDuYgNt8X8HPRNqAr8P9fv2Au/xz/S98X3uohX3/P0E4vezApghQwsABMPzqfkS61cBfxFX+qMHHAjV/c7wjQQmDJX3/vVB+Vf4lA33EXH/d/5e78z39PgL+4oHavzEDd8X1wMj/8X6kvGy9UTljvlwFsUJAAtG+2T6YAhuB+IG4wWHCrX2yutR94P6shRYCtjxjfgW8m8DsQgLCewBNAHbCw7wQv40B1MEXvko8eESago8Cnb3Et227C/x2Qe9BlQH+Q5jDrIVpf8DBPX02vMdAHXqowA975j7chXl/CUYShBaAV8Ikv73/kDmxebG/1sIKwBEApQkpAtw/kDx8tVwAFEKKBAD9cjudAxh8RoKvBgsElUJSegs2vfuewt/CuURPQXe/DX/BfV5BNgDTgBOBWv2cwICCSz6fv2t9YkCTBCfFVYcZP0a7UzybPX/7y/tt/MO9RMFyA43CucIvRLyFJP5gQAGCnH+EPo827fm4AcdD8YHz/Sk+CL+Y/9TCCcRCgqpFVkNmvQu81DwSQrv+xzyB/gD4C7pzPaTDVokDjBSIVn80/Tf9P3xs/BH9R31mOoC+5sPjyXKIvX6wQRa9AXnvwpi8s3pOAPpCBkKqvyDAbUZlAxS7ybhnfKYA1MI1Aud9eP+JfYa8DP+8P5tEjwGeg0fBwb1R/8WDkgbPvVc6hP4dvm3Bl//9/wuC2wHPAzuDPIIqxQv9JDjJuZ/2gz+vRziDiD0qfg5/ZL9+BP5/dL7RPuJ7QAFsPPvCw8WJAJwAMzzaw11AhsZ0gLn4iUNtQMsE+b9AfWC9jjcW+HL7lwdTyr7KMgKHuMp8Sf76/zfCIoCu/yB+mnkcPqkAIIETQVO9KUCFfcyDtwaBRDwB7P0dAUA+Zv0dwFu9m4AjP3Q/bcLgAdy9a/cRvRNBEAaah3E/FwTd/4FCpwN0u7x+WDiNOcu7oz6KgraE90Su/2K/ez0JQjjDb/+Ww4tA8Pq9/H68b8HZQ0aEJYZGuj0+AHu1eR3CQ75CxQQEBn/Ug6vCBoMuxNk+QXqLvp963Da/flPHLoRcAgI/pj9SO6s5I8EfRIsHCUHYwCrAO37Awfl9ZTwFekx6xb8CALZIX4iEP4XAY3+MALgDLoKw/sv4rbiLd7FB3EnOSfgHHjeltzJ9Cr0ngG/BE4L1Qhq/CP93/wKKN4U/uLI88Hn2gSiBf72Ufz7+mMcFQ/OCN39FfHx/BHzAvv3BOsGhBhr/Grg/O+/CNMT5vJTB2T+v/R1B2X7xBHkBVkPEOof1n4EWASLIZcT2fjLAavyOwXhCw8AoA+y6HLsEfa/A9YdpfPpBNLrF/PSAu35bBu3A7QR7Pic9QEE3euSBOrw495P8WMPYCACB/gVLBRM+asCcev9/UQGGgHRCPv0AwoK/wb/eP2V853uV+3aB2APtBrPCI8Iu/sn75X+9/Yi+Pv+5AGc8+v6ev6xEtcZ3v1m9ODesOuPB3EUHh6WHr8RugCU8Lbn8PA/7VjjcfAbDEcXmiH3DUr08f8S7gzvEAI6CZMQUPjc9UAL3x1tBILuKvp+6FIBEwA/ARoN9QxIGZ3slwUjA+vqCPUY5Qz72gSdFWwSXAbi/t/2hPau9a0CYQdY+7fldfi492gCAyGBGbwQMAUE+5n6ograAdvstOgNCtAFaPCfAj/yagKkDBIJqAJJ99cNQAHV+GsHuwLk/7/51+h53C/xAyPRDxj5swdtAvkI+f+6BRf7RAT8GWP0N/cT+x4CkwSX5WPwt/e4/KUSjxCNCB4R9Az9+GcJEQMk6GzxbPeIAr79cwzMEQPzu/vx7drkJ/5BCYgR0RC2FnwSc/h299LyEOXI6u//0Q8YAJL3OwazFBMKwgMA/eHx2fjB/Fb/8vdbEpMT9QkWDQz7l/nk4rfyRvZz948SfAteEX/+LvYIBS4HUweKAXf6YvIJ84b9evze+P4DpwoiCMj/PP8OBVQE6Ppo+1X5+wZrDVD7rQLd7pb6KwQY8RP/Sw3xD6v6D/+a8av4JROr/YX8qPw9+Vn7jfF/DB8y/xvXELDyaOM27f/qiQx//toB1QC7/K8G2ALxFyv+evvr7vrQ/ulQ/uQJaBk6HP0M6fql9iv1fO5FCO0LmQC6/MQB2Q8h/r4O4gsK+u34bOwcAD0E4AarCK72Hf3CAE8GiAYJ+u/1D+bD9vYFFwK7DmUUOQ2T8b3xx/wOET0IKN7R543rc/xDEgQRhSJCKDkR0vkH6oPnUvnK8r7wUwUp/rT/jwj9AbAUTw4PAekGXezr8bz5ovVsCbMFSAXSAxz1E/0/+ZD33QqYC0gFL/x1AcD8s/gVAUD+DQZxAvYHZfUmAEokNgLn8f/hQeATAwoHCgf3CpQH7wb1+6r46xCKF9IN0fUS1t3qWgdhDzwPaPd7+fb0zOvdBVgblB5KDgr6K+YM/QkHXvmt9Z/kYPvx9Tz/oR7SDAcPrxB//Yv8OAQ2+U/uLOqX+xf/+APUDFYAxgkiAsgKiAWz+YgBYujE5V/8RgtlDAsY1Ahe8IT1avhsBYsJrgEQ+Lv0Z/LzBs8bUwoUBUr/7PQS+ioBNBAtE1f+JO7V4yjkrPT0DxcQR/whBEUE3AXoDh0UAhCI+mPsvdx25f8CMglZDh0RQADB/ycFpf4B+9v/iQOuAu4Kqgb4/ynsL+Ec+nAKeBkUEKPtj/SjAk/vBwauEqUIFv5k5pwDKv8E/bUPHQpN/GDyHQ4F/wwHuwY+7f4CyAl4BLvmEe/sBkMFjQnKCgYPlwPuBGP35tm38qcVVBG++hHs9PkHAH4HEA4+/ocJvwBJ7xTzlgH3EKMNRgth+Hz3Xfv9+fINswvvA/H4c+d373r9YxDaGEwKQ/d/7Nr6xvyKDPMTsf3a8ITpb+8p7MIPuxWy+wwGmgJsB18IhQf9CZoDcAB6/T/np/bK/+ACkh4J/N0A+Pmj8qP8E/bmFz8IYv7U+3L72AJ7+wf3Hu/B+WcF7BFhASn44g7eAZXw0Aj39qXnBvvk9ugMIRAAGTcXQP5uB5gBrfZO/A339Nyn5oYGTRiiE6UVeBgd+sT05/WX7EPsPf1GBPL2APzTA5EOlhIc/pXxie7Y+LMI+QCUD6cWyPn56IP08wfHB9QOwQw5+AXy5u5J/SIfExlmBLn1hvPx+aDuwASGBSb5Yv+y+Hn7GvynCawPmf5u+83+lfvWALAFCAqxBA4IsfuM3x7vV/YDCNwPaQknBJT/ChXLC8z10/wECW/yl/C77bjwqA92DogKM/UQ/4cPe/+2AnQLdQef+DLzpPpT8wX27g7iAJ35BwVSCJ70MvjyDJD3gQeVA9T97A/H/KUBsQl79A7vQOOP828TDAeAC1f/VBC7DnD5GBaAFDYGOOp+5Prfq/kdCxMEcQKR7ygDZfiDABcQIRKgEmoCC/D96aACFv2HCB8B5e738qYDhRcbDT4F/wQxAfL02wgS/VH9DAF662L6PvOCDosWxgjPCBf4UPaP70v2xfVz+iEHHvcCB84QSv4mDJgLZw4ODsf7MfGg2D3iZgb1DloGtxtoG6/5NuZ26TkBDAThGPsJZPHfB2v9SwT1/Oz5FgtS6ZLq5eWv9GAe2Q6sDSH96A7bGg4FARAG9QPtDOlM5oLnf+fAD70QTAldH7oS3gRbD8YBMfGi8Ln+P/kO7bv3rAWCFLUI7/n29OMIIgFf6KD2hAWbF1MMUQW8A+T1Du1G+vgN8QT0Bzb9Ieis6fbxm/jrEloVjAatD7YLGgf+AeMKoQDO8EX6FQdX+SvfdfIn7hL30hr8JQ8RBv7H+HnlcwYTFHgPqAnx8rzv0N4x7I0BaQQn/SUAOP6S8YoYMy9BGRwIevy06J/lN/RT/pIHcAvEAJLyu/4gA9r/vPuz95MBcQQKDIYSoQgk/dkCH/P+7CECGfvn9x8DdAb8+A3/4wuNAfLzUf1GDSAGVA0sBzj74f2LARAAfvHb7zf3APoy/jsGYAMLD2YGrQBG/XHrVxMTBO71nw+NDTca6feY5rrvRd859TUN1wsnCCIGVQwaCoMAOv1QBdH80+qF6jLpZQR+FbET4B7gFS/8kuS+6NL1PwLn+Pz1GQtvA4gUMw+1+lIHuPEW/EMDE/e/AtkBfghV6l/sCQ6OBv78vfU4AiwDHRO8HHEIfPoO9Ozi49U7+7MNaBrkD2AFgglS8XUI0hUVDCz5heFh5m30+gycE8IDKwP38z7pcv83C3MdDw6m+5rxT+I19AgF4xFeBpz/t+797P8ERBEtH+kWqf5M5bbw5vO7AAQZ4RXR/ljlAffrAIYGdglPCkL1nufg+439UALLFPIW8Pu6AX/7mfP166jqpwaj9jUNdBmxDgIMnPHP62X2qwPZChcTfAJb+rL+p/bl89EC8wqQ+Pbvpu6PBCsNkRHAEjoD9ADu84H+OAKAAO8I6P0N8EnnWvlJBzsE/wULB3ICAQYgFLYJ8Pq/+7nw8uVX8YgJghOXBYX72fYc8qUCiQWA/xIUHRH4AM3+kPxJ/tz0wefi7In+0REpHG0TegKm+6j7vPmcAlgGVP9K9lPlKPSZBkIGfQqNBhQJAALX8k8ALwe8CVMJBuoU9DD0teHWAJr/fwvOKDIbqwey9d3xlPMf8KAA+g3DASf/HQdMCLb+Zf6g+y7wWvVx904IohoaGR8DYuwH9V3ste+8CikJ5AnoAu/3rAYjB479rwcYBKr4ovIu42/+Zg5ACcENoPuhCpT9q/sIBfHzjgn2+SP24fgU+HsMHQGTBbIFYv+9BToCLhKzBVHzsAsx+Q34wvIC4Br3HgHuF4YBHwNIF2X8iwbbAMwAPAGr48XzLAiV8q33nQLRC2YUwQ2LEir/Xfs385Pfnehb9QsLQBI4Eggd7xXpCKX/De5d7r/fDeuC9/7fBQ7yK3ciSA8+9bcCHQLX+iT7yuty9If+zvyZBnkHPxRF/djfC+1F+QsX4iKLDTP6JPmw97P4xPm5+LoNfhN//OHubPxZDx0NsPP/5hrmMfpiCIwLFBCeDL4cuQsMB+D6c/AU8n7ksv7O+RsEygyMA0D6pPQXBRAH3Qs3/kwE2vtP/T0CyutX8NX5dhYPBmP6KQRyAKsObARIAg4Cv/kjAObrsOoGGB8bZg0m+H30LQg7AScGy+zz5Ur6Q/s0CPUMMRU3Dkj+CPmw9rf91vdx50Lsuv5CEywifQ+i9ZTwl+Yf7lsIfBTpGWIJMgUM/f/tH/uU/Z8KvQOU9+z34PvGEqIQmAaT8GfrQQF7+tT57hBCC2YA5vjE6tcIjBr9DlDwINJt6CQCIQlED80kdCHw/THt++uw827/DP2D9QEAHgoaBcb8+P0xAIMHFRIdAaDzZQGX91v0EwQjAHIboQ5y7Rr4SPd8AZ/4h/hsBQoEJwyc/gPwj/1U/14FvhIpAz0UHwmj7Wb4Qvle+xT0BPnL9Of2RQEDEnsX0gVkBi8AVvp4570BRgyO+sgBFvLwA8AFG/5qAXwF3Qn86k3tLwyRCaEMEQd1ANsJnfOlAwAA9/5wEFjxqfNX9Vf9uQD9CGkKj/bx9DrzAvaR93kTxxdHEf8OWAL5/Vj2O/LD5ZDmDPSyAowHKxAiEh4fGR8cDMoA9+cM8P3ajOJK+Bf/1iFyDsUQDxrCBkv+HuvS3SLvuPvqBJP8dfaPCxP8/QaSFZgZKRrRCUj8zNzQ4yztWuwS8wf/1BEzEPgSkxLACnAMwP366OH1uwiQCRv82QDAAAX2iv4mBez+OOIK6cj62wt5IRwYSBfLBXP0Y/Rd8Nj80fsi78n1Qu5u+18PjQXsDeYJWwaCDY7/2PLs/swMYQhI+P7u2O926iL71wHrB28fTxoL/IroLQF9EX0Gm/pY6nD0SAr8BHQQ0A7LAwYD0Oi5+j73t/E2C6jv3/K/AcYPbSEkA4/6ZPFU85EKKPYLAYEHavu1AGb3//s9/4UByvpa/L8FRAsnFLgKmgL9+Nn7wgFNAsX+TPgG/x8DT/3z8V/64QaOCH8IpvFa9SoNiP8eCHAC2QA0Ctftt/CL6u/7KA/KBzMMYv6p+J79QgTSB68NePyR/Gn3//3pE+sB2hl8CNLqgeoX5Gv1vfvC+7b7zQBbEQYeOxRdGpgQefl95trcfO1M9HEHigOpAqwCTQTJCnT5EgBdAxf+2v8HB/4BsQQQ/sr4xvwl6hP8LwWJ/OkPHhiaDYf/LPBd/+T9Y/Vr/i76dwVA/W8KkQcqApoM0/Ml9mr26frE/ZcIGAkB/3b4euZW9wIHvQkpB7wKYQISCAgO/P6fCGMHmwHa6urbRPjKEsIHCQMS+n/xpgl9BVUOiAMD83sGFP5b95j7ngEvCisIxfhC+W373/L17Br17QvHHaok3/+w8mD2i/DrCx8N8gfq/KXxyPEx6Ib1hgqkGakFv/kXAuj1LgDIEHgQzgKqCUcLtPVR9pzud+np7wP6pwukC4kTNxCI9LsFQQJD/bAHrukz+1/11fUQEdH99wOrBW79z/pL+yQB6wTE+Bv+lgcQCgEbQPjW7Qr01/wlDIADtw1OAYX+NAE6ANIBtPowAOv0P+dn9mAFIAqUEZUGeQQrAdD/W/8t+ygIY/DF6HH3nvEjAPYVoxTRGtULD+c68370QPjmANf/Gx7wCorvc/uN//8IKQDo9mD9UAMNEAUAiP+fEL351uiF8xT+f/2VCU8P3PyX+SkAhPzj8w7t6QI5EosKqg80/+X7DfjR6z3+ZwGb/8L93ALQDj0PnQLpDsgSluXx6Lj8XwXGCuP1VPMFABwGLAPpAJsExRRaBePr//p6/EQCRfzx7nn18P0UGJILef6IBJH+sfyP+x0I3PLa9fj/bPT6DowUKxPnAmT4Rexv3P70uhDlHnIDlfzK+Qn/ahH3AiYSsgiq+5voStTn/d8KaxFhFmj67/359pHqNAS+CS4QBgQk61Dziu1z98QIXBJkBzb9XBKtBCQDzAJF9/UENPdP7wr+NggMEXgNAvvF+6f+BfVcAX0A+f7u/zYCEwJY7HkA2wO++NsA8/i2B5UAfv/OFKEHlQ5fDDXwnPVZ84rvFfLR8xsSsgzNAysK7gAyAWD4hgHvA08M5gdf63v8V/qFBAH/fum3/tP6/AyVCD78kw0DBjQDWvOH+TkLJA5HCN/x+vV8Bg8IxPuv8YPqbPQZDsQSWAXjCMYHn/E8+SYB/wy/HOQHBedY32Lpf/6qDtz6cQl0+OLqJA0n/oYf7SfZCF/7Q+l7+rntre+MA53vN/q1EiIUQhsDEez9N/Y16qDpA+6H/hAL9gsQCLL/agcuCRoH4fKe5jb3LPJR/z4U1hHZDvMDwfyX7pnpdgXvCVv87AyyB/UBpxPX+QjyuPNV7/X7B/sJFNcXqQf2BUL2Tesb8+D+Yvz3CqYNNfbo+zcK7Qn6CL3/Bu0C3ynv/xGEEmIXIBSw8sfpZew/+OwBuxatITMHHvxO8OTzUfrB9sUGyPsg9mwJggag/EAFVQZsDIkIrvgfBQ/w4fQa8xPhxALnBWkWEQ80CvUKqvQ0BUH6HACRA2z68PqF78QAuAQF+fMD3wqBCpoFX/Ik+bsBJQhs/U3zBhPTCi/+jPL47eH8AAN0DFL5sf4lEpcHovek7i4CABOQFIwBFOYi8ov1CPKB9/YAgxwLGXwGUf4w/9Pzxf31/N3rXRS8B872Dvxp8aoAOwg9DQ4JJQN5/28FBgIa73XySQNY9rLrK/ycAwQS/xKHFHL/8vVuAgv1xfqo/PYMbgxE+AfuOuuc+bAGzwyGAwUMOQb29tz3pguNGccK//xV5FTwcQVcAOz8oAOq//nmjPctAXsI8h+mCpsCrfVU8FEMyve/89b+Df/jCdgCWQ5nCwTzLfIW9uHvXwGZDGYAKAuIEDMQxQdkCa4GOOkm1nHgCv18/P4SEx/y+7/5NgU9/8oNRjDaGuDoCNdE4anlCO8UDasP1Aq0AWz+pv52D80rjQ4Q7sbdB+tGAJ0HUBdMBT/+uPqb5lrc9fxaGzcGfweZCEgMswtgAD74B/Ji+ljvM/euAQ0YAiZ9C1r8Duaw51LwbfT4/IX75xC0EmMRSCGGCt8G6gMu7xfgZsxa8AT15P1tFfsGyB2bFNQNIfqG8L4L1v/c+8ACdwPB6ELynfrO7a0N+hVcCesBJwWlAMT8nQCQB432Dt6l+MH+EA0AISUQ6/0c89II2QJV7Ez2SPWq9c8D8Au8DHgOcgAS5e/g4f41Hp8aWxmBDlb2Y/Aw5DzuXPNV8Z7y2fDTD90heDDmLZ8Kuux008fkwf1b81P8HwJN/sILLQPEEp8Sb/UG9Hfk9vdTDQYalx0f+7Hzpe4Z+UMB2wC4Ce0Ffgjh8jrvLPyeAbMG2PQx+f7/vwUxDC4HnAgo/MjxEfZU/Gz9PRB7EQUBsPtz6RT3iQA2AToVzBcnDrsGafZ96mv/LwPCB7j6u+PU7pzzrQ/RFLkA/fxUAVH/V/Qb+cr89Q2SC8YFZA2ICTwTIftQ4ZjvXvAr9KgFIAJc//4PrhiMBs76CwFX+qT22/dgAaoI3Pc/9Ef2TfnAC4wFEgb1EoX7vvaeCGEFJgCIBgkDyfwO/QX2NvFI8EoCogWQDLAgWg4b/U7nMuu29GzvdA+qDSP7MP7X+tT6QQPzFCIRMfyiAxcJJ/vi7ifoQvdE+skBlQ6ABBcNPA9REp4FGvQvBLz18u38+wvzVfiKBB/6+ATFEJwFqwD186nzTvgI+WwGrQ+pDCsQkw5j/6n5++NS7Fb8A/IAA/IINBazE8L/lhTSC6vyt/Xp+Y79jPWY61zz9ghZClX/YQKbBDIIDPOH9TEMewuQE9EJcvoB8CrsGPMMBi8GKPgt+Yf8VQyABvEDAARbAXD4yfUtCN4L0glB/xYIE/I2+4sRdP0G/Qzc4+gd/XkHUCV5FzYQdBDs9brsCvuM8cH16e+F820AiQKqFeEMywUoAM36oPBA8YUAG/+GCu8Mxwe0CwEJFAGC9mjsCfR+/loF4gMAAoz8bu/a+U8NwSETHI0Ip/Kg8VjxTu4LC7L8vPqZ8D3iqwZ0EaAb6hhaBm38OeaK8Gn8ePZ1Azv5WQO6CPEGwBjaDXAG8e2R5KTw0gF8BNQEXQwkBEIHNv6OCvgCpQDp9q3mhgLsA0MN2gKgAVH6BO85DgQINvoi9ZDlmPhjDKMGFR77CNT2n/OC4XYGaBKAEhgHI/md9Bfnff4zE3IUQBHkBEryLuJX6g8DZgKHCQMhmBh+9qD3NwB17tfw1PM0BXoGCw4MCPzpP/iK+UUQDgFV544AfwbhHDUPwgN9E3n04eMW2pPpJAkpB1UWiwYDDUsXevyZBO77U/th8yn01gfb/xwDBBDFBQf2B/Kk7F/1h/SbCpQNlwgDFLULtw9f7Ubs6vMS9+v/9viFAS7+pwie+1UPdBlQB0cEZ/N0+hr4BwEq/XX+K/1t8sj+UfYXA2sKmQVIDQ0BsPoFBqH2NvxfBTn+tQq385r5GQAL+8QOLQ0gCnL2Ie3U69347REZEycTVhIEABLrfe7S7Bz92wQC+38IG/sM9vH/lAL3E+YNdfmq9WXu2Pm//78Eyh0GGcoV/PKQ4l78u/ftAjb4X/iX93LqoQvMDHsWBh5GAS0FqfQa7ij5Ner1A64JdPt0ACoBowS2/fQLFw4XBmr4OuCw6/oHXxvmDUIETv177RfymP/m/z37wP3N/8QQow9GAEX55/F596cBlwKSEhoRXPiB/3LxhfiwA7QGHhLZ543x3AgUDmoSsP1R/ln5YfQA8nD4igenEP0QDvyO9mb7APkvBV345PJ+CsYAJwb+CQX/PPnz9VH0+vS5EAITFBcFCK71LP459NQBVfpS9B/4CPAr99ACpxdkIrYMJfb09rjvgAPQ/On1Ef2i6pwFEPxIEyMgKA2oHELqAueG7DH3OBFJ+2IANvYG/WwLqQSrATz+2Q26Awr4U/4SBA0DyOsj55zyivkG//wQOhPq+0sQahJjDDQZovlp7vvjhOrnB6PvQf3kDTj11AeFC2cTrRm8Ak8Feeaf7KEFWf+0+wP1bA9k7GLyNRNh++wMnfvN9aj2UP8dE84BWwuvCOz+rfAE9rwFWfmrBEMLIgZY97EAdwqG8eL4gQRIBVH5mf9NCYEBMhhgCr/6E/m172LsMeWf+MgDcwejCIIRDAUa82L/YwDpDHIP5grs/NEAQvqV7D//Q/pwASnvEu8u+wsLpiRZEz4M0uzdBGUH7ukXA/Xz1AMHCpr3k/ZI+Mv/j/fj9sYBHh+XHfX//P2r/Ar4TvbY+nQGgQSv8F3uWgTgBFAGn/0c+psFk/C5CQYH9/69EmD7mATY+Rz9dv9a+Xb5AfY0CYQCwxCqAG0G1AR+99r4HOPiB7cBZBSuCSv5BwtT6EMJqP9dBVASRO5Q+Cj4kQa2/yvsWAREBdUBBg16DbkPRut86Ij1AO6BD30NEw/gBAbwPP8V95z9kgzr914B6A8p8ej/fg8gBD7+ofx3E/YQCvO78yH7qu3T/T0DBBbdGZrzvNgg3HcQVQcsD6QMTP1aD0fvJgRZAzsKIA1x4F3lNOP5/O4V8RMzEGgNHRhuCTLvMeS/76L50//AAIcGsRy9FnYJEemd69QDbeXj8/DzEPQ3DagcriyFAk4BgwW39tP8GPxy+1TrFuxv5xLvAQqZIGgR1xIqE07xpAEJ9IwBN/K32tT7FvemGZgXPxDIB+35agqS9M/24PKP98kF8wX1CDMBiwkyEvIIqPAh9Br9Yu5v7834kAm3ERQLbwH+5/XyQftJ8O8TsRO/DikUzAJh/BDsEfWy//78LQlu/2/rbfqoA58LEQs3BPoTBPx0BTb3qOMlAjoC1glc85gBngKo+90FIPFqDsYUVBi698vasfAP/EMK4ADuGGIN/P90/EzfAfrD9439X/2T9PcOuwbvEgsPwAVZCAT0M/vX7or4fAqk/5IAhPdtCZYPWwLB93bxhPxo+J0FRBiHFzQFxOlY5Y74CgmA+TT35wAg/uQAzvyrC4QV9QaL9s70/Qi9BWgFxQIW98HzVO4L/KYF5gg6CUsFpvR49+kIAQKpBbcJMg8tAT77+/lp7Wf0RvK0CCUKmQYDDiXzs/EK+hYMjRJ2C3sMXPqk8VvsBuoY8sITSiHCBoP5Teh++R77x/1DG5UNCQlR7uDueApOCg0M6fsFAXv0EuaH9GHw/QDBGiEfMA7y97r4Y/oVA54JjQzc+OXlYQA66XX17gvzBCYFCeljDWwKgBKAIg8D1fZR3Gzw/+oG/LwY6wdFCNgDfApwAIb8Wfuk+HUBEf4TCNkIiQGB//7uagIeC84G9QRr4D7sLeyd9kwbxiaHGRP49Org2ZfyCQifF0MOAP7E+bjveg0xBdAXUgfY9XIF2fJH/fT11QPhA937xQZ2DiQK+fkH+q3oUfPlAAcASg5aAhz6K/Uk9nYNBf2DCQsNAvuoA5b0bAzk+/LxgfV66U4GgxD5JPAOWvZh9VT6GhBbCnb75fEe7CzwRfjr+wcfBiKW/I3s0vHSAAAHM/2fCs4N/e/u/e7uVQAOC1XyJf7k9/AOyQRmCmAVLATS+WXpk/QD8wf5CAXgD4ED5fg0/N333QlaF2Ib+RFN+tndKdnq9fr8NvhEE7cZeBhWBV0BDg7671r2yepY7a3/tA2rDZb8oA4K+z71BPlaAgfua+tWCUcKkRZ5AwcaxwRd7cn7O9jm9LABJ/i7EYIQkxlkExwDCgmj3FHdhwFNBnAGuADxDUIEPfr78JT6mAnJDHH2pezZHUMUnwiRAVwFVgLc0nTXmOxbBN8ZXBwtEd8ICAjJAADrcOj1AJH3mvR8AHEGehNTFzsQMfUw5tvts+aC8jQH/CRrJ5ILdRDv/XIGRfE9zUbogvBOAFQCTBDiGy4LowOCAc75ZfuWBrLrJfuvBfL9WQpuAo0SNvOD7yIDS+JD/nsN5Q8pDacCwBN9AX39nPuj+DHzWvnp+THxfBOp/+n2o/gU/nMNVvohDCwDJPfPBRYRlhho/tTiEu409Ab54whLB7oIoP2G80z4JhyuGrUEqPv77swCnvS7/8z9fPJt9NH0QwAr/ssgMBU2Gd38BNx69Y7r5g0KBon9VRX5Cn8D0P1P/Nr1lPHC89z21PYVBpENRQcHCVYIWvfvAbkJ8P0UCar/GQ0I9OnkcvaC6mX/ZwYiHq8Q+AGf/XnvHwt0/sYAuQJpA2/5RPI7BO311AE0/k8AsgMM8hgAGwzFEckJuwVaBZ75GO3E6QgA+gwyAisF2QPIBVgDZuXW8/YDFQm/Dhv+LAR494XxRgX2D+ALVA2dDwHo4ehN+B37eAouBGcFnfDH9CIBoPeLEQAQehHQALzo8ALt+yn8TQbl+H79C/ml+XYJm/4P/6YNbgnmDZgK7f1m+zHxs/L/9UbzUw8TBMj41Q3w/PP9VfdK/gYMPAKHDIwGDfwG+6kBjPd98TXugf0AEb7/vhFwDRMDPwU/7//okP7EEkQCSP33A1cGnvUC75n9Tv1QAx0HSw45BnX+mf4W7en52Q2v/pUFcBYBA5vyEflsBC//uvPm8mP8tvqh/8sPKQqNEEcJLPVu+DX8ggSn/47xcve28qPxQA6RFkYJDwXv/RD4Kf3m/NgNExDj8K7od+5gCM8WChAkDpT8QvPO96f4hv1JDYwEQend70sIbQlnA8gOhQsv9zr7Uwh/BTb93Pd387XkTexSCCYR+hR4DpsDvgZU++ztrvJU/qkSNwOy9WILjgqRA/X1MvAT+335OfVD/UIOUBNdA5n70wZtB4L3su4xAdoDjvwK+VACrBRz+lj3HACb/XkH7/xU/U8OpQgf+kb5EP92Dk/8OfXIB1X3TfR+9O4A6Asn/BMC/wdSA2n+uwFwCK0FGfzn8Kn7VgkgD9f7/+z08GfpBQIXEq4aigrC9LgEEQGCBnkFHAoiA9bryN9h79QEBwB6D2MDyg7JAW/zuRNDBEEUEP6B2TvyavlE/YcNHRYfFHH97+jg8Fn2UQGyA/oGHw3uCwsNvQNO/ZXv/upI8e/0RvzDBPAMMA5IB039+vkWDL4H+/awA1/9ofwR/Dz+AwhVCZgIXPhx+An+0gLr9w/7vfsY+RQKCQNqE24Sp/fR6wLvjPP390ADUwuFELH5afssDTQMugF582buN/5hCN727wcmDXkKlwly+tkDBvke/Hv5POiL+Qr9L/7jAvIKmxFxApkAVQysCHsBYAKl7lHmpfD+BEIRcwZkEh0HZQJXCNX2f+hV7Zb8aO8A90EP9B6GA3L3EgfC9wAMzgbU9X0B//bw7Oz0Zf68FYoTe/1mB6EBeP44BhUPS/028iT3RvdxBs//dghN+VjwyPIj770JrQ7zEMQGyPi9+Hn+8/6/CIsQFQIt8jDn8vL6/qMWFxGC/E4Efvi4+GUF7AyYGd8Ij+j86CX2BwkADfT7u/xp/mrwUPFZ/rEKDhf8BV39l/64Bt4Gyeur8xP7hPqzBiAOUQmnC6MH3vJn+yb8h/J87EDyZQtmElwSbho+FOb7evAO52TkBfem++YC5g2gB9wEQwNNDzgUtvgJ9FD+PfUY8fX3aPx2B+sL4P6C+kEBRAs4B673Bfz1AsIBoQWm/zj3/vzM+PH3dgWnEHcaCwvv+MXybvOd8hvwNQQ7/wz87wDrCLAekRGFAXX4Pu636Ufz3fGjBbIXe/hBA2MTfQxhAeX4O/lk+hj1qfzKEQ4F7AaDAvD7e/sv8WrtqevMCh0QqAOqDAMPiAYHBwYH4fUF9Bv1Z/QS+VD9jQYvBHcA5gO2BTEGiflR/6D4ivbPBaz66wr3EVcOAPn+7VH0v/MFDuEKFQrqAX/sK+SQ+gIaRhplFFQMuf0W5YrsIPF9+jj+Zvv3/ggBJgp/Af4R/QgAC8T6ieQd/kb+6RH9E9cD6v+89LrmSvbkAn0HEAecAaMJH//3/pT4iQAm9MgAMwwo/J0Tef5R+5HzU/Q3+dn2iQiEBGcQPgvhAZz+QwYJ/6z0OO4b4Sn8uQwvF5gj+xQ8/YPne+DR8oz98Qg8COQEPgTGBJIZ+AMb+v36jO6y79b8zfvr+UcLtgf2E8L7oO3rAOsCmgMi/J7/KgGgCAb5RPsEBqEANAMM/OsENgu9CX37D/E6+D8ChQQHAon+x/mD+Fn5pQfhAW38Wwu5A0AArwpT++f3Hfld76j/cgEp/xARhgA/AiUXVO5A99UC9vrbEpf8jfLi8ssE2g7iCe8CfvoJAnnvZ/Ce/VIPJRGaBAbzJ/v+DnIBVwBk97UFY/+e7xTu8PHRCGEJHBGPC4YXJA8J4OXje/Id83sDYAgUE1skKQoa+ov5kPoaAcr3QOoX9nX5XO6rAFEMrBcoFYYKtQF698T8+/nO+oz7KP3y++r7MgPo+7P3HP+1BLcNdwl7BasKmgoQ+1Pt//i+7hwE5wiW+BEH1vPh/Ej/KvsfCVsVcgX68ssLVv4AAagIT/ie/5P2juZr7zz+ywnYEIEKvQp3Cp4Dl/64/0/3mvhA/Fn4PApBBRgBLfyg6vP+ZwfP+WQMUxsdExT9RPCY5bTlCAP89kIQph3UB1AOSO1Y9zEAp+wB9xICaPvK+XUGiwx7EhcJrAZ0+dv16vAS9/QLCwKLElH7We1E+sz2ZAofEnUhDA3c9sHzj+rz+B7z/f4QAljzVgNLCgIKjAn5Cvj40fj0AWr32gBM/MsDf/is6LsEKQm6/8oARQaVBEADlPko//8PqwpfBG/2LAN7EZ//9u2u7H73MPJ5/AwOJBKkDiL+5Ac8BQv/LPra5SbyEvnEByQEMwV+DhP1wvLJ9CEPzAkGAc/9WvGpDDIE+gvv/ckA7wsK7CX+pAKzFEMSXQVK/cXm//Ut3k7wxRBRB9gPFgYVCw/+SPouCXn7cfzFBDoAvOOI7r0A3gMiHEkSPfwt844BCP2R82EHtRC0/7TtpweACAgA8wER8nrv4P4yEWAFCwRNAcP5Xfjt9VoHMwm/EFoFrvFm/4IEuAFY+ksDOP79+Zz60OlTCqMTeQHF/Pn9EP5N6o33fAF4CyYTeQle/xX/GxPcAS76suni5nYBKPSEAuUM7BqzIGb8sfMb9P78XvgL9dj65vYXDx0J7vfUAiwOJAPr/Ez9Guk8+lHv+PFADQgZnizTCLEA/fbF7Ln0evHi/Ib5JwR79pwJEyDHDMsPTPJd6vfzVO8HB10XCQ6CArb4F+Y39I0F2PtSC0795/YwBH4GNRDE+zcL3ANL8QjxiuwpBUEJxBtYCn4AiPnT4FTtXPLQF64lDBmED3EEiPaw7nDjr9yI+b3zswNdErIGpw2NErQOlv45+wnwY+oQ8uEHGQv4BdkkmRJl5TTsJvZO9eEImQ1TAGL76AIL/zX2wwT9HhkRm+yw7v/ir+5aC/wHuwKjDXQIh+81A3YEnRWbEhfzzvkf7DzxjPFB/1cR1w/rAJT34f3b+EcQYwkW/uX8jAEHBpL12vzRA5L9ZvDjBz8GYAOIDJTxQvaZ/6UPNQZqBToKffSn9nj4TggdBKkDTvaf3kX7pgBbBkAMjgnqDIIB2wne/SLwX/ZR+7ryPu70EVEIkwTHDQQGiwZX9sf62/WACQgHZvkyAucHvBmi/JgEEPoE7Db4X+qj/WQLwglG+lsI0vl3+TkO1vk0CXHxtPbaDs39aQdWBSL2u/Uf+t/wQANsGFEL5wEBAIP/Q/0t/vgE4PiI788FJgVrApMQNPu687f/Terg8RcVVBl5E+8BD/45BaLrDfb1DIL9Bwaw94HkbvWTAtkCjvmHC78SvAt8/MwCpgq974MCUfNL5Bz/u/+7AFoJXRZZCDUBbgChBp0CJe9oBLL1jf4GGTUGtAJP8TXw8u4R81EDCggqEB4DgAf5+z4JyxDv5Rj0Rvuh9LYFqAi0AXYOHAcXAhj/IuxTD84BUe3kBKz5Re7YAvUSRwurEW8Gd/+97HDttAfp+OwEkAhv80rstAkXDvP4ZQWk9Q77LgUOBvYSrAi1DSMBQO7677n6eP/s9cL1mesMDdkVpQRGGo4JnA7i+XfrZAC27cz3PwG2AZj2+vz1ANn32hHtBGEBnwJ59JIA8QP0EeAUFfpn8P7xVucn8oEF0wzQGLcJjgXYETsFYf5z9PDfN+/Q+6bxXA7aD5EQJRdu/Fn3POoN8k75hv9Z9g/9ihYsDfshLAbRAbfxAtdb9w34thZqGAYGZu3K+DcQt/s8CAD8tfsQ8Z3pNQIhApAOpBhkB/Lywvf6/TkBvQnRDPgBMe0m5yTy5vjoCs0Xyf2b/QkN5hZvGNkDBPOu4QLmK/Sw+nn+DwWeEzMFa/64BP4CxxBBAJ30L/gD98oI4QbtBI4HPgYIB+z0Y97L8qEJvQijC43/uAUrAZr4WPo4/Q4KUQIz85PswgonDeoAMAKN9l/04vRUAmL+xAulEwELrv8e8qYLvQah/v8DJv6n+R//WgWr+fUDCvzj9yX+cOqW/HEEFv4vDVIJEwqODdcHC/g67UX5VvpZ/aD+zQOfCpH9nv+A+5b+sgdo/U4DVwCg/qYCbvZb/aMALvrTCV0Gp/7+Az39SAzhCGkCffdb3zXxXPLeB68XdhgoG3L+k/V85kzxpvoqBLAOgf9JAdzzqwGFBs0CGQMs/1H9BOdDAigQQxpIGxUDc/4N4+nsB+K95q4SzA2QE88KGwV2+sb4awnz+VHxX+79/XYAKA1CHskP/go0AObxLeyH+s32a/Ol+yUEDwFi/gkd3Qzu/hUGCARr8qbsGfyq94cKRwE+/n78ePYABt/xbgX6GooFx/Y29un3uwWbHu0aqg2aAwj1nt3N2ZfscPf9/sb+2wfkESMdjCKQCqP6YusU8OLx4ud9+k8Bkgx+CoYPnQu9//MOevaJ7YTtO+lq8ykGohvaIVwfpwlnA9rl1dUf77b3YwNuFFUKqfgvC5nzZu/ABU0BiBv/CUv0Ffto+RsJahZQA8/5uvZZ4/D1gPal+/UMyQh/DNL50wFkCC0K3QrF+7L9te/aAaP/weuzCUEFAvZCBYj+KwCMGHwMEPwD6V/hCe6HAR8XrhjfH6cG+/8c9frnHv7i6lntMfvPDUwL7AnUGU0EXQNP96v5awNsBPj+4uq2+Tn/iv0/BYMEi/jy+HXtie4DDcoO0B1LF+QHIgLN9OnxpOpl9+bzagYyFCn3FAYhBo3+Aw1PAtj72wAQ/1z/CgsB/lj3sv7u5jv12wXHAqwCB/32A6wGrhT8CW8Aou7Y7QT8pu73CDIDcRMjGd0ET/739IUEbOf88T3vbfMREiwM+RR6FWQSzfHd7vfs4wL3D+j/EAkv6azwX/f8BvQDTwkCFt/sNAmiAzL1dQEx/hcJEwo6A1Xyp+7B6/j8vQ3aFFYcA/4O76nt3edDAf4S3wz9/ObzE/pkBAUQpwpKC74AeQBTAAziofNlByP5dPl6AuYFlxnIDTb89fu072r9r/hCBWsTiQhQ9jXtR/MA87sT7BcdF7oBR+Na5u/x2w9qCRgIpfqC/LcFyvegB5wK6ANh9sv35/AU/1kJvPZUCNcFLxSFC4nr1/bcAu8AnvvsCYz7f/0MAvX1xwjq+0j/zwGU/z0WVQ6cA9cHwQG736bp2vUw7nMKZgBECfsP9/zCBXoDfAFS9lD99frk+6gElPW3Db4HJf+JBioAgAFC+bj4sPKdB+4MeQw/EP/+zwcT+b3sdvNp+XbqrvJfDGAD+BFcB1kDyQQI/nwN0AYbAkP3J/oD9NP5ywgQ8DcIrwtD8N/2NQHpCvUDRw0uBkX5RPAg7IMKPfzxC80SVfiaCJH3Je4P8+UEXgjPCP0YQQSXC4H5VPBeAOTuuwAyBFf22P/XETEBVPX+/GrpcAVWCHv8dg6nBdz8AfF99yT4nRWWEMbx9wMH9RQMvRTgAR3+5PnY6sbksgR8/GQbKR9a/oP6zPYICXr7Df+P7GrrcPnW7jEXUB2iIBcQAuoP6eTtdwSiBogFtAN2AqUFoOoX91cHb/75AXr8BAIB+Ur1V/sH/3wVCRi/GkIAsOtK8gjmrgLzDdb+jfuu+K/7qQDVEcgN/wok/cDwV/j+/LAI4gAP/iTxJ/+CB+QAnhJkBPcIAvKg5xb28P26ELoNUw8982vxKvA29fMIFAXpEOEEtgiH8wHzbQi+/8sOw/aJ+QcAb/SaCTQF3gwmFqYA1u1D8V/x6vZZBuf9tgyxDEb+EAR5+er4Mfr9/CL7nQckDxEDNRCoA+7x8PZV+DL5Qf+3+dYDMQtO938A7QF/C6APYwNc9Y/niv7j/C79FwNJD1wSpPUn/PLxZ/uwFDsS1gbd9aQF5e9b79gC6/roCBT7n/3J77b4zxRnCxcQY/o6/7z0UfXaBdX6owcPAAf3BeuLALIOxQpyFv4MH/1d7W0B7Pzj/CgF5ffT9j/wwg+zFOwP2xY19ynnZONY86UB+Ae0CgoA5AM1+mQHkQZg+W0G1/L89ekHdBAn/AD8xQFO6jsAtfl7AvEKWAYDECAMzQ7N/5QEHe0y5/b1j/OwBfsOjAz3+PwEPgG4+wr4mvFaB+3+hATG+QT9kgPP+ukMG//SBv4GSQOWA6P3dwlb/RH+YQDZ+tz86/zQCeTyg/0fBbkAnQyV/9QDtPTR9ncBkQbxAejt0fxz8NIAdhPp+18GUg4MCe8CDAYe/hP6Sftt66r3a//VBHwFawKxBVYBegp4/xn7W/Xz/1gKQfvoBO74HP7WBw8I8/qA/KQGGve4Chv6h/kf+rPzWf/mB8YSvfoIDXbssuqdEGYD4RTDBUr3K+jG8JP2uAI/Dcn40w28/CwMShkSDsEME/soATbpCfpw/2r1tAFd72T4FPzWCK8EpfkRB9YAPvle/bwPWQQFAwgC++zP95j+IfkBCK0cEhSzDkj9Ie6L7eHzKgU2+1j8Pft6CS8MN/+i/gTvz/cI+h4MrwRfAMwNwOm1/1wP5gl/FaUFPfjx64L5ogTC/6UCovz3/68F8AJz9Sn4EwEu+7gB9vY5+IgCaf0i/xASvxumB5EN2e4g4An2d+vsAqoUJw5hAyMSdgZH98EGdfQf/BX/s/pz9BEBfwBK8z0R8/dMAzQPEvQwAMv6mfOA/7kO4/avAEsUDwgMDHb+hP/j/McBMP0N7DD4pvuB/ILyVfL5CdEcNRBpBVYECPZMAy8Bk+9D+Y8AJ/M+8BwDjQ/wFEUP+QRB/7IELAPw8ZjzevNF8dwIigoYAB4SKQKL6Zf3F/W5+WYKnQFE/3wImAqqCFMLNgRLBDX/OOk89zkEXfw19b8JMwFq84UTPfmWAZMGQu18ATALXQu3+eL/0/lO/1P83uvHCRMIwQtWEVwNiPpI+0/6ddw793AIXwktDsUO7P3m+NgDNeu89doELvwb+/n9iAK+A9sKzAPwBSEHBfu0/jz5V/YL/CkFoAJkDMIbgP4vAxj4VOH4A7oHfPdx803qfe1oC+ETbx0tHw4EE/W478z/kvos+ujyLO3q/wEElw2cEHILVuhQ95EGmPlTEFoCAwVc/Pn2twJGAJgO7Aht+ejkEOpy9s37khE1HsgR3AWeDyf79ftnCEr90ffk3DDhre7CAAsPEg2MH+4LsACR/3D6yQCtA7/7Buk195j33gtTD3f5twCS/LoLbQJKBvMAUO8F/WzvPfseE2gXCwphBhH5S/YaA47p3vO6/YUDtgfD/5v9Zv0kFw4HTv1DAYj6pPYv8PIGA/1XAQgAyPNsD6UO8BT0AtjoButt+lEPfgKvCMYDwQKtA2DssAPcDT75XO9O9fn0Pf4wEg4M6Ani/vAC1/zd9YAEHfViBskE+u86/0YJ7AlgCGf/m+9WAqX6FvzfE+kIOgRQ7HTxW/rrADoIVgLED93/XQL7/iHwxvrSAyL5D/cgDtb+r/1CClUEfvxJAV8Kmv+WBIP6KvhXBBIDQQEP+WIJUgFS5k/02wGDBjYKKg86CWr/E/lu64v2J/Vg/2kLjgPUFoQMdPbM7KrzffOEDa4hMP5uDBYBrPOY+eb7Owxl9WPwb/Ye+0IEDxESBgYDzghv74b6VPPP/gEb+hBmB/n44AGV+bnusO1U7acA9fjl+koWzyPPHaMQE/ZW4g3zqvBx9G8GSQYjCAT/cPvA9SD/0QhBBZAL4PgY/OEF9f4hDUMQu/8e+oX5BedL5LPzfwdSDhIJYA+uBZ4LWgir6GP2BgNI/MMKiAmx+GUEPgA07wr83/ehD7IV9gC/CV7xZ/Kf8iT9tQsFCTEeu/yR7S3sQedl+RcMqxSCA+//T/JjBRgH0P1tE9EGdfwA6XvxDf4QCL8O8P6uC34GdgAh9fn5RghW+U77YfRw+boFDAZCBaf+QgV4DXYFE/+YDHP3L+jy7dzkqgcWEdwMkQ8H+WsLRwsR9Jz5gPo17c/3AgwnDFUU+wO0+1X3D/CWDfoC0/g//6n1a/cgAywH9vbLCHAU9g0eAoTuT/7y9GL5VAQC+7sKpwHIAb8A5PjaBbf8i/am+HX6Dv3xAQMI1QuOFEUJhQPT/AX3qfpR7vX5pvUp+kwGvvvMBB39SAqtDMQKGRTqAZr5FPJF/Cb7owbB/b/ePvAr9SYNAB1GFnoWFQL/5qTmz/vABhsjIBBY86L5F97572IF7wVxEfb9AgIt+u/03QhmBgoNygo/A8bvHvBZ/eb8zART9Kz6MQF9CJ4GlflbBFL7GxHYFTwMjQh98O/qqehT9+7+DRQVCULrkQTJ/dsEgRGEATn+RgOfCFT2/vxz+RbtQPstAR8Tlw3IAV345vTj95n7FhI0AS0MURG57tX6QPrg9NX8CAEZ/t7+xwAM+LgLywfNB0kLVfXgCa3zz+xZBxb8HQxTB80FXPyA9qX86et9AzgLYg9p/0v19/7b8SUM1QLpCY4UvvUv//7znftPEcwBG/VM9qD2aPGKDf4NJQgwEvjsKfKa+MDuNQTk/5L98wKMAQYDZA+eDSwKhxD//ZH2if0dAD76Q/mb/mT3APmHAc/7NAJ1D9cK0v6F8gT+v/PU6LECTAkbBz0L8AKU9RgM7gbm9UT9FPhIAyX4tPt7E5MQyA7PEBz//vJo/43u8fMN/FjxoQA7/roBuABfAx8UpAQRANL83fIF+dr61PvX9s79BQRGDdUR1gV/FK0E3/QH9FTw3wPi/a/8APwNCRcQtvkw/N76CwgEBEn42f7o9l/8VfdUBVoPyAGZAOLxQ/mT/I373xQ0GMsP6wR+8KfjienI+T3+bwSWCmILJwp+/xsHAP6Z+18GXO+l994IXQl9/5AECAci9nj+KvklBpv7HfbBE9b7zwMHDTcAMgOI9FjzUfO88l0A9gkABer+FgIZ9K39kQnC/iEP8gTMB88ODPjGBQP++Oqz9H7+S/7x/vIBCgEHChIDCP2RB5kAlP84BrgCJfyD9GH0APhYAv794ALND90IAgU59j4FmwHp+YQAS+ur/lr+rAJzDvIB+AAf8Y32ogHwASsJdxJ+Dhj6Rf19ApX3qgFlAnv5rf9wADj6Y/qrAhv4bgI7/6ryugeqC6wZlgvI8KXw4PVO/S//OgOQ9nD6wv/f9rYJihU1CyQIKPuS6tH5zQ4TD5cH9v58APf8cOjL8xf/pfdT+OfzF/ufFfkaCw/fD8X1hPA4+s74gw4CEHcCkfmk8NvqywCtB0EL6QWX8Vj/zfQkALkQwQ7EDrb8ffKz+5EIiPGE9Zj3feaJAOkBBQdNHPIDXAeUCiXyrw6zFLn6KgPzBynxb+/a5gTjKAt3BpgGfwik8y8FvwSgA7wQ7gvjBLLxv/Fv/6EGFgam+ZT/xOfE7WME/QCdF6USBxD2AhT9dP+d9sb/nPbf7gPzxPxUBAUYWRS3+iP5Bfao+DIJWv2f++YOt/mKCJwN+wEkB97tzuQw6E75xQLODwASwAHjARgCHA2/DOz7Mvu39V/ucvvVARkUognNBdYK9u+Y/O/56PA68hD+ogMDCNcQxwdhB/XstPRo9+Dwew1eCd8DTwsLBbXvbPSQAXUIbxozD5kCjAWN+rIDEQEr7tPp++Fk6KL3bRWHFUUYuBUx89/61PdjAx8JuvnC/73smPWgB0j5agjeGNMJPvfo+I4ADwIdC5sAI/wS9J/wHPLI8CIT3BOjDfUBGf1OA4vqZfHHBTAIvAckFvr92/IlCaPxOPNMAMT6nQ8zFd/8//3l98Lu+Phs+w0K+RD2/2vzqfRy9ogNXxomDEECme9B8Ur1xfplGicYCgeg/tHlU98P9FAE3QZOE5YMnQOoDXb9BQB0/g7tN+8k77v7Hgpn/6UJ8RAE/A8Oyw1T/wQEKfgk77373wHB+MUC9frIA10Iofu5CjUE2fQS9GH9xQHrDx4GAvfJAsr4ef03APXzvP9jBdwBug1GBZ/8uv7n+Rn+gwEOCjwDd/ll+Mz37Pz2Ag0OVgD57ov6RAhFFwQX+A1TCW3uJ+bj43XoigBoBhwEaQDPELcJwwNfC9rsIfFU+xP2PgtEEcUVqw9P99XqoeSn/tgGIAxaEzsC6QQN9fn8jgXq/+QDwvL47K76ehGoDakO4QmW7/ToPugN9ioE2wO/DDsOrwelEs0BU/Xz/UL6dPpI9rT9rf3GAOMEqfoIA84DXQOMBhEIphNPA+P2cPK57o/6++4TBMUHk/xdF3QE+Pd9A70AtPrjB48IlfTYA5kD5vcM/iT4v/yQ+HfxJBG3D7wImRQiBeX4xu6B75XtkvdiA0oFHgqH/+wO3ghF/BALpP2x92f7FPcx/sYEtAR+/ywAcw27Bdv0ouzz81sIpgV8CbMP2gPS9+rs6vfdCfIT+A0J9ZvxSvEH88EFqARGA4UDw/7u+3f+aBLrDj0Iyvwu8MLyg+ziAfwDfQDQBnUBggdECJUNE/mJ+/sAq/bgDYUFSP/U++7ttP8GC4IAMP+690fwGf2aBQMFtAY1ATTqHQD7B4EDViH8//D2/P6m7mQGrAVi9A/7zfuW9Or9aQmyCZoVuxAq9ZT37ACOB7QHn/wU/X7zbvZG+n/7UwuIBpT80e8a63wDzRXTEuYHCwZx/DbsrvUO8vz2Eww0BwkHqQWM/w33C/guAoAIGxYiDpH/R/vr9/0ExgKU+1AIY/ZJ6C/t7vABD9IXjQxrBXz9jfHG7in7NPQPEeEONfYeFIT8HAJyDWL1V/5b+R77zvvMC6gDCP2iAoHvHgKEBcgKYQwtAsYAxPxl8aXq7/wQ9zr4iAFDDeoL7A2wDuT5gQH68anzj/zhBcESCwXxDlTyuuZkBO/9p/+4/7/5NvoUAv8TAg3tC/H+iO+D9VvwlgZ1BOH1kwKF/UL6FwfWDXEAC/f4+/wAswIIFOMY7gRb9sb2zOaQ4PkJ4wrrDRYTH/Wj+PkC9v8HAF0G3/sf+xf5j+Nf/y8Z8wPZ/0r4XvLuDiMQ4wfwCU4EZvvL8er9wAFo/fn5Oe3C8A/7sxTyHVINzQua9FTw1vfV+bMGa/6z/O/2Lfm1+yQIjxAsADcEzvZC8QsE2QJH/7ETUwhRAWgMbfViACz8Ve8F9jj4KQUlDW4NjP0vBqf8zvW4BiXyyfkw++766Qej/awOGRSM/j7vgfht+mr/vgiF8koE0g3kBSAGswQL+wHv5PnJ6lwEKBVoDS8SCf1Y9Bv4AQFP8SAAf/50+KEIx/AlCb8VoQhLDSwLAPdZ75n9XfbX/3755O+J/6j+4QiUD2oFNAokBN/x4fed/+T1t/Zl/isGFhHrBpYC7gIK/KL+KfvA9e0Axwe0+5cExQfxCVgKGffK+bbxDfFd/zUAKQPSBMsBTPgR/QMBS/05EEsPgAhtCT/tyPYrCp/6hP1K+ubwvP5C/+j9bxCkD4wE2gLt+mz4owQD70Lw2QrP+vQGnQWL98H/RwNpCsoITQH19HT+1QGh/0j+Lvf0A4kBW/RG/6sRZg4UCjH7BfTZ+aD1U/vyAfoKJQfFAPD4V/pnBygGIgbe+C3tpfSrBF8JWwhFD6cDEvU/8B7sQgAqEewC+gFUBlAGBv4q9PD2RPUQCCYGMAA8FWsMBwRYBRcCiveQ7hTuj/QqADX/kgw2D7IGqARk/Vb/cAADABv23/dD+h/6hADV940C8wuVA3/88PUb81L9nBHmFRoPYgx6BFjzve8c+hMBsALx/2Pw+e/aBcUK6wkKCc0Dg/d+74zyC/+rEtgc/xk4/XjvcvIA6jvzxQCw/4f45vmg/CYLORqqEDkOsPqh6mH78/kh/Q8GDgH2+lr+2gJn/KYE+gCj980G2gU5/0IHnfpg/YkNLAENCjsLt/KH7BH2P/HC+5oKZfZXB6UJQQQdFHX+c/af90jszfXID7UKqA3fEe746vR3+jkBfvpH/pEBsPjG/cH+KAxMDBMIhP9e8x77u/o+A134i/uCEvoAqP7UBIz5mvgIAuf6Lv6jDBkAvvrr+G7yL/tNEbgPpQ6kDpLvZuy98D36xwrpCqsEkPwF+GPuyA3MHQMDvQPU9V7s4PxKACMF5gbA+g/yLADyBlgGjQj0+DD7Ff8d/wEGwg6z/uTk2vxrBVMExwqKBkH8PfPl9zr9vwUaA7sNf/+g78wJrQpUAe8H7/+b58v6wwnr9tcF5gxH9Rb8AwGLBQ8gbQZx8fTz0eap8A4F3gRVBo4JiPY3/voQbQiCBAUGkO2j7H/6iflqD0UGZ/kPAf0E9AgsBqv8BPhpBbwC0wEfDU0H6/Bf8lf6f/NiB0ASZQHaBGgPWPZE7M/0Cf2FCv8DSf8A/xT7/fp5+hL69wm1CtAA/fuJ/jEHn/j6A4wE4/wMC80AP/pk+kX/uwq2CwQDIP0Q+ij5m/Rq+7gBZP2kCjoFBgCoA24AUwAzAOr7Rvfj+L/qY/M4AIMCNhPZF8YJt/2DAlLyZP2NB2T4XAvjBDgA6wdwA+b+J/u48w/nu/wuCSINcxKL+Q/14faU7JP85A88F4MYIgED6+7oyfWF/G7+Ggtr+432IgTxAnoUxyDNEwr4lumv8MXxWQJ8Cu//IQEU9WnxPgJhC8MN5gWD+M0AbgUU99n+rP2Z85L5Gve++HATJCGxCov9/vQa9tABffvJ89/0ePrs/yoF0QgSFZ8W5gH59c3yP/Oj/xAB+/rl/hQDVwsg/Zf5AAkh+tP00vlS9vADLAtaCnsUlAvmAQwApfg07fn2hgD69JEIeQbb9gr8W/N59J4L/AltD5EgDQDx/xj5NuZz+H/5nfMi+78G2fYoDLYYLQLBBQ37sPWr/n0G3wa8CTMFUQMKAdrwpfuX+9n1DP7p89z34QGmEEsbxgSkAnn5NO7W84v8WAMxBtIO6u/e8hv8mvr1C8EDnf9c+twQShHxDkgMgPTc+N3pQ/emB0T/VgJWA1L1Ue77BcgEtQWNCZn9uQKdAuEEYQHN/FL7MfY9/3D2Ff8VCbX4rQAvBJMGegy4DEEELPze//f0mext9y0CWgayBLT44wC1B+b7QQlUECoAFgTT+gHqhQRL//nxkwpNBcLzLAOhA1PwPgYRDnQMHRXc9tDmvvLD5UDx2RjyCuELbhhP+0YBCgsR+mIGpgZ26iLpp/Dz94AQBxXvBksKVv4m7yn9zgnvBeMDG/j+52T8+wI/Ae//bPuGCagE0Qf2Axz79QcSAbfxX/t5BX0COQiE/v306gQ4AlL3vf3r/2QEd/uj8dP+Iw0XC0cHJQt/+gcFhAZU7ib8nv/d8yABsgY9+c0GIP5d9XEAqfuMBNwHwP2y+2cK+/9PACEISP7xBm8ErPpk+Lj+dvc6+/QEAQcjBm763v+c/yMD9AQ4AR/+Fftv/OT31//pBGX6YvWa+RX6vwP2DQEQgQJN+d8GNQJRAX8NKwQj+wP/Nutp7qn+DPi9BxER0AnT/8QCY/2u/z8J4/U1Af/+X+6U+N74lARjDSgFugXNBlP/aPv+/OP4XfxgCjEFY/gbAL8C8v11CFcK3/x48e36G/3399gJOgBx+zT65ejFBwghjhZLD0T84uNa8EIAs/rDCycFke2z/hL+oQOgHSAKT/gG+VLpx/VqFB8HiQHbCiv03fE0B2cBaASABsvkB+5eA0YGXxkHFPoCf/yF7u/l3v3UABIAIBG4B2IEqw3aDHT6HfjW86burv3H+1oEGQpIAXIB4wGTBRcA5/2pALz3ZPis9vwBNA+zDI4Js/r99+zvHvbM/S4GyhRTAzr9cfza/Uz2ZvpDAnwFAxShCZX9LPHw8oT1NgE2BYH+OQsw/Z0AegpyAYUEgAAy8034/gaWB3oFIgej+hLr+fAi+2wJWwlRBqwIBwhnA6P69wHb+Cf1BvSY8LIEABW4BYECGxuUATX2Nvcy35PrcfUR9+AOXSUlIvYSiQKS6dXonPZv+L0SgwrW7BH6g/Ng+XcR5Q0rDGIL5vXO7Qf60wWICff6x/hw9+P4cABIBosNWwOBBXEASvr9CCIGCPuG8qD6DQA1+QUEBga3/zEACQd0//T2ewFd9t36IgupBeMDhgMo+bT5hwM8AlkMGwEz+kkIvPcD8zMEdwF6/S8HCf9r/tEKqgCg9F0Crvvz9C0BufATA8wJs/YSBXkIVwMfDFkRUQC9/G33/OwR+gQGTP98/jf/Sfg/B6oFngF4CLsJKAYPAFEIEP2v9Xv2gOpN7l4CcAcHBCMQRQad/88CGPQ9/J3+6wFIDrX7KP1wCIH6cvfqBwkF4vsNAPj97fiE+KEIpgBsAC8Mdf9fA8kFrv+R88H7eQFv+HT3sfUa/yYDiQVFCL4PWwjNAuoAkPcWB98HZfzs+YP4rPXM9+n38vk4APcG2g9XEZoLi/WX9+v1/O5yBR4CF/3sA/n6KPogD7gV0wb4/LrtyektBV4M5wz5EW/5L/KT9lzzVf/xDdoEXf0IACX+wAZXCrUAQvUB/PH2F/RyATgCPg6sCZv5uQCIAQz/rQZO+L/5uAIuBX4Gr/MG/Rb9qvxJA53/Uv5yBDQGYfV3A5ADDAa/BOL35wFdBQAJTfy5/9H3FfbEBkf49PvNBVAGwQNAB5gJqAVzCST2Xub278zxm/uKBOsE5RC5CTT08fMYAD0Jxw34BXf4efIk/5QBzASyGf4Dmvmy/K7wAQTSDy0HcwHA/fvzQvUPAQL7CAAtC2340vcj/hf25QeGBWb2IwbyB1j8KAqP/17v/wPeA973cf1GCY0CggiLCZ35XQfA/B3zLvsL+5UKEgfL+ZEBKgv2C2ICi/mY7E3o6/rK/q784AevDwgH/ApdEEz+1fZC89juP/ZODkMNMgk4DOLzGfcA/Cj+DgQ/+9n4G//pAvL42ARxBjn6ugIF+338HAiQBC4E6/6M9vzzdfoKA1IP8RfGC5ACGv4F+jb4vwB/A3n+4P0m8fPyQgKuDvgGxwCw93/vKv/B9ugBAQ95AXP8LvoW+l3+dwYAAgsHwgef/noEtwXP+QsB8gQA8HD9Pgfu/8YKqQt4/5v2rPZs+lH7XQKfBl8BcQCD94n+Xf8V+cYHNATA/lMApgefAVD/SgUx/LT/dAHf/k36W/9U/+z9BwFs9fT7lP3V+SP/xgiYESwSXA6e+BbzBfaR7WjzgP6EAawJSBZLDDwLEAQD9pn+8+3N7oYB8whEE5wJ0vfP9BcBy/Vp9r4CRf1qBbH7ffysCtMFXv7m+Vn9zP8nBO8A+QGDCIMBRAR0/pXyW/tJ/6L/DQb+DMkCj/xfAPP4cAKRAcr6mPiK/HYDsPrvCEMKsv/H//wDZwN69iL7F//mAaT+rfjq+okDzQe1AJf/dP38Aif8Jfg3AaQFYwao+c4Bngk8COsFSfGU9Vz/jvcQA/AIAgPwBqsCxP1gB70CT+u96qz3EAJQEPESHwt8DwoBLe5yAELxtuzZ/0nxVwCCGt8XVAxS/7Ptj/OQ/lHz8fay/rz8jwR6EZoRgBnWC7Drqu5t8KX0/gBiAmMGDARE/QT/+wTcBsoHVQXT94v3GwCc/Yf8lgC1AAT4W/Z+/O4MTRaME1UA9OrJ/C31HO9kAKYCrQmqCMkD1QJdDD3/bvRs91jxxwLNCAICegNUBqr+yP1pAg738gBD/xT3tAmxBYEGPgdb7/rqcve7BKYFhgw2C6/72AH+CPYICAOp+XLv2vPp+0L7XQdDEOsH3v6F9/bwSwWJDGcEjg+wCkb78Pfg6jnrMgDt92P/mQsXAhkEsgho/8z8Mw9UAS/5pPy/8zz+mAStAJ8DL/5j9ZwATAbqDB8OnQmKAD71lPZr+I79sv45Akb8PAUKC7cHCAV1/Df7FOlq88b5BQCWDQ4GOwIu/r0CjwDtBgcEDfty8m71IgrrCZcDGQAY/DTvRP/AD6sLag/x/9vwFvdv/qQB5gfq/dr6HwBG+jYAgAuV/570i/9G/rv+EAt0Cbr9ggUMAZn6vP2W8Wj3Afhr/qwISw27B5v+DQZ49qrzJ/1H/D0EqAsoATgEjgsr9xP81v2J+CcAG/5+AQ8APgPpB5UF/gW4/Pn9tf/z99D+Of85BY0IL/gr/L0DKf2E/1/+6vdBA7oCN/oJBM4IIQSw+pX4/Pei938DVAjkBJcCpgJRBJ77qPVT+Xj2mgVfDmoBzg85C+n3tvyv+8X9Wf/g90jy4P+3CxELGhIGCNr0YfDy7tHz1QbpC9UQQQtA7/TxYPj8+SkGFAyLBwT/E/du8lr+ygp+B2IDvAhc+lX1LPuv/m0SVg6oBtb7tfU3+Y7zmvicA6APXwX3ALIBNPOk8wkFDAyv//f+i/mB/eUHvgGr/wv9nP6H9l733QHvB0ENl/8m/FP7Ofm0A30AA/Vc/tIHeQccFM4K0/qTAED30OqJ/h0E/f0TBjf4uQOdEQoDtv3J/PrzrvFDCU8CqADlEbD59O/kApj9j/5GEB4GlAC3/Mjxhv8QAuT6Zwsn/o/1Swwk/BP7Swb6/H/6zP/8/yT+CwhpCzwEKP7Q+j/zN/jH9lMAOQpsDHsVu/sJ+rL+u/xg/ysA2wQt/rT5f+3r9I/8JQbFEA0K0wD3/6AAH/iMCO8IGQEKBTjyCuhv/soFZAt1E8AABvxS8zjymPyPBegEHPyFA40D+wIHBkcBE/ma9PPv7gSQEPoGXgpaBNn1JfV6AS75oQKkC7YCywOGDPAAxe9lAnT3a/Bb9PL9VwNLA4UZywrn/l8EqwFq9wT0JfS28Xz0VwMJDTYLXQ07AIT+vvtaEIANju8gAnr5Hep/BkAOzft5BVn1bPNAB04D1wwqCoT7b/NR/rD1dgEzBrDzAw6GEUz8+PlM/8Hz9P2QANL2nAB5AqEFFgeBDFoIvwJD+7n3ou/b8qgCBQI3BzYHewc/AYj+pvyaAOv/Efv1/Uz56gVUDPkLWQQ3/uTzru+q+RX8lvnR+5gL7wf3EuUI5vzXAnH3u/k48OX24ftaBcoDMgIoGHUHZwXt/D/r2Pp8/a30aQLhDMYAVwd5AoLyPwF6AnYD0gnT/PD4M/8WAyD5hwRpBlD4gwIs94j+jwuuB1AM/wEf9I3vxOyQ79ICUwqFDRMNnAJwBegBN/0bATP8jfwGBu/8QvUjAfL6HPUQCUQGlwwjE6r5k/3p+032z/2P+4v1lvzYAZ/51Ar5CP8CvgYMAn8DhwMGALP14Po16dTxDQ2lA4oVJhmw/03y/fJb81T9IAm9CGj8DO6R9lH9BQpzEg8QSgXx/RX/5fO9/xIMvAF59vX1KPnc/NP5nPkxCAUJIgsYC9P9ePfLAQf9hP2iCEjyqfVQACvzrANkFQEIBQb79wTw3AqYCYgIrgCr73zzbP1gAHwLbhpXAePw7PLE8sb4HP8KAPj/OAdfC64PigmFAFoCifmW8H8Aovso+vsFW/nl/oMP9xBh/oz5c/Fm+eH99On6A+wDTwtWCoD2NQiNBcgGIAIg/InyDvKDB4cF6Qu3Cx/+Rf34/nj7//q2CmUAevQ/93j5ZBK/BBfy1fhy/z4DlAFCCHL3GgEjCTb7ufxF+Hr8of5tBQAIbQjNCPoJVf7o8bwCoQO1+/HxtvIo/rwAfgHvA5US/xcUCAL7Fuwe6vX/hQHXB+b9HO1Q/aL6hARHGIUMFAnXDL/t5fcDEQr3pfXI8p73hwfGA7v+CfsmBi8CpwMnAHT35QjF+Y706AJK/4kDCQWCBMMEkAuDDPgAGPdr+HD6n/LP8Xf6XQwYC9cLxggu+KwAqAQTBaMDpfvG9MvoGer7A1IB1gBZE6cAAP8zDDsNNQLZ/hECN/vO+0r/PPnV7aAA8gbPCUcSrw8SADTsMPNI7br3+QKmCD0KhAYXCef6m/3lA7YDdPZl9f71nfooBxoLaBUF/qzxWPagBLAQBAZ0AUv4hPQI/fsDaQoWEFj51OjW5TH1WgiQCq0cGBFGBZ72tOTm9aT+xAMlEogMS/ci+MX1X/eLCIIKqgR6AYf+bQEMB4b/zv5z/Gb4TAMyAVX4ggEV+o/2Igo+BNYJVQSN89X8vfVY+b8LBQhQA8sJqf0k/+IEO/MU+gEArvnZAXMHxgBfB8IEqfkFDdoHIfLJ9eL1kvdBAWwAXAQ4BsX/Ygbe/+n8uQjXA2LwXvPzBwQF/AwrB4H4D/669zn7MQC5CD0OpAjG+Pz04AIk9Cj1CPs2/SgOEg2DB0j/Cvgh+n7+G/aj9uUFuwEQ/Z8FJwc0CWoNUQDC+y//jP5A9sDscvzXCF4MiAljBr4JNf758Qj0Y/P39wUIUQmKA0P/jAKkAdoC2gnv//P9y/cK8dz3qf9gA2AGhQQn/XwGogqEBDoEVQDS7kz2ywHd9L3/nQba/zUBcgSuAaUGQwgJBrEDWvTp9P/1Gf8BCC8LAwVh/lcCa/d0AccEef+Y/+z76PW+998CoAJQBnr8t/4HB78IeAU39nn0//mb8iLzMg3VCS4LpA1zBScDhgN3Ag7yswC39FD1/gTj//4K+gDoBAgGTP4A/O0CeQQO96L2PPZl+Lz/igorBYoCnP/p9CDzuvzDDHUIyQgeB0v5VP69BMH5wwHYAAb13AGcAD0LxRR0ApD1VPRB9n0Akwfh/54B7/uA95wB5grJBqT8U/fZ7gP2Zv0DB4UMWAZ4B3j/RwYJCy/9Jfw8+FjyNPkEBhsD3fk++dP5twTQCoQI+A56DrgCOwE5+Wvxq/sR9lDvpf4xCAsEVgKg+aX5VAndDkEKMgJk/HP1U/ur8KnzlxTnCHAAjwX7/UL+pvsR/U39tfwsBBb5GvwqCVAMgRdsDQUEc+wo4rjtGvL3C9YO5AmSBUT5EvtyBUT+DP2bBJr6BQPbAzYDzQKJ+AH41QSCA1P28QNB/7QAFQ2OBUf/a/SL8WgAPgEBCcQQcfjs/RkBQPhHArMHxwI4Afn7uPbU/tjt6vmtC5oGegwhDej6Ye8+CBsD2gVQBdDz8vIc8rz/QAr/EjIIkvqU8YP2Fv0rAN0I8AYbCwsAeQKkA/v+Svga6zf2xwINCmEBNwPkC3ABhQD5Bej8qgKhAxzzPPlkAdoDyf9R+J3tg/KNAu0IrgsHFPYSkvnB+2jzQfVOB739wQTGBbb9mPUh+R4ACQb2DQgJ1AYZ/CD1GfvL+tv64/1O/18AXPziBp0FOfp5Aq3+4f3aARb8VfjgCjILHwYMDt77Zf5a9DHr7Pp/A50CZAN5FuEGlP58AATyGPaD/mv+QvdYAAP+mPy+BgYFnAJx/gkFtQDoA/kN4v++/Cn4ifMPAhQAOvcjA2kFGwWCEU8FPPev/gHya/PoCA0CaARqA7/5jgJyAFL94AjzB1r8Gfrj85n3GPm6BIISYwL8B1X7V+r//PcGAwWKCcQNePdP8Yn6GvwNBoUE+fab/joJ3AjNCUwCMQx1Crb3g+ya7tX5RvNp+vkHNRPbGEoHDPt0/Uf1h/AT8yzySgE3DsERXgWw/+AEzwKgAib1Wubg8p0FKv7gDT8aIxBKAVbtQPcnAvgII/+a9tP0Ev/RDosF2wwW/rPs7vFQ9RAC9ggrC+UPOAZF+Hz+E/JV7gYA4wFcCO0NtwVY+bv5tQAJAIv/sAPu/DkArwfu/jACgPsk9QcCkP5TAFIM7/1HBN0QjfnP9v742Orf9scIAABqCn4PZAd6DZcAzAbX+03l2PQC8/v3TgZkA2oLzQ5DA58AYvvz/PQCC/oD+If/UgBE+QkDBgLp/RcLe/5D/hAMBAjUBSL/s+/b8jUAI/1KAqkCRgDLCbEHDQc6/uT38v1781nz8gJMCeEKMQqxAMT52vfn8soBXAOtAJ0RQf51+MkCYfWt+vICY/reAoMHAPqzBcUFsAYqCanzWfUK+Wb6u/7zBrUMtAp2/5b6pQWp+N78dAS2/6gGJv3F9mEDTP+z9dj9BwCeDd4Iz/sKAL0A5wCv80n1ff3DB3wDD/1t/sf4DwoTCSoBJAAqBKQCVvIY82f4pAeZDD4GgQPn+wEBEwcT/Vv/XAef/Eb2BvZ4+8QKjRMJBOn2YPvX+W372/p3/YsKNQfh9SH5NwYFBuMBI/pZ+D/8N/1O/QwBkwUFBUYA1wWMD/wGHf7z+Dz4+Poh+qr/ywGh/KYAXAZZA0MMQgyV/hn4ue086DT1uAxMEGANwgvc++T4j/3H+r/3vP3cAev6jQDVBwoIIAqMAiT8LQBE/oX4ZvuS/HIACgGb9gP7Lf5EA/MR1g8N/0X27/0s/Fb6rvvC+3cDzAEq/S4EAxKfEMX8FPiSA476tPcn8Qjwww82DKQCg/yA+cP/Sv2iA6UGmAvIArX+9/fE8aL4mP4x/zTy+AEzCWMJVgtyA8ACdwtqCA7vIfv5+4D3cgDG95f/0AeF/JMDwBL6AAsCdPxP8ZH2DgAyC4YDvArmAvP1EPvt/aL2UgAGByr6g/+sAHkMvwoMBYP+W/rb/DLxVfZA/cwKEQahA4796fn1AQzyHveC/LwDQQ0XDwUNFxF3CJHzsvh/7yjuoP3lAYYEZAj1AbgDcwWJArb9S/Ov/wf15vrlCCYIrw5R/6v86f4N/wj3Cfr7AZcDSgM1/Xv+FPkMA90ADAWsC3H6rPnp+3j+NwbgC/P8Ffb7+OfyvARqDpYA6gYyA4v6uAlpASz8f/wBAE4Jd/8f/fz7xvWu+f8CvfkDAhEGzfUW/t4DRAwdDAcCHP1C+lTwKvvwCtr+oAXS/FP7wwSEAvkE2v09BJP9yvBZ/EALkggzD6sMm/dI+wXt5+Jp870BSw/gEb8ISgFUAVn/6QAMCBIHoPyC+dH0KfkmBbr8Y/z3AeD80PtOA8QNEhc1DCr2Me0/79L3UPgY/DcErwEm/mcGTwtWEi8NSPHv9h76OPf0DW0LRgCoAtvx0vGuBFIG3Qf6/xj+dPpR/5wDPvzWBOT/MP+z+eD9BQQ0BCgE1vYw/FX0uPuPCaYESwH9B8ADefm1CyMBuQGJBt/3kvqO+23/NwAi+svzq/gv/ggQQBkxDEb7yvEt9hXzdPwlA1EK0Qmv/PP1gv7xEvYJAv1u9gXxIvYJBk4DFwVMFC0Gh/rG9a35iPef/rMDj/7cCiwK4f1V8/b12PbVATUBUAD+BH7+hQx7CP8JsQbd/5r/h/Bf7kX35f5QAOoI7QJyBPcDxP6sBDoA6v+Z/2gBuPj/AQUFMfxlAlz5XvXR/pcGaAOFBf39YABW/0H5wwOpA50OgAJn/f4BsftjALr6p/Gu+EQE5fKR9tL/4gN4FRcTrw31BQ797/Yk8jfsyPelAQAAcARzBnEOVhDkBR/18e8Y7wz+kQlyAxAOPAj+//EE2QDv94v2zO+G7ND6ngbJFPgUmwRW+z73o/W6ATYCZvzKAa78UP1lDeATXwKr/s/73vSB8WPzMg05BUD8+/8D81X8UA3bBpgIfQ7L98b5Rfne84IBKvgF9/8Cpgo6C2kMaweVAbEEP/n/89f1HvwBBOABUAA1ANAI/QKS/EwAb/g2+ij17P3JBecDBg8R+Ev8KghRAxMKKfr9+F31xP2tDGoKOwfX+gQC3vna7aX1evqD/UIBpAcqCtEM7wjRBo8BxQWz/hLo9+y27AH1LQqNDkISpRmrBp/6FP2b7oP7O/6v9YQCvAPy+kQBGAucBJwLcgBn8Fz4lfnaCH0KTP4MBJD2G/fIASj5Kw7oDuL8Wf7O+yX73/0e+X/wTv5HAY7/tgoPD8sRQg0Q/KfyfPnT8h76jwC0+hMATwiCBg0GrA2D//AA1vau7B7zY/g2Bn4AtguCEJgF3gD8AJr9IAGaAbPs9PgVAqcD/w+c/0X1FQIp8rP0JQh3AwQRhApQAPwA2wA0/AP1U/fH9kn4vPnaB6EK4hNWErH7wPtM/sX1oPdI/sv7iwx7/sr8fQrq96f0V/Vr+X0GyCC3DhP5nfdt76b5p/mCAUwDtwPjBHUCff0wAb0KLAX/BWn8CPtz/CT4yPxs/hP6agO3A0DxiAFvC/gD2xDMDAX78wAF8m7sR/3J+AEA0gXXArv6VwDjBsISAQ7//OoAfu4N/2cCMPmPCYn+//7sARz3XfVb/eT15PjlCccN/Qw3E4MHAfeR/WfsdfCW/LP9ywtcAc73XgOECtwGjwrFAHr5D/uy93j6BAdBFqMHJvRY9Nr7L/l2+fT4bvwBC7kJkAOMB7UPFQCC/NfvsuxVAoj4lQSABVwCSwSE+mP9GABxCmIJdwFe+LH7awBSCWkOzP+oAMz4zOil8AICXP7PC0kLsf0sDzkGhv93/9D1jffWA1Tz6PQPE7b5gvelBScCdQXB/zEAYgZSA+r+Mf6o9oII6At5+pb9S/c09Nv6hf9PDngP1fxL/S3yDfDzDgUQhgX4DWv+lPEM+avvOgB7CE8B5gZRDLUE5fPZ9tfy6vkW+ZoEphBZDS4MEvvPAZj/fQSY+Y/zLPhG6kL2OQBYEw8WgA0rBN39AfMH9XgCHflGCTgDwvT9+1cAOf8iDLoIZ/ZYBub9uPilAWECfwNnBED7x/iDAjAFdAlN/Gb9b/vu+xL/RfuAAAMBdAk+BV8DUfX09rj8ZPWGCe8MoQSgBXIC2PF2+7gBP/dKATkESf3t/oMKnwRn/ZH/GgW9A97+Ov6R/Lr+RgB6/h73IwDHAJ8EaARP/4MFuPf6/7P+OfUVBPoRH/858xMDK/drB3QHK/4ZDssEy/on5zjtufoyA/gK7gbpDEQISw9OBO345vvj7CryDPZC++QH1QcSCGYMUQVEBJYKmPa469X1Y/ZT/60Xvw11/6YCSvjj9pT5MvpPAIcLKwR9BhQDhPSqCG7/lPS3/sUCIQAQ+r/87/rg/D8CWwc5Aw0E4gvFAZP5d//X8db58gXI+voNFAJIBfALge7c9qUHSQJ0+pgFMfh3/XkOQATGAHoETQfx72DutfRZ/Y8HawrBEj4Ev/mw9jX2UfnBB18Kyfrj8L/8dQkWBU4RhgFP7qn4gv/t+ywJlhQkA04ECPrr9PoBvf96BNsFkPMb8jcABPorB3YQNQSs/CX1XvcbAQMKAAj3/6L3ePXP8sL2kQShDPMQiBB6A/oAKQee8GX3tQFd84L7Rfre+74M0RXkCRD9a/V99037nu6h+akH+AwgDqoI6AE191f8N/mD+iIGzf0R92H2Cf4FBawMNRN0/sj4r/v59vr+DATGBvUFewNp/nYDy/5s9q74x/Oc/NH+HgTyCmUOiAkB/58Fw/5g+zn3D/hi/Sb6EgBU/Lv3Qf+4A8MJOROWA636Mvvm81D/TAwWCQ0EMv8f7T/zyAPK/mj/rApjBbX9HPyr9IUEhAnACQ8JggFDAEr5l/hK95L60vWc+rr+9gTrDEEFvgmABOf9FwSBCef1avne9crrowY2+SwHnBrWBsUEfAY9+XD1L/4q8zj1Qv2l/6MCTAOHAhcJzgTp+ZL/QfoZA3sD0Pnj+zYH5AleAXP/d/giBij54/hKCCb7bQShB4UDFwSXCwX5XvC7/QbwrPwwCKT+9gQVDGL+/gA6AiDyeP///ZT8/AhX/0v7wwUCAqkFchES/Cz4uPir7/T5bgLNB0kGVAFH/QwGZgCG+4YEY/6XBXcGwP+4B3n6luee+Yb5G/1EFDEJhAUnCA/9mf43DdT5ku8N7d3tZAzwCB8LdgeyAbH4svbh/ST40gyX/QL+lQIr/vkIgAAtB+EIPARq9fT2O/gU+20LHgUXBxUBg/RK+j8DRQlPB6T41/bX9qP5Mf1SAm4L0AyCDWv4Mf7r997tWPl//W4JuPuKB/4LcwlrDxMJYP206J3z8O5f9TkK0wp4B04HPwo5/7P+cfZe9JL4jPfKCAMN3RBWEmL9fu0+6nf0H/x1CxsUC/5P/FoAzP47CVkMyvur8YDu++v1BggZMRa2Bv768/an9Vb54vTrAL8EPPxvAicK8QjBCUMBov+G+4rxDfrP8i8CRAlOAccBageOB9Lzg/qI+bAKbwVI/TAOSftP/ucAgvWg+FQOzfua+IwPc/0sBgcCp/Yt/2UBsP+ZAMX6w/aBAYkBGwIoBQoEB/2P/Wf7fvzQ//cIwAgH+cP+EvJn/EAGaAJDCIICdv+I+3gN4AWTABMBlusr6wb/NwgpCX8aIgOt8tzzj+6SBIoOegeACDYEi/Gj8rL74Qp7EW8Ju/en64jx3u0kA+8QdxJZD/n/LfuQ+uX+gPfw9BT/pgbxAu4I1wcwAqf+KvG5+yz9ePO99/AD7AMgEmUjbA61/5HzgdwT4Av+kgFSCYYWMQuA/gb9RP///wINz/rh9BT5PvoBEeYMSgdUBFD8l+uc79r28fNvCMUNfASxAAoIVf9E/M8CCvhiBFAMc/8C/iX6/vgw+nf6cwQYBWQJqv+n/dkK2wPOBXgDpfS/7Wf84PvmBP4MC/l4A/wDZgO4BHP9cPUM7Tv0p/dwD3sfrA8gBmj9e/Bp8X/4pv5GAvMBwfs1/IMHYQVvDYENyvqg9Iz1yPFa/XERpglfDPgI0fep+uH7w/Zm9+b5XPdqAkgLrAUJCTMFYPcC/l0CJgCgADz/XPY28O8B+v3MB7gK+fh7CTMNJgNa/w4CmfTn+PwCv/1iBGwBLgHE/FwAlfwhALMBxPXyATMFlAVfBPAFyfZx8BcEnPrG+/EKHwiIB3EHJfqC+YQAK/0M+CP14fODAhsRRwcdDdYMK/SP8x4GHfml+oIMAveJ+HL6PfwECCP/uADlAC4HPxC+CgoBh/kl/Ev7YfLN+g4HswM3/kwCCfv69dEIHP5q/yEKj/tp/t0EKAFd980DqQXi9zH08PP/A7YPFA79AgME6f2j8tX4WPoPBRsQbAWE/pD64fPCBKIQuQz0/tP10fAW51389QmDCcwN8f229CsEpABqA1gSBwXI+gvzW/WL+NMB+gkc/gcAmv0q9S/4fgI4ClgSMAn1/DH4wve8A2sJ7wp9+Pf5cfSf5KD6dgo5Ds4OJQrq/4MF5vwB+nX8cPQFASUAg/1CA6oT/gLW9PUBPfou85X0EPwu+gwGyAlNDWURdxXaB63jjfDJ79/5tQvT/4z7xf4v+Yj/DBZlBdMGoP8693MDsQCqAQ4CIAK37sT2xPx2ADgTLQe5/54GFPo08M8CHvsAAdkCS/pIBkgEBQkoBNP7kPdq/1n3SfXr/gD5QAXoBjsE2gUODHMEBAjdANftDAHa9+T35wmRA5QCqwaR8YjvRwLTCEEQbf5S/fP+PgESCr0EqwDm/L3+JO5j8SL5U/uWApgEXBHcEn8GzflV/pzxzPafB1j/VwbW/Wjzr/4CCG8D2wsYBVv1Qvrn8W77/gkID3UMegho/wHxV/aK+IH6pPo2A48IdgWrCPAF9fvK82L/+PxcAFMA8fcLBlIDhAecCKsEeQH3/Vf6Ue9t+kv6fgHNCLH/8wHaA3AD7ADuBfv9Pvny9y/4agbjB5oHTP/z9Nr97waOAKcHmAdy9yz1cfyBB7gJJQNe9Fn8xP/0A2wKu/tHAXwA2Pym+fb/D/if8jv/wv9pC9wJWAvQBN0FIPpO8iD8+PJmAq4BrwZtA0j/3wAf/VMHxgQyA4D5qwDN+Yj8/QIRABIGhv+fB3H/hPpz9bMBxP+3/GIJRve9+rAF0g4hB/EKFveu7Jr+Cf0UCtL92v379Vr5pP/Y/6IJR/4yBYUHugfP/FL/vfpdAN0Dd/U9AYj89ABF+2MA/ABuBhQK0P/XCDsEPQRS9Rb5D+vX9PIIc/+2DKAGNhA4/zH55PqT86/9gQWBBvj3XwB4/AD+avpACUAJXPlwAjfznAHpBYsJxwgkA4AAu/OM85r6LA2EAmYDJ/4M/MkCDgWYB8j60QB99BDz+vvICRQScwqM/pv09v0s+Lz5PvzTATD7pAVGCc38vhDzARz8J/li+uQAgwL7/7b3ff/R9VgDfQWgBF8ETP9FAr/7nQ4QB5IAmf6c83/uzPLvBpUGCQmhCG3/n/xi/nr1CgJdDb0DcwbJ96X+KgBb9zP9JP/x+7r3fQnDCfUHMQh8/h7wifSXBDL8kwpBCnz+v/5CAEUCDPeq9X7ySvtzCqYIlgdVDbgCkgDc/tXqWPZ1/kIIuQxlBvEEF/ok+2r5C/nb82X56AHxCRkVtRubGln7aOw75pzpg/J2BPkGTfm/Cp0ECQMLCoQOVgD49Sr7vvQN/6L7MQSb/qL6KQNJ/zkGlAlnCwj6YvZ8AJ4EXPqW/pz7qvKQBfUEfQ/+C1QGLvZd7rL4JfGY/10JLA52BxENmQPa/sX4y+jM+fT4agrtDJ8KCgID/u792vDbATj6oPpv/1ADv/96B14PIwMEAlX4v/jn798BOgLI/igKEwSTCB/+DgDP+QMBPQRb/4X10PXiA476KgnjDOAMe/UO9er8Ie9kCrINwQJU/d7/Tfob/rwC2QI2A2sDuQfn7kD2ogK5Bs/9Rv+jBbT4CQQxCEMThANM9Hfv1+2f+EoHuA+x/40CtvQ1ADMRJQ/uBSn2FPWP7hUACf1f/xQBYf3BBEIMPw5HA/wL1vNp8O35E/qL//QAiASk+FkMTglf/zcFCwDE9+bxYfYp+0oL0QdtCLUGeQCI/xL0NfoMA1L/LQGBCEb8OvuV/Kf7k//7/lEHkgenAjQBegS/+ccDrgAm7mMCqwIHAXsCcgJ+/WT2mv1r+1ABoAxODG4DtgCk/F35zPlu/i4G/v6o9Qz8wQnqAQQClQc8/ekCNgaq9/H24AQrAEj7Ev7+/hMCWgJpAgf8F/hS+Y779gGBCCkO3Qo6/oP65/Yh+vEIRAltAoX3fv5yBG/71QMp/TT82wYl/mL5aP5i/XH4HQJyAKT/qwnzAf4DP/+W+LYCwwOrAe0A4ADL+FX6q/9zAuwKGAV9+kXwzv+tCDQD/A8xBWD8X/zZ9QD22fgw+1b9ygERAXIIwApm/Z74MwOmCCoD4gQ6BND+sfvg9W/xB//tCVsBIP74AJr9e/niA0cJUgggCUT9Zfl8/Nb+rv84+x7+vAIh/zD74v7c/17+qATnAG36AAPC/eT/Bw9RBKz/9P3L+iID6wCb+Xf0mPe9/FsCvwesEHARdQLDAAL2NfVpAuT6cvskAQj6zv7ZCb/5Ivr3CJsD8QWFA6P3afh0/Of3LQC4DOkNcAj8/DfxIO65+CkBFAp3DbEIMQdtBsn6IvSt+zz6Ivhe+CIF9AZjC0gQ1P4hBIv71/Af+Lb0KfvODNkH1QX0CFD4c/0G+dr4bwLlAbwB+f/Y/9D59wfyBLYBGgAw+1r7L/VyA40FLwtHBgYCIvo3/gMGruzM/nsCIv3TCTMJIQeCBSD7RPMM/PD12f/cAs/8h/vF/moDYAWCE5EIYvsv7kz4xATeBqMHKP9FAWj0nvnu+eMD4wUz/CcI2P8vAkgCEvw9+LsBfAf3CnwIJfSp8iz4nQFuA0oKBQAN/4cAM/Do+mgDOQ2PB1IAoPu8+RL5rgBkCTkFbQuA9nz2Lfjn/P0Fhf2nBgcD2v1Y/woPCQG9/6kINvtyABwCGP8t7fD+Vflw7W/+cvyZBPUHtBhnEHwCGQBm+kT0OPbp/Df13wBJ/VABSQHgB4APNQDEBJf/Ef7p9+724f8gDTcJzP4O96PwlwnC/PT6swPO+JIAgAgrCC4MwQaN7oT79fhLA2YO8vYG/G75qPnS/oUL+gSq/2IFSv4T/uUAoglx+WX61fSV7cL7mwD4DVkNSxKVCoz2WPPB/Fj/SAboC3n+pvmI9QL+Wvv9/7UEbQKDCO3/awVzBQgIPwDs8mHuKfGI+6D/tAbN/VIIfwS1/QoLRf+iAGYG2PpX+JACSfwNAo0LLwER98X4Qvrq/VQQAgalCNMK8/nC8GPt7vvmBiwMWf0pABH71vyiEJAEtwlnAiPutOnY+00AzgKuDb0C+wRb/n0FvQAB/fYLRf418zTyIfO38AUJNg94BykYcwpT9zP06vZyAKwFvfcd8hj9mQIpA8cNtRLwCFcHl+2Q5fPxQfckCPwMThQ5D0b+pPqeAuj+/v2L/V3qW/Nd/OYB6wldBSMKKgt0BOP8lP20+Bf1iPeZ95QMzQx6+1v/M/ez/VMORwSY/ST/uP2m+e77bwCiDNkRogVQ/Ffsuu+v+6n/HwuMD10JJf7I9tb2UAQp/7n6RwfC+bL6wgOZ9ncCYhVvAiX4y/9494T3kwDSAwgJ4wkNAij7lvcXAbkEOfUP/NQG0PjK+f8HRwsUEdcGUfIk9G/11vfxATwEzwSN/2/+dghbDKgOuwe49sDpfu08+mb/qwwrDfkH2guG/ovzofQ49cj5K//Y/KYDKwo7CksKkwTGAJP+pfrz9S76C/hq/5j6WvWWEKUIewhpEJ4APfZv/JD+v/UlB8sEiwByAW729PiJ/voCRAFJ/wD6pAJq/8f+7g5CEaoLyP2U8qHlyu+09z//6QhWCQQSbwM0ApcHFwJA/pf+8/D78JsC8flsDM8L7AAQCcz9nPnD/C325PFT+0H1LgUkGTUV8ROWBbLyNfHm9jbtqvg5BO8DkwI4BakPZQuvB2cAKvUi6Dv7Hvz499gP5gZkBJD+Zfr7+v4GwPxq7Wn/APfdCTcYQQ0cBQj+/vVh+ccDTvbe+835jQEZCmADiA9ADLL5sfVW9Sbzagc5AED7F/8nACcF4v89BVz/tRDpBAL1Z/eU8rkC0f+HAkD+B/8m+z0BqgnpB6YOsfeU/qD6evOO/Pb2mgARB8wHqwvICUr6U/sE9vb5NgLc+Wv9jQVzDs0RDRJj8+3smPST8lMBXApQDUcElwZG9mz2+/rQ+6wB0vjZAOr0zgGxDo8UvBN9B5/5N+Pn7eDov/u2CikLIxEHCdcFWAIrCX/6XAEn/MTuxPNS9K3/0wrEFjgLxQmP9yHx4fvo+eL7n/UNAjcCQwo4C3YJXANo/Of6Ju1N/oEAuwAc/5YBEv6M/mYEcwHOFG3/Tf8f9vfpjwWoB9IKWQw8AO/pmvZz/A0ATxBHDDYBiews+KME1QklED0JE/cq8SvyS/EpA1IFqQOBAqsLuQTq/xwL3f8k/hL3HPjaA3gImfwc+eT4TfVVBwEGV/5LA2oJBAHdCX8Hfvwg/kHsS/S7+F4E0Qm6/O/46/4kCDkLGBL398L8yPse71QABAaXD8sF5v6A88b2+vUO+98K/P5FDrIDy/kBAgsGhwVrA7sGgvAW9Yr8BvuY/AsBYQfkAWcFHwCHAYkE3fzs+Lf/CQW3AU39gP2yAF0CjwQA9Sz8RgNRAs4Fvv2ABYH/9QCG/2kA/glHArT6C/N/+oP1p/+XBaP8ewUgAZMFHv6s/yQLmwQ6CcX/JvUL90bzWfeVBPUJ9v47+7oD9gMbCRQQTQeW+Wz0+vAG9CD9ggXGCLEEaA1GACP1XPsz+7sG+gUaBur97ffh9xz3qgBnCEcMXgCiBo35TfFFACn95QiRCtsA8fL193/6nvrrDW4S6w2E+iX48PmQ+90A2Poe/MkBIQjPBNIMrAi7/Bz0fuhM76z3tgdbDccP+w42/2b3qv6t/6L2ogQAA3v6fPwg/zIEgAMbECH++u0L+GD0nfkQC4kYKw7TBx4AY/IC8cPyZv9q/CgAHgkx/zoDaAoLALP8PAYj/SD9hgMJ+ej+Dwd6+G7+pA45/cD+IQHS9ob/0QZxA+n0ffVh9dP+dBLSF6gJ+u+2+aT/bwDECtMC1enX4a71dQB6GbUglw1Z/Rz1rPu1/H8Bi/2x+rXyu/ISBwUNJg/GBNwBXwSv9YLy3QFv/poBCg9I8qLzZAMU+4cH0w2XBcr+RPlD+CgC2wNZBmoEqfak9DL3+f8eCCkMlATj/h38yfP0+2AEZwNCAjEDiP96BbkHlfpM/DP+FPo4/Eb/lAIwBXgFJAOY/EsALALW+sH61ASUBXb8VQWF+aHyIAKwBMr8L/rM/g/35ASdBtQMsg67ABgEtvNc/f3/Gvzs+bT9fAjW+QIEEwhtB2b+9fU496n4lgAdBncJcPoRAqn/fvzQBrgCb/5+9ej6IfyKAx0N6Asa/WX5T/6E9mMBUQi7CFb5P/u5AnD6PAomA7H2MQBaA7Hwbe5wBGAJ9wzZCRH/t/t8AuUGsfwC/6gCqfbC8fP6JAJmBqkPlwmLA70FNP4p80XyvfvT+CD/VQGp/lYCiwHOCBcF4AZ4/kr6Xfkk+GwDQP7aDaQGkfjP/Aj9QAPFAYoDWQBYCVX7hPkuBzr6+ASvAxT8vfdm+/T1C/FXBtAPrhQFAMz2PvWD8wcLggr0AT0FaQD77m76GgNLALMM0QAn+QIAmAOa+TD/AA/aCpMD9ff+9MnuMvRv/MkCBgsuBbsBKgDPDjoKNAQVBCn42fhP9Yn6k/ZO+uUKSgkAAXUBBQB5/tUHZfir/ocF2/np/TD4gAIFClIEM/ah87b/pwOZAjz/hgYpBBMGd/yj+WQJGwVHAPf9gwVr+WTu6vhKAoUNMQ2FAX306/cz/GMEygp7Ckf/mfFi9oT4wAmRDLP/mvWT/RMCNPlUEDYHRfeN+uT8jfda/1cNy/UtA48OOweu/7T6ofw481gBQAAcA/z/bgEHA+/3Swyz/3n5MwFQAUcArwU3C+33ev0v+b37PwFX/Dj/AfqcBIsG4gbhAREBlfxD/FED4vXz/0X/4vrZAO7/GwFZCMMHcPpLAAT8V/lsAMUFiwSQCloJ6PbQ+O7yhQBOBosA1wCd9/n7ZQD+BwMKxA/r+P3uZPo3+OYJkAchBNQD0gN/+j/6yP9p+Dj+B/qvCMIIogTYALf17fwm/qIIo/qs/SAE7Pj1BHb/FvzWAEMFjQCuAmgCm/cuAEn8/gETCucGugJg9Ob2GQHbAwQGawpY/1b8M/0G7/r18/8ZBNcEiAi1AFj7DQXeBbsFdv6TBIf6yPEJ+Df9TAcs/rr/if28CRoJKgClD4EE4fo89uL3/vaP/QIDxP2aALcAiQRW+/8IMQzz+eD/gQQ/+y3ySQCS+G3/IxHJ+XT3ZwJKAeX4ugT3C0P/8QM2/1T9cv8XBL8AffKz/O8DIQU6BL4EYP9CAe4Hrfoa/Bn62/gd+pn/8AaqAkQJtQTiAm8EMfxm9bX2+vem+ZIBnQOaBW3+RAf5CFL9yQwGB9Dyevlh/K70wAEMA8f9SAf0/+T6XfnEAR8NnQG3BRwOJATh+tj6dPLs7uwD4QHj/D//Sf7R/ccGuRiuCZoJv/va6Rvuv+76BzUFxv3TAIQBkAJgCYUHsv0MCwH5Evdq/o76IQeJBmoDi/zGAtz/7PuHASkAr/52+I3+gPs8/MoG7gLV/4kCRwqRAqz+agBK9B36jAUMB0f7IftS+lzug/pPB3AZJBWwCD79AO91/ssBjv2R9yf9z/rU97P+1wKyEWECpPr09h/7rgVOBb4LvQHxAk3/pvrq+MT4dP9/Ad4FqfsY+08EKQ3CBNv61wDh91P54QAwBD8HrQVJ/vP4DABlAL7/2/ez9Xr+Ef1VBOcDrAPAB4QGJgozBCT/8fZ897v6WfhTAVcAmP71AnEJWwUSA7sDRfhw+yL7KwAw/4D56gj8ALYACwyi/dX3m/8Z+YD0vv8mBBAHewouCnIAZfqRAXr+6vo0/Cj77fK5/IMGbQQxDF8Fqf6k9o//HgUH+68D8/u5+pkDjAN0AiEFKgSX+3D+Wv9rAX/8Kv3qBWL9WAQcBxH42ACqAM7wnvkpB30BtP2LB5UANPiqAZQCH//nBGAAUPuRAfD5Ov7IA6UCXATi/lIGpAan/HH6gQB4/1QBVwV8/Gr/TwKd/B/5d/1EAW371v7vBjEA2QF9B7n+b/vE/6L/gPuqBxz9bPR/AgD/s/70Ao0LYf9ZAI/6dfM9CkYAdwatAqb6Uv+1+7gBMwJGBvP5PwL4/KjyKQYtBXUMBwPi/FH9rP2XBMn3iAF9AXT5ff7q/98GfAdvA9b4OPaw9xv+dALV/6MJvAH9/nsAcPgpAnIGOgEM//f+U/tY/wEFsgV5CLX9KP0V/dX1QgF3BED+SQD6BBf+UP7HA+n2OPyJB9EItAeSAZb4tvS8+xP1QfyvAfD/7gxKAz8AbAmsBPX9eAPRADH6ef+H9MnzK/zS+pkGswj0Ag8JOApNCh8Cnvon9v71efpw9ysBLQJ8CxADJfvSCXT5LQJOAe358fqe/M4C+/yMCxQEuQN4ACr7Gf4c9w4HZPwb+DwBFwGH/xsA3AKS/AYCXwGn/l8Axg4zCtX3RAJf/7v3dvmt/Q/+dPyUBLoCJ/yfBkQKcQHkA9YG+f3591H7nfC99vb/5fvYBG4B3QHAALAD+gQCBBoCJ/aiA1cDPAWCAzD3df6+/44H2gQyA1EByvtL+tzzeARcCS3+N/1b+gH6egAWBt4EnQE9APP8xfij/xIHhAJ6AnQAE/La9ykD/gBgCcULRALG+R0BVQKL+Cv+2f8Y/mL9pAPxAN//9QhUAOD6Pvt2//v2cv+ZCHn4mgPeBI4BKwgwDzADfvYi/X7xOvnr+KH6JgZOBhoQkQDm98gAeQHC+dgCvAW79DYBPAEo+xAK8Qf4/SYAP/zW9Y/9OP5o+gkDhAdFDO4K3PnM/539XPsDBZv6dvxrA639bPBKA+AK8vgm/XD8AQDFAEMOWQsS/78AHPQ79/n/0w1NBaf7efpL8kr8AQQjEG8Fmf5S/Lb0yAVkBTYDAAVdAMn4PvRH+zkBngJMBI4JlP4l+JL9jfucBGYKlf0s90z7jPvmAEUMTA32BT7/RvFG82wFNwSG/7EBxAF7+y4B8QUPANz/Nf5oBOv23PipCbf61P8iBpn/8wMEBbD4H/sUBgX81/iA9fj8IgtDDHsPUgLc9gD3fPYI+3IDzgqK/X731wCx/1cKdAky/NP51PuyAFAAmQOp/sYC0gLy+rMFIft4/Oj+zfq/CAcCcwECBYP9jPly/iICM/qX/kb7Qfy6DVIK3wAz+Vn5DfjY+E8EEgRECeAGegckCDz6rvz89E3wSP4aA3YABQd9BVL8uwh+CckEmwAZ9ZL1bPWHAAYJugBfBeMCjfX6/YAAuPjv/8YGpAWkCAII8P3E+Xf1u/7g/9D5jQN1+Uj8XQlPCrQF6AFPAO/16PvGARIERP5Q/8ABaPaxB/oFiv0M/5b1tft1A10GYQFfADP/kv9BApUB7Qc9BFgD4P3L9Nj4AvdK+Wb/iQUJDn4Gkf+lA80AgwD2/gb0t/QY/2L94wICDvYFPgNOA5/8qvuG+9j5M/TQ84wAPgoFDmoRLgeFAagDuvh19qf53/jc/If36vn9Cp4MwwXrAIH9R/2+ARQC0wH5CFX9N/Ml9HP6AAbdB+ECNPm9/5H/AvySB+kIogKK/R79yPlKAZsABf6wBqr/fQCl/JL4j/6M99L6ugfKBXwKiAoZBIMCcPdc/qH4lvicBt0A+/78/E8FwAP8BXj9yPY6/pr5dgri/wD/egO98y/6lAEJCXAHvgbF9Vf0xv+e/88DhwCpBw7+1fqgArYBDAEcAosBwwGhA1z3c/8M/fL/HQRb/G4Iw/+7+C/6sAcvBOv9rv7s990DCALzCBMD7wQBBPvxovhq+6D7ZvY8CDAD6vzOCBIAOggeAloEighY/Rf0C/JF9nUBNREOAvT6AQD0/Df7+QUOCVEExAYG9uP03wGGAcv4/QDqA38EswqC/Zr/5vjL+3f+sf5JAxr+Ggag/HQG2gV0BCAFt/DB9+L3MgMZAfv4nQQJCLoIPAJIAAT9LfxI9in80QbEAlYChP5P/NUCwAiu/ur5TfxN/nf+5QQkBX/4a/6l/BUFsApjAWr/8/pm9gf7pBG+CXcEvPyX8K0CKQHq/zP40/U2+4f+ZwcdDI8TaADl9Kj77/4Y/Bz5J/0A+VwB3gQBAn4JBAgcArcARv2L+G74w/rO/xIEzAXRBQcLDAPS+4YBx/nY+l/6g/Jj+C0IrwmLARkIxgbdA7oBB/2k9CTwCv34AOoKqgx//6r6gvP1+GIC+wrbCbT6pvlQ/58IwAsLCV39Ne0R86P5sgRVDJkMIgFS85EGHAXs/NECvvX57Zf4IAJhB8sQTwrjArv4W/amBNYC0wIMAqj4L+xL9FIBaABgDs4VgALG9SsC8vwYAgoMjP6J+BvxRPYaACsKHwn0BygDe/Xq/VD7LwAUBY4EfgRwAX4GHv7D/9z7H/TC90D6IvoQAe8GC/+kCIoHJvrZ/CsFOgNpBhQH4/jZ/kD9i/im+i8BKwG3/IECSP9yCYUFlgVPBLD6D/w39r7/L/Sp+ncGHP+xDLgKKAB9+XcBS/nI+JwHM/t/Aj4JXP8s+Rr5UP1MBZcPLwljAV3+qfQu9MT6WP+OCYIDcvg2+Hz5R/9iCosREQHGAf8DTvbJ++39Wv1EAAEHqP1A+S4Gl//K/AH/cgGVBQQGl/+g+SP7WfkUAE4FnQfmCNz/YfxMBIP/wu9w89/3kvsxCQwPnw38CsgEg/dP9/0CzvqH78b3jPh4/twSUhEFDCEHVfUR8Nn01vG6/YsM+waoD7gKW/hO/eX9W/z6/NMBEP9s+Gj94vkOBXQQ5ga0AXv+Qf0m/oH+oPhR90oCFwPiBCgGXPxyALX+Y/qDAyH+VvvK/e/8AP7ABJQKAwOJAi/9s/YH/QgFVgBc/YkIEfzl+zwHpgBWABYBe/0a+mYE4gGU+x0EFwQT+3H09vzuAxELlgoZAn7+gvmN+Bn4j/l1AygPOQEV+nD9YPUf/okKxQ2tBWgFd/sO9S8BcPuGAYQC5fWY8QH5lAPyApAG1Az4EK8LjAAb+YD2Gu/X9N8EPAXxCDsC5/MY+z8MrARMAWcHTvoB+hAAEQBb+kMCnfxB+IMOwQe/A2v64fO/9tb1HAWLCCQG3QHRBZUFVgWuBPz6nfs99Xv2lvk9AvoHqgBfBF4LkgcI+4D8jfjz+nkBB/iW+uAElgjvAWIEvwgE/0/2o/+P/mXzJACE/RD/zQlxAtUEtAbZA/T/JfnE/c4HN/2F9BgCsv3I90QCpACOBBYL9AQd+4D4UgJ8+TX6uQq8A0D/f/6R/C3/AQMKAkb/xP6/97P5r//2AhgOowmR+//+ZP36/qgDfP4u+ij3K/xj+tgDpwx7C+AHef6KACj6zAHp/Z3xCPZ6+ngH0gfmCUYCuAAH///64gBG+cL92/gX/UwEJgSWCGQH5wdN+QjztfypAnX5jQRQBhP7ZAj9APf6hQCkCOv9ff45AiD6pQM0+90BJv3k+2cDvvsH/ZP+0AQC/VwG8QVwAD/+3v48BJn2DQKM/eX/mwD/+hwDZwJNBS37XwUBBRsA3Pxe/VIA2/jE/ij6TAnpA/UBbAEc+7EFHfgkAU3+qv8OACf6LADEBM0IjPsRB0MCZwDbAvD47PXv+HH/CvadB/MKIwy5BPcA0gAh7YT6pfkiA40EaQp+Byr76AAH8lQDh/8KA0L9F/UbD2QHmwFBA1oJqfOg9cv5/fV5DJMDOv85/KgGAwPC/H79TwQmB4b0cwAQ9lH+PgKF/mAFBgO5Cn75FQRMALkBbQDV+5wFDvKLAQ8AF/90AnUGEgX6+kUHrvmO/UH9+ACv/wz7VAcIAQv+Nv4sArDxLgDlB0T+UgVm/ZH7XPoUDIX+0ASFCsz7AABf8CsDAflr+k8IEAW1B/T/1QdA9/ECTwTv+a7/GwHv/o7w7wNr/6L/aAcEA8b+o/5UB/z5CAVFAv3/d/s1+O//ofZrBIQCu/2e9W4BJwugCS0SKAAp/zbxc/O3+gn9XQgR/D/8vv7UCXUGRA5yEun4e/OE8TLyWPuxCXUBwQCMB1UC7P0mARwMEP9s/R76UPkM+h79agWB+2gDhQISA8j8Yf+xBWz71wmFBzj6qPqRBAv1EfjtByH6MgELAmQDHgTnCZgCP/iY//n9Pf8C9yYDFADo/hoCgvxxBOD8Mwje/SL6Jv8AAEcEeP96C/T33v1GBXD6mP+vAo0C+vR/AsoBQQHZA6r9rgKA/CsEBQMI/fP9TP8c+JkA5gq4+m/4Wv/pCIr93QAXA8r3IAA9BGoID/0SB5j+iPFGBFoCl/5G95L+QP2T/yULwwgJArX8TAPb9lkAqAYa/pL9LPt8Awr+YAYMBQ76D/SA95wE8f86CYUJ1wOc/6f9dPpD+xwKyfnb8I35qgHrBbQLAw5E/Tj7Qfr2+AD7NQaqC9H9gAJpBKb7av6qAxT9V/xQABf9yvh5/JEGAP3mABwIq/47/1kIWghM+Ln9H/qE9Q8BgAHMBCT8cAIXASD6jQqoCMn+1fte/9P3ef8ZDrwBff4l/wf7q/KB+vIGmQP/Av0C4P/B9xMBbgFv/iMIKwq5Bxf1k/uy+4Py5v6c/TYASARVCQgAKwHuDnsDfPrU/doGq/e+9ikAffpQABsBLgNd/aEGXgqP+ar7sf9B++/6CxEWDp/6rvjg8m/xC/7WCioB4ADDAwkAyf8/CU8MQ/WR+MX7dfcP//kIqgiA/9AH7v3p+vUCxf2J9Qz4OAIm+dkBLRJmEaMBJvzx/eX07Ppi/qkB/AFvA+j+DPjdANEHOQCO8mUEoQCO+5gKyQTxAnn8k/xN9V34QgQ7CFUHXPk0+0z3MgInEZIM/QAj/Z/9ZvBW/QMFewVkA0ECbQUh/WEBEfjj9OH5rgJQ/KD5rQo6AJAHKgh8CB4Hk/nw9VvtvP7CAsIAVf1f/64JmQICDHUFlfsh/ab8l/c//cIGhgBuBdH6GP1S/wX6WQF0+2EDjwQMA+z9jgA+BRP5i/+k/2AEtQNmAvYEffuYAL/7vfxc+sz52wP+/bcHPQraA3D+mPxS/Dfz6ANjBvr9TgIP/bz8zPwKBi0BE/vsBrQAcv3QAO4AxPrnADMKagG1/Tr6ywEEA/r+UgFE/NP+XgAf/Hv6tAhLAJLzSwQtBSIHBgrwB7z5AvG3+kv5nABvA2UBivx2/FsE7ALVB3cGEwRI+/D18gAAAZP/jgNhAPH2wPxpAC38wQQICGv+Af28B30FpwONAR/8jPol90z8Xv3cABoEVwbRASv7TwTEAGQCjwXT/m3+Vvyo9fHxAADDBxEDTgCWA/4FGQWXBiECtP4O9xP1Z/SJ/eMNIwS0ADn/9QSbBXj/1gqL/PP0E/oM+t36UQRGDjX88v04/gL6UAOWB+MKffov+Wz72vgW/A4FsxDWA+oB4fyp8db4sgXnAlv7UwVKAPf8D/+kAzQGaQRRBFP0APrDAf4A8P77+GoAPP7AAq8GiwTmA2EEUwRy9pn8HgGY+OP7pwCaAw8BQQebBRL/PQTD/N/1tvtLAEH97gDIA3r/xQAm/rwD3QCB9xQBhv7j+UoEWwkiBWEHGwXD+vr85f3a+y/27fsVBMr96gDIAHUF+gh9CegDW/jV+BLz4PqNAP8GEQhi+Xr8Vv2RAzYGBQkuBjD6jflY9fX65AJBCBAFNgOOAX79YgPV/kv/Cvwq9rb4Rf37/00GQwpi/tgF2wUN+3T/AfwN+qj/YwRrBKkEoPy8+Zf9WvxuBw0IIv6t+578MP6fAwoKpALH/Rj9d/rF/Fv9RAK0AHf1NfsQA4wEpgfHAoEA3f/qASz+Y/42BhwAJgPw+4b3D/5O+8z8kv2zCJkF6gRxAzn5zgK9AY0DmwHF/kP/8ffy9/D8rAfm/YD78QSX/1ECewKrAx4Ddv///Jn6TgbWB+v+u/c59h37Nvs7BMMHuQeNBFz9iQBQ//8Asfw8+nf/BP4kAPkApgIoBB0DYf3q+3YBFf/KANsAAQDQA6H/lf5O/wQCkP8M/LT99PsLA1f+bgJkCHECPARD/0H8EPKo+ycBx/+XB2T9qQJcA1cBmv0a/8MCrf1HA9X/0ABpAkgBpfuq+uj9Qfpi+8YBeAaNA4EIIwSjAUEBz/xv+e/48gCd/LX8qwE5DOICrPvdAtL6y/7I/ekA5QC+BD8H//qf/ncBEvxG9poCsQEx/9wG+f1QAhIEB/8v+7r5fPta/C0AaQcZDWwErv/N/kL9j/2m+jP8JP/1AHX/ZACOBJAF/vuE+jkCY/9jAD38OvwjCT0NtAIG+yT8ufYK9rf5pAN1CQMIAwJV+S0A/AaACCv8XPru/0/8EAXMAiL7g/0P/8v41v7CBusEF//V8+P9bAWWBJQGYgHk/S0C2AAu+vwBywJ2+wj4FftJ/TT9pQW0CZkKDQcDAkz6cvVT/KT/5v+iAbAEXgFX/jb/Cvqp+isAHgL/AmMDQwS//1L7e//LBCcDBwIFASD4APktADD/Cf7o/+X/x/5kApQFOQVVBckA+PpB/Qj8d/2I/wABLAfQA5D/6/yo/6H8Hf0aASf56P2uAhsFQgc5CPwCP/rw+an4uv9MAAAAxgQ5AoT+1Pqh+cn5rQEABZ4IqgrZAS//efra/BICZf1A/XD+i/xP/UoCygT9BmsDd/1i+hL4p/xZAXgIlAYsBEr/+vIx+9MFpAP9/hMBSPqs+hABiP53C+oJSfxw91P6DQE1BFcFQwU5Bf4B9fu59TX5Qv2MAnX/4P1tAkn+4gNOCDoIeP65/7T8W/KR+x3/OQJ4ACoGMgIa+xECHQCK+lj9fgvCBAcDTgQ2/HD+Yvs0/ef+agHIBPf/p/hG+MD9cgA4Aq8HXwXu/+sA4PoK/6cGdQe3ALn4j/jR9A/8bgDYBd0LLgUfAHb+/P+Y//4G4AFs+Lj69fXd+ioDBgXDArQCVf3o91YCKQdvCDEE4v1s+sb50f+/APYBOgJVAEX8mfsN/wsDhgVhBBADDQA0/Jv7kgO3ARIBpv8a9j73JP0vBM8GHA5ABRf9bP9J+aH48/jb+lj3zwNdCTMJyQ06BY0BNfbV87bzR/jpAY4GXge+BA8IoP65/FQESgaz/NX4UfvY+PMD+wiOA//+pgMvAGr3O/sp/Uj9lQEKBoQC9gK+A7IAq/wFAAMDW/3x/Rn63PdP/bAEuQCx/E4DAAPrBdYEpQC9ACT/g/2p+4X+FwLKAJn6dPkkAPQBlwbLCecCRgIx/2b2rvYI/mED4gMuBrcDGADU/Ub5xfxQ/gIEewfE/uL/V/zD9a/5MQVgCyQDRQOqAGn8G/6G/rwBmf53/lT9gPh9/+8BKv1ZAdAHegh+BNEBHP7J+o/8I//ZAIMBYgBJ9Cj5/gRWBKELswbeAgf9pPde+ib67QF6/e3+RQYCCM8IEgCl/wr63+4d8jr91wQrCIYNhQtrBEUBUf+5/Rb9Afs/8VbxMP7aA6cGKQ0zCyb/z/mE+tUB4gRTAlkArvlOAGwC5/iE+6kClAJWAlsA+fy8AgkEBgIwBIYC3vs7+Nj3yP0SBWwHUAgp/i/4PPhL+2D+0QPLCOn+u/4GAOL/4QNtB9gC+voV/Fr0i/cGBBsJBwa6AI4ARwDaA2/9hvcw/R0E1ARx/5z+tf/tAcgBPARhB1MC/vpv8Qrw5f5TB7kDrAn9CncAsPxj/LD+Kv7H+Xn5FPqQ/E4CwQctCzoLyAEH9tH0BP07Alv/ewCBBFECYwATA9IFlgbJ/xH4l/Zk+gYBjQCL//YC9wNl/e4AOAhWAy4EDwA7+J/1avU6/PcDqQZjBzoCXvsz/xEAOQGTA1IDXABD/Sb/g/he/poG3QNDA28BWf/T+B38EP7MAQAKrgF3++f47v5xBNYBowCR/uD+R/u3Afv/HP0yA6j6oP1mAzUI3QYyAsQC8PlR9ur2Of/xBbMGaQWKAUEANwAkAIH+vgNL/kf4V/jd+oYDoAQ2BQYEYwYr/XP1SPux+0EFTgRSAUoF9gMGAv341/vcAO/9R/nS9qj+UAZ3C1wGzwfsB0/+1faf7k35BgOaAn/9/P9zCpgLIQXm+U/+PP7q95L3qf+eCacJ/wR2+Db7DwIdAE37LPuE/6T+//uc/LwIngcrAFn/A/u9/DQD8wFZ/zUEXgUAApP9wvtk/W3+7Pp9/fsB1gNmB3UHTwX1/kL9qvmQ+e7+qwBh+2337f/pBYYFXQO7Bqv///xe/1r67/pe/Yn/UvuaBwkN3QQfAHf+qv0A+fv/7fpm/WcGhQJr/7b/gAJd/1/9VP9MAh7+V/9V/hH8sAPeAvn+r/7gAD0A5gLhAqL/sPy3+Vj+KQGgBkgG4f8YA7oDewDt+737fv6B+LX2dvnzBS0OlQgIAMr78wGp+Oz45/+IA7gFxPh69lX/cAuNB7wBPAA0ACr+cPe//xkDDwWyAqn6Rfhj/scBfAFaB5gKSweD+x37+fiX+PP+Q/7M/iQBYQZpAwQD2QMT/2n7FP5xADD7QfzW/sz90wFtBnACT/3U//r/Dvo6AMcCiQHZBQIEl//R+RD7Iv7dBgQG+QEF/Fr1AgO7BJ4E3AFv/Rz6fvwOBI3/OQW2Ajj7LfkU/g0C7f5GAbwAOAW9BBv/5Pye+Xb7HQFr/7EBnghEAVn8zAAnAf3/O/7F+5oCqQhTBFT6efbz+rL9Rv/SAaoFeQUfAYj9LAQ5BTgBRfya8yH9nAEIAJ4CxwTVAZ7/LQSI/3YB8QT//3j7uvl1+XT5zv5bB1MGkP9cAEH9jfl4ALwFVv4U/9MDyvwt/TYGTQYS/0L/Af2P+Ib6LwOIBPEDswmcA5L83fsCAKb7h/7iBF38PfwGA8YGsf6I+wz5QfgeAtsHrggpA0EEVf17+ML+Svtz/D4A+/2V/5kEIAcbBFP7l/rnAGoB9QBdAQH/rQGsA4v9DP9+/yj67vjN+/wFcw2KBav8sPrw/UgAGf4QBP8C//2h+sr5HwT3CWIKcwCz+/H4IPYH+sf9lwwxBlv9XQA9/P7/W/+vAJAEOgVE/yT52PwH/ZwCo/+U/AoGjQI7/HX9AAFgANoBaQOsACUDTQTF/1P17/OM+5ABPgYdCq0IhP/I/o/9bv2ZAc0BBft09Qv9cf9YBFYIswVPAgP//v6j+7b8Df5WAED8/PzTBD8CqAU3BEb7J/2QA0r+rf2PAN7/AQBb/D8DmQZvBY0AD/1r/HH7M/5l9kb6BAILB80I3gKjBckAvfvU+a31G/3uAqgD4gZOAx0BLP7x+B78lAUGB0j/MwED/bv9KwWiAV3/SP3t/wAAmv2m/zwCcPsb+JYAhwIyBOUAVvvD/LIFtwpBAlwAMwEE+mH3U/t3/1IFUgQU/goAdQOBANf9kf/i/3EAjQHqATAC0/1r/Iz+6P/8AA0A1f0R/IX9ZPw4BP0KVwTpAfH8Wf6qACf/bP+b/CP9ePxW/LwACwpSBKP7Kv0O/sMBq/9AAAsBhwP9BO77SvslAob/WP3Q/RcBFgd5A/gCWf6w+y35dPds/AEB0AhNBGkG/gS9/jX9RgAJAlD8IQDp9UD2zADcAk0DKQRZBq8A5gB0Ad4Ce/+l/5z6evXcAHEEHQQCAOT+y/tu+0H8LAHgCDEDLQRX/8v8XwWTBBX7Wv32AuP5kfsr/oH7hP5+/kQAFwOJBuQKTwq+BN7+uvoj9D32/f2Y/gX/uf+AASsDtQRUBlMBwvoF/bz9NQL2CC4Bhv5T/IX8hfvu9sL9TwBjAyQIoAgzBGUDE/6K95H9mvuB/Cr/e/9nBQ0FPQSxBFUAVf3v/YD+bvvP/ssAx/yIBeQEFgAn/1r9UwPKAm781fY4+gb9PALsBmUCLQHh/Yr7XvsAA34HawBo/dP+rv/kAWYFHwMW/hv9tv6w/q0B7gQ+Aq3+5/9u/6IAAwSo/gj+qvbO9Kz//f7nAqEJvAbsAJAEYAIO/4QBt/SF9R38pfh2ArcHsgV6ChMI6Puj/hwBpPRo+xT+wv0RB/oDJQc1A5j8cvq4+lX8rv2SAXv9uQVaAt8A8Qd0AuIG//7l9136Yfq6+C78ZwOkBSELLwMp/5QCwf2M/Xn+Ef6i/Mv9ev2H/MgEjAR//zYC4//XATn/yPxE/+T76f9HAYsGIwRu/hL8uvldAeQCwQcOAPD84f3L+p0ELQX6BK76Kfsw+9j4hAb7Bu8HCAAh+FX4+v6uA2UBugbe/xL97PyQ9+4AvAcoBLcBd/4j+x37EwD4AXcDLAM698z6YgS7C/wMLAFX+zj2HfPS9bIEIgnTBCoElP4BA9EI/gf99pzx/fly92/8cAjBDosGuQGq/Zvzb/mzBzIDqPs4AFn99f65AVoD9AN4/k4B5//F9fP/kQqF/LYCSge2+5v+PAHF+8zzK/8pBXEB9QJgBDsCUPvUBW4CUP2oBAcBSfc5834AVQKKAe0FVwSs+2r8TQMD/LgD+Qk6BCv6Ffs5Afv5WP/OBDT/H/3SA3T85veVBCcF0wFN/7oB4QNV/g39wv7q+h8A+gQf+ej6iAdzAe/8IgUGAUr9+v4DAg4DJgRcBVT7A/uJAJ7/kve//tYGkP+8AEIDywXe/WT9AP20+ikBHgJSANn5BQaWBIT8wwXAALv4K/ge/on/ZwQZB4QBxAKVAND+K/4i/R8CKQC+/LD87/pMAS4GIgajAqsAk/3A+18BNf80ALP8q/xB/ez9ag1iCFsCu/pK8wj7aP66BIj+s/0MAur/EwVXCDkMSwRu+1LxPvLV//L9jQZgBuj+FAN6AsL8UP54BqD7Hfs3AhT+zwJZBPEDXAGx/Jr40/Zr+2f/NwdIBAYEyAvq/5H+/gTU/0T3lvWT+XX7owQpA1EFSwKm/0QClfZkAWwDnf+BAv0DCQJx++EB9/hw/UMBGP0pBd8AiQMFAjQAigJWA938i/dpA5D94P5JBvr+2gIQAiz+c/tNAD0D1/mQ/mb+jf1QADcBewaj/+j9z/4M/tcAqgI+/fP6GgWDBYQFXfsZ+Rb/j/bx/3wDaARGChED+v03AowICAAJ+2r4ZPgs//36Yf9/CLwF/v+KATEAW//uA2j67vl8BF8BIv8XAS//Uv5D/XP/DAQjASgAVv6K9pz6bwGTABsHyQhNAvD8CvuY/bj/VANBAxUCzfuu+fj/FQL+BmQGA/+r/DD9O/cxAMMJoQOnBMr+t/t//7n86PqgAEcF8QHe/ZH6O/k7+RD/bgggDvkKoQCR8zjy9v9FBz4E4AD3ACv7TvcL+kUE/wZcAz8EoP5kBP8EU/8R/dD+1P9X9oT6zf7EAzcHiQL0BPr/IfdA/MUDPQNpA9j9DfXx+2QDXP9OBvsJrf/29zv40gA9BBwC1gA0AiQCVgH9+RP5yAWpBhcAaPvR/tz/KfwFAYQG3QMDAc78BPeG/64CW/3k/AsDlAGM/R8EnADH/zQBoAEnBNgApv10/zoBKPso/If+vwKLBnf9lfskAroCXf0YAdUEoQEGART8Uvw8/QL//v1B+U4G4gUk/Cn/ywEABGwEkQKL/Q78vvkb/Jz9kQHMCwcClvrq/7P/dPyzBHsHTPs4+fX+Wge+BlAAPgLA/yD6dfk79in+tAvWBRf9iwCoBAL/rfuL/8wANP8A/0P4iPc3AjgDHAKnAjIFB/7v/a8DbP+9Ao0AvQTpAID8vgGP/sP75fgx/Sn7sghvDAT+FwbNBZj/a/rYANr8XfT6/G35AQFXBlkIewMA/UAEU/yl+3b9Sv9+9l73QQyOBxcE9AJ4A2n9zf82AAXxOv9rAuj95P8DCt0Iwf1xBKb8OgDn/qD9VgL0+jX/of5h/v8CBwiE+lv6fAJs9CH9IgK4AzUFmgGDBLsDAQZJAaL8yvX3+OX4VfaFBvkFxgNeA+YDLwI4A/YJFgU+AZH18fOG8rT+Iwq1/IIDxQVXA4/+VQKHA436jPwU+9MAIP5eCAcI0fl+A///qfgX+3cBVvjR+t8J6QYiB2cEsf8O9lb2dPwA/HgHiw/IBcb52v6//u77+P2i/LX+lPuFAaQCMf5rBgwHx/6cAHIHyvn3+dkCUfwDA90DW//0+dv34/92AQIDfwP7/lP6vwIjBnQDTAnTBQ7/hPV69eX5r/nTASIEiQQ5BHkAavuE/DoHgQbIAJEAN/6c+WP9WgLCBX8Gr/hA8WL1IgDCB34FdgiYDRoG7vXj+bz7e/yzBpL+CPtU/+0DWgBt/QEEa/8K/CcD+wZC/PkBgAYE97j2bf7KAZ3+WAbxA8X57gGWAqD+Jf3VBSUAz/SvAeYFVQDB/ksAoPmW/5YHxQMhChAFZv0o8oD1bwX6Acv9A/yuAbP/FARkB8sC1Aa2++706/Le/sgEpP7KCDsHSP+n/jUGoQAw/vn8FPZZ/6EBXwbe/i37JAPm+1398QakAcD5cAfBBZX+yf+x+uf2gPimBiwEaAJqAVb48fqiBSEOwQVQBNkBJfd+8dn37P/1AmQNVwerAoQBkv1t+QPyGPuc/Ob+NQbKCM8LtgmuA6r5ifsU+Nj5Wf3P8lP7zwGuCU4QOQZRAiABDPfG83IB3//TA8sDRPffAY0FOQZd+5/yBP4eAaoCZQmFCiL9UAAl/mv1IwCyAr0DtP/v/2kCkv66AF4DrvxA++UCdvlL/WIGMwDd/wUCy/9U/nMC5v1h/ZX9/ACTA1b7oAOxBET+LQLRAz0ASf+H+rrztPmwBQwM2AQ4Bu4BGvjp/a7/4v5O/7ACtvko9Wf+2QJXBLMEuwM5+iUBjgdaAm8BtwTJAEjzy/qw/e/85wH4AzsBeAEPByP9/QDLBrYEqPms9RMArvuXAngIcQRs/Nf8//mt91IHXwKF/UX/7AWYA776/f9v/BP+gQMtBkP7+PkkBQr+RAD1A+sBhACX/br9vP7u/vsFQgrP/LEAMwOW9YH3N/vdAD8KhAbJ+6X84P9iAw8F0f9eAqv9qvj3+Pf8hwTyAqkDkgG2/hX+yf+qAFkBnQKK/Xn/Jfm0+w0IsQRQB4kF8/Va81b6lvg3BIENqwkTCZwBnP34+oX6y/1z/G/4//u9/Cn3AwUUDbcJpA2wB+n6NPZR95z4a/x1BSUEAP5oA+gCAAHRBDYFbPvm9vf6v/qUA6sIMAi9Aor88/zT+2j+6/pa+Dz2OPhZAgMJsRISDhcAwfl/9dL8egRkAWX/N/+X/fT8fwAJAugFnQLU+y7+QP4LB90GOgB/ASwBy/wa9/f53/6nBTL+qP3b/gP8GwbR/K/89QRkA24EuAQ6+6v2y/mP+V8I7QdXBgsHevj7+L8E3gSO/Y7+g/JQ9UUCEQfKEbcQfAyn/nPxp/KG+u/2tfihAK38OAg6B5QEHAoKBPH9x/ZB+g8D4wP++nz8kPva+M4AjfzoBM8JM//QAEEFLwIKA+wE3P3C/sH4ePfs/DX4gv/7BGMM1BAjBuP+j/6V96fyy/jN/1QNuwMF+Gb9evzaA6EE0wKPA6b6b/Bx/KYM0AxOBvb2rfjD+xT3NfzQA7cF9wMkAEH/HQ8FCa/5Qfsw++v7iP6i//3+pgHJ9oP6KQWgBa8LfgJuBiUIpPth9ej1jPjq9l77RwCgC5oM9AbQAewCXgWS85n11wAzBCkEUAXP/Z32mgBN+aT9awNvBeEDyPi2BP0EHP9z/yz/uvXE+aMGCP3AAoEGggaiAFv8xv8j+jX/0QByAAgBHApIA+n4xf66+mcDEf6D/ZoEqP5+A2sBigHCAVf8ivWi9+MBPgfaCND+G/sX/Xr+6watB+wEuQBI9lz1//yz/gv/UwfxA2/+FwRK/nEAkgCl/9sAPfdQAigG3APhBhMBHvsv8n/2nv7WA4cHNggM/0P6yg0dCev/oAJ09jTzRfIr9oYDMwmaCdgIdP4N+hYG8/85/b3/5fiyAE///fu4/3gArQVEB9UCuQDuAPT9SvlM86b8DwdSAosD1wWnB7gGcf8J+qT2M/i7/cn+BwCgBHYCbgJ/BFsCpQAD+6f8lv+X/ekBtAF6/Sz93QLnAWwBQwLy+64AfwA4AVoAY/7M/Vn6UQOeAVoF9gUW/hH9tf8VA277oPzi+iv8Ufx/AwQQyAb3BOX8i/Qt95T8ngLCAtcCRgIjAFL/UwdaArP3XPhb9jL8kge4CUwKjgbf/OT4eflq+9gBZQcJ/578Zv7U/BcAGAWRCuUCL/6x+zn6EAAxBhcG+vvH9vb18v+pAnoD5wSD+7cAFAOL+6j6UQSzB2z9Mf4ZCj4JtgKZ+uXv9fPn/ScDAgLbBSUHbwJTAn4EiAba+/X0CPSL9tYCaQl5C28GV/q6+zn8kPbsAEIDrgE3Cx4F0/w/Ahf68fj1AO0ADgz6Aq/5PgC++yn8cQL3/Ob1Av/N/MMB+At9B24GgP7l/Nn3h/WfAUYF6ArXCAr6ffcB9yn4VgOCAvYAwQeMA2UCEAYG/nb82vuT+jMGfwh3ArD69u839RAG8gYECWIKLf0o/qv7+f7dCQT9C/Yg9ev3YgSWB3wJHwzvBWT3du9W+lwAZ/3V/TD/1gMPBXkEeAYTCn0DEvgK++v76wNaBJT3BP8J/zr5Ov6KCDgJM//N+nj56AKi/5b/RAfoAcYAU/n1/RgGFgDV+c/3sv0iBA0BoPyuA9YCGAAgBmIKUQUw+v31+vqLAdsCtAFx+t35mPho/N0KcA0SCEP91Piv+sr+4f5jBHwGnv1Q/6f7q/4xAucADf7g+DP8hfyNAcQIJgwhB4wBKf9n+Mj58f/rALb9RvpqARkLPQIR+vn0afhIB64D6v4xCGIJcABH/lX7yAMLAoDwQvOr+eoJmgm8/eICagKe/ksCdQSu/KsFoAQR/Bv9ifaEAAUFOf73AlECQfsoARX8nviKCEUHOgCx/RD/4f9A+wL7YQALAI4A8AOI/+QCnAO2AyQB4Py+++L0Cfo/AzYHYQefCwgFH/r0/XD3cvjBA1n9H/nBAbwELQhSCAIFJ/0n8pv2JvpH+DsBtgzBCYcLhQw+AOz36vS78qz1gAW2BcEBDgJ/BEIKawHq/Yz1Ofae+Tz7Hwa+BekMwQfDAAkAHfpl/sX6t/zuAvb+DvlC/A4EEAFmBqYF9vqt/UkFRwm3BZkAWvWr7l72xgAdBSEC2QIRAJ4AKwnICT0FJQJk+cH01Py8/yn8Efw/ABn/tAMNBlsEpwyiBcH3QvWT+MT5W/zWAGMGigLX+y4C4//sBpQJwf7kAT8CvfuT8+L5FgB/AbkIUQMpAtsB1v/MAJf92/+9+Cr48gGdBKIHvgQ3/IT0FPrw/8oAZQEkBSEEK/vSAy4AmgJeDYj+1fe1/Ub+TvzK/+79UAKkAbb9UAa0BMIExP/88jz6PQVfAIAEYP8O81r61/43BXMK2wX0/xkBoP1S+4P+Gv/iBeYA/P8k/Zv5wQPFBHMHqQO/+HDyyPdkBAUHTAZWAyYCev19/pEGSvtH+Jb6cPYBATkJBgglBJ8DOwNLAQz8U/uh+63wmfzeB5EBvAbMAnT+8wSXA67/dgBm/oT5Xvkg+Vf/IAdLBMIF0ANdA2EBOP29/kX6yfwj+FT+XwNm/y0N1AxMBUb6VfSR7W347AWS+6sHgQfGCOoHdwFdBzD6V/Py7qry+vxeDd0U4AdDCmcBkPSK9ev5cP3J/PEAsAKlAU0HOweSAWX+TPad+C75hP2sCpoH1QQGBmb8Q/ctAMr30/0CBicCswfI9qD+cQb//98BHAA9An//rwSo+zr7k/79/UACM/87CO78r/kLAEH52P/NBm0HwAD3/GP87v28Anv/Vvwo/yYG2AB9940DG///+zYGmgVmCN4Civ1S9mr6UP+Y/lEBBgB+AVb43gj8C179fAPO+Zfx0fdK/04AOwlHBj7+3QSUCYkJDPth+Dr/Gvdl9rkB8QMMBAIEWwEAAP4DcQAq9RT9NAPJA9YDTAXW/3D4tvmi9nf+AQFqBZ8K4v5O+Qn/dwO8BgcELvzf/Tn7U/3XAn0CrwOG/9z3DQHcCOX/lf8N+dX4Ov7sA9oLvQrPBgz+a/nv9ZH5iflxA10I+PqM/s78QvyHBHgK8wZwAYL9cvVu9g8BwAXU/ZMBKgKV+r4AgAWiAY0AWf0y+33+kwFQCZMDhP2OBEYAhPmXAA7/MvwzAk/5MftQBZUHcAUCAY8AAwIY/6X39vtF9/X8YgamAEoOyw1v/932RPRO91L9Qgp7Amv8OQFG/k/8IvyKBfkGDwjvBe/7Jfr1+Gb+cfVZ+mwIkwHjAGH+rQNHBvEGxQW8BBIExviJ+GPuNfi7Bib+TgP0BBQKrglLAR0AQPvs9Az4UwBFA7kHEwI+/acAeAaRBtb9nP1L+O/wrvVcAb8BXQOACrYHDAiEAkn6rva9/Dj+Rvop/jkEiwRh+6QCdf6+/DoJIwWABnULAAVG9GT0PPnH/usGpwYtBJD47f5PACn1+ANICVL9UwFpAHn3lfxJA2oFyQTO/0D+wPlJ964Dtv1d/YYE7/qI/XYD0gp2CiIFq/zR91j2AfpdBXsEXgzCAbn1yfbQ9AECzAx6DUcGKPok8ykDRQYmBHoHIvqo+djzpfK5B2ILOP+m/5P9CQX6CC74DPv5/uP9GQKyBLgEowSc/Gr4PQBZ/c39kPap9ZwGQgjuB1wLQwVU/WsAdwBO+TT5dPp/+qD8nwTWBr8BKQhxAwUBZAWI+Abx/fQZBhAN9Ab3AHb+0/07+Ub9iff6AcIJTf0WB9gJhv9I+Nj1hfd1/2MF+gOeAocBPAtzBSL8gvq/8A/5xf/6AssFuwQqBZz9FgE5AZ7/ff6p+8f7gv4jCMQAhQOLBf75zvne/awClQRQB9cBFf+o/lL5JPuh/1oCnv3z95kDSgk1A10EXvcA+9YA3Pk5AYMCmAMe/o/+mAKZAlH7L/okArj/Fwv6Ay/7KAEX/2L8PAR/DRkAj/n/8zP28PxSB20PKwKyAon7tvdR/sgBBgWwAsz/APZh+LIAKQbSAkv8Bfye/AIEUwidBZcCpgAo9ib5NQAAAkoHBf659k/8fAqICKQGXv729Ln+wfmMAX0FuQWnBMj5hv4zAdcDzgE5/DD0c/s9Avr67AWqCrEKOwTy+TD+vvfy9Eb/b/uw/FQKcQN//KoHMAIv/dIBj/91/D34FQWHBb0C1Qmo/7L4yfUK/Nz8AAZWDNMDsP9p+YsBAvxIAGsKNf7+/Un8QPes/gwFTgVZBlP4NvAR+oL7aAQyD3MICg2JBTH23f3D9Sn6Fv7k8q/86gZIAmUHMBEMBuwHXvwx8b32kvWyA24KDwfy/+P+ifdZ+ekB6gDbCccAd/zi+5v93AgBCXIAXPWA+f35lfvGADwDhgVaAeQIQwLc/8YGo/cO+OP7cwTKB3T+HQJT+Pz1YAHuBKT+7gWwCOH4eQJZ///+dgSG+SX86fdH+2sCGQW7DLQNTwAP9X/9Ufdg/RgJBP1LBBgGFv6TAk4F/f9F+Pv2EPhG/sUB0wKZ/+b+0AdMAgD7Ef1i+2v9LwNwAh0GNAoVAxn58vtkAIj0lPXCABcFDw3TEPAHMgJh+zn3b/94/YX8S/vv+9b/pv7E/iQA8gSO/Z78ufux/cMMnASnBaUJCvfi8O3yq/i1AhAL3gqTA1kCjP1RAFP8awP6Ckj83gUN+qbx6/3XAVkFkwPbBVX2WPmG/qr//AZv/5EBRvtG/5oD5P9fBccDfP/I/ewDIQFg+x75B/hPACoFiAPZ/asFXwTP8ez8vQLuANkJYwYf/1/5Ffqc+AAAXQpKCHr5+/YcBAv6qwWEDVgAcgGi/VP/RwJ0A+/8Kfhs+ZX2Tfmd/1kN1QpT/y0GnwIo/DD6tfMs/S0DfgAVAyQKKQg7ANX9Iflr/gj7V/gP+h8BJw/CBD8E5wUi/b/8Af0n9w32UfxO//IInQVhBcUFdfulAGf8p/xoBjkA3/l5/2H83vnqBukAcAb1C0b90wO8/iH8EAEv+yH9TP6y+A74NQNP/VYAQgbdANIMhwgNACr/gPtB+J/4ufpc/j4D2gFqB8D+rfhDBMsEFAPoAcP7+vd++qP/ZwqoEbYKLvz39BXyVveTAPz+Af8AA8MEuvztBXcKnv1X/un9NgIu/bb+igFn/WwHQAYb+q3xmv4f/Gn7Xg3wAz7+Sv5J/2AC+wXcCSsACfgU+W4BdQHBA+YC9O1Q8f79uv15CiEVcRatCdn3D/KP81L58PtnABD9vQCZB+wBWgoSCbv8S/QH8o/4Ff8oCXcL6gWUAiQHlQKy9s/yjO4A9J//6wqHDvMO/hKLAt/3ZPq19Hb21vlDABIEqghOCYP/ZABk/qD8oPF7+d0KB/+jB7AJJP1P+0H9kvnk+SwArvlj/TcHKRNsBZf6zANd9wz5PQP9DcIGL/yz9FTsugaZD1wF5fr1+iz9J/Tt/kYIRQa9AHf+uPizAMEM2gLM/Ln65v5i+hL7uAD6+AIAJwiuCjEOFQiHAkr+xO9r9W0BaABwBEAA1fj4/E4HtgEMA4YD5/hH9G/41AkwBYQBGQLRAZz+HgFfBUb5JwTu9TPuEf8rBewF6gWpDiIESwR6+or1RPsv+5kJDQIsAsEGx/kV9OIBjAY6BSYIHft49Af2sP5qAxAEQw0dC8XzpvT7AIf5dAQICS8AF/rb+B7zJvqpDUkP9Avk/iUCEfpV8doCi/9nAEMGSQQXAhoEb//K9Qr2HfwSA0b/8AWgBsP62AFeAZD7OwQYArb4HP8hBK8BzwAUAQoCSv7Y+WH/zAB+90j/wAOZA4EJXwRHCC8CY/n79U32ev3q/tIE7/3VAlf/ivnFBqIHbAk2/jr98f61/HL79fqcAlz+LQYnBAkBqAM2++z55fbt+KH/ywLvB8sMYAfhAFT9evjQ+UcB6wGZAmP6iPQF/xP/DwdwB8EJsgSx+vsAofj0AO0BFAQeAT771v9a7kL58QoPCGwCJgdy/qPy+/2a/RwGmQx0CYL9bPDA/hIBwPhxA/cFpfhB+24AjfkxBngKJv5BAv3/VAL6ASUBhQqe/oL22fld92L3YwIhBN4H1BDkA6T75/vF9xb6FAUWA5wA2AF5/SQB+/61+kD51fj3+4wC7gDuCnMP7/pSBG8HQfsq/ZD3GPZXAJ0GqAKAATT+L/xP+877vAuyC2gH4QpD+Ybz/fdM9/j7vP2U/vkAWAIvAKkFkgUMCYMId/X/8YD0Tv+qCLgKgA6qB+L5QfTd9qD48QHZAvz/agM7Cc4FAADZBncDwfoM9Hr5h/wu9VD8zAaLBfsDZAO5/j4IGwoR/574bfiq/o37HPtjBI4EZviT+yQCuAPKESgKgvRT8Sb3/P49Ca4LdgWQBGj7Hfd9+hT6lAY0/qf4BgQoAToHpAjaANEARgN09Dr1xQH+AXwKR/4++4n52fUPBhcH7wbuBNT+/fc/Ai4I1/4oAyf6O/kG/qD65ARUBjoBrf7e/Yr99vuB/37//gPOBHsGJgRw+cL/4/k++W7+Yf/M/5EAsA2l/p37twJM/p38k/7ABB76SQjSCDb7sgMBAiv4PfI8/4MADQXACQwEEQbc/FT/WPVR9V0Le/+j++UCkP7K/+8CYAEPAO0C3fh6+Of8tvzGCfcBFQNMCZb/yQId+dXw/f6WCI0CVQed/jHzkQaVAKgCpA/SBoEBKPZW777z8/2oCIoKxf6W+qX/NPpoAJEJsAZHBXwEhvmw9jkCQADV+VL/xv5P9Vf6jv9HA0gKegtfCSQAqQHD/xP7e/sm94z08vV5AscCKAiZCZgDIg4VBD/9L/p2+fH7h/hfAsEC3QYyBRL9rPv5/UIJnALb96TxIPXBANoIzg4AB3gFBgHx8V30uP9WBI//1Pqg+8YASgorBKb9VwI2AXf8A/pIAVUCuAa7CHwAdPmW+/ACffbHABwJ/vwL/p3+R/2JAyQOzQOvAaL5x/CW9Jj0SwguDPsHaQad/Ef0hPwZBtoCVwjo/9v37f4x/cz52gUdBJgBkgbj/VL9NvwxA8ADVgHPAoj8c/ab8wT/bQDIC/4OS/qT9o78kgJXABkDYwJs/KoB6AQeBVwG9gl0/O3uJfGo78z9XA0TE1IPewRz/VDw0fGR/VoElADsAB0Auv2jCtwCbfkZ/Nf+Ev4nAbj/3vzbBcMChAZ8CKYDSvrn9XT5EgHLCgMFYAKC+Wr8uvrA9rkADAKUAo0GFw5C+e32KADd+2MAjv8RAlT5TPoD/7gCKApqCS0B5vAm/AYIrwOVBgoD5/u3/un+w/jl/oAH0gPI/Gn8RAPeAwz+FP7e/owEzwND9Qv33AKNA4EB3APTBAUC1gMt+jzvQPhE/yIE4AD+A9cJXAQWAc/67wJPBxkADPNC7m35aQUpDfEJeQ2OBw//xfam9rz90PfL+bD7OQJkCY0PewwMAYr8G/cG7dfwu/9JA3cJ8AelBQsAW//T/WX8lgS0Ap4E0vQA/bUCi/plA8P+AgGwARgJc/3z/w8MGf11/UH3a/piAnoE6f619HAAgQrXBDf4fP7RAQ36dwdgA+j/XAtc/prxgfRYAWz+dPzbAJYB0grjCb8MYQFj+Xf/P/mR9sX7SQBL/LIDhASPBQcK1v+q/Gr3L/UiAPoBev7sBdQGJASK/0f+Vf3a8aLxM//AB98IMBPPCQn/xP/69Pj4BAGGA+UADfyE+g796PqnAVAQIgG0+dAAMf3JAlAIqwIZ/Y740fRH9L3+0AjsBE///wC5BikFIwoBCi36dfOX8wf2Mf9/DKsLmAZFAeL1Svk9/ab+CQNmAFsCDAFrAagFrwBe/cT4Ivgt/EAF8wEu/lEJugGG/K39mgHFAPn//wAJ/RUF/QQCAvP6bwLLCHD4ZveD+NL1YgIUD08G7ASqAif4W/XC/NoB8/1bAT/8CwD8BM0N0wmO9ln5HPZf9jT67AI4BVoNrg6X/U0IPwUJ/Mr7ufqg+lX3RPmr+e39ywXxCoQHygRsAwH/z/pMASIBw/Zm/ID6vvdf/1QIIAawA4YHYvyd+MP+MgVUAkP9q/2++zL+SQIZB14GrAUF+Gbti/yPAN7/3gU0BAEFjwfXBAoI0gXn/D73r+0i9HEDUANQB94Jsv3K/7QAuvbB+ooA6QcgCCIAMv+Q+8z3/v6A/x/4ygUIBzr45wGgC84G5AVh/2Xzy/eW/Xj/8v9yBfAKtwO/+tz65wFD++L/2fuX8sID6QfrA74Gywyq/uL7TP7w90gCHf8bAPL5NvuJART+nwIOBssIHv9rBIr9cPGB/Lj+gftFBUkNTv8EAK3+sf3Z/R76rv6R94X//wodCv8HvA7zArfuAvjy+nv3HAK+BiP64PzfAggARQC2BmILkAPlAqcAw/tP9o762fO78yIKywjdBoAGwQNu96v6AgTn/PcA9f9iA1n5gPw1CQQBaQMBAqv9zvZE+0r+c/7HDTELrgGe/Fv5YPbV+UwFjgWZBZP9UfrSBrUFOgQsAtP2QPYl/I/4ZP5dB6r/Y//GAcMBtgmBCH8AEf+C+3f+lP+J/bwAOPwX/VD+DwDd9wr+1gvZAtEItQkA/Jjz7v3F+rD+pQcg+SD8b/t5BcEBkgCTBZb/mf13+ZwJggGlC4YJCvh5AWH90Ptm9bX/M/sp/eoBRPk5AlYEqw23CxkM3ACd9Wfz6ev29hD6eghZDhMCmQPcA0n9tP96AvL8uQCN/Ev6Ov/RAP8JzQgGAOX7NfUD+p8FywUDAxL/YPsx/dgBHgONArT+F/l2/eMEXgfMAn/7APkvAUEBo/1kB6j8rvjeAbL7e/+EB50HjfxtACIEmPzeAxICMgKJ+m74fP5F+sUAugJAAm792wQuARv6PQXQ/in+//9jAxkEfAHA/hH+dACZ+4H7h/ju/8UIzwfLAKQDTAKK/HcH8gH9/ZD7bfg68qj8wgjbAowGlvnN+tf5IP7OCYkIrAvhBL8CGPTL9tz5ZvgGBcQAUgAd/c8ApgNhBlcHqQL0APP5Bv6Q/wICX/8F+EL6I/2F/yUDxwp3CcsF4gKN+mX4VP1s+XX6rAJ4AeUBJv7tApELMQUh/w38Sveo9+f/nv9z/hYA1f4G/Z4A2gvOC/oCb/lA+Nb71P//Bjn+iPYs/pABAP80Bu8K2QA3APQCCPoQ/UUEa/sc/oABHf25/6/8L/2O/+cDeweQBVL9Ufn2ATD+NABkA9j+/QPnBR/8P/f6/Un5I/kO+dn/Vg16DCEPvQYl/5L4dPaZ83j14AOu/kcGnwdS/qr+MwWKBJD3kP5H/2YBIwSsB/UFpvvLAjH6Sff6/Un9Offb/HkKCQP5AmkHYQik/1r8F/0K8zv4q/96AeIBYgcjBFv+kwLkABr+Svy5ACr7GfmHB1MLOgMC/V7/+wFiBGj/Jvnr9xcDeQg29x/8UAXc/tj3nv1mBXYCWQdMAtb9NQL4CEr79vAO/jfzvvWo/4kHdhIGFZoQfvvP9Y7zxvSA9aEDAAx9+OIC5wfMAlADXQS8+PzvawJ7/Vr+3AcrAJH7CAT0DCUAwvvg/6L8qPoiAjAJlfuJ9rr/QvtcAXUTpQgv+H/7gPvI9RP74QccA0b9owUhAiT6+P4YCUkA4fdo/BH4pv2XB7INEwKd/bUGNPdd/RcH3gBpAHEBJv2l997+s/3o/J77NwUPCpUCFQnX/Df1HfxsAQ7/bwCaCUT/OP3C/Zr30vsvAtoBef0A/ugE8AxtCY8HDgJY8bbzovdS9Gj/mAsXCSMBxARPAToCswoO/nX4CPaB+KH9p/xpB4sKfv+2934IiAca/O4Dzfkn9/kA3QB5/QEFvQJ89Gz7/woxEUoD1vdD/ET2G/TYAwMF3gUSDMz+CvUP+0kDcfjR/NEHSgL4BTMGvgaZ+5b1K/eG+f0CRgdhBFT6/wWJAb75agXeB1wEWvk6AFb9QftqBjv/Xfiz/vAFBvh8+n8FEQFoBnkHPAEQ+aX+jgKC9xr4PgARBsACnQfbBLb2qf1X/pL+OQFZBIUC3/QH+qYDggfvB10GJPtD+4UHhv5z97v6Xf729IX/+Q3EBjsLOwUM/VT/uQFo+C72E/7/Ah0CPflkAx3+LfnJAk4BFgG5A9gFBPs7AjgESPZW+l4AWgJN/LIAawU3/2n/lv2j/JAEkgydBEACbwkRAW/33vZDAa7/ofhLAjT7TfhIA1/+9PkRCpUOGAC0BTr/LPSe+Rb9qAHd/fL/ogDs+/4A0wlzBGD6lP2r+LP7lQgeDZEH2f8iAxz5NvOZ/vT94vw+AvIADP4cBPQKsgT2+33/kv7i9bT8BQU2BcgIgAej/Dv2cvkM+sT61v4jB2AFk//6Aw39TP5zAdj+aP5a/UgDPP1n/TAD1gT6AKEB3AOd9WMAxwNm+w79sP6NAu/9qQe/B/gGpgbe/hf9EvLw+q4Bg/0k/9EDKf/I9SQBFQQLA4gGLwN9/PD+tgJi/tP8hvo/AvH/m/uk/oz5uPwxBiYJGATYCBQFLvc2/MEDVwHlAGMBe/cg9Mr+ogLE/xcG/wgIBRQA4fsZ+yb5p/4dA6sB6QAIBksB6/ja/3H+3frs/HcC8gBRA5YL7QUCAY36Afrz9xX5kAFnAecE/AilB8z8SP03/7j1wvziAHMA5wE/AtIBxP19Bl0EFPoY/L39Wf7k/f8CGAW7A2YAFf2H+iT7tgVHAcH+owUGBIv5YfvRCNMCSQAhAJf8wvmy+i8B7wAQArn+wP4kAgMHigbX90z5WgU8/xz6iwIy/9L4/P+VBZEEzgo4BhD2q/We/RMA0/tpBnMJYQBbAfIBXgA7+t0A+/50+BAAKwFM/j0BiQv3AzP94/95+SD3TfvH/pH+kgQLBowClAT3BED+SfnPACYHeAOc+ET17fY++SoIvQxsB1AGs/y19038/wS+BG74lPix+6P/tgU+DKoKRf1e+tn4Xfk4+sL9pQJXBDMMvwbsAWQCQv4+9yL3xP9o+6z9igFCAdgIpwOO/3ACNP6U/lj/8/g5+M4CpAF8/18J6QLf/f39Ef6WACkAJgQa/1cAGQOCAH78X/iw/lz/hP/c/1IEHAWuAZ8EUAHbAMYAkfxS90v7w/3a+psAkAJUBJ4FCAbpAFL9BwOIAIsB+ADH+yf6A/er/NL/+v/zBaIEUAAJAEgGpQUgAAD+kfdO+r390QFCAu/8dAOIAtcBWwER/oz/cvsa/mgCtQftBln9Vfot/A8E+QCa/X7+If37/mb6iP4fBTwGFwQeA+kCDv6ZAZr6ofa//Z78VQFrBDYD/QI7B/YFmfmy9wL5CfpWA60ImwGa/VMD6QFQAlUJXwK58C3rhPNF/zANOhCECe8FYgW4BnEAePQr8ljyOvEAAYANNQ6lD9EEd/y2+SD3UvoD/Lv+PgJOBWoD2/58Aw0FEgBq+8/2Kvge/CYC8AKqBKAIOgB7+338aAFEAEv9FQY0CxoJkf9o/DL2o/Aa+cb49AIJEOEH5wG6AwcGzwO4AN/8F/fS9VXzkvgGAnEGCAgfBTwDR/6f/ir9tf4hBmP/fgLsBrD/+v2I/Xz6wfzT/qv3y/vRBfcC6QXEC+sEXwC1/nn5vvVj+hgAhv46BUwHngEMAs0DSAAv/Dn/CvkT91j/qAOaCF8GcAIy/mz47Pmh/ZcEAQWc/vP/nP6M/Vf/I/5g/84AfgDn/8EC7QfZBmn++/zf/qP68fbe+OgAdAaiCg4IgwO1Apn/8/wk+LP7+v3D+UL3RvlPBLgIsAuvCtgD6gDU/Er5ePdK/vP8OfXo+fb/fQjCDN0KEQQ1/rX8PffG+YX+7gN5CFwEyf+9/m788vbl9+369wGyB90HTQUQA88IyAW2/qX2VPbL/ET6Zfjn+3sGFAb0BqMH0gCABKj/c/af9o3+uP48AkQGmgCeBSv+Yffp+SD9lAS5BDMHEwXKAM78/fXK+WcANQCCAIIDKwUVA8wD+QfNA/H9jvev9hf8sQC0BPkD7AXD/kv1RvcJAKYDnQQqCLL/uf1C/WH/8wIX/4T+a/vD/7H/Lv5D/i3+rgJr/9oAIAOZBl8FugJtBDH+pf3f+Jn1qvdn/oEHy/+tBB8J3QS8Bhr/6v3t/3//j/rt9sf4UvYs/LEHtAxRCWQEIPzU/JX9BPrY//P/wgGY/w3+LAJXCG0FbPxD/ZX4A/wp+/0AigvSB6gDufaP92X/lAS7AnP/QQFH+/T/EgF9/04EvwGM/kf+of1+/asAIgA1/iQC6AGh/4n+agAbCpgGff/Q/Mr2evqM/SQC5Qbc/8L83/8G/eD+Vf9l/rEDmQO/BFkCXwGmAUMAhfye90v5lPgmAfEFOgapBAoEkgN39/7+2QAW/ZMAP/v5ANYFuQMyAFwAbv9P+4D/1v3l+SMAKgPHA8EHMQUg/0/82P0f+674kf8SAwYDygL9A74AZ/+H/6j4EP2dAfX/ZADfAZYFnwRJAeP6ffj1/PP++QD4A10BvADnAd77PwA9BsQEsgEA/Z78dfnJ/ZoCPQGsAWH9E/4uAfb/pQHaA8ABCQRxABr39/pC/dn86v/RBHYGqwHkAF4AFQBZAyMD/vtI+qz8APkJ/UkGlwcpBY8Eb/+m9tn6PgA//ej/dgBSAFkANARnDE0EVf3s97z1fv/4AB4BQAB7A+gFOv9YAKUEcgEE+QH4Bf23A+gIXwM4/Tb8DPsw/cEAPv/2Ac0GEwKe+y39aP3H/C4Duf9//p8HCAEs+h0CYAaFAj3+5Pya9gz5OAXOAlwFEgbk/mz/vQEYBnD+fvyg/XzzvfciAacHywnJBl0DKf60+0P9ZP8D/wUA4f/d+xL7ZP9nAccBYgW+ARAAuP3P9zf+PgJsBr8FW/9sAFP+NP7V/dX/3wNdAYv7aPnf/8ICWQWxBo0E9AGs/l39Bvod/D3+z/tz/Lr9ZAEUAf79wQLABIIDGAQNBJwAC/59//P6/Pqg/xwCkQDC/jL/sv0dApr/fAHFCEMIMATe+3n68ftL/k38jfn8/swERgHk+/P/agGAABL/Ef9QABgJqAq0/FX8fv7V/GH+Sf+P+0j6Hf71+48BaQyqDdQG7P2K98n4V/+J/00BLgHI/JX7Bf1aA+YCSAXSAhL5+/tPAKEIrwVGAEYCb/zE+tv63fyM/EcCnQKT+ScAZgX9ArQCfwMv/mf8+gD7/xb+tQMvBHX+pQCu+8H3Hf4GAjUABwJhC3YJxwL5AIr3L/VL/3j+o//VA1P/ePri+gACUQQQBJUCE/rL9mkBxARGAxwGPQGD/poBTAEG/Lv+g/up+IMBpQEYBDcImwW4/4P+Lfxt+ToAGQVCASQBXQIo+Wf7CAEI/dz8HgEtAWoBgwdhBk8ANv5K/Pz0hf5ZAnP+CgcVBOUDMgDGALv+3PdG+8X7MwDrAUAEGwPsBa4Dpfrg+ib9MwE2/mUFiwXA/yMAovjM+O/9xQUnBTkGbwfq/Ib4IvzM/5X9+QJEBqIA5QFfAX36svvV//b1rfjhA2IC+gFQBIAG/QCDAmMDIPvkAMD+sPg8/GD+AAA3Ai4IaQQHAAkAdPwqAq4H4gK4+R35Hfep9jEIIwzDA6UAs/0g+r39CgSX+xr8GgKG/FoAfQi4BR8Ag/60+836Av48At4CdwJpA2z+7/u3AIQBhv7c/9v/k/y5AHAE6QPdBvgAofiU9oX22v9RBLwEIgdABOUCmf9k+/D+zv/8+7r6gvq7/zIFqQeJBOoC9AKz+zL6cfuzAHsAA//o/yb8YQFaBvABa/6UA239fPye/rD4fP+xAycDXvw6AxMIrAEjBhkC7P30/Dv5l/RM/C4FaAHyAGkFdAQ0AJYDov9d/pQC+fw29gv6tQAL/ZgDdgllA48CNwB3+Kr62AMIBesBn/+M/uv8zQJLBpT+0f+gAx766vAc91ABigO7BocHyQI+BFj+zvaN/YcDVwEO/V79iP+0AvUBhgMMB6IBhv+k/F384QI+Ah/+Ef0n/Lz8cQAOAngCBQOQAJL8q/zo/7j/0P28/xoAofwlADEEOAKCBVUHiv5V/Xz/i/jJ+wACr/8FBMwH5v/v/V4CRPuG+cMAgQFnAb//kP5R/v8ATAEH/CX/0wMPAc79VQEGAOv/vQKc+2L+VAcSAvH8VgUFAYP7AgOx/hD8r/0E+lP21//LC9UJmgVzAxv8GfZR/74Aofup/3//Jf1OBEoJ+gHw//v8kvvn/mv+nv91/53/FQNhBYICQQJR/aT1CPeA/ggEhQWkCNoBRfyr+wr5TP9DCa0IIwBL/s39Hv6OA0kFwP/X+0n5l/fA/pEJ+Ahk/sb9Jvum90v/5gA0/t8D1gcaA5YFegEY9jn4VP1J+8v9RQMDAjgGoAelBB0DZAR6Abf1Mfl4/M76kP/v/6gB+AdfCF4BKfxn/Qb9Cvpv/xkAqwGRBfz/1QBeAzABtPvI9wn7iP6MAb8GAga9Auz+3fiq/FMCDwU7Ad7/ZgEs/rb/lv2kACwEvwE2/BP5XP9oAcgDagRLBHsCt/98/M740P5UAHb/O/wJ+iv/2gCdBgkJtgPb/kn/4f3k9/QAigOD/DsA+f2S+sn+5QMJAhUDiQkbBuUAt/5h+4P3HPvR/mb+TAO5BrEADwDDB1X/Y/mB/Kn5NP37BU4HmwKgBfb+6vXN+3z8e/z2/cb86f7wB/EOdAcwAKf/3ffN9f36cPz9Ag4IBARgAHYBLQIl/5r9rv4R/GL/ugH6AYMKZAbV+vz05/ZG+JH8FgjHBf4EnQZbAVACsQTbAQf9IPj898P51fr0/sL/TQfvCDcAI/5JAeQG5wNCAPP75Pm2+2P90wE/AZMAB/lz82D9/glWDDsJfgcFAOn7qP3A/Wz5vPqfApP+dABeCBMAyfsr/oL7BAL4CEcDWP9j/9T9aAHSBAj+fPbv9176vfp8BGsKyAJQAEYAVft1/9oEz/3i/NwCOwKkA5IGBQJF+6j8jPt596n9OwOMBOAHPQl4AeP9dAOh/qj7F/4R+Xf5xgB8AaX90/0iALgAugB8BRwEiv6v/bD6cQFXCTYF6/up91z7dP5uAYUDbwSAACf8pf6DAbACfASKAukAFQQFAOX7tfzO+oX4Kvz1AocA5wCBB6IGYAYcA2L3g/fQ/tD9Tf1aApYEx//xAK8A2vpd/+MApftf//cFUQNjAJEEAAIM/MH+IfuG97MB6wT//ykC7ANrAEABzwOe/j/6yAFBAeP7GQSJA2H86/7n/1f6Jf1lAej6qv0NCv0KyQOEAjL7D/a4+pD8fP5wAXMFuf8S/KkERQmVAbf8DwGz/Z39QP5u/HMAnwS7Aab59P4JCMUCQv4VAsT8c/VH+b3/IQWADH8Mw/0J+cD9+vli/AEDaABq/qv/igB2ABwFPgio/8T+cf4Q+c35z/s2/noEtwhnAvD9Bf85/xf9FgJtAkH+HANR/Zz6Jv+UAD8AaQHMBEcC3wORAlb5xviN/0D9if+nBFwBnwIbBKYCrv+gATP+Y/WI+iYAdAGGBj8HCAFT/Yv/6/9YADUD8/8e/gz90PoS+rf9PwR5/w3/ZAN8BW0ERQGi/k78D/41+Yj67P6JAc4GzgSuBE8EMQC9/Mn+YPzz+fQDhAWn/aH9qAC2/SkC/QfXAFcAyAD29aX1fwH4AhP8owGjBhoBLgXmCHr8v/mzAAv49fiaAtb/EgEbCb0GP/vf/uoAr/sV/lX+Ef8vAUkDOgNMAacECAIB9a/49ABWABgDywDdAQsCTwNvAr79EgMjAcr6jPfz944ATwe9BkIFDABS+uH8o/xa/7wECwL2/s/+nf6//+UDIgJy/m/+H/wj/ggCLwMAA9wCHQQl/xL5dPok+9P7uQJ/BK8E8QhaA7b5B/ob/1T7NADaBMf9ogJ5AS39IgM4CE0CIvp8+3P5MfyfBCIISAN6/4z+aPl3AkgKpP5p+zP+z/f8+Ur/PfxR/hMGKAiLAikCBQRhAJYDYQSr/bL7q/h99t75owSKCDoAbv4u/8IEVwhdAor/ev5s/U7+U/0Y/UsAX/1h+2H8rv67Ar8E4wTTAYsFHAVS/bL58vow/XoAgwXv/zz9FwNeAR/7pP0e/7b5iP+GBYYDuQKEBIQAFv/hB+4Div6x/WT4ZfgJ/O/+7v6iAnkDu/+fAikIfQOy/EQBov3L+uv9ifqn+cwA9AcIAX0BLQI//Yn/PAHfA6H+5/sP+6P8RQUMCncLhgT5/GT4CPjB+0D/xv1w+7v+6v5GAjYHZgkHCWsC0Pvb+Ob5qPsq/6ECogGR/bb8bwMgAjP90/1P+48A7AhgBogBSQS9ARv4h/vn/fP71P+s/i7+9wNYBoIEkgKQ/5r+hv1x/kX7a/rtBAgFiQBGAA/9QP2H/879Dv/1BHcGB/+Q+ikAZP/h/0wCJgCr/qP8EQCHADgCMQaCAgb/pvuc+Uj+WwStA9oAg/7a/yj/Nv2+AtoApgDrAEb6wv2RAP//ZwI9BTMHEwGY+2n9yfyM+/8AlASz/3r7Hvkb+PMCugwFCL4EzwIi/uf5mPsd/kb6Df/t/dD5FgZCC4gF9QDC/gz86fzwAD7+Af7FAkP/AvuoAQADjgDcBSkDvfsh/Cz/V/uy/CIFCgLK/jMBYAL+AIoDHAVn/S0ATwNl+YTzpffp+hAAiQwuDX4EU/+Y/Iz5av8SB7kAKv2r+wL6x/y6BRsIZP2eAC8Bdfx0AaIDbv9j/lIEuvuJ+EcC8QC0/3ABRAHs/pYDJwO5+B/7dP7N+mf/7QaCBdwF9QX4/xz+nQCR/hn4afww/Y/8awlxCgUCm/1t+lD2MfhRBNsGrwPgBx4DWvuz/xP+5fnB/gr9aPe1+7sCrgKTBZ8G7wCm/7v/lwIEAhkAav5R+Xz+MAI+AIoCEQRu/4j5NvwEBIoDcwDpA1X+yP4WBAL/oQDxA1QB6vg0+s/9SfryAbQG/v4f/dACUgC6/hADYAEtACgGWwFz+C3/Bf1j9Wz66gGfBaAIkQes/3n/ygFH/gn9FgGg/gH63AAeAxP9jAFrBiEA9/4z/O74EQEJClQGewAnBJL6gfMl+/j+PQQABuP8VfgQAewE8AJTBe0Hjf5x9Yf5yvuTAUkFugEj/iT+OwNKAdwCewWj/sv5B/6jBcUCjf9mARb91fis/csAKv8lBHUFIAGc/8X+fPmP+NUA0v4fAB8GKgFfAtYEPwEB/3j/p/1P+a7+VQCp+ccCfQkVAtcEkQgtAC37kvxs+Ff7iwQEAKn7HwEHAwz/CAOtBQP8oPuP/pP6QwBRB4UBTAFCBdL7u/eC/0X/efvIAQsDYf2bBOAHsQDUAq0BQ/iQ+U0A/P9HBFoKHgAH9xL+eAHB/U3/OwFxAooEOgMbABT/Iv6U9lv3ugJ8BX0EdQHNAPUB7/xi+336RPkE/BwAOgXPCP0IvQKz/WIA4QCv/wT/RPpW97L7xAAmA5cK8A70A+r6bPrb9zD8lwJs/0H+HQB6AtP+hQHMCroA+/o8+p31TfsQADsA2QKMCqwJdgRYAiP8d/d2+Fn5O/xLBbUEqgAuAcYBvQH3AXwAYPgy/dEDX//ZAkMIIATu/Qn7BPeq9r3/ywctB6QIvATB/Fj9Mvy3+dD80AB1/uj+rwMSBZYDiQFJ/737Tfxh/Ev6t/kRAhYLBgg0BSoBO/qG+oH/yQDa/TQA5gPG/ID8+wKyADAAogS+Agb+mwQj/ij0EP6HA1QA2f/pA7//OwFdCIAAXPmt/Xn7XPO3/3kIXwJNBWgIEQOfADsCbfkq9e3+JP+k+lb+Rf+Z/4QF1AphB8wArf/5+bz5Tf99/3EBRv65+s7/vAXqB/8C1vzX/SL9CPy1/48B6ALeAeP+W/6o/+QBngADAIsDKgK4+oP2W/uoAIYBWQF1AtUFbwdzA8L+1P+0/879t/t8+139iP3S/An6sQPKC88DawCbAvIBw/9RAIH8Hfl//Sv9c/kjA5cL0QLWAMMED/9H+8v8r/op++wCGwTqAcIFOgTh+/3+rgQv/Bn7VwC5+U76hAH1AqUDvgVdBHr7IP+fBJr9F///Ac78X/ow/qb/Rf8RA7oFxAGZALUA5voA/Jf/fwDuAUAD8gMO/sv+pwORASH/5fty/D/8UP7ZAYf+/wOCCF4EVAO+AIz5B/gi/DP9oQDtAxMBQPuHAWsH8AFIAHz4hPRa/jIG4QTPBm4JLP7n9mz8OAAqAZkE5/yV99kAxQXQBA0D7gJW/K78KgIAAcAGyAR69/DxXvaL+sMDWw2uBooA0gHEAfr9dfyA/8/+DAKp/6z4g/1jAvoBkACXAykFAwLK/An7Kv+mAT4DNf87/U3+zv4a/k/8ywGABHoFGgVa/0/5nPqF/y7/ZAN3CDICk/zSAT7+3/kXAV0Ccv9TAKf/bvld/XgD5fzmAHcMygVl/bP9Yvn59wf/5gA7/csGyAiU+yT8cAI7ATECGwXH+zb5MQNNAR//bgYSBWP7/vlO+xf8TwHVBP0CsP8yARsCxfxX/qcBWv2j/Sv+7P5cAP4BawTBAEwAd/45/NL/xgEAAB/9VAEgBP0A5QF6AJL9NAHTBe4DMwCV/oz3RfZRALMDfQEUAkkANP2jAfYEJgSVAgL/gfZ58278Hv0fA7gMxAgSAgj+Z/v5+CwBpwT2/Zz+DgCc/tACwgeNAU7+Af7R+lj8tgBdAT//qQEBAWcBHQP3AEIAJv+I/gv82/vj/rUC/waZBDP/yv0S/OT6oAFuAswBGQLe+1D9NwCrArj/kP2UABP70P+GBO8ANQUEB3X+2/jm+/f6EPtBBMkIWwKDBMsFIvyP/nkAMPlF9138av7gAKMLDAosAHr/h/te9fP5LALLA+wDeAW2/ef5nQNIBKICQQf3/8T18Piu+876ZABqBf8ESwW5BogC4f37/b/9J/07/NP6evoY+nz9LQiADNIG1gWsAeH49Pu6/oH7of5cATP+a/9zBloDR/wKAYQB7/sp/o//CAEUA5MB/f++/lYCfvul9+ABxAGZAUgDpQLzAa0AXADS+x78RgL2/878Yv/R/HL+hQRfBdYBXv9wANn/zgHL/9D9a/4U+377ef/zAiwEAwQpAhYC3gPWAWH7yvlS/YP8tv8IA9YBZAIGAVMBJgE9/Uf79vqn/MT+AQSACLsGDgbD/Sb3Hfpd/df/DwFhBpsDf/2Z/u/9xP4lA5oD3P1X/ln/ZvtL/4wHjwWa/wD+D/ca9v0B4Af0BAAFkANF+7L8igLq/Ln+YQJA/DX70AHVCJwEkAIpAPn06/cW/7n9cQBkBnUE4gK8ALP9ef00/Lv/l/5jAowGiQJ3/iL7wQFw/6X6WgCJALn/zwP8Bp8DYwLPABX5zPRZ+W39jwISDTwJe//V/Sz9jfkM+YIB+AG5AeQFxgOSAqEAkPsX9SP6+wG5AMQEnwavAaYAKQG//d/9fADk/V35Tf2PBsAEtgMwAV37oPzV/ab+CgAYBQMEx/8Q/j79cACi/+T/9gB3//n+g/8k/4IAUQJi/kb9JwEWAtP/PgLHA+AAiwEn/ur4VvtK/woA4wHaA68ARfxj/r8AZwLoBiQEN/9LARICNPun+Mb8Gv6W/9cE1gQ0/1YAEPzZ+rYEuAS8AK/+mwBT/rH7WAIfAED+hAH1+0X70wCzAFQDsAfoBR//LPrb+1T9MwGMBk0DAQGH/3j6IPun/QoAswEhAsQAtf/0AnkADQBXAlr/lADD/4X6sP8tBwwBz/s4/3j+sfwDA2cB/PhE/1IDYf2pALIG9f+p/hoEW/3C+B/9xP4o/msIYg1NA5P+4/l/8633ZQRVBwoCawFAAQgC+gRPCGAEfv2++cXxLPIC/ikG3wbgAVsAIACN/Nv+0APUBUcHVQP8+yv7ePpg+QL7RQGkBVIChQQVAbv+mgPIAAX9Y/sQ/n37JAGdDLYHNQPY//z4OPf//uP+YfYP/FIDQAAEBK4MNgbXAXABf/eo9yv/2/1c+6UDNAnLA8MBFP5V+Dz6Nf6e/QD/cAdoCJUFcQSu/dL8bf+f/pP6oPii/a4B7QMUBOAAxf52/vf55f0NCGcI7AO0/Yf9kv1M/Uv/NP7X/JX4hvxLBBcJsgvnBCv/9/zE+LH1w/2yBgQBifvg/uMAJAKYCJ4F9f5I/wf3cPTI/mEI6wjbBUQHxvo48tP5W/uGAV0NKArS/b36IfqG+AsDfQx3Ahb8Hf3C9dr5EwYBB5sClQEY/xH76/+2ATP9BgF7BQkCjf+X/778c/wcAv8B///lA/7/0PZ49+b9KQK3B80KCgdMA7b/Bvbh8sr9nQIY/43+cwI4AdcCjQlvBY0C6P3K96329vltAN//XwQ8CVICqf/FAp//5ftI/Yf8d/nH/oIBLv2/BcIJKwD4ACsEbP18/fMAhP0//IQBZf519t4ATATtABgG/gb0AWb8+P7I+Qz7wgRuAML9swAs/7r81AE3BegDgwH8/Oj26PnXBI8IBQkLBBb8b/nf+Qn99wFnAiT/mvxO/ScAagJ+Bp4CGP+3/cH6oP3sADAFMAQWAmn/pfpB+1D/1QOjAxkByP+y/db7gf9bBVoF9wGQ/sH48vmaArwD9gH4Aw4Bgfgc+/QCmAFlAmICtPjb+3YHwgOHAZ0Cu/xW9w782wCg/j4FJwYb/HX8GALNAJ4DJwWd+jL3vf7qAgYDGAUaAnv96v0XABICoAO/Ayj8efgf+zsAwAdbBlT/Kvvw++P9ZwEzAFr9WQDKADAAfv/2BBEH7gBAAOj7Ofmh+uv6i/32AucKhQqdA0f/ffuD94L6QQCGAbwD2wQ0AQf9p/+zAUH9hPlK+tz6FgAcCswIPAcxCN7+7Pa++ev9zPkz+aQBFgLnAX8F7wDJAUIHjQPw+gP+GAGi+j7+kv99+8j9vwR3AgcBFAf2/xf5v/xlAfz9oQAvAs/8zwPkB+UBMf7VAQ/9ifn9/jf9WfuDAMMAfP1wBdgG2gP1A2QBYP3c+nP+tfxJ/qUCyP/X+yv5lvyGBOoGzQYTBLgBLASc/XP4P/pW/lf+6PvG/3oBMAbDCDoElQA//xv6wPTj+BkBzwbVCfAGw/0N/mT/ofyH/bn9x/sb+xcCTgMNAzUI1AEZ+QX+4wIFAOj/Zv+N+dr+gQhFAaz+zAK/ABT+iv/N/iL4Uf9aBMX9QwIVCdoCsv3h/zH95vxb/hD7HvofAeQG3wS3BP0BofpR+lYAyQBe/oABcAI7/2IAt/8H/yYCV/9u+w768AEjCpUDSAD6AUT+Uf/2AIT7//kh/2QBp/6/A/EGkwJfAqr8jvliAFoCM/zN+g0BwwEcAmoCs/vG+kcBvACHALgGIgRA/Tb+Ov+g/IoBBgNz+dT7vQK5A10GfwUtAKj8R/6L+2X6iwJuA1UBFwbfA9L7QfsT/nH7XfteACn9fAC0B/4EEQSOA2b/ovYC+F4AngPsBaID9v3h+cj71P6rBOIKBwqs/GfxbfmAAI4EpgYuAsH6EfsnAAoBaQhgBsX4GfTL+FEAAAZrCSgEevs0/vD97P22By0Fnfy6+r/7zvt4AlwKrATR/Y389/qQ/lUI4wOf/G38S/l++Y0BDAidACT/sgD/AdUGvwHa+cP4r/6h+xL9IghXB80DiQLU+0L5IgBr/o786AMJBHf+zgAmBakBOABa/xL4nPjQ/mkCkQcuBSn97vcb/SQEGAU0B9oCRf5i+y37DABNAU7+KfrA+jwBygiDCUYEMf/T+3f35/jL/W3+iAMJBxkF0gKnAfP6vfd0/Zj8Wv0kBeQIKgTOAqgC0f/2/5D7Qfgv/YoBMgAJApsEXQRqBKT/Tfnm+Hz9B//yAecFjv5s/JkBDv7m/N7/ogMXAjcA+QIl/REAJwNL/Or9nALzBBEBw/7v/Lr6aP+cAOb/PALLBCoGngP7++D4tv1HAV0BGwEUAN78cf5Y/Yz6jwAcAeb/ywPuBsYGLALg/lD6LPoF/pb8RP2A/zH+Q/+FBtIJ9gZZA4z+7voF95X2fP36BgYM5gcM/hj5K/y2+1H/AQYd/zn4zvmj/7gFTw3ODFz+6/oN+0/1+Po4B3MFiPyj+5b6L/4fBDMDRAGLBtcGNf0a/A//TQCi/l39ePwQ/4QEGf/t+eH8AgIfAx8HXQi+Ayb9k/RK947+bwVDBKMAiP+u+xX/LQUEBw8CXP3J+cj6N/2+AdsK5wo0B2/6o/F6+PH/OQOaA+oEAAG9/Ef8m/h++/QFQwc9AOD9Dv92+7H+mASdAWgD3f5a94f4LP+uB7IHywbtAoj8CPtF+2QAjwP1AXEEjQLq/KT7MP1sAAwDbwSI/Nf5+QDXAP4BGwbsAWX6Jf12/Sz7+v9dA8EBggKPAxT7MPxCA1ICbAGQAYb8qvV/+Q7/XAbWDfIJPAC3+pP6yvt5/iD/Lv/PAKoA+P9fApcBSQBsA1oB4v2A+9D6vP3mBQ4M7gRH/8X6uPQb+Cf9wgNgCY8IrAGM++7+6vy7/XoBT/7T/Yn8Af8KAuUHwAjx/+P7NPjU92j7cgGbBBoECwSGAbL+wv6qAe8CPAMb//P+7/1k+1IBOv0g/pwDIP0K/GIEKQv4BhwCUP0s81r5PwKa/FH+kwRQA0f/TgGEAJb8sgXr/6DzG/4lBzQI7waxAyr9Hvoe+uryXfl2B58HggI0AEsCZwUZBnn/evnF/JP/Tv5y/hsAuP/JAPwBzv7m/XEAMf+5AJ4DIADlAIsBBwAE/wD/SgEGARgAY/zn+jH+PAGIAIgAqASfAagBkQPc/C/6Yv3G/jUACAR2BAcCswGR/tv2P/zkAlT+oQB/BGwH6wOs/yL+HfpIARj/uviq/AoALQFvABMEXAGEAFkD0v0m/tcBuv9j/pn+Q/rV/KkDQgXyBXMHHwfS/PT5qfr39cr9bAWbA0QBewP0/6X6swF3AhADSgSn+pX1A/n+Ab8DGQFqAPH+fAKLAesBif+9+q0A9AEGAVIAEP96AbYB2wRWBYQBP/2B9hv39v1SBIcDwgCLA5QFTAQCAOH54fWo+00CRQaOCJMC6/x2+Lf4tfuW/WwCTgTE/6sAhwlPClwCl/tt+XT67AD4/zD6aACpBCUDLwBo/jv8yf04Adz/CQTPB8IBw/+eBOX9f/mR+yH5L/siAYUBRvuOAR8FagBMCSIMkgGg+Xf11fgQARsDkf4P+jQAvwKvAnUH3AUMAmf8Q/lu+dAB8AcEBYkCEP9j/RL8jP1d/Rb+v/4D/p/9T/2sAjwFiAb0Apb9t/zZAPwEIP/K+EL2RPtIA98GuQZ4BU0DvPxZ/awE0wPc/AP1lvUoAxEMvgrxBIP8yPRU9XL6Pv/0AykBWf+BA9ILFg0nBYD9ofKM7xr0PvskA4gHhgq+CZkHBwNp/Y/8FvmQ9dP6eQA6A0wGLAlsBPr8GPsd+gb8igA2Adz7qP0+A40HQgrGBer/ofa49a35mv4EBYQCSAAQ/yQE9gWsAXYA9fo1/fv/qP6cApUAov6V/dD61/2qA6gGagNOAsEAPPza+oT89f5g/VUAogBv/TUG2QwYCVoBXPoj9972QPos/pYE0wxUBv/5PPlg//cAFPzO/SMEwwRUAGP9j/5GA5QE/vrD9m39+QKWBMEDtAHw/k//1wFk/yT+ugBAASECjQDvAToDuf8l/fj2UPfM/eD/DwAoBLALOgkuAMv4hPeZ/vYA0v5T/gED9wfNAiT9ofw//0QAIv6V/mwAuwJCA30B+gFeBCL+b/jr+zH/RP77+xf/PgAMBdAGIv7//AYB5gPpAIsAGAHT/nH/wPtH/Er/SAIrBtMDuQCf/Bj6qv3hAK4CNQLzAcMBbP06/6QBT/2X+7/8hPzs/5AFcANRBPAGNwG/+bP5fPqc+8cG2QY7AiMBJvy+/iUBXgCi/I/73gDiA4oDjAKlAc/9FfrO+Oz/dwV+A2sAGf7rAvYE0QGS+xv5L/tC/MECMgdkCSwGg/tB98755v5hBYUES/w4+Hn+WAVmBdgGawTS/yf7PvbV+EwATwQo/g8AXQdPBbAASv1w/kACrAIj+9X4WQCnA3MAIAF/Acb9dv0E+Xv6KQJBCC0J+wH8/uH9jwGlAkT/nf9Z/Fv3j/QR/AEGsglcC6kErP5oAFcAf/0m/UMArP53+iL6lPwjABAF8QdHA8v+u/wV/60BogBqAAsA8AGq///+gv8nAFQAZfnV+d78vP/DAiACIwLAAwcF/wI+ApsCTgG6+Hn4Bv8p/1cEMwHG+KP5vgHqCXkK1AQc/Zz7MP5z/4r+8QHMA+77hflq+t77cP9I/6z/lwSJDD8IPv0Y/kj6dvhnATUC3v5NAI0AVv4bAkID4v7O/PH8C/zG/SEHjwXYAwAJMQW3/c74vfhv+rQAR/6S+NL9ogPHBXIFUApjBGn6Wfr2+8sARAPZAYb7R/3zAG3/8QFnAuP/d/q9+T37c/9IBc0JtgrM/wr6U/rd/XUBV//B/qr6yf2rBEAAyQA+BAEAxv05AEoDrgEeAmADyP9zA+gBUPcU9jz/GQJ9/7b/Xftz/wUIrQadAbwAPgCI+ob9bwGN/rz8RP68/1YCTgdI/5v5Rv12/CEB1AehA/f8zP4I/5X/QQflBnn/tfvE/GL8E/zg/Wr76wLZCdUCqgDWAR7/tPmU/GwC9wGf/uj6Kv0DBYQNuATD+Vv5yfVd9X/90gngCCQJBgkD/I/7/v/E+gP4NQDK/2z5JwKjB9sF+QYTAe71JvXK++78SAT5CxAFFgFxAuUDvgNF/5v2EvIl/IECegK4BfEELv+I/kUBaAJYBZcDmPxA95f5N/6E/+ACKQOR/1L+/P7CAOYF9gY0ATL75Pdi+Y796QJcBq0CUAC1/j79dQVuBbn+sPxO+mj59PrzAoMGmQePB3EALP66Af4AKfk9+RP5OfpGBEsE2gRIBvsFGAQ1/uL6zvWl+3L+EvyLAi0ELgSQAfgBZgCfAKAA/PdM/G8Bh/7K/FYGcwn+AigCZ/yZ+6T87vyP+XQBnAyQAZ79rv+NAMf/IABxAWv9egFLAQT8qf+0Afj7mfkT/qwAlQU1CnUD2P2AAWUA0PuJ/af7jfl0/zEEbQKMABMFIwDr/VQCzv7J/7r9evvK+xT/GAVUBQkFJ/7q9hj8+QEvBMIJZAVn/Cv4RfY1/XsGHwsrBu3+Gvqa+MH79AFTBWYB4/3g+vb8WAMwCawIHABL+Oz5s/3p/Ir9R/y5AJcFQgd3B6QENwEY+SD4lf/BBhYFfPlE8Yj1sv5BB7oJWQWoBRQCqPvy+/gEeAUD/I/5XfZp+WwDowU0AzIFbQQa/hj+hv97/+cFWAQ7/DgARQFA/l8BcgBI9672TP4Y/E//VgmiCAYC5AElAv/99/4P/J/2hvmRAdwHGwUTA5sB9/u6/Q0BmP9HANAC8Psl+9MFNgaHBIb/Efod+639KQDh/zQBZP4N+zsCjQhTBI8AJ/uH92j/ygYsCJMFkwCp9rn32QA0AB8A0f9P/bwB/gKB/fIBkwcpBa39Pfle9vL2YQFrAhcDZgpNCI77M/lAAXABBwGPAB3/yf95AM397Pu/AooLgQTJ+6j+TPoV+T8AYQIqASMD1QBG+3D7OAC1A70DzQHc+I77QQCe/PACmAlGBqv+zf2v+CH60wWxA2r/ZgAn/EX7oAQMBpEBdQQSAtf6Vv1lAE/95PxZ/Lj4q//2CEUEWwDkAJD/rv3EAAkBjgHzBB4Amf0L//0Dcf8t+4b8JPhm/H4D9Qn7B4gDZwFD+0350P1aAj0CgAGA+of4uP9jA5z/Ovrf+2b/hgERA98GIQ0rDdb/J/jP9wT2W/cP+7n9cQQiDmYF8/52BIEFTQE1/2X/u/gV+wH8NvkJANMHNQYj/Qf9HP6W/kICdv9L/N0AugImAUwGqQgcAqb8JPe68i35WwGFAez/QAfTBmIBZwaUBkIC5f2a+mXz0/W/ADUD7wV4COMDKfnI/uYBJ/ovAYkGcARiARwBoP3e/c//Qfh2+pP+Nv2J/+ECIQNJBb0HNv5O+qv92Pwq/ZgCmQfGAigEFwDL9Qb7KAIQA2L+0P8v/kv/agh/BiQEDgK3/sL6Q/t5+X73qwDcAon/dv8pBd0Dd/9tApwBoQKQAmT61PMT/gUHu//H/9MDBf9Q/uACRv9M/o8FvgJ2/J8BGQIy+Rj4gvvC/6UKGg4EAZD1O/gIAFsE+gY4A9H77Pog+Ab6xgYSCQkCDf70+u/+rQceCksFLfwI9oz0J/hBAIkEuAVRBgQDv/ze+kEC8gQ1+1b4lgFhCPUGRgQU/u73A/o2+mX6MP6IBEUGmQHmBOgIIgcuApP5L/Gj8sf/CwqzCzwJCQTt9rXviPV/+1ADQgeMBFQCQAe2CnwDgP6y+Vn1kfmC/XX+GAQsB0AATfz8/uf/x/5CA/8ETwFSB/UGZvqG+Ib+S/r69Dv9rP5k/JkGlguPBq8DPwDw+ED+wwUtAIX+oAEpAez9cv4sAPX/yP5x/ML+eQCI/GP4dv6gB9YLNg3QAjH4T/Y493n67f4QAtgB6v5C/QsCyQfzC6cLHAB09jz3PPgk+t4EdgxMBVn+Ivwg9ET3aAEV/1YD9wllA9T/HgRMAkf9w//J/Wn42/vY+z37wgdyDPgCmADwAIH7v/qoAHD/QQGIBkUAgvwG/qP/c/sV/fEG0QJs/VX+GgCh/9QCWQTT+lj7VwFG/pr/kQj0BI/9Rf0p9+73CwN0B6ECSwMrBQv/jv9p/2T5Xv2k/k72Yf2KC7IIEQHQA04DAf7K/hD6sPNx+d8BiQRtCN4KLgPe/D7+/P0m+5j77P2e/voByAkIDUAEMPmL9KL0pvt2/+ACCAjyAbr8lP2WAWAFTAYOAFT2WvhO+gP9MwdqDLkEjgH1ARb4K/dx/UgC5gTMCZAHPv9WAL36IfWW+2gEUwPjA1wDPvo/+pb8mADqBvAHrf6590X7Ffyn/2YF3AJK+DH5wgIzBSIKjQv5Ajb8aPfm8nT15gJ5DdMGzgH2AZ/9NPzUANgDlfy5+dP6XfztAhIH4gmHCLMBNPsZ+lT67vr//BL9ef3FAZICGv4yBj0LKAGI/Pz/2f6o+gv9pPvu/OkEEgZNA/gA3P4r+jH7ef9H/+0ANAQqB8EHoAV6AqcC/P1i8mTzcfiw+KH8egYtEOcLBgV1ANn4ZvrW/TD8nf7NBegBh/Zq+9QEZQSHA4QCF/ts+Mv/mQIPBEgH0wGW+AL70gDGAYAG4AXh/nv8eftr+YX8aQCg/78D0AkbBhgBgwNz/gr3tvpW+xv3If7gCCkIHQf0B9n/zvWm90f7sfxRBG4EZfz7/VEJBgZS/pICPP8i9l711/1cA1gH2wYmAKMBTgNW/e74IQBhA1P+B/7E/Fj92QScBn0DLgfiAQD2Jvd1/Ev9VQP1CvACO/rQ+3T8uPtYArcG9P9ZA+QFVPzN/BgDgwD0+df5NfnH/FAJqwvsBvkD1f3+9576hP3Y+vb+ZQJaAeAErAiIBB/9SvyG9TbzIAHkBrMB4QNeB0P9Dv4fCNoDjgGYAmX7y/Q7/JD/ovtVAuIEUf/1ABcHHAHA/WUBy/+oASgASfml9+/9Qf+tAKwGJAO3/CL9hP9e/wwJEgnP/DH9/P48//sBDQbkAMf3Lfkt+wL4Pf0iBwcHMQiXCiIGtf279w/0vfZN/4gAUv+8Br4LDASqAIj+4/oI+Nz1Iv2lCbcO4gKM/wYFMgNj/Tb4FvNZ8aj7ev1PA8EQmxA7BvEAmP/s9bX3BfuE++v9W/4cAkYErQl6CtkHHQFQ9ejuQvTyAqQJqQtVCSkA5frA/Nz9o/u7/C374fkqBfgLIQSAAJMCTvwn+BsBdgHw+9MAtADh+2IANgMG+yX8OARDAwsDHwX+/wT7sf8c/y77jf4ZATcCpgXEBfb+q/9a/S72BABWBtwCTwSlAp/8jf3eAUf+mvzpAf8CcfyX/wIEE/oI+cr9Yf1YAEIHHgdmAD4G5AjL/VT1JPbq9hz3XAWPC8UIPQea/bn4W/sHAZABggGn/4X7pAK8Ax0AZAKABV3/ePci/Wv/VP6BARAAVvxCALgCzgDaBlEKgAI8/Mj/W/7S98z1XPpI/fD8xgZVC1wJSQlOACj3J/nn+i/26vgUA/MEUgTICgEJNgLa/5D4mfNO++j/lvt3AV0I3wTNB+YLLAHK+cv4KfLj9KMCcQcLBVMKAQX++CP8/f6R+Kv5KQboAlv81QJGBeEG4QeR/nHzXfXJ/Hj+AAMMCyYIfQOA/6f4WPlk/sABu/0NAFEFhAHp/v7/RwFEAFIClP199bf4dQAuBIsHCAuOAo/97AKQ/EjylvtdBK79Z//QAgsAZQWQC7sBOvpMATT8vfT9+zUDqwXhB3YGvP6i/J//Zfqj90b9z/+LArIFuASDAXL/oP84/gP90fz+/1gAPv8EAqf/VwHvAJb8df7oAtoDy/4IAsQE0wG+AgMAyfcT9yb+hf6N/3gFkwcoAzgAjP2w+cn/YwGw+jz6mQQuCB7/Q/9GA4MEHALl+qn4Wvlh/tkDKwKiBAMJwgQZAKv+BPxY+5f3ePSo+34ENwoSCNoCGgAo/9QCNAQ3/iT8Yf4V96r4gAIdBeEGdAgwA3D3LPnk/Tf8wwLvCUoDzfwoASX/WPwtAOj/efdb9nz96gQrCWYGSAN4/qv/+f4o/Bf/BgJpAlQBzgjPBZX5J/Wx9hr63P4fBgoG2AZfCFMBiP//AnT7Mvdq/p381PrLAmMCAvwn/nX/Nf0QAoUFUf+bAsUIfwDk/aYDwwI+/SL7uvmD+4MDbQdqAVj7TfzV+xf/cwZzCh4I9wE3/o34Ovmu/en5hvorAM/+pvydBFwH9fyZ/80B/fxbC4oSMAfS/bv3iOwu7aYAFwjYB6UIpQBe+ZADxw3vAub5AffN8RH2aAR+C08JegmDAN3yKPRC+EH7GAJsBwcGAgXQB5wCTf1g/8gB4/00+0b8TP6aBlMIyQAb/QEAFPyz9sL7wQLQBU0Hggg+AHj6Ff5e+qj1if71AhH9sv7rA2QE5wWmCin/u/W9+Rn7RP3zAEMGGAZQCPMC9vfS9wv8iv9a/2UBnAIbBRcCs//eAu4Aev3o+fn7YAA8BtwDmP5UAP3+Ef/AAg8Ca/1GAIkClv8rAPkBQPuM+d396PvrAbcE1v4s/YACQwOwAHgF7ASo/s34lfbN9pr+BQhdCWAINgHt/Pf7b/pm/r8CuAOxAUP/jP6eAygJtwLZ+hX7zfjL9QP8kANsBa0JiQm9/0j6PvtC+5b9rgQ5BJYADwO//n36KP9Q/Xv5rf17Aa0B2wSkBygDsACyAg4B7vo8+sT4t/eEA7cHJAQIA/UBl/yf+JH+ZgESAvsDQAZ4Avb/4AVpAm/5g/aT9u32bABHB9sDhgclDFoBwPUX+5f7zPthA0oBpf6+A04IzQHL/kH/GvUa9Mn9dAIyCNYOJgYW/GEBlwQw/Rf4F/nb9+36kQInB+QHZAQIAFT5+vn7AtwAAf3JBJsHrwCYAbkD5vgZ84r4F/u3/wwMGQ5oAhkE8Aiq/L/10/gM9034QQJ9AaD/kQoDCgz/Wf0n/aH4z/t7AaMDMASqBTwG0gAB/O/68Pqr9nD5GgI1BRcH3An4Bcz+RgYuBKL1cfbK+9/0OfpUCtQD3gB2B6P/rvbWAjMHofu3ABwC6vw3AQ0I8wLF/Kr9d/bS9Iv+ZAJxAVQHAwwaBsf6UPxQ/2j9HQJ2AuX+Pvvt/YT8S/ygA7kBX/rQ/oAKmQfCBmQFsP4H+kn5svn99rz/CwPCAIUFgAY9/3f9Jv5N+qL9kwNPBPsB2gV4AQj4ZPov/zX/CQACAnT7AvutAzULKQnhBAgAs/cb+Zn9q/9Y/hoArwGy/43/oQTwBI39MAE4BM3+3frh+/T3UPsTCo4KVwRpA6P+n/Ig+JEBuPu3/RIGogOhAaIMcgal+W/7xvVs8TP8OQfvA/wEigslA0D+Fv8E+b/2d/7ZBEoDoQQ+BIgD2QAB/eQAxv2b+vP+sQFK/eIA9QbrAbICKP8n9iv32QWgBfP9swiqA4Lz5/SD/54AKgUSCHL7j/oiA+IBpv7TBgUF6vc1+s0B4QEuAuUDQAFq/Bz6Tv+rAjkDLwNW/rH+JgS3BUP9b/gc/nj/vv5dBbQFdPlZ+hUB8fw6AL4Gcv8I+04Bkv9s/xYK7Ahy+pr45/6o+KP4eAQNBukG7wovAoP4wvjY+rb7CQAwB/0Dffxj/VYAjQKCAhgAVfy/+U79ewBXAHgD5QZtBDD/dACAAqf6WfrUADYBeQXkBw8BR/to/tH+qvjG/uwDnfvT/IQEYQL3AS0Fsv4K+WD8Kv3H+zEAoAPu/4EArgJTAqMDHgFy/nf+8/0q/pb/pgBPBf4JYgNl+ov6Jvwg+Mb+nAfNAQsBgwaKADn73gRhA0P24vgt/+f71gAUCrsEpwDPBesA1/Lt+DcCXv6QAZ4D5gE7/53/jf2C/HYDMQLEAFgDAQQWADL6Kvv+AGL+svobAYUCBQC/AgYHDQZMB+kEE/ce9Pz8sv0j/NgEngMU/dADfgQM+5z8wgJ7/e37gQACAeYBygROAvX82v06AOT9vPvW/ioDcQPi/Yn+eANCAlIFxwW4+8H4awGsAJH84QdbCmz5GfXR+rH5yAEDDJMC4/gpAXL/4PZxBU0Nbf+D/GkBJvmz9/AE7wjtBLwEGP3Z8XX3OgENAGMD9gp/BXP+WwBuAXn/T/9pASj8EPQO9lT8CQLMCTANQgRs+Qj8fv44+8UDEAroABj6rwEyA17+NANd/bj05v7DBTj8s/ysBoQCCQAbCZkGUvos+kv7SvumAOMCqAD9/eL+ZPwh/9wFdgSWAOH+8gITBM37HvgAATED4P3nAIcDWvzT+1IA2/shAjQKgAE6/PgDXgHg95QBjQQ1+Tz7qAMA/gD/GQtIBB/8CP09/Cb8VgHgB7wEWwCb/TD6E/uf/Zv+aAHkAnYCHgON/0D/QwT+ACP45/olAdT+7QJSCbgCY/1+/rb5ZfigATcFkv55AlIImfxz+4kFtgTgA4IDZfg28En48gALA04IJwspAo/6Fv47AXT+DP5NAFj8/voPAC4E3wNgAoMF4QDo+Jv6W/lw+f8DxwXT/gEFJBD4CD/9K/xb9Ovvd/rZAucDPwYRCicEFgAwBJf+M/X49cv4aPyZCCsP0Ai7AGf9ePoV9ZT3Hv4QAigG9QcVCKYDw/+v/j76UvUZ97b9FwLgCZEOTwhZ/2P7e/X+7l/8zQb7Av0E8Qc1Ag/9dAIL/Sv4DAN8AQD6LAGxB7cCFgELA4D8dfcF/qb/6P7LBNUB4v2pAecBKQHeAm//GPyF/MT+hQAEAP7+3fr+/UcBi/2JAbAIuAZABKED1P6j/aL7IPj59mP7mwCXBI8JdwevBRwDlAEG/LD0bfktAo0Ef/+W/oEAegEKAL4ClQG0+yT9MPpg+V4ALwnMBW3/ugCT/R77OQDiBmoEhwLLAIX4nfOb/DEEjALgBcUDlv1P/wEH1wJM/2gB/vh29zIAZgTIAVAHYAOW97j4Cvz+/wIDzgZ5Ayn/R/+O/m8CFwTnAJf+wPzK9kX32P/dAr0FGAc9/mH88wFt/+L7fgT2CHf8wflO/UH97wBIB6MEJ/+JAvH8x/eC/VkDtgAJBSsKZf/R+tn8cf6r/Hr8Bv2c/+YFkQROAAkCUQKZ+qj7of3mAJwGsQHS+tr8xgD4+24CwQqhA/n5kfvr/b7+UglSBqP8xfno9X32swN+DFUFFQFAAeL+/P0mAxcCkP6q+nb1Hfr3BPMJ2AToAyoBtfx//5UB8fwf+T79ePvt/aAHWQVXAmAFfP9u9yL73ABeALUEqQbS+VP3xALkAt8ASwj1AQf6N/8h/GP6EQLoBMD+y/6oAWD/3gBrBEUB0P4tA5P7lPUr+nT/PAbaB/sDCQDGA9MBdPsy/j0BFv6a/nwBIv7w/v0Az//d/SYCAQK1+4sAjv8I+w4BUQlaCGj/G/nd9Qr4uv8IAekBFwmrBc/+3v4aACgCEgK//nD73AD4A3L7SvwGA7/9Qf6WBfgBqv1JAZIAZ/zaAXQDDPy2/sgF6QAB/h4B6PxR+iz9i/3x/c4CtQQFBOUFXASXAVsAIvtN9hv87P7W+7z+qACUAOIGSgqw/2T9ZASL/+j4v/yUAVsAawQoBCz6qvucAi0A0v9uBqUBS/fD+kgB5gQiCGYFZv5E+n38j/oC/DYCTf4v/qQC8f9K/okDagMYApsE/v1J9k/6fAQEAuv+IQHA/CgC6QszCUf/T/zJ+G318P56ApkAKgb0BhkAcgKoBJr6dPYt+6/9RP8QBFQBr/wGBFoHwgFx/8v7DfjO/bIAXf14/1YEEgINANEF3QK7/F0BMP7q9isAUwipAjEATQAD+Tn66QTUAef9qwOZAez9TAOABBH/fP5z/5X7v/vfAXAC8AIrAtD65vje/9YEPAEnA38Bvvk8/scCbgKmAtEA5/k1+SoDDgSi/5QDIgFB+hUDyQV6+Sr8gQTiAFYDIQbH/E345/7Y/4L8GgSyBQ4C6gMz/4r1BPgkAY3+HALaBjv/EP1bA1MC0P4QBOQBdvsn+xD/jP7IACUGyP38+Rn+gf9Z/6MEkQpDCI8CGfu895f6kP7g/YwCjQT2+4f8uwHQAP8DSwmO/2r5p/9i/Sr8DgnuCA74OvZr/FL8iADLCvEG5f7kAHH6VPQc/WECTP8ABvgHMQFAA+4ErP2l+dz9Vvpm+QMErwNp/iAGOwKH+SsDtwYN/qb9SgTp++f6jAdFAtr96QT4+4jvu/11BIP8vAKlCWwCAQCmBTT9sf3hBTz9ofVe/hUEwPxvADIDifph+2kBrv77AggMaAa+/gkAt/78+Cb/RAEh+BT9xwNw/voAYgmYA/r79P4/AN79/AOtBHD8xP4h/ub4eQA0ByH/V/sMAFX+C/1NBikHnv0fAFj/y/la/ggDawDXABgH/wCI+db+MgDs+g0AowRz///+2wJrAgf+wwEQAU/7IP/x/K37agNBBgQCcP9VAgv+cfjM/cn+/P7bBWoENQDpA4UDPPoM/IUEmAF+/tf/EP2s+4UD3QSy/nz/m/6Y+7z+sAHe/sb+YAL5AHMB5gULA0T8lvvX+Wj70QOEA6j+7ADTA/3+jABEBkMAsfxqAUn9DfoDB0gGH/qv/MP+0/hE/VcH2QHKAWUGc/6M+oIDfgV0+ub8Xf4Y9wP64wP0BwwJAQ4ZAqL0nPfc+p75DwEICc8B5AAPBXn9XfixAa7/XvgcAzoFWv81ArsFfwEn/zECt/v+9Lj9fgNfAMQFcgPW+e/+FQagA4cADAB5+sT4NgIgBbL/TQGX+3bxIvxSC8EI/gMaCT0C8fbW+pj+FP5wAdj+qvbQ/40K2wN2/8EFGQT4+uf7mPoE+osDnwIE/HUDWgfT+/b4ugG0BO//4QEbAW/7vwFjAxT8MvpKArEDl/8gBH8BrPz7/93/VPrG/r8GFQQFAGwA6v+I/Az9Y/pE+ucAkwSdBBAEQQaYAB/+NQAK+3b8YgD6/Bf8bAHkAbn+rQARA03/yP/CAL/+PwU4CgIEzPu6/or7sfMT+vb/DwI7BfQDwf2cARQJgwOJ+2L+G/4B98IBGwef/xEAhQAK/uP6JP7J/bv6PgK+BDAC2wNhA+r+IgGfCOIGfgC3957uWfKH/h8G7Ah6CgQDR/tH/jEEzQKv/7UBzPmJ9+7+lQCfBPsJRQaE94j0UfsS+27/OQoSCIAC4wVOAUr7q/zw/8X4K/V7/j0AWgZQEBANAv819bLykPHN+X8Hbgs8CRsIxwBl/K//d//Z9lj4jgSRATICxgg1A7v9vPsS+LL4JgEyBd0AogbgC+/+y/mz/X78hfuW/K/8ivpGAIEFrAN3BgIGm/r59poAcgOIADIGNgbk+Az5ygF6AkMCwwDI+4f6EwZtCOz9nAN2BbX4DPiG/aj9mP7vBdQEM/uq/1IA/fpVAn0Gz/4b/dv/j/ml+koHkwjs/0IAbfwt9UD9mgZiCN8Kegog+Q3yL/21/Mz//gaJAYH8Of9l//v7Uf9aBL/+fP50B4IGIAMIAf35UvVx/KEAKPy3AXAHAQGU/lgBOv7x/VgCNQMu/hkAvAFE+tQB4gfq/xn75fse+iL4nwOzCv4BugI+B9z9of5tA4T8RfuwA1gCqPZk/AYAd/spA+0FwP9yAFsFlf9U+0kBgP60+vgESQOr/S0DGv0T+L8A6QoBBML8BgE9+6P5agKXBIEAiQWjBr37pfmf+7/51/83CPv+0/Ye/QoE7QUrCh4KRPp89JH0DfPXAKIN3wwHBbIAfPn78zz+QgQMBHMJpwQq+CP6mQS+BU4CZADu9oPwQ/usBa8IFw9xD8j/Xfad9/HyJfjNBuYFDP5e/hH9wvhrAP8IiwScAU0AFfdr++QJCQW0/ar9w/sn/jAGmgfL+5D88AJt+6T9XQeKAlj69v5nAd4CpQtoBRD2xvX5+sv6zgBeC+UGi/xA/Fb5JPs/BRAHHAQpAn//I/jw+BYBGQSFBkIF2fyE95/9Nv8T/7QCFgHD++n7rAETAKAE2gp5BpP9Rfq/+u70u/1eCPIFyQPxBCcAJfhq/kIDJfz4+kMCYwNvBw4Lav809Yz3Ffz2+9wBfwLr/kgBoACMAEoBggL6//L+HQFx/Hz8ygR6BCAAUgNK/w34xPqPAOIBWgQxCcn/9/Z2/gQBQwGEBrAED/nx98EEAwJk/icC1/4H++75rf75AsoJnwn7/AH4IPyV/Rz+TAbMB/kCUf82+Yv27v0BBboCOwGa+0n4mf9tCywNXQViAnj4ku+F9BD/UwMbCAcJ8fwm/NMEQwdDAr8AofvT8NL1ngCIBj8JMQoiBl3/bf4V/Ir3c/xPAGf6UfwBBFUHbwWHBBUD+vzc/rD7mfON+ncEUgPJALQF3QQf/EL+bAHr+wUARgMC/rP+dQVJBN37I/wW+nf41gJXDNoK+gMo/xf40ffAAEECG/2m/g3/g/01As4EAQXYBFQDPPo98yr9wQKuA/IFrf4e+7H8uf5CAcABjgcOBJv5wPrp/igCDwe1BID5yPci/oH/zP4MBXwIbP/j+3n8EP7RA+UEKv61+G7+jgDkAiYIcwaxBEv/Evny8lP3pAV+BRoFkgZU/xH6Ov66A0IAxgAoAHLz8vWNB1wHhgTTB4//XPZx9pb+Ev6nABkJZAJmADYGRQV5/5v/P/7T82X3SwY/BycDOQR6/gr7rP7u+8f26wCpDBoGCQHHAJL6CftUAvsAlfso/Cn8RvirA8UPqQfIBJ7/cfYE+SQBNgOK+3z9ewBS/LEB9AefBuADyP+N+fvzZfnXA70F0gsaCx/9KvVW9L/5+P8sBMwE8gD4BvYI5gB0/zD92vnF9/D6jACXA6wGBP8c+9ECGgTo/nr8uPxv/kUEHQakAJ3+NgFX/Sf6hPw9/jUBIwU6BosCSALWAiX64vSM/SUDqAT0Bd0Ax/2RAFIDnQB/BHwCCPTT8rn45f4mBUQN/Qsu/i3+iv4P+lv/FAA0+2v7XQFWAdj9XQYrCkgBGf1J+zb29/ioARMERwKvCJkKrv+f/vz/HP2N/aL+f/pz9nH+GAKwAkQLWQu3ALb8e/tD+BL9JQXKAR35Vfyz/nAEYwm8AIz4NvrNAij+PP2qB8oFHf1a/w8BLvuh/rQD5ADY/BUEqwFf+fL/lQJmAzgDEwM8+yD2ZgJ6BTQAKv0Q/I7+8wLaCF8Iuv5z/D74AfSE/QYCrwQnBpADhgGk//sCvgDl+q37mfmj+SwAMgNMBq4JoAkYAW32SvnI+Ov3qAPIBMYB5wOkBkEG4/wc/tL8Gfdk//kD1gICBBsG1vxx9qT8+P9RAc0DCgSj+6n9xgToAI3/pAGOAGX5efrS/cL+LwfiCLgC6v5J/sL7N/pCANYCsv7IA4wGR/vZ+fz+bf82Ah0EiAFg+ur+4AUq/nf+MwT+/w/9SQG+AeL8R/9KAej6wP4zBfT/sf/oB/YI9fwX/Pb+1fW++L8CKwLP/X0E7wYkAIoDjgI2+Mz5TwC0/AD99QHYAjkDfggfBsb22vi7AbT+T/15/3X/nf7CAuEEvAFdA7MDWPg6+XoERgKWAEYDvwAP/ZABUwMu+1H8xQKj/aX7FQNpAsP+6wPIBZH/1P71/aH2NfjKA9IEY/6nAZ8DEf/c/UADNwBd+2oBSv1g+dwDrwolBiwCswHH+Sz1RP1nAOoBUQgdAbr6H//3BUQGjf3E/b/5vvRR/kcC3AGuCUsNEQQY+AP5NPrQ9oID6QUe/TsASQNkAjQDxwXf/Sj4yf45Aoj/YAF7Agn7d/zcBAMFmfps9mH+TgMoB+sH+AHW/df/Lf/r+iz9bAFI+435/QIFBf4DTAVJAx789/n+/n39aP1xBYICavpwALAEAQM6AvwBZfxz9sv9TgO4BCwIUwOc+CX5kf2x+0ABxwl2BxL/M//0/G72NPyBBNwD1f4j/68BZQJoBJ4AQfpA/Rv/o/vC/pkHUQm9Ab4B6wA89CPz3f2WAgUFYQa0Ap/7ufwHBD0BfwJIBrj9x/ndACwCeP0N/uP///qB+WoF3AVEAuwJ/gSr+kL57vuW+nT9jQUPAs7+HQbYAYX3b/0DAEL7Pv6/Az4D1AIYC58G5vbj+O7+rvpn/jIGiQLs/68C0f1A+aT/lgO+/pUAfAa/A3gCPwVfAbX3tvfM/YT8cP3KAIH/xf2YAU4E+wQ0CWYIx/1I9VP6oPuX+jIBigG8/wwDmgdwBJ/+CgHg/OD0avwcBb4DogPjBK4B2v+4AxIDYvhg9A/6cvtgAn0Grf/E/1AHfQtvAST94v9Q97v1Hf4eANP/twKUAe8BqwdYCawAcflY+pn30vooBRwG7gEqAi8DUwDU+8T+m/9J/GAC4gLM/oT/m//N/db6mP4vAtoApwYyCYQCkv9D/jP8zvX09rEBSgQvB48EIPoO+lQCRgRBAZIBIwHW+/f8QwjVB44Bnfsg8LLu+/kbB8MOtg8EClIAxPcP+7j78Pf2/xYAcvtl/f8GRQqbBOgISAGz8/XzW/fg/X8HZQliA5EBUgJt/wf80gGJAjH74/rc+/7/ewBXA74Fxf1E/04CSf/k/9oBOwEyAKv9a/qn+hv+XwSTA04FzAd4/g76dv1YABz+Bvx2/48Afv9PA2IFdgOsBXn/B/cz+sv+x/7X+yECHQZHAPUCxQV+AgACVgDW9R/wCfy+A1gC9QhhCHf8p/35A6EC6ABJAsT8nPMx/JAD1v9SA+sE8Pv9+soFywXj/2gB/AMJ/cn7FwTB/fv3Fv2pANIDAwa6/2r3C/vPBEMEnAEaCqoEefbD9rn8if9SAMgC+vsJ+wkGewYCBHIGsgST+Lfz+/0AAdIBnQdpBfr+BP+P/mP3d/s5BpUEQf3J/MX/tfyLAq0HSAES/9//rv7i+CP8rwE4ACQEvQSp/S7+ywXLAGv5oP4HBT7/L/1PBjQDCAAT/aryX/eeBP4J8gVwAT8EJ/9y+RUCYgCx+df9Gv4Y/Fz/YgekB0oCxwPo/EzzGvtDBcgCMAWJCbz9tvVC+sj8yfzOBGkH+fyt/YUD0gG/AckHZwLr9Lj7LwBa/a0EsAcVBOn+Jvxx93H29QRACc//8AEZBBL+c/xv/rb8WPzEAtUARPo4BfwKT/9t+zr7PPlR+1sClQd5BToKZwW99W/4Xv42++L7AQP2BLIAkQSCB0gCGQAO+230bfgmAsYDRwC+AzoFOQLLA5YCs/m99xoALQMm/uz+awEg+77/TAgrBtAGbgEu9OzvE/rHA5YBEgI3BgoD8QQgCi4EJv0E/Ib2d+2q9cYEzgelDIcNqABP+qP+ff2i+TP/ZgYc/q36gAU4AgT/9gTq/rv41/3PAP7+IQE0Bvb+/vaR/8ED9wJtBbIDMv+Y/4MC//p59ej4LfmR/4sKhArmB5MGrgAQ95b3+QET+/70q/1eAxAKuwxMBiT8iPf1+gb6+/+WCxcESPdU+X3/WgEjBOEISQSe+aH7gQKwBKwHbAG59Vryvvfu+40AugtFDdwFEwDz+tH20P+XC1UHFv2l9FD0P/X3/zkNFggHBqsECPtN+PsCnQY1/hv+l/7i9R74ZQbuBRQDVwjdAv723feQAGD/ywKaB3r+GPv8AGUD3f4k/JgAuvy2+5MGAAZgAXEGhQPa9/H1Nf0vAkMBEARxAuT5+f20/7n71wJTCcwEGwBqAqgC4Pq5+eH9bPhg/MEBovzlAEYMRQ2jARv+V/wK9e/20gDcBTcH9Adv/HP1OPz/ASgBHv+0Ap4AHP6qAV8DTgMUAmkCzP2s9QL8aQKrAXEHQwQk+xH7LP4/ANL+gwIiBvD8X/k4/0MC4whtBjL6wfel+Cz/RgOxAY0Ghv7I+FYD9waoBZAAWfxB+3r35f0UAxECCwdFAxn/kADG//T+BPvx/dYAUAHEBhUE//tc/BcB5f6G/Of80/yZ/hgEIwmHBL8BrQEn+iH3xvo9//ED5QTRA0z8OvdDAloDYP3HAc4BEv54+/4AhwlBB3cGM/4z8oD3I/th/n8F/wRcA64AcQM9BYn8K/8uBqICPv9895rzLPxsA5IG7wWqA1H/IPZG96cF0AryBz0D7fgR9RL29/v1BAoG+Qa8BPD+mv4z/uv9Lf/h/wP8PfeS/nkJrAvICs0HSvuP7qjuffkTAusJEhBdB44BYgCb+uL1p/m4AsH+OPzqAWEBCwC1BugEqP1TABf88/ZK+R0E3Q0gCFoB2/qj8W/5SwTEALQFLwlsBJ78ZfkiAM//cwDTAYX9aftz/5X/mQIyCvcGKf+Z9dv1f/kc/esHsgl9A/sBLQHk/db+g/1u+w/7k/2j/jr9YQbzCxYH1AIr/2P6xPZ0+CkAVQE1/1IBMAC5Ar0GFweDAgr8QP1a/Yz4cv3TAiUBuAMwATz+XPsT/S0GcwLf/7kBzfoe+ooCKQRoBiEJMQPf+Sjzn/nI/iz9oAIo/7X8Ggn5CpsHMgRa/z/9M/U69QT6gfqNAyUKEgaUBnMD4vxV+lv5Qf/2/xECcwMR/ob+CAV3CN3/6vnJ96b2/PtLBYAGfwNnB6IC7fte/EQBqgF/+jD/KQCH+fgBQQO7AcsJsQjGArv2kfWG92/0FgX1DcUDzv/dAq/+v/yRANYCTgAX/mcA6fiZ+rMEmQMYAioEzv1B9+H9TQTOBLACkwX2AZH3ofnI/cEBdAbtAVb92f33/YX+2/70BHYEtvs2/UsCIASVA1wE+AFr+Ev28Pso+2QCIwgzAukAPv30AF8AW/69BVcBb/2x/Rf7M/uOAvQI4gaO/G35k/8b/64C3QO3/o/9aftO+yUC9wffCZ0BVPj7+oz6Zf37AdAEfgjdA638r/j5+IkA3QWgANkATP2l+SEAAQYfClgEIwB5+gr1MftWAsACqv8HA9UBp/uQ/mEFmQOlASAE1P4f+cL4hvtlAIwGhgeuAG/+zAA+/6X8EP88/9L7Av1A/F0BkgvOCLAE3P6s+BH7Z/lV/DIDaAGtASsALP89Al//HwN+AZj5Df8qAwwFWgYZAoH6b/dO/GQCYQBB/hIE9f/kACEGUQJUAPD9DP5W+0z6/gE/ACr4FP5GBcoG5QqFBk/94/f9+Wn9tfrM/aEChAGSAaMFOwfXASIBSP6s9PD5IgAaAKYEdAa5Atr8f/7r/iH8AQFGBNL8zfpyBKICsAHtBO0AQ/4t+9n+IP+j/N4C+wDS/DoCPwIj/AoAKwR/AuD9e/z2AY78Fv3hAzgBGwaQBmb9bPiv+Wr8QPwFARMIaARt/lj/xv+lARoGfwT8/DD5jf13AkEB5ABVAKL9mP1N+yz9KgTaCcwHOvub9aX67v48AyEFDwMXAgn6WvhH/0MDwQkGAef4K/yZ/JADkgTXAtYGIgOrAS0A+PcD+Ej8JQHQA5D/3v4OAOz/ZwK0A8IELAfc/a3zz/fu+1IANQTkA5wEMAAe/en+Pv8qBk8G0/yx/PP7DPot+64BgQmjBNf/sf6k/nsEdAKl/EL9nf1sAFz+if1rBNkBpQAeAOf9DgG4/pj9AQBoAVsD9AJ//AX7Af6o/O0BlQNzAokC0QGOBUH9mvf4+3776gIMCZ7/IP3kAK4B1gRy/r37N/td+RQE6wTaA4kFBv4D/YoANgFxAcj9yPoa/Yn95ACEBXsFPAWH/vj7/PxS+C/9qwIOBRwD5fsjAGMDAQQBBNH93vlN+7P6ef0nBAMEgwQ0/vIAGwRM/mgEqP3k+9gBtgA1ABj9vf6cAfz/P/5hAob8zvzqAZn/uQkjCCj+cPZf9Pn/EAabBXsDQvsp9/v/IgIlBGIGyv2/+4H6kf9cB/kD7QPm/V/3G/5XAOEB1QSL/7f9uPzV/b8FggEm/voDl/40/zcE5wCM/qb5QPw9AbIDXwlWAM31CvkL/ncExQWdAikE9f9E/LD+Hvsj+9v/hQAOA9wCNv74AfYD1QPEBTP6cvZ8+ZH6/wdfC8MIVANJ9MD3nP1Q+qMCfwQuA/4FAQGy/g3+bQBKA8D8T/kC+tz5zQLmCrUIiwbc/jP3SPnx/IYByQVjAZX8Qvyv/jUGLwUcAh0ArPyg/uL5qvbA/r4EVwmBC0MDGv7t9hj2cQAsAPwC7wJa+fv5KQTQCAILXgW2+cj3m/Ug/Kr+YQICDq8Fov0+/Lv63P/6AfX+FwPVAkP+Gv5m/G8CJwUc/lL9gf84AI4BmPzxAHoE8fyuAcX9fvwxA/b+fADQAJX9Tfw++q0BQAoBBlYE4wBW+VH5ufmo/owE3wO5Ay7/NfutA9cEvQCrAMT67/nf/Sz/8gOhBugEaAUv+oT1Df2x/vUERAAYAlkIoP2F/ID+7/yyAFcCOAHSAlj+LPrP+1D/aAaGAX79PQFE/q/+DAI7AkkDkf+P+qr+WwABAtcDv/9HAZ0AaPvy+6P/vQFCBKoF8QLQ/BX4DvwN/av/GwNSAgYHaAC2/lQBAPti/2f9evsVAAP9yQCmBjgHvgs2BBL3ovsi++X5jAGk/tX9HAMMA5cA7/0AAKYGlAO9ARwB1vOk9rz70f2xC1EKlwSa/E34/ABuADMAyANd/Pz39f4PAdsGKQfkAyYFkfmn+e35kflZBJAF7QNn/zv7cvuD/gkB8QU4BnQBowA89hv4UQJyBccK6AGJ+rH7rvjZ/Q8CVALUBu4A2PoIA4YEDQFZ/275R/tk+nz8hgacBoUJPwRq+un6G/dw+1sEyv8qAV0ErAGsB84HTQR3/IDx8/Ri+Ij+uQgwCMgGAwmtAVT8bvnr9eH8e/+9A6YHnv9H/Jr84/7/BL0DNwEu/Sf2J/9OBDcDhwWS/Fz7zvyb/oIIyQbGBEX/mfIT+qwCRwH9BDwDDgCU/mL7G//X/7YA2gdIBAMCQAKe98r1I/pB/FcElAbfBrQEl/u+/Nv/s/6AABYAa/2L++L9pAasCSkEg/5N92b66/tU+xgFMgh7CrcDc/l1+sf5dPz0ARIBhAPwBZv9GP0JAIgDoQei/9n7WPgv9qz+SgUYCRcJ4P6o/Iz9//bt/vYDTQTuA4/6ofkU/ckClwciBLIBsACt+RD4mf+4A8MEVQC2/Ob5M/r3A28IrQoMBbf6ivvq+vb7+/9DABsCtgA6+7z9iwOPBpcKAQLs+E73nPMlAB0K/QaHBkL90Poy/mH5jP5VABIAggaHATMBgQZD/jj9CwJX/Fn+FfxS+BoBZAG1B5QKnwHh/0D6bPbK++UAvADlAVcCsP7Y/Sj/EQcSCXIED/5U8nv1dv3TA2IJEAOIAsv/2vnZAPICBAHjAXL+fv7n/nf/3QBf+h0APAfE/hj/Pf5q+8wDfAQPA0wC6frS+l/8sABKCRMFuv+i/nb2iPiDASABIATnAGn93AKYACcCoAXtAEsBTf1T9ln/0f81/+kDA/5EAd0AaADcA87+Af93AHz/QwMQATf6RgHkAGP9EAJJAAsBg/wU+UABrwMIA48FE/+Y+tD79v0ZB2gHPgPO/jv3i/lQ/uP9sQOYBXr/e/8f/eAAsAMuA+IJ3ADf+Hz4YvTM/MUFAgZKBVkDLQHb/ZD8dQLeBOX9j/yF+qL21P7HAoYG4At2BsH/9PcE92j9g/7cAK8Cw/7d/5AAHwC+CKMHVgCc/UX3tPq+/cH99AS+BMsFYAIa+Nj7wgAxAA0CkgHhAE//jvpC/bj+3gGyCSwE9P28+kL5T/4YAuYDyAWd/oL5Af29+qIEewu5BhMEvPqD+Rv6WPzeAYsA8P7lABMCygHmBSICXAAU/ln6M/ut9h8EjAqHBWkHrv6F+LH1uPdI/fcCSAWjBWwFCgWqC9T9nPRd+Dj0ZvnS/FEHlxDhCdAFMAAB+S75gvVl9vcEhAj2BWQBJf1HBKUAxfkQ/n79iwHlA+D/IwQLAJL9fQB0/Mz9hPyP/YkFUQZpBnsEm/wM+E71V/oLAhADCQXxA0ADEAOv/iL/dQJ3AHv9kvh2+QgAgf9DBK8FgwPXBKv8J/ky/JX7pwA7B/EDBwDv+3/8AgMvAhgGUQK79ZL58f3pApwLtwbFAC/+HP2m/ar6M/58/4r8VwEgBfgGQAeIAWn7T/kx+q74/fbL/c8ENAY9CYELhgis/sDy0PPk+QkCzAYX/H79MAE+/08JmQy2B2H9/O+R8tn+HgP4B0AHWgK8AAv4w/zcAkUErgcf/ED5y/uR+HAB9gdyBkYD0Pgp+r3/5/wzB7oJLQFZ/Cz1W/gLAZwE1AiPBoj+Dfwg98v7igYRBIIEPgAZ+mD7CP6QBYAFvP7q+5n6Nv0vBUwFOAURB7j+j/q29db47wEcAt8IDgW1/ob/xvgZ/LoAhgGGB+wGEP5w9jP2g/o+A98FxwUaBRf9xwBy/7T9hwdhAIL6e/m19jYAiQYrC6wLmP0x+SD6D/Zu/IgEsQfqB7P/lvtw/Pr9hQRoACH+l/+j+43+Bf8wBFcFCQKjBJr+Dvor/sYC8gFhAOv9X/xh+hj6bgO+B1AJYAT6+TD6SvsM+zwA2gTQBkwD//mU/FAB0f8IBe8BY/0E/gf3e/rPAS0GCw/5CLD9c/n+9fT8lgRuAfMBLf0K91f7bf09Cd8OSAWP/v31yPQh/N8A5wgLCqD8SfoM++X/8wpDBv4BmPqW8zr5g/06A6kL5AdmAlUCOfnC+VX/wwDtAOP7AAGk/4n5/f6N/xcD4QrrBCcAn/4G+7T91fxcAGMG8f28+Tv/bwFOBa4EggJoAkX5Nvpa/on9EQKF/hUAdAUTBEIDy/xl+t0BeQCf/eQA5vsR/7gDbAKeA538z/x9/UH9UQQEBJ8EWQcC/YX3Hv2a+MX/6QNaADsHfP7j/ZYA0fqAA+0EqQCCAvr5O/usAzIAtQYDB6f9r/i/9Oz5AwJVBdAI8gXf//AEZ/wk+WcAHP2mAd/93vzU/xr8cwI+CLoEHAD/+ELz0fx8BBsJswdO/gr/c/81A9oCE/ox/PP7yPhq/mYCpgpaDEcBNgEg/aL5qP6A+cn/SAPw/EMDVP+k/yUCcPq4AAMDdP9YAbb/8P0ZAtoE1QS7/Tb0mvno/B8BUgeMBHIFqQNLANwAd/8Q/Un6ffpY/Sv+nQHJBPIDxwRRArX8zv66Avr/if2U+8b8sf1EAGUE8P+RA2EFT/1z/gX/Zv4r/lj7bgDwArwFoQZV/E/+Sv+K+HD7if9ZAkED8/+dAYwBOv5hB5sCKvx4/9X4if//ApgCsQNt/sYBuP9f+gr7AADYBbUDmAHmAJD8nP0MAAYApgDP/OL8i/+BAOEEKgGp/X//Z/xSALUC2ABFAQMB3gZOA375KPpu+lD62gNJB/oFrwl9AWr6T/o8/F3+7fc7/FwFlQDDAY0GzwM6B8wDYvxN/JL4RPo9/ED+JwP6/90C6QWG/KL9EwJBA1QHMwIU/Mv4Vfrw/an8NQIWB0gBHQEVAQ/8Qf8iAI8DvgOW/Y/+Pfrc+1wFpwecCg8KyPlC8j/1TvkwBBgCwAMMAz/9rASkAMsCywl0AF75Evek9tj7yf/oBEEH0f/OAXABiv50BGMCN/8j+tz1xfuKAgIGEQkEBsr/dP+Z+0P6/vtYAfADI/3HAaECAv/aA9MBif2m/8//5QD6//v57ADEAHj+AANC/JoBHAKH/fsBAPzB/roD7P2lADkD5P2q/nL/twBTB4gD8wCw+4ryx/y/A3kDjQZO/0T5xP22AIgHHQyGBQv+zfHQ9Zj///9FB18DjwCW/1b7DgFAAwkBagGs/s78lAGr/d8C2waO/uH7KfEK+A8E/gXiCccCggBB/2X+uQWIBeD7z/hv9VL1zgTNBysLrwsxAWACz/ZS8hv6DfseBh4IBwO5AeT7hv2BBMb/g/6EArb8Df6W/dn/PAeLAj0Bvfk09zABUgGhAf0FogWRAN3+/v40/VL7xf7tAjf/6QEo/5f7+gBQ/PQCYwiPAPj9o/Y8/HEHXAW+A5f/yvsv/Vb8rv41BWcB3wR/BrT40vig+Rf+DghCBvwGUf87+N8Ai//eAccK3/p39ID7Wvc+AjUJgwYMB0sASvt59cr3vQPaBOoCiQQn/4P8ygLFAjgCjQER/LL1vPOo/4EGXgdOCXoCcgAyAiz//P3V/kb9Pvxw/dsA3AG6/gMDBgKh/2IFP/2Z+Mj9sPwkAr0HkwWgBQH8Bva//G38qwQnAzb7gf5n+BkBbwiLBKYKpgT/+Kr2XfTT+vYHNAkPCSkByPmAAkb/svwcA3X8MfvR/oX9sgYsB5YDCQCp9qn8pftP/UEGBgI2BKwDS/5t/SX5EvqrAtAE3wVQAL75GQD1/Cr+Uwb8A5YDl/y49Iz8uQb4DEgJD/wr+KTyoPX4CRsJFAXTBqr5kfV/+OP9DQgPCZkHpgCI+CP+F/8h+3oDzQC+9qj4Rvs5BNALsg36CSL+//rs9yr3zP47/7cBOQaQA04CeQBu/gn8GPu8AuoBwf57AGz4Efx6BgID/wN4Aez8+f2L+tAATwRN/VIAC/+o+bUDzwOLARwHswGFAe771/oNAST8iwLkBOz7agDrACD7bgQmApIBowSP+Nn8LP51/PcAHwDwAYIC7AEHBVMGFf6D/Ln42PQj/BH/owe9C3MIEgLS9O71Z/5dAgoHvAMV/Oj4PvtCBuMMCwnsAjby0uxz+Bb9LQ1uEScFOwIz+4r7LP4sAAkHyQIp+9f6t/Xq+mADJAH6DD8JVPzr+X71YPrDAKMDLAWzBSQCxAGc/BL8EwSF+3H7zPxy+ej/6QJOCBcMrwY4Apb4YvS4/uX+4/+7AI77VwAnBUQEoAFiAg0DCv5++0n6JfbO/ywKqAqhCUv/UfzS+P/2JPyv+hoEggbxAmMFyfxx+2MADv+VAcYAaPvT+5781gBMB5oErQSr/wr5iADRAej/Qv4F/A8A0wHvAesFoAUiAFH5A/d7AowCRQFMBYf+uwGWAC3+M/9g/AD7Dvh/ARQIGgNZAGP+4wAPApr8HP3IAAEDAAUd/7L7wftx+6gFWQZ1/FL+kf0dAOIHrgY6A2j6eflm/QP6+v/ZBBP9s/84BDkAWAAmACAEagF+/x4G8P2o+Hv6zPlfA0wIRgIZA7X/f/tF/iwAwwHO/Wf/uv+0/Y8ClQP4BmYE6fkY9JP1EP+p/rz/BQqVCL0HoQWeAN0BUf0r9hjysfZVAToDZAf+Dm4HBAD3+fLyzffJAjQNWQde/6f9B/fM973+ywK5Aw0CgfwH/Yn/LAMbCeUEGwHf/vPz0/G/AasM/Q2iAQ/3OPy6+y4BcwTFAzcFPfml9XP8/AQPCjQCcP6f/qz/WAHQ/jL9rfv9/mD++fo9/54AoQPZCaYDqAGyB+j8I/fv80b3HAWrAZgCvANpA6cGagCVAHQGpv7b9rz2w/OLAcIKWwn+CkgBdvtG9in6KwVQAeICmwN+9T7z7v6LCFAM6wh9AXf0T/RD/8UAgggGCu38LfmS+/7+4/2ZAaQIFQKnAJ38g/fe/UIAAwNIBqYEDgLu+x/6wwBe/ycD3wG5+BsCAwFU/j0DwQArASb9+vlTAFkCxwOtBBX+XwPu/pfyu/s4BRcKXwf4/OP2VvplAPYEMAkFCP396PCG90wCuwgWC00BjftY88L1bgDwAdsFxAUhBKAAIvjI+XYH7Q0dBuL3cvLi9vP3ygJOCFoLDxBx/bL3nPym/DUCugOQBbf+GPM+9sX8AQFWDeALHwLRAMH1c/VfA3IG7gEU+vz3pP3R/ykIOw/vBzUCv/aO7cv0KP21BdQItgnCBqT78vxQ/kr+9wMAAIT92/sQ+l/+AgR1CIsBivb7+VMBxwfSDSQFYv8X+iT3z/zX/UgFJQBh+c0CJgeWAyAC4gCR+GT15PiPAhMJNgrfBMP4Ovp4+CHzd/89DWAQzArl/Uj2ZvJG82P+pgfeDTIJ9f6F/38Bwv+k/7L/Rf1C9yr2M/57Be0JIAZWAnL/ffdQ9Z39lQhaCRwDLP+M/gn6N/zt+wf82QjtBK3/4P04+sz++gLGBjYGt/5M/fH/2/qiAAYClPyOATL9Vfor//sBXQcwCuYDZAA89x3uIPnYAfsJ4A04AJL+DQFa+9n9W/5bAqUABfgr/VsCkQc9Bl0AJgG5AJz5C/b3+yAAEgXyBj8HnwJ8/jf+LvpY+zb7/vwBA5gEPQHHAIsFdwzhBAL2xPcO95v6sf70/AoILwuHAvP+2vvk/tIEBfvm+if8pf2hC6UEn/+O/R72U/9kAeEA5gwxB2r9yfxd9S7+0QJJ/ncB6/yIA5EKQQJG/4/7e/YV/3T+D/qxAxgEAQXDBCECvAQn+ljzgfgO/2sKOQn1/dz8cv1B/scEMgZ0A3kAavmQ+DH73v/dB+IC8v4o/Rb6fwGNBNED5wI+AIL9LvgS/gMIkAS+AKX9R/pp+zn7R/31Ab8IPQw1BID6zvzT+3n67QJ7AM8BCQBR+IX6pv0DC9kOKQSs/tX46/PK/KwCiAPUB3/9B/26/UL8pweBAogAcwLb+ZD8CgMy/zH/uv3J/cUDmfu+AT8JFP/FA+L9RvUgACIBZv+EBGwENAPq/RD5pP1M/WoCvghr/Fb6ivwy+i8ESQllC4wJA/8j+o32o/e6/xT/Jf1GAvH93v2NBkkIIgoGA+L5+vW38lT9QgNEAzIJkwAK/6UGmf2p+4H7EvmBAUz/aP86ByEDGAUXB9sDMAKS8xbwtvfs/m0MSgpZBmIFgPqu+ED+2P3J/Qz+yvuzA+UHFAZnA1z9TAB++S72ngNiBFUAIwCN+pv6zPsN/v8K9AfOCdYKkfaP+VD65/aBAKP9//07ACoCpQt8Bvf+agQl+HLyYP51/osEMQf6A3cGhwA2/ab8FPeU/jACs/tNAu7/fv1EBfIGfAnN/w/1NPih+wAAdwWCBTsD9gBj+vj75wCoAUwEGAH4/wD90fiW/an+CQdgDt4Gdf98+BT4d/q//e0FWQX2/rH5RPUy+ZsEEQn8CZ8E+fpd+P74lgPACbYFwAE2913w6/yZCioLAAvT/ZD1Yve0+d0FagJvAhoIF/4E/4oFKgFRAPD+qPkt+tf1A/3xBRMB4wfBByP9Jfr19/P6RQfGDo4K8P4U9tj50vtS/CgGzQMY/bv7tPNK/UgL6Qn7CKQAY/pT+bf72QeiBrr+9QBS+ZL0x/sm+6wCKgwrCrsI5AEO+xn3uPR5/r0GHgcSBhv7e/fN/xEDQgJn/aP7K/sW+ksBkwk6CIcCdAA++XD4owAhAokJsAfZ/J76Ufef/LD9l/0UBmQGPgcdAaL6qAKyA5sAyQId+hn2N/1/+t7/hQb1Ao4F7wFq/fn+mfwcApUCLvlz/2UCLAGeBvIBcv9o+xr0wfvTAaMHMQ5QAdP6iv2x+54C+QAa+lj93/qH/T8G3QLjBpIIVAAuAD/5CfeA++D6+ATwCqoC9wBU+YL2hAKKAo4L9Awb+z7zxPKq+yIJbgwJB6sDvvR89Lr93P4iDVwBo/Vj/nH+GAKwBR4FqweLAnD5Y/xI8+H0GAO7BWsNVgU0+X77dP81AyMGowJ//rP4GPaQBmQMNQmhAuf0EfRP9mr6XgNiC4cLOATq+Az1KP20/uwGWQwpAPL5zvXT+kQHWQhLBO76oPiP+/b9HgnpCjkCif3I9gv2YwGxBV8J2wfO+4f5FPVb+X4E3wSKB5ECSfr8+G38HgbuC70FcwAW/2D0KvVi/YUCUA7nBor6z/lm9/wB0wY4AckGOP8o+c7/YfpD/xUGnQPrB/MBH/fK90H2jv0fCtkGuwc3/zH0VwClBZUDrASl/dD3dfgd91YBhAj0CG0K1Pvj+J/72fjbA74L0QS0/u/56vYvAvwCNgJhAqL3ZP8uBnADOwf1/wn67/+Q92v2qv4oAl4MqgeCAvwCafq6+Ef9o/sE/3EEDPuy/+8CMQDjC+MG3f2W+M/xtvqaBHIHZA+cBtn2XfYA8fH41QgGEGYRGwVg+NP1cPPZ9CkCHgSzCQMIV/np/iIEHwgSAgL4rvTH8jH6rQRLDysPeQzt/Y7sj/BG944CCQ4yEI4JbP0r+Yb5X/pHADEBxfdo91wDzAcjCqAKrwIZ++X1EPuZ+w77UwNxAq4B1wKk+4z6dQO3BNgItAgIAMn0G+4FAsYJqAVFB87+4/lVAHgEq/5TAAf9JvZb+mP+zQUDB7UEswh6/zP5M/5694b8gAVu/5b/JP5C+6T/egIoCFEHHfwSAOH/ivnxAYcDNgYRBij6zPrV+077Yv9e+zH8vQMmAoEBOAxcC/IB2f2J9CXz2Pas+w4H2AsfDQEJOPxh+Zz4jvKD/asFvgQ+CMMC3P8v/3r8bwL2//350PsW9oP/+g99B5oDofyN63H1n/99CW8VFQYAAoP9+PTT/sIB0QHCAJf6SvVq/10HmAjDB/f8D/xF9WL2fwUACYoJcwOf9mj3xPv3+8EHvgfuA7ICqPbc/IgCP/46A/cAjvuk+77/kgYrCNUFwQAA/WD5LvnA+V3+yQjRBToCT/62+Fz50vm//lYLuAr8/2gAgf/wAwYD4wAt/9vuKfOh/M8ACw+uDlAGFwRH+p/46/zk/ZsCh/pS9ykBogRPBewGZP3g+T7/uPxNAKX+rP7DAegA+AR6Ah7+TwD7ADkBPgccAV/57/XH9qwFmAg5BoABpff0+s3/0AOCCn0I4v4D9hnzMPfnAfoKXwmS/mb7x/zj+ooDuAPxADgCsQBRAcj9MgOYAJz48Pl++9UAvQlvBw78qgKGAwb/C/wl+J3+Vf5wB3oKKv3p/MH7ePjwApYIewFs+831wfpYByELcQyx/kPxI/oh+57/lQVdAiYGwv/s+WP+4wC/BAQGgf+eAAH8CPXvAj4ICwlLA9X3nPeK9lD9WggNCGkExPyb7lf8dAtkBygM5wGC+TH6hfRK/SMCLvxRADj/NAGxCaAEgAoECuX5K/Xi8pj2KPzWALQNvBH/BKv8qff/91YCx/ty/GIEDvwt/a8AAgkJDi8EZgIA/I3v+POF/igDoQl0AAn5DAC0AOEJ1wZPAfEBMfMw8xz81P4YCSwOtwK9/lf8XPxcAcb7VwRQBKX5SPme94UDpw/xCkQCvPwn9OX38P4+AicJ4/pE92j/FP/OB10KeAUaAJD0FPLD/lYCTAZqCEoEpQWu+R/2+gDFBOoDdf/4+/v8rvol/YEJPgkNBFT7BPTf/ZsBUf+5A1oDYv1t/OH+jQPzAgj9aQDyAMn/GgGB/Nf+aABQ/r8DLwVUA7f/B/mX/A8FMgB2/80B+vlQ/Q7/lADdA7b/IgJlAP38MAErBa0FCQav+b3xwPph/bgGxAtNBqT/6PMX950C5ARZBb8EFftE+O39VAEbBroAyvwKA/MA9/4X/sb7kwOAAlr4cfsjBQYIzwMgAOQGgAbf98L4MfjV9tIEnAPt/7QF4AJu/u7+3v1LACv9UfnzA+YDUAarDeEAnvfM9VHynvq9BXgHOAjaAi0AWP+U+MEBlAiXASz+xvrL+J0AsgKC/6AEfvxD+W79w/sNBhAIDgWzBrr/XvcM+UL+GAV0BUD8TwHK/R347gITA/8HSwjB+Lb2rfrh/5sHvAWiCA0H8/PX9FP+Svs1AkoE2P2K/AD9qQKZBoIGjAb9AGf5zviS99H6OAUABjEELwJPAB8Df/6o/MYDGP7b+Kj7WvtvBpQMOghhAVr3efeC/PL+EgJvBPH9XP+BAYH+BwabAr//uf/s+Sv8Tv2B/SUC2AYACd0ImvpI8ar5nv3oAlMEhAJAAGL7xAGWBeYA5f0Y/rH7V/8VB6oCWwGkAFz9uf54/YYBlwHu+jMCFgUh/0MAhf7X/HL+BAS+CWAHz/3h9GzxDPJSABYJKgrpC5ECwvrv+vYB+APC/k39n/iF8gcANhD7B5UEdwIw9A34Yv65/8cJCAdwBpkCIvUa+n77IvzWBfwCgvu4/TP8+/8ECW0Hrgn9/OPwEfdG+1oGZQ0HCMT+HPnB9iD8wgLMBM0IZP8x/Of9+PYvAW4IoQShA3r91vfG+GX7AQRaDkoIrP9G8+bwagbTCCwDO/4o9Yb95wSNB6sP+Ajp/FD1a+qe8yQEAQXsBasI0gH4/8UCcv6RAQ3/xf0M+x7wC/oVCAUP+BCEAlL2V/s3+2z4wv0hBoUJefvl9XgAbQH3BAoNbgRz/3j9oPH386L+ygXJDBQIof1Z+Kj1qAQ7DEr/hv1v+5n4TwBtA5MBMAW5Anz+dfpS+gIGKQRq/eD9MPuO+uIBaAIvBDkNvQeR/f7xyfXDA3IB9QG0Abb7gAKBBPH+xgZ/A6H8Af3x9v/8H//A/r0JYQNe//cC2fvL/p4Bv/4a/g78Lfpe+mL+vgkpDuMCCgSu/Gjzhv0p/YkBVQWp/zT/tPsN/vsIdgapA4EEkvfP9aT/rf9hAeMDJv9N/5j9Wv6KA/cCMAhMAtrzFfYy/iwCKwfoBnQCivrJ9rf+Wf4HCMUNm/7R+439G/pw/ogDDf5P/r/9RP5WANv/8gqEB3oADv/i94L7EgMNAiL+jvzU/Mv8+PpXBM4JPQdKCM7+jfql+hD3ePne/OwAxgQ/Bl0LxwoL/gP62PiR8bP27wFJBPIIHweiAV8FX/0p/B7+sf1jBG39UPwwBCUEgwCtAq3+vPgB9s/2TwdyBy4HhAX6+vX+c/yM/TMDjAT1AVv6dfhBApsDtPpSAZP/kv5OBF3/7AbzCgIDbf2V+Hz/Rv5Z8tr6dwK1Az0KzgVy/bL7S/kn/FgDwgOIBQj++fnJAzb+DgF7CjAAGvl99wv5yAARAtQFqgtjBAz+VPju9DcFZAqG/3D9aftx/ff/H/7jA+oCvP6jAlL8Wf6cBU/7//xHAub9+QBQAxcD7QLS/gwAH/5++YsBqQE1/zYBhPuB+tABKwcWB64EgAAP/jf2X/XV/kcA/QUqCuMDiQEzAvv4gPdEAa8EgQKH9mL3XgHoBBgNJww3BX/9GPEY6yn0KAbIDe4GEgGnAnT83/oZBBYD3gMHARj3VvYO/PgCBwYACJsJ7QSG+KH4hvya+ygFDAgMA8v5t/fR/eP+QAYZCfQBM/67/qz7VvtXASUFdwAu9w36Ev+iAQEMxAmw/o//+/fx8CP9igTnBQsAmP2bCKwFFgP5BOj5zfZ0+FL1Lv53CO8H3QopCRoEMv+68bb48wOe/q8CPQDM9z3+TgHqBX8KM/3K98z00fZ3CIwLmAx3D7H+Tu3v76P0tP4wCXAJTwxg/7n3SvuY+d4GLQvn+835Gfxe+ykIkwlGBCsEmPcr9Gf20vjOClUOXwZjCOH6rPfS/tP1Zv+3BSQAhgXHAtYAxgOS/k//5P6D9OnzbPiXAo4O+A0hCjL9du+89o/+1v7EB5UGwP7L/wsAbgNWBDD/APpZ+Rf9egFgAGICMA0xB3b/S/zw9GT6dQFWAgYACAEYApv7+/tJA3cDugBvASb9NvrKALgFKgQwAT8CigKQ+zP8Pv0C+sj/zQJKAREBtQHA/Xv9SgJ7BdMFp/1G+w/4jflNAnMEvQXTAL79wP9jA6kDzgNmAcL4jfoR/bn/ywaECZME7fxR+5D7+vs4+v/7o/8A/CoC3AiEBIEGWwTh+2b57vnk+3D/FwHqA18HPgPtANX87PsSAz8BPQL6Ahz74vjl+yoCywivBH3+KgOT/sr2Cv50/Hn+QgXs/V39/P1R/9gEAAQ7AwkELf0o/V4F1v4LAe8B+vVU9tX7YAPMB/sG9gWvArv6Sf0pAeD81QK4AzQAFP/1+kL8/vwg/WUGVwTo+lj+LfsiANMOOwjT/qn8qfR+97n/BwUOC///FPci+hL6lACGCsII/wMp/j/3R/oUAmcL2wkT/Ir1DfgP+HUBqQqMBVsGzv8b++n9zvy4AcwDJQUvBEb2hvER/nwCJgnzCsv9Ofa29GT5NAPiD5cOvALx9oj0wvsA/tgFyAU6AJf+VPov+rMBygrzCuYGWfyi8Q7z7v1ZC8QMRAPl+4z0KfbeAEQFDAcFBen+lvlz/d0FQgaC/i/5wf1E+9X7wf5m/9oGoAbPAXn96P1EAFkAHQJ9BOkDRABv/mX6ifwK/6X+SP8H+zEAmATgBCYHFwUrArn8DPn294n7pP8bA1MGfP/0/nwAxfzs//8Bp/6t/bP/6v76BVwHAwIzA5/7DPtD++n2I/vdAHIHuwmhBmMAy/0W/T7+1v0Y/SsAaP0oAcACOP/uATwH1wSe+qv54fl6+/r9fARQDJ0Dsv6X/V/74QKDAm/7qvsW/9cBXwMYBaIBCvow9C76wALHAlcLYgq1AqIAQPx/+m74fvol/sX/pwDUBRsG/gZ1Cl/+g/QU8brz5vrOBs8R5A00AxL7IPvW+hb9dwDz/hX/RQDDACIAnAKzBbIC4PxS/dP4yvNiAUMMFgmoBiQA5/ZG9Zj42v+3Bk8KTAW4+/37ewBO/yv/yQXQAkv43/Yv+qUDShAWD24FRfm97/DxX/bsAt0OrggF/6H6GvmfAr8JIAVwAFz14PRg/UcEAg3tC2IIZf528R/wdvl2AqMGawWHAYIDEwAc/7sDNAPV/lr4JPbo93kB8AdXBpIICwV//qX44/Tc9zr9wQVXClII0QKa/5P/OgHu/+b5RPo++qn6gv5eB1cPlQpnADL3XfQq9Qr8GgGEBV4LcwbT/2kA1wMw/nb9Jv8p+8L4kPVo+0MFyAxHDmsG6/kJ8ob0hANNEUALfv8I9Eztk/HM/OUIMQ/RDZQEXf7s/vX8Gvv5/1wBtvtg97X8AQcUDO0NiAWP9tXvmvKZ+FEFxQ8vCRH+nPd4+QX/TwazBzUA8/ut9y33PP8CCx0PFwqt/XXzePTe+PUEygp6Bm4DFfx79Sf5KwP8BbkFpwMP/V/3jPYI/tgIogs7BeH9YfNc8Cb6ggTUDjUVngwa+ADtPvIJ/MwC0AimCcUC9/yj/oIBNgHV/1P4SPgtARwCTv0gAuIJUgTR/gb9dPql+cgCIQn5BlgEZvkd85b0Lf+nBn8DcQYQB6oBSwB0Apb9V/dM+GT+ZP6uAIsLIQgAAEj8+vRY9Z7+sATTB+YGDweLBJP8tf1++jz2xv2bATj+OgDNCWgMDwZ/AcX5JfFZ9RP8sQDTCJgLQgGM+ar6L/vpACsG1gYnAfL5g/tHAVwDiQQ6BT38R/YF9fj6xgkbDX4J1QGH+AL5zvq//hcJeQjm/wP75/fj+Q0DCQWd/5H9Xfp8/f4CsQdHDpMJ1Pvp7orqoPbrCZAQ3RCCC7f6tfC18HL2zAHvCG4HcgJmALsEZALyAKYFSv/L9Dbw+PU3AMEH4AkjCsUJHQBt+eD36veX/gcAkP/qBvEEKwCVAqD/JP6s/Ir8agBD/jQA9gR8AbUBNwFA+9EAuAOf/mn9q/7ZANf70fpSBLQIHQJN/S78lPtqAOIC9gT8BL0AYfm59SL6QgAhCXMKwAcbAK74q/pY/EL83fuvALkE8gTOAkcD4f9b+oH9C/2g/8oDOgFZ/eMAiwT7AT0Aev6v/Xj8DQSoB3f/Afq0+av63PrvAckJLgr3Ab/+qgCb/x4ByvsP9Mn3U/yQ/ckFnQy/DFYHKABw957yKPpuAWsDxgQlBW8AhQEQA739Sfqv92f4Sfs/AHQGFgwPCBgGYAUN/4H8DvPm83D9zQFfArMD8gRNACwBYAKTAi4Ba/sz+ED/1QTnArMCVgIKAxz7KfnF/Cr5OPu//VICDwhNCLgDfARECEIBLflA95n5n/yp/UYB1QSXApD9rP1SAn4DvgMLAgf/cP9p/gAABAGc/O/7Nv57AYAFawbwAs/80vnG+qD8d/0lAMkDhgXBB8YFgP/h+J70V/es/9EFiAUiABL8HAH/BSYFHwEQ/rD8h/oV+hH7FAWODcUJHgOT/Y37Ef07/5n/Jv+8/Cn7avqO/WwFygg0CPIDG/4C9qvz0PoC/8sDVwehBZIDe//M+sn9+AO2Ad7/S/9S+q34E/wSBbMNLg6KBZr4IPI89TP7PgOODfcHqvxx+WL57f7bAawEbgZHAcP5Vvcf/GgG3gqZAVf/x/wG+XX8N/8XBmEHlgFp/hr86/c6+h8AsQcwDN4BwPr9+KH43f2tBYIHhQF5/rj93gJdBUcBPvrg9IT75ABDBJMJEgrjAnz8E/4+/Pj4MvwNAkkCEQAP/3n+IQFmAlMDZQH2+6r35vSN/0MPXQ9iA8D4OvjG+nX7/wC2BU8CZP86AiMCMQP0Agz9kvo/+6cAIQK7/pv94/2YA6kLngi7+jT2Jfb9+F0CkgfxBmEBtv52/YH+RwC4AlkE6/5B/SL8N/xhAnwHWgWS/bb40Phs/fcBlwhzCWj/nfjr+Ej+6QK1BfsDN/+L/jn7JPlx/Y4E1QcSBjYBKvo295n3DgC+CZ8JLAYYAdj8Bvvw/DEBzgT0APX2XfON928DVQybDKwK9AL8+dD3f/ry/BD72PvXAcwB3QIiB5AFdgM5/qb4cPqT+wT9xwENA68DegTJATUAJwAC//z+gv35/HUBfAOYAXL/tv5B/0j96vx6/4QCRAY7BvkAGP7P/E341PutAXYCkQMiAXQBTwFh/ZL+q/4J/tX+qPs+/eoHrQa1AP4EHgJe+R35Yf38/ykCsQCS+0v6PwGJBwMGSgVNA5X/hv0K+CL1v/vmAXYE0ggmCtQDsPs5+M77YwEXAsoBdftQ+HP/zwPaCM0KhASK+rbz7vMW/vAFBQexBAX8H/r3+jsBnwjFBzoCqftS+U371f+7/7MFwAUR/y/9/PoH/WsACgWJA28D7gAW/Vb7OfmI/2gEcwVpAAf8QfvkAD4Izgr5Bxj8rvYr9iL4u/2nBowI4wFJ//b9/v5UAPUBSwIKAKn4tPOQ+JQEyg58CVP+D/lc+fT94QV8B6QErv/U+CP3EP4SCZsJHQVQ/tL4O/gG+QoBjgkzCXIBxfm79bv4HAGlCdMJTQK8/RD6lfdn+6UDdgW4Akv/+fm7+K7+MApHERAM9/5J7+7pH/brAgEM6xHDDJn+7/PX8Ez2tQIRCfQIvwTn/mj6Q/1c/50C9QaN/dX4yvfh+uAFDw3hClwDhPkQ8kX01vcAB1oQ0wq3Ajb6afiF/HwCZwJOAhr5vfWw/vgCxwgzCaoDoPsw+dP78/9EAQwENQZ7/3H+WP1y/cn+Evz6+zn8J/zKAysMfgp1BmX/lvpi++X7JPw9/En+iwFvAOf9df/hAc0IAwu7AtP+GP259w73WvrqAM0HKQXQAXsCQwLM/h/6g/lY/JD+VP6h/mYBjweeDAkKi/549Tv0Vvad/koHTQfs/1f8YwBjBcUI8gOy+jz3cPX0+88HOA2BC2QAVPm8+Mj58/u2/VoA1wRFBdP9yPof/REENAnFB5D/gPW785f5awXzC+oOMQWV9E3yafa0/y8IiQfeAeMB/wDZ/Gz51PtLBj4IfwSC/BD1RPd+/rUECwj4B9MDBvx296H9AgJ1AwEAJv2fALwBfAHO/74BmwFCAjUA7Pqi+oD3Zfs0AjcFkgfLBksANfq7/AcBHAVlA1b90/hw9z39RALdBSUH9wPJARgBgAJf/w770vvJ+X790gGk/ooDRQqpBxsBp/c08+z5pwDCBRkKtQQY+wH5VP6cA84FYgPy+9D26/gmAkEJxgfIAjT8+/XM9HL+NAnbCc4HTf6a8//3ygEOBz8JNgX2+hL5MPxG/3kFLAkKB5b5MfCo9Yn/gAnwDOYGrP7X+yf5gfzzAuwD2AWx/pD0NvRW+m8EwQqzCf4HYwRs+Pbyhfhn/+MHtwhcADn6lfim/NcCsAWrCMYFHvza9f31yPyNBs4KkggQBsj98PZ4+aL9/wLYBdkCsPxU+aD5Pv+4BUUHmgWz/Wv95/2R9wz4OP/HBkIJoQcxADL9bPr8+TgEnAXP/mL45/nu/WMFZAsjBmACGPsG9e/39QN2DFoHufy+9hP4Nfk1A1cJVwTZAP390v8HBWUDBv0x/GP63vpl/lACoQZkBrsFtP5n92/4bfxiAqwJAApiAu73qvJ6+iMBHgSuB2MG5wG5/FX5gPs7/2MAPgPzAvL+GP2N/rv/+wJECH4H5f8Z95/0EflXA4wKYAgwAJ/65PlT/NMETAnaB6P+E/WK85L6LwVlBwoGRgJzAtn9E/Z4+TgCEQl8Bar+6fm9+X76fADKCg0LBgSh99/0hvlSAI0JHQl9ApP6vPid/k4EHwY8BiICo/xh+V31mvn7Ao8IUwnJ/2n3Fvum/DIAXwe9CGsGRPsX8kH3JAEEBg4HfgHm/cv+MPybAYMFxgdSBxn9JvUi9IL7rQMDC6MHT/6K+Qj5tf6HAsMIqAYL/XL5PPuC/RcAFAXxAxYCZf3q+cL9/AJ1A8z/jQH7/3L9Xv6G/6IBpQQTAuv8r/60/JP7C/5xBFkICwIj/PP7lf+mAD0FQAOv+2D5YvueAg8ErgNHAYgBvQPT/+76b/ho+hr+gQUwBlIDTQJW/hz9e/1YAVgBQ/8K/yX+2f5yAe4DmAHF/7D7F/rC/pEA8wOJCNoI+gIq+tT2iftsAjkFNAMO/ZT27PTP+RAGfwy6B90Civ2i/WoDuwStAKb6YvPd8jv8iwQoCy8MOgouBQn6t/I29ID+twf/CM4FGwS4/cb2p/lrAZQEtP9G+4n5SPz5/zEHjwxCB5P8XfUV/aMBMQL9Ag8AKv0W+RD6jf3kBfsKiQhgBDv9BflI96P6HQLhCQYJdf2U9m/3Nv4cBVwFOgKX/TD7wfyS/+MBWgdGCGn9jvfz+Er8hAKrCfQK1QW3/3b3hfW99pT9hAdaCJoEm/7j+2n7pv+fBGAGBQUV+4f1IvrRADcFNwjnA4r8hvtP+qP7qgJDB1wDDf63/0ECZgGTAMD/3f2j+pz4PfkN/2YHyQfkBBoEcQJy/XL39vkJAqQFEwIK/Cz9FQO5BdwFSgNx/mj4VPcU+sH+wAZtCGgDn/3y/SD/1v7h/wABUQGF++H5/v+cBI4BEwAIACr97/5p/ikAUwUZCLcG5ACJ/b/5xvOm9HL/LgigCAQFVQNFBMcDiP9g+lD56vwJ/hX9pQD7AhsDvgAxACUAq/4b/Xz4Ff51CCYK5ASN/ir5ZfVO+lgE6Qi5A2r/Q/4F/oD+5/7vAKoCRQGn/cD9Gv7cAc4HGghEBcH7mPGR8er5vggGEIAHMP6o99L4hQDpBcIHmAL2+pb4ifyp/rID5QWhAB3/yPzO+977mf3nA88JugfA/r34S/jD+if/XwcBCMICXP4O+RL64AFZB7IGDAMi+4P4iv1bA08HiASg/kP53vcl/aYD1gWnBEQAbv0E/dH6OvxBA/AHiwFP+Gn2kfpqAXsK0Q8CCjD+dPWS9338JP9N//v+CwJrAvMCowfNBmL/8v2V/H34dvUN9v4AbwzrDU8GAf7N9OfwkPcpAxIOTw/JCRj+3/ZV+JT6pfxH/6QBcQFHA4EDBwagBm4DygAd+O7ymPL09noA5wnLEK8OuARS+qr1DPbo+Rj+zwEhBRgE6QLLAuD/BgEWAzkAdPvm9jz5cAFhCFELXAf2/FT0GPL7+PsFQQsKCb0Cc/zV+d/5mf0QBYEHcQLF/ab3A/m9AD0IzA0fCTX97PGP8U/5yANhC6cNPAaY98Tzbvfo/8sIBAkVA2v8S/SL8gn/ZQtjD98IAgKH+n7x9/XgAEQH9Aa9AcT40/dZ/k8DtgrSDUkKW/008qfzBPcn+9QDewwQC4sCLvhQ9rb+ZwRDCKYDTvq/9YP3awM4C3oIWQVL/kH0cvNK+W4CdAjtCKAIewIT+8D4FPxeBBsJMgFn9u3zAfdPAr8Lowy+BgH7uvMj9l8DJw78C4oDHvho8Dn0If3BBQ0MOwpvAjH7SPlI/P7+qQGaAgkBqwEIA+gBaP9e/o/9KvpX+FX63P60AxIICgsDC7cGVvw1863xfvcMAU8IdQgQBSAAQvo9+/cBOgaOA2n+5fc19dz6rgLnCSoOFAuy/5r1PvOq+U8CLQZKBaD99fXC9SH/bgyuEmoL//3j82DuvfQgARsKJwx0Brj/afoc+D37yAGxB6oIof8m9mf28vo/BlwQ0AzcAFH09vBC+MkCHgxNDJsA/vT88Cv2owN8DLkM/AUv+zj1jveRABgJXg0+B4D6PPFC8x3+ZAOxBk8HygKd/Jf5d/tqAX0IdwrKCBn/P/Wh86/2r/3SBe8JQwcZ/4n3zPpuAt8I6Qn/AET42fTP90cA+whPCqgF+Pyj9VD3mfzTAZUFqwWGAL/82/2/AXYD4/9O/6UA2/6M/D3/2gNrBLcCW/8TAbUCyfuI9jb7HQS7BSoD3wKyAkj9ffnK/KD/mAEs/0H9/P+wA7wEcgIlAiv9kvca9+r8qQRRBpsDwQDuAEIBMANpAzwA9/t6+1r96f2wAK4CJgSuAY780vna/X4BNQJUBnwFzgPC/Rz2b/ec/EkC1QdKB1EDdAFk+lD3P/nN/psGLQb5ATD+jf76AJECqQIlAbD8h/dK+Fr+0gSdCQIKDwPT/Hv4qPgM/L0AWwkiCJL/gvib9l39owdDCdcCcv60+Zr2Afp7A0YKAQomBCv74fYK+BP9WwN+B+cFZP7V99v5nAK5CTELAATd+E3z8/KR+EEFQQ0JDHUFyP16+8H7/vqu+hYAgQYdBhsCO/4y//YAnf/j/XL9Avwf+eD9vAXoCfQK1QNS+c/0gPWK+LsBQAq+ClEFdf6C/OP6NvuCAI4CYwEg/Xz9+gVICSsE7Pu090v5ofwmABkEIQYEBPMBdf5j+y78nfwX/v8BIQXfBLsE3QFz/Jv5h/qtAHYCgwDQAA8CFwR6Ajz93ftV/rv7qvnv/QEDHgiYCSAEKf7q+mr37PcD/jEFfgitA3j9KfyUAC0INgbJ/qP66vfl+p7/KgSoBzUE9/9z/gv7FftS/SD8HQA9BSoGKwb6AN/51/oUASIGxwMJ/BT58Pi//ZwF/AZ4BX4Buvl6+J7/OAVPB6UD4/1o+XX47/xh/9oDZwmfBen9wfuh+07/4AMjA9UB1/5r/MT5qvrBAwAKzwf2AH75jfUa+pUAYgQWCFQH8f7c9Vb1ZvuhAhgLdA2HBR39d/Wl8V78+AetB+gFGQHU+gj6XfydAuwHAQkeAzr69PUS99/6SQG3CrAMuQYQ/db3HPqp/pQCyP/8/IH74PrB/ukFxQvECQcCEfhA8sf2mQIvC+wIbgB++In27fxNAswFzgZAA9MAWvzi+9T/EwIOA/sAbv5F/Ir7APxnAOgFKgY8AtP8u/ob/mQDrQYQBFP76vQ79K78zgdJDZQMZAZX/wr2JvJ493oBkghZB2ECTP2U+7/6rfvj/9EGcAqtAyz8G/tO/UP/QAD6/18AXv95/TT+HAKjB08IZwPS+wj1fvTt+iQD8gpJDJ8DUfqC9/X7jQEJBn0HXADd9mz1ivotAAwHggklBPL/Qv10+tP7ewDgBKEG/gKe+9H3pvvGAQoFAQUZA5b+6Ph79sD84wW3CSoG/f4y/Lj7jACBBF8DqwLE/Or2y/kVAUcDigXJBf8B+v/q+bn2SPzjBA4Jsgap/0T6u/iL+vP/HAHNAx0E3v+q/aX9BALGA04DMwEf/3v+tPpT+ET/ZQmsCq8EXfs098z3tPppBDQLGAi9/l73r/ZA/EICHgcrCzMGmfs+9gD4///CBsYGDgPe+pD0WPSX+ngJcBMtEIYEi/WM7K/zJgEgCmYMGgPv+D/0KvgHBV0ORA20AsH3EvQc+oMB+gUlBk0APf1Q/BX82P3TAm4GvQMc//P6I/gF97n+dgfWCEAImwIf/bf7X/3d//v/k/6t/T0CawP+/tD/0QHXAfABWf/n+2r6OPrB/QoFqAjRBqcAKvq3+Nf5k/55BpQJ0AXd/yj8BvoV+wAAigMBBMcAUvvv+Q0A+AV+BgAFcP/s93T1ZvrIA9YJQQlgBVT9rvMw86b6twPXCrMKigTe/jH8lfpW/GkBgAXRA57+/vmN+PIBJAgFAsn8oPqI+AT7WgVNDa4NDAbT+qnzhPEa+9UFXQgFClYDt/nG9l31iPj3AlQMUg6xBxf/c/xR+5X9T/8K/BP9U/zX+PH7UQQKCsgLkQWr/Wj7dPbU+dsCYweFBwMAvfjM9rj5af8MB8sIDgTr/cH67/6gArAF7gWYAWD8sPYG907/TgVQBqsEaf+L/Xj6O/jO/s4F6gbuBIYBbf20+0P5o/lK/ikEjge3BJsBdf/O/Y/+9wA4Am3/afqK++b/WQPSCN4IwQGp+v7z1PM+AAQIAAiOBjkA8/mT9jf6nQB/BvEHRAQpAMP7Tf3rAAABd/9a/5L9uPxe/xUCJgUuAwn+svwhAaUBHv1c+yf9WALUA9oBwf9K/wL9wPz4A5IGygDr+qL53P0kBJwFXgY3BRj9MfgX+Sf+3ARXB4wEGADG+Uv1L/tKBRoIJAi/BWT7WPS09fP8OgUgBqYBHABHAWAB0QM8A7cBBv+l9KvxjvzQBIgGUAulC7gDyftl9pb3Rf1m/1AAwQN5A/b/rf2a/kADcAXgAV7/3P6t+s38zwPEBf4Ddv6L9j31WPvH/ecFTA/lCzgFy/2V+P725fSa+CQDGwXIAjkDwQGLBHoEgwDw/SH7rflX/LMAGwNXBxQJMQSn/Kr2w/OD+agD8ASbBhwIMwF8+gr68/36BTwJSQMZ/pH3gfPQ+AUCBwkWCf4BA/vR+jr/TgWLCBkEQf3O+cb2SvggAD8GnQjwBfL9O/iB+mL9CAHiBOoEtgREAK36afyBApUFawYvAm35bvQ09DH85wWDCd4K1gqSAjH3nfeZ/SgBOwIh/nv59Pri/nYDrgoMCsL+u/Wj9M36mgUoDLcKzQE+9WP0ifuz/tUDMgfmBL8B6Pxe+vj+7wGYABEExgSrAKH9bfza/y0CKADu/uAA7f/v+rz5Jv95BvkJEATd+g/7TPte+8MA9gQtCXMH//3m93v57vuX/Vb/+ADtA2wDlgB3ARIDUgLFAQP9Q/jp+G76VAELCYcJlgU+AJ36vPhc/C7/KgFMB04GngDMADb96vuL/UT8ev5dAjwCbP+0/57/AQB6AeYCJALB/dr67/x0AywF1AMU/535ZfpL+/39iQVjCaAD9P9I/hT9/gCzAHUAPAQxAoL6uvhb/IgBWgVhA/L/t/xy++78/wHWBT0GawRx/e74V/ks+6H+IgTxBdIELwK0++777/6OAXwGgQUY/nf4jfk5/f8DQAg5BKr/rPtv+nf/AAOvAmMD/QE//gj6ePYa+m8D8AiHB8oBk/xa/Ib94v85BKkEqv+++/z7NvzA/mQDZwU1BVMD3v6y+qr7aP8/BAUG5P9T+4X7SPof/pMF7Aa1BSIA/fdV9wv7JQHVBz8ISwM7+6r19fh0Am4IbgjYBK391/k9+in8OALKCekIyP9F+vL1WvanAHsIugg3BTb+FPi1+CX8PwI8CMsHVgQx/p31UvaY/QAEsAlGBcL+Cfs99876xASECh0GBgFY/v/66vml/QsCpAQ3AmD7+PuQ/77/GQO5BbcDjAMX/lL4wP0oAGAAEQRkAo//SQAq+j36awT1A/EADgCG/jL+vP/u/2L+4f9eAKj/PwHHAdr/CALEAQv+/vvU9yf7JQK2AyoKtw3RA5n8V/i09B77nwBHAWwGhQgeA9f/qvzV+mf8WP1n/K/9CQOMBNEF8QMs/P34+PyuAIkCewOE/wMAngGo/fD+bQBX/cj9Zv4zAHwIkQdIAlYAR/pw+QT9AgCtBJUHowLE+2L5T/YA+ysFoAkiCZwD+/z4+H/69vzwAGkGIwNW/b/7mfzqAdEH7gD0+S367vrBAnsFxQPPBLUCaP2F/OD9mfyt/1gAjQIOB9oD3/oV9zD7gP/iBaYH2QRDAsP9WPnv+5kClAVqBm4A7/mG9wP3NfvaAHMDlQdPCSAB5fz+/CX8i/6TAwUCmv5UAFj7wfuUBREIWQLg/GX60PwCAo8DSgXvAp3+cf0y/Gz+PQLVAnMAo/5P+1v5Pv1gAdcEWwbuBNH/Mvo8+4X9zQAYAj4BZwUdBHb+cP3A/Xz95P9+/3X/ZgTBAIr90/6Y/dr9/wCIAkcAUf+o/8IEAwaDAQv/wvpF93322fyBBvkN7A5CBY77KvWr8vj5WQOxBjAGvAKW/tb9Uv7d/or/ufyM+jj8Av4sAk0GQAdwCM0FVPsc8/72tgCiCFkJkwDC+Zz8av5W/hADtgWDBXADEv37+Sv8Qf1L/1sCWgHTAH3/Ofwv/+UCOgMQA4b9hPcl+yIAdwEABZoFaAQtA1H8gvgz/JgAuwIfBL4Ckf/r/IT5efzvAwAGFARnA14Be/ud+ar9jgMXB8UCXPzO+HX2S/r4BEgMdwnY/zH2dPZj/UMCVQepB0UCKP0j+rX7lgGaAlMAaAKoAJv9BPwT/SQDCAc6BS0Av//G/gL8+Py+/R3/BAKeAcj+igAt/0f7zf6FAKwBJwXQAY7/iQGr/57+hwDi/0P9E/0K/a79mgJlBtcGkgOz+rj2/PzqAhAHMQa7/Hf6HP1n+sf9lANvAysGXQaS/5X9d/2++vj9igEuAdEAA/7y/rICrwI3Ao4A/vvy+f77T/4uAiYIYAjvAgj/i/jS9E/7mgGTBcgIAQaL/0D9QfxS/fUC1gKx/SD8/PtN/o8EWQSFAgECyPxm+YP6zv42BIEIrwYaARj93fh9+EH9/QFVBHgEZgG4/1z/X/1S/4sD2AFBAGgBp/19/PX9tf60AvUE8AFk/a37J/yw/oEBzAP+BI8B2vo0+oX+sAJyBgUD7ABGAuj8cPf2+m4BpAM5BTED0fwC+9P9Xf8MBmwJoQHZ/bz6Y/an+XgBXweOC2QFP/od+cL5TP03A7kDigITAIT7eP3LA3UF6gSJAFX6y/ay+Yf+8gIcCQ4IbAO6/gv5q/oIAXoBl/+dAGgBcQF4/3H74/qzA40JGQWy/z77zfqX/uv/3ADpAocAhf50/lP84PxH/z0BuQQvBpUChP44/rz+F/1T/rj+if36ABIATv0SAUgEjAU/BqcA6/p7+sv6LAGoBUoBlf3k/Af/xwGwAtMB3wAJAFP/T/8HAFL+Svz//0gD3gKdASz/df20/pz9fP0bAhoBIwEhAT/9BgFdBAsD/gA0/sP8Jvz3+wT99gAfBlkGYgIVAOX7WvrE/XT9NgCUBXQC5P9bAm4APQLQAgL8n/1h/2T7H/w/AKwDVAePBiMALvu793X5Uv/IBHMG3QJzABH9Avtz/mUBkQJTAWf9mv2pAL8AhQJRAwkAJf4i/RP/6wGiACX/AwBoAosCRgHd/vT6hfpO/RICzwZhCEUCq/qc+cb8GAMABXIBev58/T/7TvuBAo8GQgb4Av36D/a7+S//YgbEC7oFw//p+y/2IPYL/qcGzgk7BSb9cPum+3r8rADsBTMHQwPQ/kP7kfygAGABu/61/sn9l/whAdkCfQTMBOn/PP3i/Hr79/sAAOoClQd6CXYDjfu59E/ya/j1AxgLnwqzBU7/Y/so/mL/t/zA/8b/Qf6cAJD+7/4FBUYFRgHL/tf6Lfrj+9z9ZQNjCEoJVQOl/P35n/kw/kcCxgKfAe/9ZPv3/tkE5QfKBcj+UPps+lr7V/xb/nMBIQWnBi4E0f8m/VP9+f74AGL/GvzQ+7L9AwFIBN0EwAM+A00AkPv3+pj8iP7cAd4E9QFA/XH9r/3KACwElgJXASUAnf/LANb/C/6BAaUBu/tE+/n8XAAvBV8D/P4jAHcAb/zT/nkCeP/B/doC+wTRAbX/cPt0+SH9bP/SAIQEQAQTAu0Asv9X/2P95f9bAYT/P/6T/CH+mgKkBWsDSwCK/C78fv2m/Jz/lwI7BD0F6QOv/xb94vpD+9ABQwOdAqUCjv7x+H35bv6xA+kHJQW0//78yPwe/RUAmwQFBO0A//xu+bT6F/73AIMGGgmtBMT8R/d8+dkB1gYQBPwAmf7+/Xj/xv8v/qv+yQGLAKb+tP2t/Gj/igNWBOIC4wEL/zv8nftx/Nj/kAMOA6wCQgIW/hP8ovwWAUMFLwPq/kL9Ff91/mL+mAAkAKEBLQMbAGL9tPuI/O8B+wThAUb+3PxQ/PEA4QYYCLwF/f6V93n2sPvAAD8EMgcTBrYBBv68+bf5ZABMBGQDPgDa+kP4ofvNASUKeAqwAdj6rvXZ9SH+HAcPCbIFWwFW/Rn84fsX/fAAJAXKA5IAWf9v/Nr8MAFHAxQDAQRf/276xfpD+lQAGgesBQ0C2f55+TL3l/4nB/ILWAlQ/Rn07vaH+0f/cgZXBnUCFf8J+3r8hgEpBbEFcQKI/FT5IvqP/iIFEgflA5z+JPqi+UH8MgF/BrUHYgVi/9z6Hfqe+q4B0AeBBbL/rPqM96b6HgL9A7YDPAO8AP3+wP0w/nQAiwNlBRkDx/27+bT4zfrC/yoGTwj7BPf/5flM9kj6CwIkBMMFjwdyA8z/zPvh95T7ygGqAXEB5wH3/XD8Ef8PA58HQgj3/1D3APax+sMD/AhqB3YDTf7b+NX3Zvr0/1gGwQQE/xf+lf+CAa4ECga+BP8Au/hl8Xj3wQEDBugI0wSM/jL9wvyL+8D+vQPhA38DJAQlA9L9v/iv9mT6vAK6BrwFbwAJ+/z7AASZB6kDF/31+Kz8rP/uAscHNwVX/qr7Jvls+On8bv+wBKkJfwaAAXr/Ov3n+pD9VQAC/7T+eACZ/47/UwBo/8sCHQVvAf383fpm/H8CyQc/BJ392/rj+c38nAA2ATMFRwcQApT+nvyP+jP+lAHeAHIDRwOa/iH+h/6q/tYBJAUJBAz/p/hj9l/8XQMMBtIEtgLd/ir9W/2O/c0CSQJr/0UCYAId/Bz2l/dXAGMMHA0LBLT80vvk/X7+FAIEAKT7C/3R/u/+CQB/AOECSwe3A0T/UPrw9HH4+wJmDNALLQKR+df5tv0VAFgBBgF2/gP8Bf7HAlUF9gSiAdj7EfwE/8MAjgItAIj9pf2i/X/+ngLoAk0BsAAt/pL/4ALfAa//2/89/ov9FP5V/ZEBQgWHAysAs/xG++39qgPbBh8CyPzs+rv6y/+gBgIGwv+A/dD9Q/4tAc3/U/5EAngAOPzb/S7//f5sAU4EAAS/AeX9uvsF/dz+zADOAV0B+P/z/mH/LQHkAzYDWv98/hL/2v7r//L/3f6+//MA2ACUA2cCufwx/Jj9n//6APwAqP7D/l8C6QPtAzP+6/j++dP+gQJFAb0BlQI0AiQDHQIs//z8f/qG+rD/UQPdA/wEDgMa//H9Gf0b/bH+df/Y/yUDEQLN/SgCAAWkAjkBNv3F+5P+mvwR+hz9LwGiBVEIswUWAGn8WPtd+jr9xwK4Ao8BnP9d/CAAKAKZ/kz+KgDg/Qn/HwMXBEcFYAEz/v//if60/OX+LQFxAX0ChAKQ/oL5TPka/Z4DeAdIBeQD9AH9/L36tPsQ/Lj/9QPlAkz/rfwd/Jn/ZQV5Be3/pvva+yf/UwUNBuQAdf8K/uX8JP4n/Sb59/vkAmEFNwgtBqX/Mf6Y/r79L/+8/pv9E/8W/4MBXAa9BckAZv0N+Yb1JvlVAeMIdgyrB+3+Pfxk+6z6Hf+aAWL95fzfAIwAzf9m/xEAEwS3BIn/sv3fAA4B0gBDAZz/yfzI/eH/Rf8AAGr+Vv7hAXMCAANnAx8BKv0k+9378f9BA6cB7AJxA8//x/x9/YT+qPxi/U3/XQFwAh8CXAGpBGAHIALt/Y34GfWl+ucBAwWVBUMDX/8h/4L/G/9Z/l7/7wAKA6wC7/vi+R/+awMVCEsGe/3m+cP6LfuPAXgG6gNkABz9bvp8/ncCLAIiA6ADAAAA+3L5V/sQAlsJYAkcAqn8tPgD90L+OwSYB8YHogHN+UL43vuo/u0CmALv/8QAoAF8/x/+Dv7w/vABxgAYAo0Ev/9z+fT4Af+IBV8IJATC/pL8bP2SAFED5wLP/I36ofxD/1ME7QNp/+/+Kv/L/oQBqf6Y+3IAVgKXA+YDZQBU/RD8cfz7/f4BqQKvAAgC7QOgAOv+Yv/v+wP9dP+s/sMAjAJ7AasCnQOVAGf9pfuu/SsCMwJL/9f91/ym/Vr+BgLaBrwGLgW5ADf8z/kC+F36NwLrBPgCCgSM/+b9BgDz/T7+DgGvAWACRgTR/yX7X/wT/Nb8SwK2A/MBHwMdAmgAGQEN//b6TvwHAMMCcwNdAjICXQC6/Z37v/mQ+RP9/wIhCbwLGwaP/Mb2CfcE/FUDKwecBqgDz/73+eH5Yv8ZATcBDgKMAC7/vv9MAAYBrwKEALv9e/6D/6f+pv/nAHMAWQED/zD7GfzSAG0EsQZbBUcAN/6H/B77N/0s/tD+dQLMA8UDgAQVAOb5UPkQ/cwB8QgvCmcB4vqc96z3gf5YBXkFCgM3/+D4d/oxAQAEPwUKBFMA//2a/AP5avuhA6MHzAakAFz4WvcD/3EGAwybCdn9uPUO8x34wgM7CmYHzwLC/vn5Jfkg/RICBwMSAqkAbQBSAvcAXf7S/jT+NPwN/xgCHAAH/pD+SAMtCmoIsf9x+JHzWPZ0APEJSQt/BOz6pPeJ/C0AVATRBdAAb/2L/bv9AP86AVAB1wDu/zAACwBm/8MAbgBhACX/vvyX/TwAxQD9AU0FnwI+/3H9hvoW+3L8WwCaBwkKQAZR///40vdo+Yn9DAT9BrIFwQHc/UH9Tv4K/Tj+nQFPAkAFYwJu/AT9ef0W/lMChAPWAMz+o/va/D4CHAWXBLQB8vzk+NP6lwALBUUFiwJw/6n9Q/vP+eIAKAdwBeQAoPzE+xf9RPwr/m0GwweyAn8BMf4Z+zL8Wv3FAKICy/+C/iUBAAOfAMb/wQAf/3z/sgEh/2v9vf33+7UAdwY/Ax4Awf/V/R3+7QCQAKMAGAJv/6L9qv6U/uT/PAFDAF8AdgE1AAP+5v1n/gsApgOGBdkDTP6h9732uf3rBWII6QVP/374KPoDAvIIsQgnAWT57Pad+Y79CQXqCbAG5gAC+nf2E/hq/aoFSwpKCHIBkPnX+Lr9EgKWA90AkPwg/Gj+yv9EAyIFNwTWAYv8OPi3+Ev/nAYaCtMFn/9n/Tj6dvpq/fX+uQFxAo4AGQTmBSYAj/zJ/BUAIwMFApX98Pt9/ff83f1SALsCoAW5BGH/7Pxt/0L/5/6hASEAvPx++m773wRWC4IErvtM/IT+Gf74/YP+pAEJBPQCWgEKA/QBWvzy+wAA1gAO/2v9dPxAAAcD2AEOAn8ByAGDA/0AVvsy+V34yvwLBHwEXgMfAnj/a/07/2oCGASSAwsAa/ub+PP7+f9iBSMIXQGG+jn6tP7ZA84GkAQKAd78Zve09ib8HQSgCCYISAX5APX5qPbN+ar/ZgVuBfED4wC8/FL9Yv90AvIEOgG8+8j2EfWE/ToIfwyMCa0CwPxa+tP6qfv2/QsAlf+9/sH/sAHsBbEIsgRO/9r7afrI+hL8F/2SAXMGRwb3BFgCXvt79ob64v9SBOsFTAEc/Uf79vx7ANAE8wcPBer/D/vc9sL3r/21A4gG3QZBA8r9vfuJ/MH+W//hALoDvgR6Ae77I/yiAF4EEQHB/DX8q/r3+7QBXgfQCQoJVwFZ+b/1APhqAKkFcQfNBPT+mPgC97f8jgIOBE4CEgGG/9kAcgFuARcDpgBR/kL9gfom9xr7mAKOBeoIvAkLBSMAn/jF9F39GAOqAc0BSQCJ/lj/EwAwAQMFOQVN/mX5xfdE+J3/fQkeDU0LxAPo9CTuIfTh+74F1wtcCegFYQHg+cH4s/2LALsCzwGg/fD7LP3zAU8H+AXp/1T6pPh4+rD9wQQ/ClALSgbW+dj0l/aC+YoDUwtnCU4Elfw29Ar3Jf/UBCMJmgV2/2j73/rd/eD/MwLyAWAA1ABD/a36af+6APz/lwICAh8C0QFa/pv+PwI8Au4AIAFs/MX3mfqGAdAHNwgVAsj71vlr+gT+iwejCzQFuv7F+vf5MfoL+mv9vAO/BuoEIgP1/XH6JP1UACACJwIQAEn+BgF7AYb/owHn/+v7sf1x/er6BgFVCKAHzwNM/Tr4kf1/BJ4DMQJmACb64vmm/hMArgH/AfAA9gDcAvAEMQMT/935w/di+j7/pQSxB/QH7AKe+/X4PvvAAKsBAf51/cX+cwOnBQACCgKEA4T+Qfmb+fz7HQIZB0cE0gGfAFP6BPjY/ooFhAd4A7z9svuH+1/7vP3wAtEGjAalAp394/lo+3n/SQHvABH+g/y1Ar0G3ATbA+L9rPoB/Dv9av9qAIMBdQG8ApsB3P++/UL7PfxE/0UF+AeLBuoA7Pmr+SL7XPyAA94Erf9nACf+ff+WBD8BB/6q/9D/7/08/9r/1QCrAjECYwAf/rL7PvpF/woFSQTPAv0C2gHu/4H7Nfm+/bz/j/4jAUwECgOAAoQC0f+a/yL/S/2+/d/7iflz/QUDpASlBB4FsAMS/8X7z/qZ/UsBLgKRAdb+3v0s/u4AbwSyBB4EEP98+PP3D/+KBqsIBgPN+1f8Dv54/3r/A/52/x0COwLfAAD/tvxZ/uD/tgHZAg4DxP9y+fD5n//DBrkIggO5/E38qvx8+zkAOgMhA0gCvQDZ/Pv8HP/o/1UDXAMhArL/Hf3i+hL9wQNrBKgB2f40+4r6cv9wA84F6AUhADX7OPs8+7D9LQVWB7wCB/5I/YH9eP6D/kH+RALeAqQArQGAAgP/Rv5w/1j/wv+J/UL91QD/A54DLwLH/5v8yvuu/QoBjQNOA/z+SP+lAg0BD/6n+5P6IwDvBCkDdwKUAKz+Rv2I/E38jvy7Ad8GHQjGBMj9iPdw+Z7/BwMIBXIATvly+u0BvAZ8BWwA/P1v/in+8f6IAXABEgFNA4kC5/64+Of2YvwQAqQFyAf9BjABQ/xY+6b+zQGlAmgBTfyO+NX4w/7NBY0FogFcAaYA3P4+/3r/LgGxAwkChP12+lP3kPmrAUgJOAxKBkb9qfbc95j+1wM7BikFVgBW/af+Pf5eAH//Qv6+AjH/3PjC+ikCHAkPC7kE4/w4+D30v/iAAl0JgQhAAkz/bvzw+ED6xf1kAVYG3AQ8ARYAkP2w/gkBjwD8/5n/X//1AKD8n/qHAdkDBwUWA0D9ofsI/zQC0gPaA0T9Hvnt/D8DdgStAnT/oftC/zIBVf7D+0/7VP35BE8LPggnBOH8svY49ZT4YgIoCvMIZAHm+Sz4Yv5FBMcFggOE/gH5XPYB+zkGmw4nCycDFvzh+Kn3QvYb+4sCIgaDBTwDBAACAYwESQPEADP9fvkY+VX7eP6ZA8IHqgWcAFX8JPqG+87/WAPUBWEFLgAM/c/8Nf03/5gAtABAADMBrgCU/4QAzvxi+w4B8wP/A7IB1PzE/UQDRwQZAAf/oP64+T34M/v6AKAI5wvKB+X/XvdH9dD8TQQYB9MDWv6K+TT6fAKvCPsGA/6+9x/64v4u/38CBQUKAggDLv8w+j38LP+OA+8I+QIs+AX4+vpm/wsFUgb5A+wBa/8t/a//MgG6/hX/ZgBq/Zj9Av5b/qAD8wTWAikBmv4e/cv/TQGz/9T+ff7H/3sBGv8e/XUAEgJOATMCLwM1AT7+2fsT+SL8XwLpAgIE+wVuAN38jfwg/pEDRQP8/UL82v2J/qkAFAOaA0AAGPvS+sH92AMVB6UHMAb3/9P4WvWh+IQAvgcZBgIAm/sF+rX+nwQ6BykHmwIo+2/5Z/rc+3z/UgAvAI7/Pv8iAg0F+AWmA2X/O/yU+dX8jgOlAzkA+v5n/rv+fwHFAaMANv8Y/UwAdwQ6Az//IPyA+xv9DgGdBdAEtAAX/j78EP38/Jb9eQLeBNEC3/7e+7j+bQTWA4QAIQA1//H93fwl/Ij/bQQAAx3+qPuW+7z+WQSoCIgHAQNv+9D1U/vJA5cFMADi+LX2gP4jCBQJYAZ/Avz92/o/+zn8iP5cAuYB3wGHAhIBav44/sL9r/yi/YP8kP9mBNEFjQWOBL4B/f4w/rr6TPik+W7+4wONBsAEDABi/w8AjgGyArL/H/oU+ZT/VQSiBAcCCP7j/D3+wf/DAgcETgHw/t380ftH/Wf/oQJgBdMDff9A/cz+jwD7AOQAUP3T+pj91//UASUEJgTOAvsBhP+W/Oj76fre/UgEfAfuBCv+F/oL+8L8P/5rAhoEVAGMAD0B1AL/BI8DBf0u+OX4APw/AC8DDQNuAcsBeAAg/3UC3wHt/kH/mgCMAGb/aP1v+4/97//YAGgC5QL1AW4BdAJ5Acr+xf3o/D7+GgFSAFr/nv6+/g4C1gLeAdYA2P1v+4b85gCPBVMFSQDI/Lf8Ov7//fT/jgNlAk8AVP8R/oD+xv+4/poA0gPyA+AEkAI7+xj3Z/r6/7QD5APXALf9ofxU/SIBDgc8BjQCqP5s+8H7Df8zAq4APP5j/Pz8rv5I/xUCJweiB7MBQv4k/Jj7C/+kAHv/LAE3Agf/N//K/W38EAAYA1QDBgOkAi//B/2C/Rr/twDBAWb/S/wV/0oAhgBEBFYC0/1j/uT8VfxnALkCeQRrBgwDMP07+xj6kvuBAG4DqQEVAIcBHwD5APECmgAB/9L+rvs//d4CpwIUA3EBc/w0+7f93QAQAzEFQwNs/9/9+fsa+xf/vwDGAfQEUANj/xL9J/2S/Y/9Vf7SAB4EWwYXBRUAdPwA+hH8oQEFA7MApf4T/1kAVQBLABUCSwESAPMBIQHf/TP7K/sp/9EDrQRoAbn/LQHGAOL+6/yG+uH9vQLhAH4AogIbA2cDpgDo+6L5DftK/oIDygYiBakAzPun+ib+0QSqBfQB+f1M+/n9sf56/+0CAgM//9H+AAFYANAAAAEj/x/9zPy//ZUC0gYQAnz9vv77/sL8vf7jACgAhf/Z/Sj/lwPgBOkDcATj/2b5h/gq+yH/AgBCANsDigXNAsoBFATyAZD8sfvr+9j7xv2t/UACnwvqCbr+efdk9JH3pQKACC4H6gRJAMn7zv7VAwQCr/5P+/H2q/gY/4MB/AN+BiUEzAPVBNsB2f57/E/4u/jo/cYAmQKfASz+tQC1BkYGNAOAAVr9Y/rX+fL7rAEaBeoCWgBVALv9JPwa/1oBWwBmAG0Amv7zAR0EiAIlArH+B/vm+7r9ifzu/lYEAQY+BO4ATfzE+Gb7MwGMBn0GQgFh/NX7XP31/Ov/8QFrAqkDkAN5Ajn+9/ro/CYBZwMkBKYALPsi+1r/PwIWAzsDr//D/AP7I/pLABwIpAdcA6v/MPpU+Fn7yf9mAxEGhANO/kX+AP49/xICewFu/hH/V/+x/Lz9oP/lBNAIYAZq/x360fkq+uD+AQNPAt4AMQJRAdr/ZQGX/8z+z//K/pD+wQDQ//j9LACpAAv/RgDcAPf+nAF2AkP/bv2M/Y7/BQMVA7X/DQO3BYgAJ/vQ+Xz5GPuj/bb+WAQCCa0KHAsiBJz4gPTZ9737xv6DABUD3wEQAEz/aAHPBTEC3v3+/Pf9yv9lAWYB3gAAAWv+D/0L/Zr+jwIMBZUCS/7v/J79F/8aAAAB2QJDBScDL/8T/lz6Pfgw/G7/ugLTBo0G3wIwALX+Of1M/+j/h/6O/mb8f/zxAVoHRwZNA/L/kPi19pL8tgDWA7gDEP+kAP0DAAOPALr86/pL/n4CaAG+/tb9xf7lAcID5gI7AGn9H/wv/mgDXgV5A9YAE/xt+aj71f3b/tUB5QJKAwYF9QDR/Y//BP/R/L3+iQAr/47/RAALAusCigLpAR0Ct//m90j2I/3aBJ0H3AZiBNT+2PlZ9+z69wL5BVcFowM3/hv6Cvp7/bwCuQb/Awz9zPqT/mEFZAezAwj+JPtR+3j6G/xOALUDCgWMBdsBHv2k+9n7oAA6BHMCvf9V/g790f0//+X/sgHsAtgCZgGL/av5YPzlAZgEVAUaBXICc/1/+9r7cvxX/j0BgQEBAC7+PP3PA5IJ8QZO/3/5nvfy+Aj/RARWBUIDsgLuAGz8X/u++qn+YgMkA7oCawJIAbP/sAFaAzMAm/pe+Pn6cP3KAHUECQe4BbgAIPwb/Hb+mf/cAdECjgOGAI78wvve+6j/OQLzAZsBwAIsAFP9of+NANn+sv7PANQBVgT1AZP8h/xv/e3+JwH3AkT/O/1sAXoFtQbgAQP7tvbO96v8nwE5B6sHswJzAO39V/mW+M/+mQceC6wEqvy5+1X6Nvm+/P4BLgXrBBIFKwQ8Aoz86/br+ET90wDtBMEEbwCcADMCcv+E/UL+wv/jAKb/8v7pAMkC6wHb/R/82fxz/iUEcQYpAvz/9f5e/C/6vPpn//UD+wXHBJsDwABk/Fb8xfxW/UkAJgSxBG8C3P2A+qL91ADFAH0ARwBc/Uz8/QCFBvMITAQp+xz3z/rM/s/+aQBSAuMCFARuAcz9Vf3S/6EB0wKiAyj/t/vP+r79IgPZBO8Btf5p/W76F/zdAUUG3QaJBD0AP/xO+u73fPzcAUoDmATRBBgBSvwH/2wB1P4P+/n6nQHZCdkJUgJ4+9f1GvbH/KIEeQZsAXD/4wEgBrUHAgJP+Tv0HfWZ/E4GLgp9CFcDbPyx+IT4L/3/BHsHdgV/AT39fPlU+Sv9BQEVAwIEXQMz/2/+s/5SADQEYgJ4/mT70/qu+9sAXgZkBqoC8/zR+478BgDvAa0AGgMQBE4DTAHx/Fr5yPrm/If/rwOgAhgAl/+bAigGUgVCALL5b/hR+WH7RgDxBHIH8AdHBSX9tveO97j6ygJpCOcGMgGq+/z4Xvy5A9sGLAQYAM78w/o++zL9iwFqBrkEoQFZ/6v7+/uWAL4E4gSBAM/7aPuv/YT/qgGZBL8E5f5b/Pb85P2kAF//QP7BAVEFkAT1AtX+I/hm+fT8Wv9gBKEGHQJX/9sA2f/C/6v+PPvV+2cAVwKQAn8E2QJJAJ4AUP6n+pD7XP3d/9YF1QceAwz/cvt++ev96P+0ACQE/gORANT+o/7U+837KAC0BEAFzgCc/FT9KALIAtcB2gFU/WX3GfloAGUFGgdDBcoCu/52+FP3sf69BmUINASE/Cz3RPbZ/VEJhAwjCLP9u/X99Y77GwJlBVcGRwUuA5f9P/hX+Lb9DwSTA70AP//K/kcBMgSWBK8C6f7g+Wn5bPsD/lQCxAOMA14EVAOp/1L7qflS/uAD1AN8ADL+Jv0L/Q8A4gNPBVkEzQFW/ff42PYE+h0DiwgdB+gF4QNG/GD2yPiy/5UFKgRI/rr8lf5A/wkDdAfYBC//KPqL9t/4mQAnBjoJtgeWAMj72fqj+fH5bgCJBOoDlQKZAJwAYQF0AOj93f5D/u36o/2/AUkCQwP9BJ4C+f91/UH6HPqu/eIBHAVoB1YEg/9d++j3YPlvAHUGFAY9BdgDpf+M+an3O/vlAKYFewMdAFb+rv5hAjgGpATT/fj35PZB+2QA2gXnBjYEfAHh/Rv8Lfvs/Jv/swJDBeQFhQLf/Ef6N/rw/ggD2QTFBaQCYfvA91X8vAE3BsYF/gFz/UP6lPoM/lME4gQ8AFv9TP7C/r4A6gLrAScB8/xH/bIAhv89/8oAtAG7AhYEgwLs/fr4+vlT/7YC9gL+/zz/of+S/qEB3QZHBdf/hvx++774Vfe1/DIFagvZCPkBNf1w/Gn97v0kAY8BMv9L/ij/sQGFA0YDYf+L/XP9AvvT+hf/QwRpBjEHEgQ0/c/4tPaI+toB9AWMBsYDzQBa/tX84/xo/vj+VP9cAXkDCQRKAdT9e/wW/6oC8wJgANv6H/iu/TkHvQn7Azf9gvjW+Fv+mwTJBgEEAwBS/Dv6CvtD/UgD2ge2BqQDIQCu+7b3kvtWAogDVgBc/rf/zwCKAZwAbwA5Afb/9vyJ/AL+7v58A34FbwNdAKP/+P7T/Fn9Yf1B/gX/MwFRA+EEZASZ/j79AwBEAE7+8P1y+4z5Nf7pBT0KDQeWArv83vgR+Wj7dwHgBqoGnACN/v/8tfqt/RIC5QIIAkYCp//6/0kBv/92/un8/Pu0/DcA4QIDBOADrAIDAXv/gPyD+Gf6JwCwBZUHOQWZ/x/6bPje+v4C7ggQCGACSvvA+Mj7LALLBI0Cbf/d+0f7YP0y/+gCgQaBBXgCPP4G+vP5v/vL/i4CMAO6AQABvAExAuIEhwXSAT77EPcY+Pf5hv5aBGoJZwhUAnv90fwA/2r++/3b/qn/zf6M/14BOQAJ/l39+QB9BDsG+wMv/+P6VPnq+3P+YgOWBpcG3gLx+z/5tPwyAbgAqP9CAMUAqwBPAFYB2gKYA33/n/qJ+YX8DgLKAhkBJwKQAwkCuP34/XgBNwNVANr71fug+tX7BQE3BhIJLwYnAtT98vjw9fv4sAE3B0UG6QOlAMH8zfsI/Dj/fwMNBPX/yP1k/ob/OwS5BVUCvv3f+rf4O/lQ/14FTgmzB54Amvph/Mz9G/0TAS4C/ADwAH//9/uG/SsDPAUeBL//6vuv+nD7JPyMAdYJDwnRAWX62fdy+jn/kQRRB6IFrAAY/Fn4ofic/2kFHwbsAxkAcP5A/Sf8BP+FAswCwf8H/5cBvABt/sT/DQDi/O38y/91AWYBPgGmBSQK8wQM+4r0AfVr+bj8YANJCUkIFwPH/rD9cf16/db+OgE4Ao8Bzv+4/ur9qv2B/54CxwPGAVEAV/6o/58DwwOB/1v6z/nP+kL97ADpBbsKYwcTABj87/km97f3tP2QBfwJ9giHBBX/Qvnx9wX9UQAwAEQAwAJOAnP/kf/MASgDSwDj+yD7KP/S/+H/igKEA30DAgBt/Kf8+f8WAtgDSQMcANH8RPpm+878vQEWB1oI/QWE/7r5mPie+mz+gAT8BXwDBgBw/Db84f6FAFr/xf7i/7ACeASjATv+qf9YAN38cvtg/hAAtP+ZAhoFtgPj/oX7Ovx6/84CYgQCByMFGP6095b2IPon/zkFIwdNBNYB9ACfALcA9vw7+Vj6Yv7vADED6Qa+BOP+WfpT/Jn/JwB8AOkA+AMTAhT94/yzAAgDygK6/pD4U/cP/ZsGqwnTBjkBWP7P/VT9iv8jABgAQv2l/OwAAALZ/pH9dQDoA7kEXgEZAKwAgQEMAMz85vqn+U78tAA4BIwEGAN+AhgDZgJd/vj5q/Zc+RoBRAa2Bp4F1AGd/NL7LP7nAID/v/oe+48BhwYjBtEEkwJf/lz8AP05/YD9pP4YABQD9gSGAqkARP/A+ZL3oP0ZBEcHngUsAj4A0fxx+Ur6JgBYAxkD6QFEAMj/D/7k/ML96gCWAS8CRQSnAXz+wf8mAnb/1/s6+Tn7gwGUA7QE1gVlA+T88fq6/X//qwBNA5IEEwLE/xf83/o7/Lb+egPwBdUD5fz8+dT9LgLbBcAEt//g+pn5Ff1FANYDMwU9AvT9Svpr+wsAmAMGAx8CbwJuAWP/FP3d/f39Af1B/XUBWwbfBkwD+/5o/i/9DvzL+vH6Ov+FAxcGEQQ8AHz+pgD0ARQAtv8l//X7cfrr/ZEC8ASBAsD/0QDTAW3/iP1L/1MA4ABUAJ7+Q/yX/QYCnQJDA6ADPAGd/WX7hvv2/ZMCygIaAoYBJ/1E/NkAQgVsBMMBdP/D+/X5rfrK/q0C0AOMAxYDUwNW/2j7gfsR/QYAaQLDA1UBqvvZ+gkA5ATQBcsFggTd/kz59/fH+7L/ev/X/xoD+gTWAYkAyQNQAzv+QPsF+2n7v/yK/58EAwfXA4v/Dv6t/Rf85/zZAO0BUACkAsQEkwLh/VD7Ff6l/+v+4/26AFUEcgEf/7MCcgNv/0T9UP3d/Vn8D/yFAEcHMQsSB1L/hffb8m31Sv8eCI4KjAg4AaH6tvfp+t0AxAIRA8oAPv2/+0v/zgbLCnYG8fuH9Ar04viw/4MGAArjB94D/P8x/vX8yvwq/tf+UP8d/4gA9gBl/rr8rP9ZBFYEFwJ2AMUAmf9E/Qr/+gGrADD7zvm+/GEA/wOTBiEIcQQ7/6f6LfYr9qX5RwIeC1gLegX8/b74pPg2/lIEPQUhAu79xfrk+/kAhQTxBP//bfr7/FEDBgVOARkAXAC3/gP9//s8/+IB8gBT/6//hv9t/kgBWQKAABf//P+gAnQCHQC2/kf+0ftu/E0BiwPFASb/ef/RAAcC+/8h/e3+FAJcBJoDuv0t+O760ACHBD0FswG2/FT5Vvo7AegJAwlQASH8Cfqe+73+JgIGA/wA+vyv/EEBiwOnA4UCGQCz+4b5evzlAUUFXwPzANoAlP9V/L/9jwEcAcb+Wv/WAVQBPv4E/W7/bwD3/eP+XQRGBUUCSgEJAWP+LvlV97D8cgWOBp8CFQHiAHP/g/wD/F/9cQH5A8ECHwFi/479uP37AHECiAImAcT+v/vY+2D+VwCiAxgE0wMMAQP+dvzW/HgCfgSpAaf8d/j/+L4A4wiRCTwElvyl98L3TP1OA8UHRQdvAU3+Bv2i+h36xPzlABkE0wN6AyAEZwEg/VH75f0kAA3/Y/9aArMEegPY/6D9qvzY/CT+LQCoAbAA5v6gAOQCyQFmAGD/iv3s+ov7Vv9NA64GugbPA2P+E/qG+Lv7eAFIAuABSwNOBNEC/P7V+0z9GAC6/07/oABLAZr/1f8ZAcIB8wDP/Wf8dv3N/vv/mwL1BfYGwAP3/QD4Wvaj+oIAugTTBYsDVAAq/8z+7f02/mcBpAJBASEAaP///v/8f/1t/x8DawQSAuf/kvwY/eL/LQEj/0r+VQCfAs4E9wNdAZ79pvnK9i76JgAXAzgFywYOBrEDmgEy/X/6U/hE+ej+SQJ3AsAC3AWuBMgASP1c/Kr9i/46AOcBuwMUAFX8r/27/3gAfAByAfIC0AE1/b/7bv5DAqkDFQNhAZP9afth/JT/fwGoAfoAUQFkAR7/kf1h/iUBjgKgAVYANf8I/s/+5QGcA2kBvPyd+lb76/zi/7QFswqYCJ4Cnf1O99HzZ/irAGMHDgeOAbj/jgE4Acr/nwAt/4D5/vbf+7wDCQhaB1kDeQDS/0H9+PsD/Nn9HgEtAYkBhwE9Ac4ASv///dH+ZgAEAPkA5gAX/9/95P9lAtoCXwIm/9b8pPwr/0sA0QA0AFb/9QFOA70DJAFO/s/7GPos/MQAZgWOBAABR/3Y/DkAHQJtAX8Bd/9V+yL9kwCWAmUC2AF9AiwBLf55+UP5kf/0BrYIuQTO/av2Evam/HIF1Qn5B4UBMfv0+bL7iQDfBUoFNwAc+1/4qff2+iQFkw2lDGsDK/rc+Cb7hP0u/68B/AGD/gj+kgBMAVr+c/6zApUFQwQzAZz/t/zO+vH8tgLiAiX8/vgZ/iEGMgcrBekDSf+s9wP3Sf77A3IEMQGSAD0Aa/0Q/SUBfQTdAsj/8v5H/oj7yPuVAF4E4wI4AI//i//c//3//QDGAMz+5vw4/6UCSgIEAZUAcQCq/FD6cfwnAW8FKQXJBHEDQf0r9s32hf6nBL0EYQPPA5MBYv33++f++wA+AFr/z/6R/63/vP8UAwAFDwEN/fP8FP3j/PL+IgI0BSoFWAHw/Vr9jf1a/jkBSQN4AsX9e/qT+xX+GwLGBIcFmQaTBH79CfdZ9lb8pAKHAkQAOAK2BqAFV/8D+5L7Xfzs+/v9OwKHBrAEiAFVARwAzv1b+9X7Dv5FABACiAPFBHADuQGQALT8h/gc+VX9wgCYA94HzQiaBH39c/Zv9Rn7zQEoBlcFRACR/AX+lgJgBVgFcwDg+nj5bfpO/goCUAVWBQcCD/8y/U3/WwFxAckAtv5G/Pv8kAGQBGwC5/wH+kf8ygBHBPkDywFR/+38W/7aAZYDDwJR/hL8Cv1qAIoB2wBKAToCWQKK/zb8Mfxu/8YCRgM2ASH/DP7Z/Uz+ywAwAvf/9P1D/4oBjQJDAmX/8f0P/W/9eAC1AaYC2AM0BaAAqvkq+Hb8PgMOBAABt/zl+wn/ywN6CGYHwAAM+lX4kfpBAJwE3gOPAEv8Dfts/nYClwNoA74DaQL8/dH7FP1t/1oANgDCAcABzv5Y+3f8GgHWBdEGAgNc/R/5qPnu/EIBIwPXAxwD+wCZ/83+BQBW/2P/0AAAAfr+Bv3e/W4AkwLzAUcCKgBO/FL7Wf+fBVAHhAJo/GH6r/i2+oAAAQcmCaYE5/+d/B38GfuB/OEAzgQgBV4BBP95/VL+pf/3/7v+wPqC+Tr/5QYJC58JZgMs/YH25/So+VP/tQL7AqQEqgQ/A/4A4/3C/v//Rv8C/nn8T/79AiMGrAQR/jv5Ifma/IgBKgbcCKsFi/7m+Rr88P5i/tn9pf9nAosBiv+wAHEC1gCN/oL/9v/+/sz+KgH/Afz+ev3u/aT/f/9u/2IEVwYWAnD8q/uA/T3+wQAXA5EE0QKP/7X9OP2t/Bn8yP/0BPIF6QJbAN788fqp/scCmAN1/ib6GvsK/zICgQJDBIIE9wD2/e/9d/8i/hH7/PssAeAEggQtAyMCGwBK/UL9wv8zAZcAZf4J/uL+dv/WAOoBuQI8AY4AfwG6/wH+xf1S/bf8jf0hAPQCLgPhALD/BgDU/7b/SgEfAugAS/3Y+tb9twLXBMoCgP+r/Zv8efx9/jACIAVIBlIDj/5C/LP7O/w//40ErwbvAWL5y/Uz/DcFkAioBZcBKP98/O74mfmB/psCogQ7BM4CxQD4/eP8/P6JAUMB/f6r/Xr+L/8+AuUEKAPFAHD9x/qn+1P+TAHaA4gEmQJkAOD/a/7q+rb5zfynAigH0QZZAsL9AfyI+3H+zwIrBDACc/3l+hr8JADmBBcFKwEm/ST7CPyM/mgCkQXiBFIBpP1B/aj+5v77/rP/HgGmAcQAqP9m/7kBMwPAAMb9TP19/kcAcwEJAXoAjP7W/H/+lwHYAuf/u/w+/kECAwPuAOz/HQCg/5r+NP5m/hb/3f/LAcIDEQKv/oX+MwB+AdsDGAPf/iD8bP3U/27+BPzp/H4BQQWOBOMAJP4b/WL94/9/A+YCMf3S+dL7aQInBj8ELgAf/WD8DPwPAGgFZAfGBOn+8Pv5+kX6zPoOABMHEglTBN387vnK+8H/mgMRBasCtP26+tX72v6UAVcCrQGc/7P9wv6qAmAFQgPD/1b9kfu++ur6mP6MBDMIuQfSA6/8MPes95H8qAFgA3wDGATjAqf/nP/2AJz/Dfwc+vH9pAOkBLsAt/9MAV8BG/8G/dv/SgNZAtj9IfsK/E3+fgE4BNoF6QTJAGH7e/iE+kf+awG1A3ADxgIGAjn/uvxW/vYBJwL+/zD98vt0/W7/cAJyBqsHQQKb+7f5D/uf/bUBvwTcBCoCO/12/Df+7P7u/08C8QKD/yX+SP95/yH/3/5Q/9//hgAFAisELgQDAeP9qPz6+6T8Nf9uAXsC3wFPAJgAvAAh/339fP2N/lT/CQL9BMcENgE9/tb8APyO+4r9RQMKB3MFEwB9/C37Gvsn/twCZgckBnkCdv+T+yv6m/vR/g8BQQGuAPQBNQOHAUH/Zv95/4P+Kf4u/pr/NwB+AacC3AGf/qX54PlV/0QGgglpB24A6vhC+On7ff+GAZ8CHgN1Az0CEwD0/i39a/0//8UAegEXAPf/sQA9AaoApP6L/UP95P8BBJYDaQG2AN/+sfto+UD66P4ABAcHnAb9Axf/9vjV+C7+HgOPA1AB0v8WAPwB+gHk/x/+Qf2J/bP/+AGhA9AEJAOH/VL4qPiN/YMCFATAAxYDgQJTAIr9xvxI/bT+bv7H/ysDFwVJApD9PPy6/HkAFAL+ACsB6AGXAZP/8/6r/VT9cv2q/cv/5wKYBLYC9wB1AFsAPv9S/Zb7/vwGAQUDqAO5Ab3+Ff55AbMEYwNx/wX82Pp1+uz8cwF3BagGmgOj/9n7ePlR+zj/uAEAA7cCLwIrAtsA5v52/Tb8LPzi/tYCYQSeATz/kgCPAkQCdwCH/a78HP4b/yIBtwEdAMT+eP+yABUCUAOUAd7/+v31/Hf8KvyE/SH/KgI0BEMFLwQnAkf/kvtK+yP8Mf4kAWgC1gJ8A+wCDQCY/br9hP5C/Rz8Sf6sAlUHgQgwBND+Bvnn9Yz5DQB2BGoEHQP3Aq4CkwDy/CD7bvyY/94BgwJtAjYCJQEt/7D9NPxV/Bz/5QDbANgBPwMtAmwAd/+8/nr+OP7b/u8AnAEdAFj/5gALAssABv5Z+wX81ACrBdMGCgNz/XD6Pvps/aUBTwS1BM8C1ACL/Xn7r/uh/ZAACQLEAhoCdAKYAtMBDQA6/eb7Y/v+/G7/sAO9B98F1gDD/Of6svls+gH+NAPwBfQEGAS+Ao7/Vvpf+B383wCIAvYBkwJNAbf/U/+t/7gAQgD/AIsDfAM1/4P6Avrh/bEBxAIQAvsAQgGyAd0AlP+s/ab76fvj/kIBJwO+A9YDNAMg/wr7xvhS+uj/3gNuBIACewGbATcBXgCB/D36ovyNAMEDlwQgBIUA9vy7/KD+ZQEkAgEB5/6r/SD+cP+iAG0BbwKHAnkB5P8yAHsAQv6Q+xT7//xE/wEBogK7BTwGCwJP/aj6WvxyANoDDwMu/jL6d/pIAB4GewbVAbv8o/v3/K//mgKIA14DkAEvAKz/tv1H+3/7Af8oAfwAtgCTAoUEKgNkAfv++/zk+wX8Wv4HAP4ABAI6BCMEcwAS/GL7A/6R/3kC7gLWAGX/1P4HAT8DwwEP/bD7Lv0IAAsD6ANEA7L/4Px5+wr9vwCmAokDnQJNABn+N/7l/mz/z//6/af9K//aAGkCMQOSA3YCTgF//7v8x/s4/Mv+JQL2Abr+7Pxx/2gE0QedBWj/lfkT+Df7RQCkBFgFkAP8ABb++vv5+tn7Kv+gAzUFvwKXARYCdQFL/5P7Cvo9+9z9HAHfBHEHQgbuAs3+Jvuw93D3gfyRA6YHSgZRAw8COgI+/777oPnj9xn6Wf/eBUMICQb+AngAVP///D37mfxh/0UBPgLoAlIB9f7L/ZP+GgAyAAYA9v9hAGMB9gD1/yv/Xv8lAJAA6wDX/0D/ev80/pj8FPz7/SsBGgRZB6gHAwR1/WH34Pfp/DYBmAKdAusDwgMFAO/8kvyj/Qf/agDcAfQDPQW6A+IAKP1/+Nj1dvk+ATQH/Qi1BRMBJP55/V795fzH/IH99P+AAuoDegOxAcL+JPzx+9/9WACuAjYEIgPOAUQATv4N/Jf7rP45ArsEcwPPATUAbf0q+4/6wP3FAdQEDgY7BeIBy/z5+Q/68Ptt/gcBqQNIBXQFGgPS/kj7k/mT+6j+nwGyA20EwgSsAbL+IP0B/Lr7Kv7wAWUE2ASvAQb/tvxk/BT9cv2kADQDLgU9BdMCXv+G/HT7XfvT/aMBogF3/6D/NgHfA84DqgGG/7L8g/zl/IP94f7zAFEDpgLp//r+EQFgA+gDAAET/Wn6Ofpl/nUCigJ+AdgBkQL2Ar4CgACK/Fj5Ovpg/hUAMAAGAkwE2QQIA+3/QP/z/mH8pfuP/RMBiAMiBQkF3QAE/O338vjf/iwDugOWAw4EkgISACf9O/vU+yv+9f+KARIEuQW1AyH/s/ul+yr/jAEfAYf/0f2n/vEBzwR8BdEBwvps91L5ov/rBhEJlwVM/+b55fYp+ar+gQSIBuIEYQIc/4n/OADO/wD+rPvy/KwAfAN4ArYBLgFH/wn8wPox/UAAjgNJBOcEhgOjALP+ff13/QL8+fvq/G8AGQSXBfQFLAPk/yT7Wvlq+6H/ggT1BPIC2P8Q/Qz84vwa/p7/ZgHqAo8EmgM/ABP8mvqR/CX/vAE8A84DtQJEAMP+Cf3G+1j9nQEkBWUE1gBs/tH+v/8Q/7T9Ivw0/UgBcQXkBikEKQDT/MX50/jZ+xcBVQVuBq4EEwG2/HT5gfocAFMEFQQXAav+tv+yAnoCU/4I+u742vwIA54GlQVqA8UACv10+4n7Ev7mAHICuwLzAQ0B4v/z/+P/Ff/J/Qv+/QBLAgcCWwFfAO3+wfzp/EAAvQBa/pL/lwM9BWACKv6V/C79FP0D/sQAvgOuBGkBd/6W/Df8Gf7Q/hoAdgLHA18DywDb/nP/EwCF/8j9e/zH/qECZgZyBhECgfws+Jz5x/4jAzIDaQHEAc0DpAM0/7T6RPgR+Wn9aAMmB00GBQLc/h3/pP07/CX84f1PAbADtQZEBUABsP66/Nz8Lfvl+Y387QF2BowHsgZZAbT5xfYn+9ACawaEA/H+Wf50ACkC5wCt/pj8K/uq/VEBtwQpBjIF6gHf/I75ivgE/FEA3wJABREEuQD7/QD+af9G/jT9Ef4qAeYDIwQaA83/l/vd+Uf8+ACRBCgG3gZCAwL8cPeX+YQANwRXBNQBk/0M/SEAcQMVA8f+zfkF+QX9JwJ1Bt8HTgUm/3z6wPmD+zX+uwDnA5cF5gN4AAf+H/7+/rz9rP3u/4wBdAHXAYwDbALz/lz7Svrx+xP+2gB+A2sENwTQAvcAw/7k+0v8xf7mAasDNwFy/0n+3v6UAGsBAwDA/Av8dP7cAkIGAgbbAdH7fvc4+bH/HwVHBlcDav/q+1f6A/1PApsEzwMjA3YBGv9k/XD9zP7c/pH9GP7XAWEEAANYAWz/Bv8L/9/9p/6O/vr+5/8cAUEC6gDT/6j+rv48AMwB6gEDAX7/8/2l/oH/SABTAXQB2/82/h7+FgBUAmYCIQGM/4b+Pf5bAKsBQwBv/kn+RAAQAQIAPv2d/AAAVgSeBZ8C/v7D/af+xP+p/9785PqZ+1oAVQYoCAoGDAKD/Tz44vdU/BICPQb2BTEDiP48+9j7g//dAWwAnv6I/1ED0QXgA2//0Po5+CP7Bv9YAp8FrwZYBqUBcPqV9pr4C/+7BGsG2wROAT3+Hv2J/KT81Py9/gUD4QUYBRwCtv6W+1375P0GAD4Acf9jAX4FaQZrA+P+lPvS+vD6o/5cAwEE2QEFABYAt/85/mb8EP7eAegC5AHv/zb+Z/xD/R0BmQPQAg///fzR/rsBFALCAFsBuAB8/6j/TACjAFP/tP3U/ED+CwBaAd8B6wGoAnsBdgDb/kP+av7D/CX8jvzrAD4FOQV+ApQAowDb/x/+mft1/RwB3wL2AfL/j/84/3L/rP/7/8//Uv9A/4cA9QFKAf7/Jv55/U/+5v9TAFQApAIZBVkDQ/7++lX7Av+uAuECbwDA/s3+1wHPBOcCd/4x+u35Vv1iAPgBsgKnAjMCUwGW/yf+hfte/HAAJgRqBhQFKgHZ/Br7HPsZ/Rn/bQBIAogE9QX3A8IAyvtS9772u/tNAowF5wZDBXUC7f02+jz6cP1UAh8FFAXDAsX/nfzZ+0T+nP9JAGEBUAKjA1gD1wGY/5v8eflP+fH9eALWBXQFlwKM/xT8Wft2/J3+Cv/c/2oC0gUdBnACtP0N+rv6q/2iA34ENwAd/lL/YgQ2BD7/F/vf+nX98AF7B54HYwFb+Qn3NfsRAcQE1gQvAX78Q/t7/SMCogQMBGUC1v/g/T/9W/0Q/nT/OAAKANv/3gB5AjcDCgMNARf+jvoI+Wn8MwHTBPkEbQMzAxICagB//Ff5a/rc/uYEXQaWA6f/GP3L/Ab/uwJPA5UAyPw0/CD/VAHmAbQAdv7P/Ab9Jf/xAQgDzQHd/1b+yv17/WT/egMOBRQDGADx/VH9Yf4GALcBVQGe/nX8qP35AngFQQXwAkX+TfsI+4/+BwCF/tz9tP9VApkCmgK1AVQA2P5J/ygByAA1/Yv6cv2IAqoFsQO0/u77+vzU/+YBwAGF/n79qv8wAkkEZgMhAdP+FPxh/AX+QgCgAbsAjwCNALr/4/9rAU4CbwLCAAP/0v0y/Kz7n/yNAFgEkwbIBLb/Rfzo+vP8L/+wAQUCGwDz/qb/FQO/A20BAf/d/b/9+vxd/hgDEAV/AvP9DPt0/e0A9wLgAjYBRv6c+wD8HP42AToDkARPBLsA4vxo+4v9ngDaAE7/cv8EAa4CeQNGAqMAGP9b/cH8z/yA/tEAFgIaA7sCUAAP/RH8wP5wA/8D9f9S/BT8V/9eAt0DIQIu/z79TP0R/2oA4AFHAmACEgA4/rX97PyZ/qIA2gLMA8gCGwCe/Zz96/51AI0BCwGf/pf9H/82AYABYAD3/+gAJgHM/2D+Sv53/s7+5gHoA8cByv3K/H3/3gAlAL////9X/6v/TAJJBagDdv1y+Jn5G/5iAYoEwwU5BKf/xfyh/XX/TACE/qL+QQA7ArICSwEpADf/g/6M/Rn++f7cAFECbgG3AL//bf9V/1f+8/1c/x8BFgMGAgX/uv3k/YMAtAJqA6QAXPw9/DAAUASPA53/qvwi/QMAugAuAXEBoABf/xn+Vv5YAE0CtQFX/9P90v5IAbEC6ACL/bf7m/xGAG4DsgVcBBsA6P02/o7/6P1//G/9WP8uASoC1AL9Aj0COQBT/kr8I/yD/aQASQRZBJIBRP6M/aL+xP/F/6IArQItAiEA7P71/w0B6f+z/eH8Wv1i/94BDANXBDACSP0g+sn5Y/2jAvsEhgRwATH/XP6T/nsAvABBAB3/CwC4Ae4BJgC8/QL/swB6AYf/Jf0c/aoANAWIBcMBb/t7+Xv8DQHbAmUAb/1Z/Bb/OgOfBlcGIwLH/ST73PqM/Bn+lQDqAvIDhQRCA8MAdf2d/B79XP55/14A9wHsAJb/1/0F/oUAfQJlAl0Awv7q/fX/+gJAA8j/UfyB+hX8eQIzB6sGXP90+ID5sgC4BggG0QJi/6r7OPkA+/j+iQG8AuUBmP8l/6AAAQM2BbkCXf2y+5X8av6bAB8B2QCEAeEBwgD7/zj/SP50/2cBkAGY/hL8BP4JArAE1ARcAYr8EfrP+68BigTkANP85fus/aIALAOpBHUEjAFm/Wz8Ff4wACYAC/8uAEYBxAJMAif/8fwb/Mz9HAG1BDoENwF9/sT8wP17/3EBqAHN/4H9h/1RACADNgI9/7T94/y6/b3/vQM9BkwFRAFW/cf8dfzV/Pr8/v5hAbwBZwJrA9IC+gBu/wv+Xv5V/Ur8Rf1FAtcGmAZDA8D8jPg2+Iz8wgGzBFoEjACf/vn/SAPAAw4BS/x5+bH6oP49A4YFLQVWAkX/0vsK+4/+9gKuBJYCEf///Nr85P2MAC4CtgNBAh//yPzg+lT9RAH4AtkAsf///xsAhgDeAGoBPwDE/i3+0/7uAGADFgThAmn/HfsK+eb5Dv6zBLgK5gm+AvH5wPRn9lz9uQRFCIcH6wG/+9/4rfzJAtgDWwBi/J/8zf9QBE4H5AUzAd77O/eo9lH8mgQ+C1QJZwAc+Sb2L/gf/hwEtgebBjIDOwG//8D9ffr/+LL8xgHeAv0CDASjBf8EVwCK+qj1/va4/RIGjAoQBzAACvrI+BT8PwETBLYDogCj/bD8nPyI/y4DWgU8BOgAkv3m+978HQB+A0IDMQE1/gv9iv0j/4oDdgVYAoz9h/oG+x3+9v+NAc0DPgOtADX+Kf1L/wcDpgPOABf9LPvd/B8AHgKnAqwBCACv/wgCCwSXAp3+J/tL+3v80/7rAZEDpwQWA/7/r/wF/Of9AAEbAuL/Of7l/nUB6wBP/3n/UQBgALf/vgAUApsCIwC8/f/9XP5o/hf+Wv+5AgoGCwYRARX6evYQ+o8AFAYYCZ8G9/+c+CL3pfzkA8AGMQN5/3H9RP7s/8oAeAAe/vP8Zf7IAUYCVAKmAykDqv99+jT6f/ya/8gCjQR3A3v+FPvi/BQDjwVqAsv93/p4/V8BvAI5Aa//rADRAfQB6//Q/in+bPtQ+wj/4wRgByMEyQDi/oX9LPwn+4P8kf/wAq0EFQSxASz9nfun/VIApQHLAB0CuQKiAZEAK//r/TP8XP3T/6QAWf/2/1UD9AQDAsv8kfqR+1v/DgMGBCUC2f93ANoB7P9q+uv4cP6ABZgHNQVVAUf9i/tC/OX+pwD2AHgAUQBkAmUCv/+h/Q/8L/0BAOcAygCO/+v+5f+nASEEgwTKAQL+Tvzn/ZkBoAIDAEf8gfrO/EkCowYxBfsAZf13/aL+b/6S/ysAdwBo/on+ewHkASEAq/w2/b0ALwOwBMEFPQRx/sT4Vfmg/8wEawVBAxgBI/13+UP6NP7hAY8BgwDuANUBhQFHAP//PP4P/Fr83/6sAB0CpQMYBDoD4f+8/F/9rv9IAHcAdAAdAlUEZQLF/hH7kPmZ+9f/hQQ2BqIDPf60+yr+7AGlAdL9z/vl/WMBxgK3AmICaAIKAVj/lP3a+/b8U/8mA44ESQJ8/wv9Mvwj/YEBogPXAT7/fP/BAX3/nvx2/Jz/mAK4ApIBVAGSARP+tfwI/g7/qv8ZAS0EsAWcA2L9O/oM/Fz//gExA74BcP2w+xj9mgCHAsUBJgGZAEH/hv5P/2f/DQBdAKD/tP3m/Ir/sgRQCOkF2wAE+8L3fvlI/0QFWAfbBTgBN/0U+0r7Af6RAPwASQCNAEsBfQGm/8L9hP0t/yUCDgSkAqH+U/xy/ZAAagEh/2T97v09AbAEHAcYBDD9YPq8/AEAQP9r/If9fwEeBPkE6QMeAQn+DvyP/T7/HP/1/+oBswK/AF7/UwBWAcD/7f4a/6r9Pvzq+2IALAVMBWoDhgGU/yb7Wfl1/CsAzALYAgkC3QD8/sL9wv4VA2MEngI1AMf70vhm+mwC/ggVCCACMPtM+rL89v9TAhUBxP9m/9r/fQCwAAcB0gFuAVYAVv97/CP5xPkJAaUGpgVQAn//Uf5Z/ST9+/6qAekClQHMAbwCQgGU/rn8cvxU/LT9W/9rALsCQAWWBtkD6f4V/KD8I/3o/AT/SgDAAMYBjANdA4n/qfu1+ff8+wEkBXcGPQVaARH7FPkR/AQABQN4AkwBh/5e+378CQBJA6YDWQLNAfj/6/xk/Or9Kv8iAZIDPQQMAif+nv3pAG4B9/2P+3f80/5OAXMFbQenBYQC8v3T+hf5Afms+xAAbQSUBCYD0wLLARL/0Px9+3n6Rv7VBMEI8gar/+H5hvm6/T0BKAM0AlD+U/zH/QYCqQRCBIEBS/6H+y/65/tg/8YEdQe2BRMAlvod+k/9swEmA8EDPgONANX7xvp+AJYD4AKx/yn+UP6O/Tj/pgMkB7MC1/q09uT3p/xFAT4FGwcaB3QECACF+8P6pPyE/nkBjgJlA6kCeP8p/Q37//uJ/2YDEAe7BgwCr/zC+YX6+/1KAfIBYgBF/cr90gIfBTsDlP7p/HT+zP+VAbACWQOcAOr9Uv2U/Gn82fxgAawFIwU/ASn/7f/W/mH8kvsg/lIBzwPtBBIDUv/h+kz6uP14ALIBQgMHBHgEyAJU/yH9SPur+7z9NACGAbkBmQIRBLsDwwCA/ir8g/ry+sD+xgOaBQ0F1wFH/tn6Q/pv/lwCJwJg/83/JwGIAPT/wP8n/5f/PAF3A5cCyf2J+9n8OAGNA+wDowOh/gn6X/o2AAsEKwP2AXwAz/4A/Nz8DwGIBMAEmwGn/pD8AvtH+4f+wAAhAp4CuwHEAUACEAPaAPP8jPqL+xn+nP9QADcD8ge5B6wDofwQ9z73lPpmANUExAbkBYsCC/+g/Mn8uv65//H/NwAo/1z+xf6rADkDWgTEAQ/+Yv7h/jX+of6v/y0Alv/u/n7/cwF1A88DCgFX/jr7U/t9/+QADwJaAhkCfQDn/jv/mv4D/9//0wLtBbsEYv9h+hf5W/i0+2ME2gpNCXAC8PsP+vP7hf2d/zMAOAA3AKEAOwLoAZz/1v0Y/ln/kgEEAjwA6/98AQUDeABW/Mf6gP2HAU8EvwTlAfX/lv2z+v/7wv8oA4IEUwJaALIAo/8W/JP67Pzd/20C/QMBBW4DJP/9/KH8Yf6p/w4A5QGyA9wC7/5u/BL8mf1lAMgB1QBf/10AcAKzAz0CcP4s+6z5xfpAAJwFUAbzBUQEKgAg+p715/gCAaEG6QZ2BMEAhPwe+uL7ZQEUBWUE1wBZ/Zb8Q/71/2kCRQNYAV3+j/vG++T9jwJsBggFrQFx/gv9sfsV+6D9TAJiBSYCO/0Y+878kgGpBZEFlgEL/uH9xP5m/7kApAFfArMA1f6U/0T+zvvd+8kAWAUhBEgAhP6OANkBHwGm/lL8evxI/s0AIwCG/GH74/+iBhYJkAbZAI763vfr+dIAeAdHB6YBcvsf+TX8JgDxAnEEcwK3/37+GP4rAMkCZALt/nf7dvvh/Ab/2AI8BAUDHQIqANL9R/3B/osAhwHqAaoCvgP+Acv8rfeJ+NX+IAWiB2kEEv/O+ib7LP9CA/oDxQDY/Qv8RP46AhgDPQGg/x0AlADw/0H+kv4XAGsASQG5AhIDIf9W+ff4Wf7jAkwGogi6BP/8ifa29y4AdQXQA3b/e/3r/UT/zAGZA5cD0AEv/8z84vo//H4ALQXyBEoAGP5O/tf++v2Q/kIBDQNwAxoBtv02+3z8UADOA3kFiAN4/5b64/h8/RsEOAT6ALcAAgJIAFn8Kvwu/mEBcwJFAyUEmwF0/yv+6v0Q+z35O/2LA5AFtQHr//j+TgBRAgUErgS2/mT3C/an/C8EGQigBhYCMv7k+h78c/8nAgQE4QMlAMv7lvte/kcDFwVTAVT8yvoF/MH/uQU1ByEDCPxy9/z5ZgDpBFYEKgPPApoBZP5u+vn5p/28AecCdQOrA+wBfv6q/GH+SwCkACT/i/5iAFEChABE/Tv/RgNwAxcAe/wS/XIBYwISAAz+vv3b/dT90QHBBsYG/AEl/hH9LvxT+nT6Vv9uBG8FfANIAqf+tfry+58AuwOiAVr/MP5m/gf+w//jA70ExQIQ/4b92vxY/bT/mAPsBNwA/fxN+qX85wHuBr4GrQDY+5L5fPvK/tsBkQOmARr++fwf/70AAQG9ATwCKAFc/zz+Jv7T/oMB3gMZAwkA9f1r/gX/5v7+/vMAhAL7AWj///zA/bD/PgPBA6MA3f7k/f/8sfx3/7UBQgCp/pcAWwQ7A2n+0vs+/oEB4/8g/m7/RAESA6QFAgWfAM/8nfmC+XX7Kf5MAtsFXAd5BXwDjP/7+dP2YvhJ/t8DeAadBS0Dn/6Q+qb66/5FA/gDSQLp/l/+pv8RAbkBGACO/sD9Cf3n+xr+aAJUBkQIAAWH/+j6SvfL903+tAWLB7gCx/uL+SD+uQM1BS8FUQZcA2L7avWv9or+yQRDBYADPwDV+3r7dwDYBiUIhgEC+oT1P/cl/yoHeAmEBk4BiPtB+YH5Nv6gAwQFpwSTAuYAhv7c/A39wf5s/43+Xf6E/lsBgwMcBMEC5f/q/eL8A/1//Y7/OwHrA3sFrwRwAvX8fPmx+ID8ogKVBZQDcf9x/yUBqwFVAIH/jgCT/p35+PcX/UgCBAWzBgYH1wQI/ej21/fe/UMEWQQUAtH/Of0f/ugCxwYOBbb/IPqn9+v4mv5yB8kMBwoNAOf4sfZr9xz72wBNBtoFgAHA/fD9MAAjAp0Crv82/XH8uP22/ygDqgW4BEgB1vz0+xz8vP0xAWMEZgN3/lb8lP3i/1UANgK2A00C0QBBAZ4BqPzf9Sz03vpMBY0LvQsAB1/+Nvib+voAEwScAU37Vffo+o0BxAiIDHgHhf339Qv3uvzSAEcDmwN9AsgAYP1/+3P93ADJBEcEAgBz+rL3lfz5A+EJdwlDA778Hvml+Or7PAHfBGQEGgDR/Jb8WQFvBogHFAV6/l73cfMB+DMB7AWwBMwAyP8nAiwEnQM6AUf9afo4+7D/9gLNAFX+xP5FAUsE6gRTAXr7JPgm+ej+FAX7BnIFEgODAAv+ZftC+DD5bv9JBTMGGwN7AJb+pf8uA18DMgB6/Pv7dP5NAEsA1P4c/54CSwV6BBb/2Pl++hH/JwPqAgYA7vy4+wH9xwBVBg8HwQK9/fb6rPrA/NX+gwCzBFIGhQQRAQr94fuD/LH9GwDJAkUDKAEV/4AAsQJcAVv9/vpK+7v86wApBYcHtwQk/vn6dfrz/NgArwN0BJwAmfy8/fwAxgKFAmj/mfxF/J//UwNzAn7/Uv4r/1v/EP9yALkDlgSVAbb9XPqK+kj+XgPlBjMFmP9Y+sT5+/0KApMDSwIo/5T/XAKABFkEdwD8+gn3KPcK+zUDlgrSCbUDev3C+Q/4yfk1/9MEuwd+BXgBnf+w/qn8O/pF+wT/ggJ1BXoEKAPMArMAav47/WD93ft3+wL8Dv9dBaQHqwUJAez9mvy++9v7YP2hASoEOQTZARAA7QDvAGn/+vw3/Wz+kf31/JT+qgJsBRUESgHF/s38qvx5/3YDpQT7AY3+3Pw++hT5cP2BBJgIhgcvBaAAOft+9+j4swCgBLgDJgGQ/0gAggDL/zr/Gf+n/jP/XP31/PkAUgQPBbsC6P+c+7v4j/tLAhQGpAMEAFn9mP3V/RAAmQRpBOYAUP9nAM/+TPv7+yoBlwMpAQAA5gH6Ahz/8fvg/UsBAQL6/mf9nf4n//H/mAGYA1kEUAGF/WX8QP4r/hn9zf5uAv0FrwTqACD8qfn/++UA5wVzBawA2Ppu+YL90wN0CdYH0v/U9zL2Ufv2ATgG+gVEAkz9k/oY/fYA5gPbA+4Aiv8R/lz8wvz+/4oDfQX9A7z+Jfo++Kj63f/GBSUIzgW6ADj7kPoW/h8CpgFAACz/gP26/Oj+jgNIBPQD2QJAAEb8GvoW/asBiQOlAZIB1f/J/KX8CQAoBcYF1QF9+wX41fiO/RwDtAaEBz8E5ABB/T77fPs8/Az+NADPApcEOwQ8AkT/a/xg/AT/wf/q/uT+YQDxAf4B9ALPA38C4v0z+vr7uv9vAaL/T/9K/9X/6QK1BIgE9gGJ/7z8ufrw+mf9dAEUA1IB1f/3ACsAaQD2AC4A8v+y/kX/AAETAR79hvr+/MABYgWlBU8DVv5O+5n8Pv8nAc4ChAPzAlkA//tU+4v/ygP5A6EBaf0D+ob6HP8UBkMJEQbs/jr6XPoO/Mb8Ef5RARgDUAE2/nX+dgFRBL0ESwLb/ST6Ivmd/IgDhQjiB1IA3/qO+5H9xP6wAKECXgIDA80BkP+c/Yf8Nf7pADcDSAKRANn8dvpk/XkCzgPxAEb/Kv4l/0MBVQJvATb/uv7c/sz+X//jAP0CzwKG/zv9+fv++3D9VAG8B9MI/wOc/o37jfql+UD62f0WAzIIeApCB7j/Uflb+Qb81f1j/ln/1v9d//EBGAXUBzMFmv4e+uj3ovqq/6UC4QLuAvQBmv64+3/9zAIZBLQB+f5A//X/of3m/dAAjAMIBIoCVQBJ/CP5rPlN/0EGiAhEBLH79fbb+UwC7gnICXgD6/uc94X2bPkj/4cDKAZGBzsHuAMp/178ffru+Xr52/uRAesFSghNB04DUP6k+KX4hPww/7AAfgABA58EqQN5AQD9j/qV++3+PgMnBpoGTQR8/b/2dPdW/ukFCgeYAmX+Tvu0+oX8QADRBGMGVwL1/H381P2l/+oBLwI8Ak8Ahvxw+wgAhwSxBKgCXP/h/VL9BP9mAQgB/P9S/9kAvf8O/DH7/f3dAqcFHQXbArb+hvlx+U3+jgNUBYACgf6g+0L82/8XBYQHRgX9/5L6rvk8+rv8HAFKBKEF0wIC/zr9WP6+/6gAEAIsAAX9LfxH/5sDsARMAt/+I/87/6z82vwT/1YBvAI9A8wCDgGC/ar6nfxrAVAFTQRBAEf9F/sp/KD/egKvA1gC3f5K/LD8OP+vBAQH1AIP/Tv62/vV/VgBfgXKBsACcvtP+DL7JgHWA+MEYARrARf+pfkK+mv/MwSfBMIAdv1k/Rf/+wByA44CFv9+/VP9TP7g/68BSwNmA3UBnv4K/lH97fzC/2oD/APm/6j9YP4XAE4Bkv/9/kEAoP+F/RT+6/9JAo8C7gDG/2j+1P6P/Xf+FAKPBOgDBQCR/bL9zf8eAH0AjgATABMArQAWAqsBkwHo/4P9cfvw++/+1QBoAo8D/wKq/rb64fph/9MD8gRyA+f/A/63/rAAggAZ/lz8/P2mAIwBiwLUA+IDEQD5+2v7+f2PALYB3wEvAYL/6/2h/s7/4wHXAgwAmPwf/D4BaQadBGL/lvzx/MP97f5tAi4EOgKS/tj8Vf4m/wP+QvuO/AgCVQagB7QDr/3y+qT7af6aAQQEHwSq/5f8DPyf/lECVAKiAaEApwAaAOgAUwHN/53+Ef25++H7wABmBQMHTQOD/jr+zvxv+lj5/PyHAbsE6AbrBi8Dl/z3+GH60/83AyQDx/+n/OD8swArBdAEMAPm/jP8i/1C/+kB1gHc/iD8Xfwy/oMBQgUrBRoCwv8o/0b7v/ew+l0BRQY3BaUDxAN4AAj8lvsT/uP//f86ABECygLZAT0Arv0X/Kr8WgBcATcA9AB/ASMBc/8M//f/WQB3/3f+kv5DAN8D3gXQA0/+Tfoi+nr8KgBNA9oE9AJP/gf8gv5BApQD/QGU/qX7iPsO/vcBngRbBF0Cj/3v+Ir6XgFaBFwDQwIlAaz/I/ya/OUA6QR8BYYBp/3i+T35Lfy3AHAD2wSeBekCxP3e+Dn6tf8bA7UDOwT3A4b/p/sY/dgBDwI4/RX6EPwyAVYFFAh9Bsr/uPiz9u76yACSBYQGtQMZAEv+2v7y/mb9L/1K/qb9Of/6AhQFBgWSAez9jf2u/5IBJAI//4n4tPa0/ekFVQh8BgYCAvwu+Kj5Xv8FBaYGVgMl/wz+nv9+AC8Ayf88/1j+lfsl++cAAAZNBDj/Bf+iAocDTwH2/hz+xPwo+8P86v+LAe8BAwJLAaoAvAGUAlz/+Ptj/DP/7AHHAfIBSQFT/7P9Mv4oATEBSgGRAb3+SPy5/Fr/4AA/AvIEyAbTAp35wvXR+o4B/gTYBX8EuABB/VP6E/vU/8cDCQSo/+H8Yf0pAdQFCQXoAQv9pfix97D6QgLJCJYIcwNh/TH6G/xC/9oATQKLAyoBuPy++sD9MQVdCMkDIP8B/mT7MfjD+NH+CgVXBfQCSQCq/8L/hQCyAdcBEQBu/fH83v2LAPMCtgNpAT3+5Pzr/B3+ov+JAq4DVAWvBPf/q/wU+gz6Bv1tAYkFywY2AGz37fWq/PkFVQmJCAQEGv0L+QX7FQBAAksDtQII/mL41fg1/ywFlAdxBRoCG/6j+ej6VQHsBNsCBP8K/D37FP2PAEoE0gZaBlMBBfsC96H3/P3FBrgLWQkPAnb4rPMn9zH/CQZbBg4EjADK/Rb+/P8fAsYBAQBa/lH8OPl1+l4Bwwh8C2QG9/3p9q/0VfmoA5kL5AkcAij7Dvk++Rj8UQKPBooGcAIv/lD9gvzB/DoAUgMtAvb/GQBM/pT9eAEVBawD0v0L+AX2A/vbBDYMPAyVBJP6JPQO9Hj7LAalCk8GogBC/t/9ZP1j/C3+AgHQAdwAPwDmALwBeQMqAnH9QfoW+xP/yACQAQkEwAUnA/z80/rW/BD+1//zAqUEbgJn/pb7ovuF/mkCoATXApgADQBU/7D8V/rn/EoBPgQCBloECP97/A//QgFe/7z7IPzH/uoATgTHB2MIowL1+uX3RPgU+tT8gQDpBPsIPwlLA5z85vkg+gf8C/1F/zoEvgaZAyH+NP2f/l3/uv+0/+D/MP8MAHYB5gGCAQYBNQAh/pL9ofy2/YcAegRAB+MD0Px29in6zgHRBrIHegKR/vj72/oG/NwAUgSIApH/Wv25/hcAgwECAm7/Sv2t/T4A/wHcAEb/n/5j/gkAjwLMA/sAlv0C/fz+IwKbA5IDjv/x+4T7OP00AZkEFQf0BbP+y/ad9bL7PQRmCAoI7QKp+8n3qvit/k8DAAUSA/P+O/3b/noCKQRqBHsCof1s9zn1yvucBREKhwj7ARr5jfUH+7MEuwiuBkgCpP7H+mX21/cu/+kGfAdfBXYDTP+S+3L63v3AAvcE3gEl/eD6S/2fA/MGCQPP/C76hvpx/LwA1QeKCvQEZfz59qT3YvwCAQkEvwWeBNABQv2/+Tv6H/4oA+8FWQW3Aqz/0Psn+v37EgCwA7wE3gK6/+L/zwCEAJH+Uv2G/p3++Pxl/YYBRQYJBkH/DvqV+U38+wAMBkIHoQUzAh/9dPsk+o36Uf32ABQDJANjBEMEhQLD/gr8uvsS/Ar9cQBpA4IDUQEe/3cBigH8/l/8F/zn/HD+wgP5BxsJhARp/sj4JPaL+hwBpAaAB8kDTP64+Ef2NfuHA9kHvQbLAx8AZ/vx+df8ewFDAtT+o/wO//ABKAR4BSgCUf2Q+i/8Xf8/AYABHgPDA/j/gv2i/r//Y/7J/uIBmwTxAXz+zv6I/qD8n/tRAFQEQgWkAtD+fv0F/Zv+0ACqAQf/iv4YAJgCrASjAgH+3Pkm+uv8ywBvAvcCuwIPA8UDUQI2/yr6mvkr/Hr/iwDrAqsEfwIiAID9ov3A/esAVwTbBAsCcP0o/G/94f/f/8oB+ABm/4gAGQG4Abz/Gv/K/fr92v0m/V//SwIsBjcGDgPM/Zn3m/Uu+pYBFgjqCgUHuwDg+kP4Evt+AJ8EEgNz/+v/uQFxAcf/jv1N/If7R/0GA2YIPQfi/0r7HPvo+pP8DgHlA18DwwK9AswA7f9t/2X9c/rx+FH8nwGCBiYI9gVJAgL8Nfcb+ZL/wAP1A+kCeACv/BL7E/59A/EG+wTo/7P8Avx+/AcAJQPAAf7/7v+v/zv+mv/SAqQEUALn+4X5kfqi/kcEfAZ4BKb/w/xR/GP9JP6b/fv8RQCiBmAIXgWQ/0P86/r5+mj+dAG2AhQAo/+uAkADlgCU/W/+1P/D/2b+3v0qAEcCYwJkAmgCVQDc/Kr7If6XAXIDawGy/XD7XPxY/5UCZgRbAnUATwFaAoH/+/oY+mj+2gKsAn8BiQAv/1n+vv/yAjkD1P+h/WD+if99/yD/vgB1AtQCzP91/In8Kv/rAR4DPgTbACr8bPqO/RwDAgVmBCUDav9r+fb4HPw/AekDtwJ2A6MAEP3X+6f9AgHHAgoC/QB+/9D7Kv3+AZUEawIv/oD9pP6+/54CjQYwB/gB0vmX9+34M/ydAqEGDQddBIIB6fxC+Bf5g/4AAh8BQQOvBEoBJf0T+6z+TALcAOD+9f56ADoAwwFuA30Bt/5X/WH/agAZAbkB/wGaAO38Afxd/d7+b/4DAHADBQXdAh0AyP+0/gX/sv9/ANoAoP+x/WX9Af7m/mwBrAOxBFABZf4s/jv+Xv5Q/ysB5wH0ALH+JP+Z/lL+6/1Y/dX/nQJ+BAkCkf8p/3QCpwQQAqT+wfqm+rD7IwCkBXMH4gRG/8P6bfg/+4wAtgRvBHUBk//+/o39If16ANUCqgF//Sj9QQDTAc8BDALFAr7/3fsC+x/+xwBHApYELAOh/5r9Sv5SAcMBMv9b/vv9Yv1V/xMCmQHN/lH8CP5BAhkFSgcoA/37wviw+kABigXQBLkA9f28/EH9nP9GAcoA3P/WAHMADv/f/cr+PgCnAT8EHASvAAz6kfdb/JYB6wMIBLADuwJAAdT/MwFHAEP9Bf3f/P39R/++AHsC9gLkAlUBkv2l+tz6lfzUACAERwRwA2ABzv5//L360vpU/2AF0wcgBI/+/PwB/+gC6AJ4AJ3+Tvxj++/9rwJHA2QA6f+zABUBbAAZ/2X+eP5I/17/AP8v/3EAdgOkAzEAEP2p+5X9mwAaAVYCegPCAokBBv/H/eT8yfzh/h8BnAE1AdkCfAMGAEz6UPn9/J4B5gU6B7EEYv29+aD7nv7tADkBYQJcAQH+sPwSAcgGSAWh/+L9B/79/AX9uv+gAq8AKv8+Ad4C2wAh+9756/3/AQEEIgJ+/Xj6E/2+BXIKAQbM/976Q/co9sX60gMuCpAIwwJ6/+P+sv3Q/Xf/Vf9Y/oH+yAE8A2QAIf2n/bMASACp////PAAVAM4BdQTcAnn+D/uI/Gb+7v1m/hICiwRgA0gDIwQeAjr7Yfew+RL9jf/vAgwFbAVGBEcA9f1m/Mf7qfwT/w0CcgQABPn/pP42/3YANgB0//z9dvwb/zcD0QWoAgv/Hv67/VH9x/3vAeMFkAQ1/8n7f/pH+kH99gJCB7UFygD+/CX8SP35/Wv+HACRAaYDGQTXAd//l/7H/cP8Bf3v/nIBYwI6AsoDRANzAHT9+/x2/nz9M/1mAbMFOAQH/4H9Hv11/Kz9oACvBMIDqQBW/0T/zf1o/CoANAMPA2UBDAGh/xj8Nfu5/hEChQBu/2MBOARmAh/+kP4g/2P9KfyD/2oFpQX5/7T9IP+T/oj8mP0XARwBev+2ALcD+wTZAjz+1vt1/Fn+bQFkAugBRwHv/w39MfsV/KH+owH8BHcHXQWbAKr78vrR/Cv+Ov+Z/ysAav+bAAUD5gNlAMj9OQB1Aa4AJv+w/x8BzABX/s38bv0X/ngA1AOuBF0AhfvP+rn+AQIFAgcCjAN5BFQA7vyl/Iv9GP0z/QoBHQToA0cBhQCgAeYAA/2T+3T+vgImBWMCCf8B+y/5Wvut/6EDjQVcBpcCrv3k+ir8d/6FAAkCbQGkAZH/JP8AAFj/hv+iAcIELwIC/Y36N/wJAPUCywRWAx4Apfx1+3j/EgS3BQ0DFf3Y9z/28vrQA6kKjgkzA/D8sPe9+Pj/vQYoBnIAlvv1+oL8of4YA+0EbwOp/1v+b/8I/0z/WgAMAxwBN/zp+u7+iQNVA9kCaQH5/of8Pv1cAF4CwQHd/zsA//7J/68AoQAU/xj8p/1n/8wBVQMXBIYBefz9+in9QAOfAsH+yv5mAZoDogFGAGn/Pv/i/qv+KwBc/wP84/umAfAFEwYBBFoAGv22+vb5qvvdAEoFWQRZAo4BTwCG/j38X/xK/oP/PAByAq0FsAPG/5L9W/yP/Af+CQDEADUBhAGrAaD/LP2e/nwBVQMIAQb+f/6WAFECEQFPAMoAov5C/UD/VQJSAhv/bP1s/pL/5QDTA0sEdgCn/Uv+6/5e/Vv9yP87Acz/QP/wAYcCLP5F+3z/WQMAAnMAwwCeAFz/BP/lACcCawBS/9//AABG/UD7J/+HAwQEkgBl/g8BdAKyANcAwwDA/U77gfue/7wBswHCAaUArP/i/UgAdwNxA/QAWf7y/an8mv0eARcEsAF6+wb6Ov5vBEcGLwTE/8r7gPpd/PgBPgYoBkUB3vtZ+Z370gDQBCIFIgAs++D51f3rAgAGvQZIA5j+e/v5+1H+SQH6Aa3/jf3P/YMASgOTBIsClf8E/B365vu6/loBrQIUBPoD4wKSASUAA/00+lD8ff7O/ob/sAJTBHMDvwIVANP82/qG/LgBjQStA8kB6v+8/WD79fuX/y4BcgAGAA0C8ASmBNoB7P3Z+pz6lfxhAe8FfQUmARb98/sM/Bj9hf/SAiYEUAJ1AVABlwCn/Dj5rvrX/b8AAQS7B6IGvgFO/I/68v3U/xD/nP46AR8E9ATEAuD9/vq1+v/9LgOYBvcDMf+H/nj+9/3x/On9sv+z/9P/6v9NAfIAZP99AGIC8AJtATUAPf+1/U/7hPux/3cDUwQmAiEAp/6m/kUAWQENARL/eP4oAF4C8gCt/o7+Uf6V/VX+jwHgA5MDhQDI/gj/bP+rAGIBZQAO/En6hv49BBMFBQFo/dj88v5SAEcCogK9//n8YPzE/7cDJQNn/zD9BP0s/8sBRARdBRACSv50/Vf+ev5r/m//KwCC//T/WwMJBlADlfx3+vz6JPor/NoC2wnoCsMEv/wp+Ub5l/tk/oEBwAPnAvYBCgF8AbwBCv75+fP43fra/q8DqAeWCIUEEwDu/An7ePt5/LL+kgGVA2MEsQPaAJb+wv7V/6n//v1N/nAAMwNEAoj+WP2w/Rb9Jv32/2sDHQQ7AzUBPP7b+jr5iP0pBL4GiQSyAMr9l/yX/A3+hgBbALAAvwKkBKUEiQB6/P75jvr4/ecCQwYhBXoBlf3J/Jv9Ff8rALABjwE3/x4ATAJUAln/Wv4D/xn/b/7N/fv+Tv/f/24AiQIFA8gAl//+/84AQf5y/P37ov7PAugC3AGbAQwCKwHf/tD8+ft+/Nv+DgMMBnkFlwG7/UD87vxs/54C6gL8//j8Xfw6/mEAuQJqA3oCnAE1AGf/bP8P/+P8Sfu7/MMA8gOkAXn+m/98AXgARP3Q/J7/7gKBBRYFpAFJ/U/6WPpm/rcCgATSBO8Bi/0u/Jv+mwFWAlEBav94/oD+Yf7i/94B2AC0/kH/nAKrAyAAUPxp/EH+f/6z/pr/AwL7A/AD3AJEAEb+fv22/p7/uf1P/Jf+EgJRA08DQQHC/oD8Jfye/0wD6gOQAeD/Sv+F/4/+xv3M/jMAKwIPAjkBAgB2/+v+6/7YAL0ASQAUANsAwQAm/4P+B//mAO//9Py8+17+SgJgBfoFMwPQ/rj5tvhB/JYBngRHBOgCzwBBACkAxf60+yT7Z/1gAfMELARKA9kAYP1Z+478oAGeAxECi/8e/0H/uv5M/8YACQKR/yL+wv7J/1cBeAB0/2D/9QDJAp8DHAKT/Mn4NPro/7UE4QTQAicAHP42/In8MgALA2IC5f9k/8MAAAHe/yr+6v1M/3oApAChAMgBcQJaAo3/cv1+/pb+ZP9/ARgDggEI/kv7pvs6ACMETgVvAj/+ZPsa+xn+vQFfBXIFYQF7/Mv6+/1NAbEBuP8X/6//yP+TABECggNUArj+C/yh/Pv+AgGaA2MEawF7/jD8YPuG/Y4BuwQoBTkCcP3f+o37pP4aAs4EgQTO/3H8Tvya/z4CWgDy/cP92//zAU0D+gF//nb7a/yRAcEDwAMMAlwANwBt/yr+s/x0/TD/MAC9AGEC+wJZAeMAgQD7/tD82PwSAE4Cvv8e/Zb/1AIkA1L/VPzc/Pz9v/8sAngEAQT+APf+A/9i/1r+Tf1L/Uf/2gFLA24DGQJcAQYAyP1f/af95f7J/2EA1wE9A0YEwgGA/M35+/uF/xMBwQAAAcgCPAMNAeL9+PyS/ST+vf+7AaMCkQImAYr/wv9VAIL/lvwE/L7+CQHBAtoCTAEPAG7/RP/ZAOIByQBv/+b+df7d/Z7+kP9HAIMB4ALLAocBRf+z/bf9wf2p/lf/WwEtAyYDtwEz/2r9jvzR/Zz+ov/oAGAB3QBlAKYB1wFoAcn/tf1d/U3+EABqAQ0C3QF8AmACggBE/fP6c/sv/twBrQP3A7wC+wCN/x7+KP1m/Pv8h/4fAQEDegKzAVUB6gD5/8v+Y/70/hsAYgCK/2H/gACpAWUCVwJ9ANT8Rfr++0QAdAKtAcwCxAOYACz8bvuI/tn/xgC6AkoEYwPIAHMAsP9//Mb4EPqe//wDDQVOBHQD7v+5/U7+wf70/I/75P12At8FewMf/zz9s/6PAG4A2P7Q/av/PQGDApMDWQP3AOr9tf34/Ef81/w7/zcDhQVoBCwADP5k/h3/1v5K/rL+4v5N/5r/FgKbA9MBSAB//1//Cv40/r3/ogDoACAAMQBMAQkBQf9C/5cAKgEeAO/+Nf4J/hMA3gFdAwwDL/+4+vP6dv+FAr8CLAL9AjkBzf1t/CT9XP9n/yoAwwJvA7cA5v3v/qoA8ACE/3f+O//t/78AzgBJAR8B1f5u/kz/vv9WAC0BmgGyAAX/qvwr/cEAZAMzAxgBaP7v++v85wBCA/cBk/7Y/Eb+gQEEBHEEjgJ9/rT7bvy1/of/Q/8BAL4B0wOWBMUDIwHD/J753vj8/FkCvgRoBJsBkf/Y/tD+Nv+U/4T+OP3K/e//qQP/BD0DqQBl/bf7zvvQ/a4AtQL9A2wE1gMbAZn99fpP+jX9RwHTBP4E6QBT/Zj8kv0T/3EA2gE4A04C4/8d/ib9+/1y/5AA9wDeAcUCVQKRAHn9x/py+qb+IgQBBjkEsf8+/dD9QP50/04Afv8L/2oAmAIWAyMBOf6S/RT+lP+iAY8CUgIKANr+rv4h/5b/kf9tAPb/ov97AIQBpADR/rX+av+lALkABwDy/rX+L/8X/9L/xABmAtgCiQGY/+P9rf17/gkA9gBZAZMBYADI/wwAmQA6AH7+D/5B/gL/BAGmAqYDywEx/gn9Uf3Y/SD/ogHBAwkDb/+s/Pf9ygBCAvUB2gBF/1T9vv1ZAPkBGwK6/yL9Pf3v/w4DCwPIAI3+ZP7E//n/x/+7AAsBHf9G/iv/TAB9AML/rQAdA60DWAAs/df8xP28/kAAggFNAP/+SgCVA2oErwAy/Bv8Cv+AAIUBowDt/sX9Qv9zAqADsgK1/oD7Xfz//4gCEAJ5/4r+QgBOAt0DlgIUACb8UfnJ+qP+pAOxBj0FyQCC/Tb9vv7J/pb+g/7V/tMAxQHzAT8AOv/U/78AJAH5/4P/9v/1AHkA7//O/33/IgDXAAQBHQCk//n+cf6V/uz+kv8vAPUAGQHCAMr/c/9xAE4BgwCh/Xr8Ov+BAjoDWQLhAE7/O/+S/wb/Pv/x/rv+Av8dACcCcwK+AjQBFf+7/vr9j/6b/r/9Vv1D//QCQwXjBGsBzv74/TP9c/yg/UH/YQBnAVoChANXAhQAWP2y/I/+Tf+4/2cAcQEkAsMBoQG6AZj/nPz2+y/+bACYARACQgEoAC3/QgDkAJYAd/9i/dn96/1Y/6ECZQTHAz0Bmf6l/G/84fzP/6oCxgPSAgoAzv50/s3+fP5o/8kADgLAATgAm//C/tr+Ov6e/qgAoQIiAv3/HABzANAAef5g/aD+LP+x/53/UgFRAjUCEAFt/23+Uf0X/jD/egCfAAIBfAINAsMANQAwAL3/S/9n/rz97v7s/+0B+QLNAYX/ufuc+53/MwSRBcYBy/zL+jv9/v8KAucA6P78/zwCdQQ8Asb+Zfww/Or+9ADYAsMCmwFxAPL+Hf28/Hf+4wArAqwBQQEoAOz/nQAQAAT+6PsE/CcAYgXzBNkAVv3//Kj+OwB5AW4BjAF3ANP/z//a/1QAQACV/53+Xv7y/scAogC2AH8Blf+4/Zz92QCTA2oC7f+r/u/+Yf86AJ0A9v/h/ZX9TgBXAwUE9wAy/i/+jf92ABYBlgA0/vj8qPya/t8AVQHXAsUDgwPIAOz9Xf3C/Dj9kv06/2QCGQTzBDwDsv9k/C38gf4CAeEBGwHYADf/h/6e/nL+ff/a/2gBWAIEATEAof8T/3v+U/56/y4BMgJ8AcP/N/69/aL/OwJPA4IBif4x/sD+nP64/1oAtABdAmcCbwDH/nP+Z/+b/+L+iP6F/7wAcgGXAb8A4P8s/r39Wf9zAHIADACRAAoCOQLeADr/0P2h/kUA+ABDAfT/c/7D/SP+vgB5BAAFCQHK/Dv7xfzn/lEAYgEGAsUCyQHAALX/IP0M/AX9MQBSA9wCAQGYAJMAQQAgAFD/qf6y/h7/VP+z/or+EADOAmMElgNSADz9Jfzf/Lf+RABkAUQCfQNfAw4BkP4D/JP61fue/3EEuAZSBAoBiv5A/F37WvyU/zECOAJZAaMBTQIRAcP9gPt0/WD/tv/d/9EAgQHdAeYCfQOjAu/+hvvb+yX+7v4O/z4BvgMrBDEC2/8Y/tX8Nv3e/mEApQDrADsCogK+AFP+yfxJ/UD/ygBnAmoCqAAz/+v+1v57/7oA9wDlALT/Wv4t/xkBWwKkAaz+Kf06/jgAYQFUAbAAGP+Z/z8BqAAe//v+7P9cAL0AsP9m/1cAAgHrAfMAXf3s+i787P96AzQEUgNXAa7/2P7j/d78PvwX/9ICTgS6AqcA0/6H/Wf+p/8eAiECZwDY/nf+hf9p/2L/9f4qAMABmQIdAmP/lfyY+o78lwH2BU8G2QJ6/af6zfvA/jYCdgH+/y4AfwB/AecBCwFG/yv+dv2t/nMBSAMLA8wAKf6q+1b7M/65AqQF3ATdAGP9SfxI/QH/qf99ADoBMAG9AH//Hf9MAMUAAAEYAPb+O/9M/4oApAHFAM7+oP6u/5EAzgEhAVYAi//3/5H/Cf07/Vb/OAI1A+QAxv5s/xwA4ABSASwAIP+8/Wb+5v/3AAABmQA4AREBxAAY/9n9pv75ABoCIQDk/rX+z//4AKMAzf9c/xr/OP9g/+H/vwD5AOwAwwAGAOb+8P5vACkCMQJa/yP9rPw3/qcApQLgA1sDLgE8/gT9aP2F/tP/0wCQABwAbv99/+EBtAEBAHv+Hf5x/44AOQFEAYcBmABUAL3/Rv7c/Xj+jQDjAbABLADX/0AADwBF/1H+2v1O/dr+XwGPAzAEpwE5/3v+lv3H/Zz/igBzATkBvgDCAMn/d/8OABABZQAk/rD9f//dAf8BfwDp/4v/7f8lAFn/9v49/sj+xP+7AA4BTQB8ABgBogAQ/7j+Tv+oAC0CXwHZ/4H+nP0M/5QBBQL3ANL+zf0M/7X/MgEbAycDxgD6/d37z/yS/2ABjgIrAVoAuf/D/wQBkv+r/qX+9P+TAZYBXgCK/wgApP/5/gn+Y/5iAIkC7wMhAoD+bftm+4r+vwHJAzwDGQHs/43/9P6i/aT9xf7CAPkB/ABVAJT/8/9oAWgCkwF3/ln9Rv4uAGYAvP9NAFkBQwLKAO/+I/2G/Aj+gAAVA9AD2wIXACL/Vf/I/S38jvui/TcCbQUJBaICwP+h/Uf95P0h/xoAiwCJAKz/aQD/AS0CSAEY/vr8zP07/zQBBgIwAsQAh/9d/zEA6/8g/yv/tP5P/5z/TQCEATsD4ANEAVD9CPtZ/C//6AEEAjQBjf8q/hEAPAG3AZ0Amv+U/2L/g//O/mj+V/8iAosCkAA//17/oQCDALX/yf7G/nj/VQAxAk4CcACw/i3+1/76/0gAwv81AN4AqAHNAaP/HvxD/BT/pQAjArkCJgMPAo/91vr0+xX/awLVA0MDvAGH/mz81f1kAO0B0wA8/0v/4QC2AXQBhwA8/or9a/6+ADUD9AKiAEn9APy2/fX/PwJqA2kCfgA3/hn9Zv74AHIBc/+T/t7+HAHMAiABdf8Z//7/iv9+/uD+Y/8CABYAnwByARgBOQDn/18A9P+5/jb+hf8HAs8CgQFn/xH+2P7N/z7/j/+JAPQArADO/yEA9f8u/2f/sf9lACQA+v4x////TABbABEBHwKJAQP/Vv2X/bL/rwJGAz4BAv+Z/aH9Wv8oAMX/NgD3AIUB5gCa/2/+x/4UAFwA7AGDAhMBlv+2/rz+jv5o/hb/9QB+AugCjAE7/5T98/1+/9X/vP8v/04AgwI3Ak8AFv6C/aj/RgExAZj/3f36/ez+mgFKAx8CNQGd/8P+3f4Y/i3+ef+vAIACAQN2AVX/0f2k/Y7+CABDALsAEgHZAD0AiP+4AMUAU//v/nz/LQDiAJEA+v+1/hH+iv9XAf8CSAI/ANX+Y/73/dX+//8iAFEBiwDW/zn/n/7m/0EB/QAHAFf/3f8TAcoALgH7/uT8Lf5JAMEDawPN/9L8PP31/3sCjwJAAQYAfv21/MT8XP8SA4oEgwPn/1D9mf1Z/7EAwwC9/h/9bP5OAhgFywPu/vr6tfvt/rsCtgO8AQ3/pP0c/pL+9f90AQEC4wHOAIr+N/7f/n3/KwGTAX4Ac/8DANMAcQGBAFP+Kf6q/pX/2QCZAXQBkABC/8v+Ov5W/gkALwCYAMwA2gCIAW0BkwDh/p/9fP6JAKgBMAKHAcr/0f0J/c3+gwAkAQwByABZ/5z+s/+1AJwBHQHm/7b+Zf7g/q3/XwGZAIn/c/8OAOoB9QFUAXUAyP8U/kr8D/2g/xcDFgRxAykBqv2r+7T72f3PADMDHQPCATgA6/9dAFAANf+Y/U/9uf11/10BJAOKBNsC1f67+xD8I/9rAQgBtQDE/xb/8f/rAE4CaAGa//3+Mv8g/1L+wf5eAJkBIwHsAIQA2f8yAPL/eQC4/9z9bv4UAFcBIAERAHv/0P90AAkBugD+/mn+E/9lAOYA7wBiAfkAJgBk/tb9kf4z/xUAwwBSAfYAzABOAPr/xf8V/8P+jv/nAOMAXgAk/5D+jf+4AKEBYgAfAIwALQAvAPb+l/7O/m7/SwEXAykDBgFe/vH82vwH/QD+uQB+A5sExwI7ADf+Vv3s/cD+rf+TAAICQwIUAbz+T/xG/V4AiQO8AxQBW/7y/O3+pwGOAnoAav2p/O3+3wJnA2cAtP2w/Nf9xwDYA/YEnQJr/vX7FfvT/DUAgAMkBpoDgf8+/QH82v3V/24BqwEwAB0AiwA8AfcA8v/0/qD9Cv2z/fr/JwPyBI4DYgDG/FH6//obAHgFgwWYAdv9j/1r/vD/ZgB2ALgApv+1/4v/JQCeAPD/W//V/sf+Ef95AH8BwQKzAWH/Nv44/hYAIgHyAY0BcwBm/5f92/yR/TEAPAP6A2ACVAA+/r/9JP75/uP/3ACKAc8Adf/a/fb9av+bAdoCWAHp/tT9FACAAjECiv98/Uf9cP4dAHEBxwEmAWoAkf9v/yD/6f8uAcgBhgEk//f8Kv0kAAQD4gMeASr9+/sg/v4BxAM0AsL+mf0z/joAfgKpAh8BpP4X/Xv8gP2X/9ACCQSuATP+NPxH/sQAWAKGAdn/ev4M/nD/dQFzAwMD6P+B/FL7R/3hAGUDJwTkAt0AF/9N/rH/YQBUAIj+pPwn/hkB0QLWARwA5v6g/iz/mAAsAdQA/v+B/gL/a//z/04BuQH3ANz/yf5Y/vr9n/3w/jYB3wJ2A0MDRAF1/kb8ffu6/dH/wAHdArwCHwMGAbL+0/5b/1b/HP7K/fL+tQBKAvACSgIcAJT+Xv0o/uT/of8AADgAzADDAUkBHgCp/vL9g/6//1kA3ABjAJn/1v/7AJgBOAGg/6z9fP4JAKAB8wDM/l7/ZwAJAagAigDrAEwA4/7L/rr/hP9C/5//dgEYApUAk/48/rz/TgFfATMAQACj/+H+T/62/msA8AFHAtr/gf0b/WD+PgE9BDwEhgEe/hT7Dfy0/mIAfQEbAosB9ABAAQ4B6wCu/1f98ft4/FX/3wKDBNADcQEQ/4b90vwP/7gBxgLEASwAFv/0/cT9NP54ALcCKQLJ/2H9M/zW/VsA8wHlAmUBYgASAOT/VACV/8n+FP7c/q0AywEtAgMC1wFmAaz/SfxU+u789QFXBfIELALN/fj53Ppf/vABiAOIAqsAUv8G/wX/FgAcAcIBiQDO/Xv8xf12AfwDnwNgAXn+I/ye/HP/rwJ0A4wBYf/k/I/9Rv8gAWsDlgN6AbP9c/sy/Kr/yQK2AysC+P/2/pP+6P5s/8P/z/9xALH/5f8sAbYAQwAHAPz/Fv8I/qf9Vv+eAcUB4gARAD8AogBbANX/ov/0/+j/lv/5/y8AewATAVABgAAZ/hv9pv0BANQBzAFpAX4ANgBX/yf/Gf///kn/VQCNAe8A4/+g/zgAawCw//r+Xf+w//T/WwAyAHMAWAC/AKABZgHq/839+PwP/rMA3QErAcQAHwBLAJAAJf+W/rP9tf6OAXICnQJoAVIAHQBO/7H9kfyN/G7+xwE3BOgD/QAp/wH/2P7Z/X7+swCcAv0CtAAi/i38vPzz/38DkgPvAJH9lPtq/k0CfAQHA4v/x/0n/un/gwCm/y//mf6F/Qn/nAH6A34EDwJ9/jv84vuF/ScBOAPtA0wBc/5F/p3+Xv8w/9z/tADdAYUBeQC9/5X+if5r/lb/0gB0AU8B+P+M/j3/+f9pAF0BzgBJAMD/6/+4ADgAqv4P/br9nAEBBdcDKwAJ/Vv8K/6N/wAAxACrADwBRgG//1j/s/6a/kMAFAK+Acz/0f0x/ugAygFAAcf/bf8fAfkArf/j/mf+nf6Q/ywAlQAHAUgBrQGYAZcAxP6f/PX8yv+eAawBdwDz/vb+kf8+/w8AtAD+AO0BPgGM/2b+Hv/a/3wA+f/A/kD/7wAyAzICev82/cP8Zf+fAuYCSgFb/yL+TP/5/z0Avv5p/e/+EQFhAr8BVgGiAIkAvP9T/zv/6f5X/w3/JgCfADcADQAiAOj/jv6w/swAxQITApr/TP3+/Lv+6QCOAWUBCAAF/5IAAwEdAQ0ACf/B/2UAkgHxAP7/K/+2/jgAXwD3/tv+PQDwAQ0BIf6u/IP+PQEwAu4BXADx/l7+hP+hAZoBnf9S/aH9HwAjAqcC1QGBACj/Y/4T/hr/dgCFAeUBLQEhAHv/tv63/oT+nv3M/soAhALtAhsB7v+P/z3/sv9S/5v+rf5FAGUCiwICATP+l/2C/1ABewJGAb/+BP3i/f3/7QCXAAUAUADfAaoBVf8//Yj8UP5OAJYBqAGKASQCUALkAIj+4vzJ/If/kgFVAr0BHwDC/8L/1P9b/nz9+/02AIMDlQNGAUf/Ef8pAGv/Mv2b/Gv9OAFnBNED8AFp/2v+sv5Y/+P+Mf7Q/oUAJAJNAhsBbv8j/47/ewCD//b9YP4vAG0ChwEXAFX///4s/3P/LgCrAIUBHgHyAIMAM//s/iH/aQAvAFX/8v53/8sBTgIBAef+J/6E/mD+vv68/78BLQM1A0IAW/z9+kb9dgG7A/UDoQFd/1T9svwH/5UAkgGoAR8CGwIXANb9SP1U/zkBdwBT/o39d/8/Ap0DrwIsAFb+5P2J/ib/8v/tAEABTgGKANP+m/0p/wAB7wJQAgH+tfuY/JUADQMUA/ABh//L/tX97P2Z/ub/ewGfAXMB5f9B/4IAqgGzATb/3Psx/FkAlgQiBZMBi/3k+zz9OgCMAkECugD+/wIAmQCD/4z9j/2K/r8AVAJWAZQA7f/J/6n+yvzw/SMAzwIGBBYC9P+2/uD9Vf7y/9gA6wBU/4r+vv8YAMb/mv+1AFUC8wG2AOT/Zf+5/0P/tf3e/UL/3wEvBOgCLQFg/zj+m/0P/Rb+3/8+AlQDfALF/zL9lvx7/fgAAgLf/2z+qf4EAqQD4QHj/yD+9v1h/gn/OQAzAdUCuQPQAo//+vsc+079RwDVAd4BggDnAPoBegIkAZL9HPy7/P7+kQB1AdQB7wEkApsAWP/k/f39wv5e/04AiQCDAWkCJQPwABL9MvtI+2f+HQLkAuYBOQGdADYBLQEN/3v9hP2y/3sBFAH9/yT/JwAoAqYCHQE4/2P9oP0KAJwAUP/g/uwAggPaA6kB+/1d+1f70/2VAGIC8AFjAC8AbACeAF8Aq/95/0P/Kf43/s3/hAFsA/kCTwD6/aL91v/TAP3/QP+1/kj/QQHNA9sDggCe/Oz6o/yO/7cBPALLAYIBcwBO/5/+Qv9gACMAGf9R/tn/awK6A3ED6P9c/I366vr2/gkDRwXjAy0Apf6e/hP/UP4R/iEADAIsAhsA8P6U/ycASwDg/5v/N/8C/x8AvQG6AogBQ/+l/iMABwIeAUP+sPw0/Qv/QQCbAAoCrwJtAe//e/7w/aL+lP7y/u8ANQLeAagAUwAaAHz+hP3L/TQAwAIPA+MBgQAy/0v9//z3/pgB6QLaAQMA5v2p/cn/eAG9AXYAfP6M/p//XQEjAo0Aof6o/bP+5gB8AX4ARAAGAHwAlAA+/z//Nf/4/ov/hP/z/7cA/wB9AR4B0P8T/93+kv8PAJf/M/9D/60ARwIWAuj/X/7P/oj/ZwBgAHgAYgF4AW8BEwCq/eT8k/0FAP0CnwJ/AFH/iP+tAIP/y/3q/GP+IgHgAi4D/ACt/oj9wP60/o/+4P9sAVoEcQRPAQj9Ovvh/G0BtAPqATz/b/wq/s4BbgQpA5j+C/wP/Yr/qQAVASoApwAgASkACQC3/+z/JQA8AIz/5/0M/dL/hwPvBMACkv4N/B78c/0L/+UAHQI/A8ACDQEE/5z9O/66/vn/YP/s/hMB4QJAA14Bff5E/UD+aACMApgBwv60/YL/HQL6AeX+7v3D/3QB0gGR/939xPxm/lIB1wL2ApYAPP+c/rL+VP3A/NT+PwI9BcYE9AEY/nH8M/0k/+P/rv8KACsBUgIvAi8B3P5n/Yb9WP/DAIwB8gHCAe0Asv6o/Yz9vP8QAhoC0P9i/dD8sf6eAX0CfQI+ALr/JgAUALf/bP7N/g//CwCTAIUAzgBMAmcCPQDu/VT7Bv0VARAFZQVKATX9jvsV/Un/XAAjAGcACAFnAZoAov82/wwABAKBATL/df0y/dz/BANVAuj/WP1Y/uwBdQM/Auv+ePyg/MH+6//AAVYCcgINAkv/xP0A/EH9jgDqAscC2gBz/2z/yQBMAJL/Xv68/iQARQEpAUD/Av/U/5YBEwFq/7T+Fv9q/9r+jP/o/1ABAQKyAbcARP75/Qf/NwHFAQ7/7/0CAKUCfgSCAjv+2vtv+0b9KgDnAs0E/QOHAXH+9Prz+rP9FAFNBKoD0P+P/f/+TAKJA1P/xPqG+oX9kgJCBZ4DJgET/5P+uP9bAHv/8P2t/kgBIgKlACT/j/4mACsCwQFUAH39f/xi/h4AhwEaAmsClQEFAEb+Dv32/VYAPwL8AcQAif9V/9n/egBT//D8g/z//qkDgQXzAgH/Bf38/XT/p/+T/1f/dv+cABkBDAFyAPj/FgHPAaAAR/71/Er/vwJfA9YAv/yK++X9lwLHBCsC5P5t/Jf8bf7iAGAC0gJsAskAh/8D/uv84fzb/sEAewFEAVIBuQLQAqYA+fyn+x79jP9UAs8CCAKQAeQAzv8//ob8x/xP/v8BywRaA5MAa/3E/Z//+P/6/6r+hP76/9IBlQJjAZ3/FP9G/z7/jv6//kkApQGNAlMBOf/o/nb/KgC5ANf///1//TP/1QLAA/0Bz/+J/Vz9Mv2+/ev/+AKZBLMDlwDf/KX8lP1KAB8C2wALAB3/ZAA0AboAp/9X/kP/7AAnAX7/aP8IANAANwDb/dP9yv4nAlwEGAM3AGv91/w+/l8BswFcAL3/kv90AKr/Kf4R/n//IQJ8A/wAov4C/k7+BAD+/2kAMgGyAY0B8v+G/j/9i/3T/3UCYgLxAIn/T/+5AEEAVP/0/sr/HAHBAXkAJP+t/8H/9f9M/5T+rv1h/v4A8gFyAk0Bd/+F/mv+qf4jAGMB4QGxArcA7v0P/Oj9ngHvApkB1P4b/pb/DwLCAp0CwwBX/SP8+/zf/pX/MwAAAooDfwK0/9P9Yf5FAMAA2ABj/5f+gv7a/gYBIgIAAhcAk/4o/pP+IgB1AUMCcwGW/yv9df0kAYQDEwOb//v7zfus/hwC8gM0A1QAl/7D/Sn+z//y////AAD+/44ATwGhAaEAdv9y/fr78f11AZEE6AQrAlT+ZPx9/Zn/pgAOANT/4v9JAOgAdwDp/zgASACdAL4Ag/96/uf+VgD1/0L+8/6EAM4C9wPTAQX+6PoJ/P//GgNwA4sBcv8z//H/GwCy/1P+UP66/4wAKAH0ABQAKQDAAJf/vf56/kr/EwGiAX4BqQCw/17/jf8eAA4Ak/+M//n/MAC//03/lv8KATQBcQAAALn+eP9JADgA0ABbAPP/kv/0/oL+Df///w4BgwHsAJv/m/5w/xUAcACwAGkAXgCmAMT/zv7+/pr/qwCuAFsAwP+fAI4BHQEpAMb9Wv0F/u8AxwOOAzoBC/3m+0X9AAB7AcQAkQBFAfcBUgFDAI7+Pf6c/hv/Qf9m/5kAWQFaATQBAwEc/1f+u/5t/+//wf+JAF0BaAJuAQT/oP52/3gAqgDT/lT8Of27ABEFTwYvAjb+Nfxy/An/VQDm/1n+mP6mAXQDuAJqAKf+Mf5N/sr9+v1mAHwDvgRgAp7/+Py2+8z9owC8ArMB1f+e/4kBjAKlAL/+RP24/Qr/sP8SADoASwGsARIBLgHA/3D+Ef75/V3/l//OAKEC7wKYAb3+Gv4a/2wAAwD1/vv+agBVArQBMgFb/5z8Cf2d/64CcwPxAEn+2P20/Qb+t/5+ABQDbQSZAzMAzPx5+7L8Iv8RAZsCNwMdA+AB+f/X/T38vPwB/+gBbgNyAkQAzP4w/zb/6P2G/Yr+hgGlA1ECAwGd/5f9HP3W/Y4AtAKwAn8BD/+Z/Uz9+/6NAQkDIQL9/yv/y/66/wYA9/4n/7MAnwKdAooAw/42/rn9rP2r/Qv/awEsA/ADHgKS/+D9Wv2u/Rn/Nv9U/4UBSAPhBP0BDf6L/Hv91gAJAS3/sv3f/tIBiQPvAg8An/00/WD+Rv8yAEMANQFoA3oDOwFF/Zf6dPvb/i0CsgO3AmEBAwF1AND/Nf5A/Xz9a/4MALABrAL9AmUC7f8w/Tv7mfxhAIwCPgNrAeD/cf+J/zQA5v+6/zv/u/4W/2L/zP8sAB0BRwJoAjwB6f9S/1z/jv99/4b+uP7F/4QA0wEOAfL/g//A/oL+Fv6A/0QCcAP9AfX+0vxL/br+XwBZAi0CkwCj/mX+Xf88AFsB+QA7ATQAOP7k/df/DwNwA+gAyfxT++T9KwFVBJ0DCwDX/SD+uQBtAkcBFv/S/AL9mv4IAIoBcwLlAv0Bn/9Z/HH7Yf3s/1kCdAPUA88Bg/+T/S/8Fv2W/g8B2ALwAhQBpf8dAEAA0v/O/Tj9Rf+fAv8D/AH7/7D9Iv3+/iEAeQC4AEcBHwLaAPH9E/w//YoBZARQA3n/C/wY/GH/IgJPAuEAbP98ADgBGwA6/rr86v1mAMwCqAKNAYoBYwFuAJ79/PqY+pL+1QNQBvoEqP+c++X6mvyc/5UBCAT1BNIC5f/k/DD7wvwpAEsD4QOaAaf/Gf88ADAAR/7e/Tz+8/6AAAcCggKeAbT/xf3S/Ln9BgAEAowDmwIBALP9ivy4/Z7/MALrA4YD8gAa/ff7mf74ASYD1gHV/br7t/1GAU8EzQORAOf83vs8/m4AUAEPAUoB8wEtAqUAEP5V/TH+Z/83/9D9k/4ZAgAFagTNAFf9Efxe/SkAfwEEASUAXv9LAAgCsAEx/0T9pf0IAKkBJAF8/2D++v7Q/wcBHgMEBHUCqf2z+iD7Pv7WAnYErgMQAOD8YP2h/4gCaQKN/5n94/58AFoB1QGAAC7/PP3k/IP+ZwAZA4oDFgJB/3383vwUABEEtQQZAW39qPtA/Eb+XAAeA3wEfQP2AP/9nvxY/Nj8Mv4AAYgDzgOvAkABq//F/RD9//00/00A3QABAZ4CXwNoAV7+7PqI+ywAxgOQBI8BQ/4k/a/9X/8wALYArgDj/5AA6wBYAIv/Yv/MACIAe/1t/IT+7gLtBJQCN//S/b7+CgHbAnoB+P0x+yf8gQB7A9oDyQLnAG7/l/46/l3+aP/e/wYAAQB9/4oAvAG0AVAAH/5h/fz9P//JALEByAGoAc0A8f9A/7b+ev5t/g//aP8DACYBFgMWBBAClv/8/LP7Cf1i/vr/eAFMA+kEewMkAAL92Psg/c3//gAHAfoAzgDHASkB5/5l/eX8p/46AQECFQFAANgAPwEgAIP+aP0H/n0ApwILA90AEP5S/Yz+XQChAAIAoAADAjICyf98/SP+3/+5AbsBBAAP/0n+kf8qASABmQCE/6T/nQCiANT/QP///n//rv83/+X/JgCuACYAHv7q/l4ACwEnAWcApQDAAFMArwCeAM3/nv69/Sv/WgE9AZf/sf4z/64AdwE2AnkD/gEC/+P7IPuB/vcAKAJ2AZ7/Hv/4/noAagHV/zr+tv0C/x4BZgJ7AqgBYwB//sf94P76/7MAHgBY/xUA8wAZAT4B9ACd//T+O//b/44AtP/I/sz+AQD/ATsC1/9V/tz/4QBbAAX/PP7a/mP/qQBCAqYC6gBJ/ov9hP7H/wAAsf8QAGsAzwDhAIkBzwFqABv/vv0A/Vz+RADZAdIBTwGxAVoAEv/R/7r/xP4h/qn9iv/bASoCSwIUAnsB0/8V/eD79vzw/nkBggPSA3YCOf8d/fn8yP3s/sr/gwFtAnYBcwDcAP4Ag/8i/kn9S/6dAI4CdAM2AZb+8Pzd/bAAxAFhAab/Cf+8/5MA+AAaAMj/g/+K/+H/2//Q/2j/Yf8JAA0BAgG4ALEATADR/4P+yP2g/qcAXwJJAkcBzv81/jX96P3K/xsBtAG9AQMBcgD5/kz9pv0a//sAkQE4AScB5v8j/y///P8zAU0BDQH//9j+zf7+/iUAcgKhAsgA5v24/Lr+3v8WAGj/Fv8IAb8CGQNmAez+3/wS/cj+TQByAdQASQHAAeEA6f6P/Pb94wARA5oCDgAa/wH/YP9c/xL/JP+QAMEBzAGrAGv9Wvzw/V8BZATeA1sBpf7Y/bT9n/2p/kMAAwIZAUUAfwC6AKMA6P7b/Sz+Tf/2ARgEtgNBADD8Yfsc/lIBKAIXAXUAiwGIAd3/wv7F/cz9nv5z/4IAUAGTAdgBwQKxAa/+L/x++zr+6gBiAgADywIbAuP/Rv6q/Wn9+/3L/1YCNwNvAun/qv3c/Rv+df4hAB0ChAPgAhkAzv03/Jr7yfyc/40D8wV+BaMDGwES/pb6kfeS+Lf92gMACBQIkgUYAbb7K/mI+jL+HQGFAtYByQDaANsAGwIiAhj/QPux+db8FwJOBUcFIwOg/xr9fPx0/YX/pADaABUBugF8ARcAb//i/o7+Sf4K/yABKwMyBIICg/+4/PX6rPsx/igBhAN5BFYD7gAp/gb93vyy/S0ASQHEAc4BFgGvAL3+c/1N/ZX+BgH7AbsCSQLcAJn/I/5S/jP/Kv8x/zgApwGAAgwCaQAy/yz+g/2G/g8AYAEUAf3/4P+wAD4BEQDU/oP+qP6v/8EA1AFdApIAPP4F/pn/sABbAIEAKgEnAAf+kv0b/6cAfgEgAfgAHALDAbT//fy2+wb99/90AzgFAATN/078e/wM/7gAef9J/ir/+gE6BN8DbwGu/Rj7OfpH/LwBaAZ3BqwB2Pya+pf87wC8A4gE1gGF/Wz7Avz+/nQBHAJ8AtsB9wCQAJn/Sf8n/q/8b/71AF8CTwPOAi8ANPx3+p/85QDZBNYFoAPMANP9OPsT+wj9lwB4AycDqQEAAfgAKv9G/Zz8Jf3G//oBAQN2AusAPP/O/Wv+Vv/U/yYAjwBcAUAB4ABkANoAhgBM/0r+tP3o/1YBwQE5Af3+5P3O/gsBawF+APv+Hv4x/6P/4P+RADYCEQLG/0b+df11/7EB7QFuAM/+QP7Z/gYCzANBA+EAsP0K/BD85f3d/6oCgAP0AW0A3P4r/tH9mv/iAR8CSACf/Vf9mf8SAgMCawGmANb+sv3G/q4BbwItAaX91/vJ/u4BwANpArQAdv+x/TX9o/06ANUBmQFtASgBugDj/6//C/+f/v39rv1KADwDogNDAcL9l/vI/PX/+wEGA4gCoQB//y//Jf8r/gv9BP/rAToDEQNbAc//4v5G/gX+J/7//h0ADQJpAygDcAEG/nr7yfuT/QcB4wPYAwQCIv8e/Uz9b/6G/7YAmwJ+AkEBVABQ/9b+Uf59/ln/jgARASsBOQLiATEAU/0Q/Oz+mgIPAycAkv1Y/aP/swG1AZQAg/7o/TP/0ACxAakAjf70/rIB1ANcAzgAm/2a/C/9Cv9XAL0BxQHjAM//bf53/jX/pACqAdoANwDB/5v/6f8x/xn+Nf4UABYCVAO8AlAAl/3i+4H82/5OAQwD0gSnBdcCgv4H+sD4CPzI/9wC9wIQAjUC7gHHAc3/dP1Y/NT8QP//AHECLQM6A0cC1P61+yP7GP33/54BvwGEAfEAuwBiAV8BTP/G/Kz8mv7iAa0D3QEvAMX+5P18/k0ACQPDAk7/oPyX/Gz/IgKVAs0BqgAw/6r+lv/uANYAbv57/fb+8wCOAr4BXAExADf9mvy+/bkBAQQ5AkcAsP0S/ZX9rf56ANgBogJAArwBIP8k/VX+DACCAYYAP//7/7gBEAIpABj+hf2n/sYA5gEwAYQAXv9T/6MA//9c/gH9/v7eAWMDJwNvAMD+If0w/c7+AQH6AvkBqQCv/ur9Wv6n/ncAwwGAAXMAdQAiAeQACP+c/Sv+b/+fADn/MP8/AQQCYQJ1AEz/SP/P/m7+X/7c/2IBJAFkAJgAHwFgAY8A8P8RAAX/4P3T/O39fgAzA2kEVgLhALP/ZP5C/DL71/xM/9QCPwQABNECIgCb/bb7B/wF/qIAfAJzA2cDywE2/xD9jP0L/3sAgwBmADkBCAGJAEL/9f5T/7v/awCOAAABWACj/2L/hP93/9P+Pf9oAEsC6wFLABz/g/3r/YD/FQFpAbMAWAA2AAoBjwCU/j3+rP82AGT/Zv8CARkCbwFBAJL+t/17/g4AYwLfAw4Cav4u/EX8bv9AAvEC5QEu/xv+z/+JAtwBaP5w/JL8SP9gAgYE/QIGAOf8APyU/yQC9QELAI7+BP9t/zAABAH7AegAN/7M/Uv/tADoAN0AQwHTAKX/lf+8/5r/hf9+/tP/JQHf/1b+f/7YAaoDDQPwAHT+dP3X/Kv+LAGOATAADf4E/x0BzgFdAYkAFQEJAC/+/P75/9n/q/61/gYB8wGoAMD+Vf53/+v/ZAAeAWkBIgAr/rz+vQFbA98Bdf8N/gz+Vf7+/oMAigFIAfb/hP6Y/jcA8QGNA70CXP8a/cX8xf0n/xMB9AEtAUYAY/8tAL0AHwDm/5X/b/9Q/mf9u/5lAkwFeAM3/3/8Lfxx/RcAkgILAzACdv9g/VP+0v9DAXsCAAKs/z39h/0NAGwCEQIg/8X9Yf6F/0sBqgKIAicAk/yf+6T+xgFZAswBzwGCAcb/C/7m/cj/IwCH/g7/FQAQAeQAav/x/+0AcgCp/3v/f/80AEIBqADt/yP/8v56ANkAxf8tAGAAVP+S/vn+PgFyAsABMAF3ARkB8vxx+on8hQBGAx0BGQB9AQgCawAb/bD88/3k/14CrQOaA7kAKP3N/AD/VgD9/23/SACEAIsALwEaAU4BDAD6/Un9K/7h/30BggNcAoP+j/z3/W4BrwIGAvb/mv2w+wb88QCEBTUGLQLv/GD8Qf74/3IBbwE2/0r99v3kAQYFywL2/jn9Tf6u/r/9ff5UACQCEwITAQkBmgDc/9r/yv+b/kz9l/yT/8UDQwPKARoA+f6i/0//JP94/5cAcwHJAOUAS/5B+4H91wFQBS4Exf9s/b/8fP2y/s4AqgLhAQoBNAENAuL/uPxs/JH90f+sANoAswLpAukAiv5F/gv/1f5d/tn+uwD6AUoCwAIrAtz/tfxk+6n9DAFBAwIE1QI9/3X7jvvV/sgBpwJGAUH/0P4CAFIBIAMoAmb9HPoz+0YAswRcBegDyQDW/JT5Ufqe/30EfwVYAy4AIv3z+h/8ugDgBCAEfv+Q/av/bwHSAI/+v/3C/jUAWALLAy4C7v5D/fn9T/8K/wz+mf//AlkEYALk/gr8ovy3/qQAgwKgAVUA0P8SAKD/6f1c/sn/mwGfAg0CHQG6/rD9w/3G/iYB+gEoAlQBO/9a/Tj8gP7vAvUEqgO6/zL9/PyX/AT+QgHYA5YCx/7S/e3+kgAtAO3+8/9WANIAoAG8Af4BD//w+/X8awDmAuYBPgBl/5//JAA1AM4AFf9u/a79MAA+BOcDvwHi/sD7PvuC/B4BEQUkBNYAsv9V/6L+2/+WAP7/Ff2d+rj7GAFRB0cIzgaNAVP6CPZX98/+DQR+BX8DVQHxAKz/IwAtAD7+0fvD+2v/QQQlBs4CTP8h/U78Zvyy/m4CyQOgAjwAuv8u/6r+iP+c/yH/Dv5//q8AdgKWAuMA3v5I/pH+Fv8LAfwBhwFy/4/+qABjAVMAd/5e/tv+TP+tAPABkgNWAVr9e/w2/k0BDgL9AKgAaACW/47/dv/J/n3+2/4CAe0BmwE9AQ8BvwCK/m399f2B/3X/IP93AdABpAAG/1v/eQGNAaf/bP4i/3v/DP/M/6oDZQX5AYH9CftN/Xj/PAAsAqcC+QCx/c38B//wABAB4QAPAeT/wP4Z/w4BpgLxAIn90Pz4/S//iwF0A18DPwF5/rj9bf4u/7f/swCyAWMB2f5M/Qn/CwH3AVoBOwBi/9/9+Pwk/+ICIwT6AqwAKv4H/Sn92P7UAZcDaQG+/qH+Yf7+/lgBAwJmAcT/z/0n/lj/6v5d/ocA1ALTAcv/cv9UAf4CqQHb/jn9WvyX+wD9dgEFBRQFkwJWALT+iv05/uX+tP9g/zD+nv+9AnkEawOvAGD9jPxN/jsAAwGy/yr+q/6UAXkD0gKsAA//i/2I/Fv9iv7/AKcBs/8g/9YA2QNmBPUByP1Q++n7x/2QAAYDVQR6Aaj9T/43AIQBygAW/7L/2gCD/9/93/+NAoIDOQFn/dH8nv6KABEAd//b/zr/GQDrARQDKAJ1/2D9vPzP/Ur/kgDvAC8AuwDjAYcCeAHh/gn+rf6J/8P+B/6a/0cChQOGA4QDXABy+zT4wvoRAUwFDgZIA3QAC/64+8P7Yv97AhkB3f7J/hsB0wKEApEAOv0J+wf8qABOBU8FtAFJ/9X+jv7r/TX++f6K/qH+uP9uAgME3gLbAAv/Qf2g+7399wHUA3sCY/9S/g8A/wBC/03+8f97AXwBIwGEAIT+bv3W/Yr/zwHFAccBsQK3AUn/tfvp+tn9IwEiBJADzAAD/hr9G/9mAIIAbP/D//0AMAFjAHb/gwDOAGAA5/+G/yf/dP0R/owBowOZAm7/a/0Z/z4BeACm/kD+Kf9NAdwCvAJsAIH8KPyR/l0BbAI5AdP/A/+L/xkBhgLn/6T9tf57/7//yv6F/zYBNwKYAQwAJwDb/tP8HP0WAYEEMgSaAar+Sf1z/En9JAB6Ao0CWQH0/+7+BP+f/j8ADwG7/7//7f5DAJQBKwEdAeX/Uv6a/Ov9AQHCArQCdAEaABz/dP83/ygAOABN/jT9NP6KAJ4BlwLdAswCQgB4/Gr7q/wf/xABcAO6BPcCQv5p+x/9KgBSAg4CZQH0/8D+Gf/5AD4C5P7q+wX+NQF8AogB7P/1/wMAVf8+/27/R/6K/aH/hwJ9AzkChgF4AGv+e/vM+gD/wAKlA0kCxAAcAC0AYv9H/xQAUv4F/Xf+sgKeAxoBZwB9AAcBhP5A/DX9oP/ZAcAB7AAXADcA9f/1/4AAl//w/tD+if9UAGgAbAA8AIwAhAHhADD/Iv6t/fv++P+OAPYASwGrAbAA5v+U/9EA7QHJAEr+//xX/uf/xAE7ArEAkf1M/G7/lgJnBHECAADf/R/8rvyj/hoCHQIFABUAiADW/07/OQD9AUQC1v6t/B3+rACpAS8CywJOAIT92/vV/FwAiQHNAEEBjwMTAvH+ov4y/ur+kf8MAM0A6gDV/5T+uwDiAcUAgf5R/a39wP5iAfYDxwXZAiP+SPta+9/9iADnA+YDtQA3/Lf7lQATBg4GlgC/+2P4GfrI/pAEDge4Axv/qPzr/ugANwEQ/8H9/vyE/LT/BANJBV0DNAFM//r8yfsD/CoArAPNA2AAkP8wAW4BGQGi/5r/c/56/Tz+UwDDAbQAJwDi/0P/if0g/swAdwK5AroAqf8r/iz9nf6XAIcBaf8c/lMA0gPjA2kBCP9I/oP+4PyM/gwBuQEgAfL/fAECAVf/S/1Y/hsB6gCOAaAA3f8W/wf/FwEiAdv/8f2l/pYAAQEjALT/YwBS/yL+3v5+AUMCBgDU/lwBpgIUAHz9m/s1/ZT/EQEkAzgDVgJ0AJYArAGV/6/8E/z+/LT+PQFQBIYFfAIn/5j8b/zf/cP9EwB6A/UDJAGH/ur+PQDv/yr+kf1r/vz/DgDBAB8DqQPQAe7+Fv74/U393/0OAP8CXAQ2A1UANv0k+7X7MP9FA/UDSwEb/57+QADAAQ4BAAAW/4D+1/8ZASYAEv5i/aP/agGNAVMAvwCxAhACDQDy/cr9Ov0Q/bP+ygCFA9oBLADkATECjQDy/Z38+Pxj/Z3+mgGTBCoEJAIPAbj/6f3V+5j7NP4hAgYEsgOMAh4AjP4K/qn+8/2y/Yf/dQF7A40B/f7i/Xv+8v8bAOgAoAAHAfEBGwKTAHT8L/qJ+7n/5QIQBLkDqgK6AdH/r/7E/UX8GfsS/R8CRwZsBtkCCAA1/iH8WfqZ+ov++wEjBMkE5gMjAcH8Nfvw/f8BUgJVADj/NP/F/6n/MQAFAOf+Qf97ASsDYgJVAUsB9gDm/XT5dvhm/QoDHgaSBv4EPAFB+/n48/s+AKoA7f4lAMoBjwJJAbYBswKt/538ovsx/oYAZwBiAYYCHwMZAfn9qf5yAJ7/mf4q/zMAUAB4AFcCpgJ1/3f87P2aASkB2f23+3D+kQLsA/oDIQKh/3D8ffsN/0UBCAGG/xn/5AAXAfUAlgEjAWH/Mv1s/pYBMwJ5ACL+yf2R/vb+k/+0AZoDMAOsATwAq/1Z+y/8+f9pBG0ELgEc/Yn7wv1dACMD9gL4AJn/bv6W/4YAaQCp/0r+t/5//9b/LgHKAvsCOQBk/er72fwdAHED7QRQAW/9Ivzg/ScCvATAA0IAzPwe+kb7MP/iAl4EBQN2AOH+hP9+AP8A4/9I/iX97/0OAaUCxQINAZL+Ef0e/ZD/6QHeAZX/8/5kAKYAsf/b/1sBkgKyABv+Sf0Z/jMARQGtAwwF1QCh+oX53f91BeADsv4n/LH9igA6Al8CsACu/Nv5Xv3TA/MF3QNG/438s/ws/pP/jADLAckBkQI5AjoBo/+A/VL+w/26/EH9mAChBFEFDQO+/6f+3/00/eT89v1+/0QAtwKCBCAEuwBm/dT8uP2y/00B2gKrAj3/Bvu9+ov+QQLWA64DIgJR/jD9xf6cAN8BfP9W/Wj9/v91As0CugG9/ykAhP8T/jT96fz2/6sDxQYiBgYBOftl+Jz7MgG8A7gBd/4i/b/+NwMGBpQD1/1Q+dH5cv4yA2oFswP+/wr+UP7C/4QAp/70/Iv+EQJ0AzwC3QACAK/+u/x8/Rv/fP+K//sAFwV9BdUBkfxT+/X9DP+O/7r/MQH2ANcA0gHuAiYCj/7D/Ov8mf8AAK0A5QGsAHD/Z/6s/90A+ADq/0X/Of41/Wn/jQOsBqMD8/1B+pD6pf5SAhIF7wT8AF38Tfu0/Vr//f/SAKwBaAJtAcgARAG0AEH+e/uV/Hn/mAGOAgUDswLGABb+k/wX/ff9Y/9iAOoCRgSmAngAoP5a/2D/rv1N/E/95P9AA7kF6gThAUP9f/q4+lL9MABMArQDpAJPAL3+ZP6P/kQAHwDt/pX/PwCrASYDOQMmAfL8I/p8/MMBqwSzAqj/Rf0K/REAjAI9BKcD8P7F+jH72/2UAGcCDwO6Ad3/Rf/Y/o3/ef/g/+EAlgGdAWb/3/5n/9L/Ef+C/qb/pQCEAHUA5gFkAQv/rfyq/aIAgwHpAAAAPQHnAB4AUwBYAAkBw/9h/Sb9mf40AHECQwRZA1n/Cfzz/OL/EgGO/97+bAC0AaYB0gDN//L9VvzL/eoBYQRpAS39rPxHANMD2QPOARAAI//E/CL7zfxbAOgDzgOOAZ7/m/5o/hD/zwDgACgAhv8J/zIAUwD3/lD+jP7x/8UB0QPnAzoBeP1h+5j8kP65AaYDBgQ4Amn+M/37/QMAAQBkACoBxAB9AKr+KP9z/yT/xf6F/9gA0gDKAf8AjwCe/v39HgAbAegBLABq/2H+Gf5P/s3/WgL+AVEC6QD1ALD/Dfzn+8X+BQO3Ap4Ap/89ANb/8P57AEMBgf/P++X8HQL6BcEEeACu/ej77vsL/dv/YQK/Ag0CwgHOAScAhP70/SD+wv1C/rYAtgLyAr4BdgBd/17/x/5U/pj/HQBM/+n9vP6ZAGQBLQKQAqkCqv/v/AH+4P/RAUkAq/2o/U//UQGKAuQDwQPPAAL9D/tH+2X9JQB0AlYEpAMdAWD/6/8JAen/jP0z/Jb8Of5DALwCBga2BCL/Q/ze/Of+6AAlAeYAhf8D/Xj9fQBwA84C2gBJAFT/Hv6A/Cb+uAJpBPIBHv9y/Q79GP8EAlsE2ALk/s77YvvU/c3+NwBXAy4FxQObAG3+av18/b79aP7g/sP/vwJsBRcFIAEm/az7Ef2E/9QAaAFtAR4A+f3z/Q8AZwLoAb3/2v64/qv+Mf5FAL4C3AEC/17+CgGTAvQBjP/5/pX/zv8PAHH/RQC//xj+I/4X/3EAQgJ9A3oD3wGt/S/6OvpJ/S8AHwK2A1sDxQEqAKsA5wHg/5v8NftT/cQAggI3A+8BQABZ/kD8tf3r/98ByAJdAgABSP5L/ZL+ugFAAtb/k/5X/z0Amv9mAGwByADb/lf/3wHgAS0AL/0t/fn/RwH5AIIAvgD1/7f+r/6g/yEAaf+S/sAAFwQDA+//4f1K/dL8tf0dAZ8DdQOmAToArP7K/NL7cv3nAmAGpwRDAPX8QPwQ/Vv/KQLLAmoA+f25/f//7wAJAVsBbQExAaX+4Pze/bwATgL3AEv/0/0i/XQAEQUzBV0AwPnc+Hz9mAJHBd0EEQPx/4H85/qv/SkBtQI7AikBAwHK/gv92f0kAAwCrQHmACcBeAAh/4X9hfx1/mEAKQL1AtYCEQEr/sT8Rvym/gIArgBRAgcDBAOLAOz+8P5h/xX/+P1e/lAAGwJUA/cCHgAg/UX8UP24/4IC8QI/AW7/n/5R/0T/L/+2/zUA0wCzADQA8wDZAcgAA/7e+tD7Z/9KA7QFQQQMAQj9FvzJ/UIAOQJpAR8Aa//C/ycArP+g/t/+LwCVAYsCXwEZAAL+Jf06/Qr+lwC+AqYF/wQAAnP++fnW+FD71P9zA0MF/wNNAlgB//8a/8n9TP2Y/Db9nf4zASMDawIkAkQBEAAW/rT9P/+p/63/Jf9LAEYChALQAWoAif9r/oz9Of7X/74BZQKoAVT/aP3z/ez+bQCLASQC8gGv/zP9Ef0g/4kAdgD2AM8BigHr/xL+nP7Y/z4BlwHvACcBiP4H/fD9//9TAokCxwFeAfoAxP7W/VT9Mv1S/Z39TwGqBK4FcQMaAUT/b/zy+hv7qP4tAhkF2gWGApz+YfvA+/T+3QHFAkgBF/8P/kv/ZQDWAIgAu/+k/7r+o/6MAIcB2gG8AMf+Qf6k/l4AWAEhAbsAp/4k/qr/1gA4AWwBWwEqAWoA9P3L/Nb9HP8yAIEB9gFwAe8AzACrATYB2P6U/N38R/4r//QB9QMwA6kBAwBt/vv8FPup+1n/0gLaBJsDagE7ACP/hf4E/oz9d/1F/hsAkgIgBHEDkQGj/83+JP8V/1X+MP71/jYA8gDrAAECrgKVANv9Evxs/CL/LwHXAgUDEgKgAXsAcf+2/S788fvn/eoBMwStBAMDQ/+3/dT9qv1n/iD/PQDPAZMCDwJH/w/9gf0L/+IA9QGjAtIBpf6y/D795/+oAjoETQOg/xD9lvxJ/t8AfgJ1AmgA8v74/tz/nwA8/4T+Pf86/zAAzwAjAfcASf6y/GH+ngGVAwgCrf8f/8r+B//f/3kA3AAqAOz/agAXAYEAFgC2/5/+l/8WAJYA8v9n/jv+eP/hAUICbgI6AQH+Wv1W/uP/+AC9AJkAMQD4/+3/+/+LAMoAfAD8/5z/Tf+6/gr/CgC2ACQBnQAiAPL/af4c/SD+bQBlA9UDRwFp/kj8Y/2F/2UBhAL2Al4CKf/g/C79QP+pAIYAqwBLAMIAwgHDAY8BRgC4/Vf87P1JAHsAfwCdAGIAhgCq//X/UAE2AYEAG/8d/bP8NP4KAKIC0wN8A0ECn/9b/Xv8E/3V/Un/EAHhArsD5gKAAhEBl/0z+iD67vyE/30C5gRABRYEFgCe/Af9XP6U//AA7QGDAPv+Y/50/8gBtAH+AFn/H/6P/bL+cwHEAs4BbP2W+1v93QCAA+EChwHC/tb86Pzq/1MEfQSqAY7+iP0o/gz/EAF6AXIAXP5w/PT+/gL9BEgDY/8//Ir8Cv+sAMMByv82/3T/JACTAm8B/f+n/kv+oABnAn4CCgDG/If7avyH/ikBswJuBNoDOwE+/pD7o/vD/L0AmQNfAwECGwBGACwA1v8Q/3r+3P8TAOT/2/8s/8b/kQHNAngBAP9M/gD/zf8D/yr+ef8rATECBQKgAQACyP+V/AD8ef28/34AYwHNAlYC0v87/Vn+8QDQAB3/9v6KAHsBcgCt/lL/awF3Ah0C4f9z/fT7SP3EAW0EagPf/wD+kP53/8f/FP/K/5UA9wHxAQkAu/5s/Zr+agC9AbcAwv7Q/kn/3/8dABwAMQHvAQQBJwBJ/vz8OP23/8gCswOMA2MBYv+Z/aH9bf1+/Az+VADeAlYELAU7Ay7/kvs9+un7F/8FA3EFQQXeAfD+YPxh/E7+ff9zAcgBWAK9Abv/XP0//KH9uP/CAXkCVgIHAIL+z/1x/mIA9ABbATYACQAf/zb/ZgFfArgBjv9V/Y78Gv9WAvADtgL0/hb8B/v9/aYCpwWPBCcAof3O+1P8LP4dARUEcgNMAtL/Tf7M/k7/BAA//3P+6/3V/h0BWAN5AyQBXP7B/NP8Jv5IAeICOQJr//r9Wf+8AEcBjP9f/7UAYAFZAVoAvP+P/+b+0f4PAP8A6gC6/lP+Tf9SAMkAWwCUAY0BHACk/ZP9s/8+AdwBVgB8/1//nf/LAIEBwwBG/iH84fz6//UDIwUXAzMAdf1t/Gv8//3y/8EBfwOEAyIB6/10/VH+LwCZAeEBmQF9/7z+Ef+b/0j/ZP6Q/44BJgHv/4z/qP/LANQAcACQ/5X/sP9q/3oA1f8C/xr/yP+pAQYCFAGGAPb/Qv7t/HP+pgA2AgwCBwCz/m3+dv9wAEgCMwMIAZn+o/xE/Kr8Gf8FA+oEnARpAev+9P2K/G/8E/2H//kC5wTiBAkC6P6y/G77+Pwq/5sA4AH5AhgDtQAi/qX8Mf25AGkDowNdAWT+V/1x/YD/WgHxAZQB2f+H/jz9xf19/9UAuQJoA5UCjwC7/T/8u/wj/bn++gGMBFgFEAPW/9393vyp/J/8K/6qACoD/AQgBb8CTf6q+uP5Hv0FASIDQQJQANv/fP7D/T3//wFMBLgCIABL/8j+zf2X/bf+VQA4AMgAyAGXAZsBIwBL/pT9af3K/WD/xgIuBGcCl/+U/av9jv/dAZ0C9QDJ/sP9ff6r/7MAYgEcAcgAxP8H/6H+Iv+DAMAA4QBhAP//WACvADIAGP+1/v7+wv9yAIIA+f/Y/4YARwAU/7b+qP/3AagCjgBZ/nj8AP1A/+gAUwJoAicCigIzAXf/KP29+zn+PwC/AUgCgQE7AaP/gv+Q/yD/K//+/ln/hv9//yMApQJOBCMCWf51+/b7VP/OATUCOwFA/2f+yP9iAcQB/wCE/0b++v0A/yUASwB/AMsAmgD4//T+XP+MASUDMwKF/+f8pfwz/gQAZAIVBAkDnv9P/ez80f2c/jD/LwFPAx4EUgIhABv+0/uU+8D9kwFoA9ACXgFmAJQABP81/eb8fv8sARIBlQHbAAMBzgAO/zv+zP1H/kMAcQK9AhABd/41/en91v+fAbgCYAOlAQb/UP2q/Ej+lgDvAdwBjADa/xYAzAAHATIADf7j/Jn9Sf9KAXECtQIxAWEA3v/i/oX/rP78/cT9h/7jAMkCPATKAg8AZf2B/KT9jP4NAW4CEgKCATIAAAAeADX/d/3c/Fj+4ABTA8oDvwK7AID9G/uo+83+TQLrBM4E6AEi/nn7Bvxj/k8B8ALzAZQAu/4e/jn/bACkAZMBPwBg/uD9o/6p/xgB+wGoAXcATwBEAA8AUf9x/k7/uv8wAN0A7gFiAjUBw/5y+zv6Mf1HAnMFBAX/ACr+qf2U/aX+HwA4AvoCYAH+/nH+QP5U/sz/zQHEA90BMP8q/cL8K/7u/e//xgIQBJwDtABY/Tv8LP3x/ukATwGeAa8CkgJ4ASEABf5N/b39+P5/AVsB9gDFAAAAZwB6/zz+7P1l//oBFgL6/zr97fwd/4QB5gInAjsAlP6q/kv/HwDW/yb/IgDGAKcBTwHWAFcBkQBN/+L8afwb/gYBeAMLA+4BDABr/gr+x/55/zr/TgCsAe0BkQAd/mH+5wBPAi0By/5T/oL/CQAq/yr+OP4DAL4COwTHA4sAXv3r+xr8KP47/2EAjwJhBJwDU/9c/Gj8Pf/OAXECJgHy/2AAZQCLADL///1v/qD/MAGfAEMARADcAPIAk/9e/r/9zP+DAo0D/QAw/bz77P2tASID2wI7ADz+N/64/jH/Cv9qADIC8gIRAkf/EP2D/cj+KQAHAQEB7wDgAIgBwwCU/v/8bf1PACUC2wGYAB4AhQA6AAr/JP2j/e3//gE3BDEDwP9y/XP9r/+LABoAfv9T/2wAMgAtAJ8AbQBkABwA5v8E/5f+nP8MAlcCVv/U/Hn8zP96AgACewAv/33/TQBZAckBTwE//1f9M/4Q//L/jQAvAUcCuwGn/1P+Gf+t/1UA7QBqAPz/Sf+F/xcADgAVAAYAuP/D/qr+bv9uAIABmwHzAIL/HP7o/ZD/mwFVAooA2P1//U//LAIgBEsEOQG8/I/65Pvs/rcB1QIeAkQC2QHu/yv+pP3v/mUAjgDD/iX+ff8PAR0DXQPtAJL+OP22/S0A1QAXAR4BgwA6AEz+P/3+/Zv/ygKfA8QBn/62+wf9NQB8AmsCRwDJ/oT+UQCuAfwA+P/l/v3+HQAQAQQBcAAJAXQBIwBZ/r38/f21AGoDcAMzAL79lfzU/b//FwEiAuYB/gCy/0j+Pv30/U3/2QEXA3QB//7z/YX/WAGoAtkB4P8u/UL86P0lAEEC3gEuAUEAjACLAFEAhADi/ov+pP6Q/2cA0AAtAfMAAACG/mn+Df8CAcYBTAGxAAr/If4A/nb//QCrAXMB7ACmAHf/YP7q/nv/bP/5/t3+MgCIATUCvwG6AJz/I/6p/uT/VwC0/13/JQApAfIB5wCZ/wv/3/56/k3+NgCgAV4CHQK8AEv/JP7Y/Zz+kwBBAfAACQC1/5wASwBJAEX/E/51/hkALgH1/4D/eP/yAPsCUAImAKj9wvyW/n8BegHm/6D+Of9SAsQDIwKp/hP8jPzp/x0CxAFmACL/mv/8/9r/9f5V/qH/0AF7A9cCj/+4/JL8b/5LABcB/gBWAZcCZALG/838ePtA/hsCfgQnA5L/uPyN+1j+tQAvAlkB7f8nAfcBowGu/tP8VP1n/2UBOwGoAIgAawFDAbYAO////BX9Df/oAncEEAL2/ib96/0//zX/of9xADgBTQFnADH/Zv41/6wAzgLqAqwAGP7i/Hv+ZQCMAYIA5P7+/iEBMgIsAbz/C/6J/iX/+P6T/yAAegGqAusBTgDN/Qj8B/5gALQCYQOLAdT/U/4K/xkAHgCo/8X/JwB2/+7+ff8pAeUBuADn/nD9Jf7zAGoC6wE8APP9tv1P/2YBjALpAa0AWv89/8X++P3u/f3+owG/Az8DPwHz/uv94/3a/fH+AAAZAfgBHQIaAlwACf4//Cr9IQBsAc0BqQDP/+v/tf8s/9n+/f8rAa8C/wGC/8H9w/xq/pEApAItA9wB9f8j/uX9Bv59/lT/hAHcAioDYAF9/mr9Lf2//+AAFwF4ABUAcgFFASMA5v0+/Z/9qf/5AY8C5QFj/z3/GgC1ALT/T/6E/sH/tAGQAY4A/f4+/3IACgGDAHD+ov0X/80CvATKAp/9nvqY+2j+oAH1AbABbwHcAVcCAAHc/fv6JvxaAPoDpQNsAV//uv6a/+b/H/+k/eb+UwHUAlYCh//g/Ub+ogCaAdX/9v2Y/Y3/zwGFAkQBVv+V/mv/JwExATD/Rf7U/jAAwAEfARUAQQBBAKAAHP/K/B39Iv+iAvYEgAM+ADz94/uN/e3/8QBGAVUBDQGpAKsAAgDl/zgA9/+O/7f+xf40/0EAZgFTAd3/P/6//jYB4gKYAfX+bfxM/JH+EgGRAngCTAGCAA8BlP8Z/b/7AvzE/3sE1gZwBMP/h/xY/Fv+ff8//3L/mAHIA8sDDAIG//n8K/3C/Yf+A//1/8oBbQPCAzMBbP1N++f8SABQAiICBABO/3gAiwHTADz/nv1r/ZL/pwFyAtEAx/4+/rX/cQGWAev/VP7q/s4AuAIQAYP+uv1J/vcALAJJAXH/rP7C/40BswHw/+X9JP2b/osAQQJuAU//q/4RAKcBJAHi/8/+ZP8nAGsAzv/0/v3/OwG4Am4Cx//N/Cn7R/0OAVYDowK8/0X+mv4XAHgBVAB4//H/EgE4AUv/9P1X/vUAAwM4AqD/evyx/D8ArwPLA+EALP7O/cj/UQGrAK7+Cv60/3wBowEAAMP98vwR/0YBsQGhAHP/FAFsAlQCOgA3/R38YPwY/8gBHwNiAkcANgDp/6L/ov8M/5r/zwAXAVoAyP7A/lIAgQHyAY8A3f0l/Lj9iABhArcC5QCp/3D/0QD5AD//sv06/uEAOwKKAeL+aP5O/wkAiAAGAPH/xf8pAMgAOwEfAKj+sv4ZAI0BWAAw/+L+xv/TADIAnv69/gEBnQKqA6wBcv4s/Hf8Ov+fAc0CJwEIAPj/DwBE/779N/2i/c8A4wM6BNgB+P5Z/rz+w/7q/ZL9hv6SAWQF5gXHArv99PlB+r/94AFmBFUENAOvAWP/Z/zJ+Xn63P1/Ar4FhgR4AYv+8P0S/2j/Nv+a/rj/9wGZA90CDgBb/T38/v0LAEEB8QDuAE8BMgHOAJH+g/2o/Vz/tgF3Ah4Ba/5j/WT+lQExAz4BI//7/QP/fwD6AAIBaQAnAOIAzQCC/6b+Ov4z/yoBdQFKAJ3+B/65/1EBAQIfAff+AP6i/qUAZwL/AYAAw/7u/Zb+n/75/tn/tAHkAicCVAF6/5v+6v1+/fz9Qf8hAr0DIwTUAd39Pvvz+gz+3wEiBMYDggGG/y//Q//6/hz+7/2T/zYBCwNiA84BRP/L/Er8L/3M/lEA/gFWA+MD3wK//3L7t/kr/DkAfgNpBBcDAgHr/8z+3P1F/sf+nv/IAH4BTQHAAEgAiwAmAQ0Aa/2Y+1b9BAHjA78DQwDG/QX+IACJAh0DGQEY/vz7dPyw/hoBYQIWAiUCZAJjAZb+s/uN+6D9pgB6AgwCLgFmAHMAGgAj/xX+e/2B//wBlgMUA24A0/5S/ur+X//s/mP/vQAMAmECkQDt/fX83f18AHcC2QE7ANP+gP7g/ygBwADa/4b/BAD0AAoBBv8G/ef9mADUAqwDWgJu/3X99/w5/rT/gQBRAZkBTgJMAXn/kv1c/Ij9B//EADYBzwGBAr4CXQGX/tb8Rvy9/usBnwPJAjwAhP7u/fX+CgBrAOb/6f9/AbECCgKx/wz9KPx2/ab/pwG0AfoAhQBpAK4AcgCo/+v+nv4n/77/BABeAEcAZgF7ApAB4P8M/in9Bv6n/x4ANgD0/3UAUQIVAz0Bh/78/KD9qP/JAPYA7/+S/+AARgKWAioAT/1S/AX/MAI1AycCTP8w/gL/UwB4AD7/Hf5f/pkAWwLAAWcAjv+B/x8Agf9S/TD8Q/4EApME2gMzAAv9Yv2r/6YAFwDM/lP/CQFgAyUDqv+b/Uj8pf7sAQADxwHy/pr+mf86ATQBhv83/j/+DQBDAdkAZAASAHH/qP9T//P/vwDoAF4BHgBN/q384fwTAHYDRgRSAvz+RP2L/Yv+Vv/J/4oAIAFLAgoCQQAs/uX9ef/tAMIBoQCD/zb/EwAEAjACeADu/df8vP7EAX4CwQDO/S395v5qAZcCxwGaAC/+6/1D/pv9bv7k/60CzARDBAQBYP3l+6P8Sv8oAc8AfgCZAe4CtQIPAFL8E/uk/Y0BxgOmAiIAP/5S/gAA+AA/AOb9of03APUClgPkAJj+S/65/6YA9v8W/+r+8v/1ALkBFgFw/6T+Yf/yAN8A9f59/T3+MwFgA1gC5P8j/lD+NgChANv++fwt/bMAkgRBBb4CLf6g+zz8/f6nATMCvQE3ABsAZgBp/2n+uP3x/vsA4wEyAQgAEQA3AREBhf9n/Rf8Qf4OAv8E9APw/3L8Rvuz/qQCVQN+ATH/SP79/0UB5P+Y/UT8cf7yAW8EAAQ9ARj+IPyh/fL+2v9UAA4AdAFjAoIBmP9b/jj/CAGKASkAaP5b/pj/TQE2Ak0BQP+W/Y3+WwCtAS8Bm//i/jb/gQCNAAwAj/+u/3gAqgBaAAj/pP5L/38AlAGXANz/hP8F/+v/OQA9AHn/tv6k/xYBEwLGACL/pf6m/yYBRgFVAAr/2P70/sT/gQDV/03/8wAMA/8D3wKo/sH7pfvT/b7/aQD8AIIBnAJ7AlkAdv1G/Gb93//qARMCawBo/5L/AAD7ALL/vv6S/hQAUQImAnYBGv+k/sf+wf+yAAsAhwA6AEEAzAAeAEn//v4n/w8A9P8WAJUAlgA3AX0AR//4/TD+k/9YAecCYwHh/gX9p/3hAGEDtAK2/3v9//xn/ukAUgINAbX/Ef+//wwB0P/d/iX/PQANArsBfQDN/vf9R/9yABgBnQD//+3/xQB/AVAABv9Q/ij/hAAFAcQAaf/t/uH/qgDAAJz/3v1F/nkAdAKSAs//E/33/O7+ugGIAj8BIf/+/ej/VAE0AcX/ov7f/4kBvwL6ACn+w/w9/mgBpgLoAYr/Pf7i/h0AxQD2/zj/SP/4/5oBJAJzAN/+S/7G/mL/aP8B/1X/DwFbAqUC7QCv/oH9bv0Q/5wACQEUAa8AUwDSAKUACACc/03/sv+NAPcAUwD7/rn+Tf+AAPoAuQAQAXMANwDU/5H+vP7//uL/NQHwABcAwv+h/4UA7ADV/7z9r/yl/dX/vgJAA6QCegGv//P+hP6b/oX+Jv/6/14BKwKWAe0Atv9L/yT/Ef9I/17/PQA2AcgBeQEGAA/+If1S/ksArAE8An0A/v6b/oP/awAGAAgAT/8gAKcBCALRAOf9vfxE/tAArwJTAiX/Uf0E/gsAxAKZAgkAPf6E/kMAvgEFAW7/tf4o/2kASwEhAYcAMQAhALr/ef6B/S39ef/fAuoDAwP0/179YP1K/10Asv8A/x//aADPAioD2gDj/QD8b/3j/xMCvgInAUIAGgB8AFEAaf9i/gf+tf8bAUkBJwAp/4X/uv9dAJYAPv+1/oD/zgDKAYMB6v/Y/mT/AADRAEUAH/8v/wcA7gGVAqIAHv6I/RP/bgB5AJX/Gv+qAFACngL/AJz+fvz9+yL+GQCWATUBSwHiAXcBxQBj/t/9Zf6FAEcC4gH6ACP/if7N/gQAzv9v/y3/vP5rAMMBygElAXAAhv8RAP4A6wD0/3X+9v2U/sL/JwCtAHwAGgBqANsA5AB6/4H+vP6v/xABNgF4AMz/5P7w/iz/Zv9b/77/dQEiAucBqwDh/rP9O/7u/28B8gHuAAIAvv9EAGgA2f+0/kT+1v6oAC0CugFkAVX/Z/7O/g//3f9O/3z//P9PAVUCmgH+//f9GP5///v/yP9I/xz/bQBKAh8DrwHz/oX97/3a//kAMQA0/3//+wBXAo8BZ//j/PH86P8LAtACywCb/s7+oAB+AUYA0v5k/c/+lQEbAj8B1v+s/m//XgA+ALP//f47/5EA3wF7AT4Amf77/Qv/BgAXAbEA+P/u/6r/LQDa/2z/c/9q/zgB2gFSAbYAL/9+/ub+dQDsAFEAQv8Z/6UA5wDBAGf/Iv5T/vT/bwHyAYMBq//6/k//EQD5/1z/z/67/kMADgEDAUUAi//Z/8cALgHzAGf/+P10/oP/SwGCAfUAcQBg/zT/Kf+y/9H/4f/c/y4ACgFhAPL/8v/o/3wAUgBw/8/+7P57AJIBhgFyAPH+e/7e/zwBjwCu/7v+g/4pAHIB8AFdAYH/wv7e/vX+hv/0/nf/rADHAVcCagDx/hr+xf7s/wwBswDQ/m3/pABwAs0C+QCa/mX8nvyr/pUBJQOjAoEALP8+/zD/kf9W/+j+Rv85AOYBnwIKAY3/zv6u/kr/Jf+6/lb/pwDcAcMBtgBC/yn+Jf83AHsAt//v/uH/dAGxAjkByv5T/SD+sADKAZ4Br/9E/jn/MgFYAu4Ahf5T/Tn+WwANAtUBXwDO/+D/FgAuAN/+df2q/QAAAQPbA0MCL/93/WX9I/9/ACUA7/+s/8EAEQIQAisABv4i/aH9rP9dAVQC0gEDAYAACQAh/wz+Af5m/lMADQIkAhEBAgB7/yb/FwCuANP/Df8M/8b/tQDZAN3/7v5C/z0AMAG6ANL/4f6u/j0A3wBIAJj/+P9MAH4BrgHA/3j+cf1C/qsAdALyAUEAvf7//qgABAGTALv+wv3E/tAA5gFUARUAov47/zYA6wD8APP/kf+H/67/HwCm/0T/tP/cAGMCGQJkAF7+Qv2Z/QP/GgCeAOkA4f+0APUBzQHYAPf+4P2E/mb/BwA8AIX//v/WACYBNwEbANj+Tf/JAEYBCQFw/6r+dv+SAKUA2v++/nn+SgA9AWoB7P8T/tH+rAAbAk0B1P48/Sj+ogBlA/wCTwDx/Qn9aP/EAKkA4P+2/nv/KwFpAQABdP8r/nr/BAELAab/t/4Y/3kBSwNKAp//rvzH/LT+PgGTAtwA2/5p/mMAlwJgAr7/6/13/ub/IQH9/03+tP3S/kAC4wMyAsD+PfyX/QMA1QFwAR7/Kf4Z/9QB/wKwAc3/BP6p/vH/ggBbAJn/VQCzAJgA+/8Y/rb9A/+6ATsDDQJT/0396v3h/8IBygF1AF//sP50/9kAbwDX/4T/9/9QAdwBpAAe/nj9yv39/9oBowGDAT4AQQDJ/1n+3Pxd/IX+pQFjBGMFVwNG/6X86/sR/bn+BADbABACUwM1A9UBH//X/Of7mf3PAAUD8AL8AJ3/pP7W/mr/U/+7/gb/2wAdAxYD3QDI/ub83f2Z/7wAmAC5/4T/HQDRAbQBywAQ/wz+0P4uAMwACAC9/wD/nP/4AG0BDQH3/6D/Fv8V/xH/Ff+7/0sAUQHMAeABTgB0/lv+8v50ADABVQDb/5f/KQAQAZYAyf+g/o/+aABmARUB6f+w/j//UAAMAbkA5v7x/QD/kwAcAWIAcf8+/10A0QGUAWD/OP5M/p//pQFPAQMA9v6k/+MBNQKxACX+1fzq/ckAAAMXAoX/8f1e/v8A/AKEATb/HP1r/af/DQK+ArEAB/8//T7+HQDIAPAAvv9QABsBKgHOAK//gv5R/ov/9P81AOL/2v+OABkBfgFWAE7/nv51/18BwgGgAIP+Nf4G/0EAcwHFAOr/af/q/mH/YABUABMAmAA/AWYBlwAI/5z93v0a/4UApgFqAdsAWAC2/6P/E//p/Tn+TP/+ALsCWgMaAqn/q/30/CT+iv+/AP0AyQGvAUAB0gBe/5P+VP1j/lYApQHpAX4AU/8n/2oAgwBb/yL+6v3V/osBBgPVAcv/y/10/iIAEwKTAZD/8/0C/h4AywFoAnwAxf+A/wgAnAB6/1f+s/2x/u4AsgKqAc8APv8m/woA3/+3/0r+qP5Y/w8BOAIsAlkBof+A/5H/nv8u/4n+Fv7t/vX/1wA8ARUB6gC7AEYBvv9m/j/9Cv5xANIBeQKYAD3/Kf88AMYA/ACb/0f+Lf9mAHwCLgI5APv9q/1x/wIAQwA1/6P+BQAiAh4DcQG9/lP92/1zAMkBSQG+/1X+hP9OAdQBdgBk/pb9Z/9vAX4BWABV/kv+k/8HATcBPAAv/1b/rAAsAe8AIP+s/c7+rwE5A6YBK/82/cv9KQAtAvYBOgAy/4f/gAF5AbT/Dv4Z/YH/nQE2AuAAv/5n/g//nQB4AAT/DP7B/iEBcQL+AaoA6/52/oL/l/8jAHv/qP6q/7oAfQLXAbQA2P8k/87/DQCw/4H+jv7o/2UBAgKaAbwAUv+X/hb/hP87/3L/NwAxARYC4gF0AMH+W/1Z/WP+KgBQAfEATwEBAa8AUgBm/2b+xf1L/s7/pQEUAkAByf9F/2T/k//W/4j/Vf8+AJUBCwKQAQAAOf/F/qL/gQDf/4b/SP8KAOEAvwFVAbX/WP7//Rz/VwArAUQAM/8v/+//DgEPARgAyv4f/vH+bACjAfcAUv9M/8L/SQHuAYwAE/85/oL+yv/dALYAQwCv/7UAGwHhAC8Axv4y/1f/tgAaAWAAc/9r/pf/wQDFAZkAVf/z/ij/YgC2AEEAQP8J/x4ADgHlAPn/iP5q/mb/EgFiAZwA3f9N/vz+DACEAJsAXwAcACMA1AA/AG7/Uv5z/tP/vAGUAkIBs////pf/mADmAO7/kf4b/g8ACgL6AeIA0v6B/TX+LwA+ATcBnf+8/h8A6gAYAVIALf+Q/u7+kf8MAOz/nv8xABIB4wEtAQcAGf8t/xUAvgCGAFr/1/66/rf/mAHZAYIAPP9Q/vj+nQAFAd4Azf8f/5z/CQG9AUcA1f70/YP+iQCrAeoA7v8I/1f/igBbAc8AUP+j/oP+yv8bAHsAgABV//n/LAAsAHL/H/8jAIUBaQJ5AZv/uP3q/TP/6wBqAnEBHwAw/3H/vAClAHr/OP5f/dj+WgHpAp0CLgDg/Xb94f5oAFUB/QBlAB8AkACXADr/Lf5Z/ef+qwEcAycCogAY/9n9r/7a/80AowATAMT/o/9r/x3/hv9PAF8BRQEjAbQAAAD+/s3++/4X/34AYQB0AWMB0AB0AGX+/vxJ/fX+9ABtAyMDqQFi/7D9FP54/uj/IgDWAMAAGwGKAUIAnv8H/8v+zv9KAPj/VQD8/zcA+P+e/4v/9f5m/0IAMgKGAVUA1v4u/mz/qADkAdQAzP+R/l3+w//3AAcBDgCo/53/mgANAaYAl/9R/hP++//wAE8B6gDO/j7/Y/8uAJkA3f9n/1X/+QAyAikCsAA2/9z95f1S/1oA7ACFAHUA8P8ZAJMAewDW/73/8P8L/5n/jf/A/+IAWQAlABb/ef46/1IAegG1ASsBj/+2/tb+rv9MAFYALgBf/wIAcQD2ALoABwBMAMz/+v/m/wEArf+m/g7/QQDGATcCPAE4///9UP7F/8oAawD5/vr9Rf9+AX0COAL3/179fv3K/uQAzQFKAUUAqv/y/ycAtwATAJ3/HP/Z/vL/PwC8ANsA5gCNABYAXf9f/pv+Qv/+AHUCbQIXAcf+df2K/bX+OwCBAHgA2gAmAQICagFz/6z99/xe/jMAgwHYAQ8BegD3/4L/pP4P/pL+7/+9AY4CXQL6AB//Dv+A/wkAHAAn/67+DP+XAPUBmAGeABf/e/4L/+3/NAAx/2X/rP8qATkCMQGm/7f98/2R/4wAygAvAAv/yf8OAeYBVwFI/6P+e/5EACEBhQDI//7+EADOAIEB3gB5/87+l/41/xIAaAChAFIBNAGZALb/O/8M/x7/ff/C/wAAnABmAXsALwD6/rr+kP+6/x0Aaf/3/+kANQH7AI7/Yv4m/jr/WwEhAhkB6v8L/1X/m/8AAP3/MQDKALwA6gAmAHH/aP+E/87/CADJ/x4A6AC3AFkAW//J/t/+hf9QAKMAmgBtAEwAMgCX/1z/1/+q/wkAlf/a/mb/iADvAWoBRwDK/n3+x/8YARkBrP+m/uH+yQDDAc0B8f+Q/vD+Lf/oABsBrgAvAAkAiwCLAK7/F/4E/tT+lAD/Ac8BdwAZ/8f+Lf8bAJb/K/8O/5L/PgG8AdIB2ADe/uH+Ev80/73/Tv8BAC4BwAF1AU4AGP8c/sX+/f/9AHEB+wDI/4D/vP+R/yAAtP9+/7P///+aAF4AKAAWAHYAuABhALj/lf5Q/l7/vABoAfMAf/8x/8D/tQCZAScApv5F/qD+wwDSAWEBNgAp/9H+MP8XAOD/jf/H/3YAvgH2AZoAy/71/VP+7/+pAMcAEwDq/8kAPAElASAA5P7R/cr+NgBGATgC/QA8ANL+Xf77/qj+iv9iAN8AZgEjAYgACQBM/+7+//7H/zsASgAjAPX/5f/c/+YAMAHAAIX/j/5z/ob/rQDlADcBBgCv/9L/LQCkAFX/TP9M/7X/vwDtAMYAZQA1AOz/W/+0/qz+bf+IAPMBPwIsALD+Ov78/ocAzQDn/7X+wf4XANMBcQIcAYz+y/1Y/k8A8wHBABQA/P6O//4AXAFYAHj+VP7G/toAKAKmAaD/yP4Q/9n/IQFjAK3/Jv+A/10A0QAhAEr/7/+ZAHcBxwB9/1z+U/55/0UAxQAiALT/SwAWAU0BWgC//sT9VP4oAJ8BvAENAeD/KP8D/3n/SQBrAEcAiwD0/4z///+z/53/+f9LAEgAMwBnAH4ASAAmAOn/Y//r/uf+yf8LAXsBwwDB/9v++v7I/88AMQGv/1v+OP62/34BYAJwAZT/pv6T/q3/KAAaAFH/hv8pAS8CGAL2AM/+LP0V/mj/HwE5AccAkQDc/7sAIgCP/0D+df3d/jUAYAKOAvIA6v7L/Zb+sP/nAAYBgAAyAGgAQAGqAJT/NP9E/hX/UgC9ACEBTwCSAJIAyv9c/6n+S/8/AA8B8wA3/5L+eP7P/0IBJQHcAHb/1P5a/yMArQBCACcAVAAwAFMA7wC2ADsAhv/D/mT+Rv+RAEgBIgGL/6L//P/hAPwAHv/8/Z79gv9sAY4CngGG/5j+A/+YAJ0Auf+6/gn/CQCOAQ8ClwB+/5n+nf8tAM3/A//C/noAggE/At0AEv/W/vr+XgDLAB8AJ/+t/q3/9AChAcoAZ/9h/m/++P8SAagBogCs/9b/cf8aAFgAzv+k/iD/fwBBAaYBz//P/nj+kf8tAZ0B3QDS/mn+yf5sAEoBjAAzAEL/p//HAMIArf/C/pT+v/9sAW8CdAELAE//xf6n/37/Rf8g/43/QwH0AbMBAACP/jD+uf6u/0oA6P+3/yMApwClAf0A1v8I/4z/+/9oAKYAD/+B/qn+kABPAioCzwC2/lL+sP70/5UAoQBOADMA5QBvAPn/Jv8w/uT+CwCTACsB7wDF/6H//P97AEYA1/8n/67+6P9TAQMCKQEm/4L9Lf4PAMEBdQIpAML+af7B/qMAywBZANP/0f8EARcBz//W/lz+Q/8BAZEBTAHs/0D/ef+M/7X/Hf+T/2kAdAHSAcgAzP+p/mf+/P5d/7b/UgByAdMBSQE4AHX+cf4X/8z/UwA3AOUAvQANAQoAkv6p/uD+ywCFAc4AnP+h/of/0gAnAX4AKP/P/tj/4wDNASQA6P5C/m7+nQB5ARAC1wAf/1T+Y/7C/28A3QBmABIAcAAkAHAAgAA2/0z/Mf+4/8EAjwBiAFn/GQBRAVMBhACq/nH9Of42AIIBsQH5/z7/q/90AAcBNgD6/uf9F/8OAaoB+gBKANz+Mf9iAOH/EQB7/47/HwCMAI0A3f+D/57/bACOAAwBdQDf/9n/ov/Y//j/gABNAA8A7/+4/3//G/90//r/PwAjAGwAUwAyAB0Al/8K/83+pf+ZAGgBVwFuAGL/tP7h/oD/HQDZAFoBaAG2AD//Xv5//jj/8gA2AeEAiACw/z8AuwATAK7+HP55/v3/6QE5ArQB9P8l/+f+YP9NAOT/OgC6/9T/2f8z/0n/LP8cAJkAxgAdAI7/u/8zAH0A2f8LAMH/DQCPAN0AvAB9//3+xP49/zkARgG8AZIBAAHO/0D/3P7z/gn/I//K/7sA0QEcAuIAyP43/SL9Ov9uAQMCUAHu/5//DgC+AIcA0f5+/cH9sv+SAXcCwgHW/0X/Bv/L/ywAkv8AAKD/w//9AN8AYgB0AP7/VP9e/2j/1f+1ABMBQgF6AET/tf+2/+n/HgAX/wj/4P6t/9kAKgHcAF0AeP93/j3/3v/5/30AcADl/0sAawCIAOsA/P+9/+H+df7a/tr/LQGlASUCngCm/+b+4P6g/xQAlAACAOL/ov81AGwAWwDV/wD/Vf8PAMYAggCdAFgA9/95/3D/wv/l/3IAYAA/AJP/RP8b/93/wgDwAJgA0P89/9b+xf8yAGcA5P93/ysAfgCDAQsBOwAY/4X+u/5Z/zUAswBIAdYAIAFiABD/kv78/mYAdgG2AeEA2v+q/oD+gP/I/6z/jf91/9f/0wBEAYgAd//U/sH+LQDgAPoAlADR/8j/jP8AABkA2/+J/zAAYwGiASUBK/8R/pb94/5xAbwCagKsAN7+sf1J/kL/4f+O/3b/dwA8AXgB7wDa/wf/mP4N/y0ANwH1AVMBdwCZ/y7+Of4A/5f/YQBPAUkBYQCEAAgAx/5P/wz/Tv86ACUA4QCGAIEAKwAxAG8Ayv8BAEL/r//2/1QA8QBKABUAV/9L/8j/JwBNAGcA4f9T/0n/U/+EAIcAjQAKAPn+Iv+o/+8AXgHbAC0AaP/H/tT+MwDRAEIBqQBN/63/xP8UALcAVwDT/yf/zP83AOAADAH3/4P/7v49/4D/nP+z/7n/rAAWAZoBhADF/k7+4P4TACYBcAF1AGX/Qf/j/7UAlACC/wj/K/+eAKYBXQHx/3n+q/5Y/0gAlABHAKz/DwBqAG0AnQCj/0f///52/9X/lQA+ASQBJwGB/9r+UP4E/24AFgE7AfX/bf9r/1IAAwEwAa3/Vv61/rb/XQFrAVsAWv+k/8P/CQD9/7j/qP9z/x4A3P9xAOD/0/9NAC8AxgA8ACYAJP8A/7r+Uf99AKsAGQJlAYcAlP+w/jX/cP/F/w4AOwD1//n/jgDmAOEAwgBd/6j+ZP+L/z0ArACuAHIAov+c/wkAvf9w/1v/lP9NAJUAAgCs/zEASACnACUAUv8D/5L+cQCCAYkB/gCV/23/T/9b/6j/y/9oAL8AwgBFAGL/O/9Y/2AABgE+AOj/h//h/y0AgQBaANH/X//b/q3/lAAqAeAAwP+T/7b+P/9EACsAdgCW/zf/EwDnAAgB+v8e/9X++f8vAXsBVACs/nn+Mv8kAcwB3QC5/xP/QwCqAJUA4f+M/tX+w//vAJoBwQDh/wH/7f5l/0z/zP9SAFoAfgDpAGEAfv9c/zr/x/+kAMkAXADQ/1f/r/9JAEsATwCI/1P/u/9IABYBwgCDAM7/Vv/e/53/s/9g/7X/RgDEAFQBfACR/zz/ef+r/6n/4v+5/wgAzQBlAZoAYP+a/qT+mv+HAHIBHwHEAK//xf/0/1H/Of+b/sH/yQABAcEAwf8r/yz/OwDRANcA+/+J/zn/2P+vAJgAxAC0/4D/QP+Q/0gAdQB6AFv/ev9U/2gAggHhAFYAmP88/2j/8P/x//L/h/8iAL0ALQDL/9P+Yf83ANwAiwGeACr/iP4V/y0ApQCnAKAAJAD5//v/wv+S/5n/DwBMAFQASgCHAHoADwC5/w//rf4d//v/agDSAH8AeQA4AHf/Uv/1/qH/oQCHAdEB3AD2/+j+K/9+/+z+ZP9X/77/6AD/AHMB9wCH/yf/qP4r/+3/zgDbAMUA3gDA/8T/QP+f//f/uP/p//r/zwCQAMgAEgD9/vf+S/8IAAcAOgCB/+n/MgBGAPcACgDQ/9/+z/6p/34AWQGRAbIBZABi/w3/+/4i/9P+Hf/N/7QAQAJ/AgUBf//r/ar97v6JACwBIgHvAIwATwCW/9b+Rv6i/qn//AAHAosBXwAe/6n+4P5H/+X/wf/0/4MAHAFIAiABJv9k/jT+p//tAPIBTwFQ//P+9/7V/64AewAwALv/of/W/xEAlgAMAHr/hP9Z/2EAYQBTAAcAZf/C/wwAhgBFADQA+v8QAN8AJgAV/5v+p/4aAKABsQEDAe7+Rf5u/4AAgwGbALL/4P7//tD/tQD1APv/AADk//L/i/9C/6H/+P92AOQA/QCOAAAAQ/+B/yr/P/8UAA8AnwCjAFoAKgCEAIkAlf/s/hH/UP8eAOEAAAECAUsACwD0/8n/V/+v/rL+CP9oADMBLQEhAWgAtP8q/8T+9f4//9b/wwD3AB8B7QB0AJT/v/7z/nf/BwBVANIAxwDTAOAANAD//8j+z/7o/1MAswDs/0L/Jv9AAA0BOwEFAfz+dv6E/l7/ugDNABgBGAD4/wYA6P87AMn/Of8X/x3/M/+zAPAA9QDiAM//WP+Z/oH/pgAnASwBswBm/6H+tv/W/6AAMQGuAGoAFQDC/xwAHAD5/5D/xf6t/zEARQDz/9b/Uv/3/p//fv97AHUALgBkACEAFgDM/5f/o//6/zYAGAEVARAB9f+t/nD+tv4JAAMBvgHTAEoAEQC4/+L/jP+Z/5b/ZACiAPMAYABE/3D+3/71//T/0QA8AAEAdQCY/9f/+/+8/+r/BgAJAOIA1gBfAKX/pP6W/kf/lABLAf4A7/8G/yf/3f9mAGUAegC9ALUA+wAeAML+2/7D/rz/NQBrALcArQDRAF4AyP+w/i7/Xv+NAJEB0gB7ANv+Rv94/4n/HwALAPX/4f+4AIEAxQAoAMb+t/5G/z0A8gA7AaUAvv/f/hX/CgDDALUAPwCl/yH/BQBiAEIAvv+K/+n/QACHAN//l/8GALQARQEuAfH/4f67/mr/NgDM/1z/Kv8YAJwB7QEOAdb/uf6A/iv/ef/J/xwAtwDFAAoBjQCi/xD/kv5a/5//TADeAPYACAFqANr/Iv9E/57/CQDc/zMAEgBMADEBTAANAEb/T/91/9//WwGXAK4AQwDN/9r/KP94/1D/Vf+s//v/lwCEALkA2wD1/4P/N/9U/9z/GwBUAD0Ar/+5/+r/XQDRALMAcwBd/5/+//7B/2QA0QDxAPv/kP8TAJsAeABeAIz/+v7P/5UArQAsAPf/Tf+i/7H/TP/q/9r/kQA8AQ0BOAA7/+j+X/8RAHcAlAD+/wn/9/4eAKoAAwEtAGf/G/+M/wsBmwB1AKD/2P7i//EAWgG/ADr/V/5u/zUALgEDAb7/Kv9P/3EANAGDALb+jf5m/kUAxQFiAR0BH/8A/6r/CwBjAKb/l/+k/yoA2gC/ABUAjP9U/2D/4/9LAFIArACiAFUAMAB1/8P+z/6i/0MAbwFlAdH/Vv8v/6v/WgCBADEAzP+U/zwAfABFANn/Vf+A/7//oQChAIoA3/+L/xIAHABrAFIALQCA/zD/Wf+v/wQAFwCaANP/7/9FAI0A6AAnACv/6/05/rL/LgHzAVgBdwD+/wsA/P+A/w3//P53//f/qwAkAS0BsABZAM7/IP9M/07/u/8xAAcATgB8AHcAHgBX/73+M//X/zcA0wARAAAAgQBOAKsA3//t/j//Y/8uADwA6v9MAI4AHgFXAbsATf+8/rr+Tv++ALEAWgDO/47/t/8sAM8AaQC0/w3/Mv/L/8wArQEJAbL/Xf5l/uT/NwHLAXsAFf8V/xP//P+jAPL/Qv/Q/mP/XACnALQAtgCtALYAVABq/8H+5P6p/wIARQAhAHIAZwF/AUwB8P8U/6H+cP63/4wAzgCMABsAvf8kABQArv+m/4H+cv+EANkAoAF0AGr/0f6R/hoAugBoAC0AZf+8/ywAiwCzAAUABACS/4D/6v9mAEMAMQDm//b+JP93/7sAKQERAUYACP+S/57/lgAQAQcAjf8CAFcAcQAtAIH/d/9M/+b/DwDT/zYAowDkAHUA1v94/oP+af9PAPYA1gA3AHz/j/+T/yYAVwDx/+//uP86AHIAvADjAHIAwf9A/1D/CAC2AD0Ad/8Y/1L/eADlAFYBTQAm/1X/0f7a/63/n/8eAP7/dQEmAYgAof+e/or/8P8sAI4ACgBPADsBqwALAL7+VP4b/+3/KgEVATQAe/9E/4X//v/S/4X/ff/i/34AEAGMAXIA6v+I/zH/y/9AAOEAhQDB/zf/vv6f/9kAJgENATUA2P5L/6j/rP8YAOD/vP/g/2gAxwB2APH/E//+/j7/0P/xAIcBOgHAAFQAJP/S/pj+xP4yAA0B/AA5ANv/sf8VALEAjgCU/37+/P47AE0BEwFcAGT/+/7J/4IA2wAJAEn/cP/G/2wAfQDF/7b/DwBLAGAAngAkAKP/q/+c/8n/KQBCAK3/1v/j/9L/xf/L/y0ANQBsAJX/1P9gAKsALwGXAIH/dP6F/mb/TwAaAScBKAAmANn/AwCMADn/f/9k/y4AWgBIAD8AjP/HAE0ALQB0/y/+HP7e/4AB8gEiAkEAPf+P/iX/qv/H//D/5f+aAGgATQFZAI7/Ef9e/hf/g//YAHgB9wENARsAmP9G/jr+uf6H/8AATgGeAX4B3ABXAMj+fv7F/hL//gD+ALsA/P9e/wYAAwBlAIv/u/42//z/TgEmAS0Akv/i/mX/ZwDdAHsA7v/1/jf/+/8YAKkAZwAvAPb/IgBhAFcA8/8CAMX/Gf/s/xwAGwHmAGYA+P+h/jz/iP+lAN4AAQAl/8/+xv9OABwBHAD8/hv/Pf9IAGoBAwGOAOr/fP8+ABsAAgCV/2//hf/+/5YAngDdANf/s/+C/7P/VAD4/xwAl/+Q/wMAvgA2AW8Axf+G/r7+BQCyACYBVgBe/8z/jf+1/4MACwDZ/9H/1P9WAB4AJADB/6X/tf/O/1UAAAAEAK8AMABWAJ0Ar/+p/0T/Wf9AACsAYwCr/8D/YwBBAG4APwAqABUAegAkAKL/6v4F/7b/IQAVAacAQQC3/7b//P+5/9H/Pf+n/0sAsQDGAEsAcP9G/0v/v/8yANr/UQAtAIkAfwALAO3/eP91/2//DwDtADoBrwCEADkAo//w/zYAGQBV/9X+sP54/0wA6wBcARMAwP/Y/03/zf/p/+z/TABSACcARQAjABv/BP8h/xr/yv/zAOUBUgGpAOH/NP9k//P/FACQ/1b/vP+3AFgBFAE1ACj/qv5c/1kAmACsAEIAZP87/7v/j//f/8T/lf9ZAGAAAwHhAGkAFQC4/ywAz//u/zj/H//K/+n/bQAoAAEACgAdAIEASwDP/5L/Jf+d/2oAUQBmAFcAXQAMANH/7f+D/2L/tf8PAIkAxgDWANEAQQBw/67+Df9w/wAANQC7/2r/JQBYAT4BQAHm/6X+Mv9i/wEAmgB/AD8AygDGABUAJP8I/vb9wv47AHYBWAKVAWAAX/+i/iH/kv/T/8D/9v8gAAoBeQGNAC0Azv5k/uT+m/8FASIBLAHsAA4Azf92/63/7v8cADgAzP98/3P/r/9xANAAOACl/0f/d/+a/+z/pwAAAEUAzQBoANz/vf+K/3P/tQCIAIoA8P8c/6P/Tv/F/9b/mv/0/xMAcQAuAQIBbADP/x7/Tv8k/33/KgDNAJ0AtgA6AFz/xP/d/6IAjQAJAOf/TP+4/wYAUwCfADYAt/+C/5r/5P+O/9D/EgAvAHgAMwDY/zH/dv+m/9b/owBnANf/MwAFAfcAtgDz/2n+c/4s/wAA+QDMALwASwDU/wAA1v/n/1UAnAAPAOn/3/+V/w4Ayv/T/x3/Ef9GAPwAkQGTADz/eP4N/0wAHAHBAIf/Rf+C/3IAsACi/9X+Rf88AEUBaAFKAGP/2v5O/4YAdQB7ADcAyv8iAGQA3/+D/8f/NgD8/wgArgCQAHkAw//l/rL+zf4vAA4BPgGmAKH/Zv+P/9z/3//L/33/tv8TALkAWAETAWoAK//k/vb+w/+NAFwABADc/xYA5AAYAbn/4P5a/vf+nwClAYMBTAD6/6r/yP/+/2z/d/6c/sP/kwDSAccBtwDc/2P/Mf/f/uT+mP9VAGcBOAFlAIMAs/+X/1b/A/81/3T/jADyALEAVwAjAI//rv9b/wr/wf8oAN8AtwBJANT/2/9vAFoA///d/5v/wf91AB0APAAkAOX/6/9WAIEAIgD0///+Mf/1/lH/oACsAG4Apv/U/7z/vv8uANP/xP+r/zcANwHkAHIADQBR/1MANQDo/yEAsf8kACAAPAD3/3z/M/9l/+D/iQDAANr/JwDc/7v/fwBfAIoAOgCN/yz/Bv/H/4IAKQDZ/8P/6v+WAMYAWAA9/6v+PP8NAHUA2gBdAJD/GQDPAPIAYABd/3X+zP7B/4UAOQFxAdsAFgDB/3r/Vv91/6n/1P/A/1wA8gCpAJcAFQA3///+wP5o/wQAdwBVASABUgBH//f+Gv+H/08ANQC7/wkALAA0AKYAlABAACQA9P+W/6z/4v/3//r/if8MAHEA+ADCAD0A8v/B/tr+XP/B/5IA8ADxAPAAoQC4/1//sf6S/vP+Z/+yAFsB7gGRARoACf8H/oj+Zv9jAJsA7P9OAB4AFwEyAQYAY/8i/t/+KwD6AAYBwgAjAH3/SwCLAIEA/v9D/+v+Ef9r/0IApABaAPcAigA3APv/Zv85/wr/Yv/q/3cA1QA7ASABUgBT/7b+8v5m/+r/RwB3AHcA/QDEAHAA0//x/jP/fP/p/+//KwDL/+r/NgAwALwAQQCx/3H/dv+H/8r/fAB/AHgArQDkAJMAAwDi/pD+Rv///+EAAQFvAOb/kf/g/0oAKwDk/0//N//T/5cAGQFAAL7/2f7I/ur/UwDWADIA6v+y/7j/gAC+AOsANgDL/1//TP9t/7f/yQBvAE0A+/+2/3UAlwBfALv/w/7S/mz/AwBcAaIA9f/u/3P/qwCWADcAU//0/p//ZwA4AVwAk/8o/2P/IgBzADoAjf9z/9X/7gBAAaoAVP/U/mT/5f9MAPX/4f+9/0kAMgE3AW0A3f9H/w7/jP+N/+f/9v8uAI0AqQBWAOP/EQB8/2j/Wv9y/yUA1gDQAAoAff8//3sAlQBxADEABv+z/18A3wAuAQoA3f7U/jH/GABzAGoAzQDm/w4A1f89/5P/m/9HAB8AGAAwADgArwBFAIf/Rf+v/y0AogCqAOL/pv+I/9//fgAbABoABwAVAGYAr/+Q/03/nP8eAEkAxgBUAHcAHwDm/6n/av4c/6j/2gDOAZcAJADE/yz/vf8hAOb/HwDP/ysAcQBmADEAZ//s//n/4v+H/7H/aAByAM0AEwAh/9D+Rf9VABABsQDP/2//If/9/2kAcADHAEAAQABzAN3/9/9l/x7/vf+F/xUA9v/GANwARgA4AAP/R/96/4UAnQCf/1cAEgAGAHcAHwBu/zb/I/8eAIsAcwCgAL7/WgC3AOAAgQBG/x///P6j//n/8f+v/67/FQB5ALwAjQANAEP/n//+//P/VgCdAD8AwgA8AKL/j/+5/rn/7P8QAKIAhABuAMf/u/+V/xkAcwAfAKj/4/59/3AAJgFHAQ4Awf4E/8r/EwE8AQcAQv+w/nP/xwDpAAYAcf86/+//hgBGAGsA8f9v/wAA+v8GAFEAvP/O/xgAFQAwADgAyACAAOz/Lf/Z/qr/TgC0AIgAnf9c/7b/OABpADAAGwAaABQAawBJAJ7/eP80/w3/9v9SAGkAYwCRAOkArAAnAFv/IP9a/8v/VQCsAKEAUwBX//n+Uf+g//sA8wCCAM//Pv+k//P/egCp/3X/QP+6/7MABQHwANj/1f+v/wUAZAB/ACwAaP9//zr/ov8DAIkAxQBTACwAtf9F/4L/6f/D/9j/aP/O/yUB8ADnAOL/1v5y//n/iQByACEAzP+S/1QATwCSABMAU//V/87/TABkABoA3v8BAPL/h/8cAPP/2/8gAJj/Ov+n/7//MgAhAbQAAwDF/+T/BgB2AN7/Af+//wkADwEMAdv/xv+W/6T/CAAOAPL//v9DAIsA0/8v/0j/WP/7/34AcAB3AHUAawAyAM7/Ev+7/lD/xv85AAcBEQG9AJEA9f9S/2r/kv9RAPsA/QA2AP7+H/9A/1QAtgD7/w4ADv+V/88AjADu/x7/rv5I/zsApQAtAXQA4f+6AJAAAADL/zf/kf/E//n/TgCA/zIA3AABAXYAiv8l/+T+rf/h/97/qf8HAPQA4gDtANb/cv/L/9b/FQAIALv/7/9bAFcAWwDn/4n/SP/v/+T/1P89ANT/RgCq//H/aAAoAOb/NP+9/6z/egDpAKUAXQDK//P/0v8LANX/mf+p/9T/wgAFAX8AwP8p/3P/FwBKAAMAwP9h/0z/SgC4AJIA+//H//j/9f95APb/ov9o/43/gQDPAIEAFQC3/yr/sf9f/2P/DwDg/4wAzwDaANsAVwCt//7+9/64/xUA7gBXAWwAzf/z/mf/MgBZAIIAo/9H/9T/IACCADsAjf9p/2D/GQBdADAAIQDh/+P/nP8kAA0ATACdAB0AiAASANH/wf/O/87/yf8VAOr/ewCWABkAtf9D/yb/7v+SAHQAbQDr/47/ZP80AIwADgAqAHT/gf8nAG4AxgBXANb/8v/t/9f/AACH/9H+Pv8ZANUAAAG6ALgA7v+K/3r/Sf9Y/+v+FACPADABmgFRAKH/t/5x/2AANQAjAH//kv+X/80A/QDr/9n/TP+4/zMAAgAxAAEA+/8kAHoAkQAuAC8Abv9D/0f/dv/8/0gA5gCMACwA8P/p/zMA+P8//5/+7f71/5IB+gEhAZX/jv7+/vn/9wB6AO//V/+6/7QAmgAcAEj/Av+c/5IAZgBbAAAAVv/L/x4AHgAcACYACwCQAHUAuf9r/97+X/8jAMQAawElAXYA6//w/nL+5v7a/uz/xADVADcB7ADUACMAWP9s/wz/5/5b/xEAHgGtASkB/v+A/8H+7P4HAN7/JgAWADoABQHUAEwAgv9Y/0f/V/83AAAA9P8MAA0ARAAFAEUAxv/H/xUA0/8bACYAYABVADMAFwCw/8n/z//0/yMAAAC3/xcA9v/n/wAAHQABAA8AMQC0/zIA8v8lAJgAEwAJAIP/kf/P/2EAYgA/AAwARf99/4T/CADV/+L/EABXAMUAcwCiAJn/Hv9W/17/EACfAMAANABKAGcASwB9ADYAhf8n/xT/kP+HALwAwwD+/yT/4P51/40AngD9////v/+h/6gA4AB3AL3/Lf9v/4P/LgB5AFsAgwB0AKQARACa/xr/8/6b/wwADwADANj/sv/P/yYAMABVALYA0AA1AMH/w/9H/xsAawBbAAAALv9TAKQA1gBiANH+pP6A/4sA4gCtAKH/EP97/z0AQgBu/2z/b/9rAPQAQAGCADz/R/9r/zwAUwAuAOT/k/9AAGEAngClABEAzP8//zD/4/9IAPAAsQCl/1v/af+k/8cA+ACs/5L/g/+q/7AASwDE/2r/U/8WAFMAGQDv/5//7v+PAN8AlQADAFUAIwDd/7//NP+N/9X/4v/6/1f/hP9nAI8A1wA3AH//o//W/5AApQAnAKn/Tf+p/2UAggAFAJ7/cP/J/6oAFgH2ADwAMv+z/83/sP/B/0b/rP8WAKkAkwAMAPT/Mv/7/pb/2P9EAN4AqADWAGwABgBDAJ7/h/83/wf/wP+SAD8B7AC//1L/av+q/5gASwC6/2//WP+NAMoApABaAGX/Xf/7/xcAJAA0AJL/9v9UABkApQDo/woA6v92/3T/K/8sAK0A/QBIAHr/Sf+O/z0APQAzAAv/o/9zANMAGwENAIn/Yf/D/0EAdgCJ/7f/2/9+/0IARABpACsAPQBJABgA3f+K//j/gf/9/z8AtwCdAA4A1P9F//j+uP41AHQA+AD+AEIAnAB8/4n/Lv/4/nn/7P8CAS4B7gApAJz/T/80/43/rP+fAO4A2ABUAGj/U/+y/+7/wf/G/5X/RwDjALMApQBv/zX/vv9RAPoAcACF//v+OP/+/34AJQDx/73/yf9GAGEAeQAcAOL/mv+C/7L/DgAJAOL/QwAEAL8AXgDL/xgA9/4M/3EAtADOAJMAx/+p/1T/6v9XAAoAkwD0/8v/NADJ/wIAAAC3/+v/V//Z/2cAKABUACUA+P90/5n/9v8sAKQANAAAAHcA7f+J/xMAzf/X/+H/z//4/x0AcACW/7P/CAAOAHMAUwDz/4//+P8JAAcBtwC6/8D/+f5C/w0AxgClAIL/DP+q/14AvQCaAOb/fP+D/zAAFgA9AN3/mP8CALj/mABHABYAqgDK/73/AQCq/+r/HAAXAB4Asf+9/wYAVgCoAPb/9/+w/1H/SwBDACQA/v96/6r/LwDXADoAsv89/wX/7/+mANQAKQD0/5f/2P9gAHwAPQA5/07/AABiAGAAlgAEAIH/l/+2/1EAVABLAN//MwBIACgACwDa/9r/2f6j/+j/7v92AHoAegD9/ygAlf9OAI8ANAAPAIP/bv+C/+L/7v/q/03/FACNAGkA3wBEAKT///7K/6v/9//ZAJwAqgAzACwAkf9Z/2//Jv8rAHsAbgDEACwAMAAGAIj/2f8ZAPj/cv9a/2f/AwCoANUAkACs/4H/bf9s/7//JAAzAFgAIwBpAJ0ATgC6AAAAOv/w/sP++f/3AOMA4gAnADf/3P/X/wQA9P+E/97/dQD3AGwATwBr/+v+j//0/x0A+v/s/zsAxwBIAAIAa/8w/7v/2v8rADkAZQBgAE8AKADv/4z/av8GAC8APgAUAPz/8P/F//7/UwC2/57/IAD5/6kAmQBOAPz/Hf9+/+//zwClAM7/AgCo/4//+/8gAMz/ff/J//r/WwCaAE4AFgCf/0X/lP+4/xQA0AC1AB8AcP9M/8r/zAD/AEEAxv8H/8X/dgDoAHMAfP9e/z7/1QAfAQsAcf9+/rn+3//xAOUAewDh/7L/EgBbAAQA/v+M/0r/4f9HANUAkQClAND/6f6d/8X/NQCeADEAq/+1/9P/SABOAOX/2f+H/6j/sv9tAM8AWwArAFr/XP8DADUAxgBOALT/p/9f/zIA3gDpAGMAwP92/2n/3f+d/6P/O/+y/xIAZgD2AHkATwDM/8X/1v/Y/+D/xP/s/zIApABzAB0Aff+3/+H/uP9HAAAA0v8jAEoAUwBWAAIAxP+o//X/vf+q/5X/5f+RAE8A7QBIAJ3/d/91/yoABQBBAHz/f/8uAMgAzQAUAKv/Hv/D/8P/3v8FAAUAagBrAIUABADB/8P/LACDAAEAef9U/9r/UQCsAJYA2f9R/9X/DwAOAOP/jf8LADEAdQALAFr/sv/y/5QAuQAzACcA0//e/yYA+v9k/0f/xP84AL8AnwAEAJL/Vv+W/8n/yv/C/1sAAwH+AIAAkP8G/7P+k/+RAO8AKQGRAAwA5/+K/9H/5/9o/yL/hP9yAPoA0wBtAL7/wf46/8D/+P9tALn/cADAAA4AOACG/5D/cwBpADYAzf9L//H/EwBMAFAAev+r/woAjwC7AA0Ahf8n/3v/RwCpAH8AAwCM/x0ARgBnABwAVv+A/1f/9v+DAJ0APwB8/4z/xP9AAJQAtQD2/2j/lf/L/+X/FQD7/wIAkgBpAEIA7P/N/wUA6P8BAGr/r//V/7AAEQEdANf/ov5y/20AtAD7AIH/v/7u/hAACQGlADAAc/8s/wgASwBrAEkAn//N/2IA6gDjADwA1f+c/7v/iP/a/wIAHQDB/6P/x/9n/+b/0f8mAIkAWgBfANr/7v/8/1QAMAC2/5D/kf9YAFUAfwAuAJ3/wP/4/1gA9f/r/7L/pP/z/yIAwAA1AAAA/f9+/wEAov/H/4gAXQBSAB8ABwAnANb/0f/m/2P/Xf/Q/0gADgDW/wQAzv/b/yUAFwAiAG8ALAD8//f/FwCVADgAXgA1AKX/0P/N//b/0v+o/4T/sf8BAHMAnwA8APH/lP+C/5H/HABZAH0AcQAvAPb/of/v/xYAggDU/7L/+P+s/2YAGQCW/1L/j/9JAEEAawADAFb/v/9xAGEAFwCv/97/DwDCAIcA5//2/2n/+P9QADoA7v+T/8f/BwBsABQA///x/x8Aw/+3/yYAdP/V/ysAOgC1AD8AwP/J/7j/1f86ADsAt//Q/+T/XwDrAGIAAAD1/sb+Z/+w/3MAjABiAMz/dACGAOj/MQBr/9//FwBEAJcAIwAjAAwAIQDp/7r/cP/X/xsAGgARAJr/u/94/wMAdwBDAGIA9f+i/9j/uf/8/2cAyP/y/24AhACjABkAyf94/5f/6/8XADcAtv+N/9//HwBoADsAKQDJ/7z/fgA3ABUAuf9d/zsAiAAcAJr/Zf+c//b/fACXAOD/sv/9/2kA1ABPAGP/Gv9e/8n/zQDWAOL//f8WAAEAJwAuAKr/Rf+1//v/3v9fAOX/yv8oAAUAfwAjADMA/f+d/9v/2/9CAGEAbgAAAOz/qf+r/7n/y/8HAOb/fgAyAHwAHQCt/9r/JwAMAPf+sP9w//j/OwG+AGAAvv+a/8v/OwAJAN//v//T/wAAMwBgAMT/mP+w/x0ASABxAPz/tP/9/0wAkgCb/7T/Yf+a/5oA1ACaABwA+v9M/67/z/8OAAMArP8iAKz/ZQB+APz/xv+K/8T/x/8qAFwAsABSAEkAWQC1/6f/A/9D/wAAcgCfABUAb/+v/3UAogBpAG7/ZP8BADoAvAAvAEr/ef/v/0AAqAA8ALj/qP/n/8kAkQAGAGT/JP93/2kAxwAyAAEAd//J/+v/CwB3AL//uv/p/x4A5P/0/wsAx/9fAE0ANwDQ/1H/nP8cANoAeAAYAJ7/zv9MADwAkgB2/6f+ev8rAPUAAwFKAG//V/+3/28AagDC/1r/bf8rAMMAwAAYAMr/gP/B/4EAYQD8/47/qf+4/+j/FQBxAAcACAByAK7/LAA5AO7/qf+C/+7/yf8tAD8AJAACABgAOAD4/8f/p/+z/woARQA/AE0Ab//h/y8ANwBOANP/qf9h/08ApgCfAFYAl/9Q/83/ZgApACkAcP+H/+3/agCbAN7/nP+a/xcAWADLAD8AYf89/2f/BwCxAP0AcgCb/xD/uv98AL0AaQC5/yz/OP82AGwATQCN/zH/Rf/Z/wUBFAG/ABYAx/+k//7/2f8BABUAlP9kAAAAvv8fADwAtwAQAKH/8/4h/7D/GgAeAU4Avv9z/5L/oQDgAPgAx/8G//L+yf/oAJwAagCc/zP/xP+IANgAfADv//H++P4BAPkA4wBpAG//Jv8t/wQAdABMAG4Aev/r//L/SQCSAO3/9v86/03/lf9PAKwAoACtAMz/wP+p/8j/QwCUAPb/wf+i/27/tADgALIAIgD7/tf+Xv9TAPwATgBe/yT/cv8KAKUAFwH//43//P/2/7QAYwBNAAUAQ/+n/7z/BQBDAHwALQB7/0r/df/1/+v/kgA/AJX/0P/w/5MAdwAyAP3/1v/b/w8AlwAHADUACgC5/3oAEQC1/6P/k/99/9b/8P/a/20AcQAdAPn/ov+E/8P/QwAwAAkAFQADADYAggB6AFIAHQCJ/5v/8v8oAEUAnv9T/x7/s/9KAPIAxQAFAP//Yv/0//z/9P9qAJT/ff/P/z0AqACdACwA6P9Y/9n/SAD7/xYAp/+z/6H/dgDUAEsAAwB6/2//gv8QAEEAcADz/xYATwABADYApf+7/6r/LABCADgAiAD2/1YA6v+S/87/Pv8i/y8A3wCcAIcAbf/+/kL/wv+tACEBcwCR/9L/rP/8/78AzQANAF//N/95/6cA8QBxANH/6P4V//X/vQDBAP//K/8l/9L/igDYAJwAs/9U//7/ZAC9ACUAKv9D/zv/HQA4AbQAUgDM/yz/x/99AHMApwDS/83+M//a/0YAnwB9ACD/OP9EAMoAJwF0AK3/uP4g/3AA5QCdAAkAc/8Q/+z/HgA4ACUAa/9GAFIAawCrANb/sP+1/xIASwAwAO3/d/+S/5f/KAClAGsA+P+S/wEAs/8QAFkAzv+3/3f/+v+IALMATgDz/8P/wP8mAA8ADAD6/9P/gv8PAAYA3P8fADMAUgA5AIwA9/+y/1D/2v6R/yUAkwCwALcAQAAEAD8APwDn/zv/C/8b/ygAjADmAOMA+/+n/0H/XwBVAOz/KQAt/5T/y//J/3YAHADF/4v/l/80ABABJAGuAMj/9f58/04AQABjAL7/H//a/zMATQBPAK//Uf+8/7QAygB9AC8Amv+a/33/4P8jABcAyv/h/ygAHgCAABIAnf9h/7z/EwBQAJsA7P/M/4L/FgCLAEYA4/+M/yQAEAB+ACcAyv9q/x//WgBSAHAAVgAhAOb/vv9wAEoACgC5/3n/hv/X/4AAmABDAH7/RP82/8H/CwHBACoAuP8N/9P/hgDqAF8Ab/8j/4D/XQCbAMsAKgBt/zv/of8rAFQAegD0/7//2f8KAJAAJwDe/9b/ev86AFAAQABuAIj/nP+m//3/iAAjAL//Dv9n/3MAygDNAEEAPv97/2EAoACkACQA7/7K/u7/RgBTAf8AbP8m/+r+4f+CAHIAIwBi/6X/3f+PAAIBfwAXAF//af+8/4r/igCPAM///v/j/yAAtQCCAO7/qf8g/5D/KwA+AAcAtP/1/+T/MwB9ACEAtv/o//b/NABJAPP/7f9w/9v/1P/3/1AASwBYAGr//v/g/1IAcwD4/z4AY//y/zsABgD3/8f/q//X/3EAbQBLAMH/gv/X/0AAbQBIACYAgv9O//P/ZQAxADcAjf+A/xgAxf+dALEAFwD4/3n//P/7//v/ZQCX/3T/zf9LAOEAPQAtANT/IP/N/xEAJgA4AA8A3P/H/wkA9v8xADsAAACe/4v/0P9SAJwACgAfAK7/yf9CAKIA7QDY/0j/Cv+0/w0AtgCQAPf/HQAz/ysATADg/yAAyv/I/6L/nP/t/xsATv9pAEEAv/9bAOr/ogBYAK8AhwBk/73/8f8JABEAvf+n//n/0v8XAMz/sP9vAGIAPgDd/67/o/8MAHgAqAAmAGv/R/9T/ygAogB3AAsAWf+I/+P/YgC2AFsALADy/+H/KwBFAAsAyf8EAHj/kv/+/8f/EQBpADAAgf+0/1T/l/9cALwAeADd/1QAAABDABgA//8LAMz/YQASAEEAsv8E/5D/BwClAJgAyP9//zn/xP/YAAQBZwC+/1H/5P4iAN8AOABHAOL/iP+k/3IATwBKANn/KP+9/6v/ZgDIANoAgwDl/3D//P6V/6H/CQAYAPn/FgCw/4IASgAnAHAA1f8TAO7/w/8kAFAAFQCi//3/2v9WAFwACQAaAIP/e/+L/0kA8f/x/zoABwA/APT/IABMAAIAlv8rALH/0v8SAJL/PwCg/yQAXACzAI4A3P/8/8X/AACg/wIAyP+Y/0EAIwCVAEcAvv+//03/Pf9bAGkAfwAzAB0AFwA2/9f//P8gAGYAXwCq/8f/7f/r/7kAAgAcAJr/t/8GALb/PADY/0IAKwAmANr/xv8JABAAigANAOP/pf+E/7//VgCyAOv/AAD5/4j/9v9JAOH/AAA4AJv/FwD2/5f/UgBWAEoADgCN/9f/HgDv/xAALQC9//3/LQDw/+T/GgAMADwAIwD3/xYAjv/x/wwAhgBBANv/0P9k/24A4/9AABEAUv8LAPD/KADi/yEA4P9mAC0A+v8SAOT+NwDf/2wAigBp/10A9P99AHYA0v+A/1n/9f/2/1kAOwDf//j/BQDW/7n//f8jAF4AewDv/3//rv8KAFcASgAOADAA5v+0/+n/SAAaAMX/QADP/2P/v//E/0EAiAADACwA3P9o/8X/OgCpAFAAWgAlAMr/JQCK/y4AIwB9/6X/df8JAHEAUQAzAAoAu/9z/7j/LQAJACMAIgAUAJQAHAAqAAAAbf+Z//n/+f8bAKYACQDi/8X/LQBoAEsADwBG/53/ov8HAI4AeAA7AK//ff/H/+n/GAAhAPn/NgAIAFoABQDH/5//Lv/0/w8AdQBMAFgARAD7/3UAnf+2/xAAwf+//w4AGwD5/7QAbQDT/5P/V/+X/wIAPQCMACQAw//e/77/dwCbACQA+P9v/3T/+P/g/0YAcQA8AN//lv/R/6b/XgB4ABIAHAB3/7L/0f8iAEkAfQAWAND/sv/Z/5UA3f8KAAIAkv/X//b/XAAXAE8AAADk/0MAxP/b//j/qP/g/ysA4v9KAD4Am/8IADMAMwBTANn/rP/X/5X/2f8UAF4AhQAYABIA7/9///3/WADl/0EAwv9U/97/BQCLAGsAIQCz/8r/CABdAEIACwBGAFL/Z//O/xkAFgAUAC0Aof8PACAAyQBoAN//9v9o/wAAEgAvADEAt/+0/1z/7P/2/7H/TwASALX/BgClAMYAgwBVAJb//P5t/4wAkQCWAPX/Z//I/0P/SAByAO7/8f+W/w8AMgA+AKUAMwBx/8H/eP+f/xcAEgB+AA8A8v/N/zIAowBiABEAqf+y/3v/4P9pADAA7/+Y/5f/uf/c/00AWgBMACMA1/9qAB8AOABHACQA+P9w/5v/l/9HABwAKQAmAG3/u//9/1cAoAD6/5X/+P97/w8AdgDp//f/2f8VABcATQD+/zMAAACU/x0ADAApAOz/9/+e/+D/ZQATADYA7P/i/6r/BgAaAMP/5v/Y/5gAWwASACsAtP/5/7z/tP/M/+P/ZABHAAYAGwDe/7f/YAAFAKH/0f/1/0QAIgCjABkA6P9+/67/gwAcANMAtP+E/67/iP8MALr/VwC2/xIAMgCB/zEAUQBlAFEA2f94/8r/1//3/74AqAD5/53/lv+y/zsANQAQAO///P8rAMT/3f/l/zIAOgAMAGwAlv/O////TQCBAN//3P8d/8X//f8pAGQA3/8nAIn/JgBKAPT/NgAmAAgA3P9OAJP/sP/1/zUATgDh/+T/pv/O/xYAmwAyABwAoP87//f/XwD2AK8A4v9B/4P/g/9JAA8BKQDd/1b/h/8DANf/agBFAK3/y/+h/+T/KwAaAKgAUQALAKL/pf/9/1YAlAA7AOb/av/j/6z/CwCoADgAAACc/4P/mP8VADoAmACTAC8At/85/53/t/8IAFwARAASAMH/y/85AE8AQAA5AOX/1f88/9r/MwDk/44AVgDb/6//tf/I/4IAjAABADMArf+r/zAAQwBaAAAAsf+Q/5v/5//D/wEAkgD8/ysA+v+t/w8A1/+PAGoAzf/v/8z/LQDr/9n/QQDJ/+X/EgD+//T///8EABQAQQDF/8T/KwDG/xUAOwA3ADcA2f+5/3z/xf9hAFMAIwAsAOT/Vf+W/28AIAA6AGgAwP/h/xEAQwAaAAAA7/+w//r/wv/Z/zEA0v/+/04AAQATAFAA9//L/0MAxv8xAF0ApP8pANv/3f8IAMn/1//k//z/0/8zAP//DgD6//P/5v8cAIcA3v8GAOX/vf8GAGMAWgBEACcArf/g/93/l/+P/9P/eP8WADYAHQC2APn/MgATAB4A3f/5/0wAvP/4/zMAcQABAAYA5//U/7D/wf/s/1T/4//K/1UAogA6AFsArv9k/9X/UQBTAI4AUQATAJv/u/9LAP3/+f/W/53/m/8HAEsAUgDn/5b/wf+E/xMAiAAdAM3/9v86ACQAaQBUABQAIwDS/+L/EwAkAPr/m//I/67/CwAQAAIA7v/Z/xgA2f/d/+r/cgA9ADUANgDO//H/EQA4AO//QQCs/zT/1v/G/1QAlABoAAkA4/+o//X/9f/c/zQA+/8GAPH/pv/j/0AAQABuAPr/KQDn/0z/NgDO/2wACABb/0gA+/8mAEUA7P/b//T/9v9JADAAGQBIAMb/r/+Q/6v/rf8PAGwAFAABABUAz//s/4kAPgAAADAA7v/n/wwA///a/1//3f8KAAkAnwDT/+D/7f8HAKkAZQA6AH7/O/+I/0oARQABAAgAx/8cAPT/WwAvALL/EQDT/8j/9v/c/yoATgAuABcAxf8DAMb/AwB2AO//JQAsAP7/4v+S/+f/IgD4/wsA3f+k/x8AWwBeAGkA0f94/4f/2P8XAEQANwDl/xAA1P8pADMA7f8pAOH/KwDP/5n/ZQDl/8P/KACa//r/cwAMAPT/0f8nABoAYwC5ANz/hv+e/6r/8/9eANb/EAAPAOP/SQACAPf/nv+b//7/MwATAAQADADd/x8AMwAqAPr/GgAaAAkAJwDE/2MAGgAGAAIAjf8NALP/w//G/47/9P8UAGsAbwDo/xQA8//L/xIADgDL/wYAXgB+AGwA7v/T/4T/yv8PAOz/YQAPAAYA0/9p/97/cP/O/0IAHQB5ACAAXgCYABMA4/+v/9P/p//H/1sAAwDX/yUAEQARAA0ABwDz/+n/DADm//z/qf+p/zMA/f9EAPX/CADt/+f/ZgAGAFEAQgAGAPP/AQAtAOf/i//Y/9r/nv9bADMAIwATALT/LwDP/7//RwD5/7b/5P/a/6n/KwBuADIAOAAaAEoAVQC1/wwAuv/p/xwAtv9HANP/0/+9/8v/EgDm/1AA3P/7/w8A5/9vAB8ADwBkAEcAyv/g/+z/yP8aAKj/2v/r/5r/NACLAIUACgCQ/23/j//t/5IAPgDK/0kA3/8PAF4Au/8xACEA7P9mAMb/o//w/7v/CgDx/x4AggBAACsA3f+M/5n/yv8HAEEA6f/c/+r/+f9HADEAcADo/9r/2P/d/1AA9//y/+P/7v+L//f/WwAYAIkAFwAbAMT/x/8SAMn/PgCy/6D/LgD5/yQANgDa/zgAeQDi//T/xP99/xwAJgDH//L/yf/d/zUADwCgADAA4/97AMz/8f/M/+f/6f/R/xwAnP8AAAAAKwBJANX/5f8AADkA4/8NAFgA9v+q/woAHwDi/xkASwAtAJv/DADI//H/LgDM/0IAw//p//L/+f93ANj/+P+p/4P/HQA2AEwAdwAOANb/DwCx/5z/BAD7/0AAlAAuAA0AIADr/+n/AQAIAKf/+P9FAIT/uf/D/8X/PgD7/34AaACp/6X/AgBNAKv/8P/V/8f/SQApAKwAdwDO/xEAw/+9/xUAFABtAPD/T//H/+X/+/8jAE8A+/+c/8//RQBfAEMAUADo/7L/eP8eAEYAx/8IAL3/5v/a/y8AcgDi/04AJgAKAFUAq//X/+H/pf8aAKL/7/9QAAsARQAgAN7/wf/X/+r/FAACABYABQDy/zEAFgBLAOH/9P8aANr/6P/o/1kA/v/e/wgAEABuAOf/DQALAFT/5/8YANz/3f/x/ycAnP/+/3cAzf8xAF4ACAACAAsAJwACAN//9v8ZAJ3/r/8iAOz//f/R/wgACwDa/1EAJwANABwAOwD+/9H/EgDF//r//f8NAEwAUQApAO7/2v+o/6f/wf8cAOr/5P8DABcAVwBDAHAALgCu/53/lP+h/yUAMQBNAFAA2P8ZAKH/uP89AAAADADs/8f/7P9LAGgAWwD2/+v/OAAQAPb/JwDw/+r/CgCl/9f/kv9w/+P//v8qAP3/LwAeABUAOwAFAC8ATQAMANz/8f/x/xsALAD3/+j/4//W//L/NwAoADMA9v/8/8T/d/8uAJ//CAAJAJP/UgDW/0UAoQAWAGEA/P/g/+H/u//1/yAAt/+2/y4AFgAiAEwADwDR/9//LAAUAOf/EgCp/43/CwD8/xEA6P8rADwA4P8yAFUA4f/g/xoA///+/+P/HQAAAPL/+v/x/zIAIgAfAKr/5v8TAJP/OwApANb/HQDR/8H/MADQ/wkANgAfACwAEQBFANr/EgABANz/9P/z/ycAzv8DANn/rv8eAOn//P8iABcA2//t/zIAAABTAC4A+P8RALz/+P8JADcADQDl/y4AtP/B/+v/DgCy/+//BADd/yIA5/9lAEcABgAMANj/BwDC/9T/EAAWAA0ATgA8AAIATwA9APz/hP+M/9f/pf8jAIkALAA2APn/7//z/9b/oP+e/woAuv/j/wEACQCMADUAKwAgAOD/7f8EAB4A8f/4//D//v8TAPX/HQAFAPr/HAApAMn/1v8lALT/XgD2/5n/AQDO/3oAUwBKAPL/tP/S/9f/0f/H/0QAiP/u/w4AIgBUAN7/PwDJ/2QAbgA4ACoAnv/b/8b/9//M/ykA8v/x/0EAyf/+/+H/yf8IAA0A9P/3/+L/+v/j/+L/FgAAAIMAZgBKAEoA3v8GAPv/5P80AMj/eP/p/7f/+v8dANr/KgDv/zIASwDs/+T/yP/d/8b/4v8hAPL/PwBUAFQAYQDC/9b/5v/V/xcA8v8WAO//BQACAOX/DwDg/w8ACwAuAFIA5//0/xAAx/99/8r/FAACAMb/RwAHAJn/dgBDACAAMwC7/wIA8v8HACAAvf/b/w4A9f8WAGwAQwAwACkArv/x//b/pP8AANz/9v8dAPb/7/+c/63/JABTABAAPwBAAKP/LAAAAC0AOwCw/wgAnv8AAD8AEgBjAAwAl/+f/5j/0f9nAC4AawA2AMH/4P8PABcA8P87AML/IQD6/6L/JgDq/wUAIABQAPz/zv/l/8v//P8VAOr/AAAAAJb/8P8LACwAWAA8ADUAAgA5AOD/BgAyAAYAw//B/+P/wv9OAA4ALAAwALj/BwDL//P/9//o/+7/oP+j/8T/DAAPABYALQBjAGgA5v9NAF0ALQD+/9b/7f+b/y8AIAAQAAEAsv8LAAoA9/+Z/8n/HgC//9H/DQDs/ycAUQAAAB4Awf9PAIEAJwBqAMb/rP+b/6H/+P/l/xgAJgAcADAATgA0AA0AQgC3/5z/6v9i/7D/5//X/97/dwBbABAAcwAqAHgARgBCADkApP91/0H/q/+p/+D/HgAHAOX/IAAxAFIAZgDb//n/FwAWAN3/FQDS/6v/SgDk/zAARQAqABQAEQAJAK//AwDo/4r/9f/d/8D/bgBaAEIA9f/1/0QA1/8ZAOH/t//f/9v/0P/t/+X/zv9IAAUAHQAoADgARgALAN7/vv/H//P/9f9aAE0A6/9DAOz/HgDu/9b/YQCi/+//t//O/00Axf8QAP//3P8UACIAJAAsANf/2v+5//r/KwAyAGUADQDq/4j/CgBKAOT/VAD1/4z/CADZ/7r/BwDF/zcAHAAAADoAsP9gAAwACwB2APj/IwDg/+j/7f/W/xEAEAAJAMz/6P+o/9n/PQD9/wYA///9/zQAIAAeACQALADv/5j/KACe/5D/PgDg/zIAOwDa/9r///8wACoAZgAIAOT/FwAdAPH/8//l/3P/NQAHAJ7/9P+6/2kASQAVAEkA7P/0/y4AXAAOAGT/qv+j/6T/CAAMADsADgBnAHsASQAvAOH/MACO/9D/9P+m//j/m/8tABMALQBBAOL/3f/G/z4ASABBANH/0v/l/3n//P8AAFcANQD1/1EAtv8+APP/wf9vAGX/xP9gAOj/VAAGAPz/IAAhAFEAIwAAAOj/2P9//9z/2f+n/z4AJADd//X/LQAAADsAGQDO//P/+//m/xYASADQ/y8A0v/T/3AAyv9jADMApP8VAN7/0v/g/yEA3/+2/1AAGgAjAAYAzv/i//L/MwDj/ysAPACZ/7f/8f8WAEYAjAAgAEEAGQDG/yMAfP+x/8j/i/9LAAEA+v88AN3/LgAOAOP/FgAhAEsAKgAqAM7/2f+q//3/GACo/xEA2v/u//H/FAAnAC4AOwADANr/6P9TAPb/NADS/8H/IgAYAIcAwf/P/7//AgDh/6z/XADQ/wsAGwASANb/2/8AACQATgD7/wYACwAZAOb/EQAVAAQA+P/v/xEAzP///7f/4f/F/9H/TgC7/0sALgApAI4ABgD0/8H/yv/J/wgAUAD9//r/+f8TABsACwD+/7H/lf/d/xcAAAAgAEoAVgAkANz/oP/j/xgAIwAyAO7/AwAAAOL/8/8yAOz/5v8bANT/FAAWAOv/8/9IAPv/0f8SAJv/6P/t/x0ANAADAC4A7f8SALj/EABXADcARADC/9f/8v+7/+3/xv+9/woA2P8pAG4AMgBSADoALwDp/8P/0f/P/6z/qf8lAM//AgBzADMAbABOAC8A9/+f/w8A4v/k/yYApv+//9//r/+//+L/FwAnACAAHQAAACAA+v8jACkAEAA6AB8ANgD2/xcAFAD//+//8f8JAL7/7f/a/6r/1P8XAOX/+f86AL//3v/p/yAALgBNACsA7P8hAKT/yP8DAEIAQgASAFgA9f/s/0gAaAABALj/pP+i//D/0/8NAP//mP8JANj/5P8pAFgAgAA7AAsAqv/9/6v/xv8GANj/HAD8/1sALwBjAF4AwP/u/83/pf/u/+z/kP/j/xYAFwAnAHEAKQA0AGUA1f9JAJn/m//D/5z/HwCI/2AABgDP/1QAFQA6ACoAKgAwABsA+//M/7j/7v/U/87/CgANABwA+f8rAPz///8OACAAxf/x/xcA1/9eAMr/5f8fAPb/MgAfACgA4P/y/8P/AgCo/4j/MADh/wYAfQAwAOn/NgDe/0wA///z/zEAcf80AAkAvv8qAE4AHQDW/1cA5f/8/xwA0f+6/1b/4f8SANz/JwBMAPf/+f/j/9X/YQA/ADQAKAAAAC4A3/8kABUAqP/n//r/sv/d/yEACAAxAN//FwDt//T/SQCd/+r/4P/j/wcAEAC4ADIADAAcAP//wf/q/7r/nP+4/+//HwDa/2MAFwA0ABQAzv87AAAATgDW/+P/8P8iABsAt/8kABMAIgAjADUAMAAQAGH/lP/K/4H/IgDf/00AVQAJADQA///J/7j/egApADwAHgD5/woAu/+Z/4r/AgDl//v/NAD//3AAPAAaAFUABAAaAMv/3P/L/6D/3P+//0QA7f8yAGoA1f+PAPv/uv/x/63/wP/v/yYAIwA3APX/4f8EANP/3f8FAAEAEAD//1gA8/8HADoA7v94ANH/qf8oAA8AMgAPAA4Amf+s/83/1//w/wAACgDb/8z//P9eAEQAWAAsAPX/zP/3/wAA0v8UAOX/GAAxADcAJADr/x8Ax////yUAPAAPAJ7/5v+r/7//0/+u/1oAz/8MAC4A0P9BADEATAA0AB4Ayv/p/+//5/8PALf/6v/9/0EANQBCAHMAMQD0/7P/pP+L/6r/oP8oACgAXACFAMf/DwDu/6n/9P8qAP//w/8PAAIAQwA0APD/LwDQ/7b/MQBcAEgA+/9IAAAAdf+r/7f/GAAPACIATADm/wEAuv/G/7n/iv9TABwARABQANL/PADw/+j/OQDu/7H/QgA/AK7/FAAdAB4ACwDK/wIAAwADABAA0f8JACQA9v8vABoA7f+t/7T/0f/4/x4AIgD7/97/bAAEAH8AcADz/woAeP+p/77/6/+0/ywA6v/p/1oAlv85AAAAAgBLAAgAHgALAOf/9v9EAPf/+//x/xcA2P9gAHkADgASAI//0P+T/6v/xP/3/xQAFQAVAPv/MwDt/ywAOgAqAOX/IgAEAK//+//S/wgA7/9sAOz/GAAcAIT/LwD4/+v/AgAPAOz/BgDR/9z/SAAmAEcACAAAAO7/XgDw/7X/8f+w//n/6f8ZAPn/EQAoAOn/zP+5//T/4v9CACoAeQBLAP//TQBx/6v//f/K/wsAEgAWAO7/PQBPADwA/f/L/8T/hP8MAA0ADQAnAN//OACv/67/HQAhAEoAjAD1/9D/LwCn/x0AKgA0AB4A0f/G/6j/zP/l/wIA9v80AGf/8/8YAAUAlQCj/zsAGAAVADwALgAgADsALwC//0YAbf/c/+7/BAAmALX/MwCe/7H/yf9MANf/z/96AM//GgDk/wkAVwBcAFIAJQAGAOb/CgD+////BwADAIH/rP/N/73/LQBEADgA5P/l/8D/CQAGAOz/DAADADcA0/8IAPL/PQBrAOz/QwD4/9H/IQAaAPT/0v/6/7z/wf/P//z/PgAjAJcAZQCG/5D/5/+4/9b/WQAkAM//8P8TAMj/GgBRAGMAaQCb/+P/uf/Y/zIAIwCBAMH/3//j/8z/yP8SAHkAmP/Z/xsALADQ/zAATADG/9v/jv/B/0kARQAVAMcA5f+5/1sAt/8BAAkATADW/+z/9f/a/+n/1f/2/1f/IwAAAAAAKwDu/0AAIAANAOn/BACd/y0ATQASADgA6P9LAC8AGADQ/9r/MwAsAL7/3v/U/6v/KQACABUA5P/o//r/HQD0/zwA9/9L/2IAnv+5/wAAHgCAAMz/ZAAQACsAJgARAFQAFAD7/+n/HwCP/77/3f/9/9b/yf9EAMr/pP9EAHMApP/u/zUAEQBdAK3/LQAlALH/agAiAOv/+f8MAB8AqP8LAAQAu/8mAAQAMwD9/5v/CwD+/8D/JABEANz/4v/3/87/LgAjAPH/EAC0/w0AOwDU/+7/OACBAAoA6P83AM7/PwAAAM7/FQBc/8b/7P/e/3QARAA8APj/4f8AAMz/q/8IAGAABADJ/8//0P8SAHoAJAABAEAA3P/J/xgAFABrABYA1P/o/63/zv+u/z0A2v+u/wQA4/9TACQAnAD1/5//CACO/9//6v9KAFkALgAtAP//vv/t/00ABQBMADcAAwCs/6P/0v/9/24A4//T/4r/rv8tAOP/WQAqALD/7f/R/9H/ZwB1ADgAiwD9/83/yP/A/z8AFgA/AA8Auf+i/73/QAAmAA8Ahf/z/ywAk/8HADYAbwANAL7/CQCb/1v/TgCBAEgABwD2//H/2v95AD4APgAiAOH/v/99/w8A+P8uADEAu/+i/8v/wf94AH4Avf8RADn/7/8BAM//xQAnAE0ARwD0/+X/7P/W/y4A9P/j/y0Af//r/8j/+P9zAF0AJwD1/7D/cP8yAC8ATwAoALr/wf+m/+z/dAA8AAgAxP+r/xkAiP9yAKUA9/9OAOT/DQDZ/8//9//i/yoA2//R/6r/tf9DACcAIwBiAN//AAADACAA2f/W/0gA4/9VAC4A9f/H/7X/FAC5//T/LwDn//D/HwDj/xoAMgDm/yEAzv/H/+r/KgAfAAkAGgDd/wkAIAAbAFgACADd////yv/5/83/v/9lACEALQDz/3b/0v/H/ysACgC6/ygANwAuAE4AbgDl/xkARwCe/7H/xP8mAEIA8f+4/6T/tv/O/ykASQBRAAYA7/8OAB0AIAD1/+3/IAAnAMT/OgDJ/5b/VwAWAPD/3v97/87/SAD6/18AeQA8ADkApP+0/+7/2P8jABoAzv/l/83/AQBGAEUAzv8SAFoApP+0/xoAWAD9/x4A8v99/wYA/P9/AO//m/8vAKr/8P80ADcAgQAWAMz/1P+m//z/NQA8ABgAvP/m//D/6v/P/wAAKAAPAOf/AADM/8z/HgAuAJMAAQB1AAYAr/8TAJ//IQDj/zIAGgCb/8f/KQAQAA4APgBy/8P/3f/n/wIAFwCQAE4ALgDh/8r//v8zADcAVQDK/7z/uv+M/1AAHgALAP7/5v+Y/0z/LQBpAB0ALQAjAPT/4f/8/2wARQAmAF8A4f+S/7v/5//K/yIASgBPANb/f//F/wAAAwA8AJMAYf/F//X/z/9cAEcAkQCC/wsA5P+5/1IAyv+OAM3/6//H/6T/VADm/0oAFAAEAMf/HgA5AO7/awABANb/wv/a/8P/3P9AAP//+f+n/wgASgDp/zcAgAAVAOb/EACm//X/2P/3/y4A/v8YALP/wP8hAAkA/f9GAOb/0//e/7X/NgDE/2MAIQDX/2oAwf9QAN//8f9PANL/WADs/+D/PAAbAB0A7P/4/9H/vv/W/+X//P/Q//f/5P+q/9X/EwBSACgAmABcAM//+v/n/xUAQgDt/4r/1v/b/6L/HwBSABEAdwBUAKz/DwD6/7f//v/D/+b/1f8aAGUA9v8DAEAAHQCo/wAAAwCN/6gAGwARADoANP/p/9D/NwCMABcAWgCc/27/hv/e//n/vf9FAOf/IwAeADwA3gBuAEsAAAD9/3r/mv89ALn/YgAOAH3/2P/h/9v/BABBAOj/8v/r/+r/BwD8/x4AEQDt/6n/wf/Q//f/nQCPAEAAbQDC/9//AACj/5AACQD2/xAATP/2//v/4/85ABcA2f/m/63/CwDr/xcAfgDV/zUAyv/u//f/5f+5APn/zf8nAMb/xf9hAPD/EwAfAG3/AACN/9X/pQBHAE4A8v9j/7r/9P8kAEgA9P9tAMP/1f9fAPX/UwAhADMAfv9O/6P/nv98AHQAOAAuAOz/zv/J/wgAewA2ALr/TgDC/4P/5v+KAFsAuv9wAMP/wf/h/7D/KQC+/yYAOQAPAKX/3P8YAPL/ZwDJ/9L/7v/0/woAGABIAN//bQAQAN//y//m/3IA+P8yAOj/w//u/yAAMQATABYAiP/V/9j/0P/i/+X/PQAFAAUABwDi/ygAw//x/9oALwD6/yAAZP+L/zwAngAWADgAFADF/9j/1/8dAAIA1/+p/xcA0v/6/0UAv/9CAMv/HgApANf/LADy/0EA1v+z/+T/2//T/xEATwAJABEAQABQAOH/GQA/AAIACADe/7z/3P8XAAcA4f8gAA4Avf/5/8b/wv8AAD0ANwDp/xQAoP/w/zgAIQAsAKX/+f9CAOf/EABAAEIAXwDv/9z//P+O/9H/0v8qADUAxf/n/wkAvf8cAEsALwDX/9n/QACh/0cAQADH/9f/AgBrAHX/HgA8AEMAVgDj/zwAWv/y/xUA3v/h/8v/GQCP/+b/DQAmAHYAZgCDAKH/z//e/6b/cAAuAAIAs/+U/+f/uf8rAC0AEAD2/2cACwAtAOQAj//h/7f/Zv8eANX/IwAqAEAA7v+O/9z/7/8ZAC0AMQADAN//0/+8/wMAYwBEADkAHQCr/97/8v81AFAAXQAZAD7/w//M//b/bAAQAPr/0/+5/+L/QgBqAFEATwCZ/3D/tP+8/0cAXQBZADkAbf+V/9j/AwBUACMABwAwABYA+f8hACEAGgDn/xAAAwCa/8P/7v8uAGIA8P+1/zMA1P+b/7f/rP+fAEcAHwAhAKT/7v8mAAkAJAAfAKH/7P/k//j/PwBfALQAKwDn/wUAhv9v/zQAFQAZACAAof/k/8X/8/9OAOj/jv/g/8H/6/9OADgAYQAmACAAQgD4/yIAPQDf/9f/rf++/9H//v9NAPD/BwD4/xkAyf/T/00APQA4AA8AHACG/7b/zf/x/wcACABcAOb/bAC6/wAASwDs/1AAj//S//v/RgD1/xwAKAC6//b/Zf8NAOv/CQBfAC0AbACU/5f/JQDX/wwAiAAeAEMA6//1/zwAzP8BANb/wv/a/wUA1//v/2gAKAAmAMn/kf/W/wwAQQCx/+H/KQC3/1cAMgDK/ygAtP8tAGgADQBYAPj/1P/y/9v/GQANAAUADQA2AAkALwAMALv/5v+o/7r/5v/y/5v/0v8VAKb/QQBmAEcAPwBBAB8A7v8AADEAMwDK/zsAnP/s/yEAkv9zAM//tf/o/7T/BQAvAGYAHwDZ/5H/mv/c/1oAWwAbACEA+f8CAJ3/+P99AAAASwAuAMf/7P/Z/xkANQB8ACYAt/+q/3T/8/8JANz/1/8dAAcA4P88APf/4v/d/xgAGQDx/+H//f9hAA4AGgAdAL7/tf8SAGwAVQAgACcAIADP/5r/6//5//L/IgCt/6b/wP/2/1sAQQBTAAsA5f+5/+X/AQDe/2gAMwD2/9j/6/8TAEAAIwDy/w0Axf9y//T/fQAMAEoACACs/+b/mf/I/y4AhgA+ABoA1/+C/67/FgBKAOL/RgDB/83/3/8bALQADwBaAOn/2P/7/63/CQBRAGQAqP/X/4X/Rf8rABYAKAA9APH/3v8HAN7/JgBMAKkAegD6//j/hv/H//z/IQAQAPP/uP+V/ycAGQBPAO7/CwDD/yv/pf/4/3wABACYACwA2P9XANz/YQDY/2EA5v9//0MAjf81APz/BgAyALj/5P/I//z/MwBkABoA7/++/4f/7f/X/wEA2QBBAPf/IQCA/wwAQwAPAE0ArP9+/9n/AAD6/y8AXgDR/+H/FADo/xcAOADt/xYA4v95/9P//v/w//7/DAB2ABcAKgBYAPX/IQAIABEApP8AAA8Awv8bAK//CgAOADUAPQD+/8v/qP+9/4L/HgD2/x4ADQDj/2AAz/9TAKsARQBKACMAtP/h/xIA7f8nAL7/AwDO/6b/tf+r//f/AwDX//L/LgDF/3YAOgAjAEoAiP9WAPX/x/80APr/7f8TAKwA6v/Y/zwAs/8VAMf/l//E/8v/OAAZAOH/DwAbAPj/IQAZAC8ANADr/yYA0v///yEAzv8+AOT/CAD7/8n/qf+n/wgAEwBQAEoAIADq/xMAFgAeAP//z//+/5n/4f8WACAABADN/wkArv/i/y0AKABaABUAGAAWAJj/1/81ADcAWQAJAN3/8v/H/zEAGQDs/zEA3P+x/5j/+v8sAPz/1//o/7T/uv9yAAkAiQAyAA4AnQCv/wsAvv/j/yEA3v8qAOz/2v/y/wsA/P/m/+z/NQA1ANr/vP/g/wQA/P9/AO//EADz/4X/2f/j/zIARwBGALP/0//r/xgAIAAFACEApv///xUAZQBIABIAawDs/47/r/+i/+7/aQD2/6//3f/j/9T/RgBTAGsASwCb/xoA6/8LACYAAwAJALf/9P9z/zsASAANAHIAqf8kAO3/tP/k/xgAEQCq/yMA0/+l/9X/+f8uADsASwA+AC8A7P/2/woA3//4/+3/CAAXAM7/LQAwAFQAfwAcAOr/vf+N/5v/1//s/x8A4//j/8z/2P8DAAIAgAAnAB0A0v/P/w4A+v9TAPz/SwD9/9X//v/e/zMA+f9VACMAy/+x/6H/IgBFAPr/FgASAK3////l/wQA+v8DADEA1f/x//b/jwAwANr/AABv//n//P/l/0sALwALAPb/6//1/8X/xf+3/x8ASAD6/0MALQA4ADYAHgAKALn/3P8MAPr/FgBHANb/x/8hAMz/sv+i/+D/BgAPAD0AMgAYAPv/7f8SAOD/3P/9/xIAOQAeAEMAMAABAPT/BgDV/83/z/+8/w8A9/9LABkA8P8EAAAAJgDv/yMAsP/u/zcA5//d/8P/3f/0/38AEgDo/xsA/v/+/9j/fQDY/1QAMwC4/y8Abv/5/+7/0f9QADIACgDl/xQAyP/d/9D/3//f/+j/HADn/1sAVQARABQAEgAAABAA7P/1/wYAh//h/zAA9v+0/yoAcQAzAAwAHQAeAHX/GQDG/6b/iwC0//j/NwDm/0gAKwAhAOv/w/8FANX/9//8//H/PQAHAOr/zv/9/9L/0/+mACsAyf/h/8n/q//+/ywAQQA2AMz/DAAEAB0AQgATACAA3P/K/0AAEQCi/woA0P+f/+j/IQAiAAUAIQBGADMABAAsAPL/3/+u/7r/5v/a/wMA9P8nACQALQADAE0ALwCQ/zUA3v/f/08Asf8bANP/3/9/AOP/wP/u/8f/NwAmAPH/DwDb/0AANAC6/0MAEQDY/9v//f/Y/zcAXgAAAB0AqP+f/7X/OAAhAM3/IwDE/z8Ax/9DAA0Ahf8iAAQAMADX/y8ACABjADMA0P9VAMD/LADv/+v/BQDn/w8AAwATAN//LwC3/9L//v+l//L/AADE/9v/QQArACoAJAAPABAAvv///+3/BAD6/9L/RABdACgASwA0AOf/9f/5/8H/qv/u/x4A7v8YAAAAyP/p//z/BgDv/xwA+f8qAPn/uP8bAJ3/OQAlAP3/+v/v/yYA/v9LAHYAGQDW//v/k//2/zYA4v/y/9T/AQANACwA8/8nAB8AxP/8/+L/DgAHAEQA+P/p//3/9//x/9P/8f++/+b/5v/7/04AEQDM/wUA2P8sAKgABQBIAA0A3//n/xYAKADL/wwA5v+5//7/EQCt/zYAPQCi/wIAMwAAAAwADwDx/z4A0f/h/+r/rf8gAOv/CADU/8P///8vADkAAwBlACkA3f81ANP/w//9//X/KwBCAA0A4/88AMv/AwCIAL7/CwC//7j/vP/I/wAADwBZAMH/LAD+/7H/bgDm/6X/DgDn/x4AHwDP/zkANQA8ABwA/P/5/y4AMwDn/xAA2//q//3/sv/L/wcA4P8TAA4A4f/q/8r/MADm/0AALwDQ/yEA6P8GAMf/EQBtAC0AEgAAAAEA2P8IAOn/2v8nAB0A2v/x/8f/x//e/+X/MwDQ/wkADwDv/6MAOQAJADIAq/8hABQA4f8NAN3/JgC9/9T/DwDN/y4ASgBmAMr/jf/P/x8AJgDt/y4AzP/k/w0Awf+l/9//FABOAFYA8v8vADsA2//0//b/xf8JAHIAKQAYAPz/tv8iAAEAIgBsANb/vv+0/7X/lf8AANn/9v8jAJf/ZgAUAOH/LwAEADgACgA7ANX/JgBNACAAcAAKAN7/4v/W/9//AADw/+b/q/+Y/wsA6P86AFsA5f8XABAAxv8TABwAvf8qAOL/mv9FAOX/AAArAOH/FQBLAGsA8f/q/x8AJQD3/+v/JgAQAO7/iP+m/+r/fP+v/zoA7f8VAHQAVgBMABYASgAVABAAMQAZAAEAkP/N/6z/zv++/+r/VgAUADMA6P8HABQAqv+q/wsAIwAtAEcAFADp/yYAMADo/8P//P8kALj/3f/2/7X/AQAgAEoA+f8xADsA5/8rANz/MQA4AI7/z/8FAND/RQDi//n/PADc/2AA8P8HAA4AvP/r/9v/DQC5/97/+P/w/4YA9f8nAOv/m/80AOr/9f9DAEkADAAHAB4AMQAHAMX/LwDt//L//v+7/6D//v8rAAMA7f/U/x0Aqv/q/+j/rP9sAAYAbABBAPz/bQD0/6j//P9BAJ7/8P8CAA0ASQAXAC8A0//E//r/IgDt//v/2f/N/wUA7f8NACsA8f+v/z8AIwD3/2kA1v/w/0IA9P8cADUArv/e//j/wP/U/7D/CwAgAEMAPgD8/xAAxv8HAAAArf9OADcA0v8SAO//+/84ABkALADq/67/BwD9/+v/NQAAAKL/4P/6/9b/VQBIAPb/EQDA/+j/RgBEADkANQAmAPf/2f+F/9X/sP+B/zAAyP8bADkAKQCYAO7/EwDt/6X//f8DAEsAIQAuAA8A7P8OAMj/xf8MABAAyv8yAOP/1//x/6H/HAC4/9n/OQDi/yAAbAA2AAkAYQBJADAA8P/O/+n/wf8FAPz/2//p/8v/4P8LADwAIwBuAB8AnP/4/53/2//y/6L/BQAFANX/AABVAJQAQQDZ/3QAKADP/x0AqP/I/8T/DQAIAAMAKAD9/0IAqP/s/9n/4v8hAMP/PwC5//z/EwAfABYAwP9eAOf/5/8xAOj/eAAbAMz/TQAHAC8AzP+q/wEAsv8oAP7/2v83AOP/u//a//H/9f8WAAAAIAD7/wYARgAAAPv/IwBqACsAAADN/+z//P/L/+7/KAD5/7b/MQD6/87/8//5/9T/8f8dALj/TwAKAAIAAADM/zYACAAOACwAXgAJABAAzP+H/9f/7v9RAEMAMgAFAMT/uf/o/0kA6f8bAEsAtf/t/yYA+v/x/7j/BQAgAA4AHgA7AC8AmP/E/xgA4P/j/x8AEADe/wAAEQDx//7/ZADm/9H/AwACAEQA7v8GAAIAhv8JAAkA/f/e//P/VAAdAFwA9P/O/+v//f+NAMv/9f/T/5//DQD1/y4ApP9UAF4Asv8+AAAABwAVAPr/EQC4/67/HwACAOX/5/+P//L/KwBHAEEAAABAAC4A5/8JAMj/AADn/9L/PAAZANz/FAAhAPr/NgAiAAAA6//R/8j/1////8//2//O/z8AIQBTAJUAEwC8/5b/4v/I/9P/GAARAMz/xP9yABsANABWADIAPwDM/+j/EAC0//r/vv/S/2oA3P8eABAA3P89AMD/y/+9/8//GAAHAPX/GQBHAC0ANQBzAM7/p//I/9T/TgAhANz/zP8dAPL/3/8SABEAUgD6/zgAxv+h/yQA2//L/x8A+P/B/y0AYwB+ABkASgAoAJD/1P+a/+f/zf/w/+n/mv8pADkALwAyAC0ACAAOANn/3v/M//b/NwAcADMAAAABAOX/2/8rAD8A7P8SAPb/ov/j/9L/BgDE/wwA/v8wAG4AwP9LAPL/CQD5/7z/fwCz/yAAUQCQ/xUA2//4/xQAAwAGAN3/DwCF/xAALwDp/0QACgAiAPT/LQDX/+f/KACv/wUA4v8MADAALwDk/0kAHgDZ/zEAl//R/83/4v83AP//1/9GAIIA9/8oAPT/vP+1/+X/UgDn/x4A4//W//3/zv9GALz/q/8TANP/EQBfAGMACQAuAC4AGQA/ABwANgAkANT/tf+z/3//0v+7/3b/vf/X/0QAAQBiAEkAKwB5AP7/YgDz/0EAQAD6/8P/Wv8uALn/NQDk/3n/WQDL/0gAEADJ/yYAof+y/ysAPgAaAGUAEABOACcAuf8bAMv/jP/c/+L/0f9aAAAAMgApAH3/WAD+/xQAHQD1/woA3f8cABwAIwAdAAQAyf/y/7T/x/8AAPb/8v+W/zkAAQAfAGQAAAAgAN3/BQANAB8AJAATAOz/9v/7/+P/RgAaABYAyv9+/wAACwApADAAsP8AAOX/iv88APz/BgBEAAoAFADw/xYADADe/0YA6f/z/1gAfP/t/zcA6v/w/8L/PgDx/0cAXAAgACEArP/Z/8r/8v/t/y8ALQDE/+f/7v++/33/JQA4AEwAhAASAFsANwD6//z/lv+H/4//mP/0/zcAOwACABIADgA3ABAAMwA9APb/IgAJAC0Arf/H/83/vv/4/wsAJADQ/14AOwDq//r/AgAtAPj/OADG/+P/5f/2/xgAq/8GAPH/mf/f/0IALAA6ABIA8f8MAOf/YQBNANj/5f8XANv/3f9pAFkA7P/m/+3/qP+b/+X////w//j/1f/M/yMA1v8mAFwAAQAaACUAAAAXADwARQAvAO//if+3/9r/5v81ACEABQDq/9P/PADj/+X/cwDg/y0ATADU/+r/9v9XAOD/ev/f/9L/+/8dAOf/3v/u/+L/QgAcAO3/RwAbAB0AJwAlANn/+v/v/6j/GADx/xYAGADh/wAAKwD4/+z/HwC7/wAAJAC6//H/YgAVACEAPADS/9f/xP8iABYA5P8rAPf/EADW//P/DgDI/xgAIAACAMn/mf///ygA3f9GAEsA8v/x/9r/DAAnACMA9f9LACcAyf8YANz/9//p////+//q/9f/IwAOALD/SQDc//v/GADv/0cACADY/9//AQAFAPn/y//0/zQAGADg/8r/DgDi/yYAfQA5AOX/KQAaALz/DAAIAPX/wf/y/7v/0/85APr/HwDR/wMABAAHAGgADwBLAAgAuf/3/7b/u/9BAPX/3f9CAOX/1P8XAEMA1v8PAA8AlP9MAP7/DAAfAO7/KACd/+H/MgA7APP/3/9TAKr/HgA6ALj/4P/u/yIA9/9dADAA9v/y/63/DgDS/xkAEQCR/yEAFgAdAFMAHAAHAOv/6v/c/+f/7v/n//X/1v8fAGkAtP/5/1MAnP8NAB0ALwAVAAMA7P/U/zkAwv/7/xgA7v8rANj/z//H/0gAIwAAABYAOwA1APL/EQC9/xIAvv/S//7/c/9iAB8A4P9OAEQA5P/f/z8A3v8qAIz/1v+JAMH/LwAAAKX/8v8CABoAPwDC//v/awD//xcAOQDt/+3/+f/T/6n/k//6/z8A8P8eAAsAEAD5/wsAMQDT/0EALQApADkA1//d//D/xP/r/0MA+P8tAN//nf+//4v/AAAaADYAagDj/93/eADs/xYANwAXAF8Amv/l/+X/2/8rAOD/NwDt//D/MwD6/9n/GgD9/7P/v//B//X/6//t/9z/MAA/ABoAnQBAANH/4v/9//7/5P8RAAsA3//p/ygA5v8ZAEoA6/8LABcAxv/Z/0QA2P/N/xAAtf/I/+r/HABCAAgA3/8UADsA3P/2/0kA/f/X/w4AAQAwANX/NAD9/8b/KwCb/yAANwADACsA5/8VANf/yf8nABoA1//V//b/7f/S/1UAHgDy/+v/t/9MAO3/IAAcAMf/IAA9AEMAAwAIAMT/+f8fAMD/9v8RANf/zf8TALz/4f9NAA4A/v9jADUA7f8YAPL/+P/5/wMAtP/m/7//0v9dAL//EAD2//z/RgAgABcADwAyALT/IgBGAMT/6f/J/x8AEAAuADMA2v///73/AQDs/5L//v/Z/xMACgAWADgA2f9iACEAJAAgALr/CQD7/ykA6P/y/x8A7f/U/8D/LADw//7/YgAKAKT/KwDh/7H/fADB/9f/KwDI//7/5v9LAAcA8//5//H/JwAHAEgA/v/z/+3/3/8FANX/+v8cABAA+/8ZALr/6P8uAD8AIwC//wIA8P/r//v/mgAGAOH/OgB2//H/xf8xAEUADAAgALX/8//c/7r/3P8rANX/LABvAKj/5/8NAO3/MwA3ANX/GAArABQA+f8UAAMAuP+PAEAAq//h//D/wP+i/0MARgDp/+L/4v/K/4T/QgBLAAIAWQDV/yAACwDX/y4Av/8mAOr/6//J/+D/OQBHAG4A3f86AAAA+/8QAMT/zP8nAO7/0f8mALX/NADl/9r/NwDW/+7/uv8lAAYAVgASAN//5f+q//v/DgBRAP7/GgA0AB8A6P9IAAAAAQD+/5v/WwB2/+//7P/H/ysArf+MAAUABQAUAAAAOQAlAC0A8v/5/5z/DQDl/7f/8P8cALj/CwBtAMX/XwAkADQA0v/o//P/f/9ZAJ7/XQDy/6T/SQALAFcAif9PAND/9v92ALH/PgCw/wgAyf/p/ycAsP9cABMAPwAIAOz/TAArAA8A3//h/63/nf+y/wIAIQAHAFsAQwDP/+3/AAD//wAAEAAyAPn/BQAlAAUAGgAdAMX/0/8hAMf//f/7/7X/CAC4//v/VQALACcA0v+8/1IA//8LAAQAAQBRAMv/SwAFAHP//f/1//X/BwD5/x8AFgAfACIAEQAHACkACgD3/yEA3f/K/+//GwA4AM3/0P/w/6//w/8nAPj/MgASAOX/SwCO/8n/DgDk/1IAFgA8AC4ALwA1AND/zP8HADEAIgDc/+T/6v/7/wIAtP/2/woAFAAwAPL/7v/g/wUAJAAfANP/sf+u/w4AJgAIAGgA9v8QAEQA9v8RAA0A+v/U//v/y/////7/u/8EAAQALgAWAO7/IQD1/wkA+v8OAGkA1f8jADQAdP///wAA//8WAPX//v/l/w8A3f8XAMT/h/87APz/IgAXAB4ARgD//+f/BgAwAJr/5v/4/xEAHgAHAAoA1v8+AP//PgAeAO3/MgDf/6n/w/8CAMb/RwDe/9r/TQA6AFAACQDv/6v/KADn/+P/JgDj/yEA6P/o/87/GQDq/8j/LAD8/+X//P8lAPT/CAA8ACYA1P8dAMb/9/9XABwAMADg/yYA1f/m/xgAzv8zAP7/3//s/wwAn//w/wAAj/9DABAA+P9cABUAyP8yABAACwAVANT/GAABACwAVADe/7//FADB/8f/CADZ/wsA/f/5/+D/EQAsAEQARgAgAAUAAQAHALX/1//5/+//0P/j/wAAAgAgABAALwAOAO3/+f8MAOz/IAAZANr/KQC0/8j/2//T/wIAEgArAAAAJgAQABQAdgAPAA4A/v/n/xIA/P9MAM///v8CAIX/AwCE/+v/4P/j/z0A7f9EAPD/bAAhALT/OAC2/+H/XAD6/w0AWACz////TADE/+X/IAD1/8P/LAAHABkAAAD+/yAAvP/T/9X/EQCY/xsAJQC7/3cAq//A/xAAIwAtABYAawD1/ygA/P8PAE0AAAA1ADUA4v/C/ywAvv8OAKT/Wv/t/2H/AQAFADUABwDo/wwA1f9sADcAUgAjAEEALgAsAIEA8v8dAIX/vv+4/8r/KgAOAC8AhP8VAN///P8HAMj/GQC4//H/tP/3//n/AgBhACoARADU/3EAEAD8/2wA8/8UACwAOgDT/xYA2/+R/xYArf+0/83/0f8PAOj/y//w/+7/EAAlACIAEwAPACsA9f9aACQALgBwANz////Y/+//4P/O/9n/5f8mAEEANADf/+v/u/8JAOv/BAAcAMT/1v/L/+z/6f9OAFEAHwD1/+P/FQDr/0YANADS/8//DAD1/yEAWwAWAAcABgDJ/6D/2//j/93/IwAAAMb/OgAPAMP/LwADACQACAAVANf/KwD//43/TgDr/2AAWAD0/0YA2v/a/8D//v8LAMv/GgD5/6L/1f/O/xgAFQDE/xQAMgBMAAwAMQAUAAMASgDN/zQAJwCP//P/7//F/+//+v8BANH/BQAVAAIAJAAyAFoAzP85AC4Azf8lAJj/8v/O//j/5f/G//f/FABLAMr/NADs/xAAPQCQ/2gA8f/h/2cAFQA4AAgAEwArAKP/7f/a/6n/7f+y/9j/AAAMAOz/1/8QADMAUQA/AEoAEAAAAFQA9/8xABgAzP/3/5r/CgDr/8v/9f/f/zIAh//k/6v/1f9iAKz/ZAAiAPT///8LAGcA3P9cAFwAJQDN/97/VgDU/9r/FwD6/wMA9/+d/wQA5v+k/2oARAD7/+//AQAVAJH/2P8AAJ7/6/9DANb/CgBtAAwAVwAFAAUAcQDX/y4ANAC9/9f/DADr/9f/3P+P/9f/2/8AACMACgBDANH/DAAEAAMAZAAoAB8A+f8AAMz/1f8IABQA/f/k//j/+P8iAP7/IgA8AOH/IAACANT/3P/x/z4A+//V/+H/z//o/9D/6v8LAAMA+P8TAFoAIwAFACAAEAAhANb/BwA7ACIAGwDo/w8A5//e/w8Awv/j/9r/lf/v//n/5/81AAgAAAApACwAKQDt/6r/IAAKACoAbAACABwA4P8UAPP/xv8UAA0AOgCg/wAAEACm/wIAqf/A/+b/AgAkACgANgB8APn/0/80APL/FQAkANT/AQDw/+n/AwDb/ysAPwDF/xUA9v/0/w0A1P/z/9z/5f8KADkAIAD0/+D/zv/e/yUAOgAWACoALwBDANT/oP/l////QQAiADIAHwCE/9n/SQCo/6X/9f/B/+v/PQA4ADAAJQDY/+D/t//3/4kA6/8bAE0AFwBJAPf/8//H/+D/CQDL/zgABgADAAoAxf/q/3j/9v9UAK7/TgAaALv/RgDI/0EAMwDH/1YAx/8BAPf/AQD8/wcANgCk/10AJQD0/wMA7//X/7b/OAATAE0ACgD+//P/tP/h/9//CgDa/xgA1v///+7/wv9cANb/SwA7ALP/OgDy/xYAQgDX/xQACQDp/2MAPwDP/x8A+//J/87/1P/A/9r/WQCl//v/AAB+/0kAFQAzABYAZgA7AMz/7P+v/2kAFQD1/wwABwAcABEALADO/woAtf+Q/+r/1v/G//L/GgDf/ykAGADP/1kAOQAWAFYA1v9NAB4AGwBHAOH/1P+L/7n/9v/t//r/UgD5/w0A+v+5/w4A2v/v/+T/NgD9//7/KgAUADAAzP9fAPn/0//i/zEANgDR/zYA5f8nAMb/3f/Q/93/AwDh/xgA/P+BAL3/9//R/57/UwCz/xQAEgAhAF4A6/9KAB8A6v8UANb/QwABAC0ANwCY/wAAxP/S/6f/xv/h//b/IADl/1YADAADAPX/GwD5/yIAUQDK/wkA2/84ACsARwBWAAcA5v/F/wcA0f/R/7j/AwC7/+P/IgCc/0AAHwAkAPn/yf/k/8P/BABHAOr/CABhAEAANgABAA8AFAD4/xEA///z/1YAJADH/9z/vP/K/5L//v/V/9X/LgAEACYA1f8FAOv/8/8zAA4AGQBHAH4A//8nAPD/0v/H/4X/AAAYAAgA2v83AGAA7f8hACYA6//o/7//AwDv/8z/OwAZAMD/4P8RAL7/NABCAAkAIQDX/wcA3P8BAO7/6P/R/yEAfwDE/6UAPQC3/ycAl/8IAN3/oP/6/+T/HwDb/77/AACf/zMAOgAgAI0A9P9ZAN3/5/9oAOj/7P8VADAAuP/t/wUAu//T/9b/BQCW/xIAQwDO/zEAGwDZ/x4AMgD0/w4AAAAkACQAAwDY/+T//v/y/04ASAAdAJP/8f8TAJv/OADd/+z/LAADABcADwA8APb/0P/c//T/8v/y/wEABwDU/9z/zf8HACkADwBVAFIAawAsAK//n/+w/53/BAASACgASwD0/1AAw//k/zwA5/9SAOX/y//7/7T/rP8kAOj/IgBNAP3/XQAUACEABgAOAAwAEQDV/+3/AgBy/y4AkP/K/xgAxf9VAOT/AgAHADQAAQAFACQA7f8ZAOz/EAAiAPP/PQAwADwAJgDA//z/nP+8/woAuP/r/+L/bAAbAO//9/8KACAArv8yAB0ANgD3/9b/GwC0/+r/FwDP/97/dQAqABkANAD0/xQAAgCx/8f/5/+3/xcAKwAhABYADACm/7f/HwDa/zoAIwAVACgALQAAAPj/DgDV/xwA+f83ACMA2v/t/7P/1v/8/w8AFgAjAPv/JwDJ/9b/4v/g/xoAsP+JADMAyv8VAMD/8f+x/ykAcgABAAAAUgAQAN7/TwDl/8z/xf/Y/xAA3P8LACMAOAADAOj/EQD7/z4AAQDf//f/ov/i/9L/BwAwACMA/P/p/yUAxv9OACcAof/Y/9T/BQAiAFgA/f8hAD0A4//w/yAAFwC9/wQAvP8PAFIAnf/0/zAAIAD4/xoAGADq/9T/9//8/8r//f/y/yUAIQDm/1MAEADs/yoA8f/7//7/4f/V/+7/4v+5//X/CwAZAC0A/v/d/xgAKgAjAG0ABwDt/zAAz/8bADkAs//8//T/0f/q//b/3v/H/+v/2P8YAPT/r/8XAPD/KABFAEEAAgAPAAkAMAAjAPH/HQDf/xUAEwBeAPj/pf8MAI3/QQAVAOz/1f+z/0AAmP8cACUA7v8KAOH/7f/d/yAA8f8GAAcADAARABUAaQAmAAwA/P/Y/xwAKgDz//3/1v/h/w8A0f/s/xUAx//q/xkA9//a/9//EQDb/xkAHgA6AE4Axv8fAM//AAAoAA8AXgDh/zcAtf/n//T/qv9oANH/2/8NAMb/FgAvANb/AAAIALz/NgAqABAAAQAUAK//3P8IANH/BQALAJkAKgBKADIAyf8sAMz/MQCa/6n///8MAA4Ag/8ZAAIAHgDJ//j/BADx/1YAmf8WAPj//P84AAIAIAAuABUAPAArALz/OwCZ/7b/FAC9/0AAKwDm/xkAjgApAB8A2f/b/+j/tP/W/3D/NgDH/6b/HwDW/w4ALwAjAB4AXwDh/xUAcwD+//j/AwDT/x8A/v8HABcA1v8zAAUABADJ/8r/IQDL/x4A1f/Q/+//9P8hAP7/j/8BAD8A7/9UAN3//P8sAIUATQAHAD4Am//b/+P/OADd/7H/DwDP//f/CwASANz/xf8vAPL/rv8VAPr/CwBbAEIAAwALABsAAgABALz/KQC4/87/GAAUABEADgBBAMn/KQD0/+j/5f/2/3gAzv8EANr/1v+Y/zoAJwCT/2oADABxAO//8v8oAJr/EAD4/wYA8v8DANb/xv81APz/4f85APT/yP9tACoARAAOALj/GwDN//z/AwDQ/+T/DAD3/9//9P83ACgA//8dAAsACgDp/7D/n/8FABIAJgArALD/FQASAML/BQD5//v/OgAVAIAAVAAxAI4A1v8mANL/l/8uADP/6f8MAGj/5//b//f/7v/J/zAAZAA8AEoA3P/G/+P/CQBWADAA8f9bABcArv+FAAEA5P8kALT/BwCY//T/BQD//xIAkP/n/+//0P8cAEIA8f8dAP7/DAA9AKH/SQA4APT/QAAmACwAn//6/wsAs/9AAOn/DgAqANH/RwC3/wkAwf+x/xIArP/n/7v/LwALABkAZwAkAFIAJwBpAO//y//y/4z/1f9SALr/JgBJANT/FQC4//7/jf/V/2IAWQDq/8P/QQC8/zQA5v/6/1kA9v9MAPL/+v9NAAgAqf8wAJ7/9P8qAIz/FgDD/77/QAAAALv/YgAHAPf////6/2YAqv9OAPX/GwARAKz/DwDX/5wA9f/z/xwA2/8BABQA///x/zsAsv/9/+v/yP+//9T/VAAeAEIAYwD0/+7/HQDM/8D/zP+H/7z/DQAQACIAHQAAADoAKgA5ABEAxv8JAB8AGQBJACsA3f/g/8j/IQDp/9v/NgC4/+D/3v8LAO3/x/9HADsA+P8oADkA2v/I//7/8f/T/zgABQAGACEA5/8dAPH/6f8DACsAHAAAAPD/2f/t/xIAIQDC/7b/5P8BAN//CwAYAPj/PwA0ACoA+P8JAOv/SwA6AMj/NgCm//7/QgDe/woAy//K/9H/AgBDAMT/tf9OAMf/3v81AJP/FABMAAMAXQBWACsAGgDw/+f/JgAFANT/5f+p//X/8v///+n/xv+HAMX///9CAKn/FwCO//L/NwDc/xYADAAYAB8AWAAKABgA9P8MAD4A4P85AOH/EgDT/43/AADB/8f/CwCAAND/7P8mAOL/TADi/yoAHwDs//v/5//T/9D/NgDP/xAACQAhAG0A0v8PAOj/yf9WAOz/nf/X/z8A2P8lAGIAtf8lAAYAAgAmAKr/TgDk/8v/PQDX/97/DQDs/97/3f+u/wYANwAkAE8APwDR/wwAKQDv/yMA9f87AFEAtf/L/8z/tv/E/8j/NAD6/+H/IQAmAFwADAAlAB4Atv/e//j/0/8aAIAAMgBCANz/tf/R//D/CwC2/ycAqv93//H/NgATAN3/fAAcAPr/ZgAiAAgAIQAZAMv/0f8CAOT/AADl/7P/EwAaAA4AVwAAADAABgCO/+f/7f+9/w4ADgAoADwA0P8mACEA1P/1/xIA9P/K/ycAof/Z//L/p/9uAFwAOwAIAOL/GQAlACYA+P90AJ3/0f8mAGT/hgABAHn/SQDc/0sA1P/u/z8Aav8WACcAzf/6/0gA4P99/2QA9/8jAG4A/v8+APb/3v/x/2cAFADH/xwAtv/M/9v/y//K/7j/9f8mAAkAJwBCAAUALQD5//3/UgD5/xwAHADS/x0A+v++/xMAEQDJ//z/IgD4//3/yP8SAIb/3P9hALT/RAAnAD4A/v8TAOf/1f9oAOb/SAANAOr/ov/2/1YA4v8TAGn/DgAcAMD/MAAeAPX/4f/q//T/TQACAPn/9f+Y/wQAJQAMADgA0v8IADUAIABkAPL/aAAJAMb/7f+7/zAA5/8sAMn/3f8PAN7/IgDb/97/nf+//9r/uv/J/xYAQwA9ADkA8v9sACUAGwAwAPP/2f9OADsAvP9DAOj/CwAZAAoAFgADACcAbP+W/9L/pP8FAAAAAAAAABwADADP/xgAFADC/1YAHQAAAFIAHwA1APT/0v/U/wQAAADy/xQAFAAQABcA+f/N//L/p//i/0gA+v8WABQAEADw/zEA0f/P/zMAov+u/wgAVgD8/yQAHADw/yIALABVABcAQwC2/+//MQCy/7z/4//R/7P/RQAmABwAEADC/8v/DQAfANP/EgAUAC4Auv8RAC4Ayv/y//D/KQDK/x8ALgDi/xMAcAAiANr/TgAaAN3/9P/v/3H/s//U/9X/ggAZAP7/AAAQAAoA0v/c/xIAZgB0AD4AIgD6/8P/LwDO/3P/wf/T/53///8IAHz/AAAvAEkAUgBCAE8AIgAhAMv/LQBWAOD/zv/+/8L/7//4/+L/NwCB/4v/YwDu/+//YwDx/1AAJADu/0AA8/8pAML/DABIAH7/GwArAIf/2f8TAM//0P8BACsAw/8HAPn/BQB9APz/XwBNANn/DQC5/8//CgDY/z8ADAAZACcA/v8oALr/zf/3//H/uP/r/wkA5P9QAB0A2P///zwADgD1/ysA0/+6/wkA7/8pAPH/KABaAJn/YgC2/7v/oAC1/7T/6f8jANH/HQD+/xkAFwDf/0IAyv9UACAAAAAvANH/AgDi//v/z/8AABcAvv+n//z/zP8rAEsAUQAEAH//AQDP/2QAHQA7AFAArP8VAKf/LgAcACoANwAKAO7/w/8fAOf/NQC7/6z/DADb/wgAzf+3//D/6/8nAHoA8/8QAPj/yP/Z/z4AfAArAIMAEADq/9T/ov81AAYAzf/2//r/zv95/+r/MwCW/xYABwDp/04ADgBpAPX/9P/r/9//TgDd/3YAKgC6/2MAz/8PADgAnf8+AOD/ov8hAN//zf8ZANv/iv8jANr/y/9KAAoAFgAcAOv/RQBeAOX/QAATAND/LQACACwA8/+4/xkAov+a/x8ADgDc/wwACQAWAMr/2P9wAHcA7v+q/1IAp//z/0QAZP9fAPv/9P9SAMj/EwAPADUAMQD+//z/BADP//z/HADh/97/7P8aAOf/AgDX/7f/DwADAOL/8v/+/4H/NAA9ABYAVgD1/zUA5v8XAFgA5//q/+T/HgAsADsAUwD9/83/BwD2/8D/+v8DAOf/4//7/8v/Zf8FAAUAwv8lAML/4v8ZADoABgA2AEEAGgBzADIATQAWAOb/9f/f/zEA0//a/93/qP/2//P/u//s/xUA5P/e/7v//v8mABMAhgAoAPb/SwAaACQA+v/i/zUAzP+p/+f/1P/6/wIAIgBjALf///9JAH3/KgA3AIX/CQDi/zMALgC6/1YAtf8FAFkAoP9hABMABAAJACQAbQCk/8//6f/p/+v/BwA6AMH/z//c/8D/DwAqAOT/TQAMAMT/TAANAD0A0v+x/xoArf96AFcAzP9lAOP/sf/a/xwAKwD2/yoAwv8NAOz/wf8gAN//BQDi//H/TADo/wkA1v+p/zgAsv8iAGkA7f+ZAOf/CQD+/8L/TwD1/0wAJQDP/w8AoP/B/7D/wP8IAM//QwAJACMAHgDi/xoA1v8AAPD/PgABAOX/PQDP/1EAKQD1/x8AIQDY/+D/DwDh/1MAwP8rAAUAgv81APH/2//h//b/y/8QAP3/zf8sAPv/AQAyACsA/P83AP7/1f9CAPf/MABFAMn/IgA4ANb/sv8SAMH/uf8aAM3/4v/J/xYAt//o/yUAwP+EAEUAOwBLAGMAGQBn/z4A1f/O/wgA/P9hAOH/yv8IAOH/7P8oANT/of85AN3/3/9gAOb/MwBFANb/HADA/xMA3P+4/x8A8/8IABUAXgDu/wcAEwDF/wQA4f8YAAgAGwAfAMv/OwAKAPv//v8WAAAAkf8WAAIAl//Q//b/8/8gABsAJgBeACgA0f8JABcAyf+5/+f/PAD2/ygAcwDL/6j/BAANAAYASABRADoA3v+j/+P/qP8SAEYAfAD5/+f/AwBp/zwAAwDv/6z/ov9nALn/2P/v//P/FQDz/ysAEAAuAG8ABwDg/wgA2v82AAAADgATANH/FQAaABgA6v/V//r/QgAKAAQAFwCT/6L//f/3/wQANQARAP7/5/8jAAcA7P8XAOf/IwAiAL3/2f8/ALz/QgBGALf/UAC5/woAMQDr////+f8cAMn/HgDJ/+j/xf/Z/3IAyf8FABYA6f9QAPL/7v8lAPr/NQDs/9f//P/a/zwABgDD/+P/BwAqAEUASAAuAOH/4v/J/+v/PwCu/wIAwP+o/z8A/v88AB0Axf8bACgAvf8KAEwA6P/8/+v/AAC8/wQAAwD5/zsA3v+BAAMA+f9EAMr/CgAMAPv/1P8vAL7/3f8yALH/y/+D/7v/OgB4ABEAWABVAM3/WgDH/xcAwv94/08AAgBjACUACgAsAKv/tf/6/73/7P9zAA4AGQDG/73/EQDO/+n/uf/M/xkADwAqAG8AXQD3//D/hAD9/+D/JACd/wcAEgATAEIA+f8DAL3/kP+V/+v/GgDf/yYAwP/D/zMAJwBkAAsA/P87AB4ANAAAAEMABQCr//T/IwC5/8//IwB9/xUAAgDt/x0A4/+WACkAAwDS/wAA+v98/ygA9P9GAOz/zv9NAIL/4f9BAA0A5//O/3EAOwDX/1sATACw/zYA2//L/0IAjf8ZABgAtf8GAO3/JgD6/xoATQAGAOz/3P+h/+//8f8CAE4Auv8AAEAA+f/+//P//v+0/xYALQAMAAkAIwAsAL7/CwDw/w0A9f+3/38A+//w/xYA2P85ABEASgDg//3/IgDb/+D/yf9jAI//kP8bAK7/JwAPADkAHACf/wQAfQAsAAgA8v++/woAqf/Y/xMA4/8JAC4ATAAPAE4AAwDr/xYATwDj/7r/QQCS//j/5//G/x0AzP/+/xkA8P8jADkASQAaAKv/HwDa/+T/LgCq/yMArP/r/x4ANgBJAMH/GgCx/ywAIgDk/14AxP8GAPP/LgBuAIf/PgAwAFP/GADk/87/KgArABcAxv/p/+b/IADd/zwAZQDw/38Ahv/V/ykA7f8sAHf/0v/T/y0ASADG/yIACgDx/yoAAAAgADkAHwAyAID/y/8TANb/2P8JAAcA+/9UAOL/JQDk//D/LwDC/5QAy//l/0QAq/+T/7X/DAAHAGgAPAAfAAAACwAQAA8A8v/J/14ABAAxALX/tP8AAMf/RgANAN//sP/1/w0A4/8kAPH/3P/2/0sAOAA0AFEADADk/9z/5//6/5b/3//9/+X/SwDu/zsAPgCg/8z/7P84AEsA3v8lADYAof8gADMAyP8SACYAvf+6//v/pv89ADMAAgBXACUABQAbAAQApv8IAOj/AgA3ANz/NwDh/8T/QwDH/9L/w/+R/yEA5v9YAHwA9/9YAOf/KQAAAMD/xP8hACIAv/9UAP3/6v/w/w4A8//l/xYA2/8sAPD/+v/k/wQAFADH/yIA+/+y/6r/PwAoANn/KABqAAUACgBrABEA7f8PABsA4v/7/xwAnP+p/7v/3P8oAO3/CAAjAOr/MAAjAPD/5f8AAAAA2//4/yYALQD2/yAAFgA2ABQAuv8cALT/HgAmAN//AQDc/8D/8/8rAA0A7/+v/1sA3f8eAKkAWv8CAEsA3//y/04AYgD7/+r/xf/f/9L/BgCk/xQABgCT/4cA0//E/zQAFgAhABUANAATAP7/CwCw/+z/5f/o/4IA5P/N/+b/wv8pACQAVQDa/w4A8v+x/1wAOQAQAAUA7//X/wQAyf8DAC4A6v8AAOH/JQAYABgAAgDm/6//q/89AN3/HQARAMb/4f8RABAA6f8gAPr/PQAWACsAWQD4/yMA/f/Z/+b/7//0/x8A3f/N/20A0v/L//b/rv/2/xAA9f9JABgA1P9aAAcA6f8QAN3/1P/X/+D/+/8ZAAAAEwA3ADYA3v8VAO3/HwBpAM3/FwCV/wQALQDp/0AAbf/x/ygAPQAGAM3/+f/1/xoA2P8MAOH/+f/5/wgAAwCk/zUAHADn/zIAYQAZAP//GADr/8j/2v8sAPL///8TAGoAFQCS/xkABADo/+b/ov/f/83/z//4//n/KgDn/3IAdwALAHcA6/8QABAArP9NAN//ZP9zAA4Auv8cAJf/HgCf/wIADADB/1YAzP9aANr/8v8dAPz/7//i/1AA3v93AHAAPQAGAP7/vP+5/6//jP9VAK3/BgDk//T/GwCO/14ANwAfAML/NQApAC0ADwANAGkArv91ABMAo/8iAN7/1f+3/+X/u/8AABQAsP/q/0MA7/9CADoA3f/2/8L/LQDz//b/WQATANP/8f9VAMz/nv9+AEkAFAAOAAUAFQCq/9r/2/+2/8v/FQBGALX/AABDAAwA1v8TAPD/yv9yAD8AKgD9/zUAEAAQAO7/X/8FALX/OQAGALX/HQC7/xwACADz//r/HQBWAPz/EgAbAA0A6f8OAPb/9//4/7b/NAAoAL3/MgD6/7T//f/7/xcA/P8lAF4Ak/8iAAcA+P93ALz/3//L/wsAAQAIABcAyf88AIj//f8fACAAAQDZ/xwAqf9yAOX/KgBwANL/NgDY/xcA+/+m/+f/CgCv/wgAKQDy/xwA+v8tAK7/EAA1ABgAEwDm/1kA8P/V/83/EwDj/xIAMwDQ/zcAAQALAMf/1P8iADQAuf/G//D/uP9KAPf/3v/o/ysAIgD1/zQA5f8WABUAPQDt/+X/LAAVABYAEwBfAPv/+f/0/wcACQAaAMT/cP+0/7b/HgDV/97/3f8AAPv/1/8+ABIAUQBCABkA6v8qAC0A5/94AEIA/v8AAPr/vP/Y/+f/1P/o/9n/yP8ZAAgA8f9SALr/1f8GAPj/9f/5/ycA4P9mAMf/7/9OAP7/UQD4/24A2v+U/yMASgBdAMz/FwD9/77/1//I/9H/2P/D/8H/9P/P/wsAmQANAMj/2f8iACwA7f9NANX/YAAhAPH/mADF/zgAxf/h/9b/uv9YAH7/FgD2/87/PAAcACMAIAD+/8//KQDx/wkABAAYAAAAuf/g/+n//v/f/xcAxf+1/xoAGQDl/zMACAD5/0kAAQBbACAAGgD7/zwADwAqAGEAgf8cALD/+P/u/7z/6/83/0wAAQDB/0wADgC3/zkAuP/J/4EA6v98AN3/8/8CACcAhwCT/1EAzP+Q//P/AQAMANP/pgBxAPP/2v8FABcA1f/e//L/BgDX/wQA7//W/yoA4P/X/+X/uf8pADQAuf/Z/wEA8/8BAB4ALwAqABoABgBSAHwABQCCAPj/uf/T/3b/MADG//X//v/J/0kAlv/7/wQAFQAMALT/GgDF/8H/LAArAA0AAQAbAEQAAAAyAG0AAADu//L/AADq/8T/CADl/+P/GwDv/0QAz/+z/w4Awv9iAA8A1P/m//P/GACi/14A5/8CAFYACAA/ANf/BQD0//n/7//g/y4A8f/i/+D/bAAoAOP/HwDL//b/8f/v/wkA0f9BACkAxP+//7r/IQD1/9b/IQA5ADEAAABTAMH/IgBOAGP/SQDo/8j/LQDV/xwAFAD1/+f/KQAdAEgAQgCc/+n/2/8AALP/3f8TAN//hwDW/yQAAgDW//z/6f9BANH/aQDA/7f/KwDo/0MA/P8oAPT/NwDv/5T/CQDz//b/IQBZAKj/rP/k/wcAKAAAAAgAKADy/83/TADV/14ARQDp/zUAvf/m//7/FQDm/zsA0//z//T/Uv8QAPj/QAAAABcA7P+Z/2oAJgBEACIAMwDv/wIAPgDI/xYA//+q/w4AAwCN/8z/9P8JAPn/KAD3/6v/NgDX/+f/IgD+/xsASAA9ANX/TQBLADEANQCY/y0ADwDf/xYAo//R//r////x/9z//f+v/wAAAQDP/9z/IgARAAsAUADl/0sAdgA2ABcA2P+g/z4A/P+G/5EAn//F/yMAnP8yAOL/AQDr//L/FAAKAAYAIQBGAOL/OwAMAPH/JgAcAAAAqf+9//j/4P+j//T//P/4////TABuAOv/eQAnAMH/DwAmAPP/5/8xAKr/wv8MACEA/f+Y/z8AOADZ/woAwv+0//H/WABJAOX/EwDJ//3/CgCl/4IAqf+r/5UAz/8XAC4ADAAxAGMANADL//f/uP/i//j/2P+W//L/FQC7/0oAOAAMAPb/BgAPALT/AABSANz/t/99ABMA+P88APf/CQD2/wUA/v9VANv/nv8RAM3/vv8QAAIAuP/+/xcAMQA4ALv/AQAaAE0AWgCv/yAAo/+O/1UA8/9aADwA7f/G/xkA+//5/wUAnv8cANP/PQAAACUAdQCJ//v/k/8iAD4AHABxAPP/DgCc/wIA/f/B/xYA+f/b/7f/DgAEALH/HgBVAO//OQAjAFYAYQCx/9r/1//M/+r/4v/l/+H/HQAhAD0A2f9DAH0Arv8NABIAKQACAML/+P/b//f/zv/p/7b/FQAbAOf/WAC7/xkAOQAYAOn/1f8iAOj/EQD9//X/sf9oAPv/7/9mAOT/VAAeAIL/9P8SAH3/HgABAB0AawAuAB8Ah//e/6//EADH/+T/WADM/3YACwDw/9j//f8sABcAPwAtAEEAm/9DANn/YP/q/8b/9f/2//z/6f9uAB0Avf8UABkAKQBjAEgA6v/+/wQAv//M/w4Awf8OAE0Avf+l//r/1/9jADAA5/+PAAAAzv/h/xMAyP+1//r/iv8JANX/TgBqACcARADr/9v/zf8hAC0ASADd/z8A3f/k/zgAmv8hAAsA7v+1/7D/u/8sAPf/FgAZAL3/nQAFAHYA3v+9/zwAgP8NACsAGQAMAGAAu//O/wQAwP8SAOn/8v/f/1UAJQD5/3f/MQAeAFX/bwALAEcADAAXAEMAyP8YAPv/IQAFAPX/EwAbADEAtf+J/zAA2f+i/0IAzP/N/zUAAwAFAAYAqf8RADkA0P8tAEsA5v+t/18ANQCi/60ATwDc/zcAnP/8/w4A6v/k/8f/RQC6/wIA0//c/wAAw/8AAJz/VgAmAAwAiQADANz/BAAmAOL/BwD//0wAFADy/8X/0P/q/9P/cADx/+j/QwC2//L/AwCu/xcAFAAsACMA8f81AK3/BwAKAE0A5v+z//X/nv9AAOn/EwDY/xQAGQAbAGsA8P+XAJr/vP/k/6z/JQAOAEUA6/8DANr/2v8/ABkA9f/y//P/RgD5/9//JgC9//3/9v9eALn/9v89ALX/eQDG/8L/1v/Z/9X/w/9qAG4ADwASAAMAqv8sAKz/AQBzANL/RAAVAPn/OgDw/7z/xf/E/xEADwDy/+f/6f9cADgAOAAfAO//1f/z/7H/tv8IAOL/GQAAAB0AUwAEANz/RwAFALr//v/s/1IAJwD8/8n/LgDt/23/DgAPABsAEQAJABEABACE/+7/KgD2/48A/v8fAPb/MAANAJj/GgC0/3AA/v+Y/1cAmv/r/zAA0v+2/8T/NwABAC0AJQDc/zkASABSAOr/7f/V/6f/JQAQAPf/FAAgACEAGQABAOT/yP/p/+7/GgDo/+z/TQCM/wYAAADx/wcAtv9YANb/PwBgAAIAPQDI/8r/7f/o/zkACAC5//v/HQDp/9T/0gAGAFj/UADA/9L/8v8hAA4AHgAIANX/SQAMADwAz//8//b/5f8vAMT/AQDB/+D/9/8FAAEAEAB1AOj/AQAAANj/AAAiAAYA+P9BAAkA9/8TAMr/0//4/+//7f/h/7n/EQAkANz/VQB7ANn/+f8/AMT/7f/3/+P/IQAUADIAKgDZ/87/s/8qACkAw/8RAOX/0//7/+r/UwA5ANP/HwAKANb/6/8vACIABwDc/+b/MQCF/zUA8/+6/2gAzf8PAOH/BwA5APz/MAAcACkA8v8nAM7/EQATAOX/AgCv//v/wv9BACQA1//p/77/HQDD/9b/EQD8/x0ASQAgAO7/DgD3/xcAyP8yAC0A8P9NABEATAAWAOP/1f+l/8D/yP/v/wYAEQAiAAkA/P/n/8b/9//s/z4ARgD+/+n/5P85APP/FgAmABwAEQDT/xgAKADy//7/AAAYAPT/0P8RAGH/z/9EAKz/DwAMAOX/sf8xAH8AOAABAPb/DwDn/1IALAA5ADQA4f+o/9n/NwAjABoAkP/C/4L/q//4/xYAXQDu/xkA+f9KABkA4v8CADwA8v/4/3QAn/8zAOD//f8IAKD/NgDY//L/pP9KAA8A1/9XAOv/PwDN/yIA+f/l/zEA5f8gAPf/JQAaAA0Avv+5/+n/3v/6/xkAJwD0/xIA+f/G/wkA+f8QAEYAMAAeABAAOgANAAkA8/+f/9D/BwD2/+v/GgDn/wIArv/S/zsAgv/P/+n/y/8SAFoAbQArAHUAOwAWADYABgAfAEoAuf/e/wkA7P/X/5T/EACk/0//JABVAIn/y/8HAIr/FwBNAIMAagBGAC0AHAAQABYAFQA3AC4Ao/9KAM7/xv8FAJf/yP96/9T/x/8sAFAACAA2AM7/RgD0/wMANgAgADgAzv8LABkAvP8CACUAqf+v//j/+/9SAE0APwBIAOD/FwDN/+H/0f/b/0IAx//8/8T/5/8XAJr/HQApACwAAQAjABYA2P8eAP3/FgA7AOf/6f8jAOr/m/81APb/RQAsAKD/WgDE/0sABwDU/1EAp/8yAOX/AADE/57/AwCi//v/DwApABcAAACN/10AUQDK/60AEgAEABYACwDZ/+v/2v/X//b/7f9xAPL/5/+7/ygAgf+9/4wArP8xACAAMQAmAAEAMQAzAOb/DwA4AKr/4/+i/yAAxf+F/wAAyv/0/0cAlgD7/1AAOQD7/+f/3//E/ysA+v+s/7oAqv/b/xIAv//j/+H/KQDt/z8AKgB2AL3/7v9IALj/7/8z/x4AKADm/4cA+v+0/zEAMwDb/x8A0f/M/zEAAADb/zsA+f8OADIA3v/8/7v/EQAhAAoA8f/0/2QA3f/u/1UAvf/k/y8A4P/9/+7/KgD7/4H/+f/m/6z/GQA2ANb/RAAlAC4ALQDK/4UA6v/7/x0Ayf/2/7z/+v/l/wgADQA3AA0A6P95AMb/w//+/+X/6P8VADUAf/8BAA4A7f8/AMz/4f/n/14ACQDU/6gAFADU/woACAAFABsA+P/+//7/nP/y/9v/8f8ZAAIAEQDi/8L/DwBSAAoAeQD6//r/3f+A/yEAzf8kAPz/BAAJALz/GwAIADYA+P98AAkA9f9UAOz/EQCw/6D/iv/+/wMAMABAAMX/jwC0/4b/FwDZ/xQA4/9MAFEA3f9LADQA3P8RAMr/CwDa/9T/NwAQAOz/wv9ZABAA2v8hAAgA+f/G//j/wf8AAAcACwAaAPf/AgC5/ykAXgAnABEA2v/r//b/4v8sAO3/BABSALr/FwCS/6T/RADt/yQAMABlAPb/8/8mAL7/uv/R/zUAAgARABYA+v/6/xQAHQCW/+n/WwANALv/CAAHAKn/9/9MAFMABwAWAOT/3f9lAOr/8P8OAPH/MQDA/7b/NAD+/53/2//0/9D/KABhABIA3f8nAAYALADp/wAAUQDl/+j/LwAhAAMACgAGALr/tP/w/+X/yP8FAAkACgDI/wIAIgDh/0EAJwAWACcA5//L/wsAHwAZADsAAAAxADEA1P/P/7b/zv8JAPD/sf8mAOb/9f9hAM//JAAWANr/gAAeANv/QwDk//n/5v/D/xcAxP8bABoA+f8cAOT/5P/Z/zYAyP/O/w8A+//y/8v/BwACAGMAHQAhAB8ADQA4APT/EwDb/y0AFQDM/+3/4v/q/6v/AwATAPD/+v/Y/wMA2P/Z/10ADgD2/xUA8f8nAMj/HwBlAPb/VABAAA4AFgDb/9f/rv+9/xAA8//+/9r/HQDO/+P/GwCu/0MAAAAwADQA3v/7/wsAtP8QAFkAm/+DAPL/4f9kAOb/BgDR/zQA/f/s/8j/2P/Z//v/NgDh/9f/wP9lAPD/GABHAOr/YQDe/+T/OwD//xMAFgDb/w0Atf/U/8D/AgAWAL//CgDh/yQAAQBDAP7/EwBEAL//JwDs/zwA4v/8/wgAvf8NAPL/6f8EAFcA4f8VAC0A+//U/z4APwC4/9r/xf8gAKf/CwAvAM7/LAAQAOX/4f9CAKD/NQAbANb//v+3/3oAHAAFABMAyP8WAJoA9/+8/xAA1//z/6//6f/i//L/5P81ACIA0/9WAKj/EAADABsAagDh/zUALgAGAO//7//U/wAA3v/Q/xMAxv8UANz/7/8LAAAAdgDJ/xwAGgD6/zoA//8hAL7/NAAEAIn/FgD6/wMA+P/V/8n/v//U/wUAPwD6/2MASQCt/w8ANQANAHIAQADW/8z/zP/T/wQAEAAfAMP/4f9FAA0ACAAOAEEAgv+d/0AA5//K/xUARwBI/x4AbwDA/00A3f8ZAA8AJgBWAOn/BQAFAN3/2/8xAB8AHQDg/9H/EgATAOb/3v8TAOb/3//S//z/BQAYACwA+v/u/0kA/v/J/yEAmf/E/w8A9f8xAFkALADa/zAAEQDx/woAFAD6/+v/2P/8/ycAAAARACEAz/8GAKT/f/90AI7/6/9xALT/LgD+/wQAJgBCAPn/TwAqAOj/GADM/0wAi//O/x8Aov8vADoA5f8OACAA+/8oAMv////H/83/9f8LAGcA5P8QAOD/RQDK/+X/AwDC/04Ai/8iANv/6/9NABsAUwDt/1MANwAEAPb/FQDb/8D//v/L/zEACgAAAAQAsv/W/zAA9/+//xgAMwAcAO//2P/5/+L/9f/0/9z/DQDz/97/fwAQAL//KQCv/zMASwA0AFkA1/8hABcANAAMAMj/+P/I//b/7f/Y/8//2/+8/7f/3f8HAAYATgBcAKr/KwDy/9z/mgANAOP/JQAAACYArADs/ykA9/+u/wYAiP/B/6H/CQDr/+3////H/xUACAAtAAYAYQAWANP/CgD//zAA2P8sADUAFQAAAA0AKACy/93/DgCp/9P/TQDB/8f/4//s/yAALQA+AO//HADv/y0ALQDj/yAA+P///7//IwDZ/+T/aAAHAE0AAgDK/1MAMwBx/+j/xP+B//n/vv/J/9D/XAAVABEApwA7ADIA1f8lAM7/FQBCAMb/LwC4/9b/BQDM/wcACgDw/xsAIAAqABgAFQDW/5D/AwCp/8L/LAACADUAFAASACwAUAA6ACMA5v/h/xQAk//M/7v/9P9LAOb/CQD0//r/DgBBAOf/2v+KANv/NgAjAMD/AADA/wUA8f8dAB8A8P/X/8//0v/B/zAABgApAEMAKwDH/yMAFQDU/zIAqf/e//L/GwAhAND/6P/h/zkAHgBTAEcANQATACIA9v+x//L/pP8AALH/1//x/8v/OwCX/yIAJQD//2kAJgDm/zYAPQAoAPr/xf/1/6H/GgADABIAFgDE/zcA1f89AAgA3f8oAL//5P/6/xMA2v/5/+P/+v8WAP3/GwAPADEALgDx/wgALQD0/xkAFwDz/6f/wv/Y//j/FgDU/yYA0//p/wkA9v9RAE4AJwAoADwAEADz/9L/qf/I/9//8P8+AP7/BAA8AKr/2f8RAB4A6/8kAC0A5v/s/5T/GwDY/x4AJQDk/0QAKQAJAN//6//Q/0YAHAATAOX/JAB1AB0AHQC0/8n/yv8FAM//7/9CAOb/+//o/+z/1P/B/+v/LQDE/zAA+P8JAEoAw/9+AA4A8f/Y/xgADwBaAEkA4f9OAFn/DgC3/8v/IAADAA8Awv/q/+n/qwCi/xAAOADY/wsA4f9JAKj/ZAAdAOX/JwDS/6v/vv/T/+j/PQDP/18A1P9HAHgAwv85ANj//f/n/yIA6v/R/ykADAAiAPH/DQDU//H/2P/6/+T/EwAOALr/MAAHABwA0/89ADQAof+BABEA/f/8/yAA5f+e/wwArP/Y//b/4f/6/xgANgDx/yQA0v8SAJQA6f8rADkA5f8NAA8AyP/7/x8Av//m/9T/+v8oAOj/DQAPANj/HgDs//D/DgCw/yIA+//3/y4AHAD1//L/NgDZ/ykAFQDu/wMA9P/t/9P/9/8NADMA4/8rAHIAFQDt/67/3P/P//j/AAAFAOD/7v9KAAMABwAiACoAFgD5/7D/5/8fAKH/+P8lAMz/VwAyAHX/LQDx/ycATADM/0IAt//N//7/JwACABoAMQDl/xQA5v9MAPn/9/8dAOb/2P+g/8r/BAB2APz/DwA+AAYAKQD5/5n/q//3/3H/LQARAN7/cQAoADYAAQD2/+b/QwAYAP//agAgAAsAwv8yANX/bf8HALv/t//N//z/7//v/x4ANgAIAPX/QQD3/wwANQBRADgAFADh/8r/SgDc/8H/JgC9/9T/5/8CAPf/DgDl/yYADgApANP/DgA4AL//VgDm/zYA9v/9/8j/+P8qAOr/GgBV/ycA3v/P/0sAMQDb/z4AFwD0/0EAGgAoAGn/OQCM/wQANQD2/+f/sP8rACUAVQCm/+UAzP8bAPj/u/8PAGz/WADP/z8AGwAPAH3/YAC0/yQAOQBg/2kASf9qAHX/SQALAE0AZQDA/1sAxP88AFT/nQCJ/x8AJAD7/ykABABbAIP/NQCt/5wAZP9WAM3/+P80AGL/UwBT/2gAev83AK//EgDu/3wAQAARANQAdP+XAFb/EwHS/2UA2v/f/wIA+/5GABH/YgAV/64AOv/KAP3/zP9fAPz+8QAf/0QBEP8GAaj/PwAmAPz/2gDi/nwBR/5bAf3+hwAzAIL/AQAW/+AA2P7NAaz+uADl/g0BLv9fAMT/uP+MAIj+8wHp/uQB+/4zATb/awAkALD+QQHo/XQBvv6IAeX+ywBa/8n/1AA6/m8CiP17Asn99AH1/goA3ACq/ngC6/1RApr9VQL9/AoCw/94/r8Ahv0vBLT8HQQK/UsETfWVB2MC/fY0DHTxgw3Q960EpwE9+RUHk/jtC//yoAd+/uP8Ggfp9c4IpPg9BH//fv1wAyL9LAJ3/ooBG/5vAhz+CAHD/6T+2AKp/LECW/+S/zsA6f+4APf+1gC1/zAA4f9tAK//WQDI//3/VwBl/9YAuP55AA8AM/9qAJn/dgDG/wsAEgDf/+f/8v9cAMr/iwC+/0YA7f+2/2QAav+AANL/JQAvAPj/OgDz/ysAgf8iALD/FgD2/xwA5//r/5AAh/9VAPD/8f/i/wMA6f+0/xwAkP8MABUAGgAOADAA+f/u//z/7P8TACkA7/8cAFoA5/9TAKb/hQC3//r/KAB7/9gAff9xAJH/6f8gAKv/DABF/08AXv96AJz/MgA5AKT/bgCi/+QAxv+gAPX//v9DAI//XgC0/xUA4v8lALf/yv+X/z0Asf///ykAjf+mAKT/oAC3/zQAGwALAEQAs/9zAM3/UwCR/xIAdf8DACAA5f8ZAI3/PQAw/6YAIwDR/x4AAQAsAPv/XgDI/08Avv+AALL/OQAhAGv/rAAh/1QAFgDK/zAA1P/F//D/7/8NACoAoP9sALj/GgBZAA0ANgDx//f/IQC3//f/TQB4/y8A4/9hAJH/2/+NAKj/aQC4/z8Arf+//+H/LwAaAOX/mQC//1gAsP/Q/7H/2P/b/yoAhwDL/6wAvv8LAOz/LgCy/9D/RAA//zwA+v8uAB0ALgDU/zUA6P/i/7AAkP97AM//OADa/+H/XQBf/ygAnv8GAMz/+f/a/9L/5v/r/6UAqv9/ABsADgA6AOj/AgCI/08AHwB8/+H/RAC//4kA3P8QAAEAxf++AJb/HAAkAIz/NQAUANf/TwDa/wwAtP+s/9D/w/82ALH/cgD+/wsAPgDKAFz/HADyAMf+CAFp/1oAwf+T/6UAzf7zADH/HAD8/5D/pABc/04ABAA0AHEABQBiABIAXf+SAKj/nP9FAKv/TwCW/1YA/P+m/ywA8v8bAC4A0//+/zAA5f89ALH/dwDj/5v/rwBt/z8AMQDP/1AAWP9DAJP/gv91AFv/7QB7/zgAUACK/xUBiP/SAMD/3P/e/4P/FwC9/38AYf9yAPf/JQAAAGMA0v8t/7cAev8kAOD/VgCR/xYAIQBm/48Apv+TAHz/jgBUAK//PwBw/ywAlf9CAPL/IACx/zoAiQAIALkAyP9CAHz/CgAhAIv/0v/C//b/lv/w/5v/dwAaAN7/1v/t/5cA6P/AALH/eQAZAGn/agBg/2wA/f/s/ycA0f8IAKj///8PAAgAwf9WAA0AKQDD//b/OAB5/5kAmP8mAAgA3f9gAGn/EgDF/1kA3f8RACsACwAWAMj/MgCY/2sA8P9/ABAA7v8sAE7/fgAB/3gAIwB5/8EAcP87AIz/LgCJAGz/KwAcADoA8P8dACEAHAA5AMD/DgCM/wgAQQCT/+v/oP/O/6D/aQDh/3EANQC1/xkBQ/+eAMj/BgD9/4z/JAED/9QA2/+v/ycA7v7MAN//hf9DAAQA//8jAGb/fwD6/+7/+f/M/0YAb//oAGn/gABKAJ3/2wBw/1MAcf/5/wYAyf9uAF7/JQBpAIj/ogDf/3H/hgAX/7sA0f/3/60APf9RAKj/VADv/9v/UADD/7z/dQDC/+3/gQCQ/6MAZP9+AC0Anf8QAKb/zwAm/4wAyv+y/+j/4P+EAKj/pQCq/14Awv+h/zIAZv9OALr/HgDl/zwAcACj/0sAAgAGAAgAuP9mAPP//f9SAIr/5v9bAOb/GAArAMz/CwDV/9j/0P8jANv/5P8jAFr/SQD//3EA4P8KAEkApP9uAIP/ZgDA/1AAIwBYAEgAgf/bACn/kQCh/3L/QQDs/l4Ax//k/2UAVv8+ADcAuP84AXn/GwBPAK//QwDx/2oARf/3AHH/HgDo/33/4QD1/v4AKv+GANv/bP/FABv/hAA0/5MA+/8BAFcA4v/w/+D/mwAY/28AzP+SAD4ATf+7AJj/MAAIABkA5f+x/14ADgD7/2b/0//q/8X/EADp/0oAq/86AJoA4P8qAWj/OgCIABj/bwAs/x8A8f9S/1MADACl//v/YAB6/2MABABRAHsAAQBwAGn/EgDB/6D/dQCl/+3/FACu/1QAq/8JALUAuv9VACkAx/8IAAoAMACI//T/9f9+/1kAAADi/1MABwAWAAAAXgDo/+P/7//1/xAAeP9AAMP/7f/5/7P/eACy/7wA8f+o/3gAjP+HAK7//f9PAIf/ogD8/x4Ayf++/wQA/v8tAGX/TgCr/zAAUgDB/3MAgv8OALH/x//7/3kASgAMADwAZP98AAIA0f9DAPj/3f/g//L/xv8/AJz/MQA/AHP/ggAfAPb+uAAUAN3/yABi/50Amv8lAEgAPv9bAJn/RgDX/wIAMwA0AHz/CgApADP/zQBk/zYACQDO/6MAIACKAJr/cQBr/xYAPwB8/30AfP9CAML/DwD8/5L/KwDe/14A1P/K/x8Awv8KAD4A9P/u/0IAVgAqABgABwDs/7T/CwDi/7T/OwBb/yAAuP/z/4QAv//wAHP/KQDt/yUA0AB8/8UARv8HALT/oP97ACX/jgC1/87/QgDU/93/OwAVABAAogCP/zAADwDh/zkAFwCw/+X/YQDE/yoA2/+b/x4AFwDN/zQANwDP/zMArP+3/+P/5v+7/3IA6//Z/5kA6P9SAPj/RgDQ/+H/TgAAAEMAxf+lAAIAp/8EAJb/kf+p/+v/AQDn/9L/FQCm/8YA+v8dAGQAr/8QAVD/eACz/z3/fgBD/1gAfP9rAFAAAwCNAPD/TwDn//T/Yf8gAL3/8v/Z/+//aQB9/4cAjv+CAH7/EgC7ABv/6gCT/y0A+//I/zAA8/8LAO//xwBH/yYA0//l/6//o/++AOH/XADC/zoAv/9vAB8Auf8uAET/wgA4/woAIwCX/8EAsv8AANf/KAAWAOP/BADh/yYA9v+PANP/sP91ANL///8GABQA4P9r/7MAwv/K/08Au/82AF//UABTAH//lACr/wAAbwCI/5IAhv/d/5UAOf9nALv/LgAEAPL/SgCW/4MAHQAmAO3/tf+W/8AARP83AMMAsv4gAR3/cwBqABz/iQBv/zsA7P8YAEcAKgCM/04Ae//X/5UAZ//cALr/ZwCg/xMA7P+y/18AS//RAJ//mwDL/9T/ZABz/3kAmP/y//n/FwDT/z4Aof8rACgA3v+vABb/sACy/+3/NAB4/1gAbP9gAPn/TgArAKj/ZgAGAJL/rf+jAC4A3/8lANb/2/8mAA4AGADu/9j/+f/6/8T/9P/0/6X/WQDs/yUA7//Y/0IA3v+YABQAwP8zAKn/EgAqAIH/TwDw/yIAbABX/2wANwCl/4IA2P8WAB4A+/5LAHv/ev+7AJT/0QCi/8n/mABy/5gACQADAHgAq//V/1sAZf8pAPL/y/9HAJf/awDi/xoArv8aAOX/SgB0AFv/zQAx/3QABQCW/7IAWf8xAPX/KADC/ysA4P8PANT/GgBHAF//EAF4/ycArP+8/ywAef+8ACf/qACV/+r/ogCl/3kA+/80AML/dQB4/xkAnf+z/5gAcP8QAan/eQDL/4b/qQBh/3MAfP/3/9b/9f9kAML/GgDJ/y4Akf8SAB0A+v8UABQASQCe/yQAFAAnADoA9////9r/EQDn/yYAPwDi/zkAqv/K/zAAdf9iAK7/NwAhAGH/uwAx/3EAAgCV/90Aev8TAL7/JgDg//z/bQARACUApP8GAcL/uP9bAID/SQCe/0UA6P+c/0sAUP8HAIz/w//GAKf/UQBOAIf/HwCHAAcA1v90AMD/EQBtAL7/5//x/x4ALQD0/+L/8/+o/8T/zv/q//H/CACCAP7/NQD4/wEAtf/R/zoAkv9gAAEATQAmAAAAjACf/wkA3f+7/wQACwDK/ygA5v+t/6sAe/+JAN//i/+bAPz+swDG/2b/ewDC/2UA/f96ACwA8P+2/w8A9//D/0cAf/+PAL7/HABvAHj/OACd/9n/GwBwAM3/ZwApAGv/IQDV/yAAx/+HAKj/JwC+/3f/DAHi/ksABgCI/7IABwBGABgAJQDh/8L/of9RAE4A4f+FANn/1f8XAMX/5P++/5r/BADE/1IA/v8aACgAjP/oANT/5f8pAMH/lwDR/wYALQBg/x8AKwDo/58Aqf/m/7b/BQBhADr/ZgDT/+7/GQDP/1QApv81AEEABwAdAO3//v8EAOv/IQC9/wwA7v+5/0sAzv9FAF3/SAAwALT/nwCu/10Aqf/y/zYA9f8oADwAPADE/y8A1P9/AK3/wv8TAFz/ZwCW/8L/1f+l/08A4v9JAEIApf8ZABQAdABTAPb/dwDb/yMA4f+0/y0A2v/p/+X/5f8eAAsA8f8zALX/3P/n/wkACwDv/2gAeP9IAAMAjv8hACQA+f+8/+//zf9DAL//SgBJACgAPgAnAIIAVv9FACsA3//I/y4AIQB+/5oAXP8VAAAAlP+hAGr/PwBMAEL/GgDG/8H/XgDy//b/SwCx//r/PgCS/3sACgDk/1IAxv9yAMn/fwBOADQANADT/wsAOP8cAJP/4//k/8D/CQDe//j/n/+IAAgARADw/w0AfADl/z0A9P/2/+r/agBT/xUAFACW/1kAkv9NAAsAbQCm/xUA+P+W/0wAS/98AIz/5v9TAOL/pQDk/5UAGADu/08Alv/L/9z/sv8UAMn/yP/v/0wA7f/f/50Aiv9lADIA9/9TANH/QwB9/xAA7f/C/xQAPABFANH/+P9aALz/cv9hAJP/SACl/8D/lgAH/7sA9/8RADoAz/9fAI3/2QAMAMj/FgB8//H/+v8NAOH/cgC3/xMAx//G/2YAdf/SAOn/5P9sAPD/lQDK/8P/3f+m/4j/HwDg/+//CAAIAAoA8v+ZAF3/ewD6/5P/0QCi/3YA2v/S//3/3P88AIz/UgA9AF7/MADz/73/hgCW/3MA0v/2/6wASv9+AND/p/9QABMAGAA9ALz/+/8yAF3/CgDM//n/+P/8/w4A1/9MADwAEQAVAC8A1v+GAJ7/NADu/2r/dAB6/2AA0v9LAOX/mP9XADD/NwD7//z/KQDv/14ARwDU/8r/3/9EAHAAFgBdAM3/DQC7/8//6//f/xIAyv/j//X/NgDk/zgA4f8XANH/BgBkAED/OQDb//n/bABvAL7/YQDm/0z/DgEi/3UAJgBU/7MAiP/A/wAAPQB7/z0ABADd/40Aqf9fACUA8/8OAO//BgD0/x0AsP/8/+r/kv9OAJT/BgDz//D/igCe/1YAPQAPACwATwDm//b/MQCH/2kATv9tALT/l//PAEn/agCn/wEABgDU/97/7f+CAK//bwC0/y4A4v8iAHUAt/9UAJf/iwDv/7v/SgB3/2QA5P/2//3/d/9WAPz/9v8AAHD/8f9fAPj/GAA0ABIAJwDN/0gA8/+T/44Al/8pAA0Axv9YAK7/OgC6/8f/agCf/8//agCC/wkAUQAAAEYAiv+fAPn/+P9xAHP/PQCo/1wA7P/r/6cARv+FAP7/Vf8/AI3/y/8AAB0AQgC3/+r/FgA5AMv/1f8oAOb/HwAUAKUACwAaAF8Ab/91AP3/4//v/3j/PwDM/3v/7v/p/+3/YQDT/+b/SQD7/ycA+f8oANL/DwByAAAAJAAUAOD/MgBQAEz/8P/k/8b/fACM/1oA2v/F/38Anv84AJb/pv9fAL3/GgD4/y4AEADZ/5AA8//p/xAA0v/y/6n/YAAQACwAoADM/z0A4f9T/woAxP8HACkAJgA4AOT/QAB6/7D/8v/U/0YA1v9wANX/4P8GAOf/+f8iAGsAt/93ANP/NQB4AIL/ZgCp/4j/AQAUAOT/HgCw/67/DQDv/6MAzP8lAEAAlf8bAGkA0f/q/2QAuv8bAMH/MABQAF//MgCH/9r/KADV/2UAGgA2AOz/DQB6ANH/7P/E/wgAGgC//wUAyv/D/2wAKgCk/4oAAADT/wMArv89AIn/8f83AEYAGgCu//7/AAAqALT/TwAAAPP//v8fADkAdP+TAJT/JQAmAJv/SwC1/3cAx//y/xgAAABGALz/cgAyAKf////x/83/2/81AC4Apv+8/xMAwv8cAAIAKgAPAHj/KADe/wQAUgCa/zgAUACm/6gASQC//5EAeP9CAOH/+P/ZADD/gwA8/6X/fABM/6cA6v9hAKT/rv8oAKL/DgCI/0wABQAAAAEAVwDk/wIAPQDB/8UAiP+PACMAoP8LAKn/MgCK/1QA/v9xAL7/1f9PADj/hQBn/+//9P8IAC8Anf+3AL//TQCz//v/cwCS/4QA6v/x/wMA2P/X/xUAJgDb//P/3f8RAGMAcgDF/6oAx//5/0AAQ/84AB7/KQDs/7P/DwBz/8YAwf8uAB0ABQBKAH7/EwA3AL7/IwC0AJ7/ZQDi//X/xwBQ/yMArf+J/ysAu/90AEUA6v8MAJ///f/b//j/CADb/1IAq/8IAPf/kwABAKv/VwB5/1YAGAARAJL/IwD+/7r/wQDM/40AGQAZANj/0v/4/2T/0f97/00ADAAvAN7/GgACANH/tQD//0MA+v/t/w0Ax/+2/+7/ef87AIkA3/8vAF3/OADK/0AAWgCs/34A8P9YAM7/OwDs/wQA4/9l/yEA2P8JAMP/7v/G/zkAUwC2/woAAwBIAGMA6v/b/0YAt/+jADQA1f8EAKv/GgCb/+H/nP9vALr/yf/AAJb/bgDH/wAAAACt/+//qf9TAPL/IwD4/zcAawD8/yAAwP8QAAAAsv8QAAcA9P9KAO//3P/X/9v/TwB+/0YANQCt/6wA2v/g/7//4f8GAA0AEQCa/7UAlf8/AEoAUv/LAMf/JABzAMj//P/B/+z/AADe/xEA1P+5/zsA6/8TAIL/4v/X/8L/rgDn/x8ALwALACQALgAFAEIAEgCZ/10AHAD0/wUA7/+5/9v/8f/h/xMA2P8rANX/y/9JAB8Amv/9//3/y/9HACEAGgDH/2YAWQApAEwAx//m/+j/pv/H/0sAuP80AEEAwf8oAL//8P/h/+v/if8PAIsAxP94ABEAHQAcAFj/bgDb/5b/XQAFAL7/EgBkAFf/WAA7AJ7/sgAgAFUAk/+3/+3//P8CANz/YACt/yYA8P+E/87////0//f/kwAgAOT/RQA2ALv/GwAFAAYABQACAFAAuP9kAM//yP///3T/h/8fAE8Aov9BAND/HQBtAAAAiACq/wMAIwCn/4QAtv8UACUAkv9YAJL/4v8eAFQAUwDy/xsArv8fAIb/wv+M/9n/NAAqAJ4A3f90AP//RwCh/9P/aQBf/xkAgv9LABQAwv98APH////6/wYAAAAYAPr/fwAJAOP/OgDQ/7b/bf8AAMT/RAADAJP/RwDR/1EAbgDz/zAA9//o//L/tv+XAOP/wf9NAIf/NgAaAO3/AADv/ysA8f/i/+z/9P/g/ywArf8CAFkA5v9SAB4ATgCo/4j/LAANABYAFwD3/7H/OwDx/x0A3f/c/xcAuf+VALb/AAA+AIr/CwDv/zUA5/8HAEEA9v/6/woAs/8BAGAA0/9PABQADACK/+L/OwDL/xQAv/93AOr/wf8VACMATQDO/0IAz/9k/+v/TwBqACIA6f8cAN3/2v8eAIr/1//e/ywAJgARAND/FgA4AKH/nADa/7X/KADn/1EApf9RACMA0f9RAJ//HwAKAAsAZwDg/xQAyf+n/8r//v8mAK3/0P8vAE0A9P8ZAA4A+v/I/xcAIgDG/zYA1f8YAOn/XQD3/xUAmQCY/4wAwv/K/5n/mv/6/5f/NQDE/1QAov9qADwAp/++AKn/OgA4AAUAVQDm/9X/EgAOAM//DgC7/7L/4P/F/8L/3P83AB4AIABxAM7/NAARANb/RwDi/1UAFQDv/x4A6v/B/8H/r//D/1IA/v9AAOH/CADo/wUAPwCm/8cAwf9EAGsAg/8pAML/8f+N/9b/9f+A/xsAhQDs/x0AQgDf/wQACgBdAAsABQA0AKr/6P/s/7n/7v/w/+j/3f8JABUAsv9CAEMAMgBNADUAOgDG/woAAADq/yEAyP/w/w8Ad//g/xkA/f8JALH/QQDg/wYAGwDG/2QAmf8sAI4Aq/+JACYA6/9EAKT/1v/y/+P/tf/R/wEAzP80AOv/RQAnALX/9v9EACAA1v+QAP//6v/h/8b/HwDc/xEAHAAPAMP/HgD4/08AHADs/yIAkv/4/6P/8/+y/6//OgAtAE4AIQBZAP3/LQBYADIAcP+1/xcAlf9JAKf/OwD4/7D/cwCP/z8AQAD1/yIACwCEAN7/wf8WAJj/MAAUAFD/JACm/zMAxgCs/w0AqP/H/zMAIAAvAI//zf8iADQAYgBEAAIAIwARACsAKwCl//D/wf/l/4v/tP80AOn/TgAYABQA5v/h////6P8lAEEAAQCs/xcAxv8WAE0AUQAsAPb/9f+j/yoAxv8VADoADAA0AJr//P8dAMn/zf9PALn/1v8vAPf/OQCV/wMASQCZ/83/iAAlABcAUADZ/0EArf/L//D/3v8sABcAPwDq/wIAvf+X/w8A/v/R/1wAEQAIAJkAGwAlAML/2v9hAOL/GADz/7//V/+M/1sA7f/v/xwAxf/q/xIADwAfAFAAiQDU/yEAXQB4/0AA0P/u/ycAc/8vAMz/AwDf////mgDG/+z/cQApADIAAQDX/wUA4P8dAJ3/nf/T/7L/UQAQAEsA8f/g//f/f/9oAMT/nP/UAMP/OgCaAMH/hgCd/xoAiQCZ//X/tf8VALr/GgAbAMP/CQCi//b/LwABAN3/OwDp/zsA/P+z//n/6f83AI//8v8fAGAA/v8hAEwAt/9sAMb/HgD3/0IAGgC8/4cA/P/y/7L/9v/P/+b/eP+z/y4Anv8KAOj/twD6/+L/fwC8/z0AQAAbANr/JwDn/wkA4P+//y8Aof8WAMf/m/8fAFQAPACv/zMABAAJABoA3f8kAAAA5P/3/zoALQAsANP//f/p//D/OADZ/wsAqf8zAPj/wP9qAPH/SAD5//X/CQC8/9D/0f+h/93/KwDX/1gA4P/+/28A3v9ZABAA0P9mAP//1/8yAID/RgDw/8b/WwB9/zwA5v8dAPL/t/8GANT/jwDb/ykASwDm/yAA5/8qAOT/w//9//H/LwA3AND/8P/J/67/1v/L/+3/PQB7ACsAFwDh/wwAOwDc/xoA8f+z//3/BwDk/wsAHgDg/+7/7P/j/zcAMgDZ/wQAHAC6/zgAVgDF/0EATADY/yUAof/J/xkA0f8sABsAyf/3/wAA3P8RAL//8f/1/wkAgQDU/4MAIgCY/w8AcP8PANr/dgBIAIT/NQDZ/wIANAAQAO//WQD5/+//6v+L/2AA1//p//f/AAA7ANf/dAAAAJr/x/+///L/SAD0/2IA+f/v/3QAzv9KAL//BwA1AOP/4v/j/+b/3P9hAK3/1//y/9r/CwAWAF4AnP89AMr/LQAXAKz/TwCm/1QAQwAjAOX/DAA3AKH/6v/3/9j/IABpANr/AQDD/9X/DgCX/3wALgAOADAA2f/N/8D/CABjADwAv/8AAM7/QQACAJ3/MwDH/9z/xf8JAAUAxf9HAGgAUADN/ycACwAjAE8Acf/S/xYADQA6AMD/DwALAEn/BQAkACMAcAD+/0gAvv+o/y8A2P+y/yUAgwCd/83/7/8FADwA8/89ANX/FAAyAN3/MQAdAFAA/P+x/9j//P8nAMf/xv8dAL3/EAD1/7T/2f8FAH8ACgAHAFgAIwD1/8T/IABkAPv/0P/Z//z/yf+q/y8A9P8pAAgALABRAL//HQCJ/7z/CQAJAFoA7/8MANb/EgA8AAMA5v/1/9b/6f8tAI//OQAfALP/VwAaAPz/JQBSAOT/XgAsAAYALgB2/9f/4P/X/9X/sP/6/93/1/8TABgAKAAgANj/NgD2/wMAKABTAHcAFQBHAJH/uv/H/5//OgDr/+H/CQD1/8X/TADm/wgARACB/4cA+P+l/y4AOgA4ABMAJAAXADAA0f8ZAJ//hv8CANT/+P+h//P/+/8FAEcAVAApAA8AXwDJ//H/LwDA//7/bQDj/+L/8f+b/yAA9P8HAPb/FwAXAMP/GwC+/wcA3v9LAHkAmP9tAAkAnv8zAPz/+v/e//z/8f+q/0UAOAC+/+r/3f89ABYAKACJAMr/AQAYAPP/3P/4/+f/mv/s/5H/4v88ABIAQQCw/woAEwDz/3AANQD3//b/OwAFABEAVgCs/83////H/xEADADu//z/6f8AAMn//f9QAPj/HgAFAEkAGwDU/2IAzP/7/wAAxv/w/27/yf/0//P/EgAjAOj/7f9+AD4ABwDf/0kAPQDN/xMAxv/4/x0A2v/z/xsADgDq/8v/qf/s//v/PQAxADMALQAjAO//yP8nAOX/4v/y//D/dwDe/+T/HgB6/97/CgAVAEIAov8tACwACwB0ANn/4P/1/wAABgAUABYA9/8AAMv/FACu/6L/JQDt/xkAcgAvANz/PADb/9X/AADf/zAA5v/5/yoA0P+3/+3/GwDv/zsAMwDY/1IA4v/X/14A5f8WAA4ABQDV/9z/GQCf/ywAzP/O/zcAuf+VANT/sv97AND/GAA7ABwA4P8KAPb/MAApALH/OwD7/+X/DwD2/8v/uv8lADgA1v+N/ygA6f/1/woA3/8TAGT/HQBIAD8AXwAtABwAEABlAMH//P/h/+T/2/+L/2kAsP8qADsAqP8bAAMASQDp/1wA5f/t/zQAnv8aAOj/3P/2/wIA3//T/yUA+f/z/ygA/P/Z/xMA0/+TACEACQBlAIz/OQCf//H/DACd/1gAqP/+/9v/tv8gAAUAyP8mAJsA3/9UAKAAMgDH//P/+v+p//f/2v+1/8r/LwAMABUAFwC3/0IALgAAABAA+f8gANz/8f8iAKz/2f/o/ygAMwCc/zUADgDC/wIA1P/H/8H/SAAdAEAAGAATAH4AKQBHABIA8f/3/7L/zf/6/wAAvf8BAAYA6/8uAOj/qv/O/9z/LgA5AOb/OwAAANX/8f/q/z4ALQBUACQAz/+q/+n/DgDe/0cA+v8lACgA7v9/AOb/2/8KAF//6v/8/wUAMACc/wMADwC3//j/YQAsABkATwDk/zUAAgDX/xMA2v/N/77/wf/c/8v/7f9mAAYABABaAB4AUAA2AAUAEgDs/xwAOQDb//v/3P/Y/+P/Yf8AAOT/9f/l/wsAVQB8////KwAKADMAUgDf//7/YQC8/4MA+/+o/wUAvP9SAFwA5f8VAE4Agf/Y//n/xf83APr/2f/m/zEAkf/z/+T/yf8zAPv/MwDU/0QACwDl/x4A7P9HAFUAUAD//z8Av//+/xoAw/8UACgAJACb/wAAsf+e/67/+f9VAHf/KwD9/wMAyP8kAJcA8/9GALj/+f8rAEEANgA0AEMAwv/I/97/0P+M/ywA//8eAA8A6/9HAKH/GADn/yMAIgDa/5IA1f/l/+//o//P/woAAAAMACAAKAD///n/IADg/zEAAgD4//T/5/8NAN3/RADo/w4AHwAvABEAn/8SAML/NgDt/8r/YACO/+X/IgAUABcA0v9JAPP/u/8vAN3/CQAsAL//8f8AAP//QwA0AAkA8v/o/w0AAwAKACUAs//9/xQAzP8NAPj/MQCy/xMAQgCT//7/GwD0/wAAJABBAAQAy/8+AGIAHgAoAOv/uv+Z/wAAq//q//P/0/9SAL3/+f8OACkAGQAQAFwArP8eAGIA7v9jAOn/Tf8LAK///P92ADcAUADg/97/w/8aAMb/9P/w/6D/NgCz/0kA+f8lAAIAy/9BABgANwAJACYAqP8zAAQA7f8KAJL/nQAJAAsABQDI/67/FwAQAO7/HgB0/wsAjf8TAJwA5/8xACgADwDK/wAA9P8KAOD/LwAoANv/JQDZ/wgAEgAFAPH/HADd/9z/7//H/1EA+f8DAFoAFwAKAPH/1f/L/7//0v9CAAYA9/8zAOD/GQD9/woADwDN/xIA1v8DADcA+v8gAPr/AgA8AP//BQDr//r/JwCh/+T/MQD//woAAADB/57/FQDn/wsA7P8LAGMA1P9TAAIAOgAkAPn/MgC//xIAGwAlAM7/2v+r/8f/0P+b/ygA9/81AFIAZAANABQALQDg//D/9//s/7H/FwDp/woAJgDP/xUA5P/e/+7/4f/j/xYAJAA4AAgANACVAP3/8f8CALb/2/8YAMb/DgDr/w8AAgCb//3/jv8pAOL///9kANL/hwA8ACkATgAnABUApP+2/zAAzv/G/+P/ov/h/+z/HwDa/wMAHQDo/zQA7f9ZAOX/OgCIANH/YAAQAO//9//q//z/sP+t/9///v8AAA4A+f8XABUAv/8KAPr/9P8qAPD/GQAeANn/NgC8/9z/YAD0/3sA4f/Z/0MA5f8gAK7/wf+r/7z/4f/X/1kAKABhAEkAGAAyAOb/EQD7/wcAJADl/+z/7f/D/7T/+v8cALz/KgAkAPL/DgCt/wIA7P+i/zIANQDx/2gAEQDl/yYA8/8tAAIAFQA2ANL/AgAZACwAzP/+//n/sP/0/+D/zf8PAPv/5f8wAMv/DwBaAMX///8SAFEAPQDY/1gAGwDZ/+7/cP/n/+T/wP8MAOX/RgA7ADwAGQD3/ykA6/8dAO3/CgAiANT/2P/Q/9L/wP/f/xIASQAmAAMAKQANABkAvP8sADYA0/86AB4ASgDH/3r/3f/q/73/HQAUAJT/8P8XAAYA6f9QADsALQBzABkADgDd//7/8v8TAB4AAADD/7f//f+z/wUA7P8zAE4A4v8LAJb/ov8XAEYAOgAeAPH/3P8pAPr/yP8lAAAAFgAgAOr/SwDc/+v/wP/s/y8A+/9OAOX/EQDG/+D/GwDm/3IAEQBTACwAuf/F/5n/4P/R/97/BQCU/xIARwAZAEUA6f9HAOj/9P8MAAAAaADf/00ADAAdABwAz//F/8X/NwDD/+3/zf/f/+D/9v8fAO//RwAAAB8AHgAlAAcAzf/f/9P/QADO/yMABwDR/wIAAwA8AKP/WgBMANz/VwDk/1oAxv+o/w8A0v8+ALj/RgAEAI3/AQBV/xsA6//o/2kAu/8jABYAVgBgACIANADx/ywA1v/x//3/9P/t/9z/QQCP/6T/AAD8/zEAwf81AAwAOwBkALj/8v/a/+L/+v8HAB0A7/8fABgA6v8LABsAKwBFAMr/1P/B/87/HwDm/xAACQA5ABEA+f/Q/+r/qf/d/0MALAA3AOT/RQDy/+X/JADG/woA9/8kAAAA3/8XAPv/3//l/yMA7/8NACoA8P/j/woARgAIAPX/SADd/6n/3////zcA7P8LABcA8P/B//b/EgDA/xsA6f8ZAPr/MQAsAMb/ZgDC/xoAUADJ/x4A8v+z/xcADgDR/wkAg//d/1cAHwBSAOf/BQAvAN//JgDz//T/HQCZ/yIA6v/E/14A/P8cABkA3f/D/ysA/P/W/0MAtP9CACAAx/8aAMf/3f/j/wgAKwA5AFQAKgDW/8r/AQANAEUAAQAcANz/af/M/8L/1v8gAOj/MgAsAAwAdgATANL/7/++/3AA/f8UAFMAtP8dAAcALgDl/5f/AwDn/+n/BgATAKr//f8nALL/DAAuAOv/BQD8/yQANwD4/2IAAgD6/0UADAAEAMX/BgDS//3/y//g/yEAwv8EAKv/3v/y/wEANwDw/zEAMwA8AAMAKQDL/83/UADm/y0AFADb/yEAt//5/xsA2P80ANX/CQAiAPP/LADv/+v/3f8dANn/rv/D/zgAKgDQ/1sAAQD+/zQALABIAAMA9v/Q/8D/9P+9/7j/EwD9/wEA+v8UAAcAHQAMAC0AHACz/3EAwP/r/2MA1f80APD/9v/s//b/1P/y/xEAEQAOAOL/OwC8/xoA5//E/14AFQDt/ykA/P/I/x8Avv+x/zEA5v8IAPP/FABbAB8ACAAHAPb/FAD1/+T/6v/U/7T/zf8NAAgACQAcADMAEgBGADwAHwAyAPr/pP/V/1AAwf8TAL7/m/8SAP3/DQC4/yIA+P/2//v/OgAtAAgAmQD//zUAKADf//v/v/+J/8H/DADS/xgA9v8NAMf/vP/7/xQAMQAiAGsAFQACABQAJwC+/xkA8//u/6kApv/3/8z/1//8//P/1P++/ysA2P9YAN7/w/8vABEAOQARACQAGgA5ANL/AAD7/x4ADAC5/w8Ayf/8/8P////n//r/BQDW/z8A8/8gALv/9f8kAAUAFAAcACwA4P9iAA4A4v8FAAgABwAEACgAqv8JAL7/8v9sAKT/CABTAMf/AAD+/8X/KADn//D/2//W//f/JQADAOf/+//U/0YA9P89ADQAEABbAPr//v/y//r/4/8rALP/BwAIAKn/kwDW//P/5/+g/x8AyP8tACUADgAoAPn/CADl/7v/NwDn/8P/TwAfABsAOwDu/53/+//Z/87/+/8iAP7//P9AAAoAWgD6/8j/+v/E/+n/KgADAAsAYADn/z8AKQDP/9r/rP+7/+n/+f/P/0wAJAANACkA/f8qAAQAGAABANn/GADI/93/FQDQ/y8AFADb//v/vP8VAEIAJwD6/zMAz//M/zEAyv8yAOj/7/85AN7/IAD7/w8AFwC4/ycALwDn/yEA8//o/yQAmP8NABwAo/8UALf/NQDn/3X/PAAWADwA7f9HAB0A0v9nAPf/YwArABMADgC0/y4Av/+n/xEAyv/v/1QA4/8IAJ//4/8KAJf/VQDv/wQALQDt/wkAQgBxAPD/y/8dAPL/tf8bAPz/IgAIABQAMAD+/+H/uf/y/wEAMADh/xgA7P+7/xcAvP8SANL///8ZAAwAPQDy/y4AHwDf/xUASQDt/xAAHQACAMj/5//5/8v/8//G/04ADgAhAD8Ayf/+/6z/4P/Z/0kA5f8JAFIAr////wIAZQAOAAgAHgAHAAQAyv/o/9H/RQDf//L/JAB6/xEACwAIAPr/EABCAAAA4P/i/xEAyv9uAA4AEABDAIb/NwCi/y8AOADG/0IAP//3/xQAuf9lAFIABwD9/yAA3v/4/yIACgAXAAsAsf/h/ycA2v9oACQAqf8YAAYAFADf/6v/FgDq//H/RwDt/8H/BADy/97/LAAZAAAAzP8bAAwA3/9WAOf/+v9kAC0AJAAxAIr/9f/0/6P/KgD8/1AA5f/z/+3/6v/d/+n/GwCC/z0A2v8dADIA9f+yAOj/PwDz/7z/FADB/yQACgDe/+T/pv+w/+7/FABSAD8A+P8nAKf/u/9cAB0AaABVACAACQC0/+D/p/8cAOb/5//e/2X/OAAKAOr/JgBtABcASAAfAPj/QADD//X/vP/5/+//BQAcAOv/IwDa/+3/tf/o/9H/OwAMAM3/TAAKACAAJwB1AJX/CgA1ALn/PwDi/+r/uf/G////EADW/xIAFwD//0YA9//g/xIApAD8/x0AJQCY/+P/n//3/+L/BQBpAAIAAgAaALT/HQAIAJ3/CQCr/+v/3v8lAIAA/f8cAA8A/P9FADcA8f84ANf/+v8UAMr/3v+M/+7/7f8AABgA/P8KAAYALgAuAFAAAAD+/+z/CQDC/7P/BgD6/+f/4v8cAOf/FQA5AMz/8P8IADMAUAACAAMAHgDW/5z/MwAaALv/YQAtADIAHABz/+L/9P8nAB0A3P/n/+H/yP/7/2cA+v/C/w4A5P8WABMAEABCAOT/0/8UAP7/DAAfAOD/FAD1/9j/SADT/+L/0//U/1gABwAVACYADQDj/9//8P/h/+//FQA2AP3//f8MAPn/GQA0AOn/MAA8APL/1v/k//n/ef8JAOX/yf8JAMH/WQAwAEwAMwD1//3/5f8QAN//yv/W/wsAAAAJAAEANgATALD/EwACABcASgBYABgA5P/K/8//y//5/xEA2f8uABwADQBFANr/EAAJAGz//P8AANr/EAD0/xEA9v/E/9P/RgDa/1AATwD2/1MA1v91APb/BQDv/8j/CwC//ycAzv8uAN3/4P8AAB4AJgD6/xYAiv84AKH/BQBFAMb/MADY/yoArf8QAE8A6/8AAP7/5P8gAEkA5/8XAMH//v8sANL/GAA6AOP/1/82AMv/MQAZAPz/IQDB//f/BQDV/9H/GgAUAA8AMgDC/yYA6P++/2MABAAjANv/1P/y/6X/IwDn/1YAMQDv/1YAvv8AAAUA+f/J//3/JQDV/wQA2f8cAPj/YQBCAK3/DQDq/+f/zv8aAC8Auf8cAPv/+P8hANP/HwALANn/MgDE/wMATgDU/zIACQDZ/yQA2v9bAN3/yv9BAPj/3//J/xYAfv/r/18A7f9NADAA8v9AANX/2/9AAHb/GQD+////HACw/20Ay/9NAD8A9/9kAK7/1P/3/9D/3P8bANf/FgAxAKD/qP////n/+/82ANj/HwBEAPP/EwBbAC8AfQATALv/JgBs//n/4P/x/wYAzP9JALH/9v/X/wQAHQCg/z4AKQAAABYA+f9LAOT/w/9GAPn/MgAEABUAJgDX/x0A6v/4/+L/2v+//wAABQAJAD8ADAAyAMH/uP/M/8b/IAD+/yYABAD4/2MAIQBoAA4Az/9VAHr/HQAKAJH/6//m/zkA4v9OALz/AwAmAMf/TgDy/0kA7v+x/9P/0f/m/wQAggAmAP//AgACAPL/EADK/zIA8f/P/7b/gP8RAPP/WABaAEMALQCj/+f/AgD5/y4AUwDu/2wAEQAEAEcAcf/f/7j/uv8HANz/9P/N/yIAFAC8/xgALAALABgA3P8LAHcACQCAACwApv8oALD/9v/G/+v/DACv//n/+P8HAAMAOAAHAOL/CQAQAFUACgD8/////f/R/8D/wf9FABEAAQBJALH/6P/g/yQAyv8EAPD/qP9iAO7/dwAnAD0APwDV/xwA6P84AOf/5P/T/7//rv/n/8T/v/9EAMX/NQAoAAYAZQBEACkALwD//9b/LgDk/8v/+P/j/7H/9P/h/wQA/P+O/zcA2v/7/2QAIwBEAAoAFgBcABEAKQDZ//X/DAB9/w4Azf8BALz/2v9NAJf/WwD1/7b/LAAuACkAFAATAM3/HADW/9X/LgASAAMATQAGAPz/NwCo//L/7//U/+n/0P/b/2QABwDb/x0A7v9vABkARwAMAM7/6P/A/x4A6f86AOr/zv/g/97/CADn//T/1P8QAKn/AAAlABAAMgDy/6MAGwAyACYA8f8/ALb/GQC7/+P/9/+T/x8A5//O/xoA0v+3/yUA//8zAD0A7P9CAAgAOwD8/xEAWwCX////IgDB/+j/CgDw//H/GQC9/wMA1v8jAB0A0/86ALf/t//w/wYAaABkAFMABQACANX/zv8GAOr/3f/2/xAA8/8AAC0A+f/d/7n/AwDM/8r/UAA7ADcA+v8SAA8Ayv8OAD4A/f/3/+j/GgAUAOX/LgAGAAkA0P/T/8z/0f86ANT/SQDz/wwAZwDu/6L/sv8zANn/RgA9APf/+//g/9f/sP8xABsADQDr/9H/VAA5ALj/PgC9/7D/dgDl/14AEgDb/yEA7f/v/+P/CADW/zsAEgDd/8b/6//Z//P/YgDd/0EA8P/k/woA5/8qAPX/6v8CAAIAzv9RAOb/BgAkAN7/UwD7/+j/q/8UAAMAJAAhALz/JwDf/x0ADwASAAEAwv8iAO//8v/n/w0AEQAcAAEA5P8AANj/yv8CAC4A4f/3/y4A2/8XAF0A+/9PAAAA1v/g/8H/5P+5/xEAJQAgAFEANgAEAB4AMQDq/9L/n//j/7j/GQARABgATQDF/ygAy//Z/8r/9v8cAN7/dQDM/xQA9f/p/ywABwBhAN7/TgDY////AgCk/0sArv8ZAOH/yf8LAPj/NQDI/2YAEwAOAAkA6v8eANX/IQDi/wgAyf/m/zwA2P/h/97/TwADAC0AEgD//ygAn/8jAPL/if8VAAkAs/8qACAA//8zAPf/VQDw/83/SgD3//b/DwD//77/w/8UAAYAy/8WAEoA8P8XAFAA9f8KAAMA/v8EAM//FgDk/xsA0v+W/w8AxP8wACsA4P8rAAgAs/8PAFkA3v/4/z0ABgAEAPb//f8bAAsA8v/0/yoAxP/q//L/0P8zAMv/GABLAAgA8v+y/0EAEwDe/zMA3f/5/+D/9P8pANP/AAA0ABAA4v/r/xsAFgBFABoA8P/0/+b/7v/j/9P/qP++/w0ARQDx/0UAMgAIADYADgBHAM//DwC//8b/BwCu/wgA9P8+AAsAMwAWAOj/FQCU/y0A7v8TAEsAxv8QAAkA2v/i/9z/CAArAA4Ax//W/zYA6P8yAOb/4f8pALf/ZQAOAP7/OwA2AFEA8P/y/8b/BAAQAOX/zP9//5T/9P/M/wkAcAAeAEUAJwDd/7//9f8WADYATwANAFYA2P8vACgAyP87AHP/9/8AAKL/EwDO/8D/BgADAKb/KwBFAAgALwAJACAADQDq/zsAJgDt/yMA9f8SAAAA9f+q/8f/IQDS/zgAIAANADUA4P/f/+D/5P+n/+n/9v9GACMAGwBKAPj/LAD6/8T/sf8SAOT//P8lAOf/ewADAEsADgCY//D/o/+m/9X/EwAoAFsAJgBZAC0ADgAFAJ7/FwDI/+r/MgDv/9r/JADW/9z///+Y/yUA8v/5/wIAQgBOACEALgDq/0IAs/8jANz/u/8TANH/IwC1/2EA7v88AAgA6/87AHL/SgCd/8//awDt/wEACwAPAJb/NQDs/87/DQAWAFIAIwAiAEUAPADM/zcAy/+l/+z/iv8MALr/CQAzABoAJgAMAE4A6P/6/9n/6f8AAA0AHQAgAFwAnf/O/4//4P84AMv/JgABAA0A+//4/z8AQwAvABEA///2/ycADwDx//v/yP/4/w0A7P8DALv/1v/q/8T/8/8EAFUAPgBFAD0AEQABAM3/0f/l/7v/AQBNAKr/IQAiAHz/CAAPAPn/NgA1AOz/UgAAAL3/bwAIAPn/CgDZ/5v/wv8JABQAGQANAAYAHgDy/xMAcwAHAA4A1f/H/7j/yP82AMT/GgDl/9D/IAD3/xwAEwBSABUAGwBAAPX/sv/C//z/5P8TAOb/CQAcAPr/LQAKAPf/BwDZ/+P/4P8AACEABgCAAEkAsv8PACkAzf/+/87/uf+c/6v/+v8AAFkAEQAyABYA4P9gADUA8P8DAPP/xP8vABsADAABAJz/UAAIABcAJQDe/7v/sv/v/9v/GwD3/xAARADq//b/8v/Z/wwAGgATAEUA+P8VAEkABQBKAMj/zf/7/5b/6//H/wIAFADm//7/GgAnAOf/HQC+//v/OgAsAHIA8P9CAMv/DABDAOP/5v/Y/9//kv8AAL7/BQDn/9D/VgDH/wQAUAA4AP7/QADt/+//RADr/x4A/f8EAPj/4/+z/8L/JgADAEQAFwAJACcAwv8BAOv/1P8sANn/+P8WAO3/KwDz/wAAIQDb/wwA+/+H/ysAAQC6/1QABQAxAP//OQAlANP/RAA7APT/6P8WAMb/sP///8b/v//9/x4Az/8BAB8A3f90AGAA9v9TANH/GADk/6H/BQC8/ygA7f/s/woArv/h//f/JAAvACUARwAaAOf/SwAiAAYA2//x/zIAEQAUAMr/6v/C/7T/4P8vAOP/zv8pAL7/NQAnANf/BwDr/9X/8f8UAA4AewApAD4AIwDM/xEA+//u/wIA/f8EAN3/9P/W/+f/DQDA/0UA3P+6/1cA0P82ADkACAD7/9f/5v8LAAIAJQAGAJf/HwD1//3/9/8RABEAEABfANb/KgDu/7b/zv////P///8/APr/RgADADIA/f8IAAkAwv8dANj//P8KAMv/5v8QAJz/6/9AAND/NADb/wcABQAUAHoAFABVAOz/m/8TAOD/yf8kAOD/+f8GAL3/YQDp/9n/UgDU/wcA+v8CABUA9f9FABEA2f8DAOP////l/8L/NQAYAAcAGAD2/zUA/P8fAPT/6f8LAMf/4f+7/8H/EwAHAOr/MwADADIAKQAGAIgAAgD//xIABgDD/7L/zf+q//j/+v9AAOL/FwD6/+H/EgD2/3MA5v8pAOj/2v9tAOr/PgAKAN7/5P+z/9v/9f8FACgAyf/n/+//+/87APn/SAAWAO7/BgAGAAYAFABBAAgAAgAjAPT/2P8bAKz/v//5/43/CwDE/zMAMADZ/y4AEQD2/xMABwD1/2kA5f/4/zgA8v8fAN//LQDf//7/7//N/+v/uv8YAMH/AAAKABIAXAD9/xMAHQBHAAAAEADr/8z/IAAbAB4Axf/h/8f/6v/I/x4AUgDY/z8A0/+8/67/7P87APL/WgAJACQA+P/x////7v8FAN7/WQAgACcAIwDX/+v/9//V/+X/JwAMADIAAwADAAsAxv/r//3/zf/W/7f/tv8wADUA8f8XACsAFwA1APr/VwDX/+3/jgCd/z0AnP+O/xMAtP8aAPH/kQAeAO7/GgAeADQA8f/0/9j/sf+b/zQA9P/x/xsABQD7//j/FADs/0cAsP88AA8ABABrAKf/QwDk//n/AQDp/xMA7f/n/w0AHABg//L/x//n/18ACgBcAAwADADx/w4ARAAQAOT/+f8cAK//7/8rAP//zP/I/xIA5//J/2gAMQBDABcA0/8RAMD/FwDg/+//3f+x//v/4f87ABMAKAAhAEMAEwARAP//yv8UANf/KAC1/+T/GwDI/0kA3v/x/yYA6/8HADAABgDx/+f/zP+7/wQASQATAEkAPgAuADUA6P8bAOf/n/+f/8X/uP/0/yMAzf/W/wEARwBXAC0AIQAXAA8AMQAdAAsA4v/A//n/t/8LABgA2P/z/wIA8P/d/1QA8P/p/zsA4/8zALP/7P8oANf/MAAHAPT/FQD+/w4A+//n/zMAAgD4/2AACgAdACoAxf/m/8v/AwDX/8//z/93/xEA9P/5/w8AEQAwABYAdgAQABEAHQDq/yMA3f8cABsAxP/k/xIAGQAkAOv/9//7/4//MwDp//z/EgC8/y8A3P/v//3/IACd//b/iADO/24AGwD8/2UA5//C/+H/2f/c/0IA5f9BACAAxf8+AMD/DQD6/+7/AQDT//b/xf/5/7f/KwAsANn/IwDC/0EAOADs/2AABgA3AFQADQDH/+v/IwCg/6z/AAC9/8//CgAbAAcADAA3AFIADgDn/9X/3/8DAPv/BADv/9r/GgADAPr/EgARAB0A+P8dADgAFADh/73/EgDc/wkAAwDL/+H/8/9tAPr/9/9IAOz/DwDo//H/OQDZ//D/MACy/87//v/U/xcAAQAFAAgA1v9ZAD4A1v8SABMA9f/M/wIA3P8FAF4A9v8SAPX/5v/w//f/MQACACsA2f8CAFYAl/+8/wAAjf/H/xkAKgAjAPj/KwAoAEwAHgAqAOb/uf9cANX/6P9eAL//4v9GAJP/3P8GAMr/IADr/xcAEADy/0MAEADZ/yAA7v/J/zgA/P8FAPz/3P/s/wUALgAFAP3/0f8TAP3/vv8+AEIAAwDW//v/2v/f/3AA+v8CAEkAzP8mAO7/+v9AAHH/zP/1/9f/LwD5/+H/SAAwAOn/TgC5/0IAEAB7/0QAvP8WAEMA//8RALn/HgDj/zQALQASADQAiv/X/xAAzP8OABIAz/8EAN7/FAAhAAkAaADl/wIA2v+i/w8A9/9LAHgADQD6//n/fP/J/9H/xP9RAAkAUgA2AKb/zP8TAB0A+v8VAEsAQgD9/w4A6/8CANb/+/8mAOP/EwD9//v/3P/2/9n/wP/m//D/7P8XACwAuv8UACgAIgAdABcAEgDM/wIA3v8XAF0ASgAYAPn/AADL/x8Auv+C/w0ADgBeADEApP8WAMP/r/8DALf/8f9ZACYAMgBoANH/BAD1/9T/DQC//yoAJgDq/0gAUQACANb/BAC5/9H//v/r/+T/DQDr/xMAMgDp//7/FAAPANT/8/8fAO7/2f8ZANr/3/8tAAIAJgAbAEoABQAYADgA+f8mAMf/BQCm/8T/9v/a/y8Av/8KAO3/4/9DAPP/6v8hAFYAIAD///v/HwACAPH/2f/f/8v///8nALD/MAAaAPL/PQDi/xUA9v/N/xEACgD5/wAALADs/+r/FQDZ/xMAFAAtAFsA2v+c/wQA2/8PADUA1P9KALD/AQBFAJ//PgDx//P/KwD8/xgA6v/G/6H/CwDk/xsAbADy/yIA2P/w/ygA/f8rANH/7/8PAOr/SADm/yUAIwC+/ygABQDX/xQA7P/n/w8AEgD1/xoAvP/m/wwApf8VABcAJAA0AAsA9f/r/xEABgDl/+f/7f/1/woAFwAqAAUAKQAMAMb/TADV/wkAPAC1/xwABgD3/+3/wP84AAoA1P8nALX/1f/6/73/JAB//wMAGAAbAFgAOgChAA4ALgA1AAMA1//d/+H/yP8eAK7/IADz/87/EADQ/y0A6P+r//n/7f/6/xIAEQAFAA8AIwArAA8ADgAnACAA7/8nABIAGwDG/8j/z/+w//L/x/8cAB4A6v9DAAsA//8JACwARgAgAC8A9/8AAAwAof8jANX/vv8kAMr/JwD9/9f//v/M/9X//f8SAPT/HgCs//D/UQDo/10ASwAdAFMA2v/y/9f/6v8tAOr/8//s/97/3v8pAO3/1P/g/+P/JgA7AMgAgwBFAEYA9//o/zH/6P47/5P/1/9oAI4AqwCEAKn/zf+w/+b/0//K/+T/QwAHAV4ASgD7/7T/i/+J/xYAGwBtAHcAjQBOAID/pv81/2b/VP+U/2MAQACnAI8AUgAJAKv/ev+H/xMANwBxAJwApgAsAPr/rv9i/3f/o/80APD/PAA+APH/5f+5/9j/rv8JACIAIwBAAI0AMwAXAB4Ak/+7/83/CQBDAFcARAA3AOv/pP+j/63/sP+Y/0EAJgBMADoADQBEAHz/z//A//7/ZwBNAHkAHAAAAIP/HgAVAGr/KgAnAOn/UgAMAPH/+//i/xgAzv+R/57/+//5/wwAXQAdAAoAUgAaAJ3/9/8bAPn/cQBaAMb/CADJ/77/SQDj//f/NgDv/w0A8P/8//L/xP8EAMb/vv8/AAAAJAAlAML/IQDw//b/QABBABoA2f/x/xgAuv/L/zoA8P/o/x0A5P8pABAA2P/d/9r/IwAQAAYAYQATAOj/JADC//f/BADH/w8A1P8PAEcABwDz/xIAHQCJ/ygABgDb/1EA0P/1/+L/EwD2/93/DQDL/zwABAAUADgAUAA1ACkAMgDl/9T/o//x/7f/ov/2/wcAKgDJ/+b/CADm/yAASgAgACMABAACADYA6f8UAP3//f/g/+L/KQCy/+D/4//s/x8A2/8TACUAVQA6AAgAMQD5/wIAEAD2/8v/rP/e//z/8f8jAA8A2v8IANz/DwANAP//OwAbAB8A8//O/wQAzv/j/+b/MAAaAOX/LADg/wIAFQDn/zMAAgDq//7/CAD0/1cARQDQ/+r/tP8CAAAA5P8qABAAAADa/+f////V//7/+/8JAPj/GwBGANr/PgDU//j/NADT/1gA7P8UAAkA2P87ALL//v+p/wUATgD7/0cAvv+c/9D/6P8wADYACQApABgA//8LAA8AAADO/wwA9P/b/yUA5/8OABMAtP/j//X/HgBAABMAPgAhAP//BAAfAO3/qv/k/87/5v/3/zgAAAAZAEoA9v8AAMz/0v/c/83/6/8OAFgAFAALABMAxv8iADMA5P9HAPX/5//x/97/HQDO/zUARgDK//7/FgDp/9T/LQDn/6z/PQARABMA9v/0/w8Ayf/k/wQA7/8dAFsAGgAOAPb/pf/p//T//f8eAB0A//8JAAAA7v84APb//f////L/xP8GABsA0f8EAB8AzP/j/ywA/v8gADwAKAD9/20APwCR/wEAvP+S/+z/zP8WABMA9v8TACEArf8kAFEA5f9jAAwAIQAjAKL/DQDv/+3/+v8AAAAAn/8RAOv/9/8NAOP/MgAeAOn/FQCVALz/+P89AG7/9P/b/9f/FADk/zMAPAASAE0ADQAgAAcAwf8rANH/OwD4/9L/+P9Z/wgAwP8UABcADAA+AOX/KwAiACcA1P8rAPP/2v+dANn/8v8zAIz/3P8JALP/5v8hAMX/AgAmAFIAKAABAGcAAQD0/y0ACADT/8b/7P+F//f/FQDf//7/2f/4/xgAGwANAC8ABAAlAPv/2v8FAAEARADw/04AHQDv/yYAsP/1/7f/1//f/8D/DQDm/yoABwAuACMADQAqANb/LAABACEAHwDH/0MAx//u/xAA6f80ABoAHwDG/8b/zP+S/+f/JQDz/z0AQQD3/zIA6/8MAAEAuf8nAAoAxv81AGcA2/8tAOL/2v/2/8H/KgAJAAMAAADx/97/6f/Z/x4AFwDe/1AALwAXABUAUQAAAOD/AwDM//b/m//L/93/EwAfAOr/FQDl/9//5P8xAOn/2f9+ABIAHgAhAPb/MgDq/+P/5P/c/7j/SQBhAPP/QwD0//P/5P8TAPD/0P/t/3f/KgDf/xIAYgAQAEIA8v/x//7/zf+8/w8AwP8rAHkAIAA9AOD/2v/Z/8H/2v8HAAMAHAAKANn/PwDW/yEADADZ/yMA5/9FAAsA0f/+/9//8f8YAA8APwAxAM//AQDI/6b/EADb/xkAHgAEAFgATAD2/+T/LQDP/9r/CwCN/w4A8f/Z/04ABgDw/xAABQDm/xEAGQAbADMAy/8WAB4A5v8bANP/AwDy/8//SgDn/9L/AwAAAPH/EwDR/wgA/P/r/20A4v8mALz/CgAIALf/gADF/28A6f/q/+z/kf9bAMH/LgA2ADAA0//S/w0Ay/84AOD/4f/2/+n/HgAqANv///8uAAsAIgAAAPH/BQDo/xMAJwABAEsADwDq/+L/+f/y/+v/JwCl/7D/zf/V/9T/0f8RAAAAQwArACwAKwAoACQARgDw/xYAJgDI/xgAtf8UAOL/zv8qAAEAFQDz/0AA1P/z/xwAKgDi/8v/IQCV/8n/7P/M/9b/HAAZAEIAbADf/00AGwC6/wAAFwD4/8//SgAsANL/ZgAWAL3/AADO/8X/4//1/wsAFADs/wEA1f/8//b/2/80AK3/NgAAAM7/LgAcAH8AGgBqAAcAxP8TAPP/xv/f/wkAvv8NADMAPADV/wEAEwCq/+r/oP/p/+z/GwAlAOX/bQAOAPj/CQDq/+z/5f9UAD0ADAAzAML/uf/n/w8ABwDa/ycAqP///y0A4/9LAEAAIgALABUAIAC8/8X/6v+S/+P/EQANADMACQANANj/FAC5//f/QwAEAIgAHwDj/6v/7f/c/83/7P85AGgAEgBPAPP/0P/e/+n/4//l/xEA8f8zAAgAMwD7/7P/HwC7/wsACACo/xoADgDt/yQA3//g/zkA9/8qAE4A+P8eAEcAFwAtAL//wf/I/9H/EADP/xIA7v/r/yMAp//y/w8AxP9AADgAIgA+AAEATwDx/97/NgDh/+H/DAAEAOT/CwDm/+T/5v8TABoA/v8WAL//MAACAPf/CgDA/wEAnf/1/ycAFQBdABUAuf/1/0AAvP9QACQAuP8UAAsAFADg/ykAHwAiABoA2f8KAKX/AwAHAND/8P/M/xIA8v8ZAOj/FwA6APL/BQAbABQA1v8MAOP/FADa/6j/JgDe/y4ARgA8ABIABwDy/wIAIwDc/2gA+P/H/7H/r/+r/4P/UgAEAEAAMQD9/0QADwApABUAFACx//f/2f/t/00AFABSAB0A3//N/9b/m/8GACEAzP/7/+D/HQDr/zcAIQAUAFsABABOAPf/0/8FAK3/2v/Y/8H/EADY/8T//v/r/yEAFwAwAFYAHQAaAGcAEQAXADoAt/8bAK//tv/c//P/GADH/x4Ay/+p/97/RQD5/wAASgDU/18AEQAsAO//+/8pAMH/KAAfABMA3/8IAKD/5f/+/8j/SwCQ/0YAOwDq/yMAOwAgAMj/QwCp/+3/6P/B/z0A0v8qAOb/4/8DAAgAQgD5//H/JgDS/w4AEgATAEcAwv83ABcA2v/1/7/////C/xoAOABLAAQAEgAtALX/IACr/3n/1P8XAAMAIwDu/8z/QQDw/0gAKQD8//b/9/8KACMApgABAFkA6f+R/9z/sf/N/9T/EwC3/wEAKQAdAC4A0v8xAAgA8v8QAA4A8P8JAAUAzP/f/+L/BAALAOj/+f8HAAUAJAB3AFkA+P8WANz/6v////n/DgDQ/xEAtP/R/ykAFwD7/8L/8f/w/xoA9v8NAO//8f/2/wkAFACh/xwA/v8rAHcASgA1AAUA9//T/yIAyf/k/+b/3P8DAAgAMAC0/xMA4v8PAO3/qf8dALT/PwA7ABgAEgAbAA4AEgD3/8//3v/S/0IABwAtABEADgAkANf/RwD5/8D/+v8HAMb/4f/y/8b/CgD3//7/9v/q//n/SQAMADIAZwDQ/x4AJADc/7v/6/8FAN7/EgADABcAHQAOAB0Azv/h//3/1f/x/+n/BQD8/yMATwAJAF0ACQDN/87/7//L//f/UQDC/wkAEAAQAP//GwD7/6X/DQCS/wgAAwAtADEAEgBTAO3/QQDn//D/9f/c/+7/xP/9/w0ACAAGADsArP8hABYAy/9sAMn/IQAgAL3/5/8qAB4ABgAFABEABQDH/xoArP8IAAAA8f8iAAAAXADZ/zsA2//i//b/8v8lALD/IQDb/xoADADZ/+D/zv8sAN//9v8hAEMA0/9GAEAAyP8NANL/8//t/xkAFAAsAEAATQAoAJ//w//q/+T/1/9qAL3/zf/4/83/VADs/3YAw/8EACIAzP9vAJL/FACV/9H/BQCq/2YA1f8eACkAIAA1AEgAAwD8/0gAzv9RANT/2v8HAMn/GQCm/wsA0P/U/2MA0f/f/yEAt//8/zwA3f9WAAAA8v8wAND/LgDR/+7/NwAEAPn/2v9zANf/+v9BAOD/9f/l/wYA0//N/wgA///u/wUAEwDy/ygAJQAeADAA+//e/9P/7/8AADAA4v8BAB0A4v8KAOb////i/w4A+v/j/x8Awf8+AAkA7v80ALz/BAA3ABMAJgDz//T/HAACABkADwDN/9j/uP/A/8//uv8SAFAAGABPAB4AHwBSAJX/YgAmAKL/XgC7/x8A+v8AAP//qv8QAKz/GgAXAAMAEgDT/+7/DAD//97/IwDX//z/6v8dAPT/DQCHAPX/GADx/xQAqv/8/08ApP9CAAEAJAD5/0AA7P/b/xcAw/8kAJ7/IwC9//L/DgDX/zsAt/89AMr/IQD7/wQAJwDK/1UA8P8sAM7/cQACAL3/bQB+/0IAIADS/xsA6f/D/wkA6P8BAEQAuP8PAKX/6/8iANH/fABIAPr/PADZ/9L/JAB8/wUA4f/+/20Ay/9aANf/3v9TAN7/6//n/xEA7/8IAC8ABAD7/xwA///F/+X/EwC8//r/GwC//0wA9v/q/2IA/v8pAB0A2//m/xcA6P/h/xcABQD8/+n/1f8IAAcAFABAACIAGACg/6b/uf/6/yAA8f90AEkAXgAGABcA7/+v//b/g/8KAJ//2v8cAAkAVQDe/z8ADABfAEQAKQAeAL3/CQC9/8T/zv++/+n/EADv/zIA/v/Y/ysAAQD8/wkALQDq/zgA+//5/xQA0P8wAPz/QAAUADsA8f/V/wsAf/8FAKX/x//k/yMAQQD6/18A8P80APD/BADz/8P/fgDj//T/8P+r/wEAEwAnAB0A+P/l/+z/AAAlAAgAwv8hAAgAgv85AAgA1/8YABEAHAATAGwAGwAUANX/CQAeAJn/6v+p/+j/DAASACEATQBIAPP/FQCY/7f/7P+e/x0AJwAAAE4AJwAAAAYAxv/Y//j/AAA9AHAA//8HAOH/+f8RAK//9f/l/woAwf8uAFQAx/9hACUA8v/X/9z/rf/1/zcA5/9JAOr/DQA3AEEAHAALAKn/tf/q/37////j/ywACQATAP7/6P9qAKz/MwAGAOX/+P8GAFYA4P9OAFIAYQDO//P/9P9D//n/3f8ZADUABAA7AAcA6f9EALT/0f8LAHX/FwDt/wQALQD5//z/2P/5/ykATQAEAAkADAANAOX///82APr/LAD8/xcAtP8TABYAwv9pANL/2//9/67/CwDo/+j/MAD+//L/MgDg/73/SwAeAAIAKgDZ/+z/3/8UADsADwBGANv/w//a/8P/BgD0/00ARwDo//D/9v8HAOf/AgArANr/+v8lAPL/9P/2/yAAt//S/zkAFQBDAP//6P/6//b/DgAKAN3/2P9HALf/y/8iALj/TgAKANz/VAAAABoAJADv/xgAKQDL/wAACwDY/+z/EgATALL/EgD9//P/PwD9/xwA7//Y/9D/7v/m/8z/AAASADcAHAA1AB8AHAAVAOX/wf/G/0wA8f8VAEwA4P+s//D/3//r/30A9v8eAPb/rP/X/7L/HAABAFcAUABOAAgA1f83ANb/+P/5/7P/0P8NAPT/HQDQ/77/LAD1/x8AFwAEACMA6/8IABcAKQD1/87/EwD+/w0ABgAOABsAzP8iAOn/zv8lAN//2/8HACoAvf9NABAA1P/K/8//YwCU/1wALgDq/2AA7P8sALD/BADr/9X/BwAiAEYA4f8qAMH/NQAhANn/BwDy/8r/of8hANf//P85AAwAzP8gAAQA6v9MAJz/LQA7AOr/MAAxANj/y/8QAMb/IwAZAAIASADX/8z/HwANAAEAPAC6/+z/+v/K/xkA7f/M/+//BgDu/ysA+f9rAGAALwBBAMH/1v+R/+r/8f/p/x4ADAAAAMX/KQATAML/HAAfAKP/MgBNAP7/JgCh/wEA1v/Y/xkAIQA/AB8AXAANACQACgARAP7/tv8BAH//1P/o/8z//P+d/wcAJgAnAE8AWQAaAPb//v8OACAAtf8dAO3/oP8PANz/AADt/xIAQgABAAwALQAPAAwAMADq/yUA6v/n/xwAt/8SAN3//P+5/9n/MwDH//r/JAA3AB8AKAD+/+j/FADk/wQA3v/r/0UAIwD+/w8A0P/P/63/4P8PAAAAMgDO/yAABwD+/2oADADr/xQADgDV/3wADQAGADQAnf/9/+f/z/8KAPz/8v8TAKb/5//j/6P/RAD8/0YA+P8XAAsA3v8FAL//TQAHAKQARQD7/4AAp//9/8L/wf/F/6P/4v8FALn/8f8SAOL/dAAaAAYA/v8WAPn/FQCAALz/YQDY/+b/FQBd/xgAxv/q/x4ADgBXAAMAHAAjAAMA4/8KABkAu/+u//j/z/+3/ycAKQAOAPb/GQBUABcASABwAPX/BAD4/4D/2//I//3/CAAAAC4A0v8GANz/sP/f/xoARgAdADsA8f8DAP//x//s/9z/EwAJACIALQA8ADsABwAfAOD/HwDl/9P/KgDf/9L/zv/4/8j/t//w/wMApP8BAG0A9v8sAAMAGwA2APz/TgBSABAAHwDp/wEAFgCD/xEA9f/I/+D/uf8OAJb/AQD6/0wAiAAYAB4A5f///5H/y//m/xcAPgDU/z0ADgD5/08AOwALADMA6/8IABAArv8yALj/3v/k/7//6/+//+r/OwBAAOn/9v+u/yAA0/8wAGsA5v9lAL//JQAeAMX/KAADAK7/1f+GACoAGwDz/wQA7/+S/wYAyP/1//T/3v8DAF4A7P8wAGcAw/80ALT/6/8WAPP/FwD+/zIAyf8FAOz/BwASALT/7v/Y//D/y/8WAD0AIwBWAAQA9v/I////GwAAADUA6/9AACoA3/8KAOX/3//D/8r/1v////v/FwAxAB0AHADh/xgA4P/k/yAA+P9DAPP/GwDn/8H/CADO/yUA4v8KAEcA/v8BANv/HwAUAPL/JQDN/y4A+v/R/2QA7v8OAMn/4f8KAJX/DADq/+z/AAAAAEgALQANAPz/AQASANb/RQA8AMD/KwCq//z/CgCy/0EAxf9MABkAFQBEAKv/7//3/9//yv8YAPr/3//z/wIANADQ/0gAKwDv/+//8/8hAAwADgAAABMA5f8GACMAAgDj/xgAHwCv/+3/JwD6/9T/FQDh/73/3v8eACEAtP8gACwA3/8RADkALAAtAEEAMAAAAJ//vP/U/9n/8P8AABcABgAAACYAQgDn/wAAGAAEAOv/0v/1/yMA//8gACoAyP8HAMb/x//g/77/JwAKAEMA+/8rAE0AEAAWAOD/5P/q/08A/P8FAPr/5f8DAOj/EADQ/xEA3v/w//r/yv/x/8b/KQAVAAwATQAFANX/FgBfABcACADx/73/5P/i/yoAZAAeANn/4f/0/63/5/8wABgA3//9/wwAz/8WAPb/RQAeALX/LADo////CQA1ABgAwP8TAIr/xf/8/x0AVQAJACYALwDp////CADJ//b/zP8SACkAIgBQAO7/QwD0/8n/1P/C/+v/zf8lAPD/DwAeAAcAMQDG/xIAAADR/yAA5/8uAE0AJgAXACMApf+l/yoAt//z/0gA7v8EAAAA1P/t/+L/4/8gAPr/EwAgAAkAAADV/ygAUAD7/+D/NwD+/+//jAD4/wcA7//R/9//vv/5/7b/4/+8/+3/NAA6AA4AEwBzANT/AgALAPP/AQAHAPv/2f/o//T/JQDa/+T/yP8XACUAAgBTABIATgDz/zAAvv/D/zgArf9KAPj/NwAGAOf/8P+7/+r/bv/2//v/5/8NACMAOwDy/yMALQD5/xcAJgAAACQA/P8PAPz/DAD3/97/MwCz/wMAAgAAAAsAyv8cAPD/3P/l/z8AEQDd/woA3f83AMj/6/82AB8AKQD+/9n/y/8dAPL/BgBFANP/1f/4/+T/7v8uAC8ADgD8/xwAyv/S/yMABQBjAAgAKAAGAJL/PQANANT/1f8pAPr/jf8IAM3/7f8PAPn/DADI/9z/UQDm/zMAkAAWAF4AVwAYANP/8/+F/8j/JACN/9n/tf/1/w0AKgBRAO//EgA/ACMA5/8OAPf/+P/5/7f/AAD+/xkA/f8zABAA4f/p//7/PwDP//z/+f8uAAoA3P8LAAUAAAAJAPD/rv8gAOr/FQA1AN//MADX/xoApP8YABoA1P9NAKf/VADj/+X/IQDf//r/u/9MACIAJQBLAFEAAADh/+v/rP8cAOL/CADH/+L/9P+t/xEAAABLABUA6v/m/+r/5v/6/yQAYgCOAAUAAAD4/+P/lv/3/wwAxP/5//v/CgDr/yIA9/////j/HwD7/9D/MQDy/ycAFQD+/1EAKQDX/w4AFwC1/y0ADADn/5z/nv8LAOT/4/8RABwAz/8SAA4A9P8xAE4AKwAuAA4AIwDw/9b/UwDG/+//AgDg/93/jv/y/9j/CgA0ACkA6v8gACwAwf8DAE8AXQDo/xkA9v/i/xsAFQDh/6v/+P/M/wwA2v/u/9P/mf8mADgAFQD6/2sAAwAjAEsA2/9XAOb/JwAkANT/MwDp/+j/yP/V/6b/p//r/7T/6/8CAFgADwDh/yYABgBAAEwAVwBQAOH/CQDK/w4A9//d/0sA0v/p//X/6//m/wAAIwCm/8T/3P8XANb/DwAtAA8ANgDY/wAA1v9eAM7/CQCVAN//bADj/+L//f/6/83/8f/1/33/EgDk/0wAx/8VAFcAvP9DAN3/QgAAAML//v8PAOH/3v94APf/+v8wAAAADADL/9j/GACu/8n//f/z/yoADQBRAE0Axv/O/ywAw//q/1UALwBKAC0AEgCQ/7r/1//e//T/5/8bAAoADwDo/xwAJQAJAC8A9v8NAPn/+//D/9j/HQC1/+z/KAAAAAcA5v9iAAwA7v9aANP/AAAjAML/6/8dAO//9f/f/wEABwD+/z0Azv8JANj/JADd/wMAagDS/3EAGQAAAAgAqP+3/woAFgD7/x8Asf/h/6z/vP/u/x0ANwDy/3gAaQABAOj/LwDt/xAA2/8iADEAtP8RAM//9v+5/+n/6/8mAP7/IABVAOn/BADA/xIAs//9/xcA7/9LAOr/KQD0/ywAGQDx/8P/BgDm/+n/QQATAFgAyf8oACYA5f+o//L/PgC2/ygA0f/E/57/0v8SAA0AKABCACAAvf9IAMv/IABYADMAaQAgALz/uf8CAKz/EwA2AOz/CQAhAOH/EADQ/87/BgCn//3/AAA4AMX/GgAMAML/EwDS/ycApP8zADkA9/9/ACEAdgAHAM3/PAD9/7H/NgAOAL3/0P8TAN7/xf/2//P/5v/W/0EAAQAkAOz/IgAAALn/JQCb/zAAu//7/1YADwBmAMb/PAAQAML/AwAXAAMABgAiAPT/+P8hAOz/t//C/6v/NwAOAFkASQDl/zsAx//X/xkADQDN/x8A8f/1/x8ABADL/8L/CgCn/xoAAgAVABEAOABgAOz/bgDS//H/5P+p/wIAEwD9/+P/9f////f/sv8yABwA2v8RACAA4/8OAHcA6v9IANf/2P8vAMz/GQD5/8D/CgAUAMX/LgDx//3/EQDk/xUA9v8eABIA4v/2/yoA0v8YABwA5P9QAPL/zv8RAN7/uv8rAOT/FAD0/9j/FADg/x0Az/84AP3/4v8gACMAZQD+/ycACwD5/9L/3v/n/+//KgDi/xEAhP++/ywA9/9bAEwAKwAtAAkACwDD//T/7/+p/wkAsf/j/+j/5f8VABUAQAA1AG0AGQD4/8v///8KAMv/HgCw/zQAEQD9/xoA7/8PAMz/AQC//9//OgBGABkAWwD+/6//JABx//b/LADV/0IA2//v//v/zf8eAPT/8f8PAPn/KAD7/wMATwAaAFsANQDU//b/3P/E/+j/x//2/wIAJABYAJr/IAAbAMP/aAAHAMX/FACx/+j/+v+M/2oAHQDZ/yoA//8FAK7/XAAwAOz/HwDm/xEAGQBPACYA+//U/9H/7//w//H/5f8kANH/JQASAM3/AACt//3//v/n/xcASgAIAOj/RwDn/9X/FwAOAAkA+f+w/+3/YwAZAOb/LwAZAP3/FwAtAOz/5v/y//j/BgDw//H/5P8VAK//9P8/AOL/LgDT/+7/8f+///b/FgAMACMARwAAACwAOwC+/wEABgDS/xsAw//k/zAAsP9HADoA6P8tAEgA9v+w/wEAvv/b/yYAHgDt/6H/0f8dABwAegBHAN//QQDu/8T/+v8uALn/2f8WAO//IADx/w8A2f8TAPj/3v8ZANf/8/8SAEoAJQAmAPb/9/+L//v////O/3sA3P9aAMH/AwAWAKP/JgDs/0oA6P8lAN//AwDR/wMAHACE/2gAzv8DAPr/+v9PAAUAaADo//r/EADw/xQA+v/P//X/7f8EAA4A5//9/9//4f+//zMACQAPAB4A+v8eAPb/JgD0//f/0P8VAPL/4/8yAAIAOgD8/ysA2//E/wIA+f/a/9H/CwD1/xUANABXAP3/HgDK//j/DgB1/z8A0//d/2MA+v8kAEMAAwAkANv/x/8uAJ7/OgBIAJ7/BADy/8H/2//V/wMAOgAAAFAARQDk/9L/m/8nABoA+v8+AFkAFAD7/2QAyP/b/wwAi/8vAJ//+P/v/7f/OwCf/x8ADgAiADgAFAD0/w4ADgDm/2sAxv8dAOf/3f8hANT/OwDT/ywA9f/2/x8AIQANAPH/MQDM/xUACACd/8P/EgDK//7/yP+3/1IApv8gACkA3/8/AHsARwDh/zsA9f8WABYAOgAWABYATgDN//T/kf9a/27/j//5/9f/MwA6AOz/gABRAAkAHgDy//3/0/9DAFsAaACFAPH/CwD//4H/4P/w/9X/FACG/37/mP+N/8f/9f9AACIANAA/ACkAIQATAGMAWgBmACcADABKAAYAEACe/63/yP+I/8n/CwD1/8P/LQBCAOT/+/9XANX/pv8+ALj/PQAAANT/CgDX/2gAAgAhADkAw/+6/zwA8P/2/1sA+v9cAOn/CwDU/67/6f/G/1IAAwBTAOP/7v+9/4T/2/+y/yoACQBrAEAAPwAcAO3/KADx//L/zf8iABIAFgBkADQAov/o/+//hf/2/9H/4v80AC4A7/9XABAAv/8JAHD/EgAGAOj/ZwAtACQA///e/9L/GAAQAAoALQApAMD/GQDi/7z/KwCu/ysABgAOAFIA0v/1/7b/2f8oAO//8v/5/xwAYwAaAAAAGQD5/9r/6//c/+n/RADw//7/OgAzAOL/x//B/9X/HAAVACkABAAyAO//zf8EALT/AgAdAEIA+P/7/+7/s/8BAM3/NgAxAPP/AADv/y4A7f8hACsAEABCAP//6P/4/+T/AwDo/+n/+f/m/xQADADq/wEAyf/5//f/7P8FAMX/9f8iAB4AKwAUACQAKgAbACoAHQAdAMX/4f9CAOv/5v8lAMD/x//C/63/5f8VAAQA/v8LABMA8P8nADMAGAA+AM//8P/3/9X/fQA3AEsADgC//wQAqP+q/5z/2/8CAPP/QQARACIAGgA8AA0A9P8dAKb/8/8OAAEAJADU/ywA6P/L/04AGQBMAAcACAArAKr/IADY/6j/+f/P/9z/6f/a/xEAVwDA/+3/TwDk/0oAMQAEAEsA9v8NAOD/o/8LAAkA3//4/xQAxP9IAAcA6P+KAOD/IADn/8r/6v+4/z0A/f8DADkABACv/5z/vf/d/xIAMABLAAAAFAAeAO3/OAA9ACgA7/8jAAwAxv8TAP//8P/Z/xIANQCK/+P/zv+9//b/7/8YABIA9v8HAEoABAAnAP//4P/0/wMAYAAVAEwAPgDL/9n/1f/K/8z/1/8AAGcA0P8tADoA8/8eAM7/xv/K//7///8bABkAIgAuABwA8f/n/+L/nv9UAPP/+P88AL7/y//n//r/tv8cAPT/DgAhAAMAcwAxAE4AJwD+/zYAzP+0/+f/o/8IAPj/yf8ZADIAKgDP/0gA2P8CAAgA0/8PAJf/UQDa/9z/NQD//xsAGQBmABwA/P+y/8z/BwDu/woA/P8NAJv/w/81ACYADQA2ACgAAADB//D/JQDe//b/BQA3APj/5/9CAAYA5/8CAAEA5v8DAPf/JwDa/8b/TADI/+3/fAAaAPD/2f/e/7z/+f8mALH/WwABABcAOAC4/zwAxf/i/8z/5/8IAAAANgDh/0QAAwAnAEIA5v9BAOn/2P8JAM7/m//y/y8A+f8VAEoACAAAAAYAFAAHAOH/BACZ/9H/AQCx/xEAGwAuAP//BQAmAPL/OwA+AA0AGgBDACAA9f/a/7D/AACO/5r/AQDm/wcADQARAPr/DQAaAOv/RwBTAPD/RwAjAAkA0P/S/w0Avf/v//7/IAAsAPT/UACk/9//AACk/wsA7/9DAPn/8P8KAOP/GAAXABUABAD+//z/dQAXAOL/GADO/63/0f9IAP//GwAVAJP/6P8JAMn/6v8pANz/KgAnADAAVwDX/wcA6v/5/zcAJADr/xAA9f+9//n/0//h//v/xv8UAAYAAQAqAAQADgAgADMA///x/xMAtv80APP/7v8jANv/DADT/w0A2v/+/30AIgDt/9L////5/83/NwD3/63/DgDt/wgAFgAMACEA1v88AOD/7P8qAPP/GgDn/+v/4v///w4A+/8OAAkAPADG/wAAKwD3/+z/HwBcAKD/8P/y/7L/JgCv/zIAIADS/1cAJAAuAAMA7f8zAOL/MwAnAMX/DwDO/6L/pf/r//f/zP8tAAoATAASADcAMwC9/wMA8f8tALD/+P/3//v/XgDU/1IAJgAHAPT/6f/I/wIAAgDL/yEAmf8vAOH/3P92AM7/7/8EAC0AFABJACIABgDa/6z/8//k/xcABwAMAL7/RAAFAA4AYgDL/yYAuP/o//b/8f8KANT/AgAbADIA5f85APz/EAAHAOT/4P+Q/1EAs/8fAFEA1/8JAOz/7v+U/0UAHgAWAB4A9/8pANL/NADn/wcA/f/S/1kAx/8AAFUAIAAaAAEA8P8NAAYAuP+//7z/+f/j/wQAFACi/+b/KwD9/wYAbgAoAA8AHADq/xgAHgDn//f/AAAfAAAA4v8mANX/2v/v/+H/CAABAEEA7P8FABEABQDi/+H/UAAAAP3/EgDh/5P/2v/d/+f/KQDd/zoAIQAuACIAJgAVAMb/OwD0/wYA8//4/8X/+f8wALH/OwAoAAkABQDZ/xcACQDX//n/CQDn/xsA0//r/wcA+/9GAAIABgAfANT/pf/g/xEAAQAxAAAAKwDd/wwAPQCe/ycA/f8DABUAGwBqAM//8f/z/9n/p//h/x4A6/9BAPn/JwAPAPT/AQD7/8L/sf8kANj/NQAsAGcACgAqAFoAo/8bALz/4//s/+T/FwDP/zYAHADt/wgAz//E/wkAzP8TAMr/o/9FAPH/OgBBADEAMgD3/1MAuf/9/x8A9/8lAA0A/P/k/w0A6P/j/9T/t//4/6P/RwALANb/jwDL/1cAGADM/xkA7P9RAO//NgAkAJf/rf+2/+L/GQAMAAUALAADADMAAAANAFMAqv/M/xkA3//7/zIAAgDo/yAA8//q//X/4P/p//L/7v8nADMA4v8QAOX//v8pAOv/PQAOAPf/IgALACUAEAAnAKP/DADf/6L/WwC2/9r/DADV/0gA5P/t/x4AGQA8AA0AJwAdAMz/f/8AANb/5f9RAAMAIQDO/xgAFAD2/2IADgAIAMz/z/8MAPX/9/8HAPT/xP/u/xYARgAsABgACQAZAOb/9f9nAM//x//I/5n/4//M/ysAIgD1/0EA6f8GAAsAEACNAAYALADz/8f/MADH/+n/7v/x/wEABwA9AMT/0f/5/67/KwDe//X/OgC1/4EA4/8tAFkAe/9+AOv/5f/l/83/8v+3/y8A7/8lAFkA7v8zADMAy/8HAOH/+f/q/73/OADo/wYACADh/xUA3v80ACMA3/8tABcAxP8bAAsA5v8YAOn/7v80AKz/nf8SAPD/NQAdAAEAAwBIADgAJQAfAOv/2/+R/zcA+f/X/+X/uf/y/8P/JAA4AEoA+f/F/wcAAgARABoARQABACIA+f/x/zIA3v/g/zUABADp/8D/+P8gAJv/FgABAOr/CgAAAAkADgAqAOL/VQAVAAgA/v+w/9f/yP///8z/5/8lAEMACABKAFIAz////8b/6P/k/xAAGQAOABUA0/9bABgA/v8xANT/LQDw/9r/3f+B/8P/x/8LAPv/IAAzAB4AOgDk/0UADgBBAAsA3/8aAHb/DwDv//D/AQDX/ygACwAlAC0AAgAuAFUAIAAFAMb/3P+U/1P/uf+d/93/JwBsAFIAZwB0ADMA/P/f/8f/t//z/wkAWQAkAHwAPgDL/z4Amv+R/6T/4P/l/7T/wv/J/wMA1/9JAGUAXQBAADgAOADd/xEA/v/X//7/zP/j/+b/7f8dACUAMQAtAPr/z//n/w8A6f/l/wwAzf+a//L/CQA0AGAA/v8DACEA3P8QAPT/AwA0AAEAUgDy/87/2//m/+//sv8oAA4AKAAGAAEACwC9/ycA+f8lAP//+f8cABoA6v/t/+7/rP/c/6v/RQAhANj/hwAdAPL/IQAmAOv/wv8HAL7/wf8uADkAHgANABAAEAAMACIAFwDw/83/2/+9/+H/IAATAE0A/f/t/+X/1f/u//3/6v/l/0YAAQD7//j/FAD4/8T/+v/X/yIAOwAbAEAAPQAXAAwA6P/y/0cAz//m////nP/k/8n/7f9iAOD/DgAWAJ7/IQDp/wgAagAgAA8AHgACANb/6//c/+b//P/t//b/PwDv/+T/TQCE//7/FQDe/0MAKwBBAMn/KADm/7v/RQDf/0QA8/+w/yEA3v/d/xkANgAiAOr/EwAJANr/CQAEAAAA4f8LAAIAFwA2AMH/3f/i//X/5f/9/woA6f8FAO7/KgDb/xkA3P8KAFwAAQCFABAA7f/2/xQA6P/f/yAAAQAIAKf/+f/d/+z/6P/A//v/AAAgAPj/UgAIAPD/KACs/wIABwDl/zgA1/8BAEMAAABnABEAGQAjAML/HACv/+3/GgCy/ykA5P/g/yQA8P///+v////T/+D/MQDq/0QA8P/y/ywAzP8sAC8AAQD4/zcA8P/n/wAA//8/AOj/8v/1/7P/0v/c//f/gQArAOr/AACe/w8A6v/P/wEABQAlAPL/IQA5ACQASwBSAOj/KQAIALn/zP+i/xEAlf/T/2YAk//s/wQA7f9VAPv/dAB3APn/7f/Z/9P/u//x/w8ARwDt/wQAKgC9/xYA8P/R/9n/NgAbAE4ACQDk/xYAsv84AMT/QAAGAKP/OgDN/zAACADW/+n/2//N/y4ACQDc/wMA8/9OANP/MwAOAAkAPgDK/4sA/v/d/wQAuP8TAO3/wP8sAP7/AAAbANP/HgDv/wwA8P/V/w8Azf8EAOz/DAAqAP//EQDy/9j/JAAeAP7/MgBEABcAxP/k/+n/BwC3/xIAMADm/xQAvP8TAC4ACwAfAN7/2//R/wkA8P8AAPH/xv8pAAgA4v82ADUAIwA/AEQAEgDm/wUAAwDV/7P//f/d/9L/7//n/ywABgAcACMA7P8jAAIAu/8oAPv/8v8yAOz/JwDf/+f/4P8WAEgAiv8GANr/AAAWAND/dAAGAAQAOQAGAMH/BQD//8b/EAANAPD/GgBHAOb/FQAAANj/CwDt/7f/+f8cANv/VQC9/wIAXQCm/1gAOADo/8H/IgDi/+D/GgDj/0QAyf///ycA8v/0/+n/zP/x/zEA7/8iAOr/WQAmAC0AGQC3/xMAtf8IAN//AgD5/wAAEQDF/xIAvv/+/xMA6P/1/w4AOQBWADAA+v8uANP/7f/h/6j/FADr/9z/jAAFABAAOQCU/+T/2/8tAAAAHgANAAAALgD3/+b/c////9v/7f8lAOP/NgAmAFIA5P9TABEA7f9hAOb/6v/P/9L/yv+//wcADwDd/ycA0P8LADcAHQBPANT/+f/W/77/zP8wACkAxf+FABYAz/8fAAEADQA6ANz/UQAqAK3/FwCw/8j/wP/8/w0AIQAmAND/PwC9//D/GQCy//j/EQAfAO//OQA+AOf/2v8EAEMAIwA0AAkAn/8JABMA6//K/wMA6v/7/+r/vf9IAOT/MAAcAPT/PwDI/xsACwAoAI//9v8RAIz/RAAiAFMA9f8zAEoAtP8uAEYA8f+0/9L/5P/h/8b/BADS//f/8f/Z/zUADwAYACkASQAYABUA6P/g/+H/5/9aAMr/KgAQAMn/CwDn/xsA4f9NAPD/tP/y/+z/BwDh/woA3v8hACcANQBPACYACQC//8r/5P8PAOD/9v8qAAgA6P+z//f/EAAQAB0ASgAEAPv/HgD0/zsA6P8AABQA7v/K/9b/3/+I/x8A4f/y/zUA9f82AAEABAAiAOz/CwBFADAAAgDC/wkABAD0/wgA3f8dAM//AQA4AO7/DgArAPz/8f8iAKD/AQA/AOj/KQD+/w0AAQB+//D/HgDS/wQA9v8mAB8Auf/+/+H/9v9KAA4AQgA4AAEAAAD+//v/0f8SANL/7/82AA0AEADl/yEAv//1//X/9/8FANf/PwDW/y0A2v/5/xcA1P8yAOP/AwD7/+z/+P8QADgARgAnAPX/HgAqAKz/x/8QAJD/HAABAPX/8f8AADEA5v9LAPn/BQD8/+r/yf/4/1UA1v/7/ykAz//7/y4Ayf9AAO7/4v8YACMAIwABAD8A5f8VAJL/yv/h/+X/ZQDN/0QAuf8EAB0Arv/+/wEAFQAFAF4AOwA6ABMA3v8HANT/vf8XAO//wP8CANP/LgDQ/+3/GwD9//7/EABCAPb/WADo/x4A4////04Aq/86ALr/7v/u/7v//f+2/1AAAAAeAGAA7P8sANn/3P/W/wIAQgDf/3sALADD/xcAwP+0/9L/v//B/y0A2/8AAEAACwAcAE4ANQD5/y0APwD5/+7/5/+U/wAAzP8YAEoA0P87ALj/LgD3//b/OACu/yIA3f8PAMf/4v/c/wkAdADq/0kADwDG/xQAAgDQ/w4A3P/k/yQA/v8iAPv/HgD2/wsABwADAAAA1v8XAL3/LgArAO3/HwDj/yUAxv/H/xQAAgDh/yYANgDm/9z/EwAEAMj/+P8vAEUAOAA0ABcAyv/p/7T/yv8RAO7/3v/N//f/zf/g/2AAKwAbAJgADwDu/+v/z/8XAL7/IQDw/8v/HwD1/zIAtf8kAPr/8/8oAJ3/MgAnAB0AIQD1/+3/BQAdAPz/2/8EAP3/3f/t//j/GQDk/x4ADgDp/xwA/f/5/97//v8BAPj/RQAeAAMAHADe/zkAxv/V/zAAYv/d/8X/8P8PAAkAUAACAFsA+f84AEYAQwBDAE8ACgB//wAAp//E//L/jv/K/9f/DgD3//7/OwASAEEAQwD3/y4A1//z/9v/u/9LANz/CQByAEMAzf8BAMn/zv8AAP7/JQDi/y8A4v/n/xQAyv8zANr/AwAYAML/QgC+//P/VgDo/yEABAA4AMP/CgD4/8j/TgC9/0kAGQAkAMT/qv8jANf/MQAVAEcAwP8YAP3/4f8ZAPv/EgDk/ywApv8CANL/wv8xABMA9/8GAEUA4/8vAP//KAD0//X/HQDb/w4Ax/9MAPv/BADe/8D/1f+l//7/FQBZABMAXAA8AOz/4P8TANj/s/8mAMj/KgAhAP7/+/8iACMAAgAKAMf/JQDG/+//HwDV/xIABQAKANX/9v8UAKn//P9eAOL/IQA9APH/DgDk/xUA2f/p/w4Amv/6/xMAIgAoACcAZgC4/wAAFQDn/yMA0P9NAPf/5f86ANH/1P/M/+n/0v/p//r/BQAAABsAGgAlADQA4//1//P/AwAMAFQA1v/G/0AA/P9EAOP/HwAnAI3/CQDZ/9P//v/6/+v/6f8HAP//CgASABYA/f8OADIA4f83AE0A+//3/zcA+v+u/wkA1P/K/7//7f/7/9D/MQANADMA/v9QAGAAw/8cAMn/9//l/8X/OADj/w0AIQDH//X/DgDz/ysAGgAaANP/xP8KAPr/NwA0AA8ALwD//xcAsf///+3/of83AOX/sv8DAN7/1f8RAAwANgAgAGYAiADU/ysA8P/Q/+z/BwDO/7b/LQDB/zQA+/8EAAcA3/8QAK7/KwAFAAAAGAD5/8L/AgDW//P/dADr/2cA9v/1/ywA8P8IAC0A5v/r/yQAsf8HAJz//f/f/xoARADk/2YAzv81ANn////2/7v/PADE/woAHgAJAO//1//g/0kA1P/X/4QA4/8dAAAA1/8aAPb/AABJANz/PAACALr/WgCZ/+f/zv+v/0IA//8vACYA5/8bAO//9v8xAAMAIADK/9z/3f/l/0AA4P88AAQA6P88APL/HgBWANr/+/+3/7n/EwBn/zgAFgDc/ycA+v8RAAQANwA+ABEA3/8BAPr/IQAIAHMAAADq/0cAZf8GANn/+v/6/8//DgC+//z/o/8AAO//CAAZAEwANAAVACwAxv8wAAEAOgD8/xAAIwB0/0sA4P+t/04A/v/v/8D/AgDv/8H/SgDl/yQAQADn/0QA7//u/+//AAAUAPP/8f/X/9L/9P9AAAAATgAYAAUALgDN/8r/z/8BAPT//f/b/zAA6//b/1UADgA6AOn/+f/1/xwAEAAFAAoAuP85AM7/CAAIALT/QgC1/wwAvv+w/xgACwA/AB0AdwAZABoAFADj/w0A2v/d/+L/5//6//b/2v8jABoAAwDO/8n/4P/a/04AIwBCAC4AVAAhAPH///97/y8Axf/N/zYA3P/4/+z/LQC0//7/QQAkACsA5P8uAN//yP/8/+7/6/8XACsA0v/W/xcA9v8fADMARAAnALP/MgAYALT/+P8MAAYAAAAiACoA0v/e/9f/yf/k/7P/+f8TAOz/MABBADUAAAANADoA3P/M/zcAt//u/zcAwf8LACQAEgAjAAsACwAWAMb/HwDo/8L/MgD4/87/BABWALb/OgAUACQAZgC0/w0Akf/Y/67/sv8GAPD/EwAZADgA8v8yAP7/NwAKAFIAFwDM/zIArf8yAKH/4f8TANz/WgAFAAIA1/8lAOn/HQD9/wUAFADG/xEA/f///9X/4v/f/9j/+f82ACgA9v8jABwABwAKADMA7v/b//L/8/8rABgA8P8DABkA9v/9/+T/2f/Y/wYADgDp/9r/DwD1/9H/UAAbAAwALAA1APv/HgAoAN//uv+H/yEA8f/3/+L/BQA0AM3/NwAwANb/GwBIAL//FwDw/wYAAwDM/xYAz/8fAA8AIQD+/yEAVQDY/yEAxP/C//H/7//v/+T/1v/l/0QAGwAEABQA1/85AB8A8/8TANH/BgDf/xUA+f8VAC8A5f9kAPH/EwDb/6b/6f/Y/wwA8f8qAOT/JAAKAAoAMQDD/w4A/f8PANT/NgAOAN3/GQC7/wIAQgA9ANH/GAA1AL//6P+7//H/DgD0/1MACACc/+//9P/t//7/CQAtAOz/BwAzACoALgDa/y4ADwAJAAMArv89AKT/+v9cAOv/HQDg/+z/DQDy/67/LAAgAND/GQAQAMT/6f81ANn/AQAVAPT/2P/f/0gA4f8DABgA7P8eAA4AIQAAANb/QgAgAAoAMgA8ADIAzv8TAG//jP/8/5L/LADw/wsADgArACgA0v8AAAAA+P8GAFUALgAVAC0AMQDK/yEADgC6/xwAe//s/8n/6f81AM7/RgDY/wcAVgAgABkA9v+7/97/AwAkAO3/CgBbAOH/AwDd/+n/GgDr//H/s/8OAC4ARgADAMb/5/8WABIA2P87AAYA3v8gADwA7//x/zUA+/8CAIj/yP8mAL3/DAAnABUACQD2/yMADAC8/woAJQAEAAEA9P8WAP7/8v8JAC8A9//2/+n/8/8VAOD/XgAGAP7/9/+T/+v/8v8hAPL/+P/j//v/CwA9AAAA1f81AOj/TgAYACIABQDa/04AAAAJAN//8v+0/9P/AQC5/9X/6/8XAPf/IQBBANH/GgAIAA4AYQDb/yMA/v+1/+7/2v9EABIABQAMACkAIgC6/xUA7v8RAPb/6P8zAMj/AwAsAOb/w/8WAOv/u/+v/9T/GwA0AAgAOQBbANv/KAAwAPj/VQAWAMf/AgDn/+f/KwC8/+r/AACt/wcACwC8/xgAKgATAAQA1f/7/zkA5v/C/zYA8/80AEIAJAAAALj/JQCn/yYAKwDJ/10A3P/9/zQA2//Z/7X/r/8oAEcA8P8zAEAA6/8fAP3/9v8LAM3/3P8BAPj/vf/G/+T/CAAFADAAQwA4AG8A8f/0//b/2/8hAN//KwDq/8j/KAD//+b/AQC7/+T/4f+i/zUA9f/2/zIATQAbABsAPwD3/9//5v8iAKj/5v/k/+z/FAA4AFQA3/90AP//BQAgAPD//v++/yoAwv/k/xAAw/+x/wQALgDD/0UAAwAIAAkA+f8mAMr/2P8OACcA+f/i/wMA0/8TAP//0P9lABAADQAZACkAKwDT/woA0/+x/yYAJwDt/wgA+/8CABMA1v8pABcACADx/ygABADg/93/tf8yAMf/BADt/5T/9v8gACkA9/81ABsAUQBGAPP/AADq//3/w/9DAEIA1v8oAAMA6v/b/6v/0//R/+X/KQD2/xMABQAKABoAAgDp/9P/BgDg/xgANQDv/wYASwAhAAcAFADV/9f/FQBOAAAA///8/9H/OgCM//b/LACf/00A0f/5/zcA8v88ABQAIwDf/+f/3v/e/wkA2//y/9j//f8tAEEAJgAEAPL/AwBAALH/3/8UAKb/HwDu/8z/TgAMAD0AIwDp/ysADgD7/7n/GgAPANz//P+R/w8A8f8oAFoAtv8rAPT/9f8EABkALACo/zsA9v/T/ycAj/8tAAAA+f9xANP/6v/6//j/+v8MAFoA0v8BAE8A8f8fAPr/5f/O/5P/DwD9//f/fgDy/xgACwDZ/y4A1/8MAO7/+f/9/63/CQDn//X/DAAmAOv/+v8SAOj/XwC3/xAAMADq/0MA7v8VABgAEwDx/9H/x//z//H/DgBsAOf/9/8XAO3/8f/m//3/BgDg/97/1P/L/xQALQAoAAYA9//0/wQADwAWADUA+/8wAPT/DAAxAPj/RADH/97/6v+F/wYABAAdAP3/qv8+ACIA2f8ZABsA4//Z/+r/IAAsABIAKwD7/yUA8P/W/+n/6P8GALj/PwAPAEYA+P+1/2gAl/8GAD4AGAAMAPT/DADC//T/u/9JALn/zP8hAIz/LgDP/zMAVgDz/xcA9v9jAPr/MwBjAHf/FQAQAPD/PwDh/ywA9v+8//f/6f/w/7D/xP/n/xkAMgAQACYAzv/H/wUARAAZAEUAQwCx/xQAGgDi/wwA3P8lAPP/9f8dAOj/EQDr/xoAv//P//n/zP8CABIAGQANACIAAAD9/wkA9f/8/9n/7P8yADYAFwAfAOn/BgD7/+j/PwD2/xMA9f/k/xMA1f/V/wIACgD//8L///8rAJr/EgAMAPH/VAD2/3gAEgDo/z4A5P/s/8f/8P/d/8r/DAD3//3/9P8AAPD/FQAoABMAIgAYAPb/GwAcAOH/JADu/+H/SAABAMz/3f+l/7P/8f9LAOv/9v9SAP7/JQDz/y0AHADZ/w0A1v86AOv/IwAeAN//6v/y/x4Awv/7/9X////7/wgANwD3/xoAov8KACQA6/8xAIQA9f/G/zsAx//+/6v/BgDv/8v/SADO/x4A5v/3/yoA7/9AABwAEQDt/7P/AAAAAPT/QQAAANL/3v8TABIAz/9LAC8A//8BAPX/TQDK//r/AwDe/x4AwP8EAAoAu/8JACMAAgDK/z0AEAARAAEA6v8WAL3/FADt//j/NQAWAAIA0P8AAOX/HgDp/yIAOwCC/wQAIAADAC0AFAASAAEAOwAJANH/7//W/93/AAAFAMT/5f9NADMALAAsAAcAkf/r/w0A2P8TABMAAQDc/wQA4v///w4ABwAsAA8A8P/w/wAA4P/X/ysADgANAE8A6//j/wwAz/8JAOX/GwBdABAA5v8VANf/2P8SALX/JQAVAO//IQAMANb/z/8+APX/BQAaAPj/y//L//H/CAAyAAwASQD//xwAJQDD/xIA5f/r/8j/9v8PABoA5//7/1YAu/8mAAUAAAAlANP/AAAHAOH/4P8nANr/MgDR/9D/RQDW/ywA9f8fAAgA4v8lAAsA8f/z/x8A7v8NAPT/RgAfAPb/FADm//X/jv/+/+T/zf8NAOr/IAAQAN//6f9hAOH/EwAeALb/FwD4/z4AJQA8ADEA+v8QAOD///8JANP/uv/s/9H/AAD8/+7/EgAVAPn/+v8WANL/CAAyAAoAHQDf/+7/+f/M/0cAKwAJACwAy/8AAAwA6P/n/yAAAgDY/xoA9f8zAN//7/8hAK//JAAWAAwAEQDO/wMA6f/t/xsA+//f/w0AMwD9/yUAGAAbACIAzf/q/+z/CADr/+v/3/8FADIAx/8sAN7/yf/j/wQAFwD5/z4ACAAjACwAAQDP/wEA8//u/yUA3/8fANH/OABJAL//IwAMAMf/7/8SAAUA8P/0/x8A3v/q/+b/EQAJAND/QQDR/yYA4v8IADcAzv9DAOH/BAAJABcAGgDG/zcA4P+Q//X/AwB5AA4AMwBIAKL/FACz/xEAIACm/+D/5v/T/8X/KgD9/0kAMgBIAC0Auf8OANr/PQDR/9j/MgDg/yYADQD+/83/JwAXANX/rP8eAOr/1f9AAM//NAAgADsAQAD0/9v/+/8KAPT/OQDX/wUAGADJ/87/1v/E/8b/FgD9/9r/ZwAcAPf/bgAhACoA8P8HAAIAaP/8//j/3v8PAHkAZACz/+r/6//G/+T/BgAXAB0ANgD1/+//+v/k/8L/8f8AAO//LwAwAAEABgAVAPL/CgA+AOH/EwAZAMX/5f/Q/wIA5/8TAAAA+P9GAND/MAAIAOX/8v+5/xUA8/84AB4AKQBQANz/NwDg/8L/CQCV/wwAKgDh/xAA7//t/+H/7/8iAA8ABAAaAAUACAD7/8z/v//i/0AAGgBKAD4A3v8RANn/+f8LABQAFgAFACMA2v8XAPr/2/8sAN//uv8AAAYA+v8AAPP/+v/H/6r/PwAKAPH/LAAQAAEACgAcAO7/AwArAEcA7P8CABoAtf/5/w4ACQDd/ykAw//d/0EAyv9FAOb/GAA6ACUARgC///j/zP+e/7z/u//x/zoA/P8wAB4AEgAzAAYA4v+6/0gA2P8gAFAAyP87APP/IADu/xgAJwDU/8j/u/8CAP7/7//5/0MA2P8GABAA7P8fAL3/AwDn//v//v8sAGoAUQApANb/NAC2/+n/2/+T/yIA3v8gAEkA8/8yAAIA2f/g/5X/BgDh/9X/DgDr/z8AIQA5AD4AAQAlANP/8//4/+7/7f/y/y0A6P8AABsA//8mAP//IAACAPH/6f/Z/yYAwf/1/xEA9f8QAPT/RQDc/xYALgDE/xsA1f8TAN3/0v/u/6//JQAbAPr/LwA4ABkA3v/g/+j/NQD4/wQAQQDQ/xcARgAAAAIA5v/m/wIA2f/+/+j/+/8DAOD/IwDi/yQAJAD2/y0Auv/N/9//CQD4/+b/DQAWAAAAFQA7AOv/TwAYABQANgCp/w8A4f8QADEAzP8+AMn//v87AGf/9v/s/5n/IgAFAOv/NAArAOv/BQC2/wkADwAVAF0AFwBDAAoABgD1//n/7P/1/y4A1f/9/8v/CQD9/7L/EQDh/wQA7/8DAB0AGgAxAAwAEQACAOz/1P8SAN7/5P8vAAsALQAaAOL/CgANANP/oP/M/xQAzv/6/yQABAAiADEAKABkAFgA1v/p/+b/2f8MAO7/+v8aAPz/AwBUALr/0P/5/4P//P/p////8P/u/xsAFgAvACgAEgDr/ysA2/8IAOv/1P9YANT/VQAeANX/FADT/2cACgC8/+D/DwC4/wEACwCW/zcA7/9iABQA3P9KANP/BwDc/w0A+/8KAM3/+P8OAIX/LAASAN3/AgBCAP7/IwBbAMr/RgD0/wAAFAALACsAxf8CAPX/0f/E/yIA4P/C/1EAEQAVANv/tP8JAKD/9/8oAPD/RgAnACIAHAD8/yMA/P8DABQAGAD6/9z/BgALAOH/6v8KAP3/2v/A/zYA/v/V/zMA1f8LADMACgAbAOn/FADI/+7/EADD/y0A5f/w/xUAAABJABMALAAwANj/DAAHAL3/4/8hAM7/1P8gABkAzv/z/xYA1f81ACgAAAATAOP/9//N/87/KgARAOv/+f8RAB8A4v9SADwA8/9IAN//MwDY/+L/EADr////mf8vAH7/AwArAJj/egDA/+f/HADz/wAAMgA6AFEAJwDi/ysA6f8JAN//8v/S/7n/xP+t/zgAv/9pAEcA0f8mABkALAD7/0IAFwD9/wgA7//v/wgAzv+b/xcA5/8WACsAOwAbANv/8v/h/7//qv8MAO7/y/8yAHEAuP///3gAz/9oACwA0v9LAMz/1f8HAAQAUADT/+f/JwC3//L/DgDU/6H/DgAPAMv/EQDy/87/yv8pAE8AXABMAHAARwDF/wEA8//b/7b/MQDe/5r/GgDq//3/0P/q/0wAIQC1/zkAEwDw/9//6v8AAL7/FQDX/y8AZwAyAB0AAAAMAL7/NADu/+f/AADl/ysAEAAmAOT/w//i/+j/+/8fAJn/CAAZALX/XADc/0YAFQAjADMACQDy/77/QgCU/xgAFAD1/yoA4P9FAPP/1v/1/xIAsv/5//f/EwBWANX/EwATAA8A+/8xANb/7f/e/4n/+P/W/y0A7P8VAB4AFgBwAD0AMwDu/wAAwv/f/wwAAwDi/7n/DQDz/wMA8f/6/+b/1v8qAEUAFAAxAA8ACQDq/wQAAwDM/0sA+P8CAAQAv/8BALf/+//3/0gA+v/U/yUA0f81APX///8sAOz/HgD9//j/6f///wkA8v8CANX/FgALAND/TgAWAPb/vv/+/0cA6f8AAMj/BwDK/zAAXwAXAAkAyv8dANf//f8CAOv/FwDA/woAIwAQABIAEAAmAAAABQAQAMz/CwDj/8//DQCi/xsA6f+s/xYAJAAOAEgAGADW/zUAGwAxAOT/HQDW/5z/FgDN/1QAw/8AAFgA8v86APn/GgD+/+H/CwDo/+b/EAAHACgABgDX/+r/5/8CANj/MwC2/8b/DgC7/1wADgBTACYA4f8fAHH/FgAmAOj/LQDv/z8ARAATAAIA9//8/8f/AgD2/7n/6P+0/zwAKQDy/yoAFwBaAMr/NAAAAI//+v+N/+T/FgD7/wwAQAArAA4AXADh/8H/1/8fAPH/+f9eAP3/AQACAOj/3f/s/0cAJgDL/w8A3f/W/w4AAAA8AP//EwDU/+//FwCg/+z/1P/t/zYABQAmAEAANwDZ/+b/aQAtAMD/PgDo/6D/2P+2/+b/BAD7/yEA/f/7/xkA8v8MACkATwA7APH/2v/u/xQA4f8bAEAA2v/f/8n/4P8LAM//MgD//8v/TgDx//r/QwC7/+7/TQDe/wgA5//a/zkA9v9AAPD/4//8/9P/FgANABQA7f8eAOL/4/8eANv/HQD4/x0AKwDo/xkAAwDc/9r/0f8LAMv/FAAeAMX/igAqAF4AIwCq//3/t/8HALX/DgACANT/PADg/9//AADq/xkAFQD3/2QAz//3/zUAuf9CAB4A6/8WAOP/2v9FAL//8f8lAIr/8v/b/w4AHgA0ADoANQA4ANH/AADU/xQAMADx//n/3//w//n/FgAeANf/0P/t/9X/mv8IADUA6v/a/yEAHgDd/4QAXgAwAEcA6P8IALb/DgC9/9T/eADR/xQA0f/O/+D/+/8HANf/PgD8/83/GwAjALb/HgAZAMP/AADS/wgADQAtAAUAKgBvAPv/HQAoAO//+f/S/97/KACw/xEAFACk/7z//P9GAOn/DgAEAAAA8v/u/1wA5f/W/////P8LABQAGAALAAQAOAATANX/DAAKAOD/6f8aABMACwD3/xMA9P+6/zoA9v/F/xEA8f/T/wAA/f8JACkA7/8WAPH/7f8IAO7////g/wAA3//Y/0wABwAsAHEACgALAAkA+P/v/xMA+f/3//X/yv8ZAND/KQD9/7z/HQDC//z///8cAAsA2f8yAPn/6/8PAAQAJwAkALD/7f8CAPP/FwDX/0YA4f/C/2IA9/8UABQABQAXAM3/RAAWAOD/JAAJANz/1f8YAPH/z//6/77/xv9BAEEADgAMALj/+P8MAOH/MAAcABwA4v8aAAkA2P/u//D/KgDz/zgARADF/xIA8v/U/+f/5/8GAOL/CwA8ABYA8/8YAAwAzv8hAB0A+v8cAOP/8f/B//b/EQD0/ykA+v/8/9T/4v/U/9j/JwALABsAMQBFABAADgAzAMT/2P8DAAwANwAAACQABACt/wMAHgDt/+H/9/+V//v/PADA/zoAzv/x/7f/1P92APL/WAAWAFMALwDF/0YA2v/r/wIADADY/+v/KwDm/yIA9f/P/8//5P/L/xkA/P/x/1wAAAAUAAEA7P8nAO//JgC1/9r/RgDf/zgAGgAGACIAAAA9AO//t/8NAO//m//3//7/vv/f/wUA9P8ZAC0ANABNABgAIQArAPH/tv/Y//z/r/8CABMA8//1/xUAMwAGAPH/BQAeAMr/ZgAsAOz/AgCu/wgADAA0ABUAJgDG/5r/QADY/6f/7f/6/+j/GwAmACcACAD4/wAA6v8nAOT/JQA0AP7/FwAeAOX/yf/r/+T/DAD4/+L/YgDK/8n/IgD8/zoAGwAFAOv/0v8qAPL/1v/4//D/8P/1//3/OgAqAA4AGgAAAAwAHQD2/7j/DgAoALT/MQDu/7L/4//Z/yAA8f8HABUADgAaADkAMwDl/x8AAADw/+j/AQA1AMv/3/8iAOD/wf9CABkA1//w/9b/SQCt//P/JwDE/1oA0P8aAPv/1P9rAOD/MwAuAO7/RwDT/8X/7v/P////PwDr/yAAGgDB/wcA5/8BAAEA2f9fAP//9f/9/9f/DADv//D/8//c//T/HgD9/xcAIwD+/yIAPQDw/w0AJQDY/8//xP/+/7//PwA1AAAAQgDS//3/z/84AN3/wv9FANz/JQABAP3/qv8IADkA+/8SAOf/JwDl/wsALAAoAB4A9/+5/wAAFgC9/wUA2P8KAO7/QQBSAOD/0P/B/yAAq/8SACsA1f8dAEAALQDm/+H/GAAjANL/AAD8/+D/GgDy/9P/DwAuABwAKgAAAOr/uP/8/wQAx/8sAP3/KwAUABQARgD0/xkA4f+4/+P/xv8sAAgA9f8hAOH/IwDt/+//GQCX//z/MQARABoA9f8MAOL//P8MABUAJgAOAEQA6P8LAPH/1//q/9v/RQD2/zkAGADK//j/oP/G//D//f8hAPz/+f8yAN//UAAuAO7/IQDl/zUAwf8VANH/BgATANT/dwDR/z4Auf8FACcAgf8/AOX/x//C/w4ADQAOAAIAGgD9/ycAVACi/44ACAC1//T/0v8MALD/JQAbABQA6P8AAGwA8v8tABoACAA8AAIAtP/U/8n/kf/I/9H/0v8hAEgAOAAOACAAFgDL/6//DwAMACgAGQAEAE0AFgD5/yAAOwDS/8r/EAD6/yMA+v/9/+7/r//5/+j/u/8pAPD/AAAyAPX/eQDr/xwA6//F//z/dv8HAPb/UAAWABMARgDB//X/6/8UAAAASgAuADMAHADF/wkA4//Q/73/8/8OABkA5P8cAOL/oP8wANL/CgDY/wAATwD3/1UANwDr/xgAOQD8//b/8f/v/9P/5v8aAN//FgD4/9v/FQDs//X/IwDY/wgAEwDu/y4ABAD8/+r///8xALz/EgD4/9L/JQDg/z0AEgDu/+z/yP8EAOT/LQBCAFIA4/8aAEwAtf87ACAAPQDA/8b/vP9R/+T/rv/0/zkAFQBWAA0A6/9lAAEA+P8CAO7/YACz/xcARQCi/wwA/f/p//7//P8XADwAKQAIANf/EQCv//P/LgCv/xoAqf/4/xMAwv8fAPz/CQD5/wMAQwBCAAQAUQD//9X/IwDZ/zEAEADS//r/1v8mAOn/yv8fAL3/2f8WANX/8//t/08AJgDM/zwAAgAdADQADgA7AL//vv8kAAAAxf8NACEAuv8/AP//tP/f//v/JwD3/00ADgA8ABEA2//q/+T/GACZ/wkA8P8bADoAuf/v/+X/DgDG/wwAJgAWACkAIgA2AB0ACgDx/9f/3f8oAOr/6P8FAAUA+P8MABMAw/8cANr/AQBLAOv/8v8DAOP/yf8kADEABwDj/+//HwAKABcACgDl/+H/8P/5/9b/9P8uANv/7v/9//z/AAAvAFEA+f8tANb/6P8QAP3/OAAlACIA/v8CANj/7v/Q/+H/IQC1/wIAGwDt/xoA3P8EAPH/z/8KAPT/FgA0ADAA8f/w/wAA4v84ANb/CwDl/wEAVgAkAHEA4f/q/yMAr//o/ywA5f/2/8T/2f/n/2n/NgD3/wMAKAD1/yMAwf9NAFYAAAAYAEsABgDi/wcACQD6/+L/DQDB/9j/LACu/w8AFgDi/0UA5v8KAPP/wf9HAO3/+f8cAOj/+/8TAB8AVgAeAN//KwDN/9f/tv+i/+z/7/8SAP7/LgAcABIADgBDAEcA4P9DABcA3//s/+T/4f/8/wYAj//e/xgA/v8MAPn/GQDk/93/QADy/wQAHgBQAAwAzP8EAMP/CwDF/1AAfgD5/0gAAADk//v/sP/h//r/fP+8/87/1v8pACsAOQDf/xoAVgBdAB4AIgAdAOz/7v/9/w4A3P/7//r/wP8JAPX/3P8JANv/yf/y/8n/IAAIAAEAHgATAEYAMQA8AFMAGQD1/9H/w//r/6L/EgAtAP7////W/zIAFAAZAN//6//W/7X/DgAEACcA8P8mAOv/3v/e/+b/NQDt/yAAHQANACEAXQD0//X/HgC0/w8A6v8CAA4AEAAoALL/LwAFAKr/DQDD/6j/4v8VABcAUABIAAUATwD7//j/KgDp/+P/CADG/6v/CADL/yEAIQABAAwA9v8HANr/GwD3/wIAJADh/wgAHQAXABEAGAAXAPb/r//O/xwAJQDi/zAANAC0/+r/4P8JAB4AJAAGAOj/EAD6/xUA9v/Y/9z/8f///z0AzP/g/yYA6P9HABwAKQDl/+7/NgDk/8r/xP8BAN7/4v8vAEUA6f/2/zYA//8nACcAEgAqANr/6f8YALv/8v/x/6z/sf+1/0EA/P8HAGIAGAA2AC8A8P8UADAA1v/+/ykAov8MAAcAsv8YAOr/1v8/AAwA4/8+APb/tv/0/wgABQDe/zwA+v/b/yUA6v8jACIAOQDs/yUAEwDq/ycAqf8IAOX/rv///zYABwAxAEoAwf/u/7T/JwDv/+H/+v/f/9n/BgBwAOf/LAD4/9L/CgD//yIAIwAPAAIAMADE//P/1v/O/yMA7f8zAP//JwAAAML/CwDf/xEAAQAwAPD/0/8dAP3/+/9NABkA7P8mAAQA4v/f/9L/+v/X/+j/AQACABEACgATADAAKQCk/wMA8P/Q/wwAz/8NAD0AGgAVAHEA+f/z/0AA/f8nAKr/+//P/8v/6v/H/zYAuP/W/woA8v8UAGsAKgA6ADcA5/8CAMn/6P/e/+v/HAAwALf/1f/f/+v/SAD1/28ABwAfADEAmv/u/+P/0//F/+X/7/8kAD4ARAAWAO//IQAAAPz/+//t/8H/7f/8/0sAMwDq/0EAAwD9/87/5v/1//D//f8EAGQAnv8RAB4A9v/7/5D/NQCB/+3/UgDp/2oABwDy//j/MwD6/wYANAALACkAtf8JACIA8P/U/+X/4f/V/xgAvf8uAPX/3P///+z/EQA0AEAAuP8xAPH/GABGAB0ALADo/z4Arv/N//H/KwAXAMP/MgDm/+j/zv/U/7b/9//n/xwARQDM/1gAyv8WADAAKwBaAPj/MQDZ/+X/uP/I/yoABgBEACEABwD1/6f/6f8AAOL/QgD8//H/3/+//wsA/P8DAO//OgAWAOf/WwAAAPv/BAAUAAoAvv8mAM3/6v/i/9b/KQDl/xkA4/8gAD4AAgBDAPz/NQADAA8ADgCb/8v/tf/R/xEACgAjABEA0/8bACQAGABTAC0ARQDj/6L/IAC0/9f/BwCk/+z/0/8FADAA8v82ABAANAAxACgAGwC9/w8AMwDq/xMA3v+2/wcAp//V/w4As/8AADoAHQApAOn/EwBFALX/KgAgAAsAYAAPADMAOQDq/77/4v+9/7H/+P/z/+X//P/T/+P/KAARAO3/FQAdAC0APQD5/w0ALwD0/9b/2f8jAOT//v9aANb/wP/Z//n//v/n/wkANgAQAAgAKwD//+j/7P/+/+3/9f/h/yAAFAAZACUA7/8XAOT/6P/F//P/2f/k/4YA0/8kAEkA5f8iAN7/EADx//7/EQDI//z/FwAhAAQAHAD4/7z/EQAPAO//LgDY/5T/CQDy/7T/HAANAC8ASQDu/xMA4v/c/yQA6f9JADoAAAAkAN7/AADn/+n/+v/n/wcAxv/X/yoA8v/1/1cAHgAWAPL/+/8KAL7/5f+5/ykA8//3/04A9/8rANT/NwAqAPT/9P+x/yIA7P/i/0AAPgDu//z/DgDr/9n/4v/q////FwDq/xkAp//3/z4A1f8wAPv/JwADAAAAUQD0/wgAAwAZABAAtf/U/xEA6//n/ysA9/+0//H/cgAaAAIAKQDi/83/yP/2/wAA+v/4//n/FwD9/wsA+f8AACAABQD5/xAA8/8QAB8A0v8tADoA9P8hAAgA+P/6/5v/AAAIAHj/EAAoANP/bwAZABMAGQDI/ywA+f/6/zsA8//m/+7/yf8AAPL/tv/o/9L/7v86ADQAOwAPAO3/CAAlADAAIAD4/wsAEQD0/xgA7f/w/+L/9v/v/5r/6f/6//b/3P/y/xAAtv8uACgAFwA5ADkATgAJABsABADo/+r/LwD3//T/8P+3/xsABAD1/8P/zP/n/97/FwAzABEADAA+APz/GwCt/+3/KwCw/38Axv/4/x8Aw/9AAMb///8CAND/+f8sAA4AGwBkABoA/v/7/wUA3/8sABIAyP/q/8X//f+e/xIA7v+d/xwAQwBDAPn/QgAoACEA7//k/yQA3/8cAPL/6f8MALz/7v/u//7/FADn/8f/7P/d/yQALgA+AGgAAQADAPb/8P8JACEAGAAAAPz/zv+g/83/IgASAPr/FwDR//r/OADW//7/EgD0/wIA8f8wAPr/MQA4AOH//P/u/wMAyv9JAB0A5v/m/83//v+d/y0AOwADACoA9P8bAOf/9/8AAOj/FAD//77/BgACABwAGAD5/0cAwf/K/8z/GwAaANb/iAD3/ygAEgD2/0UAov8LANL/kv///zgA//8mACcA+v8zAM3////8/9H/3v87ACsAvf8jAMr/3P8VAO7/IQADABAAMAA5AAoAIwD//9n/rf/X/ycAz/8HAPr/y//m/+3/3f/v/1EAHgBkAEQANwBAAMv/JwD6/4z/p//c//3/5v8jAFgA0f/x/x0AnP8NADkAz/8PAAcALQAEANf/TgAhANz/KgD5/+D/JwDz/ygA6f/k//D/pf8gAOD/BwBDAOn/AADI/93/x/8LACMALgBYANr/NQAKAMv/EQDj/wcAQgAsAOP/AgDb/8v/5//6//j/FQA9AOr/EwAKAPb/+v/v/y4Asv8uAPr/3/8nAM3/VQARAOv/8v+y//z/xf/q/wQAuP83ADIAIABoAC0ATAAKAAwABgC5/8//0f/X/8X/CQD2/woAIgApAGkA4v8kALT/n//0/7X/HAAmAAwAGgA4AO7/5v8BAPX/AAATAEMAAAAsAPb/2f/p/73/HAC1/7f/8f8kAEwAMAAsACQANgAaAOv/7v/9/+f/EgD6/wQA6v+m/9P/8P8cAND/HgD//7v/IADn/0sACgAuAC0A1/8rANj/+f8ZACcAAAAiABEA3P8HAOT/JQDt/9D/7/8aAPX/0/8YAMv/MQDW/xkAGwCe/x0A7/8RAN//9v8uAAMAJgALAAsA8f8QAFQACwAKAPr/CQAMAMT/6v+S/9b/NgCy/zsA9f8YAG0A5//4//X/zv8IACcAQAAnAN7/NQD4/6//AADy/wYA9P8SAOj/8P/o//X/JQDa/xcA/v///73/IQAaAMX/OgDo/0wACAAAAFsAGgD//8X/5P+//zwAAwD///r/pP8aAKP/4//w/wsAOAAiAD0AAAA0AM7/NwAuANH/IAAAAPr/6P8WANf/5P8VANn/HQDB/8T/7f/6/yAATQAWABMAKQDd/xgA/f8VAA4A3v/w/9H/GAD0//3/GgDh/+L/5/8IANb/CAAHAO//RgALAO7/JwD9/xEAGgAAAA0AHwAGAPf/4f+w/xAAMADo/yQA+P+5//X/+/8aACYACgDt/+7/GACI//f/GADn/1wASAAYACQAIQCf/9b/+P/H/00AGQAvACIAwv/2/+b/qv/3//j/4P8fABQA8//a/0IAEgD6/08AEAD8/wAADQD4/wcAyv/c/xMAIAA8ALn/BgAEANn/GgANADkA8//O/wMA5/+X/yEA+f/n/zQA6/8oANj/TABGAOf/TACn/7///v/c/+7/JQA+ABoAHgDY/xgAJgC6/xMAEwABACoA1//l/9L/3P/L/+f/CQAOADoA7P8nAPH/9f9LANn/RwDv//r/9P/Y/zAA0P9JABwAGwAuANz/2//Q/9z/v/8YAAsAz//9/yMACgALACYA+P8KAPf/JADl/+P/DwDH/xgACQAdACQALgD2/8v/NQDo/xMA7v/A/87/6/8MADgAYQD5/97//P/G/93/CQARAAcA2v8AAAgADgBHAMb/FgAvAMr/DAAFAB4AQQDp/wIAAADH/2EAFQD1/xUAlv+z/6T/1P/q/1sAAgDn/zIAzv88AEcAbAAcAPv/AgDn//X/qv8wAPL/+v/i/8v/CgCV/xwADgAWAFwALgC+/7n/IQDO/0IAJQD4/2kAJADR/wkA+f/T//r/4//N/+X/HQDz/xQAFQD3/xAAr//C//X/LwAiAPP/ZwANACMAGgADAB4A4f9lANX/qP8GALj/AwDy/w8A5P/5/9n/tP8AAOb/FgA9AN//FwBcAAcALQAeAPf/8f/H/0EAxv/9/ycAy/8eAOf/RwDZ/+v/EQDt/yEA2P/9/+n/8f/t////aQAIAEIADwDI/wgA1P8BACQA6v+//zgArv+Q/ygA3/8hAEEALwAsAPz///////L/FAAUAPX/QQC5/8D/6P8AAP//r/9gABcAGADt/w8AKwCQ/ywA7v8VACcAsf8XAOz/EAAVABYAPADA/x8APADi/y8Anv/O/zEArf8nABwA+P8cANr/DgDy/ygAVwAAAB8Axv/T/7T/vP/m/6T/HAAXAFoALwAUADsA6f8TAAsA+f+6/wUAHwAoAEEAJgAOAKr/t//9/8H/yP9QANr/EQAsAAsABgACAE8A1P8fAJ3/1f8uAMH/GwDb/y4A9f8EABsA1f8LAA4AOQASABcAMgANAM//SADj//T/SgDC/yEApP/M/9b/xP8GANb/4P/F/zAAEwDt/0AAFQBfABoA9v8pABUA7v/P/0EAEgDP/xIA7v/e/xAA5f8kAD4A1P/0/+n/5v8QABQAHwDM//n/2v/C//j/CAAtADoAKgDl/+D/4v/3/x4A7P/K/1gAUADu/xwAwf/F//r/JABCAA8ADADr/+j/zf/v/x0Atv8HACMAp/8oAAcA+v9VAP//MgBRABoAtP/Z/+//7v/v//H/GwDB//z/8/8MAOX/KABTANb/MQDf/xcAIwD5/8n/7v8DAL7/OwAUABgAFgDp/wkA8P///97/7v8GAN7/+f9AABcA5v8UAA4Ax//j/xMAKwD+/ysASQD6/xMA5P/a/w0A+v/T/9H/GADZ/wEA4P8JAAIA5f8eAPb/CwD9//j/IAD9/yMAJQDe/wIACQBBAOf/8/8vAOf/BwDE/wgA9P8fAAcA3f8pAMH/NgDG/wAA2v/o/wEAzv9FAMv/SAAhAAkACwDK/x4ABABJAFMABADn/+X/r//x//j//f8MAM//CQAYAPT/5f8lAMj/DwDk/zMAcAArAEIAqv8GAMX/BgC4/+r/LQDA/woAgP8bAPD//f9aABMAGAANADAA+f8iACUAHwAVAPz/BQDq/9r/uf/M/8//2f/1//v/OAA2APr/LgDz/wwA///e/zIA0P87ADIA/v/8/+3/DgDK/wAA5f8QABUAtv8lABQAxf86AA4AAQAUANX/GADk/wIAsv8CAAMA3f8wAAQAJQAJADAA7P8cAPv/3P8UALX/GAAFACQABQADAMz/JAA+ALr/FQDV/wwAyf8rAC4A5v8xAPH/LwD1/xkAxv8oAOX/tv8gAIb/IwD1//z/HAAPAOD/6/9HAPT/VADy/xMABQCf/x4A/f/v/yIAOQD5/xsADQAcAPX/7P/n/73/NwCu//v/+/+4/0UA8P8YAPb/KQD8/w0A+/+v/zoA8/8xABQA9/9UAOH/IgAFAK//SgD1/8f/+f+K/wYA9P/i/2UA+P/r/x4A///w/0oAAAD1/0AAnv/U/wUA9//0/wQAKgADACcAGgAPAAcA2v8mAOn/l/8vADMA6/8aAEgAAAABAP7/z//j/7n/yf8rAND/4f80AAcADQAQACsAJQAOAPL/yf8OAAYAHAAuAPn/2//r//T/tv/1/8f/2P8wACUALABVAEMAqf///ysA3v8oAOr/BAA5AOz/SwDz//n/HwCu/+j/pf/t//j/4v/2/7L/JADJ//n/aQABACIAPgAdABYARQDl//r/RgCi/+L/EgDx/+7/BwDr/97/6v/a/x0A0v8uAFkARgD6/8T/UQDA/9z//P/I/wcAov8iACsA9/8+APD/9v8KAPz/LQA0APr/EwD1/wAA7P/x/xAAAgAGAAYAKwDV/yUAAACz////xP/J/+H/DgDH/9j/ZQA0ACMAMQAVANv/BQAaABEABwCv/+3/DgDO/wYATAAFAPz/6f/J/wYA8f8TABcACgA6AOz/8f/p/0gARADY/wIA+//1/8j/1P8WAAsAAwDj/xkA+//Q/xIA4v/q/9n/AgBfAAgASAA0AOv/JADn/+T/1v/T/+b/2f/2/yIANgAdACYA4P/b/yEACADf//f/9v/4/+3/PAA/APL/AACY/9P/+v/c/1wACgD+/y4A8f8YAAAA9v8NAPD////T/yMAIAAMAF8A/v8LABkAxf/v/77/kf+z/wgAAADy/zQADgAzADIAEAAlAMz/LQDe/+T/FAACACEAEAArALf/5f8ZANL/3f8fAAYAFAAyANv/EADK/wwAAwDW/xYA//8pAOf/GQDR/x8A///H/1UACQAVANT/CADD/6r/AAD6/yUALABIACQA5v8oACkA7P8DANf//P8NAB8ABQDZ/yIAnf/g/wQA7v/X//z/HQDp//z/MQAqAKn/GQAbABoAJQD+//j/BAAzALz/RwAIAPP/KwD7/xQA1v/U/7v/CAD4/8f/7v8GAN7/MQAgANL/LgAIABEAJAApAPH/DAAZAEMAFADO/xgAsP+7/9f/FADh/w8ACwAIACEAAAAyAL3/EQAeAKf/8/9SAOP/8/8MAMj/UgDs/0IAOwDp/8H/+f8iAO7/CgCd/z8A5v+w/w8AGAA2APz/WAAZAOb/2/+//67/EwAeAFgAdAC+/xgACACc//r/8v/V/+f/9v8oAN//HgDs/8r/ZwD6//z/QgBBAOX/CAAKAAYA9P/A/0EAuf+z/wwAAgDx//j////4/x8AFgAdAAEA6P8vACQA1f8sAP//AQAAAOL/4/+K/xIA7f8jAO3/DgA8ABcARwAQADQAm/9BABwA5/8OACgA2P+U//j/h/8PAJf/NwAlAOT/RAD0/1YAiv8EAB0AKwAvAFUATQDq/z4Axv/5/9j/vP+2//T/0f8MABwALgAVAKf/SACQ/x4ALwAXADIA6P8WANv/SQDv/xIA6//m/ykA8/8AALP/6f/h/xkAQAD7/wAARQDW//P/AgD8/wQA0v8CAMv/JADU/yEAHADI/2UA9/86AEUA0f8GAM3/0f8OANv//P8oAA8ANAAGAN3/5f/q//z/2//C//f/7f8IAAAA8v8AACkAIgDd/4IAMABSAFUAAQAuAKL/tP+b/wYApv8WACMAt/8gAPP/IQDI/xAAQQDJ/ykAOQDL/xQAvf/t/z8A6P8rAOr/RQDH//z/CgDO/zEAvP9KAAEA6/8AAAsA3f/b/0EAHQCPACgA6f/w/9X/5P+1/9z/DgDF/9L/IwDd/wMAGQDt/wQAIQAEAEkAEADy/+b/GgAWANz/jgD3//n/AwDb/+L/2f80AJn/t/+3//v/3/86AC4ACgBZAMf/bgCz/x8AYQDE/zoADgAOAAkADgDi/+b/sv/X//D/rf/t/yAA9v8cADwAOAAGAJz/XgADAE8AIwDC/zkArP8QAAgA8v+V//3/7v/e/x8Axv8rANb/VwAvABUAPADa//H/8v8qAO//IwDm/+X/DwD5//v/4f8NAPn/7//6/ygAAgDh/9T/u//Y/zUARQArAGkAJgAVAB8Arf/M/+D/3v/7/+D/yf8KAOj/6v9CAOH/FQAwAPX/KwDy/ykA4v8vAAsA3v8pALb/GwD8/zwAAgALAAsAt/82AL3/9f/B//X/HwAJAAoA8P9eAAwA7f/5//3/uv/n//T/CwAJAO7/GgDe/zMA4P/z/yoAAAAIADYAKwBHAB4A2f88AJb/CQDE/xEA/P+B/zkAfv/y/+D/CAAFAPz/aQDz/xwAMAApAOz/cgD2/wYANADU/xEAsP/0/+D/DQAFALr//f/N//T/MgAIAAwA2P/g//n//v9vAN3/IQD9/6r/MwAIAGAAVgAYAAsACwDA/+H///+q//X/rf/L/8r//f8pAO7/UAAAAB8AYwDw/xcAGQDT/7f/+v85ACoANgAKACQAvP/g/w4Aw/8cAOb/GwDt/8j/AADm/8//6f/8//7/KwAYAGwA8//v/yYA0v8oAOT/FwAuACQACgDr/x4A7P/R//3/2v/n/+//if8YAA8A8P9RAPH/BwATANX/AgA3APv/BwAcAAkAGgD3/8z/KwASACsAVwD9//L/iv8FAO//uv8UAKn/xf/f/xEASABPAB8AKwD1/9r/CADc/wIA7/8EAAQAIQBGABgAFgAcALn/7f8UANL/IADH//H/7P+O/wcAEQDU//j/BAASAIkAIAB9AGIA4v/y/9v/BQDE/x8Ar//p/8P/qf8VAN7/QQDj//D/FAAzAPn/+f/g/9z///8IAGIA/v9UAOH/GAA+ALP/UAAKAPH/8P8XAPv/wP/t/w8Ao//Y/zwAtv8tABIA2v/t/+7/KQA2AOX/3f8XANb/bwAzAAAAGgD7/xEAx/8uANP/xP8IANn/8f8AABcAIAAgANj/CgAHAB8AQAC9/yQAr//Q//b/r/9KANT/KgBFABQAIgDv/wAA/P89ADgAAQAjAMv/u//w/6v/8v/V/7P/HQDn/1sAHwDY/zYAAgDs/yoAOQARAEsA/f8xAPz/wv/6/93/BQDS//H/r//r/8n/xP8gADMAVADi/zUAxv8SAGIA2/9MANj/9f8fAPr/RQALAB4A9f/A/+3/lv/y/wQAr//V/6//GgBTAEAAMAAxADgAFwDn/7b/BgCq/xEALAAnAC0A5v9MAAUABgABACEACgB9/6T/0f/v/9r/XQDI/9n/cQCh/wcAMQD//0gAOwAfAP7/IQCz//P/BgCl/00AwP8LACQA+P8ZAA0ASADu/ysAJQDU//D/4P/z/6n/0/+5//z/+f8XAGkA8P8GABIA/f8NABQAFQAEACMA2//W/wIACwDm/+b/BgAKAEIA3P8AABIA1/8eAPD/EQATAN3/MwAhAB8A/f8rAOf/3v8CAM3/0f+9//P/9v/7/xoAAAABAPj/6f/P/y0AQQAdACUAWwA/APD/4f+0//n/AAD3/zUA7f8YAAwA5v/6/8v/7/+j/wQADADo/ysAz/8VAAMA7/8TACYASADx/xgA9P/y/wEACgAbAND/6f8+ABwA+v84AD8A/v+h/wIAqf/K//7/CgABAJL/HADp/1AARAAaAGwAnf8MANX/2//K//X/KwANAE8AIQBiAM//DgDX/6P/DgCg/ycABwASABQA+P/3//n/0//k/wEA3/94ABQAFgAiAO3/JQDq/ywADgD6/+z/1//d//H/+//y//z/AAABAAAADAC//8v/z/9JABMABgBhAMX/WACl/zEASgCQ/3oA3v8AAB4A8v8RAA8AFgDP/+X/8f/c/8n/CgD1/wYA6P8FADAA1P/y/xMAFgDw/zEAFwAVAAQAIwA5AJj/RwDW/6L/NwDn/x8AKADU/8r/HQDz/wYA9f/u/xUA8v8XAAwA3f8AADwAAAAwAO//zv/s/xgADwCp/xcA7v8TAO//uP9AAPj/DQAoADEABwA1AEIABQDv/6v/DADo/8j/KgDN//X/4f+Z/w8AFgAAACEAFgBGABIALAAXAMX/HQABAOX/NwDe//j/AwC3/zwAJACx/xYAGwDi/+L/y//j//b/AwA1AAUAFgACAN//MgATAA8A/v/2/wEACAAXACkANgCr/+j/CADG/woA9v8hAO//8f8qALj/9v9NANj/zP/q/wwABAACADoAJwAlABAA5//w//f/xf/6/yQAGgA5APz/AgDA/8P/EQD0/7P/DQA9AAsAXgAAAEgA2P/0/zUAjv86ANb/3P/W//P/EADM/xAA4v88APb/8f9CAAQA1/8zAAkAvf9RANP/IQAAAP7/MQDJ//v/t/9DAPr/8f9AAOX/1v8zADIADAABAMP/4f+j/+X/AAAtACUA6P9kAOX/+/8VADoA8//q/zgAs/8BAAwAAQDs/wsA7//w//H/y/8RALv/FgAOABgAUgAFACAAAAAjAPj/FAApAHn/4f+7/+n/OwDk/0MA8f/K/8//LQD8/xAARADe/1QACgA1APH/EgArALT/BwDd/xsAuv8YAPL/tv8pAK7/EgDY/9L/HgA4AEAAPQA/AAwAMACj/8X/EwDL////8f/6/xoA5f/3/wIA4v8bAA4ASwAnAOb/MgDW/9P/KAAGAAAA0P/m/9n/vf/l/w0AJAD5/ysAWwAjAAAA4f/+////AAAMAB0Ap/8AAAQA0v8sABEAUQD4/+X/BADP/8j/9/8DANb/MwA0AC0A7P/2//z/1//1/zsAIADk/08A1P/4/wgAyf+9/+v/EwD+/w8ArP9iAAEA+/8wABwADQDO/y4A0v8VANf/AgALAA8AUwDt/yYA9v/p/8j/8//v/53///8KAOr/MAA1ABYAEQAaAP////8XAKf/9v/d//X/IAAMAHsA1/84ACgA4f8bANL/5v/V/8P/w/8dAPj/HABGAOT/BQDg//v//P/+/1EAzP/V/xcA5/8XACEASgDo/+//2v/y/xwA+f9VAO//QgD0/9f/2v/E/xIAzP8OAJz/JAAkAC8ASgDH/wYA8v8GANz/LQAbAEQAFwAVADUAy//p/+j/9P+Y/yUAtf///wcAn/9fAIn//v8HAM7/KwAYAGMAVgAqAA8AAAAgAA8A9v8dALH/yP8EABQAJQAYAPD/zP/2/6z/NADq/+L/TgDj/wAAvv8FAA4Az//9/zIA6v8BABEANQAmADQAFwDB//3/ov8ZAOn/KAApACQAeQDf//3/xP8KAL3/+//V/+L/FACW/4IA8//8/xoA4f/I/7j/KgACABoATQDX/+j/BADH/5sAJgAqAD8A7P8sAK3/FgDL/+z/q/+//wkAtv8GAP7/QQAZAFUATAADAPf/x/8TAPL/CADp/8z/+//e/+P/+v8+AD0A8P9RANH/5//0/7n/EgDF/zEA9/8gAAoAAABNANT/CgDH/xwANgD5/xAAQQD9/73/9v/C/w8A5P8+AB4A3/8gAOn/AwD0//j/7P+k/7j/VgDF//X/LgAGAFQALQA8ADoABADK/zcAs/+8/+X/1f9NANz/OwD1/8T/3f/j/+3/+f86APj/KwBBACgABwABACUAIAC2/w4A1/+k/0UAs//h//7/AADO/xAA//8UAFYA9P9MAA8APgC2//T/+v/i/1IAs/8pAK7/9/8BAPv/PACz/1EAGwDS/zkA9//H/yIA6//s/+H/4P/0/ykAJAD1/yEA8P8bAPf/DQDg/+j/GADd/xUA3/81AOH/8v8zAP7/CgAQAA8A5P8HAP3/z/+0/+v/AQBjACkAPQA9ANP/QwCj/9j/EQApAPb/v//7/63/8f/U/y0AOgDp/y8ACQD1//r/4//R/z0AHAD8//v//f8bAPP/PwAYAL7/EwAgAPn/GQAjAPf/BQDe/8v/7v/K//T/4v/r/7H/2/8JAPL/rAAcADEARADz/zYA1f8UAAcAx/8LAEQAsf/O/xgAsv/2/9f/LQD2/+v/LQAvAA0ABwBFANH/EwAuAJz/vv8AALj/8f8TAAsAPgAOAEYAFADP/+r/CQDk//L/JgAGABIACQARAAUAQQAqAPn/9//W/8f/0v/P/wkA/f/b/zsAmf8UAEQAv/9fAOX/CgABAOP/KgDQ//3/CQAeAE8A8P/r/yEA2v8nAB8ABwARAOn/7/+u/93/7P/D/yYABADc/y8ASAAjACYAOwAfANH/4//E/8n/1P/8/wUAMwAAAA4A+f/w/0sAv/8wAAMAw/8yAKb/HQAuABQAEQALAAQAu//J//X/GwDr/ycAAAAiAD0A4//9/yQA4f/e/yQA5P/V/xgA9P8aAAEAAgAdANb/7v8LABkAAQDo/wcA7/8bAPn/KwAVAPj/RQDX/w0A3/+S/+j/uP8AACYAzP8XADEAOgBGAPL/JwAGAAAA4v/J/wgAKABZAAIA7f+4/7T/AADx/xMABwAbAPj/AAARAMb/3//Y/wUAIAAeADYAIAAeAP3/IAACALv/8f8AAPr/3P/h//j/BgDo/xUAOgD1/wwAJQASACEALwDq/xcA/v/g/9H/mP8RANP/8v86APr/HQAdAAoA8f/l/9b/JgAGABAA0P8+AFAAxP9OAJH/rv/z////CAABAFIAEADv/+//GwDE/ysAFwAZAGcA2/8DAOz/7//j/z0A5f/i/wkA1v/O/9H/DwCo/0EA5/8DAHQA4P89AN7/OgDZ/w0AWwCb/xMA7//s/yMABAAbAOv/4v8xAOT/HQAKAKv/DADC/8H/zv/8/zQACwBzACwAOAD//+7/AQC6/zMAx/8SAAwAxP8wAPT/TwDO//7/IQCz/wwAy/8dANj/GQA2AN7/3/+i/w8AEgAxACEAMgAmAPL/egA8ABkA0/+S/6T/kP/N/83/9f84APn/IgAqABIAMABIAGUAOQDg/+n/3/9v/xYAIwCr/20A5f+W/yAA9/8NABcA//8AAOj/FgBGAL//5P8yAPb/KQAvAA4A0P8UAAgAoP/Y/wgAw//+/0cABQApAA0A/v8RAAsAEwASAPP//f/z/wcADgCh/woA+v/X//X/+f8KAPr/RAC//w4ANgDL/woA9/8ZAEQAQwD0/+f//v/G/xAAGAAXAB8A8//1/7//4v8RANX/8//q/xIACgATAAgAiv9SAOT/6/9HAAIATwDK/0AAPQAIADsAAwAJAKf/3P/r////0P+i/+v/BgDg//D/aQD4/y0AGQD//wwAwf9HAO3/+P/l//z/MgADADwAJQD2/8L////Z/w0A4v/r/w0ApP9JABkA1v8AAO//+v8DAE8AGgAlACQAv/8pABMA6f8xAKr/6v/x/+n/KgDZ/y0A8v+5/xMAuf/3/zUAAABFABoADwAgAMX/8f/8/yoAHwDr/yIAlf/l/x8A2/8CAAsAHAD7/xMAOAAZAOn/+//a/+r/9v/+/w8A/P8NABQA7P/A//n/1/9WABIACQBjALb/GAAPANL/FwA1APb/1P8XANX/BwAdAML/3v8XAMT/9P9RAJv/DAA3AL//FADh/97/DgD2/zQAKgBmAFwAEQACANz/5//u//P/NwAlAMD/4/+x/9j/1//4/04Asf/c/yIA9P/w/yoAHQA/AFUAHAAUABYA9f+d/9z/DADf//T/8v8NAPH/AADt//X/MQDe//7/HAABACoAwP/n/wEA6/9SAPf/HQAhAB8ANAAZABIA+v8QAJr/4//T/7T/9P/h/1YA8f8QADcAyf/3/+f/of8/ACoA5v8pADkARgDW/w0Ayf/Y/9r/DABCABEAOgDn/xAA+v/u/x8A+/8qAPT/4//A/xMApP+9/yYA3/8FAOf/LwBDAB0APADX//v/KQDO//r/9/8tAMr/AAAPAMf/hQAhADgA5//z/9z/qv8VAM7/NwDb/+j////i/ykA6v8QAN//OAAZALX/7v84AOz/GgD6//v/WwAEACgA7v/E/+3/BAAPAB4AEgDE/+f/x/8DAAgAGQAsABMA9v+y/+//LQADACUATAD0/+//0//z/93/AAA6AMn/HwD2/9X/HgAkABQACQD0/wQA8f/A/ysA4/88AOf/6P9YAKv/DwDw/xgADgAGAPT/3v82AOL/MwACAL//9//S/8j/BQBdAB4AIwA7AN7/6P/9/8P/GwAbAMb/DwDw//H/AgAaAHMAtv8PABAAlP9zANH/1v8wAMH/AADd/+//QAA5AC0AKwCo/+z/AgDl/ysALAAHANf/EgDN/w0Av//K/w8A4v9LAPH/FwDa/+z/PwDC/00AVQAJABcADAD2/+r/GwDd/87/AgDn/wQA6v8wABUApf9EAAEA0f8CAAAA/v8XAAUA3/8GAMn/EQDy//T/SgDy/wwAMwDv/9z/AQAHABgADwAWAPr/BgDU//j//f/Y/x0A7P8NAOj/HQBQABgAHgAKABUAiv/1/9j/wf/n/wAANgC2/yUA7//o/wYAKAAdAP3/XAAwAAQAPgBPAIr/1//0/8D/NQD7/wQALgD1//D/3v+G/+b/DQDf//f/MQATAPj/PgAJACQABADn//j/AgDv//f/QQDm/zUA6v/w/ysA8f8zAPr/9v+9//r/1f/Y/0sAAQARAD0AKwDT/wYAov+j/9z/ov8sABMATQBHACAAWQDu//z/9P/V/wEA/P/f//7/NgD5/7///v8sAPr/7/8HADsAxf/k/2QA8v/9/+b/+P+//7v/JQAIABYAKgBLANf/AQB0AMP/EQBAAND/6//B/87/9f+5/xIAFQDt//j/AQAIAPT/JABHACcAAwDx/wMA5f8BADgAxP8LAAQA9P88AN3/RADx/+D/GwCd//L/v//z//f/1P8rABEALgAqAPz/GwDm/8T/UwDw/y0AOQDY/xcA1v/x/w4ADQD+/w8AIgDu//z/8//S/9X/6v+1/zwANgAdADMA4//L/8b/EADY/yEAGwDu/x8AAAAmAAAAIgAtANr/LADv/93/CwCn/yIAx//z/xkAv/91ANv/GQAbAPz/7f/o/x8Ao/9MAOn/JwD+/8P/NgDk/x8AOQAvABMADADN/w4Ao//z/1AAmP/6/wEABADP/wwA9f/s/9P/3/9oAPP/UgBBAAYA2/8NAAoA7P9lAOL/5P/0/9P/yf8pAAIAxv8BAPn/HgDD/zQAPgAsAAwA+P8GAOH/BQCb//v/6f+8/0cA//8fAB4A5f/3/+j/AgBJAC0A4/8gABIA0v8+ANf/+f8JABwABACX/0YAyf/w//j/8f8lAML/BgAqABsAAwAeAMn/EQDk/8X/SADS/1wANgAYABAA+P/B/8f/FAC+/xUA4P8AABIA//8QADIA+P8dAA8AmP8NANz/NQAJAA0AAACA/wUA7/88ACgAeQAWANL/LgDO/+f/6v8+AAAABgD4/xYA9v+F/+X/1v80AP//DAASAML/KwDw/9f/JAAFAC4ALwAOAEwA5P8OAAMAtv/3/7j/6P8EAC4AIQDS//X//P/m//D/IgDc/1UARADG/0sACQDL/wIA3P8DAAkACwA/APD/CgD4/9L/EwCb/w4A6f+x/x4AAgBwAPb/QAAWAKv/MAC8//j/7/8/AAAAt/9AAM7/FgD2/xAADwDm/zQABAAgAAAA1f/7/xsAyv88AOb/2f8oAMT/IgDv/14A1//O/yEAwP86ABAAIADe/x0Ay//f/wcAsP9pAO3/9P8iAP7/+v/d/xgA8P/S/w8AFAAWACMAJQBjAPb/yv/9/7X/qf8dAAQABQA8ANb/LwDc//v/CwATACAAjv9XANj/CgAIALb/VwDg/z4A3v8eAB8A5P8nAMn///8mABcAuf8mAPf/0P8gAJT/2P8CAA0ALwATACwACgAFADgA3P/N/ysA3P/v/z8ADAC6/+3/FwACAAUALwDs/+j/LAADAAgA4P8EAAcA3v8QANb/v//p/+r/UQAPAPD/awDe//z/TwAAACcAuf/c/wAAwf8lAA8A2v8WAPD/FAAlABkAGwCq/ywALgDH/xIACQDK/8v/IgASAN3/7v/5/+T/3////xEADgAnAD4A/f/Q/8P/AABLAEAAJQA5AAIA5P8KAMn/8v/D/9D/7f8AADYA3/8mAB0AuP8mAFsA7v8/AFwA6////8z/s//X/7X/lP8PAP7/xP87AAkAKgAeAE4AQgDV/0YAMQD0//3/CwDX/83/6f/D//D/7/8bADwA8//4/wgAzf/U/xYAAgA+APf/GQA1AN3/SgDF/xAA/v8aAFgAtf/j/7j/xv/k/xMA9P8PACoACQASAOz/OQDD/z8ABgCl/yMAyv/r/+f/SgD7////OgANAGAA9P8MAC4A4/+8/9f/6f+j/xUACQDO/xcA0f8kABYA9v9IAOT/TABAAO3/SgDy/8T/AwDQ/wsA/v+W/zwA8/8sAEAA0P8vAG7/0f/w/9z/AgAMAFcA+f8qAO7/FwAqALb/NwATALz/TAAdANr/eQD4/9z/BQCd/9T/9/8KAC0A9f8OAAkAp//9//T/2f8mACEADwAGABAAPAAhALz/QgD0/+j/8f+0/2sA3//S/xUAu/8gACcA1P8rACcAzv8vAN//8P8+APz/zP/w/x8A4f8wABkAxP8ZAPz/3f/t/8L/CAD3//L/AwDa/y8ACAAhADsAKABQACIAKwBAANz/0P++/1z/2P8dANL/IQAQAPv/DQAkACsA2P87ABIA+v8vAO//KwDF/77/BQCu//r/+f/T/wwAHQAkAO//AQA2ANL/IgA7AP3/BgD//zAANAD2/wkAGwC9//H/1P/J/wAA2P8nALX/AAAAAM7/RgAcAAUAFgA4ANb//f/q/w4AIQDK/yIAIwAFAPf/XQAVANH/EAD2/wEA2/8oAL7/7v8gAKv/DgAGAMr/AwAEAN3/AwC7//b/JwDv/x4ARAAbABQAKwAJAC4AHgADABoAAwDm////xP/U//v/5f8sALP/+v/o/8j/IADf/z8A1P8TAOT/8f9qABMAUwAIAD4A/f/Y/yYA5v+c//H/DgDW/xAADgDw/+//4/8JABwAqP/q/xEAvP9DABcARgBxAP3/BAAUAOP/DgAgANH/4//T/yEA5P8KACcAwv8cALz/KADf/73/CADs/zIA8v8YAA4AFgAJAOf/AwASAE0ADADN//f/vP/T/24ACgALADEAwf/H/9T/MwD//wAAHQDl/xAAFwD9/9b/NQDX/xoAUwDA/yAAtv8SAPz/yP8+AN7/KwAwANr/6f/Z/wwA/v8SACcA6f8OAAMA4v8LANv//v8DAN//1P8OAAUALQBlAPr/LwDX//P/HADp/0kA8v/6/+3/5P8VAKD/6v8DAMv/IgBVAOX/vP8BANP/qv/4/yUAIgAhABMANgAoANz/NwABAAMAPAAMAHgAwf/j/zgAi/8MAOr/vv8AABIA4f/L/yYA1f/2/wkAw//v/0IAPQAXADcAFQDy//v/5P8CAAMA2f/k/+//3f85ADgABQASANH/4P/S/+L/DAAyAE0A8f8jAAEA4v///wAAGwC5/+T/8/9CAGAAAADB//n/7v+0/3sA5//8/xMAvP/r/+v/FwADADwA5P8LABwAwv/U/8v/MAD0/0YAFgAJAB0A+/86APL/DwAMAM//+P/j/8D/IwAmAAQA8P/L/83/yf/u//v/PAAVAEUALADl//z/JAALAP7/EQDj/2MA1f/+/xwAuP88AKj//P/v/9z/5f8VAB0Alv88AA4A9//7/77/GAAEAAwAPABBAPn/QgA1AO7/AAAGAMP/3f8WAN7/MADW/8n/DAD3/wYAGgAeALz/CwDU/8z/7v8EAC4ACQBxAAAACQALAAgAAwCT/0EA0/+v/xcAFQAuAAsAEwD6/wcA2P8xAPn/tP8XAM//RwABAAcAFgDY/wIA/v8lANX/cAAkALH/SgDL/8X/4/8CAPb/x/8kAMf/2f8FABIAXADv/xoA6/8AABsA5P9iALz/+/8QAOX/TgAMAEcAEwDy//r/7P/w/6z/JwDi/8D/+v/g/9j/6P8rAAUA8/8jAPX/8P/z/+7/DgA9ABoAMQBfANX/DgApAPn/SgASAN//xP/H/87/oP/3/xYA1P8LAA0A2v80ABoATgBOAJ//EQD4/7b/DQARAB8A4P8XADAA8//w//L/EAAQAA0ACAADAP//IgD2/9D/EQCa//P/BwDc/2AA5f8IAAsAx/8nAOf/9P8lADkAEQDe/+P/tf8JAAAACwBIADUAFAAAAPP/nf8VAP//6P8WAM//EwAaACkARgASANj/6P8MANj/BQANANj/6//q/wgA/f/r/xwA8P/5/zUAJQAjAOf/NQDn/+j/EgDR/+v/t//f/9P/8/9OABYAIgBOAGYA2f8bAPL/pf85AK7/xP8pAOv/3P8eAC8Axf8EADMA5f87ABkA9v8KAMH/KwDf/wwAIAB0/0AACQDf/zoAy/8uAOH/5/8XALX/MwDn/+T/IADi/1IAMgAPAEAA1/8GAPb/4v88APT/LgAnAAsA6f+f////HADg/+r/CACm/9H/CAAUAOH/l/8MAPr/EgBlACUADwAgAAoA8/9VABsA3v8gAAQA2f/u/9//9/8dAOj/HgDx/wEA+v/Z/87/wv8mAOr/3/8LADIA8v8pAGoA9v8aANn/NwBCAM//6v8FAM3/t/89ANb/EwDs/87/JQDi/z8A3//q//b/GgBFAPT/NwAMAOX/CQD9/+f/+f8AAM3/4v///+f/IgAUAD8AIQDH/yYArf+y/zsAlP8EADMAEgBuAPr/EAAaAAAADAAPACcAo/8bAA4Av/9aAM3/wP/c/9T/vf/b/xwAMgA5AEUAQQC8/xcAGQCe/xIAIwA1AAAAGAASAMb/+P/o/+L/yv8kAP7/+f87ANv/DgAZAOX/EQDw/xYA/v/k//f/2v9LAAAA9v8LAPv/GgD9/yIAEgDc/9D/EwC3//L/EgDQ/zAAyP9NAAwAqP8oAAcAFABQAB4A9P9XANj/+P/e/7n/DgDZ/zwA+f/j/wQABQDd/8D/GwCn/wUAHwASACkAJgBmABgAMQAyAOT/vP8AAPb/0/8IAAQA8P8LAOv/zP+0/6b/8//4/wAAQQD/////cAAwADIAOgAKAAkA3P/9/9X/4P8RAMj/7v/3//D/8P83AOn/7v8rANn/FgAlACgA+////ygAGQDj/+P/GgDR/77/KQDe/9j/6f/d/+3/7/9kACcABQBUAOn/BgDt/wsA1/8GAM//5/+AAMn/TgBpABEA+P8AAPz/lP/J/8z/4f+4/wwAy//5/0kArv9IAPv/KgAxAO7/VwAHAO3/MwAlANT/2f8JACAA7//z/wIAIwDb//7/JwC6/93/y/8NAKn/AABZANv/YAAdAAUA+v8pAC0A1f/j//v/EwCw//f/9P8QADkADgAPAAAA2v/a/wcADwD3/97/GgAAAOX/OwDX/+//GgD4/zkANQDa/xoA1//I/xkA0//7/xEADQALABYA/v8AAA0Awv8FAA0AAwAnAAsAJAAbAPb//P/v/xAAlf/S/zsAnv9EAAcA3P8rAOP/IgDT/xMAQAD+/xMAGgAMAA8A//8OAPb/v/8JAM7/BgDe/9D/BwD9/xQABQAaAOH/GwAdACkA2v8XAEEAxv9bAPX/EQALAOn/JgDB/+T/zf/9/8L/8f/i/9T/8v8vAAgABQBXANX/WQAxAOD/DAAFAPT/+v9AANL/CgDG/9X/CwDX/z0ACgAlABEAzf/2////2/87AB8A1f/6/+T/LgDv/+z/CAD8/x0ADwDq/9r/5v/y/z8A8/8EAFEACwAAAAQAAgDk/5//6v8hAOj/BAAGAAcA4P8jADQACwA4AJX/zf/0/xkAOQAmADIA3v8jAPv/yv/8/+z/AQALANj/IgD//+z/NQDK/+3/9P8HAAMADwAFAPT/BwDq/yIA6v8jAPj/DAAwAM//9v/X/y0A6P8nACcA0f9oAAAA1v8iAO//q/8AAOb/9//l//z/IwDv/w0AAAD6/4D/JQAnABkASADs/2MA8P/g/zsAAADi//H/0v8aAOr/4/9eAPj/SgDr/xYA7v+7//j/f/8fAIb/CgAmAMf/RQAgAFwA9f8hAMf/DwAzAO3/RQDt/93/v/8LAOL//f8NAO//NgA5AIIA/P+0/wMA1//R//3/9v/0/+b/yP8GAPL/7f9BAC8A+P8UABIADwDk/z0A9P8SAEUAk//3/73/4f8FAAwAUQDv/w8AzP/o/zAA/v8MABEA6f8AAAoA9P/P/wgAGADO/20ACwDl/+P/5/9ZALr/JAAdALb/+v/2//f/FQAIABwAMADi/wAA6P9YAAYAzP/d/8H/NgDH/xEAQgALAMX/FAAQAIT/DwASAC4A5v/+/xkAJQA0APD/YgDN/8r/9//m/+7/AQDx/wUAOADc/x4Awf/S/xkA+f8hAPD/LAAPAP//0P8gABwACgBCAPX/HQDn//X/FADN//H/pP/d/wwA1f9IAA0A4v8IACoANQAYAAQA3f9GAMz/2P/+/87/DgDd/zYA5P/o/wsAEABIAOL/VADD/9X/GgDQ/zkAMQBZAPH/1P/W/83/6v+4/xcAAQDr/1AA8v/T/wEAKQAQAAIA/f8WACAA+f8oAM3/9/8NAPz/GgDU/yIAAAAGAN//3f/u/+z/CgD//2UAAAA3ALL/ov8GANv/OAD1/yYAz/8XABIA2f8vAN7/JwAFADgA3/89ABEA3f8+ALT/QQC//8j/CQAnAN7/ov80AMj/IQD7/xEANgAlABUAxf8BAKf/zP8tAOP/MQB9AO//WAArAKz/uP+G//z/HwAjACIAOADr/wkAMgDt/0MA2v/d/+7/3P/W/xwA3P/P/zwAvP83ABwA1v8lAPn///8RAAsA0v/1/8j/KgB1AB4AFgBQANf/nf/6//P/MwDt/wwACgDq/7L/5P8cAK//NAD5/wUATwDI/+v/UgAbANL/HwDw/wEA/f/s/wEA8f8gAOP//v/k/wQAFgApAAQA/v89AMr/6P8UAOP/6f/V//z/AwDw/zsA4v8aAFwA6v8dAAoACgDe/+b/FAC8/+v/LQDd/9b/KgDz/wEATgD9/wkAAADf/xUA3f/7/zMAs/8EAN7/LwAPAK3/YgDm//D/VwDq/xMAPwAtAPD/pf+z//v/zv/3/9n/CAAjAAcAZgAbABkAHwAoAN//8P/p/4f/xv+7/xUADgAAAEIAGgATAB4AIQAsABAAAAArAOf/4f8IANX/9v8FABgA5f/a/+b/7/8QAOn/AAAMAOn/AgAeAP//1v8LABkAAwAuAC8ACwDp/8v/FAD//6P////5/xUASwAlABkAy//h/9f/DwD3/zAARwDc//v/CgArAMf/7f8dANL/HQD8/wQA3/8FAP7/OwDy/8z/AwCl//L/2/8BADYAWgArAEMAKACz/zEA0v8fAPv/vf/3/6j/7f/S/zkA4v8BAHMA0/8fADUA6P8jAC0A2f8eANz/9P8AAMH/CADA/wUAKQAAAPv/BgAaADsAJgCo/xUAtf+s/3QA//8vABcA3/8WAND/EAATANv/BgDz/wQAvf/O/z8A+f8BAD8AOwD6/xwADQDn/xgA9f/v/9//2v/d//H/5f8aAEAABgBGAOD/5f/Q/7L/HQD0/zUAGQAJAA8AAgAyABkA+v8qANv/6//z/7P/CAAJAC8A6P+3/wgA0v8BAAEA6f/x/yQAPADy/yIARQDv/zIAIgCo//7/NgDr/+L/MAALALD/7P8LAPH/2P/6/ygAHgDs//D/zf/S/yMAFABCAPP/9//9/x0AHQD//1sA9P/0/+b/MAC3/8b/TQCs/1gA7//G/yMA0P/H/7D/9/8EABwAvv8lAGgAEgBhAPX/EQAqAAcAKAAGAMj/yf/4/9n/9/8GAPL/6v/3/wAABQA9AAAABwDu/5P/NAAhAND/NwDr////WwD1/ywA4v/Z//X/mP8QACQA9v8XAAsA+f9CAEIA8/80AMP/0//g/8H/JwAQAPX/9f8QAOb/4v/m/wgAQwATADsAzP/R/wMA9f/x/1EAJAC2/x4A4//y/xcAAAAcADMA8v/S/xcAvf8uABsAof/6/8v/AQAvAPL/QwAhAP//MQDK/9X/GQAQADMAOwAmAAIA6//3/8H/xv/A/6v///8CAPr/BQD1/0IAEQAhAE0A7f8pAPD/7/8KANL/KADG/9P/GADc/yMA5v8EAD4AKwAbAPT/CQDp/wMAAgAMAAAAtf8FAOr/+/8fAM//GgAHAOP/CwBIAAkA2v/j//r/EwDp/ygA//86ACQAwP8bAMn/9/8NAPr/FgDP/9n/5P/i/w8AQQApAOH/3P8WAAoAzv8mACYAxf8LACMA6v8xAAAAEQBPABAALwAzAPH/y//v/8f/7P/U/8r/5v+l/9j/q/8TAD8AHQApACIAHwA5ADQAEQBPAPb/JgA2AO3/4P/L/+z/nP/u/wkA0v/z/xIABADw/+j/z//2/wIAQwA1ACcANwAAAP7/4v8AAAAAAAAAACYAFgDt//L/lv8KAOb/5v9kAOX/+f/3/8//IgCa/yYAQwD6/14ACgAhAPH/9P8CAMb/AADp/wgAJQD5/zIADwCo//r/4P/Z/0gATADw/8H/9v/c//D/CwAnACEA1//u/+P/KAADANj/UgALAEQAHwD4/+//mv86AOz/FgAYAMH/FQB+/xAAFQCq/wsAJABJAPT/KwAlAOj/9f8KANH/QwAhAMf/XQDp/9j/+//j/8D/1P8BANn/OgA9ACoATwDp/wYABACH/wkA0f8bANT/4v9PAOr/XgDd/1AA+P/m/3MA2/9mAMv/sv+s/4r/9//t/xQAJwAQANz/CwDU/yAAKgAeADAA4/8EAO7/9v/x/zYAAwAuAD0AEQACAOv/+f/V/+//1P/n/+b/BADs/xkA9//2/xIAtf9QABsAaADc/9z/PQDC/xEA//8AAOT/GgCc//L/EgDD/zoA3P8tAAAAIgATAOP/BQDw/0cAJQAbAAEAGgCz/+f/HQC5//3/9/8PANb/EQD4/7j/VADq//7/FwBMAPD/xP8lANr/GgAeACoAUgD5/yYA4v+//6b/6v8bANL/LAD1/wEABwDT/8D/7P8xAOX/MgBVAEAAHADp/yAA///O/9b/6/8FAPX/+//w/8T/1P8OABIAIgDz/wgACADx/5oANgAiACkA0P/A/8z////G/+f/FQDZ/8///P/h/0gAZgC4/0MAIQDj/yQA/P/L//D/w//7/w0A4/+RALn/FQAZAOP/bgDY/z8AFQAEALP/7//W/4r/TACw//X/5v8oAFMA5P8OAAcAHgDi/yYADADV/w8A9v8EAPH/wv/6/xoA9f9FACEAQQAqAO3/AwC6/9P/9P/r//f/8v/0/zoA+f8bAAAA2P81AP7//P/7/+3/3P/n/ycADQDz/w8AHQD3/xoA5f/p/zIACgDn/8v/CADy//f/gwD3/9j/HADA//n/+/8WAN7/xv8jANb/IwARAAcAOQDf//v/JQAAAEsAOgDi//j/1//J/9X//P8AAPX/4//5/0kAt/8NAA8Av/9EAN7/EAAcABMAGgAAABwA5P8BAML/GQA2ADAAMgC+/wQA/v8TAAsAAQDQ/+T/FwCl////wP/j/zEA6f8OAAcAPQAAAAwALQD2/xEAAgAJAE4A6f/t/woAxP/s//X/BwDn/+j/7v8PAPj/CQA7ANP/BAA5AC8A7f8cAOr/+v8AANj/JQC+/yUAAAAFAOr/wf/s/5n//P/W/1YA/P9OAHAA3v9JAOH/9f8BACIA+f8ZAPz/BgDu/+L/IQCm/0sA8P/c//D/nv8LANf/CgDx/0kAXwAmAB0ABAAAAOH/3//8/9P/xP8WAOD/8/8OANr/5P9DAEUABwBHADQAEgDg/+T/5//r/+H/qv8kADUAJwD//wIA2v/l/+H/vf8jAAMALAAtAA0AIwDK//b/GwAcAPD/AgD9/9//MgCk/wAAVgC4/wcAEwDi//b/zv8VAGEA8/9DAA8A1v8bANn/GQDI//f/AADd/wQA4/8aAMf/LgAZAAsAAgDk/xwA8v/7/8z/9f8dAO7/LQBXAA8ALAAWAOv//v/3//H/qv8YAKr/3/9eAAgAHgD7/xwArf/t/+f/9v/Z/xUATwCX/5EA7P9YAC0AvP85AEP/TwCU/87/OgCv/20AHQA2ABMAXADc/wgADQCe/xMAjv///9v/4P9WAA4A6/8UAEQA5/9RACcA/f///+7/GgCu//r/zf/l/w4A3f/k/+3/6f8WAOr/AwBXAPL/LgDr/1UAYgDR/yAAn//y/w8A8/8MALn/+f/Y//n/AAA9AFQA2v8AADwA5P8KABoAGwDe/7L/BACz//T/CgAHAAYAEwAlANj/MAAEAPv/AwAGAMP/1P9RANb/TgAFAMX/GQDW////SwDT/+//KQDX/0gACwDq/zoAqf/M/zcA+//5/wYADQAOANj/OwBIAAoAAADa/+P/pP/i/93/CAD3//H/DQDa/ycAFwA3ANb/NABEAMn/UQDn/y4A3v/H/0oA0f8gAAsA7//7//L/FAAsAM7/r//7/6b/6f/2/w4A5//3/0kA9P87AAoAHAAJAB0AWwANADQA6/8jAJT/4f8jAKn/TgCu/xUAHACf/w4Asf/t/+n/FwAhAD8AYQAEACMAsv8jAOr/pv8LAMX/QQALAPD/KAD9/x0AAAAMADcA//+2/wcA3f/a/xMA+f8HAOb/AgAFABQADAAwABEAu/8TALf/6P88APb/TwAtANH/IgAPAPT/GwDY//3/yv/F/x0A9f/k/xYAEwACAOD/CwAUAPD/dQDq/x4AJACz/9X/+v/l/7f/JwAAAD4AOwAvAAQA0f9PAKf/JgD+/6P/FADq/+P/1v///97/WwAFAOf/z//N/xsA9P8pADYAEAAYAEQAAAAGABYAAADm//f/GwDK/+z/DgABAAgAJAAPAAwAwv8OABQAzP/w/9n/BgCw/+//EgDT/2sA7f8OADkAzP/i//T/HADf/wwAdQAFAPb/TQAAAMn/EgDV//L/9f/d/zUA7v8PAPb/3P8LABQACAAOAEMAlf8IAOT/u/9VAAIAHAD8/9//8f/x/w8AAwAAADUALQAGAE4AtP/o/9v/2f8TAND/PADx/zcADQCw/+z/yv/f/wwANAAaADQABAAiAB4Axf/l//r/FAD3/x8ASgDm/+v//P8CABAAwf/k/9//7/8UAAoAEgASAPX/AQAVAJX/CAAOAN3/OAD2/xwAFAD1/zoAOwAxAD0Ayf/+/y4Azf/g/33/u//K/8//6/8qAEkADgBDAN3/OAApAA4AQgDx/xgAuf/j/9P/IQANAKL/YADz/7D/IQDr/9T/PQBBABAADgDh/83/DQD3//r/CQAPAA8Ayv8AAAAAl/8XADEAEQBFACAAPgDx/+X//P/e/xYA9/8OAAgA5v/V/9//6f/W//7/IQBKAM3/HAAYAOr//v/G/xIAAwDw/wYALwAIAAMAOAAGAO3/CgAyAO3/AADf/7f/NAAAABgA+P/Y/ysAxf8tAAcA1v8QAIn/IQDW/+//NgDq/zQAwf82AOb/FgAiAP//dgDK/x4ADgDq/1MA5v/m/yoAAAAoAO3/vf/t/8D/DADP/8P/xf/E/+z/7v8HAEMANwBKAIIA0P8gAGAAwf9dAC4Anf81ABUAm//g/7//p//D/9v//v/5/zIAIwAAAAwA7f8bADMAEwBUADMA//8LAOX/CQDi//n/AgARABIAyP/d/9z/3//l/wYA/P/q/+b/EgD0/87/DAD6/zwAPwBIABwAKgAdAPb//P8KAAAAAgAaAPP/AgCy/7f/wf/B/wAAcv8dABcA4v8/AF8APQAmAFoA4f8gAC0A9f8ZAO7/yP/I/wMA6v/5/wwAw/8DADEA7v8CAMn/z/8RABcAJQDl/+b/7f/4/xEA+f82ACkAEwBYACsAGQAkAPj/BADO/93////V/8H/2P/M/6b/2f/x//j/YgBYADsAMgAYAMP/y/82APr/EgApAAUAGADm/wIA9P/C/83/DwDf/w8AGQAAAFEA5f/1/9T/y//5/+v/EwDz/1QAHAD+/0AA+v8LADkA9P/c/9L/xf8XAAYA7//k/yYA4//F/0cA0P8HADEA/P/w/+3/CwDy//j/CwAyAPz/CwAfAOP/JwAbAAIADgAcAA0Ayv/U/8//7v///wYA7v8mAEgAxP/Z/+j/yv+4/wEAEAD0/2YAHAAsABUACAAdAOL/UAAOAAQA/f/3/wwAtP/v//P/zf/5/zcA8P85ACkAx//5/4n/EgAEAMj/IADs/w0A6v/8/zIAPAAgABwAFgACAAUAEQAuAPz/0f/N/97/tf8KABoA9/9fABcAxf8nANj/s//+/+7/LQACAPv/BQDi//L/CwBOAN7/7//9//n/WADo/0cA5f/f/xYA6/9DAML/6P/j//T/NADv/x8A7/8AAPz/+v8GAPH/KwDj/93/4P8rAAcAzf8KAA4AHgAUAAAAHgDm/+j/MADi/w8AFgAHAPD/sP8IABkAAwAgAPT/7P8gAAAA4P/j//f/HQD4/8z/HgBSAAEAJwDi/93/LwCu/8r/JQDk/9f/RQAkAAEATwAJABgACwDk/+v/xf+5//T/+f/W/8D/cwB6ANf/bgDq/4z/5/+8/wQA9v/1/1kAMQDv/wcASwAdADYA9P/P/xEAmP/W/+7//f8TAAEAOwDW/wYAOADO/+L/5P/Q/0gADwDl/yUAoP85AC8AJABCAOf/QACx/9//BgDv/wAA3v89AOn/AgDX/8f/CwDQ/0EAPADt//D/zP/T/zEAJwD3/xgAJwAqANb/RQA8AL//9P/Y/+v/zv8ZAC4Auf8PABEAHQAsAAEALAD0/+L/GwC2/5j/p/+y/+X/CwBpAGgAWwA7ABQACQDm/wsADADg/8z/JQDf/77/MAD2/8r/5v8TANj/IAAmAAkAIgANABoAyv8UAMr/rf8LAO3/JwBPACMA4P88AOj/AwAdAO//QwDM/9j/FwDT/7b/RgD9/9f/TwDd/8//z//0/7r/GABXABwAJQDj/wsAEwAXAAkAbQDe/8L/TwDn/x4Auf/s/+z/0v8cAJz/QwAhAOP/CwCz/+b/FAAtADUAGAAhAOv/+/85ANb/FADS/9//VgDV//j/MQABAL7/KgD7/8b/KwDC//X/AQDG/wMA/f8KAEkAAAAUACkA+P8jAP3/AwAEAOj/6f8TAAkAvv8NAOL/FADo/8j/LwAAAAQAFQBFANn/+v8ZABcAHwCy/wwAzf/6/xIAEAAbAAEADwDR/yQA+f8YACQA+v/+/8f/9v8OAOH/3P8HAPX/IwDm/wAAKgCz//L//P/e/zgAVAAUAHoAAwAHABEA2f9DAMb/zP+b/8X/uv/B/xUACwAxACYAOAC1/1kATwDF/zcAx//c/wgAEgDh/1YAGADo/2YAGADp/8H/6P/U/83/7P/w//X/0v8NAB4Ax/9JABYA8P9ZAOH/MADz/yYAHgCo/zUA7P/y/yoA+//g/woA2f/f//P/yv83AOD/1f/o/wYADAAgAGAAZQAhAOr/LADX/8n//f/s/8n/2v/2/+z/BQDf/zEA6v8CAEcAHQDq/woAGgDA//7/HgAsAAQAJQD5//3/FwCZ/wkA8P/m/wAAHAALAAEAIwDD/wcA9P/6/xkAJQBNAPP/7f/o/w4AAADa//7/1//H/+//tv8SAPH/v//7/y8ASwAsAGwALgA+ADwA3v81AOn/v//z/wkAvf+3/xoAiv/N/y4A/P82AOH/5f/v/+H/QgA4ABMA9f86APn/HgA7AP7/cADz/wAA5f/H/+P/x/++/9z/CgDB/x8A0v/q/woAs/9HAC8APAAwABcA7//t/xkA0v9nADcAMQAVAMr/+f/K/9P/3f/0/xoAAAAaABIAFQABAOT/uv+f/wsA5P/+/wAAzv9jAOb/8v94AMf/GwABAOv/UgAeACgANAAVAK7/GAARAN//CQDK/yYA+v+q/+r/1v+3/wUAEwDl/00Ayv8nADgAz/8rAAQANgDq/xkALQD7/yMAxf8WANz/0f8jAB4A+/8PABQA2//p/7v/r//7/yQADgARACAATAAEAO3//v/D/xoA8/8yAAYA7/8aALL/2/8fAFoAJADn////+//q/9X/BQDZ/+T/4v8PAAAA+/9aABIA+v8kAOT/1v8ZAPf/9v8TAAYAAAAAACgADwANABYACAAKAOz/wf8DAOD/+v8GAP3/HwC///b/EgDO/+r/GADR/zEAJwDp/1YA4P8IABAA6/8EAEgAUQC//ysA+v/Q/9n/CQDa/+H/DwCr/+X/uP8QAP3/MABjAOz/PQA2ABEA7/9YAPj/+/8TAOP/2P/v/yEAt/8dAKb/1P/x/83/FAC//zYAEABcAEwA6P8IAOH/7f/c//b/IQBCAPj/MQDo/8X/NgD6/+r/8v8FAA4AAgCr//r/FwDv/+H/JQBGALr/ZgBdAB8AOQDn//3/5f+R/7b/7P+A/8z/8P8lAD8A3P9jACIA5f9GACoACAARAPf/BADv/8v/EQA/APv/rv8MAM//1P8VADUAPgDp/xAA7P8DABsA+v8PACIABwDZ/97/4v/Z/8v/6P/u//f/8/8SAO//RAALAAAAagD//0MA//8DABMACAANAOP/HgC8//D/1P8cAPf/u/8SAOv/EADr/x4A1v8JACIA6P9HAPP/5P/h//P/y//5/yIAXwBVAAwAQQDH/9L/2//K//H/FQAWANH/6/9AAPb/FQAhAN7/EADW/zcAGgDr/+7/kv/9/8r/DAAxACQAXgD0/ysAuf/b/w4A8/8dAOD/JgBEAOv/HgD8//f/KADN//T/qf/i/x8AtP9IAAMA1f8kABMAJQAAADIA//////7/4f8ZAO3/8//q/wIA8//T/0MAOwDN/+3/8v/2/yEA1P8sABsAyv8hAMH/+v/I/xgACwDe/3IA//8/APj//v8NAJr/IAArAMz/LABWAPD/NADt/8b/+/+1/97/+P/d/xkACwArAAsA3v82AKr/6//1/8n/OAA1ABMA9P84AAIAAgCl/xoALADu/3QAs/9QAAoAu/8vANr/AwDt//D///8fAL3/8v/Y/9L/NQACAEcAvf/8/yoA0P/w/+r/IwAJAAsANgA3AO3/QwADAPz/DwC2/z8A4//Q/+X/8f/Q/7j/PwAcAMT/AABIALT///8aAP//6P8aAHgA5/9EAPD/8P80AP3/SgDn/wMAeP8AACYAj/83AMX/5f/f//7/KgDs/0oA9/8EAPH/6//8/9P/DAAuAFYAbQAHAPn/CgC9/9T/yv/c/+z/xf9tACAA9v8zAC8A/P/u/9r//f8aALj/MQD6/8L/GgDy/yEA1f8SAPj/+f/6/9P/MwC7/+r/FgBvACAADQBeALj/NADS/7H/0v+0/yoAwP8eAPz/JAAbAOD/UQDR/xMAGgAcADUAEAAwAPP/7f/P//v/sf/P/zYABQAGAAUAHwDw/wEAFgDY/9n/BwAdABUA5f/4/8z/6P8JAL7/RwAMACYAZQD8/xcA9/8AANv/AQD4//P/8f/W/ywA5f8HAO//5f/z/woA4f8JAEcA1v8sALH/JAAzAMr/aQD8/yMAMAADAPf/4P/j/7D/1//y/yoA/v8qADgAu/8LAN//pf8QABAAAgAKAAEADQAtAAIACAD+/yEAVQC///X/2v8HACkAn/8/ANf/0v9dANn/FAAGANb/PADg/9D/BgAGABQA4/8uACQAyf8OAAcAHQAIABUA7v/o/wEA5f/m/8P/AAATAMz/HwBJANz/MwBZAOX///+7/w8AEAC//0MAKwDV/zYANADK/+v//P/N/9f/4//8/xgA1f80AF4A6/8eAO7/1/8UAN7/JQD//6f/KgAIAMH/IAAKAPL/VAAZAN3/BADH/wEA6/+8/24A8P8fAHYA+f8iAM//tf8PAOf/7/8oANH/0v/m/7L/HwDd//v/YQACAP//AQAUACwAJwAgABkAKwDq/10AFwCn/wkAu/8DALf/i//z/6T/BwD8/xcAQwBGAE4AHgAPAOr/KgDy//7/HAAJAAYAlP/i/8n/xv8uANj/+f9fACgA7f/u/ygAJQDp/1MA9P+1/xkA2//c//D/GAD1/zUAMgDK//r/BQCs//n/CAD3/2sADwATAAMA7P/9/9v/6/8QACAA3//5/7b/DAArAOX/JQDJ/1QA+//q/14A6f8aAMP//f8ZAPv/+P/O/x4A5P9CADAAvv8EAMf/vf/6/8v/6P9eAOD/FgBAAPH/VQA5AEkA5f/p/xMA7P/k/9P/3P/J/xgA3v8WANH/+/8fAID/VgAJACkANQA1ABEA7/9XAMz/AwDZ/8f/7v8QABEAKAAqAIz/CADM/93/7f/t/xsA7/9KAOr/HgA2AN7/CQAFABIAJQAcADsAIwDz//L/xv/d/7X/1P/4/wwAIgDz/yAA7/8NAA0AyP///xsA8v/F/zQAIwD8/zsA9P/7/9f/DwAeACEAHADR/0QA0P/R/wwA2P/5/9X/RADs/xIACAC//ywAvP8WABsANgD5/xEAGgDK/y8Ax/8hAPr/2P8sAPH/CgAiAAAA6//9/+r/FwDm/wQA9//9/xgA6/8YAIf/vv8BAPP/DQBiAPv/DwBrABEAWQDM//b/4v/B/wkAtf8DAGMAQADf/xwArf/f/xcAxf8rANL/1/8KABgAHwA6ACQAEgD4/+n/GQCy/9v/HQD4/wAABQAUAEAABgDm/zMA4v+e/+j/AQCj//3/EgD3/yMA6P+BANj/HgBNAO3/NwCk/xYA/f/i/xwA5f/2/wAAFAANAC8ADwDR/9L/5v8BAA8A+f/9/wsA3P8AACAABAAdANX/PAAVAMf/HwDN/9P/0f/b/x8A8v9bADUADQA8AAYARgDE/xsAFgCF/xQA0f/c/9n/+P/9/8z/UQADAPj/AgD9/wkA9/9CABsABAAgAAAA4f/9/woAAQAjAPb/3v/v/8P/7P/q/+H/NAAIAF4ADgC6/1cA2v/W//X/qf8nAOv/FgB9ACQAGADW/yMAvP+5/0gAn//8//f/6/8FABYAYQAAAB4AUAD8/7L/5//2/8f//P8WABIA8v/x//L/6P/O/w4AMAAvAA0A0/8PAB8AMQD9//D/+f/x/+L/0/8mAPz/LABMAPH/BgDm/wAAMwALAMj/CADh/4r/EQAPAJL/CAACAOn/QgAmAD0AGAAdABsA7P/j//7/CgC+/xsAKwDc/+//4f/u/y4A+f9MAEAA6v/1/93/7//Q/9T/+f8NAAgAIADl/6T/KAAYABwAKgAeABMACgAeACAAQAC6/9n/tP+r/xAA1//c/w8AAgDy/zMAGgAaADQAz/8fAAEADwBZAM7/CAAjAAEA+/8dAP7/9//v/3D/2f/5/9b/KwABAO7/6/9cADgAKgBfAMX/wP/T/+P/8P/7//X/6v8gAEcAAADs/wAA8/8KACQAOwAGAAQAAQAKABcAuP8WAMf/9v8nALH/VwDe/7D/2//P/xYA3P9BACoADQAZAPb/AQDv/+v/MwACAPr/fwAAAAEAQgDc/+3/AADs/7f/AgDU/8L/EgDN/wMAEwDl//3/AAD4/0oA9P8rAFEA7f9RAAkAFgAHAMT/3f/e/9T/7//x//T/IADT/ywAHQDa/wEA7f/0/8b/GQAAAOv/bgAcAP7/MwDp/yUAPAAGADYA7/+r/8f/2v98/wMA+f8SADkAmP91ANb/CABnAMz/bADi/wsAAgDv/w4A2P8sAPD/FAAgAOf/of/P/+3/yv/g//T/OwAzAAMACQAqADcADgATADsAAADT/x8ABwCZ/+n/LgC1/yQAOwDP//3/HgDY//z////k/ykAy//m//j/6P8NAOv/MAAkAOX/DgAHAAUAHwD0//z/AgDf/yUAHQDh/xkAQQD6/xkACAAJAPf/0f/d/8z/8//8//T/DQAmAML/LQA0AOz/NACg/+v/t//i/0QAAwBtADQANwD3//3/rP+3/yYABwBGAPv/0v/P/9X/0v/2/zQAMwAsABMAHQC+/wIA4f/V/wAAJQBAAOb/JwALAOz/0P/K/7b/GQBnAO3/YgAhAPr/8v+3//X/0/8aAAUA+/9iANf/AAAuAKj/3f/9/wAA6f8KAEQAEgDq/+X/AgDq/yQAIgD0/yAA+/8OAN//AADa/7//JwDS/zYAEQDw/00AtP/7/+v/9/82AA0AOwAgABkAv//Q/wcA4P/6/zEAHAC9/wIATgD7/xIA4//1//7/yv8wABYAzf/W/+D/6/+l/ygAJQAVAEMADwABANX/JQAIADAACAAbADsA1P9gALv/6P/w/5X//f/8/wgAGgAPANH/FQDV/+T/JgDy//b/4P8sAP//EQBQAB8A2f/w/9b/tf8tABUAFQAVAPn/+/8mACoAJQBQAMD/mf/X/+//NAAYAB8ANQC6/+//uP/b/9j/tv9IAPf/IwDn/xQALADy/x4ACwBGACUANgDy/zoA2P/D/w8Axf8dAOX/yf/C/+T/xf9JAFoA9/8xAAIAwP8GAOb/6P8jAKr/RwDf/wQAagDg/3cA5v/i//H/LgD0/woAKwCP/xgA0f8PANn/BQDx/83/BgDG/wEA0/9BAPv/3v9UAG0AGwAWADkAyP8BAA8A+P8FADEA0P/z/+f/1P8EAJP/XQDO//j/DgC5/xMA1f/o/xQASAAXAE4A9P8YAAwAz/8VAOb/CAALAFwA0//x/wAAm/8ZAOv/DQACABkAOwD///r/9v++/wkAIAAYAPT/1P/K/+n/GQDS/z8AKwDm/ycAGgAqANr/BgA2AAAA4f/g/63/vP/R/wMAZQAeAFcABwD6/zUA+P/z//z////v//T/l/8LAA4A2P8TAPr/1P8aAEkA3f/+/x0A9P/i/wgA9f8lACwA9f8QAB0AKwD0/xoAyf8QANH/qf8OAK3/VAD9//v/PwD6/wAAAwAfAPL/EQD1/ykA6v/z/x4AmP/r/9T/+v8dAOr/JgAZAOn/JgDx/wMAUQAAAAAADQDp//T//P8AADcA7P8WABgAz//J/5j/FwATABwARgDk/97/1P8AAAoARwA/AOD/HgDM/9L/LAD1//X/z/8iAPf/8v9CAM7/LwDT/zIAFwDC/xoAyv/8/+P/LQD//xEAGgApAAIACABZAML/NwDs/9//5f/N/+D/nP/b/9r/JwD9/yEAGAAHAB0AGgBOABoAWQAYAMf/vv8SAL///P8AAOb/YwD8/yIA6f/K/6T/x//j/93/GgARAEQAEwBmAPr/0f8wAO3/EABIAPj/2//3/+n/JgCo/+7/w//8/xoADQBxAHf/HAD1/77/HAAJAEcAGwBGAOf/JgDw/yYALAC6/wEAqv/p/zQAAABDAN7/8P8tAFz/CwDO//z/cwCQ/1kA9f+c/yQA/P87AC0A+f9ZAOf/9P90AMf/7v/L/+j/IAAMAAoApv+p/+H/HwDg/zMAFgAHACkAAADv//n/iADx/+r/EQDt/9z/NwAYAMD/IQDG/yYA1v/P/yMAEwAiAPv/JwDK/8n/3v8kAMn/6f8MAMP/TQD4/xUAMwAiABcAUgAQAEgAHQCs////qv/l/7P/9P/g/83/RQCv/wUA1/82ADkA5v88AB4ADQDc/18AGQDl/0YA4//B/wgANgAMAPH/7v/d/8j/7P/y/9v/1f8CAOb/0v8yACoACQAWADkAeQAaABkA2/97/8v/8P8+AAwAQwAdALT/HADU/97/9/8gAD8A8/8PAOX/0f/P/zQADwDg/x0Azf////L//v8vABoAQwDu/wgASADh/+T/5v/c/7L/BwDj//L/TwAHAHYA3f/+/0EAs/8vAKb/r/8CAML/yP82AOX/FQBLAAEAnADt/87/MgDy/+7/4v8yAPX/GgAnAPD//P+8/wIAFgDz/+7/3v8CAPn/5/8xAOP/2v8sALv/xP8MAOP/HAAFAF4AcwAOAFIA3//4/x0A1//r/+j/AADv/8r/9P8VALb//P8SAPP/2P/T/1MAs/8uAEEA8/8gABkALgDU/xkA9v/0/xAAAQBKAPb/AAAPANv/+f/4/8z/8v/4/9L/q//Q/yUAJgAzAEIACgDh/wgAv/8hAEMAuf9YABYAAABtADEA6//S/9T/5P+o/77/PgDg/93/FgDt/8//JwA1ANf/DQAOANn/CgBbAP7/OwANANj/EgDB/zUA0/8TAEsA7f/Z//r/CQCi/wIA4//0/wAA7/8UAAAAIQAwADMABAAhAAEA/v/6/wMAEgDE//T/yf////L/7v9AAA8ANQDg/9L/xP/v/9T/+f9HAKv/RgBzAAAATQAIADIAw//h/wwApP8QAMr/8/8JABQA/P8mACcAtP9pAMD/7P8rAJT/PQCy//L/FwDL/yoA+v8qAD8ADADz/y0A5v8lADIA3/8wAOT/DwADALb/HQCb/9P/9//W/ywA9v8TABUABwApACcA3f/L/xwAAAAcAAsAKgDj/9D/SADl/yIAEQD3/87/AgANALH/PQC+/ygA+v/w/0sAy/8xALv/DgANANT/DgD0/wIA/v8jAPz/DwC5/+v/FgAeABIA8P9pAJb/LwAlALz/XAC5/y4AAwDs/woAx////+b/+v8vAPP/8/9hAA8ACQD1/9z/0v/T//b/x/8mANv/RAAtANr/SgDK/wsAEQDq/2EASQDq/+L/w/+6/x0A0f8PAPf/0f8JAP//MQAbABkABgDg/6n/MQA5AAAAPwDo/+b/2v8BAO3/AAD+/9X/GQDq/zUA3f/7/0MAvv83APX/DQA0AP7/FwDe/xYA+v/5/wUAPwD//83/FgC7/+b//v/7/yAAzv/8/8//6v8JAAAATQAlABgA8f/5/wkAsv/I/wYAGwAXAOz/IAAQAPv/XwAYAAoAGwD0/wcAvP/8/+X/9/8oALL/+//C/wEA7/8FAGQA2P9HAO//7f8zAPH/IQDk//7//f8JAPP/6P8OAOr/HQAkAN3/DQAUAOr/1f+o/yYAwf/s/z4A3P9+APX/EAAQAOf/GQAVACsA3v8YAMb/EAAXAO7/5//N/zMA8/8JADsAEQDP/ykA4v/0/yIAWf8MANH/h/8AAFMAWgARAFgAEQAGAMr/0f9KAPf/LQBqAO7/yv/z/7b/AABaANX/vv/X/7X/EAD9/zoAUgDN/yYAGAANAB8A3//d/wkA6P/p/xUA9P8NACUAHgD5/wAA9P/g/77/4f8GACgAQQDL/x4A5v/q/zMA9P8LACMANwDY/wkAp//U/zYA9f///9D/IADp/0wASwAIACYAs//i/xYABAD5////2P/x/8r/HQAoAOX//P/U//7/7v8GANT/TQAkAPP/MAD6/3YAGgBEAOv/8f/+/7r/CACi/73/nf8IADIA4/8eAFQAAwDZ////tf8JABoA+//v/00ACAAPAFUA8v9HAN7/uf/0/xIAs/8+AA4Avv9bAMT/FACy/9//PwDi/+//7v9EAD4AFwAAAP//1v/V/9z/RQBiAOb/IQAAAML/0f/5/+T/BADd/93//v/c/z4A/v8VABIA9v8GAA8A+v/z/0QAPABIAD8AwP/i/8r/m//9//n/BADU//r/HACm/zgAHgAdAA0AEgBWACcAEwD1/+L/2v8MALX/JgCa/37/HADm/00A9P98AAEA4P94APb/+P8hAN//3P8UALX/FgDo//3/MgD1/zUAxv8qAN3/GAAVAL//MADn/+3/5f8ZACIAz/8XANn/mP8rAAYA9/82ABsAMwACAPf/DQAWAAgA1/8GABwAw//+/wAA9P8lAAEA/P/4/xEA1v9EAOn/rv8+ALL/JwDW/8//NADc//z/EAAqABkAKgAhABcAAQACAOf/6v8kAND/CgAlAPb/OwAAAAUA2v+P/xkAkP/j/zwAzv80ANz/CQA9AA0AAgAnACcA3/84APH/AwALADQABgDQ//v/ov/v/9T/tf9IAAMAyf8kABsATQAmABsAEQDT/yUAw/8TAAMA+/85AOP//f/g//7/CwABABQA/v/H//X/yv8AAOf/+/89ALb/ZAAAAAMAIACk/yQAwv8+AFwA5P9AAC0A/////7f/7P/6/9j/DgDW/wIA8P/q/y4AEwACAN//BwAAAMj/FAD3//r/AAD6/1oAEwBZAOj/AAAmAMX/SQDO/0EAvf+o/9H/m/8LAOf/cADP/zYAVgD7/w4A+v8xAK//5P/1//H/5f8NACAA5P/0/9j/JAAhAPb/5f9DABsABQBZAAkA+f8KAA4A/v/+/xMA4P+c//H/r//C/wwA7/8aAN//DAAZAB8ALgAjABoA9//o/ygAeADO//b/CACv/7X/BwD8/+r/RAAkADYAyP8QAPv/xv8rAPn/+f+o/97/9P/C/wgAMgAqAFsAQAA2AGsA6f/o//P/vv+2/9b/p//H/yYAzv8MAGUA8v8BADUAVwAyABUADgDc/9//4v8AAPL/6v/0/6n/FgDg/9n/VgDp/xUANgAkAN//2/8HAAIAKQDl/8f/7P8RADIALwAMAOv/+f/0/wEA/P/7/z4AEwDe/woAOAAAAAYAAwCs/7H/5v/C/+P/JADl/xAAGwAuACYA6v9XAOL/JAAZANr/OADz/zsA9f/4/wIAzf8GANv/1P/V/9v/yf/0/xsALgDx/xkA3f///1cA5v8tAP3/HQBTAPb/GAAIANX/HQD3/9X/FwCE/yMAKgDi//f/5v8WAJf/CgAcAMb/EgBIAAkAIABDAN7/UAD1/yIA+v/G/+f/wf+3/7D/AADP//z/XQAOAC0AjAAuACAAOQAdAMH/5/8FAJX//P+0//j/yf/j/ysAt/8fAPT/XQDl/zUASQDB/zUAuf8aAN3/IwBPAPr/HgAAAOH/7f/Z/6v/AADp/yYAGAAPAAgA+P8YABgAOwCu/xMA5P/Q/xEA+/80AN7/BwD1/+3/4f8yADoAlf9TAOz/5f9gAO7/LwD3/83/2f/0/x4A0v9HAEAACADn/9b/0v+t//r/CAARAAcAHgAmABcAGQAHAAgAz//h/9T/CgDw/w8AUwDw/wIA1f8IALb/LgBLANX/XACR/yEAIQCj/2UA7f/2/xUA7P8OAAEAIADz/7P//P+2/9b/GAAgAD0A9P/8/1MAIgD2/yMA4v8GAAcAwv/3/8//EwAXADAAFwC0/zkA3f+x/wQAtv8UAMv/3P9bABkAcQBXAPj/4f/M/5P/9v9jAN7/UAASALr/SADH/zAAQQD5/y4A3v/P/5T/rf8JAAEA5P8DABUADwDl//L/NAABAC0AJAD1/yIAAAAkAD4AFgDt////6P+L/+b/FgD1/0IA8f+5/xIAw//O//j/+P/j/wsAMwBFAC0AHQATAPP/RABHAND/+P8kANT/5f/8/x8ADQC6/+f/8f+x/9P/SQDm/+3/AQCi/yYACABbADUA2f8cAPn/HgASAFoAAQD5/9b/kv/6/9H/MADV/+X/KgDf/zoAEQD9/zgAGQAFAC8AHwABAMX/CgC8/8X/IQDf/wQA4P/h/w8A5P/9/0IA8v8eAFkA1f/p/x8AAAD9/0sA3v/S/wYA3P/Z/97/KwD8/wAAHwAdAPD/6f8SANX/DgAeABUAKAACAO7/GgAQAPj/BADe/8D/n//w/x4AJgA0AP7/CwADAOX/AgAEAOz/DAABAFwAGwD1/xYA3f/C/+b/CACt/wYA8v89AOT/2P9+AOn/UAALADYAxv/K/yIAwf8RALD/BADt/wAANQAtACEA+v8aANP/BADK//f/9P8BABUAl//x/wkAGQAHAG0ATgDv/xAAEAAlAOP/+P///5L/vP8RAN3/CwDh//z/KADe/zsAIAAQACMADAAAAAYAMQDR/+v/IQAOAPP/CwDe/7z/6//4/wAA+P8eADoA7v///xMArv/Z/x4A7/8EAB4A2f8DAFEAOABLAM7/8/8SAM7/RAD6/wUA7P/Q/7j/3//q//T/TACJ/xQAMgD5/z4APgAZAJf/+/8iAAoA/v8GAAsA5f8AAA8A7/8zAE4AyP8sABIAyv/u/+b/GQDQ/wAACgDx/wAA0P8PAN3///8sANH/CQALANf/FgAAAEkA6/8eACcA8f9PAND/DQDL/xsACACe/04ABAASALb/FwDl/9z/LQDW/xsApv8cAC0A3/8cABAAFgD8/woAEAArAMb/7P8QAND//f/7/zMAEwApAPj/BwAAALj/JgD6/xkAJADf/wEA6v/6//T/8v8MAMf/8f/h/+H/LQANAE8ALwDI/xYA6/8OAGMAEAAwAP//3//O/3f/2f+y/+X/LwABABgA8P9pAC8ANABKANz/+f/5/9D/HwD+/93/BgDj/wkA8v8PADQAtf/r//v/6P/w/ywAGwDm/xEA4f/2/8D/DwD2/+//9P///08ABQCHAEkAOAAWANX/3v+F/0EA///1/xUAzv/j/6z/+v/6/xUABACr/yEA7v/2/zQACwAtAPf/IQAyAP7/4/83AC8Atf8vAOr/1P/2/7b/1//W/y8Axv8xADwALgA8AMH/PADq/zwACQDR//3/zv81AOb/HQC5/+D/BQDU/xMAuf86ABYAKgD5/+L/VADt/xgADgDQ/8T/4//S/xcAOwARAEwA8/8YABkABgA8APn/+v+y/9n/1f95/8//6/8QADYAAwBcADwAGABVABUACgApABIA4/+u/8X/yf/S/9//+v8lAAEADAAsAAAAEwDk/xQAAQBIAPT/of9cAO///P8NAPj/IACm/+D/9f+j/+v/7/8iAD4A6v9PAEUAHQBjAP3/CgD+/+f/zf/u//D/CwDt/xEAOACO/yoAAgDA/6X/zf/4/5j/SAAiABwAAABHADwA4P9aAND/DAADAA0ALQD1/w8A5f8JABoAOAASAC0A6v+b/+n/2f+e/9H/DQDN/wcA8//8/zsAEwBDACsACwAiAAAA+//4/8H/DQBNAAEAAAAXAJb/3f8gAI7/IgAMAEUAIQD8/xEAuv8fAPD/HQAUAMj/FgD3/8D/AAAxAL7/TADc/wkAVwDQ/0MA7P8FAB4A7//y/8z/HgAAAO7/DwD0/+f/JgAIAOn/2v8AAB8Avv/b//7/3f8ZADcAGAD6//z/NQDh/wAAYwDK/zMARQCg/xUACADJ/w4A6/8QAPf/BABLALH/JwDT/8f/CwDN/xIAuv/R/8D/MwAdAH8ATwC0/2YAzf9EACUAGgDZ/63/UQCw/yUA+//w/9D/q/8fAOv/yP8hAD4AHQAWAAEALQC0/wkAMwC6/w0AzP8FAPz/gAAoAAAAHQC4/+v/wv8TANr/EwDp/8r/FACm/zwAMgAAAB4AHgAAAAwAEgDq/x0ACQAYACgAyf/i/wwA2//9/xoA+//4/wIA3f8EAAgA7f8xAMP/5f8HACUABQDL//r/3v8AAO3/OgDx/yIAVAD2////6v9CAN7/DwAlAPT/VADf/wIA9P/P/+f/lv/A/8b///8gACQAWwD//xYABADw/xEA0v93AP3/NgAtALL/UwCg//H/4/+0//n/5v8jAN//+P/6//D/8f/d/yAANQAGAGsAMAAKACoAxv8EAMT/1f8ZACsAzv8EAFQA5v8AAO//GwCw/7v/DQDK/xAArf/5/xkAAwBdAD4AJwAzAD4A6P9DAPf/sf8PAKT/DQDS/+L/MAC7/ysA1v/a/xgA2P84AOn/4v83AAsAAwAOAPr/AABIABIAHABQAOL/xf8MAMD/r/8DABMAGADi/w0ALwAOAO3/6//e/9D/+v8SACsACgAuANv/0v9qANz/EgBEAL3/FAAgAKX/3/8BAN3/BwAPAOv/7P/Y/+f/VwBRACkAAgAKAEMAv/8aAP//kv8bAAAA8/8xABMAJwAoAM3/GgDN/8T/4P/k/zgAnP/x/+n/w/8pAE0AIADE/0MA9v/h/y8AEAABACUAQABRAC8Ap/8AAPP/mv8OAAIAuP8VABkA0/8UAPD/+/9EAAAA6v/8/+r/5P8BAB4A5v/q/xoA+/8jAPL/BAAdADQAKQAOABYAw/8XAN3/3f8HAMn/9f/x/+T/8f8VANf/EQD7/xwARwDp/x0AAAAoAEQAEAA0AB0AxP/d/+n/xf/u/77/ov/N/7n/6v+VABEACABaAA0AYgD4/y8AQwDU/xgA/f/P/wsA4P+v/9b/rP/o/wAAAQAuAAoAFQA0AEoA+P/3/zgA/f/O//H/zP/B/zAA9//2/+r/wf8KADIADAAjAB4A8f8uAAQACQDx//T/EwDr/x0AFwBEABcA9//i/8n/wP+o/yEAq/8RAPX/0P94ALD/MwAuACcAOQDP/10A5v/w/wMA1f8hAPH/5//l/xAAMADZ/zgAGADL/wYAw//r/77/9//h/8T/WAD5/y0AAQBOAEMACwBLAMn/BgDg/xEA/v/j/+b/9v/+//T/1P/l/xsArf8YAPH/JQAVAFAAKwDq/3kAgv8xAN7/xP8PALn/LACx/yIA0v8EADsA8//u/xoASwAwAFAA5v/m/8z/0//q/yEAAQDI/0cA9f/0/w4AMgDc//X/2f+Z/wMA6v8AAPT/KgAAACYAHQDw/0sAEQBEADgA8f8BACAA/v+w/+H/7f/Y/6j//P9BALj/3f8tANj/EwAkAAEAUAAaAPz/BQC5//3/LQAWAPr/BgD+/9D/6f/u/zcABAAtABEA8v9MAK//1f/g/8//3v/u/yQAMQBAACMA9P+1/zYAtP/6/1cA5v84ABYAKADm//v/6f8IANL/8f/M/9z/SQDG/yEABwAvAB8AAgALAPD/+/+7/9n/g/8qANz/KgBCAML/ggD7/yQADQAAAO7/6f8GADEAWgDm/zIA/P/O//3/sv++/xwA6f8TANT/uv8kAOv/CQDk/ykAIQAMACoAGQAAABoAFQDZ/0QAsf/5/w4AuP8rAA0Axv/v/+3/yf9XAPP/CAAwAAgARQAVAB8A9f/4/wMAz/+Q/wgA8//P/yUACAD7/xEAAAAUADcAuv9QAO7/2v9OAOj/PADi/97/FADZ/83/wf/h//r/1v9JACwADQB4AAcAAgDy/wQA1/8WADIA1////8D/PACn/xcAMQB5/zIAAgD5/+n/DwDt//3/MQADAFoADAAlAEQAvv8GAMf/uv8AANL/BADb/0UA+P/f/0QAy/8cAPH/LgACAND/AQDz//3/6f8AAPT/HAD6/z4ASwArADsA5f/v////sv///+3/of83AOX/6P/f//z/AADc/zEA3/83ABwAGQAxADYA3v/s/ysAh//4//7/EQD0/x8AFwAfAFQAAQBAALz/+P/d/8P/8v/8/9f/1/8gAK3/IgAkAKn/HAAuANb/cAAnAAoAPQD7/xkAt/87ALb/zP/s/67/WgDN/zEAJgDZ/yMA2P/9/xEADAAkAOf/NwDr/+L/MQDY/ygAw/8DANP/+P9QAKb/RAACANT/BwBJACgA5v/U/8P/FQC2/10A6P+//z4AyP/4/xUAJgA6AC8A/P/w/xUAMgDn/yAADQDj/xAA+P/Z/+b/LgC//xIAu/+I/9//i//z/yMAPwBlAG4A+P9TABUA5f8EAND/TwC4/9T/EQDe/9j/EwAjAAwAGwD3/zYA7/8BAO//9f8tAPD/+f/G/8L/5v8YAAgADQA4AL//BgBGAPH//v8FABUADADQ/+H/QADT/+f/YQDu/y4ADwDs/9r/x/8IAMn/9v8cAB4A8/8UACIA7f/U/xEAEwCZ/2wAyP/r/zgA+v8TANv/TQD1/3kA6v/k/0AAlv8WALz/wP/0//b/+v8mAPb/7v8kAPn/AQD7/wgA9/8aABEAQgDZ/z8AJQDB/1MA7f8wAPb/CQCt/73/5v+E//z/EgACAOP/RwDR/zQAbwArAEQA5P/q/4H/9P/T//T/JAA6ACIAwf8vAOf/TgDv/x4APADG/9P/3v8dAKP/CADr/+7/AgDo/5AA+f8LAB8A4f/u//f//f/z//7/+P8eACAAGwAfAP//qP/L/9j/zP9lAOn/DQAtACkALgCu/w0A3v8oAAQA1v8VAAkARACY/0MA0P+4/0sApv9GAN7/KAAFAIj/XgDM/zwAUgCw/wAA5/8yACkAOQB6ALj/1f+j/8z/AwD3/0IACwDs/8P/LwDl//n/OACt/wcAGQADALX/7P8AAAEAFADd/zcAHwAgADoAaQArANv/OgAlAK//ov/b/8X/3P/f/9n/+v8bAAMAIQBJADcA7v/z/ywAnv/S/xwA8P/4/+b/QgAYABwAJwD//1QA6P8PAA0Awv+u/3j/IgAjAAQAKgDz//T/6f8QACIA8f8QABAAvf/w/+f/BACDAAAARQAyAPX/4f+h/+D/s/8IAAAACwAtAPf/PADs//D/RgD8/9b/NQAYAN3/LQDG/8H/5P/u/x8AGgA9ABsAAwDa/8j/4//o/woAAQD//ygAHQD5/1MAOwDS/+P/+v/o/53/vP8cAO3/HgAoAAEAGAAUAAIACAAYADcAPQD9/8r/6/+5/9L/KADU/+f/HgDn/wUAFwD2/zkAKwDa//v/8v/+/yAABQDq/xUAGwAmAO//xv8XAPn/EQDk/9D/AwDo/y8A/P/+//L/FgALAM//ZwDn//n/2v/E/zwA+P/l//3/CwAGADoACQAXAF0Asv/6/xsAuv8YAPH/0P/g/9P/4/8NAE0AHwD3/wwA7//+/xQA9v8RAOj/AABEANX/HQBKAPX/CwDc/wgAGQC8/8n/8f/5/7n/9/8mALT/EAAmAPr/HgAwAEIA2P8VAGgA0v86ADsAz//r/5r/3f/b/+7/MADt/x4AyP8RADUA4f80AAQA+f8AAA8Aw//B/xwAEQAYANf/AQAmAOX/GwBPACYA8P/+//X/rf8PAO7/7v8aAMP/GwACAC4AIwAzAPz/0f85AOr/+P/V/8j/GgDh/9f/KQDw/ycAFACd/yEA9v80AP7///9EAK//OwBfAAEABAAOAMr/uf+s/xEADADh/0kA0v8IAMf/KQBJABgACADI/wAA6P9mAAAAGQAEANn/CADK/+b/pf8LANP/9v8AAPz/JwAhAFMAEAAIANz/EADn/+f/IwAXAAIAFQBFAAAAVQACAO7/4P+9//T/yv8XANn/1/+l/8P/IgDz/z8AGwAVAPj/0v9QAA4AFQBbANz/8v////n/OgDL/yAANwCk//r/JQAKAAUA1v/r/+j/6f/s//H/6f/q/yYA8f8DABwAAAAcAOf/4P83ADYAIgAuAEcAAgD2//r/3P8CAJj/9v8VAMH/CQD1/93/1v8CALz/EgBNAAMACAAoAE4Az//o/xQAzP/b/4EAIADe/0gA0P8uANz/LgAYALT/OAC//77/4f/c/wcA9v/i/xUAEwARADgAGwAHAOH/xf/C/xEA3v9IAE4AEgBQAAMAOAAQAMz/1f/p/8v/OQDr/5v/BgDP//7//P8XAO3/EQD7/wAALADg/0YA6v8DABAAIwAZAM3/8v/s/yMAw/8JAOz/GQA9ACwADwD//xwAuv8mAPf/FAAcAMj/5v/2/7r/wv88APj/5v/j/zgAAAAAAHsA3P/8/+T/BAAiAAIACwCv/0kABADf/wUAn/8CAOb/LwBCAAAAZADx//r/0//u/+H/0v89AIX/FQAbAA8APgAyADEAu/82ALv/1/87AND/MwDw/9z/5P/S/yEAAgAbAAkA5f9qAJz/5v8dALD/UgDR/y0ALgDn/zMADgAvANn/AQC3//v/OAD+/y8A4P8XAML/0/8KAJ7/JgD8/xEAKADe/zgA8v/t/+7/DgAsAPL/QwACAOH/rP8mAEQAjP9DAA8AAAAuAN/////m/xIA8P/8/w4A7v9XAM7/FADv/6b/LwDM/wAAAADZ/0UAFAD5/0kAEwC9/97/5f/u/93/BAAAACsALwD3/zwA6//8/xMARQA2AOD/w//J/8b/+P9WAOT/QgAhAMX/0//S/w4As/8zABAA8P9CANv/1/8gABoA4P8aABoAGAA8ACgA7f/3/7b/yP84AMX/GgBBAML/9v8dALT/2/8EANn/YAAeAAcAWQDE/yIAIQCh/zYA5P/l//b/ef/1//b/TwAwACoASgDW/ygAFAD4/9z/BgDk//7/PwAcAA8Ayv/g/5v/rv+5/wIA+P/t/2oA8f81AC0AXABNAOj/MQAVAAAAvP/x/9X/AADs/+P/FgCL/zsAIAD//zAAuf8aALP/9/82AK7/JwDp//n/EwAHAIsA/P9IABAAx/8SAPD/6/+L/ykABgDM/z0AAAAkAAUADQDk/8P//v/L//3/CgDq/zwA5v8QACUAsv8pAAMAAAAqAB8APwDZ/xYAFQDo/xUA5P8BAOb/v//5/8b/4f8DAE4ANADq/0EA3f8aADMAr/8mAMf/8P8uANr/OgD0/y0A7/+l/+v/2/8AAKr//P/1/9//aABFABIASwAaABoAPQDY/zwA2//U/yQAof8nAM3/9f/T/+L/FQDc/0oArP8lABkAzP8mAOP/4v/b/wkAFgD3/+3/TwAOABgAiQBAAAEA+f8lAKr/0v8DAMj/yv/S/xIAFAAeAAIATgCo/73/3/+z//3/5f9pAAwAFQANAPH/OQA+ACoA5f9nAL//7P8DAOb/NgDb/ygAsv/4/8r/4/8OAO3/MADf/yYA9P85APT/tf8NANr//f/P/1YAMADU//L/EgAUAOD/YAAzAAYA7P/F//D/7f/8/xIAAAAfAA4ADgAKAMH/2v/R//7/4f8rABYA8P9MAAQAMADf/yUA5P/S/yAA1/9KAMn/IQADAMn/6f/u/0MAmv9GAOT/qv/7/wAAdAAyABYABAD6//T/8v+v/+3/6v/+/zQAIwCDAP3/LwDt/6//IADY/zwA9f/a/+n/g//B/8T/4P8hABwAawBeAAYAKgDy/9b/wv/6/yYA3P9FAC0A8/8ZACgA/v/0//r/+v/q/wgA3f+u/wwApf/s/+D/rv9yACcAGwD7/xgAQgA1ABkAIgA6APb/+f/A/+3/5//Y//z/8v8hAJ7///8GAO//RAC1//P/CADE/w0AQwATACQA9f/h/xUAFgBMAAsALQAoAPX/8//k//j/vP86AAEA4P87AJ7/CAAPAJP/3P/e/8r/AQAGAPP/QQDe/+7/UQAFAIYAPAACAFAA5P8aAPn/5f8DAL7/5v8HAOD/HgBDAL//xf+z/9D/HAD9/+//FAAYALv/+f8rABoAHwAuAFgAAQD+/xQA2P/0/83/0P8PAN//RwBkAPb/DQDD/wIA0P/Y/z8A1f/p//f/8//0/yEA//8/ADoA6v8tANr/sv/f/wgA2v/y/ysAAAD6/xQAOwCz/zgA/P8UAHwA0f8tAL3/z//r/6v/LQDx/woA/v/5/xQAIAAVABkAFgDN/w0A2v/H/zMAHwD2//D//v/5/wUAyf8UADkAAQBRADUAGgDb/4b/GgDY/7v/IwAAABcAzv8BAOf/0v9LADsAKgDK/1AA1//I/xkAnv87AOP/QwA1AMj/IAAFADkA0P/l/xoA7v/n/wEADwD5/wgAGwARANL/IgDY/4L/GgDg/w4ATwAiAPv/EAALANL/QwAGANn/FwAKAA4Ayv8AABkABgAHAN3/AADO/+X/EADH/wsAMAAhACQABABEAOz/2/////T/8P+5/xUACwD5/xkAGQAHAMf/KQAeAPn/AAAeAOP/yf8GAJL/DQAlAAYAPQD0/zEAEwDo/7z/LABgACcADwBAAPj/fP/V/9D/0//p/xMAGQDj/x0AzP///1AAHQD///3/uv/2/zIA7v9JAA0A7v/8/ysALgDi/+b/tP/4//P/KQAjAP//VgDq/+j/2f/H/8X/wP8AAP3/5f8LAEwAWAA4ACAAHADe/+v/AQDx/x8A4P/R/wYAEwDT//D/OACz/1QAEQDF/zsA2f/+/wMASADK/9X/PgDV/ysA8f/u/9T/2/81AP7/FgDr//P/BgCz/ysAPAC2/z0ADgD3/z4A4P8iACIA5/8OAB4Awf/Q/y8A6//z/xMA6v/y/wUA8/8hAOL/7/8SAC8ADAARAPT/rv8BAKb/AAAkAOT/KQAhAOX/+P9XABAAcgDv/9X/HQDQ/wwA8v8MALj/9v/h//f/LAD+/w8AFQA8AHr/EQD//83/AQDq/xoAGABnAOz/UQDx//X/OQC8/xYA+v/2/63/GQAFAM//7/+9//L/2/8OAAIA8/8NAAQAYwA3ABsAMwAOABMAz/8qACcAlv/8/8P/2f8TADwARgD7/y8AxP/I//j/y//x/8L/3v8cAAQA7v9HABoA6P8yAPT/KAD7/8v/RADX/+z/JAAHAD0AMwA/ANn/3f/u/6T/BQD//+z/AADh/wsAp/8LAD8AGwBjANb/8f/Y/+3/MAAHAEEAy//0/9T/5f8AANr/+P8LADIAJgD0/+z/ZgDm//r/LQDi/ysAAwD7/xsA1P+l/xMAz/8EAAMAEQAiAKz/SACM/xkAKgDs/4AA4P9PAOX/5//q/8X/1/8DANn/6P9kAB0AbwBCAOf/uf8hAOL/jf/6/8b/BwD0/zIACAAcADAA1f9PABIA4v/0/8f/1f/+/yIAFQAYABYA6P8WACgA8//J/8j/BQDH/yoA7f/g/woA7f8OABQAQgA3AFMAHQBYAOr/5P8GAJb/uf/f/83/bP9WAML/NABPAL//WwCt/0oA8f81AA8A/P9FAM3/RwDm/0wAtf/5/xsACgAXALn/7/+R/0oA+v/6/y4Auf/0/xMA6v8AAAwAEAAdAOn/7P/k/wAA9v8cAPn/+P8wAOv/OAAiAAQADwARAOb/+/+n/wQAXACj/1MA8P/o/wEA2f8NAPH/KQAIAB4ACAAUANH/9//8/8f/SADb/9D/IQDN/+7/2v/o/2IA1/9KAAEA4P9BAMr/YgDl/yMAFQDi/+f/xv9GAAMAMQAkAAYA5f/G/9f/8v8AAN3/+f/6/yMACgAVAOD///+w/+f/JADI/28A3/8WABcAFgAHAOb/bgDZ/yYA9/8hAC4A2f8AANn/uv+z//L/+v/L/w8AJgDg/zEABQBRAAAAKgBvAKb/MQCj/xcAFwDO/10Aof/w/+L/BwC6/7r/XADm/zcAMAAXAOz/8/8tANf/AQDh//3/5P/r/18Awv/3/y8As/8/ADoABwAuABEA4v+k/xgANAABAAAA7/8NAJ7/xf8mAA0A8/+X/xEADgAcAFkADgAQAOn/egAbABkANwCI/7b/u//x/8v/EgAaAAEAAwDf/0wA2P/4/zMA4f8cAPb/KQAxAAUAFgAMABAA5P/d/x4A2v+t/w4A3v8BAC4A+v9zAN7/5P8CAIj/8P/l//P/yf87ADkA5P85AAAAKwAuACkAHwDE/8b/IgAIAN//SAAFAAgAw/8TAAAAzf8xAMf/3P/5/wkA6P8EABMA8f/k/xkATgDx/xUA7//6/9j/LQA2AMf/OADv/w4AGgD//7j/1P8rALD/EgAaAA0A+P8kABkApP8LAP3/6v8pAPX/OwBJANj/NgC6/63/LQDG/yMA8P84AFMA5/83AL//5//U/8P/BgD0/xUA7/8UAOT/4P8pAGYAJADI/zUA6v/H/83/AgAFAP3/PwA9ADMAuf8AABQAGgDw/wEAPQC5/+r/AQDv/8r/2f/Z/+D/SADg/+j/QwAKACMAEADP/wcACQAYAA8ACQAfADIAFgDY/7z/nP8VAPT/zP8iAOL/GwBHAC0AKABVADQAxv8ZAAMAlP+6//7/AwDq/8T/8f/x/xAALgAPAAwA/f8DABUAUQDO/+P/NQC1/+z/NADm/9//QAAKAAgABgAQAPj/w/8DABYAHADy/y4AAADn/9v/v/8MAMj/AAAhAFcAIQAOABsA1/8JAM//BwDs/+D/FAD2/+j/AAAAAPT////S/yMAFQApAHIA/v/P/xsA0f/b/zYA4/8AAMv/8P9JAOb/FQAqAAQA/f8DAOr/6//F/wsABADL/xUAAwAxAOP/EAAmAPX/BQDX/wkA+v/n//D/BwAHADEATQAmABcAxf8AAOT/8//t/9D/JQDR/7v/JwAJANP/OQAjANH/HAAXACAAHwDy/wQANADX/8f/CgD1/xMABAAjAPb/6//1/9H/rP+3/x4AEABDAEkAQwA2AOP/GgDt/9b/EwD3/+n/JQD5//v/BQCc/+3/CgDV/x4A/f+q/+////8nAC0AEwCAABwAAAAlAN//GwDU/9z//v/X/wsA0v/x/x0Aqf8fAAYA/P87ANr/HAD4/+j/KAABACUA7//k/zUA+P8DAEsAOADf//X//f9o//D/5v/m/wYA1v9oAAIAEwA0AAYABwDr/+z/x/8BAAUABwD9/+z/9/8pACQAAgBDACIAMgDe/8H/uv/p/xEABwAbAN3/VQCr/+f/CACt/0kAxf8GACgAGwAeAPT/CADd//f/7P8VAA4AJgA7ACAAGQApAP3/uf/S/63/9v8OAAkA9//7//D/tv/r//H/FgA3ABsAJgAoAO//CwAmAN7/9f/2/+3/0/8uADAAAgBKABEAJQAkABgA0f/H/+z/qv+t/6z/8P/h//3/RgAgAP//DAAvACEA4v8nAGAAzP/1/8n/2f9IACYARQAgAB8Anf/u/+H/tf8/AKP/SAAJAOn/OADs/7n/1P9VANz/KwA/AMX/MQDL/63/QADu////IwDv/ygA8P8LAP7/BQD7/ywAFQDd/yIAqv9EAP//DwBHAG//0//J/+n/2P8CAB4ALQBaAD0AQAANAO//+v/9/7j/JADn////0v9+/04Auv8RAGUAFQAeAPT/FADP/9v/AQAhAKb/1/8GAAcANAAQAFAAIgA7AAYA2//w/+D/AwASANL/qv8cACkAzP8eAAAA5P/b/xQAPgDE/yUAHQAHADEAxf8QAAsAFADs/0QALQCP/zEAof/R/yUAw//6/9X/AQAcACgA6f87ADUA9v81AP3/BwD9/7P/BgAiAL//LAAmAM3/LQAgAAQA8//O/8//8v/e/ysAIwDl/zQA2//3/97/5v8mAA0AGgA5APz/wv81AOD/JQALAMb/MQDm/9D/2//2/9//EgAgABgAVwDx/0YA7P/b/08A2v/y/xcA+//A/8X/EQDK//7/QQCq//P/DQD0/0kADAAiAOX/GwDV/7n/TQDu/zsATAARABYA3P/O/83/+//r/9n/GQDb/9H/NQAtAD8ACQAUABYAz/8pAEEA7v+m/8T/s//h/wAA+v8WADQAJAAnACQA6f9iABUA9v8LANv/LgCq/8L/CQDa/9P/vP/m/yoAPAAIAAkA/f8hAO3/DAAqAP7/AgAFABMA/f8mAP7/6P/S/83/x/8gAEsALgAXACEA6P/M/y8AqP8RACcApP84APP/6//q/9//0//y/yIAOQAJAPL/cQDJ/+r/JwD//yAA6v8iACoA4//C/woAEQD3/xAA8v/i//n/RgCy/wQABAC//xIA3P9NAL//FQA/AI7/LgDm/xkA8P8IADMA8/8oAPz/bgDo/wQAEADc/yIAnf8/ANb/6f8qAP//9P+d/zwA0//o/xEA7//9/wQAJQDG/xkADQAvAB8AOwAHAND//P+n/xAA2v8JABUAGgBqAO3/AAATABcA9/8LAL7/xf/C/6L/RADs/yMAEwDI////9/8VACYAZABaAB4ABQAdAML/9/8OALX/4f+2/+//5/8CAB8A2/8QAMH/OwAjABUAhgDg/yMA4P/c/y4AvP8eAMT/GAAjAKn/QgDx/+T/7/8EAA8A3f8AAAUA7//2/yYA3f/4/z8AJwAjADcANgC///X/AADc/+f/7v/z/+n/RAAhAN//zP/+/9L/mv/9//D/QQBJAAAABgDI/y4ANQAKAB0A7f9EAAYAAAAhAMz/BAC//+j/8v/R/zQAKAANAOH/EACf/+H//f8AAEkA+f8XAOL/HgAsABMAEADx/+P/IwA9APv/QQDA/+//9/+Y/7n/CgD8/5f/NQDs/wQAIgA+ADgA3v8xAOr/9P8lAB8A4/81ACEAAgDx/9v/TADH/x0A8P/y/9b/o/8qAJ3/CAAxAMf/BwD1/xkAKwAIAC4ALgD//xwA8P8DAP7/3/8JAMz/7P9CAOv/HwAmAN7/JwCi/9j/3//P/y8ACwAwADwAEADd/0AA7f/t/zAA3P8fAKX/0v8kAAQA5v/M/+T/z/88AAMA6/83AD8ABwA8ACYA+/80ANv/HADy/wIABQCx//r/lf/5/wMA1P8UAOP/FAASAPb/LwARAA8AQgDm/+T/AgC1/wcAQQAgABgAOAAVANT/0v8mAOr/v/8PAOT/EwDy//3/AQDA//r/8v8aAN3//f8rABgAKAAeABUA2f86AB4Ax//0/wsAFQAIAPH/GwAbAPj//v/G/8r/nP/M/+//+/9YAAQAVgDT/xMAagDx/y4Av/8jAPL/KgD6/7f/aACh/+r/OACY/93/BgDz/yIAvv8DAEUAov9WADoA8f8tAB0AAwACANn/2P8hAPL/EgD4/wYAKAD8/zQAAQDx/7H/0P/z/wYA2f/x/0MA9/8UABEA1/+X/xEAQQAOAEUAHwD5//L/1P8BACUA0v/z/xIAwv/2/yEAJwAKABUA4/8RAAsA3/85AA0A5v/j/xsA4v8MAPj/7v88ANP/AQDx//j/CQDc/xsAKgDo//L/BgD2/wkA+P8YAMj/IQAiAMD/BAD0/woA/P8gAPv/VgBAABsANgCG/wUA4v/f/wYAq/8PAMX/0v8KAAAA/v/0/ysAHQA9ADgA+f9fALn/6P8PALX/eADU/wsAMQCK/83/HwAOAOj/UQC8/xsAAgC//y0Aov8NAOf/HQAqAN3/OAAOAC8ALADS/+//GwDQ/xAAIQAWACcA/v8oAOL/2P/w/+z/s//W/+D/qP8WAPH/KQAOADoAMAD//x4A+P9SAAgAPwAYALr/8f/k//r/6v8zAOL/JQAHAIf/+P+4/9r/DgD0/1gAIAANAAIA8P8RAOz/OgDu/wAAIwDs/+D/7f8tAJj/RADx/+f/UwDe/38Ar/9DADAAlP8rAL7/FQDD/9j/3P/l////6P9QAPf/OQBHACgAOQAMAPD/IAC1/5L/+/+b//T/8P8bADAAAAD3/+r/EgDY/z8AKgA4AOf/IgBJANj/DwDy/0EA1v8NAAgA1/8CAKj/MwCx/+X/zP+7/x0A8P8UAPP/VAD2/0MAOgBUAA4Aov8YAJP/DwAIAAQA9f8JAEgAoP8VANb/5//2/x0ASwDt/ywAKwD7//z/4f///zUAv/8EAP3/tf8iAPb//P8MAAUA8//e//X/EQD2/yEAGADb/zwAw/8kAFEAq/8uABcA0v8fAAsA8P8kAKP/wP8PAPT/EQDr/0gAKQD5/yMAFgDi/9f/yf8pAA8A5f8jANH/DAAAABQAKADM/9v/zv8HANb/GABIAAcAHgDJ/xYALwAOAE4A9v8ZAP7/+v8rAMD/IgC2/5T/JwDW/+n/9/8oAN7/AQAjAN//FAAGACgAGQAbANX/FQAzANr/HQDp/y0AwP/U/+X/AABEANX/NwDM/+L/8//y/x8A5P8rABYA/f8OABYA8v9bABYA4f8mAOP/LQAEAAMA1P/K/7v/yf/z/+//1f/E/ygA7v8cAEMAKQAmAC8AOwAPAGAAx//3//7/uf/i/8L/GACr/wgAAQDY/ykACwD+/+z/LQATADwAEQD6/xUA0P/q//v/EgAqABMA6f/w//X/w/8EAAsAAAAxAPL//P/n/+D/hADC/zEADgCa/0QAt/8oAAgAzf/E/+X/IwAyACUA1v8SAN7/AAATAPP/9f88ADAA7f8qANf/HQDd/ysA+v+c/wIAvv8hAOX/VAAiABEAEgDM/ygAof8AANX/QQARAEgAEwDM/10Alf9zAM3/2//x/5D/EQCi/1EAu/85APv/3/9uALb/TQC5/zoAQAD4/1wABgDz/wMAFQC6/wAAz//m/xwA/P8tAMT/DgDS/7r//f/f/w0AJwAxABUAIAD5/wEAIAAPAPb/HgAeAMX/7/8EAMn/zf/z/7n/7/8fAB0AYAAyAPr/SgDt/9v/8f8ZABsAuP8xAPr/z/8DAMz/CQAMAEEADQD8/+P/5//r/8f/DwDV/wMAKwAEAFEAJwAKAAUA1/8GANn/nv/w/xEAIgAbAC8ACgAeAO3///8GAMX/NADC/0EA1f/A/2IAff9WAO7/9P8+ALr/QAACADQA9f8yAB4A1v/q/8z/+f+I/y0ADwD//0cAl/80ADkAuf8yABcAwv80AC8A4P/j/+j/7v/M/9P/MgANAPz/LQD//3AAEQAgAC0Ayf8TAKv/3v/S/+3/4v/I/yQA5f8qAC8AAwDw/1UAEADQ/0oAAgDp/9H/DQD1/7P/CwBFAPr//f8LAOn/KwCl/ywANADf/xUA3f8jALr/JABTAP7/EgCd/9v/yv++/yQAIADo/xYAIgAmADMAMgDo/+7/HADf/0sAxv8QACUAu/9YALH/BwDs/7b/HgDH/zgA4f/9////5f8uAMb/CAACAA8ATADn/z4ADwC//2kA1f/7//7/u/8AAO7/KgDk//r/0P89APL/tP9tAOP/DgDF/xcAJAD//2YAwP8WANP/0/9iAAUACgD8/+X/EQD6/9H/IACt/8L/GwDb/yAACwD1/yMAAgDo/yQAJQAUAD8ALwAqANr/6P/u/9X/9P/0//P/8f/V/7//AQCf/+3/DwDk/28ACQB9AFcADgBGANv/IQAFAAwAFADK/9v/hf+5/+v/3//6/xYA4f/c/yYAIQBGAPP/zv8XABUAMABUACMAHwAwAJn/CAATAOr/CQC1/+T/uv/L/wUA/f8WABUA0f8KAFIA2f9hAPf/BgBsAKj/NgDt/+P/CADj/0oAwf/u/wQArv/g//L/8f84ABEACgAtAAEA+P++/+P/MQAdAA8APADP/7r/NAAaACMA6//5/wAA2f8OAPH/JwDq/6b/8v/1/8b/KQB1AAUAHwAOADkAAgD//yMAwf/a/xIAzf/0/yIAyf/0////BQDu/xsALgDT/1oAuP85ADoAjP8pAKb/BgAbAMT/5v8LACAADQBHANX/GwDf/wsALwDr/24A4f8wAAoAef8MABEA2v/5//z/CgACAP7/MADw/wQAAADf/xQADwDf/+T/6v+f/+r/7//t/24A9v84AFYA4f8mANr/AAAjANT/LwBmADoA4v/6/wEA2P8iAOz/zP+x/9X/BQCv//z/7v/f//r/DAAmAO//YAAUABUAVwDk//7//f/8/xUA6P/U/wUAHQD8/wQA7f/9/xEA1f8ZABwAx//Z/7T/2f85ADAAJwA6AMP//v9HAAMAMgDw/zoA2//W/0MAr//b/6T/HgAVANn/LQDn/0EA3/8QABoAyv9ZAMn/AQDb/9z/QgAOABoAAQA2AM3/7/8OAJX/CgA4ABAA4P/0/ykA7v/T/ysAHADp/+7/KQBBAK3/HgAbAN//IQC2/x4A8P/N/y8A7v8TAAgAv/8DACcA8v84APb/GABAAAQAJQC//7v/AwD+/9//MADX/73/8f/0/yIA2v83AA8A4v8+AAcAMADu//n/DQAlAM7/xv9GAMP/OwA7AP3/6/8aAB8A2P9mAAUAAgDr/6X/mP+E/9//0/9EAFwAGQAPACQA9P/r/yAA9P8VAMb/FAAEAPH/7P/j/0UA3f+IAEMABgBPANv//f+P/8P/1v/l/9X/4/9bAAMAGgDQ/wIAAQDN/08AGgDh/+T/FADb/wkASgACACEAEQD4//j/+f/e//7/AADo/wcA/P8fAML/7/9aAPD/AAAHAP7/LgD7/xUAHADI/ygAu//C/wMAq/8uAAAA+P8eABQADQDU/w8ABgAqACoA7v8VABgA3//v/yEAGQDM/xcAHAAKABUAw/+s/8j/0v/8/+D/RwAjACoARADB/zgA5//Q/0cAAAASABkAMgDx/wQA1P/O/97/qP8jAPP/ZQBLAN//PgDo/8j/iP+x//D/FwDq/xIAYAD3/1wAMgAWAB8ADwDo/63/SQDP/xwAVwCl/x4AsP+p/+j/4//0/w0AXQD+//b/AADe/+7/4P/8/w8ANgDn/1oAKgDy/0IA2v8iAPz/2v8BANH/DgD1/9v/uf8FABMACwAjADgABADp/1YA3P/y/wkApv/f//T/KgAkAPP/HgAFAKb/QAD9/87/9P+t//n/GABSAFgAaQD0//r/IgDB/wAAsf/j/6//sP8tAPD/GwA/AD0AaQApAMn/7/+w/53/HQD+/zQAOgALAPH/DAAWAO3/DQDI/+L/1/+x/yUANQAAANv/EwAUAAcAAgACAAQACAA0AEMAMgArAA4Az//m/+//kv/Q/77/zv8+ANv/DwDo/+r/HAAOAHcAIgAcAAgAFwAMAMH/AQD6/x4A6P/d/ywAFgDr/xgA8//E/87/9v8LAMX/TQDz//3/EQDk/0sA0v/7/x4AHgAKACYA2/+5/x0Anf9FABYA4v8qAN7/GwAOAOv/BQAfAMr/IQA6AKr/9v85AOj/EgBOAAwAAACz/w4A9f+x/y4A0f/E/yYAAwDl/wQA/f8JACAAAQAqAFUAJwAVAN3/0f/e/7P/4f8aAEMAGADy/+7/CQDi/wgAXwD0//T/8/8AAPj/yv8ZANH/9//y/zUADADN/yEA3P8QAPX/OgD3/8r/GwD//0MAFwDw/97/2v9lAFYAtv/Z/+H/zf8aAPr/OQD+/93/+P/P/93/BQAAAOT/EgDA/x4AMwBIAC8A9f8cAN3/IAAjAOn/HgA/AK//2/8PAJL/+f/R/00APQAQADgA8P/k/4///P/+/wAADgAUADwAsv/y/xQA4f8DACMAIgABABkAIADa//H/GQDY/8r/EAA/AAkA0v8aAOv//v8iAN//IACo//T/LADY/0sA5/8LAPb/MQATAL//dwDO/wYA7P/i/yQA8P9CAAEAHwDI/6//1v/j/woA9/8yAAcA5P8bABkABwAlAOz/7P/U/+z/GAAsACMA8f+VAOj/3/8QALX/+v+u//D/wv/R/+L/HAAsAO//GgAxAEYABABdAOb/JQAHAJb/KADJ/wwAzv8iAB8An/84AB8AAAAXADgAtv/B//n/nf8WAB0AIAAfAOf/LgAlAA0ADAD9/1EAy//e/ywAxP8BAAIA5v/0/6r/8v////v/FwDV/ykAAQAMAGQACgBUAAAAxv8oAAAAwv/7//z//P8iAPn/WQDj/87/4P/d/8L/yv9PAK7/5P/d/9f/4f8PAHEAEgBFAP3/SwA1AFsAUQAhAEEAnf/l/3//rP/b//f/IAAFABAAiv8VAMX/EwD5/+L/WAAQAD0ALwAtAOD/8f/t/wYAEADN/xwAq//Q/+z/AAAOAAoA8f8gAG4AJwBBAP//zf/i/9b///8gACsAAAAAAPH/9f/n/8b/5v/s/8r/3/8NAAwAHAAyAEUAUwAVAP7/4v/j/73/0P91AN7/GwAmAHP/IQC3/y8A0//j/14Auf8jAAUABgAyABkAMwAOANH/CQA+AAgA6f/Z/xYAw/8KAL//vf8lANz/KQC4/zsA/v/v/z4AAAALABAALADJ/3YAyP8LACkAgf/8/7X/kgDr/x8AWwD7/xUAd/8PAJr/2v/y/83/CAAAADcAGABLAMf/4v8tAA0AQQBTACUA3v/l/wQA9/+5//X/BQCV/xAA8v/b/2AAHgAjAN//LgA0APn/bQDj/9H/lf/x/+r/i/98APH/CgBLAAwA5//V/+v/w/8VAAcADADz//b/BwAQANH/JgDI/wMAWwDb/6MA4f8JABoApf9oANT/3v/0////zv8aAMP/5f8/AND/XQDZ/9P/KQA0AOD/JgAnAMH/GwCw//L/7v/I/y0AJgAEADcASQCy/x8AAAAKAPL/y//b/xEA9/8GABwAxv9vAOr/7f9BANv/IwD+/xAA3v+6/+j/DwD5/yQAJQDp/w4AAgDR/9n/CgCd/wsAzf/y/3kA9P+BAC8A5f9KACwA3f/E/8z/GgD5/9r/LQDw//r/CgAcAAEArP+1//v/+P8FACkA8v8PAM7/+//u//3/JgASAFsA8P96ABkA8f8fABMA6//V/xwAov/c/+H/5v/S//j/8//o/0cA9v8uAAEAIgAgAPH/KwDV/9j/+v8NANL/5v8SAEMAKgAxACsA6P/g/7b/+//o/wkA/v/P//f/GgAOAO3/4f/j/0oA8P8zAE8A8/8VAAcA8f/K//X/5P8IABoA9/8OAP7/9f/y/wAA+/8TAPb/KgAHAA4AGgDI/wIAwP8FABkAzv/z/+7/8P8QACEANADY//X/SgDy/xgADAARAA8A7//t/+3/4f/7/y8A1/8oAN7/2P8eAJz/9P8KAE4AIwAKAAoA/P8QAOT/LwD+/ycATgDm/73/2P/O/8L/1P/n/yEA7f8dAEMAJwAUAD8ALgABADcA2P/s/7D/3v/d/6r/FwDU////7/8kAD0AAABBAAgAIQAAABUAQwDT/+7/0//K/wIAwP/g/y0ADAAIAAcA+//d/yYASQAAACsA3P/9//P//v9hANT/7//V/8//JADf/xIAKgAGAAAAFgC//8X/FQDs/xIAMgD5/wUANADY//P/AwAzABoA0v85AM7/7/8aAMz/7//o//b/5f8KAB4ACgAaAPj/EAAaAOb/OwDw/wEAMACc/xwA3//S//D/AgApAA8AXwD+/+b/z/+9//b/MQA8AOf/OQD6/77/IwDX/wcAEQDr/ysA9P8NAO//xv////T/GQABABEAMQAeAKP/BgACAMz/MgC//zMAJAALADMAIgAFAAAA7P+Q/yEAxP8WAAcAvP8AANb/KADL/44AIAAAAE8AyP8FAO3/QQDZ/yEA0/8AAEoAo/8+ALX/8f/m/+P/NADo/yAAyv/A/7j/3v8XAA4ADgA7ADMA0P8kAFwAUwA1AAIA9P/S/wkAFADf/wgAGQDk/yYAmv/Z/wgAlv9DANP/CwDW/9D/XQCz/wAADwAZAAMAJABoAAEAHgAMACcA2//E/wMA7P/H/9n/LAAOAAoA+/8OAAgA+P8XAPz/+//u/wMA9P/8/wAAEAD8/xkAFgD2/9j/mf/r/wEAVAAxADQAVgDQ/woA0//X//n/FwAGAO//QADW/wEAEwCq/97/1f/Y/+P/GAAnAAQAKwATAC8AAgAHAPD/AgA1AM//UgCx//P/TQDN/0MA7f9IAJD/DAAfAJr/PQCg/xsA0P9GAEAAMQA3AIr/8P9z//n//P/Z/0kAGgABADkA4v+v/ywA1f8uABUAaABAAAUAbADA/+f/+v/X/8f/+//C/9f/AQDj/w4ACQBKAOb//P/E/x8A0//S/0oA+v9QAO3/bwA0APP/IQDu/+3/xP8hANz////y/yAA0P+e/wwAoP83AOn/CgAqAA0AJwDs/yIA3P8dAC0A7P8CADYA9v+g//D/AQAMADoAEwAWABMAyv/v/wMAAAD9/+7/AwC+/xEAOwDc/zgAJwC5/wUAAQDL/z4AEAD2/x4Awf8HAPT/BgBRAK3/LwD9/5H/6P/J/zMA7f9YAE4ACABeAOT/3//g////9P8kABoAAAD+/wUA2/+t/zQAlv8FAPr/iv9aAKz/MABJABgAJwDp/3AA2v8aACkAGgALANb/o/+y/wkA2f80ACcAQwD1//f/HwBW/0IAKQAJABEA9/86AK//FADl/xMA/v/W/yUAAwD9/43/1P/a//f/XQAqAA4AXwA3AAwAAADe/0gAzf////r/o//I/+T/EgAAACAAwv8yAPr/CABUAAAANACw/0IA0f/h/yIAtv86ANH/9f/8/w0ACAD4/0EA4/+4/xoABgD+/z0AHgAWAOX/AwDo/8//AADW/xgAHADm//f/KwDh/wUA4/8bABsAu/9uAPD/EAA5AMv/IADo/w8ALADg/8j/6//+/7b/TAAEAMP/TAC7/x0A6//j/wwAtf9GANn/TABGAOj/CwCj/xMALwACAAYAMAD7/y8Ax//r/zMAk/82ANL/6f8UAPL/DAALAE0Apf8NAAoA0/84AAUA+f/0/ykAIgDj//z/7f/o/xAAuP8eABgAtf9NADEA8//x/ycA6//d/xEA2f8GADgAHwAZAA8Awf8ZAO7/yv8bAPv/9v/K//7/yP/E/ywAvf8pABsA4f9wAD8ABQAfAA0A6f8RAAgAAgA1AOf/KwD0//7/4//j////qv8rAJr/2f8nANH/JwALAAkA1P86AOH/CwAvACEAPQDw/0IAov8NAD4AxP8EANL/yv/C/yYAHwAXAOj/1f/9/y8AGwD0/1wA4f8EAOH/uf/p/wgAUQAoAFEABgAFANj/0v8XALv/9f8EAOT/AAD0//7/+P/3/xUA+/8zACAA6v8hANr/8v8NABkAGwA9AEEAq//T/93/oP8IANH/2P8oAOL//f8QABwAMAAcAG8AGwDs/yUA9//Q/93/AgD5/+b/+//D//X/6v/5/zsA3v9mACMA/f9GANj/NwD9/+j/9/+C/+3/4v/U/zMAJgDl/+T/RwD2/9z/QQDk/+P/EAALAPz/AwAIAAsAGgDc/zwALQDA/yYAAQDh/wkA8//p//X/CQARAN3/4/8hADsA4P8FAO//vf8NANj/MADt//j/UgAwAEwA4P8iANz/4f/X/7r/6/+p/+n/AwAwADYAGQDU/ycA//8WAEoA/f8nABsAAgD0/1YAuv8FAP3/bv9HAML/8/8YAOP/lv8HACcA5P9BANX/PAAKAOX/NgAVAOj/JgAXALz/EgDS/zMAAABFABkAJAAuAMj/HQBm//b/3//z/xcA4/8BAKX/DQDY/xgALQAZACsABwA6APz/3/8aAPP/vP9qAB8AOAAsAMz/QAC9/+z/DwCh/+7/BgDN/xMA/f/V/xcAof/w/w8ABQAsACEAagDd/9//QwDm//D/BQD2//H/8v8RAC4AAAAEAPn/9P/n/xsAPwAQACkApf/a/yEAkP89ACwA5v8wAO7/9P/c/8b/+//8/xgA/f/9/wwA3//d/xsAVQAWAOj/GAAgAND/AAA1AOr/MgAYAB8AAADQ/wsAnf/s//r/vv/8/xAA///r/0QACgAVACQA1v/r/yEAzv/+/4MAv//t/xQA4/8RAAAAHgANAOj/AABbAOT/+f/m/8L/xv/e/wwA4f9LAP//9P8NAAAA/P/i/y4AAAB/AAkAAQBLAJb/0P/L/zwADADk/xUA9P/+/5X/LwDw/+H/IwDx/xEAEwATAPf/LgANAOD/OQDj//L/BwAeAPv/6P/7/8//UwAAALn/CQD7/wAAv//s/wgAyP86AAMASQA6AMz/PwAQAAIALwDC/8n/CQCv/+//IQAcAAoAGwBIAL7/FQDt/83/IwDE/yQANQC8/ysAXAAFABcA/f/c/5X/qP8PANf/BQADABEA///r/xAA1v8VAFMAXQAfADEACQDl/+L/u/9HAPv/7v8eANL/AAD8/xIA1f/x////6/8lAJr/3//7//P/OAATAEMAAQAXABEA/v/a/wMAGAD3/1IAw/8xAPP/3/8NALX/JQCp/wsALgDo//3/IwAiANj/4P/O/xIArv87AGIA7/8yAO7/HwBAALH/+v/3/4v/TwAFAAkAMwDw/xIA3v8mAPP/DwAMAOz/9//8//3/xv/p//H/6//T/1gA7/8BAEMAyP82AAkAAADv/xMA/P8aAE4A/f/f/9P/PgDi/97/+//7/+3/2/9dANL/4v/8/wgAAADg//7/y/8aAPH/CQCDAP7/MwAAAMn/HwCw/8j/EwAqAPv/5P88AMz/4P8MACMAAwAqADcA//8VAAAA8v/B/ykAAgC2//f/n//U/xQAAAAUAGMAHwDf/0oA1P/+/y4A4f8cAAwA5//x/wQA5f/0/yQA9P8fAPn/vP8tAOb/+/8gALT/9v/l/yUAQgD3/wcAAQDy/9//BAALACkAMgA7APD/1/8CALj/FAC5/wEA5P/2/1MAu/8cAO7/EQAxACAAOwD8/w8A7f/O/xUA5P+z/y0Atv8OAC0A9P84ANr/UgDg/8X/LQD9/8r//v8MAMT/gwAFAPv/RgDZ/wIABwDr//j/7//d/wwAw/8EAMf/2//U/+r/QgBDAGUACgBHAPz/FwD3/7z/6/8RAPn/w/9SAML/IwAJAN7/KACk/yoA4P8BAB4Ayf8RAOP/jv8oACMA+P9gAB0ABQAHABUA1/83ACkAAAACANn/4//e/xUAtf8kAN//EwArAO7/WADC/xIA8////8H/1P8OAOr/IADq/3UACQAhADMA7v8aAK//4P/u/83/7f8oANX/2v8bAM//HwAEAO3/fQAFAA0AUwA/AAAA2v8KAIn/3v///6P/8f8CAA0ALwA7AAIANgCY//z/FADr/24A4/8LAAIACQD9/w8Aw/+z/zAA4v8QAPL/DQDz/xEAHwDg/2cAEwDx//v/4//Z/9n/BwD3/9X/AgApAOj/EAAyAPr/BwA2AOf/+f8qABMA6P/u/wwA8P/h/xIAGQCq/wQA1P8SAPv/u/9JAM3/YgAmAA8ANQCd/xsA6v/9/wUA/P/d/9P/GwDt/wMAEgAnAEgACgAQAM3/AgA3AAMADQC8/+z/6v/D//z/yv8NACIAAgAcACcAAABzAPf/7f/1/5r/KgDY/0gA0v/G/3cAvf/8/wAA9f/J//L/CwDy/ywAEAA3AAAAGgAIAMj/KADo/9n/GwADAPn/5/8MAOn/+f8sAAsAMAAtAAcA5P8IAMb/1f/9/x4AQwDd/zEA///S/8v/2v+U/5//MQC9/1AARAAeAFwAHgA/ANr//f8pAM3/AwAeANX/IAAXAKL/7f/U/xIAIwDy/ywADQAHACsA/v/J/+v/8P/N//r/HwATACUA2P8hAOP/oP9MAOv/DwD6/9j/fwAEAPz/LgDh/wEAs/8eADUA2v9tAOf/5v8bAN3/AQDM/7b/wv/8/w0A/P/2/xIAFAAHAAMAHwAeABsAMQDK/0AABgDn/2AAtP8HAB8AuP/q/8//5P++/yMAOADe/+7//P9YACkAGAAmAP3/2P/y/xkAvP/0/8H/AwAlAAoAIwAPABwAzP8xANT/7v8kAJj/9//n/w4A/P86AB4ADQAEAPT/WgDs/3IAGQDj/+D/tf/P/4P/OgDf//r//f++/yUAxf83AGEAXABMAAAACwAYALj/0f/9/5f/7v/n/9z/IwDn/yEAPQApAAAAFAAbAK//KAAcAAQALAD1/xoA4//W/+7/0/8BABcAAwD3/yYA2P/D/+r/6f/u/y0AIABAAB4AuP8JAAoAGAD1/ygASQCr/xYABACO/wcAAgABADkAyP9VAEwAtP9wABgArP/d/7T/qv/q/ysAHgAVACkAEQDa/97/5/8MACAATgAIAAoAFQDf/+7/3P/X//f/FQDg/9n/FAAJAAYALwAjAP//MADW/w0AJwDP/xUAAAAbAOD/xv8EADEA/P8iAAUA2P89AH7/7f///53/LQATAPn/JQArAPT/OAD2//H/GQAqAAIA+v8BAOn/EwCD/woA5P/X/28AFwCKAO7/1P/K/77/+P/U/zUA2v/q/y0ACAAeAE8ACQD+/wMA3P/0//P/DQDi/yAA9v+q/wsAIADW//z/zv8gAOz/y/+TAPP/VgBTAPP/LACe/wMANADI//T/MQDl//T/tf+4/+D/qf8yACIACgDl/2AAQADJ/ykAKwDh/+n/FwCl/83/BwAOADwAWwDy/x0ASQDY/14At//v/7n/2/8KAH7/FgDc/yQA6f8iAD0AAAAYAO3/YAD4/wUAIwDn//H/AgCc/+P/GAC3/wwA2v8oAAoAJQBzAA4A8/8AAML/1P8AAOP/RgACAD4AAQDu/73/5f80AAMARwDj//b/yf/+/8f/7P8eABoAFQD2/3sAxP85ALn/7f/T/7P/bQCg/2QA1P8MACgACABVAL3/GgDY/xkA5P/M//H/+v/Y/xMACQATAHYA5v9CAOv/9f/f/xkABwCd/xYArv/Z/x8AGADS/0wAMAAoAB4A0P81APL/6//c/xsAr////xoA4v9eANH/IwCz//P/CADR/0UA5P8JABAAIADj/zUAFAD0/zUA7//1/wQA1f+2/2EA3v/k/zwA8//3//n/FADb/xIAAgAFAOr/IAD//6j/AwCQ/wwA/v8/ADIAGQAmAMv/VgDv/0QA6/+y/xwA/f8xABkAIgDN//f/CQDm/9T/6v/c/wEAOwCs//j/9//f/w8AKADh/+D/KwD//zAAAgB0ACIA9P8DAO//JwC1/zMAuf+t/8P/DwAqAPH/XwABADAA7//3/wgAy/9HABkA+//n/3//vf8CAOb/PQAfAIYA2v+W/1wAs/9BAPr/DAAFAAEACwDL/wMAqP8eAO7/OgBaAP//+f/3/1QAPQD7/6v/KwCx/77/NgCq/6X/9P8RAB8AFQCx/xMA3P/m/0cASwAdACAAYwAWACEA6P/0/6j/uP82ABAA7P8SACEAqf9CAOP/6////9P/BgDQ/18A3P/+/0UAAADo/7b/BwD8/xIAHABFAOP/wv8LACIAGgDq//z/3P/u/yIARAD6//v/BgCr/8D///8GAAwAHQAxAAAAzf8AAAMASgD5/z0ALAC9/wcAzP8UANf/KgD9/wAAUADV/yAA0v/j/7f/CQD7/9n/EQCm/y8ABQAnAAAA7/88APL/IAAaAN//GABAAMT/FQAuAO//LgANALX/7//X/7b/HgDx/0kA///M/wsAEABTADAA+P/L/wgA7f/E/9H/7P/H/8H/6P8hADMAOwB+APv/QQAxABEACACu/1IAk//H/wIAz/8YANz/IAD6/4r/BwBJAKb/SwBSAO3/KgAMAD8A4f/4/zcAuP+2/ysAKQDO/xEAw/+z/xYAAwAXAOr/NwAhAN3/OQABAOX/9//1/wMADAArAOT/t/9QACYAMgAuAMP/MwB6/6r/LQC6/0kAQwALAN7/AAAcAAgAFADC/7v/wf/4/+L/IgBBAN7/+f/x/zcAPADo/yMAPgDm/0QAJQANAP3/8P8PAJ//+f/T/+D/BQAIABQAq//8/xgA1P/w/x4Arv8pAD4AKABdABgADADA/ygA3v80AB8Ayv/M/7n/CwC7/2kAAgAEACwAsv/f/wkALADo/ygADABoAO7/5v/v/6L/6P+//4AAHQDm/+j/EwAKAOj/KQDy//7/VP/Z/zUADwDz/wcAaADg/+n/SABkAEoAPgBGAEUAxP+d/8b/3P+H/1//LgDi/yAA4P8XAE4AzP95ANr//P8bAPP/1P/2/1wA4v/7/woASADI/woAbQASAAYA0v8KALX/oP/1/wYA5/8fABwA4v9dABEAv/8/ALf/i//2/9T/VgA/AOr/PwASAAgAHwBOABQAyf/s/xkAvv/c//7/5/8HAJ//ewBsANf/PQDB/+b/xP/U//H/AQAyAK//KQDB/8//rAAQAGAA8P9Z//P/5/9UAGUAAADY/9j/7P/u/1EA///V/xgAv//9/zoA9f9NACoAHQDn/6P/LwC+/9//NwDU/y4A2/8GACcAnP/7/+n/DgBXAA8A9/+1/+X/LAA+AAcA+f/z/73/DACGAFsACgACALP/rf+z/7P/OQAxAOL/sf/e/xgAAQAjADMADwDx/ysAegAIAPX/LQDi/8r/7f/z/9v//f/m/zwAGgDN/zMACgDX/7P/FwDo/9T/+//P/2UA2v/u/2oA7P/n/zwA9P/8/x0AOAB/AJj/+/8BANn/8P/7//L/nP8UAAsALQDm/zAA4f96////wf83ADsAbwANAPf/SwDx/9//EAAyAMH/CADz/ysA7f/o/w0Alf/U//v/KwDg//f/BQD1/yYAcgBCAEQA//9p//z/Uf/I/xEAHgBpABUALQC7/yIAAwAdADUAYAAFANL/5P/F/wwAVf8VABcACQADAB0AQgDS/0EA9/8hAMT/ZgDo/5v/FQC7/xAA6f8BAMz/8v/W/00AFgDv/6sA5P9aABkAQQAAAHr/9P+o/7X/x/8dAOn/FwBwAB8Arf/f/wsAxf8nADsA+//Q/zEAAAD4/zsALQASABwAQwDq/+T/nf8NAP7/2f9DANf/if/g/y0A5P/g/w8AXgDz/x4ASwDq/yYAjv/b/9T/HgCHAC0AHwCz/9f/JAABAOH/JAD8/8v/7/8DAE8A4f/h/9f/vv8bAC0AIgD9/wQABwDt/8j/9v9GABQAEwD1/wEA+//q/wAAov9AAFIA1/8YACgADgCf/xgAKQDa/+7/+/8DANL/OwBnABoA0P///93/fv/P/zcALwD9//L/8P8AAAsAYQADAIP/BgBLACwA/P9oABEAZf+e/zYAUgCx/+b/3f/8/0QAHABwAMr/b/8+AEAAvv9QAAUAqP9CAP7/DwDE/37/IQAuAFgAAQDw/9z/9P8qAPD/4//j/y0AMwATAPP/of8dAHQAOwAfAOz/wf/Z/8z/5v/2/7v/3/8FABsAJQDx/x4A/f/w/2cAAAD1/wsAMAD3/3z/HQAcAEAALADx/8X/3/9BAAcAzf8EAB4Ag//q/yIA6/8kAPr/6P/y/00A0f8vAIIANgADALz/7v+o/9T/of85AC8A4f9GAAIA4f/I/zIAzv9IAGEA5P/R/x8AQADM//X/x//T/5L/DQCgAD8A6f+Z/xcABQBOAIIA4//j//H/s//U/xIA+P+o//v/QgDX/y8A+P9JAD0Asv/V/xUAWgC9/yQA1//C/8H/2v92ACAAFwCx/x4AAACj/08ASwD6/+D/GwDy//v/GgAmABcA7v+J/+P/MADZ/yAAJQAjAA0A8v+9/xgA5f/e/z8Auf90AB4ABwAgAMb//P/f/7n/vv8rAPL/HABXAO7/yf/b/yIAXQBDANn/z//r/zEA7f/0/9D/nf8BAA8AQAD1/zEA+v8JAEcA/v8bAMf/6f/x/zsAPADu/+H/+P8CAAQAAQDH/+b/w/9pACQA0P/g/4D/BwD9/+//4//2/1kAhABEADUACADG/yQAMAD0/2f/2P8+AAgAEgCZ/6H/7v82AHAARwCf/8b/NQAjAC8AHwDA/6b/7P8VAGwADQDO/wUAVgB7AI//q/+o/4z/NQA0AC4A4v+1/0EAFgDz/2wABQDR/xwAIwBWALD/t/8+AMj/NQArAIj/6f+J/9z/ewBdAEAACQD4/wYA/P+H/5T/vP8IAGoAZgB+AO3/sf/8/wUA+//n/9P/0f82AEcADgAvANj/lP/u/7T/EQBdAPD/bAAfAJT/5v9JAM//3v9XAMv/xP97AEsAnv/P/xgA0P/q/xkAcwDt/7r/xgABAH//FwC9/5n/9/+iAEkAov/7//3//P8uAAYAqv+u/4f/9/95AD8A5f8NADAAEgDn/0P/WADd/wsAAAHq/ywAEABBABUAs//1/8//2/+t//T/QAA/APv/1P/D/4v/kf/u/2kAPgAwAO//WgAXANf/XwDk/+z/yv/3/xwAi/8uAJYAYADh/4T/LwC//8P/HgDO/1D/7//CAPj/UgAxADMAUQCu/28Axv8H/83/VABl/+//mwDR/3YA4v8/ADwAZ/8+APT/BwDr/1oAkQDW/08A5P9z/5z/lv+y/y4ANAC6/0gAbgD5/7L/PwBJAOX/LwDU/zIAFQDY/8v/sf8dAF4AUwCO//f/HQCJ/wAAWABaAMP/s//6/+j/yf8vAEIAvP/I/zkANgCp/1gALADp/18ABAAXANj/5P8vACIApv/D/9r/qf9PABIAh/8iAIoAn/8EAJkAAwDS/+n/VwD6/8r/aAA4ALP/8P9BAEoAVP+3/j4ACwCj/6wANAAaACUA/P/2/77/bf/P/3AAaAAJAQUBjP/+/rP//f9JAMD/rP8AAIr/tgDfAPP/rP9L/7v/ov9m/2oAsADn//j/PQBrAHMABgCy/9f/QADl/z8ADwAKACkApP/v/wIA0P+C/+X/vP/p/xIAUABIAKX/OAAcAGn/pP+GADsARgCTAL3/1P++//b/PwAmAIH/HABcABIAswDW/7j/o//1/8H/lv82AD4A3f/c/+QADQDs/+f/vP/k/wcACQC2/20A+f8mAP3/W/9Z/8j/UgDl/5EAGgBLAE0AQgDF/6n/cwCf/wwAAACAAKr/Zf+tAL7/yf8bAJ8AFQC7/wsAwv+H/1X/CgBQACkAVwA6APz/LACq/63/owCnANr/3v4HAFoAMwBzAPb/YP9H/50AtwC9/zj/tv+LANX/FAALAIH/AwA+AHMAYwAIAPT/wf9gAKsAr/+T/+7/of+v/yAAmf9A/1YA+QBCAML/Zf8tAP0AMABgADkA+v5I/3IApgDk/9//p/8B/x0AnwBrAKv/B/+8/2MALAHdAD0ALP8E/2oAiQBLAMr/V/+I/wcBBwCC/2oAKv/v/wYAZQCgAAwACgBg/7T/ZP+2AFIAcf/9/0j/mQDFAFIAnv/n/x0AKf8mAJkAowCp/1P/2gCJAHv/s/9RAO//Xf9uAGoA8/6j/9YA4QDx/tv+lwDQ/+X/cwCGAKX/fP/8ANsAAQD4/+v/Fv9u/0cAjwAFAHn/pf/b/9j/awDeANv/yP8n/wwAGgHx/4UABwDC/8z/Xf8kAJ4Ab/+O/zkAsv/CAB8A7/8AAKn/OQC9/xwAtv/U/+H/XgBrADkAgQBk/wUAff9MAGUAe/9aAPH/gwAcAM3/Kv9i/2EAxv/h/0YApgBq/3j/BgA5ABsAsv+7ACkA3/9yAEAB9v/O/oAAyP98/+L/dgCBAIb+qP+OAGcAQgBz/+r/K/83AGwBEv/j/zoBYQAgAGr/9v4C/wIACAFOAFIAYwDF/+j/xf9rAD4AoP6s/xABBgAGAKUA1v+k//P/MwBi/0f/WQA4AGb/oQC9AVz/3v6J//j/DwCNAAoBLP9r/1cAqgB2AB0A5f+6/tP+NQHsAb7/zP8V/0b/OQD+/wgBpP8I/9X/mACtAGMAXP/g/u7/EwCkAKP/ev9dAEUB5QGz/0P/Q/8+/zD/T/9BAQIAWv9qAX8Ayf9iANz/K/4a/2UBCwD3/24AqQHDAS7+mP7x/7b+Nv+HAMkAMAAXALoAJQAVAHP/lAAyABD+GwDZ/0EBCwHq/2EAn/40AC3/RQCtAY//yv5u/24Bdf9w/8YAYP8J/08AyADQ/7H/EwHsAMn+lv9IABMA+v9PACoBHgCU/y3/+v9pAB7/O/9F/38AtQELAMT/6v/V/y0Ay/80//T+TwFSAKT/9gAdAMUAVP+vAMwAMv7H/s/+9gDjATMBxf8h/1//Xf4UAOoAaQCG/pj+ugLiAT0AU/9a/3H/Xf4QAdwA8f9i/1AA8wCw/kkBKQBj/gQAbgCuAMD+qwB7AYT/CADT/+v+J/6H/9cB3ABa/44ATADr/+b/HgBSAMr/EAHt/7H+1//3/+D/EABoAav/E/4D/37/NAJ2AjUAxP5L/hwA3f9aAPkAEP+F/g4AdAKIAVr//P1M/zMAMP8sAjoBbP6g/ksAEwKFAE7/7f6y/2j/0P/FAVEB4/9l/p3/YgCn/zoADQA3/2f/nwAqAVkA6v8a/yb/pABe/9oA9v/o/kYBpwBJAa3/cf/a/v7+CQCYAIoBmv7eALQA5v8m/+P+QQDf/5sAvv11AZABRABzAPf+NAFc/wb/yv5pAXb/X/75AbMBngCM/SkAZf9H/4YAoQBWAK3+MAEuAUgAVf+cACv/PP6Y/y4APQFm/2ICsQCe/87/V/6G/z/+MQF3AHv+oAA+AtsBQv9R/4H/wf1D/nYBfgIlAcf/3P/R/2f/ZgCU/k39u//IALUBHAIFAXj/Cf/9/zr/BP+D/iUBPQKL/zMA6f9xAWn/Hf5UALb/4f5s/m4CowKoAM7+OP+6/8D9qwG0AUH/Rf3LAA4Cuv7VAGEARgBC/Rv//AFtAPcApwAJATb+3/9FANH+sP6A/zMCV/7S/2QCeQFs/2T+AwCU/0kAJAAcAZH/8/7rADwAhABW/3P/sv7E/zoChwD6/2b/Ov/i/xIAeAAC/8P+NAClARUB/f+eAH3+cf73AJUBKAAu/s3/uwAnALAAuwDe/mr+oAA+Aj4A1v31/9T/lgDfAW7/WP3J/qgBMgAJAZsAEv6b/rACVAMY/rL+Lf+1/u0AqALxAdj8kvtvATkDPf6c/y4Bmf4lAHsCngHQ/h3+YP87AS0B4P0l/pYBOAFw/xEBZACB/WL/VgIZAjz/Bf+BAJz/Iv+y/zoBnv6U/VcCEQMZ/n/9dAI6ACX/wwBF/v39MABcApcBvP8x/8gAZf+I/q0BUQDk/v//DACqASIBav79/4n/kf5u/+8AuQF3/gX/cAE5AfT+UwAaARz/9P2C/scCWQA8/30A9P/YANb/i//j/n4AMQA9AHEB8v8p/nf9wALlArn+1P7M/Xr+bwLkA+gA5/3E/YUA8P62/zoEg/7G/AUBBAOyAPb8NQBs/wT+///oApgB9/vR/3sDFAE7/tf+df+v/x4BHgF5AL7/c/8F/3ICYQAs/UX/2//aAVwBwv+u/zgAyP2IADICOPyT/+kCEgDu/0EACf/t/1b+GwAwAgT+zABtAk8A8P1uAPkAp/yhAfMB5P2R/tMCQQEf/iMC3P9L/Sn+1//LAPQB7QHJ/df/zgDXAEb/Af5wAvT/vP0NADECiv+w/l4BFP+O/vEABwIL/rwA+QO5/qn8W/5AAcMAggHH/n3+0gE2AHQBbP+X/mD9W/4eBY8By/xk/0ADLf8u/UgELACk+ln99wOjBSf9VAA9ATT9iP7qAegD2Poi+w8COwLu/0ACogJg/of9mf23A6//SP0kApn/AP+1Ad8CDv8s/nz+bwH3AJz/YgCU/bD/TwMJA8H9bv+S/q76m/0RBUMFYvtj/iIDNgMo/hwA2wFb+TT8IQO0BnwAl/6WAWL/fv2TAHUCwPsI/YH+XwLlBbAA3vyQ/nACw/0m/pgCjACY/qUBDwMH/5T7xP5BAxH9t/xWBDcERf1uAf8Gu/1g+X78HAGq/3QBcwTY/AH+OwI+A20BbPz/+zn+XAAuA98EiQH1/r/9k/5UAB4A8v8//Kz+ogIGAVkCEgOL/1L6G/54Aob9Xv41At0D4wJj/1v/jv+W/ir+Z/4q/pIA1QPsAPEC3ANx+qH6ZwCwAB0Ak//uASABWACrA/MAyfsz+jT+bQIrA6AFFv8L+g0CbwMT/+39xv+N/S78PgQ3Bur+0fsnANQAcv3h/n4DPf8N+zUEcgXH/8H++v/h/D/7bQHtBMQCwfxv/0gDnQDK/OX9GAMr/or8xf9hAwMC4v3uAJADNv8N92wC7AOg/CUDOgCeAiT9dv60Bk38efxC/kEEIQKQ+psCCgLP/nL9xALfAdb7x/8xABUDU/87/ej/U/7nAOUCugLY/QX+uAD9AUgBRv88Aaf72PtzArsEGACk+/QCUP8r/ZgDaAFj/yP+CwDU/1f6wv0kCf4GKf4T/M78G/3R/4oG9QB9/cr7LPwIBOkI1gW8+IT6DPnCAnoJ/PyO/ub7HwJhBXkD/f0c/Kb+qPqfAxEBdgARAQL/egA4AB0F6P52+pf8nP/yBRQDn/wBAJsB9AJb/Pv7AANGAA8A4/sOAgEDJwDs/4H/6/7N/JMERwEx/mj/6QT4+qn7cQQs/cEAg/4jA1n9eQQFBeX2cP63A98I/Pkk+roD3/8R/i4ElATu9Pz7sQfmBeb7QftBCIf/M/NKBggGDflU/i8Dugcz/H7/7wGP9RQAlw5f/h33qAAuAIYDGPqCBi0EOPU//IkDHAlz/2wB9vl7/Vb+GwAeBvn9ZQZh+oL51QElBjABKPn6A4QCuf1LAfMCg/31AV7+z/pi/pn+kQFUBHABD/8VBGr/hAAI+if9HgUt/zz7bv22BZkATALk/nAFgv9/9r7/dwBQBqL7tADpAGYCvwIR/ygGTfgk+Sb6vgYVASr8gwhdAgMGmPYFAKwIb/bi+lsEtvwG+RMLEAAj/UoH5v/a/sP6jP/TAE79ov9GCTUExvaDApwBqf2u/Dz+uQGN+GP/kQqLCZP6ef5tAlv01AUBB0T1kfsUA14CrATeB2QADPb2+BUGiwKX+osGlwOF8jP9tgaXBdEAEf0/BNT4Ivt4DH4HHfSh9/sFGf5Q/uECYAlMAO34IAF/Agz+hPsGA0n5yP9mBlwG7gA5+DoDVfxV/2n9+QAMA5P85ADD/ycKAAfc/KT4V/yN9GH/Jgxi/qb6rgQKEIH3BAHG/mD2Sv/V+GoMG/2BA5sJqPpZ94gApg+o8ivxKQrbCKL66wqTChzsPvV8DckCHPPLAP4ERgXg/GIJ3AQj7Kr5ov/mBK8HNw68+kPtXwlsD2T3gfQHCEf5ifMnBtcQDwMj9x8CbwYJ9i/2NQr5/Nj4rAKgDH0BAPgcCd//lvaW/wP/cvLoCNIQav8H/Pf/PAve+JLsBQEzD+P3fPbKCKkGfANQ+8n9SQDkAIH4kwCxBD7+jwOfAQwGW/fN/dEIMQDA9379KwvH9Rz+xP5CAksOIvdB/vD9Owh9B9T22/XG+JENGvy1AQcKTQAR+oL1wwsg+b8CRAeO+XT/sfWfCEUH+ABC/Cn8vgWI+5//W/u9AcsKc/F2/0gLm/nbAvb9/gduA1vzd/27BZkG+vQGB38HOvfD80EDqg0Q9eoAwwtaA9TxgQINCKjy8/vzCL0GfvI/CKcIfP1n+jT14QecAYb+z//vA0z9ygEDCAL/qP6I91n5S/70CFsFFf6m+/oBkwPq86sFJAhJ+nsACPwNCIQJ4e8T//gDR/4rAbv4JAMU/3EDvwdTAocA6vWR/In81gc+COL3owGH++sBZAeZANQAH/Tr/oj8ogPaBnb6OQt4+Ez9FQhi+DoCnQDu9kgHgQQB+i8LTvgCAFAACfmcEFL6xvC7AQ8O/vM+BJYQo/I8/vv3qghw/Sj6CA49/p8BAPbnCCkEqO2DCIoEifUnAfoJC//SBTMFrfev9/r1jwRJAaf+Lgz/A0n6jwRjCZzprfb0ERT8OvmUAUAJS/l3/U0fzvvj44j+jgGy/VsF3xJsAkDqsv7xCj4G6/iX9R795fhUCpsI8wMPA0X2KwKMAHv84QIg/7n5uf/rBOMEigPg/ZX6XfpWByECpfax918N3w3f7k0GlQTm9yYCH/pLAwkEw/il/foFvPOUCKgWk/qZ9dL0tAU8AaMAZQnzA7H4T+7TBWcEYPzJDEcEwvFVBWAGQPgs/sT5BwVcBKv2lACmDvb4+QP2Eu/nze4zCbkB5f14CzwFLwCh/Jv7qwmC/6f4y/O5AXwEjP3sAXgJGwRr+ysJN/MS+ssB/vhkA8oCJPthAnwRr/yx/479pvlBAacD9PRT9eIROf9eA+sCaAmt+nXzsAkX95wEW/3BBaH9ufffCZYAXf/q7AcBAwaXBmoDbv4vCBXzkwD2A+3/VANfAlr56PstDCL2T/3t/ef4gReSApHrAAYPDlQCYfvU+XL7afh69QYG2RuG/Mjusw/AARbvPwHZB3T3WPTVABochg2V3RkGAxvg7R/0SwM48q77jhFODu4GAPcZ9wT9iv1nA9YHGvYU60INfQWSFegYieJq6NQC3QjG/9IDVfDtASwL7/eqGY37SvfYBYL82/K0+kkOZ+WFBokapQHWCO3zHP0eAKnx0QNQAlntQP2NHfsRf/AyAXACpvgJ/xPwTQRgAP8BZQzo/x8HqPkN/G76VfvxAD0ACghZ/uYBLgR+ADcA0ACS+eH7k/qFAOUS1fV2/xoFufW7/g4AAxOe+AHsNQHoDN0NV/oXCGP0u+ZCB8wGpgnLBhn6YP4O/D8EFAIU/wwDCu61+wAF6w4VFlrrSfcfDdX4K/HEBJ4Clvr0DbEB3AGV/t0BOA2M9drsTfFEBTQC3BXgEofs8f43+f8BafamACYT/+Y+AWANdAp9Amv7WQQa9oQAB/Q3+fYB0wyoGGvvBvXVDLft9f0yHpD1tPdK/qsDAQvh6aoBEQjH76j5ZhUsDVf2XvuECdsDvfGJBm0AffRT+uUMbwHY9EEaIfx261P8QBD4AJH4VxGU6Hj5bwjeDncRKeI5+y0K/f1pBPsI9PoT4/35wxd8CT/73Q/rAoPePv2MG3v5+/C7AvoE8QU67ob/1iTbAibsxfg4/uH1PvlrGA4N8+w1+wAQSwC69jEAMffv/LD7kANBEfYFlAmR9VoDxv7j6Ib9f/d6D4QK8f9u9lcABhTY900K0fLb/Fzve+/pJxD0TQuTBqb06wTm9PoAafriCsv5JQxmBHnq7RYkAEL6hPmD9qTzuvn1F/gEWwBNBvcK7vVX5qQHLgDQ+HwRLwDcBcAMpemgAQT4oO5fFtMLNPKMDCUbo+Ha/hMDxekbB6bn+/+6H6MNnQIPBiUAY/BI+KH6DPcS+Ir9QRYfJJX72fLF7g0HqvkR694jQeZx+uEQFQwqGTrmXfuY8hz1kf0VBksC8ASdEg0BjBio+V3oJu5h+MkCxv6U+8QNgicf9r0DYPrq32b/SfTGEdUQgv9aCPnuvwJfAPv30fu27sYMMwXsDdwIdvtDB3v44QSw8lXpCP6dBkgEixuU9Nrr+x809fsNSwSU6KD3SgFcDsj0eAjz+vb49wH6+bkMkQgaAI/xQAP9A77uXQ79DVPyiPvrCCL+u/zzBs74WwcT76n46BQwAVYIve6rEtP7vfuiBZXkhgsu8ysMTwNP/YoLJAjV+NP7lg6X18gKxg42/hn9/QC7AZz2LhAn8jwUzvsM62v/3QdWCecBqAKZ80ATzegS/X8GjfiEBTf3ewqEBAQBh/60I3jsat16CikGV/wg90cX++2jC2UFhP+6Cr/dZg1m+HzskRWfE94OJ/9F4Ar8QgDQ+F0POfv99e/70hNOAuIaUfcD5nMlxtVc+S0KLe3CDfsJowkN8AAI8Qw+Cn0FF/LO7EzsRAK9B24KRwkPB/D57A4//9HkKgIY5Sz1zioEC+XyERhpASzt/AP481Lxz/vZ/RX0NwyMK7kcWPrN6gztNep+9lYJKAg1/uYHGAhlEej3P/w7DAbhR/vOCZIByfmdCzIIpvkaELkBaeHb5VUlr/kP7D0Kah1OFAPZkgrzENXxmNq3C1724fHQLGv4Jg1s9mcNnxB577/qwPhkAublCiSy/X4DmA2dA6/wN/NnIRLdmwZRBgEMeASE3ykEgwMbAyj7LRWz/Zj3CwAyDiDnqPCeHEbx7Bxe/DsA6un2+S0Ya9wtHE71hvNpB2oKQxvF+4H3rvHHCwbisv+JI/nhCvNpF/kEof6iFssNT/G94ij+TP4v/6oKcQAcA4XtHg7zJbnyW+CEBwD53e9rG7UML//F5koJyiLg3ejyjv/08RUJxAefEvsOgAau/c/9Vvcx3SAIwQGJ8EkIAPwZ9S4EoDUnD3TvzAS97Ofiju4oF5AhR/wX74AE1gSdAAnrZgIs+nrgYixmEnINWguv+wDtxtj4EIP4WP1L8cP+cSbVCkP3S/TWBPnv9fY49wcbyxR59k0X/Q2n157QICWU+9fuAAqCFWYYNuTbD1L8rwCaA8fs5wpy9Uv0GeZbCVMyvQGF62j+1Aa0Ai8DUAPl99Dej9/HEeojohFNGIz/juGs+d8FUPMl91n5XA6lACLhDTWMKS3RfvP9GWPfO9tkIS8OOffo9W4OjyCE7t7wkBaHAujgZvqEC6r6aPj1+18VBRlp90bwyvwkAvjzjgD6Cu366u6G9vUfdBjJCY3q7/F9Ap/soA7pBgr0KOMDGeEY2PdNEqLrEQLlBAX9N/AQBPcHpOsjA7wIUhw88/r/yONe5FcojwTWB6AKzv176CH+KBAzEhL1M+G+9K/9ACWZCZgPrOMh0FgfmSMWB/Dz2PBP6FwVSAzo+/T4suTFAs8OQxO+DpIJntxf39EMcQVK7T4axCAO8KQXFPc88gj25d3FAs4GNP3eEkwu2gM9/bHexuiKG97nmecW/QUj8R1S808OZA591LffJR8D+97rFQ8pBqwMGxClB2cEbeP21ij/oh2kDvYClQ4g/n7ujfgMAO3/+vmxCVEOKObC8kYYbxrA9ljdIA7gDvj0ewegGJXoRtsBEfUK5uid5fkkkwLIA68whPOo73DmFAXeAwnuTAT1BqgXueyy8fsnRfKw3NE0Lh5B2rTm/Avo8gzrBx7i+kcAc/6rFfEGqN2uG8PsW/JcCLv+fv+p7Zs37BYVwgnuQCLeDOfnvAfHC73UE/4FNhoof9l6x9kxs/mG4N0oRej91xH+gi7PD1nqbCWh+kLv9/57Bg/4vcanIqAuwuGz7WUkpAYe1oACKQjF+ifvNxgVQUUAOrvi8rwHMt8wImUFCvqWF9z5cAnj8gXuE/bzAocgEBO7AoPqLxbnCYy85RCJ+crevf+4/upC8B9vBeP1QPTIw87mmCZf+lgrnPZy8bjz8QulFPjt+gCj46wKmPgQLNQaFNQmBuAAKeXi+LIUqPFP+4EIMh0y7YURAAlVyG8RovByJef9Vu3dQGLv5MSmA58VTempCDIeTA8w0cP6rzquCMPa4/K2A9Wx/wEVWMcmoubU8awCxdhq41kWMCZ44PANUjGc7mTqSwN65hDybyJS+vYEeyLYBMnyNvow4boESO2X2g4ruhC6EfsGwhOZEpvZIdsz/W/3LwJDH8v5bAo87LD9OQtM/GwEcwHH/xfeYCvm+2DqShMs9XkMFv8ABrkEFusE1hkExBvU/P/51CvfDnXwES5i8cvuluefx20D0hOZ/6AP5yK++FLyGQJeBYH8reHp9nAbPv3vGDwfiOIr2NDoVRfGAxcETBS3B6XCpATaUafSDA9+Hh7itugrBvYQa+cn+4juvBr1/NDqSDtoDUX+ZA2Q0u3iIgH/8ar98/IlHxUgLBsJGiHrrOnJ3Ff91/g39KEDRAbAHLQScAl4+kXp29+5AEkWwO8l9GcivwzmAd0RlvZC3ojlYRXeIOPzxuL/CicCzxRJ+GHjOjHt364J/yh529r6H/eRBwjy3v0ZEP78hwGyDGAvmdo6umQSWhNU/WILEQRu/goRX/2r/gwAMtmrDCoLKu2bErb+vBEo/Zjo6gq8/aP6jfkFEun/1QqfEWjm9AHs6RntGgZzD9UaQwVWFtLog9cVDL4DW/Id7lQS0hdV8ZAMhBw4/U/4qf4T4rH1W/r/+Fw28uoo8T8apfWrDnDvYARH7SsDCwGi45csa/0qAgv9JhQ49sjS8x8NEP0AcOCcFFkS/tpy4D0TZCns/m0BOvcbHWfSOAAiJcPb1gTW8fkDvevtFMcsNSDSt5K5qT5f7acp+gNXDW0MY85mM9X+kfA24Rf7rNit3xNAzQxjBC/4rRkgEez3Qfq++r/97du4Kk4LVNhQDQjrNP5FEkbxjgS5EQHpQQHAIdb1bikXCeTSPv2d3Tj5AwIH4l0Ipjb0/qoAshR4Bhoy1MVC47377NrsIAMDxh7X/VL1uwk79JEGkvV3/kEBRO9UAwbzRum2Hu4EOCV5E0j4Suf+y9xLJ/Rh4GQB3M3VG2QJsxpORAHqGcGwDlv/ouGy3WAm7ywu2cNEUBIA1BLk+PbFB9K+SgH0FskD+yCfP7cOr9z8Ft3jYs7Q4Nv5UjTB9/bmwihxE3nh8hGPG7TjHuG/+l4xSfQa4YEUFwa7E8/eaAkNC0DJEQE4IWcGzwDRI4XtAfZsAlcOsP2o3JUHuNXwHq8M3dx4GR0I2hfSDUv43fRMBpnT/efAK74F7PsKB7PwvvB5JXsIugBN7lv1wRTz2mMNdCUoEJcCwNw89SLjrdhqMUgYLvU9IxoLvOxn6KkXvOzlyR/xtAs6N+wVIwnE+WoDRfQSBvgOdb3U863zURPpLGn3owtiBD4A4/8QB1UFWQIw3wfvUwUP9bcHyuPYEHgl1/O2948ZwRNzBLcDKseNy2r0ES6HMnQLqvJ6+gT8JtkQG+ULk/Xp85IFTx04BMcTROeP3MjfSg+nITX/MvXdFW4YGO88/LnYARH/6M4EVDgo9bL8veJIFijSYQZmEl351Ur20jbvnhpk6bLPujSjHaHYWx2V7X8U6fq/3vEIeuWQ13AlejnS+zD80/VfB2bWV//qG6v25zG/AMbvE+Pt6FwU5vx48kbqsS8uGObYNTG/BbnW+/Tn+fIRKfy7IDgFkvP97T7LaBfA+yHzQAhzIVoXhurpK6YCrOSm1/DZvS9DHcT7qAz7/VHBDABcKHvr0PrD9FoqOhfv4eoRBgsAA7XTyvHkCfbqmwuuF/MLKvqkFgXqq/gj+/fyFjzq5FD+Xwv9yJr1+g25C1YcfCY04P/jyvKf+ZAZkPmw1Rzs+C33OqE1SfPb0AzVE/iMDgb7bhEU1AwVlCLB4+0N4RR5Dc3nQvuR8D8U7APv4j8nxQ0730K/cAivB0AfljZk3uX7fvNy/tcCl/XQBhgH7/kQGuQQj9PXPKDzu7HJ953ejSFVK8Men/usBtQQFOPzFnnDqAJILGzAxwB2CVsSUwQMLyUAwrUvFY/+rBFfINwNxuaR1ffKaQ+yXJHjfvx++AYBTg2N/LMCzeUXEiPRHwZjK8L5r9c7D9krTNF7EIb6XAEIBOgM7w/F+gIPIudVHn/4VP029trtov8Y+3ofEtl1F0EFtOT2Aj4B8RY/6IX2s+dmI7gM3PArOG7YduX7/zgXYR2u4WQaqtiGzj0WOQL0I6UR8gV3JcQcRdMCyXwBjNAWBZotu+ahHlAe2OhGHAD7fNqz9NLrpwWlAjYsOzaGCk/1bNNA+2HFdccYNP8ylQyF6/0V7wLFzyECBhZf6aHqMhqKCgYNXQvnFVkfENdS4qXya/WIGjD8kABo/Yn6EiYv7bf1ijnI+va1dgMZKGDGIggVHYHk0Qe4/Z8K9xVdAxXxARUh7inNhA+AKLIN99aGDYUTHRAU6/D/zTwhwjYHNgPGztsJXOaF/aYf3yqNDYsQhd81zcQb7fpY/SASu/uJ9LkYlwNe4UcQQfAf7k/kPgBySosSM/6p/c3vM959/Zj8tvB8GKz1IArXFFoVa/RQDln+zLi8AqMAexgg9hk6VjvpuybnMtstKG0QMOKsAgrkyOaTJIdIbAg1/A3TV8u202wUWDGbCYoQvQD1Qo7038kU7U3kk+Yp7hVLPA7Q+lwZNQYaCEnf0f6j32bzJyH16GL/tgtUGJ/yoOQ5KmsAO9/8HjA1gOXj36v2IvVO+dbte/cQEhMe1vt0NhXgj9RmUF7kDNKbC54NwddaBAwT/eBjDSAK0jF9BZrMxwfwDaX0ESbgD9/jpdRR3q849v1oBm0R5Ltg+PQx+Ozf+loj8uclM98OaNg5F1Tqhd4YDK/0xdfgAUL7SRp+RtwaY/PxFfTe9sJ7FsHrAeFCEbg0Mt/B830f2ePDHfbXQgNoMYEEkhRo0QgHhSTF4Ob3pvrV6C0BcAV3K2QVrclr9KkSEfRVHXkGpdakEnXmtAPaODHW49agGZws4hur7L3hIQ6HwybsIkBf3jYTcx3tBPsZSuoRB8L38OrVFNkDI8P3Cq0w4bB0AzwkPxglG1nXAw/d8rUF+PfPDism27Ym/wghFPZP95k4hPMCvywbh/9W+HoHjx1q+dDhHQQoEM3tHgcIJJ/UcNiFBds7dPLr/on3/AgQRly8ly2f3fe0WAqHArxNGOa/Hhj4SfsbH9XOohMt40zUHvDwRLsN99NvRHL0eO15Hc/Km8YaBaAEXS8QFzAHNg0q4hA4p+XQzm3wDuUAN5PymBSFMgcBEOwL8HwFVs9t6jwY8xqfBesazRYm567fYOTo5Y/ZUhonLWc0ZAeX7UYlv+MZvjrnRBAj9Y4+CjVR5tgTfOho+KfZKdt/9VcSLS7MAMBMlOkG1fgE68reFMPuYvGMJNHuBvIEDVwfYwLK6HgpC/5u88/4Su6gSpbSKN4QDH7lyCYX8yslDhH22hHgH/ULBgbx7Rq0Bk0nP+gzAjU3r79R4B78J+1XB3owIwGHHd39BdYpPWbSod8UDHzzgwB1BY8n9BLhJhfWcN0jFtz6+OnqwNz23BWRKpnqDQdcUVXsaQ1KEPvyOOI4yMD4kevW+0wx+if1BZMG+Pt4Bsvx2c2f99UFcRxwCk36PRseLYHGxrd0NCnUNO/REcQOMUfx3Yop1xUtvlnqAdDc8mod2CbFHWYdN/VL59sNsgA2BPfzw84Y8E4cZPDKDX0VBAYLGBjjmxRz8bLvAQ9N1pYVjAXF72HtEfBjEK0X2SaeHmX+58DB9ysjR/gW8RAT3gNj4b0QVBuPFOHR7/faBkfgMTzF+DnW6OtW+Af8aih7OCnNyfPp4IcmQD5z388GrrPvzUYwLye4HLcnpvC45f0bt/17ItLgSqvS0hgIUBKGE79U9dta/80MIPHWFkzHTh7GC9fcO+L3KKYgb8fJN+wMCNkw4ZUa2RpU3ZUYIxXY8eP8njbmvyHophart7cJc/agOXEIkPsBRczim+/n2w70MvqN5mwDizmjIy8Qh0u/55TeXtN07fjlk848OVzoVvIfJmk5MP7YvwL+ivTw9mv3sjm6IF/pLu5AC5PvLs7wJxjUhSFPQKjk9Ry4D4z8l+TxFLTPkAXXKkbljiWgvqPkZeeS+5gxTuk7/tjzkjvEHR4knyIU1dTNgbiaDqroNw5wJ2b7ehXr6lMakjUREbq7tNhL8QUTTTOg64IfRQ1Z4eq6iBjJ/ge0lEPJF6YmtS876WHyOeIt0HILOQz5CZUPT/iDRt76a+0nyObFyOX+2CY4JAqtWSUVQd/LLaT/o+Wr2Fb3wes/ELPsLSJuHSrFJQnZNUD4C+tFGnKvmR7/B0sM62Ob1lP3P9k1AxjrXdCD9TriORVWE9s4lDE0H8XuPOw92szfSgZw3rAXHwb2CBQYsCMtBy7UfgkT2MTzegbAFOccZc8eLLsHRNVcAwP5a/KZ5+Eje/sUEmHwj+XodU4TgPIO+W3HO+KRCk3slOp0KEPjiQoHPz/pRPL2CrbnFR4B96YKzi/4vlgHAdaA6GkQrcxAD/whtFoqEcn8HhZi8SITtNHOwkbjyeci/0oWaj5FJFHYLfgo/E/5XgFW7uH+f9SoJEdGJval+P0GhyED6wjiwfl/0dv7chMzL7UcB97jIfzlWtAvB7r1mAB40es3mDYZ8EMlmvgh/qznr8z/4c79JAfWH1InYOWPEzc66Rj+xEDFtAGaDuIUNe3BGgroIPcyDsbQEhtl0DLcYB3rNE8oJCgONTqUQvwgQZjsydr/7grmBMwqRMsNyikFE6/uPy9KsQDzMRZt4dfKx9U0EBM35TTjBMsz7PFdz/gAK+qO2LYCKhsL9csftQxPAYXij9+FGoHSBwRTNBwWjS9WQEYwds/svp7RrY560MIb+OqFPN5cTTUnLvDflhuc05iJq/6K7o0RQBlDMrowP/kR/dDNRPNRyMXWFhtoDx4vHCxNHav4twMC+sTQ88fZFcj/r9dOQTMbMAbB8pcRlvOhxX4CW/kFLM7+Iy6lHlbvi/iXw9sSBtim3TL2ryoKN3nmwjC45vzuL9aBtk9Hnexf8whXahwNLIHsTfBk+VrIsgaxt0MHCCErH0BK482mEyrqueg89fb65zqfzcfw5O5A80QP4hO3QkzaC/a/LHLN8AlRBPzaPwrw8vYR8xuDQqL4kN3Z5J6sySOKAqYc+Ajx66Ynkh6fHVTG3+plywXLJwfhM2EWNBlFVE3XlCIu6z3UP/Q2vkoBRORzKs8PvxsCHVIN6hBisiX02+hcD84pLAaDCbrq3vyuKIgaB8rd2/PRRwArOypDKjC56CjdebqSBZkEwfTJE9/b+A/yTsD/6eoSH9KYUNHV/A4uDWqCvTcXkfmb2OMKBwaAF03sEQItCME+8+qE96UTNLG9unHxYiA+JMZQxf2eFvgNRPhcAQ21/flvub7paTyoLtEH+ezCH1HvnAm+NWPnBsKp/9vabio+JCjDdBA486Aaiz2CB+i8nfm06ELT+UgUBY89auwnvWkrD/aO6/XedROF/7/70kKoEefrKe3OBY/pn9uvCOv1qRiJFff4qzD1AFPxzvLO1I7ubAr1A5H5Xy1OG2oUgektwvHoy9YPBTANlh8ANcYbLgk7E1s7e8hitHXEJcE4E7Id5UOtJp8LFfNYER8XlKii9kLalPaeQojz8zPLFwXzJ/Fk9HUVtL1E/SEh+OT+FsTVrP56Tnrw8vKa7ozjlw0KEDkif//lxkAUbxOd82MmHejW8bv43Oxs5DDzdE31JHMSH+92HKntZatZM2bqXeRS6Bb04zth6Rf+og2MBlL/iAWiH5Dre/bk/EoObi8Q/n3qkxchAw/HSQEr4tG0tgKzArAjPii0FYY0nRL7+mznec+K3UTLWPfRX5Ybd/cAKTwJrvTX3iH3EPYut7L5Cy+CD19GmCdn5U7jmMti6ywM3/901Bn+ufW9Ck5hegwJBAztKOjCB4TgTivwKOXav8dv8Ckynfak4+Qv6/TD484PSg8+IS/gCdsXAC/ypR6hAzvx2CwiDMMCcfzy/6sLq7x83RwG0/W25I4sE1HTAkQ/J/oTyo7WhrZCF3n/D99WDIUlgycbPMUsPNVh0VHo4cU9xwgaXBBeD0FIsj/wD5b1tP5a2TPKfajmA9UndvQlUyIWaBJvDcrsRgvSzmjhacBY074y0ivCGXoiPiRF/SfqBeRUvfjdpAMfDPhpLypQ6U73usFY4DQn3TOCqhD2MEDw48Uz0Qp89wn5xMUS8ZfiA+KINGAvovcSFwQ0kQp8uGfoVBK6CmUS6/E0EKnm5elE8VLdny80NsIbXPjpxe3eqRsXB9f+3+N/xUH6WP3JJ/VKXz9eBSbNpfqmA+/6jeoezGTjbRCILMAeR/qCIrcflfIE+L3FRdmj4kTxkiLcH7gbkvCHHArz7e2ZFSy4dvCrJagj+QXJE3UVx+UjHDcFoQEfynPQrxY115sT0zFtAYnukxcvAwvrui9P8kLm5djwzogRUA4N4Egt7WUz4jwZNRgaBkvnSYY9G5Pn5OUePm0XbRGY7zgMbe3FBfomotel4kEDvP25BDz71yAEB9PXyQBUDXktrOJ/BOsul90Y/VDskvo46of7LThC8YfcwRCd4lQOsCP/0QAQMt/MAzMndhsdGdf0KB3xwj78Lu6YxeMgST6kGAHaZBToCEn4x/OUEQX2QsZ45UMxvy3i8WY4f8ZLxKPzadNg84cxGGeyH9wJjNNX98vn4PRd8izOOQWZ7qdZBjudNBj4ha5v6D3dOAWo38IJofXQEdU5HQxMNovYLKz//aUTztJ2Gy1NV+gFBx8Zx8056V0VWwTn+nHbsQoKIvoI6h5zJZbw3r5OBLHwZMzEDDwCJ+X3J4VEdvJJ9SbzywEPL0XTfuma/FjtMzyw7TbtURbG4U4k4FaCEazRwsR9w4QjgB5HrNj9/D736IkhrTqh6/D3rtvyHUDfUMlVFOvYyziAGxw8cgK/kIUtQwGF2kY43jA20G7hK/6K9u4b7QSlEUfvatGb/mgfEA6sDG8RZd7N6jrfl/HmGcP/Fz/WCBnY1ibA+5YQAAIb86naCaKyFB4kayNbJpcQQd/oz6oNcvPzHBAC7Q45IInYOgDo+1ny4NzG2LAX0xOSC9InYxcFCD3vDwQPHA/p1O1V4+P9qO5u6rk5CQdI4JfxIxhIIOUETAPQ+K7hfdZICbUUWwmUGNkP7volzEjbEvim/jcvGBrpIcMEjt9LIHEF9g3t0biyQARk+v0QxyDTT5wEhclAC2vcrgpxBkLkrxJdCV/5kuppGh7+1NYsD1LZhP6sY2QQc/wr8WHWZwTa4KX+aAbS/6oYHff775HkURx/LJ8edeCo2hwofe0TCjwhuf1Dtwq/6iHvKCUf2h2/NE3RS+jXKBvhl9bH2pHqyPmXLu4E8SJuIQ/ZWu5Q0rcCYweHIvQNEP7PEJnygSjk7vTzoOJ20poZTgYkFP8djSUa+J/k5OgczEoRiDcHFO4LBwJN13Thw+2Z7BoAUftZHfccgP6LEI0RbuCpzebl/AkiM8sOBDMFNGLWD9ks1OHVqfwgE5bmIBlfMy0R0SqgDRQFiKdhyQEWmB1fCtX5UFb16fHY0Nmz0SQMbe6NGRAm9yQM03wNUS1n73T+07rJIpMTG6/+H2E9RdcN0s0rpBF2BmglgtJeCLo3+7H07fgC6NO0GiYq3ShBGbAKP+so7ATnn+Fj3v3owCp0EYQ800MI3i21Nsbv88MRqDrEA+DydAv//z0v3POXzT7qp+aOAI8PfAfeAgARHQCUBOoL/g2NJzMMherb3sfwMsf8y0A1AEDlHaThVP4LPTbtF9Zb4wnrQ/knBb40wAOJG9sprN2TrfOs9xpzEBM9CT3m8T0JZQXMBim/POHT28jqoSp+POIz5fn+ElG1nf0VGgDmPRR43JP4VByeATXKmDIhE+T4VBdg0+EX7u9GMY/5BaVYAfgLewug4jI69Sv06TwTtNI02Vn7wQH8OfERfhoy/sTKnQn63WgByOdK1tgqLh3CI5kI9g9V+bzmjfs/+YP/5P7M/i/zUfmI4qLozw0JJZ0Qhhg+GT/zRg6O9WbtK+2R7trzzgaCJu/xYRzn6be2FCTp6I0T4EeI15IKRzdI+1Xegtamw9v9shbuKIUw0M/zE3MSoPxHCJj5NRKIt0QEgjJG7pbkgAsTAjjIej4rInIByi9L0DDod/IjxxP7QvL7Bd03gh7lHRkaWv/X3u79s9g5xd4jawF4GUcbhO06Gs/OqMMVHIUGkBItMS7zDPLiKCfs5t78DNrojS9SE3Le9BRfx8DwFSnlIhgBEsZ7A4To7fvRINboIxfU7pPr0jSzJzQjW9bZ7wANXN9j+OfpqxVA7WTdqFhXKsbDFeKIDm4Dmv94GV8IKPAy9HzRFjwN+VObaBapzBMmrUQ5KRpVdcUE0B3tCjE0GvK1ag06L/P/YMjMHbIZAb9i9rbg0PHy9uEPj1Kl9T0DSxeOCOUEKLpb4zYRa+aX0lI+ACuK9aI5CPDhDS/+zfBlKorS5/k9/YX+O/H46TwHk68VF4ksKzP8LhO48BWQ5V64TAs4G+wFM/h/EUUpekTzAYb14tk/pj3GywglI/w/+WPu6Z4Rg/5hsZ3uU/Eezq27KU9BFvL1ZkwVHaASC7ujzLkQWu8L014HsDbvOMIXiPQ19RjZogAH9yD8KAr58qf1wv0SEaX/CR8f/JP7JAnzFYkVNNCo/Dvhjv6S8VDauT6c9vTyCDk1BMDSzfzZFgUlLBEk+FcOv7+Zw0ryMvtQDiMGvxL3JeM3uPmZ6BwD3AuwAZLy//795EMCncql4pE4lulXFCM8vfFCFHg8rL4G0lUQeNKk9JL7YxC5L50ZKe4k4yvgKe+eGvcTZhcbCdo4GgAc2+4lwOCItie9tAJBGwwcwzdZD/EChu2XBugZ9eAR8c39HtRK+7gP7BtaFZT7MAU956Dr1OtIBSATzi9KL3H/GuOZxQP7G+BQIRcgM8xz//nsMwueF4YsRiZB7+i05PRTVvvPJAocVEHi7Nr97BX+pBVg3kv8XxaRzPASvPHx1EcAmhqwWUMFkBLG5hLwrjgwob3FF+dEEVdPsxOiLL/whPMp6y0BiTnx6vHqA5SZ9f9/DSJ/+ZrOf9nS3vj9BAoZ/PkMnxnJPiP+jeweIO4LdtjR2R/azfUGAxzhNDZ5NKryz+cvEiwcifKzOALxbLBXCfHwYQmoJI/fI/DXIy0XTsub5GkSYgsRH8DyghHVBsX0pxgA+d4Ax+bp4QfnP/wHAyLvMh7FF7MKCiJtHsH4nemc/Hb+096+6T8CFf9i/B8eGTgL3Xn/Cwfe4b4Cr6E34SRR80JOOMYWjubEtBPb0A3M0lYMszbayyYVLyiZMqATg8RYAS+t1hP1Ia7e/x0m8AgrcwETJyYGMdtd/g6UmAOVFOAzXjjHxLEa+zWo+KXVLgDE9ZDQWeaFEC4cuAPHGGsi1gMK07T3/+lH+sUhFgKc6/XekRjy+hIoZhmayRTcdw/BNiD8lSXn8ev/i/+A4JUnpuvn72/NTQCCGNcCbxHs7U4KnfBq+1UVKESQ623JiSye7fUKTB+IxurHJf0Z7FUGhhepGh46BwWmCuD/ptYH1erscCLHBpwTwTKp0TgRMTwL4hjZl6F/ANkWLQPBRYkblfe7u4Mycw7wx/owKN9m5uLgdvvyOIX7IQSxAdEKmxLr9r/8jfVc/AULr/bcBAARtRZcDNsDWQkRmpjDNgj36tMdvPkoIK0PS/5ZRXcumA0w1m/votXv9lUVUQQqJ/7YwQtlJz/4wOOC8cToDNwOCdQKazHAyc/55DVOwO32AB6cKRT7ROm6+4UKMCOm/NQKMOqRs/D5uUHQGXH+PRGnCuj02fSO8XIDgwrTxEbXYhjGIOgZ1AqF9O3+S/JO6UwU0fJn7IMblTrYJETd9OcgA1LwfQcL+qPZk/mOAHIMgR6OJVDyt9LO3tzvDiuyEhPzR++G9aXv/BuqM8b1uB53DJbezgt/Aczmxw9M4ve1s/n9OuU9xg/X9JXfbQ013eT8YDdMxNX4wg796Rw87SSDyQYNWLgPw0tKqNLj/Z44MFioHBP5MBcdwuvvm7asuoLeFhnyV0cdwWKEK2vZV+Pp4s3TDMRb7Vf6gyJuSogi8gU9/fzm3+8m+B3mCMzf39cd0kYeQYL6beVnC1H3ANc0EjkcDrMitYEOVzTpEBgYqUgeBMLGia4t9h4zMPfxPq4c3NfCIuX7J9F6Blbh87DLICA1sDHcLITwZBSF6W233eOG8wPyDh0rHyENMvmT0AjjPRzYIff6mg8aAOE1vDvxwY7R3vpB4JnVQxWGIfIZHiAXKwwKMtdszMrC3g3kAhod0STG7pTtIPuCKZDvMw4L9X2rMwsHTt0tQBNp7nrVYO8H3koYNOnj/aYSJtb4NnQKCCIP8cXXhA4c4GEKZtgXGbs7gwtj+U7qHg7Zz4EA/CYXDGwIr/KK+sj6/gc+8UIF5foR0nf7HSUrDkv4bhRMDQsDuq8R5CEnbffbGDsdoEyk4ivVZ+Wm3R1En8a/9AoWQRIIFo/55UXH4TjLVMrW8p0vLB2HH+Ix8QRMnpzdbvAUHvcFuO7xHTbwuyiYFz0U9dAJr7TvsP23VEUnof2JFYbn4NlzAHoLvAJU7koK0/kPxFw4aifq9wEUzwAk9ObM7AgaDMPzn/Hc4DUcAAVrDvMXK8ZOGyonb9Hv9LbnVwK4MKxJLAT6xu/7bNqG/yn6wQQMMZHidPyYFpkItUMN/pmKHfmvGZwGLxMSBDkcqdJk/FUgCvIo4pHS4/5XEfv6aBdyVQ7iRt+bRuUCYuMq7uW/YKIxPc4z09OjLgcbJgqXATsO5AYbzS8MIAPF9w/cTvFzYxUC8tB59f4MpxTF/4YQ7+Sq8qPc8+ZiMMocMSjqGn/cXdF38/HxvP/O4DTT/wxlLxUuPQtdGWn4lgGC4TrMgCR9Cy/8QOJdGNkqLNYXHXoV0N69AAAW2vHusXQYhyXB8Qomud9oD6AEvedEHkjKMOAZ+p4iBBXGFddRjes/zHXWteYiHGoDk+TaIHgcc/8lM0wdPugitJzbJ/XS5wpAPQ2GCz4V2Mz6FCHl1BAOE4TqnTSVrRETIR+H4G0aleXNITP3WBwm4hzuZlqFxS4EQezms/IVhuevHixULfTy5pfzBgGe+rkUDxRZy3MAj+nnI9ovcOo/K3fnQ/5lAyvV0QoWCczb1czpGLZMDi+KACL6v+QPqNmkDh7IPSwUr0obGxDoPvYz22znZwYs1cn6PDKb+YQegyiUEr/4D7922vUKpSP/7bji0zF4/f780hIYxysbShBw6eoOIe0rBgfVK/hNKcMWSjDnC7MWkuUJxHwCFO1K6zAJs/RV/noDlxafFL0JlSh1vXfkfAom7a1hrxqE7aLWUdGV7ZML1UOvzIT7fyB1+fEKCOTDDyYCJuXHBxMf6A3rGBgKT+Vt5H/TmeH4+P8Sgg2IMEEUEe6D+gUHOxXPzi/k1e1LNoYx8+JSL8nwc9BS/jvr5O2CCCrmaf4RHf82KFfb+v/Vksdv+lb0UvJcAjvu/wyP+KdV/PmAsAL2RehrAJIqlWBV+PXSdOQ+DJoWN+zEGnnTDNtk36EoSWtD1CPlH/AS6aoZkQpBHAkJFvEv9g4G/gkKBP7xVthHCPwNfvi0ILEqPfIu5EDRHNnbFNHksC4IO2/riSBw/uj7+P6JwurVHfZl4fUg80q1IhkMLu6QAFTvGuG00ZzymhVpCu1CKDjmHC7/z+Ffv063ZPQrCD7pbxmQO2EInTfyBibq79dkwqEXI++VBesXLB/GHTgJHhbc2iPYO7tx4o8iNBliG1gK5xD4Cbsi4gRTyYTuuN8JupEPP0iYJKkmff8X6oAU0PlP1nn3quJg854p2vJPHK0XVQQzD/+/KtrXC1Eob/A4/dsuOPk69qHrbPSl30bkCghbKLwhnxvtLMnWUNxMHhj/X8dR8jfqDfaFGCcHlEkSHXUCsOrEAxYBD9iJ/RfJ4Ajxx330fnjLBqsg7gJw1lbzgfg6EXPw8Pv83G0GNGg554v2AwIKs68HY+mIBmoc4RfdHujUNhb968XswRaFxIQysyzc7G1PSwlKuEThPgVR3nPE+Bu5ElbzYCARMpoYHNhC5OX2IPnGMkUN8Q66CJ/ldRkwvurVnx/09PT8CB7LMRLnb/lSAwjgYuOKBCgrIwD59BcJzSuT9RX09fTXsunOMCRuPa/pXh85FgEFCSfs/ukI29XP17kOXSOM+If3awNU3nnT7gIAKDXKtxsjHIXtkkEhBeAThfMz8+L5fKlS48wiuR73GHk0HPdj7FXV1dPYKusBQg0HAT8AywHtK/cTpsPj5gjEACa29xMN7Czd2CQ+SQtxM8MDwM2A0+3KFhA66O8d/A1SA+P6lhUjKHzf2+qczdHpKfdwP2o/xNtkJe4hlOzV8izbXr+a4WkVDxCHOK0iQgGuKFTpBB998oyqst3UyAc+zz6tCLXgnuTYE6P6kwt/+Kj7Tv7fIwzUpdmMH2MMFyaM9aokrdg2uh3/PSeRNKzeNAHABWsgCw+bBsr9xrM04HoNAxupCGomKgmL5uLL+szoIUEI8yAUDAAL/SWf7tP4Ve72HjbrYb7D73gEvlkq/1v2oxFIwNL2wfD5Cvc6ghIx0VXkgS0S6GYAiyaQz47/XQff/pc+2v2f2aHzTfhD1xcMfje8+QA6rQpdvYn5cvrM+AkUw+vB67wF8tnQGjwdgArtHm/shPxdKe4ghcFDxw3kWd3ZRFgieebyLv8H/xNrGTXVjtszx6D9evAxDYw0gg5dGIn0jwGV2xP+4+8+79gv3R75KM3o+/tV1uTekvvt2TADvgaYNZMs9xIH7FwGyRUU60TzcvL9ByzfC/o+DZTvogoSCQ3k1fdkEccDeSEz8lD77gXV7mIAS91fB8IP7QjXM6L5os2P8RPlTi1zOaPjnwhQ2ZPmwy4MIO/nlgOYMvLr4hs72uPeXhSBvM/usf/bJ+DwI/ZsNb34zBpK9mb15wRI+sjvSur+B53lNQxMHJMVHvsew7sHwi5ZNHMTY9sWB5vosAFfIN3c8f5S3kDNUt/AMhFH4uyYHdXig+KH/UAFKQmJ55Q1VfrE8ocYewuHDqL8BOTtxBD9Hv18IQRKavp4zFPf7/nWAakUdBxz+Tn2TiZS35DsEwuwC14MEpmKPSg9TLUp/XkbSTYk24T86iB3HrUQ0+BZD8utXruXBNgcCAQKElhIJujsIQ4SZNfdAwjZGb2h29oaSw3ZFJoibwkqG1koYB1eAVHfdbdmzxH0BfAQLPg1VfnJ+13ytRhiLLHqO+Jb3ibdFydxR0ELt/kz2Xvo+RWY5m7wQRle7f7s3BcM+LoxaxPrwbD7Fgot8YgU1il24y4YkfGMzbISQRERE2P2zPgzzbQacQxT88Yoz+UhHeoHNuf6EsIN68Ko98f+TdjyKVAGrRPHEQ0eE9xG2IoV1vT6QzEgGfbYAObZSazb7NUQtRt7BmHe8Uig1v/wLmnR2dTHehxY5Wfb5EPp+Gb25ylE4tn02jQmAu7Kp/oI9i3r6gyeDo0lfD/TxMjROyLZ3OcOsvNI4osoQBJTEgofAPg46GAGs7ERyxcN4eT/Sno7ZBwvSEnJjMBc5vCfzwYbMMbtLkomPok30hd+oFusfrvgCIEi4D7RJS4NYjh0z0UR9Af0vCTcc9erFv8AJAMLVBwNdbBC9EoJx/d9CGEPW+ck+cIsSOleEILyPdqQII0WhCZ4+gbPF/J8/Vn8ARa9A3IbSRhACvIevgca5eih28MHA0IRkyJVSQTzT/6aSKfskvWtoCGartVkAI1MrDqFRvIcmez+8EEWBubX9CPo1caGC14Ley4IGRpJKPOXh5j4LwYN/SYEfEcVMnzLOdr68m0D+woP/A7rSNjxEzMWOwE8NabYF82kDDYEzQtLO5RLveRbz17sxP4XG8jZwrJ+GrsUKvt6At3yVzk86oT5FR7d+iUayd4bA8I3thqUxknZEQNUxLYO3Td1ARzy//CUErYgEORG7T8wzvfk3ZcUeOEw7woVw9GsLbJRNcgG3RkGGgYXJOL+8u1l5uHqje8bQpY8L8JqF2n11fatGOHgh+0j7qkexOh4MusNn+JuLXTnfBwU8j3ZTscYAZoxzOCMEO8TZw4w0BTpcSbFBQzg8glrKVzlmA4nAUkMrO9OBhwvG+MO9kvFzjSBQsbSvwrN+ifPONyAHhP6G/gyBw/+zw6oHBks1OxSAR/S6gIzDz/WVCMKxeIzdDOrzEwXq+dRGI8VWuC0zAcD5hUs8NImaAZiBrrwL9vpCosKBP7S/GUEgQmrAzPiyAGbHO8RufpO/RIYjwfDGrbwveuq7maoguRpOjUZkAJdMS0HFwGqA8/ese0m15frNuJNJzwqq+f6O4kEXijv+1mM6yV5DLnSqw0kDHsH6w1rDwjqv+6fFAMhbgu61cILQRQ445MLgOuYFi0oxPVF8Ei0Z9lKGv0Xm9rRGyxZtf7IB8cPYOohvB3LrdXoAdQr+QNnO2ARFxo9QwTvMv5oxxqjIgdPP8RAK9z+4Hsgotd79ZUMexqBCqmWQBBOZHblZwfXF6zMQ8TWwNAnLjbP+lwq3glM2L7p7ylmAxb3mElID57ikN8W8Hj5TfpSBwLAFeWyCOogN2Y3NWQiLcpCvAniWsJfDUoA2+3mAEk29D+hHEUaEMEE3+Mcp/sTyyn11REw8cY9YAksvhr70Phn3fsrG1/x+aTV4+M97C0bE+Q7/mYgVeMPLAAz+xiS82bMQ+6cvBD4ozF7Efsw7ewF6qEwK+ns6s/3utdy8goV1CsEMDL5ZagZ88Ln2/UpO336RvlB+Z8nyAmFIVQcrs6zHq76e8Z06fMY9xZsIkQCwPAL/H+7T/hOC5H/9hE16lLfjzCbPpkEJTU2A7qYr7fV3zgJMS3W+EISEhU5IBdC6wI9AyLkctljyj4NT01p4BXhpex+3DIeKAxp7is64OA00gBF4RUG+DHvJv/67lbr1i57CdvgkvcuA7cCZ+gyC5f5ff3fR9L72wCOA/MFUeyOtxUNhfej3e3mWDKXVeP3Cd/7FmQHgvp4BAbPYBQv2cv1t04o+In8axLbLFrAWtUWDkjNL/2p+XkWFC3rKj0OgPhFCLndiO79zTHtNTiM74P9qhT8AnkONR7x9ULxYvKBtXcmcQtpCdVP7vuyBR/ltbm164ZHB+o+2j4TBvdjCcDgc0IkKEMNm/VFpo3cIepeKMsZThq2E6IAZxHg+VLtIu9//UPMN+RBIMpCrjd7HUreO7/56kPeCQ0m4+0QPEKq3zk1qiJx1UL6hM3AwYb3qiN/HqUU4i+3EfYEIvsrzmHcnR2UGFrQXu6sHg0BFfzVL/cAZ7a2AR1CHgCMB9IcNp1W3No1oBLnC4rePefQ/d4esh+//CXwl/Mw88Io2Tni5XrtgsHB4lkODfdRGf0YrDxr+yIPkBcT2Iraib7BCjYGchFmFqDqEAaHAEML594a8BET4wDFAF8arDF4EYwDVe3A8yziLPZy/u7OEfRkBSUYSjeoNizyC+4JGRMIquAo2wfgnacN5AwdNFIENbMDtxWc1WIBuu+ADSsML/DMAcHm9zT0+oAgNPuFrxEAGufzJKEJyOjeE9kQHfXcCPI+f9wU0pz77NuRCbM37g1f5af0rxVx/M/2zipm3CD90AxWx7EtpRPtAPIW7OyrwaXdOC/b8vQCyAs9A0QPYghnL5cCE/VkzLjYy/y+D1tSRQwH6EDyP+TX9Hb32ON+AT4HRRJ7JoXx4yG8EPz4H+iT1jIoyOri5jcLyAaw+lnsFCQBDRn3BvpZ+Ogcyztc+TS5YuYr+S/uuvveKUgBwdyMDQUNlh79H9gJJu0u19n+jQTaC2sJEuHt9PvaO/xpTwALCQs1DobLIMKG90tUnStG3gTrVu7P6WcXqCJT+JPziAIi+I792Bbs+rYFKBGkDwfg1cdEGx/tuOllJ34n99hn4DpMZPFB91MRzcnw7aX0JQJsIpoJsQ3QJPwbzQFd7wXlPsz+E6gDeO7KB/LYxzV8C+wCyw3l1g8DhgjeRnfiXNHo62XUoByJ+Y0nmRni+dj74P466//b/Cim7GEIgzGhIXsU1NrV3WvPqeaF52P2/Bh3Ml1OhC2sAvP6kvAFrE+8Dd52/rUV7SYwMUQeEDl33V7tY/YMvYb6QfKuB+T9CQlYL0YlgTXE+nrI4tZzugDfoh83AVc1wTaS9I4aRxEt60XlDdZF5mvkLPjCJp0npDN+BY0EmeJb2F0F0tgqJ6Qi6vdj+tntDQIW6iLeiDLyUV+1AswyJJoQIu5XGNwXSMaTEp8S+glIEeEuEtO5oE38ssn5EK0iYzqUA1EJ3zuQ1DYtKvEy5fAE+r2IzB4QcT/P/rAfqPRm2kwZOvv07/AGXBcpBWX2je7ENLEey8/84cHbAeuX7QYwLSYfvZ8EHELEHVAR+ANf2ja+9+IKJuEOnxAn96n7Ezz58wQoO/GEylz8pc8A8kTg3FG9GkYK2jelvyoR8Ak0+27N89i17z27JSAfK08VRiVZGQYBLiFmD/rf8drOCAr80tWcKiTeHPibQm8DDutG3/T2nf/pEygQTff64fADywcAAeTtaQj4KdHJNhqYJyzr5/tVE4P2oMw6IZT4MxK3LIMHYxeyy9bV2Q1S6g3ho+xs3y8ttirkG4sN4NOFG1TjpeV+ISsO/gzT4fAq9R5lAaLve7KwM6EfY88V5AblIwi9GuszzNFox1MfePUlFycPxgCYII3oFxEtIN732g694ojwu+zv9TItw+fG7+H/D/NM6Ib1S0G7K2cDke0+3rHfpOzqE18Ljc+7ACM5rwjY7JPrUyfzBhkOmS+wyawYVTVf7EX2/N/Bzmzd+R6xGFj1XArT/NfvLAH3DH74RxOZ+cLaERcvC8L9r901+EcVkQArJh7x4PmvF6kIqO/t954aN9rREGkQx/VkH8LVgPrjMOHT49jNMCXpM8XRAeooPSodDnkYW+Yb0e/QAwiUMooGbxSP7rAPnP766mks+PtADHcA2M3I3FUBoPnwAYZGdyrN9LjhwObry0foxyCjKGAVF7dlBHdN//et5TMA5AMb6mTsFOyLHa05HO/aB6j859KrJtr1H+k1SNr+XdJWDRP8tNedEQIS/BUNLJ/fG+Qo8sO6yuv8JwX1vSWgLY8bZStJ8E7bMbgj4fe34+7TOMYtL3vMCWoxewucm+Xb+sLexBjgpj9mM5IpoHi+GY/SsdN7tvTpJOQ73bASleewBjAyYFdTLxX9ouZ9r0oE3PyJ67vql/ANN70kWBeaHVjuMKDjxHEpGg/3/uIv5+VAKgJYv+ns9IK70Jnz3a5ASgDIBu5WqPuJJ4L11NXCAULW2v/XFwQN2fjZ4ZMBmRVHNLoWY6xe52frmAnJPj/zIA7R0pjim0JD/ofonR48FtwAjes06nsNFApB9znYdvpgDiwGLfW18FMdiiPyHVQPbf57xt3fid/s6SU2lBJD9hD4lBPyGgEmEuAqtNDF5AwJSwMLsCeL6JwMjCX878QPeN/81zvEfhBZ+nUZtlNQ8LsWpuTd5Y7vlcqVDHwhIgmVAkEwuRnR7tHisdbj03/vIBChHDoZZCLRQdXXKO5qFdG0TfHj/ZMErBM2IpU52AC/1uvD5uIE3F0UyUeAJOzo/+8eJ8PoCwnU0We8xicMM90ua/6bHNzR7qdb8QP36C+6HGkV2xSbEukQ4c7a9Xr1/+vGGI3+fd6oyKwQmS3YFigQtdy4EbosLxMoBrP0csvptafkhxmTTdkJUwSgKJXpVOZO8gXdqPXOBB78jDID84kDgycu24H5fNYu5f4W6DXOHRwJ6h933Qv5dO7JAxD3vcE2CHYQ6CyiBJ0VehkmxeXg8dByElIcReAcFZITHfiIA6MrGQzH4r77zACqEiAVVBQD9YfBIO8n6EIDTSqY7HIQTAUm/XkSShIbBY3P+eUv1xYFcCDPCpk3bCgm+6HTqOKnACX/6u2nDysU4QXdAg3t0hDED53tadTjBHYVdQ8xCZfrH/mo8ecaKwbp8tXZnfP8RCn3n/mwDUro1QqiI+v9bAi5EEzS7exrBRnqLQCe9/LWAgcFKr4FFR3wI/zh4Ao+/brhZ/Jo20cycxlb+aUSGv16/8/qUMuV1uIzhBhW/1MaURkz8nLRJxnHDm4PdvY4xAL3kigtEtTRcNZfEsgI3vT7KnwhMRd2FesbFABp1MbowdtQ32zZSSPjHQvjBiYhCtsDaw611eLifAIrEREBmOX5KWU1/hyw6wPTNwPXx334DxEhA2Qn9irZR3UF+fRc4HzSOMMvnkj7NBfQEdYVth+AJMIkaRuj0A704PkVyE/r0CvmKbHahBkTNB0CkyZ094i6uuNr7tQL3Cc2447yreRfBPUpf/REFhABoBO3/oTk0wDfCcTtONAxMg0BC8qC+E8cGRaEEI8nrBV5G8XfFO79CA7ZLr9V50r5egzpPlPuDxM1ART7CktICrDuutWZ4wX1kgHKC3kR7wlb4izp9f8gJ0Ul9Qc91dIGwg4Y2bUDB9/RFuEeI+Hy/NUISyW8AQUENxAaBvTvIss4AUftXNefHIULRvXJNq4V1vvjBN/PZvsqAB4PGxET4DAc3xUkE7kJjtsS2CS/bxskNHbw/CjtIEYPXdcUwhUyZQvK5JHjIQDeFZHKWQqbLiT93geDCjEBn+049u8bnxvR9AXYHu9r/m4CQPpy/H9UEiCYtPvY+AbpJZoOQe8AAOXuLOeTFQ0NO/Er48H0jhhRFMEuMCVX80jT1exZAwsQU/BWrOnzvg36F85A5CgXHFDxmd2P8qXrCe6121DbMyo4M7gkRwxo/4H++sD8+OoRW9q7+CUbGRR8ErcUOvQF/X8B8df0EuMcbt5G+zL3tPg5EF0JLP4cDpn94eG1BSb/RRYuEFwJGOP1yIYFzgcES3MnrNe+0bjMefUVDa4C6eskD20vbz8JMD7/rd7S7a0D2unb1U7aZP6nCMUMEjElIHbHwgUdJ03kyAgw9fjo69m6/p8sCxn5ACrntg+u61TUJu7ZEuAwpxADFncGUOCACQYQT+VJ66zxghAnDVoO6hIhCTcXZejR1fvmhNwJ0LgNLUPTSkkUvOlWECb2i+iaBHTwgZNS3SUimRt7TSQNcQ92AX4DfeIJ5mIS5s3cBS0XlS4yBPPsg/4h7NYcvN6q8GjyxgO9ECEJpyBjx3MAiRmRFawiFtr+49b01uz0A6z6U+0RMFQodR55B9vguf8N4e73PPof5E0L6geTBo8arAjsAav1fODJ+zgKzBk18ML9nBqp7noIXfq576L5W/2ZEIMHKw8jFxrmGPLTHNPv+tSr6b4c9weA8VgAJhCHDpfsf/wC5TkYtUCE/VXpnQC8/gz7Rfeu6bggr/YD1xIEJyPwG2zqXel62I8FdCNuAqoVO0ii63u3VhnbzxHlByh/5pcH5hvzCyUyQSz80OS/ju0i0IoCfzLcJpU9hwMiBjnKCbslA+zlVBRz91/o8PGaILNFDBNGIYAGIO8g0uD6dCCs/0zEJ+k8N0j4Bg9j7nj1Cw9F8HUAYfK2FITrrR/gEjHpSCBBu6vlXAHm91ouZxfDBRn5jynHAmT1MOzttdEZiAVg8sc/QSjJ8uDsbBU73wvC0Qe1CF8JgPLx7REpKBLyDkT8C+aFBC7/reOJ4vcddRa3AWb+MCayEz7b4vzO4mcHAfls/rMOqPf8CzzfzilFBGzUtCNP/KbS6vWJPUAvDwk59t/CN9zIE+j3fSE6J2fRMNZ3/4w48Q4q/gkbaNgDwBHQBkdsS1Xacgse5vfnKAJT84VMFvM/3K/7tgLHQSH01AIx1hO71R2FAuUT2BJrBXUP1hHbIjzTWu/07JmrPQq/Hu8wuh3Z/WwExv7xA4LACuVr+AcGEgktDBcsPBNJK3kAwvpLzGPQbebA+blNzvVG9uL7TwSqEj4lLhcxqzzgN+egGbkkAvv8HeEEORWT8loH9Adxu+TXpu1KD6IlZiHJJJrv1ekvCVv4eNjR5+w9aiCX+NX8Xslp4iDkTRGZTqcweAnf1CX0vPjo9/wV/Pg/8VTZIgTTO64b8yXN7FSmpeYv3b7ulDXuFTATPgmACtDsn//1HDPUOiFsFq/hJwPE/g7wk8GmEuYRQfcDHsQeXT6ew1TpBlXc6RLqVeM8yyv3WgF6GLMXTfTs7tsCdvdMGNY6q+n57aH9hNQ3DDYl2gI74aQRAyVB4gHY7vG4H4brVgk8PpXYegJJLpDofvHv7XDa1i+GB4PoUBWl5hwiAxzm+gcHM+PptCTRCTL9Hi8n/A9fAJwbMAOSBR7aGLrA04AIY/hnDWxRBSMY+qkM1Qc51iLoQ+e82HcMFffgAec/HTWzDkkFzwhA1JTNJuiD5BgHSCQMHT30NxAb//fuVg7o8vgCSevDA9r1KAKKI9gaKDMawSrukAEf0ar4YvCaHiQieQ+J9K4Lwv2p5SQHy/Tb9YMMXQfO4gsejAPH+o4Z5ecrNRLWqtNuNO7aciN3LLbmUMd+3YMaJ+g5JEcZHeq9FHH7kCUmG3P94eMVs8DZzfyqGY8pTxrvBb7/RgwN+OvmA/9F/431Seg5Bf83XSag/XLWYuvT+yjun/KgArkR4hBKHZ0giAHT3nbltc0O8GsmtxwUGfQKVuBy66tCguQs1nLmlroNHVgvOjYtK3IXjN0l9THl2NH9KuzML/NcA5TyzAZ8KZguWd8HQ0H+Qtzt9Wz2VyCWyCzrWATlGsEc3+brDUv67eH9DTcESgTp/aTj4hFoBSAIAQwD84b5cPfbD7wUuP6i1F/7fyo/9zX7qimp/4HgSOtz8Zb3aOeFI0gDXgaiIVD3ODDG3Ib/vhF0zjkO4uD0AKjra/EeEbPrxUzx/7vljBXo8SwXI+ODCjYg8tRs+hwc1COGAXUGXe7FrYTmAvc59fA7Ti7q9SQ2UzeQ6szkGq3DuIPeVwOBRgoe2SfD/BD9ExZG0m/5n/MaFXcFRQvwKkvZEv+M/x3srdnYA3YIO+36MTQVDxGU+V7n0+2X83LpGhXWNqbpkQyE8irY2eBxJPM8Jvj6F8fYhed9EiEHYOpX0wD5Ev5MKhk6HSBg3hnz5A/m2TvQsf2JNTnxHuaoGUQh3uFY3EEeWPWFIH0Ex/A/IazmFhV7GqPHN8S4EyUsoPGe7GcLThjlA7wsEB+h4rzaU8tw/FL5+PTREIQJBxquC2QPcSfmDN/LkrrA804dVwgCAHkOBROlFkYItP+i6fjPXd70Cc3hrhkZdmvjbd+rEkT8eRSX8ETy0ud8C8oFEeRiBL3PvyNlPgfjiREHCon7pPJY/2kb2AJM/pfYTfghDh/tAgIv6YL/DRXj3iQLHxefHJkpL+a1Bz/lzcsfBech2RwFykDttwkh9n8fzTd0BEX9agWE48/5ruTMC3vsnue1GUABgS8TG7gKzuCU5vn2SeICAQj/nwJg3xcFMBd+ImYouOSYFfcFudix6mrrVgXA74gGYxsJ/+klBRnS/+Xub/MFCIjuDuqx98/sMfzSLZX5QCO5LqjIp6z71PAoEh2aVU4k0+ZL/s/qj/6etfjotAeu1q8N6TqQJgQ6DiIp2Fjt8rEgxj3y+Ss1YA/5Ae8iCIjwjPLTCPf4V+356D/3mxLwNPgC5uRSBpPXuzPsCivlnSh2COb1ctICIiDiStQVDAPpqjXd/SgIhyxo3TfmLgfUFlL6mvvRBcrU2ev7K+AbXewkCAQbbfgs+dj+gO9S7GACQ+07CUUlO/7XEooH+ur51XsJ/Ra/5VMchPOH22DnOvkDOpQBshpTBsfdPC8mDE8Dre/A+NkH9Pf/Anvap/4p22Hs9ifOAlfpZgjzJlUGTSn8DK7o6K0l3L8akRAVVhQCjewR64gG6wn29dUAyb9JEj4UaBdOK6bUl8lVAdIesxGkA/r2FtYVyNQijjSRD0YFlgpg28b3aR8Y6+EXhtiCCiYqiAdKM4/2GNiM3rDvnLbp/q4oWCj+LQroPh7M7h4FDPlwvHrv18Ly7eE/jjrVLSId8/ax4PT+mQjq/bzt1sJyAgxK1yHH8nADweaAynoWMuhg0G/hRyQVRoMYg0bF+y/ok9GV4Y3t1syIFDDVuDSBWtD35TKbJSHMzJs75TYD/PlCIJIfojr5IWnpE+9E4MrSaell6Q7SpBX5NT8QRi86JE8XOPIZw+/P/ugGK14q0/CZ+TcQcvW689gSc/Mh0MD+RRLyBIsAXh4qG/ztBQ9s/MwRh9P4wG8a4Nw4RSE2Zs3M7In7sClVAgDuKgM7+w/vyPkaD7UkGgXD5DrsKAXoIqXcRgBn9+flCggY1kc1tCPI+I0FAv87KnHko/dr/9vsgAXpwIsBiRLpANEpT/syJA3mMeYfMfjcwRMaBoTsb/kW1LIfZw5jEBXhDdeGQnXyLg3aD47urAgt0a8tjxSt2UgEIt+h8q4rQDkl6jjrCvuT02H6Ovcc/CYPAvjBE7Q5Mw86B+fgJcvvH3H3EvsMKln7r91R+0ANAubuFV4IV91j7mcEazIaKK0opOutxLbbROueHpUQjBM8BKbOeu5nEGEdeBjk1ezuPPpB1zhJ0jMo36v8QA9OCL/kPQq6EgzyWt7g1XMaXRxhB/wKGfUdAgv2fwID+IHmlwxz9yAYFA4z/a4Z8u59DiH61+iSGMTSad1VC5jjwBap7tPzHmHqGsQK3g295jXptQyZ+5bNafaP8n8bGhPm9SAeV/Il1kn9wxRK+UcN4B9yCI8RPgE6uw3hdhan+GwJs/j0ACMaABeVEC39FNrx5F4DDcw5DCJJIBeB8voO8C4i+1XoNbkoxMwRYx8zGKr05ddeHbFfpAtFzm7otgZ9+Lz6GgxC5G8MzBoZ9tQIWA5zBSzNU87B/i/sqSK4KlTvFzLcJ5vcfPCq5Vnm4/s99UQDrvhwJdFB/e/1DU0Og9dBA6DbxQHxBXfKtSKMGZAiOwTe/fcKbbVF7fX1yBUJDI/1rRNp8ooE/wWeIWbxBvMx84PeexVQBuUUOCTDOrng9cP0Ac8a5whatK3/EQhGAW4dMgQ2FM/tON5QEcAh3Paz7SoIBiB74fn6MhMT1FYY8+pq6GYYJPmk59L+70IACoILkfvE5Xj53urUJHTsBeHP/DYL3jKNIuMPxLuR4MjrW9+8PMoqqBD9/Jz69uop8jMOjugs6H3rVeiiJ8NRlPl5/ckTeNIMuDTfjDjVO9E3svRd13//7Pzb+bbMyuHP5N//9ChAMahJt01fERuf17B52GDrzOsZ9mog+SX1JIIESBfWLLcTs8ycwYsNZgTy+tEpfvso4HIS4Nqb5WUDyvMQBp8NnxCQ8io0BTi/4+zw6Px72iLN2uoVEPMg2woY7oAJZTGKBMoLX+/3y3jzff+RL6QZ3Qdd89sRnxKR81zxhsBkDO/xK/CyE94ZXAqO7kcgMvmNCjLc3d67+ZkQbhJP2owSHOpCGsUluyrVB+batAPpuAELJBlcCBb+1eUx718KCkUm6GgSHA1H8AAXCNDm6+rosuKdBM4SMCDXD5gzSQnHzJzp7uB/Af0OmR1fB1r8Hyys8kMELe7t2lffS9qwNrUjG/4S+2DnsvVCJbYIzPIM5Vzjjyj2DV4epiit9vi8vNPnGNMXwRof5owDvRHc4xrruOdBAgsY+yicHmgObSGq8gHKMdcX5Qvs5+ARFFcZzS26EWHgARJI6b0U5Ag+BW731+0DKqT77iYc/tH7HbRWvM0vGvY4EG8JnSq9+yD8ERiY7FTk3tKFE2oBBhyxGQAFlwFk+8oL+d170XboRBLpC9469iZAEEb7x9SAAhbrcw48/oLN1Nt8C8UTf/oiBOUDu/a1/M8hZAXwMTkWVu8oAcD3H/CI1rERnN6s/mEmbAY19mjc4y1TF2LfuNys9HEB/xQJD30fthpo7XjvDeY9FhnoZwoC3Zu1pixj9TMbVk+PL330PfSe62DdvBU7+Jb42hsQ+HW2Se8qB4gJ3AnbDPYSke2kILwIYEKvHdrCBeb4xqbqCO6+C70ZeQ0MHIwOzhQh93rzC+0d0inu0xCnHyoqSwvq7rL4rPRX0gzjpPSHEZkZ4+20Rz5NSQ5B2DjAZfPL8xH7sul6Er81cDZ+DsTNq8ud1ebshfjsE+8UTwdaChlEExUtCrcUAZ35p3rMmiLDHvk30kLe5sMUDQ8T8tq8lfb6HbHwfuFs9s4kdBu3K78FtQdT34DJwuZhCyAq5yDSI1rC4NB/6hsIgxcS60Do6wFdRJIg9QttDHTawJ/SBXMnFRy0MtPWUvVB6IMUVhSU+jPsatZwMiYNuxd6HZcIs8/AzGMA3P2CBovptgVSCjAijAq6+xvhg9bY++UABD5/D/QPpfpc/kIRh/BJLZT6hLGD2DAdDfi48HQHCvtCBTEWwxuJ+CsBlQBv7/bzyBYEBMQTiw3u6PcDvOOY+2zs4g2EGQ4M5ygX6Vv+rwQ1+8Hn+s/p4oT5yw85Klwa0eNy+MsP+hP/4tjgN+Uh/IgvMhBxFnE1zT9Jz5bS5Adb6b/1zdUFB1EOeg7mE3gFsyQ29g73INOfpR70ajNKPH0G0w407Fm4yyYKIgP2J+PN+mMKwP1FWCog8t36zEnaO+tM8HoKjTCWJ2q6Nic5LTQkX/jbnSgAMMftGiw7Lwcr3PXeNji5A5QiqRHl3wq5tPEFMLAohDbi+STeCNAT6eHeXwlBG40MOg3b5/4Wwvkq+kf/VOIW5VsDgzdoNOgSVvrb5jrWpghTB4fsttKKHLs5V+/GIPL03Mh05zwKkwejHokddAAPIRL9Xufu0p3yZPpB+U/gegTEPdr2JB4L9ZL1Juaj8uhOfw0X/WbThtVAFGocT/D2+2/4GPGdLW7t0OFFHIQC29cQIgEmvvDJD+kTovNcytvrj/kTEAv89RAGKCbmLBpAHJEAkMzeuXrlswYvS+gy8f7c+tESjhAp7ZHYueUl9s3ayPToD8sDxiD0GUYIqecA9icm9PW1AOUJiQlxCNII5/0N3XQRMgUP2HfG+SOTGjLXqRL0DhcnU/lJ3Y72GDBZFKnZnAQr5hwESPeEECX6KtAt/YHhBzKLQzEmIR7r6FHbquF8ASj5udUvB/oRx+97GJIPmfqkHX4lV9dHxefbit6nG1w28j7PBrrmsu9M+zAdkfuL0Cn/MRtLx20DoiiACxIKVO1zERf8LQEr77AAKxrY/dQJtuEB+A709xdZH3PeROKEx1D4+ibJKbD/bgwvN2vicufLIzn9RcNQ4Fb6RCQ6Ec35VzRD6pcNMiL11FbrdOwH3E0O1FEjGjD6F+Zl5wrz1d9lAxT4QOWl5AElszozF0soaRKo0jL1iwo3zqL0Jc8U2TgbAEWAUsjgiAN+HcvPEdUfIF4Cmb0J+E8bdxSaB64cefux56n/MO6KFa4b2AKH8XXkWup/CHUchwMPEUkXz/eA8wX6lgUZDWTHVcbn9xryYjAXJlwl3xxt557+O+N7AlABnPVj40jqhDHkCGIjuvmI0uj7Jvga7ooefU3YDnEOv9/X3Z/Sy+0ONw7yguqR3LfzE/WoQxxKOtiM1A+7WPsiKnQwMxwVFQzkq/9vJ8/HPycj/VDY6wcoBGgLLrrRDHEB8/IAKR8QVjaf6Przixm6927nCcSL/u/YEuztG7X6ZSloDcMKEx+8FBkAHe0pCu4MNPJ4xV/5tC/S+2bjx+kKPLwY+7XcKDHxecbLJTkPbRtvD64hAusp1gT/FdKHA3oVOPh2/BvwJPz+Ft0DADa8EDfmKOzVwrYOfg+QEGT+URjEC4fm9ioXArIfI/rItuvUEQ+96sMFOE9d8/vyU9Xg9fktxBlb8KnYvfmhA7wrrQuA/K8FuOza2pX8Uf19EsE3eeio2Sz7kA+GCflC0hDk2MgAOdCa6y7pkvuxAy0AxBt3JUMhucyY7mH/w+JcJKAcYfYcDKkSpQI+Gk34EbXl4J/sCu9pHrU28CO3/VURAObf5/Xa4OG5NXETTxgQ5nL7GT/H4G7yzSC2yqfAc/NLFM0lBwNMDsjs+/l/IAceSh8k3anRHNy4A6wNYCe0HXDZnQAY/Fz9zw6R3W/iDxcEPO1J1u/w7tQXnckcys3DMtqAIMANHCbTRoQUdAll1y3n/eujwNg43h/47a3/jAukCePyUgfh7aT/x9y89tIsqixzNDrHNNZDEa3vJBkCFqLmpMny6Bwz0BGkE8v6VOUW/bzzpBjcCs8IofVS/fwUdSIGBKDFzOAs034ALzANFWn67vn1BqYjfAkz7BUDm9ct2+Dyqz47HM31zRqgzD35Gh5C8Ob6n//w31AN6ibNDRX4A/8JBy3pJwAH/Jn+qNpQIJYRa9XVK5IPRxDg8mLWEMHgCOgTC+OzIdgjDFJGKbwFuOj43d6+K6+RCNT8yCn2N9D1SfGTDr7yuQ+mGu/RGd6u/PoSdBSIDRjtM/937NfQ+goFMkhExA/M3lP6eRFj5If63AIf3I/v0AvT9RH46xlmA1YhRwKHD+oDBt608SXXQQglDNIdNfWYFlsjQ8dFKBwNeMw07czkw/6eJ+wDhQ7lJQPhxeg6EGvvFeaHKg0KDuotFcPcruT9CpHq2/bgEo43HRIFFlE8OMZquIj5Zg8IALcXXhKd4PQHJQvhIQPtQuLnxXXZyEKlE8UzGRIQ+KjOUq6V8wgwhyEz3mwdrfb2GaYUeu4zF3vShQDOAo7yFwTNIqgfugQ6HP7qptUo6PLwzeRq+lgPahjIBGHtSi51Bqfn6vT32ycK7BLXMqQp3OSt77D0/voky1AMlDA00DMCJxDzGHoUwveD9urW5uS48CjztiJYJ/sAmStm91ff7PtYBy38NL7RFbP4mhPIQ1UGSx+n+UgAOOcL6035Cdac9pEFkw4hCnX5CyV9HInOP/GI2p7rQh20+1YZkeWY9DZSYR/C5a/5Xt9/C9UOXfOqD9zGHxCP80zch0FQFLf08eL9C/gJ/jfYHFbOcRE27jTZdf+YDwLSYN/JD9EEcRq0FWoyB/iq9RMIGc4K4fb8Vy7lBMPvNAHm47kAEAbcAfML1g+x9eDuGxZYCArm/vlFEcz8YxWOGpLqTP6JFuoPvOyN4lQHa/sdE14TSeq/8KPsIArv8uL6Ihv63+D0wQfMB4UVjSJWDbHUOcKQ2tAa+Q/FOOQs0Oc0+57Y8grrR9UNp8YY1A67iuqbWUcK+yoISH7h2+Ep/va+jOGWLmL4xP1N/soKtxA1EZMMCwfkDzbJnOyVALgKiBsU5t3i+QjyAAH2ZgoY2sX9sgvWHUMu3RqPAFLJIiPQ5zXlxv2V2jslvPEyDwIsXDP1GMzaLPlh37DbnOP00PUBtEhxMkcGU9Fe3w8R+gaxFFP0KgXC+pnX3PzAIVs4jv/ByNHNXhotMIMVVhQoCnnetp8G8MgY+QXsFfwNBAC9+c4gXRVfJW8PW9ml6hbjEPZY+dn/QBy5IBLvN8kI9fEa6wuh+tEG39jI4eQjVi/aD84HchrjzCKxkAWVMBj7qPMwBe4KsCyLEgoHbuOt3erVEuWWM8kaXw2hABgdwQ4UvmQGBiXnzX3aHhS17074HgXJC8Il5fLQFfwsRgwX+77PWPxNHzAZbtfovQIDN9hlBiw1pQLu8sjU3xLqOyoWzw51FGvqksOi+40ZPPL65czqwgbBJSMmMj419WjT6vG7s0jxejEWFTH7F/B+CDQFCDR7Nji389BZCsjfKAmBAYraH+0TMLcnE/89I0X+TQEi777+Di2K8L7ulgQE8aP9TA1GumTg2SWhAVv7A/rRDukPeCeVHmbvbtvaAwv7+NZcBAsBtSLwANsAPyZN8Qn6Le7R8Wntf/uRE7gHxj2mHIG0G+9mDhTi4AraA/bwZ931/s0JeQ/mR+n4l/6//qzvMfoo5xwkovIF/ZYQROdSAiHv1x6BD370GBtd0zrh3CigCCPgIyg8KJHBnuXw98Lt//jyEfIju/X1FvwcnQkeCy7fEeQ4+xX3awWrC7ALThfT+rjutuLL2oXuOv+oCJ0QcDOGJtQsyBws3rvISOEm29u3QxRuKC8i6iIwGgkztO1u+FXNlsKYLgUTN94kAYYVhv+JAbfTBet++TvwqCc6Jq4O1vmbFbzg7vBQKl/yTuUq9jEc5wd7KO4aNN621Yrih/bZ5H0rmvTu9ngohADsCeXisA8x+lvg5AqjHr/ylNN1MWknoPnp+LElXPHWzmkDZxBhQFfY+cF/AhEG3/Td5dYzMQ/i4Ajs6RPsJOj/DfuB/FoIY8zY3bgMpRiqKIn5efkN8MYLlAl48kMVuu9wDD4Vmt7LBkDrsuzWRoj5eeFxByTfEvZAAZ4zzCtw6lLkeNx+GRMUZOdRDGIEZvKF+CL42wtl8Dr7ShF688gV8wEd+Az4ABIiNxPc9Oby8ZPiXhXoFX38n+U3F08NmOMaDrsWZgMR+pr9ieCcA/029xCf+/30r/+xxv7DI+6JBuNEKBOEBmoU8RkKB14OKAJBrc71NAgx7DXR/f64JHwX5k3240PY0eLB1NAuAESQMEMC58Ic3HwzH/b68ZoE46iL1cxMbhIr5HwxVAdFIbvwcduCPWDCAN79MUHhHhOEHGTmTRGJ9KvpAuwV6iYO8xsyGT3uagJm6s0BCj4r++nq7wyn8GbnuDLBFlDO/8qJ1QAANTMPIBQdXezi25lA6wbi9dD5wvbR8in71RqH9sn9xrJMAcP9e+rfRtwQpQobAGIx0QAWBK3iEcQHFUnkkgbr7WQWQRGf/+oKTPZrH1zAEASnFnrpPQokEJ4v5Oq28TkQoOCv0mwcWxiX+x0hLfas6qreHgBYGFMKRAbn7BoJsPbcCQQlNCMM6XLCwP8Q4g8BPioqEJ3lq+YhBjv14/5MJGZBpfL/54Pw9PR3//n2Gxif5JsQgRz29nHdMBrDFPWREe1hDlY1ljkkCngF0AofE5XZBxcR4FK87O9X6vIMiEI6QZTRsthcBEYHgfGk9pcd8vSTAq4i6h4WCfT6lvZkz47ZM/fV5MH63RJRFiErLQqN4NcYRBYG/vg+Nf2f0//gG9uX7D79MB0R9YjnLw/WGAbakAw5HTf9WzzbAs4KbQd78ynzbOYh3BPTz/2i4YUAvznbQmDtB+0PJr8J5RRA5fDay+LFDSsHnhVHKyG9uOsF5pnwxzKOBiVIWRWIvk36kRH+6ZbH7hg0ENgb7RwLwi0OdBOG5VLAc/JhJoUmMCSJ8HQkn/uR+aP/g+QQ50v3ghhH+egSoRCOMpTcKsV9/WnWzQtYCOcFNgVMM4ANEOy4CzP/5yUr2c7QiwXj5YfZTQP7IHwj1xmSEGkZU+O2BWIuasQ+1gYiS9nD2Skc5wig8E4O8QVS/nchTgj9ATwGdgRe1Nf1Cx7hAfQZfvYZCKjKPMBfK/MlyP/k/7YF8uGO/mE1ckk99rK5YrSu7FI9Lgtj/WzyAPDg9Pr4oSVNHiPqCgU+BV3+1x//IiwkfazNz5T5AOvtGIYZIim57tz1c/VHF90EwecU5Sy//fpBGMpCyzP9HwbpMOQ33TjHJw7lAeEOsAx1E7YNSwj6/WIexviCwP8N1fBdBSUKlw47CPUPjglm398Q09Vb17cB2R8IH88CUe/x71EIa+vkDBAHJQwX8LnQQyjyOaAWCAL59IL2Xe+s257QU9+iHGUXxw0FHc0T+TL3BH7GydlRCtMnQfduEOsUv8GmC/LWI7/+KCYRjgVV9ygoURE+AvX+Nv9kEaroHgY/3zP5ofYGIp8mpLst9+4QJAPm9IcTvRuCGR/8dOcA/5/7Mf8e7PgYAu/07qA11wgYz2/xEvJy69wyF+p49esb1PhEAxYJXg5d/ir8zwXuEXACQAsf0dHmMAcd6QsPUvKvJRYVvevlABQEUxuzBqHUTelNM6nwBQBQJ0v6FtQf95EUy9MbLSj+XfJvG1LURxsf/xrtDPZv+hELQQrRESwDwx0j5vXbG+t09zD+hP+ZKZYXKiRu+BcLvwvg8dH6sdx8B2vb+w4tA4TtuR8y3cY0SAEA0CH9MuaAEKn5zSFyBmzjFhPW6NkRLghn8GwVAA+lFqP5E+2wAhH6vuuXE57tzO4mCx3S/RzSMS0aAOZn4H8Z/PNQAvQKuujh13oZJCSbI/ENHNUIyJXqp0N28KH/mA0T2HcP8S5RJovSw9vm8krrTPoDCrYimCZx6Oj8aCgy3nTafPhmEAbk0yIUIk31YTRY/yz9vOe/57bdRuLdAfUr2AJS1Mkx8Ppb9w3tIxXWF7H+4x3L5twZi9WL4v/3atVeCvgTCyepEGAnP/4j5cEw4wU5v13oiPTY41YGnzH/HwvzYwM0/vPp5Mq5BPclkwlqD6n8AAta773nzAQgDC7uEwTl+bHk/xrR/4kbYh5HDoz8oe6d/RjxOhOZ9er6ZQR50bTXKwMOGmcUcBRA+cbvxRTHDvvrYPhyAdAYYw8y6SQLewjSES0HFLq16Lng1NVRSXklNRFbH+cAFRcE8oXH6vEzBUfbhBJiJ0IQGBAt697ouezh3y3ctzH5Id3/ZxwND1YtIODEyZwMTv7/6tcCnuuk4oMYQft2DQooaB+r79PLDRZtFb7+iffn4yf3kfjkBU0r3Aa+7WPzZgkxHs3rx/aO3efqZBg5FqhFEC3wASKiMcQEC/nr+Rep9kL7ehlhGpYFnfTMDHkM9gWi5b/yYvQUAOcCpOxmAwI0hQclqH8AqSfBF+83WDgx+KS7Z+IIwlDYgCl7CUkESxfw//QLG/mGGDERGtdDIRzlc+UHIkD/vQVgAJD1Xd2y+SkLDx+U/QrnKgxR8/kG9UIqME+7suCBA5/pkBW7CAb0Ds7l+qE+9hnL99INIOXxxRn4Vw+JJ6H/aAVdJcMDWe1m3G/5t/Sj+IcGQuC1CQsuOxKfJJgto/tbz2PTLe8J57LioiLGInPurunLASougCjWFn/b1eZjC0ndlg9EBzEBtf1YBewY6tcD9w7iGPyA9w3TNzL5FKIfKyAvCKwhIQO49O7X2c5Osa/0TVB4LLoaugDSAZb+j/CW4AvvDQiX7IEJwRIbHU8xnfbkyCLcw94M/Sz6POgIMigPzReSIxYRKxsnwM/kPwrc9EgPEDAnHTzOPP+ECk3JywbyHATnS+UU4vX0RBU4I5Y4ohNV5q0J2ecwsRgMdCYbFZwTudhb2+YEtR3SMbYd1cDApq3uizWzZGkxiAh58f+u79FH7kETixqRyb7+2wylFLg6LyBp8nrDzPeZ9VvxpRidHRgBhQpNBpXrwSKB6Z7d+uOqBI4K1O9JTRzs5vARFDHzkA+m+28AT7BB7IUz6QZRFoQSLfxgCLgQGdkWC7H/T7ks16YbKFLQIA81DdvOtAQhLAFbAdrW5N137i0CdDHwHkI9gNqz1b4Bf9ZuHFALM/GHMLIa/+sc/jEOFQ9+y4TOlQ5M6l3qfhhdT2AT/uhxC1a+ceyzQCvySOHLC/fzU+ijEhkuwAOx4oH4BxrXFjMKofw52PXkBwINEc/7LCGRGOja1Bqa8T3X0tCM0YdJYDIFDCQao/iZ6Db1cycBBxTHnNr65kcLFCLXNSACHc2YBcHIigfrOLwI5CDS7aMNTel27UURhMmNEGA01gMzClMXoPUM1ozVUOck3vwRtCA5/+hG4Sw+GiHpP90B77XPV/h0vAj7NSpaBC4f+y/5B8TqNwzD5DcFSdfQH3AriNsSTs4FEgix0mjETvu859wK2eAOFUkHEfuC3Enn/00DQmUTTgLfFYjG9eUn8FzXcx3PALr2BhxgIY7mhftZCX7hZeL3/IwmOS+hMR8SUeaS3zL3tN8e6ZXtX8md4aUVPDaoHn04bgt15D0HNuzRE3kdnvhh6prZiPEc98QDvwPY4z0aTxqQ+Jv0M/ZVKFIQHvt2GF3u4M7sGF8KcxPyBZzZBiXfypjm2gf03e4ijiABJDn5Xe4Y9GncDuAiKusUed93GIrxoAajNNAajMCby9Tt+NfYSUhD6RMdEsABa/eeBeESvuBP1mbhh/nB/aQN2BfY8xzqkP4M9PzqHCqmF1wEFwrR5yQPgwEQ7L32qvRpGQ75ROrQ/S8AXSmYFZj1IP4SCl8WZNmOzZ73dehgPLorQPiPKanmS8c+4qgq2exvzRQnBt56AkFODyxoGy4gWdai0ob3dPWn6Zm3dBaRDLv3FTDAI1PwsO5V/lvnaCQF9AwYNvcZ6ukXPuz3NdD40P93v3S7wvhpB6ZNWBKTPIUEYwQ5EB7kSP+L0fLVYNnM+7wbiTjTD9IDVP2eyeP1w/Yf9jQYOTR3E10DvuDB83sYpfPjB/bdDeQe3bYW4l+TCBL9Bvtj583gU+wmCxYdb+7F4+IEgO/SN7kjRdaeDrkTquwm9WX0qvYpHp0FKdq7A94rtf+I6NDvAO+9MCoeR89J2Uf/3Cay/5fkXxUzAiz2RO7wAqApkvSmBcjxc+0BNSgA6vQT8BUC6xuk2WbfTwQuJtsbEfkmBJX4CO2h5bP6YiJFAFf9ovkT5yQQoe56/rAc8wucC/sCdwK41k8X8h0k6hT+xd7j/F8LYgFNAKgckiWb7AHghfLn9x3hF/Vo/RsreDI86mr8muJo+EsxVPg17KgaH/yU6KooaA332onvMP79AKb78PuUB2sLDwAwGCIUHtj81NHvnAZDHlQMM/kM8fDvYToEPMvml93l4XvyxAcVCrEOhgI2+kz+kRWZHXnlQM8c8VQJYxgYBMYorvj8tmQcYhRF97L04PAt8MTdtDZeK0LrhBbKA77rsgQD+68T8gvi9f7iFPGzH+rWWP5NAQDlIx0G9KkTsRwFChb5rOGDAU4Qrw2hGgEdVdCjyi0AngMr9EYUXx/657QT7hw1BJL+kcbh6LICU/ztFBkFGw7/IlweB8v1uLQNkNYw7+g8nxedPAYupeu7+gj+i/Zu2nfIYuFODpUpxA90E6IPZeHNteX3ky29ICggJ9v97D79px/cLpYCBfZB0SYU1g6T6KjIqemkQ/QA0PAEJEgQ8/KYDsDiatbB9ZUUWhAi5V8W7e5RA/cWSONX+QwKKgjmAB4lsCokDmbZ59+f3gbzgS9I6bb1CigeKsIFVcgq0A/cjfhfB2YdECLLFlU+dBQv9+j3f8fEoXXjWT6oHHUk+gOI/koI/wNZ/qa02RKG+azeHhEJG6ofIAKDLGDaVMNb6Jv+0AwLGNMHixWyST3YHugX+t8MIOWs0Igzl/dqEy8BfPNXD3n79v7c6Rz8euTMA9xJdfU87/4Mu9FnEwT8b+ckEfYMZhyoHfUJS78Y40XsR/nOFc0bHg2e9oEcw/g8H5vxauBj/JnhkPuRA1Ybz/7m+bXqevxGE7s0+ERnAJze9O/u0TiwHBqzCUkUSwwW8qf/XeUoHLPsIwt49gn50grJBBQ3MuxTCfIDKgQT9zLxEgyz9kn1Z/fYMeLuLAt1+hLSyirY7Gv54PKCCAoaxdW0ARv+qwQZBt7o5x2BFYvZTvzNAr34/i3PEo73aPIR+TQJEgHI/Bflqg6K767JphRtL0ksFwDc7PgkIv7BwzXxiefi+q3f/vQjTur9cTn6I4Xf4PKN5mobQOWY+lkCzu5oNt0GnsTq04j0+AFeCLULPiCfEzUSmA88B+L+8epr5ZW+ixHdIDv/niJR6Tn6/xU0ASXiQPSZDYsFpB53B44QJw6bCdDofbyf1gLUVPmqI7REFRrgDcElCOAsBNMSt8krq7T4wjGvES8hDi/Q/SvgSgf3yh+2/BbXJlD4zwlsOPMKq/3qBEsFlgsU5WDsvAHwy4fkfSIVCs0KwQKH5VDtPi9KGmXxAv7uDi4Bsd+ANIb9XtCo+KAF9vQh8AMwM/epCdr2U+5sBa0FcQ9L8kYsQPxyCc0FDeq3BCjbELyKtEsMFS+/HgEUHjwWQE/6gtJVA5wTOLqm5zT+KBDrGwjnL/xOJmb/r+GmDaXxiBFkF+nqTvVHECMnjP4J3qHm6QXN67XY+QQTIe0EEvHA/mItzina8wf8kdBF8Yn0Qe3bOpX+EgJUI8/tRufcAiIBGP+N5fXknR4BF4Mv6zUKA20FVOhYufCtL+uDGT35jgSlGWMnQAmu+xwN4fIC7v72Ewae/GwkQwp27B0NghCVA5q9Idhe1/4VHDdsNqIuRuA2Mu3o1uZL8zzQIQWw+ZQZ2OqGCykf9wUo4frZMgH08KgDr/tmGrQbkC2IBRXydvHSyM8BOfLhD30QBxPx9HnpASDX/7b85bn+40IsqUjqNvIINQ702G/yn9631MffAdPI8649/lf0D2giFAfK8X/GzLvf9Czil/yrF4pUryWKAf8aSeivyvPKf+E9168F6jkrUpwhtBO7D7PbGAhg0N66ZvAVGI8Kff/XKRsOvSP/CCHVPQP8A+PCnrzOCP1XVC3v8aADPOTbvSrzriB75PYXjTcXCZLv6g+DLibqUh2P1T640wXl8xgH2i9fI8Dft+oKyT4rxSH6y5svyAYD6OECeSJf4tz0ECLu0MwBUhzd+0vq7uGFCsAffAxwDrYHNAwsAg7+Ee5Y1HDiG/QPBb8Cj0HkJX8Bu/Yo/lvwyN6hA+iryDKrIivhVkdwAG8NbQXM6rXLcu3O9I/sIRw1GlQbEuOV9dH8eRCxODkfv/DuvoXaPAGOH5UvUPww3CflY/o8KswYcB+N9C7Rpu0u59QRoQvBEgjpD80mAnAepRzAKoIH7eyeFXjH3f2IzizUJS5Z1RxF1zPEEhoIy+3aKmvU1fFoAfzGMOTeDxdGbhjI6cr4EfUm18nmWx9XCe00Qg029D49xt+hxF3yJOhXzc0d3BRDAWkuTQSlGs/OiNTDAaARcQr5CdYmmtwMKFEx9+tE9fUDD6BLssYeQ/oDMLYW9jmrLhDwkRE94cLezN6A4abOc/pCPhAytxloAd3na9Nq+rcZCQOg4/sMkxjz/d8aSBib+zjqJNsm2vvzohm0Da8BGg7YAdEhsuoU2KMLkfJEGhAM3/kt/8oSExqC17r1TBM0Csb8POulBHPkNOH9EFv9cTLeHmTZRBKL7mH+8ApQyRwR/vWW7hcwkfVeEYb/mPloKyX/Y9dE358WMfVRMGUeLOVSG+Panva96CLziCDk7aXaC/wyDJ/xHx1pCaDuJQCeIwkAD+vmNRseEP5w4VfKCuRTEOnwRRNlMuMHgSF14S7kPQYf5drzygfQAQ4P9v5PBdEjQeV8AlkLp+j85fMFQg4p4Egj8QKa6AIS0O4w9WQLWCfIJOv7hPXk4TXT4vclCTX9nOxQ+2EQbC1DMwL59MmQ/ocTZszz+88pAT2/9HnqoUdc76rf3eV1zJTKDfgxFn0dwCyc/O//8PkSHdzvB/pI9mS5VhdOGCs62io7ANz82+mE1oXSf+fD+pAYouf4RQwuZQXIG+3aqA2c2Rbxc/BTxS/qPQn9PiMtz+Llyxkc/gqfCMAa0Rlc957tdDlDCST4OMjSx9Xv6vEYM2sfSw995/DeyyycC3jn1fAv5JUYYAerAxoVttCsGT8ZL9aiBln5S/F3+8boVBe/HsMpRDfV3kHXzACqA5/pfB3TGPa+ldSe8/AtRCGYB2gYAesesvbxeyltD85KRgMe3JHjQO+TFOvwDyAw5ALYUvuiIpxD9+5PDDnx7skr4FEO4BdK3IkQMBvME+UmhRBK7pnw5uXu3yYEGNoWJpIrpt/LFYn7UvQA/YL1uf1NHnkjcvx0HRQEEsEA577XB9U3IcDyYQweB2wGdkd5DzER5Agr+hrTAOh+A1P3+AlOCcEPsPMYGRwEwAbQ4xjQEfZp1UgVeBqPF1Ew3jvF7kHTe+qj4Fvwy+YiB+r8ATVnF8D+MhQV9s3gTO38HxbHsgE1IEgdmCG+AOgjzs/S2L3rRNTU/OEtwCDn59LvHzafHFn5xgoF3CHbO+y+FRD+iA7+DL7/B/1v7LEwysKt1SgLPAMhIEwp6zuT7OzgXvCg85LN6+/DBTIAjBFe/iYtZB0BGXIJ3Ny/1hb9/Bb6EAb2VPRl+wkEGBBj1t4H8PIX7bIJLRkQKnf1oA6Q5dkMWQaV36P5NOtj+vn/7+mp/otWHxKo/5T2YNYt2sz7NCxf8jQvuQzM8dzolPkhJbDK9Qsp9b/WVw7NIuoDUOb7IKrpAf+NGE4djSHz14kIZPnV1kQGPy2n0ljEQysCAJguiSHm+GjRmspIGQH20BB+EEYQhtUR9qsy1fRxFent0fLP7TcJfTB2767oiQqkCprsQecK/2MQaeUfLpoNmNLnNUQl/Ptv6JLc8cuB9zEbOAcN8bIWTxHr+3IoXP5nG54BHOdtyTXiuke49JDu+Qr1AVzq0vPGFnTuxtXWEFouYfRO/FryuQakHJvrov+tLhgTNOwf5LTgLhhLFt7iQd6iBbgGQgSvPH0WNwhbGMzJo78+4UrqOCX0LLYKqfmsA+QuMPQ+xx7/Ks5m0q0xsR2iPH81SOvK4Xv+QAlw2jTglNfT4jskOikwBYYxNAKzzZkRsfHgD+Dvsu6DBEr+hjTNCWwOvfOEAUXoxfn0Dcrnsxse4ZL9Oezq/PojNe5l5KHwHSFn7FwhUQAy908hDNs1B3n1ARiHAMMAeQti3M0UJQ0F8IvMMBvQFJv0KCAoEp4ctfKyAPn6a/Oe48DgH+W2+dAwVQweDuzedQykApvzYjhI6Xruw9vo9a0ZGA3D/ezdIhkFLfseTPsx34zG4+mpAs7yyje6FabuuBs2GXgo9wWQ3dPtTMRH1sQCNiyVJ1f2xuok0vsW6hivCS4v3fiT2g7eeurJAjP5rBFfPX3yNPKnA0oZlzGc57cMYdWiuDLukPxbIJYUYiic89EAFBFb+pAdT+TU6kbQudtvH0oGVirQJwT3aPbDD+HkEOZOFIfpEfz7BDT8+SK9FrDj8QOt/BPj6Bmu7nr/pw4T6moJWQdpAAIBBQtzEIvxQuHU+fHoCv08H6MOfP/8DPk41gXg2PbTRdvV94oG7DTOPaoCzPnP/SLkDveJ6TPhVtLs5RUlSjNpEO//YirG5MnlLhJM74f3CRNyGOkFzOPEz3sMWO9lNeRHDb+TBDoWkee30iULLS2g+I/5J83wDoYd0eYjKvD4TvSLERfok+fc5OQTbSPKE6H3Ofnn/a7xzvIR7kQrZia3COfcxvVjFHwJqgP8ynPrUerMDwYBPwS1NlImrBEc0V7l6MU/+JsrYBYYDcD01A4dEh0lfwA+4XjRat7f0f36GESZC8zuygc0IVwXgSWB8MDhGtBW8PMZtPZHHsjqMhJt57XYmyDYErMCpP5pD5TCTCZDFLAGJUMy713WeL0vEl38bfkfFlT/owjzAwYdK/0fFoP9uNb6yC32aAzK+6Q+cvhlG18bO/IqDwO3Huaz66bd9gRYE7A2QRZHIFgjgxKz94TR2MwtBBr34s1WMW39/+9/FPARlDnO8YAF3OL+zAMG//L+ESgILf7l+8LugR73HmPslOm24wcAiByE+MckvjQ65KnW5w2SGpXcZtu4FZj/tffzCeEFtvzz6NQdDwrV3qwTDP9DD8gekOXe/QkQsu5K9K0Lw+2g9Xf6N9J2C/FDdiY08ckFdvxT76H3Jef+8RHPTwXpAgAMVyNsFO0yJPn+7oDNiB8s/6vDRyAlCeAsYAGq75AQPy7E3la3+f2I3wMryxN7FSUpftlB3KHrL+jf9+0hjgIT7PYWyDFBI4wTEsZUy/YTIvwk7jb3owmJ/WAeThh5/esKu/9D6CUK4v+PwVjq3N6JH0MHDw2sSw/3sSBVCYD2lRDe5b+5mvweJwj72OXV+FEQp+QSGoEPQCRO8g3l+SZd6vEyO+yW0ZLq993nAy4XLheYA2gLi720FT4th/Z8/9Dp2gRmAJsg2gU7990HGRKlCGTiCPG8BaPhvN6GDVP1yiRzAwzxqkfcKdHxudMw/fz/ROUVAhXx8N8EC9z3f/DW/egNFUUJD/T3Lgpm7PHn0wx/AWPxJ////m4Gwgm4KBruHvHj7yPWW/w97acVywdbKKwVQgHYNVjpX9LQ2Hnb5/LVIF8kixiAGNMLtuZozxsGLu0uCJXy8OqCRb3zrwn0SN4FQ+RO11rZJMEl4FQ74heAF31AV/Hp0S4JtA9Q6gfg7du7B5Iq8SS+Hs71aAoZHQHFQMRYINP0terE/DH2ZyK1E4EgMy1UD3muhcoIKBDshODw9XIYrgS2BepKdDCA1TzLfu5l1+4INyNi+W/wFhGvHBInFCZC2y+8n8WgCKwq2SWbCybkuBLdCm7nnwDbBU331/c811/lrhbwQHc2guaV5GUA4O3V4ms10QUFyv0P+emU7sNASTpV7wXosdmv9r35aQgTKfPDkQnWAwDpfhlN/IUhJwPHBxoNeN3X590Hxf43Az4KcvF29U79RhfaEm4apfl15+rfwtgYQushVw9+EU7DSdT66Cgtey7L8q7+QN0/8Pj4g/WQPYYI3t2pCxD+AAUX+k0ZrjDBvIXg3iSF+I/bhgNPMyHkDAW7FsrmLuJl/ucssuHgD7IYs/jMEsXfpfvVB1H7JQVM597qzSMlAxz6sSRyJI/+fNGFFtwAdrql/bcry+Mi8jkosPwoBgcQoQWs1GzsjP101OEQiRwyH7QTBQGLAoPaBgflHOPdcP0PBJTgbv49F6ouZDF5DU/tCfBg7sXdaOB/IiQHnuPyDejRkgJ1Hp0U5ASOzS8GFB+ZMXoXlOcTx/XbzweMBhsLlguDHLr0juZMCTEnzfSM0QHnKPeeFAkY8z0wBGD1X+yb1iwFnfL4IAQnywMB7B4FqApY5VPz9+Do1xYCDD4jF1cw8huiyDHqS+A3D5ADBOAj70H1wRC+9ggGmSFWD0P6Jf2aBVAeifBr9PEm/sRy97wD9+GGOGYC0//4IVb48OJl7p3+6fIp/iHqEPD8Qj00ZO44AbUQmdw07aEFoOLx9SsBthTHDHwEgjZQAwW2A9RE4hHqcUGqFX4KgxHhE19BS9oGAST3SMtC2yTnjBpZAtERWQCoCqfvcyk5LgHflBOS0xTcJgmTHnwRcerC5CvwcPReBf9AQ/6S1O77SCiX6agApR0x+SE3K/Gb+T74u8tq2ibzhQQs9CUsCDXy/Dv8DR3d6ZfaJ9gcAuf3FdfRSXc/8R8PJboDf7CR0n/0rdYTDl78aQhwHqI3py40AyvNiPTQ8xqtDw6t9hzrfAPAOylI9+vCGejvpNTZ9s7toP/K6hbtAzutNsgC6+2v6P/7NggjIlzjjNpTBTvsGQqLSrY3sd120mq3segXHPkNSycI5Bjz+ABLCuUzG/TW+DcFPeY8830Jof1kAhnz6e+2KVgH2xNiHYnmFPf07+sEOOvN7A4mJ+7IA2QN2/YGCtEFfCrg+kW5xdFF99/vPR8VNIzuWwVt//gOaQaYKwceeang+cAVnR3A+QALmAwGtZ/ckPQMHfn5vhhZD+z20yS8HPggrAezAIuw/9a80jT1QC9r84E27u0e5yopqyTl+YzU7fFtArELfPX1F3Qt5QG08DQMPtmP27bsG8Op9ksg1yP7LUNfaAHd1f8MtNUg4gX46e99F0IXCfHxAu4EUQ9L7BjbVAGC5oTyQkc8SpAO0wCItnfUtuN//lcbJvoRG0TrDCyk9vPVhyOyB/35s+pC878Cp1JQFy74xQ8x6m7JsdFw//LRfAcQC24bWQniCa5pwPwS0tX/BQiCxynVUiDb97AA9+HB6hkxjSbKIP7w3uPg/P39EQygJwsyMekjztrMpvP3DIcIABfLEUARq9xOH3jqs9H9IqbURvRz/WMi6z1SAIwHLBy17XXEafZ36OnLYPdVGYoiPED5MrUPOdHhxW7yKOp3Kn8nQ+b0GhM+ncn1yD3xTdv++QvxaiHACC4xgSXP7fUe/OlzFXWrc7cSTWkCfx6JILIHttqn7MIbucux+hn3YeaqFYU7LkQr89P4jP2M5x3xzQjxz+/vmBcvy3sgcQq6FIvz+fBSPAjAKASACWj5EgkaFWU2de1HA1jVOu1YCVMUciGN1hftjf3vAO0Ccz9TAdvvOw9ru1UbDelX4TsfEv7wDA7ofgzlELoTPu/bAAD6lc01BdXs8DIcJfMSYPz27BkWrvH0HkfKtNinA0Hogh2cA44TIQlV91cTYQiZCe74QNMnB0EW7u9+8k8pxy5mw3bJLRGPFhrxGey3/xkJov3LOmUy49RHDbflkM1J+bESXRdN8AT2Tgm39Hv+qS/T0JDizRnlE/n9lxIEOxH5OxZk4pXjqeGs+6YUjsId7y70BgwKKtZd1y+L67Ppw7bfxIUYUCzo7MzfE788DtU5Riq2FmLe3u8W/ILsTfcnXUEVlOFv7pTtuP70/3QpWwSjEM7wAwLG2rvCICO7BLHMWOk6IwoEFVopMDzvdfQFstXqOfnwCq73LQ7VIpPwDRVfFrj4AOh/xs8RdDox9JUFhuBdB+knpv08Cij5IAxz4O21S+G1IO0HWRsUJbnkehQHEHADN/l/DcImoee0sZXIhxhtDUIvRhzj2/UjEgkD+J7rWtDmDkD2Ewq0DkHrzzUVRqDyJrNC6tz03emVB3j8xh7xC/UE9hnTBqwMSvTp0YjFVP/zIHoB6g/wK7Aa1AJUJdfw78dz6Tncy+1pH5Ahf+DS+okZbhxS9pr3vx2SqDf5CD8C/X4dfh6J9aDJqN7PCyv0vNZgEAwX6RXBFXAw8Rm/3qQR4rj9ycITnilaD8nfmjYq6j3nYiLP0Yro6Q23+IMddyXLE5n3luCg7wru+Br8+ezjOPNZHNo62/DUAowNWsu9wCcROBfxEKYlmgao7I32hxUW8GzrHN2e58cUESP9GvYFTxibAKvyrP7FB8f9T+tO8b4CufP4D4gSN9BX7qkV+TaOCHfXR9tZ2AQO4isiLrEIJ+hLCMvY7dV+RBoFS/0M7JrYOiNI9YQ5TA+t2/Yd4f9UzfD/nTut1OXhXRMdADT9kR35+f3NWBuT+DvRd/65OBILOfR+NwDg8d/rAsXuIh8Q3fbvGP0y97dMvSR3Fafn0+O14jfyRRGf4V724AHhOGkKJhasI23ot+bd4uXso8E7HNUOAvVrD0YExR8PAawS8gYd2IfBLhHLDSEC/zHJL2UI+N8bBv3dNPk04/TLivw5IeU0IvhVD8UZzQys4GvowP3a/4cHJ/zaC0DfnxnqGLfVQPrVDbEGeNzx+zgiVwSaIEXuO8taBbsNLhSv6w0SBAn1/7Mv0vyo9PHDhM7E9SkcXgxTBnkuhPgUG00YzRY09M7Dh+iW9Eb7PP5UB/jnTyCVH/P0Gy+HAaPQX+K757AIayPAC2IREgo/+Or7xQKf9y3Vy96J9df39wkSNnP2aBLhM0LSDwAN+v8VFw4G/uMwGtoS6n7zbf2s7RHRP+bb8QgnCyxWSmshQgcj4cPzQ/9usF/91uNVzGLsMDWDP74ElSPLCm4Lh/5Q6jLSD/NyF1sGx/Le9M8heiJB/Jv0WB+YwC3PhAU+8w8k1hYXBHveAhqNLMDuMQaJJFjWduo1Ixvycuc7yxoG6tHUEoNNDgpsO8/h0e/VANH1Nwb+6tPYsOcSBIn9CTirJ43nKu8mC8neO+UkFXML5vbMDsc6wRP69gP2+vSr6kEalQCJ4hz7uPZZ31nxKUKS4d3zYRgLCCjsjumjS3TyKeEj9Pzlht6mJoY+ZA2rD2Ldqg7X9VsAsxuj3uPTqPZsD2/65RwOH5j0fujpFyMTmuac4czw3+l0ACMPGdUTCLU2QhgpEBYUiA7iD7XhGQb59hLe0QYZvXUerBaSC+MI6dRhCAEHUx013z0JseUB7g4YHAaFLwXyqgkixWTnfgP4/uY9rvfQ/T8dvyT19ogCQPOM2xjmxNe2B88MyUUPKEDdd/2Q0xfjOAwX4uL7ZiOGI5wREv6nGBIg1OR84aXQz7jvB5sI6zAEOqcY8BaJzCrb5AMlBKja+gE3J/IKt/yR86QDh/XiCsvkJuCD+kEZmCkZEOQ42/5P2Uj7MgTp7UDkt/DL3oneoR7xRg8f7CLMAnvoQQEg3X7VnfsE3vLqJQ+xEesj2BLoIuMKEQfm6azlRP9S29r0RtkKDdIMlwBUQHcXIgW7AL4K4AAx7/v1v/k60OrK7+/D/lw5Lz7QB5sOZAqr7cgMrc8FzU4mnwnJ4dMUIh278X8LN+pgEZsZ+AaS+HC5iOtH/zcXfwI8GUHodvINXKL3Nf7RENfed7gzAgwcCu9fFP74heFW6a1CGScY6xL0uRJ3B4TmckkQGwrkFM1Q5x/rJN5cNgIA5vJl9scR+Avq7r8TVfdi4jbxiievAnUC6wvOHE4AccGSIHr29u2EA/7mKeJGAiEu+glVSFsdvvE98Tu5gOXiDSwcrRwy3nDMqR7VG3MjIObV3l8B79bIHvXkkS6uKhC3lCuKNl4M6Pkh70/Tps/G9UcZ1OLc/OwzrejiD0sJ+BeABdEBIgWGuC/6UyLANSLuFfizIO/F982LHhIoefPCM0b3Z83d+FL1ASTXATvlT+ZdE0D0iyV/TJLUquvJ6fbjzeDBKKQjsNNBFwvmvPRpG/ErLB1S4bv0PO5T+boH5ig8Cu38WdrmyeEdNBgMB8fhH+z3+yU2WArH2DM4ndvr8IUrD+KP5QQUyOgt2NgeKAkHFAEZ2COLDnDo+/8S4cXbgPXi+6D15QjZGLUf8A/DFX8D/cg74sToN+1wDoUMNALvNe0oh+ja+Mb5EApr+xrRWAJyCi/Rcg/2NoDy5wJ7HhDr0PotBwzsCBLOARMQTvImuoUEOfPp6mo51CfU8B4Y7h+o650MT/jj3dkLackC8kEf1OgXC0kMAh3K/+4YkvEY60Yt0N3uDMvuuPPZ7VzimhvHAO0OdPHMCW8DeRl1AxHwQAx2/m3438fHDe8Lghu3GjkBOAGk5K0H+d039xIMHBB4CU0JSwCj3hkoAitg9OTWzvzS8yPewxF+8BLySSVy+8nsBRIMEPD/yAM0HtTvndTbD2UJHez7FmIY8/M92NDsZSDaHJQIXdiM+H0CiiTcE3vg4SHg4Gni2PltG6EODP8eIWzgvPNL/Ob3DtgFDEobCwCEIRz9IABSCJ8D6sw21Hn0Sw4wCeQMgSjnCDcFThCnJ73fI9qZ1onWIgiPGvQKov6ERvUbrSFQ/RbpqehV0MzxydYQIlYXd/CD81j6iRUKHu/93P+N9+C1/AXOACckf1uzAK7Nntdf6EgXIhKfxxT7IuhXC/hENUWjK2vzmPTYoJb+EBeE3KMXAvBjDykl9wNmARHqXtk63EDtrf6LGHo2AyeJFuUTogW03mjZIMeuwOEW3CcbKWwQzgtT667flAvh3p0PfBU1/44AhyNNH8XuCgltyWrgKQIP5Az94xwGNKIdp/Xu/M8GMNuB9Pgk5gkB5XX4Bfyo+J0R5RYY8zHm3whA6+T2WA7i/Zbb/fioJIPntBEyMf37Yuoi8ooI1yFXFk/8CPQj1TzVhhG6Jw4LKSw/+lDBGge7DY76TAS6Cansd8hRDbAqJQD/IaDySuFx51j21RXgAgVMYwgF9hbuefNcCxm/7PwK24cPoxkwHfcs6d9hEC3us/0s1QQKoRk63wAYsezkHKr4Qvgo+X/ZCPuaC007c/xfFNEgwQlFAf0LZ/pfuuzzwugbFYQXqAXEBwzUfOlM4EITEQ/2D7Ady+kp8MIzdSQG2lQBvcNbynEahiWiHnkGyRZ+93bdAfiEM979KvHZ84PRAhUTIz0e5ehr8eMTRvH/55n7verT4o0YCxF/CD0g1yCJ4d0GCQIZ6rUJLN7iE1L/ohbBGRHrevxU5pPrcufDA8zwuQ8yD2QPBCtbB8AD8cOB5KLtlQKqIVMLKyrC/5MOgfxr9/UIud7n5wD0UxcDDDUd2hTr9zASROZ20LPs1wj93rYF1gaD6mZXUx2l2qTpU+WW2KUMGTXQC8YXgvTA4pEV9h2d8lEDjtv73MP/xfqNQvoE1u2s7AkDyw6m8t0AFgXgET73xCj15TLrEQlE2ogDyQsK9Jfr/S9B8tkUrC6XBrX2SM1q9rHf1gG/+8ILBASBAvoh0wNO66fkAyJPAO/5nOH6FkIkf/iXILrVzeU4GpX+0+ObIJf8sfksAYbPoisbBc/ogwjECzsCeh2CFGvmKALH2T3sTgTWD00UqebUFYcHk+AvErX2yPVI+2HtLiWWG3XrxQjpDwjhTiDE5pLVjPkg5V095iDQKmXktec3B2zHPQDnBOwTj9R7/a8/8znFDA/oTQv13coSEN91uOPkfABcO5sJCQ5UAw32LBU8C2oDOv9FBqHNevIfJJjixP2M7ln67gzGCeQXnwX0GFLoQPwC9IkGVRD8+9v+S9NFL+IBnvo0EXv7Lv962dXkyOtNL2AT/Qa/DVAztRfH6vzvJKts+v/dtwu8KYbvigrx/S4MOdudKAIRKcu8GIYPaP+PF1A3cuZnx2n3LOZZ/6MV3QgI+CzkTvZ9LUkzqwdh+sfrrfd6Adr3TfDT6+YAcgs7ByTUfS7UM9bE+/j/AnAcrggjC4oL8+IS9v/t3QjuBEMAc/Xi90DwM+FlHVBK/PXD0xwVsfQQA630qO57/jUEsAV++GkfxfTY8pMMuA4jD38dM/GU+0Ughd/OAiHrXuiB/nP8o+dr6YgPRBEhKZEB0inBDHbuiupY2rII5dyw9Cb3jwWLEKADdwcY+8YpDyvXBfvdm+rg+kvtTufkASgbwQVxBEsEpAyKCrD/5AQt+W3ytuYF238F1RUQLZglfP0T7mLKHg2+EGfqPPCS/u/+rfIwEzwDoCM5/yH2+fWo3FgHigfNMwMWkPoh01rj1vBrAEMzZeoPFSv8aPjYDVIC5R9g9Vjdtf9WKHjq0P4G1mTv+hbk5nsSaNVRFbQcZSPYNiPyMPWrzcHdhPyXC8kS8UDP+bLj5wku3Aj45+vuH27vkdtNCdHnoSQQSHMp9f/f3n++a/G/F3EMoe3iB/oFDsFSCSE4Mju5CKztwOrQzVntBBRjBn/jDg42H4EZlQQrFEblKtaZC9XXXP69C0cQDA878GgEZhq26SfW5SmhEBkKJxfHC3P+pO9g6GTq1ej25bAxBATWC4IU+smoCdEMhf4g7i7pcy0O/oT/JTqTCRb6P9DQ12bs1vimMvIGOArOH832HdwFFDbipsAdIfoQzw6gDywx1Q404VXpnu00/Cva2Akn6cPrPvuOMXlkuPXLCT7jUt3X/sMFfw476mYSpuDg4EgHSCQUIffv6vjm2Mn/IAZXByINWAfNJybxNAPrEMTiadea7RXoD/zWKGkWCBMU/3kTZ+bs86wOJMvdCT4JufzjBlAUnSBz/Vz3Q/oF4XDXWxNrEacL1hRUEoToqO0cPMMmwOf/xSbVP8s89vA/E1DG+QDyswBwrI0bgi4yDzf85tAn0j/msEChNVgcD/QW+1/McdLTF6LmkwFq+8MhIy/OHAMRPPA3/YPtaPYn/n76OO6c71fyBSSmJXDo0vrD6PzjHBDG9Wj42yfUAOcNKQ29+C3+/e3jD8P4JPKyC+0BEPYqDUrzLOBTC88Dl/nmBdMojg83CPsAffSG32LfNxsi+2LzrwhLF+/emfvhGebcbv0uFpEqkQBjCeINMAsR8x7vqfKJyaUh7vrE9yTplxCfLQnIKBE88tn/HRBH40D+YRupGzsL9iJF6/D48gWz6eT7Ofn58UP3mP5u/IkiDBGo5v0Tcxot37n1ngqZ+ubn9g6FKADXqvMYAmDoA//iD1r78gB5BIDpkBYwB34h1AfYzKXyoBzpJRIJTRkk8jvlgeMCD1rs49ZQNizj7wBmF4sIniIpBH4F3OHD+JrqL9fe3YvuG0NPNrL/EhE4CSnTW98k+MUAThVt8NzocQxcMuE3Sgb0EZ3sMclM1prZy+1C+a9BaSTRGkYmrfRu2l3Hdv8X9v/3NeLZF7s8pxHKO1Hy1vF93A3OuPk87iL1PginSVEhJwreBobmateF2kX4Hed795ApiCgu5FATxTqw8+f3AfbI4pXw4uYU4CAQkSTYHS0b1BHe/436e+FT0eQGJvgSH2IqsNjWAPoBpgYXEVXVbeGQ3av3hSQ1JSM2chIZ7frftf0K+0f81xKK4QP3NxrEEDH7jQTY59vovwH9/6MZRuE7KXYw6ONM3ff19QXuzconuxfu8O3zSwZOGLTd4TNvGmzT/df5FGgIjvv4PsXuY/1ZBV/sLtdf13cOjeFEAoE0Gx9A/lgRvRmZ5iTvEPrnBFjoJ+yWHDv1pwc+Gint2dLgAYkmxxHTLQP44wNQDojmA+ZCydj+IeE49o0EySPdRsz19g6X5NoAYxPx8qTFN96cXakN6QLKE0UFu9wS0Un6wN7qIOYSMOHb/5w2jyoCCiUIU9xM3KnRmPMzDNvwgCecPBDTw+q0MW/mff4RCKr63wad59AKHBxuE4cErPPR79/2U+LZzyD8XAnJKpEuRQfOCpT8ePjc8NLkXvSsFvsBt+jYAF8IOBJH7xsLPR6l83Dux+eCEYcF1wOPCPfvsOvc9K8sjgWq1sf5DSFaEGIAVP6P7S/37RGkG7DTb+rl+bb0VxnVFLYywO66+p8F3+ZlEMb26P8q3jj0uRvh93YNvwQG9fcTbgfjxQfzLBNpChMr1hqVGOXfcNUNCaP2nOKf/SwTiNNo+Acv7wMBAXgCHvA3EcA1TwzwFLv17thl3CbQZhO7HIoM4+yv/k4K0wlHE5zghP9MCKAKwP7W/UbuGP0HHyzwCRjqAdTsJsQ16zU76gPPD2/lDeSm/IEMDSBiIhI40P//55ryk+oq5NHs3uvxAXzq89hvJbEaeSIwU8gHqt452CC2rvtTEF83whEc8kZIWe5x8Wv+F+cjwAPXTAgf7Lk1fPmYJJkycf63EcvpQOzM1twKegBy/HIBbwG5+ZXfQBGP7Z4Sbht6BeQTjw3tFGH3cwao76faA+SZ69kQpe/zHjg4ZPhqKSD6iQFo6WavF99H3Rw4f/Ln2nQv0VZCHBrt1DnA3cLx793Y2zXLQ9b0UlQgWRfJ59P16NuR/nYGwu9tSgESjuUwxKI2yEEU/1XfBsnO6f348DUD8vkNMATF66sD1O6M/ckD6Q2g/sAwQftrAUAEDdc46PrzK//z2+sVhgLEE78p3hOsAYzp6f6J2hQAHB6hHnzbNPTcK8/xLwFXCqn6Mstp4jAbkSKH74LcGAcRJ5gc3u+4DsH1ruekDTv/itgZBk0clQMiHMf2qQsj9Q3utAA24q0UOgxh9cr69wOn/jb0ng6k61fdoB/AAkgEvSMg/Cr4Wf3LFd/2rQGU8rDXBhiNE+IcP/5O52b6OPpX/TgSCfo465sULvH5+m7/SxOy/ITJbQa4JHQXoeGR7Yr2p/vIKZEhWv0d9GEK/A7nG4vxQuxL4XPeS/jY5ag74StN4ljtOg09H8/r6OZq/m72mfch8pb+HDO6EjH1jQb4AyT9ueEn8PD6HA4C+KsI/h9C72UMfhWLBHXaEQOGARjv0BOJ0LT/exylJGb2cu9cGuLWYA1uB9ETP/xy1ToNTueY+vEf/CCQ/jX5rP949K3xmwWFFM7rWvln5pnvVvHmCKRLuwfXAKUAgb5r/P8zU/JoKC86jtsw137Bggb3Ninu3ATWAOTJzvHQEFkeoDAl8Yb2WQ7N6PsEvQBR9ar4PPGKCEz+lgtuCW0ATgit9E4CYP2iGQIYJtrH7IQKQgmxE8n6+vU8B6HKYexSCPQDeSD47tjsO/lWIe0rOSB/EUjWut+M9DMBMvHg8DbmLPXPKNcyTjf/BMLnENB20hjvki2cLcXhUCLh7RLXqxpM79L+EPtR6BbkgxReJJgJZDGCIXwCadKjxYvpTOYt7cwzni3n+NMXt/O19zQENwMg9NbRe/xCAQErajZ+D+naftw1/J3xzes0CC8+5elGEp8RGej+GbXsQwUJx+HoQwEe6og0wBjKJDr+ffgGEH7XUuyUCaDMRfUxNkrQr/thPisXigRG7kYiWelf2wIwVOCc6FwSEv0YB9D/CBlLA3neIeoo7QTzRix3LInrLQI4IkL65cVY7d4VQAN3+jIEixnYFFYQjfowzMH1axeG2XbjRQHhA9r2DiPWQPcIlwse/ezydsX97ogngRSH+jXUc/tq64cnhDnSDDXh7dEn5Ub91lC66ZXp6AKzBb0cTeteCZr4ZPmP8Gn5j+xVBgscCt576kVBIivG3fwRI+AU+DILWBNCHZ/vphH23+TRM72YHRgnkPDCH8Xy//sLJg0tKdx7CAgkCvQ1yprc5hK/2Sch6f2B/aoZIfu/IMfVzhOxEzbKDBWwAyjZcxNkKAD3+hdMHOzYl/4t/r/x2PffxRP9DhnB/FgXexdhBgAlFwL70UEIGRRQEo7lWeYL9WjJhRQ9Fv7fG/8cJBsj+/h/DVIUKvrrDo/ao9blG3IYjPzh5gftGQxn+4TtXC0w/SvuKgR86ykZJxCmI8n7ot9O90YFrQwZ3VHigvPyDnj/Ig5k+S8c3ShEyv8ntBDd2YoVeAHs5c4CNQBPAx0Lc/AhAI7sUxauAODosAbm/y4WqfW6FOb7Z/UDHU7fJdajBA8cVwA052zkchnGH5sWtxoU6AYLPAPi6g73xeNOAN8BawzZ+nvwwzCZBADKaAGFIxsGffxf7iX5s/c/Gb4KN8ttL9oHwfmzFor6ngVKzOoZf/kQxOwGyw+rGQwnbiV95m7ddu1U79Lu9wDYBS0R9RT39w8dsRt4CBbUcddmEfj7pPqnFOn9I/OjGSIFlQi3/jnt6AMa+Fb93wof9IDtZBJh78P1oSgi8mXqog7X7M/2KBsrMkAWiO6kCaLXpdvoBmAVduQ+1OgcffU7/c4q1k77/4Hchvx00iDxkRC6Ou3l0Pu6BLu16xVR/y38Twba6YEXqzFVC9YD3QlR65IXGesFxqb1jAaVDeTw8BCmCJj/BBYX91Uy7fZFzG744MuGDJAcGTZYGkbKVxKqDtflQ9isB/oISv4jHrbub/p071wROSyFDskmxdduyaXaqOiSILgQewf67RUPrRsgGikYvOL85xbSXNBG9RA7yyFV/tsb5vA++I4F/Qut5zr1pBGf9HH1QgjYPgsNR/Du6+jHmePn8YoAWSINP2Yn+OsP7a7zqutM95PkeQlICJwGtRzW6E3xFxheJu3nSt2k8PTgPAoROvUwSfKQ9UcHR/F8AEgYrM6W5fsAbOi0FosPCiLw7Rrv0Azs+LgIFStzHIfL/e1dBv8XbvTy/CoDJNggB+z2vup/7KUykSaP6578uvio9M4EiRxj7RHvcgVXDv4BSwZDDN7hANxbBT0MOATmQWwOTuzp9ej1TxJm+7zXl+15EMYDmz4BBXTc8+SG1IbvkvieO/4NmQB1B3zrl/aeDN4YS/r8C+748OPo2kIGgxNwGoopYM3T8FIhpfRa/4sHcvqT+zvldQ04IskUCBit07Hcufa/Ax8Eu/DCB6oAMgo7FYIRfAHbAEsDYOkY4Pn87jSK1l7QADlu8rUxPypAvuzwZwvn9prSwhhRIbj5duTm+k0utPf6FMv5ithH3C8GlhcsC1VO9gg375HWb/kME33R4vp26CcBqgw4B5zv9P6sXcYIGe329/P3uA1rya7ij/YSKeo33+Ls3f3uzRqW8yv0qAVWFcAkYf6gG6787hjf3s/Cp+Pa0CYR8R+aQ8H1IgzWIQXdWOKx4oUy9O0b62kcwgvACTUOEhYi1E3yJd5j5d4PiwZNJ3wAjOch7JMA6hj5GZP0mwXzEDjkUBeiBID1aAbK5f/flhFpJ7jvSfA925QwkigH2p4wBfYF6Ub6mgB7DX7lZtNe3zwM9QCfOLoUNvITC/cRTDD58pD2ysdLyW8F1w2LBrP/6y+I9LUZSiEk73cEr6qc4VgUN/GeEt8J0CUSFZ72KwEm8GvsgwlQDVfmrhBLB+MkoCTvvdD/wgDJ6SH5wt4fD1Mx9f6h5bUS8hNV80P3TP6f5Jr27fuZ+u4PpxVZET/yO+x4+a4d5AvRDwEcou6P18MJKgmkyRYlse+J1E0GVO5oMyoWnhEABloGxyKZBGj8LuVH61bKgMyA9/0InirKHHAm5gY58echjewX43n1LREpElntWu0P4hIPQtv/CAcTuPFtFUTl9jT3GPceYPii3DANmeQRD4bRDwvHDwsClxwb9F8cXeWJ7jPeMvvjLuYdgvDhxrcq9vm98XUfieaa/McEGeXR4hEiBCTJBdEG8A6L/jDL4QAK82/2ITh4Bn3vJNJg9SwR8wsuIJL1NCh5FXPmbwsd4O7R4OFAA8UMDAySK/ERhwdVCZ0POevJzL7vp+4L+ochUjgG7Gjo1gyQ/7QWPuZw8dzpk9cnAHoO7RPAIzgaqOK8+iUFey2LIE347erWwNPvhutTHosXBvFOCLjjYxmqHksU9iA03vzsa+slwvgaACGn6xX1MAaIIv0V3vui6q4EpgFn6STmFvdSEAUbhgXf+0Qp0f20BTHvXNSSGvf3P+cS/VIF1gUPEt4DpPBc7hEA1gw7874O3v+u+QMQaBnGGvLxMe3O56zWUBLuMAoRQwsP4LHnGfuQ8Z/9eAGjEIEHrw0TEhQKYwRdA9fVvNMVDJsRug9M9jwFQgmNAcb4Hf104+DAGR5ZFx378RjgL1MuYwkP/Q/ZpO/K4jDL8OwV8gwViSxuEK0Fuz1cJgvh1eL84E3e9O9xCZftzBVKRv3+jA4FHzDSPr5a1JDiEP/rCKs3j0QR/iQIdArb5HXtAhrG64+tMwWXMm8M/hcjF7Xm4QPLBC3Jrd+GK2v/XN0ARr0J4vFsCAr2Uhag+P79zOeb5G/3gBRzCW7tqxAk/VT1xgmBRSUApsmcDnr8L/Jc5CP7wgRMCv8Gn/neIfPTMOJfFif4LzCWHST1xPB/8gP9pfoy9+EGLSEDBcwFV+9F+m4Vjw7M4W6r/Qvn9772RVTGKuPj5PMpAxfmqiDAAUbugA0r+lziye+HFHXtzwwTHXoFfw4TDR7fWeicBM4QyR69zDHmOu70A4UGIe0hOTsaPP1q9bL/8+6XDAIdZO7tBrz+7+7A1A0ErB3QC34J0wV/BKnpKhXqDBkDE+Ec3rcQk9HGHrQMxcbIQoobB/4LBHX7exW2zBfK6fwJHRghtiUR9ZL2ZSws1R/CTv1qGuzzxgKW+4sDeT3zEagf8+Sy6iPporh18dUFvRyTLa1A6fpS9x0AEOOt5XfTbAKvASUXwhHeBtYOzw1VDKnTpdre8dj3M/WpHI8lwQx3C5cTxAm/wtXoLCORAGTbGhPgLkEVoAPk4uf9R+G5/rf38tShE70OJQlX7w4Vggjb6TssdBs09ALyXw5B5kLECPovG9XW0/9TUHXmTBYELMrzhvuc7Agm7/1Cx3fh/u4l998anhfu9hoc5Aci4ozuSRp5IFL1WwjGCfDpFAfJEYjd6Ov9AcvZafQwK3YZOPbp8TMeGg4f3+0aYBlC0XfcQB/wEDPtzAC3CQb7XwlPJzPSF+HTCT/n/xHWEE8iWhTY6FD6Ofui2uoCagk76/owhhijEiPrKcEu/6fWp/DnMNsXdQnPH+YfEgxD7+rVr9jg4Rbxyff+KgBE/RC1+Er5RN5I5hwQeAVYBiMLJANKFHILEfg172rZueyJ83rd1O/wDEgt+SnYGjIRH+j95oMbEfFy2dImBBDa4IT7ChDV8mH1HQmtGpryf9erA1npZC9aLDsDYRoi5dnrDN+19ngT3/SM2wrs3htrCP3pphClJT0VCyKU72r+Qwey0kLzIQEqDOYNWu6lAb0Pz9Io//kLXfMCGkj79QGL7RvyQCHaJhUY+AOJ/P0KA96wvvoKp+H//MoMuPGvRsQRgduP+mwPnxux96zUTR7YHjbr0euV+PQISMq16F4N2PdYGQEoPh5oDRXtpSJnKAO7ZN9ZBhAGmPtYANgSmAbs9X/TmuuH+i8hzwriAeD+KezH+LL+OyvtBfQZBPzI5DTW8N5KJn8axjzS+qrl7evQ983uNtgAACcDc0O1HMgPO/aL9SwnC9qqxYPbEeaj9GwsQSt1JRUS8fGu9Pja3BFC/X6/+QWuMk4efRucCKLxx8aSyT3/XiDUPCL5i+LGACv7hiDYLv77Iu2E40zYaeXb5FkcUPzPIjJBmNqHF64XbABc9DO9TOMr7rMH+wiv5wYWeCa9KMUqt//y/kjvEtWUCx/+feJ5E4rtIPMCAXQNlySp9Cogzvdm78j+KOHl8rXdfRCy9Rn7TwmP9LgpKjeMJe30wd8zvir+Qg1Q6yAXWwBPK/8N7+yQBe77g/x7x33o8h2NKkENLgViQiHe4MNOAzrcg/a0CPz+EAXSDmICcwEWJEYcMPBSy6YHqQ9M00f8JhJt+tINbBY/FW0R9uAj7FHqEdYgHKoOfvPNNTUcvvAR/U7v/+8O8OwGdhagAOIAyhBVDKb50O4U2Q7x1hKmA/L31xA4Af/5Qx9tAD73GusN6xkDkfoKEBkKOQmT/cDrLhA/AUb8gicMFpfgxN82/1f8Zg0vEJcJNvFK5qcIl/bqDQkSXAgR2Bry+D3m+sfqkuVn+CbWBxC0SgntyumwCfIWb8o0F2EyyfdN6enSMyM6BrwYOB4+6dfH3QJZGULoITT+AVvQEuIXHjcXqfhBLXj4JNTs98oEA+6m8DAQzjfD+jjx6x9N4qiyaSwkTU+e+QucCtDKqDzJOi4E6rmmCpQdWAT544LoAwoQ15wRKy/6HO75Xglv1f/CgjB8GVLykf0Q+p33GjZ/HL/YOv9JB5fHVNC3+GgKLTNBHHcc0/XZ4sgC8wHW5Fj3ajTp6w/2DROQJpEUKfhG+YKy1/gi7A/r3xkUGi8WX+4LGaXlywEwJhkDvA6Z3g7rOvtgD9X29ebgEsPwLvn+FK8UIwk6FLspXv4M6bDsC/Ni3xzulhg/++cM2xX+7uvQQPm/KV7w3en1+K0e3CfmDa4S8N/m/vXw98MTCp0jFQj6AUUNgPcyC4omfva12A0Glv2X6pMViAFb/4z9hg4t/dTTvPSBA1oOWfA9CGshtCYS9yTohxod3JMItujw34sIoNsOGrUrayLt9VAKuQ174Ov+TPSl558H4xTx2AUHJA717gsVRwsvGXQfyARE5h4FhNL01YUECOz2Ii71EP2BPcYg0f2P8Cbrm+Hm4yAEzRBn9eYfU+ldClUzrtwADGP1Qt2Q32MbkUF5GF7oQr1dEcH1jhJ9Jjr0CweQ1Sv5YAnZBxgagRSH7MDMauJ2Aak1hxTnCKMNpv2K+JPz4QCs+oLyY+6Y+cIAPB+x8eHU0QEkGH8duf1eHFIFs+mZAT8HTwr5+TXoM/5uCK23M/BAHe37GRQeKfkzxvERBFsEbNObC/b+1c1D/uMCtPShHgX/xv5IEIj4dhmPCQ3UqfBHB+UbmSPvDDTvKOSRA5bfVPkB9VXuGxh6Ce8KC/YuJ8380PbnDKvnW+r62jkagxIjJ+8KLhFUDw7EpRhz6L3ISexUEdoDSQzNXh7/Xve1E0nUdNS2DpYBS+tuHwTxVfFV/qfwghRhCv8Z2PHI59oHH+ZuAIQiLhNA+Qwbuvoy1gn3iPa5BAvx7xTvDLr0vhzaHIUHvuYk+aTdydtjGN4Xte0hEolHn/f8wqj6mRI8AuUQ0vo18QDZPfQzDBLrjy/XLo3vM9ZR+jT41w8JFYHx7f8Q5tUM1fMCAKsGvxHJIVngtwgi5qH7xyQdGVYI5eZE/ozlDfoEJa4NSuLT6fgOigXc/YoLB/ql/WH/bOv39bIMnBIy8gXpMuTZCuAdVCeXFJzz0vLI3usP4+EY9VcKAPgBENENcjMqCuf9a8wbAC8dpeIq9+r1jAwFAGghJvjo94L/GOr3E+7pDu1BD4syRgso4AoCIROQxk/OgBa/ADcbPh7fDJ4JAh7K7ETc5e0J43LnMNSyKf4/bzLoFYT/suE53WgEI+ZfDNn5wABVCi8kGiR5/kr6Xb007ynmLgsJC+HlZi3mAfcNLyY/CGXKKsgc95nxsA+4MBQxkvSwAkgJrteI9d3wKBDJCMHu9B2NA2b1I/QTDOsCSP7xENTjIgg6AgsCdBsLEU/7pddf3MjUZw8tKsIprQ173Ej1yBGHHw3ql/SJBLTf9tNwAcw1N/of9PMNOQtXGMX+lOYJDLkD7N9wABsCt+5RHRE35OA8B8cYWtfvAXDoCwgC8ADq4huD6ZgqBxgH9fjtbAFnF3XHLAaRCdPm3gaZITcZAvnWHb8BReaSx03px/KM7mFNfCSY9pIMGTAIzKjPNyPp2A0LpPEg4zsLkxVMKYAUDxOP43rccc7eAPEepP3lKfMhuA8C+KH1JfUa4yTr0fxx97fnHRIVIqT2GvHgCwIBFAVaBFPv6/JgFG8VwPsvFwT53cyF3b7naxDMPLQesRtb8sXeJQ+0CtsgsOoX80zdqeT/K6T04h3lCMPtQMW38PEM0NnWPDU3DCLc5Dbvl/Xa68r6s9hrDh/mfyH0B8Tq1iau+pz9N+FXHcQGNARTV1oEGbTl71Ax+99+3OYDJOcR+NcbghtHBAgOPw3o+SviMuC5+fLvBhUSLpLylfXVA6gV4gIw4zwbDfiY4C8EyfLR+hcTtg92Ap8UOQOl5/vzrfufHGQB+wBELXvU77gm9zcA6QK0KxodOeDKH8kkzuPbDiwIDupM/KDkNupZ2TIGmk8C8roDzRIa1j3fVOtEHUI1aC3F8eXNhf+nNA78vcuNDDnrKs4KDh8fVhNAKmIPW9vVwNfptS5oB0ATviXd+4IJJhaW6mrBqcwY8ePl4/hSTkI3TBeKHLr8H9w59/cBGtUZ5q7wd/UR8GYdE1p/MbT1C+2K6Ny8n+ZL/zIByi9vFKEN7SD58vr/KvWU1cv7JN397CkGJxEhEl8XOyoL+P8PLfGMzZYIvBQl8Jbyhg9REY8IGPOV+2Lx+PG16w8B7gTj98otDQTT/e4qkwr+8PPvSeO6+lfx4/eVGwnxgvuoKOgd/t9c+bLu5dkHDkEVjw678ywxsxQ57LnpReR74I7XSyYR9AsPVyUYCJP35v5TPrTs0RAj/T2vPuMsDH0N/gKuJ0sEhgr2BDjr7gWt6rAFi/D14j4eEvIE3lsiXkDnEOIbaRJrydzMNcROEQoXrf+0IfzNbuxhFd8t2Bms9acCuNMh+TcQPhQqDEX+svMD7z0IXeyj9+b0gPTXD90fng3G7P8OtR5XJdcHeuZl6CXOSdk59QEKziowI+oPVADt4RXyOupf8/4VEPQxDsAWCx/cMfLkyNL9zuHMMAvzH1QA1hF+LhUQrAMh9q7tgu++4t3hkPa9MGk/siAlBuDPItIx+v3wSu4M/kQZoRoHKdQhB/PY2Zngh/3+zxcUFh7W4vgnhxAQFcYNcgmQ+X7Tq9TA1AwM3gEQF3kY3ARrKQkuVvPX64EMwr7PyTziuAYmICQWHzrUDdXsTPT3D+Hcxec5G0/+YAPIAhoq/BNdANvzGcp99rAD3etU6QIGDR/iEGcVYBDg6r7zGvZ69VP+5g4ICaLchQT3FP8Dxft1AMfyqPHPHBL98A89BCzuFPB883gaMvlzJhAo7ve38e/VrfeHAvzpj/CGCFgArxEpGVMBaBLLC6n65NX911kCSAuQESIN3x61+6TaGQWg57oHCwRT0jokgB15II0Es+8oHNriTfueCrMAvc2V0J801/Sy+VI5xQK425PhMvM5Isos0wcnBd8GMfJ/9rQR/Qcn4gnKpfPa9W8TpzRC/b4ALucC8ZHwwQNqNE38UO40FhkjMfUCDwv1U8RZ25HQwPTCFSxMmEEkHHMWn9dGz0D11QjG/NvwXf1G+sv8xyDoI4j5h+3g7R/ZVPBcAJAOAfpjD0c5sNbYBLojTvRG814dggoFrhUHT/CiBkoj6xCtCLvA7Q1KEfgXAQ4DE3/d7eajKPTsKiPC4MbsSM2I34NWVhag++7cNQhX/78Y3xvi80/a2cB5GAIEohj8JPAT8QvuCpX7d7v18M34O/Wv6QYLERUN4qRVGE426NrwSc0Eum30ghkYPJwv8QuPAYnRLOHUE8r27MkC4M/ynhyfU6YjWv9K+Bf3Fuqm3fXW8+i1KegRWCG+Dw7tORNZ5WjYSOk1LWgYdeZwC3XvYx77NycnUfR+yu/ZH9gi4XnzKjT+DvEChA6C/Cko6weg6j/h9fwy+DYSYidK+JkVf8mlzAEVvO5a7AIU/iMOAZsasB+nB1Loy90/2uyxNTOzXyIAhwANBF30tOzuCZ8XZPXE4Eb0qO2o/IA08hme+wTyUMb63r8hVyUwOI0jUOLK3wDjfNwl3PkI3RoQ3EgAqE0mDMgG8xxy48P+MRMy6ke+6Oy7G4b2OgahILj7gv9MF5IBGQbk3lAM8hIu2dQGIgvqEM72iv529w4Z4CXe6GXYANzzNgblcNpFHxATThj7+q4B0shd+XsWkfSKD9IftA0K2RrtEgkt9lMGkjqtupPXX1Fi9CUAmxW4EcnvWrt8CI8ic9jCP8gbe7VNQpweC+5Z6H/rWv+F2ejnexfwGZjlSRgBBUn5zA+7/Kr12eF5IioXZexqBikf5e+mzhv7jhM27uznlBYeBB8TcA9MBiIG0gFHEov3A9wQ7GAMK+M7A8sonv/f/5Ug8wHD4UcOwvHV24HuCxC1HPn/lfVEFyYLNAd8KbfhG9eb65v0c99sFZ4wLvTDBlflsAO17/P/hRPuBkgT7P02H2YJyhse5RHvI9CgwqAn1f8MK1oQlv1g+57+RQY66jYY4/ag6OwN4BLD3GECyBSS3nkNNhVP2vrfpBj1Ft4bTA9z9NzdWuAmA6UWwQqPEq4t8/fq80UJqRHo17/nlP/6spb+3SdYGQ0SijCFFhPscN2EyzANcQRoIDMCKeIF+kcVrPxV0FE+A/A/44AafuQLA9MLhjQ8F0HdR/mzAhHBAvQINTrwpRyU/3voPSDZA5r+WtB52NMG+RC8J80ZRwyh/w4fXg7yySPhwNsS62oLsQxpMvQLrPDv+ZIU6QdR1qX9tvSOC5UKSxQ4DqXflPHnyRkWWv+WDDwbDtc5NWYSpQlO+Hr17gT3/arud98aHm7/Rikx/y/2jQ5VxuzcGPp5IDgQFhajCwz0ePnsIdcJddKE8wDVK9ny4xQAyh5uPFI4jgzUDKH4SwFf2JnStxeRB2D2ZCva/BvwIwIJ5YcFBPIT/wnr6fc/J7U3Nygv91n5W9d86XPdwfH7/rb3xPppCixIHggUDtfUv9PlCLDsayGX6z8AKRsfFDwuCw0P/vXtDus5vKbYfQVz9dwhbhxFFu0NjSbIIyTwvA7R3q7cEe415d/mS/BfK8n3GgYIE1QYxeqowzwvi+sx/RQcQQpLG4X+9htB7OfrW+Mb8F3/TgCCLeEaziZW2KXYk+JyygH4BAReNXwQoB4QGoENMDIDDW3TKbmi3JC/uwpGKBgd4SC98iMJ6NjWFqwg6ft2DHMAeBIO5U/rlf1R6o7TlPQoCO8BiyAZIKsNrudMDPsomOll6ELq5uXXJOX6sRIRLbkQ1AgZyCT7ueSlBfX7Sf66MPfPXyBoEH7togxQCSjtK8qS38j4cyhgDfckGfnK7agP+t8b15wEyTRp7dIH5im8JeQJ/uwSGXPc7cH/930AvgZYHWkBARML/UrwFRsF7SbVjN9xEuAH5RMKNmv5gQfA+AHCafcnD0394ASB5QP92RfGD8cT1xdaG0nmYOV9/cHlzQGkCiLxhRqhAlnpPg13+ugI/AZ7AGkGrfhG92MEax466xHkNgNy6vD6eA+SIU4Zhut41pkJQCihAiAEe+n84Lrl3/v7IuQGhQRdBAj14OUUDRweZwuVDm70hOyDDa0SyeftAeQA1Qcs7yfi9Bal/aEHtxpjHfe82+pUOJH2Pugz91QX/dIsIEAQ8ugKN5vZgdAn3CEekULzBiEFhvBv618XJwLH44oA8gH6/9r3cxamG3wQC+fZ550J1O+JGffxEeHk9vD9IRA2EWEcMuPe6EUZ8xHF8uj3SwgUDjf6YOJp/0b2XAUKAHj8YybkCngXnQ+s0vHi0fhqAsAdcwq06DcMufQM3+cc3Q1E/U3z+uDO6UcDeh2fMaogGOwf6IHiJO8l5BAn1T1R9tcV2+ib8dkNpAMM+pjJb+pw9+75VicMPxMHe+PyCZfn298B/isQmB/P7msN7/YnDcUuvc3Z92noYN551+P3qjDDNac/0Ag1GpvVyfz06ajHmwAg3ksGt/RhNeQUNg/lCmbJgAEr8koWXA7M7oj4SBLHBNMYwRo49nLmPMlEEAv83AEmA6HyIwa88tISBBuGF8X5Ev719Uj5qwvJ8in8bPfM+Sj2TeYTCDkWABCOFUbste6aG64swvbk2KjxhPZZ/Rn7jA1OEkwxm/OI0Ab7Jvso/zjVHwO9FhQMKgPqCYwZOvb7BTEOuflE54T+n+8WEYUl2fNtCwQFbuTj4Cna0/AYL/UaxQxn/nvtRAmQFV35d+kXFobqwODQ+vMSqQG1FXgdRqo4/mgpwwlaAhT3CRvw9ugF6xIF8NDysAe+A6D3PPylBhAJNeu27nMOZQz7B3Pu+OJcA+0g3BCZ3igKGwLJ+s0PzwhRIHrL1fUG+qbU5TrNEsnYjMzq/tMgnRiOM1EJGAmU/VPbxf5E7GLq+RFA997udhRz/xUXABvr4FP1EeivFjYD5wNpNabb9QT9B/wICBAiBvjpWLZA85jd4xjpIhwCMwQ+5yMhbx3ZCertjPYs8kXk6f77BIobwSIyEVbq3AVnBlnwD/gz68z4tOkz7MwOEh8hLm8svvCFw/PkRQScCtIYVhW25crhvvva+igH/AiwBuUHCv/09KAHZwHk+IoXe/svEL8FhNjh+4Tz8wG4Bej+Kw699HYA0yUF/MPu4QLp3jEPlxy2+/H/aPcpBb8KCws//GLwROEa7pH1++80NzMsSfVlCZbsLej+AkIBxvnz88MVQPKy5lYN9Cb/JFH8cf8m8njbb9N5F5INuPCWFssAtejt64pMrw3n6FYW2NAO5SwI+h1mE3gISwPG9GbmV/uVBYbke/2x+rb83PzsFr4m/vFpA0cg1P4u6Qv4u+U+1HIOIh+/H2oy1Obt5t71deJmBIEG+/m7+oL8TPyPKiIqcQva0V3wWPidxRELQgeXLFr8Oes5F3EK2gXN78ATzN1WHaYO0dHL/Qgsry1juCrzXhHrAl7/fBST+gXpvSqzzkzYu+0HFrQcXd+hDhP95AwbIVwSkgKV8CYO4v9M7P8GM/ak5gjsQO0yDmYZXv0/FpEl8vUOIQ8ojeYa2+3qIPP46rD+w/dQ9H34xv2JF8f7T/4fIvfvk+4TDgv87/o7AOgqwP/L6FoVs//o8hMUZwlk2IgO9+4Z5zESrglxEDr2zBVt84EFayjz8Pbdsd62+db72QM38zcMkB8GC00e9/yt5RLf7uqOA5QE3iOnCJbqjyRbIzf/B/Ww8bbVJMyDDeUTkfRgCiYmcQW98PL6xfSY8Gr4eijBF1v6FBRuEErx9d8x95z99fYcAvcHN+0U6CIFDA6GHU0S1O8Q7FD1tAcXG0YS/gq38qLbFAEX9cHfUQM7Ft8XpgkiFV77uu1aDOfW3fReQyESaOLcA5EJKemh5Z3mOPqK92oD1hq2A4sPghPVBcL+ewDIAL/iv/JRAwv+oQGwHM8z7fgV+FLlSdZmFsLwq9ufBtwcmvCMBAIeIv2VDUQFfxR+1iTrFQ9k3LgL+BCTDP7yrAT+B3IBeRDTBrn4H+WUPMHom9FHNxQKwti/x90LpeG7EdxK7+8/CfcATfkZ3eUE3A6I5E4L0+jCIMAY/RA9DVLrXQtC2LAN6/gv/8kDLuZREETgIC2pEHoAo/PV0+UQaeTmF3sIdPvDAJr3owgTADsYguPD/zj4eAcNOPEL9fazzAIC1QSl/iYpzOGPz+f9gBjA/H0es0Be2Ofk+wl+6YjqdfULCsX5PSU6Hr7t2/VV99v2oOGsEmkWXOKR760xuB2bDigsutP14Q7X0ubyBYzjoy3QEAcUGg6QAS4cz9zZ69DifeNhJNke8hCuGEsAjQaw79O+2AKc9uHj3xYh7joNpjKWCvkCnwLWCjcBC/An8qvcYusMF6UMyBshDC/ybPqH1kMJ7wAi5wcgNA/W/Bb8fQa6/zcsgBOFzfbtkP4pB6n0Og6dFB/sENZO/9ghlgyTGPL9DfnL/Isa8v7P2TjmV/AP+Svwvi+3CXgWGvUjyMYPCAP0CYMAxA/A8/UPhwLPBQgc4dlCCYr0hBQk89wEng222oUU88UM7NYYWDDjKLcC7Qhq92YB09MjB53m2rlu/PQAryhXMqo0cQ0X0z/sXOIaBgEWFNNg8HUZtBke/QIFPzDtEVbHVdaaAnoEgipz8rsK/x9jC2UInb+A7iPidu5HDr8P5Q56D3gXG/EKMmAE7evA82Teg+5/+UYmDvtbEkr8YdAK3NLxDxfaEwIkd/vIJGEVnfGvGUfu3fgR16nUt/LrBbYxPAHmDFESfOyfDcAV6eU03xrpCPr7LjMRPhPtBPbe1vGe8RENz9Hl4P8Lq+8ZKLweVw0/Sk4uucX44gb8i+An9x36Avlu5aMRjTFNCigMJgOl2mLNXfDUG0wU4AkGJRwGner5CfD0XNga+54dhxB/8XoGsv6w7mIHB/dv8/3gHgTsI3UJex/4I6QLCelT3HzfAvad3fPsrAb1FYU81uVjIDAyfedoCN/Pod0+GPb7kAeLE+PkaxBpF7f6XRnD9LzUCMX1ASkfvxZJNMwHm90Q3G0Sq/9T64QYOfq+BhYAT+gjFJcJLgC2DJfmKe02DTX16PP+DwMFWPrOGGMESAMiLDMExt9c9z0NCOLH3HzzU+C5/GATnhucJ2QNiwFI+Z3WqxvsFvfrgRsw8EoAR/Dw+JoZP+SqBGXt29X1+KUCdCF3P/MWAxAv8mzbCRqN6vbfkPqy+q/vn+lsJHQaRvXpEu7zgMNgAGgeCxrODrksrCMV7wD8oerH1vDHBPnb+6HfPw94M3ImkSHHAgbUjfM14ZMW3wUd97ETD+fmIzcHUxT8Gvns991KxfDQCv7aM5sEaiEMNr0CS/p6CeL289EB+mj3D/va+7zyLxBt5tcBrRhS5vAdCA0z/vP98vN+H7j6DhH9EsYGQe3S5tjkS9LaBDMK6yk9Cjsn+AB21Z0F1t0ZFiEM3PjX6xsMdxkc/9IQ+fTP/J3aJQCu/KP+mQW46cIpZSAOGXv0N97b20LSK/i3JFkYWw0dFRzhRhE1EC8DgAsF3m7wL+ji/xMU5xHG/OngkfopITElJA6zGAPvwuHC43P1exOw/U8QJ+ZP33vrtQvcJ5HsAvBSB/wwhQdjKpow6dOhDgbDXaGq70QaFR9KBEYKR/d+HRoPrBbw9dTBOvuv7k4KayDOT3QFcsWqK9rguN6z7xbY0/E4B+Ye7An+K+EMKRG1/loCtjjf5/no57v9xtoKSAY3JsQBtezvA3rzjQZuOsrmI/JnFkDqCR6S6wD5GBv+AxYB3910+lQEtge19Nf9aRhr7/nukxkBMFnw6ABl/vnTIhwh/lsSLA+D5xjsmL+8ACAK4SssCevbQjTw7lj3FR+L5y/pihTvH4cGrf4pAcb2DeBQ73X2+uxk9GMW/QpIGfUi7fZOFmAPfgT47xXjFvEn9VHp1OKIAgXntCXkRn4RlgMP8Mv1q+ny+o0VBg91+krucOr65vURSwJ38jAdlfX9/+EDl/nZML8DRAM5+vPdjvEq8sgRXgOY/fkMnfAp9MslsQ7W+9jmUtEG9YoQhzfwEzgBiwfqAb/GBOamTKYQpuUz2D8GxuaV/octfunn9b/3jR7d218ERji+5kf1twHHEh7cbhEAJiDsWfrrI0cZ+7cmCd/2Jc4oHXgHReby6kFAMxp77agcDQRnApbys/5p543QjCUoCxDyDAl9Agv15NQGCSwG1eyyMD442Ppy/90VYu6h5HHmuQii6Obg5BH82+sPKSIwFbQihva+C8TvOuvZE6YHqAVLCfv06N7I3EzpHiDXJpUGdAr767TPUfwEDGn2eiQIBSbh7g6aB1EilAas6NUE3eUC6k4XtB/d2ND8iR9J83QHkQcgMBvv19R/CjTfufk9KOIZTs0R864UEd1E+cA5WjYP3g3inOfX7WYK+yBgCD6+mhBtBUL+cUQFBBUF0+rjvDUG0yWnFMIM7OAt64kOHu/0GXsdoO4DCN/xofNa58wFrSxx2kn+AQtK4zgE5SL2G33itBVMF2nCt/REGtX++PL4+v8IaPBz51Ic1hag1nIX8jaB+BX++gCo/RjZtAVuABHH+hMyDyb+vBFcKfP0dvvMIMPdgurN7Z0xZRbpzJz7iQW1/eLwNvkN7owUzBpz+B4BgxOq/jPezvhp95kSERzRCl3zjPBiEcIegQja0Ynuz/W/3ar18RReGpAqBSw2983xOPcL9Kngydn07wIPWhz1BlwSPwqwChgNnszQz/oSOSLm+TvwqSB3GMgU+/tV/FkDBsnaAu79ZPdVIOoDXtil2XILLARlFBv9ShgNEHf1IT1uCanoZdxW4eHcKt9LJV8cPw3iHXgE5NnBCfMYCdC+8YsRbe0QLWscbuw9HvLjhN8OAZMHQRSF2EP1zBlv/fIJOAdF+R74pgPcFaAJwwGCDCf0ZtM39wML9veCAcr3GfJ7HtApyPcXAAwCYN756n4DLAkpCRcK7u5lBEwMUgHPCkXjMAiwGNjlLAosKMIGt9ZrzF4Jmw8R+Twh8gji+KQlLfIy4rQA5QozG0PF+uDbEpHjkBoyOiYBqeZ6B1HpHeveA/Yb5Rjx+HbrH8V1F2UkZxo1Affx5Av73IMN+wJDFNcNseoy8WXWEQViF3f10/QXJ0YNlBP+EVfZk/yODo/ho9yq+rQM3iWv9/4FVfqw2E0LXR6VDIz4tPaa1nQLwww8LOMUNtxuBmbbAAuy9PUX3xNP1Xv8L/1J9iHtMFYnJRH14+qj4KH8dPo3M6XVZtpm7NXtLf9IDO5HcRT5E33dg/CN/3ztJBos6Rz+3yUVCFPL9PuoBD0HThh/2EL9/vkxHHMPUP2KCdLuXCB5/gwJH/Ub8FXymLIGDUM80hxnDlL7Jt458JQMCPxj7vwK4i9l+rDkWfyr+Vr7WRJODDDx5eAeAz8ewxbTLaTcU9m+A6LmseNBB9oh2u0yAGf/0iS2LpX3eefDv2sHhDGwBZn6XRFQ94Dj9e2P+Ej2Eff8JPP/NRoHLOYRRwEf8uf6Z8FO32DoiOy7AqIRCkKzC74BYxEp7jrcifbrBnQKoTvqEM3iM+X11ND0l/VEEGorU/LA+RUjyvyf9K4NHQEu+3/RCAYJDi/n4SlSC8r/1AIAE+/7ztP/Cu8C9t46/qoRw9J9CbM2FyNW+t/gPQoJ5UsE4vbW7AkFzgdRLigKZvxBE3vyjLE+6g4DEPH3JxI+Hxze7XEQ6QgG35/ueAUn8IrkLgJdCFHp6BZIRbjfq9z686n7qRJYAr0I0ONi+90hTQ3d6nwQKCl1+lrh5dHpAUT+LPs177sEsD3z/YcQLAKW9sQFAu+sBVjzaRG2/176XA3eAZLqddM18+vu6yH0+7YaLENf94QJjPW8+bLi7vB/1dzjfShkC/z+0u+qNq0NQ+y13TL6Hyxq9jkUbtto5GoryyhL+3IBM+vSwiYPdwgKBtkkcRgp1o3fnfUkDkMQWAjeGPy8FQk+MI8RFAXO6Fvznuv0C20G9ex98BouaOuB6n4XyAtGCU3R5f5b8hYssRyS8tcCD/r+BWDPRQMA9QMi7hhS9noHJOFzI1D+t/cS6coNJBfl4AsXG/TO+M4ArfVv6Or18wUxCCwqswc9GMD/gNyY+dvwHuSeCOAVO8iD+P4vKRvQI6UTsP2E6pMHx/W00vj/hyHD0bLulVKO3J/bPyQYEb/aZtkZMKjz7uEgQ68wJtJb7Z4Ln/AI7q4XhRe8uukFEBxR/KAYNBal+7zCLvTJ+2YhwDafBWj68+Ab8s0FZw1O96n/I/na61wHaxZ+FE7i9OTj9hPp5AETL8wVyetKDOQehwQm7R4AqvwN6JYTRAesyqLt2x37DpL90AZaAGv0kf8TKMQdOfBXE17v0s7j6qvwGRWZC3j52Pva+ogMchPw8B4IbCsI5f/Wtw9u9Ejp1i6iGfzwLPVzE8oIwuN+EpDw1dEk/CgVn/4e+dUxQv5e404s1AvB5mMHtf4rDyf7Bd28+Wbwl/Q94TDiACxfQOQa6vpC4zIIvwbV3XMGlvcs3vX7GRsGDlgpmCkq5Q33R9j88i4CKe6MFOb+zg+KDS4H8fGk+Gb5adfl96wb60fbCCXyy/q58ifqOrctBdsUDQBW9gAJqimXKOwtX+MS7yLmqeDECToRPBw9AMnQ19HlIhIWxC3W/jvBT+nY4cobwRdoPcUqG9s71I3x0wGx9cc10ezM3DD4He01Bmb8EjLoC+z6pQDy21cNOR4yD1D/4eYo9034/PoaDlrubOJQA1IaxRvXI/gLI+vpxW7Wcgs4Cycqsu599Z8zfhJMFwrxre5oBlLQVsWVFtUf0fNF8bv47g/xAmMGICIPEHj7//rL4rn1NBGa52j4wxrcAtINd/4f4iEcyBH/Ac8CrdDv3hEBtSGhG9sGuRaV6GfMpgnZF54U+/v37nsGYwH8Ht3ZErqdAygDoBIDKSwlzh3k0/bKSB99G8MXPtuL1gXsI+qsQEQDlP4aBaX2bhAY8xUCf/R7CPsQ1Q8z8Cnv3SP06EvhFwsSEXbsrfdZKgTlnfKPNCsHeN4m5R4W7OI8560lcvpeFGsPpf7O5NHyWERxBR/E4gDAB9/c+BIcCrX7CRg2/mPtM/KfBKgLxw6vCIsHkPoLCNkMMPtf3UTw2wGzzqYAuRkcIMQNkAPwA7AE2BKk7XsSB9RH1g0EUwnLLegbyhTDyNXY2OxU7bUcXRdRBZ8VFijSBFIMIean/bD5jrIo+ZXqcfhXSb0OYQcqEV3zlQRx+6EJAtNL2P8M+PJOMCUfnQS1A5Pkw/OdCy4DswpRBsDL8f2zAr0YHC7p80P0t8oO/nsaAA5iOCUPH8cd0sIJR+2BAVgZshEl+cvtNBgs2Yr7siQy8x4AKx0dCLzRCxAhFigbTAwyyZ/rE9uK9MIbyxxUD1coVQejy7H/huUWAyAPBBmmA3/eAzTy8Kzq2iR/7xvJxv+eCYPkTxnUArAFQuKdB89oTfmaDqsL4KlJ1FoRuAiE52AjzAD13WQG1ggZMB4MmvcG7tvg/ui++IUgFzSJUXbuwbq+4Njece2N/LMG6fiOG2QWnwRYGoU89hZVxirVDuEY6PLu0yKZHTkKiCNLIGDoU8m/I4zIWMkNGejr2hZWIXcqmhRBCYL9qfZ57U7hewl67YL4tPHH4zILVhh8+OXw0CRWGVQLLRYUGyr6JOchAo/XjsJi+RoMBxIFLGInCxbACWbzlcroxNLemRBVFyj4gyTZBpEKMjn58mH0jv3sxg7L6PFsJjgtTP5zBEz+gObfHVcnoO7/DP7+p99rD7/9tvtfBHv53dy92JsFRRXQGKoGhB9pE+H1Gfhb983xVfN1Cu7ka/CxDooYWwWWADoI4ftDGPgAQeTezNMKbSYHDRH32+biD4vjPAVWA2bv/w3QDisI9/t/Fxj3khN98yrbiv1CDrgluOlmA0384v7mFPjghfIMHCv41OOIFDoHbBcBIVDuuNNR37Tu6gXh+vz4IT/lCqP3mAoc/ooDyAZgELjD+Oe1JqUITvbHAxMe7vrHAMf5zOeO7cnqsgR2ACQTQCNuA5H9yf4h9E38hhqcADLTiAAgC9fubgjFAzT4CP0oJJUq8PxbCWPaw8j6CVMICueaIdsqQb6S77n3gP/fMu4NOQ1Y6JcKd/SL8ccHsRmxOB/Z1fcY2yXlfwz46K7+hAvSSNwInOpn2wTj0yEYG7EQQ8xu+wYMUe4OAQf8Ih+bEx32I+tC80AIxw+/8hHvNRCPFqwXJvlY5qnuHRGyE3TtnxKwBD/VxutYARMNIQvjE4b9C+UG6C4GzCmmJi4QP87b+NQDdfh9HAXf/vT8Atz0D++wD6YUaN5Y+8/1wC1JQDkMdQI91SjVwRMzI/bphOW75HzXlw02L1kWwxnZ+/DSyQPOCiUP+R0k3X3Z5CDHAdD85iMU7zrXqOmh9WT/vBYUCE8K2hdwD88HV+HiCYkmTQ3B503kl/kQ0BPtqiczBIsKwwWswW4RVyuHDT0MoernAXLg3/40JVkIVA3g/ofIJNPIIIkh1BjJEgIE0uXM91TtntSF+0UScDCG+lwaAhhX6XcWl/U5627fwdlo5Kv0lglvIRcj4jFCKvXT2txMAQIkxuK91o8fq/DPEXkPb/RxBbTyUfOx0QPYYDu2JRD+qjBB+eTj7Pcp6Sz36xBSCAjpSQPgF5kXVQzKANDk3+SC8Jrn9BNGD1IbpTL+CNEM0OuIq/LwGgk+4pkj7B9X/AHtM/pUHwEBCgRC7j3WE/r7IFEocgnRAXf5QfkC+ggFfPto7Tnyt9fZDSUq9RHh/b7irv64+d78l/zmFK00OgBv8Nb+JQZX89Lhtdqt6q8iwC+H/ibjgh88DOrtpSZ1AGHZk+db7j73WPRDIlQt5/n78qn8zOTczGkNXy0oEj8FvvzY+nj7ByIt/lH9b/8a2Pf/1AM0FcUP3xmrBN/SpfWG7Dv8X/tn1Sr28BNxHY0suRQLCcUDY/ch9c72NgQZ7RvqnOCQ8Tz/7xe3Jtrphg2sC8EM0DBQFn3pduyw62/E3fea/on+HPzrHhcZY+rlGlbvmQa3Bf/9Ph6J55vkZvtICCQOfiBl9J7yJgPNAgsW8uY68R4Jwfk44BwEZQdPAm8PjuiLCdgJUS63GgXcTdy042sp/vas6SwOagoaBgTmY/xACowvz/MI1kINFPAWD1IUUReb/qjrvQny0Dno0RwnCYDik/B/IKgYpQtrDQ0Di9MRAA4hAdrzDEZBrPwx3knsvuoJBR8Ly/gs503X8QPRJykhnyQZJnT4z+cl2j2/xwCRHFoFk/5iDHALpvalHfgnQOqx1UD9Wuyy4sES4SXZAtsGRBiL1jLlOBeRLtPsmNR7IZ7mEQzbNN74yeGF7WYKFvj/A+IdsAmN3qkHTNlJv0oqCCEyIDYDUPsjDwTxZu9B9pr60fYACmH6ug+CFL/g0fkFDAn/kQkJDBX3twZuFur+rPRlAHMJ7f7x8cbzVudsA/34c94LJncngi7j8SvEA/+V27T2ngrOGLk0XBwy/ZXtQQHq8iHbKtS8+wEFQvPoBwcmCyK7KegnL+Ni853yA9yx0THxmCQJ9eoeEyJx5PMKLA760/zsRSl4BonragrPC5PWVPp1Iar4VBolFqfm3uTxA07w4M6RF2IZoemP9SMtsSkx77YDnx/DAam8pAyuAJ++kkc/L+Dv+Pq7AzfsINaKATz/sNnk9NJPVSFsCTYToOoCzivi/Rgo5UkJQxTB66brkxh4PMPmDPp5AFr7KAtN8vIJigdmBh8NI+BP09sYXPzC7ekV9+2EEQAK2OrjFIIV8San8nXdPw6G48bc/BBSHuXx4/lDBaAOQge0BP4mdc2v9NESrci353UswThU8+3+EeWC8aIYtxQNBqvArPxoGN/+cwUFIYkRMsoB9ggE5fUSH4Al5PZF1AbgoPLuIHglzfsk3Bz/WDgnA2ju1/o8EgkHbeQL6X/oVCEX7NkDgihF/0YbxOzw5un2EhKa5WAErP/a2QQpXPk0BOn5aytbHRDkePF84WL/LdQCHnQmSQ2l8ifckxGnIAMjGeJ08R/n2hIp+yrWYf7i9XgsdwwAHEsCSPfRB9jmRfQ6ARoSbuah3EHv3R7cD4gRmiM7D+4Xx+bE44PfHuo8AJQOYOkR9D4i/fuJGsYEvAbzCaDtxvQo+r0GpwshFmXd5euD/6YJ7P+Vz8Yf8hYnBVcytwI+77H8TdzK2QADPBEU95L1ZCS0BA76kjhhHsvhNuey7O3kcvZq8Hga4B2//z4kOgV04kbvEfsK4w/7/CdeCjD13fmrBqjXoN1tBYwEBCWhNUEdmObg7Ij9dvQ/5jH2nv847w4yiiV06JEIQyCe30TZdhWO82LUrPZaMR4zOQ8mED8C7drN5MLL09fvKBIAngEvE+wkDx8g4EsH4P282tn5VAkv7OUKtR2VADT3I/TlCTr+Uh8m+R7wvAYc6ToQaewzJPY14eRZvN7Z6Q1z7fQhIwsSFboacviEIwnm//VH/YXcf++NE/fpWe5lNe/7UAai6SAnfjEu3QoFor1w3hD0yAJrLEYskTRN4lrsC/Q2/Cz3YwNy+nXJ8xKTCBUivR+9Da8BlMADDcgGuQoWAj/jNv9l7t4aFvzsC0kFmdOmAPP4KweSEW4ftv3N/FQQvPzhBM/rOAZG9zb3/ftOBVv9leZCG8j1aP3NBBoWmg+v5KMD4/0lCr37ywJt/X3lOeVWApj6xgNMPkvlFAVUIPQCmgjj2QP58vNlBOEEWgnDHo3/aAaO857o0PJ87v71rARP+i8VRyHNElsGpulW+w3eQABiEJvnIhNVA4L8xA77ITIELN8J9lfakutdGhYlOw2U9ooVTQQP5qMSYgqu1BDdFurU79IEByySLLjxQ/BmIA4BnAvmGcbYJ/Kx6Rv2/gH2FbdVyPcFxsnlGQHe6vDhdxWMEjr9QjqMJtjDtB5G+szPjg+M+1TvV+uVAEbVphVLQ5EbbOWD1GocFfXyD0Qu2QVa5lD6AwIw3ekBGwYhxkK8LSOVOtM5jj5QEt3eActm7i7o7QegF8D1ic3rB9QwhRlLL7Pgu8OM2zYF6Q03+dAT7gUsCun8jB9qJOjij+Yg4lbmeQiDIV4M2/oh/gbuyAadEocPSPOsAAIm7dqy7LcJLQbYBqPloRgCBQTqExUMBrLtNgx59vDuwgYW6V8QL+VC9GoprfkKGUQA1/2d7IveVQe+ARYryQ2H/BcAmeiaB38LcPMh4DAQ7hPeCo8DOgbZLGnwQeGZv+/unCtnAicb3PnL8wHv3fhiBM/7bfbF86YMavY/NYkpDg2ZCz3B5c8u6AkL0h+cClQHxxbsAd4LOBbF2O/kJuBi2yX4hBnEUiwwTgdr4rrHj/j790bnjhakDsjkEhSb/soR6ysd45f4jsMG9rMoegNrNoAdiQRqwzHq4wEE3lYCt/p//YkN/0pFFaviEfod9Ov4oujN98kLkQ94BZQIrQu+A6Tq+uqD28Dxjx6E92H7nvrRKkszQxa/9b+6ge/SAGT5FRBPIA0iWQ636Zfv8uhh4Pf/a9hf9V8nehMzIxY2GRKAA0Tk88o/1Oq7nPyBL8IhTB2iF1ro5Po7Irv+/g/E30LROeFC9jswoSe+DtAKQRlb6LnpVusC2ITyvABIDGgTMjA0Agv5swiQ+9b99vCbDjHqTtWX+DMZDgjU8yktbQ8Q3rbYfRZCC5Hn1CAf+Q8Vaxdg8S7+ygUb9aTd9e4exyEhiR7kBf428/mbGScEWPTd6rD9TtuWwPURKPVOJ1UhTQ4VFS3rffI59Ob7eezg9uL4lBAwJ002eBzt2ubjq9lM7RT6qe8GCdIGbBgSHF34LCNIE9Dj8AJq4dbPG/WRHgn7aA6cJL7pLRB79kbwreQ87H8kLv92EbEQDRGgDHcHvwaMxpvcJxx5CrHqQA6X/r7pHAt6Bs8GJAj8/WX0tAJN98fzcg+zB4v3s+38AksSLh41/5jwy/Yq77MsPPrY3DP02QNkI7Xlzhp7IIfqIvj/9TwCQ+VYA0URXwC971IVFjC+0ULpBQiP/zLSyeyePK/5/xxqJJj+8AFH4ILqet6i84QUtAOv7dINADgh68vu1iaV5xb0BAEx5m0H/h5tOYQV6vEgCK/gd8H+6VLwmu9+BvcfvjCWEQcViAmI2UXJTfreA3Lb/QhDJuwnBxnrCXTZHs8y87j4cwUOHkMr6NTsFp0dmtqwIC4TjQH7yUzayAx5I+ETJQ1VBm652/lX+fDnRQohKFotFgb+HKz9APHvzqDISgHu7UoG0xbSB6IgbjGhHgPfo9xn6mfgm/Hx7TAOmxa/IQEWLBOdMQP14c15wBzcEgGfKkA2aver7IQlRPwmzusWT/7q/WPtG+bEIfYdgByvCifrTOLxArbF/ewzEbQC9z5A/qH2YfxLEf/82OWWBSryBvzL7cwGCiCWHe4IM/NT21Dm4Ak++CQE1h4cFNn1oxqKDLjjhemyBxMEDc4gC8wjGgND+/QBivzk+Iv4t9ztBeAjwB+f/6nrEBRuEnHQ5eNdJaHpsvjRIgHqce5ID8QFgOU0DKgpdv7sBGgA4+436ScIwRic1hvyfDPdDmLKv/EMI4jkYufeLQMUrO3iHYICDvV1JHQWEPfI1ADidd7h1eELGzCSCx/8mDAtEZvwWggS7MLivPKRB0z5y+1zNjYOyNqTH9kQr8zi3ssAzvFD+78i5yiD+tAeKCO37t3tU9868RjkKBCeEoj5ViR9EH/Xs7F4GzsU39S+HGEnfPqJG2pEzAJ69MTodN6Auevaqydt3nsLtiRI+/cXFiuICRXvNgi48eEGs/bH+LELlt29Fx8SV9wg5KH6CwVBAMEN0BdEDtrn6wFjBT0TLBms6+sAPuqL9cTkQvXcHlAK1hW19HEXnOsw2w4Vau04C9wRLfcL9SYN8hEeAMEM2wGa7dLmDvAI8bDzpBA2GyUHtQc7D477pPTaBKQFjR81CVPf1fgE57z4jg/LGFX9wtqADG/62gAvDYUCrAgp9GUKMvY/yTv27SMACdgL6Bnv9Rvu9/VmAtYQIRQSFcHllPOOBzTUI/bLD40IthSnHQcOQOaV55YHpQGe87ooqfnPxw0RzRdR4jHh6BiW/XjxXBjO6xMFly0JJNwSXeUkECblI6qBCH0WqN4W/RAyBw/GJs4lHuG9uWLuVSU3+uUZhuOq7ln7c/bdIRL0wyTECYjp+9SJKd8i9cisJbzr+OaMAZ0FCALh9ZcZfCfvCnHdGQK84EH9/w46Blr7GNif+dDbpBCfPuIigPtaEFr6os6vHKT1Ruoj+EHtKgLM+/oEJRAaIIsOQBlE+MbgVfUF2eMNehR/CBQSAwdi/bnbpPtm/Qb/uvIo/z8SyvnkFm/7ywvYB0wL+PjB1gEGhvKy+9EENTySB+XOIBRQ2HnWPRt2BzLqEB8EHqcVBxRICRL64NjND7/1Y8ns2J0RoQ/h8WIoYzclHTLyBOyCyagBBSSc8ycEyuJw/NP6afj6ELMRuBx58Rvwx/E5AEz7XewyCW725hqoHbTsCAi6GqMRgOy08ssBjfLoDZsJMMWCyEs4mBYz8Zc6Vx0T+gXZ7OGU9d7e6Q0KEInjmANpLQYQfRIoHp3WdtbvFvUEVtT07LgXzQhdGRcp0+qK2xz3fv5OAQ8akTTy+Yrt2vmx8WTvI+eeGjfINtlqOjMnojSP+P/6uuOK7yoOOvArC0Tj3fbOAwsrdyJ97WfpGN5KF5Pq0OhLB+Xxoh0wLmIRYP3D95D7K+bX4FEVNQx2HQv9QN58CGv6wAl/Fo73ethJHKEHqd+RCa4NOASf4tD7r+HWBuQ4qjEtFhLBb9OM3nnxpgQpGe0ykxJQ91H2bwI/+SInrxlXvl3chxJt6iAB8kLEHSr/ivoa2CvUUuskFMj2BtpjOqUjGgGSDqr8Mu5bxJUORh7g+mb+cQyI+uHiVB6SBZ4QfgeL5SXZ4ugaMtr9vxdHP3f2LOCw/3btRdYH/vrt3f+/BAIMRUMyDXX3p/pm36vlkuif7x/8mjjUKNPezAAUI0MMq+gK/Sn8Tt8d4XbcOwmLOzBGyh2i6m3fue8h9M/ks/oq/oXgJvSeEgIb1T8dLob0yeFm5p/v+/fk/fX3JPrS8FodWCOICAoGxeey3Lfd4jZMHGvngRjB5x7fgBVMHRX8KO/H4eL/XfzPCBcdc9+DFvIO9OXE8aoXfB0w7NcC2vP7DJ4Zigyx7KPn0RqQ9APqN+b5/GsCvPgiDuUEKh1YMRUURt7A9eby0dZJ9BcD/hsbBhb/ePzN74IJqvGk868GegYPBaQB5h3DERf4vPV7CqHnNcev/AUB9xpNC0kZHR3D+hwd/MWt29z6zQCYHQEDsCm0+xoi2hEL1xTkWueg99+/NBVrDhrsxiwyK+gYE+LyF/D2G8ZR9r4VchFeAcAz6/aL3W3y3e1+7qHoTw8B/jkb9ic+CU0YFypFCuS4rcGi2O/uJxnZ/McacTQPC4kkrurO7oENX8Jq7Q75vRX2JAQRve8L+CY2AdXD3ObZD+r+F9EKVlMz/7joKh487XnnRRLS+nfVgu4iEzwgDOn7HOA4cuIF3doLA/Kz3gkCBvE8FI4hlCRnBuXWaeRV2iP5zwtaEucWuiS299zucwHwBqYs4de541z4+P31Avvrnix7KfcVH8902UwT5va662oMHhnh3zUNsB18/2L7pvsS8lPaswoZFq4LbAP0F3wBh8piC+ck89xW5lgdk+aY/N015QOi8D4H8Qat4CrpsgIO+0sOWTONFi7tFvEG7qrg9eewB+X9ZxH3HL4LLhIBGNYkEONkzW/BNMt4KrAXVCTbCafcjCtFCK7+hhf49gXfZNH760f9qFAKK1DzDP27yw//R/De/a78/AMuEy3p6RTgA1xBZwSc2MTUGr+UQC0G0hTgEdkI3ANX0kr9IvFIKF3QTvMxER/zm08a+vIZfgui5LjHMNYVEjXr/Dp3ATrzegv8BVQcXuUGBaXYgM/f+rQfsDQXJdcSwvCx+vPa5B/V9dLCEQupyc8DXSTFFXU3fhq79h/WQescBc0DZ/B6GskKJuTH993XGRR8H6YYWw8Xzsnz+gmkHNf/uA74Aja+4BLU/qLxhvqz+LofLPYrKMgf7gib+EbKg/yW7hf17OaY3/AUoC0BK3sSDCm55/Huegjg2Ub2hd1v/6P99wPrHc0TqhH+z1QFSfvC8SQA4eSYClgNTzWVGnQWwhFY+/HtIM+u7MfKjPRkBxn9FwoNDD8qBu/u95cN5iKSR04CD9hu4Zf3++7Q3xP3y+k/5nj4ahg0KEcsW1T8+HTOQwqR493U1AC8AePjQxuXJHX2buYA+HEFeOEgAswXeeV1+txJph2AHtcSW9yl9D/Gyek48+D2fRiGEIoTwgh1CEfrkQBk1xng6BsfFooXPwLmHgoBNvrkFZfQKsLu+or0mfWBDuMg+ypLDLoIlfV3++PvnQXPDDLv6SVm/8z1lPRu4un3avM39Wz0cAgrGo0jUfZ6FmQqE+0W+JzaDOeY77bbAgzaF2wVYg1bEbAFw+eIDcztodmABcnvgvFtHSxTFR8L+h4YutWCwwXmyQ6LBFrp1RKUBoHxZhZxM6YQue96z6W27/rsKo0cVBGcJUkM0OIl843zru4u0q0Dswkr7v5D2hVxA3gMfeUR8fr5rgXY97wLBvtfAXEDwfhjIRb4QfDp/A3kyOPKHEkRCAKCOfwDQ8NvySclOxp54WMboRZt9Bnf2PrmEa8GgQA5Bgr5Ju5HC7D7IBkMEzb25+y72lkMrwBp/9kfPQvIBJkG59cf68IkMQgY77/3QRRY+7fvR/tKFOoExtG7/N/+EhAgJbQhw+mV7IYGWOPGHrL9iAcL6vXkqgcp4gENsvR+IEIGphNlKFX8+AoG0RD98vK24sTyIg6ADo/6BickD+kJaPyECffVp+ehH2jtAO7gAGsqVeMN6+EPtPmRA+0OGjN56poDrRqN4aXmnPbcBjf2XPpX7vTrqvfUHgEtEAq8EuQJWvMz8kwRPdBn0SkY2eJ4J+wqD/1gEYnfM+0t4PX0fRMKEJ8aQhDbIinqd/+rF0LYmuxk/Z/q0tpTBaAB8wVNNrAW5AbjCMj7TNyN36DxVhW/NksJgP7q60b3QA+v8HbkJM2s89796xL4QY8bpS/7Cg/MwNnZ+nsEaOj4+oDn7/ZRJp0tJhNU6av+KdRy4KAS4Pf/H3Ez0xQTBzP9m/Mn7b/sNP9/5cnP9R3EHc3pCQUiEjsHWvIJ+dUNZvHGGwM6i+zj6skMZ/rl1JLhNhY+6Rr3LRrV538ggSmJAlT0rPdTIP3rO9/671UFJQFM9toW2wyfHgL/Uvn13gjx1/umyug4Dhn5C50gpu+dCFEDNvJY4y//8O5++YXo3/+kK5L3ARYx5h/snCIwDi7t+vFbGXj36/s7E+wIPfn9IMryysSWB9MBm/OL8UMP5QyOCUIbvxVJ6HvrwSZ11Fbc2gUFA14VvhPtLd733d/U9VXhRdKbEroiHQCjOW4XhuCN7/nskf+h/BHY1gfZDUXtFDGDDpsA3SMo627dseHZ+kYHaPQcEhAlLgP3+DsHgPd78QD7gfoIBnAVV/CjBqgZDfDxBZ3lswj9EY3c5hNk/vr7sPcb8J8G1vUqIZ4hVPpJ+fTzr9WK8IsFmulm9tkAsC45Gl/7jDfXHZHi9tsZ+xbkjd0JJVv+KAAHNDQBg+EaATMh+vJL1nf83AQS59wJQxyU/1cNlO/FAInzBAGvCBriRBIo6EQb1x/a5eHtkeTeF5YDtymtF2jh9As4FWQTgOuL8lbj+cX/4UsikTWE8dH3IwGc/BcKGh6JF8HjmPlmDZAeEgF43TjokdR3B3f8jA55MAUMZQk360fqkPNOGIn5kv+9DKzu9gwG6r7wVwiSOOrmQtxrDSrO5hjlDRsgqwMv8Hb6PdoLJBMX2SveCMDwE/ux3tvs7fK5D2TmZe9hGEsU+BGQ8Uz4AvGw26wJ+hBfEZAdzg0yAjYERhfl4I/Z8tZA8REMYQAhPUcH3QNxCzUM3wgS8dkBI9LY/C3xffl5IPH9sv+I9vH9JgUo/kr7Ygqc9VIJIgJDANwN7N6IDFALF/2I7rYEmB3T8Z0Cl/hu++PybhpvGrfwLCKo7O+zreaeMSj/X/+mMvjyfP4JADUR//2K7XTuzcHn+soXc0PcHtf1XPVE4lkSuP04CPrny+OQ+NQIFihg9XT+F/UJ8EzqfhgAH2/6PxaO7T4ECQkZAWj2mOPUALEHFvxD+f0kZvK62HUlYSxK9J30Sfqb4g4V6RIOAeHjbOiEGOrbtv5LIhkAVvaP6NwOL/rC+a8nkhlv6D79wxiV4+MAsuAd5mAWoBaBLdf7xQdm7mfxfunU8BYQjN0CKe39VfCQHU8Z0SRY8CH8KNiE20cKrfow8WoYcTJt9efbq+XoA/YW3wuYD2AIt+SHAGT5DeEOMRUDfua2FJb8ReQg6CAfUhLH6Fn/Ih1/+pPomRJ3/4T/sxnUGjPwavN2CRHL4P9VIkb3mu5a8d0GqfTkFtslwQFv8+ABQQThyF8CmDQx6g3isBYjIdYHb/G85QzbjuBaDb4RZQudQ1gs6t/3/XENIOWi0DblcwL55YD0RxRQHF0oKRiz+nr/vPrH4iEDNAHmDekCB/qNB+THoBExLkTgePYnBAIMqA4g/X8U5gVH5dj1Ate+B78nau6g93zgiwY0ErcAZiIZAwH41fDw/K7+sQxuCnHxW/T/8bsmTwaq/IT5Lha6IHDPbQ2F33jsYQND/9oue/VtH5TqT9xJ/ML+6BBHDTkbddeY76XtWQncDf7ulyDv1Vr3siyl/D0AJhSQETbz3OtIC2/2f/SuIyEErvCm9KcLBfZm4VQHaAkP9G3ruieyFEUMRRJZ5urxtPalBE76lBhGD6rYfusU9b7/J/Xj8QIUFAtqDLo/vBWS4CD4Nfg/4DHo6gqPARL84wpaHan/G/BrEZLkPtH37+kaiSbpIKo5cQqb8yf6oeBR1Ma41fGz/qXjjDwBI8QUTiLz+yH74OwRGAv/nt9BAGAPLvMI9eIid/h+DQnx1d8Q9iba8xEnD8cXlBktCDQApPlCAITTlg3gHsfdb/duFpf/CtCD/jUg9vVQHtEgLuzFzEkGdDyxCeIbQ/Uw4LbrcfZ+ABW95xVyJ+v6zRPYBv8Nmf3F5iDizvtDB3sTTPWl9v8dAQQO9DUGiCTs+Nb9SvKt2h7zeOJFFWkaUygVFhPZswMp/s4bJhK45Vn5RdybBAjuBPiDGTvqtCPU7175GCc291wEYAO49af3tAyW59r8fO3y+L0Y/fkVME/1nwixBFLymA04rrcGfSoC834W+/pE+aITIAbv+IEIXBYx33bPQ/4VCh0I2RsDGb7nXexvB34a2erc+h8TJtpZDHf2LQYkCwEH2xBP5nEQyehP68YMViAe9ALvoxCy+CYUaeJDHg8K0wbxDmjDpACJ6rQcU/mfDscsH+HLDz3Yq/8W740PgT+I25j3P9bM+EIbs/cyAcgO7/8z2VwYlA5B/0AeDAOO8lcQhAcW0IYBKweb95n0cAKdKQ362v1t6nnoAw8jDxogD+3s90AesuOS7gUPHv+RH6MC9brv58cSNgkV8q8P+jfZ+/D6VweB8QH/9AwMBODRx+lUBgAHwQD8CWsh6PSe+1XvMwIGGwwDevud15IPpBr7+mQTzxcq55fP8f/y9L0TxRn+4XDnXwXWJVsViAUJ8q/ki+en74MjlB9hEhoR+tnQ5fP+JukTHL4gL9575cESIBL28KEs0iyB3yXhWu3dC1Pnw/3dKuj0JO8b7ggBNwceFKr++O/EDP36+w4f+/7yr/me9l4S6xAMDLUNPgV00uPiUBFsAWwUqhDr+9H4M+5iAUn2ZQyuBnPk8gYV+Vj8yws9K1EEHf6TA9HMwQdq6tgRywip8uojyu2W9ejyKyUfAITz3vpn/9s34ex2BkPVScw5Fp4CSA3m+1EdvCOt7cXiugJ8/B/lCQZBF0IBMgDWH8gNvt0P8tEYjeXu6NcW5+zF9MkXVA62BeoUIQsT+Enq6ejIEu7epAS9KCDPPxCaENj4OgVbBRQBWOJeJuoQ/+VN55YKxfL84IgpyvgHCqIXqQhX/Crz5g/S6bvspASs9W0JfjXBC9XzsemqAQjcOMYTLH32qv+6K5kbX+WO+FIsUvV59fX0jQhxyLQWOj2Kx1sSwRZ+2wfLCg/yFMboKRfYOMz6rOL3MZHuruAN8Fn0zBLR9dISBewa6sEY8RH3BdMaZQ090i0KgQipAkENhNvR98DxU/kYIEwi+fY16Y344eE1FUIEAvTPADTdOfu9KtkuIf0EGioH0Myw8iv8letv64kE+QzJFbcUmQ2i8LboaAUXBDwB6/TpHmwbKOJ08sMIXAEuCPf3TOdQBMb0l/XACwYe3RR58jzqUOBVDJ8fLxcGDafgNOcE7EHpTBY9Ld0Mwtf93kMGkQoIHqslMAYB4lHzlv+c6ioLEh9h9bzGo+33L3gSoftXHbIBGf+gJRoAb9M6zjjiGeyXE98z6CHqE5kIBfeE6iXq4N3q7wfzJxxrFo3zeTmVArjfou6UBdQdOsxW7CkTcwNMGB4Z5g4y5w7w3AMM9FgFHAqx+KDrQh1SEkDNwwTOELEONwHz7R4G3eSgCkoXuCKYCiXjVPniu1b5WCDOER4LB/sTHnXtrA3E+UPrOQFU0AsKogoYCY4PixplBdHaNxWu9UfqXAnoBKv93vy+Im4T7ejE9Q4Ju/WU8Y/jVu4MILsbHgLA/NEOgw2z58rgYwkf/5zz8BRr+PzySBhIE7PzFeyh/3ToagEcHnUWaxPu5xUSiPVu0jMYnQ1W7g7zHSFE+sn4Jg7D7uLnBeXVKgAfDgD+77f9jQOU8asZcO+D6Ur5ahYTA53x0SqZAFz3GvOq20r7kxBvEGIKT/ZX9HgJ8xNq/C7zjQDF5pkBihxmCSvzHgXhDi79Ju8Y3CwNlfuVCfUTffNcEUz18g0fGNn2EuSH9w0HjOOJD1Yi7RYR8wTPEwii7G/t+DU+A1bvDwkjAF32ShLMGmrxnvYiAHn9vdZE9h0P/+7qFm0egv6T2SwqmCk+4W3+F+0QCPIH3/2/5trbYRKPCoMHcAYjGuwLUvSd7tnS/Ap9FRDqPO7NDWETmQ1cJzMGd+W43BEP7x3i4qsFD+fL5qsU7BIqHtX5xvqz7djsVgV6//0ZGDXh9zHEVQLS+6AAnQjT9LT3wt84EboQShZUIvoZqOnMqQ4UevOZ9nY3keje8k8NNCUc7XL4piwF8SjmaO4k/yP9jBxCDv/wLtZsAAVIbdYg8qIh1vc19MAHfAlm6RAg9QDr1SzrxhahBPLvQxY6+RAXGQ45ArLyj++rDSjzDPs23NH+RB2AClX/sAJjKzb5ze9t/uX0vusV85QLGtkZ/EJANSCy7lXyDh6R4qC2whxhKa/8DQvn9n30B/5/MeIbKcEg9tQKC9+N6NAcrAFr7WcgkAk3/2QQGzOe3wWtaQpYFmsdjgCu+IPnS+PfKQ0Kx//NFfgKHuwUz4H70BH2EzQHt+Z3B+ACkuVx+FkWMxxYGaD949ATAPULZAn18Szy8AxE2x0O8QPICvwcR/0TBu3cLArrF40Isfz64ljgFAITMqvlfOV8KEAThewg+p8GM/NRA9EBCOVq8yU3hCtl8F73+Pzo5gPfXxAAHUbXzuB2EWEIJBNyGd0Usw4x5THLy+qgCeQSkA2M/zwPeQgdDTEY3eStzowFUxee7AHneBoiKaXiNPszJDf1kfxECaLe3MzXCdUmUBfkCXoZqfF9u2MaFA2U2tsTUgpy9NLsYRJKK+b30AEaEe/dU94JB+f+GflMC/wRbfc8BZ45SPSx2In5avJ1BVzi9OghItMvYBz4DHnt3/Gs/aDFhguIAyvrVzBU83fcpv+uLOIWZv6g/EfruQp5+zkTwN/0z1clqwsbHR0Hcufc/mbgmOB6D+UcjBXM/dj0tiIp7T4Miizdxavcj/XnC3sW2fes8aUICALk/U8DufhDMq//i/L76wvrDyssEl39/drwA0/eF+2+Dxn5nzrwByX/+c4B5xg4+RXb/6Lg5AVOAUsNcAsc4ovmPfiKKd/wiv8eJ9Po4wfd94Tc+fZSHCMJ3ePnLpkRwvfV+ezzXAFO6y0CBu3z/3oUOxUN5yb3oBUL0L8WVBagB00AVPVSD7P77wJS9uD3jOkqDSruF/jKLNz37R5nIRURZu2O2N7Z0sZKANYZ7RUiKz0ygPaV9akaKfTpyBy+VOk+/eId8TOrHBAIIf+kGkfZHNwB9irXOCF2G84EYuvzCsUy/eRS77MRMQ8p5V7mlvnYDHsnvhBa7/XLZwhYGKXyteeXGwZFwAFq+5gDs9/UxK/oA+3j9Boimh7KJtgeWRZN6Z3Jld4XAZwPg+6w8ewAExEwIvcb6AW8CsQFheJl4XH2hxfSAHr/wgL90psG+iSE/zvweBXcDMbfrxiAF2jppd6HD6LwqudvMHv0vguWCM8GwOvU4V4YZ+V+/8nxGCJEBXkAdDlv7yYAOOiW84HSq+NYAxsT9jD8+CE5NgFS5nn71vYW6GDK3yR2E2oWRQ3d/qoIcf92EjHX5PFb85fmh/ZzBttGNwvu5K/lPfjlBrsFwSOb7qUAlhu1AoXlMvpFCR+9QephD0AZPB/7KlT9cMJmHT4J0PJH+NkXawRo1+EUBuuuAGEBj/18+i/63kdJ8ejZeBHTJGX8ZOFRCqXsfvVc/GkEhPj9B/crBfQ244ncCOzRAXodORyv/6MLRh/RCljFAwfSAy3fQA7H/YUHABCpKIT4HuGy/pgLxPkB0AAMAfGZAkYnVutX/YcuLy4K4jDfbO7a3ejrGACAMIkMJPfKHLroXuceHqkfeO1n46sWzBmcDUL4j/jT1NzpfxH59w8UZ+njE+MOyd6PETQP0Prg1ycJ+ANDBNYUkxYqBY3ZFSvr6unmBxjF6N73M/BjGdwLX++X/B0VihpG8sz4FOmC+DwlGCHW5ifv7RHrz6nhRwlyHW4iq/Vv62nshxQ1I/kKZ/sW//rrbNvrCuwDQviu/L0AbRNODeYDiQPn48bRAQ9RFpH/agQNDNoMehSvDmjqPPu6+M4Btflb64IIt/Ke7dQKPCndFSQGvfj41JDbEw+UMrn1Au0HFH/7Yt2E7K0T1iDD7W7odg8a4PcmBCam4tgPN/7JB2Xnwwr/B+X3uidI5/T7sOWoAsbzpNfeHODyFTKBLj8E6Qd/9DvhcND5AQ4HKAFq38QFXCEp7kQb0CN3/PTyrPr27kPlyBxIF0rUaQAwEUDjIv8oM4fzwtzPMfT+TPu5BCwOafpvwbgEDvc9C5sb6g96+oQFDiye1N3chgAoCTTra/8OOS3zAvNvF5gLF+A5440NTvKW7ar8uwlyITUVtRaM9vXtFQUh33n1qv2TBUUbdQPOCnoWNAIK9bb08dBM77EK5++1Gl0vUe5V+IcXG/z5/1XkqgE0/aDd6gLWGGsnHAPl/vntFO056/X4dxQV7cT/fBLvHksDliIxJ1XgbeEm4HUFgN7I+hAi2uLlBi8rFhkA1mDoBfxj3dwMcCNBJowfPxBw+z7rVej13Vfaf+rV+y/7UxePNfAk1v7GCGcHJdWd5HP9YvnREjIId/2hEtARgBgW6v3hTec40nQeExw1AOIOwAjL8KDhwxAlJDsDE+hDB9r8DvWUDkoDDwlK+CzjvNznBX4gmQaj8coCTgiV9o0hPPhl5ZYWaAoyBbb3GRHSCyPdGv+qDCLsyvP9DOn0OMvtAyk2Nge0B3gRs/WWAjEbrvBJ0g0JiPPt3vcRyRNOF+UJn/qg6vXw3xQ9/p3h9/wRK5IC3fkhDd79swkAFQICVtnK/6oQyvrwv17nDDgcAgIHbgyoCgXinwBq/p3gfzELGLEfzuS81yUKivdHFIIFCeue4Vj1SduI+eM21xTGEt4YSP1q6l4UICua3+7C2flL/yD5rAlWGR0NPQOqByoLz/J13hkKkOJs5wEQLhe1G5YDpAOPA84SXO5f6XvhOfOS/gv4xCRXBU8RhBA4EYfYvNFEId33KP0UGNcc6/TQ+zcVE+vkA8IOR+JAw0TkvCXJBrLuEhrYGGgO6BGwHZ/yB/wlBZ3suup41VUMfexIC4cSRvu2MIgKLQn/3k7xJuvG4jAOfQGdE6cHNidvEgrkDfcf6gzzxwcJ8Vn6Y/NUBKYy7gmlCUofQAKoxurgWwQc9qsOCSUs/cjQv/6q9XoNIRxmDwkPa/iXBerrsvF5+NIaaQKG1V30RgsZ/REQOUOr7+r7wflw3cn5su78FfjvmP6qCC/45CNQFUsbpgLNwinOifsXCYESwSj9D1b6+fLe95sUpeeVAs4R3dmu7PQH4xrnBOsLGeNe04gd8hGv//QP0yfpBAPfJP2zBdT1Nv3xBgnhWeFNIsQHFvuKE8P6DPwsAhIWxwC/BpbwB+hZ+VD44CaH4ZPvpfIG+44j1A5AFoXxeQLT80YEYPLT9f8T7CToEBTZ/CDY3IruMgms/GoAdOWzDnDVfgTHFacOmgmCFH0SQtYXGJMA5QH4/VfthP3u5lsCIu0/6R0d3D4vBIDiTyEz+ovPHQsOEdz65xugGcPbOOYxC0P2SOPb9vQlvwaL8dEI1ANi+UMWMSlu8ubuY+6j1FXZZygGIR30hSWa6MjrZREZCHEMtvss/s/bROE5HmYgyvR5/WQErvWUCLoeMf0E3XkFG/Jk6H0UyRDeBfgN9Qng5pf27BLF+isDRBekA4DYQfXXGrnn7+/9JbwJxNF+EeAWIObaCgwDJgUI52P6FQsD7nYNUBpJDI3npxkGAsHcyBPoA4Dx4PeF/dbph/hREw8hbhnABt/iBt3GDhXwW/s3FfsDNhba/gfmwQ0eDJz4yvR573gMcfZICoUXUeaI7PMO3iOJ+tX6ifuh60cKufUICpwJ6fY2BrXRkvf1CcYEawujACwuZfcRDrsNg+iy+g3q2gii+ukDkf/R8Y/hQwPQFEIFbSOy98UTrux73t0GjAgTF6UCLAhU7j8DzO9r+N/6JdkDBIsCiAe3Hno1mRnIAnnOW9XYAZn1owql+doPywZqD9UBue60D+39te/dzhMWpQXT/mQ7FPHNDLMLae3DA4nnA+Rg9drqpPKsCRwbBi0d+7QORCci7JTm9+fV9sr3Swf7FL0U0RMS7L/60+c34BsKR/qp69Qmpi6O8cwfxAN+6/cGWuAu2JDcUwlG9cgL0x7+EVYnrfIjCRrwyu5eCt8E5wlLBNYnf99f2zv0v/vP9jjw/CxV+Ff3Iv8cDUMRlQ5cCkzIsAosBAb3oyKb91XgFgDE/e33awlfCYoyfvT45h4KDv+XB5wBiwEw1jIGRAx48vr/wRVW++y4PAfDHYEcoPNxDxIrjcaqB04aVwEABLP8F/dD1GsAWR0LB+gHx/0Z7Fn/TgS2/k4HaiF0HoLe4OEg+WzaBt0p/PYNRxSqGGUZWiOFJrvt5Otm5JzRnw5W7lL/XCbOBtkJCOdD/mA01AZq3qv0+ejF7s8TMBlcDpz0bvUI+Evq7OnsEPYa3QsuAZL4/QtOE9gRhM1m45wMi/aOK6AGNQdSBa3k6PA829sMpwz0+cTig/dlRWwNmRQhMb7gTrqi97IPft1i/sQBuPlSDioCTjuhGXz1Sgc600Xe8PPcIkgRAgmDEgTRwPxR+FcErf2M4PMF2hl7FFLyozNdETX2P+Lmz9oLld2oA9MBeuTgGrwy0v3QDoQeZuNTAZ7V3+z1EtAQ3glk7P8DXhh+GBrjjPr/4V4H+Q8N64MkxvlSH4nzcPNY7j2+jRek/4cCngDfQShCVck368fY9OIqIhcUWADJ72cQgSBD4GriUjAgEUnRKemN8XINYicPEZgDyfZL/TDnyuxZA6zkb/1XOMcZO+vjIMwfbNoP48cNJ+A/1RUQWwqPFo4REB1V8QzPYRAJ+Wb09QG9E1AM6hr2AcDIiwfs9ZjuXf2pHVEPEOs4F9cA6Q18JdEZE7b+yoYRWuNU/CAQ/y6U+BsKISQg5/z7XP1U5h7ZsS3/E2L4hxXP6RT5ufV4GO/xr8x6F6sVwe5qDCMuv/HN/FchyuIH0f0LWxP2zHP/ujkP+eb1kxWg+HrSihd8IVTxUfca5kAQ6w7KDasEXvQp+l7/1ARY0RcZJwfw8/sMVvaaKTII6fmc504HuhiM7Vnv0ejR4g7pZjaVH2X5pROpBDkBvfZ85sDmefs/FnoDgNtrBlI2rAbQ2pQOu/4v+7AXbP18FNED3AXIxUDNJTLPERj1qvl49tLuORvSAzr1oh0jGDn3K+bdCLAPfAWH63728ufFFLQiuNzA7J8C5QeT3+cdnBai+JMLlvO5+mrq5zwoBDDqpwcs2eQFWfX8B2D7n+znCPkQs/0YBW8h1OYHCnoEIQnYJJ7r3xFl4p3QlxEC4NrnyR+YB7780glF4C7vwiBtD5YG1QQzEgYhofOh+ZUSnfYqAMDGWLk5J5kS4NTvEJopygaTI8UhWfYmyy/7Higz3pf9swkJ8i4GjQ9eB6TkE+uG++r8b+fPGSEoAAj1CoIHCA2q9a8CKtG23db9+/Z3GHz+cw8a/30WwOQo61kza+M4DyAACPMo/toAUhX/BY8mTPgvAwT0u/Ph97vrGxYz5iTieedFHnf+lvfQMTYO6w0g5wEqrQIhxBAOHP/Z4031Ggfk7KAKy/j2+535JwcdOy0JUhQU8lr7+hm8AbTndNMq9efyogOvDUf89exOKpAQMNLkG9QqbA7R75L+Rfy2APj11eA476vqmiLr9X3nzw8gCjQdQRREB6LUtfEFBCfs2vwWAnYrtBz+AeneT+XnB1L5vRupATj41ghk83ILpgfTA0kG6doX5nsbhhGgDiAD/fPg8rPvNQ0FA1v95/mE+NQFugeBCwQAxu8Q6FsHFgT98+oIaBpnIjAP2venAUjy+tEK5X312A2LCsUPRwhf9MgZGBmk+YrhHAW06hbmqRWzCgsVagwMDlHdO+UFGYX/gvmdB0XvaPD9JzADu/3TAs8DJAat1BHjLhIHJoP01ghMEPP7fgbP2W3X1QRpHjX2JR1RJYMZahrQtmXeYALvAtAdKukIySj1eiZXFPUZzh9SEA/wutjZ3kD6qy0DBr/eoM4WByE8dQtvGKDuotisC6wQ1OLt7fIh+QWKFHcQ8AFf4wbyhBtCy2vq3guh7xgB/QxoLYcqNRGm923TpvBfBUPi8/YW/Qj+GxVZHkgRT/abCh/p6cqa7u4kWyZf5iAgVSEF2WQR6PSh2dgLOwslAr7ovglgFjMNAv2S47fqZvChEubcF/1tHQUReTJz9GkF7/2u+Vn5GeIM//73EwL4/HQAJQ3zHCoK5QEZ6rz3Fyrc0qrh3P2W7SARUyVHFcb/Jhix71bcJO+TH9YAY8mnDer7pvwsKYQi8fJg7vYOE+ab6b0ODi0R/6ncoQZA4rf3chGVD0QSiNIq/HAEaAOIMTwECAZq5G7qYQe388QaFif7CJrKvOIs+pEQYyYN9ifw0N1/+v72NQgGL7YR+hGj9YP3XP9g/aAJovoA01TjFAIdDw83iQG517QGpxH75TsECgOq/YAdyP2yJdYE7gXc/ke7Ktve9zUVN+y/FA8SCPJGMVAJhfss5BbxERj5C+0Sv/zrAL3zHujD2TvQyBqQCr8KEh419hEQSx4OKKfwUfk1BI3QyOM93Ssm3hbM+J76bth4FiMkOA3D+PAJJvML8fQD+wkVD3bk/QgH8271RRkKD3L5feUW/Un7vvqNBC40dvIC3e0BSdNL/wslwDmo/Zr2Uw+Y6BXpZd6gEyL1lQJRITLbOxW1PIsUG9a68kAGxciQALwIJv9aE9AUaxeU2pP8/CUp5A/V1/3W5vb/1kQ6E7QRBAPy0LbmIxanCS3s+Re97Ijp2f11F4Av4O4OFZ8BEMok5EcWQBFZ7oAXdgH18VEPbRQQ+Xrq7wkG7NvbCxPJF2IGOBEFCqj61ObJ9WvjiePqFS/8HiLdPjALTvai9iHsxOkC+BDhD/yaD5QLuxf58GUXeCc+17Hj+RMN8lTq1RTbDnEHOgcqCZLqfeVHCM7j1QSnE8UNDg4s/OcSLt5D7Oz4ww8LFMP89Sum4QHq9hzS/dHjABLsBqbLrA2t/yn9gQ5lGNQDPwVXJ9rsSuVyzSvtXwzMEUYmu/1p5XMBihHI6yMHkQRGCTD+jwBL98ncbDSsD9v5s/6l9U726gVyBKbZawy5BEgVqAB8AaQLxeHv82PvRP1BBHk6K/5j6snnm+cIQSHu1f9V/pn7nAoe/3MFQex0KOTdkeg/Ddb+BxKC+iIQUeK6CcAZKfhCDAb4BwOj+Vrodf5iEOnzJujWF8kPtfDDBqLgAPZBLNEYyRVK91kI9Or8v4H0sxdJ8mXzgh5/+b0ZES5fHi3TbcbqHDLZpfuCMKMK8P0iDrgU1tTS6ComuvwYxpr6+Q98//IG+BdaCDHujBWz+pURTBzb6J3hXOXyCdL4iQtSEmzzOOII3UsW7hhGHKoSG+Ku/7cxtP9A2FIJaANc70r83w6u6r/q2STO7xPs4xndMwcavMLE5BgFef2TGAAML9H/5HIssPd1CoksCvx76IrOSwL25OUAg0LO8kYADgPoF1MKPQJVA0fRsgAJ8bIX//5b8UYpKvHtBT39LQED81L3FQ0n4QXrCgB0I5gcSCBF85rdxvrb7isQWfTlCc8PUelYCvgHRAbU7Wf/eBIn2aj9Dxdy8/X/eQuqBikNOixPFDLN3L/Y8kMNPwO6GFsLj+Zo7gIRLBp3DvMRRQuK+v3yQPQw9V8EURBz8YTeefb+C4gVoOWe9dcUMP3/HorxX/rtEGT1bAAw9d8LmQRb/Pn63gzq9PPs6SwwFCzjYedT/qHemAV+L8sBD/VYD40Ihu1ZDkYBvugAAFEdP+491mP0kv0uBe7reDFBHATjlxV58LzxPTpLHtveyuFs7+zyXfU0JcwUQuJz/LwIkfd0BRUMsfPABU787R9v7LfQEB6W8A/zJQsKIK8BUht7EJDemPZG9Lkg6MZa8gQXCvwsMjj0VQa88KXrvfRp8h34cCHWK/n1qCrf18rrVhAf3U30fOam+4f4iivUChoa9T4y8X/4k80f1W/2jhCbD+XubgiyGecJq/8SGl/riOiZ7uL1IwKv9S0mWPwR7CEBdRe+Jewe9haI0ra34eZnF9gAAiHnFMLiuQDt+H8C/v2i90jpegDNFCMADzXtHknpse4R5FbpL/gW+K0EPg+tGeQbgwJR/or9/PKd65zlHwZTBWj4ghfWArz9ChRPCcP5ZfXO30T0Sg9S6ywT2gtE+b36NxWeMZjdcQbUDsbaTu6HDBcAKNtpAkAaegP99eMwcu6Ky8oodRIY79EAqRMa1p/vqBx+Ki8T+t8d+hjKx+jKE2wQ8wjtHU8f8NZO9bbnCAeWExXzewaqAn0ivvK1AXQOjfOW+0HmbxFI8OHcs/6rEfoWwQuoFcrkDPuSE3r5E/ZgGxQiWNHs+XP5ze/mGHrrx+gu2SHzFzFxJsgNvQ59BUXXovL7HtMYe/RX2cj+T9YVAFM/Te6/FuoP7uWh8Jj3fxqVFUUcj+pR1p7q2gOACqb+KRQQ918BMwLTGVcYPvXh/S3d6uCH/HMV1urOBmosjOR+E7MpGApf9O3lKezX1SUB7Q2R7tr5lh9RH6vzJhPt6AfGmwOdG1IcK/PN8CEBpgB4CIUxSgyv9m4ZjLQ+37MKZvwsGgX43RUiCqQIef/T56v/3P5SBpz9SxjrCU/0sAZT8TIMP/0n7YkDne017VT40gxYEJkZOAG0A0r/hNeYA+LuDRDX/4flRA4q9qoo6yDpB3zuQO747vz5YAAV6Z4gEQHjDVMoeiYh5uPbzgcyyVHsa+YMH2EYivuyImjx5hfTEV/7ZNy72SzcDvwNH+oBCD04Dubo/f+87uH7gQD95ZD0bic9Im4iQveE5I/lVO71CIvuRwHABYQPAgvN+20WcBu29HzbVPSY3ov81iJ8Dc8IDQuKBv3sH/NjAff4/uDiAOoBi/RwFy4aPCDb6xDzg/yB8N4QESA86uG2sSPs67rnnU2kJywLPu7zEcTg0sfQ/mAXQvkP8vgY1fd6HHIY8xSy4dHYH/5fyIv7pxEwLYceshXE69DdcBT75SwGbeZr+SANkwsnJDER1CAI5FnvudGs6PwQHwQEC7HxpDBW+0IPjQ7zy3ncOue+GPnuEyC8GusCXi0rB+EPdvBc5MnMMNXk+osSxy2HA9YMtga9AqsPHPvG6oLT2+NTBv0veSGc+f8Ac/NlAoIEXeie6uHx5xP8AIYDUx7D/IALnf498HwFwxSC+yXLyQSlGmzzev/4EMT3Qtw4A+kLLAdgEzsBnf+f+ksX4h+N/B/4rPCT5RLXzv8ZBrf90COoAGT9Uw9hDmMEffTk6uDo0Bas+2ff4QOfCS8KOgjxAuTwZgJQFmbsSfX9FfQS6wiN++r3hf17/H399QeY7VYbwSi00TjmRfyU8V/s9gISEy8AgCGSIzT6Qv4pCUfiU91X4jwCMAJu7GIV1wtrN9Iy7QDm6m7Of9zE3d77Gg9dIKMSTw2oC4kAGiu7AGvVvM2P65wBnvfCKMMEUfPSIPgSKPVx6UQZ0PqD0fT95w81F4ATThiM6WvkxPgN3RnyogyVJlgCy/iNBFYKORFC7Hz8IQQHBbUBB/BY5er+VwHU/70pahKB9/LhreT47SwM3ChaFeEKwgNLCv3xtgFuBXPl5NpJ6zcLKv1GCZr0G+woDfgtdSWj7WkWfAcS393ste/5D8YGUgVi69LdgRrqJx7tZNwLGWkC+QEM8ZD7qCpfAuIl4+3z6WwI4u7s9Ubc0gOXBXcfM/Ap7u4S2O9vJQwLmgv96KL5ugE90X8jiAlMA+/iFOPNDecCATef8acPKwq8umIHAwwHCAvz9f2c7T8BVz7ZHMo3p+ht3/flkM8G+kXkNhRd+lj/3AgTBUBAzRiI8pAB7fxn1PP8ew5u4uT3xQ1H3rvv6ycdDK7y5/biKJUF7uCLD+seQwlCAVDwRMyT/p34I+gED5Iz2BbM+7oNoPEjDEb3xfmW7KjUNgqh8rj7gzlONhnvnN+p8fj1yurJAycEf9plGgEenQPFBwkZAQRw5TYQLd338G4VhexWBIEKIB7L9gDv4wWc4v4Gevn9Fz4cQfFUDxHvG+g8+GcZwg7BCbkXWeRf0SLsGw3D9MoN3hB/+BgO4hpMEKjpevu494/38vzZ+YoLSfpw7bUUiw4g4BMXvxCY2L78oxLj+L8KIxJqBMQHevF98gL90Pzu37n7DiK3H0n9BOxVCTP15CZUETbrj+VH0oH69/51E/Ab8iW6933jIuBJ8+Iob+fV8wYIRg3uG+MHjQTlB9cUp/QW1RXn2g6U5wvPyxUJPgQajArHE6bvIOnk8hMEq+sN7E0KkOf4Ccco6RBWBzcJCu8E0IYAOwei+kQe0A0iBi/4ZepX+uTmEvaTCQ8NLRFgEwQLLu/0B5QPFu9p30PnS/UcHR0pKvvrHHoTB+y++PfiP+6D5yT2oxtc9lsLRz0cDBf75fYT1Y3vfcpd6Yoi7QqVPrIc+uC3/g4gy/uC28f+E/PE4vkJ1CsuDsUKrfKj0IrjZv+jKRYBl+oDIYgWb/M/LEsO2+BJB93S4tng8jz5NAV/ChUjMhTWBzsE6fPw2IYAiBD6CxMMqQFNDmLjNP3wAiXmnhIwCL7vTftgD1EC0N7Y/jw0NylX91jr0exX47sABPJ38JkK0QqNFf0Bh+pz6hUerhRJBwoL3PEBFhL5lOfeADcH2QjzCY/+y9zA674HTPyR7d0UwxkhC8ATkvtc0E/xgR0h8nj+SQTTDz0PivsECcDnq/y2A4Lo/ONZC9YovgG+EWUHafr6IBz34L/3zlAbuSl/5bgCECBw/sz68Pl/5EEOZUMEAhPRkOppI/QQwff4BUTn7/9j/sL3S+Ts8tEmLv9z+N7+iAcY+wUFowORzdYAXCewDPP4ahDtCdnphAjg7lDl8BcFG0P5RPSmBVkK8g/c/ToB0fyu7WLlQ/drGykM1Rtr7AHTcwET9pIScCnE/ifr0/mz7HMWGRfWCiUCAsqD8br6dhIXBWH5kAcP9CQaHAtiGSQLKuSl1nz3RwtWA4gQ0s8jIlIeLet/JHD6zwyC5wTl0vht45o6yyh87sb3xv+b5iDbVgLF/rgFnQjRDpz0f9Z+NtUwevZ29VnaONpH70ciCDf7FHUEk+nE39EOsgEk8670ygOeHYjbDP+vGvkDQwjI7PkJA+v4AF0Ui9hkBFcwaxP21bv0OelR1+81TxcD7N8FxCU0/IrrRg/Q35YN5/pu8BQN2e4bJs0TOgbR9BPvIufB5k4KW/ZjKqAK7BTjE9jQpgFZ8E/zMfJs99oRMgUjC3IMUxreBmD2q+Dx59cAQd7473YT8ySiGXwOYxVdBfIKBeTJ4Qv5wu2eEMD6/eYJ/24ZxSJfD8H4dNreBMwT898M4/gSnC7DCmT6iAHl5nbuM/c42bPupixrOY0QAvAJAlUTaueu9xIK7ssGACMbJd7VBJEaP/mLAm4DNfeS8e0V1Bw27ZoONQyj86z2FRX1ARbSsgwd+KnvR/dXHuMZo89rEYMLW/vxDRkyqQ39zgkHQNrbxGXvCgGx8/UJhExuIyz0qxa4Fc/R4e5PNcX0AtmEHMLmW8rKE0Mi3gVe6Hj8YfRT2k4dakpQ+SEAaCDsxv7jnhgvAFz4c/Xv5+nkCBiYRvoFC9aWDsj88uyYG3AVT+Ob+eQN6eIu6rUMKiGT7bEGZgPkx0YONRuHFdwMuQ1HEZvc7M3V+4kWogRnI5EKje+j/OP0ZwegCqAAt+Zn6G/zDwssEpD+PgWUCpgYzPfrARD7NNzO/b7s2P6vEaEVTwUj8JnwmeObMg0m8e9zEP71FvU8DLfzZ/Dm+3L9Mf1K6lAAWjKPHUjiDAAa/6HeQAWpBUcH3Ox4DmwQf+kwEbkP/QzI0T4BRPpwyFwetSN6IdPo/fl8Cgnm5RO5EoQDkfph+SjmFPpu97HsngGh7e89hSS4y6wakQXF9XoTFQWhEtXXD/b597HwIB7TFRYP/7qbAmMKNenNIL/51QNs8FkJJQ8ICkcEAAZzAFrF6BhqErXyKfuk3pcHoxSPAsUHYwGPAVYbGvalCh8VqerEBbT9Vdyf68QPW/HC52AJ3Qcp70IV5Cq3/NQOBQCO/lHvjOvBHvsB3PMY/YcBS+ua+wITWuoL8T0JSAqGBuIccRAI6x737AhLE9LtDO1NHPvVh9PsIL8CgQ+0DHDgCugZCooopf8oDBEqlwGM52X8AgOi4XT17Pe18pffTAZZQaTrNxt1NofixOyz/9UOKNRD5ncZ3Oxb+o4cOTRYBcX3KgH6xF76qwzn7Hb1Svn3GZvnRgibMPr0ZRTpDZ/0Fe2mA+/zIeOwF0kCYgdS9Zb+vf904/kV5QRs+64MxRq7C6gP6RQA3nLl+ffh+S/2OPwxBvD3mu4sEZshtP5l6oMB9w5dxC7ndTFkB9IK6TRIEeXaGPjVDKrs4c9yCLILvetfFTISmANUBg8fh/LN6DgJrv3Z8x3uNxyhAP4DjReY4ufXUPXW+xgIjxO37aAj/xAG/W4VmuDQAWH1p+M9D0QnfA569MkEneO91yv+sA9b+fr1JRLM9ZIJr03oBeLh7Ahp8KbmAOn2EZcel/Z6EGEUvNW55vITAfkF23X8aRY55u0MWy7sDgkD9/U/AYL0UQ4oA8DXxv5IIbPr8s3kG2YHE+nzA0EM5SS3ISYjhviu0RvyyOC50dQCsRNrFvUKXhE4JAbiUPIdESHq2Oua9W4J4/zaFHUdQwqmFe4HfwW0y9bQmgKc/VP6GPnuCvEFjBJTBjYC4g9uAG0GYPyQ9+H4tOkM+Pj9qeAyGGAhQxpbH1fkmu9B6wQO9Qzr7C76bPOB71cLHiyh+OUc5wIc3QPx9ez4IcH68f89/yTnmvNPCNoOdgD8GCD9tOuV+LsqeQZ73ScM+fNb8vv6Vvcz/goVnRjh/YT5HxNJEy3jjdZI8gcFEwTrG4oN8P+uJrr6Vs/QABL8evFPCF/wygLQCMn6dh6iGZbeDQ9NHwDl6fb24JAM4Ade8r8R+vlDDB75y/VB6tr/AhgM+IQDngiUC/sJ6Ay55vXwEgFi5D8Xjhig/f72afITDKrx7frjFGboZu7n+7UdjiQVEcMgSO+Q3bzihPjUAg3yHvs74B3+kx/MEicxWy7ZC4HiAMsa6nThmvdCCQIbDjCG33TyI/JT9Zwynfwe62b4WATkBEYBsQvH/q4OjgeV3/DhQxSHG/b7lAAX5zMOVxsc6AIiwu8S0Nrvf+oZHHQt/Cdv/Hv59eOj7oMHbfa4HLL5RuJh5JcMmg9VHdApC915/c8A+PMK8JjyUw4TEd0MX/eO8zT/sxsC6AblffoW6wwZtwIi9lsdPRFxA/AMl/FbEBkOzNUA50jpvPqaGEM0nAoM4wj8lP4A+m3q0heuGRX2yP2k7yj5hwKb+wj+NgCZCAsk1fxg0P8JKwWl8gAPwAm3B2v0IAJW+WfvqwzqAZYPRgCi+XHjIPxQGjnsbxlOANj+kvpC3TkVkA37CnYP6RdL5orqrPtL4nUoygdR3R/8WR7DAOLrcBp1EOoDq9zv53n7M/zpD27owANACjz/eyFaDK0OovsS/IQOI9Mx7DAbSgl77DrwJv027h8qHCXS8UoKDf+D7zzxs+Y99lYTvQOgAy8DuAVFGf/rFwZ2BxzcshvI+vvVGfmOEfgoVfZRCosp5d3FxDodzx4E0hEV8BlI5SsA7f+Y30sCYDXsCTbjpPlJKKPod9tWH2EFWNTK484iP/3UIBUoB/FJ+1TulPSV11b7rRIFBoQANQdBEmkSjCWS7Vb2hQhQ8VDKZPXPEqvhzCLrBv//sCXdG9H3leEt//DtjAZ56Az5hiAU3/3plAgjBdoUeRZD+Z0Rex9T+prcSNo589gGQRzJCej+nQYZAlf7aOXL/KcIXxOVDgnXzfvNGhwMlwYJ/Tb9ovuO+ObWKeozBhYZmilfH1UTHfRsAP3WmtHd8kn+lCqdEsgazgHrzP/7NwnY4kvsnhWjC2X3vxIYEnMNtxO3COnrw9JIBxz3bfXzAssC/jST+/n/Ogiv8qf8nPTD4iEVzzG01nb/fuTZ5p8kbhtCCE7i2ged4ur4KRC8JDEQce8nDUbVjO3W3oUQIhCw7y8opvy88XonfDFL3ocTjOWZwrgTAtteCKAcrjHpJMzYQM9g8HMLevoHFlP8wwp4GNr9IhN03dTyzR3P4sjt9AFXBcka/fJ07yENl/Zr+X8FHPQuFlkdjP0d/p76nw0J7mbZNf799coEbRrj+JMNSSbZ6BTnhQlbBgTqZv3pIX4T8BupBMzkI+RR/JnyW+oxARb1IAuJ/KoLsx3w90oKIOMw2rcWph0LCtwRXh9w6CTmnPtR9SzoqvVlIvXbMhHOKwLlNQ7QCvQN4t4PAM0Kreg4IiMRav/35+sOfOUl05IQyPO7+mTojCJoMaf0zCZwGVjolQFf5+PztQaR1hP39ACv7swJ/Sh+/qoPZwrB5OsAnORLIKP59+/nC5IFORgd5KIW4/BL99QRvgWvAVvvXg/o+xL3178wB3IRNgLwODIFayDB+ibtjeDo3NT6sQfmFyrvo/RbDWolpvCM/C76UNZPEPoU8xuS/f4Ixx7NBzXVnOYRF7HGLvdYE+QNeyTm7XAM1/D9yzQMLh5q+MkRvyej9g7xXu6KC/EG/+XNCersyNTFAq0PEhioLPz9CwaS/MXT6g4R9Jz+4yGi+WQM2Pcp3BEVfgWz4kwEmgrnFTbqVPh3GZAJfxr1AhHj28j9A/YGlwKW/GEOWDGo3BEIVe9N92oVWuai8779txtXADoV1/SE8TP0m/8SIHPvoQ2i8L0Gzvrv+q8VAANoFlLmQOkM5GMbHyWa9c/4Tfgf/ODxMx5jClIQsAqW6qf2yuRi6Lz3lgnt+dgCJwu0CUARsAoz9CDwJA/5Ah0C/PyB5Jftmw00+7oZwStN7PYXT/AB0wgcmv9A71H/6wIXDjQdMAw37Y/u1PXTBKHt8upt+6LlOBPdIdQmdxVZ7RIMONoT5OwIpAHPAtXyvRhZBdL/Bg6B7gnj2+6+BsQFfRgRCF7l4gQHGGcKKf7tC0j2d922B570hP2KIwT/OO2j/bQp5QbT4VkT/QGQzoj7QCybBqQBJifK7jGsR/ucGPnym+2xFM8DNcp8GwsdshpDFwwWMf7sr/gCTQyBAkMLeh1aAz3bsvcH3PwESRhwJkzqkuWSKfXvxwuiPWcPDdNR93Ple9TX6mIB3jb2/gH7sAuq8/ANwBB58zv8aeavAUQk5/lUHjYEM+xU4LfdAe334u8KNhbVMy8iyRjk+YzqHf6T0kD4wfYyCfkhgAhTEacEtPqO8anV1sy4G5QqOgl7EHP7JQgnDK4LbO/azxzsKu61/FQFBx4WNNIXCxV53nTIkPjBBkIDVPpP+Sj6mAly/6AAWRvYFD4EyO++82r1BvzLJqf5LsWKC2QWrwGJDQ0JMfoq3T3ptQjkIV8SKhopBkDhYf2/+gfwZ+WHAjoERQWA/vPmXw+pIaATL+9qDxD/SdrpBP0Yk/bc9HEtBuvs3psEmfiW4Y/+Uj9KBSDudxkFK6PUnMsZFTwAMfaSDiADV8dEEao73fPJ62IjKQhKzDEEMQ0zB2/41BFuBAvuBRAK2CfpjwCODuP7gh+6Q8vNtfLyIOHrQumkF3gFTcAP8+cANfydI8QmuxwB9s8FR+8SwdLyUi8cF1DXkyzaEivJswUN/bX10v/lGq/ygPrcHlQBgw05/Qb9YNth8GQIAvNABXf4fyLcIbzxfPvD7k/i2QP599zr5Rq8IBAFyA2u+rnwJwNp56oGbALrDbgfAvCu9Iv4KSnsBpDRduZw62ruyf9YJOcNkhm8FRnscfTyC0MUgeZOxl77Exs3+1IEcg5hBln/7//V7fAQOzPy707sfgAoCtv5fO5l9Wb+iBpR8cnlrvOHA1YbggAm730NTCqI/SPscRKv4FfsAxSK8b4YgwyGBocAweYU97z5oQda5i4HewvQARcV0AZsAcP1LSJT8EDhGu9025sJHgo5DzEcohnc+5v/P/ZxAIIa8O0l9hLh4eEnDF8VoBx9DYbvvujWCWz8a/x2EJkBI+Wnx0P2KxmUJ8dGsxIs5g3xBeKD8OQDSftEDj/fMek1MU0NXibsKxfrPsib1hYL/fedDhMcau8V8T0Iaw/e+1oJj+od2iwbuyCp/Af8jQGC5gjy5AMq/7wEOv6gEyAKM/hDDn8NBAJy+KD91um4/4QMV9stB/MPSQBaFqkZ0QQH/UEjk9J+vgQUpBSe2ZTVeCzsDKb8CRiFF/XzVtBEF33U4PY1VGwSxvPt4bkW6P+v+Ur+atDN7mX6eBpr7ughWDeR7d4JO+CAFQ79y+MQJnvoBQHj95/cKwPXClgITwGKBKYPkwxk6EkCQw/B9+kDFgxC/6zxRe933nj7ChDsMjQccd5t8Hfp0f2f/fgZW/3A7XQW4d2q/xAbHEPkBwzbVQ7Nyfr35gtY+R8CgP0WCAcCRvM+7QAveQi7+z4R6eSbCkT87ddy6TsR/iklAKnwKwVmDR/6h+e+/enpHgQvKMH8nf+sDKwV//T27/MG4u0s+EIJfPpiADkyQgCO6PkC8+9e8HLamv2C+W8OLDliGYwPnd3E/z778c84Cwf9O+w3+dsQlh1CEp8PGAgI4NPSfxQH/Jv4FhA1D9IMNgCUJUbm2eP4C4H7Qe/8AvoPreE2GFwUl+3W1Ur+GDPq/xwHCAxgCSHj5PnxAtrlWQBQARQGUuSaAHAlBP+F9Z8QEvvrBRIHjuT4+7fx5fjGCpgdIQD6EgkSvPYFDofT0PbrBH35ZPbVDMQZCuPED5whyf5m6ij3bOEE9K4OXRCoDAnqLRbaD+YCIwJtB8bwl9sX/M3z1PedAOgH6fPBE8QPZvFCIDwmRf8M+zUPIdGm1Aj/jgfSGMUJtfc0/4gL9eeA+wwV4vc6CrccpvvHCkjxN9EIB1jiRvdzJb8J8AEZBKYG0/rYHd//sdmJ7Wb0Ex5DCQMAuxz4DeoH++QH05PwCgah/g3/tg0bGwIUmuE84qX7CR1WEfnz2wblACX2r/NJMN0Jgtxn/5zXb+UYDt8keiQTF+kOwOyRwSXokP6F9w4lehQuBKf6NQcj+lMDovJU7dMOoeSYKdj4RfdwFgzspgvT77oPdPKGE4ENFuFTAQftOBQz+44NSwMX70MqQfgC15v9kgtSDQUR8dpt0l8CJhhpFa0KEBfDGTj71uPV9oT5JvgI8XnpWPKPCysrHgfJCA4cxPRT9gD33O8rDqkO6eF6428h5gt54voFrgu3C9MM//EB4h/uSQ6mFJP5OA8bL7byod3C/kPvyuMYCRcmhQXtB+sGis0w5bgW2hfXCQMUc/7vve34FRnUGBclqPGG8wTnSvnv+wL/UjCPGWP0M+xkFPT+FOMY4hj/CQvc9HAeieiG7GwwcxXr7lMGev9C4xv09uIZIsj2xe3OH8TrDRY+F+wjqeM02hsD1diwEvoPYRAIBwMiagpI4KwLt9cuDtTzhO3LIV/qiBXD8sD+jwvK9toB6doGKd0W3//sBZnhZQww/UnreszUBNEXdPV+ILb8XCUkFhf1qvzu4GYNeOwV3db8mwoiHPkSbBAaC4Tt0Ojo/1TsIfRXFwwJIv6HCfn7RAYc+Urxiv4f+7ofzgDvCSgJeP9BB3HY0fE+8M709/8oE572DAj5QBX/Eu1I51gLQNY7zu8uSwlQFkUokAKh6JH1iBAgAB7UpPJzALr2IDMALPH8vvRsDX3jduhpBUL/DvJc4kgOjeDwGmNBuvHy/goNfPfI0zrqowpTCjcELBwq7/ffDRldCYj4fAgbIY/sHvU6DMgHuAuK/lX9acuZ5yL8NgQbJQ41EyQ/9Kbt7+0d5YbbORqP+5LNJQn6/twAtDQaMf73t+zv7oP1evkH9VAU9xZI9PMAZ/jJ9mMciOhc5gTv+gnCJjEOiiJL8WXrTxKuAd/kB/Nv9LTkHvwYBIIdNQfWD7sPi+ixBfAL8/7I5oAFcRKD3KABZCetCxb0D/RX8cHaIP8XFPXzHO4NF30dVf3+HxcLWP6+9EXu9+3F4VUqPfWt4nIOqCf4HSDx6Q3S1GLcGAQ6B9oGHBlNJ9LjZfGg9cL7+/9M/jIFg9AT3BcV6iEkEocwUR6/68Hpl93W9bgKGAIE/MboQ/vSP2EvzuYr9ub7C9gM6ucIzg02DO8RVvGB5tQf2he769Dp+OkP8bcOffdCB/sqwf+ODgXq9NhbJ9ABVdf1FIsOMOjcDx37hfy6D9v+rxKm6DPzix+m8Ff0ZBFwDOX9NPlUBiPfL/a+KPz51+meEi8V/PHL+N7zG/0C/qHnvBTeD+DneRzCMRnm3v/mCAvWkdvO74EGNummFx4/IA3c8E4Bqf7g2/UReSXM8Jj3iyWI6sTTSyzgGSzjI/GI+wm6efIORisD8AXlKA8bT9PW1VggN+Ng4N8uKQIf6QApBRD42Sn7fhRJCSLl5PLBDl3oLg4OHrv9bhPG/M3j8vCOCzYOB/PV9JvuCuw+E20n1Q2u6qbvjvCk+QQgCxm0GS8A0+E65dz/ai8vFO3q6dxF8RDhrvCSLVsFwA6fAEv1yx5d9DH9wAxt9X7sCenJ+c/6Ng0vCGkJkRVf/xYcpAI/3Wbshfo78NbloCBxHhASJxIrA/P4D+ac+5zySPUr+fkI1Qw08OoKQRKyCiX1FAuyDsXbIemo+58cthNjBnb7Etlb/DwFBAoLBsQNe/6l2WgAAv8eCmT7Tf8hCK72mS7WJlj+peqo7zfNVeEOAELzLRp0E5AvBwfI+IAH8gIZE37m8AHx6SH0QA96+Gf0bvmjAjjwdg2g7Koefxqz2AMYwPvCA0kGOwwNDMfYaPF6/fX3wd7KCmAIU+/iPsUiFQb1+ivtse1e7+wslQFh3WYL6f3p1xb7TCnJARsElw5R6ePkhg2VJyAFcvG9BiT3pt5O83/yXAIUINcUWfel7TELdQO/7G4Grxql+YLzoAVO/gMK1P/x/skBTdkI7ksQFhrKD4UTwSRyxCHcCQpK5qAi4i24Kr720tS25qjoSuK69nky/PQB8doRRgg2/2sdYj5b4TXYg+yi5jHwYgbsLz0bXgMSBCPk3s0F/TQSawe62BwNrD5q97sn4huc7jvu7tim4aXksRCTElD9rw94FkUDdfcf+hfmhwMLEo/1ugMQE4cORvHN344FiSkwAaHZTej59LMJFAvd/pMHoRewDfTxTOqf/kEaxBwVBN/5pwsv5qHXlNjn6aUjVDKUG1PRD/uLExTzzwobCPP4y+gkFKn8APu8GtEsVgVQxYgIIN4uy+gLoBxDAZsT0yuX6ecGfAyDBscDde7y+3vM+uCuIPP5KA34MUDf4vF6Do/rsQ+6FcoESQLH8h/5yAdJ6nfaufyfGDAicSKR/RvzhfZ07bniABCXL7zTOffrCBj5SxjdHVgx9vFj52rbR+fL4v8GQS0A1w8B3AjsEUEQePm9Dm/0oPE/BSsVcwX8Ef/p0+5gAzjYvPG0F/0R4d/lBEUaLiBnGZbv2vNX1QH/mxQ7/FsQ2BIl+xfp8PYR7GgCeBmcCH/1ouhBGqEGdecCGwcQMBSyDLXSuOK2BhcI6Qam/L7jc/DqAl/+iPftD08nZvOaAaMewgVvGQ3roN9j9I7RfgxIH0sENQ3NFPT9WNzXBwz2N/ipFTv0DQTNEb0K6PwMEPwIj+fL6fXpVfEU9bwM0x42HhD6t/DvEDPreux5EwX1auvZEP0dOxP7DJ0KFdedtMPd/SGZOlYAtgkvFV3yJPzkCKEB8+N98J3RreXKLsUjBC9mEOL9m/1YBlv4n8eq4eXwEhOqB8YExxoiBTcGUf5dFBD3KfCt/YPmafM0AYYj6RPW96TrxvIhCDb0ZwpPClXlV/GcA/gq3Bzf9sQMhvOg6wTh8vw8IMIBehYD5UrQRBPSIXYO+f937O4HNfwm0jQjxwiYC18mrN+66pjrmP4pCcgCDuoC9jofbgk5+gT3ehHXCw0JcfRU5sv4rvtyD4T+GhYUElr+a/mb7/MNWvI7DMIHNNH49LAEovsIDxcqdBPgFr4CkOXk9bTfmOEh4fj/BP64FPYVe/GhP40X8/ip8lXwvufb7b0vFdiJ9q0dLPM+4yn/vCXE8oIFFvMrG1oEqeMSM1/w4/FCJj0aEeKX6bjy+tCBBbATIRxiEPQSZ//r2mcHr/hU+PX2svkNDhf68AoWDqH9ROkIA3nqZu+cIZ3dABcHFrUJ1ykS8u0NB9PJ9AISgc4H8AYXZyUDBgkjUO846t8W7OQl84XvXRZd/gHoxxCWCD4mbh3f5VC2Zeg8ENoEIRoiD5YKsvs8DmwkXfTz4hbjhtUx9hUCnfzhK5sjLAKk+jf7A/sn9m0NyPrn8ccMgB7OAK7kuiiuDurRBOUB5q/unwLqISYS3v3lFYEV+fO46yQW3Pdx4uzvvOTOBswHdg3wGSsQHhAc/NDiYNtE/Vz12xGtNazyMQxSGu3iqPVzCH0AVujK5okE6wspD0gSSQnm9xr8lPTS3ir4bQ9sGqL+MPn6DU//OSSUA2DkmPSv0Cfa7P5CJp8OthePKQ7uZOhz7fwLxfMX5gMOxfqmFwERzgzcFrUJVg+W6bTfJtMc/ucM5OdEG1sHTxgNHCUBRyDC7tDkwOQf6DbgcP8fMgTrbv+j+MH/SR1m8B8P4+QvAuMePuwsGHUTXfmO+zUKIuow8uYe3umD1MPyJRzFJ0Mk3gnp57fu9vmaE8Tv4fSlB6zbivv8BpACVgsVDlwJiNyS9n4e/Q8aDlkDBu4z/RwLKvSV6GfmxvRA/AcXbis370jzTxgIDmMClgVj+qnU6veiI3kIoPOVCbv6hNvt+P8b2hJx/SQKx/hI560DmiajC1zZFPytHH0CPebZBIP8AOem6f3t5Q69EbggfgBd/fsFFgU7DcLp4gRI7TDtaQlP/zvzhBMCIx/SDfyzE1gHMxUVG34JJcz9+/MIVerKBoQeC/CG1Mj4RA84A9kHIzgU9z3Y1/+HG+kBtuIYFv7pc+5QCVbwgv8hMf0NdNMPBonvxRoXDiTnbg5U78gTsvvW7sEN0gN48p/yRAll7PkJCBH7+aUFNwI5F+vwxe7FKxkCQ+fZ6SbqjfskEjIatvd5J5kHBNzK+aD98B3/8NnwEdu75OkNZAvCMmMMGhMR9WfpbwRA/Lz23OvpDnnlPfz1B7L99CCXA88C4up495sYKvyMBSsZ+9+05UMXegYm8TXqDhS1C/X9MxU8H4ILweCR7Ezm3/zUExrwheWK8wYWGRyNF+MYvQHb+qfeq9Xf9YUJExE39tYZFBQP7gEDpffu8UrmiRNFCwr3RB19FIoF6BE4N0a/A6aL/cEALRxvA30N2wez9RIKlRlOA7rs/Ral6Z/f/AebECYQ3ez9+az4LvDq/MP+Tgm7DG4cgwEv5R/5PPrv/+z7aQkuCF3waRnwIHL+qAX4/NvQ4OBZCVYaxw01AyoR5O2O5un8thJ2C5v9u/5S653/jQ3bCc3uug4PBPPZX/l17sUgDhGGCXIOId9FCM0ML/q25hQIne4f85YbAwg2QcrtyeLmAtHiowgV52IGjv8C/E0cewYLEKABogT/75v9DvtC69f5yuLRHBMNAAmdMwr8KNvP1IDwgw1YHwINGAfS/6LfVfQtCLgYowHg+oTvDvuvFG4Jtxni6YHyQPQK65wFdfXxG24L9QjxB0fp/ws2Btn4KuPb+iEUp++mJZgKQ+NhEAjy7/ld+g8BUgGI/EAH7fsoE/TpOA+nDqzpXxZp8zX9l/0pEVYSOOsP7y/WXvAOBQMQryeYGS3/gAFvCrjudN1+4BUJNxe1AJkcrgZt45kCAP2W8T4DFRusAj/JagL5QykLPQYzGXDEd9RrDtTspveOJtgh6fNX+WwSC/SO0+v83v0o6+QuUjdu8+PiWif9AXPTIAde7hvYU/eiGYb3EAqASN4AEtRv8Av6v/1RDh0TtvTs9BUjUhw345HpOxZy6SLjbB7G9t7oVx04FT/VGP74LY0ElAwUCKrpm9IPDZAQP+CIARz5Bgm7++cMihlw81sTYQe85TDiQhWw9qXovyqiBSP9ggDeEAr9//l7Ir/TKeCJEbzwiPH9COMiFiKm+MTyHwhd6Dv3UhZv7tHoVxHZ+Rby6QvkBIkVi/0sC9vpJedwKBPgAQVLIK4PMQNP1Ev2xfK4/GwPfx1y+dzr2wMa6T8xpiyS4cPqMPge9lHwAwDEDiwF0fviAWr/gwx+IPL/nOds//EEYAyt/criVe8I//wJUPc7BLLwwOzqH40UQAzOAGMG8O2+8SUFi/KHDVgN7weS6CX3gxDn/rjyKvItH+HxkOmGHPERvQYCAtoFke4q6+kOVAlZ8qAIAPrD5Bb57RF5Gc/iJPcXHDn1FAxcICDxyPbR+0PnkxP3EGMBEfRU4XbzOOjvG4Y4Jfv89ngL2Nr9wUcUDSjtEWwWDgnYBHnht/xD+XDgAC24BPrJnOWxFjsaIwXEORAccdkz8JH93NRs9iQjEAPGAMED/voD534bOxuu3AAXs/z509bkzvYGDoL3JDPsLbv2RQAwAD/wIMVKFJsHvOfEKkD/mvNW8BAbExQtCjz4gdQaDtzzeRjj/4MKGxjm4lsH2+Pq+zT4MP3r7o4BRS08BXoXk+49++Dn6PHWFYPpUABEDfkSwQUZEoT68Oc19ef8/Af56O4CoQS8DnQdI+/M6JENxhDY56r5/QSkB5sNMO5z+3T6FBM7FnHpc/3L790QJA8l5VkJGANFDGkN2PFh4WsNORR89w4ZE/jY8dj7Zu/l7hzvlQmYGtITiPw6+0ToKvJpFfMBnAvMASDm5QeTFvkk/wCn6z4SRdxTz3D4NBKfBkUSRx8FAicCU/i8IWrj9M6HEovh3eqGIj8urPSm9YUH0eJK87YcYPp/4ascR/wI59ITXTGfC0r0XQMi6uX1ROAbCokTKvvQMLXzj9a7Cab88vGHIboClNYL9Cn3gQp9BoEcdCwW5tLsnADK8j0JSxCkBdrrtu2GEuMEGO/D/S7vD+XBIKkzjf4vDrEGL9bF+loFcgZ7/e30UwDu7FX27P67ImME7/UsBojshxWKAWMD9/q+EgcoZ97w6R7qHe/v8R0OoxQcBF8Kt/9EFYTWQ9+SCgoE+ghRE3wnCPl2B4f9EuEJAcgOwQwS6lrodQP99Q/eURCELy4ejgP/9SrzntpDFoohZfOjAGHy7dVh6ZgJ7AhzIawQXuZX9TMAbwhn95/xdwMfFcQdvRKMIZPpZediGfzfJeB39TcUQvx25ioXq/UFDSsnKg3p1orgCRoZ9yn9RhAtDPDzQf5WDbP5Z/6Z+DXoFNUZ+/olqyA8B10X3v/j7twqn//N8LP4gOCn4gjraRStFxwLjfur+RIQTfk6A9EG7eCT7eL3igo+KFozawmlBJz1ubD72LjsMB3ZGFgKDhIV6MYQcgzNIZXo7vebGLfY3u9t5uEdrRW1IC76Nbx1BfISPwSp6NAWN/1s/ZIma+yl8eb0mAkxBsD6RiUmFkH6pPN24G7kRPxXAj/xzvcs8mgOSCXKGC8wVesh7dDlQtMj/TP/pTfiIKoPwvDI9PYBROymAhzlSf9U6Srl8Qg7KWFJehd380Hlku3X7r/5TgVC3mPOSAXYDbgQaiYrIiYLUs846c33G/sRKQ0lzuef8s4mYvfG+kcUaPlG6Tbv5uQh/db/RP9WFAj9zhte9wL4eCiZD0XvPvg+DJ7qT+9PALr6itDD8sQL0/06Crgc6Tjr9FkCxPxm5FUGIQWq9yznkvj9AtccM//aBIcNpfsx7cneZw0wApkFxv9BBSwUZw0SBWAMtxBP6jwKoejG0Lv1Gfyk90cINyDWAtoMHfqq+7AC9u5BDvIKSwAI/3rz5Oko/bYPLO9L8oIviguK/FQWG+Zr/lwEJfnk8xf3nRvt61HqbR6MI4n5xgcSDMeuQucSC6v0hRmLCSgmQgjDC7wQXtaCAlP7H+yc5rAP8BQv/rMXnuWkBYTye/9rFDLefAna8jj7uRYIMMsFN+HA/3TS5BPo+J0CZSon5L0ecN1n4GomvBjKF/fO8v5JH0XtDN9fDPUbKvWwHF706OYu4bMA0ioP2ZAEkfRc6j0dvB5OJkP3G/+K7WnmFPilBEgYIgLu8B/pPRUfFAMTivMZ0tz6SvYeFT4DvvhvJF4YBPX28+oLiOyv9QQDn+1i86kWYgaV4REnaxe25Lz0z/RxE/MI3wIcGAfs/fbjA3Pf2QQFCwj8gvyJ+Iv9HvAAIaIbo+v9DG4HUNRd1fEM1AsaGYs8Bgjo+30HffTN6lPnPQFb8FTHuQAHIsX68y/eLyDnigDbBnPpi94o8v4Q7wwx//gIOgAc/Z0ik+117DYXyt+G4cjtrgbHHs8C1yakExTsVBMT9PDr/u5n7/D9nPAxGK/0jA5vJ63++hJV5UraINt8F3ojQwDBLkoWPQp065/fGths2k0AAv1/B58TlTOf/YP31hqD7N71I+V07fPp1Pq2NkwPbhvFFaPnxOgi6nLwHv23FjP+Ef63EC8aYADw30oT3uM66l4Zx/AGBZoknRq06uj1UwJx7C7gn/70EBrzzhV9/wH4vQliDscTutR2BQoktekR/TT4KQIxJZkO0vyD3szhk/Eu+a0EUAO8FtADNQcMBegN9viH8yYq2vN5CtUIQ9Rz7Ev4EOgJ9isypAX9/8f60PKXENX5Whr/+NDxYRiEBToA9frx/pnrluQdCwIOQOLU+CARmO9zBAUhUhnREKMFw+WR9MsKwuszDqkF2e07/N7YVxlaF9Lk5gyLBQr6/t4yFCAsqwEYCbnjRPxQAHXtR/qx/6IHjQImDr/rxhn+HzzhFfTz3qEFTSGBCiMEhv8SCOX2/vBA8uoNtve96T0X2whV/Z4Oog/r4cnkBQgC/vzlAAf+Movsnv12J9QQ7g+V7sbkONE76fAjMR7z8b8ASRwF3Ifc+QuGGxgHNQDhDUL7/PJW+ZMdovIx6YkWwAC/8OzvURuo9q7sowVE+QUVOv6w/eX8qgrc/6kD7yrQ+UvwJPGv8HPvWweZC3bpTgwEDtoAROjc+eIsHgOW5ggCJAyEBFT7/+6P88D3ZRVVFFPf8u6JC6Ej8h0t5ljyOAwWBJP4iQlpCNrxZwpu5uDjV/CyBZks/usUB1khFQJ87q0GJADs1esUW+/g6W37pRH8Qf/zOQBsDDrfS+bPDcUAJO7OGVYNxwgR/un46ALK4mT/lA1z+fMLmu5U3Yj/WiHSGMD+MRUTBBjZRt1EHMYfzf9l+0HfjvhL/jgf5iAE5gkFDgIF6Lb4vP3O+CwKBwCJADgDzeU6F2MPs/ERD5b/XAZb+YsLhgme3zYFPu3S+eURABC1DjnpzgkTCaj7rO/v/Zjwv+d8LGMMSPqk+ioFwgj47XL1TfloBqj50vc2/MQGsw8PE0MHIfukFmoE5e1W4kb38gb+7lsIPAFh9nMSRhTRDVf6AADJ+MbqMP9CAmwD8/ys/kfvXAh1GPQJzQHI1LsIpw1P9u8IKgDQCW/8TPg9/RsI0/yh/9UXkwmU450BiASCzOMBwxwWAr7yfg7pC6jpCRQVJ6z2Uep4C9Tw9N7p7JIYFf3b+/8wDBGWAyDqCPNb3Gn+MyILAY38+uckAuUACww/+UgRKAau6agUwu3oD/wGNOwnFUYB6djPDy0VBNmmEDQjMv9A47b/RQor+4cKmB4DBQHVdgUo94Pd1frsDBTw7+wGJ8wOGARbF6ok2/PN0RL7Z9f1Bg1BePOm+CX/BOPY+08H3By9EUwKwPI9zd30OgSlILJAWvuQ0ln06Pi976gMQR28BWPzgc0s+mEh+PftElwJTPAv8JsRGRk/E0YAU8po8CD/mhBmE8AEPuw98YURNe3f90YN/Bwp9tQD1hEp9PMPAgwv/VLiDgoWFZbwidA4+Mr/KO+2LAL1IA0HGoAU0Psx0Lj8zvQhInoEtOz+3TcQdTiE2o4XkQe35Ur0LfRJ87348Bzi4lT4uxjcPmQlj+8/Ce/Dlud3CR8Io/8V+MQUs9KwAfsu1QuZ6032kwL5yi0DuC82GjwJThHf+pXLg/fx/e/3ChOgHUkGc9M47BAKNfNoExMTa+Qo+gUOShxEJWEJ7/aG8CTiTPUW8k/fVA/j+kX+UzV/BxsEHiEG9k/RSenRDecGKw7sHLnv4vAiId360d8TBNMEjvgf9eT1cfdABusM8v5aADH1sAlTBdn1FSFpA//aQQcAEtv04vxw+0b8mwBOALjoSgMSP9IPd/ly6HboD/eT/toGa/uAFCsClBSGAmQDtg9v2yTrVd3Y9osCdBTnJxMCdABi9NkHmAbFByf40t2BEPsA9O8xFksHze/J7vn/CvS41xIMHi4hCtUKwinvC7b6SQMK2nK57djNIHISAxvJNj35lfaFCWAAo+Ur94r/2t5XB0wYnSV+CN/omfrG1yT3Dwcc9uz2eAUR/lXv3zZRHa4OiRVOAAriS786+Z7fFwAoMbccuROkAtsEFuMmBMkHvfxB5V/bVxsJ+7QF/RQF9JUHNC2TE8jT/O1x7yDe4AYZHjQXM/3BFWMTLuAvAGAU4uQb2GP9uwFGAqAl1iz/5/PIqQ1mEi38Jui+5Fz3SQWdJVcZ6A0yDhH3L9Q9/MUGgPMHI80L4/y9BPEDUwYP9JXn5etP8Bj3xBWsGMsHJR8yEGPOcOxq+bTvJv+lDucIOexQEL0CJBgWFvkNxf/3wIb3AQI4B1kOdBmO/JPlOxZf+MvsvfoJJN4Fjeaw+BD3DRLfCQoWH/LY58cG6+nv97DzoAG7F77/pgc/BEsUghA6+Ur3JdkB+lckJhdw8EoANvxfz8f4dvFRBS0orhfhGcHr0OcwDon/SPXtATXq6+ygEX0P2BwFEGfyYwan79XjKgHVCeDyMPpqLvQBTvCPESIRYfFe1eYIyw6Y8+PyAQc2/fTqLQtkC/bkSPyXJYABGglKBuHvUfOJ8/QNpBvE+FEBcyA50PH9Ux79CD0LP8T0+BcATQaqBl4C7Bxf6Hr6hvFFDsccXAS5Btbp5AWH6uX4tvYV4cEmEQGLGDwgZfLTBbfzmgB+27L5xCHm7zv5WfT/82QBPCmCG7X/PP/h4ELiG92MBngWzv8tBbAH4hWnByMLrBbk9Vr2gQVZ5gbiG/lWCbgP3AntDfsElP2LAT/4lO5D/cgJVvUn82YHKgGjAFQSAhYV9EjuXxqhB37e9Oap8r/oHg+MIcL8mQHgGNcRcd/dD4EfRfAUCWnmE+V364YEBB4j67MAwyH7DajtfQJuASfv2Qu+9bUAFw1nBFX7kOVEB7YELf6P/cP8MwtlChkMWOA7900WbAGhBhf72vrx/NYHZfkY7PEEYwLYCJEPyQlqBsz6KvlF5dfkBQpaE9r+c/MRGZ0LV/9OAYntSAjX/t4D0fmY+BsO2BcVCYjl1fAX5nz6gQAhFPICMQNkET/ljBokA0gOZABe4uztG+G9D4IGDie89lf7qwl/5somwfvI+Qb9Xfs9AXkCrxc4AS33Ie2ACyLvavPNEp7fDO+GCIIK1RKKDkz/pggE/5vsfg3pAIzxv+887sf/1wTMLCUXZwRsCX7rUfiN4BwDhAFi7ssfZAFX/Ev69xZuBujWSvPn8sL25wxzJkT+pRRiHmTk4vlv8YALJf2t1BjhzP9OMLIjNSBEC9X1yupzzYnZAfzODjEHuxGfDHELexaBDqcLi+ip2fPmtOLWBTkRm/tXHdExMBzC/MoG8fPr2S/9JuJX96kJAffnBS34jQShBpAQlgnPCej3xeLjFIP7DwLdEKXyOOhV+OMSDt+NBF8eMvQdB0oCsxbvBmsBMROp58bwYAS+84vq6/1TFZsBwukgDSIlrQx59/DzM/ne7I//Av3F9wD8WQNWGWQKSRs5+pz6/fO900L9ePVNDegM+wg6Ag/86RXxBEwJffx07+PngAIwABT9rh62AXgXKfpJwtrz1vXy+jor6AI8/SIvkBwF5svsbQ/63iDiPQfq+E/tZA3GFyH3LQaNGGIgYOko+N8Rfs3R9vYRa/fBBGwVcRGD9ALv5wp2+Af7eQ1p9/P7CfsyEln9WexHAVv3hAg1FbAYb/867Qn4zQeZ7x7tQPPa5L8RowRgE1ohdQqvBe7jDvpXATMFTRbE+CjsHwPl9+78nQlj5CwGXxLhDPcFEeOYIYsfe+Pr9SUUgfWi0h32S/mc+wwVJSW1F2zyFAG83r3BKQFAKuIZCBUSEaPipO3WBGECxg9zC/0J8Ono5IAHHv13/s/84PQjBIEDHAjtE6UHbv5+/WruzhnIFB3kqQIM4ynjLAfSABX+EhNSMdHzVN8uAJIQ9/1lBlckvdwh6/ETB/QQ/qsSy+zL2nwPpgLL8PIUGx1tBE/7igUB/lLhMAr7PcfibtwuGIzmlPXpFz75SP5QEWD9rM3C2Zw1MBUe+aRH8gnjyizvOwOE5nzmeCQt+/z0HTCxCAfgMPM1HfXmttumEaD+Yh0yFzAZzw8a/HkXmb6Z04AEZeJs5Jr0zDVFHnod4iht9cbthfpO51HC9hNDE7/qWgjaB0EriRfKA5PovuFj9k7zX/zd+jAirw2ADcABI+80Dezj2AwX9Vbn7ys1A7b1G/E99jLxOPvpC8YHBR/G+mUNMwl58YYK3v0UBLH2mugX07PyWxmbFdEHJALSJ4z5HvhH8MTgBgwZ/EQHmw5AAyH49f/P7yrysgQjCWYN/QPSGTHg5wDOE1LixBdAB0PvGPCKBlcGFAhVGokEw/fW5u/zR+W2Be0ukPRQ7boI9xi4CXDlsgUd/yrTLvwXDrr0QhwpITvmKQezAkr0cQ1N9ZoNdO8w6hr9+PnQEowImhiWBJLqt/KzJb8e1+ms8XLiy/KI7T8VsTAS9Q8AR/QY4QT90h6EEyHthPhgBXT+BAf4ECvv9uiLEMcKJ/Uu/SAH8uNb4t8cHROl/uATkP1r5UcDrRemDHgAxgSn8MjTngjPEd7uIwCjAaMKdhHJB/QKfgRr9ccC1PJq7RMHUOPXBfUYaek//uAPDQtf/KIN9AdG61n1zv3D/p/q/hqlGuTpjg/l9sLw/AU5BDf78u5JJOcEO+wgIb/1QtNzBkoc1v6I/5gJ2/956BTi5gpV/uMEKCwu7inxfQx9+boSdQEFCgsBivUJAq/k6/Vj7x35ZviX+bcePyRrJO/uwPdX+0DsnvCG9ywjW+Mr/IIQrN4tH/4QawFnCFQFrgza5q31oQQX/R8AUgXk/WLtERRTAF3psBINBUXvuOAjC5oRQflOHi7vDPt8D+L26wkzArMU1erR5z/8SOZpDzoSJA7y+pAEjAGL84glTgs+Bk75hO545Pi98ROsJWj2IvusDu4Dg/G+KWwaIwE/+HjpMOdX5skwnwos4fj2p+46BBcAuyjQE3juDfo57SkLvQihBpL9z+zU8z3vlPjKCqQdnRD5/mz1vut+BUImAvzJ2Cv9oQ1zAwnypANEBnAGKw9B7hvqpQzpIgb6TwKH/VbpdxvN9034Wwwf86kBMPG26AMDgRpGGkDzO9cL6VMSCh4TB9wIowN1/gXqy+kYH7YLM+ps3r78GPE2AdFIMw4RCMPwlPfDBpXe/Bg+/hr1EQN7DqgSof2OFt7rhe4p/zjutOEG8VQAm+8UIIQNSwpJLiIJQgP495bn8NfO2mcFVgkdBBEHnQbXCwcdDQg15JkJ1eln36EOrgo/PCMjKABa79rHR/z3EnUC5ukh9MEDrPJkB/ML+v8KEuAFPNlMAQsc9RKTEt7pHucXAWH5UPSjITj3Ss1g88oDaR2ODoEltgww1qfs//rXDMMIdCdyEJLdcvpFBybtK95BCNsIAfTPFL8bcf7gBj75/NxVDHcPfPcHDu0Ex/hhBaMH8vyS1rzrSQ5H6XbsSRuCLV8C0gdDBfTitAMKDhn4kOgeD6v/5/JCE5QPCBd27mv4A/F03IoYDQrl7UYFgQuCAWkDaxoHEjLqpwfP8XLDt/fXFtsESPyiFx3/QvHICgwW2vDv68hCWPuB0QYIBAJ5Be/2fgbj+N7kbQrWDWvnXgWHIDX6rADX++4SPQNr7sMNWeWo/kQIqen++7IRewqR9r7+8O61JR4ahOztBE7xcPck0gkN8xt447MrGxLk9FL17gC3CArv/PYsB2X93dogDpP+2f8PNNEGHgzEBEvyo93s3zf7avz9C2gY/SUq9Uj8uQVd6KkJ5faSANP0dOC491YHFjKaF1oPRRA52hDctAEL8mrvwCFi/e7yFgZ3+5YURAmOF27/sdcYEAYNo+2rDIwMTeY05i7zceKd+iRGfjFI4ETzVBJ/BdkDSvpk7wHdweaF+8T5oh0/LToSN/JT/4wWKwGK943jYetP/p4FwQUKCFcakfQn8JPziOZl+2YL7RSP/pUTfyU4/x3x8uov4bP3EBjB+zz3PQ84AKHzm/myEJYKmQs3AqHz0fhg/ccRpQOcE+DwY+QQBi7ktgP57h8DcCT++KASexRS8ILrrB5X9b3dEgjsA0IIne0AEpkQK+8IBqIGKPrg6wUCDPNZ69oFEBMKFo0DlBOuFdP+KvZq8N/pYOHB+yv5o/c4HrIPkB3fDwz3//ik59gI+fOnCGENAfV8CAPfTvd2/ewLBhYa+3oJd/Ro4i3t3Ch3EPL2HCHWDFvkesy2/u4YYRGnD7UFK+h+4NUPiQpBBQUQOBUU7czk0gT59RL24PngGSv+kggBJeXnZ+a46M/65gs+A/cA2wQHAzwIpxAI+t0WWwvT2NTi8/UV9ioMdiVpDK8LPhKp8XDl6vlXAW8ILPyX8Ij6yvDk/psUKwfC+/wl5xmJ62Dufff7/Yf1zfQb8o8GrPGr97ciXQ+mC6z5d/dSAL4OtQ6a8dXttvugAnr6TvhmBQwSYPcu8ALwgxkjE0L0Ywv17s8V7vlY5YQKVQxbE7Xvi+Df2Tgd4x0oAaAaBwCQ80Pk7AWoFXEDmf8S/Bv0oehhA+Ad+xqQ/yDtJOPv/70PGuQ++a0QbftMDIj09fVvFqsCzABS7Hv26QsCGu0JMOwfDKMJwAfY9C3uUv0N9THtHvkQH5ETEgQGCZ//qvApB4EHj/O++Tv3DP3y/6kJ1f9v9KbwPhLRHQfxiuYoAb4MgewvEQcHgAmQHETwtvsb2qH7AA3d++wEK/zOFRXq5/XZABEL0RvK9TISHOiO5Z8NIxHfFlz2xRAG+irwW/aG584QeQh//MHfZvKUEfYfFC1J63nksfwX/2T3TwXYDv8QZPjLz1n//vqJAO8q9Avg5/AQCQqw34kHifcYDJYVxPwA8SzlfRRfAF8ARBjS/QDkq/QtFs/0sOvsFu0OKeiH/ucNv/cmAbocFfzX3P0XfyOw6Sf3MxeQ2EXl9CnI9AToVBF5AZH+4Pbh/P4XGgCHGBH52dA6JZQE/t8GDOwEYfmS/tEbjfTZ4NIkuQDt3vQCmhjNBHQBPBiz0lLmOQwKBgsgtgGp+fLmFvGc/Tkj8Clh4avbseLeCzIICQVXItgaZdBszqRNZyPU/ukPLePWwBLuah9/7ZcVriAx4dfdogj+FEP74uxWF6U+OOGk8pIMyeKvB8sGOPvo6CP+sP/g8uP2bg0DL9D1XQQ7D4IC5hek+BP1/ePy9AMX9+z33AcGEAOB+V4YEQTGB0QF8QHxDdHiRv+rHIcKjvL25bX4uv1tAo721AGAGkofXQfd4wb2z/fY5/X+qA3QDAEKv/Ee9OAJnfrE/wIWyvPk+RENk+OTEyQkCQBWDO3w4/Ux7Aje9wyJAh/zJxkmNUsQA9uv9wsLSvXy5bf/8gh916QJ9hSq+TMK3QVfEffkie9LCGoM3w/99isKAOa0+kcgFfVkCjkQLe4j8BXrafN+DNwX4B+s+pvzfAo2DIoGEAA/Bw3gyej6B1XxA/kxCfL6t/LsDwz7rv0SIN8Jyf+r6dr0CgbpB5YMY/hN8Xb6RgZN55YMohE0+jQhhP28Ap3jlfa8K2joHPdWED74lvHfCSsN1/47+jnvAvQQ8coAdxi1H7kSdPrd/2L5YuPs+9LyyfNtEYUiNxIs2RQAx/U35QvsUxJ5LrrgMwj4Ce4QShMXBZcK1N8mAvDotduhAPUbI/mKBUYes+8XGeUFN/4//Y76UwQg7T0AYAGU9sbtvvvf/ycEXAEv/Ub1wAZGKl0Bj/lAEE0EUu2y+E3z9PEd/37+jAb6/qsm8wvH5EoGngfS/qsAZ+yR2jcOvAnR8uEV7hgVBTHvwfMOAkwDsfd4BYcL/+pZFGodk+lV/WgCm/YB9HH/XQRV7Uv/LA2dBGIBhRTiBrPmQuwgDxwWwdlhAdcbyfB0BD8FKPr08r4DZwZX/GgZQRQm4jbOBxljIIj5iRv5/STj/eO+D4AOAuQrIkoH58sQ3a4lGhQ7BhYzuub9CKoYXgLX7e7d9hPe2ffgIAqHAokAixB7EvPw7QriCeD38wFgChT/pNfj6vgXbfs+FywdFPkN/SvufQpd7KQIAx1J7nf4GfWa+wXlZh6qIQ/8IQue9kX5sPXMFmIG2eB55jECYv7K/pUfOu6m714XfQ+H6qkQkzOU99z3sfNK39rpnge7AtnmPgmWK84M++a18jn1hf7VC7wBJe7y+9clPxKUAnsHvg0KAZLgEOuf4oT80x5++ygHuBZWAfkCxAVH8JL1hghX573tSRaGHjALSvjxA0j0YNtt40oUZBFO78YMZfvH/lUX6AIr/m8CRBTl+BTnAAEaCGYMfQAx+MP0evDS9C0C5QUPAskSHBTGAeIEMRFq+Xnqff/1CHbzivnk/m3lxAVnAED+2/rT8Bwn0vYu7xQZYhhLCQr7yQxj2QbojQZACIsApgPCLQfdj9+t9nEGgzVuAAEAvuh45vsB4RbQGNgBHxp967DhNOA96oAMUvHTCukU8hgNEDL6aPK/7CQGoQzHDN/8qQEvAhn3yAad9nT/iBavALXxxPJ76i728vu9Cs42fxbg73L2z+9e+5TuO/OEBUsAGAmq/+EY+van7HMKZO0QGIQSHP8I2oDqShR7+vUqGBFHE4bsZtmCAxvfEhQ0GyMHyee5CDgOZd58C+7tSwU5/i//8heY+Tsb/wCB9sX1avyjCAn0FhKm8cTcPxCdAgr73RZJDLvt7vVaDeHxeALcHJEG5PJD8mICnvCmBOL4UO56/0r6NygG+Hr52iZYBbcLIfv35P/XFAkKEkTpFQlbEuQVaQsrCwno5euXDILimwLT+qYAHhdM71QCrxnbA6DmdfgQ748FR/qx3lAy2RGf8eMZvg2w7mboYArt+O73syXIDSrwxfvp6t7gTALvFLgG5AEbDhgTbwXIDEsLRtzX0Tb02QEk2XgMVkDfAoADYwuf8vLxYRGD63jbGvsYDmczDPSpEV0pJP4U5CTG6AfE6x3zJROx+DMMyw5GJewSo+j67tgONvS06V8SwQjg/8z9HPdc7QL2agaJCRQA2ArAFGcEXf5e9xMENfaD+zj2f+kMAYvx+wmwKfccz+cX7E37E9gb6jMNiCfRARcJASRMD3v///moBmXZ/+zqBYj30gL8BBUOY/RACSkbm/RI7pb6NPZVCGQlE/8xAakKbssW4YT/gPINBdgKwg2VC/ALdfj1C7r+jO7xHR32gQKy/tcICBMs92cTE+zN6CPgXvmV++rw1SHlI1QRF/3lLDfmdc8lD8PsAeoC+5kUUfPe754iHxS96XET2hgw31X2hQPu6pzo3SXOIV33sg3xFqLen9tQGVbvT+0IFZQK4uX7+KAoRvXq8JMg1vcvxTL8USWAEvAXPxWP5ezjkQD5BnQPOPp/Bub0AOm1BMICbAMlE7kXltuT790X8vr/9SAAmvnh/ZgVnfpp+l4Cb/6aCboCyvo25cz9iw409gUBsAjPDZMU5AN19SwCuPQ19M0SUufm/LEb4fX6AwkH0fEt6rMEi+5b8N4KlSNNI8jkZQTsDTQSLfdu9DH9q9JTAgsAXfulDcQ9FAHbxS0K/vuKCHoGB/Uf3UDuzSg6GTLmDQFAM/rphtWaAsgSa/DYBW8mUel98VAZbv8A2rEFrQyd//8WKxT3+trmVQoNAL7xmgMCCSr0D/3ZD8jiC/J9B98PZfkx9H0d/+YlAX4geOox+IwdCxd81hLwchNpEO0Hxe66CoPecekl/1bn0wJfJe0+ff76+wARDfng+nz6nt+U2uIFgAGgA7r7CQnYF0v/QQR/BQT9vwFD/i3k/e3oC+spvAuKCzoCi9Pw9FDzSQqO/CkB3QkC6V0UaAwS9Rr/JSUvBcfxCgU/8wkKr/Mw7eDvVfwFBDoJGw8I8pQYFf6EAW8OWfH1DwTtOfa4+Tb6OwGTB8scD+Vu+QX9tQfr/tL4+SN64tH0zhQ8EGP9APiLCnP3yfVw+lYULu85AjcShfGU9mP+MCrH9ybkM/v36P7zpAgtHEoa0Qnf6fPgtPEuDn8Z5gmtDLP/luGS/UQFDgOgHkX9DdV6760sTATT/SMSFOMV0qrqFTBtANoSoi/Z2wbb5PKCFs4DEQGHFb3+L9rp+1cpOPaJEsUWLNsH6QgImAVuAPIJkiFkEpzfmPiD/LvqdfR57MT28/9LBxMqyBO86EAJvvR72RT2Hg60GTIFcfrDCKYGAv5iHrcIjOYr/E72aeWg9EsbzA4I/KoOYxAb6LvnYv9q7sgU1BlBBR8VwO176hseuvn00//vpe6Z8yUIzx8jFygJexSDFAUCxtsb8ij0SOmPCU8ZYRQdBg8ASuCQ4mIAKwYN97AU7xrk+GAX8/Ko6fX8Rv01F/YF+PdRAN4FuPY7FIoB7u7K/YzguvfF/68TwAuJ9UEPhAm9/yT95/to+/r3YvkPELoBUPSaBLkEoeLV33oTuxrPH2b0xvK0FYD7fgsUB+HwF/yUEGrwwts7BzEcZPiA7IAHnfYn/woHZ+8zAFEedRFXDo/3IffdESTiGP3Z8DXVkRahHpcFOQOdCG/9mQcoEeUJNNnn6OgEmNl4BWAnfBv6EPz9RdOj02b+3SHMIHrxeg3gBcjizAaHDmrpqQjGFCLexOZr+GsdZivDEKL1BOpg4sf6hhx9APEFeO8HC8EaMPLDA0/mSPrqBWfzEw/BDiIWSvuo2pHniwfbI3z7KurJ7KoK9iaU/g4KB/XS9Xz3rOugClf5mAn1Evb/w+tZF4ga6u+lBCwBYPMw1vwERRTH8OIF2wxbBMr4bA7E+ojtvQgK/LL8gwGzAFwC+Os3FXEkF/geCqMLnuZ+13/8G+rkBMUsfgctDOPyvv4Z/EoKbxka6tLpafvT8prrsxV/BxYJTwdV7uT8bwq+EFz5O/bXAJAij/2x7/oAQuhT+rwC+hb2/Fv7Gg7x4y7qbB0nDkr6RACd9GcUcf0G8XkBcQAVE6QEg+6R7s4CawDRC5AMz/90AWbyGQZO+hjmVRiZ+xLwrRh/7vQHriG1CTrm2N/yEAYCZPlj/lj07/l1DDr9PPmOGXAZ6RGQBeDv5+WX+2cBaP056Wr+lxRV9s38oP4EF0EHBv8VAknjc/ZsD1gQ6PeuAir/GgK8BGHmLPimBjoNww7pAgD+gAbbA6XmvOflB2cQvwdZ8SUBGQYsA80bf/6MAqftOuxV/Ez55AHS+TUiBPoQ8hEEXwo/+77i8SFs/lT9hhNaCFT/qfjV91vrxf7X3Lj4FwjaDvIofgvBBFDxQ/9h/gMCtQNN9rf0WffWDFUDFBUn+eXrZQ5z6H/zOhnc/ITyiwoE+az/VRfsBEoIEfFE7lz/fuPrC4gYfPjP/JfxzwwoDR78uBU3DJr98PZCBSQW0fNW8QoA0+QF44YIPxbE9Or/9wp087UDVBG8IEDuld/dDvjl3uhkEXAkWws59JMO8fjD7u0MMRCS7rnvJA1kBwH6zv1KDzILvPmL+YD38O18CBUK7O1K/tIFuAQU+yT89gbl+q8CnQiw8Mrs6RmuGG74TgR4/2XztvqcDKMIaulf95QKnPKZ9UIUYw9k7x3zNwiMAJgNYhyQBBr0n/MaAJMA7fEn+sb8QAP1Cqfw7vOzGpgWpv1gAaXvxO6NEcbzkwCGEj7jxQHTCLL+uAC0//IEcd66/GIGMRFXGzABug4M5oH6wAmM+sX8UvwIDoD16xeSB03tUBZS90zd0vglD/L/Ju4+6IsFlRrPHN4Gj+EtBM0H3+NGAIsVfwcsEMb6eu5w60/1aiLJ9mHxqCLRDUzojfFkC3D08fqTGKf4aufhDs0Z/gCJ7A7/FxHM+An7pgeY6l3yRBXn+Z3/HwvvEKIFQN7M/Xf7ZQ4LHOXqQuywAG0O+QR89iILJ/d60vAQKBnL6fMAPDTkBWTOihLjB1D7xQPeIqMHTsDjGKgCN9NR9kMkDfwy3aIq0fa8+KIY9CUsBKjXuRxv247Dexe8FjT1IQT+G77safD4JnAMpuUL8JAMqAxg7KIXThoX8Mz5NO6o9gL5WQy4CJLmaAFDEfEBeQQK/MHwoQb167MItyvuCJ0HuvZ38hrlUvN3AOIC2w4E/GP8+ub2CFcSZQDMHegGDftw94MCNgqR9d38yvyn64b35/338EQCiB5kHbT3FAAIFX/qiuIFBTnxo+gEHacRe/hEB5EOBQdC6afqe/HO7ugNcB8oATf1cBa6FngGbAu9+CABhf6U17zeJviXETEBaRSuKioAZPeW51rrY+wnAcgrPww059EBIxHm5tD97xJq+evvjvNf9Wz8zBvwHAQM1+JL9/sQ4PS3B8cFqf8sAALxufvMHET1x/CDETLmDPlu+PgK5Crz8TsBvBGJ41/61h4t9ODrIwqoAc/ygvB4D3ETBuh9AAEDS+MbGWIgp/yf9XL7KgFd76QAPBgb+gD1pRAU+T/3Rg6mDY/5ZuXE8Lb0UfhvCT0oaQnl/NEaRPuc7eX22wGE7bP/NAxW6vz/bQvbCS71zf7+GhEMjfCo5BIKHg2k+FX80fAh76gRAxnFAq8NlwmD9HnqmOY2/LcF6v6BAO4GjQuBCloO5PhO9Un7EvrOCJj4tRJwEu7zlfuq/IoH4OxY7Rf32AMZBi31QxQSBZsc+xR27lXxl+wsEBTtG/lvC4P2RQdv9bUKKfoV/XQHx/W+CrgG1QK//Z4Ovvro7Yv6swsRHN/oFwWzCjDqGQFe8Nf7mBe7Ch7oSuxdDoQcnBTZ/swSdPI+1R3/uOxk+soQGA0JBy/w9QbZAn77xAngAH7lSfoWEMD4pgUTEIYs3Qrk6JT7fuAQ4hvyNgbP/lsHiCXiBK/uZws1FdEJW+9F5rsE1OyiA9Qd2Qg8Btz22+lI68EeqgM65ccIXQqY9ejw7A+cDT4Mqe+p7vf5U/9bHZ/xHvoTID0IXNv47yEKHvlWGxcKGerm9wsfyROH2FQBmgyJ8aUCDAgPD1f0D/m+AfjYtgd0GL3u2A5QFr7mk/AwIcgUOwQ6AE7ntujd8Fr5ag1xATMWih9e3Lz3fwlO7K0NCQYS46MDrihy9ND6qwS4/uwJQ/ATBrn27w2OB+rv4PWr/TItOuxi9LEBp+0lABL8DA+ADdgjGvrN7LP7dODF5R0BOQxa9X0eASEH+fDyHwQr/PPwngMoDJUDgeKYEUsfbPaF/VkOXPKA4kP/vPLmAdIGYg7HFH8MCA8s+ULlxuo1/u31QfzB/nQeFBVq9Ub5pfD4AKXuX/Vf96gF2ha1Fx0U0/ugJdMML96y0tHTEP+BB4YIPxOzHmITi+cL9m0E0/01FmP7cvWZ/Uf4bPt9+yMPMAwP8y/shPdo49cLDxonDtUGIOuPI/n8pezVFvr0tereEXECMeZjGZwC5OYM5uX8Jw+TEocxQgbi8xf1EOtH92j6GgBtC2j4/vBiEhsH2fAoDucjmP/P4z3UxvDYIoMOwAHf/v3yRABABn/7LPYBD0cZ7fi/+wH7xggu9bDr6wHF7VsqjAxkBz/5HNDKIt4NA/b94C8Atv78/ZgvvQV4B/nuIvXF5/njPxhDD1vlnuxMI278MP5gHmsZ5feK6osHeAEr/Ov1NwPg5+ABhyf2ABbtiedDB9j2tP1WCi36sSBpCcjkuO7aC4YLfwtdFXPf/vamD234MfrN65MIJf909woCMgVGCa4AQSzm89br+yih72TkuwQDCjrkXOzBEpv/hP8rBTkYaPuX6a0HPefAC/skmPiy8Ez7uw+B/jAKWw55717toPej9wrvuxmFBBbxewjq/WYYBBWEHyb7ccxX9TjqJfaVGXEJweWsBTkfL+dQ/wIWYxOa8UnUnxMP+VcEtDyBBG3kBf9WAkbecPJDCzz97vjB+lgmEhk4+M4V2fSszuTkLBC+EyL9BAaM674DdxFNA3EU896J6qUFEfzwCDQN2RFdCUEGVvRc9JwGkQnp6ZHd8AT3DkMWxRlaAN/2Lv136uHwNABUC/cGBOR7+xYPbxK9DvX/FP6F8zr8QAYx7+8JUCc04z3vd/rK5IURcwz/AYQLTAwn91wJJABE7vATBeJ+5X0SNQT0Dn0CS/HqCWERAQgi70/kPAdcDJICWAvQI0IJGObY767eQPZAFOsBGdm17H4iDRRJHasJCvBy/0Puh/04++r6pQfKAHgQxQCwDYkDNvas/B/y0xAv7pDyTguq/t/rG/uoNKDya+k4EyIA+vynEdQTu+kW4iL/uPw2310dDRuI8fIUf/3f6pf07glnDi0LcwWt/9v5TPgx/iX8svmS/ngVV+iZ+GoI5unWD/QOs/uqFXQhVd097A/8DvwBDCX6aAuj7wILfwf39voTlReH+GTSyfna/wn9BAI2BkXxHgPtHb8BNwfwBTIOmeZw5R8E0vdE/xYbJBM25kb+N/p/42sEAhRq98YPkBj5A38M5PdRBuTwnPxh/BHWqgodGOX30vd5AlH79gupAoT8KwcH8QACTg398tcY2yVU9WD6t9rU5RkFxgUF9EjnQBGg748NlSqVGu8eWPJVzMPl9QqsBpskffM65JgJDfxA/SgDiR5IAfrnL/R3CK/0Qv8gIacH8AT98vj62e7h9uATmOS27IcUWg31Di0AAeZ180QQmiSG/XECHBGM8SbidfLoFIv2kwiVB1Ttn+v2BWQrQgaMCBnkGt/cBngI//oR7GQaigwm+kkMaP+J/OkU0P+j2PUHyCbK9wjlaAkrBU7sOfdhG1X1T+c1IqfzU/BIDegFPu9C3sgfsBWu+uQLNgaq/jHxHgMbAPMDogWc5Izl9fHNGGUhhxj9CLz/phqL4P3SsAbvEADofO1aGbbk9wQVGeT4pQFDA2kcKAB9+9AN3vv9xuH2NDlc4t39+h0G78/osfwiECX+0yITEAbkOvJ5+A76zwBsFdzsYvipBVz3tB+VA48C2fT856cTJx4+GN3xKvZk64neFfxS/cIEWAuOHsTx/ekRLXoG9vQQBPPtEe0t9PD5afMiAYYVoh2LEWT2LA+4BLHn3/Ar6ALxURehIdDyWxOGI/bUQ+5iAOnw2w6W/9738PnR/lYmdf+99cIWk/Lc53zpTvxCArsMRRgxCJcEGATSCXDkmfr+Bl72mfqJ7tQJmwErHAYMseTe9w7z3f8F/tcQwhGhBecV1f/b69nkOOFCCCgPy/cdDlANtARVGS8Iu+aaDtr6ZOFc/djtqA0XA4MG4BJi8Vj5Pwnm/SfyiQtJ+TH4kwMhFJAKbQHZGjv09ecM10vq+wpXE6kQuAOfBrb70gNq8zYI/wW69/4E5f6/AVAVYB3F3z7eQu97AMIHuP8bBxL9GBSRDRAMKv+OBfUF8t6x5AH3TwMt9Y0OyRy+AkUGw//r8Vvux/WlCWL9dhCsFJz0hQz68cD+QArG8ib2Ff/REAn7ogYLBwgLROI45iYJvuyB/ZoHwjCyFjACsPYm59HvYAWsJETa0Pl4DqX3V/nECpoWH+e9Foj7JeAS96ENXCBn8y4F4QL+6Sz8Vhda9QTnLB+V9+vZfQuiHZAHlfikFl/77d/PCPQDOvRQAPcXN+x27s4ltg6U+a3q4Ph/5nIAsB9JB98N4vpq/hPkyAdQG4fqMwdTB7T0A+nyBaEb+guFAeX0tPUz57fqyAdyBmz8ZBDrDEIE3QpkA07upfAfB4b2zgf0D20FTghA6w/3P/hl/QYbYAIE+/H+mPTQBY4NAAu1Bd7wa/ww+G/qPhTMDLn1kQUN+/TuKvmxFEEQ8fNp9knyl+x/D9APe/EBDMoaJgM27uYAyxdr7TDz9hOa5q7sxSBS/3nfegO7CBz4ZBIuFEMBvvsw/SgFRf8OD4MEkd675BQDqwjYBFsTr/7f+r4SiQX+96kM7gt726Dh4xEVA7P+bw/S7ZLyXf/e+I/03wBcGhkFwhhFFCzgVOc0DU/+0+x6FRUIn/TVBuQb8w6P6mz7eQMI14v3+SAY8FgOuBAq/5MLQf14/+HtGQlg8hXm/QQMEBoHwvO7J872iOUtC2rv3PxE+7gJvwDa8LMNCQTx+ycD5fZP7xvyMRDFHqb8zAmOFA36ZAFnCDz0NetZ8vb11gVDCUkNfxOp/GUGIgwf7uP4YvVq4A38nw1kCyIGlwItBhkBafOlAhEcr/EL5M34afBWEosZcvZsAHz/Z/I1CAoTxBFH797qLgzP8Pb8RhB/ATr/XAUjAoveIQpLIcTjyumbFyYO3/HwIZAa5d3w/E4JC/bD7NH82A158lj+nv8yBHwLYgirER7Z0PZSC6/s7g7lChQCt+ytCiwPtfkXB4rmHgNF+2HuVw5XCqH7iPY8FFD++wANIpQRLfWx497+J/999uEFSwUR+9TtnwJMCm3wOhmlJ3vhqehh+eTnoAOCDRQXahRC+dT44v0IAjf9GvhA/dX37fQk+6b6JQYDFv0bFAwH6fL7Uw8v7tffKQG7Ge74IALTDqvhewFrFU3q7gSxEosCdw0HAqD/WADb+fYM7wGJ2s/2gA4N5Zz7KRXkB7YXqg0196rhq/P9DWD0gf4eBlb3p/yWBdsB4AzSDB/qYPsl+JHzmQtoGBIjqwET+94C0wRE+O/z3ega4IAHl/kHCdoLnAlkGizs/wAXC0jv3hFSCYfdo//vBOXzEw/3BBjxufJK/3AKZw6IBz8LQvkc9X8TyQGO/qIOAfnN1hDxWAjX/SID8wWD/x7vshATCfrwwSgQF+TaDOqPASEVOgUC+aseeu0n5X4VWPhW40MN6Az9zAQBHBxeBcAn/QwP/C/27evhBDroE+KXDU0Io/mLCHoft/22AhMQ2Oc199QFRwOH9XgHmAQICrYd5vDn4iX4ghi580j7U/1M42oDFeoCA+Mctw1sBlwQXvhE9pQMGPXUFJrv5e/9CLDnHPnSBAUV4ACfAjQLLfnn/gUCzwBn9S4Kegs4+Ir4ufTfCbQCVfsnClD8KQU79S31BA7u80n82wTW8tv0rRl+I+IDZAXU/NnuAvKN/NzwKe0vBv0EOAV1/IkAdwa6EoYbp/cV+rH5oeu24UsLWiNx85YbRBGQ2QfxmxYIDJT4FwIr7g7pyNviEoEpnPuvIMgFhtis+kci/AbsBOwG7ts84Lf0mxNHC4L6UuwV7M8XDh5oGaUb9P3560np+uiBBbT/uv1/8cDtjBUEG0sJafz/C47oQt7QAKIE6w8bJLQRWOjl98kCsw98/SUC6/AZwd72QxV6EdkFMh8N/R3mEha2BcoJbRCKCSbTeNdLDegOQAk560/8pwFO++oYSwUs5g///x6yAdrhwwUwC2IHHRQL/R4G2fcx8WIHmfu08YP5W/+J9Jv/dREIDvMNrBLz5unXA/TsCdESdv5mA6oLwghp7L4ECAQg7U4T8vbj587zHR2aFD/2qhWa/LzzlwiJFKgIcfKR/2T6OtJV828q4wcO7cIC/fMy5Ssc6Bux8D75WBdF7jLa0SVQEaTrFALl/g7lv/+yHUv83vcPD18W1/FL+XUaHPbk5eP84vVi96cbRBM38bv5DRYnA6Pihfn6DUvqvvUcESwFAwg6Bj4CU+zwDe0VOAFB+wrxshD34pbvgwo7+bYOCAmB/wv/Jgyg8T3tIfvqCqMB2PdSCS3zxBC0Cv3xDgStHf0UKulG7Xf0qgA8/EMK3PkD4WogZg278pEBF/HOAycE/gM4CYAG3A9cAXH+1+Yw63sUAgaZ90r3QvjxA7UEPwKOASgOXBnb+sP79etG69gO0fWKBHMDHfeVAAgAz+0l+HoRlfxRHCwMlQeCCcb6DQIh3Kf3qvny7tgL5Q9//IIDjhVxEoMFxvKhFi3+yc3V5LEG+QZyDL4MIP1kA9/31BCy8TDtJRLP96gAAgzfCdL1wvt07IvwbhDJC3oMMfvTA632kPuQELMIvwFh9cMEtOHX6A4gjQBf/xwSVw8k8ibslCa0/x7siQjZ9n3tcgfkEFrhrQnq+VIAIB/B7i4ZLOcM7XoMKu1DEA8I+gmi8fD9kvwp8sQjRPcv323+Jhb7BwMKIR1E7CkBOhq18r3T7O2pHOLtXfX2GEgIjwIhB3oP+t8w8RQdBPbk5O/8yB/b/s3y/RnH6Qj2NyV3+P7o2fpOByMKthUw/Qnvag62/KnrxOo7BKEHTgpSAksDRScL+EYFSP3L1rj7QgSq9qDozxHTDiz9ahgG9e7xxRI5+aPr3AF4DygF7AxOEFntK/VP5Hr13gdi9NYfMABW914SGRBJCf8Coh8Z9D3aifYQ9ef0EvygBaQMBgv19Zby+fer+jsgFBx+/sv3GPF2ABvzvfiSC5H66O0T/ZwJMuXcEWcmV/Ld+nMPqww8+WEV5A6k4U3maALXCgbryvemG+336+0nFpX7cwDyHaAGP/CK8EoFVAP79sDzMgXc92ICTxDR5pEGaw/1+wX+++49AVkQvwk9++Ps7PbtB3sQZQn+AHj/q/YUATwDBREmEgH4V/bz23P1yBTtCq8PEO8+3CH+tBzRF3YRAf1l6+z5pvXs5IkEURiV9i4I3QfI8BELUw+s94PvePmpA5cC1fVyDVEMOP2uBxnxnP9ZFNMIJ/fC74X8fO553TQEXCm9BgQKdCNz/Mft4Q+wEaXfCtvT+ToBXQSa9Mz9lwt1+ZoWaB1V9nr9sv9Z5xnrbP/vEEchGf5m8RYAxOjJCsgQlfwO/xz58wovARgSqAhh5ff2iPtrAKP8NAY39wXxkxFl/XL6ZATyFiwBfeG8EbQQ9AOxCaX+8uXM3b0BxAatArUM4R6EBlPxw/kN7lABdfjz/MUSJAQt92wAWhVbAvT4vfcQAfH0MuluC6gBvvkDDxUb+vRa7nUVEQGP7YL8fRUQBEb7ZBIB/73bNOhrC+7u6/EkJiQbm/Pn8QILLgzx+/sIZgan2ZPykhoGB1kFChLS/Yvh3fM8Bvr09OyHEf8QB/ueIXkdffQU7eT9M/c24ZXv2gqB+7n4jB2/9nf5jRlhCBQKQvTm/hsF7AWWAyjqxPT1/fQIo/VC/aoNxfl3B5DxkvQgG8oTmwNwAAb7KuyyBWkBw+jgBtgLof3HABUB8P1aBVn1AABnDOrw6wcbAOn8dxXCBK3w3Pn8CCTm6PbtAXrt6wvLEmoKawFjEIgTPPZC+a4HVvnx45T7T//y6IH+JhK3DPUG2BShByXn7v0yBrXzfgFrC036z/tJ/tHzevo5AtIQVQT+9HEBRQOz+mINfg0PABkUKunP4n3vYAOhG+nvJgYV/t78DwJZ+ysUEAguDqL41PLZ75r/hwVq7tEYQRMPE/4HIOKs7+/lM/bkC/oGzxPw/i0Dvv4D+rUhEvaE67n5x/dw/vHfMwR+Eu/+CBTjJBsCN9xXB+HxAty9EKoRHgzdAWgEiAp68/D+EglQ9WbuRRboCVbb3wq7GSz1lfw2ABf0igFBCGjr3f2eHGX8PgUMEv7+Pe7g4EQAnvKy97kYrQvn9Evz9he7A+sMNRmx+Pbfr/H8KXH4nvQNByjlvQHDCBP4Bf0JCcgM+AYb/PP6PwS0Czz43e9BCK3zs+eFCHMGXPiiCxsSswwnCQn6d+5X920DMAJ29/L0BQcp/Gzn/QHdIzUDhAWEFvrspgADEsgEUvMUDL//ctGvCoz6nd5oB0QPDQEKBJoJEf+rDcIKwArw+y/jsgMxAbjfRQf7G83sFPhaE+HxW+0OHO0WgfHM+6gWJAzA9l8DJPs17NcPcxKa5Bja3AEAH2f1RuyEBq0AHQr9DQP4Yu1CHJURYO+qBbQJ1QdX8KfujOUm9z8ifALe9hgCFwERCngNWgcY+831YwQp/h3t8/gRGYv3NdLIEzYNb/5QIkwGnedK9ygVpwNn4yXxyxgx9IXo1B0CA4T3yw5QBsL+JxIxEW3lyuTRB+cDCPnqAUj9z+TH/OQqtgMj+ZgK4/r567zyqB0iASjyVgrS/vD7uASYE8D7Vfdl96Tp+QQ+BIMNOwv09aL4kd1JE4Ev0+qF9k8H6v1y+F8MXhSl7x74tPd63i/mbhuJLFAH/QlTAlry/v4kBjT+3u1y8lP+6gHeDBkXUf4n93UN7+tf5qACMvtO8rAKJCW5AIHwjgcgFDf5m/HjA0jwo/lE/7wNvv2P7OkFAP9MB8gGshWeF3f3A+Zs9nsNGgkkBWL7y/6p5H/7Xxrn94r+lQUuAbXjDuaLERMMvAAGFOoRh/Cw+AYQtwAW6lnyfwd96g3m2CSqEewEdhEi+C7/b+9rEroaN/Jk+q30Je71+PQMyP+nCW/9NOy5A9D8xw1CEfYYfwfb2y3yc/YO9KIWRhDe+TD4/PZb9sj7jAhICLMGCfJF/If6oPynKucNwf6e9LbxRO7b+sEPiu3RB3AT8gMG6ksAlhRe91gRwQQD/U3v4vagFF3zofo4FVQC8+uk/GoAguLP+xUZ8vtFAdoTCQ0M+MT+/AXu8ucAr/+VAaTzz/87DZoB5BCa8sboL/azAXL84gs0H6UF3+sk90YYpuzyBKYuWfEA0uD/OgPe1/8PZhl+9GL6eQYEA2/xWyDhKp/k7enzFvX1rvSsC9X1/uZtBKEVafeTArQF4fk990wLjAhA8TsnnAQZ0lMDexAeAkf54g/S9wfRZQ/kF4ju3/0dFyD6CN74D8MVjfe7BBoXAfad6XAaU/5C4o36gAJo/+EA2QiFBT7/1/qTACLzkvfsEMH/2P/CGaICHusZFHILgN9nB7gQ1uEm6c0EDAfgBO4kOiMs9TD1x/Fj5R7sQgdjETT1jPsyFu8OzfBU/doJd+6c/dnyNuIpEqsOTQn/EPv58/fx+eMKfgLC7PIEJx0KAib6AxQT/bLoGu2N+4H4RwCtDTcCxAJn+vIHRApgBJYFBwYGB6T0zPk4+CoFUAXI7Wz4NOZC9NMhFQDK8IINuhKWBo/ztQTLBwf3+/vE/C340AzwIi31Nug8/q/5l/3E+roAQgD7CesH+/LgAi8RDhNOBf8Cgvba50QA4/HD9A/++wR3FXH9vgV8Bozz9+a3CTgHBOoQIGsDRPKSA+oM+BJs9u0Q4fnG5C7pyfmaDgj0XhGeEHX55vfBBXIT/eQI864KpQIfEpYIhvuK9U8Gz/s35ysANwbSBFX/NP6b/A4CAhDGCzf4XeRbFLoSEuwVEHwJfO88/bH/xu0P+nUNRgVO9bf7pBM//Gf+Mg109Ob+hvpG8s0Fm/6dB7gFj+8cC1YPV/4JBI4GSPg09JcCxunQ99UTAwXV+zoOSxaY8Aj+9/KU83sKdgQYEqH0KAeSB8/2bvTQ9RAO+e8IABXzlO06DxEKswpt/rQRKAau+EIE/P4XB+b76PFK9RYEx/2A/R0To/An7fv/k/z7FkoRBgSGAYMG2gJu7rv4qQBDA17+VPgg8d0LBBOx+eH8Aeq6Ba0Yk/1H+gYDQvoy+MIG+/ECCMceHPtS8SkBg/O69x8DxPn8+4v7ABYj/zbsGhJVEuH+0wZQFOv1u+3/+3Xz7ecAEiklIO1j6gYPCQnu+vsRggEG5Jj57hjrBxX1gAQ8/tj8L/UJ/277XPrDChPwvOxdA+UNEAsdDy392vmmBsP8Mf8MAmIBQgQeD/ABWfau77j4SwPG9B8AhgyqEHYDSQlnAtnuDvqN+FoBS/0sBUcBIu6dAMwGTwmGBQYLJvny5noG5vYC+hAHtQLZC6YCwhHm9mv6sg2i8Xf24/cmGS8Hz+pT+qzpj/cYEigda/irDYktsun16a8CPwXn+E/vtQMM9b781glbBgn62gHgEIDqcuK989oJKgp7DpwYXfx9AbIIrwHn96X7H+/E5woArAGTERYARgbAEb3l1vyIEZcRwxWl993z1vzTDN0L++zb7tH7jPw45lYFBCamBM8Dt+nX5TP6KP8mHiQKU/jW+3AF5wKn9oYgzwi96YXykuKV+NP70A48EhD4bQYcB2oIoAdXGu4GkOLW+Pj80Oz4/mIiZvkm48QC+exV+lcmsg5l/tv+cO198FUErRhOEI36HPCB/+730QSaHjz8Dfn55QvmRPrhCfoMq/GiDh4JOfQABDMcxgrn8ZIG1PW77JIGJA9M/fz83Pxx9Xz3hPuNFSgP4fxoEBnsK87LDTwW1BBtFoP++PG86TwHsP9q+pwW+gw13TvaOQX9+uYUCRks/Ff2yfReEQYDWwNVFwABQN8YABMUuuXwDGj7/tgN/+0IOxv2DqYZTgbN3Oz8EQpm9r37Wwq/7Cvz6wY5E58OoPO2CXz1U+J9+9wBGwR7FPcOmwF6Dc8C3vla7bPrTPVa4CD89Cs0FfgLYBiT+STh/+l7+bAHoQlb9yQHTgsT/28N/xNuCYr1/fHe3GX0yxfxC2r7YQDF/Une3QsoDTwElAtm83AOKfni8rwBeAhZCify+e3T7TMJNxZ8C8kRzgfZ9OjsQ+qp+tcK+g/2EWACkve990/6jv2vCuUJlvq28C3l9A0eCvjuqBaJ+bEBCRUe8z4CTAYFDCbugPDYGIMNY+cX7FQJi922CVcrwgQp+T/7Gg6d7m4BfRND/433ffV587Tv8xFHDfz2ufdyAc32EfqiG1wELvemCrYEtwXBAUj2J/BN9uYPuPu39zQLuwqK9dXsdBcpEKb8UwBI/ZLdp/cYH+n7HQtXAGvzn/6+B4UPPfNg9SIBn/I68xUP5RD+C1sFn/Ml8XkLXQ/dAqT7O+XE9l/5TQWWCxT+AQbdBAH0Wf5FG4v1LwjYCGjnzPRTDAMZm+/pA7L4LO7gAg/+OxfdAKcDngUa5bv2jg5/DdwQ3f0C5UjzSf4uAswB0fn7ATgJ8P6QA2gHWQYp+4zvxPbnA0wUhgWdA6P70PBf+JEBrhLWBFX/xPNU/RwNewV1DWr/1/Nd5dTygQlq/mgQhRyWBLjrX/0WDt30cPfFADrzEuhs9toMvwdcDlUPzfdp7L4BDBKQAA4EcQpr7xv3OxVm/0nzDgkcD0nw//TtEiP4QP+KBm7wi+crDg0eguksBagIafL9A9YGMRSHA8f6pv+w4KbpFBxs+/zsvhQy9bPqBRnFGir3hwj1CAThBu2lGOUJ6enKC6D2bO/hCZgSdCA57zIDgQY73JMGbQ8/+2P9PATd7uD5SR2/B3j53gHV/vryNgQG/yzl8/wUCT3/UfsLCL0VgATG9OTz9/VbD2gRJ/OI9/AF2Qtp+gr6oQrQ/Fv7zvWN+F4CYgl6AejvYwd6DjwBBQvREiv5dP+KDuvt5uZ+7Q78fvfM9gQNggXsDP4Yxw9P+ir6AgZZ/X7ntOA5/J0NeRXTD2MAK/z6+1/8mQMA/zP2FAv3/ZLpAv77EzcRvv8r+L/vUvh1DwwY/QAD8Yr6sfch9hICjAL1/+L+VvT9AgAXxBpiAxv4l/K/4sT1rfrJDHz/nwJlHH325fhuCj0Op/0d/if1rOejCHwEEgN7BGgLVQq6+uwAFv0f+wYEE/1v8Pr7AP3aAV/t+/ZCF3QBMRfPDw7xlOVs/zQWBvmhCo/1vfa1Bjz5IQ9H+U8C9wcI/bf4pe8BCLr/QgxBBGgDJA2u8L4S//wu7PD/8PHd+NjsKgU/EiEGVxUIBdvqhPiAEJz0r/QIFUAAvfXeBkcGF/O88eEJlAAf9msSIw9p+KkGJAtc773w1gsyCXno+uyPDK0CyQdpGRELuvjg7jD1e/R28+AGAgg2/hsLtAgP/PQBIQYfAGf9C/5p8jv6jwe7DJgKvf86/8Dp4/ONA6T0Ygp7FWr/o/jW/5X8hgMiBC0RqwwC5rMGig+N8jzyvvji+N72+wPg9UMCVQaDBjcUeQGGDhQK8/056G7lrQTKBgIBGPNIDCcDsfUMFcMGHPbS91oJWf71+IYP5Ba/Biff0/ZIBB0A2//u52ABafxzCvIZAvKlAyQQPPog6ur7rQ0HEIX62OavEfcEOfgaA1b33+479NYXKfcC/nEd1QRI+FvzsBK+B3v6IwAp9ibvh+dzC8gM7wL6EjoGtfiCB10Vpfv992P87+ek87ABBQgQFIAB9/eI+FbuvP31B7z5CfZBAaYIrhC3EgUJpf3sAm/4CuMB7HXsGAhDEygBNQVPDbIWlwX7A/L0yPFZCCIBTu1W9vEkPQA752f+LvsCBbUD+wVN/Ln35wpLED3u5O6qFK73n/D3/lL81gvNCm8EXvKi+nQLOvp/Cbn/v/PT/AP9fwI99tokYxwg4uH7rwOp91/4bRAoAjTYxPx8HeMNpAY/DUH4XN9o/hkFg+fWBD4igf6S6xUKQAJd9scOAREU+bjo9gB//s/rNgs0C9DzvweeAMHwBQs4EZX6X/CxCuUS0woIAr37avvQ8TD78vbHAqMNEv0V8pz1+P0OEdAgkPrs8Rj5mvmcAQYFYgb2A6ELbvd66zfkN/XNGI8KmvrACZsGNgGNEpILQfuz9csA+fWS9KPmzejEFzQHIwZIDzMW8f876gABAQBdBaYC/xF8Bhfne/hoB6j6evkeBH/uDfJiCsD+tfYiAeMOgiBDD3f78PNm/Or8IfFS/1v5HwKf9RIKYwul7rcJUfcABRP/QwWMGlf7DPzABYL6DucMD58N3O6j8xrxQggPDOUOxhOS6qjy0Q/c70r5lwxGEK/+X+/xDDgDYAQIDrj2mtv56wD8IAHvGvQNgwZb/PMEogEy6i0VmRQa44vqmAqOBiIACgNQ/j/9TAJmB7HtDvJsFTz+FPBeBx8PHAFCAOIIHu6j/REjGQZF5Xf4qPYs6y0PNAlQAj0K8Q5HAyThGQgUFlPxyPbhB3bxVf8pGtjxe/BpDL8JyOgF/s0LZvGyDjsEtvja/AwN9Aqe9EcIEfjS7vP04AnPAnX5JxyuBsrzgfnIBM31V/wNHs75svSLBmn4q/+FDY8DvPgzDNUC79ku7esSdA1R/+UDfP2F8pQI4gmU85/z1wpIBE399gqRCBsDMOjv/0EM+fWYBCUBT+mV8TgVnv/NCtoTlgTzAuXrUhAhCM7wYgMgAe/2n+7c9MH/dQfcB6kZOALb6pQLtAR+9IUBlPdT+Vz/bu9bCXMNPv4pA3L7ofd1/C0DmwNyA+T8tgZ4CdEFIgSP+b//SQHaBK37EwHCCSPzTvZcAMXy2fvRGQoOhPeo+gUFm/MJ82ca8QKM65j+U/RL7I4COxgQEA7+TwULBg/lDvkEGTb4Z/lOCFD9TvjR+zr+7/imCOIUrwmdAdwKD/tk67EFGwAT9wIDZAKb+OfxPwS9A+L/sQ3AB1L7FvttD+X6iOUaBGYRggOz8EQJWf5l6wcGZAFO9kj6RA8S6j///yGP+lcIVP+dCh4HTfu8B471Q+gn7P8G+PwOFaUbevNh+mL8cQKrBEgEsQRZ7drvtAUbAv4KJBF4/0Xuqfvi/LzqiQZABqcJlAk78vkB7wXA/0b+yfyX/5wJWwIrA1QJffJZ93kOPAQc9x/7bPDc9az8BAoyFi8JqQyU9WL1zAWV99ACHAII+nwEPAIQ/acA0ff788EDOPs48wsIWAvn+IkEJBw4BLUJvAka49fz4/ha90f8rQATFrYFS/Ra9k8D8ALr+ooUNg/f6yj5xxFD+oz2pQzJ+L72YgCk9qwCoQLZBKcK0/gfACIQyv8n9+AE3/Oi52UFhg4zDv8NPP7e5APbqwYqDfQExhfWBWb7lAbGBnD4tQjH+t/r6gCS7KcDyAr/+ugN6/qR8J8P8Q+/9s3+/f/s/joNBgB68VL/iwMz/Uv4mAYJAXj14BU2+NTqWw2LGIMHU+g96+P3UgsMChkXdwR18b0LK+/L5q0IpRLq8nP4/Psu8qcVMxKBAA36+wTgAHfzmQTHADP/9/3hAYQE0f10B731m/U/8UgJcB4l6aMIXAq7+uIJx/wrDpwDpO/g4jb+6fdG/8Mebv7b/4z9jgKj+Zb+wA4Y+4T2zfM9+osGNxiXChr/OvtS/Y0HUu5f75P/bQI8BYIJ4f7U9A0OyA5Y95T8LQAYBqX+bvN6Ab79vwJ1AoH5U//oBekDdPSX9u4DpQf4BlsNbwc4+EX5Jfd/9hsJ1gLh8iD2Hf5iDf0QaBE6+2DtXvK+92EGkv+QAzgT7ghZ+zANsf7r8OMPAvjt3S/7sgE9+6EBZAZ/E34JewYKCDP0g+PRAWMS9fOJBiQOOwUc663syQBY/ykH7vf/BAYQlQgk9msKlgRT+GwT0/sE6nrw3Rdt+TT23QyD/sIAdu2FDEwCWfVtAIMOqguP9S4IhABC8cnzCQAbAd4SlAY59f0DXvwO7xH+whEb9J0Eggg88lYDkQ3//PntYQiCDBz7SvRHBE0GxARpHVQOA9iz4FQRHfu57PMJVwft+YMOMxJiACn5QRPVEUPiCuMhAE0M3/bn+5LzT/JxEeschgas4qoHfwxuC4gGGvs9/z32DP4C754KGQlWCLAR0ewT8tP53vck/7D5/PQeEf0MFwPKEx8JgPZvAUX9xO41/CrzzPjr8u0BMBJiBUkSrv2Q9Or8KAWJ/bEKMyg5BrzmcecU5yXwXxPgF6z5ivJCDBQKX/qZD/wXjv4+24XxIfoL7ikYuRqn/875YQisBLfrZfM4/6D9k/r7CN8Ptv3g/dgAgv2CAVT5a/RgBwwOOPqY/PsPfASIB+AEae/z7iPk4wLSDjUF6x6MC3z1rvg0Ac/yce9RD3UG++si+78LRPuV/4wakAaT610Fc/uG6aj6/xQqDurzwhplBYPgNwS+DPrvdvijBpfuAPpWET0YZPtw9+kNi/7N7Xj/x//s88kYSAPh9PsB7QQd/WfvEwZL/2793weKDV/yzvhJCTH7vwEJ/RMIHgIrA38CgQON9Zj4xgls8gkGIvjg7tMCAglgAvf7NRj0GC/8Je2y9Tr3PwmkCIj2+BK6CNXhl/Fg+MD/RhhJBN/4SP+/BusIDAWj8Jv5bBD685b+tAQ//ykCtgD//HfxTAR4/sX65QeqAjX86hKKG5zvw/9tAU/bcQMJCA37HQdq9lgDNwaO/E0SRQEc0bD8hySv/l4CThR5BBfoHPbgCPP81gMNAtHpyfrWBIL7HCB/B/3r/fjy+xQL6A2OCsIIivx06aUCrfLd6Y0Mvvlj9F8FrhzuErEHRw3z9w/pzfWhBKvqrepNEuQLMQJdEVoOB/eR8IMHXe//6cMByRNUC7HnvRZSFgP8lgDG/snqrOEmHkcPyezm/RsbgQCk4jsCvvor843+cxWdBmv2FRsaFzj0ovW2Aa3qw+HfAsIKBwMVDHUL+wl38QoAMAmL43bzJQnv+w/8hShyDs3+zwwm6Ln0yexf9VYBbeYQB6chywnSBZ4Q5AE19Fv4DQMuAdn8vQJ69gz9URhi9Jnz7gbc7mD4gv1DByQB7gNXC8T5oQPECAUGKvgQ890D4P4R80oR7BKi+E0FT/t5347zFwLi9QYRow20AD0CLwv5HmkQrwUz73LuQewf6Trw6vaaDwURaRUi+Yf1IhpcE3L8NO7F8DX0BvLB+cYUpw3b/64USvsp3hj9kAl89VP75gzJ/zsDShZYBBH0n/jHDuTza+1zF4z9RvQ6+wQFcwnM+ikGKPV37FAKpxYYBDwEmw59/hr9n/YK6eH46wtR/B7vpgbzAG3+HQkVAEkBwgECE2UJlOsK8bwRSAzW6hUB/gNw+6H4NQFPA6/uihHQE6PuFvIjGTMUmeY2/RgOlO52+O4NcwKp+eL8nAZH+ELxowgY/hDycBGGEvn59QnYEAT6TfBQBFD9uu5M/fr0ne8bARQRshBXDQ8CxgmtBB3sl/uW+aT3RPuA/kAGJgozDRQFjwFl8BDzXwqPCpX2tvgr/XftXgJXDVUEhQ6DEbkDWeml87ANTP1wCdr+3NyF9W8A8wr2FawRwQXD/cT5z+7Q8Lvw/hPwBl7q6BTqD/n+CgM5Am/+G/j8+7X2qP+LDuMA3PBs/bUPQQbaAuD6xuqr/9sFXQW4Cg8BYwPiAV37KvCw9gX/ywQZA7Xwlw7tD4XyEPw2B9z6Fvt1EngH+wGp/iD62vES+zIhQQEv8Cv04vHe+DDwdRKGFH4EkRk5CCHoN/ZlD1nzde0ZC7L+x/6DA9v3Df2rA7QFfvcW85EEWAcZ/RMOhg42AcUJhflH/BYCkAK087PuwQ1IA6b23/dFA7rpVfbvH/UD2wX9DE8NlvqT99IIVf7z85n3IwPH8Ob7R/p0+UsLef59+7MBhBUSB7XzLf/mEh4LMP/dA/znL+fG/qIEqfTBCdsk5f4f83gKvQBd8XgJhvpG7aYD1QQPB6n7LhbNHQXq9+Rl/wn3nuszB/L8AfhZExwMmQGhAUMR/wdI9U/9w/ZB+HUCp/18/4P+Mv7pDQoCTO9l/EYCAQGeCgEAvfJE/UwOhw5g+6cH6gRk893yrvbOBekEmw16/8v4+vNSBXwS2N0IAAIKevpGDccEqws0Ac4CHPwe9T//rAJm98fwWAClARwDa/yWAHoCLwFmBAwBCAqLBrgCfAPjAfr4dP/Y/zzv1fzZ9/z3OwmxBP0J6/y6/OkJpAO+DgQAf/cv8hz8vQs67fUGwBBgAVACZ/bM9UPvAQfJEUz98OmT/8IW3/xeCRIMmvbk+lcH7vmO7h8Psw4b9bDkAfwmEVX6DAuQBRTvRu5ABc8jRQvdCfQEGvHH84H7vv778HX3XPjpAPMAzgBgGYoYQAg07wnzMv2l/5v97PlKCcD+ogbeDwj3GPfW+GvwBfhJ/FgEIBJoCt4NIAx87bz0+Qgd+A313QTH/GL4Dg0FC4P81vds/3MHWu3d9MQZ+hHR+QsB6QIW884J9QGK7ar2bvwVCoX+XQTiFnkL6PrI9kH5HfPI/0QIm+366mAQcwnqBj0TqAF3A0fyCPom+zPsUgWuBhwFAvyfB+MEePa7CvcDIvnP9B0ToQki6u4HMAzqAoLwJwNnCy/cnvP4Dir32+yOHAMuG/py+eD+Numv7W0LQA/TAj4Gg/3o8/DsJAlIDn0B1wnD+jr2MfaZCTcJGvvU/Gj5tv9hEIQJKeOv/a8LWPuXAbQG2gst+xn85f+t85Dn4A53GOHuWgeFDgLrfO8SEoEMdv8LAGf1we4RAFIQRwscCMr71Py/8hwCExd0Brr9n+vu9CMBzv/O/Y0BKAp6BoYEawRkBrP0xvN7+3vnAgLSH7b/W+7d+XQVtQ4m/0H+k+SJ+mkFVgRFBpf9zQMxApX+VvbGBaMB5gDBAsnviwDiGZEQCwDR/HbxWfVo7Kv39AmSCdwAEgaFIMgGrAKf8Q3pXvU08Ob9Kf7jEYEITASbArH1aQl8+8b03v0xBrcTrv8R9wgCJf95/1L8ZQLg+Ff81f+Z4yT/Ix4AFYQMiAWd7g7wjfw4+x/+4P50EiIFfPRPAaoVaAid6aryS/eB89b1sRuDELj8dhZeBMrxuu1eD7IFA+Lg8yACO/6E978qhAzW0b8LghO67Uvveg+MCmr6hAVF/1UA/gbeGE8A/+ZX9TL3/ACD9YUALQQhAsYhBv9p7xANwv6N9gUE+A4s+j/tuAFW833y+wJsEdoSmflsAK74Vug7/8EOYgRl/WML3xM3+JIAEw0D5TLu6P45AaT/+ARvB6X+xAj49SMGpwd4+zT/XvftCQv7UAWMDzMEOwFC7SL+vfmO8A4A8/xxAogCRwkfAR8COhf4ARb9WPYs8cz8NQH7BhL7ova4Ai4HkverBZ0J0f1LB54EkPtV8hcM4wDo6wcHFg6Z/Hf5Pw4c+Zrwagf0C9f8y+zgC6f/o/XjG/n6Wu1B+ooKNAwH7LIJ1v1X9+gCPf8tC2oBNh9Z8kDQwPw/BgEM5BA4D7n4kgDCDwX1JuoZCMkGe+Et6e0KHRJiD48MiAKQBB/yAf9b/irqZw5OBOX3TQdNDHQHcfVi9hP6S/IrALQG5AP0Cib3wgklC2nwc/51AvT0OOR5BqEUzwjBEzEKWAk9+WrzI/lr7F/ubf15CXH1Eg0fI8L8fgQaAivwhPnSCeIBkO+NBxYCVvk5AVD8lP0h/PIBGAJo/+YCoQZOAWn/YQoiC5D63vt09YHlsAv5B1v07g0xBoX31fLp+SMFqxNdEr34tPOP+GoM+P4E+3EQZfo2/wXzpvQHDAoCMwQn8kjxnQMhD1UH7wkiA5Ltrw9NBQv8qgNz+af5Ue7AAGX9ggGQDf/8ZADa+rvzPf9RDyUAVgNuFbgJfwgT7R7pGvzu/QMDi/91CuL6Kfqj/03w3wr/FrQG7AG1BOnwc/VxD8kApu4UAxMLYe2R9c/+TwpaCfT48AktB6gEYPjk9Mj1qwh7DW7snhOeDwX7UvnK6Xz+Wvk3Bk4E0fQ+AEkQVAr786UQzQil/a36nPQTB+r4qQYZ92zwMQwZ9fj9Ww2IB14G1/oV/jcEHP0pAQwJlvmK80sJX/Tm8EUNwACa/9gBzgwA82DqPx1wDq32EvaPBscEJfE1BDkGN/t8CNsI4et69ZkSOAyG/5kAdvue8Tf65wAQ+5X+lQutBLT60PvGAdICZQpnDcT1xPx5+sPrD/y0AzD4+PMTFAIc6AC9/lML1vxU8tQLJAVP+PT9P/ui9JnwkAvjDUH7Mf4xAfTyhfKCEvAOXhQ8C+rrcf14/FTxUvLDBDkFvuub/ToFaQKtFWsLzv3C+u7+aAV58PryGRF/D3vvowWOCinkFwoQC4/tyf73A9IGLgyyCED/6vUNB98F8Oi++BQLAQZo99YKzwD25KQQkxIB9tzn5ge6DmL6Wgrs+xDv1O7FC6cGkPp8C0IFIwJ0/sH/+PiWCe8PW/Ul7hj5lAMCCX0Gwvtu/QL+1vrm904Acwi9CU8I3wMdAFAAwQIC/57/WfTy81X7/wHAAM78VATKBjD7oPhcHZ8ITfBLAXH+GfV5AJIO8OyW9p8NCAbU8IfvNg/5Bo8CqgZ8BMv3C/1zA1L3HQ2sIOIJLOF46zHy6/aJE3IHWwWkAX7+mwiA8wL3oAyZ/sT7QAGf8533wAHyDskVMgqtAsj3DOaP4bcJWQY19wYY1w33/8z2iAl6Bvzo8AL4/RXxFQIpEtwHOPoaADEESALP8sr5twOk9g0CUAxj/o8Hawn3/Iz1cv1rBR4A/P8RAGUKTvbE+AwEe/p29X/4MROgAXr8rwaSCin74fdADbHs+flRD7L8d/kk/psKXQMF+68IUgFX+vP+pPKW8m0N2BJZ/tIOhfqe8gEArvF2/sj5/An1CHoE7QY2BpX2muq5BQLwIf+BCYoM5gom81UINwNUAXX9mvovBt3/4vTaBPsHdPRXAmMJIwTf/Ff1t/g69HD6rBY5B8gDXRAw+DDwuffSBkX7JPv0/Fz9pAb3CGkM5e4d/cwKLvzK/AYJZg9k9gnzWfkKA0kKCAa+ACj6vPB8+pcPVfuIBHcTkO236fUI8RJqB5kClf1P9OjoxPejHbYDKvfxEJr/LuXX89kMzwRZEJoMEP2h9KD3Iw/NArbx0vQkA8n8aAl/ALv1Mg1GBNT+s+7VBrwN2P3e9pzqfwXfC6APAgQz93L6nQW4Bgv0R/9VAAj6fgLABr//2foyBoQGdfEV+oYMPgqz+Rf41P3A780E9xPOCeX6mQhTBF/rRP7J/xr95fdyBn36HfV7F9gOuAc7+xn53vXV8aIDSwfl/KP8ZPvr8DwFDxuDD4YCAPoi56by3QOVDd4LggPuCpX18uvO9fr6RAt2EMD5CvpVBJwGxAcrBSUI4PAg7WH7QgaC8/oC1Rj0+S4IywJkAT8Chvlo+MX49Pmn+ygQcAM4CgT64PYoAx71rAA+9MH8qwYBDo0PHv+EAskEQf3T8W0ARwHF8eP7EvgG+jsOnQkiBOADIgigAq75r/jb96kKoQUk/5/+dP5iAU7ySfML/ywR6gR59gIJqwVuBSv/9/xdBPvxEAIBAArzhw8wChb5NfiC/mMCQvt96av74g/S/wQJPRLcChj+N/zK99f+TQT++oHzmPFv/VX6nxKKDTAFcwqX9SP9LPZK+x4RWgd99tAFhf0/+AcIkQA8/Ef2pQZD92Drav8TCWMJff0fC0wTYwPU+Tb9ifIW9GkHRgLC97IQdQbY6Df53/QLBZULuA0bCxvx0QBLA0784AJWEKkFcPGC9Mb+rf4O+WUJNgsh+g8D0wXs72L2CPy6CVENnQWiCDr4NAPVAoT4l/Cn8iP8+fm//n8AFQsZCU4G0gmJDMwARv/PAyz1zesL8b4EbQsWFY/+Ivb3Bm8AIvYv74sD5wEEBmMRoAjQ7nX1NBMb7x7riQzCDrj+vAHQCuz0ofhqDucAUfBG+JP8S/NcBkwaAQSVC1cAe+3j8q37+hfh9xYCXgoY5MwBAxiQClL0q/5J8w3hPASDFeYN6QEqClQG7enoBSId3PE068wC1PoZ75ECegO69B4OWQjr+7cGSAaV+En0SQhjCTH+OQFUCp3taPMsGYL/O+07BYEMbfN29dUEzQOi/vQTDhH27bD4evz9CjH8JfC4C18JtACq8c8AaPfZ7tYDvwypAn76qB1eAC3h8ftwFcsL0fXvD1EFGucH7uMCoP50+UQVCQSR8WAOtAdY7ZjuVArwEL/6yhJtBlrqjfr6+0D7FvrUE1sGau41/5oGEAxf/jMAjviw+1kJ4gMvDRf9Xvo/++Hz8voYAFENA/lj9ZAKyPrf+NwIrA5Z91Hyjg9jBuT0C/kvBXr31PigGRYGLfScCJsFdu/q+5IO9AkB/Ef60QeM70DwLAmL+zn8RwoHDT4AAPeIBBsM4vz08en+EwNnBA4L+fYU7/LzUgH2Cfv5iAUtAFAJpAo/61YJ3hNKBPL2IPYBBrf0CO/3C3gKfeyVCCEP6e9XBR8XkP4l6LYBnhL69ln2rxMPAnPtBvynAfv62PubE8H+++5uBL8DHAFN/h8HTf2S/tcL//dl9e8FewtK9/T3cQHn9d0G3gf6/uIGyf3v/8z4i/bLCXUFjwHMCX8CPPd7/q/81wLxAybtbfERCSwKCPyOElIOuvRp9+32d/MT+IwW4Qge/gcHJf2aBDL0EAMfD6P0pfXU+M71tf8eDRsA/v8xDbEDNf5w/ZoEdv249HICv/9y/FgD9QVi/Wb+WgeUBu8BZPOLAhsBRvOBAQ4Dj/5l7qH6VwmyDD8Z/gs+9dXhg/hqA2DtHwZ8Fp0A0/mBBzcL+wYLCTj+IfGV7Lf4Lw0gAWL+9Adb/k38HgNHCK8DCf4b9H3vxP6WBUD/GgQ0Cn/3c/nCEncGNPoXAqwHc/7h5x77fwgO+W36QgbXBWb8mRSsB2fyxgGBBNf+EfFyCeMElfI7BlYHWv++6uwAug2C8lMH6gSF+hsPExKhAVbgxPl1DJXumPpvB7YJ+/tVB1YPSuys84sMVwXW6sn+dQdV828JdhPiD34AGP8yBxTtevF1+ZH3kQdyBCYGcQKBD1EMUu9e/6j4X/lrAvYKuwa+7AEEd/9Q95X/+ASEBwj8GwRg9MDtgwTPEcIBEvu+Chn8HffU/84HbgH1CFQVnutO9VUIc/BU+cQCpQc/AQEIUwnq9nP91gEP/onuQAbeFUL5yPrKBJUDEvjD+8v22/1JFugE6vFL9hcFYQRBCGL8fu/fCRUD0vfb/wQFXgsnAlz/dvu+883/OApy+jjy+ghbBCL9RwnfBiX82/mPBffpN/bNG6oK2gZC+un63PvT+fcCiPwSAF7/3v5R90wK1A0L9dv27PanCq8GGQbdCUP15QPy+RvwGgwuFYj47Oa7AuICmfWJBu0JSftCAyQSL/bE8jAVIQ0n8VHqRANcCRv+3ALe9qz6YPaUAwwV4/PJALoMnvgb+xcQaweV+8gBie3IAkMA1/kmCvD3Lf7PAj8AofIGCsAOLu5VAlQKRgU/A7kE5vSI8ur9pv6PCNYAIAnUB9X4VPPs/KkMQwJq93f4ygGFBBkC/wkQFbv3JvFgBpzuE/0JFOr9aest8jcFOABZAIoV5AUY+bYE0vYA9agBFBVlCQn1dvth8F38UQayB6b5/v0lFRPsnPNYF04BC++oDT0cl+3195MTOf1a8g75fg46+/jpnwwl/EHuLhAeFo/3kfj4FCf1aPOSAiL+Gf/G8KUM+fwm+1QNxP+oBXrymAvZCXDzYvOT+XwRZAV+B4Xxyf6bBtDxsxCB/jP7hwNJAIX7P/dDD+MNkP6a9gMCc/sX9sT7+/rPCVkATQkyCBPzMwaQCN73W/I2AG8D9vxj/j35qgvj/uf8OA6S7wz4WAHlAqUHcgj1DeYBNfxc7pIDEwIqAPQKM+uM/HX6HvtiDjsEuw2sCDP2CvVo9yn8twxgBdQHfwwO8azys/uy9BECORKXAjv5twOk+2/yzw3SD7/3SPcS+8kDif3/BCULKvxi9AcF8f2+6UwVdAxN95L+3f6zAqj43wz0DnX5HvPA/xn34P5fD40D+QT79Rb3Af/VCej5+/l2BhPw7ggMCHv8aQ2mFNb03+GH/icFDwPhAtEAgPfQ/owAxQPlBfj5RxE9DlHrJvaMD8b1xewcAUQNtg5xBy8BoPSx9Z327gOTBtMIUQsc/BjvFujKCDMROQVSA2T7M/Ze/tP/kPffDSUR9wSs9/32VAOK/876gfFG+1EJHwHh+iX++QJaFCQYjPnD7w7+RPyF+FPyRQXSESb4HgOA/CcBXw54Br39tN/xAEMGNvKHCTwWDQly/AcH5v0b8V3mqArRAvjvRx7+BSwADQOf+JL66epo+ZEKTv4GAGsPUP0qC8wK++/k/iQDEQJV9HD12g+jAxPxxwRlAiIA3gs49pr3LgNuBtAC5QD0BbUJ0AMO9Z0Aa+4Q76cFywM5BiwDnAhO+Bn7eAN0AR4Ay/cVCK0DKwGrA5cBOgA5AEwGtwDJ+QXyLfX77s3wiwriGYgSAgrJACz6W/2C+nQO9gGV6zT3Fvfc+XwIIRZLA9f4WAKv+47xrv/bDzMGOgXR/hD69/dk+yAKUQJX+uwCmgfQ8pL08w3zAmD3N/vE+077ZwHrDSgHmvvtAVkHo/4XAZYEpPBp9q8BwQFjDboADAHl/kvm4QMoEqz+2AtlBVznqO3dDGgR2Qt/APMC5/1t6uoELgkBAej4svEK8e3v9QzGGTsNv/TnALUAQgA0D8X8eAJ4+HH39vlN+AAAlAnOASHpoAbSDcgETAEVBbcBGvFFCmwCZPiEDckJzfeq7Fj3zw8bAGX8EBVS83DnUwQzA1H5EQqAExICifniAcED0/2lDe38c+f29S32dPpEBAAA0wHnDxcJcvf39g8VwxHC5+b5Uw+x92XzUhIkDkzvLP+zFgj0zeN3BVH8ffqfA8wB3goOBXsEfAnoBmz5oQIT9xHzXwES9voKSvhm9KwIbASbAYH57wvz++/4avlpAbEaxAKzAnL5XfNlAo8F7ALV6qPtRA33Bfj9FRJxApP3qPhD/MMAg/8TFj8XCP9A8XoAbvg19CMKxPEJ+4kO+e3L8YkRGhAm+T4DfRP66OXraRk2BqPwHwSmGMzyu+DLEAoJv+MSAlwUP+Pv+sAntQP09toEVgpMBPD+Xv1S8VX1lwR2DFEATfsQB/AHTfgJ6Pr3jAb5CJQGhAF+A0MBywbKBGf/cexS9d4JgO7I/TAILfxqENMNqvYw8ysKRgyc/vj1L/tlAY3s/Aa2Ei//qwuiAQX/TOva+mQVQfmuA3L0bvIBBE4KRAk2/nQN5PG0+b8CFfyXD5n/RPuO7cz3TA6jELEGyvfV+6zsL/F4ASAQWBAKFLIGq9K38BYPLQdcCJIF/fvk62sQIxDz8wkGBwa4+Ev6KwT2+Yb+CgRh80D4vQA8Da4H7fO0AJkJwfaa/BkPPQDkAcYKqfOS7Q0KAgvh7/v5Vv0YAnYTHAVWAh0IHAhj7R/w6wVe+jIKiAB39MfvfPwjEMn47gUtFMIJMfC29T4HlvQzAQkRvgEn9HoD3v+I+Cz9pgNoByn6GQpgCOH8cPh8+U766PdmD+MJxQvbA9zvNwCQAr8AK/lV+a322u5yBY4JMAFWCQ4XbwV/7qj6QQGlC2b98O909bPws/6ACewJBAC5EaQN9O5q94UBwA9t/XH2nQQy/gj+Uvu1Bb7+T//gFFoFgu7o9sEAPfLD/DcLGQeYC1T5mf4lArjzNg75CJr25fm9BNr2Vt6l/YUR1AGG9jQOphLAA/YKZ/ym+HX5/P6V+GztbQh7Ddj7CPwQDFwP8wRpBAAAw/V4/Rr7AffC+kj7HgzCBQr/cQJMAOv5x/EXA1sKJPwK+/YI7/ka+dsBnv/XCHf94wSR+lr6+wmbAp79lvS1BQz/2fp9BRYK2vmc7dcNbQlfEB8OwP4K9WjpAwNk9z/yyAYsBZr8QwZ7DQUBBg2iB+b2nfPH7d//jP8K+gEWVQxi8A/77Qhl8sr2IAZc8hIAGASwDBYMZgEADA/5DfqfAWb9u/TTBqYBI+rQBMgJWgojCmsCKvav8Jz6xgzc+4f5tSL2A4r61vrmBJIACOAGBLH8v/gA/hUDPwyr+B0B4QVPCjUBWALT/XHtjAOYBjME3gEc/igE5fSm9X35O/nVD6kKNPOq+dEO8wpNBQwDw/9WAiP+kgs79IbkRQeIBVLyPPVsElUYpv8b/Kn8pvBb93MEGQPDBKkBAQtCCM7ulPzfD773derkAfkGMvZn9iwKwAff+dARlAoK7PL+JAwB+NPm5gaMHYYJHwIx/pb5Wubd82b+8vl9G/UYFBAH/f30qATd9aHt/O0DAJ8Dhgo5ENn/GwPF99D5c/sG9VUHzwCl9PoD4AsoA58HvAzT+/HtCf+R/YXlageYIN4AEvyaDYj7I+yy/K8I/wQ+7HUEEhqK8ZMEhxLf9aPwmP4L/F/w5xVTERzzqf9WBFoAFgEG+mf1TAh0+wb8zf8N+TIXZQWE9Bb3fPuPAiMCzgQ3+EYOCw3X6l/ofAiwEWr09gl+B+b3rw1PBEv5cf2lCCAC6/RM9or2mQzHDHsAUvab8LwLLgQ1AWcA/P5zBAH27gYD+gr4pQrJ/wH2QfuGBsL/bwYS/K//CQfp/mD/FvYnAGEI8g32/crykAEECJv6LvMsArEGMw3q+rv0Yf35/mEMYgOG9VT70g61/znxGwN0CIANMA17+z3yVfHP+hMAtvT9AUwK/wYG/bgAuQq88y3+Xw2ABNj4//s1AeHzBfxiBhEJ1P0C+2sQHP8v7voHRv+n70UGcARPADMPxg0LAr7zTuqB+zYGMwe5ERQB5uyx7Ur+bAarCuYVi/qe/QYGoOuM+acESg4J/iP1ggbx/dgMc/z09Bf0dfo9D7X0sQAeCHMDrPD0/fMdKAMKCuAAVfQT6V/0DxEfAbUK4QjZ9jHpUPxxEVD93AK8CasDDvuU/osJcwV8/8/1d/dj+hIDQAAw77gB2QVnB14TPQI966vw/AWM/JT/qwq+FAsKiO8l/DL4efaZA80ESPpmAIUMsP/c+00D2QRL+LsI8Alx/RL7QvjEBUD5FALM/QvxBP8VB7kFfvs6Afv3GgzkEoTyx/12Cl/1T+jDBQAUBATf/BIEqf6f8+wCogLc4UT2MSDo/rr5BxazEKv1cPvDEj/qKfADEXT9Veym/HARDQPeAM0HE/pq7S0FzxV29IDrbxQ+Drz0QwZ194L83AmI/Ln9bvAd7XMJDBQP9BoF6xBS7lUBKxLI/q/4AgBRBDAFvPRm+l4RSADf7zz5N/2aAAMNIQPO9Y/+lQycASUBVwqY/Ij/5fo+9DH7Mwh0+Jv1ARE4+uT50Aj1AYUD9wwB/aLvbv88+V8CSANJC8YPJfGg8+4A/v8F/bIQMAdD8cL/FPg3/iMMKf/ZAasAL/tRA5cBUf/791/77gVFBYkDcwBJB133e/Dc/5oCwQEHB+AFveiK+g0aGw+q9w7wEgo7/vf46QvhAgH6tPo4B28Ae+3o+88QRffI96sUH/4X8hv4iAw0EF4BERBm+wbiQPICDnEJl/8dCD8AUvaR7KMIyQGS6icQcxPGBfr8jwX0CpL9N/Ky9noCt+zm/X4AZ/8UDzMCdA+p/139XQIz8/X2Xf5GCZr54gE3E2EFvvTz9Mv/H/ogCJIAl/AWDDgKXAM+BIr0B/7l/Xv1VwYoCnP9Of5NBvf7yfwxCEj5R/11/5vtTAUjDrf/WQiJDO/4Fu/gBvr/VPXHA74J6Ptw8oYJZwht/vb/dgp3+NjlOwx4CiMEeQ6pBxP0Tt4w974HcP/7A3YcgwvS6r4H9wAK8bf/fAGv/qPw/v74DPoGVQP8AOMFhAAR+5P5mPkJ9Gv8KghE/sUEkA5ZE4QN7O7s6wf2c/MZB5sMCwNa+o3+ogZx/lELXw1h/H70YQCD8Yr28RKu/Jr5zfmTDE8FHv2TEUX0H+7f+ZUD3/2iBpgSDQCt8/oA6QIU5f8GnhOF/kP9BgPoFNTwRffzEK/uz/c8DmoF/vOi9M8HkgKQ/P4AxxGrA9T6WQUA8hsAQPyABwAHV+wy/kECufYC9CAY2A5C/QcArPbT+Fn1CxLNDQH4pfoAC2kDVu76/RUASfvRAFEK/f8XA2IM3f22+c/5aP9SBY/5pfajARL8Twe7DxAFTgCa9kDz7P4MAKkFRAgy+0r/p/CeAPYIBAUNCLLp8v7EAxAG2gPX/FMMt//1BMjuwPBTCw0HsQG68EYJvhh99nD39weJ+pT3dg82AJLktwzkEnHx+P5YCLUHRv9G9pMBH/Iz7uQKfgom+Cf9BArK/3MJDwiI/q4Fyf6/+DLoeAG2A3jxNwohC6f/cgF2Cu/14fuQDmcIuP0I9l//JPfA8oH/xRiMCAPxpPir9wIHVwwNAgv9kvxxATAHugJ5AWn7Afm09wj2DQjOCh//evi8BSr+ogRvB/Xu3QJeANP7sge6/jQCXQ2m/Eb5KAUN/+D+sPbw8mcBfQ9C/RUGTQ2x8+b+fP88/d/+I//P/qACxAAyAdT+p/B+DR8HPP+FBtH2tf1682f8nwiZARELawDk70z/5g3e8wECQhvx95b5WfoP+PAAhf8yGCn67OhYDiMF9+yp9YsGagxYC8YL8gAe7En+xQjG+Z/+jgNi+MgJWAgv3hEAbhZWBCf9e/Eg9rH8SxVLGgj8xe4PCJv/9+VJA3AIZQGLB7H8VvIa+WsUGwkJ8EsCWv/b9g8CbhQSDNbrvQUqChXyCwLPALPmZfPAEY4JzQgfCTb8Hfi+8gT/8A7zBZAHL//t6LLu+gGvE/0H0wTx/D30oQCo+38OPwmD9kj+AAAQ9/HtSwokEmL5w/6VBiD6MvgtCesGrfnpBM0KLP+W6in49gkm9aUEkw8oAr34V/xNA1n+HQutCEP4dPVP/YXzqQo7EhjqjAy9FH70evIz9HX7VvyO/r4H6AoOBSUQygL+6WEB2RCl9/3qxfyj/PH6UBJ/FlL7A/yoAkP2xvpi+9MDlQAPA+AFmO9QDm0QWfnzAnnw2PIpAhoG+wVO/+wC+wdc/xTzMwbLAC/s/vtjB2sFWgg6DO761vibAz//0Pbj/kMG2+8d93cDYQhvEEsK1wi58+vulgBYBLr79QJsC6j2cQJzAzD2lgu2CkMI3fc16kv+pfap/SsM6wKz/o0HKhPX+l3vpgToCIXqTfIXD8Lttv/RF236cPsADf8PUPeF7C/+4Qx/9iX6wQti7RoF4xSV+wf+uQMEBhL/hAIX/oHzBvuyCdoL1/dCCK4L4PRr9Cr4zAqy9nX7sxGW+TH1Hv7dE4b0avWoFcD0N/0TB1cEJvi885AJEAPL+VD/DQF69YMHzwyP8XH/EBwdBSfxUQjbA63qB/E6DIn+evscEk4HnfLG8fYMhf2a93gTIgUh+9QFEgRn73v2Zgv8AOv3DQWZEXD8oe9D+qnwTf7VEbwDmfs7BZUJLv3/BooC1fxv/77sXPfJ+qX/rwU2BJoC0QaQEAX99QRMADP09Pn07UMHSxr4A9L9gP5S9H7yFf+XBmj35wocDkT27P3DBGsRtfUO+0QHMvCKAIQKRAUn5yj9jQx69pUCbAi7Advz4QQCAAX+7gqjDFcElvIb/VDuXfhNDUkJxv97+2wF0P/H+9X4rgaLAaP8tgoIAh7vcf9LEyn8JfuZ+0kM4wWJ86sHVvih+NgM1Aqx7rX2tgaR7yD6NBJAE177V/9XBAzul/nFCfIKVf6A/FIA8uen+8YQ7QL+/J31TwMjAb0NEA+M+lIDoQbtBEjqCACICBLy5f60/s4GWf4hAXr+2vt7+Ib6lBYz/DL+4QunAKMB3PxnAB/rOO7cCfMGgwCN+QIKWAsU9vQEkweU/WwBAAAX+ov3fwCBBcoBMgPz+AT3qwq1/6EArhGN/ub0RgIOAUf76gRYAvP4m/V7AX0GiP6QDbcHL+9E8Vz3G/rjDOIREgo2/Cn81QaM9OsDygon69frxvZr/EQI4xmvG5sA5PTv+PzxvvsHCQIM0wAt+5IBGPwd/Jj7vwKdCmkB5u+B+xoK/P+yBCQC2gEh//f5iAYM/XPwqQxWBXDptAdGCWL2sf2tAZz8svSLANQRkwjQBg0QWP5R7Av4PwaN6vn4lxTe/Z7+5Q9fFC7uWvUzDAT1b/mVCA4LT/My92oDufZy/UIYORHW7AL1LP48+gcDsQw7Cgr7u/N/AygAvuz2CxUVtPO199H+VvDqCXcRbAK7AobqZQZ2EiHuQvu8DtgHPP5HAJT6M/oTAKP8OPtr/En+KQzDCZj53gkABXn7qwFKAMn2EvItA/72v/erAxUJCATl/tMVl/tt9sYBcP9AA67z6AZzA1n8Uwt0/+X0kvY5AT723vgEEjgPLwUv+t3/WgB79zIUUAMZ5/X7Iv578hj7JR1fEC3/YAR67jvt6QCzF94FS+r1+IoNFwtR+eEBbflC7sYKOf+X+HgRogWIAJf94fW9+HAFZg2r9xjt1/gvDpAFHQgIHAEDGu289OP8nOrb+tkVHAE7/4MOFAQIAbYIB/yq9EzpZfuSFQz8ev/pCJn1ngWDEj0G4vIA6qH89Paz/FwK0gpqFl8G1ecK7mgFMv0kC0cC3/PsAin/4hFyAR34JghiBMDyxvAQBEv81AhFCD8Bif+SBRcYEfEC5FT82v/4BdsDrQ4NEAfvs/kDCs34jfcSBqwGb+929V4KfP+E9mYNxA7q9MLxeP1zCRkDewLvCxL+//kXCkT24u2gBl4EPfkd8U4B8QrYB+4TLQqw+CICVAsK8F/rPwDNAaX/GwPPBnv/Jvmg/hMCvfru9kwBygnL9gQAgRvICG33wf+IBObyTPhw/5T3uPtZ+9wD6vn2/PASZhBXAE7+/wz/81PrGA7oDhD+gP5AAMvweOoI+nUBxgjJCmAIKweH/WwLMQdp8JT6MQCj9Mv29wQJBOEEKgrhCwb/IfddAFDoq+faBUYJsQNKCNkUFRWnCCb5tuzv6IP6HP/g+f0IzwpEBsj7EALfCt/4IQJoBPfoA/NLD9AO5gp4ATf8uwjc9RXiB/iQ/icBxgy0A9gUvxG99Wj4S+9j8TIGFBHo+tjygwtoBWQBJf5RBDsCofPh/63yafyTEssFHgD+A08K/fYM7d721QBXCUIK1A9b+ID9JhAO8f/yvAUV/PXw6fx4CTQGvRIOFmT5WeUH/BAGXPFj+NoEu/ss9cgOjRhN+O78xgwo/EP2/vmM9Sf9Cg51EF4C3flBA3X+hPNa8uABcRF6BlT8sPBn+oALFxQTCwPvRvs9AR8AZ/hc9NEP0gf0813uNv71BlACXw7kAigD5goJ9rP0iP/w98z5vgijAq3/DwfTBn8FZPS0+KYBofhUBbkEbPs9AwUQGAUz9SID4QSa8XT31gYL64jz9xr4Bcb6JxX7CePvCvZy9dH4mPo9DEgY8/R3/2oMd+0U68UNXgtx9SAI7Qmk/SABhgLA9w/8EQd9+5j2kgKdCvoGFAjRADD0c/nRCTb4kuK6D7YfVvTp9uQLbfc89eQHEQAI8FAAPhPe9EXsdhB9GG7+ewP3/pbp8/ww/8X1GPVSGL8YqvZXCPP+c/X1+JoEDP2B/pESifu4AOH5Sfvb/Tj9uwsJ8nf5tQdVAw36jwUwEaDzyAPlDLzo0fvwDenvW/OXDBEPxfTr/j4TI/Jo7qsPjAsD7n8FJwvA+xsArwotCzvlmgShAznnrA+gBJD3/AAGALMDMAkhCU39G/+D/qT+zQZz8ij9lgHj78MBiwDFB/UI1glL9M/tPgks9sgIvAk9AVIGYANRAs70Vfou8D8CEARb/C0ShAc/+7z5Q/uG/DH/0wjJEJH5YPa4Atb50gAkCisPfv7e7djybvyZ+Pf+fxD/CSYSegZu7Z/4jfKy+YkMYAHMA4L+DgYmCHny1vtoB3D+UvL4A4n5Z/AbCTgRNRCt+F7/qwfn86H/Ig9J9ivzuwiAAUH3lf1NE5T/Burj/7wLyfkNAKUSRf3M+koDhwlY8+r0Mhdi/GDnBQCyDDv1tP5xBRYAhgGG+/IMzPcF9LALjwPj+8EGZxEo+rj7RAnp81PoHPa7CsIClfweB0b/af8+Dp8XfvXj9Y4Wnfhf9WH7VPxp/6X2Svsr+LwEEwkEA5v6+wIfCFH+ogtUAOX8KQAF+CH5VfUq/zIJnvv8/vYNDPrv+pIDTwPvB03/+gXX+i72VQXxAXj3zQDhEAcAjQBW/1T0hfmJ/SkI8wIXA9QBqvwCAH/5d/+LAan5MgUOBToBTxFe9R7rqgnw+Rz1QxAcBbnyCgFNAZX9rfh7CIsX4/zm+br7LPX99y4OqQce9FcE1Qn/BfXx7wBdEJj+Xfh78Gf43APTEQUHefT+AAIEEgFaAyn59fmpB7P8V/Sd+y8MFQiA/o0P8/kg6Pf8TQDW+uEA3AkEBPX8/v8HEfQL3e96BbD+cOQmAkwH/gAGCPcDa/oH9JTxFgcZE3kBzgKhAAIKJQY4AIAEVPTW/mzzp+Iq+RkUew8BBRUIyQEBBvX22++89jn+ZQV7AD4GDQSoDh4CPfITCuMCpeuX7g72TPEXEGYfqfzC+4sELBG/BDLmtQoUCpvndwRuFOj4EvM+CX3+y/MrAccLIAcM9FsAZAJnAIYIb/wMBEYCf/NBATECkPCPAswIBvVN/0QPegCD7uv1qgYwDpX7kQncFEvoPe5cESr6nurFDgwU5vh/9nkVHv4r578Qnglo+sbwEwEMAnj0vxPhE4oCQ/nbCOzsjOnsByIA0gWPAYEOG/cy8rcKJv4t+Mr2hQTiAub89QF8Cy39j/JCDTENn/f2+T79lfZK+goDKRseBAnxDwV695P2NwdVEk77lvcNDG/4Cvd9C+AFavcL+c4BHf7EAXAUe//88Dj8vPv69XECLxST+koBhAM68vj4QgEEE675v/IYA90EbP568ycNSQsBAuoJIf5/7uH2LgVH9vQGKQrfA1gI6+sCAuwRmvbE+KUT+gKu5vICaAX6+Tr7GQh9C93wzvoNF3MCQuDVB7EPTOFp/rMejQII9h0JgQXH8Wz1agQi/D8AXg/nAgb2cP6FBEP5N/5ZBzAHOPKZ8IwVff9G/h8gu/kc+9gGWOIE84kFewXH/Uv8ngMTBQoMzPjJ+mr96A0ZGIHy5u5h/UEHRPK7++YP+/OO/4wFPfG4+m8UDxJfAWf8wvqJ+jjuc/hQCbgBSwlVCH0HIQe0+VMCG/819lXsevb3AvgC6Rv6Bgb9nfhi+JwLz/OJDlcMuO0u8jv1CAdxAZoUhQfp6Dr46PWXBAgAWAXxGG0ArfwU/uj4nv4gARD5zPbtB64GTwQxCgn1I+sIBlUPlQFACMoH+fWu8Jb4OgH+AqgQxRA28+znPgeOELDv+/qmDIL5bfOeCXgM5fTRAkMHQPQW+BwK2gxP92b6dw1YBkP2G/vw+NH8CQYS+T8DmgR8//cBpQA5A4P8DAtECNrxD+uZCtgWYvKKDeAMZe257aH7sP226DUYnB3Y9ET6EBmpAmHhxA8l+n3n0PoBCwgC8+61IUITzfak++IDtvVg4vQQfgbr4UsEFx73/DoD5B2f9qzqNfw+987zkv56FYgQ5/si+DT8Nvh9+LcdnAPX5bEDNgBq+qX/oBtYC8b7RPah58//jPQjDWMJK/jiC0YEgwIg9/0FkPgj9/IEhPLBDL8PLQCd9S3/AAqa83EAJf9o+bT7Sf5hCiD7dQ4yCVH2iv8E+9f+QPZjB0gEkvXEBsYIe/+n8sUM1Alv7FAGqgrO+ZL+FwcNA7fr0PsxBwj0FQA+B44ItQAlBF4DJf/dDKH3HvCh+iv7j/zTCTEJU/yY/Kz4KwQ5BLUJ/BL58wHnWvzaBdILyQs1/5wAGgLH+2HyHfj0CJ8DDfO1/Nr/Q/c9E8US5vq3/zoMIf4i7osBOP1h7wn7GRDbCiD2XQZ6/+TrjPp0CjoIxPVTBw8P9vpGDLgR5AHH8rzvxvZ/8hL7kAzoCxL9x/mpAZ4FNgGXAy0Jtfvg8noH8QqD+CIBQgG5+VT3LPYX/tT6b/3eA6IIgg57DwMF5PDR86770PirBkkXPAxb8kP+V/JU544aYQa39UMCJflRBDcCrAuaBKMAbgGiAKL0i+65Frj6Tu8iDgf4tfPaDqEGmvAH/8wFdgNaAIcG6wx99xL6zQu18JvsIBFsBM3zL/33BekK/AzSAmPu6fz7BHj7c/4jA/kI6f2z/mIAqPJeCPsO/fbZ7+8CsQjQ758IqBVP+y0DiQWX7u7vKASL++sBPAp2AToAlwHoCHz29PTTB+8AffW3AZIMsv6TAgkItwDc8N3+IhLO7tPzGAXw/ZMFAA5TBIrzZQke/iXxfAcRBSL6BftMDKj4+/vqEzgB//JP704AxP2dAHwZWAiy9W35qwVgBl3zf/9FAufxv/pIAL0FIwcDC2sAewAr/BbwjgUR+U3+/wdoCRoFIQV9DnbtgfJT90gCHQJU/ucPIQMMCL/1mvt9AiAA3Awn+OTxIfEiBKoNaguuAYT8AApV56TvMgvM+isBkATuC70AA/KXD5QHWfE+/oEHMf4r/9kHF/ia9cEBBgmf/kr+zw9//JHy6QTpD3UBU/ic/yry0PkuCOEE9wfB+U/x6wicCu36VgXT/mDtdfWy+uQHwhfXCg7+nPVv7Zz5QAYZBk0ELQxxBer0FvqMAvAEhf62A1cDzvvdBvT6X+7n/PMKEAaY/jcHgAeS9pLwfv1VDMMKMAJB//HpG/I7BusJAw0D/f0BPfWU77v+HQXPDiQD5wBC/hX+0gIVDk8AJfF4CioCQfeT9v//1/yJ9xwNcgd2BQMAWf89+2/3tw0PCYH/hPn6/I/5Z/XlBYX1RfjQDgMGFPqt/VsDnQRdB1r4JPok/7sCbAdz/D4Gv/8R+m38XwGkAbD39gwIDF/2ofqKB6zwTPCWEuEOEwYh/gj8AvsV+nMANwd1CY39fP7F+zT2jved+qsGRv4M+EQKUgV4/m4BRAN4BGX0WgWMEYv+Xfo/+M/w8PEID38TKP7ZAb8KK/Vl5XX9/wNoBLoQqQwI+VL6jgwtAyb+wgGg/U/0gPZzA0T4x/YvDn4PRvbk95kGp/tX+JcIMw8FAUT8/wNRCP78BOtP9KYI6gF77pP4vQs5C1EAoQeTCnb7DfrQ/DwCW++8BsMeJfrZAVX6V/ab/1D6T/+7+Fb91vWJC7AMlwAzF6YBP/9x9s/vyQaICIEDVvsL/uzoROpmB9gIKAF/Ax0Nxfh4Ag8QKgHv/f8A0wTy7yrvZv9CCdIFBgKW+8vyQgfUC98NI/pC9VgDNvVRBA0PYgVhBQUEYuag8skMzv7FCS0DfPtY/F/4bQHJ/6z9ogqbAz32HgI9AP4I+gCg8X/43vllDvMAd/BkAiQEn/4HCToL+PHP/DUSQAIJ+FMHbxE49Q/tfvnu8IgC5R0xEGfv+PQAAcD2WQXPExUAe/DeBSEDlPH/BNALUP8L+SH/YPeW8sMC1wemAxYEPxAYAAz0owaq9xnpLAanEZjzIfdHD4kLdwUxAg8CYvQY7CUEWAiJ+ioN8Axd9KX3CfGEAw8UAgKqBpP65v7sBtP3qfaS+079sfWFApj75AJhEYcFwg0n80T8pw53+SD61vQg/RX42PsuEa0Ljv7++pIFK/Fs9TITKAcc/OEDuhBq/UPx3f+X9a3zvQQeB3gB6ASNAcb8D/nH/WwP5gGn+uYGHPWE9xEP8QXW/Yn7LfIP7xoGjg8e96kMiQ0Q8NP35QMSESoGUv01+MTz3/xU/3QMrvuv+RQSwAMM+w7zQfcBBvj9nP0PA0sRqwXU/KYMXOuR8xAaqQLF76v1aANc/SvyvPtUA80MTBHrBW70pPjLBHAMLwaj8mX+CgPPAOn1P+l1Cw4I3ehR/kIZtQtmBLgHr/Re89sIdQvg+Cj9fgmz+JfqIQA4C0z/WwUR/nX5tPlZBT8RIPAk/pUY/fTe+M0PGfnQ+ooNOfym6RT7BQX7/Ov4wv+nD7/4+/0KEXwL6QQb+e4Fzu6l8XUIAQKlCYv93fYw/60Mqf4t/SYCueoz/HACkgR2DyAE+hFRB3nvnAA09Szp7v4uBLn/xAvuBuj5RAI9950DawJO+lMR0vZP+UcUQQKd7t8AdAiS8lIB3gjb9YTzBwuwDhn6+f7xBgkB7vSW//8HgPT0AOIN8/uu9P8KdBKo7/314f7B9AgBXAO2EJoCif1OBl/zBe619noY7A3H+4EJxwD668HqbxQbBn70Jg1HBmz8wO7ZBXQR2vLz/qwUHfiT6EoRqgrh7Bn96Q2Z/hf2EQkEAKP2IfkJCksNUPMw//oNxv1R7tIAqwWu+90EFfkf90sMAwab9mAFZQPD+ZACHAZq/2L/vwSG93L4zf/ZDbsNefWb77/6BQnVBgEK2P+1+ukDrPGg7kUSExNQ+o8Ks/Wa7Xb+Gfg+BT4G1Q2TAFz3ZPxO/KwD7PsKDs77deyoAc4Dpw2O/3AGCwvj9ZD6tvu++hP2RgKbCHb/7goVCdj/qft29G/+Ygh09gP50Q/rA1P7HQtvAMz8nQFZ93v7vOg+/OQRsftrAC0KTxbl/Kj4ogD99EX3EP6xE+vyzPCNB3MGsgI0+QQEyvYKCkYHP/ftBYEC0g3HBp8AQPR1+Ov+cPZgBfL+mggm/tjx9QxFBuPvB/z4EFb51AYaFsf0J/RRATQIL+3k6O8LbA7S9y326A9+ADH7jw1ICvb98/K1AID7hfMk/6gEEAmSAyMEZQUj9U70WwCTAtoBj/1sBgYRzwbm8Zn1UQgl/6YDJwLD82QEkwOs9OX2MgiaE9X+wvHYBo8Fk+9oALYEcPvXAEMCBhNB/jLtNwDT+7v3UAdzEXwBl/0m9h/13/ZJ/csasw2CCfn4Fu3VBk4DHf/h8hj3AgOhA7D/RvviEBj/XfUyFDEJXfjM9+4AaPz17NUC9QxWAXT/MAYJ/xP1zgb2BCXvjgFpEaPyS/pxCyX9CvHeAA0SLfMW/7MPeQcW/yr21wFO86b3bRNbCXnsPgJ0C83xCfq4Cs8M3gFRDL8ABfAU+h7/cfnF/jwOtPUO+xYMjQewBDv4jPpk+0X1wABgCaL0hQRUFs75E/YcAYP8YgJJBkj6PPrf/oH/hfzWBecBSfpwA4wJwQhv9joDzwXUAJADCP7u+wr0rwoK+fztSv1CAWAXmQ4LC+b+UvKq8+/3t/cW8UobixLj8BL7pfXi+bUIIhK8/gf6Uv5R9KT54/qdER8TjgnZ/Sf4lvfK6LoIYAKJ/64MMgBLAHH6/Qbo+moCkQnV/4ILCvg19jQCcP4E7wv2hQ2aBaMAzfre9lAEAQPMDvANA/LM/67+APCv9JgIcgzR+AAQfgFt9DIGO/109nbpGP9EEroMkwZsBK4HkQFYCj77Wu/s8nH3Gwl8/XUC+wnaAW/+CPnFBRQCHQBX+5XsvvVQCWwUAQUuCCAKYvSP7S/1BggUAXn38QIfApf4fgRLD3oAeAVKBbP0l/qXB6EEPvVR+QQD5PgcAlAQD/nU+/cMkP03+cP77gSDBvv3MQKIAoD46xLbC+DtcvoIAND1HvfuBZUAnAUKDx3+ZfYb8RIJzgU8BP0MC/ZXBEX/ofBY6ln/0xSWAqQA4QVQCCXtlP79ErD9pgg/Bojyv+WXAfUDf/LEBH4Sphaf/X8AJwRH8kr2JPlJA9gC1QY1A1T0k/UZ+qIK8Qg4Ck4NKvsy8oPsgPe8AWwKCw5bBmwJ7v0i9y327vO09y4FqQhV9z4Lywk3/LUM5f7w/Z78fv3VB1r1zfzMBNv4TvsZC4EFqfQvBGT/K/kJCKwHkQC++ocGzwRA8hL2cf4j+x/4nQqzEEb+NwjPBHTvt/FOBWwC0vJAFQUM4vHPAcoJzvzc60MPbA9e8Kvutw8SBnLfzBvqF3npYPe9C1gAfe8jDngG4frh+x4Hkf5+4PQSihIX7bIFdw5n+vjt1we4AIfsUQbHCZkFzfAhAKsYEPgmA9/9j/pwBp752wRY/RP4C/2fA3IIXAGsAv8DFv2t7mP6Mg6kDPQHUf2c8e70z/2HBXQHxQUHC+r5l+4/+MbzUAJmD70D3v7DAisJ/QTcBdUAAvZA/F/7hPY49G4BGAbs/78GUwZjCL4EtP+59dD4WAcbAiX8i/Y6Cu8Ls/LIAtAQXfos8rj7HfP4/XIQwAbs+Tn99AuJ/Sn0KQme/eX1Qg7xAgj1kvz1ApsHXe/KAgcZs/gTABf+ie9Q9jENtxSb8l4DJQ1v94L7t/5C+n7xjhIwFfLtzPqfAuf6qvoG+C4DGQt0BygGWP8S9av/Jw6HAZT8oQCq9V/6u/2d9Pr7YBDNErL6nP0LBBzqpvX3DngC8AE7BmkIJAqA8IHyhAdrBAv6zAGrBwLv8AAmClb6IgVS/g8MMA07883tyftiBC4GcAkI+gcMEQeH6WztWPnEEM0JvgVC/WX2cQMv/JoGRPxP+dARjAMk8TP4jALr/QYQowVl7EkOJwOk6pvyIQh2CnruzxUDGs/1WQgkELftAdzwBQsPAPV29YIRmgj05VgPThvW9zr9k/Ui7BYCdxPLBX3y1wILBO/32fmlBLcTH/Z/8nj5UvOZE30Uhfvj9HME3wVw+Uf7Ivkm/DAGZghABsEFBwle/PjgxPOSAjQI2RwbD+T/4+gv7awHEgo9C8kDR/fg5n/vRAZvCxkNcgylDdf9U+3l9SYDmAWz8LD3EQet/18I0w4ACrTpG+rGBIIOQQTg9bIT1gFn/FwMG/dA9Wn90grn+SP3rQLPAYkA2PtUAVL7Vw+KGtfxlOYQ/z0H7gOHAq8HTvrH9uoC5vq79wn54ArKAUj8WQnX/5P2cvg2EjD8LfkUEWv7bAEwE8/+6+bO/UsIWfiA9Er/UQ0pCDP8kQFpAff3VRb3EbDwrPFh/+L5me1qBt0EMQAeC40ETf649sD50AkaCTz01v51ATrxU/vSCmULEgFx/aX/3ARE+Rn7ng7zAFDzvAQYAWzvuAWrDSn78vJiCLwRRPjlCYAWe/2b553wOwZ6/KX9RwUoANbswv3VGvEAmgTnBUTxaeqX9n4QUQQlADELUQoO+t79fgiz7572U/ve9bwEff8XBpoTOvxNAPkP7P+lBhMEBftJ+tPwVvXeDYYFePANBa37UfXHA9gG4f+gAd0PHP11+zQBJwGO/R//ZQFM8/X9TAN+BVP68/AB/OgD4gxuCmAAjf6gB2v/+v2YA3UAKvqtAroIFexp+U0KGfQ48rMOLBQr/LMDyAMH/B/9Qfy9Ck77mP6tDIXj+fNcFt8NHP5p9ZwEVvfR98T/hv5w+qUEgxB9/CkJffq6Bev/wuIXCfEB4vylBkUPAfoa8LYJqAGv/hD1EBQDB/HkQxDND4nzGPb/FOn/WeSvCF0C1PDtBXEUIgNe/BQGp/MJ8Oj24P4fBTgCAA37ALD7gQt7Axj9OAr99tznpwyWBPDsNAE6DuX+nPZ+CtILVfkJ+6MC8+7l9x0W6AuFAFcEaP4T88/6IwMBACb5FwHmADT6OxOSAu3tUgmBCGX60f9j+1MCHwkd+y0B6fPk+EYWc/t56vgBSwA5968WpA7R9bUDIf5l+bnymgLHEynzcfn0DG31vPa9EYcUP/wI7oj9H/7P+icScwxm7MTwsAYzB+EDGgN2B4742OqKBVwCsv1hEcsB2/Ot/YEKPQer+WD+1P0E9RL2+PsACP8IXQdMCUf92e4LBAcQYOu6+3IOPv03/Vv8kwjr/p3+2gmcAubzz/uXDg7s2fvyEv8AtgTRAhkAU++h+aUFwgNLCoEEdAPv7dPx5wLsA24Mev22+Cz9If9bBr0FFAVV/Rb9Mv3Z9YwA0wI8+9gEbQN2/gEBa/96B3wA8/j2Dh0SGvNi8ToACfE7+SETGg6O+0z0vfsHBd0A2gPhBk37efgI9xYHPwWO/msLJgLt9Fz1vQ5d9Y7tXQov9RUCFwz0DtwIdPYcC0ABs+lw+kgPGwTP8tMGAAms6mECxQyE9UT6Uf4kABH/MRFOEGkAyfqn/lII+O28+DsCx/Y9AOr+4Ad+ACz+aQZnAf766fY9CbIMa/hd8yUBpwZVBFsLLfl+5XP7PQg8AeD8CQDUFC0MKvaO/1n/0gHKCMLyqu2+DP0QC/mu/DIDpPOc/rccjwBe3JQDhhQ++PzvN/4kFD/+vv51Do7vmfYuDVsIPelM8D4Q2wXqBuX8kvc/9/MChBTgAXT4PfRlC+YD/e4TEOwOBPC+8j8SGwEz7l4OCAeQ5xX2ABeNDMv6ZgOEBDz25e2cDRkNo++kDYEFieGE+h0QVfrT/5IPovD7+pIRSgmU+ED3qgJU7Vj6Lhb8CTrxEwFSEyjy8fMbFfAH+eqnBesCvuEhBAkZ7wEt/F0M/woL76f0pgrp/4n8LACr+4j2bQpqAgfqz/uMAqcaUQMs+d8O1ve5ADn3HPwABT4A+/qz9oj4ye6FFp8Vs/ovAIEIkwYJ7wv/ZBIT/rHtowHMBGr0RwZsCrz79fzy/8r7Gfa5/dkLbAwe9y/xaQehCasJVQCNAx/5B+NIBCQAFf18A+wKRAxz8iECEQSKDCj76fapBZXpwQS1DfUExgWV/0L5qfRRA9H0lgN4Cjr+jwq3AdcAp/M4BSEPvuo99EsAAQKSAeYOkw3e7Gz4QAXD/gr7/wXDEAb9SvQ0/a788vxWCeIDFu6U8K4LEg9vAvMT3Ar07w/1Pv5EAqfy7feaENoJo/kQAkkR2e3f700Q1gAr+MAAOwmt8B/+cw1R+B0FggvGCSDuqO3wAAsB+AcbA7MEXPNcAGcOOfFnAtIMcvo5ABv/NP4UAgIGWwkK9jn53wSkAcv8pPvF+/X59AY0AiQFiQVf/k8Je/3K9XT+SPuu9eX+wAchDegDyflYBaQC8/IS+6EHwvkW+bMB8QBg/IgOZhUn+373jPRT/Sr2DAK5Fsb6FP8xARP69PlzAxsAeAD8Etb2XfSi+Hb6HRDuCagNTQNY8tD5WfO09NMHLQ2W/7b6yQHO/7sCePod/wUJX/lIAYcCsQEBB5n63PaRAZkGAQXeBLrsnes/CAYRBgVR/hsMMv9M9hoCcACm/CkCBQmi7j3xNxEjAyX6bPgl/Z4DnwNJEcn4pPJ1Bi0JWgPy/PkIpvNa8KMIMgK1+G4IbQ4o683w2AnrCWsKWAjTA7D8EfTc+y4DrPajDa4NZOty8SsGfQbx+ZQENAodBRT6LPH/9+sBMApQAnAHFQ0u+1P0lwUh/Z3t+QRfDG31d+49ClUGMfSgD/0Xy/ms7cj/1wE1+v4FnRdqBorqUfoxAOn7SwyJBjnzLOrQ8XYHbQwOF50OPfmDBmDzSel9B/0R+/x99WMEPPJj/IwHI/1f///8vQLK+pcLVQV89oUIrwB5BdD9GABRDe73uvDe/mT8KPvqEHACIvNcAkUMj/vg7JYTOg+k6tYAkAs5AJYHC/+07m72oAAKCJgCpPIdBGoIW/a7ABwAifyuA6kNuw2i/dH22fcuBMYA//30+9j3CwSH+0D4bfyFB0gbxAvp95f22PQzA3gGcPz1/6IA8gJnAZD+evnP+7wB5gJq/mL24QHxBnoHvQKN/AIAPAI1/q79kv1s9lUAcwDu/gD/FAWICnH/tgCmAej7ivs7CQwCmvpg9bb8RQ6Z/UsDoQqZ+lDvkfxeAl0AdgkgC/35KeojBD8IgQeG/xH8EAU09oMAHgImAb/+vQXVAh/0JAPD+9X6kgJH/HQCgQe8CBwQYwBG8+v9j/ih9qQKawXE8ab3kvueCBMEiP5WDy4KEf3D+m8AdfWL/nMHF/ne9TMCrws3BPACq/U08kT/QAbTBdIKLgSU9qL+UfhIBLkO8/5U/Yf9ofcX+q0AfgbNA+39F/1A+KEGJgWoBJsGgfZ3+GUH9Aqc938F/fsm7xf9OPnEBFkCLgv7CiL4sfd5ClEGRfN7BoP8hvdmCGQHGQED+XAJrQMO8b76kQfBC+bwUeuJ+ZD6sA5mE/kMVgWjA137ifiUBKX1G/tt/zL3zfZ6/iYG9vlU/xkK6QuIC6MONgaf9oH0MvTo+w8DkgUc+Tvp1P8pETv9SAN8CbD7SgZKBfD3IgDXBM4AFwBY+5oA4AS9CFT9AOtz9JgAnQRO8JX+txr6Bnz7LAk+BmfxLQ0MEEDxq/l7/mf77/PY9jQFKAI794UGYhAI+dD8VxPPAwz+ogqy9v7yF/4UAjj6zvXvB0cDAwBu/r78hQR7Bv78gfk9ACLxbwuGFdIBjg0H+2P2df/S9bH47AFF82P5rQUd+R8K5wdUEGgImu5+Ax4FhgL9+i76vgGg/UPzaAABFvD52vCmARMIJPbN8gATOwp69vwELAoO/nv7TP+0Ckf8YO9FByEB8vK5A3UHP/0sAUIAef7o+fn5FgU4B3QHlf/U/qgCK/9qABwFl/uj+dEDI/k8+En7eAA3C5T+uPqCDh4FKPLCAMoCbgMyBmj/KwQ3/V771/z69FPywf1/DOsAowHDCawH4gRuBRQOCPgA9b/7F/BN9M72QgdKF3YKnfX1/Dz+pv04ByL+o/zc/+8J+wF+85P2aw5dDrjoi/eVCVf8Ff2CC+0Ggf6tBigJTPnp45b5dQ2i/Ob2mBZsFjb4wvg3+C/5pfYRCCwLe/cJATkFzAXa/5n/o/8v+Mr8w/3r+VL7PgyJElQAlPdJAwYFLPKA9gsBEv4hBvP8YPjD/zIFmhKPB9bxt/VMChX+l/aMCM4AfPwTBwEGVPan+Vb96v+tAuL8IhKbCFD1pPf09rH9xQNFD1cDpfxrAtD86QBg/VL+9PoJ+0kGMfwN+NgBmP6m/ZIKCg1kCeX/1PoJAu3z/+xAAgsISAidCvb1jvaC+o/8hAsBBgsK9fqJ9YX+Wvx0BGr7nwp5Csz4FPv++dIBUwQCA5f5IgCOARX61QtqBpv7QPst/Ib9T/lEA5oTcQzu+Ov7XPXD788F6gmm+p74uQHv/6oA6QYjCGv8y/7pDJj7DPii/1/3uvDm/uoEDAzJGZnzlPPSA7D/Wwen+TMAFwAC+XEE4AsX/U36wQqQAOb8qfg5ANkFsfY49arzwQBrDpsVABJq/8L4Evaz+OT6WP5R/4L60/oo9wD1RQNyFH4OSwPqAzAIUPkj81cCvgEn+Lrxvg9FCF3oOf9QBvH+JAPuFB4D0fUSCfgDuvk/9O8BSf8zAecCkf4PA5P7yf/U+Ob+pACTAsYAVfiGCO8AjwM0Bu/9F/4oAP//VPVq/ycDTvny+OT/KAKm/70K9gSdAZYLJQOi/q32qvcdBEIA+Pi+/q4Ap/kKDKkMtP/p+Hn8TA7m87XudAV3/4X/IQsiA576gAZlAs71dvDB/akJ8APEAQkCcQAc/pEKaADd8EgGyQTJ+WAA+v1eBWMFxfbs/UYIkAZLAGzv4/ReESYLSQI4Bv/5AfXD9oDxnvN0DGAZygFa9Q4CygD1CjsPpvgb9APzh/09/AL0NAhSDdUDFQByBAz+z/ndCQf/gPBh/v8NlQ1++s7/IPqR8uwAA/gFCJUMegX3ASf0YP7jBrYBLP2eAuz4P/oW/6IC9AqdB1ICfPL59+PyGfhBCS8IIwMbA0QNz/+wAPsCmf7e8IrwqQm7A+H80v8HCsX5b/enFJMFoPUeAesBzO1v+L4VSQ4eAnoBVfvz7E/v2wf1Bqv+OgPKAMr7/v25DvkGHfO8/74EHPim/0AAavxFCjQMI/8b7jL51ATcAD7+WPTq/BsSdRFp/nQAafw69Zr8XvkC/bQMigkz/pf/IvZyBtoINPzT+1vu8PYW/UQR1xBz/CcI8wjq/gL7AO/18P4P0v1S85QM9f7G+hoMqwMU810Eigjj+kr6A/qy+6QG0wkcCQwJFPX1AcsCm+kZ+RkKsAWQ/9kD2vXr9Qf/mgSuFPkFdQc/B0Xueehs/FgMggDUAEwLzwHb7oABqgoX9ED8FgfPAiz4H/i7AkYRowoM94r2J/sjCs38VPkBBwD/qgFUBt4EP/cH/6EI/ADO9f/rtwU4Bgf9MhOzBmr5AgW9/Vj2wPu5AHEB9QMJ/db2XwGJBaEHNPoK+L7+MP2xC6b//PfPBGQDAAAY/zEJEAwc+Yj3EAEb8pbv3AdMDgb9wgFcB4L8PACYBdICP/qKBb8Nlf0/6x7wDgl+Aef99gVRBEcC6fr3/iX7U/7sDh8HIfYk7z/8Hgu7/YYCVwe9+LwHAwujA5z5n/TU+nT2DgT8Acf/IwEhCFoO0O/K/1cRJPzd+/sEsvm/8p0ENwMc/8H/JwORBDP8EP6u/Bj7f/7xBcMAFf1oBsQCY/97/+f7xf1BA2QGJv9h+BD5dPMk//YD1Af4FDAFFf4j/hz+Hf3G/7D+LvjC+oH3ugVaAbP8Dw4gBoz+WALv/JP8zwSz/zn6svTs/J4FVAAFCAAMTwe394nxf/yj/v7+oQjXBkr3Lfs8ACz7HwGDAQIMrhCF7bz3mA/x+0z7fP8E/pMKswm+9WX0W/IO/RMNYQNHCT0Fpfxx/i/2w/lICxMH4AFM/pf0Mghu/MbxJAPS/WgHYA7t+f319AZg+Ev0XQuDAg0K3RfB/Jjv2fA4/zcL1vwuAEf0M/CJAcMAEQuZEb4ObQ/GAOHwQvgn8NL0iARC9xP8gwuxCh/+DQbIAzf0x/7/Bo79q/gfBpz97vvhC7EUpghN8vP0XvKr80f25/8aCksH/gWaAvH/egCvEU4C4/WJAZD3G/sxA2r9IPl/A8H/Nv+MBMIA2wg6/rz5wgC6BRwHOAHX/Vz3A/qm/uX+V/bqBKIPXvd79uf8XAeTDOICfP9I/Dv9pgNq/2zwjQNCBmn1IwVfA+YD2AZF+av7ogWGAooDSQJ08xIEig7f/Jf4sQCX/o7raveoC5YM7wax+jYFlAhn+6r/BwSK9tz1MAf3+ADwAgc1C638qfjWBO0G7gAsBOkAYv0oAdEEvATM+Of5zAc9AC3yc/uSAyn96gxmBg70a/5K/0cHTwZq/wkBTwA1/y78IgPQASD+/PtJ9V3zDf6pCr4JQgRa/i79vwGcBC8DMAhu/TvyPfb/9vcCOQ3JCoL73PkI/gsAnQqIBjT4ovpgDN35i+qxAjwV0geO96z/lP4TASj+H/bj+bf8yw2QB/zsffzfEp0G0fsq/+L2S/+QEyb6m+/K+8X/rgpe/cP53QmrB37/xgRF/jj8SgddAkT25+7v/CEESgemALv8iAjQA74AHPbb+UkEzwPuAMUB5wR99in49gOOBOwFnQuM/ljtM/QdA3QJKQR7Ba4En/pS+tT6b/yGEIsJtvjjADr6yu8NANcLBvwU/S0BMAqI/4zytA4KAuHsw//hEGD9KgCrCjb+I/fl8yEL3vfc+5oNNvrQ+pD81gj2/c4BTwOUA/0F2vTsB3cAzfkaA+z+af3M/00AkPQM+UQBEQ0TCpv+9gdwBMX02PU1CTUFmexw9boE5v08DEkRw/zx9/sGaQU/62D2ZwM9CzQKN/n6CLEG0fl096X7D/vA/UoDNv4eC+n7Kf72Bz/2ZgCtCHH/pPPg/o0FSP+D+zcLjRWl98L4PP2H7cX1/gaBBoQFZg3xCP32MPDUAzIGVAIRBPP8yfo1/Tr/I/10/4wBkwet+VLxbAVBAVcAqgyxCQsGAvy99Nb+cfg9/WwKqwMe/9n64f6p87T4SA+SCMT/ZPREBugQIfkTASIIrwB5+qP17/rI/ej7ivuW//L1xv2cFXsPGf/Y+pUJCwJK9LQJGg/L+tD2hPmm6dDskwtQEDr8OQCVDxsHB+6kAxoVf+4P/MAR3/gs6gEKKBCV60DyZAQwDgH8wgDNDCH39PKuAIMU6QMoA24AXvWS93YBkROe+xD2OPO9+wUBfPekEpsSZgGF+EUCeQBJ94wFHQSU87byjQeSA+n+fwqN/f/31QTv/6f99PxI+OIEpP2TAU0QGAE2/N38Cvgy/S0KWQRP+gcA0fsL+gj+gwOB/+oAUBEEBPz8IQNiA/gDj/hL8u3y4vr2/SMGfglNAgEOMAIM95P/fPp6APQA//q1/v3+YQQr/p/83QQuAnYAh/b2/7IMEgB19L0JdxKP8Hv8yQbU/loE6f/E/uDujvq2EXwEyPBp/KMJS/VP/T8G5QJjEKcG3fiP9s/3nwSWA4L6VQHDAZP6nv3KAxkBkf2hB7MHKfeN/LIH0P/S/F/5vv3DBqP98ATgC1L6k/hwAMb8JPurALn82v7DBn3/AgbpBrD+DgMpAr0Aovdv91v/HvY6+0MIuggzAqL8nQlf+QjpxQnlDu3+mQCeC2MBPflsCBkAhPS79xcLLAC87TAFDQRH+/7+SgYYBCD0kwOECQ37JwjgB/j50vxEAjj6v/BD/m0ApfrY+dYDgArhAUkWmxGX8ej0yQPJ/E/6JASB/Pv72AUuBgL8T+2V+mASsvqx+iAUxwIZ/eEGZwTF9Cj+FQgo9PvvBPuHArn+dgaaDBoEsflQAu4HcPUs97z87/baA3AV0QbA/4kEPgVe+xnxEf4K+t39uAFq9lD5ng+xD7n/9gUe+gP/DgwV/SXz3fuVAFcDzABs+10Jcf+89GP5FP1U9RcBfxbhBHQKfgmZ9JH13f3S+AL3ewa5BYUBEwQXAEr7ef9zAz0HI/4r9dr+iwHvAYUHLwoUBXIDxfqq70Hxb/47/wP6LwGG/r0K6RGmCcX/GP4S+sXxJQLo+DkCFRdB/634lPvzAqcCOPX5AzUEOPXU+QgH5gLj/vUUAQVK8MLxEAQJBZzsFgwgBdLz9groBZ74DABQCB/1cPny/rkAWgJk/scSDAuP9JsA6ATM8gb9RwUB/VYBzwf8/aD2if0O/N8EhgJlALkIKQiAAi/3HPtI/cf/aASi/p/z0PE2BmANcQTIBdj/j/vdAOsDYgM+9Z365wWh/Rb51QbICm36ngQm+//uNwU2Bl/73f7fBW4DoAAd/XoGeAMN9b0Fkgxw/Qj2+QEg/5zus/xBC0YEQwGGCNEDvvXK8SoBJw04/b7/qwbO9R39xw7aCU/9YPpi9un4DQSiAFD8zf1GAh8Am/Y/BusO6gKRB5D8ivVi/7H/qwQuAEr6WvQ4+Db+3QJVCA0BMgjnBSsIOglm+5X2ovp//970ZPjrAHoJLgZ/BswM5fdn/pIA+e599OQDsAn7BgoDMfoG/S4L9gsA9J32YQp691jwR/79BAAGNwNFAiz2tPcsC5sM4v31/10WMv7V6mP/f/UH9mMLVQu78zb7VxK5AB3/EgVl/MT6f/tX/V/7j/sQCCIR4wMr/jsBpPrK+bT7m/Y++8IHoQFF/t8EgQV0AqgCo/zZ8tQDqwuxAjEAc/4L/ZH79PmU900Eegg7Dsn9R+SwBBYHbv1yDFIEjf7kAG7/zPyh/vQD1gjG/L3txO/h+iYLqxF6BEz/uAgf/x70OPYiBHAIif9DBeD8sO3QBEARs/QL/yMIiPte/Qr1lgBYA7ACggWs/l0DMQRsBeP1ZACxC//wCgC9CSMAVfji7v8AOv4N/hkMnA50A/j57xFz+x7rfgRlBjn/bvjID2sDkOym+RL7x/tn9K4OaRIA8Rb/JAlaBK8FFAnCAgf1WPm8+k/5p/yoAYIGiwDB/Jr+6QNOCEkANvdkAuIGwQAsEOAEDfA0+w0G5/tb630CagY99gH+rQLxB0//lQnzC1z3vvgzAef+GfSoAkQKPQbeAkEAO/ux82f/0/im/WwIi/0q+zwG3gt/CxQJswG+/1fwjPwq/uHyDQLnBfwFSfVOACQLf/1U+m8A2QF0+5YG6AJu+cv6vwhUBc3/hQMiAPT+t/NRABL4T/pBBm79QQLz88H+GhIkEVMJYAFZ/lr22/ZhAMAEyPxXBAoKsvEf7iQILwaM9kX3Gw2KDn/+rwuZBZv5EPOW+WX7pPNYAHUDywXH9oD+exGjCUECiQBFAeTxKfruAXv8ev09BgwTTwKE+4//APf29Ir+DQIA/GoFABB1AQf4GQT7BDf6vPzdA2f2OPQoAJUGxgkAAY4CfAOpAVsEJ/668WP00/2G/zkMkANM/7//bP0vBIT5OQIFB8kI1AIDALn9NfCtBjEA+P4zATb8eQNs8UX78f9J/zkG3wtdDykBPPsh+i39L/lN/xAAk/yeBdoBtPtp9B4FNgu1+6/9Q/kpAwEIR/2YA9QFywRXBFgKJ/e17joFFvXq8xr4tAbaEyYCXwmYAhX4lv1sBzz88vrQBB/6j/1I+30GKQKT+VIAKPeN+dQFkQbi/sgLPAU3/Ln9TPzl++H1DgdgBX8B7Ar+Cmr5d/N+Cc/1K+5dB4H/mPPTBDoRoQRXAYQQtAc37uD1i/+J9F7yqgh8Dnf3lAawD5X1G/OTAvoDlPUGAvQPJwTv+mL67gjkAX34pQXwA5T3gPiYAIT6OvsBBIYGDf8p/5r+vfoNDlgLZwIdAxb/5fXJ9Q4CuPb2/jQGegNrAwH3UwFuAsgDEQlFAn/77fceBWz+tQBlCHv2W/vT+FP5qwBz/6YQoggv+Ov0V/3FB1cADQfjAz38tPqgATgRVvoo9I8DPPiV9I0Ddw0z/Br38wiZAdr8kgowCjr/pPks+4L4DP6HC1UDBfdI+2YEdP9g+/4GJAQ/9aH53gHQ/GUOJBWE9Ubu8f3nBT4FfgFcAAf2ee0UAE0MIAJ3BGoPjgFp7qr7zAV1BXoDbgA2ANH3Ff9JBAf/E/2y//kKzgJR+RX8MfdAAdkE8QE9A3n5nf47+XADnwv0/vgHcARaAb/vRu9oBQ4FF/+j/HwGGP1yAo8PvP8V92YDfwew8brxeAd9BJD5dg5+DvvxfPMZAmX7Z/l+DqwIsvKY/4sVmf8R9iAHQP2+8Ur4KxCqBH7zLgko/9XwPQTjCtf5Q/i/C5YBc//HCnsAbQIu9aX5Wf5G+lb/Mvr6Dor/2/wJCggErvwo7FIG3gDb74cMrBns9jHvKBNJ/XruMwyfCzrxofW8ESMAbujDC8AX0fgX9cYCi/v68kIMCAsu9G/8FQ8IBKv2rgeUAub0Ivg5Bd0BEv2S/3T5hP+g/yEEGwbJBsP/nvaTA7QEGv7b/oMAGfxf+Wr5zAPxBML7Kwi4B5X1VPlDDH8FzfklAIMFmAOy/jH+G/5O9T71XgsxBeT4ngXIA8D+vf8GAXT9dQK8Cq//3vvU+Sr65QRk/4n6jfysAIP/6f9eBZf5OwdYChv2H/2mAMUFTgb/+xX4yABZ/Z/6QhJDB/r6OfpN8yD3R/pmEKUP/AS1AFT6gv4/9icBbAJ0+XkBdAUV/Qn6Qg9SAOf1ygT+AGb+wPdm+2oBigNoBdYHpQbZ++gAXP/u9kX4tv46/ujxiv02DJwOJgpn/Gr9cvwA/asIwAdN+E/5AgQs+jH2dQftCl/6bwQfBg33X/ZAAUsKoPQS+TkI/gIq++oIGBV/+xr+f/7t+DHwcvLVBaXy1wIMFkYC5/he/z0POAwhAO/89v8/+sv0FgAz/eH/vAUc+nr1w/mDD6kO1/+4+IH6eweL/hcBqgBwBl8EBPWB+yL6ZQb1DA4GH/XH7HUFBA0Q9tzweAPKCn8HjwKlA/nyBv0DEyoFYfmR9TwCwfSS8hP/hf10CP0HHRC9Ajn0yggSD9r5F+/p/K/8rP80CcEL9AO69mUC2v5M71D7gAd7ADD1qACeDCIEt/41DQkL0vPU+2sAb/LE8yQCRgqR/oz3oQeOCWv5lv2rA8wD2wGJ/bT7CwRQBUoCUApm9crwJ/9L/9z/DgIIAnb6RwNnBKAGmQIh+3wDfvv9//EGdwUuAYf7//T99MoI3AYzAfoBG/Ay9QgIXwRFCVIJUP+V/Z7zUffYCEQSqAL/9UD67fKA+JoGkw/7Bk73jfcB+bsDWQuyCfUB2Pa/ANoGAfIqAjYYGvN67oYPsAMU62sCcgj361P61RaTCSXq9f/FE9L+pvs6CloMo/j999f6OfiS+MIAjQUY9RcB3BDCBVv9lf/f/n4AuP7b/OMEPwR1AA36//vZ/9IA2wKf/K72HgXLBg3vwwWrEIj9/wqeBcXxufmZAWn+uP3T/10H1AJr9cz4jABo/xICeQXVBQEDEvud+s4E7gPV+ocEQAPt+Y3zvQLoCvjw9QQDC8X3Uf3bDHEJPvL3BZgMGPcS8aABCgxL908Aiwd+8ez77grE/wX31/2rCTD9ngI5Cw75Nf/1AKD9fwJHBB8BNPNT91sG0v9p87kDAw2T/YkGywBg++MIcv40AGX+nQshBqLrwPY8+RgCzATfB/gCJP1sBP//HwAg9BkCfQ6L91L3nQqvAzkDjwTh/Jn/gPGu+j78+/lK/QoI1hD371j+8hPBA7L+yAxbBt3rwfQ6Acr4mfj3DbMR/vFr740OOwTW9xIHbwpP/pD+zgWL9e31b/8iC7D9/fd+C9f+9v3C/Fj/APzb/LIAW/hbBaH5UP1VEsYJ4ALBB/EJPPg671r8A/7n+KP2oQBw/5/3xRUqD/D3RAgzCp3y9u7iBuEHMvx8/d4Gbv2j9LkC2wxB+53vNQYDA4P79wSlDtj+PPaMCyEA+Pj8/ff/Rf26+OD5mgEUB3H6rwQYC8T8cPyq/xH8QvypBdoR6QTC9rT+APa79IX3yf98DmYEiwH/CAX+Q/TEBbYH+wDo/p33nAEw99D5SBEFAiD+KgWmA1EBpO0S8WcLDQkp+TcGzwKk+qkQKgeO9BXvvv7UB1X23vuoBEEL1gNy+tr+ufyA/b0FbQSW84EBrAosAkEENveV/mEDq/hABb8AefTmBygOY/nY+PAD0AHhAMD8SwH/BzDy+fkQDkwBqgGUAZT59vG4+RgEBf37/+4L1ROA+VHw+QkcA8H69P0++O39kQI1BCoKmPj9+kwI4wEV+9v5xwrPCAgCG/Qn9qgIRAJHCL/+iviJ9Q33PA2WBqX9wgbxBhbx8O7UCHoJ1P1FBPb9nvED+hAMag3J/VQDywJU8QLy2Ay7BVD37w8A+fbwhwoCDdcCePTjALsEIvsd/HkOiQFd5VkIig3b7sn9wBSLAq7sOP7oA6UAdgV8BAsFA/vs/b4DBf3y9Nz7dAFj8v8DsQ9nCecByPUUAk4CqATcA7357P8J/Tz4xP3iArIDIQo8+XDqlweEDjABq/4Z/qQBnAG1BJb/hf09/kH5BgPT+pf92g6/Anv38vok/Bb2NQizDr/9vf2AAtcFi//zAP//mfqo/JL3zfjg+rn95Q0UDzv8FwQGAy72kgIzAB8BvwS99N3zegNrBbf/5wDJBOEA7PorCSsGlvRhAiUMd/nr9skCLAD+/Rr+YgNh/y/59Qh4AurwTQdUDYP7QP4Y+yP6AvucBpMO5AA4AVMBpveG7qX+CgE++G0HkgRi/u7+OgMpCJ0OeAcI/DcHAPiC7e75t+7I+tUNUwveDrr/XP/bAWH+kAOO+AX4tfmjCLYAnPssDxT9ufMy9kEIOggh9loMYwUK53v1ug+2C/79TAQSBZDyRPnDB48EYwFSBeABL/ZD9l35dv6C/dsFDQ76CxQHFP45BOz3UfNA/mT8OgFaAab9dPx3/yUJqQyq/jf1Z/2gA4vzAfaYD54CCPtBDJ0Ja/XF9CAI8QFf8kcA+wsU+H32aA2JAwTySgouEPT2PvZeBooPqvks+60IrOxO7osIrwx8AlMDcgQf8TTyNQ3ZEWEA0P65+svycvquCOMPWAKf/B77w/q3/GX3IwAgBUgDc/v79qYHmQXD/aYPnArX9zD91gaP/w7pTPy+CInslvQpCSQQ6gY5BTwTgP1P7FMBgAPz90MB9AWt9Xb3MAoJCFcH0P0k/wP+S+sJAEgFcvsu/5ILjgyo/BH9YAWABTnyQgEEBzXzgPw5AAv8o/shCB8AofYWBGQQLApv+SMB+QEI/uL8N/089M33kBEuAv74af38ACgDP/uOA4f/ngEdAh/9FQY/BfoGkwJSAdv2yOnqAq4FbvQbAg4IZv6Z/90IUQ00/bHxHv20/sb5uQikDFH+Kv4BA1742O0aBckK7f2aAej90QB2/oACvgcCB8f8T/bBAOr6YAakBuv9mQCw+L3zZgNbDyr4OfyPBBr+5/qcBfARuPxU+xv7O/e89bj6eRNODa36lfoeAI76AQHTCs/7wvoEBbYCb/fl+bsIJwDv92ED3Qq4+U/8Dg5L9kL5Jg0jDTz5CenQAcUBMfVABdEY6AKt98sBsvKt+YgBOwp1Bfb5UgUOARj1dPyUDOD/n/jg/2r5xfa7/0MMCAtVAIz6jwO5BbT2rAKxCZL1K/gRA78KGQCl92gEwAD89G76LglP/O76iAcuDIgDLfyDBaX4zfss/c/36fizBK0QwwAd/HL/owSA9sT8nwdh+9IDHQFi9ZH7pQnbCvEMYAIl9dLw1PgD//b9hAoSCNQEafLg+/kKHvxz+YEExhC7977+4gQo+aUErQHv/M79nAFB/aT5cfYO/RsEVwWNBJAJowIC9xoGvvpEANsK7P/F9Of0Nwd2+x7/AQWX/qQDQ/rL+WYGkgSYBJMMtQTs/On6VvSP+M4JYQLg+74DV/dN9LMCiAjbAdYIOAZV8oL36AalBlsDeQWh/mP30fqzAR8CmP/E/Ab7f/n0BMgPcwIh+T342f8hAykIdgaz+DT9kgGj/sz3QQauDUP0EfcnAKTwNARDFrr/HP/4AJ39cwKxAnoAp/yX+ZP8JATU/dIDkwkb/AD+LgNB+CjyUQLsBdf5RQijDN3/0wWWBJH77OyP+LALO/vF+9MLQgTv8ywF9Qif+1n82AEzBFXwa/15CSn/FAbLDXcFaPJO9432APXcBe0Gtf6ZA9gO1wZ89MT5LwEh/Yv+cQIkBGX4lgDIDRwD6fnl+jP+g/vCBg0E8ftZ//z/NgZNAjT1yvrJCE/4Qv9XC9P4y/+YCOAAUvin/j8H/ABq82H2PQgg/7kGQBcZ/VDvdvrw/rr60AHRDa8Dw/YJ/fYFyfks+acLZgwf+ub2xv/w/CsB6wPLBmr7NvmMB2L/nvc7/eEMBwWEA1v3HPEKC8QFEv8598EDtQPy+BUEYP1g/2v/pQKc/Lb34wvQCWX3WPbe/NwCFgrwCc38TfCGAT8GMf+SDLUIfPNr9Cz5B/fLBmoLFAvC/UD3lAivCIH9k/sSAG/xOPhdAOj+RQdGA47/5vp9A3QF+gjMCKX5fvLq9cUAKwLvBfwGjAaG/2X6kvxz+238Zv1UAjEGKAl6/bD8iP29+9YIlQMm/2z9sv1zABj5EPk8BxoF7wOMAzfyIQAYCYUA2/jLAMsICv3gAIf4mfyDANACewhb9IL+6gTk/ncA1QJLB4v9lgJvBtb4Gvai/9v+lPh0B6cG8/clA6wEDP97AjcFqQdg/ND2H/sV/8r9B/9QCHv9u/wCCtP7TvIE/N8BnwrmAqb7ege2A13+5f0tCEEISvVg+pv6xfX4AT4Aav3O/hL81QqUDbkGzweQAtj3uPICAOb94QJWBiLvivPSAosIwwHQAUMNaAGt/SwFiPoy/I0Cwfi0+18AkQN2By74//aXCIEEPP1//4377/17AiP+Zf9uARAFWwtQAH4DKwBD+dr/wOue+OUFvgQ1E8cGgvcy+EAF2AKd/lX8L/dQArkCu/02AfQGcQoF/r/v9vz7/0v+NAE7AgX/rvRPFbETy+8U91r/6/q3ATIEQPuHA+8FtQh6/gL5h/tB9WwDvvik+QsJUQ1bAdL7rw1oB4EAA/VU+1r3JO0aBQUOeQndA8YEGPSZ+igHUPcCAOMDigCq+wgDVQk++QoCkwpL/Cv3F/obAND4a/rKD58DGv3wA2X/EvcZ+iwNFP1U/40WVAXM7az4pv+F8WcATQq4AuT6vgXiClX6Vf0CBD4Lk/jO9sAG7vq8+fz+OgUf+vsEnw4u9s/4qfm6+4QElATXCogL4P9y74z3ggTF+msDCA4K/JH4Sv/D9678VAkfBx0Buvuq+3kFtAaB/rYEyADV8AoH6gqr+Cr7H/f+AwoF4wFjBrD6GgPX+Kr1QgXfB8IN4ACW+yzxn/dTB8T6QwXgAIH+RwKY+YD88P6VBMH9PwcoAzr7EAgT/YL9DATuDHH/RfYs/2D1GwDx+ob9lA2YBNMCaQMAAN78rQYd/n30bwfU/h/6tf469igIFQOJ9x8G9/oz/zYJKfwB+JsF2Agk/C8A2wB8AKz1G/uECJL5RQSCBCn8dgPCAngGMQYS+8j5c/z/9xADhwpDBff9iwM9AHv2mQak/sP6kgUq+gn3JAfzAov5bQNr/UwClADjAJ8IKfPE+tYNmP5V8hMHYgCu8HYF1gZmBOX+SQWbCGbxrfdaA2UE1wA8BbsHiALt/5P59wH2+nj7zQEs/YX8GP+yC4b91/+HBdL/+QU9AFr6NvTp+yz+RgLU/FT+8xPH/tT1RwSa//77DgMMBMX/wfxIAP3+SPJz+38JGAvsBUwD7Pql+r/8BvlzC+0Gxf2A/SL7zP1MAKwKdAV/Anr6IPKm+wf/OgJlA8sEAgAt+1oMNgau8/L9lgFa/oj4pP5nAp75cATkBQ0Clfr3C9EUW/AK8BH/WQO8+gED4Qfe86QBbQRhAEb64gDkDmoARf37/L8FqfxX+U78G/PnCoMNkgKN/I/+6f1v9ZQBRgW7B6wGLgAT97vyuAN3C2kCRwHM/Rb3Zfzp+2sA4gHvAEsL2QA29CAHzwOC7jcH9g1u+Pn4MQXAAqX2Ov8YBuUDLPyEBPED+O4w/VgM9Ac5/58AGwR0+GH7VgiY/Zn3Ow7+A+Xtq/eR/1AF0wQuBgUKx/wK8976pwDt/p8EMAlLBQ72CvbKBysGFv+y/d77kfWV/m0FpfooAXsJwQj3AC4ATQM4/Iz7o/0M+0P7Dge1DNwCQPfe+CUAwgBVAtX+3QFECZL5AvaRBYYFXQGC/LgEIgLu870AaATs+b37VAKR/DcDEwLj9l0GJAjXBUUBA/gG/SwAcwDZBDsEE/cX/fUD9/6a/4wDuA6pAKfw8/fEAVAGdvwCAWEE5fof/ZoDyv3n9IEMjw81+sz8tAEu/dvzdvnzAAQF9wzIB8/60/Ug/RcJHwAn/OQHGvvs+LYBRQPz+yT/SAz3/0L2CP9KCSz6DwIkCy71ivOY/kYBE/rGCbkEmP8XBeYB+wm0/IQEAAPS7oTyAAGH/4v+oQoC94MBKRXSB23+9vNl+vj9ifw7ADUDHwJu/PwHzf01+VILfACs+EfzJfe4Ah4OoBLo/Fz6Ov26/LT/7/96Aw7+fvoc/lIFuQXRAn79/vaR9s78XAsPBx4APwS5BsEBTfdxBUj/BfZp/Sb4R/+f/msKOgWaAfEHRv3LAA/w8PzB/hj9uQYTBGYNGfbtAPEC8PiYALX8JP34+uoI4AKqBC/+Yu1kCJIFKPgsD7kB9/ZABx4DGgV5+gf96wBy+jz36P1jCIr3lQwsC0L5If2H/hcII/RY/HoJHfes+V4KHAfK/XH/b/eC86L3PAYiDQP/XwKbDDr/cP7WBEz+X/5YAdEDuvDo9IULxQBT/DMBvQPc+2kH+Q4I+Uf6DwH+BFUAK/wq/Lr4+v4H/6T+4/9ZBPj+WfzZALH8MQRQEc8HZfOw/9j82vCd/XEGcQMd+2gHWgXY+x77QAcEAurssgpMBbTzuwpQCU/7ff8CDgEDFfds/4H7B+0M7YsJPxrlBqUAaAat+FPzwANNAEv5CAjIA3v4yPde/KoHBgnG/Df7DP4B/iwEawM/A+oBawT2+Y71E/3G9n0EwgPTA/MMFwyWCF/65fuM8RXxV/3C+0cGXwO6BuIHTfmmCGMPeP5u9fn6ufXj8/8GFge1CFb8VvvuBzv70/5JAaD/l/hk+xMGaAcJBPf6jwWb+JTwVgniCPkH4whD/an1cvDJAUIIevZQ/GgIKP+C9wATyxHL+gb/CvyY+Ezz4f8qB7H3UvboAKYKRwRHB9gNcfz78ln/8ga6/fH38P6c/O/6qQEhCnIMnv1I/lwB2vHm9WEQSwtG81vzePu0/wwG8hB9B/H7Yf/+AfD5qPajAkP+rvkb+O8CyglLB4kOE/tc+TsDLvn5AH8Erfw5+S/7bf7r/L4H1QuaBSX9KvruA6v5fvz0BqL7p/bIA3AHF/OtA9QW2vm/7+IGNAaC9u37Rwq+AgzxugJOCzD3T/jiCfUAi/AdBvMQEv0r/JYI7/3w9wkEJwSY+Lj95wcs9Bb8CBPkBSb8Nv9cAsLw0vFJEOoDovH1/zcP3wII+g4Rrv+y663/Qf0+9yYEgQh8/OP6ygJWAQUE6g7LBXD2Z/y+/Db4V/spBKsGP/3H/aEAsfcs/ZgNKQtcCJ8Hzfco8oEEYQKa8qoBVP707l//EQ6hEJsEVwUPAy7sCfXrAJICsfwiAG8EGv8VDZb8Gvm/BOD/0fnU9ncJYv4T/DcIEwGz+iUAdw2Q91HwvAj3ByX+VQdhBW36EPtM/p78kPRFArIIgfybA9IQMgUc/zEMb/Vo5xb40QDIAiUEIwkH/xn7hQKiBdAA6vm7ART96fhW+rv+FAbdAw0MbAIU9tj6UQKnAnv1TPyIBSgEngLnA7cC0vyN/V0ClQRz/VYAewKpAzwDyPoF+qL48/4CBI8DG/+EBDUIUviLARgFwvod//r6Mftm+QP60gmYCMoAa/2x/SIBU/va/kEE+fp9+3UKMwHv9VgHygjN/hf72PvpAZgBhf+n/SUEdAm7Bcv5TfInAbsImwKz/K4FCgMo+k8Fy/Id8QcC4gEaCAgEfwOvA74Bkf9c/hv7nPpvBp//LvaT/OP9avyHCYAJdf4nADIAtv/09yb8QQic/3QAAggD9vj58AtX/Ob8Zf+Z/80REAJj9bkGUfqn9jcMvPs09ssIEAHH/loFnALUBUT9hu55+rD+UP18CDsJAQjj9un1uAm+/8r9JgKm/eD6T/vOA7oC5f3EA20HRfuT+hECCv20/uoAk/z0//AGawufC8X/jvaB7nz5BgzqAZb+4AOW/rj8rQRW/nwCOgPz+m0GhP+a/LH7/P8W/Sr85gXeANsH2fq++UH60foiBVwE7wn0+uwCpgAo96kE4P6Y+gAB7wip/Xb+r/1r9MgBPw7iCtP3j/9LBR75hPuQBNYJVPr3/cwBp/Ib/G0MiQ3K+SD6GAMN/M/+FgBeAN3zdgCKC0P2SQSrDN0AM/l6/UQBYvrl+gn7GQXP/vYAhQT4+4cMXwEd/dQA/vsKCp4B6vqx/QMD8Qbe/IT3Z/asAa8Fdv7tBfUG2f55/YP/WwAy+eL4GAZ+BFL5NgDaBkP+DvzyBUIGQ/Yo9xn/nvs5/mMDeQasBTYLggZM+s/6PvpV/f37JfzS/T39JQkQCHf8swDbBWQDgQBg/fz5JP6RAdD8FgCqBz4KSPm88rL+AP7NBO4Hqf809dP/cQPS/v8RfgM99qz1evVABIcE/AVEAjL5fv1ICFkCnPVNA3kEUvGY/XQOWAS6/4YHHgJb9MT4bQNpBBz9yf6tBRj+6f1HCFj8re80BDoKEgLO+zP7HghsAS4BnQMl/Yz8fP6//pz1VPhB/g4F1AzrBFv7sgAWCUH9Lfp+//370/9nA08H1P0i9zgAIAPm/aH6aQlUBFIARQA3+dQD7P32BEUBSPs7Buf5N/80BP76xPpp/Tb8gQOqBH34UgT6CWf8A/9bBvD/hfmEAP0JxgJ899f3Zvvm+ycD+wzPASr5t/5/AGD21PwXEqwHOwPUAzby8PRDBMgHzQE0/ksC3fx78x4AzAdf/Bn8tAOBARL+bgR/CZ4C8ftY/6IBcPp8/hgFT/xt+mH4NPkY/XgAEgtyCj8BcwK/BpX3mftVA3n7TQOCA9MDBfyZ9tr8uAAUAob/+wN++WD7Vgm+BdoE4wk8BlL4qvoh/iv+gvtm9bT/e/o2/aEIFwiDCr363vx9/JT23QJeBloKFf09BB0H2/MT8O/6LQ6T+i//IQYe/GADC/2DBJT9eQQUBa33Jf4pAYYIlfdwAgwKF/6Q/nb3YQSB/Mz+VQcl+z74MgSBC+T5lv/KAz8HVAB17aj/6wfCAicBXP8e+CL10gGXB9wCAAQ2AaH6J/qO+ygFAgDL//MDoAXVA6z78wUt/Lb64wFY/Cr7KgC3CkX9YftfCYUBlftCB/T88PWoAgUCKQbV/FH+lAge+6757f8//jf9UwCUANj7G/20B6IH2fmd+0sJhP+i9Sr9jAdAC8P7Lv/n/1b6tAMr/uH/F/2X+jAIKgNb80YBFg74+3kByQVe+UUE2wXN/Ev+Q/q2+YsCCwM1/s76VACpBVD+tf9gB9wAIPwWAPL4Df9tCQoDogZq/DP28v8v/Fv6cv6ZAzoBsAJOBGb8WfvMAwcN8gTC99b+3QFX/CwAnfj8+NUC4gipCe731vWlAVsFof0vBBkGCPZxAKACavsm/yUKhQyGAMn72/fg+4D9Ef95+cz5kgXu96MLyRXP+Ir6ZgCGA7H7NAOQB2L43f6z98D8dvwC/AoJpQFHBOIDp/77+bYG0Qh883b3JwdABbj5sv8E/fH7SgQaB/4IOP/b+MD4/vsw+J3/lg+ECcYCEQFfAaD63Pd9CWP/tfDx+s7+TQkOCrwDvvlj+H4IBgWQ9wbyMAXjA3P44AQJAlYCPAi8Ad3ymPrcDaQEZvWX/NkEHAF7/PABTQif9rj8XQNX+f0CkgaqCF0AUADqBY38bPUR+HIDDP7GAuAHSPiC/LsDlv8v+6sEOAmc+ZP7dwANCmAC4fKYCcL4TO06EQAPHPMq9eUFAPsJ+oAOIhFyAer3Nf5J+O3z9AWaCeb9QAEeCW4C9fEq+U4JhvmA9FgO7A5E/vwA9P0Q9qP6+gR+A2r8r/7QAfEBCvjB+j0HzgTP/RoDHwbM9or7sP/b/LQBqgG9DtsCofYe/5v7Ov3Q//gHHf2G+P4HpgT2ACf9dwiA/2b1JQdfA/n7qfiQASv9QPYlA98GVQPO/YAJLwMU7m/55AnjASb+0wZGAOf7CP7WAwIC0vKY+uwPlwRN9tkDoQRH/Tr/dwC9/I/8LQZTBk76wvU6A0UOnQE1/r0AdPAU+ucI+//x+MQDfgw9+bv9FwdhAEwERQGH+Qn4jANIAJP6mgRQANgA8gAH+ur/wf07AOIG+f+s/mcHzgg/+V39sP5n+X4GQANs97/5HAdn+ob5MQQ/AP0FuQPrAxP5PgRxDYT96v6J+Xb7X/ui/jsClfqI+48BhwaW/27/uAebA/H75QPQBBH5FPybBLkBcPp5+rv7ggJMAxT48AJqDRz+5P+nAPj1P/9bDcEJFPZc+g0FRQNt/GD5dv5w86z/uAnx+nsBLA32B9n9tABBBKv4ffc7BiP/FPSb/TMK8v0S9eoKxghi/uv+I/9tARH5X/m3BAMHAADy/08D6/Qa9pMPWQkf/cb+p/qv+ucAOwGm/OkFAf72+zAFj/4OBG8BIwByBtv5S/URCKME1vZm/lUFIQAe+6gHTQV2+aYBlQSk9Jr82gw7/nb9YwK3AIj8xPvYAUz/0AFGA+D/ePWT+UQOpwBS9sMLQQWL+DIBYARo+u/6HwzT/sHwAf0ICHz9ZvqnB0UFewgs/mEAtf898+kIewTr9Dz7GgPs/tr+CwfC/dr/mAVA/0b/dvy8BOEJUPjm99z////H/WH9FgdMAhL6CgTo/0T+ewQyAMEI1fm48t38Rv9KA0H+MRLFCMMARvtk7NP//Pb7/z0IhQTEAG37ygoEA/0FZgU0/gn5cvIMAEv8Df4aCUf/lv0xBWT9SPuoAeABGABEAOcFMQH1/bUEOQLT95j1fQBE/Nb9yAwXBIECVwepA6b2hu75AJECHP/4CKMIZfyU/FgFKwD6A9/8IfPH9rv2egbUDMv/vQHjC6UDh/AJ+OYImQUyBlj9oPW090D84gxwBE/3hPscDX8C0e9eCUMDd/4rBQT7cv2L/ccG2AA9+EsAxAHQA90FtgLX+6343flMA5f/MvzYCGMA/fpWBI8A1fgsBMEMxQCV/AH88v+fAtP30Pq3/XH/Ywl8APX2D/9FDQsJZfjR9oL5H/2DBAoLG/8vAr8Mp/m49jb3oACOCggBW/4N+hz41/tLD9YIk/iLBroDkfzz+xEAgv9F+qECCQUTAFD6ff6o/Nbx6QRyEQcEhv6G/q0AJPxP+20E0gJHAe0CePlT99gEjgfh/8/xafCuB74MA/6/AYcFo/tECfwHafzRBUz5ZvqI/f3ry/tuEDwJtwQMBUT+EPp8+/f8zvfq+1cP9xOnASr4KP6D+Z32Jv3yAMH8FQAzDGn5jvIFC04K2AGM/dD1B/cCBZwQDv1+9yoMBgbY92D3vQDm/QD3vAFLALAD0REXDsD8ZfQN/lwAXfeT+EYCJgO/AHgBBAV1/BL8Lgs8ALz5P//YAqT+jfyYBDr8K/j7/dcGBQK2/AIBQQGh/pv7bwvJAsT6tQIs9Rz3ugPvCgUIWgZ4Buj6xvKj9KQByQNgA7kKBPvX9egIVQq0ACn+dPw++G/3rvwfBvT7NP7FC9P4ZfyECxAH3/uv+UQAlv7HA3MH6ANv8hbzQAQO/mT/swxeCjr66vosBicDvfrg+u76DgDnBo3/pQWDCL/3tfw1AnX6TAS7/Af8EgeL9sr/4wcv/qcFHAH893n+Mv4ZAFoB7/iSA2MKMwF8/rn9hvUv/c0G1wPYA5YBZgeh+w/xRfwRBpEHxgBZ/yr/XQbeAgH7/P60/D7+2wWC/0j3xv/BApD+xP8IAn8AdQXe/i/8XQcG+oz91wYq+436AQKmAeP4rP50CXwAmfo4/ywHSQLP9zYJSAEi92wE8P4M/sb+XwcTA9/3Wvh3/0YImP83CBwCyfjhBGn4TvZECT4FrvgIAXwFYwHx/MgBdwVi9nH4zgQa/q72TQr2CsT1SwJuAmH7wgCAA70HBvpf+4YBMvxQB5YKDfmg7nn6YwaICHYEywL+Agz8HPYz/GMC2gOWCu0BC/j2+Kb+sAjCBLD7Wv30AYz+D/io+KgEUwFIAU8OyQpNAyv5mvbG8Tf5lwhZBhMJlgCo/DX9BPmr+yn9TwizBW/6xPtLBfcJnP5wA4YA7va3/6gCCP2a8x8CPgFv+VEJdAb8Bd7+7vwPAS/5jwCUAh0AHgXtBEH9APiyAxT/cfQMBL8CvQa7Ajj7MQGa9xUFCv36/KgDK/yHCDv+uQFxAgcERgJV+o7+3O+5+b7+kgQJDSUBhAeB/7f3CgD/AscBogOMBRX7JP11/ywBOAEB+88Bj/rI+vf91/5IArABWg0MBUkGogb39Ur3Nfqq+Hf6iAbQAxz6C/96Acj9LgQ/Csn9yvUoABILPQIPAloGqPwB+e/5TAKO//H7VQeL/4L00AFMBwL8swNbDfn9v/fbAYoHX/zJ9jEEJP8nAp4C6fjLABP22Pw5BsH4FQVpDcgG9PtW+Bv/FgG6Bq/7TP5VB+Px7vVKA+z+M/+DCAcO9AGL+z8Cofm59sIHsQZz/Or0WwYBEpb7jvirA4kCIvbgAWABLO+e/+ENEwFM+HAHVwP//Fr++AMkCOz1O/rKAKX+7v1sAwgJlf4W/Rb8y/az97wBbAk0CpAGgQNoA7v7MffR92UCGQQZ/A8FvP7B+LsHQQib/fL82/vf9d8BsQOwAA4HWP9JBlkJg/6d/lwAhPeq8iL3e/WaA7sMLQSYCcsHJPpg/o7/Tvy+/VUBtAlX/Qf3//nyAisDSP03CpD/APyp/LD50/+c/zUKbAspARz3C/uhBA/9TQCZBxkBVPyN+u8C0fnj8cEJ0Qcu+Uz6YwlMCQL+3AS1Amb7QPekA3QA8/Fi/6QFOgCM+9MCegZV/vUBhgR2/tH74QIcCbL9+vp5AHn64f0WAVf+Fv9MBO0H5QM7+xf7uwLY/Cn3WgBcB7//XgC+BSAD/P0g/F4Eg/2s8n33vQJ0AscAYwujCQ8AUwKgBgz8ofOE9l77tv9+BbgFBQFdAZP/iPyY/VIEjAGL/m8DAQV1/sH4S/2UAsYFUv6e/2L+D/1HA8j/T/2s+EgHvgv6+qj1DP6mA4j6Bf6/CG4MFQVPALH7mPQR/BoCePw6+tL+yP1+BYQG5gUiCLr+TgDC/MH+uv0Z9i0D2wCk+rP+kgSQA2P8vgszBLL2DwCxAAn9P/owC7QDCvboAcwAhf6++NAFZwVE9EUHoweX9RH/wAyf/+HuX/7jAjP55wWbDA0GgvSI/vEKLfZj/MgE0QLP/zf7h/s7+isBbwzWDJb82f/9Agf2MPQw+HoCPQhACZQITv+u+FoDYQHa9M7/qwUI/28AhwA6AMD/XPm//jcCR/rZ/AEEyv9PAt8JMgIZAWYAMfqh/E78LPcFAKYEV/6QBB8Kyg3u/WD1kgBa+UP0Mv6OCggF8QRzCBj/UvfD+L8CBAAZ/57+z/oGAGkFcAINBNYBhPf7/Yz++v/KAXsChAeDAJr8i/wKAvT/U/p/95D4QgioC/4Al/4XBSwCAvt7AtoHVPVl+H4Lwvht8joF8AgLAjsA+P+g/jABwAJQAsD9a/9j/6/6nvxWACAD1ASrAuv8Q/yY/DUEuQMK+4v+4fjN99cHQg2QA/cGywR09kz+Af9g9i79RAPyAGT7bvxzAe0C2gVdBa8EdwIBAOf+nPVL+S0ESALp9zf+XwfF/b0CJQRPAwUFqgBV/hT3v//K/Qz3eAE4/LP8YAm9Cu0HQAYkAdrz9vQn/UL7RwI9/x0FIAfO8cEAaROsBqADvQhM7y7nxgMmAoz6FALMBWkFuAFJA9AGIAHq/V0Evfp78ln98wD//uD8nvqiApgLghFFAgHwEgTPB+j22/e4+3n6X/8WBUb8hgPlBGgB7gy+ANUC9QmK+T7x1u2w99oFvQLaCYEOAf5M/Wz/nftLBNkL4f4d7oX1rvo8/CQEzREbDlr9+QoW/fHmo/pDB60At/rfBHUERP01Ab8BHQSN/i4ATwIA91ED8wNr+cYDbABX+Pj+NwpF/sz8lgs0AUT7xPwKA+r+k/q4/Vz2Hvt9AxYG+wPUBGcDaQH+ATj/xPld9/37rfz1AokFEA0QBbH39AJ2ACn7Vf0NAav6PAGKBc3/BAQb/4oD4P6p/bf/fwAcADD5Av8w+jj9hgR7B4z+fPd8A80BJAMeBY8GQAfW+ez3SP1C+Db3+/aoALwM+gU5Ay0E3QcD/2373AL8/CD+EgH1Adf3x/kuCTMIGP/P/EsBsPgT/E0Bjv6SBOMEPAFo/ocD5/5a/Df9s/qnA47+dgOUBsf20/y0Ak/7m/lLBFcGEf/HAF8DcAXF/TIFmQq69kD4dfvj9rv+ZAJJAJ8H5wbuAUIJgf09/Iz+ZfgMB+78I/sBBh/3dPwIA6n/NwXsBzUBYfM5/FkBePwZBaUDtAZp/bb4mwPC/D/+gABiAuf+PgBTBdf+ZAEf/K/9fP7KAAEJxAOO+sP18wTWBsABUwHCACMCofeB+WD71fkVBRIMxQSKAc8BXQPb/131pv1J/F35cvvq/jcEJQJsCo0B/ALSBqD+DwSl9X7w6ffU/zcKPATrB2sJ//kA9noBiQGp/lILQAEj9Rn6Q/jDA34JcQe4CVf9GvM+9kX6ZwFQCu8IywAE/20AZ/Mc/AgPMgL1++j/IgLf/o/+Svqq+JQC1Prm/bwDYQVOCi4FfAKR/ib+IgAM/tn2hvay/94DAvx4/ZMNUgeC/lEG5gIr8wz6owCj+xMDkgOOBC0BKQSDAYH1Y/wjAhIEiPusAjEFkPjt/dr/Uf9lAYUKdgTY/Vb9Wfp2/v37igIB/hEACAPa91P7PATXCp//xwKCB2H+Uf1a/+T9TPTm/xUGd/0n+LsAjgzoBT8EMvzS+mn9X/3k//z6XwALC2YJcfWD9ycFdQFpABoAnAMRAGf+qgQ9/d/3lAHqAmf8k/x/AkgGafrh948F3AMi/QMJNQNj8/r/hQOK/i4AJwYiBpX/cAA4+rf2hPgsArMFlgC8BBYAsfzyApUFXf5nANoD4vvd+r/8CQf8AIf4RQWw/034K/wgBHcEm/+zBRoAlPsvAYEEFv86+Q4DVwIp/T77Y/c4AgQIJAKE/5P+QQDwBpIGhPrx98ABwAafAu72HPwMDUgD8/aZ+lH7uf55B0QETv2z+/b9TAa7/tj8uwobAtf2qQG2Awz7YAHq/6r7HP27/BYCt/33/REEDgJZAYcFTAeI/BAAngUw9wv9kwQM/xP+I/pj/mIB4AqgBh/4iv7q+FD+egNHA1sCoPu0BygB/veO+T8DFwX9/HoIcP4K9vD7awA4AEf6AwYQB07+TgEWBbX7f/iYC5MLmPli9Zb29P7VAxkBrgUN/6H+6QLUA/AGFv3KAPwDg/qF99cA8Aey/8kDW/7a8Zb79QD0ATMC1f+SAbcA7QEwBdoDcvua/ZMAGfg5AV4CEP8T/X76lgpgBVH8PQTVAKz0dvzXBY4C9wIGAH4GpgAs9WL/SQod/BDuBQDWCKgCjQGPCdUAA/N3/80IGwGg97MA8P0C+NkFGAjHAyUC3v0s+NH7UQAXBmwHzPiE/kwC7fdxBUYG1v4r/4r6DgFh/8gEswVd+kf4bvT9/5EJvwoyBWQAp/s29v0DLACT/jwHKP0V9/b7gP/TAzQLZAO9APv+bfeU/MT+BQP7/uj/EgZiBPICSPpH/qj9bPpy/vcIFQcT89QBYwLr+P4DxALwAvIC1fyc+lkF0f9s/m0HSvtl+Jz+y/1H+LoBGQitCi8LC/+f/b701P20BN7+XQMR+kgB4fzY9xEHegWW/bH6hgPa+dX52wpnBRAAKACNBmMBMvlq/iX+vPFJ9hgN3Qef/0QIfgfC/Kz30PlWAjMCXAArBwX/wfxGAX4HNv1I8Qn95QTXAwj41wLHBAL+XAEQ/8cLrwKG/O/7EvDL+aEHNAVX/jgHpwa0+9T+ngDj+7r7xv+JBtECpft0AjkEi/zw/rYG6Pz29Ef/zAbd/p/8IQh7BrL6VPbWAtMGb/mk+yYGnvse+GIK1gX++1EGZgcI9QXx1fyVAsMEpwbvDvQB7PSWAN39ufbw/40Hsf3a+ucDxgIaAFoE4whv/Gzzjv7c/RP7uwDwBWQFtQT3Ckn/fPiN/ND5N/hm+B8GbQVS/hoJwgJk+aoDlQil+sfypQFWBHX9nAUQBN776/dSAUkGnvWF/3kQZQIS9ZoAQgkZ/RwACgSe9lP3VwQvBnsA4AL2AXL/m/tz+acBeAGn/GD6nwflC0v9ifkH/+kHnPsg+1kEGP6Y/dsBYQWc81b6FQ4lATf5sP7kBWz9ufzZCkQE8Pr0AmYEL/fg9aACPgC4+lsFjwbu//b6Af+uBDP/5QRwBav63v7zA4EB2fqL+WcCjP4HAB4DUPvi/xEFVf4H8+7/7w7oBhD7ov2iAeX0bAOYC+P9wPmhAR0J+/E09WUKcQWD+qkBRglX/IcFggIY+uv8kv6hCzX55/VP//v+HQVz/GgBYgBAAWsFefwN+aoCyBJe/A3z+AG+A1kF/PuD/T3/ePjZ9bP9fAYlAOEIRA95/sL7rgmEAWLxavorBpMEUfsO+2//5vke/g0CZv/PBrsJYwHC+dz82gIkAe//VQJ1ANr7hft4/6D+avwfA/YBk/xW/JIGcQbh9MQBPg7pBtP6jvp1Cbf/hvWF+C3+n/jT+/oKEP0E+90MugyD/cH8t/7j+2UCUwKyA9//Cv6s/On3kP/LARD7P/xKC2QCRPexBMIHwQP6AEUAwfZF+IMJwQRg+UP9FAQT/iL6MgduBoH3Yv08/x/2RAIGEPoFgP+iBUT/QvXj9GsA/QGq/DcCggJ//OEAiQft/GIBtADZAH8ES/jbBSX/i/29BtL8OgAD/sT/GP47+3z5Of5AC70CPgJ9Bdj7z/6NArj+wPii+QMGIATbAhgAlPs7AR3+2f6s/Ir+UQIDA8QA+PqsA+MC4gLzBW39zveH/Z4Erf8bAmX/A/nYAtv/rv4oBIb88P4+ALIBxwjmBOP77gCeA4HxevocBygB7gAbAL76JfrdCkgCUPSrAfMH3/+N+1IB2f+n/5wDqwTU+WP1dQisCIvzJPe6C7wC8/qbCPUHCPzs/K8EEvk4+dkHuwFf/0kDEv4a+rD+vAT//t36QQH0/Xv6eANOCZkE5P0LBMcAZvW0/P8DbAIy/Bv8qf82AAz93/4VBdQGtQDb8P3+8AjKArUGHgeoAR/zvvwo+0f3/AEbCmQM5fgDAfsEof05/gwEhAHi8GgFUgXm7dL7dBJ9Ccb63wBL//773/gE/q4IFPq2/BESOf5w8JgC6gaQ+fL34QVcBhQF8AEn/vn8hfzxBU79K/WK/uICygGiAS8FwALB/8oCIgP2+pT3CQK8+y77Ugp+A9ACcArT/6HyT/h8+138rwEQA8kMlQGx+PYEXwJJ9ygDNws79sL3wANbAXT7egdtDAP3PfOr+ioB8vzmA2sOBgX2BVMGg/v88PD5AgTH+Jv28QSoCK0B2wMVAu8BgwiM/6H48PYm+jQBjAAFAMYABgpJBxP9S/k/+/39LfvxBNkD2f2I/YUDWwO7/lkIjATX+lP91Qg989vupQqFA+765gAABhL62f+jCfEB9wGbAnoEl/UY92wEqv4I/Oz/MwBB+hAC1QZm/cwHogs6/D/5Tf2jA8H4NvkxA8v3kv8YDY0K2vwR/ecHlgIT+aP7cwKU9zf4kgTzASwAggVDCKkAQPg8/KEA/P9rAqIDXvys/BQDQfwA+/f+nQgOAp78CwoU///9uPsm/RUDlfp6AWUC6/um+fwE4giqAO8ByQSc/gf2D/c5/QsDaQGOCVsFXAGEAVr8cwNK9OT88gWe+NT+hQhkBvjyWf6JBHb9ewkwBfUATvk5+vT/xv+qAaX/KQbc+337EwJk/i8H8AYmAmn1U/lu/zz77QOuA3IFi/2r/40EKvwnAaECsgLa+Tb5Kvy2+LYDfwqBCV7/TgGgAcb28f42/Fn9AgdnAjwD8P209e/+2QN4/oEGmgX6+10AU/5R/RgDXgIQBKgE+vcI+d/9q/ntAjgDCAf/CUH61/xoAFH01/fJBXMI3AJNA0IEaPvF++oCPQEj/DsAQgLy+MX+qgSp+0/+MwaPBVv9NfplAr78Uf5iCG0AS/8gAugEJfqp9P0EPwPw/WsEBgJi+SIEOwXp9gT+RwUcAOj9wQYrBYT4lPwbBhD/v/M4/NUF9v41AYIDu/xh/VQDjgsrAFf3kQEyAA/8s/7sAC0AWAfTCfL6Ie9f+rAEBP4X/rQCTQ28CJf/sAOU907zJANyDH77CvfeCHEBL/1w+nr5egbQAX8C8v+H+fr96QBV/7j+fQtiBOMAcQGX8xX1ev1ODSYDNvnYBrsE+/0l99z5t/wLAvgNrwNs//r/mvx4A9L76PlNALoIkQVT9+r9F/6AAAD//gIyB9D8vAAF/TX/oP/hAQEEdf2uAe/8zPtJAFQCCf2V/YYCavu+/3gJUgGu9dn7mgLZAzMF9gZUAYf5ZQDHABj75f1FBK3/gPoP/cP+JwVDBZ0FlAHM+Jb8zv4d/+sCPQXeAd7/oP5Y/T4B1wBXABr/hv/F/eb5GQBtAvL8Kv6RBuT8If2hDQYD//hj/OICcQLu/OAAof93+Az4dANvBEb8fgrmCsj3QPpzA6EFxQBt/5L8nPfmAQMH3f/n+E//RgES/i4CjASqCH/+IPq2+IbzkwR1DqYFMf3nAb8AC/qq/6H8EADAABT2sP5yAXsCSQZoBBQEt/waAUEDoP2i+s35DAJLA1QAbAABBeP+pPQS/rYEWgWDAg8AjwXk+br0ngWbBpf8M/qr/+sApgEeBhoITgPM+5YB9/ZR7/T9lgCqCEML0/3W/pQJ0wVb+uH3F/3S/uH1Yfx1CS39tv/fDn0AtPdVA9EFWv54/osBZPoO9Y8EjRAt+DP3bg6s/j3zBgBSBDz8Bv7aDB8ETPN+/H8JC/yx9joJwALi/4gHWfz3+ScCbgV7+kH7MQIp+Gr2ewSeD7oE9P8RCu0BBfWF/23/OPEP/TAEjPzq+bEDBg/gBR7//AAV/O/9TQJC/8YCvQBm/En5v/qnA3IDAQSTAf8ArPmv+4IFRv0QA7sAqfyUAXT+If5TA8MFi/7FA8wAtvdJ+DwBVQQT9PT+xQrN//cCvgsQA476Y/5DA5n9UfQJCDkIGPE+/MAIxfxp+98GGwK8ACAAFAC2Aa/6LQHT/o31DgIpAzj80wZ+B8gAOAJZBzL7xO/N/FADx/1O+AsJwQQ29toILAxgBW79tf15/ST1wvr3AWACrQFgAvkAcf4Z/ToBMgGRAuX/+PwK/4AAmgyq/5L43QU6ATv6bPk+/z391PuVBjYGg/vN/YsCmP4m/TgCNgYRBbMBp/xj/UP4PwDaCMz7WQLa/S3w1v/ICwIC+/45CJL+o/bUAqsGeAO3AYD+nf83+Er0HAT7BZwDLAVT+n/1bAJWDNb8OPooBEAAqf93/uX7Ov0SCikLoPr7+EsBjwFw+i/4/P0IBqIBqAWGB934twDyBvX1gPYHCx0C/fYU/pUBSgncAxH72PmHAa4FY/qy+0cCGgCmBA4E+/Ze/+ANoAKQ/Kj94/bi/qIFhQAN/qf+GgIL/m/6WgDpA+v+MwUDCdb7IPpBA8AD7vlr/nT/3faAAOIInvwJ934LlgvK+ZQA2QVk9Rv2sAUfBOT5kgEtDWf8I/c1B80FJfi3/2oE0PUJ/noHGQITAcX+rfy7AN4AfwTf/2352wDd/Gz+jP+8At0GNAJgAGD9kP3s/M77yfrfBV8DLwLhC9j7O/M//D4FSv2o/r4K5gRf+/74mwLtA2MAowQvBCv+uPfM9wn9tPeWAfQQ4AcyBWj/2/Yb+Tr8igF4ByQEe/5s+vzysPg9BWELXgbuB4sDIfga/jn7Gv4qBML7IftZAG0ApgTNB74APvlqANQH9Pzr/Mz7p/rYAc7/BgMABlsGRwDD+Zr5P/oOBCMG3Pw5/hD+IgBFCMEDVv+9/Tn99fjJ/uMHBgT8Ak3/hvyt+eX8evzKBHIKPf7T/3b+9f8v/pkBqgPP9g75TQMzBO37rgOgB6kCLwByAZ4Blfak+1sA5fuL/FAEywXwAWr9pvslA4IAIv+GAuoGFQHa+xEA9f+n+OL2Rgs+AnL7eQpoAMj2Kf1nDEoGVfef/sEGavbl7YYCQgv+CDIHi/4A9E/3kv5n/O8B/QoOC3r91f2tBAb7swA3Ay39V/rg+XT+SvnuAwMKBwKA/77+kwZk/xT7TgC+/Sr70f/HBMMA5wdVCGv7SPZw+Cv/bwDo/U4DhQXr/9X9QAPlAmb9fAq6BEnxfvaDBmQFVvYP/40BVP6PBHcFTf3C+YEFawRk/jAAZAceAKf5q/7T/br2S/uJCw38IPuyCDQDqQGfBcX/MfcYASwAuAKk/yz3Wf6CA4UEIf6LBK0F6P2S+GX5Mv30/GcIiwgQ/mr8wQMsAnL9GwM8AaIAM/7w+XH5rPuJCa0DE/2uBdf87fxzBrwF7/Qy+cYKufvN/Q0HCAHp+un9FgWo/1n+J/2e+vH7YQEABs8JywSG/ob+w/gW/gj+7/+TCJoCOPrq+ckA8wPKBvQE/PpR9Vz8UALVACEFDAPJ+2MAZQKu/Qv/HAPRAnf34vaaBfUFsf2aBhcKmfiV95/8DQHpBFQCkv9t+3f+wwAABtcClv6C/Q39ngVu+0T17QFlCVgARf3TBa4GKP+99ZgCIQMn+jUFGwP7+yP8Jf51AdAE8//M+FH/BP64+dYCogPlAQwDVwLUA3T9hf4wA3wA/P+B+Ir4ywFcBbMCXv3p/WUDAAh7AbQAEgNG+ywAJ/wy8uX5dAchCU38nv+OAsABvgdkBUABmfzO++v3y/ez+9YAggg2BFMC8wPyABT+MgHjAC/5ZPv3/Sj+hQBi/ekB1QQl/T0AjgSAA6MC2gJ3AIf7VP4e/c/7DgAe/rr9ugaJBY0BywXWAgkDEf0Z+Yn8e/l6+Ez7NQWyBA4HDgnb/igBAP8h+6f48/o+A0UAr//T/84ARAKdBG8BjvoF/6f+9AIWAI36zf+lAdcENf+q/Rb9igWYClX9B/7I/AD9XwC4/m38HwHjCA4Ezf5A+mD9qgUBAtP67AHj/9b49QHG/hn9uARZBNT+rv99/4f3dfwVBIADH/5uAH0JVAII+uv5HwD8A0P9lAL9/Wr64QygC6D2y/G1AVL9Nf53B0gDPgW8/UYDnQKX+qsC/ACl/qf+VvxE+XH+3QRa/kz8XQfPBm0BlP0E/sUBOfdX/Jj8iwErCiYAWwXG/XL6nvr8+mkDIgCwCJIGivsQ9eb8qgwWBegC9gAc/Ez99PgW+kb++QK9BGwFvgYMBSr9YPY5+yH9Of6aAg0INQbsAAAALPqL+Rb8ZP+oAcYAHAJBANf5v/z2BYUH6wZ/A+H9APXV/GX/e/XRBOoMRQjL+Yv0zQAi/jP+RwZeBJT7ygM/Dv8BAvZT+/D6V/lvAwYAQwIDDO8FCP62/ygBF/pH+Jr71/r3/LMERQkRBFr9xwFV/+D4GgMrA+T4Pv0sAYb8uv6dCOwJbv2+/doAs/T++DwHgQZ7/dn/XwemA5/+GftRAFQC2/nSA7sG+P1PA6j8pfrY/IL91wQQAsb/QPk5/2ID6gN6DK//Xf00/pT3Jfik/XADc/4EAcQBU/z//loBZAXRBsUBuQOO/Q/0l/wbA4AEJQHv/1cCq/0t+6L+/ADu+5cAXgvtBdD+jwFQ+8PyYQEwE4IFQvc1BBz9vPDe/e0FHQCz+/7/BQPsARv4HAIbDe38igKrAAL0EgG2CR79mvTX/NoAXAQ8BYED1AE6/HwCrv/M8wr5pgfnDhcB6/mWAbr+vP5oBT0DwftA/p8Ag/2p/Sj5NwLCCAb8KAVXBjb6TAPKA1D+VfX/+3AIFf0J/nf8g/3f/Xr8XgjZB9f/9v25CMb+y/fK//j6nPxi/wgDTwGZAiIDegS0A2X6/vtR/r0EuwPX9sXytwDjB+gEjwbqBfEETfuI/msB//yP/878efk09///5QJkBHQIkv+//bsB8/q5/VQMjAJx9Qj2Q/7uCTACqvwtBNwDhwDW/+P5w/qoBGoAr/hN/7ADBAHSAtUDWACuAD4KDQOM8Nn9JQUZ91L62QXABWr9cP7JA74EjAJYAwn6JvAkAxYLtvsK+CMGfAQB+vf/zwLYAYcAkQRg/ln5MgbDBVX6e/Z7+z791P8PBJoGcwfdBIX9r/sxAv7/d/3O+yT55Pj7BOcHEP6uAiELYAav8tf7WAjMAMT6VvvLAcv6igVLBrD6EwDE/bkDdP9A+cMGxgIn+kL9kP/U/8z/PQnvAgL61wDa/Gf7tP/+A7AABP19AT4CUgHG/Q39agQ4Bz3+Afw3A6cAG/P892EI9Afi/wQEtgWC9U34Aga6CeP+HP+/CrX32++F++cCdv95AfcN6wZT+hj7oAA/+RP9VgrrANX5dgPu/3H56/+QA+4BYf0PAyYAR/n6AGUEkP7D/YAI/ARA/r36Efo1/0j9nwEZB6wDV/+cAZMAtPi2+HgEVAZ0+sD+9QdqAkEA6gEp/Dz56PrmAawDAP1Z/+UD4vxn+xEH2AMMAEIBuP0W+8j/Bge+/Hn9vQVABCD6YPldBpcAKPyO/r8EtwHl/DgGHP8N+iz/zAQMAUr6LgXoAhP4IP/HBTICZAGq/zD77/t7+9v9mv+LAYYGFQNPAYcBiQIa/1X8kfxP9DX/PwPN+Z4BFgfJCJ4CLgPLBsP5wf2fAUv0g/hNBkQLWf8V/dQKgP+p9ev9UAST/vX76wXNAlr4Z/fYAGcAIQObCl4D/vc+95cJgwUZ+vr+5/4++gr60gRGA4D+hABvAvUA7wA3CXcHfvcl85L+Vf38/wsIawc7Arv61Ppr/r4BOAY9Axf26vxmBd4Bk/9mACgHTgHF/1P+ovwO+of/MQfh9BL1zf1eAnUGSgGcBo0JTAFwAMgBiPsM/Er/JgJ5/Yb76vy++679cP8/CbADDQBUB8oDBPwH+UH96wEGBtX/bAEyABf6Pv8U/0H9Bv24A5wFuwBT/XP+kv5+/a8B5AS7Bpv87Pq8++b1tfz5BjELXQP8/0cBPwBM/BD9kATG/Nv6kwVkAvT84P5IAZIFafwB9zQCuAeFAiH7PAIbAHH/lQTh/Pj6QfzKAiH+Q/w6/Pn9dw3eBXH9+AFIBD3/Zv/u/L/5cACP+gABUgMa+5n5TQDVBT7/RQhrCCIB6QSV/4b19PpDAJz+NwEU/Tn/dv0/A8sH2//x/vD6ZALl/fL71AjwBTb+k/lbAZX+9/05Ccj+WvlN++388f9A/ZEFHQX+/Pr/JgGe++cBeguWAosB/P8l/kX4BvcVA+X8OAEEANP/IAchBr8E6PjX/SAAuQCH+0H3UAM3ATMEiAIBBMABT//jBd/46fk/+435nf+BAi0DDgAGCr0IhwUuAEH3qv1W+NwAzwA09//+wPtAAVMDoQGIBRAIXwKE9jb+TgFfBN4DjQPyBInvWvVkBjoBEP40Cm0Mlvax90n+wv7h/W0BswzG/R33q//mAIUAIAsXCzP1w/ia/Jr2u/uvAr4BcwA9B+kEff/E/XoG5QLr+OMAOv+l+cb/mQUVAHP+DAH7AagBVf5yAc7/Ffp2/iEGegGs+kr+HgPlAREAwwV7Aqb08vljAw3/4PzCAM8L6AG5+GAB1/g1+54NbBMu/uXywP7B/9T8jv3LAcD5kPTh/jYAnfxmCLgUfwmr/JX+0fwt+E8AEwIS9ijykgEMC4AF+wRPByIEifYQ+o4BNfha+KEL0wsH968EFgfW9+75m/56A4f9OP8+BcX7//YfAu8GWQG0BKcI+fwp+h/91vvjAXIBXggM/TX3gQE19pL+GAWhBxEIt/9y/x3+pP5Y9ST6UQYABDcFhgcJAMP2I/5IAC3+jgHHAKMAXPz8/IIBmgBx/YoHnwyD+L0D7wgy8Lj4VAM//sT4JQJKCxr7wPhf/3T/VQemC3YEbvrr/l0Epveu8v39GQfsAXkAIwhN/JP7egmA/knzuP+cDFsDpfme+0X41/rOB28OeQhV/u/7PfxT+zn8AgEbAKf9KQWD/DP3sQM0BjQCv/9dBMsCDP0qAsQBfPnN9lD94gDv//oFEQgb/Z31hgSKCz7+cwBWANr4ffr+AIoArf3TB/MFfv+m/aID+QHU9ET9T/42+aL8vAgqDOn7+v36A5P9sQJiC3z/qvXR+Yn/CAEd/zMD+P6c+mMAP/5n+JYD2wzPBIoAKfxw/vMAPf4qBxn/0fFYACgJ4P9j/DgDaANl+1n8Gv2N/Y4C4wN7A70AHQCTAFICWQNAAE79Cvx8/7L6T/nq/ngC/AXkArwHzf+L9/gBjwNUAyb/T/qf+ZIAb/1m++8LoAWJ+9D/3gCP+Xv6NQSQBngAv/liAqQBDAIjCBcFcAA593760PmF+qEDFwE5BIkIGgGq82z5IgzzBYD8wf+4Aij/VP40BnT3v/BaAjIKTAJL9nICeAbd+lQAUwdvBhUA0P4U/xz2EvocBIsCKANbA6gFEf2w+TkEQPsz+lsBAQKs//wCAwVR+14AawEo/lL/6wAtBov+t/2x/2v6ifu9AO4GYf8HASUHRvkU+YQCTAPA/Gr8agRjASj9dwLbA5f+wQD5A40Envsn/H4DKfc190kA6wXwAQECcQcg/b3+sARYAAD7fgI0BH/xn/YTCGcGrgEJAbQD6gLv/dMBcALN+cn4XAP5/YrzbQXUDP4ABwCUAHX/+fxR/IQAsPo7AiEEbPT//BEHfQljAFf/LgGC+mMF6AKdAbT5PPeVCkoBX/gzArwEhvvw/mcGcvtM/F8FtQbm/uz2pv9LAncDpQOM/dz6FvsPDAQFePMQ/6QHtvtU9Q4Fwv/A+pgEFAeyAP/3QAMZBgT9Mvz2BGEBPPfmACQFT/0w+N4EBAgB/TMC5QCb/qcEPQCN+tL6aQHTBD8Acf/LA+IDsfm8+wsA5v+3BmoA/vgU+kkDuQOFAQsEhv8cA2T5kPT2/mUAaAEUB4gIDPnc/CMER/uFAnwB8v0CALT/oQDO+SD+/AezBrf+Lv/CBM/+JP7iABz8QvfiA1oL1PoB+3QFvv9t+igCjwVs/qv/tAJq+6L98P6W+3EAKgEUCR4E1/ho++j6IP8JAfUFAQUaALYD/f2c+XX7mwO8CBr+5vpPAiwCr/yY+zL+pQCyBDsCuwMQBVP57Puc/rH5iAMUCTIBkP7i+yb7AAZtArn7fwUxBXv9nv7Z+BP59QIiAQT+vv/MB9YFRvwe/TX6zvc9BHMJrP/B/kAB6wfIAVz1b/24APH/CAMGBOL17/jxC67+bf4RDwUI6ftW/9b+w/Th+Lj9FPzC+5n/vgT9BLcExwIlBR39QP5oBw35SQCNAz34cvru/0sFCf54BgoFd/q4/z/8MABdAZP+fPx/AXwGof6m/5kCLwNW/nT/pwAe+roAOgKA/qf6ePkuAYYAkQQ2C63+OvpRCkIGxPFR+agJQPvN9ioKrgMs9tn7bwbk/gr5YQx6DLz5jfL3AeQBvPbdCNsJff34/QEHkgGV9x0DqP9l+/D5ofrXA3T9CgAgBxoDsgAaBhsKCvtY+VcBvPh59uP9mAS9/df9TQVqAeAAC/90AmgAKf3fBRkF1f9m/wcA5Ppt+SwCxQZUAVgAfwKq+ub4+QBUA7L+OwCwAgP9vP3XAzUAHgInCpUFq/+b9t7z7PoH+k7+hgRJA3oErAqFBwL8Av00/k77j/6C/x0BoADv/qr+h/1qAigDqgH+Apv9rvkY+cv8lQXzBCIC9ARVA3IBkwJLADr+s/se+yMBVfwz+5z/igD1Amb6dP+OBy4FNQK1BQ0J0vey9vv6CfrYAY4HbgJz9Yv90gbZAFb9jgSiAer9VQcG/9f1dfvlB6sBa/jiCP4OwP9H9LT5/frB/joHkQXa+470kAECAbX8pgigC8kHaP2n+nv6yPsnAkb61frFAG4AAARTAGgDxwYLAMj6oPu7BvMCX/2//Tz6YADF//7/9QaNB3L/6/sp/Iz4VgEkCEH+P/Qv/PgEAQXjAQcCfQcjAQ4Aif/K+fcBogb186zwnQOoAKQErA7rBgb5pve9AJv98vu5AnUMdv2G8akD7QEV/bMFPQYEAQT9EgJOAEf2ff1mAi78igFICTb+2ftrBnsBOQLt/mcBTwRs+Lz6jv2R+fj0OwdbCfv+EApPAooAYvzL/OT/svYAAr0GXQR9/cb9LwPs90v94ARnAgMFFQNF/b32L/o1A94DbQaNBfb8YP9pAHv80wDGA9gBpfgG+dn+zvyk+37+DguqBbb/gAjtAyoAYvzq+n/5X/rS/wv/rwEG/JP/kQkuAzgF8AQVAlcCe/ti+YD3H/qp/ln/UgOVBTsDBgNbAXj+4gTUADH6Qvzu+kf7ff8bA+sFbg0lBGj6Ffya+M/8Cvyq/zAEegMiBaL8Uvou/14CRwO0A1UA4PsvAM8CugK+++H9oQaq+oD1j/7xAjkCDgULBQcB6gSBBi0BIPLr9SgC/PmGAe8IKARU/2D7sgCA/Jv7FA4yCVv1Lf2yBYT9g/rMAZX9bfcuAYACT/un/E4I1Qk+/cL+xQew/iL6cv9E+xkCCQnnAqv6WPtRAFX+sP6y/noA9v6WABIFlAMECN0Iw/8J9rv0j/fM+lwC9QkjA+P48QDaA0n99Af1DOX6B/qX/uz2XPiv/aIEBgjVBIIA+AKu/bTzGwDiBUn7vALsDMj7YPeP/6D7ZQW5Cm0AEv96BqD/UfXS+tr/4wI4AQ38PP+iAXn8of+qA+T7awZoFGn/evFQ/mD7MfSjA5oIfP3iAJwFXgHP+tD89AL7+y//7waxAv79zgDSA9b6O/usAtX/of+eA0r8lPTr/sEJOAK2/1sIev/6/TYH+wE/+V33//sW/98C4gW+B+n/9vje+Ub6VQQrCuIFv/7+/Jv3ffVmBEYIGgJW/s//HACI/aAE7AZM++T2lf5mAML97gOyBj7/Pfpf+7sAAQEXBk4KLABK/Nb+8Pyg98f9/gRTATwDgAJdAav+pPrlBasDK/gpAcQF0/ur+s4GUf6M+YYGaAIEAPX6yfl6/W3+4QIzBBoDlP2oBYoDCf1NA+D8nPmT/NL9K/8mBE0G6vys/okDmfZ2/l8KOgSyBFgC4v5p9pv+8AjT/tf4D/kXA0QAKAAwCYYDoP7lAEkDrvgJ93ADI/9B+WkAVABsATcIUgU8AB76XvoXA6D/Ofq1/hf+U/4hCBMKrwAm/0L/GPvw/Gn/NgPNBFcD4v0y9y78OwQCBvcBcf1F/WP+Tv7LASECvPxDAcoDJP3bARAGj/2y+3QAVv4Y+8QB2AIK/tH8HgC7A/v9mQYoDDf9fPpOAnv5t/efBZL+IPmX/44GpgKp+1H/RwIpBgsCZQBF/KH8HgG5/gAASPtbAUUGnANqAr77wvvuAEAABfoV/+kHWv/B+oYC2gA+AxkDZP+0AYj7lvslAQUC2ftD/fwEXgLy/Z7+FwY7A3X+fwEn/7j8QwA/AGz/rv+F90T93QDg+oYFmwksA/ICKgE7/d393fhw+1AA+vtUBL4Eyv+GAUUB6gFuAH0C8P8D/h/9f/15AUP/jAJWAnH9VPvbAgwGnvoc/MIEcgPD+jEDJAU9+A79AwTFAWD43wKnCwv/tPsa/oz78vepBbgJGfpJ/SEHQ/x0+LwB6AHKBHEFKgKQ9wz2YwBmBNQGXgFIBlv+PPQ4/o7/RAQPBH0EtAHg+nP+Ev1YADwD0QBsAjoCFP1+/a8ALgCs/RT7+wBIAzYD9/77+akAxP9G/44CKwIkALb8/P6pAdYAPgPAAAT6Zv+6/xf8VP6+AA8FOwMnALIEeQcS/0sA4vsr9Gz/5QMdB00CQf1h/q3/R/8q/J0D4f5//v39QfwCBuAClQQ//wn40QJ7AhD8TP/2/fr91gAOAJMAaf4fAaUCeQFd/Un9HARtAGf9GP+tAp3/Ov/mAkL/G/64/iwDhwTdBOEAcP7S/zr7c/1o/s78Rv4oBhgEgfpYBMQGafvM/GECMv6E/Lb9pwAh/gT5pgPdBHYAGgJCAOb99v6NBX0CJPi++I8FhwUC/xAEy/0c/VkFTvx/+c8CMgVfAkr9IvuU+zb/XQWnBFoDqQW6Bs/8Fvfu/Kz8ff55ANP/Lft4+WkBNQXoA4EDfgdMA+z9vPyM+qj97v2a/7wCiAHk+gH/Vweq/Z4BuAI59yX/IgRsAgf+2QBCBhP9p/9SA9AAqPyM/RYFpPlI+MkGmgVb/JkAGAYK/qj6lgA4A4H5vP0ACZsDYv2h/bMDtf1O+v79rfem+/4DugflBAMBxAaL/iv4pAJXAEv8CAJUBEj8DvwZBxIDdv3N/e7+kAB8+WD6zgHg/+4ELgckBJQHQwFI/AH6vvn5/mz8N/2AA6kCDv7VAIIERf54/p8GfQFL/df85v0VArz7YwLbAVr5sQGfATT/v/5WA34I4//g+dT9DP4f/kcC8PwT+58FHgl6A2MCUAJFAGf6LPem/r39ef/4BU39xPf4//8KIQhE/W0CwAL5+Db73v1E/HYC8AY1/cD7+v0g/jsFoAJAA7UEvf8P/zv8F/ml/vsEWAQCAfH9rv80/w4ELwHW+MMB8wJWAKUA6/1o+JX5dgTIAXn+BgURB4n9xvilAvwCwwD4AiH+DvwF/Y8Bqf4p/LsDCADX/dACmQchALH7zwIB/1L7dv7xCfgHTQAY+7jzeP5i/0L/jAPLAH39jf5rBZkAPQGtBPgFQ/sv8aEDJAQ+/k4D6f7X+Oz98wXj/mz8lPy//4z+fQD1ERcH+v7ZAsX8SvoA+EADLgJL+Nz+6v0g/AMDuAcjAn/91v+zAcMGBAFW/rQB2fqb/Fz+HP1j/L4A7QVm+g/5bAjdC0r/5P09A6n5BvfBBN0EK/omAdkKWwSV9/ACPAir75H4AwpZ99f0pgt1CF/7ogOCB1z/dfx6BR8EKfWd+U8Glvv790IHDQBC+csG7wRl/KP/oAOb/zH8iQXrAdP3pwJfBTD9rP9LAlcBkQAF/Yr7UPoH/DUDIAhZAwT9/ABXAT0BZgFvACwA2v17+0b6XgNZ/tP5ygaAA/T71wHmBtECqf8E/Dj7DgDa/yn/dwAcAL77UgBJBuP+ggBvCHgESP2Q+6P9Nv4M/Zz8jQAQAMP+fAhjBKv+dgOG/wr8TP4cAyMCVPod+C79ovub/RYIvQTX/W4BBAjcALb5tAHUAeb59PpfAloC4f74BHMKNv4R+aIEJwNL+Iz37AFc/FL4jgURCWsIuAGSBfUDKPdZ/T/6s/lc+mn+jglj/o/9EgQkAGv+AgLQB7r+Qfo5B8ICcvgC/yH/rPyd//4BAQFc/egAKwr+A+H0+/2LAxv5bP4BBcX5Vv6UCaX+ywK5CPsFhQJg9c/0g/t7/0IBMQF1AA/+9f+9BvoC8P0aBz4Gsfvp+UEEhwWj/Qv8Nvjc+qP9QAALA3T7lwByBxz9s/7qB0YFywCZ/8n+DvqO/q//yfiLAtAGJwOt+nT4hQT0/zn/FAYrBB0BkQH0AMP3Xv2tAmX+LgQTASj6mP9cBawB2vuG/xYECvpq+gUHggBL+S0BagieAFX7XQfOBiT8HwApAa/1jPO5/pYE0v7Z/nsD+gH5/kwDBgleAe7/1AYD/Bn1+f0IABP9ngDDCcYBxvckAKABZv+e/RUEXgWc+Hn+qwYx/kH8WAc6Ae766QWwA4b4Vvn0Al381PXD/gwB9ABCCMQMwAD0+2kGCAJN+iH8MgFj/nf3i/rQ+lX9/wX3Do0FAvxHBYz6ZfoXBI8CvQDo/MMAT/t2/CADgwNcAs78BP+P/rj/kwGV/fb+PAJ0/gj8lQKXA1L/nQaxCxT92fN4/uYDRfqb+ugCDAAc++X+LAaWAfn/wgh3B7z85/j6AOD9i/nzA28DM/wQ/qIAYADSAnkCH/40/Gb7jP6m/x8CqAV8BQwAvftbBpoCu/xnAnT9CfZY+LQBhvtC+4YEMAp5C+D9AQB2Btr9svtbAGECvP2X/JD/fvrp+90D6ALd/vr9mQVUA+v6k//UATr/Bf8CA4ECeP/R/zz7wvqK/hoDvgcQARj8dwDb/pr25vqsBOME+QbaASf+cALKAvMAw/2u/Uv8kf1v/+H+gf+BAG4EQANy/GD9KAb8BQr9pPqB/4b75f4NB/UApv9GA8MCd/mD+Y78kvxoA7gDqAShAnsBxQLG/mL6XPwuAFL/DADMADcBKwBl/0b+QQJmA4YAWgHF/Zb6b/qaAWYDuwFcBy4I/fzX9l7+PgFRAOL9RALcA+b+0QF7Auf1XvX4B0QB6/34BuEDgf+5/h8Eg/9w/6L/1Ppy+dj5HwMwAy4B/gC7ACcADP5uB4IEuvm9/5UB/PgX/QkHXwPO/Y7+1P+E/Tn7qQGJBTH/VQFCBeYBJwCQ/jkFAP+690kCj/wz/NcDYgLs/Wv97wJwAF8BUP0E/Z8B7fpjBP4A8PWHBF0GqP+i/iMBQgOv+jT9UgMz/8/+igYwBBL5Svud/ngDpgHH/xoGhf65/RIFcAPW/pj+9f5u/M//ff2l+UH93f9IBjUFKQLOBP0BRQHz/J3/j/038z77APuo/NkGbAg+BywBWgI4AE/8UgRSA477eviQ+Sn+1P2P/54J2QkU/yQAwADE9qz76wSOAjv/qgJeAYn8zf+wAUUD3/8B+2P+B/92+18AhgYJAOoArwOR+4z9ngWqAuP/8wBS/OX5tf6dA7D+nvu3AdYAOv3HAPgEUwOVAT4DBgCT+SH9jwPY/IX0YQMHCWX7RAazB277BQD6Bdb9SfKWATcGyvox/NoAsAZpAGv+wAKU/6f9KwSEB932bffJBd7+/fsRA1sEFwIc/rb83/5+/h7/3AblA0b6HgBEAg7/4f0i/r8BdgHwAiMBsv9W/b/65gA6A9wCGABg/s37wPsYBZwAFfu9AnsDRQD4AFID1f1O+qoBwgB2/7P/vAFF/1f4jgE2A6IBQQM6BhcGOPh7+2X/pP27AcQB6v5M+KgB1wW0+fD9wgZEAVf8zAQ9AuX8xv+9/AIEWAHY/VMFCP2W+IsAmwcvAKn73f/g/17+uvnn/i8CxgWHCAUB6v5f/jkE3QKS9gP5XwCX/Dz7ygJiAVEAzQYzB7gDQ/4S/kIA0fxq+pf/NQRT+z//bwUO/cP+aQPHAeH8WwHW/uz4awHq/w4BkAARADgHLQLp/qgChwBe/NUA0f8o+NP8kv+7/Kj/MgJyAzQETQjcBzL9sPk+AFQE7f1m/OX8OPkC/YsBugXm/mf8MwI//8kBx/8D/vYDmwTs/1z+YP88/Zn/LwGZ/uX6Gf9eBA4BSgBZ/8wBE//M+7oAaAIHBU0FRQPK/hH+VgSj/hP1svySAET6Uf3gAvQDKgCnBpMGRfy5AAEFNAD68gH8XQXS/DEAuwDKAwEB1P8YAJf4Zv04AyECBvvEAJIEGP0GAosF0QE2AakFJf9U+B/+4wCX/v751vrlAI4FcwU7AVUB2wCY/6MC2wH7/m79yfye/rr8N/s2Aw4Htv1K/FECiwAD/vQBBATt+9L9BwPsAAsFIQGf+lL7Nf73AkgD5wBGACoDZftY9Hj9ggJvBIEFPQOp/y/8Xf7xAwICs/5tAsr/QP2Z/KL/VAMZ/r4BpwWmAbkAXgDl+3T6FPw3AocCEvxLA1sCLv9PAf4BTP5x+dgG2gTa+mH7F/4sApz6tfi5APQFegUZBpwFdvtk+e0Baf5l+kcDkgd2A2L8bPg++0EEbgUSAiMB8f+4AOT5k/uhAUMBpQHrBo0If/65/Mr99Pvk+rYCVwWl+RP7uf7J/qL9lv1mB2wIMAOFBPz/hflL+2H+k/k7/JMFlv9dARwGcwFt/U3+tgKJ/6z/e/33/W4Awv+QAzkCVQCIBMMHR/8C/OL7rfrJ/aL6ev2FBVYFRv+aApQCbf5v//z/nAP1/hv/hwF3+9H5Tf6rAZX9J/93BKMCcf43/0H/JPvWApcI0wKSAdoAkf90+vv8qQTc+vz69wG5AbMAb/90Br8AL/u1ApID6PvW97ECAQdFAj8BsgHx/mv89P1p+qv70AFxBQP+CfmTBDoGugVzAVf7kfyd+8oB/gCa/MIASQeiA/H7UQD8/B77DgA3AR8BqAAqA4gAqP69/xcDYgNO/fH/AgF5+RH7MQXCBfH/of2A+a36JgIYBG8DDwAn/3oCNAByAP8A2v56AdQCB/2z+4IBgQBH/Rf8GfwEAAUE5QOBAXQBdP40ANUI4wUl/Q79Xf9r+rD4Af1Z/1cA5//JAKIBCQShBHAEBwMP+7/9b/3Z+4ECZ/yh/AwFFQGY/OwGsQi9+Un8vgNG/Gj4fv9pAsP/8gIQB1IEJf2C/pgB+vvM+lQAZ/9c/awDrf6P+ucCnQHRAL0EBAeTAs789gFf/2/61f5z/P34QgCvAyYATALPAX0BFQSbAeL/Gfuz+2UCcADr+d/8xQROAzIGUQIT+uAAEf/W97r5XP+2BNkGwARsBHID5/0L+07+LQA++5kBCQTs+2H+hP/Z/+b/7ABbBX0EHfzQ+sQCxv9w+1IB8AI9AAMGGwOy+gv60/t//gf9LQXGBd/9vAAwACD/FgGNAsUCpAG9+wT+yQDO+bP/fgMC/dT7iQElAugA9wOF/+IBCARe/+cEIAIX+SL+JAKA+Bf10gOpCHIDagYTBFD8jfrg//P7KvdS/0IC4wLtAfECsQSq/nwDiwea/H70hPpk+2/3fAHSAQwA5wb8B1AEiP/3Ag8CpwGvAG77uP1p/Or9yvyN+owBYAXyAy8ERwas/637XAHdAgb+i/w1/Tz85AL0AWb63f9nAjsA8gBgAfn9HfuuAG/9yfpO/kcB0wrsA8T6hwMeBCL+uAH7ANb65vvu/YL7MvwJAWwC1AevCAMEDwQ8ApT8jvdg+U/7CwJlA4gCrwbSAAb9yf/pAaT7k/31AEj75vrY/C8H9gddABr/5P9pArP8VfvLACD85PvMAV7/0PvTAMIGXgC7/soAqwKSBbIELwc2/n36GP11+6v5m/2JBeb71v6HCB4DHADJBF4F7/z4/OX8Df8aANr9rgE1+kL7QARb/+H/MwP4ANb/aAH1/3j8vQDV/jf8fgIBBu4CWvt6+3H/2wPRAxP9dPrB+wH+uP8dA0UEbwauBzsCW/49/qcCqgDf+Or2Afv9AkwBaQG8BCf+Bf/9A8UCKgCwAuH+pvkgATT9IfwcCP0Gff38/XL/E/sM+w79CwBa+N/3iQppC/r+MgNVC60Cuf2K/+/7a/f4+UwA3vzk+vsDBwXI/qkEIggOAB4ApQO7/dz7Gf/WAnkC9f3IBLr/rPXC/l0Ch/kL++YFBQK3/hIDUgKJ/nj/aQXYA/f+4QAXBgr9JPZG++z6mPnb+1cCLgKZAncIzAITABIHsQZk/dr5yv9h/MP3df5eAfT+7AGUB8cCoADiAbwC8P+S9uf/rARL/yYB2P7Q/Yj+lQDPAfEBGgKUAAj9VvtV/jv+w/1h/zr8Dv26BLADfgWUCz8Dpfs4/Ir6+v24AR79wPu9/L3/kv4O//wH9Qa0BokEXPo4+ar+CQJeAu7/h/n9+/gBEvyO/zEIIwRIBaoCqvkT/tz+yfwyAZb+pfp6AEcGfP9p/nwIWgWO+9X53vqP/YH9QfzmAUsDmgBuAzEE1QKEAu4B2P8H/tL8ZfyX/YP8tPsC/14EewX7A7ADVQRiAhD7lvxGASr+Yvvr+7H/JP1n/SEGCwaUAMsAagOg/6b+IAL6/lj92vp5+UD+KQK8BuoE5QAi/xn+AADPARAD5/23+1H9DfxE/J/8IQVgBwH/AwNGBhcBLAEX/nX4Gfxl//EBJgYLAIn7agFSAfL9sADOAsMBLf6z+RX81wDrAUIDRAR/A0sBif8V/hf+S/2R+lz7/PxTAswF9wO8AoH9cf+vBfYCpgGuAEr8dfpn+wP8uvxZAzsEAP94AsUCMgBYAe7/ff/qAHEBSP+W+o/6DwFDAx/9qgA+CRUEfAJDAj76j/mF/ln9qPeT/h8EIAFwA2YEtwWaBI8EswHr+Bb4VfsF/L75Mf36AY8C6QMXB3EGjwCjAEcB0QDg/m/7q/1U/cj8lv8lAtQCbwA3/yz+HAFNBVIADP28/cH8uf/tAJj/MQMbBXb/HwF1Aln7BAB1AN74afow/8IE0wI0/ncB4wXkAL78OgbdAjL7GAG0/5n5C/mgAf8Csf0SAZoBf/8L/yoC3AThA8oCGQNn/hP4Wf9r/eL3awAbAsP+SQHIAkIA4wIXATj+EgEK/rz94f+vAL0DgQJI/94A3v9GAJIBEfwUAE8ALv3pAP39UAMuBRL+k/wQ/S8BowAH/yn9m/7nBM0E+AH4+9H8m/22+ugADQJXA3MIzQLv+838P//AASsA0vuq/ZEAk/81AtcBCf5gBUYHjP1J+gX9kPqL+BkBkgUwAh0CmgSjA0gAzPpI/CIFFASm/wT/jP6k+4v/2gGd+6T7S/5nBdkDqv16AeYDHwNfAtYCXfyS+W/+nv1E+xb/dwUtAw//ZwAFAJP9UgJDAqT83P8iA2wBOf2X/sH/Fv4xA7oETAAY/8oB7P5N+KH6sALFA0H/Lf75+2b8awebDZ8HqwF1/1j8rvn49bvzm/60BxYEDgHR/2kDnAZVAmkBtf6V+dL8Z/oN9Sn9RAYnCKQI9ggNBEz9Cfst/Hr62feV/tT+/vobAygJlwVPBJIHmAgYAyX4wfa3+vX7W/pN+mb/zAEpA0QCvgX5BTACzAQz/pf2F/+MBIf8Xvpm/P0AlgJVAB4CBwIYBUQC4fs3+eL9fQKZ/Uv/WQJdAokAoADZBt0Euv5f/zX8cPsO/737RvwNAUsBvf9TAj4B0QLnB+X/mfwgAW7/ffy5/UP8l/vK/3UDYQSNAaMCvQLF/UX7oADjAQ7/WAAk/lD9OgC/AQcAkgJBA/IAY/6n/Hn/cP4b/eT7pQBvATcAEgajAf79BgOYB3QCDv0f/nX8rPqi+oP8hQB+AhoCOQSsBlQE0/8RAr39bvmk/Fz6lv4hAFn/EgKxAnUCVAP5BdkA2/ys/Sf9SPtW+xn+4wErBdADHwHR/1UBRP+7/GP/6f8+/uv8cgBOAzz+lwD6Cg4E5Pca/zYDiPx2AU0EUP0V+177+f2jAIj/IwOvB1sARP3qBDEFbP+2/ir8ZvVL+XL93/yXALwDuwb0CV8IegPbAMD4u/Pp/Lv+WvnL/i8FEwbNBHP/cwDFBicDOv64/dX3LvliAboB8f8qAIgEiQYnAdT8zAD5AFP9Xv4D/87+qfymAl4AKPdkAMYErgD9Aw4HX/6P+mQAPP4i/pwBJQSkAVH4ef4JBej8WABEBwYBQfn5/oMF2P2S/oQFEP0M9Tz+iARK/8QAEQeNBxsCdf6DAHH9HfiG+7P8/viA/6AHGgMqAp8HOQS8ABUBBv4s+t/73f0y/jH/5f6SAqsFCQQXAOD9VP6F/gIACf56/UUBowTaBSIAd/lZ/SkD4Pyu+rcBtQM8ASH+1Pze+hsB+QoBA2z7LwHoACb9OwCyA5cDD/+G/Vz+9Pjl+mUFTwOi/FQEDgb6/aUAUAXG//D2HvlVAlMCivwLAhEFkv3RA8UHaP2e/EgDP/1d9CD7GgHMAGMEYQMHAV4D5wPWAvT9gvuP/mgAhfxd+LD+SwF8AKED0QT2BNMAxftL/zsBlf5V/6f+jgAzAPz+xf/i/swEIgWp/iL/swGt+k796gRI+9r7ewO4A+4BOv8YAksCkfvO/XQDtP3W+9cBsP9P+54AugIA/w7/JAJwApj+IQFc/6D77ABgAaD/DQA4APkAUAF4AUECiAAq/rYARAA6/ZMAxv/G+ioBRgfwAVT/ugKEAYf8d/1lAC79Lf0DA7IBhfuN/KsDWQKQ/DsCaARe/JD+fATg/q36fwAJAv39uPuX+zADdQTj/y4E2APd/LL8ZAJ8/0H9dgNOASP+uQCM/+/+kQNIA9X+TP9u/ov9l/+q/v8CrwQAALsCfgBi+af8MwGU+wD8UAPzApkAEQCVAM3+bQB1Ap4ATAEFA7D+RPlS/iX+gv4fB5IFXvoV+JsBFQHd/SsEgAZ0ABYAvwXp/w/4CP62At/7rPu3AeYACP44AA0DOwHYArkF+gA8/Z39L/su/IEAsAN8BSMChv63/HT72f4bAzgBfwF7Azv+Yf6CAHf7wv8XA+/98f0J/UoAJAQk/wT+pgPQBnMDgv4R+8j54Pow/uMBkwKlAogGiQTC+oD6vwEVBqsFvP9g+m37/P0W/8z/BP/AAB0AOwErBmcAsv2zAnr+ZvsdARQD7vxo/dYCB/48/LcCLgaeAar8ZP9E/h/9YQFcAWT70/pGBfYFR/7MA/wDhPm7/dUFigAM+0IAzf8C++L+NgGQAl8B4wI3BwIB0/umAD8Clvq9/Cj/1PfH/coGRQSKAcgE8gMm/W7+vQIt/8f4hPmQ/Rb/z/+lACkE3QI5AkoGKQOq/0T/of3K+Rj4iPzk/xcDMgR6/vX/1gabBf0CoAIBAcb71fn3+LL5IAFwAR0EdQaT/7sAAwbuA8j+9f0i/Zr6Ovzo/n7+tf4YAgkE5AAcAD8D0f9y/M4B/QAE+qj9nwTd//j5UQHFAgr+TAI3AiD/B//ZAakB9P0s/CL+BwHD/aoEgAea/1METQS+/Dn/SwGv+pv2WfxiAJT+EQPoB1AGdAOcAHP/8QCe/nb67f18+R33AgCSApEC2gLnAYv/HAD6/pwBRAUO/Nv6ZADv/an/lAP//6T+qwO7BJH+ywLmCPP9A/svAAz/Zfw9++T+WAEj/Dr/VQysCWD/iAFHAvv2uvfV/4T7afhI+8L/9QIMBYUDogWxCPUBs/5o/qD6t/lf/T7+FgCa/6j9iQPoBHcDngMBAkH/t/5iAKL9nfuPAAYClfwx/ckCOQRHAngBmwGl/jD7OQB7A4L8wfx3AfP8ffp0AhQGawQNAsT/oP+w/Gf+jP/8/dMAOADx+Wj6OANDBLoBRgEqA/QC2f7jAqkD4PpJ+7ABJ/6z+p4AfgZtAHX5sgKXB/j/Ff9IBEYBEvo2+wn+g/1u/nYCwgPb/3MCCQVT/Wn9BQMM/TP52f0MAAcBWQJhAHL+qwEbB7YEcPyN/YYBtf40/Q37Bv2sAeQBLgQlBCEBgAA8AIj/YgEDAF79AAC8+wr7cQHm/5L93ALtBwMEaP8G/uv94v0c/KX7p/uIAFgFHQAgANMEgAL5AT0DSQLN/Rj7I/75/f75e/x1AYb+1QBuBmYESwI9AlkA5/7nAdwBfP2y/Dv+cfv3+nv/pwLxAhMFigbcAKcA4wD8/vb8oflH+0j8uwCqAdECMAR0/3UD7AHh+h3+swGB//n7PftA/5wDngJnAWwECAGA+vj+iAF5/6P/zQLbBTMAHv1sAf0Bkv2g/dP+Ff2L/bP/+gPRAi7+NwK/BKz8sfmuAM4EnP8B+1P/uP8A/n0DWwIT+yz+igdaBLT5F//HBHv7QP19BJb+0fxPBvAC3vcd/OcDaQFi/UQDQQMm/YIAMwQMAQT6fP4/BCb/AgCPBDcCDP2t/ff8AfwgAbgBuwKnAzj9ufzJAH4CMgJj/of8ufzf/g3+pfxzAf8F0gQTAFcDGgW5/Zv4P/vA/ov9pwUmCLz8D/kL/0oAX/00BK4H3QHT/n//df7c/pwEfAKk+hf7av9u/Vv++AQvBAz+lP0HAnwANP4o/0T9Lv1TASkEhgMsBNgD+/7/+uD7L/2d/T8A0AFd/6D9cgDQBK0EhgHIAnoAWPmU+iYBUgNx/0r9G/+T/+n+PwEhBIcAJv9dAwUAEf2QAREBsP0q/+AAiP/4/m4CxwIb/Sb6Zv7xApoDdwPI/3P8lf22/wUB0/0w/ZsD3QQIAfcAiQGy/9z8kfzn/1r/IP08/7j/DvuA/j0JYgihAr8CFQKr+i73L/7fAAv++gATBPH+Yf0uA/gBRvv7/ZMGxwQk/kb8Zv3v/nsAkwHE/639yv+0APL84v/lB4cEBf5NAjYAwfdp+/8BFv/W/VICHgICAur/qQBFBJIBPwEn/7P6bfpA/9n+Dv3KAcAC0AMfBLgBkP/XAVMDKv9p/MP6nPpo/ET+Sv6vA6oGlwLFAvUBmf/M/6r/6P05/sD9t/z8/oICbwNJATP/zP72AbP/Hv4aA93+yvhpAMwH4QC+/i4D8P5e/EcA1gHd/4P+wgC3/vz5qf1bAUsAOQJ3BZoCc/9oAeUA6v0+/mABTP0L+pwBBAL+/e8BLQPK/1T/if5g/6sBd/8FA0oGTP6D/KYCXgBK+cD7LgAQ/Ub83QFeBAEAtgHXBnsEkP8SARcARfU2+JkDRALQ/zgEVwFt+3AAswK//zQAZgOuAor96vzJ/rz8tf86BkACKv15/foCvQGD/NcAcAEsAEsAiQF1/sT6s/wT/SUA/P/vAEoGSAQEAED/5f7SABgBhf2D/Sz+aP7y/Av+cwOPAx4C1wTdBTf/WPyh/p78ivxo/0gCgQQeAy7/Wf2xAJ0CHP/i/iH/tPtk/asBtgE1/nX9iwCdAUEB7AKeAlj8wfvg/8L9Z/5WA5wBn/yaAHECQf5DAWkEHwP4/yL/MP9w/kr/X/4v/4EBuQJFAgMBjf8b/J/8kAF1Aw0CRwCP/6D+c/ve/hkDi/+6/1UB6P2//EICigPd/44BkQJM/zn8qfs2/g4BP/4Z/aYB2P+sATkFL/83ADQFrgIn/Zn9MAFP/uH8w/1I/0P/Qv9dAZ8BMgN1BJYGHgG2+rT/z/259RL9MQmnBXsDSQDR+Vv/cQGU/8n+8PvU+/z8bPuB/G4Ewwi+B9gDOP5J/ooAUf4B/HD+WQAX/vD9pf6a/F0A4QPh/9kAaghpCG4Bcv+a/fL7d/wo/UMB5gBf/wb/TvzL+u0ArwjiA9gA7gGJ/nn8VvwI/iMBYwQCBaD/qPuH/en9L/+7ALEAK/+t/wkBufpj+0IBjgHO/3wCMgY3BGAE2QEq/8z9w/wU/s/72vsK/9/+6f3MArkGRQUcBVMDcP6pAJ8CgvmL9qT+8gB3/OIAZQQR/hP/5QLM/tD79gJjB1UBTftW+t3/5P8u/88DY/98/r0ESgFC/JH+1wAaA2QC0vrN+oD/2QC+A1cE7gNOA/UAWQAF/4b88/2m/QL96f44/TD/dgJfAvID7gKD/nL+3v6O/QX+vv7nAGMCSQIFAPX/CwC7/aL9Ef5oAZb/Yv1fATcEdgSzAdUAbv9K/kf/UP7u/bX+JwDTAU8BJwCvAPQAsQGWAQP/Of33/Z/77PvzBNgH0AJZ/4797vxW/Jr+hgGG/2oBQAKx/SX8zP2HAhUEmAHj/44BeABq/UYAhf/5/s0CQgRbAxP+RfrZ/Jn+GP88AR4Cgf6A/WcDKQMJAEcEgwZv/p/43vsV/az8JgCkAyn/JPyOAeEEkAM3AVUCMQBq+lP8EALF/5j8MwHJAgIBoQBbALAA8f5m/Nr/YwH4/7ED5wHT/If/NAK0AY8B2gF9ACj79/uVANP9bv3wAST/F/xzAwsE2P21/9ICpQFL/e/+BwbPAsH7zPyj/hH/zwDiAE//2f9tAkAC0vzI+6gB0wGwAOb/AP7xAg0GDQAB/REAqQG2BNoAvPoR+oj4KPtM/h4CQQeLBwUD7ABaAeH9ev3L/+QAgP59/I7+1P1I/EQA+gMAAbsBvQT6ACX9JP+6AokANwCxApP+2/rk/Kr+Nv5BANYCEANqAKgAUgb/A7b88vme/Bf+Yv/HAmAB4wDA/9P++f7I/hEAfQGqARr9k/7C/87+WAKaAYYBogKPAMX98f4OAS4DWgCB/PYBuAFU/Xv9ff9a/8X+nABX/4IAPwEXAigCpv7M/+8CXwNt/Tv6mfys/cP+B//1/2EA7QG4A5YB7v+MA5EFpwCy/UH/r/70+z/9gv5e/XX+8ALlBP8Akf/aAN4AbP9MAj0Evf5N+x3/9P8u/Bn+bgExBCsCI/2M/HD/tALR/yz+ev4z/9kA+gEAAIP/pQW6BOL/Zv7o/tL+Gv6A+yL5O/2ZAjoFowPZA0YE2gIdAcb/UP5p+Zz4bv1jAA39OgD/BpED8wHGBDkBRvxz/tn93Pqd+3T+kgBZAnkEwgKaAswCW/8y/Z38z/5aBHIDAv4A/uL+2P5+/j8ACwOHAqf/+P/dACf93P67AI796v7ZAOL+tf+eACoAPwJvAIEAUwE2/BL8SPwD/H4ESwcoAcEArwM+BFIBtf6WALf9NPkF/R7/1PtGAOIHfAPJ/acB0wReACL+kwDz/1/9svrn+uv7Zv7YA/gF/QNSA/cDFv05+Uz8JP95AkcAjP6J/YT8nwPlCMUBjP6tA1sA6PxN/er83f+HAP/+8ACUAOf/GQQwAlP9q/4CAFv/mAC7AG79rPtS/dgBMgSCAsMBYQDf/qYA1QBNAKH/ePsf+0n9df1AAUgFywVXAy8BmgLZAuwAzf6h/db6zPm6+/f7UQDlAoAEnAZkA6UAaP9P/rL7pPu0/e7/ZAEiAKgC1AOBAK3/oQEr/6v8u/91/xr+5gCAAPD98wFJBd8CoP9+/QgBMgJH/ncALwG//CX9Tf8M+ib33f+QBWcDpwLdBekG4wReAUb9wflZ9H/4EwDu/o4A4gU8BMX/DANgBeYD6QGB/3z++Pta+1T/gADqALoDnQC0/B79CAG2APz70/9+Atr/JQATAQL+aP2zAB8CSQExADkD5wNU/836MP7dAMb79vsx/r3+PAC2AUQDEwV8BhwFugBl/lf+uf2a/Ej8HP3g+///dgYoA5T+OgTXB1kA5fok/Fj9vPxmARACMP/t//T9Mf8/AK8AaQDBAb4DAf+6+939WwBB/Pb+0QX0/yP7KAE7A6H+yAILBlQCXQH1/w37tfep+jMCPgP0ABwEuAET/zEBOwL1AdMAHv8C/6kA9v0Z/qD/7v+AABv9k/w0/g//wgC7AXv+gQCNBHMC6gJvAUoAmgCE+8b56PzG/RgBMwL9AFsEwwAs/Db/FQIuA9oDqAFa/tv99v7fAP393/2jA5MCy/5l/rH9cP1sAAIA6f7SA/AE4P+P/oL/c/94AKEA4/7k/AD+Gv7p/pMAvgAsAkgA+P5K/xgC0wLa/7v/KwAuAYD/rv6q/2kAPf8a/MD+YQDc/jMBRgKOAV4ERwTaAR0Aov1Z/sz+A/4W/9f/TgEqAj/9F/x4AB//BADLAtD9+fxhAeX+mf0gAbED2gRWBL4Byf1S+W/6nAAM/5P9oAK2AyMAM/+2//r8MACaBqsEegAfAZ0A8v0Z/14AfP+UAIMCQf9r+Yf5c/4t/sz/MwdWBf4ARQIjAbT8tgD6BFf+6/yLABH95vdm+jT+uADcApkDigJi/+4DhweA/+j69gHiACP5Tv79/pn7uQECA+H+IwBnBNYDgv+Z/oYBJwL+/zQBPQJe/pT/PANz/ij9YQNKAfj4c/mu/gr+Xv9MBQQDkP9xA04CQ/2N/l0DMQJ7+yD6ov1r+0j5iwLXB3YCfwAvAPz+DAHzAxkCCP99/uD/qgCe/o0BfAXxAQL9gP7QAXcAKv4V/5YBZ/51/Hv/3/8LALMDdgZiAq/+I/43/jL6RfkEAT8ASfv7/dYBKQAKASwElwNWA9H/g/2p/1AAegBpAGn6A/tsBCkDWv+AAC8CFQKh/+UA2wM9AlAAAQDM/Ej5xvuBAhQDbgAtAhcDmQDtACEBSfy5+7j9W/x7/VkCagIMAT0CWwH//8H9UP/fAbX/Jfwk+83+UgGhAd4CWwVnBdQAOP3c/Vb81PpnAbMEyf8u/8sDNwK0+1r9IQNwATb+hwDIAmcB0f/rALr/gPzv/FT/XADr/or9R/+4Ab//JP+MBIoDyv1Q/mAA5/22+8f/SASFBNsDBAG7/HX7If6O/oz7Bv4GBHkFUATgAz8DogAZ/7r/YPwn+Wn8wv9p/UL7dP0AApsF2AQgBjIEWP1r/gQDrAH+/nb+5/v8+7f98P2D/U/+NQK7AhsDGQXNBAYB2f+vATX9S/ov/VD/V/+0/zABZgDN/rT/awGqAQz+5PslAP4B5v+8/3wBAgKeAt8DwQHU/Nf80QHB/Yb46vwNA+0CPAI+A7n81ft2A1QEPf/uAQoG+QCj/VX+6f8Y/UD8rv/a/eb8yADTAFv+XAOHBNMAmgIfBDn/y/hp+Wr9PwBlAsEDhQBC/E3/bQKA/9v9wgGdAhL/Uv6gADgCDARDBEYBR/7r+47+bwCz/RP+6v9w/5MAqgHm/i7/LwN2AlcASAE7A1ACaP20/Kj9Gfxs/aUBLAEG/X3/qQGo/u/9YgOxBTgB+f6h/qT+8Pyj/QwBWALAAdMAwAAY/2b/mwGwA6QAj/yd/fX9wP/D/zj+FwKsA+oAdQPuBGn/Sv6C/vn6L/r6+oj95QN7BgUCpP/RAmoCJf6d/dUAGQBW/EP9mv74/nz+0wIcCXQDYv+yAW39uflC/UD//QDlAaD/pv6+/Xr9ef+3A50FCAXNAu3/XwCX/37+xv+B/iD54PiU/vX/2/1hAQYHXwVyBI0EpwLO/iD7ufwS/Vn7N/sOAMsD/wBx/yMAPwB3Ad0CEf+I/esAJgCW/ez+AANZA3QCWgPK/yb8sv+EASf9Nv0IAZ0AV/wr/PMBZQMlAZsCTwPUAEYDugQC/oj5PPyx//T9aPyS/ab9i/6gAZcD7QHAAnQECQJ5/rD91gCe/jH6ePyuAaoCNgCgACUCJQEpABwCHgDS/J7/ewAo/Yr9OgQoBs3+0f0PBIkBCf4oA6YCVPwE/Cz+Pvzh+0cB4QJ8/LL7DAJ4A4kBOgJ8Az8CUgKsATf9Nvo//OL+pf1f/0QBwf4c/7QBiwJSAbMCZwaNBCP+evx7ABkBSv94/mn78vj4/PUDYwU5A70Acv54/uv9LP8ABMMEuQDM/Jr6MvzXAOIBigEHA9kBSv5E/n/+kPzZ/hwDsQE9/hb/fv5k/lEAnwMcCLoEhAIKAZ/7Vvuz+gv6J/5RAjcB//86AdwBCwSWBDoBxv7K/RcA/AFE+xz6TgBh//H+AwPeAS7+WQE6BC8AU/t0/70DXP7v/fYAd/4q/VQCKQUuAY7+ZwCBAg0BQv5n++X5TPx8AdECAAJ1AhoCLALZANf/IAApAdIDNgN1+uP1T/yDAasBSgCBAgUCkf/CAdYC0wGEAKL+0f1x/l39aP+dAFH+Fv1BAF0EZwJlAiwAsvqj+fj8m/+1ArsFoQLMAX0Atf/I/5r+GwHjAsn+0Pre/7f+cPrd/qEEJAbWBMcEfQIY/3z8aP/mAHP8tP3j/zT7XPly/bsBZAanBQgCDwGP/+b9dv3F/Tf+0/8q/zL98Pzs/7ED5gNkAj0CJQDf/ZcBSQIgADj+nv02/gj8Jf5jA6QEDAPIBPYC4/2n/tH+gv6c/kv+Lf3D+zD+MgGPAVYEEwc9Az799vs6/p78Jvy6/fv9/wDKAm8B5QCsA/EGTAU//0z7tPoy+1H9uf44/Qn/WwMtAzcDOAShA00CigJnAj792/pK/pP+zPvt/f/+YvyE/BkAVQR5A4UChwepB/b+o/35/0f81frT+tL6A/xf/h0CSQTTA6UE5wKW/sEAWwIV//r+lQL1/pP7/wF0AsX8Uf2dAEX9rfqqAPQF3wL7/iADCgUQ/2T9+v+5/Ef9ugLW/0P6Kf60BGgBOP4mAOX/jf3R/y0Dxv8HAGUEtQR3/xD9jwFbABX82/7gACX8+PxnAFf+Kv/JAjIF8gNYAToBoQCF/Rf/6wGs/db6B/00/iT+9wD5AUAAogIQBZIAEP2WAu4DyP9F/Mf6hv6N/0sATwJZ/9b+/AL5Aa7/jQEhAQz/Qf0G/HT9JQEkA0QBYwEeBAYDif9L/yP+APzd+wD9fwDPAkQB2vwl/vgCdAM1BGoEGAIv/lj9Of6q/Lz8m/9bAF/8OfscAR0FlwPYAo4C4AAv/7L+UgFH/0X6nftZAGgCYQGPAtkDfwFb/pX+M/x6+Xr/CQU9BHr+hfxnAuYEOAHIAKwCEQGPAXb/Afk3+dn9xP5w/pD+M/9RBIkHnASFAv8BIwDx/4//Bfs2+oL9Mv0H+yP9dQSsBNwBygVhBOT91PyRAe3/+fn9/l4Def/u/vkBXv9Z/h4CggHp/2sAQQMwAYX5TPqyAEYCSAUCBlb/JQA6A9j/yfxe+2/65ft7/5T/O/3S/ssDsAT1Ap0DtgOXAdsAWP0x+sL8Lv1B/vD/PAB0APsADAOqAf3/JwJtA4cBFgL1Af79rvvp/UkAD/0d/dcA8QDg/bX+rgJzAlUCrQKv/kD9UwHDAUv+OPzN/SgAmwA9/5/+DgJ5A1oB5v28/Pb9VgAnAl8AbgAxAbP/bACsAlEBagHLArUAT/8I/+P96Pt0/cMAcAGp/kn/BgFaADEBQQDG/3sAEgQZA/r7DfyR/3T/0P6f/5T/aP8S/nD+8/5PAFYCTQAkAFUCGwTcAqkCpAO0Aan+av0+/RP8Nvwd/PP8Gv4qA1wG5QLXAfsAqgFpAs8AzPyt+uz9Vf0r/EgCOAbsABX9Kv///+/8MP7bAvIBL/9QABID/QBKAeIEAAKx/e/9+/+c/wT+Afu++nIAmwIz/xX/agMGBRUBp/7yAbMCY//GAFwBZvs6+20AywAg/xb+R/zR/awCDQGG/7kC9gF8AToC0gD9/3ABBQEn/rD9QftB/A4C0gPcAs/+bv01AJsAiP+tAIwBeP8SAkkEWAAy/RMA4gFK/Er6Q/7LAK4BdQIxAJj97P44AAP/4f0YAVACWABkAQUDEQI0AfsB6P/1+9X86//S/Wz6kfzhAmME/AOQBGUBtgB8AdgARf/Q/cf+Fv89/Fv6vv1P/lD+1wOmBF8ABgL4BLwCqv8o+9v6ePxa/pMDSQOBAE4BhgIbAmoCJwFw/rn+fv0E+6j7i/9+ApUA8P/SAW8AMAHKBM8AlvzA/5oBGv4f/KP/F/5u+4X/AQKPAJQCigcnA279KgAiATL9x/yp/9f+wf+CA0UFsQGU/yoCav4s+w/+D/2F+j//5gDX+3L/9AZBBScBlALuA74A+P1cAQL/xvc4+4P+a/xc/osCFgRLA9YC9QJpAxcDgQSvAj75CPjH/V79b/7DAQwAtf2m/jUAtQCZAFsCjwRAAJr6kP3NAyoDjABcAkoCkv6m/or/wv1j/lb+Yv7m/pX9jP6jAdYCUgHZA4cFOQUgBNT+TPxV/Gr76fp3/hv+3/rQ/3cCp/9ZADIEdAbiBRsAq/uj/QL+iP80AOT94Pyv/pcCjACx/tcBvAPBA44BQ/+x/iYBcQLKAUr/mfvS/iUAof10AP0A5f1wAKoCUf7x/BcAJQG+/3v/8wAXAEL9NAD5Al7/6f6cAXABI/3G+gr98/67AXYFUgYsAFT+9QJqATj/xf4X/nX+nP2I/rkCDwWRAz4BsP6Q/qAAIP/Y/cH9gPvC+7EAOAS0A4YDCwJE/Mr42f1JAmEBJwIoAkv/3vy0/rcAyP0O/j0C7AG6AEEDNgTVABL+2/8f/+T7f/30/5n+xfwaALcEnAWKA9kDFwOu/K36+Prk/BEBuQFnAqYBgP5K/jQBvQCS/ab9AQBRAED/5f+hAe0CMAHl/r//uwC3AEUBqADX/af+PwE+AMr9Mv88AEX9Mv7lAI4AAACkAkECJf6RAY8FugEP/UH/7//b+Ur6tP4p/7D+owH3Alj/nQL+CSgH2f/h/vj+Tv03/Rr9f/xD/tn/BACG/3r/lQLIAhYB6gFIAdj/0QBuAR/+RPwz/eb9j/yt/coCZQE0/XIArQSxAtD/IgAu/z/8D/5RAhEC9wAoAyUEcgBN/n3/VADK/ob9Lv88/z3/EwB8/+r+DwHkA6kDvgHR/l381Pvg/44Bwf0B/3cB8P1++y3/9APkAmcBuQNTAfH8Cv7JAO//Jf7yAQcD6v6t/k7/Zv9z/4oAIQKs//n/LgKRAJ//MABr/5D+tgARAG39nv6L/9n+Sv3z/tsDPAM1ALwAov8z/90B0wLwAGb9Q/tA/FT9Z/5XAQoCXQP7A5wBXAE3AYT/S/6J/xn/SP74/98AlQCs/2sBFQF//6D/Lv6I/fz+yv+TAH0C6QLIAZ3+7f2V/w8AIQAV/3D/kv5t/p7/pv4E/kEBngNzAmgBtP4k/1ECKAIqALH+5f2P/s/+tPw7/RwCtAXVA/UAS//P/tz+kf8VAKT+kv8yAdUAnP4iAEwD2gAv/tn+TwC9/X/8+P2Q/nwBhQWaBD4AhQB4AFj8HfycAbwBhf7j/+wAuP8O/sv/kf9d/sEA5QIuAo7+5f81AYv/Hf+d/qz/DgBh/hf++wFjBFcCswKgAln+5ftR/Ej9vP3N/cEA+gLYA3UF9gNzAMj9jfzz+xb96v4t/u3+ZwKsA9oAEQCUADkADAJ2ABL+8v6s/4kAKAFqAMP/+/8v/mH+Bf8n/e//igKOAKz/wv+MANUBqP8vAWYF7wGK/bT94P5Z/5H/Af/2/Tr9Sf6HAMgAJwLFBAoFZQG9/50AiP5L/Rj+Uf0C/I3+wQDU/9wAYwN0AYv+ZwG9AqUAbgDY/nv7Z/ypAbECeAAnAZACQABa/nT/Ev8V/Xv+QgGq/yT/owHFADz/TgCHAmEDuQIVAj0A4fyN+rv7HP7O/2YBygGHAJP/1gBrA7ADrAHxAfUAmPuG+5D+mPxs/GkAoQLwANYBhAV9AUL9qwCuABH85fuj/2EAKP+L/8X/wQAuA1kDuwCpAG0BWP5D/GP9/v5wANsAzADh/xgBEAaxBXEBrwC5/+v84voy/Cb+7vwl/ZT/ewD2AqsFiQNgAWcBgf+l/Y79ifzX+yP9Cf/s/mr//AJaAyMCiAEiAXEDigI7AAIA9P7r/Q/8W/tz/g4BBwGdAmMDjACCAFYCAAGLAHICtQEK/r38Kf38/Fz+JACKAIoA8wCw/7z+vQGWAoAAfv8R/xP+v/us/L//QgCyAawD4wETAOMBjQIJAID/XP+3/b/9Hf7W/Xn/ZQD1/9EC4gRbA54BbgL7AFn98v4jAEr+9/ty/eb/Hv74/l8BHAHyAGcDbAO5APf/lP+j/in8Tftv/Eb+vAEoA/MAMgDtAKYAeANABHH+Pvzg/6H/mv0g/2QBjQLYA0kEgf+N+jX8MACk/4H8xP4TBIUEGQFU/kv8fPzuAO8DpAJ1Ad0AgQEEAHb7I/vf/sIAif8u/3f/LAEoA8cD6gRuAmX/xv6s/qf7BPhp+zEASwIQA4kEywOr/2n/CP8a/f78cf+DA9gATf2cAOkBmP8jABYCtP/H/jkCYgDL/L//swKnAEj+uf8GAdP+DwCRAjP/n/0gAv0AsvsH/xsCO/9Z/1QDHwKx/FH+EQLz/xj+LwB4//P9ewG2A8n/lf18AEsA5/2t/oAANwByAQ0DQv/h/YIBYAKa//P+bwB+/6b+RwGUAaz/MQDKABUB0P+5/vf+qP2g/WoAggLmAlMB5/0s/KD8s/09/0gEvASx/n/+yQD3AGn/w//EAE//H/++ACsB9/2M/4QDQACx/gkDlATM/3P7NP3//q/+3QHJA7YAdv25/2UClADM/qP+HgCs/4b+S/5b/OP7SP4NAS4DLATPApkCHwK5/vv9GAGxAcT+Yv2L/Uf9of5iAYUBIwANAgEFBwMGALr/9v+C/uL8i/7o/iD+X/93AIr/7P0tADIEXQRhAfD/aADl/zT+2/tZ+8r99/99AR8CEAL5AvsBHgDG/1UAnv8n/x3/Ofz9/GwByAPzAc4AqwGP/1P+m/20/Yn+8P9fAigCygGzAqUBR/1z/IT/GP9J/ZT+YwGsAZ7/aP+1AU4C/AH6AQwBwf12/ET/kf9V/p8AygN+AI38WAAeBJkB4P6i/wQAQP+B/wUAlv4q/tn+Cf0l/tQD2QRuAjAC/v+z/Y39dv0I/Y39MAA1AUD/hf9SAmYD4QJGBPAFGQOZ/SX5Mvdw+TX9u//EAksF4gSaAkj/Of/5AbIDcgKu/tz8Xvto/Hb9Qv4iAgkDlAPaAhMAuv4c/6L+KP4cAK4AYgCJ/6n9bvzz/Y4AiQPxBaoENQF9/f/7tfx4/4sA7/9cAI8BfwHv/cz+JwJMAuMAIgHNAKv9mf5AACn/8PzX/pABMwAyAakA9/w8/ZkCOQP2AFgCoQEOAJX/t/+n/Zr8Gv9q/rj8if0tATUCsAH1AvcAkQBRA9oEegAH/RQAqv2t+B78TAPQAwMBJAGw/2n8//yIARMDywAgAU0EsgFP/FP98ABiAaEAjwDq/kT+T/4d/Rr9bf8eA8ICLQAJ/1r9Vf0KAuMDLgGoAaYDwgGq/N77KP6P/Yr+bgL7AEj+DAFJAqD/fP5SAywEBQH0AVYCYf9x+578pPwy/Kn+9QDeAWT/WgAdAm8BbwHvApYDogB7/xH+Tvxt/Hr9+v+9/wn/gwA9ATECogLvAM//SgHAAo0Bmv6q+yX8ZvxF/PX/7wKSA+QEdQXZAI/8vv1x/xz9NvxyAKABKQKlAnoARwD6ABIBOAC8/gX9Vfw6/nf/Vv57/0AFvQbYAjMABf+M/PX6xv7+/5T+UQEDA7AADf52/sP/VQIgBd0B/P0O/7YAf//o/dn/vP8L/SH/swBA/h3+BQFvAeL/RgFGA3EBFP9MAEgAAv4C/0MBcwJpAxYCuv1l+5H85v7h/pT97/+GAicDqgJ/Aen/cv8wAroBSv4r/oH/if3S+q/9HAE+ArsDOANqAdD+3P7V/939Xf8SAowA6P0d/9QAsv6F/zECcAGbACYAUv9I/k3+LAAOArMCbAKuAEj9hvy8/SX+9v4t/7//BAHeApkDjQIcAIgAfwNrAV/9evs9/dz+lf6A/28AjQEuAnUCAQGN/yYAkAB6/3v+gf/r/gX+vP7W/0oAyP8XAPsAUwHGAUIBF/1Y/C4A6QCn/z//UQEUBOgDdwIiAXj/3v0d/cT71vpi/UD+7//qA6ED/wIjBdoGKQIe/aT+EADQ/P36Iv2C/Ev8P//AAh0CLwDzA1sEq//c/o4Ajf9I/6IAUP+n/Ar9Q/8R/0X/5QALAigCNALvAZr+cP0JAXUCSQCH/jv/Tv+C/t0AbQISAv0BWQFmAJ7/fP7o/B39vv0XAEQBfADFATUBWP/o/7EB+/8G/bb+FwGK///+cgC6/3b/fv/c/kD/4AAuA8ACd//X/In9IgG7BMkEDAH8/Pj7MP1J/WL/nwNMBFIBLv9U/uH+cgHaAckAkQAWAK4AaACp/Z38rP5x/1z/k/8x/3EARgB7/9b/GAJGBHgCDgCv/qP+uf1C/iH/L/5//Gv94gGoAVgDLgWoAsQAHwEsAr/+Lv6V/zz9B/rq+/X/aAANAycG7gQWACwAhwFy/q39pv05/PX8qf+2/7f/CQJuA/EBUwF9ApcAqv75/vP95/rw+pn+fQD7AOYDHgYZA7EAEQJMAe39Df17/OT6Dfx3/n//owCiAsQDrARJBXwDmgBLABD/Vf3h/Cn8Rf3n/Uj+gv9gANoAogImBC0DgwK//w//7wD6/tL8E/6X/gX9OP/JA0MD3P2D/fH/T/6k/joBOQJRAe0AGAE3AAoB9gL8AJ79v/0z/Tv8sf7GAGkAaQCMATcAqf44AfYEUQOv/zYCZwN0/mP85P4D/1v8ZP1r/uP8h/5tAoICSwBFAcYCEwP7AmEBCv+G/un+Zf6J/jr/KAA3/5r+B/8c/v/9HwCKAqEBdgE6AcP+2/1u/rgBuQO5AqMBZQDc/5f9VvuG/kQBJACD/wv/7v5x/sH/iQJsA4oDLgSeA7IALf9a/fb7M/wf/BL9Iv5y/q7/mgKdA+QE8AX8Ajz/bvxl/B78lPuP/fz/3gEQBDgF1wBf/ckAOAIM/1T8Rfy8/icAtAC+/2r/OgMKBdUC9ADWAOP/lAC4ApH/Gfyp/Ln8lPq8+h7/fwG7AcYENgb2AtoByALzAP/8Dfxx/WP9Yf59/4T/YwAvARAAbv7l/+wAbf7r/kICywIHAi4DKwKS/jz/GAF//vz6PPwRAMAAlQEpA6AB9gCIAdMAIP9m/kz/C/98/l7/HQFbAYsAMf9f/av9wf7o/8r/PP/P/4UA4wHsAPv//QDqAUkC1QD4/vH/iwIOAn3+uP2W/t391f7d/3j9WvwfAc4EIwTvA5YDwAHi/Zr78vvw+1v99P9YAVEBMAEaAcIAQQJcA5L/DP1b/vX+eP4w/3H/uv14ADMEUAK8/u/+CAEQAPr90P9LAz8BEP9u/6z+XP6HALYCgP9Y/jsC8QKjAAYApABV/+/8jP0rAQYCZAFD/2X9b/49AHYA9f3m/b3+IP+jAfgCbQGIAZoD5QKK/rf7sP14/vj8rPwP/0kBeAIABeQEeQIDAT8Afv9d/yb94fub/n0A3wAo/7r/XQH9ANYACwAo/6/+AAF8AjL/If0g/q7/gQAnAFEAjgCw/3MALgF7AFABXgHD/3X/9/2z/GD9nf4dAbQCGwSLA3AALQAYAMn9+vua/kMBaf/A/yUC8QBa/6gAdQG5AC8ALQCS/gX+jv+O/uf9mv/FALQASADmAGgArwCzAqsCyP9p/j8Agv7p+oX88f9s/7D/MAK1AwYFxwMvAiMAgf7o/h/+bPzk+57/rAEPAM3+Of6D/60AjQHZAPv/8QG1AtQA3/6d/7MAWf8m/uT9Ef4w/x8CawI9/kr+XQGfAQQAQQBRAev/mAAiAg4BQADHAEQAff5q/u79y/xx/Rj/QAAAAZICqgIGAeIAlAAP/4n/NQAi/2n+Zf4A/3P/Gv/7/hkAlgHzAUgBsAF3ArMA2P7h/vD/mgAnAOP+Rv5y/yQA+v5b/r7/XgFBAk4CKQKXAY0AtAAe/5P83/z0/Kf8b/7O/24A0QFmAqMDYAQVAmz/7f1//bH9Mv0p/rsA8ACmAJMB7gHkAGQA2QDLAEkCmQNdAlr9qvp++jX68/0WAN8AIgLEBEgG3AKuAOwALAAo/f78yPu/+MT7HwA5AYsB1QQyBlwETgNdAPz9v/6Q/w0AIv5j/JD+sf6R/dz+pQCUAOcBhAS1A4oCAADb/d38h/xp/Wb9/P5MAJ0B9gJqAnQBBQHsAIAAawAT/+T9gf5X/oH+Iv9s/g8AYwIGAjUBeAFJAqcAegAfAksAOf6I/h3/Ev9D/wb/Uv7o/tAAcwC8/QP+kP+cAI8CRgTZAVb+AAB6AXr/7/z4/RMA//7y/qH/JP/H/mIBmAOZAkoAJP90AfQCfwK1AQsBAf+U/Pv8j/2T/Un+IgDQAOb/OgDDAbsBtAAYAGv/OgFxAusAG/6w/C7+O/2t/dcAYADO/+wBCAMsAvYBJQI0ABv+p/1t/pj+v/4tABgBHAIDAggBjQFaArb/7/oD+6r+xQBO/8b/KgCm/p0AkQHJANMAgwNRBW4CvP/S/8f/ZPyc+vf7M/vH+zkAxwJfBAYGOgVbAqAATAJ3ARv9Nvro+xf+QP5i/5v/AAA8AUAC2/+L/hMCZQMIAqkA1P/Z/oz+Z/78/Z/9bf7eALQB/QEoAxEDdQB6/u78x/sz/Fb9XABfA7EEJQSbA2MDHQKN/5n8RvyG/On7rfto/S8ByQKRA6oEZQOVAc0AiQAA/2z8wPtQ/Yn+x/4v/4H+yv1FAKQE6gWiBBkE6AK/AHj8Kvmt+Qb8W/3k/dkA6QMrBLUEygXWA94A+/6Y/S79b/x4/VD+lfyv/UkClQMlAWIAkgBZAF0B9ACa/z3/nP8X/1j9mv7PAAsCOwLYAZQBWgBeAc4CDwDr+mL58voD/OL+oAFCA8EDJQSdBF4D2AENASQAeP7W++r4nvlC/V7+lP2cAJEF3gbyBDoEUwRHAlcAvf0Q+/r7Vv43/rb7wfvB/h0D5gSQAj3/8f87AzoBgf7q/zgBtv8P/g/+sP5qAMoBJAH3/nv+cf81AOH/X/6s/uj93/0zAY8CxgPVBfcEDQIj/yv9+/y7/PX7bf29/vP+uwFaBAADgQAnAacBkv8T/6kA0v4W+8D9gQFs/3H+KQIZA48ANgFRAkkAb//s/6L8vfkp/Hb/6v87AeIDqATbBP4DrQIKAbr+NfxE+ff5OP0R/b763f0bBKgGsgXOBE0FEwTiA0YCvf1f+9r7g/x4+cT3mfpY/2oD5gQDBZsEYAWHBVkCEP+3/dP8Jvzi+4L7WPvo/JkAuQJUAuUCnwQZBc8C8f49/Wz8i/ve/L795/3K/uMC+gZ0BUgDWgOAAtT/gPwq+W74yvpk/vMAUgGVBP4HIgdhBL0B6v8v/vT9NP2r+Wb3ivo4/7j/Df88AqMEEARvBVgFfgIYAaf/9Pur+Qz6A/rZ+qP9EwLVBBIHkAgvBkQCRf8D/aP51fhc+7r+jwGjAv4DfARUBHME0wJGAPP9rvrJ+Bb68P39AEkBFATiBWoD0gDf/+b+tPwI/t3/Mv2A+qj7Av4//6cBVwSBBIcDbwW7BZkAC/2M/ff7fPrU+477p/xSAmcHzwVDAmYDYAUbA+r+u/zZ+rL5i/ww/7P91f4PBGUF/gKnAfoB8QAd/5L+nP4D/kj9Tv0d/cv9bABkAUIAuwFaBM8DRQAC/sj+ef5N/n7/H/9V/hsApwOaBGECEwILA70Ajf0S/CT7JvoN/BH/JgCrAdgDCATEAvoC8wK9AFr/ggAM/qj55Ppq/a3+xgBZAwEEAwOQAtQBCgDr/vz/pv+M/oT+D/6t/F39PADkAAICcQONA/UAkv4J/v/7bf26AYIDBQEB/an9pv8jABQBPQJfAhwB4f+h/o/9F/1d/i4BVQL+AjcDLQJQAN/++P4c/uX9rP6Q/yL/0/5NAAsAsgEqBOQDnAJRATkBgv2F+Uf75/x9/E39vP65/sf/RAOBBWwFFQU6BSEDjgAO/1r8OPkd+nL9Sf0y/n4AEALkAqMB7ADWAOcBOwKlAU8AxQGiBDcCjP+I/WT7yPrb/Hv+Rv0Y/bv/NwF//mz//QOZBQEFLATSAln/ofyQ/hIAIP2F+9D76fvb/Jv/sgK6BFQFOwWgBIkBDQCe/un7nPtF/WT++v7TAaYD8AIqAfr/m/5U/l7/p/9R/279S/5BAM0AzgBQAXoCdAIAAjcBu//W/Zj9iv0U/nr+Ov4u/1X/D//J/qEAHgTXBbcEKgIlAJ39ePxW//EBcP+I/af+fP48/Db8uv9FAUsALAGyA58EGAWeBKoCVwBH/8L+UP1//Vv8gfrZ+5T+Pf8w/5QAgQEZAt0C8QLYAf4B3wLDARv/sv2x/u396vtZ/H/9aP6rAUgCtv9H/+4BYgKg/2wBGwPoAW8BOQLZAkgA3/7t/mT+PP3N++P6IfyCAFkCDwEhAZQCRwI8AY0CtQI/AHL/oP5d/un/VP79+ov6w/wF/2cBjAJIArsD7gNoA+gBjP9NAIcAQ/4S/Hn8cf4pAS8EgALK/5X/nf5X/U397f2R/U7+dQHDA1sDZgNwBLgCVAFHAacAcv63/H78F/u5+Rz62/zN/goB0AKWA48G5gcCBnYDRgLr/739MfxF+an3Lfcf+zr/oQDKA3MH+ghOBkoDAAHS/7//d/3w+s/5EPwg/nT9ov7pAQsF6QWkBHECawG9ANv+s/vr+WP8TwCHAfb/FQDvABoBgQHbAK8BiAIzAqb//PpD+pn8xP1F/7gAAAD2AOMDaQQMAuUAiQEFAb7+Kvx6+rD63v6wApwDsQNZA60DVAIvATAB6P5y/Ur/Zv5p+2z9IQH+AEj/lf9j/+b9o//NAXEB1ACEAXABGf+s/mv/qP64/sP/NQBnANsA4QBN//n+sP96/o3/zAGVAc4AEQDwAJ4BTAMNBFQB/f74/Pb74fsm/A/92f/GAcsBWQJJA24E0gLMAbMBqv8i/fH7zvwU/PP7pf3n/uz/IAKPAzMCcAD0/0wAmQCZAjoC+f/v/zcAL/9Y/rn/2f/c/0cA8f4S/b3+BgLp/1L98P6VAaMCZQSfBYIChgB9AXz/DPuA+e77Kv5A/l//1/9QAAsDlQNBAaf/TABvASwBkwCa/83+9gAFA2IB3P7N/eb7hfks+qP8egDMA6cFnQV4Ax4B0QDqASYBt//R/gX/zv2K/On88v2p/jz96/+2AiUDWgO+A48DxgELArcBdv/b+yf87vy1+n370/4mAiYCzQHeAHf/RgCMASUBhP+GASsDiAFgAM8AtACB/y/+JPwP+l77Z/9bANP/CAFPA2QDbgMgA1QAGwC0AsoCVP5G/T//fv1d+5H8cP7O/swA8AIUAgMAjgHJA6MCjAG8ALf+7vxO/NX8Iv1H/1EDdQSBBEEDJgCm/YD8/Pso++78TP/4AMwAQwH2AvQDbAVYBU0C2/06/Qj9hfve+nH74f1MAJYCRAGO//4ANwVBBooDRAJfAVYBff7C+kr4bvjP+8j/ZwGqACUClgRUBxgGAAIm/qf82f53/yX+GP1Q/xwBSADj/rX+TgCoAPL/V/0S/N/9aABGAvYCPwORA7wD7gHn/z//UP/i/gP+1f1z/QH8LfzB/lUAKQBSAkkFNAbcBJABzv7z/Kv+8v7x/GX9Tv7//l7+IgCkAXEBAgONAmT/Tf7hAPwAiv6+/hABswDA/0j/u/2i/aL+8P9y/w8AHAKjApABjAFSA38DmAL2//b+ZP6p/Mv7Mfv4+0T9KQDvANwAUgLRA/AEIQT/ArMAUv0Q/eT+0/3M+/77X/4kADcBtgMvAtP/CQFdAoYA4/7GAAQAKP6n/1gBQwGsACQBRwHZ/wr+x/0u/kf+2P5K/mX9Cv90AuAD3wLrAh8CaQFLAQAAp/1i+9j7yvxi/Qn+7v8MA/0CbwIFBK4DPwFGAUABxP6W/Dz96P24/Gn+IwEdAc/+cP/yAeEAKAAXAhkC3/+GAAcBjf4k/94BggCl/UD+FADEAB0AF/+X/UX92v5cAEEAbgDGAk8CmgHEAhECTAD3/gH/e/1r/BT+mv8qAM8A9QFyAcQAzwAFAacA7P7K/e39ff8gACgAuABLABwALwCjADAADP9uAEgCiAFj/sT8UP6K/2f/e/9SAIkBFgKhA8kEIgIV/2L+Cv4S/Ej7Fv0//jT+TP9fAl0E0AQpBDoDbAEQ/3P+Pf5z/dH8w/z3/L/9zf+yAbkC8gFiAT0CSQJ4AgMCo/6+/H795P2M/XP9sf/1AZgBdQGGAZcAHwCTAVoCif+o/X7+MP9r/4P/H/9U/xcBtwKCA20CNgAZ/kn9Dv4J/vP9Sv61/1IAGAC1ANwBEAMCBNwDCQGM/9H+N/7z/TX8hPxl/qH/Sf/h/k///f/jANECAgUcBOsCHgE6/u/8nf0y/rL9cv5yAOIBxQAD/xT/FgC/AXwCNAGjAG4BkAA6/pr9Qv+AAAUBawDp/tT+6gAQAdz+XP/UAM7/Xf4y/kn9xf5IAhMC1f9+APgDaQMqAJ79PPxY/ZP//wBf/9D++QEoA8X/WP4U/8b/dgEYAgkBbP8XAA8CkgD4/eH+BAEyAeb+Qv2Y/jUAkAGHAN3/yv/u/4QABv/k/pz/LwHdAdIAJQDkAEwBGQA0/tD7Tf0U/57/9//S/7EANAHPAjYD6AAjAIsBcwHD/g386Ptq/oUADwDu/nv/FwI9BM4DzQHg/2cANAFS/7H7YvrG/F3+0f47/1ABLQOGBG0FRQOCAS4BRwDN/tL+e/4v/Ez6gPyK/4b+9f8BA9sB5v/9AVIC3v4R/wkCNAFm/X79gADxAKT/qwDBAfn/tP4K/2D/zf+Z/wv+cf93AqEDKQKSAdACCwHr/44A/P/c/E/8Vf5X/Yv8af7eAGoAegCvAj8DmAGmARADnAHO/6X9XvwW/F799v7Y/aL+mQBzAtACnwJDAmMAc/8H/4z+pP6iAL4CgQKPAewA1wCHABn/5v2s/RX9Bfzq/OL/GQI0AQcAowLwBLwDLgF6ADoAGf+8/vv7MvrE+0/+rf4M/XD/+QPTBhsGkQN6Ac8AvAFHAB/9v/tU/C/8nvyr/6gB2QGyAhYEQAJd//j+ev/+AFIB1f/A/Ub8wP5mAPn+Cv+hANcAygBHAksB3v5t/zQATf7q/l4CmgE4/uD9cQHRAXz/X//+/xgBWAG2AD3+U/w1/3QCpwHJ/zEAyQAVAeIArwDyADACoAFE/kv88Ps0/CL8Uf6YAHEARwG8A/QE9AJ8AhADogD0/Wz9a/zb+hv7QP2t/xYB/gMBBdUCdQGXAAgAEACHADn/FP5K/9X/jP4d/t0AQQJCAN3/iAA/AAsAlQARAYT/fv5n/5X+Lf01/nwA5AE7ArUCJAIPAUwA2P7N/Y39i/6k/2//QQBDAToBowB5/73+l/48/zYAEgBZAJUBHgNBBMICy/89/mT+t/2h+1j7e/3+/hUA1AL9AkkAuwAyAzUDGAFWAUoCFgFj/+L9l/vL+u38U/6m/Wr+qgEIBWIGvgVdA+kAgv/b/v38BfpW+gP9Uv9oAF4BNAMCAygCZQGxADL/l/4uAF3/X/7b/kP+gP0w/3gBvQFZAXACcwNPApYBKABZ/cL6GftW/Q39Xf5TAfEDXgW6BVsFRASwAgEAHfwd+SX5EfoE/eD/jgE4AvcCjgTEAjEBUgGIAEH+Sv10/lf+I/yE+3n/EwHKAc8DLgRwAqgAZgGMAIT+U/6Z/tj86vsc/Yj+TAE2BFQFKwPKAfsB9f9Q/Qf9ef0J/c3+EwI/ArcAAgEHAooBrv8U/13/Dv/u/Yf8/v3c/3UA6QDzAEkAHQDnAdIC9wEQAbAAi/9x/dL8g/wc/Oz98AADArQCCQQoBJ4D8wF0AL/+Wvwe/M772vtV/VT/YwKxBI8EWQKrAZIBFQB3/kL+dP/e/jr/jf8+/qL9p/8EAloBLQHBAPz/IwBbAN/+Xv0q/7L/sv64/nYAMQFiAYEDKQRAAxcBWf9E/fr6m/rp+jv8Pv+QAqwDbQTtBM8EjASyAjX/6/tE/If9Av3v+wn9O/9iAGMBTwEAAZAB6AMJBL0BAwFGAR8Bz/4S/Xj8WvxY/J79l/8tAPIAyQE8AgoBtv+i/5X/vf/J/wAALQDkAaMDKwPOAPX+Lf8K/t378vtl/cv+IQBiAPz/CQGcA+QEzwTxA1gCVgEaAAr/Mf16/HX8/fqy+or8J//j/2YBjANXBL0DJgOkAnYBnQAQ/wL+WP0//a79H/00/Qb9xf1aAHQBqQCzAFYCVQMMBC8FEwXBAnH/7v/+/6392vwS/L777Pv//FL9t/3K//gCmAYSB00E5wEaAyQCHv44+0X7A/0o/Lr8W/3j/Iz+UwKSBOoCsgGHAjwCu/88/8r/Kv8rACUCjwAk/uz/KwFY/zb+p/9j/+v97v7g/8j+Q/8UA38DoAFNAlMEBgNu/1v+tv5O/hL9QP0I/Mv7H/6k/hr+zP+RA9gEqASPBNcDjwF+/0j/cv3P+kT7dv4+/rP8RgBhA0kC4gF5AxUCIv9///AAvP9F/ycAGv/x/lUAwABW/8D+Fv/5/igBmwIgABr+Z/91AAb/2/1n//MAGAJHAxkBCgBfApUDbAGp/oj9E/yQ/FH+p/0t/Y7/JgFEABQBVwNsA9EAm/9tAI0AfQC9/x/+Kf5X/8r+j/7Y/zIAnwAeAmUCzP+v/4MC1gFW/9L+Jf/O/kX/0QCa/zL+egALAicBOQBZ/2D+Sf5Y/qP+5/6Y/20B5wHYAa8BZAHrAUcCCAF7/xf/MP6f/Cr8j/1k//4AEQHG/20AbwFVAYsAhgD5AMYAMQCO/03/Tf87AMoByQDU/uv+h/56/hT/2/7W/iP/ZgCnAKQAiwJeBEQD5gJbA/QACP7w/ID96/uD+vT7p/0i/p3/YQKsAngDNgVdBp4ESQEmAGP+4/ws/OX7J/w9/Ib9EP/i/0MBdAIQA/IDCAP9AdwA7P4y/wMAZf/G/rP+d/99ADUAg/5P/fD+5f+O/nH+ZwDsAWABKwKcA/0CbgGcAcMBbP/j/RX9aPxt/LH9vf5F/sf+twAlAukBoQKKAz0EJgRoAY/+TP1V/af8w/uD+3n8//5BAQwDVAQxBT0EKAImAHL/zP/O/rn8tvpd+4b9zv+GAfQBiALuAoMD0QLaAToAR/7m/Sf95Pxh/Yn9Z/2G/u8AAwRiBaQEowRoAywBOP7I+3z7fvte/F39A/++ADgCBwX5BWIDiQDV/9n/gv2A+4/7X/zi/dT/gwGKAXIB2wLHAoMAzP8QAJIA7wD8/Qr8Sv7/AEEBAwCl/8kAZgKOA5sCEv/V/XT/oQBw/mb8A/9UAfYAsv+xAN4BnQF1AZ//X/04/GP9Gv/8/4D/OQD8AW8B0gEWArcBKgG4/zD+8v1z/jP9av0DAEkBlQCTAX0EagQFAcj/kgB9/oL8PP4U/wT9O/0TAE4BkwAuAZkCSwLGASgC1gGn/739Wf16/TD9/Pze/Qz/GQESAnoBGwK6A+YD3gHa/3H+yf2B/UL+HP/P/TD+vQB3AnMCSQG7AMD/6/8zAZkAy/8O/1L+mP7z/wIBh/8d/+QBlQK3/wX+Hv5g/oX+ff/BANP/yQDcAqsCIAGf//sAXwGh/2L9TvuQ/Ef+hP+iAR8CqwGeAjQD/QGPALn/IgAHADz/Nv5T/cX9J/0Z/YD/cgH3ALUApANdBMgBiwDdAKn/fv2Z/eb9bf0M/sYAkQEiAB4CZQTnA70BZP/f/DH8v/13/an9av7x/7IBpQEHAuMBtALxAjYBpf84/Zf8Rv3f+yr7Nv6hAuADyAP7BOoEQQOYAcf/sv3V+2n7cfv1+4j9FwC/AScD1AVLBeQChwHbANT+Nf2c/WP8Avwh/Wr+Zv9m/0QB/gKtA6ADJAMhAlMAaP6J+3362fvK/TT/hQD8AeoBNQPaBJYESgMdAVT/M/1v/N/88Pzo/FH9of9FAaQAmgGOBN0EKQPyAVIANv+B/hH9cfoB+pH8Vf7L/54BFAMTBJME0ASCAyoA8/7S/Sn8vvy5/fH9Mv0m/gEAWAG8AgwEagVgBKUCmQD1/s39C/xn+6n7D/3G/ZL+KAGsA1IEjAM3BIIDqADL/Yv8zPxk/J79T/47/sP/zAEuA3gCBAKIAkMDHwL3/8v9ePvp/BD+c/0X/bj+9gH6AkYEpwSDA8wCEQHO/Y/6YvvX/NP8uf1d/5sBEAMzA+MC7wJdAycDxwCR/SH9sPwj/KH8D/37/ikATAFwARoB+gJwAzoCpQE8AZr/N/7I/Xr9kv39/ZX/cgF1Acb/4P+NAdYBowAdAP8BCQKm/4z+f/5H/hz+1v9PAcT/Qv8pAPT/9f7d/joAVQGGAdAAagBfANH/gf84/20ABgEwADr//f7P/2r/ff8eAE//4f3b/l0AJQA3AFUAXAEVA6MDCQOPAV//nv6b/p/9k/yM/Ob9gf/FAPIApgCGAmQEJgT9AeMAyAAs/+D9Hvw8+ur65v0ZAAgAjwDlAVsD1QOsAzMCoP9M/wn/Bv5e/Iz8iv1R/kUBEwM4A5QCqwI6AnIAf/5d/OT8P/9MAAUA3f9iABwCsAPfA8ICIQGR/6f94vtL+sr5LPtG/rf/sgCZA20FFAYQBTwEZQORAEH9YvuU+W74MvqK/Ln+gQAuBGMGkQbEBnMErQF5/5T+9Pzl+i77UvwD/d39dv8jASQDMgRWBFcD2gK6AZT/ef7C/M/8xf3Y/r7+wP4qAUoCogESAREBTf9n/dv8gfzC/OT+JAEhApEDFgQnBRsFagMpAez+RP6b/Lb6qflX+oX7Y/zW/koB1gN0Bi4IvAcbBnYEDAJc/tL6MvjY9sf3Dvro/KD/YAJQBBsGVwfXBvEFewMEAZ3+Qf3p+zr6x/rk+zT8svzs/hUBKwLYAicEhQV9A3YBQABk/4P+kv3O/aj9AP4V/0IAlgA5AAEAYgArAegB/AHdAaQB0f+1/vH+1f8g/xD9kf4NADUAXADoAM0B5AFUArwADv9u/mn+eP+o/m/+sv+U/ywAngDo//H/TAFvAuUAQ/94/yj/Iv5x/fb9uv68//MBMwMBAmYAuADGAdIAxf6d/hz/1f/x/3n/9/+AAFYCaQKOAJD//f65//H/SP9l/mr+q/+fAKIArf+X/3AAjgHlASIBoP9r/1L/nf2V/ZP9C/6Z/6cArgBn/9D/PwEGAicBPwF2AvoBLQBJ/yYAz/4h/f39fv8T/1b/0wGnAtEB2AE6AwMCHf+Y/kD/c/6l/d3+Jf+f/43/wv/E/6H+M/9d/0cAcQH+AdMB/wEhAvz/av5n/q/+G/6P/sX/x/8z/vD9ZwDWAFkAzACaAR4B/QBMAr8BcgCTAP8B6wFX/0D9ov1c/sb+U/+D/tX+BgFWAloBpv/z/kIAUAIJAoD/ev6c/4sAUQBP/s/9Xv4e/zMAFgC4/3j+0v9nAsoBDAG8AcUCxwGV/17+cv3V/Xb/9/8z/3r/UAC8/wf/WwAXAVkA0QBVAm8CGAHEAKAAaP9L/20Aq/+9/Xj9Pv5F/qr+qf92ABoBEQGSABT/jv+MASABDQF+AUgBCwCdAHEBUf6d/IH9LP8R/3P+bf+f/5v/rgAzA1kDdALgAv0CswE9/zn+J/74/WD8N/u4+4T8p/5kAYADHgRsBLQFSwb+A6sAQP5D/cD70vn/+bX6nvuu/UoBNgMZBPsEegVEBQUCfv8M/ln9jvxP/KX9dv5U/7n/OQGSAngCAgL1Af4BuQBG/0P/P/9z/dn8Cv+YAFb/1f/hAjADIAH7/2IBzADT/hn+1/zP+0D8S//PAcMBZwLAA1cDNAKtAN/+hv4J/i3+f/6L/m//Hv/P/iP/Df8jAPEAowGEAfr/gABMAewBMwI+AVUBIgFjADz/q/6b/xb/+v2v/dz8iPxg/Sn/ewCcAZwD3AUwBrIEiAOjAdr+2PuE+a/41/hA+nb7nP0dAY8D9wUqCLIIxAalA6QBs/+0/P75q/hb+H75lf3UAMgBEwLEAxYG4AX6A9cBfwGIADv/0/35+h77oPw4/q//4wCpAQ4CFANRAUb+Fv3m/T3/lf8j/5X+6/+NAQUD/gO0A4kDJQIJAPH+nvwN+1j7Ufvw+yv+3wD3Ad0B5gNXBTYFjgT6AsYAx/6w/Z/7i/ly+VD8mf9xAHAB/AIlBDwEYAQMA3oAnf+n/5P/N/3P+yf8wvzi/Qj/RgEzASoBtwEtAdQAZwAzAKD/sf/V/wAA2v+TACUBCwGUARcBbAAr/8/+af5p/fz9Ev8xACAALAHdAfYAbAH6AfIBZAHMAEUAV/9x/sP+Mf4//dD9A/5Y/mT/TwCTAFEBHAL4AR4BogDBANEAEAEpAEf/9f5Q/7L/av59/bb9kf6H/zsAugDzAA8BZQLFA9YDJwNiASYAmP43/fz9zv2Z/Tj+2f57/xkAugBrANf/lwB2AZgAmv/4/8EAxADiAKABnACS//r/qv+C/Vr8uv0z/7T/Q//i/1oAbwBSAiYDBgOnAiwC0wH9/x3+Yv2a/cD9Lf2V/SX+Af/JADEC1QO2A2UC2gEDAYX/bv7l/kn/N/91/5z/N/9C/r39wv0U/uf+IQAKAX8BoQK1A1IDdQJ+AZgAm//Y/mD9rvuR/Mj9sv7C/o//VgFWAa8CzwIEAi8B/gBFAfP+K/5U/p/+xf5n/+MACQG5AckBCQFrAAkAPf8//gv+Av7s/tn/jADeAOAAVgEeAhMCpQBUAPP/x/4//lH9W/2Y/az+OgB+ALUBVgJAAtoBuACdAJj/vf62/dT8Kv0F/gAALQFbAjMDggOpAikBZwFcARsA0/4y/lj98fzs/e/+VP8SADMBRgIjAiIBHAG+ABoAdf+v/lv+Iv5r/rX+Nv+u/+H/dADtALAAYQCAAc8BCAGuACUARf/M/eX8e/2e/vz/7ACEAXMCuQNUBO8CUQDC/t3+sP7k/aP9gP26/vr/UQCfAKQA+QCWAQkBNAB/AKQAYwDW/8j+wv1y/Rj+q/4u/3n/+f8bAWIBegERAtEBYgGEANr/H/+A/qX/uv/b/0ABIwFMAMj/S/9i/2X/pv+7/7r/rgBGACP/Cv/w/60A1wAkAdgA8ACZALH/5P6c/qr/m//N/v3+lf9E/7v/HgBsABAC2QL9AuQAXf+p/iT+yP4o/pP+Z/8fALT/YP5Y/woBGwJhAVwBSQKUAa4AJgAi/xb+3/6GAGcAPP93/x0Aqf+E/+7/PgA+AGQANAC3/lD+eP/k/1AAdgFxAlECuQGlAKj+D/2O/db+Xf5n/o7/lwBrAcgA+f+TAPMBfwLwAGz/2P5J/oP+nv9xALH/KwAzAl0CfgD5/mb/tP9RAIIA3P91/7r+t/8oALv/hv5E/08CuAJVAZL/t//JAGEAyP8O/5n9bv04/t39SP0q/pQAKQIoA68CsALlAmUB7wDr/xD/9f2T/eb96f2H/s397P1b/2MCTwRFBM8DOwMhAxYCPwD1/Sv8xftm/ND7fPt0/Ez+dAH1A50FwAXRBFoEYQPt/4f8dvtN+836bPqg+/78Sf+6AcgDUAUcBs8GHQUsAp7+mPxY+2D6jfqt+/b+zQBnAewBZwOhBHYD4wIoAngAP/4P/Sr9+/xM/lT/u//5AM4AgwEhAqMB6QD5/0AApv9Q/lL9T/0J/uP9Xf5DAPsBawKCAnECqAGDAKj/H//Z/v/9bP3Z/lMAJQFwAbQBfgIvApoB8gBn/7H9r/wE/aT9//2B/+EAnAFnAjQCGQKeASsAfv/G/0f/2v2c/S7/cwADAV0BCQJGAuYB3gHE/zn9EfwN/JP8vfxN/iv/agDPAg0EsAT/BIwEqwLnAC3/Evxq+Wv5MPsg/f7+DAEsA8wE5QVwBYADcQE5AMX+nvzw+l76d/sW/ej+vQBTAmkDNgQLBRIEgQJkAOf+af78/AD93/zI/Nb9B/9rAPsAWAI3A3MCrwHqADj/bf24/Wf+Iv8fAFIAaAC9ANABPgIPAQkAZv9D/wv/Af5O/Vr9Iv+SACoBSAJ/AuMCsQK1AbcA+//t/2X/H/7P/GX8nfxY/er+1//gABUDkgRkBK0DjgIQAvMAdf6j/N/6K/q2+vD7Ov5l/9gBqwSEBZwFZQQUAwgB9/6c/WH8tPv3+ij8qv0e/yEBnQKBBCYFYQQiA0oBnP+b/gD+nfzu+wn9Zv4RAIwBXAL1AkMDWAPpAPH9w/wO/Dz8ivzX/Fj+lQCSAlsEPQXmBMcE6AMKAsb+SPue+U35+vnL++39qP/KAdwDCgUaBcMErwRrA+oA7v5t/X38DPzF+w/9av4V/xgA1gBUAVcB7AFHAj8B/gDqAJQA0P/U/tn+MP/B/uH+g/9f/5X/zP8NAFz/s/4pAIkBQgICAsQBMALlAK7//f6E/uP+s/6O/j7+pP20/lgAGQFGAdkBbwKLAeb/9f72/m3/9v/fAMABrwEUAYAAdQDb/1v+Ff4j/oH9gPyW/MX90P4FAWYDKwQSBF8EDAQKAkkAPv9e/p/9GP1b/P/63/ob/Sz/BwEcAwoFXQb9BSIF2wI4AEP+CP3f+zn69/k5+lb8+P6pAD8DQgWLBkgGIARIAkgAw/3B/HT8pvtD++T71P2O/6kB4wN8BAwEwwNLAxgB7P0I/FX8D/3i/CL+MgDBAa4CwgIcAvcAiQEVASH/uf0U/TT+Rf/B/zX/e/9bAUEC4AFwAD4AXwDj/6H/zf5r/sz+Bf99/woAJQCNAdMClwItAm4B/P/0/Qj9af3V/WX+Af8DAHcAQQFwAoUBiQCLADwBbgEhAPH+2f1m/ngALwBz/jD+n/8TAHj/TP/J/2UBJQOaA2ICAADl/z4AbP+3/k39MP6f//f/0/+7/mD/gQARAakAmgD3ABcBZgHMAMz/av/g/+L/p/48/cP8Kv0P/lT/3f9sAbsCCANlA14DxwInAe//6v/k/wD/Iv4F/oL9bP1W/q3+Af+KAGcCWQNTAxICrAGtAZQAkf7i+4j7svw9/dH9sP4GABACUwRlBW0EpAHS/7n/Ev5M/Hn7P/yU/vL/+QAoAf8AQQLvA8MDFgKsAPn/WP8a/qD8x/w+/r/+RABYATkBvwH+AVsCywHhAAQBEgBE/pb9Tf7q/T79n/1K/84AVACf/53/rv9vALMB7wEaAZ4AXgHxAbEAsf4s/jb/iP/i/g7+jP6X/4cAfQEIAbQBRQKEAocCDwF5AAIAyv8e/wD+A/5E/m3+Z/1X/Zv+rP4M/7H/QgHkAsUD+QOvAhoCtgHbADT/pP1M/YX8X/xS/Ln8K/6b/4IBrwL0AmcDoANTA3sCwgBw/zD/P/63/Wv9rv2T/i7/RQD6ADQB6gFvAooBe/8m/2//hP7q/cn+/ABXAXUAcQAoAT0B8v9Y/3X+Lv40/gX+Q/7R/Rj/rwFSA04DiAINA3IDAQMFASz/lv4m/Vf8tPs5+tv5q/s7/6gCKwQaBYkGpQayBdEDbAHq/gH9mvzQ+0L6QPmU+gn9hP+0AcoCfgPSA40EZATQAkkBxQAKAcr/Zv14+7b6Ffs8/Zn/3P+MAOQBbgMfA1IB8wBDASQCcgEpACn/gv1r/az+If/W/sf+o/9tAIz/Qv8IAFwAGwF1AuIDfALz/2n/H//M/9f/m//I/xX/Hf+v/qn9NP1D/iYArAGJAggCmQEAAikCggH0//3+ef62/Yf9Nv1L/Qn/xAB/AYoBkQGnAQUBngA5/wn/dv+H/ycBBwHmAIsBrwCHABQAif8s/8H+xP61/qn+rP4U/3T/DADzAPUA0AB+AR8CWAHTALsAg/9F/yT/Df4g/Sb9BP4A/3wAfgEjAqwCoQK+Ao8BlAA4AHj/xv7Q/dH9k/7N/o7/owC2AMYAAgGuAHYAvP8R/+/+s/61/hv/vP9oAGEB9AEiAvcBrgGrAeEAf/+H/uL9z/yE/Kr81fxG/u3/ogGJAhEDaQSEBE4DwAF9ADH/bv71/V79dP26/ej+P/9B/7b/0v/eAA8BPwCz/zgAXgGfAcIBcAFaAYoBqQB8/+b9qfyr/Gf9BP52/q7+CgATAlICVALlAoUDswPNAmwBIwBA/uH81fxE/PX72vyM/goAIwGnAbkBXQIIAq0BWgKfAUYAiP8+/83+EP6k/tb+Xv5U/zIAl/+E/nD+h/88AVsCOAIMAmUCcQJzAWP/qv5F/zz/1/4+/QH8RP3Q/un/tgB2ATYDHQTnAmcBZABgAEsAr//g/nj+Cv5k/Zv94f3O/i8AIQGKAXwB5wESAlQBWwADAEoAAwDP/iH9+/wL/nn/UwDHAG4BywFGAqwBZwBY/7f/lgDt/yr/cP79/uz/cP9Y/7P/xAAEAk8ChwHVAD8APv+1/v79B/74/Sj+af5e/icAngEnAp4CzANYBIsCdgCO/t/9yP0O/ZL87Pst/Xn/yQDAAA4BOAPNBMIEsAPNAYr/0v0//cL8N/zY/Iz+ZP+r/2QAWgEcAmQCAgL4AcUBqgCY/83+Sv49/w4ACQBw/6T+sv7M/vL+M/+e//gA2AEHAoUB2AChAG4AZwBw/+P+tP6r/ff8IP0w/sv/RAGBAuoDxgMhAwIDkgHRACIASP63/Kn74vv0/D3+of95AQsDrQPjA0ACKACY/zr/0P0U/Qz95P0S/8T/cwHvAXsBDwL/AXEBXP8//Rr9sv2P/mP/9/+6AHkBwwLxAyEDmAH0AMsA5/56/Fn8w/yZ/YL+i/+iAH0B9gL4AlsC9gHrAZkByP/8/Vj8E/wS/bX9bP0m/nkABAIPAwwDegOjA/oCgwJ3AKr+uvy5+zD8+Pt6/OT9IACHAdQBZgKAA8QDCAP0Ak4CxwAV/839Av2Z/Df8FvxZ/ff+YQC2AV4CbgJ+AioDIwMgAgsAxP5M/1X/HP59/LL8vv5KABoACAALANz/qgDnAB8BKwGqAXcC1gGeAJD+G/51/v/9av5f//X/pv/q/3AAwQAQAbcALgF3AeEAcv+L/kv/CgBoAKoAwACYACYAgv8t/4v+lP5A/x7/EP/w/gEA2QAhAHwApQHUAukCigEAANn/gP+h/o39m/yB/cP+VQDIAKgADAKDAuQCjAGk/yf/1f51/w3/U/4h/o/+WQCcAeUBBALpAUQBcQBo/13+/f3L/QD+jv7J/7cAngD1AJsBGgL2AYwBrgBb/zf+e/1N/Rj96v3Y/34BhQKaAesAOAEYAQ4BEwHrAH4Az//e/kf+KP5Y/oD/TQBhAJoAXwD//8P/iv8pAOYA0gAbABP/wP4J/5H/EADLAI8CBQPPAXEAEf+h/mP+RP5g/rH9K/6m/xIA7v8hALQBRQNzA8kCsgGHAD7/S/4p/d78gf34/ZH+HP9VAOYAkwHBAgsDKQP2AhcCiwDk/tn9/fyx/ND8Sv1J/lH/r/+b/+MAWwLcAncDZwOhAgkCAAHi/7/+df1J/bT9RP0S/eH8yf3Z/w8BCgLVAoADHARpA4EB5f/o/pf+KP6p/cv9nf32/cP+Df///5IBawKpAmICmQFbAfIAPwCy/1X/wP6m/av9if7A/kn//v/oAJ0BmQE5AYgA0//K/zQAn/+8/xMAHQCPACwA8v88ADQAbv/S/m7+k/4F/y3/1/+HAFYBXwEyASwBdAHmAYwBugBH/0D/Qf9+/pn9bP2C/Qb+6/7j/pIA4gH/AmQERQQzBOUCBwH6/h391vvi+sL6M/ur/FP/PwGJAgIE1wQHBmEFLwPQAGD+y/y6++365/rs+4b90v9HAV4CSANeBOAEVAQQAx8AYP4F/RP8v/s4/Hr9dv6OADkCUwNqA/sCWQJ2Aav/q/2q/E38zv2F/lX/EACDATwDlQOzA98BoACM/3v+qf3V+777Hf3P/pUA8QBvAl4EKAQEBGsC1wAV/9n8GPwM+7H7TPw2/qQAoAEzA/oDIASMA0ACUwHcAG3/sv2a/MP84/w9/cH+l/9BAdwCfAPyAg8CeAH+AAwA4f12/Lz76/uv/Oz9pP9zAU0DdQRjBckEBQNwARkA+v4C/j38iPrB+kD8Tv5g/80ARQLEA0QFcQQNA5MBBwEeABD+mvyl+/776/zZ/aL+aABiAs0CyALlAQQC3gFVAFz/V/+M/0P/rP9u/23/+v9KAHkASf+z/oD+k/67/s3+rP/mADgCEgJQAl4CIgLAAZUAyP5B/UT9Lf1M/SL99/0e/ykAxgH+AesCQQOsA3cE9AKxAR0AWf7P/Ar8B/zV+4z8K/2d/uz/lwCoAlUD+AOkBEgEZwMlATD/Bf5V/eL85/zR/Mv8FP0g/s7/LgAlAW0CAAM3A8QCAwINATwA9/90AJf/5/5t/ub9iv5M/gf/mP+p/wQAEAEsAqoBrwHBAN4A3QHpAMH/pf57/v/+1v7e/bP9P/63/oH/9P9ZAHcAigGIAg8CzwBiABsB8AAlAP7+iP6W/hf/4v+1/8f/mv/+/5sAMADL/7//vQBaAXwBkQGNAAEAfgAFAaMA+f9+/5b+hf4e/lj9D/3o/Iz+EQBJAdkBfgFxAk8DOAMFAgwBzf+i/un9/vyt/JD8iv46AN0A+wBLAUQCAAImAq0BzADd/9/++f4A/2H/of/l/8AAYQE3AVwAh/8GADQApP+6/rP9XP6A/if+vv6r/88AoAGlAokCbwHxACgAOv8P/w7+pP1b/Zr9Lv9PAPYB6wJpA+sD9QMiAvr/1P4a/eL8v/y4/Pr8xf0GAN4BkAP+AzoEBQTvAisBZ/5I/PH63Pv//C79jf2L/qAAmAKWA70DjAMLA88CkwFc/yz90Psw/Or8jv1Q/vH+bgDxAWsCdwLOAocCAAKQAQ8AVf5D/cH9Wf7a/gQACAAeAEkANQG0AWMB7QAcALEAbgCN/7L+s/7m/xUATgDQ/3L/AABJAKf/3P7U/rL+ev+G/x//+f/3AKsBIAGmADYB9AEhAuoA3/+g/zv/tv6p/Wr8vvwZ/h3/0v8oACIB0QJtBOUDMgLRAX8BLAFa/wn9T/w4/Sj+Ff4q/t7+CgBcARsC/QFLAuYCxgK3Aeb/M/+8/l3+2/11/XX98/3M/lT/nf9LAJABiwGVAdEBpAFwAU4BEAFUAJX/nf6m/pb9DP2W/db9sP4c/w4AHwEyAuwCtwPlAyMDzAKzAVcAHf6i/DT8/fvG/B39Sv4pAKcB3gLkA3ID5QKtAs0BdwBp/jP9l/yR/Pz80vyp/dL+FgBOAQwBFgL/AqACOALyAFUA+P/f/iL+Uf6h/mD///9t/1X/AADtAE0BhwEWAVcBOgLzAdcAl/8t/5D+cP5a/nH+wv7s/joAEQEmAXwAegCDAH0AQQBp/3//rf8WADkAuP9J/xP//P6x/qn+Cf9Z/wwAIQGZAdABdgHIAY0B9wCsAPX/pf+9/r/+xv5s/jP+7v4gAC8AxwARATAB3AGlAXwBQgF/ABAANf9d/m3+Ev6C/qP+2v46/4P/rgAeAEMAvwBEAdoBpAGyAc4AHgBo/xv/0P6z/vD+GP96/0P/3P98/yAAtwGpAbsB2wBkABMAtv9g/xD//v4I/9b/pf/o/oX+9f/YAOYA4ACYALwBvAHjAOz/Fv9a/zEAPQCZ/5v/hf8JAHUAhwAtAHwATwAp/87+Jv4u/kz+uf7E/5IAWgGoAR4ByQBTASwBFAFnANT/R//j/o7+nv3Q/b3+awDFAIIAtwCNASoCnwHkAU4B/wCdAF3/Vv5z/V79QP4G/5D/tgCDAfkBcwEjAU0BFgFYAAv/gf64/db9Ff6+/Wj+ZP/MADYCTwK6AbABBgLzAS4Az/4F/pf9zP2w/aT9Df7W/8UBXQNCA+kCgQNcA1sClwDq/oT9XPwP/Lf8jPxv/Vr/3gBwAtkCfQORA6UDaAJ6AHz/3/2+/Nn7y/sM/J797/4AAIIBUwLxA8cD8gJwAowB1wBW/wP+Y/1i/cT9J/7R/hkAMwF+ATMB8QDsAPIAXwB4/1b/T/+T/zr/cf+5/3oAFgLDAXMBtQBZAP7/t/7i/e78ov1N/u3+3f9fAD0CFAPuAuQCVQKZATkAiv5G/Wz8iPwD/T79v/1e/8kBtAI0At0C+wO1BLEDVAEx/+L9Af1u++H6rPpK/FD/7ADsAXQC1wNZBXgFXwONAXcAff91/hf8jfuP+5z8q/5B/6X/PQC2AXsCaQLrAS0C6AFKAfEAUf+Z/jX+cv5F/hL+2f53/xgAFAD3//D/4ABBAQ0BFwH0ALcApQCXAKL/8f/v/zoAFgDl/hz/+f6Y/6D/1/+z/13/zP9b//7/IwDCAAoBEwFfAXEA+f/K/9X/gv+w/4b/fP9E/3L+gP+h/3UAtwHnAYQBeQCbAL8A8P9I/8L+Pv+n/7P+QP4G/tD+ZwDOANsAcwAHAUMBZwE5AVgAsgD/AGQAtv6Q/Uv9Y/6I/7n/XwBEAfcBqQFGAWEAuP8d/3//5v8M/0D/WP9KAFsAfgDxAC8BgAE5AMv/5P7P/rT+cP5I/8z/SwBXAOIAhQDLANcBbAF7ANH+OP63/nf+uf26/az+qf/tAHgCwQKRAtMCigLtAf8ATf8n/r39cv2x/Uz9y/0D//D/VwF+AlQD1QK+AgcCRgAD/479Av0U/X39aP4J/5X/1AByAQ0CgALwAXcBhgC5/3r+jP3//Y7+NP+T/1wAngGRAQkCGwIMATgB0QDh/2z+U/3q/L/8lv2J/r//KAEjA+0DuQOdA5cCaAHS/8H+yv1E/bz8bPyl/Iv9v/5PAA0CAwKSAkcCLALxAdMAVAF1ABYAeP+l/sL9Z/y1/HH9Y/4e/9v/fAAnAdkBigLBAhkDkQOJAyoDAgE0/0n+EP0I/Kz74fu//Mj9Av84AHABrQOGBP4EtwQ9Ay4Cvf+Z/UX8avtp+yL87PxU/YD+tv8VAUoC5QIaA0QDZgNwAhYB6f9k/0j/L/9G/sb94f1n/m7/Ov9u/+f/GAG5AeMADwH0ALIBRQJHAikCRAGpALT/0/7Y/dX8nPyk/PT8Qv1Q/mj/nwBRAm0DJQSJA4AC1AEYALD+4f18/Tj9ufz9/Gj9cP4HAJwBogKLA7QDkQMxA2ABWwDB/+X+a/4F/p39jP0b/i3/vwCWAfEB4gHGAQ4BIwAv/0/+v/5H////Yv+g/wAA6/8uAUIAef+q/2L/If8R/pP9lv7A/zcBPAI/AmACvQHAAdwAg/9y/mj+JP8U/uv9Rf5R/3IACwH0AXgCfAJ5AgwCOwAe/5X+b/46/s79F/5W/rP/9gByATcCeAJIAhIC1wAt/9n97/wH/WP9Bv6F/lD/jQBsASsCYAKvAs8CMgKuAYYA3P5Z/Wr8SPxG/DT9LP5T/4UA3AFsAzYEvwQ8BIsDdQJrALr+L/3/+1D8pfyD/Jv9Tf5B/4QA0QHdAu4CrAN5A1YCvwAQ/zf+Qv7H/Xr9Sf70/sH/8f9hAHgA8ABZAfEAlQBI/yb/PP9J/+3/ggAvAZsB1gGoAWIBJQCG/0v+I/3o/Kb8OP2r/aD/GgH4AcwDagSgBNwDxwL+AK7/b/4M/KX7Xvs8+4b82P15/0gBFgNYBAYFYATmA+YC+QCi/5b9vPx4/KH7IPwK/Vn+iAB5ARwCdAJ8ArMChQGoAP7/4f6G/qT+BP7t/dP+7v9BAXkBAwLkAS8BqwA8AA0A9P69/lr+nv4e/0b/HAClAPEAXgEdAvIBeQFvAML/wv8I/2z+yv1n/af9Rf4A/xkAZwDOAMYBUQKBAu4BvABFAB0Afv8Y/2v+H/7b/nb/oP9q/4D/cQDIAfcBpQH1Aa4BVQHHAHj/if4q/uj9if22/Wz+u/71/7AAbgH8ARoCRwJvAfwAqP/P/nb+I/6D/jv+Nv4H/00A8gDNAekBNgIfAqsB4QA1/yL/T/58/nH+CP4M/3T/oQDpAf4BjwGqAW8B5QA9/0X+P/5V/TD+tv6g/hr/TwCeAQICJgJyArECuQFEAC3/X/7R/Xr9vf1J/t3+lP8wABcB1gEwAtoCYAInAU8Awv/i/sr9VP3Q/Z3+Fv+i/7//pgDfAToCWQIZApABlQCX/5P+W/3F/Nr9h/4F/y8AvwDDAS8C6wHgAdQBIwG/ABkAFP9y/sX99/3m/Rn+Uf+UANcAmQDFAF8BDwKsAecA3f92/7b/0/4Q/h7+YP9WAG4AfQD//1oABwHkAGUAGADfADMBJwA+/93+5P6E//H/XP+M/wwAbQCgAPT/1v9WAIoAbwDD/x3/7v5p/zkAyP/k//QAQwGuAe8AngCJAEkAAwDb/ln+3f3Z/Qr+Sf6M/78AvQFJArwCtwJRArIBgQCH/4f+8v0u/Sn80Pws/jH/8v8EAU4CTQPbA5EDqQKhARQBCAA4/oX89fvX/EH95vzb/Ub/0wBvAv8C/AIGA9QCIQIIAVL/PP4i/in+Mf6z/V3+Tv+o//X/oQBkAVMBIQJ2AXkAdQBiAHoA/f+w/7v/QAAsAPL/qP+X/8z/u/+k/43+bf6K/ov+7P5U/67/nQDdAfEB5QGVAcIBnQGiAN7/M/+i/hP+L/7u/Zz9jv5v//z/2ABsAfYBaAJBAn4BLAFHAZMAXwA1/9b+rP49/mr+Lf7U/lj/YAB2AFEAmwD0AEwBFAFoASsByADd/0X/+/5u/nP+sP4K/7L+Xv9G/6X/KgAhAE8BlQFhARYB0gCwABcAIgBTADoAFgAKAJ7/wv6i/q3+Af+T/7v/8/8TAGsAxACxAD4BNAJ3AoACDgKzAIH/cP7e/U79//xE/Zz9jv4K/7P/wQCKAQwCtgJvAs4BBwHH/8j/xv9U/wD/6f7S/tX+nv5h/qj+YP+rAB4BVQGVAWgBVAFgARABrgCaAHEALQDh/nv+bP4r/pj+j/52/0EAkwBIAQwCIwI4AuEB0wA/AFT/1f7X/Xz9kf2r/a/+zv5A/1//8v96AasBwgGkAlkC5wGxASQASv8G/ub9vf5Z/hf/fP/j/9QA5ADnAKkA1gDoAKwAZQDr//n/BADx/7H/PACnAOr/sP8R/+L+MP/E/t/+bv8LAGYAdgAmACAA1QBNAUYB6ABwAB8AEgAY/6n+Lv7Q/UX+hP4d/43/TgDTAA0CdgNlAzsDMAKdAdoAKADD/tz8Av1z/Rj+H/6I/oL/9QBeAlAC7wFhAUkBUgAl/4L+K/4h/hj+jf65/q3/sQASAQ0BgAEUAk4BTACU/zj/H//i/sP+xP7k/tv/9QAfAZ0BTwKrAlgCXgHw/zP/3f7a/cD90v3t/b7+lf9IAMQAbgGSAh4DlwJmAY0AAgDs/rr9Lf28/PD8zf2X/iL/zf8nAfcBCALjAfwB6wGEAQ0BpP+z/5f/k/9z/5D+u//4/xIAMABY/1L/eP/D/0D/S/85/7r/nwBtAGYBqwGAAe0BCwJfAXEAU/9f/lz+9f3y/ar+X/7j/hcAawCwAAgBfgFgAoQClgGcAI7/m/4V/qL9af2I/cr9z/7C/0EA6ABjAUYCBwPiAmECRQH4/1T/9/75/uz+0/46/8r/PwBS/yH/1v8rAOUAbQA1ADIAcgAIAdIADAEXASQBRwFdAML+4/2r/er9k/4R/iz+Hv8eAHIAwgCxAcMBVgIOAr0AYv8Q/tz9U/1x/RT+F/+tADwBTQI1A7YDIwQ3AwwCxgB4//P9hfwF/L/7Cf2Z/gUASgEPAlsDQAO1AsMBuABaAML+u/z6+yb8M/yj/Vr/uwDOAqUD2QOGA1cCAwFhAP/+Ev2C+wf7V/xL/ZX+vACPAn0ELAUWBZAEQQLRAM7/Hf6e/Az7JPsA/ET9qv5fAPYBcQPEBNQE4QNqAmABxv90/nn9YvxU/GH8Hv0X/kf/jAAnAtoCYwJIAnYBWACn/+f+iP5J/oX+H/9v/9v/ZQAwAR0CEgJFAUUAu/8G/w7/pP5F/v3+Tf+qAJwBHAJMAm4CvAKYATsA6/50/X/8WfzL/Nf9LP5l/+AAlgHjAg0DDwPHAjwCRgG1//z92vxf/BX8BP2m/SX/BAFHAgIDLgM4A50ChAEeAML+iP2G/V39CP4z/8H/agFPAuEClgIfAtEBgACq/4r+qv3I/Nz8I/29/Uz/dgAqAuMC+wI6A48CGwKSAJ/+PP1A/OD7UvyD/G/9tv9xAQQD6AO/BNMEFQT9AgIBtP8X/rH8k/s0+zT7Tfwl/lr/jAH2Au4DfAQ+BIADbQJXAX3/mv7c/dz8YPz1/DD9rf3m/hoAGQFpAQACLQLnAn4CzAGEATMAbP9I/hz+9/1+/Tb+sv7X/l//HQBbAKMAbgEsAlwCUgLwAWsBoACe/wD/hv7n/cb9+v3Q/ZL+RP/H//0AXwEMAo8C/wGmAfoAnwBHAJj/af/e/rn+Pv6Q/n3+Y/64/ywA6gBBARkBHAEeAd4AcQAgALD/CAC2/13/ff6H/s3+rf5E/x//4//QAOMByAHyAaMBcgGNAU0AiP+V/jD/p/5K/kj+TP5+/2b/iwBpAJsAkAH7AQ4CgQFmAdYAfgBu/5L+IP7W/eL92f2w/in/2f+CAAMBZgFtAZsBnwHsAE0A5//6/rL+Sv5D/qb+Jv8yAMEAmwH5ATECmgIBAnwBbQDM/vj9Pv31/IH99P3x/lIA6QD2AY8CFQJwAhACWQGLANT+p/0j/cv8HP2q/Vn+c/+ZABYCBAPeA30DzAJ4AvIA1P9O/oP8yfsy/Lf83f27/pD/XAGIAqMD+QOmA7MD8QJ/Aav/QP0a/Iv7VPte/Pf8if49AOQBoAIoAw4E1AMnAzsBsACN/6H9BP08/Jj8pf2B/hz/MAAOAXoCUwMJA5gCNgIHAtIAIP+i/Sb9a/3V/dr9pf6n/1QAUwHwAFEB8AD/AGQBNwAMACT/BP8g/9f+SP9S/xQAJgHRAN4A7ADjANUAHAC8/2D/nv+1/4H/dv81/x4ArwBXAAAAuP/7/1EA9f+b/8D/+P8JAAUAEQAXAKoAhACIAEkAaP+4/6P/Of+6/uT+Wv/S/z0AhwDpANkAOwF6AQsBWAA5AKn/Uv9Q/2P+gP7N/ib/t/9GAH8AuQC/AaYBbAE5AYkA8f+6/0//sv69/oL+mP4H/xb/1v8nAB4BLgEGAc0BIgFGAZcAkP/T/xz/L/9L/l7+z/4a/08ABAA8AK8AfQG5AR0B6wAIACAAGgBv/9v+tv5C/3b/b/8A/zX/6P/s/0sAsgD9AB0B8wBFAQIBtgDJAFsAcgDc/+X+zf48/v39ev6i/jD/o/9dAJwB/wFQAoUC0QIZAp8AWf8x/mf9cvw7/GX8Yf1V/m7/cwCHAaEDUQTrBBEEvALtAY4Arv7U/Kb8Qfzf/KL9w/32/qL//AC+AV8C8gKjAmwCuQHCALX/Hf+I/sD91f0J/uj+Pf+M/1oA0gCOAREB2QC4ACgAPgDK/7X/Xf++/zgAQACrAFkAKQABAFr/7v6r/qH+Vf/5/iP/AACKAF0BjgElAl4CcQLRAeYA0f/I/mn+dP1d/Xz9Jf6h/gX/yf+MAAECRwIHAukBqQHYAXYB4//8/gn//P7O/hX+1f2P/p7/9/9xAFcAfQCgAU8B2AAWAC4AaQCB/2D/Qv9X/4j/qv/e/0sAjgBqAKoAdwACAAMA7f9w/17/iv8x/+L+Af8AAKsBwQFYAagBfAGOAeEAnf/b/lP+Ov7v/Vb9Wf3s/Tf/WgCXAU0CpQJ4Az4D4gITAsoAPv/E/c38GfwQ/Jv7l/xb/iEAEAKcAvgCHgRDBKQDBAMXARgAZ/93/t79kPwV/KD8cv20/a/+fv+6AOcBHgIzAxoD3QKLAu0BUQFpAJr/4P6C/t39Uv3t/Ov89PzA/bb+e/+GALABMwPnAwwEwgOIA6YCmAEJAMf9uvyQ+w37k/tf/M/8M/4iAK8BjAMeBNsE5QSTBMkD4AEYAOj9evy2+zz7sfoQ+8P8s/64ANUBKAM6BIgEzQTmA7cCLQGA/5r+Ov21/OD80fw3/aD9mf5o/0YAzgBpAQ0CTwKkAp8BcQEuAbQAQAB8/+3+XP5+/kL+c/53/iH/6P8CADQAKwDgANcADwFMAQEBIwE3AQ0BogAqAJ7/hP9J/8T+hf59/iX+Sv79/un/dQDaANYB7AGkAisCFQE4AE//Pv+P/qb+/P15/p7/oP/Q/7f/WACrAE0BAwEeAOT/4f8wAPz/cf9B/2cANAAkAA0AVv9uAFIAdABOAED/Sv8B/y3/Yf/5/+YAeQEDAtwBvgHZATsBmADv//X+Vf6+/Rn9FP2U/SP+1f7S/zQB8gFDAq8CvwJtAukBxQC+/8z+av09/bj8bvxu/TL+4v9lAS0CBAPzAskCZgK4ATABs/8z/33+9v0w/pr9dv5Y/wgA9gA3AYsBcQEYAQ0BcACc/5T/Uv8A/0v/w//9/zQANwCHABIBYwCz/xj/Ov7v/fD9A/5b/iH/RQB2AVICvALmAtICEQKGAf8Afv8H/hr9uPwW/Y/92v0O/2QAxwHnAsQCoALYArACGQLOAN//D/81/m/9+fxz/Z39QP4L/2D/dgDGAOoATgF5AbsBdwEKAUoAQwAAAJr/m/+3/tz+Kv8d/3P/BP9A/+H/awAcAQMBaAFfAWcBaAG2ACYAGP/n/rr+uP7//qz+uP/z/5UAGwHUAOgAmAC8AGwA6P91//f+IP8l/0b/uv/f/zUAmQDiAMkAsQC+AOL/Uv/1/oT+ef5u/jP//v8RASgCnQKAAiECtQHSADT/CP6r/T/9J/19/Qr+3f4HAJkBUgInApwC0QIXAoABlACk/1f/+v5i/sz9eP24/Z3+jP/5//EAgAHyASgCXQGaAfEAMgDP/7/+u/4Q/or97v2J/jj/1//IANoAUAGqAesB4AEZAQcBVADR/4T/Qv5K/on+sf51/97/XQCfAAcBvAGIAUYB3QDt/6L/p/4V/iD+5v0R/6X/fwBqAWgB1gEAAsYB8QAyABz/6P5B/qz9w/13/W7+Vf9SANAAggEuAr4CtgIyAr4BbADu/4n+Lv6o/SP9o/1Y/sD/ewD8AWMC2AJSAsYBbAFD/3T+bP09/Tj9s/22/m3/PQH0AdwBiQKgAgACqQHP/5D+nv0W/TH93PzM/QX/kwG5ArcCRgNaAzYDVAKGANb+nv1+/DT8SPy4/BX9Yf9PAYEC1gO7A4oEegOZAjEB6v5d/az7BPyn+xb8o/0M/3UAHQJmA7QD2AN9A5sCKwEEAGn+XP3B/Er90v36/UT/EwBiAY8B8wHbAaIBvAGMADkA7v6F/jn+qf1i/mT+2P4IAHAAtwCfAQsC1wFmARMBzwAnADv/2P7r/o/+Ff9e/9b/fQCAANwArwDSAPQASgBOAA8AcP9c/wz/Q////u7+Rv9i/8//uP+rAEABDwFSAf4A6ACnAHsAIgAn/9v+m/5n/qD+c/7M/nj/IgDUAG4B0QHjAa8BbAE6ATIA4/+M/wf/Gf+u/sD+Tf/F/wgAXQCsAMsAgwBrAJEAUACpACsAkv9E/wP/yf6k/rX+m/4f/y7/yf8hAG4APwFlAdgB2wHnAaIB+QCWAJL/5/5T/s/9Q/5Y/nP+GP/O//AAbgHPAYACUwJWAo4BXwCX/5X+of0s/Rv9dP1P/v/+jgC/AToCNwNeA9sC9wFMABP/7/0K/aT8Sfya/I79Hf+lAKcBsgJ/A7MDZwNcAgEBKgDI/kr94fyX/Bj91P1L/h4AZAFYAnkDowNxA6gCUgL9AD3/7/0w/cn8mfwe/cL9p/9KADgBmgJNAnECEAJmAUAA2f4P/rH9mv3l/Sj+zv7f/8EArwEyAdgB3AFlAYEBJQDf//f+lv6G/jT+gf7t/tP/zACCAXoB1QGKAXEBZwGaAIEAyv8D/8D/Lf+D/qz+yf7V/6v/MABWAA4AVACs//f/zP8OAOr/wP+2/4v//f+g/+7/5/8XAF0AlgBDALf/k/+T/6sAPQBuAIcALgBmAB8AAQDI/0UAdwCEADQAAQDz/wEADwBP/zn/g//a/xAABQC0/4T/bgCMAG8AeQBMALUAsAAaANb/p/+x/5L/Sf+3/pn+4f4n/5P/1f+dAJkA6wB+AXABTAGBAB4A4P82//v+qv50/un+N/+m/1IATAAyASQCKwLtAYQBVgGaAN7/h/97/vP99f2q/SD+cf4T/5kA7wBlAVgCYQKbAuYBbwAUAAv/4P2M/Un99/2D/uz+4v8pAAcBugGFAb4BuwF9AdoA3f9C/4f+kf6P/kT+rf5H/4IA7gDSAD0BhQGKAbEBPwHHAGEAav8K/9L+h/7A/hP/lv+b/93/awDfAIwAOwBtAHcABwBd/5f/Pf9B/77/q/8uAFQAiQCQABAAUQBgADUAGgDu/7L/of+s/1r/3/5S//H/FgDk/48APwHOAOUAbQBCAF0ATgABALv/gv/h/2MAqv+//87/GgDL/4n/NP9v/4IAJgAsALP/hgDDAJUArADO/10AAwD8/yj/jf77/vP+DP/E/kr/0P8EATcBOwHoAfkBBQKoAbQAqf9X/3v+Cv4w/Uz9Ev5A/pz/IwBbAXUCpwIhA/ACIQIyAdv/if7Q/SD9Hf2J/TP+Hv8vACEBEgJyAtUCRwJ2ATIBqf9F/1v+c/2y/Vj9Gf7y/o//agCYAWgCRgIIAvcASwDM//n+kP7U/QT+w/5Q/1sACAHuAYsC8gLsAoQBBwAd/wn+xPyG/FD86/w7/m7/FQGEAq4DYwS6BD4EFwN4AX7/lv2b++L6rPre+pb7Hf2o/40BlwMEBa8FIAZJBbgDfAEY/+T8hfud+rT5L/qA+9395f+FAZADZQQuBaIFMAWzAwMCQQBZ/uf8zvtZ+5P7QPwi/dj+aQCaAYICuQJGAwYD8QHLANr/ZP/8/l3+Wf69/k//9v/7/77/5P85ABMA+v/R/6v//f9LAC8AJQBeAMkAKwE5AWEBFQGpAKz/OP8b/0D+F/4n/pb+J//K/2QAyQA5AVIB1QG7AZYBzgAjAKr/L/+S/h7+Zf4n/vb+pP/4/xcAbADdACABVQEiAUABugBMAAQAlP9x/2L/BP/Y/mn/ZP97/wAACgBEAN4AjQCLAA4A0/+ZAKYAxgC7AAABVwG0AA0ArP8M/57+RP4o/vr99/1h/4v/uv+2ABwBtwEjAvkBrwFPAVEA7f/7/jz+pf2B/R/+Af5B/ykAlQFKAvMCZwOhAhgC1ADq/2L+if0d/eT85/3v/vn/0gDcAcsBOgLtAfgAxwAoAGP/i/77/Yn90f09/q7+jv+mAM8BuQIzAowBZAGdABQArv4j/r39tP1D/sv+0v9lAAwCawJlAm0CtQH5AAcAef+N/k/+zP0l/gn/8/4rANIAIQH7AdwBrgGXAZcAMAA5/2H+pv5b/rb+y/76/tr/lAC+ANgAxABRAAEAVf/P/mH+cf7D/m//zgBUAZYB2wGfAekB/AHeAB4AOv9a/jz+1f2v/Vr+Pv+hAMwBKgK0ApMCMgKZAVMAjP+H/qr9Av1S/aH9If4n/wIAkwFjAtgCfAIOAhkBzf9a//n9s/3f/ZT9Bf6k/rL/ogBVAQ4CAAILApcB9gB1AH//WP8d/xz//P45/2H/mf8oAH8AIwH2APQAXQHEAAgAKgD2/6X/iP/o/mb/cf9e/2v/Ev+a/8b/9/8WAA4A9//4/8IA9wDuAPMAAwHVANb/g//m/kH+YP76/Y7++f6g/2EAoQB8AbQBDwIdAiYC/AFaAWcAZ/91/qn9v/2W/a39Hv5h/1QAJwFNAogCTQOUArIBGAGB/13+wf1V/ST9tf3P/Ub+F/8sAMkBcQKRApkCIQIIAhsBU//Z/hD+xP0x/iH+Yf4V/8z/wgBwARwByAEsAvoBcwElAIb/Yv/v/ob+c/5y/in/wP9oAA8BKAGCAcYBQwFFAAEAfv/u/sH+uv4S/zX/TP9g/3f/UP+f/5L/HQAMAfkAYgEZAQIBNAHXAHsA1/+d/6//Xv8g/6r+eP4u/zf/ev8OANQAugEVAkMCtwFkAQEBNgAK/7D9+/yv/EX98v2a/h0AfgEpAqMCuAJ1AgYCmQG9AIn/5f6m/fn8/Pwg/YX+W/9NABUB0AGjAncCEQJhAd0AQQCc/8b+C/4c/p/+A/9F/wgAGwAzAd8BYwGAAdcAiQAZAFX/uf5Q/m3+Gf/6/ib/DwD1//8AtACQAPoAKwCLABIAFgC3//L/BgDC//H/6P+cAAoA6v8hAEYACACj/6X/Fv/U/9z/KwBqAHoAGwHiACEBawC8/6D/7/7P/t3+0/4a/27/BQDgAAkB9AAnAbAATQAaAHH/Zf9B/27/O/9g/9v/w/+RAKUA2gAuAeUA5AAMANj/Tf/z/sb+i/6I/7D/UACPAEEA3wC8AJYAYgD2/wMAnv+W/7T/of8OAPL/hQDRAHoAlgBnAI0A+f9r/37/Fv/y/iX/af+w/+T/TACkAJAApACnAD4Ax/+D/9T+wv5s/zv/hP8IANEAZgHbAakBeQFfAQ8Ao//E/ib+Ef7c/cz+Y/9SAFsB4gH5AUsCIAJ9AcsAIf9S/q39HP07/Qf+jP6n/4wARQF0Al4CegK9AeMAQwAX/3T+5/1w/fX9qP7T/i4ARQH9AWsCWwJaAtABsQAm/2j+2v2H/Zv9v/2t/vr/LwFQAmICRAJPAgcCiQHj/+3+uv1t/Yr9SP2A/sP+x/+tAH8B9wH7AX8CygGOAYcAo/8Y/yL+/v3D/ff9sP5C/+v/6gAJAdYBIAKUAaQBQAGIAJ7/XP///pr+f/6x/qP+uP4u/6T/6P9gAPAA+wBrATkB6gDVAA4B4gA8AEQAuP9e/zv/wv7o/g7/D/9w/4//3v8UAGEAGQGFAckBVwHsAF8A6v9k/4z+ff4j/mD+af7E/qj/7P+mAAgBUwGpAT4BXgERASUAPQCq/0H/Yf8w///+7P6X/6j/KwDIANwAUgFIARwBbgCF/1L/W/8z/1z/W/9X/9//VQB6AIcAZgCMAL0AkgBFAIH/Gf96/lD+t/6B/vn+t/92AA4BawGjAesBBgKWAdQA7v+A/7z+Xv7T/Qj+wv7Z/p3/HADyAJsBJgLBAigCmAEeAUYApv/X/gT+Fv7b/cj9cv7Q/o//QADHAIEBxAHeAc8BTgHAAEUAgf/q/rv+p/7H/t7+3P5u/wQASACcAH4AewCFADMAOgDz/9X/PwBkAF8AUQB1AJsA7QCPAGgAPwCE/5v/GP+J/rf+wf5X/9T/AACHADMBfwG5AbYBTgGzALr/A//P/h/++v09/q3+tv6Z/0gAdwBeAUMB5gFxAfwAPgH8/3T/6P78/uv+F/9j/63/CgAVAKYAiQB1AFkAOwAgACQAGwANAPH/j/9RAFEAnADRAIAAkgDM/5n/kP8x//H+B/8x/0v/fP/S/z8AgACSAMoA3gAAAQwBegAiAOT/Z/9a/1T/E/8J/zH/Tf+d/5T/ggDIAJEApwBzAHwAKABEANj/fP8fALIAVgCoAJ0A5v8nAG7/wf+q/2L/2/97/87/wv/o/0oANQBRAPcAwACHAO8ALwDX/17/6f7R/jf+Pv7c/v7+p/+BAMMAdgF2AY0BkQEiAc4AOwAsALD/hf/p/mj+w/6//lX/Nv/o/rb/FwAcAY0BmAH5Ad8B5QEqAWwAv/8v/97+8v3O/av95P3Q/m3/FwDCAIgBDgJ4AjcCvgE2AUsAgf9a/uj9yP29/Uv+L/7J/tL/egAgAY8BAQJjAjEC+QFJATEAxv/X/nH+4f3N/VH+y/4FANb/xAB8AXsBRwKMAU4B3wAJAK//xf7j/QD+SP4y/nr+SP8CAJ4AiwH+AS4CxwGAATYBLABq/6b+O/41/oz+zf5Y/+D/VgAgAVsBOwETAQoBxgA8ABgAKf/u/gL/eP4s/zf/lv+cALMAFAEZATUB4wC6AFEAg//i/qH+Uv4X/oj+GP80AOsAhgEAAgYCwAEzAb8Azf93/x7/dv7K/R/+jf6p/qb/BAAYAcUBKAIDAsQBwgE3AXkASf/H/qj93/3//bT92v61/5MAHQGkAa4BugFYAdsA/P9M//n+K/4J/hH+4v5//xwA7ABVAe0BGgIwAnUBawDh/0r/qf5n/gz+jf78/sn/7QA1AWgBigHhAdUAQgBm/5T+kf4a/n3+qv4v/9b/sAD8ADMB5AGoAboBcQGlAKz///71/ZP9Sf1I/Xr+Rv84ABQBBQJmArICxAILArAAtf80/0j+Lf5//fn94P58/4UA7wDaAQwCNAK3AfUAYwBx//f+O/7I/ez9Jf4h/7P/hwD/AGgBKAJgARoB+gBeAIj/3P6N/gr+g/6e/lH/7v9SABQBngFZASYB+gD5/9n/Ff8J/3z/aP/9/z4AxACIAOIAmwAUAAYAyv/p/03/Hf8K/xH/ff/4/wsA+ACGAUkBvgH/AHEAJAAy/4D+2/3R/dn9kP7Z/vD/OwH0AacCNgJnAtkBjgAmABD/Ef5r/Zb9l/33/dP+s/+mAE0BKAK7AtcCSwLjAUQBMgAU/1D+FP4//Xn93P10/mX/CgAmAeMBtAJpAvEBSAGCAAUACv9k/u/96f1i/uL+UP8zAHcAlwDhACQBUgEGAewAKADN/5j/V/9V///+5f5y/zUAIQCzAPcA9QAaAaEAUADy/6f/Y/9Z/y7/Q/+I/wYATQBCAJUApwDFAGMA5/+w/1X/gP9W/0P/OP8g//L/6f8yAPoAwgAOAfQAywBVANX/zP9f/0D/Hf8f/y//j/8BABEAnwDNAPUAKQEnAbEAdAAGABX/Cf/y/tT+s/4b//j/agDMAGMBiAFgAZ4BiQA7AN3/0P6z/hv+Tv5M/p3+G/+2/08ATgBUAb0BGgKyASwB7wD//9X/6f6Q/tz+u/4U/1f/tP9ZAJEA5QBEAQgBIQF+AMb/fP9p/3j/SP/q/hT/yP/8/5YAdQCnANsAsQAGAUEAMAC7/6v/c/8j/3v/VP9x/77/UAAJAF8AlwBuAGgA0P/3/13/cv/f/5P/dP/G/+z/0P9yAJEATABzAJ8AqAB+AC8AJwDy/9X/CwCM/2j/R/+D/x4A/P9kAKIArgDqAKQAOwDN/5//cf90/1v/Iv+X/0f/mv9rAMn/JgBkAEMAigAtAB8A3f/O/y4AIwD+/xUAAwAIAEAA2f/h/1YAJQAeAN7/pP+V/zf/dv+v/67/8v97ALMAxAD9ADsBZQEhAYgACAC+/xz/rv6n/n/+0f6H/5v/zf9ZALoA2ADjAM8AwgCWABcAjf/p/sX+4/6T/v/+gf8CANQAQAEsAUABaQEDAWoAMwCg/9j+5/5b/un+jf8CAPMAwwBIAVoBTQEXAU8A3f9E/9r+df6m/oX+Pv/L/9T/IQE5AS8BGQGzAMEAWwDT/z3/Jv/D/qP+Bf8c/4D/UwDgABYBEAHyALgALgAGAEz/JP9F/97+df9U/9f/TAAWAEUBUAFRAfEAgwC4ANL/wf9G//D+bv9x/87/nP8FAGkAdACeAMoALQD7//b/FP89/xL/bv+m/xgA2gCFAPEARQDi/7//Lv8K/+f+Qv9e//P/YgAoASwBWgGaAXkBRwEFAO7/5f6P/kv+of2G/jv+Gf8LAKcApAFsAlYDBQNWAlEBGgDU/u79Zf0i/RX9t/1R/kL/vwCqAXECtAK+AhkCOgF5AJb/i/74/Zz9Yf1w/q7+bv9NAFcABAHlAcABpgGUAaUAmAAg/97+SP9d/hL/UP+9/zUAogA5AT8BTwHpAKwAJAC9/4D/2/62/sT+2P5U/xMANwBYAKcArACuAHMAOAAeAPz/lf9i/5j/1f4d/zr/ff+nAFsA8wAYAQMBbgG6AG0A8P+f/3//O/+y/uD+Of+T/zcAYgCMAMcAkQCtAM0ATgBYAAwA/f+t/yD/Wv8p/4D/pv8PAFUAfACzAHcApwBQANr/tP8O/8/+DP/n/ob/rf9GANwAjACcAUMB6ADTAFYAHgCv/2r/Hv+Q/lL+tP75/pH/AADVAIgBiwGxAa8BvQEtAdoA6f/v/mn+Ev4G/uH9xv4B/6X/bQC/AHUBpgH5AdQBMAG2ACIAJv+V/i/+I/45/lP+N/+g/9L/ywA5AT4BqAF6AaoBbAG8AJAAwf/w/jX+uv3I/WH+i/6W/wAALABtAZgBDQIOAiIC2AGNAQIBvP8M/xP+uP14/Yr9G/4r/9b/IAA/AYsBxAHBAZMBHgH3/5L/Zv/m/pr+wP65/uv+kP/w/2cA2AAKAQ4BKgHlAHIAzv+U/4D/a/+G/6v/xv/1/14ATQB3AGQAQAA+AN//lv9z//P/sv/a/z4AHQDJAFAAUgBKAB8AQwCU/9j/SP8//1j/XP+q/2j/PABWAE8AYQCwAKEANwAZALr/tf9a/5b/of+x/6v/hf9NACAAcwD4AM0AZQEuAWUAhADl/4//u/8G/wH/4v4i/0z/Xv/+/wMAywDtABsBFwGfAAUBHgCU/4L/Av/3/sT+q/7X/iv/hf8FALMAkgGwAQwC0wESAZYA3P9P/9X+6f5V/oL+uP4F/8n/sf/+AP8AOgGaAeYA1QB8AHEApf+H/wv/r/4P//3+o//I/4EACQFCAU0B4wCjABoAmv8H/xv/4/7a/l7/e//S/2MAkAC3AIAAlwBiAMn/PACf/8j/5P+0/z0Apf8aAN7/5/9WAA8AXABeADcAXgB5AMn/wP8MAMn/2//F/9T/Yv9m/4//lP/q/+T/IABbAH4AZQCBALwAfwCEALEAhADo/8r/kP/n/vD+4f5K/7H/5P9iAHsAqgC+AKEA1gC3AF4ACgAi//v+1v5//in/h/8jAHkAgwD4ACwB3wDBAJ0A/f/9/53/iP9o/+H+eP+2/9z/KABvAH4AhQBoAEcANAAMAO3/4v/I/4T/Rf8m/53/vv/b/zgAWACJAO4AFAG5AKwARgD1/6r/X/9M/0D/QP8H/4//0v8wAJsAjQCtAG4AjAClAPf/x//3/4f/OP9B/zj/Zv9s/9D/IwB+AMIA+QAbAcYA+ACtAE8AvP8H//f+J/9d/wv/fv8RACcAxQDBAJwA0wCGAFsAAACX/2//pv9//9X+av+c/wUAVAD1/+8A8QDAAJ0AFQANALL/wP9g//f+Gv83/4r/1v/W/0cAxgCiAI0AEwENAboAogAsAAwA1/9z/z//w/6C/3X/gf+d/y3/CQArAAUAcwCgABsBQwEJAdEAYwAMAIf/Gf/Z/jv+h/6b/uL+zf/t/3MAQgHcAQACCwLaAQYBAAEeABH/df5n/Wj9qP0G/sr+jP99AIEBDwKfAt4CgQLZAfQAAwAO//f9mP1v/ef8ev2e/lz/NAACAd8BcQKrArQCLwIqAVsAo/95/tD9nv2K/az9dP4//zAATAHwAWkCgQJeAtUBGwHc/xf/yf79/fX9r/3H/Yv+IP/y/64AYAEiAm8CfgItAhwBnAC+/7H+T/7G/bn91/13/l//AADWAIsBrAGbAY8B8wCjAN3/K/8C/3v+8v7h/hP/4v8oAMUAqAD5AB4B3AAYAUkA6f++/4z/if93/43/+f87AAwAFgA4AGsAIQDl/43/U/81/7f+Q/9i//D/UgCEAHgBJwFCAU4B9ACCAKP/Mv+i/hP+I/6r/tX+h/93AKkA+QA8AT8BCwFdAW8BrQCxAL3/Hf8H/4H+XP5E/vX+Tv/i/8UArQBbAZsBqAHOAUcBzQBRAJv/3/5a/rH9wP2M/n7++v4FAFEA5AAkAaQBCwLaAaQBwgAZAJX/8f5o/vH99v0W/pX+Qf/Q/7wAcgHeAZ4CcgLeAU8BoQA2AGH/0/4//if+bP6P/vv+T/8LAK4ANgFDASIBKAHLAIMAIQDY/1H/+f69/qP+E/9J/4n/sf8qAIcAhADyALgAqACrAGEAfwAmABYAKgCQ/5r/qP9Z/53/7P/L/+b/8/8FADUAUAA/AF0AVQA4AC0AHQDx/6D/7v8tAPz/EADZ/+//5P+i/6H/0v+p/9f/KQAIAG8ABwD3//r/tv/V/6n/9/8LACoAYwBOAEkAcwA+APz/kv+9//j/hP+z/6r/iv/+/6oAjQCtANMAQQCAACYA9v8HAL3/hf+j/4z/OP+i/6//0//W/w0AIgAjAE8AYAChAGUAdQB8ADQAzf/P/0n/Vf8m/xD/tf+V/20AJwB4AH8AXgD1AF4AeQDY/63/df9s/7b/xP86AJH/FQAsAD4AcgBPAIgAJwAAANH/EQCc/+z/TwAkAFcAvf8vAAkAw/8KAJ3/vP9//8H/tf9R/xgArf9MAAkBYADxAAABtQCQANr/iP8X/8f+j/5P/oP+Ff+W/0cAqgDxAL8BIAL1AaIBHQGtANb/HP/g/ij+0/0E/kD+2/6r/6cAXgHEAVECUgLCAYEBlgDo//L+Gv4g/p/95/2b/hv/2P+qAE0BkAEjAhUCmAHzAHwAn/8//6j+9/06/gn+jv4M/6j/eADOACgBVgFgAcYAqQC7AC0AHgDW/4n/tP90/2v/uv/A/xwAXwBvAHkAlQAcAMj/yP+H/2n/Zf8iAFoAhgDkANgAgQDx/8//fP8f/8/+xP4C/9/+CP/K/xIAxgBQAUsBzgFzAT4BCgEwAB0ANv+Q/mP+4v0b/oT+FP+8/74AWwHeAf4B5wGoAUAB0wDw/47/EP/O/rr+rf6g/r3+Rv+N/xkAZwCjANgA8AD7ABIBtQAJAD8A2/+h/4b/gP82/+r+Uf/9/lX/T/+5/1EACADXAEUBogFiAZwBTAFyAK4AtP8K/83+Nf4a/lD+qv4V/6//kgDzAKIBEAJlAR8CNAGzAG8ACP8B/xz+Ef4x/kr+k/76/ikANwATAZEB3gHEAZQBRQGUABQAr/9x/5T+rP5g/j7+2/4D/6f/XABFATsBiQHEAWYBQgHkAHcATwD1/x7/Av8x/gf+if6E/tD+Yv9aAHEA3gA6AV8BZQFDAQYB8f/o/3H/9P4h/8z+x/5V/8//gQCuALcAIQHnAOMArwBIAD4A5/+o/y//Df8+/1P/rf8DAOH/GwBiAEIAbAApACUA7v/P/7P/hv/v/3r/8f97ADwAeACGAE8APQBMAPr/xf9k/23/T/9t/53/M//y/3EArwD2AC8BUAHoAK0ADwDO/3//AP8V//L+v/4R/3r/sP9PANgAOwEjASYBEAFgAFwA0f/E/2L/5v4L/53+HP9z/6P/DQApAG0AngB5AJgAwwAtAFcAbgD7/+f/w/8IAA0Akf/C/7H/QP/u/+v/CgBgACIAogDIANwApgBZACIAt//V/3X/Uf+M/yT/CP+K/5H/k//p/9r/dAC4APgAaQElAQ0BmAAkAGH//v78/qr+v/6Y/gb/of+6/yoAngDnAPEAUAF9AfkAJwGcAND/JQCS/1v/Gv+t/vT+1v44/4L/awB0AJ4AcQErAYABFQHIAGEA2/9T/8X+8f4p/mP+kP7K/or/1v93AMEAMQEkAT8BRwH2AAMBgwA0AND/Uv87/wH/gf6u/ij/Ov/O/yYA3QBuAdoAWQE1AXYAjgAHAPH/tP82/0P/LP8z/zX/VP+T/7T/JAA0AFUA5ACqALEASwHiADQAKAC7//f+VP9D/zr/V/8q/7H/uP+t/+L//v+GAIAAxwAYAdMAswCkAEgAOwDO/7j/qv8p/23/lP+B/7f/of8AADwA8v+YALUAXACnACcAKQBNAPP/z/+K/2j/lv9v/1D/hP+b/xAAAwAYAHAAmQDiAL8A3AB5APv/p/8Y/1H/3v5z/7//c/8VAOT/DgBKAIUAzwCzAOoAwQC4AFoAKwD9/4D/eP+E/z3/SP+M/4j/0f++/yQATQBOAH4AWwBhABoAVQDw/83/IgCm/6z/lv9R/2P/sf+e/wIARgARAI8AkwCNANAAXQCOAJkAUwAfAFj/dP8q/zf/Pv8F//P/6f8vAGAAzQAAAZkACwEgANz/l/9Q/57/ZP+U/wMACQA3AJoAUwA4AGoA+//C/xkAkP8z/zf/B/98/33/LgC1AMoAGQFHAR4BmwBxAJ3/d//m/kz+m/6J/vv+j/9cAOgAbwHmAUECEALAARcBZQC//z/+DP6G/Uz9gf3u/QX/cf8JAe0BSwKmAqgCWAIzAW8Ax/8l//79if12/Xb9R/4W/+D/0wCDAe8BYAI4AusBUAGIAAEA7f6J/kP+Sv5d/pv+ev/G/0gAxwBjAVkB5wD4AE0AJAD8/4f/Q/8L/9z/0P/E/0IANACdAFUACwAOAFH/cP+D/zX/a/93/9H/VwCPAAEBNQEeAVQB7ABIAML/Jf8h//T+mf7u/t3+Bv/k/3oAGQGDAbgBkwFgAcAA3v9W/9r+2/7E/lv+U/75/s7//v95AOIABAEhASIBDAGvAKEAVwDa/3z/MP9B//v+Tf9d/1D/7v8BADwAqgDnAJEAqQBpABwAjwA+AAsA0v8jAMb/bv9S/xn/g/8K/2P/tP/Q/zAAfgCaAMwAPwG4AAQBzAAPAKH/Q/8m/+T+Gv8u/17/Wf8MAGIAVQDuANoA1wDYAOAAdQDd/7v/if/g/jj/q/85/6//w/8RALcAoAD1APAAxQCfADYAPQCD/xn/Lv+7/iz/E/8s/9H/KwB/AGEAiQB5AE4AawBvAEgADwAmABwAHADE/9L/OgCz/wkABwCV/63/W/+j/8b//f9fAIQAnQCzAMAARQBRAPr/5/+0/5T/kf/x/kv/Dv8R/2f/CQDYANAAWgFsAYQBSQGcAHYA0/8G/4n+Nv4C/iD+dP7a/pr/qQDVAHkB9wHxASEC5wGiAWwAn//4/oH++P2x/Qf+X/4b/7b/tgAhAYwB6QH8AeIBNwHJAND/ov/T/vD9DP45/k7+qf54/9n/tgBhAd8B/gFhAX4B5gAnAL//Sv///pX+vf7U/gX/y//e/5gA8wALAQMBXgA7AP//DQC3/6n/wv9m/9X/+P/+/9r/LQD1/8L/t/+q/xsAAAA3AGcAfACXALoArQCpAGAABwDK/0T/HP+3/j3/Yf86/4//bf++/0IAsgDdAEYB+ADMANkASQAqAL//Pf/w/u3+Tf+i/x4ACABPAPwAkgC1AFYA9/8pAO7/7P9Z/1T/gP9//wAA2f8hACoAHwBPAEIA7//k////AgDD/6X/JgAMAC8ArgCFAIQAkAAvAF8AAABM/0b/4f4h/zj/qv/F/8//WABRAFQAkADPAGwAqQDWAD0A6f+N/4H/eP+t/3T/z/+4/6b/gABDAJwAzwCdAGEAQADd/zz/Iv8E/1z/wP+K/xQABwAqACwAVAD/AIkAggCvAIoASADX/6z/T/9k/zn/t//L/8P/KQDi/z8AGAAsAHUAUQAuANr/o/+g/6//W//P/9z/VwCzAHQACAG+AJAAbwCm/0j/W//r/h3/Qv8g/+n/NQDAAAABMgEyAQABzAArAPr/i/9R/6n+cv6y/gf/Y/9f/0IADQAHAUUBLwHbAfYAAAGSAAkAdv+x/sL+h/7C/tv+cv+Y//L/oAC7ABsBQwGRAfQAkQBTAIr/i/9E/zn/RP94/2D/fP/A/5n/HQAdAB8AjgDCAPQAxACaAKgANQD5/8T/p/+1/9f+GP9E/+z+af9v/+H/EABfALEABAEcAa0AYwEZAYMAXQDO/4f/2/6//rX+sf4B/yj/uf8CAIAAEgFCAYIBjAEnAfoANQDd/6r/0v7B/mH+bv7l/gT/hf+//5AAIgHyAIsBTAHIACABfACy/9T/7/7l/g7/2f6I/4b/CQCxAJ8ApwB1AOUAWAA2AD0Awv9XANj/jP+f/zD/iv+Q/5b/8f///1AASgDw/w0ALgAUAAoATAD7////ZAAdAHwANgDd/zMAuv+1/7f/8/++/+3/9/9a//H/5v/5/04AIgAbAPL/AAAQACsAVQDAAGsANwB3AO//kP98/3v/Xf9+/7H/cP/O/wQAZQCwALcA9ABwAGUAhQCx/4H/av/7/jX/FP9L/5X/yP9ZAHAA9QAfAf8AIwHSALYAUQDE/7z/O////ir/5/4h/y3/AABAAGQAwwBiANUAPAAxABwAs/8HAGv/wv+k/8v/RwACABYAEAD//8L/zP/f/8L/yf95AGEAHABtAFgApQClAJIABwABAOz/jP+Q/+P+5P7o/kj/qP/J/0QAiwAyAW8BcAE5ARcBzwAWANz/AP+0/pv+ZP53/lv+7P4p/9T/vgDpAOAB2AHKARgCdQEsATQAU//U/kz+0v2q/SP+MP4Z//3/cgBQAZ0B3AHyAbkBrwE1Aa8ABAB0/y7/Qv6b/tb+bf4E/yj/W//0//H/lQDhAK4AdAFZAdQA0wA1AAoAo/9w/4n/7v7+/j//Rv+v/2f/sP9kAE8AewB7AMMAwQCwAA0BwAC1AI0AEgCk/2b/B/+r/rn+pv4m/xv/ov8GAP7/uAAvAeUBhAF+AVUBwgBWAMP/i//o/jr+P/5O/mD+0v48/wcAqQDaALsB8AHvAbUBcQG3AD4Ak/+U/pf+Jf4O/kf+lf5B/6L/DQDtAK0BsQHrAeUBlQG8AH8AJAA7/+n+bf5X/lv+hv6j/gf/tf8JAMsAfQGLAXEBfwEaAZoAaQAeAG7/Vv9a/x7/L/8Y/y//LP/u/xQARgDVAEMAkwDmAK4AaAAvACkA+f/F/9v/wP93/5H/sv+r/2z/z/+e/8T/BQDv/zcAEgChALUAuAAYAbcAZgAXAN//nP/m/uP+5P6t/hH/ev/R/xgAawD7AP0ADwFWAV4BRwEjAZIA5f8w/77+dv7T/Ub+a/4X/87/QQBAAUwB1AEAAqEBWwGUAAEAYv/8/pD+fv5H/pv+Gv8E/8D/0P9zADsBXQH3AWIBJgHrAFEABACI/xP/4P7d/rj+T/9c/7D/OgADAI8AnQBYAG0AwwB5ADYANAAbAEkAx//W/8L/rP/E/7r/5v/J/97/kv/T/+j/sf8bAE4AoADVAI8AvwC8AC0ACQDb/3X/Vf8D/+3+5/4O/0T/gf85ALgAwQASAQcBrgC9AM4AoAAOAOT/ov8n/wf/IP/6/iT/uv/v/1kAtADbAPcAlgBsAGAAbQAHAOD/f/86/5r/M//r/xYAzv8uADMAIgDU/y8ABwABACkARAA5ACYAVAD3//T/AwDx/8D/9f99/4H/kP8G/9P/Tv/p/20AgQDEAGEAMQG2AOQAcwAoAOz/RP9b//v+aP8W/3j/tP/K/1QAcQDlAEQBSgHhAM0AVgCD/0P/Wf8S//H+Jf8X/3n/n/+1/1YAvACRAAcB3ACVAG4A+/8fAFP/c/9b/3L/vf+H/9r/CQA8AFwAvQBuAIwAXgABAPf/4v8oALn/8//X/wwABQBm/7//pf+3/7b/sf8LAAMAbgCwAIsAkQBXAOYAuwBKAC4AZf+M/7r+sP75/ob+M/+i/ywAlwD8ADwBLwErARMBgABsAMz/JP8O/53+rv7G/jz/vf9RANsAKwGBAXABIgGoAI4AeP8N/1H/1/7J/kD/kP+d/+r/TgC8AKAAxwC+AFYAUADl/4z/j/9X/0b/1/+M//3/NgA9AOYA2gD0AIAASQDl/5D/h//Q/vT+OP8d/8X/CgBNAO8AAQERAcUAhADv/8v/Xv8K/zX/1v50/yP/6f+aAFwARAFDAakBdQHuAKQAQwB0/wT/lP5a/mn+Iv7m/i3/y/9ZAEcB3AGBAckBPQHVACcA8/+S/yr/MP/3/ib/Hv9S/2//0v8WAGwAhgBuAEwAQwBiAEsAQQAjABgAyP+k//D//v/c/8X/7v+5//X/RQBPAP7/EAACACkAOwAwAGcALAD2//3/IACD/7j/ov+V/+//p/81ANj/HgAoACoAkwDn/yUABwA2ACQAAAANALf/tv/G/5z/ov/q/97/8P83ABUABwBJAAYABQAXADEAZADr/2IAWQAAAB8A4P+k/+D/of+B/6T/ev8MACwArwDFALQAjQBMABIArP/T/0n/If9E/1n/1f8IAEgAdgCDAGAAnwB7ACUA+P8YANT/Pv+p/1H/F/+S/+7/LwCeAL4AoACKAAwAQwAAAOn/zv+C/5j/qv/w/wMAMQByALwASgAcAGYA6v/z/97/Uf9R/1n/Xf/D/7n/9/+UAMAAtAADAZ8AfgASAMT/qv/l/ib/Hf9J/7n/xf9PAC0AoADcAJ0AngCRACkA1v8FAJb/f/9J/zv/jv+e/wcAMgBFAMEAkQBrAJEAMAAsAOn//P/X/8X/wP+1/1oA3f/h/z8AGQDd/+L/tv95/3n/f//6//z/fQBFAGUAnAAVAHcAOgDr/4L/Y/9K/3X/ff95/zEAFQBdAG4A2ADFALQA1gA7AHwAlv/G/73/IP9k/0n/gv91//z/CwBJAIcAdQAEAYIAKABlAAkA8v+G/4n/Wf83/7v/qv/2/z0AaQBwAEUAEwC9/ysAqf/R/wYAqP/1/zwAJQAJAGkAKgA5ADQAFgAKALj/kv8i/2//WP96/1oAlABwAM8AyACxAOEAnQCcADoA2/96/9j+//73/gr/c/+s/xoANQBmAN0AygDaANcAOwA+AAQAi/+X/zn/CP8Y/zT/Wf81/8b/QgC/AOMAFQGOAQAB3wB3ACoA5v+D/4D/KP/g/qb+Uf8Z/1n/7//H/2YAzADMAEUBcwELARoBqABoANr/Xf8Y/5P+Tf/H/in/mv+O/5kASwCOALAAtQBVAFQALgCb//X/kf+2/5b/kf+E/8v/WwDt/0YALAA5AFcAMwBRAA8Atf+9/wMA2v8gAGwAPwA5AA8AAAB7/47/x/+t/+v/1f9VAA0AGwCHAFIAjgCIAKAAGgDR//H/uv9E/1r/gP8L/2L/av/X/0AAiwDHAN8ABAFWAH4A6/+j/9D/Tf+//5D/hv/L/wYAGQAxACwAyP8BAPD///83ACwAXQApACgATQD2/wEABgDF/woA6v86ACEAJwB7AKP/mf/f/7z/bf+4/9D/pf8QAAkADwBdAI0AawCBAE0ABQA2ALX/7/8PAKb/t/9+/3D/p/9o/63/EgArAEIAlwC5AFgAjABBADkAUAAfAAQAwv/T/13/g/9v/6P/BADO/wMA8f8oAEcAiQAuAFkAsQAMAEIAwP+k/5r/Pv+Y/5P/w//H/8T/LgC/AKgA3QDXAJIAWgCm/4v/Sv9i/3P/qf+d/57/IQDW/3EAaACEAPsAUACVAP//vv+k/zn/rP9Y/zn/4v/L//3/TABcAMAApgBnAGwA0v+v//f/oP9o/57/6/9IACQAcwBzABMAIwA/AD8A0f9HAPT/iv+7/3j/uP+d/9b/7/8dAAAAOQBfABUAdADv/z4AWADX////uv+1/7n/qP+6/yEAAgDb/wcA4f84ADoAHgBIABMAFAAjADUARAAJAB0A9v+2/8b/oP/E/5P/rf8wADIANgBUAHgAHQD8/2UAUwAPACUALgDa/5r/pP+E/5n/r//E/ycAKgAwAGsAIAA9AA0Abv+y/2H/KP+g/5v/DAAxAIsAFwHkAJUAaABcAFIAKgDq/9v/bf9Q/1f/I/+E/8f/AgCeAK4AzgA7AcEAjADm/zn/SP/E/gf/F//6/nb/JgBTAMoAegEHAT8BGQHYAGAAe/+O//L+ov7F/rn+2v5N/+L/dQDKAO8AQgE4AQQBCgEUAH//gv/i/rD+vP7+/q3/HwDDABIB/AAbAfYAnQCCAGcAjv9a/0//rf6s/gj/V/+P/xYAzwDfAMkA4ADpAKsAZwBnAK3/U/9U/xv//f4H/1X/wv9ZAFwAzwAvAaMA8wDGAEoA7P9+/3r/Nf8G/wD/M/8k//T/PgA9ANMAmwD/APsA1QCpAPX/0P+N/3z/b/8n/1n/nv+//1EALgAvALoAfQCQAJoAYgDK/6v/fv9h/4v/kv/A/5H/x/8pAA0AMACVAN8AgwBkAHAAwv+N/3f/Qf92/2X/HAD3/8f/PwBKAJQAWwCJAIAAcwA5AO//KwB5/3n/hf9J/5j/4//s/xcA/v8KAGsARQA9AEQADQAPAJgAPQBFAEQAwv/q/7H/sP9T/1X/pv+r/+v/JQBwAFYArQCVAJUAjQAeACkAif90/yb/v/7s/u/+Uv92/+n/hQD3AGcBrwGjAVMBdAGQANj/Wv+h/tL+Nv49/r/+DP/S/zYACwEdAVcBoQH0APgAmQA3AOv/RP/B/l/+ef6W/jj/1/84ANoAtgAjASwB3QA+AVQA5f+k/1D/zf7V/lT/HP/s/xQADwC+AGYAiQCcAF4AJQASAC0AyP+q/9L/rv/X/+D/QwBmAHoAjQArAIAA9f/k/8H/Vv9j/+X+ZP9y/5v/SQCNAN8AJQHzAO4AfgALAIr/Iv/p/qP+G//c/i7/uf/1/7MADwElAW4BngHwAOMASADV/3b//P4g/5P+9v4B/2L/zP88AIUAeADvAMYA/QCWAKcAcAAXAEsAhP8z/3L/eP8h/3n/Yv9v//3/7v9EADgATwBkAFkAWAA/ACkAFwAxABgA2//Z/wEAw//g/8v/hv9w/6//FAATAFkAnABxAHIArAB8AGkAHwAEACwAvf/N/5T/Tf9T/z//av9l/6v/OgBEAHYAsQDjAL4ARABrACgA7v/Y/4f/Qv9I/0L/Wf+B/7P/5v/T/yoATwB8APcA3gC9AAEBnAA6ABoAi/9R/zb/QP9U/3D/n//w/zkAWgCxAMwAzQCRAGEARgDz/6f/vP+f/yv/Uv8J/y//Z//O/1wAsgDbAJAABQFTAOP/2f9W/3n/W/+6/8f//v9BAFoApwChAG0AQAApAPb/rv91/4f/Yv/A/+r/5/9KACEATACMALsAngCqAIsAfABiAHf/Rf/N/o7+3v78/mP/s/8kAMEA7gDwAE8BBwF6AFMAsv9k/13/3f48/zr/Rv+i/8//ZwB/AOUAKAFGARsB1ACAAPb/Of8K/zv/0f4+/1L/jf/M/yAAuACNALIAowCTAH8AmwAWAOb/vP/6/mH/Av86/6L/0/9DAHEAnACvAMgARQCSAA0A4P/K/z3/jv8Q/3v/hv+O/x8AFwBnAGoAYAC7AMoAWgB0AA4A/v8KAJD/8v+o/2T/n//5/0YACAATADMAZAA0APT/EQC4/+D/vP/Y/x0Ao/8EAAoA7v/S/wAACACu/z4A+P/z/xAA3v85ADoANABFAP//6P8vACEA6f/1//j/EQCs/8b/9//N/9D/wv8bAO7/8f8MAO//aABPAGkAhgBnAIcA5//U/9T/gP+m/6f/i/+C/+n/agAnAEcAWwDCAM8AEQD6/8v/pP9h/yr/MP/9/mH/P//o/0AALwD7AAQBHgEmATUBiwBGAPb/Pf8R/7/+Ev8s/7T/EQD9/5gAcgCqAMEAoQCpAEIAAACI/0v/VP/9/vj+hP+N/+7/iQDZAP8AKgHqAJAASgAUAMP/U/8R/+j+9v4Z/6j/GQBsAOUAuABuAGIAWAD9/8r/wP9X/1r/s//R/xIAQgA5AN8ArwCPAOIAWQD5/7n/yP+5/z//SP9h/0D/Xv+f/y4AmwBcAAQBGgG+ALYAPADb/2r/BP+f/qb+qv7j/nH/KgCfAPoAvQGZAakBwgHzAEoAMQBD/73+ef5P/sv+Qv78/pn/kf+qAB4BhQGJAXcBNgHoAG0A5/+g//3+tf6h/s7+qP4n/+//IADLAPQAZAFWAb0AFQGXAPD/tf8x///+b/7F/t3+cv8AAA0AzACCAIcArwC3AJsAUgBKANz/7P/A//f/SABHAE8AYwD8/6f/dv8f/3b/9P5y/6j/m/9YAFIA3AC9ALQAvwCWAPQARwDn/3X/DP8C/8T++f7+/iv/wf8cAMkAGAFaAVsBWQEgAXkAJQCY/0b/+P5u/uf+Rf8i/xAAggDJAC8B3QD+AH8AbAATAHj/Tv/u/vT+DP9O/2D/5P9BAH4A8ADgAPcA7QBtAEgA5v9Y/7H/I/9J/6H/dv8uACMAtgBxAIIAtwC7/yIAzf93/53/eP97/9r/4v8PAGUARwCgAHQAnAAYAL3/7/9u/57/nP+f//n/BQA8AFUAPgBiAHIALgAYAOb//f+S/5v/xP9L/6X/zf/X/zIAjQC8AIQAbgAXAPD/GQD5/7f/s/+A/3f/2f/D/woAGQBaALQATAAkALX/yP++/7f/wv/l/x0A4P9xACoAZABbAHEAnADT/+P/k/9z/2X/q/+p/3j/PAAoAGcAgAA8AI0ATwAtAHkA4P/b/43/N/+e/2b/m//M/xIAWgBgAIUAsACcAFcAbADq/7T/d/9e/5X/Tf9D/5b/sv/p/14AaACxANYAVgCTAHMA/f8mAM//sP+z/4b/0f+t/5D/tf8hAE8ASQBDAEkAbAAPAHEAEQAMACYAw/8TAJf/af+I/33/wP/u/5//4P8qADkAhgBcAMQAiABbADkAEQCZ/zT/dv9V/5b/Uv/s/xQADwCWAD8AyACMAIcAfwASAHQA6P99/7D/ff9K/6v/nP/9/1EA/v99AGwAAwBHAFwARQAKAMb/yf+T/6r/8v+o/9////+I/xEAPQDI/y4AHQAJAPf/HQAmADkAggAbAGkAOQArAC8Asf/Q/5j/j/84/6T/nP+I/yUA+P9EAKgA6QB0AG4A0gBGAB0A9P+z/3D/if8h//v+ff9u/6b/yf+3AOUAEQFVAWgAegARAMj/wv9K/0T/H/+0/6D/qv/8/8b/LgA3AFEApACYALgAhAB5AHIAJADK/4//iv/Z/iv/L/8U//b/zf+7AHsAdQAeAXcA0QDmAGEAIwApAGf/zP4S/6r+7P79/lz/BABSAO4AbAFvAWsBPQGjAFsAeP8//9T+nv7l/sj+pP/T/yIAdgCzAMgA6gAhAbwAlgBmAP3/gv9I/wT/6P7R/gD/Vv9P/8X/OAAwAUsBcgGOAQwB8wDt/67/O//D/hH/y/4M/57/iv/d/3QAqwDBAJYACgGlAEoAWgDE/wkAsv+T/8z/sP+//67/8P/X/4r/4P+Z/9z/CgCy/1oAKAAwALMAuAAMAcEAUwATAK//EP88//X+AP9J/xr/s//i/2AAvgDtADwBJwHNAOkAnwD+//P/QP88/9j+uv72/jf/yv/h/6sAhwDgAD0B4QDQAHMAHwD2/5L/B/8y//r+Uf+X/5r/BAAPAEgAcwCqAIoAZgBeAEcAAADG/8T/qv/b/9v/w/8CAPr/i//+/+D/0P/o/wUASgDc/3cAVQBsAIsAYgCCAEQAYgADAML/fv9u/zr/X/+J/4r/9P/k/3AANgBBAIYAlwBqAD0AOgDg/97/aP+X/47/vv/5/+3/AwDz/+D/qf9OAEoAWwA7AO3/GABh/7f/9//g/ykAmABXAD4ASABFAHwABwDU/63/ov90/53/4/+0/xEALwBrALYAjQCiAKUADwAlALL/XP9a/+X+hf9L/x//CADJ/w0AVwBhAOsAiwCmAFQA8P8kAHX/tP9K/5P/+/9+/zwARQBrANsAjgCMACMA8/8oAPP/xP+G/7f/5f+f//b/0/8ZAPf/AgB0ABEA2v/N/wEAof/R/8r/1f9FAGwAfwCPAKIAQQAQAKv/wf9J/9b+dP9E/2v/v/8GAEEAogC0AKcA5QDbALMAVAAlAI7/h/8s/07/Uf8w/8X/zf9ZAGMAvQASAbkAfQCwAGoA3v/+/0T/Lv8I/+X+TP9b/8n/CQBTAKQAmABbALwAmwB7AEEADAAVAIz/i/9z/3//T/84/3r/zP9FAFUAYwCIAKIAogCdAGgAYwAGANv/zf9m/8r/eP+m//X/mv/F/+3/NwAAAEAAsQBoAJ8AZwA/ADoAzP/M/83/Y/80/wj/3/6E/8P/1v92AKMA6gDeAAEBwgBvAHcA3P/c/2z/Nf/z/sv+BP9V/9b/HADFALgACwHzAAABtwAeAIsA3/+9/2v/LP8E/wT/Vv/L/zUABACbAHwAfQB8AEAAZgASAC0A5v+e/xEA7P9//wwAi/+X/97/Lf/Q/+D/EgAAACwAZQAiAJwAvgCMAF0AWgDx/87/rP9c/3D/W/+L/5j/fP8SAJwAdgDeAEIBEQF3AJEAgAADAL3/Bv8B/4T+pv70/hX/xf8FAI8A1gAiAQAB5wD2AOYAHQDP/8f/vP4N/+H+yP4n/1L/t/8UAI0AywBlAUQBHwEcAYwAWQD4/6f/M/8+/xH/1v5+/5//2v8pACYAxgDBAMMA9wBcAHcA5v/0/5//GP9O/+3+f/8p/1r/6P+h/10AcwDfAAMB6QAkAYUAfAD+/33/X//b/hf/D/8Z/5//i//x/5UAngDpANoA9wAFAaAAaQDu/+j/hv+B/2r/G/+M/2v/CgApADgAcAB7AGoA+P/6/67/6v+k/83//v+n/73/kP9MACoACABzAAQAEAAHAMH/BwATAAAAPQATAGgACQAMADIAs//1/6r/yP/i/8L/6v/8/0QAIwA8AGAASwBcAA8ACQDI/6n/vf/B//T/o/8rAAAAqP9JABkAGgA/AHAA+f8JADAAu//7/9D//f/I/3n/pv+x/9T/5v/v/ykACQBWAJYAZACRADQAJAAFAP7/5/+k/9D/m/8jABEABADv/4f/4v/9/1MA/P8xAHsAEgAAADMACQDC//H/l/+D/4z/cf+D//P/dQAVAJYA6QC1AOwAjACyACgAmf98/4H/ZP/D/iv/HP86/4H/9P+WAFIA2wDmAPsA8ABUADIAyv91/8H/Yv8Q/6P/ff/B/wwARABOAGgACgGoAOcAVwB9AEMAjf/O/xX/Xv8h/yr/Qf9W/w4A2P9PAMkA9wCgANgAmQAHAEQAwf/W/63/G/9W/1P/e/+3/6n/XwBQAIEAxwCBAJ0AZwBCALz/1v+p/27/wP8n/2z/8/+y/ygASABEANAAfQDcALUALwB8AAYAuP9f/4v/K/9J/5n/Zv8LAN//TwBPAEoAawBSAJgACgAzAEQA8/+I/6r/sv9P/8v/3f/U/+n/DAD+/14ALAD6/3EARQBtAH8AmQAaAKP/1v9m/7j/if9B/4T/nf8AABwAPACBAMsAFQH5APUAsABMANT/EP8R/6P+dv4E//7+Xf/N/zkA6AD4AG0BfwFRAT8BZwA4AMr/0P69/nj+Wf6x/jb/Xf/e/88AIwGCAaQBegHhAGAA7P+N/2H/g/7U/vH+3/6b/y4AfgDwAFsBBwHRAHMAMwCq/1T/Uv9I/1z/Wv8PAN//UACjAHcAowAxADwAIwD5/5X/hf84/3T/d/+0/44AXwCvALQAwwBVAAQA9v/T/9P/Q/+h/zT/Nv+s/8n/IwA/AHwAoQCkANMAdgBVAOj/ZP+2/4P/hf99/7n/3P8IAFEALwBvADQAYgDm/yUA8P+w/zIAsv89ACsANwAKAEAAPQAOAC0Aa//g/43/pP8//4r/yf+d/x0ADQC2AJIAFgH5ALAARgDY/9T/PP9m/+P+QP8U/zr/BAAUAGgA6wAqAa0A0wByAF8A6v/2//v/qf/n/yH/Wf8c/xL/cf/i/0wABAB8AJIABAHCAIgAswBUAHYAKwDa/4H/Qf9e/+z+7/4M/0n/sf/h/2oAlQAbAUgBRQFIAa0AdADZ/1f/Lv/P/qP+1/7u/ib/6/9vAKcA1QAdASgBGAHzAL8AaAD4/5b/O/8e/8v+wv4h/1z/af/r/x4ATgAJAR0BCAEQASgBOQD0/9T/HP84/x3/NP+C/5T/fP/S/x8AHAB4AGAAewDgALEABABaAAUA0//v/93/+v9t/7H/gP+Y/7v/1P9SACUAgQBgAIoAcQAZAEMAAQD//xkAt/9N/8z/hf9w/+j/zP8NADEAJQD3/zYAHAAqAGMAOwBRALj/+P+4/6L/EgDR/5EAHgDR/14A8f/G/+z/5f+8/7L/2f8EALb/DwA4APH/RgBXAJAAgABJABEA+//P/9T/5v+c/wgAs/+E/+D/uP8SAHkAggB+AFQAQgA7ALH/w/+O/yX/df/y/j7/rP/C/1wA+gD2AC4BIwGqAJkACQC4/3f/cv/T/gj/Y/8p/xMA6f9kALUAWQDaAL8AbgBaAFcAj/+r/3z/gv/A/7X/AgC1/0IAXQBFAGUAVgB9AC8ACwCW/4L/cf+c/6z/h//z/wIADQASADAAHwA8ACYAWQAQAIn/tf9v/wAA6f90AJkAxf9tACQAHAD//9z/UAD+/w8AawADAAQAUwDJ/wAAFQDg/x8Axf+k/8L/xv++/8H/2P/3/wgARgA/AC4ADADn/9P/sf+5/7D/2P/u/xMALwCFAOcAlwCyAGIAyv+3/7X/Uf8G/9r+PP9X/7L/MgCaADQB5AAyATMBsQDDAFcA7P9X/z//AP+W/vr+6P5l/w8A5P+lAM0AMAE7AcoAFgH8/wIAff/G/ib/eP4X/zT/Zv8OAIsA7QAsAUkBAwGoACEARACZ/2r/kv8X/1f/d/+w/+P/XgBxAFYAAAAeAFgAKQAoAPz/NgAiAOj/AAAWAPH/6P/7/+T/JgD2//D/y/+3/5b/n//N/7j/9P8aAMf/UQCGAFAAwQBTAAoAIQAfAOb/mv+x/6f/aP+K/8H/rf/0/wEAXwBpAGIA8QBSAKkAnQDJ////zf+x/7P/xP+m/5L/vv/f/+f/NAAQAP3/DQAvACoAEAAYAOv/PQDr//P///+R/8X/5f8EAMP/1f/1/8n/+v9EABgAWABXADQAiQD+//r/3f/v/9L/DgAQAL//KADE/+H/0P/I//D/9v8FACYAgAB5ALcAjwC6ABoA2f/O/1n/FP/P/p7/Yv9e/+r/MQAyAGAA0gCGAJ0AgABIACIAJAB6/2D/b//Y/mD/of/G/1YAqACwAOwAuQChAEMA6f/g/3v/gP++/1X/a/8fAAoAoADqAJAAtAB3APL/0//C/zX/Z/8s/0L/Qf+o/1IA+P95AEcAswCdAIcApgAJADIAm/+g/zj/Nv9G/0r/4v8PAFQAjADNAHEAmgBnADIAlwAzAE0ACgCT/6n/Yf8U/1//W/+j/9T/AwBwAIsAngB+ALAAQgBAAIsAFQD8/5n/wv+Z/zL/ZP+c/1n/i/8CAPn/iQB3AHEApgA9AEAAQgAyAMn/h/+O/3r/vv+G/+f/HAAbAGoATgC6AIwAVQBHADIAQQAAANL/p/+8/03/e/+J/3z/MQA7ADsAbAAjAC4ARADi/xsAEQDo/+n/8v/j/4j/uf+y/9j/2v8pACkA9P8lAE0ATQDo/5QACgCq/yoA0v9DAO3//P8tAO//0//o/wYA1P8+ABsA7P8OAAMAMwDY/wwATADx/+n/GAAZAJb/lP/L/7j/AAAaAKwANwAYAFwAxv8NAOL/g//M/6P/jf/A/8H/MgArABAA1ABtABwAQQDr/8L/gv+///3///8/AEUARQBNAGQAKQACAAUAAAADAOL/zf/Q/5v/mP/A/4D/vP8vAE8AggCJAIMAIQAJAPH/wP/p/5f/xv9m/9L/vv9//xsA6v9LAEYAoQCUAE8AcAD//yoAnf+w/37/a//b/43/yP9AADIAagC4AIkAYABlACsAGwDd/1v/R/+P/7n/7f/1/zgAjQB8AEIAgQBLAAYA0f+B/9X/e/98/0T/M/+5/9r/MABGAFEALQBVAEsAeQBNAEkAfwDV/yMACgCz/8T/uP/k/63/r//Q/+P/CQBOAG8AkABlAHMALAD5/9X/sf+u/5b/vf+8/4H/iP/B/7D/PAB9AGIAvQCEAOgAhQA/AA4AnP/k/2P/bP9c/0n/V/9s/7//5f8ZADUATgCmALoAmQCtAFoAiwBdAMz/wP9K/3L/sP/Y/5H/qf/h/8b/XgD2/wIAYwAGAI4AmAAZAHQAbQAWAAAAu/9b/1H/UP9a/6P/p//D/0cA/P98ALoAagDpAJsAmgBBAOD/o/+Q/1T/A/9e/1j/zP8cAIYAwgCVAMoALgA/AAAAvP8FANz/HwDf/2b/lf+q/5b/nf/d/8j/w//1/xQArgBrAKUA3ABfAIoAGABYAAAAp/+h/2j/c//l/nv/hP+c//P/KQCaAOsAJwECAfoAVgAzAMz/T/9J/8f+Fv///i7/4P8AAJ0AAQHHAOIAsQC3AFgA0P/N/zT/HP/j/jL/Ov+g//X/9f+/ALQABQHqAGAAowAuALH/8v++/6j/qP+a//X/ef/5/wwAAwBlAHMAkwB9AFYA2f8KAI3/lP+c/7P/6//N/yoA+v8qAOL/4P+L/7D/sv+n/wQAw/8iACQAVQA5ALUAnACIAIMA7f8IAGz/3v9C/2T/sP+s//3/3P+iAJQAGQGjAKwAqgDR/+D/if9r/xP/VP87/4b/rP/M/20AhgCYAJ8AwwCKAJ8AFAAUAID/Mv+6/y3/df+a/8b/yv8ZAP//DwAOAPj/RgANAHAAUwAiALj/8//L/73/cQAYAJYAGQDu/1wA+f9iAEgAFQAsABEA4P/f/wMA4/8PAO7/t//3/57/nP/H/5n/p/+C/8n/0f+9/1AAVgBXAKUAxQCNAFUAgADs/13/mv9s/xX/N/+Z/7P/PgAXADIA8gCsAAMB1wC4AE0A4/8YAGD/g/9U/9L+2P45/6f/2v9xAJ8ABQEvARwB/wB4ADUAof9l/23/E/9x/z3/U/9p/5D/QwAWAHIAKwBbAK4AOACWAGUA8v+V/4v/lP9n/5f/DQAQADgArwBTAHAAfgAgAOr/z/+E/8X/5f/j/1gAOABlACYAWgBqAOn/xP+Q/6L/KP8G/1b/iP91/zoA2ADZAEIB/AABAWUAYABSAJr/cP8D/3z+xv7j/tb+0P9HALEADwFFAXEB8QDGAJwAEgB3/yH/yf69/sn+9v5H/8L/lQDhAOcABgEoAbUApABVAO7/9P9K/8P/rv+A//D/af+a/+3/6P/u/2UAegDe/0QADADt/yAA4f8FAC0AJwBLAB4Azf/G/6T/bv+Z/5T/l//K//j/AQCPAHwAagCcAEIAXADv/zAA9f+e/9D/XP/8/9r/CwAcAPT/lwA1AEEAVwA2AMb/7v/w/3P/iv9y/8T/1//k/3QAVwCvAKgAXwCBAAUABgDZ/1X/lv+Q/13/wf+b/4r/KwDn/0gAjwBAAGEA2//F/6r/o/8HAOj/LABxABYAeABqAEwAhQBJAEMA+P+u/5n/wP+U/2P/0P8DANH/FQB9ABoANgAgADYA///E/yMAtf/j//z/wv/W/9n/MwAjAD0AdAAzAPX/5//a/8L/j/+P/67/l//M/+z/DQA5AGQAhgCbAFIAaQBkAA0AYADs/xUA1/9t/3v/JP+H/3P/zf85AFsAoQBXAFQAWAAYADgAPQDv/xQA2v/I/x4AxP+y/+X/1f/p/xkADgDY/w0A3f+3/6D/zP8IALL/SABoAEQAbgBXAC4A5f9gAL7/LP+k/2z/s//j/xwAfQBZAIoAcAA9AJgATwAaAA4A1v/5/0T/lP+U/4n/0P/Z/yEAEwCzAH4AdwCDABgAHwDk/9H/T/80/9D+Rf/A/9D/kABVAOYA9wBEAH4AIQCS/4n/kv+L/03/sv/y/wsAegCIAPUAawCfAHYALAC+AMn/4f9T/8H+Mf/U/jb/ef8GAH8AlgAXAegA2gCTAGoARABy/8j/Lv/n/lb/JP8AAB0AagCNAHUArQB4AHsADgDy/7z/nv9d/13/gv+D/9b/+P+EAGQAkgDcAIAARgDs/9P/Sv9f/5D/if+v//f/RwA+AOAAuQBwAG4ABAAxALv/p/+t/0j/3f+J/5v/7//f/10AiAC0AGgANwA0AOj/qP9u/0P/R/9c/6b/2/9tAKsAzADvAKkAnAAIAAAAt/90/63/Rv+J/3r/mf/Q/7D/DgBrAKkAowD8AIwAiwAbANP/EwDE/4f/o//N/yL/s/9x/1v/IQARAKUALgBeAFAA8P9kAFkAGQALABUApP/s/9f/pf+y/9P/7P+8/y4A0//5/yMA7/9oAE8AjwCcAGAAOgD6/wMAqv+m/7T/lP+O/zv/kv+u/9b/KQB5AJAAkgCsAGwAsgBFAOr/9P/d/4//J/9B/zL/n//7/xgAPQBDACwAWQCtADkAcABAAAsAUQDk/5b/qv+Q/3P/rv+y/8X/xv/2/yoAWwCNAHIAggBdAGMAKQALAP7/gP/f/7r/aP97/9H/0f+2/1EAFAA/AG0AGgCRAIAAawBEAPD/0v91/0H/Vv9q/0r/2v80ACQAqwBZAG0AegDq/2MACQDo/2wAtf8OAK7/iP81ANb/PwAzADsABwDy/+D/dv+i/4P/pf+//+//WgA/AFwAnQCQAD4AdgAbALn/wP+s/8X/h/+x/7v/3/9BADoAdwCTAHoAbQBJABkAmP9G/w//EP8b/2j/xP/2/6MAjAAiATMBvwDCACEAJwDP/4j/ZP8K/1n/Of+C/9H/sP8cAJgAwwDiAK0AdwBgABMAt//L/7f/of+c/4n/0/+U/83/BQAOAFwAYQBYAGMALgDu/0QAvf/B/woAlf/h/4X/9P8jABIAaABBACIA8f81ALj/xP/h/6T/6f/5/0wAEQA5AGIAJQAaANn////1/+L/6f8XAOb/qP8QAL7/5f8dAB8ARwAQAEQADwDl/xQA2P8pACAABQBCAOP/h/+3//L/v//Y/yEA5f8qAN3/2v9AAPb/GQADACUA//8mADcA9/84AFAAJQASAA0Asf/Z/5D/2P/n/5X/YwAcAB0A8f/4//3/lv8KACAAHgA3ACMAFQBcABEA8//w/8T/EwDX/wAAz/8nACMAu/9KAMf/6P/t/9b/+f/W/ysA5v8LAB8ATwCCAO//NQDe/8v/w/+b//T/c/+Q/wkA8/8EAFAAUAB5ALoAfgCBABgA5f+4/1P/e/+W/5D/6v8JACMAUAAuAJcAjwBLAGgAJgALAKn/kP95/2r/tv+t/6f/z//U/zUAcwBPAHYAMwAUADMA8v8PALj/af+2/7b/1f9EABsAdwBhACIANACv/+b/4P/M/9L/QgAaAAoAjgDM/zMAfQDs/1IAFQATAAUAvP+W/4r/uP+u/9z/BQAAAP3/CQBgAF8AIgASAK//g//B/8L/BAD0/xoALwAcAEkA3v9TADIA2P+JAPT/+P8TALz/zv/R/4r/tP8FAA8AUQBUAGoAdQA/ABYA+f/k/9f/mv96/8L/lP+9/wAAYwCBAIEAzAA4ACwAwv/M/9r/Hv9+/6X/1v/e//r/bgAjAIMAdwAkAEAAEwD9//T/2P9Z/zn/SP8j/3n/LwBBAIQAMgG/ACQB6wCKALEAlv+l/1X/5f4s/2D/lP/T/zcAMwBaAFcAWABLAGwAIQDg/wkA3f+K/1D/tv+//9H/2f8FAE0AAQChAJkAYwBdAOf/BADH/2X/jP98/97/9P/w/1gAOQBEAG4AaQBjACUA4P/k/9f/qP/e/4P/kv8AALj/VgANACQA0gAmAHcAKQAOAA8Ao/84ALH/h/9f/6L/mv8v/+D/qv8NAEUAXwAGAf0ADQHBAIwAIQCo/5b/ev+9/ib/Qv86//P/y/9JAIIAtAC9AIEAhgA7AEgAAwDH/9v/w/+N/3r/Pv91/6H/qv8eAHUArgCiALYAjAB7AD4ACwDk/03/qP9U/6H/1//S/0YAAABzADAAHwAbANz/GQCd/8j/8//V//f/1v/e/yMAHwAeAFUAdABJACUAIwDT/1r/UP+v/wAA4v9AAJkAZADDAI4ARgBmAOj/vv+P/z7/0v7E/v/+LP/2/0UAngAVARcBTwFaAeIAdAAvAM//Uv/c/qv+1v78/mj/j//l/8EA2QD+ABAB8QC2AFMAGwCu/2v/L//q/iD/hP8R/6z/TwA9ANQAlgDKAIkAVgBJAPH/EgCi/9L/+/8AAMj/l/8UAMr/5P86ADUAKQDl/wYA+f+t/67/GwDY/9v/NwBiAFwAPACJADMAy/+6/3v/nf+P/5n/h/+M/8n/AQBnAOIA7wCiALQAcwBdABgAtv+W/4P/2v7g/jn/7P4SAAwAgAD3AKgAGAG0APwAUAAjACwAqv+V/w3/Zv80/xv/eP+d//b/NgBgAJMAHQFzAIcAeQAUADEA6P8GAJn/lv+K/zn/lf+P/4b/+v8kACUAUwBNAGMACABZAHoA2P8+ABcAGwDh/+L/eQDk//b/+v+l/5//jv+0/8v/DgApAGAASwACACQAFwBSAHwAGQARAOb/yf91/4//xf9v/9j/FwATAPv/VQBhAE4AfgBJAIkAUQDW/93/kf9Q/0D/J/91/7r/sv83AEIAlQC5ALwA0ABqAIEAAwCs/6v/rv+N/4r/f/+S/93/m/9HAEUAVgCHAGwAwABFAIAALwBCAOz/ev+g/0X/Xf+i/5j/k//N/9z/NABFAD0AhgAgAIoAPADt/+v/2//w/6n/8f+s/+v/LQAkAFQA9v81ALr/6f88ALP/OgApAB0Axf8eADwA5v9uAP//LwD5/4j/AACM/4z/sf8MACcAHACUABwAZQCUADAASwBMABQAc/9o/0H/F/9Z/3z/q/8gAI4AegCrAMoAhQBWADYAz/+k/1D/Zf++/wf/xP8jAEYA2QBgANAAjwBYAB4ABAAJAIj/2f96/5//zf+q/xUAMABvAGEAOAAhAPn/Yf9d/93/nf+3/8r/2P8oAD0AxQDyANYAaQBKADcAv/9Z/1T/Jf/9/m7/Sf+I/ywAIgCpAAIB7gC5AK0AQwAXAAAAl/+P/zb/XP+m/6v/+/+AAGgAiQC8ACAAMgDM/9r/tv87/5P/TP8IACwA5P+ZAK4AXgAzAGQALwCm/+3/uf+V/4//jv8oAMT/8f9EACYAjgBcAHQASwD3/6b/3v9t/zb/i/84/zgAHABAAIwASQDUAE0AXAApAM7/2P+A/7j/df+y/zYAAQBOAH4AUQCAAD0AGADf/8r/zf+X/4f/gf/K/xUAPAAhAFQAUgBOAEcABgD0/7j/wv+e/4f/ff+3//L///9DACEAcQBmAEYAOgD2//z/vf/E/9X/OwAMAPj/KgALAEIA6/8iAOv/JAAGALT/AwCa/xsADABYAGUACQDjAGQA9//i/57/Tf8i/0z/Qv+F/8L/zv8GAFAAlwDPANYAywCXAIYATACm/57/Ef/x/nT/IP8y/wMAQQBwALgA4gAnAY4AsgDXANT/2v+Z/1n/a/8t/4X/Vf9a/6j/HwB0AH8A2QCmAH4AQwArAAsAp/+c/7T/tP+N/8n/xP+7/8P/8P8PAOL/RQD9/xoAPgBSAIEAHwBaACkAaABaABQAAACL/53/eP+f/6f/1//t/7H/BwAjADcAbABkAHAATAA6AFkAOAA6AN//Yf99/4b/Uv+U/6z/ev/7/y4AeACJAGoAoQB9AFMAXwBKAO7/vf9n/1H/L/8F/3v/lP/R/ygAgwDqAPEA6QDtAMcARAD0/3b/Rv8v/8/+Vf9B/7X/bAA4ANgAqgDgABEBSQCWAP7/c/9j/x3/K/9n/0z/2P9VALj/ZAB/AI0A0QAuAG8A4P+R/3//av92/3z/uf80AJUAeADMAIoAbABvACwAAgBj/4n/if8a/0n/hP9+/ygAVwCrAAEBsAAsAYYAHQD8/17/aP8z/2X/Nf9A/8D/1/9MAIMAqQDmAJcAxgB1ABQA4P/J//j/Xv+G/0P/b//C/37/FwAKAEEAdQBaAE8AIgAGAM//MwBPAP3/EgD7/8////+0/+j/6f+b//L/xv/N/9X/FAAWAFgAXgBDAIUARwB9ADMAeQD5/woAAgAx/5f/Sf+J/5L/qv/l/xwAWAAfAIsAHABpAC4AIQAEALv/IgC6/x8A3/+//yIA7/+6/9L/2v/o/ywA1f/s/ysAPwCxAFgAGwBtAAQAFgCk/5f/6f8c/6//Wf+9//r/9P/AAGkAvwBaALEARAD9/0kAnf8gAF7/kv+b/z//t/+L//7/GwBOAMYAjABpAKQA//9RANr/YP/6/0v/0v+R/4H/CADy/z4ANwCNAA4AHAD1/8b/MAC9/+z/CQDX/xgA9/8HABQA6f8tABkAHgByACAAUAAwAAQAv/+S/6T/rP/A/9j/aQAfADsAdgBIAPf/8f8PALX/s/+q/8r/nf/b/wIA8/9DACIAVAA5AEsAUwD1/ysAzf+4/9v/TP+b/8r/yv/E/w8A2ABeAG0AoAACAFQAOAABANL/oP+f/+L/qf+3//b/6P87ABEAhQBOADEAZwD//yoAwf+k/5f/pv+M/8T/s/+f/xUAOwBMABkAlgAdAPn/YQDx/zIAAwAdADoA2f/B/7f/uP+Z/8L/of/P/y4ABAAxAJ0AcgB5AE8ALADo/6n/8/+e//z/6f+8/ysAvv/M/+L/7f9PADoAYwC8AF0AWwBMAMv/0P9c/6T/ef9g//v/if8PADYAFwD2/9j/BgDc/xMA1P8tAAkA8v9QABAAcAAqAFYAOgAjADoAzv/g/+z/sP+E/7v/mf/Z/w4AhwB4AIIAyABQAKIAEADb//b/kP8y/x//cv8Y/5n/4/8/AGEAlADfAFoApQA5AOz/0v9Q/zr/R/8p/5b/IgAYAI4AxgBkAJsAbwAVAHoAHwDN//j/uv+9/6z/zP+k/wEAXgD9/1UAJQD5/3YAnv/s/x8ATP/9/wUA7/83APX/JQAoAPj/OgAWAN//EACl/+L/yv+M/8//xf/2/+//EQA3AGUAWABxAFIATgA6AHH/sf/A/5z/t//k/xQA8P8SAHwAiwBKAIoAJADX/+X/sv/U/5b/rP/S/53/9v/1/yUAgwA3AGgAOQAVAD0AFgAPALr/nP+F/4b/l//1/+b/DwBqAGIAhABHAFgAtf+1/5D/fP/K/3X//P/F/x0AigBMAFUAmABkADsAKgDH/8T/ov/l/6L/y/+6/9b/ZABXAO4AkQBiAEAA/v/N/+//4v+K/17/Rf9b/zn/BgC3/wEAkAAqALQAaQB3AHUAWgDj/7n/sf9f/4D/sf+//+T/KwAdADUADQABAEkANwA7AGUAAwAnABsA3v+CAMD/CADn/wAAWgCC/xYAnf++/6//+v8VAKr/kgDz/1MATQD3/0wABQAmAAgAz/+C/37/iP+O/3r/pv8KAPj/agB5AF4A0wBqAIMAJgDr//H/Wv/T/3T/rP+Z/8X/QgAZAJUAMwCXAD0AdAB7AOz/PQC9/ycAmf9s/4r/X/+v/8j/BgDy/xUA5f9AABgAIABYADIAPwAsAD8A9v8aAKf/t//6/5L/y//I/7f/pv8HADYAXwCLAIUAcQAsADUA3P/l/6X/gv+F/9X/8P+5/0cAFwCAAIAAOwCJAFQAaADB//3/oP9X////fv+o/2f/lP/o/w8AawA9AHEAAQAoAE8AKwD0/8f/BQCO/8H/5/+//xoA/P/2/zQAYgBXAH8APABTABYAqv/0/5v/lf+w/9n/+P/y/x8ADgBZABUAQgAZAOT/XwDp/zEA6f+Y/8v/wP/r/+f/z/8AAF8ABgA1ACcACAAAAPf/4P/9//r/OP/P/7v/BgA0AO//lQAcAE4ANwBBACEAJwAuAMn/w/+6/+j/s/8tAPv/JgDb/wwAMgDh/7wAuP9+AEsAof8jAHv/qP89/0r/ZP+u/xcAWgBkAIQAwgB6AHwATgBOAM//+v/R/5//xP+J/8z/Yf+o//z//f9ZAHgAYQCOAGcAIwArAAQA8/9m/3P/iv9X/6H/3/9gAFsAigCfAIUAeQAUAEsAuP92/3j/Xf+Z/5H/DADw/zkATQBCAHYAz/89ALv/4v/u/7b/MQCI/yUAvf8zAD0AKgCfABgArgA9AH4ACACn/wAAp/+Z/37/gP+h/yAAov8yAF0AMAB/ABYARQDf/8T//P/4/5//zv/r/6v/HwDf/+L/BwD4/34AmAAvACYA1f/m/63/df/7/+f/EQASAHcAPwArAG0A9/8LAAMA4v/t/8r/if/p/87/s/8/AP7/agDKAG0AXAAQAPX/sP+K/9r/gv9E/4//g/+//zMARwCFAIcAgwCTAAMAEAD8/3z/Y/+V/8D/eP/f/+P/+v9qAHwAqgCyAJMAXwBAAND/6P+E/77/nv+O//n/Tv82ADIAIwBtAJ8AdQA5AIAAjf/R/4z/ev9h/2b/xP9Q/xAADgBbAH4AhQCuAHEAVwAzAAAAlv+2/3b/nP+F/7f//P/j/xgAHwAbAAQAcABNAJYASADu/y8AtP8HANP/wP/s/yIAIAAOACsA4v8rABAA1P8IAPX/wP/u/wQAu/8JAAQA//8TAP3/+//C//3/yf/g/xoAvf8wAEwANQAvAO7/SAD8/+7/KQCp/8T/wf/Z/+L/1/8xAPT/TAAyAD8AhQAcAFwANAArAMf/h//s/2z/d/+H/yEA3v/m/8MAAABUAKsAQQBpAAUArf+5/9z/6v/R/6n/qv+0/7j/CgDY/ygAagAgAFUALQD1/8v/AQABAMz/5P8sABcA5P9kAAIAVwAtAK//GQCZ/9L/pv+8/w4A3/8KAEQARQA0AHoASQAkAAkARgAqALv/CADT/6b/eP9I/3X/fv/L/1kAXgBRALYAnQBfAEkAVgBSAAAA+/+x/0L/Nf8r/x//ov8AADEAiQB5AKEAlgB9AHcACwDo/9//2P+4/7v/3v+F/6P/0v/P/wYAHwAkADoAUwB2AIcAlQCnACoAIwDC/xn/8f4m/xD/t/8FANz/iwAgAKMAvACIALgANQBNAOP/2f97/3z/e/99/9X/rP8HAOv/EABSAG4AOwA2AFYALwARAMb/HgCi/9v/7//U//f///9IACwAZgDc/w4A0P/B/+j/dv/O/47/GwALACcApQBmAFUAZwAnAMb/6f/R/wkAz/+1/6P/xP+4/9H/IgDx/3gANwBxAC8ABgBOAOr/SgAKAPv/z//R/6j/mv/w/7v/7v/G/wAA3v///+7/CgBiADUAegA6AGEAAwDP//v/r//y/93/5P/R/97/4P8fABYAOwCJABMABwD8/+T/AADG/7z/zf/Q/wMABADf//7/+f8lAHEAOAATADMA2/8QAP//o/8jAPL/AgAxAMX/9f8MAOz/3v/c/xYACACx/9f/9v/m/xEAOwBcACAAXwDBAH4ABgDk/+L/uv+G/3H/WP/2/mz/bf+z/1kAdwATASIBSwHoAG4AbQABAFP/Tv83/6b+Bv8d/8T/CQDh/30AwQDZABMBCgF5ALMAQwC//7z/7P4F/+X+Cf9R/2X/3v8NAKoA9gD7AP4A2wBTADwAGwBw/4//R/9U/2j/j/8bAOT/eQBfAIEAkQAxAJgAyP8AALX/XP/Z/3n/AAADANH/YwBOAEQAcwAtACAAm/9q/7//Wv+f/63/yf/E//b/jwB5AAsBxgDwAF4A6/8PAEP/Vv/p/h//Y/+D/xgAMgCgAPsA2QDxANYATAAuAM//Tv9L/1j/K/8//8n/l//4/1IALwCdANMAtQCHAHoA2f/c/7j/Q/9q/0z/jf9m/8b/awBDAIMApgCyAD4AZABTAOT/6P+D/5H/iP9s/4b/u//F/wsAggCSALcAZQC1AHwA8/8RAM//w/9P/3n/kf9r//v/+v8BAF4ANAA4AE8AKABSAFYARAAZADUAzf9n/6n/Hv9w/77/iP/o//P/TQCmAIIApwBuAE4ABgDd/wAAvP/l/7j/7//Z/5//2v8SAFsA5P9hAEQAwv9JAEwAJQBYAAsAv/8QAIz/ev/F/7r/wP/O/wkAHQAaADUAcwAIAC8AAwD6/xoAFgBCANz/LAB8/4P/wf+a/yEA7v87AMz/OABgABsAcgAIAPz/BAAJAP//LwAWABEA7v/O/8L/kP/b//D/9f8AAE8AEgAQAKUAJwAUACsAAADj/wUA5P+K/+H/x/+j/9P/vP/L/+3/+/9OADAASABpAFAAXwBtAP3/oP+g/7b/rv+A/9//CwALADkAaAA9ABIAPQDC/yEAZgDu/+X/0//a/5H/AwDu/83/CwDr//7/9P/s/ykAMAA1AIcAaABiAGUATAD9/4//t/9c/5r/i/+R/7//XP/g/+P/HwBXAIIAxgBlAJUAeQBFADEAtf+Q/5L/nP+Q/2X/lP/g/+H/egCZAKYAsABvACcAAADf/07/uP+v/2H/sf/B/9r/9v8rAD4AjACKAIQAawD4/yMA9f+6/6z/nP+t/4r/Zf/e/yoABQB2AC4AXACHAJcAugAQAMf/uP+H/yb/f/9j/03/TwBbAIgAoQCZALQAQAAMAAwA0/+F/7T/lv+2/3r/zP8WALP/3/+9/ykA3f8KAGIALQCdAFkApgARAOv/5v+i/+D/qP/9/+r/LQBAAFEAQAA4AEEAu//m/8L/wP+b/6P/0f8ZADsAzP9MAPv/FQBVAC4AHAD6/9X/tP+4/43/6f+l/9z/SQBIAF8AVACVABYALQBHAP3/pv9//6P/mv/B/7v/vv8KACEArgCSADwAgwAXAOj/6v/d/0MA3/+5/9P/rf99/8z/5v8KAIAAFwBAAI4ACAAOAPz/0f/k/5v//P/Z/3r/AwDt/wMABgA1AAYAGwA0AO3/ZADX/wUAVABHAAsAEQBqAN3/TQDZ/5f/iP9H/5H/hv/d//3/GAAGAEAApAB1AL0AZQAzAE0Ayv/W/67/P/+Z/4T/4f///7b/+P8lAGoANgCVAJYALgAXAAMAAADc/8f/sv/J/5f/+f8eAMH/ZgAHAEAAJgCw/wIAbf/o//b/v//3/1IAGwA3ANUAAgBDAB4A5f+2/7L/xP9p/xEAxf/+/6n/9P81ADIA8QBzALcAZQATAMz/a/+X/37/jv99/5n/if8ZADYAgADSAJ0AeABNAFkA5/+V/4r/gP9T/6b/xv+i/xMABAAxAHUAdQCfAHUAWQBfABMAz/+M/5n/cP9t/9P/vv8FAAYAJwBFAFwAGAAqABEAzf8fAMv/JADh/yQA///8/z4A0P8MAMv/VQDt/yUAVQDI/xgAAQCg/2z//v+o/zAAFAD6/zUANABxAAMAawDA/xwAu/+d/9H/ev/u/8b/VwAiAGcAfgB2AEEA4P8XAJP/0/++/8f/0v/r/xQACgCz/wAAGwCH/zkACgBVABQAUgBYAP3/RQCS/wIAzv+7/w0A5/8PACQAHAAVAFEA9P8uABYAvf+i/6D/8P/Z/6D/AwAvANr/XgA7ABgASwBOAFEAJwBKAAMAuv/L/3X/Z//H/5f/2P8UACsAOQA/AKsAQQBtAEQAKQAyAJr/T/+N/6v/Wf/U/7P/q/8GAF8AmgB3AOMAtQCLAFUAOACi/5T/Y//2/lr/Ef93/8D/UgCVAHsA1ACmAIYANwBGAAUA9v///4z/q/9v/1b/Zv/E/8X/LgB5AI0AfgCEAKsAXQBhAAQA0v/J/17/Qf8f/4D/hv8CABYAAQBwAG0AmgC6AIQAdgA3AKP/+v+r/xf/s/90/8f/rP+//wQA4v9OAGwAuQB5AFYAhwAaAL3/1f+Q/2H/tf+5/8//BgBWAG0AYgBeAF0AjQAAAMv/8P+p/3v/mv/r/8P/j/8OAEIAEAA5AA4AAwD9/+z/AQD//xkACADk//L/CQDv/ykAUAAuAAUA1P83AAwAyf8IAOH/wf/U/6H/w//K/9//CQA4AKUAKwCeAI0A9f+LAMj/0v///6//z/+c/+z/tv+k//z/AQAiAFcAEgA8ABsAzf8TALf/7v/9//b////N////1v8NAA8AAwD0/xkAOwAdAEEA0v8aAPn/w//3/+//NQAeADkAMQAkAOH/EADF/4v/7v/u/0QA4f9IAAYA1v9YANv/GAD7/xEA4P/x/+r/5v8oAIT/8v/p/xEA4v+2/0UA9P9LAIoAXQBCADAA7v+q/4z/l/+q/43/5v8rAP//QQBGAAAAeAA5AAUApwD2/wMAEABR/9L/af+t/8j/sv9UAPj/hgC3AIMAswBLABsAQgD2/1L/dP8h/0j/Qf+X/xEACQClADUAkwCxADoAeQAGAAcAx/+1/3r/e/+F/7H/EgD8/4QAbgDEAIEAOgBkAL3/IwC8/6D/of9I/5//Uv+3/7z/vP9eAFUApgCnAG4AbgB6AEEABgBYANP/v/+k/y3/d/96/8n/5f/x/ysAIwB0AE8ATwB7AGEAFgAaAPT/u//H/6P/mP+r/87/sf/O/xEAHQBBABkAPQBYAD8AUQD7/wIA9f/E/wIAmf/T/xMAk//+/93/LACZABwAfwA+AOr/DwCx/wMADwDm/wcA3f/I/+z/vP/X/zsAxf/X/0gADAA+AE0AHQDw/xgAIwAbAO//jf/t/13/ff8CAJz/+f80AAQAZAA+AB8AqABDADIAcgBVANT/uv++/2f/y/+2/8j/7f/9/wAAJQCnABYAYQCsACoAKADs/9z/lf9Z/3T/kv9u/63/4v8MABIAPAC0AI0A1QChAFkANQDI/9r/hv9S/4z/cP+e/5D/of/6////mAB8AGYAlgBXABAA+P88ALL/4/8MALT/AAD//wAA5/8VAPb/EQD1/xIAbgACABcA8P/m/97/5//c/6H/uP/C//z/AQAxADgANQA5APz/HwD1/wcAAADe//n/tv/k/w4A4v9LAEEAMgATABgAEgCq/93/+v/t/6T/q//c/9n/KwDS/zEAWQAnAIwAawCQADkANAAFAMf/wP+F/yAAbv+Q/wAAk//a/5r/CQBvAJYAhQBWAA4A7f/U/4L/qv9d/7H/0/+y/xkATACEALIAtgCPAHwA+f/9/73/c/+d/17/Y/+C/9j/uP9XAFoAhQDVAJ8ArgA1AFEAvf+j/3r/Of+B/2b/jv+8/ywAQgCRAKsAkgCwAHIAMgC1/3z/cf9n/0n/pP92/5f/FQAcAG8AlgCQAH4AjgA7AFUAFwDe/6D/Uv+G/y3/y//R/x8AhwBxAKIAYwCHAGYAIgCg/wQAsv9i/6r/Xv+x/+z/LAAxACMAXgBuADoAigD//5L/DwB4/6T/gP+p/8D/zv9DAB4AYABRAE4AQwB3AAEAEgADAJf/2P+D/8r/tv/0/+f/CQAxAPn/pAB9AFkAOQAeAC4ADQC8/8r/nP9L/+D/df+e/xAAEABrAJIAvwCcAF8AXQAwAFD/2/90/0j/vv8l/5z/nP/4/+T/PQBkAE4AHAGuAOIAPAAWADMAUP+X/zf/Hf+e/4b/2f/6/+T/WgB9AIoAlABgAGQAOwBQAAUA8f/7/7L/q/93/7D/lf/P/9D/3v82AML/gABbAGgAbwAcADwA3/8aANz/n//2/8z/rf/f/+7/6/8IAOL/QAAIAO3/GAAeACoAGwANABwADgCH/xAA5v+R/xsAAQBIAN3/NABaAA0A4//R/93/cf8TAPH/BABNADgAYAA0AFoAXQBKANv/kf+d/63/sP/m/+r/oP/6/+r/BwB7ADsAgACAAO3/JQAXALH/qP/E/7r/eP/K/+P/3v8BAFEAcwBaAGgAGQAsANj/u//p/6//uP+h/7f/r/+3/3kAbABjAMcAdACKAGEAJwD4/6v/n/9Z/33/Xf/G/+3//P8lAAUAZwAvAHoASQAiAB4Azf/p/8v/2v80//T/+/+0/ygAFACUAFYAUgBOAB8AFgDP/7f/lP+B/9v/2v+S/+X/DwAtAGkAcgBDAGgATwAZABAA2//o/8T/0f+l/9L/8P+//x8AJQAyABcA3v8XADAA1/8NAE4AzP8jAPb/tP8VAPH/EwARAMj/xP/0/w0A8v/1/yIA5v8rAEoA8P8iABsAs//c/wQAAADz/+T/QgDX/+L/JgAgADcAFAAqAMT/+v8yAND/VQARAND/LQABAPb/+v8fAPL/rv/k/+T/8v8EAOH/xP8AAPb/5f8xABsACwD0/ywA/v/Y/+f/o/8aACIAGAAHAAMALgAMAE4ASwAiACIA//+K/8D/2P/F////BgAdAPT/NwAtABYAWwArABYAVAAaANT/7v/l/7z/fv+u/4n/h/8GAND/HwAGAAAApwBRAFEAUQBBANn/ff8BAK//8f8jAOn/+f/e/wEA5P/7/1IAQQBcAFwAPgBIAM//nv+2/yn/wf+///n/VQAUAH4ALABPAC0AEwAbAO7/MwCl/7f/yP/J/xQAsP8EACIABABGAPH/MQAtALT/LgDO//L/tP/x/1UAe/89ABEABwA4ACwAKwDr//P/2/8HALD/4f8aANf/5/8EAMj/8P9SAC4AUgDx/00AWAAaAHsA///7/67/jP+w/77/6v8DAAIA5/8hACwAAQAtAEcAy//G//L/nP/S/+r/5P8gAAsA+f9jACQAEQAyADAAUgASAC8A/f/D/+7/sf/6/+f/qv/c//D/1/8LADYASAA6ACoATwDZ//3/FwDL/xIA+P/X/5L/cP/j/+P/xv9dAFIAKwCcAF8AIQAFAOT/7P+3/7L/rP+3/6X/2v9wAEgALwBXAEYAMwBWAC0A8P/L/57/hP/M/97/+/80APr/FAD3/wUAQgASAAMA+f8NAND/0f/0//v/NQAGAO7/GQAcANX/IQD//43/FQDT/+T/OQDZ/0gAKADS/0YAAAD7/z4ASwBEAO//EQCv/3j/3f/F/+H/HwBMAEsAMQBCAAUA7f8EAPv/1P/M/+X/g/+n//D/rv/x/w4AMgBEAD0AXgBXAOn/BgA+AOX/GAASANX/yP/Y/w8AKQAHADcAUADE/yEA5v+P/5j/d//4/7n/CgAuAEMAcwAhAH0AYgAMAB4AGwDl/7b/iP9//5v/lf/g/+3/ewB3AHcAxgCIAIAA+//d/33/KP89/2H/jP+g/9//wf86AIIAfADuAK0AngCVAAUADwDp/2z/e/8+/2//k/+U/wAAQwB1ADQAmwB4ACsAggD//xEADQC6/2b/jv+U/3H///8iAAsAEQA+AE8AFwAvAIMAQwD2//3/p/8+/6z/of+V/yIAEQBVAIIASABAADYARQBAAD4AEQAJAJz/lP+A/4f/1v+q/yEA2/9aAEUAHABoAD4AZABLAEcA4f/e/wAA6/+h/7b/m/9H/7L/qP8jANL/aQCHAPX/fQAfAJAARQAeAPP/8//G/2//BQC7//L/9f8UACIA1f/e/9//9/8XAB0ABwBfAAcAIQA4AEkAeQAYADgAx/+k/7D/qv+D/3//q//F/57/9/9MACkAYQBtANcAWgBQAEgA7v8mAJH/nv+t/5X/wP+r/6X/IwA+ABMAvwBlAGoAfgDW//T/wv9j/2z/kf9k/6//0v/r/3cADAApANYArACeALUAaABBAN7/yP+z/5T/T/9J/3b/d//U//T/5f/s/2oAOQAVAKwAoABoAGEA+f/Y/+L/k//+/6n/iv8hAOP/y/+x/1kALQAjADgALwAlAA4ATwDp/x8Auf/4/+3/if8JAN7/6f/1/1wA/f8dADYAAQAmAJv/9v+4/w8AHgDs/xcAzf8oAAAAFAAAAAMAOgDS/7H/DAAFAIr/LgA8AAkA8/+CACQAyP9EANf/HwDu/xkARQDu//X/6P8iALv/3P/u/4n/nv+t//H/DwALAGEAawAuAJMANABXAB4AsP/o/3n/GQCX/37/8v/g//v/AABMACcAOgD6/ywA8P/j/yUA2P9NABEA8f8KACIADADV//P/mP8PACEA5P8NAAYA6f8UADYA/P8UAA4AIgAjAOP/3f+z/wQAHQBz/yYA5/+x/1QACAALACgA/f/p/2oASgD2/wsA6P/W/6f/xv/S/zMAsf/F/xYA2v9hAGkAcgBoAG0ACQD4/ysAr//6/+D/Yv+h/8z/zf/x/wYABADe/+7/1v9RAFMACACUAAYA5/8qAPP/AAD3/+T/BADQ/7z/HADR/0gAUQD4/08A1v+2//P/6P/Y/+T/4v8CALj/NwA+AOz/hQDN/0MA/f/Z/2EAsf9jAPv/7P9AAIT/u/8VAPr/3v+s/xoAJgCi/1UAHgAmAPD/1/8VANb/UgDK/wgANwDO/xwADAARADoAUgDI/wAACwDJ/wkA1f/n//L/wv/q/x0ACwD0/9H/GQDT//7/QQAaACEA+/9JAAcANgApAPH/+/8WACgAuP/9/6D/lv+u/4X/AwAUAC8APgBQADYAJQAYAEYAXgATABoAz//e/5L/of/Q/7n//v/8/w0A4/9CACoADQBeABsAHAAxAAgAuP8CAMb/lP/5/+v/3v8JADAATgAQAAsAIwApACQA/v8PALP/3v8CAN7/6f/W/yQA2v/x/xoABAAGACIARQDf////vf+0//T/1/8lABcAOgBiAE0AGgAUABYA5//Z/+H/rv+5/+T/5P/P/wUACQDa/zoATAAlAEQAVwA1AAkA+v/D//v/3P+j/9X/ov/O/8f/7v80ABMAgQBlAGMAawDf/yoAuv9P/8X/kP8CAOL/9v8WAPX/dABJAG8ARwAyAAAA+v/i/53/hf+k/9H/lf8wAPn/NwB+AA0AhQA0AEUAFQDm/zYAnv+c/8D/iP/C/9L/AAD3//v/VwAiAI8AbwBMAEUA0v83AMT/sf/U/67/h/+t/87/tf8LAPv/dQA8AB0AegARADkARADs/+f/DQDY/9v/nP/s//D/6v9zANH/QwA8APj/+//F/xwAyP84AAcAtP/K/8P/9P/C/zEAFwD//1cAUgBSAAEADAAoAOn/4v/S/8H/AwC4/+//DgACAFwADgDx//3/AQAPAOn/1//8/77/FQAKAOr/PADl/+f/CQAcAO//VQBhAOv/TwDQ/+L/tf+a//v/wv84AA8ABwAfAMv/IwAKAP//MQABAAQA+v/O/wYAFwADAP3/MQAdAA8ABAALADIA6v/t/xQA6//G//v/6v/T//T/2//u/9L/AQAoAA4AKADs/9//7f/f/xcADQAYADoA9v82AMv/NQBLAPv/dADS/xgA/v+N/7X/yP/O/wUAQAD5/18ACwAwADgABwAPAPD/DwBz//L/tf+F//r/wP/1/xgAEwBLAHwAGQB5ADYAIgAZAJD/6v+3/7L/1v/T//b/8v/b/1QAKgAFAHsA6P9PACQA3f/w/3//1P/E/9j//P8VAAwADgBLAIAARgA4ADQACQD6/8P/FADi/9H/u/+m/+j/kf/w/y8A+f8vAEMAuv8gAOT/lP9kAOn/DwAIAOD/TQAqAO3/FgApAAUAQwDe/ycADQCe//r/8v/I/9j/LADM//j/PADu/x0AJgAAAEwAWQDW/w8AGADe/9v/sv+0/87/1/8MABwABwAnADMATQAWADYA6f/a//z/xf/y/7f/y//R/+z/5v8VAD4AJQB2AO3/TAAtAN7/TAAHALX/u/+5/7X/EQAxAN7/u/8KABsACgBIAGAAQwAAAPf/u/8RAPb/9f/a/9L/CwCU/w0AGAAQADcAbABaAO//7f/B/9r/3P/9/8n/BwALAK7/IgD8//r/TABRACoADAD4/xEA+//C/8X/if/q/8//s/8xAEgAGQB8AFoABAAoACMACADa/93/nf/a/7v/nf/0/77/SgB0AFUAZQAoAA8AQQAjACEA9/+9/+P/av/F/37/pf8MAKL/CgArAGcAEQBkAE0AHgBhANL/WAAfAML/KwD1/+7/1/+w/wAAj/+A/wYAuP/l/9//LgBZADMAjAA6AEAAUgAiAAwA3f+a/8b/1P+O/7T/of/y/0EAJABdAHEAbQA+AEIA/v+5/7b/yP/J/3//z//b/+D/MwBQAIAARACGACIACwAPALT/8/9c/7f/qf/K/yYAvf8BACcAHgD+/xoAAQBJAD0AFABNANb//f/1////zf/l/zgAx//1/x0ABQDt//P/+v8oADsALgAQAPv/BwCr/7z/3f++/wwANQApAAMA1v8zAAsAHgBzAPX/5/8HAJn/sv/z/+7/GAD2/w8AKQAVADAA//80APP/tf8KACMA///b//T/vP+d/8j/EwDS/wQAdwA6AFsAKwAcAAMA3P/q/wMABAD5/x0ABAARABUAEQAKAA4AMQAKALf/xv+M/5n/1////zAA5v8yABwAzf9QAA0A0f8nABkAHAA0ABwAIwDo/8n/6P/D/9X/GwD5/8//IgAUAMr/DwAaAN3/JwAkABQAGwAQAFwAPQAUABMA7/++/7j/vf/I/wsA9/+5//j/KQA/ADMAFwBhACEAv//v/83/zP+a/+7/AADH/wYAKQBSAP3/FgAFAAkAMwD8//r/6/++//f/FgDI/0AAFwABAC4A1P8aAN7//f8QACgAVwAdADsA3v+8//X/pP+w//r/IQAWAAAAEAAIABAA6f8oAOP/7P8AAK7/QQDi/zEAKgASAB0Ay/9XALb/HADd/8D/8f/k/xkAxv8hAMf/OwAEAMb/OwAiAFgAJQATAMX/OwDN//z/SgDe/2cA3P/0/wkAyv/V/6f/7P/p/+r/JAAGAOn/BQAUAPH/QAAMAPD/JQAQAPP/1v8dAOr/t//f/9P/AAD1/zoAWQAOAB4AWgAyACEANgCr/7z/2P/B/73/xv/y/+b/BAAmADgA7f/4/2MAIgDz/zAALgDy/zIAIQDb/xYA0P8aAPP/z//1/7T/+v+w/+j/FQAqAC0AyP8wAMn/CAAZANv/BQDz/wcA0f8QABcANgAyAA4AgQCx//T/+/+t/yYA5P8lAO//u/8LANb/+/8fABYAVAAwAOH/GgAwALj//f/N/8r/+v/r/+r/4/84ADYAVgAiABsANwDY/8P/AADj/5H/1f+7/7v/HADx/0IAWgALAGsAcQAAAN7/9/8AAPL/2//e/8f/f//r/73/xv9jACYAPwBJAJkAZgBTACcA9P/q/0j/rf9t/37/g//Y/xQA4P++AHsAugBhAHUAPgDN/yUA4v/S/3T/1v9W/2//1v+b/zUA7/81AEsAOABUACQATQAGAPH/RgA9ACsA0v8EAPz/Xf8iAM7/0f8NAL7/yf+l/wUALwBgAAMAYAAyAAcAaQDa/w0A3//z/+7/xP8UAPb/9P/L/4r/7P8zABIAVABDAEwADQD2/wMABQAOAOP/DgCj/8j/4P/w/wYAzf8JAIf/1/9DAPH/PQBwAC0AWABUACcAVwAIANb/7v+i/5z/bf9Q/7L/+f8nAF8AWwBEADQAQwBdAD8APQArAPj/nf+R/+b/e/+2/9//uP8FAPD/WQABADkAbQANAEgACQAdAAUA6P/M/9L/6v/5/yoA0f8JAPD/5/8QAAkAVgAeABUAMgDw/8r/1f/C/+j/x//N/w8A4f8IAB8ADwAWAA0AMwAzAAUA7v8OANz/yv85AA0AIABpAB0A7/8LAOv/2P87AMn/4v8GAGP/rv+4/+f/7f8iAD8ASgBWAPP/cwA1ANX/BgDK/+j/+f/Z/xEAHQDN/+//HQAIAO7/1v/t//H/3f9IABkAAAAeAB0AJgD9/zgA0v/a/zMA6/+6/zEA+f/p/04ABQACAOH/9/+T/83/1//J/+r/9v85APz/XADx/1YAcQAdAFgA+P8SAJD/uf/W/+r/wf/7/+X/rP9SALr/PAAdACsAdAD3/1sA+v8zAA8A6f8xAPf/7f+5/7D/wP+Y/8r/7f/3/xwAFAA5ACsALAD//xAAPgD6//H/IgD9/7//6/+K/9v/DQAQAEoADgBrAB0AGQAeAOP/1P/r/+v/0v8BALz/OQAEAOv/TQAHAO//1/8vAOj/8P85AA8A6f/J/xEAuf+n/xsAEwAeAD0ARgAlAAAAEwAKAMv/2f/z/+b/GADe/+D/DwAMAD4ACgAUAO3/vv+k/9D/DgAIAEAAFAANABkASAAtAE4AeAD6/wEA+//D/7L/g/94/63/kv/s/y8AAQBPADsAVgB0APj/CgD3/7j/6P/6/y4ADQDV/yAAy/8XACMA5P9FAAEAFgBUACAAFwAxAOv/6v/i/6P/v/+2/5D/w//O/5z/0v8bACEAcQB5AIEAkQBBAF0ABgD7//r/rv/3/2X/gP/I/7P/4f8DAF4AFgAcAEcARwBIAOz/AAD6/9n/9P++//D/8f/Z/04Az/8QABUAFQBVANL/AAAHAAgAtP8nAOH/3f89AOr/IADJ/xAA4P+l/ywAGwARAAsACAD6/wMA/f8XAAgADwBHAEoABwAHAOf/1P/N/4v/2v+s/zoA6v8AAFQA8f+OAAwANQAkABIA2v/m/zwAnP/c/9b/5f/h/7v/3v8SAN7/OgATAPX/WADS/2MA5P/v/2YA8/+fAPX/3/8+AKL/4f/l/8v/wv+3/8v/3/8AAPv///9YAEYAUAATABkAJADQ/zAA6/+5/97/sv/S/wYAWgBcABcAFgDm/7P/2f+9/yUAIADx/zoA+P/l/yIAtv/C/zQA4//6/xgAHABUADAAQAAhAO//CQD3/9z/wv/X/wAA0P+//93/HQATADYAaQBHAEAA2/+K/8D/xv/E/yoA4P/b/yQAwf8/ACgANAB4AOT/CADi/9//4//Q/zsAyf/e/xoABAAyAB0AEAAkABwABgD6/wAA5//5/+b/CADV/8L/LwD2/wMATgD8/y4ASwDB/7b/FgD8/4z/3v8ZAMj/7f8tAFUAJgD6//3/1f+6/wkATAA6AOT/MwAAAKD/z/+6/xwACgAfAA4A+/9GAC4A9f8CABgA0P8FAN//WQADAMv/gACs/+7/6v8tAEcAAQBRAMP/9v+3/6n/xv/A/6v/2f8IAPD/WABBAHMAKgDl//v/+v/T//H/BAAEADwADQCJAMr/9//j/5n/MwC9/zsAIQAOAAAA6v/7/83/DQACAO//5/8qAM3/9/8OAP//OwAAAPD/3f8pACIAMgAVAMr/3//S/+3/GAD1/+X/PwDd/7//JwAHACEAAQDY/zcA9f8AABMA5/8MAPf/MwAHAP//IgDs/+H/FQAsAPr/BgD8/8z/1P/6/wwAEwA6ABgA1/+3/+f/2f/K/+n/8v/x/yAAOgA1AFYAJQBJAOL/DQAdAMv/KwDW/+L/5/+Y/93/p//F//7/BwAgADAARgAWAEMAOQAEAFYA+f8mACUAAAANAHb/z//J/4r/p//W/wkAKwBmAIcAXABEAF4AAwD0/8f/hv+0/3L/xP/d/6L/BAAjACgAYwA0AIUASQDb/0kAEwDj/+X/5f/K/5n/7//b//T/BQD4/ysADQAbAAYAQgATAAcAAADj/zYABwAHAAMACwDw/+D/sv/2/yYAsf9ZABcA8P8CALj/+//z/9b/3f/b/8r/ZAAuABAARgD6/zQAFABEADMA6P/O/9H/vP/i/y4A/P8VANr/9f/N/+n/CADI/9z/CwAaAAgAfAD4/wkAIQD1/wkA3/9KAP3/8f8xAAUAFQAIAPD/x/+e/+n/+P/b/00AUwA5AB8A0v8XAN//wv/6/8L/uf+l/+H/4P/s/2gAQABPACUATwA9AAAA+P////7/tv8FALH/u/+x//P/AQDo/5YAEQByAEEAHQAdAJz//P/Z/8z/2/8eABQA4/8EAPv/3P8jABoAz/84ALb/FABDANf/OgBiAOn/7v8IAKP/5//h/+L/5v8GAO//5/8RAJT/XQAYABEAiAApAE8A5//o//X/qf/E/9z/7/8YANz/7/8AABwAOQAnAEQASAA8AAAAOgC//7n/1f+h//7/bv/S/9r/EgAlANP/WQARAEIAOwBAAGQAFABRAAwA7v8bAOD/yf94/5P/hf+S/wsA7/9IAB8AJgBEAP3/cABJAAAAAQAnAOD/h//Y/+3/CQDW/wkAMgAAACsALwA3AAgABwA3AOP/xP/8/8P/rP+t/6//HwD8/xgAhwAnAEIAUgDt/yMA/v+9/5T/qv/5/9T/5/8UAOz/JAA1AEgAMAAfAC4ALgA/AAMA3v8NAMv/kP/r/7v/1f/p/4z/CQD+/ygAWQBPAFsAVAB1AA4ALACv/4z/rP9k/4z/w//g/+H/XAA3AD8AdwALAPP/IgAeAPP/ggA8ABkAJgDP/+X/qf/I/87/yP/L/+P/AQDC/w0AQwDs/xcAIADu//b/RABWAA8ARwD4/x0ANADT////ov+y/5r/xv/o/xoATgAAADgA4v8LADsA7P8JAAkAuP/5/wIA4v83AOX/OwBFAP3/QwAJANr/uP/0/97/vv8YADcAFgDp/0AAHgDe/x0A8/8DANL/sP8WAAEAKwDa/93/5P+q/yQA2/8DADkAUQB7AFQAIgDI/9T/p//f//L/u/8XANn/m/8nAB4AHABhAIcAhABBABkAwv+9/4X/nv/R/8f/zP/z//7/0/8NAOD/JwBpABUAZwAlABwAIQARAPj/IAAsALv/5v8JALf/9P8sAN//MQDi/3b/DgC3/7//LQD2/wcAIAAQACQAAwArAB8ACAAkADoAAwD///n/iP/N/9H/BQAwACYAUgBNAAQA2//i/77/3P/+/+b/0f8EAAYAIwAFAN7/VwAPAAMACgDX/8T//f8dAOn/XAAeACIAHgAHAAQAyf/Y/8r/AADY/xsA3P8TACAABwAvALX/JADs/wcABwDR/xwA/P9KAAcA/v8EAM//1v/g/zsAHQAIAPv/AAApALz/7P/r/7j/FwDB//X/PgAbADMAVAA+ANf/BgABAAkA/f/Z/wAA+P8nAKL/2P/6/8n/TwDn/wcAGAD2/0UAzv8TAP7/2f/2/wgALQDq/zcA3v/s/wUAEwBbAOn/HADs/9T/AQAJAAgA6f/a/+T/7P/z/wYA6P/r/w0AHgDj/zcACgABACcAvP9PACIALgAdAAsAJACR/83//f8gAMv/AwCk/8b/JACW/y0A2P8zAG4A+v9yADQAGQDR/7T/DwDF/yQAlAD3/xEA/v/v/9j/wP/k/8P/1//A/34ADwD+/1MApv9NAPP/uP84ANv/5/8LACoAIwDW/wMAyf/c//v/AABjAK//LQAWAMb/VwANAEQA9f/a/8P/3P8KAOD/BwACADgA7/8EAB4AGwAIACUAYwABAPP/zP8XALr/nv/E/53/7P+w/x4ACQD6/4MANQBCAGoARwBDAD8A9v/J/7//h//K/8j/9//M/7P/+f/F/xoALwBVAGEAaQB3AAkANQDQ/+v/sP+l/+v/bP8MALr/rf/9/xIASwAuAGIASQAlABsABAARAPn/BAD7/+X/EAASANb/nv+e//L/EgAjABsALgAIAOf/6P8HABcA6P8XABIAJwD2/wUAGQD1/+//qv9EAOX//P8vAMj/PQDn/8v/4f8ZACUA/v8fAOj/9//l/z8A6f/p/z0Ayf8dAMr/t/8MABEAFQDj/wcABABlACsA/P9RAOj/IAD//wUAOQDY/7T/w/+2/8f/KAADAPD/9v/H//7/HQAfABEATQAqAAMAMQDg/+L/AADK/9L/LgDr//X/CQDE/xgA8/8oAFoA+/8cAPL/SQCr/+7/OACl/wkAjf/3/z8AAAALAC0AOQApAFwAz/8RAOf/3v8OAM7/KAC2/8X/xv/A/+P/x//i/9T/ZAA7ACUAXwA9AGgAUwDo/w8A9P/V//3/1v/F/8L/yf/I/xUABgDL/zMABQAAAF8AMgAGADIA4f8LAAIA4P8hAML/wf/m//7/JgA1AE0APADG/8P/nv9//wAAzP8sACYAMQBBABsAVgDv/0MARgABANn/0v/E/7X/BwDf//j/wv8eAPv/IABmANj/UQDe/8//9/+7//v/9v8SAN//HwAxAPT/OABGAEIAJQAaANT/v/8KALD/z/+8/8v/+P/r/y8A8f8OAEgAKABJADMAEQBJACsAlP+w/5D/xv+2//P/dgDF/ycAEwAKAD0A8v9JAPL/GAA1AB4A7/+u/8D/0//m/5j/RAAqAAAAXAAuAEYA9v9fABQAGgDn/3b/qv+K/9z/hv8iAAUA1v+jABIAegBLAOT/HQDk/xgAOQDr/9z/4v/y/8//3P/L/9f/8v+Y/y8ANgAAAEgAIQBOABUAOAD7/7H/DwASAMv/5P/a/6b/4f+f/x0AOgBKANUAQACLAAAA6f8NAND/8f+1/6b/iv+//6v/h//R/97/HQA3AGMAjwCVAE0AGwA/ANb/8/8KAL7/0f+1/8v/mv+i/yUACgA4ABYAPQB0AC0ARAAlAPD/3f/T/7P/7v+g/6H/9//J/xEA9/82AHAASgBkAFIAHAAEAP3/CgC1/3//3f9f/9r/6v/S/zAA9P9kAAwAGQBWAAwAAgBQAP//1v9OAM7/DADz/+f/GADb/9z/4f8sALf/9f8KABYADADT/20ACQAlAFMAFADr/+3/wP+g/8P/wv8OALv//f8VALj/LwAoADMAbAAdAAAAUgA3AB4AMAAcANz/qv+w/2n/uf+4/7n/AQD6/14AOwBqAFsAOgBjAN7/0v8tAMn/m/8KACMAr//R/xEAqv/X/9///f9XAFYAWQBpAF4Ay/8IAOr/oP/j/6b/5P/D/wAASAD2//b/+P8HANv/DgA2AOX/+P8gAD4AGwDq/3QA2v+3/xgAiP/m/8v/5P8jAAAAHAASADgAHgBhACMATgAQABAALgCZ/+n/rv++/27/rf85AMz/NAAgANL/FAAqABgAUwBKAB4A9f/f/9j/9f+1//T/QADa/1wA1f8sAFEAwf88ANv/7/+O/87/+f/Q/04ADQBZAC8ASAAPAAYAFQDd/w4ApP/U/6r/n/+3/6r/CAAkADYAMQBlAIEARwBSADkAvv/G/8D/wv+w/4v/FADj/wkAIgBLAHMAJQA7ABEAzv++/w4A8P/T/+b/2f8CAK3/5f9pADQAEwBtACkA8P8FACUAy/+f/9j/z//E/9f/EQAHABEA4/8XAE4A2/8+ADMAGgB0AGMAy/+Z/8H/wP/w/8b/JQDz/9v/8v8qADQA1f8yABcASQDA/7r/BQC0/wYA4/9HAD0ACQALAF4AJwDb/yMAuf/Q/+L/GAAvACQA7f/e/xsA7/8LAN7/GADO/7r/CAADAOT/r//Y/4v/+f/r/zcAigBYAIkAWgBdAAkAGwD//+n/8/+S/6H/mP+V/4z/8v9KAEsAKwA1AA0AJAA6ACIAHgAVAFsAu/8QAPz/p/8KAK7/8/+1/woACACn/+H/tf8AAN3/NgBWACoAiwAiABEA+P/6/zAA5f8QAOz/sv/x/97/6P/Z/0YA/P8cAIgAz/8LAPD/x//w/xIA+f/D/w8Ayf8pABEAAwBaAOP/0v87AMT/x/8jAO//RADe/xsAGgDt/ycA0v8lAM7/BgD5//L/TQC+/9D/uP/V/7r/YQBOAO3/SgAGAEQAMgDr/w0AQwDl/xMA4f+s/wYA4P8SANX//v/2/67/6f8LANv/5/9uAPb/GwBIABAAJgAcAAIA5P/w/7L/7/8cABIA4f8BAOj/qf8SAAMAGgD8/wsA+v/2/0oAUQBHABoAWACm/83/1f99/wUAw//V/+n/FgAuACsAGAA3ACQAFQAkALn/IQDx/+j/KADI//7/FwDQ/8H/+/8AAPr/PQAwAAcAQwArACIA+P/C/wgA7/+2/+T/nf9h/ykAuP/+/1MAAgCEAFoAiwAVAAoADgAkAAgAbP8vAJT/2v/n//H/SADG//n/qP8jAOb/RwA5AMz/MgDL/xoA/f9OAFwA5/8WAP7/qP+w//X/yP/l/+3/SAABAO//OwDx/y0AKwD8/+X/7P8BAA0A3v8eAC4ABgBCANv/MADy/9H/FADR/wMAyP/M//H/3f8CAD8A6v88ABgAzP8ZALb/CgDz//r/KgD9/zkA5/8TACoAFAA9ABAANgAGAOf/PgDE/3n/zv+5/8b/u//s/8r/8v8fAEkAdwAWAG8ASQA4AFoAIQDP/5f/oP+w/9///P/+/+b/MAD//9r/+P/k/yUANwAsACEAPwDJ//T/7/+5/zEA/P8kAP7/EQAkAP7/GwD6/wwAyv/v/9f/pP/p/7H/2v88ACUA8P8sAOv/FAAsAEMA9v8xAGQAAAAOAM3/5v/1/+7/3v8PAO//t/8FAM//HAAlAAsAMwDv/wMADQD1//f/+f/T/yUA3/8fAOv/4/9RAOn/cwAQAPP/JACr/wkArf+W/9H/3//i/zIA4f8UAGoAHwBYAPH/IABdAA4AQAAhAMP/2f/k/7L/1//f/9n/6P8OAPj/CAAqAMn/AAApANv/CwAIAPv/RgAfAPj/DAAhAOH/w/8AAOr/4/8AAAQAFQD2//j/CgAjAN3/IQAmAEAAXgAXAPn/yv+2/9z/5f/6//f/AgAGAJv/4v8NABcAbAAaACIAAwDI/wEADwAEAMb/1/8OAOb/ov9OAOH/wv9+AB8AJAAWAFAARQDv/wQA/P/L/7b/BAAAAMX/yv/V//H/z/8NAD4ADgATADIAPQAsAAEABQAgAOL/0/9IAPz/tv8HAB0A+P+4/+T/q//F/1cAvv8fABkA7f8uAO7/WQAYAOj/TADF/ysAFADP/zgA0P/l/w0Awv8SABAADQAWANX/4/8KABAAEgAeANz/6f/M////KAAfABgAHgBtAN//AwArAMf/zf+r/wIAOQDP/+H/4P+g/yQA7P8KAF8Apv8kACwAOQAQAPv/QQAWAPv/7P8MAK7/9f8AAND/3P/4/zMA4v8RAPb/WQAGACEAbQDE/0wAxf/J/9L/wf8GAA4AKwDV/0MAHgDc/wAA9f8WAND/zf/7/+r/8/9LAL3/BwD4/7H/WgDc/1UAGwDw/1YABAAOANv/FgAhAOr/EAAQAKv/1P8VAJ7/6//i/+b/JwBUAPb/QwBuAJr/dACy/5//UwDl/ykA2f8FANf/4v8hAO3/NAAZABMA/v8KAP//2v+9/7j/BAD3/ykAFgDi/xEANgA0AA4A0P/g/+D/AQAHABgA+P8EABoAnf9WAEoAAwBYAN7/5v/r/+H/7f/n/9r/2v8KABYAGgBBADwAwv8sAN//rf8YAMT/AADr/w0AAwAAADYABwBNABEAFgDc/wIALQCi/xUA+P+I/8D/AgDk/9D/TAAmAAUASQAtACcA6v8fACgACgD3/y8A4v+T//T/4//f/7z//P8GAAMAIQAkAEwABgBdAAAA0f9SABcAGQD0/87/1v/N/8r/pf+6/9//+v8MABgAEgAfABcAIgAYAH4APgAEACUA9P+u/67/IgCZ/+n/7f++/xIAnv9DAA0AVgBYAP7/ggDZ/zcA8f/1/w8Aaf/2/+H/3v9qACcA8f80APr/5//5/9f/yf/l/xEA7/8+AOL/+/9JABIA/f+e/+j/6P/R/xMA//8fAAYA/P9LAPH/u/9QACYAAAAxAEIA4f/p/xYAAADx/xAAGgDu/+L/pf/j/9D/s//3/xAA3f/4/14AKgAcACIAMAAJAB4ACQDw/xoAv/8vABsA/v/5//T/rf+9/yAA4/9BAO7/PgAJAOv/EAAPAAcAn/8JAJr/+P/m/+P/EgCm/0AAHwAsAHUALADo/xsA4v8OAAkA+v9fAAgAHAACABcAuf/T/8b/nv/p/9D/OAD7/y4AGgD+//7//v8LABAARQCy/xMArf/m/zAA5v8JAPX/PwDy/xIAFAAGAOX/DwAXAPD/IwACAHcA0v/u/yMAu//r/9v/5P/4/yoAtP/9/+z/zf8KAPb/dgA6AAMA2f8mADcAu/8KAMP/jP/y//X/JgD7/wYAHwBHAEcAIgBOACAA8v+w/+n/tv/e/xIAHABgAJj////T/9L/KgDn/ycA2P8+ABcADQD4/zAANADM//n/lP/4/9r/3/86ANr/HQAiAN7/+f/+/93/XAA0ADQAOADt//D/5P/7/x8ANwCH/9//2v/C/x8A4P8lANr/GgA6ABsALwA/APf/m/83AL//0P8jAML/CAAEAB8AKgAOAAwASwDx/y0ACgCT/+v/q/8RAMn/1/84AOr/TwDX//T/FADx/zUAHABRADYAHQAVAOD/nP/Y/y4A5f+Z/8b/2//w//b/NwBjAA8ARAAsACcAKQDC/8r/8P/q/+r/7f/l//X/AAAxAA4AMQBHAOf/EwDG/wIA5//o/+r/3/9kANj/8/+8/+7/4v/w/0wA0P8uAMX/PgAjAPj/XQDG/xYAxP8DACUA4v9MAP7/8v/8/xwAAAAlAKr/2P/3/7n/PAAAACgAKgAmAEUALAAFAPj/+P+h/7P/nf/+/9H/0v8fAAIAOwD0/04ASQAtACMAIQAIAKT/5v/S/9r/kv/F/+7/8f8mADYAWQD4/7IABAD+/40A5f8UAKv/2//1/8n/7v/Y/8T/0P/7/8P/7P8JAB4AbwB8AB8AEwBYAOH/sf/y/9v/t//l/73/EwAIAML/dQBGAAcAHADd//b/2//7/0EA+//x//n/4v/N/wAA8/8KACQA3P8PABwAHwABAAAAGgCQ/8r/YAAmAPn/agAmAPv/4v////z/p/8NANL//f/P/87/DQATANT/AgBvAM7/lAAJAOr/VADm/0EA2P8AALD/qf+W/7j/2f/N/1EACAAuAAwAKgBiAJwAkwBXACAAo/+b/4H/nP9J/+z/2f/O/0MAHQB4AB4AaQBIABwAMgAGAM3/sP8FAJb/5P/K/7f/GQDs/87/9f8EABQAWAA9AGIAJQAqAAsAEwAtAMT/AADX/7n/wf8FACcAFwAlAO//+//k/9v/6f/Y/8r/HgAEACIASQAOACQA2P8UABMAAAD1/8b/IQDQ/////P8VAAMABgATAKv/JQDK/x8ARgDX/ysA1v8dAO3/AAAyALD/9f/Z/woAJgD8/zsAOQAwAAcAJAAOAJ7/+P/F/9z/FADq/w0AAQDu/7H/JwDa/+T/QwD0/3MADgAPADUAuP8/ANb/2/8lAPP/9P/M/w8Atv/M/zMA6f9DAFsAIQBAABcA+f/w/4j/fP+z/6f/BQATABIAaAAQACoAXwAcACAAUgALABcABgDN/9r/nf/O/wYAwv8HAAAAn/8vAC8A6P+FAM3/5P83AMX/GwANAAUA5v8dAAwA6P8OAN3/NgAJANb/LgD1/wAABQDr//v/6P/+/wgA2P/9/1QAxP8AAB4A2v83APP/PgDu//D/yv8DAC4AxP9HAML/RQADALj/WgC4/+v/FQAAAPb/5v///xsA8v8IADAABwA1AOX/NwASAPn/AgD0/7P/qP8AAJf/CQDa/w8ASQDZ/zIAJgARABUAWgARADoAKAAhADkAkv+l/8X/zf/W/+H/3v/W/9D/HQA5AA4ATABJADAAGwAMABsAGgDc/8v/PwDy/7n/AADC/8T/s//t//b/o/8wAAwAXwA9ACgAoQDg/xYA9//m/+D/FgADAM//MwAJAOL/zv/l/73/zv/h//T/HgAmAEMAIQBCAPf/BgDx/9r/CAAeAO3/4/8JAKL/6v8hABIAFwCQABIAvv9xAIv/1P/u/53/yP/B/wEAKQBlAP//VQAJACYAPAAFAPT/tP/h/7r/KwDZ/+H/FQAwAB4A9/9EAMD/UQAGAN//RgD0/0AAwv/Y/7v/jP/z/xwAVgDe/zoA5P+v//L/1f8hAPf/RAAhADQAGwDV/z4AGAAZAND/8v/O/8//DQDO//v/BwBSAL7/+f9DAPT/LQAOADIABADd//T/AADO/ycA/P+8/0YAm/+0/zoA5P8eADoAGAD3/+n/UgAAAAwAUQDd/wAA2P/G/wUA0v/Y/6v/HQDq/73/gAD8/xwARgDn/xsA/v8zAPf/HAACAPT/IgC5/yEA///5/+f/7f8MAKD/8v/B/wcAVgAwAD8ABQApABYA3f/q/8f/vP/P/+//EgAJAEkANgAjAPj/4f8NABIADgCp/xUA2/+o/z8A/P/p/wAA9P/l/wEAFQATAEsAUAASACUA///c/x4Azf8HAOz/3/8RAKD/JAARAOn/AADX/xkA6P/v/wUAEgAYALz/FQBeABcAQQAiABYAMACb/9T/GgCh//b/tf/w/ysAvf8lAOr/7v8QACMAAgAdABwADABvANP/YQC//7n/KgDJ/yUAuv89AOH/4P80ANH/EQDs/+v/8P8RAO3/SwAEAD8AKQDS/+7/uv/8/wIAIQDA/zsA+P8AAGEA7f8cAM//1P/A/+n/zP8ZACQA5P81ABUA9/8SADoAv/8FAOf/+f8GACoAOADM/5AAAwAVAAgA+//S/7H/EgB//wMAy//f//D/CgAMAAEAXQCo/ycABwDu/xAA/f8hABkAWQAdAFkAFwDv/xsA8v/M/9b/RwCk//z/SQCT/9X/mf97/+L/s/8bAG8AIwAnADYAHwD5/xMAIwApADYANQArAEQAyP/q/9D/Wv/a/+z/PQBQACIAEAANAAMAtf/K/7//+P/S/8j/6v/c/00AIgBDAAoAMwANAAgAfwAEACEA8f+t/wAAov/R/wsA2f8zAD8AEgAFAOL/IwDf/6X/KgDi/8P/bwATALr/OwAHAOD/LwD//zYALACk////zf/J/+z/zv9DAP//PgA7ANP/OgAGAC4AKgDn/+3/FQDs/6v/5f+z/w8A3v/m//D/xf8PAAIARgBIACcASQA0AAUAIADV/87/+P/K/yYA8P8lAM7/3v/Q/53/VAAFAGcA9f8BADAA1P9AAAAAHwDJ/9n/5v/w/xEA6v/0/8b//v9FAA8ADgAmAAMAJgC3//X/CADp/0cA2P8qACMA4f/c/93//f/X/w0A5f/J//3/KQAvAC4A5v8/ACAA/v/6//f/HgCZ/+3/2f8OAFIA5P84ABcA6P/h/wsABAAoACUAQwAZALb/AQDD/8//vv8AALP/p/8CALD/7P9NADkAIgC7ADIAOABMANz/RgDX/+L/vv/Z/wMAtv/2/+3/wf/R/wkAAADj/xMAYwAfAEoAOACd/9b/7P8IANX/BgBKAOr/KABQAAQA6P8CAP//t/+p/wEAPAANAA0ACgDQ/9T/BgAFAPj/DwDy//b/TAAPAAkAEgATAA4A4P/Z/9v/GADV/yYAPADf/wQA0/8DANr/9P8gAPH/EgAVAAcAAQBBAN//AgDs//L/6v/s/3gA1P82AA0A9P8aAK3/FADJ/wgAx/8aAP3/gv9AAB8AGQAhAEgAyf/u/0YA7f85ANr/4v+l/8r/2v/6/zgADwBaABUAMwD3/wAAHgDx/wEAqf/N/83/GwAnAAAAJQAYAOf/0//h//7/VQBNAGYAQwDe/97/6v+2/6//3f+0/wkAJQAFAA4A6P/Y//P/BAAPABUAJQAOAM3/+//8/wIACgAtACIAGgBLAOH/DgAxACwABAATAOr/3/8bAH//nv/k/7r/RQAIANz/KgCe/1sAKADi/4AAoP/7/wIA3/8KAN//PAAUACgALAALADoAKgDg//3/3P++/93/nf/4/9b/wP/s/04ADAD9/1gA6f8jAP3/WQAqAOT/MADW/wsA7/8JABQA7P8AAPv/9v/K/xgA9/+v/wMALQDC//X/bwDs//z/AwDd/ywAx//t/wMA9v8MAOP/JQDZ/wwAKQD//z0AHwBBAAMAJADA/+X/EwCt/woA5/8AAP//JQA+ANL/CgDe/8r/1P/F////6v/1/0QAFQD//wUAAABSABQADwBdAO//7v8XAAsAAAAEAPX/3P/e/7j/5f+8//f/QADy/xAAOgAPAM//IQCy/wAAewDO/wQABAARAOz/z/8nABcAGQD7/x8A2//k/xQA8v/9//T/GADH//j/BADj/w0A+/8bANr/EQAuAA4AMwDS/xQACgCM/0UASQDv/0kAJQDG/7b/uP/g/wgAzf/X/1MAbgDm/y0AfwDi/8n/EgAHAMf/+//d/9D/z/+h/xQAJwASAD0AFQDX//X/CABJADcACQAJAND/7//l//L/BwBVAL7/vv81AK3/XAAEAPP/PAC1/xAA7P8fACcAxf8VAOr/AAA/AM7/FADx/9P/GwD5//b/3P8mAOn/EgAmAM3/+//t/0oAz/9kAEIA4v85AGf/LwDr/7D/TwD/////CwABAO7/5v/0//3/6P8LACoA8f8AAD0A9P/5/wgA9P/d/73/MgAIABwASgArAAMA+P8IAJ7/q//Y/9v/5v8aACgAz/80ADwAOQAwAOH/9P9CAOb/MgAKAMn/MwCu/wcAxv+5//X/4P8TAOr/EgDm/ykABgAUAGAAAQA/ABAAOQAzAAgAz/+z/+//1f8NAMX/6v/w/6P/6v/5/+r/BQBbAB0ACgAcAPz//P80AC8AyP9MABYAzv9DAOv/sf/H/x4AKwDZ/+v/LQD2/83/BADd/+z/LgAVABQARgACAOz/1P8RAPf/z/87AO//5v////L/4P8GAPP/FQBAAP3/ewDp/7r/7v+5//v/6f8NAAUA9v8AADAADgAJAD0AFwBCABMAKADH/83/3/+K/8D/1/8TAOH/6v8fABIAGwBIABMABQAoAOX/MwArAAQA7/8MABcA+/8eANb/wP+8/97/v//J//f/MAAiADYAcQDd/zkAAAAKAFwA0f/5/6v/0f/d/9v/FQDh/0UA6P/m/xIAAAAhAND/HAALAAMAKQDa/z8A//8GAD4A1/8SABAAxv/e/yMA/P/0//3/yv/7/wYA4//x/8b/DQAYAAIAZwARAP//9v8bADcAp/8AACwAwv8cABwAuv///wcA/v9zABIA6f/u/8j/1v/V/9z/DwD0/wQAEAAJAD0A5f9SAB4A1/8JAN//LADT//7/BwDx/0UA3/8AACoAvv/w/00A6f/6/ykAsf8tAPb/vv/g/8H/GgD2/yoAJQCz/1IAHQAAADQA9f+T/+//+//r/0oA3/+KADcABABhALL/HADQ//z/JwC3/8f/0//d/8r/1v+8/xsA0//y/08ADQBCACIAYwBbAPn/MQAAAJP/GQD6/7L/IADZ/woA7f/T/4kA6v8EAEMAwP/T/6r/lf/8/yYAEQAiACgA8f/o//j/EgBKADQAPAAaAAEAvP/X/+n/6f/f/wgAEAD4/yQAGgAdAAsAJgDn/7n//P/L/9b/4//x//7/FgA+ABYANgAIAGkADADY/xwAov8PAJP/EgAYAGj/QwDg//n/8P8AAEQA2v9eAFMAQQA5AEMA8/+q/6f/5f/3/7v/AwC8//T/LQAPADMAxf/1/+j/wf80ACgA6/8JAEUAJgAGAB8AKAAYAP//CQALANH/+//z/+3/BADK//X/uv/Q/zUA9v/m/ycADgAPAPT/6f8tAO3/BgBYAFgAz//f//j/wP8MAAgALADK/+T/AgAEAC0A6v8nAPz/8v+4/9z/9v8HAEcA5v9AAN7/3P9NAB0AJwD9/xkA3v/c/yAAmv/D/xcA1P8ZABIAzP8RABsABQBAAEgA8f/V/x4Ax/8DAEwA0f9XABIA9/8cANb/BADG//3/+v/o//r/vf/r/93/z/8HAE8A8P89ABgAs/8hAPn/HQDe/xcAJgDa/zYAGwAYAC8A/P8JABoA8//d/+L/5v/d/8//3v/6/0EACgA+ACQA2f8hANL/1v/r/7T/BAD5/8H/HwA1AMT/YwAwAOr/fADp/xsASgDo//n/8f/d//D/HwDC/wMA6//P/+//DADu/3X/QQC8/73/VQDf/zYARQAtACsAXAAIAB8AJAD1/xwArv/3/9b/oP/J/+f/CgD1/xgAAAAuADMAFAApABIADgAHAOT/4f/G/7P/BwAXACsA+f/u/0kA8//I/yYADADV//X/+/8MAOD/BQAaAPv/MAAPAP3/HAALAA0A8P/i/yAA6f/B/+z/EgD8/9f/HADt/x0A8P/r/1oAyv9vAFIA1f85AK//z//X/9//2v+O/zkAHwDp/1sAUgDx/xEA6f/K/xMAzP8qAEcA+v9KAN7/0f/4/8j/FQD1/+b//f/8/9X/GgAgALT/EwABADEAUgD5/1MA0P8MAP//2/8cAAAA/f+1/wUAzv+6/73/z/9tAPb/VQBuAEIABQDk/zIA/f/e/+r/CQDQ/97/v/+4//f/8v8pADQA4v/b/yMAzf9CADMAGQBnAAQABACk/9H/1f/h/1oALQACAOz////7/z0ADwDm/wcA0v/x/w4A1v/0/9z/GAAlAOL/IQDQ/+T/5v8UABAA5v8aAPD/TAAEAD4A5v+9/2MAjP8YADQA+P9gAOP/6P/s/+L/xv/P/yAAEAD7/ygABADz/1cA9v/6/0sA+f/Z/9j/9f/M/77/6v/C/zQAu/8vAGgArv+XADoAAQBBAAIAEgAEAMD/1/+7/6f/+/+7/xMAFwDI/yYAEQBMAEUADwDy/wAA0v/f/y8A6P81AEcA9P8AAOn/4P/F/93/QQDl/xkATAD7/yAA2//J/woA5f8LAOf/r/8OAPv/AgBnAAQABwD7/+j/JQAIAPj/JAALAN//AAD1/7j/2v/y/yoAGAC9/0kADADS/10AAAD6/8D/MwAuANP/BwDq/wUAmP88APP/t/86AOP/KgAiABoA7P9EACIA8P8LAOH/HQCv//z/BgC6//7/BgD//xcALgD+/w0ABQBCAPb/AgARAM//y/+Z/9T/CADV/z8AOQDt/2AA3v8BAEoA0P8gANn/8v/n//b/NwD1/xkADgAwAPb/2f8GABsA+f8OAEsABwDs/7L/0v/m/7v/AADT/9L/9/8PAG8ACQAnAEwA8//i/8//LAAQAAsAm//t/ygAk/9QADsADgAsAEIAMgD2/+//pf/B/7z/7v////3/XQAUACEAFADF//f/HQDo/8P//v8dAM3/QgAVANX/QgAEAAwAvf8ZAAEAAwBUAOj/EADc//v/uf++/yoAGAANACAA1f+p/0UABAAcACUACQDg/wYAXADJ/0IAxP/c//v/7/8hAK//MQDl/zwA8//C/1UA1f/e/wMAJQAVADEAAAD//9T/qP8LAN//3v82ADUA6/9QAP7//P8jALf/BAD2//D/4/8mAAAAMQA0AM7/GQDp/yIA2v/8/9b/1v86AKf/KADe/wIAJADv/w0AwP8tANv/DQBSABoAWwBEAEUAyf8FAPT/ef8IAKn/yP8vAOL/AgADAAMAwP/f/wQA8/8nANX/ZwBvABIATADi/+X/2/8CAO3/5f8MANz/JwD3/wcA9P/R//H/EgAvAPX/AgAkADwABgACAO//u//t/+3/CQAHABEAEQDJ/9X/xv/z/w8ABAD1/yoANQD0/xoALgAKAN//SADg//b/UwD8/zoA/f8bAAUAyv+u/93/9v+v/yoAy/++/6j/2P8lAP//hwAoAGIAYwD1/zUA3f/o/6n/AAAPAND/+f8aAOP/yv8kAO//CwDk/woAEAC1/zYAIQDe/+3/CAD//ycAAwBTAEcAy/9dAAEA3f/n/+3/JADm/+7/uv/R/63/BgAZANH/IgAtAC4A8v8ZAA8A7f8GAB8A5P/y//z/9f82ALv/AgD///P/QQAOACkA+v/U/8j/AQATACgAVQAlAB4Asv/U/+j/vf8BAOD//f///+f/FgD4/y4AKQAuACgA2f8SALL/+P/m/63/5f/V/0YAEACNAFoAFwBpAPb/+v/a//7/nf91/9P/7/+9/+j/IQD8/4IAEwA4APP/t/8gANr/YQAQADYAPwDz////8v8CAJn/s/+9//b/+//Z/wcA+//7/w8AmABBAPH/HAD4/wEA6/8XAFEA5f/X/xUABACm/5z/BAAQAPr//f81AND/zv9dAOn/9v8aAA4A0v/l/wIAPgBGAPD/WgDe/+b/EwC6/wEAFwDo/9L/HwDI/wMAIgDQ/ygADAALAAkA+v/n/z8AEQDp/+X/2v/O/wgAXgDo/18ALADu//b/z/8CAMn/HQCg/x4AIgDA/ywArf/a/xQACgD8/0kAJQAcAD0AGgBgAJj/uf/u/5//AQAaADIAHAAaAOz/5f/z/wkA7P/v/zcA6f/g/zMAYwDj//X/8P+r/9n/6/9yAM///v8XANH/WADh/1gAGADX/wkAtP8zALv/vv8AAPz/FgAjADIA1P8xAPv/7f84ALP/KgDm//3/MAC8/wMADQDN/y4AIgDU/wQADgAfAN//0v/8/+z/BAAvADEA9/8eACAA8//P/zAABwD+/ysAsv86AMP/qf8UAJn/9P/l/x0AOgAqAEcAMQBGAFAA8v/z/8b/lv/3/57/qf/1/xIACAATACgACAA9AA4AOQACAOj/BQD6/w8AGAA/APb/UwDA/9j/1v+h////cP/j/9b/EgBeADgAIQAvADEAzv9iANT/5P9CAPv/5f/r/xkA9v81AO3/GADJ/xEAFACj/1oAv/+S/+r/AADk/wUA/v/+/xAA9P8wAOH/ZQAjAEIAVQD//0gArf/u/8n//v/f/+z/KADQ/xIAmv+8/+f/9f/1/xUANQAmABwA+/8wAM7/6v8OAEsAHQADAFUA6v8tAAIAEADn/7X/AQDG//7/8P8PAAAADgC//8f/FQCz/+7/9v8aAOv/EAAAANb/cQATAFMAXQAeABUA5P84ACEA/v/z/+j/qf+f/93/1//o/83/AAA5ADQAHQDz/yMA5v/L/zMA3P/t/yQA7f8oAAwANAA0AAEAHAD6/0MA0f+0//7/wf8UAL//7v/t/5//AwD3/zoAFQBUACUAMQAhAML/PADn/+f/s//p//z/0/9PAMn/FwAxABEAeQDd/+L/HgDK/x8AGwD3/yQAxv/5/8z/rf/t//b/MgDe/9X/9v8YAAIAMABDACkACADc/0MADQD8/xgAz////5v/of9XAND/v/9LAPj/MAAuACgAHwAjAAIA8P8oAKf/6//0/9H/FgAbABcAs//q/wkAGAD1/w0ATQC//9H/JgD7/7H/SQAhAAgAFQAYACEAzv89ANT/9P/o/9b/7v/G/wAA+P8FAOf/WQAOACsADADU/1MAyv8vAAkAAQAjALP/GQDp//v/2/8FACcA4P8CAOv/IwDc/73/FgDy/wsAJgD6/w0Ax//z/zYA6f8ZAD8ABgA7AD4Au//g//f/AgAvACEAKwDg/9T/6f+v/+z/CgDF/wgA5f+i//H/EQAzACUAAgAdAA8A1f8iAC4AMgBXABkAUwAAAN//9v8WANr/af/Y/8P/+f/S/wsAGwAvADMAz/9TAIn/HAA7AK//QQDG/zUA/P/9/0MA5f8KAPb/FQAIAEMAHwAsAAoAyf/6/9f/nf/P//v/l/+7/wQABgD0/ykAOQAkAJQA/P97ADsA8/8bAKz/2v+8/wUA//+0/93/AwAXANr/LACv/8L/HADT/zQASQAlAFQAKgBDABoAuv8JAAMA0//L/9r/vf/i//z/1v9hAOz/IQBuALn/JAD3/+D/AADP/yoAAQD7/y4A8P8VAO7/HgDu/7v/aAALAPL/rv+///v/e/8eAC8AKQBaAAkAaAAoACcANgCa/8H/wP+f/8j/9v8gADUAYgAZAP7/TAAFAND/FQCd//P/6f+J/ykA4/8zAPn/7f9MANP/agA7AP//BwD8/w8A3/8LAAIA4P/e/8b/3v8zAKj/LwBFANv/JADM/9//8v83APf/OQA5AAgAWQAFABgAuv/v/9H/xv/w/8P/0f/9/yMA1/8LAOb/YwADADQAVAC3/4AAtv9nAAoArf9CAHH/r/+z/z0A9f8yAD0A9v9LAJ7/OQD3/+//7P/R/ykA8P8KAOH/LgDH/+D/9P/N/xcA7/8mAEMAWAA9AE0AHQD8/wAAq//m/7L/1//T//T/EwAFADMAof/u//L/7f8nABsAPgD4/2wA9f8XAD4Av/9OAMr/s//Z/xkA8P+Z/y0Aw//q/0gAHQAFABQAGQDW/wsACwDw/xsAEgDy/zMAIwDr/zkA2/+7/+j/y/8HAOL/CQACABoA+//E/xIA3f8OADcAUwASAAkARgDQ//j/8P/f/+j/CQDj/xYA9/+l/ywA8//o/8H/NQA3AP7/hQAFAC8A9/8NAPj/zv8MAJL/BAD5/+X/EwDW//T/BADl/+n/DAAfAOX/+P9XABEA4f/6/0AACwAZAEUANAAFANr/4f+i/wgAHQDR//P/6v8qAA0A3/8AAPX/uf8EANv/6v87ABoAMAAZAP7/CQD0/9D/8P8EAB4AKAAAAAcACgAXANf/KAD6/7r/RgAVALT/7v81ACcAJQAMACAAzv+L/7v/0P+7/xwA8P/U/2gABgBTAB8AHgAbALn/hgDn/xIAMQDy/+z/2v/v/7b/AQD+/xYAzv8oABkA4/8AAKL/MADQ/yEARgDi/wQA0v8EAFQA9v/w/yQAfP/u//j/9/8yABgAXQBKADUA9/8YAMP/4f8MAL//MgCz/7L/HADV/wgAFgCi/xsACADo/0wAJgB8APP/JwArANL/+f/U/yIAyP/w//b/tf/H/+n/DAAFAEcAGwAqAOj/DAAPAA0AFgC3/woA/f/A/7v/GAAsAAsAFwAcADgA7v8OACoAFgBJAAEAvP/V/8n/u/8BAOL/sP/4/y8AEgAuAEUALAAzAAQA9v8VALL/6P/3/7z/SQDj/87/NwC1/+z/8//9/zwABQAvADIAEQD+/ykA5//w/x0A0P///wcA7/9OAM3/7v8ZAIb/4//8/9X/DgBVAPT/4v8wAMD/UAAWAC0APgDD/0kA0P/p/zkA3f/Z/+j/ef/6/zEA0f+CAPL//f8EAO//HgDj//T/2v9CAPj/XABZAM//BwD4//z/xv9FANb/yf/x/+v/HwD+/3AArv/p//j/yP/s/6L/EwCr/x0AIgAKAFMAEQBPAOz/HAAXAAQAMAAVAAEA6P/2/xYAHgCt/7P/cP/G/xsA6/9+AE4AEQBCAFAA3P8PAC8AhP8TABEA4P/9/6n/v/8JAOr/qP8eAOH/5/8rAFoATgD8/yUADgD1/0gAMAALAA4Axf/N/8j/pf8NABkA2f9HAPv/u/87AOH/FwAWAPn/SgAIAPL/AQA9AOL/BQDc/67/AADL/9P/1P8iAN7/MQBZAB8AJwD+/ywA+f8vABcA6f/R/8n/y/+6/xwA4P8aAEQA5f8LACwA9P/1/zsABABFABQA2f8AAJb/AgABALz/DgDZ//v/HADo/yMAIwDd/xEAAgC7/zoAFgD4/0oAGgAmAFsAHwDc/8b/2v8AALD/x//n/9P/3//u//3//f9TAAsASABCAOb/NAAPAAYAJgADAMX/0//D/+z/9v8lAAAA7v8bALX/VwAGAM7/CQCT/wwAMAAjADMACwD3/z0A6v/Q/wwAlf8NAD0A1f89AEEADwAZAP3/BQC0/9j/CAADAOT/r/8aAPH/4P8HAB4AAAAqAC4A6P8nAOb/agAiAMD/HADZ/8j/CgDn/7D/UgCz/2MATgCU/2AA0v/t/9T/AwD0/+D/LQD+/w4A7f8wANL/7v9DAAUA2P/w/wAA4v8PAP//SgDt/xIASwDv/xEAHQAoAND/EAC9/8D/1f+G/wYA+f84AA8Axf9AAOT/DgAmAO3/KAApAP7/IQAVAAAARgANAN//KACj/9n/LwAcADMACQDS/+D/sf/m//X/7/8VAMf/LQAJAJf/9/8QALT/LABbAP7/TQABAGQAKAD1/1MAmv/5//H/xf8hAOv/3//d//3/DQAGAAIA2P/Y//3/SAAvANr/VgBDAPb/HAC7/9P/8f/X/8H/3P///wUA8f8HAAkAKABsAB8A2v82ANX/7v92ALT/CgD9/4n/OADo/yAA6P/3/ygA0P/u/wEANQD3/zYAMQDU//n/x/8GAO//yv8rAPn/CAAcAKr/BQDX/w0AYQASAEcAHwA5AOj/8/+l/5b/CgC+/1IA/v/V/xkA3f8kAPb/MwAkAEAAQwDm//v/vv/D/6b/w/8IAD0ARQDx/zcAOAAwAO3/AAD7//X/GADS/zcArv/D/yQAuf/R/6//DAAIAO//SQBVABoAIgDt/yUASQDw/x8Am//6/+b/t//9/+3/BQAUAEQAwP8qABkADgBXABwALACv////0v/A/+f/vP8CAA0A+f+FABUAyv8/AM3/6/+5//D/KwAOABkA9f9CAMv/HQAAAMj/+v/u/yIALQARAMz/RQAaABkALQD2/8n/xf8MANv/CAC//+f/yv/i/zoAz/9hABkA9f9FAN//HQAgAPX/TQAbAAgALgDX/7j/sP/5/9r/+P8VAAUA7v/z/zkA2/8oAOv/2//0/8H/LAABADEAKADp/zkAIgCl/zEA9//A/0MAs/9cACkA4P8pALP/4P/h/+n/2P9FABYAMwASAP//KgC//yYA2/8yAPb/1//n/7D/XQDQ/z4ADQC7/+7//f8hAPr/NwDv/yoA7//6//H/7f8VAOH/KACj/xAAAQC4/xkA+v8xABIAHQC1/+7/HwDp/5IAFgBpADwAnf/f/7//+v8WACwA3P/4/wIAmP/3/+T/+v/r//b////5/1gA9v8yACAA6v+2/+3/NgARADMABQAVAPD/+f/V/9f/7f/9/wcAv/88AAoANwADADwAXACs/xsA7/8aAPT/3v/v/5r/z/8AACgAAgAKAAEAGAD5/yAAVwC0/xsAEgD8//v/3f/f/8n/7//e/0kACQC0/zkAyP8HAG4ADQBUAAwACwDt/+r/RwDT/8P/tP/F/9n/+v8PAA4AKwA3ABsA8P8uAAMAMAAiALX/DQDY//j/+v/7/+7/3P/0/87/FQARAFIAMAAWABAAt//k/+T/9f81AEwA6//U/7//5/8nAP7/HgDm/+j/xf/1/xIA+v9DAA8AEAADACYA1f8FAGIA+/9MAO3/u/+r/+b/MAD+/wsAEABEAKH/1f8rALv/EwAIAOf/HQAaALf/8P8EAPf/HgAIACgADAAMABoAOQAWAPP/IwAYAAkAxf8DANr/7v/2/6X/5v+s/+3/7P/l/2QAEgASABIAIAA/APb/IwAZAPX/4//4/ysAxf/q/8v/7/87AJL/UgBLAOD/UgD4/wAAHgD//xQA8P/O/+v/3//d/xUABQAJAPr/5f/d/+3/+f83AOT/EAAYAPH/MQDf//L/GQDo/xcALQDi/zkAJgDf/0QA4v/n/xEAjf/T/zMAkv/b/1oA0/8SACcASQCw/+z/fQAGAEMA0P9ZAN//zP/+/6v/LwC8/1cAHQDR/ykA4f/n/9//FADp/yUA3//a/+z/7P8LAOj/OgDl/xIAKQD8/x0AEQAkAEMAHQAPADYAmf/N/wQAo//p/9n/8v/Z/+P/GADk/z4ACABPABgA0/9AABEALQAZAD4AAACZ//j/vP/d/wAAxP83AEIA7f8iABwA3f9GAMz/yv8SAMf/xf/4/xUA4f8tAA0AQQAQAEYAHwCm/zIAzv/m/wMAAwADAB0A7/8AAO7/zP9kANb/DAD9/8v/8P/r/yIA6v8jABIAFQDe/woAEgDr/0YA1P/y/9r//v8eAPb/GQDl/7X/JQAlABUAaQAIAPz/zP/9/+z/5f8NAOn/egDW/+P/6//V/wMAvP/z/wQA9P/I/zcADQDt/wwASAAbAAMAcgAQABAA8f/6/8b/AgA5AIv/GgDI/9z/7P8EADoA0/8SAPv/8P8XAA0A+//Y/+v/IwDg/woAgQAWABIA8v+7/wkALwASAA0AVgD8//H/y/+g/+X/4f/i/+b/BwDH/7L/MgASAC0AUwAZADwA6P8RABYA3/8YAO7/RQDe/+L/KgCW//3//P/8/xcAt/9PAOL/vv9aABUACgADAP//4v/m//v/0v8mACUAIAAnAAkAEQDp/wsA1v/b/yQAsP8iAAYA6v9XAND/FwDZ/77/CwDi/xYA+/8XAP3/QgAYAPL/WADN/+v/0/8QAPf/w/85APT/+//z/ycABQC//wQA5/9JAAUANABdAKT/KQDq/4f/8P/y/0cAFwAiAN7/wP8LAOH/BgAOAAMAAAAbAP7/TwA0ANr/NQDD/+H/8v+4/x4AFwDM/xkA7P++/ywADgAZAPX/KAD5/wsAIADw/0QA3P8iAOD/zv8oAJ//x//0/9r/DQBgABIAIQAKAP//LwC7/0gAJQAaAAAAxv8aANL/zf8GABMA7f/o/83/GADr/73/VQDN////RAD0/y0AKgAUAN7/GADU/8b/9P/1/1kAIgA3AAEA8/8SAM3/NQDY/9T/GQANAPT/1//1/+j/8P/N/+z/iP8BADgA2f+OAPX/TwA+AC4AYQD9/wkAnf8uAMr/3v8RAKz/4v/K/woADgD1/93/DQDK//j/MAAIADoAJwBqAA8AEwDb/+r/9P/R/wkA/P8PANT/agAbAN7/wP+d/wYAtf9WAD0AJgDP//v/EACf/zIACQD1/xQABwDz/wUAAQAAAOf/+v8UAKn/XAAyAAkARQAGACcA3f+g/+3/CQDU/ysA5//x/zwA/P8eABsA3v8FAAgAw/8TAA4A3//Z/8D/AgDx/wgAFgBhAEIA1/8RAFMA6v/d/10Apf/X/73/W/8PAMz/JABEAP//TgAqACIADgA5ACoA8/8YAMf/zf/y/97/HAD1//D/CgAJAPr/vf8kACsA8/8oAPn//P/i/8z/KADz/wIAGAAEAO3/5P9dAAQA4/8kAAcADwD//6//xv/o/6z/PwAIANT/LwAWAD4AIQD0//n//v8bAOP/AQAeAOX/UgAcALb/9/8XAOz/k//X//X//P9iACoA+/8ZAP3/4f8bAP///v/i/8z/HAAMACsAJwAQAOb/+/8RAOL/6P/t/wAA+//Q/wYALwAGAP7/+v/Q/8X/GwBUABQA//8PABUABgAkANv/n/8WAAAADwA9AND/1v8IAN7/BQAaAAgAGQARANX/KgBAAOL/IADa/8j/4v/n/xYA9/8SAOn/5/8jAEsAEQAmAAAA3v8tALf/MwDu/8r/NwCz/zYApP/G/zEA2v8hAOT/GwDl/8T/LQArAA0A5v8eAC4ATQBFADUASgCu/7j/7f/R/woAIgAkALz/f/8UAJL/3f8ZAA8AQgDq/z0AHAAkACMAKQAJAJf/DgDd/xoAJwALAPr/8P8GALH/yP+3/wEALQBdADMAJQBBAPL/JwDN/9r/1v/n/w0A2/8lANn/xv/+/w8ANAAXAC4AFwATANb/GQAnALj/2f/T//L/wf/5/yYA+P8OAAAAdgDy/ysACwC2/1MA2f8MAAgA9//u/zsA6/+2/zgApv8zAN7/4P/0/77/UgD+/wsAHwAzAAwAAgD8/xEA4v/a/w8Ayv9dANr/BwAAAN//uP+w/0IA5P8oABEASgDj/zwAUQCf/0UA0P/f/93/WwAEAK3/IQCN/xIABADz/z8AGgAFAD0AGQAbAOz/q//n/9L/BQAEAEcAyf/+/xgAxf8QAPP/RgDt/zsA+//a/1UAkf/h//X/6P/1/w8ARgAjABoA6v8yAP7/1f8kAAEA0/8EABsA3f8sAPr/tv/U//f/1v/2/04AEQA0ABQAr/8qAM7/7P8nAMn/HAAdACgAXQAJAM3/9//W/8r/AgAfAA4ADwDX/xEARQDZ/x4AtP/m//b/vP8JANX/SwATAB4ALwDg/+f/JgDy/9v/egDT/+T/QwDj/+z/AgA2AAMA9f8wAAAAvP8ZAAsAyP/v/ykA3//I/+v/vP/Y/+L/JgD3/w0AKwAdADEARQBTAO//AADg/+H/RADW//T/9//d/xgACQDY/wYA9f/h//f/EQD2/wUA9P/v/0IAHwAWADUAEQDQ/wMA5P+6/+T/1f/+/8T/EgD5/0IAOAASAE4A5/9kANT/FADd/+v/JgCY/wwAyf8LANr/xv/9//P/8//g/zEAMABVADQAUgDn//b/1P/K//b/vv9DAAQAv/8vAC0A8v9QAEoAKgAAALz/7v+M//D/xf8IABsAwv8mAM3/+/8iAOT/HABSAAQABQD4/w4A/v/p/yYAMQAhALP/GgDd/97/5P/f/10AuP8gAA0A9//8/0MAaQDj/xcA9P/r/7z/4f/n/+z/CQDg/wQAqv/3/8X//v9JAAsAXAApADMAFgDq/xkAEQDh/9r/6v8DABAA3/83ABcA6P8UAPH/7P8GAMD/6v8qAL//DAAZAL//PwDl/+f/GAAVAEoA/f8MABMABgD+/y4A+//Q/ysA5P8QAN7/+//s/6D/DgDY/9H/DAA4ACwA3f///xEA1/8FAOv/UAA2AN//WgD2/yEABwD3/y4Aj//H/wUAxv8AACwA3v8AAND/+f86APj/VAAlAPv/AAAdANX/FAAUAL//MADM/8n/IADd/wQAJQDu/zMACQDy/1IAtv+m/00Ao//I/4gA/P/s//X/4f8gACIAKwDy/+T/uf/M/z8APQALACcALgDY//X/AgAVANb/CwDf//X/DQDi/wQA4P8iANP/OQD4/7D/6//1/08Auf9FADQA8f/h/xYA7/8JAJIAAwBNAOr/+f/U/9//AADj//D/l/8nAJ//GAD1/wAAMADy/0AAof9uAAcABwA6AMH/6f+v//H/7v8AAA0ATAADACQA+//2/x4AnP9SAEQAMwAtADkA7P9w/9j/if/G//7/AwAmAEIAEwDu/z0Ar/9bABEAz/9yAA8AXgARANP/sf+L//L/nv8XAMr/8f/i/9f/ZAANADUAKgA8ABQAQAAUALb/MAD4/+f/qv8CANH/zv///9n/SQDa/2kAUgADADgABAANAJ//uP/q/7b//P89AC4A7P85AFcA+P/6/wUABAC7/53/0f/0//v/5/80ABIADgBBABsAKwABAOn/w//u/+z/0/9IAL7/8P8qALH/5P/9/2IAVwBwAFAAIwAPAHb/z/+w/xgAIAACAEEApP8cAMv/0P8PAKb/IQDy//n/GwAdAA8AFAD7/zMA+P/b/0wAAABDANH/3/8RAPD/3//0//L/lf93ANj/3/9UAMf/NwDv/+j/RwAMAOz/IACS/+T/+P/s/z0A9f9AABoAHwD0/xUA+v/5/+v/9P8hAJ7/NQDZ/w4AXQDh/+j//P+0/+7/iADa/0IA/v+i/9//pP8rABoADgDu/xcAwP/l/zcADABKACoAFQAvAEEA0f/t/xQA0f/o/wAAPwD+/67/0f/Y/53/xf8bAPb/EQA8APz/WQADAOj/gADI/9//NADf/+P/EwDo/w0ABgDq/yQA4v9NAA0AVwBCAL3/SACK/+X/p/+G//b/7/9CANH/XwBWAPP/HwDe/8//HgALAAwAWQDM/9n/4/+n/+j/2f8CADcA7//6/2MASAAHAPT/6//e/xMAOgDn//f/NQD7/wQA7P/u/woAt/8RAOv/s/9GAL3/GQBHAKb/cgAZANz/IADS/zgAHwAzAAgA3//X/7r/HgCb/xYADACM/wAA4v8RAB4ATgAaAPL/MwAYAAgADQAOAAAAHwA2ANj/0//W/+r/9//k/xUA9v8dAB4A//8HAO//4//h/08Avf8RACoAqP8VALb/5f86ACkA9P9WAPT/qv9DAPT/OQAeABcAAADJ/8H//f8bABgABADq/wYA3f/1/5f/KgARAPn/FwALAIwA0f9cAP3/8P/0/3r/GACn/83/3v/+/wUARQA3AEUAUADr/+L/x/8gANH/KgABAPv/0P/7/4sAvv8cAB4AFwDk/9n/1v+//xsA9f9BAOP/LwD7/97/+//F/xAArv/3/x8AJAAJABYANgDg//7/KAAqAAgA5//Y/9b/6//6/wQAAAA1AEkA6v/l//T/yf/a/xQAQAD+/yIAPgAZAA4AAwATALb/BwD1/87/AgAKAOH/s//3/4b/3v88AAoAKgAeADIAUgDs/0IAHgCo/14A0f/7/w0A6v8oAJz/BADL/9H/+P/0/xIAFAAHAOn/PgAEADoAZwDL/9P/BQDO/yUAPQDg/x8AzP/Q/wEA///w/9D/JwD+/wQAFgD0/w0AMwD7/xMAGgDH/wEADwARANf/2P/s/8P/7//+/yQA8v8vAC8ADgAyAO3/KQD+//T/7//G/+P/6/8OAOz/WQAKAOL/FgDr/1IA8v8EAPH/2v/8/+X/BQDt/zQA8f/5/xgA7f8BAO//HQAgAOX/yP/d/+D/KgD7/xkA/v+8/yEA9P8LAP7/JAAnACYABQAQADsA2/9CALr/6v/p/9D/XgDn/wkA7/8WAOD/x/8RANX/DAD+/+j/7//p/97/JAACAAIALgAlACoA5f8yAA8ABwAPACkAEQC7/w8Au/8DAOP/1f8WAOT/zv+K//r/IAA2AHYANgAeAA4ARwDs/xsA3P/0/yYAof8YAMf/zf8MANr/MQDP/+j/LwDv/yIARAAEANX/z/+s/yIAGAAEADIA5f8hAPn/HAAQAPv/MwDb/xEAvv/i/zwA3P8BAOH/NAAhAND/QgAgAO3/PgD8/7r///+//8//7P/J//j/LgDb/woAQQD4/zQAMwAqADkA///D/+L/zP/J/+3/9/8OAPT/WABWAAMAKAAjALn/2/8kAKz/AADZ/zQA7f/K/x0Aof8UANT/NwDr/8v/QgAAAE8AHQAdAPL/CAD5/ykASQAIACUA5/8VAMX/4//j/5L/5P/b/93/DQAYAPX/HAAhAEgAyv/z/z8A8v8qAPD/7/+7/ycA+//N/0cA2/9AABoAHgAoAKz/KAAcALH/5f/o/+//9/8mACwADQA+AN//2v/3/9D/BgAGAPj/5f8+AB0A7f8YANj/AADC/8j/NAD6/wcAKgABAO7/HgBoACoAGwDv/4X/y//N/xkAIQASABMAsv8SAOP/tv8aAAkAKwARABEAOgDO/w0ASADw/+7/CwD//y4APQDo/wwACgCl/7//n//W/+7/KgA4AAQALwDw/yQA+P8AADoACwAaAA0AAgAhAP7/5/8bAMD/bf/f/7L/0/8lACUAPwAdABgAOwDa/xoAHADJ//r/0v8LAB0AMgBDABkAQADb/+z/5v/I/+f/tv8uAPn/0P8GANP/HwAbAHQAEwD4/wIAmP8SANP/8P/1/6r/HAD5/z4AWwDz/y0AAQDs/xoAIAAQAM7/HgDI/yoAAwC3/zwAkP8vAAAADwAGAJb/bgDz/xMAHwAQAJj/yv9kALH/RwAbAPP/EwDc/9//5f/g////6v/m/z4A3/8yAAgABAB/AP3/QQAVAPr/EADS//n/FgC+/7P/+//a/+r/EAATAM//6/8YACAAEwAkAPL/6P8BAM3/NQASAMr/KAAeAO7/KQAnAPf/SQAFAOz/0P+d/9b/3//5/+//CwD2/yYAPgApAEIADgDX/xEAHgDo/x8A/v8rAPT//P/s/7j/AQCp/9f/lf+w/+v/7P9XAG4AVABYADMAJQA+AJv/+P/H/8P/UgD4/+X/3/8IAMz/BwBAAAIA/f/g/yYA8/8PAA0A+//k/xAA0/8KAAkAdP9OAMH/2f8ZABUAdAAcACQAPgAZAMv/MAAVAAAA1v8EACMAk/8RAKn/3P/E/6f/FADV/wQAIwBcADoAIwBKACoA9//4/xIA//8nABUA9f+p/4v/tf/K/8X/FQAmABQAXwA3AB0AAAA1ADoA/P9EAOD/rf/f/+3/9P/3/wMA0v+J//P/6v/9/0IANwA7AAAAGgAXACAAHwDw/0MAAADn/8v/wv/f/8n/CQABAOP/AQDR/+z/UgAsACIAJgAIABIA6/8PACsAj//m/zAArv8qABIAEgBSAN3/RgAaAMX/7v/Y/93/q//H/wcAvv8TAEAAvf8tADwACQBeACwANAD6/8D/JQD0/7P/MgD//wsAHADo/x4ArP8DAPj/u/8GANv/EADN//r/SwAOACUAHwAmACIA8f8bAA0Avv8VAM//lv/p/+P/HAADADwAHAAIAFwA4v8gAMz/+f8bAPH/6P/L/+z/o/9ZAPv/2/9NAMH/GgAfAEcA2f87AFYAwP8cAL3/9P/a/+7/MAD5/xIAAADM//3/4P/y/yYA3v8rAO//FwAbAMn/SQDs/+j/+P/n/wAADgA+AAoAFgAyABoA0f8AAN7/mf8MAOb/5f8FAOL/DQD9/wYAbQD+/1oAUQDD/xMAov/t/yEA8P/K/77/6/+3/yUATgD8/zMALgAXAAcAFwDx/97/5v/t/w0AzP/c/wcAEQBZANz/KQAvALD/bQDv/6//+P/M/wEAAgDp/xcA6v8AACkAAwA1AAIAEAAUADkAFgCr/+v/uv/8/83/DgD5/9b/RgAKAFcAwP8fAPr/if9KAAAABQAJAPH/3P84AAIA+P9GAN7/QwDz/w4AJgD0/xwADADi/5b/6f/5/wAAAQAAABcA9f/V/7z/5P/J/7z/MwARACEAfAAjAG4APwD1/zkA1v8dAOf/yf/Y/+//3v/X/9f/p/8XALv/+v8tAOn/LgA1AEMAGgBHAB0ADwAsAPr/wf/h/9j/of8bAND/6f9MACIAIwABAPD/DwAaAJP/vv8IAC8A7f8hAGAAtP9AAPb/BgAmAI3/GwDL/00A7v/3/z8Aqv8nAMD/DwD0/wMAQwDu/xYA5P9IAM3/DwAtAAoAAQDe/zkAkP/r/+X/o//W/+7/OQD+/zcAGwBEACgAJAAqABcAMADT/wQACgDQ/43/zP/z/+L/3/82AFwA2v8kADYA1v+q/xsAGgDT/zwAx//m//3//v83ACUATAD1/zMAzv+u/y8Aq//w/+3/5P8CACIAcwAeADEA3/8HAP3/vv8RAK//AgDp/9L/3v/f/yAACwBIACkA/P8DACQACQAxADAAJgAyABwAz/9k/7z/rv/4//j/PgA+ALz/JgD5/wsAEwAhAN//w//o/+f/PgA7AFoAFgAIAMb/rP8IAOb/5/8hABMAuf/d/xMAFQAYAE8ANwAVABkABwAUALX/IADi/+r/q/+X/wkAv/9jAD4ASgAAAA0AAQCo//P/ov/2//H/YAD6/wAAIQDF/0YAZAB/ANT/OwDo/5L/IQC+//D/t/8PAL7/1v8EANv/LADo/wIAFABVAA4AEgAhACUA3v/p/3gAyP8kAPv//v/h/4T//f8FAAoA5P9CACQADgDz////6f/u/wAA0v8uAKf/IQAlANP/OADr//L/BgAgAA4AOgA5AOr/HwAJALT/1f/q/8D/EwD3//n/7v/g//z/9f8EABIAKQBOAFcAJQA6AM3/BADZ/53/BQDO/2cA9P/8//D/wv8DAPv/9v/N/wQA0v87AAsADwArAPH/DADl/wwA3v9iAOj/DQBUAPD/QwDY/wEAzv+q/9r/+P/g/+j/KAD0/+z/MQAZAEEASwALAAEA0P/V/8L/3f8YAOT/6v8AAEUANgAlADAA9v+t/+X/9/++/+P//v8qAO7/QAAtADgANAAZAEYAt//E/5n/rf/f/9j/BgBKACEACQA0AAAADQDD/y8ADgDi/yIA+/8dAA8AEgAOAPr/nf/2/+//7/8nAO//GADa/zoAKwDn/wkAMgC1//r/KADL/8z/kf8dAOv/RQBRADEAQgDG/wcA5P/+/+L/AQARAAkAAwDy/xMA3f9aANr/+//i/77/LgCy//r/IQAXAB0AAQD1/+P/4f84ACgAAAAUAPT/NQAXAAEA8//Q/97/9/8dAOj/3f/q/8z/GAAUAOr/RQDX//n/UAASAAsAOwAfAJ3/FgDj/w4A3f+S/zsApP/I/1QAXQAfAEwABQDR/0IAzf8cAN//3f/6/6n/LwD//8z/5P85AAsA2f8lAM//8v/v//X/awDs/ysAVQAaAAUA6/8VAP3/IwARAAAAoP+i//P/5//y/7f/IAACACsAOwAEADgA6/8VAOL/zP/x/9H/5v9IABMA+P9KALv/OwAhAPX/LgDl/xEA4P/k/+n/7v8oAOD/6P/V/wkAMQDu/0cAu//Q/ycAvP8oABkAHgADAC4AcgDS/wwACQD2//f/vv/t/7T/v/8GAPj/HAAuADIAIAARAC4A4//0/wkApf/s/+v//f8VACAABgDt/04A7f8NAA0ArP82AN///P8yAMz/DADn//T//f/c/yMAHAAiABMA7v8gABgADgDc/9T/8P/Y/wcA0P/Z/0UAIwABAAAAKAD1/xMA3v8nAGEAvv9LAAkAuv8RAL7/6//O/+H/JAC7/8n/EQBGACIAGgAvAO//+v/m/+L/NwD+/xcAcQDO/9L/HAC2//n/XgDs/87/+//A//7/3P8VADEAzv9HACkAIAD7//T/JQCU/yUACADP/z8A2P8GAA4A2P+1/9n/2v/0/wkADQBKAEoAkwBCAAAADwC///v/+v/N//7/3f/A//7/2P/m////2P9FAC8A2/8TAN7/2P8TAD8AFwABAB8Avv8FAPX/GQBFAA0AdADj/wQAAQC3/9r/gv/+/97/1f8DAB4AHQD1/14A8//d/yoAMgAwABgABwDg/93/7f/P/woAKADS/wAA4f8bABsA4v9eACAALwD0/4//1//K/+j/FgA4AAsAr/8VAB4AtP/6/0oAGQDy/zIACQD1/z0AVwApALb/4P/o/+z/BwAPAOT/iv/Z/6r/5v/m////VwBVAEwASwBAAN7/5//T/wUA3P8QABwAwP9ZAPf/FQDr////FADJ/zAAxv8rANz/+v8HAJ//GgDP//X/8f/1/zIAMgAeAAMABADq//3/4f8rADEAIAAfAAoAFgDg/wcA7/+4/8D/3P/j/wcAHAAWAB8A0P/1/ycAFABoAC8A7v/0/6X/6f8AAOT/AgDr////JgAaAB4A8/8TAOv/2f9qALz/2v9ZAMD/AgAHAMX/8P/U/7b/FgBKAGoAUQABACcAxv/6/8L/5f9LAJv/RADt/+z/PgDJ/xsA4v///+X/6v8YABIAGgAmACQA8v/l/+3/1v/Q/9T/+/8DAPH/FQApAOD/FQBMAEQADQAXABcAEQD7/9H/NwCv/8T/CwCl/wYA5v8EAEoA6f8MAA8A5/8ZAPr/EwDa/wcAEADD/xMAIQDv/87/QgAXAAAAiwAJAPr/CQCg/wsA3/+j/wwAJQDc/wAAVgAGAOn/3P+k/wQA9P8YADgAGQAvACQAFwAKANb/pP8RAPX/9f8EAAsAAADE//T/AwBDAPz/AgD6/+r/EAAJAEkAAAADABEA+v/g/ycAsP/R/1UA3f9GAOj//v/6/+r/JgDE/97/1v8cAPv/LgA0AOv////f/+L/EQAnAN3/QgAaAPP/BgDy/wIAnP8AAO//6/8yAAAADwDv////PgAtAOj//v8xALz/zv8WAB0AAgD1/yUAif8ZAEYAzP+KACQAzP/p//j/yP/G//f/LQAMAN//RwDp/+b/DwDT/+X/5/8zADkAJwAlAAEA+/8dAPL/9P8AAPX/xP+y/+v/uv/0/wkAJQD+/yQAAQAQAF0AGgA5AAoAGADx/yAAFADe/wQAjP/Y/+j/5f/O/wEAOQAyAPL/CAAtALL/IQD2/zIALADQ/+r/7P8JAKz/BAAKAPT/7v8MAEcA//8gAC4ALwD//zUAAQAKAPv/j//h/9b/5P/v/x8A/v/u/ysAAADQ/+n/4f8oAEkADAA9AOD/0f8UANb/HAAwALr/KwAcANr/HQAFACAADAAmAKP/v/8aALH/EQALABcAXgAGABsAVADK/73/8/8MAI3/2P9hAG//AAD9/xoAHAACAEoAIgBNAND/OQDR/8v/FAABADoAx/9EALv/3v84AP//7v8dABMA4f8aAI//FgDs/83/JQAKADIACQAAAPz/IQDe/8//+P8dAN3/FAAiANX/MAAVAC0ACQDo/+f/+P8PADIAHwANAAoAsf8tALD/y//s/4X//P/5/+P/8f9uACkAOwBMACIALwDQ/zkAHwDh/ywApP/i//X/df8HANj/4/80AAYAGgD7/xYACAA4AOv///8JAOj/HwDN/zQAOgAmACEA/P8AAPD/5v/F/+P/zP/V/xYAJwAAABQAyv/+/zMAwP/9/wIABwD//zIAAwAHABcA2v8TAO3/LgBJALj/NQAbAMX/TwDl/8v/VwC1/8r/wP/G/z8A4f8xAB0AAQAPAN7/GwABAPT/JQACAP7/7v8QAOn/AQDl/8//EQD+/zoAAADY/x0AFgD3/0cAIgAWADEA8P/0/5X/+f8AANr/1//P/wgA/v89AAMAKADx//H/NQAYAM3/8P/o/2//WQDT/zsAQQDf/0cAqf9OAAIA0P8RACQADgAQAPT/DwBQAOn/OgC1//H/sP+o/1IA0v8QALX/KABCAPX/OgAAANX/EwC2/63/TAC8/xUAXQDv/wsADQAaAAIA6v8XAPb/AQA9AOb/GgD5/+f/FQAMAM3/zf/i/6L/NADZ/xIAggAFAD8ADQAKAM//3v85ANX/wv8RALD/+P86AOn/LwAWABMA5v/t/7//EQA7AOr/IwDs/xYAAQA5ABUACwDm/7r/CwDh/xIAsP86AOT/DQBXAKT/PQC2/+v/JQAkAB4AIwD3/+3/9/+R/ywA/f9SAM7/yv9YAHn/EwBhAAIACQBCAPb/BAD9/8//DgCz/xgA+P8eABIA4f8PAP3/KAD0/wEA7P/w/9n/IwAAANP/LwDQ/0gAAADO/+T/wP8LAP//CgA8ADQADwBnAAgA8P8YAOH/4v/V/+H/p/8RAOj/9P9BANr/QgAOAA4A/v8QAPz/5P8sAAUA1P/3/yQArv8SAAAABAAGAMX/QgDk/zMAEADv/0oAsP8bAAkAyP8MAOr/+P8aAAAA5v8tAPr/7v9IAOP/zv8AAAwA9v8HAPT/0v9DAAYAHADt/73/NwD0//D///8iAAgABwBIAKD/FgAlAOP/PQANANT/4/+q/+v/2//2/2YA/f8ZABYA9//N/x4ANgADABwAuP/t/6D/HgDy/+L/dwDp/y4ASwAlAOL/6/+7/wsACgDS/1EAn/85APj/8/9qAOT/AADH/wAAvv/c/wwAFgDj/wQA7//q/yMA4f+FAPv/7f86ABUAQQDR/xQAnf/N/z0A5f8aAOz/5f8aAAcA/P9FALv/EQDa/5r/6v/W/zUA6f8PAPL/IQBkAEQAfQAmAAsAz/8CANT/zP8cAND/JADZ/6b/6P+7//P/LADz/zcA2f/z/1UAsP80ALX/CgBhAMP/LwDO/y8A5f/+/24A6v9OACQAMAAdAP3/5//L//X/w//J/9H/2//y/9j/MADQ//r/IACR/1IAMwDd/1AATABaAAAAIQDZ/9//JgDi//b/uv/Z/wgAzf8vALf/lf8fANL/MgAeAFkAiADP/zYAAgAPAPf/HgABAMb//v+s/yEAtP+//wYAHgAaABUAHgDB/wgAEgAxAB4AKgAAAAEACwC7/wUAr//7/+3/EQDt/wYALwDs/x8A8f8FAOj/0f/r/14A+f9BACcAqP9bAOv/HwC7/zMACAD9/1EAXf8UAK//NwDs/+T/TwCu/0AA0f/j/8r/1/8rAEcAWgATAPr/BwDy/7P/QQDs/+z/WwDw//7/HQC6//3/RQCf/+D/0P/s/ycA5P9qAPD/tf85AAoAQgAeAPn/QgCq/wkA8v+w/7b/1f9NANL/MwAPABgAKgD4/3UAyf/0/wkAz/8JALv/GAAPABcAMgApAEMACQA0AOf/QP+z/4r/sv/y/ycAAADz/1UAPQA7AAAAUQAtAO3/LgAsAOz/2v8lANb/KgDf//3/IQDL/9j/qv8JAKL/9//8/+f/GQDx/zMADQBNAOv/AgArAAUANgDc/2IAKAAAANr/kv8dAJT/NQAtAIz/CQDQ/wAAAQBVACMA6/9YALf/LQAqAKf/6/8DAOf/+f8fAAYABwDt/xgA2/8vAOf//v8lAMn/UwDq/zEAMADU/xQA0P8OAPP/oP/v/+T/oP8KACgAKABNADsAQgDp/8r/HwDK/5r/TwDj/zgA/f+p/zAA9v8eAO3/bADs/+L/CQC+/ygAxf/8/0IAMwDT/zsA3//3/x0Avv9FALP/FAD+/9b/JQDN/9//7v8UANf/IAAAAPT/RADt/00APQADADQA5P/l//X/4f/M/8r/IgD7/0UA5/8lAPr/hf9DALX/GwAlABcADQCp/zQACAAaAPj/EAAaAOX/EAAVANH/HwD+/+z/NACg/ywA1//b/yUAAgD+/+H/GgDJ/xYA3v81ACUAvP9PACMAIgDm//P/7v8IACEA8v/1/+r/KQDj/xIA/v+g/+z/CADv/xwAMAALAOr/EQBLAOL/5f/P/w4AEQD2/x4AtP8EACAA2v83AA0Azv8jANH/RAAWAMb/YwDm/y8ABgDt/wcAsf8VAKH/4P/d/6//SgDk//7/SAAkAG8AQgDq/x4A7/+U//7/DADr/zwA/v8SACYAyf/y/wUAJwDD/+n/8P/M/xMAGQDV//3/BQD9/yIACQAIACIADgDM/x0A///v/x8ArP8uABkACgA2AP//xf/L/yYA/v8sAAQA4f/E/83/3P/7/20ARwA2ANP/9//h/8D/GADm/zAA//8CAAUA0v9VAOr/7v9fAL////8EALb/IgASAFgAGwD1/+3/wP8pAPf/6P/G/8r/x//f/ykAIwAeAAsAUwALAMv/6P/v/zoA7f8nABcA1f/+/97/MgDd/9T/bADs/xoAOQDS/9n/FgD7/wUABwDq/xAAzv/n/9z/6f8bANT/IwADACoA5//K/z8A0v8QANP/KwBiAAUAQgASACoA6f/w/8n/of8GABAALAAXAOv/uv8XAP7/1f8lAOn/s//P/zkA//8oABIABwAsABEARgDp/zUA9P+p/+L/s/8+AAMAYABjANj/GAC3/6f/4f/m/+3/9f/u//7/4f/3/z4ANQAQAPH/RAAHAAMARQDU/wwA/v/a/0YA6f/+/x8Ayv/0/7f/DQAAALT/VgDd/9v/BwDp/xMAy/8PADMA8P8/AA4A2/9PAPj/AgAwAPz/FQAOAPj/tP/S/9r///8FAPz/EwDo/xoAJAAwAPj/9/8dAAEACgDH/9T/7v/V//n/2f/7/+n/OgBEAPL/YgATABEAJwAcABwAwv8RAMf/2//N/7H/5v/5//n/CgA+APP/ZQAVAB8AKQB2/yIA3/8EACMABAAAAOD/4v+//yQAAwBEAMf/1f8bAOD/QwDb/zUANQAtABQAzv/n/7T/LwDh/0cARwCL/yQA2P8WAE0A7/84APL/9P/k/9z/vv+P/9v/JQDd/yAATwAAAEUA8/8qAD8A4P8QANT/4//7/wcA//8GAPv/AQDP/9j/dwCo/+L/SADr/xAA7P87ABYAvP8fACQA3P/l/+H////b/xQAFgD8/wwAIwA4ANz/LADj//j/AwDU/zwAFgBBAPj/EgCs/8X/8/+s/xwA2f83AA0A6v8fAAAAJQDV/xAAEQCk/wMAAAArAI0A6v/r/+3/rv/6/xYASwAWAPj/AgAgAPL/5//w/9r/7v8HABIAw//b//z/AgAHAPP/IwAsAM//PgARANP/eQALADwA3v/z/xcAqf8DAN3/9v/O/ywA9//d//7/2v9IAAoALADX/+j/9f/W/+v/JAAjAAUAVgAFAPb/7//T/+j/LQDF/1cAagCl/zEA5/8SAOz/AADq/8T/+v+2//3/7P84AND/HQDx//r/UQDf/zEApf8RAC0A9P84AEYAu//E/yQAsf95ACoA/f8oAAAAAwApAOD/hf/9/+f/3//8/woAp/9BACkAu/9nANn/BAAbABYA9//c/xkA8/8ZACoAOQDm//T/MAD0//v/7v++////5/+o/wIAFgD3/wQAGgAVACwAMAAOAND/t/8HAN//IwBBANv/GQAMAPf/LwDL/xgABADD/yQA1/8UAOD/5/8zANv/7P89ACkAGAAZAAYALwCk//H/FwDI//j/2/8HAKb/JwDg/wgAjAALAEEA9P8cANn//v8NAKX/AwDv/9r/8f8oAPz/AgATACcA9f/C/0cAEwAdABoAz//W/8T/IgD8/+r/GQDR/+v/GAD6/+7/TAAHACgAMwCq/xQA+P8GAFAAJAAFANb/9v/c/+3/9f/R/53/NQA3AKr/EwD4/+//JgAXADgAGAD5/wUAGAArACwA7P8NAPD/3v+6/77/vf+7/wAAJwAgACoARwD9/w8A8f8pAE0AAQApAPH/7f/c/wsAzf/1//v/xf8CAND/9P/u//D/AwAeAA8AIwA3ABEAFgDt/xwA+v8BABEAxP/o/7v/v/87AD4AKwA2AO//6P/1//D/JQAEAAwAJwAdAOf/y//B/6n//f81AMX/UwAIANT/HwCv/3cA2f/i/z0ABQASAMb/MQDo////JgAAAD4AAgDV/wYAKwDk/wQABADL/8//DQDN/+v/JwDj/xcACAAOANv/GgBFACgAEgABADkAtP/K/wMAEADq/7z/2f/G/+X/XAByAAAA/f/7/8X/+f9LAPH/MQAhAJn/EwDV//T/+/82AFsADAAWAPn/5v+n////o//+//j/qf9dAPP/BgAvADMAFQAEAHYA+v8XABEA3v/6/7P/DwABAKX/7v/Q/8j/BADi/zcAJgDy/zoASQABALT/3f8hABcAEAAlAA8ADQD7//D/IADT/9j/4P/p/wAA5P8sABYA+//v/yIA6P8EAC8A7f8tAPX/zf/d/xQA+v/w/xgAEQBDAPT/VAAWABgAKgCf/83/pP/S/+L/CQDo//j/AwD//zYACABRAPH/IAD+/+z/8//R/0IAmv9KACAAtv9YAMb/QgALANP/GwATAE4AFwDL/5v/+/8CAMH/+v/j//j/EwAGAA4A6v8vAO//JABxAOT/CgAAANH/5/8QAD0A9/8GABcAhP/F/xYA0v8JAAoANAAnANj/IgDl/+b/+v8iAMn/6/9iAAsAnAAMANr/+P+z/wUA2/8nAPT/2f/q/7//6v8RABcA1f8aAMT/LAA2AA0ASQDX/x0AFQAAAAIAAgAbAMT/GQAWAMz/8f8fAMX/GAAjALb/RQDT/xcA8v+P/y0A1v8sACsAJAAbAMH/7//9/yAABgAUAP7/AAD1/+T/CQACACcAyv9GACkA3v80AOr/FQDV/wcA9v/r//P/3P/9/7z/9//+/xAA5P8LAFYA0P8OAC8ABAAyABkAgv8VADYAFwAfAAIAQQDA/xkA/P+z/8D/tv8PABMABwACAFIA9v8zADsAuv8hAMj/1//x/+b/KADl/7v/EQAIAAYAWAAXACgAKgDE//f/2/+r/1EA6////0AAt/9iANL//P9vAKP/EgBGANj/AADo/5j/w//+/wIAFAAcAMD/JQASAMf/agAbAAsAVADx/x0Awv/E/ywAMQAOAOr/8v/0/8z/8//6/5H/9/8FANv/IAABAFUAQABVABwAw/8xAMz/7//1/97////N/2sA+//c/zsAl/8dAP7/uP81AA4ALQAMAOr/DwCl/6b//P/2/y8ALwBGAFUA5P8ZAAUA+f/+//D/EACw/83/5P+//9b/PQA3AAcAXAAOACcAEQABACsAyf/g/9H/wv/R/+//KwA3ABkABQDs//3/z//3/1AA6v/9/9//CwD5/+X/MQDn/xcA3v8LAO//HABMANT/TgAhADkAHAADAMf/kP/F/7///f/o/zMAAQDd/yIADAAOAA4A9P/c/zYA8/8yAEsAFABDANL/EwCl/8j/FACH//T/0P///9j/IQBvAOj/ZwAgAC0AHQC+//T/6P8aAN7/FAD2/9n/+f/i/0cAs/8IAEEAwP8CAPD/VgAeANT/+P/I/woABAA3ABIAJQAlAL//CwDP/7f/+v8dAPb/DAAxAKj/3/8qACQAHQA+AFEABgCz/7r/MQDP/wEA4/+9/wUAzf8aADMABAAJAEIAEgARAOb/CAAKALn/EwDv/yMA2//z/xAA6f84ADAAJAAIAAMA4v/7/4z/+v/v/5D/JQDd/1cAVwAWABsAKADy/wAAOwDU/wEA7v9OANn/n/8gAJD/BgDw/8z/+v8HACsAAgALADkAHwAoACUA8/+9/+H/BQDU/y0A9//q/xAA4P8rALn/SgA4AOT/NgDD/yYA5v8MABAAvv/9/8H/DQAAAEwAGADh/14A+v/h//P/JQAAAAUA9//g//7/4v8YAND/5v/m/+r/CgDy/wMAvv88ABgABABbAA0A8f/z/x4AxP9cAAUA8v/2/6f/IQDU/zsA7v+h/yEADgATABUAIwDw//X/MAAtABUA6f+s/wUA8P8CAGoAwv/8/yUA1P8aAM3/rP8vAAAAzf9RAAAANQAcAJ7/GgCz/93/LwACADEA/v8NAC4Ay/8MAAMAu/8pAOP/7/9XAAYAOgBkAKj/2v/1/7///f++/9P/2v8eACYAAQB5AOn/RgAMAPv/JgCh/xoA6P8UACcAGgDx/+j/CwCf/wgAtf/o/yEA3f8SAN3/NgANAO3/MwAoACwAQQD8/wwA2f+0/xcAiP8QACsACgAuAM3/NwDP/xoALQDD/wAAmf/j/xAAKAAyAD4ASAC6//X/7P/r/+//6P8tABUAFAArABQAAgArALz/EAD//6H/AwCt/9////8EABYA9/8uABAA5v8AABAAAABYABoA+P8PAAsAFAAFAD0Anf/E//v/xv8gAPn/GwAOAAQA/v/6/wQA4P/7/+H/DwAlANr/QQAnAMH/6P8AAPH/7v/x/7X/LgAnADwAaQArAEYAlf8gAOT/uf8WAJ//SADv//j//P+s/woAzv/j/0YABADa/1QANgDr/ycAFwDx//r/NADq/9P/OQDA/8//IQCy/0QAJQAOACcA6P/+/8P/4//c/xQA3v/l/yQAGQA5AMn/SAAEAOL/MgDn/9L/3f9HAN//5/8LAAMAKQDn/0MA7/8JADAA9/8pALL/EwAVAL//6/+y/wAAsP/o/0MANQAoADgAAQAAANf/8v9SAKz/PQD2/7j/YQD4/yAA9//v/8///P8DAOv/7//L/yAA+P/0/ysAGQDL/zMAEAD+/w8A1P8pALv/JAAFADkAPQDx/ycAs/8VALv/HADq/7f/PADI/xsAAAD//+T/wv8pAAkACAA/APb//P9SAAQAEQATANn/9f/1//X/9f+y/9P/IgAsADgA//8jAMP/3v9AALj/BAAqAMv/AAD1/9f/EwAkABwA7f8bACMA0f9DAEkAxf/1/wsAmv8EANz/BACFAMv/IgADAMn/HQCh/wQA5//s/1EA5v9JADkA8f/a/+D/wP/k/1sA3P9EAPX/wv8fAPv/IADt/ycAJAD0/8L/LAAXAAcAWgC1//D/yv/L/+D/8v8YAA8AFgDw/+D/xf89ADEATgA1AOn/BgDC/+z/2/8BAPv/FAAfAND/5/87ACcA1f84AB0A4f8IABgA1//v/+7/kf8jAEAAl/8dAF4A6/8RANH//f/6//v/XAD5/zIA5//E/yYA8//a/+7/PwC8/wsAQAC8/yYABAAAAPD/+P9AAPz/AAAnAO//nP/F/yYAAgD+/yUA8f8BACUAuf8IACMA+P8nAOr/LQAgABIA3//W/xoAsv/3/9n/7/8pAFEAFwDq/zUA9f9bAM//6v8GALL/GADB/+//IwAQAAMAIwD2/47/8/8BABgASwDu/zoA7P+e/18Azf8FAD0A8f8CAOL/GQDi//P/8f/o/wMASgBIABIAJwDK//7/0v+Y/wQALgDs/wIAHADi////2f9HAO7/4P8HAAIAUgDa/yoAFgDt/+j/AgAqABsAGQCy/+b/2f/m/+T/zv8rACEAJgAWAPH//P8rAC4A1/8AAAYAt//R/zgAIQDO/wsAAgAAABoA8P+NABQA3//S/9H/8f+y/04A/f/v//j/yf8ZAAoAOQAfACcA0//j//3/1P8yAMf/0f8wAAoAIAAMAPX/EwAFAEEA6P8AAEAAif89AN3/8/9OAKL/7P/d/wIAt/8XADkA1/8ZAOn/JgDy/xEAIQDx/x8AGQD4/xEANgDh/xcABADC/wYAyf8DAAQAw/9NAOb/+v8gAN7/SQD6/yEARwC3/6v/9P///wIAAwDN//3//P/w/woAyP8SACwAHAAhAEkAOAAKAPD//v/a/83/RgAKALL/4f/+/wsAEADo/wwA9P+n/wkA+v8eACIASgAqAML/OADJ/8L/agAAABgAAwCz//P/+v/+/wAAKAAAAM//GgAuACAAmP/o/97/xf8vAAIAJADv/zYAEADH/0AA4v9MABcA3v8+AM//FQDj/wEA9P+4/wIAy/8JAA8AEgATAAQAGQDQ/0gAKQDC//f/EgADABYAGwAKAOP/0v9HAO//BABAAKD/4f/O/9j/1v/D/yUAEgAlAB8ANQAEAMX/UwDu//f/XAAVACMA7P/5/8j/BgAiAOX/PwC9/8X/3f/6/7n/v/8hAMz/GgBEAFQAHAAYACEA+f9QAL//EQD0/7z/SwDX/wsA+v/V//D/8v+//w8A9f/e/2IAwf8rAAwAMwB1ALn/LADk/5r/FwAQAKz/AQD5/wYARADw/0EAKgAjABYA+v/Z/6H/x//V/xgAAQAsAOr/DgADALv/KAAKACIAKQDI/8j//P/k/z4ASwADACIA9/8XACIA6v8RABEAn/8SAMH/yf8MAKf/QQABABoAJADW/xUAJwD3/0wAXgB+/zoA+//M/0AA2/8IANj/+f/T/xYAJQDH/+L/sv8TADYAyf9MAAsAqP9eAPL/AwABAAMASgD4/0kA+/8HAAoA+v/8/8T///+8/xwA6v/S/0YAq//y/1sA1P/a/ycA+f/k/0sA7//e/zsAAwABAAEAAAAAACkAGgCv/xgABQDT/9v/KAD6/9f/HQAIAEEAAQAWAAAAvf8QANn/3v8qAO3/BgAGANH/HQD//+T/EwA5ACkANgAJAMf/JAAVAN//7P/L/+j/EwCf//v/HQC0/xQAEABuACEARgAHAMn/AAC8/+f/5v8gAPj/KAAFAOb/KgD3/+v/6f/7//n/+//m/54ACgDZ/2UAz/8aAKT/xf/5/9//5f8WAC0A4/87ANn/JwD5//D//P/O/2IAyP8XACIA7f8LADMAMADh/+P/2P/y/9j/+v8YABYAwf80AAcArP9WALr/8f8EADgAIgAFAB4Auv9cAPD/JADn/8j/6f/H/ysAnP9LAPn/IwBqAKb/DADi/xQA9/8FABoA+f8fAAUAKwAAAPX/BwDX/8L/HQCx//P//f+z/2cABQDx/yAAKADJ//X/UgDV/zIACQA3ABsABQAeAND//P+i/+3/6/+2/xMAGAD9/wsA6v8tAAYA2P8zANT/8P8eAP7/8f8yAEAA0/8cAAgA8P82APP/7P8FABAA3P/7/zIAy/8IAPz/o/9pAOT/vv8tAMr/8f/h/+3/BwBAAAUA9/9FAN3/KQAwAPf/YAAKAPT/GgCe/7r/t//p/xMAAAAfAOj/BgAJAAsACwAzAPz//P9ZAMn/5f8CAMD/0f8YAND/FABSAOH/QgALAMf/GgBBAOz/SQAZAI3/LQDG/87/HADh//D/IgAAAO//AwDz/xQA0/8lABMA7v8uAB4AAgDl/1AArf/D/+X/q//9/9z/JwAmAGkAEgApAD0AIgAMAP3/TgC1//T/sP+//9r/3/8AAM7/KQC+/xsAEwABACMA1P9KAAMACgA2APT//v/p//7/MwACAB8ADACv/0cAsf+0/0kA9/86AMz/VwAHAJf/YADp/63/6//y/8P/BwA4APr/IAAGACIAHQAhAOf/o/8VAOL/9v8QAEUALACt/wAAHAALAAAA7f/Z/9b/LQAfABMAMwAQAOD/8v/8/wwAwf/n/zMA2P/Z/wgA+f/M/xIAKQAJADEAJAAmAAUADgDZ/97/AAD3/w0APwD7/7z/EADn//3/7P/Z/wwAFwD//9j/6P8DADwAAABCAD0A+v/+/+//AQCP/y8A///y/xQAqP8TALT/CwARANL/YAD7/w8ANgDz//H/RQAjAPL/KwAJACoAFAC9/+f/7v/i/+r/CADC/9v/0v/9/y4A4/8SAKP/AwArAO7/XAAeAEAA+P/x/+T/5P8vABoAKAABAAgAFgALAA4A/f/j////+//N//3/wf/T//D/zP8iADwAyP/c/z8ACwDm/+j/GQD+/zgAeQApAAYA8v/0/+f/4/8YAPj/5v87ANT/vf8KAMP/0f8jAPj/8/9EAPj//P/K/+X/CAArAGIABAAzACcA8P/8/wwAzf/n//b/1f8AAMT/9P8PAPX/0v9EAFsAxv8LAC4AEQDY/ywAAADp/0sAAwADAP//6v+p/xoAFQC8//b/+P+o/6v/DwAdACUARAAyABYAFADc/0AA8f8OAF8An/8jANn/FgAvALn/CwAxABwAt//2/5r/vf8qAKz/AwD9//H/UQAoABAAOgADAB4ANAC8/9v/CwDt/zIAFgDq/yUA0f/8/wMAw/8JABEA6v/a/wEAMgDm/+D/DADv/xsAMQAAAFQAEgDg////GgATABUADQDL/3b/2P/n/8v/TQAZAPz/7v/s/04A0//8/zwAs/8DAD0ADwA7AOv//P8FAPD/KgALABQAIAACAO///v97/+7/AQC7/1IACwAoAN//zP/0/9b/OwD9/yMAFwD1/zYA///9/yQACADc/wwABQDK/5j/CgAcAO7/HwA1AB4A2P8nABIAtP8yAP//DAAQANn/OgCy//L/+f/k/0kAEgAoAOf//f+a/9b/PwCi/wYA3v8/AFAA5P8fAPn/UwBMANz/LQD6/+r/FQDF/9b/q/8AAMv/rP8LALj/XAATABkAYQAAACIA+/86ADYANgAOAOX/3P/k/+f/2v/v/8L/6f+g/8L/CQDu/ywASwBTABcALAD7/xcABgCs/y0A4f/O/xEA/v85APL/FABLAAgAJQCk/83/2//A/0UA+P9ZACoA4f8aAPr/8/+P/+b/0v/e/zwAxP81ACYA5v83ABYAHwDc/wMAJgAJABQAq/9NAOT/z/9tAO//UADd/9n/v//H/1kAh//s/wgA1v9ZAAkAFgAAAJf/JgBQAP7/GAAxAAwAz/8UACYA1/9GAM//9f8TAKT/4/+q/+3/PQAcAAgAJwDv/+T/NQAuAD0Azv/f/xMAo//m/ygAKgAKABMAIQDr//r/DQD4/7b/4/8ZAAkA5f8NAOv/7P8AABoATgDX//P/YwDq//T/IQDV/xEA9//4/xIA9P8NAO7/LgDo/8T/4//B////6/8QACQAHwBCABQAPAAPAJX/IwDr/97/SADP/x4AhP8GAC4A0f8WAM7/OgDy/wgAPgBEABMAKwAsAMP/GACm/9T/uv+P/wcAzv8QAFEANAAiAEwABgAlAAUA9P8SAAEA6f/q//n/yf/v/xAAAwD7/+n/1v8JAAcAFAAYANT/FgANAPv/sP8gADwAJwAyAOv/NACg/2IADwDE/+f/jv8hAO7/AAD8/zAAsf8fAAQAmv95AM3/MQAcABAATQAcAEAAv//I/7r/zP89AB0ACQBAAMr/5v/d/yEAMAAGAGUAm//V/8D/5v/+/9X/JgDg/yEA1f/u/ysAOQBIAGAACQAOAOL/vv8DAI//+v/h/xAAy//c/yUA7f97AB8APwA4AB0ABwD3/97/4P8JALv/EwCz/97/IADe/xEA2f8FAOj/xP8DAIYAEwD0/x0A+f/3/yAA/P/s/x0AyP87APX/JABeANb/UADo/77/1//L/9j/1v/c/wAAFQADABcAHwD4/ykASQCr/woAHQDE/xoA5f/4/x4A+v8fACAA2f9BANf/+f8kALv/ggCb/xgAHAB3/3sAz/8EAM7/1f/8/93/TwDe/0EAJwAhAP//xP8oAMH/KwAlAOb////w/xMABgBAAL3/x//9/7v/LQDc/0EAKAC5/2QAx/8iAD0A8P9cALb/4//T/8P/IQDT/9z/2/8AABYAIwAbAHQAFgDx/zwA0P8XAAwAvv/8/xgAmv/V/xQA7/8jAOj/+P/O/wcANQARAEIADwAAACEAAwANAAAAtP85AOz/4P8gAIv/HAADALT/LgAxAOn/QgAuAOb/7P/j//H/3/8sAPD/MQDg/7v/LgAFAE4AuP8ZANv/EwBxALX/UgDW/8P/LQDg/6//9f/l/9f/9v8MAIcAEQAlAG0Az//v/0IAvP8fAAQAkv/7/7T/xP/y/ygA1f8uAPn/8f9sAPr/IQCe/x0AGgAyAJYA5f8gAPH/rv/m/xAAqP8SAAAA2/8QAKH/UAAjAN7/AgDt/+X/DgDh/wYAUQDY/w4A9P8gAEEAz/8kAC4A6P8WAOb/0P8oANX/NgAMAK//wf/I/xoAAABGAAIACgAOAEQAAwAIABUAxf8bANX/FADD/+b/4f///24Ayv/5/9z/8P/x/wQA+P8EAA8A4v9cAD8AHAAHADIACAD//ywAUgDY/8D/BgCN/8j/tP8EAB0AuP8VAP//AADn/wcA8f/4/+b/5/9CAAEARQArACkAJQARACAA0/9GAD4A9/9HALv/1v+t/4b//f/a//f/xv8WABcA/f8pAPr/QwACACYACgAwAB8A2v8XAOD/7v+y/xgA9/+X/wAA6f8oAPf/NABdAFcAUgDT/xoA5P/H/ycA7f+W/7r/x/+i/wwA9f8LADYA0f9bAHAAUQDy/+D/OQDl/+b/+P8dAAIA9P9LAO//sv8IAO3/CAD4/4P/JgDF////VADu/0UAuP/4/zYAGAAhAPn/NAD4/+b/3v/s/xAA6f8AAOT/NwDg/yIABwBx/z0A0/8EACAA9/9fAPL/KAAwAOf/7f8lANz/FwD5/4n/HgCO/9P/RADx/xEAPgBPADAAJgAmAOb/xf8LAOb/CQDu/7f/AgCu/7r/z/8qADAAPgBaABgAAQA5AC4Awf/h//T/GADU/9H/DADY/8T/JAAcAOD/UAARAD8A+//k/0YArf/x/+v/6v8HAO3/x/8dAA8ACAAfAPH/+P+g/0MA/P8DAEEAxf9dADEA7P8pAPH/FwAlALf/DQDj//j/8//i/wMA3P8BAPj/8/+8/0wAAgDd/y0AoP8lAAcABgDE/9n/aAAeACAAEAAwAPf/3P8yACAA9/8jADEA2/+9//j/wv/l/zsA1f/2/7b/AAD+//H/8P/n/3EA0f85AAgAvP8qAF4ANAD8/xMA5P9GAK3/4v/k/6X/KAD5/xgA1f/+/+3/z/8rAAYALQBlAOz/HgA/APP/UQDa/8b/zf/V/7T/AAAyAL3/IAAJAP3/AwD5/w8Au//g/yQAzP/+/3sA7/9QAFsAvv8MAP3/DwAvAPP/+/8WAOf/pf/8/7r/fP8/ABQAGgAcAFAADQADADIAkf8nAMz/s/8vABcAWgDn/8z/JAD7/wEALQCn/4wADwDK/yQAmf8cAJv/MwDw/xIABQBp/04Akf8RACAAAABIAO7/dwBBAPX/VgAMAJ//FgD8//v/OgDv/+D/AACg/8v/AgABAOT/pP8nANP/AwAgAAYACgDb/1UASABUACQALgDm/wQAKQC3//D/uf/O/9//FADB/+X/MwDq/zUA3P8HABEAMQAtAO7/IQDl/8r/IwD7/w8AFwDG/xEAAAAeABsAIADX/6n//f/X/yoA1v8fAE4A4P///ygAAADQ/wIAGgD6/8//RwDy/z8A4f+m/zcAn/8RAKn/GQDo/9n/mgDq/3wALQAZABYAo/8xAAMA2/80AOn/6v/A/9v/EwC//zEAsv/q/+P/5/8zALX/QwDK/3MAQgDg/40A+P9bAJf/DADz/5X/TgCs/z8A0f/k//P///9XANb/VwAPADYA7P/s/xAAbP/2/7X/8f/P/7z/IQAtAHUAKwApAOD/EABcAOz/6f8QAN3/xf/Q/xIAFwDU/woA1v8iAB4ACwAdANL/YwAIAAAA3//g/zUA3f8EAPz/AwDP//L/EQD3/wQA8P/b/wwA/v8EAFoA8P8aAPT/7/8iALD/+//t/+r/7v8eACcANQDk/ysASACN/0wArv/X/zUA2P8oAO7/MQAiANH/1/8jAL7/KQA/ALj/LgDO/x0A4/8AABwA8P8EAOb/OADT//j////p/0AA+P/9/zUA0P/a/xoAzf+hAP//t/8iAHr/EgDX/wUALAAFABsA/P8wAPT/AAAFAEsA5//s/0AAk/8HAOL/7v/3//D/gwDF/6P/GgD2/+f/KQAQACsAMgAEAC4A6P/f/93/qv8KAPf/u/8jAC4AIgAKAP//FQD3/wQACwBEAPf/0P8uAOr////6/+r/CwDx/9f/0P8LAOb/HABCAAgALAAAAA8AtP/U/wUAs/86ACYAJAD2//v/GAD7/y8ArP/+/+X/+f87AKb/NAAYAO7/HwAMADcA5v9FABcA3f8RANP/jv/A//L/5/9HAAIAGABJALX/GAAfALT/3f8wAFcAAAAXACwA0f8UAOH/GwAXANn/QgDI/wcAxP/e/xYAmv///9b/GgATANv/MwAKABMA8P8aAC8ANAA9ADYADADI/wcAqf/w/97/zP9RAAAACgD+/7//qf+u/wUADgAKAEQAagBHABAAJwDO//j/awDU/7T//v/e/0oAIACx/9//tv/H/xwAHAD+//3/5P/s/+n/QAD7/zsAYQDF/y4A8f/9/w8ACAAqAP3/FwCy/wAAx//M////rv8pACAAMwANAAYA5//c/97/9v8wAOz/LgAXAIMADwDs/zcAh/8wAA8A3f/f/5//OwDD/+3/HwALACYA6f/0/+3/0f++/x8AGgDv/yIA+P9TAEAASAA9ALH/7P+r/6T/5/8dACoA6f9HAA8AGQDy/9P/5v8DAC8AMQAcAP7/SgDM/8b////V/9L/5P///wAANwDR/x0ATQDR/9v/5v8YAOz/DwAfAOH/CQARAC0A1/+l/xYADQAXADcAyf8IACsAAwBqAC4ABgAVAAYA6/8AAM7/m//C/4z/CgDt/wsAUgDk/1QA0f/A/0sA5//x/zEAJQDL/yIAMAAXAD0A9f8uAP3/xv/Z/+b/FwACAAIA//8UANX/xv8jAI//wv9HAAgAEQDh/xMABADm/yIACgBFAD8A8f8dAC4A7P++/ykAMADY/wwA+v/T/wUAvv+9//7/HwAsANv/4P8rAAgA9v9MANf/8v/Z/+//MwDJ/z8A+f8AAC0A3/8NAAgABAACAAAA5P8CAB8A9P/s/zwA/P8BAA8Apv8SAMz/AgA4ANL/LAD1/5f/HAANAOD/SgAmACoA8f///zsA1v88AN3/vv89ALb/6P8fAOb/RQDj//f/GwCv//7/oP8lAAcACAAmADIAPwDE/44Awf/1/ykAwf8AANr/XgC3/73/yf8OABYArf82APH/CAAYAGIADgDV/0YAxf/6/yMA8f8PAA4ACwAGAOf/KQAmAPL/4v/N/8f/8//H/7v/VgAgAAAA//8ZAOH/y/9EAKP/BgAVACwAegDv/00AIAAcAB8A7v+p/7j/MwDs/+L/7P+7/wkABgC///f/7v/v/0YA//8FAP7/8f8YAAQANAADAAkAXQAAAC8ASgDB//r/fv/a/ygAw/8sAPD/FgD9//7/JQD8/+X/3P8SAMz/AQAQABUALwDk//f/KQDQ/wcAPQCr//b/zf/5/zwA0f8sAPn/CwAKAAsAQwATAEkALwDG/w8ABQDT/wwAZ//n/0UA1v8BAOL/AAAPACMA2P/v/ycA1P85AO3/DQA5ANv/OQDm/+n/PwABAO//DgDl/9P/BgDd/x4AEwDV/ygAIwAaANr/zP8BAB0A4/8NAC0A2P8qAPz/JQDG/6v/CADo/x8A2/8EAAAAEAAnAC8ALQAKADoAwP8DANT/EgDQ/5z/XgDq/wUAPAAnABQAIAAdAPj/3/+4/+7/q/+j/9n/8f8SAAAAJQCYAFEABgAvAN3/BwAzAAcAw//2/9f/vf8wAM3/1//9/9v/+v8ZAPL//v/7/xgAGgAaABkA/f/y/wsANQDz/yYAEgDd/1sAEQD0/+//tv8aAAIA1/8uAPH/BACc/4L/KQCi/xEAIgDa//f/2f9SAEcAcwAdADIAUADz/wUAMgASAML/BgDC/3n/7f+T/8j/CQAEADsA8/8XAAEAFgA7ABEAggDp/wcABgCW/w4AHwD5/+X/+P8pAAMAxf/+/+P/AQDo/8X/6P8NABYAGwA4ABcAOwDm//X/8v/M/yEAEwAYAAsARQD5/1YA7P/b/yIAY/8IAI7/9f/A/83/dADj/zUACAAcAO7/LQAEAFwAQwC9/yIAuf8tAKL/CQD5/4X/NwDc/yIADQADAA4A7f/H/zwAVwAWAF4ALgBAAM3/5P+p/6L/4P8CAAQAzv8YAKb/6f86ANj/DwBIACgA+v8AAC8AQQAJACAACQAGAP//6f/3/8X/zP/H/wIA+P/Z/+z/xv/P/1sALgAWAGkATwB3AOD////S/3r/AQDL/+D//v8BABEA8f/l/w4AMgA+APj/MwAgAAAAFQCf//f/7f/c/+b/CgABAMj/PADB/xYADAAWADUA/P8yAOj/CgAAADAACgA2AMj/2f9qAIT/3P/y//3/5/8HAPz/s/8wAP7/DgAWACUA5P/x/+7///8XAJ3/SwAjAHgAPwD7/wsAov8aAK//JQC4/93/HQC0/0oAz/8iAPn/AQBMACMAFQDi/0MAnf88AAYA2v8jAKz/NQCY/+z/8f/B/y4AHgASAMn/QwDl/0MAJQDB/xIA3f8aANv/PAAVADYAMAC5/0IA5/8XAA0A9P/x/7b/vP/i//r/w/85AMz/CwAsAA8AUQAGAO3//f86ALr//f/3/83/BAAGABYAzf8eAAMALgAjADQAJwAKANz/uv9GALb//v+o/93/UADR/zsA8f8RADsAHQAIACEAnv/w/ycAjP8aAMv/MwAdAMz/MgDn/wkAJwAkANn//f/N/zcABwD8/0cAs/9YAPv/5P8rALH/6v/g/+7/IADl/+f/+//G/yQAKgAQAAQADgBYAFUAXgAYAMH/wP+1/+3/0v/J/9n/wP84APb/9P86APr/OgDO/wwALQDb/yUALAABAO7/RADf//T/5v9BABMAwf9qAJ7/KADf/wsAHQB8/z0Ahv8vACwAnf/t/8r/PwAkABUAGwBFAA0A1f85ABIACAAaAOj/z//k/xoA+//4/ysAEwANANv/qf/s/8z/7v/c//f/CgAYAC4AGwD4/xMAZQAVAAQAJAD3/wgA2P8hAMb/u/84AA8ABADv/zMA0v/N/+v/n/83ANz/IQAKACcASwCh/1oAw//f/0IA5P9ZAPD/uv+p/9n/7v8NAEkAHAAtAAgAEQBJAPz/uP8nAO7/+/8pAOj/JQDe//L/FQC1/xQAFQCy/87/1//k/0MAAADu/yEAEAA+AE0A9//z/8r/zP8ZAPz/FwAIAPT/LwBTABIA+f/A/7j/5v/0/1sA3v/z/yYAv//z//T/AwDX/yYALgDp/9j/GgARABkADADq/y0A3f/W/xAAOgDP/xoAPQCX/zkA/f8HAAwADAAKAOz/OwDf/zkA0//l/9T/6/8FAKX/CQC2/y4APwAJADIA7//r/yIABAAPAAUAvP9EAMP/LQAMAAYAKwCU/48AfP8GADAA0/9mAK3/JQDH//H/FgDj/zoACwAZACcAuf/O/+3/y/88AOf/BAAiAPj/TwDp/9P/w/8KABUAQgBQAKj/2/8XABgAFgAEAAgAIgC+/ygABADk/0AAzv8RAN3/4P///9f/8f/K/zkA4//Z/xIABwAsAN7/NwAbAHYAJADK/xkAp/8nANr/3v9qANP/wP8OALn/pv8ZAKT/VQAfAND/VgDx/7cANQD3/xkA4P/t/8r/DgDB/w0A0v/+/xMAyv////L/FwDY/2EAEAC9/xcA8f/9//f/VQDx//f/FQDe//3/5v8HABgA9v/n/ycA2P9mAD4Azf8DAMz/6//w/wAAxv8CABQA8/8oAKv/HAAsAOz/SgAqAAUA5P9AAM7/tf9iAMP/vf/7/+b/FwASAA4Ayf8pAG8A7f+6/+//5f/n/00A4/8EAE0AMAD+/xgAHgCt/9z/9//3/wQACADF//z/MgDM/9f///9YAKH/RwAyAIz/dAANAEEAyP/H/93/kP8TAAcAVgA+AF8ADwDv/8T/BgDw/77/QgDM/xAA7v8GACAA//8UAOX/3v/R/zEA7/8GAMH/4f9lAC0AJQDY/xMA0P/e/y8AAAADAB8AAADu/7//zv8IAAAAkwD8/xsACQDV/zcAof8QAAEA+P/y//D/4v8wAK7/2P9uAIL/VgDf/+//ZwABAEgAsf/q/8n/WABDAAQA/v/e/y8Au/84ANj/1P8oAOz/BAD0/wUAof/B/+z/JAAkAOH/MwAxAB4AOwAyABcA6f/S/+f/9P/h/0cAAQD3/xcAw//U/3j/DwAnAD4AaAC+/zoAsv8MABwAwv8jAMn/OADV/xUAJQAAABQA1//1/97/AADt/2EA+v/v/z0ACQDs/7f/VgDp/7T/LADO/xIAMwCa/xsA4v/a/1oA/P9jADcA7v/X/8P/BgA0AP//yP8SACYAKADc/zAA1f8TAA8Afv+y/5T/3f/K/1cAHwAGAEQANgCYANz/QAA/ACQA5P/q/+v/mf+y/9j/AACq/zEAIQB0ADsAz//v/9j/BwDA/y0AJwAQANj/EQDN/83/hQDN/zMAyf8hACsArv8bAJ7/DwD4/9T/KQAAAOL/HgBXABcA9f9DADcAuv8xAAQAi//K/+b/7P8CANv/+v8rAE8APQAQACwA4v8dADMA/P8QAOn/qP+e/7P/2P8aAOr/DQDr/1oAGwDR/1cAxf9rAA0A2/8KAND/QQDc/yYANwDk//7/+//O//L/tP8AAEAAtf8CAA8ALwDO/wMA6/+v/20AOAA/APb/MADz/7r/IAD9/x8A2v/V/w4Avf8KADEA0f/t/9f/8f9wACcA/v8dACgAZwDq/4z/5P+Y/8X/zP8EABcABwCYACgA0P/U/2UAJQDV/0UAz//p/x8A/f+l////AgACAA4As//i/zYA+/+P/x0AFQBWACkAKAAhAK3/PADM/xUAAQASADEANwD3/4L/7f+Q/zEAEAAMAD4Ax/8ZAAkAGQDa//X/zv/t/ykAy/9IAC0A5P89AA8A9f/1/87/HwAaAN3/6//b/9n/7/8oACcAPQBmAMf/wP8wALH/OAAGAOr/HwDH/ycAav8VABgAuv8eAOT/SAAhAE0ABgD7/wIA3P/O/+r/GADQ/y4ACAADACsAHQD4/7D/VQAwAN7/CADy/xwAGwDd/+f/jf+1/ycAJgAFAAIA9P/V/y0A6f8DAFYA7v8NAA8ADgAnAOn/2v8OAPH/JwBxAOz/f//u/yYAqP/v/+H/rP/o/x4AZQBWAF8AHgAfACUA9f/Y/+T/6v/q//b/m/+w/9X///8jANf/MwBdAAcAVAAOALH/LgCb/+n/WAAXAAwApv8HAM7/5P9WAAsAKQDj/xUA6//1/0AA5f8nADQA4f/9/wgACgAGANf/9//r////EgCr/9L/3/8UAN3/GAAnAM3/IwDh/zMAFQAgABUA8/8NAOX/AAD1/yoACgA+ADIAIgADAJD/3v/u/+v/IQBDAMD/CwDc/7v/BADa/0QAwf8DAAsA3P9FACEAJgAIACAAJQDd/wsAEADX/8v/sf/n/8b/IAAmAMn/jQDr/zMAbAD9/xMArf/V//3/KwAfABAAwP8jALn/cf9JAOL/EgAOAMn/NwAlACUARwAHAK7/OgC5/+D/+f+p/zMA4P84AAAA9v9SANb/TgA7AAwAGADG/+X/6v/t//D/AAAUAP/////V/53/MwAnAAAAPQCw/+H/AADq/1EAAACJ/y4ALgDb/3cA+v9eACIA1P8cAMD/HwCz/xoABAD2/+3/ff9ZAMj/5v8VAPb/HwAwAAgA2f8XALv/6/8kAPz/LgAoAOv/IQA4AAMAHQDf/y0AEwDV/9L/4f+m/8z/OACq/y4AQwCw/+H/RQAsABoAGwDj/zUA0f/A/2UAxP8EAFoA4/8wALr/5v8NAM//IgAFABAA+P8HAJX/NwBaAKH/hwCi/+z/IQDn/0UAkv8TAA8A/v8eAAEAGgAHANL/5/83ANH/HAAIAPz/KQC///H///8SANb/zf/u/xEAaAD//w0AIAC6/9X/BwD8/0oATQA0ADcApf/f/wsAv//k/8X/NwDw/+r/IAABAPP/7v8KAOP/QQAkANv/XADt/5r/SgACABIALwCS/xsA7/+x/woAv/8QACAAyf89AC8A7/9MAC0A/P8LAMD/DgA0AI//QAD8/7H/cACk/z4APQDu/wgAwf83ANP/DgDX/6P/2//J/xwAKwBXAPb/8P8lAKn/AQCdANT/7/8AAP3/WgD1/x4Az/8XAL3/9/8UALT/MADU/3YAz//E/yUAy/9UAOr/BgAFAKX/FwD+/+X/IQD6/0YAHwCa/zIA8v8kAB0A3/9YAOP/0v/d/6T/LAAAANL/MAAKABMAFwDw/yMAKwAAADoAFQDi/xcA2v+U//n/6f/W//3/tf9BAAgA/P9/AAwAOwDP/wgALwB8/+T/6P8KABsABgAWAMz/2f9UACkANQAJAPD/4/+q/y8AAAD1/1wA7P/O/+7/2P/h//n/1P9RAEMACQBwACIAyP+4/+D/wf+S/xQAEwDs/yEAIQBUAM//DgBxAPD/KAD5/9H/EgDe/xYAwf+s/ygA6f8QADAA6f8YAAQA+f/a/9H//////87/IAA9ABEAWgAUAFoA5v/i/2gA2f/h/9b/nP/B//j/tv/n/zsAbQAxAMb/OADG/+T/HwCk/+H/0/8aACUAOABXAP3/IAD5/w0A7f/g/yEA4P9JAPn/BAAGAKb/IgD9/wEAzP8VABoAkP8lAOX/5P8sAPv/NADQ/93/LQAOAP7/EgAAABMADQDh/0kA+f/5//n/3/9BANT/DQDk/6v/ZgAEABQA7//P/+//sP8LAB8ADAAeANT/PgAoAOL/SQDD/zcAFgDY/zUAqv8dAA0Ar//3/8v/2f8eAD8Azv/w/wYAxf9gADgAHQBPAOL/GQC2/9P/HgD9/wcA8f9gAOb/EwD8/4//FgDd/+3/EgD7/8f/CAABAOb/CAAOAC4AHwAiAAUAYQAgAB4A+P/E/5P/lv88AMv/LgAjAAoAPQCB//L/LQCx/y8AMwDd/0sA1v/y/+j/2/8TAOD/VQDz/yMAOAAtABEA8f/u/6n/2P8eADAAuf8OACsA/f8AABsAFQDX//L/DAD8/7z/HgDS/wMAKQANAAkAtf9EAMb/0/8mAAkACAAjAFQAy/8TANb/AAAxAIX/AADV/8z/QQBeAFMADAAcACwAAQAQALL/3P82AJv/0/8CAMr/LgD9/zQAHgCG/xYA//+x/2MA5v/V/14ADwAcAOr/4v9PAA4AEgDo/wkA7//9/ykA9P/W/3r/AwAGAPz/BgAoAFAALgD5/wMA3v9w/wAA3/9RAD0A2v82ANb/CwAzAEwA0v/P/+//KQAWAN//CACi/wMAvP8rACkA7v9NAAUALwDQ/ysAov+h/w8A+P8mACAAQwC3/xEAJAAAAP7/GAAiAN//LADT/yQAAgDV/yAA7v8KAAcA8/+y/9H/zv/y/0sAHgBGANX/sP8XAMT/EgBWADcA+P/n/xgAxP8CAD8AEQAFABgAOAAuAA4Av//R/6b/0v/G/wAA2/+3/2UAEAB6ACQA8//2/9H/MQD8/1kA5P/6/83/lP8dAL7/BgA7ACYAJAArANb/9f8fAMT/WwD2/7X//f/s/w8A6v8DAAMAz//1/w0ADgBGADEAOQALAAkA3P+6/0UA6v+8/9f/6v/Q//X/GgD3/0gA/f9EADYA4v9AABEAlf/d/zsAAAAvAND/lf+i/6z/PAAIAAAANwA1AGUARgDn/wkA/f8BAAAA4v/V/+D/BADt/xkAl//v//n/6P98ACIAXADw/+P/+v/q/zQA///T/9D/8P/1/wYAv/8FAB0AAAApABEAHgAuAAUA/P8CALP/RQDT/9X/HwC6/0EApP8vAB4A3f9xAPv/GwDv/9j/EwDO/6T//f+n/xQAdwD5/ygAIQDl/wIAVgD6/xsACwDX/28As/+S/zEA1/+7/yMAAQDx/+r/BgAUANf/HQA+ACoA4v8RAMj/q/9NABsA5P/b/+z/4f8aAFMAZQBQAPP/HgDa/8T/5//C/7f/sP9BAPz/9/8gAMf/OwAeAFAADADo/wAA8v/s/xUAQQDt/wUAzP/D//7/zf/a/2MAIgDw/4kA2f/+/+X/2/8qAOz/zf+3/z8Aif8NAIcA6P89ACgA+//U/+L/t//Y//L/SQAqAO//aQAcAOP/CwAcALL/AAAkAAYA2P/6/yMAm//s//z/9//B/xAAOACy/zoANgDd/yMANgA3AOz/x/8pAAIA/P/3/9v/+v/+/zUALQDc/8P/6P/J/wYADAACABoA/P8lAAAAMQDK/xgALwB3/2cAPADn/wAAQQCz/9P/KwDW/w4A1v8PAPP/GwDZ/9j/IQDx/xAA3P8YAPL//f8SAPX/HwAyAP//vf8HAMP/QgA5AN3/WAD1/z0AVgDy/0EAwv+Q/+H/xf/Y/9f/9//g/4n//P8UACUAZADz/28AQQDd/0QAGwDY/6D/NADV/8j/RQD0/ysA/v8AAPX/JABqAMn/y/+b/5//6f8vACYAEAAtAPP/NQDW//3/HwDp/zwA8P8NADMA+P+7/wMAxv9t/z4AKAAZAA8ACQDr/+H/NADt/28AGAAPABIAvf/d/+T/BQCq/ysA/f8pADkAv//2/7f/EAAVAHUA1/8hAPD/v/82AJT/SADr/+n/FwAtABgA/f9AAOz/YgDc//b/5f/2/wcAkP/p/4P/BQAgAOn/IwAwAO//+/8EAPH/IwAtAAUAAABEALv/PgAAAAgAGQC//2YA0f8sABoAq/8rABAAqv/E/wAAzf/W/wsAMwDI/+//MAAJAPn/5/9SAPn/EgBIAAgAHABJAPP/FQAdAKr/yP/O/9b/7P8FAPf/FwD7/9H/qf/c/wEA5v9qAAIAgwAfAPn/UwD8/zsArv9kABgAwP8DAKf/uP+w/zEAGwAXAB4ADAC7/8T/xP/e/x0Axf9xABoA7/+BAEwA/P8iABEAzP8kAKX/6P/i/6v/IwDv/+T/8v8lAN3/HgAvAOH/AwAjAC8ABQAyAOD/1f+7//D/HADT/z8AAgBRABoA3/8jALj/BQAqAAAAzf/V/xUAu/8SAD0ABgAFAOn/BgDf/wcAHADt/0QABwAAADAAIgD2/4v/wv/1/83/IAAeAMr/+/8kABwAPgAqAAsAIAC4/97/9v+m/yIAAADm/z4AFAAmAOj/OQA/AA0A8P/g/wIA2/8AANr/5/8YABAA+//T/wgABQDM//v/BgC8/9r/HABMAPH/5P97ACIATwA8AP3/8/9X/wUA8f+X/28AGwDg/yMA4f/S/+3/AAAlAOX/GgAYABUAUwD4/xgAt//S/9n/8P9dANf/BAAMAOb/5f8QAOP/3/9DAAEAMgDz/+P/FQD4/wUAGQD4//b/RwDr/xsA6v/S/0QAmf/Z/ycA+P/9/ycA8//1/wMA4/8ZAOH/5v8jACMAKwDl//v/+f+2/ygA1//h/z8A4v9CADUAAABDACMA/v/n/8H/6/8pAPD/BgDz/83/9f/7/7r/DwACAJL/NwA0AC0A4f85APP/uP9+AKj/IwAMAOb/UQDA/0oACwARAA8Axv/5/wMABwC1/9r/2f/U/2MAMgDD/w8AQgA4AOX/9P/v//z/DwAjAFoAAwDe/8n/tP+W/9v/3P8NADUAy/9rAAwA3f84ANr/HgBmAPX/1//r/+z/XADz//X/6v/p/zwAyv8sABIA2v/4/yIACADQ//3/3f8VAAYA1f/5/0IA///O/1EAvP/Z/zEA+f/5/xQABADv/wEA4//a/9//OwAuAOD/VAAyADIAJwDv/8L/o//y/9f/BQDa//T/IAD+/9X/GwBLALn/bwBBAB4AVQCU/wcAm//Q/wsAyf8BAOr/CwABAEIAMQD4/ysA3//J/9T/MgAyAG3/FgAnAML/WQAgAOf/LQAiACUAAwD+//n/5/9XAOn/lf/W/7j/BQD3/wAAIQDe/yEA/v/u/2QA8P8IABQAx/8HAOb/UwD4/+b/dQDs/wQA2P+3/w4A5//k/wIABAAFAPn/DwAZADQA9v+7/0kArv/z/zMA7v8eAJH/GgDz/wAAWgAdABYAKQBSAM//4f/C/+L/2//q/wIA2v8dAO3/5/8TAB0ALgBMAPH/+v8ZAOL///8ZAC4A3f8GALn/0f+7/3r/WQD4/x8ATgBDAGsAHAAvANz/mP+5/yQA2/8zACAA2f8jANT/8//1/9r/0f/i/9b/RQAyAKn/PgAkAOz/CgAaABMA5v9pABMA1v/l/6D/SgA3ACQA+P8hABIApP8KAJf/2P/k/7v/IAAcAA0AFAALAPz/VgAAAP//AAACAHEA9P8gAN3/sf8rANr/IAAFAL//9P8AAPn/2f/q/x4A//8XANz/+/8LAND/QgDt/xYADgDv/0AA2v9aAM//q/8FANf/TgDt/x4AGQAFACMA9v8HAPP/EADl/wYA3/8DAEkArv8LAAAApv/Y/+v/7f8BACsAPQAWAA4APgDG/7z/BwAHAAkAUAAXAB8AHQCd/xoALADp//H/9v/q/9n/GQAAAPL/BgA3ACkAuv8cAPb/nP/3/5//GAD3/6n/XwADAGEAJwAgAE8A4f/x/xQAPQCx/wcAxf/U/0EAvv8aANr/2/9PADoA4/8JAAAA7P8LAMf/1v+9/wIANgBZAEIAHQAQANz/tf8yAOD/nv9xALr/7/8LAOL/CADY/wsArf9MAMv/LABbAPD/UwAAAGsA3/8gAB0Azv/E/5v/zP/6/zsA6P86APz/2//4/+3/IADy/93/zf9IANz/NABaANn/ZgDR/87/MADR/8L/0v/+/xYAIQAwACMAFQD7/8T/AADp/+3/AADw/y0As//H/y8A6P8dABEAawA5AP3/EwAaACQAwf8OAAUAxv/u/ykA3f+P/xgA3//G/7b/DQAhAAIARwDq/1UA+v8sADIA9/83AOD/0v/r/+3/8P83ANn/5P/U/7r/NQAeAB8AAgBGANj/SQA/AKj/MQAAAAsArv/Z/w4A/v8AAA0AHACk/wcA9f+B/9j/KgAdACUAbADu/xEAIgA0AAwApf8uAA4A7v8HAPj/4/86ACUAwf82AKj/8/8yANz/KwCM/+H/6P+t/xkAKABIAPL/5v8PADQA8f8kAFYA3P8PABkA//8KAAAA3f8eAM3/FQDx/+v/HgBn/zAAnf/t/2wA1v9dADYA8v8GAOj/9/9CAKH/GwA6ANT/LACi/ycA3v8dAPb//v9GAJX/ZwDb/8L/EAAbACoA9f83ANX/0P/v/xsABADC//z/8v/y/x4AQAD4//3/AQAEAOv/JgDU//b/TgDO/wIAwf9bAFkAw/9kAAEADQDk/9v///+T/8n/3//w/+//HAAwALz/FgAoAAUAHgAbADEA5P8fABAA6v8pAP7/AACt/6v/FwDu/y8AIQDH/wEAIgAhAHoAQADD/w0AwP+e/93/zP9EAAoA3v8BANH/+P/M/xMALAC//2EAPQAzAFwA9/9IAM7/yv8cAJ3/5P8XACwAHgDZ/+7/3P+g/8f/KADQ/wwAVQDO/zYAxf/Q/2oACwBYAC8A7f8EAEUAMQANAAEAzP+z/6H/KwDU/9b/HwDi/zIAy//j/9v/BwAtABMAZAD2/yoAIAAFAKL/pf8TALX/DQAuAPj/FgBOAL7/7v8aAAcAhwDo/y4AIACy/+P/CwD0//X/EAC7/0gAnf/P/zMApP9DABIAIADg/xYA0v/w/4oA3v9JAAUA4f87AOP/nP8ZAL//0v9pAM7/UAC5/wsACQCB/zYAw/9EACAA1v9OAO3/HwBCAOz/EgC4/xwALwCd/2MA3/////P/1P9RAOH/JADT//L/6P/z/z0AEwD5/+n/MgCc/8r/6v/j/wIA7f9HAPT/IAA0AB0ANgDp/+3/AADT/+7/DQD1/wcASABdALX////6/7T/SwA5AO7/x//h/7z/BAAoAK7/6/8cAP//GwAbAAsALAD0/zcA2P/y/2wApf/w/xcA8v8IAB8ACQDS/wwA8P+7/9T/BAARAEAAWwAwANr/8//w/7j/wP/P/yMA+/9hACgA3P/w/7n/7//1//7/+/9rAGAA4f8eAPb/1f/Z/zMACQA1ABgAzv8lAND/LgABANj/0f/s/97/fP8dAJX/IgA0AOr/igDk/28AHQC6/ycAIgD//8P/XADq/7H/8f+o/wAAVwBBACoA7v/P/zAA+f+Y/yQA+f+g/yQAz/8aADEA2f8gAPH/3/8UAEsAUAAqANn/BAAXAL3/OADk/4X/CQAiABsAEgD7/xQA5v+0/xEA3//K/9j/9/8MAAAANgAlABwAJABbADMA0v8tAA0A3f8jALb/5f/9/6j/9v/O/xIAJgAdANH/DwAgAJD/FwD+//b/HwAZACMAQQADACgATgDZ/xgA7f/+/+b/vv8AAKb/rf/2/wMA8/9AAAMANwAVANr/VwDb/xsADwDs/xIA7f8tAOf/0/8gAOT/yv/8/xcAMADY/wMAQgD5/wkAUQC3/+v/LQCj/yYA6P/k/9n/2f8XAOT/+v/9/1IAuP8bAFsA9/8YAAwASADV////EwAZACMA3P8kANP/x/8JAOL/w//W/+b/AADo/9X/JwAAAEEAhADw/97/AgAxABcAw/80ANH/6f8gABsA6/+f/18ARADz/5L/3f8IAM3/FgDQ/z0AKQANADQAIwDe/wEAHgCS/+T/3f8/ABcAKQA4AKH/BADm/xAA/P8oABwA6f8hAPP/6f+V/xAAyP8bAFEAs/9XACQAEwAUAM3/DgASAM3/9f9AAMj/JgAZAOX/HADG/9j/v/8BACUA//8VAM//IgAGADEAQAC4/0kAGwDx/x8A3//O//X/CQDB/zoA9v/h/3wAtf/U/+n/3v88ALX/SAAcANr/UgDu/xoAAgDL/9H/LADa/6r/awC+/wcASAAOAEAA8P8KAMT/VwDw/7r/EwCb/xwAFgD1/8v/HgAOAOz/IQCm/w0A9P8WAFIAFgBjACgA2//g/zUABQDo/+b/2P/i/6b/9f86ANz/AgAXABEA//8CAFUAs//m/wMAEgD9//P/GADY/1EAuf9BAAEArP8HAMz/ZwDe/4MABADP/zIAuP8XALv/5/+x/ysALwD1/1MA1P8TANL/JABVAOX/8f/p/9r/r//Q/0kA0P/i/20ALAAvAAAAEQAVAAQABQACAO//rv8DANz/HADa/77////6/yMA5v/3/xIAFAAxADwAKwAcAGwA+P/g/9P/sv8VAJ7/zv8HAPv/2//u/z8A6P8EAOD/8f8pANr/UQA0ADwAOAADADcA6P/o/zcAy//N/+z/0/8AALX/BQDq/9L/+P/n/xsA9P82AAMAMQBQAOr/GADq/9f/GQBuAPP/3f/k/wUA+//a/yAABwAGAAIAGQDo//j/8P/s/wUAzP/5/8z/NwDs////JADu/xgAfP8BAPr/JACLAO//2/8dAFgATQAdAPD/5P/r/+D/AwDN/4H/6P/6/97/HAAGACcANQABACwAFAA7ADYADAD+/67/0v/b/xgA1P+3/0gAyv8MAC0A5v8JAMv/6//2/w4AUwDz/yUAOwDg/2YAHgAAAPn/5P/Z/4X/GwDO/+b/HwDo/z0AzP8VADgA8v/5/xkACwABAP3/BwDx/9r/CgDF/08AOADg/wgAAADT//r/GwDm/xIA//9SAPX/0/8kALL/4//K////AgA8AFMAGwBkAOH/q/+o/9z/FwAKAAIAvP8DACoAEQAfADAAMADy//r/CgDz/5b/vP8sAOj/NwAiAMT/MwAUAOj/GQAvACQA4v8TAMn/nf9GANX/DwAdAPn/KQDQ/yMAAwDX/woAFAAwAAsA2f+A/+//RgAXABYA0P/c/x8ACAAXANr/EgBjANv/BgDl/w0AOgD1/+z/2v/W/87/FQAdANv/BAA1AM//HgAbANT/MgAlACcA3v82ANL/AgAmANL/CQDR/woAxv/9/9b/GwDr/wAAXACZ/1YA3/8VAEkA3v9AANL/8f8oABMAwP8jAOH/mv8AAOP/AwAJADUAAQAEAAYAMADu/y0AHQDM/xUAvv/t/wgAMQDv/y0AHACw//H/+v81AOD//f/X//T/VwArANf/9v8gAJz/MwDy//z/DwDH/xgA4v9GAAMA4/9DAPH/JgAEAPH/UgAFAOb/4f+b/9X/tf/1/xgA9P8pANX/+f8QAAQAYQAmAPj/8f8oAFoA0f8mAC4A5f/2/7n/GwD1/6v/FwATANb/8/8cALP/zv+x/wUAUQAsAHYAEAA5AAwAlP9MAPr/z/8cAPv/v/8IAFMA1f/B/yoA+f+3/zMA4//n/yEAwv/t/9P/IQAFAAkAXwAFAB0AGAAuAAgA2f8wAPb/5P8SAP3/0//s/+z/q//p/zcA7P8AAGsACQALAD0Aw//c/+z/2//L/wEAEQDX/yAAKAAoAPv/5v8XABMAHADa/w8A9P/2/yIAMwAYAOn/FQDw/xAAyv/U/8P/0f/v/9v/YQA6AAIADgBHAKj/3v8nALL/JgC8/14ANgDX/0EA2P87AM//CQDh/5r/DwD6/zUAJAAWAP//GQAhAPX/6/+V/wEA9f/X/wYAIAA4AN//FgAiAPz/VAAtANn/sf85ANH/rv/s/7H/GwAAADkAJgALABgA5v8vACQAJAC+/xkAu/+V/3oA2/8kAA4AAADq/7r/XADx/+X/8f8UAO//FAAXAKr/PwDu/yYAMAC0/zAACQDm//P/FgDU/7v/QQAsAAAAEgAlAOT/7/8dAPj/yv/V/xcAJwANAMf/FwAFANP/3P/1/+z/uP9EAEIAOwA9ACgA+//j/zcA6/8UAAYAxP/d/9D/EgDD//T/5v/x/wcA0f8sABIALgApAOv/IAD0/+D/EQABAAcAJQD6/0IA4v/C/04A2f8NABUAqf8RAAAA2/9GANz/xf8hAN//0f8kAPv/6f8cAA0AFAAXAAoABAAqACoA+/8lABcACAD7/9T/mv/b/+b/yP/6//z/DgAaABIADgApAPD/UAA/AM7/FADw/y8AAQDn/wEA8P8AAKb/1v/Z/yQA9v8iADQArv8lAPH/9f/R/8r/aAAjADMAJgC8/+L/1P8nADQAGQBLACAAHQCn/wgAGQDW/+v/pP/D/+r/AQDA/yUAIQD2/0QAw/9MAAIA7/8TACcAfgAOAEoABwCa/+f/8/+z/8X/JgC9////VQC3//r/HADn/y8A7//f/y4ADAD7/10AEwCy/8//5f8rAMP/BAAoAOX/KADo/1MAEQAIAA4Ay/8AAPT/PgDg/+n/QAC//xgACgCu/87/AgACAPf/KQDu//3/xf8uAB0AIQCLAKv/OAA+AMn/4//K//r/tP8jAAYAHwD+/8X/OAD+/wgAJgAEALv/QADW/+n/9f+D/1IA9f8ZAAIA+f8fAOH/QQAZAM3/AABFAOb/WwDm/7v/XgDX/xwA2//Y/wMArP8vAAwA0P9aABcA1f8IAM//MADt/8z/IACX/xIA5f/k/0oA1f8fACkARwD+/x0ARQDV/0MA9f/a/wUA1f8DANb/7f8iANn/4v8TAA4ACAD3/zEA5/+3/+D//P8nACsATwDN/xgAEADS/xUAn//6/8z/LAA9ALj/TQBXAAoA/P8MAM7/6v8hAMv/0P/1//3/HgD2/ycAVQDX//r//v+7/+j/z//o/1sAEQDs//v/LgBRAPj/RQANANH/7f/S//P/EQAbAJP/9P8YAAAAGgAWACkApP/o//P/4f/T/ycAQgD4/wwAFwBRAB4ACwDx//H/4//6/1QAEgDO/+P/xf9s/+z/7//4/1MA8/8mAEsA9/8gAFkA4f/4/+n///8WAMD//f8AAAMAHwAaAJn/JQAIAKn/UgAHAP3/EgAoAAMAFgAmAO//0P/6////kf/J/8f/BwDp//H/GABMAGAA5v9fADEAHwACACYA6//1/xAAnv8QAL3/+f+P/5X/QQDX/zMAKgBmADMAHgANAAAALACk//H/4v/D/wAA6/9dAAEA0v9HAO//BgABALn/1v/e/yAACQA0ABoAJAD7/8r/MwC///v/AADd/wgA3v9LABsAHABBACAAIgAMAPr/tf+n/6z/8f8KAO//GwAVACoA7f8TADIAwP8WAJ//+/9jANz/WwATACEA+P/v//j/4P/W/7z/MwDV/woACgAKAAkA7/9CAN3/DAAxAOr/8f8DALz/HAD6/93/QQDz/0YA0v8kADkAzf8iAOf/JwD6/7f/xf/9/8j/7P/O//T/eQDI/18AGADz/zMA4f8AAM7/AgD3/zkAKwBTAPv/if8rAPD//P9EAAoA6P/W/9H/CQC3/6f/DQAbADwA6P88ACkAJgA4AOX/MwCt/5v////U/+H/TQAnAAEABwAJAPr/8v8KAJz/4v8AABMARwAIAND/9v96AE0ANwAFACoA3/+d////wf/e//7/CwC+/+X//f/j/y0Au/8WACoA4v8yAGUALADv/0oA//+g/+r/HwAAANP/BgDq/+D/FgAHABsA+f8eAAMADwAEANT/HgAVAP7/7v/0/8D/DADg/87/RwDY/yAAyP/q/0UA1/8HANP/CAApABEAZgB2ADUA4f/g/6z/FgArABAAFgD1/wYAm/8BAPr/hf/7/7z/z/9NAOH/y//b/7n/NQAyADMATgAUAGYAMwATADcAPwBDAOT/8//n/4v/x/8DANr/0//u/8b/1f+h/wUALwD//0oA/v8sAEAAGgBUAML/+v8kANX/zv/h/wwAFQAYAE0ACQDJ/w0AOgDY/9P/JAAqAKn/0P8fALr/rf/5/yMA6P8GAFAAHAAaAD8AIAAkAPb/z/8DAKL/BgD1/8b/TgDz/xgAKAAAAND/HQA+ANf/HwDr/6n/vf/u/wsA9f8WAFAAEgD//xAA8P/+/8T/VAD9/yMAIwCk/xQA7P86AN//3/8aAPL/4f8hAIEA3v8GAO7//P///8b/KAC8/8L/9/+a/ywAFADu/z4A9f8KABYANwAXADoAXAC5/+f/rv/U/+//8/8UAAkAOgA9ACUAAgAVALj/xv/H/97/yP8LAHMA2/9DAB0A9////6T/JwD5/9f/VAAOAPb/0f/i/ycAwP9WAEUA7/8VAAkA8/+y/zEACgDM//f/XgDF/9D/OgC2//n/vv9OAAUA7/9EANL/QAD1/x8A+P+u/ygA9P/N/wUA0v8tAC0AAAArAM//7P/k/1IA9/8aACgA8f9NAL3/5v+5/xcAGQATAP3/q//f/7v/IQDo/wcA8/8kAD0AGwAwAAAAHQANAB0Awv8VAOv/NgD0/9//UABs/+f/AADn/9/////5/zAAVgAnAAgA6v8gAPL/OADX/+z/3P+i//L/EAAtAKH/eQAXAOL/UQDn/9z/9f8cANr/8//M/+r/5P/3/wYAVgBzAAQADQAbAA0Avf8GAPP/2v8FAOT/1f8WAOP/iv9lANX/9P9nAAwAFAD7/yQACwCs/+n/UAC9/yAAGQDR/zsA8f9HAAgAAAAHAO3/7f/t/+H/EwAAALH/GwDG/+n/KQApAPz/9P8bABAA7v/7/xAAr/8gAC8ASwAkAOH/LACn/9v/IgAKANL/AAAHAOL/4f8OAO//GADp/wsAbgC3/0oA9f///x0AoP9FALb/vf/1/yQAAwAQACQAAgAbAAkAKADT/0MA6f/n/ysAsf8TABgA4P/j/+n//f8+ABEABADu//H/AADf/yIAxv/k/yAAIAANAPT/wf85AA8Acv9XAN3/7P9nAPj/ZABjAP///v/r/9//2f+w/xAA0f/E//H/yP8DABgATADy/wAAJgAOAG4AVgARANn/KADY/4b/5v+5/+P/CgACAA0Awf/5/wwACwBeACsAGQDy/0sA8v/t/3AAdP/t/w8Avv/9/77//P/O/yAALgDH/10AggA8ADQA4P+m//L/4P+x//b/vP/9/wUA8/9oAMz/DwAkANz/OgASAE0AKQD0/zUAtv/B//f/z/8TAOL/AwDS/93/cgDw/yoAMwAtACwAAwDn/4T/v//K/8r/1f8MABAA+/9GAAcA3/8LAGkAVgDw/x4APgDl/7r/QgD1/wEABADN/xIA0v/s/9H/8/8SAM//LQDr//b/CgDg/zsA9/8LAD0A0//o/wQABQAGADwA7//l/ycArv8tAOH/6P9PAPH/FADS/9T/BQAgAB0AMwBCAN//NAABALr/qf+g/wgAxf8OADUAAAAEAO//LgBmAD0AAgBbAOD/ef/6/+n/yP8DAPv/EgA2AOL/QgDt/7b/KwCk/xAA6f85AE0Aqv9lAAMA3v/4/xIA2f/d/wwA/P84ALr/QgAQAMz/UgDM/yIAwf9k/+f/CgAwAHkAWABIABgA7P8KAC4AJAB9/7D/uP+P/+D/HgAvABkATwA2AN3/z/8TAOP/BgAYAAMA7f/Y/2oAHQAzANb/4f/p/63/PgAEADcAAgDm/6P/JADo/7P/SQDQ/zEAGgAaAK3/NQCBAJT/fgBlAOX/2P/s/5X/kv/l/+3/OAAHAEwAOgD9/87/rv/i/+j/GQD9/ycAHwBAABEAtP8zAA0ABQDz/8P/IQDv/zYAUgAMANb/8//X/5f/GwC5/wAAJgAOAG0AAwD1//v//f/U/+7/oP/c/1UAHQBPAOT/EQD+/w8APQDe/zcA+/+9/9z/1f/L/xIA5f/+//P/HABLAPz/JgBRAOD/7v9GAKn/EwAbAPD/9P/Z/8//xP9AANT/OAADALL/6P/G/0kA//8tABkAbADk/+f/FADL/ygAzP9VAAYABQABAAsAGACE/1gA9v/q////3v8EANL/GgDO/4X/CgDy/9L/cQDs/w8AMgALAGcADgA+AO//NAA+ABkAIgCF/+P/lv98//3/xv88AAUA+f8dAOz/DgAGAAQABwB2ACQA5//n/wUALgDd/yMArP/c/zAAOADv/8z/LAD4/x8A9//7/4P/rP/f/+r/mwA/AI8AJQAAANr/uv/n//D/5/+T/zcA4P/V//T/PgA0ANj/bQDe//n/IQAiANn/kP8tAAsA3/8SAFQA/P/d/wgAwP/4/+L/SwBAAKz/bgArAOX/+f+k/1AAEQCp/+z/9v/U/w0AKgAyAOr/kv9QAM3/AABFAAAALQD6/y8Auv8PANn/3v9EAPP/DgDW/xwA6/8XANn/v/9SANT/FAD+/9r/EgDf/x4ABwAnACUABgBGABcAFAA0AKL/tP8jAMD/9P8bAPT/FAC0/wcAFADH/9H/xv8eADEANwA0ACwA0f/i/+T/7v9yAB4AJgA9AAYAGgDk/+//rf+i/wYA5v/z/+D/z//s/w4A+v8DAJMAFwA0ACwAwf/x/63/OgCv/8r/kgAKAPz/5/8lACMA9P/3/wUA8P/L/xEA/P/x/+//MwAJANf/7P/g/+D/UwBmAMr/+//4/+n///8/ALL/FwBFAKD/IwCV//T/yv/q/ywACQBoAC0ATQANAEgA6/8KAMP/l/8VALz/EgDD/x0A6//J/0sAJQAAAGgAOQDE/xUAo//V/9r/rv/6/wsACwBFAF0ACwCDABQACgC7/93//f/h/yQAjf8nAMv/vv8FAOf/+f8SAGIAwP8bAPf/HQAFAAcAMQDU/yUAw/8wAM7/HwBfAPj/OwDl/woA4v/2/+P/sf/M/8f/+f8VABcA4/9KAPD/1v92ADAALgAKAA8A8v/V/w0AJQDJ//7/LwCA/9v/DQDh/+v/5/8TAMz/YgAAABQAHQDc/zsAmv92ABcA1/8bAOr/TQDs/0EA8//X/9j/z//e/x8AYgCM/8X/qP/v/ycAUAAzAAMASgDb/xQAwv/1/8//MQAbAMz/eAANAEAA/f///+H/7v+9/63/RQC9/yMA9P/5/1kA5//l/9n/v//0/y4ALAAlANr/CwDH/wAASgDS/xgAIQAHAPz/VgBAACcA6P/T/77/kv8TACgARgDB//D/+/+G/wEA5f8GAEMACgAxADIA6P8kABQA4P8aAAkAJQD1/8z/sP/x/+3/FgBRAM3/CwDY/+D/7P8SAEEAvf83ACsA+P8+ACEADAAJAPb/3P/s/+f/5f/M/+L/DQAiAAAA7v9GAMb/+v/7/8j/GADI/yUAYQA9ABMAFgD4/7L/LgDf/xkA7/+l/0wA5v88ABoA6P9VALH/+v/Z/8z/KQCU//z//f/l/yQAGQAFAAoANwDO/+f/FwAwABAANgAmAOP/FgADADsAxP8HAOP/qv8uAOL/EADh/1MARgCq/+r/rf/q//L/IAAyALr/9f/6//P/DgArABkAAQD3/w8AAAD7/zEA9f8PAFAAHwA0ANL/vv/U/67/+P+z/zMAKgDD/zwA+f8BAD4AAgAAAP7/8P8UAO7/BgD3////EADI/yUA5v82APn/z/9WANH/RAAhAO3/FQDf/+7/9P8CALb/3P/1/w8AAAAGABUA1/8BAPD/+v8qAOH/3/8PABAA+v8PAGEAfgDz//7/KgDm/+3/CgATAPX/xv+y/5f/EwDy////LwDx/yQAwf8TABMAwv8EACoARwAJAC0AKgD5/wYACQD5/zAAnv97/x8A2/8PAA0ANAAkAOD/BADt/9f/+/8CANL/WAD8/yAAfgDN/wAA7v/X/+z/BAACAPL/+P+r/wAAAwDu/1UAEgDv//3/BgAMAPb/MAAEABcAHADl//T/FwAXAOn/0/8DABkA3P8eABAA6f+7/8j/NgCc/9r/9/8MAFIAKgBjAAYAXAALAPf/AwCn/wgA5P/S/+n/tP/c/yAAyP8hAPD/IgBIAPb/gADO/ysAKgDf////vv8fANL/EAD4/xQAEQDx/zIA6v/h/9//7/8TAAYACgAwAPX/8P/D/+n/GQCl//P/2//z//n/HQAXAD4AaAAQAE4A5/8tANz/w/9EAHn/1/8bAAUAMAD8/yQA/f/a/wMAMQD8/8T/8//y/+X/vP8TAHUAvv/n/2AA+/8MABMA3v8KAN3/2v8wAAUAJQA8AN//wP9AAMb/uv9tALf/PQAXABkABACl/y8Aof+r/wIA7v9WAC4A3/82AP3/4f/n//H/CADw/1UALQBIABMADQDq/2z/AAD7/xQAKwBKANH/z/9LAPT/4P/X/9X/pP/5////3f92ABEA7P8fAOf/HwD3/8r/KwCr/x4AdAAKAGkAGwAIAOz/p/8JABwA9v8vAK3/7f8LAGf/wf/7/1IAFQA4ACYAuf8GAN3/IAAJABkAEADV/xAAEgAsABgA7v8QANv/4P8qAPn/+//8/0wA+v+z/x8Ayf8BAAEA5v+z/97/1P8fAFMABwBdAPX/FAAHABsA7P/y/2IApv8dABAABAAjAA0AFQCj/wYArP+V/7X/8P8gAAMALwA0ABcABwApAAAA0v8IAEAALAAoAM7/BQAgAMn/DwDt/+r/FAAKAOf/8/8iAAoAqv8MABMA+P8FAOP/MgDZ/9r/4v/6//z/KQBlAOD/GgDj/wEAEQDh/ysALwA0APX/0v/D/+z/pP/7/xsApP9EACIAKgAOACgA+v/x/yUA3P8oAM//CADH//X/iQDM/xUAHADk/w0Azv8uAGIAx//a/9n/zf/B/7j/RwAOAEEAGwD1//H/oP8BAAAAHwAgAAMASAArABQA+P8DAN//wv8cANr/HABHAJT/LgDU/+T/JwDn/2wA4f/9/9X/FwBBAMT/SADN/6L/7P8hANv/AQA+ALP/RQDX//n/UADe/1kAEAABAC0AwP/h/wAAzf/9/+D/8v8nANL/AADY/1QAHQAZAFYAq/8qAB8A6/8FANv/1v/M/xIAyf/y/08ASgAGABYAGADP/8n/AwDp/5z/QwDt/z8ARACZ/wIA6f8+AM7/FwA7AKP/PgD//xUAHgAQAEkA7P+8/+L/+f+n/y4AQwAAAPf/2P8QAOj/1/8LANb/FABPAB0AKAAlAOX/xv/L/5P/HwD6/wcAbwD0/z8AJQARAA8A7v/c/8n/CADx/xsA9f8IAPT/9/8DAKr/2//T/w4A+v8dACEA4f8oACIALAAuABsAKgBEAA0A3v/h/9b/4P/n//r/AADn/9z/9v/b/xcA4v/N/xEAyf8sAE8AIgAxABcABgBbADAAvf/0/7z/3f/W/w0AMwDQ/ykAx/+4//L/+P+8////GQABAHUAGwAIAF8AEQAPAEAA7f/q/x0A9/8GAGX/2P/t/9L/QwDe/9j/3P8OABsAEgAoAPn////p//L/JABjANP/5P9CAAoAFAAVAPb/r//2/+b/GQAvACQA/f/z/xUAtf/s/5D/PwAjAM3/jgC+/wwA+/+8/xIA3//Z/xUAQQAmADwAIADx/8r/2f/Z/wcABAAQAAcA2/82ANf/NQAzAMz//f8VANv/xP8uANj/IAALANn/TgA6AP3/LQAfALD/tv/R/+X/pP9EABQACQBiAN//UAAcAOD/qP8EABYAvf/5/yYAUgDG/9j/DwA2AJ//z/9CAMX/JwASACMAeAAjAPD/x//h/8n/xv8tAP7/6P/j/+n/KQBVAEUA4f9GAPT/vP8UACAA3P/y//3/yv8+AKP/HgDs/5L/NADg/3oA0f/+/z4ABQD2//D/WwC4/x8A1f/6/xoAvP8sACkA3v/z/xsA9/9DAPL/AAADAPb//P/U//z/2f8rANX/AADv//f/TgDo/9P/3/8VAO7/IwAiAB4A5f8DACMAPQBoAOT/AAC4/53/4v8JAOn/EgBPANv/LADU/xoAOADR/xoAAgANAK//6P/f/+D/GwD0/xgA2P/O/yUANQAqAAUANwAfAPP/HwAGABAA2v/p/+P/rf/H/yIAMgDI/+7/7f8bAAsAOwBbABkAQwDS/wcAwP8BAB8An//z/+n/DwBVAAkAqf/+/8n/uP8bAOL/YQAAAOH/RADb////+/9OAEYAAQAuAC0ABgDF/8P/1v+u//n/LQDx/zIAIgDQ/woA8P/k/+L/AQASAOT/IwDi/woAEwAWAAkA2/8qADIAVwDT/w4AGQCs/yAApf8HAA4AzP84ABQA1f+u/xMAHAD2/+b/DAAgAAAANAAeAPT/xv/v/wgAMQAxACkAKQCZ/+X/DgDQ/7j/FwArAOD/VAA+AEIA5P/q/xIAmP/T/wEA8P/M/9H/tP89ACwAIQA0APX/NgDX/10ACwDf/zgAq//3/9z/7//j/ycARQDt//n/DgAWAAkAAADg/z4A3P/x/+//uf8iAL//+P8lABAAOwA5ACAACwCq/8f/+f/e////EAAYANf/DgAPAOj/RQAZANj/DgDz/9z/UAAFADAABQDT/w4Ay/9DAOz/s/8MANr/4f/r/2AABgDm/zYA6/8WANf/AAAhAH3/8P9KACoAFAATAOf/7/8DABoA3/8IACoAk//7/woAIQBEABUABwDI/wEAHgAZAOn/PQDi/6j/zf+z/0kA+P8IAPj/GwAEAEsAOwCw/1oA1/8SAPb/vv8WANT/CQDt/yUA6/8TAO//IQAaAG//IwAOALT/NgAwAFwALQDJ/zAAxf8cABcAr/8lAI7/2f87ABIA3//L/9j/9////yQAbADh/0QADwD0/wMAAABBAPr/JQAYAO//8//Y/9r/+f/s/4j//v/r/+j/JAALAEUAMQATAEQA8//y/wwA3//n/6r/+P9KAP7/GQDg/7v/VQD2/wkALADY/xAA9P8NANT/AAAjALb/KwAqAPn/+v/S//r/AQAEAN7/+v/i/9H/TQAzAPj/IQD9/yIACADF////HgArAPb/LAA/APn/BgDs/87/wv8FALf/3f8CANL/+P/M/y4A//88AGIACQAQAOn/KAD+/wEA9f/7//D/0P/w/+j/6v/+/yYAzP8+AAUAEwBcAMT/cwDt/+3/7f/t/xUAnv8eAO7/JwDe//P/JgCK/zIA+v/6/zEAsv/s//T/DADz/0sAVQDj/3kAzP/a/0QAAQAtAMz/FwDK/8H/+v/S//r/y/81AAQAtv/g/yUAYQAgAO7/DAAMALr/7v/l/wMACQAqACsANAAWAOr/GQAEAAUAEADb/wYAGADy/wQA0//l/6z/t/9PAO//+P8LAC8A+P/d/yYAHQDR/+n/MACS/zwAIAAQAGYAuP9QAO//9f9IAMP/8/8KAN3/8f/U//X/7f/f/z4A+v8cAOj/+/9WAOP/u//p/xQADwAnAC8A9//p/ykAGgAnABcAtv8FAPT/zv/b/ygAwf/L//X/2P/8//n/aAAoACwAAABUAOr/w/9lAJj/FQAZANL/AwC8/wAA+//D//f/SwC+/0AARQDS/08A4f8LAAQAvf9FAPn/xv8GACcACQD5////2f/p/x0AJwD+/ysAz//C/1kA2//x//H/9P8FAA4AVAAJAPv/1v+t/xAAFwDU/yQA6v8FAH4Asv/q//v/s//h/xoAKQA5APf/8/9RANP/+f8ZAAsA2v8kADUAn/8eAPr/6P/9/8T/HQARAO//MQAHAMn/OADv//X/+v8XABUA6f8XAOj/BwCe/+b/OQDl/zoAKAAaABwA/f/s/wAACAAXAP3/4P/T/8X/CgA6AAQA9f/7//D/0f+i//z/+f9QAEsAGABaABwA9v/v//n/rP/I/yMA7//z/0kAJgDL/1IA5v/Z//L/vP8JAJD/MQBkAAMAJADR/+X/AgAgAAQAVAD2/8b/ZQDZ/w4A7v/Q/+H/nf9HAP//AwAtAND/7P8LAAAACQB5AMX/EwAoAJb/GAARAAoAsv/W/0AADgDL/xAAMgDe/woA3v8RAPb/EwAvAAEALgD6/2UA2f/K/woArv8DAM//5f8rAN7/9P9gAPX/6P8bAO//6f/Q/x4A9P8zABgAIgAHAMT/WgDA/yoAFQDr/0EAo/8oAPf/fv8eAP//4v9RAPX/x//8/8j/MQD2/+r/OgA0AMz/GgAyAOb/IgAFAEUAIgCo/+H/2P/Z/+7//P87ABwA0v8EAAIAv/89AD4A5f8mAPD//v/c/8P/RwC2//T/FwBRAG8A4/8+AK//wP/Q/8T/8f+8/20APgD2/9T/DgAEAOb/SQD5//v///84ABcA9f9PAOf/2/8AAPT/t//Y/z8A7//w/wwACQDQ/+//HAD5/wIA0v8EALX/CABRANr/OwAkAEsAEADw//3/zv9SAAAA4/8mAMj/4v/z/zIAEQAWAB0Auf8FANX/AgDf/2P//P/g/xEAEQD6/wIANQAzAMT/WQAIAFAANQAGAEAAKQAhAND/LwC+/8v/CgDF/+n/qf8aABUAr/////7/uf++/x8AKADa/zYAEADz/zwA//81ABYASgAWAND/SAAAAAEA5P8AADIA4v/u/wwA3/8JAP3/uv+r/7v/3P+9/ycAJQDt/zYA3v8NAEQACQBNACIA7/8cAPv/SgDs/7//KwAKABEAAQAfAMb/1f8IAM7/0f+l/woAMgAYADEAKQD2/xEAAAD1//3/lP/d/wkAIgArANv/CwAkAAUARwAmAPT/AQC2//n/DQDg/wMAIgD2/+7/SgDk//b/JgCi/9j/7f/u/w4A+P9AADQAGAD4/w8A1f+w/yQA1f9JACkA0P8+AOX/AAAZAAYA4P8SAOX/0v/4//P/DgDn/zYAIQDq/y8AIgDR////PAALAI//v/8YANf/DgAQAOn/AwBXADEAFgD2/7D/LQDe/xkA8f8FABwA3/9zAJv/6v/f/7b/KADl/wwABwAGABYAOAD//0EAIgD+//b/1v8AAAUABADY//z/u//c/xoADwA9ANH/5f8PAAgAEQAUAB8AjP8RADkAzf80AOn/CwACAAAAGgAYADsA2P8+AMT/7f/2/9L/TgDe/zwAe/8GAFgAnP8xAO7/EgDR/+H/MgD4//j/IwAnAOD/w/9TAE0A+f9FAP//8P/z/8j/6/+4/6j/u//T//r/VwAhAAUAMQAPADUAXQAtANb/AADe/wYAMwDu/7D/xP/m//D/IQAqAFEA6//v//L/2v8WAOH/DQD6////HADj/wAAHQDW/8f/GwD0/ygAWAAtABoA4v/G//X//v8BANn/8v/Y/8X/QACt/wgAOgD//0MAGgA6AOT/KAA2AP3/EgC4/wsA0//V/wMAyf/q/ycAMgAGABYA8P/p/8D/0P8JAMr/BgA3ABUAHwA9AEQAEwACAB8A/f/m/83/j//t//f/AAAtAPz////M/1EAKgACAAcAq/8rANL/1/8mABUANABXACMAov/n//L/7P8GANH/AQBRAPT/CQBvAKn///8ZAKb/GQD+/wcA1P/n/wEAAQBQANb/uP/r//3/q/8bAGMAs/9QAGMA2f/7/zgAAAAAAFMA9v9AAPr/0//4/6r/+v+2//7/IgDt/zMACQDK/+j/FQA3ABUA8f8UAN3/7P8OAMz/5/8SAAsA6v/r/+P/y//1/zoAFgBWAFEA1/9CAPT/zv8TAOP/LQD7/yMAIgD+/+f/sv8nAKr/uv8CAKP/JgD8//r/XQD//z4AIQAOABEA9f8rAO7/OwAsAK3/7//L/w4A2//s//b/0//j//7/AADb/zAAEgARAAMA/v80AAYAJADs//z/SADc/8X/IgDG/ygAVADW/1cAy//1/+D/sP/1/9f/SQALAC4A2f/O/xQA8v/y//b/ZgAWAOn/8P/a//H/DAA0ABcA9//Z/9D/JAA7AKr/DwAmAMD/VADj/wsAOADM//r/AwAGALb/6v8WAAMACAALAF0Au//7/zYAxv8cAOf/EgALAC4ADgDs/+n/wf8hAMf/y/8NAAgAFQAoADsAEwD8/9X/GADm/9//MQD2/w8A5P8VAFMAAwANAOP/wP/Q/97/0P8GADAA1P////3/DABLABAAGQDk/wMA+v/p/w4AEgDs/xIAJADY/z4AFwDx/yEACAD4/97/FQDn/5n/0f/1/57/JwA1ABwADgDF/04AHwA6AEwAAwC0//T/FAC1/zEAFgADANz/5/+f/93/SADv/zMA8v8lAGMAIADb//7/1/+6/0kA8P8FAAwA8f/G/6v/MQAdAPP/BwCz/7//JQAhAFUAOwDI/x4AEQDh/xEADQAKAOD/7P9vAP7/IQAqAO3/2f+n/+r/vP/m/ycAGgCl/+b/KAAEAB4A9P8nAPz/LAAzADwAKQC4/w4AAAACAAAAMADD/+H/yP+M/yIAoP8tAAUAwP9pAAMATQBpAC8A0/8GAM3/tv8UANf/DwD3/z0A0v8PADsAmf+BAMf/BQAWAPP/ZwDg/y8Ajv+q/+3/EQDs/7X/ZADl/z4ALACw/yAAEQDE/wYAKQCV/xsAKgAGAB8ADwAwADoAQgDb/zwAy//L/ysA8v/e/7n/JACU/6v/EwCz/yQAMwAZAP3/of8NAGIA/P8QAFIA1f/x/1UAOQBXABEAzP/i/7j/7/8lABwAv//M//P/4P8CAN7/IgDv//T/PQAVAPD/xf/+//X/2/8bAGUALADU/zYA9f/I/+b/4f85ACoAEQAeACAAAAAyAFoAFQDm/9X/vP+x/7H/uP/f/+r/AAC8/+v/MgArAAoArf8mACEA7v9XABwAXwBbAP3/VADf//f/RQAMAPX/yP85AKT/vv/2/4f/y/++/yAArf8lAPX/u/9eAPv/fgArABgADABJAE4A1v8GANj/6/+X/yoAsv+4/7sA6//U/ywA5v/T/xMA0/9BAOj/AgA3AN3/LQB2/z0AEwD8/0AAFABJAEb/FQABAMH/WgDd/9n/7f/v/9z/+f82ACsAMAByAD4A1f8BAOD/BgAIAML/KwD4/9v/LADD/8n/0v/Q/+X/AgAHAPH/FAAoAC8A6/86APH/EgCOAND/1P/3//z/DADq/9v/wP/1/1gA+P/z/1IACQAyAPr/DwD5/8//5f/x//b/wf///7//7v8kAN7/LgD0//b/FgAMAD4AJgAiABoA6P/s/+L/CQDz/8L/LADx/7z/DAD1/1kAPQAKACQA2f89AAQA1f/1/5j/CwDl/9X//f8gAAUA+f+HAPv/2v/1/9n/m//r/wwA3f9VAAEAHgArABIABAALADUADAAbANn/8f/i/+v/1/8jACgABwA1ALn/4P+X/8f/+f8jADcA0P9iAPH/JgBkAMP/8//k/+//BADa/wEAQAD4/xgAFwDc/9//AAD4/87/LgA+ACIAGgDa//T/8/8aAPP/m/8SAOH/s/8yALP/MwCZABQAOgDy/9v/7v/6/zUA+P////L/EQCw//T/IwCS/wgA2P8YAPT/AABoAMP/NwDx/9//EgDp/0YADQD9/+n///8ZADAA//8NAOn/2f8nAPf/IADs/wYA6P/a/0EA1f/y/9j/6v/c/2//RwAZAMH/iQD5/zwAfwDD/18Axv/Q/ywAsf8gANr/JwARANr/+P/S/wkAPwAZANf/8P/I/wAA6P/h/ygA6/8VAGAAQAC6/wYAHQD7/wMALAA1AKb/0v+c//z/6v8bAEwAnP9UAOj/tv/v/97/IwAEADEAOABFAEQARgADAC4ADgCx/9n/uP8LALf/sP8JALz/AAAYAO7/FAAbAB4ARgAMAPz/DgDu//v/OADH//X/NQDv//b/xP9IAN7/CgA5ALL/DAD1/ywA1P/x//P/z/8wAOP/HwAEAPf/5v/y/wkAMwAnABwAOgDg/wYA1P/b/wwAMADp//z/OgCE/ywA8//k/+//mf9YAPL/LgArANT/KADj/zAADADe/ykA0P8jAB4Axv80APj/KAAAANz/AACX/8L/4//v/1kAQAAPACkA0v/i/woA9v/8/+b/CgA4AB8AAAAZABIA/v/j/wAADQC//9b/6f8EANH/HwA4APv/YwDn/xYA5v+o/1MA7v8AAPv/0P8SAPD/IwArAOT/3v8jAP3/6f8KAMn/DwDU/w8AOwD5/0QADgA/AMT/z/8CAK//CwDb/xoAAgD4/ysAu//u/w8AFQA0ADIAOABNALX/0f8bAN7/FAAdACgA7v8EAPz/sP+g/5n/BgAlAAoACwBDAC4ADwDj/wYAMgCf/yAAKAAKAPn//v81AAIA5v/z/xMAl//8/9H/7f81AOn/dQD7/wAA5v+n/9v/yf9VADYALgBbAPj/7v/5/9b/HADq/wkAJQADABcA2P/x/8f//v/+//7/FwC1/zEA7//R/wAANgAuAO7/OwD6/73/+v8zAND/9v/x/9f/PwDz/zsAFAD+/wwA3P///w8AIwDj/wgA8f/z/wIA4f8JAEQAz//Q/08Axv/n/yIA3v8CALj/yf8vAPb/IgBUAPj/RgAgABYAGQDF//P/8P8mAPf/IAAtAP//1P+///7/k//m/9//7/8lAO3/QQDs/xYAKwD7/xoA///Y/9v/9P9XACEA2/+JAPT/7P8fAOL/7f82AOT/av9EALT/8v8vADkAagCW/zgA6f/b/9b/yv/n/8X/AgDi/4kAzP/x/1oAu/8oADQATwAAAPP/CAARAOn/8v/q/8H/ZQAFAKr/KgAtAO//0P/u/xkA5//C/xcAFwDe/xYAFQDc//v/5f/u/y0A+v8zAAcA8v87ABQAMgAOAOr/5P/W/yIAu//h/yAA6f8GAN7/6v/a/wIA8/8mADEA1P8bABYAcgDu/0EAUQCL/wAA2v/Y/8H/HgCo/xAAYADZ/4AA9f8KABAA///j/6z/+f9i/xUA9//7/0QAEgAuANr/CAAVAEMADgBPABAAjv80APj/AADa/+f/4/8AADcA3v8hAN//3f/i/xIAAQDu/1QA9f8xAAQABQADALz/2P+P/yEA8v8XAG8AEwBCACYA6P/Y/woA3v8pAB4As/9PAN//6//j/4//GADG/97/NQBBADAAEgAaAPD/6P8bAN//nP8eAOX/zv9IAB8A0/8iAC4A7P9JAAIA7f/Y/0EAUQC3/1cAwP+W/woAAAAjAAYAHQDt/xcA4//l/w8A3f8JANn/xv/h/+j/5v8+AAcA/f8KAC8AWgASAC8AGgD9/9H/KwALANv/7P/M/xIAxf/2/+f/8f/5////OQDw/+n/0P8QABcAJwA5AAMAEAAgABQA0/8vAPX/yP/6/+r//v+o/+r/EADu/yUAIgDo//n/+f/+/x8AIQAgAFIANQDm/xwA0v+i//b/EgACABMAxv/d/z4Aqf8NACQA5/8dAAAACwDa/yYA9//h/wQA4/8pAAUAYAASALL/IAD1//v/CwArAP3/8f/C/+j/JwDH/woAKwDI/zMAKgCy/wYAIgCk//v/QwDZ/+7/JQD8/x4ABADe/0sA/v/z/yUA6f/2/+T//P8JALP/UwAfAOj/cAC+/w4AJQDz/wAAwP8gAND/8P8NAK3/AgDe/8X/TAAbAA4AZQAHAOP//P/6/+z/AQDX/8j/RQDn/wAAbQAmANL/GAAAAIX/IwAdANL/EAAtABgA0v/q/+v/4f/w/8f/NwBQAL7/SgD0/ykAPQDt/0oAk/8cAMf/if9jAKj/CAA7AAoAJgDt//z/LADu/yAAQQCj/+f/8v8hAAoA7/8JAI//+P/7/xsAOABMAPn/3f8+AND/4v/V/+T/GQAKADkA9//l/0wALwC5/xoADgDb/wcAvP/V//b//P9EAOX/4v83ALn/NQAcAOT/HQDm/0gAzf/p/xYA9v/2/zwAPADu/z8An//w/+T/x/87AOf/LAAEAO//5v8pANn/+v8zAND/KwDM/9v/0P8LABEAJABvAAsATwAEAOj/lv8CAA8Ap/9YAA4A8v///wIADwDN/6T/7////8f/PgBMAPn/LwBRAAMA5v/0/9L/4v8WAAQAt//7/xIAAgDv/zoAWADt/xUAMQC7/6//0P8RAD0Aqf8oAN7/6P9EANf/LwASADgADAAAAPn/zf/0/+//JQD4//3/8//w/wwA1/8VABcA4f8cADcA0f9hABEA//8zAIX/6//P/+L//v///wAA9f9PAM//KgDZ/9H/GgDS/2cADwAyABIAu/9HANP/xv8ZAOL/5/8kAOH/7/8IAP3/IwAMABsA+v8gADAAIgAhAP3/9P/R/+v/+P/T/wcARQDA/9P/4f/P/x0A1P/6//T/9f8UAP3/AgAjAOP/9P9iAMb/QgA3AEcAKgDs/ysAvP8TAOn/JQD3/8L///+9/+j/y/8xAAAADwA8AM//1f/6/9n/0f8cADQASQDS//3/PgA8ABUAMgAAAJ7/KAD4/+v/8P/l/+D/7f/o/9v/AgDH/97/AAAzABMASQALAPz/SADf/ykAFAAHAOX/JwAAAPj/KAD1/xwAof8PAOT/qP8qACEA+/8AAAAA4/+i/+H/MADN/3AAEADf/18Auv8SAAcAzP/7/zAAAQAhADkA0P8nANP///8hALP/KAD//9v/EQDM/xAAFQDT/zIAFwD5/+v/HAAwANP/+//0/+T/7v/3//L/AAAzAPb/HAAfAPT/+/8nAPT/6f8bAMT/KAArAPz/MQC6/9f/tP/l/x4Av/9LAOj/8v9bAP3/3v8YAE8Avv9XAEQAp/8tAO7/6P8AAMf/5/+3/+L/TwACADoAFwDL//D/EgAGAMr/BQD9/xYABgDy/0oAKAAPAAsA6//N/9L/p//Y/+//RgBFACEAhgDz//n/IgC1/9j/7f/6/xoACgDI/zQAAQCv/yQA3//b/8T/BwArANv/JgBXAAQA6P8gACoA5f/6/wQAxf/l/wcADABEAAQAyf8RADMA+f/b/y4A8v/H/7r/EQAiAAsANgBCAFYAq/8AAOL/kP8YAMX/9f/A//b/FwBFABEA3v8eAPz/TQAPADMA+/8IAPP/3f9sANj/JAAZAOP/4v8JABYAtP/a/8b/+P+Y/8n/CAAsABIA7P9mAOn/AAAdADgAMQDk/+r/GgAvAOH/RAD+/8r/7f/y//b/+f/6/8b/BgDl/yoAIAAWAA4A+v8XANH/HwC7/wsA/v/d/zEA3f8/ABYA/v8KAA4Ayf/W/xgA5/89APP/EQAPABcA7f/y/wAA3v8RALz/BQDM/9P/4v8AAEsA//8uAPP/EQD8/0YAmgDi/zYABACx/xUA1v/u/9L/5P8kANL/CwDw/xcA/v/v/xwAfv/y//v/HQAsAPn/TAAZAOD/1P/x/9v/5v/n/xkAJwAtAEkAMgBHAOf/7f+7/xcA1v8LADAAmf9oAOf/3f8QANX/5P/U/+L/7/8WAAAAVwBAAAAA7P///8P/yv8aABgAIgDt/yUA3//b/xYAMgBFAPL//P///xcAv/85AK3/mf8lANP/DwDP//3/4/8wAEgAIwAoAP7/YgDj/83/JwDi/6f/HwAHAAcAPADv/xgA///v/8z/LAD1/73/+//X/w4A9P8RAAMA4//n/00AGADu/+v/7v9TALL/UwAgAKT/TADN/18AIADR/zQArf/f/wkA2v/+/wIA6/8lAO7/7/9RAO//UgAHALT/GACI/9f/EwCr/zUAJQDy/y0Az//G/3EATgAWAEgADwDu//f/tf/H//P/CgAVACQAFgDT/9H/yv/4/x8A4P8yABIA8/8BAP3/JADJ/ysAcwAWAP3/0f/a/+L/9v/m/xcAAgCa/zIADAATADwA6P8rAPP/rv/B/9b/EwALABgALAAlABEAZAD3/w8ACQCW/ygAyf/x//v/zP9RAA8ALQD+/wsA5f/F/ycAyv/z/+7/uP/h/wsAMQDw/yYAJQAGAC8APQA6AN3/5/8IAPv/5f8QAAYA4v/6/87/5v+y/+r/8f8xACUA2f9rAPf/9v8tABoADADo/ykAu//t//z/HgArAKT/AQAJAPP/HwAXABwAJgD6/yQABgC7/8T/jP/U//X/8f8RAP7/PgAzADcADAASAEsAJgBpANT/wP/k/8H/FAC//+7/+v/l/+3/OAADAOn/cgCj/8//IgDc/yoA0/8oAP3/3P9LAAwA+P/v/wcA3v/r/wQAOwALAAAAVwC4/xMABgDW/zsAp//w/yQA6f8rAOj/8f8sAP//DgADALj/FAD8/+7/AwCw/wAA9P8bAAYA/v8YAOP/PAAFADwADQDo/1IAzP8WANv/+P9YAMv/UgDz/+f/IwCi/xkAxv+7/xwAzf/U/yEAov/g/zAA0P9BABcALQBdADMAMQD//xgAwf/6/+D/vP8gAPH/9v8IAM//1/9eANr//v9kAM3/UwDp/+z/GAABAFIA5P/9/+r/nP/u/xgA2P+i/wMAKQDo/ywAPADE/wsASwArAPn/0v8xAPv/xP8QAAwAMAAQANP/8P/X/97/9v8tADUA+/8FAOD/0v8IAAkACQAIAO3/GAA5AP3/EgAYAN//0v/R/xsA+f/b/yIADADX//n/GgDz/woA/P/q/wEA6f9CAEwAAwDr/xgAHADJ/wQAIADl/wwAAQDf/wUA1P8DAEEAwP/z/9j/0P/J//v/QgD1/1oA/P8SACsA/P82ABQAaQDC/97/7P+U/xgAz//0//v/GgAzAAAA1//i/8T/9/9KAP//KgDq/87/NgDr/ygANQDw/y0A8/////b/rv8qAML/6v85ANT/SwBGAOf/CgDV//b/FADP//f/DAAVADEA8v8UAND/pf8xAN3/1P8OAPf/PwDx/wMADwDS/1IAUQANANv/MADm/8//agCX/9z/DwDw//z/o/+v/xcAMgAhAGcAHAAMANn/SgAxAJ//6P/L/wYAxf8LACEA1/8yACIA+v/z/+T//P8kANX/BQD3/8r/KwAVADIA6v8bABYAAwD6//b/KwDv/yEAJgDq/w0A8P/S/xUAxP+8/9z/vP/8/97/NgAcACoA+P/X/z0ADgBJACgARwDg/+X/+P/a/1cAJwAFAPv/4v/H/+X/2f/j//f/8//w/8j/DQCO/wUA9/8SAE0AFAA+APH/LwAJADwA8v9JAGsA4v9ZAOD/4//U//T/u//L/8j/sf82AMH/IQDT/7P/AgAhAPr/BgAeAM7/cAD6/0oAQgDm/10A3P8YAO//EAD1/5X/PwDp/9v/RADn//3/+f/o/woA1f/o/yoA9P+k/+r/7P9FABkA9v8qAP7/SADq/14ARAC8/xAAyP8FAOn/zP/Q////xf/a/y4Aiv8YADkAEAAlAC4ABgAcABcA6/9EAPz/DAD4/+D/9P+9/xgA9f8BACQAFgA1ACwAOADt/8P/AQDY/9H/m//R/w8Ap/8kAN3/BgBxAB8ARQDV/wMADgDf/x4AFABrACYA0v/8/9n/AADp/+z/MADd/wUAuP/Q/+T/vv91AOr/IQArAL//QgAPAA0AFgAjAKj/rf8OANX/6//+/2wAKgAFADYAwf8JAAYABQBHAPL/FwAxAP3/w//T//r/uv/1/97/2P8SAO3/MAAxAB0AGwAvABMAu/8BAN//tf+6//L/+v8eAEwACQA6ANL/IAAbAAkANAAYAB8AvP8yAMH/nf/d//f/IQDx/2IA6/9EACAA0P8jAKL/2P/Q/zEA/f/U/zIAFgC0/9L/IQC0/1cAJwDy/zoAxf/2/xQATgAsAPv/XQAfAN3/NgADANX/y//j/8X/of/S/+X/5/8JAFMA5//7/wcAwf9OACIAJQBZAD0A7v/T/9n//P8AANr/EABDANn/6/8dALn/CgAJAAYAHwCs/yEAPAAWAP3/+/8fAL3/GAAIAJD/9//2/7T/5f/e/w4ALAAtACAAGgBpAP3///8PAPD/QgArAPD/7f/6/zUAHQDS//D/4f/Y/9b/vP/T/+b/5//u/2MA4v/D/zoAIAAEADwAQgDe/wEA6/80AFAAu/8ZAPL/tf8LADQA0/8DAOX/vf8eANP/w/8LANb//f80ACYASABgAEMAUQAfAKr/JQC2/5H/IACl//r/x//7/1oA2/80ANP/EwD8/8j/TAAJACkA/P8KAOb/4//l/93/7P/6/1QArP8+AD0AoP8dANb/GQD5/wgAcgAQACAA+v8OADwA2//T/yMA4//D/wgAvP/8//P//P8NALb/KQDy/xwA6/+g/xQA5v9EAB4AQAA9AOT/NQASABgACAAKACAA0f/U//T/zP/M/wgAkv/k/xUAFQBaABMAFwAWAPn/BgD//wkAGgDc/9z/QAAKAAYAAQAkADkACwDQ/4n/0v+C/87/JgC+/y4ALwATACMA9f82AGAAMgAhAPj/8P88AOv/6f/1/8P/UQAAAN//5/+0/9j/nf/h/+L/+f8zAP7/RgDs/yQAFwASACwAAABYACYABgD0/ywA1P+4//f/0//k/xkAWADH/0EAIADQ/yIAu/8FAFz/z/8FALj/eQDZ/zQANgC5/zgAMABDAAwAJQAqAPv/0/+2/wEA5f9FAP7/5f/2/6D/CwDx/yoAGQBDABUAw/8MALX/8/8HABEAxf8wAGAAhP9SAP//yP8wAOX/IgAiAOf/DwAGANn/JQD1//n/CAAAAOH/5P/4/+n/RQDX/1QAKADu/2QAi//B/9b/sv/z/yYACABMABMAzf9HAPX/HgATAPD/BwDq/xMA/P/w/xMA+f8SADUAtP8BAOP/k//2/wMAJwAMACcABwD3/xgA8f8HALb/IAARAPz/UgD4/zcAPwAAACoAuf+F/9r/0//l/w0A4P8tADUArP/+/zgAGgDi/wMAFwDS/0EAZQBNAD8AHACu/+n/9/+o/yoA2v+y/5n//P87AKT/FwAAAND/+/9AAA4AIQA4AAoAOAAgAEYAFwAvAN7/3v/5/+j/EwB//yoAx/+c/+f/p/8TAP3/IQAbAEMAbQA9AA8AHQACAPL/6f/L/yAA2f/v/zAABAD3/+7/9v/4/x4Aov8RAOb/gf8TANf/SQD1/yAAQgC4/zAAJQD1/xcATwA3AC4AEAC3//3/2f/J/9b/x/8AAPb/9v/F/0EAXwArABgAu/83APX/rf9TANH/3P85ACoAXwD7/wcAFACX//j/kf++//r/sP+NAM7/yf8XAAoAFgAQAIkA6v8yAEIA4P8PABUA9//y/xUAzv8YAJP/vP/2/7b/NwAGADEA7/88ACIA2f8JAM7/MACe/+z/MwDZ/yAAJwD//wcAAAALAC0A9f85ACkA/v8aAOv/xP/S//n/5P/q/xgAAgDC/wkA3f/q/0cA2/8mACAAQwA8AAQAAACp/wIAw/8KAAQA5/9jAOL/AgDb/9r//P/M/w8AJQA6AAcAPQDw/9j/IQCg/yoAGgAaACIA3P8mAK//HwDz/6b/7f/6/ysA/f8cANn/5//p/ycARQAIAH4A6P/h/1kA1f++/z8ABgC7/8T/tf8JAK3/FABJANT/9P8WADYACwARAC4AHAApANf/wf9GAPj/6/8PAOj/AADI/y0A/P/w/wcABAApANf/OADl/+b/2//o//T/4f89AN3/BADl/y0AWgC1/ysA9v/R/0EAOgC1//j/KQAhAD8A8f/+/9n/8f/8/wsADQDt/9r/nf/C/8X/7/8YAD0ASgD4/0sAJgANABgA8P/3/+z/DwDN/+j/w/+9/zMA5v8lABwAJABcABkA9P8JAAQAr/9nAA8A+P9FAGn/1//4/8P/DwAYANX/CQD7/7H/+v8IAAUA/P8YAAAATAA1AP3/XQD6/zQAEgA+AAEAwv8PAKj/2v+x/x8Ayf/n/9//7v8vAKn/aAAKANv/KAD7/9n/3/88APv/ZQATAB0AHQCs/y4A8P8hABkAsP8ZAAUA0P9AAA0AuP/z/8D/sP8HAAwAAwA3AO7/AwAsANL/DABHAE4AHQDx/x0Az//9/x8A5f8YAMz/xf/x/+D/3P8VAPv/rf9EABAA9/8+ABcAAQD3/xwA2/8sAP//AgAeAP//7v/M//r/BAAXANv/VgAAAOD/WQCu/xAA3/+7/8//GAD4/97/bQDp/1oA4//S/yIApP8jAB0AIwAuAPb/9P8AAN3/EQAAAAIAAQCh/xIABgDl/xwAGQDt/xsABgDh//v/uf/d/zwAIwAVAGsAJwDH/8f/BQAXAPX/8v/m/wAAQwA/AOD/AQABALv/4//6/93/1f9DAOv/EgDh/6b/ZADT/10AKgDV/18Ao/83AGoAwP85AO//nv/s/8//rP/R/+7/6v80ACEAQAA8AOL/GgDl/zwA9v8lAHwACQAnAMz/uv+p/+7/6v+Z//v/BwAcAPH/IgAsAB4A+f/1/zkA5//4//X/EAAcAA8AIAATAPr/3P/B/8r/5P/q/w0AHwAzABoACQD//xIAGACp/wQA4f8XAPr/BgBCAHD/AwDz/+P/awDM/zYATAAWAEkA9v8oAOf/gf8OANn/7P8tAKX/2/8nAC4AHQAQAEkABgDf/83/of/q/9L/6/9QABwAKABfAOX/qv88ACsA8/8LANL/MgDT/97/NwCe/w8AOADl/+b/BQDt/7z/AQANABUADAA/ABsALgAVALT/PQDl/wsADgDk//n/zv8CANr/KgAWAAgAJgC1/wwA8//n/0MA7f8FAAEAoP/C/wgA+v8fADIANwAzAOb/FAAoAAIAFAAKAAwA3/8KAK7/pP/w/8j/2//u/zYABgBDACUAEwAyAN3/MQDP/x8AQwAGACcA+P8RANP/tf+8/9b/wf/s/xUAHQAtAPz/KADd/wIACgArABwAHgBrAM//QAALAJj/1f/O/y0A6P/g//r/f//r/wAAAQDt/9//XgArAG4APwD2/2YA+f/1/xgA0f/Y/x8Az//5//3/t//S/6//FgDq//T/CwAmAPv/6f8QANb/WQAnACYABwBkABcA0P9TAKD/9P/o/wAAJACb//n/AQDe/xUAPADb/xsAKADy/wsAxP/s//X/1P8OAB4AIwDr/zAAFQDb/xMA6f8LAKP/6v8UAOj/UgAsAEoA/P8wAPD/s//9/+v/GADo/+z/yP83ABUA2P8cAOn/xf/Y/y4A9/8iAA0AOAAqAOb//f/T/z0A4//v/wQAAQDz/wcABADa/zYAu//1/wgABgBXACEANADi//D/HACl/+3/BADY//3/zP/z/wkACQAJAAoA8v/4/0MA9v8+AOL/JADk/9f/UQDx/0gACgApAN//4v/l/7//HwC2/zoA3v/4/wQACQAJANH/NACv/wAAHADy/zAA+f/s/wUA0P/2/zcAHQA2ADsA/v/Q/x4A4v8/ABAAy/8/AL3/xf+a/+b/tf/+/1EA/P9OADoAawDR/+j/EADf//P/5f9AAOv/+P80AAUAHwDt/6r/8f/g/8H/NAD8/+D/GwC+/wgAIgAgAG0A/P8tAPr/jf8JAM//CgAbAC4A4f8PAEwAr/8oAAwA0//y/zgAvf/o/wAAlv9LAOL/LgAaAPX/GwBHAGAA7v85AL3/xv+1/8T/JADk/0AA+P/T/woA7v8lAC0AsP/o/xYAzf/2//X/MADs//r/PQBLADsA2f9cANL/1f8eAJz/QQDp/83/8P8SAD0A0f80ABoAIQAOALv/6f+9/+f/8v/u/yUAt/8UACgA7f92AAcA3f/o/+b/SQD5/0oASgDQ/9n/BwDl//3/IAC9/+P/mv/K/zAAzP85AAAAAgBmANz/MgAwANj/RQDe/w0APADr/wQA2P8IAL//AAARALn/9f/g/xIAsv8mAF8Azv8+AB4ACgAMAP7/BADR/xwAIwD4/zEA8//F/xIACwDN//b/rP8NACIA8f8rANb/DwDn//L/MQDf/zQAPADz/87/3v/s/97/+/8oAC8AIAAiAPf/1f8cACEAz//x/1YA2v/k/zAA5P8rACsAEwDK/5v/JAB+/xYAKwDS/zMA8v8/AOP/CQDL/+v/QwAIAB8A8f84AKT/FgAXAKj/LgDM/0UAKADf/+j/GQAvAMj/SwDu/9v/QgDW/+n/AQDm/8H//v8fAOv/XAD1//j/ZwDe/y8AFwD1/8T/vv/Q/8X/JgC//x0ALwD9/zUA3v8IAAIAy/8yAAEABgAxAOL/HQDn/97/7/8kADwA4v8zABAA0/8zABYA9f/9//D/6P8AAOD/3//v/+v/0f8cAOH/GQDk/8L/RgDG/zUAGgAoAFUADwBIAC8AMgDV/87/v//Z/+j/u/8aAJb/+/8IAN3/SgAbAAIAZADm/+7/RwDI/zEAGwAXAOf/+P/X/6L/YADZ/xIAAwDf/wYArf/7//D/GAARADYAGgAjADAAwf8mAAAABgDr/97/UwD3/53/6f/O//L/BgAfAA0A2/8AANL/JAAJABkASgAjADMA1P8WABgABQDr//r///+u/wkAJwDQ/+7/yf/b/y8AOQA1AAEA8v/4/8T/EQDy/9f/BwD4/ykA+v/K/ykALQABACIABgD4////6f8KAPP/+P8lABsAHwANAAAADwDc/+z/GwAPAKP/yf/w/8L/BgCx/wIACAAsAGQACQBxAAwA1/8fAAgA3//2/+f/1f8XAOX/+f8TAOn/DwAvACoABQDj/woAAADe/9H/FQALAM//FgAPACQA8v8cAB4A1P/2/+z/AgC8/ygA7v/g/wcAvv8gAAAAKQD4/08A6//0/00A6v/k/+j/XAD1/3EAVwCi//H/xP+y/9v/2v/6//H/FwBQAIn/AgALANz/OQAfAG0An/8rAPT/6P83ALf/dADr/y0AKgDb/xEAuv/Z/+z/9v/h/83/AQAPAO//8P8fAEIAxf9OAFIA2/8cAMz/FQCW/zEANQDR/x4Ayf86APL/6//Q/w8AFQDu/1gA0v8qAAAA6v9AAPX/3P8WAOz/yv8fAMz/7v8dAAkACwAYADQA9f/i/9r/AwAjAM//CAAHAKf/DAAIAPv/9v/R/zUAEwAQADgARQAYAOP/GwDv/xsA2//z/yYAzP+//9z/yf8oACsA8v8oAO7/FgAnAAAA+f/M//T/JAAcAN3/HwC1/8//NgDs/0MA4P8SADcA8P9UAP3/i//3//n/uf8sACsAJAAoAC8A1//W/ykAjf/k/8T/6f8rAPr/NgA1AAUACQBbALr/EwAIAOb/AAAAACcAyP9BALb/GwAgAMv/3f/4/+3/m/9pANL/FgADABcAcgDt/1oA+v/H/8//KQDI/z8A2//h/0UAav9IAKz/yv8aACcADwDO/1kAAABbAOf/8//t/+7/JwD8/0MA8P8IANv/8P+4/xIAFACn/xMA6/8SANf/PAAzAAAAHgDn/zwANAAzABgA5/+w/+3/7/+e/xYAyP/E/wMACgAQANH/QwAmAO3/QQAhADUADgBHAM//sf8zAKH/BgDo//j/NwDW/yMA9f88AAMA8v8dALL/1/+s/wQA4/8dAHEAwf8xABMARgArANL/FACr/wgADgANAAkA3P/K/8r/GADh/zgAUQBDANL/1f8EALH/UADn//n/VAC5/zEABwDV/0cA+v/E//T/vP8JAPv/AgAjAOz/aADM//H/IADi/0AA3v/m/9T/xf8oAOz/MgBDANf/EwDh/xEADgDy/2EAOAAXAP//7v/H/9P/z//u/yYAwv8rAAYArv8GAP3/7P8PAAYA6P8GAOP/NwA1AOv/GwDv/y4ALgDk//r/LgD+/ycAvP/t/yMAzP87AK3/BQAjAPf/CADn/xsA0/8EANr/DQDk/zEAGwDX/0AA5P8/AOj/1/8JAN3/2P/r//n/2/9BABwA+/8vAA0A7v8/AAAAEwD+/+P/NQC//ywAj//k/+z/o/9bAKD/LQD7/ysAXQANAF4AJwBTABMAwf+n/+f/jv8FAAkAx/8aAMj/LwAMADAAEQAMALb/zP8yAMD/XAAYABsA5P8PABUAqv8kANj/GADn/yYAGgAEAGUA5P8eAAsA1f8nAMD/8f89AJn/2v/k/yEA+P/H/1kAvP/W/yAAAAD+//L/GQADAOH/GwAdAB0ARADw/yYA7P8GAN7/6v8dAOP/UQAcABYAyP/4/+X/qP9gAOL/6f/g/wgA8//p/ysA2//7/+X/7v8tADsALAD1/9n/FAD6/wcA8v/c/ygA3f82AAoA5P8KACkA0//x/w4Alf9dAN3/DgBBAAwACQDP//v/mf8bAMj/MQAfAPv/PADr/3YA0v9PAOz/4v8UAOT/DwCL/2YAtP/4//7/ov8xANH/BwDh/xgAGAAXACMAPwDm/wwAKwC5/1MAu/8YAK//AABeAJr/UwC//xEA6f/Y/ygA7/8LAOb/NgDu/xEABwAeACUA4f8TAPT/8/8CACQA7P88AAcAzf9HANT/m//Q//7/0/8IABYADQAIABMACADp/x8AHABMAM//AQD+/9P/+f+i/w4A9v8WACgAOwAUAP//NwDS/zgAzv/w/+j/9v/k/+H/egC1/0IAIADT/+f/9f9AAKz/RADk/8T/DQDh/xMAEAAMACMA9P/P/1gA+//l/y0A3f/S/7j/7v8BACgAHgBYABYA/v8JAMj/CwC//wAA+f/c/+P/IwALAOb/HQDo/04ADABJACUA5P8IANT/HAC0//f/JgDZ/+7/7v9BAAIA/P8fAA4Ay/+U//b/9f8TADAA9v85AAIARAAiAMb/CQCh/+f/2f/p/y0A7/////H/NQAsADEAIQBKABwA8P82ANL/DAD5/9v/yv/R/8r/vf/2/7X/5v8FAP//DgAMAAMAOgBGAA8AOQAtAC4AQQDu/+v/3P+u/w4A0f/i/zIA9v82AMb/KgD2//f/KwDf/woAlv80ANr/9f8RALL/MQCj/ykANgAcAEIAFgA/ANz/4//q//D/zf+3/zQA9v/2/2cAJgA1AAkA4//r/7v/CgDT/w8AUwD8/+j/LwDe/6n/EwD1/9n/0f9PAPD/3v8EAMr/FwAXADMA7f9WAC8AIgAiAPL/9P++/z4A0f8/AOL/wP/Q/7b/LQB+/4AAMgC//2cA4P/j/8D/8P81ANn/EQBxAO7/QgABAN//6/+8/wAA0/8+APP/HwAXAAEAAgAPABEAsP8DAMP/JQDN//3/JQDN/zMA3f9dADQAJgALACMA5f/8/xMAkv8CALP/LADr/x0AQAACAO7/5P8XAIr/HwC4/xgAHwD4/zgAGwBZAOL/OgC5/9D/CQDT/+b/AAAcAMj/OwDm//b/DgAMAPH/DgAQAMD/YAACAD4AKQAVAKb/8/8YAK3/TAC4//7/wv/z/x0A0v9YANT/SQAAAPj/OADK/xMAUADo/+r/FACD/zIAFgDP/w8ABQAAAOL/GgD+/8f/FAAfAAUAEwDi/x8AAwAdAAoA1f8RAAMA+//p/woA1//R//L/SwD1//X/fgDK/0AA9v/c/+7/wf8FAK7/8P/w/zkA/f9AAAsAGQAsAAYAawD2/0sAwv/d/8H/nf+z/+X/HgCz/5gAwP9dACQAsP9zALT/1/+s/x8Aqf8VAHcA+f9DABAAKwAWAAcAu/8xAPn/6f8zAAoA8P+4/x0Amv/t/+T/AAD2/9n/TgDs/zkAFQABANH/OgA/AAEACAAJAOv/wf8TAJj/eADW/ysATQBq/0MAl/8oAOX/4/8rANL/GQD6/0oA4/9VABUA4//a/wIA7v+x/10Amf9WABUA1/9FAAYAAAD7/1UAtv8cAM//uv/w//P/9/+5/y4Axf91AOj/IABIAKP/RgAIAEcACQAPAOX/IQDY/9H/FAB1/0cAwf/0/xAA2/80AAoARQDt/xMAPQDp/8z/BwDg/8P/NwDJ/9//AAAUADoAHgAnAAsACAAsAAAA5v/1/+D/y//W/+P/4/8FAFAANQDd/wcADwAEACYAFgAwAOL/8v8EAOL/0f/2/+7/jf8DADQAEQBpAPH/6v8RAJv/+P/Z/xcAKgD7/4gA8v8SAPj/wv9FAM3/9/8oAAQAyP8eACkA8f8XALn/1//s/8b/DwAnAPv/EAAoAPv/RABQAPf/PwD2/77/wf+F/wAAt/8ZABMAEACGAOL//v/+/5//0f8PAAgAFgDp/0YAHQDg/4YAFgA4ABQA4f8WAHr/7f/y/wEAIwDb/zIAv/8TAAEApf/9/7H/+P/e/xEAPAAlAFwADABPALb/BwAVAK7/KQASADkAy/87ANb/0P8lAOz/OwDg/x8Asf8KABkA5f/0/7n/EgDE/y4ADQD9/x4AHQALAL3/NQDX/+X/AAAEADEAGgA1ADkAFQAXAM3/7v/w/57/1f/P/xgA3/8AAC8AKAAuAPb/YQC+/+7/FgDW/wAA7v9vAOH/IgDd/8v/TwDU/xIAs//S/9v/6P84AAoANgAcAP7/CAAZAL//FADs/+j/EwDy/wAAuP9tADIA8v8jABsADwC0/zAAqf+0/yUAxv8MACQAHwAZADsAJgDQ/8X/GAAHAP3/OQD7/7D/AADk//T//v+Y/zQAwv8PAFUAHQBQAMr/JAD9/zoAvP8oAEoAuf8aAKT/MgCn/xEADgDk/yQA4v8+APj/MgDO/wwA5v/j/w4A+v9aALL/7v++/x0A+//5/yMAvf8rABwASAAdAAMADgDN/ysAHADK/+n/0v8QAOn/5v85AO7/GgD2/xgAuf8AADAAx/8hANH/DgDC//n/GQBSAFYAt/87AMf/y/8AADkAJgAkADcAvP8AAPj/5f/6/+n/8f8eAO3/1v/6/+b/FwATACsAFADe/yUA5f8YAPj/pf8eANP/ZAD+/w0AYwC//wcAov8QAKX/BQA3ALf/aQDe/1oA6//e/wUAyv9KACIAWQDd/wsA9f/M/+X/vf/p/x0A/v8IAAwA1v9IAOH/zf/Z/xAAHwAWADkA1/8KAOL/CQA5ADsACgDu/+D/3f/h/9z//P8BAFgAyP8QADQAxv8fAFYAEQAEADwABQAJAKP/4/+9/5X/1P+d/wAA2/9AAPn/BgCBAPb/PgB6AFEAIQAOAE8A1v+y/x4AjP/k/9n/rv8OAHP/BwARADIACQD3/1AA0/8kAFgA+v9RACoAyv/8/7T/3f8DAO7/GwDq//3/3////wIABgD8/yEAZgDJ/wcA/v/d//v/FwAVANr/BQAAAMf/6//2/9n/JgAkAEkARQD2/zkAAAAUANX/BwAnAM7/8v/L/8j/vv/4/8X/w//e/wQAOQAbAJUAHAA6AAkA4v/R/8T/GQC+/z8AAQAAAFQALwAUAPX/TwDL/xEA6v/u/9L/4f/2/63/8f+p/zQABwDk//P/GQA5AMn/SgAjAPD/2v80AP3/8P8WAAwAIQDJ/ywABwAOAMz/RwA1ALX/LADL//H/mf/P/x0A2f8sAB4ACQBDANP/HACeAMX/awD7/6//FgCh/xEA2P+w/+v/8f/q/xMAAAAEADEA8f8XAAAAHgD1/+L/IgDv/w8AEQDP/0sAIQAGAHAA4f/p//r/yP/P/7D/uv/o/+3/BABnAC8AKAA7AAUAEADp//L/LADv//j/0v/E/+7/0f8bAAkANQANAPj/BwDZ/woACAAtAB0AAADw/wEAj//h/9v/4v9oAPH/TQAUADcA8P/2//n/nv/7/wQANADO/3wALAAxABkA6v8eAHD/AQCl/9P/u/8nABYAyf9cAND/JwDJ/zoANwAuAGUApf/X/87//P8UAAUAGQBIAPb/AQAgAP//tf/C/wgAzf8JADUAKQDn/zQA2f/Z/yEAyf/3/wMAGQDS/xYAAwA/ADoABgAfANX/LQCv/ygADADt/x4AxP/g/8j/+//t/x8Ayf/s/x4Avv8JADMAOQA3AGUA5/9XAC4Aof8FAKz/pf/l/woADwAeAAYA+v8BAC0AIAD3/xYAAwCz/wsA5P+q/+z/6v8KANr/KwA3AAMAIgAwAD8A3/9VAPv/9P/9/8n/BgC3/0gA8P/S/wsAyP8MAN7/AgAWABAADADh/xQAHwAFAPn/DQAkAPP/wf83APL/0f8mAAgAHwD9/wUAIQDJ/9n/GwDn//j/GwDK/+3/6P/D/wEANAAvAA4AQQACABkASQACAB8A4f/C/+L/5//s/xgAvv/E/zAA2/9aAOv/MAA9AMD/HQCy/wEADwDR/1wADADv//3/sv8gAB4ACgAMAMf/CwDd//X/+P/x/zYAAwAUADcAJgAJAAUAGwAeAKv/DgAEAJD/BQCs/xMADwDz/0UA0f8JAMn/6/8rAAYAYgA/ABUAFgABAL7/AQAFAM7/FQDW/woAIQDi/+z/vP/K/8H/NgA3ABcAIQAiAPf//v8qAND/CAAyAPz//P8xAMr/+/87APL/v//y/wsAg/8eAP//JwAQAPf/SwDX/xwA3v8wABwAGgD5/9n/6P+9/ysA5P8wAAsA6v+m/ycALwDO/3AAvv8qAPz/////////4v8NAHAAw/86AOL/3P/a/83/l//Q//j/p/9DABYAbwAYAHMAMwDV/zMAuf8oAOH/HwARABMAAAABAAoAuP8OAK7/5//d/9H//f8VABQAEgA5AAAA8v/u/0AA5/8NAB8At//6/x0AHgDk/wAAAQAdABgA2//c/woA+f/x/yYAIADi/+H/GwAnAP7/5//R//b/8f/k/ygA6f8fACsA2/9AAP//LgAiAO3/+f/+/+//v/8AAM7/AAAZANL/EwAXAAgANQCv/wsAUwCu/xUAEAD+/7//CAAFAMP/JwAHAEoA9/8uAAAA9/9fADEA8//e/+7/lf/j/7z/tf8RAEEA9f8WAEEAyf9uAOf/BQAGAN7/IADF/zQAFAAOAAcAAQDU/y4A2f/o/0IAcf8DABcA3P8IAFUAEADd/yUAvv8ZAA4AEwAsABQA2f+w/xIA1f/z/+r/+P8rAPD/JwDv//L/IADm/xIANwAMABIA+P/t/9//VwAoAMb/MADx/wYADQD+/zQAyP/L/8L/3//k/7T/+/8HACoADwAdABQAy//2/xAASAAYAAwAIAAYABAA0/8zAPz/7P80AOL/4f+6/8v/BAAGABQA8P8WAP//AAABANr/EAAdACAADgBTACEAyP/V/7b/zP+q/wcA6v9CAE4A7f87APD/HwAzABoA7v8bABEAtf/v//P/HQDq/wcAEgDD/ygA9v/b/+D/9f8bAB0A8f/c/w0A4v/7//3/sf/7/xoAEwBJAF4AGgBhADAA5P8pAMb/HQDF/7b/6/+Z/wQAi//p/xIA5/9uAAMA+v8iAEIAIQAAABYARwDm/wYAEgDb/9z/7P8AAJ3/8//d/+f/QwD+/y0A4f/3/y0A5v8XAPr/BwAdAP3/SwAVANr/9v/3/zkA1v/e/ycAvf/8/wwA6v8PAM7/0P8PAMT/PgAkABMA8P/v/w8A0P81ACAAIQARABUA7f/c/1QA/f8TACcANAARAM7/1P/l/93/o//9//H/w/+n/9P/AgDe/zcASQALAE8AUABHADkA8/8SAPX/2P/2//j/BAD8/ykA2f/A/yUAlP+6/w8A6//t/zgAMQDm/zIAEAAAADsA5v83AC4A6v/W/93/JwC//9b/KwD//9r/HgAgAOX/DQDO//n/HAAPAC0ACgD1/83/6P/d/8P/IAAJAAwA9P8HAC4A7v89AAAA/v8ZAAkAKADh/xEACwAEABkAGwDf/6X/JwDM//X/+/+g//v/AwAkABYAGgALAAIAyf88ACoAyv8NAPn/8f/x/x0AFQACABQAAAACABEAFQDr////+//Q/93/OgAcANP/OQDq/97/6v/Z/0IA5//K/wgA5/9VACIAEABhANb/yP/9/8X/5/8kAOz/4f8jAOL/MQDa/+r/HwCk/xkA+P8VADQAJAAaACEAVgADABkA2v/X/9n/3v9CAOH/9f/I//z/FQC//yMA5f/k/wMA7f82AAMAHwAOALL/MwD0/wwAMwDF/ysA4P/b/xUA7/8xAAkARQAvAPH/EwACAMz/tf8CABkA6P/e/9z/7v8GAKj/6P8DACQANQDP/0sAGAANAHUALQApACwA3//g/9T/3/8NAM//BAAAAO7/yf+I//X/7v80ADkAGgBLANL/BwAiADcADQD0//P/u//e/8z/AgDC/wAAdAALAAwAGQD1/xoAKQANADEA2f8AAPT/m//o/8H/1f8rACsA5P8JAEcArv8gAEoA6/9TAAEA1/8YAP//vP/2/1gADwAOAPv/4P/U/57/CgDx/x0A+//6/1kAsv8MACwAAAASAP7/GgD9/wYAnv8MAA4AAAAHANX/SgABAC0ALAAUAOb/zv8wAJr/1f/r/8P/CwAIAO7/9f8mAMb/KwBDABQAkQBNABwALwCx/8j/vP+9/+7/q/+z//7/UgA9AEcAWwDp/xsA2//K/9X/uP8TAOL/6//c//r/KwBdADYAXgBvANr/BwCq/+H/x/+//0kAdP/1//b/gv9TAAYAKABtAPz/CAACAOf/MAA1ABQAAAAPAOv/2v8LAC4A5f/3/04Auf/T//D/yP/+/9X/CQDt/8j/AwAXAPr/8P8NABMAJgA9AF0ARQAeAAMACwDF/7T/EQC1/9X/EwDt/+r/PgA1ALz/DgDz/+b/AAAAAAAA6P/8/xcAFgDs/wQA7P8OABMAFwBOAA0AOwAQABwA4//F/wsAr/8dAPz/9P/F/8H/GADG/9z/7/8mACUAIAA1ABwAQACx/7j/8P9+/+f/QwAfAGEAGwAvAGsANgAeAAkAOwDY/5b/3v/Z//P/n//T/wAAx/8tABcA4v/b/+7/QQAHADwANAC+/xQAFgAHAOb/YAAUAML/MwDd/x8AAwALAOH/sv8OALP/4v/k/yEAxf/o/24AEABNADcAFQDk//b/CwDC//b/z/8TABkA4//o/woAAQAMAEcA/P8YAPr/3f/u/8P/JAA2ANj/8/8QANv/CgAHACEA2v/M/4wANQAnACMABwALALL/6P+G/3L/6v/O/w8ATgD7/xgADQDV/yMAMQBDAFIA/v9NADAA4f9MAJj/z/8UAIH/9//i/+j/CgDl/9j/9f8XAAAAgAALABMAOwDM/wUAwv/7//7/y/9QAA0A+P8WAAYA/f8EAN7/EQDl/+3/DgDA/w4A5v/z/zUAKAAcACAANgApAPz/0//o/7z/rv/p/yUA/P+y/xQA9v/S/w8AaAA4AAAANQA7AP7/+f8BAM7/8P/a//7/KgADANP/6f87AMb/8/8YAAAAAAD0/zIA3v8VAAUAxv/z/9f/+/8rAEAAGADn/yIAHwC6/zIABwDi/yIA6/8SALb/4v/j//b/HgD6/wQAvP8eAF0AEgAtAP7/8/8JABIABAAiAAwAxv+0//n/ov+9/zcA6v9RAB0A2f85AAQALgAHAOb/RADV/ykA+//I/y4Aq/9MADEAuv9PAM3/xf/U/wkA3v/1/zcA8f8EANf/4f8UAN3/yf8CACUAUQAcAPP/XADJ/w8AQQDl/yYA5P8kAPv/vf8hACUA9/8GABcA1f8TAMD/0v8iAMr/9f8KAPf/q/////b/9v9MAMD/XwBSANT/VwDq/8P/MQDN/9r/NwDn/wYAMQAJAPT/9/88AOn/2/8NAOH/3P/E/yEAFwDo/wsAEAAsAOT/FQBGANn/BQD//xQA1//Y/zwA3f8PAO//0v8NAMz/OgAYAPX/8v/z/xAAv/82AOX/wv8qAMn/LABPACIAPgAaADgA3v/N/1AAqv/n/xQAuf8aAAEAr//w/wUA2/8PAAEAx/9KADIA6/8OACAAMgAKABsARAD5/83/uv/F/8X/3P8xAN7/1v/4/ykAXAD+/+z/LAAsAP//RQA0ANz/9P/x/6r/u/8eAPz/+P/r/x4A8f/Q/zUA9/84AMv/TQAkAJ7////u/y4AqP9bAC8A3v9pAAkAWgDA/9T/uP+///T/v/8bAAMAEwDx/xkA9f82ABkAtv8xAOL/AgDf/xcAPwD6/w0ABwAQAM7/HwA1AKL/FAD6/7f/GgAHAAoACwD+/wQA4f/9/w0ASwAoAAAALAD0//3/4f/u/7z/nf8VALv/tv/6/+//NwBAAGoAPADc/xEARwA8ABEAAgDP/+H/FADX////2v8AAB0A/P/a/77//P+8//n/8//a/+b/HgBLAP3/YgA4ACkANQD8/x4AvP8lAP//sf/j/8j/wv/K/w8A/v/s/1cAPwA4ADgA+P/w/5v/7P8XAOj/WgDj/+D/GAC4/zQA8v/7/zYA+v8dAOb/DgCz//z/EwCW/zMA9/8eACIAEwBZAOb/8f/O/8X/DQDv/08AFQDa/0cA+f/e/9T/5P8mANf/LwDp/+b/BADT/3IAEAAtACQArf/a/9v/4//8/xgA/v82ADEAGADf/+L/DwD8/ycA5f8WAOf/t/8iAAIAvP8qABkAGQDt/6P/ZQDT//3/OwDZ//7/3f8xACwASgDf/wkA//+X//n/sv8UAPX/HgAjAN//LwD0/9n/QAA1ANj/GgAqAOf/1f8jAOb/5v86ALn/MgDt/+j/OQD6/+b/7f9CAMD/8v80AMb/DwDT/+T/UAABAPT/CADP/8j/3v8OABwAJADl/xIAEQAvAGQAVQA/ANb/GwDy/9j/NgCZ/7//vP/C/87/wv///zwAOgD9/0sACADZ//3/9v/1/wYAEAAUAPv//v83APz/FADo/8n/VgDw/wAAMQDH/wQAFADw/y0ANADo/wEA0v+8/7f/zP8HAK3/CAAEAOD/bAAGAPP/agAtAP3/NwAJABgADQDp//P/6v/o/+n/PADi/yEA9v/Q/x4A0/8oAMP/v//T/w0A5//1/zUAvf9KAPb/LgAQAA4AQgDN/0gA9f82AO//yv8BALD/GgC5/xsAIgDs/yYA4f8HACkAJgADAPH/HQDe/9z/PgDQ/wkAIwDl/+L/yf/S/+3/KADy/2EA3P/+/0UAsP8uAO//+/83ACUA+f/w/wUAy//d/wYADQAAAD0A8//N/xEAkP/c/0EA9f8/ADUAAAANAPj/7//S/xAAFAAGACgA/v/2/w0ACQAfAOD/tv8kAN7/AQAuABQANwC1/zgAif+F/0cA5P/u/yEALADd/ygA7v8LACoAAABzANH/GgADAMH/FADr/xsAPAC6/xUAZQCU/zYA9P+z//n/yP8TAKH/MQAhAJr/4P8LAAgA/v8yAO3/FAA5APf/LABfAA0ACgD7/w0AIAAIACwAx//b/9n/2//f/wAAAADy/9H/1v8wALf/HAALABEAFQAJAFUA9v8LAN//VADg/+3/RQCp/xUA3P8UAB8AHQC3/93/9v+L/3cA0f8AAEIA/f8eANv/KwAXAO//+P/w/yQA6f8DABAA0f8jAAQA9P/6/8j/8P8IAD4ADQBDANr/7P8SAKn/MQAdAOb/zf8NACwAJwABANL/KwCv/x0A8v+b/yMABgA9AA0AKQAHAPX/PAACAP3/zf+t/+3/9f8IAOv/4f80APv/JAA1ANj/RAADAPD/HAC0/wQABADc/x4ABgDg/wgAHAA+ACgA0v/8/7//t/85AO3/GwAuANP/JAAEAAAAFwDo/wcA0v/Y/yUA2//l/0AAxf/+/2AA/v8cAOT/5/8iAOv/+/8DADAA7v8RACwA3//x/+z/0P/W/xYA8f8kAMH/EwAuAMz/YAC4/y0AHgDr/zMA8f8GAM3//P8hAAcA0P9CAC0Arv9PAAoAyP/8/+v/4//8/9//8P/F/9b/HgDk/y4A9P8hAEUA8/9jACEA7/8nAAcAKQAHAOP/+P+8/9r/3/+v/83/NgAvAAoAOQAdAO7/u//U/83//v8MAO7/RAALAFsA/v/r/1EA4/9QAOT/1v8VAJz/2f8lANv///86AP7/BgDG/wwAEwD6/z0Azv/7//f/6f8oAOT/FgDq/9f/8f8DAA8A1P8fAB0AGwA1ADwANQAAAOL/FwDp/9H/XADu/8D/yP+3/8b/8v80AP7/JgDy/xwA+P+x/y8A1/8eADMADwAJAMT/JQACABsAWgDz/w8AGQDG/w4Aw//2/yoAqP8IANr/sP8xAB4AOwAMANr/GQAOABUAPwASABEAGADd/8D/7v+M/w4ANADh/08AAADw/9v/yP/j/93/MwAJACwAHQAFAFgAtv/q/yIAtP8RAD8AJQD3/yMA1P/o//X/4v9JAND/BAA5AB8A4v/E/wAAif8PAAIACwD3//H/UgDY/2wAEwDx/1kAtP8mACAA0f9NAL3/lP8GAI7/BQAMANr/XQDJ//X/OADP/x4AHQAOABYAGQAmABsAOQAHAPj/7v/2/9D/p//x//L/RgD7/woAOAC+/yoA+//G/+r/1/8lAAUAHQAJAPH/AQDU/xYA8/8nAAcAAwAqAL7/JgDP/woA8//e/0cAIwBBAAEABwDQ/woA4f/q/yUA3v/z/9b/HQC3/wgAIwC1/zoAQAD3/wgAOADO/xcA9f/W//b/j/9IAAkAIQBEAO7/WQD4/8b/HgDZ//3/vf/r/yAApP8kAB8A8v8IACIAKwAcADgABAABAMb////I/+n/CgDj/+7/0P8oAPP/OQASABcA4f/Y/2EA3P8jABkAAADy/6f/CADb//T/BAAqAEUA+P8GABoAwP/T/wwAAQAyAPT/GADy/+H/VgDU//f/CACy/10A6P/m/x4A8/8TAB8A3P/m/wgA1v8FAPX/MgDQ/wQA+P8OAEEAlP9dAML/3v83ALD/OQBrADEAu/9gAL7/BwAcAKf/aQDT/7L/1f/7/8z/KQArAP7/XwAGANX/wP8BAOz/8v86AAQAsv8cAAoAzP88AOf/LQC3//b/UAAVAFQABwA7AM//qv/0/wAA6v8kAAUAzP8UAMr/5P8RAA0ACwDj/xgACgAfAEEA+P8IACoAx/8HAAoA7v/7/7D/6P/v/wQAYgAjALv//P/2//b/BgABAA4A3/8eAPr/BABBADsAHwDu//3/5v8CAPH/5//U/wMAkv/J/zIA6f9DAAkA+v8BAPv/BgApAIYArP/Q/xIAx/8/AAYABABFANP/CgDg/87/AwCz/wUACQA2ACwA+v8KAOv/MAD8/z8ABQDY/wcAv/83AOP/8f8gAAgABACh/+j/zP/V/ycAMgAlAPL/9v8kABsAIQAqAOT/HwAAAN//6//x//T/sv/8/wYA8v8SABQABQDX/zIAFwAUAM3/9v9QALf/FwAeAOn/MADI/zEA5//8/0wA1P8yANL/+f8NAN//RQANAPr/0v/e/9r/+f/h/wIASgDP/wQAEQAVAAYA1v8UAO7/7P8YACsAIQDg/wYA/v+b/wIAwf81AEMAKQCPAOH/RQDH/6f/yv/W//7/6/9fANv/8P/v/wAAJQDV/xIAMADo/+P/UQDp/xUAGgD8/wUAt//4/ycADgDk/zsAoP8bABAA0f/6/6T/YADa/9T/AgAeAA8A4v+CADkACgDw/+P/7v8PAOj/yf8uAMf/CABEANH/8P8rAPL/8/8eAC8AIQARAPX/vP/P/9//IAATALj/DQD0/+r/BAD5/0cAEwDq/w4ABAAAABgASADb/+v/AQCg/y0A2//v/woAyv9yAPv/OgBrAH7/vP9tADoAdP+s/3kAHgDQ/w0Avv/Y/wgAcwA4AKT/uf8uAC0A8f8JAO3/JAAsAAwA3P+e/+3/GAD2/+f/XgASAPb/HAD0//r/nv/Q/xsAMgABAAQAEwCu/2EAXADr/+n/wf/6//D/MAAuANP/7//x//T/BQAaABMA5P8fAL//9/8HAM7/GAAHAFEAyf/g/wAA4P9EAAUAYABKAPz/IgDO/wUAAADD/9L/7P/s/+D/BgAKAKz/6v8cABkAMQAOADEA9//b//v/5f/7/yMACwAnAPr/DAATAND/SQAAAOb/2//A//P/zf9ZAA0ADgAbAA8AEwDB//H/5f/y/xcANgAUAEMAFwDf/xMAkv/Z/9r/4f87AOf/OgDx/87/CAAZABIAAAAfAM7/CwA4AB4AJgD6/+//z/8iAA8Ayv/k/+f/3/+s/wEAPgD6/1UANQDo/xYAHAAAAP7//P8HABcA8f/d/+T/z//1/zIABQAHAMT/uf85AOH/8f9QABcAEwAcANr/AQD8/wcANAA1ABwAqf8aANP/3P///4n/VADk/w4AIgC8/1EA0//g/0sACgDc/xsAKgD1/+n/KQDX/8H/IADh/xkA1v9EAD0ABwAFABAAAwCc/2kAsf/0//z/yv93ALr/PADf/+n/CwDy/ygAtv9eAOb/4P/8/8b/6v/n/9//GgArANT/YgAlANv/KgAYACgAAQD8/xMAAAAdACQA6P/k/9T/6v/N/+D/BwDK/xIANAAGAMb/AAADAN//ggAdAMr/6//X//D/5v/c/0AAKQAbAIsACgAIAAEAqf8AAOb/6P8FAM//yf/4/y0AJwAeAAYAEgD5/8L/vv/w//T/MAAvABwAAQCx/2EAJQDz/xAA8/8MAJD/LQDw//z/LADg/1EAi/86AA8A3f8LAMT/SwC7/y0AHAACAPX/1f9EALb/KQAZAOX/3P/6/yUA2f/w/zYANwAGADsABgABALf/EQD1/5T/PADJ//T/1v/p/yAA3P8tAL7/RAA9ANX/ZgAZAO//AwAoAP3/8/8iANT/vv8AAND/HQDV//3/SAC1/10A2v/V/0YA1P9EABQA3f/v/+7/JgD7/wwAEwDr/+b/9f///+r////+/xkAJQC6/xcAQwDk/xYAYQAVAMz/IgCh/8n/8f/C/0cA3f/w/+D/0v/w/yAAKwAgACUA1f9JAAEA0v9JAB0A9v/x/yYAz//8//n/6/8rAB0AOAD2/+7/AgDu/+H/EQC3//D/5P/U//v/wP8aAOr/DgAjAPj/OAA5AP//8f8lABQAMgAeACkAuv/C/1QAxv/X/1AAIADK/wAAyf/2/8n//v9pAKj/DwDV//T/LgDa/wYADwATAPj/IgDH/+j////n/1wA+f8AAEsAFQA6AF0ACQDK/9T/zf+//7L/4P/9//P/GgBHANr/IgAMAMr/2//7/18A5P9AAAcAz/8nAOP/FwA8ACgAuP8qAMf/xf9TAN7/EQAMAPj/0f/R/+b/6P/9/woAIAAAAEQA1v/4/xoAAQBHAPT/RAD1//X/AADO/woA1f/N//r/OgDm/w8AFADd/+//0/8eABgAOwAaALT/6v/i/wAAOQD///7/JwA2ADQA1//8/wsAo//0/+j/y/8kACQA6v8TABgA/P8IADUAGADo/+v/0v++/7H/GAAXANT/GwBBABgAKwAwANz/FgD8/xcABwDj/00A7/8qAAcA1P/l/5z/JgD4/9H/EwD7/xQAvv/F/wcA2v8PABEAYwDR/+L/QwDM/2YA3P8lAEYAFgBkAKD/+P/E/+f/IwC1/wEA5f/p////1/8qAEQAEgBwAAQA5f/w/7L/7v/Y/+//GQArAN3/5P/u/+v/CwBGADIABgAKANX/EQA7ADcAAADu/7r/3v8AAL7/EgDc/zEA6f/+/2YAsv8DAOj/qP8SAAQA5//8/wwAUABPABwANQAQACEAFAD4/+b/wP+m/+n/5f/o/zEA8v/9/+n/QgD6/xkACgDY/1gA2v8XAAcA4P/B/+P/BgDH/wMA4v8qAPz/OgAQAAkAPQD+/xUAKgAFAOL/IwDD/y0AFQC+//f/tP/G/+b/CgDb/2AAOADZ/zUA8f/e//b/BADz/wgASgAdANn/DAAWAOH/GgAWABsAxf/W/yUAv//z/xoAsf/1/9j/CAAxANf/RwA1AE4AFwD3/xoArP/R//n/5v8KACkA4/9LAPr/0f8gANj/MgDr//L/EAC//8n/DgAKADEAdAD8//P/7f/r//n/8f8VALj/5P8ZAOH/GwDl/9D/IQDr/zUAOwBSABkA3f8SANj/DwAmANj/3P/v/8T/7f8FAOv/JQBYAPj/CQDa/5H/SADS/xgAHgDc/yAA1P8wAP3/KAD3/xYAMQD0/xgAyP87AOT/GAArAMz/1v/s/93/lv80ANz/7f8JAA0ARwAlAFMAQADm/+D/7P+G/+D/6/8eAA4ABgBUAA8ABAAlABIAzP8mANH/xf/v//n/CgDd/77/vP8pANr/bgBcABEAOwAEACoA5P8gAMz/6v+q/9z/PwD9/ywA7f85AN3/DgDu/7b/KgCw/yAA9/8ZAAwAwv8tAOb/CgAPAML/VgDa/xwAPADL/2UADgBJAPn/vv/P/9z/2P+z/08A8P86AB8A4v/t/9j/xv/9/xoAu/8tAPj/TQAqAN7/KQATAAUA4v8lAOP/MACg/xUAJQC8/3YAwP8OADIAzv+9/w4A5f/i/0UA2f8iANf/8P9DANH/GQA7AMv/BwALAAAAPQAPAA8ACQACAO3/7//h//f/AADM/6v/tv8pAAIAKQD3/+T/QQANAGEABAAnAP3/zf9DAAgAHAAfALn/+P/S/9//9v+J/+7/8v8wADEAcABiAND/HQDC/7X/1P/4/+P/7f8SAOP/WQAQADsAKwDz/wsAEwACAKX/+v+5/77/HgDh/w4ACwANAOj/LwBdABcAeADy//3/GQCL/xsAyf/b//b/9v8RANn/OgDb//L/AACc//X/DADZ/1IAbAAMACwAAAAeAPL/OQDz/6X/EACh/yYABADz/zsA9//8/9T//P/0////3P/f/w8A8/8rAA4AAAAUAAMAIwAhADUAvP/Z/yMAlf8OAPz/AwBbAOb/XgDq/wEAGADa/wAAEQA7ANb/9P+T/5r/yP/5/1kA+f8pAN//6/86AOX/HwBWABUAJwAAAMT///+//xYAJQDY/zEAFAAcAPP/BQAMANX/AADt//H/5v/y//n/GAAJAP//BgD6/wAAwP/g//j/3/8fACUATQAvABgALwDu/yoAxP+W/yIAwf8FAAwAzP/4/9D/MgA4AAwARwAWAMT/2v8HABIACAArACkABAD9/wMAKgDV/7n/6f+//wQA///v/xIA7f8GABQA//8CACAA3P8sACYAAgAlAPr/4/+m/w8A9P/4/wsAFgBRAPf/XgDS//z/5/+p/x0A6f8VAAAAUwDa/8n/CwDN/xQA5f9LAMX/OQAaALX/VwDD/+D/5//x/yIAEQDg/zkAYAD4/1YA4P/1/+L/5f8BAIX/3//P/9//JQBUAAMAAwAgABwAMQDV/woAxf/9/wAAwP8ZAOj/NQBKAAcARAAgAJv/0/8RAAcADgAPADQABgDr//f/+/+2/8X/TgC7/8z/OwCv/yUAAADi/2AAyv8PACUAHwAKAAAAPQAOADUA3v/c//f/zf/m/9r/AQCr//v/JwASACMAGgA8ANj/4//8/xgAFwAGACYABwD2//v/FwDr//7/6//k/xgAEwD+/9b/4v8GADIA+/8FABQAkP/k/9//vP9NAO//TABlAML/9f8EADcA+v8sADIA2/8DABYACwDM/+f/s//p//z/IgAyAMf/IAATAPD/BwBIANb/1/8gALn//f/r/w8AIgAMAF4A8f/V/wEA4v/J/wkADwARAAMATQATAP//8v/q//X/xP/3//f/BgDz/xMAt/8BAEUAsf8lADUAKwD5/0wAJwCu/x4A2P8XAP7/4v/l/xIA8f/w/08ABQDd/wAAzv/x/ywAyf8YAPn/mf8qAOr/LQA+AO3/JgDt/wkAJAD2//v/8P/7/w4A0//z/xMASwAkACMA4//e//n/mP8lAPr/5P/4/+n/AADL/xkA8f9NABUA3f9PAM//BAAuAD0ALQAAAOf/AgAZALH/8f/b/wgA2v+s/zcA1P/h/00A9P/0/+v/CAA1AAMAPgAQAPj/FQDs/0YA4f83AC4A6P8SAKX/4/+x/9j/1//4/wsA0/9GAOX/GQAXADAAHADz/wkA3/9VALv/yf9iAOT/PQBSAO//4//Q/wAA4P+d/x4AGADp/woAvP/l/xwA9f83ADkAFwBHAOf/8P8qAMf/uP/l/+j/JgBCAPf/TAAZAOz/8P/K/wEADgD3/wQAFgC7/+j/KQDL/ykAAADR/x4AJgAHAAIA8f/o/+f/wv8mABIAtv8QAD8A5f8CAFgADAANAFAAIADy/7H/m/8mAOL/7v9jAAgAAADt/xoA6P/Q/ygAuf/Q/xoABwDx/xIAIgD+/wcA2P8YAJQA1f8nACwAjv8JAOT/CACr/9n/EQDO/zwAvv8EAPb/DwBHAP//LgAZADQA+P9fABYA3P/N/5T/2P+y/1wALQAbACgACwD4/7b/MgDt/w0Arf/Z/w8Ao/8tANv/GQAsAP3/LAAYAAwALwA5APL/AwAKAO7/0/8AAOD//P8JAAAAFQCH/wIA//8AAEYA2v8+APD/2f9NAM//9v9CAAAAPAAmAB4A9f/1//D/pf++/4//2v/u/xgA+v/w/18A7P9bAA8A6v9/AO3/HgAJAMb/JQAKAMP/EgD0//L/8v/m/9b/1v8iAOn/MADy/wwAXgAMACQA5f8KAKD/DQBPAM7//v/S/y0ADgDg/ykA5/+e/7H/8//y/yEAOgBBAD0AFwAAACkAyv8nADIAzv8YAIb/4v8GALr/NADk/zoANAC9/93/9P8DAEQA8P/l/1EAEAD7//7/DADc/9f/9/8zACEABQBGAOD/GAAEAMD/5v+c/9j//f/4/yIAGQAgADsACAAVAPz/t//+/9//1/8eAP7///9tALH/HABrAJ3/NwDc/xEADwDx/1wA+v8xALn//P/j/6H/IADT/9r/1v+0/8L/KwArAFUAOgA1AC0ACABGAPv/+/8UAAwAv/8+AAMAZv8BAMf/v//8/w4A/v8fAB8A2f8bAAQAIgAfAPL/BAAoAAsAEwDP/9v/9f+z/0EA+/8OAEAA1v8SAPn/FQAEALj/CQAkAPj/8P/w/wEA1/8oAE4ALAAuABYADgB8/9j/8P/i/+3/3P84AL7/SQDl/8b/VwAcAHQA+f/u/87/7f///8T/HAD1/wsA7v///wgAGwA8AA0A///c//b/z/8hAEUA0f8HAPn/1f/l//H/IwABAPH/7P/v/wIA6P8lAF0A5v8aADEA8v8WAO7/AgAKANX/6P8oAP7/zP8WAA4A3f/I/9T//f8hAAgA7/8OAN3/9f8vAC4AHAAdAOb/VAAtANr/bgCi/8z/AAC4//v/vv/6/wAA9v/o/ykAAwAAAFEAAgBgAAQA4P/p/8f/5f/Q/9z/wv8iAA8AMgBbAPj/JwAfAAgAFQDv/xEANwDS/wwA+v+b//D/r//e/+7/4P/9/xAANgACAHEA6v8VACgAwP8OAMr/HADZ/zgAOQDh/3QAxv8iAC0Arf/T/6f/CgDc//T/RgAhAO7/GAAAAKH/+/8AAPn/IADv/ysAHAADAC0A6v82AAEA1/8IAPf/qv/9/zQAm/8AAOf/8f9AABIAWwAVAE0A8f86ADYAhP8PAMj/qf/b/xMA+P/d/+P/+/8/AP3/OgAaAPn/9f/0/9v/8P8ZAOn/TgAKADYA8f8DAD8AyP/T/7X/8/+3/+r//f/y/1IA9P8cAAgANwAUAEUAHgD4/08Aov8hAAcAzv8SAMP/8//i/+r/CgDx//P/6P/0//D/DQD1/+3/QAAEACsAOgDn/zkA4P/6/xIA2P8PAOX/xf8OAP3/9v8cAPf/NgDi/9j/DwDN/wYAMwA2AAcAPgDx////9v+6/zkAzf/7/+n/CgAYAPL/BgDM/7b/4f80AO//IgAtAPn//f9FAPX/IAA+APL/GwCW/zkA7f/V/0cAqv/7//z/FgDD/xsA5v/5/0gA7P8QAN7/NQDt/wAA4v/Y/wMA8/9NAPj/LAAkAAwA/P8LAL7/u//f/8P/OgAgAGEABgD///r/3P9JAO3/9P8CAO3/nv/k/9f/6P87AA8ASgANACIA8v8DAAsA2P8UAN//JwDo/w4ABADx/xEAwf8OAOT//f8nAB0A+v8eACwA5/8kAM//4P8TAMz/DAAQACkAz/+1/wUAIQAPAAQATgD6/8D/FwC4/9j/FwDZ/1cABADO/1EADwDt/wYAPADv/9j/MADB//H/JwAHAPb/7/8jAOj/DwAhALj/BgDd/7T/NQATAEQADwAbACgA1v/z/7//GQANABAAUAD0/8//zf/e/8L/5v8KAOj/6v9DAP3/EwA5ANr/OADo/xUAKwC3/wMAEQD+/ywASwALADcA1v/q/xsAs//y/5j/zP8lAP7/7P8rAFQA7//n/xsAuf/X/zIACgAfABgA9/8PAPL/GwDb/xEADwDj/0oABAAUAPr/9//K/8b/DgCp//7/AQDr/1AA8/8/ACYAtP/m/x4Av//u/xkAFQD6/zQAMgD3/2EA9P8AAB8A5f9AAPT/GQDQ/8b/0f++/8n/rf///83/AwBMACYA9/8ZADgADAAsAAEA+v/5/wcA6P8tAC8A5v8vAO3/9f8fAAQAGgDz/83/2P+c/8L/BwDb/yoA/v8gAOz/8/8/AAAANAAfACsADgDH/9P/7//0//v/HQAeAA4ALQAaAAoAGAD+//n/h//l//D/z/8YAOv/GwDw/2QACADY/zEAwv8ZAK//GwAaAD8ALADJ/xcAz/8cAO3/8//q//f/JwDc/zQAMADG/7T/IwD5/+b/GAAHACcA8P8aACsA6v82AAEA4//W/9X/DwDa/z4A0//0/yIAyf8DAMX/RgDs/y8AdADI/0IAxf8hAAQAy/8EALT/9v/k/yQA8f8dABYAEADj//v/MADM/w4APAA8AO7/7v/v/+P/4P+7/x8ADAA3ACgA///n/+v//P/3/wEA+f9SAOn/z/8KAOL/qP/D/9H/AQAhABkAdwBIADYA/f8/ADkA2v8jALj/2f/s/83/7P/i/xYA9/8qAPn/w/8PANX/AQALAL//YgDq/83/AADo/zUA7v9YAP3/IwBpAA8AIAASAPb/rf/v/9n/3v/x/9P/JwAGANn/7//V/93/EQDC/1cAOgAYABIA2P8uANz/WwAgAAoAMADn/xEAs//c/73/qv/z/w4A6f8FABgAFQAVAPz/NwDz/10AGQAPAEoAxf9EAP3/4P/s/+L/AwDL/+f/zP/s/7n/xf9cALf/3f9KAA0A/v/f/0UAEwD8/xwAEQA1APD/WABIAAkAMwCm/5D/8v/g/8D////4/ywA///3/x0ABADe/9//RgAfACIA9v8HAOf/zP8/AAMA8v8eABMA4P/V/8j/DQATAOv/EADr/xEA0/9CAC0Aov81ABkA0v8TAAkAzv8/ABEA9/8tAMf/0v/F/8v/YgAbACwAPADq/xMA4f9EAOL/2/9gALn/GQALAKz/1f+d/+L/MgD3/wMAMwAbAOT/sv/5/+3/CwAfAFMALgDW/0cAJwAEADYAHQDu/wsA3//y//r/qf8SAP//8v/Q/wcAw/+4/ysA6f8rABMABgC//zwATgDT/3UALQAMAAIAjv/3//b/mP8pABwAEgAYAOH/GgDi/xsA4/8AAAIA6f8+AAEAFwD1//H/1f8DAMr/7v9HAOb/TQD9/zIA2P+w/yEAtv8GAAkADQBGAPz/KABGACwAFADX/+H/2P+6//f/0f/F/xkA1v8AABkA4v99ANb/AgB5AOb//f/7//v/uP82AOn/MQBAAH//gwCR/+X/ZACv/1IA9P/f/+b/7P/l/8z/QwD9/9z/CQAvAAcADgBhAPT/GgAmAJv/EADN/w4A9f+l/+n/pv8qAAAAJgAdAPH/MgDz/18AOQAQAFYA4v/e/yAAzP8eAO3/w//p/6r/DwDS/xcAvv+3/1YA0v9JABAAKQAjANj/7//Y/wsADAAqABsAHgAdACUAIgDx//L/8v/x/xcA7v/l/+7/yv/0/wkAEADN/9r/5//0////CABFABgAJwD0/7X/9f81APT/QwBiAAMAVwCz/8b/4//1/9X/v/8dANH/SADn/wwALADn/yYAMgAvAAgAWQC+/7b/qv9s/9//xP9nAF0A7/80ACkApf8GABIAGAAaAP//QwDj/yIABwA5ACsAu//z/8r/1v/u/wcA3f/n/woA5v/0//H/DwASABMA7P9WABQA4/9IAPb/9f/b/7j/LAD3/xMALQAYAEsAz//y/9r/t//Y/+P/CQDq/yMA/P8hABcAOQAnAAoALgCj//7/9v8aAAAA8f/4/wcA8/+0/0EA0P8kABMABwDx/5f/OAD8/wcA9P8jAPT/IgBQANP/OwDQ//D/5//z/y8Azf8AAAwAHQAEANv/AADp/9T/7P/+/xcA7v8UAAAAPAAeACYAZgDt/xkA5P/V/6f/tv8MAPP/KwDx//7/6v8ZAOz/5/8tALj/+P8DAA4APwA3AAUATAAFAOH/IwD7/w0AEgBQAMn/DAAJAGr/9f+x/7T/tP/4/wUA2/89ACkA6v8XAFoAMAAlAGAAAwAWAEIAt/8mALL/tv8tAOf/BgDe/0QA1f/H//3/qv/6/+7/7f8aABUABQBPAPH/+v8BAOz/NwD5/ysA7//u////FgASAAAAKwDO//f///8dAOT/KAAZAPD/HACW/wEA8//5/+7/wv9lAM//zv8nAMn/AgA9AOn/FAAPABoAHQDm/xIA8//m/0QANAAwAPz/tv+q/9v/SwAAAFMANwC9/wwA3v/H/8L/yf/W/xwA4f8qAFoA4f9LAMj/CQArAOf/agD6//b/9P/z/wAABADq//j/8v+5/+z//f8VAOv/RwANAPz/RAAMABMAs//Q/wAA5P8QAP3/9f8BABcA+P/e/1IAIgDr/0oAzP///z4Av//y/wsA3/+l/yoA4v/S/zIAGgBrAMb/HAAbALf/TAACAPf//f/I/xIA1//Z/yQA5//A/0AAAADi/xAA9P9kADAADgA9AM//7f/w//H/8/8oAND/3v8RAJT/CAApAAwA4/8kAP//+/8jAPH/KwDz/0MA6P////z/qv8iAOL/FwDg/w0ATQD1/ycAAwD8/9v/3P8XAAcAJAAcANr/8P+2/6T/+//a//z/BQBFABwA4P9fACgACAAuAB8AYgArAM3/IwCE/5L/KwCX/7n/8f/P/yYA8//G/yoAGwBaAEgANwBQAP7/IwARANn/y//W//r/yP/5/xEAvP/g/wUAAAAMACEAQwDs/y4A+P/3/+n/vf9GANP///8IAPP/FAAWACEA4P8hAC8ARwDY/xoA4f+A/+j/s/8rAPj/IgAYAOf/MAC6/ysA5v/W/w0AwP9JABwABQBbAL7/HQBLAN//AAAQAD8A+/8LACkAtf/6/+T/5//c//T/JwCl/xAAAACn/ykA+//m/xcAIgAWAAAAEgDx/xkA2/8hAEEA6f8QABMAzv/p/z0A5f8ZAPr/KwAFAKv/KQDa/8T/6/8CAPX/GQAPAO//CgCh/0kAAwDy/00A4P9gAAwAWgAgANL/GADI/9r/DAAgAM//3v+x/+j/EgDH/y8A1v/0/yAACgDK/9D/LwDY/z4ARQAnADwA/P8SAMv/KAAOAPL/eADA//7/CwCu/9r/5v8JAP//EgD9//D/wv/e/wAA3v///+z/SQA7ACEAOQD5/wIABgD6/wAAOQD5/xkA0f+V/xoAxf/0/ykACAADABsAFAC8/x8A7//L/xMA5v/x/z8AKAAyACEA3P8AAOj/0f/1/9X/EAAgABcAOAAJAAkA0P8XAPP/uP8fALr/DQApAP3/DwDV/1MA5f/o/yMA+v8bAOX/HgAnABYALwDs/9T/r/+n/9n/xf/k/zMATAAbAA8AJQASAC8A9f8cACsApP83APL/tf8NACsAQADt/xIAEADS/93/yf/T/93/2//i//v/DAALACgAGgA8AEYA/v8OAO3/3//5/y8AQwDV/ygA6v/Y//v/1P8WAPz/7f++//T/9v/F/xYA/f8cADkANAAqAPb/BADV/9//IAAHAC8ABQDu////EgDw/8P/BgDJ//j/HwAiAB4Ax/8PAPD////6/xUA+v8VAEoA0v8vAAUABwD3/wcAJQCx/9D/yf8DANH/DwAhALv/NgDo/0AAPADu////xf8DAPD/+v8rADMAIwAWACYA/v/n/+r/7f/9/xAA4P/X//P/zf8TAAwA4P/5/+7/MQDx/zMACwDq/3IA9f8hAN//6f8kAMH/AQC1/+v/JQAvAPf/DwBAANL/CQDQ/57/5f8PABcADAD6//T/9/8LAPH/+f86AC8AJgAfAFwADAA+APj/tf87AJj/DADi/7//EADI/+z/h//v/+b/BQBPABsARADy/yoAJgDp/x4ACwAAAAUA6/+q/+n/AQAQADMACAAoAOL/EwApANz/QADf/w4ABQDH/xgAz//l/+X/9v/y/+b/DQATACEAx/8cAPb/vv83AAQA/f8ZACgAYwBXAAoAIgDF/+v/7/+s/zQAzP/S/9r/rf8DAAgAAAAzAAUA1f/i//P/LAAgAGwAGAAUAG0A8/8eAAEA4P/o/6b/7f8bAL//9f/Z/37/+//7/1AABQAXAB8A6/9bANj/PQAwALX/BwDS//T/IgDz/9D/GAATAPX/RwD6//D/IgANANj/BQANAL7/8v8PAAEA/f/v/xQA1v/2/zMA/v9QAB0AJgAHAPT/HADl//D/AADM/+v/0f+S//D/FAAYAP3/yP/+/yoASwAqADsA6f/D/woA6/8iADoABgDP/yYA7f/F//7/5v/h/wEAMAApAEkA7/9XAA8Aof8jANb/2/+r/wsA3v/B/ysA8/86APz/MAArACIA///s/0MA3f8lABgA7//z/67/5/8RAAcA1v/q/6b/vP9BAN7/IgBRABwAQwDi/xQAYQDI//v/+f+n/y4A8//l/0EA4P8sAC8ADAAPANT/4f/B/+7/0f/z/xQA7v/t/wAA8/+w/zYAQwAdAFwAbwBZAN7/GQADAMn/uv/G/8P/yf8JAPP/AwDk/xwAGgDg/yYA9P8tAA0A3//o//L/0v8CACwA4P9xAFoA/P8AANj//v/a/83/LQDr/x0AJADd/9j/zv89AL7/9v9mALj/RAAUAN7//v/z/wsACAAgAMn/AwAFAPn/RADY/wQA///u/ykA1f9QABIA+v/p/4H/y/+c/wMAMAAOABsAFgBKAOT/JAAoAGgAGQDf/y4Aqv8GAPz/9P8jAOL/zv+8/+T/uv/2/wsACwBeAPX/FAAiAOL/JQAZABwA/v/s//P/6f8PAPf/+P/s/wIA8/8HAAMA2f81AOP/QwAXAKv/+v/t/y0AAgAhAOj/AgAAAMn/+f+M/w4AKgAOAEYAFwAmAA4AKQAhACMA8v////P/wf8LAL//n/8JAOD/3/8NANf/CQD//xoARQASAD0AIwASAEsAFgACANn/7//D/8//EQDf/xkAJADS/wsA4v+2/yQALwDP/0cA1//N/wYAuv9rAAcACwBdALv/BwDq/9//FgAjABYAGgDU/wYA6v/R/2EA+f8uAOL/2P8MAKv/NQAGAN//EgDm//z/+v8HAA0A2v8JAC4A3f8YACUACgDg/8P/zf/e/ygAWQBaABcAMwDZ/8r/AADx/+v/BQA5AKf///8CALT/fgAgANz/DQD6//v/7P/l/7z/2//y//b/QAAbACEA+f8bAAEAmP91ABcA5f8TAA0AFADf/0AA3//0/+P/EwD//7z/RQCn/9H//P8VAEgABgBQAN//t/8mAAYA2v/W/8H/3/8gAE8ADAAiADcA2/8sAAsA3f8bAPP/7f8uAPf/AQD3/+L/DwCp/yMAFgCF/+T/GwAbAP//KQAsACcA6f/1/+//4/8/APr/GgAKAMr/RAD9/7z/HQDQ/9j/MwDh/w0ABwD2/+L/7f9VAOr/FQBRAOj/6v8HAPn/oP/V/y0A+P/U/yoAAgAaAHUAQAAKAOv/AQDg/93/BADE/7f/1/8jAMD/EwAiAP//QADf/yEA/P/e/yYA6v/6/xMAYwD2/x4ALAANAC0AnP8MANL/uP8DAOT/8f+B/0MAFgC7/y8A4f87ACAAAwAgAPf/KQBYAB4A+v8AAMr/BQDC/9D/+//3/zkAKQAmAMv/AADI/8H/4//g/zgADgAUAO//WgDV/wUARwC8/3MA8/8qACAAmf8PAKT/2f8HAPb/MQAEAMT/CwAUAPv/CgAEADYAs/8DABIA4/8iANP/LQATAPf/SQDv/yEAGAAAAOT/1//w/7r/IwAPAOj/AADy/yIAAADv/9z/HAD3/8z/OgAaAO3/KwAcAB0AFwC//xMAzv/p/wcACABzAOX/PwDJ/5//AQCr/y0A1f/z/+v/0//u/y0AMQAWAEAAGABHAAIAMAAHAAoA6/99/z0A///4/xsACQDu/7X/8v/b/9T/y/8TAOj/wP9cAAEANwAlAAwAegAXADAACQCR/9z/+f/s//b/MAABANr/KAArAPn/wf+4/6P/0f/0/xoALwAPAA8AVQBTAL//ZAAgAPf/IgC2/zUA1f/B/8v////V/7n/TADQ//n/6v8FAFoAAQAAADcA7//C/1oAPADv/wwACwDg//f/AgAuAOv///8tAMH/7v+m//v/JQDx/wAABgDf/9H/PQDL/xMAAQDF/x8A/f9AADQAUABQAPD/9P+i//L/AADC/woA6/8UAPL/CwAyAOD/TgD//9X/+v///8r/0/8jAKb/AAAXAEwAKADr/0kA6P8ZAOz/DQABAAgAPwDj/zsA4f/c/w8Atv/i/+z/vP/Y/+3//v8KAN7/WQAUAAAAZAD2/x4AOwAXAPH/wv/2/wEAEwAJAOX/7/8BAPv/zf/Y/7z/8f/q/00AQQAlADsAtv87AO7/1/8IAOz/PwDM/y4A+//v//n/8v8nAMP/IQAkABEABACr/9z/1P/O/2wAQgAJAGUA7f/0/ysA0f/3/xMAov8vAOX/sv8aAKj/AgDF/+j/HAAPAFsA/f/f/ykAMADt/zsA8P8rAFAApv///x0Ayf/d/yMA/v8GAAkASwAAAK3/+v8EAAYA3P9CAOL/wP/S/8f/HQDo//3/u/8WAGMAIQBcADcAAAALAPP/2f8gAO3/IwAAAM//8P+9//3/5/8HAPz/EQDx/67/+v/9/xEA9v8XAHsAFgAlAFwA7v/R/7r//P8cAAwAGwDL//n/9P/k/2UAu//m/+P/of8kANz/9v8wAPn//P8dAPj/LQBEAPf/VwDm/w0AHQDo//X/7f8DANX/HgCo/8n/4//B/zYAHAA1ACEABAADABAA7P8SAD0A3P8AAAEA9P/t/8L/0v8MANr/NQAAAAQAggC7/1QA8//Q/xYA8/8zAMT/QgDH/9T//P/b/yIA//9LABQA5v/Q/zYApP/h/zsAv/9IAKv/5f8yAOr/RQBQABMA/v80AA4A6P/T/wAAxP/8//z/+v8EAJz/FwDo//D/6/8lACQAxP80APD/PwAdACUAIwCy/wAAzP9rAFsA2P8FAMn/2v8QACkAHwD4/9P/4P8RAP3/uv/z/+n/9v8ZAOX/SQAsALj/HADR/8//NgD5/yAAMAD8//7/8v/h/wcAAQDz/xgAHABsABUA/v/8/8D/+v+2/wkA7v/U/+n/0f9HAAEAIgAhAPT/0f8ZABIANQAHANT/OACX/xMADADf/wQACgDm/83/UgASAIQAEwDh/wsAyv///+D/+//Q//b/uf/3/xgADAAtANr/LwDa/wYAOADQ/ykAAADQ/9z/6/8UAPb/ZQBZAPX/YwD0/8X/pv+V//7/AAD2/1QAQgC2/zcA9//m/yMABwAEAOb/KQDz////DwDd//z/0//F/zIAzf/0/04Azv/1//7/LQD9/wEA+P8QACoA4f8tAOP/BQDV/0sAHQD1/wgAzv/8/6j/jgBJACUAt/96/wIAEQCbALf/0f+6/+H/LgAzANr/fP8SAPT/VACy/8//ZQAtAF4AGACw//X/UgAkACEAoP/0/0kACAAZAOX/8//P/yAAFwDi/9T/0P/g/9H/BgDe/7b/2//T/yMAKAD7/1sAUgCaAGYABgBnADIA+f/u/+D/gf/H/wUA5f/P/47/yv+3/+//AADi/9v/4/8oADEA5v8rAGsATAA1ABcAPAADAA4AAgAWAAsAzP8AALv/1v+1/w8AIQAMAFAA7P8KALj/6v8UAPH/7////wcA5f8OACMAAAALAA8AAQAiADkA9v/f/+P/zP8KALz/8f9EAOz/+f8BAC4Axv8HAFEA5P9EAPD//P8AAMv/4f/+//T/8v84ANz/+P8XAOP/IAA9AAAACgAOAAAAIABEAAQA0P/8/9f/uf/2/yAA0P/V/+v/t/8+AOj/7P9FAL3/AABEAA8ALQAeAEsABQAkABIAtP8vABMAJgAJAKL/yf/G//X/GQC7/8z/FADa/z8AJwAxAPn/0f8jAM//8//v/3oAGgAbAEwA3P/2/5X/0v/Q/xwA/v8mAEMAEQAcAKL/EwDR/9P/HwBDAO7/IwA4AOf/UgB3//T/x/+7/zoA7v8dAP7/GADi/zkAGwDu/ywAHAAcABUA/v/G//T/4v/O/xwA4f/w/xUA4/8EADAA4v/p/wwAEQASAB8ALgASAAwAEQCw//X/1P+i/1YAAgD1/woA7v/+/zEADgBLACYA1P/k/7j//v+b/xwAJwDm/1IAp/8eACMACAAKAP///P8YAEAABwBiAOn/CADQ//n/PgDm/93/hv/I/9T/CAC2//n/HgDS/0sA7f8WADkAKwA6ADkA7P/w/ygA0f/v/xkA5/+2/+3/AAAZAAoAKgAMANT/DwDc/xoAKQArACMAx/8lAPz/vP8qAPr/7f/m/67/1f/k/xoANQBJAPj/6v/1/9T/HQBAAG8A0f/X/+v/mv8jAAYAIAAbAO3/8//e/w8AAADt/wMAHgD1/yYABQDp/xUAKgD6/xcAIgDQ/0AA5f/u/xoAy/8FAJj/RwAYAN//LwDS/xEApf/K/9n/wP8fAAAAKgAxAPz/NwBPABsAMgDy//r/CgDZ/wcA5//m//b/1//3/xcA8P/g/xQA7f8GAAkAAABPAFEANwD3/xUA5//B//b/lv+r/7f/AwBKAGYAWAD//y0Awf/i/9v/z/8uABQAKwDC/ykA6f++/x0Atv8IABgA9/8SABMAEgAEAAwAEAAsAAsA3v8cADcAwf8hAO3/0/8OAPT/AQDf/y8A4//b/93/1/8SAPv/QwAOAA0ANAD8//n/HwDc/wAAEQDE/+n/1//+/yEAPAAXAOb/z//a/w8AKQD8/w4ACADr/wcA4f8JAAQAAgARABcAQADs/wYAHwAIABMA3P/c/9D/w//t/97/BgA2AOr/CwABAAsALADm/xgAPAAAACQA+f/T/9P/AAAkAMT/+//V/8r/FAAgAEwA7v9IAA0ABgAcAN3/RgCj/woAEgCX//3/3//k/+D/DgDz/y4AIQAzAEQA1/8fADEAPQDY/+n/GQDY/+7/9//Q/7L/5P++/+7////l/zIA+v9QAPz/AACOAAUAVQAQACsA0P/b/zIAlf8PALP/FAD9/8f/HgCW/x4A9f8YAPP/GQAcANj/KQDV/ywA6P8qACsA/v8PAMb/4f8DABcABQAzAAAAKgA3ACUAAwC2//T/l//j/zQADwDC/+f/JADS/wAA/P8kALr/1f9LAPj/SwAZAPH/FADu/yEAGgDq/+//9P8uANj/AgAJANb/IADj/wsA9//h/wQAFwARAP//LADe////DwAVAAYAFwAMAMz/2v/m/woA2P+5/+7/OADh/zgAXwD7/2sA/v8UAPH/BADi/8P/CQDm/wkArP8OALf/s/8rABUAJQD1/xcA5/8LACEARwBDADcATgDd/w8Az//m/9X/zv/2/6v/x//s/wQA3v8+AP//CgBIAOb/NAAFALn/8/9MADsAHQAlABQAxP8AAHwA2P////H/sP/a/6H/yP8AAAMA3/9AAPL/3f99AA0A/f84ABcA2v/N//j/HAAQACIA/f/c/97///8DAPn/HQDc/x8AVwDe/w8A7v/Q/+P/u/8SABUA7v8VADUAJAAHAN7/9v8fALf/IgA6APr/GwALAAAA6f/5//L/7v/t/+D/IAD3/8f/xv/5/xcAGABbAAMA2P8LAOP/aAAuAOD//v/I/yAA2v/y//L/v/8PAB0AIQD4/ycAAwD//wkAQQAAALT/AgDz/9H/rP8HAPb/QgARAC4AXgDG/xQA2v/4/yEAuP8VABgACAALAMf/MwAcAKD/KwDJ/9f/DgABABgAIgAVANf/YAC+//7/EQDj/zwAzP8vANP/JADc/wAAIAD1/yMAu/8/APD/GQDX/8j/8v+s/zoA6f8kABgARgArAOD/RADk/9D/6P8RAPv/8P8TAPr/7f/3/+L/BQD9/wcAGgATAAAA9v9CAAwABwDZ/+3/EgCM/00AAADK//v/xf8TAPj/8P/z/z8AAgAeAFQAEwAmAPX/RwA6AOL/AwC9/7n/2P/e/+T/z/8CABwA8P8tAA4A8P8kAPb/0f/v//X/IwDn/wQAIgDE/zUAJgAAADIAHAA0AMv/4f/9/8n/FgA6ACcA7v/5//3//P/R/+n/AwCl/zIA+v+2/wAA6P80AEkAIgAYAA8A7v8iAPT/3f8MAO3/IgApABUABAAQAMz/1P/O/43/0P/w/wYA/f80AAsAFgA5AEcAUwDU/z0A7/8ZAA4A9v83AKr/NACj/7X/4//+/woAv/9fAK//6/82AEcAKADp////nf/1/+H/+v/+//j/IwAQABcANgBOAAsAHgAUAAkAGQDk/+P//f+o/zYABQCk/ywAj//X/83/7v8tAPr/hgD9//3/4//Q/z0A9f8zAD8A3v8eACwA2v8uABgAw/+s/+P/HgDN/woA9f/u/00AFQAdACkAyf/+/9T/1P85AAUASADW//L/JwDc//3//v/G/7P/LwCt/x0AHwDq/1wABAApACkAIgD9//X//v/l/+j/7P/9/93/7f/s//3/CAAcAAgA8v/d/wMAXQARABEAGwAaAMP//f8lAO//MACy/9r/5P+3//H/BQBHAAAAFAAoANz/GQBBAPj/xf/O/wMA9/8AABQA2v/u/xgALgA0ABQAKQDc/xYA+v/c//r/7v9HAOD/CwABAI3/SADc/wcANACs/+z/2f+7/9b/FwATACIAYAAwABMARgDp/+b/RQDw/+7/7f/u//3/zv8AAP//CwAcAOr/7v/X/+D/EwARACoA+//k/wYACgAZAAIARwDx/+7/PQDs/9D/0//N/5z/AQAQAAwAKAAmABUAJgBFADsAAQDh/xMAkv8AAPT/nf8wAKv/GAAAAAMAJAAKAF0AAAAhAAQAGwAFAAMA/v/B/wYAyP+8/8//x/8UAAYAOgBcABAAHgAFABIABgDW/xMA6/9DAPb/9v8aAKv/6P+d/8r/3/8BACUA9f80AG0AKgAeACAA9P8gACEAFwCr/8//1/+r/zYA4P8yAAMA+P8aAK7/GADF/x8AcgDp/xAA7P+m/wsACQDi/04ADgDh/xMAAwAJAA0AGwD3/w0AJAC9/ycALQDI/y8A7v/n//L/3P8JAOj/zP/u/+j/qf8iADcACAApAB0ACABDADwA+f9CAPv/4f/9/8P/1f/w//H/AAD5/9v/BwC///j/NADi/zgADQBIACQA4//u/wIAJgDF/yIAt/+o//X/7P+EAA8AJQArAOP/+f/q/ygAGAAyAP7/+f8AAJ//GQCu/8b/AQDC//H/2f8NAAQAOwBgABYA5P/7//7/OQBRANn/RAArAAcAGADU/9z/xf8PABMA5f8OAMv/4v8VAKH/w//r/+n/7v/q////DwA4APv/QQBGACcAIwD2/1sA7f8wACAAzf8SAI7/7/8vAMD/FgAHAP7/HgALAO//3v/z/+7/0P/w/7H/8P8HAOH/KAAVAOb/NgAYANf/IAA6AGwAaQAtACwAAwDa/7X/3f+t/7n//v/O//P/MAD2/7L/FgD3/97/OAACABMAGwBhABYA3/8yAL//IQD8/9r/EACv//f/AwDj/xwAKQA4AAAA//8JABkAAAAXANn/oP/+/+n/4//z//P/6v9LABYA+v9NAA0ABgAAAP7/FQAcANb/7P/5/8n/FgC0/wgACwDY/04A+f8GAAAAJwAbAM7/GgAVAA8ACAACAAoA/f8NAAIA0P8KAO3/0P/u/9b/0P/J//r/WwD7/xEADwDo//f/6v9zAD4AHAAhACoACwDo/yYAmP/X/7f/wP8uANr/MAD4//r//v/o/wwAPABZAPz/KgAcAPP/9f+j/9b/sv8KACoAu/8/AAAA4v8qABQASQD6/xQA5v+2/y8A+f/D//X/HgAHADEAIgAFAPT/9//q/8r/OQDh/9L/3//E/9//HgB1AP7/+v8JAC0AEQD1/zkADwD3/+r/DQC+/+T/CAAoACQAvf9BAMn/GgAvAN//MAC6/5P/JAAWAK3/JgDZ/xcADAD7/2wAiP8bABMAzP8fABIAJwDe/ywADQBAACcALQAzAJT/8v/P/wQA5//L/wcA4f8UAPX/9P/1//n/x/8KAPr/RgBlANH/IgD2/xUA7f8rABkAx/84AKn/AQD3//L/8v/Z/+//GgATAOf/TwCi/xgAHgDP/1QA7P9DABUA7v9HACQAFgDe/+n/4P/N/9X/0P/T/wQA9f8YAAsABAApAPL/JwC2/9r/KgDj/z8APQAkAAMA4//W/8j/2f8gAPL/FgANAOP/XAD6/w4AQAAzAPv/AwAsALv/8//J/wkA/P+T/wEAAgDZ/9j/+//1/2IAIAAiACoArf8AALL/+P8SAAUAHQANAO3/JgBpAMD/WgASAOv/NQDk/xgAsv8aAMD/tf/w/+j/9v++/1AA8P/7/xEAHgAWACwAZwDE/ykAAgD6/wAAr/8yANb/1P8BAP3/BgD9/7X/7//c/93/RwBBADcAEQBNAOb/+P9EAOT/LQDb/+j/7v/H//3/uP8KAMf/8/9CAAIA8f/e//j/CQAVACkAPQD8/+r/KQAbAAIAKgC9/8b/FwDg/w0AMQDs/ykAQQD9/xkAzv/T/7//AAArAG//QQDz/7P/KADM/zAAKQAjACkANAAWAOf/FADI/9//QAAiAOL/+v+L/9L/GQCP/1IAJgAPADsALwA+AC0ADACm/x4Azv+4/xUACwAeAPn/JwDX/+j/DADk/9L/wv8VALj/AwBIAPn/CgAjAPn/HQBXABYAAAAcAMb/zP8oANj/PQAiANj/VwDz/8r/1f/s/9D/1v89ALn//P86AOb/6f/+/wsABQA7ADIA//8MAPb/EgAPAMf/FADa/xEADwDH/+//7P8JAPH/RwAkAOX/5P/p/+P/2/9ZAPv/KwAkAA0AXQDf/wwAv//v/xMAz//n//T/7v+p/w0A8P8pABkAAAArAI3/NgBeAPn/PwAhANT/zf+1/9//PgD8/0cA6f/L//z//P94APT/OAALAJ//4f/e//D/FgDY/wMAUAAMABAA2f8uAOX/6/80AK7/MgC+/wYAKwDL/xwA5P8dAMz//v8AAOr/HAAoAGEA6f8pAA0A/P80ABwABQC+/+H/yv/D/7r/6f/D/+b/UgAHADUAVQAIABYAJgDX/xEA2//t/wUAzv80ANn/HQATAP7/KAC9/wkA+v/y/wsACQAUAAgA2P8iAP//3/8+ANz////1//3/2P+k/yEA2P8cAGYAOgAAABcAEADT//z/wP/9/8z/RABPAM7/NQDZ/9f/3f/Z/xUAQADw/wAATADu/x0AEwAWAPX/CQDX/8D/4/+a/9f/AABNAAAA6v8bAP//DwAMAFAA4v84AEEAwv/4/wcAUQDV/wUAGwDq//n/rf8LAA8A1//o/w4A3P///wIAw/8MABgARQApACIA7//x/w0A/f8aANL/9v/E/+r/9P/v/xoA+f8uAA4AMgD6//n/FADA////+P8FAAwAHQAHAOL/CgBTAOX/8/8+ANL/JQADABUA7v+h/6//3f89ANH/KADx/9j//f/Q/1oA5/8gACEABQBKAAQAJADs/yIA2f8JABIA3P8wAOX/EAAEAO3/t//A/xAAzP8dAOX/wf8OAAEAXwAxABQAKwDS/zMAWgDI//D/DwCu/+b/EQDh/9n/z/8WAOr/AQAfAPf/OAD2/18AQgDK/1AA8P/Z/93/1f/W/93/AgDu/zkABgAHABQA4/85AP7/EwD//8r/FADl/+v/GQDp//3/3/8LANL/AQAqAC0ADgDx/zUA1/8aABwAvP/0//r/NAAVABwAGgD4/xoA0//N/+v/x/8AAPf/9P8eAO7/OAASAP3/GQDh/xkA4f///ykA5/8YAAQA3v8sABQA9v8mAIf/s//K/+L/LQAOAGAA6v8FAFoAyf8EAD8AEQBVABcA8P83AIL/5f/U/5r/SQC+/yMAKADu//v/o//z/wUABAA9AFMAGwAUAPL/7v/g/9D/BgAUACYA5v/y/yIA8/8SABAADAATAM7/sf8AANn/EAA6AOr/MQDW/wAA/v/X/zgA+f86ACsAAQD6/x0AUQC4/xMAzv+H/wgA0P8MACoACgDs//r/9v/P/5wAIAD1/xMAvv/e/6//RgDL/83/HAC9/0sAIAAyAFAAKQAoAM7/6P/p/+r/IgC+/9f/IAD8/xEA///m/43/4f8iAOb/SgAzADAAKgATAAQA/f8fAAIACwAXAOD/3v+p/wUAMACo/zgACgDT/xkAiP++/+f/9/8UADQAXQBnAEEA0v9OANz/l/8KAOX/GQC3//7/FgDt/x8AAQABACsAEgAeAEYA1P+5/97/9v/3/9//OAAnAP3/AgAQAPn/+v8GAAkAEwDP/wEA/f/r//D/r//g/wwACAAHAO//AwARAPP/EwAYADgAXQAFACkAJgDM/wEAKAAVABAAp/++/93/kv8tADAA2v8rAOL/3P/6/8n///85ADYABQA+AAAA7v/a/6//FQDs/xQARgAUADAAUgBHALn/GQD+/6f/4//b/w8Auf8rAPH//P/0/5L/PQAFAAQABAASAAsAIQA0AMr/IgDC//v////o/0AAEwA9AOr/BADa/+X//f/U/xgAOQAXAA8A7f/C/xQA9//C/ysAJQDa//7/LADg//X/KgAKAAUAKgALAPj/7f/a/woAz/8HAOD/7P8RAMX/ZgD5/9//KADQ/woA8/8GAAUABwAKAAAAQQBLAA4AEwAOALb/uv8VAO//LAALAPb/KwCz/8L/0f/E////AwAxAAwA3/8GAAEAAwA9AAQA+P8rAP//LQAKABIAOwAqABYAzv/U/9n/+v/R//j/1P+7/xgAAQAfAA8A6/8SAEwAu//O/zIAsP9IABIA6v85AOH/GQBcANr//P8nANj/BAAYAPT/xv8UAA4AxP/3/8//IAACAAAAKADz/+f/8/8xANH/EwAmAPT/3f8NAP3/9/9UANb/BwASANL//f8UADgA/v/6/wUAMAAEAOr/zv/F/6D/4v9AAMj/KwAKAOL/XQAWAA0APQAkAB0A6v/R/0EA5v/g/1YAz/+a/6b/rf+X/xwAOgADAD8AdABJAA4ASwCt/wkAQQCG/yoA4f/Z//b/p/8jAPP/SgAnAMz/HwDZ/9f/FAAJAOr/CAAmAD8AMwD8/yAAzP/p/yAA4//7/87/1/+5/9H/AgARABoAOgA1AOn/JQC5/+7/HAALAJcAFgAEAPj//P+3/53/MwAXANz/+f8hAMT//P8YAO7/HQDu/xoA6v/i//7/GgAKAOf/DwAHANv/HAASAPL/TwD5/87/HgDy/x8A/P/3/zcAFgC7/5b/5f/5/+z/LwAXADMAHwDp/yEA3P8OAAsA/P8oAOj/JwAWAPn/2v/1/77/CAAQAJf/DAC0/9r/IQBGAG0A+f8RAOf/GQDg/xoANQDq/xcA9f8MAO3/PADf/83/UADT/wIAFQDH/7H/5//Q/9v/RgDh//j/CAD6/yAAJQBBADkA+P8AAAMA6/8kAEcA7f/0/xwAyv/M//r/if+0/xsACwASAAkAIgAeAPP/TABGAPP/DAAUAM//y//e/wcA8//C/1YA8//5/woA+P9oALj/8P/z/7T/GwAlAEAAGwDo/7b/FADx/xgADQDE/zAADwAXACQAFgDT/wUA5//Z/9j/0P8mANb/PADx//f/XQC5/2UA8f/7/0MA4v8RAPz/uP/j//D/0P8nANb/LgAtAK3/ewD4/8T/VADg/9L/IgD1//r/8P/7/9r/7P8wAAoAOgAgAOX/8/8vAAEApf8JAND/8f8FACwALADi/2IA1f8LACEA7/8VAHP/vP/S//b/NQABAFYA/f/7/00AJwDz//T/DwD//+f/6//U/+v/FQDz/wAA+//u/yIA9/80AAkAKAAxAJf//P/E/zkAbAAGAB4A+f8VALz/4/+z/6P/3/+l/yEAv/8yAIcADQBlAAkA6P/3/+f/AAA2APv/PAAdAN//+P/p/xkA2/8qAAUA4f8sAM7/yv+l//L/8//c/x0A7P8eAPT/KAAzAAAAKwAiAE8A7f/z/ysAkP8BABIA1P9CANv//P8aAMb/AgAuAAUA4v89ANn/kP/2/x8A7v8PAC0A5v8XAMP/KwBOAAIAVAA2AP//pv+r/7j/5f/L/w0A7f/z/04A4f9+AEMAGwA3AOn/BADL/x4A1P/a/yMAxv8jAN//o//X/8T/4/8KAD8AEgAaAIsAKQANACQA5f8KAPH/JgDM/7D////H/97/JQA4AOj/IQArAMr//v8kAO7/4f/s//X/MAADABIAFQDc/93/4v/q//P/CAAhAOj/7f8dABkAWQD0/wQAGgDd/y4Arf8nAA4AyP8LANz/JwDQ/zIAGADS/9//EwAsANX/QwD4/+3/BAABACcA4v8EAPn/5f8TAPH/7f/7/4n/7f8YABQASgAzAEoAtf8JAAsA8P9PAAYABQDZ/+7/3v/0/+b/1P8JAMb/DgA0AEEAIgANAAsAxP/5/+z/9v/V/9v/HAAUACsAMgAtABUAEADg/9f////b//b/9v/3/97/AADP/x4AKQDN/xQADwA2ADUAAwDq/xQAGADt/0IAAADa/7r/sv+6/+b/EQAaAFQA7f82ACoA9f8cAPX/7v8FAPT/3f/j/8P/DQD//9//UAATAPT/AgAYAPr/+v8XAO//SgApAA8AMgDZ/+P/v//B/w0Anf8IACQA0P8NADoA7P/y/yEAHAAxACYAGQDk/9j/5f/U/yMAAgDl/w8AWQAPAAAA5v+x/8r/t/8nAOX/5v8zACEAMgA2AAgA8v8RAOr/HQAYAPf/5/9AAOj/DQA2AI7/LQDs/8v/HADT/+n/AgDY/8n/AADd/yQAHgAnAAAA4v8eABMAKQDt/2gA2v8sACUAr/9IAL7/PAAeAJv/7P+3/+z//f/S/1oAMwDV/2cA1f/u/xYACQAMAJ3/+f/z/6//IgAJAMn/ZAD4/zAAVADT/ywA2f8EAAwA8/8OAOT/4P8YAO7/3P9RANL/KwAbAKH/7P/T//n/AwBCAAkAMQAWAPj/VQD7/wAADADW/73/+/+7/+j/AgDp//z/4f9HABMA+f8kAPP/+f8MAFkA+f/+/zUA6P8SAOv////d/8D/4v/Q/wQA+P8CAFoA8//3/yIA1v/6/wEA+v8gAD4AKAC4/x0AIgD2//n/3//j/+n//f/g//P/AAAlAOT/8/9eACgAFAAhAB8Axv/i/8r/xv/3//n/JQAPADkAAgAAAPL/IQD9/7T/FADJ/04AGQAiABAAv/8jAMf/GAC1/7b/7f/n/zAA9P8gACgAHQAkADEAMQANAAUAGADk/8v/7P/w/0IA2P/o/9X/0f/+//r/tv/z/xcAwP97AAAA/f9DAOb/ewA5AA0A//8AAP3/wP8EAAYAiP/6/+//mv9lAAAA9P/w/+T/8f/9/xQAw/89AAoAAQBGABAALABQAEcA///x/+f/1P8cAM3/0P/w/8r/DgDP//n/zf/B/08A0v9AACEADwAHABIATQAbACUA+v/w/4z/AAASAAwAPADQ/xgAv//s//n/AQByAOj/9f8HALD/1P/g/+//FwASAHsACgAtAAAAAQAMAKH/NACP/woAAwDm/y0A0v8yANf/AQALACsA5v8MAFQAvf8cACAADgCk/xAADwDl/1kA1v/4/+D/2f8EAA4AAwAAABgAFABEAAsAAwDu/+H/6P/E/7r/AgAaAPv/IgD8/+n/5f8DABYA6f/o/1sAKwC//ykAQAAnABQA+f8fALH/u/9DAPb/z/8TABYAEwDX/wwA1P/L/xEAyf8aADQABADt/0IALQDX/xsA5//q/9P/6v8hAM//NADo/xcAHwARAEoA7v8PAMr/1f/T/xwA3//G/zEAs/9AANP/SQBHAO3/ZQDV/0EAJwAdAOX/1P/M/6P/0f/U/+z/4v8pAPr/YAAaAOj/SwDs/ykA4/8gANv/8v///8//NwCn/wEAFgAEABcAz/8fAAMA6v9cAPX/BgBFALf/HAAhABwABAD0/wIAmv/Q/8r/6/82APf/5/9QAOb/BQA9APH/AQD8//n/wv8qANP/KABNALP/RwDY/+n/9f/x//P/BQBTAPX/JQAoAMT/BAAHAOv/EwC4/wwA2P/R/zUAs/89APb/JwAUAOL/cAAFAOn/BQAEAM3/FgACAOr/PQDk/wkAGADI//f/AADb/wEABgDE/woAHwCS/zYAJADI/1QA7/8rADcAJgAVAOz/5P+5//L/v/8qAAsA0//N/0IAQAD0/zwAEwAxAMr/FAC8/8H/VADU/zoA0P/j////8v/h//r/CQDd/30AJwABAO3/8v/1//f/6//b/yoA4P8sABUA0P/e/xMABAAYAB8A2/8cAOn/MAAJAA0AGADU/yAAuf/s/+D/3/8MAOH/IgAKAOX/DgBaAAcAw/8kABsA3v8jADMACgDl/wkAMwDR/+b/JwDg/73/6f+//9D/JQD9/zwAHwDy/zsA7P8JAO//8v/3/+7/TAAfAA8A9v8CANH/o/8UANT/DQAeACQAMQD7/+7/3v/r//f/AgAmAF0ANQBLAOj/wf8QAKr/0f8RAOr/5P8MALL//f8wAPT/AADD/83/BwBEAPP/SgArAP7/VQDh/00AFwBUAAAAwv/N/5H/xf+y/xMAzP8DAPz/GQA2AP//RQAQAGAADQA+ACAA3v/j/8r/EACz/9z/9P+T/9P/FwDO/xQAVQAbADMAKwAgAMb/8/80ABcA3f/t/xMAxv8vACgA6f8oAPH/hf86AAcA0/9UANr/KAASANz/LwAAAOX/sf/0//D/1/8/AA0AAQAXAOr/NQD2/wAAOgD8/+n/CQD7/6L/8P/Y/xgADwDk/1sA6/8vAEsA7v+l/wgAOQDd/zkADAAlAPP/yP/t/+T/1P/s/9//0f/i/zUAMgDb/0sA9P82AAAA2P82AL3/OwDf/yIA/f/5/xMA6v9sANH/KgDV/8n/AADZ/0QAzf9hAOz/sP8+AKP/9//6/+P/+f/f/x4A+/8/AEwALQAwANf/CwCO//X/OADz/y8ADgAtAKz/0//e/87/+P/1/2QA+f8UAOr/DQDO/8X/RgD5/0EA8v9GAPr/7/9WAL7/AADp/wcA+f/j/wMAAwAPANr/IQCd/4X/1f/+/zUAKgBoAB4AcgBUABsAHQC2/w4Ax//B/9//8P/D/93/JQDY/xYA/f/l/wYA8f/5/ykAMQAHADUAAQDZ/ykABwD1/zwA3P/W/+f/AAAZAKj/SAATANv/LgDK//7/CgD1//n/CgAEAMz/MgApAMD/KgA+AMX/CQD1/+3/7P8LACcA4P8tADIA9f8LAAQAoP/0/+v/6//w//j/GwARAFwA7v8kAAMA//9YAMX/0P8CAP7/qf8eAOj/BQASAJD/KgDu/woADQAPAAMAKABRABUAGgC5//3/3P8hAPv/zf8OAMP/+v/x/1AATgDw/xIABAAIAOz/3//p/9f/1f8sAOn/zP9CABgADwBMAAAA9P8WAOz/KADs/8D/9f/N//b/DAAWAAoA2v8YAP//AAANAOv/HwDz/wYA9f/8//T/sP9NAP//EAAZABsADADp/24AJQARAMn/3v/P/8z/IADM//j/2v/e/wIACQBEAC8A2v/e/zcAyf8hAFgA+f/+/9f/DAD8/8v//////w0AEwAGAPL/6/8TAP7/DwDu/xcAKADa/2cA7P8MAMb/jv/j/6r/MwD+/0YAVgAdAEwAEwAXAPb/7/+y/6n/2f/3/+D/AwAkAOH//P8AAEkA+v9MAE8AvP8oAMP/6P8YAOn//P/d/8b/CAA4APn/OQDl/wIAHgDJ/1YA4P/R//n/2v/u/0AAVABCAAIAtv/2/8T/9/8DAO7/KADG/xYAEwDZ/+v/EwALAAYAEgD8////zf83AAgA//8IAOf/EQDW/3AAQgAQABoAuP/6/63/4/8cAOT/AQDo/wYACAAWAP//8/8WAAoA5/8pABoA8v8EAP7/6v+5/xYA/v+v/xsADQDD/yQAHQDk/y0AGQAPACUAOgAgAPP/EQD0/xkAx//0/wkAsv8kAND//f8FAPv/AgCa//////8dABEADABAAPX/PQAiAAAA7v8AAAcA4P8RAK3/AADn/9//MwDe/zMAFADa/yEA8f8DABsA7v8CACgA1/8fACQA9/89ANv/4f8AANf/JADy/6//wf+t/wUARAA0ACcAUgD9/9//CgD2/wgA6P8RAO7/0v9GAPD/MgDg/wsAHgDf/xMAsP8DAOv/MwAnAPL/AACb/zUA2v8RAEcA7P9TAAwA/v+v/+L///+v/wwA0f/z/0AAKgANAAsA/f8FAP3/7f9IABsAGQAuAPj/vv+2/+X/5//t/x0AJQDi/+7/SgD1/0QARQDZ/+j/1f/P//z/6v/X/0AAy//Q/yAA9/9FANH/AABEABsAVQAuAAMA9/8wANT/mf8pAMX/pv8PAOP/7f8CAA8AIQD//9P/7//p/yMATQAWAC4A1v8CACcACwBMAOb/zv/x/+n/OAAEAOf/AAC7/8r/HQDY/wAACQAAAEIAxv8ZAEAA7f8kAB4A+/8BAAIAvf8AABQAyf/v//j///8QABgA//8nAPP/sv8yAOf/7/8gABsAIwD7/xwA8//f//b/AwAKAAAA+/8hABQA/P8WAB0A/v/p/8P/t/8YAPX/8f8ZAOb/+f/c//3/EAANACcA+v/0/wIAAAAcAEMArf/4/xUAn/9rAEwAXABTADAANwB5/8j/rf/e//f/GgBYAAIADwBn/6j/dP9i/7z/kv8yAC8AbgBZAGsAjQBCAFAAHABGADcAQgBHAAIA5P8QAPH/uf8FALD/nf+w/4T/r/+w/8f/wf/K/9z/KQAPAE0AXAAaAFoA0v8hAEwAJgBwADQAKAALACwAqv/B/wgAvP8IAL//9P/n/+T/HADl/xAAFwAXAML/2P8hAMv/TABAAAgASADV/6z/HgDn/wUAPAAJAPr/4//N/+X/6P/i/20AHAD8/wUA1P8eAOL/JQAlAMD/5//W////BwAbADAACwDq/wUAIADz/yAAFgALAAAAEgATAMj/9v/9/4L/0P/k/5f/5f8mABQAOQBLAGoAKgASABMAAwA+ABoADQDm/8P/0v/e/+f/4f/w//r/GwAZAN//CADZ/8n/HAAcADQAAwAFADsAFQAJAMn/5P+x/6X/KgAAAD4APAAKAOT///8NACEAQQAdAB0AxP/R/93/o/8OAMv/HwBHAOb/MwABAOn/PQA0APD/2f/e//L/4v8GABcAy/8lAP3/AwDe//r/FwDG/y8A9P/2/xYA//85AAAAQgAWAMf/OgAAAOD/SwDs/+P/7P/W/wMArP/4/xEAv/8LACUA+f/l/woA3f8tAFIA/f8xAAEAEQAVABIA8P/f/wAAv//r/x4A/v/6/wUA8P/Z/+L/7v8HABYAOQAoABoAGwDh/9X//v8uAAgADQDx//3/5//r/z8A8f+h//L/2v/J/xwAEQAZABAA8v85ACEAHwDz/yEADADk/2cA9f/8/wgAuP8BAOz/7v/7/7v/sv/i/9n/LwAuAA4AJwDt//3/+//k/yQADQAtACsAMwBKABEAFgABAMj/5P+S/+P/9P+S/z0ABADc/x8ACQDy/+z/JQAKADQADQAvAEYA2v8SAMv////v/+n/9v/W/zgA6P/6/zgA1v/T/xwABwAKAEwAHADv//H/u/8GAMv/m/9DAMb/DABoAL7/TQARAEIAGQC8/w4Aov8cAMT/DwBRAMb/RwA7AB0AxP/w/yIA5P/i/+X/IAACAAAAFwDo/6r/BAAKAOX/QwDI/ygAHgCq/0kACAACACgAAAASACUA8P/+/zYA9f/4/7H/pP/t/6n/2v9OACEAMAA/AMT/7/+r/wYAOgAMAFYA3v9YAAIAGgBlAPD/9v+//wcAu//R//3/AwDd//b/RgCY//L/BwAEAPj/9P8sABsAAgDP/24ACwAaAF4Alv/8/6b/sf8IAL//PABBAAcAIgAEACwALAAXAO3/8/8dANv/2P/2/wQA/P8RAOL/v/8IAOn/+f85AA0AAgDv//b/7v8IAO7/AAAZAO//LwAuACcAGwD0/+3/zv8VAOT/EADt/9z/DQDh/xIAov8bANH/FQA4AOj/dADU/zoA+v/2/1MAq/8rAPr/BwAlAM7/9//i/9r/zv/e/wgA9/81APH/MQBzAMT/PQC//+b/CQCu/zsA2f/x/wEAGAAGABkAHgABAAwAAQAUAMn/FAD0//7/5//6/x0A2v81AMb/5//v/9z/EAAeAPv/+//y/wAAeAD2/y8AHAAbADsAuP8dAM7/4P/q/9T/EQCX//H/IgDm/x4A6P8VAB0A3f8HAPf/RABVABoAHwD//5r/x//1/wEAMQDy/yQAOADL/9//+//u//n/8//z/wQA9f8LACUAIQAaADsA8P/X/zoA6P/Z//D/CQDP/xUACwDa/+7/0v/0/+7/TgAHAAsA///5/y0A1f8nAOD/EQBCAJP//P/U/8v/TQAbAF8ABwD2/0sAu//a/9X/HQAjAAYARgD7//r/2/8RAOP/zP/h/9T/x/+x/yMAyv8zAHUAAgCXAAAA3f9xAN7/2f/o/9b/BwCm//7/KwAUAC0AFgASAAkA8v+t/wAAvP/1/yAAxf/z/w0A5v/o/2kACQAPACwA5f8+ABEA9v9GANn/9v/M/8v/3/92/2kADAD6/20A6f8iAML/SgAkAMf//v/+/yUA1P8oAAcA5f/I/9z/6//d/zsA+P8bADcA7P/W//v/AgD6/wYA8/8xAAcANQD0/xYAPgC//wAA9v/j/wMABAAPAM3/5/8EAN3/6f8qANr/xv8AAN//NwAEADMAOgAeAGwAIwAfAAYAGwDl/3X//f/f/7f/4/8JAOf/GwDV/8f/YADk/zIAHQD1//7/s/8IACkADgA3AB0ACwA2AP//CAAVAN//3//h/+P/9P/9//L/4P+l//f//f8SAGEAHgAuAAYA8f8cAOr/0/8DAA4A9/8uAPL/CQAEANf/FQDS/5z/CwAdAD8ALAAAABIA1P/k/zMAKgDo//D/9v+o/6z/KgAyANT/NgAFAP7/TgAcAPP/JAAcAND/UQD9/8H/FgAEABEA6P/s/9//5v/P//H/DwCH//j/GQDL/zcAMgDp/+f//f8OACkAlAA8ABMAIgCo//7/JwAKABEAyv/F/9b/of8BACYADAAzACMA+v/x/9L/1//T/xEAMAAtACQA8v/o/+f/BQAVAPP/AAAvAAkAAgDw//b/FADQ/xIA4f/b/2YA+v8GAOP/4v+x/xMANwDz/0wA2v8tANj/6f8rABEANgDt////mf8yAAoA8/8dAJj/LgDR/xUAJgANAOP/+f8sALj/DgACAOH/yf8mAA8AHgAjAN//OwDO/yYACgDu/zMACgAAAPr/9f+H/zsAFADw/1kA6v9FAN7/t/8XAJ//3P/Z//r/GwDo/yYAAADw/wkANQDc/yQAcADL/1gAMwDv/zcAu//U//L/y//a/zcA///h//7/CwDM/wUAPADU/ywAAADM/woA2P8VAPz/yf9AADAA0f8uAPr/4P/0/+f/" type="audio/wav" />
Your browser does not support the audio element.
</audio>
Conclusion
We observed that as the order of a filter increases, the steepness of the transfer characteristics from the stopband to the passband (in case of high pass filer) increases, making the filter more selective. The influence of air between the mouth and the microphone was evident in the unfiltered audio. But, the final filtered breathing sounds does not contain the audio of air.